針對麻醉用藥的個體差異,術中麻醉維持的復雜性和不確定性,以及當前監測手段存在的缺陷,傳統麻醉深度PID控制器不能滿足其非線性控制需要,而以往麻醉深度(DOA)模糊控制器的規則完全依賴于經驗調節,因此無法達到預期的控制效果。本研究建立了以大腦狀態指數(CSI)為反饋變量的模糊麻醉閉環控制系統,并采用粒子群算法同時優化基于CSI的變化和異丙酚輸出率之間的模糊控制規則和隸屬度函數。通過系統仿真將CSI值的目標設定在40和30,并加入高斯噪聲以模擬臨床干擾。實驗表明,該系統能準確、快速、平穩地達到CSI預設值,且在噪聲干擾下,無明顯擾動。經粒子群優化(PSO)過的基于CSI模糊控制器應用在DOA閉環控制系統具有較好的穩定性及魯棒性。
引用本文： 湯井田, 曹揚, 肖嘉瑩, 郭曲練. 基于大腦狀態指數的粒子群優化-模糊麻醉閉環控制. 生物醫學工程學雜志, 2014, 31(3): 532-537. doi: 10.7507/1001-5515.20140099 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
臨床麻醉的表現主要有三個組成部分：肌松、無意識和應激反應降低，三者間的平衡調節與控制是麻醉學一直以來的關鍵問題。多年來，麻醉師對麻醉深度(depth of anaesthesia,DOA)的判斷主要依賴于傳統的麻醉臨床體征和個人經驗，缺乏統一測量方法和量化的評估手段。而在現代麻醉中，由于筒箭毒堿等肌松藥物的應用，使得麻醉師失去判斷DOA的重要體征，例如呼吸頻率、肌肉松弛程度等。
由于意識的產生源于大腦，隨著信息化技術的發展，對原始腦電信號的快速處理與轉換，產生了一系列源于腦電，可用于監測麻醉深度的數字化參數，如腦電雙頻指數(bispectral index，BIS)[1]、聽覺誘發電位(auditory evoked potential index，AEPI)[2]、大腦狀態指數(cerebral state index，CSI)[3]等。其中，CSI是一種通過自適應神經模糊推理系統(adaptive network based fuzzy inference system，ANFIS)對四項腦電信號的子參數(爆發抑制比、βratio=log(E30~42.5 Hz/E11~21 Hz)、αratio=log(E30~42.5 Hz/E6~12 Hz)、(β-α)ratio=log(E6~12.5 Hz/E11~21 Hz)進行計算得到的指數。該系統的主要優點是不會假定一種固定的、潛在的函數來描述腦電指數和患者的臨床反應之間的偶然聯系。CSI同BIS、AEPI一樣，屬于無量綱的簡單變量。與CSI相比，BIS刷新間隔長，有延遲現象[4]，AEPI由于采集方式特殊，對環境要求較高。因此，CSI在即時性和穩定性上均優于BIS、AEPI。同時，多項實驗表明，CSI能較好地反應異丙酚靜脈麻醉中濃度變化[5-6]。近年來，隨著以麻醉藥理學為基礎的靶控輸注技術(target controlled infusion，TCI)[7-9]的不斷完善，麻醉計算機輔助設計已由單純開環TCI逐步朝著自動反饋控制系統研究發展[10-11]。
本文建立以CSI為監測標準的DOA模糊控制閉環系統，并采用粒子群算法對該系統模糊控制器中CSI變化與異丙酚注射率之間模糊規則及隸屬度函數進行優化，期望更精確地指導臨床麻醉用藥。
1 藥代藥效房室模型
房室模型[12]是按藥物在機體內轉運和分布的特性，將器官抽象地劃分成不同的模塊，并用藥代動力學(pharmacokinetic，PK)參數反應藥物代謝的過程。效應室(effect compartment，EC)[13]為描述效應部位藥量變化的假想室，與中央室相連。效應室濃度Ce和藥物效應(pharmacodynamic，PD)的即時對應關系可用S型最大效應模型(Sigmoid Emax model)描述。
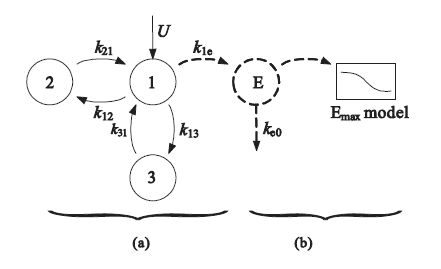
圖 1(a)為藥代動力學模型，圖 1(b)為藥效模型。U為輸注速率，1為中心室，2為快速分布室，3為慢速分布室，E為效應室，k12、k13、k21、k31分別為中心室與周邊室之間的轉運速率，k1e是中央室到效應室的轉運速率常數，描述藥物從中央室向效應室轉移的快慢，ke0是描述藥物在中央室與效應室之間藥物平衡快慢的參數。PK-PD模型描述了藥物劑量、血藥濃度、效應室濃度和藥物效應四者之間的關系。本文的CSI數據來自中南大學湘雅醫學院麻醉科，采用Schnider等[14]藥代動力學參數預測Ce，并用Sigmoid Emax model來擬合CSI與Ce，可得CSI與Ce的關系，即：
| $CSI=100-\frac{100\times C{{e}^{2.1}}}{{{7.6}^{2.1}}+C{{e}^{2.1}}}$ |
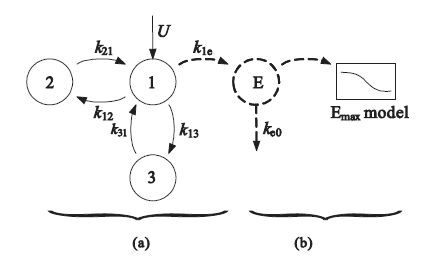圖1
藥代藥效模型
(a)藥代動力學模型;(b)藥效學模型
Figure1. PK-PD model(a) PK model; (b) PD model
2 粒子群算法優化模糊控制
2.1 模糊控制
模糊控制是以模糊集合、模糊變量和模糊推理為基礎的數字控制方法[15]，它是目前智能控制領域的一種重要、有效的分支。因其不依賴于被控對象的精確數學模型，且具有較強的魯棒性和抗干擾能力等優點，在DOA控制領域已得到了應用[16-19]。
>1999年，Elkfafi等[16]以AEPI為監測標準，先后實現了離線和即時在線的模糊麻醉控制，并進行了21例臨床驗證。2001年，Allen等[17]建立了以AEPI為標準的神經網絡模糊邏輯自動閉環系統。Shieh等[18]實現以麻醉醫師的經驗和自組織模糊學習算法為基礎，雙層結構的DOA控制系統，并于2006年實現了以BIS為控制標準，適用于在麻醉維持階段的遺傳PID控制系統和遺傳模糊邏輯控制系統[19]。
以往，DOA模糊控制器中的模糊規則往往是憑操作者的經驗和專家知識獲取，這樣無法保證規則的最優化，從而達到最佳控制的目的。其次，有學者采用遺傳算法優化隸屬度函數的形狀[19]，遺傳算法由于其自身的特性，存在重復分析次數過多，局部搜索能力不足，參數選擇復雜等缺點，易導致搜索速度較慢，早熟收斂和不穩定等現象，這些都影響了控制系統的響應和穩定性。粒子群優化 (particle swarm optimization,PSO) 算法是近年來發展起來的一種群體搜索智能算法[19]，它源于對鳥類捕食行為的研究。其不但具有較強的全局尋優能力，且易于實現，近年來在生物信息，臨床醫學等領域也得到應用[20-21]。
2.1.1 模糊規則
Mamdani型模糊控制系統是最基本的常規模糊控制器，它的輸入輸出變量都采用模糊集合形式的語言變量表示，其模糊規則的一般形式為：
| $\begin{align} & {{R}_{j}}:~IF~{{x}_{1}}~is~{{F}_{1}}^{l}~and~{{x}_{2}}~is~{{F}_{2}}^{l}~and,\ldots ,and~{{x}_{j}}~is~{{F}_{j}}^{l}, \\ & THEN~{{u}_{j}}~is~{{Z}_{j}} \\ \end{align}$ |
其中Rj為第j條規則(j=1,2,…,m)，xi(i=1,2,…,n)為模糊控制系統的輸入變量，Fnj(j=1,2,…，m)為模糊控制的模糊集,Zj(j=1,2,…,m)為模糊控制系統的輸出變量。模糊系統的輸出可表示為：
| $u=\frac{\sum\limits_{j=1}^{m}{{{Z}_{j}}}{{F}_{1}}^{j}({{x}_{1}}){{F}_{1}}^{j}({{x}_{1}})\ldots {{F}_{n}}^{j}({{x}_{n}})}{\sum\limits_{j=1}^{m}{{{F}_{1}}^{j}}({{x}_{1}}){{F}_{1}}^{j}({{x}_{1}})\ldots {{F}_{n}}^{j}({{x}_{n}})}$ |
即
| $u=\frac{\sum\limits_{j=1}^{m}{\left( {{Z}_{j}}\underset{i=1}{\overset{n}{\mathop{\Pi }}}\,{{F}_{i}}^{j}({{x}_{i}}) \right)}}{\sum\limits_{j=1}^{m}{\left( \underset{i=1}{\overset{n}{\mathop{\Pi }}}\,{{F}_{i}}^{j}({{x}_{i}}) \right)}}$ |
2.1.2 隸屬度函數
隸屬度函數是模糊控制的應用基礎，它將論域劃分為不同大小的模糊子集，從而將不同的輸入量轉換為各個模糊變量的隸屬度值，進而利用模糊規則進行模糊推理，它的精確調整對于實現良好的魯棒性非常重要。其確定有調查統計法、例證法、專家經驗法和二元對比排序法等，具有一定的主觀性。常規模糊控制器往往用二維模糊控制，即誤差和誤差變化率作為輸入，傳統模糊子集劃分多采用統一形狀，均勻劃分的方式，對于DOA控制的非線性特性、均勻劃分的隸屬度函數并不合理。
2.2 PSO算法
2.2.1 PSO算法
PSO算法在求解優化問題時，每個粒子的位置代表一個可能的解，根據它相應的適應度值來衡量粒子的優劣。每個粒子根據其自身歷史最優位置和整個粒子群的歷史最優位置，來更新自己的速度和位置，通過迭代方式搜索并收斂到最優解。
假設種群規模為m，第i個粒子在D維空間位置為xi=(xil，xi2,…,xmD)(i=1,2,…,m)，速度vi=(vi1,vi2,…,vmD)，決定了粒子在搜索空間迭代次數的位移，適應度函數由實際問題中待優化的函數決定，更新每個粒子的個體最優pbest=(p1,p2,…,pD)和種群最優值gbest=(g1,g2,…,gD)。粒子通過動態跟蹤個體最優值和全局最優值來更新其速度和位置，如式(5)、(6)。
| $\begin{align} & {{v}_{ij}}\left( t+1 \right)=\omega {{v}_{ij}}\left( t \right)+{{c}_{1}}r\text{ }an{{d}_{1}}({{p}_{j}}\left( t \right)- \\ & {{x}_{ij}}\left( t \right))+{{c}_{2}}ran{{d}_{2}}({{g}_{j}}\left( t \right)-{{x}_{ij}}\left( t \right))~, \\ \end{align}$ |
| ${{x}_{ij}}\left( t+1 \right)={{x}_{ij}}\left( t \right)+{{v}_{ij}}\left( t+1 \right),$ |
式中ω為慣性權重，t為迭代次數，rand1、rand2為均勻分布在(0,1)區間的隨機數，c1、c2為加速度因子。
2.2.2 PSO模糊控制器
本研究中Fuzzy控制器采用二維模糊控制器，兩輸入分別為CSI誤差(CSIe)和CSI誤差變化率(CSIec)，輸出為異丙酚輸注速度。每個輸入、輸出變量的模糊子集分割為5個等級，即負大(NB)、負小(NS)、零(ZO)、正小(PS)、正大(PB)，模糊規則為25(5×5)，為使誤差較大時，收斂速度快，在兩端采用S型隸屬度函數，即：
| $f\left( x,a,c \right)=\frac{1}{1+{{e}^{-a(x-c)}}}$ |
而在變量接近零點時，為了達到更高、更準確的控制精度，在中心區域采用陡峭的三角形隸屬度函數，即
| $f\left( x,a,b,c \right)=\text{ }\left\{ \begin{align} & 0,x\le a \\ & \frac{x-a}{b-a},x\le a\le b \\ & \frac{c-x}{c-b},b\le x\le c \\ & 0,x>c~ \\ \end{align} \right.,$ |
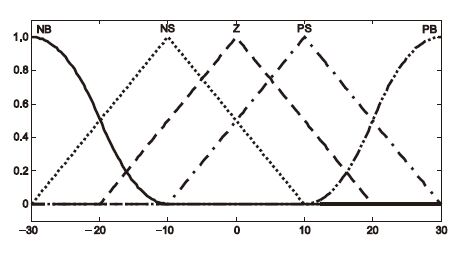
其中a＜b＜c。其優化前的隸屬度函數如圖 2所示。
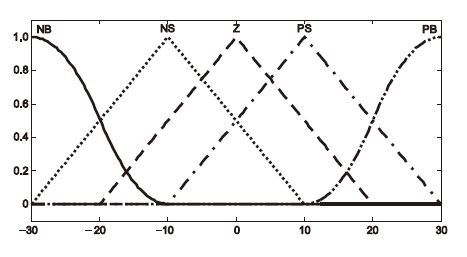圖2
隸屬度函數圖
Figure2.
Membership function
采用粒子群算法同時優化模糊控制規則與隸屬度函數，具體過程如下：
(1)初始化粒子群，確定群體規模，隨機產生粒子的初始位置和速度，給定算法的最大ωmax、最小ωmin權重因子，迭代次數。
(2)選用誤差積分函數計算每個個體的適應值f(x)，適應值函數為：
| $fitness=IAE=\int\limits_{0}^{l}{\left| e\left( t \right) \right|dt}$ |
(3)將其適應度值fi與其經歷過的最好位置的適應度值f(pbesti)作比較，如果較好，則將該粒子的位置取代其當前的最好位置，即f(pbesti)=fi，pbesti=xi。
(4)更新粒子的速度和位置，將更新后每個粒子最好適應值f(pbesti)與全局最優適應值f(gbesti)進行比較。若f(pbesti)＜f(gbest)，則用該粒子的最好適應值取代原有全局最優適應值，同時保存粒子的當前狀態。
(5)判斷適應值是否滿足要求，若尋優達到最大進化代數或評價值小于給定精度，則結束尋優，如不滿足要求，再進行新一輪的計算。
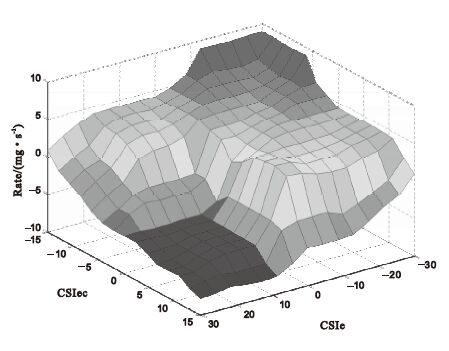
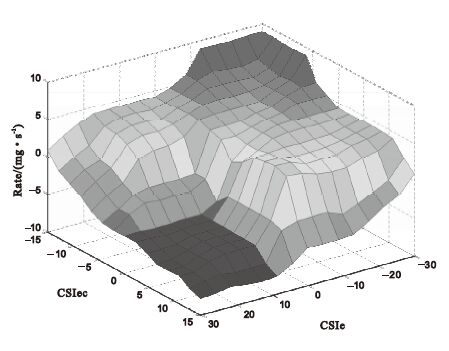圖3
模糊規則
Figure3.
Rule of the fuzzy model
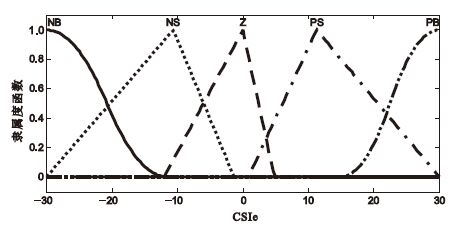
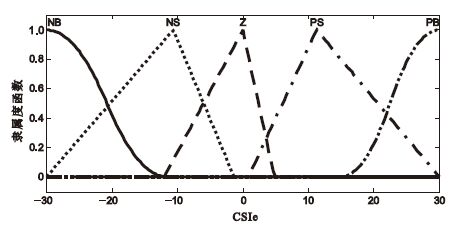圖4
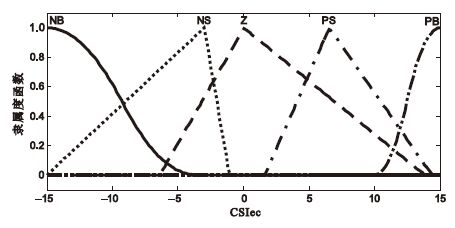
CSI誤差隸屬度函數
Figure4.
Membership function of the CSIe
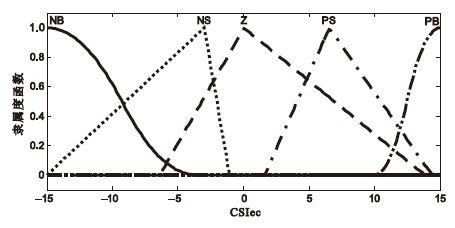圖5
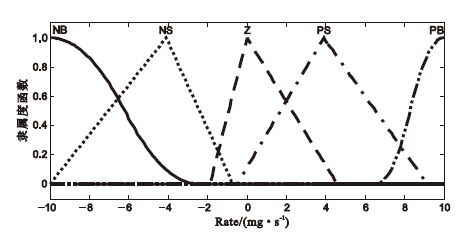
CSI誤差變化率隸屬度函數
Figure5.
Membership function of the CSIec
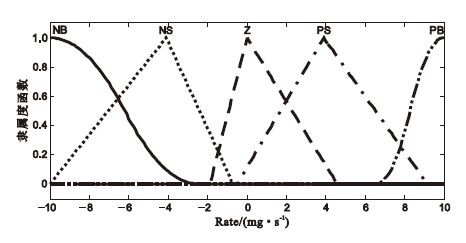圖6
異丙酚輸出率隸屬度函數
Figure6.
Membership function of the infusion of propofol
3 基于大腦狀態指數的麻醉深度控制器
3.1 控制系統結構
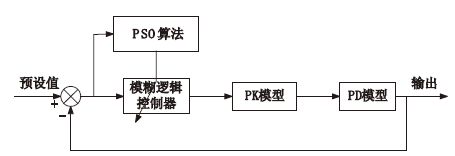
基于CSI的DOA閉環控制系統結構如圖 7所示。
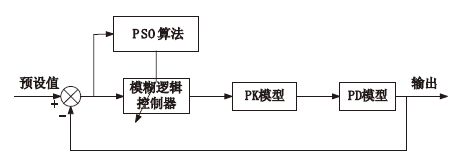圖7
PSO-Fuzzy麻醉控制系統結構圖
Figure7.
Block diagram of the PSO-Fuzzy architecture for anaesthesia simulation
本研究中模糊邏輯控制器為模糊二維雙輸入單輸出控制器，輸入為CSI設置值與當前值的誤差(CSIe=CSIsetpoint-CSIcurrent)，和CSI誤差的變化率(CSIce=CSIe(current-CSIe(previous))，輸出為異丙酚注射率。該系統采用異丙酚的三房室PK-PD模型，其對應的傳遞函數為：
| $\begin{align} & {{G}_{pk}}= \\ & \frac{(s+{{k}_{21}})(s+{{k}_{31}})}{{{s}^{3}}+{{s}^{2}}({{k}_{10}}+{{k}_{12}}+{{k}_{21}}+{{k}_{13}}+{{k}_{31}})+s({{k}_{31}}{{k}_{21}}+{{k}_{10}}{{k}_{31}}+{{k}_{12}}{{k}_{31}}+{{k}_{10}}{{k}_{21}}+{{k}_{13}}{{k}_{21}})+{{k}_{10}}{{k}_{21}}{{k}_{31}}} \\ & \\ \end{align}$ |
| ${{G}_{pd}}=\frac{1}{\frac{1}{{{k}_{e0}}}s+1}$ |
假設一位患者，身高為170 cm,體重50 kg,年齡30歲，通過Schnider參數，計算得到傳遞函數近似寫為：
| ${{G}_{pk}}{{G}_{pd}}=\frac{2770{{s}^{2}}+195s+6}{26251{{s}^{4}}+38123{{s}^{3}}+12896{{s}^{2}}+472s+1}$ |
根據臨床麻醉手術的需要，將CSI值設置在50以下，選取CSI=40和CSI=30為設定值,通過Matlab Simulink進行仿真，并在全程加入高斯噪聲，模擬臨床手術中的實驗儀器的測量噪聲與外科手術刺激等干預。
3.2 仿真結果與分析
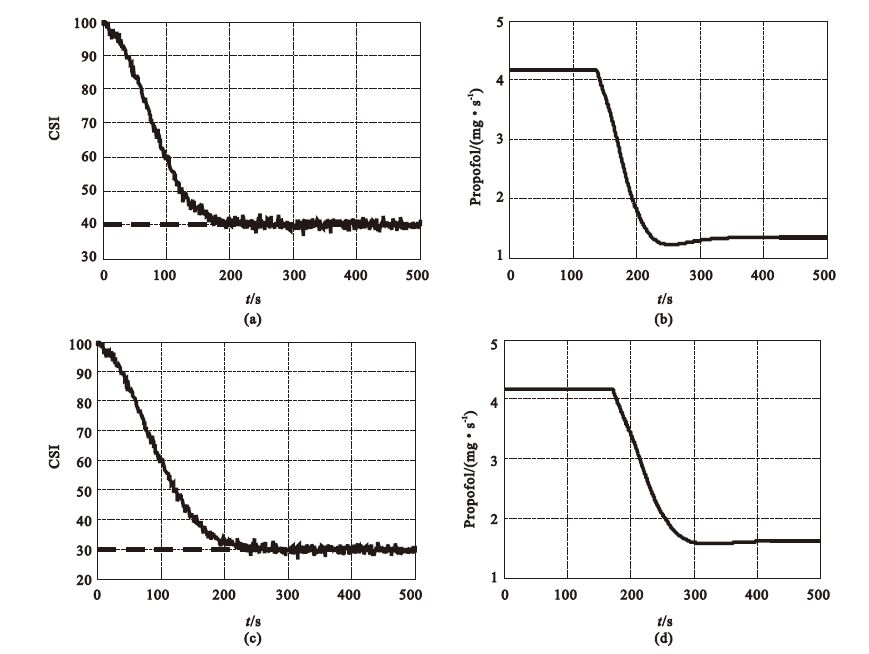
圖 8為DOA控制系統的響應曲線。在兩種不同的CSI預設值下，系統達到穩態的時間均為200~250 s范圍內。CSI預設值40時，由于DOA相對較淺，因此高濃度注射時間短，圖 8(b)中，注射率在130 s左右開始下降，相較圖 8(d)中異丙酚注射率直到180 s左右才出現下降。同樣，在DOA維持階段，圖 8(d)的注射率也比圖 8(b)高。圖 8表明，該閉環系統響應速度快，平穩的達到設定值，即使在有噪聲干擾的情況下，幾乎無振蕩和過射現象，達到預設值后一直平穩的保持。
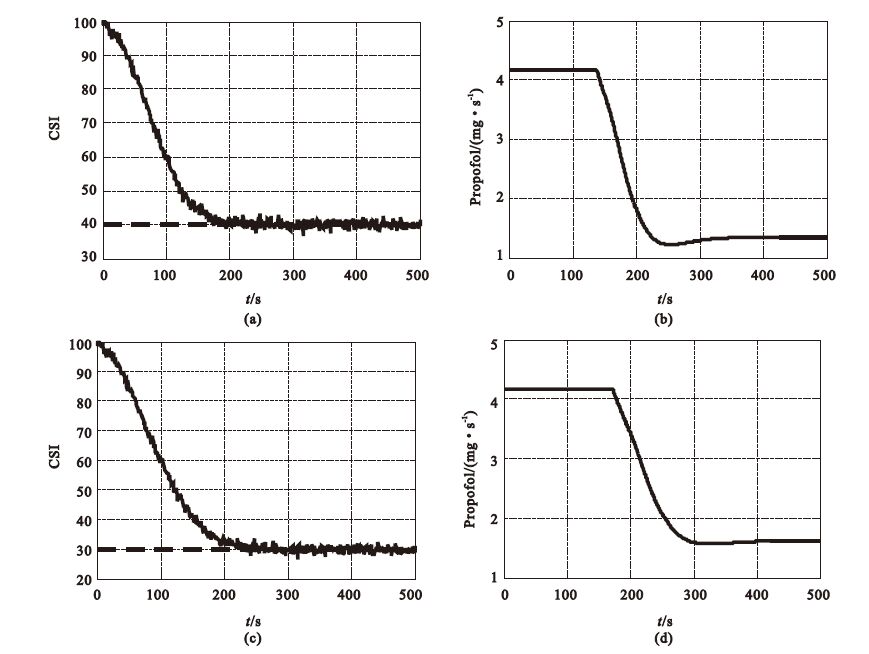圖8
DOA模糊控制器的響應曲線
(a)CSI=40時系統響應曲線;(b)CSI=40時輸注率響應曲線;(c)CSI=30時系統響應曲線;(d)CSI=30時輸注率響應曲線
Figure8. Responses of fuzzy controller for DOA(a) responses of CSI=40; (b) responses of propofol infusion (CSI=40); (c) responses of CSI=30; (d) responses of propofol infusion (CSI=30)
4 結論
CSI是一種將腦電圖通過神經模糊算法轉化而來的量化指標，已逐步在臨床DOA監測中得到應用，實驗證明其與異丙酚效應部位濃度有很好的相關性。本文首次提出并建立了一個基于CSI的DOA閉環模糊控制系統，以異丙酚的輸注來維持DOA的平衡，并采用粒子群算法同時優化了該模糊控制器的CSI誤差、誤差變化率與異丙酚輸注率之間的模糊規則與隸屬度函數形狀，避免了人工選取的主觀性和以往優化算法的弊端。通過仿真實驗，驗證了基于CSI的DOA閉環模糊控制系統的穩定性及有效性，該系統在噪聲的干擾下擾動小，并無超劑量或者低劑量所造成的DOA不穩現象，魯棒性強，響應迅速，達到預設DOA過程十分平穩。基于CSI的DOA閉環模糊控制系統使患者進入麻醉狀態更加安全，進一步減輕臨床麻醉師的工作量，減少藥物的浪費。未來可對該系統進行臨床驗證，并簡化其傳遞函數求取方式，設計人體化的傳遞函數。
引言
臨床麻醉的表現主要有三個組成部分：肌松、無意識和應激反應降低，三者間的平衡調節與控制是麻醉學一直以來的關鍵問題。多年來，麻醉師對麻醉深度(depth of anaesthesia,DOA)的判斷主要依賴于傳統的麻醉臨床體征和個人經驗，缺乏統一測量方法和量化的評估手段。而在現代麻醉中，由于筒箭毒堿等肌松藥物的應用，使得麻醉師失去判斷DOA的重要體征，例如呼吸頻率、肌肉松弛程度等。
由于意識的產生源于大腦，隨著信息化技術的發展，對原始腦電信號的快速處理與轉換，產生了一系列源于腦電，可用于監測麻醉深度的數字化參數，如腦電雙頻指數(bispectral index，BIS)[1]、聽覺誘發電位(auditory evoked potential index，AEPI)[2]、大腦狀態指數(cerebral state index，CSI)[3]等。其中，CSI是一種通過自適應神經模糊推理系統(adaptive network based fuzzy inference system，ANFIS)對四項腦電信號的子參數(爆發抑制比、βratio=log(E30~42.5 Hz/E11~21 Hz)、αratio=log(E30~42.5 Hz/E6~12 Hz)、(β-α)ratio=log(E6~12.5 Hz/E11~21 Hz)進行計算得到的指數。該系統的主要優點是不會假定一種固定的、潛在的函數來描述腦電指數和患者的臨床反應之間的偶然聯系。CSI同BIS、AEPI一樣，屬于無量綱的簡單變量。與CSI相比，BIS刷新間隔長，有延遲現象[4]，AEPI由于采集方式特殊，對環境要求較高。因此，CSI在即時性和穩定性上均優于BIS、AEPI。同時，多項實驗表明，CSI能較好地反應異丙酚靜脈麻醉中濃度變化[5-6]。近年來，隨著以麻醉藥理學為基礎的靶控輸注技術(target controlled infusion，TCI)[7-9]的不斷完善，麻醉計算機輔助設計已由單純開環TCI逐步朝著自動反饋控制系統研究發展[10-11]。
本文建立以CSI為監測標準的DOA模糊控制閉環系統，并采用粒子群算法對該系統模糊控制器中CSI變化與異丙酚注射率之間模糊規則及隸屬度函數進行優化，期望更精確地指導臨床麻醉用藥。
1 藥代藥效房室模型
房室模型[12]是按藥物在機體內轉運和分布的特性，將器官抽象地劃分成不同的模塊，并用藥代動力學(pharmacokinetic，PK)參數反應藥物代謝的過程。效應室(effect compartment，EC)[13]為描述效應部位藥量變化的假想室，與中央室相連。效應室濃度Ce和藥物效應(pharmacodynamic，PD)的即時對應關系可用S型最大效應模型(Sigmoid Emax model)描述。
圖 1(a)為藥代動力學模型，圖 1(b)為藥效模型。U為輸注速率，1為中心室，2為快速分布室，3為慢速分布室，E為效應室，k12、k13、k21、k31分別為中心室與周邊室之間的轉運速率，k1e是中央室到效應室的轉運速率常數，描述藥物從中央室向效應室轉移的快慢，ke0是描述藥物在中央室與效應室之間藥物平衡快慢的參數。PK-PD模型描述了藥物劑量、血藥濃度、效應室濃度和藥物效應四者之間的關系。本文的CSI數據來自中南大學湘雅醫學院麻醉科，采用Schnider等[14]藥代動力學參數預測Ce，并用Sigmoid Emax model來擬合CSI與Ce，可得CSI與Ce的關系，即：
| $CSI=100-\frac{100\times C{{e}^{2.1}}}{{{7.6}^{2.1}}+C{{e}^{2.1}}}$ |
圖1
藥代藥效模型
(a)藥代動力學模型;(b)藥效學模型
Figure1. PK-PD model(a) PK model; (b) PD model
2 粒子群算法優化模糊控制
2.1 模糊控制
模糊控制是以模糊集合、模糊變量和模糊推理為基礎的數字控制方法[15]，它是目前智能控制領域的一種重要、有效的分支。因其不依賴于被控對象的精確數學模型，且具有較強的魯棒性和抗干擾能力等優點，在DOA控制領域已得到了應用[16-19]。
>1999年，Elkfafi等[16]以AEPI為監測標準，先后實現了離線和即時在線的模糊麻醉控制，并進行了21例臨床驗證。2001年，Allen等[17]建立了以AEPI為標準的神經網絡模糊邏輯自動閉環系統。Shieh等[18]實現以麻醉醫師的經驗和自組織模糊學習算法為基礎，雙層結構的DOA控制系統，并于2006年實現了以BIS為控制標準，適用于在麻醉維持階段的遺傳PID控制系統和遺傳模糊邏輯控制系統[19]。
以往，DOA模糊控制器中的模糊規則往往是憑操作者的經驗和專家知識獲取，這樣無法保證規則的最優化，從而達到最佳控制的目的。其次，有學者采用遺傳算法優化隸屬度函數的形狀[19]，遺傳算法由于其自身的特性，存在重復分析次數過多，局部搜索能力不足，參數選擇復雜等缺點，易導致搜索速度較慢，早熟收斂和不穩定等現象，這些都影響了控制系統的響應和穩定性。粒子群優化 (particle swarm optimization,PSO) 算法是近年來發展起來的一種群體搜索智能算法[19]，它源于對鳥類捕食行為的研究。其不但具有較強的全局尋優能力，且易于實現，近年來在生物信息，臨床醫學等領域也得到應用[20-21]。
2.1.1 模糊規則
Mamdani型模糊控制系統是最基本的常規模糊控制器，它的輸入輸出變量都采用模糊集合形式的語言變量表示，其模糊規則的一般形式為：
| $\begin{align} & {{R}_{j}}:~IF~{{x}_{1}}~is~{{F}_{1}}^{l}~and~{{x}_{2}}~is~{{F}_{2}}^{l}~and,\ldots ,and~{{x}_{j}}~is~{{F}_{j}}^{l}, \\ & THEN~{{u}_{j}}~is~{{Z}_{j}} \\ \end{align}$ |
其中Rj為第j條規則(j=1,2,…,m)，xi(i=1,2,…,n)為模糊控制系統的輸入變量，Fnj(j=1,2,…，m)為模糊控制的模糊集,Zj(j=1,2,…,m)為模糊控制系統的輸出變量。模糊系統的輸出可表示為：
| $u=\frac{\sum\limits_{j=1}^{m}{{{Z}_{j}}}{{F}_{1}}^{j}({{x}_{1}}){{F}_{1}}^{j}({{x}_{1}})\ldots {{F}_{n}}^{j}({{x}_{n}})}{\sum\limits_{j=1}^{m}{{{F}_{1}}^{j}}({{x}_{1}}){{F}_{1}}^{j}({{x}_{1}})\ldots {{F}_{n}}^{j}({{x}_{n}})}$ |
即
| $u=\frac{\sum\limits_{j=1}^{m}{\left( {{Z}_{j}}\underset{i=1}{\overset{n}{\mathop{\Pi }}}\,{{F}_{i}}^{j}({{x}_{i}}) \right)}}{\sum\limits_{j=1}^{m}{\left( \underset{i=1}{\overset{n}{\mathop{\Pi }}}\,{{F}_{i}}^{j}({{x}_{i}}) \right)}}$ |
2.1.2 隸屬度函數
隸屬度函數是模糊控制的應用基礎，它將論域劃分為不同大小的模糊子集，從而將不同的輸入量轉換為各個模糊變量的隸屬度值，進而利用模糊規則進行模糊推理，它的精確調整對于實現良好的魯棒性非常重要。其確定有調查統計法、例證法、專家經驗法和二元對比排序法等，具有一定的主觀性。常規模糊控制器往往用二維模糊控制，即誤差和誤差變化率作為輸入，傳統模糊子集劃分多采用統一形狀，均勻劃分的方式，對于DOA控制的非線性特性、均勻劃分的隸屬度函數并不合理。
2.2 PSO算法
2.2.1 PSO算法
PSO算法在求解優化問題時，每個粒子的位置代表一個可能的解，根據它相應的適應度值來衡量粒子的優劣。每個粒子根據其自身歷史最優位置和整個粒子群的歷史最優位置，來更新自己的速度和位置，通過迭代方式搜索并收斂到最優解。
假設種群規模為m，第i個粒子在D維空間位置為xi=(xil，xi2,…,xmD)(i=1,2,…,m)，速度vi=(vi1,vi2,…,vmD)，決定了粒子在搜索空間迭代次數的位移，適應度函數由實際問題中待優化的函數決定，更新每個粒子的個體最優pbest=(p1,p2,…,pD)和種群最優值gbest=(g1,g2,…,gD)。粒子通過動態跟蹤個體最優值和全局最優值來更新其速度和位置，如式(5)、(6)。
| $\begin{align} & {{v}_{ij}}\left( t+1 \right)=\omega {{v}_{ij}}\left( t \right)+{{c}_{1}}r\text{ }an{{d}_{1}}({{p}_{j}}\left( t \right)- \\ & {{x}_{ij}}\left( t \right))+{{c}_{2}}ran{{d}_{2}}({{g}_{j}}\left( t \right)-{{x}_{ij}}\left( t \right))~, \\ \end{align}$ |
| ${{x}_{ij}}\left( t+1 \right)={{x}_{ij}}\left( t \right)+{{v}_{ij}}\left( t+1 \right),$ |
式中ω為慣性權重，t為迭代次數，rand1、rand2為均勻分布在(0,1)區間的隨機數，c1、c2為加速度因子。
2.2.2 PSO模糊控制器
本研究中Fuzzy控制器采用二維模糊控制器，兩輸入分別為CSI誤差(CSIe)和CSI誤差變化率(CSIec)，輸出為異丙酚輸注速度。每個輸入、輸出變量的模糊子集分割為5個等級，即負大(NB)、負小(NS)、零(ZO)、正小(PS)、正大(PB)，模糊規則為25(5×5)，為使誤差較大時，收斂速度快，在兩端采用S型隸屬度函數，即：
| $f\left( x,a,c \right)=\frac{1}{1+{{e}^{-a(x-c)}}}$ |
而在變量接近零點時，為了達到更高、更準確的控制精度，在中心區域采用陡峭的三角形隸屬度函數，即
| $f\left( x,a,b,c \right)=\text{ }\left\{ \begin{align} & 0,x\le a \\ & \frac{x-a}{b-a},x\le a\le b \\ & \frac{c-x}{c-b},b\le x\le c \\ & 0,x>c~ \\ \end{align} \right.,$ |
其中a＜b＜c。其優化前的隸屬度函數如圖 2所示。
圖2
隸屬度函數圖
Figure2.
Membership function
采用粒子群算法同時優化模糊控制規則與隸屬度函數，具體過程如下：
(1)初始化粒子群，確定群體規模，隨機產生粒子的初始位置和速度，給定算法的最大ωmax、最小ωmin權重因子，迭代次數。
(2)選用誤差積分函數計算每個個體的適應值f(x)，適應值函數為：
| $fitness=IAE=\int\limits_{0}^{l}{\left| e\left( t \right) \right|dt}$ |
(3)將其適應度值fi與其經歷過的最好位置的適應度值f(pbesti)作比較，如果較好，則將該粒子的位置取代其當前的最好位置，即f(pbesti)=fi，pbesti=xi。
(4)更新粒子的速度和位置，將更新后每個粒子最好適應值f(pbesti)與全局最優適應值f(gbesti)進行比較。若f(pbesti)＜f(gbest)，則用該粒子的最好適應值取代原有全局最優適應值，同時保存粒子的當前狀態。
(5)判斷適應值是否滿足要求，若尋優達到最大進化代數或評價值小于給定精度，則結束尋優，如不滿足要求，再進行新一輪的計算。
圖3
模糊規則
Figure3.
Rule of the fuzzy model
圖4
CSI誤差隸屬度函數
Figure4.
Membership function of the CSIe
圖5
CSI誤差變化率隸屬度函數
Figure5.
Membership function of the CSIec
圖6
異丙酚輸出率隸屬度函數
Figure6.
Membership function of the infusion of propofol
3 基于大腦狀態指數的麻醉深度控制器
3.1 控制系統結構
基于CSI的DOA閉環控制系統結構如圖 7所示。
圖7
PSO-Fuzzy麻醉控制系統結構圖
Figure7.
Block diagram of the PSO-Fuzzy architecture for anaesthesia simulation
本研究中模糊邏輯控制器為模糊二維雙輸入單輸出控制器，輸入為CSI設置值與當前值的誤差(CSIe=CSIsetpoint-CSIcurrent)，和CSI誤差的變化率(CSIce=CSIe(current-CSIe(previous))，輸出為異丙酚注射率。該系統采用異丙酚的三房室PK-PD模型，其對應的傳遞函數為：
| $\begin{align} & {{G}_{pk}}= \\ & \frac{(s+{{k}_{21}})(s+{{k}_{31}})}{{{s}^{3}}+{{s}^{2}}({{k}_{10}}+{{k}_{12}}+{{k}_{21}}+{{k}_{13}}+{{k}_{31}})+s({{k}_{31}}{{k}_{21}}+{{k}_{10}}{{k}_{31}}+{{k}_{12}}{{k}_{31}}+{{k}_{10}}{{k}_{21}}+{{k}_{13}}{{k}_{21}})+{{k}_{10}}{{k}_{21}}{{k}_{31}}} \\ & \\ \end{align}$ |
| ${{G}_{pd}}=\frac{1}{\frac{1}{{{k}_{e0}}}s+1}$ |
假設一位患者，身高為170 cm,體重50 kg,年齡30歲，通過Schnider參數，計算得到傳遞函數近似寫為：
| ${{G}_{pk}}{{G}_{pd}}=\frac{2770{{s}^{2}}+195s+6}{26251{{s}^{4}}+38123{{s}^{3}}+12896{{s}^{2}}+472s+1}$ |
根據臨床麻醉手術的需要，將CSI值設置在50以下，選取CSI=40和CSI=30為設定值,通過Matlab Simulink進行仿真，并在全程加入高斯噪聲，模擬臨床手術中的實驗儀器的測量噪聲與外科手術刺激等干預。
3.2 仿真結果與分析
圖 8為DOA控制系統的響應曲線。在兩種不同的CSI預設值下，系統達到穩態的時間均為200~250 s范圍內。CSI預設值40時，由于DOA相對較淺，因此高濃度注射時間短，圖 8(b)中，注射率在130 s左右開始下降，相較圖 8(d)中異丙酚注射率直到180 s左右才出現下降。同樣，在DOA維持階段，圖 8(d)的注射率也比圖 8(b)高。圖 8表明，該閉環系統響應速度快，平穩的達到設定值，即使在有噪聲干擾的情況下，幾乎無振蕩和過射現象，達到預設值后一直平穩的保持。
圖8
DOA模糊控制器的響應曲線
(a)CSI=40時系統響應曲線;(b)CSI=40時輸注率響應曲線;(c)CSI=30時系統響應曲線;(d)CSI=30時輸注率響應曲線
Figure8. Responses of fuzzy controller for DOA(a) responses of CSI=40; (b) responses of propofol infusion (CSI=40); (c) responses of CSI=30; (d) responses of propofol infusion (CSI=30)
4 結論
CSI是一種將腦電圖通過神經模糊算法轉化而來的量化指標，已逐步在臨床DOA監測中得到應用，實驗證明其與異丙酚效應部位濃度有很好的相關性。本文首次提出并建立了一個基于CSI的DOA閉環模糊控制系統，以異丙酚的輸注來維持DOA的平衡，并采用粒子群算法同時優化了該模糊控制器的CSI誤差、誤差變化率與異丙酚輸注率之間的模糊規則與隸屬度函數形狀，避免了人工選取的主觀性和以往優化算法的弊端。通過仿真實驗，驗證了基于CSI的DOA閉環模糊控制系統的穩定性及有效性，該系統在噪聲的干擾下擾動小，并無超劑量或者低劑量所造成的DOA不穩現象，魯棒性強，響應迅速，達到預設DOA過程十分平穩。基于CSI的DOA閉環模糊控制系統使患者進入麻醉狀態更加安全，進一步減輕臨床麻醉師的工作量，減少藥物的浪費。未來可對該系統進行臨床驗證，并簡化其傳遞函數求取方式，設計人體化的傳遞函數。
