針對表面肌電(sEMG)信號信噪比較低的問題,本文在Donoho通用閾值法的基礎上,采用了一種基于自適應閾值處理的小波去噪方法。相對于通用閾值法,這種方法可以根據sEMG信號的不同信噪比自適應地調整閾值,更有效地去除噪聲、減小信號的失真,從而提高信噪比。仿真和真實sEMG信號實驗均論證了這種方法的優越性。
引用本文: 婁智, 鄧浩, 陳香, 姚博, 楊基海. 基于自適應閾值處理的表面肌電信號小波去噪研究. 生物醫學工程學雜志, 2014, 31(4): 723-728. doi: 10.7507/1001-5515.20140135 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
表面肌電(surface electromyogram,sEMG)信號是人體在自主運動或者受到外界刺激時神經肌肉活動發放的生物電信號在檢測電極處時間和空間的疊加,它反映了神經、肌肉的功能狀態。這種信號的特點是信噪比低,隨機性強且非平穩。由于sEMG信號是通過置于皮膚表面的檢測電極采集獲得,采集過程中容易受到周圍環境的影響,其噪聲來源主要有以下幾種[1-2]:① 檢測和記錄設備中電子元器件的固有噪聲;② 檢測電極與皮膚接觸面的移動偽跡;③ 電磁輻射引起的環境噪聲。而且,sEMG信號的信噪比會隨著肌肉收縮力的增大而減小。
相對于針電極肌電信號,sEMG信號具有無創檢測的優點,應用范圍更廣,但正是由于它的信噪比較低,處理起來也就更加困難。sEMG信號分解是肌電領域研究的熱點問題之一,其處理過程對信號的噪聲十分敏感,為了獲得更好的分解結果,如何采取有效的算法對肌電信號進行去噪預處理就顯得尤為重要。
目前廣泛應用的小波去噪方法是一種信號的時間-頻率分析方法,由于小波變換具有多分辨率的特點,通過對母小波不斷進行伸縮和平移操作可以實現對信號的多尺度細化分析,在去噪的同時又能很好地保存有用信號的尖峰和突變部分。本文根據sEMG信號的特點,采用基于小波域閾值的濾波方法。再針對一種基于線性變化力采集的sEMG信號分解算法的要求,此時需要利用不同肌肉收縮力水平下檢測的sEMG信號,因此進一步采用對小波域閾值參數c的自適應選取,以提高去噪效果,從而提高分解的正確率。
1 方法
根據使用的模型小波域濾波方法可分為貝葉斯法和非貝葉斯法兩種[3],其中非貝葉斯法又可分為以下三種: ① 是Xu等[4]提出來的空域相關濾波算法;② 是Mallat等[5]提出的模極大值重構濾波算法;③ 是Donoho等[6-7]提出的小波域閾值濾波。綜合分析三種濾波方法的優缺點,小波域閾值濾波在實現時操作最簡單,同時計算量也最小,因此本文采用基于小波域閾值的濾波方法。
對于小波域閾值濾波,閾值的大小很大程度上影響到濾波后去噪的效果,目前采用的確定閾值的方法中,主要有通用閾值法、假設檢驗法、BayesShrink閾值法和極小化風險閾值法等。其中,Donoho等提出的通用閾值法(t=cσ,其中c為閾值參數,σ為噪聲均方差)計算簡單,故得到了廣泛的應用。通常,最佳的閾值會隨著信號信噪比的不同而發生較大的變化,而sEMG信號的信噪比是隨著收縮力的大小不斷變化的。為此,本文進一步采用一種參數c自適應閾值選取的方法[8],通過構造一個濾波后信號的均方差函數的近似函數,作為參數c選取的依據。
1.1 小波域閾值濾波算法
小波變換的定義為
| $Wf\left( {a,b} \right) = \int_{ - \infty }^{ + \infty } {f\left( t \right)} {\varphi _{a,b}}^*\left( t \right)dt$ |
變換的核函數為
| ${\varphi _{a,b}}\left( t \right) = {1 \over {\sqrt a }}\varphi \left( {{{t - b} \over a}} \right),a > 0,b \in R,$ |
其中φ(t)稱為基本小波或母小波,它一般是時域上以t=0為中心的帶通函數,在時域和頻域均具有局部化(緊支撐),且均值為零,即
| $\int_{ - \infty }^{ + \infty } {\varphi \left( t \right)} dt = 0$ |
小波域閾值濾波算法一般采用以下三個步驟:首先選取合適的母小波,對信號進行小波變換;其次,對小波系數進行閾值處理,將小于給定閾值的小波系數當作是背景噪聲置零;最后,將處理后的小波系數進行逆變換,得到重構信號。為了更加有效地濾除噪聲并保留高頻信息,在小波閾值去噪中,母小波及閾值的選擇是算法的關鍵。
1.2 小波域閾值參數c的自適應選取
對于均值為μ、標準差為σ的高斯白噪聲ε,我們知道其值落在區間[μ-3σ,μ+3σ]的概率為99.74%,即
| $\begin{align} & P\{\mu -3\sigma <\varepsilon <\\mu +3\sigma \}=\Phi \left( 3 \right)-\Phi \left( -3 \right)= \\ & 2\Phi \left( 3 \right)-1=0.9974~ \\, \end{align}$ |
也就是說對于高斯白噪聲,若選取閾值t=3σ可以抑制99.74%的噪聲。然而,一般來說,最優的c值會隨著不同的信號、不同強度的噪聲而變化,而通用閾值顯然滿足不了這個要求。因此,通過構造信號均方差近似函數,計算不同c值下該函數的值,從而得到該函數最小化閾值參數c,這樣可以做到閾值參數c的自適應選取,具體計算方法如下:
設對觀測信號小波變換后為Wf=Wg+Wε,其中Wf、Wg和Wε分別表示觀測信號f、真實信號g和噪聲ε的正交小波變換。類似地,有 A U f= AU g+ AU ε,其中
| $\left\{ \begin{align} & A\hat{W}U{{~}_{g}}\left( i \right)={{W}_{g}}\left( i \right),A\hat{W}U~\varepsilon \left( i \right)=W\varepsilon \left( i \right),\left| {{W}_{f}}\left( i \right) \right|\ge t \\ & A\hat{W}U{{~}_{g}}\left( i \right)=0,A\hat{W}U~\varepsilon \left( i \right)=0,\left| {{W}_{f}}\left( i \right) \right|<t \\ \end{align} \right.$ |
同樣有 ,其中 Af 、 A G 和 A G 分別由 AU f、 AU g和 AU ε重構。濾波的目的是選取最優的t或c,使得濾波后的信號 A G 的均方誤差值達到最小。
令 x= A G ,y= A G ,經計算最終得出的誤差函數為
| $2[{{\sigma }^{2}}-\frac{k}{2erf\left( c \right)N}\int_{-c\sigma }^{+c\sigma }{{{x}^{2}}}\frac{e-{{x}^{2}}/(2{{\sigma }^{2}})}{\sqrt{2\pi }~\sigma }dx\left] -E \right[A\hat{W}U{{~}_{f}}^{2}],$ |
其中。
2 實驗結果與分析
2.1 仿真信號處理結果
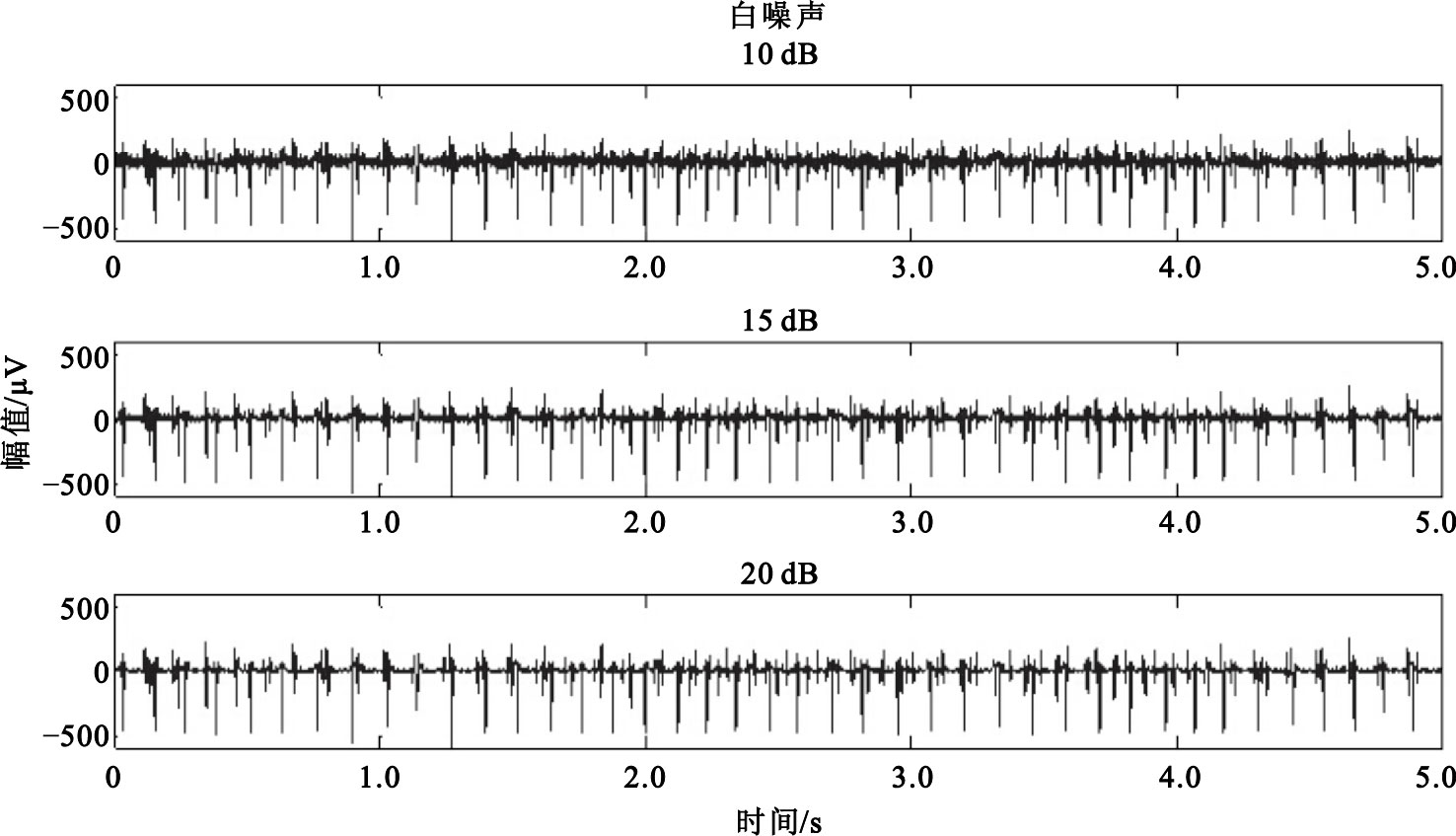
為驗證本文算法的有效性,首先利用仿真sEMG信號進行去噪實驗。仿真信號采用實驗室已研制的“基于電生理過程的sEMG信號仿真軟件”產生,其中sEMG包括5個運動單元。仿真sEMG信號產生時,設置采樣率為2 kHz,電極間隔為5 mm,電極配置為單差分方式,其它參數與文獻[9]設置相同。為了觀察在不同信噪比下自適應閾值法的去噪效果,本文在合成的仿真信號中分別加入信噪比為10、15和20 dB的白噪聲,如圖 1所示。
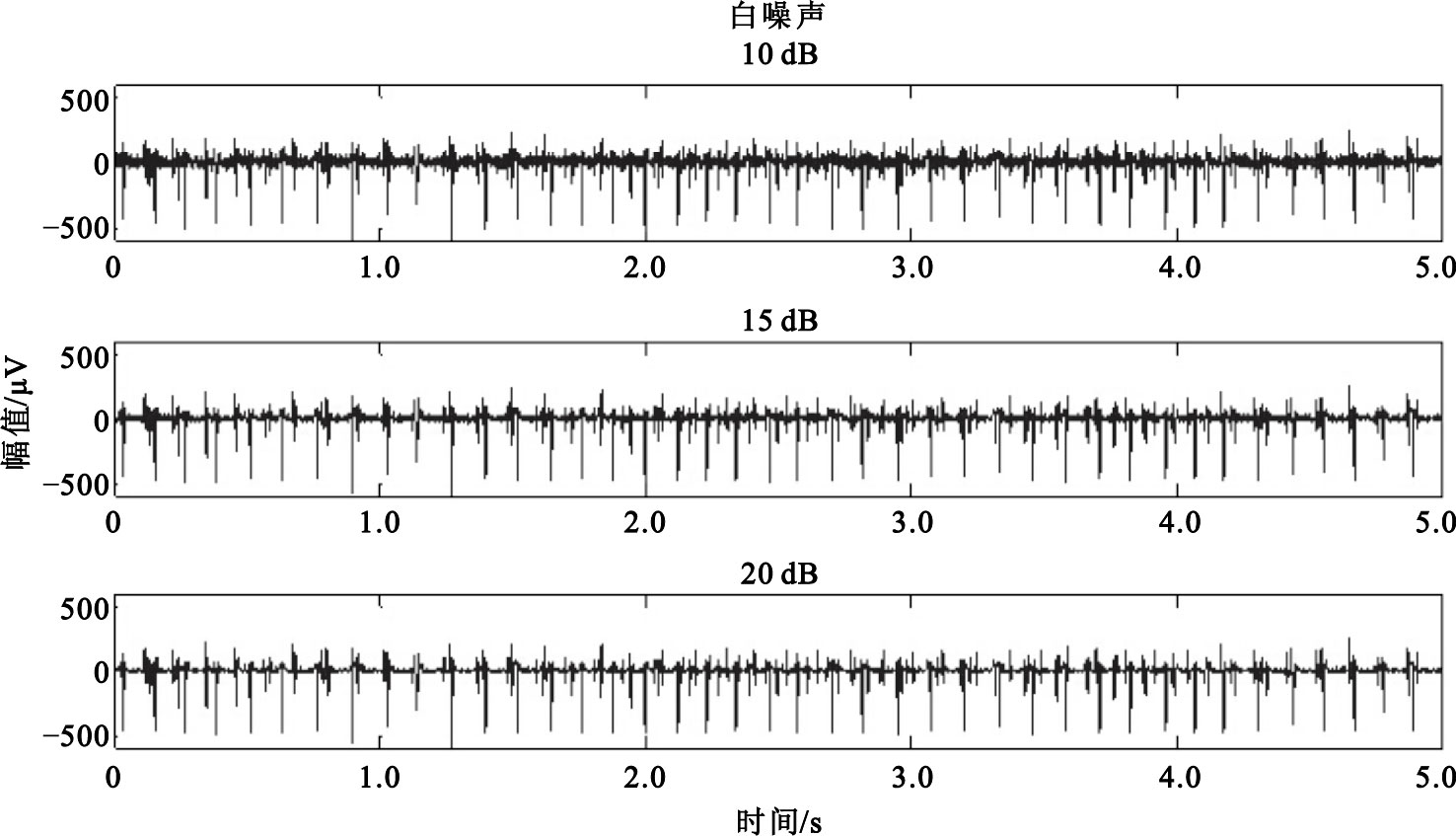 圖1
仿真信號合成
Figure1.
The synthesis of simulation signals
圖1
仿真信號合成
Figure1.
The synthesis of simulation signals
根據對sEMG信號的去噪效果的研究,實驗中我們采用“sym4”作為母小波[10]。小波分解層數的選擇對于去噪結果也有較大的影響,層數過多會將有用信號當做噪聲一起被濾除,而層數較少又不能有效地將噪聲濾除干凈,依據實際經驗我們將分解層數設為兩層。
仿真實驗中,我們主要是利用不同信噪比的仿真信號對比研究Donoho通用閾值法和自適應閾值法的濾波效果。首先研究在不同信噪比下兩種方法的閾值取值與參數c的對應關系。
對于通用閾值法,一般參數c的經驗取值范圍為3~4。我們采用通用閾值法對信噪比分別為10、15和20 dB的仿真信號進行處理,當參數c取3~4時,結果得到的閾值取值范圍分別為31.6~42.2、18.0~24.0和10.1~13.5。可見,在各個信噪比情況下,閾值的變化范圍還是較大的。這樣,若參數c取某固定值,則獲得的閾值并非一定為最優,從而也影響到濾波的效果。
相對于通用閾值法,自適應閾值法可以根據信號信噪比的大小自動調整閾值,表 1所示為不同信噪比情況下自適應濾波自動調整獲得的參數c值及其對應的閾值。
從表 1可以看出,在自適應小波閾值去噪中,閾值的選擇很大程度上依賴于信號的信噪比,信噪比越低,閾值越大,反之則越小。這也證實了在不同信噪比下選擇合適的閾值在小波閾值去噪中的重要性。表 1還說明,對于不同信噪比的sEMG信號,自適應閾值法能夠自動調整參數c值獲得最佳效果。如果采用通用閾值法,雖然直接在區間[3, 4]內通過實驗選取參數c值大多數時候也是令人滿意的,但是與最優解結果還是存在一定的差距。
表 2給出兩種方法在不同信噪比情況下的去噪結果對比。其中,對于通用閾值法取參數c為[3, 4]的中間值3.5,而對于自適應閾值法,參數c值自動分別取為3.3、2.8和2.1(見表 1)。
由表 2可以看出,對于不同信噪比的sEMG信號,自適應閾值法和通用閾值去噪算法均達到了較好的去噪效果,去噪后的信號相對于原始信號的信噪比得到了較大的提高。對比兩種算法的去噪結果可見,自適應閾值法去噪后信號的信噪比均大于通用閾值法,而且這一結果隨著原始信號信噪比的提高變得更加明顯。這也顯示了自適應閾值處理算法相對于通用閾值去噪算法的優越性,不僅可以隨著信號信噪比的變化獲得當前信號去噪的最優閾值,而且在算法操作中也更加方便。
2.2 真實信號處理結果
真實信號數據采集設備利用實驗室研制的陣列式表面肌電采集裝置[11]。電極結構為2×15圓盤電極陣列[12],采用單差分方式配置,極間間隔為5 mm,電路的放大倍數為1 000倍,帶寬為20~1 kHz,采樣率為2 kHz。sEMG信號采于肱二頭肌。試驗時,先對收縮力水平進行定標,將肌肉收縮力最大值記為100%最大收縮力 (maximam voluntary contraction,MVC),然后將MVC 20等分,每次按5% MVC增量采集sEMG信號,相鄰收縮力采集時休息5~10 min以充分放松肌肉,避免肌肉疲勞對信號質量的影響。
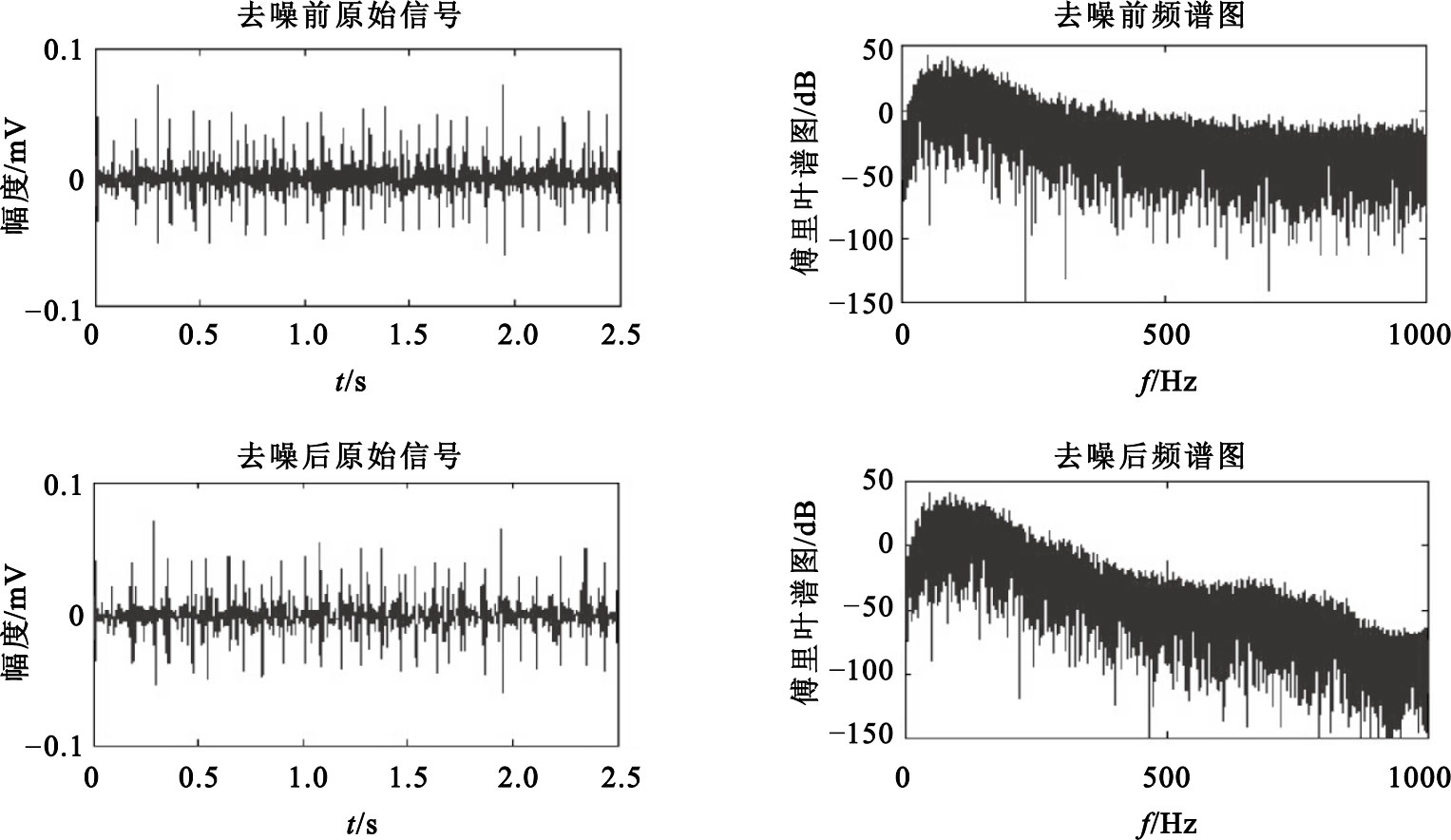
下面以健康男性受試者的肱二頭肌上采集到5% MVC真實信號為例,應用自適應閾值算法進行去噪處理。圖 2、3為其中一名受試者所采集到的去噪前后信號及頻譜圖,圖 4為去噪前后信號局部放大圖。
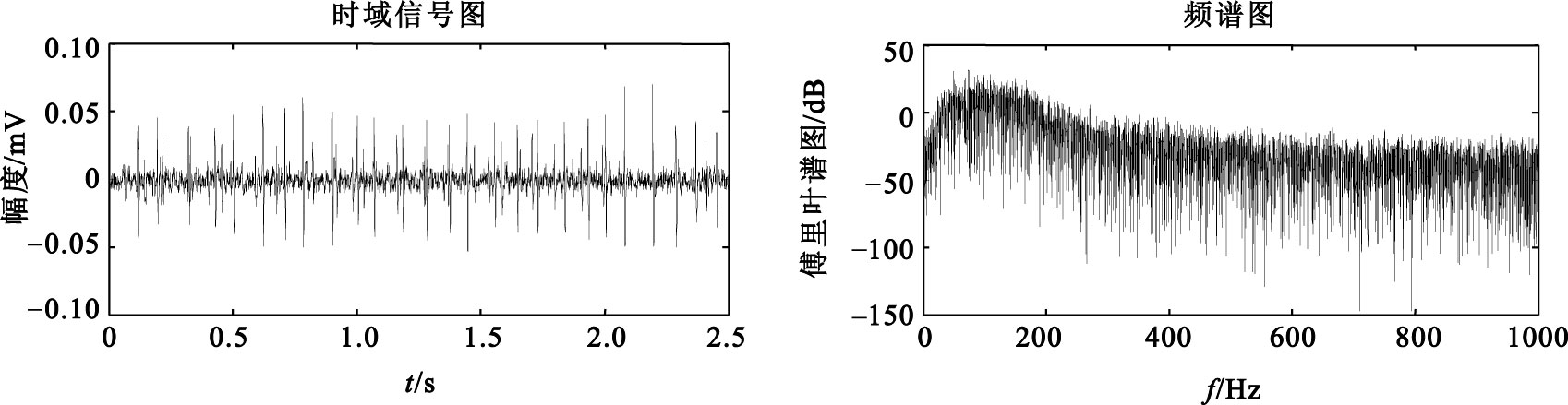 圖2
5% MVC sEMG信號去噪前信號及頻譜圖
Figure2.
The sEMG signals and its frequency spectrogram before denoising at 5% MVC
圖2
5% MVC sEMG信號去噪前信號及頻譜圖
Figure2.
The sEMG signals and its frequency spectrogram before denoising at 5% MVC
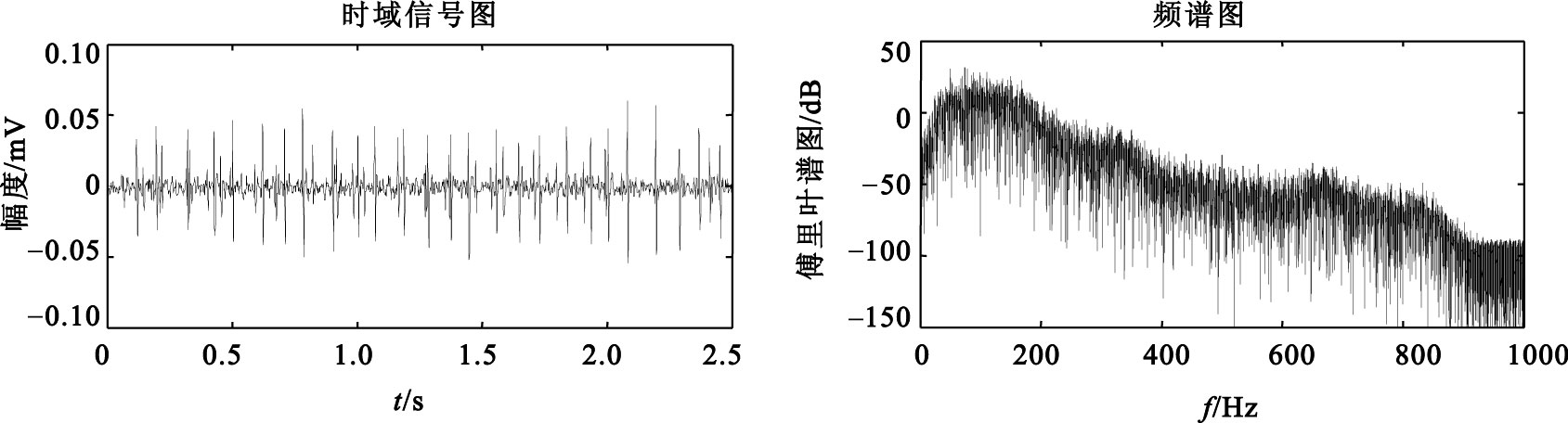 圖3
5% MVC sEMG信號去噪后信號及頻譜圖
Figure3.
The sEMG signals and its frequency spectrogram after denoising at 5% MVC
圖3
5% MVC sEMG信號去噪后信號及頻譜圖
Figure3.
The sEMG signals and its frequency spectrogram after denoising at 5% MVC
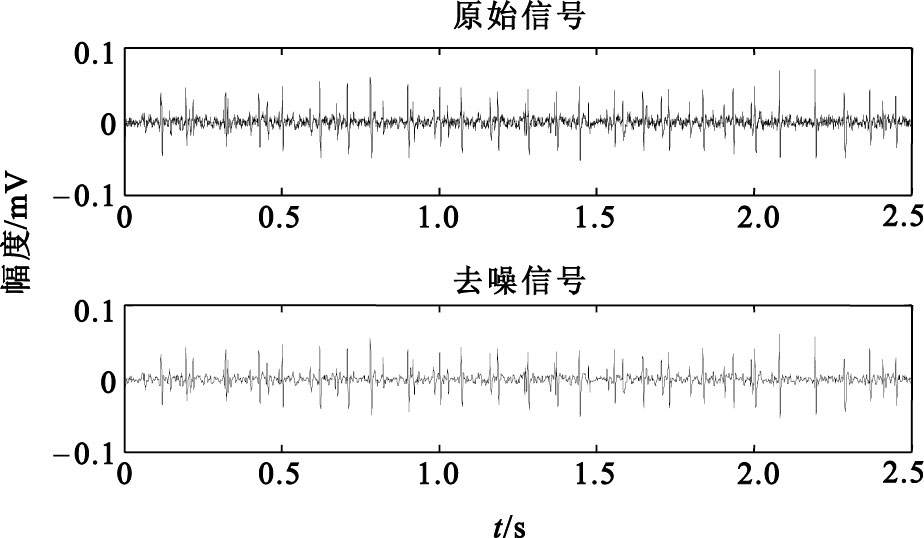 圖4
5% MVC sEMG信號去噪前后信號局部對比圖
Figure4.
The sEMG signal and denoising signal at 5% MVC
圖4
5% MVC sEMG信號去噪前后信號局部對比圖
Figure4.
The sEMG signal and denoising signal at 5% MVC
由圖 2、3的信號時域圖可以看出,信號經去噪處理后,基線噪聲得到了很大程度的抑制,從圖 2、3的頻譜圖可以看出,原始信號經去噪處理后,在保留原始信號低頻成分的同時,能夠更好地去除高頻噪聲的影響。從圖 4的局部圖可以看出,去噪后的信號在有效地抑制噪聲的同時,尖峰成分得到很好的保留,從而使信噪比得到較大的提高。
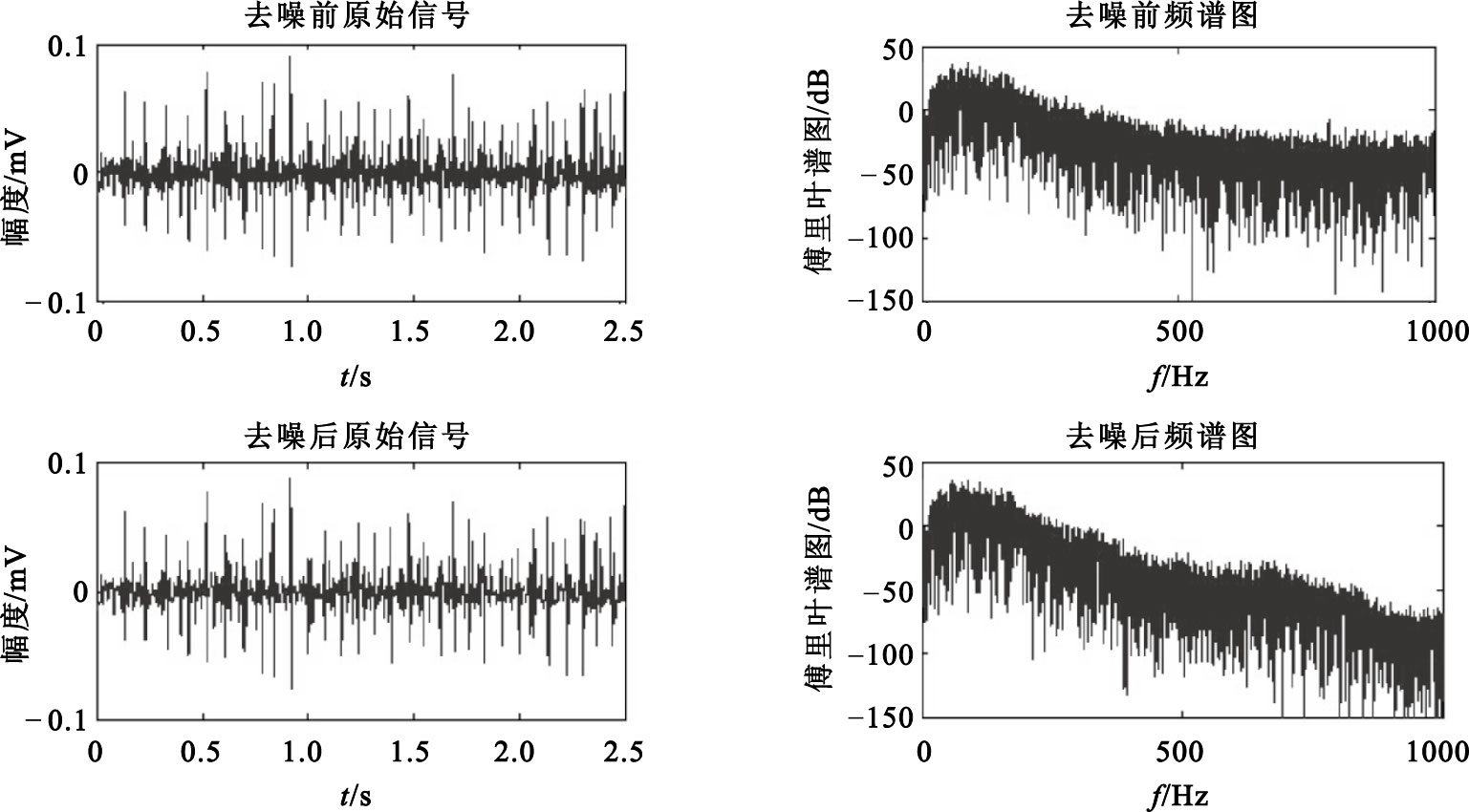
同樣利用該方法對15% MVC、25% MVC真實sEMG信號進行去噪處理,處理前后時域圖、頻譜圖如圖 5、6所示。
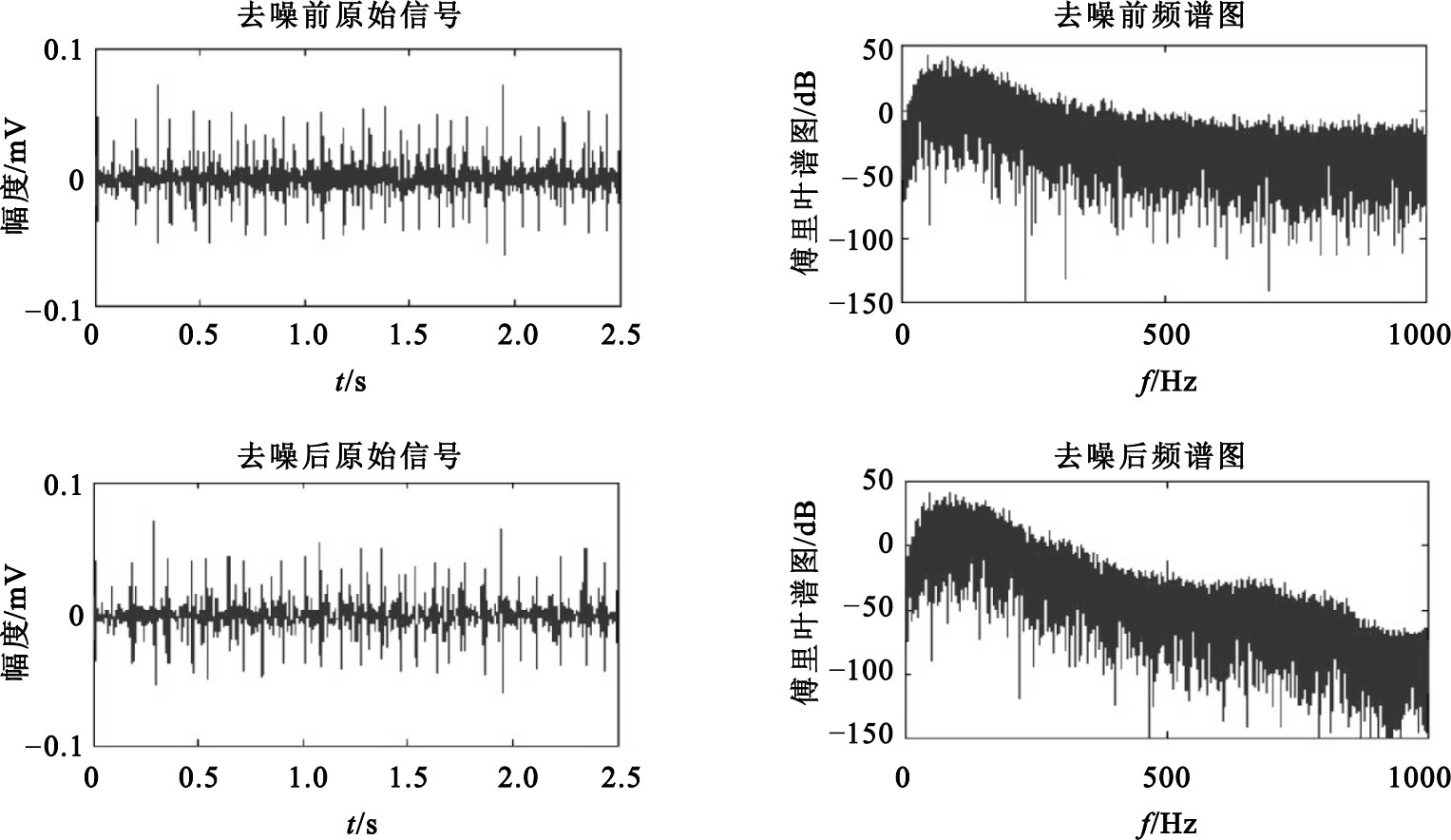 圖5
15% MVC sEMG信號去噪前后信號及頻譜圖
Figure5.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 15% MVC
圖5
15% MVC sEMG信號去噪前后信號及頻譜圖
Figure5.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 15% MVC
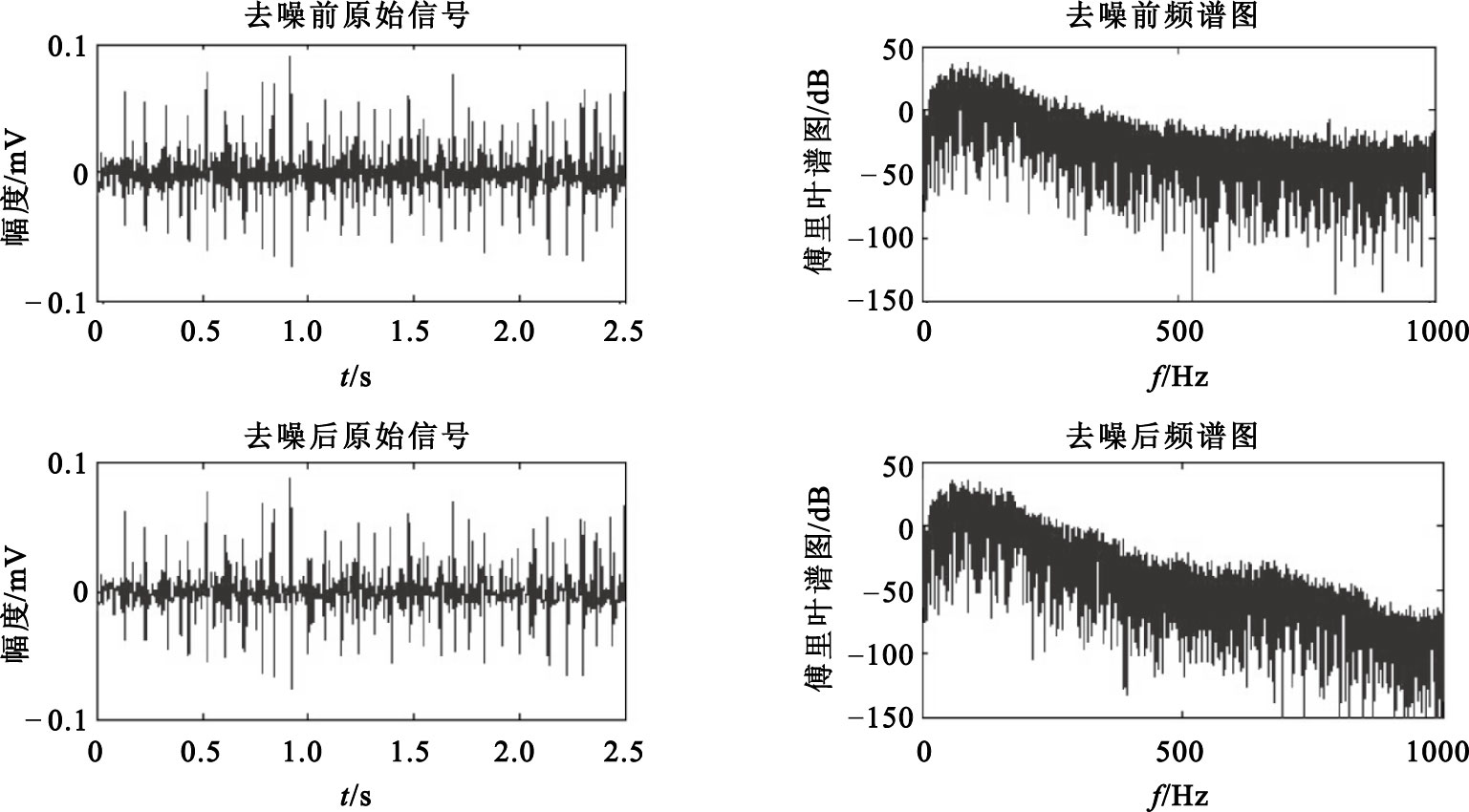 圖6
25% MVC sEMG信號去噪前后信號及頻譜圖
Figure6.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 25% MVC
圖6
25% MVC sEMG信號去噪前后信號及頻譜圖
Figure6.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 25% MVC
從圖 5、6可以看出,該算法在較高收縮力時依然具有很好的去噪效果。表 3中給出三種收縮力下信號去噪處理前后的信噪比對比結果,進一步證實了上述結論。與通用閾值法相比,上述算法可以針對不同收縮力大小的sEMG信號自適應調整去噪的閾值,不僅可以獲得更好的結果,同時操作起來也更加方便,因此更加適合于不同收縮力下sEMG信號的去噪。
為了進一步驗證去噪算法的有效性,本文對多名受試者不同時間采集的sEMG信號進行預處理,處理前后的結果如圖 7所示。
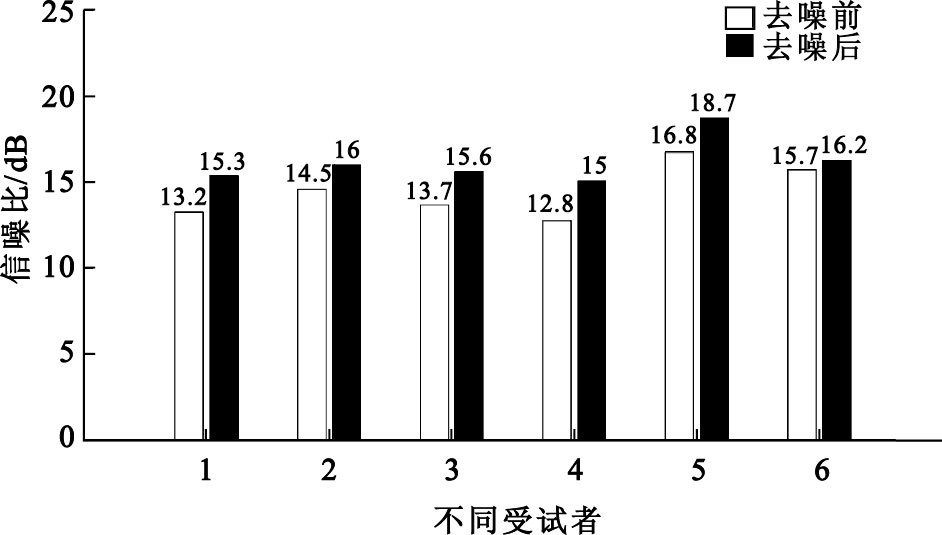 圖7
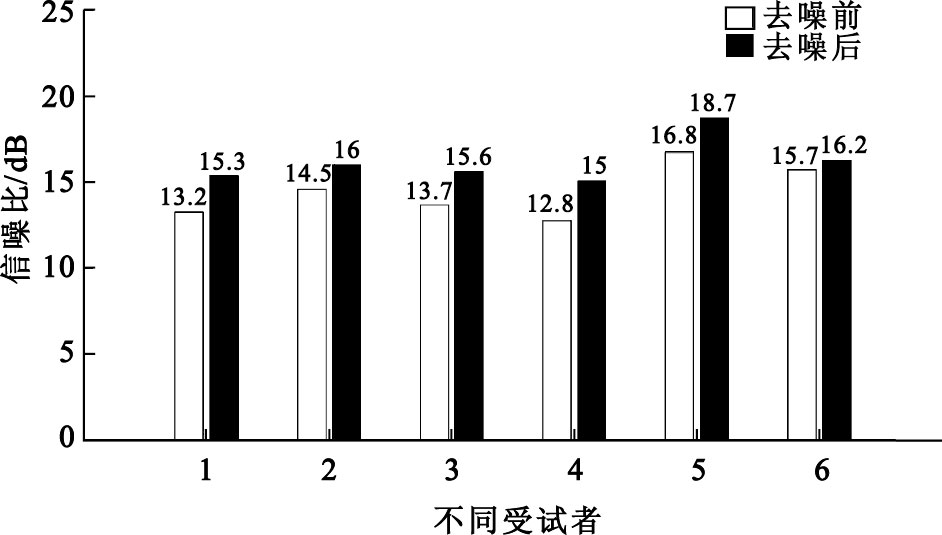
不同受試者的sEMG信號去噪前后信噪比對比
Figure7.
Comparison of the signal to noise ratios of sEMG signals of different subjects between pre- and post- denoising
圖7
不同受試者的sEMG信號去噪前后信噪比對比
Figure7.
Comparison of the signal to noise ratios of sEMG signals of different subjects between pre- and post- denoising
由圖 7對多人多次數據處理結果可以看出,基于參數c自適應閾值選取的小波去噪算法能夠有效地抑制信號采集過程中混入的噪聲污染,顯著提高了信號的信噪比。其中去噪前的平均信噪比為14.53 dB,而去噪后的平均信噪比為16.2 dB。
3 結束語
sEMG信號產生機制十分復雜,導致采集到的信號信噪比較低,因此信號的預處理就顯得尤為重要。針對sEMG信號的特點,本文采用一種基于自適應閾值的小波去噪方法,去除信號中的白噪聲。鑒于小波變換具有多分辨率分析的特點,在去噪的
同時可以很好地保存sEMG信號中運動單位動作電位(motor unit action potential,MUAP)的尖峰部分。同時,該方法可以根據信號的信噪比自適應地調整閾值,相對于通用閾值法,去噪效果更加明顯。仿真sEMG信號和真實sEMG信號的試驗結果驗證了這種方法的有效性,能夠有效地抑制信號中噪聲污染,明顯提高信噪比,從而有利于對sEMG進行分解并提高其分解性能。
引言
表面肌電(surface electromyogram,sEMG)信號是人體在自主運動或者受到外界刺激時神經肌肉活動發放的生物電信號在檢測電極處時間和空間的疊加,它反映了神經、肌肉的功能狀態。這種信號的特點是信噪比低,隨機性強且非平穩。由于sEMG信號是通過置于皮膚表面的檢測電極采集獲得,采集過程中容易受到周圍環境的影響,其噪聲來源主要有以下幾種[1-2]:① 檢測和記錄設備中電子元器件的固有噪聲;② 檢測電極與皮膚接觸面的移動偽跡;③ 電磁輻射引起的環境噪聲。而且,sEMG信號的信噪比會隨著肌肉收縮力的增大而減小。
相對于針電極肌電信號,sEMG信號具有無創檢測的優點,應用范圍更廣,但正是由于它的信噪比較低,處理起來也就更加困難。sEMG信號分解是肌電領域研究的熱點問題之一,其處理過程對信號的噪聲十分敏感,為了獲得更好的分解結果,如何采取有效的算法對肌電信號進行去噪預處理就顯得尤為重要。
目前廣泛應用的小波去噪方法是一種信號的時間-頻率分析方法,由于小波變換具有多分辨率的特點,通過對母小波不斷進行伸縮和平移操作可以實現對信號的多尺度細化分析,在去噪的同時又能很好地保存有用信號的尖峰和突變部分。本文根據sEMG信號的特點,采用基于小波域閾值的濾波方法。再針對一種基于線性變化力采集的sEMG信號分解算法的要求,此時需要利用不同肌肉收縮力水平下檢測的sEMG信號,因此進一步采用對小波域閾值參數c的自適應選取,以提高去噪效果,從而提高分解的正確率。
1 方法
根據使用的模型小波域濾波方法可分為貝葉斯法和非貝葉斯法兩種[3],其中非貝葉斯法又可分為以下三種: ① 是Xu等[4]提出來的空域相關濾波算法;② 是Mallat等[5]提出的模極大值重構濾波算法;③ 是Donoho等[6-7]提出的小波域閾值濾波。綜合分析三種濾波方法的優缺點,小波域閾值濾波在實現時操作最簡單,同時計算量也最小,因此本文采用基于小波域閾值的濾波方法。
對于小波域閾值濾波,閾值的大小很大程度上影響到濾波后去噪的效果,目前采用的確定閾值的方法中,主要有通用閾值法、假設檢驗法、BayesShrink閾值法和極小化風險閾值法等。其中,Donoho等提出的通用閾值法(t=cσ,其中c為閾值參數,σ為噪聲均方差)計算簡單,故得到了廣泛的應用。通常,最佳的閾值會隨著信號信噪比的不同而發生較大的變化,而sEMG信號的信噪比是隨著收縮力的大小不斷變化的。為此,本文進一步采用一種參數c自適應閾值選取的方法[8],通過構造一個濾波后信號的均方差函數的近似函數,作為參數c選取的依據。
1.1 小波域閾值濾波算法
小波變換的定義為
| $Wf\left( {a,b} \right) = \int_{ - \infty }^{ + \infty } {f\left( t \right)} {\varphi _{a,b}}^*\left( t \right)dt$ |
變換的核函數為
| ${\varphi _{a,b}}\left( t \right) = {1 \over {\sqrt a }}\varphi \left( {{{t - b} \over a}} \right),a > 0,b \in R,$ |
其中φ(t)稱為基本小波或母小波,它一般是時域上以t=0為中心的帶通函數,在時域和頻域均具有局部化(緊支撐),且均值為零,即
| $\int_{ - \infty }^{ + \infty } {\varphi \left( t \right)} dt = 0$ |
小波域閾值濾波算法一般采用以下三個步驟:首先選取合適的母小波,對信號進行小波變換;其次,對小波系數進行閾值處理,將小于給定閾值的小波系數當作是背景噪聲置零;最后,將處理后的小波系數進行逆變換,得到重構信號。為了更加有效地濾除噪聲并保留高頻信息,在小波閾值去噪中,母小波及閾值的選擇是算法的關鍵。
1.2 小波域閾值參數c的自適應選取
對于均值為μ、標準差為σ的高斯白噪聲ε,我們知道其值落在區間[μ-3σ,μ+3σ]的概率為99.74%,即
| $\begin{align} & P\{\mu -3\sigma <\varepsilon <\\mu +3\sigma \}=\Phi \left( 3 \right)-\Phi \left( -3 \right)= \\ & 2\Phi \left( 3 \right)-1=0.9974~ \\, \end{align}$ |
也就是說對于高斯白噪聲,若選取閾值t=3σ可以抑制99.74%的噪聲。然而,一般來說,最優的c值會隨著不同的信號、不同強度的噪聲而變化,而通用閾值顯然滿足不了這個要求。因此,通過構造信號均方差近似函數,計算不同c值下該函數的值,從而得到該函數最小化閾值參數c,這樣可以做到閾值參數c的自適應選取,具體計算方法如下:
設對觀測信號小波變換后為Wf=Wg+Wε,其中Wf、Wg和Wε分別表示觀測信號f、真實信號g和噪聲ε的正交小波變換。類似地,有 A U f= AU g+ AU ε,其中
| $\left\{ \begin{align} & A\hat{W}U{{~}_{g}}\left( i \right)={{W}_{g}}\left( i \right),A\hat{W}U~\varepsilon \left( i \right)=W\varepsilon \left( i \right),\left| {{W}_{f}}\left( i \right) \right|\ge t \\ & A\hat{W}U{{~}_{g}}\left( i \right)=0,A\hat{W}U~\varepsilon \left( i \right)=0,\left| {{W}_{f}}\left( i \right) \right|<t \\ \end{align} \right.$ |
同樣有 ,其中 Af 、 A G 和 A G 分別由 AU f、 AU g和 AU ε重構。濾波的目的是選取最優的t或c,使得濾波后的信號 A G 的均方誤差值達到最小。
令 x= A G ,y= A G ,經計算最終得出的誤差函數為
| $2[{{\sigma }^{2}}-\frac{k}{2erf\left( c \right)N}\int_{-c\sigma }^{+c\sigma }{{{x}^{2}}}\frac{e-{{x}^{2}}/(2{{\sigma }^{2}})}{\sqrt{2\pi }~\sigma }dx\left] -E \right[A\hat{W}U{{~}_{f}}^{2}],$ |
其中。
2 實驗結果與分析
2.1 仿真信號處理結果
為驗證本文算法的有效性,首先利用仿真sEMG信號進行去噪實驗。仿真信號采用實驗室已研制的“基于電生理過程的sEMG信號仿真軟件”產生,其中sEMG包括5個運動單元。仿真sEMG信號產生時,設置采樣率為2 kHz,電極間隔為5 mm,電極配置為單差分方式,其它參數與文獻[9]設置相同。為了觀察在不同信噪比下自適應閾值法的去噪效果,本文在合成的仿真信號中分別加入信噪比為10、15和20 dB的白噪聲,如圖 1所示。
 圖1
仿真信號合成
Figure1.
The synthesis of simulation signals
圖1
仿真信號合成
Figure1.
The synthesis of simulation signals
根據對sEMG信號的去噪效果的研究,實驗中我們采用“sym4”作為母小波[10]。小波分解層數的選擇對于去噪結果也有較大的影響,層數過多會將有用信號當做噪聲一起被濾除,而層數較少又不能有效地將噪聲濾除干凈,依據實際經驗我們將分解層數設為兩層。
仿真實驗中,我們主要是利用不同信噪比的仿真信號對比研究Donoho通用閾值法和自適應閾值法的濾波效果。首先研究在不同信噪比下兩種方法的閾值取值與參數c的對應關系。
對于通用閾值法,一般參數c的經驗取值范圍為3~4。我們采用通用閾值法對信噪比分別為10、15和20 dB的仿真信號進行處理,當參數c取3~4時,結果得到的閾值取值范圍分別為31.6~42.2、18.0~24.0和10.1~13.5。可見,在各個信噪比情況下,閾值的變化范圍還是較大的。這樣,若參數c取某固定值,則獲得的閾值并非一定為最優,從而也影響到濾波的效果。
相對于通用閾值法,自適應閾值法可以根據信號信噪比的大小自動調整閾值,表 1所示為不同信噪比情況下自適應濾波自動調整獲得的參數c值及其對應的閾值。
從表 1可以看出,在自適應小波閾值去噪中,閾值的選擇很大程度上依賴于信號的信噪比,信噪比越低,閾值越大,反之則越小。這也證實了在不同信噪比下選擇合適的閾值在小波閾值去噪中的重要性。表 1還說明,對于不同信噪比的sEMG信號,自適應閾值法能夠自動調整參數c值獲得最佳效果。如果采用通用閾值法,雖然直接在區間[3, 4]內通過實驗選取參數c值大多數時候也是令人滿意的,但是與最優解結果還是存在一定的差距。
表 2給出兩種方法在不同信噪比情況下的去噪結果對比。其中,對于通用閾值法取參數c為[3, 4]的中間值3.5,而對于自適應閾值法,參數c值自動分別取為3.3、2.8和2.1(見表 1)。
由表 2可以看出,對于不同信噪比的sEMG信號,自適應閾值法和通用閾值去噪算法均達到了較好的去噪效果,去噪后的信號相對于原始信號的信噪比得到了較大的提高。對比兩種算法的去噪結果可見,自適應閾值法去噪后信號的信噪比均大于通用閾值法,而且這一結果隨著原始信號信噪比的提高變得更加明顯。這也顯示了自適應閾值處理算法相對于通用閾值去噪算法的優越性,不僅可以隨著信號信噪比的變化獲得當前信號去噪的最優閾值,而且在算法操作中也更加方便。
2.2 真實信號處理結果
真實信號數據采集設備利用實驗室研制的陣列式表面肌電采集裝置[11]。電極結構為2×15圓盤電極陣列[12],采用單差分方式配置,極間間隔為5 mm,電路的放大倍數為1 000倍,帶寬為20~1 kHz,采樣率為2 kHz。sEMG信號采于肱二頭肌。試驗時,先對收縮力水平進行定標,將肌肉收縮力最大值記為100%最大收縮力 (maximam voluntary contraction,MVC),然后將MVC 20等分,每次按5% MVC增量采集sEMG信號,相鄰收縮力采集時休息5~10 min以充分放松肌肉,避免肌肉疲勞對信號質量的影響。
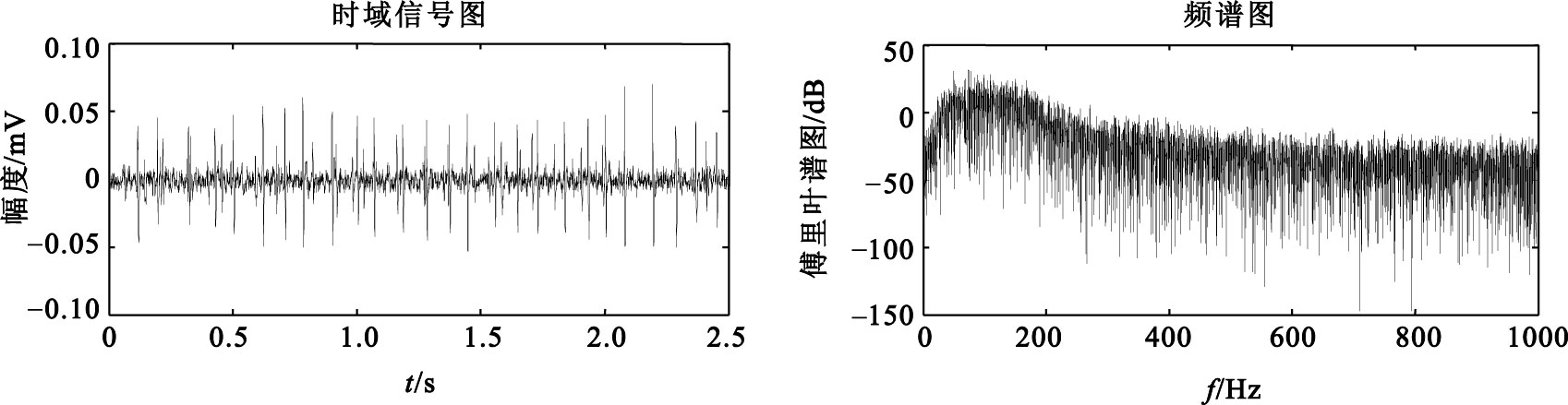
下面以健康男性受試者的肱二頭肌上采集到5% MVC真實信號為例,應用自適應閾值算法進行去噪處理。圖 2、3為其中一名受試者所采集到的去噪前后信號及頻譜圖,圖 4為去噪前后信號局部放大圖。
 圖2
5% MVC sEMG信號去噪前信號及頻譜圖
Figure2.
The sEMG signals and its frequency spectrogram before denoising at 5% MVC
圖2
5% MVC sEMG信號去噪前信號及頻譜圖
Figure2.
The sEMG signals and its frequency spectrogram before denoising at 5% MVC
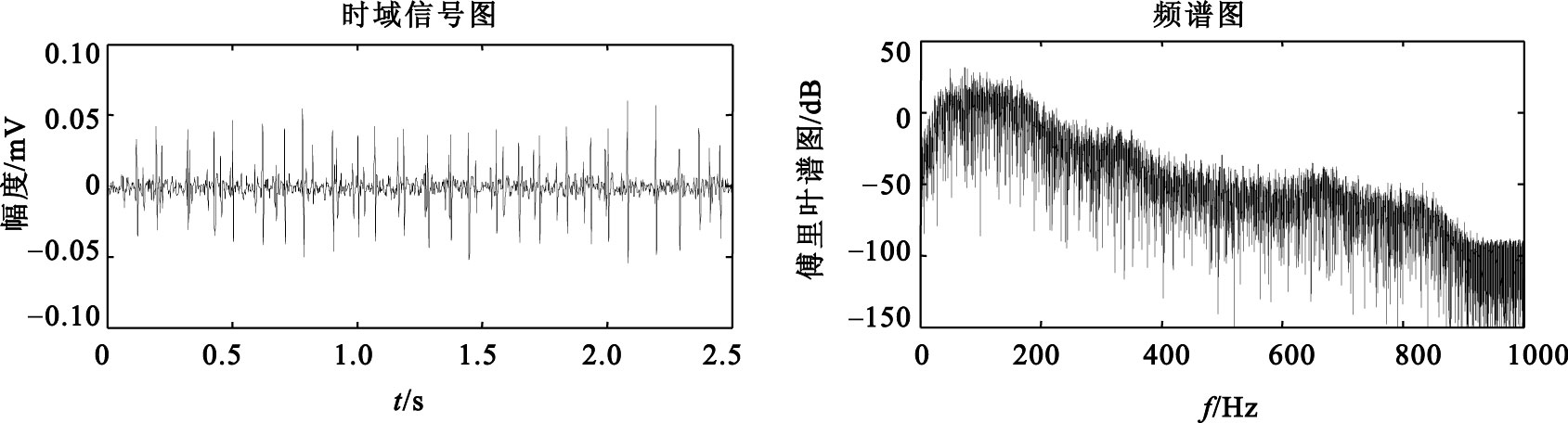
 圖3
5% MVC sEMG信號去噪后信號及頻譜圖
Figure3.
The sEMG signals and its frequency spectrogram after denoising at 5% MVC
圖3
5% MVC sEMG信號去噪后信號及頻譜圖
Figure3.
The sEMG signals and its frequency spectrogram after denoising at 5% MVC
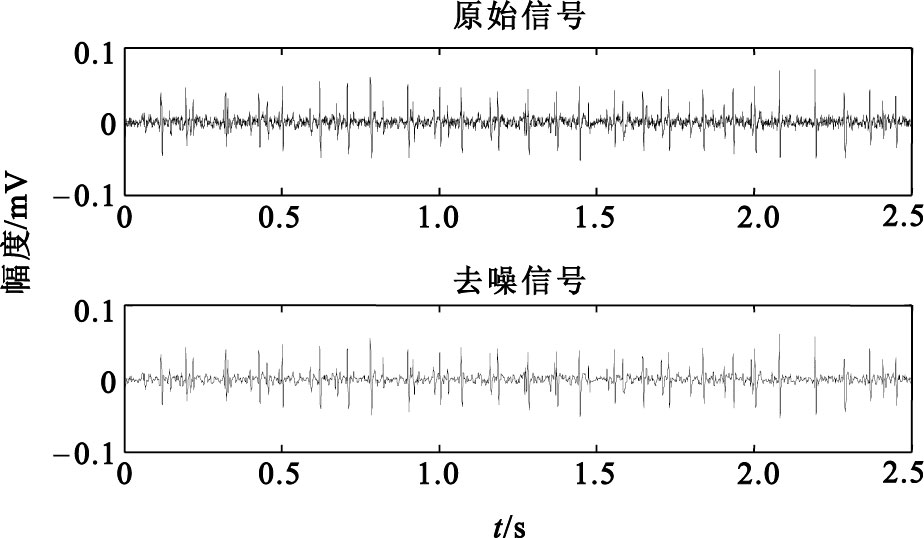
 圖4
5% MVC sEMG信號去噪前后信號局部對比圖
Figure4.
The sEMG signal and denoising signal at 5% MVC
圖4
5% MVC sEMG信號去噪前后信號局部對比圖
Figure4.
The sEMG signal and denoising signal at 5% MVC
由圖 2、3的信號時域圖可以看出,信號經去噪處理后,基線噪聲得到了很大程度的抑制,從圖 2、3的頻譜圖可以看出,原始信號經去噪處理后,在保留原始信號低頻成分的同時,能夠更好地去除高頻噪聲的影響。從圖 4的局部圖可以看出,去噪后的信號在有效地抑制噪聲的同時,尖峰成分得到很好的保留,從而使信噪比得到較大的提高。
同樣利用該方法對15% MVC、25% MVC真實sEMG信號進行去噪處理,處理前后時域圖、頻譜圖如圖 5、6所示。
 圖5
15% MVC sEMG信號去噪前后信號及頻譜圖
Figure5.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 15% MVC
圖5
15% MVC sEMG信號去噪前后信號及頻譜圖
Figure5.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 15% MVC
 圖6
25% MVC sEMG信號去噪前后信號及頻譜圖
Figure6.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 25% MVC
圖6
25% MVC sEMG信號去噪前后信號及頻譜圖
Figure6.
The correlation of sEMG signals and denoising signals and its frequency spectrogram at 25% MVC
從圖 5、6可以看出,該算法在較高收縮力時依然具有很好的去噪效果。表 3中給出三種收縮力下信號去噪處理前后的信噪比對比結果,進一步證實了上述結論。與通用閾值法相比,上述算法可以針對不同收縮力大小的sEMG信號自適應調整去噪的閾值,不僅可以獲得更好的結果,同時操作起來也更加方便,因此更加適合于不同收縮力下sEMG信號的去噪。
為了進一步驗證去噪算法的有效性,本文對多名受試者不同時間采集的sEMG信號進行預處理,處理前后的結果如圖 7所示。
 圖7
不同受試者的sEMG信號去噪前后信噪比對比
Figure7.
Comparison of the signal to noise ratios of sEMG signals of different subjects between pre- and post- denoising
圖7
不同受試者的sEMG信號去噪前后信噪比對比
Figure7.
Comparison of the signal to noise ratios of sEMG signals of different subjects between pre- and post- denoising
由圖 7對多人多次數據處理結果可以看出,基于參數c自適應閾值選取的小波去噪算法能夠有效地抑制信號采集過程中混入的噪聲污染,顯著提高了信號的信噪比。其中去噪前的平均信噪比為14.53 dB,而去噪后的平均信噪比為16.2 dB。
3 結束語
sEMG信號產生機制十分復雜,導致采集到的信號信噪比較低,因此信號的預處理就顯得尤為重要。針對sEMG信號的特點,本文采用一種基于自適應閾值的小波去噪方法,去除信號中的白噪聲。鑒于小波變換具有多分辨率分析的特點,在去噪的
同時可以很好地保存sEMG信號中運動單位動作電位(motor unit action potential,MUAP)的尖峰部分。同時,該方法可以根據信號的信噪比自適應地調整閾值,相對于通用閾值法,去噪效果更加明顯。仿真sEMG信號和真實sEMG信號的試驗結果驗證了這種方法的有效性,能夠有效地抑制信號中噪聲污染,明顯提高信噪比,從而有利于對sEMG進行分解并提高其分解性能。