本文介紹了一種心音信號預處理新方法,利用小波變換對心音信號進行多層分解,對分解后的每層進行雙參數閾值去噪,最后對閾值處理得到的層進行重構,以達到濾波的目的。對重構后的心音信號,分別采用了小波變換、希爾伯特-黃變換(HHT)、數學形態學、歸一化平均香農能量等算法進行包絡提取,對提取后的包絡作了初步分析,并對每種算法提出改進方案。用以上方法對隨機選取的30例原始心音數據進行預處理,得到了滿意的結果。利用改進后的方法進行了包絡提取,所提取的包絡與原信號有很高的吻合度,不論是低頻部分還是高頻部分的信息均能很好地反映,原信號的更多信息得到了保留。
引用本文： 張磊邦, 唐榮斌, 蔣建波, 張帥, 池宗琳, 王威廉. 心音信號的預處理與包絡提取算法研究. 生物醫學工程學雜志, 2014, 31(4): 734-741. doi: 10.7507/1001-5515.20140137 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
心音是人體最重要的生理信號之一。心音由第一心音(S1) 、第二心音(S2) 、第三心音(S3) 、第四心音(S4) 及心臟雜音等組成，它含有心臟各個部分如心房、心室、大血管及各個瓣膜功能狀態的生理、病理信息。與心臟疾病有關的各種信息常常反映在心音中，因此心臟聽診是臨床診斷心臟疾病和其它相關疾病的重要手段，對心音信號的分析有著重要意義。
由于心音的采集可能存在噪聲，以及不同儀器采集到的心音數據尚沒有統一的標準，因而首先必須對采集到的心音進行預處理，才能對心音信號進一步分析研究。對心音信號的預處理，包括濾除噪聲、心音成分提取和定位、心動周期分割等。心音信號的分析、定位和提取常常采用心電圖定位法，如Baykal等[1]利用S2出現在T波之后來提取S2，Wang等[2]采用QRS 波檢測算法抽取S1[3]。近年來，有很多學者通過對心音包絡提取的方法來對心音信號進行分析、提取特征，文獻[4]利用小波變換來提取包絡，最終準確定位S1與S2；文獻[5]利用數學形態學對心音包絡進行提取，最終對心音進行準確定位；文獻[6]利用香農包絡、希爾伯特-黃變換(Hilbert-Huang transform,HHT)提取包絡；文獻[7]利用局部峰谷點進行插值運算獲取心音包絡，最終準確提取心音特征。所有心音研究都基于心音包絡，包絡在心音研究中體現了極其重要的價值。
本文通過介紹新的心音信號預處理方法和對預處理后的心音信號用數學形態學、HHT、歸一化香農能量、小波變換來提取心音信號包絡，并對相應包絡提取算法提出改進，在原有基礎上得到了峰值點突出，包絡平滑，更能體現原始信號特征的包絡。
1 小波變換對心音信號的預處理
生物醫學信號由于受到本身及外部環境的影響，存在著很多其他一般信號沒有的特性，如信號比較弱、噪聲比較強、頻率比較低、隨機性比較強、非平穩，正是因為生物醫學信號的這些特征，使得生物醫學信號處理方法成為了現代信號處理技術中一個非常重要的領域；小波由于具有時-頻窗多分辨性、伸大拉長和折回重疊的特性，已在生物醫學信號處理中得到了廣泛認可與應用。
1.1 小波變換理論
函數f(t),對于?f(t)∈L2(R)，則它的小波變化為
| $WTf\left( a,b \right)=\int\limits_{R}{f\left( t \right)}{{\psi }_{a,b}}\left( t \right)dt~,$ |
其中。 式中a為尺度參數，b為平移參數，ψa,b(t)為由小波母函數ψ(t)生成的小波,在小波變換中對被分析的信號起著觀測窗的作用。原信號f(t)可以通過WTf(a,b)重構出來。在連續變化的尺度a和時間b的作用下，小波基函數具有很大的相關性，因而信號的連續小波系數所含的信息量是冗余的，通過將小波基離散化，則解決了這個問題。函數Z(T)的離散小波變化為
| $\begin{align} & W{{T}_{Z}}\left( m,n \right)=\langle z\left( t \right),{{\psi }_{m,n}}\left( t \right)\rangle = \\ & {{2}^{-m/2}}\int\limits_{R}{z\left( t \right)\psi ({{2}^{-m}}t-n)dt,}~ \\ \end{align}$ |
式中m=aj,n=kajb。文獻[8]指出Daubechies系列小波(簡寫為db N)對心音信號的分解效果較理想，且N≥4時，重構后的近似系數可以很好地反映出原信號的特征，1≤N≤3時，重構系數不能表征信號本身的特點，此次研究所有小波分解都取N=8。小波變換實質在于將信號按照確定的分解層數N進行N層分解，如圖 1所示(此處分解為8層)，把信號分解一次后出現了一個高頻(D)、一個低頻(A)，N次則出現了N個高頻，N個低頻；然后根據分解后的各層特征值進行處理并重構，即可達到相應目的，如去噪、包絡提取和奇異點檢測等。
圖1
8層多分辨分析樹結構圖
Figure1.
Structure chart of eight layer multi-resolution parse tree
1.2 小波閾值去噪
小波閾值去噪主要是根據實際需要確定小波分解層數，對含有噪聲的信號進行N層分解，分解為N個低頻、N個高頻，由于噪聲往往包含在高頻系數中，因而結合實際情況，選取適當閾值及閾值函數對高頻部分進行閾值處理，把閾值處理后的層進行重構即可得到去噪后的信號。
1.2.1 小波閾值函數
硬閾值函數表達式為
| $Y\left( x \right)=\left\{ \begin{align} & x,\left| x \right|\ge T \\ & 0,\left| x \right| ＜T \\ \end{align} \right.$ |
軟閾值函數表達式為
| $Y\left( x \right)=\left\{ \begin{align} & sgn\left( x \right)\left( \left| x \right|-T \right),\left| x \right|\ge T \\ & 0,\left| x \right|＜T \\ \end{align} \right.$ |
在小波閾值去噪中，式(3)和式(4)一直是兩種經典的閾值函數，在不同領域都有很好的去噪效果。但由于自身的缺陷導致在去噪中得到的效果并不最佳，“硬閾值函數,在+T和-T處是不連續的,會產生一些間斷點,從而造成重構信號有一定的振蕩;軟閾值函數,雖然是連續的函數,但當|x|＞T時,會存在著恒定的偏差,造成高頻信息丟失,邊緣模糊等，從而影響到重構信號與真實信號的逼近程度”[9]。依據文獻[10-15],本文選取一種經過改進后的雙參數閾值函數進行閾值計算[16]。
其表達式為
| $Y\left( x \right)=\text{ }\left\{ \begin{align} & x-T+k*arctan\left( b{{T}^{2a+1}} \right),\text{ }x\ge T \\ & k*arctan(b{{T}^{2a+1}}),\left| x \right|＜T \\ & x+T+k*arctan(b{{T}^{2a+1}}),x\le T \\ \end{align} \right.$ |
其中： 。
M∈[-1, 1],a是大于0的整數。其實不難看出，當M=-1且a→∞時,上述表達式等同于軟閾值；而當M=1且a→∞時，上述表達式則等同于硬閾值。通過合理調整a與M，即可取得很好的去噪效果(此處a與M的調整旨在從硬閾值和軟閾值之間選取較為合理的閾值，從而避免由于硬閾值和軟閾值的自身缺陷帶來的振蕩、邊緣模糊和信息丟失，由實驗中可得當M→1時邊緣振蕩較明顯，當M→-1時信息丟失嚴重)。
1.2.2 閾值選取
四種經典閾值，如表 1所示。
表1
四種經典閾值
Table1.
Four classical threshold
此次試驗中，我們選取了經典閾值中的Sqtwolog閾值，其第n層的閾值估計為
| $Th\left( n \right)=\frac{{{\mu }_{n}}\sqrt{2log\left( N \right)}}{log\left( n+1 \right)~},$ |
其中：。
式中N為信號長度，μn是在小波分解后所得n層的噪聲估計，Median(|αn,k|)為n層上所有小波系數絕對值的中值。
1.2.3 預處理
本文分析的心音數據是由加拿大蒙特利爾臨床醫學研究所錄取，采樣頻率為5 000 Hz。所選的30例都是心臟瓣膜經修復后的心音數據,其中心臟功能正常和不正常的心音各12例。每例都同時在二尖瓣聽診區、三尖瓣聽診區、主動脈瓣聽診區和肺動脈瓣聽診區各采集了一組含有30個心動周期的數據。本文所采用的算法全部在MATLAB 2010平臺上編寫完成。小波閾值去噪算法步驟為：① 由于不同儀器采集標準不一,采集環境不一,采集心音的幅值有所不同,故先對心音信號進行歸一化處理，其公式為x=x(i)/max(|x(i)|)。② 采用db6小波對歸一化后的數據進行8層分解，如表 2所示。③ 對分解后的各層信號采用1.2.1 中的雙參數閾值函數和Sqtwolog閾值進行閾值去噪。④ 最后對閾值處理后的各層小波信號進行重構。
表2
歸一化后的數據的8層分解
Table2.
Eight layer decomposition after data normalization
小波分解后的各層信號如圖 2所示。
圖2
小波分解后的各層信號圖
Figure2.
Each layer signal after wavlet decomposition
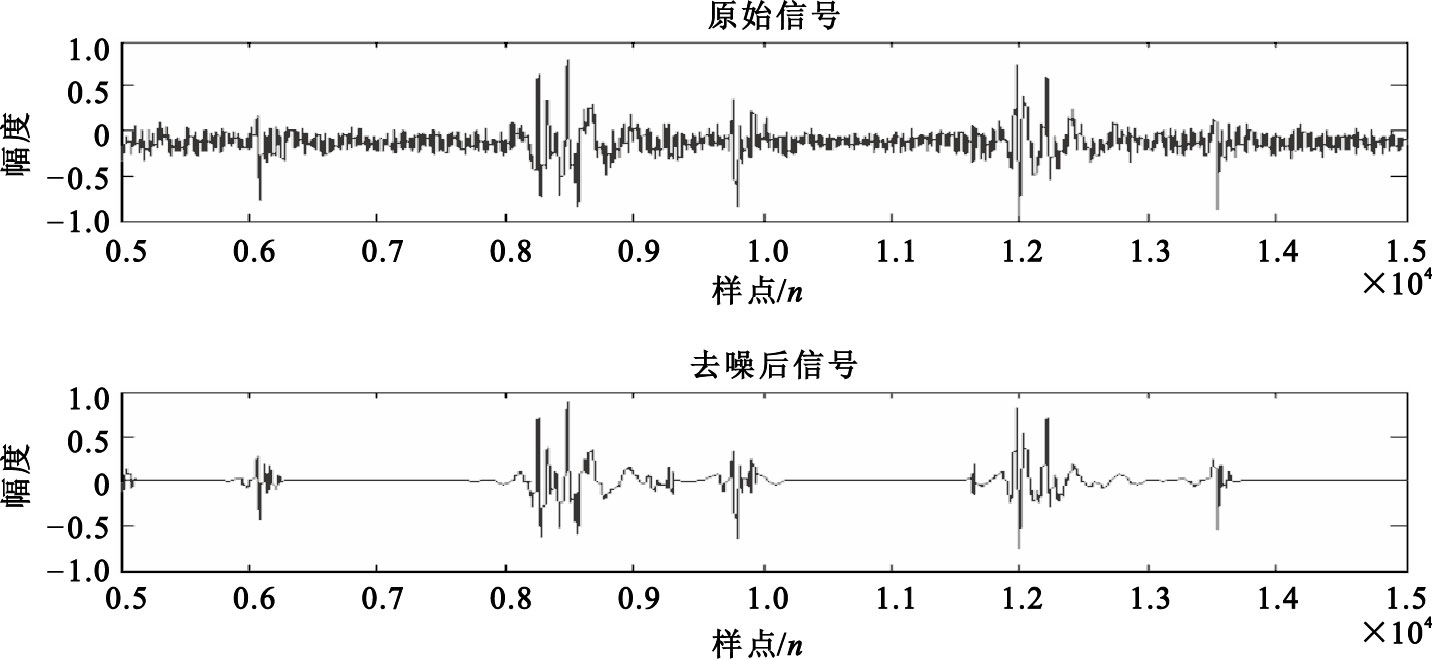
按照上述步驟進行小波閾值去噪后得到的心音信號，如圖 3所示。由于篇幅有限，此處僅給出一例去噪后的結果。
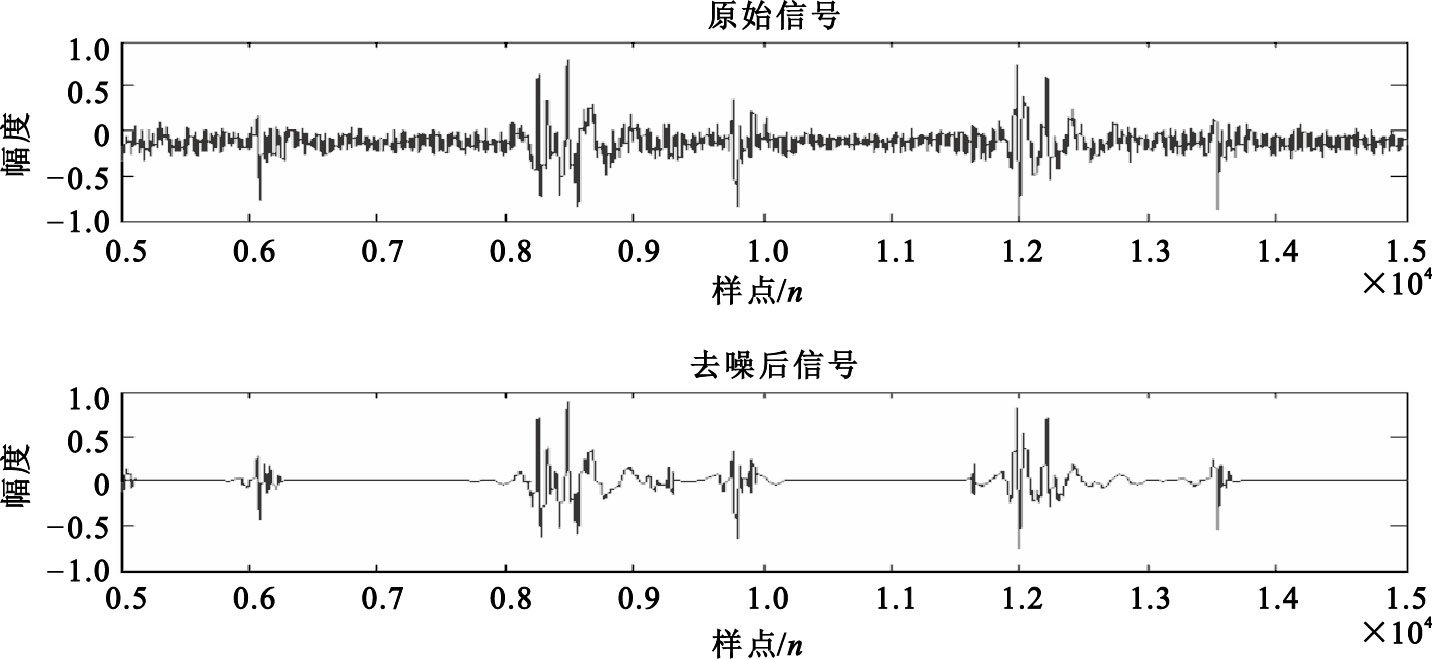圖3
原始信號和去噪后的信號
Figure3.
The signals before and after denoising
由圖 3可清晰地看出去噪效果，小波分解可用于實現帶通濾波，不僅去除了心臟雜音的高頻部分，還對低頻干擾進行了濾波處理，去噪后依然保留了對心音信號分析時所需的信息，本實驗所有數據在提取包絡前都經過該方法的預處理。
2 心音信號包絡提取
盡管上面對心音信號進行了預處理，但由于心音信號十分復雜、變化劇烈，為了更便捷地對心音進行分析、提取特征值，許多學者都用了提取心音包絡的方法，通過對包絡的分析，即可得到大部分的心音基本特性。
對原始心音數據的研究升華到對心音包絡的研究，所研究的包絡的好壞直接影響到后面對心音的定位、分析和特征值的提取,本節通過對預處理后的心音信號分別用數學形態學、HHT、歸一化香農能量、小波變換來提取心音信號包絡，并對相應包絡提取算法提出了改進方案，在原基礎上得到了峰值點突出，包絡平滑，更能體現原始信號特征的包絡。為方便計算所有包絡提取都取20 000個點進行試驗。
2.1 小波包絡提取
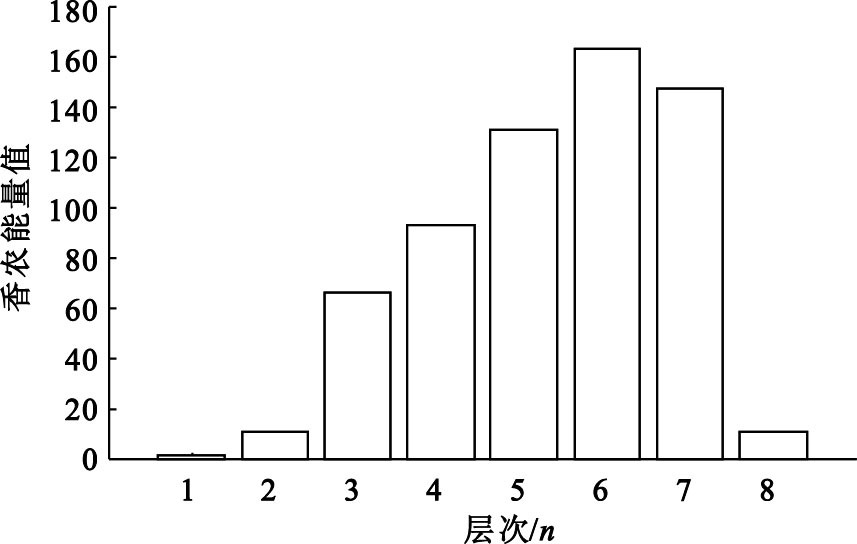
通過1.2.3 節中所進行的信號分解，計算出這8層中各層的香農能量值，如圖 4所示。
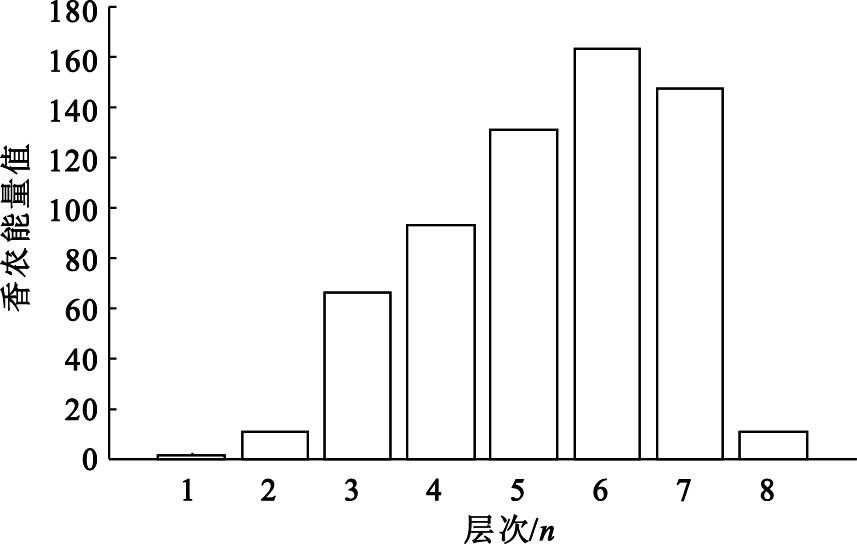圖4
各層香農能量
Figure4.
Shannon energy of Each layer
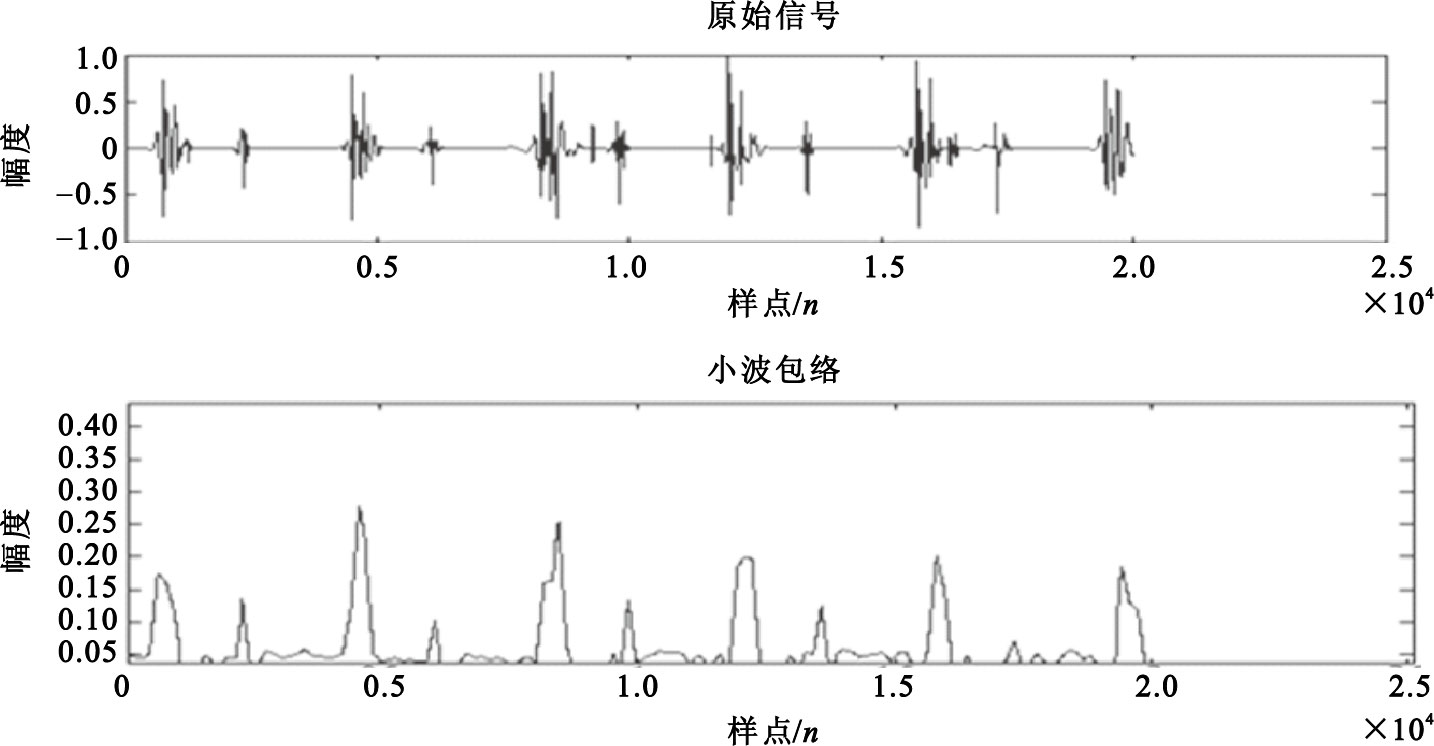
由圖 4可以看出d6層中的香農能量值最大，我們以具有最大的香農能量值的層作為預處理后心音信號的包絡，重構該層即可提取出該心音信號的包絡，如圖 5所示。
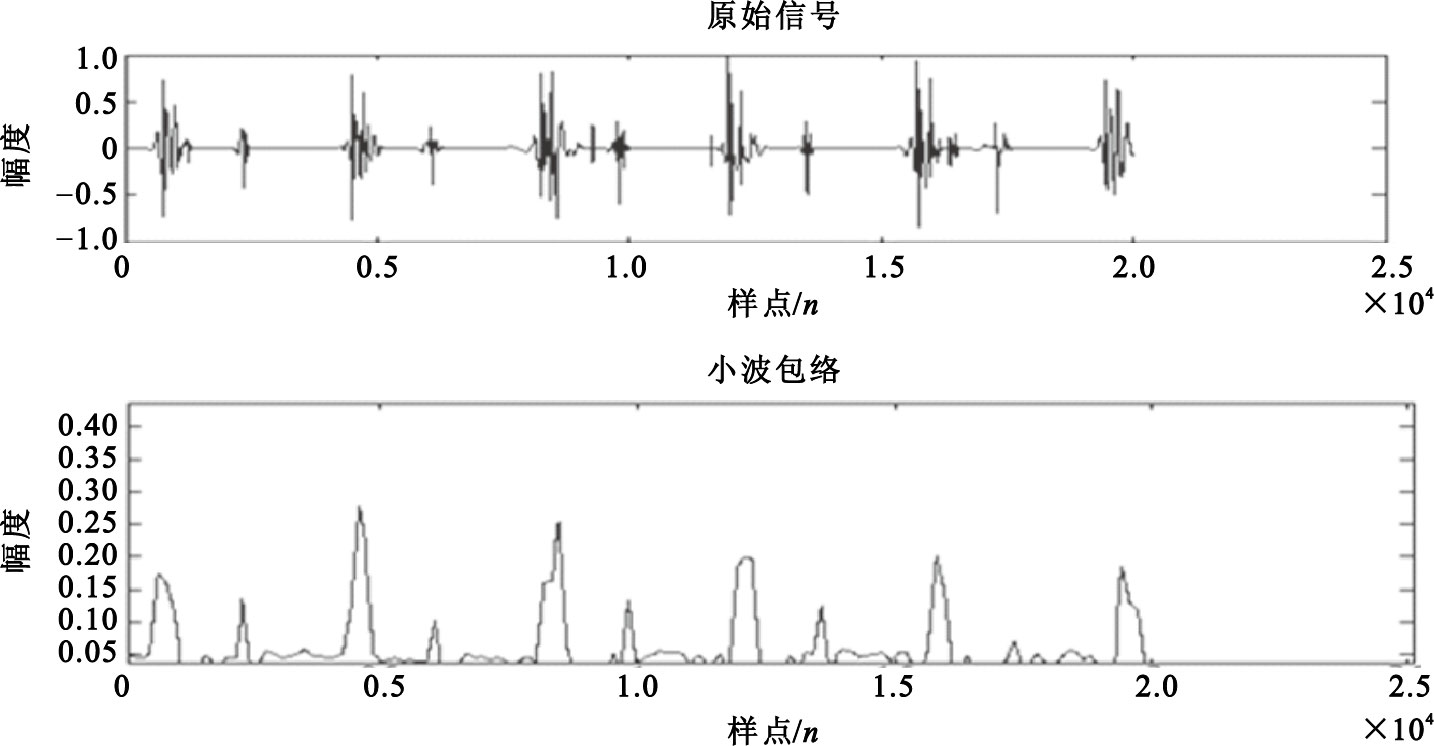圖5
原始心音信號與小波包絡
Figure5.
Original signal and envelope of wavelet
由圖 5可以看出利用小波變化提取的包絡與原信號有很高的吻合度，不管是低頻部分還是高頻部分都能夠很好地反映出來，很多細節都被保留,所包含的信息更加完善，利用該包絡研究心音將能得到更加準確的結果和提取出更加完善的心音特性。
2.2 HHT包絡提取
HHT的創新點在于本征模態函數(intrinsic mode function，IMF)與經驗模態分解(empirical mode decomposition，EMD)的提出。HHT包絡提取步驟為：首先對預處理后的信號進行EMD，得出IMF，再對IMF進行HHT，以黃變換信號的幅值作為復數的實部，希爾伯特變換為虛部，再對該復信號求模，即可得到所需的包絡。計算公式為
| $x\left( t \right)=x\left( t \right)+jx*\left( t \right)=A\left( t \right)[cos(\varphi \left( t \right))+jsin(\varphi \left( t \right))]~,$ |
其中x*(t)是x(t)的希爾伯特變換,其表達式為,,即為信號x(t)的希爾伯特包絡。
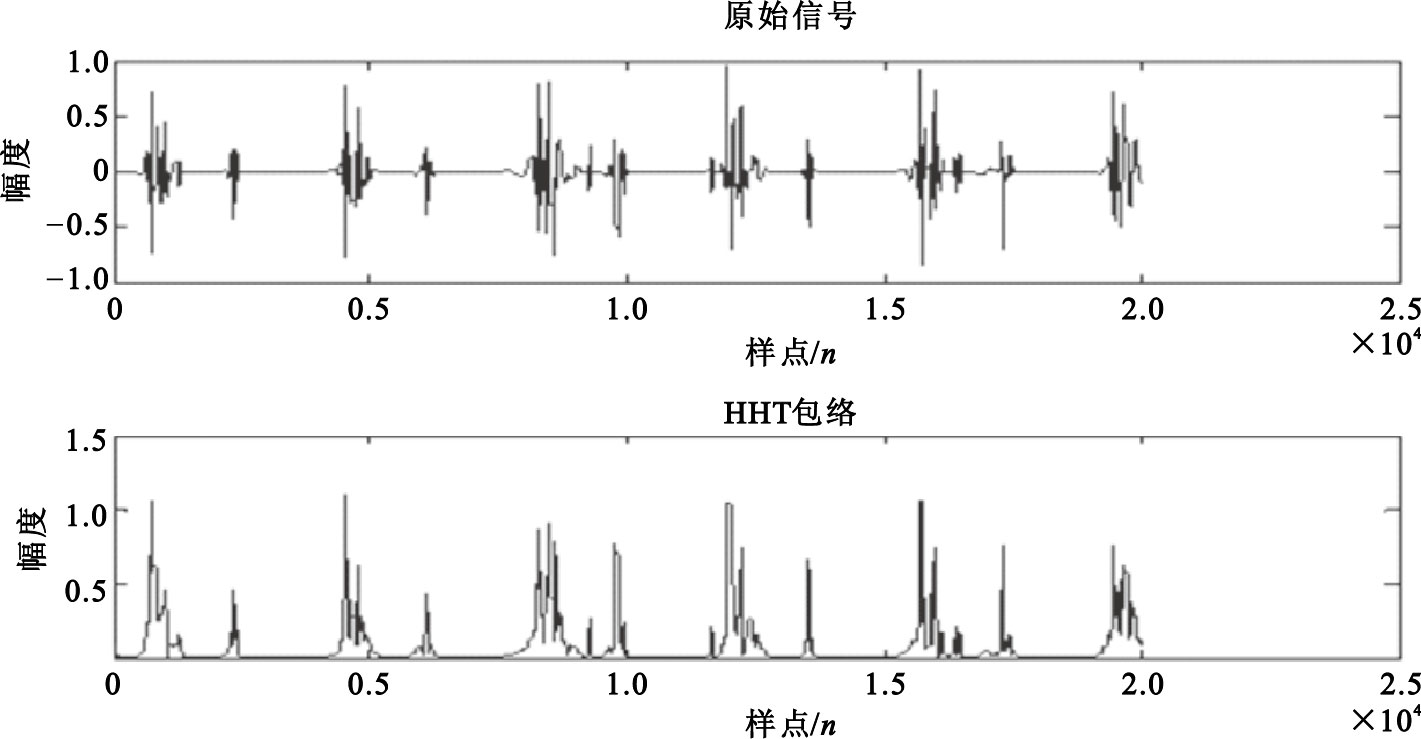
實驗中所得到的包絡如圖 6所示。
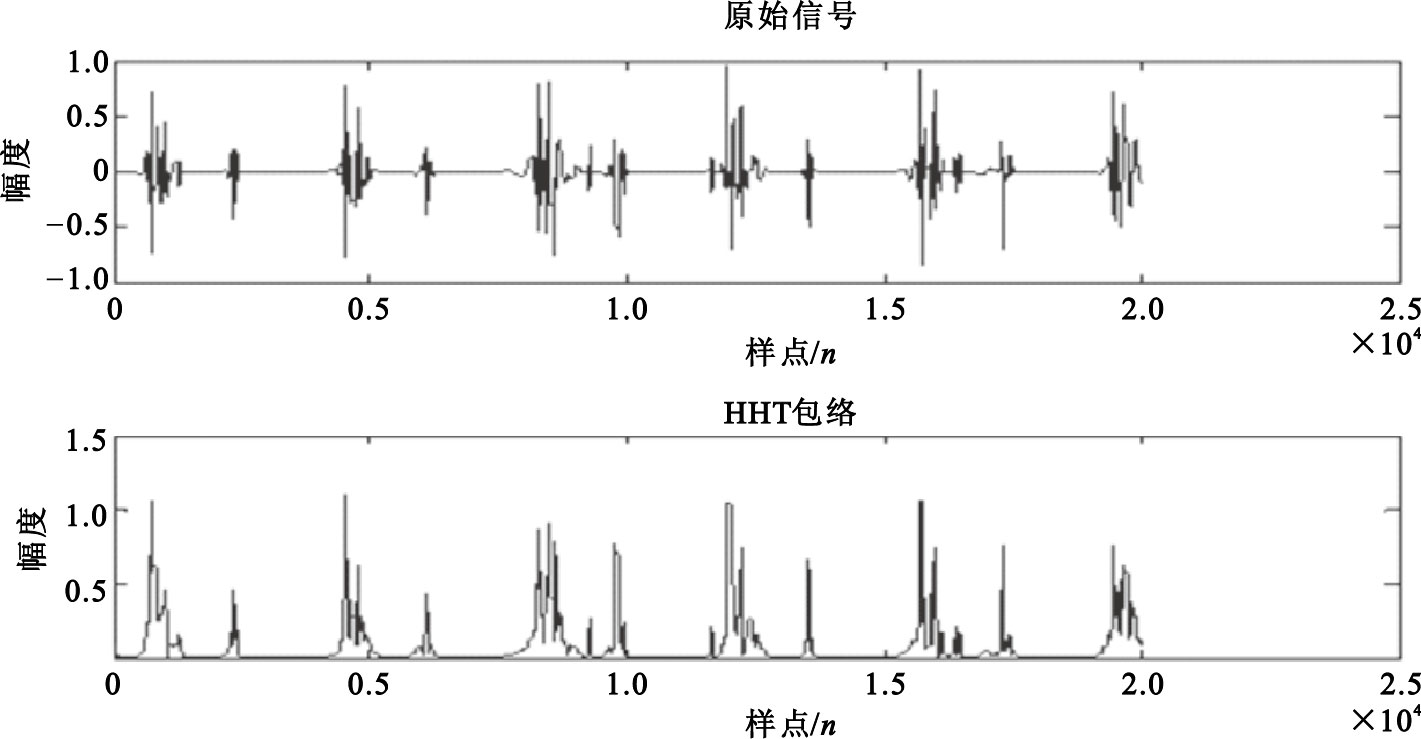圖6
用HHT方法提取的心音包絡
Figure6.
Original signal and heart sound envelope by HHT method
由圖 6可知，利用該方法提取的包絡依然很復雜，毛刺過多影響后期的心音定位與特征值提取。通過多次試驗，得出如果將該方法得到的包絡進行多次插值計算，將得到平滑的包絡。具體步驟為：① 利用上述方法得出原始信號的HHT包絡，如圖 6所示。② 將得到的包絡進行極大值點的提取。③ 將找到的極大值點進行樣條插值處理，得到比較平滑的包絡，如圖 7所示，可以看出經過樣條插值處理后得到的包絡更簡潔，便于對心音信號進行定位與特征提取[17]。
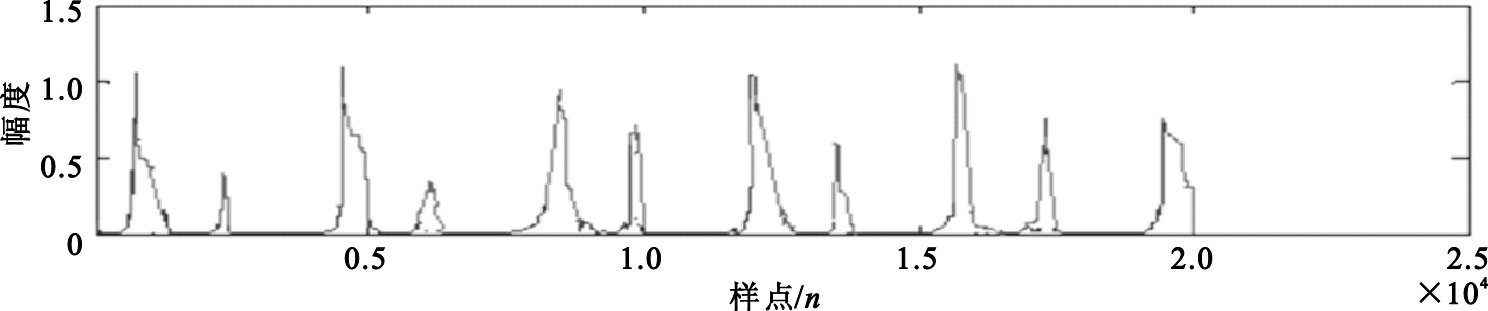圖7
樣條插值后的心音包絡
Figure7.
Envelope after spline interpolation
2.3 香農包絡提取
對預處理后的心音信號進行香農計算，按照分段規則進行每段20 ms，每相隔10 ms取出一段進行計算(此處為二階香農能量計算)，其公式為(8)。對ES進行平均香農能量計算，其公式為(9)。
| ${{E}_{S}}=-1/N\cdot \sum\limits_{i-1}^{N}{{{x}_{norm}}^{2}\left( i \right)}log{{x}_{norm}}^{2}\left( i \right)$ |
| ${{P}_{a}}\left( t \right)=\frac{{{E}_{S}}\left( t \right)-M({{E}_{S}}\left( t \right))}{S({{E}_{s}}\left( t \right))}$ |
利用該算法得到的香農包絡如圖 8所示。
圖8
用歸一化香農能量提取的心音包絡
Figure8.
Original signal and Envelope of Shannon entropy
如若把二階轉為高階則提取出來的包絡會更加平滑，文獻[18]利用三階歸一化香農能量提取包絡，取得了比較平滑的包絡，但在實驗中發現高階香農包絡有自身的缺陷，文獻中指出：“高階的歸一化平均香農能量在S1、S2幅值當時所提取的包絡較好，若S1、S2幅值中有一個相對較低時，高階歸一化香農能量的計算將導致幅值較低的那個被削弱導致信息丟失”,如圖 9所示，其中在心尖和心底部位所采取的數據都會出現該情況[19]。
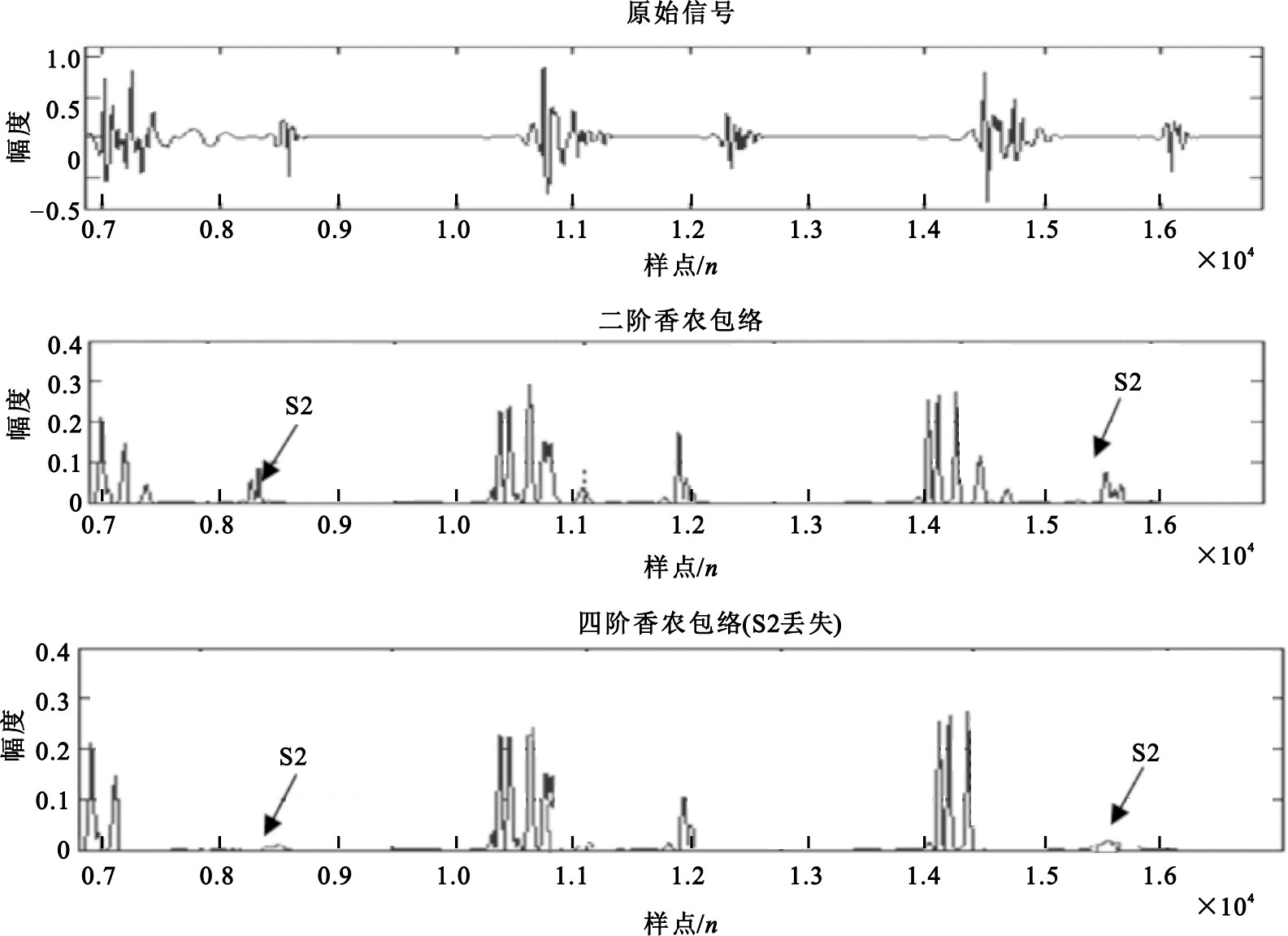圖9
高階香農包絡
Figure9.
Original signal and Envelope of high Shannon entropy
2.4 數學形態學包絡提取
數學形態學是一種非線性濾波方法，一般都是用在二維圖像的處理中，近年來，國內外很多學者將該方法引用到一維信號的處理中，如Trananias將其用于QRS波的檢測[20]。利用數學形態學實現心音信號的邊緣提取，保留原信號的一些必要特性[21]。文獻[22]中指出“形態學閉運算可以填平峰谷，開運算可以消去波峰”，形態學提取步驟為：首先將預處理后的信號進行形態學閉運算，再把運行后的結果進行開運算，所得到的結果即為利用形態學所得到的信號包絡。
閉運算表達式為
| $S[n]=y[n]·k[n]=((h⊕k)⊙k)[n] ,$ |
開運算表達為式為
| $S[n]=y[n]?k[n]=((h⊙k)⊕k)[n] ,$ |
式中y[n]為預處理信號，k[n]為結構元素。
經過計算得到的包絡如圖 10所示。
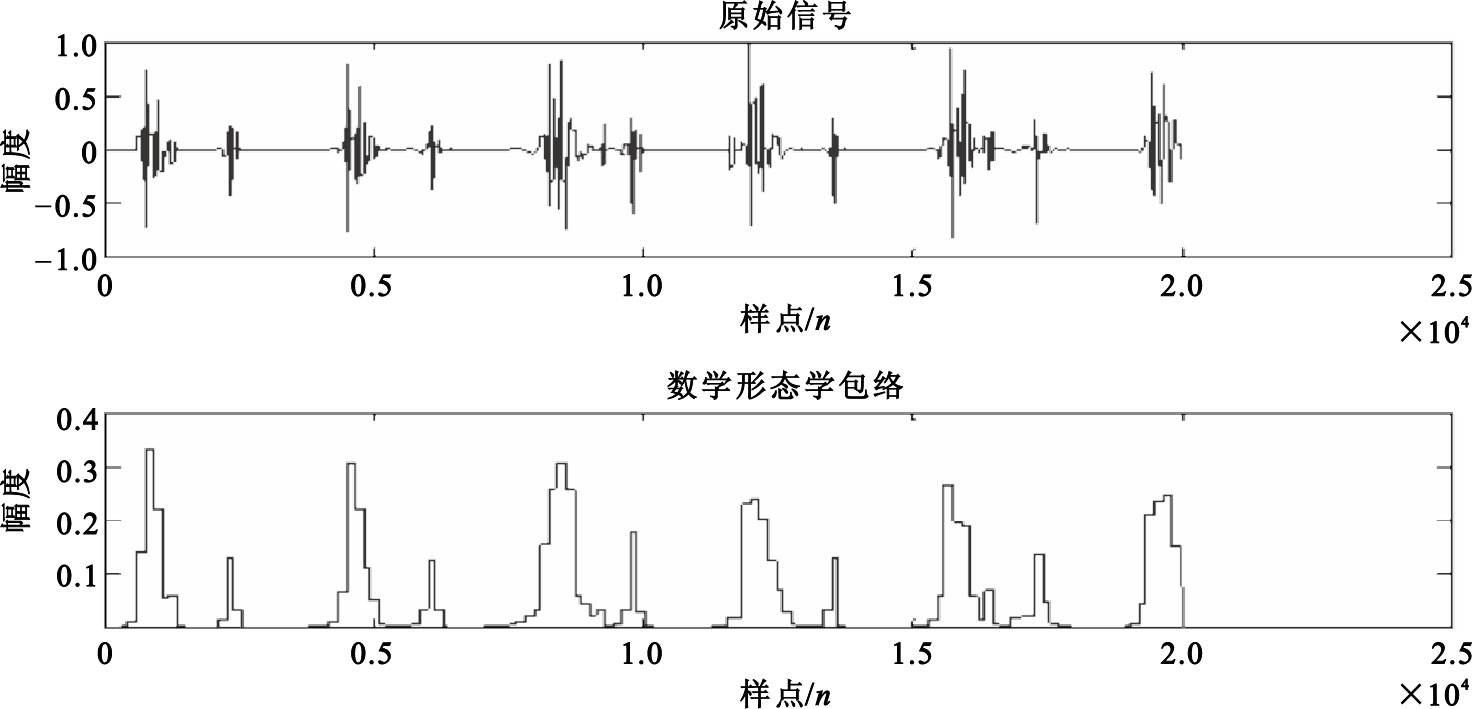圖10
用數學形態學方法提取的心音包絡
Figure10.
Original signal and envelope of shape
由圖 10可以看出，傳統的數學形態學包絡比較簡潔，但峰值點不突出局部極大值過多，不利于后期的心音定位和特征值提取。為了解決這個缺陷，本文提出一種較好的解決辦法，由于該包絡具備了作為信號包絡的基本條件，因而只需在該包絡基礎上做一些改進，其方法為：利用包絡每一數據段內最大值點作為該段內的表示點進行N階線性插值，此處每隔150(18.6 ms)個點進行一次分段(實驗中發現以150個點進行取段效果最好)，共進行了4次線性插值后得到的包絡，如圖 11所示。從圖中可以看出經過N階插值處理后得到的包絡更加平滑，峰值點突出，更利于后期對心音的分析與特征值提取。
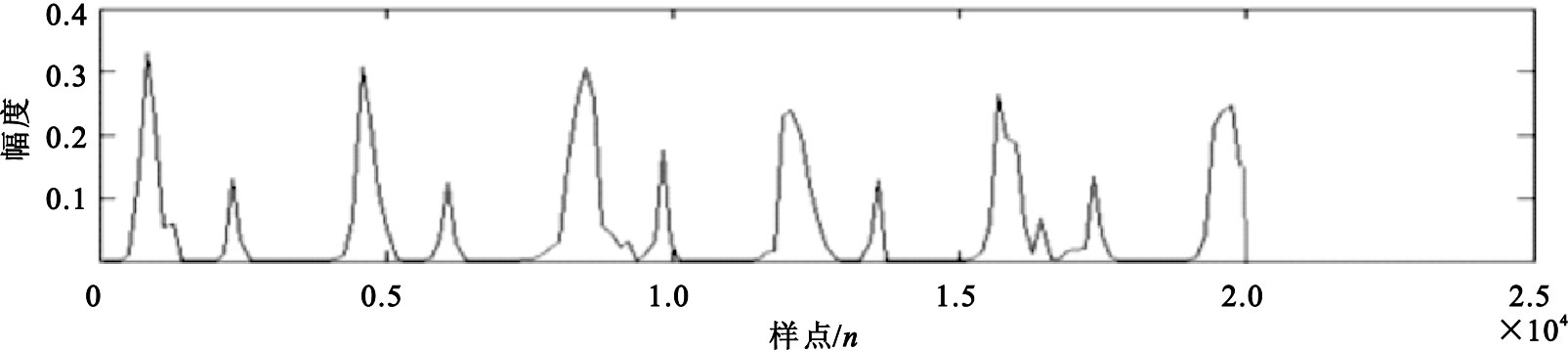圖11
四次線性插值后的包絡
Figure11.
Envelope after four linear interpolation
3 結果討論
通過對加拿大蒙特利爾臨床醫學研究所錄取的30例心音數據進行小波閾值去噪，發現該法是一種很有效的去噪方法，對去噪后的結果和原信號比較后，還發現此法不僅去除了心臟雜音的高頻部分，而且對一些低頻雜音進行了處理，簡化了所采集的心音信號，但心音幅值沒有削減，心動周期沒有改變，去噪后依然保留了心音信號分析時所需的信息，為我們下一步進行心音信號的處理和研究打下了很好的基礎。在該算法中合理選取閾值函數和閾值是成功關鍵的一步，本實驗選取雙參數閾值函數是比較合理的，通過小波閾值去噪能較好的去掉心音數據中的高低頻噪聲。
心音包絡提取在研究心音中是重要的一步，包絡的好壞直接影響到后期的分析。在此次試驗中，分別用四種方法提取包絡，發現HHT算法提取的包絡毛刺較多，不夠平滑，利用樣條插值的方法進行改進，得到了平滑的包絡，但依然有小部分毛刺；香農算法利用了平均化的思想，因而會產生S1、S2位置的偏移，對于高階歸一化平均香農能量提取包絡的算法，可以提取出比較平滑的包絡，但有局限性，當出現S1、S2峰值點有一個比較小時會造成較低一個峰值點被削弱而丟失信息；數學形態學包絡簡單明了，但結構元素k[n]選取比較困難，得到的包絡峰值點不明顯，局部極值較多，對S1、S2的定位不準確，通過改進后能很好地解決定位問題；利用小波閾值去噪后再進行小波變化提取的包絡比較完美，S1、S2峰值點突出,與原信號有很高的吻合度，不管是低頻部分還是高頻部分都能夠很好地反映出來，保留下來的信息更多，且小波變化已有成熟的理論基礎，受廣大學者青瞇，因而我們將在后續更好地利用小波變化對心音信號進行去噪、包絡提取和特征分析等研究。
引言
心音是人體最重要的生理信號之一。心音由第一心音(S1) 、第二心音(S2) 、第三心音(S3) 、第四心音(S4) 及心臟雜音等組成，它含有心臟各個部分如心房、心室、大血管及各個瓣膜功能狀態的生理、病理信息。與心臟疾病有關的各種信息常常反映在心音中，因此心臟聽診是臨床診斷心臟疾病和其它相關疾病的重要手段，對心音信號的分析有著重要意義。
由于心音的采集可能存在噪聲，以及不同儀器采集到的心音數據尚沒有統一的標準，因而首先必須對采集到的心音進行預處理，才能對心音信號進一步分析研究。對心音信號的預處理，包括濾除噪聲、心音成分提取和定位、心動周期分割等。心音信號的分析、定位和提取常常采用心電圖定位法，如Baykal等[1]利用S2出現在T波之后來提取S2，Wang等[2]采用QRS 波檢測算法抽取S1[3]。近年來，有很多學者通過對心音包絡提取的方法來對心音信號進行分析、提取特征，文獻[4]利用小波變換來提取包絡，最終準確定位S1與S2；文獻[5]利用數學形態學對心音包絡進行提取，最終對心音進行準確定位；文獻[6]利用香農包絡、希爾伯特-黃變換(Hilbert-Huang transform,HHT)提取包絡；文獻[7]利用局部峰谷點進行插值運算獲取心音包絡，最終準確提取心音特征。所有心音研究都基于心音包絡，包絡在心音研究中體現了極其重要的價值。
本文通過介紹新的心音信號預處理方法和對預處理后的心音信號用數學形態學、HHT、歸一化香農能量、小波變換來提取心音信號包絡，并對相應包絡提取算法提出改進，在原有基礎上得到了峰值點突出，包絡平滑，更能體現原始信號特征的包絡。
1 小波變換對心音信號的預處理
生物醫學信號由于受到本身及外部環境的影響，存在著很多其他一般信號沒有的特性，如信號比較弱、噪聲比較強、頻率比較低、隨機性比較強、非平穩，正是因為生物醫學信號的這些特征，使得生物醫學信號處理方法成為了現代信號處理技術中一個非常重要的領域；小波由于具有時-頻窗多分辨性、伸大拉長和折回重疊的特性，已在生物醫學信號處理中得到了廣泛認可與應用。
1.1 小波變換理論
函數f(t),對于?f(t)∈L2(R)，則它的小波變化為
| $WTf\left( a,b \right)=\int\limits_{R}{f\left( t \right)}{{\psi }_{a,b}}\left( t \right)dt~,$ |
其中。 式中a為尺度參數，b為平移參數，ψa,b(t)為由小波母函數ψ(t)生成的小波,在小波變換中對被分析的信號起著觀測窗的作用。原信號f(t)可以通過WTf(a,b)重構出來。在連續變化的尺度a和時間b的作用下，小波基函數具有很大的相關性，因而信號的連續小波系數所含的信息量是冗余的，通過將小波基離散化，則解決了這個問題。函數Z(T)的離散小波變化為
| $\begin{align} & W{{T}_{Z}}\left( m,n \right)=\langle z\left( t \right),{{\psi }_{m,n}}\left( t \right)\rangle = \\ & {{2}^{-m/2}}\int\limits_{R}{z\left( t \right)\psi ({{2}^{-m}}t-n)dt,}~ \\ \end{align}$ |
式中m=aj,n=kajb。文獻[8]指出Daubechies系列小波(簡寫為db N)對心音信號的分解效果較理想，且N≥4時，重構后的近似系數可以很好地反映出原信號的特征，1≤N≤3時，重構系數不能表征信號本身的特點，此次研究所有小波分解都取N=8。小波變換實質在于將信號按照確定的分解層數N進行N層分解，如圖 1所示(此處分解為8層)，把信號分解一次后出現了一個高頻(D)、一個低頻(A)，N次則出現了N個高頻，N個低頻；然后根據分解后的各層特征值進行處理并重構，即可達到相應目的，如去噪、包絡提取和奇異點檢測等。
圖1
8層多分辨分析樹結構圖
Figure1.
Structure chart of eight layer multi-resolution parse tree
1.2 小波閾值去噪
小波閾值去噪主要是根據實際需要確定小波分解層數，對含有噪聲的信號進行N層分解，分解為N個低頻、N個高頻，由于噪聲往往包含在高頻系數中，因而結合實際情況，選取適當閾值及閾值函數對高頻部分進行閾值處理，把閾值處理后的層進行重構即可得到去噪后的信號。
1.2.1 小波閾值函數
硬閾值函數表達式為
| $Y\left( x \right)=\left\{ \begin{align} & x,\left| x \right|\ge T \\ & 0,\left| x \right| ＜T \\ \end{align} \right.$ |
軟閾值函數表達式為
| $Y\left( x \right)=\left\{ \begin{align} & sgn\left( x \right)\left( \left| x \right|-T \right),\left| x \right|\ge T \\ & 0,\left| x \right|＜T \\ \end{align} \right.$ |
在小波閾值去噪中，式(3)和式(4)一直是兩種經典的閾值函數，在不同領域都有很好的去噪效果。但由于自身的缺陷導致在去噪中得到的效果并不最佳，“硬閾值函數,在+T和-T處是不連續的,會產生一些間斷點,從而造成重構信號有一定的振蕩;軟閾值函數,雖然是連續的函數,但當|x|＞T時,會存在著恒定的偏差,造成高頻信息丟失,邊緣模糊等，從而影響到重構信號與真實信號的逼近程度”[9]。依據文獻[10-15],本文選取一種經過改進后的雙參數閾值函數進行閾值計算[16]。
其表達式為
| $Y\left( x \right)=\text{ }\left\{ \begin{align} & x-T+k*arctan\left( b{{T}^{2a+1}} \right),\text{ }x\ge T \\ & k*arctan(b{{T}^{2a+1}}),\left| x \right|＜T \\ & x+T+k*arctan(b{{T}^{2a+1}}),x\le T \\ \end{align} \right.$ |
其中： 。
M∈[-1, 1],a是大于0的整數。其實不難看出，當M=-1且a→∞時,上述表達式等同于軟閾值；而當M=1且a→∞時，上述表達式則等同于硬閾值。通過合理調整a與M，即可取得很好的去噪效果(此處a與M的調整旨在從硬閾值和軟閾值之間選取較為合理的閾值，從而避免由于硬閾值和軟閾值的自身缺陷帶來的振蕩、邊緣模糊和信息丟失，由實驗中可得當M→1時邊緣振蕩較明顯，當M→-1時信息丟失嚴重)。
1.2.2 閾值選取
四種經典閾值，如表 1所示。
表1
四種經典閾值
Table1.
Four classical threshold
此次試驗中，我們選取了經典閾值中的Sqtwolog閾值，其第n層的閾值估計為
| $Th\left( n \right)=\frac{{{\mu }_{n}}\sqrt{2log\left( N \right)}}{log\left( n+1 \right)~},$ |
其中：。
式中N為信號長度，μn是在小波分解后所得n層的噪聲估計，Median(|αn,k|)為n層上所有小波系數絕對值的中值。
1.2.3 預處理
本文分析的心音數據是由加拿大蒙特利爾臨床醫學研究所錄取，采樣頻率為5 000 Hz。所選的30例都是心臟瓣膜經修復后的心音數據,其中心臟功能正常和不正常的心音各12例。每例都同時在二尖瓣聽診區、三尖瓣聽診區、主動脈瓣聽診區和肺動脈瓣聽診區各采集了一組含有30個心動周期的數據。本文所采用的算法全部在MATLAB 2010平臺上編寫完成。小波閾值去噪算法步驟為：① 由于不同儀器采集標準不一,采集環境不一,采集心音的幅值有所不同,故先對心音信號進行歸一化處理，其公式為x=x(i)/max(|x(i)|)。② 采用db6小波對歸一化后的數據進行8層分解，如表 2所示。③ 對分解后的各層信號采用1.2.1 中的雙參數閾值函數和Sqtwolog閾值進行閾值去噪。④ 最后對閾值處理后的各層小波信號進行重構。
表2
歸一化后的數據的8層分解
Table2.
Eight layer decomposition after data normalization
小波分解后的各層信號如圖 2所示。
圖2
小波分解后的各層信號圖
Figure2.
Each layer signal after wavlet decomposition
按照上述步驟進行小波閾值去噪后得到的心音信號，如圖 3所示。由于篇幅有限，此處僅給出一例去噪后的結果。
圖3
原始信號和去噪后的信號
Figure3.
The signals before and after denoising
由圖 3可清晰地看出去噪效果，小波分解可用于實現帶通濾波，不僅去除了心臟雜音的高頻部分，還對低頻干擾進行了濾波處理，去噪后依然保留了對心音信號分析時所需的信息，本實驗所有數據在提取包絡前都經過該方法的預處理。
2 心音信號包絡提取
盡管上面對心音信號進行了預處理，但由于心音信號十分復雜、變化劇烈，為了更便捷地對心音進行分析、提取特征值，許多學者都用了提取心音包絡的方法，通過對包絡的分析，即可得到大部分的心音基本特性。
對原始心音數據的研究升華到對心音包絡的研究，所研究的包絡的好壞直接影響到后面對心音的定位、分析和特征值的提取,本節通過對預處理后的心音信號分別用數學形態學、HHT、歸一化香農能量、小波變換來提取心音信號包絡，并對相應包絡提取算法提出了改進方案，在原基礎上得到了峰值點突出，包絡平滑，更能體現原始信號特征的包絡。為方便計算所有包絡提取都取20 000個點進行試驗。
2.1 小波包絡提取
通過1.2.3 節中所進行的信號分解，計算出這8層中各層的香農能量值，如圖 4所示。
圖4
各層香農能量
Figure4.
Shannon energy of Each layer
由圖 4可以看出d6層中的香農能量值最大，我們以具有最大的香農能量值的層作為預處理后心音信號的包絡，重構該層即可提取出該心音信號的包絡，如圖 5所示。
圖5
原始心音信號與小波包絡
Figure5.
Original signal and envelope of wavelet
由圖 5可以看出利用小波變化提取的包絡與原信號有很高的吻合度，不管是低頻部分還是高頻部分都能夠很好地反映出來，很多細節都被保留,所包含的信息更加完善，利用該包絡研究心音將能得到更加準確的結果和提取出更加完善的心音特性。
2.2 HHT包絡提取
HHT的創新點在于本征模態函數(intrinsic mode function，IMF)與經驗模態分解(empirical mode decomposition，EMD)的提出。HHT包絡提取步驟為：首先對預處理后的信號進行EMD，得出IMF，再對IMF進行HHT，以黃變換信號的幅值作為復數的實部，希爾伯特變換為虛部，再對該復信號求模，即可得到所需的包絡。計算公式為
| $x\left( t \right)=x\left( t \right)+jx*\left( t \right)=A\left( t \right)[cos(\varphi \left( t \right))+jsin(\varphi \left( t \right))]~,$ |
其中x*(t)是x(t)的希爾伯特變換,其表達式為,,即為信號x(t)的希爾伯特包絡。
實驗中所得到的包絡如圖 6所示。
圖6
用HHT方法提取的心音包絡
Figure6.
Original signal and heart sound envelope by HHT method
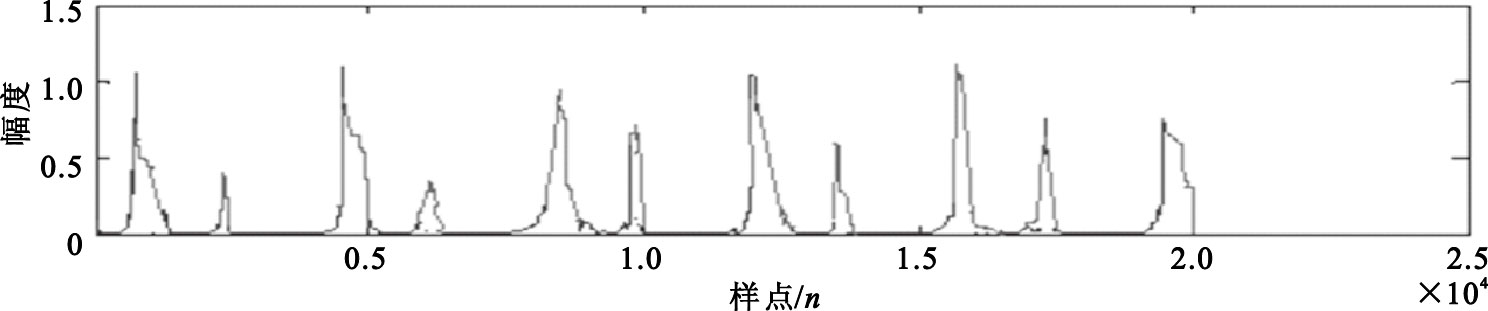
由圖 6可知，利用該方法提取的包絡依然很復雜，毛刺過多影響后期的心音定位與特征值提取。通過多次試驗，得出如果將該方法得到的包絡進行多次插值計算，將得到平滑的包絡。具體步驟為：① 利用上述方法得出原始信號的HHT包絡，如圖 6所示。② 將得到的包絡進行極大值點的提取。③ 將找到的極大值點進行樣條插值處理，得到比較平滑的包絡，如圖 7所示，可以看出經過樣條插值處理后得到的包絡更簡潔，便于對心音信號進行定位與特征提取[17]。
圖7
樣條插值后的心音包絡
Figure7.
Envelope after spline interpolation
2.3 香農包絡提取
對預處理后的心音信號進行香農計算，按照分段規則進行每段20 ms，每相隔10 ms取出一段進行計算(此處為二階香農能量計算)，其公式為(8)。對ES進行平均香農能量計算，其公式為(9)。
| ${{E}_{S}}=-1/N\cdot \sum\limits_{i-1}^{N}{{{x}_{norm}}^{2}\left( i \right)}log{{x}_{norm}}^{2}\left( i \right)$ |
| ${{P}_{a}}\left( t \right)=\frac{{{E}_{S}}\left( t \right)-M({{E}_{S}}\left( t \right))}{S({{E}_{s}}\left( t \right))}$ |
利用該算法得到的香農包絡如圖 8所示。
圖8
用歸一化香農能量提取的心音包絡
Figure8.
Original signal and Envelope of Shannon entropy
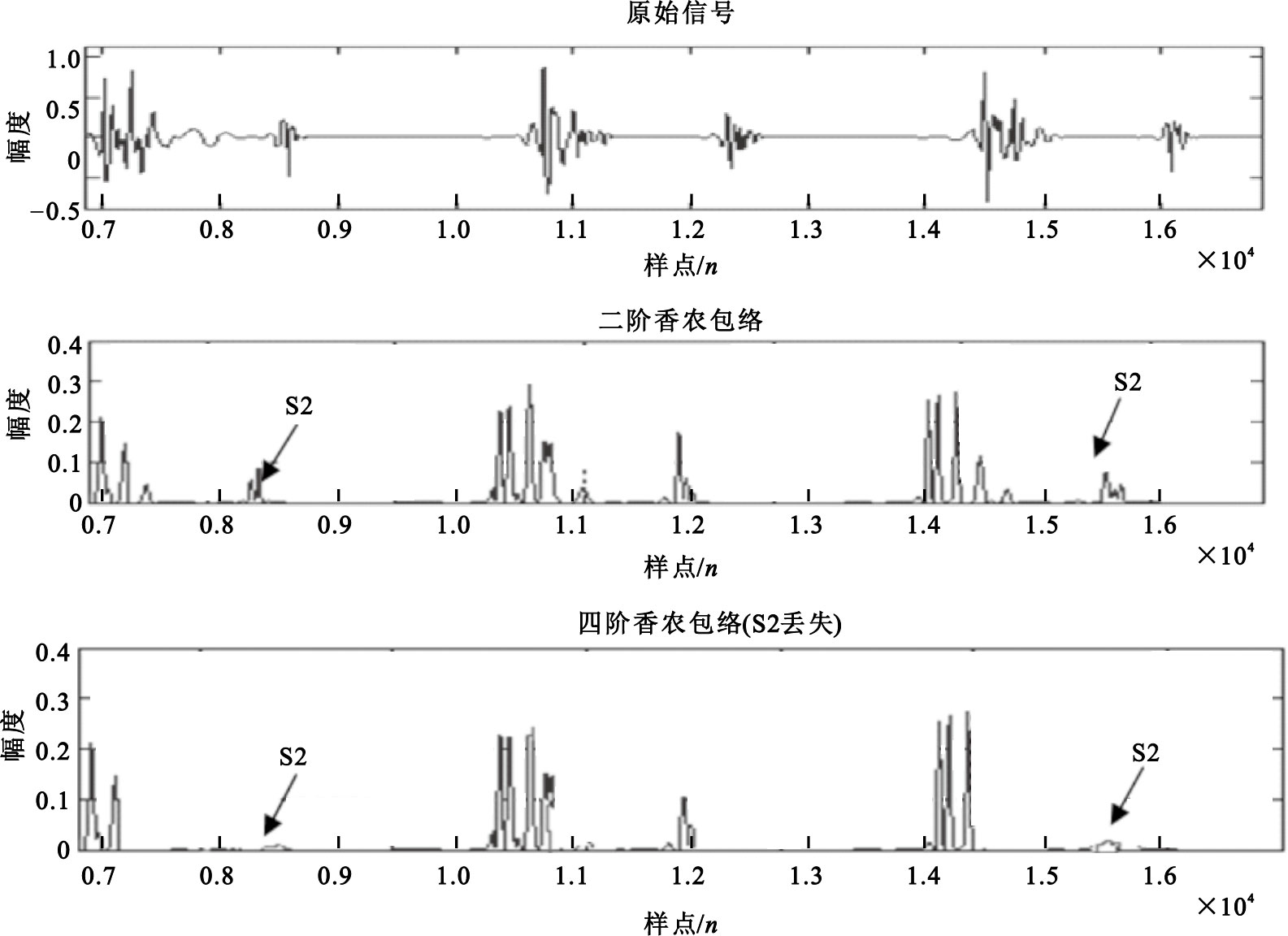
如若把二階轉為高階則提取出來的包絡會更加平滑，文獻[18]利用三階歸一化香農能量提取包絡，取得了比較平滑的包絡，但在實驗中發現高階香農包絡有自身的缺陷，文獻中指出：“高階的歸一化平均香農能量在S1、S2幅值當時所提取的包絡較好，若S1、S2幅值中有一個相對較低時，高階歸一化香農能量的計算將導致幅值較低的那個被削弱導致信息丟失”,如圖 9所示，其中在心尖和心底部位所采取的數據都會出現該情況[19]。
圖9
高階香農包絡
Figure9.
Original signal and Envelope of high Shannon entropy
2.4 數學形態學包絡提取
數學形態學是一種非線性濾波方法，一般都是用在二維圖像的處理中，近年來，國內外很多學者將該方法引用到一維信號的處理中，如Trananias將其用于QRS波的檢測[20]。利用數學形態學實現心音信號的邊緣提取，保留原信號的一些必要特性[21]。文獻[22]中指出“形態學閉運算可以填平峰谷，開運算可以消去波峰”，形態學提取步驟為：首先將預處理后的信號進行形態學閉運算，再把運行后的結果進行開運算，所得到的結果即為利用形態學所得到的信號包絡。
閉運算表達式為
| $S[n]=y[n]·k[n]=((h⊕k)⊙k)[n] ,$ |
開運算表達為式為
| $S[n]=y[n]?k[n]=((h⊙k)⊕k)[n] ,$ |
式中y[n]為預處理信號，k[n]為結構元素。
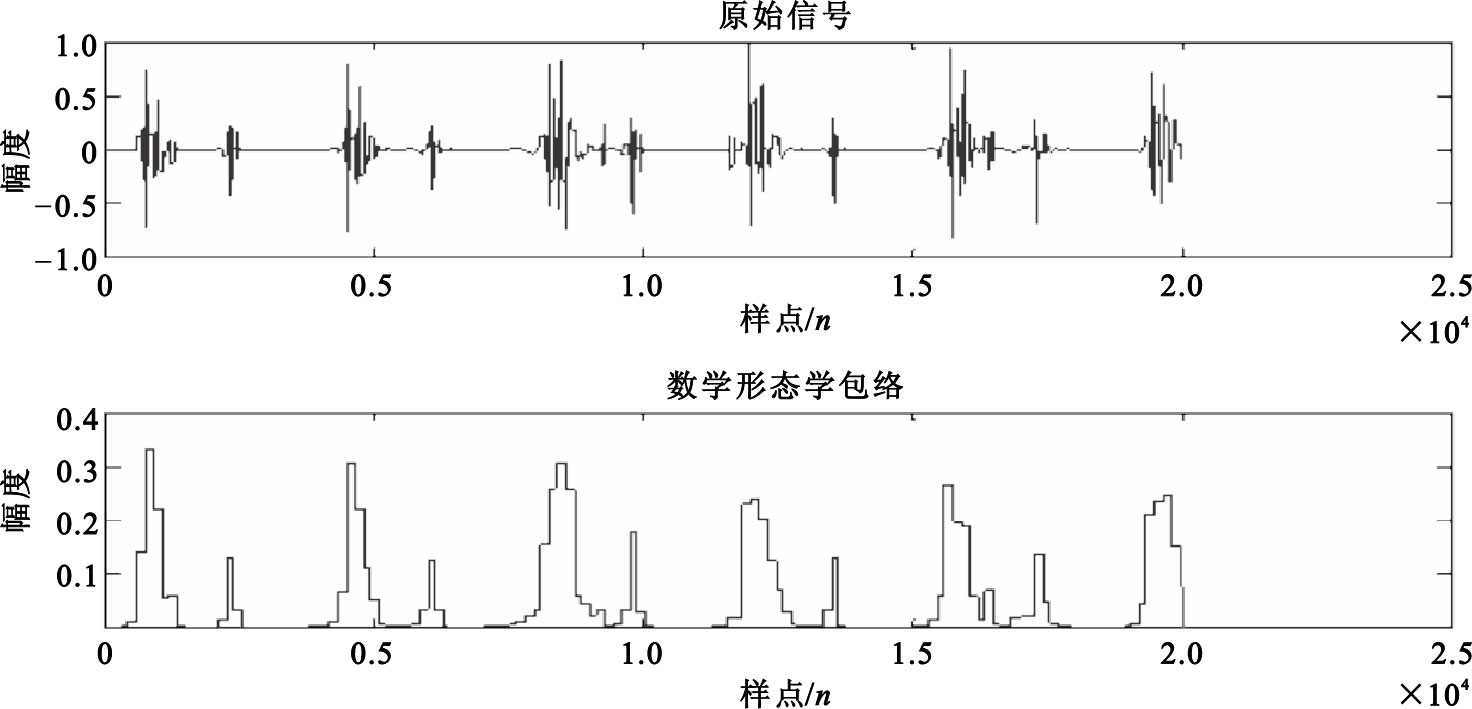
經過計算得到的包絡如圖 10所示。
圖10
用數學形態學方法提取的心音包絡
Figure10.
Original signal and envelope of shape
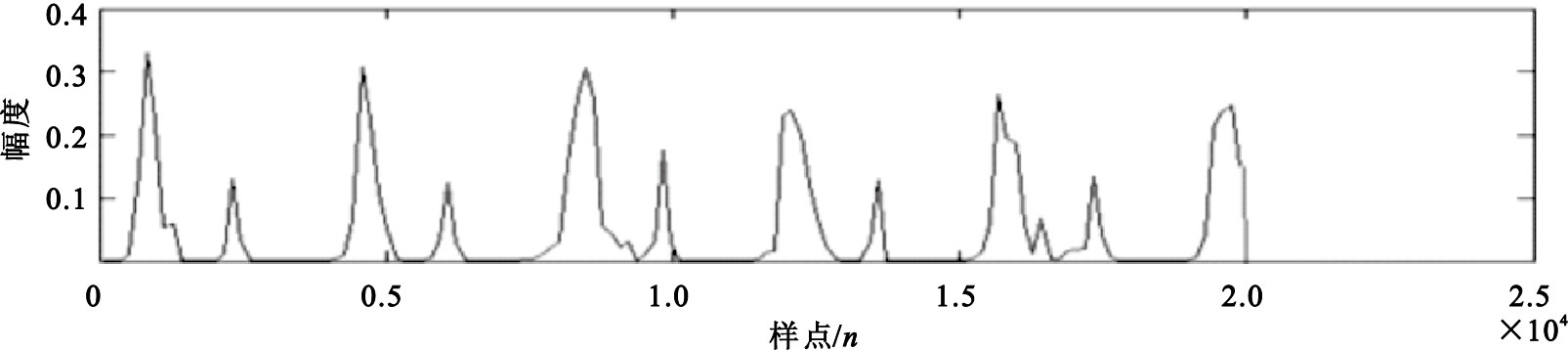
由圖 10可以看出，傳統的數學形態學包絡比較簡潔，但峰值點不突出局部極大值過多，不利于后期的心音定位和特征值提取。為了解決這個缺陷，本文提出一種較好的解決辦法，由于該包絡具備了作為信號包絡的基本條件，因而只需在該包絡基礎上做一些改進，其方法為：利用包絡每一數據段內最大值點作為該段內的表示點進行N階線性插值，此處每隔150(18.6 ms)個點進行一次分段(實驗中發現以150個點進行取段效果最好)，共進行了4次線性插值后得到的包絡，如圖 11所示。從圖中可以看出經過N階插值處理后得到的包絡更加平滑，峰值點突出，更利于后期對心音的分析與特征值提取。
圖11
四次線性插值后的包絡
Figure11.
Envelope after four linear interpolation
3 結果討論
通過對加拿大蒙特利爾臨床醫學研究所錄取的30例心音數據進行小波閾值去噪，發現該法是一種很有效的去噪方法，對去噪后的結果和原信號比較后，還發現此法不僅去除了心臟雜音的高頻部分，而且對一些低頻雜音進行了處理，簡化了所采集的心音信號，但心音幅值沒有削減，心動周期沒有改變，去噪后依然保留了心音信號分析時所需的信息，為我們下一步進行心音信號的處理和研究打下了很好的基礎。在該算法中合理選取閾值函數和閾值是成功關鍵的一步，本實驗選取雙參數閾值函數是比較合理的，通過小波閾值去噪能較好的去掉心音數據中的高低頻噪聲。
心音包絡提取在研究心音中是重要的一步，包絡的好壞直接影響到后期的分析。在此次試驗中，分別用四種方法提取包絡，發現HHT算法提取的包絡毛刺較多，不夠平滑，利用樣條插值的方法進行改進，得到了平滑的包絡，但依然有小部分毛刺；香農算法利用了平均化的思想，因而會產生S1、S2位置的偏移，對于高階歸一化平均香農能量提取包絡的算法，可以提取出比較平滑的包絡，但有局限性，當出現S1、S2峰值點有一個比較小時會造成較低一個峰值點被削弱而丟失信息；數學形態學包絡簡單明了，但結構元素k[n]選取比較困難，得到的包絡峰值點不明顯，局部極值較多，對S1、S2的定位不準確，通過改進后能很好地解決定位問題；利用小波閾值去噪后再進行小波變化提取的包絡比較完美，S1、S2峰值點突出,與原信號有很高的吻合度，不管是低頻部分還是高頻部分都能夠很好地反映出來，保留下來的信息更多，且小波變化已有成熟的理論基礎，受廣大學者青瞇，因而我們將在后續更好地利用小波變化對心音信號進行去噪、包絡提取和特征分析等研究。
