醫學三維掃描體數據和二維圖像配準在臨床診斷、手術規劃等領域應用廣泛,特別是在手術導航時,三維掃描體數據和二維圖像的結合既需要保證配準的精度,又要達到手術中即時應用的要求。本文提出一種混合幾何和圖像密度特征構成的相似度度量函數,對術前CT和術中X線圖像進行快速的2D-3D 配準,其實現方便、計算量小,同時計算精度可以滿足正常的需要。另外,整個計算過程非常適合高度并行的數值計算,通過采用基于CUDA的硬件加速算法,能夠達到手術中即時應用的要求。
引用本文： 李玲芝, 鄒北驥. 基于CUDA的2D-3D醫學圖像快速配準. 生物醫學工程學雜志, 2014, 31(4): 905-909. doi: 10.7507/1001-5515.20140170 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
在外科手術和放射治療等臨床實踐中，由于二維掃描圖像的成像時間短,可以做到實時或者準實時的跟蹤，并且二維掃描的相關成像設備的輻射較少,對患者和醫生的損害較小，方便在手術中使用。另一方面，CT 或者MRI 等三維掃描可以提供人體解剖結構和興趣區域更準確的三維結構信息，但是掃描操作很難實時進行，一般只能在手術前獲得。這樣，需要應用2D-3D 醫學圖像配準技術在手術過程中融合兩種不同維度的數據,即時得到興趣區域和結構上更多的信息[1]。
目前，2D-3D 醫學圖像配準方法主要分為基于幾何特征[2-5]和基于圖像特征[6-8]兩類。一般來說，第一類方法使用物體上的幾何特征進行配準。幾何特征點的使用又分為外部植入特征與內部本身解剖特征。采用外部植入標記物的配準精度高,但因需要進行侵入性植入,臨床應用有一定爭議。總體而言，采用幾何特征的方法一般需要精確重建物體邊界的三維表面模型,計算量較大，準確性也差一些。而基于圖像特征的方法,大部分是采用數字重建的X線片(digitally reconstructed radiographs,DRR) 算法，即通過從CT三維圖像生成二維的DRR 圖像，與直接掃描得到的X線圖像進行配準。由于生成高質量的DRR圖像通常使用光線投射算法，計算穿過體數據光線上每個體素的衰減值[9-11]，計算量非常大，使得配準過程難以實時或準實時進行，成為臨床應用的瓶頸。因此，如何提高2D-3D 配準速度是一個研究熱點。眾多學者提出了多種改進方法，如使用降低分辨率和壓縮灰度級的方法[12]，計算感興趣區的相似性[13]，使用壓縮分解的加速方法[14]，以及使用逐步衰減域加速方法等[15]。
雖然眾多研究者提出了各種優化方法，但是由于要處理每個體數據中的每個體素，從三維體掃描數據生成二維DRR 圖像的計算量仍然比較大。而在實際的手術導航應用中，既需要保證配準的精度，又要達到手術中即時應用的要求。針對這些需要與分析,本文提出一種采用混合特征信息的2D-3D 配準方法，綜合利用三維模型的幾何邊界信息和二維圖像的灰度信息，進行快速的配準計算。
我們認為，物體興趣區域(如脊椎骨骼)的幾何邊界輪廓提供了充分的信息進行三維數據與二維圖像的配準。同時，對于物體興趣區域的幾何邊界信息，并不需要顯式的表達為三維幾何模型，而是可以直接用術前三維圖像分割生成的二值邊界體素進行表示。而三維邊界體素模型可以進行高效的二維投影生成一個新的二維圖像，新圖像能方便地與X線二維圖像進行相似性的定量比較。在整個流程中，從三維體數據進行圖像分割生成的二值邊界體素表示的過程計算量較大，但是只需要在術前進行一次預處理，不影響后面即時手術過程中的配準計算。另外，由于近年來顯卡技術迅猛發展，圖形處理器(graphics processing unit,GPU)的通用計算能力和可編程性使其已廣泛地應用到醫學圖像處理領域。而本文提出的2D-3D 配準計算框架中對于三維體素和二維像素的處理計算都是高度并行的，可進一步利用GPU 并行計算環境，提出基于CUDA 的2D-3D 的快速配準。
1 基于混合特征的2D-3D配準方法
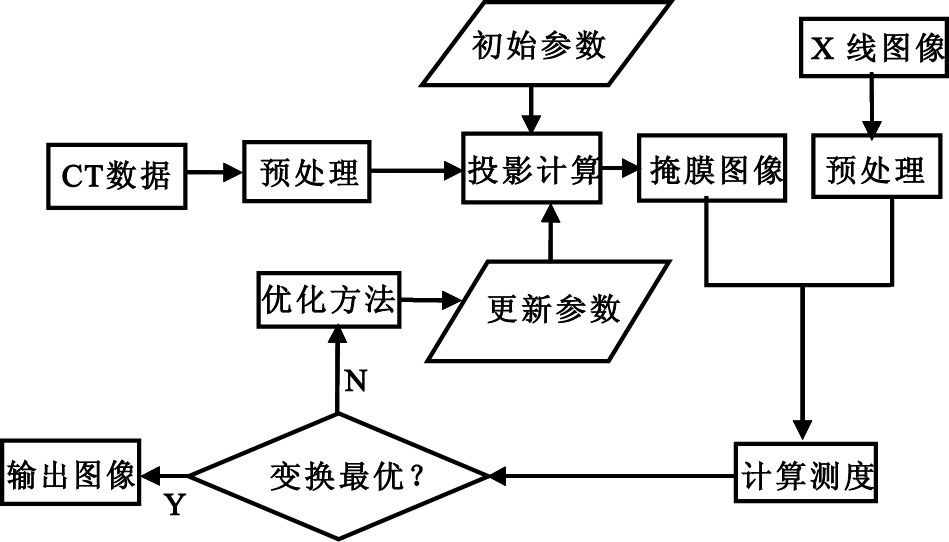
本文2D-3D 配準方法的基本過程和以前基于DRR重建的配準算法類似，如圖 1所示，每一次迭代過程，都基于三維的CT體數據經過投影計算生成一個合成的二維圖像，然后和X 線二維圖像進行相似度測量。但是，我們并不需要生成計算瓶頸的DRR圖像，而是利用一種新的混合幾何和圖像密度特征的方法進行快速的2D-3D 配準。
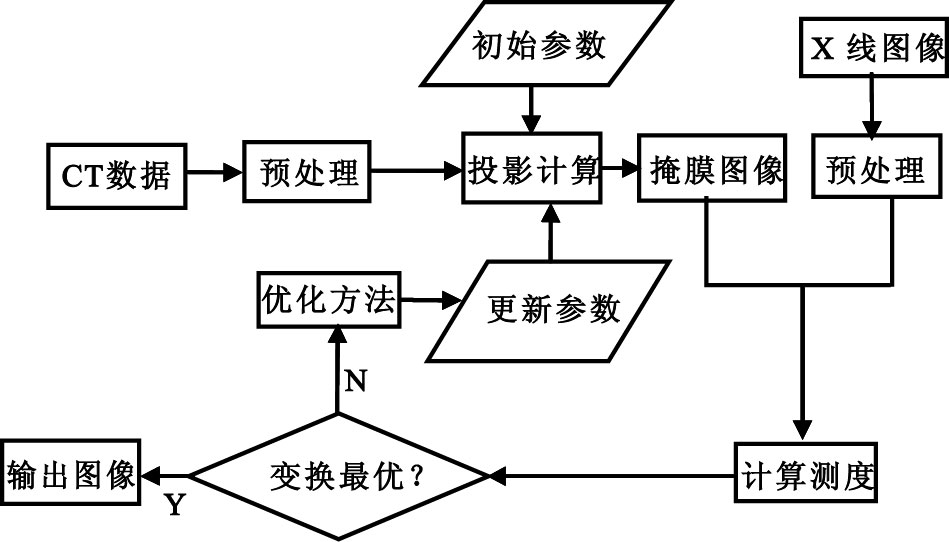圖1
2D-3D配準流程圖
Figure1.
The flowchart of 2D-3D registration
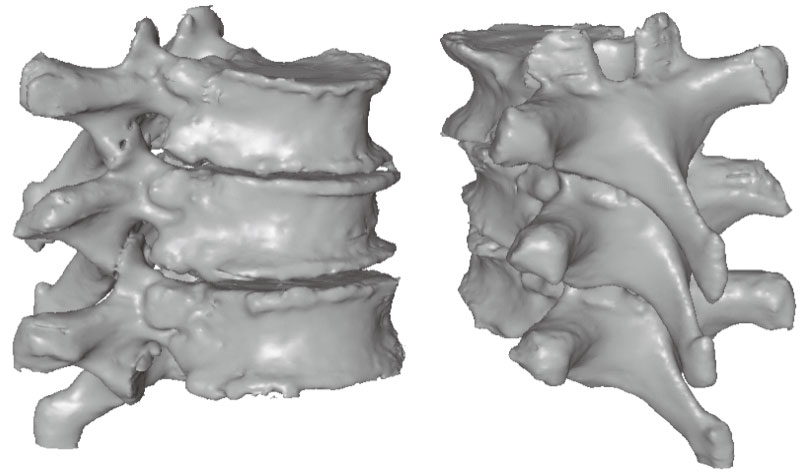
本文算法的第一步，是對三維CT數據進行預處理和圖像分割。由于CT數據是手術前得到的，我們可以采用半自動的方法配合手工交互修改，得到準確的CT圖像分割結果，如圖 2所示。但是，本文并不需要計算出幾何的三維模型，而是將圖像分割得到的二值化區域結果進行腐蝕操作(使用3×3×3的模板)，然后進行布爾減操作，這樣得到興趣區域的邊界體素。得到的邊界體素數目一般只占直接圖像分割結果體素的12%左右，這樣大大減少了數據量。這一步操作只需要在手術前進行一次，將結果保存之后備用。
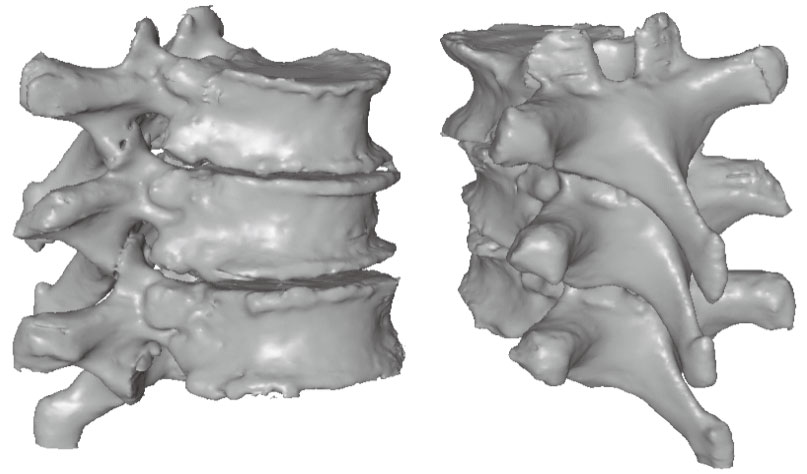圖2
CT數據的三維重建模型
Figure2.
3D reconstruction model from CT volume
2D-3D配準算法的主體過程是采用一個優化迭代的進程，確定一組最優的CT體數據空間的剛體平移和旋轉參數：(X,Y,Z)和(θX,θY,θZ)，將二維、三維數據在統一的空間坐標系中進行配準對齊。算法的關鍵是要定義一個合適的測度，或稱相似度度量函數，然后搜索，使得三維數據投影得到的二維圖像與X線圖像在相似性測度上達到最大的空間變換。
本文提出一種新的相似度度量方法，不需要從CT數據計算DRR圖像，而是直接把預處理圖像分割得到的三維邊界體素投影到X線圖像所在平面，得到一個二值掩膜圖像，如圖 3所示。可以看到，盡管只進行簡單的直接投影計算，二值掩膜圖像的興趣區域基本上完全填滿，這樣可以穩定、快速地抽取這個二值掩膜圖像的邊界像素。同時，本文采用一種改進的Canny邊界檢測算子抽取X線圖像的邊界信息，如圖 4所示。這樣，可以將兩種圖像邊界之間的加權和定義為相似度度量函數的第一部分。注意到X線圖像的邊界信息不是完整、連續的，本文采用一種局部的度量方法，定義一個半徑距離R，對于每一個X線圖像的邊界像素，計算其到二值掩膜圖像邊界的最小距離Di，如果(R-Di)大于0,則認為這次的距離計算有效，定義E1為
| ${{E}_{1}}=\sum\limits_{i\in imageBoundaryPixel}{(R-{{D}_{i}}>0)?(R-{{D}_{i}}):0}$ |
顯然，當二值掩膜圖像的邊界和X線圖像的邊界重合時，E1值達到最大化。 相似度度量函數的第二部分，則利用圖像的密度信息。我們注意到X線圖像興趣區域的像素密度值比背景區域小，這樣可以根據二值掩膜圖像每個前景像素點的坐標取X線圖像中對應像素的密度值，然后定義E2 為
| ${{E}_{2}}=\sum\limits_{i\in imageBoundaryPixel}{({{S}_{i}}>0)?(MAX-{{S}_{i}}):0}$ |
最后，定義總的相似度度量函數為上述兩部分的加權和，即
| $E={{w}_{1}}{{E}_{1}}+{{w}_{2}}{{E}_{2}}$ |
可以看到，通過迭代優化使得上述相似度度量函數值最大化時，將會使二值掩膜圖像和X線圖像對齊重合，同時也就確定了一組最優的CT體數據空間變換參數。
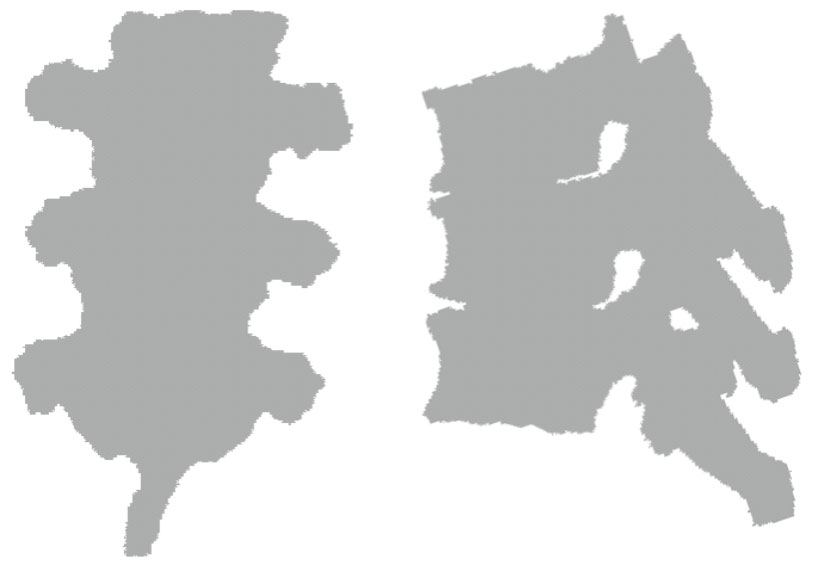圖3
CT數據投影的二維掩膜圖像
Figure3.
2D mask image by projection of CT volume boundary pixels
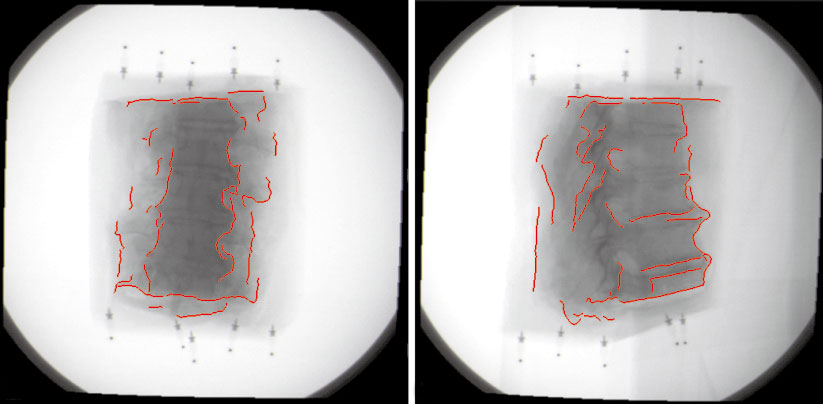圖4
檢測X線圖像的興趣區域邊界信息
Figure4.
Detection of boundary edges of the region of interest for X-ray image
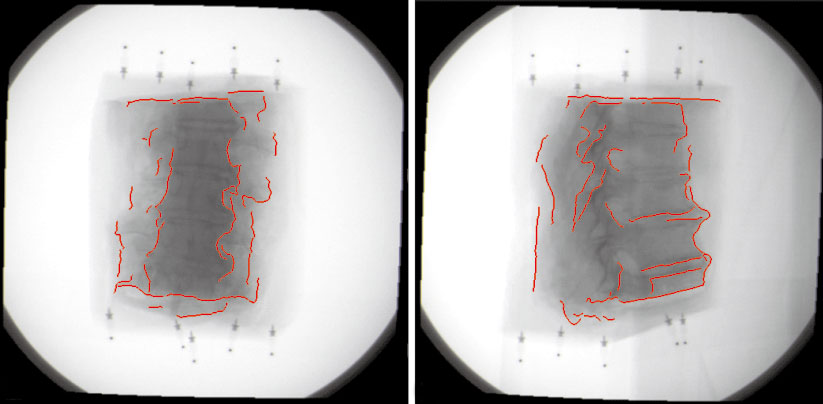
優化計算的過程采用Powell算法，這是一種方向集算法，它只需要對搜索函數進行估計，而不需要對函數求導。對于配準問題，參數空間一共包含6個自由度，由于每個自由度分別有兩個變化方向，因此一共包括12個不同的變化方向。當CT圖像的位置坐標分別向這12個方向變化時，便能產生12幅由預處理圖像分割的三維邊界體素直接投影得到的二值掩膜圖像，另外包括一幅未經變化的初始圖像。對這13幅二值圖像與待配準X線圖像進行相似度計算，可以得到13個不同的相似度測度，在其中尋找一個最大值，即最為匹配的相似度。將此相似度所對應的位置作為下一次迭代的起始位置。這樣反復迭代，直至得到滿意的匹配結果為止，如圖 5所示。
圖5
配準的二值圖像與X線圖像
Figure5.
Registrated 2D mask image and X-ray image
2 基于CUDA的硬件加速算法實現
我們注意到新提出的相似度度量函數兩部分的計算都是高度并行：第一部分針對X線圖像興趣區域的邊界像素點進行計算；第二部分針對二值投影圖像興趣區域的每個前景點進行計算。同時，從分割的CT邊界體素生成二值掩膜圖像可以通過對每邊界體素并行投影得到，參數優化過程中的Powell算法也是一種成熟的可以并行計算的算法。因此，本文進一步采用硬件加速的方式。我們選用NVIDIA 公司的CUDA，主要因為其芯片的執行單元多，同時和高階CPU 相比，顯卡的價格較為低廉，另外CUDA 的執行模式是單指令多數據(single instruction multiple data，SIMD)模式，故可進行高度并行化的工作。
采用CUDA 框架對配準進行加速時，首先需要在CPU 上做必要的準備，如拷貝圖像數據到設備內存，進行線程的分配等；其次，CPU 端調用核心處理程序Kernel，程序跳轉到GPU上并行執行核心算法。對于本文的配準算法，我們用一個三維數組的形式記錄CT數據分割得到的邊界體素的X/Y/Z坐標，而X線圖像則以二維紋理的形式傳入。根據數組的大小確定GPU 上Grid 和Block的數目，即可調用并行計算的內核函數。由于我們并行計算中處理的像素點是完全獨立的，可以很方便地修改CPU串行實現的代碼作為并行的內核函數。
本文所用計算機配置為：Intel P4 處理器 3.0 GHz、內存4.0 GB、顯卡GeForce GTX 465，該顯卡的靜態存儲器大小為1.0 GB，擁有352個流處理器。實驗數據統計結果如下：當采用單幅X線圖像進行配準實驗時，平均配準精度為 7.8 mm(位置)和3.3°(方向)；當采用兩幅不同角度的X線圖像進行配準實驗時，平均配準精度為 4.2 mm(位置)和2.1°(方向)。采用CPU的串行算法時單幅X線圖像配準過程平均需要3.5 s,兩幅X線圖像配準過程平均需要5.1 s；而采用CUDA的并行算法時單幅X線圖像進行配準平均需要0.08 s,兩幅X線圖像進行配準平均需要0.13 s，可見本文基于CUDA的2D-3D配準完全可以達到手術中即時應用的要求。
表1
采用單幅X線圖像的2D-3D醫學圖像配準實驗結果
Table1.
Results of 2D-3D medical image registration experiment using a single X-ray image
表2
采用雙幅X線圖像的2D-3D醫學圖像配準實驗結果
Table2.
Results of 2D-3D medical image registration experiment using two X-ray images
3 討論
在外科手術和放射治療等臨床實踐中，CT 和MRI等三維體數據提供了組織內部準確的三維結構信息,但是三維數據的掃描獲取目前達不到術中實時交互要求。為此醫生只能先在術前根據CT等三維掃描數據對興趣區域進行分析和定位，進行術前手術方案設計。而在后面的真實手術過程中，患者體內病變組織的空間位置與術前CT掃描數據的空間坐標不同，因此需要再次定位興趣區域。目前，一般只有X線圖像獲取能達到實時處理要求,但X線圖像是二維的,缺乏準確的三維空間信息。如果能將二維圖像與三維數據信息相結合,進行2D-3D配準，更有助于手術的實施。
傳統二維圖像和三維體數據的配準方法，主要為采用實物標記點的方法和采用從三維體數據生成二維DRR 圖像的方法。前者需要進行侵入性植入，臨床應用有一定爭議，在使用上受到限制。而以DRR為基礎的2D-3D配準，主要時間消耗在DRR產生環節，由于要處理每個體數據中的每個體素，計算量比較大。梁瑋等[12]為提高生成DRR圖像的速度，將CT的分辨率從512×512降為64×64 (軸向的減半)，同時把CT 數據灰度級均勻壓縮到16級(常見的為4 096級)，但是這樣的處理明顯會造成數據和精度損失。徐建等[16] 利用GPU 并行計算環境，提出了基于CUDA 的快速DRR 生成算法，該技術雖然能夠大大提高2D-3D 配準的速度，但離臨床的實時性要求還有一定差距。在實際的手術導航應用中，二維圖像與三維數據信息的結合既需要保證配準的精度，又要達到手術中即時應用的要求。
針對這些需要,本文利用一種混合幾何和圖像密度特征的方法對術前CT和術中X線圖像進行高效的2D-3D 配準。其基本思想是，在術前進行一次較精確的預處理和圖像分割，生成物體興趣區域(如脊椎骨骼)的幾何邊界輪廓的二值分割數據表示，從本質上進行信息數據的降維處理。三維邊界體素模型提供了充分的信息與二維圖像進行配準，并且每個三維體素和二維圖像像素的處理具有高度可并行性，整個計算過程非常適合高度并行的數值計算，利用最新的CUDA并行計算平臺，設計了GPU加速的2D-3D 高效配準計算框架，其計算精度可以滿足正常的需要，同時計算過程能夠達到手術中即時應用的要求。
引言
在外科手術和放射治療等臨床實踐中，由于二維掃描圖像的成像時間短,可以做到實時或者準實時的跟蹤，并且二維掃描的相關成像設備的輻射較少,對患者和醫生的損害較小，方便在手術中使用。另一方面，CT 或者MRI 等三維掃描可以提供人體解剖結構和興趣區域更準確的三維結構信息，但是掃描操作很難實時進行，一般只能在手術前獲得。這樣，需要應用2D-3D 醫學圖像配準技術在手術過程中融合兩種不同維度的數據,即時得到興趣區域和結構上更多的信息[1]。
目前，2D-3D 醫學圖像配準方法主要分為基于幾何特征[2-5]和基于圖像特征[6-8]兩類。一般來說，第一類方法使用物體上的幾何特征進行配準。幾何特征點的使用又分為外部植入特征與內部本身解剖特征。采用外部植入標記物的配準精度高,但因需要進行侵入性植入,臨床應用有一定爭議。總體而言，采用幾何特征的方法一般需要精確重建物體邊界的三維表面模型,計算量較大，準確性也差一些。而基于圖像特征的方法,大部分是采用數字重建的X線片(digitally reconstructed radiographs,DRR) 算法，即通過從CT三維圖像生成二維的DRR 圖像，與直接掃描得到的X線圖像進行配準。由于生成高質量的DRR圖像通常使用光線投射算法，計算穿過體數據光線上每個體素的衰減值[9-11]，計算量非常大，使得配準過程難以實時或準實時進行，成為臨床應用的瓶頸。因此，如何提高2D-3D 配準速度是一個研究熱點。眾多學者提出了多種改進方法，如使用降低分辨率和壓縮灰度級的方法[12]，計算感興趣區的相似性[13]，使用壓縮分解的加速方法[14]，以及使用逐步衰減域加速方法等[15]。
雖然眾多研究者提出了各種優化方法，但是由于要處理每個體數據中的每個體素，從三維體掃描數據生成二維DRR 圖像的計算量仍然比較大。而在實際的手術導航應用中，既需要保證配準的精度，又要達到手術中即時應用的要求。針對這些需要與分析,本文提出一種采用混合特征信息的2D-3D 配準方法，綜合利用三維模型的幾何邊界信息和二維圖像的灰度信息，進行快速的配準計算。
我們認為，物體興趣區域(如脊椎骨骼)的幾何邊界輪廓提供了充分的信息進行三維數據與二維圖像的配準。同時，對于物體興趣區域的幾何邊界信息，并不需要顯式的表達為三維幾何模型，而是可以直接用術前三維圖像分割生成的二值邊界體素進行表示。而三維邊界體素模型可以進行高效的二維投影生成一個新的二維圖像，新圖像能方便地與X線二維圖像進行相似性的定量比較。在整個流程中，從三維體數據進行圖像分割生成的二值邊界體素表示的過程計算量較大，但是只需要在術前進行一次預處理，不影響后面即時手術過程中的配準計算。另外，由于近年來顯卡技術迅猛發展，圖形處理器(graphics processing unit,GPU)的通用計算能力和可編程性使其已廣泛地應用到醫學圖像處理領域。而本文提出的2D-3D 配準計算框架中對于三維體素和二維像素的處理計算都是高度并行的，可進一步利用GPU 并行計算環境，提出基于CUDA 的2D-3D 的快速配準。
1 基于混合特征的2D-3D配準方法
本文2D-3D 配準方法的基本過程和以前基于DRR重建的配準算法類似，如圖 1所示，每一次迭代過程，都基于三維的CT體數據經過投影計算生成一個合成的二維圖像，然后和X 線二維圖像進行相似度測量。但是，我們并不需要生成計算瓶頸的DRR圖像，而是利用一種新的混合幾何和圖像密度特征的方法進行快速的2D-3D 配準。
圖1
2D-3D配準流程圖
Figure1.
The flowchart of 2D-3D registration
本文算法的第一步，是對三維CT數據進行預處理和圖像分割。由于CT數據是手術前得到的，我們可以采用半自動的方法配合手工交互修改，得到準確的CT圖像分割結果，如圖 2所示。但是，本文并不需要計算出幾何的三維模型，而是將圖像分割得到的二值化區域結果進行腐蝕操作(使用3×3×3的模板)，然后進行布爾減操作，這樣得到興趣區域的邊界體素。得到的邊界體素數目一般只占直接圖像分割結果體素的12%左右，這樣大大減少了數據量。這一步操作只需要在手術前進行一次，將結果保存之后備用。
圖2
CT數據的三維重建模型
Figure2.
3D reconstruction model from CT volume
2D-3D配準算法的主體過程是采用一個優化迭代的進程，確定一組最優的CT體數據空間的剛體平移和旋轉參數：(X,Y,Z)和(θX,θY,θZ)，將二維、三維數據在統一的空間坐標系中進行配準對齊。算法的關鍵是要定義一個合適的測度，或稱相似度度量函數，然后搜索，使得三維數據投影得到的二維圖像與X線圖像在相似性測度上達到最大的空間變換。
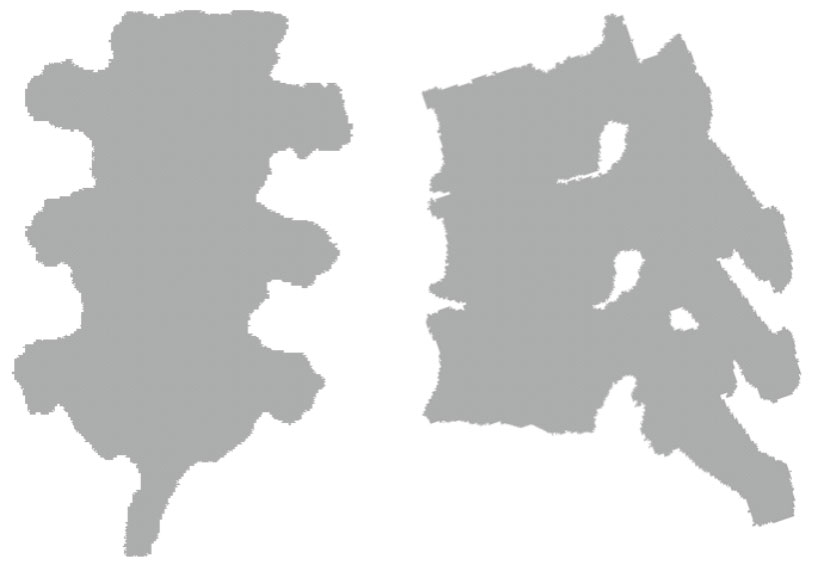
本文提出一種新的相似度度量方法，不需要從CT數據計算DRR圖像，而是直接把預處理圖像分割得到的三維邊界體素投影到X線圖像所在平面，得到一個二值掩膜圖像，如圖 3所示。可以看到，盡管只進行簡單的直接投影計算，二值掩膜圖像的興趣區域基本上完全填滿，這樣可以穩定、快速地抽取這個二值掩膜圖像的邊界像素。同時，本文采用一種改進的Canny邊界檢測算子抽取X線圖像的邊界信息，如圖 4所示。這樣，可以將兩種圖像邊界之間的加權和定義為相似度度量函數的第一部分。注意到X線圖像的邊界信息不是完整、連續的，本文采用一種局部的度量方法，定義一個半徑距離R，對于每一個X線圖像的邊界像素，計算其到二值掩膜圖像邊界的最小距離Di，如果(R-Di)大于0,則認為這次的距離計算有效，定義E1為
| ${{E}_{1}}=\sum\limits_{i\in imageBoundaryPixel}{(R-{{D}_{i}}>0)?(R-{{D}_{i}}):0}$ |
顯然，當二值掩膜圖像的邊界和X線圖像的邊界重合時，E1值達到最大化。 相似度度量函數的第二部分，則利用圖像的密度信息。我們注意到X線圖像興趣區域的像素密度值比背景區域小，這樣可以根據二值掩膜圖像每個前景像素點的坐標取X線圖像中對應像素的密度值，然后定義E2 為
| ${{E}_{2}}=\sum\limits_{i\in imageBoundaryPixel}{({{S}_{i}}>0)?(MAX-{{S}_{i}}):0}$ |
最后，定義總的相似度度量函數為上述兩部分的加權和，即
| $E={{w}_{1}}{{E}_{1}}+{{w}_{2}}{{E}_{2}}$ |
可以看到，通過迭代優化使得上述相似度度量函數值最大化時，將會使二值掩膜圖像和X線圖像對齊重合，同時也就確定了一組最優的CT體數據空間變換參數。
圖3
CT數據投影的二維掩膜圖像
Figure3.
2D mask image by projection of CT volume boundary pixels
圖4
檢測X線圖像的興趣區域邊界信息
Figure4.
Detection of boundary edges of the region of interest for X-ray image
優化計算的過程采用Powell算法，這是一種方向集算法，它只需要對搜索函數進行估計，而不需要對函數求導。對于配準問題，參數空間一共包含6個自由度，由于每個自由度分別有兩個變化方向，因此一共包括12個不同的變化方向。當CT圖像的位置坐標分別向這12個方向變化時，便能產生12幅由預處理圖像分割的三維邊界體素直接投影得到的二值掩膜圖像，另外包括一幅未經變化的初始圖像。對這13幅二值圖像與待配準X線圖像進行相似度計算，可以得到13個不同的相似度測度，在其中尋找一個最大值，即最為匹配的相似度。將此相似度所對應的位置作為下一次迭代的起始位置。這樣反復迭代，直至得到滿意的匹配結果為止，如圖 5所示。
圖5
配準的二值圖像與X線圖像
Figure5.
Registrated 2D mask image and X-ray image
2 基于CUDA的硬件加速算法實現
我們注意到新提出的相似度度量函數兩部分的計算都是高度并行：第一部分針對X線圖像興趣區域的邊界像素點進行計算；第二部分針對二值投影圖像興趣區域的每個前景點進行計算。同時，從分割的CT邊界體素生成二值掩膜圖像可以通過對每邊界體素并行投影得到，參數優化過程中的Powell算法也是一種成熟的可以并行計算的算法。因此，本文進一步采用硬件加速的方式。我們選用NVIDIA 公司的CUDA，主要因為其芯片的執行單元多，同時和高階CPU 相比，顯卡的價格較為低廉，另外CUDA 的執行模式是單指令多數據(single instruction multiple data，SIMD)模式，故可進行高度并行化的工作。
采用CUDA 框架對配準進行加速時，首先需要在CPU 上做必要的準備，如拷貝圖像數據到設備內存，進行線程的分配等；其次，CPU 端調用核心處理程序Kernel，程序跳轉到GPU上并行執行核心算法。對于本文的配準算法，我們用一個三維數組的形式記錄CT數據分割得到的邊界體素的X/Y/Z坐標，而X線圖像則以二維紋理的形式傳入。根據數組的大小確定GPU 上Grid 和Block的數目，即可調用并行計算的內核函數。由于我們并行計算中處理的像素點是完全獨立的，可以很方便地修改CPU串行實現的代碼作為并行的內核函數。
本文所用計算機配置為：Intel P4 處理器 3.0 GHz、內存4.0 GB、顯卡GeForce GTX 465，該顯卡的靜態存儲器大小為1.0 GB，擁有352個流處理器。實驗數據統計結果如下：當采用單幅X線圖像進行配準實驗時，平均配準精度為 7.8 mm(位置)和3.3°(方向)；當采用兩幅不同角度的X線圖像進行配準實驗時，平均配準精度為 4.2 mm(位置)和2.1°(方向)。采用CPU的串行算法時單幅X線圖像配準過程平均需要3.5 s,兩幅X線圖像配準過程平均需要5.1 s；而采用CUDA的并行算法時單幅X線圖像進行配準平均需要0.08 s,兩幅X線圖像進行配準平均需要0.13 s，可見本文基于CUDA的2D-3D配準完全可以達到手術中即時應用的要求。
表1
采用單幅X線圖像的2D-3D醫學圖像配準實驗結果
Table1.
Results of 2D-3D medical image registration experiment using a single X-ray image
表2
采用雙幅X線圖像的2D-3D醫學圖像配準實驗結果
Table2.
Results of 2D-3D medical image registration experiment using two X-ray images
3 討論
在外科手術和放射治療等臨床實踐中，CT 和MRI等三維體數據提供了組織內部準確的三維結構信息,但是三維數據的掃描獲取目前達不到術中實時交互要求。為此醫生只能先在術前根據CT等三維掃描數據對興趣區域進行分析和定位，進行術前手術方案設計。而在后面的真實手術過程中，患者體內病變組織的空間位置與術前CT掃描數據的空間坐標不同，因此需要再次定位興趣區域。目前，一般只有X線圖像獲取能達到實時處理要求,但X線圖像是二維的,缺乏準確的三維空間信息。如果能將二維圖像與三維數據信息相結合,進行2D-3D配準，更有助于手術的實施。
傳統二維圖像和三維體數據的配準方法，主要為采用實物標記點的方法和采用從三維體數據生成二維DRR 圖像的方法。前者需要進行侵入性植入，臨床應用有一定爭議，在使用上受到限制。而以DRR為基礎的2D-3D配準，主要時間消耗在DRR產生環節，由于要處理每個體數據中的每個體素，計算量比較大。梁瑋等[12]為提高生成DRR圖像的速度，將CT的分辨率從512×512降為64×64 (軸向的減半)，同時把CT 數據灰度級均勻壓縮到16級(常見的為4 096級)，但是這樣的處理明顯會造成數據和精度損失。徐建等[16] 利用GPU 并行計算環境，提出了基于CUDA 的快速DRR 生成算法，該技術雖然能夠大大提高2D-3D 配準的速度，但離臨床的實時性要求還有一定差距。在實際的手術導航應用中，二維圖像與三維數據信息的結合既需要保證配準的精度，又要達到手術中即時應用的要求。
針對這些需要,本文利用一種混合幾何和圖像密度特征的方法對術前CT和術中X線圖像進行高效的2D-3D 配準。其基本思想是，在術前進行一次較精確的預處理和圖像分割，生成物體興趣區域(如脊椎骨骼)的幾何邊界輪廓的二值分割數據表示，從本質上進行信息數據的降維處理。三維邊界體素模型提供了充分的信息與二維圖像進行配準，并且每個三維體素和二維圖像像素的處理具有高度可并行性，整個計算過程非常適合高度并行的數值計算，利用最新的CUDA并行計算平臺，設計了GPU加速的2D-3D 高效配準計算框架，其計算精度可以滿足正常的需要，同時計算過程能夠達到手術中即時應用的要求。
