腦機接口(BCI)是在人或動物腦與外部設備間建立的直接連接通路,信號分析功能模塊是其核心部分,其中特征提取算法的效果如何是腦電圖(EEG)信號分析算法的關鍵。EEG信號本身信噪比低,傳統的EEG特征提取方法存在著缺少空間信息,需要的特征量個數較多,分類正確率低等不足。針對以上問題,本文提出了一種基于小波和獨立分量分析(ICA)的時間-頻率-空間EEG特征的提取方法,分別用離散小波變換(DWT)和ICA提取時頻域特征和空域特征。并用支持向量機(SVM)和遺傳算法(GA)相結合的方法對提取的特征進行分類。實驗對比結果表明,所提出的方法有效地克服了傳統的時頻特征提取方法空間信息描述不足等問題,對于2003年BCI競賽數據dataset Ⅲ分析,最高分類正確率為90.71%。
引用本文： 王月茹, 李昕, 李紅紅, 邵成成, 應立娟, 吳水才. 基于時-頻-空間域的運動想象腦電信號特征提取方法研究. 生物醫學工程學雜志, 2014, 31(5): 955-961. doi: 10.7507/1001-5515.20140180 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
腦機接口(brain-computer interface,BCI)是一種不依賴于人體的外周神經系統和肌肉組織，僅通過采集和分析人腦生物電信號即可在人腦與計算機或其它電子設備之間建立起直接交流和控制的通道，以達到通過腦來表達意愿或操縱設備的新技術。其首要目標是增強有嚴重身體和交流障礙的患者與外界交流或控制外部環境的能力[1-3]。
BCI系統通常包括信號采集、信號分析和控制器三個功能模塊。在信號分析模塊中，特征提取和模式分類是關鍵環節。特征提取直接影響識別效果。常用的特征提取方法有：
(1)單一的時域或頻域特征提取：僅利用時域平均算法或頻域功率譜估計[4]。主要包括信號時域平均處理、功率譜估計等。信號時域平均處理可抑制混雜于原信號中的隨機干擾，但其要求精確確定感興趣的周期分量的周期，易導致嚴重誤差[5]。功率譜估計可通過信號的相關性估計得出接收到信號的功率隨頻率的變化關系。這兩種方法抑制背景噪聲的能力有限。
(2)傳統的時頻分析方法：主要包括短時傅里葉變換、Wigner-Ville分布等。短時傅里葉變換假定待分析數據是分段平穩的，不適合用來分析頻率隨時間而改變的信號。Wigner-Ville分布是信號在時頻平面上的聯合功率譜，雖然克服了短時傅里葉的缺點，分辨率很高，但分析多分量信號時存在嚴重的交叉干預項。
(3)模型參數法：如自回歸(auto regression,AR)模型、自適應自回歸(adaptive auto regression，AAR)模型等[6-7]。AR模型適合于短數據處理[8]，其計算量小、速度快，但參數不具有時變性。AAR模型采用自適應估計的自回歸參數用于當前時間序列的頻譜分析，對非穩態的頻譜分析有著較好的分析效果[9]。該方法能有效應用于變動大、無規律的時間序列預測中[10]。
(4) 小波分析法：小波分析具有時、頻同時局部化的優點。其可將信號能量強度或密度變化在時、頻域上同時表示出來，使我們能夠更全面更直觀地觀察、分析信號數據[11]。
由于小波變換適合處理非平穩信號，近年來在信號處理領域得到廣泛的應用。王攀等[12]將時域能量熵和離散小波變換相結合，提出了一種基于P300帶內帶外特征的腦電圖(electroencephalography,EEG)信號特征提取方法，克服了P300信號識別中對電極數量和EEG信號疊加次數的苛刻要求。何慶華等[13]的實驗表明，小波變換域特征向量提取方法能有效地實現信號的去噪、降維和特征提取。
上述方法中，前三種主要用于分析平穩信號，小波分析法雖是非平穩信號的分析方法，但仍局限于時頻特征。考慮到傳統方法的不足以及EEG信號非平穩低信噪比的特點，國際已開始研究基于時間頻率空間域的特征提取方法。Ince等[14]提出一種單次實驗EEG信號分類的新方法，這種方法是基于空間-時間-頻率范圍中的自適應主體特定運動想象模式，自適應地提取與EEG模式相關的主體特定運動想象。經試驗結果證明，提出的算法平均分類正確率為96%。 唐艷[15]設計出了時間空間-頻率濾波器并應用于運動想象分類任務。
本文基于小波分析和獨立分量分析(independent components analysis,ICA)，研究EEG信號時間-頻率-空間域特征提取方法，首先利用小波變換提取EEG信號特定頻段的時頻特性，再利用ICA提取信號的空間特征，將兩者組成最終的特征矢量，結果表明，提取的信號特征更加有效，提高了分類正確率。
1 實驗數據
本文采用的2003年BCI競賽數據dataset Ⅲ是由奧地利Graz大學BCI實驗中心提供的想象運動時的EEG數據[16]。實驗數據全部來源于同一受試者(女性，25歲)，由位于C3、C4和Cz三個電極前后各2.5 cm位置的雙級導聯記錄EEG信號。
實驗內容是根據提示來想象左右手運動。實驗共包括7組，每組40次實驗，每次實驗持續9 s。前兩秒鐘被測試者處于安靜狀態，不做任何思維想象，在第二秒時計算機發出由低到高的提示音，計算機屏幕中央出現“+”圖像。第三秒時屏幕出現向左或向右的箭頭，提示被測試者想象用左(右)手按箭頭指向去移動屏幕上出現的條狀棒。采樣率為128 Hz，并進行了0.5~30 Hz帶通濾波。在獲得的280次實驗中，選140次用來訓練分類器，另外的140次則測試分類器的推廣性能。
2 離散小波變換及獨立成分分析
2.1 離散小波變換
小波分析是聯合時間-尺度函數分析非平穩信號的一種有效的時頻分析方法。小波變換的實質是將信號分解成一系列小波函數的疊加，小波窗口大小隨頻率改變。在低頻時，時間分辨率較低但頻率分辨率較高；在高頻時，時間分辨率較高但頻率分辨率較低。由于其多分辨率的特點，適合提取非平穩信號的特征。
信號f(t)的離散小波變換(disperse wavelet transform,DWT)和逆變換的定義為
| ${{C}_{j,k}}(f,{{\psi }_{j,k}})={{2}^{-j/2}}\sum\limits_{n=-\infty }^{\infty }{f\left( t \right)}({{2}^{-j}}t-k),j,k\in Z,$ |
| $f\left( t \right)=\sum\limits_{n=-\infty }^{\infty }{\sum\limits_{n=-\infty }^{\infty }{{{C}_{j,k}}{{\psi }_{j,k}}\left( t \right)}}=\sum\limits_{n=-\infty }^{\infty }{{{f}_{j}}\left( t \right)},j,k\in Z\text{ },$ |
式(2)中，ψj,k=2-j/2ψ(2-j/2t-k)為小波序列，ψ(t)是滿足一定條件的小波基函數，j和k分別代表頻率分辨率和時間平移量，fj(t)表示信號f(t)在某一尺度的分量。在實際應用中用Mallat算法對信號進行有限層分解，可得
| $\begin{align} & f\left( t \right)={{f}_{L}}^{A}\left( n \right)+\sum\limits_{j=1}^{L}{{{f}_{j}}^{D}\left( n \right)}={{A}_{L}}+\sum\limits_{j=1}^{L}{{{D}_{j}}}= \\ & {{A}_{1}}+{{D}_{1}}={{A}_{2}}+{{D}_{2}}+{{D}_{1}}=\ldots , \\ \end{align}$ |
式中L為分解層數，AL為低通逼近分量，Dj為不同尺度下細節分量。由此，信號的整個頻帶被劃分為若干個子頻帶，假設信號f(t)的采樣頻率為fs，則AL,DL,DL-1，…D1各分量所對應的子頻帶范圍依次為:[fs/2L-1,fs/2L-1]…和[f2/2L+1,f2/2L]，[fs/2L,fs/2L-1]…，對應的逼近系數及各層小波系數為cAL，cDL,cDL-1,…,cD1。以三級分解為例，離散信號經三尺度分解后，得到逼近系數cA3和細節系數cD3,cD2,cD1。
2.2 獨立分量分析
ICA以非高斯信號為處理對象，在一定的條件下，能從多路觀測信號中較完整地分離出隱含的獨立源信號，并且具有很好地提取信號的空間特性。ICA算法具體描述如下：設x1,x2，…,xn為n維隨機觀測混合信號，由m個未知源信號s1,s2，…，sm線性組合而成，假設每個混合信號xi都是一個隨機變量，而不是時間信號。令X=(x1,x2,…,xn)T為n維隨機觀測向量，S=(s1,s2,…,sm)T是m維未知源信號，則ICA的線性模型可表示為
| $\begin{align} & {{X}_{nm}}={{A}_{nu}}{{S}_{um}}=\Sigma mi=1{{a}_{i}}{{s}_{i}}, \\ & i=1,2,\ldots ,m\text{ }, \\ \end{align}$ |
| $Y=W·X ,$ |
式中X是觀測信號，S為源信號，且各分量互相獨立，其中n為信號通道數，m為采樣點數，u為分離出的源信號的數量，一般情況下n=u。A是一滿秩混合矩陣，ai是混合矩陣的基向量。W為解混合矩陣，Y為式計算法的輸出，即對源信號S的估計信號。ICA算法的目的就是尋找一個最優的變換矩陣W，并計算出S的估計值Y。本文選用Fast ICA方法來尋找最優的W以及估計信號Y。
Fast ICA算法又稱固定點(Fixed Point)算法，是一種快速尋優迭代算法。Fast ICA算法有基于峭度、基于似然最大、基于負熵最大等形式，這里利用基于負熵最大的Fast ICA算法來分離信號。Fast ICA基本思想是以非高斯性極大作為其目標，尋找投影向量W，使得X在W上的投影WTX非高斯性最大[17]。
3 分析方法
3.1 數據預處理
實驗中，左右手提示出現在3~9 s，只需選用時間在3~9 s的數據。由于電極Cz的位置與運動想象功能區沒有太大相關性，處理時只選用C3和C4電極記錄的數據進行特征提取。
研究表明，大腦在想象或實施左右手運動時會顯著改變某些頻段成分(如μ節律、β節律)的功率譜強弱，這一現象被稱為事件相關同步(event related synchronization,ERS)和事件相關去同步(event related desynchronization,ERD)現象。ERD對應于功率譜比率下降，ERS則對應于功率譜比率上升。并且，對應于大腦主觀想象肢體動作思維提示所誘發被動思維的ERD/ERS在具體表現特征頻段和運動皮層區域均有所不同。比如，對應于手部運動的ERD多發生在10~11 Hz及20~24 Hz頻段。所以，本文將通過分析想象左右手運動時ERD/ERS現象最明顯的EEG信號段，選取合適的時間段、頻率段進行之后的特征提取及分類。首先對原始的280次EEG試驗信號進行三層小波分解，母小波采用Daubechies4小波。再提取第二、三層的細節系數重建原信號。根據Mallat算法得到原始EEG信號中在8~30 Hz的部分，此部分剛好包含μ和β節律。然后按照以下公式計算各導EEG信號的平均能量：
| $p\left( j \right)=\left( 1/N \right)\sum\limits_{i=1}^{N}{{{x}^{2}}\left( i,j \right)}\text{ },$ |
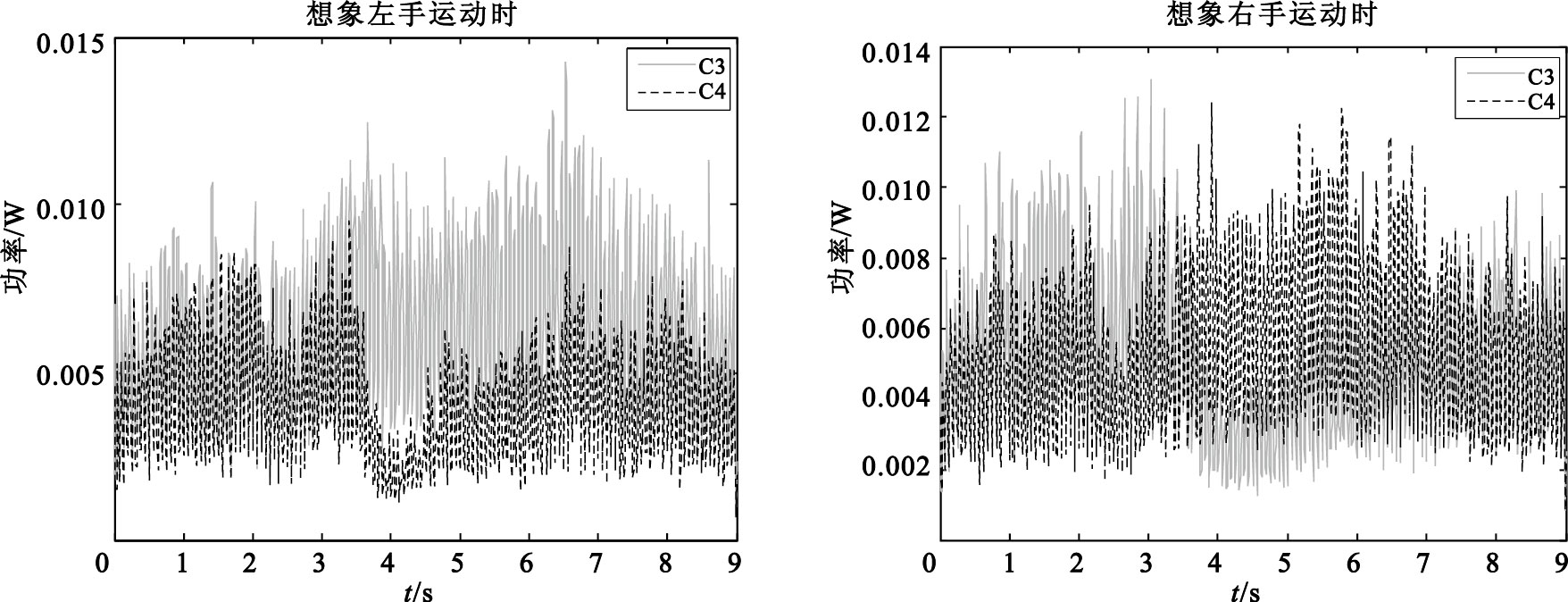
其中x(i,j)為第i個信號的第j個EEG數據，N為信號個數，p(j)為第j個數據的平均能量信號。計算想象左右手運動時C3和C4通道EEG信號在8~30 Hz頻段的平均能量，如圖 1所示。
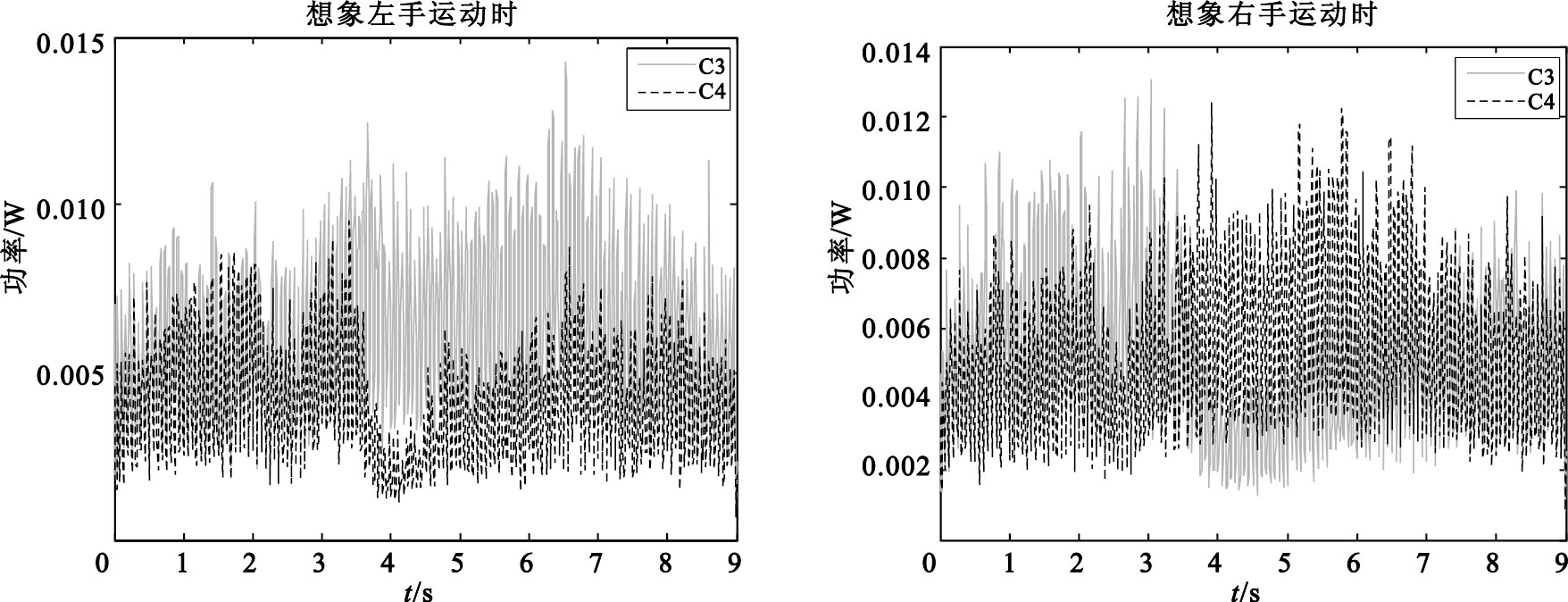圖1
想象左右手運動時C3、C4導聯平均能量變化
Figure1.
Average energy changes in C3,C4 with left and right hand motor imagery
由圖 1可知，在進行左右手運動想象時C3、C4通道的平均能量在3.5~7 s內的差異最明顯：想象左手運動時在C4導出現ERD現象；想象右手運動時在C3通道出現ERD現象。因此選定3.5~7 s時間段內8~30 Hz的頻率信息作為分析對象。這樣不僅提高了信噪比，更降低了計算的復雜度。
3.2 特征提取
3.2.1 時頻特征
離散小波變換通過將信號分解為近似信息和細節信息來分析不同分辨率下、不同頻率子帶的信號。對于一個已知信號x[n]，在分解過程中，每一層包含兩個數字濾波器以及兩個下采樣。第一層高通和低通濾波器的下采樣分別輸出為細節信息D1和近似信息A1，A1進一步分解直到得到所需的頻率信息。
用DWT分析EEG信號時，選擇合適的小波函數和分解層次尤為重要。比較了Symlet (sym2)、Daubechies (db4)、Biorthogonal (bior3.1)和Coiflet (coif3)4種常用的小波函數。分別用這4種小波函數進行特征提取并用支持向量機(support vector machine,SVM)做分類，SVM參數指標如表 1所示。較少的支持向量個數可以減少SVM分類過程中的計算時間，而大的分類間隔說明SVM分類器具有較好的推廣能力。db4小波函數較其他幾種
表1
不同小波函數得到的分類結果對比
Table1.
Classification results obtained by different wavelets using the SVM classifier
函數具有較好的分類正確率和較低的計算復雜度。因此，本文選用db4小波函數做小波系數的提取。
分解層次的確定依據所需EEG信號的頻率分量以及信號采樣率。μ節律(8~12 Hz)和β節律(18~26 Hz)被公認為是較好的BCI運動想象EEG信號特征，所以只需提取包含μ和β節律的信號特征。已知原始EEG的采樣頻率為128 Hz，小波分解后不同層次所對應的頻率信息如表 2所示。
表2
小波分解128 Hz采樣率所得各層相應的頻率
Table2.
Frequencies corresponding to different levels of wavelet decomposition with a 128 Hz sampling rate
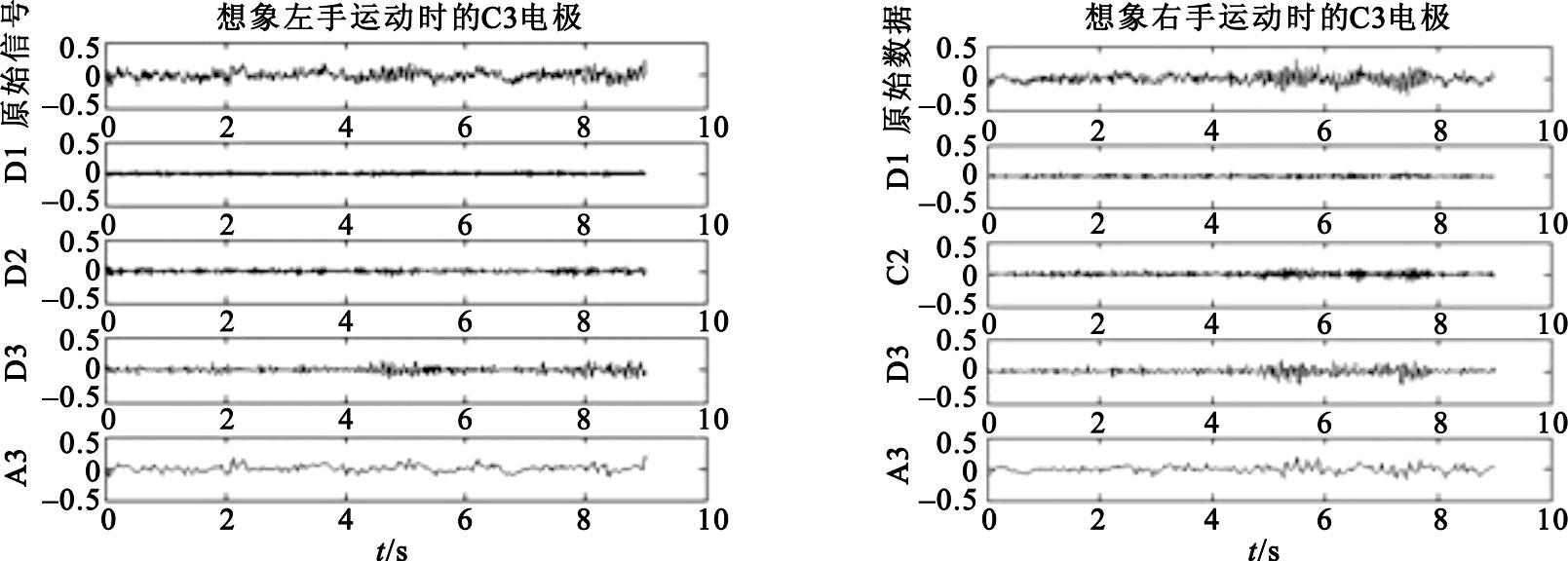
由表 2可知，μ和β節律主要包含在D3(8~16 Hz)和D2(16~32 Hz)兩個頻率子帶中。因此選擇進行三層小波分解(見圖 2)。圖 2為想象左右手運動期間，采自C3電極的EEG信號的近似信息A3和細節信息D1~D3。為進一步降低特征向量維數，在此基礎上進行了統計學處理：① 計算每個子帶中小波系數的絕對值，再取平均值；② 每個子帶系數的標準差；③ C4、C3兩導小波系數能量差的平均值。
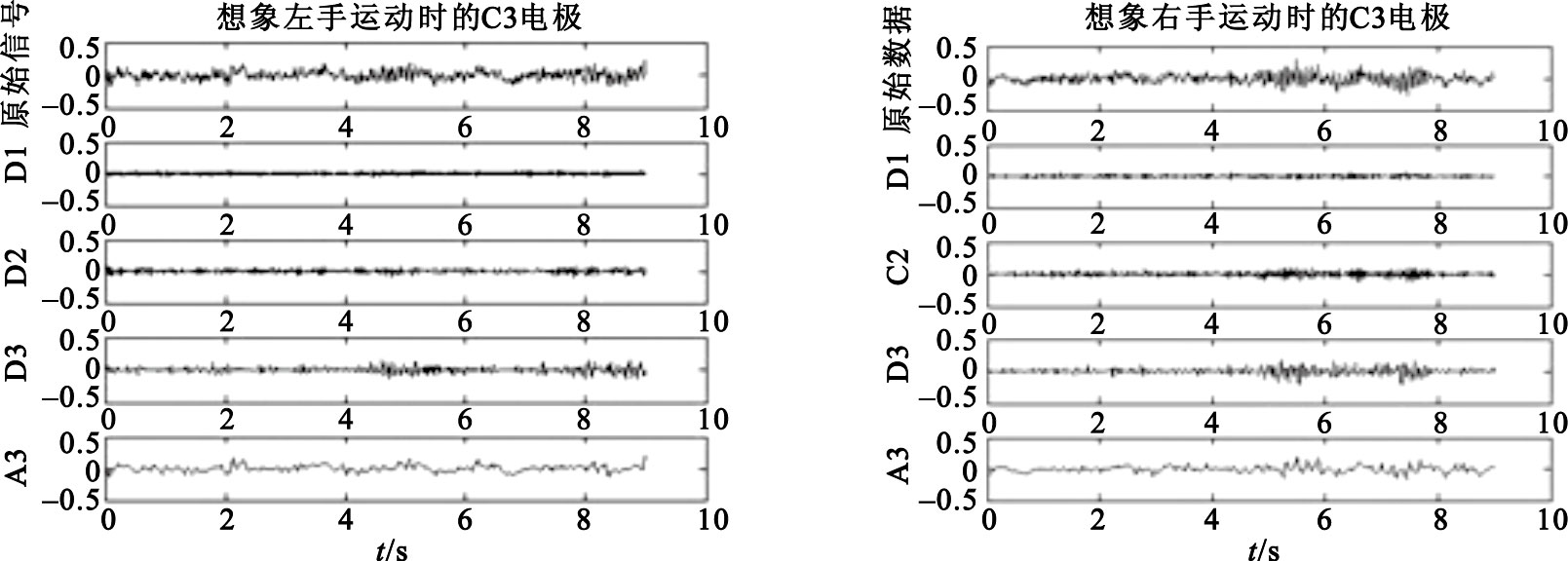圖2
用db4小波提取的C3電極想象左手運動和想象右手運動時的近似信息和細節信息
Figure2.
Approximation and detailed coefficients of Symlet order two-wavelet decomposition on an EEG signal taken from the C3 electrode location during left motor imagery and right motor imagery
由于信號已通過0.5~30 Hz的濾波，所以D1層(32~64 Hz)小波系數可以排除掉。而基于子帶D2和D3層的特征將用于進一步的EEG信號的分類中。
3.2.2 空間域特征
在進行ICA之前，首先對這280 組EEG數據進行中心化，令其均值為零，然后再進行預白化處理，這兩個預處理步驟的目的是簡化ICA算法，再用主成分分析對其進行降維處理，這一過程可以預防過學習。在預處理之后，即可運用Fast ICA主要算法進行特征提取，非線性參數g選用pow3。ICA之后得到獨立分量yi和2×2維的解混合矩陣W。由式(5)可知：
| $\left[ \matrix{ {x_{c3}} \hfill \cr {x_4} \hfill \cr} \right] = {W^{ - 1}}\left[ \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right] = \left[ \matrix{ {w_{11}}{w_{12}} \hfill \cr {w_{21}}{w_{22}} \hfill \cr} \right]\left[ \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right],$ |
式中yi為ICA分離出的獨立分量。通過上式可以看出，Wj-1是估計信號Y到觀測信號X的投影，由于觀測信號從大腦不同位置測得，即Wj-1表征了獨立分量在大腦頭皮上固定的空間分布模式。由圖 3可知在進行左右手運動想象時，C3、C4電極處的事件誘發電位在大腦頭皮的空間分布不同，而解混合矩陣W的逆矩陣正好反映了這種空間分布差異。所以將此逆矩陣的4個元素作為表征EEG信號的空間特性的特征提取出來，作為最終特征向量的一部分。
最后將由小波提取出的280×10維時頻特征與ICA提取的280×4維空域特征組合，作為最終的特征向量，共計280×14維。
3.3 模式分類
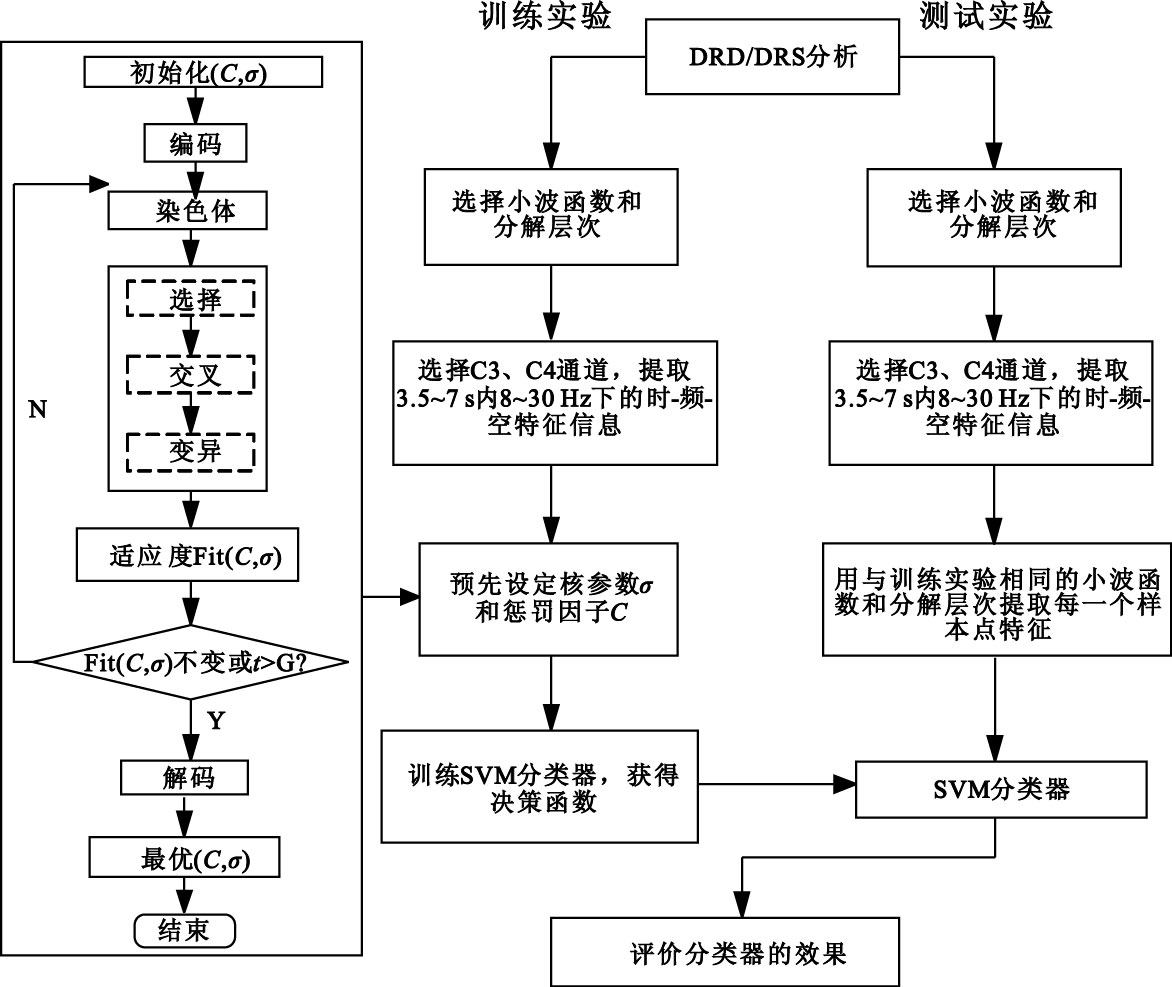
SVM在解決小樣本、非線性及高維模式識別問題中表現出許多獨特的優勢，非常適合用來研究運動想象EEG信號的分類問題。本文選用C-SVC模型以及RBF核函數。本文以GA來尋找最優的C(懲罰因子)和σ(核參數)。首先選擇實值編碼策略，設置種群大小取20代，最大進化代數設定為100，交叉和變異概率分別設為0.4和0.01。基于遺傳算法的參數尋優過程中的分類流程圖如圖 3所示。
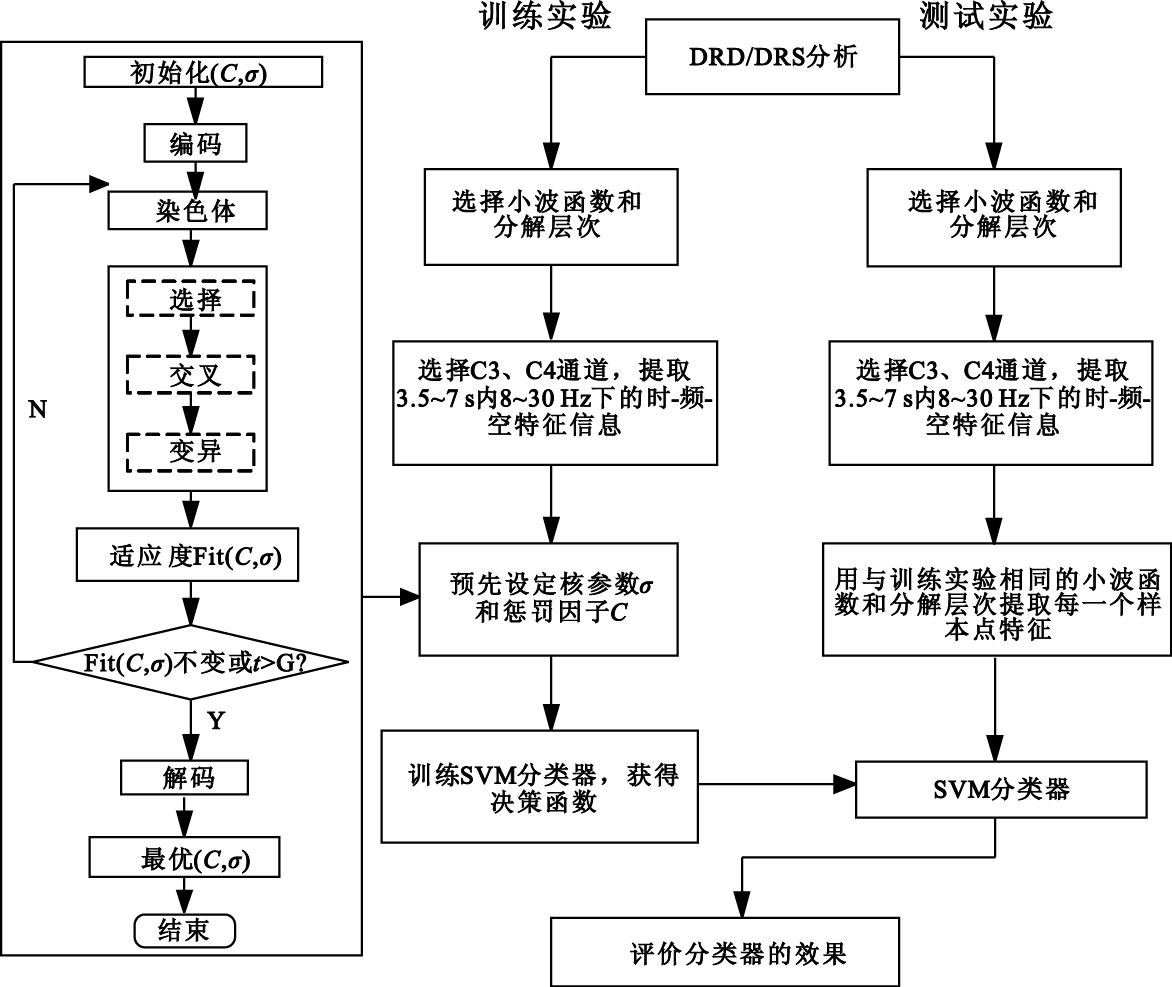圖3
小波特征提取BCI 2003 EEG信號并由經GA優化的SVM分類的算法流程圖
Figure3.
Flow chart of the SVM improved by GA classification with the wavelet-based feature extraction on the Graz datasets in the BCI Competitions of 2003
4 結果與討論
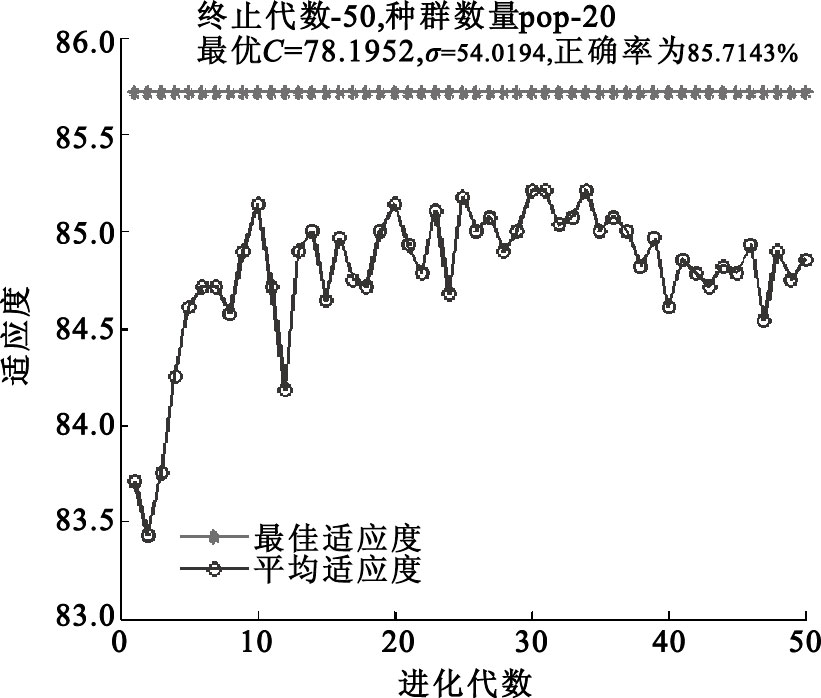
依據提出的基于時-頻-空域EEG信號的特征提取方法提取14維特征向量，送入SVM分類器，所得結果為：最高分類正確率90.71%，平均分類正確率88.57%。圖 4所示為分類器尋優時所得最優的懲罰因子C和核參數σ以及尋優時運用n倍交叉驗證所得分類正確率。
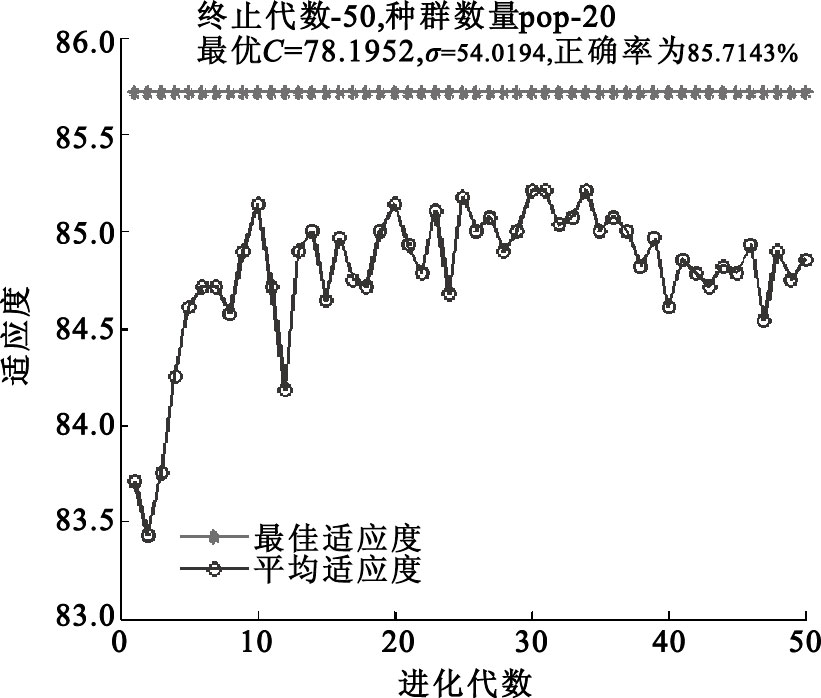圖4
GA參數尋優方法尋優時的適應度曲線圖及分類正確率
Figure4.
Fitness curve accuracy using GA when searching C & σ
為了證明本文所提出的時-頻-空特征提取算法提取特征的有效性，將所提出的算法與只用空域特征、時頻特征提取方法得到的結果進行了比較，如表 3所示。
表3
不同特征提取方法的分類結果比較
Table3.
Classification results obtained by different feature extraction methods
通過對比，本文方法與只提取時頻特征、空間域特征相比，分類正確率顯著提高，最高分類正確率提高了3.28%，平均分類正確率提高了2.12%。
將本文算法分類結果與BCI 2003競賽結果進行比較。2003年BCI競賽結果前三名的最高分類正確率分別為89.29%、84.29%和82.86%，通過對比可知本文方法所得最高大分類正確率與競賽最好成績相比也有所提高。
所提取特征個數也是衡量一個優秀的特征提取算法的重要指標，本文所提出的方法所需特征數只有14個，這較少的特征數提高了提取和分類時的運算速度，大大提高了算法的效率。
5 結論
傳統的時頻EEG信號特征提取方法因其計算簡單而廣泛應用，但EEG信號的信噪比較低且某些干擾成分與信號具有相似的時頻特性，單純的時頻特征提取方法區分度不夠，從而影響分類效果，因此需要性能良好和效率較高的特征提取方法。針對這一問題，本文提出了基于小波分析和ICA的提取時-頻-空域特征的方法，在傳統的時頻域特征基礎上組合了空域特征，組成最終特征矢量，并用SVM進行了識別分類。通過與單獨使用時頻域特征、空域特征的對比實驗，表明時-頻-空特征提取方法能夠有效彌補EEG信號信噪比低的不足，提高分類正確率。
引言
腦機接口(brain-computer interface,BCI)是一種不依賴于人體的外周神經系統和肌肉組織，僅通過采集和分析人腦生物電信號即可在人腦與計算機或其它電子設備之間建立起直接交流和控制的通道，以達到通過腦來表達意愿或操縱設備的新技術。其首要目標是增強有嚴重身體和交流障礙的患者與外界交流或控制外部環境的能力[1-3]。
BCI系統通常包括信號采集、信號分析和控制器三個功能模塊。在信號分析模塊中，特征提取和模式分類是關鍵環節。特征提取直接影響識別效果。常用的特征提取方法有：
(1)單一的時域或頻域特征提取：僅利用時域平均算法或頻域功率譜估計[4]。主要包括信號時域平均處理、功率譜估計等。信號時域平均處理可抑制混雜于原信號中的隨機干擾，但其要求精確確定感興趣的周期分量的周期，易導致嚴重誤差[5]。功率譜估計可通過信號的相關性估計得出接收到信號的功率隨頻率的變化關系。這兩種方法抑制背景噪聲的能力有限。
(2)傳統的時頻分析方法：主要包括短時傅里葉變換、Wigner-Ville分布等。短時傅里葉變換假定待分析數據是分段平穩的，不適合用來分析頻率隨時間而改變的信號。Wigner-Ville分布是信號在時頻平面上的聯合功率譜，雖然克服了短時傅里葉的缺點，分辨率很高，但分析多分量信號時存在嚴重的交叉干預項。
(3)模型參數法：如自回歸(auto regression,AR)模型、自適應自回歸(adaptive auto regression，AAR)模型等[6-7]。AR模型適合于短數據處理[8]，其計算量小、速度快，但參數不具有時變性。AAR模型采用自適應估計的自回歸參數用于當前時間序列的頻譜分析，對非穩態的頻譜分析有著較好的分析效果[9]。該方法能有效應用于變動大、無規律的時間序列預測中[10]。
(4) 小波分析法：小波分析具有時、頻同時局部化的優點。其可將信號能量強度或密度變化在時、頻域上同時表示出來，使我們能夠更全面更直觀地觀察、分析信號數據[11]。
由于小波變換適合處理非平穩信號，近年來在信號處理領域得到廣泛的應用。王攀等[12]將時域能量熵和離散小波變換相結合，提出了一種基于P300帶內帶外特征的腦電圖(electroencephalography,EEG)信號特征提取方法，克服了P300信號識別中對電極數量和EEG信號疊加次數的苛刻要求。何慶華等[13]的實驗表明，小波變換域特征向量提取方法能有效地實現信號的去噪、降維和特征提取。
上述方法中，前三種主要用于分析平穩信號，小波分析法雖是非平穩信號的分析方法，但仍局限于時頻特征。考慮到傳統方法的不足以及EEG信號非平穩低信噪比的特點，國際已開始研究基于時間頻率空間域的特征提取方法。Ince等[14]提出一種單次實驗EEG信號分類的新方法，這種方法是基于空間-時間-頻率范圍中的自適應主體特定運動想象模式，自適應地提取與EEG模式相關的主體特定運動想象。經試驗結果證明，提出的算法平均分類正確率為96%。 唐艷[15]設計出了時間空間-頻率濾波器并應用于運動想象分類任務。
本文基于小波分析和獨立分量分析(independent components analysis,ICA)，研究EEG信號時間-頻率-空間域特征提取方法，首先利用小波變換提取EEG信號特定頻段的時頻特性，再利用ICA提取信號的空間特征，將兩者組成最終的特征矢量，結果表明，提取的信號特征更加有效，提高了分類正確率。
1 實驗數據
本文采用的2003年BCI競賽數據dataset Ⅲ是由奧地利Graz大學BCI實驗中心提供的想象運動時的EEG數據[16]。實驗數據全部來源于同一受試者(女性，25歲)，由位于C3、C4和Cz三個電極前后各2.5 cm位置的雙級導聯記錄EEG信號。
實驗內容是根據提示來想象左右手運動。實驗共包括7組，每組40次實驗，每次實驗持續9 s。前兩秒鐘被測試者處于安靜狀態，不做任何思維想象，在第二秒時計算機發出由低到高的提示音，計算機屏幕中央出現“+”圖像。第三秒時屏幕出現向左或向右的箭頭，提示被測試者想象用左(右)手按箭頭指向去移動屏幕上出現的條狀棒。采樣率為128 Hz，并進行了0.5~30 Hz帶通濾波。在獲得的280次實驗中，選140次用來訓練分類器，另外的140次則測試分類器的推廣性能。
2 離散小波變換及獨立成分分析
2.1 離散小波變換
小波分析是聯合時間-尺度函數分析非平穩信號的一種有效的時頻分析方法。小波變換的實質是將信號分解成一系列小波函數的疊加，小波窗口大小隨頻率改變。在低頻時，時間分辨率較低但頻率分辨率較高；在高頻時，時間分辨率較高但頻率分辨率較低。由于其多分辨率的特點，適合提取非平穩信號的特征。
信號f(t)的離散小波變換(disperse wavelet transform,DWT)和逆變換的定義為
| ${{C}_{j,k}}(f,{{\psi }_{j,k}})={{2}^{-j/2}}\sum\limits_{n=-\infty }^{\infty }{f\left( t \right)}({{2}^{-j}}t-k),j,k\in Z,$ |
| $f\left( t \right)=\sum\limits_{n=-\infty }^{\infty }{\sum\limits_{n=-\infty }^{\infty }{{{C}_{j,k}}{{\psi }_{j,k}}\left( t \right)}}=\sum\limits_{n=-\infty }^{\infty }{{{f}_{j}}\left( t \right)},j,k\in Z\text{ },$ |
式(2)中，ψj,k=2-j/2ψ(2-j/2t-k)為小波序列，ψ(t)是滿足一定條件的小波基函數，j和k分別代表頻率分辨率和時間平移量，fj(t)表示信號f(t)在某一尺度的分量。在實際應用中用Mallat算法對信號進行有限層分解，可得
| $\begin{align} & f\left( t \right)={{f}_{L}}^{A}\left( n \right)+\sum\limits_{j=1}^{L}{{{f}_{j}}^{D}\left( n \right)}={{A}_{L}}+\sum\limits_{j=1}^{L}{{{D}_{j}}}= \\ & {{A}_{1}}+{{D}_{1}}={{A}_{2}}+{{D}_{2}}+{{D}_{1}}=\ldots , \\ \end{align}$ |
式中L為分解層數，AL為低通逼近分量，Dj為不同尺度下細節分量。由此，信號的整個頻帶被劃分為若干個子頻帶，假設信號f(t)的采樣頻率為fs，則AL,DL,DL-1，…D1各分量所對應的子頻帶范圍依次為:[fs/2L-1,fs/2L-1]…和[f2/2L+1,f2/2L]，[fs/2L,fs/2L-1]…，對應的逼近系數及各層小波系數為cAL，cDL,cDL-1,…,cD1。以三級分解為例，離散信號經三尺度分解后，得到逼近系數cA3和細節系數cD3,cD2,cD1。
2.2 獨立分量分析
ICA以非高斯信號為處理對象，在一定的條件下，能從多路觀測信號中較完整地分離出隱含的獨立源信號，并且具有很好地提取信號的空間特性。ICA算法具體描述如下：設x1,x2，…,xn為n維隨機觀測混合信號，由m個未知源信號s1,s2，…，sm線性組合而成，假設每個混合信號xi都是一個隨機變量，而不是時間信號。令X=(x1,x2,…,xn)T為n維隨機觀測向量，S=(s1,s2,…,sm)T是m維未知源信號，則ICA的線性模型可表示為
| $\begin{align} & {{X}_{nm}}={{A}_{nu}}{{S}_{um}}=\Sigma mi=1{{a}_{i}}{{s}_{i}}, \\ & i=1,2,\ldots ,m\text{ }, \\ \end{align}$ |
| $Y=W·X ,$ |
式中X是觀測信號，S為源信號，且各分量互相獨立，其中n為信號通道數，m為采樣點數，u為分離出的源信號的數量，一般情況下n=u。A是一滿秩混合矩陣，ai是混合矩陣的基向量。W為解混合矩陣，Y為式計算法的輸出，即對源信號S的估計信號。ICA算法的目的就是尋找一個最優的變換矩陣W，并計算出S的估計值Y。本文選用Fast ICA方法來尋找最優的W以及估計信號Y。
Fast ICA算法又稱固定點(Fixed Point)算法，是一種快速尋優迭代算法。Fast ICA算法有基于峭度、基于似然最大、基于負熵最大等形式，這里利用基于負熵最大的Fast ICA算法來分離信號。Fast ICA基本思想是以非高斯性極大作為其目標，尋找投影向量W，使得X在W上的投影WTX非高斯性最大[17]。
3 分析方法
3.1 數據預處理
實驗中，左右手提示出現在3~9 s，只需選用時間在3~9 s的數據。由于電極Cz的位置與運動想象功能區沒有太大相關性，處理時只選用C3和C4電極記錄的數據進行特征提取。
研究表明，大腦在想象或實施左右手運動時會顯著改變某些頻段成分(如μ節律、β節律)的功率譜強弱，這一現象被稱為事件相關同步(event related synchronization,ERS)和事件相關去同步(event related desynchronization,ERD)現象。ERD對應于功率譜比率下降，ERS則對應于功率譜比率上升。并且，對應于大腦主觀想象肢體動作思維提示所誘發被動思維的ERD/ERS在具體表現特征頻段和運動皮層區域均有所不同。比如，對應于手部運動的ERD多發生在10~11 Hz及20~24 Hz頻段。所以，本文將通過分析想象左右手運動時ERD/ERS現象最明顯的EEG信號段，選取合適的時間段、頻率段進行之后的特征提取及分類。首先對原始的280次EEG試驗信號進行三層小波分解，母小波采用Daubechies4小波。再提取第二、三層的細節系數重建原信號。根據Mallat算法得到原始EEG信號中在8~30 Hz的部分，此部分剛好包含μ和β節律。然后按照以下公式計算各導EEG信號的平均能量：
| $p\left( j \right)=\left( 1/N \right)\sum\limits_{i=1}^{N}{{{x}^{2}}\left( i,j \right)}\text{ },$ |
其中x(i,j)為第i個信號的第j個EEG數據，N為信號個數，p(j)為第j個數據的平均能量信號。計算想象左右手運動時C3和C4通道EEG信號在8~30 Hz頻段的平均能量，如圖 1所示。
圖1
想象左右手運動時C3、C4導聯平均能量變化
Figure1.
Average energy changes in C3,C4 with left and right hand motor imagery
由圖 1可知，在進行左右手運動想象時C3、C4通道的平均能量在3.5~7 s內的差異最明顯：想象左手運動時在C4導出現ERD現象；想象右手運動時在C3通道出現ERD現象。因此選定3.5~7 s時間段內8~30 Hz的頻率信息作為分析對象。這樣不僅提高了信噪比，更降低了計算的復雜度。
3.2 特征提取
3.2.1 時頻特征
離散小波變換通過將信號分解為近似信息和細節信息來分析不同分辨率下、不同頻率子帶的信號。對于一個已知信號x[n]，在分解過程中，每一層包含兩個數字濾波器以及兩個下采樣。第一層高通和低通濾波器的下采樣分別輸出為細節信息D1和近似信息A1，A1進一步分解直到得到所需的頻率信息。
用DWT分析EEG信號時，選擇合適的小波函數和分解層次尤為重要。比較了Symlet (sym2)、Daubechies (db4)、Biorthogonal (bior3.1)和Coiflet (coif3)4種常用的小波函數。分別用這4種小波函數進行特征提取并用支持向量機(support vector machine,SVM)做分類，SVM參數指標如表 1所示。較少的支持向量個數可以減少SVM分類過程中的計算時間，而大的分類間隔說明SVM分類器具有較好的推廣能力。db4小波函數較其他幾種
表1
不同小波函數得到的分類結果對比
Table1.
Classification results obtained by different wavelets using the SVM classifier
函數具有較好的分類正確率和較低的計算復雜度。因此，本文選用db4小波函數做小波系數的提取。
分解層次的確定依據所需EEG信號的頻率分量以及信號采樣率。μ節律(8~12 Hz)和β節律(18~26 Hz)被公認為是較好的BCI運動想象EEG信號特征，所以只需提取包含μ和β節律的信號特征。已知原始EEG的采樣頻率為128 Hz，小波分解后不同層次所對應的頻率信息如表 2所示。
表2
小波分解128 Hz采樣率所得各層相應的頻率
Table2.
Frequencies corresponding to different levels of wavelet decomposition with a 128 Hz sampling rate
由表 2可知，μ和β節律主要包含在D3(8~16 Hz)和D2(16~32 Hz)兩個頻率子帶中。因此選擇進行三層小波分解(見圖 2)。圖 2為想象左右手運動期間，采自C3電極的EEG信號的近似信息A3和細節信息D1~D3。為進一步降低特征向量維數，在此基礎上進行了統計學處理：① 計算每個子帶中小波系數的絕對值，再取平均值；② 每個子帶系數的標準差；③ C4、C3兩導小波系數能量差的平均值。
圖2
用db4小波提取的C3電極想象左手運動和想象右手運動時的近似信息和細節信息
Figure2.
Approximation and detailed coefficients of Symlet order two-wavelet decomposition on an EEG signal taken from the C3 electrode location during left motor imagery and right motor imagery
由于信號已通過0.5~30 Hz的濾波，所以D1層(32~64 Hz)小波系數可以排除掉。而基于子帶D2和D3層的特征將用于進一步的EEG信號的分類中。
3.2.2 空間域特征
在進行ICA之前，首先對這280 組EEG數據進行中心化，令其均值為零，然后再進行預白化處理，這兩個預處理步驟的目的是簡化ICA算法，再用主成分分析對其進行降維處理，這一過程可以預防過學習。在預處理之后，即可運用Fast ICA主要算法進行特征提取，非線性參數g選用pow3。ICA之后得到獨立分量yi和2×2維的解混合矩陣W。由式(5)可知：
| $\left[ \matrix{ {x_{c3}} \hfill \cr {x_4} \hfill \cr} \right] = {W^{ - 1}}\left[ \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right] = \left[ \matrix{ {w_{11}}{w_{12}} \hfill \cr {w_{21}}{w_{22}} \hfill \cr} \right]\left[ \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right],$ |
式中yi為ICA分離出的獨立分量。通過上式可以看出，Wj-1是估計信號Y到觀測信號X的投影，由于觀測信號從大腦不同位置測得，即Wj-1表征了獨立分量在大腦頭皮上固定的空間分布模式。由圖 3可知在進行左右手運動想象時，C3、C4電極處的事件誘發電位在大腦頭皮的空間分布不同，而解混合矩陣W的逆矩陣正好反映了這種空間分布差異。所以將此逆矩陣的4個元素作為表征EEG信號的空間特性的特征提取出來，作為最終特征向量的一部分。
最后將由小波提取出的280×10維時頻特征與ICA提取的280×4維空域特征組合，作為最終的特征向量，共計280×14維。
3.3 模式分類
SVM在解決小樣本、非線性及高維模式識別問題中表現出許多獨特的優勢，非常適合用來研究運動想象EEG信號的分類問題。本文選用C-SVC模型以及RBF核函數。本文以GA來尋找最優的C(懲罰因子)和σ(核參數)。首先選擇實值編碼策略，設置種群大小取20代，最大進化代數設定為100，交叉和變異概率分別設為0.4和0.01。基于遺傳算法的參數尋優過程中的分類流程圖如圖 3所示。
圖3
小波特征提取BCI 2003 EEG信號并由經GA優化的SVM分類的算法流程圖
Figure3.
Flow chart of the SVM improved by GA classification with the wavelet-based feature extraction on the Graz datasets in the BCI Competitions of 2003
4 結果與討論
依據提出的基于時-頻-空域EEG信號的特征提取方法提取14維特征向量，送入SVM分類器，所得結果為：最高分類正確率90.71%，平均分類正確率88.57%。圖 4所示為分類器尋優時所得最優的懲罰因子C和核參數σ以及尋優時運用n倍交叉驗證所得分類正確率。
圖4
GA參數尋優方法尋優時的適應度曲線圖及分類正確率
Figure4.
Fitness curve accuracy using GA when searching C & σ
為了證明本文所提出的時-頻-空特征提取算法提取特征的有效性，將所提出的算法與只用空域特征、時頻特征提取方法得到的結果進行了比較，如表 3所示。
表3
不同特征提取方法的分類結果比較
Table3.
Classification results obtained by different feature extraction methods
通過對比，本文方法與只提取時頻特征、空間域特征相比，分類正確率顯著提高，最高分類正確率提高了3.28%，平均分類正確率提高了2.12%。
將本文算法分類結果與BCI 2003競賽結果進行比較。2003年BCI競賽結果前三名的最高分類正確率分別為89.29%、84.29%和82.86%，通過對比可知本文方法所得最高大分類正確率與競賽最好成績相比也有所提高。
所提取特征個數也是衡量一個優秀的特征提取算法的重要指標，本文所提出的方法所需特征數只有14個，這較少的特征數提高了提取和分類時的運算速度，大大提高了算法的效率。
5 結論
傳統的時頻EEG信號特征提取方法因其計算簡單而廣泛應用，但EEG信號的信噪比較低且某些干擾成分與信號具有相似的時頻特性，單純的時頻特征提取方法區分度不夠，從而影響分類效果，因此需要性能良好和效率較高的特征提取方法。針對這一問題，本文提出了基于小波分析和ICA的提取時-頻-空域特征的方法，在傳統的時頻域特征基礎上組合了空域特征，組成最終特征矢量，并用SVM進行了識別分類。通過與單獨使用時頻域特征、空域特征的對比實驗，表明時-頻-空特征提取方法能夠有效彌補EEG信號信噪比低的不足，提高分類正確率。
