本研究擬開發下頜螺旋軸軌跡的三維顯示和分析系統,用于定量分析下頜的三維空間運動。采用6自由度的超聲下頜運動記錄儀測量下頜運動;利用計算機斷層掃描圖像重建上頜、下頜顱骨的三維數字模型;通過結構光三維掃描儀將顱骨的三維數字模型校準至下頜運動數據的坐標系。基于Visualization ToolKit和Open Scene Graphics Library開發了本系統,利用下頜運動數據計算連續變換矩陣來仿真下頜運動,通過特征值方法計算下頜的螺旋軸軌跡,并實時顯示螺旋軸軌跡與下頜的空間位置關系。本系統可以計算并輸出下頜螺旋軸的參數(旋轉、平移、方向、位置),用于精確評價下頜的三維空間運動。因此,本系統為采用螺旋軸理論研究下頜的三維空間運動奠定了一定的理論依據和實驗基礎。
引用本文： 陳磊, 張豪, 馮海蘭, 張鳳軍. 下頜螺旋軸軌跡的三維顯示和分析系統的開發. 生物醫學工程學雜志, 2014, 31(6): 1233-1237. doi: 10.7507/1001-5515.20140234 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
下頜運動是在神經系統的支配下，通過肌肉、顳下頜關節(tempromandibular joint，TMJ)和
為了克服運用參考點的運動軌跡評價下頜運動的局限性，1997年Gallo[3]運用夏萊定理分析下頜運動，引入了螺旋軸理論。螺旋軸理論將下頜視為一個剛體，描述整個下頜的三維運動。下頜在微小時間段內發生的空間運動可表達為兩個運動的聯合：既繞某個空間軸旋轉，同時又沿該軸平移，該空間軸被稱為瞬間螺旋軸。整個下頜運動過程可以劃分為若干個微小時間段，每個微小時間段均可以計算出個瞬間螺旋軸。這些瞬間螺旋軸在空間內改變位置和方向，描繪出一個線生曲面，能夠近似描述整個下頜的三維運動。
本實驗通過整合顱骨三維數字模型和下頜運動數據，實現了下頜運動仿真，同時計算并顯示出下頜螺旋軸軌跡，為進一步研究下頜螺旋軸特征奠定了基礎。
1 材料與方法
1.1 下頜運動的測量
征集一名健康的受試者，制取上、下頜牙列的硅橡膠印模(ESPE Express，3M公司，美國)灌注石膏模型(Die-Stone Ⅲ，Heraeus Kulzer公司，德國)，并在模型底座的側面貼三個掃描參考點[4]。本研究通過北京大學醫學部倫理委員會的審查和批準，試驗前取得受試者的同意，并簽署知情同意書。采用三維六自由度的超聲下頜運動記錄儀(ARCUS digma，Kavo公司，德國)測量受試者的下頜運動[5]。
受試者垂直就坐，背部無支撐，不固定頭部。將超聲下頜運動記錄儀的頭弓和超聲接受器安置于受試者的頭部，在
1.2 頭顱數字模型的三維重建
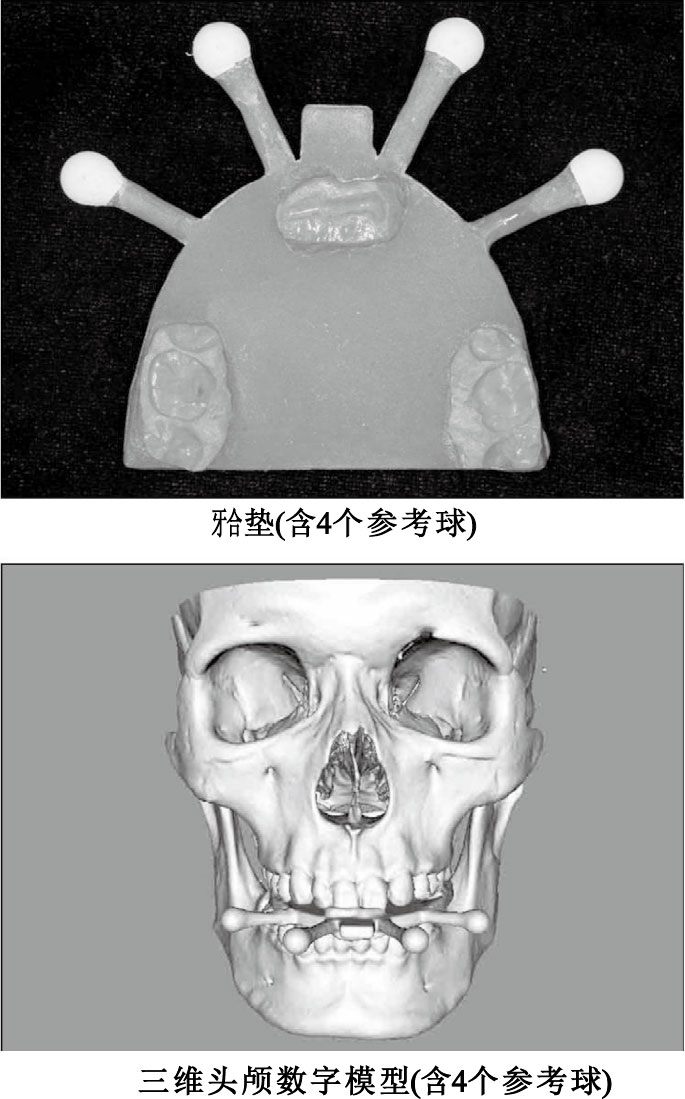
采用計算機斷層掃描(computed tomography，CT)數據重建三維頭顱數字模型。為了將頭顱數字模型配準至下頜運動數據的坐標系，制作一個帶有4個參考球的
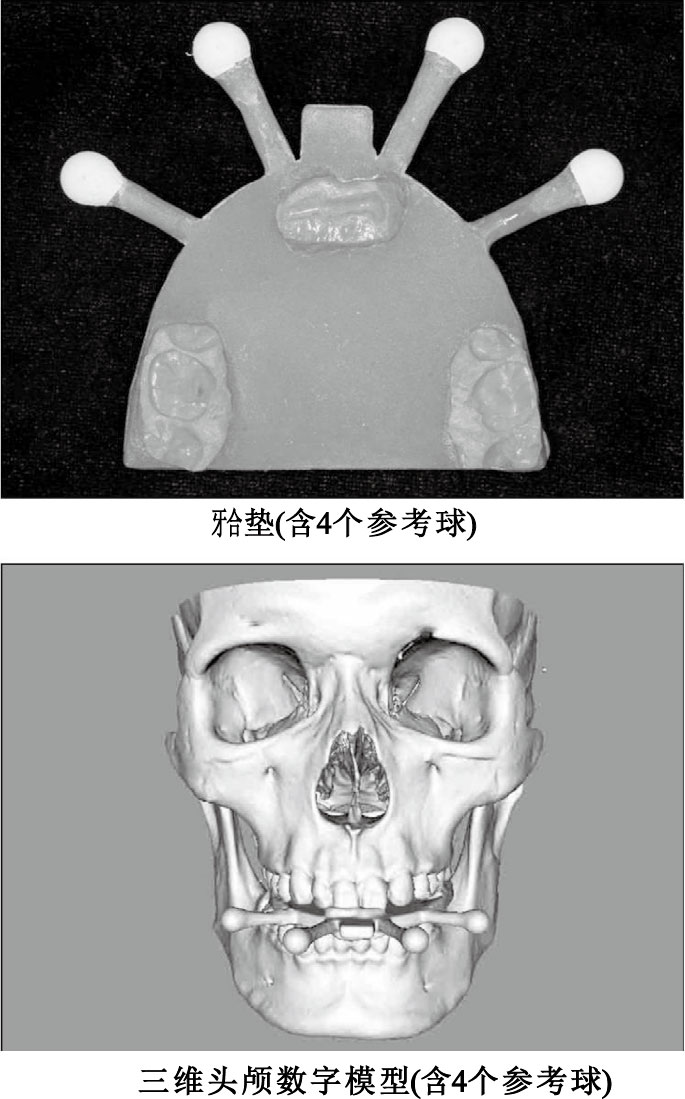圖1
利用CT圖像三維重建頭顱數字模型
Figure1.
The three-dimensional skull model reconstructed from the CT images
1.3 頭顱數字模型與下頜運動數據坐標系的校準
1.3.1 三維重建數字牙列
為了將三維頭顱數字模型校準至下頜運動數據的坐標系，必須將
1.3.2 三維重建位于牙尖交錯位的數字牙列模型
將上、下頜石膏模型固定在牙尖交錯位[4]，三維掃描并重建位于牙尖交錯位的整個上下頜數字牙列模型。
1.3.3 三維重建數字化
超聲下頜運動記錄儀輸出的下頜運動數據的坐標系與
1.3.4 將數字牙列配準至數字化
在結構光三維掃描儀系統軟件中，根據模型底座側面上的掃描參考點，將1.3.2中位于牙尖交錯位的整個上下頜數字牙列模型配準至數字化
1.3.5 頭顱數字模型校準至下頜運動數據的坐標系
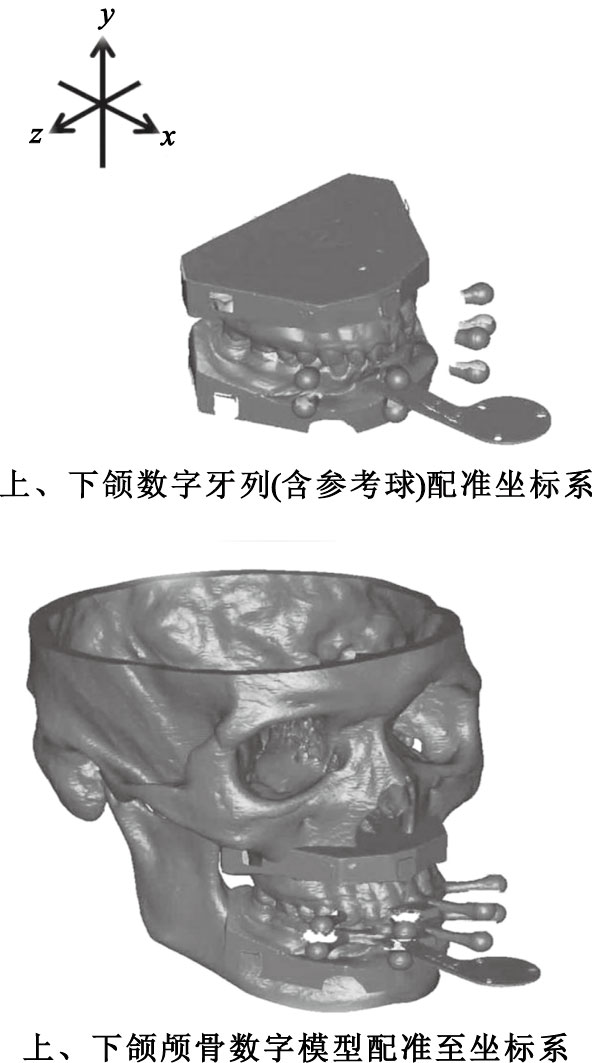
將1.3.4輸出的三個數字模型導入軟件Geomagic Studio 8.0，根據參數“a”和“b”[6]定位下頜運動數據的坐標系。然后，輸入上、下頜數字顱骨模型，通過參考球將它們分別配準至運動數據的坐標系，如圖 2所示。最后，輸出上、下頜顱骨數字模型分別保存。
1.4 下頜螺旋軸軌跡的計算與顯示
基于Visualization ToolKit和Open Scene Graphics Library開發虛擬顱頜運動仿真系統。本系統設計了一個程序組織下頜運動數據，計算連續變換矩陣用于確定下頜的位置，從而仿真下頜運動[7]，采用特征值方法計算并顯示下頜的螺旋軸軌跡[8]。當一個剛體在空間發生運動時，其坐標為
| ${{q}_{i}}=R\cdot {{a}_{i}}+v$ |
式中i=1、2、3，a1、a2、a3是剛體上任意三個非共線的點P1、P2、P3在運動前的位置向量，q1、q2、q3是這三個點在運動后的位置向量，R是旋轉矩陣，v是平移向量。根據每20 ms(超聲下頜運動記錄儀的采樣頻率為50 Hz)的微小時間段確定旋轉矩陣和平移向量，每一微小時間段的下頜整體運動可被描述為沿瞬間螺旋軸平移ΔΤ，同時繞該軸旋轉ΔΦ。
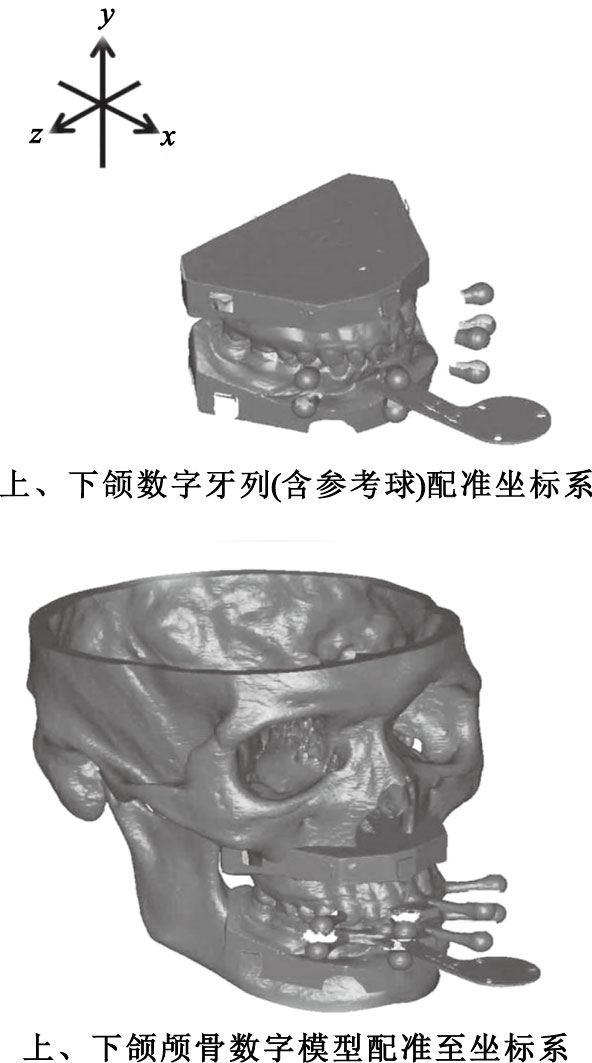圖2
三維頭顱數字模型與下頜運動數據坐標系的配準
Figure2.
The 3D skull model registered to the coordinate system of mandibular motion data
用旋轉矩陣R和平移向量v計算瞬間螺旋軸的位置和方向。除非連續的采樣時間點之間下頜運動的旋轉角非常小，否則需為該采樣時間點計算沿瞬間螺旋軸的平移ΔΤ及繞該軸的旋轉ΔΦ。在計算下頜螺旋軸時需要給旋轉角預先設定一個閾值，當旋轉角低于該閾值時不計算瞬間螺旋軸，該運動步幅被認為僅發生平移。本系統在計算下頜螺旋軸時，旋轉角的閾值可設定為任意角度。對于每個采樣時間點的瞬間螺旋軸，本系統計算以下下頜螺旋軸參數：旋轉、平移、方向和位置。
2 結果
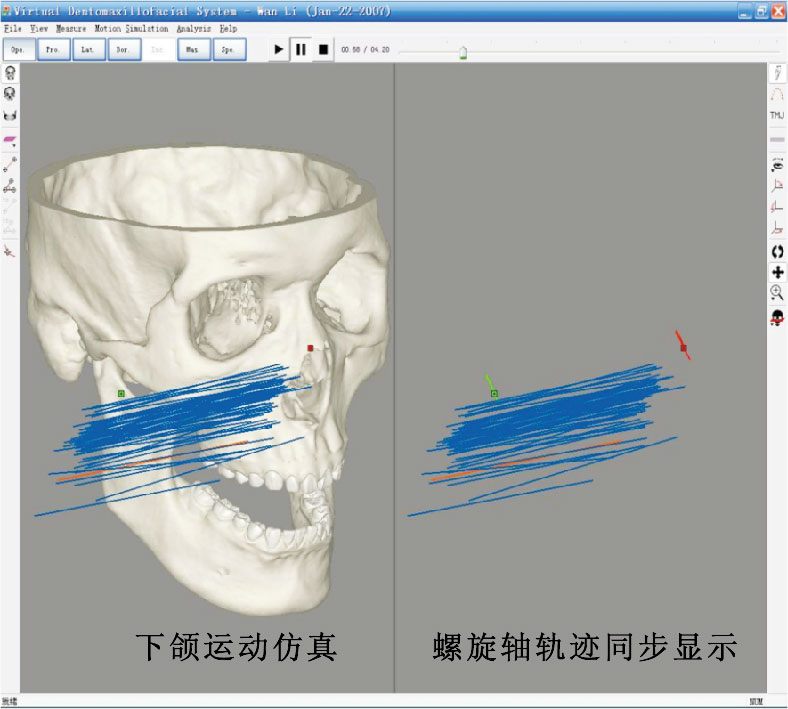
采用虛擬顱頜運動仿真系統打開上、下頜數字顱骨模型和下頜運動數據，仿真下頜運動。如圖 3所示，下頜運動的仿真結果顯示在窗口的左側，運動的形式取決于所記錄的下頜運動數據，如開閉口、前伸后退、側方、邊緣、咀嚼等。通過窗口頂部的控制面板和右側的視覺工具欄，可以操縱下頜運動的整個過程，并能調整數字顱骨模型的瀏覽角度。在下頜運動仿真的基礎上，該系統計算下頜的螺旋軸軌跡，并在窗口的左右側同步顯示。下頜運動過程中，當前時刻的瞬間螺旋軸顯示為紅色，其它瞬間螺旋
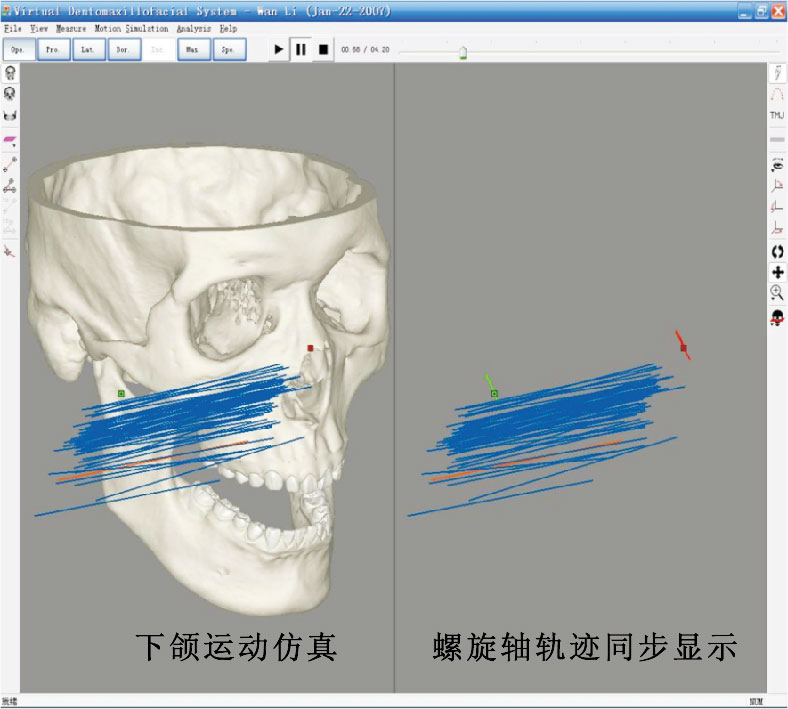圖3
下頜運動仿真及螺旋軸軌跡的顯示
Figure3.
Simulation of mandibular movements and the visualization of mandibular helical axis pathways
軸為藍色。當切換下頜的運動形式時，所顯示的下頜螺旋軸軌跡也相應地變換。本系統可以計算下頜螺旋軸軌跡的參數并以txt格式輸出，如表 1所示：旋轉Φ，下頜繞瞬間螺旋軸旋轉的度數；平移Τ，下頜沿瞬間螺旋軸平移的向量；方向θx、θy、θz，分別為瞬間螺旋軸與x、y、z坐標軸的夾角；位置d、xd、yd、zd，d為預設參考點(左、右側各一個參考點)到瞬間螺旋軸垂線的距離，xd、yd、zd為該垂線在x、y、z坐標軸上的分量。
表1
一個受試者習慣性開閉口運動的下頜螺旋軸參數
Table1.
Parameters of mandibular helical axis during habitual jaw opening and closing movements in an asymptomatic subject
本系統輸出的下頜螺旋軸參數可用于計算下列參數：繞螺旋軸的最大旋轉角Φmax；沿螺旋軸的最大平移量Τmax；預設的參考點到螺旋軸垂線距離的最大值dmax；xdmax、xdmin為d在x軸上分量的最大值和最小值；ydmax、ydmin為d在y軸上分量的最大值和最小值；平均角x、y、z，螺旋軸的方向在空間內總體波動的平均值e，計算公式為
| ${{\theta }_{e}}=\frac{\sum\limits_{k=1}^{n}{\sqrt{{{[{{\theta }_{x}}({{t}_{k}})--{{\theta }_{x}}]}^{2}}+{{[{{\theta }_{y}}({{t}_{k}})--{{\theta }_{y}}]}^{2}}+{{[{{\theta }_{z}}({{t}_{k}})--{{\theta }_{z}}]}^{2}}}}}{n}\text{ },$ |
向量d確定了下頜螺旋軸相對于預設參考點的空間位置。xdmax、xdmin、ydmax、ydmin代表下頜螺旋軸在矢狀面上相對預設參考點的最大位移，這4個參數界定了下頜螺旋軸在矢狀面上的移動區域。e能揭示下頜螺旋軸之間的平行程度：若整個下頜運動中所有瞬間螺旋軸完全平行，e即為0；e若偏離平均方向，則增大。
3 討論
為了克服采用單點的運動軌跡評價下頜運動的局限性，學者們運用螺旋軸理論描述整個下頜的三維空間運動[3, 9-12]。該理論已被廣泛用于研究人體復雜關節的運動，如肘[13]、腕[14]、踝[15]、膝[16]、頸[17]、脊柱[18]等的運動。TMJ的解剖特征使得下頜運動同時包含旋轉和平移的成分，因此螺旋軸理論適合于評價下頜運動。本實驗通過整合三維CT頭顱數字模型和超聲下頜運動記錄儀測量的運動數據，運用仿真技術實現下頜運動仿真，計算并顯示下頜螺旋軸軌跡。下頜運動的測量精度明顯影響下頜螺旋軸軌跡的計算精度，因此必須采用精度較高的下頜運動記錄儀。目前，三維6自由度的下頜運動記錄儀主要有兩大類：光電原理的記錄儀，超聲原理的記錄儀。與其它研究所采用的光電記錄儀相比，本研究所采用的超聲記錄儀的精度能滿足測量下頜運動的要求[3, 9-12]。此外，為了能實時顯示下頜與螺旋軸軌跡的空間位置關系，必須將三維CT頭顱數字模型校準至下頜運動數據的坐標系。本研究通過三維掃描超聲下頜運動記錄儀系統附帶的
為了能夠完整地描述下頜運動，下頜運動記錄儀必須有較高的采樣頻率。隨著采樣頻率的增大，下頜的連續運動步幅將變小，這會增大下頜螺旋軸的計算誤差。當旋轉角接近于0°時，下頜螺旋軸的計算誤差將趨于無窮大。為了避免該誤差過大，只有當下頜的連續運動步幅之間的旋轉角大于某個閾值時，才計算下頜螺旋軸，旋轉角小于該閾值時則不計算螺旋軸，此時的下頜運動主要表現為平移[3, 9]。但是，若為旋轉角設定較小的閾值，可計算更多的瞬間螺旋軸，用于完整地描述下頜運動的整個過程。因此，旋轉角閾值的設定需要在兩者之間權衡。對于連續運動步幅較小的下頜運動，如開閉口運動的起始結束階段、咀嚼運動等，旋轉角的閾值可設定為小于1° [3, 11-12]；對于連續運動步幅較大的下頜運動，旋轉角的閾值可設定為1°，甚至大于1° [9-10]。當對比不同研究的下頜螺旋軸參數時，必須明確所設定的旋轉角閾值是否相同。本實驗在計算下頜螺旋軸時，旋轉角的閾值預設為1°，同時旋轉角的閾值可設定為任意角度，為進一步研究各種形式下頜運動的螺旋軸軌跡奠定基礎。
下頜螺旋軸的位置參數d、xd、yd、zd描述其相對于預設參考點的位置關系。Gallo等[3, 9-10]選擇髁突內參考點描述下頜螺旋軸的位置，結果顯示螺旋軸不位于髁突內。Sadat-Khonsari等[11]用坐標原點作為預設參考點，來描述下頜螺旋軸如何在空間內移動。通常選擇有解剖意義的參考點作為預設參考點，從而揭示下頜螺旋軸與這些參考點的位置關系。本研究將運動軸點作為預設參考點，同時也可以設定為其它參考點，用于研究下頜螺旋軸與任意參考點的位置關系。根據方向參數θx、θy、θz所計算出的e可揭示下頜螺旋軸的方向在空間內總體波動規律，能反應螺旋軸之間的平行度[3, 10-11]。該參數適用于評價對稱性的下頜運動，研究個體內或個體間下頜螺旋軸的變化。此外，下頜運動數據的坐標系是影響螺旋軸參數的另一個重要因素。通常采用矢狀面和冠狀面作為兩個坐標平面，但第三坐標平面存在差異。Gallo等[3]采用鼻翼耳屏平面作為第三坐標平面，Sadat-Khonsari等則采用眶耳平面作為第三坐標平面。因此，比較不同研究的下頜螺旋軸參數時，必須明確他們是否采用了相同的第三坐標平面。本研究中超聲下頜運動記錄儀系統記錄下頜運動數據的坐標系與其附帶的上
本研究采用超聲下頜運動記錄儀測量下頜運動，運用特征值算法計算下頜螺旋軸軌跡，描述整個下頜的三維空間運動。此外，將三維CT頭顱數字模型校準至下頜運動數據的坐標系，仿真下頜運動，從而實時顯示下頜與螺旋軸的空間位置關系。本研究開發了一個軟件用于計算、顯示下頜螺旋軸軌跡，同時能計算并輸出下頜螺旋軸軌跡的參數，為采用螺旋軸理論研究下頜的三維空間運動奠定了理論依據和實驗基礎。
引言
下頜運動是在神經系統的支配下，通過肌肉、顳下頜關節(tempromandibular joint，TMJ)和
為了克服運用參考點的運動軌跡評價下頜運動的局限性，1997年Gallo[3]運用夏萊定理分析下頜運動，引入了螺旋軸理論。螺旋軸理論將下頜視為一個剛體，描述整個下頜的三維運動。下頜在微小時間段內發生的空間運動可表達為兩個運動的聯合：既繞某個空間軸旋轉，同時又沿該軸平移，該空間軸被稱為瞬間螺旋軸。整個下頜運動過程可以劃分為若干個微小時間段，每個微小時間段均可以計算出個瞬間螺旋軸。這些瞬間螺旋軸在空間內改變位置和方向，描繪出一個線生曲面，能夠近似描述整個下頜的三維運動。
本實驗通過整合顱骨三維數字模型和下頜運動數據，實現了下頜運動仿真，同時計算并顯示出下頜螺旋軸軌跡，為進一步研究下頜螺旋軸特征奠定了基礎。
1 材料與方法
1.1 下頜運動的測量
征集一名健康的受試者，制取上、下頜牙列的硅橡膠印模(ESPE Express，3M公司，美國)灌注石膏模型(Die-Stone Ⅲ，Heraeus Kulzer公司，德國)，并在模型底座的側面貼三個掃描參考點[4]。本研究通過北京大學醫學部倫理委員會的審查和批準，試驗前取得受試者的同意，并簽署知情同意書。采用三維六自由度的超聲下頜運動記錄儀(ARCUS digma，Kavo公司，德國)測量受試者的下頜運動[5]。
受試者垂直就坐，背部無支撐，不固定頭部。將超聲下頜運動記錄儀的頭弓和超聲接受器安置于受試者的頭部，在
1.2 頭顱數字模型的三維重建
采用計算機斷層掃描(computed tomography，CT)數據重建三維頭顱數字模型。為了將頭顱數字模型配準至下頜運動數據的坐標系，制作一個帶有4個參考球的
圖1
利用CT圖像三維重建頭顱數字模型
Figure1.
The three-dimensional skull model reconstructed from the CT images
1.3 頭顱數字模型與下頜運動數據坐標系的校準
1.3.1 三維重建數字牙列
為了將三維頭顱數字模型校準至下頜運動數據的坐標系，必須將
1.3.2 三維重建位于牙尖交錯位的數字牙列模型
將上、下頜石膏模型固定在牙尖交錯位[4]，三維掃描并重建位于牙尖交錯位的整個上下頜數字牙列模型。
1.3.3 三維重建數字化
超聲下頜運動記錄儀輸出的下頜運動數據的坐標系與
1.3.4 將數字牙列配準至數字化
在結構光三維掃描儀系統軟件中，根據模型底座側面上的掃描參考點，將1.3.2中位于牙尖交錯位的整個上下頜數字牙列模型配準至數字化
1.3.5 頭顱數字模型校準至下頜運動數據的坐標系
將1.3.4輸出的三個數字模型導入軟件Geomagic Studio 8.0，根據參數“a”和“b”[6]定位下頜運動數據的坐標系。然后，輸入上、下頜數字顱骨模型，通過參考球將它們分別配準至運動數據的坐標系，如圖 2所示。最后，輸出上、下頜顱骨數字模型分別保存。
1.4 下頜螺旋軸軌跡的計算與顯示
基于Visualization ToolKit和Open Scene Graphics Library開發虛擬顱頜運動仿真系統。本系統設計了一個程序組織下頜運動數據，計算連續變換矩陣用于確定下頜的位置，從而仿真下頜運動[7]，采用特征值方法計算并顯示下頜的螺旋軸軌跡[8]。當一個剛體在空間發生運動時，其坐標為
| ${{q}_{i}}=R\cdot {{a}_{i}}+v$ |
式中i=1、2、3，a1、a2、a3是剛體上任意三個非共線的點P1、P2、P3在運動前的位置向量，q1、q2、q3是這三個點在運動后的位置向量，R是旋轉矩陣，v是平移向量。根據每20 ms(超聲下頜運動記錄儀的采樣頻率為50 Hz)的微小時間段確定旋轉矩陣和平移向量，每一微小時間段的下頜整體運動可被描述為沿瞬間螺旋軸平移ΔΤ，同時繞該軸旋轉ΔΦ。
圖2
三維頭顱數字模型與下頜運動數據坐標系的配準
Figure2.
The 3D skull model registered to the coordinate system of mandibular motion data
用旋轉矩陣R和平移向量v計算瞬間螺旋軸的位置和方向。除非連續的采樣時間點之間下頜運動的旋轉角非常小，否則需為該采樣時間點計算沿瞬間螺旋軸的平移ΔΤ及繞該軸的旋轉ΔΦ。在計算下頜螺旋軸時需要給旋轉角預先設定一個閾值，當旋轉角低于該閾值時不計算瞬間螺旋軸，該運動步幅被認為僅發生平移。本系統在計算下頜螺旋軸時，旋轉角的閾值可設定為任意角度。對于每個采樣時間點的瞬間螺旋軸，本系統計算以下下頜螺旋軸參數：旋轉、平移、方向和位置。
2 結果
采用虛擬顱頜運動仿真系統打開上、下頜數字顱骨模型和下頜運動數據，仿真下頜運動。如圖 3所示，下頜運動的仿真結果顯示在窗口的左側，運動的形式取決于所記錄的下頜運動數據，如開閉口、前伸后退、側方、邊緣、咀嚼等。通過窗口頂部的控制面板和右側的視覺工具欄，可以操縱下頜運動的整個過程，并能調整數字顱骨模型的瀏覽角度。在下頜運動仿真的基礎上，該系統計算下頜的螺旋軸軌跡，并在窗口的左右側同步顯示。下頜運動過程中，當前時刻的瞬間螺旋軸顯示為紅色，其它瞬間螺旋
圖3
下頜運動仿真及螺旋軸軌跡的顯示
Figure3.
Simulation of mandibular movements and the visualization of mandibular helical axis pathways
軸為藍色。當切換下頜的運動形式時，所顯示的下頜螺旋軸軌跡也相應地變換。本系統可以計算下頜螺旋軸軌跡的參數并以txt格式輸出，如表 1所示：旋轉Φ，下頜繞瞬間螺旋軸旋轉的度數；平移Τ，下頜沿瞬間螺旋軸平移的向量；方向θx、θy、θz，分別為瞬間螺旋軸與x、y、z坐標軸的夾角；位置d、xd、yd、zd，d為預設參考點(左、右側各一個參考點)到瞬間螺旋軸垂線的距離，xd、yd、zd為該垂線在x、y、z坐標軸上的分量。
表1
一個受試者習慣性開閉口運動的下頜螺旋軸參數
Table1.
Parameters of mandibular helical axis during habitual jaw opening and closing movements in an asymptomatic subject
本系統輸出的下頜螺旋軸參數可用于計算下列參數：繞螺旋軸的最大旋轉角Φmax；沿螺旋軸的最大平移量Τmax；預設的參考點到螺旋軸垂線距離的最大值dmax；xdmax、xdmin為d在x軸上分量的最大值和最小值；ydmax、ydmin為d在y軸上分量的最大值和最小值；平均角x、y、z，螺旋軸的方向在空間內總體波動的平均值e，計算公式為
| ${{\theta }_{e}}=\frac{\sum\limits_{k=1}^{n}{\sqrt{{{[{{\theta }_{x}}({{t}_{k}})--{{\theta }_{x}}]}^{2}}+{{[{{\theta }_{y}}({{t}_{k}})--{{\theta }_{y}}]}^{2}}+{{[{{\theta }_{z}}({{t}_{k}})--{{\theta }_{z}}]}^{2}}}}}{n}\text{ },$ |
向量d確定了下頜螺旋軸相對于預設參考點的空間位置。xdmax、xdmin、ydmax、ydmin代表下頜螺旋軸在矢狀面上相對預設參考點的最大位移，這4個參數界定了下頜螺旋軸在矢狀面上的移動區域。e能揭示下頜螺旋軸之間的平行程度：若整個下頜運動中所有瞬間螺旋軸完全平行，e即為0；e若偏離平均方向，則增大。
3 討論
為了克服采用單點的運動軌跡評價下頜運動的局限性，學者們運用螺旋軸理論描述整個下頜的三維空間運動[3, 9-12]。該理論已被廣泛用于研究人體復雜關節的運動，如肘[13]、腕[14]、踝[15]、膝[16]、頸[17]、脊柱[18]等的運動。TMJ的解剖特征使得下頜運動同時包含旋轉和平移的成分，因此螺旋軸理論適合于評價下頜運動。本實驗通過整合三維CT頭顱數字模型和超聲下頜運動記錄儀測量的運動數據，運用仿真技術實現下頜運動仿真，計算并顯示下頜螺旋軸軌跡。下頜運動的測量精度明顯影響下頜螺旋軸軌跡的計算精度，因此必須采用精度較高的下頜運動記錄儀。目前，三維6自由度的下頜運動記錄儀主要有兩大類：光電原理的記錄儀，超聲原理的記錄儀。與其它研究所采用的光電記錄儀相比，本研究所采用的超聲記錄儀的精度能滿足測量下頜運動的要求[3, 9-12]。此外，為了能實時顯示下頜與螺旋軸軌跡的空間位置關系，必須將三維CT頭顱數字模型校準至下頜運動數據的坐標系。本研究通過三維掃描超聲下頜運動記錄儀系統附帶的
為了能夠完整地描述下頜運動，下頜運動記錄儀必須有較高的采樣頻率。隨著采樣頻率的增大，下頜的連續運動步幅將變小，這會增大下頜螺旋軸的計算誤差。當旋轉角接近于0°時，下頜螺旋軸的計算誤差將趨于無窮大。為了避免該誤差過大，只有當下頜的連續運動步幅之間的旋轉角大于某個閾值時，才計算下頜螺旋軸，旋轉角小于該閾值時則不計算螺旋軸，此時的下頜運動主要表現為平移[3, 9]。但是，若為旋轉角設定較小的閾值，可計算更多的瞬間螺旋軸，用于完整地描述下頜運動的整個過程。因此，旋轉角閾值的設定需要在兩者之間權衡。對于連續運動步幅較小的下頜運動，如開閉口運動的起始結束階段、咀嚼運動等，旋轉角的閾值可設定為小于1° [3, 11-12]；對于連續運動步幅較大的下頜運動，旋轉角的閾值可設定為1°，甚至大于1° [9-10]。當對比不同研究的下頜螺旋軸參數時，必須明確所設定的旋轉角閾值是否相同。本實驗在計算下頜螺旋軸時，旋轉角的閾值預設為1°，同時旋轉角的閾值可設定為任意角度，為進一步研究各種形式下頜運動的螺旋軸軌跡奠定基礎。
下頜螺旋軸的位置參數d、xd、yd、zd描述其相對于預設參考點的位置關系。Gallo等[3, 9-10]選擇髁突內參考點描述下頜螺旋軸的位置，結果顯示螺旋軸不位于髁突內。Sadat-Khonsari等[11]用坐標原點作為預設參考點，來描述下頜螺旋軸如何在空間內移動。通常選擇有解剖意義的參考點作為預設參考點，從而揭示下頜螺旋軸與這些參考點的位置關系。本研究將運動軸點作為預設參考點，同時也可以設定為其它參考點，用于研究下頜螺旋軸與任意參考點的位置關系。根據方向參數θx、θy、θz所計算出的e可揭示下頜螺旋軸的方向在空間內總體波動規律，能反應螺旋軸之間的平行度[3, 10-11]。該參數適用于評價對稱性的下頜運動，研究個體內或個體間下頜螺旋軸的變化。此外，下頜運動數據的坐標系是影響螺旋軸參數的另一個重要因素。通常采用矢狀面和冠狀面作為兩個坐標平面，但第三坐標平面存在差異。Gallo等[3]采用鼻翼耳屏平面作為第三坐標平面，Sadat-Khonsari等則采用眶耳平面作為第三坐標平面。因此，比較不同研究的下頜螺旋軸參數時，必須明確他們是否采用了相同的第三坐標平面。本研究中超聲下頜運動記錄儀系統記錄下頜運動數據的坐標系與其附帶的上
本研究采用超聲下頜運動記錄儀測量下頜運動，運用特征值算法計算下頜螺旋軸軌跡，描述整個下頜的三維空間運動。此外，將三維CT頭顱數字模型校準至下頜運動數據的坐標系，仿真下頜運動，從而實時顯示下頜與螺旋軸的空間位置關系。本研究開發了一個軟件用于計算、顯示下頜螺旋軸軌跡，同時能計算并輸出下頜螺旋軸軌跡的參數，為采用螺旋軸理論研究下頜的三維空間運動奠定了理論依據和實驗基礎。
