腦卒中患者平衡功能嚴重下降,完成蹲下站立的動作相當困難,因此有必要對人體下蹲站起過程進行深入的研究,并對該過程做準確的動力學建模與仿真。本文將人體簡化為7剛體模型,不考慮上肢和頭部的運動,建立人體下蹲站起過程坐標系,利用Lagrange方法分別求出下蹲站起過程中膝關節力矩和髖關節力矩,并利用Matlab對該數學模型進行仿真。在機械系統動力學自動分析(ADAMS)中建立人體下蹲站起幾何模型,通過仿真驗證了所建立Lagrange數學模型的有效性,為進一步研究下蹲站起康復訓練器械提供了良好的理論參考依據。
引用本文: 王建輝, 徐秀林, 安美君, 胡秀枋. 人體下蹲站起動力學建模與仿真研究. 生物醫學工程學雜志, 2014, 31(6): 1250-1254. doi: 10.7507/1001-5515.20140237 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
腦卒中是中老年人常見病、多發病,發病率、致殘率高,據統計中國每年發生腦中風的患者達200萬,發病率高達120/10萬,致殘率高達75%,而每年中風患者死亡約120萬[1]。大多數腦卒中患者平衡功能嚴重下降,完成下蹲站起的動作相當困難,傳統的藥物治療很難對腦卒中患者產生理想的治療效果,患者還需借助一定的康復訓練器械對其蹲下站起和平衡能力進行長期的康復訓練,而設計一種適合于腦卒中患者的康復訓練器械,首先要對人體下蹲站起過程做準確的動力學建模和仿真。
過去十多年間,很多學者針對人體不同的運動或動作建立相應的多剛體模型,對人體動力學模型的建立做了不少有益的工作。Blajera等[2]為了研究雜技演員在蹦床上翻筋斗的動作過程,建立了一個9自由度10剛體人體簡化模型。Anderson等[3]在研究人垂直起跳達到最大高度過程中的肌肉協調性時,把人體簡化為10段、54塊肌肉的23自由度模型,并在此模型的基礎之上計算了人在行走過程中行走距離與能量消耗間的關系。本文是在Hanavan[4]所提出的15剛體數學模型基礎上,忽略上肢和頭部運動,將人體簡化為7剛體模型,利用Lagrange方法[5-7]對人體蹲下站立過程進行動力學建模,并使用Matlab對該數學模型進行仿真,通過與機械系統動力學自動分析(automatic dynamic analysis of mechanical systems,ADAMS)仿真[8-9]結果的比較,驗證了Lagrange數學模型的合理性。
1 下蹲站起過程動力學分析
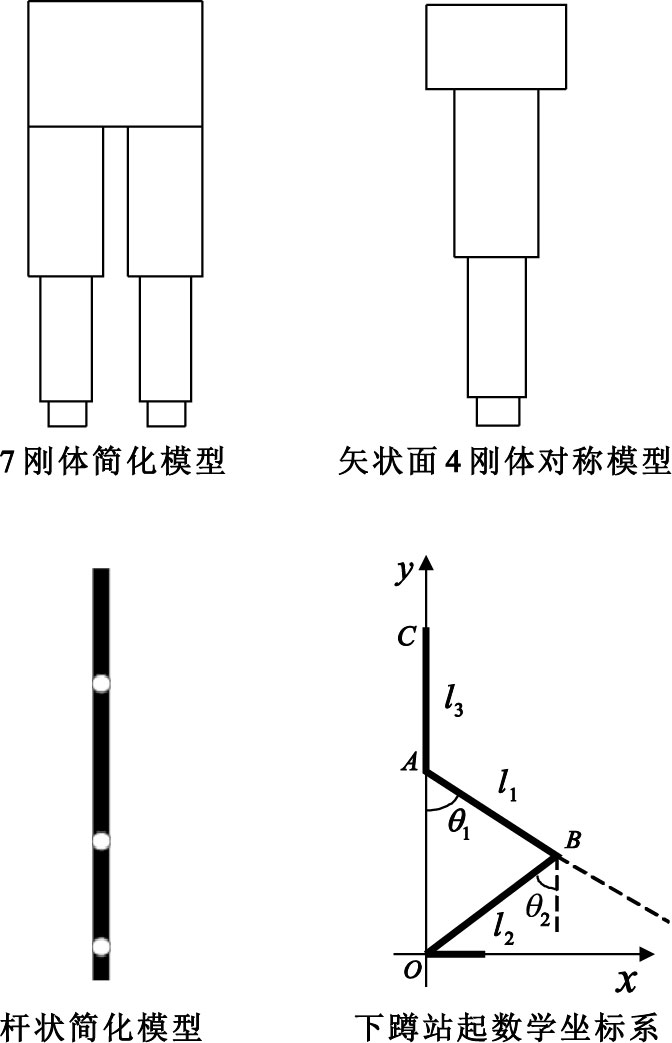
著名的Hanavan模型是將人體劃分成15個剛體段,各段之間用球鉸連接。由于本文研究的是下蹲站起過程中的動力學模型,故不考慮上肢和頭部的運動,將人體上軀干部分和下軀干部分合并為一個剛體,從而將人體簡化為如圖 1所示的7剛體簡化模型,由于人體沿矢狀面是對稱的,只需分析人體左側或右側部分的運動情況,故本研究著重考慮矢狀面內4剛體模型,各部分分別等效為一個桿,建立4連桿狀簡化模型,其中頭頸、軀干和上肢等效為一個桿,大腿、小腿和腳分別作為一個桿,即可建立下蹲站起數學坐標系,該系統只有一個自由度。
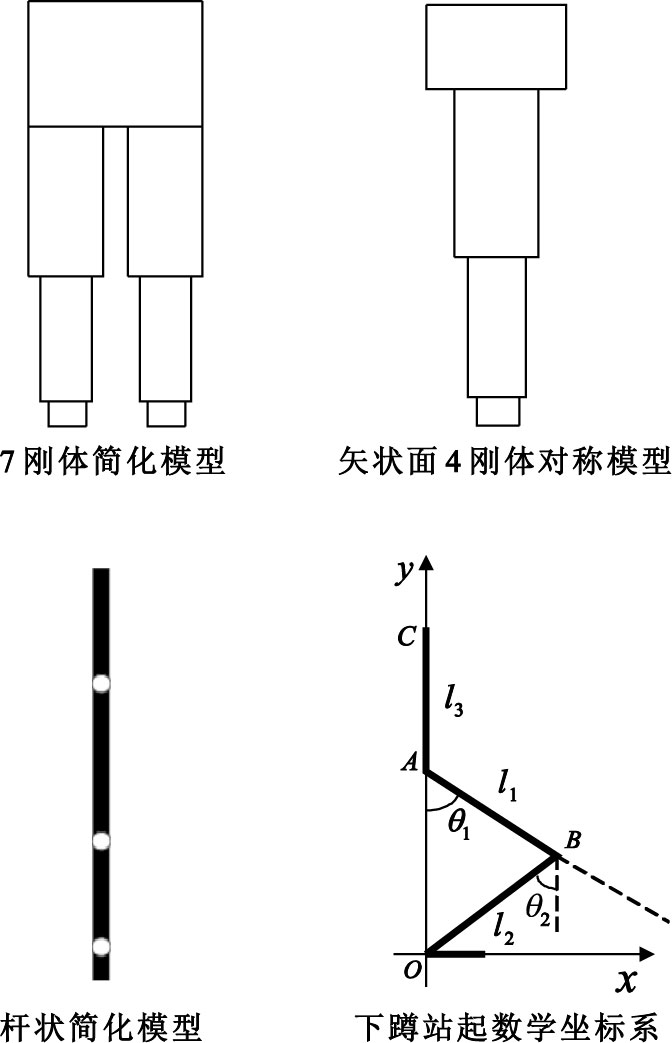 圖1
下蹲站起模型簡化
Figure1.
Simplification of squatting-standing model
圖1
下蹲站起模型簡化
Figure1.
Simplification of squatting-standing model
在下蹲站起數學坐標系中,AC代表軀干部分,AB代表大腿,OB代表小腿,大腿、小腿和軀干的長度分別為l1、l2和l3,質量分別為m1、m2和m3(將桿件的質心簡化為桿件中心位置),大腿和小腿與豎直方向的夾角分別為θ1和θ2。
選θ1為廣義坐標,運用Lagrange方法建立該系統的數學模型,根據下蹲站起數學坐標系可得大腿、小腿和軀干的質心坐標分別為
| $\eqalign{ & \left[ \matrix{ {x_1} \hfill \cr {y_1} \hfill \cr} \right] = \left| \matrix{ {{{l_1}} \over 2}sin{\theta _1} \hfill \cr {{{l_1}} \over 2}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} \hfill \cr} \right|;{\rm{ }} \cr & \left[ \matrix{ {x_2} \hfill \cr {y_2} \hfill \cr} \right] = \left| \matrix{ {{{l_2}} \over 2}sin{\theta _2} \hfill \cr {{\sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} } \over 2}{\rm{ }} \hfill \cr} \right|;{\rm{ }} \cr & \left[ \matrix{ {x_3} \hfill \cr {y_3} \hfill \cr} \right] = \left| \matrix{ 0 \hfill \cr {l_1}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} + {{{l_3}} \over 2} \hfill \cr} \right|. \cr} $ |
系統的總動能T為大腿、小腿和軀干三桿件動能T1、T2、T3之和,總勢能V為三桿件勢能V1、V2、V3之和,其中
| $\eqalign{ & \left| \matrix{ {T_1} \hfill \cr {T_2} \hfill \cr {T_3} \hfill \cr} \right| = \left| \matrix{ {1 \over 2}{m_1}{v_1}^2 + {1 \over 2}{I_1}{{\dot \theta }_1}^2 \hfill \cr {1 \over 2}{m_2}{v_2}^2 + {1 \over 2}{I_2} \cdot {{l_1^2\mathop {\cos {\theta _1}}\limits^2 {\mkern 1mu} } \over {l_2^2 - l_1^2\mathop {\sin {\theta _1}}\limits^2 {\mkern 1mu} }} \cdot {{\dot \theta }_1}^2 \hfill \cr {1 \over 2}{m_3}{v_3}^2 \hfill \cr} \right| \cr & \left| \matrix{ {V_1} \hfill \cr {V_2} \hfill \cr {V_3} \hfill \cr} \right| = \left| \matrix{ {m_1}g({{{l_1}} \over 2}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} ) \hfill \cr {{{m_2}g{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} \over 2}{\rm{ }} \hfill \cr {m_3}g({l_1}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} + {{{l_3}} \over 2}) \hfill \cr} \right| \cr} $ |
其中v1、v2、v3分別為大腿、小腿和軀干的質心速度,g為重力加速度,I1、I2分別為大腿、小腿相對質心的轉動慣量(I1=m1l12/12,I2=m2l22/12)。
因此,拉格朗日函數L1可表示為
| $\begin{align} & {{L}_{1}}=T-V={{T}_{1}}+{{T}_{2}}+{{T}_{3}}-{{V}_{1}}-{{V}_{2}}-{{V}_{3}}= \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{1}}^{3}si{{n}^{2}}{{\theta }_{1}}cos{{\theta }_{1}}\cdot {{{\dot{\theta }}}_{1}}^{2}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}+ \\ & [\frac{1}{2}({{m}_{1}}+{{m}_{3}}){{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}+\frac{1}{6}{{m}_{2}}{{l}_{2}}^{2}]\cdot \frac{{{l}_{1}}^{2}co{{s}^{2}}{{\theta }_{1}}\cdot \dot{\theta }{{\cdot }_{1}}^{2}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}+ \\ & (\frac{1}{6}{{m}_{1}}+\frac{1}{2}{{m}_{3}}si{{n}^{2}}{{\theta }_{1}}){{l}_{1}}^{2}{{{\dot{\theta }}}_{1}}^{2}-\frac{1}{2}{{m}_{3}}g{{l}_{3}}- \\ & (12{{m}_{1}}+{{m}_{3}})g{{l}_{1}}cos{{\theta }_{1}}-({{m}_{1}}+12{{m}_{2}}+{{m}_{3}})g \\ & \sqrt{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}} \\ \end{align}$ |
由此可得,髖關節力矩M1為
| $\begin{align} & {{M}_{1}}=\frac{d}{dt}\text{ }\frac{\partial {{L}_{1}}}{\partial {{{\dot{\theta }}}_{1}}}-\frac{\partial {{L}_{1}}}{\partial {{{\dot{\theta }}}_{1}}}~=[(\frac{1}{3}{{m}_{1}}+{{m}_{3}}si{{n}^{2}}{{\theta }_{1}}){{l}_{1}}^{2}+ \\ & \frac{({{m}_{1}}+2{{m}_{3}}){{l}_{1}}^{3}si{{n}^{2}}{{\theta }_{1}}cos{{\theta }_{1}}}{\sqrt{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}}]\cdot {{{\ddot{\theta }}}_{1}}+ \\ & \frac{[({{m}_{1}}+{{m}_{3}}){{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}+13{{m}_{2}}{{l}_{2}}^{2}]{{l}_{1}}^{2}co{{s}^{2}}{{\theta }_{1}}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}\cdot {{{\ddot{\theta }}}_{1}}+ \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{1}}^{3}\cdot [{{l}_{2}}^{2}sin{{\theta }_{1}}(1+3cos2{{\theta }_{1}})-2{{l}_{1}}^{2}si{{n}^{3}}{{\theta }_{1}}cos2{{\theta }_{1}}]}{2{{({{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}})}^{\frac{3}{2}}}}\cdot {{{\dot{\theta }}}_{1}}^{2}+ \\ & \frac{{{m}_{2}}{{l}_{1}}^{2}{{l}_{2}}^{2}({{l}_{1}}^{2}-{{l}_{2}}^{2})sin2{{\theta }_{1}}}{6{{({{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}})}^{2}}}\cdot {{{\dot{\theta }}}_{1}}^{2}+ \\ & \frac{({{m}_{1}}+{{m}_{3}}){{l}_{1}}^{4}\cdot (\frac{1}{2}{{l}_{2}}^{2}sin4{{\theta }_{1}}+2{{l}_{1}}^{2}si{{n}^{5}}{{\theta }_{1}}cos{{\theta }_{1}})}{2{{({{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}})}^{2}}}\cdot {{{\dot{\theta }}}_{1}}^{2}+{{m}_{3}}{{l}_{1}}^{2}sin{{\theta }_{1}}cos{{\theta }_{1}}\cdot {{{\dot{\theta }}}_{1}}^{2}- \\ & \frac{({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{1}}^{2}sin{{\theta }_{1}}cos{{\theta }_{1}}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}sin{{\theta }_{1}}}-(\frac{1}{2}{{m}_{1}}+{{m}_{3}})g{{l}_{1}}sin{{\theta }_{1}} \\ \end{align}$ |
同樣,如果選θ2為廣義坐標,則可求得該系統的Lagrange函數L2為
| $\begin{align} & {{L}_{2}}=T-V=\frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{2}}^{3}si{{n}^{2}}{{\theta }_{2}}cos{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\dot{\theta }}}^{2}}_{2}+ \\ & (\frac{1}{6}{{m}_{1}}{{l}_{1}}^{2}+12{{m}_{3}}{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})\frac{{{l}_{2}}^{2}co{{s}^{2}}{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\dot{\theta }}}^{2}}_{2}+ \\ & [\frac{1}{2}({{m}_{1}}+{{m}_{3}})si{{n}^{2}}{{\theta }_{2}}+16{{m}_{2}}]{{l}_{2}}^{2}\cdot {{{\dot{\theta }}}^{2}}_{2}- \\ & (\frac{1}{2}{{m}_{1}}+{{m}_{3}})g\sqrt{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}-({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{2}}cos{{\theta }_{2}}-\frac{1}{2}{{m}_{3}}g{{l}_{3}} \\ \end{align}$ |
由此可得,膝關節力矩M2為
| $\begin{align} & {{M}_{2}}=\frac{d}{dt}\frac{\partial {{L}_{2}}}{\partial {{{\dot{\theta }}}_{2}}}-\frac{\partial {{L}_{2}}}{\partial {{\theta }_{2}}}=\frac{({{m}_{1}}+2{{m}_{3}}){{l}_{2}}^{3}si{{n}^{2}}{{\theta }_{2}}cos{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\ddot{\theta }}}_{2}}+[({{m}_{1}}+{{m}_{3}})si{{n}^{2}}{{\theta }_{2}}+\frac{1}{3}{{m}_{2}}]{{l}_{2}}^{2}\cdot {{{\ddot{\theta }}}_{2}}+ \\ & \frac{(\frac{1}{3}{{m}_{1}}{{l}_{1}}^{2}+{{m}_{3}}{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}){{l}_{2}}^{2}co{{s}^{2}}{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\ddot{\theta }}}_{2}}+\frac{{{m}_{3}}{{l}_{2}}^{4}\cdot (\frac{1}{2}{{l}_{1}}^{2}sin4{{\theta }_{2}}+2{{l}_{2}}^{2}si{{n}^{5}}{{\theta }_{2}}cos{{\theta }_{2}})}{2{{({{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})}^{2}}}\cdot {{{\dot{\theta }}}_{2}}^{2}+ \\ & {{m}_{1}}{{l}_{1}}^{2}{{l}_{2}}^{2}({{l}_{2}}^{2}-{{l}_{1}}^{2})sin2{{\theta }_{2}}6{{({{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})}^{2}}\cdot \theta {{\cdot }^{2}}_{2}+ \\ & ({{m}_{1}}+{{m}_{3}}){{l}_{2}}^{2}sin{{\theta }_{2}}cos{{\theta }_{2}}\cdot {{{\dot{\theta }}}^{2}}_{2}+ \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{2}}^{3}\cdot [{{l}_{1}}^{2}sin{{\theta }_{2}}(1+3cos2{{\theta }_{2}})-2{{l}_{2}}^{2}si{{n}^{3}}{{\theta }_{2}}cos2{{\theta }_{2}}]}{2{{({{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})}^{\frac{3}{2}}}}\cdot {{{\dot{\theta }}}^{2}}_{2}- \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}})g{{l}_{2}}^{2}sin{{\theta }_{2}}cos{{\theta }_{2}}}{\sqrt{{{l}_{1}}^{2}-{{l}_{2}}^{2}sin{{\theta }_{2}}}}-\frac{({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{1}}^{2}sin{{\theta }_{1}}cos{{\theta }_{1}}}{\sqrt{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}}- \\ & (\frac{1}{2}{{m}_{1}}+{{m}_{3}})g{{l}_{1}}sin{{\theta }_{1}}-({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{2}}sin{{\theta }_{2}} \\ \end{align}$ |
2 Matlab數學模型仿真
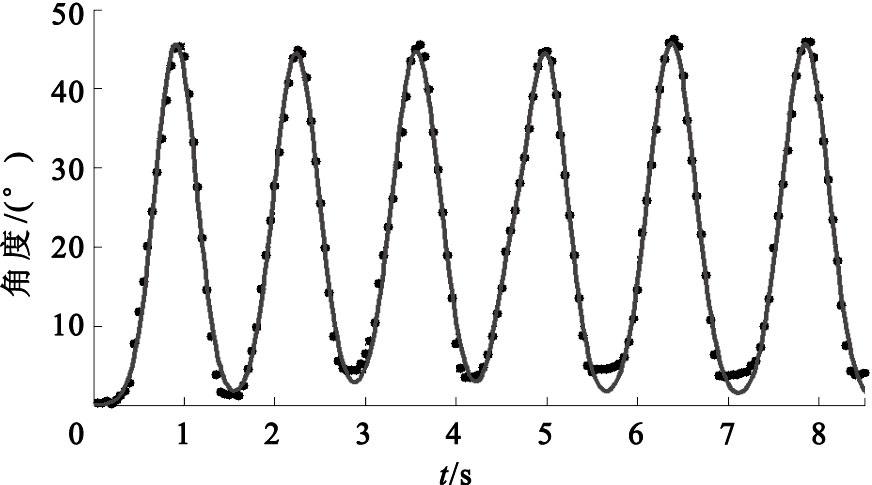
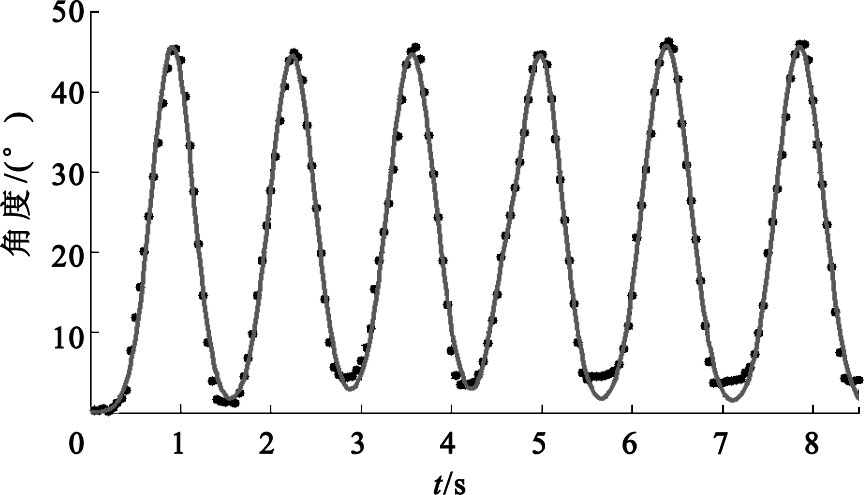
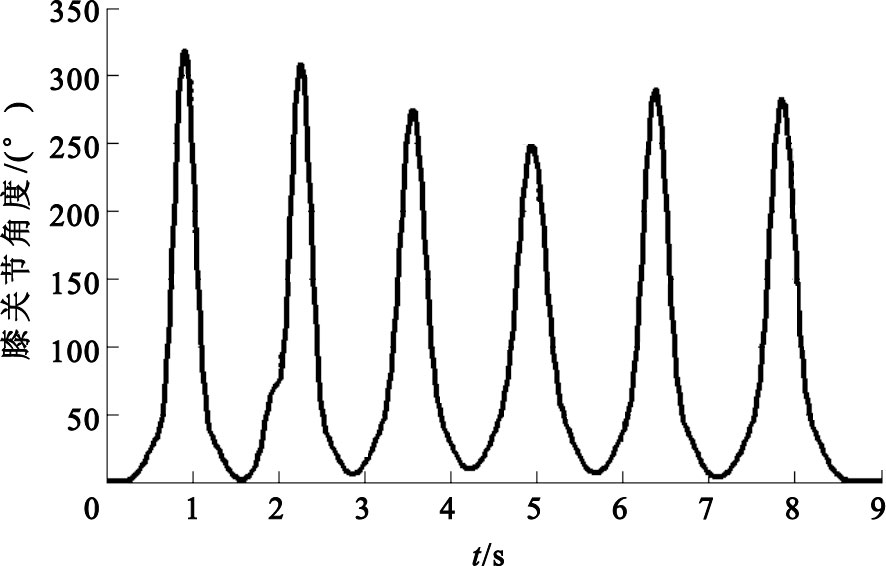
利用膝關節角度傳感器測得受試者在8.5 s內下蹲站起過程中膝關節角度變化數據,其中采樣周期為50 ms,根據下蹲站起數學坐標系,利用三角形的性質可以分別求得大腿和小腿與縱軸的夾角θ1和θ2,將所得的角度數據在Matlab中利用Gaussian 七階曲線擬合的結果如圖 2和圖 3所示(曲線中的黑點即代表間隔為50 ms的θ1和θ2的角度值)。
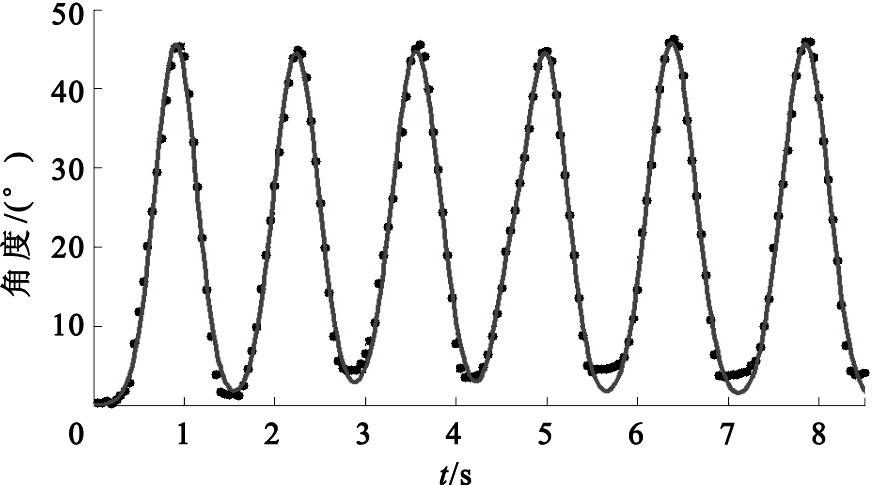 圖2
角度變化曲線
Figure2.
Changing curve of angle
圖2
角度變化曲線
Figure2.
Changing curve of angle
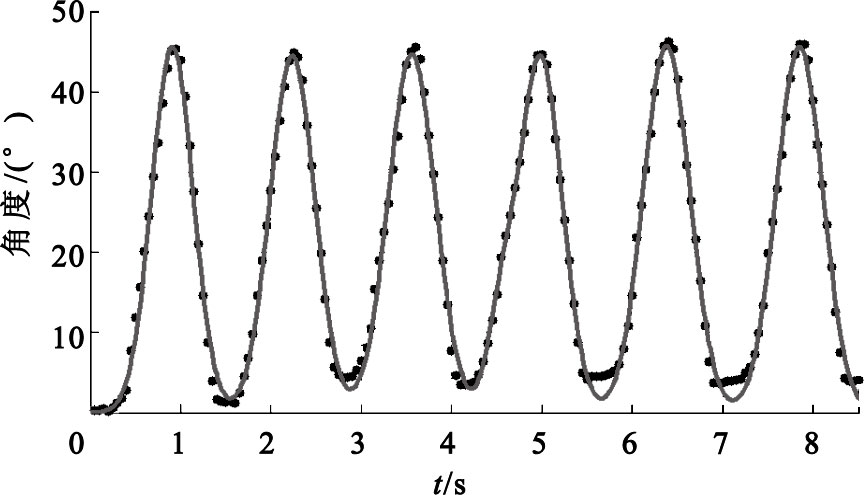 圖3
角度變化曲線
Figure3.
Changing curve of angle
圖3
角度變化曲線
Figure3.
Changing curve of angle
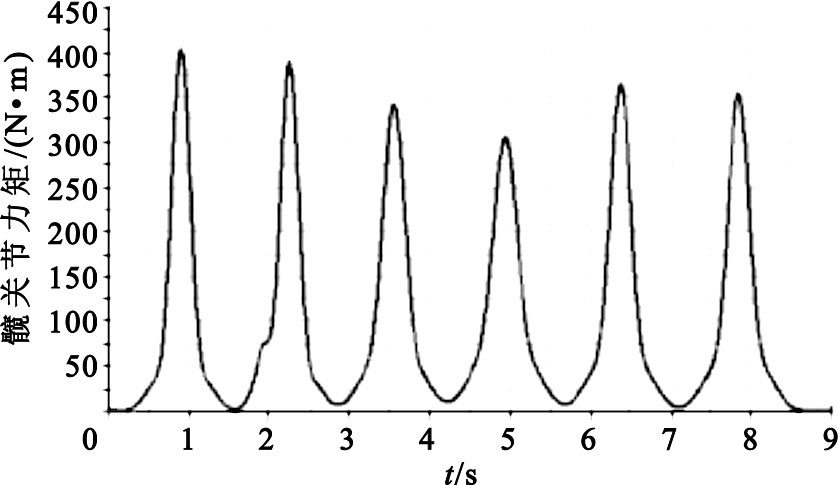
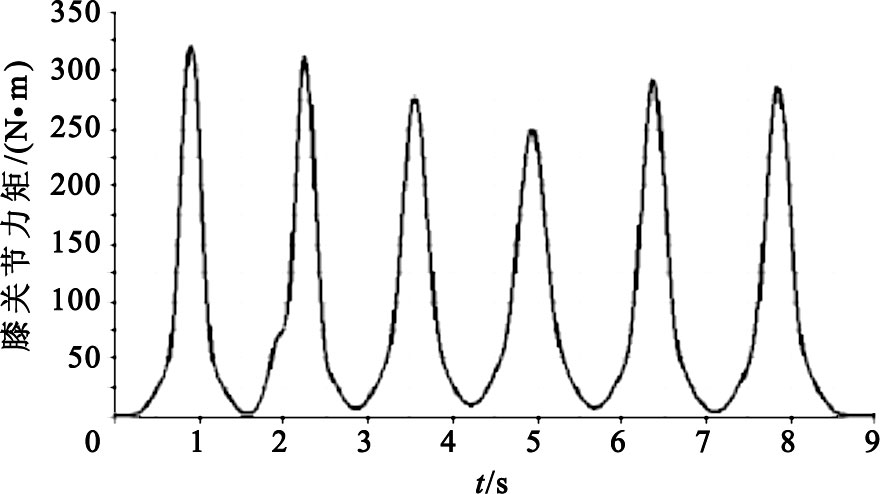
將Gaussian擬合所得的關于θ1和θ2的連續表達式代入髖關節和膝關節力矩表達式M1和M2中,參照如表 1所示的人體各段參數表[10],分別設置人體大腿、小腿和軀干的質量與長度(本文以男性為例),利用Matlab即可求得如圖 4和圖 5所示的髖關節和膝關節力矩變化曲線。
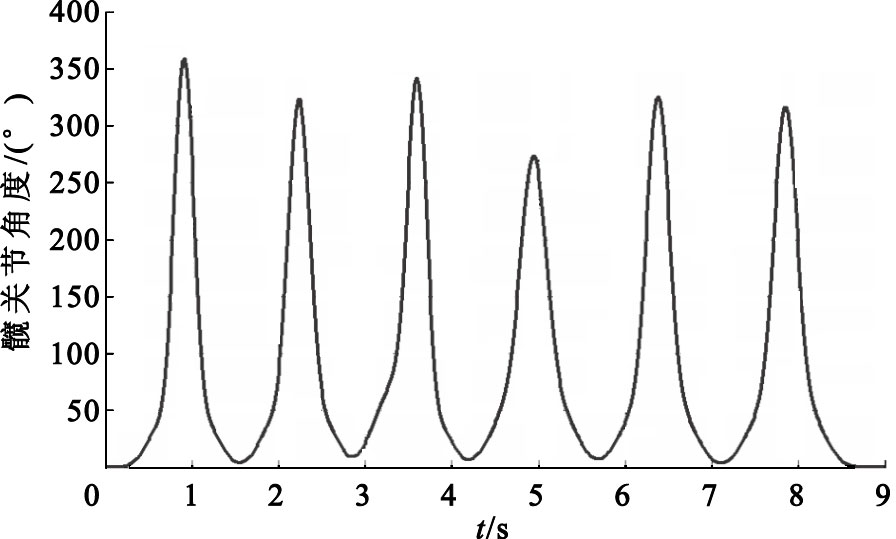 圖4
髖關節力矩變化曲線圖
Figure4.
Changing curve of hip joint torque
圖4
髖關節力矩變化曲線圖
Figure4.
Changing curve of hip joint torque
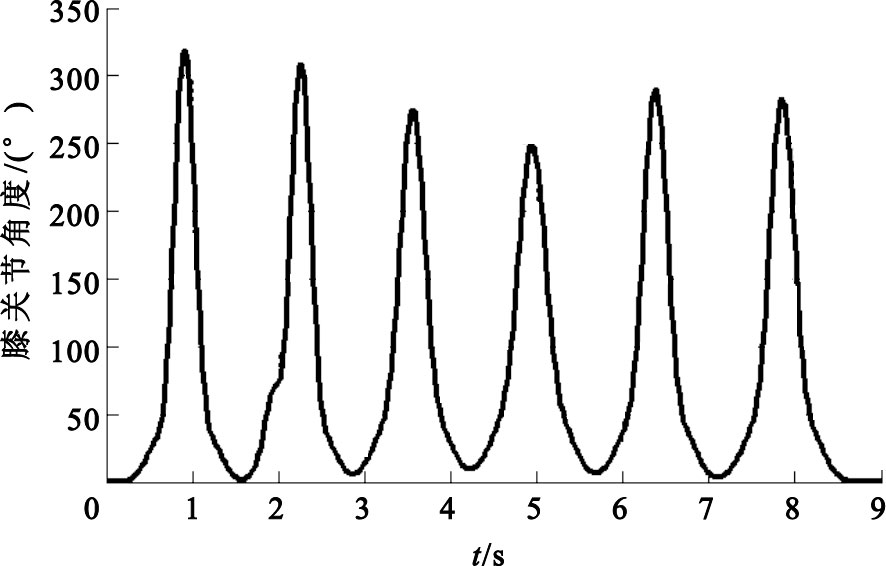 圖5
膝關節力矩變化曲線圖
Figure5.
Changing curve of knee joint torque
圖5
膝關節力矩變化曲線圖
Figure5.
Changing curve of knee joint torque
3 ADAMS下蹲站起建模與仿真
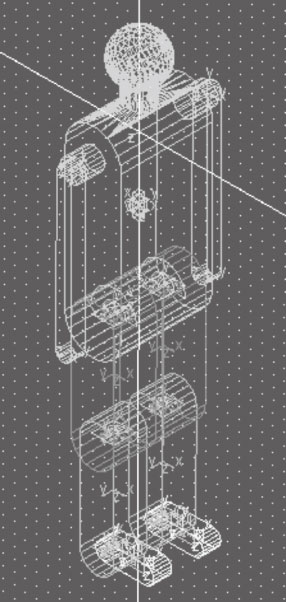
在ADAMS中建立如圖 6所示的人體幾何模型,下蹲站起過程中不考慮上肢的運動,故將頭、頸、軀干和上肢部分連接為一個整體,均屬于軀干部分,由于忽略了軀干在矢狀面內的小幅度旋轉,故只在軀干部分添加沿豎直方向的平動副。在髖關節、膝關節和踝關節地方分別添加旋轉副,由于下蹲站起過程中腳基本處于靜止狀態,故在腳與大地之間添加了固定副。
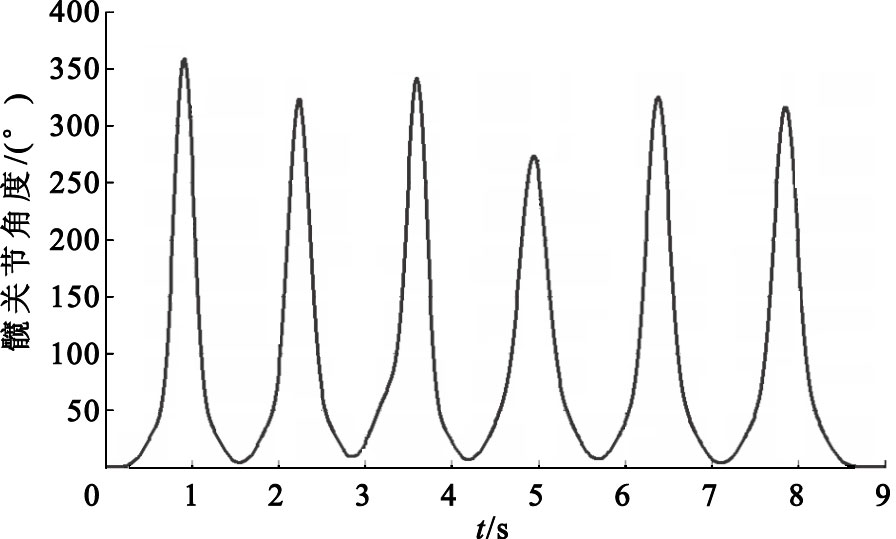
建立幾何模型時,各部分的長度和質量完全按照表 1中的人體各段參數來設置,在添加好各種約束之后,于髖關節或膝關節位置添加運動,運動函數按照Gaussian擬合結果來添加,設置仿真時間為9 s,仿真步長為0.05,最后可以得到如圖 7和圖 8所示的髖關節和膝關節力矩變化曲線。
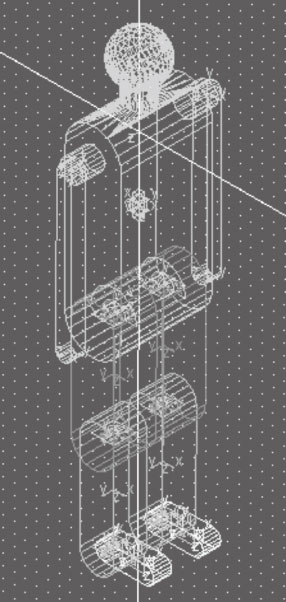 圖6
ADAMS人體幾何模型
Figure6.
Geometric model of human body in ADMAS
圖6
ADAMS人體幾何模型
Figure6.
Geometric model of human body in ADMAS
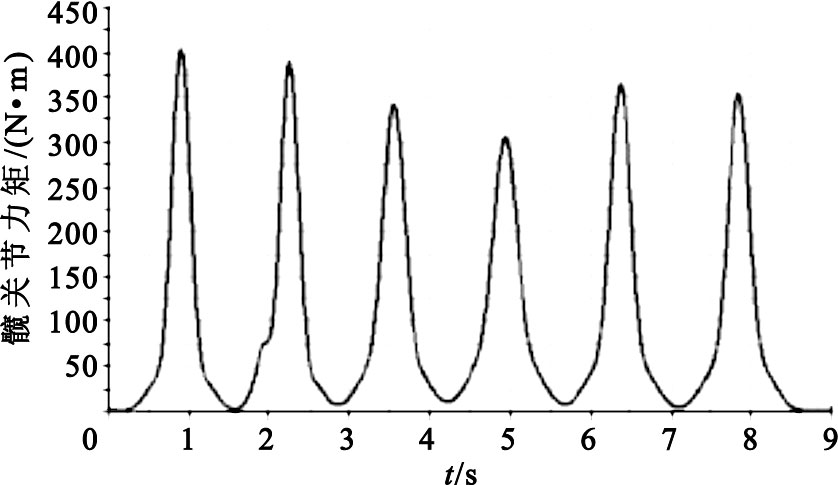 圖7
髖關節力矩變化曲線
Figure7.
Changing curve of hip joint torque
圖7
髖關節力矩變化曲線
Figure7.
Changing curve of hip joint torque
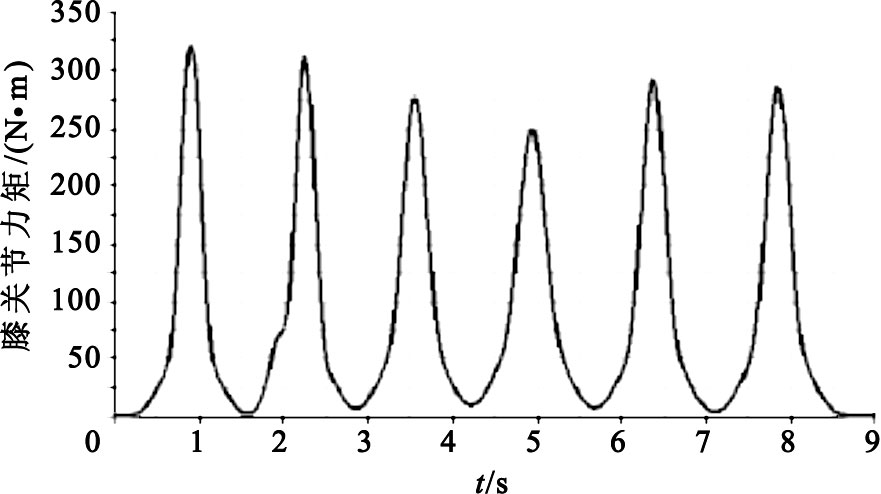 圖8
膝關節力矩變化曲線
Figure8.
Changing curve of knee joint torque
圖8
膝關節力矩變化曲線
Figure8.
Changing curve of knee joint torque
4 結果分析
分別從圖 4、圖 7和圖 5、圖 8的曲線中每隔50 ms采樣得到一個力矩數據,將所得數據導入Matlab中,利用corrcoef函數即可得到經Lagrange數學模型和ADAMS所求得的髖關節力矩的相關系數r1和膝關節力矩相關系數r2分別為
| ${r_1} = \left[ \matrix{ 1.00000.9927 \hfill \cr 0.99271.0000 \hfill \cr} \right]{r_2} = \left[ \matrix{ 1.00001.0000 \hfill \cr 1.00001.0000 \hfill \cr} \right]$ |
可以看出二者的相關度很高,通過觀察也可以發現圖 4、圖 7和圖 5、圖 8的曲線基本吻合,即上述Lagrange數學模型計算所得到的膝關節和髖關節力矩與動力學仿真軟件ADAMS中仿真得到的結果基本一致,說明所建立的拉格朗日數學模型是合理的。分析髖關節和膝關節力矩變化曲線,并結合圖 2和圖 3所示的角度變化曲線可以發現,人在蹲下站立過程中,隨著下蹲幅度的增大,髖關節和膝關節承受的力矩也逐漸增大,在直立過程階段,力矩則隨之減小。因此,對于那些髖關節或膝關節受損的患者來說,應該盡量減少大幅度或快速的下蹲站起動作,以免發生意外。
5 結論
人體是一個復雜度較高的多體系統,除了骨骼系統之外,還有諸如肌肉和韌帶等組織,并且人體的運動要受神經系統的控制,因此要完全真實地模擬人體的運動還需進一步的研究。文中忽略這些因素的影響,將人體簡化為7剛體模型,利用分析力學中的經典Lagrange方法對人體下蹲站起過程做了動力學建模,將下蹲站起過程中大腿和小腿與豎直方向的夾角數據在Matlab中做Gaussian七階曲線擬合,得到角度隨時間變化的連續表達式,并利用Matlab計算得到下蹲站起過程中髖關節和膝關節力矩變化曲線。然后根據人體下蹲站起運動特點,在ADAMS中建立人體下蹲站起幾何模型,通過仿真得到的髖關節和膝關節力矩變化曲線與在Matlab中得到的曲線相吻合,從而驗證了Lagrange數學模型的有效性,為進一步研究下蹲站起康復訓練器械提供了良好的理論參考依據。
引言
腦卒中是中老年人常見病、多發病,發病率、致殘率高,據統計中國每年發生腦中風的患者達200萬,發病率高達120/10萬,致殘率高達75%,而每年中風患者死亡約120萬[1]。大多數腦卒中患者平衡功能嚴重下降,完成下蹲站起的動作相當困難,傳統的藥物治療很難對腦卒中患者產生理想的治療效果,患者還需借助一定的康復訓練器械對其蹲下站起和平衡能力進行長期的康復訓練,而設計一種適合于腦卒中患者的康復訓練器械,首先要對人體下蹲站起過程做準確的動力學建模和仿真。
過去十多年間,很多學者針對人體不同的運動或動作建立相應的多剛體模型,對人體動力學模型的建立做了不少有益的工作。Blajera等[2]為了研究雜技演員在蹦床上翻筋斗的動作過程,建立了一個9自由度10剛體人體簡化模型。Anderson等[3]在研究人垂直起跳達到最大高度過程中的肌肉協調性時,把人體簡化為10段、54塊肌肉的23自由度模型,并在此模型的基礎之上計算了人在行走過程中行走距離與能量消耗間的關系。本文是在Hanavan[4]所提出的15剛體數學模型基礎上,忽略上肢和頭部運動,將人體簡化為7剛體模型,利用Lagrange方法[5-7]對人體蹲下站立過程進行動力學建模,并使用Matlab對該數學模型進行仿真,通過與機械系統動力學自動分析(automatic dynamic analysis of mechanical systems,ADAMS)仿真[8-9]結果的比較,驗證了Lagrange數學模型的合理性。
1 下蹲站起過程動力學分析
著名的Hanavan模型是將人體劃分成15個剛體段,各段之間用球鉸連接。由于本文研究的是下蹲站起過程中的動力學模型,故不考慮上肢和頭部的運動,將人體上軀干部分和下軀干部分合并為一個剛體,從而將人體簡化為如圖 1所示的7剛體簡化模型,由于人體沿矢狀面是對稱的,只需分析人體左側或右側部分的運動情況,故本研究著重考慮矢狀面內4剛體模型,各部分分別等效為一個桿,建立4連桿狀簡化模型,其中頭頸、軀干和上肢等效為一個桿,大腿、小腿和腳分別作為一個桿,即可建立下蹲站起數學坐標系,該系統只有一個自由度。
 圖1
下蹲站起模型簡化
Figure1.
Simplification of squatting-standing model
圖1
下蹲站起模型簡化
Figure1.
Simplification of squatting-standing model
在下蹲站起數學坐標系中,AC代表軀干部分,AB代表大腿,OB代表小腿,大腿、小腿和軀干的長度分別為l1、l2和l3,質量分別為m1、m2和m3(將桿件的質心簡化為桿件中心位置),大腿和小腿與豎直方向的夾角分別為θ1和θ2。
選θ1為廣義坐標,運用Lagrange方法建立該系統的數學模型,根據下蹲站起數學坐標系可得大腿、小腿和軀干的質心坐標分別為
| $\eqalign{ & \left[ \matrix{ {x_1} \hfill \cr {y_1} \hfill \cr} \right] = \left| \matrix{ {{{l_1}} \over 2}sin{\theta _1} \hfill \cr {{{l_1}} \over 2}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} \hfill \cr} \right|;{\rm{ }} \cr & \left[ \matrix{ {x_2} \hfill \cr {y_2} \hfill \cr} \right] = \left| \matrix{ {{{l_2}} \over 2}sin{\theta _2} \hfill \cr {{\sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} } \over 2}{\rm{ }} \hfill \cr} \right|;{\rm{ }} \cr & \left[ \matrix{ {x_3} \hfill \cr {y_3} \hfill \cr} \right] = \left| \matrix{ 0 \hfill \cr {l_1}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} + {{{l_3}} \over 2} \hfill \cr} \right|. \cr} $ |
系統的總動能T為大腿、小腿和軀干三桿件動能T1、T2、T3之和,總勢能V為三桿件勢能V1、V2、V3之和,其中
| $\eqalign{ & \left| \matrix{ {T_1} \hfill \cr {T_2} \hfill \cr {T_3} \hfill \cr} \right| = \left| \matrix{ {1 \over 2}{m_1}{v_1}^2 + {1 \over 2}{I_1}{{\dot \theta }_1}^2 \hfill \cr {1 \over 2}{m_2}{v_2}^2 + {1 \over 2}{I_2} \cdot {{l_1^2\mathop {\cos {\theta _1}}\limits^2 {\mkern 1mu} } \over {l_2^2 - l_1^2\mathop {\sin {\theta _1}}\limits^2 {\mkern 1mu} }} \cdot {{\dot \theta }_1}^2 \hfill \cr {1 \over 2}{m_3}{v_3}^2 \hfill \cr} \right| \cr & \left| \matrix{ {V_1} \hfill \cr {V_2} \hfill \cr {V_3} \hfill \cr} \right| = \left| \matrix{ {m_1}g({{{l_1}} \over 2}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} ) \hfill \cr {{{m_2}g{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} \over 2}{\rm{ }} \hfill \cr {m_3}g({l_1}cos{\theta _1} + \sqrt {{l_2}^2 - {l_1}^2si{n^2}{\theta _1}} + {{{l_3}} \over 2}) \hfill \cr} \right| \cr} $ |
其中v1、v2、v3分別為大腿、小腿和軀干的質心速度,g為重力加速度,I1、I2分別為大腿、小腿相對質心的轉動慣量(I1=m1l12/12,I2=m2l22/12)。
因此,拉格朗日函數L1可表示為
| $\begin{align} & {{L}_{1}}=T-V={{T}_{1}}+{{T}_{2}}+{{T}_{3}}-{{V}_{1}}-{{V}_{2}}-{{V}_{3}}= \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{1}}^{3}si{{n}^{2}}{{\theta }_{1}}cos{{\theta }_{1}}\cdot {{{\dot{\theta }}}_{1}}^{2}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}+ \\ & [\frac{1}{2}({{m}_{1}}+{{m}_{3}}){{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}+\frac{1}{6}{{m}_{2}}{{l}_{2}}^{2}]\cdot \frac{{{l}_{1}}^{2}co{{s}^{2}}{{\theta }_{1}}\cdot \dot{\theta }{{\cdot }_{1}}^{2}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}+ \\ & (\frac{1}{6}{{m}_{1}}+\frac{1}{2}{{m}_{3}}si{{n}^{2}}{{\theta }_{1}}){{l}_{1}}^{2}{{{\dot{\theta }}}_{1}}^{2}-\frac{1}{2}{{m}_{3}}g{{l}_{3}}- \\ & (12{{m}_{1}}+{{m}_{3}})g{{l}_{1}}cos{{\theta }_{1}}-({{m}_{1}}+12{{m}_{2}}+{{m}_{3}})g \\ & \sqrt{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}} \\ \end{align}$ |
由此可得,髖關節力矩M1為
| $\begin{align} & {{M}_{1}}=\frac{d}{dt}\text{ }\frac{\partial {{L}_{1}}}{\partial {{{\dot{\theta }}}_{1}}}-\frac{\partial {{L}_{1}}}{\partial {{{\dot{\theta }}}_{1}}}~=[(\frac{1}{3}{{m}_{1}}+{{m}_{3}}si{{n}^{2}}{{\theta }_{1}}){{l}_{1}}^{2}+ \\ & \frac{({{m}_{1}}+2{{m}_{3}}){{l}_{1}}^{3}si{{n}^{2}}{{\theta }_{1}}cos{{\theta }_{1}}}{\sqrt{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}}]\cdot {{{\ddot{\theta }}}_{1}}+ \\ & \frac{[({{m}_{1}}+{{m}_{3}}){{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}+13{{m}_{2}}{{l}_{2}}^{2}]{{l}_{1}}^{2}co{{s}^{2}}{{\theta }_{1}}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}\cdot {{{\ddot{\theta }}}_{1}}+ \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{1}}^{3}\cdot [{{l}_{2}}^{2}sin{{\theta }_{1}}(1+3cos2{{\theta }_{1}})-2{{l}_{1}}^{2}si{{n}^{3}}{{\theta }_{1}}cos2{{\theta }_{1}}]}{2{{({{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}})}^{\frac{3}{2}}}}\cdot {{{\dot{\theta }}}_{1}}^{2}+ \\ & \frac{{{m}_{2}}{{l}_{1}}^{2}{{l}_{2}}^{2}({{l}_{1}}^{2}-{{l}_{2}}^{2})sin2{{\theta }_{1}}}{6{{({{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}})}^{2}}}\cdot {{{\dot{\theta }}}_{1}}^{2}+ \\ & \frac{({{m}_{1}}+{{m}_{3}}){{l}_{1}}^{4}\cdot (\frac{1}{2}{{l}_{2}}^{2}sin4{{\theta }_{1}}+2{{l}_{1}}^{2}si{{n}^{5}}{{\theta }_{1}}cos{{\theta }_{1}})}{2{{({{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}})}^{2}}}\cdot {{{\dot{\theta }}}_{1}}^{2}+{{m}_{3}}{{l}_{1}}^{2}sin{{\theta }_{1}}cos{{\theta }_{1}}\cdot {{{\dot{\theta }}}_{1}}^{2}- \\ & \frac{({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{1}}^{2}sin{{\theta }_{1}}cos{{\theta }_{1}}}{{{l}_{2}}^{2}-{{l}_{1}}^{2}sin{{\theta }_{1}}}-(\frac{1}{2}{{m}_{1}}+{{m}_{3}})g{{l}_{1}}sin{{\theta }_{1}} \\ \end{align}$ |
同樣,如果選θ2為廣義坐標,則可求得該系統的Lagrange函數L2為
| $\begin{align} & {{L}_{2}}=T-V=\frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{2}}^{3}si{{n}^{2}}{{\theta }_{2}}cos{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\dot{\theta }}}^{2}}_{2}+ \\ & (\frac{1}{6}{{m}_{1}}{{l}_{1}}^{2}+12{{m}_{3}}{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})\frac{{{l}_{2}}^{2}co{{s}^{2}}{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\dot{\theta }}}^{2}}_{2}+ \\ & [\frac{1}{2}({{m}_{1}}+{{m}_{3}})si{{n}^{2}}{{\theta }_{2}}+16{{m}_{2}}]{{l}_{2}}^{2}\cdot {{{\dot{\theta }}}^{2}}_{2}- \\ & (\frac{1}{2}{{m}_{1}}+{{m}_{3}})g\sqrt{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}-({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{2}}cos{{\theta }_{2}}-\frac{1}{2}{{m}_{3}}g{{l}_{3}} \\ \end{align}$ |
由此可得,膝關節力矩M2為
| $\begin{align} & {{M}_{2}}=\frac{d}{dt}\frac{\partial {{L}_{2}}}{\partial {{{\dot{\theta }}}_{2}}}-\frac{\partial {{L}_{2}}}{\partial {{\theta }_{2}}}=\frac{({{m}_{1}}+2{{m}_{3}}){{l}_{2}}^{3}si{{n}^{2}}{{\theta }_{2}}cos{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\ddot{\theta }}}_{2}}+[({{m}_{1}}+{{m}_{3}})si{{n}^{2}}{{\theta }_{2}}+\frac{1}{3}{{m}_{2}}]{{l}_{2}}^{2}\cdot {{{\ddot{\theta }}}_{2}}+ \\ & \frac{(\frac{1}{3}{{m}_{1}}{{l}_{1}}^{2}+{{m}_{3}}{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}){{l}_{2}}^{2}co{{s}^{2}}{{\theta }_{2}}}{{{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}}}\cdot {{{\ddot{\theta }}}_{2}}+\frac{{{m}_{3}}{{l}_{2}}^{4}\cdot (\frac{1}{2}{{l}_{1}}^{2}sin4{{\theta }_{2}}+2{{l}_{2}}^{2}si{{n}^{5}}{{\theta }_{2}}cos{{\theta }_{2}})}{2{{({{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})}^{2}}}\cdot {{{\dot{\theta }}}_{2}}^{2}+ \\ & {{m}_{1}}{{l}_{1}}^{2}{{l}_{2}}^{2}({{l}_{2}}^{2}-{{l}_{1}}^{2})sin2{{\theta }_{2}}6{{({{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})}^{2}}\cdot \theta {{\cdot }^{2}}_{2}+ \\ & ({{m}_{1}}+{{m}_{3}}){{l}_{2}}^{2}sin{{\theta }_{2}}cos{{\theta }_{2}}\cdot {{{\dot{\theta }}}^{2}}_{2}+ \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}}){{l}_{2}}^{3}\cdot [{{l}_{1}}^{2}sin{{\theta }_{2}}(1+3cos2{{\theta }_{2}})-2{{l}_{2}}^{2}si{{n}^{3}}{{\theta }_{2}}cos2{{\theta }_{2}}]}{2{{({{l}_{1}}^{2}-{{l}_{2}}^{2}si{{n}^{2}}{{\theta }_{2}})}^{\frac{3}{2}}}}\cdot {{{\dot{\theta }}}^{2}}_{2}- \\ & \frac{(\frac{1}{2}{{m}_{1}}+{{m}_{3}})g{{l}_{2}}^{2}sin{{\theta }_{2}}cos{{\theta }_{2}}}{\sqrt{{{l}_{1}}^{2}-{{l}_{2}}^{2}sin{{\theta }_{2}}}}-\frac{({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{1}}^{2}sin{{\theta }_{1}}cos{{\theta }_{1}}}{\sqrt{{{l}_{2}}^{2}-{{l}_{1}}^{2}si{{n}^{2}}{{\theta }_{1}}}}- \\ & (\frac{1}{2}{{m}_{1}}+{{m}_{3}})g{{l}_{1}}sin{{\theta }_{1}}-({{m}_{1}}+\frac{1}{2}{{m}_{2}}+{{m}_{3}})g{{l}_{2}}sin{{\theta }_{2}} \\ \end{align}$ |
2 Matlab數學模型仿真
利用膝關節角度傳感器測得受試者在8.5 s內下蹲站起過程中膝關節角度變化數據,其中采樣周期為50 ms,根據下蹲站起數學坐標系,利用三角形的性質可以分別求得大腿和小腿與縱軸的夾角θ1和θ2,將所得的角度數據在Matlab中利用Gaussian 七階曲線擬合的結果如圖 2和圖 3所示(曲線中的黑點即代表間隔為50 ms的θ1和θ2的角度值)。
 圖2
角度變化曲線
Figure2.
Changing curve of angle
圖2
角度變化曲線
Figure2.
Changing curve of angle
 圖3
角度變化曲線
Figure3.
Changing curve of angle
圖3
角度變化曲線
Figure3.
Changing curve of angle
將Gaussian擬合所得的關于θ1和θ2的連續表達式代入髖關節和膝關節力矩表達式M1和M2中,參照如表 1所示的人體各段參數表[10],分別設置人體大腿、小腿和軀干的質量與長度(本文以男性為例),利用Matlab即可求得如圖 4和圖 5所示的髖關節和膝關節力矩變化曲線。
 圖4
髖關節力矩變化曲線圖
Figure4.
Changing curve of hip joint torque
圖4
髖關節力矩變化曲線圖
Figure4.
Changing curve of hip joint torque
 圖5
膝關節力矩變化曲線圖
Figure5.
Changing curve of knee joint torque
圖5
膝關節力矩變化曲線圖
Figure5.
Changing curve of knee joint torque
3 ADAMS下蹲站起建模與仿真
在ADAMS中建立如圖 6所示的人體幾何模型,下蹲站起過程中不考慮上肢的運動,故將頭、頸、軀干和上肢部分連接為一個整體,均屬于軀干部分,由于忽略了軀干在矢狀面內的小幅度旋轉,故只在軀干部分添加沿豎直方向的平動副。在髖關節、膝關節和踝關節地方分別添加旋轉副,由于下蹲站起過程中腳基本處于靜止狀態,故在腳與大地之間添加了固定副。
建立幾何模型時,各部分的長度和質量完全按照表 1中的人體各段參數來設置,在添加好各種約束之后,于髖關節或膝關節位置添加運動,運動函數按照Gaussian擬合結果來添加,設置仿真時間為9 s,仿真步長為0.05,最后可以得到如圖 7和圖 8所示的髖關節和膝關節力矩變化曲線。
 圖6
ADAMS人體幾何模型
Figure6.
Geometric model of human body in ADMAS
圖6
ADAMS人體幾何模型
Figure6.
Geometric model of human body in ADMAS
 圖7
髖關節力矩變化曲線
Figure7.
Changing curve of hip joint torque
圖7
髖關節力矩變化曲線
Figure7.
Changing curve of hip joint torque
 圖8
膝關節力矩變化曲線
Figure8.
Changing curve of knee joint torque
圖8
膝關節力矩變化曲線
Figure8.
Changing curve of knee joint torque
4 結果分析
分別從圖 4、圖 7和圖 5、圖 8的曲線中每隔50 ms采樣得到一個力矩數據,將所得數據導入Matlab中,利用corrcoef函數即可得到經Lagrange數學模型和ADAMS所求得的髖關節力矩的相關系數r1和膝關節力矩相關系數r2分別為
| ${r_1} = \left[ \matrix{ 1.00000.9927 \hfill \cr 0.99271.0000 \hfill \cr} \right]{r_2} = \left[ \matrix{ 1.00001.0000 \hfill \cr 1.00001.0000 \hfill \cr} \right]$ |
可以看出二者的相關度很高,通過觀察也可以發現圖 4、圖 7和圖 5、圖 8的曲線基本吻合,即上述Lagrange數學模型計算所得到的膝關節和髖關節力矩與動力學仿真軟件ADAMS中仿真得到的結果基本一致,說明所建立的拉格朗日數學模型是合理的。分析髖關節和膝關節力矩變化曲線,并結合圖 2和圖 3所示的角度變化曲線可以發現,人在蹲下站立過程中,隨著下蹲幅度的增大,髖關節和膝關節承受的力矩也逐漸增大,在直立過程階段,力矩則隨之減小。因此,對于那些髖關節或膝關節受損的患者來說,應該盡量減少大幅度或快速的下蹲站起動作,以免發生意外。
5 結論
人體是一個復雜度較高的多體系統,除了骨骼系統之外,還有諸如肌肉和韌帶等組織,并且人體的運動要受神經系統的控制,因此要完全真實地模擬人體的運動還需進一步的研究。文中忽略這些因素的影響,將人體簡化為7剛體模型,利用分析力學中的經典Lagrange方法對人體下蹲站起過程做了動力學建模,將下蹲站起過程中大腿和小腿與豎直方向的夾角數據在Matlab中做Gaussian七階曲線擬合,得到角度隨時間變化的連續表達式,并利用Matlab計算得到下蹲站起過程中髖關節和膝關節力矩變化曲線。然后根據人體下蹲站起運動特點,在ADAMS中建立人體下蹲站起幾何模型,通過仿真得到的髖關節和膝關節力矩變化曲線與在Matlab中得到的曲線相吻合,從而驗證了Lagrange數學模型的有效性,為進一步研究下蹲站起康復訓練器械提供了良好的理論參考依據。