離心血泵葉輪形態是決定其內部流場剪切應力致血液細胞損傷的重要因素之一。對具有不同葉輪形態的離心血泵進行流體動力分析及數值溶血預估有助于提高血泵的綜合性能。本文采用低雷諾數修正SST κ-ω湍流模型,對四種不同葉輪形態的離心血泵內部流場進行計算,包括壓力場、速度場以及剪切應力場分布等;并運用快速溶血預估模型計算各血泵的標準溶血參數值(NIH)。分析結果表明,雖然四種血泵的壓力場分布均符合要求,但對數螺旋線葉輪血泵流道中的渦流和回流得到了明顯改善,高剪切應力區域體積只占總體積的0.004%,NIH為0.008 9,對血液細胞破壞最小。
引用本文: 壽宸, 郭勇君, 蘇磊, 黎永前. 基于快速溶血預估模型的離心血泵葉輪特性數值分析. 生物醫學工程學雜志, 2014, 31(6): 1260-1264. doi: 10.7507/1001-5515.20140239 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
目前,對于心血管疾病的治療方法主要有藥物治療、微創手術、心臟直視手術以及使用人工心臟進行輔助循環甚至代替人體心臟。這其中,利用體外循環技術(cardiopulmonary bypass,CPB)進行的心臟直視手術是心臟外科治療心臟病的主要手段。離心泵是目前在體外循環手術中使用最多的一種血泵。在美國,離心泵的使用非常普遍。資料顯示,休斯頓醫院每兩千多例體外循環灌注中75%采用了離心泵。在歐洲和日本,離心泵與滾壓泵的使用比例相當,在中國這一比例約為1∶3[1]。
離心血泵葉輪旋轉產生的剪切應力是導致血液細胞損傷的重要因素,而采用實驗的方法來測定血泵內部剪切應力分布是非常困難的。因此,計算流體動力學(computational fluid dynamics,CFD)技術被廣泛應用于離心血泵的設計和分析當中。許多關于離心血泵的CFD研究均采用standard κ-ε雙方程湍流模型和標準壁面函數[2-3]。但是,該模型假設流動為完全湍流,并且分子粘性的影響可以忽略不計,這使其更加適合計算高雷諾數流場。而使用該模型計算離心血泵內流場會過高地估計湍流動能的增長速率,從而導致剪切應力的計算結果偏大[4]。因此本文使用適合低雷諾數湍流的SST κ-ω湍流模型。該模型混合了κ-ε模型和κ-ω模型的優勢,在近壁面粘性底層使用κ-ω,而在邊界層外湍流充分發展區域則采用κ-ε,并包含了修正的湍流粘性公式,考慮了湍流剪切應力的影響[5]。
對于數值溶血預估,目前大多數的研究均采用的是Lagrangian顆粒示蹤的方法來進行計算[6-8],然而這種方法很難計算低流速區域的顆粒軌跡,并且對于一些結構相對復雜的流場,這種基于概率的方法很難全面地反映出其溶血性能。基于此,Garon等[9]提出了一種快速溶血預估模型并用于血泵標準溶血參數值的計算。該模型考慮流場整體平均效應,對剪切應力場進行線性場積分,使其能夠更加全面地評估血泵的溶血特性。本文使用低雷諾數修正SST κ-ω湍流模型,對具有四種不同葉輪形態的離心血泵內部流場進行了數值分析,對比了壓力分布、速度矢量分布及剪切應力分布等特性,并運用快速溶血預估模型計算了標準溶血參數值,為改進體外循環離心血泵的葉輪結構提供了參考依據。
1 離心血泵數值模型建立
1.1 三維建模及網格劃分
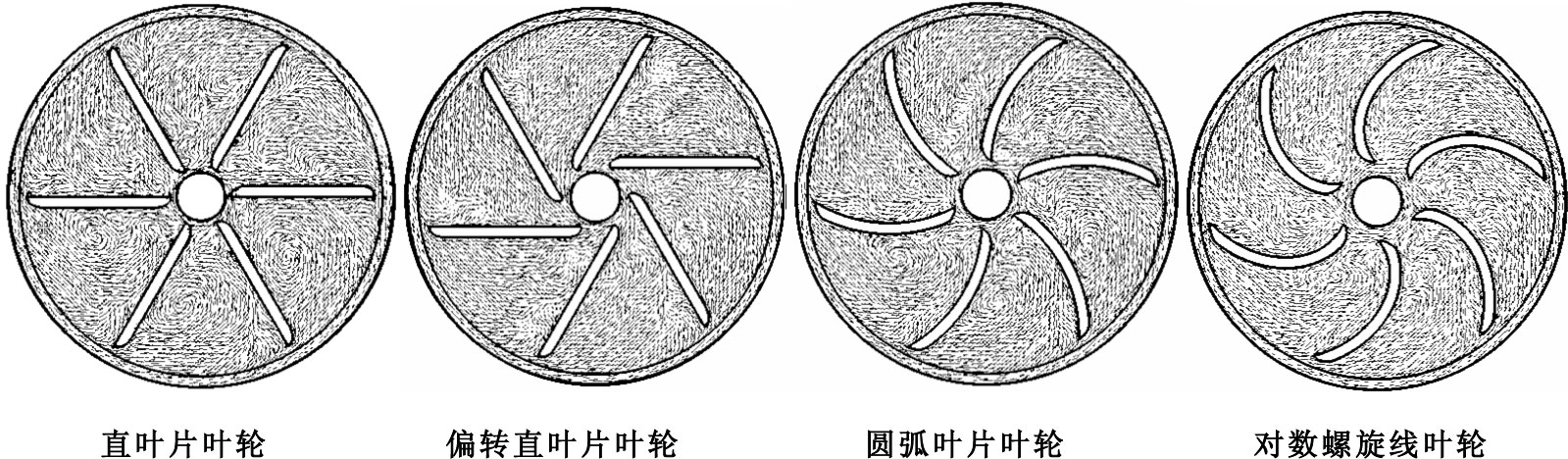
體外循環離心血泵較心室輔助泵(ventricular assist device,VAD)和全人工心臟泵(total artificial heart,TAH)最大的區別在于其尺寸相對偏大,并且能在低轉速下產生較高的壓力。本文中的離心血泵設計工況為葉輪轉速2 000 r/min,流量為5 L/min時能產生200 mm Hg壓力。目前體外循環離心血泵常見的葉輪形式有四種,分別是:直葉片葉輪,如Nikkiso的HPM系列、Medtronic的Affinity CP系列;偏轉直葉片葉輪,如Terumo的Sarns系列;圓弧葉片葉輪,如Sorin的Revolution系列以及對數螺旋線葉輪。葉輪的三維模型如圖 1所示,本文研究的四種葉輪分別為:直葉片葉輪、偏轉直葉片葉輪、葉角為86°的圓弧葉片葉輪、螺旋角為60°且葉角為120°的對數螺旋線葉輪。四種葉輪的內外徑均為14 mm和63 mm。
采用非結構網格進行網格劃分。根據低雷諾數修正的SST κ-ω湍流模型的要求,需要計算第一層網格質心到壁面的距離,并保證其對應的無量綱值y+<1,且近壁面區域至少有10個網格單元,以此來獲得準確的計算結果[5] 。計算區域的血泵網格劃分結果如圖 1所示。網格平均質量為0.85,泵殼壁面和葉輪壁面均為y+<1,符合計算要求。
 圖1
對數螺旋線葉輪血泵三維模型及網格劃分
Figure1.
Three-dimensional model and meshes of centrifugal blood pump with log spiral impeller
圖1
對數螺旋線葉輪血泵三維模型及網格劃分
Figure1.
Three-dimensional model and meshes of centrifugal blood pump with log spiral impeller
1.2 湍流模型及溶血預估模型的建立和計算
1.2.1 離心血泵的雷諾數
離心血泵入口處最大雷諾數為6 000~7 000,大于管內湍流臨界值2 300。而葉輪區域雷諾數表達式為
| $Re=\frac{\rho \mu {{D}_{f}}}{v},$ |
式中μ為葉輪出口圓周速度,Df為特征幾何尺寸,ρ和v分別為輸運液體的密度和運動黏度。經計算,葉輪區域雷諾數為120 000~150 000。由于不是管內湍流,葉輪區域的湍流臨界值在106量級[10] 。因此,低雷諾數修正的SST κ-ω湍流模型更適合于計算離心血泵內部流場。
1.2.2 流體剪切應力計算模型
血液中的剪切應力包括黏性剪切應力和雷諾剪切應力,其張量表達式為
| ${{\tau }_{ij}}=\mu \left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-\rho \overline{u{{\prime }_{i}}u{{\prime }_{j\text{ }}}},$ |
式中最右端為雷諾剪切應力張量,即
| $-\rho \overline{u{{\prime }_{i}}u{{\prime }_{j\text{ }}}}={{\mu }_{t}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-\frac{2}{3}\rho k{{\delta }_{ij}}~,$ |
其中μt為湍流黏度,k為湍流動能,δij為Kronecker算符。
Bludszuweit[11]利用米澤斯屈服準則(mises yield criterion)將剪切應力的張量形式簡化為等效標量形式并將其用于數值溶血預估:
| $\tau ={{\left[ \frac{1}{6}\Sigma {{({{\tau }_{ii}}-{{\tau }_{jj}})}^{2}}+\Sigma {{\tau }_{ij}}^{2} \right]}^{\frac{1}{2}}}$ |
1.2.3 溶血預估模型
Garon等提出的快速溶血預估模型基于雙曲型輸運方程為
| $\frac{\partial }{dt}+V\cdot \nabla {{D}_{l}}=\sigma ~,$ |
式中V為速度矢量,Dl為線性溶血指數,即
| ${{D}_{l}}={{D}^{1/0.785}}$ |
而D則是Giersiepen等[12]根據實驗得出的溶血百分數與剪切應力τ以及暴露時間texp的關系式為
| $D=\frac{\Delta Hb}{Hb}=3.62\times {{10}^{-7}}{{t}_{exp}}^{0.785}{{\tau }^{2.416}}~,$ |
從而源項σ定義為
| $\sigma ={{(3.62\times {{10}^{-7}})}^{1/0.785}}{{\tau }^{2.416/0.785}}~,$ |
在計算獲得一個穩定流場后,考慮流場整體平均溶血特性,可計算
| $\overline{{{D}_{l}}}=\frac{l}{Q}\int\limits_{V}{\sigma dV},$ |
其中Q為流量。最終得到標準溶血參數值(normalized index of hemolysis,NIH),即
| $NIH=Hb\times D(t,\tau )\times 100$ |
1.3 邊界條件設置
血液僅在低剪切速率的條件下表現出非牛頓流體特性,故將血液視為不可壓縮牛頓流體,密度1 050 kg/m3,運動黏度3.5 mPa·s[13] 。使用多重坐標系模型(multiple reference frame,MRF),設定葉輪壁面為旋轉壁面,轉速2 000 r/min,泵殼壁面為靜止壁面。入口為速度入口,出口為靜壓0 Pa,且出口段長度延長至其直徑的三倍,并認為出口邊界處的流動已充分發展,出口區域有一平直段且離回流區已較遠。所有的壁面均定義為無滑移固壁邊界。
2 計算結果與分析
2.1 壓力分布
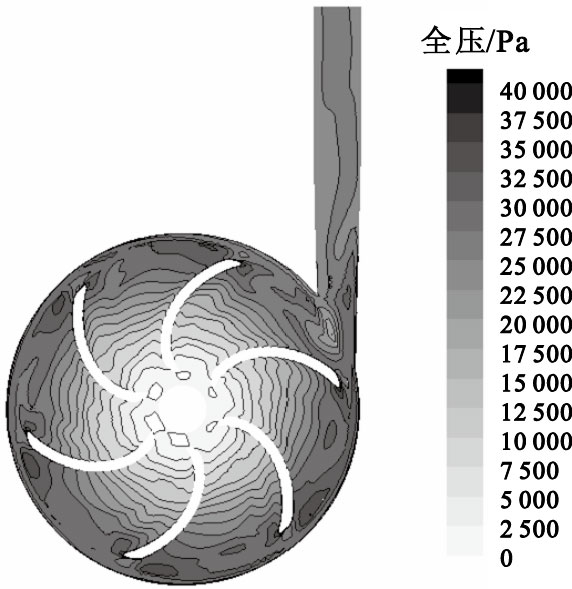
圖 2為對數螺旋線葉輪血泵全壓分布剖面圖(y=6 mm),各血泵壓力分布沒有明顯區別。當血泵運行在設計工況下時,四種葉輪各流道內的壓力分布都較為均勻。在葉輪的帶動下,動能不斷轉換為血液壓力能,從葉輪入口至葉輪出口,壓力逐漸增大且呈現出較好的梯度分布形式。
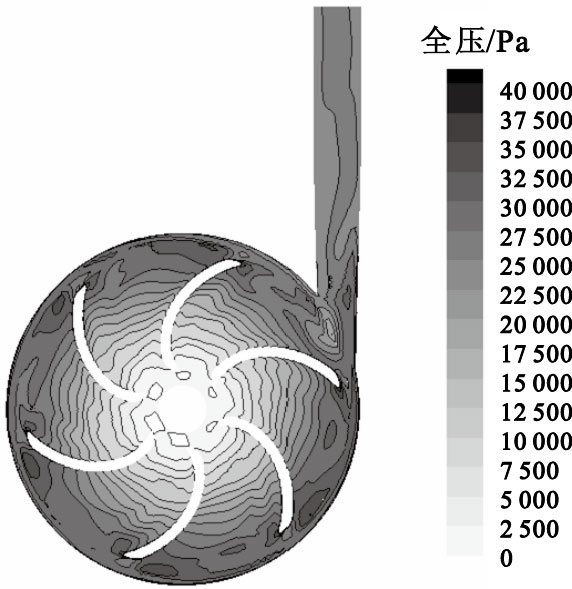 圖2
對數螺旋線葉輪血泵內部流場全壓分布
Figure2.
Contours of total pressure distribution in centrifugal blood pump with log spiral impeller
圖2
對數螺旋線葉輪血泵內部流場全壓分布
Figure2.
Contours of total pressure distribution in centrifugal blood pump with log spiral impeller
2.2 速度矢量分布
圖 3為各血泵在6 mm葉高處的相對速度矢量分布圖。各流道內,入口到出口速度逐漸增大,且吸力面速度大于壓力面速度。其中,直葉片葉輪和圓弧葉片葉輪流道內流動較復雜:大多數流道內的入口處存在部分回流,并在流道后半段出現一個較大規模的渦流,其渦流區域幾乎占整個流道面積的1/2,而過大的渦流區域會導致高剪切應力的產生。因此可以推測,這兩種葉輪對血細胞的破壞較大。偏轉直葉片葉輪和對數螺旋線葉輪各流道內大部分區域的流動相對規則,但均存在部分回流現象,且后半段出現規模較小的渦流。總體來講,后兩種血泵內部流場流動模式均得到了改善。
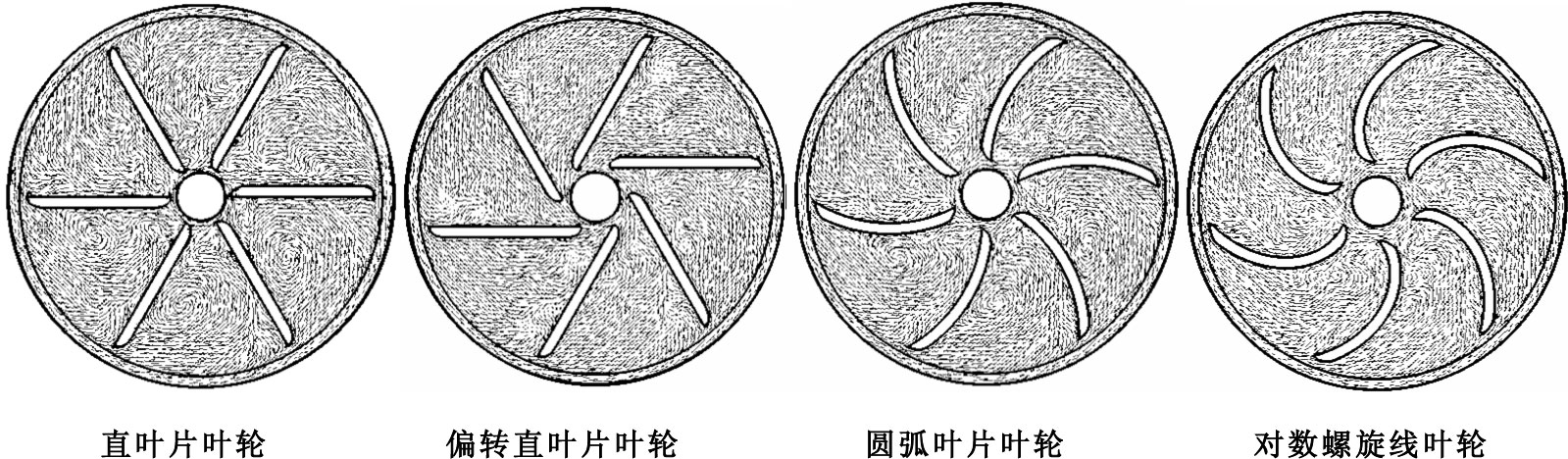 圖3
離心血泵內部流場相對速度矢量分布
Figure3.
Relative velocity vector distribution in centrifugal blood pumps with different profiles of impellers
圖3
離心血泵內部流場相對速度矢量分布
Figure3.
Relative velocity vector distribution in centrifugal blood pumps with different profiles of impellers
2.3 剪切應力分布及溶血預估
引起離心血泵內血液溶血的原因有很多,例如血泵壁面粗糙度、所用材料的生物相容性、機械摩擦產生的熱量以及旋轉流場的形態等,上述各因素的根本原因在于紅細胞在流場中所受的剪切應力對細胞膜的破壞。研究表明,紅細胞在一定剪切應力(約為150~1 000 Pa)作用下開始變形,當剪切應力高于某一臨界數值(約1 000 Pa)或經過一定時間的累積后,細胞膜破裂,血紅蛋白進入血漿,從而產生溶血效應[14]。
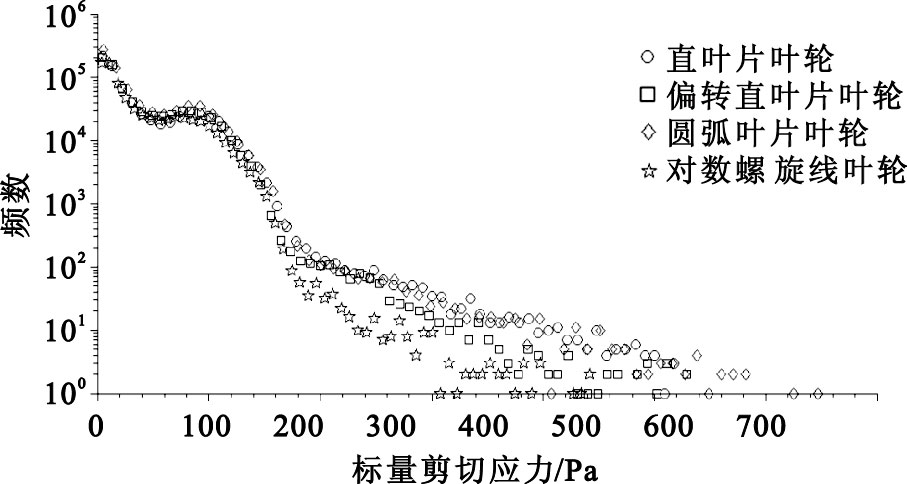
四種血泵內部流場等效標量剪切應力的分布情況如圖 4 所示。血泵內部流場的等效標量剪切應力極值和平均值如表 1所示,其中對數螺旋線葉輪對應的等效標量剪切應力最大值和平均值最小。剪切應力主要分布于葉輪吸力面的出口位置以及環形壓水室的隔舌區域。等效標量剪切應力頻數分布圖如圖 5所示,血泵內流場中等效標量剪切應力值多分布在0~120 Pa之間,所占區域的體積約占總體積的98%;高于500 Pa的區域所占體積則約為總體積的0.035%;而對數螺旋線葉輪血泵高剪切應力區域體積僅占總體積的0.004%。最大剪切應力區域出現在泵殼隔舌部位,這是由于環形壓水室中流速向出口方向迅速增大,與從葉輪流道中流出的血液相互碰撞從而產生較大的徑向力。使用螺旋壓水室可有效降低這一徑向力,但其結構相對復雜,多應用于心室輔助泵和全人工心臟泵中[15]。
 圖4
離心血泵內部流場等效標量剪切應力分布
Figure4.
Scalar shear stress distribution in centrifugal blood pumps with different profiles of impellers
圖4
離心血泵內部流場等效標量剪切應力分布
Figure4.
Scalar shear stress distribution in centrifugal blood pumps with different profiles of impellers
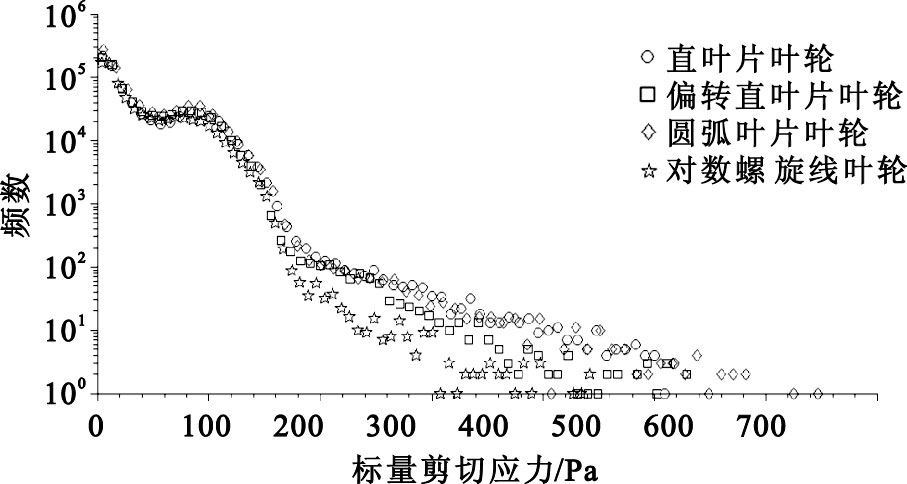 圖5
離心血泵內部流場等效標量剪切應力頻數分布
Figure5.
Mass distribution of scalar shear stress in centrifugal blood pumps with different profiles of impellers
圖5
離心血泵內部流場等效標量剪切應力頻數分布
Figure5.
Mass distribution of scalar shear stress in centrifugal blood pumps with different profiles of impellers
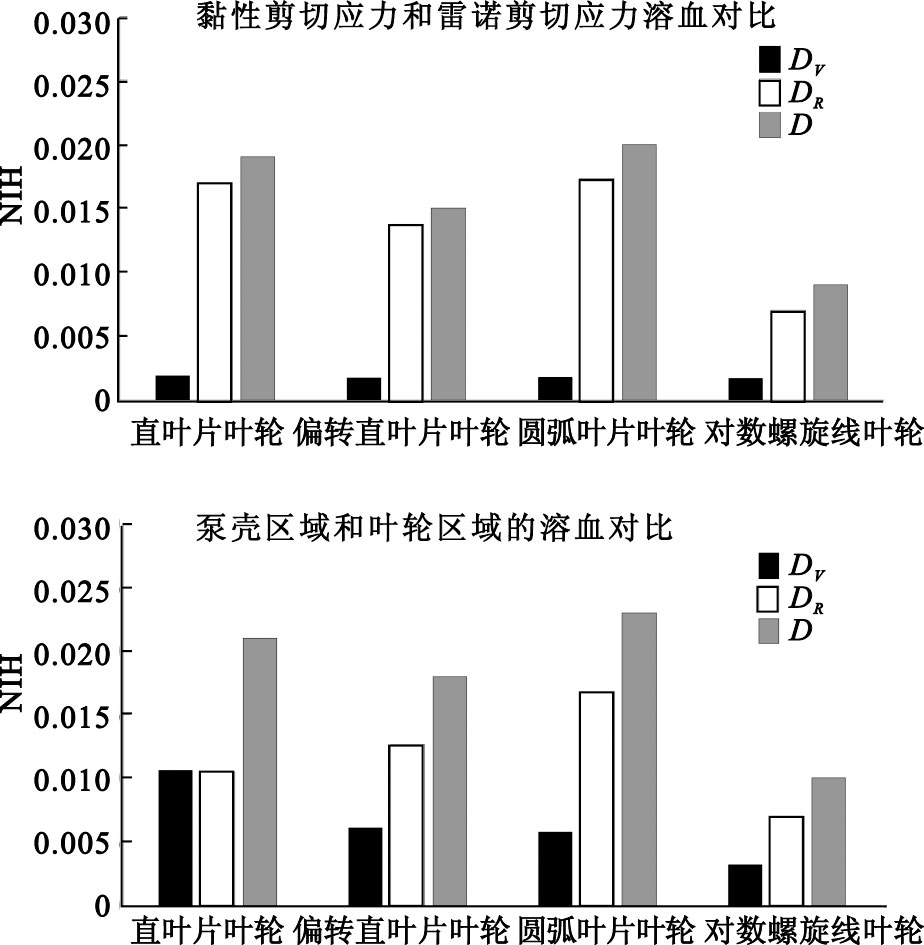
根據Garon等的快速溶血預估模型,在得到穩定的剪切應力場之后,可計算出相應的標準溶血參數值。黏性剪切應力及雷諾剪切應力均能夠破壞血細胞而導致溶血[9]。如圖 6所示,DV和DR分別為黏性剪切應力和雷諾剪切應力對應的標準溶血參數值,D為總標準溶血參數值。可以看出,四種血泵的內流場中黏性剪切應力造成的溶血程度基本相同,
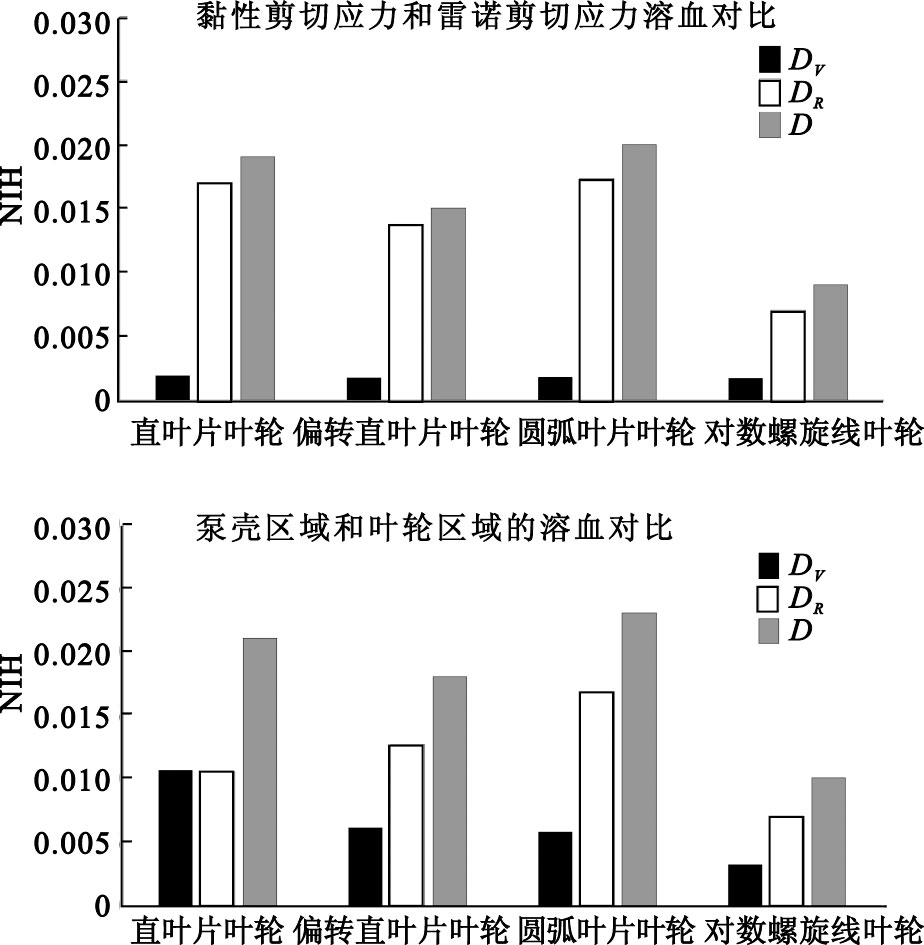 圖6
標準溶血參數的數值預估
Figure6.
Numerical approximation of NIH
圖6
標準溶血參數的數值預估
Figure6.
Numerical approximation of NIH
而雷諾剪切應力的不同是導致標準化溶血參數存在較大差別的主要因素。由于流道中流動模式的改善,對數螺旋線葉輪血泵流場中的高雷諾剪切應力區域最少,使其性能最佳。由于快速溶血預估模型是對剪切應力場進行線性場積分,故該模型能夠對流場中不同區域分別進行溶血預估。圖 6中DI和DC分別對應泵殼區域和葉輪區域的標準溶血參數值。可以看出,葉輪形態和泵殼結構共同決定了離心血泵的溶血性能,其中對數螺旋線葉輪區域的標準溶血參數值最小。
3 討論與結論
本文應用低雷諾數修正SST κ-ω湍流模型以及快速溶血預估模型對具有四種不同葉輪形態的離心血泵綜合特性進行了對比研究。其中,相對速度矢量分布對比表明,對數螺旋線葉輪能明顯改善流道中的流動模式,從而減少流場中高剪切應力的產生。對等效標量剪切應力的分析同樣表明,對數螺旋線葉輪血泵內流場中的高剪切應力區域明顯少于其它三種血泵。
從對標準溶血參數的計算結果來看,Garon等提出的快速溶血預估模型全面地反映了血泵溶血特性。采用該模型對四種血泵的仿真計算結果表明,對數螺旋線葉輪血泵無論是在不同類型剪切應力作用下還是在不同區域的標準溶血參數值都低于其它血泵。相對于Lagrangian顆粒示蹤方法來說,這種預估方法還可以應用于多相流血液模型中,并且若在獲得穩定流場以后直接計算輸運方程(4),便可計算出流場中各點處的標準溶血參數值,使得血泵的改進更具有針對性,這也是溶血預估模型的發展趨勢。
引言
目前,對于心血管疾病的治療方法主要有藥物治療、微創手術、心臟直視手術以及使用人工心臟進行輔助循環甚至代替人體心臟。這其中,利用體外循環技術(cardiopulmonary bypass,CPB)進行的心臟直視手術是心臟外科治療心臟病的主要手段。離心泵是目前在體外循環手術中使用最多的一種血泵。在美國,離心泵的使用非常普遍。資料顯示,休斯頓醫院每兩千多例體外循環灌注中75%采用了離心泵。在歐洲和日本,離心泵與滾壓泵的使用比例相當,在中國這一比例約為1∶3[1]。
離心血泵葉輪旋轉產生的剪切應力是導致血液細胞損傷的重要因素,而采用實驗的方法來測定血泵內部剪切應力分布是非常困難的。因此,計算流體動力學(computational fluid dynamics,CFD)技術被廣泛應用于離心血泵的設計和分析當中。許多關于離心血泵的CFD研究均采用standard κ-ε雙方程湍流模型和標準壁面函數[2-3]。但是,該模型假設流動為完全湍流,并且分子粘性的影響可以忽略不計,這使其更加適合計算高雷諾數流場。而使用該模型計算離心血泵內流場會過高地估計湍流動能的增長速率,從而導致剪切應力的計算結果偏大[4]。因此本文使用適合低雷諾數湍流的SST κ-ω湍流模型。該模型混合了κ-ε模型和κ-ω模型的優勢,在近壁面粘性底層使用κ-ω,而在邊界層外湍流充分發展區域則采用κ-ε,并包含了修正的湍流粘性公式,考慮了湍流剪切應力的影響[5]。
對于數值溶血預估,目前大多數的研究均采用的是Lagrangian顆粒示蹤的方法來進行計算[6-8],然而這種方法很難計算低流速區域的顆粒軌跡,并且對于一些結構相對復雜的流場,這種基于概率的方法很難全面地反映出其溶血性能。基于此,Garon等[9]提出了一種快速溶血預估模型并用于血泵標準溶血參數值的計算。該模型考慮流場整體平均效應,對剪切應力場進行線性場積分,使其能夠更加全面地評估血泵的溶血特性。本文使用低雷諾數修正SST κ-ω湍流模型,對具有四種不同葉輪形態的離心血泵內部流場進行了數值分析,對比了壓力分布、速度矢量分布及剪切應力分布等特性,并運用快速溶血預估模型計算了標準溶血參數值,為改進體外循環離心血泵的葉輪結構提供了參考依據。
1 離心血泵數值模型建立
1.1 三維建模及網格劃分
體外循環離心血泵較心室輔助泵(ventricular assist device,VAD)和全人工心臟泵(total artificial heart,TAH)最大的區別在于其尺寸相對偏大,并且能在低轉速下產生較高的壓力。本文中的離心血泵設計工況為葉輪轉速2 000 r/min,流量為5 L/min時能產生200 mm Hg壓力。目前體外循環離心血泵常見的葉輪形式有四種,分別是:直葉片葉輪,如Nikkiso的HPM系列、Medtronic的Affinity CP系列;偏轉直葉片葉輪,如Terumo的Sarns系列;圓弧葉片葉輪,如Sorin的Revolution系列以及對數螺旋線葉輪。葉輪的三維模型如圖 1所示,本文研究的四種葉輪分別為:直葉片葉輪、偏轉直葉片葉輪、葉角為86°的圓弧葉片葉輪、螺旋角為60°且葉角為120°的對數螺旋線葉輪。四種葉輪的內外徑均為14 mm和63 mm。
采用非結構網格進行網格劃分。根據低雷諾數修正的SST κ-ω湍流模型的要求,需要計算第一層網格質心到壁面的距離,并保證其對應的無量綱值y+<1,且近壁面區域至少有10個網格單元,以此來獲得準確的計算結果[5] 。計算區域的血泵網格劃分結果如圖 1所示。網格平均質量為0.85,泵殼壁面和葉輪壁面均為y+<1,符合計算要求。
 圖1
對數螺旋線葉輪血泵三維模型及網格劃分
Figure1.
Three-dimensional model and meshes of centrifugal blood pump with log spiral impeller
圖1
對數螺旋線葉輪血泵三維模型及網格劃分
Figure1.
Three-dimensional model and meshes of centrifugal blood pump with log spiral impeller
1.2 湍流模型及溶血預估模型的建立和計算
1.2.1 離心血泵的雷諾數
離心血泵入口處最大雷諾數為6 000~7 000,大于管內湍流臨界值2 300。而葉輪區域雷諾數表達式為
| $Re=\frac{\rho \mu {{D}_{f}}}{v},$ |
式中μ為葉輪出口圓周速度,Df為特征幾何尺寸,ρ和v分別為輸運液體的密度和運動黏度。經計算,葉輪區域雷諾數為120 000~150 000。由于不是管內湍流,葉輪區域的湍流臨界值在106量級[10] 。因此,低雷諾數修正的SST κ-ω湍流模型更適合于計算離心血泵內部流場。
1.2.2 流體剪切應力計算模型
血液中的剪切應力包括黏性剪切應力和雷諾剪切應力,其張量表達式為
| ${{\tau }_{ij}}=\mu \left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-\rho \overline{u{{\prime }_{i}}u{{\prime }_{j\text{ }}}},$ |
式中最右端為雷諾剪切應力張量,即
| $-\rho \overline{u{{\prime }_{i}}u{{\prime }_{j\text{ }}}}={{\mu }_{t}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-\frac{2}{3}\rho k{{\delta }_{ij}}~,$ |
其中μt為湍流黏度,k為湍流動能,δij為Kronecker算符。
Bludszuweit[11]利用米澤斯屈服準則(mises yield criterion)將剪切應力的張量形式簡化為等效標量形式并將其用于數值溶血預估:
| $\tau ={{\left[ \frac{1}{6}\Sigma {{({{\tau }_{ii}}-{{\tau }_{jj}})}^{2}}+\Sigma {{\tau }_{ij}}^{2} \right]}^{\frac{1}{2}}}$ |
1.2.3 溶血預估模型
Garon等提出的快速溶血預估模型基于雙曲型輸運方程為
| $\frac{\partial }{dt}+V\cdot \nabla {{D}_{l}}=\sigma ~,$ |
式中V為速度矢量,Dl為線性溶血指數,即
| ${{D}_{l}}={{D}^{1/0.785}}$ |
而D則是Giersiepen等[12]根據實驗得出的溶血百分數與剪切應力τ以及暴露時間texp的關系式為
| $D=\frac{\Delta Hb}{Hb}=3.62\times {{10}^{-7}}{{t}_{exp}}^{0.785}{{\tau }^{2.416}}~,$ |
從而源項σ定義為
| $\sigma ={{(3.62\times {{10}^{-7}})}^{1/0.785}}{{\tau }^{2.416/0.785}}~,$ |
在計算獲得一個穩定流場后,考慮流場整體平均溶血特性,可計算
| $\overline{{{D}_{l}}}=\frac{l}{Q}\int\limits_{V}{\sigma dV},$ |
其中Q為流量。最終得到標準溶血參數值(normalized index of hemolysis,NIH),即
| $NIH=Hb\times D(t,\tau )\times 100$ |
1.3 邊界條件設置
血液僅在低剪切速率的條件下表現出非牛頓流體特性,故將血液視為不可壓縮牛頓流體,密度1 050 kg/m3,運動黏度3.5 mPa·s[13] 。使用多重坐標系模型(multiple reference frame,MRF),設定葉輪壁面為旋轉壁面,轉速2 000 r/min,泵殼壁面為靜止壁面。入口為速度入口,出口為靜壓0 Pa,且出口段長度延長至其直徑的三倍,并認為出口邊界處的流動已充分發展,出口區域有一平直段且離回流區已較遠。所有的壁面均定義為無滑移固壁邊界。
2 計算結果與分析
2.1 壓力分布
圖 2為對數螺旋線葉輪血泵全壓分布剖面圖(y=6 mm),各血泵壓力分布沒有明顯區別。當血泵運行在設計工況下時,四種葉輪各流道內的壓力分布都較為均勻。在葉輪的帶動下,動能不斷轉換為血液壓力能,從葉輪入口至葉輪出口,壓力逐漸增大且呈現出較好的梯度分布形式。
 圖2
對數螺旋線葉輪血泵內部流場全壓分布
Figure2.
Contours of total pressure distribution in centrifugal blood pump with log spiral impeller
圖2
對數螺旋線葉輪血泵內部流場全壓分布
Figure2.
Contours of total pressure distribution in centrifugal blood pump with log spiral impeller
2.2 速度矢量分布
圖 3為各血泵在6 mm葉高處的相對速度矢量分布圖。各流道內,入口到出口速度逐漸增大,且吸力面速度大于壓力面速度。其中,直葉片葉輪和圓弧葉片葉輪流道內流動較復雜:大多數流道內的入口處存在部分回流,并在流道后半段出現一個較大規模的渦流,其渦流區域幾乎占整個流道面積的1/2,而過大的渦流區域會導致高剪切應力的產生。因此可以推測,這兩種葉輪對血細胞的破壞較大。偏轉直葉片葉輪和對數螺旋線葉輪各流道內大部分區域的流動相對規則,但均存在部分回流現象,且后半段出現規模較小的渦流。總體來講,后兩種血泵內部流場流動模式均得到了改善。
 圖3
離心血泵內部流場相對速度矢量分布
Figure3.
Relative velocity vector distribution in centrifugal blood pumps with different profiles of impellers
圖3
離心血泵內部流場相對速度矢量分布
Figure3.
Relative velocity vector distribution in centrifugal blood pumps with different profiles of impellers
2.3 剪切應力分布及溶血預估
引起離心血泵內血液溶血的原因有很多,例如血泵壁面粗糙度、所用材料的生物相容性、機械摩擦產生的熱量以及旋轉流場的形態等,上述各因素的根本原因在于紅細胞在流場中所受的剪切應力對細胞膜的破壞。研究表明,紅細胞在一定剪切應力(約為150~1 000 Pa)作用下開始變形,當剪切應力高于某一臨界數值(約1 000 Pa)或經過一定時間的累積后,細胞膜破裂,血紅蛋白進入血漿,從而產生溶血效應[14]。
四種血泵內部流場等效標量剪切應力的分布情況如圖 4 所示。血泵內部流場的等效標量剪切應力極值和平均值如表 1所示,其中對數螺旋線葉輪對應的等效標量剪切應力最大值和平均值最小。剪切應力主要分布于葉輪吸力面的出口位置以及環形壓水室的隔舌區域。等效標量剪切應力頻數分布圖如圖 5所示,血泵內流場中等效標量剪切應力值多分布在0~120 Pa之間,所占區域的體積約占總體積的98%;高于500 Pa的區域所占體積則約為總體積的0.035%;而對數螺旋線葉輪血泵高剪切應力區域體積僅占總體積的0.004%。最大剪切應力區域出現在泵殼隔舌部位,這是由于環形壓水室中流速向出口方向迅速增大,與從葉輪流道中流出的血液相互碰撞從而產生較大的徑向力。使用螺旋壓水室可有效降低這一徑向力,但其結構相對復雜,多應用于心室輔助泵和全人工心臟泵中[15]。
 圖4
離心血泵內部流場等效標量剪切應力分布
Figure4.
Scalar shear stress distribution in centrifugal blood pumps with different profiles of impellers
圖4
離心血泵內部流場等效標量剪切應力分布
Figure4.
Scalar shear stress distribution in centrifugal blood pumps with different profiles of impellers
 圖5
離心血泵內部流場等效標量剪切應力頻數分布
Figure5.
Mass distribution of scalar shear stress in centrifugal blood pumps with different profiles of impellers
圖5
離心血泵內部流場等效標量剪切應力頻數分布
Figure5.
Mass distribution of scalar shear stress in centrifugal blood pumps with different profiles of impellers
根據Garon等的快速溶血預估模型,在得到穩定的剪切應力場之后,可計算出相應的標準溶血參數值。黏性剪切應力及雷諾剪切應力均能夠破壞血細胞而導致溶血[9]。如圖 6所示,DV和DR分別為黏性剪切應力和雷諾剪切應力對應的標準溶血參數值,D為總標準溶血參數值。可以看出,四種血泵的內流場中黏性剪切應力造成的溶血程度基本相同,
 圖6
標準溶血參數的數值預估
Figure6.
Numerical approximation of NIH
圖6
標準溶血參數的數值預估
Figure6.
Numerical approximation of NIH
而雷諾剪切應力的不同是導致標準化溶血參數存在較大差別的主要因素。由于流道中流動模式的改善,對數螺旋線葉輪血泵流場中的高雷諾剪切應力區域最少,使其性能最佳。由于快速溶血預估模型是對剪切應力場進行線性場積分,故該模型能夠對流場中不同區域分別進行溶血預估。圖 6中DI和DC分別對應泵殼區域和葉輪區域的標準溶血參數值。可以看出,葉輪形態和泵殼結構共同決定了離心血泵的溶血性能,其中對數螺旋線葉輪區域的標準溶血參數值最小。
3 討論與結論
本文應用低雷諾數修正SST κ-ω湍流模型以及快速溶血預估模型對具有四種不同葉輪形態的離心血泵綜合特性進行了對比研究。其中,相對速度矢量分布對比表明,對數螺旋線葉輪能明顯改善流道中的流動模式,從而減少流場中高剪切應力的產生。對等效標量剪切應力的分析同樣表明,對數螺旋線葉輪血泵內流場中的高剪切應力區域明顯少于其它三種血泵。
從對標準溶血參數的計算結果來看,Garon等提出的快速溶血預估模型全面地反映了血泵溶血特性。采用該模型對四種血泵的仿真計算結果表明,對數螺旋線葉輪血泵無論是在不同類型剪切應力作用下還是在不同區域的標準溶血參數值都低于其它血泵。相對于Lagrangian顆粒示蹤方法來說,這種預估方法還可以應用于多相流血液模型中,并且若在獲得穩定流場以后直接計算輸運方程(4),便可計算出流場中各點處的標準溶血參數值,使得血泵的改進更具有針對性,這也是溶血預估模型的發展趨勢。