麻醉意識深度監測是臨床中保證全身麻醉(全麻)手術順利進行的關鍵手段之一, 腦電圖(EEG)作為檢測大腦皮層活動的主要信號, 是評價麻醉意識深度的重要工具。本文根據腦電信號隨麻醉意識深度變化的趨勢, 提出結合腦電分析中的時域、頻域及復雜度方法, 采用決策樹分類器與最小二乘擬合法計算麻醉深度指數(DOAI)。利用臨床采集的40例丙泊酚全麻手術患者的腦電信號和麻醉專家對信號的分類、評分對此方案進行驗證, 實驗結果與目前臨床上廣泛使用的BIS指數進行對比, 結果顯示DOAI與BIS指數的Pearson相關性可達0.89, 從而證實此方案的可行性與準確性, 為麻醉監護工作者提供了一種思路。
引用本文： 劉軍, 周雅琪, 陳紹賓, 徐天昊, 陳梟, 謝斐. 基于樣本熵與決策樹的麻醉意識深度評價指數的研究. 生物醫學工程學雜志, 2015, 32(2): 434-439. doi: 10.7507/1001-5515.20150078 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
全麻手術中，為使手術順利進行，會使用麻醉藥物使患者呈現意識消失、全身痛覺喪失等狀態，準確監測患者麻醉過程中意識變化情況可保證患者不會發生術中知曉，同時減少麻醉藥物的使用量[1]。麻醉過程中，麻醉藥物會對大腦神經元突觸間神經遞質的傳遞產生影響，表現為對大腦神經元的發放活動產生抑制，進而改變神經元電活動[2-4]。腦電圖(electroencephalography, EEG)作為大腦神經元電活動的直接反映，含有豐富的大腦神經元電活動信息，可用于評價麻醉意識深度[4-5]。基于腦電圖特征研究麻醉意識深度領域經過70余年的發展，目前主要分析方法有時域分析法、頻域分析法、時頻分析法與復雜度分析法等，這些方法中用到的腦電參數眾多，如頻域分析法中有中心頻率、邊緣頻率、β比率等，復雜度分析法包括Lempel-Ziv復雜度、狀態熵、反應熵等。
已有的麻醉意識深度監測研究大多是探討一種或幾種腦電參數與麻醉意識深度之間的關系[6-8]，或利用部分腦電參數評價麻醉意識深度[9-10]，但未說明如何選取以及如何聯合使用腦電參數。
本文從麻醉過程中腦電參數變化趨勢的角度討論了腦電參數的選取與組合，運用決策樹分類器對麻醉后腦電信號進行分類，并通過最小二乘法得到麻醉意識深度指數(depth of anesthesia index, DOAI)。實驗結果表明DOAI與目前臨床上廣泛使用的BIS指數在丙泊酚全麻手術中有很好的相關性，可用于表征麻醉意識深度。
1 實驗方法
1.1 參數選取與分類算法
1.1.1 腦電信號參數的選取與計算方法
目前應用于麻醉意識深度監測的腦電參數眾多，選取合適的參數是一個難點。文獻[4]總結了腦電信號隨麻醉深度變化而表現出的趨勢：隨著麻醉深度的加深，腦電信號的平均頻率呈現先上升后下降的趨勢，且頻率在中度麻醉時期變化迅速；腦電信號的復雜度是單調下降的，并在清醒至麻醉時期變化最為劇烈，但在深度麻醉期變化緩慢(見文獻[4]圖 7)；在深度麻醉期，腦電信號會出現爆發抑制(burst suppression, BS)，麻醉深度越深，出現的爆發抑制越多。
基于腦電信號隨麻醉深度變化的趨勢，可進一步獲取如下信息：①由清醒至麻醉這一過程，復雜度單調下降且變化快速，而頻率先上升后下降，非單調關系，所以相對于頻域分析方法，復雜度是量化該過程的理想參數；②由淺麻至中麻再到深麻(分別代表淺度麻醉、中度麻醉和深度麻醉)這一過程，頻率單調下降且變化最為劇烈，復雜度則變化不大，故該過程可用頻域分析方法進行量化；③在深度麻醉時期爆發抑制增多，由爆發抑制得出的爆發抑制比(burst suppression ratio, BSR)可作為此時量化麻醉深度的參數。
從以上信息我們獲得如下啟發：①麻醉深度難以用某單一參數量化，結合三種分析方法可更好地評價麻醉深度；②復雜度可用于區分清醒與麻醉時期，頻率信息可用于區分不同麻醉深度，爆發抑制比可用于量化深度麻醉。
本文結合三種分析方法評價麻醉意識深度，具體參數分別選擇爆發抑制比、邊緣頻率、樣本熵。
當腦電電位不大于±5μV且時間超過0.5 s時，認為發生爆發抑制。BSR即抑制狀態占一段腦電信號的比例。本文計算60 s內爆發抑制比。
在頻域參數中，本文選取邊緣頻率。邊緣頻率是指一段信號的功率譜中，功率積分達到總功率95%時的頻率，計算步驟如下：
(1)計算一段信號xk, k=1, 2, …, N的離散傅里葉變換，；
(2) X[m]中前N/2點即包含了這段信號的頻率信息，將X[m]利用此段信號的采樣率fs轉換為關于頻率fi的表達式：X(fi)=X[m]，其中
| ${f_i}={f_s} \cdot m/N, m=1, 2, \cdots, N/2;$ |
(3)尋找某一頻率值，使其滿足關系式：，公式中積分區間為1~47，這是采用截止頻率為1~47的數字濾波器的緣故，獲得的頻率值即邊緣頻率fSef。
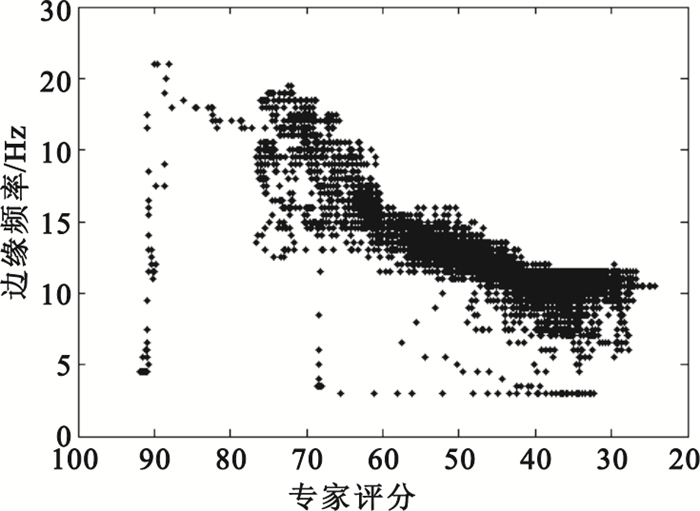
圖 1顯示了一例全麻手術中邊緣頻率隨麻醉逐步加深的變化趨勢(圖中存在一些奇異點，但不影響整體變化趨勢)。橫坐標為麻醉專家評分(麻醉專家分類與評分方法見1.2.3小節)，分數越低，麻醉深度越深，由100至20表明麻醉深度加深這一過程，縱坐標為頻率值，此圖說明在麻醉時期隨麻醉深度逐步加深，邊緣頻率單調減小，故可用于區分淺度麻醉、中度麻醉與深度麻醉。
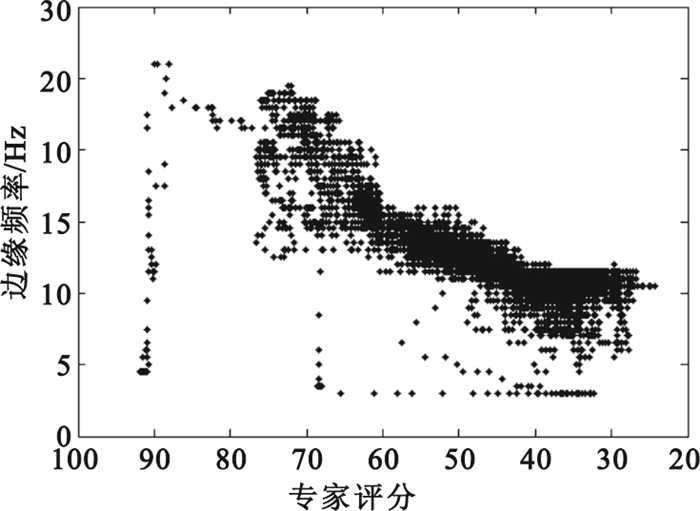圖1
全麻手術中邊緣頻率隨麻醉逐步加深的變化趨勢
Figure1.
Trend of changes in spectral edge frequency as anesthesia deepened
熵作為一種復雜度與頻域結合的方法，能很好地反映麻醉深度變化，已有學者將近似熵用于麻醉深度研究[6-7]。但近似熵存在結果不一致的缺點，Richman等[11]針對此問題在近似熵基礎上提出了樣本熵。目前，和衛星等[12]已將樣本熵應用于睡眠分期，并取得了良好的效果，而睡眠腦電與麻醉腦電十分類似，所以本文設想將樣本熵應用于麻醉腦電分析中，亦可取得良好的效果，實驗結果也證實了此設想。
樣本熵可用SampEn(m, r, N)表示，其中m為嵌入維數，r為相似容限，N為數據長度，樣本熵的計算方法如下：
(1)確定模式維數m，將信號xk, k=1, 2, …, N映射到m維相空間，形成點集{bi}，i=1, 2, …, N-m+1，其中bi=(xi, xi+1, …, xi+m-1)；
(2)計算{bi}與{bj}間的距離，d(bi, bj)=max｜x(i+k)-x(j+k)｜，k=0, 1, …, m-1, i, j=1, 2, …, N-m+1；
(3)確定相似容量r，令且j≠i，num{d(bi, bj)＜r}表示滿足d(bi, bj)＜r的所有{bj}的數量；
(4)對于參數m可得；
(5)將維數m加1，令
| $A_i^m\left(r \right)=\frac{1}{{N-m-1}}num\left\{ {d\left({{{b'}_i}, {{b'}_j}} \right) < r} \right\}, $ |
j=1, 2, …, N-m且j≠i，可得；
(6)此序列的樣本熵即
| $sampEn\left({m, r, N} \right)=-\ln \left\{ {{A^m}\left(r \right)/{B^m}\left(r \right)} \right\}。$ |
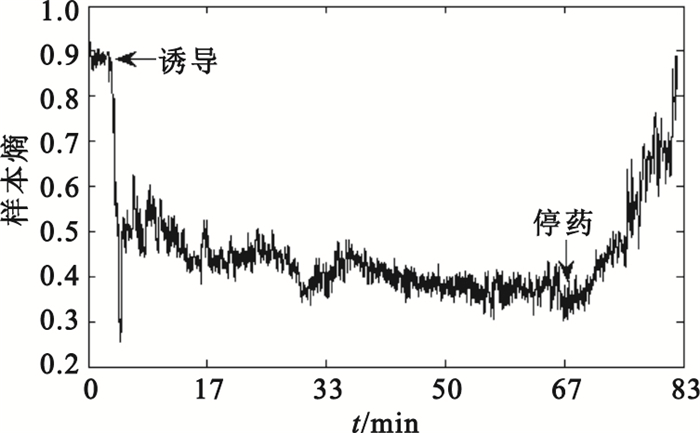
本文選取15 s腦電數據作為計算單位，故N=15·128，r為此段數據標準差的0.2倍，m選取為3。圖 2顯示了一例全麻手術中，患者腦電信號樣本熵的變化趨勢，并在圖中標注了麻醉誘導時刻與停藥時刻，可見樣本熵是刻畫麻醉深度的理想參數。
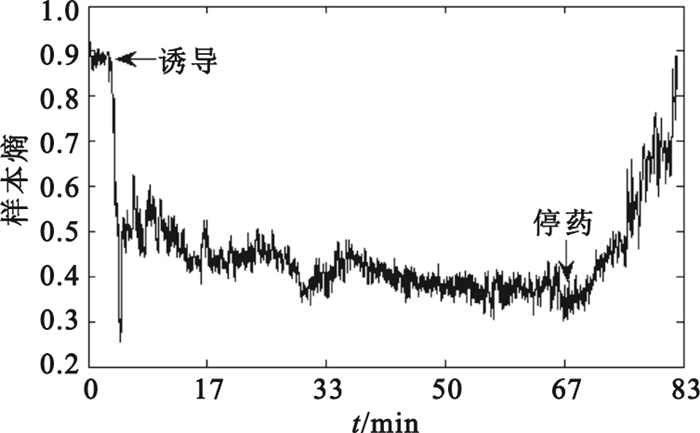圖2
麻醉手術過程中腦電信號樣本熵的變化趨勢
Figure2.
Sample entropy change trend during anesthesia
1.1.2 決策樹分類與最小二乘擬合算法
選取腦電參數后，需選取合適的分類算法利用這些參數將腦電信號分類并得出DOAI。Ortolani等[9]采用神經網絡方法，將13個腦電參數作為神經網絡的輸入，麻醉專家給定的麻醉深度評分作為輸出，利用150例患者的腦電數據訓練出麻醉深度監測算法。
該算法計算結果與BIS指數具有很高的相關性。但由于神經網絡方法的推廣性和解釋性不強，使得該算法在實際應用中并不占優勢，如它無法為醫生解釋算法的原理，且算法的維護和升級十分困難。
考慮到神經網絡算法具有以上缺陷，本文決定先采用決策樹算法對信號分類，而后通過分段擬合的方法計算DOAI。目前廣泛使用的是C4.5決策樹算法[13]，此算法具有如下優點：①分類精度高；②可運用專家知識，符合人類思維，可解釋性好；③訓練速度快；④對噪聲信號有很好的健壯性；⑤邏輯清晰，方便查找錯誤和調整分類器。這些優點使C4.5決策樹算法適用于腦電信號分類問題。
選取腦電參數和分類方法后，算法的整體流程如下：計算腦電參數(爆發抑制比、邊緣頻率、樣本熵)，將其作為決策樹輸入特征，將麻醉專家給出的麻醉狀態作為輸出，訓練出一棵決策樹。決策樹的訓練采用以下三個終止條件：
(1)信息增益為0時；
(2)D(輸入特征和麻醉狀態分類的集合)中某一類數據的比例大于一定量時；
(3)D中的數據少于一定量時，這時用D中出現最多的類來統一判斷該節點的數據。
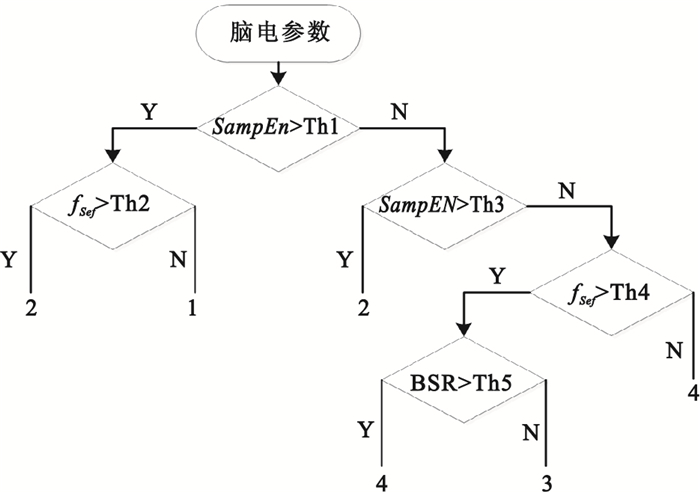
訓練結束后根據實際情況對決策樹進行剪枝，剪枝的目的是：①在保證精度的同時盡量使決策樹簡單，以提高推廣能力；②排除過度學習的可能，盡可能使分類器與生理知識保持一致。最終得到的決策樹結構如圖 3所示。
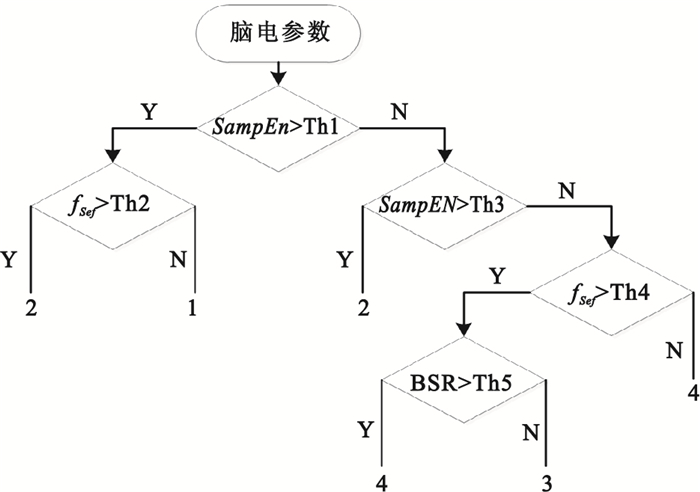圖3
決策樹結構
Th:閾值；1：清醒；2：淺度麻醉；3：中度麻醉；4：深度麻醉
Figure3. Structure of the decision treeTh: threshold; 1: awake status; 2: light anesthesia; 3 general anesthesia; 4: deep anesthesia
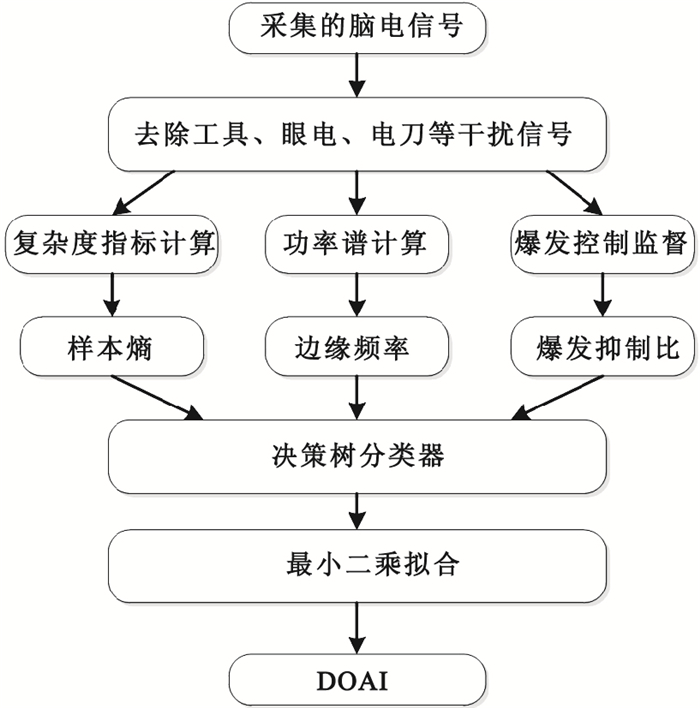
獲得決策樹輸出的麻醉深度類別后，利用三個參數在各類別中擬合麻醉專家給出的麻醉評分。由于在各類別中麻醉深度與復雜度、頻率等參數基本呈線性關系，故采用最小二乘法進行線性擬合。這種方法雖沒有一些復雜的擬合方法精度高，但是它的簡單性會在一定程度上保證算法的推廣能力。算法整體流程圖如圖 4所示。
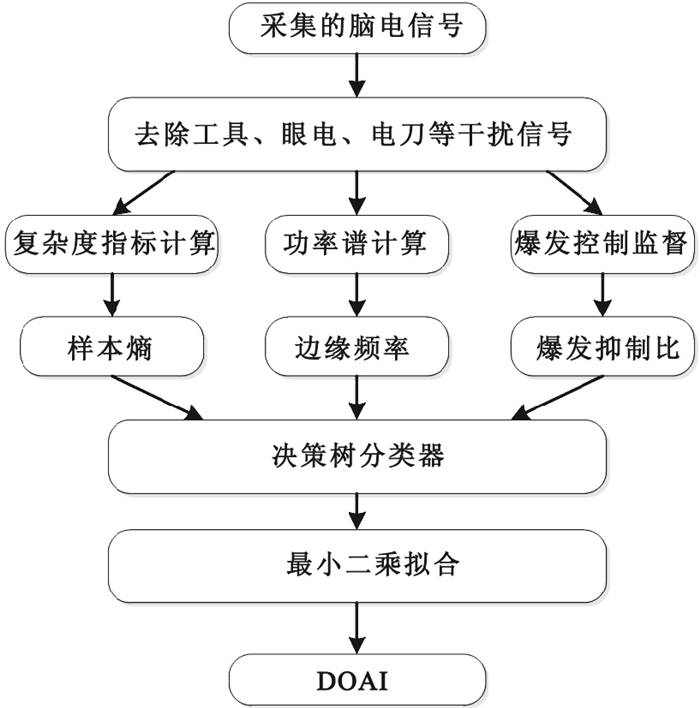圖4
算法的完整流程
Figure4.
Flowchart for the calculation of the DOAI
1.2 腦電信號采集、信號預處理與麻醉專家分類、評分
1.2.1 患者選取與麻醉方法
選取全麻手術患者40例，年齡24~73歲，身高155~175 cm，體重52~80 kg，性別不限(最終男性17名，女性23名)，ASA體格狀況分級為Ⅰ~Ⅱ級，排除顱面部手術者、精神疾病病史者及無民事行為能力者。所有試驗均是在獲得醫院倫理委員會同意，患者或家屬簽署麻醉同意書后進行。
患者在手術前8 h開始禁止飲食，并且不使用任何麻醉類藥物。麻醉誘導期依次注入鎮靜類藥物咪唑安定0.1 mg·kg-1，丙泊酚1.5~2 mg·kg-1，肌松類藥物維庫溴銨0.1 mg·kg-1，鎮痛類藥物芬太尼5μg·kg-1。麻醉維持期用藥如下：每小時追加2 mg維庫溴銨，0.1 mg芬太尼，以30~50 mL/h速率恒速泵入濃度為10 mg/mL的丙泊酚，10~25 mL/h速率恒速泵入濃度為20 mg/50 mL的瑞芬太尼。由于不同患者人體機能存在差異，在手術過程中，麻醉專家會根據患者體征，如心率、血壓、呼吸等，適度增加或減少麻醉用藥。在手術將結束時逐步減少麻醉藥物使用量。麻醉過程中藥物均以靜脈推注形式注入患者體內。
1.2.2 腦電信號采集與信號預處理
采用BIS VISTATM型雙通道腦電監測儀通過USB口采集BIS指數及原始腦電數據。原始腦電數據中包含工頻、眼電、電刀等各類噪聲，不可直接用于腦電信號分析，需去除這些噪聲。首先，利用截止頻率為1~47 Hz的數字濾波器對信號濾波，而后人為去除濾波無法去除的眼電偽跡和電刀干擾。
1.2.3 麻醉專家分類與評分
信號經過預處理后，將每例手術腦電信號以5 s為一段進行劃分，最終獲得共計時長79.5 h、57 271段的腦電信號。麻醉專家根據改良警覺鎮靜評分(Modified Observer’s Assessment of Alertness/Sedation, MOAA/S)，并結合腦電信號及麻醉記錄單(常規麻醉記錄單中并無瞳孔與眼瞼反射等記錄項，在此采用專為此實驗設計的麻醉記錄單)中患者體征(包括心率、血壓、呼吸、瞳孔、眼瞼反射等)的變化趨勢等，為每段信號分類并評分，最終類別為4類，分數區間為0~100(分數越低，代表麻醉深度越深)，具體分類和評分標準如表 1所示。如某時段處MOAA/S評分2~3之間，則麻醉專家將此段信號標注為淺度麻醉，分值根據具體信號評為60~70之間某一值。
表1
分類與評分標準
Table1.
Criteria of classification and grading
1.3 算法評價方法
隨機抽取1.2節中的30例腦電數據作為訓練集，余下10例作為測試集，訓練集與測試集患者信息見表 2。
表2
訓練集、測試集患者信息
Table2.
Patient information included in the training and the testing sets
利用訓練集通過1.1.2小節中算法訓練出決策樹，并得到擬合系數。而后通過下述三種方法評價該算法。
1.3.1 訓練集評價法
將訓練集作為算法輸入，通過決策樹得到算法分類結果，而后利用擬合系數計算DOAI。將算法分類結果、DOAI與麻醉專家給出的分類、評分分別對比，計算分類準確率、DOAI與麻醉專家評分的Pearson相關性、平均絕對誤差、最大絕對誤差、均方根及95%置信區間等統計量，從而評價算法。
1.3.2 測試集評價法
測試集評價法與訓練集評價法類似，只是輸入數據變為測試集。
1.3.3 BIS指數評價法
BIS指數是美國柯惠醫療推出的BISTM監護系統結合腦電雙譜指數、爆發抑制比、β比率等參數將麻醉過程中的腦電信號歸一化為0~100(其中0表示無腦電信號，100表示清醒)的無量綱值，用于表示麻醉深度，目前廣泛應用于臨床。已有研究[14]表明BIS指數可指導減少麻醉藥的使用劑量及術中知曉的發生率并可縮短術后蘇醒時間。本文將DOAI與BIS指數進行比對，評價本文算法。具體評價方法如下：將全部腦電數據作為輸入，通過算法得到DOAI，計算DOAI與BIS指數的Pearson相關性等統計量。
2 實驗結果與分析
2.1 訓練集、測試集評價法實驗結果與分析
訓練集數據共41 951段，約58.2 h；測試集數據共15 320段，約21.3 h，表 3為它們的實驗結果。由表 3可知，訓練集數據的DOAI與麻醉專家評分的相關性可達0.943。相對于訓練集比對結果，測試集比對結果在各統計量評價指標上，性能均有一定下降，但分類準確率與相關性仍分別可達0.87和0.941，DOAI與麻醉專家評分之間均方根誤差為7.143 7，平均絕對誤差為4.921 5。
表3
本文算法與麻醉專家評分結果對比
Table3.
Comparison of classifications and scores annotated between results of anesthesiologist and the results with the present algorithm
以上結果表明DOAI與麻醉專家評分相差不大，Pearson相關性好，從而說明算法訓練出的決策樹及獲得的擬合系數對于訓練集及測試集均能取得很好的效果，具有推廣性。
2.2 BIS指數評價法實驗結果與分析
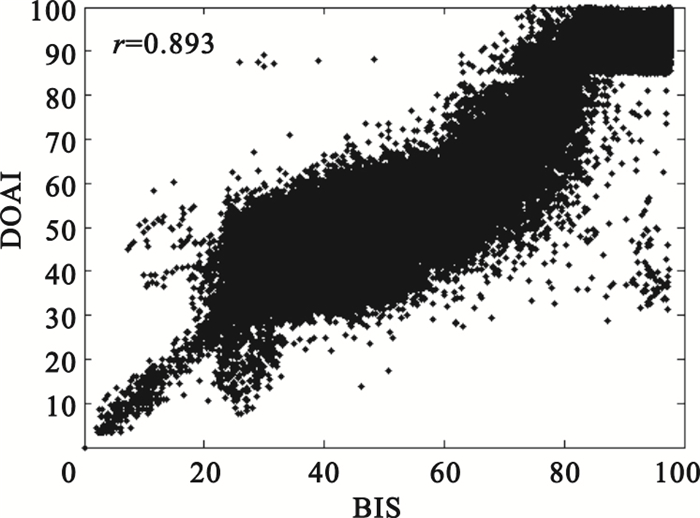
全體數據經算法得出的DOAI與BIS指數比對結果見圖 5與表 4。圖 5中，橫坐標為BIS指數，縱坐標為DOAI值，可知DOAI與BIS指數基本呈線性關系，兩者Pearson相關系數為0.893。圖中，DOAI值與BIS指數主要集中于20~80分數段，這是因為在全麻手術中，患者主要處于麻醉狀態。由圖 5可知在出現爆發抑制的深度麻醉時期(圖中0~20分數段)，DOAI值與BIS指數線性關系很好，這也說明了爆發抑制比是量化深度麻醉時期的理想參數。同時可看到在清醒期(圖中80~100分數段)，DOAI值與BIS指數線性關系稍差，提示本文區分與量化該時期所用的樣本熵與邊緣頻率需做進一步優化。
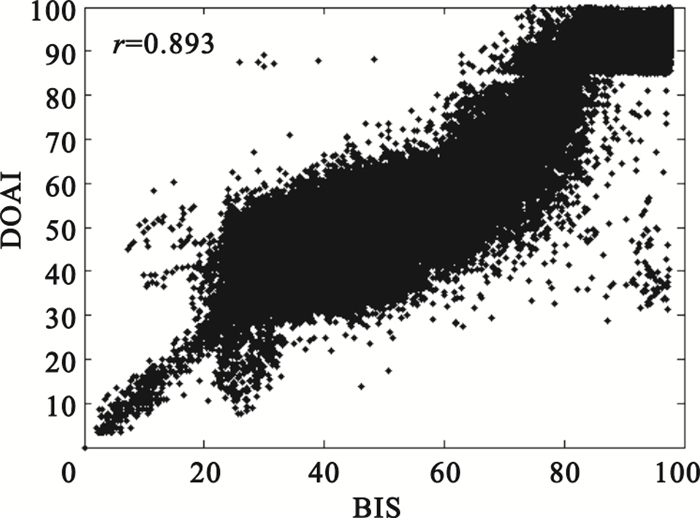圖5
DOAI與BIS指數分值對比圖
Figure5.
Comparison between BIS values and DOAI values
表4
DOAI與BIS指數結果對比
Table4.
Comparison between DOAI and BIS values
由表 4可知DOAI與BIS指數間最大絕對誤差較大，體現在圖 5中即存在少數偏離線性趨勢的奇異點，通過查看與這些奇異點對應的腦電信號，發現其產生原因是手動去除眼電偽跡與電刀干擾時存在遺留，若能更好地去除這類偽跡，DOAI與BIS指數之間的Pearson相關性等可進一步提高。
總體而言，DOAI與BIS指數兩者之間的Pearson相關性、平均絕對誤差、均方根與95%置信區間等統計量均較理想。證明經本文算法計算所得的DOAI與BIS指數具有很好的一致性，可用來表征麻醉意識深度。
3 結論
目前，利用腦電特征研究麻醉意識深度成果很多。封洲燕等[15]探討了不同麻醉深度下腦電復雜度和功率譜的變化過程。李小俚等[16]則發現相對于時頻均衡譜熵，希爾伯特黃熵能更準確地區分麻醉和清醒狀態，更適用于麻醉深度檢測。Ortolani等[9]采用13個腦電參數用于評價麻醉意識深度。但這些成果均未對如何選取、組合腦電參數用于監測麻醉意識深度進行論述。
本文根據腦電信號隨麻醉意識深度變化的趨勢，嘗試了麻醉意識深度監測中腦電參數的選取，從分析結果來看，腦電頻域特性可較好地區分不同麻醉意識深度，而爆發抑制比可用于量化深度麻醉時期。引入樣本熵可反映腦電信號序列的復雜度，對清醒與麻醉狀態有較好的指示作用。通過這三類參數的聯合，可完備地描述麻醉狀態變化過程。在此基礎上，我們選取了一種決策分類的方法來對麻醉狀態進行分類分析，由此得到一套計算DOAI的方案，并對此方案進行了實驗驗證。實驗結果表明本文算法得到的DOAI與目前麻醉深度監測中較成熟的BIS指數在丙泊酚全麻手術中具有良好的相關性，可用于表征麻醉意識深度，從而證實本文提出的腦電參數的選取方法是合理的。
引言
全麻手術中，為使手術順利進行，會使用麻醉藥物使患者呈現意識消失、全身痛覺喪失等狀態，準確監測患者麻醉過程中意識變化情況可保證患者不會發生術中知曉，同時減少麻醉藥物的使用量[1]。麻醉過程中，麻醉藥物會對大腦神經元突觸間神經遞質的傳遞產生影響，表現為對大腦神經元的發放活動產生抑制，進而改變神經元電活動[2-4]。腦電圖(electroencephalography, EEG)作為大腦神經元電活動的直接反映，含有豐富的大腦神經元電活動信息，可用于評價麻醉意識深度[4-5]。基于腦電圖特征研究麻醉意識深度領域經過70余年的發展，目前主要分析方法有時域分析法、頻域分析法、時頻分析法與復雜度分析法等，這些方法中用到的腦電參數眾多，如頻域分析法中有中心頻率、邊緣頻率、β比率等，復雜度分析法包括Lempel-Ziv復雜度、狀態熵、反應熵等。
已有的麻醉意識深度監測研究大多是探討一種或幾種腦電參數與麻醉意識深度之間的關系[6-8]，或利用部分腦電參數評價麻醉意識深度[9-10]，但未說明如何選取以及如何聯合使用腦電參數。
本文從麻醉過程中腦電參數變化趨勢的角度討論了腦電參數的選取與組合，運用決策樹分類器對麻醉后腦電信號進行分類，并通過最小二乘法得到麻醉意識深度指數(depth of anesthesia index, DOAI)。實驗結果表明DOAI與目前臨床上廣泛使用的BIS指數在丙泊酚全麻手術中有很好的相關性，可用于表征麻醉意識深度。
1 實驗方法
1.1 參數選取與分類算法
1.1.1 腦電信號參數的選取與計算方法
目前應用于麻醉意識深度監測的腦電參數眾多，選取合適的參數是一個難點。文獻[4]總結了腦電信號隨麻醉深度變化而表現出的趨勢：隨著麻醉深度的加深，腦電信號的平均頻率呈現先上升后下降的趨勢，且頻率在中度麻醉時期變化迅速；腦電信號的復雜度是單調下降的，并在清醒至麻醉時期變化最為劇烈，但在深度麻醉期變化緩慢(見文獻[4]圖 7)；在深度麻醉期，腦電信號會出現爆發抑制(burst suppression, BS)，麻醉深度越深，出現的爆發抑制越多。
基于腦電信號隨麻醉深度變化的趨勢，可進一步獲取如下信息：①由清醒至麻醉這一過程，復雜度單調下降且變化快速，而頻率先上升后下降，非單調關系，所以相對于頻域分析方法，復雜度是量化該過程的理想參數；②由淺麻至中麻再到深麻(分別代表淺度麻醉、中度麻醉和深度麻醉)這一過程，頻率單調下降且變化最為劇烈，復雜度則變化不大，故該過程可用頻域分析方法進行量化；③在深度麻醉時期爆發抑制增多，由爆發抑制得出的爆發抑制比(burst suppression ratio, BSR)可作為此時量化麻醉深度的參數。
從以上信息我們獲得如下啟發：①麻醉深度難以用某單一參數量化，結合三種分析方法可更好地評價麻醉深度；②復雜度可用于區分清醒與麻醉時期，頻率信息可用于區分不同麻醉深度，爆發抑制比可用于量化深度麻醉。
本文結合三種分析方法評價麻醉意識深度，具體參數分別選擇爆發抑制比、邊緣頻率、樣本熵。
當腦電電位不大于±5μV且時間超過0.5 s時，認為發生爆發抑制。BSR即抑制狀態占一段腦電信號的比例。本文計算60 s內爆發抑制比。
在頻域參數中，本文選取邊緣頻率。邊緣頻率是指一段信號的功率譜中，功率積分達到總功率95%時的頻率，計算步驟如下：
(1)計算一段信號xk, k=1, 2, …, N的離散傅里葉變換，；
(2) X[m]中前N/2點即包含了這段信號的頻率信息，將X[m]利用此段信號的采樣率fs轉換為關于頻率fi的表達式：X(fi)=X[m]，其中
| ${f_i}={f_s} \cdot m/N, m=1, 2, \cdots, N/2;$ |
(3)尋找某一頻率值，使其滿足關系式：，公式中積分區間為1~47，這是采用截止頻率為1~47的數字濾波器的緣故，獲得的頻率值即邊緣頻率fSef。
圖 1顯示了一例全麻手術中邊緣頻率隨麻醉逐步加深的變化趨勢(圖中存在一些奇異點，但不影響整體變化趨勢)。橫坐標為麻醉專家評分(麻醉專家分類與評分方法見1.2.3小節)，分數越低，麻醉深度越深，由100至20表明麻醉深度加深這一過程，縱坐標為頻率值，此圖說明在麻醉時期隨麻醉深度逐步加深，邊緣頻率單調減小，故可用于區分淺度麻醉、中度麻醉與深度麻醉。
圖1
全麻手術中邊緣頻率隨麻醉逐步加深的變化趨勢
Figure1.
Trend of changes in spectral edge frequency as anesthesia deepened
熵作為一種復雜度與頻域結合的方法，能很好地反映麻醉深度變化，已有學者將近似熵用于麻醉深度研究[6-7]。但近似熵存在結果不一致的缺點，Richman等[11]針對此問題在近似熵基礎上提出了樣本熵。目前，和衛星等[12]已將樣本熵應用于睡眠分期，并取得了良好的效果，而睡眠腦電與麻醉腦電十分類似，所以本文設想將樣本熵應用于麻醉腦電分析中，亦可取得良好的效果，實驗結果也證實了此設想。
樣本熵可用SampEn(m, r, N)表示，其中m為嵌入維數，r為相似容限，N為數據長度，樣本熵的計算方法如下：
(1)確定模式維數m，將信號xk, k=1, 2, …, N映射到m維相空間，形成點集{bi}，i=1, 2, …, N-m+1，其中bi=(xi, xi+1, …, xi+m-1)；
(2)計算{bi}與{bj}間的距離，d(bi, bj)=max｜x(i+k)-x(j+k)｜，k=0, 1, …, m-1, i, j=1, 2, …, N-m+1；
(3)確定相似容量r，令且j≠i，num{d(bi, bj)＜r}表示滿足d(bi, bj)＜r的所有{bj}的數量；
(4)對于參數m可得；
(5)將維數m加1，令
| $A_i^m\left(r \right)=\frac{1}{{N-m-1}}num\left\{ {d\left({{{b'}_i}, {{b'}_j}} \right) < r} \right\}, $ |
j=1, 2, …, N-m且j≠i，可得；
(6)此序列的樣本熵即
| $sampEn\left({m, r, N} \right)=-\ln \left\{ {{A^m}\left(r \right)/{B^m}\left(r \right)} \right\}。$ |
本文選取15 s腦電數據作為計算單位，故N=15·128，r為此段數據標準差的0.2倍，m選取為3。圖 2顯示了一例全麻手術中，患者腦電信號樣本熵的變化趨勢，并在圖中標注了麻醉誘導時刻與停藥時刻，可見樣本熵是刻畫麻醉深度的理想參數。
圖2
麻醉手術過程中腦電信號樣本熵的變化趨勢
Figure2.
Sample entropy change trend during anesthesia
1.1.2 決策樹分類與最小二乘擬合算法
選取腦電參數后，需選取合適的分類算法利用這些參數將腦電信號分類并得出DOAI。Ortolani等[9]采用神經網絡方法，將13個腦電參數作為神經網絡的輸入，麻醉專家給定的麻醉深度評分作為輸出，利用150例患者的腦電數據訓練出麻醉深度監測算法。
該算法計算結果與BIS指數具有很高的相關性。但由于神經網絡方法的推廣性和解釋性不強，使得該算法在實際應用中并不占優勢，如它無法為醫生解釋算法的原理，且算法的維護和升級十分困難。
考慮到神經網絡算法具有以上缺陷，本文決定先采用決策樹算法對信號分類，而后通過分段擬合的方法計算DOAI。目前廣泛使用的是C4.5決策樹算法[13]，此算法具有如下優點：①分類精度高；②可運用專家知識，符合人類思維，可解釋性好；③訓練速度快；④對噪聲信號有很好的健壯性；⑤邏輯清晰，方便查找錯誤和調整分類器。這些優點使C4.5決策樹算法適用于腦電信號分類問題。
選取腦電參數和分類方法后，算法的整體流程如下：計算腦電參數(爆發抑制比、邊緣頻率、樣本熵)，將其作為決策樹輸入特征，將麻醉專家給出的麻醉狀態作為輸出，訓練出一棵決策樹。決策樹的訓練采用以下三個終止條件：
(1)信息增益為0時；
(2)D(輸入特征和麻醉狀態分類的集合)中某一類數據的比例大于一定量時；
(3)D中的數據少于一定量時，這時用D中出現最多的類來統一判斷該節點的數據。
訓練結束后根據實際情況對決策樹進行剪枝，剪枝的目的是：①在保證精度的同時盡量使決策樹簡單，以提高推廣能力；②排除過度學習的可能，盡可能使分類器與生理知識保持一致。最終得到的決策樹結構如圖 3所示。
圖3
決策樹結構
Th:閾值；1：清醒；2：淺度麻醉；3：中度麻醉；4：深度麻醉
Figure3. Structure of the decision treeTh: threshold; 1: awake status; 2: light anesthesia; 3 general anesthesia; 4: deep anesthesia
獲得決策樹輸出的麻醉深度類別后，利用三個參數在各類別中擬合麻醉專家給出的麻醉評分。由于在各類別中麻醉深度與復雜度、頻率等參數基本呈線性關系，故采用最小二乘法進行線性擬合。這種方法雖沒有一些復雜的擬合方法精度高，但是它的簡單性會在一定程度上保證算法的推廣能力。算法整體流程圖如圖 4所示。
圖4
算法的完整流程
Figure4.
Flowchart for the calculation of the DOAI
1.2 腦電信號采集、信號預處理與麻醉專家分類、評分
1.2.1 患者選取與麻醉方法
選取全麻手術患者40例，年齡24~73歲，身高155~175 cm，體重52~80 kg，性別不限(最終男性17名，女性23名)，ASA體格狀況分級為Ⅰ~Ⅱ級，排除顱面部手術者、精神疾病病史者及無民事行為能力者。所有試驗均是在獲得醫院倫理委員會同意，患者或家屬簽署麻醉同意書后進行。
患者在手術前8 h開始禁止飲食，并且不使用任何麻醉類藥物。麻醉誘導期依次注入鎮靜類藥物咪唑安定0.1 mg·kg-1，丙泊酚1.5~2 mg·kg-1，肌松類藥物維庫溴銨0.1 mg·kg-1，鎮痛類藥物芬太尼5μg·kg-1。麻醉維持期用藥如下：每小時追加2 mg維庫溴銨，0.1 mg芬太尼，以30~50 mL/h速率恒速泵入濃度為10 mg/mL的丙泊酚，10~25 mL/h速率恒速泵入濃度為20 mg/50 mL的瑞芬太尼。由于不同患者人體機能存在差異，在手術過程中，麻醉專家會根據患者體征，如心率、血壓、呼吸等，適度增加或減少麻醉用藥。在手術將結束時逐步減少麻醉藥物使用量。麻醉過程中藥物均以靜脈推注形式注入患者體內。
1.2.2 腦電信號采集與信號預處理
采用BIS VISTATM型雙通道腦電監測儀通過USB口采集BIS指數及原始腦電數據。原始腦電數據中包含工頻、眼電、電刀等各類噪聲，不可直接用于腦電信號分析，需去除這些噪聲。首先，利用截止頻率為1~47 Hz的數字濾波器對信號濾波，而后人為去除濾波無法去除的眼電偽跡和電刀干擾。
1.2.3 麻醉專家分類與評分
信號經過預處理后，將每例手術腦電信號以5 s為一段進行劃分，最終獲得共計時長79.5 h、57 271段的腦電信號。麻醉專家根據改良警覺鎮靜評分(Modified Observer’s Assessment of Alertness/Sedation, MOAA/S)，并結合腦電信號及麻醉記錄單(常規麻醉記錄單中并無瞳孔與眼瞼反射等記錄項，在此采用專為此實驗設計的麻醉記錄單)中患者體征(包括心率、血壓、呼吸、瞳孔、眼瞼反射等)的變化趨勢等，為每段信號分類并評分，最終類別為4類，分數區間為0~100(分數越低，代表麻醉深度越深)，具體分類和評分標準如表 1所示。如某時段處MOAA/S評分2~3之間，則麻醉專家將此段信號標注為淺度麻醉，分值根據具體信號評為60~70之間某一值。
表1
分類與評分標準
Table1.
Criteria of classification and grading
1.3 算法評價方法
隨機抽取1.2節中的30例腦電數據作為訓練集，余下10例作為測試集，訓練集與測試集患者信息見表 2。
表2
訓練集、測試集患者信息
Table2.
Patient information included in the training and the testing sets
利用訓練集通過1.1.2小節中算法訓練出決策樹，并得到擬合系數。而后通過下述三種方法評價該算法。
1.3.1 訓練集評價法
將訓練集作為算法輸入，通過決策樹得到算法分類結果，而后利用擬合系數計算DOAI。將算法分類結果、DOAI與麻醉專家給出的分類、評分分別對比，計算分類準確率、DOAI與麻醉專家評分的Pearson相關性、平均絕對誤差、最大絕對誤差、均方根及95%置信區間等統計量，從而評價算法。
1.3.2 測試集評價法
測試集評價法與訓練集評價法類似，只是輸入數據變為測試集。
1.3.3 BIS指數評價法
BIS指數是美國柯惠醫療推出的BISTM監護系統結合腦電雙譜指數、爆發抑制比、β比率等參數將麻醉過程中的腦電信號歸一化為0~100(其中0表示無腦電信號，100表示清醒)的無量綱值，用于表示麻醉深度，目前廣泛應用于臨床。已有研究[14]表明BIS指數可指導減少麻醉藥的使用劑量及術中知曉的發生率并可縮短術后蘇醒時間。本文將DOAI與BIS指數進行比對，評價本文算法。具體評價方法如下：將全部腦電數據作為輸入，通過算法得到DOAI，計算DOAI與BIS指數的Pearson相關性等統計量。
2 實驗結果與分析
2.1 訓練集、測試集評價法實驗結果與分析
訓練集數據共41 951段，約58.2 h；測試集數據共15 320段，約21.3 h，表 3為它們的實驗結果。由表 3可知，訓練集數據的DOAI與麻醉專家評分的相關性可達0.943。相對于訓練集比對結果，測試集比對結果在各統計量評價指標上，性能均有一定下降，但分類準確率與相關性仍分別可達0.87和0.941，DOAI與麻醉專家評分之間均方根誤差為7.143 7，平均絕對誤差為4.921 5。
表3
本文算法與麻醉專家評分結果對比
Table3.
Comparison of classifications and scores annotated between results of anesthesiologist and the results with the present algorithm
以上結果表明DOAI與麻醉專家評分相差不大，Pearson相關性好，從而說明算法訓練出的決策樹及獲得的擬合系數對于訓練集及測試集均能取得很好的效果，具有推廣性。
2.2 BIS指數評價法實驗結果與分析
全體數據經算法得出的DOAI與BIS指數比對結果見圖 5與表 4。圖 5中，橫坐標為BIS指數，縱坐標為DOAI值，可知DOAI與BIS指數基本呈線性關系，兩者Pearson相關系數為0.893。圖中，DOAI值與BIS指數主要集中于20~80分數段，這是因為在全麻手術中，患者主要處于麻醉狀態。由圖 5可知在出現爆發抑制的深度麻醉時期(圖中0~20分數段)，DOAI值與BIS指數線性關系很好，這也說明了爆發抑制比是量化深度麻醉時期的理想參數。同時可看到在清醒期(圖中80~100分數段)，DOAI值與BIS指數線性關系稍差，提示本文區分與量化該時期所用的樣本熵與邊緣頻率需做進一步優化。
圖5
DOAI與BIS指數分值對比圖
Figure5.
Comparison between BIS values and DOAI values
表4
DOAI與BIS指數結果對比
Table4.
Comparison between DOAI and BIS values
由表 4可知DOAI與BIS指數間最大絕對誤差較大，體現在圖 5中即存在少數偏離線性趨勢的奇異點，通過查看與這些奇異點對應的腦電信號，發現其產生原因是手動去除眼電偽跡與電刀干擾時存在遺留，若能更好地去除這類偽跡，DOAI與BIS指數之間的Pearson相關性等可進一步提高。
總體而言，DOAI與BIS指數兩者之間的Pearson相關性、平均絕對誤差、均方根與95%置信區間等統計量均較理想。證明經本文算法計算所得的DOAI與BIS指數具有很好的一致性，可用來表征麻醉意識深度。
3 結論
目前，利用腦電特征研究麻醉意識深度成果很多。封洲燕等[15]探討了不同麻醉深度下腦電復雜度和功率譜的變化過程。李小俚等[16]則發現相對于時頻均衡譜熵，希爾伯特黃熵能更準確地區分麻醉和清醒狀態，更適用于麻醉深度檢測。Ortolani等[9]采用13個腦電參數用于評價麻醉意識深度。但這些成果均未對如何選取、組合腦電參數用于監測麻醉意識深度進行論述。
本文根據腦電信號隨麻醉意識深度變化的趨勢，嘗試了麻醉意識深度監測中腦電參數的選取，從分析結果來看，腦電頻域特性可較好地區分不同麻醉意識深度，而爆發抑制比可用于量化深度麻醉時期。引入樣本熵可反映腦電信號序列的復雜度，對清醒與麻醉狀態有較好的指示作用。通過這三類參數的聯合，可完備地描述麻醉狀態變化過程。在此基礎上，我們選取了一種決策分類的方法來對麻醉狀態進行分類分析，由此得到一套計算DOAI的方案，并對此方案進行了實驗驗證。實驗結果表明本文算法得到的DOAI與目前麻醉深度監測中較成熟的BIS指數在丙泊酚全麻手術中具有良好的相關性，可用于表征麻醉意識深度，從而證實本文提出的腦電參數的選取方法是合理的。
