多層感知器(MLP)神經網絡屬于多層前饋神經網絡, 具有高度智能化的特征與能力, 其可以通過網絡自身學習來實現復雜的非線性映射。雙相障礙是一種嚴重的精神疾病, 具有高復發率、自殘率和自殺率。大多數雙相障礙以抑郁發作起病, 容易被誤診為單相抑郁癥而延誤治療, 影響預后。雙相障礙的早期識別對雙相障礙患者非常重要, 由于該過程的非線性特點, 本文探討了MLP神經網絡應用于雙相障礙早期識別的效果。樣本數據分為兩組, 包括復發抑郁組143例及雙相障礙組107例; 通過對兩組間的臨床特征進行統計學分析, 篩選出具有顯著差別的42個變量作為神經網絡的輸入變量; 本研究通過選取不同的神經網絡內部結構, 隨機抽取部分案例作為學習樣本, 其它作為測試樣本, 對于雙相障礙的識別均獲得了較好結果, 說明MLP神經網絡可應用于雙相障礙的早期識別中。
引用本文： 章浩偉, 高燕妮, 苑成梅, 劉穎, 張可, 丁宇清. 基于多層感知器神經網絡的雙相障礙早期識別研究. 生物醫學工程學雜志, 2015, 32(3): 537-541. doi: 10.7507/1001-5515.20150098 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
心境障礙是指由各種原因引起的、以顯著而持久的心境或情感改變為主要特征的一組疾病[1]，單相抑郁癥與雙相障礙是心境障礙的兩種類型。雙相障礙的臨床特點是反復出現心境和活動水平的明顯改變，有時表現為心境高漲、精力充沛和活動增加, 有時表現為心境低落、精力減退和活動減少，最典型的形式是躁狂(或輕躁狂)與抑郁反復間歇交替或循環發作。
現有研究提示，相對于單相抑郁，雙相障礙具有一些較特異性的臨床表象，可在不同程度上預示其雙相的病程特點，包括：雙相家族史、藥物轉相史、混合性抑郁、非典型抑郁、精神病性癥狀、伴環性心境障礙、心境障礙頻繁發作、甲狀腺機能減退等，均可增加雙相障礙發生的可能性。但具體到每個患者，上述因素的出現概率不一，相互作用不明，尚沒有研究綜合評估各種因素與雙相障礙的相關性。
目前普遍認為，雙相障礙與單相抑郁是兩種不同的疾病，具有不同的發病機制[2]，治療方法也不相同，但臨床上早期區分卻存在很大難度。據統計，約有40%的雙相障礙患者曾被誤診為單相抑郁癥，平均誤診時間長達7.5年，約1/3的雙相障礙患者因未使用心境穩定劑而影響療效[3]，因此，雙相障礙的早期識別對雙相障礙患者具有重要意義。但迄今為止，還沒有切實可行的早期識別雙相障礙的工具和方法。
人工神經網絡是在對人腦神經網絡基本認識的基礎上，從信息處理的角度對人腦神經網絡進行抽象，用數理方法建立起來的某種簡化模型，具有高度智能化的特征與能力，其在醫學領域中可用于判別分析、生存分析等[4-7]。多層感知器(multi-layer perceptron, MLP)神經網絡是近年來應用較廣的人工神經網絡模型，屬于多層前饋神經網絡。這種網絡的顯著功能是可以通過網絡自身學習來實現高度復雜的非線性映射。而在區分單相抑郁癥和雙相障礙時，其實質也是由收集到的各種臨床資料，通過分析而獲得診斷的過程，這一過程具有非線性特點，因此本文將MLP神經網絡應用其中。
1 資料與方法
1.1 樣本資料
早期識別雙相障礙是指在出現明顯的躁狂發作之前即可判斷其發生躁狂的可能性。本研究假設，在雙相障礙患者出現躁狂發作之前，僅表現為抑郁癥狀的時候，就有一些指標可預測其雙相病程。本研究樣本數據來源于上海市精神衛生中心，共包括250例患者，設雙相障礙和復發抑郁2組，其中復發抑郁癥患者143例，雙相障礙患者107例。入組標準為：①既往或現在符合DSM-IV中心境障礙的診斷標準；②年齡14~65周歲；③初中及以上文化程度并愿意參加本研究；④有足夠的視聽水平以完成所必須的檢查；⑤排除目前患嚴重軀體疾病者；⑥排除嚴重自殺企圖者。
本研究為回顧性研究，從患者首次出現抑郁發作時的臨床特點以及HAMD、HAMA、YMRS等10項共336個條目的量表信息角度來篩選與雙相障礙相關的指標。由于各項量表條目所采用的評分等級不一致，本研究首先對所有患者各量表條目得分進行歸一化處理。在對具有相同意義的條目進行部分剔除處理后，初步篩選出87個條目(變量)進行第一次因子分析。
因子分析的數學模型用矩陣可表示為：
| $ \left[\begin{array}{l} {x_1}\\ {x_2}\\ \vdots \\ {x_p} \end{array} \right]=\left[{\begin{array}{*{20}{c}} {{a_{11}}} & {{a_{12}}} & \cdots & {{a_{1m}}}\\ {{a_{21}}} & {{a_{22}}} & \cdots & {{a_{2m}}}\\ \vdots & \vdots & {} & \vdots \\ {{a_{p1}}} & {{a_{p2}}} & \cdots & {{a_{pm}}} \end{array}} \right]\left[\begin{array}{l} {f_1}\\ {f_2}\\ \vdots \\ {f_m} \end{array} \right]+\left[\begin{array}{l} {\varepsilon _1}\\ {\varepsilon _2}\\ \vdots \\ {\varepsilon _p} \end{array} \right] $ |
簡記為：X=AF+ε，其中，X表示變量矩陣；F表示因子矩陣；A稱為載荷矩陣，表示變量在公共因子上的權重系數；ε：稱為特殊因子；p：代表變量個數；m：代表因子個數。
由于載荷矩陣A的不唯一性，可以通過旋轉變換使因子載荷結構更加簡化，使公共因子的載荷系數更接近1或更接近0，也就是使每個變量僅在一個公共因子上有較大的載荷，而在其他公共因子上只有較小或中等的載荷。對于在所有公共因子上都有較小載荷的變量，可予以剔除處理，這樣能夠進一步精簡變量。
本研究共進行6次因子提取及旋轉，最終提取出13個因子，共包含42個變量，可以作為神經網絡的輸入變量, 記為：
| $ \boldsymbol{X}=\left({{x_1}, \cdots, {x_k}, \cdots, {x_{42}}} \right) $ |
即本研究中, p=42，表示包含的變量個數為42；m=13，表示提取出的因子個數為13。每次因子分析的信息記錄如表 1所示，部分變量如表 2所示。
表1
6次因子分析信息記錄
Table1.
Information records of the factor analysis for six times
表2
部分變量列表
Table2.
Part of variable list
1.2 MLP神經網絡方法在雙相障礙識別中的應用
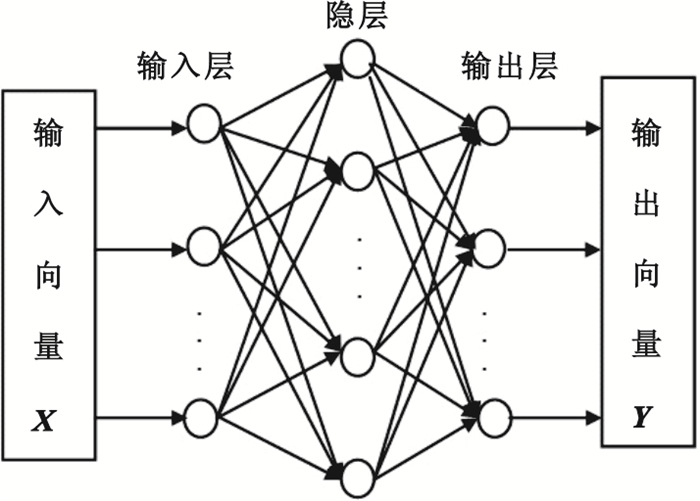
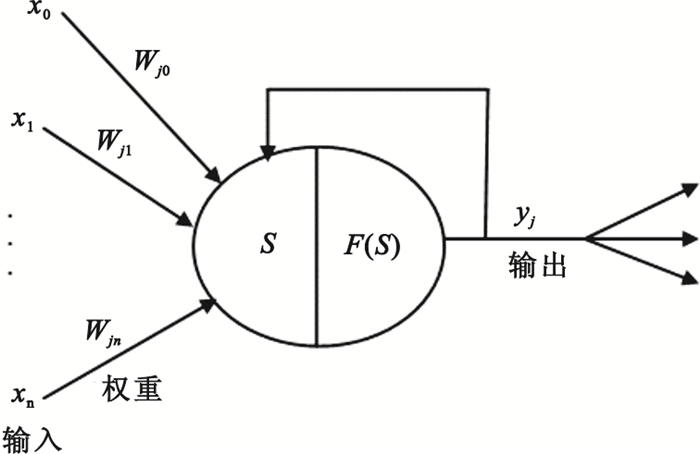
MLP神經網絡一般包括輸入層、隱層(一個或一個以上)和輸出層，其三層結構如圖 1所示。三層神經網絡(只含一個隱層)的映射關系如圖 2所示，其用數學表達方式描述如下：
| $ \boldsymbol{Y}={F_2}\left({{W_{m{\rm{ \times }}j}} \cdot {F_1}\left({{W_{j \times n}} \cdot \boldsymbol{X}} \right)} \right) $ |
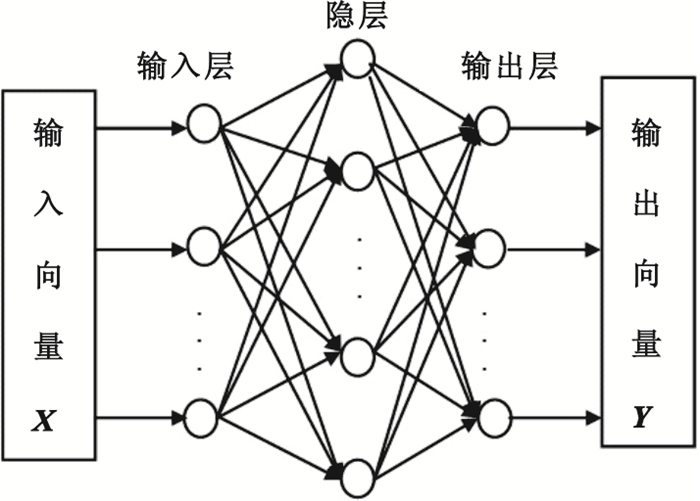圖1
三層神經網絡結構
Figure1.
Three-layer neural network structure
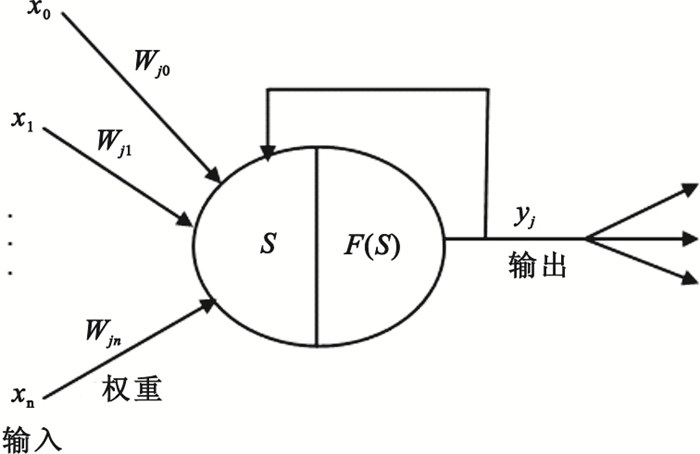圖2
神經網絡函數構成
Figure2.
Neural network function
式中X=(x1, …, xk, …, xn)，為輸入向量； Y=(y1, …, yi, …, ym)，為輸出向量；Wjk表示輸入層第k個神經元與隱層第j個神經元之間的連接權；Wij表示隱層第j個神經元與輸出層第i個神經元之間的連接權；F1表示隱層的激活函數；F2表示輸出層的激活函數。
MLP神經網絡應用在雙相障礙早期識別中的原理為：將收集到的患者變量信息X=(x1, …, xk, …, x42)組織成學習樣本，輸入到網絡中進行學習訓練。具體過程為：輸入的患者信息向量X=(x1, …, xk, …, x42)從輸入層經隱層逐層處理，并傳向輸出層，每一層神經元的狀態只影響下一層神經元的狀態。本研究中的神經網絡輸出向量為Y=(y1, y2)，(1, 0)表示單相抑郁，(0，1)表示雙相障礙。如果在網絡輸出層不能達到期望的輸出，則轉為反向傳播，將誤差信號沿原來的連接通路返回，通過修改各層神經元的權值，最終使誤差信號最小。
輸出層的單元誤差公式為：
| $ \delta _{t}^{k}\left( y_{t}^{k}-\tilde{y}_{t}^{k} \right){{F}^{'}}\left( r_{t}^{k} \right)=e_{t}^{k}{{F}^{'}}\left( r_{t}^{k} \right)\ \ \ \ t=1,2$ |
式中δtk表示輸出層單元誤差；t=1, 2代表本研究中輸出層的兩個單元；(ytk-tk)表示網絡希望輸出與實際輸出的絕對誤差etk；F′(rtk)根據各單元的實際響應調整偏差量，可見若etk為0，即網絡希望輸出與實際輸出相同，不進行誤差調整，若etk不為0，則通過F′(rtk)對其進行調整，這里的函數F即為激活函數。本研究中，激活函數F1、F2均取為Sigmoid函數，其表達式為：
| $ F(c)=1/\left({1+{e^{-c}}} \right) $ |
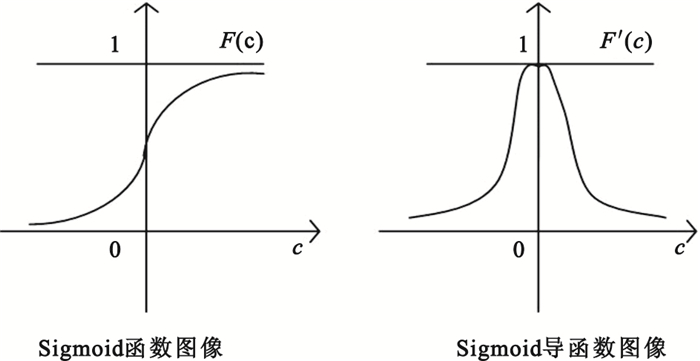
其函數及導函數圖像如圖 3所示。
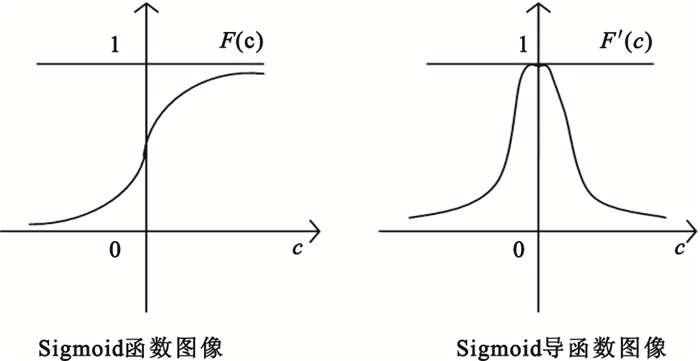圖3
Sigmoid函數及其導函數圖像
Figure3.
Images of Sigmoid and its derived function
由Sigmoid函數及其導函數可知，當輸出層某單元的輸入rtk在0附近時，其輸出變化幅度較大，而此時F′(rtk)正好處于峰值附近，當與etk項相乘后，增強了偏差的校正作用。反之，當rtk的絕對值較大時，其輸出變化幅度很小，而此時的F′(rtk)正好處于較小值位置，與etk項相乘后，減弱了偏差的校正作用。
由于誤差反向傳播，每個隱層單元的校正誤差都由兩個輸出層單元校正誤差傳遞而產生，根據計算得到輸出層和隱層單元的校正誤差之后，沿反方向調整輸出層至隱層、隱層至輸入層之間的連接權值，直到使誤差信號最小。
2 結果
本研究采用三層神經網絡結構，輸入變量為X=(x1, …, xk, …, x42)，輸出變量為Y=(y1, y2)，激活函數F1、F2均取為Sigmoid函數。對250例樣本進行兩次不同的比例分配，分別進行神經網絡的構建，結果如表 3所示。可以看出，無論對于學習樣本的檢驗還是對于測試樣本的預測，學習樣本比例較高組的結果均優于學習樣本比例較低組的結果。神經網絡的構建依賴于對學習樣本的學習，學習樣本的充足度能夠影響神經網絡結構構建的準確性以及對雙相障礙預測的準確率。同時說明神經網絡模型的可發展性及可完善性，隨著時間的推移，對不同地區樣本的學習能夠進一步發展神經網絡模型，提高其對雙相障礙的診斷準確率。
表3
三層神經網絡結構對患者的識別結果
Table3.
Identification results for patients based on three-layer neural network structure
上述結果還表明，激活函數Sigmoid能夠滿足雙相障礙識別過程的非線性映射要求，在輸出層和隱層的誤差校正方面都達到了較好的效果。而雙曲正切函數的函數特性也具有非線性，可以用于雙相障礙的識別過程。雙曲正切函數表達式為：
| $ {\rm{tanh}}\left(c \right)=\left({{e^c}-{e^{-c}}} \right)/\left({{e^c}+{e^{-c}}} \right) $ |
本研究探討了不同神經網絡結構對于雙相障礙的識別效果。與多元logistic回歸分析比較，神經網絡具有高度的容錯性，能夠通過自身學習來實現更為復雜的非線性映射。與logistic回歸分析方法給出明確的方程不同，神經網絡在分析自變量和因變量之間復雜的非線性關系時，能夠從學習樣本中挖掘規律，并給出具有確定算法與結構參數的網絡結構。因此，神經網絡能夠更有效地表述實際問題。
考慮到神經網絡的學習樣本要盡量多，同時也要保證一定數量的測試樣本，遵循隨機分配學習樣本和測試樣本的原則，按照20%的測試樣本比例，部分神經網絡結構對于測試樣本的具體識別結果如表 4所示。其中單相的正確百分比即為特異度，雙相的正確百分比即為靈敏度，準確率為模型識別患者的正確率。表 5為logistic回歸模型對于患者的識別結果。由結果可以看出，神經網絡對于雙相障礙的識別結果優于logistic回歸分析對于雙相障礙的識別結果。
表4
不同神經網絡結構對患者的識別結果
Table4.
Identification results for patients based on different neural network structure
表5
Logistic回歸分析對患者的識別結果
Table5.
Identification results for patients based on Logistic regression analysis
3 結論
正確及時的診斷對于雙相障礙患者意義重大，對臨床醫生來說也是挑戰，目前已有大量研究致力于區分單相抑郁和雙相障礙，所用方法多為基于Logistic回歸分析[8-9]。與傳統回歸分析方法給出明確的方程不同，神經網絡在分析自變量與因變量間復雜的非線性關系時，能夠從學習樣本中挖掘規律，并給出具有確定算法與結構參數的網絡結構。因此，神經網絡能夠更有效地表述實際問題，特別是當有些問題不需要或根本無法找到明確的數學公式表達時，神經網絡就更顯示出其優越性。本研究也進行了Logistic回歸分析，結果顯示，神經網絡方法的分析結果優于Logistic回歸分析結果。
本研究用MLP神經網絡方法實現了從單相抑郁癥患者中識別雙相障礙的目標，選取不同的神經網絡內部結構，對雙相障礙的識別均獲得了較好結果。其中，當采用三層神經網絡結構，激活函數F1、F2均取為Sigmoid函數時，對雙相障礙識別的靈敏度為76.7%，特異度為75.0%，準確率為75.9%。
通過從實際病例中學習，MLP神經網絡能夠完成對雙相障礙診斷信息的自動獲取，其分布式存儲和并行處理能力，使之具有一定的聯想推理和自學習能力。本研究結果表明，神經網絡方法用于雙相障礙的早期識別是可行的，但仍需指出的是，神經網絡結構復雜，其在識別雙相障礙中的應用仍有進一步的探討空間。
引言
心境障礙是指由各種原因引起的、以顯著而持久的心境或情感改變為主要特征的一組疾病[1]，單相抑郁癥與雙相障礙是心境障礙的兩種類型。雙相障礙的臨床特點是反復出現心境和活動水平的明顯改變，有時表現為心境高漲、精力充沛和活動增加, 有時表現為心境低落、精力減退和活動減少，最典型的形式是躁狂(或輕躁狂)與抑郁反復間歇交替或循環發作。
現有研究提示，相對于單相抑郁，雙相障礙具有一些較特異性的臨床表象，可在不同程度上預示其雙相的病程特點，包括：雙相家族史、藥物轉相史、混合性抑郁、非典型抑郁、精神病性癥狀、伴環性心境障礙、心境障礙頻繁發作、甲狀腺機能減退等，均可增加雙相障礙發生的可能性。但具體到每個患者，上述因素的出現概率不一，相互作用不明，尚沒有研究綜合評估各種因素與雙相障礙的相關性。
目前普遍認為，雙相障礙與單相抑郁是兩種不同的疾病，具有不同的發病機制[2]，治療方法也不相同，但臨床上早期區分卻存在很大難度。據統計，約有40%的雙相障礙患者曾被誤診為單相抑郁癥，平均誤診時間長達7.5年，約1/3的雙相障礙患者因未使用心境穩定劑而影響療效[3]，因此，雙相障礙的早期識別對雙相障礙患者具有重要意義。但迄今為止，還沒有切實可行的早期識別雙相障礙的工具和方法。
人工神經網絡是在對人腦神經網絡基本認識的基礎上，從信息處理的角度對人腦神經網絡進行抽象，用數理方法建立起來的某種簡化模型，具有高度智能化的特征與能力，其在醫學領域中可用于判別分析、生存分析等[4-7]。多層感知器(multi-layer perceptron, MLP)神經網絡是近年來應用較廣的人工神經網絡模型，屬于多層前饋神經網絡。這種網絡的顯著功能是可以通過網絡自身學習來實現高度復雜的非線性映射。而在區分單相抑郁癥和雙相障礙時，其實質也是由收集到的各種臨床資料，通過分析而獲得診斷的過程，這一過程具有非線性特點，因此本文將MLP神經網絡應用其中。
1 資料與方法
1.1 樣本資料
早期識別雙相障礙是指在出現明顯的躁狂發作之前即可判斷其發生躁狂的可能性。本研究假設，在雙相障礙患者出現躁狂發作之前，僅表現為抑郁癥狀的時候，就有一些指標可預測其雙相病程。本研究樣本數據來源于上海市精神衛生中心，共包括250例患者，設雙相障礙和復發抑郁2組，其中復發抑郁癥患者143例，雙相障礙患者107例。入組標準為：①既往或現在符合DSM-IV中心境障礙的診斷標準；②年齡14~65周歲；③初中及以上文化程度并愿意參加本研究；④有足夠的視聽水平以完成所必須的檢查；⑤排除目前患嚴重軀體疾病者；⑥排除嚴重自殺企圖者。
本研究為回顧性研究，從患者首次出現抑郁發作時的臨床特點以及HAMD、HAMA、YMRS等10項共336個條目的量表信息角度來篩選與雙相障礙相關的指標。由于各項量表條目所采用的評分等級不一致，本研究首先對所有患者各量表條目得分進行歸一化處理。在對具有相同意義的條目進行部分剔除處理后，初步篩選出87個條目(變量)進行第一次因子分析。
因子分析的數學模型用矩陣可表示為：
| $ \left[\begin{array}{l} {x_1}\\ {x_2}\\ \vdots \\ {x_p} \end{array} \right]=\left[{\begin{array}{*{20}{c}} {{a_{11}}} & {{a_{12}}} & \cdots & {{a_{1m}}}\\ {{a_{21}}} & {{a_{22}}} & \cdots & {{a_{2m}}}\\ \vdots & \vdots & {} & \vdots \\ {{a_{p1}}} & {{a_{p2}}} & \cdots & {{a_{pm}}} \end{array}} \right]\left[\begin{array}{l} {f_1}\\ {f_2}\\ \vdots \\ {f_m} \end{array} \right]+\left[\begin{array}{l} {\varepsilon _1}\\ {\varepsilon _2}\\ \vdots \\ {\varepsilon _p} \end{array} \right] $ |
簡記為：X=AF+ε，其中，X表示變量矩陣；F表示因子矩陣；A稱為載荷矩陣，表示變量在公共因子上的權重系數；ε：稱為特殊因子；p：代表變量個數；m：代表因子個數。
由于載荷矩陣A的不唯一性，可以通過旋轉變換使因子載荷結構更加簡化，使公共因子的載荷系數更接近1或更接近0，也就是使每個變量僅在一個公共因子上有較大的載荷，而在其他公共因子上只有較小或中等的載荷。對于在所有公共因子上都有較小載荷的變量，可予以剔除處理，這樣能夠進一步精簡變量。
本研究共進行6次因子提取及旋轉，最終提取出13個因子，共包含42個變量，可以作為神經網絡的輸入變量, 記為：
| $ \boldsymbol{X}=\left({{x_1}, \cdots, {x_k}, \cdots, {x_{42}}} \right) $ |
即本研究中, p=42，表示包含的變量個數為42；m=13，表示提取出的因子個數為13。每次因子分析的信息記錄如表 1所示，部分變量如表 2所示。
表1
6次因子分析信息記錄
Table1.
Information records of the factor analysis for six times
表2
部分變量列表
Table2.
Part of variable list
1.2 MLP神經網絡方法在雙相障礙識別中的應用
MLP神經網絡一般包括輸入層、隱層(一個或一個以上)和輸出層，其三層結構如圖 1所示。三層神經網絡(只含一個隱層)的映射關系如圖 2所示，其用數學表達方式描述如下：
| $ \boldsymbol{Y}={F_2}\left({{W_{m{\rm{ \times }}j}} \cdot {F_1}\left({{W_{j \times n}} \cdot \boldsymbol{X}} \right)} \right) $ |
圖1
三層神經網絡結構
Figure1.
Three-layer neural network structure
圖2
神經網絡函數構成
Figure2.
Neural network function
式中X=(x1, …, xk, …, xn)，為輸入向量； Y=(y1, …, yi, …, ym)，為輸出向量；Wjk表示輸入層第k個神經元與隱層第j個神經元之間的連接權；Wij表示隱層第j個神經元與輸出層第i個神經元之間的連接權；F1表示隱層的激活函數；F2表示輸出層的激活函數。
MLP神經網絡應用在雙相障礙早期識別中的原理為：將收集到的患者變量信息X=(x1, …, xk, …, x42)組織成學習樣本，輸入到網絡中進行學習訓練。具體過程為：輸入的患者信息向量X=(x1, …, xk, …, x42)從輸入層經隱層逐層處理，并傳向輸出層，每一層神經元的狀態只影響下一層神經元的狀態。本研究中的神經網絡輸出向量為Y=(y1, y2)，(1, 0)表示單相抑郁，(0，1)表示雙相障礙。如果在網絡輸出層不能達到期望的輸出，則轉為反向傳播，將誤差信號沿原來的連接通路返回，通過修改各層神經元的權值，最終使誤差信號最小。
輸出層的單元誤差公式為：
| $ \delta _{t}^{k}\left( y_{t}^{k}-\tilde{y}_{t}^{k} \right){{F}^{'}}\left( r_{t}^{k} \right)=e_{t}^{k}{{F}^{'}}\left( r_{t}^{k} \right)\ \ \ \ t=1,2$ |
式中δtk表示輸出層單元誤差；t=1, 2代表本研究中輸出層的兩個單元；(ytk-tk)表示網絡希望輸出與實際輸出的絕對誤差etk；F′(rtk)根據各單元的實際響應調整偏差量，可見若etk為0，即網絡希望輸出與實際輸出相同，不進行誤差調整，若etk不為0，則通過F′(rtk)對其進行調整，這里的函數F即為激活函數。本研究中，激活函數F1、F2均取為Sigmoid函數，其表達式為：
| $ F(c)=1/\left({1+{e^{-c}}} \right) $ |
其函數及導函數圖像如圖 3所示。
圖3
Sigmoid函數及其導函數圖像
Figure3.
Images of Sigmoid and its derived function
由Sigmoid函數及其導函數可知，當輸出層某單元的輸入rtk在0附近時，其輸出變化幅度較大，而此時F′(rtk)正好處于峰值附近，當與etk項相乘后，增強了偏差的校正作用。反之，當rtk的絕對值較大時，其輸出變化幅度很小，而此時的F′(rtk)正好處于較小值位置，與etk項相乘后，減弱了偏差的校正作用。
由于誤差反向傳播，每個隱層單元的校正誤差都由兩個輸出層單元校正誤差傳遞而產生，根據計算得到輸出層和隱層單元的校正誤差之后，沿反方向調整輸出層至隱層、隱層至輸入層之間的連接權值，直到使誤差信號最小。
2 結果
本研究采用三層神經網絡結構，輸入變量為X=(x1, …, xk, …, x42)，輸出變量為Y=(y1, y2)，激活函數F1、F2均取為Sigmoid函數。對250例樣本進行兩次不同的比例分配，分別進行神經網絡的構建，結果如表 3所示。可以看出，無論對于學習樣本的檢驗還是對于測試樣本的預測，學習樣本比例較高組的結果均優于學習樣本比例較低組的結果。神經網絡的構建依賴于對學習樣本的學習，學習樣本的充足度能夠影響神經網絡結構構建的準確性以及對雙相障礙預測的準確率。同時說明神經網絡模型的可發展性及可完善性，隨著時間的推移，對不同地區樣本的學習能夠進一步發展神經網絡模型，提高其對雙相障礙的診斷準確率。
表3
三層神經網絡結構對患者的識別結果
Table3.
Identification results for patients based on three-layer neural network structure
上述結果還表明，激活函數Sigmoid能夠滿足雙相障礙識別過程的非線性映射要求，在輸出層和隱層的誤差校正方面都達到了較好的效果。而雙曲正切函數的函數特性也具有非線性，可以用于雙相障礙的識別過程。雙曲正切函數表達式為：
| $ {\rm{tanh}}\left(c \right)=\left({{e^c}-{e^{-c}}} \right)/\left({{e^c}+{e^{-c}}} \right) $ |
本研究探討了不同神經網絡結構對于雙相障礙的識別效果。與多元logistic回歸分析比較，神經網絡具有高度的容錯性，能夠通過自身學習來實現更為復雜的非線性映射。與logistic回歸分析方法給出明確的方程不同，神經網絡在分析自變量和因變量之間復雜的非線性關系時，能夠從學習樣本中挖掘規律，并給出具有確定算法與結構參數的網絡結構。因此，神經網絡能夠更有效地表述實際問題。
考慮到神經網絡的學習樣本要盡量多，同時也要保證一定數量的測試樣本，遵循隨機分配學習樣本和測試樣本的原則，按照20%的測試樣本比例，部分神經網絡結構對于測試樣本的具體識別結果如表 4所示。其中單相的正確百分比即為特異度，雙相的正確百分比即為靈敏度，準確率為模型識別患者的正確率。表 5為logistic回歸模型對于患者的識別結果。由結果可以看出，神經網絡對于雙相障礙的識別結果優于logistic回歸分析對于雙相障礙的識別結果。
表4
不同神經網絡結構對患者的識別結果
Table4.
Identification results for patients based on different neural network structure
表5
Logistic回歸分析對患者的識別結果
Table5.
Identification results for patients based on Logistic regression analysis
3 結論
正確及時的診斷對于雙相障礙患者意義重大，對臨床醫生來說也是挑戰，目前已有大量研究致力于區分單相抑郁和雙相障礙，所用方法多為基于Logistic回歸分析[8-9]。與傳統回歸分析方法給出明確的方程不同，神經網絡在分析自變量與因變量間復雜的非線性關系時，能夠從學習樣本中挖掘規律，并給出具有確定算法與結構參數的網絡結構。因此，神經網絡能夠更有效地表述實際問題，特別是當有些問題不需要或根本無法找到明確的數學公式表達時，神經網絡就更顯示出其優越性。本研究也進行了Logistic回歸分析，結果顯示，神經網絡方法的分析結果優于Logistic回歸分析結果。
本研究用MLP神經網絡方法實現了從單相抑郁癥患者中識別雙相障礙的目標，選取不同的神經網絡內部結構，對雙相障礙的識別均獲得了較好結果。其中，當采用三層神經網絡結構，激活函數F1、F2均取為Sigmoid函數時，對雙相障礙識別的靈敏度為76.7%，特異度為75.0%，準確率為75.9%。
通過從實際病例中學習，MLP神經網絡能夠完成對雙相障礙診斷信息的自動獲取，其分布式存儲和并行處理能力，使之具有一定的聯想推理和自學習能力。本研究結果表明，神經網絡方法用于雙相障礙的早期識別是可行的，但仍需指出的是，神經網絡結構復雜，其在識別雙相障礙中的應用仍有進一步的探討空間。
