警覺度是人在一段時間里保持持續注意力的能力。為了探求在工作過程中警覺度隨時間的變化規律,本文設計了以三位數加減法來誘導警覺度發生變化的實驗,并通過警覺度任務(PVT)實驗結合腦電測量該變化過程,提取并分析了11例受試者腦電信號排列熵(PE)這一復雜性度量,并與非線性參數樣本熵(SE)做了簡要比較。實驗結果表明:該算法可以很好地反映警覺度下降時腦電信號的動態變化過程,且運算速度快,抗噪能力強,對腦電信號長度要求低,可以作為衡量大腦警覺度的指標。
引用本文： 趙云龍, 王學民, 薛然婷, 王曉璐, 高翔, 明東, 綦宏志, 周鵬. 基于復雜性度量的大腦警覺度分析. 生物醫學工程學雜志, 2015, 32(4): 725-729. doi: 10.7507/1001-5515.20150132 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
警覺度[1]是指生物體能夠維持注意力并且在較長時間內對刺激保持警惕性的能力。隨著現代科技的進步，人類在工作中的角色逐漸發生了改變：越來越多的機器代替了人類的勞動角色，使得人類從原來機器的操作者變成了機器的監控者。在氣象、醫療、軍事等多種領域中[2-3]，我們所從事的工作就是對機器上一些特定信號的發生進行監測并做出快速反應：一般情況下這些信號發生的概率很低，甚至很多時候是偶發或不發的，但是一旦發生而機器的操作者沒有及時做出相應反應，就會造成無法挽回的后果。因此對于警覺度的研究也越來越廣泛。
警覺度的研究發展到今天，已有七十多年的歷史，對警覺度的檢測方法包括主觀評價、生物反應測試、生理信號檢測、生物化學法[4-8]等四種主要方法。其中生理信號是直接反映人體變化的信號，在警覺度檢測中的應用越來越廣泛。由于能夠比較準確地反映大腦警覺度的變化，腦電信號的研究越來越受到學者的關注。但是由于腦電信號一般比較微弱，且容易受到環境的影響，因此對于腦電信號的研究目前還屬于實驗室研究階段。
針對于腦電信號微弱、信噪比低、非平穩性等特點，本文提出了提取非平穩信號排列熵的方法，應用這種基于復雜性度量的非線性參數對腦電信號進行腦警覺度研究。排列熵作為一種較新的數學統計方法，最早是由Bandt等[9]提出的一種衡量時間序列復雜度的平均熵參數，該算法受到了國內外學者的重視，并且應用到了包括醫學、生物、氣候、圖像處理在內的多個領域，效果顯著，具有很強的適應性,在近幾年也逐漸引入到了生理信號諸如心、腦電信號的分析當中[10]。在醫學上，Nicolaou等[11]通過提取信號排列熵特征實現了對癲癇患者腦電信號的分類識別；Frank等[12]利用排列熵研究了心率波動復雜性與行為狀態之間的關系；劉建平等[13]通過提取腦電信號排列熵這種復雜性測度研究了排列熵與腦疲勞程度檢測的關系。以上研究都給本文的研究奠定了基礎。因此本文試圖用排列熵的方法對腦警覺度進行研究，分析人腦警覺度發生變化時腦電時間復雜度的變化趨勢，為警覺度研究開辟一條道路。
1 實驗方法
1.1 實驗環境和受試者
本實驗的受試對象共11名，均為在校學生，6名男性，5名女性，平均年齡為23.3歲,平均受教育時間為16.3年。被試身體健康且日常作息時間規律；均為右利手，無既往疾病史。實驗室環境舒適且安靜，室溫保持26 ℃，盡量排除因環境因素所造成的警覺度發生變化的影響。所有被試在實驗過程中均使用同一臺電腦，保證了實驗各項參數不變。
本實驗使用奧地利EMS公司生產的Phoenix數字腦電系統來記錄腦電信號。極帽電極放置位置遵循國際標準的10-20系統，以右耳(A2)為參考電極，記錄19導腦電數據。腦電采集放大器放大倍數為4 096，采樣率為256 Hz；腦電儀內置帶通濾波器，濾波范圍為0.05~70 Hz。
1.2 實驗流程
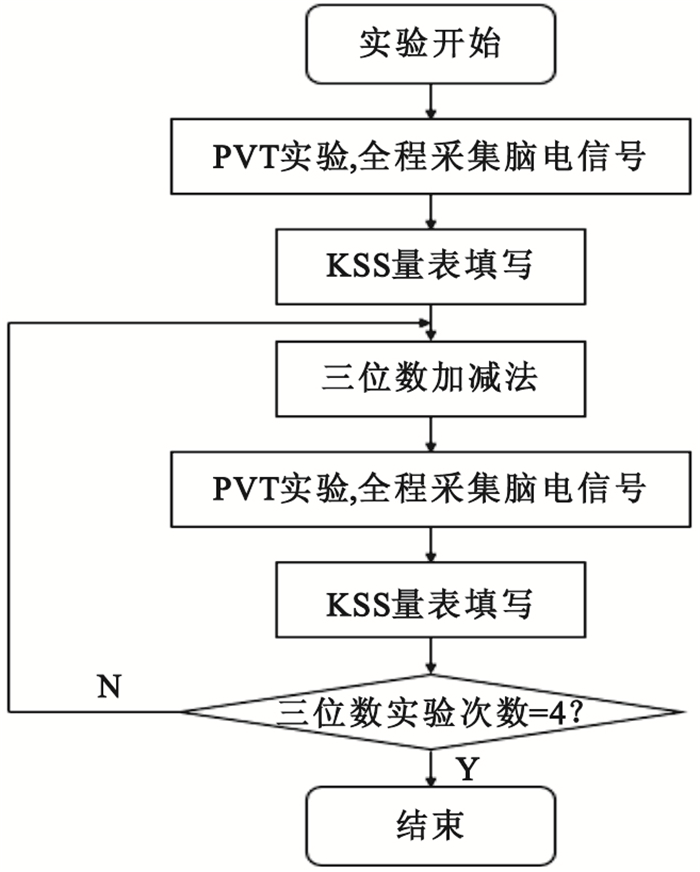
實驗要求受試者實驗前一周不可飲用含有酒精或者咖啡因的飲品及藥品，并在實驗前一天進入實驗室了解實驗程序和要求，嚴格按照流程進行實驗操作，實驗過程中不可退出。被試者在實驗開始前一天要正常作息，保證充足睡眠；實驗當天上午不進行劇烈的腦體力勞動，午休半小時后進入實驗進行持續時間2~3 h的實驗。實驗于14∶00開始，實驗室內無時間參考裝置(環境無時間)，保證被試不知道當前時間且不預知整個實驗流程所持續時間。實驗共分四個模塊，每個模塊包括兩個任務：心算任務和警覺度任務(psychomotor vigilance task,PVT)實驗。整個實驗共包含4個心算任務和5個PVT實驗。實驗流程如圖 1所示 。
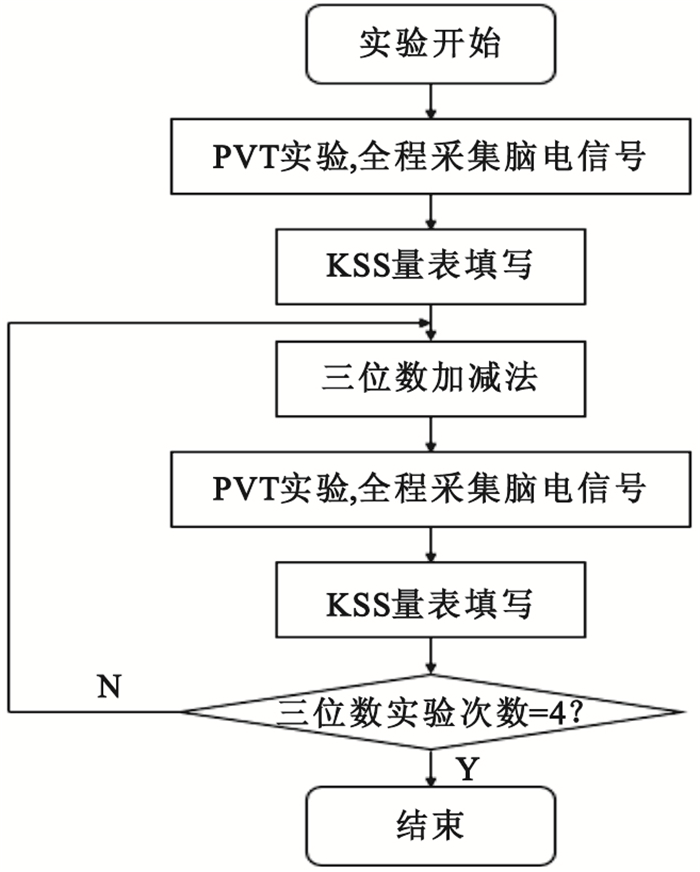圖1
實驗流程
Figure1.
Experimental procedure
(1)三位數加減法
即為心算任務，目的是為被試增加精神負荷，使被試警覺發生改變。任務要求被試完成出現在電腦屏幕上的160道三位數加減法計算題(其中80道加法題)，心算任務無重復題目。
(2)PVT實驗[14]
單次PVT實驗持續時間為10 min。該任務要求被試對以不確定時間間隔出現在電腦屏幕中的一個黃色警報標記快速做出反應，當警報標記出現在屏幕中央時，被試就按回車鍵作為響應，此時毫秒計數器就會停止計數，持續顯示1 s后消失。黃色警示標記以隨機的時間間隔(2~10 s)出現，避免了被試對警報標記的預判，提前按鍵或是按錯鍵均認為是發生了錯誤。將五個PVT實驗記為時段1到時段5，實驗過程中同步記錄被試的腦電數據。
(3)主觀量表
在每次PVT實驗后，被試者填寫卡羅林斯卡嗜睡量表(Karolinska Sleepiness Scale,KSS)，對當前的警覺度狀態迅速做一個評分。該量表將警覺度狀態分為9個等級，分別為：極度警覺(計1分)；非常警覺(計2分)；警覺(計3分)；一般警覺(計4分)；不太警覺但也無困意(計5分)；有一些困意傾向(計6分)；有困意，但是不需要太多努力保持清醒(計7分)；有困意，且需要一定的努力保持清醒(計8分)；非常困倦，需要極大的努力保持清醒(計9分)。得分越高說明當前被試者警覺度狀態越差。
2 數據處理方法
2.1 預處理
腦電信號本身較為微弱且易受環境和被試因素影響。本研究采用腦電記錄儀處理來自環境的干擾,在采集過程中對信號進行了帶通濾波(0.05~70Hz)和工頻干擾濾波;用直接剔除的方來處理體動干擾，而由眼電偽跡等小信號所引起的干擾則通過獨立成分分析(independent component analysis，ICA)的方式濾除。
2.2 復雜性度量
排列熵計算簡單且快速、抗噪能力強，同時對數據量的要求不高，僅需較短的序列就能得到一個穩定的值[15]，因此本文提出了用這種方法來進行腦警覺度研究。算法[16]如下：
(1)設一個長度為N的一維時間序列{x(i),i=1,2,…,n},對其中任意一個元素x(i)進行空間重構，得到一個重構向量：
| ${X_i}=\left[{x\left(i \right),x\left({i+l} \right), \cdots,x\left({i+m\left({- 1} \right)l} \right)} \right],$ |
其中，m為嵌入維數，l為延遲時間。經研究發現，嵌入維數與延遲時間影響信號的區分度以及信號的變化趨勢，且嵌入維數m取3～9、時間延遲l取1～4范圍內最佳，最終在本文中m取值為5，l取值為2。
(2)對Xi的m個重構分量進行升序排列，得到：
| $x\left({i+\left({{j_1}- 1} \right)l} \right) \le x\left({i+\left({{j_2}- 1} \right)l} \right) \le \cdots \le x\left({i+\left({{j_m}- 1} \right)l} \right)$ |
(3)如果存在x(i+(ji1-1)l)=x(i+(ji2-1)l),此時就按j的大小進行排序，也就是當ji1<ji2時，有x(i+(ji1-1)l)≤x(i+(ji2-1)l)，所以任意一個向量Xi都可以得到一組序列符號
| $A\left(g \right)=\left[{{j_1},{j_2}, \cdots {j_m}} \right],$ |
式中g=1,2,…,k,且k≤ml,m個不同的符號[j1,j2,…,jm]一共有m!種不同的排列，符號序列A(g)是其中一種，記錄每一個符號序列A(g)的出現次數Nk并計算其概率P1,P2,…,Pk,k≤m!，其中。
(4)由Shannon信息熵的定義計算排列熵：
| $H\left(m \right)=- \sum\limits_{i=1}^k {{P_i}\ln {P_i}} $ |
當Pi=1/m!時，H(m)達到最大值ln(m!)。
(5)用ln(m!)將H(m)進行歸一化處理，得到
| $0 \le H=H/\ln \left({m!} \right) \le 1$ |
排列熵H(m)大小表示了時間序列x(i)的隨機程度，H(m)的值越大，說明時間序列越接近隨機；反之，則說明時間序列越規則。
3 實驗結果
3.1 數據標注
本文的目的是為了驗證排列熵方法研究警覺度的可行性，因此需要先對信號進行標注，作為驗證該算法的先驗知識，同時也能驗證算法效果。本文的數據標注主要結合兩部分內容：KSS主觀量表以及PVT實驗的平均反應時間和錯誤指標。
3.1.1 主觀量表結果
從表 1中可以看到，在時段1時大部分被試的KSS評分得分為4分左右，這與大部分被試在任務剛開始時的警覺度狀態相符合；在時段5時，KSS評分在8分左右，即有困意。可以看到，11名被試者的KSS的平均得分在整個實驗過程中逐漸升高，即為警覺度下降趨勢。
表1
KSS主觀量表得分
Table1.
Score of KSS
3.1.2 PVT實驗
(1)平均反應時間
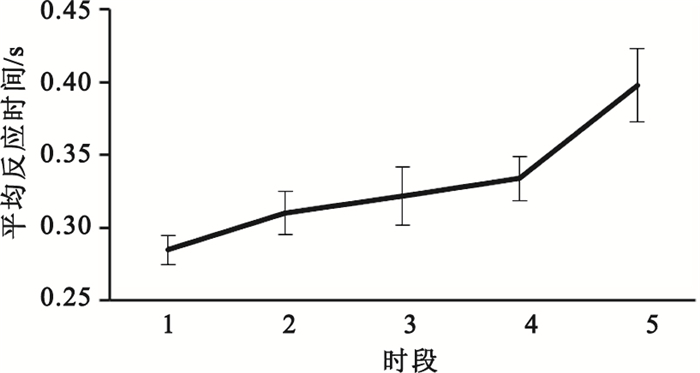
本文對十一名受試者5個不同時段的PVT實驗做了統計，并對11人5個時段的反應時間做了平均統計，從圖 2中可以看出，隨著實驗的進行，被試者腦力負荷不斷加大，警覺度下降，被試者平均反應時間呈現明顯上升的趨勢。
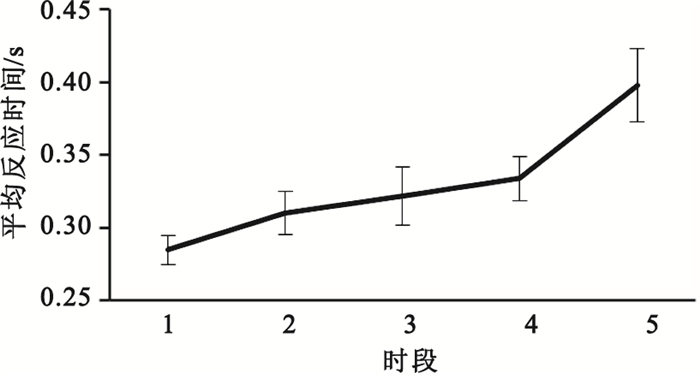圖2
PVT實驗的平均反應時間趨勢
Figure2.
Trend of average response time of PVT
(2)錯誤指標
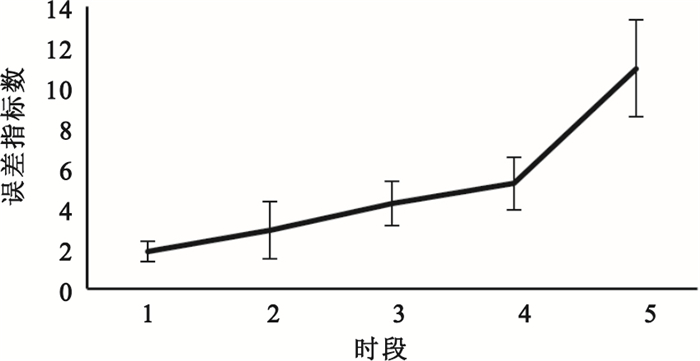
本文將反應時間小于100 ms的錯誤信號及反應時間大于500 ms的失誤信號合并為PVT錯誤指標并做了數據統計，其變化趨勢見圖 3。從圖中可以看出，隨著時間的增加，腦力資源消耗增大，精神負荷量逐漸增加，被試的錯誤指標數呈現明顯的升高趨勢。
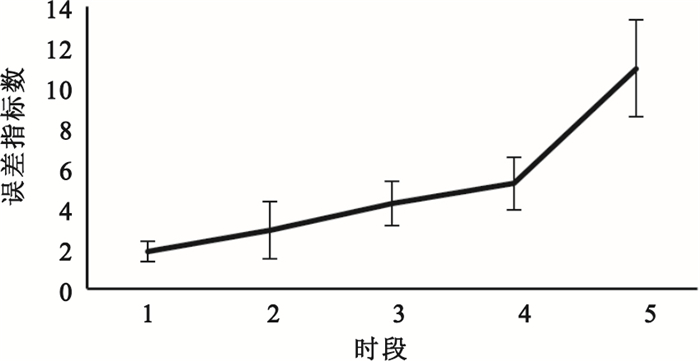圖3
PVT錯誤指標數變化趨勢
Figure3.
Trend of error indicators of PVT
3.2 腦電信號分析
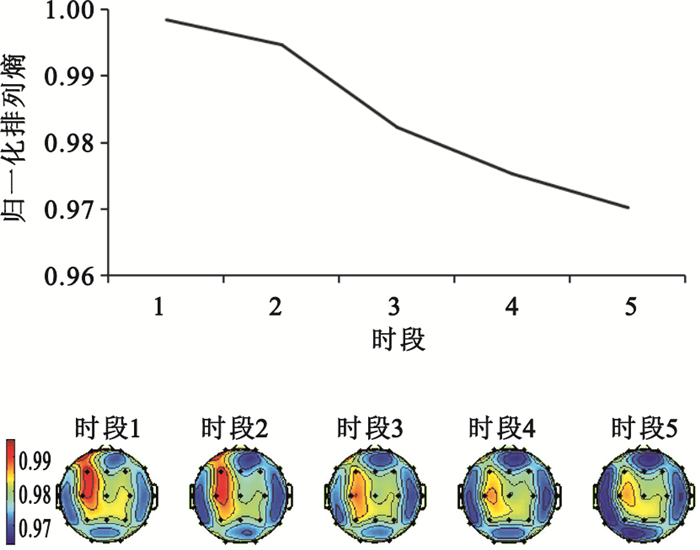
根據上文所介紹的方法，本文計算了被試者19導腦電信號的排列熵并繪制了腦地形圖(見圖 4)。
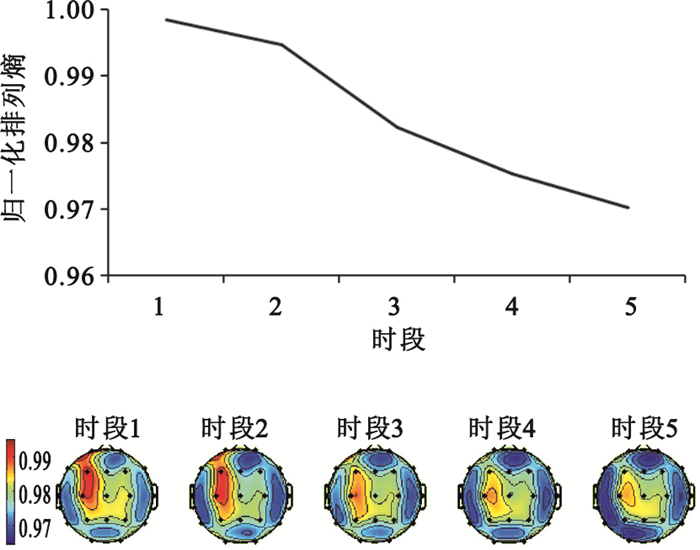圖4
排列熵變化趨勢
Figure4.
Trend of permutation entropy
在圖 4中，排列熵在實驗中一直處于下降的趨勢，下降趨勢體現在整個腦區，這與KSS量表和PVT實驗統計數據相吻合，且從時段3開始腦電復雜度明顯下降，體現復雜性的排列熵值明顯降低；同時，通過圖 4也可以觀察到，排列熵主要分布在腦區的頂葉和額葉兩個區域，這與頂葉、額葉負責思維、演算、相應數學和邏輯相吻合，且隨著負荷強度變大，被試者出現錯誤的概率提高，排列熵在以上兩個腦區的熵值也呈現出明顯的下降趨勢。
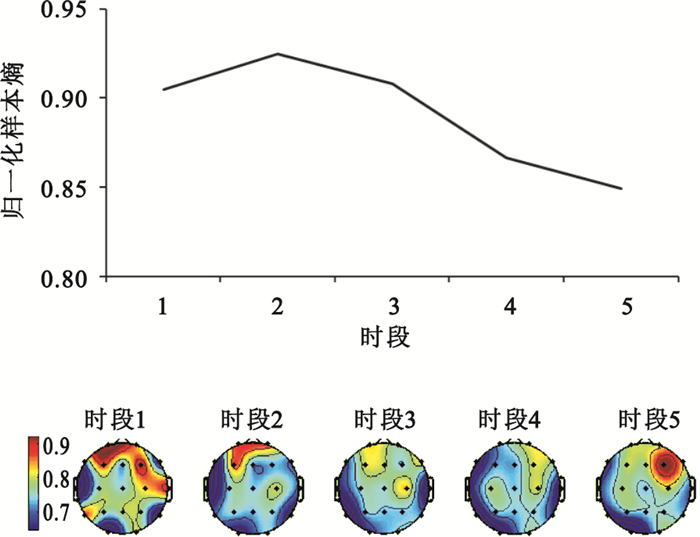
在得到排列熵算法計算得出的被試警覺度變化趨勢后，為了驗證該算法的優勢及正確性，本文又提取了被試者腦電信號的非線性參數樣本熵做簡要比較。在樣本熵算法中，所采用的數據和實驗方法與排列熵算法相同。圖 5為本組受試者腦電信號樣本熵的變化趨勢圖。
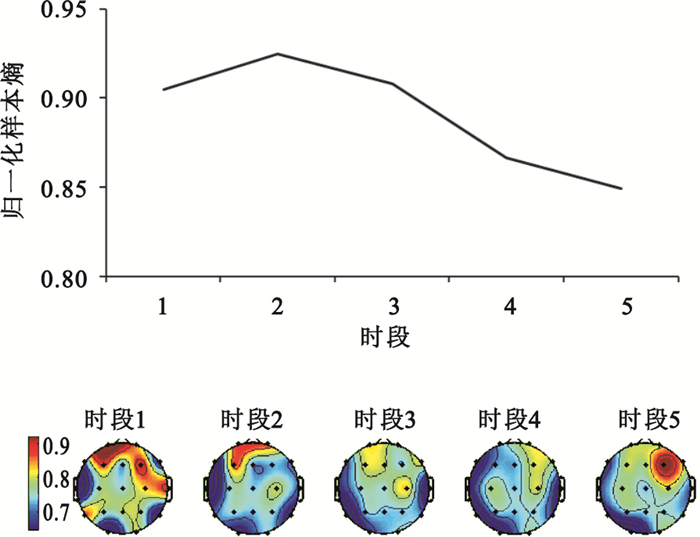圖5
樣本熵變化趨勢
Figure5.
Trend of sample entropy
從圖 5可以觀察到，被試樣本熵整體趨勢為下降趨勢，這與前文所述KSS、PVT所得數據以及排列熵所分析結果相吻合，但在時段2有一個明顯的上升，與前文描述的趨勢有一定差別。與排列熵相比，該算法同樣有一定抗噪能力，僅需要較短的信號長度就可得到穩定值，但樣本熵在算法原理上對數據有一定要求，需要限定在75~5 000，且在該算法閾值r的選取上也有限定范圍0.1~0.25，超出這個范圍會導致滿足條件的模式發生偏差。
通過上面的比較可以發現，同樣作為非線性指標，排列熵較樣本熵有著更簡便的算法，對數據量的選取沒有嚴格要求，且所求結果更接近警覺度變化趨勢，所以本文得出的結論是排列熵算法在警覺度研究中切實可行。
4 討論
在警覺度研究中，以往的研究大多著眼于長時間腦力工作以后警覺度狀態與初始狀態的對比研究，而忽略了警覺度在整個過程中的變化趨勢；研究方法大多集中在時域、頻域分析，對于腦電信號非線性分析應用較少。本文針對這些現狀，提出了用排列熵描述腦電信號時間復雜度的方法來研究在負荷狀態下大腦警覺度的變化趨勢，設計了三位數加減法的腦力負荷模式來引導被試者警覺度發生變化，并結合PVT實驗的平均反應時間、錯誤指標數及KSS主觀向量表對警覺度狀態進行標記，計算了腦電信號排列熵并與上述標注數據及通用的樣本熵算法進行了比對。結果顯示該算法下整個腦區的排列熵峰值出現在頂葉和額葉兩個區域，這與本實驗設計中所采用的三位數加減法以增加大腦負荷有直接聯系；隨著被試者警覺度下降，整個腦區的排列熵都呈現出明顯的下降趨勢，且頂葉和額葉兩區下降趨勢尤為明顯，這與PVT試驗中的平均反應時間、錯誤指標、KSS值的變化均相符，即該算法能夠反映出在警覺度下降過程中腦電信號熵值的下降趨勢。在算法比較上，本文將排列熵與樣本熵做了比較，從結果中可以看出，與樣本熵相比，排列熵更能準確地反映出警覺度下降過程中腦電信號熵的下降趨勢，且算法簡便，在數據長度要求上比樣本熵更為寬松。綜上所述，排列熵可以作為研究大腦警覺的一種方法，且在今后的實驗設計中，將繼續加入諸如心電信號等多生理信號的聯合分析，使實驗結果更加客觀可信。
引言
警覺度[1]是指生物體能夠維持注意力并且在較長時間內對刺激保持警惕性的能力。隨著現代科技的進步，人類在工作中的角色逐漸發生了改變：越來越多的機器代替了人類的勞動角色，使得人類從原來機器的操作者變成了機器的監控者。在氣象、醫療、軍事等多種領域中[2-3]，我們所從事的工作就是對機器上一些特定信號的發生進行監測并做出快速反應：一般情況下這些信號發生的概率很低，甚至很多時候是偶發或不發的，但是一旦發生而機器的操作者沒有及時做出相應反應，就會造成無法挽回的后果。因此對于警覺度的研究也越來越廣泛。
警覺度的研究發展到今天，已有七十多年的歷史，對警覺度的檢測方法包括主觀評價、生物反應測試、生理信號檢測、生物化學法[4-8]等四種主要方法。其中生理信號是直接反映人體變化的信號，在警覺度檢測中的應用越來越廣泛。由于能夠比較準確地反映大腦警覺度的變化，腦電信號的研究越來越受到學者的關注。但是由于腦電信號一般比較微弱，且容易受到環境的影響，因此對于腦電信號的研究目前還屬于實驗室研究階段。
針對于腦電信號微弱、信噪比低、非平穩性等特點，本文提出了提取非平穩信號排列熵的方法，應用這種基于復雜性度量的非線性參數對腦電信號進行腦警覺度研究。排列熵作為一種較新的數學統計方法，最早是由Bandt等[9]提出的一種衡量時間序列復雜度的平均熵參數，該算法受到了國內外學者的重視，并且應用到了包括醫學、生物、氣候、圖像處理在內的多個領域，效果顯著，具有很強的適應性,在近幾年也逐漸引入到了生理信號諸如心、腦電信號的分析當中[10]。在醫學上，Nicolaou等[11]通過提取信號排列熵特征實現了對癲癇患者腦電信號的分類識別；Frank等[12]利用排列熵研究了心率波動復雜性與行為狀態之間的關系；劉建平等[13]通過提取腦電信號排列熵這種復雜性測度研究了排列熵與腦疲勞程度檢測的關系。以上研究都給本文的研究奠定了基礎。因此本文試圖用排列熵的方法對腦警覺度進行研究，分析人腦警覺度發生變化時腦電時間復雜度的變化趨勢，為警覺度研究開辟一條道路。
1 實驗方法
1.1 實驗環境和受試者
本實驗的受試對象共11名，均為在校學生，6名男性，5名女性，平均年齡為23.3歲,平均受教育時間為16.3年。被試身體健康且日常作息時間規律；均為右利手，無既往疾病史。實驗室環境舒適且安靜，室溫保持26 ℃，盡量排除因環境因素所造成的警覺度發生變化的影響。所有被試在實驗過程中均使用同一臺電腦，保證了實驗各項參數不變。
本實驗使用奧地利EMS公司生產的Phoenix數字腦電系統來記錄腦電信號。極帽電極放置位置遵循國際標準的10-20系統，以右耳(A2)為參考電極，記錄19導腦電數據。腦電采集放大器放大倍數為4 096，采樣率為256 Hz；腦電儀內置帶通濾波器，濾波范圍為0.05~70 Hz。
1.2 實驗流程
實驗要求受試者實驗前一周不可飲用含有酒精或者咖啡因的飲品及藥品，并在實驗前一天進入實驗室了解實驗程序和要求，嚴格按照流程進行實驗操作，實驗過程中不可退出。被試者在實驗開始前一天要正常作息，保證充足睡眠；實驗當天上午不進行劇烈的腦體力勞動，午休半小時后進入實驗進行持續時間2~3 h的實驗。實驗于14∶00開始，實驗室內無時間參考裝置(環境無時間)，保證被試不知道當前時間且不預知整個實驗流程所持續時間。實驗共分四個模塊，每個模塊包括兩個任務：心算任務和警覺度任務(psychomotor vigilance task,PVT)實驗。整個實驗共包含4個心算任務和5個PVT實驗。實驗流程如圖 1所示 。
圖1
實驗流程
Figure1.
Experimental procedure
(1)三位數加減法
即為心算任務，目的是為被試增加精神負荷，使被試警覺發生改變。任務要求被試完成出現在電腦屏幕上的160道三位數加減法計算題(其中80道加法題)，心算任務無重復題目。
(2)PVT實驗[14]
單次PVT實驗持續時間為10 min。該任務要求被試對以不確定時間間隔出現在電腦屏幕中的一個黃色警報標記快速做出反應，當警報標記出現在屏幕中央時，被試就按回車鍵作為響應，此時毫秒計數器就會停止計數，持續顯示1 s后消失。黃色警示標記以隨機的時間間隔(2~10 s)出現，避免了被試對警報標記的預判，提前按鍵或是按錯鍵均認為是發生了錯誤。將五個PVT實驗記為時段1到時段5，實驗過程中同步記錄被試的腦電數據。
(3)主觀量表
在每次PVT實驗后，被試者填寫卡羅林斯卡嗜睡量表(Karolinska Sleepiness Scale,KSS)，對當前的警覺度狀態迅速做一個評分。該量表將警覺度狀態分為9個等級，分別為：極度警覺(計1分)；非常警覺(計2分)；警覺(計3分)；一般警覺(計4分)；不太警覺但也無困意(計5分)；有一些困意傾向(計6分)；有困意，但是不需要太多努力保持清醒(計7分)；有困意，且需要一定的努力保持清醒(計8分)；非常困倦，需要極大的努力保持清醒(計9分)。得分越高說明當前被試者警覺度狀態越差。
2 數據處理方法
2.1 預處理
腦電信號本身較為微弱且易受環境和被試因素影響。本研究采用腦電記錄儀處理來自環境的干擾,在采集過程中對信號進行了帶通濾波(0.05~70Hz)和工頻干擾濾波;用直接剔除的方來處理體動干擾，而由眼電偽跡等小信號所引起的干擾則通過獨立成分分析(independent component analysis，ICA)的方式濾除。
2.2 復雜性度量
排列熵計算簡單且快速、抗噪能力強，同時對數據量的要求不高，僅需較短的序列就能得到一個穩定的值[15]，因此本文提出了用這種方法來進行腦警覺度研究。算法[16]如下：
(1)設一個長度為N的一維時間序列{x(i),i=1,2,…,n},對其中任意一個元素x(i)進行空間重構，得到一個重構向量：
| ${X_i}=\left[{x\left(i \right),x\left({i+l} \right), \cdots,x\left({i+m\left({- 1} \right)l} \right)} \right],$ |
其中，m為嵌入維數，l為延遲時間。經研究發現，嵌入維數與延遲時間影響信號的區分度以及信號的變化趨勢，且嵌入維數m取3～9、時間延遲l取1～4范圍內最佳，最終在本文中m取值為5，l取值為2。
(2)對Xi的m個重構分量進行升序排列，得到：
| $x\left({i+\left({{j_1}- 1} \right)l} \right) \le x\left({i+\left({{j_2}- 1} \right)l} \right) \le \cdots \le x\left({i+\left({{j_m}- 1} \right)l} \right)$ |
(3)如果存在x(i+(ji1-1)l)=x(i+(ji2-1)l),此時就按j的大小進行排序，也就是當ji1<ji2時，有x(i+(ji1-1)l)≤x(i+(ji2-1)l)，所以任意一個向量Xi都可以得到一組序列符號
| $A\left(g \right)=\left[{{j_1},{j_2}, \cdots {j_m}} \right],$ |
式中g=1,2,…,k,且k≤ml,m個不同的符號[j1,j2,…,jm]一共有m!種不同的排列，符號序列A(g)是其中一種，記錄每一個符號序列A(g)的出現次數Nk并計算其概率P1,P2,…,Pk,k≤m!，其中。
(4)由Shannon信息熵的定義計算排列熵：
| $H\left(m \right)=- \sum\limits_{i=1}^k {{P_i}\ln {P_i}} $ |
當Pi=1/m!時，H(m)達到最大值ln(m!)。
(5)用ln(m!)將H(m)進行歸一化處理，得到
| $0 \le H=H/\ln \left({m!} \right) \le 1$ |
排列熵H(m)大小表示了時間序列x(i)的隨機程度，H(m)的值越大，說明時間序列越接近隨機；反之，則說明時間序列越規則。
3 實驗結果
3.1 數據標注
本文的目的是為了驗證排列熵方法研究警覺度的可行性，因此需要先對信號進行標注，作為驗證該算法的先驗知識，同時也能驗證算法效果。本文的數據標注主要結合兩部分內容：KSS主觀量表以及PVT實驗的平均反應時間和錯誤指標。
3.1.1 主觀量表結果
從表 1中可以看到，在時段1時大部分被試的KSS評分得分為4分左右，這與大部分被試在任務剛開始時的警覺度狀態相符合；在時段5時，KSS評分在8分左右，即有困意。可以看到，11名被試者的KSS的平均得分在整個實驗過程中逐漸升高，即為警覺度下降趨勢。
表1
KSS主觀量表得分
Table1.
Score of KSS
3.1.2 PVT實驗
(1)平均反應時間
本文對十一名受試者5個不同時段的PVT實驗做了統計，并對11人5個時段的反應時間做了平均統計，從圖 2中可以看出，隨著實驗的進行，被試者腦力負荷不斷加大，警覺度下降，被試者平均反應時間呈現明顯上升的趨勢。
圖2
PVT實驗的平均反應時間趨勢
Figure2.
Trend of average response time of PVT
(2)錯誤指標
本文將反應時間小于100 ms的錯誤信號及反應時間大于500 ms的失誤信號合并為PVT錯誤指標并做了數據統計，其變化趨勢見圖 3。從圖中可以看出，隨著時間的增加，腦力資源消耗增大，精神負荷量逐漸增加，被試的錯誤指標數呈現明顯的升高趨勢。
圖3
PVT錯誤指標數變化趨勢
Figure3.
Trend of error indicators of PVT
3.2 腦電信號分析
根據上文所介紹的方法，本文計算了被試者19導腦電信號的排列熵并繪制了腦地形圖(見圖 4)。
圖4
排列熵變化趨勢
Figure4.
Trend of permutation entropy
在圖 4中，排列熵在實驗中一直處于下降的趨勢，下降趨勢體現在整個腦區，這與KSS量表和PVT實驗統計數據相吻合，且從時段3開始腦電復雜度明顯下降，體現復雜性的排列熵值明顯降低；同時，通過圖 4也可以觀察到，排列熵主要分布在腦區的頂葉和額葉兩個區域，這與頂葉、額葉負責思維、演算、相應數學和邏輯相吻合，且隨著負荷強度變大，被試者出現錯誤的概率提高，排列熵在以上兩個腦區的熵值也呈現出明顯的下降趨勢。
在得到排列熵算法計算得出的被試警覺度變化趨勢后，為了驗證該算法的優勢及正確性，本文又提取了被試者腦電信號的非線性參數樣本熵做簡要比較。在樣本熵算法中，所采用的數據和實驗方法與排列熵算法相同。圖 5為本組受試者腦電信號樣本熵的變化趨勢圖。
圖5
樣本熵變化趨勢
Figure5.
Trend of sample entropy
從圖 5可以觀察到，被試樣本熵整體趨勢為下降趨勢，這與前文所述KSS、PVT所得數據以及排列熵所分析結果相吻合，但在時段2有一個明顯的上升，與前文描述的趨勢有一定差別。與排列熵相比，該算法同樣有一定抗噪能力，僅需要較短的信號長度就可得到穩定值，但樣本熵在算法原理上對數據有一定要求，需要限定在75~5 000，且在該算法閾值r的選取上也有限定范圍0.1~0.25，超出這個范圍會導致滿足條件的模式發生偏差。
通過上面的比較可以發現，同樣作為非線性指標，排列熵較樣本熵有著更簡便的算法，對數據量的選取沒有嚴格要求，且所求結果更接近警覺度變化趨勢，所以本文得出的結論是排列熵算法在警覺度研究中切實可行。
4 討論
在警覺度研究中，以往的研究大多著眼于長時間腦力工作以后警覺度狀態與初始狀態的對比研究，而忽略了警覺度在整個過程中的變化趨勢；研究方法大多集中在時域、頻域分析，對于腦電信號非線性分析應用較少。本文針對這些現狀，提出了用排列熵描述腦電信號時間復雜度的方法來研究在負荷狀態下大腦警覺度的變化趨勢，設計了三位數加減法的腦力負荷模式來引導被試者警覺度發生變化，并結合PVT實驗的平均反應時間、錯誤指標數及KSS主觀向量表對警覺度狀態進行標記，計算了腦電信號排列熵并與上述標注數據及通用的樣本熵算法進行了比對。結果顯示該算法下整個腦區的排列熵峰值出現在頂葉和額葉兩個區域，這與本實驗設計中所采用的三位數加減法以增加大腦負荷有直接聯系；隨著被試者警覺度下降，整個腦區的排列熵都呈現出明顯的下降趨勢，且頂葉和額葉兩區下降趨勢尤為明顯，這與PVT試驗中的平均反應時間、錯誤指標、KSS值的變化均相符，即該算法能夠反映出在警覺度下降過程中腦電信號熵值的下降趨勢。在算法比較上，本文將排列熵與樣本熵做了比較，從結果中可以看出，與樣本熵相比，排列熵更能準確地反映出警覺度下降過程中腦電信號熵的下降趨勢，且算法簡便，在數據長度要求上比樣本熵更為寬松。綜上所述，排列熵可以作為研究大腦警覺的一種方法，且在今后的實驗設計中，將繼續加入諸如心電信號等多生理信號的聯合分析，使實驗結果更加客觀可信。
