超聲衍射層析成像(UDT)具有分辨率高、對致密組織敏感等特點,具有很高的臨床應用價值。為了抑制偽影,提高圖像重建質量,傳統的插值算法需要大量的投影次數和采集通道數量,導致成像耗時,系統復雜。本文提出一種基于壓縮感知(CS)的重建算法,在有限次投影條件下,實現圖像的高質量重建。首先用平面波從隨機選取的角度以有限次數照射目標,依據傅里葉衍射投影定理,獲得目標空間頻率采樣值。然后,通過研究目標在變換域的稀疏性,根據壓縮感知原理,構建目標重建的逆問題。最后,通過共軛梯度算法解逆問題,重建目標。實驗結果表明,通過壓縮感知,在有限次投影情形和較少采集通道情況下,提出的方法能夠準確重建目標。這不僅能夠節省成像掃描時間,避免組織運動帶來影像失真,還能夠減少系統復雜度,降低設備成本。與傳統的插值算法相比,本文的方法能夠有效地降低重建誤差,提高結構相似度。
引用本文： 花少炎, 丁明躍, 尉遲明. 基于壓縮感知的超聲衍射層析成像研究. 生物醫學工程學雜志, 2015, 32(5): 975-982. doi: 10.7507/1001-5515.20150174 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
超聲衍射層析成像(ultrasound diffraction tomography,UDT)是一種重要的醫學成像方式，與傳統的B超顯示人體組織結構影像不同，它能夠提供人體組織聲學參量，如折射率、衰減系數分布等，是一種功能性成像，具有分辨率高、對致密組織敏感等特點，具有很高的臨床應用價值。例如，在乳腺檢查中，與X線檢查相比，它無輻射危害，而且可以區分良性和惡性腫瘤[1-2]。
在弱散射條件下，利用Born或Rytov近似[3]，可以建立傅里葉衍射投影定理(Fourier diffraction theory,FDT)[4-5]。通過傅里葉變換，FDT將目標的空間頻率信息和測量到的散射場聯系起來，因此可以用來重建目標圖像。根據奈奎斯特(Nyquist)采樣理論，對UDT而言，為了抑制偽影，必須增加投影次數和超聲探頭的接收通道數目[6]。對實際成像系統而言，這會增加掃描時間和設備成本，同時對系統的控制精度也提出了很高的要求；此外多次投影還導致采樣信息中包含大量的冗余信息。因此，在有限次投影條件下高精度重建圖像就具有重要的理論和實際意義。
通過有限次投影重建UDT圖像是一個不適定問題。雖然傳統的插值算法成像速度較快，但在有限次投影下，Nyquist采樣條件不再滿足，導致重建的圖像偽影嚴重。由Candes等[7-8]提出的壓縮感知(compressed sensing,CS)理論，利用目標在變換域下的稀疏性，通過優化算法，能夠從少量采集的信息中恢復出原始信息，從而突破Nyuist采樣定理的限制。目前，CS理論已經廣泛應用于醫學成像領域如磁共振成像(magnetic resonance,MR)、計算機斷層掃描成像(computed tomography,CT)、正電子發射斷層掃描(positron emission tomography,PET)及光聲成像[9-14]等。在超聲領域，國內外的學者也展開了廣泛研究。例如利用分布式壓縮感知理論，Zheng等[15]提出一種自適應波束形成方法對點目標進行成像；呂燚等[16]將壓縮感知應用于合成孔徑超聲成像；國內外部分學者也通過對超聲成像機制的研究，結合CS來降低系統數據采集量，減少設備復雜度[17-19]。
本文的主要目的是基于CS理論，提出一種迭代重建算法，在有限次投影條件下高質量重建UDT圖像。首先，設計采樣方案，根據FDT,獲得目標空間頻率采樣值；然后，研究目標的稀疏性，在CS框架下構建逆問題；最后，通過共軛梯度(conjugate gradient,CG)算法重建圖像，并通過仿真實驗對我們的方法進行驗證評估。
1 相關背景
1.1 UDT和FDT
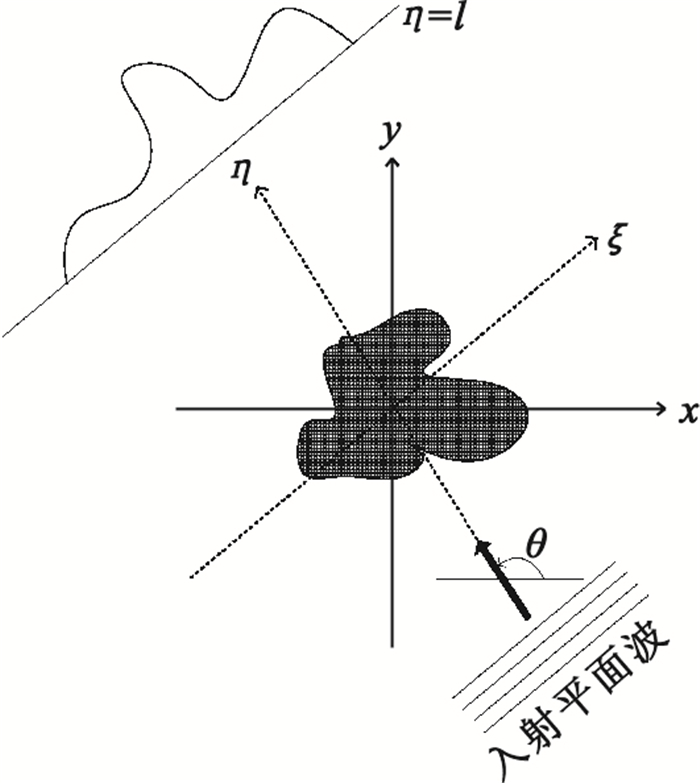
圖 1為UDT示意圖。目標f(r),r=(x,y)浸入均一媒介中，平面波以波數k0從θ方向照射物體。由于目標的非均一性，聲波在傳播過程中，在邊界和目標內部發生散射。如圖 1所示，我們建立一個笛卡爾坐標系(ξ,η)，使得η軸與θ方向一致，接收陣列位于η=l上。空間散射聲場滿足。
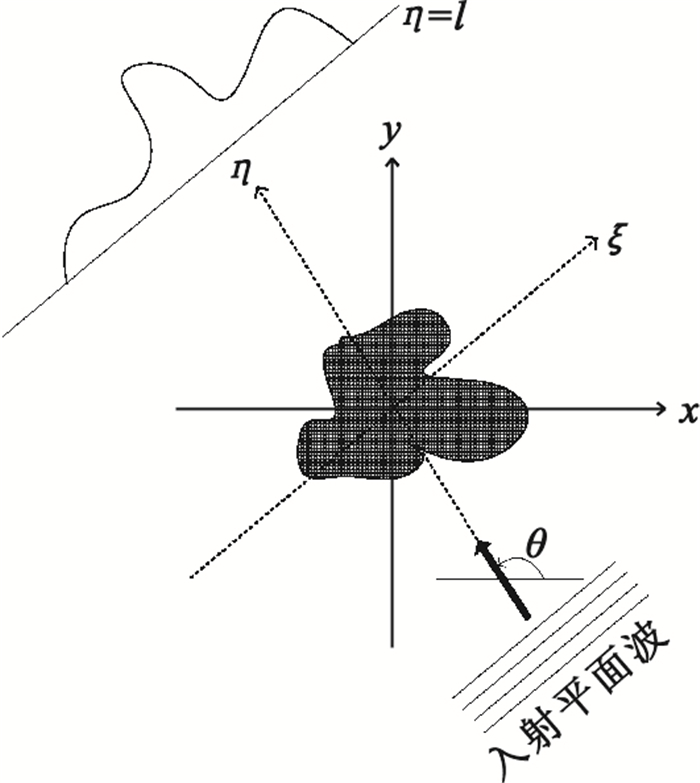圖1
超聲衍射層析成像示意圖
Figure1.
Scheme of UDT
在弱散射條件下，利用一階Born或Rytov近似，我們可以得到如下的FDT：
| $ {U_{s,\theta }}\left( \kappa \right) = \frac{{k_0^2{U_0}}}{{{j^2}\gamma }}{e^{j\gamma l}}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {f\left( \boldsymbol{r} \right)} {e^{ - j\left[{\kappa \xi + \left( {\gamma - {k_0}} \right)\eta } \right]}}{\rm{d}}\boldsymbol{r},} $ |
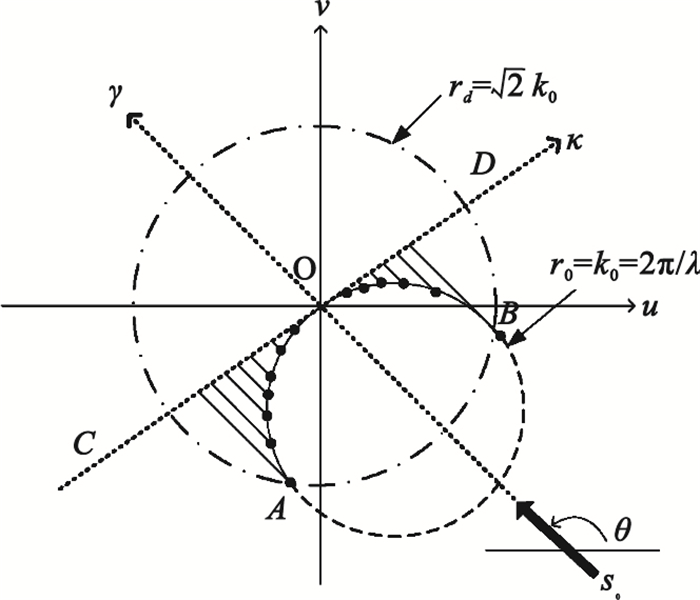
其中為接收到的散射場us,θ(ξ)的傅里葉變換，即：。分析FDT公式，我們可以發現，其右部積分為目標f(r)在半圓環AOB上的傅里葉變換(見圖 2)。
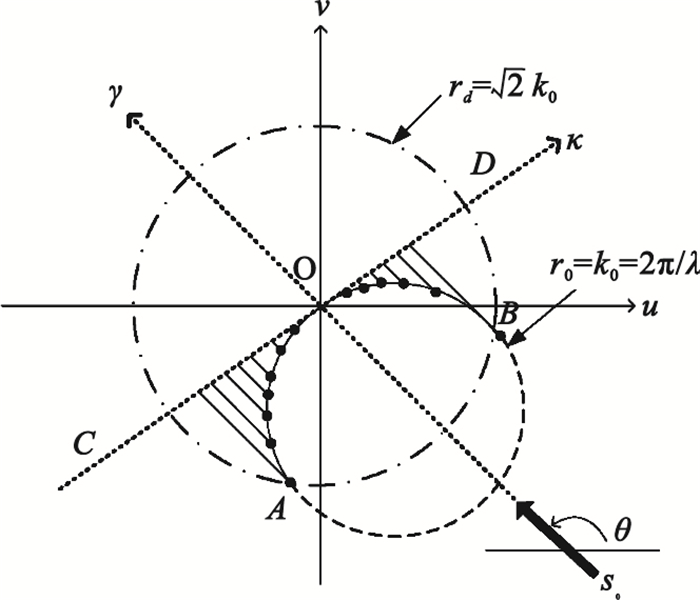圖2
傅里葉衍射投影定理
Figure2.
Fourier diffraction theory
其圓心為-k0s0，s0為平面波入射方向的單位向量。因此，UDT圖像重建可以表達為下述逆問題：
| $ f = \boldsymbol{\Phi} \left( f \right), $ |
其中F為空間頻率采樣，Φ為傅里葉衍射算子，f為重建目標。
1.2 CS
CS是一種有效的信息采集和重建技術。它利用目標在變換域的稀疏性，能夠從對目標的有限次投影測量中以極高的概率高精度地重建原始信號。其理論可以通過如下的線性測量模型進行闡述：
| $ y = \boldsymbol{\Phi} x, $ |
其中為未知的目標信號，y為觀測值，Φ為m×n(m＜n)觀測矩陣。在實際應用中，Φ往往取決于實際成像設備。在本文中，Φ為傅里葉衍射算子。對于真實的物理信號 x，我們往往能夠選取合適的變換域Ψ，使得x在此變換域下能夠稀疏分解,即
| $ x = \boldsymbol{\Psi} s, $ |
其中分解系數s的絕大多數元素為零，記其非零元素個數為k，我們就稱x為k稀疏信號。將式(3)代入式(2)，我們得到：
| $ y = \boldsymbol{\Theta} s, $ |
其中Θ=ΦΨ為感知矩陣。當Θ滿足有限等距性(restricted isometry property,RIP)時，我們可以通過如下的l1優化問題[20-21]，以極高的概率高精度重建x：
| $ \mathop {min}\limits_s \left\{ {{{\left\| \boldsymbol{s} \right\|}_1}:\boldsymbol{\Theta s} = \boldsymbol{y}} \right\}, $ |
其中。文獻[21]表明，當觀測矩陣Φ為部分傅里葉矩陣時，我們能夠從m=O(klog(n))4次觀測中重建目標x。
上述CS理論要求x是稀疏的，而且觀測模型y=Φx是嚴格成立的。在實際中，信號x往往是近似稀疏的或可壓縮的，觀測模型往往也存在誤差。Candes等[22]將式(5)拓展到如下形式，即
| $ \mathop {min}\limits_s {\left\| s \right\|_1}:\left\| {\Theta s - y} \right\|_2^2 \le {\sigma ^2}, $ |
其中σ為誤差估計。
問題(6)是一個凸優化問題，可以轉化為如下的規則化問題求解：
| $ \mathop {min}\limits_s \left\{ {\alpha {{\left\| s \right\|}_1} + \left\| {\Theta s - y} \right\|_2^2} \right\}, $ |
其中α為規則化參數。
2 基于CS的UDT重建
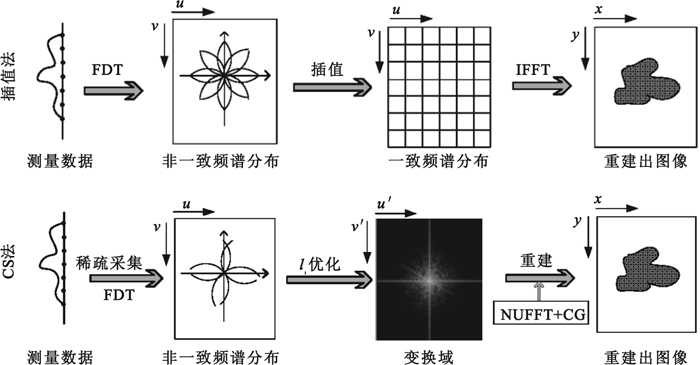
在本研究中，我們提出一種基于CS的UDT重建方法。圖 3 顯示我們的重建方法及與傳統插值方法的對比。新方法主要包含三步：①數據稀疏采集；②基于壓縮感知構建逆問題；③求解逆問題，重建目標。
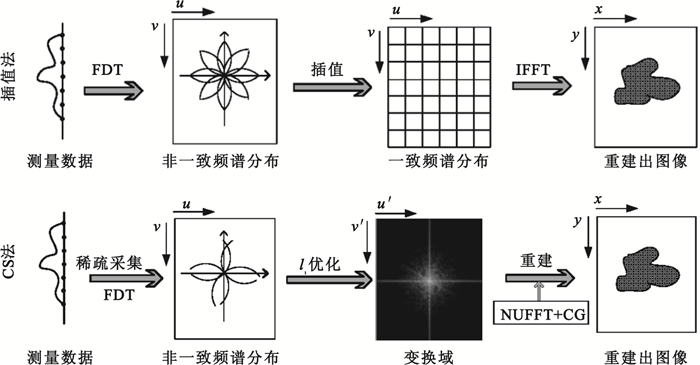圖3
不同重建算法示意圖
Figure3.
Scheme of different reconstruction methods
2.1 數據稀疏采集
如前文所述，當感知矩陣Θ=ΦΨ滿足RIP條件時，我們可以通過求解問題(5),重建x。但是，對一個矩陣Θ，驗證其滿足RIP條件是很困難的，尤其是當矩陣的維度比較大時，驗證RIP條件往往是不可能的。因此，尋找滿足RIP條件且能運用于實際的感知矩陣尤為重要。文獻[21]表明，當觀測矩陣Φ為高斯隨機矩陣(矩陣中元素從高斯分布序列中隨機挑選得到)或部分隨機傅里葉變換矩陣(從傅里葉變換矩陣中隨機挑選部分行得到的矩陣)時，我們分別能夠從m=O(klog(n/k))和m=O(klog(n))4次觀測中重建目標x。
對UDT系統，根據FDT,采樣算子Φ為傅里葉變換矩陣，這使得通過l1范數最小化重建目標成為可能。在本研究中，我們從隨機挑選的方向，以遠低于Nyquist理論要求的投影次數向目標發射平面波，利用FDT，獲得目標的空間頻率采樣。
2.2 構建逆問題
在上一節中，通過FDT，我們獲得目標的觀測數據，為了在CS框架下構建逆問題，需要建立感知矩陣Θ=ΦΨ。本研究中，Φ取決于系統成像機制，Ψ為選定的稀疏表達基。
因為實際情況中目標尺寸是有限的，假設目標f(r)或f(x,y) 的有限支集為[-C,C]×[-C,C]，即當｜x｜＞C或｜y｜＞C時f=0。假設為目標的離散形式，其中T為x軸和y軸的采樣間隔區間。 F(u,v)、Fs(u,v)分別為f(x,y)、fd(n1,n2)的傅里葉變換。根據Nyquist理論，我們能夠找到截止頻率W，使得當時，對｜u｜＜W，｜v｜＜W,Fs(u,v)≈F(u,v)。
另一方面，因為實際中的接收陣列通道數目是有限的，所以接收散射場us,Θ(ξ)可以記為:,其中n為接收通道數目，τ為采樣間隔，也就是超聲探頭陣元的中心間距。的傅里葉變換。當。
依據圖 2，利用空間坐標變換，頻率(u,v)可以通過(κ,γ)表達：
| $ \left\{ \begin{matrix} u=U\left( \kappa ,\gamma \right) \\ v=V\left( \kappa ,\gamma \right) \\ \end{matrix} \right. $ |
函數U和V的詳細推導及表達式可以參閱文獻[5]。
根據上面分析，當τ足夠小即充分逼近Us,Θ(κ)，且｜u｜＜W，｜v｜＜W時，有。記Ω1={θ1,θ2,…,θN1}為有限投影角度集合。對κ∈Ω2={κ1,κ2,…,κN2}，通過對接收聲場做傅里葉變換，我們得到。 因此，離散目標可以通過觀測求解：
| $ \begin{align} & {{{\hat{U}}}_{s,\theta }}\left( \kappa \right)+{{n}_{s,\theta }}\left( \kappa \right)=\frac{{{\left( {{T}_{{{\kappa }_{0}}}} \right)}^{2}}{{U}^{0}}}{2i\gamma }{{e}^{i\gamma l}} \\ & \sum\limits_{{{n}_{1}}=\left\lfloor \frac{-C}{T} \right\rfloor }^{\left\lceil \frac{C}{T} \right\rceil }{\sum\limits_{{{n}_{1}}=\left\lfloor \frac{-C}{T} \right\rfloor }^{\left\lceil \frac{C}{T} \right\rceil }{f_{{{n}_{1}},{{n}_{2}}}^{d}{{e}^{-2i\left( {{n}_{1}}u+{{n}_{2}}v \right)\left. T \right)}}}} \end{align} $ |
將此公式寫成矩陣形式：
| $ \boldsymbol{\Phi} {{f}^{d}}=\boldsymbol{F}+{{\boldsymbol{n}}_{s,\theta }} $ |
其中為逼近誤差。通過式(8)，得到逆問題(4)中的Φ。
壓縮感知利用目標在變換域的稀疏性，通過最優化重建目標。根據FDT,采集到的空間頻率值分布在一個半徑為的圓環內，即采樣數據為目標的低通濾波。另一方面，大量的觀測表明，自然圖像尤其是醫學結構圖像，具有分段連續的性質，即其梯度具有稀疏性。因此，在本研究中，我們通過小波變換和總變分(total variation,TV)對目標進行稀疏表達。前者能夠很好地對目標值變化劇烈區域進行稀疏分解，后者除了表達目標的梯度的稀疏性，還能抑制震蕩噪聲，保護邊界[23]。
對離散目標，TV定義為：,其中Dhn1,n2、Dvn1,n2分別為橫軸和縱軸方向的差分算子。
結合小波變換和TV，l1問題(7)拓展為：
| $ \underset{s}{\mathop{\min }}\,G\left( s \right)\alpha TV\left( \boldsymbol{\Psi s} \right)+\beta {{\left\| s \right\|}_{1}}+\left\| \boldsymbol{F-\Phi \Psi s} \right\|_{2}^{2} $ |
2.3 逆問題求解
在本研究中我們采取CG方法求解逆問題(9)。目標函數的梯度為
| $ \begin{array}{l} \nabla G\left( s \right) = 2\left( {\Phi \Psi } \right)'\left( {\Phi \Psi s - F} \right) + \alpha \nabla \left( {TV\left( {\Psi s} \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\nabla \left( {{{\left\| s \right\|}_1}} \right) \end{array} $ |
因為絕對值函數是不可微的，我們利用，其中ε、μ為充分小的正數。那么TV和l1范數的梯度分別為
| $ \begin{array}{l} \nabla {\left\| {{D_{{n_1},{n_2}}}\boldsymbol{f}} \right\|^2} = \frac{{D_{{n_1},{n_2}}^h\boldsymbol{f}}}{{{{\left\| {{D_{{n_1},{n_2}}}\boldsymbol{f}} \right\|}^2}}} + \frac{{D_{{n_1},{n_2}}^v\boldsymbol{f}}}{{{{\left\| {{D_{{n_1},{n_2}}}\boldsymbol{f}} \right\|}^2}}} - \frac{{D_{{n_1},{n_{2 - 1}}}^v\boldsymbol{f}}}{{{{\left\| {{D_{{n_1},{n_{2 - 1}}}}\boldsymbol{f}} \right\|}^2}}} - \frac{{D_{{n_1} - 1,{n_2}}^v\boldsymbol{f}}}{{{{\left\| {{D_{{n_1} - 1,{n_2}}}\boldsymbol{f}} \right\|}^2}}}和\\ \nabla \left( {{{\left\| s \right\|}_1}} \right) = \frac{s}{{\sqrt {ss' + \varepsilon } }}. \end{array} $ |
3 實驗仿真
3.1 仿真過程及參數說明
為了驗證評估我們的算法，我們采用圖 4所示的模型。此模型與常見的評估CT算法的Shepp-Logan模型類似，由十個橢圓組成，但是我們依據文獻[5]，改變其強度分布，以模擬UDT。背景聲速設為1 500 m/s，傳感器陣元個數為128，超聲波頻率為1.5 MHz，陣元間距為一波長λ，兩個接收探頭陣列間距20 cm。
圖4
目標模型
Figure4.
Original numerical phantom
3.2 重建結果
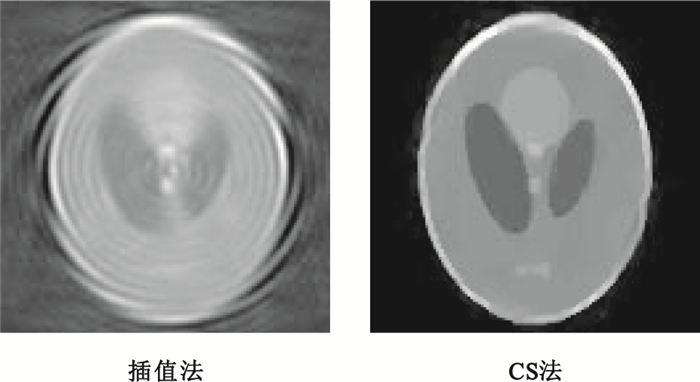
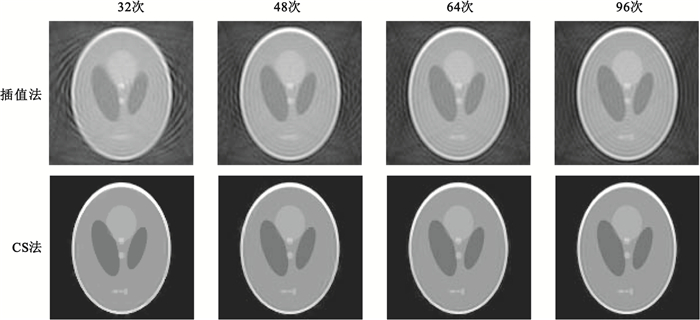
圖 5顯示插值法和CS方法的重建結果。為了顯示基于CS算法在有限次投影下的重建效果，投影次數設置為16次，稀疏變換選取Haar小波。圖 5(左)為傳統的雙線性插值重建結果，圖 5(右)為我們方法得到的結果。
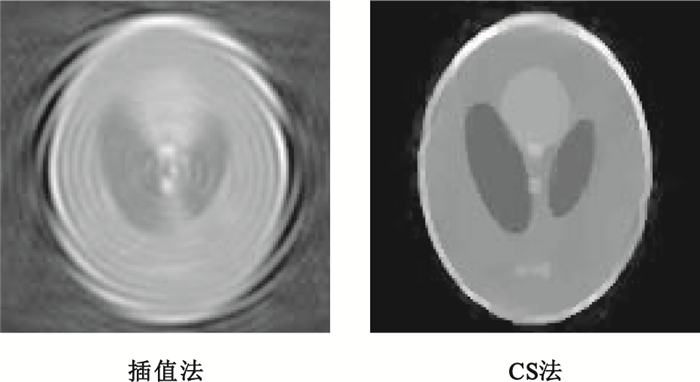圖5
重建結果
Figure5.
Reconstructed images
從圖 5我們可以看出，在有限次投影條件下，基于CS的方法優于傳統的插值算法。由于投影次數遠低于Nyquist 定理的要求，圖 5(左)存在嚴重的偽影，除了比較大的結構輪廓可以辨識外，細節幾乎全被偽影掩蓋。圖 5(右)除了部分外形輪廓出現失真以外，整體結構清晰，尤其是底部三個小橢圓，雖然不能完全分離，但整體輪廓可以分辨，表明我們方法具有更好的分辨率。
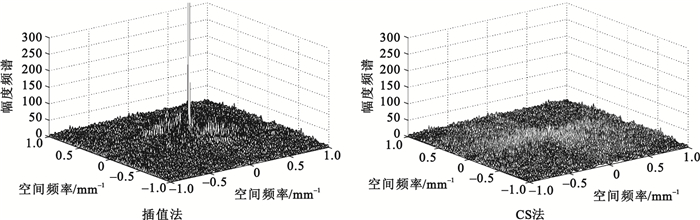
圖 6顯示了兩中方法在頻率域的誤差。圖 6(左)為插值法誤差，圖 6(右)為基于CS的方法頻率域誤差。因為插值法的最大誤差(4 311)遠遠大于我們提出的方法(54.2)，為了更好地對二者進行比較，這里截取插值法誤差于區間[0,300]內顯示。圖 6(右)中除了中心低頻部分誤差低于插值法，在中心頻率外部區域誤差簇群分布較圖 6(左)更為整齊。
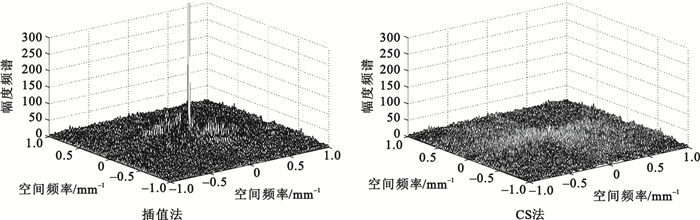圖6
頻率域誤差
Figure6.
Error in frequency domain
我們通過相對均方誤差(relative mean square error,RMSE)和結構相似性(structural similarity,SSIM)兩個指標對圖 5中的重建結果進行量化評估，前者評估算法的重建精度，后者衡量重建圖像的失真程度。插值法和CS法的頻率域或空間域RMSE分別為0.796和0.254；重建圖像的SSIM分別為0.291和0.527。與插值法相比，通過CS方法，SSIM提高了81.10%，RMSE降低了68.09%。
為了更全面地評估我們的算法，圖 7顯示了在其它投影次數下插值法和CS法的對比。圖 8顯示隨著投影次數的變換，SSIM和RMSE的變化。
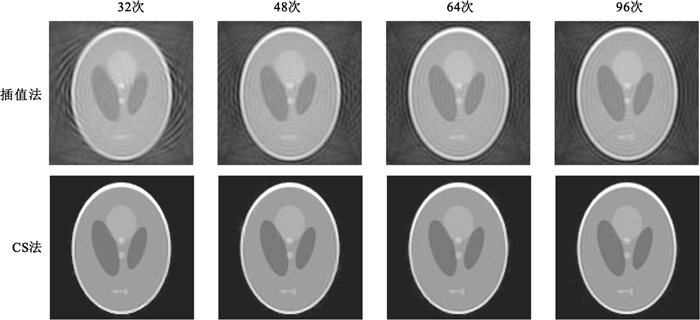圖7
不同投影次數重建結果
Figure7.
Reconstructed images for different views
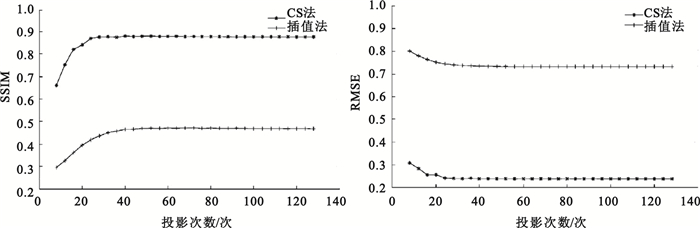圖8
CS法和插值法在不同投影次數下SSIM和RMSE變化情況
Figure8.
SSIM and RMSE for CS and interpolation methods with different number of projections
從圖 7可以發現，在同樣的投影次數下，通過CS重建的圖像質量高于插值法。隨著投影次數的增加，雖然偽影尤其是背景部分逐漸減少，但偽影始終存在，圖像內部細節無法清晰地識別出來。當投影次數為48時，通過CS的方法，模型內部細節特征已經能夠徹底地重建出來。
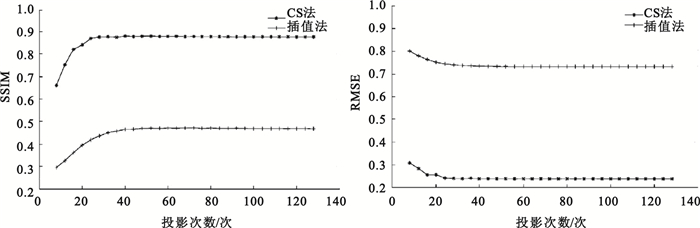
圖 8表明，當投影次數從10次增加到約40次時，對插值法和CS方法，RMSE和SSIM都逐步提高，但就SSIM的改進速度而言，CS方法快于插值法。當投影次數高于40次，對插值法和CS方法，RMSE和SSIM都趨于穩定。
3.3 噪聲的影響
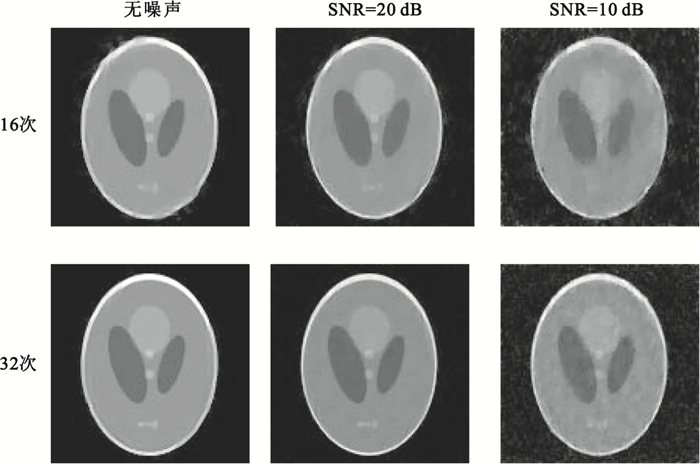
在實際應用中，測量到的聲場信號不可避免地受到噪聲影響，如換能器的熱噪聲、放大器的電子噪聲。除此之外，根據FDT，采集到的空間頻率信息為原目標的低通濾波，即存在模型誤差。因此，考察我們算法對噪聲的魯棒性就很有意義。通過對仿真聲場添加高斯白噪聲，評估我們提出的算法。圖 9顯示不同噪聲情形下的重建結果。為了更好地評估噪聲對算法的影響，分別評估了投影次數為16和32、SNR為20 dB和10 dB的重建結果。
圖 9表明，當SNR=20 dB時，與無噪聲重建結果相比，圖像雖出現一些顆粒噪聲，但細節部分仍能夠識別，目標內部結構層次清晰，邊界完整。但當SNR=10 dB、噪聲污染嚴重時，重建結果出現嚴重的顆粒噪聲，雖然整體結構能夠分辨出來，但內部細節損失嚴重。
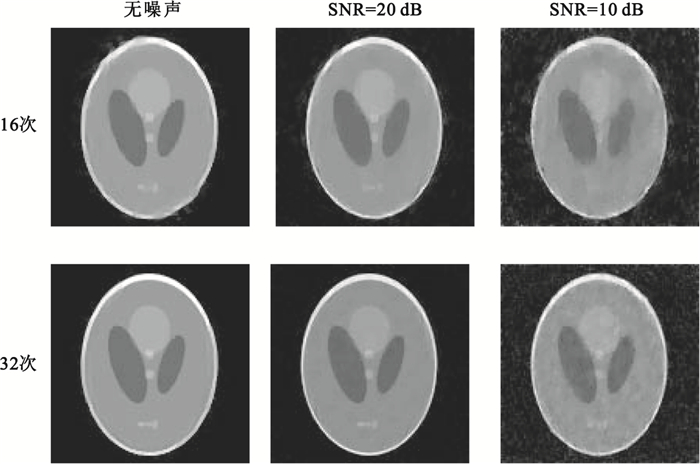圖9
噪聲對重建算法的影響
Figure9.
Reconstructed images with noise data
4 結論
基于FDT，本文提出一種基于壓縮感知的超聲衍射層析成像的方法。本文提出的方法能夠有效地在有限次投影條件下重建目標。對實際成像系統而言，此方法不但能夠降低系統的控制復雜度，減少掃描時間，還有助于抑制成像過程中人體呼吸運動帶來的偽影。通過仿真實驗，并與傳統的插值方法進行對比，圖像的分辨率、對比度、相對均方誤差、結構相似性均有顯著提高。
引言
超聲衍射層析成像(ultrasound diffraction tomography,UDT)是一種重要的醫學成像方式，與傳統的B超顯示人體組織結構影像不同，它能夠提供人體組織聲學參量，如折射率、衰減系數分布等，是一種功能性成像，具有分辨率高、對致密組織敏感等特點，具有很高的臨床應用價值。例如，在乳腺檢查中，與X線檢查相比，它無輻射危害，而且可以區分良性和惡性腫瘤[1-2]。
在弱散射條件下，利用Born或Rytov近似[3]，可以建立傅里葉衍射投影定理(Fourier diffraction theory,FDT)[4-5]。通過傅里葉變換，FDT將目標的空間頻率信息和測量到的散射場聯系起來，因此可以用來重建目標圖像。根據奈奎斯特(Nyquist)采樣理論，對UDT而言，為了抑制偽影，必須增加投影次數和超聲探頭的接收通道數目[6]。對實際成像系統而言，這會增加掃描時間和設備成本，同時對系統的控制精度也提出了很高的要求；此外多次投影還導致采樣信息中包含大量的冗余信息。因此，在有限次投影條件下高精度重建圖像就具有重要的理論和實際意義。
通過有限次投影重建UDT圖像是一個不適定問題。雖然傳統的插值算法成像速度較快，但在有限次投影下，Nyquist采樣條件不再滿足，導致重建的圖像偽影嚴重。由Candes等[7-8]提出的壓縮感知(compressed sensing,CS)理論，利用目標在變換域下的稀疏性，通過優化算法，能夠從少量采集的信息中恢復出原始信息，從而突破Nyuist采樣定理的限制。目前，CS理論已經廣泛應用于醫學成像領域如磁共振成像(magnetic resonance,MR)、計算機斷層掃描成像(computed tomography,CT)、正電子發射斷層掃描(positron emission tomography,PET)及光聲成像[9-14]等。在超聲領域，國內外的學者也展開了廣泛研究。例如利用分布式壓縮感知理論，Zheng等[15]提出一種自適應波束形成方法對點目標進行成像；呂燚等[16]將壓縮感知應用于合成孔徑超聲成像；國內外部分學者也通過對超聲成像機制的研究，結合CS來降低系統數據采集量，減少設備復雜度[17-19]。
本文的主要目的是基于CS理論，提出一種迭代重建算法，在有限次投影條件下高質量重建UDT圖像。首先，設計采樣方案，根據FDT,獲得目標空間頻率采樣值；然后，研究目標的稀疏性，在CS框架下構建逆問題；最后，通過共軛梯度(conjugate gradient,CG)算法重建圖像，并通過仿真實驗對我們的方法進行驗證評估。
1 相關背景
1.1 UDT和FDT
圖 1為UDT示意圖。目標f(r),r=(x,y)浸入均一媒介中，平面波以波數k0從θ方向照射物體。由于目標的非均一性，聲波在傳播過程中，在邊界和目標內部發生散射。如圖 1所示，我們建立一個笛卡爾坐標系(ξ,η)，使得η軸與θ方向一致，接收陣列位于η=l上。空間散射聲場滿足。
圖1
超聲衍射層析成像示意圖
Figure1.
Scheme of UDT
在弱散射條件下，利用一階Born或Rytov近似，我們可以得到如下的FDT：
| $ {U_{s,\theta }}\left( \kappa \right) = \frac{{k_0^2{U_0}}}{{{j^2}\gamma }}{e^{j\gamma l}}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {f\left( \boldsymbol{r} \right)} {e^{ - j\left[{\kappa \xi + \left( {\gamma - {k_0}} \right)\eta } \right]}}{\rm{d}}\boldsymbol{r},} $ |
其中為接收到的散射場us,θ(ξ)的傅里葉變換，即：。分析FDT公式，我們可以發現，其右部積分為目標f(r)在半圓環AOB上的傅里葉變換(見圖 2)。
圖2
傅里葉衍射投影定理
Figure2.
Fourier diffraction theory
其圓心為-k0s0，s0為平面波入射方向的單位向量。因此，UDT圖像重建可以表達為下述逆問題：
| $ f = \boldsymbol{\Phi} \left( f \right), $ |
其中F為空間頻率采樣，Φ為傅里葉衍射算子，f為重建目標。
1.2 CS
CS是一種有效的信息采集和重建技術。它利用目標在變換域的稀疏性，能夠從對目標的有限次投影測量中以極高的概率高精度地重建原始信號。其理論可以通過如下的線性測量模型進行闡述：
| $ y = \boldsymbol{\Phi} x, $ |
其中為未知的目標信號，y為觀測值，Φ為m×n(m＜n)觀測矩陣。在實際應用中，Φ往往取決于實際成像設備。在本文中，Φ為傅里葉衍射算子。對于真實的物理信號 x，我們往往能夠選取合適的變換域Ψ，使得x在此變換域下能夠稀疏分解,即
| $ x = \boldsymbol{\Psi} s, $ |
其中分解系數s的絕大多數元素為零，記其非零元素個數為k，我們就稱x為k稀疏信號。將式(3)代入式(2)，我們得到：
| $ y = \boldsymbol{\Theta} s, $ |
其中Θ=ΦΨ為感知矩陣。當Θ滿足有限等距性(restricted isometry property,RIP)時，我們可以通過如下的l1優化問題[20-21]，以極高的概率高精度重建x：
| $ \mathop {min}\limits_s \left\{ {{{\left\| \boldsymbol{s} \right\|}_1}:\boldsymbol{\Theta s} = \boldsymbol{y}} \right\}, $ |
其中。文獻[21]表明，當觀測矩陣Φ為部分傅里葉矩陣時，我們能夠從m=O(klog(n))4次觀測中重建目標x。
上述CS理論要求x是稀疏的，而且觀測模型y=Φx是嚴格成立的。在實際中，信號x往往是近似稀疏的或可壓縮的，觀測模型往往也存在誤差。Candes等[22]將式(5)拓展到如下形式，即
| $ \mathop {min}\limits_s {\left\| s \right\|_1}:\left\| {\Theta s - y} \right\|_2^2 \le {\sigma ^2}, $ |
其中σ為誤差估計。
問題(6)是一個凸優化問題，可以轉化為如下的規則化問題求解：
| $ \mathop {min}\limits_s \left\{ {\alpha {{\left\| s \right\|}_1} + \left\| {\Theta s - y} \right\|_2^2} \right\}, $ |
其中α為規則化參數。
2 基于CS的UDT重建
在本研究中，我們提出一種基于CS的UDT重建方法。圖 3 顯示我們的重建方法及與傳統插值方法的對比。新方法主要包含三步：①數據稀疏采集；②基于壓縮感知構建逆問題；③求解逆問題，重建目標。
圖3
不同重建算法示意圖
Figure3.
Scheme of different reconstruction methods
2.1 數據稀疏采集
如前文所述，當感知矩陣Θ=ΦΨ滿足RIP條件時，我們可以通過求解問題(5),重建x。但是，對一個矩陣Θ，驗證其滿足RIP條件是很困難的，尤其是當矩陣的維度比較大時，驗證RIP條件往往是不可能的。因此，尋找滿足RIP條件且能運用于實際的感知矩陣尤為重要。文獻[21]表明，當觀測矩陣Φ為高斯隨機矩陣(矩陣中元素從高斯分布序列中隨機挑選得到)或部分隨機傅里葉變換矩陣(從傅里葉變換矩陣中隨機挑選部分行得到的矩陣)時，我們分別能夠從m=O(klog(n/k))和m=O(klog(n))4次觀測中重建目標x。
對UDT系統，根據FDT,采樣算子Φ為傅里葉變換矩陣，這使得通過l1范數最小化重建目標成為可能。在本研究中，我們從隨機挑選的方向，以遠低于Nyquist理論要求的投影次數向目標發射平面波，利用FDT，獲得目標的空間頻率采樣。
2.2 構建逆問題
在上一節中，通過FDT，我們獲得目標的觀測數據，為了在CS框架下構建逆問題，需要建立感知矩陣Θ=ΦΨ。本研究中，Φ取決于系統成像機制，Ψ為選定的稀疏表達基。
因為實際情況中目標尺寸是有限的，假設目標f(r)或f(x,y) 的有限支集為[-C,C]×[-C,C]，即當｜x｜＞C或｜y｜＞C時f=0。假設為目標的離散形式，其中T為x軸和y軸的采樣間隔區間。 F(u,v)、Fs(u,v)分別為f(x,y)、fd(n1,n2)的傅里葉變換。根據Nyquist理論，我們能夠找到截止頻率W，使得當時，對｜u｜＜W，｜v｜＜W,Fs(u,v)≈F(u,v)。
另一方面，因為實際中的接收陣列通道數目是有限的，所以接收散射場us,Θ(ξ)可以記為:,其中n為接收通道數目，τ為采樣間隔，也就是超聲探頭陣元的中心間距。的傅里葉變換。當。
依據圖 2，利用空間坐標變換，頻率(u,v)可以通過(κ,γ)表達：
| $ \left\{ \begin{matrix} u=U\left( \kappa ,\gamma \right) \\ v=V\left( \kappa ,\gamma \right) \\ \end{matrix} \right. $ |
函數U和V的詳細推導及表達式可以參閱文獻[5]。
根據上面分析，當τ足夠小即充分逼近Us,Θ(κ)，且｜u｜＜W，｜v｜＜W時，有。記Ω1={θ1,θ2,…,θN1}為有限投影角度集合。對κ∈Ω2={κ1,κ2,…,κN2}，通過對接收聲場做傅里葉變換，我們得到。 因此，離散目標可以通過觀測求解：
| $ \begin{align} & {{{\hat{U}}}_{s,\theta }}\left( \kappa \right)+{{n}_{s,\theta }}\left( \kappa \right)=\frac{{{\left( {{T}_{{{\kappa }_{0}}}} \right)}^{2}}{{U}^{0}}}{2i\gamma }{{e}^{i\gamma l}} \\ & \sum\limits_{{{n}_{1}}=\left\lfloor \frac{-C}{T} \right\rfloor }^{\left\lceil \frac{C}{T} \right\rceil }{\sum\limits_{{{n}_{1}}=\left\lfloor \frac{-C}{T} \right\rfloor }^{\left\lceil \frac{C}{T} \right\rceil }{f_{{{n}_{1}},{{n}_{2}}}^{d}{{e}^{-2i\left( {{n}_{1}}u+{{n}_{2}}v \right)\left. T \right)}}}} \end{align} $ |
將此公式寫成矩陣形式：
| $ \boldsymbol{\Phi} {{f}^{d}}=\boldsymbol{F}+{{\boldsymbol{n}}_{s,\theta }} $ |
其中為逼近誤差。通過式(8)，得到逆問題(4)中的Φ。
壓縮感知利用目標在變換域的稀疏性，通過最優化重建目標。根據FDT,采集到的空間頻率值分布在一個半徑為的圓環內，即采樣數據為目標的低通濾波。另一方面，大量的觀測表明，自然圖像尤其是醫學結構圖像，具有分段連續的性質，即其梯度具有稀疏性。因此，在本研究中，我們通過小波變換和總變分(total variation,TV)對目標進行稀疏表達。前者能夠很好地對目標值變化劇烈區域進行稀疏分解，后者除了表達目標的梯度的稀疏性，還能抑制震蕩噪聲，保護邊界[23]。
對離散目標，TV定義為：,其中Dhn1,n2、Dvn1,n2分別為橫軸和縱軸方向的差分算子。
結合小波變換和TV，l1問題(7)拓展為：
| $ \underset{s}{\mathop{\min }}\,G\left( s \right)\alpha TV\left( \boldsymbol{\Psi s} \right)+\beta {{\left\| s \right\|}_{1}}+\left\| \boldsymbol{F-\Phi \Psi s} \right\|_{2}^{2} $ |
2.3 逆問題求解
在本研究中我們采取CG方法求解逆問題(9)。目標函數的梯度為
| $ \begin{array}{l} \nabla G\left( s \right) = 2\left( {\Phi \Psi } \right)'\left( {\Phi \Psi s - F} \right) + \alpha \nabla \left( {TV\left( {\Psi s} \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\nabla \left( {{{\left\| s \right\|}_1}} \right) \end{array} $ |
因為絕對值函數是不可微的，我們利用，其中ε、μ為充分小的正數。那么TV和l1范數的梯度分別為
| $ \begin{array}{l} \nabla {\left\| {{D_{{n_1},{n_2}}}\boldsymbol{f}} \right\|^2} = \frac{{D_{{n_1},{n_2}}^h\boldsymbol{f}}}{{{{\left\| {{D_{{n_1},{n_2}}}\boldsymbol{f}} \right\|}^2}}} + \frac{{D_{{n_1},{n_2}}^v\boldsymbol{f}}}{{{{\left\| {{D_{{n_1},{n_2}}}\boldsymbol{f}} \right\|}^2}}} - \frac{{D_{{n_1},{n_{2 - 1}}}^v\boldsymbol{f}}}{{{{\left\| {{D_{{n_1},{n_{2 - 1}}}}\boldsymbol{f}} \right\|}^2}}} - \frac{{D_{{n_1} - 1,{n_2}}^v\boldsymbol{f}}}{{{{\left\| {{D_{{n_1} - 1,{n_2}}}\boldsymbol{f}} \right\|}^2}}}和\\ \nabla \left( {{{\left\| s \right\|}_1}} \right) = \frac{s}{{\sqrt {ss' + \varepsilon } }}. \end{array} $ |
3 實驗仿真
3.1 仿真過程及參數說明
為了驗證評估我們的算法，我們采用圖 4所示的模型。此模型與常見的評估CT算法的Shepp-Logan模型類似，由十個橢圓組成，但是我們依據文獻[5]，改變其強度分布，以模擬UDT。背景聲速設為1 500 m/s，傳感器陣元個數為128，超聲波頻率為1.5 MHz，陣元間距為一波長λ，兩個接收探頭陣列間距20 cm。
圖4
目標模型
Figure4.
Original numerical phantom
3.2 重建結果
圖 5顯示插值法和CS方法的重建結果。為了顯示基于CS算法在有限次投影下的重建效果，投影次數設置為16次，稀疏變換選取Haar小波。圖 5(左)為傳統的雙線性插值重建結果，圖 5(右)為我們方法得到的結果。
圖5
重建結果
Figure5.
Reconstructed images
從圖 5我們可以看出，在有限次投影條件下，基于CS的方法優于傳統的插值算法。由于投影次數遠低于Nyquist 定理的要求，圖 5(左)存在嚴重的偽影，除了比較大的結構輪廓可以辨識外，細節幾乎全被偽影掩蓋。圖 5(右)除了部分外形輪廓出現失真以外，整體結構清晰，尤其是底部三個小橢圓，雖然不能完全分離，但整體輪廓可以分辨，表明我們方法具有更好的分辨率。
圖 6顯示了兩中方法在頻率域的誤差。圖 6(左)為插值法誤差，圖 6(右)為基于CS的方法頻率域誤差。因為插值法的最大誤差(4 311)遠遠大于我們提出的方法(54.2)，為了更好地對二者進行比較，這里截取插值法誤差于區間[0,300]內顯示。圖 6(右)中除了中心低頻部分誤差低于插值法，在中心頻率外部區域誤差簇群分布較圖 6(左)更為整齊。
圖6
頻率域誤差
Figure6.
Error in frequency domain
我們通過相對均方誤差(relative mean square error,RMSE)和結構相似性(structural similarity,SSIM)兩個指標對圖 5中的重建結果進行量化評估，前者評估算法的重建精度，后者衡量重建圖像的失真程度。插值法和CS法的頻率域或空間域RMSE分別為0.796和0.254；重建圖像的SSIM分別為0.291和0.527。與插值法相比，通過CS方法，SSIM提高了81.10%，RMSE降低了68.09%。
為了更全面地評估我們的算法，圖 7顯示了在其它投影次數下插值法和CS法的對比。圖 8顯示隨著投影次數的變換，SSIM和RMSE的變化。
圖7
不同投影次數重建結果
Figure7.
Reconstructed images for different views
圖8
CS法和插值法在不同投影次數下SSIM和RMSE變化情況
Figure8.
SSIM and RMSE for CS and interpolation methods with different number of projections
從圖 7可以發現，在同樣的投影次數下，通過CS重建的圖像質量高于插值法。隨著投影次數的增加，雖然偽影尤其是背景部分逐漸減少，但偽影始終存在，圖像內部細節無法清晰地識別出來。當投影次數為48時，通過CS的方法，模型內部細節特征已經能夠徹底地重建出來。
圖 8表明，當投影次數從10次增加到約40次時，對插值法和CS方法，RMSE和SSIM都逐步提高，但就SSIM的改進速度而言，CS方法快于插值法。當投影次數高于40次，對插值法和CS方法，RMSE和SSIM都趨于穩定。
3.3 噪聲的影響
在實際應用中，測量到的聲場信號不可避免地受到噪聲影響，如換能器的熱噪聲、放大器的電子噪聲。除此之外，根據FDT，采集到的空間頻率信息為原目標的低通濾波，即存在模型誤差。因此，考察我們算法對噪聲的魯棒性就很有意義。通過對仿真聲場添加高斯白噪聲，評估我們提出的算法。圖 9顯示不同噪聲情形下的重建結果。為了更好地評估噪聲對算法的影響，分別評估了投影次數為16和32、SNR為20 dB和10 dB的重建結果。
圖 9表明，當SNR=20 dB時，與無噪聲重建結果相比，圖像雖出現一些顆粒噪聲，但細節部分仍能夠識別，目標內部結構層次清晰，邊界完整。但當SNR=10 dB、噪聲污染嚴重時，重建結果出現嚴重的顆粒噪聲，雖然整體結構能夠分辨出來，但內部細節損失嚴重。
圖9
噪聲對重建算法的影響
Figure9.
Reconstructed images with noise data
4 結論
基于FDT，本文提出一種基于壓縮感知的超聲衍射層析成像的方法。本文提出的方法能夠有效地在有限次投影條件下重建目標。對實際成像系統而言，此方法不但能夠降低系統的控制復雜度，減少掃描時間，還有助于抑制成像過程中人體呼吸運動帶來的偽影。通過仿真實驗，并與傳統的插值方法進行對比，圖像的分辨率、對比度、相對均方誤差、結構相似性均有顯著提高。
