在眼底圖像分割效果的評價中,針對傳統評價方法只考慮像素點重合而未考慮視網膜血管拓撲結構的不足,本文提出一個新的評價方法。該方法首先利用數學形態學和細化算法得到血管的拓撲結構,然后統計并分析視網膜血管區域3個特征參數的分布情況,即以互信息、相關系數和節點率來獲得基于拓撲結構的眼底圖像分割評價結果。該方法的實驗數據取自STARE公開數據庫中專家手工分割及其腐蝕結果。實驗結果表明:互信息、相關系數和節點率這三個特征參數可以從拓撲結構的角度來評價眼底圖像視網膜血管的分割效果,且算法復雜程度較低,該方法對眼底圖像視網膜血管分割評價方法的補充有重要意義。
引用本文： 盛韓偉, 戴培山, 劉智航, 張文妙韻, 趙亞麗, 范敏. 基于拓撲結構的眼底圖像分割評價新方法. 生物醫學工程學雜志, 2015, 32(5): 1100-1105. doi: 10.7507/1001-5515.20150195 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
眼底視網膜圖像在如今的眼科疾病診斷中起著十分重要的作用[1]。研究證明視網膜血管結構特征的改變和許多疾病密切相關，比如心血管疾病、糖尿病、中風等[2]。在視網膜血管分割的研究中，由于獲取的圖像多，人工圖像分析費時費力，計算機自動眼底圖像視網膜血管分割成為一個重要的方向[3]。目前已開發出許多自動分割的方法[4]。
對于疾病的診斷，血管分割結果的好壞顯得十分重要，而判斷這種好壞依靠評價方法[5]。一般來說，目前的分割評價方法分為兩類。一類是基于像素點的評價方法。其中，傳統的基于像素點的評價方法有三大指標，分別是準確度(accuracy)、靈敏度(sensitivity)和特異度(specificity)[6]。這三個指標是將分割結果與金標準進行像素的比較。還有一些基于像素間計算的方法。如Uyen等[7]提出了一個新的評估方法，它是基于精確性和完整性的概念。此方法的一個重要特性是對細小局部錯誤的容錯性，這些分割錯誤不會影響所需的血管特征。但該類方法沒有考慮形態學的特征。另一類評價方法則是基于形態學拓撲結構的評價方法。Gegundez-arias等[8]構造了一個基于連接度、區域和長度的函數，用于表征血管結構，作為血管分割結果的評價指標，該結果證明利用該函數對分割結果進行評價更適于樹狀結構圖像的分割評價，是對現有圖像分割評價方法的補充。
目前大部分自動分割算法所用的評價方法是傳統三大指標，沒有考慮到血管形態學結構的特殊性--樹狀結構[9]。為了更好地評價眼底視網膜血管圖像的分割效果，需要將分割結果的拓撲結構信息融入到評價方法中。為此，本文提出了一種基于拓撲結構的眼底血管分割效果的評價方法。該方法利用細化算法提取血管的拓撲結構，然后計算細化后的血管與細化后的金標準之間的特征參數，即互信息、相關系數和節點率，以此作為評價圖像分割結果的指標。
1 實驗數據的獲取與預處理
對圖像分割結果進行評價需要有一定的標準和待評價的圖像。對于眼底圖像來說，金標準是專家手工分割的結果[10]。在STARE數據庫中，有20幅眼底彩色圖像和兩套相應的金標準圖像，分別標記出了10.4%和14.9%屬于血管的像素。本文采用STARE數據庫中第一套金標準進行實驗比較。
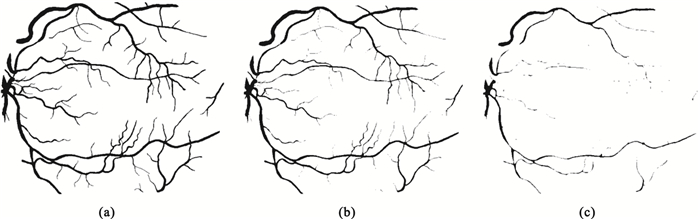
在確定了金標準之后，關鍵是獲得待評價的圖像。本文的設計思路是采用形態學方法對金標準進行處理得到待評價的圖像，即分割效果較好和較差的圖像。具體操作是對20幅金標準圖像進行腐蝕，腐蝕程度越大則代表分割效果越差。進行了兩次程度不同的腐蝕得到標記為好和差的圖像各二十幅。圖 1(a)是STARE數據庫中第一套專家手工分割中某一幅眼底圖像，圖 1(b)和圖 1(c)分別是用不同結構單元對圖 1(a)進行腐蝕的結果。從直觀角度看，從左到右圖像的邊緣信息丟失得越來越多。這三類圖像代表手工分割的結果、直觀判斷分割質量較好的結果和直觀判斷分割質量較差的結果。
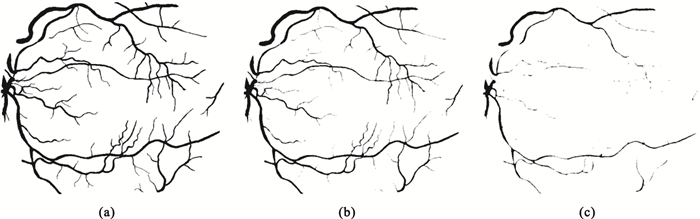圖1
金標準腐蝕獲得的待評價圖像
(a)金標準;(b)分割結果較好的圖像；(c)分割結果較差的圖像
Figure1. Going-to-be evaluated images with erosion of gold standard(a) gold standard; (b) the better segmented image; (c) the worse segmented image
為了對以上分割效果進行進一步量化分析，采用傳統的評價指標來對上面直觀的評估效果進行驗證。在視網膜血管分割領域中，廣泛使用的傳統分割評價方法是基于準確度、靈敏度和特異度的分割評價標準[11]。
| $ 準確度\text{=}\frac{TP+TN}{TP+FP+TN+FN} $ |
| $ 靈敏度=\frac{TP}{TP+FN} $ |
| $ 特異度=\frac{TP}{TP+FN} $ |
其中： TP表示正確分割的血管，FP表示本來屬于背景但被誤分割成血管，TN表示正確分割的背景，FN表示本來屬于血管但被誤分割成背景。
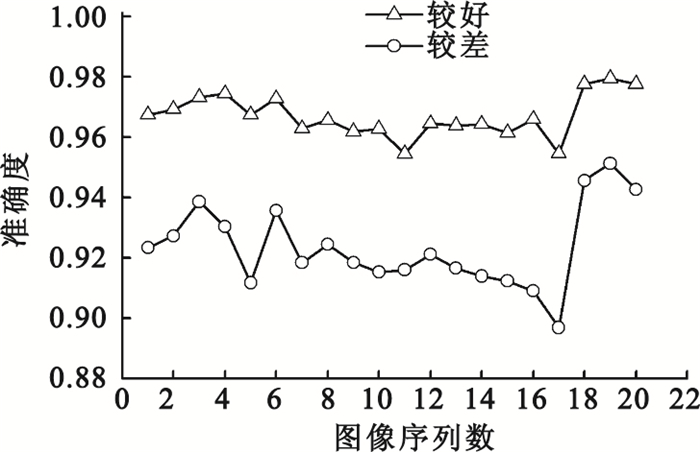
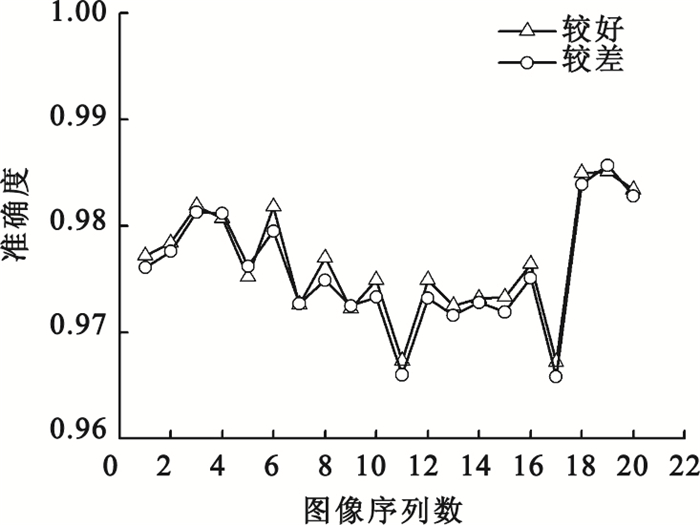
本文只采用準確度來評價腐蝕后的結果，它是代表正確分割的血管區域和背景區域占全部圖像的百分比。對直觀判斷結果為好的20幅圖像和直觀判斷結果為差的20幅圖像分別計算準確度，結果如圖 2所示。直觀判斷結果為好的圖像準確度都是較高的，結果為差的值都是較低的。而且由于腐蝕程度的一致，兩條曲線走勢也基本相同。因此，這樣獲取待評價圖像的方法是可行的。
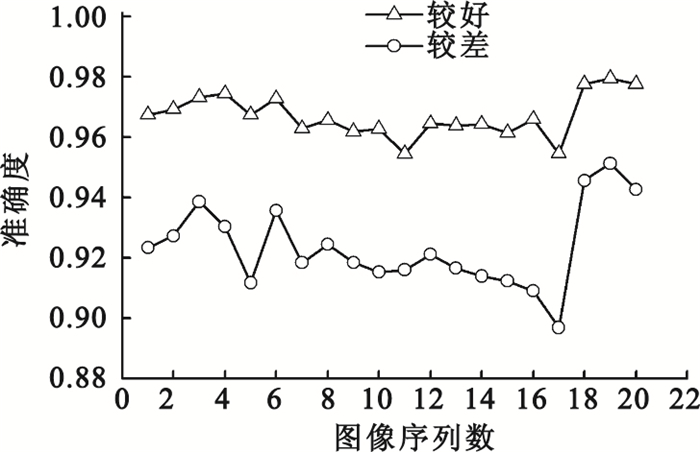圖2
獲得的分割效果較好和較差圖像的準確率對比
Figure2.
Comparison of accuracy of the better segmented images and the worse ones obtained
2 評價特征提取
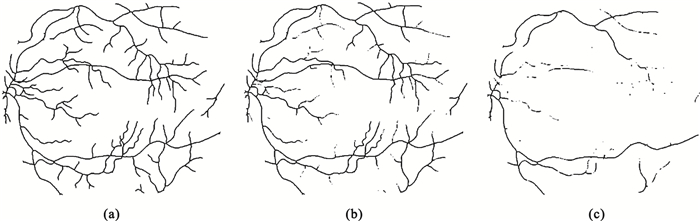
由于本文是從拓撲結構的角度來進行評價的，在確定待評價圖像后，首先利用細化算法來提取血管的中心線，即體現了血管完整的拓撲結構。本文所采用的細化方法是MATLAB軟件中的數學形態學函數bwmorph。圖 3是圖 1中三幅圖片細化的結果。
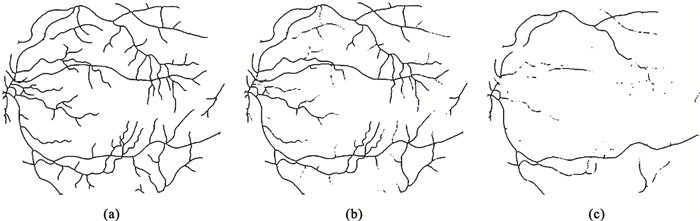圖3
金標準及其腐蝕后圖像的細化結果
(a)金標準的細化結果；(b)分割結果較好圖像的細化結果；(c)分割結果較差圖像的細化結果
Figure3. The thining results of the gold standard and its erosion(a) thining result of gold standard; (b) thining result of better segmented image; (c) thining result of worse segmented image
如圖 3所示，細化后的圖像體現了血管當前的拓撲結構。對于評價特征的提取，本文用到了3個特征參數，即互信息、相關系數和節點率。選擇這三個特征參數的原因是互信息和相關系數均能表示自動分割結果和金標準的相關性大小，節點的數量能表示拓撲結構的復雜程度。
2.1 互信息
互信息是用來描述兩個系統之間的統計相關性，一般用熵來表示[12]。系統A的熵為
| $ H\left( A \right)=-\sum\limits_{a}{{{\text{p}}_{A}}\left( a \right){{\log }_{A}}\left( a \right)} $ |
其中：a∈A。而互信息函數為
| $ I\left( A,B \right)=H\left( A \right)-H\left( A|B \right)=H\left( A \right)+H\left( B \right)-H\left( A,B \right) $ |
其中：H(A｜B)表示已知系統B時A的條件熵，H(A，B)為兩系統的聯合熵。
互信息值越大說明所包含的相同信息也越多。因此，對分割圖像進行細化后，再計算互信息，那么結果越大則說明兩者之間的拓撲結構越相似。自從互信息作為圖像配準的準則被引入以來，已獲得多數研究者認可[13]。但是由于互信息測度對兩圖像的重疊區域大小比較敏感，因此Studholme等[14]又提出了正則化互信息，其表達式為
| $ \text{NMI=}\left[\text{H}\left( A \right)+\text{H}\left( B \right) \right]/\text{H}\left( A,B \right) $ |
研究表明，正則化互信息有更好的魯棒性，故本文采用式(6)計算互信息值。
2.2 相關系數
相關系數是測定變量之間關系密切程度的量，可用于表示兩幅圖像間的相關性[15]。通常以ρ表示總體的相關系數，以r表示樣本的相關系數[16]。總體相關系數的定義公式是
| $ \rho =\frac{\operatorname{cov}\left( X,Y \right)}{\sqrt{\operatorname{var}\left( X \right)\cdot var\left( Y \right)}} $ |
其中：cov(X,Y)是隨機變量X和Y的協方差，var(X)和var(Y)是隨機變量X和Y的方差。而樣本相關系數的定義為
| $ r=\frac{\sum{\left( {{x}_{i}}-\bar{x} \right)}\left( {{y}_{i}}-\bar{y} \right)}{\sqrt{\sum{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}\cdot \sum{{{\left( {{y}_{i}}-\bar{y} \right)}^{2}}}}}} $ |
其中：xi和yi別是X和Y的樣本數據。
相關系數越接近1，則說明兩者越相似。因此，對分割圖像進行細化處理后，再計算相關系數，結果越大則說明兩者之間的拓撲結構越相似。
2.3 節點率
以上兩個評價參數是先細化眼底血管圖像以突出其拓撲結構，然后用互信息和相關系數分析血管分割效果，間接地評價了形態結構的相似性。而眼底血管結構錯綜復雜，對于這類結構的拓撲分析在醫學領域中應用廣泛[17]。而眼底圖像的節點數是一個可以直接反映拓撲結構的特征參數。
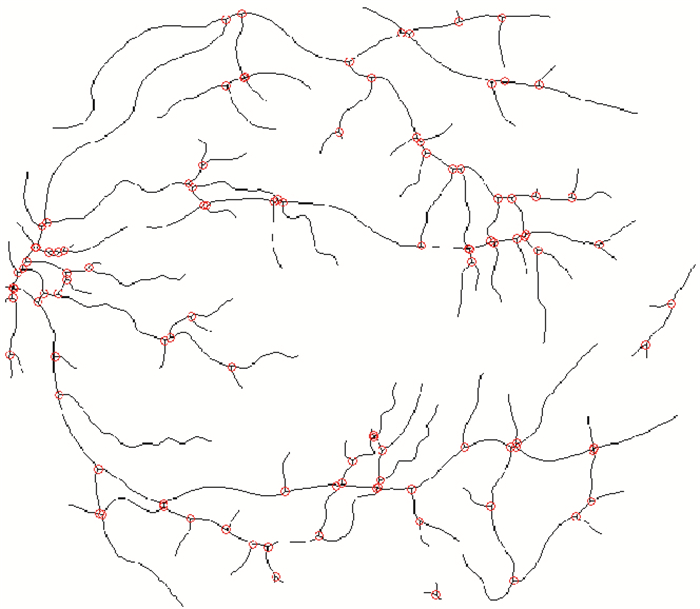
在拓撲學中，節點是網絡任何支路的分叉點或網絡中兩個或更多支路的互連公共點[18]。因此對于一幅眼底圖像，節點包括了分支點和交叉點。統計分割后圖像中的節點數，與金標準中的節點數進行比較，兩者結果相近，則說明分割結果較好。為了能更好地顯示節點處所標記的紅圈，進行了細化處理再展示節點，結果如圖 4所示。
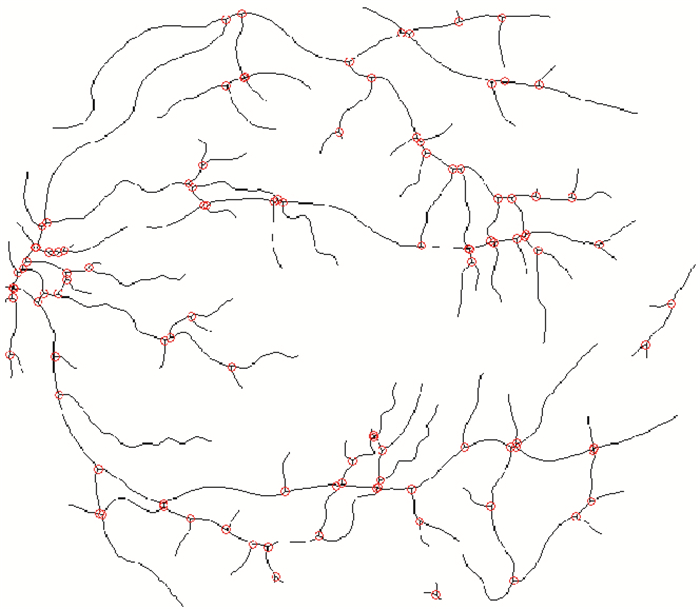圖4
節點圖
Figure4.
Image of nodes
為了與互信息和相關系數的計算方式統一，本文提出一個新的概念--節點率。節點率等于待評價圖像中節點數和金標準圖像中節點數的比值。該值越接近1，則說明兩者越相似，即能反映待評價圖像和金標準的相似程度。節點的數量能反映眼底血管分支結構的復雜程度，因此這方面的拓撲分析對眼底圖像分割效果的評價有重要意義。
3 實驗結果與討論
實驗環境采用的是酷睿i7四核CPU為4 GB內存的PC機，在Windows 8平臺上，編程軟件為Matlab R2012a。原始數據是STARE數據庫中的20幅第一套專家手工標記結果。將這20幅原始圖像都進行如圖 1所示的腐蝕，再進行如圖 3所示的細化處理，得到60幅細化的圖像，即包括了20幅金標準、20幅分割效果較好和20幅分割效果較差的細化圖像。
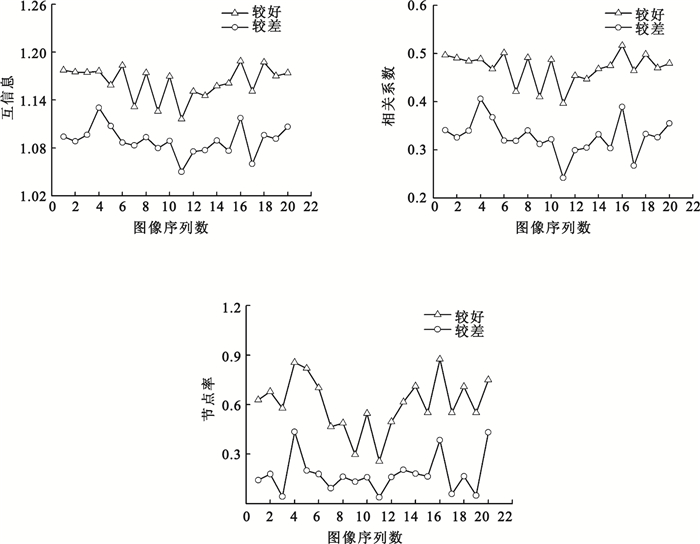
最后分別計算這20幅效果較好圖像和20幅效果較差圖像相對于各自對應金標準的互信息、相關系數和節點率，結果如圖 5所示。可以看出，直觀判斷結果較好圖像的互信息、相關系數和節點率的折線都在結果較差圖像的折線之上，與預期符合。而且每幅圖中兩條曲線的走勢也基本相同，體現了對20幅金標準圖像每一次腐蝕的程度是一致的。
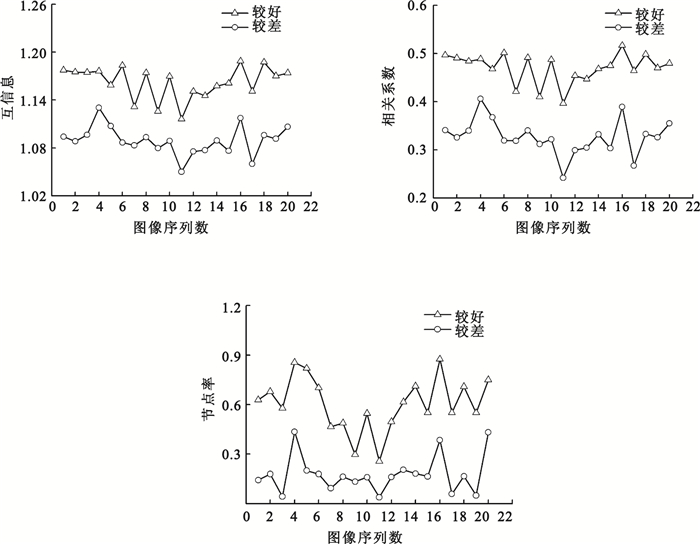圖5
評價特征參數的折線圖
Figure5.
Chart of characteristic parameters
綜合以上實驗結果可知，細化處理后的互信息、相關系數和節點率能夠評估出眼底圖像分割結果的好壞，并且是符合直觀感知的。此外，為了區別互信息和相關系數跟準確率的差異，又對這20組效果較好圖像和20組效果較差圖像的準確率進行了計算，結果如圖 6所示。可見，較好圖像準確率的值大部分處在較差圖像準確率的值上方，但十分接近，而且有幾個相反的結果。此結果證明，準確率與互信息和相關系數在算法上有所不同。進而說明，細化后的準確率不能用來判斷眼底圖像分割的好壞。
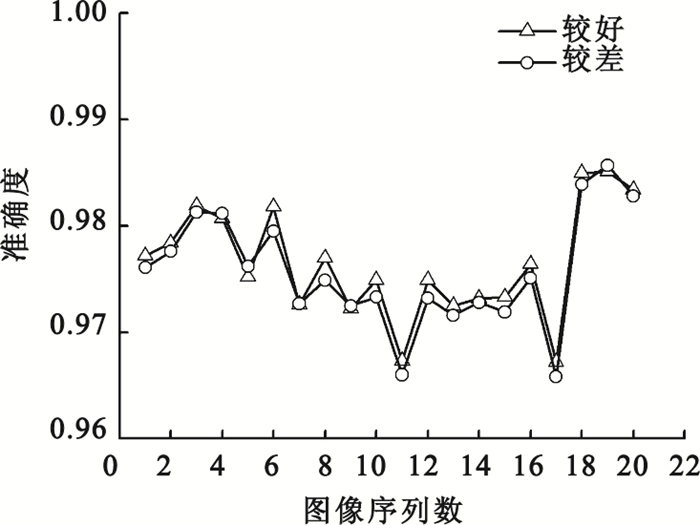圖6
分割效果較好圖像和較差圖像細化結果的準確率對比
Figure6.
Comparison of accuracy of thinned results of the better segmented images and the worse ones
最后對本文算法的復雜程度進行分析。算法的復雜度，即算法在編寫成可執行程序后，運行時所需要的時間和空間資源，包括了時間復雜度和空間復雜度，其中本文重點討論的是時間復雜度[19]。首先結合式(6)及其相應程序代碼，最復雜的是雙重循環，因此根據復雜度計算規則可得，互信息的時間復雜度是O(n2)。其次結合式(8)及其相應程序代碼，最復雜的也是雙重循環，同理可得，相關系數的時間復雜度也是O(n2)。最后，節點率涉及到鄰域搜索和除法運算，因此它的時間復雜度是O(n4)。在此有個經驗規則，時間復雜度由小到大依次為：c＜log2n＜n＜n·log2n＜n2＜n3＜2n＜3n＜n!，其中c是常量。若一個算法的時間復雜度為c、log2n、n、n·log2n，則這個算法的時間復雜度低，即時間效率比較高 ；若復雜度為2n、3n、n!，則稍微大一些的n會令算法運行困難。綜上討論可知，本文算法的復雜度較低。
4 結論
針對眼底圖像視網膜血管分割效果評價的問題，本文提出了一個新的基于拓撲結構的評價方法。該方法是利用STARE數據庫中的信息，將專家手工分割圖像及其腐蝕后的結果進行了實驗。首先是運用細化算法提取血管拓撲結構，然后計算互信息、相關系數和節點率的評價特征參數，再進行對比和分析。最后實驗證明，提出的評估方法能夠評價分割結果的質量，對補充眼底圖像視網膜血管分割評價方法具有重要的意義。下一步工作將研究把互信息、相關系數和節點率這三個指標結合起來評價眼底圖像分割的效果。
引言
眼底視網膜圖像在如今的眼科疾病診斷中起著十分重要的作用[1]。研究證明視網膜血管結構特征的改變和許多疾病密切相關，比如心血管疾病、糖尿病、中風等[2]。在視網膜血管分割的研究中，由于獲取的圖像多，人工圖像分析費時費力，計算機自動眼底圖像視網膜血管分割成為一個重要的方向[3]。目前已開發出許多自動分割的方法[4]。
對于疾病的診斷，血管分割結果的好壞顯得十分重要，而判斷這種好壞依靠評價方法[5]。一般來說，目前的分割評價方法分為兩類。一類是基于像素點的評價方法。其中，傳統的基于像素點的評價方法有三大指標，分別是準確度(accuracy)、靈敏度(sensitivity)和特異度(specificity)[6]。這三個指標是將分割結果與金標準進行像素的比較。還有一些基于像素間計算的方法。如Uyen等[7]提出了一個新的評估方法，它是基于精確性和完整性的概念。此方法的一個重要特性是對細小局部錯誤的容錯性，這些分割錯誤不會影響所需的血管特征。但該類方法沒有考慮形態學的特征。另一類評價方法則是基于形態學拓撲結構的評價方法。Gegundez-arias等[8]構造了一個基于連接度、區域和長度的函數，用于表征血管結構，作為血管分割結果的評價指標，該結果證明利用該函數對分割結果進行評價更適于樹狀結構圖像的分割評價，是對現有圖像分割評價方法的補充。
目前大部分自動分割算法所用的評價方法是傳統三大指標，沒有考慮到血管形態學結構的特殊性--樹狀結構[9]。為了更好地評價眼底視網膜血管圖像的分割效果，需要將分割結果的拓撲結構信息融入到評價方法中。為此，本文提出了一種基于拓撲結構的眼底血管分割效果的評價方法。該方法利用細化算法提取血管的拓撲結構，然后計算細化后的血管與細化后的金標準之間的特征參數，即互信息、相關系數和節點率，以此作為評價圖像分割結果的指標。
1 實驗數據的獲取與預處理
對圖像分割結果進行評價需要有一定的標準和待評價的圖像。對于眼底圖像來說，金標準是專家手工分割的結果[10]。在STARE數據庫中，有20幅眼底彩色圖像和兩套相應的金標準圖像，分別標記出了10.4%和14.9%屬于血管的像素。本文采用STARE數據庫中第一套金標準進行實驗比較。
在確定了金標準之后，關鍵是獲得待評價的圖像。本文的設計思路是采用形態學方法對金標準進行處理得到待評價的圖像，即分割效果較好和較差的圖像。具體操作是對20幅金標準圖像進行腐蝕，腐蝕程度越大則代表分割效果越差。進行了兩次程度不同的腐蝕得到標記為好和差的圖像各二十幅。圖 1(a)是STARE數據庫中第一套專家手工分割中某一幅眼底圖像，圖 1(b)和圖 1(c)分別是用不同結構單元對圖 1(a)進行腐蝕的結果。從直觀角度看，從左到右圖像的邊緣信息丟失得越來越多。這三類圖像代表手工分割的結果、直觀判斷分割質量較好的結果和直觀判斷分割質量較差的結果。
圖1
金標準腐蝕獲得的待評價圖像
(a)金標準;(b)分割結果較好的圖像；(c)分割結果較差的圖像
Figure1. Going-to-be evaluated images with erosion of gold standard(a) gold standard; (b) the better segmented image; (c) the worse segmented image
為了對以上分割效果進行進一步量化分析，采用傳統的評價指標來對上面直觀的評估效果進行驗證。在視網膜血管分割領域中，廣泛使用的傳統分割評價方法是基于準確度、靈敏度和特異度的分割評價標準[11]。
| $ 準確度\text{=}\frac{TP+TN}{TP+FP+TN+FN} $ |
| $ 靈敏度=\frac{TP}{TP+FN} $ |
| $ 特異度=\frac{TP}{TP+FN} $ |
其中： TP表示正確分割的血管，FP表示本來屬于背景但被誤分割成血管，TN表示正確分割的背景，FN表示本來屬于血管但被誤分割成背景。
本文只采用準確度來評價腐蝕后的結果，它是代表正確分割的血管區域和背景區域占全部圖像的百分比。對直觀判斷結果為好的20幅圖像和直觀判斷結果為差的20幅圖像分別計算準確度，結果如圖 2所示。直觀判斷結果為好的圖像準確度都是較高的，結果為差的值都是較低的。而且由于腐蝕程度的一致，兩條曲線走勢也基本相同。因此，這樣獲取待評價圖像的方法是可行的。
圖2
獲得的分割效果較好和較差圖像的準確率對比
Figure2.
Comparison of accuracy of the better segmented images and the worse ones obtained
2 評價特征提取
由于本文是從拓撲結構的角度來進行評價的，在確定待評價圖像后，首先利用細化算法來提取血管的中心線，即體現了血管完整的拓撲結構。本文所采用的細化方法是MATLAB軟件中的數學形態學函數bwmorph。圖 3是圖 1中三幅圖片細化的結果。
圖3
金標準及其腐蝕后圖像的細化結果
(a)金標準的細化結果；(b)分割結果較好圖像的細化結果；(c)分割結果較差圖像的細化結果
Figure3. The thining results of the gold standard and its erosion(a) thining result of gold standard; (b) thining result of better segmented image; (c) thining result of worse segmented image
如圖 3所示，細化后的圖像體現了血管當前的拓撲結構。對于評價特征的提取，本文用到了3個特征參數，即互信息、相關系數和節點率。選擇這三個特征參數的原因是互信息和相關系數均能表示自動分割結果和金標準的相關性大小，節點的數量能表示拓撲結構的復雜程度。
2.1 互信息
互信息是用來描述兩個系統之間的統計相關性，一般用熵來表示[12]。系統A的熵為
| $ H\left( A \right)=-\sum\limits_{a}{{{\text{p}}_{A}}\left( a \right){{\log }_{A}}\left( a \right)} $ |
其中：a∈A。而互信息函數為
| $ I\left( A,B \right)=H\left( A \right)-H\left( A|B \right)=H\left( A \right)+H\left( B \right)-H\left( A,B \right) $ |
其中：H(A｜B)表示已知系統B時A的條件熵，H(A，B)為兩系統的聯合熵。
互信息值越大說明所包含的相同信息也越多。因此，對分割圖像進行細化后，再計算互信息，那么結果越大則說明兩者之間的拓撲結構越相似。自從互信息作為圖像配準的準則被引入以來，已獲得多數研究者認可[13]。但是由于互信息測度對兩圖像的重疊區域大小比較敏感，因此Studholme等[14]又提出了正則化互信息，其表達式為
| $ \text{NMI=}\left[\text{H}\left( A \right)+\text{H}\left( B \right) \right]/\text{H}\left( A,B \right) $ |
研究表明，正則化互信息有更好的魯棒性，故本文采用式(6)計算互信息值。
2.2 相關系數
相關系數是測定變量之間關系密切程度的量，可用于表示兩幅圖像間的相關性[15]。通常以ρ表示總體的相關系數，以r表示樣本的相關系數[16]。總體相關系數的定義公式是
| $ \rho =\frac{\operatorname{cov}\left( X,Y \right)}{\sqrt{\operatorname{var}\left( X \right)\cdot var\left( Y \right)}} $ |
其中：cov(X,Y)是隨機變量X和Y的協方差，var(X)和var(Y)是隨機變量X和Y的方差。而樣本相關系數的定義為
| $ r=\frac{\sum{\left( {{x}_{i}}-\bar{x} \right)}\left( {{y}_{i}}-\bar{y} \right)}{\sqrt{\sum{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}\cdot \sum{{{\left( {{y}_{i}}-\bar{y} \right)}^{2}}}}}} $ |
其中：xi和yi別是X和Y的樣本數據。
相關系數越接近1，則說明兩者越相似。因此，對分割圖像進行細化處理后，再計算相關系數，結果越大則說明兩者之間的拓撲結構越相似。
2.3 節點率
以上兩個評價參數是先細化眼底血管圖像以突出其拓撲結構，然后用互信息和相關系數分析血管分割效果，間接地評價了形態結構的相似性。而眼底血管結構錯綜復雜，對于這類結構的拓撲分析在醫學領域中應用廣泛[17]。而眼底圖像的節點數是一個可以直接反映拓撲結構的特征參數。
在拓撲學中，節點是網絡任何支路的分叉點或網絡中兩個或更多支路的互連公共點[18]。因此對于一幅眼底圖像，節點包括了分支點和交叉點。統計分割后圖像中的節點數，與金標準中的節點數進行比較，兩者結果相近，則說明分割結果較好。為了能更好地顯示節點處所標記的紅圈，進行了細化處理再展示節點，結果如圖 4所示。
圖4
節點圖
Figure4.
Image of nodes
為了與互信息和相關系數的計算方式統一，本文提出一個新的概念--節點率。節點率等于待評價圖像中節點數和金標準圖像中節點數的比值。該值越接近1，則說明兩者越相似，即能反映待評價圖像和金標準的相似程度。節點的數量能反映眼底血管分支結構的復雜程度，因此這方面的拓撲分析對眼底圖像分割效果的評價有重要意義。
3 實驗結果與討論
實驗環境采用的是酷睿i7四核CPU為4 GB內存的PC機，在Windows 8平臺上，編程軟件為Matlab R2012a。原始數據是STARE數據庫中的20幅第一套專家手工標記結果。將這20幅原始圖像都進行如圖 1所示的腐蝕，再進行如圖 3所示的細化處理，得到60幅細化的圖像，即包括了20幅金標準、20幅分割效果較好和20幅分割效果較差的細化圖像。
最后分別計算這20幅效果較好圖像和20幅效果較差圖像相對于各自對應金標準的互信息、相關系數和節點率，結果如圖 5所示。可以看出，直觀判斷結果較好圖像的互信息、相關系數和節點率的折線都在結果較差圖像的折線之上，與預期符合。而且每幅圖中兩條曲線的走勢也基本相同，體現了對20幅金標準圖像每一次腐蝕的程度是一致的。
圖5
評價特征參數的折線圖
Figure5.
Chart of characteristic parameters
綜合以上實驗結果可知，細化處理后的互信息、相關系數和節點率能夠評估出眼底圖像分割結果的好壞，并且是符合直觀感知的。此外，為了區別互信息和相關系數跟準確率的差異，又對這20組效果較好圖像和20組效果較差圖像的準確率進行了計算，結果如圖 6所示。可見，較好圖像準確率的值大部分處在較差圖像準確率的值上方，但十分接近，而且有幾個相反的結果。此結果證明，準確率與互信息和相關系數在算法上有所不同。進而說明，細化后的準確率不能用來判斷眼底圖像分割的好壞。
圖6
分割效果較好圖像和較差圖像細化結果的準確率對比
Figure6.
Comparison of accuracy of thinned results of the better segmented images and the worse ones
最后對本文算法的復雜程度進行分析。算法的復雜度，即算法在編寫成可執行程序后，運行時所需要的時間和空間資源，包括了時間復雜度和空間復雜度，其中本文重點討論的是時間復雜度[19]。首先結合式(6)及其相應程序代碼，最復雜的是雙重循環，因此根據復雜度計算規則可得，互信息的時間復雜度是O(n2)。其次結合式(8)及其相應程序代碼，最復雜的也是雙重循環，同理可得，相關系數的時間復雜度也是O(n2)。最后，節點率涉及到鄰域搜索和除法運算，因此它的時間復雜度是O(n4)。在此有個經驗規則，時間復雜度由小到大依次為：c＜log2n＜n＜n·log2n＜n2＜n3＜2n＜3n＜n!，其中c是常量。若一個算法的時間復雜度為c、log2n、n、n·log2n，則這個算法的時間復雜度低，即時間效率比較高 ；若復雜度為2n、3n、n!，則稍微大一些的n會令算法運行困難。綜上討論可知，本文算法的復雜度較低。
4 結論
針對眼底圖像視網膜血管分割效果評價的問題，本文提出了一個新的基于拓撲結構的評價方法。該方法是利用STARE數據庫中的信息，將專家手工分割圖像及其腐蝕后的結果進行了實驗。首先是運用細化算法提取血管拓撲結構，然后計算互信息、相關系數和節點率的評價特征參數，再進行對比和分析。最后實驗證明，提出的評估方法能夠評價分割結果的質量，對補充眼底圖像視網膜血管分割評價方法具有重要的意義。下一步工作將研究把互信息、相關系數和節點率這三個指標結合起來評價眼底圖像分割的效果。
