為了提高可穿戴設備中血壓測量的準確性,本文提出了一種基于多脈搏波參數的人體血壓檢測方法,該方法通過對脈搏傳輸時間(PWTT)、每搏心輸出量、波形系數、升支平均斜率、脈率等多脈搏波參數的多元線性回歸分析,建立了基于多脈搏波參數的人體血壓計算模型,利用該模型計算出血壓值;以心音信號為參考計算PWTT(PWTTPCG),克服了以心電信號為參考計算PWTT(PWTTECG)需要更換電極、有導連線穿戴不方便的不足。分別對基于PWTTPCG和多脈搏波參數的人體血壓計算模型計算血壓進行了實驗驗證,實驗結果表明利用PWTTPCG作為PWTT計算人體血壓的可行性;利用該模型計算的收縮壓和舒張壓的平均誤差分別為1.62 mm Hg和1.12 mm Hg,較單一參數分別提高了57%和53%,具有較高的測量精度。
引用本文： 苗長云, 穆殿偉, 張誠, 苗春澆, 李鴻強. 基于多脈搏波參數的人體血壓檢測的研究. 生物醫學工程學雜志, 2015, 32(5): 1113-1117. doi: 10.7507/1001-5515.20150197 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
隨著生物醫學傳感器的小型化，信息處理、無線傳輸技術的快速發展，基于可穿戴設備的多生理參數采集系統的研究已成為熱點[1]。可穿戴設備能夠長期連續檢測人體生理指標的變化，避免了傳統監護設備存在結構復雜、體積大、不宜穿戴、限制患者運動等問題[2]。
可穿戴設備對于心血管疾病診斷、分析具有重要意義。近幾年，國內外在可穿戴設備血壓(blood pressure，BP)檢測的研究方面取得了很大進展。瑞士聯邦理工學院研制了一種腕式集成化的遠程醫療監控系統[3]；美國VivoMetrics公司研發了能夠采集心電信號(electrocardiogram，ECG)、血壓、血氧等生理參數的生命衫(LifeShirt)[4]；中科院研制了能夠采集心電、血壓、血氧飽和度以及心率(heart rate，HR)的人體傳感器網絡[5]，以上可穿戴設備對血壓的檢測都是以袖帶方式，缺乏舒適性，需要充放氣，無法實現血壓的連續測量。2009年香港中文大學采用基于脈搏波傳輸時間(pulse wave transit time，PWTT)的血壓檢測方法研制了h-shirt。該方法同步采集心電和脈搏波信號，利用PWTT間接推算每搏血壓值，實現了連續的血壓測量，傳感器對測試部位影響小，擺脫了血壓袖帶對身體的束縛[6]。上述方法中，心電采集使用氯化銀(AgCl)電極或織物電極，AgCl電極需要定期更換[7]，不適于長期吸附，織物電極阻抗高，不利于信號的獲取，且單導聯的心電采集至少需要三條線，導聯線過多給穿戴者行動上帶來了不便。
心音信號(phonocardiography,PCG)能夠反映心臟及心血管系統的機械運動狀況，第一心音(S1)的峰值點準確標記了脈搏波傳輸的起點[8-9]。心音信號檢測可以通過單一的壓力傳感器，能夠克服心電信號檢測需要更換電極、有導連線穿戴不方便的不足，且在心血管疾病尚未發展到足以產生臨床及病理改變以前反映出心臟的重要病理信息[10]。影響人體血壓的因素很多，如心搏量、動脈順應性和外周阻力等，也會影響到脈搏波波形特征，因此基于PWTT單一參數的血壓檢測方法波動性大，準確性差[11-12]。
針對上述問題，本文提出了一種基于多脈搏波參數的人體血壓檢測方法，通過對多脈搏波參數的多元線性回歸分析，建立了基于多脈搏波參數的人體血壓計算模型，以PCG為參考計算PWTT(PWTTPCG)，克服了以ECG為參考計算PWTT(PWTTECG)需要采集ECG、更換電極、有導連線穿戴不方便的不足，能夠實現可穿戴設備中人體血壓的連續檢測，提高了測量精度。
1 典型脈搏波及特征參數計算
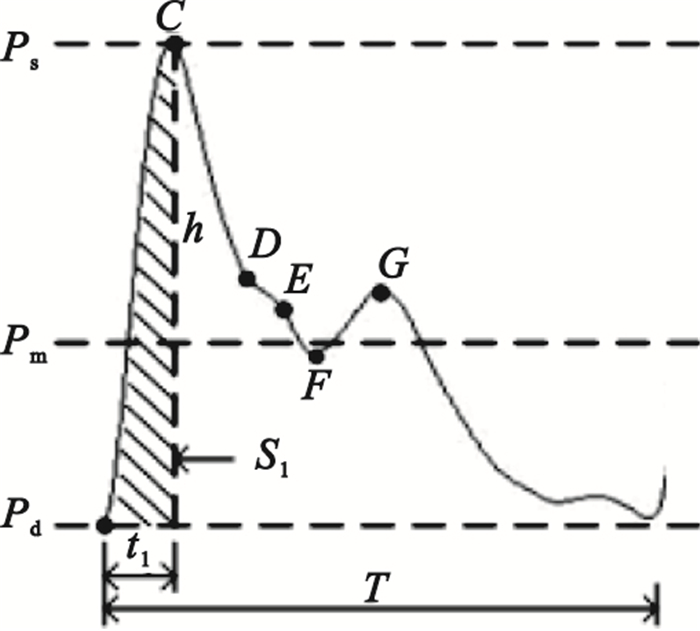
典型的脈搏波波形如圖 1所示。其中B為脈搏波的起點，表示主動脈瓣開放；C為主波峰值點，表示收縮期最高壓力點；D為主動脈擴張降壓點；E為左心室舒張期開始點；F為重搏波起始點；G為重搏波最高壓力點；Ps為脈搏波主波幅度、Pd為脈搏波起點幅度，Pm為脈搏波平均幅度，h為脈搏波主波高度；t1為上升支時間，表示心動壓縮期；T為脈搏波周期；S1為上升支面積。
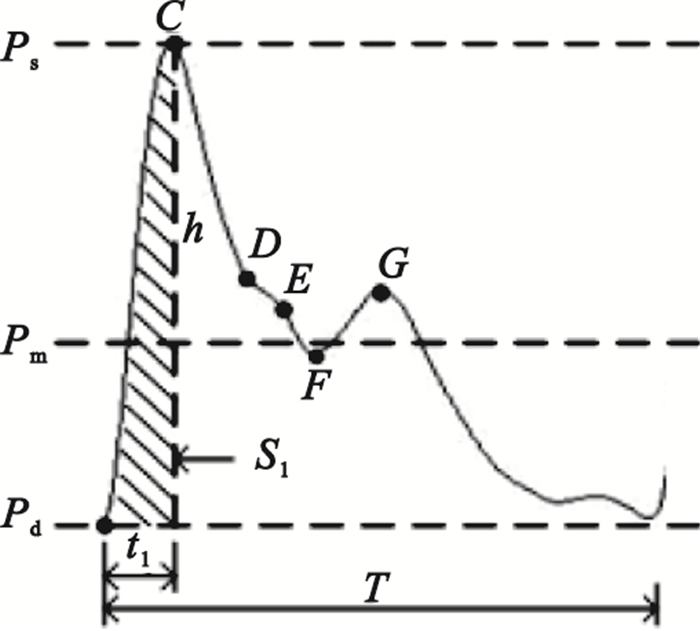圖1
脈搏波波形
Figure1.
Waveform of pulse wave
根據B至G的脈搏波特征點可以計算出各脈搏波特征參數，主要包括PWTT、每搏心輸出量、波形系數、升支平均斜率、脈率等，這些特征參數包含了豐富的心血管生理和病理信息[13]。
PWTT是指動脈脈搏從心臟收縮開始傳播到某一動脈分支血管所需要的時間[14]。根據血液動力學理論，心臟射血后，血液在血管中流動產生的脈搏波滯后于心臟射血點。如果血管的彈性保持不變，則血壓的變化與PWTT的變化成正比，二者的線性關系如式(1)所示。對于同一個體，血管彈性在短時間內不發生變化，參數a和b也保持不變[15]。
| $ BP{\rm{ = }}a + b \times PWTT $ |
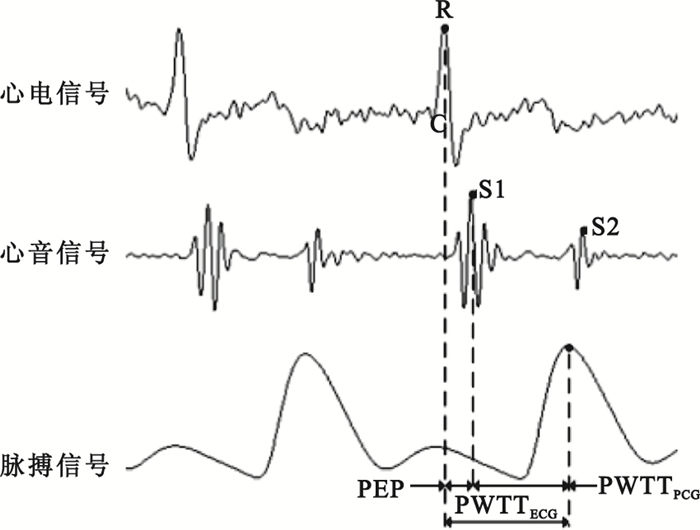
PWTTECG是以ECG的R波的峰值點為起點，脈搏波上升支的峰值點C作為終點。PWTTPCG是以心音信號S1的峰值點為起點，脈搏波上升支的峰值點C為終點，如圖 2所示。
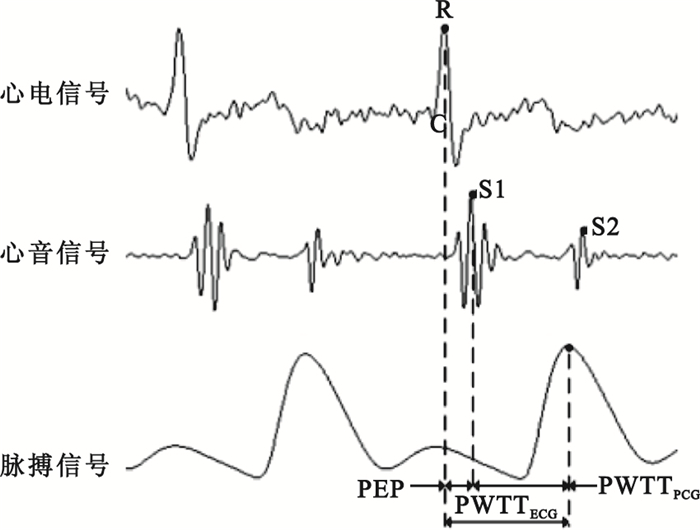圖2
PWTT計算
Figure2.
Calculate of PWTT
PWTTECG包括射血前期(pre-ejection period，PEP)和PWTTPCG兩部分，即
| $ {\rm{PWT}}{{\rm{T}}_{{\rm{ECG}}}} = {\rm{PEP + PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
其中，PEP為心室除極開始至心室射血開始的時間，是以ECG的R波峰值點為起點，心音信號S1的峰值點為終點。R波峰值點是心臟左心室電興奮時刻，并不是主動脈瓣開放、心臟射血的時刻[16]，在PEP期脈搏波并沒有開始傳播，即PWTTECG不是真正的PWTT，因此本文采用PWTTPCG計算PWTT。通過對脈搏波原理和動脈彈性腔理論的研究，表明除PWTT外的脈搏波參數包括每搏心輸出量Z、波形系數K、升支平均斜率k、上升支波圖與整體波圖面積比值S、脈率HR等，計算公式如表 1所示。其中，每搏心輸出量對血壓的影響主要表現在平均動脈壓方面；波形系數是典型的脈搏波面積參數，可很好地反映人體心血管系統中血管外周阻力、血管壁彈性和血液黏度等生理因素；脈率則主要影響舒張壓，心率快時舒張壓低，心率慢時舒張壓高[17]。
表1
脈搏波參數表達式
Table1.
Expression of pulse wave parameter
2 參數人體血壓計算模型及實驗驗證
2.1 多元線性回歸分析
通過皮爾森相關系數計算多脈搏波參數與血壓之間的相關性。皮爾森相關系數r公式為
| $ r = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \overline X } \right)\left( {{y_i} - \overline Y } \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \overline X } \right)}^2}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \overline Y } \right)}^2}} } } }} $ |
式中，X=[x1，…，xn]和Y=[y1，…，yn]為長度為n的2個變量，
根據多脈搏波參數與血壓之間的相關性，計算多脈搏波參數的人體血壓計算模型。多元線性回歸模型的一般表達式為
| $ P = {\beta _0} + {\beta _1}{Q_1} + {\beta _2}{Q_2} + \ldots + {\beta _m}{Q_m} + e $ |
式中，P為因變量，Q1，Q2，…，Qm為自變量，P表示為Q1，Q2，…，Qm的線性函數，β0為常數項，β1，β2，…，βm為偏回歸系數，e為殘差。
2.2 人體血壓計算模型
為了建立基于多脈搏波參數的人體血壓計算模型，本文選擇54名志愿者(32名男性，22名女性，年齡22～46歲，其中10名血壓偏高)，并搭建基于labview的多生理參數測量系統，如圖 3所示。PCG和脈搏傳感器分別選用壓電薄膜型傳感器HKY-06B和HK2000B，PC機通過數據采集卡NI USB-6259，以1 kHz的采樣率同步采集測試者的PCG和脈搏波信號，并對相關信號進行預處理和特征提取。
圖3
多生理參數測量系統
Figure3.
Measurement system of multiple physiological parameters
利用水銀血壓計和多生理參數測量系統采集每名測試者在運動前后、早晚間等不同時段、不同狀態下的實際血壓與PCG、脈搏波信號。分別以每名測試者的收縮壓(systolic blood pressure，SBP)和舒張壓(diastolic blood pressure，DBP)為yi，分別以脈搏波參數PWTT、每搏心輸出量Z、波形系數K、上升支平均斜率k、上升支波圖與整體波圖面積的比值S和脈率HR為xi，代入式(3)，得到SBP和DBP與各脈搏波參數的相關系數。
以測試者1為例，與SBP具有強相關的脈搏波參數為PWTT、每搏心輸出量Z、波形系數K、上升支平均斜率k、上升支波圖與整體波圖面積的比值S；與DBP具有強相關的脈搏波參數為PWTT、每搏心輸出量Z、波形系數K、上升支平均斜率k、上升支波圖與整體波圖面積的比值S和脈率HR。
為了建立基于多脈搏波參數的人體血壓計算模型，以P表示SBP或DBP，Q1，Q2，…，Qm表示多脈搏波參數。選擇SBP和DBP與脈搏波參數相關系數大(絕對值大于0.5)的脈搏波參數為Qi，與脈搏波參數相關系數小(絕對值小于0.5)的為0，將每組SBP、DBP和脈搏波參數分別代入式(4)建立多元線性回歸方程，計算β0，β1，β2，…，βm，得到基于多脈搏波參數的人體血壓計算模型為
| $ \begin{array}{l} {\rm{SBP = 128}}{\rm{.03 - 69}}{\rm{.22}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} - 63.19 \times Z - \\ 10.96 \times K + 7.61 \times k + 48.83 \times S \end{array} $ |
| $ \begin{array}{l} {\rm{DBP = 30}}{\rm{.85 - 67}}{\rm{.33}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} + 7.44 \times Z + \\ 205.33 \times K - 1.51 \times k + 143.31 \times S - 0.54 \times {\rm{HR}} \end{array} $ |
2.3 實驗驗證
實驗包括兩部分，一部分為利用PWTTPCG作為PWTT計算人體血壓的驗證實驗，另一部分為基于多脈搏波參數的人體血壓計算模型計算血壓的驗證實驗。對54名測試者按照年齡段分成3組，第一組年齡22～30歲，24名測試者(14名男性，10名女性)；第二組年齡為30～40歲，15名測試者(9名男性，6名女性)；第三組年齡為40～46歲，15名測試者(9名男性，6名女性)。
利用PWTTPCG作為PWTT計算人體血壓的驗證實驗中，同步采集54名測試者ECG、PCG和脈搏波信號，同時通過水銀血壓計測量實際血壓作為參考，每人采集15組數據，分別建立PWTTECG和PWTTPCG的單一參數血壓計算模型。以測試者1為例，PWTTECG的單一參數血壓計算模型為
| $ {\rm{SBP = }}239.37 - 482.18 \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
| $ {\rm{DBP = 139}}{\rm{.74 - 239}}{\rm{.28}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
PWTTPCG的單一參數血壓計算模型為
| $ {\rm{SBP = 184}}{\rm{.32}} - 347.29 \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
| $ {\rm{DBP = 130}}{\rm{.55}} - {\rm{259}}{\rm{.73}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
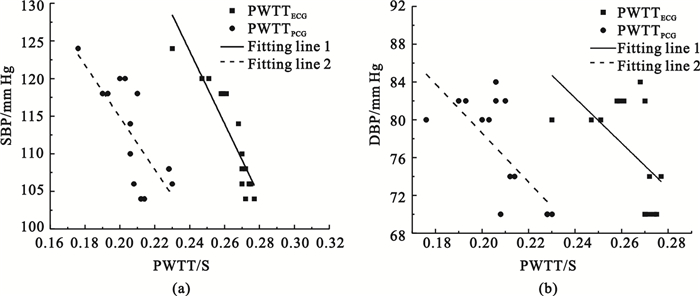
SBP和DBP與PWTTECG和PWTTPCG的擬合曲線1和2，分別如圖 4(a)、(b)所示。
從圖 4可以看到擬合曲線1和2變化趨勢相同，即PWTTECG與PWTTPCG的單一參數血壓計算模型具有很好的一致性。
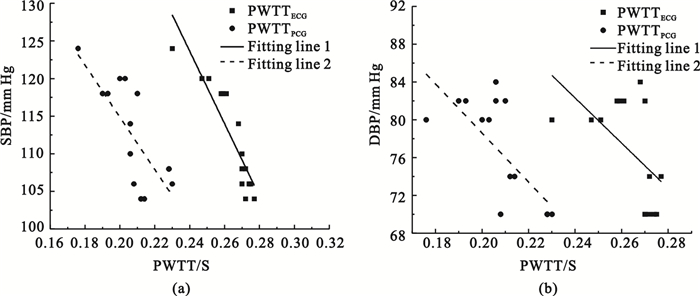圖4
SBP和DBP與PWTTECG和PWTTPCG的擬合曲線
(a)SBP與PWTTECG和PWTTPCG的擬合曲線；(b)DBP與PWTTECG和PWTTPCG的擬合曲線
Figure4. Fitting Line of SBP, DBP and PWTTECG, PWTTPCG(a) fitting Line of SBP and PWTTECG, PWTTPCG； (b) fitting Line of DBP and PWTTECG, PWTTPCG
分別通過PWTTECG和PWTTPCG的單一參數血壓計算模型計算得到的血壓值與實測血壓值的誤差如表 2所示。
表2
計算得到的血壓值與實測血壓值的平均誤差(mm Hg)
Table2.
Average errors between calculated values and measured values of blood pressure (mm Hg)
由表 2可見，PWTTECG和PWTTPCG的單一參數血壓計算模型計算血壓的誤差都在±5 mm Hg以內，能夠滿足臨床血壓測量的要求。因此，可以利用PWTTPCG作為PWTT計算人體血壓。
基于多脈搏波參數的人體血壓計算模型計算血壓的驗證實驗中，分別利用基于PWTTPCG的單一參數血壓計算模型和多脈搏波參數的人體血壓計算模型計算得到每組測試者的血壓值與實測值的平均誤差，如表 3所示。
表3
計算得到的血壓值與實測值的平均誤差(mm Hg)
Table3.
Average errors between calculated values and measured values of blood pressure (mm Hg)
從表 3中可以看到，基于單一參數的血壓計算模型得到的收縮壓和舒張壓的平均誤差為3.74 mm Hg和2.37 mm Hg，基于多脈搏波參數的人體血壓計算模型得到的收縮壓和舒張壓平均誤差僅為1.62 mm Hg和1.12 mm Hg。由此可見，基于多脈搏波參數的人體血壓計算模型具有較高的準確性，較單一參數的人體血壓計算模型在收縮壓和舒張壓測量準確性分別提高了57%和53%。
3 結束語
為了提高可穿戴設備中血壓測量的準確性，提出了一種基于多脈搏波參數的人體血壓檢測方法，建立了基于多脈搏波參數的人體血壓計算模型，利用PCG計算PWTT，克服了利用ECG計算PWTT需要更換電極、有導連線穿戴不方便的不足。分別對PWTTPCG作為PWTT計算人體血壓和基于多脈搏波參數的人體血壓計算模型計算血壓進行了實驗驗證，實驗結果表明可以用PCG信號為參考計算PWTT，用于人體血壓的測量；多脈搏波參數人體血壓計算模型計算收縮壓和舒張壓的平均誤差分別為1.62 mm Hg和1.12 mm Hg，較單一參數分別提高了57%和53%，具有較高的測量精度。該方法能夠實現人體血壓的連續檢測，應用于可穿戴設備。
引言
隨著生物醫學傳感器的小型化，信息處理、無線傳輸技術的快速發展，基于可穿戴設備的多生理參數采集系統的研究已成為熱點[1]。可穿戴設備能夠長期連續檢測人體生理指標的變化，避免了傳統監護設備存在結構復雜、體積大、不宜穿戴、限制患者運動等問題[2]。
可穿戴設備對于心血管疾病診斷、分析具有重要意義。近幾年，國內外在可穿戴設備血壓(blood pressure，BP)檢測的研究方面取得了很大進展。瑞士聯邦理工學院研制了一種腕式集成化的遠程醫療監控系統[3]；美國VivoMetrics公司研發了能夠采集心電信號(electrocardiogram，ECG)、血壓、血氧等生理參數的生命衫(LifeShirt)[4]；中科院研制了能夠采集心電、血壓、血氧飽和度以及心率(heart rate，HR)的人體傳感器網絡[5]，以上可穿戴設備對血壓的檢測都是以袖帶方式，缺乏舒適性，需要充放氣，無法實現血壓的連續測量。2009年香港中文大學采用基于脈搏波傳輸時間(pulse wave transit time，PWTT)的血壓檢測方法研制了h-shirt。該方法同步采集心電和脈搏波信號，利用PWTT間接推算每搏血壓值，實現了連續的血壓測量，傳感器對測試部位影響小，擺脫了血壓袖帶對身體的束縛[6]。上述方法中，心電采集使用氯化銀(AgCl)電極或織物電極，AgCl電極需要定期更換[7]，不適于長期吸附，織物電極阻抗高，不利于信號的獲取，且單導聯的心電采集至少需要三條線，導聯線過多給穿戴者行動上帶來了不便。
心音信號(phonocardiography,PCG)能夠反映心臟及心血管系統的機械運動狀況，第一心音(S1)的峰值點準確標記了脈搏波傳輸的起點[8-9]。心音信號檢測可以通過單一的壓力傳感器，能夠克服心電信號檢測需要更換電極、有導連線穿戴不方便的不足，且在心血管疾病尚未發展到足以產生臨床及病理改變以前反映出心臟的重要病理信息[10]。影響人體血壓的因素很多，如心搏量、動脈順應性和外周阻力等，也會影響到脈搏波波形特征，因此基于PWTT單一參數的血壓檢測方法波動性大，準確性差[11-12]。
針對上述問題，本文提出了一種基于多脈搏波參數的人體血壓檢測方法，通過對多脈搏波參數的多元線性回歸分析，建立了基于多脈搏波參數的人體血壓計算模型，以PCG為參考計算PWTT(PWTTPCG)，克服了以ECG為參考計算PWTT(PWTTECG)需要采集ECG、更換電極、有導連線穿戴不方便的不足，能夠實現可穿戴設備中人體血壓的連續檢測，提高了測量精度。
1 典型脈搏波及特征參數計算
典型的脈搏波波形如圖 1所示。其中B為脈搏波的起點，表示主動脈瓣開放；C為主波峰值點，表示收縮期最高壓力點；D為主動脈擴張降壓點；E為左心室舒張期開始點；F為重搏波起始點；G為重搏波最高壓力點；Ps為脈搏波主波幅度、Pd為脈搏波起點幅度，Pm為脈搏波平均幅度，h為脈搏波主波高度；t1為上升支時間，表示心動壓縮期；T為脈搏波周期；S1為上升支面積。
圖1
脈搏波波形
Figure1.
Waveform of pulse wave
根據B至G的脈搏波特征點可以計算出各脈搏波特征參數，主要包括PWTT、每搏心輸出量、波形系數、升支平均斜率、脈率等，這些特征參數包含了豐富的心血管生理和病理信息[13]。
PWTT是指動脈脈搏從心臟收縮開始傳播到某一動脈分支血管所需要的時間[14]。根據血液動力學理論，心臟射血后，血液在血管中流動產生的脈搏波滯后于心臟射血點。如果血管的彈性保持不變，則血壓的變化與PWTT的變化成正比，二者的線性關系如式(1)所示。對于同一個體，血管彈性在短時間內不發生變化，參數a和b也保持不變[15]。
| $ BP{\rm{ = }}a + b \times PWTT $ |
PWTTECG是以ECG的R波的峰值點為起點，脈搏波上升支的峰值點C作為終點。PWTTPCG是以心音信號S1的峰值點為起點，脈搏波上升支的峰值點C為終點，如圖 2所示。
圖2
PWTT計算
Figure2.
Calculate of PWTT
PWTTECG包括射血前期(pre-ejection period，PEP)和PWTTPCG兩部分，即
| $ {\rm{PWT}}{{\rm{T}}_{{\rm{ECG}}}} = {\rm{PEP + PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
其中，PEP為心室除極開始至心室射血開始的時間，是以ECG的R波峰值點為起點，心音信號S1的峰值點為終點。R波峰值點是心臟左心室電興奮時刻，并不是主動脈瓣開放、心臟射血的時刻[16]，在PEP期脈搏波并沒有開始傳播，即PWTTECG不是真正的PWTT，因此本文采用PWTTPCG計算PWTT。通過對脈搏波原理和動脈彈性腔理論的研究，表明除PWTT外的脈搏波參數包括每搏心輸出量Z、波形系數K、升支平均斜率k、上升支波圖與整體波圖面積比值S、脈率HR等，計算公式如表 1所示。其中，每搏心輸出量對血壓的影響主要表現在平均動脈壓方面；波形系數是典型的脈搏波面積參數，可很好地反映人體心血管系統中血管外周阻力、血管壁彈性和血液黏度等生理因素；脈率則主要影響舒張壓，心率快時舒張壓低，心率慢時舒張壓高[17]。
表1
脈搏波參數表達式
Table1.
Expression of pulse wave parameter
2 參數人體血壓計算模型及實驗驗證
2.1 多元線性回歸分析
通過皮爾森相關系數計算多脈搏波參數與血壓之間的相關性。皮爾森相關系數r公式為
| $ r = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \overline X } \right)\left( {{y_i} - \overline Y } \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \overline X } \right)}^2}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \overline Y } \right)}^2}} } } }} $ |
式中，X=[x1，…，xn]和Y=[y1，…，yn]為長度為n的2個變量，
根據多脈搏波參數與血壓之間的相關性，計算多脈搏波參數的人體血壓計算模型。多元線性回歸模型的一般表達式為
| $ P = {\beta _0} + {\beta _1}{Q_1} + {\beta _2}{Q_2} + \ldots + {\beta _m}{Q_m} + e $ |
式中，P為因變量，Q1，Q2，…，Qm為自變量，P表示為Q1，Q2，…，Qm的線性函數，β0為常數項，β1，β2，…，βm為偏回歸系數，e為殘差。
2.2 人體血壓計算模型
為了建立基于多脈搏波參數的人體血壓計算模型，本文選擇54名志愿者(32名男性，22名女性，年齡22～46歲，其中10名血壓偏高)，并搭建基于labview的多生理參數測量系統，如圖 3所示。PCG和脈搏傳感器分別選用壓電薄膜型傳感器HKY-06B和HK2000B，PC機通過數據采集卡NI USB-6259，以1 kHz的采樣率同步采集測試者的PCG和脈搏波信號，并對相關信號進行預處理和特征提取。
圖3
多生理參數測量系統
Figure3.
Measurement system of multiple physiological parameters
利用水銀血壓計和多生理參數測量系統采集每名測試者在運動前后、早晚間等不同時段、不同狀態下的實際血壓與PCG、脈搏波信號。分別以每名測試者的收縮壓(systolic blood pressure，SBP)和舒張壓(diastolic blood pressure，DBP)為yi，分別以脈搏波參數PWTT、每搏心輸出量Z、波形系數K、上升支平均斜率k、上升支波圖與整體波圖面積的比值S和脈率HR為xi，代入式(3)，得到SBP和DBP與各脈搏波參數的相關系數。
以測試者1為例，與SBP具有強相關的脈搏波參數為PWTT、每搏心輸出量Z、波形系數K、上升支平均斜率k、上升支波圖與整體波圖面積的比值S；與DBP具有強相關的脈搏波參數為PWTT、每搏心輸出量Z、波形系數K、上升支平均斜率k、上升支波圖與整體波圖面積的比值S和脈率HR。
為了建立基于多脈搏波參數的人體血壓計算模型，以P表示SBP或DBP，Q1，Q2，…，Qm表示多脈搏波參數。選擇SBP和DBP與脈搏波參數相關系數大(絕對值大于0.5)的脈搏波參數為Qi，與脈搏波參數相關系數小(絕對值小于0.5)的為0，將每組SBP、DBP和脈搏波參數分別代入式(4)建立多元線性回歸方程，計算β0，β1，β2，…，βm，得到基于多脈搏波參數的人體血壓計算模型為
| $ \begin{array}{l} {\rm{SBP = 128}}{\rm{.03 - 69}}{\rm{.22}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} - 63.19 \times Z - \\ 10.96 \times K + 7.61 \times k + 48.83 \times S \end{array} $ |
| $ \begin{array}{l} {\rm{DBP = 30}}{\rm{.85 - 67}}{\rm{.33}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} + 7.44 \times Z + \\ 205.33 \times K - 1.51 \times k + 143.31 \times S - 0.54 \times {\rm{HR}} \end{array} $ |
2.3 實驗驗證
實驗包括兩部分，一部分為利用PWTTPCG作為PWTT計算人體血壓的驗證實驗，另一部分為基于多脈搏波參數的人體血壓計算模型計算血壓的驗證實驗。對54名測試者按照年齡段分成3組，第一組年齡22～30歲，24名測試者(14名男性，10名女性)；第二組年齡為30～40歲，15名測試者(9名男性，6名女性)；第三組年齡為40～46歲，15名測試者(9名男性，6名女性)。
利用PWTTPCG作為PWTT計算人體血壓的驗證實驗中，同步采集54名測試者ECG、PCG和脈搏波信號，同時通過水銀血壓計測量實際血壓作為參考，每人采集15組數據，分別建立PWTTECG和PWTTPCG的單一參數血壓計算模型。以測試者1為例，PWTTECG的單一參數血壓計算模型為
| $ {\rm{SBP = }}239.37 - 482.18 \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
| $ {\rm{DBP = 139}}{\rm{.74 - 239}}{\rm{.28}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
PWTTPCG的單一參數血壓計算模型為
| $ {\rm{SBP = 184}}{\rm{.32}} - 347.29 \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
| $ {\rm{DBP = 130}}{\rm{.55}} - {\rm{259}}{\rm{.73}} \times {\rm{PWT}}{{\rm{T}}_{{\rm{PCG}}}} $ |
SBP和DBP與PWTTECG和PWTTPCG的擬合曲線1和2，分別如圖 4(a)、(b)所示。
從圖 4可以看到擬合曲線1和2變化趨勢相同，即PWTTECG與PWTTPCG的單一參數血壓計算模型具有很好的一致性。
圖4
SBP和DBP與PWTTECG和PWTTPCG的擬合曲線
(a)SBP與PWTTECG和PWTTPCG的擬合曲線；(b)DBP與PWTTECG和PWTTPCG的擬合曲線
Figure4. Fitting Line of SBP, DBP and PWTTECG, PWTTPCG(a) fitting Line of SBP and PWTTECG, PWTTPCG； (b) fitting Line of DBP and PWTTECG, PWTTPCG
分別通過PWTTECG和PWTTPCG的單一參數血壓計算模型計算得到的血壓值與實測血壓值的誤差如表 2所示。
表2
計算得到的血壓值與實測血壓值的平均誤差(mm Hg)
Table2.
Average errors between calculated values and measured values of blood pressure (mm Hg)
由表 2可見，PWTTECG和PWTTPCG的單一參數血壓計算模型計算血壓的誤差都在±5 mm Hg以內，能夠滿足臨床血壓測量的要求。因此，可以利用PWTTPCG作為PWTT計算人體血壓。
基于多脈搏波參數的人體血壓計算模型計算血壓的驗證實驗中，分別利用基于PWTTPCG的單一參數血壓計算模型和多脈搏波參數的人體血壓計算模型計算得到每組測試者的血壓值與實測值的平均誤差，如表 3所示。
表3
計算得到的血壓值與實測值的平均誤差(mm Hg)
Table3.
Average errors between calculated values and measured values of blood pressure (mm Hg)
從表 3中可以看到，基于單一參數的血壓計算模型得到的收縮壓和舒張壓的平均誤差為3.74 mm Hg和2.37 mm Hg，基于多脈搏波參數的人體血壓計算模型得到的收縮壓和舒張壓平均誤差僅為1.62 mm Hg和1.12 mm Hg。由此可見，基于多脈搏波參數的人體血壓計算模型具有較高的準確性，較單一參數的人體血壓計算模型在收縮壓和舒張壓測量準確性分別提高了57%和53%。
3 結束語
為了提高可穿戴設備中血壓測量的準確性，提出了一種基于多脈搏波參數的人體血壓檢測方法，建立了基于多脈搏波參數的人體血壓計算模型，利用PCG計算PWTT，克服了利用ECG計算PWTT需要更換電極、有導連線穿戴不方便的不足。分別對PWTTPCG作為PWTT計算人體血壓和基于多脈搏波參數的人體血壓計算模型計算血壓進行了實驗驗證，實驗結果表明可以用PCG信號為參考計算PWTT，用于人體血壓的測量；多脈搏波參數人體血壓計算模型計算收縮壓和舒張壓的平均誤差分別為1.62 mm Hg和1.12 mm Hg，較單一參數分別提高了57%和53%，具有較高的測量精度。該方法能夠實現人體血壓的連續檢測，應用于可穿戴設備。
