針對現有二維分割方法人工干預較多及存在分割缺陷、三維分割方法對突變異常肝臟分割錯誤等問題,本文提出一種基于圖像序列上下文關聯的肝臟器官半自動分割方法。利用肝臟器官組織圖像序列上下文的相似性先驗知識,結合區域生長和水平集模型,并以少量人工干預輔助應對肝臟突變情況來進行肝臟的半自動分割。實驗結果表明,本文方法分割肝臟精度高,適應能力強,對變異性較大的肝臟分割效果較好,可較好地滿足臨床應用需求。
引用本文： 張美云, 房斌, 王翊, 鐘南昌. 基于圖像序列上下文關聯的肝臟器官分割方法. 生物醫學工程學雜志, 2015, 32(5): 1125-1130. doi: 10.7507/1001-5515.20150199 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
圖像肝臟分割在肝臟診斷、腫瘤分割、肝移植等臨床應用中起著關鍵的作用。從腹部CT圖像可知，由于肝臟自身變異性較大、形狀不規律、圖像對比度低和相鄰組織有粘連等特點，使得肝臟圖像的分割成為一個具有挑戰性的問題。目前，國內外對肝臟分割方法常用的有基于形態學分割方法[1]、區域生長分割方法[2-3]、基于圖論分割方法[4]、均值漂移分割方法[5]、基于水平集分割方法[6-8]等。
以上分割方法雖然在實際應用中都發揮了一定的效用，但這類分割方法對圖像質量要求較高，且在實際分割過程中，由于個體臨床CT圖像存在很大的差異性和變異性，分割結果會出現過分割及漏分割等現象；而且觀察醫學器官的斷層掃描圖像可知，圖像序列上下文關聯較大，其本質為三維圖像，而現有二維分割方法多考慮單張圖像，未利用組織器官的圖像上下文之間的關系。針對這些問題，三維分割技術漸漸得到了發展。現有三維肝臟分割技術主要有基于半自動[9]和全自動[10-12]的分割方法。這些分割算法對圖像質量同樣要求較高，且要求被分割對象形狀和先驗模型接近，如果被分割對象變異性較大，往往不能正確分割出肝臟，因此實際應用效果較差，難以達到臨床應用要求。
水平集模型是在解決火焰表面進化問題時提出的，平面閉合曲線隱含表達為三維連續曲面，將求解計算從低維上升到更高一層，是一種高精度的分割方法，在分割過程中存在曲線演化表達的簡單性，以及處理拓撲變化自然性的優點，而數值化的求解方式具有很好的穩定性，其中基于能量函數模型定義具有直觀的物理意義，容易加入約束條件。而在利用水平集自動分割的過程中，如何精確設定初始分割位置非常重要，初始分割位置離實際邊緣越近，收斂到正確位置的可能性就越大。
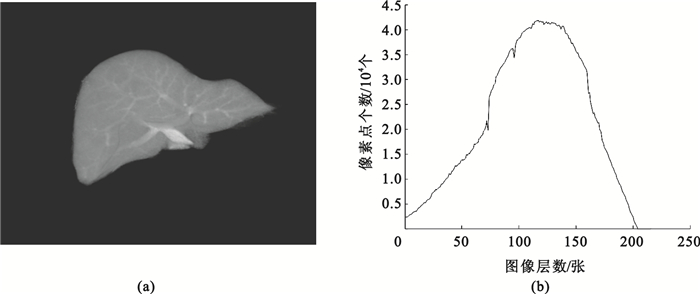
考慮肝臟CT圖像的三維形態，如圖 1所示,圖 1(a)為醫生手工分割獲得的標準肝臟圖像，從二維圖像上對肝臟面積進行像素統計可得圖 1(b)，由圖 1(b)可知其軸狀面中肝臟面積變化較為平滑，相鄰兩幅肝臟圖像中輪廓具有連續性，其輪廓形狀在一定的空間范圍內按一定的速度進行變化，因此可以根據相鄰已分割圖像中物體輪廓的位置、形狀以及它們的變化趨勢來估計并分割當前圖像中對象輪廓、位置和形狀，以估計輪廓作為水平集的初始分割輪廓，這樣既可以提高分割精度，又由于初始輪廓接近真實輪廓邊緣，降低了水平集的運算速度。
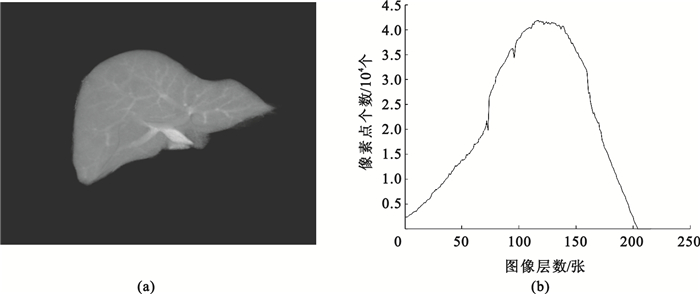圖1
肝臟面積分布圖
(a) 肝臟原始圖像；(b)肝臟面積分布圖
Figure1. Distribution image of liver area(a) original image of liver; (b) distribution of liver area
基于以上原理，本文提出一種基于圖像序列上下文關聯的肝臟器官分割方法，由于醫學組織的變異性較大，因此醫生可以采用手工的方式利用工具在關鍵部位選取3~8張圖像進行輪廓勾勒，然后將醫生勾畫的肝臟輪廓作為初始輪廓，再采用水平集模型進行自動分割，同時將分割的結果作為相近圖像的初始輪廓，繼續進行分割，直至所有圖像分割完畢。該方法雖然要利用部分人工交互，但是比起完全自動的方法，可較大程度地提高整個肝臟的分割精度。
1 基于圖像序列上下文關聯的肝臟器官分割方法
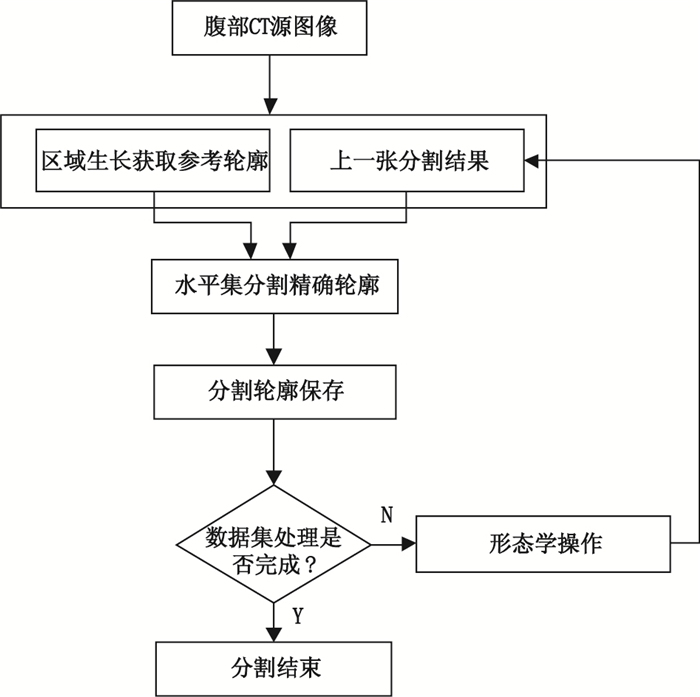
臨床上，由于人體之間存在差異，不同人體獲得的腹部CT圖像有所不同，而現有分割方法實現時均會出現一定的分割錯誤，本文方法不同以往，主要通過一系列的有效操作來進行分割，并將分割輪廓映射到原始圖像中，使用者可以對每一張圖像進行查看，如若出現錯誤，使用者亦可人工干預進行修正，獲得更精確肝臟器官，本文實現分割的具體流程如圖 2所示。
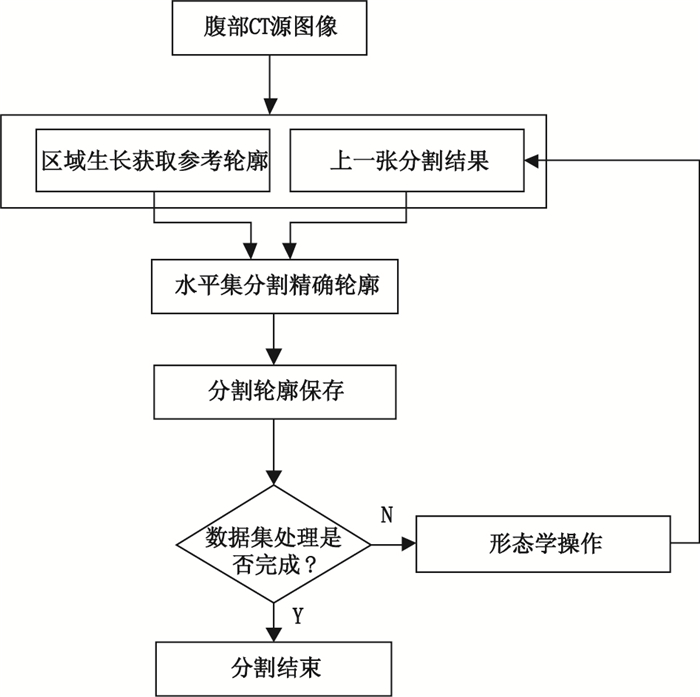圖2
基于圖像序列上下文關聯的肝臟器官分割方法流程圖
Figure2.
Flow chart of segmentation method for liver organ based on image sequence context
1.1 初始輪廓的獲取
初始輪廓是本文實現分割的基礎操作，在分割精度上要求不是很高，但是在速度上要求比較高，因為 初始輪廓的獲得需要一定的人工干預，需求的時間過長會增加使用者的負擔，因此最終選擇操作簡單、算法快速的基于區域生長[2]的分割算法，利用區域生長，醫生實時調整閾值，并通過繪圖工具進行修訂，可快速得到單幅CT圖像的精確肝臟邊界。
1.2 水平集分割算法
經過多年發展，水平集方法現存多種改進算法，經過幾種改進方法的比較，本文最終選擇文獻[8]中的基于距離正則項水平集分割算法作為本文系統的基礎分割算法，其算法分割效果較好，消耗時間較短，且不易出現突變情況，具有較強的穩定性，對實際應用意義重大。
傳統水平集函數[6]在演化的過程中，由于演化的不規則導致退化的水平集函數中符號距離函數不滿足其自身條件｜Φ｜=1，為解決該問題提出的重新初始化卻為計算帶來沉重的負擔，水平集演化速度變慢等消極作用，因此引入新的方法解決符號距離函數的問題即：水平集能量函數中嵌入“距離正則項”來維持符號距離函數的性質，水平集能量函數定義則修正為：
| $ \varepsilon \left( \mathit{\Phi} \right) = \mu {\boldsymbol{\Re} _p}\left( \mathit{\Phi} \right) + {\varepsilon _{ext}}\left( \mathit{\Phi} \right) $ |
其中μ＞0，為常數，為距離正則項，定義為：為外部能量函數。
水平集函數達到穩定性要求其符號距離函數本身固有條件，，因此距離正則項定義中勢函數定義為：
| $ p\left( s \right) = \left\{ \begin{array}{l} \frac{1}{{{{\left( {2\pi } \right)}^2}}}(1 - \cos \left( {2\pi s} \right),{\rm{if}}\;s \le 1\\ \frac{1}{2}{\left( {s - 1} \right)^2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;s \ge 1 \end{array} \right. $ |
以此勢函數定義距離正則項，并以此距離正則項定義水平集能量函數即為：
| $ \varepsilon \left( \mathit{\Phi} \right) = \mu \int_\Omega {p\left( {\left| {\nabla \mathit{\Phi} } \right|} \right)} {\rm{d}}x + \lambda {L_g}\left( \mathit{\Phi} \right) + \alpha {A_g}\left( \mathit{\Phi} \right) $ |
| $ g = \frac{1}{{1 + {{\left| {\nabla {G_\sigma } \cdot I} \right|}^2}}} $ |
其中，Lg(Φ)為梯度信息加權的輪廓線長度，Ag(Φ)為梯度信息加權的輪廓線所圍區域面積，可以分別定義為
| $ {L_g}\left( \mathit{\Phi} \right) = \int_\Omega {g\delta \left( \mathit{\Phi} \right)\left| {\nabla \mathit{\Phi} } \right|} {\rm{d}}x $ |
| $ {A_g}\left( \mathit{\Phi} \right) = \int_\Omega {gH\left( { - \mathit{\Phi} } \right)} {\rm{|d}}x $ |
式中，δ和H分別為Dirac和Heaviside函數，μ、λ為常數，參數α控制演化過程中輪廓線的收縮和擴張，當α與輪廓線內水平集函數值相同時，輪廓線擴張，反之則收縮。則于距離正則項水平集分割能量模型定義為：
| $ \begin{array}{l} \varepsilon \left( \mathit{\Phi} \right) = \mu \int_\Omega {p\left( {\left| {\nabla \mathit{\Phi} } \right|} \right)} {\rm{d}}x + \lambda \int_\Omega {g\delta \left( \mathit{\Phi} \right)\left| {\nabla \mathit{\Phi} } \right|} {\rm{d}}x + \\ \;\;\;\;\;\;\;\;\;\;\;\;\alpha \int_\Omega {gH\left( { - \mathit{\Phi} } \right)} {\rm{d}}x \end{array} $ |
1.3 迭代水平集求解整個肝臟CT圖像
1.3.1 上下層關系判斷
臨床上患者腹部CT圖像是由一系列圖像組成，其中相鄰的圖像存在一定的相似性，肝臟器官的主要形態不會發生很大變化，所以本文選擇利用上一張肝臟分割結果作為下一張圖像初始輪廓進行水平集運算，這樣可以減少人工干預的工作量，并且最終所得肝臟不會出現較大形態上的差異。
本文方法在用上一張圖像分割結果指導下一張圖像時，必須要進行上下層關系判斷以確定需要進行的形態學操作，本文主要使用的形態學有兩種：腐蝕操作，膨脹操作。本文中形態學操作的判斷主要是通過上兩級肝臟面積差作為依據，假設獲得參考輪廓n1，n2，n3，…，ni,將全套數據分為1~n1~(n1+n2)/2，(n1+n2)/2~n2~(n2+n3)/2,…，(ni-1+ni)/2~ni~end段，分別以n1，n2，n3，…，ni參考輪廓圖像作為初始輪廓進行分割得到精確輪廓m1，m2，m3，…，mi，在對nm張圖像進行分割時，先求出上兩級肝臟面積差dm=mm-1-mm-2判斷進行的形態學操作，判斷定義為：
| $ i = \left\{ \begin{array}{l} 0,\;\;{\rm{if}}\;{d_m} > 0\\ 0,\;\;{\rm{if}}\;{d_m} < 0 \end{array} \right. $ |
其中，i=1時進行形態學膨脹操作，i=0時進行形態學腐蝕操作。
1.3.2 水平集演化
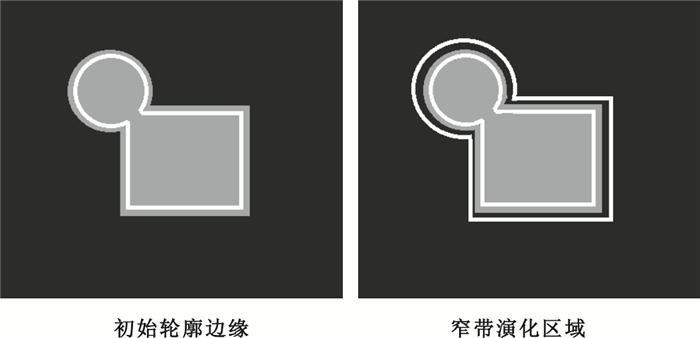
在水平集演化的過程中，若對全局圖像進行水平集能量函數計算，則計算消耗較大，且運算速度較慢。在本文中由于根據先驗知識已經獲得肝臟初始輪廓，所以水平集在演化的過程中可以不必針對全局圖像進行演化，只需對初始輪廓進行修正獲得合適窄帶演化區域即可，因初始輪廓接近真實輪廓，因此將初始輪廓向外擴張一定數量的像素點獲得演化區域來進行分割，而擴張像素數值大小通過多次實驗可知當addpixel=30為最佳，具體實現如圖 3所示。
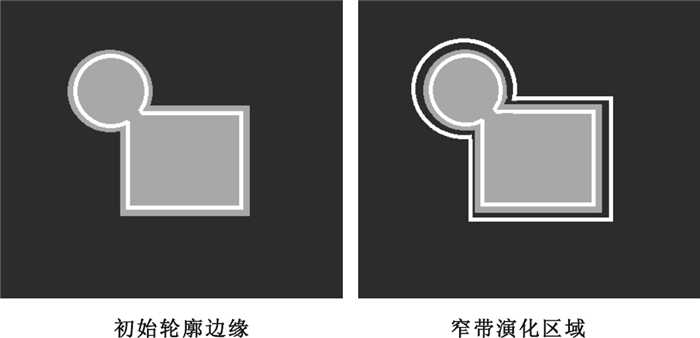圖3
窄帶演化區域示意圖
Figure3.
Schematic diagram of evolution of narrow-band area
如圖 3所示，灰色邊緣為目標對象真實邊緣，內部白色邊緣為初始輪廓，通過擴張，得到外部白色邊緣，則兩條白色邊緣之間的區域為水平集演化區域。
2 實驗結果及分析
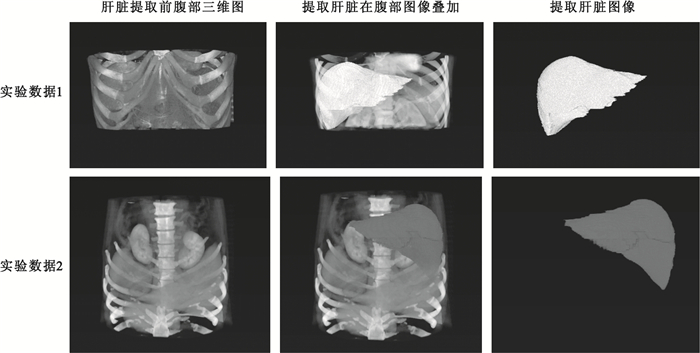
本文所有算法均采用matlab實現，實驗數據包括：數據1，健康志愿者，女性，44歲，數據圖像為512×512×216；數據2，健康志愿者，男性，53歲，數據圖像為512×512×304；本文分割方法具體實驗效果如圖 4所示，分別為腹部圖像三維圖，肝臟空間疊加圖以及三維肝臟分割效果圖。
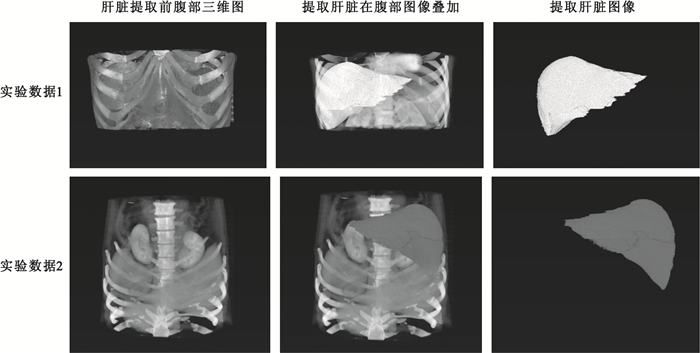圖4
三維肝臟分割效果圖
Figure4.
3D liver segmentation effect chart
圖 4顯示兩套實驗數據使用本文方法進行三維肝臟分割的效果圖，為進一步驗證本文方法，從上述分割結果中分別隨機選取實驗數據1和實驗數據2中12張二維圖像數據，具體效果如圖 5所示。
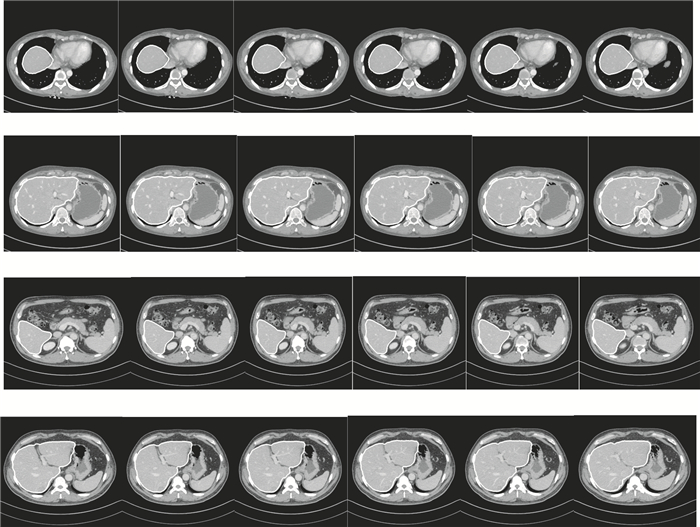圖5
單張肝臟分割效果圖
Figure5.
Effect chart of single liver segmentation
由圖 5可見，每張圖像中白色線條為本文方法分割肝臟邊緣，線條包含內容為分割肝臟，由上圖可知，隨機選取的12張圖像均分割正確。
由圖 4、圖 5分割結果可知，無論是從三維角度還是二維角度來看，本文方法分割效果良好，分割肝臟與對應原始圖像肝臟吻合度高，形態變化差異小，且準確定位了肝臟邊緣,錯分外圍器官組織的情況較少，只是在與心臟連接部位由于像素值近似而導致少量分割錯誤，但可通過少量人工干預進行調整，且三組實驗數據使用初始輪廓均介于4~8張，操作簡單易行，且時間消耗控制在有效時間范圍內。
為進一步驗證本文算法的準確性，本文邀請醫學專家從實驗數據1中隨機選取15張實驗數據原圖像進行手工分割，以此作為分割標準，并將其與本文算法分割結果進行實驗對比。從醫學專家手工分割結果及本文分割結果圖像中對肝臟部分進行有效像素點統計，具體情況如表 1所示。
表1
有效像素點統計表
Table1.
Statistical table of effective pixels
由表 1可知，本文實現分割方法是可靠的，若以醫學專家手工分割結果為標準，本文分割結果準確率可達90%~97%，能滿足醫生基本分割要求，具有一定實用價值。
3 結束語
現有圖像分割技術的研究往往集中在理論知識的改進上，較少提供完整的肝臟器官分割方法，具有較少的實際應用價值。本文核心內容在于以現有成熟分割技術為基礎組成一套完整分割流程來實現更有現實意義的分割，提出一種半自動的基于圖像序列上下文關聯的肝臟器官分割方法，并提供可人機交互的人工干預工具進行輪廓修正以解決異常突變情況。
實驗測試可知，本文方法實現的分割比手工分割更簡易、快速，比自動分割更精確、靈活，能很好地平衡速度與精確度，具有重要的實用價值。在今后的工作中，本文可以在提高速度和精確度方面進一步開展研究，希望以更快的速度達到更好的肝臟分割效果。
引言
圖像肝臟分割在肝臟診斷、腫瘤分割、肝移植等臨床應用中起著關鍵的作用。從腹部CT圖像可知，由于肝臟自身變異性較大、形狀不規律、圖像對比度低和相鄰組織有粘連等特點，使得肝臟圖像的分割成為一個具有挑戰性的問題。目前，國內外對肝臟分割方法常用的有基于形態學分割方法[1]、區域生長分割方法[2-3]、基于圖論分割方法[4]、均值漂移分割方法[5]、基于水平集分割方法[6-8]等。
以上分割方法雖然在實際應用中都發揮了一定的效用，但這類分割方法對圖像質量要求較高，且在實際分割過程中，由于個體臨床CT圖像存在很大的差異性和變異性，分割結果會出現過分割及漏分割等現象；而且觀察醫學器官的斷層掃描圖像可知，圖像序列上下文關聯較大，其本質為三維圖像，而現有二維分割方法多考慮單張圖像，未利用組織器官的圖像上下文之間的關系。針對這些問題，三維分割技術漸漸得到了發展。現有三維肝臟分割技術主要有基于半自動[9]和全自動[10-12]的分割方法。這些分割算法對圖像質量同樣要求較高，且要求被分割對象形狀和先驗模型接近，如果被分割對象變異性較大，往往不能正確分割出肝臟，因此實際應用效果較差，難以達到臨床應用要求。
水平集模型是在解決火焰表面進化問題時提出的，平面閉合曲線隱含表達為三維連續曲面，將求解計算從低維上升到更高一層，是一種高精度的分割方法，在分割過程中存在曲線演化表達的簡單性，以及處理拓撲變化自然性的優點，而數值化的求解方式具有很好的穩定性，其中基于能量函數模型定義具有直觀的物理意義，容易加入約束條件。而在利用水平集自動分割的過程中，如何精確設定初始分割位置非常重要，初始分割位置離實際邊緣越近，收斂到正確位置的可能性就越大。
考慮肝臟CT圖像的三維形態，如圖 1所示,圖 1(a)為醫生手工分割獲得的標準肝臟圖像，從二維圖像上對肝臟面積進行像素統計可得圖 1(b)，由圖 1(b)可知其軸狀面中肝臟面積變化較為平滑，相鄰兩幅肝臟圖像中輪廓具有連續性，其輪廓形狀在一定的空間范圍內按一定的速度進行變化，因此可以根據相鄰已分割圖像中物體輪廓的位置、形狀以及它們的變化趨勢來估計并分割當前圖像中對象輪廓、位置和形狀，以估計輪廓作為水平集的初始分割輪廓，這樣既可以提高分割精度，又由于初始輪廓接近真實輪廓邊緣，降低了水平集的運算速度。
圖1
肝臟面積分布圖
(a) 肝臟原始圖像；(b)肝臟面積分布圖
Figure1. Distribution image of liver area(a) original image of liver; (b) distribution of liver area
基于以上原理，本文提出一種基于圖像序列上下文關聯的肝臟器官分割方法，由于醫學組織的變異性較大，因此醫生可以采用手工的方式利用工具在關鍵部位選取3~8張圖像進行輪廓勾勒，然后將醫生勾畫的肝臟輪廓作為初始輪廓，再采用水平集模型進行自動分割，同時將分割的結果作為相近圖像的初始輪廓，繼續進行分割，直至所有圖像分割完畢。該方法雖然要利用部分人工交互，但是比起完全自動的方法，可較大程度地提高整個肝臟的分割精度。
1 基于圖像序列上下文關聯的肝臟器官分割方法
臨床上，由于人體之間存在差異，不同人體獲得的腹部CT圖像有所不同，而現有分割方法實現時均會出現一定的分割錯誤，本文方法不同以往，主要通過一系列的有效操作來進行分割，并將分割輪廓映射到原始圖像中，使用者可以對每一張圖像進行查看，如若出現錯誤，使用者亦可人工干預進行修正，獲得更精確肝臟器官，本文實現分割的具體流程如圖 2所示。
圖2
基于圖像序列上下文關聯的肝臟器官分割方法流程圖
Figure2.
Flow chart of segmentation method for liver organ based on image sequence context
1.1 初始輪廓的獲取
初始輪廓是本文實現分割的基礎操作，在分割精度上要求不是很高，但是在速度上要求比較高，因為 初始輪廓的獲得需要一定的人工干預，需求的時間過長會增加使用者的負擔，因此最終選擇操作簡單、算法快速的基于區域生長[2]的分割算法，利用區域生長，醫生實時調整閾值，并通過繪圖工具進行修訂，可快速得到單幅CT圖像的精確肝臟邊界。
1.2 水平集分割算法
經過多年發展，水平集方法現存多種改進算法，經過幾種改進方法的比較，本文最終選擇文獻[8]中的基于距離正則項水平集分割算法作為本文系統的基礎分割算法，其算法分割效果較好，消耗時間較短，且不易出現突變情況，具有較強的穩定性，對實際應用意義重大。
傳統水平集函數[6]在演化的過程中，由于演化的不規則導致退化的水平集函數中符號距離函數不滿足其自身條件｜Φ｜=1，為解決該問題提出的重新初始化卻為計算帶來沉重的負擔，水平集演化速度變慢等消極作用，因此引入新的方法解決符號距離函數的問題即：水平集能量函數中嵌入“距離正則項”來維持符號距離函數的性質，水平集能量函數定義則修正為：
| $ \varepsilon \left( \mathit{\Phi} \right) = \mu {\boldsymbol{\Re} _p}\left( \mathit{\Phi} \right) + {\varepsilon _{ext}}\left( \mathit{\Phi} \right) $ |
其中μ＞0，為常數，為距離正則項，定義為：為外部能量函數。
水平集函數達到穩定性要求其符號距離函數本身固有條件，，因此距離正則項定義中勢函數定義為：
| $ p\left( s \right) = \left\{ \begin{array}{l} \frac{1}{{{{\left( {2\pi } \right)}^2}}}(1 - \cos \left( {2\pi s} \right),{\rm{if}}\;s \le 1\\ \frac{1}{2}{\left( {s - 1} \right)^2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;s \ge 1 \end{array} \right. $ |
以此勢函數定義距離正則項，并以此距離正則項定義水平集能量函數即為：
| $ \varepsilon \left( \mathit{\Phi} \right) = \mu \int_\Omega {p\left( {\left| {\nabla \mathit{\Phi} } \right|} \right)} {\rm{d}}x + \lambda {L_g}\left( \mathit{\Phi} \right) + \alpha {A_g}\left( \mathit{\Phi} \right) $ |
| $ g = \frac{1}{{1 + {{\left| {\nabla {G_\sigma } \cdot I} \right|}^2}}} $ |
其中，Lg(Φ)為梯度信息加權的輪廓線長度，Ag(Φ)為梯度信息加權的輪廓線所圍區域面積，可以分別定義為
| $ {L_g}\left( \mathit{\Phi} \right) = \int_\Omega {g\delta \left( \mathit{\Phi} \right)\left| {\nabla \mathit{\Phi} } \right|} {\rm{d}}x $ |
| $ {A_g}\left( \mathit{\Phi} \right) = \int_\Omega {gH\left( { - \mathit{\Phi} } \right)} {\rm{|d}}x $ |
式中，δ和H分別為Dirac和Heaviside函數，μ、λ為常數，參數α控制演化過程中輪廓線的收縮和擴張，當α與輪廓線內水平集函數值相同時，輪廓線擴張，反之則收縮。則于距離正則項水平集分割能量模型定義為：
| $ \begin{array}{l} \varepsilon \left( \mathit{\Phi} \right) = \mu \int_\Omega {p\left( {\left| {\nabla \mathit{\Phi} } \right|} \right)} {\rm{d}}x + \lambda \int_\Omega {g\delta \left( \mathit{\Phi} \right)\left| {\nabla \mathit{\Phi} } \right|} {\rm{d}}x + \\ \;\;\;\;\;\;\;\;\;\;\;\;\alpha \int_\Omega {gH\left( { - \mathit{\Phi} } \right)} {\rm{d}}x \end{array} $ |
1.3 迭代水平集求解整個肝臟CT圖像
1.3.1 上下層關系判斷
臨床上患者腹部CT圖像是由一系列圖像組成，其中相鄰的圖像存在一定的相似性，肝臟器官的主要形態不會發生很大變化，所以本文選擇利用上一張肝臟分割結果作為下一張圖像初始輪廓進行水平集運算，這樣可以減少人工干預的工作量，并且最終所得肝臟不會出現較大形態上的差異。
本文方法在用上一張圖像分割結果指導下一張圖像時，必須要進行上下層關系判斷以確定需要進行的形態學操作，本文主要使用的形態學有兩種：腐蝕操作，膨脹操作。本文中形態學操作的判斷主要是通過上兩級肝臟面積差作為依據，假設獲得參考輪廓n1，n2，n3，…，ni,將全套數據分為1~n1~(n1+n2)/2，(n1+n2)/2~n2~(n2+n3)/2,…，(ni-1+ni)/2~ni~end段，分別以n1，n2，n3，…，ni參考輪廓圖像作為初始輪廓進行分割得到精確輪廓m1，m2，m3，…，mi，在對nm張圖像進行分割時，先求出上兩級肝臟面積差dm=mm-1-mm-2判斷進行的形態學操作，判斷定義為：
| $ i = \left\{ \begin{array}{l} 0,\;\;{\rm{if}}\;{d_m} > 0\\ 0,\;\;{\rm{if}}\;{d_m} < 0 \end{array} \right. $ |
其中，i=1時進行形態學膨脹操作，i=0時進行形態學腐蝕操作。
1.3.2 水平集演化
在水平集演化的過程中，若對全局圖像進行水平集能量函數計算，則計算消耗較大，且運算速度較慢。在本文中由于根據先驗知識已經獲得肝臟初始輪廓，所以水平集在演化的過程中可以不必針對全局圖像進行演化，只需對初始輪廓進行修正獲得合適窄帶演化區域即可，因初始輪廓接近真實輪廓，因此將初始輪廓向外擴張一定數量的像素點獲得演化區域來進行分割，而擴張像素數值大小通過多次實驗可知當addpixel=30為最佳，具體實現如圖 3所示。
圖3
窄帶演化區域示意圖
Figure3.
Schematic diagram of evolution of narrow-band area
如圖 3所示，灰色邊緣為目標對象真實邊緣，內部白色邊緣為初始輪廓，通過擴張，得到外部白色邊緣，則兩條白色邊緣之間的區域為水平集演化區域。
2 實驗結果及分析
本文所有算法均采用matlab實現，實驗數據包括：數據1，健康志愿者，女性，44歲，數據圖像為512×512×216；數據2，健康志愿者，男性，53歲，數據圖像為512×512×304；本文分割方法具體實驗效果如圖 4所示，分別為腹部圖像三維圖，肝臟空間疊加圖以及三維肝臟分割效果圖。
圖4
三維肝臟分割效果圖
Figure4.
3D liver segmentation effect chart
圖 4顯示兩套實驗數據使用本文方法進行三維肝臟分割的效果圖，為進一步驗證本文方法，從上述分割結果中分別隨機選取實驗數據1和實驗數據2中12張二維圖像數據，具體效果如圖 5所示。
圖5
單張肝臟分割效果圖
Figure5.
Effect chart of single liver segmentation
由圖 5可見，每張圖像中白色線條為本文方法分割肝臟邊緣，線條包含內容為分割肝臟，由上圖可知，隨機選取的12張圖像均分割正確。
由圖 4、圖 5分割結果可知，無論是從三維角度還是二維角度來看，本文方法分割效果良好，分割肝臟與對應原始圖像肝臟吻合度高，形態變化差異小，且準確定位了肝臟邊緣,錯分外圍器官組織的情況較少，只是在與心臟連接部位由于像素值近似而導致少量分割錯誤，但可通過少量人工干預進行調整，且三組實驗數據使用初始輪廓均介于4~8張，操作簡單易行，且時間消耗控制在有效時間范圍內。
為進一步驗證本文算法的準確性，本文邀請醫學專家從實驗數據1中隨機選取15張實驗數據原圖像進行手工分割，以此作為分割標準，并將其與本文算法分割結果進行實驗對比。從醫學專家手工分割結果及本文分割結果圖像中對肝臟部分進行有效像素點統計，具體情況如表 1所示。
表1
有效像素點統計表
Table1.
Statistical table of effective pixels
由表 1可知，本文實現分割方法是可靠的，若以醫學專家手工分割結果為標準，本文分割結果準確率可達90%~97%，能滿足醫生基本分割要求，具有一定實用價值。
3 結束語
現有圖像分割技術的研究往往集中在理論知識的改進上，較少提供完整的肝臟器官分割方法，具有較少的實際應用價值。本文核心內容在于以現有成熟分割技術為基礎組成一套完整分割流程來實現更有現實意義的分割，提出一種半自動的基于圖像序列上下文關聯的肝臟器官分割方法，并提供可人機交互的人工干預工具進行輪廓修正以解決異常突變情況。
實驗測試可知，本文方法實現的分割比手工分割更簡易、快速，比自動分割更精確、靈活，能很好地平衡速度與精確度，具有重要的實用價值。在今后的工作中，本文可以在提高速度和精確度方面進一步開展研究，希望以更快的速度達到更好的肝臟分割效果。
