估算動脈血管壁所受的應力以及產生的應變, 對于評估血管壁的彈性和預測斑塊的發展趨勢具有重要的臨床參考價值。本文利用計算流體力學(CFD)數值模擬技術, 對從動脈血管內超聲(IVUS)圖像序列中重建出的三維血管及血液模型進行單向流固耦合模擬, 得到用偽彩編碼表示應變分布情況的三維血管模型, 直觀地展示血管的三維形態結構和三維應變分量及其分布情況。
引用本文: 孫正, 劉存. 基于血管內超聲的動脈血管壁應變分布的計算流體力學仿真. 生物醫學工程學雜志, 2015, 32(6): 1244-1248. doi: 10.7507/1001-5515.20150221 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
0 引言
急性冠狀動脈綜合征多由粥樣硬化斑塊破裂造成,而斑塊是否可能破裂取決于其易損性。有效預防急性冠狀動脈綜合征需要及早識別出動脈中的易損斑塊[1-2]。斑塊破裂的位置與斑塊內及其附近區域的應力有關,文獻[3]指出58%的斑塊破裂發生于最大應力處,83%的斑塊淺表潰瘍發生在高應力區,偏心型斑塊的最大應力區通常在薄弱的纖維帽肩部。因此估算斑塊所受的應力以及產生的應變,對于評估其易損性和預測其發展趨勢具有重要的臨床參考價值。
血管內超聲(intravascular ultrasound,IVUS)是檢測血管病變的一種常用介入影像技術。它可提供血管壁、管腔及斑塊的橫截面圖像,根據動態圖像序列還可獲得心動周期中冠狀動脈血管壁和斑塊的變形情況[4]。
目前,利用IVUS技術測量動脈血流動力學參數(包括血管壁應力和應變的分布和管壁的彈性模量等)的方法主要是分析超聲導管采集的原始射頻(radio frequency, RF)信號和背向散射信號[5-7]。考慮到原始數據的高精度,分析RF信號的方法比灰度圖像處理的方法具有更高的分辨率和精度。但是只有當血管壁組織的運動方向與RF信號方向一致時,采用RF方法才能可靠地估計應變。同時,斑塊組織的變形包括徑向、周向和縱向三個分量,而RF方法得到的只是一維徑向應變[8]。
雖然對于RF信號和背向散射信號的高級分析有助于更好地了解組織特征,是測量血流動力學參數更客觀的方法,但是目前臨床采用的多數IVUS成像設備的標準輸出是常規灰度圖像[9],不允許采集原始RF信號,因而限制了RF方法的廣泛應用。文獻[10-13]提出了基于IVUS灰階圖像配準的血管壁應力/應變估算方法,該方法采用的圖像數據是在兩個不同管腔壓力下相同位置處獲得的血管壁橫截面圖像。由于心臟運動和管腔內搏動的血流會導致超聲導管在管腔內產生復雜運動,所以獲取滿足該要求的圖像比較困難。
由于生物軟組織的變形在三維空間中是不均勻的,因而測量三維應變張量有助于全面了解動脈血管壁的力學特性。本文以常規采集的動脈IVUS灰階圖像序列作為數據源,對從圖像序列中重建出的三維血管及血液模型進行單向流固耦合(fluid-structure interaction,FSI)數值模擬,估算由搏動血流引入的血管壁應變的三維分布。
1 方法
動脈血管壁是有彈性的,而且彈性管壁隨著搏動的血流也發生變形,這樣動脈血管壁就與血流構成了一個復雜的瞬態流-固耦合系統。在前期工作中,利用同步采集的X射線血管造影(X-ray angiography, XA)圖像定位超聲導管回撤路徑,實現了血管的三維重建[14]。本文利用此血管模型,進行血液流場與血管壁之間的流固耦合數值模擬,估算血管壁的受力變形情況,直觀展示由于搏動的血液及周期性心臟運動引起的血管壁應變的三維分布。
1.1 建立動脈血管的流固耦合模型
1.1.1 簡化與假設
考慮到血液流場與動脈血管壁耦合的過程非常復雜,本文在以下假設前提下進行三維流固耦合計算:①所研究的動脈血管直徑都大于1 mm,這類血管中的血液可以近似認為是不可壓縮的牛頓流體;②血液的流動為定常層流;③動脈血管壁是線彈性體且不可壓縮;④忽略血液的重力;⑤忽略溫度的影響,即不研究溫度和流動以及應力的耦合,不考慮血管中的熱量和其它能量形式的交換問題。
1.1.2 血液流動基本控制方程
采用Navier-Stokes方程
| $\rho \left[\frac{\partial u}{\partial t}+\left(u-{{u}_{g}} \right)\cdot \nabla u \right]=-\nabla P+\mu \Delta u$ |
和速度散度為零的連續方程(即不可壓縮方程)
| $\nabla \cdot u=0$ |
來描述粘性不可壓縮的血液流體的流動[15]。其中,ρ和μ分別是血液的密度和粘度;u和P是流體的速度和壓力;ug是網格點速度;t是時間。
定義分析區域即血液流體部分具有光滑邊界,血流的進、出口速度邊界條件為
| $\left\{ \begin{align} & u{{|}_{\text{interface}}}=\frac{\partial x}{\partial t} \\ & \frac{\partial u}{\partial n}{{|}_{\text{inlet}}}=\frac{\partial u}{\partial n}{{|}_{\text{outlet}}}=0 \\ \end{align} \right.$ |
其中,interface即血管壁內表面;inlet和outlet分別表示入口和出口;n是邊界上的單位外法線向量。入口的速度矢量沿血管軸線方向,徑向和周向速度均為零。
設置血流的進、出口的壓力邊界條件為壓力隨時間變化的函數:
| $\left\{ \begin{align} & P{{|}_{\text{inlet}}}={{P}_{\text{in}}}\left(t \right) \\ & P{{|}_{\text{outlet}}}={{P}_{\text{out}}}\left(t \right) \\ \end{align} \right.$ |
1.1.3 血管壁運動控制方程
采用獨立的拉格朗日-歐拉(ALE)方程作為血管壁的運動方程[15]
| ${{\rho }_{s}}\frac{{{\partial }^{2}}{{v}_{i}}}{\partial t}=\sum\limits_{j=1}^{3}{\frac{\partial {{\sigma }_{ij}}}{\partial {{x}_{j}}}+{{\rho }_{s}}{{f}_{i}}}$ |
血管壁的應變-位移關系為
| ${{\varepsilon }_{ij}}=\frac{1}{2}\left(\frac{\partial {{v}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{v}_{j}}}{\partial {{x}_{j}}} \right)$ |
其中,i, j=1, 2, 3;ρs、v(vi, vj)、σij和εij分別是血管壁的密度、位移向量、應力張量和應變張量;fi是作用在血管壁上的體力分量;xj表示三維直角坐標系中三個坐標軸的正方向。
1.1.4 設置血液與血管壁的耦合邊界
血管壁的內表面為流固相互作用的界面,即耦合面:
| $\sigma _{ij}^{\text{f}}\cdot {{n}_{j}}{{|}_{\text{interface}}}=\sigma _{ij}^{\text{w}}\cdot {{n}_{j}}{{|}_{\text{interface}}}$ |
其中,σijf和σijw分別是血液和血管壁的應力張量。血管壁的外表面是自由面,即
| ${{\sigma }_{ij}}\cdot {{n}_{ij}}{{|}_{\text{outwall}}}=0$ |
1.2 CFD數值模擬
在ANSYS Workbench工作平臺上,采用ANSYS+FLUENT單向流固耦合模塊,對三維血管及血液模型進行血液和血管壁的流固耦合數值模擬,估算血管壁的應變張量分布。基本步驟包括:
1.2.1 有限元網格劃分
三維血管和血液模型是非對稱的,且幾何形狀非常復雜,因此在網格劃分過程中很難劃分出特別規范的均勻網格。同時對于狹窄段,也很難保持原有規范的網格形狀。因此本文采用智能型的網格劃分模式,將血液與血管的三維幾何模型離散化,在遇到形狀突變時能按照合理的劃分方法自動加密,以獲得更加理想的網格單元[16]。
1.2.2 建立三維血管有限元模型
首先,設定初始條件,即定義血管和血液的物理屬性[17],如表 1所示,其中各參數均取人體正常生理條件下的平均值。考慮到粘彈性材料可能使流固耦合的迭代計算不收斂,因此本文不考慮血管的粘彈性。設置溫度為37℃。
然后,設定邊界條件,即對血管模型的入口和出口設置為固定約束,限制血管內血液的流動范圍。對于固體部分,血管外壁面只設置一個自由壁面條件,不加其它約束限制;血管內壁面(即血流與血管接觸的內表面)設定為流固耦合界面,并假定無滑移邊界條件(對于定常層流,假設管壁上流體質點的流速為零;對于不定常層流,假設管壁上流體質點的速度和管壁速度相同)。對于流體部分,將邊界條件設定在血流進出口界面上,出口壓力設定為零。
其次,設定血液流動的載荷,就是血管入口處給定的流體速度。為了實現流固耦合中數據的傳輸,將血液對血管壁的壓力作為加載流,將血管腔內表面上所有的流體動力都加載到血管壁內表面。
最后,定義時間步長,設定求解開始的時間,選擇迭代求解方法,設置收斂準則,誤差要求、輸出信息控制等。
1.2.3 計算結果的后處理
為了提高計算結果的可視化效果,用偽彩編碼顯示估算出的血管壁應變張量分布以及瞬態的流場變化,直觀展示由于搏動的血液及周期性心臟運動引起的血管壁應變的三維分布。
2 實驗結果和分析
實驗所用圖像數據的采集是在河北大學附屬醫院的心導管室中由醫生完成。IVUS和XA圖像分別是采用Jomed Endosonic超聲成像儀和Philips Integris CV單面XA機采集的。在進行IVUS檢查的過程中,XA和IVUS分別同步顯示超聲導管和探頭在血管腔內的位置和相應血管壁的形態結構。IVUS圖像的采集速率為30幀/秒,導管回撤速度為0.5 mm/s;XA的幀率是30幀/秒,圖像大小為512像素×512像素,灰階為256,像素尺寸為0.3 mm。對一個IVUS圖像序列進行處理后的實驗結果,如圖 1~圖 5所示。
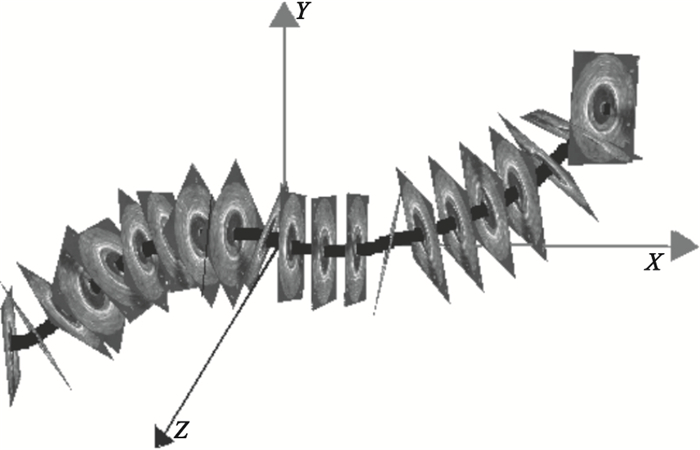 圖1
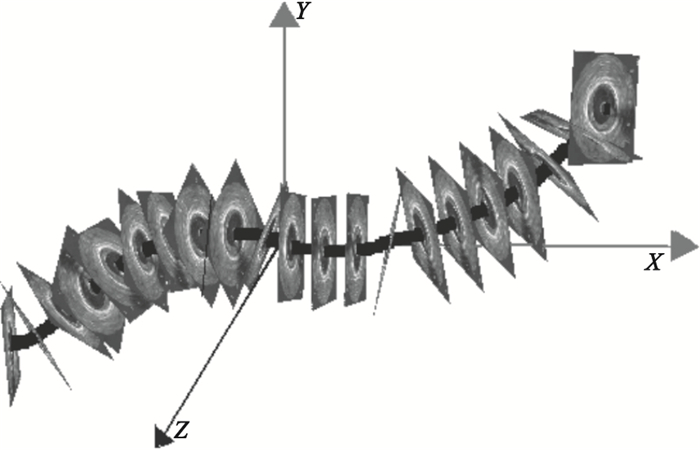
21幀IVUS圖像沿三維導管路徑順序排列
Figure1.
Alignment of 21 IVUS frames along the 3-D catheter pullback path reconstructed from angiograms
圖1
21幀IVUS圖像沿三維導管路徑順序排列
Figure1.
Alignment of 21 IVUS frames along the 3-D catheter pullback path reconstructed from angiograms
 圖2
三維血管和血液模型
Figure2.
3-D vessel and blood models
圖2
三維血管和血液模型
Figure2.
3-D vessel and blood models
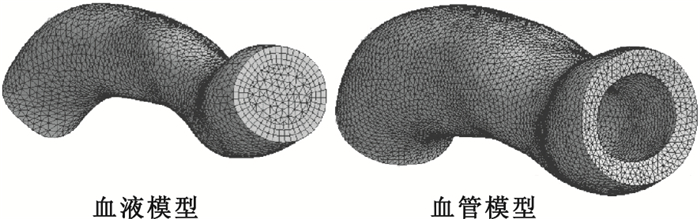 圖3
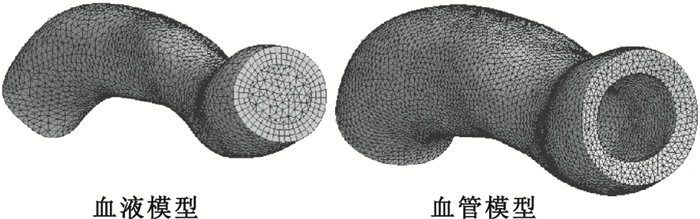
網格劃分后的血液和血管模型
Figure3.
Tetrahedral meshing of blood model and vessel model
圖3
網格劃分后的血液和血管模型
Figure3.
Tetrahedral meshing of blood model and vessel model
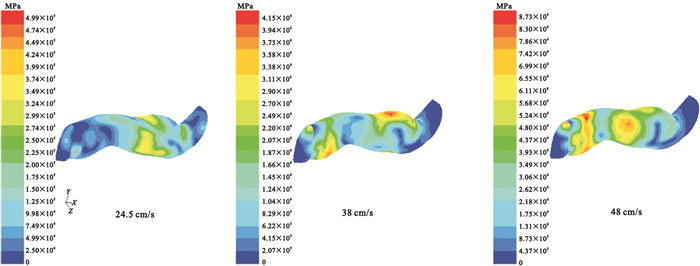 圖4
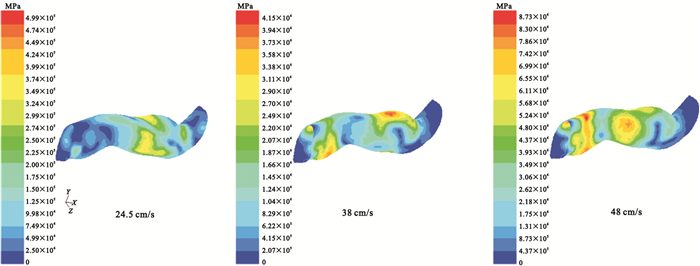
血液流場計算結果圖
Figure4.
Numerical simulation results of blood flow
圖4
血液流場計算結果圖
Figure4.
Numerical simulation results of blood flow
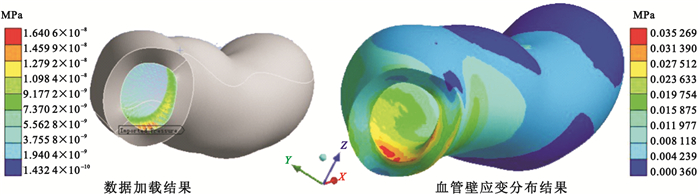 圖5
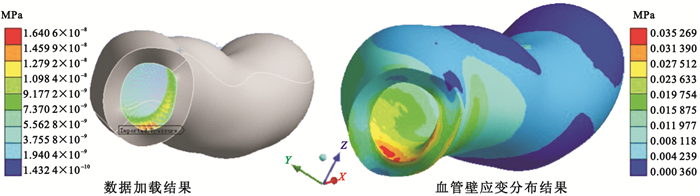
血管壁數據加載和應變分布計算結果
Figure5.
Load of the hydrodynamic data and strain distribution on the vessel wall model
圖5
血管壁數據加載和應變分布計算結果
Figure5.
Load of the hydrodynamic data and strain distribution on the vessel wall model
如圖 1所示,將部分IVUS圖像沿從XA圖像中重建出的三維導管路徑順序排列。計算出各幀IVUS圖像中血管壁內外膜輪廓的三維坐標后,得到血管和血液的三維幾何模型,如圖 2所示。
對三維血液模型進行網格劃分,其中生成的網格總結點數是15 793,總單元數是49 839;采用靜態結構(Static Structural)模塊完成三維血管模型的網格劃分,選擇自動網格劃分,生成的網格總結點數為30 013,總單元數為150 061,網格最大畸變為0.840 075,網格質量滿足計算要求,劃分結果如圖 3所示。
利用ANSYS Workbench下的FLUENT模塊計算血液流場,總步數設置為150,調整能量殘差收斂標準為0.000 01,迭代計算在第70步時達到收斂,流體區域的計算結果如圖 4所示。
利用“輸入壓力(Imported Pressure)”命令將血管腔內表面上所有的流體動力都加載到血管壁內表面,以偽彩編碼血管壁面應變分布,由紅色到藍色,表示固體組織的應變逐漸減小,如圖 5所示。對于沒有明顯分叉、狹窄和彎曲的血管段,管壁組織各處產生的應變分布規律是越靠近血管壁內腔表面處的應變越大,而越靠近血管外膜輪廓表面處的應變越小。對于彎曲的血管段,在曲率大的區域應變較大,且彎曲段外壁上的應變要比內壁上的應變大,這些幾何形狀變化劇烈的部位往往是斑塊阻塞滯留的位置,對于這些區域,在動脈粥樣硬化的致病因素中血流動力學的因素占有較大比重[18]。
3 結論
本文在從常規采集的IVUS灰階圖像序列中重建出的三維血管模型的基礎上,結合力學知識,采用CFD數值模擬技術估算由搏動血流引入的動脈血管壁的三維應變分布,得到用偽彩編碼表示應變分布的三維血管模型,直觀地展示血管的三維形態結構和三維應變分量及其分布情況。無需獲取IVUS成像設備的原始RF信號,而且較基于RF信號的方法能更全面地反映管壁和斑塊組織的彈性特征。
本文方法的局限是對局部應變的估算結果很大程度上取決于血管三維重建的精度,圖像采集、二維圖像的分割、沿導管回撤路徑確定各幀IVUS圖像的軸向位置和空間方向等步驟中存在的誤差都會累積在最終的重建結果中,進而降低對管壁應變的測量精度。在后續的工作中,考慮在采用虛擬現實技術建立血管模型并模擬血管支架植入術的基礎上,對支架與血管壁的交互受力情況等進行定量估算。
0 引言
急性冠狀動脈綜合征多由粥樣硬化斑塊破裂造成,而斑塊是否可能破裂取決于其易損性。有效預防急性冠狀動脈綜合征需要及早識別出動脈中的易損斑塊[1-2]。斑塊破裂的位置與斑塊內及其附近區域的應力有關,文獻[3]指出58%的斑塊破裂發生于最大應力處,83%的斑塊淺表潰瘍發生在高應力區,偏心型斑塊的最大應力區通常在薄弱的纖維帽肩部。因此估算斑塊所受的應力以及產生的應變,對于評估其易損性和預測其發展趨勢具有重要的臨床參考價值。
血管內超聲(intravascular ultrasound,IVUS)是檢測血管病變的一種常用介入影像技術。它可提供血管壁、管腔及斑塊的橫截面圖像,根據動態圖像序列還可獲得心動周期中冠狀動脈血管壁和斑塊的變形情況[4]。
目前,利用IVUS技術測量動脈血流動力學參數(包括血管壁應力和應變的分布和管壁的彈性模量等)的方法主要是分析超聲導管采集的原始射頻(radio frequency, RF)信號和背向散射信號[5-7]。考慮到原始數據的高精度,分析RF信號的方法比灰度圖像處理的方法具有更高的分辨率和精度。但是只有當血管壁組織的運動方向與RF信號方向一致時,采用RF方法才能可靠地估計應變。同時,斑塊組織的變形包括徑向、周向和縱向三個分量,而RF方法得到的只是一維徑向應變[8]。
雖然對于RF信號和背向散射信號的高級分析有助于更好地了解組織特征,是測量血流動力學參數更客觀的方法,但是目前臨床采用的多數IVUS成像設備的標準輸出是常規灰度圖像[9],不允許采集原始RF信號,因而限制了RF方法的廣泛應用。文獻[10-13]提出了基于IVUS灰階圖像配準的血管壁應力/應變估算方法,該方法采用的圖像數據是在兩個不同管腔壓力下相同位置處獲得的血管壁橫截面圖像。由于心臟運動和管腔內搏動的血流會導致超聲導管在管腔內產生復雜運動,所以獲取滿足該要求的圖像比較困難。
由于生物軟組織的變形在三維空間中是不均勻的,因而測量三維應變張量有助于全面了解動脈血管壁的力學特性。本文以常規采集的動脈IVUS灰階圖像序列作為數據源,對從圖像序列中重建出的三維血管及血液模型進行單向流固耦合(fluid-structure interaction,FSI)數值模擬,估算由搏動血流引入的血管壁應變的三維分布。
1 方法
動脈血管壁是有彈性的,而且彈性管壁隨著搏動的血流也發生變形,這樣動脈血管壁就與血流構成了一個復雜的瞬態流-固耦合系統。在前期工作中,利用同步采集的X射線血管造影(X-ray angiography, XA)圖像定位超聲導管回撤路徑,實現了血管的三維重建[14]。本文利用此血管模型,進行血液流場與血管壁之間的流固耦合數值模擬,估算血管壁的受力變形情況,直觀展示由于搏動的血液及周期性心臟運動引起的血管壁應變的三維分布。
1.1 建立動脈血管的流固耦合模型
1.1.1 簡化與假設
考慮到血液流場與動脈血管壁耦合的過程非常復雜,本文在以下假設前提下進行三維流固耦合計算:①所研究的動脈血管直徑都大于1 mm,這類血管中的血液可以近似認為是不可壓縮的牛頓流體;②血液的流動為定常層流;③動脈血管壁是線彈性體且不可壓縮;④忽略血液的重力;⑤忽略溫度的影響,即不研究溫度和流動以及應力的耦合,不考慮血管中的熱量和其它能量形式的交換問題。
1.1.2 血液流動基本控制方程
采用Navier-Stokes方程
| $\rho \left[\frac{\partial u}{\partial t}+\left(u-{{u}_{g}} \right)\cdot \nabla u \right]=-\nabla P+\mu \Delta u$ |
和速度散度為零的連續方程(即不可壓縮方程)
| $\nabla \cdot u=0$ |
來描述粘性不可壓縮的血液流體的流動[15]。其中,ρ和μ分別是血液的密度和粘度;u和P是流體的速度和壓力;ug是網格點速度;t是時間。
定義分析區域即血液流體部分具有光滑邊界,血流的進、出口速度邊界條件為
| $\left\{ \begin{align} & u{{|}_{\text{interface}}}=\frac{\partial x}{\partial t} \\ & \frac{\partial u}{\partial n}{{|}_{\text{inlet}}}=\frac{\partial u}{\partial n}{{|}_{\text{outlet}}}=0 \\ \end{align} \right.$ |
其中,interface即血管壁內表面;inlet和outlet分別表示入口和出口;n是邊界上的單位外法線向量。入口的速度矢量沿血管軸線方向,徑向和周向速度均為零。
設置血流的進、出口的壓力邊界條件為壓力隨時間變化的函數:
| $\left\{ \begin{align} & P{{|}_{\text{inlet}}}={{P}_{\text{in}}}\left(t \right) \\ & P{{|}_{\text{outlet}}}={{P}_{\text{out}}}\left(t \right) \\ \end{align} \right.$ |
1.1.3 血管壁運動控制方程
采用獨立的拉格朗日-歐拉(ALE)方程作為血管壁的運動方程[15]
| ${{\rho }_{s}}\frac{{{\partial }^{2}}{{v}_{i}}}{\partial t}=\sum\limits_{j=1}^{3}{\frac{\partial {{\sigma }_{ij}}}{\partial {{x}_{j}}}+{{\rho }_{s}}{{f}_{i}}}$ |
血管壁的應變-位移關系為
| ${{\varepsilon }_{ij}}=\frac{1}{2}\left(\frac{\partial {{v}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{v}_{j}}}{\partial {{x}_{j}}} \right)$ |
其中,i, j=1, 2, 3;ρs、v(vi, vj)、σij和εij分別是血管壁的密度、位移向量、應力張量和應變張量;fi是作用在血管壁上的體力分量;xj表示三維直角坐標系中三個坐標軸的正方向。
1.1.4 設置血液與血管壁的耦合邊界
血管壁的內表面為流固相互作用的界面,即耦合面:
| $\sigma _{ij}^{\text{f}}\cdot {{n}_{j}}{{|}_{\text{interface}}}=\sigma _{ij}^{\text{w}}\cdot {{n}_{j}}{{|}_{\text{interface}}}$ |
其中,σijf和σijw分別是血液和血管壁的應力張量。血管壁的外表面是自由面,即
| ${{\sigma }_{ij}}\cdot {{n}_{ij}}{{|}_{\text{outwall}}}=0$ |
1.2 CFD數值模擬
在ANSYS Workbench工作平臺上,采用ANSYS+FLUENT單向流固耦合模塊,對三維血管及血液模型進行血液和血管壁的流固耦合數值模擬,估算血管壁的應變張量分布。基本步驟包括:
1.2.1 有限元網格劃分
三維血管和血液模型是非對稱的,且幾何形狀非常復雜,因此在網格劃分過程中很難劃分出特別規范的均勻網格。同時對于狹窄段,也很難保持原有規范的網格形狀。因此本文采用智能型的網格劃分模式,將血液與血管的三維幾何模型離散化,在遇到形狀突變時能按照合理的劃分方法自動加密,以獲得更加理想的網格單元[16]。
1.2.2 建立三維血管有限元模型
首先,設定初始條件,即定義血管和血液的物理屬性[17],如表 1所示,其中各參數均取人體正常生理條件下的平均值。考慮到粘彈性材料可能使流固耦合的迭代計算不收斂,因此本文不考慮血管的粘彈性。設置溫度為37℃。
然后,設定邊界條件,即對血管模型的入口和出口設置為固定約束,限制血管內血液的流動范圍。對于固體部分,血管外壁面只設置一個自由壁面條件,不加其它約束限制;血管內壁面(即血流與血管接觸的內表面)設定為流固耦合界面,并假定無滑移邊界條件(對于定常層流,假設管壁上流體質點的流速為零;對于不定常層流,假設管壁上流體質點的速度和管壁速度相同)。對于流體部分,將邊界條件設定在血流進出口界面上,出口壓力設定為零。
其次,設定血液流動的載荷,就是血管入口處給定的流體速度。為了實現流固耦合中數據的傳輸,將血液對血管壁的壓力作為加載流,將血管腔內表面上所有的流體動力都加載到血管壁內表面。
最后,定義時間步長,設定求解開始的時間,選擇迭代求解方法,設置收斂準則,誤差要求、輸出信息控制等。
1.2.3 計算結果的后處理
為了提高計算結果的可視化效果,用偽彩編碼顯示估算出的血管壁應變張量分布以及瞬態的流場變化,直觀展示由于搏動的血液及周期性心臟運動引起的血管壁應變的三維分布。
2 實驗結果和分析
實驗所用圖像數據的采集是在河北大學附屬醫院的心導管室中由醫生完成。IVUS和XA圖像分別是采用Jomed Endosonic超聲成像儀和Philips Integris CV單面XA機采集的。在進行IVUS檢查的過程中,XA和IVUS分別同步顯示超聲導管和探頭在血管腔內的位置和相應血管壁的形態結構。IVUS圖像的采集速率為30幀/秒,導管回撤速度為0.5 mm/s;XA的幀率是30幀/秒,圖像大小為512像素×512像素,灰階為256,像素尺寸為0.3 mm。對一個IVUS圖像序列進行處理后的實驗結果,如圖 1~圖 5所示。
 圖1
21幀IVUS圖像沿三維導管路徑順序排列
Figure1.
Alignment of 21 IVUS frames along the 3-D catheter pullback path reconstructed from angiograms
圖1
21幀IVUS圖像沿三維導管路徑順序排列
Figure1.
Alignment of 21 IVUS frames along the 3-D catheter pullback path reconstructed from angiograms
 圖2
三維血管和血液模型
Figure2.
3-D vessel and blood models
圖2
三維血管和血液模型
Figure2.
3-D vessel and blood models
 圖3
網格劃分后的血液和血管模型
Figure3.
Tetrahedral meshing of blood model and vessel model
圖3
網格劃分后的血液和血管模型
Figure3.
Tetrahedral meshing of blood model and vessel model
 圖4
血液流場計算結果圖
Figure4.
Numerical simulation results of blood flow
圖4
血液流場計算結果圖
Figure4.
Numerical simulation results of blood flow
 圖5
血管壁數據加載和應變分布計算結果
Figure5.
Load of the hydrodynamic data and strain distribution on the vessel wall model
圖5
血管壁數據加載和應變分布計算結果
Figure5.
Load of the hydrodynamic data and strain distribution on the vessel wall model
如圖 1所示,將部分IVUS圖像沿從XA圖像中重建出的三維導管路徑順序排列。計算出各幀IVUS圖像中血管壁內外膜輪廓的三維坐標后,得到血管和血液的三維幾何模型,如圖 2所示。
對三維血液模型進行網格劃分,其中生成的網格總結點數是15 793,總單元數是49 839;采用靜態結構(Static Structural)模塊完成三維血管模型的網格劃分,選擇自動網格劃分,生成的網格總結點數為30 013,總單元數為150 061,網格最大畸變為0.840 075,網格質量滿足計算要求,劃分結果如圖 3所示。
利用ANSYS Workbench下的FLUENT模塊計算血液流場,總步數設置為150,調整能量殘差收斂標準為0.000 01,迭代計算在第70步時達到收斂,流體區域的計算結果如圖 4所示。
利用“輸入壓力(Imported Pressure)”命令將血管腔內表面上所有的流體動力都加載到血管壁內表面,以偽彩編碼血管壁面應變分布,由紅色到藍色,表示固體組織的應變逐漸減小,如圖 5所示。對于沒有明顯分叉、狹窄和彎曲的血管段,管壁組織各處產生的應變分布規律是越靠近血管壁內腔表面處的應變越大,而越靠近血管外膜輪廓表面處的應變越小。對于彎曲的血管段,在曲率大的區域應變較大,且彎曲段外壁上的應變要比內壁上的應變大,這些幾何形狀變化劇烈的部位往往是斑塊阻塞滯留的位置,對于這些區域,在動脈粥樣硬化的致病因素中血流動力學的因素占有較大比重[18]。
3 結論
本文在從常規采集的IVUS灰階圖像序列中重建出的三維血管模型的基礎上,結合力學知識,采用CFD數值模擬技術估算由搏動血流引入的動脈血管壁的三維應變分布,得到用偽彩編碼表示應變分布的三維血管模型,直觀地展示血管的三維形態結構和三維應變分量及其分布情況。無需獲取IVUS成像設備的原始RF信號,而且較基于RF信號的方法能更全面地反映管壁和斑塊組織的彈性特征。
本文方法的局限是對局部應變的估算結果很大程度上取決于血管三維重建的精度,圖像采集、二維圖像的分割、沿導管回撤路徑確定各幀IVUS圖像的軸向位置和空間方向等步驟中存在的誤差都會累積在最終的重建結果中,進而降低對管壁應變的測量精度。在后續的工作中,考慮在采用虛擬現實技術建立血管模型并模擬血管支架植入術的基礎上,對支架與血管壁的交互受力情況等進行定量估算。