本文采用小兒腦癱患者步行時下肢的表面肌電信號（sEMG），對其步態運動的特征參數進行分析，擬達到對小兒腦癱患者的臨床嚴重程度進行評估的目的。首先采用綜合輪廓法（IP）、樣本熵（SampEN）和平滑非線性能量算子（SNEO）三種方法分別檢測仿真步行狀態下，下肢雙側腓腸肌激活時的 sEMG 信號，并對這些算法得到的結果進行精度和運算時間的比較研究，最后確定了三種算法中性能比較優良的 SNEO 算法，然后再利用實測的小兒腦癱患者的 sEMG 信號，對患兒步態活動段進行檢測和標定。研究結果表明：三種算法在 sEMG 步態活動段的劃分中精度的差異沒有統計學意義，但 SNEO 算法具有運算速度快的優點，適用于 sEMG 信號的步態活動段檢測；小兒腦癱患者的腦癱程度與其 sEMG 信號的步態活動段平均長度呈正相關關系，三種不同程度腦癱患兒的步態活動段長度差異具有統計學意義。通過本文研究結果，我們提出或許可以考慮將步態活動段平均長度作為一種評估腦癱程度的輔助定量化指標的新思路。
引用本文： 婁智, 姚博, 楊基海. 基于表面肌電信號的小兒腦癱步態活動段檢測研究. 生物醫學工程學雜志, 2017, 34(3): 342-349. doi: 10.7507/1001-5515.201512064 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
小兒腦性癱瘓（cerebral-palsy，CP）簡稱腦癱，是指從胎兒期到嬰兒期，由于各種致病因素所致的非進行性腦損傷或腦發育異常所導致的中樞性運動障礙[1]，典型的腦性癱瘓多具有運動發育落后、姿勢異常、中樞性運動障礙等體征。
近三十年來，隨著產科技術、圍產醫學和新生兒醫學的發展，死胎發生率、新生兒死亡率均有明顯下降，但腦癱發病率卻不減反增。根據國內外報道，腦癱的發病率在 1.5‰～5‰，發達國家的發病率較高[2-3]。雖然小兒腦癱患者的腦損傷是非進行性的，但如果沒有得到適當的康復治療與訓練，患兒生活難以自理，甚至會引發包括心理障礙在內的一系列繼發障礙。步態康復訓練是腦癱康復中運動障礙康復的重要環節，步行能力是生活自立的基礎。步行者在步行時，雙腿交替邁動顯示出明顯的周期性，借助人體步行運動的生理學特點，前人許多研究工作涉及采用不同傳感器對步行時的運動/停止狀態進行檢測和記錄，本文采用的步態表面肌電信號（surface electromyography，sEMG）來自左右雙側的腓腸肌，從某一條腿獲取的 sEMG 信號來看，其信號變化周期為一個跨步周期，我們將每個跨步周期定義為一個步態活動段。看似簡單的步態活動段其實是神經系統平衡中樞、運動中樞和眾多肌肉相互配合、協同控制的結果。因此研究步態活動段對于揭示神經肌肉控制機理，對腦癱康復中的步態訓練具有重要的指導意義。對步態活動段進行準確的定位，獲取步態活動段的時域位置信息，可以進一步實現對患者步態、步頻、步幅的精確分析，對于小兒腦癱患者康復的評估具有重要的現實意義[4]。
sEMG 是由運動單元動作電位（motor unit action potential，MUAP）序列在檢測電極處的時空疊加形成的信號[5]，能夠反映運動神經元的活動情況。從受試者小腿腓腸肌采集到的 sEMG 信號可以充分并客觀地反映在步行運動中肌肉的力度變化以及邁步頻率等重要的步態特征，由此可以在一定程度上對受試者的行為模式和身體狀況進行評測。但是目前對步態檢測的研究常限于健康受試者運動狀態的研究，如步行者航位推算、導航和運動數據評估等方面，而對腦癱患兒的行為模式進行探索，并通過試驗結果對腦癱患兒的功能性運動障礙程度以及康復情況進行評測則鮮有報道。因此本文采用一種基于 sEMG 的無創且方便的檢測方法對步態活動段進行分割，并對小兒腦癱患者的步態活動段特征進行進一步的探討。
為了對小兒腦癱患者的運動狀態進行客觀評估，針對他們的步態活動段的精確定位，本文采用了三種常用于肌電信號運動周期檢查的方法，即綜合輪廓算法（integrated profile，IP）、基于樣本熵（sample-entropy，SampEN）的活動段檢測算法和基于非線性能量算子（smoothed nonlinear energy operator，SNEO）的峰值檢測算法，分別對仿真信號的步態活動段進行檢測，并比較三種方法的處理效果，選擇其中針對 sEMG 信號步態活動段檢測的最優算法，并將這種算法應用于真實腦癱患兒的 sEMG 信號的步態分析，以提高定位精度，同時把步態活動段定位與小兒腦癱患者的臨床評估相結合，完成對小兒腦癱復雜進程的初步定量分析。
1 試驗方法
1.1 試驗對象
本研究中，由安徽醫科大學第一附屬醫院小兒神經康復科協助招募的 18 名（8 位男性；10 位女性）不同臨床嚴重程度的小兒腦癱患者自愿參加試驗。對于腦癱患兒病情程度的判斷，臨床醫生通常采用國際通行的針對腦癱患兒的標準化粗大運動功能分級系統 （gross motor function classification system，GMFCS），用分級評定的方法來評估痙攣型腦癱患兒粗大運動功能級別[6-7]。其中 GMFCS 分級評定系統將腦癱患兒分為 I～V 五個級別，I 級為最佳，V 級為最差。在本研究中，小兒腦癱患者按其主管醫師的臨床診斷分為I～Ⅱ、Ⅱ～Ⅲ與Ⅲ～Ⅳ三個級別[8]。18 名試驗對象中每種級別的患兒各 6 例。根據研究的需要，選取的試驗對象包含以下篩選條件：① 被診斷為先天性小兒腦癱的患者，即出生時便患有腦癱疾病；② 具有明顯的步態異常癥狀，但能夠獨立或在他人輔助下完成邁步行走動作；③ 無其他可能導致下肢運動功能障礙的疾病史；④ 在治療過程中未接受過任何類型的矯正手術。所有受試者在參加試驗前，由其監護人代簽知情同意書，本研究的所有試驗方案遵循赫爾辛基宣言并受中國科學技術大學倫理審查委員會（Ethics Committee of University of Science and Technology of China for Human Subjects）的審批和監管。
1.2 試驗方案
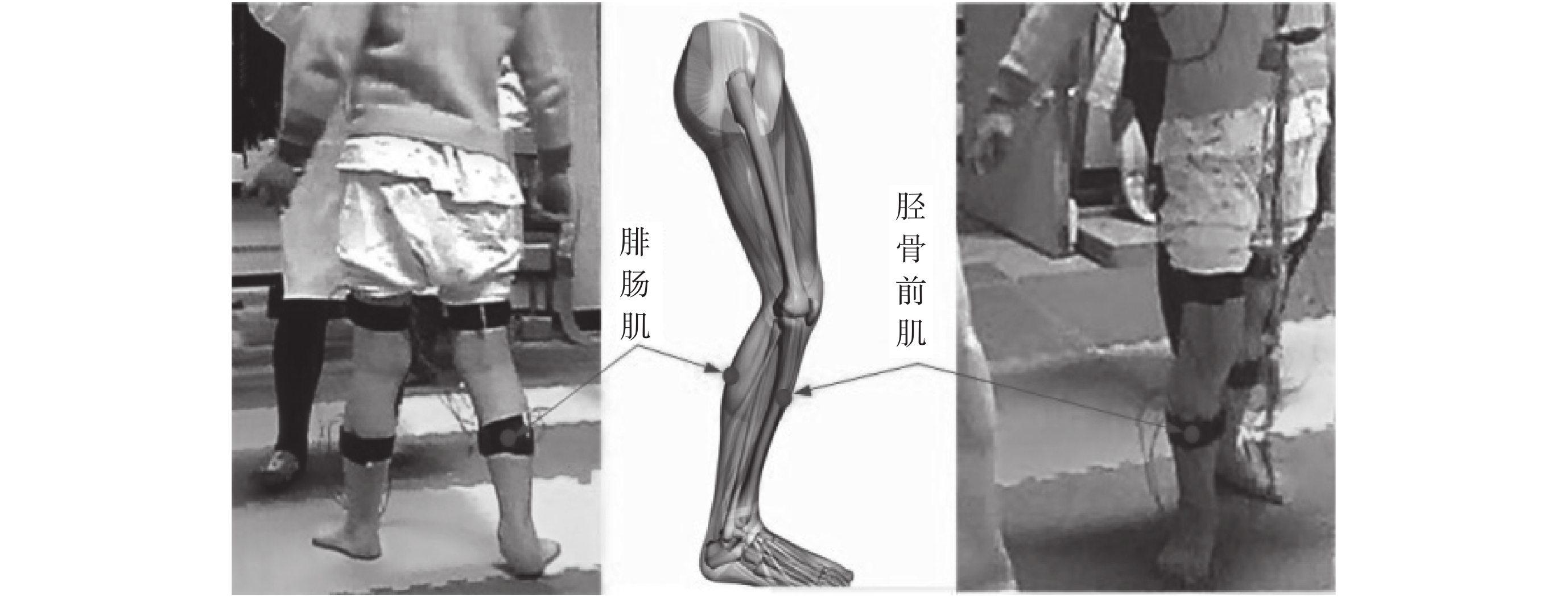
人體的步行運動主要受到腿部肌肉的控制，小腿后側的腓腸肌是一種踝關節伸肌，提供了體重支持與行走的主要動力，而與腓腸肌具有協同關系的脛骨前肌是踝關節屈肌，與腓腸肌成對作用完成行走的動作，因此從腓腸肌-脛骨前肌這一對肌肉采集的 sEMG 信號包含了步行運動過程中檢測步態的主要信息。據此本文試驗設計了腦癱患兒采集 sEMG 的電極放置位置，如圖 1 所示。
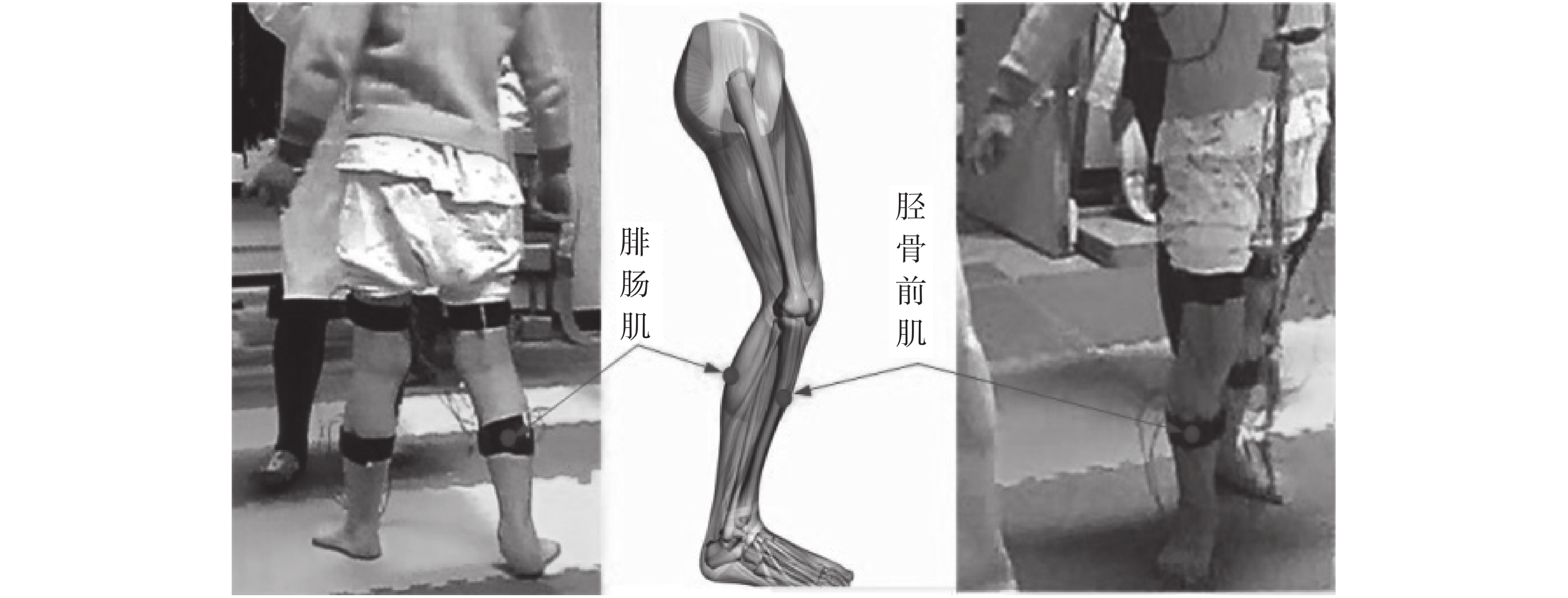圖1
腦癱患者 sEMG 信號采集方案
Figure1.
sEMG acquisition scheme for cerebral-palsy patients
為了提高采集信號的質量，試驗前首先刮去體表毛發，用專用砂紙打磨皮膚表面，再用酒精擦洗殘余物，以去除皮膚角質層，并在皮膚表面測量區域涂以少量的導電膏，以降低電極和檢測表面的接觸電阻。電極與皮膚的接觸電阻是影響信號質量的關鍵因素之一，本文采集設備及其配套軟件具有分別檢查各個電極通道與皮膚接觸電阻的功能。然后把 sEMG 采集電極通過有孔（使電極與皮膚接觸）薄雙面膠貼附在測量區域皮膚表面，位置盡量放在肌肉的運動點和肌腱之間，初始朝向選擇陣列平行或垂直于肌纖維方向，同時在腓腸肌與脛骨前肌的合適位置放置參考電極。
進行試驗時，由家長和主治醫生協助患兒完成指定動作。試驗動作包括站立和環繞康復室的行走與轉彎，要求腦癱患兒以合適的速度環繞康復室行走 2～3 min，并完成左右雙側至少 30 個邁步動作，同時利用采集設備記錄 sEMG 信號。
采集設備采用 DELSYS Myomonitor 4 表面肌電與二軸加速度分析系統，采樣率為 1 000 Hz，采用 2～500 Hz 帶通濾波器以減少采集時的背景噪聲。
2 數據處理方法與驗證
基于 sEMG 對運動周期定位的主要研究方法有以下幾種：① 利用信號包絡的方法，如 IP 算法；② 基于信息論的高斯性刻畫方法，如 SampEN；③ 基于信號幅值與能量的 SNEO 方法，這三種算法的詳細介紹如下：
2.1 IP 算法
IP 算法由 Santello 等[9]于 1998 年提出。在此算法中，信號的線性包絡由 A（xi）綜合表示，它的定義為：
| $A\left( {{x_i}} \right) = \mathop \sum \limits_{j = 1}^i f\left( {{x_j}} \right)/\mathop \sum \limits_{p = 1}^N f\left( {{x_p}} \right)$ |
其中 i∈（0，N] 為采樣信號的樣本點個數，xi 為采樣信號在采樣點 i 處的幅值，而函數 f（x）定義為：
| $f\left( {{x_i}} \right) = \left| {{x_i}} \right|,\;i \in \left( {0,N} \right]$ |
信號的參考基線為：
| $T \left( {{x_i}} \right) = i/N$ |
采樣信號的綜合輪廓的代價表達如式（4）所示：
| $G \left( {{x_i}} \right) = T \left( {{x_i}} \right) - A \left( {{x_i}} \right),\;i \in \left( {0,N} \right]$ |
采樣信號的運動周期起始點與終止點的定義為 [Min（G（xi）），Max（G（xi））]，對于本文采集的步態 sEMG 信號即是活動段的開始點和結束點。
2.2 SampEN 檢測方法
SampEN 方法是一種利用近似熵方法改進而發展起來的信號復雜性測度方法，最早由 Richman 等[10]提出。一組信號序列越復雜，其 SampEN 值越大，若序列的自我相似性越高，則 SampEN 值越小。SampEN 相比近似熵精度更好，與已知信號的隨機部分有更加緊密的一致性，因此更加適用于分析生物醫學信號。針對 sEMG 計算方法如下：
（1）采用疊加窗技術將 sEMG 信號分為連續的信號幀，每幀的長度為 128 個采樣點，幀間重疊為 50%，即 64 個采樣點。
（2）給定 sEMG 的信號 s（t）， ，N 為步驟（1）中信號幀的長度 128 點；
（3）按照信號序列組成一組 m（m<N）維延時向量，該組向量共有 N–m 個，如式（5）所示：
| ${X_m}\left( p \right) \!=\! \left[ {s\left( {p \!+\! k} \right)} \right]_{k = 0}^{m - 1},\;p \!=\! 1,{\rm{ }}2,{\rm{ }} \cdot \! \cdot \cdot ,N \!-\! m \!+\! 1$ |
（4）定義兩個向量間的距離 d 為兩者對應元素中差值最大的一個。
| $d\left[ {{{\rm{X}}_m}\left( p \right),{X_m}\left( q \right)} \right] = \mathop {\max }\limits_{0 \leqslant k \leqslant m} \left\{ {\left| {s\left( {p + k} \right) - s\left( {q + k} \right)} \right|} \right\},\;1 \leqslant p,q \leqslant N - m$ |
（5）選定閾值 r，對每個 1≤p≤N–m 的值，統計 d[Xm（p），Xm（q）] 小于 r 的數目（稱為模版匹配數）Nm（p），并計算該數目與距離總數 N–m–1 比值，即計算如下函數：
| $B_r^m\left( p \right) = {N^m}\left( p \right)/\left( {N - m - 1} \right)$ |
其中 1≤q≤N–m，且 q≠p。對其所有的 p 值取平均，可得：
| ${B^m}\left( r \right) = \frac{1}{{N - m}}\mathop \sum \limits_{p = 1}^{N - m + 1} B_r^m\left( p \right)$ |
（6）增加維數 m 到 m+1，重復步驟（3）～（4），并統計 d[Xm（p），Xm（q）] 小于 r 的數目 Nm+1（p），同樣有：
| $A_r^m\left( p \right) = {N^{m + 1}}\left( p \right)/\left( {N - m - 1} \right)$ |
其中 1≤q≤N–m，且 q≠p。對其所有的 p 值取平均，可得
| ${A^m}\left( r \right) = \frac{1}{{N - m}}\mathop \sum \limits_{p = 1}^{N - m + 1} A_r^m\left( p \right)$ |
（7）最后得到樣本熵定義為式：
| ${\rm{SampEN}}\left[ {s\left( t \right),m,r} \right] = - {\rm{ln}}\left( {{A^m}\left( r \right)/{B^m}\left( r \right)} \right)$ |
對第 i 幀信號 si（t）， 計算 SampEN 特征序列如下：
| ${S_{{\rm{SE}}}}\left( i \right) = {\rm{SampEN}}\left[ {{s_i}\left( t \right),m,r} \right]$ |
在已有的研究報道中，一般將 r 取為信號標準差的 20%～25%。針對本實驗室采集的數據，我們按照經驗閾值取 m=2，r=0.015。在進行 SampEN 計算后，用閾值法確定活動段的起始點與終止點。
2.3 SNEO 算法
非線性能量算子（nonlinear energy operator，NEO）是在研究非線性語音建模時引入的一個數學算子，其輸出分量可以看作是信號經過高通濾波后的瞬時能量成分。
對于離散信號 x（n），NEO 的表達式為：
| $\psi \left[ {x\left( n \right)} \right] = {x^2}\left( n \right) - x\left( {n + 1} \right)x\left( {n - 1} \right)$ |
為了提升 NEO 處理非平穩信號的能力，根據已有文獻[11-12]，在 NEO 算法中附加一個窗函數，這種算法即為 SNEO 算法：
| ${\psi _s}\left[ {x\left( n \right)} \right] = \psi \left[ {x\left( n \right)} \right]*{w_s}\left( n \right)$ |
其中 ws（n）為一個窗函數，而*代表卷積過程。
根據當前已有的肌電信號相關研究表明，漢明窗在肌電信號處理中具有良好的效果，因此本文在具體實現過程中采用該窗函數對 NEO 進行平滑[5, 13]。同樣，與前述 SampEN 的起始點、終止點確定方法相似，采用簡單的閾值算法標定運動周期的起始點與終止點。
2.4 算法有效性的驗證
為了檢驗算法的有效性，本文利用健康人的真實標準無噪聲 sEMG 加入不同信噪比（signal-to-noise ratio, SNR）的混合噪聲構建半合成信號。這些半合成信號具有明確的活動段起始點與終止點，因此可以較為準確地評估算法的精度和有效性。半合成信號中的 sEMG 采用健康兒童的步行 sEMG 信號，由具有經驗的研究者手動標定活動段，并采用基于三級濾波器的 sEMG 降噪處理方法進行預處理，最后獲得標準無噪聲的 sEMG 信號[13]。
此外，為了準確地仿真腦癱狀況下的 sEMG 信號，本文加入并混合了腦癱患者 sEMG 信號中常見的三種干擾噪聲，以驗證三種算法在噪聲干擾下的效能。這三種噪聲為：背景噪聲、其他肌肉由于痙攣產生的 MUAP 干擾以及工頻干擾。
2.5 統計分析
統計分析采用 SPSS（SPSS，Inc.，2007，Chicago，IL）工具進行分析。在仿真實驗中，不同算法組與組之間的差異性采用雙因素方差分析（Two-way ANOVA），而在真實信號試驗中，采用單因素方差分析（One-way ANOVA）研究腦癱患兒臨床嚴重程度與 sEMG 信號步態活動段長度的關系。當 P<0.05 時，結果差異具有統計學意義。
3 結果與討論
3.1 半合成信號實驗
半合成信號由一組（共 10 個發放序列）同時持續發放的真實 sEMG 信號段構成，分三次分別加入 SNR 為 0.6、2、5 的合成混合噪聲信號。合成噪聲由背景白噪聲、工頻干擾產生的 50 Hz 及其倍頻噪聲以及移動偽跡所產生的周期性尖峰噪聲構成。sEMG 采用前述的 IP 算法、SampEN 算法和 SNEO 算法分別對無噪聲與加入不同 SNR 噪聲的三組半合成 sEMG 信號進行了處理，相應實驗結果的一個示例如圖 2 所示。
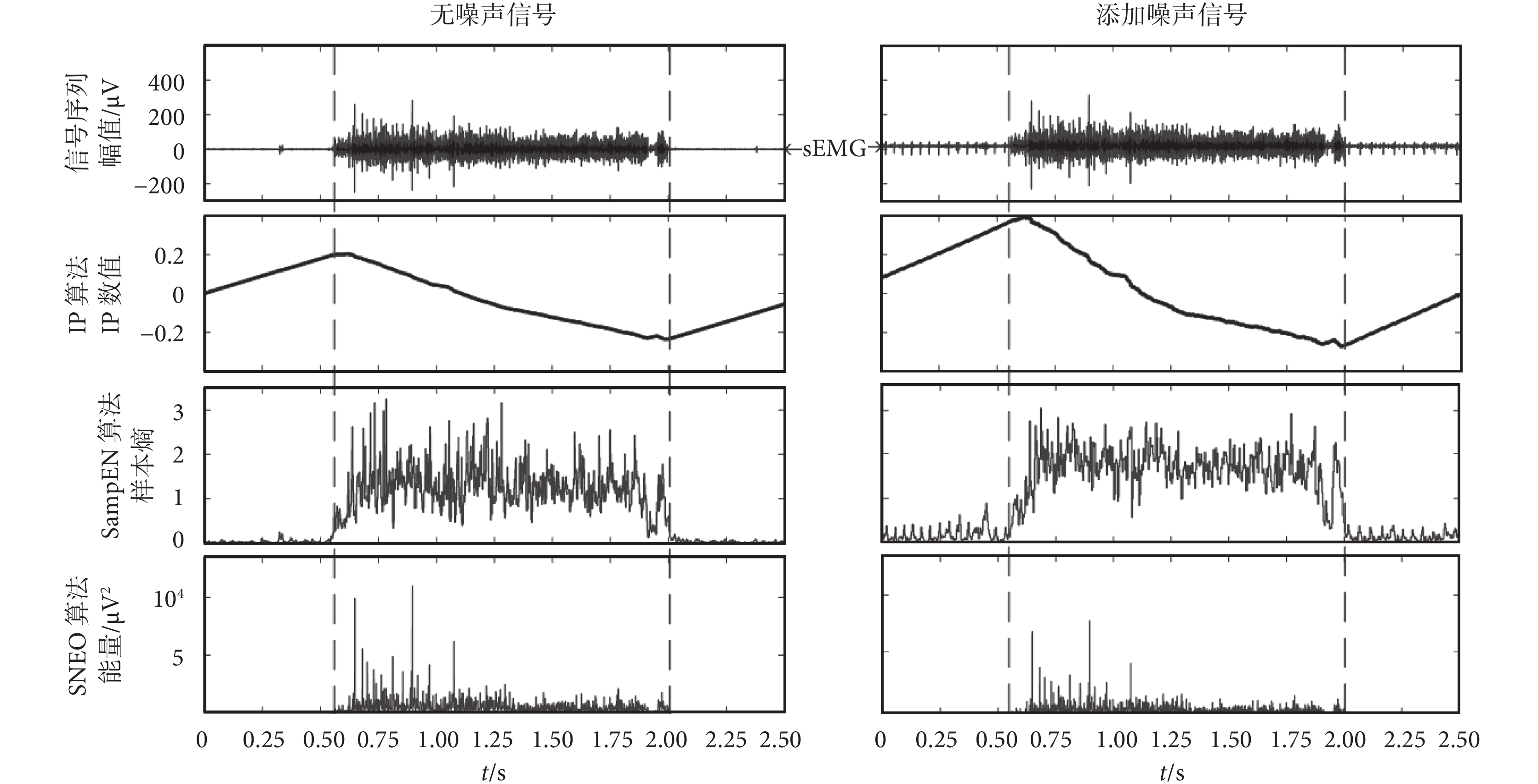圖2
信號仿真及三種活動段分割算法的實驗結果
Figure2.
Signal simulation and the results of three different segmentation algorithms in simulation signals
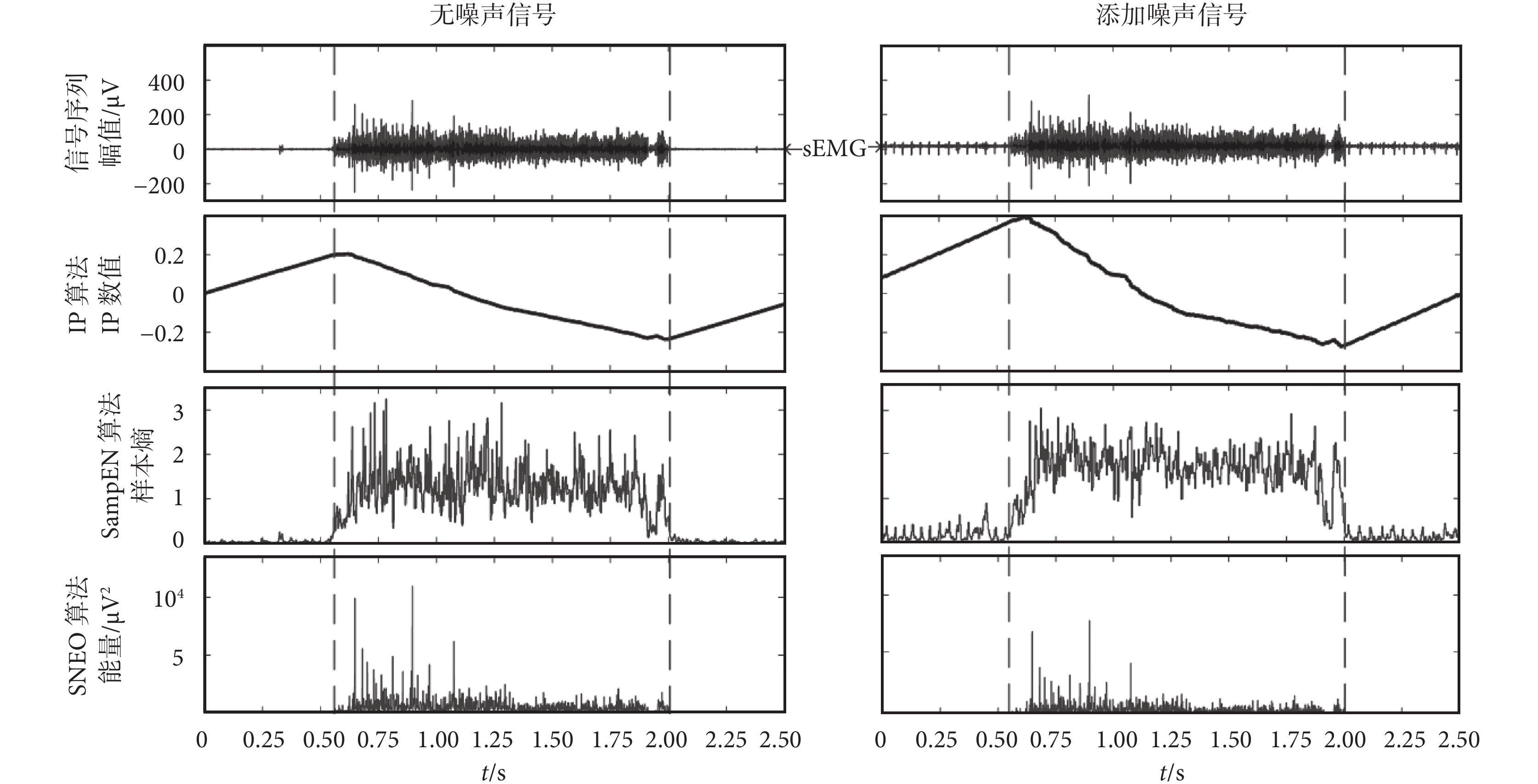
如圖 2 所示，無噪聲信號部分的最上圖為無噪聲的半合成 sEMG 信號的一個周期活動段，其余三圖分別是三種算法的實驗結果。由圖可見，IP 算法在起始點和終止點都有一定程度的偏移，SampEN 算法定位的起始點略微先于 sEMG 信號出現，而定位的終止點又比實際周期延遲出現，相比之下 SNEO 算法定位的起始點與終止點與 sEMG 實際發放位置比較接近。添加噪聲部分的最上圖為具有尖峰偽跡的半合成 sEMG 信號（SNR：0.6 dB）的一個周期活動段波形，三種算法的實驗結果與無噪信號試驗結果類似，同樣 SNEO 算法的定位準確，并且抗噪聲干擾能力也較好，因此這種方法適于步行中 sEMG 信號活動段的檢測和定位。
為進一步驗證上述結果，在仿真實驗中，將三組（共 10 個發放序列）添加噪聲的半合成信號采用 IP 算法、SampEN 算法及 SNEO 算法分別獲得的步態活動段長度和運行時間進行比較，并采用雙因素方差分析進行統計，結果如表 1 所示。
表1
半合成 sEMG 信號中三種算法的定位精度及比較
Table1.
Comparison of accuracy and computation speed of three algorithms in a semi-synthetic sEMG signal
如表 1 所示，三種算法在分割活動段長度上的差異不具有統計學意義（P>0.05）。然而結合圖 1 可以看出，IP 算法在實際活動段的劃分中，在活動段起始點的標定中有一定的偏移，且起始點遲滯和終止點提前導致實際估計長度的均值（1.37）要小于實際仿真信號長度（1.47），而 SNEO 算法與 SampEN 算法所獲得的活動段平均長度（SNEO：1.47；SampEN：1.50）與實際仿真信號長度更加接近。在計算時間上，SNEO 算法與 IP 算法顯然要大大優于 SampEN 算法，這兩種算法在實際應用中能夠用于腦癱患兒肌電信號的實時分析。而 SampEN 方法，由于運行時間較長，僅能應用于離線分析，也不適用于數據量比較大的步態活動段分析。根據以上分析，本文選擇了活動段起始點偏移較小且運行時間較短的 SNEO 算法應用于腦癱患兒的步行 sEMG 信號活動段劃分。
3.2 腦癱患兒真實信號試驗
對于真實試驗獲得的 sEMG 信號首先進行去噪預處理，采用一種基于三級濾波器的 sEMG 信號降噪處理技術[13]，即采用頻譜插值法去除工頻干擾，采用形態學運算去除基線漂移，采用經驗模態分解去除白噪聲。然后采用前述的 SNEO 算法對去噪后的步態活動段信號進行檢測和分割，小兒腦癱Ⅰ～Ⅱ，Ⅱ～Ⅲ和Ⅲ-Ⅳ級三種患兒的典型試驗結果如圖 3～圖 5 所示。
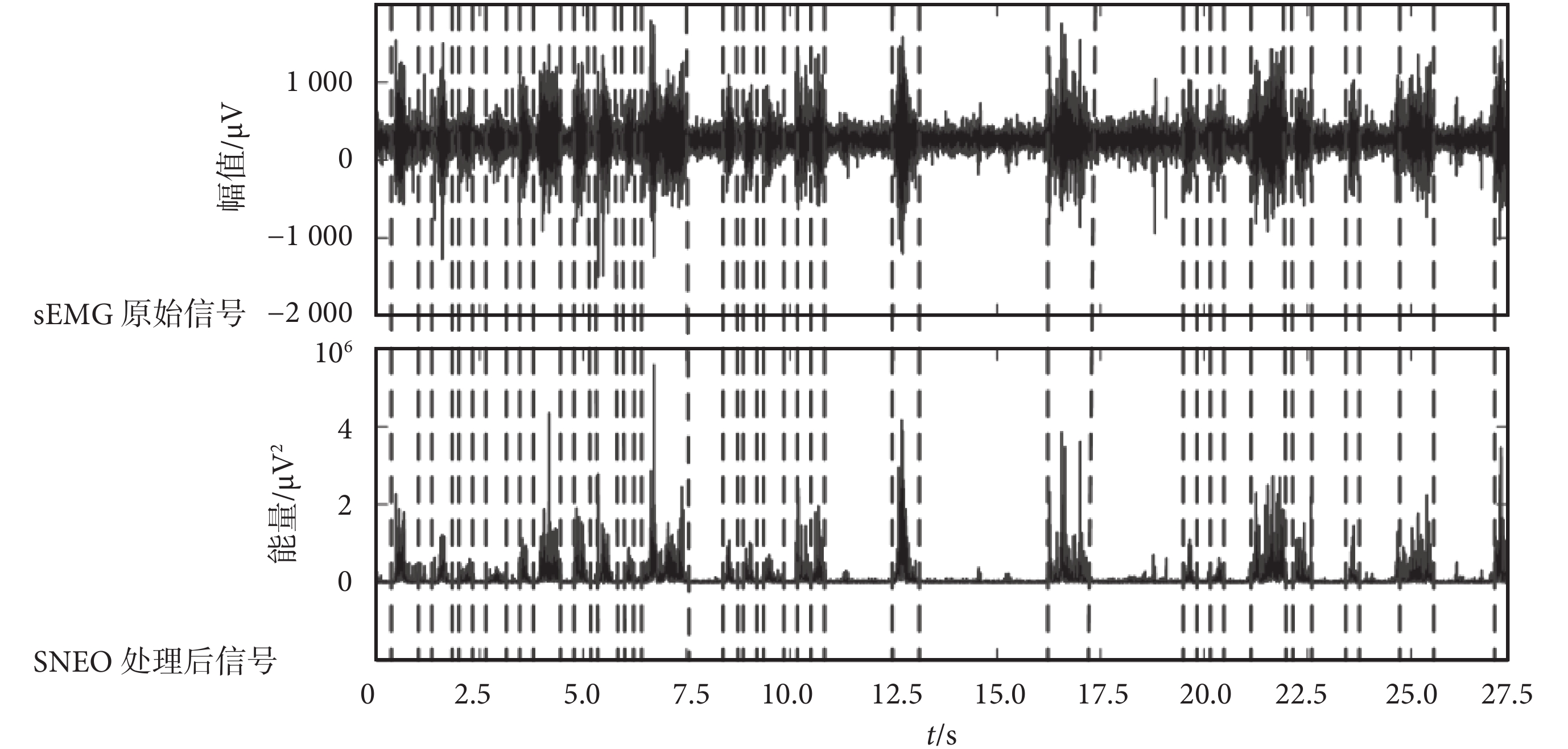
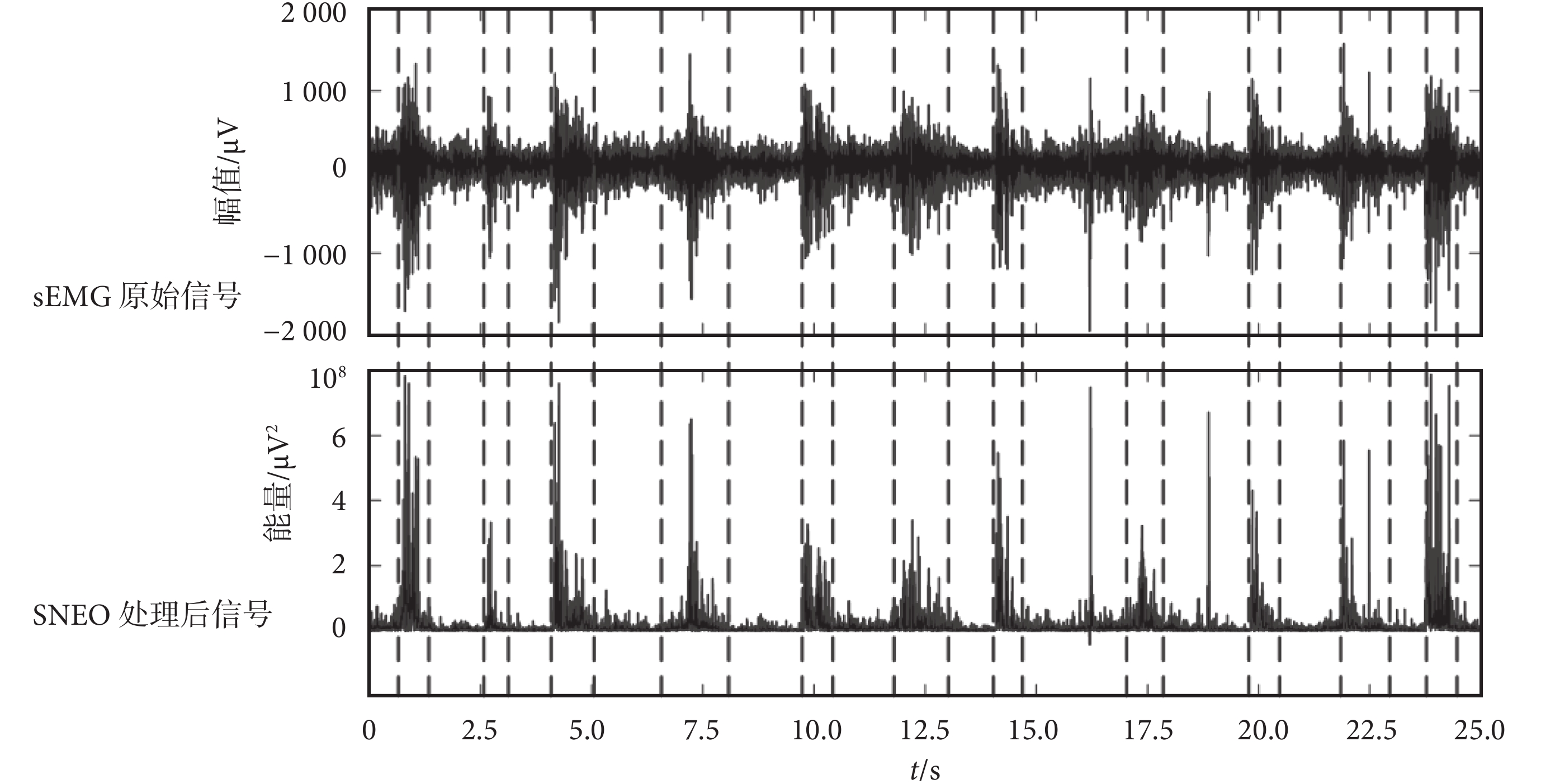
如圖 3 所示為小兒腦癱Ⅲ～Ⅳ級患兒步態活動段檢測結果，其中上部分為 sEMG 信號，下部分為經 SNEO 算法處理獲得的結果，虛線表示該結果對應的 sEMG 信號活動段分割情況。從圖 3 中可以看出，小兒腦癱Ⅲ～Ⅳ級患兒的步態運動周期是不均勻的，即步態活動段的周期性較差。患兒原始步態 sEMG 信號中引入了較多的噪聲，這是由于該級患兒的行走十分困難、步態很不穩定引起的。另外，該級患兒處于肌強直或者肌萎縮病態，其 sEMG 信號中也呈現出較粗的基線。如圖 3 所示，經 SNEO 算法處理后，顯示出了較好的抗噪聲能力，通過選擇合適的閾值就能夠比較精確地對步態活動段進行定位和劃分。
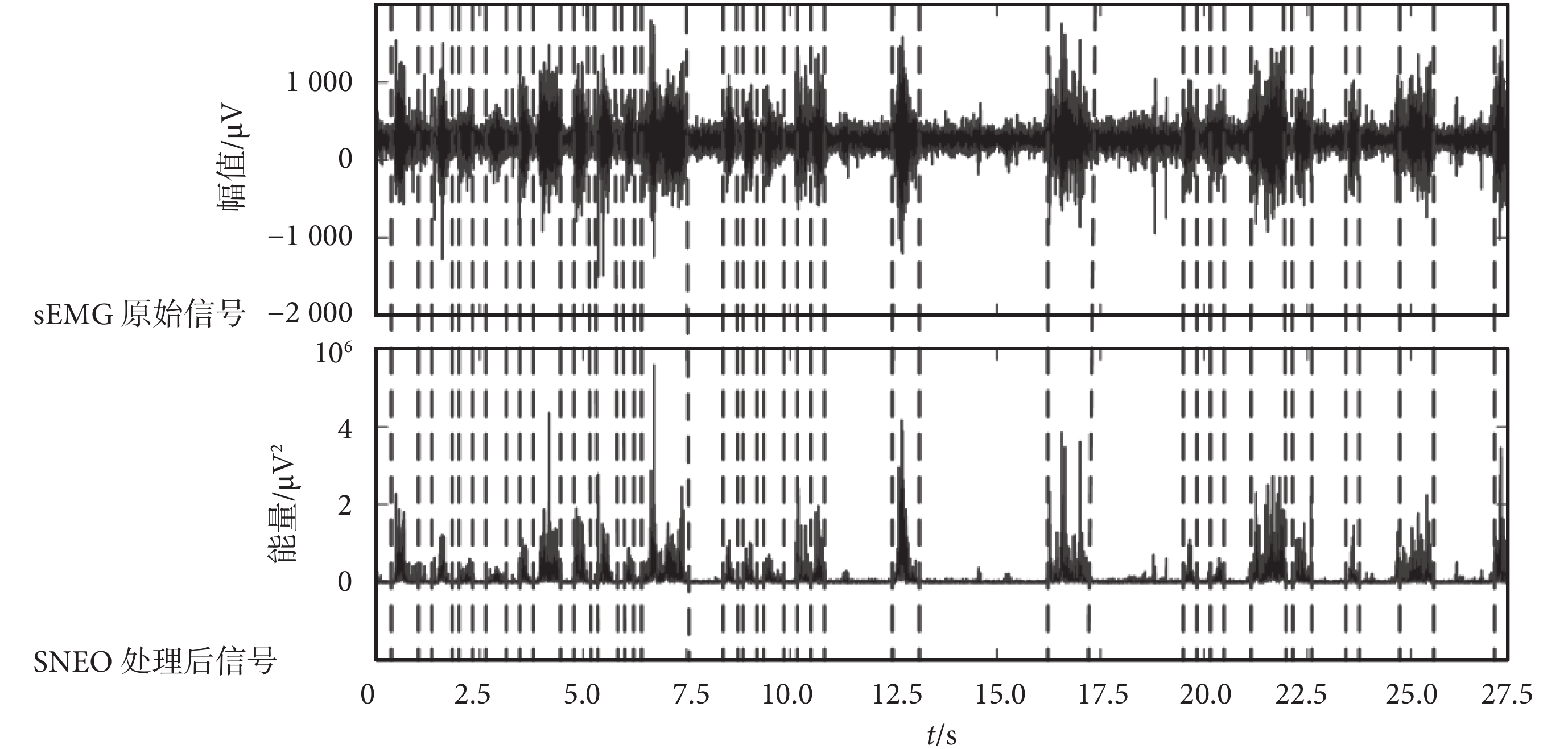圖3
Ⅲ～
Ⅳ級腦癱患兒步態運動周期劃分結果
Figure3.
Walking sEMG segment calibration in cerebral-palsy III～IV subjects
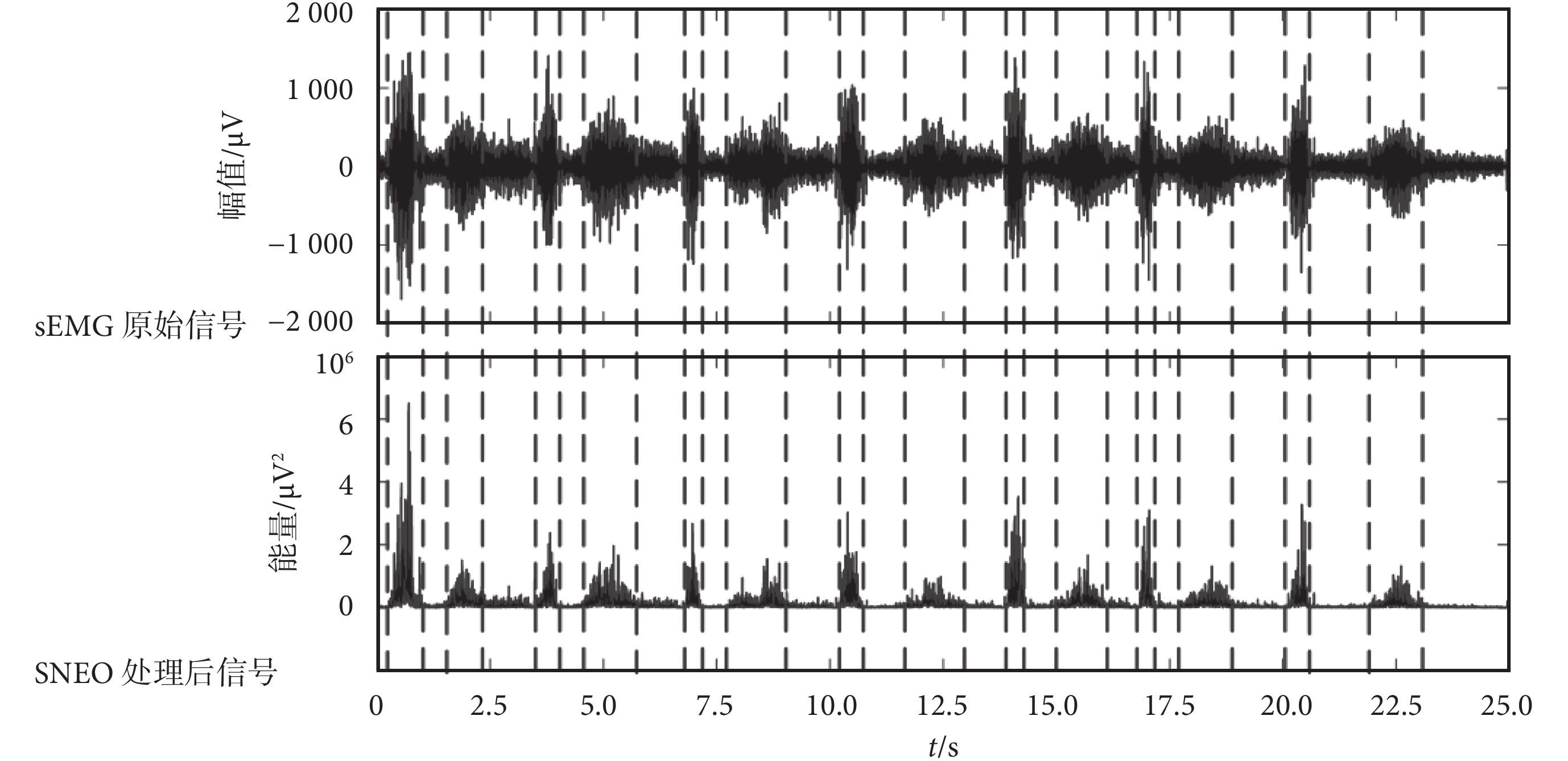
如圖 4 所示為小兒腦癱Ⅱ～Ⅲ級患兒的步態活動段檢測結果，與前述小兒腦癱Ⅲ～Ⅳ級的患兒相比，該級患兒的步態運動周期較為均勻有序，周期性比較明顯，但是由于這個級別的患兒運動障礙仍比較明顯，sEMG 的發放并不穩定，步態活動段也顯示出長短不一的不均勻狀態。
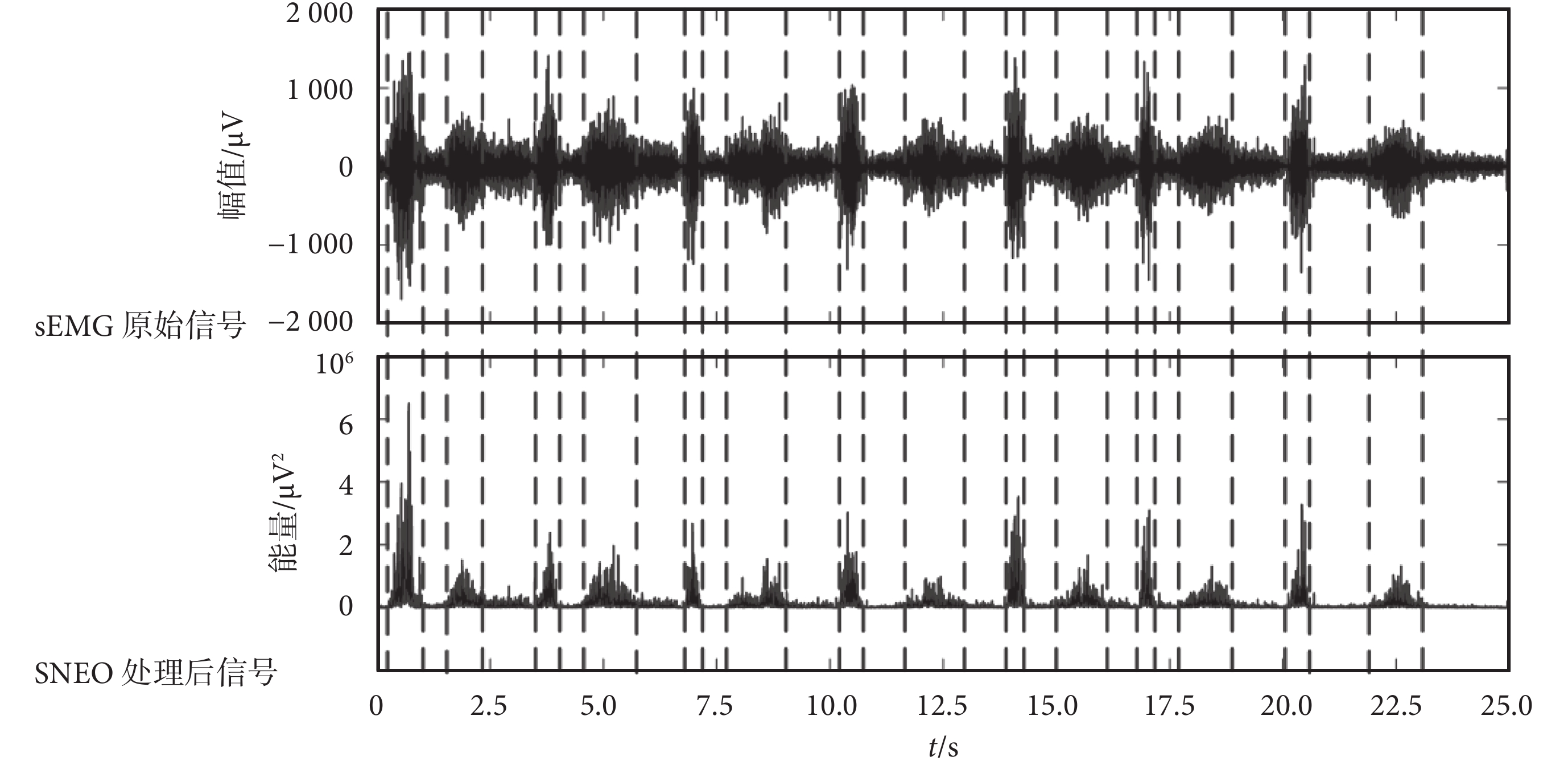圖4
Ⅱ～
Ⅲ級腦癱患兒步態運動周期劃分結果
Figure4.
Walking sEMG segment calibration in cerebral-palsy II～III subjects
如圖 5 所示為小兒腦癱Ⅰ～Ⅱ期患兒的步態活動段檢測結果，這種情況下的患兒無運動障礙或者運動障礙較輕，sEMG 顯示比較穩定，已經接近于正常人的表面肌電信號發放，但是 sEMG 的基線仍較粗，說明患兒還存在著一定的肌肉緊張現象。
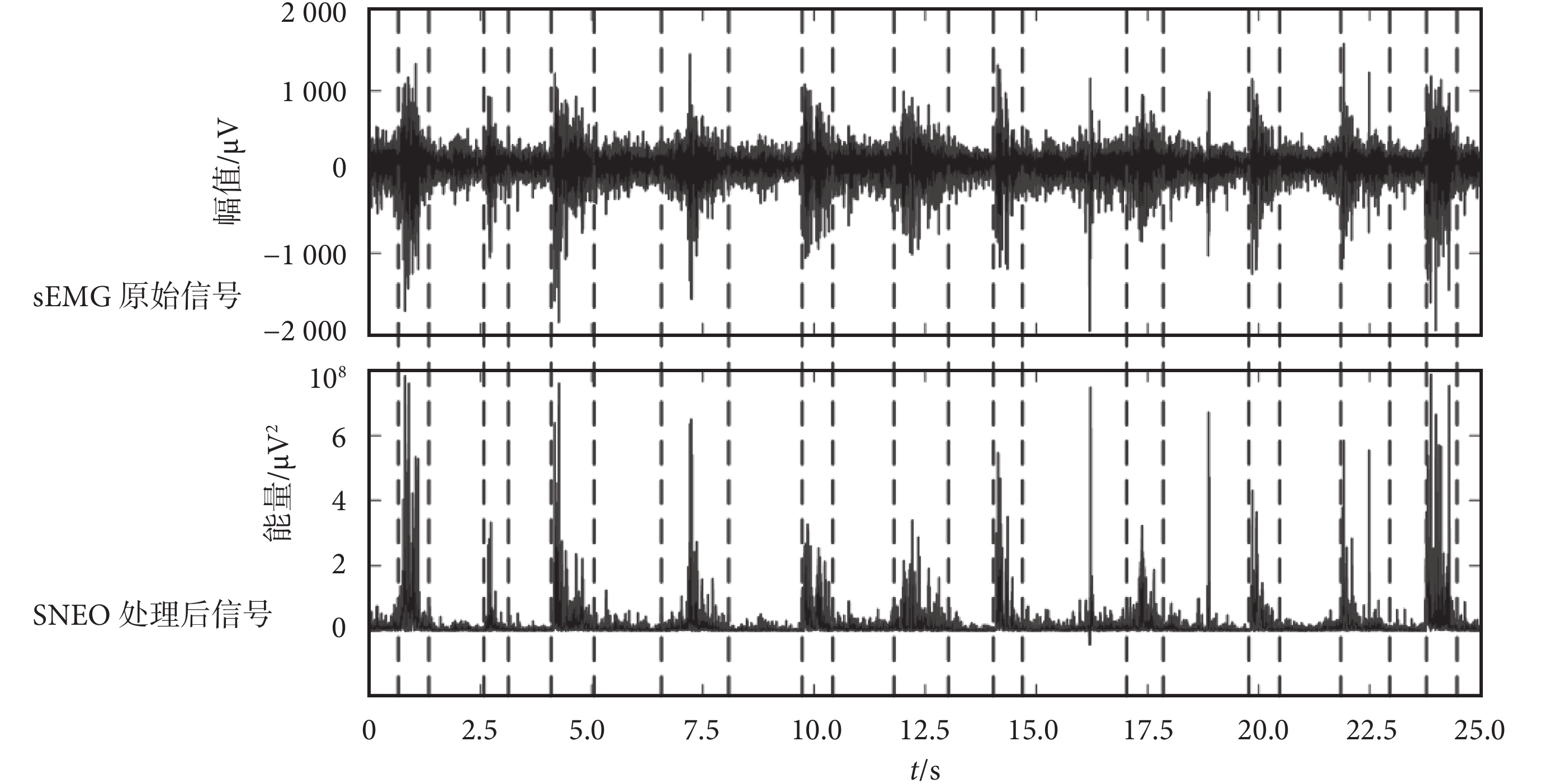圖5
Ⅰ～
Ⅱ級腦癱患兒步態運動周期劃分結果
Figure5.
Walking sEMG segment calibration in cerebral-palsy I～II subjects
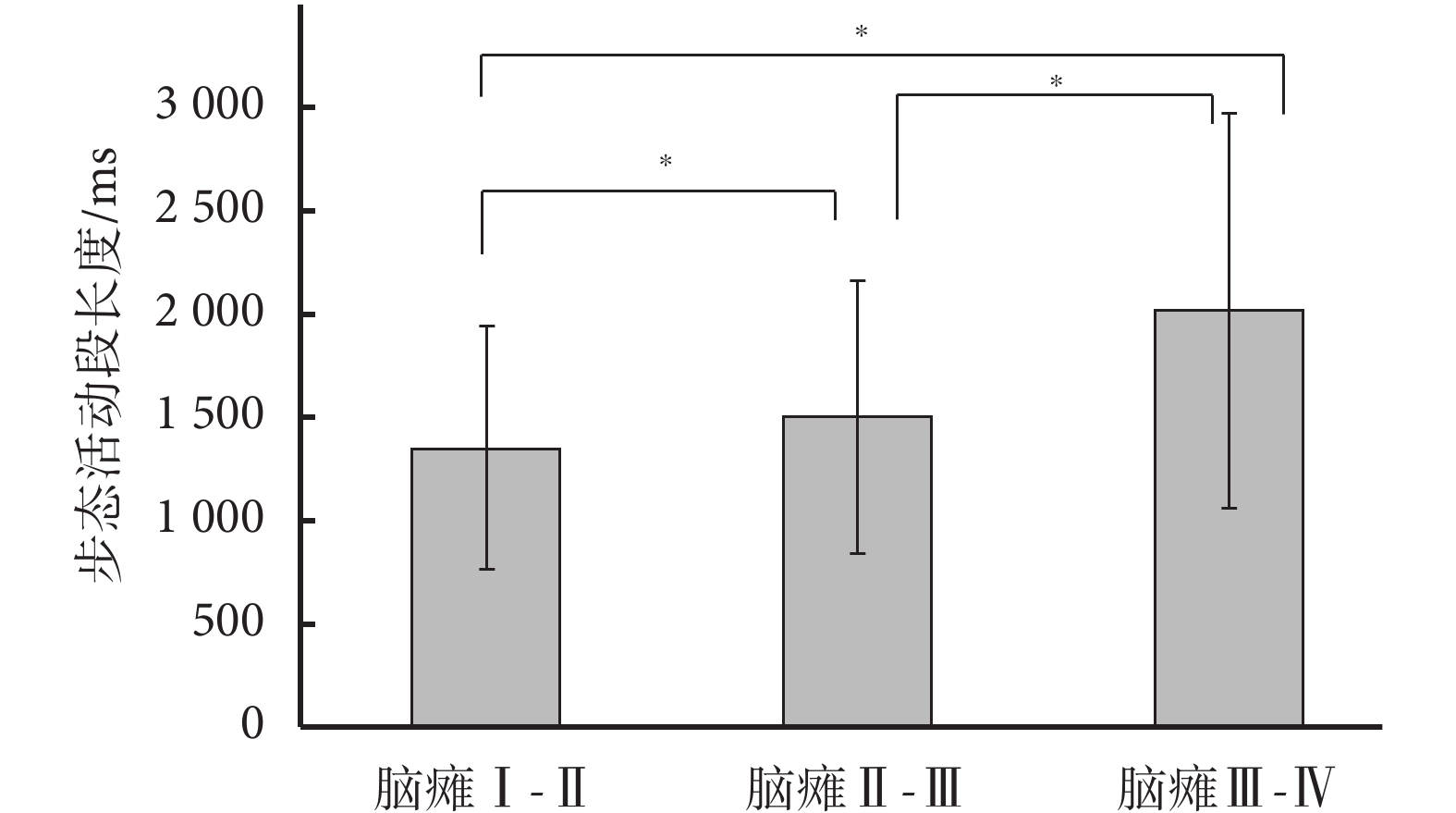
在對三類不同程度腦癱患兒的 sEMG 信號采用 SNEO 算法進行步態活動段劃分的基礎上，我們進一步對已有的數據進行統計分析，如圖 6 所示為三類不同程度腦癱患兒步態活動段持續時間的均值與方差。小兒腦癱Ⅰ～Ⅱ型的活動段持續時間最短，并且也具有較小的標準差，這說明小兒腦癱Ⅰ～Ⅱ型患者行動具有較好的周期性，而且動作比較穩定。而小兒腦癱Ⅱ～Ⅲ型患者及小兒腦癱Ⅲ-Ⅳ型患者的步態活動段長度呈上升趨勢，同時標準差也不斷變大，說明隨著腦癱嚴重程度的增大，患兒行動更加困難，站立和行走時間不斷增大。如圖 6 所示，采用單因素方差分析對三類不同程度腦癱患兒的步態活動段長度數據進行處理（腦癱Ⅰ～Ⅱ級：1 364±623；腦癱Ⅱ～Ⅲ級：1 508±732；腦癱Ⅲ-Ⅳ級：2 033±975），在三組患兒數據的兩兩對比后均得到 P<0.05 的結果。試驗結果說明這三類患兒的步態平均活動段長度差異具有統計學意義，因此步態活動段長度可以作為一種輔助評估腦癱程度的量化指標。
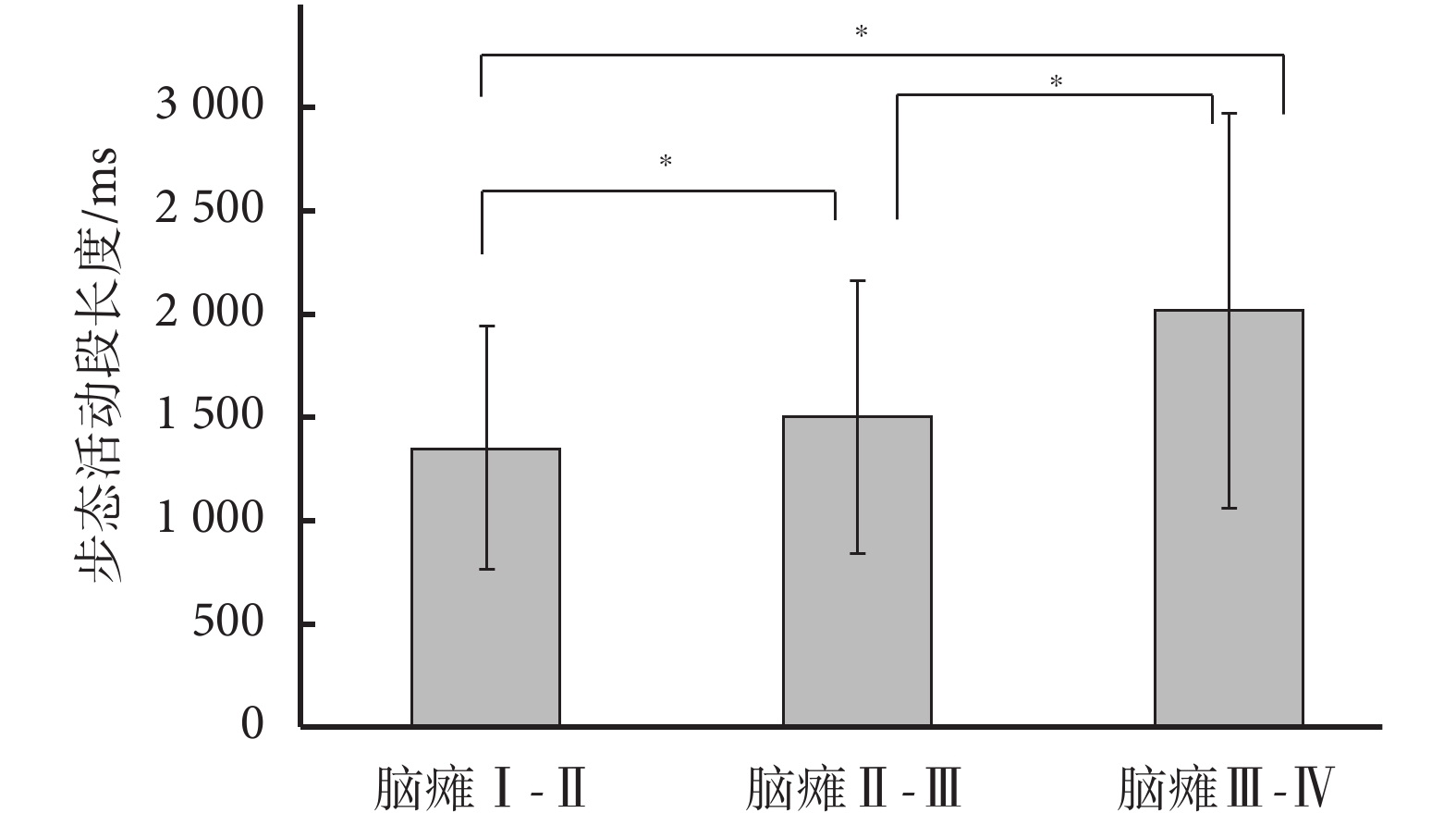圖6
三類不同程度腦癱患者步態活動段長度的均值與方差
*
*
4 結論
本文采用 IP 算法、SampEN 算法和 SNEO 算法三種方法對 sEMG 信號運動周期的定位問題進行了比較研究，在此基礎上，選擇性能優越的 SNEO 算法進一步對腦癱患兒 sEMG 信號步態活動段的實時檢測和定標進行了探討。
研究結果表明，SNEO 算法對 sEMG 信號步態活動段的劃分是具有定位準確、抗噪性強和運算速度快的優點，可用于對腦癱患兒 sEMG 信號步態活動段的檢測和標定。對小兒腦癱 I～II，II～III 和 III-IV 級三個級別腦癱患兒的步態 sEMG 信號初步研究表明，患兒的腦癱程度與步態活動段平均長度相關，且差異具有統計學意義，因此步態活動段平均長度可以作為一種評估腦癱程度的輔助量化指標。
引言
小兒腦性癱瘓（cerebral-palsy，CP）簡稱腦癱，是指從胎兒期到嬰兒期，由于各種致病因素所致的非進行性腦損傷或腦發育異常所導致的中樞性運動障礙[1]，典型的腦性癱瘓多具有運動發育落后、姿勢異常、中樞性運動障礙等體征。
近三十年來，隨著產科技術、圍產醫學和新生兒醫學的發展，死胎發生率、新生兒死亡率均有明顯下降，但腦癱發病率卻不減反增。根據國內外報道，腦癱的發病率在 1.5‰～5‰，發達國家的發病率較高[2-3]。雖然小兒腦癱患者的腦損傷是非進行性的，但如果沒有得到適當的康復治療與訓練，患兒生活難以自理，甚至會引發包括心理障礙在內的一系列繼發障礙。步態康復訓練是腦癱康復中運動障礙康復的重要環節，步行能力是生活自立的基礎。步行者在步行時，雙腿交替邁動顯示出明顯的周期性，借助人體步行運動的生理學特點，前人許多研究工作涉及采用不同傳感器對步行時的運動/停止狀態進行檢測和記錄，本文采用的步態表面肌電信號（surface electromyography，sEMG）來自左右雙側的腓腸肌，從某一條腿獲取的 sEMG 信號來看，其信號變化周期為一個跨步周期，我們將每個跨步周期定義為一個步態活動段。看似簡單的步態活動段其實是神經系統平衡中樞、運動中樞和眾多肌肉相互配合、協同控制的結果。因此研究步態活動段對于揭示神經肌肉控制機理，對腦癱康復中的步態訓練具有重要的指導意義。對步態活動段進行準確的定位，獲取步態活動段的時域位置信息，可以進一步實現對患者步態、步頻、步幅的精確分析，對于小兒腦癱患者康復的評估具有重要的現實意義[4]。
sEMG 是由運動單元動作電位（motor unit action potential，MUAP）序列在檢測電極處的時空疊加形成的信號[5]，能夠反映運動神經元的活動情況。從受試者小腿腓腸肌采集到的 sEMG 信號可以充分并客觀地反映在步行運動中肌肉的力度變化以及邁步頻率等重要的步態特征，由此可以在一定程度上對受試者的行為模式和身體狀況進行評測。但是目前對步態檢測的研究常限于健康受試者運動狀態的研究，如步行者航位推算、導航和運動數據評估等方面，而對腦癱患兒的行為模式進行探索，并通過試驗結果對腦癱患兒的功能性運動障礙程度以及康復情況進行評測則鮮有報道。因此本文采用一種基于 sEMG 的無創且方便的檢測方法對步態活動段進行分割，并對小兒腦癱患者的步態活動段特征進行進一步的探討。
為了對小兒腦癱患者的運動狀態進行客觀評估，針對他們的步態活動段的精確定位，本文采用了三種常用于肌電信號運動周期檢查的方法，即綜合輪廓算法（integrated profile，IP）、基于樣本熵（sample-entropy，SampEN）的活動段檢測算法和基于非線性能量算子（smoothed nonlinear energy operator，SNEO）的峰值檢測算法，分別對仿真信號的步態活動段進行檢測，并比較三種方法的處理效果，選擇其中針對 sEMG 信號步態活動段檢測的最優算法，并將這種算法應用于真實腦癱患兒的 sEMG 信號的步態分析，以提高定位精度，同時把步態活動段定位與小兒腦癱患者的臨床評估相結合，完成對小兒腦癱復雜進程的初步定量分析。
1 試驗方法
1.1 試驗對象
本研究中，由安徽醫科大學第一附屬醫院小兒神經康復科協助招募的 18 名（8 位男性；10 位女性）不同臨床嚴重程度的小兒腦癱患者自愿參加試驗。對于腦癱患兒病情程度的判斷，臨床醫生通常采用國際通行的針對腦癱患兒的標準化粗大運動功能分級系統 （gross motor function classification system，GMFCS），用分級評定的方法來評估痙攣型腦癱患兒粗大運動功能級別[6-7]。其中 GMFCS 分級評定系統將腦癱患兒分為 I～V 五個級別，I 級為最佳，V 級為最差。在本研究中，小兒腦癱患者按其主管醫師的臨床診斷分為I～Ⅱ、Ⅱ～Ⅲ與Ⅲ～Ⅳ三個級別[8]。18 名試驗對象中每種級別的患兒各 6 例。根據研究的需要，選取的試驗對象包含以下篩選條件：① 被診斷為先天性小兒腦癱的患者，即出生時便患有腦癱疾病；② 具有明顯的步態異常癥狀，但能夠獨立或在他人輔助下完成邁步行走動作；③ 無其他可能導致下肢運動功能障礙的疾病史；④ 在治療過程中未接受過任何類型的矯正手術。所有受試者在參加試驗前，由其監護人代簽知情同意書，本研究的所有試驗方案遵循赫爾辛基宣言并受中國科學技術大學倫理審查委員會（Ethics Committee of University of Science and Technology of China for Human Subjects）的審批和監管。
1.2 試驗方案
人體的步行運動主要受到腿部肌肉的控制，小腿后側的腓腸肌是一種踝關節伸肌，提供了體重支持與行走的主要動力，而與腓腸肌具有協同關系的脛骨前肌是踝關節屈肌，與腓腸肌成對作用完成行走的動作，因此從腓腸肌-脛骨前肌這一對肌肉采集的 sEMG 信號包含了步行運動過程中檢測步態的主要信息。據此本文試驗設計了腦癱患兒采集 sEMG 的電極放置位置，如圖 1 所示。
圖1
腦癱患者 sEMG 信號采集方案
Figure1.
sEMG acquisition scheme for cerebral-palsy patients
為了提高采集信號的質量，試驗前首先刮去體表毛發，用專用砂紙打磨皮膚表面，再用酒精擦洗殘余物，以去除皮膚角質層，并在皮膚表面測量區域涂以少量的導電膏，以降低電極和檢測表面的接觸電阻。電極與皮膚的接觸電阻是影響信號質量的關鍵因素之一，本文采集設備及其配套軟件具有分別檢查各個電極通道與皮膚接觸電阻的功能。然后把 sEMG 采集電極通過有孔（使電極與皮膚接觸）薄雙面膠貼附在測量區域皮膚表面，位置盡量放在肌肉的運動點和肌腱之間，初始朝向選擇陣列平行或垂直于肌纖維方向，同時在腓腸肌與脛骨前肌的合適位置放置參考電極。
進行試驗時，由家長和主治醫生協助患兒完成指定動作。試驗動作包括站立和環繞康復室的行走與轉彎，要求腦癱患兒以合適的速度環繞康復室行走 2～3 min，并完成左右雙側至少 30 個邁步動作，同時利用采集設備記錄 sEMG 信號。
采集設備采用 DELSYS Myomonitor 4 表面肌電與二軸加速度分析系統，采樣率為 1 000 Hz，采用 2～500 Hz 帶通濾波器以減少采集時的背景噪聲。
2 數據處理方法與驗證
基于 sEMG 對運動周期定位的主要研究方法有以下幾種：① 利用信號包絡的方法，如 IP 算法；② 基于信息論的高斯性刻畫方法，如 SampEN；③ 基于信號幅值與能量的 SNEO 方法，這三種算法的詳細介紹如下：
2.1 IP 算法
IP 算法由 Santello 等[9]于 1998 年提出。在此算法中，信號的線性包絡由 A（xi）綜合表示，它的定義為：
| $A\left( {{x_i}} \right) = \mathop \sum \limits_{j = 1}^i f\left( {{x_j}} \right)/\mathop \sum \limits_{p = 1}^N f\left( {{x_p}} \right)$ |
其中 i∈（0，N] 為采樣信號的樣本點個數，xi 為采樣信號在采樣點 i 處的幅值，而函數 f（x）定義為：
| $f\left( {{x_i}} \right) = \left| {{x_i}} \right|,\;i \in \left( {0,N} \right]$ |
信號的參考基線為：
| $T \left( {{x_i}} \right) = i/N$ |
采樣信號的綜合輪廓的代價表達如式（4）所示：
| $G \left( {{x_i}} \right) = T \left( {{x_i}} \right) - A \left( {{x_i}} \right),\;i \in \left( {0,N} \right]$ |
采樣信號的運動周期起始點與終止點的定義為 [Min（G（xi）），Max（G（xi））]，對于本文采集的步態 sEMG 信號即是活動段的開始點和結束點。
2.2 SampEN 檢測方法
SampEN 方法是一種利用近似熵方法改進而發展起來的信號復雜性測度方法，最早由 Richman 等[10]提出。一組信號序列越復雜，其 SampEN 值越大，若序列的自我相似性越高，則 SampEN 值越小。SampEN 相比近似熵精度更好，與已知信號的隨機部分有更加緊密的一致性，因此更加適用于分析生物醫學信號。針對 sEMG 計算方法如下：
（1）采用疊加窗技術將 sEMG 信號分為連續的信號幀，每幀的長度為 128 個采樣點，幀間重疊為 50%，即 64 個采樣點。
（2）給定 sEMG 的信號 s（t）， ，N 為步驟（1）中信號幀的長度 128 點；
（3）按照信號序列組成一組 m（m<N）維延時向量，該組向量共有 N–m 個，如式（5）所示：
| ${X_m}\left( p \right) \!=\! \left[ {s\left( {p \!+\! k} \right)} \right]_{k = 0}^{m - 1},\;p \!=\! 1,{\rm{ }}2,{\rm{ }} \cdot \! \cdot \cdot ,N \!-\! m \!+\! 1$ |
（4）定義兩個向量間的距離 d 為兩者對應元素中差值最大的一個。
| $d\left[ {{{\rm{X}}_m}\left( p \right),{X_m}\left( q \right)} \right] = \mathop {\max }\limits_{0 \leqslant k \leqslant m} \left\{ {\left| {s\left( {p + k} \right) - s\left( {q + k} \right)} \right|} \right\},\;1 \leqslant p,q \leqslant N - m$ |
（5）選定閾值 r，對每個 1≤p≤N–m 的值，統計 d[Xm（p），Xm（q）] 小于 r 的數目（稱為模版匹配數）Nm（p），并計算該數目與距離總數 N–m–1 比值，即計算如下函數：
| $B_r^m\left( p \right) = {N^m}\left( p \right)/\left( {N - m - 1} \right)$ |
其中 1≤q≤N–m，且 q≠p。對其所有的 p 值取平均，可得：
| ${B^m}\left( r \right) = \frac{1}{{N - m}}\mathop \sum \limits_{p = 1}^{N - m + 1} B_r^m\left( p \right)$ |
（6）增加維數 m 到 m+1，重復步驟（3）～（4），并統計 d[Xm（p），Xm（q）] 小于 r 的數目 Nm+1（p），同樣有：
| $A_r^m\left( p \right) = {N^{m + 1}}\left( p \right)/\left( {N - m - 1} \right)$ |
其中 1≤q≤N–m，且 q≠p。對其所有的 p 值取平均，可得
| ${A^m}\left( r \right) = \frac{1}{{N - m}}\mathop \sum \limits_{p = 1}^{N - m + 1} A_r^m\left( p \right)$ |
（7）最后得到樣本熵定義為式：
| ${\rm{SampEN}}\left[ {s\left( t \right),m,r} \right] = - {\rm{ln}}\left( {{A^m}\left( r \right)/{B^m}\left( r \right)} \right)$ |
對第 i 幀信號 si（t）， 計算 SampEN 特征序列如下：
| ${S_{{\rm{SE}}}}\left( i \right) = {\rm{SampEN}}\left[ {{s_i}\left( t \right),m,r} \right]$ |
在已有的研究報道中，一般將 r 取為信號標準差的 20%～25%。針對本實驗室采集的數據，我們按照經驗閾值取 m=2，r=0.015。在進行 SampEN 計算后，用閾值法確定活動段的起始點與終止點。
2.3 SNEO 算法
非線性能量算子（nonlinear energy operator，NEO）是在研究非線性語音建模時引入的一個數學算子，其輸出分量可以看作是信號經過高通濾波后的瞬時能量成分。
對于離散信號 x（n），NEO 的表達式為：
| $\psi \left[ {x\left( n \right)} \right] = {x^2}\left( n \right) - x\left( {n + 1} \right)x\left( {n - 1} \right)$ |
為了提升 NEO 處理非平穩信號的能力，根據已有文獻[11-12]，在 NEO 算法中附加一個窗函數，這種算法即為 SNEO 算法：
| ${\psi _s}\left[ {x\left( n \right)} \right] = \psi \left[ {x\left( n \right)} \right]*{w_s}\left( n \right)$ |
其中 ws（n）為一個窗函數，而*代表卷積過程。
根據當前已有的肌電信號相關研究表明，漢明窗在肌電信號處理中具有良好的效果，因此本文在具體實現過程中采用該窗函數對 NEO 進行平滑[5, 13]。同樣，與前述 SampEN 的起始點、終止點確定方法相似，采用簡單的閾值算法標定運動周期的起始點與終止點。
2.4 算法有效性的驗證
為了檢驗算法的有效性，本文利用健康人的真實標準無噪聲 sEMG 加入不同信噪比（signal-to-noise ratio, SNR）的混合噪聲構建半合成信號。這些半合成信號具有明確的活動段起始點與終止點，因此可以較為準確地評估算法的精度和有效性。半合成信號中的 sEMG 采用健康兒童的步行 sEMG 信號，由具有經驗的研究者手動標定活動段，并采用基于三級濾波器的 sEMG 降噪處理方法進行預處理，最后獲得標準無噪聲的 sEMG 信號[13]。
此外，為了準確地仿真腦癱狀況下的 sEMG 信號，本文加入并混合了腦癱患者 sEMG 信號中常見的三種干擾噪聲，以驗證三種算法在噪聲干擾下的效能。這三種噪聲為：背景噪聲、其他肌肉由于痙攣產生的 MUAP 干擾以及工頻干擾。
2.5 統計分析
統計分析采用 SPSS（SPSS，Inc.，2007，Chicago，IL）工具進行分析。在仿真實驗中，不同算法組與組之間的差異性采用雙因素方差分析（Two-way ANOVA），而在真實信號試驗中，采用單因素方差分析（One-way ANOVA）研究腦癱患兒臨床嚴重程度與 sEMG 信號步態活動段長度的關系。當 P<0.05 時，結果差異具有統計學意義。
3 結果與討論
3.1 半合成信號實驗
半合成信號由一組（共 10 個發放序列）同時持續發放的真實 sEMG 信號段構成，分三次分別加入 SNR 為 0.6、2、5 的合成混合噪聲信號。合成噪聲由背景白噪聲、工頻干擾產生的 50 Hz 及其倍頻噪聲以及移動偽跡所產生的周期性尖峰噪聲構成。sEMG 采用前述的 IP 算法、SampEN 算法和 SNEO 算法分別對無噪聲與加入不同 SNR 噪聲的三組半合成 sEMG 信號進行了處理，相應實驗結果的一個示例如圖 2 所示。
圖2
信號仿真及三種活動段分割算法的實驗結果
Figure2.
Signal simulation and the results of three different segmentation algorithms in simulation signals
如圖 2 所示，無噪聲信號部分的最上圖為無噪聲的半合成 sEMG 信號的一個周期活動段，其余三圖分別是三種算法的實驗結果。由圖可見，IP 算法在起始點和終止點都有一定程度的偏移，SampEN 算法定位的起始點略微先于 sEMG 信號出現，而定位的終止點又比實際周期延遲出現，相比之下 SNEO 算法定位的起始點與終止點與 sEMG 實際發放位置比較接近。添加噪聲部分的最上圖為具有尖峰偽跡的半合成 sEMG 信號（SNR：0.6 dB）的一個周期活動段波形，三種算法的實驗結果與無噪信號試驗結果類似，同樣 SNEO 算法的定位準確，并且抗噪聲干擾能力也較好，因此這種方法適于步行中 sEMG 信號活動段的檢測和定位。
為進一步驗證上述結果，在仿真實驗中，將三組（共 10 個發放序列）添加噪聲的半合成信號采用 IP 算法、SampEN 算法及 SNEO 算法分別獲得的步態活動段長度和運行時間進行比較，并采用雙因素方差分析進行統計，結果如表 1 所示。
表1
半合成 sEMG 信號中三種算法的定位精度及比較
Table1.
Comparison of accuracy and computation speed of three algorithms in a semi-synthetic sEMG signal
如表 1 所示，三種算法在分割活動段長度上的差異不具有統計學意義（P>0.05）。然而結合圖 1 可以看出，IP 算法在實際活動段的劃分中，在活動段起始點的標定中有一定的偏移，且起始點遲滯和終止點提前導致實際估計長度的均值（1.37）要小于實際仿真信號長度（1.47），而 SNEO 算法與 SampEN 算法所獲得的活動段平均長度（SNEO：1.47；SampEN：1.50）與實際仿真信號長度更加接近。在計算時間上，SNEO 算法與 IP 算法顯然要大大優于 SampEN 算法，這兩種算法在實際應用中能夠用于腦癱患兒肌電信號的實時分析。而 SampEN 方法，由于運行時間較長，僅能應用于離線分析，也不適用于數據量比較大的步態活動段分析。根據以上分析，本文選擇了活動段起始點偏移較小且運行時間較短的 SNEO 算法應用于腦癱患兒的步行 sEMG 信號活動段劃分。
3.2 腦癱患兒真實信號試驗
對于真實試驗獲得的 sEMG 信號首先進行去噪預處理，采用一種基于三級濾波器的 sEMG 信號降噪處理技術[13]，即采用頻譜插值法去除工頻干擾，采用形態學運算去除基線漂移，采用經驗模態分解去除白噪聲。然后采用前述的 SNEO 算法對去噪后的步態活動段信號進行檢測和分割，小兒腦癱Ⅰ～Ⅱ，Ⅱ～Ⅲ和Ⅲ-Ⅳ級三種患兒的典型試驗結果如圖 3～圖 5 所示。
如圖 3 所示為小兒腦癱Ⅲ～Ⅳ級患兒步態活動段檢測結果，其中上部分為 sEMG 信號，下部分為經 SNEO 算法處理獲得的結果，虛線表示該結果對應的 sEMG 信號活動段分割情況。從圖 3 中可以看出，小兒腦癱Ⅲ～Ⅳ級患兒的步態運動周期是不均勻的，即步態活動段的周期性較差。患兒原始步態 sEMG 信號中引入了較多的噪聲，這是由于該級患兒的行走十分困難、步態很不穩定引起的。另外，該級患兒處于肌強直或者肌萎縮病態，其 sEMG 信號中也呈現出較粗的基線。如圖 3 所示，經 SNEO 算法處理后，顯示出了較好的抗噪聲能力，通過選擇合適的閾值就能夠比較精確地對步態活動段進行定位和劃分。
圖3
Ⅲ～
Ⅳ級腦癱患兒步態運動周期劃分結果
Figure3.
Walking sEMG segment calibration in cerebral-palsy III～IV subjects
如圖 4 所示為小兒腦癱Ⅱ～Ⅲ級患兒的步態活動段檢測結果，與前述小兒腦癱Ⅲ～Ⅳ級的患兒相比，該級患兒的步態運動周期較為均勻有序，周期性比較明顯，但是由于這個級別的患兒運動障礙仍比較明顯，sEMG 的發放并不穩定，步態活動段也顯示出長短不一的不均勻狀態。
圖4
Ⅱ～
Ⅲ級腦癱患兒步態運動周期劃分結果
Figure4.
Walking sEMG segment calibration in cerebral-palsy II～III subjects
如圖 5 所示為小兒腦癱Ⅰ～Ⅱ期患兒的步態活動段檢測結果，這種情況下的患兒無運動障礙或者運動障礙較輕，sEMG 顯示比較穩定，已經接近于正常人的表面肌電信號發放，但是 sEMG 的基線仍較粗，說明患兒還存在著一定的肌肉緊張現象。
圖5
Ⅰ～
Ⅱ級腦癱患兒步態運動周期劃分結果
Figure5.
Walking sEMG segment calibration in cerebral-palsy I～II subjects
在對三類不同程度腦癱患兒的 sEMG 信號采用 SNEO 算法進行步態活動段劃分的基礎上，我們進一步對已有的數據進行統計分析，如圖 6 所示為三類不同程度腦癱患兒步態活動段持續時間的均值與方差。小兒腦癱Ⅰ～Ⅱ型的活動段持續時間最短，并且也具有較小的標準差，這說明小兒腦癱Ⅰ～Ⅱ型患者行動具有較好的周期性，而且動作比較穩定。而小兒腦癱Ⅱ～Ⅲ型患者及小兒腦癱Ⅲ-Ⅳ型患者的步態活動段長度呈上升趨勢，同時標準差也不斷變大，說明隨著腦癱嚴重程度的增大，患兒行動更加困難，站立和行走時間不斷增大。如圖 6 所示，采用單因素方差分析對三類不同程度腦癱患兒的步態活動段長度數據進行處理（腦癱Ⅰ～Ⅱ級：1 364±623；腦癱Ⅱ～Ⅲ級：1 508±732；腦癱Ⅲ-Ⅳ級：2 033±975），在三組患兒數據的兩兩對比后均得到 P<0.05 的結果。試驗結果說明這三類患兒的步態平均活動段長度差異具有統計學意義，因此步態活動段長度可以作為一種輔助評估腦癱程度的量化指標。
圖6
三類不同程度腦癱患者步態活動段長度的均值與方差
*
*
4 結論
本文采用 IP 算法、SampEN 算法和 SNEO 算法三種方法對 sEMG 信號運動周期的定位問題進行了比較研究，在此基礎上，選擇性能優越的 SNEO 算法進一步對腦癱患兒 sEMG 信號步態活動段的實時檢測和定標進行了探討。
研究結果表明，SNEO 算法對 sEMG 信號步態活動段的劃分是具有定位準確、抗噪性強和運算速度快的優點，可用于對腦癱患兒 sEMG 信號步態活動段的檢測和標定。對小兒腦癱 I～II，II～III 和 III-IV 級三個級別腦癱患兒的步態 sEMG 信號初步研究表明，患兒的腦癱程度與步態活動段平均長度相關，且差異具有統計學意義，因此步態活動段平均長度可以作為一種評估腦癱程度的輔助量化指標。
