為解決用傳統粒子群算法估計磁共振（MR）圖像偏移場會陷入局部最優的問題，本文提出了一種自適應權重粒子群算法估計MR圖像的偏移場。針對傳統粒子群算法的缺陷，設計一個衡量早熟收斂程度的指標，根據此指標來自適應地調整慣性權重，確保粒子群有效地進行全局尋優，避免陷入局部最優。本文利用Legendre多項式來擬合偏移場，多項式參數利用本文提出的算法進行尋優，最后對MR圖像的偏移場進行估計和矯正。將本文算法與改進的熵最小方法進行對比分析，本文矯正后圖像熵值更小，對偏移場估計更準確，將矯正后的圖像進行分割，分割精度提高將近10%。研究結果初步說明，本算法可應用于MR圖像偏移場的矯正。
引用本文： 王昌, 秦鑫, 劉艷, 張文超. 一種自適應慣性權重粒子群算法在磁共振圖像偏移場矯正中的應用. 生物醫學工程學雜志, 2016, 33(3): 564-569. doi: 10.7507/1001-5515.20160094 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
磁共振(magnetic resonance,MR)成像具有非介入性、非損傷以及對軟組織分辨率高的特性，目前在臨床醫學中得到廣泛應用。它已成為腦功能、病理和解剖研究的主要檢測手段，以及腦疾病(如阿爾茨海默癥、多發性硬化癥、精神分裂癥等)分析的重要工具，而對腦組織(灰質、白質)的精確分割和定量分析是研究的基礎。然而，MR圖像經常受射頻(radio-frequency,RF)線圈、MR設備、腦組織容積效應的影響[1]，導致圖像的統計特性分布趨于平均，人體相同組織的灰度不均一，不同組織之間灰度產生交疊，圖像的細節信息被嚴重模糊。
偏移場為一個緩慢變化、平滑的乘性場，帶有偏移場的MR圖像可近似看成原始圖像與偏移場的乘積，附加噪聲的影響(可忽略)。許多學者對偏移場模型進行了分析。將原始圖像與偏移場分離，對偏移場進行估計以矯正帶有偏移場的MR圖像，成為當前主要的研究方法。偏移場有基于多項式的、基于離散余弦變換的、基于薄板樣條的等諸多模型，利用Legendre多項式基函數擬合偏移場是當前的主流模型[2]。Likar等[3]將信息熵的概念引入偏移場的矯正，提出基于最小熵的方法，但沒能解決參數的尋優問題。傳統的遺傳算法和標準粒子群算法在偏移場參數的尋優過程中，容易陷入局部最優，導致無法得到全局最優的參數，最終無法對偏移場進行準確的估計[4]。王利等[4-5]將傳統的遺傳算法進行改進，得到了較優的偏移場，提高了分割的精度。劉軍偉等[6-7]提出了改進的熵最小化的方法，首先利用基于空間連續性的自適應模糊聚類算法來對圖像進行分割，對聚類結果交互式選擇像素點，用于粗略估計偏移場的參數，最后利用傳統的粒子群算法進行尋優，但該算法需采用改進的聚類分割算法作預處理，標準粒子群算法易陷入局部最優，其估計的偏移場不能保證是全局最優。當前粒子群算法發展迅速，提出了許多改進的模型[8-14]。董平平等[9]提出了一種自適應慣性權重粒子群算法，定義粒子個體尋優能力，避免了陷入局部最優。韓江洪等[10]、邢萬波等[11]提出了改進的自適應鄰域粒子群優化算法來避免粒子群陷入局部最優的問題。
本文將自適應混沌粒子群算法應用于MR圖像偏移場的矯正，省略了基于聚類分割的預處理步驟，通過設置自適應的粒子群的慣性權重，有效解決了參數尋優過程中容易陷入局部最優的問題，可應用于MR圖像偏移場的矯正。
1 算法
1.1 預處理
腦部MR圖像中，非腦組織(背景)占據圖像的一部分，背景部分不受偏移場影響，但其灰度值近似為零，對偏移場分析影響較大，故需將腦組織提取出來。本文利用OSTU大津閾值法計算出閾值，利用閾值進行二值化，可以有效地將背景區域的像素值置零，設計腦部的模板，消除背景對偏移場的影響。
1.2 偏移場與信息熵
MR圖像的灰度不均勻效應是在原始圖像中加入一個空間變化的光滑乘性場，其數學模型如式(1) 所示
| $I=bX+N$ |
其中，b為偏移場，X為原始圖像，N為噪聲(可忽略)。
本文利用Legendre多項式來擬合偏移場，其基函數如式(2) 所示
| $b\left( x,y \right)=\sum\limits_{i=0}^{k}{\sum\limits_{j=0}^{k-i}{{{p}_{ij}}}{{P}_{i}}\left( x \right){{P}_{j}}\left( y \right)}$ |
其中，b(x,y)為擬合的偏移場，Pi(x)、Pj(y)為Legendre多項式的基函數，pij為多項式基函數的參數，k為多項式的次數，圖像坐標值定義在[-1,1]。多項式次數越高，參數越多，偏移場擬合越準確，但計算復雜度越高。本文在偏移場估計中，選擇k=4，則需要估計的參數為(k+1)*(k+2)/2=15。
Likar等將信息熵的概念引入偏移場的估計后研究證實，信息熵越大，事件發生的不確定性越大，從隨機變量中獲得的信息量越大；信息熵越小，圖像的偏移場越弱。圖像信息熵公式如式(3) 所示
| $H=-\sum\limits_{x\in \left\{ graylevel \right\}}{pdf\left( x \right)}\log \left( pdf\left( x \right) \right)$ |
其中pdf為概率密度函數，x為通過矯正偏移場所得到的圖像，矯正后的圖像像素值為浮點型，需對其作取整運算。利用信息熵的公式計算矯正后圖像的熵值，在此僅計算模板內的像素的信息熵。
1.3 傳統的粒子群算法
Kennedy等[8]在1995年提出的粒子群優化(particle swarm optimization,PSO)算法是一種基于群體智能的進化優化算法。在PSO算法中，每個粒子對應一個待優化問題的潛在解。粒子的速度和位置分別用Vi=(vi1,vi2,…,vin)、Xi=(xi1,xi2,…,xin)表示，其中n為粒子的維數(多項式基函數的參數個數)。 Vi取決于粒子的方向和速度，Xi取決于初始位置和更新的速度。粒子的適應度fi 由位置決定，其為衡量粒子優劣程度的指標。粒子Pi的當前最優解用pbesti表示，當前整個粒子群的最優解用gbest表示。
對于標準的粒子群算法，粒子Pi更新自己的速度和位置的公式如下
| $\begin{align} & v_{i}^{k+1}=w\times v_{i}^{k}+{{c}_{1}}\times ran{{d}_{1}}\times \left( pbes{{t}_{i}}-x_{i}^{k} \right)+ \\ & {{c}_{2}}\times ran{{d}_{2}}\times \left( gbest-x_{i}^{k} \right) \\ \end{align}$ |
| $x_{i}^{k+1}=x_{i}^{k}+v_{i}^{k+1}$ |
其中，c1、c2為學習因子，通常取值c1=c2=2；rand1、rand2是0~1之間的隨機數。慣性權重參數w對算法影響很大，較大的w值有利于跳出局部最優，進行全局尋優；較小的w有利于局部尋優，加快算法的收斂。傳統的PSO容易陷入局部最優解，無法收斂到全局最優。
1.4 自適應的混沌粒子群算法
PSO算法中，粒子群的多樣性是算法能收斂到全局最優的前提條件，在求全局最優的過程中，粒子的多樣性會逐漸喪失，表現為強烈的趨同性，算法雖快速收斂，但易陷入局部最優解，發生早熟收斂的問題。然而，降低粒子群的趨同性會影響算法的收斂速度。故此根據粒子群早熟收斂的程度來自適應的調整慣性權重w。
對于早熟收斂程度利用指標[10]來進行評價，采用的定義如下：對于粒子群的種群大小為N，第k次迭代過程中粒子Pi的適應度為fi，最優粒子群的適應度為fm，粒子群的平均適應度favg為當前所有粒子適應度的平均值。對優于平均適應度的粒子再求平均favg，則定義的早熟收斂程度的指標為Δ=fm-f′avg，Δ越小說明粒子群趨于早熟收斂。
根據個體適應度不同，采用不同的調整策略，使粒子始終保持慣性權重的多樣性。慣性權重較小的粒子用來進行局部尋優，較快收斂；慣性權重較大的粒子跳出局部最優在全局進行尋優。具體的自適應策略如下所示：
(a) fi優于f′avg:表明該粒子是較為優秀的粒子，賦予較小的慣性權重，加速其全局最優收斂，其自適應策略如下所示
| $w={{w}_{\max }}-\left( {{w}_{\max }}-{{w}_{\min }} \right)\times \left| \frac{{{f}_{i}}-f_{avg}^{'}}{\Delta } \right|$ |
(b) fi優于favg但次于f′avg:表明該粒子一般，不改變其慣性權重，其慣性權重定義為常數。
(c) fi次于favg:表明該粒子較差，對其慣性權重的調整采用以下策略
| $w=1.5-\frac{1}{1+{{k}_{1}}\times \exp \left( -{{k}_{2}}\times \Delta \right)}$ |
1.5 自適應的混沌粒子群算法描述
偏移場初始化：假設k=4，每個粒子需15個參數,在[－5，5]范圍內產生隨機數,得到一組參數后計算偏移場。一般情況下，所有點的偏移場均大于0.3；如果某點的偏移場小于0.3，則舍棄這組參數，重新選取,直到生成合適的偏移場。
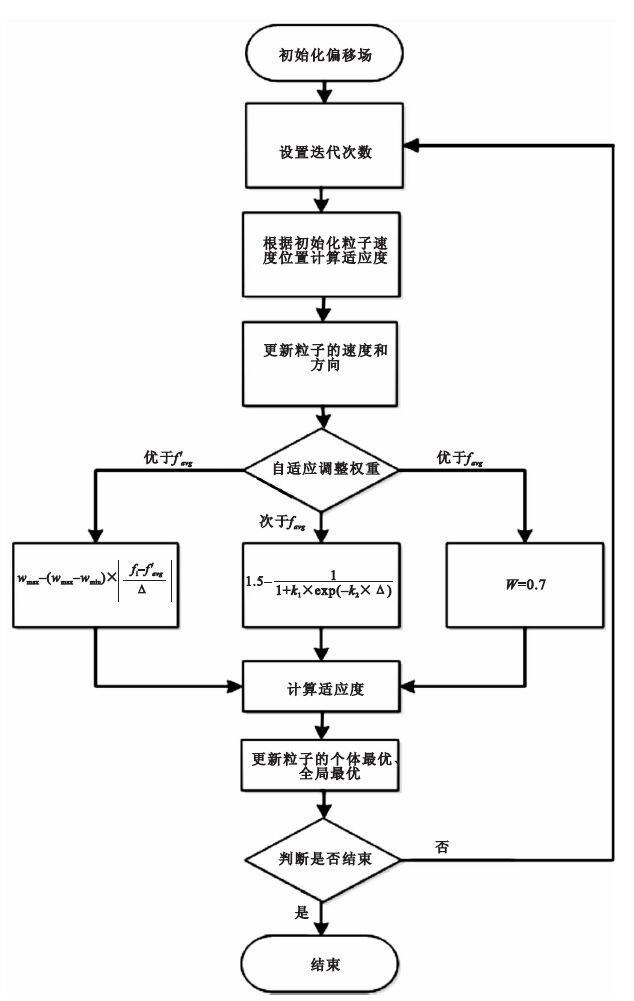
粒子適應度的計算：利用觀察到的圖像除以偏移場得到浮點型，對其取整，利用公式(3) 計算圖像的信息熵，對于偏移場值小于0.3的其信息熵定義為較大的常數。算法的流程圖如圖 1所示。
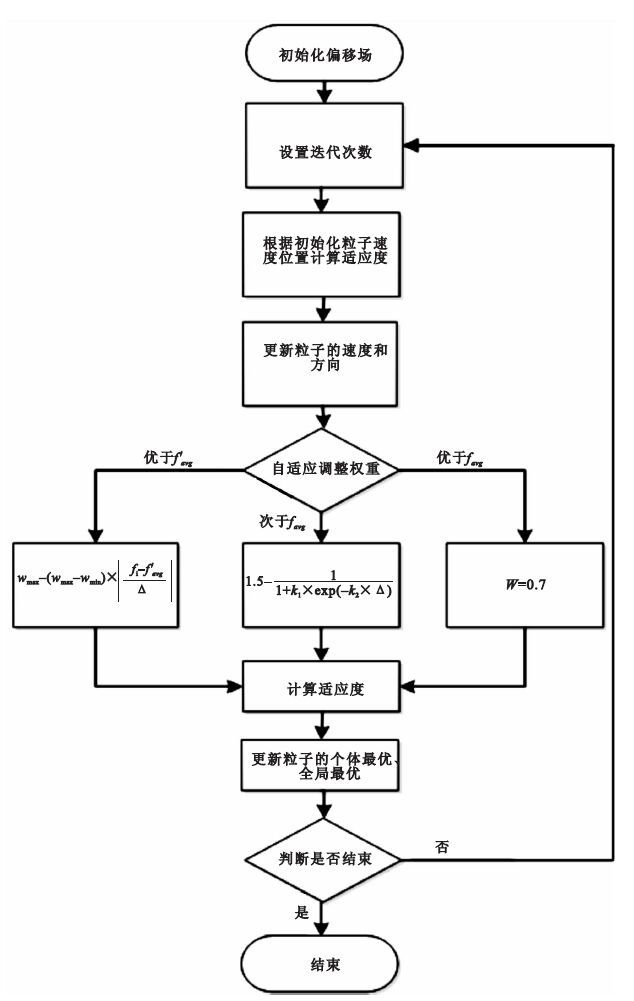圖1
算法流程圖
Figure1.
Algorithm flow chat
2 實驗結果與分析
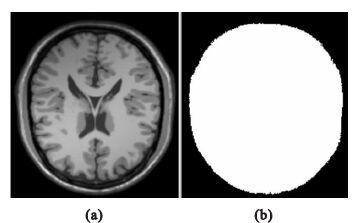
本文的數據采用McGill大學Montreal神經學研究所大腦成像中心的Brain Web仿真腦MR圖像庫，選擇偏移場強度為100%、無噪聲的仿真腦，圖像大小為217×181×181，取第90幅圖像為例。為減少背景對偏移場估計的影響，計算腦模板，其結果如圖 2所示。
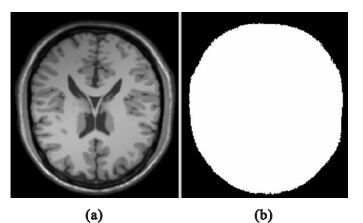圖2
預處理結果
(a)原始圖像；(b)腦模板
Figure2. Results of preprocessing(a) source image; (b) brain template
圖 2(a)為帶有100%偏移場的原始圖像，圖 2(b)為利用OSTU大津閾值法計算閾值，提取腦模板的圖像。
本文算法的參數設置：粒子群的種群大小20，每個粒子維數15，搜索空間[-5~5]，迭代次數設置為200次。
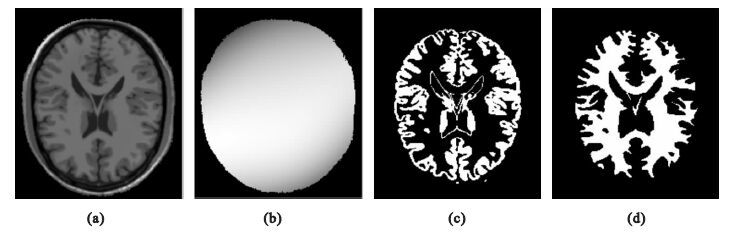
利用本文提出的自適應慣性權重粒子群算法估計MR圖像的偏移場，圖 3(a)是偏移場矯正之后的圖像，圖 3(b)是估計的偏移場。對矯正后的圖像進行聚類分割，分割出腦灰質、腦白質，并利用二值圖像表示，圖 3(c)是腦灰質，圖 3(d)是腦白質。
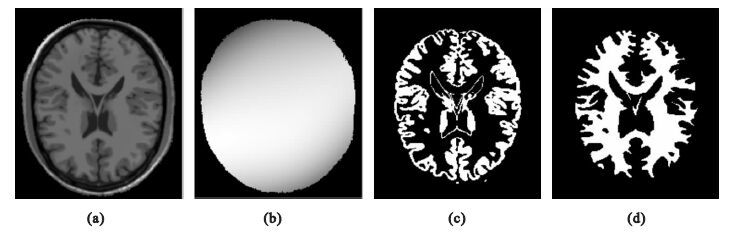圖3
本文算法結果
(a)矯正后圖像;(b)偏移場;(c)灰質;(d)白質
Figure3. Results of the present algorithm(a) corrected image; (b) bias field; (c) gray matter; (d) white matter
2.1 信息熵的比較
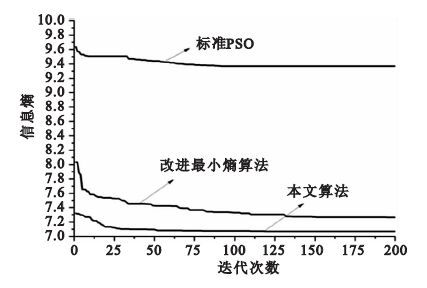
本文采用Brain Web仿真腦MR圖像庫中相同層的圖像，計算腦模板中圖像的信息熵，無偏移場的MR 圖像信息熵為6.816 3，帶100%偏移場的MR圖像信息熵為7.852 1。 將本文提出的算法與傳統PSO算法和劉軍偉提出的改進熵最小化算法進行對比，信息熵的變化曲線如圖 4所示。
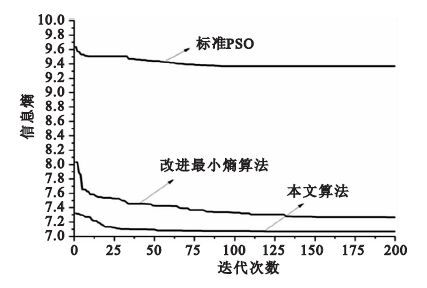圖4
不同算法信息熵變化曲線
Figure4.
Variation curves of information entropy with different algorithms
圖 4中的三條曲線是針對相同圖像利用傳統的PSO算法、改進熵最小化算法和本文算法來估計偏移場時，經偏移場矯正后的MR圖像信息熵隨迭代次數的變化曲線。用傳統PSO算法來估計偏移場，其矯正后的信息熵為9.335 0，在進化過程中陷入局部最優，無法得到全局最優解。改進熵最小化算法對偏移場進行了估計，矯正后的信息熵為7.447 2，降低了圖像的灰度不均勻性，減少了偏移場的影響。本文提出的算法對偏移場進行估計，矯正后的信息熵為7.063 2，信息熵是三種算法中最小的，與沒有偏移場影響時的信息熵最為接近，因此估計的偏移場最精確。
2.2 參數分析
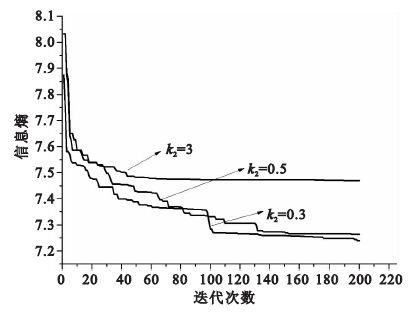
本文算法中參數k1、k2是慣性權重自適應的主要參數，對算法性能影響較大。k1主要用來控制w的上限，k1越大，w的上限越大，本文k1取1.5，使粒子的慣性權重w∈(0.5,1.1) 。 k2控制公式(7) 的自適應權重的大小。
圖 5中的三條曲線，分別代表參數k1設置為1.5，參數k2取3、0.5、0.3時，利用本文的慣性自適應權重粒子群算法來估計偏移場，矯正后信息熵隨迭代次數的變化曲線。經過實驗驗證，若k2偏大，雖收斂較快，但早期容易陷入局部最優；若k2過小則權重自適應的調節能力不足，到后期不能有效跳出局部最優。故本文中參數設置如下：k1=1.5，k2=0.5。
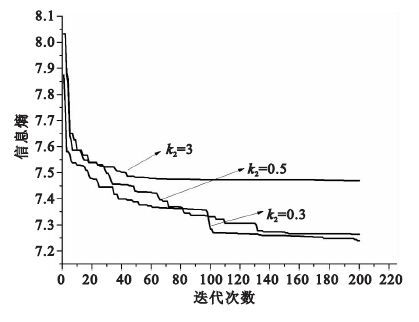圖5
參數對信息熵的影響
Figure5.
Influence of parameter k2 on information entropy
2.3 偏移場矯正后的分割精度比較
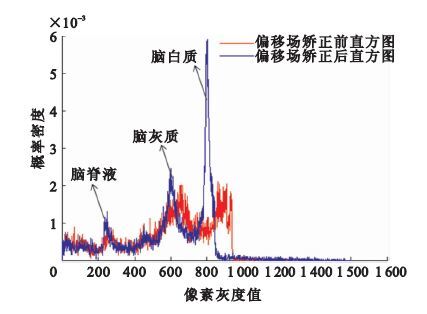
偏移場矯正前后的圖像的直方圖分析結果如圖 6所示。
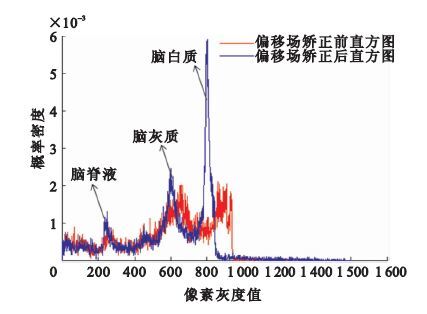圖6
本文算法矯正前后直方圖
Figure6.
Histogram before and after correction with the present algorithm
偏移場矯正后MR圖像的腦組織直方圖分布特性滿足三峰，分別代表腦灰質、腦白質、腦脊液。矯正后圖像均采用聚類進行分割，將本文的算法與改進熵最小化算法進行對比分析。利用Jaccard Similarity(JS)指標[見公式(8) ]判斷分割的精度，通過定量分析的方法來驗證利用本算法矯正偏移場之后分割精度的優越性。
| $J\left( {{S}_{1}},{{S}_{2}} \right)=\frac{{{S}_{1}}\cap {{S}_{2}}}{{{S}_{1}}\cap {{S}_{2}}}$ |
其中S1為經偏移場進行矯正后的MR圖像利用聚類分割的結果(腦灰質、腦白質)，S2為無偏移場影響的MR圖像利用聚類分割的結果。
從表 1可以看出，采用本文算法與改進熵最小化算法估計的偏移場經矯正后，用聚類進行分割，通過JS指標比較，本文算法比改進熵最小化算法分割的腦灰質、腦白質的分割精度提高約10%。
表1
不同偏移場矯正算法的分割精度對比
Table1.
Segmentation accuracy comparison between different bias field correction algorithms
3 結論
本文針對傳統粒子群算法在估計MR圖像偏移場時易陷入局部最優的問題，提出了一種自適應慣性權重粒子群算法來對偏移場的參數進行全局尋優，有效解決了由于粒子早熟而出現過早收斂的現象。與改進熵最小化算法相比較，本文算法矯正后圖像的熵最小，同時分割精度提高了10%左右。通過分析參數對熵演化曲線的影響，即可獲得合適的參數，因此本算法可應用于MR圖像偏移場的估計和矯正。
引言
磁共振(magnetic resonance,MR)成像具有非介入性、非損傷以及對軟組織分辨率高的特性，目前在臨床醫學中得到廣泛應用。它已成為腦功能、病理和解剖研究的主要檢測手段，以及腦疾病(如阿爾茨海默癥、多發性硬化癥、精神分裂癥等)分析的重要工具，而對腦組織(灰質、白質)的精確分割和定量分析是研究的基礎。然而，MR圖像經常受射頻(radio-frequency,RF)線圈、MR設備、腦組織容積效應的影響[1]，導致圖像的統計特性分布趨于平均，人體相同組織的灰度不均一，不同組織之間灰度產生交疊，圖像的細節信息被嚴重模糊。
偏移場為一個緩慢變化、平滑的乘性場，帶有偏移場的MR圖像可近似看成原始圖像與偏移場的乘積，附加噪聲的影響(可忽略)。許多學者對偏移場模型進行了分析。將原始圖像與偏移場分離，對偏移場進行估計以矯正帶有偏移場的MR圖像，成為當前主要的研究方法。偏移場有基于多項式的、基于離散余弦變換的、基于薄板樣條的等諸多模型，利用Legendre多項式基函數擬合偏移場是當前的主流模型[2]。Likar等[3]將信息熵的概念引入偏移場的矯正，提出基于最小熵的方法，但沒能解決參數的尋優問題。傳統的遺傳算法和標準粒子群算法在偏移場參數的尋優過程中，容易陷入局部最優，導致無法得到全局最優的參數，最終無法對偏移場進行準確的估計[4]。王利等[4-5]將傳統的遺傳算法進行改進，得到了較優的偏移場，提高了分割的精度。劉軍偉等[6-7]提出了改進的熵最小化的方法，首先利用基于空間連續性的自適應模糊聚類算法來對圖像進行分割，對聚類結果交互式選擇像素點，用于粗略估計偏移場的參數，最后利用傳統的粒子群算法進行尋優，但該算法需采用改進的聚類分割算法作預處理，標準粒子群算法易陷入局部最優，其估計的偏移場不能保證是全局最優。當前粒子群算法發展迅速，提出了許多改進的模型[8-14]。董平平等[9]提出了一種自適應慣性權重粒子群算法，定義粒子個體尋優能力，避免了陷入局部最優。韓江洪等[10]、邢萬波等[11]提出了改進的自適應鄰域粒子群優化算法來避免粒子群陷入局部最優的問題。
本文將自適應混沌粒子群算法應用于MR圖像偏移場的矯正，省略了基于聚類分割的預處理步驟，通過設置自適應的粒子群的慣性權重，有效解決了參數尋優過程中容易陷入局部最優的問題，可應用于MR圖像偏移場的矯正。
1 算法
1.1 預處理
腦部MR圖像中，非腦組織(背景)占據圖像的一部分，背景部分不受偏移場影響，但其灰度值近似為零，對偏移場分析影響較大，故需將腦組織提取出來。本文利用OSTU大津閾值法計算出閾值，利用閾值進行二值化，可以有效地將背景區域的像素值置零，設計腦部的模板，消除背景對偏移場的影響。
1.2 偏移場與信息熵
MR圖像的灰度不均勻效應是在原始圖像中加入一個空間變化的光滑乘性場，其數學模型如式(1) 所示
| $I=bX+N$ |
其中，b為偏移場，X為原始圖像，N為噪聲(可忽略)。
本文利用Legendre多項式來擬合偏移場，其基函數如式(2) 所示
| $b\left( x,y \right)=\sum\limits_{i=0}^{k}{\sum\limits_{j=0}^{k-i}{{{p}_{ij}}}{{P}_{i}}\left( x \right){{P}_{j}}\left( y \right)}$ |
其中，b(x,y)為擬合的偏移場，Pi(x)、Pj(y)為Legendre多項式的基函數，pij為多項式基函數的參數，k為多項式的次數，圖像坐標值定義在[-1,1]。多項式次數越高，參數越多，偏移場擬合越準確，但計算復雜度越高。本文在偏移場估計中，選擇k=4，則需要估計的參數為(k+1)*(k+2)/2=15。
Likar等將信息熵的概念引入偏移場的估計后研究證實，信息熵越大，事件發生的不確定性越大，從隨機變量中獲得的信息量越大；信息熵越小，圖像的偏移場越弱。圖像信息熵公式如式(3) 所示
| $H=-\sum\limits_{x\in \left\{ graylevel \right\}}{pdf\left( x \right)}\log \left( pdf\left( x \right) \right)$ |
其中pdf為概率密度函數，x為通過矯正偏移場所得到的圖像，矯正后的圖像像素值為浮點型，需對其作取整運算。利用信息熵的公式計算矯正后圖像的熵值，在此僅計算模板內的像素的信息熵。
1.3 傳統的粒子群算法
Kennedy等[8]在1995年提出的粒子群優化(particle swarm optimization,PSO)算法是一種基于群體智能的進化優化算法。在PSO算法中，每個粒子對應一個待優化問題的潛在解。粒子的速度和位置分別用Vi=(vi1,vi2,…,vin)、Xi=(xi1,xi2,…,xin)表示，其中n為粒子的維數(多項式基函數的參數個數)。 Vi取決于粒子的方向和速度，Xi取決于初始位置和更新的速度。粒子的適應度fi 由位置決定，其為衡量粒子優劣程度的指標。粒子Pi的當前最優解用pbesti表示，當前整個粒子群的最優解用gbest表示。
對于標準的粒子群算法，粒子Pi更新自己的速度和位置的公式如下
| $\begin{align} & v_{i}^{k+1}=w\times v_{i}^{k}+{{c}_{1}}\times ran{{d}_{1}}\times \left( pbes{{t}_{i}}-x_{i}^{k} \right)+ \\ & {{c}_{2}}\times ran{{d}_{2}}\times \left( gbest-x_{i}^{k} \right) \\ \end{align}$ |
| $x_{i}^{k+1}=x_{i}^{k}+v_{i}^{k+1}$ |
其中，c1、c2為學習因子，通常取值c1=c2=2；rand1、rand2是0~1之間的隨機數。慣性權重參數w對算法影響很大，較大的w值有利于跳出局部最優，進行全局尋優；較小的w有利于局部尋優，加快算法的收斂。傳統的PSO容易陷入局部最優解，無法收斂到全局最優。
1.4 自適應的混沌粒子群算法
PSO算法中，粒子群的多樣性是算法能收斂到全局最優的前提條件，在求全局最優的過程中，粒子的多樣性會逐漸喪失，表現為強烈的趨同性，算法雖快速收斂，但易陷入局部最優解，發生早熟收斂的問題。然而，降低粒子群的趨同性會影響算法的收斂速度。故此根據粒子群早熟收斂的程度來自適應的調整慣性權重w。
對于早熟收斂程度利用指標[10]來進行評價，采用的定義如下：對于粒子群的種群大小為N，第k次迭代過程中粒子Pi的適應度為fi，最優粒子群的適應度為fm，粒子群的平均適應度favg為當前所有粒子適應度的平均值。對優于平均適應度的粒子再求平均favg，則定義的早熟收斂程度的指標為Δ=fm-f′avg，Δ越小說明粒子群趨于早熟收斂。
根據個體適應度不同，采用不同的調整策略，使粒子始終保持慣性權重的多樣性。慣性權重較小的粒子用來進行局部尋優，較快收斂；慣性權重較大的粒子跳出局部最優在全局進行尋優。具體的自適應策略如下所示：
(a) fi優于f′avg:表明該粒子是較為優秀的粒子，賦予較小的慣性權重，加速其全局最優收斂，其自適應策略如下所示
| $w={{w}_{\max }}-\left( {{w}_{\max }}-{{w}_{\min }} \right)\times \left| \frac{{{f}_{i}}-f_{avg}^{'}}{\Delta } \right|$ |
(b) fi優于favg但次于f′avg:表明該粒子一般，不改變其慣性權重，其慣性權重定義為常數。
(c) fi次于favg:表明該粒子較差，對其慣性權重的調整采用以下策略
| $w=1.5-\frac{1}{1+{{k}_{1}}\times \exp \left( -{{k}_{2}}\times \Delta \right)}$ |
1.5 自適應的混沌粒子群算法描述
偏移場初始化：假設k=4，每個粒子需15個參數,在[－5，5]范圍內產生隨機數,得到一組參數后計算偏移場。一般情況下，所有點的偏移場均大于0.3；如果某點的偏移場小于0.3，則舍棄這組參數，重新選取,直到生成合適的偏移場。
粒子適應度的計算：利用觀察到的圖像除以偏移場得到浮點型，對其取整，利用公式(3) 計算圖像的信息熵，對于偏移場值小于0.3的其信息熵定義為較大的常數。算法的流程圖如圖 1所示。
圖1
算法流程圖
Figure1.
Algorithm flow chat
2 實驗結果與分析
本文的數據采用McGill大學Montreal神經學研究所大腦成像中心的Brain Web仿真腦MR圖像庫，選擇偏移場強度為100%、無噪聲的仿真腦，圖像大小為217×181×181，取第90幅圖像為例。為減少背景對偏移場估計的影響，計算腦模板，其結果如圖 2所示。
圖2
預處理結果
(a)原始圖像；(b)腦模板
Figure2. Results of preprocessing(a) source image; (b) brain template
圖 2(a)為帶有100%偏移場的原始圖像，圖 2(b)為利用OSTU大津閾值法計算閾值，提取腦模板的圖像。
本文算法的參數設置：粒子群的種群大小20，每個粒子維數15，搜索空間[-5~5]，迭代次數設置為200次。
利用本文提出的自適應慣性權重粒子群算法估計MR圖像的偏移場，圖 3(a)是偏移場矯正之后的圖像，圖 3(b)是估計的偏移場。對矯正后的圖像進行聚類分割，分割出腦灰質、腦白質，并利用二值圖像表示，圖 3(c)是腦灰質，圖 3(d)是腦白質。
圖3
本文算法結果
(a)矯正后圖像;(b)偏移場;(c)灰質;(d)白質
Figure3. Results of the present algorithm(a) corrected image; (b) bias field; (c) gray matter; (d) white matter
2.1 信息熵的比較
本文采用Brain Web仿真腦MR圖像庫中相同層的圖像，計算腦模板中圖像的信息熵，無偏移場的MR 圖像信息熵為6.816 3，帶100%偏移場的MR圖像信息熵為7.852 1。 將本文提出的算法與傳統PSO算法和劉軍偉提出的改進熵最小化算法進行對比，信息熵的變化曲線如圖 4所示。
圖4
不同算法信息熵變化曲線
Figure4.
Variation curves of information entropy with different algorithms
圖 4中的三條曲線是針對相同圖像利用傳統的PSO算法、改進熵最小化算法和本文算法來估計偏移場時，經偏移場矯正后的MR圖像信息熵隨迭代次數的變化曲線。用傳統PSO算法來估計偏移場，其矯正后的信息熵為9.335 0，在進化過程中陷入局部最優，無法得到全局最優解。改進熵最小化算法對偏移場進行了估計，矯正后的信息熵為7.447 2，降低了圖像的灰度不均勻性，減少了偏移場的影響。本文提出的算法對偏移場進行估計，矯正后的信息熵為7.063 2，信息熵是三種算法中最小的，與沒有偏移場影響時的信息熵最為接近，因此估計的偏移場最精確。
2.2 參數分析
本文算法中參數k1、k2是慣性權重自適應的主要參數，對算法性能影響較大。k1主要用來控制w的上限，k1越大，w的上限越大，本文k1取1.5，使粒子的慣性權重w∈(0.5,1.1) 。 k2控制公式(7) 的自適應權重的大小。
圖 5中的三條曲線，分別代表參數k1設置為1.5，參數k2取3、0.5、0.3時，利用本文的慣性自適應權重粒子群算法來估計偏移場，矯正后信息熵隨迭代次數的變化曲線。經過實驗驗證，若k2偏大，雖收斂較快，但早期容易陷入局部最優；若k2過小則權重自適應的調節能力不足，到后期不能有效跳出局部最優。故本文中參數設置如下：k1=1.5，k2=0.5。
圖5
參數對信息熵的影響
Figure5.
Influence of parameter k2 on information entropy
2.3 偏移場矯正后的分割精度比較
偏移場矯正前后的圖像的直方圖分析結果如圖 6所示。
圖6
本文算法矯正前后直方圖
Figure6.
Histogram before and after correction with the present algorithm
偏移場矯正后MR圖像的腦組織直方圖分布特性滿足三峰，分別代表腦灰質、腦白質、腦脊液。矯正后圖像均采用聚類進行分割，將本文的算法與改進熵最小化算法進行對比分析。利用Jaccard Similarity(JS)指標[見公式(8) ]判斷分割的精度，通過定量分析的方法來驗證利用本算法矯正偏移場之后分割精度的優越性。
| $J\left( {{S}_{1}},{{S}_{2}} \right)=\frac{{{S}_{1}}\cap {{S}_{2}}}{{{S}_{1}}\cap {{S}_{2}}}$ |
其中S1為經偏移場進行矯正后的MR圖像利用聚類分割的結果(腦灰質、腦白質)，S2為無偏移場影響的MR圖像利用聚類分割的結果。
從表 1可以看出，采用本文算法與改進熵最小化算法估計的偏移場經矯正后，用聚類進行分割，通過JS指標比較，本文算法比改進熵最小化算法分割的腦灰質、腦白質的分割精度提高約10%。
表1
不同偏移場矯正算法的分割精度對比
Table1.
Segmentation accuracy comparison between different bias field correction algorithms
3 結論
本文針對傳統粒子群算法在估計MR圖像偏移場時易陷入局部最優的問題，提出了一種自適應慣性權重粒子群算法來對偏移場的參數進行全局尋優，有效解決了由于粒子早熟而出現過早收斂的現象。與改進熵最小化算法相比較，本文算法矯正后圖像的熵最小，同時分割精度提高了10%左右。通過分析參數對熵演化曲線的影響，即可獲得合適的參數，因此本算法可應用于MR圖像偏移場的估計和矯正。
