本文旨在利用模仿生物神經細胞同步脈沖發放的交叉視覺皮質模型（ICM）對生物視覺系統的輪廓整合機制及注意力選擇機制進行初步探索。將生物神經元“興奮-抑制”振蕩子的思想引入到ICM中，同時引入目標輪廓鏈碼作為高層反饋控制輸入，提出了擁有自底向上（BUTTON-UP）及自頂向下（TOP-DOWN）機制的興奮-抑制交叉視覺皮質模型（EI-ICM）。仿真實驗顯示，本文提出的模型可有效抑制噪聲使得光滑邊緣同步發放，從而完成BOTTOM-UP過程；目標輪廓鏈碼的引入可得到與輸入目標鏈碼一致的目標輪廓，而其它目標由于與輸入目標鏈碼不匹配，無法形成閉合輪廓，從而完成TOP-DOWN過程。結果表明本文提出的模型可模擬視覺皮層V1區輪廓整合及注意力選擇機制。
引用本文： 高山, 畢篤彥, 任宇環, 魏娜. 基于興奮-抑制交叉視覺皮質模型的V1區輪廓整合機制和注意力選擇實現. 生物醫學工程學雜志, 2016, 33(5): 963-971. doi: 10.7507/1001-5515.20160155 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
視覺系統是人類和高等動物認知世界的主要渠道，是了解腦的認知功能的突破口，研究它有利于闡明腦的接收、加工、儲存和利用信息的機制。而且這方面的研究也有助于推動工程領域中圖像處理方法的發展。目前，視覺研究已經成為神經科學發展最快的領域之一，已廣泛應用于生命科學、農業、工業以及軍事領域。
輪廓整合(contour integration)指視覺系統將物理上不連續的刺激整合起來形成整體知覺的過程[1-2]。一般認為輪廓整合的神經基礎是V1神經元通過長程水平連接進行的交互作用。視覺系統能夠從外界環境中提取我們需要的信息，其中很重要的一步就是識別物體，而輪廓整合是物體識別的重要中間步驟，因此對輪廓整合的機制研究一直是視覺研究的熱點問題。
視覺注意力選擇是人類視覺系統的一項重要機制，它主要是通過大腦中的視覺系統對眼睛所接收到的信息進行精簡和處理，從而將提煉后的信息傳輸到高級的中樞系統[1-2]。通過這一功能的實現，人類能夠很快地注意到視野中有意義的顯著區域。在計算機視覺和人工智能領域，視覺注意力通常被作為預處理的步驟，用于實現后續的目標檢測、圖像分割以及圖像壓縮等。目前，視覺注意力的機制可以分為自底向上(BOTTOM-UP)和自頂向下(TOP-DOWN)兩種。
在視覺系統的初級階段，單個細胞對處于它們感受野中的刺激做出反應，視覺系統必須首先把這些局部的單元信息匯集成具有全局意義的特征，才能感知視野中的目標。Li[3-4]通過對視覺皮層神經機制的研究，提出了迄今為止最為完美的V1區輪廓整合模型，完成了BOTTOM-UP過程[5-7]。雖然Li在模型中也嘗試去實現高層控制對視覺目標的選擇(注意力選擇，TOP-DOWN機制)，但她僅把高層控制信號作為負的視覺輸入直接加在振蕩子的抑制單元上，抑制了非目標神經元的振蕩，并沒有解決知識的表達和利用問題，還不能根據先驗知識有選擇地提取輪廓，即未實現注意力的選擇。然而，TOP-DOWN機制對于模擬人類注意力選擇功能十分重要，甚至是必不可少的。
交叉視覺皮質模型(intersecting cortical model, ICM)直接來源于Eckhorn等對于哺乳動物的視覺皮層神經細胞研究成果，是從模擬哺乳動物的視覺活動而得到的人工神經元模型[8-10]。對于傳統的人工神經網絡模型，ICM利用了生物神經元特有的線性相加、非線性相乘調制耦合的特性。同時還考慮了哺乳動物的視神經系統的視野受到適當刺激的時候相鄰的神經元會同步激發35~70 Hz的振蕩脈沖串。這種處理過程非常接近實際的生物視覺神經系統對于圖像信息的處理過程。
基于此，筆者嘗試利用ICM對生物視覺系統初級皮層V1區輪廓整合機制及注意力的選擇進行初步探索，通過深入分析Li[3-4]的輪廓整合模型，將“興奮-抑制”(encitation inhibition, EI)振蕩子的思想引入到ICM中，同時引入目標輪廓鏈碼作為高層反饋控制輸入，提出了擁有BOTTOM-UP及TOP-DOWN機制的EI-ICM，來模擬視覺皮層V1區輪廓整合機制及注意力的選擇。
1 交叉視覺皮質模型
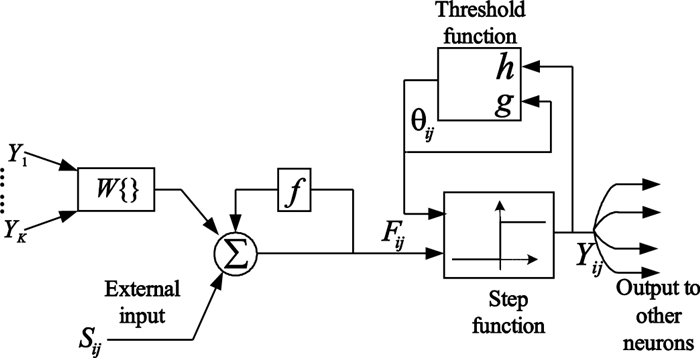
ICM源于Eckhorn對哺乳動物視覺皮層神經元脈沖同步振蕩現象的研究[8-10]，是具有生物背景無需學習的單層神經網絡。如圖 1所示為ICM的神經元架構圖。
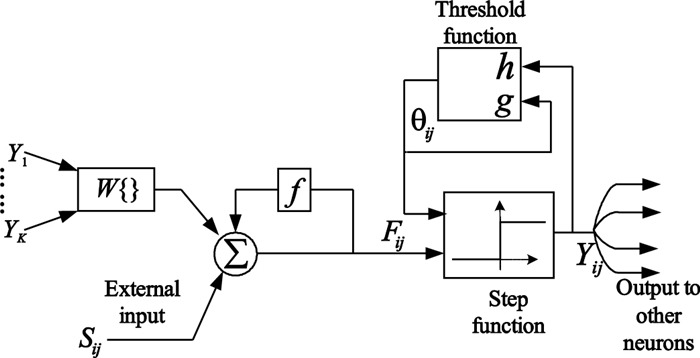圖1
ICM神經元架構圖
Figure1.
Architecture diagram of ICM neurons
ICM神經元含有神經元輸入和連接部分，神經元間通過突觸函數w{}進行互聯構成復雜的非線性動力學系統。ICM中每一個神經元對于上一個狀態Fij[n-1]具有記憶功能且狀態Fij隨著時間的變化其記憶內容會發生衰減，其衰減速度受到衰減因子f(f＜1)的影響。ICM的數學表達如下：
| $\begin{align} & {{F}_{ij}}\left[ n+1 \right]=f{{F}_{ij}}\left[ n \right]+{{S}_{ij}}+{{W}_{ij}}\left\{ Y \right\} \\ & {{Y}_{ij}}\left[ n+1 \right]=\left\{ \begin{matrix} 1 & {{F}_{ij}}\left[ n \right]>{{T}_{ij}}\left[ n \right] \\ 0 & \text{else} \\ \end{matrix} \right. \\ & {{T}_{ij}}\left[ n+1 \right]=g{{T}_{ij}}\left[ n \right]+h{{Y}_{ij}}\left[ n+1 \right] \\ \end{align}$ |
Sij為輸入圖像對應像素值，其中i, j為各個像素點的坐標。Tij為動態閾值，Yij為每一神經元的輸出。f, g, h均為標量系數，g＜f＜1，保證動態閾值隨迭代最終會低于神經元的狀態值。h為一很大標量值，保證神經元點火后能較大地提升閾值，使神經元在下次迭代不被激發。
ICM用于圖像處理時，其為單層二維局部連接的網絡，神經元個數與圖像中像素點的個數一一對應。輸入圖像中較大像素值對應的神經元首先點火，輸出脈沖，其閾值突增至較大值后隨時間以指數衰減，直至再次Fij＞Tij時神經元第二次點火。同時，點火神經元通過連接函數對其鄰域內神經元產生作用，使滿足點火條件的鄰域神經元相繼被捕獲點火。
2 Li的初級視覺皮層V1區輪廓整合模型
格式塔視覺心理學表明，整體特征的整合是隨著局部特征的接近性、相似性、連續性、封閉性、共同的運動以及對稱性而加強的[11-12]。目前為止，大量的生物實驗也表明，初級視覺皮層細胞對于光刺激的反應，不僅僅由其感受野的光輸入決定，而是受到了其感受野周圍的光刺激影響[13]。Field等[14]發現，人類視覺可以很容易地從具有復雜隨機噪聲的背景中確認出一條光滑的輪廓，這條輪廓由各自獨立的甚至不連續的邊緣段組成。接著，Kovacs等[15]發現，當輪廓線閉合的時候，人類視覺對它的敏感性會大大加強。1990年，Li[3-4]以上述實驗結果為依據，試圖探索腦是如何將局部特征整合成更有意義的全局特征的，提出了迄今為止最為完美的V1區輪廓整合模型。
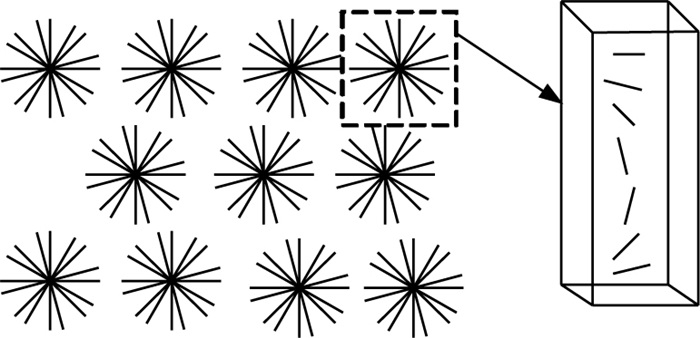
視覺空間由三維結構的神經元組成，如圖 2所示。每個位置i上都有一個由N個神經元組成的V1視覺方位柱，用(iθ)表示處于位置i具有最優朝向θ的神經元，其中θ∈{θN｜θN=nπ/N, n=1, 2, …, N}。
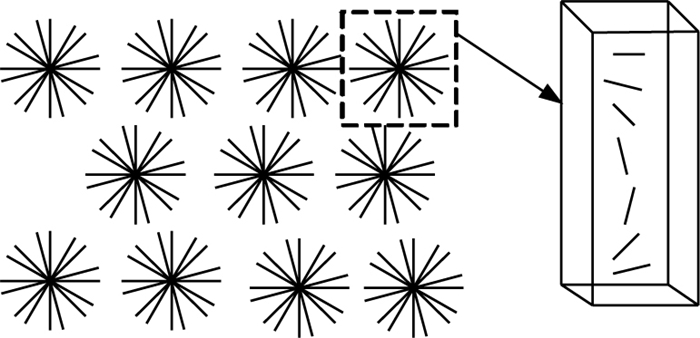圖2
視覺空間及方位柱
Figure2.
Visual space and orientation column
Li[3-4]的模型中，一個振蕩子由一個興奮子xiθ和一個抑制子yiθ組成。視野中的圖像經過V1內的邊緣檢測后，其邊緣狀況作為外部視覺輸入Iiθ送至視區相應的空間位置i上：
| ${{I}_{i\theta }}={{{\hat{I}}}_{i\beta }}\Phi \left( \theta -r \right),\Phi \left( \theta -r \right)={{e}^{-\left| \theta -r \right|/\pi /4}}$ |
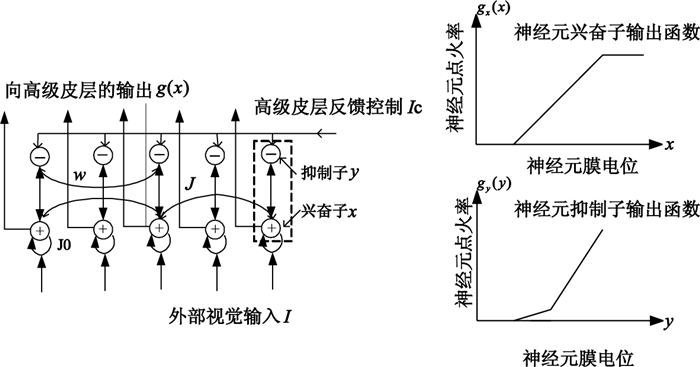
其中Φ為指數函數，r為視野中邊緣段的朝向，θ為方向柱中各個細胞的最優朝向。神經元構造如圖 3所示。
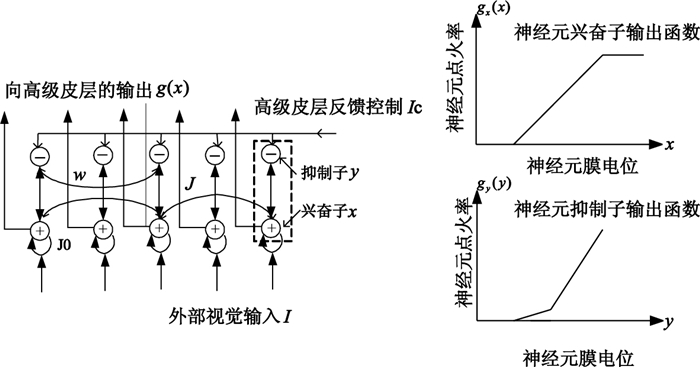圖3
神經元示意圖及興奮子-抑制子輸出函數
Figure3.
Schematic diagram of neuron and outputs of Excitation-Inhibition
關于Li的振蕩子模型工作原理可參見文獻[4]。網絡中每個神經單元都是一個振蕩子，具體方程如下：
| $\begin{gathered} {{\dot x}_{i\theta }} = - {\alpha _x}{x_{i\theta }} - \sum\limits_{\Delta \theta } {\psi \left( {\Delta \theta } \right)} gy\left( {{y_{i,\theta }} + \Delta \theta } \right) + {J_0}{g_x}\left( {{x_{i\theta }}} \right) + \hfill \\ \sum\limits_{j \ne i,\theta } {{J_{i\theta }}_{,j\theta }} gx\left( {{x_{j\theta '}}} \right) + {I_{i\theta }} + {I_0} \hfill \\ \end{gathered} $ |
| ${{\dot y}_{i\theta }} = - {\alpha _y}{y_{i\theta }} + gx\left( {{x_{i\theta }}} \right) + \sum\limits_{j \ne i,\theta '} {{W_{i\theta }}_{,j\theta '}} gx\left( {{x_{j\theta '}}} \right) + {I_c}$ |
神經元具有膜電位xiθ，1/αx和1/αy為隔膜時間常數，gx(·)和gy(·)分別為興奮子和抑制子的輸出函數，滿足：
| ${g_x}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} 0&{x < 0} \\ {\left( {x - 1} \right)}&{1 \leqslant x \leqslant 2} \\ 1&{x > 2} \end{array}} \right.$ |
| ${g_y}\left( y \right) = \left\{ {\begin{array}{*{20}{c}} 0&{y < 0} \\ {0.21}&{0 \leqslant y \leqslant 1.2} \\ {2.5y - 2.748}&{y > 1.2} \end{array}} \right.$ |
J0為自興奮項。Ψ(Δθ)為抑制子對興奮子的權重，定義為：
| $\psi \left( {\Delta \theta } \right) = \left\{ {\begin{array}{*{20}{c}} 1&{\Delta \theta = 0} \\ {0.8}&{\left| {\Delta \theta } \right| = {{15}^ \circ }} \\ {0.7}&{\left| {\Delta \theta } \right| = {{30}^ \circ }} \\ 0&{other} \end{array}} \right.$ |
Jiθ, jθ′、Wiθ, jθ′表示興奮性和抑制性連接強度，分別定義為：
| ${J_{i\theta ,j\theta '}} = \left\{ \begin{gathered} 0.126{e^{ - {{\left( {\beta /d} \right)}^2}}} - 2{\left( {\beta /d} \right)^7} - {d^2}/90 \hfill \\ 0 < d \leqslant 10\& \beta < \pi /2.69 \hfill \\ or \hfill \\ 0 < d \leqslant 10\& \beta < \pi /1.1\& \left| {{\theta _{1.2}}} \right| < \pi /5.90 \hfill \\ other \hfill \\ \end{gathered} \right.$ |
| ${W_{i\theta ,j\theta '}} = \left\{ \begin{gathered} 0 \hfill \\ d = 0\;\;{\text{or}}\;\;d/\cos \left( {\beta /4} \right) \geqslant 10\& \beta < \pi /1.1 \hfill \\ {\text{or}}\;\;\left| {\Delta \theta } \right| \geqslant \frac{\pi }{3}\;\;{\text{or}}\;\;\left| {{\theta _1}} \right| < \frac{\pi }{{11.999}} \hfill \\ 0.14\left( {1 - {e^{ - 0.4{{\left( {\beta /d} \right)}^{1.5}}}}} \right){e^{ - {{\left( {\Delta \theta /\left( {\pi /4} \right)} \right)}^{1.5}}}} \hfill \\ otherwise \hfill \\ \end{gathered} \right.$ |
神經元(iθ)的鄰近神經元(jθ′)可以通過興奮性突觸Jiθ, jθ′gx(xjθ′)發送興奮信號或通過抑制性突觸Wiθ, jθ′gx(xjθ′)發送抑制信號。另外，每個神經元還接收來自較高級視覺中樞的反饋輸入Ic, 可以起到增強或填補輪廓的作用，但不會產生視野中不存在的輪廓。反饋輸入Ic避開接受輸入的興奮神經元而發送給抑制神經元，或者是不接受輸入的興奮神經元。增加或減小Ic，只是增加或減小抑制，而當輸入刺激小于一定閾值時，Ic不起作用。也就是說，對沒有刺激輸入的邊緣段，Ic不會讓其興奮，而對已浮現的輪廓，則可以通過Ic得到增強或抑制。
興奮子接收外部視覺輸入，其輸出gx(xiθ)通過連接權Jiθ, jθ′與周圍的興奮子連接，使得周圍的光滑的邊緣段得以興奮，通過連接權Wiθ, jθ′與周圍的抑制子連接，使得其周圍的不光滑邊緣段被抑制。這樣設計連接權值的目的是：位于同一光滑輪廓線中的邊緣段，其反應應相互加強，而由噪聲生成的獨立的邊緣段，其反應應被減弱，或者至少沒有加強。也就是說：如果在邊緣段c(iθ)和c(jθ′)間存在光滑或彎度較小的輪廓線，則Jiθ, jθ′應取較大的值，且隨著彎曲程度的加大而減小；若邊緣段c(iθ)和c(jθ′)剛好是一條光滑輪廓線上的兩個支線，則兩邊緣段應通過Wiθ, jθ′相互抑制。
3 EI-ICM模型的構建
對于原始的ICM，定義神經元(i, j)的鄰域為：N(i, j)=[i-k/2, i+k/2]×[j-k/2, j+k/2]，可以看到，原始模型中神經元與它周圍的連接并不存在權重，只要其鄰域神經元有一個點火，它就可以接收側向輸入，而不管這個神經元與其是否屬于同一目標。如果要利用ICM來完成輪廓整合功能，就必須對其權值的設計進行改進[15]。基于此，我們因此提出了一種新的具有“興奮——抑制”振蕩子的EI-ICM模型。
3.1 輪廓整合機制的引入
這里，借鑒Li[3-4]模型中連接權值的設計思路，對ICM的權值進行重新設計以達到模擬V1區輪廓整合機制的目的[16]。
在ICM中，將F和T看作一對“興奮-抑制”子，這樣就可以把式(8)、(9)中所定義的連接權引入其中，提出用于模擬初級視覺皮層V1區輪廓整合功能的EI-ICM模型。于是
| $\begin{gathered} {F_{ij}}\left[ {n + 1} \right] = f{F_{ij}}\left[ n \right] + {S_{ij}} + {v_F}\left[ {J \otimes {Y_{i'j'}}\left[ n \right]} \right] \hfill \\ {T_{ij}}\left[ {n + 1} \right] = g{T_{ij}}\left[ n \right] + h{Y_{ij}}\left[ n \right] + {v_T}\left[ {W \otimes {Y_{i'j'}}\left[ n \right]} \right] \hfill \\ \end{gathered} $ |
其中，vF為興奮系數，vT為抑制系數，J是興奮性連接，其與原始ICM中權W的定義有本質區別，J由式(8)定義，與邊緣段的朝向有關。通過興奮性連接J使得光滑的邊緣段之間能夠相互加強，而不光滑的邊緣段即使發放脈沖也得不到加強。另一方面，孤立的噪聲點由于得不到足夠的J，發放頻率將很低。式(10)中T比原始ICM中T的定義多了一項，其中抑制性連接W由式(9)定義，該項用于抑制神經元鄰域內處于不光滑輪廓或噪聲位置上的神經元的發放，輪廓線上的分岔由于周圍鄰域神經元的抑制性輸出使其閾值升高，發放頻率也會降低。因此，提出的EI-ICM模型具有輪廓整合的功能。
3.2 高層反饋控制機制的引入
依據生物視覺系統視覺注意力選擇機制[17-21]，深入分析Li[3-4]模型存在的不足，嘗試引入目標輪廓鏈碼對先驗知識進行表達，并且將其引入到EI-ICM模型中作為高層控制信息(TOP-DOWN機制)，目的是在視野中搜索出一個先前已經記憶下來的目標，從而在視野內模擬目標輪廓整合的同時根據先驗知識實現注意力的選擇。這不同于Wang等[19-21]的振蕩模型，Wang等的振蕩模型是通過同步振蕩可以使得注意力在感受野中不同的目標間移動，但不能實現擁有TOP-DOWN機制的注意力選擇。
先驗知識是認知過程中必不可少的，也是生物腦中最深奧的一部分。在EI-ICM模型中，先驗知識定義為目標的輪廓形狀，由目標的輪廓鏈碼來表示。目標輪廓鏈碼在輪廓匹配過程中，被編碼成脈沖送入神經網絡。具有最優朝向θ的神經單元都將接收控制信號Jθ，且神經元均以間隔τ為單位發放脈沖，其點火周期為T=logg(1+h/sij)。
| $\left\{ \begin{gathered} {J_\theta }\left( {n\tau } \right) = \hat j,\theta = c'{'_n},{\text{or}}\;\;\theta {\text{ = }}c'{'_{L - n - 1}}\left( {0 \leqslant n < L/2} \right) \hfill \\ {J_\theta }\left( {n\tau } \right) = 0,{\text{else}} \hfill \\ \end{gathered} \right.$ |
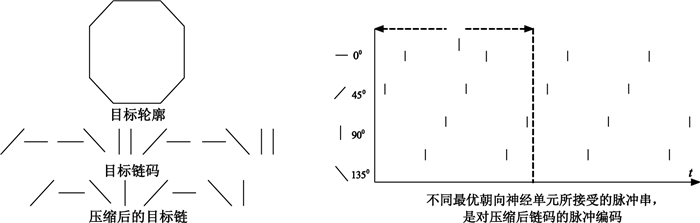
其中，0≤n＜L/2，＜0為常數，τ為每個脈沖寬度。在第n個時間間隔τ內，最優方向與目標鏈碼段方向相同的神經元都將接收一個負脈沖信號。如圖 4所示，描述了從目標得到控制脈沖的過程，輪廓采樣點起始于目標左上角，假設神經單元的最優朝向有四個，K=4(即：0°, 45°, 90°, 135°)。
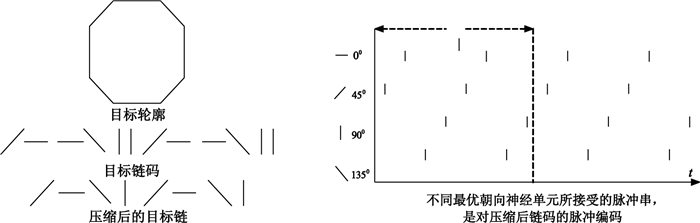圖4
目標鏈碼及脈沖示意圖
Figure4.
Target chain code and pulse diagram
根據Li的模型，令抑制子接收高層反饋控制。對于EI-ICM來說，即在閾值Tij上增加一項Jθ(由式(11)定義)作為高層反饋控制輸入，以實現注意力的選擇。
| ${T_{ij}}\left[ {n + 1} \right] = g{T_{ij}}\left[ n \right] + h{Y_{ij}}\left[ n \right] + {v_T}\left[ {W \otimes {Y_{i'j'}}\left[ n \right]} \right] + {J_\theta }$ |
3.3 具有BOTTOM-UP及TOP-DOWN作用方式的EI-ICM模型
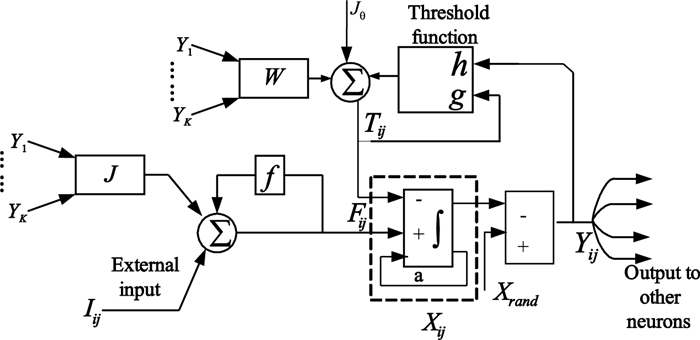
這里，為了模擬神經細胞的累積發放機制，在模型中較原始ICM除了對Fij增加興奮權重J、對Tij增加了抑制權重W和高層反饋控制Jθ外，還增加了一個累積電位Xij。如圖 5所示為EI-ICM模型示意圖。
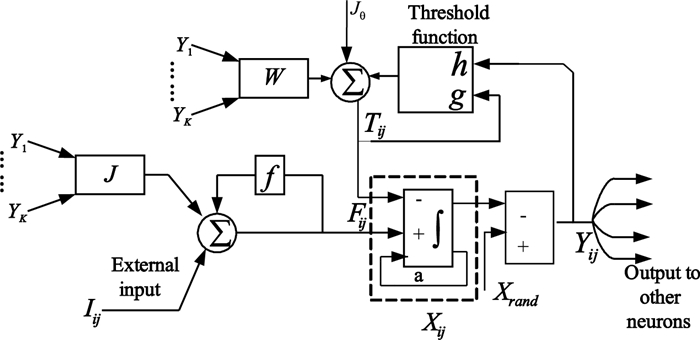圖5
EI-ICM模型示意圖
Figure5.
Schematic diagram of EI-ICM
EI-ICM模型的數學表達式為：
| $\begin{gathered} {F_{ij}}\left[ {n + 1} \right] = f{F_{ij}}\left[ n \right] + {S_{ij}} + {v_F}\left[ {J \otimes {Y_{i'j'}}\left[ n \right]} \right] \hfill \\ {T_{ij}}\left[ {n + 1} \right] = g{T_{ij}}\left[ n \right] + h{Y_{ij}}\left[ n \right] + {v_T}\left[ {W \otimes {Y_{i'j'}}\left[ n \right]} \right] + {J_\theta } \hfill \\ {X_{ij}}\left[ {n + 1} \right] = {v_x}{X_{ij}}\left[ n \right] + {F_{ij}}\left[ {n + 1} \right] - {T_{ij}}\left[ {n + 1} \right] \hfill \\ {Y_{ij}}\left[ {n + 1} \right] = step\left[ {{X_{ij}}\left[ {n + 1} \right],{X_{{\text{rand}}}}} \right] \hfill \\ \end{gathered} $ |
這里，累積發放機制通過膜電位的累積Xij[n+1]與閾值Xrand的比較來控制脈沖的發放，若大于零，則Y=1，發放一個脈沖，否則不發放。
4 計算機仿真結果及分析
4.1 V1區輪廓整合
在進行輪廓整合及注意力選擇實現之前，首先要進行邊緣檢測。如圖 6所示分別給出了原始輸入輪廓、疊加了強度為0.2的脈沖噪聲后的輪廓以及(0°、45°、90°、135°)四個方向的檢測結果。
圖6
原始圖像和疊加隨機噪聲的邊緣及四個方位(0°, 45°, 90°, 135°)檢測的結果
Figure6.
Edge of the original image and the superposition of random noise and the results of the detection of four square bits (0°, 45°, 90°, 135°)
如圖 7所示，為選取實驗點的網格示意圖。紅色的是邊緣坐標，藍色的為噪聲點。仿真實驗中，這些點每次都是通過程序隨機選取的。
圖7
選取實驗點的網格示意圖
Figure7.
Gridding sketch map of selected experimental points
在典型參數下類比過來的參數設置：f=e(-1/1)=0.367 9, g=e(-1/30)=0.967 2, h=0.1, vF=1, vT=0.1~10，鄰域連接距離N_d=3~10, vX=e(-1/0.5)=0.135 3, Xrand=6。
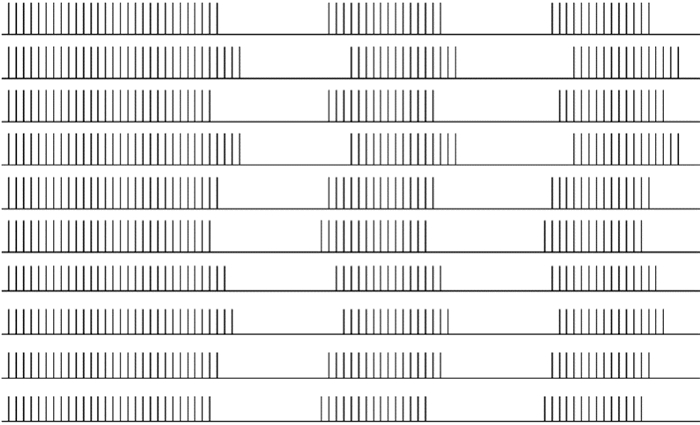
(1) 首先在不加噪聲的情況下，任意取得10個神經元(依次為[4, 20], [5, 7], [9, 32], [12, 32], [13, 32], [15, 32], [31, 32], [30, 10], [18, 14], [23, 5])看到，模型可以使得位于光滑邊緣神經元能夠以脈沖群同步形式發放脈沖，如圖 8所示。
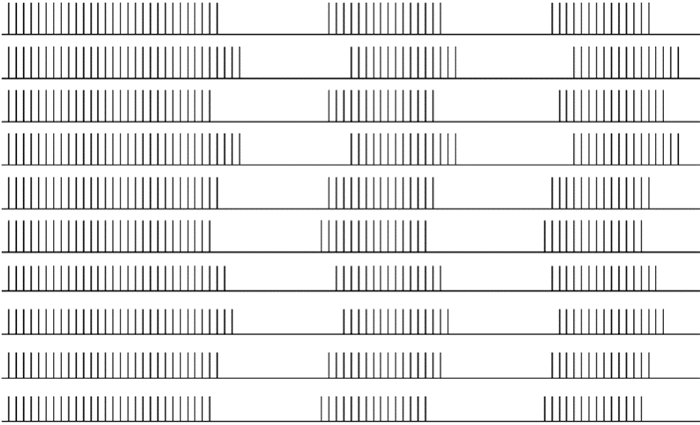圖8
不加噪聲的情況下，位于輪廓線上的10個神經元脈沖發放情況
Figure8.
Pulse distribution of 10 neurons in contour line (without noise)
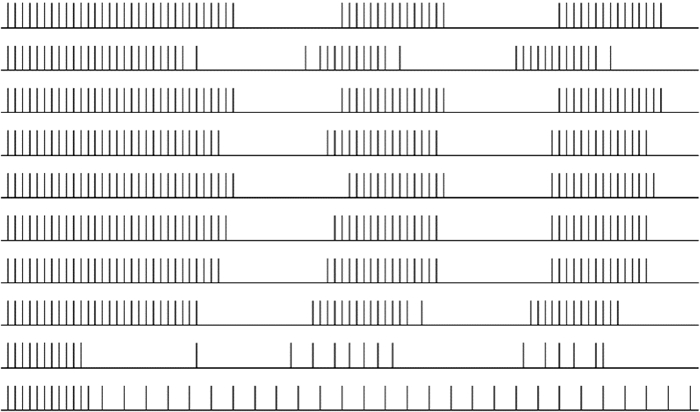
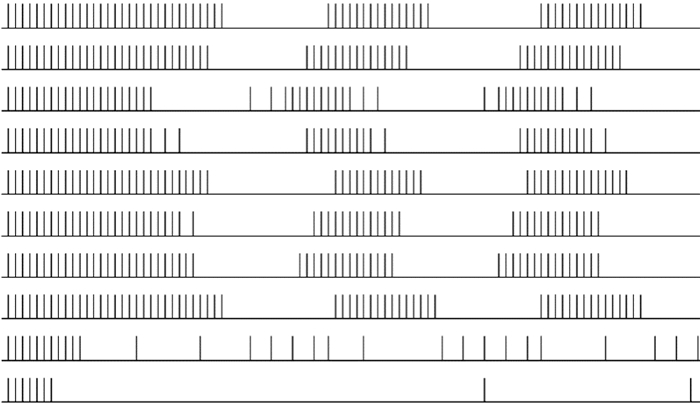
(2) 為了比較J和W對于輪廓整合的作用和影響，調整增益系數觀察結果。輸入圖像加入脈沖噪聲，固定興奮系數vF=1，首先選取抑制系數較小值，任意取得10個神經元(依次為[4, 32], [4, 16], [7, 30], [8, 32], [10, 32], [13, 32], [13, 32], [30, 10], [16, 15], [20, 17]，其中前8個神經元位于輪廓線，后兩個神經元對應噪聲點。觀察其脈沖發放情況。如圖 9所示，在抑制系數vT為0.2的情況下，噪聲無法被完全抑制，導致光滑邊緣上的神經元同步較差。
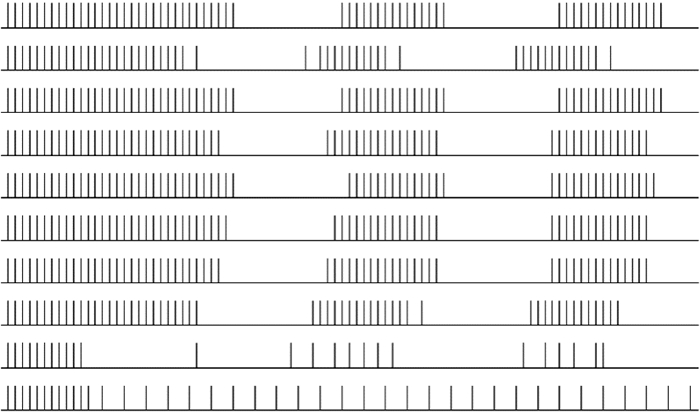圖9
加入椒鹽噪聲后，vF=1, vT=0.2時，神經元脈沖發放情況
Figure9.
Neurons pulse distribution in the case of salt noise (vF=1, vT=0.2)
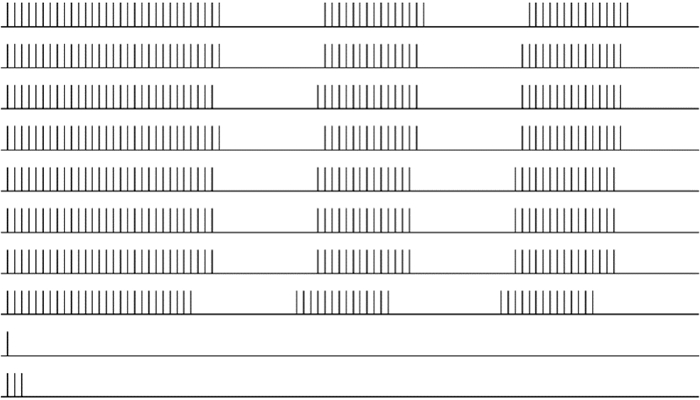
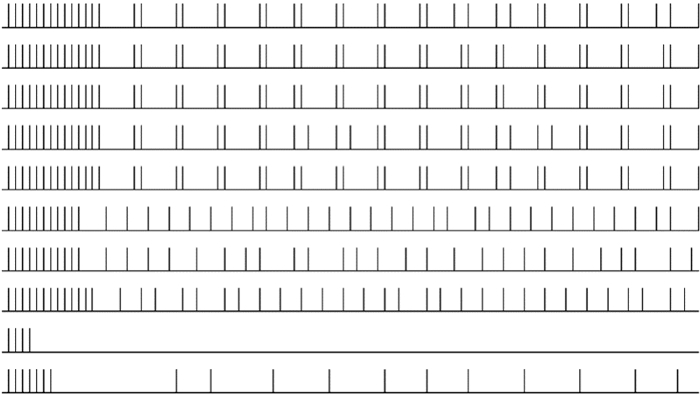
(3) 對于以上噪聲輸入圖像，神經元選取方式同前述所示。加強抑制系數vT為15，神經元的脈沖發放情況如圖 10所示，可以看出加強系數即可以抑制噪聲(孤立噪聲和非孤立噪聲)光滑邊緣上的神經元同步發放。
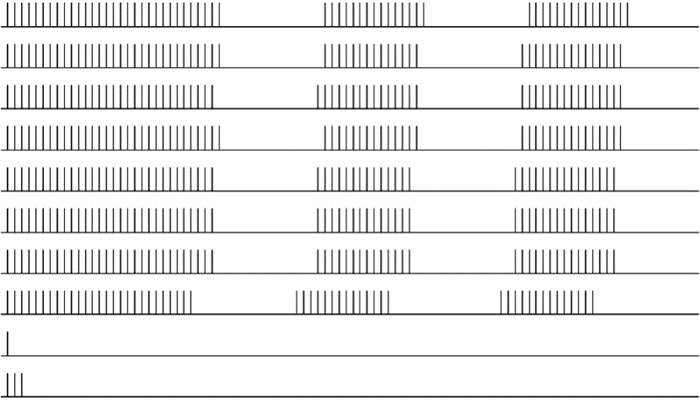圖10
加入椒鹽噪聲后，vF=1, vT=15時，神經元脈沖發放情況
Figure10.
Neurons pulse distribution in the case of salt noise (vF=1, vT=15)
(4) 文獻[15]只對抑制系數進行改變測試脈沖發放情況，實際上從模型可知，J和W是以“興奮和抑制對”出現的。為了測試兩者的關系，首先令vT為1，輸入圖像及神經元選擇同(2)。當vF=1時，如圖 11所示，不能夠實現對噪聲的抑制和光滑邊緣上神經元的同步發放。
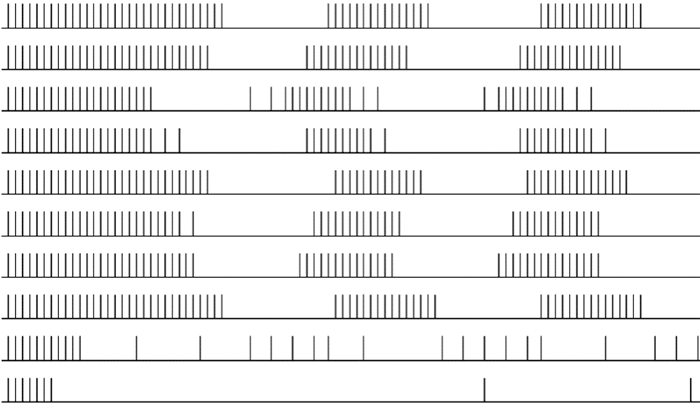圖11
vT=1；vF=1時，神經元脈沖發放情況
Figure11.
Neurons pulse distribution in the case of salt noise (vT=1;vF=1)
vF逐步減小到0.1，如圖 12所示，噪聲脈沖發放放緩，但也出現沒有完全抑制，且光滑邊緣的同步性稍差。
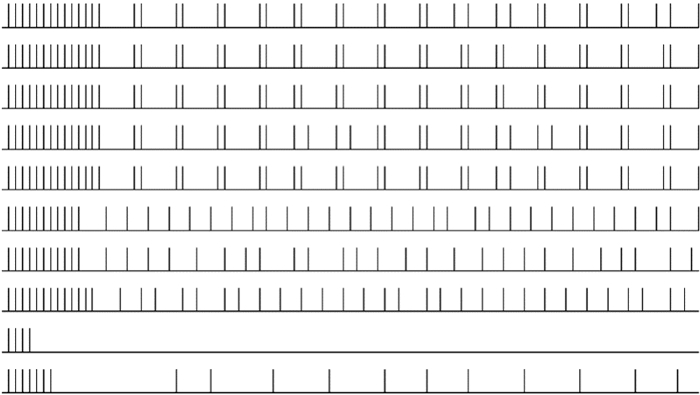圖12
vT=1；vF=0.1時，神經元脈沖發放情況
Figure12.
Neurons pulse distribution in the case of salt noise (vT=1, vF=0.1)
而vF增強大到10，可以抑制某些噪聲點，但對于部分噪聲點雖放緩發放頻率但基本不起太大作用，結果如圖 13所示。
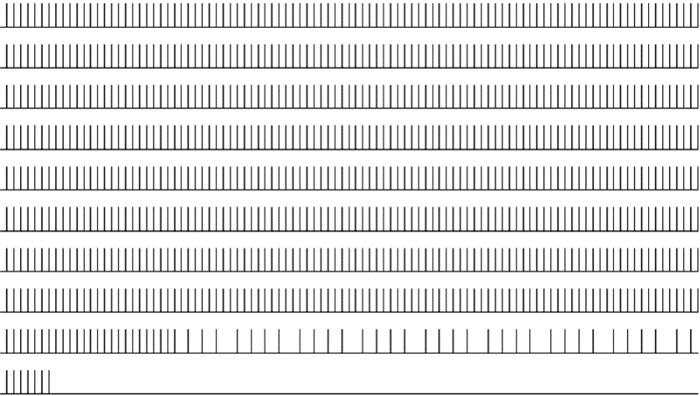圖13
vT=1；vF10時，神經元脈沖發放情況
Figure13.
Neurons pulse distribution in the case of salt noise (vT=1;vF=10)
(5) 根據(4)的實驗結果，設置參數為vF=1, 固定ICM的興奮-抑制系數增益參數，考察鄰域連接距離N_d以及抑制系數vT對神經元脈沖發放的影響，即噪聲(孤立和非孤立噪聲)的抑制。逐步增大N_d。(vF, vT)取值如表 1所示：N_d越大，所需要的(vF, vT)越小，即強度越弱，達到一定的鄰域鏈接距離后該值趨于較穩定值。
表1
N_d與(vF, vT)相關表
Table1.
Correlation table between N_d and (vF, vT)
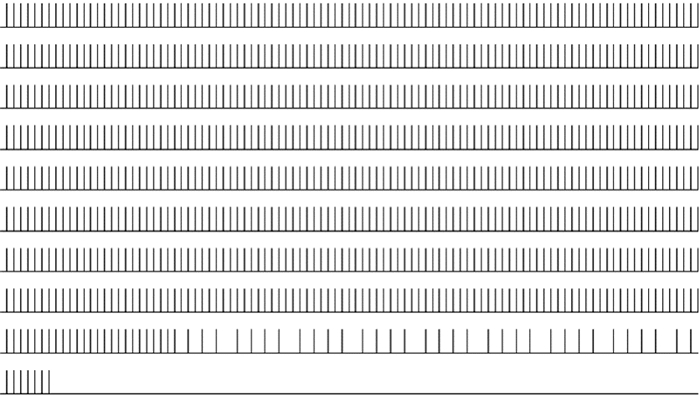
這里給出N_d=5、(vF, vT)=(1, 9)，輸入圖像及神經元選擇同(2)時，神經元發放情況，如圖 14所示。噪聲(孤立噪聲和非孤立噪聲)被抑制，光滑邊緣上的神經元達到同步發放。
圖14
(vF, vT)=(1, 9)時，神經元脈沖發放情況
Figure14.
Neurons pulse distribution in the case of salt noise ((vF, vT)=(1, 9))
本文實驗的脈沖發放圖是從最初模型點火進行記錄的，省略掉周期部分，可以清楚地看到脈沖發放規律。對于孤立噪聲點像素在進行邊緣方向檢測時就已經被抑制。在模型迭代過程中，由非孤立噪聲導致的不光滑邊緣段即使發放脈沖也得不到加強，噪聲點由于得不到足夠的J和較大的W，發放頻率很低。這樣通過輪廓整合機制，就可以在實現視覺信息通路中將噪聲等盡可能去除。
4.2 注意力選擇
經過輪廓整合“興奮-抑制”1~2個周期后，EI-ICM可以有效抑制噪聲使得光滑邊緣同步發放，從而完成BOTTOM-UP過程，隨后引入目標輪廓鏈碼來表達先驗知識，作為高層反饋控制輸入即可實現TOP-DOWN的機制。
首先以一個最簡單邊緣為例說明注意力選擇過程，其中包含了幾種簡單典型形狀，通過程序自動選取所感興趣的輪廓并標定起始點。圖 15中選出的上方目標輪廓以紅色打叉點為起始點，順時針選取得到壓縮鏈碼為：1→3→1→3→1。
圖15
簡單形狀及相應壓縮鏈碼示意圖
Figure15.
Simple shape and the corresponding compression chain code
注意力選擇過程中目標輪廓鏈碼與圖中各目標匹配的過程如圖 16所示：
圖16
注意力選擇的實現
Figure16.
The realization of attention selection
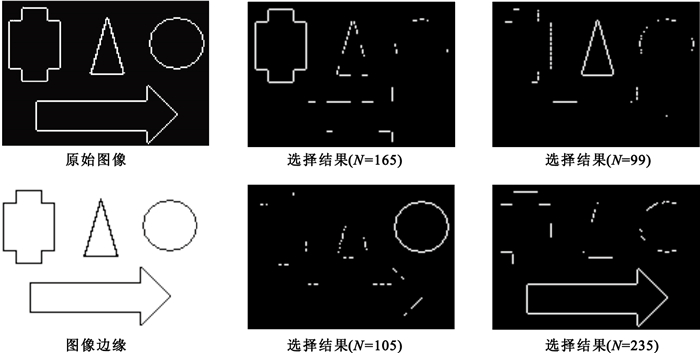
以四種典型邊緣為測試，分別以不同圖像為各自注意力選擇對象，最終輸出結果見圖 17(N為模型迭代次數)。
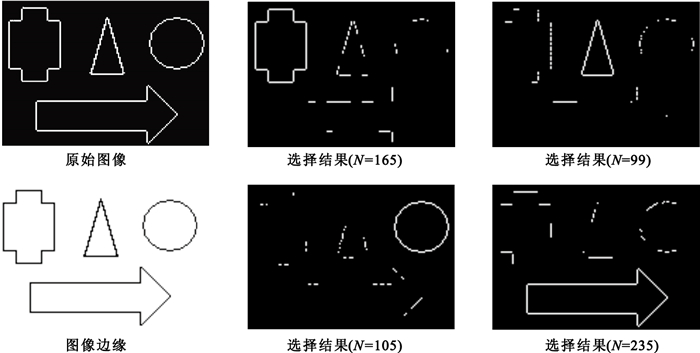圖17
不同目標注意力選擇的實現
Figure17.
Realization of different attention selection
從上可以看出，最終得到了與輸入目標鏈碼一致的目標輪廓，從而完成了注意力的選擇。而其它目標由于與輸入目標鏈碼不匹配，從而無法形成閉合輪廓，選擇失敗。
5 結論
本文旨在對生物視覺系統某些機制(V1區輪廓整合機制和注意力選擇機制)進行初步探索，借鑒Li的輪廓整合模型中連接權值的設計思路，利用模仿生物神經細胞同步脈沖發放的ICM來模擬視覺皮層V1區輪廓整合機制，完成了視覺信息處理通路中BOTTOM-UP一個很重要階段的任務；在實現輪廓整合的基礎上，通過引入目標輪廓鏈碼來表達先驗知識，作為高層反饋控制輸入，得到了具有TOP-DOWN機制的EI-ICM模型，利用先驗知識(感興趣目標輪廓鏈碼)在感受野中注意到相匹配的目標，從而實現了注意力的選擇。實驗結果表明，本文提出的模型可以很好地模擬V1區輪廓整合機制和注意力選擇機制，為后續目標檢索、目標跟蹤和識別提供了理論依據。
0 引言
視覺系統是人類和高等動物認知世界的主要渠道，是了解腦的認知功能的突破口，研究它有利于闡明腦的接收、加工、儲存和利用信息的機制。而且這方面的研究也有助于推動工程領域中圖像處理方法的發展。目前，視覺研究已經成為神經科學發展最快的領域之一，已廣泛應用于生命科學、農業、工業以及軍事領域。
輪廓整合(contour integration)指視覺系統將物理上不連續的刺激整合起來形成整體知覺的過程[1-2]。一般認為輪廓整合的神經基礎是V1神經元通過長程水平連接進行的交互作用。視覺系統能夠從外界環境中提取我們需要的信息，其中很重要的一步就是識別物體，而輪廓整合是物體識別的重要中間步驟，因此對輪廓整合的機制研究一直是視覺研究的熱點問題。
視覺注意力選擇是人類視覺系統的一項重要機制，它主要是通過大腦中的視覺系統對眼睛所接收到的信息進行精簡和處理，從而將提煉后的信息傳輸到高級的中樞系統[1-2]。通過這一功能的實現，人類能夠很快地注意到視野中有意義的顯著區域。在計算機視覺和人工智能領域，視覺注意力通常被作為預處理的步驟，用于實現后續的目標檢測、圖像分割以及圖像壓縮等。目前，視覺注意力的機制可以分為自底向上(BOTTOM-UP)和自頂向下(TOP-DOWN)兩種。
在視覺系統的初級階段，單個細胞對處于它們感受野中的刺激做出反應，視覺系統必須首先把這些局部的單元信息匯集成具有全局意義的特征，才能感知視野中的目標。Li[3-4]通過對視覺皮層神經機制的研究，提出了迄今為止最為完美的V1區輪廓整合模型，完成了BOTTOM-UP過程[5-7]。雖然Li在模型中也嘗試去實現高層控制對視覺目標的選擇(注意力選擇，TOP-DOWN機制)，但她僅把高層控制信號作為負的視覺輸入直接加在振蕩子的抑制單元上，抑制了非目標神經元的振蕩，并沒有解決知識的表達和利用問題，還不能根據先驗知識有選擇地提取輪廓，即未實現注意力的選擇。然而，TOP-DOWN機制對于模擬人類注意力選擇功能十分重要，甚至是必不可少的。
交叉視覺皮質模型(intersecting cortical model, ICM)直接來源于Eckhorn等對于哺乳動物的視覺皮層神經細胞研究成果，是從模擬哺乳動物的視覺活動而得到的人工神經元模型[8-10]。對于傳統的人工神經網絡模型，ICM利用了生物神經元特有的線性相加、非線性相乘調制耦合的特性。同時還考慮了哺乳動物的視神經系統的視野受到適當刺激的時候相鄰的神經元會同步激發35~70 Hz的振蕩脈沖串。這種處理過程非常接近實際的生物視覺神經系統對于圖像信息的處理過程。
基于此，筆者嘗試利用ICM對生物視覺系統初級皮層V1區輪廓整合機制及注意力的選擇進行初步探索，通過深入分析Li[3-4]的輪廓整合模型，將“興奮-抑制”(encitation inhibition, EI)振蕩子的思想引入到ICM中，同時引入目標輪廓鏈碼作為高層反饋控制輸入，提出了擁有BOTTOM-UP及TOP-DOWN機制的EI-ICM，來模擬視覺皮層V1區輪廓整合機制及注意力的選擇。
1 交叉視覺皮質模型
ICM源于Eckhorn對哺乳動物視覺皮層神經元脈沖同步振蕩現象的研究[8-10]，是具有生物背景無需學習的單層神經網絡。如圖 1所示為ICM的神經元架構圖。
圖1
ICM神經元架構圖
Figure1.
Architecture diagram of ICM neurons
ICM神經元含有神經元輸入和連接部分，神經元間通過突觸函數w{}進行互聯構成復雜的非線性動力學系統。ICM中每一個神經元對于上一個狀態Fij[n-1]具有記憶功能且狀態Fij隨著時間的變化其記憶內容會發生衰減，其衰減速度受到衰減因子f(f＜1)的影響。ICM的數學表達如下：
| $\begin{align} & {{F}_{ij}}\left[ n+1 \right]=f{{F}_{ij}}\left[ n \right]+{{S}_{ij}}+{{W}_{ij}}\left\{ Y \right\} \\ & {{Y}_{ij}}\left[ n+1 \right]=\left\{ \begin{matrix} 1 & {{F}_{ij}}\left[ n \right]>{{T}_{ij}}\left[ n \right] \\ 0 & \text{else} \\ \end{matrix} \right. \\ & {{T}_{ij}}\left[ n+1 \right]=g{{T}_{ij}}\left[ n \right]+h{{Y}_{ij}}\left[ n+1 \right] \\ \end{align}$ |
Sij為輸入圖像對應像素值，其中i, j為各個像素點的坐標。Tij為動態閾值，Yij為每一神經元的輸出。f, g, h均為標量系數，g＜f＜1，保證動態閾值隨迭代最終會低于神經元的狀態值。h為一很大標量值，保證神經元點火后能較大地提升閾值，使神經元在下次迭代不被激發。
ICM用于圖像處理時，其為單層二維局部連接的網絡，神經元個數與圖像中像素點的個數一一對應。輸入圖像中較大像素值對應的神經元首先點火，輸出脈沖，其閾值突增至較大值后隨時間以指數衰減，直至再次Fij＞Tij時神經元第二次點火。同時，點火神經元通過連接函數對其鄰域內神經元產生作用，使滿足點火條件的鄰域神經元相繼被捕獲點火。
2 Li的初級視覺皮層V1區輪廓整合模型
格式塔視覺心理學表明，整體特征的整合是隨著局部特征的接近性、相似性、連續性、封閉性、共同的運動以及對稱性而加強的[11-12]。目前為止，大量的生物實驗也表明，初級視覺皮層細胞對于光刺激的反應，不僅僅由其感受野的光輸入決定，而是受到了其感受野周圍的光刺激影響[13]。Field等[14]發現，人類視覺可以很容易地從具有復雜隨機噪聲的背景中確認出一條光滑的輪廓，這條輪廓由各自獨立的甚至不連續的邊緣段組成。接著，Kovacs等[15]發現，當輪廓線閉合的時候，人類視覺對它的敏感性會大大加強。1990年，Li[3-4]以上述實驗結果為依據，試圖探索腦是如何將局部特征整合成更有意義的全局特征的，提出了迄今為止最為完美的V1區輪廓整合模型。
視覺空間由三維結構的神經元組成，如圖 2所示。每個位置i上都有一個由N個神經元組成的V1視覺方位柱，用(iθ)表示處于位置i具有最優朝向θ的神經元，其中θ∈{θN｜θN=nπ/N, n=1, 2, …, N}。
圖2
視覺空間及方位柱
Figure2.
Visual space and orientation column
Li[3-4]的模型中，一個振蕩子由一個興奮子xiθ和一個抑制子yiθ組成。視野中的圖像經過V1內的邊緣檢測后，其邊緣狀況作為外部視覺輸入Iiθ送至視區相應的空間位置i上：
| ${{I}_{i\theta }}={{{\hat{I}}}_{i\beta }}\Phi \left( \theta -r \right),\Phi \left( \theta -r \right)={{e}^{-\left| \theta -r \right|/\pi /4}}$ |
其中Φ為指數函數，r為視野中邊緣段的朝向，θ為方向柱中各個細胞的最優朝向。神經元構造如圖 3所示。
圖3
神經元示意圖及興奮子-抑制子輸出函數
Figure3.
Schematic diagram of neuron and outputs of Excitation-Inhibition
關于Li的振蕩子模型工作原理可參見文獻[4]。網絡中每個神經單元都是一個振蕩子，具體方程如下：
| $\begin{gathered} {{\dot x}_{i\theta }} = - {\alpha _x}{x_{i\theta }} - \sum\limits_{\Delta \theta } {\psi \left( {\Delta \theta } \right)} gy\left( {{y_{i,\theta }} + \Delta \theta } \right) + {J_0}{g_x}\left( {{x_{i\theta }}} \right) + \hfill \\ \sum\limits_{j \ne i,\theta } {{J_{i\theta }}_{,j\theta }} gx\left( {{x_{j\theta '}}} \right) + {I_{i\theta }} + {I_0} \hfill \\ \end{gathered} $ |
| ${{\dot y}_{i\theta }} = - {\alpha _y}{y_{i\theta }} + gx\left( {{x_{i\theta }}} \right) + \sum\limits_{j \ne i,\theta '} {{W_{i\theta }}_{,j\theta '}} gx\left( {{x_{j\theta '}}} \right) + {I_c}$ |
神經元具有膜電位xiθ，1/αx和1/αy為隔膜時間常數，gx(·)和gy(·)分別為興奮子和抑制子的輸出函數，滿足：
| ${g_x}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} 0&{x < 0} \\ {\left( {x - 1} \right)}&{1 \leqslant x \leqslant 2} \\ 1&{x > 2} \end{array}} \right.$ |
| ${g_y}\left( y \right) = \left\{ {\begin{array}{*{20}{c}} 0&{y < 0} \\ {0.21}&{0 \leqslant y \leqslant 1.2} \\ {2.5y - 2.748}&{y > 1.2} \end{array}} \right.$ |
J0為自興奮項。Ψ(Δθ)為抑制子對興奮子的權重，定義為：
| $\psi \left( {\Delta \theta } \right) = \left\{ {\begin{array}{*{20}{c}} 1&{\Delta \theta = 0} \\ {0.8}&{\left| {\Delta \theta } \right| = {{15}^ \circ }} \\ {0.7}&{\left| {\Delta \theta } \right| = {{30}^ \circ }} \\ 0&{other} \end{array}} \right.$ |
Jiθ, jθ′、Wiθ, jθ′表示興奮性和抑制性連接強度，分別定義為：
| ${J_{i\theta ,j\theta '}} = \left\{ \begin{gathered} 0.126{e^{ - {{\left( {\beta /d} \right)}^2}}} - 2{\left( {\beta /d} \right)^7} - {d^2}/90 \hfill \\ 0 < d \leqslant 10\& \beta < \pi /2.69 \hfill \\ or \hfill \\ 0 < d \leqslant 10\& \beta < \pi /1.1\& \left| {{\theta _{1.2}}} \right| < \pi /5.90 \hfill \\ other \hfill \\ \end{gathered} \right.$ |
| ${W_{i\theta ,j\theta '}} = \left\{ \begin{gathered} 0 \hfill \\ d = 0\;\;{\text{or}}\;\;d/\cos \left( {\beta /4} \right) \geqslant 10\& \beta < \pi /1.1 \hfill \\ {\text{or}}\;\;\left| {\Delta \theta } \right| \geqslant \frac{\pi }{3}\;\;{\text{or}}\;\;\left| {{\theta _1}} \right| < \frac{\pi }{{11.999}} \hfill \\ 0.14\left( {1 - {e^{ - 0.4{{\left( {\beta /d} \right)}^{1.5}}}}} \right){e^{ - {{\left( {\Delta \theta /\left( {\pi /4} \right)} \right)}^{1.5}}}} \hfill \\ otherwise \hfill \\ \end{gathered} \right.$ |
神經元(iθ)的鄰近神經元(jθ′)可以通過興奮性突觸Jiθ, jθ′gx(xjθ′)發送興奮信號或通過抑制性突觸Wiθ, jθ′gx(xjθ′)發送抑制信號。另外，每個神經元還接收來自較高級視覺中樞的反饋輸入Ic, 可以起到增強或填補輪廓的作用，但不會產生視野中不存在的輪廓。反饋輸入Ic避開接受輸入的興奮神經元而發送給抑制神經元，或者是不接受輸入的興奮神經元。增加或減小Ic，只是增加或減小抑制，而當輸入刺激小于一定閾值時，Ic不起作用。也就是說，對沒有刺激輸入的邊緣段，Ic不會讓其興奮，而對已浮現的輪廓，則可以通過Ic得到增強或抑制。
興奮子接收外部視覺輸入，其輸出gx(xiθ)通過連接權Jiθ, jθ′與周圍的興奮子連接，使得周圍的光滑的邊緣段得以興奮，通過連接權Wiθ, jθ′與周圍的抑制子連接，使得其周圍的不光滑邊緣段被抑制。這樣設計連接權值的目的是：位于同一光滑輪廓線中的邊緣段，其反應應相互加強，而由噪聲生成的獨立的邊緣段，其反應應被減弱，或者至少沒有加強。也就是說：如果在邊緣段c(iθ)和c(jθ′)間存在光滑或彎度較小的輪廓線，則Jiθ, jθ′應取較大的值，且隨著彎曲程度的加大而減小；若邊緣段c(iθ)和c(jθ′)剛好是一條光滑輪廓線上的兩個支線，則兩邊緣段應通過Wiθ, jθ′相互抑制。
3 EI-ICM模型的構建
對于原始的ICM，定義神經元(i, j)的鄰域為：N(i, j)=[i-k/2, i+k/2]×[j-k/2, j+k/2]，可以看到，原始模型中神經元與它周圍的連接并不存在權重，只要其鄰域神經元有一個點火，它就可以接收側向輸入，而不管這個神經元與其是否屬于同一目標。如果要利用ICM來完成輪廓整合功能，就必須對其權值的設計進行改進[15]。基于此，我們因此提出了一種新的具有“興奮——抑制”振蕩子的EI-ICM模型。
3.1 輪廓整合機制的引入
這里，借鑒Li[3-4]模型中連接權值的設計思路，對ICM的權值進行重新設計以達到模擬V1區輪廓整合機制的目的[16]。
在ICM中，將F和T看作一對“興奮-抑制”子，這樣就可以把式(8)、(9)中所定義的連接權引入其中，提出用于模擬初級視覺皮層V1區輪廓整合功能的EI-ICM模型。于是
| $\begin{gathered} {F_{ij}}\left[ {n + 1} \right] = f{F_{ij}}\left[ n \right] + {S_{ij}} + {v_F}\left[ {J \otimes {Y_{i'j'}}\left[ n \right]} \right] \hfill \\ {T_{ij}}\left[ {n + 1} \right] = g{T_{ij}}\left[ n \right] + h{Y_{ij}}\left[ n \right] + {v_T}\left[ {W \otimes {Y_{i'j'}}\left[ n \right]} \right] \hfill \\ \end{gathered} $ |
其中，vF為興奮系數，vT為抑制系數，J是興奮性連接，其與原始ICM中權W的定義有本質區別，J由式(8)定義，與邊緣段的朝向有關。通過興奮性連接J使得光滑的邊緣段之間能夠相互加強，而不光滑的邊緣段即使發放脈沖也得不到加強。另一方面，孤立的噪聲點由于得不到足夠的J，發放頻率將很低。式(10)中T比原始ICM中T的定義多了一項，其中抑制性連接W由式(9)定義，該項用于抑制神經元鄰域內處于不光滑輪廓或噪聲位置上的神經元的發放，輪廓線上的分岔由于周圍鄰域神經元的抑制性輸出使其閾值升高，發放頻率也會降低。因此，提出的EI-ICM模型具有輪廓整合的功能。
3.2 高層反饋控制機制的引入
依據生物視覺系統視覺注意力選擇機制[17-21]，深入分析Li[3-4]模型存在的不足，嘗試引入目標輪廓鏈碼對先驗知識進行表達，并且將其引入到EI-ICM模型中作為高層控制信息(TOP-DOWN機制)，目的是在視野中搜索出一個先前已經記憶下來的目標，從而在視野內模擬目標輪廓整合的同時根據先驗知識實現注意力的選擇。這不同于Wang等[19-21]的振蕩模型，Wang等的振蕩模型是通過同步振蕩可以使得注意力在感受野中不同的目標間移動，但不能實現擁有TOP-DOWN機制的注意力選擇。
先驗知識是認知過程中必不可少的，也是生物腦中最深奧的一部分。在EI-ICM模型中，先驗知識定義為目標的輪廓形狀，由目標的輪廓鏈碼來表示。目標輪廓鏈碼在輪廓匹配過程中，被編碼成脈沖送入神經網絡。具有最優朝向θ的神經單元都將接收控制信號Jθ，且神經元均以間隔τ為單位發放脈沖，其點火周期為T=logg(1+h/sij)。
| $\left\{ \begin{gathered} {J_\theta }\left( {n\tau } \right) = \hat j,\theta = c'{'_n},{\text{or}}\;\;\theta {\text{ = }}c'{'_{L - n - 1}}\left( {0 \leqslant n < L/2} \right) \hfill \\ {J_\theta }\left( {n\tau } \right) = 0,{\text{else}} \hfill \\ \end{gathered} \right.$ |
其中，0≤n＜L/2，＜0為常數，τ為每個脈沖寬度。在第n個時間間隔τ內，最優方向與目標鏈碼段方向相同的神經元都將接收一個負脈沖信號。如圖 4所示，描述了從目標得到控制脈沖的過程，輪廓采樣點起始于目標左上角，假設神經單元的最優朝向有四個，K=4(即：0°, 45°, 90°, 135°)。
圖4
目標鏈碼及脈沖示意圖
Figure4.
Target chain code and pulse diagram
根據Li的模型，令抑制子接收高層反饋控制。對于EI-ICM來說，即在閾值Tij上增加一項Jθ(由式(11)定義)作為高層反饋控制輸入，以實現注意力的選擇。
| ${T_{ij}}\left[ {n + 1} \right] = g{T_{ij}}\left[ n \right] + h{Y_{ij}}\left[ n \right] + {v_T}\left[ {W \otimes {Y_{i'j'}}\left[ n \right]} \right] + {J_\theta }$ |
3.3 具有BOTTOM-UP及TOP-DOWN作用方式的EI-ICM模型
這里，為了模擬神經細胞的累積發放機制，在模型中較原始ICM除了對Fij增加興奮權重J、對Tij增加了抑制權重W和高層反饋控制Jθ外，還增加了一個累積電位Xij。如圖 5所示為EI-ICM模型示意圖。
圖5
EI-ICM模型示意圖
Figure5.
Schematic diagram of EI-ICM
EI-ICM模型的數學表達式為：
| $\begin{gathered} {F_{ij}}\left[ {n + 1} \right] = f{F_{ij}}\left[ n \right] + {S_{ij}} + {v_F}\left[ {J \otimes {Y_{i'j'}}\left[ n \right]} \right] \hfill \\ {T_{ij}}\left[ {n + 1} \right] = g{T_{ij}}\left[ n \right] + h{Y_{ij}}\left[ n \right] + {v_T}\left[ {W \otimes {Y_{i'j'}}\left[ n \right]} \right] + {J_\theta } \hfill \\ {X_{ij}}\left[ {n + 1} \right] = {v_x}{X_{ij}}\left[ n \right] + {F_{ij}}\left[ {n + 1} \right] - {T_{ij}}\left[ {n + 1} \right] \hfill \\ {Y_{ij}}\left[ {n + 1} \right] = step\left[ {{X_{ij}}\left[ {n + 1} \right],{X_{{\text{rand}}}}} \right] \hfill \\ \end{gathered} $ |
這里，累積發放機制通過膜電位的累積Xij[n+1]與閾值Xrand的比較來控制脈沖的發放，若大于零，則Y=1，發放一個脈沖，否則不發放。
4 計算機仿真結果及分析
4.1 V1區輪廓整合
在進行輪廓整合及注意力選擇實現之前，首先要進行邊緣檢測。如圖 6所示分別給出了原始輸入輪廓、疊加了強度為0.2的脈沖噪聲后的輪廓以及(0°、45°、90°、135°)四個方向的檢測結果。
圖6
原始圖像和疊加隨機噪聲的邊緣及四個方位(0°, 45°, 90°, 135°)檢測的結果
Figure6.
Edge of the original image and the superposition of random noise and the results of the detection of four square bits (0°, 45°, 90°, 135°)
如圖 7所示，為選取實驗點的網格示意圖。紅色的是邊緣坐標，藍色的為噪聲點。仿真實驗中，這些點每次都是通過程序隨機選取的。
圖7
選取實驗點的網格示意圖
Figure7.
Gridding sketch map of selected experimental points
在典型參數下類比過來的參數設置：f=e(-1/1)=0.367 9, g=e(-1/30)=0.967 2, h=0.1, vF=1, vT=0.1~10，鄰域連接距離N_d=3~10, vX=e(-1/0.5)=0.135 3, Xrand=6。
(1) 首先在不加噪聲的情況下，任意取得10個神經元(依次為[4, 20], [5, 7], [9, 32], [12, 32], [13, 32], [15, 32], [31, 32], [30, 10], [18, 14], [23, 5])看到，模型可以使得位于光滑邊緣神經元能夠以脈沖群同步形式發放脈沖，如圖 8所示。
圖8
不加噪聲的情況下，位于輪廓線上的10個神經元脈沖發放情況
Figure8.
Pulse distribution of 10 neurons in contour line (without noise)
(2) 為了比較J和W對于輪廓整合的作用和影響，調整增益系數觀察結果。輸入圖像加入脈沖噪聲，固定興奮系數vF=1，首先選取抑制系數較小值，任意取得10個神經元(依次為[4, 32], [4, 16], [7, 30], [8, 32], [10, 32], [13, 32], [13, 32], [30, 10], [16, 15], [20, 17]，其中前8個神經元位于輪廓線，后兩個神經元對應噪聲點。觀察其脈沖發放情況。如圖 9所示，在抑制系數vT為0.2的情況下，噪聲無法被完全抑制，導致光滑邊緣上的神經元同步較差。
圖9
加入椒鹽噪聲后，vF=1, vT=0.2時，神經元脈沖發放情況
Figure9.
Neurons pulse distribution in the case of salt noise (vF=1, vT=0.2)
(3) 對于以上噪聲輸入圖像，神經元選取方式同前述所示。加強抑制系數vT為15，神經元的脈沖發放情況如圖 10所示，可以看出加強系數即可以抑制噪聲(孤立噪聲和非孤立噪聲)光滑邊緣上的神經元同步發放。
圖10
加入椒鹽噪聲后，vF=1, vT=15時，神經元脈沖發放情況
Figure10.
Neurons pulse distribution in the case of salt noise (vF=1, vT=15)
(4) 文獻[15]只對抑制系數進行改變測試脈沖發放情況，實際上從模型可知，J和W是以“興奮和抑制對”出現的。為了測試兩者的關系，首先令vT為1，輸入圖像及神經元選擇同(2)。當vF=1時，如圖 11所示，不能夠實現對噪聲的抑制和光滑邊緣上神經元的同步發放。
圖11
vT=1；vF=1時，神經元脈沖發放情況
Figure11.
Neurons pulse distribution in the case of salt noise (vT=1;vF=1)
vF逐步減小到0.1，如圖 12所示，噪聲脈沖發放放緩，但也出現沒有完全抑制，且光滑邊緣的同步性稍差。
圖12
vT=1；vF=0.1時，神經元脈沖發放情況
Figure12.
Neurons pulse distribution in the case of salt noise (vT=1, vF=0.1)
而vF增強大到10，可以抑制某些噪聲點，但對于部分噪聲點雖放緩發放頻率但基本不起太大作用，結果如圖 13所示。
圖13
vT=1；vF10時，神經元脈沖發放情況
Figure13.
Neurons pulse distribution in the case of salt noise (vT=1;vF=10)
(5) 根據(4)的實驗結果，設置參數為vF=1, 固定ICM的興奮-抑制系數增益參數，考察鄰域連接距離N_d以及抑制系數vT對神經元脈沖發放的影響，即噪聲(孤立和非孤立噪聲)的抑制。逐步增大N_d。(vF, vT)取值如表 1所示：N_d越大，所需要的(vF, vT)越小，即強度越弱，達到一定的鄰域鏈接距離后該值趨于較穩定值。
表1
N_d與(vF, vT)相關表
Table1.
Correlation table between N_d and (vF, vT)
這里給出N_d=5、(vF, vT)=(1, 9)，輸入圖像及神經元選擇同(2)時，神經元發放情況，如圖 14所示。噪聲(孤立噪聲和非孤立噪聲)被抑制，光滑邊緣上的神經元達到同步發放。
圖14
(vF, vT)=(1, 9)時，神經元脈沖發放情況
Figure14.
Neurons pulse distribution in the case of salt noise ((vF, vT)=(1, 9))
本文實驗的脈沖發放圖是從最初模型點火進行記錄的，省略掉周期部分，可以清楚地看到脈沖發放規律。對于孤立噪聲點像素在進行邊緣方向檢測時就已經被抑制。在模型迭代過程中，由非孤立噪聲導致的不光滑邊緣段即使發放脈沖也得不到加強，噪聲點由于得不到足夠的J和較大的W，發放頻率很低。這樣通過輪廓整合機制，就可以在實現視覺信息通路中將噪聲等盡可能去除。
4.2 注意力選擇
經過輪廓整合“興奮-抑制”1~2個周期后，EI-ICM可以有效抑制噪聲使得光滑邊緣同步發放，從而完成BOTTOM-UP過程，隨后引入目標輪廓鏈碼來表達先驗知識，作為高層反饋控制輸入即可實現TOP-DOWN的機制。
首先以一個最簡單邊緣為例說明注意力選擇過程，其中包含了幾種簡單典型形狀，通過程序自動選取所感興趣的輪廓并標定起始點。圖 15中選出的上方目標輪廓以紅色打叉點為起始點，順時針選取得到壓縮鏈碼為：1→3→1→3→1。
圖15
簡單形狀及相應壓縮鏈碼示意圖
Figure15.
Simple shape and the corresponding compression chain code
注意力選擇過程中目標輪廓鏈碼與圖中各目標匹配的過程如圖 16所示：
圖16
注意力選擇的實現
Figure16.
The realization of attention selection
以四種典型邊緣為測試，分別以不同圖像為各自注意力選擇對象，最終輸出結果見圖 17(N為模型迭代次數)。
圖17
不同目標注意力選擇的實現
Figure17.
Realization of different attention selection
從上可以看出，最終得到了與輸入目標鏈碼一致的目標輪廓，從而完成了注意力的選擇。而其它目標由于與輸入目標鏈碼不匹配，從而無法形成閉合輪廓，選擇失敗。
5 結論
本文旨在對生物視覺系統某些機制(V1區輪廓整合機制和注意力選擇機制)進行初步探索，借鑒Li的輪廓整合模型中連接權值的設計思路，利用模仿生物神經細胞同步脈沖發放的ICM來模擬視覺皮層V1區輪廓整合機制，完成了視覺信息處理通路中BOTTOM-UP一個很重要階段的任務；在實現輪廓整合的基礎上，通過引入目標輪廓鏈碼來表達先驗知識，作為高層反饋控制輸入，得到了具有TOP-DOWN機制的EI-ICM模型，利用先驗知識(感興趣目標輪廓鏈碼)在感受野中注意到相匹配的目標，從而實現了注意力的選擇。實驗結果表明，本文提出的模型可以很好地模擬V1區輪廓整合機制和注意力選擇機制，為后續目標檢索、目標跟蹤和識別提供了理論依據。
