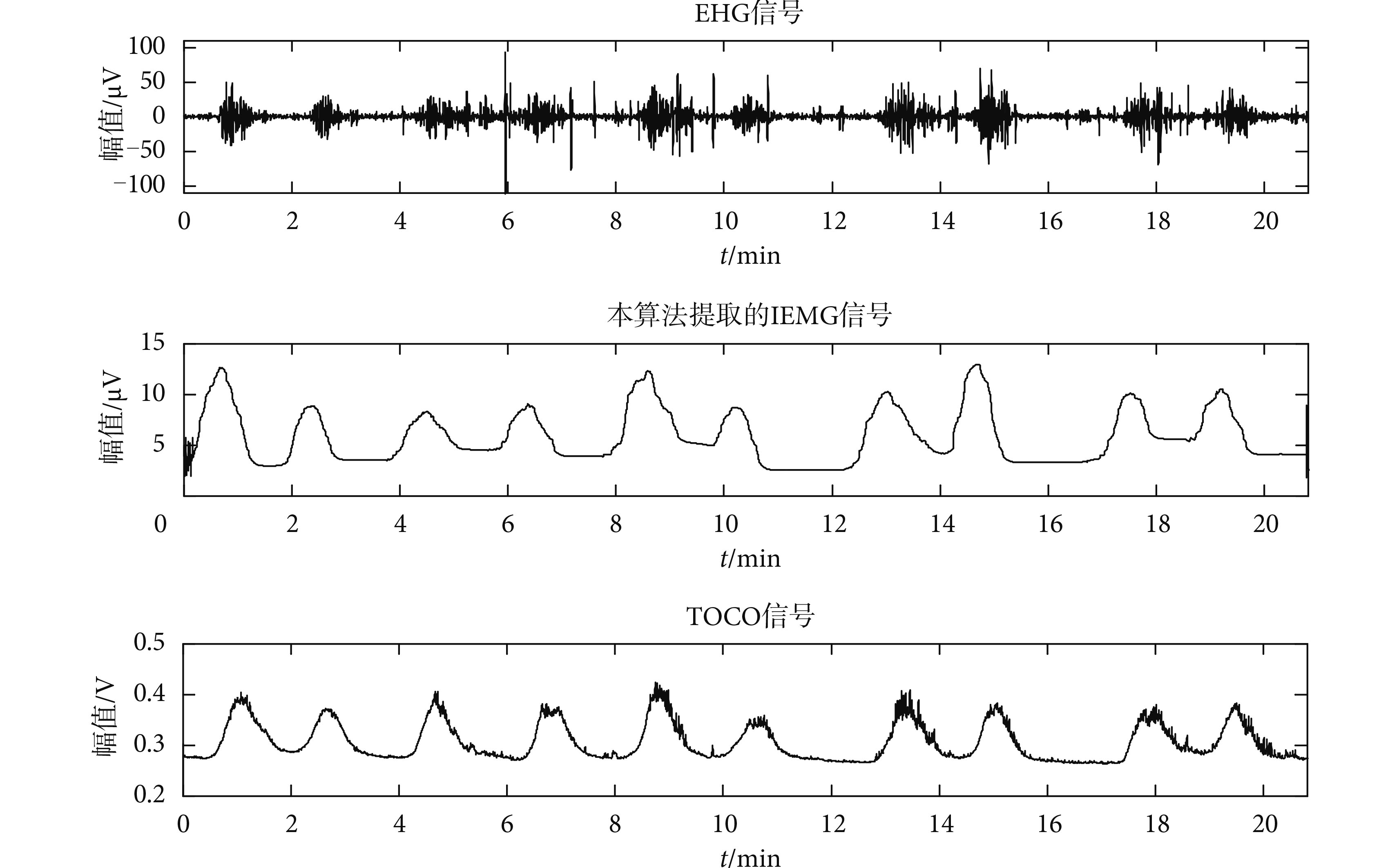
基于腹部采集的子宮肌電信號（EMG）提取子宮收縮信息被認為是一種最有可能取代分娩力描記法（TOCO）的新方法。傳統均方根（RMS）算法對子宮肌電信號中脈沖性噪聲的抑制能力有限，為了有效克服上述問題，本文提出一種改進的子宮肌電包絡提取算法。新方法先對原始子宮肌電信號進行過零檢測，識別出爆發波并分段，再對分段后的信號進行不同窗口寬度的平滑濾波，最后采用均方根法提取子宮肌電強度（IEMG）作為包絡。為了評估本算法的性能表現，本文將該算法與兩種現有子宮肌電強度提取算法進行比較。結果表明，該算法在抑制子宮肌電信號中存在的脈沖性噪聲方面要明顯優于對比算法，其測量靈敏度與陽性預測值（PPV）分別為 0.952 和 0.922，不僅明顯高于對比算法一中對應參數的 0.859 和 0.847，同時也高于對比算法二中的 0.928 和 0.877。本研究表明了該方法的可靠性與有效性。
引用本文： 陸堯勝, 潘杰, 陳朝霞. 一種改進的子宮肌電包絡提取算法. 生物醫學工程學雜志, 2017, 34(1): 92-98. doi: 10.7507/1001-5515.201605025 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
分娩力描記法（tocodynamometer, TOCO）作為一種檢測子宮收縮的方法，被廣泛用于產前與產中的子宮收縮壓力檢測[1]。但該方法在測量準確性和靈敏度上存在一定局限性，因此，近些年人們試圖利用從腹部電極采集到的子宮肌電（electrohysterogram, EHG）信號提取子宮收縮圖形，即子宮肌電強度（intensity of uterine electromyogram, IEMG）。由于子宮收縮是由子宮平滑肌細胞周期性極化與去極化引起，因此，通過從腹部電極采集到的 EHG 來檢測子宮肌電包絡與傳統 TOCO 法測得宮縮信號十分相近[2-3]。為了進一步研究兩者之間的關系，很多學者提出了各自的子宮肌電包絡提取算法，Shulgin 等[4]通過對 EHG 的慢波（頻率為 0.005~0.3 Hz，幅值為 0.5~15 mV）與快波(頻率為 0.1~3 Hz，幅值為 0.02~0.5 mV)進行幅值解調法來提取IEMG 信號；Horoba 等[5]、Shulgin等[4]先根據均方根（root mean square, RMS）統計法提取子宮肌電信號包絡，再利用漢明窗補償功率泄漏。此外，為了有效去除腹部肌電中由電極位置、皮膚阻抗等造成的干擾，其通過在基準值上加上檢測窗口中最大值與最小值差值的 0.25 作為閾值來進行收縮檢測，此方法能夠有效檢測出宮縮波，但是由 EHG 信號中混疊的脈沖性噪聲所引起的小范圍波動也被當作爆發波檢測出來。
對于包含少量脈沖性噪聲的 EHG 而言，很多現有的子宮肌電信號包絡提取算法都能取得較好的效果[5-8]，在宮縮次數檢測以及包絡的形狀方面相差不多。但在實際的臨床檢測中，由于各種因素而產生的脈沖性噪聲疊加在子宮肌電上，對 IEMG 的提取造成較大影響，這主要表現在所獲得的包絡圖形中可能出現虛假波峰。
由此，本文提出一種子宮肌電信號包絡提取的改進算法，用以解決上述問題。根據 EHG 信號的過零率（zero-crossing rate, ZCR）將其劃分為爆發波段與非爆發波段，并對兩種波段采用不同窗口的信號處理方法, 最后得出子宮肌電包絡信號。
1 子宮肌電信號 RMS 處理
由產婦或孕婦腹部體表電極記錄得到的 EHG 信號被稱為體表子宮肌電[9]。為了得到該信號，臨床上通過貼附在孕產婦腹部的 Ag-AgCl 表面電極記錄腹部電信號，由于記錄的信號中包含 EHG、母親心電、胎兒心電、脈沖性噪聲等，因此需要對采集到的腹部信號進行帶通濾波，去除不需要的成分，保留 EHG 信號，并由該信號提取 IEMG。RMS 統計法是一種從 EHG 信號中提取 EHG 包絡的常用方法，其中 EHG 包絡表示子宮肌電動作電位振幅圍繞一定靜息電位的變化[4]。采用標準差用以衡量數據值偏離均值的程度，由于相應的常數分量在前期的信號處理部分已經去除，EHG 信號的平均值為 0。因此，標準差等于信號的均方根：
| $ RES = { \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{x_i}^2} } } $ |
其中 xi 表示 EHG 信號中第i點的幅值，計算窗口長度N的選取對于信號處理的結果有較大影響，根據實驗分析可知，一般選擇寬度 60 s、步長為 3 s 的移動窗口得到相應的 RMS 值。此外，為了抵消頻譜泄漏，移動窗口選用漢寧窗，表達式如下所示：
| $ {y_i} = 0.5{x_i}(1 - \cos \frac{{2{{π}}i}}{{N - 1}}) $ |
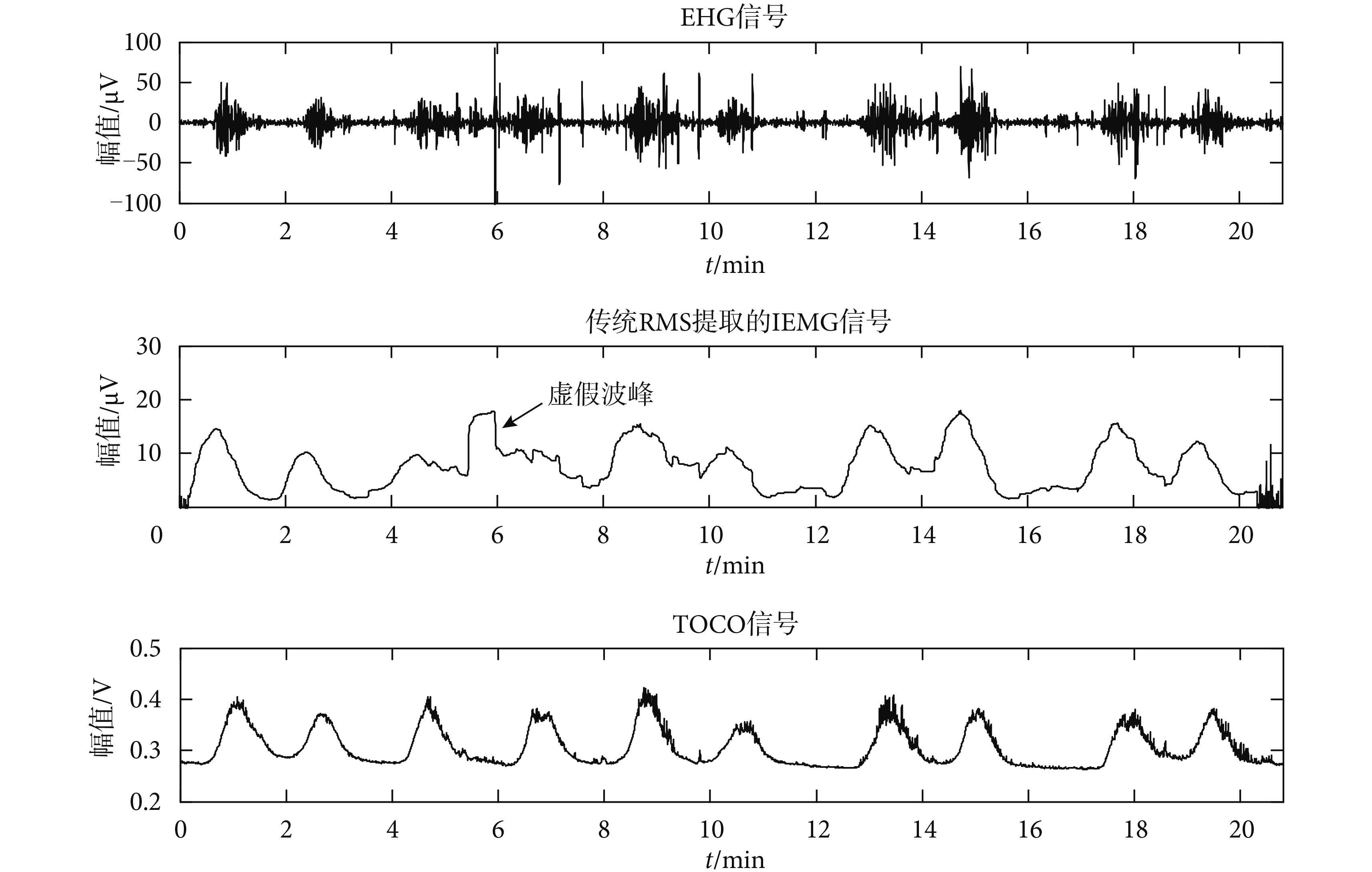
其中 xi 為輸入信號，即第i點的 EHG 幅值，yi 為對應的輸出信號。圖 1所示為一例 EHG 時域信號以及通過上述方法提取到的 EHG 包絡信號。由于在實際的臨床測量中，獲得的 EHG 信號會混疊由電磁干擾等因素產生的脈沖性噪聲[7]，從圖中不難發現，在記錄時間 5~7 min內出現明顯的脈沖性噪聲，使用傳統 RMS 法提取到的包絡出現了虛假波峰。這可能會誤導臨床上對宮縮的判斷，因此，為了克服 EHG 信號中脈沖性噪聲對包絡提取造成的干擾，本文對傳統 RMS 算法進行了改進。
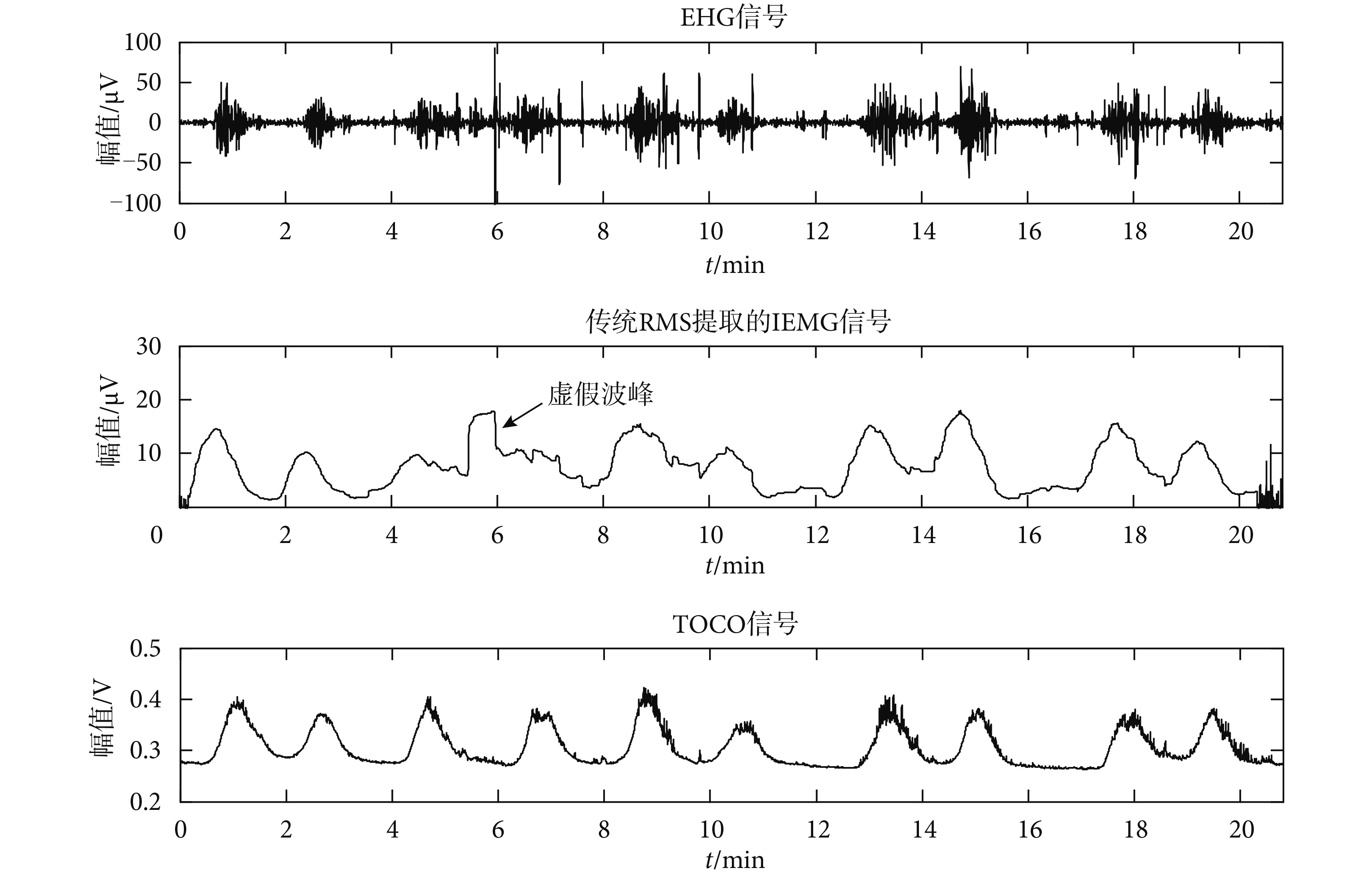圖1
傳統 RMS 提取的 IEMG
Figure1.
IEMG extracted by the traditional RMS algorithm
2 改進 RMS 算法提取 IEMG
2.1 EHG 過零檢測識別爆發波的可行性
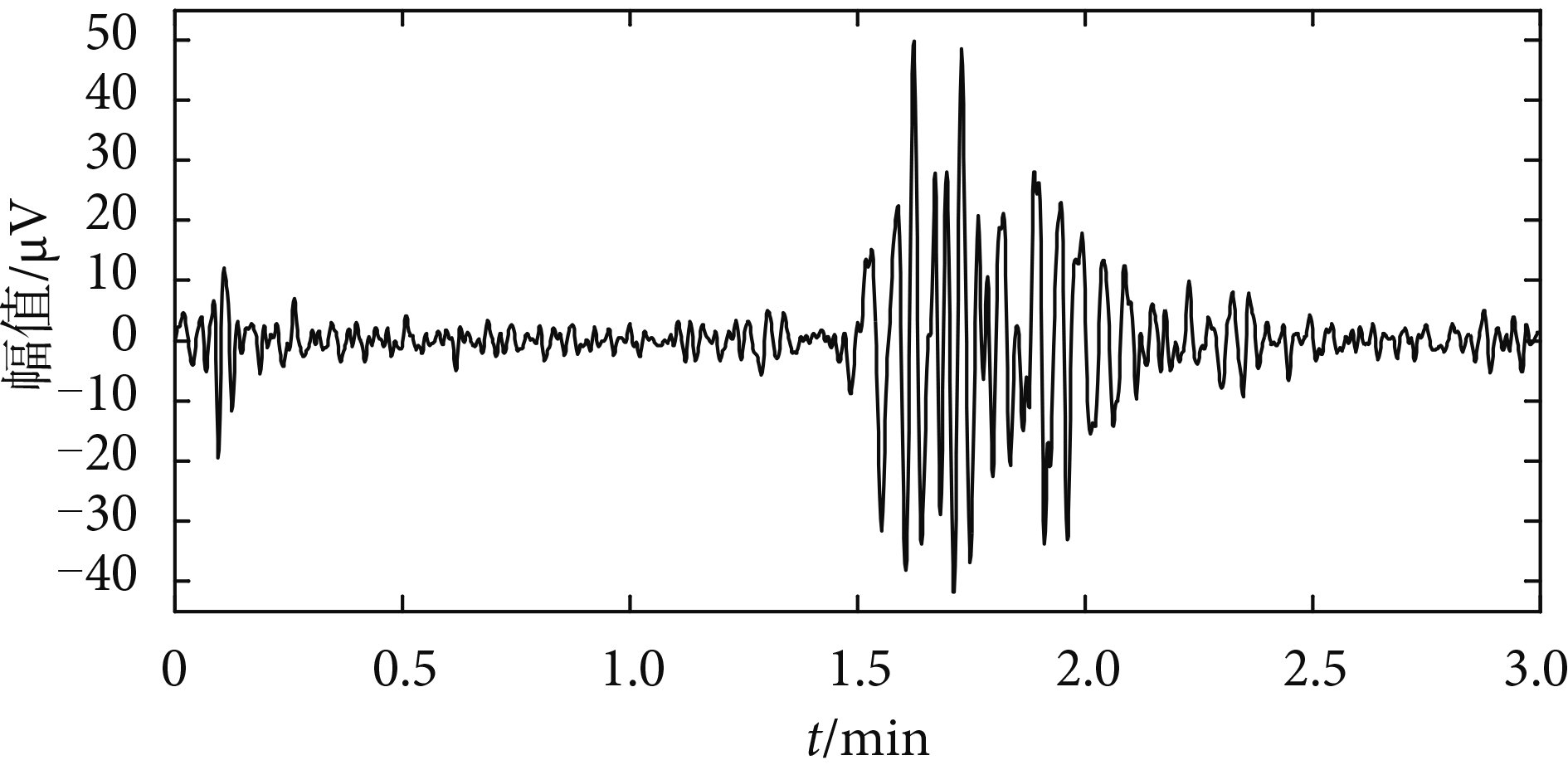
在傳統的 TOCO 監護中，通常采用兩個指標識別宮縮波：宮縮幅值與持續時間，即當信號的幅值與基線差值大于設定閾值并持續一段時間時，該段信號被視為宮縮波。與 TOCO 曲線相比，EHG 為非平穩信號，其表現為峰電活動較為頻繁的爆發波[10]，振幅變化范圍不確定，因此不能根據振幅來識別爆發波。理論上，EHG 信號爆發波段（宮縮期）信號過零點數目明顯不同于非爆發波段（間歇期）信號過零點數目[11]。圖 2為 EHG 信號的局部細節圖，從中可以看出，在宮縮期，峰電活動頻繁，信號的過零點數目明顯大于間歇期。方法上，過零檢測可以對小范圍信號進行準確檢測[12-13]，從而提高爆發波的辨識度。因此，利用過零點數目來識別 EHG 信號的爆發波段是可行的。
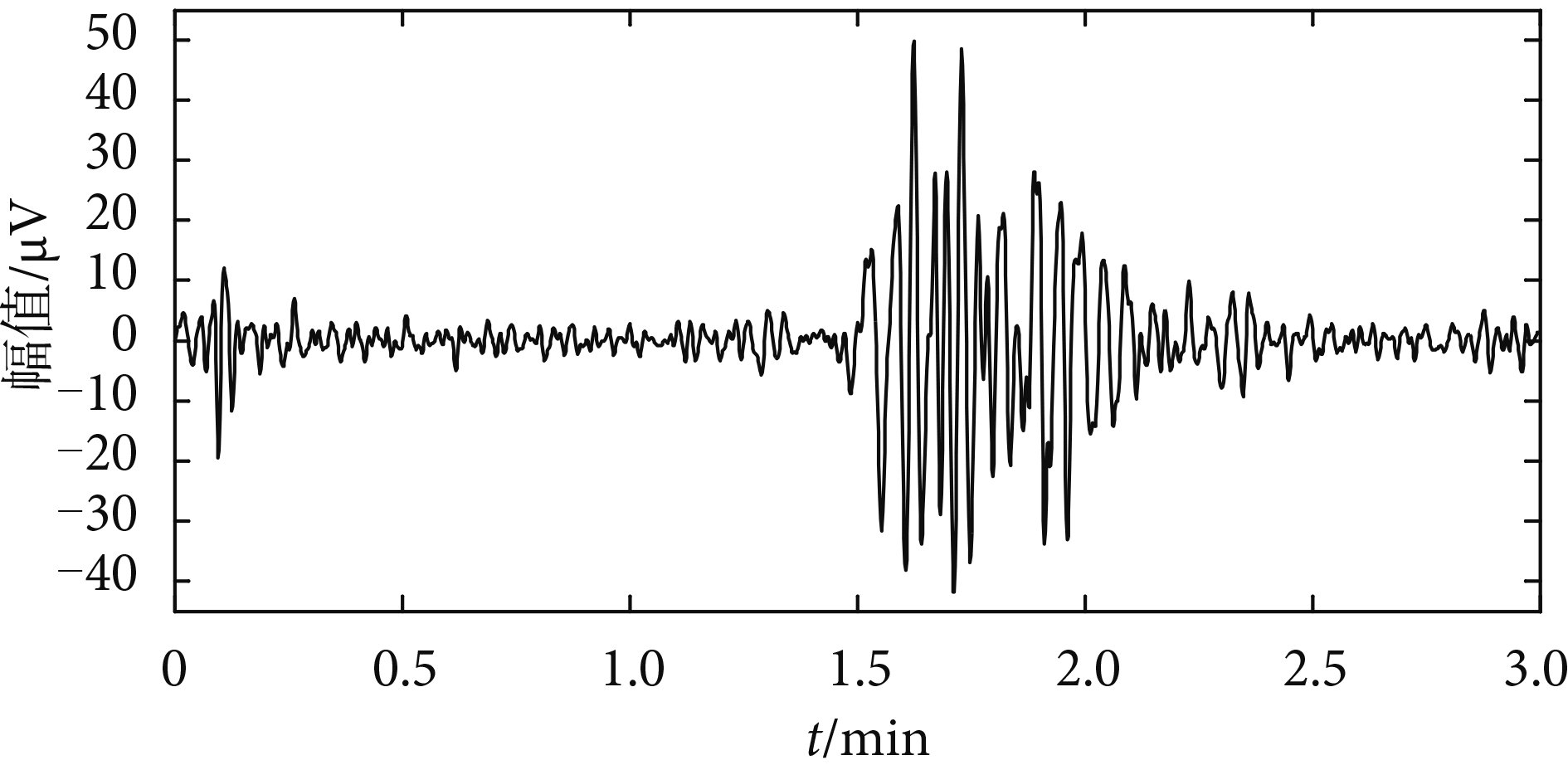圖2
EHG 局部細節圖
Figure2.
The detail views of EHG
2.2 EHG 信號分段
本方法主要根據信號波段的過零點數來區分 EHG 信號爆發波段與非爆發波段，對于一段長度為 M 的 EHG 離散信號而言，其過零點數可由下式求得：
| $ {\rm{ZC}} = \frac{1}{2}\sum\limits_{i = 1}^M {\left| {{\mathop{\rm sgn}} [x(i)] - {\mathop{\rm sgn}} [x(i - 1)]} \right|} $ |
其中 ZC 為過零點數，為了不受信號長度 M 的影響，本文采用過零率來識別爆發波。過零率的定義如下：
| $ {\rm{ZCR}} = {\rm{ZC}}/M $ |
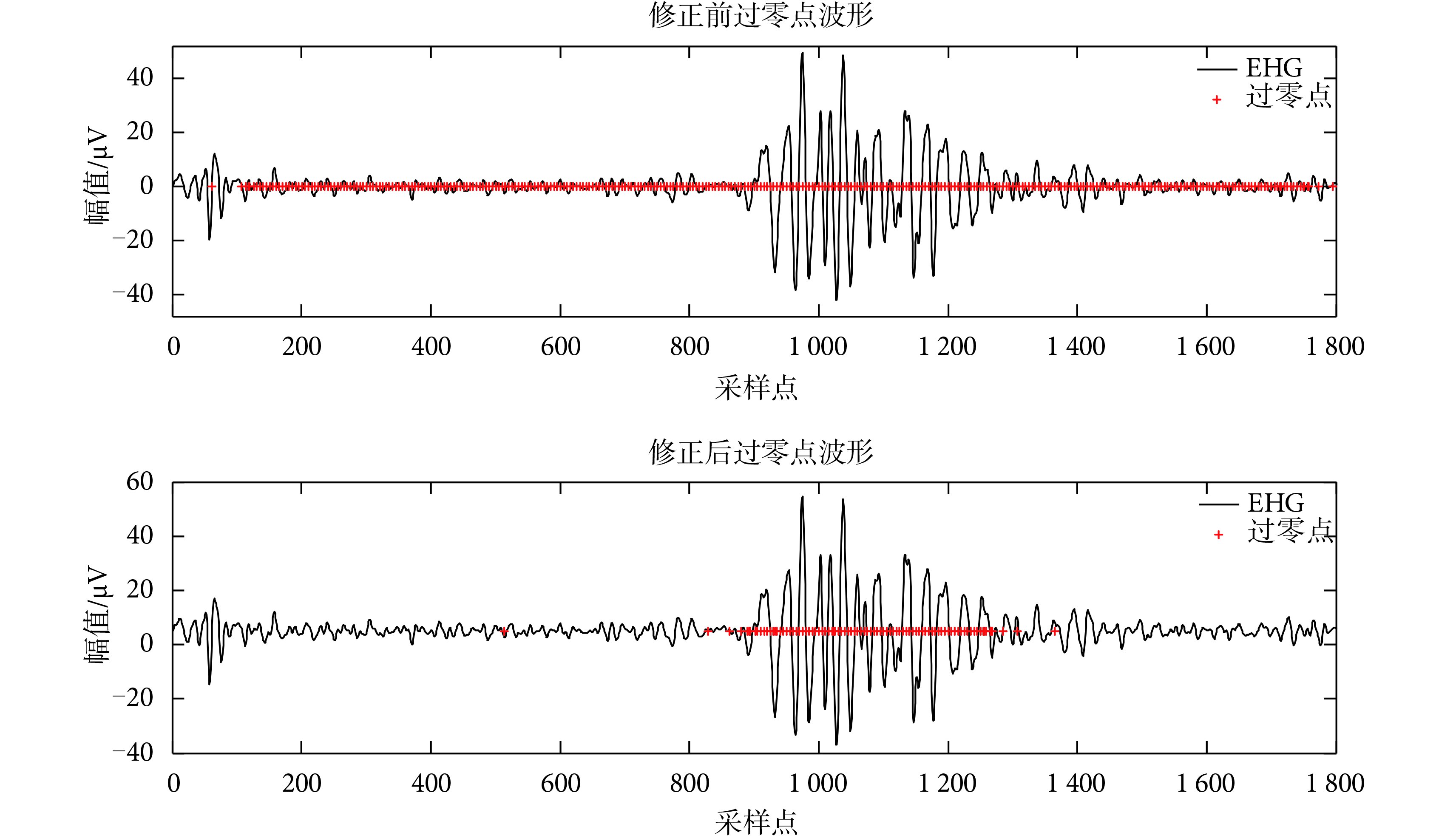
其中 ZCR 為過零率，本文設置長度為 300 個樣本點、步長為1 的滑動窗口，該窗口長度的選取既能有效濾除虛假過零點的干擾，同時也避免了窗口過寬造成計算量的增加，根據公式(4)計算出滑動窗口內信號的過零率。設某采樣點坐標為i，并計算出[i—100, i+199]范圍內的 ZCR 值，若 ZCR 值大于設定閾值，則取該點為過零點，反之，為非過零點。對于實際采集到的 EHG 信號而言，在 EHG 非爆發波段可能會出現一些小的波動，通過上述方法判斷后將得到大量假過零點，如圖 3頂圖所示。為解決上述問題，本實驗在計算過零率之前，先將 EHG 信號整體向上小幅度平移。由于信號微小波動的幅度遠遠小于爆發波的峰電幅值，因此，直接將 EHG 信號向上小幅度平移既能有效濾除假過零點，又不會影響爆發波段的過零點數目，文中采用的上移幅度為 0.005 mV。根據修正前后的過零點波形可知，修正后的 EHG 信號中過零點大部分落在爆發波段，這有利于后續信號的進一步處理。
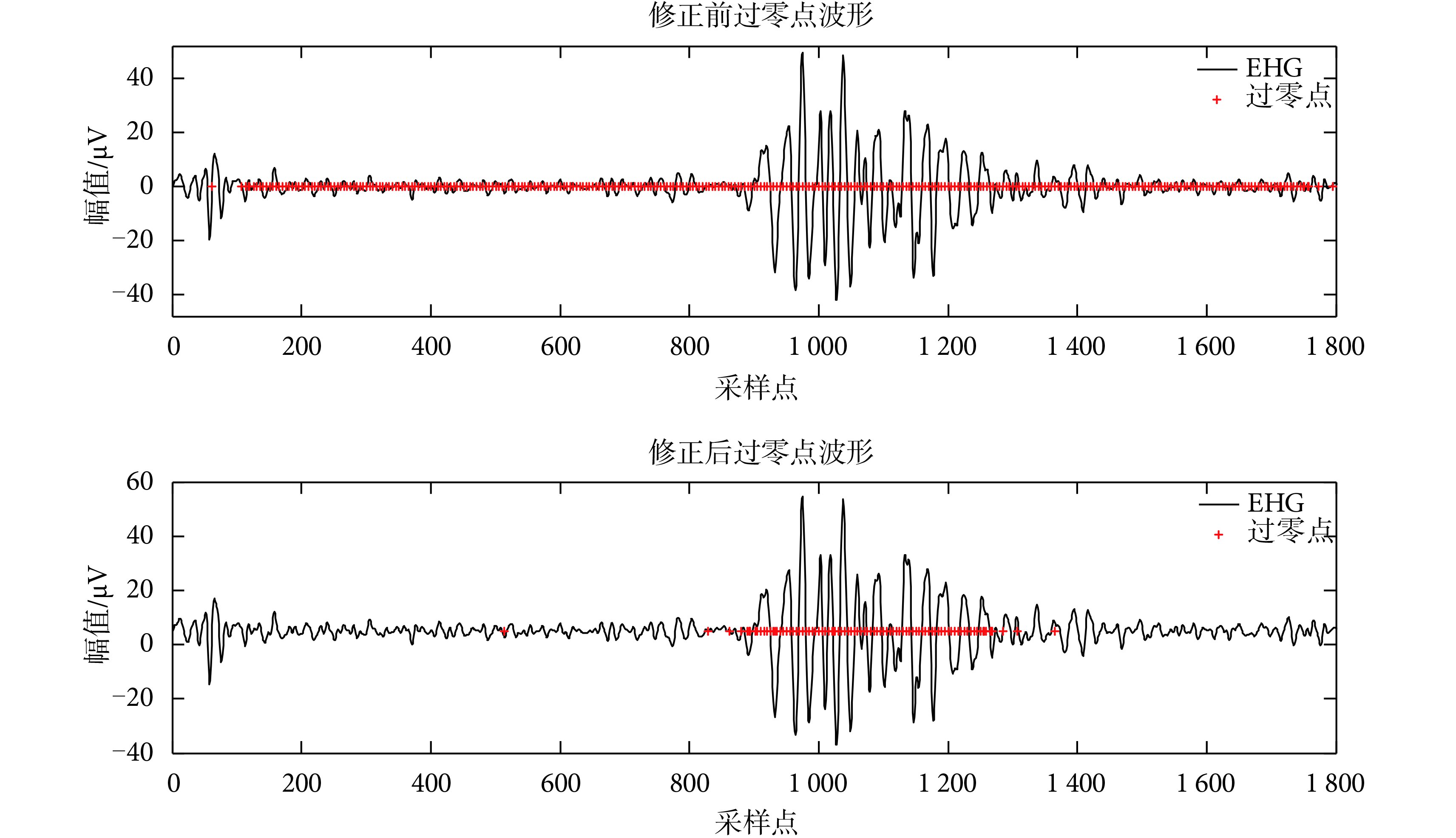圖3
過零點修正前后對比
Figure3.
Comparison before and after zero-crossing correction
2.3 EHG 信號平滑
RMS 方法對脈沖性噪聲的抑制能力非常有限，影響了信號包絡的提取精度。當脈沖性噪聲出現在非爆發波段，這種干擾將更加明顯，提取到的信號包絡容易出現虛假波峰。為了有效克服上述問題，在應用 RMS 方法之前，本文先對采集的 EHG 信號進行平滑處理，去除脈沖性噪聲。常用的平滑處理方法有均值濾波和中值濾波。均值濾波速度較快，算法簡單，但該方法是將噪聲進行分攤，因而只能稍微減弱噪聲；中值濾波是一種基于排序統計理論的非線性信號處理技術，算法簡單，能夠有效抑制噪聲，對脈沖噪聲的濾除效果較好[14]。因此，本文采用的是中值濾波方法對 EHG 信號進行平滑處理，濾除脈沖性噪聲。
中值濾波是基于排序統計理論的非線性信號處理技術，基本原理是把數字序列中一點的值用該點一個鄰域中各點值的中值代替，從而消除脈沖性噪聲，其實質是以誤差的絕對值之和達到最小來確定濾波器輸出響應的方法。由于 EHG 信號是一維的數字信號，因而這里只介紹一維離散情況下的中值濾波算法。選取濾波窗口長度為Ld=2d+1 (d為正整數)對離散信號S(n)( n=1, 2, , N)進行中值濾波處理。設在第n時刻，窗口內的信號樣本表示為：，且n—d≥1，n+d≤N。其中S(n)為位于窗口中心的信號樣本值。對窗口內2d+1個信號樣本值按從小到大的順序排列后，取中間值Y(n)替代原來的 S(n)，即將 Y(n)定義為中值濾波的輸出值。這一過程的數學表達式為：
| $ \hspace{-10pt}Y(n) = Med[S(n - d), \cdot \! \cdot \! \cdot ,S(n), \cdot \! \cdot \! \cdot ,S(n + d)] $ |
式中Med[·]表示所求窗口內所有樣本值的中位數。
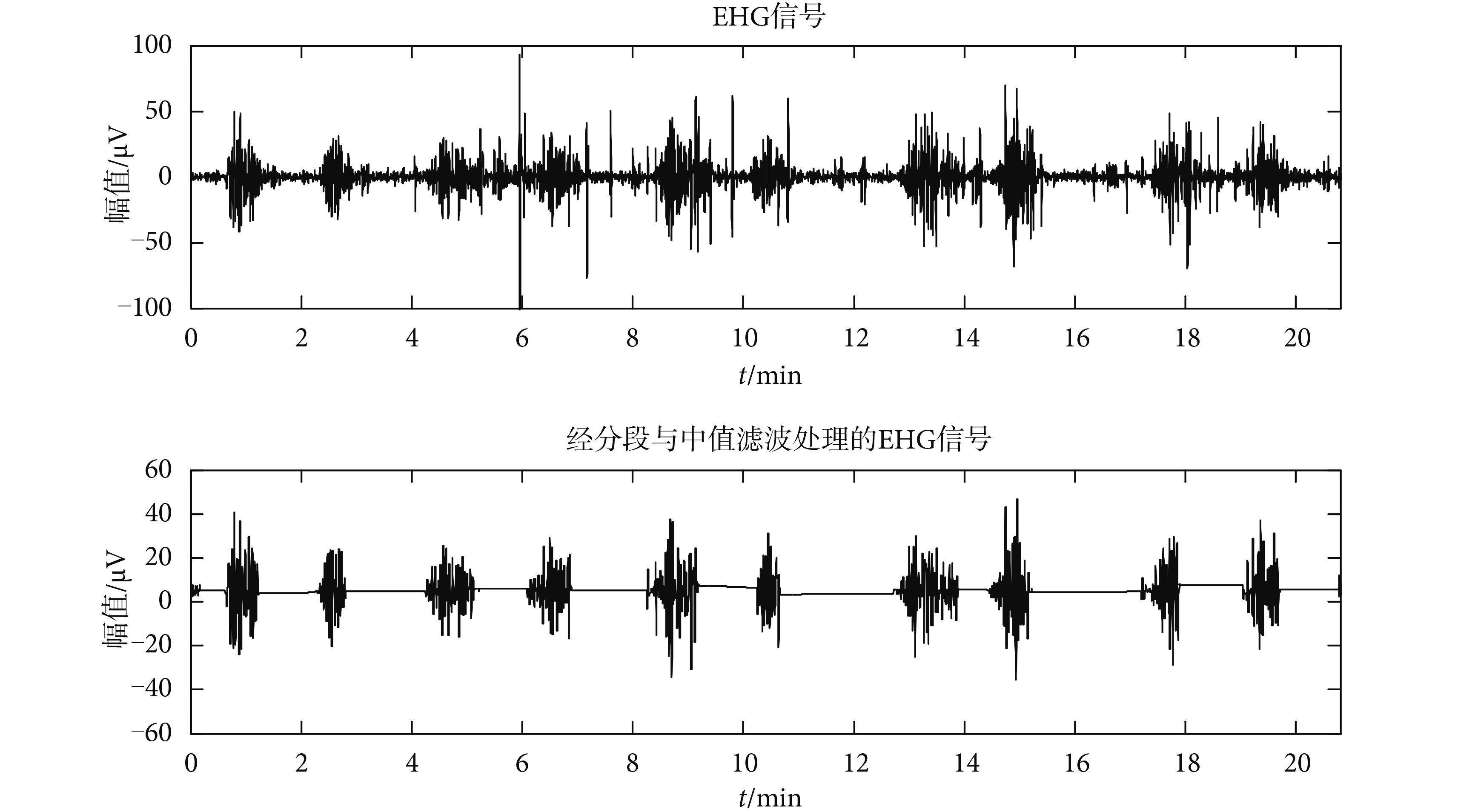
中值濾波的效果取決于濾波窗口的長度。若窗口取得太窄，去噪效果不明顯，處理后的信號中會殘留脈沖性噪聲；若窗口太寬，不僅計算量迅速增加，同時還會導致有用信息的丟失。為了能夠有效去除脈沖性干擾，并且不丟失過多的有用信號，許多學者提出來改進型的中值濾波算法，自動調節濾波窗口長度[15-16]。本實驗結合實際信號特點，改進了上述窗口選擇方式。在經過上述信號處理后，已經將 EHG 信號分為爆發波段和非爆發波段，這里可以對窗口長度為固定值的經典中值濾波算法進行細微改動，對爆發波段和非爆發波段分別應用不同的窗口長度。由于 EHG 信號非爆發波段理論上不包括有用信息，本文對該波段采用相對較寬的濾波窗口，窗口長度為 70 個樣本點。而爆發波通常表現為振蕩波形，脈沖性噪聲加載在信號上，由實驗得知，脈沖性噪聲的寬度通常很小，若窗口取得太寬，勢必導致有用信息的丟失，因而本文采用的窗口長度為 10 個樣本點。 EHG 信號經過中值濾波后的效果如圖 4所示。從圖中可以看出，經過分段中值濾波后的 EHG 信號，脈沖性噪聲基本被消除。對于強脈沖性噪聲，濾波后仍有少量毛刺存在，但是幅值已大大減小。
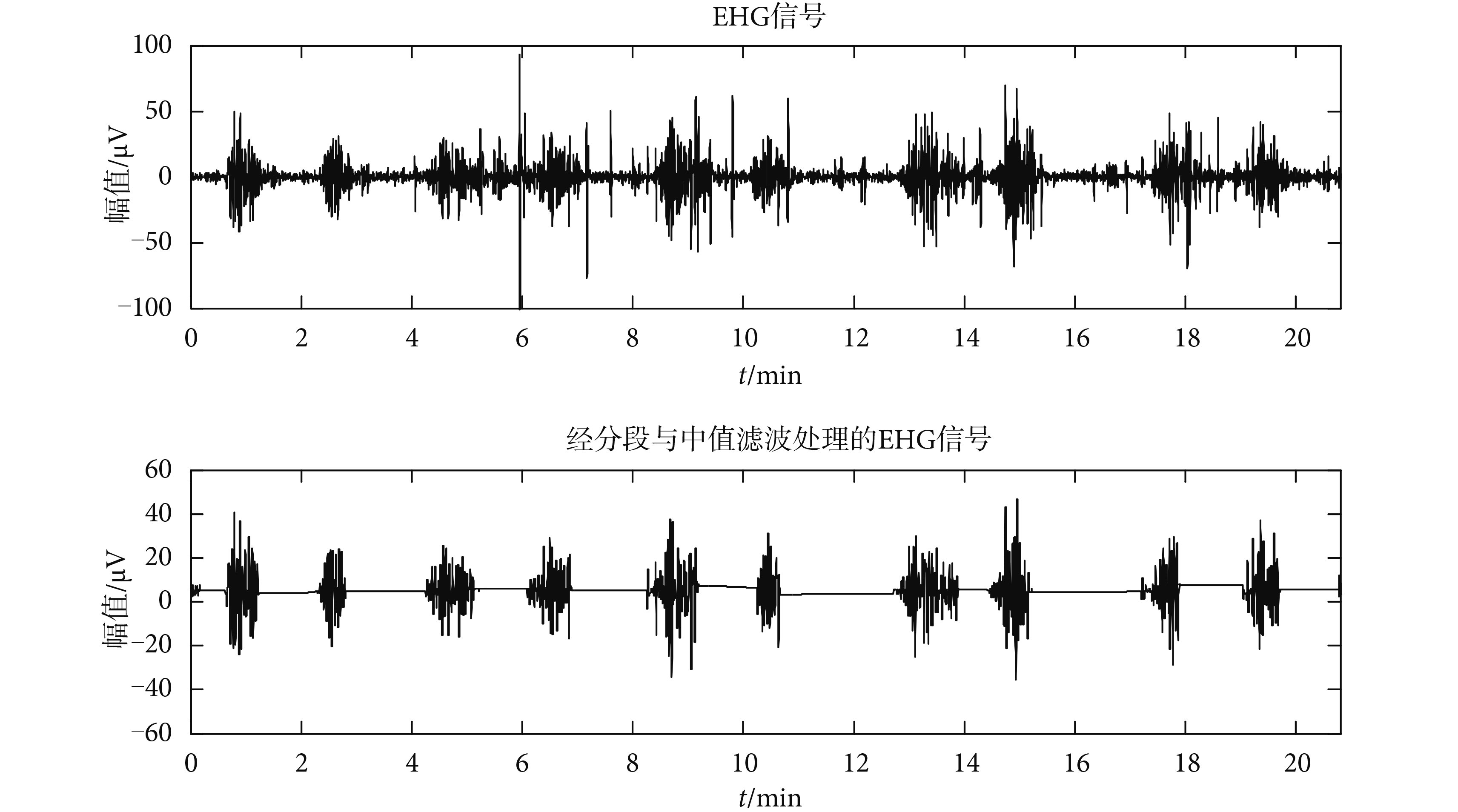圖4
經分段與中值濾波處理后的 EHG 信號
Figure4.
EHG signal after segmenting and median filtering
2.4 IEMG 信號提取
本文采用的 IEMG 提取法同樣為 RMS 統計方法。經過上述改進方法的處理之后，非爆發波段的脈沖性噪聲基本上被全部去除，爆發波段疊加的脈沖噪聲也有一定衰減，濾波后的 EHG 信號中保留了較為清晰完整的爆發波信號。使用上述 RMS 法作用于濾波處理后的 EHG 信號，同時本文選用的移動窗口為漢寧窗，長度為 40 s（400個采樣點），步長為 1 s。在 400 個樣本點寬度的窗口中，第i個樣本點的幅值應取[i—100, i+299]范圍的 RMS 值。上述參數的選擇能夠保證 EHG 中過零樣本點被充分利用，并且避免爆發波段邊緣出現明顯跳躍。改進后算法提取到的 IEMG 如圖 5所示。
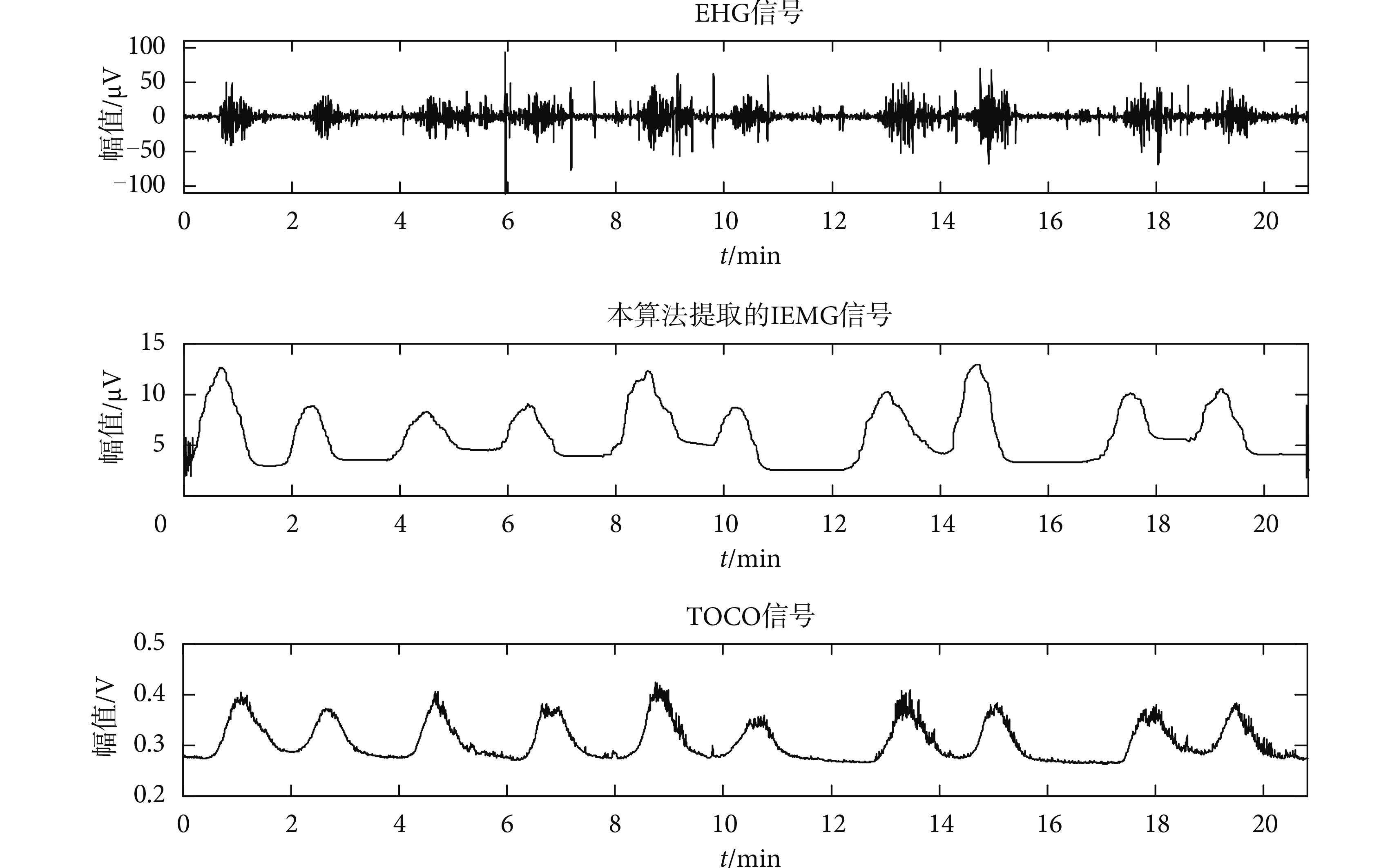圖5
改進 RMS 算法提取的 IEMG
Figure5.
IEMG extracted by the improved RMS algorithm
3 實驗結果
3.1 實驗說明
在研究期間，本實驗記錄了 58 名孕產婦的子宮收縮狀態，實驗中所使用的平臺來自于 ADIntruments 公司，其型號為 PowerLab 4/26，最大采樣率 100 kS/s，24 位 ADC。在進行子宮收縮信號采集之前，孕產婦被告知使用腹部電極采集腹部 EHG 信號，同時利用臨床上廣泛采用的宮縮壓檢測方法 TOCO 同步記錄子宮收縮狀態，經孕產婦同意后方能進行相關信號采集。
本實驗中信號采樣率為 1 000 Hz，每例信號的采集時間根據臨床實際情況而定，其中大部分信號采集長度在 30 min左右。在信號的實際處理過程中，為了提高信號處理速度，并且在不影響信號固有性質的情況下，我們對原始信號進行 1/100的重采樣。此外，為了評估本文提出算法的性能表現，實驗中使用 3 種算法對 58 例信號進行分析：傳統 RMS 統計法（記為算法一），由蔡坤[17]提出的基于數學形態學的 RMS 法（記為算法二），本文改進的 RMS 法（記為算法三）。其中算法二不僅能夠大大減弱脈沖性干擾對 IEMG 提取的影響，而且對 EHG 信號中的白噪聲也有一定的抑制作用。實驗中對每一例 EHG 信號分別使用三種算法，并得到對應的 EHG 信號包絡。
為了對比分析三種算法識別爆發波的性能參數，在對 58 例 EHG 信號處理后，統計三種算法對子宮肌電爆發波的識別靈敏度及陽性預測值（positive predictive value，PPV），研究中以臨床上常用的宮縮檢測方法 TOCO 為參考依據，對比分析三種算法識別出的 IEMG 信號與 TOCO 檢測出的波形，若算法識別的 IEMG 信號與 TOCO 檢測宮縮波相對應，則將該信號記為正確識別波形；對于在 TOCO 信號中無宮縮波且 EHG 中沒有出現明顯子宮爆發波時，而 IEMG 信號在對應位置出現宮縮，則將該信號記為錯誤識別波形。對于每一例 EHG 信號，分別利用三種算法得到靈敏度與 PPV。其中靈敏度為該算法正確識別子宮收縮個數與 TOCO 法識別數的比值，PPV 為該算法正確識別子宮收縮數與識別總數比值。
3.2 三種算法效果比較
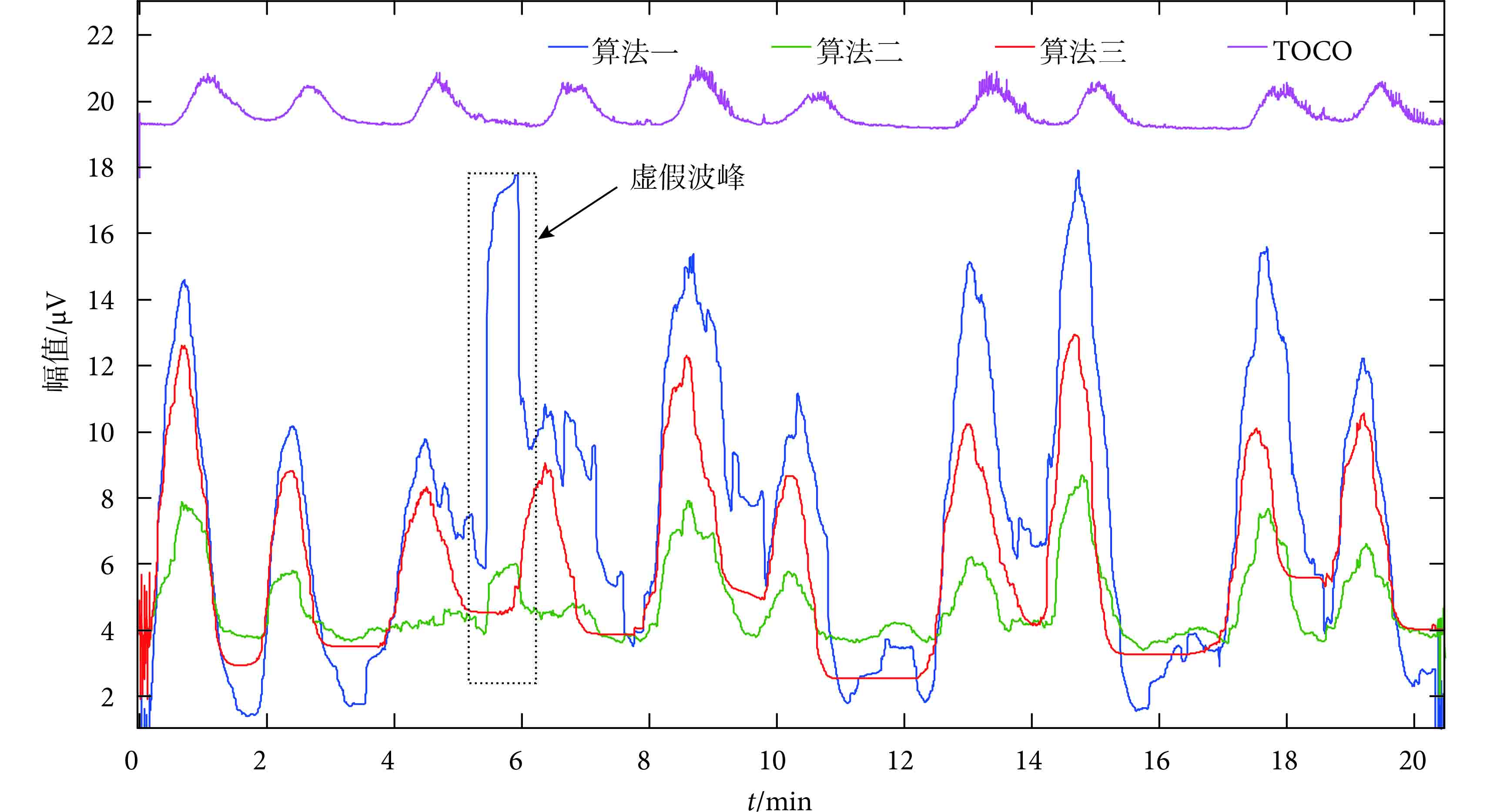
三種子宮收縮爆發波識別算法的分析結果如圖 6所示，算法一能夠識別出清晰爆發波段，其提取的 IEMG 信號幅值要高于后兩種算法；算法二提取的 IEMG 信號在幅值上低于算法一，但該方法在識別爆發波個數與信號平滑方面要優于算法一。然而，這兩種算法均無法抑制脈沖性噪聲對 IEMG 提取的影響，在波形中的 5~10 min 范圍內，由于脈沖性噪聲的存在，導致提取的 IEMG 中出現了虛假波峰，同時也對真實波峰的識別造成了干擾。相對于前兩種算法在克服脈沖性噪聲方面的不足，算法三在經過過零點檢測、分段濾波后，能夠有效濾除脈沖干擾對子宮肌電包絡提取的影響，并且從圖中可以看出，由算法三得到的信號包絡與 TOCO 信號具有更高的一致性。
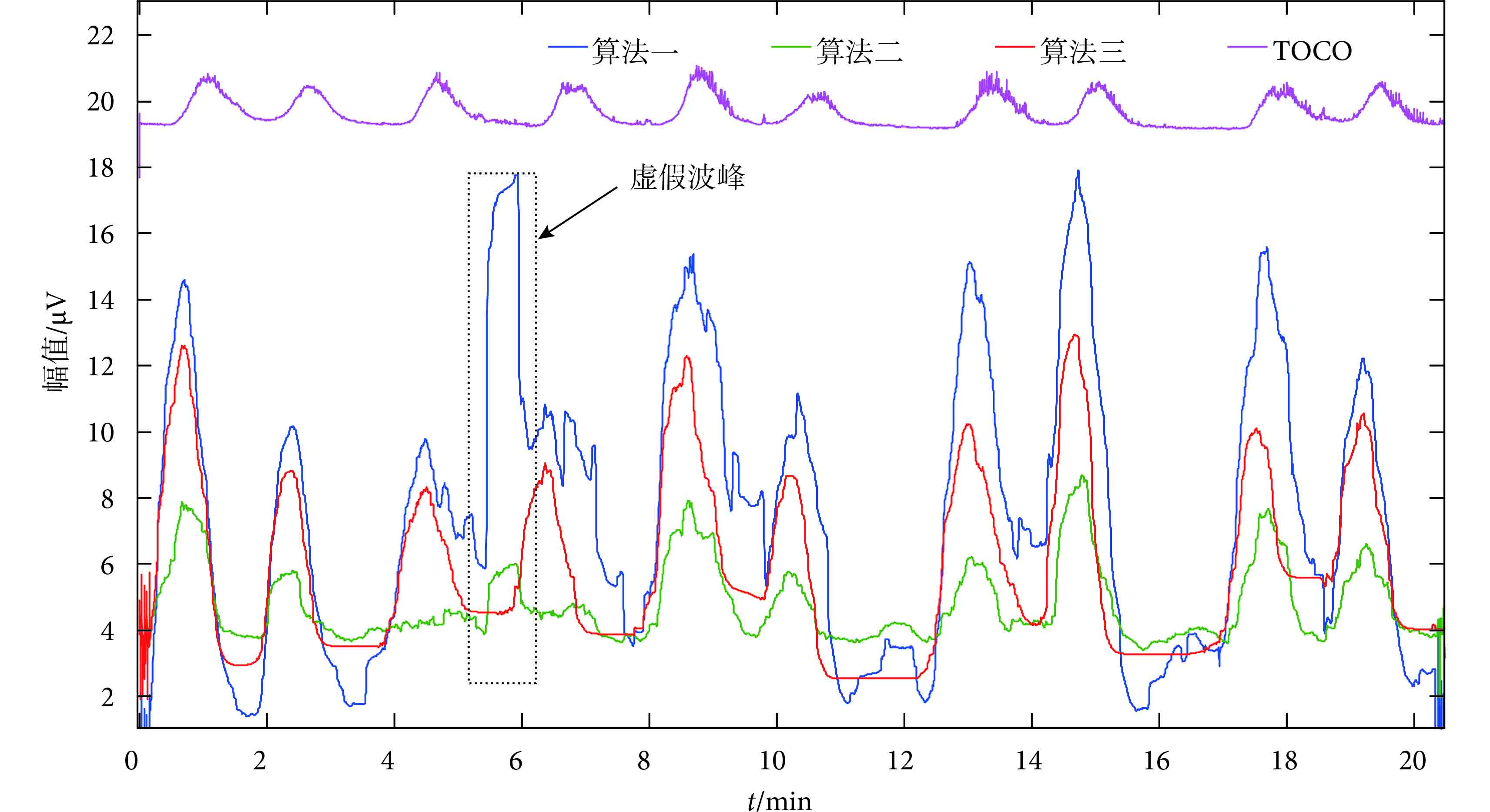圖6
三種算法提取的 IEMG 與 TOCO 比較
Figure6.
Comparison between TOCO and IEMGs extracted by three algorithms
三種算法在提取子宮肌電包絡上的表現如表 1所示，本文主要通過提取子宮包絡反映子宮收縮狀態，爆發波檢出率在很大程度上反映了算法對子宮收縮的靈敏度。通過對 58 例臨床上采集的孕產婦 EHG 信號處理結果的統計分析可知，算法二與算法三在子宮肌電包絡提取靈敏度上要遠高于傳統 RMS 算法；同時，算法三在 PPV 方面也要高于前兩種算法。
表1
三種算法識別IEMG的結果
Table1.
Results of uterine contractions identified by three algorithms
4 結論
本文提出了一種改進的子宮肌電包絡提取算法，其能夠有效抑制 EHG 信號中脈沖性噪聲對子宮肌電包絡提取的干擾，并且使獲得的 IEMG 信號更加平滑，子宮爆發波識別準確率更高。在本算法中，先根據 EHG 信號過零率將信號分為爆發波段與非爆發波段，再對兩部分信號利用不同窗口寬度濾波器進行平滑濾波，最后經過 RMS 統計處理，得到平滑、準確的 IEMG。
對比分析三種算法處理 58 例子宮肌電的統計結果可知，本文算法能夠有效識別出子宮肌電的爆發波，其靈敏度要明顯高于前兩種，此外，該算法所得 PPV 值要遠高于前兩種算法，這表明該算法在檢測真實子宮爆發波方面擁有更高的準確度。由此可見，本文所提出的方法能夠實現子宮肌電包絡的準確識別與檢測。
引言
分娩力描記法（tocodynamometer, TOCO）作為一種檢測子宮收縮的方法，被廣泛用于產前與產中的子宮收縮壓力檢測[1]。但該方法在測量準確性和靈敏度上存在一定局限性，因此，近些年人們試圖利用從腹部電極采集到的子宮肌電（electrohysterogram, EHG）信號提取子宮收縮圖形，即子宮肌電強度（intensity of uterine electromyogram, IEMG）。由于子宮收縮是由子宮平滑肌細胞周期性極化與去極化引起，因此，通過從腹部電極采集到的 EHG 來檢測子宮肌電包絡與傳統 TOCO 法測得宮縮信號十分相近[2-3]。為了進一步研究兩者之間的關系，很多學者提出了各自的子宮肌電包絡提取算法，Shulgin 等[4]通過對 EHG 的慢波（頻率為 0.005~0.3 Hz，幅值為 0.5~15 mV）與快波(頻率為 0.1~3 Hz，幅值為 0.02~0.5 mV)進行幅值解調法來提取IEMG 信號；Horoba 等[5]、Shulgin等[4]先根據均方根（root mean square, RMS）統計法提取子宮肌電信號包絡，再利用漢明窗補償功率泄漏。此外，為了有效去除腹部肌電中由電極位置、皮膚阻抗等造成的干擾，其通過在基準值上加上檢測窗口中最大值與最小值差值的 0.25 作為閾值來進行收縮檢測，此方法能夠有效檢測出宮縮波，但是由 EHG 信號中混疊的脈沖性噪聲所引起的小范圍波動也被當作爆發波檢測出來。
對于包含少量脈沖性噪聲的 EHG 而言，很多現有的子宮肌電信號包絡提取算法都能取得較好的效果[5-8]，在宮縮次數檢測以及包絡的形狀方面相差不多。但在實際的臨床檢測中，由于各種因素而產生的脈沖性噪聲疊加在子宮肌電上，對 IEMG 的提取造成較大影響，這主要表現在所獲得的包絡圖形中可能出現虛假波峰。
由此，本文提出一種子宮肌電信號包絡提取的改進算法，用以解決上述問題。根據 EHG 信號的過零率（zero-crossing rate, ZCR）將其劃分為爆發波段與非爆發波段，并對兩種波段采用不同窗口的信號處理方法, 最后得出子宮肌電包絡信號。
1 子宮肌電信號 RMS 處理
由產婦或孕婦腹部體表電極記錄得到的 EHG 信號被稱為體表子宮肌電[9]。為了得到該信號，臨床上通過貼附在孕產婦腹部的 Ag-AgCl 表面電極記錄腹部電信號，由于記錄的信號中包含 EHG、母親心電、胎兒心電、脈沖性噪聲等，因此需要對采集到的腹部信號進行帶通濾波，去除不需要的成分，保留 EHG 信號，并由該信號提取 IEMG。RMS 統計法是一種從 EHG 信號中提取 EHG 包絡的常用方法，其中 EHG 包絡表示子宮肌電動作電位振幅圍繞一定靜息電位的變化[4]。采用標準差用以衡量數據值偏離均值的程度，由于相應的常數分量在前期的信號處理部分已經去除，EHG 信號的平均值為 0。因此，標準差等于信號的均方根：
| $ RES = { \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{x_i}^2} } } $ |
其中 xi 表示 EHG 信號中第i點的幅值，計算窗口長度N的選取對于信號處理的結果有較大影響，根據實驗分析可知，一般選擇寬度 60 s、步長為 3 s 的移動窗口得到相應的 RMS 值。此外，為了抵消頻譜泄漏，移動窗口選用漢寧窗，表達式如下所示：
| $ {y_i} = 0.5{x_i}(1 - \cos \frac{{2{{π}}i}}{{N - 1}}) $ |
其中 xi 為輸入信號，即第i點的 EHG 幅值，yi 為對應的輸出信號。圖 1所示為一例 EHG 時域信號以及通過上述方法提取到的 EHG 包絡信號。由于在實際的臨床測量中，獲得的 EHG 信號會混疊由電磁干擾等因素產生的脈沖性噪聲[7]，從圖中不難發現，在記錄時間 5~7 min內出現明顯的脈沖性噪聲，使用傳統 RMS 法提取到的包絡出現了虛假波峰。這可能會誤導臨床上對宮縮的判斷，因此，為了克服 EHG 信號中脈沖性噪聲對包絡提取造成的干擾，本文對傳統 RMS 算法進行了改進。
圖1
傳統 RMS 提取的 IEMG
Figure1.
IEMG extracted by the traditional RMS algorithm
2 改進 RMS 算法提取 IEMG
2.1 EHG 過零檢測識別爆發波的可行性
在傳統的 TOCO 監護中，通常采用兩個指標識別宮縮波：宮縮幅值與持續時間，即當信號的幅值與基線差值大于設定閾值并持續一段時間時，該段信號被視為宮縮波。與 TOCO 曲線相比，EHG 為非平穩信號，其表現為峰電活動較為頻繁的爆發波[10]，振幅變化范圍不確定，因此不能根據振幅來識別爆發波。理論上，EHG 信號爆發波段（宮縮期）信號過零點數目明顯不同于非爆發波段（間歇期）信號過零點數目[11]。圖 2為 EHG 信號的局部細節圖，從中可以看出，在宮縮期，峰電活動頻繁，信號的過零點數目明顯大于間歇期。方法上，過零檢測可以對小范圍信號進行準確檢測[12-13]，從而提高爆發波的辨識度。因此，利用過零點數目來識別 EHG 信號的爆發波段是可行的。
圖2
EHG 局部細節圖
Figure2.
The detail views of EHG
2.2 EHG 信號分段
本方法主要根據信號波段的過零點數來區分 EHG 信號爆發波段與非爆發波段，對于一段長度為 M 的 EHG 離散信號而言，其過零點數可由下式求得：
| $ {\rm{ZC}} = \frac{1}{2}\sum\limits_{i = 1}^M {\left| {{\mathop{\rm sgn}} [x(i)] - {\mathop{\rm sgn}} [x(i - 1)]} \right|} $ |
其中 ZC 為過零點數，為了不受信號長度 M 的影響，本文采用過零率來識別爆發波。過零率的定義如下：
| $ {\rm{ZCR}} = {\rm{ZC}}/M $ |
其中 ZCR 為過零率，本文設置長度為 300 個樣本點、步長為1 的滑動窗口，該窗口長度的選取既能有效濾除虛假過零點的干擾，同時也避免了窗口過寬造成計算量的增加，根據公式(4)計算出滑動窗口內信號的過零率。設某采樣點坐標為i，并計算出[i—100, i+199]范圍內的 ZCR 值，若 ZCR 值大于設定閾值，則取該點為過零點，反之，為非過零點。對于實際采集到的 EHG 信號而言，在 EHG 非爆發波段可能會出現一些小的波動，通過上述方法判斷后將得到大量假過零點，如圖 3頂圖所示。為解決上述問題，本實驗在計算過零率之前，先將 EHG 信號整體向上小幅度平移。由于信號微小波動的幅度遠遠小于爆發波的峰電幅值，因此，直接將 EHG 信號向上小幅度平移既能有效濾除假過零點，又不會影響爆發波段的過零點數目，文中采用的上移幅度為 0.005 mV。根據修正前后的過零點波形可知，修正后的 EHG 信號中過零點大部分落在爆發波段，這有利于后續信號的進一步處理。
圖3
過零點修正前后對比
Figure3.
Comparison before and after zero-crossing correction
2.3 EHG 信號平滑
RMS 方法對脈沖性噪聲的抑制能力非常有限，影響了信號包絡的提取精度。當脈沖性噪聲出現在非爆發波段，這種干擾將更加明顯，提取到的信號包絡容易出現虛假波峰。為了有效克服上述問題，在應用 RMS 方法之前，本文先對采集的 EHG 信號進行平滑處理，去除脈沖性噪聲。常用的平滑處理方法有均值濾波和中值濾波。均值濾波速度較快，算法簡單，但該方法是將噪聲進行分攤，因而只能稍微減弱噪聲；中值濾波是一種基于排序統計理論的非線性信號處理技術，算法簡單，能夠有效抑制噪聲，對脈沖噪聲的濾除效果較好[14]。因此，本文采用的是中值濾波方法對 EHG 信號進行平滑處理，濾除脈沖性噪聲。
中值濾波是基于排序統計理論的非線性信號處理技術，基本原理是把數字序列中一點的值用該點一個鄰域中各點值的中值代替，從而消除脈沖性噪聲，其實質是以誤差的絕對值之和達到最小來確定濾波器輸出響應的方法。由于 EHG 信號是一維的數字信號，因而這里只介紹一維離散情況下的中值濾波算法。選取濾波窗口長度為Ld=2d+1 (d為正整數)對離散信號S(n)( n=1, 2, , N)進行中值濾波處理。設在第n時刻，窗口內的信號樣本表示為：，且n—d≥1，n+d≤N。其中S(n)為位于窗口中心的信號樣本值。對窗口內2d+1個信號樣本值按從小到大的順序排列后，取中間值Y(n)替代原來的 S(n)，即將 Y(n)定義為中值濾波的輸出值。這一過程的數學表達式為：
| $ \hspace{-10pt}Y(n) = Med[S(n - d), \cdot \! \cdot \! \cdot ,S(n), \cdot \! \cdot \! \cdot ,S(n + d)] $ |
式中Med[·]表示所求窗口內所有樣本值的中位數。
中值濾波的效果取決于濾波窗口的長度。若窗口取得太窄，去噪效果不明顯，處理后的信號中會殘留脈沖性噪聲；若窗口太寬，不僅計算量迅速增加，同時還會導致有用信息的丟失。為了能夠有效去除脈沖性干擾，并且不丟失過多的有用信號，許多學者提出來改進型的中值濾波算法，自動調節濾波窗口長度[15-16]。本實驗結合實際信號特點，改進了上述窗口選擇方式。在經過上述信號處理后，已經將 EHG 信號分為爆發波段和非爆發波段，這里可以對窗口長度為固定值的經典中值濾波算法進行細微改動，對爆發波段和非爆發波段分別應用不同的窗口長度。由于 EHG 信號非爆發波段理論上不包括有用信息，本文對該波段采用相對較寬的濾波窗口，窗口長度為 70 個樣本點。而爆發波通常表現為振蕩波形，脈沖性噪聲加載在信號上，由實驗得知，脈沖性噪聲的寬度通常很小，若窗口取得太寬，勢必導致有用信息的丟失，因而本文采用的窗口長度為 10 個樣本點。 EHG 信號經過中值濾波后的效果如圖 4所示。從圖中可以看出，經過分段中值濾波后的 EHG 信號，脈沖性噪聲基本被消除。對于強脈沖性噪聲，濾波后仍有少量毛刺存在，但是幅值已大大減小。
圖4
經分段與中值濾波處理后的 EHG 信號
Figure4.
EHG signal after segmenting and median filtering
2.4 IEMG 信號提取
本文采用的 IEMG 提取法同樣為 RMS 統計方法。經過上述改進方法的處理之后，非爆發波段的脈沖性噪聲基本上被全部去除，爆發波段疊加的脈沖噪聲也有一定衰減，濾波后的 EHG 信號中保留了較為清晰完整的爆發波信號。使用上述 RMS 法作用于濾波處理后的 EHG 信號，同時本文選用的移動窗口為漢寧窗，長度為 40 s（400個采樣點），步長為 1 s。在 400 個樣本點寬度的窗口中，第i個樣本點的幅值應取[i—100, i+299]范圍的 RMS 值。上述參數的選擇能夠保證 EHG 中過零樣本點被充分利用，并且避免爆發波段邊緣出現明顯跳躍。改進后算法提取到的 IEMG 如圖 5所示。
圖5
改進 RMS 算法提取的 IEMG
Figure5.
IEMG extracted by the improved RMS algorithm
3 實驗結果
3.1 實驗說明
在研究期間，本實驗記錄了 58 名孕產婦的子宮收縮狀態，實驗中所使用的平臺來自于 ADIntruments 公司，其型號為 PowerLab 4/26，最大采樣率 100 kS/s，24 位 ADC。在進行子宮收縮信號采集之前，孕產婦被告知使用腹部電極采集腹部 EHG 信號，同時利用臨床上廣泛采用的宮縮壓檢測方法 TOCO 同步記錄子宮收縮狀態，經孕產婦同意后方能進行相關信號采集。
本實驗中信號采樣率為 1 000 Hz，每例信號的采集時間根據臨床實際情況而定，其中大部分信號采集長度在 30 min左右。在信號的實際處理過程中，為了提高信號處理速度，并且在不影響信號固有性質的情況下，我們對原始信號進行 1/100的重采樣。此外，為了評估本文提出算法的性能表現，實驗中使用 3 種算法對 58 例信號進行分析：傳統 RMS 統計法（記為算法一），由蔡坤[17]提出的基于數學形態學的 RMS 法（記為算法二），本文改進的 RMS 法（記為算法三）。其中算法二不僅能夠大大減弱脈沖性干擾對 IEMG 提取的影響，而且對 EHG 信號中的白噪聲也有一定的抑制作用。實驗中對每一例 EHG 信號分別使用三種算法，并得到對應的 EHG 信號包絡。
為了對比分析三種算法識別爆發波的性能參數，在對 58 例 EHG 信號處理后，統計三種算法對子宮肌電爆發波的識別靈敏度及陽性預測值（positive predictive value，PPV），研究中以臨床上常用的宮縮檢測方法 TOCO 為參考依據，對比分析三種算法識別出的 IEMG 信號與 TOCO 檢測出的波形，若算法識別的 IEMG 信號與 TOCO 檢測宮縮波相對應，則將該信號記為正確識別波形；對于在 TOCO 信號中無宮縮波且 EHG 中沒有出現明顯子宮爆發波時，而 IEMG 信號在對應位置出現宮縮，則將該信號記為錯誤識別波形。對于每一例 EHG 信號，分別利用三種算法得到靈敏度與 PPV。其中靈敏度為該算法正確識別子宮收縮個數與 TOCO 法識別數的比值，PPV 為該算法正確識別子宮收縮數與識別總數比值。
3.2 三種算法效果比較
三種子宮收縮爆發波識別算法的分析結果如圖 6所示，算法一能夠識別出清晰爆發波段，其提取的 IEMG 信號幅值要高于后兩種算法；算法二提取的 IEMG 信號在幅值上低于算法一，但該方法在識別爆發波個數與信號平滑方面要優于算法一。然而，這兩種算法均無法抑制脈沖性噪聲對 IEMG 提取的影響，在波形中的 5~10 min 范圍內，由于脈沖性噪聲的存在，導致提取的 IEMG 中出現了虛假波峰，同時也對真實波峰的識別造成了干擾。相對于前兩種算法在克服脈沖性噪聲方面的不足，算法三在經過過零點檢測、分段濾波后，能夠有效濾除脈沖干擾對子宮肌電包絡提取的影響，并且從圖中可以看出，由算法三得到的信號包絡與 TOCO 信號具有更高的一致性。
圖6
三種算法提取的 IEMG 與 TOCO 比較
Figure6.
Comparison between TOCO and IEMGs extracted by three algorithms
三種算法在提取子宮肌電包絡上的表現如表 1所示，本文主要通過提取子宮包絡反映子宮收縮狀態，爆發波檢出率在很大程度上反映了算法對子宮收縮的靈敏度。通過對 58 例臨床上采集的孕產婦 EHG 信號處理結果的統計分析可知，算法二與算法三在子宮肌電包絡提取靈敏度上要遠高于傳統 RMS 算法；同時，算法三在 PPV 方面也要高于前兩種算法。
表1
三種算法識別IEMG的結果
Table1.
Results of uterine contractions identified by three algorithms
4 結論
本文提出了一種改進的子宮肌電包絡提取算法，其能夠有效抑制 EHG 信號中脈沖性噪聲對子宮肌電包絡提取的干擾，并且使獲得的 IEMG 信號更加平滑，子宮爆發波識別準確率更高。在本算法中，先根據 EHG 信號過零率將信號分為爆發波段與非爆發波段，再對兩部分信號利用不同窗口寬度濾波器進行平滑濾波，最后經過 RMS 統計處理，得到平滑、準確的 IEMG。
對比分析三種算法處理 58 例子宮肌電的統計結果可知，本文算法能夠有效識別出子宮肌電的爆發波，其靈敏度要明顯高于前兩種，此外，該算法所得 PPV 值要遠高于前兩種算法，這表明該算法在檢測真實子宮爆發波方面擁有更高的準確度。由此可見，本文所提出的方法能夠實現子宮肌電包絡的準確識別與檢測。
