本研究采用腦電信號的整體子波熵和分尺度子波熵研究腦電信號的信息復雜性，探索兒童失神癲癇（CAE）發作的動力學機制。研究采集兒童失神癲癇患者及正常對照的腦電信號；采用連續子波變換提取腦電信號的時頻特征；采用子波功率譜分析提取分尺度功率譜特征；根據分尺度功率譜計算整體子波熵和分尺度子波熵，分析整體子波熵和分尺度子波熵隨 CAE 發作的時間演變過程，并與正常對照進行比較。結果顯示：CAE 患者發作期腦電信號的整體子波熵顯著低于正常對照組，也低于發作間期。CAE 發作時第 12 尺度（對應中心頻率 3 Hz）的分尺度子波熵顯著高于正常對照，α 頻帶（中心頻率 10 Hz）腦電節律的子波熵明顯低于正常對照。腦電信號整體子波熵可以反映腦電信號的復雜程度，CAE 發作時腦電信號的信息復雜度明顯降低。子波熵降低有可能成為癲癇發作的特征神經電生理參數，為癲癇發作的神經調控技術的研究提供依據。
引用本文： 張美云, 王晨, 張瑩, 陳英, 吳波, 張玉琴, 王鳳樓. 兒童失神癲癇發作期腦電信號子波熵分析. 生物醫學工程學雜志, 2018, 35(4): 530-538. doi: 10.7507/1001-5515.201701002 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
腦電作為伴隨人生始終的神經生理活動，記錄著人腦在各種生理、病理過程中的神經系統電活動行為，與神經系統的生理、生化、病理過程密切相關，包含了非常豐富的人體神經生理活動信息，是一種高度復雜的信號，是不同尺度電活動信息的綜合。如何從腦電信號中提取有價值的定量信息一直是腦電研究的重要課題。
傳統的衡量信號有序無序程度的指標是譜熵，它的計算基于傅立葉變換的功率譜[1-2]。譜熵在 20 世紀 90 年代初開始被應用于腦電信號的分析[3-4]。由于傅立葉變換應用的前提是信號為平穩信號，且窗寬是固定的，而反映大腦生理過程的腦電信號是高度不平穩的非線性復雜信號，因此譜熵在腦電信號的分析中受到限制。子波變換可以同時顯示時域頻域兩方面信息，且不需要信號是平穩的，所以非常適合腦電信號的分析。子波熵作為衡量系統的有序程度的指標已被應用于腦電信號分析。
癲癇是中樞神經系統異常放電引起的發作性神經功能異常，腦電圖可以記錄這種異常放電的全過程，是診斷和研究癲癇的重要手段。目前臨床工作中對癲癇腦電信號的識別主要依賴于醫生的視覺識別和經驗性判斷。客觀定量分析腦電信號，從中提取有價值的信息和參數對于癲癇的臨床診斷和發作機制的研究具有重要意義。但是癲癇發作過程中，尤其是強直陣攣發作，經常伴有大量的肌電偽差，甚至將腦電成分完全淹沒，影響腦電的定量分析。另外癲癇發作腦電信號是瞬時急劇變化的信號，傳統的基于傅立葉變換的功率譜分析應用前提是信號是平穩的，因此對癲癇發作的腦電分析無能為力。子波變換和子波熵在癲癇發作腦電信號分析方面發揮了它的獨特優勢。
近年來，國內外學者用子波熵研究腦電信號、誘發電位（evoked potentials，EP）、事件相關電位（event-related potential，ERP）等的復雜程度，進一步揭示了大腦電活動的動力學機制。其應用主要在睡眠分期[5]、癲癇腦電信號的動態觀測[6]、網絡成癮[7]、麻醉深度的監測[8-9]等幾個方面。Rosso 團隊[10-12]提出了子波能量（wavelet energy）、子波熵（wavelet entropy）、相對子波熵（relative wavelet entropy）等概念，來研究短片段的自發腦電信號的頻率分布（子波能量）和有序程度（子波熵），及刺激后腦電信號的子波能量和子波熵的演變過程，提出腦電信號反映了不同頻率電活動的綜合，ERP 反映了腦電活動從無序到有序的過程，伴隨著腦電信號在一定頻率上同步化的增強。這一方法可以顯示受到刺激后腦電信號頻率上同步化的動態演變過程，從而加深了對腦動力學機制的理解，成為認知功能研究的一種新的方法。Emre 等[13]采用連續子波熵研究聽覺誘發電位（auditory evoked potentials，AEP），結果顯示較離散子波熵可以發現更多細節特征。
臨床工作中，對癲癇腦電信號的觀察多集中于波幅、頻率的檢測，或者是某個頻率上能量的改變。不同的癲癇發作可能出現特征性的腦電波型，成為臨床癲癇診斷分型的依據。然而引發大腦神經元異常放電的動力學機制是什么呢？推動癲癇的發作、擴散和終止的因素是什么呢？子波熵的改變可能是癲癇放電演變過程背后的動力學因素。本研究試用整體子波熵觀測兒童失神癲癇（child absence epilepsy，CAE）發作全過程的動態變化，總結子波熵在 CAE 發作過程中的演變規律。假設整體子波熵在癲癇的發作過程中降低，在癲癇結束時升高，那么它可能成為癲癇發作的自動監測指標，也可能成為評價癲癇治療效果和預后的定量參數。
1 實驗過程
1.1 研究對象
兒童失神癲癇組 15 例，男 6 例，女 9 例。年齡 4～15（8.0 ± 3.1）歲。病程 2 月～4 年。全部病例臨床表現和腦電圖均符合 1989 年國際癲癇與癲癇綜合征分類中兒童失神癲癇的診斷標準。對照組 12 例，男 4 例，女 8 例。年齡 5～15（7.6 ± 2.8）歲。均為健康兒童，生長發育正常，否認神經系統疾患。該研究經天津市人民醫院倫理委員會通過，所有被試者均由其監護人簽署知情同意書。
1.2 腦電信號采集
采用由日本 NIHONKOHDEN 公司生產的 EEG-2130 型數字腦電圖儀和 Ag/AgCl 頭皮電極，按國際標準導聯 10/20 系統安裝，以雙耳為參考電極，電阻抗 < 5 kΩ，被檢查者在安靜、清醒、閉目狀態下描記腦電信號，采樣頻率 200 Hz。在描記腦電圖前未使用過抗癲癇藥和鎮靜藥。兒童失神癲癇組共記錄 20 次失神癲癇發作，發作時間 4～30 s，對癲癇發作期全程及發作前 4 s 和發作后 4 s 的腦電信號，以 2 s 為一個數據片段進行分析；同時選擇同一患者背景信號平穩，無偽差的腦電信號 20 s，對照組選擇背景 20 s 腦電數據，按每個片段 2 s 進行分析，每段數據包含 400 個數據。腦電信號分析程序采用 Visual Studio C++ 6.0 編寫。
2 腦電信號分析方法
腦電圖描記后，對 16 位 A/D 卡采集的 21 個導聯的 20 s 原始腦電數據信號，以 2 s（400 個數據）為一段分析單位，采用連續子波變換提取腦電信號的時頻特征；采用子波功率譜分析提取分尺度功率譜特征；根據分尺度功率譜計算分尺度子波熵和整體子波熵。分析分尺度子波熵和整體子波熵隨癲癇發作的時間演變過程。
2.1 子波分析簡介
子波分析（wavelet analysis）是一種新的數字信號分析方法，通過信號與一個被稱為子波的基函數進行互相關運算，利用子波基函數在時間尺度上的伸縮運算功能對信號進行多尺度細化分析，將含有多尺度成分的復雜信號在局部時間段內進行頻帶分解。其中子波基函數是由一個子波母函數經過平移和伸縮變換而得到的一族外形相似但尺度不同的局部波動函數。子波基函數在時間上代表有限尺度范圍內的具有特定物理過程的“事件”或者“局部擾動的小的波”。
本研究采用的是連續子變換（continuous wavelet transform，CWT）。一維腦電信號
的連續子波變換定義為：
 |
其中子波函數族
是由子波母波函數
經過平移（參數
）和伸縮變換（參數
）而來：
 |
子波分析可以將貌似隨機和雜亂無序的多尺度非平穩的復雜信號在每一個瞬時按照頻帶進行分解，使大尺度低頻信號與小尺度高頻信號分離，從而同時提供時域、頻域兩方面的瞬態頻率信息。子波分析應用于神經電生理的復雜信號分析具有獨特的優勢：① 子波是定義在時域有限范圍內的局部小擾動，不需要信號是平穩的，可以自動分解和提取信號瞬時變化的時間局部多尺度特征；② 可以進一步提取信號時域、頻域的多方面的統計信息。
2.2 多尺度功率譜分析
根據子波系數
，腦電信號
的分尺度功率可以用各尺度子波功率譜密度函數表示，描述了分尺度腦電信號的功率強弱：
 |
2.3 腦電信號的子波熵
子波熵是基于子波變換，衡量非線性信號動力學行為有序、無序程度的一個量化指標。它可以提供信號非線性動力學過程復雜程度的信息，是衡量系統復雜程度的指標。
腦電信號的總功率是各分尺度信號功率的總和：
 |
用 p 對 p（a）進行歸一化，得到各分尺度功率在信號總功率中所占的百分比：
 |
本研究所采用的的子波熵為無量綱參數，腦電信號的分尺度子波熵
衡量了該尺度腦電信號成分所含信息的復雜程度，而整體子波熵
則反映了腦電各尺度成分在人腦活動過程中所包含的所有信息的總體復雜程度：
 |
 |
2.4 統計學分析
統計學分析采用 PASW Statistics 18 軟件，兒童失神癲癇患者發作期與發作間期腦電信號子波熵比較采用配對樣本的 t 檢驗，兒童失神癲癇發作間期與正常對照、發作期與正常對照腦電信號子波熵比較采用獨立樣本 t 檢驗。P < 0.05 為差異有統計學意義。
3 結果
3.1 視覺腦電圖
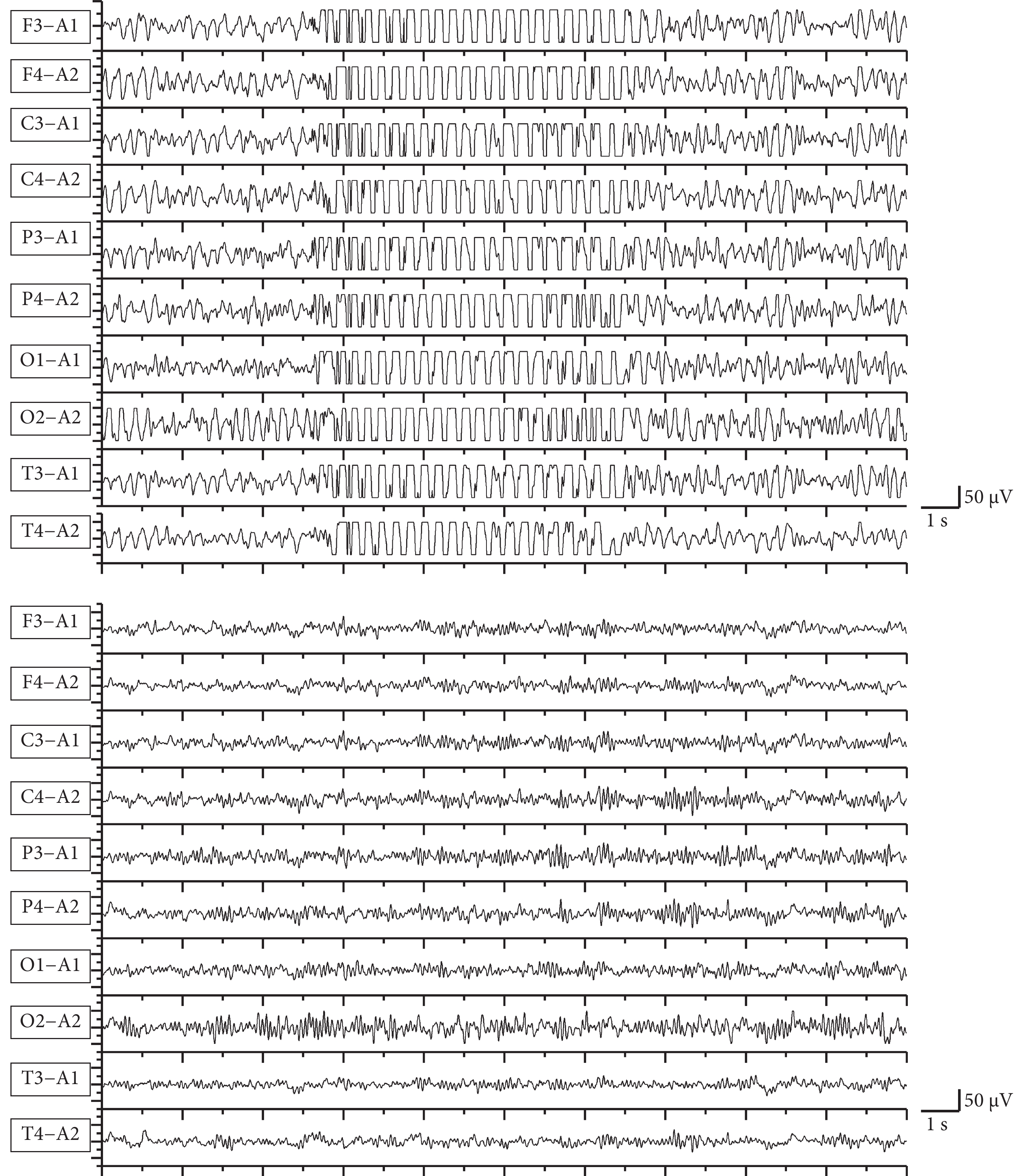
圖 1 給出了某典型 CAE 發作期腦電圖和正常對照腦電圖。發作時腦電圖（圖 1 上）表現為高波幅或超高波幅的節律性 3 Hz 的棘慢復合波，雙側同步對稱，發作、終止較快。正常兒童視覺腦電圖（圖 1 下）背景節律以 10 Hz 左右的 α 節律為主，α 節律枕區優勢，調節調幅好，未見明顯異常波型。
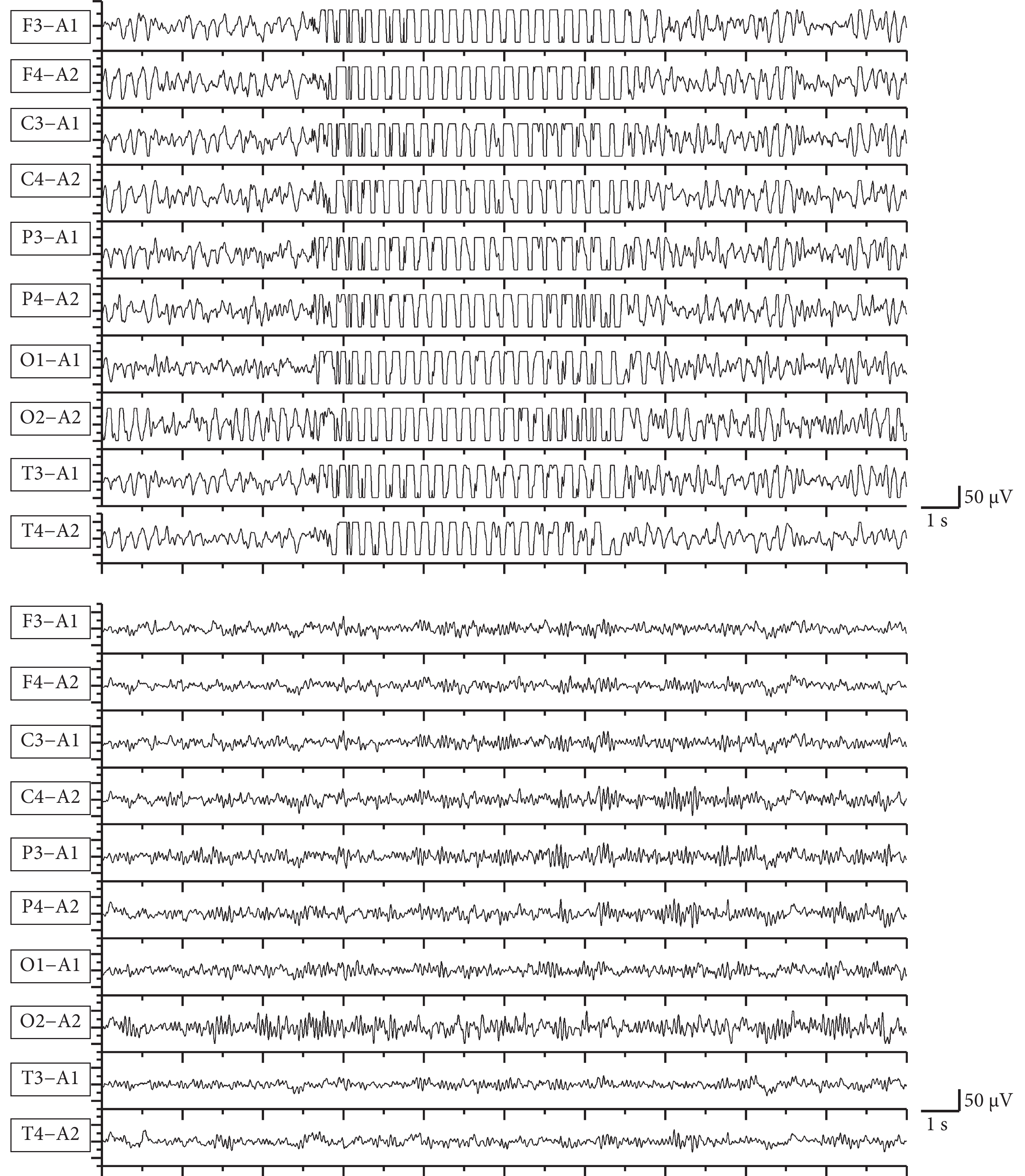圖1
CAE 發作期（上）和正常對照（下）腦電圖
Figure1.
Ictal EEG of CAE (above) and EEG of normal control (below)
3.2 子波系數等值線圖
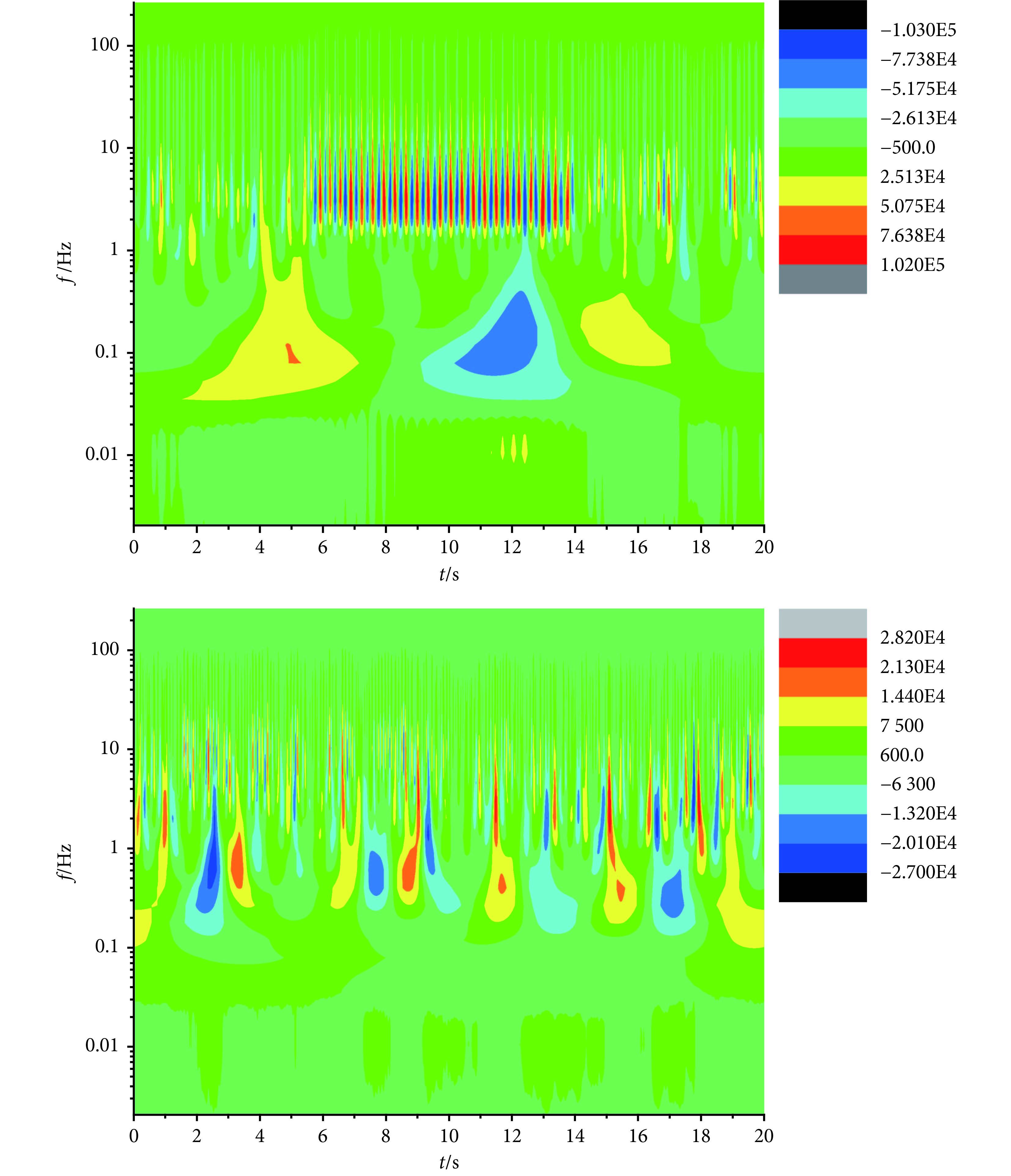
圖 2（上）為 CAE 從失神發作開始到結束的腦電信號進行子波變換多尺度分析的子波系數等值線圖。從圖 2（上）中可以清楚看到，CAE 發作主要表現為 12 尺度（對應頻率 3 Hz）的節律性增強，此時患者的臨床表現為雙眼凝視前方意識喪失，對外界刺激無反應，這時大腦神經元中的高波幅或超高波幅節律性 3 Hz 的棘慢復合波抑制了非線性多尺度關聯范圍的正常電生理信號，大腦神經網絡不能進行正常的信息的感知、認知活動。圖 2（下）為正常對照相應導聯腦電信號進行子波變換多尺度分析的子波系數等值線圖。與圖 2（上）相比，圖 2（下）中的 12 尺度（對應頻率為 3 Hz）的強度和節律相對較弱，沒有超強的節律性活動，正常對照兒童腦電信號尺度分布比較廣泛。
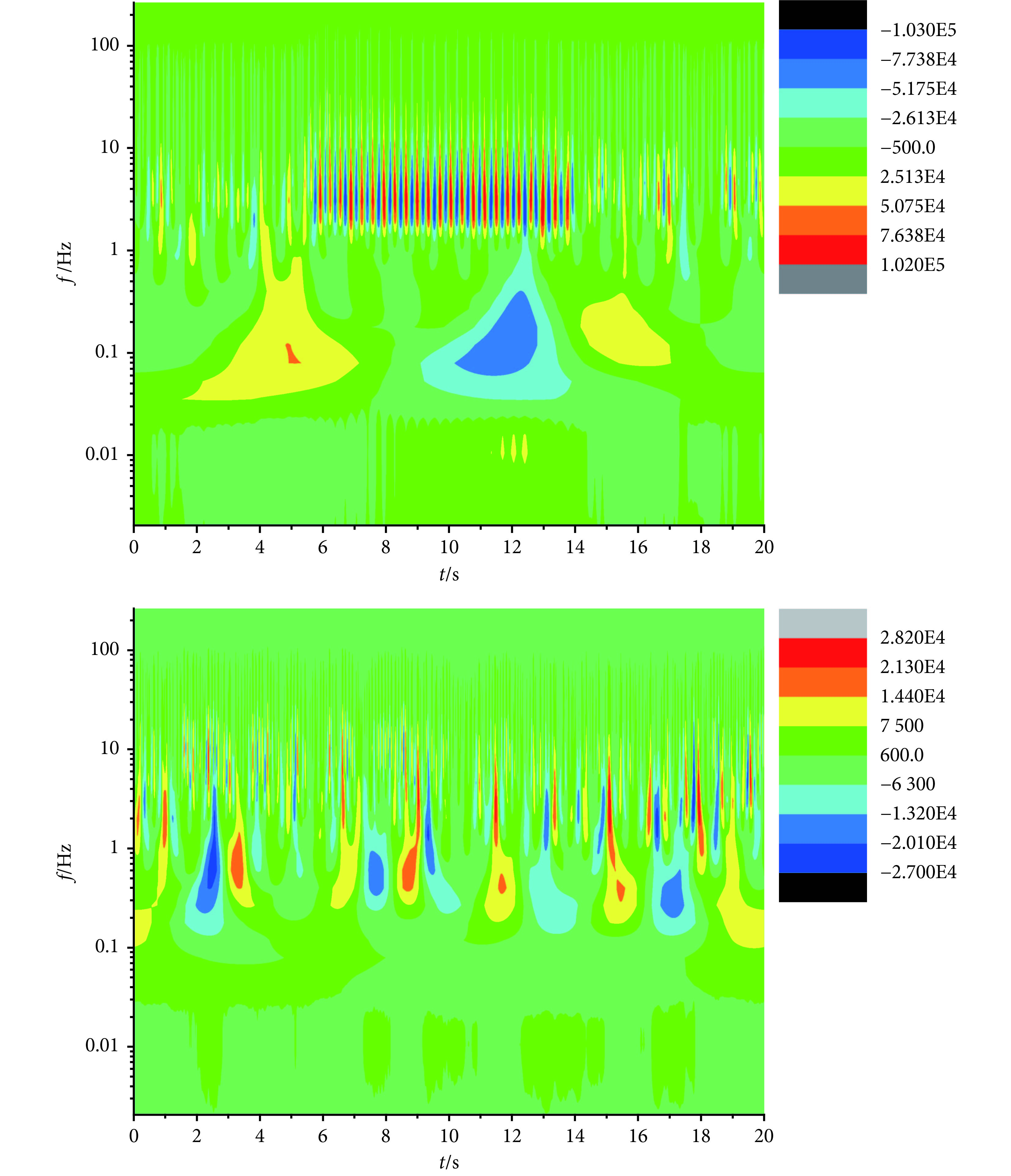圖2
CAE 發作期（上）和正常對照（下）腦電信號子波系數等值線圖
Figure2.
Contour of multi-scale wavelet coefficients for ictal EEG of CAE (above) and normal control (below)
3.3 整體子波熵隨時間演化
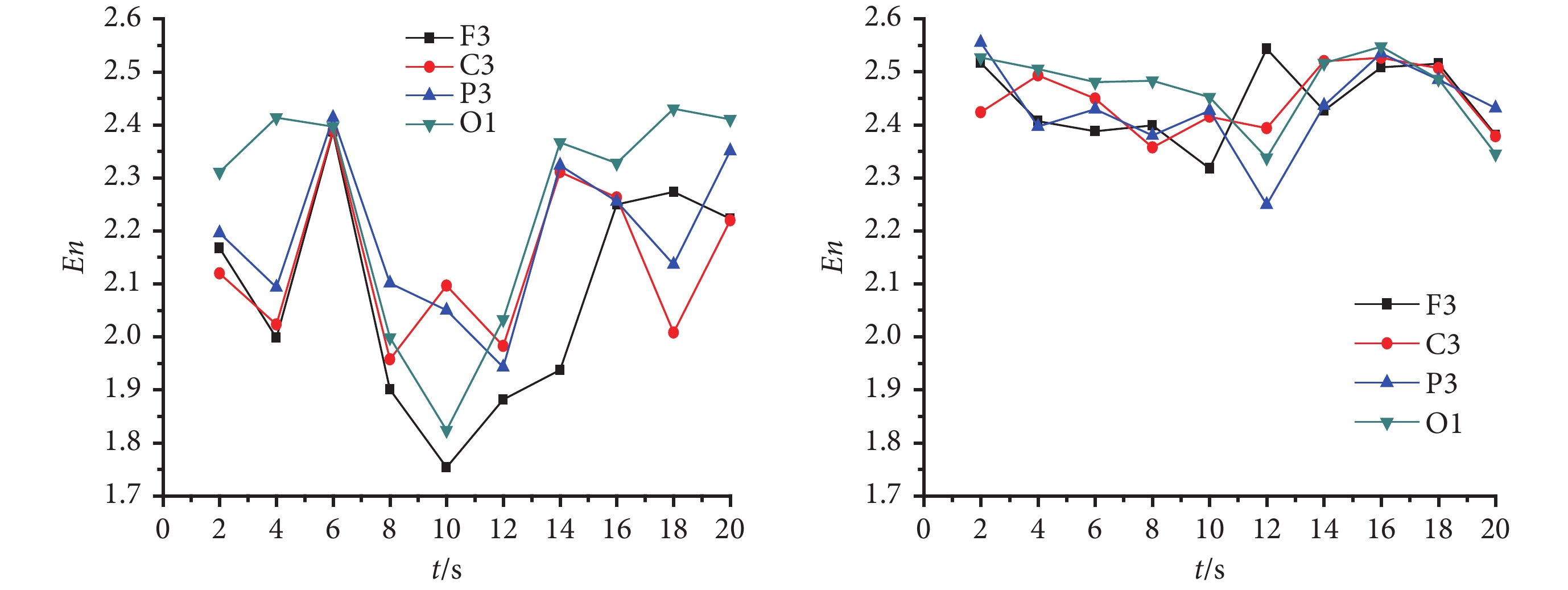
圖 3 給出了 CAE 發作期（左）和正常對照（右）F3、C3、P3、O1 等 4 個不同導聯腦電信號的整體子波熵。結合圖 3（左）和圖 3（右）可以看出，在失神癲癇發作的 6～14 s 期間，腦電信號的整體子波熵明顯低于正常對照，也明顯低于發作間期。表明失神癲癇發作時腦電信號的信息復雜度明顯降低，腦電信號中包含的信息量明顯減小。
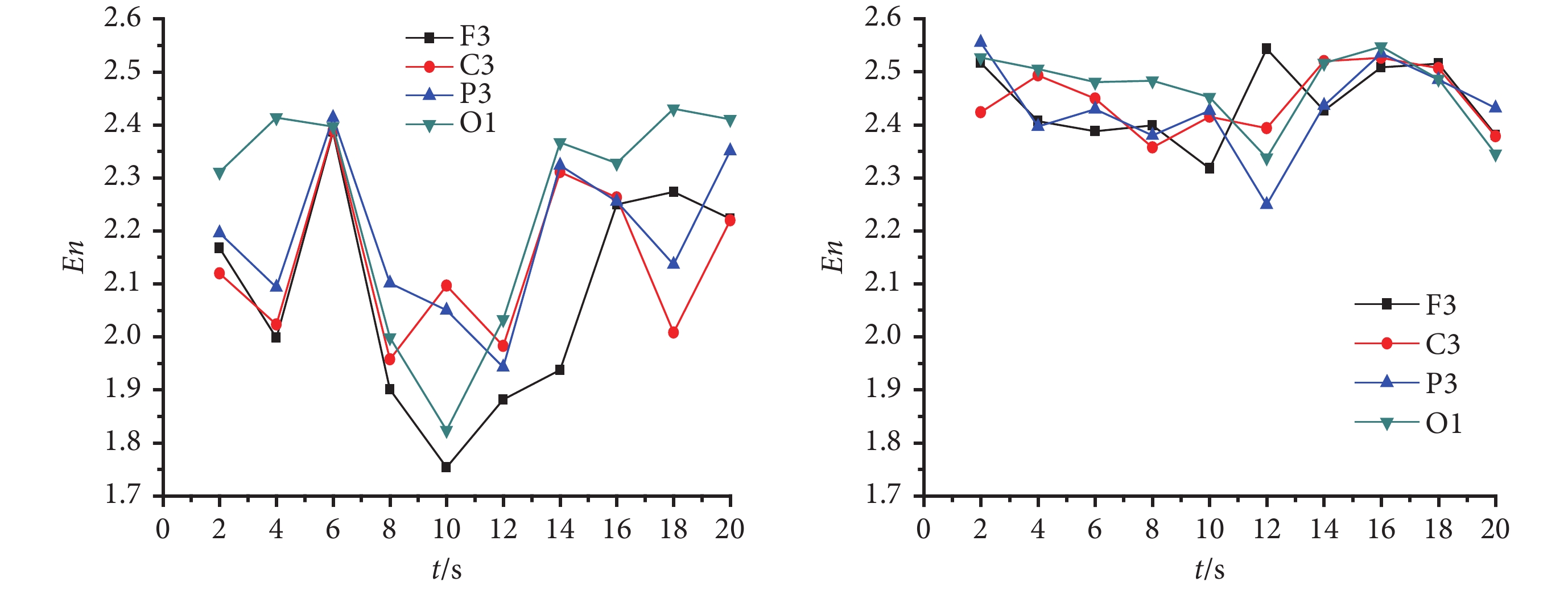圖3
CAE 發作期（左）和正常對照（右）不同導聯腦電整體子波熵
Figure3.
Integral wavelet entropy for ictal EEG of CAE（left）and normal control（rihgt）at different lead
3.4 分尺度子波熵隨時間演化
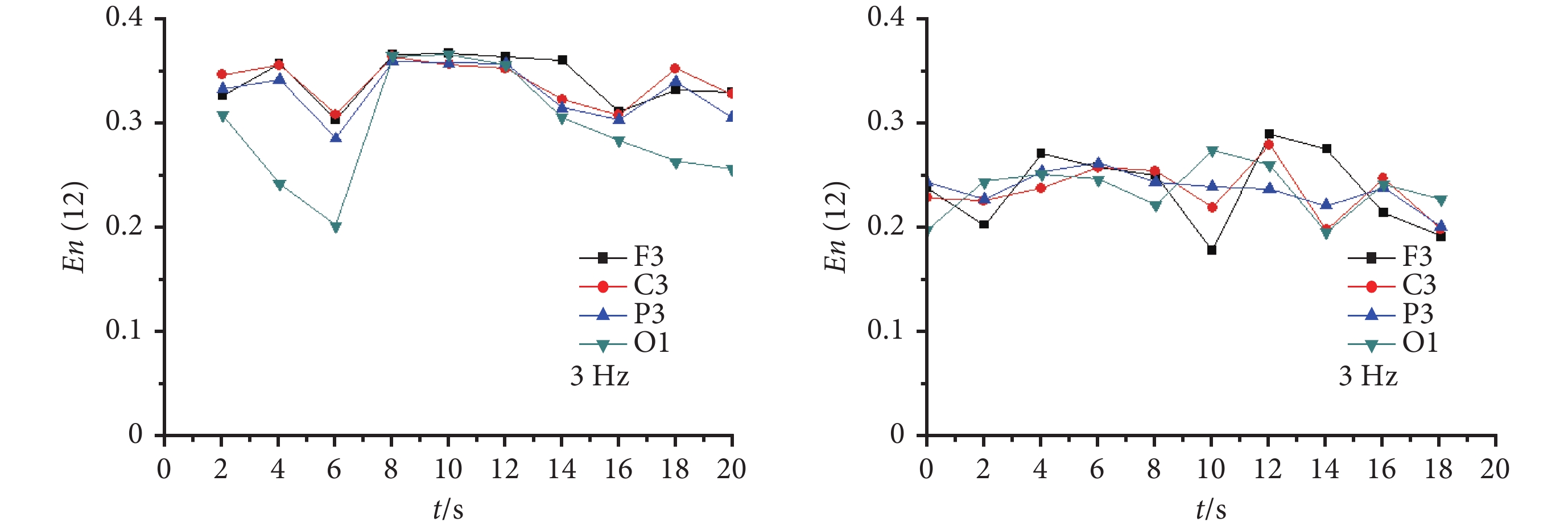
圖 4 給出了 CAE 發作期和正常對照不同導聯 3 Hz 腦電節律的子波熵。從圖 4 可以看出，CAE 發作期 3 Hz 腦電節律的子波熵明顯高于正常對照 3 Hz 腦電節律的子波熵。表明大腦神經元中的高波幅或超高波幅節律性 3 Hz 的棘慢復合波過強，抑制了大腦正常生理活動和功能。
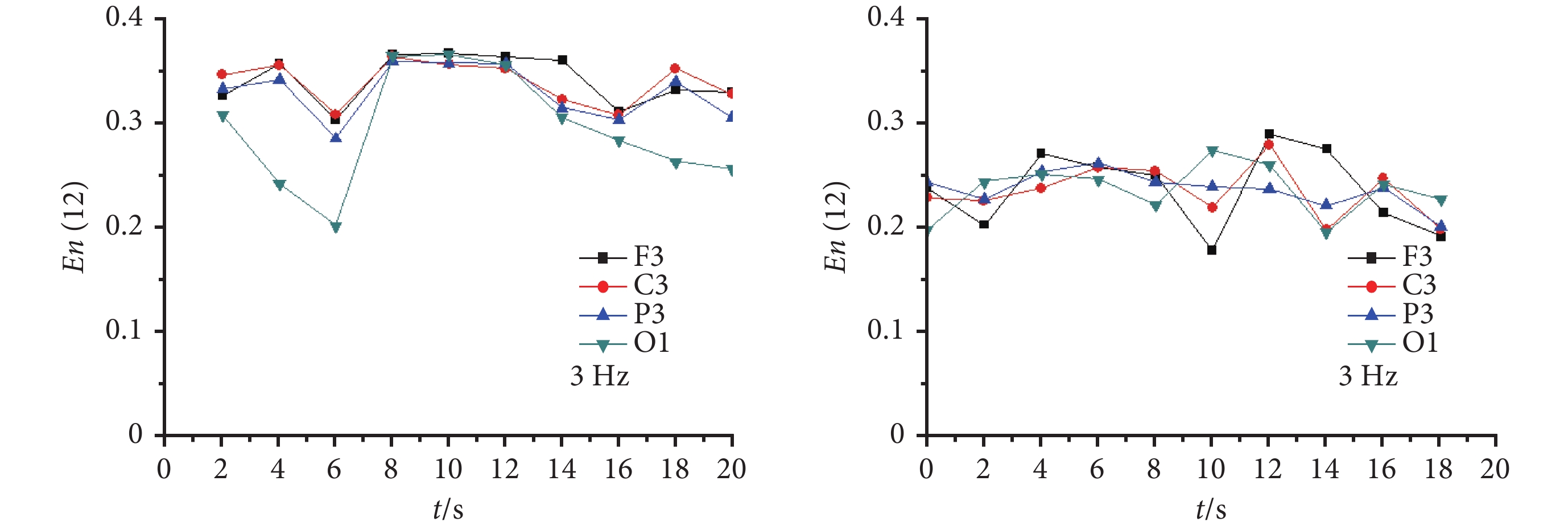圖4
CAE 發作期（左）和正常對照（右）不同導聯第 12 尺度（3 Hz）腦電節律子波熵
Figure4.
Individual scale 12 (3 Hz) wavelet entropy of ictal EEG of CAE (left) and normal control (rihgt) at different lead
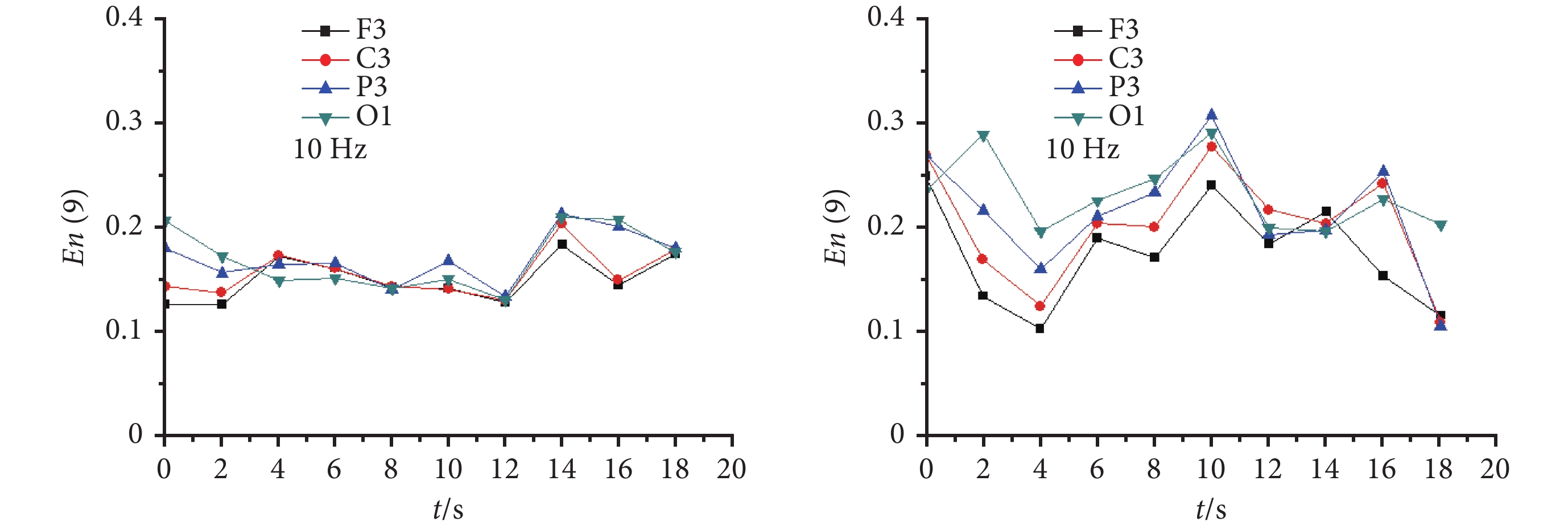
圖 5 給出了 CAE 發作期和正常對照不同導聯 α 頻帶（中心頻率 10 Hz）的腦電節律子波熵。從圖 5 可以看出，CAE 發作期 α 頻帶（中心頻率 10 Hz）腦電節律的子波熵明顯低于正常對照 α 頻帶（中心頻率 10 Hz）腦電節律的子波熵。表明 CAE 發作時大腦正常的節律性電活動受到抑制。
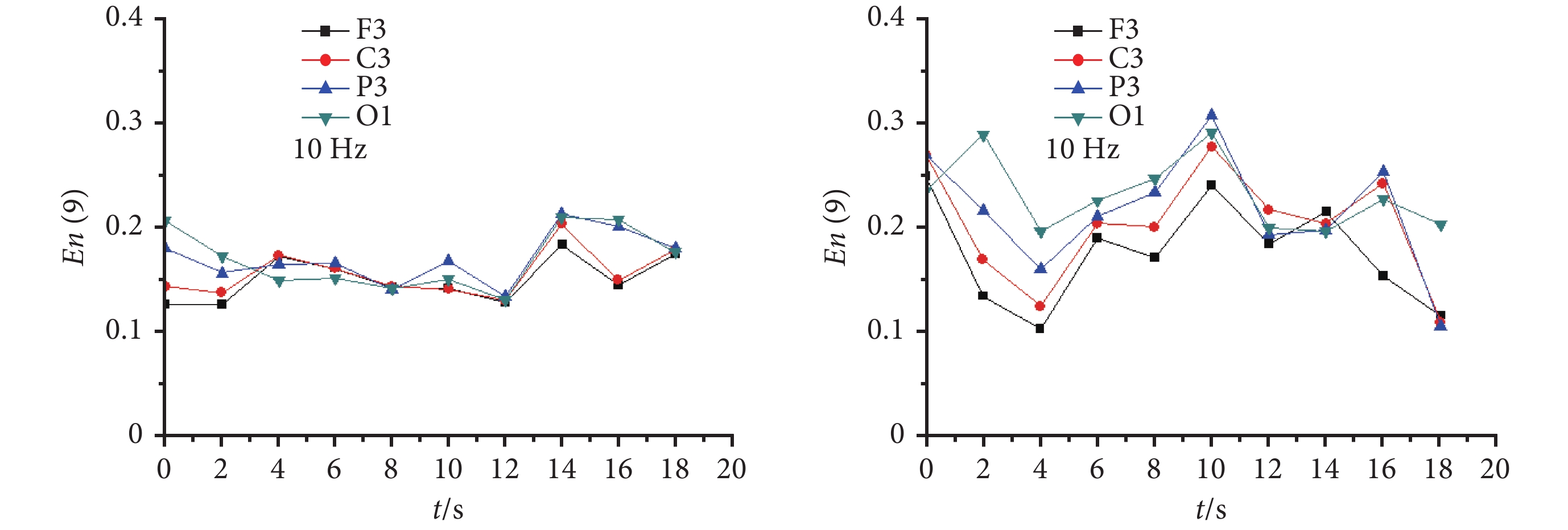圖5
CAE 發作期（左）和正常對照（右）不同導聯第 9 尺度（10 Hz）腦電節律子波熵
Figure5.
Individual scale 9 (10 Hz) wavelet entropy of ictal EEG of CAE (left) and normal control (rihgt) at different lead
3.5 統計學分析
兒童失神癲癇發作期與發作間期、正常對照腦電信號子波熵比較見表 1～3。結果顯示：兒童失神癲癇發作期腦電信號的整體子波熵 En 低于發作間期，也低于正常對照兒童；兒童失神癲癇發作期腦電信號的第 9 尺度（對應 10 Hz）的子波熵 En（9） 低于發作間期，也低于正常對照兒童；兒童失神癲癇發作期腦電信號的第 12 尺度（對應 3 Hz）的子波熵 En（12） 高于發作間期，也高于正常對照兒童。與正常同齡對照比較，兒童失神癲癇發作間期的腦電信號的整體子波熵顯著降低，而 10 Hz 和 3 Hz 的分尺度子波熵，兩組比較差異無統計學意義。
表1
兒童失神癲癇患者發作期與發作間期腦電信號子波熵比較（
）
Table1.
Comparison of wavelet entropy between ictal and inter-ictal EEG for CAE (
)
表2
兒童失神癲癇患者發作期與正常對照腦電信號子波熵比較（
）
Table2.
Comparison of wavelet entropy between ictal EEG for CAE and normal control (
)
表3
兒童失神癲癇患者發作間期與正常對照腦電信號子波熵比較（
）
Table3.
Comparison of wavelet entropy between inter-ictal EEG for CAE and normal control (
)
4 討論
子波熵是衡量非線性信號所含信息復雜程度的一個量化指標，它可以提供非線性信號復雜程度的信息。目前的一些研究表明，這一參數在癲癇發作過程中存在一定規律。
Blanco 等[14]基于子波系數，結合 Shannon entropy 的定義提出子波熵的概念，當時稱作 Information cost function，并將它應用于強直陣攣癲癇發作期腦電信號的分析[15-16]。此前強直陣攣發作由于劇烈肌電活動完全淹沒了腦電信號，無論是視覺識別還是定量分析都十分困難。臨床上嘗試應用肌肉松弛劑減少肌電的干擾，或采用傳統的濾波技術去除肌電所在的頻率成分，但結果仍不令人滿意[17]。研究采用視頻腦電儀記錄 1 例癲癇患者強直陣攣發作全過程，從視覺腦電中可以發現發作開始時出現高頻放電，強直期這種放電波幅增高，陣攣期由于肌電干擾淹沒了腦電信號。為了定量研究癲癇發作過程中腦電活動的動力學機制和演變過程，作者應用子波變換將腦電信號分解在不同頻帶上，應用子波熵來定量描述腦電信號的有序程度及演變過程。結果顯示可以去除肌電的影響，提取癲癇發作過程中的主要頻率在 10 Hz，發作結束時頻率減慢至 4 Hz，在發作過程中子波熵明顯降低，這表明發作過程中腦電活動的復雜程度降低。它直觀地反映了腦電活動的動力學過程，而且提取了發作過程中不同頻率腦電能量的聚集和轉化過程。
Rosso 等[18]采用歸一化的總子波熵（normalized total wavelet entropy，NTWE）研究兒童失神癲癇發作間期背景腦電信號，并與正常同齡兒童進行比較。兒童失神癲癇是年齡相關性癲癇發作類型，其視覺分析腦電背景是正常的，然而通過此研究發現兒童失神癲癇發作間期的背景腦電信號的 NTWE 低于正常同齡兒童，在發作期的腦電信號中 NTWE 的降低更為明顯。因此在未記錄到典型的 3 Hz 棘慢綜合放電的患者中，背景腦電 NTWE 降低為兒童失神癲癇的早期診斷提供了線索。而且 NTWE 作為腦電發育和成熟度的指標，為癲癇的發生與腦電成熟度之間的關系的研究提供了電生理依據。本研究結果表明，兒童失神癲癇發作期腦電信號的總子波熵明顯低于正常對照兒童，其發作間期腦電信號的整體子波熵也低于正常對照兒童，具有統計學意義，與 Rosso 的研究結果一致。
Rosso 等[19]對 8 例繼發性強直陣攣發作癲癇患者的 20 次發作進行分析，結果顯示在 1～3 s 的短暫的相位去同步化之后，出現波幅迅速增高的 10 Hz 的癲癇募集節律（epileptic recruiting rhythm），10 s 之后出現與陣攣項相關的低頻成分的增強，在每次肌肉的抽動均伴隨全面性多棘波發放。α 波和 θ 波的混合節律的出現預示發作的結束。NTWE 在發作前、發作后和發作中有明顯差異，在發作過程中 NTWE 明顯降低，表明腦電行為更加有序。這一現象提示癲癇灶觸發了腦電活動的一種自我組織狀態，影響了大腦對周圍事物的反映。Pereyra 等[20]采用基于子波變換的 Jensen-Shannon divergence（JSD）這一參數作為描述癲癇發作時腦電信號不同頻率成分的動力學過程。通過對強直陣攣癲癇發作腦電信號的分析，結果顯示 JSD 在癲癇發作過程中出現 5 個明顯的變化峰值，這 5 個峰值分別提示發作的開始、癲癇募集節律的出現、強直項向陣攣項的轉變、癲癇募集節律的結束以及發作結束。因此可以用這一參數定量分析癲癇發作過程中不同頻率成分隨時間的演變過程，并提出它可以應用于癲癇發作過程中不同腦區腦電信號的動力學特征的比較。Acharya 等[21]和 Wang 等[22]應用子波熵等參數設計腦電信號癲癇波的自動檢測系統，使癲癇的診斷和分類的準確性大大提高。
本研究采用連續子波變換的方法對腦電信號進行分解，以 2 s 為觀測單位，提取兒童失神癲癇發作過程中整體子波熵的演變規律，結果表明，失神癲癇發作期腦電信號整體子波熵明顯降低。國外學者對全身強直陣攣癲癇發作期腦電信號子波熵的研究表明其發作期腦電信號明顯降低[18-20]。推測子波熵降低可能是癲癇發作期腦電信號的共同特征，它反映了癲癇發作的動力學特征。熵的概念來源于熱力學第二定律，用來度量系統中的混亂程度，物質的平衡態是能量和熵相互競爭的結果。簡單地說，能量是有序結構的支柱，而熵則是無序結構的靠山。1948 年貝爾實驗室的電氣工程師香農（C Shannon）將熵引用到信息學領域[15]。能與熵何者更為重要，是一個不斷爭論的話題，能量可以看做事物存在的表現形式，而熵決定了自然過程演變的方向。因此對于癲癇腦電信號的熵的研究可能提示癲癇發作和終止的信息，不同類型的癲癇發作可能具有相似的動力學機制。對于子波熵的進一步研究有可能為癲癇的神經調控技術提供電生理依據。
本研究在研究整體子波熵的同時，進一步研究了兒童失神癲癇發作過程中分尺度子波熵的演變規律。結果表明，兒童失神癲癇發作過程中第 12 尺度，即 3 Hz 附近的子波熵明顯高于正常對照，而第 9 尺度，即 10 Hz 附近的子波熵明顯低于正常對照。這反映了兒童失神癲癇發作過程中能量在不同頻率間聚集和轉化的特征，提示不同頻率腦電信號攜帶的信息量。對于癲癇腦電信號分尺度子波熵的研究可能提示不同類型癲癇發作過程中能量和信息在不同頻率上的聚集和轉化的過程，為每種類型癲癇發作的動力學機制的研究提供幫助。
本研究顯示兒童失神癲癇發作間期的腦電信號的整體子波熵比正常同齡對照顯著降低，表明即使在發作間期，其腦電信號的復雜度仍低于正常，這與 Rosso 等[23]的研究一致，提示可能與兒童失神癲癇患兒腦發育相對落后有關。而兒童失神癲癇發作間期的腦電信號的 10 Hz 對應的第 9 尺度分尺度子波熵比正常同齡對照稍低，但差異無統計學意義，可能是由于正常兒童腦電信號中 α 節律優勢并不明顯有關。3 Hz 對應的第 12 尺度分尺度子波熵比正常同齡對照稍高，但差異無統計學意義，在部分受試者，正常對照組反而高于 CAE 患者發作間期的腦電信號，考慮為正常兒童中 3 Hz 腦電信號的復雜度也較高。兩組間分尺度子波熵是否存在差異，仍需增加樣本量作進一步研究。
目前的研究表明，子波熵對于癲癇發作的研究具有重要價值。進一步深入研究并緊密結合臨床，子波熵可能成為臨床上輔助疾病診斷和評估的電生理參數，同時為疾病的電生理機制的基礎研究提供理論依據。
5 結論
本文對失神癲癇發作期腦電信號和正常兒童腦電信號的整體子波熵和分尺度子波熵進行了分析研究，得到如下結論：
（1）腦電信號整體子波熵可以表現腦電信號的信息復雜程度，CAE 患者腦電的整體子波熵明顯低于正常對照組，CAE 患者發作期腦電的整體子波熵明顯低于發作間期腦電的整體子波熵，CAE 發作時腦電信號的信息復雜度明顯降低，推測這可能與 CAE 發作過程中腦電信號中包含的信息量明顯減小有關。
（2）分尺度子波熵表明單一頻帶腦電信號所含信息量，CAE 發作期 3 Hz 的分尺度熵增高，α 頻帶（中心頻率 10 Hz）的分尺度子波熵降低，推測這可能顯示了 CAE 發作時大腦正常節律性電活動受到抑制。
（3）本研究的結果顯示，子波熵這一參數在癲癇的發作過程中存在一定的規律，子波熵有可能成為癲癇發作的電生理參數，為癲癇發作動力學機制的研究提供幫助。
引言
腦電作為伴隨人生始終的神經生理活動，記錄著人腦在各種生理、病理過程中的神經系統電活動行為，與神經系統的生理、生化、病理過程密切相關，包含了非常豐富的人體神經生理活動信息，是一種高度復雜的信號，是不同尺度電活動信息的綜合。如何從腦電信號中提取有價值的定量信息一直是腦電研究的重要課題。
傳統的衡量信號有序無序程度的指標是譜熵，它的計算基于傅立葉變換的功率譜[1-2]。譜熵在 20 世紀 90 年代初開始被應用于腦電信號的分析[3-4]。由于傅立葉變換應用的前提是信號為平穩信號，且窗寬是固定的，而反映大腦生理過程的腦電信號是高度不平穩的非線性復雜信號，因此譜熵在腦電信號的分析中受到限制。子波變換可以同時顯示時域頻域兩方面信息，且不需要信號是平穩的，所以非常適合腦電信號的分析。子波熵作為衡量系統的有序程度的指標已被應用于腦電信號分析。
癲癇是中樞神經系統異常放電引起的發作性神經功能異常，腦電圖可以記錄這種異常放電的全過程，是診斷和研究癲癇的重要手段。目前臨床工作中對癲癇腦電信號的識別主要依賴于醫生的視覺識別和經驗性判斷。客觀定量分析腦電信號，從中提取有價值的信息和參數對于癲癇的臨床診斷和發作機制的研究具有重要意義。但是癲癇發作過程中，尤其是強直陣攣發作，經常伴有大量的肌電偽差，甚至將腦電成分完全淹沒，影響腦電的定量分析。另外癲癇發作腦電信號是瞬時急劇變化的信號，傳統的基于傅立葉變換的功率譜分析應用前提是信號是平穩的，因此對癲癇發作的腦電分析無能為力。子波變換和子波熵在癲癇發作腦電信號分析方面發揮了它的獨特優勢。
近年來，國內外學者用子波熵研究腦電信號、誘發電位（evoked potentials，EP）、事件相關電位（event-related potential，ERP）等的復雜程度，進一步揭示了大腦電活動的動力學機制。其應用主要在睡眠分期[5]、癲癇腦電信號的動態觀測[6]、網絡成癮[7]、麻醉深度的監測[8-9]等幾個方面。Rosso 團隊[10-12]提出了子波能量（wavelet energy）、子波熵（wavelet entropy）、相對子波熵（relative wavelet entropy）等概念，來研究短片段的自發腦電信號的頻率分布（子波能量）和有序程度（子波熵），及刺激后腦電信號的子波能量和子波熵的演變過程，提出腦電信號反映了不同頻率電活動的綜合，ERP 反映了腦電活動從無序到有序的過程，伴隨著腦電信號在一定頻率上同步化的增強。這一方法可以顯示受到刺激后腦電信號頻率上同步化的動態演變過程，從而加深了對腦動力學機制的理解，成為認知功能研究的一種新的方法。Emre 等[13]采用連續子波熵研究聽覺誘發電位（auditory evoked potentials，AEP），結果顯示較離散子波熵可以發現更多細節特征。
臨床工作中，對癲癇腦電信號的觀察多集中于波幅、頻率的檢測，或者是某個頻率上能量的改變。不同的癲癇發作可能出現特征性的腦電波型，成為臨床癲癇診斷分型的依據。然而引發大腦神經元異常放電的動力學機制是什么呢？推動癲癇的發作、擴散和終止的因素是什么呢？子波熵的改變可能是癲癇放電演變過程背后的動力學因素。本研究試用整體子波熵觀測兒童失神癲癇（child absence epilepsy，CAE）發作全過程的動態變化，總結子波熵在 CAE 發作過程中的演變規律。假設整體子波熵在癲癇的發作過程中降低，在癲癇結束時升高，那么它可能成為癲癇發作的自動監測指標，也可能成為評價癲癇治療效果和預后的定量參數。
1 實驗過程
1.1 研究對象
兒童失神癲癇組 15 例，男 6 例，女 9 例。年齡 4～15（8.0 ± 3.1）歲。病程 2 月～4 年。全部病例臨床表現和腦電圖均符合 1989 年國際癲癇與癲癇綜合征分類中兒童失神癲癇的診斷標準。對照組 12 例，男 4 例，女 8 例。年齡 5～15（7.6 ± 2.8）歲。均為健康兒童，生長發育正常，否認神經系統疾患。該研究經天津市人民醫院倫理委員會通過，所有被試者均由其監護人簽署知情同意書。
1.2 腦電信號采集
采用由日本 NIHONKOHDEN 公司生產的 EEG-2130 型數字腦電圖儀和 Ag/AgCl 頭皮電極，按國際標準導聯 10/20 系統安裝，以雙耳為參考電極，電阻抗 < 5 kΩ，被檢查者在安靜、清醒、閉目狀態下描記腦電信號，采樣頻率 200 Hz。在描記腦電圖前未使用過抗癲癇藥和鎮靜藥。兒童失神癲癇組共記錄 20 次失神癲癇發作，發作時間 4～30 s，對癲癇發作期全程及發作前 4 s 和發作后 4 s 的腦電信號，以 2 s 為一個數據片段進行分析；同時選擇同一患者背景信號平穩，無偽差的腦電信號 20 s，對照組選擇背景 20 s 腦電數據，按每個片段 2 s 進行分析，每段數據包含 400 個數據。腦電信號分析程序采用 Visual Studio C++ 6.0 編寫。
2 腦電信號分析方法
腦電圖描記后，對 16 位 A/D 卡采集的 21 個導聯的 20 s 原始腦電數據信號，以 2 s（400 個數據）為一段分析單位，采用連續子波變換提取腦電信號的時頻特征；采用子波功率譜分析提取分尺度功率譜特征；根據分尺度功率譜計算分尺度子波熵和整體子波熵。分析分尺度子波熵和整體子波熵隨癲癇發作的時間演變過程。
2.1 子波分析簡介
子波分析（wavelet analysis）是一種新的數字信號分析方法，通過信號與一個被稱為子波的基函數進行互相關運算，利用子波基函數在時間尺度上的伸縮運算功能對信號進行多尺度細化分析，將含有多尺度成分的復雜信號在局部時間段內進行頻帶分解。其中子波基函數是由一個子波母函數經過平移和伸縮變換而得到的一族外形相似但尺度不同的局部波動函數。子波基函數在時間上代表有限尺度范圍內的具有特定物理過程的“事件”或者“局部擾動的小的波”。
本研究采用的是連續子變換（continuous wavelet transform，CWT）。一維腦電信號
的連續子波變換定義為：
|
其中子波函數族
是由子波母波函數
經過平移（參數
）和伸縮變換（參數
）而來：
|
子波分析可以將貌似隨機和雜亂無序的多尺度非平穩的復雜信號在每一個瞬時按照頻帶進行分解，使大尺度低頻信號與小尺度高頻信號分離，從而同時提供時域、頻域兩方面的瞬態頻率信息。子波分析應用于神經電生理的復雜信號分析具有獨特的優勢：① 子波是定義在時域有限范圍內的局部小擾動，不需要信號是平穩的，可以自動分解和提取信號瞬時變化的時間局部多尺度特征；② 可以進一步提取信號時域、頻域的多方面的統計信息。
2.2 多尺度功率譜分析
根據子波系數
，腦電信號
的分尺度功率可以用各尺度子波功率譜密度函數表示，描述了分尺度腦電信號的功率強弱：
|
2.3 腦電信號的子波熵
子波熵是基于子波變換，衡量非線性信號動力學行為有序、無序程度的一個量化指標。它可以提供信號非線性動力學過程復雜程度的信息，是衡量系統復雜程度的指標。
腦電信號的總功率是各分尺度信號功率的總和：
|
用 p 對 p（a）進行歸一化，得到各分尺度功率在信號總功率中所占的百分比：
|
本研究所采用的的子波熵為無量綱參數，腦電信號的分尺度子波熵
衡量了該尺度腦電信號成分所含信息的復雜程度，而整體子波熵
則反映了腦電各尺度成分在人腦活動過程中所包含的所有信息的總體復雜程度：
|
|
2.4 統計學分析
統計學分析采用 PASW Statistics 18 軟件，兒童失神癲癇患者發作期與發作間期腦電信號子波熵比較采用配對樣本的 t 檢驗，兒童失神癲癇發作間期與正常對照、發作期與正常對照腦電信號子波熵比較采用獨立樣本 t 檢驗。P < 0.05 為差異有統計學意義。
3 結果
3.1 視覺腦電圖
圖 1 給出了某典型 CAE 發作期腦電圖和正常對照腦電圖。發作時腦電圖（圖 1 上）表現為高波幅或超高波幅的節律性 3 Hz 的棘慢復合波，雙側同步對稱，發作、終止較快。正常兒童視覺腦電圖（圖 1 下）背景節律以 10 Hz 左右的 α 節律為主，α 節律枕區優勢，調節調幅好，未見明顯異常波型。
圖1
CAE 發作期（上）和正常對照（下）腦電圖
Figure1.
Ictal EEG of CAE (above) and EEG of normal control (below)
3.2 子波系數等值線圖
圖 2（上）為 CAE 從失神發作開始到結束的腦電信號進行子波變換多尺度分析的子波系數等值線圖。從圖 2（上）中可以清楚看到，CAE 發作主要表現為 12 尺度（對應頻率 3 Hz）的節律性增強，此時患者的臨床表現為雙眼凝視前方意識喪失，對外界刺激無反應，這時大腦神經元中的高波幅或超高波幅節律性 3 Hz 的棘慢復合波抑制了非線性多尺度關聯范圍的正常電生理信號，大腦神經網絡不能進行正常的信息的感知、認知活動。圖 2（下）為正常對照相應導聯腦電信號進行子波變換多尺度分析的子波系數等值線圖。與圖 2（上）相比，圖 2（下）中的 12 尺度（對應頻率為 3 Hz）的強度和節律相對較弱，沒有超強的節律性活動，正常對照兒童腦電信號尺度分布比較廣泛。
圖2
CAE 發作期（上）和正常對照（下）腦電信號子波系數等值線圖
Figure2.
Contour of multi-scale wavelet coefficients for ictal EEG of CAE (above) and normal control (below)
3.3 整體子波熵隨時間演化
圖 3 給出了 CAE 發作期（左）和正常對照（右）F3、C3、P3、O1 等 4 個不同導聯腦電信號的整體子波熵。結合圖 3（左）和圖 3（右）可以看出，在失神癲癇發作的 6～14 s 期間，腦電信號的整體子波熵明顯低于正常對照，也明顯低于發作間期。表明失神癲癇發作時腦電信號的信息復雜度明顯降低，腦電信號中包含的信息量明顯減小。
圖3
CAE 發作期（左）和正常對照（右）不同導聯腦電整體子波熵
Figure3.
Integral wavelet entropy for ictal EEG of CAE（left）and normal control（rihgt）at different lead
3.4 分尺度子波熵隨時間演化
圖 4 給出了 CAE 發作期和正常對照不同導聯 3 Hz 腦電節律的子波熵。從圖 4 可以看出，CAE 發作期 3 Hz 腦電節律的子波熵明顯高于正常對照 3 Hz 腦電節律的子波熵。表明大腦神經元中的高波幅或超高波幅節律性 3 Hz 的棘慢復合波過強，抑制了大腦正常生理活動和功能。
圖4
CAE 發作期（左）和正常對照（右）不同導聯第 12 尺度（3 Hz）腦電節律子波熵
Figure4.
Individual scale 12 (3 Hz) wavelet entropy of ictal EEG of CAE (left) and normal control (rihgt) at different lead
圖 5 給出了 CAE 發作期和正常對照不同導聯 α 頻帶（中心頻率 10 Hz）的腦電節律子波熵。從圖 5 可以看出，CAE 發作期 α 頻帶（中心頻率 10 Hz）腦電節律的子波熵明顯低于正常對照 α 頻帶（中心頻率 10 Hz）腦電節律的子波熵。表明 CAE 發作時大腦正常的節律性電活動受到抑制。
圖5
CAE 發作期（左）和正常對照（右）不同導聯第 9 尺度（10 Hz）腦電節律子波熵
Figure5.
Individual scale 9 (10 Hz) wavelet entropy of ictal EEG of CAE (left) and normal control (rihgt) at different lead
3.5 統計學分析
兒童失神癲癇發作期與發作間期、正常對照腦電信號子波熵比較見表 1～3。結果顯示：兒童失神癲癇發作期腦電信號的整體子波熵 En 低于發作間期，也低于正常對照兒童；兒童失神癲癇發作期腦電信號的第 9 尺度（對應 10 Hz）的子波熵 En（9） 低于發作間期，也低于正常對照兒童；兒童失神癲癇發作期腦電信號的第 12 尺度（對應 3 Hz）的子波熵 En（12） 高于發作間期，也高于正常對照兒童。與正常同齡對照比較，兒童失神癲癇發作間期的腦電信號的整體子波熵顯著降低，而 10 Hz 和 3 Hz 的分尺度子波熵，兩組比較差異無統計學意義。
表1
兒童失神癲癇患者發作期與發作間期腦電信號子波熵比較（
）
Table1.
Comparison of wavelet entropy between ictal and inter-ictal EEG for CAE (
)
表2
兒童失神癲癇患者發作期與正常對照腦電信號子波熵比較（
）
Table2.
Comparison of wavelet entropy between ictal EEG for CAE and normal control (
)
表3
兒童失神癲癇患者發作間期與正常對照腦電信號子波熵比較（
）
Table3.
Comparison of wavelet entropy between inter-ictal EEG for CAE and normal control (
)
4 討論
子波熵是衡量非線性信號所含信息復雜程度的一個量化指標，它可以提供非線性信號復雜程度的信息。目前的一些研究表明，這一參數在癲癇發作過程中存在一定規律。
Blanco 等[14]基于子波系數，結合 Shannon entropy 的定義提出子波熵的概念，當時稱作 Information cost function，并將它應用于強直陣攣癲癇發作期腦電信號的分析[15-16]。此前強直陣攣發作由于劇烈肌電活動完全淹沒了腦電信號，無論是視覺識別還是定量分析都十分困難。臨床上嘗試應用肌肉松弛劑減少肌電的干擾，或采用傳統的濾波技術去除肌電所在的頻率成分，但結果仍不令人滿意[17]。研究采用視頻腦電儀記錄 1 例癲癇患者強直陣攣發作全過程，從視覺腦電中可以發現發作開始時出現高頻放電，強直期這種放電波幅增高，陣攣期由于肌電干擾淹沒了腦電信號。為了定量研究癲癇發作過程中腦電活動的動力學機制和演變過程，作者應用子波變換將腦電信號分解在不同頻帶上，應用子波熵來定量描述腦電信號的有序程度及演變過程。結果顯示可以去除肌電的影響，提取癲癇發作過程中的主要頻率在 10 Hz，發作結束時頻率減慢至 4 Hz，在發作過程中子波熵明顯降低，這表明發作過程中腦電活動的復雜程度降低。它直觀地反映了腦電活動的動力學過程，而且提取了發作過程中不同頻率腦電能量的聚集和轉化過程。
Rosso 等[18]采用歸一化的總子波熵（normalized total wavelet entropy，NTWE）研究兒童失神癲癇發作間期背景腦電信號，并與正常同齡兒童進行比較。兒童失神癲癇是年齡相關性癲癇發作類型，其視覺分析腦電背景是正常的，然而通過此研究發現兒童失神癲癇發作間期的背景腦電信號的 NTWE 低于正常同齡兒童，在發作期的腦電信號中 NTWE 的降低更為明顯。因此在未記錄到典型的 3 Hz 棘慢綜合放電的患者中，背景腦電 NTWE 降低為兒童失神癲癇的早期診斷提供了線索。而且 NTWE 作為腦電發育和成熟度的指標，為癲癇的發生與腦電成熟度之間的關系的研究提供了電生理依據。本研究結果表明，兒童失神癲癇發作期腦電信號的總子波熵明顯低于正常對照兒童，其發作間期腦電信號的整體子波熵也低于正常對照兒童，具有統計學意義，與 Rosso 的研究結果一致。
Rosso 等[19]對 8 例繼發性強直陣攣發作癲癇患者的 20 次發作進行分析，結果顯示在 1～3 s 的短暫的相位去同步化之后，出現波幅迅速增高的 10 Hz 的癲癇募集節律（epileptic recruiting rhythm），10 s 之后出現與陣攣項相關的低頻成分的增強，在每次肌肉的抽動均伴隨全面性多棘波發放。α 波和 θ 波的混合節律的出現預示發作的結束。NTWE 在發作前、發作后和發作中有明顯差異，在發作過程中 NTWE 明顯降低，表明腦電行為更加有序。這一現象提示癲癇灶觸發了腦電活動的一種自我組織狀態，影響了大腦對周圍事物的反映。Pereyra 等[20]采用基于子波變換的 Jensen-Shannon divergence（JSD）這一參數作為描述癲癇發作時腦電信號不同頻率成分的動力學過程。通過對強直陣攣癲癇發作腦電信號的分析，結果顯示 JSD 在癲癇發作過程中出現 5 個明顯的變化峰值，這 5 個峰值分別提示發作的開始、癲癇募集節律的出現、強直項向陣攣項的轉變、癲癇募集節律的結束以及發作結束。因此可以用這一參數定量分析癲癇發作過程中不同頻率成分隨時間的演變過程，并提出它可以應用于癲癇發作過程中不同腦區腦電信號的動力學特征的比較。Acharya 等[21]和 Wang 等[22]應用子波熵等參數設計腦電信號癲癇波的自動檢測系統，使癲癇的診斷和分類的準確性大大提高。
本研究采用連續子波變換的方法對腦電信號進行分解，以 2 s 為觀測單位，提取兒童失神癲癇發作過程中整體子波熵的演變規律，結果表明，失神癲癇發作期腦電信號整體子波熵明顯降低。國外學者對全身強直陣攣癲癇發作期腦電信號子波熵的研究表明其發作期腦電信號明顯降低[18-20]。推測子波熵降低可能是癲癇發作期腦電信號的共同特征，它反映了癲癇發作的動力學特征。熵的概念來源于熱力學第二定律，用來度量系統中的混亂程度，物質的平衡態是能量和熵相互競爭的結果。簡單地說，能量是有序結構的支柱，而熵則是無序結構的靠山。1948 年貝爾實驗室的電氣工程師香農（C Shannon）將熵引用到信息學領域[15]。能與熵何者更為重要，是一個不斷爭論的話題，能量可以看做事物存在的表現形式，而熵決定了自然過程演變的方向。因此對于癲癇腦電信號的熵的研究可能提示癲癇發作和終止的信息，不同類型的癲癇發作可能具有相似的動力學機制。對于子波熵的進一步研究有可能為癲癇的神經調控技術提供電生理依據。
本研究在研究整體子波熵的同時，進一步研究了兒童失神癲癇發作過程中分尺度子波熵的演變規律。結果表明，兒童失神癲癇發作過程中第 12 尺度，即 3 Hz 附近的子波熵明顯高于正常對照，而第 9 尺度，即 10 Hz 附近的子波熵明顯低于正常對照。這反映了兒童失神癲癇發作過程中能量在不同頻率間聚集和轉化的特征，提示不同頻率腦電信號攜帶的信息量。對于癲癇腦電信號分尺度子波熵的研究可能提示不同類型癲癇發作過程中能量和信息在不同頻率上的聚集和轉化的過程，為每種類型癲癇發作的動力學機制的研究提供幫助。
本研究顯示兒童失神癲癇發作間期的腦電信號的整體子波熵比正常同齡對照顯著降低，表明即使在發作間期，其腦電信號的復雜度仍低于正常，這與 Rosso 等[23]的研究一致，提示可能與兒童失神癲癇患兒腦發育相對落后有關。而兒童失神癲癇發作間期的腦電信號的 10 Hz 對應的第 9 尺度分尺度子波熵比正常同齡對照稍低，但差異無統計學意義，可能是由于正常兒童腦電信號中 α 節律優勢并不明顯有關。3 Hz 對應的第 12 尺度分尺度子波熵比正常同齡對照稍高，但差異無統計學意義，在部分受試者，正常對照組反而高于 CAE 患者發作間期的腦電信號，考慮為正常兒童中 3 Hz 腦電信號的復雜度也較高。兩組間分尺度子波熵是否存在差異，仍需增加樣本量作進一步研究。
目前的研究表明，子波熵對于癲癇發作的研究具有重要價值。進一步深入研究并緊密結合臨床，子波熵可能成為臨床上輔助疾病診斷和評估的電生理參數，同時為疾病的電生理機制的基礎研究提供理論依據。
5 結論
本文對失神癲癇發作期腦電信號和正常兒童腦電信號的整體子波熵和分尺度子波熵進行了分析研究，得到如下結論：
（1）腦電信號整體子波熵可以表現腦電信號的信息復雜程度，CAE 患者腦電的整體子波熵明顯低于正常對照組，CAE 患者發作期腦電的整體子波熵明顯低于發作間期腦電的整體子波熵，CAE 發作時腦電信號的信息復雜度明顯降低，推測這可能與 CAE 發作過程中腦電信號中包含的信息量明顯減小有關。
（2）分尺度子波熵表明單一頻帶腦電信號所含信息量，CAE 發作期 3 Hz 的分尺度熵增高，α 頻帶（中心頻率 10 Hz）的分尺度子波熵降低，推測這可能顯示了 CAE 發作時大腦正常節律性電活動受到抑制。
（3）本研究的結果顯示，子波熵這一參數在癲癇的發作過程中存在一定的規律，子波熵有可能成為癲癇發作的電生理參數，為癲癇發作動力學機制的研究提供幫助。
