本研究旨在確定能夠有效模擬沖擊載荷作用下腦組織力學特性的粘性–超彈性本構方程。本文運用有限元仿真與優化算法相結合的方法，開展了腦組織粘性–超彈性材料模型參數求解。首先，基于腦組織動態單軸拉伸試驗數據，建立最大拉伸率為 1.3、應變率分別為 30 s–1 和 90 s–1 的腦組織動態拉伸有限元仿真模型。然后，以仿真預測的工程應力–應變曲線與參考試驗測量結果均值曲線的擬合誤差最小化作為優化設計的目標函數，利用多目標遺傳算法進行材料模型參數求解。結果顯示，運用本文所確定的本構方程的腦組織有限元模型能夠準確地預測不同加載速率下的腦組織動態拉伸力學特性。應用本文獲取的腦組織粘性–超彈性本構方程于顱腦有限元模型，將有利于提高模型在動態沖擊載荷下的生物逼真度。
引用本文： 任立海, 蔣成約, 陳勇, 胡遠志. 基于動態拉伸試驗數據的腦組織粘性–超彈性材料模型參數求解. 生物醫學工程學雜志, 2018, 35(5): 767-773, 778. doi: 10.7507/1001-5515.201709022 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
道路交通事故已成為世界范圍內嚴重的公共健康和安全問題。根據世界衛生組織的報告，全球平均每年因道路交通事故致傷人數約有 500 萬，其中造成的死亡人數超過 120 萬[1]。道路交通事故統計數據表明：人體頭部是最為常見的損傷部位之一，而嚴重的腦外傷是導致人員死亡的主要原因之一[2]。
隨著計算機仿真技術的不斷進步，具有詳細解剖學結構和較高生物逼真度的三維頭部有限元模型已成為研究碰撞載荷下顱內動力學響應的有力工具[3-8]。其中，利用有限元模型開展真實頭部碰撞事故的仿真重建獲取顱內動力學響應，并結合損傷記錄確定相應的腦損傷評價準則和耐受限度，是頭部有限元模型的主要應用之一。例如，Sahoo 等[7]通過對 109 例真實頭部碰撞事故開展仿真重建，提出了基于頭部有限元模型的腦神經損傷評價準則；Kleiven[8]通過對橄欖球運動員頭部碰撞事故的分析和有限元仿真重建，提出了針對輕度腦損傷（腦震蕩）的損傷評價準則。然而，現有的不同頭部有限元模型預測的損傷耐受限度仍然存在較大差別。為了更為準確地預測顱內動力學響應并進一步量化損傷評價準則，頭部有限元模型中生物組織，尤其是腦組織的生物力學特性特別重要。因此，對沖擊載荷下腦組織力學特性的高精度模擬是保證頭部有限元模型生物逼真度的關鍵因素之一。
已有的頭部有限元模型主要采用線性粘彈性材料模型來模擬腦組織具有的粘性特性，但是這種材料模型無法模擬腦組織在大應變時的非線性力學特性[9-10]。近年來，研究人員運用集成了超彈性材料模型和線性粘彈性材料模型優點的粘性-超彈性材料模型來模擬腦組織在動態載荷作用下的非線性力學特性[7, 11-13]。然而，已有的腦組織粘性–超彈性本構方程中材料參數的求解通常拆分為超彈性和線性粘彈性兩個模塊，然后再分別參照試驗數據進行求解，求解后再進行組合。此類方法導致組合得到的新的本構關系已偏離原始參考腦組織力學特性試驗測量結果，因此其生物逼真度并沒有得到有效的驗證。
本文將采用優化算法和有限元模型仿真相結合的方法，對腦組織粘性–超彈性材料模型的參數進行整體求解：構建基于真實試驗的腦組織動態拉伸試驗的有限元仿真模型，將腦組織粘性–超彈性材料模型的關鍵參數設為待求解變量，以仿真預測結果與參考試驗結果的誤差最小化為優化目標，運用優化算法對有限元仿真模型進行迭代計算，最終實現腦組織粘性–超彈性材料模型的參數反求。
1 材料和方法
1.1 粘性–超彈性材料模型
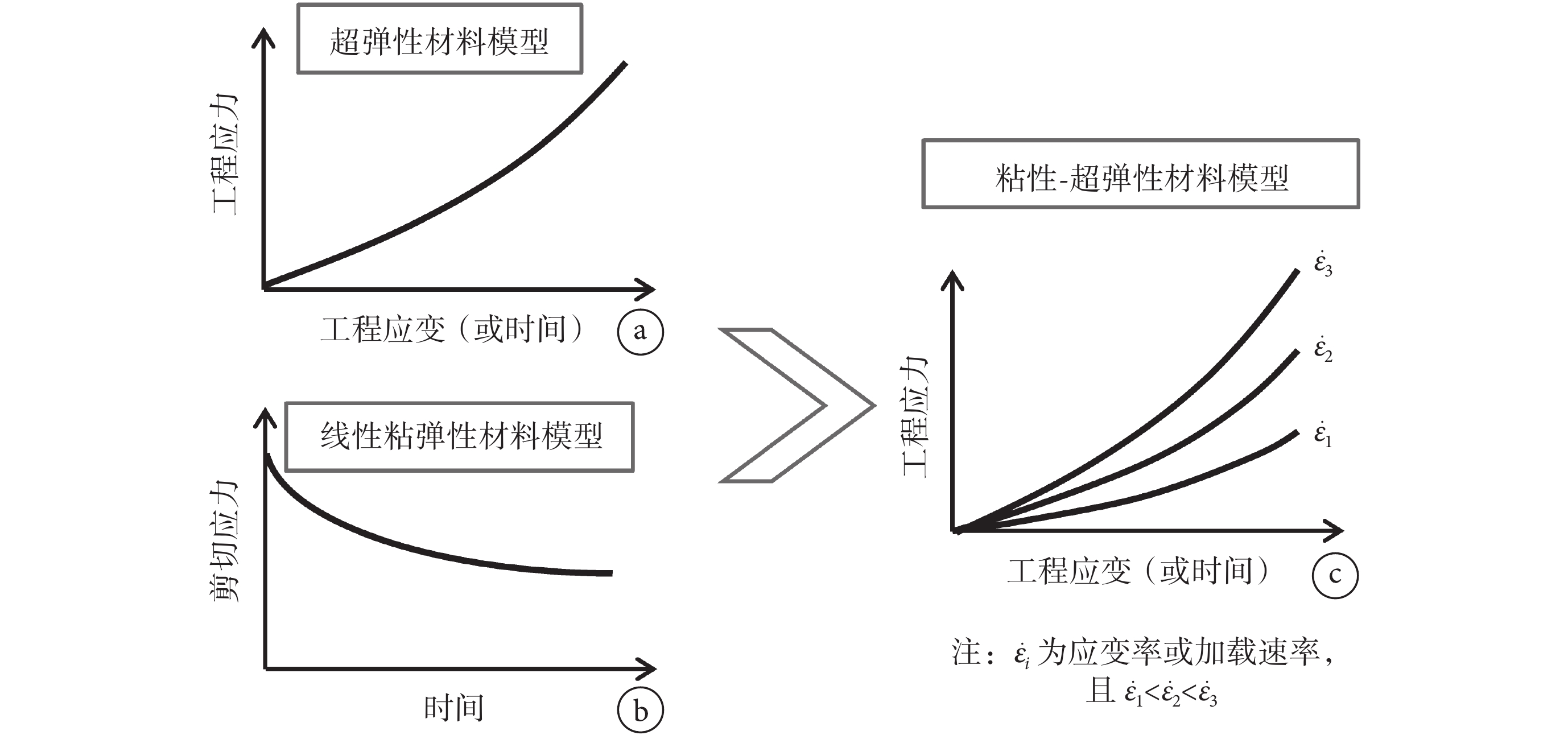
超彈性材料模型利用材料應變能函數（W）來描述材料的力學特性，通常能有效地模擬腦組織在大應變時出現材料硬化的特性，即應力隨應變增大出現非線性上升（如圖 1a 所示）。但是超彈性模型不能夠模擬腦組織作為生物軟組織材料所具有的粘性特性，尤其是無法模擬動態載荷下的應變率效應（即隨著載荷速率的增加，材料剛度顯著增加）。以超彈性材料模型為基礎，通過集成線性粘彈性模型（見圖 1b）引入對腦組織粘性特性的模擬可以構建粘性–超彈性材料模型（見圖 1c）。粘性–超彈性模型能夠較好地模擬動態沖擊載荷下腦組織的非線性力學特性，尤其是腦組織大應變時的材料硬化特性和動態載荷下的應變率效應性。
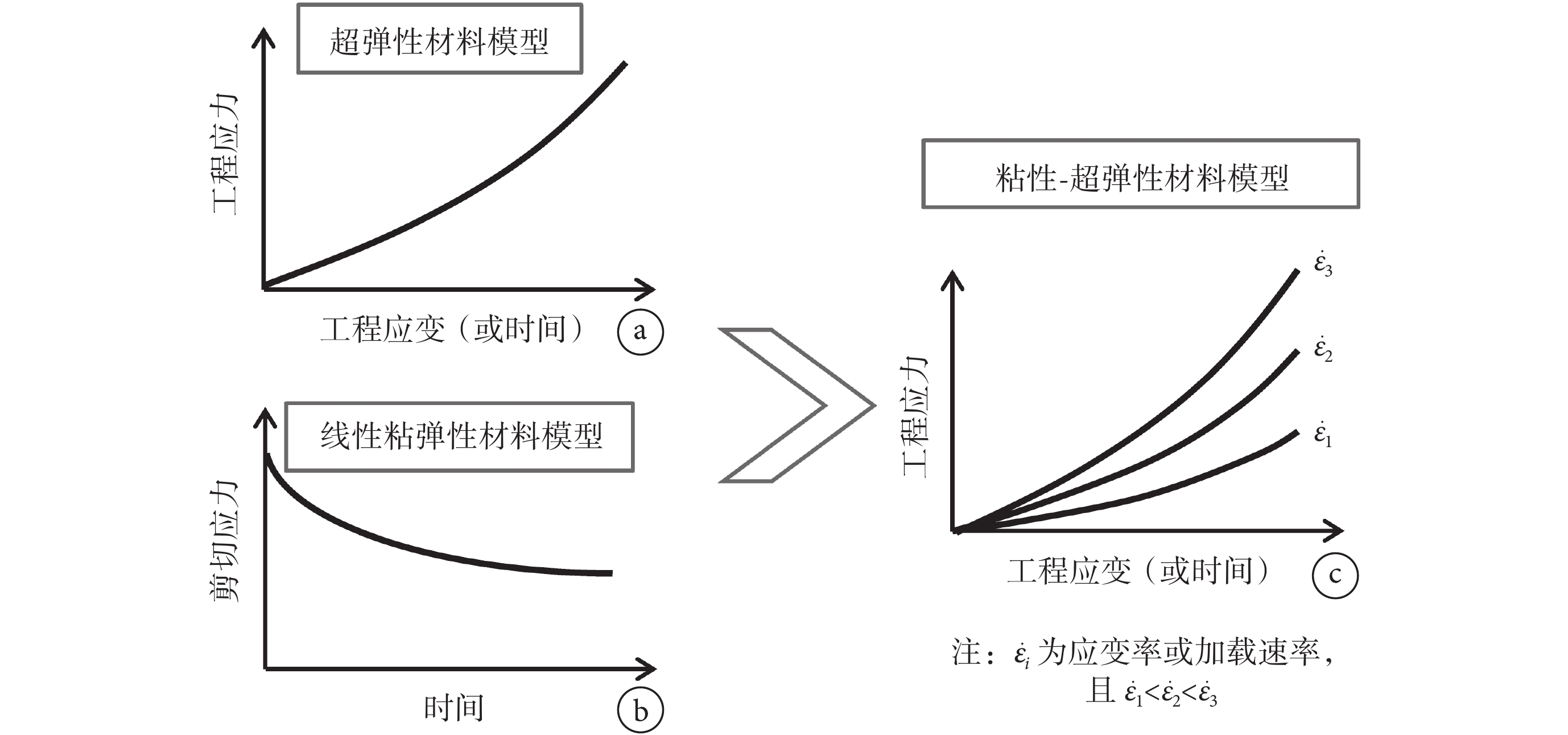圖1
粘性-超彈性材料的構建及基本應力-應變關系示意
a. 超彈性材料模型在動態單軸拉伸載荷的應力-應變曲線；b. 線性粘彈性材料模型的應力松弛曲線；c. 粘性-超彈性材料模型在動態單軸拉伸下的應力-應變曲線
Figure1. Schematic diagram of the construction and basic stress-strain relationships of the visco-hyperelastic material modela. stress-strain relationship of the hyperelastic material model under dynamic uniaxial tension; b. the stress relaxation curve of the linear viscoelastic material model; c. stress-strain relationship of the visco-hyperelastic material model under dynamic uniaxial tension
本文以 Weiss 等[14]和 Puso 等[15]開發的軟組織材料模型為基礎，構建腦組織在動態拉伸載荷作用下的粘性–超彈性本構方程。以 Moony-Rivlin 材料模型作為基礎的超彈性模型，其應變能函數（W）描述如下：
 |
式中 C1 和 C2 為材料參數，而 2（C1 + C2）為材料在小應變時的初始剪切模量；K 為體積模量；
為單元變形體積比，其中 F 為單元的變形梯度；由于生物軟組織材料具有不可壓縮特性，即 J 取值為 1，則式（1）構成應變能函數的第三項為零。式（1）中
和
分別為右柯西–格林應變張量（C）的第一和第二不變量：
，
。
以超彈性材料模型為基礎，引入線性粘彈性材料模型后可得到粘性–超彈性模型的基本應力（第二類 Piola-Kirchoff 應力（S））計算公式表示如下：
 |
式中 t 表示時間；
是由超彈性模型的應變能函數（W）決定的材料彈性特性部分產生的應力響應；
是由材料粘性特性引入的應力，參考 Fung[16]提出的運用卷積積分引入生物軟組織材料的粘性特性的方法，該部分的應力計算公式如下：
 |
式中 G 為腦組織線性粘彈性模型的剪切應力松弛函數，可以利用 Prony 級數表達如下：
 |
式中 Si 為歸一化處理后的剪切模量分量，即
；Ti 為應力松弛時間分量。
綜上可得當前粘性–超彈性材料模型的應力計算公式如下：
 |
式中 C1、C2、Si 和 Ti 為材料模型的待求解變量。
1.2 腦組織動態單軸拉伸試驗的有限元仿真建模
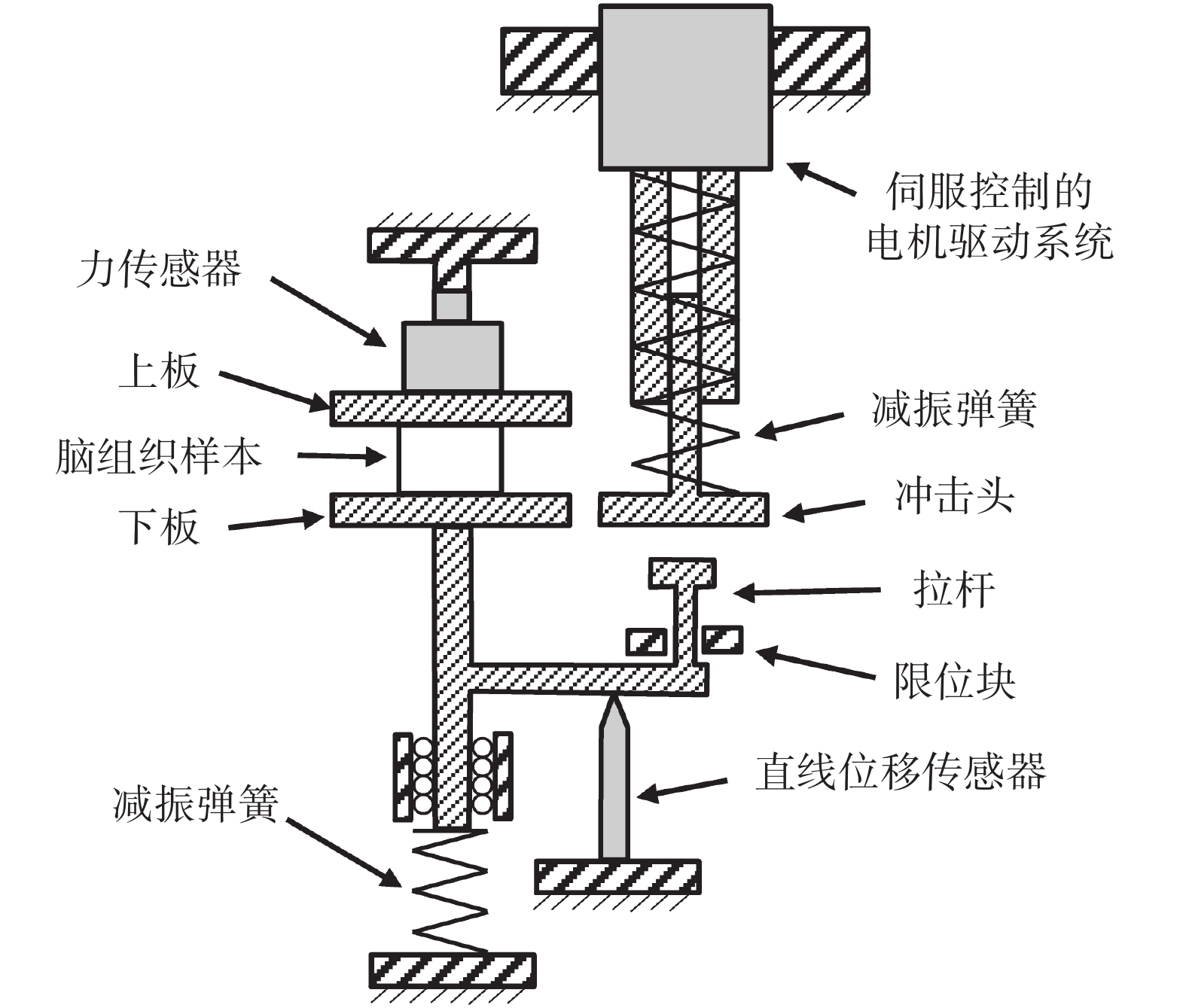
Rashid 等[17]采用自制的生物軟組織高應變率力學特性測試設備（high rate tension device，HRTD）開展了一系列腦組織動態單軸拉伸試驗。如圖 2 所示，HRTD 測試設備主要由伺服控制的電機驅動系統、力傳感器、直線位移傳感器以及一些機械結構組成。參考試驗測試的樣本組織取自新鮮的豬大腦，測試樣本為腦灰質和腦白質混合圓柱體，其平均直徑為 15.1 mm，平均高度為 10 mm。試驗前，將腦組織待測樣本的上、下端面分別與測試設備的上、下板通過一層薄的低粘性醫用粘合劑進行粘接。試驗中，沖擊頭在伺服電機的驅動下向下運動，對拉桿進行沖擊；拉桿帶著與其固定連接的下板整體向下運動，從而實現對腦組織樣本的拉伸。為保證腦組織拉伸速度的均勻一致，電機驅動系統設置有足夠的軸向運動空間避免觸底碰撞；同時設置有減振彈簧以減少沖擊產生的振動。試驗中，運用力傳感器和直線位移傳感器分別測量拉伸過程中的上板受力和下板位移，用于確定腦組織樣本在特定加載速度下的工程應力–應變曲線。文獻[17]中，對不同腦組織樣本施加工程應變率為 30～90 s–1的勻速單軸拉伸。在本文中，將參考文獻[17]中應變率為 30 s–1 和 90 s–1 的試驗組分別定義為低應變率組和高應變率組，并將文獻中相應的試驗結果作為依據，進行腦組織粘性-超彈性本構方程的構建。
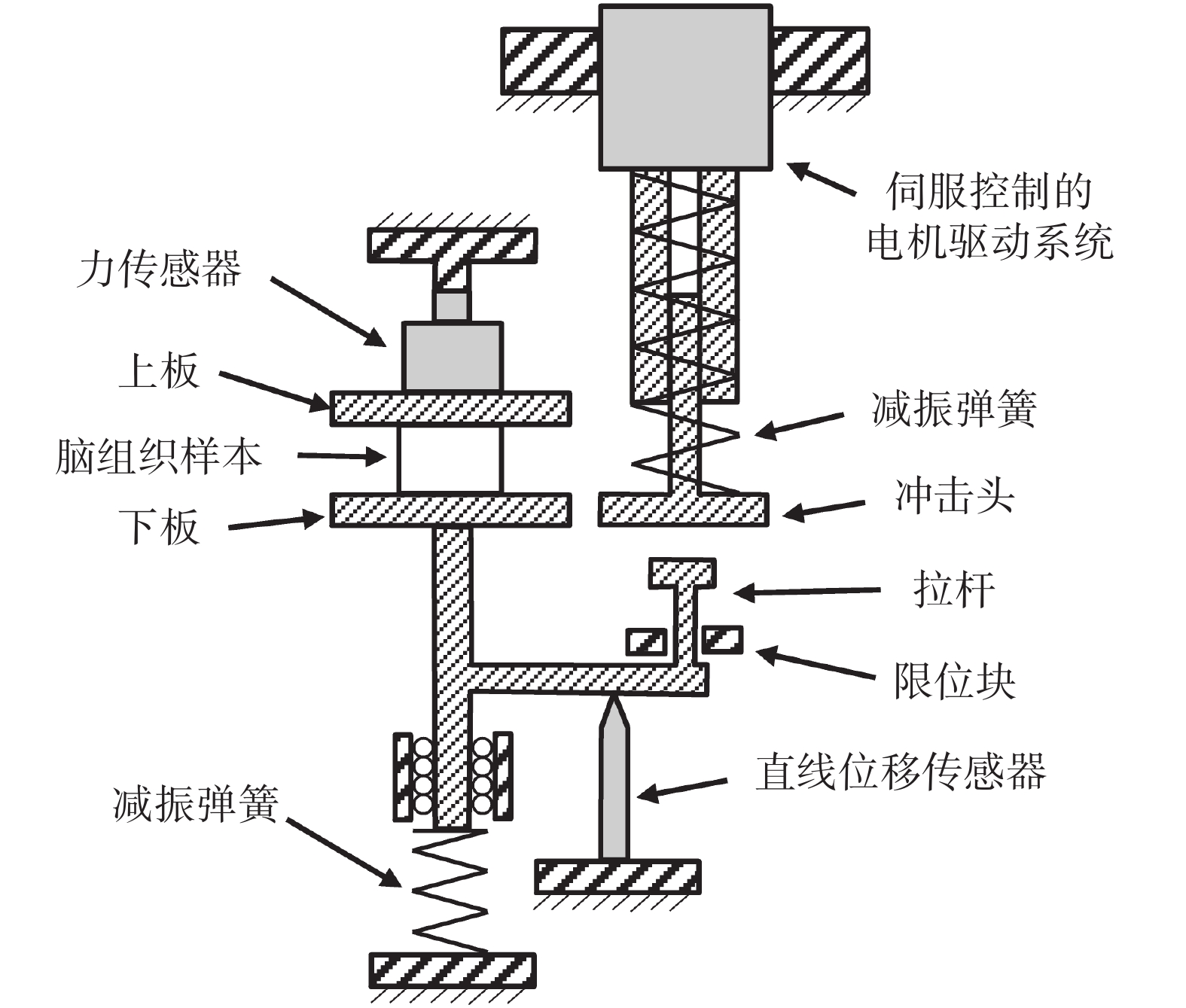圖2
基于 HRTD 測試設備的腦組織動態單軸拉伸試驗原理圖
Figure2.
Schematic diagram of brain tissue dynamic uniaxial tension test by using the HRTD
根據參考試驗的設置，在 LS-DYNA 軟件中建立腦組織樣本的動態單軸拉伸試驗的有限元仿真模型。本文采用規則的六面體網格來分別建立腦組織樣本和上、下板的有限元模型。仿真模型中的邊界條件及載荷條件按照參考試驗測試方法進行設置：① 由于在腦組織拉伸過程中未出現腦組織端面與上、下板表面的脫離或徑向滑移[17]，因此在仿真模型中可用共節點的連接方式分別將腦組織的上、下端面與上、下板的對應表面進行連接；② 依據參考試驗加載方式，在仿真中固定上板并對下板施加強制運動載荷，實現對腦組織樣本的拉伸；③ 仿真中輸出腦組織樣本與上板之間的截面力時間歷程曲線以及下板的位移時間歷程曲線，用于計算仿真預測的腦組織樣本工程應力-應變曲線。根據參考試驗中載荷速度的變化，分別搭建應變率為 30 s–1 和 90 s–1 的兩組動態拉伸試驗的基礎模型。
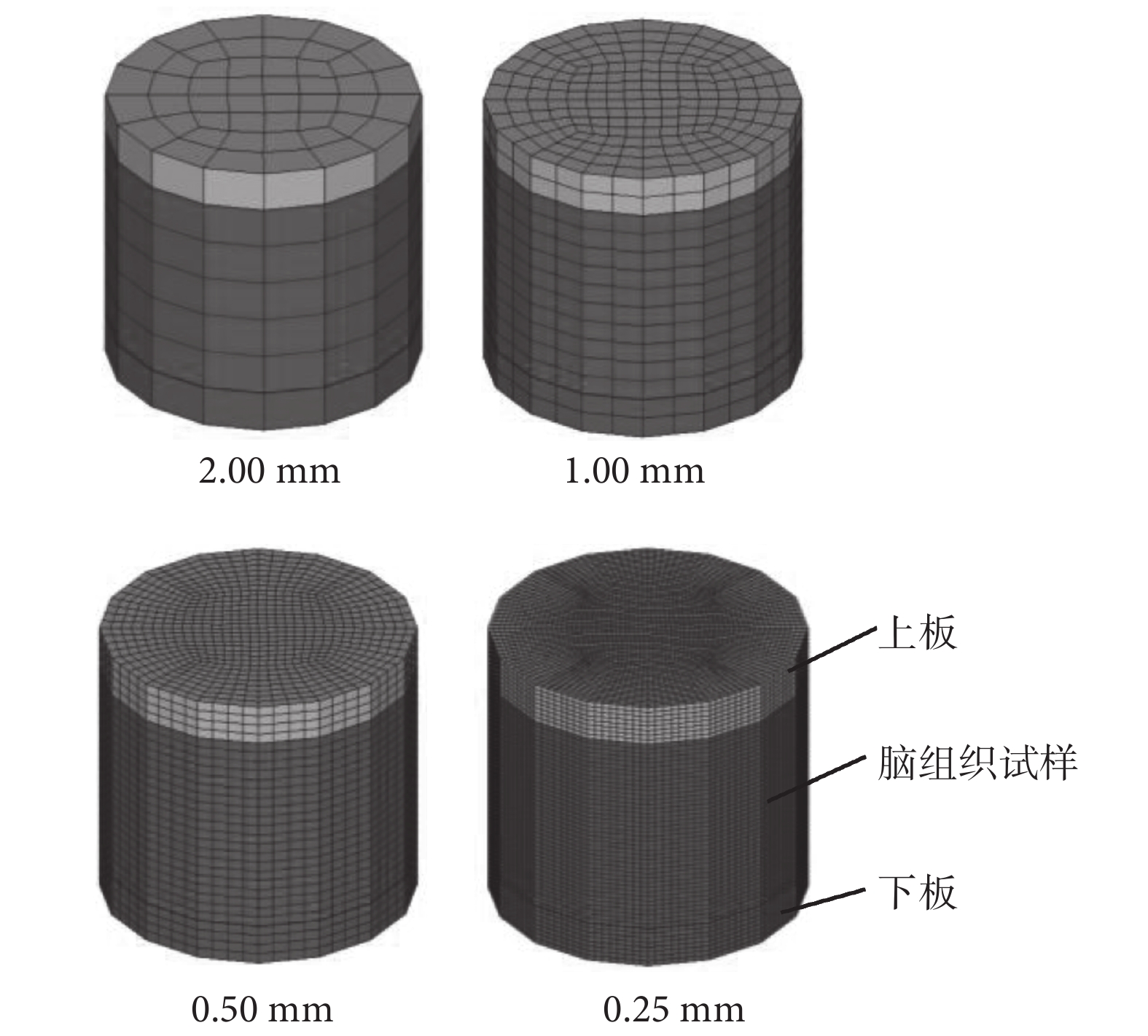
對建立的有限元模型開展網格收斂性分析。分別建立四組腦組織單元的平均邊長為 2.00、1.00、0.50、0.25 mm 的仿真模型（見圖 3），根據參考文獻[17]中腦組織材料參數范圍設置適當的材料參數。開展動態單軸拉伸試驗的有限元仿真，計算在最大拉伸率 1.3 時腦組織的工程應力以評價模型的網格收斂性。
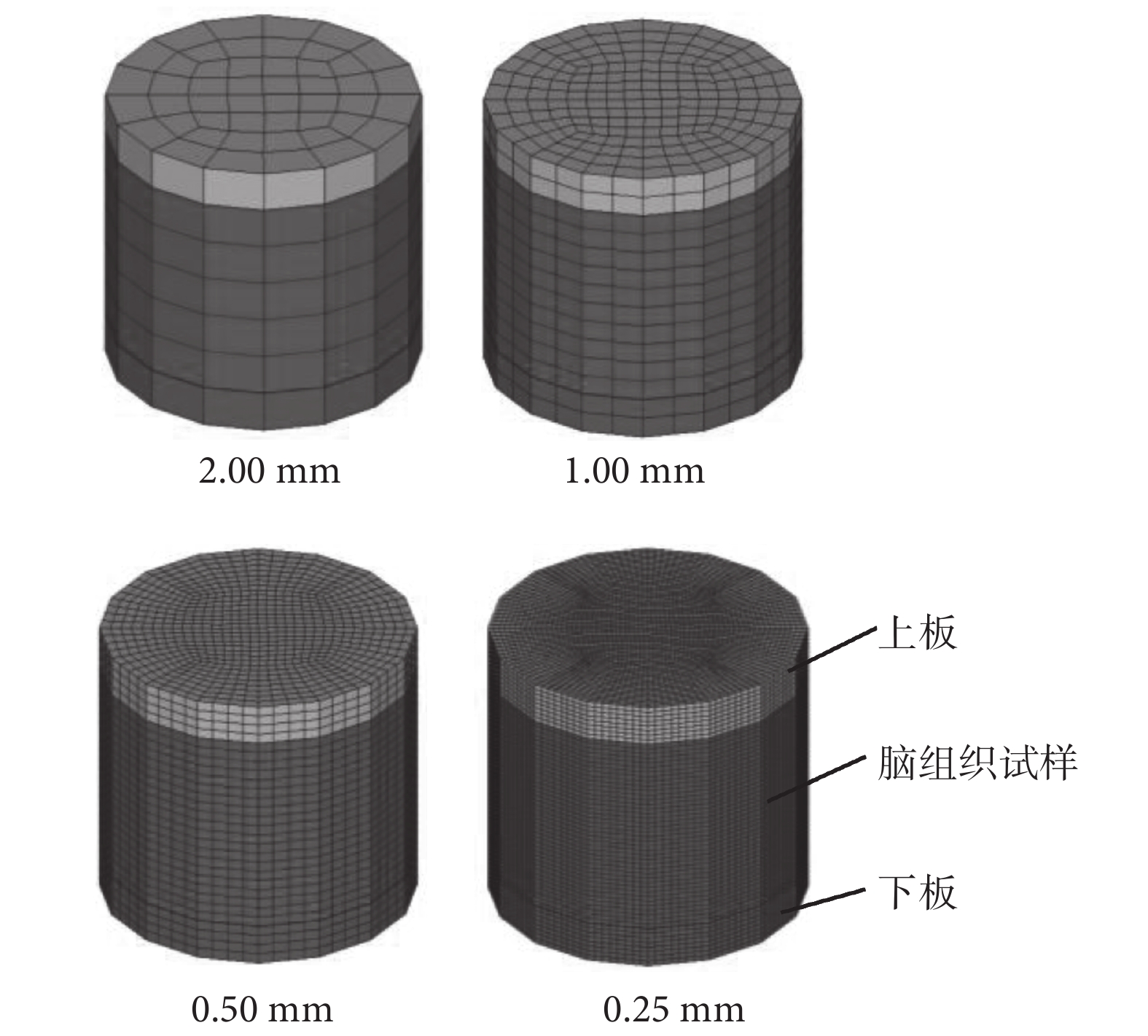圖3
網格收斂性分析模型
Figure3.
Finite element models for mesh conversional analysis
1.3 材料模型參數求解
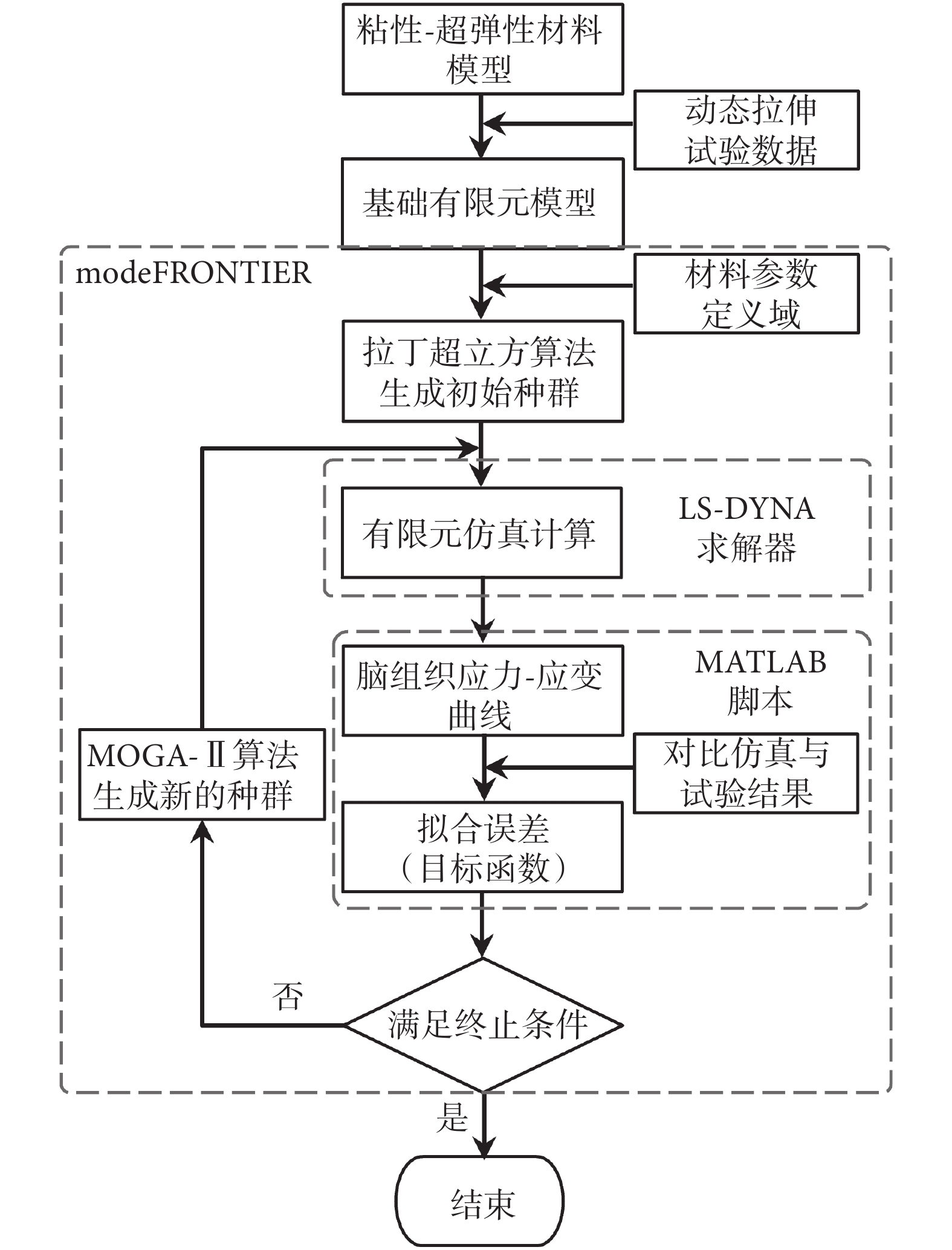
本文建立了基于有限元模型和優化算法的腦組織材料參數自動優化求解流程（見圖 4），并在 modeFRONTIER 軟件中搭建了相應模型。首先，選擇拉丁超立方算法生成樣本數目為 60 的初始種群。運用多目標遺傳算法（MOGA-II）進行參數的優化求解，設置 MOGA-II 的遺傳代數為 20。MOGA-II 是使用精英策略的多目標遺傳算法，能夠在保留最優解的同時避免過早地落入局部最優前沿[18]。同時，本文通過編制 MATLAB 腳本實現數據的自動化處理。
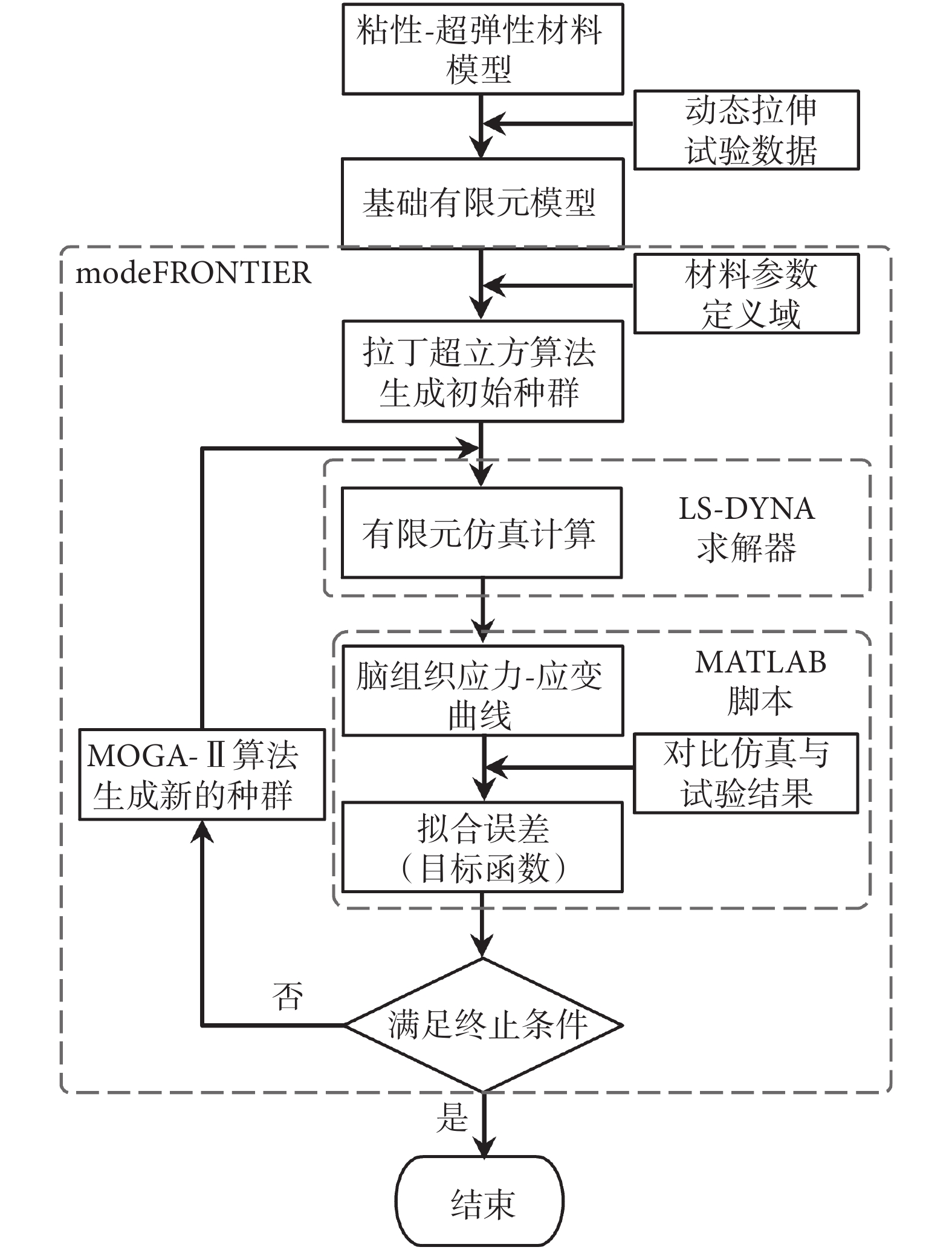圖4
腦組織材料模型參數自動化求解流程圖
Figure4.
The automatic procedure for the identification of the constitutive law of brain tissue
本文以仿真預測的腦組織工程應力-應變曲線與參考試驗測量結果均值曲線的誤差最小化作為目標函數（F），其中參考試驗結果均值曲線為對應拉伸速率下參考文獻[17]測試的 10 組腦組織樣本試驗結果的均值曲線。如公式（6）～（8）所示，分別采用最小二乘方法計算不同應變率下的仿真預測應力–應變曲線與試驗均值曲線的誤差，其函數表達式表示如下：
 |
 |
 |
式中 f 代表仿真預測和試驗測量的腦組織工程應力–應變曲線，下標 l 和 h 分別代表低應變率和高應變率，下標 s 和 e 分別代表仿真和參考試驗數據，F 為仿真預測的工程應力–應變曲線與參考試驗結果均值曲線之間存在的偏差（擬合誤差）。在本文中，每條曲線均勻地選擇 30 個樣本點，即N = 30，用于計算曲線擬合誤差。
本文根據腦組織力學特性文獻報告的試驗數據，分別確定粘性–超彈性模型中基礎超彈性材料模型和線性粘彈性模型的參數取值或取值范圍。
（1）超彈性材料模型參數 C1 和 C2：根據本文參考試驗的腦組織工程應力–應變曲線測量結果[17]，可以參照理想不可壓縮彈性材料剪切模量的取值約為彈性模量的三分之一的關系來估算參考試驗測量的腦組織（工程應變小于 0.1 時）初始剪切模量，即在當前載荷條件下測量的腦組織初始剪切模量小于 10 kPa。由于在超彈性材料模型中 2（C1 + C2）為材料在小應變時的初始剪切模量，因此可以初步確定 C1 + C2 的取值范圍。而 C1 和 C2 不具有實際物理意義，可由 C1 + C2 的取值并根據優化計算情況進一步修改確定它們的取值范圍。為了更有效地進行自動優化計算，將公式（1）中的 C1 + C2 和 C1 分別設置為計算變量 x1 和 x2。
（2）線性粘彈性材料模型參數 Si 和 Ti：首先本文將公式（4）所示描述腦組織粘性特性的應力松弛函數設置為二階 Prony 級數，即公式（4）中的 n 取值為 2。同時由于
，可設置 S1 為計算變量（x3），取值范圍為［0, 1］。參考文獻[19]中整理的大量哺乳動物腦組織應力松弛測試數據顯示：不同測試條件下腦組織應力松弛曲線變動范圍較大。因此應設置 T1 和 T2 較大的取值范圍，同時設置相應的指數函數形式的計算變量 x4 和 x5。
此外，材料模型中的體積模量 K 設為 1 × 104 kPa（高出剪切模量三個數量級）以模擬腦組織的不可壓縮性。為避免遺漏可能的最優參數組合，以上述材料參數的初步取值范圍為基礎適當擴大了部分參數的取值范圍。用于優化設計計算的材料參數最終取值或取值范圍設置如表 1 所示。
表1
粘性–超彈性材料模型的參數取值或取值范圍以及對應的計算變量
Table1.
Design domain of material variables for the visco-hyperelastic constitutive model and corresponding calculative variables
2 結果
2.1 網格收斂性分析
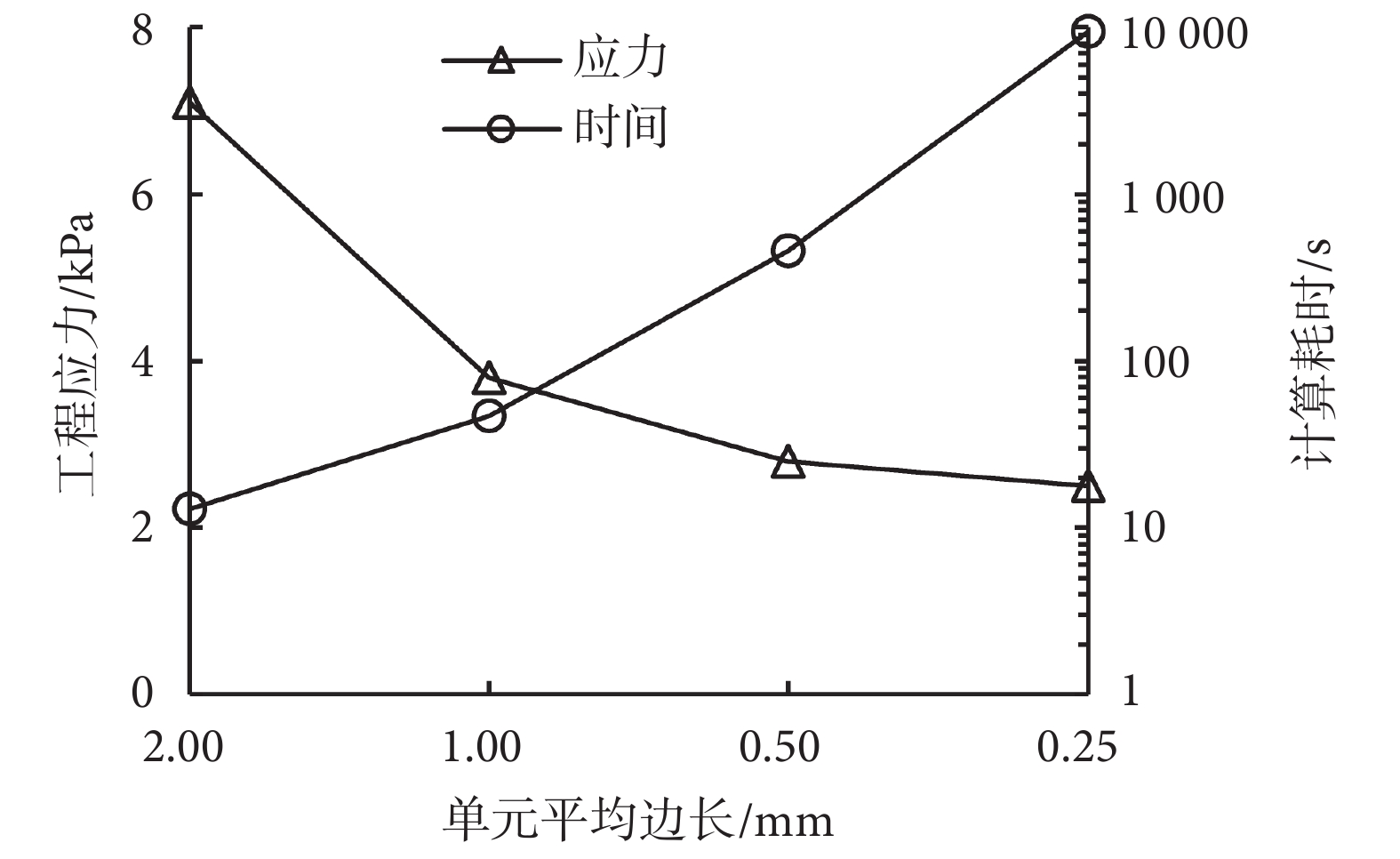
圖 5 和圖 6 所示為應變率為 90 s–1 下的網格收斂性仿真分析結果。由圖 5 可以得知：隨著有限元模型單元平均邊長的減小，當腦組織拉伸率達到 1.3 時仿真預測的工程應力呈現明顯的收斂趨勢。即當單元平均邊長小于 1.00 mm 時，隨著單元邊長的減小，仿真預測的最大工程應力變化較小。同時，腦組織的應力響應云圖（見圖 6）也進一步展示了這一收斂趨勢。然而，隨著單元平均邊長的減小，計算仿真所需要的計算時間會快速增加（圖 5 所示為運用 i7-6700 CPU 計算具有不同單元平均邊長的模型所需要的時間）。考慮到應用遺傳算法進行優化設計時的較大計算量，本文選擇使用有限元模型的單元平均邊長為 1.00 mm。
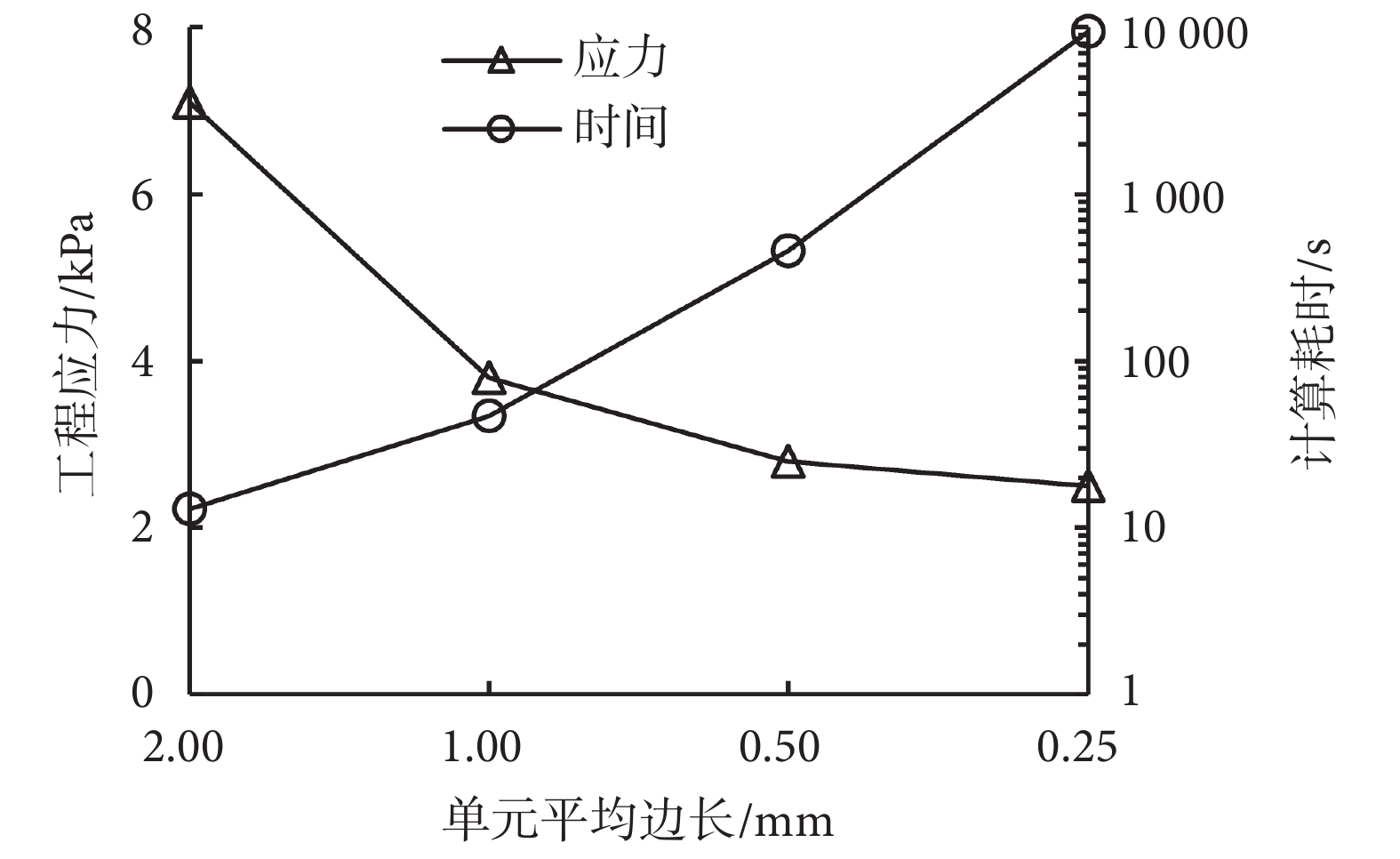圖5
網格收斂性分析結果（拉伸率為 1.3 時）
Figure5.
Results of the mesh conversional analysis（at stretch ratio of 1.3）
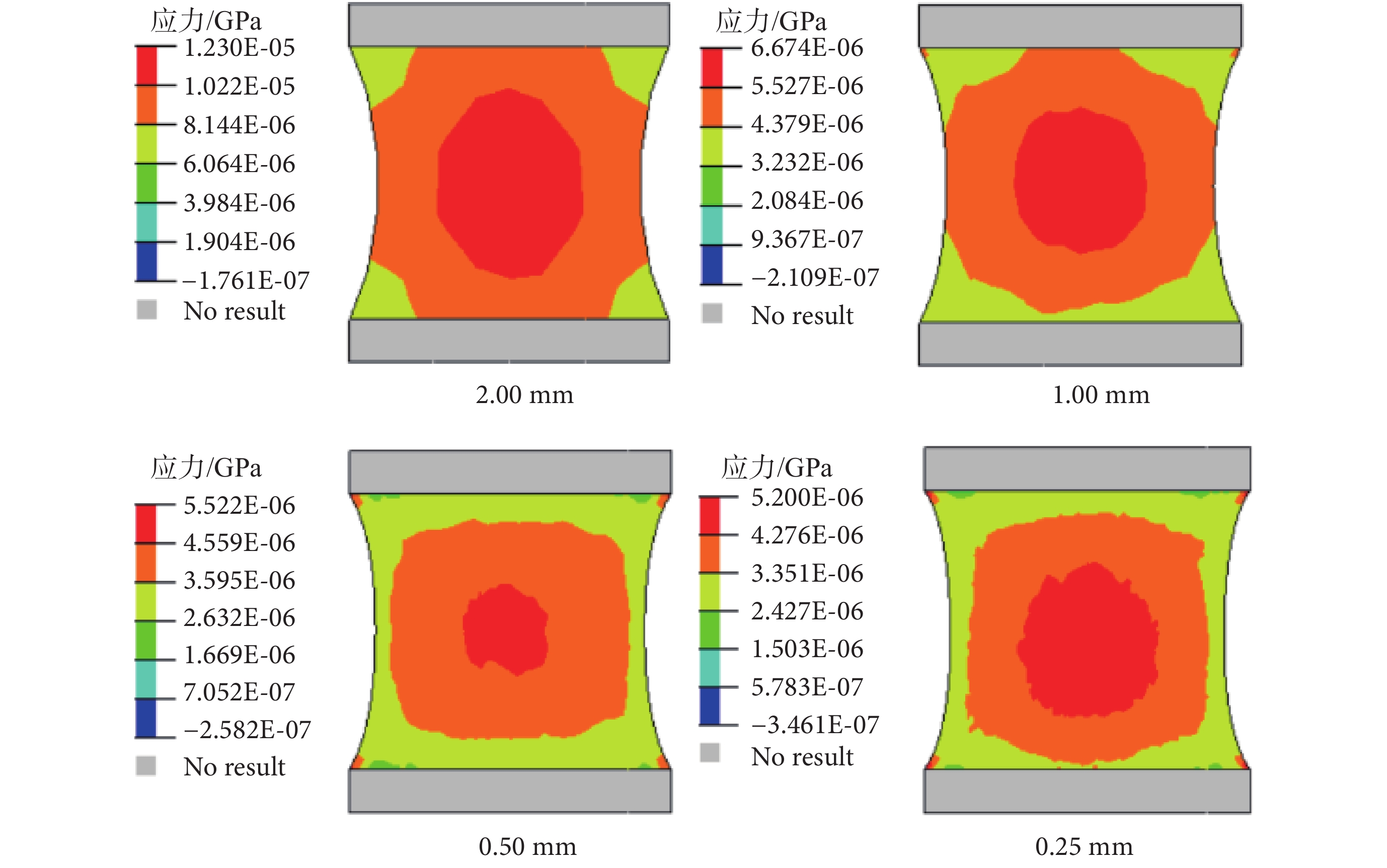圖6
腦組織中間剖面拉伸方向應力云圖（拉伸率為 1.3 時）
Figure6.
Contours of predicted stress in the extension direction at the middle cross section of the specimen （at stretch ratio of 1.3）
2.2 材料參數優化求解
通過進行 20 代的運行，整個優化設計過程共進行 1 200 組（其中有效組數為 1 105）有限元仿真模型的計算，其中每組分別包括一個低應變率（30 s–1）和一個高應變率（90 s–1）的動態單軸拉伸試驗仿真。圖 7 所示為優化設計計算得到的所有樣本點的仿真預測誤差分布，其中某一個樣本點的低應變率仿真誤差和高應變率仿真誤差分別為目標函數公式（6）中的 Fl 和 Fh，即該組有限元仿真模型在相應加載速率下預測的腦組織樣本工程應力–應變曲線與相同加載速率下參考試驗結果均值曲線的誤差。同時，可以看到仿真模型曲線誤差的分布具有明顯的 Pareto 前沿（最優解集）。綜合考慮模型對不同拉伸應變率下腦組織工程應力–應變曲線的擬合精度以及數值計算的穩定性等因素，在曲線擬合誤差均小于 0.1 的 Pareto 最優解集中選擇一組材料參數（如表 2 所示）。
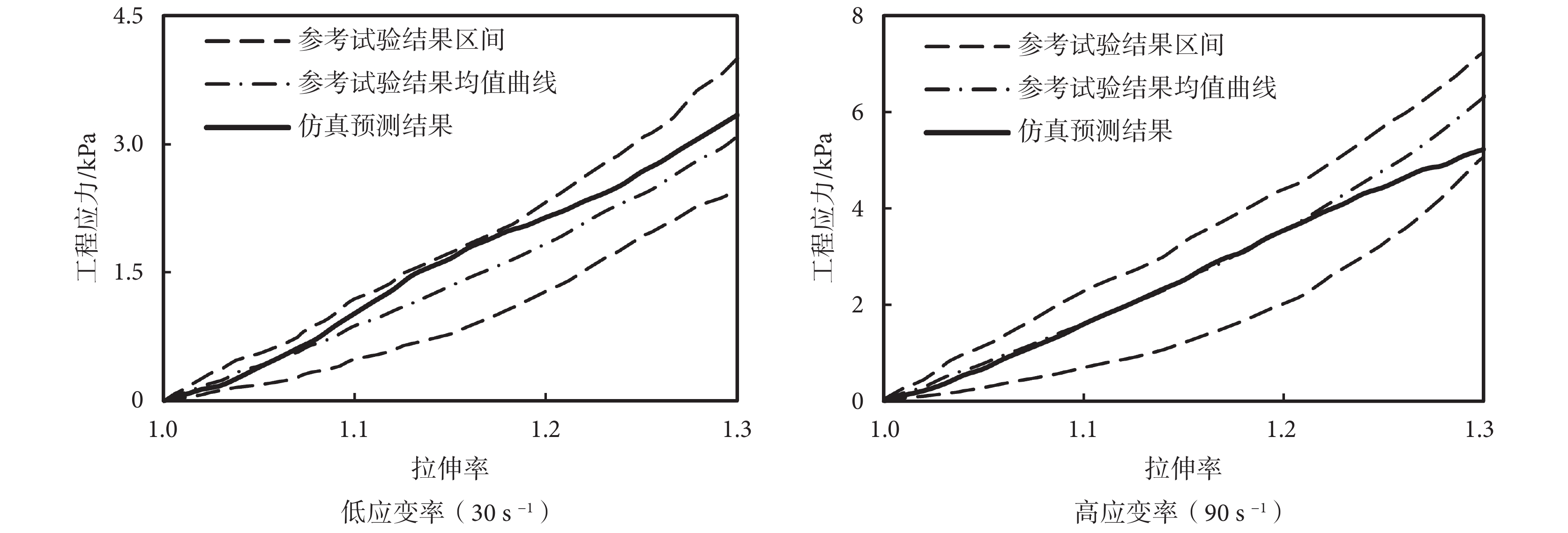
圖 8 所示為應用最優化材料參數的有限元模型在不同拉伸速率下預測的工程應力–應變曲線與參考試驗結果的對比，其中“參考試驗結果區間”是由相應拉伸速率下參考文獻[17]測量的 10 組腦組織應力–應變曲線中具有較高剛度特性和較低剛度特性的兩組試驗曲線構成的工程應力–應變曲線變動區間。如圖 8 所示，在拉伸率小于 1.3 的試驗范圍內，仿真預測的應力–應變曲線均在試驗測量的曲線變動范圍內。尤其是在高應變率情況下，當拉伸率小于 1.25 時，仿真模型與試驗測量數據的均值曲線擬合度較高。
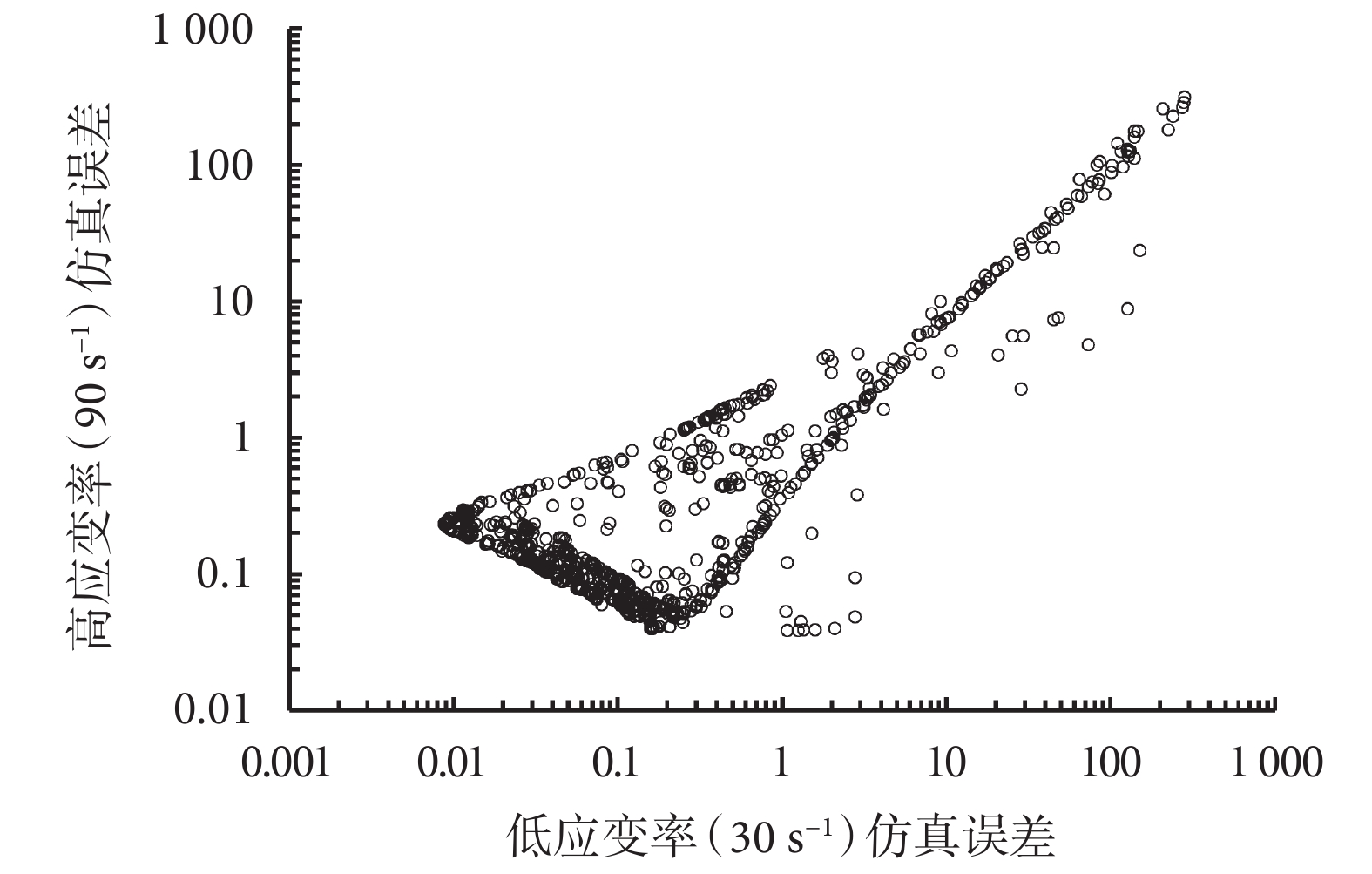圖7
仿真預測誤差分布
Figure7.
Distribution of the fitting errors
表2
優化得到的粘性-超彈性本構方程材料參數
Table2.
Optimal material constants of the visco-hyperelastic constitutive law
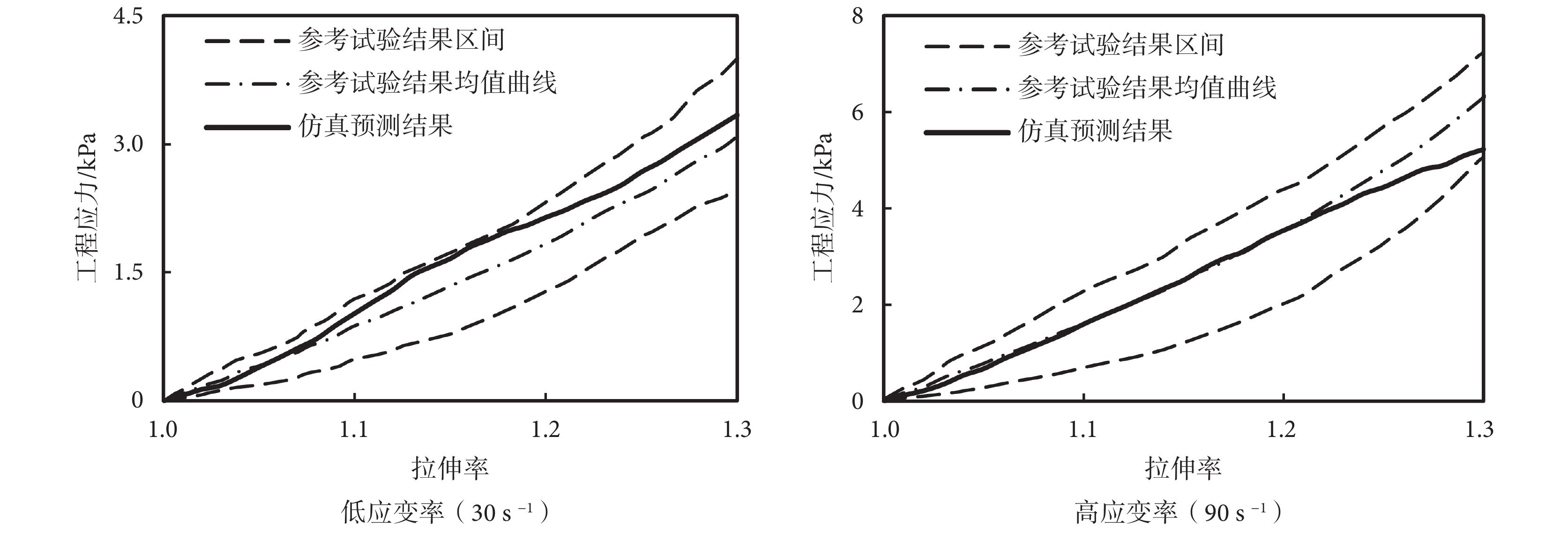圖8
基于優化得到的材料本構方程的有限元仿真預測結果
Figure8.
The stress-strain relationships predicted by finite element simulations assigned with the novel constitutive material law
3 討論
本文運用了有限元仿真與優化算法相結合的方法來確定腦組織粘性–超彈性本構方程。以仿真預測的應力–應變曲線與試驗獲取的均值曲線的誤差最小化為優化目標，建立多目標遺傳算法和有限元仿真結合的自動化材料參數反求模型，確定了能夠有效預測動態單軸拉伸下腦組織力學特性的粘性–超彈性本構方程。
由于腦組織存在的非線性力學特性，基于粘性–超彈性材料模型構建的腦組織有限元模型相對于單純基于線性粘彈性或超彈性模型構建的有限元模型，能夠更為有效地模擬真實頭部碰撞載荷下的腦組織動力學響應。然而在已有的研究中，研究人員在確定腦組織粘性–超彈性本構方程時，通常是將粘性–超彈性材料模型分為超彈性和線性粘彈性兩部分；然后，依據腦組織力學特性試驗結果分別進行腦組織超彈性本構方程和線性粘彈性本構方程的構建，再合并得到腦組織粘性–超彈性本構方程，如參考文獻[7]、[8]和[11]。然而組合得到的腦組織粘性–超彈性本構方程的力學特性已偏離原始的腦組織力學特性試驗測試結果。相反地，本研究將粘性–超彈性材料模型中的各部分視為一個整體，直接以真實腦組織力學特性試驗結果為目標進行材料模型參數的求解；因此，新確定的腦組織粘性–超彈性本構方程能夠更有效地描述腦組織真實的力學特性。
同時，雖然已有基于單一加載速率的腦組織力學特性試驗測試數據確定的材料本構方程，通常對試驗測量的應力–應變曲線擬合度較高；但是，此類本構方程并不能用于描述其他應變率下的材料力學特性，尤其是基于未考慮材料粘性特性的超彈性材料模型構建的腦組織本構方程（如參考文獻[17]、[20]）。為了能夠適應真實頭部碰撞事故中載荷沖擊速率的變化，本文基于不同加載速率的動態單軸拉伸試驗數據完成了腦組織粘性–超彈性本構方程的構建。圖 8 所示的仿真預測的工程應力–應變曲線與目標均值曲線雖然存在一定程度的偏差，但仿真預測曲線仍在試驗測量結果通道之內，這說明預測精度是可以接受的。值得注意的是，在應變率為 90 s–1 時（見圖 8），當腦組織的拉伸率超過 1.25 后，仿真預測與試驗測量結果均值曲線誤差逐漸增大。導致當前誤差的可能原因是：為了數值計算過程的穩定性，本文在仿真中添加了適當的加載緩沖，延長了加載時間，從而導致了粘性特性中的應力松弛抵消了部分超彈性特性中的應力強化作用。
此外需要指出的是，本文僅研究了單軸拉伸載荷下腦組織的粘性–超彈性本構方程，然而在真實頭部碰撞過程中腦組織會承受更為復雜的載荷形式，需要進一步探究當前本構方程在其他類型沖擊載荷或復合沖擊載荷下的適用性。同時，為了將來更準確地模擬沖擊載荷下的顱內動力學響應，需要考慮基于粘性–超彈性本構方程的腦組織各向異性力學特性的建模。
4 結論
本研究運用有限元仿真與優化算法相結合的方法，通過對腦組織動態拉伸試驗的仿真重現，實現了對腦組織粘性–超彈性材料模型的參數求解。新獲取的腦組織粘性–超彈性本構方程能夠對不同動態拉伸應變率下的腦組織力學特性進行有效的模擬。
引言
道路交通事故已成為世界范圍內嚴重的公共健康和安全問題。根據世界衛生組織的報告，全球平均每年因道路交通事故致傷人數約有 500 萬，其中造成的死亡人數超過 120 萬[1]。道路交通事故統計數據表明：人體頭部是最為常見的損傷部位之一，而嚴重的腦外傷是導致人員死亡的主要原因之一[2]。
隨著計算機仿真技術的不斷進步，具有詳細解剖學結構和較高生物逼真度的三維頭部有限元模型已成為研究碰撞載荷下顱內動力學響應的有力工具[3-8]。其中，利用有限元模型開展真實頭部碰撞事故的仿真重建獲取顱內動力學響應，并結合損傷記錄確定相應的腦損傷評價準則和耐受限度，是頭部有限元模型的主要應用之一。例如，Sahoo 等[7]通過對 109 例真實頭部碰撞事故開展仿真重建，提出了基于頭部有限元模型的腦神經損傷評價準則；Kleiven[8]通過對橄欖球運動員頭部碰撞事故的分析和有限元仿真重建，提出了針對輕度腦損傷（腦震蕩）的損傷評價準則。然而，現有的不同頭部有限元模型預測的損傷耐受限度仍然存在較大差別。為了更為準確地預測顱內動力學響應并進一步量化損傷評價準則，頭部有限元模型中生物組織，尤其是腦組織的生物力學特性特別重要。因此，對沖擊載荷下腦組織力學特性的高精度模擬是保證頭部有限元模型生物逼真度的關鍵因素之一。
已有的頭部有限元模型主要采用線性粘彈性材料模型來模擬腦組織具有的粘性特性，但是這種材料模型無法模擬腦組織在大應變時的非線性力學特性[9-10]。近年來，研究人員運用集成了超彈性材料模型和線性粘彈性材料模型優點的粘性-超彈性材料模型來模擬腦組織在動態載荷作用下的非線性力學特性[7, 11-13]。然而，已有的腦組織粘性–超彈性本構方程中材料參數的求解通常拆分為超彈性和線性粘彈性兩個模塊，然后再分別參照試驗數據進行求解，求解后再進行組合。此類方法導致組合得到的新的本構關系已偏離原始參考腦組織力學特性試驗測量結果，因此其生物逼真度并沒有得到有效的驗證。
本文將采用優化算法和有限元模型仿真相結合的方法，對腦組織粘性–超彈性材料模型的參數進行整體求解：構建基于真實試驗的腦組織動態拉伸試驗的有限元仿真模型，將腦組織粘性–超彈性材料模型的關鍵參數設為待求解變量，以仿真預測結果與參考試驗結果的誤差最小化為優化目標，運用優化算法對有限元仿真模型進行迭代計算，最終實現腦組織粘性–超彈性材料模型的參數反求。
1 材料和方法
1.1 粘性–超彈性材料模型
超彈性材料模型利用材料應變能函數（W）來描述材料的力學特性，通常能有效地模擬腦組織在大應變時出現材料硬化的特性，即應力隨應變增大出現非線性上升（如圖 1a 所示）。但是超彈性模型不能夠模擬腦組織作為生物軟組織材料所具有的粘性特性，尤其是無法模擬動態載荷下的應變率效應（即隨著載荷速率的增加，材料剛度顯著增加）。以超彈性材料模型為基礎，通過集成線性粘彈性模型（見圖 1b）引入對腦組織粘性特性的模擬可以構建粘性–超彈性材料模型（見圖 1c）。粘性–超彈性模型能夠較好地模擬動態沖擊載荷下腦組織的非線性力學特性，尤其是腦組織大應變時的材料硬化特性和動態載荷下的應變率效應性。
圖1
粘性-超彈性材料的構建及基本應力-應變關系示意
a. 超彈性材料模型在動態單軸拉伸載荷的應力-應變曲線；b. 線性粘彈性材料模型的應力松弛曲線；c. 粘性-超彈性材料模型在動態單軸拉伸下的應力-應變曲線
Figure1. Schematic diagram of the construction and basic stress-strain relationships of the visco-hyperelastic material modela. stress-strain relationship of the hyperelastic material model under dynamic uniaxial tension; b. the stress relaxation curve of the linear viscoelastic material model; c. stress-strain relationship of the visco-hyperelastic material model under dynamic uniaxial tension
本文以 Weiss 等[14]和 Puso 等[15]開發的軟組織材料模型為基礎，構建腦組織在動態拉伸載荷作用下的粘性–超彈性本構方程。以 Moony-Rivlin 材料模型作為基礎的超彈性模型，其應變能函數（W）描述如下：
|
式中 C1 和 C2 為材料參數，而 2（C1 + C2）為材料在小應變時的初始剪切模量；K 為體積模量；
為單元變形體積比，其中 F 為單元的變形梯度；由于生物軟組織材料具有不可壓縮特性，即 J 取值為 1，則式（1）構成應變能函數的第三項為零。式（1）中
和
分別為右柯西–格林應變張量（C）的第一和第二不變量：
，
。
以超彈性材料模型為基礎，引入線性粘彈性材料模型后可得到粘性–超彈性模型的基本應力（第二類 Piola-Kirchoff 應力（S））計算公式表示如下：
|
式中 t 表示時間；
是由超彈性模型的應變能函數（W）決定的材料彈性特性部分產生的應力響應；
是由材料粘性特性引入的應力，參考 Fung[16]提出的運用卷積積分引入生物軟組織材料的粘性特性的方法，該部分的應力計算公式如下：
|
式中 G 為腦組織線性粘彈性模型的剪切應力松弛函數，可以利用 Prony 級數表達如下：
|
式中 Si 為歸一化處理后的剪切模量分量，即
；Ti 為應力松弛時間分量。
綜上可得當前粘性–超彈性材料模型的應力計算公式如下：
|
式中 C1、C2、Si 和 Ti 為材料模型的待求解變量。
1.2 腦組織動態單軸拉伸試驗的有限元仿真建模
Rashid 等[17]采用自制的生物軟組織高應變率力學特性測試設備（high rate tension device，HRTD）開展了一系列腦組織動態單軸拉伸試驗。如圖 2 所示，HRTD 測試設備主要由伺服控制的電機驅動系統、力傳感器、直線位移傳感器以及一些機械結構組成。參考試驗測試的樣本組織取自新鮮的豬大腦，測試樣本為腦灰質和腦白質混合圓柱體，其平均直徑為 15.1 mm，平均高度為 10 mm。試驗前，將腦組織待測樣本的上、下端面分別與測試設備的上、下板通過一層薄的低粘性醫用粘合劑進行粘接。試驗中，沖擊頭在伺服電機的驅動下向下運動，對拉桿進行沖擊；拉桿帶著與其固定連接的下板整體向下運動，從而實現對腦組織樣本的拉伸。為保證腦組織拉伸速度的均勻一致，電機驅動系統設置有足夠的軸向運動空間避免觸底碰撞；同時設置有減振彈簧以減少沖擊產生的振動。試驗中，運用力傳感器和直線位移傳感器分別測量拉伸過程中的上板受力和下板位移，用于確定腦組織樣本在特定加載速度下的工程應力–應變曲線。文獻[17]中，對不同腦組織樣本施加工程應變率為 30～90 s–1的勻速單軸拉伸。在本文中，將參考文獻[17]中應變率為 30 s–1 和 90 s–1 的試驗組分別定義為低應變率組和高應變率組，并將文獻中相應的試驗結果作為依據，進行腦組織粘性-超彈性本構方程的構建。
圖2
基于 HRTD 測試設備的腦組織動態單軸拉伸試驗原理圖
Figure2.
Schematic diagram of brain tissue dynamic uniaxial tension test by using the HRTD
根據參考試驗的設置，在 LS-DYNA 軟件中建立腦組織樣本的動態單軸拉伸試驗的有限元仿真模型。本文采用規則的六面體網格來分別建立腦組織樣本和上、下板的有限元模型。仿真模型中的邊界條件及載荷條件按照參考試驗測試方法進行設置：① 由于在腦組織拉伸過程中未出現腦組織端面與上、下板表面的脫離或徑向滑移[17]，因此在仿真模型中可用共節點的連接方式分別將腦組織的上、下端面與上、下板的對應表面進行連接；② 依據參考試驗加載方式，在仿真中固定上板并對下板施加強制運動載荷，實現對腦組織樣本的拉伸；③ 仿真中輸出腦組織樣本與上板之間的截面力時間歷程曲線以及下板的位移時間歷程曲線，用于計算仿真預測的腦組織樣本工程應力-應變曲線。根據參考試驗中載荷速度的變化，分別搭建應變率為 30 s–1 和 90 s–1 的兩組動態拉伸試驗的基礎模型。
對建立的有限元模型開展網格收斂性分析。分別建立四組腦組織單元的平均邊長為 2.00、1.00、0.50、0.25 mm 的仿真模型（見圖 3），根據參考文獻[17]中腦組織材料參數范圍設置適當的材料參數。開展動態單軸拉伸試驗的有限元仿真，計算在最大拉伸率 1.3 時腦組織的工程應力以評價模型的網格收斂性。
圖3
網格收斂性分析模型
Figure3.
Finite element models for mesh conversional analysis
1.3 材料模型參數求解
本文建立了基于有限元模型和優化算法的腦組織材料參數自動優化求解流程（見圖 4），并在 modeFRONTIER 軟件中搭建了相應模型。首先，選擇拉丁超立方算法生成樣本數目為 60 的初始種群。運用多目標遺傳算法（MOGA-II）進行參數的優化求解，設置 MOGA-II 的遺傳代數為 20。MOGA-II 是使用精英策略的多目標遺傳算法，能夠在保留最優解的同時避免過早地落入局部最優前沿[18]。同時，本文通過編制 MATLAB 腳本實現數據的自動化處理。
圖4
腦組織材料模型參數自動化求解流程圖
Figure4.
The automatic procedure for the identification of the constitutive law of brain tissue
本文以仿真預測的腦組織工程應力-應變曲線與參考試驗測量結果均值曲線的誤差最小化作為目標函數（F），其中參考試驗結果均值曲線為對應拉伸速率下參考文獻[17]測試的 10 組腦組織樣本試驗結果的均值曲線。如公式（6）～（8）所示，分別采用最小二乘方法計算不同應變率下的仿真預測應力–應變曲線與試驗均值曲線的誤差，其函數表達式表示如下：
|
|
|
式中 f 代表仿真預測和試驗測量的腦組織工程應力–應變曲線，下標 l 和 h 分別代表低應變率和高應變率，下標 s 和 e 分別代表仿真和參考試驗數據，F 為仿真預測的工程應力–應變曲線與參考試驗結果均值曲線之間存在的偏差（擬合誤差）。在本文中，每條曲線均勻地選擇 30 個樣本點，即N = 30，用于計算曲線擬合誤差。
本文根據腦組織力學特性文獻報告的試驗數據，分別確定粘性–超彈性模型中基礎超彈性材料模型和線性粘彈性模型的參數取值或取值范圍。
（1）超彈性材料模型參數 C1 和 C2：根據本文參考試驗的腦組織工程應力–應變曲線測量結果[17]，可以參照理想不可壓縮彈性材料剪切模量的取值約為彈性模量的三分之一的關系來估算參考試驗測量的腦組織（工程應變小于 0.1 時）初始剪切模量，即在當前載荷條件下測量的腦組織初始剪切模量小于 10 kPa。由于在超彈性材料模型中 2（C1 + C2）為材料在小應變時的初始剪切模量，因此可以初步確定 C1 + C2 的取值范圍。而 C1 和 C2 不具有實際物理意義，可由 C1 + C2 的取值并根據優化計算情況進一步修改確定它們的取值范圍。為了更有效地進行自動優化計算，將公式（1）中的 C1 + C2 和 C1 分別設置為計算變量 x1 和 x2。
（2）線性粘彈性材料模型參數 Si 和 Ti：首先本文將公式（4）所示描述腦組織粘性特性的應力松弛函數設置為二階 Prony 級數，即公式（4）中的 n 取值為 2。同時由于
，可設置 S1 為計算變量（x3），取值范圍為［0, 1］。參考文獻[19]中整理的大量哺乳動物腦組織應力松弛測試數據顯示：不同測試條件下腦組織應力松弛曲線變動范圍較大。因此應設置 T1 和 T2 較大的取值范圍，同時設置相應的指數函數形式的計算變量 x4 和 x5。
此外，材料模型中的體積模量 K 設為 1 × 104 kPa（高出剪切模量三個數量級）以模擬腦組織的不可壓縮性。為避免遺漏可能的最優參數組合，以上述材料參數的初步取值范圍為基礎適當擴大了部分參數的取值范圍。用于優化設計計算的材料參數最終取值或取值范圍設置如表 1 所示。
表1
粘性–超彈性材料模型的參數取值或取值范圍以及對應的計算變量
Table1.
Design domain of material variables for the visco-hyperelastic constitutive model and corresponding calculative variables
2 結果
2.1 網格收斂性分析
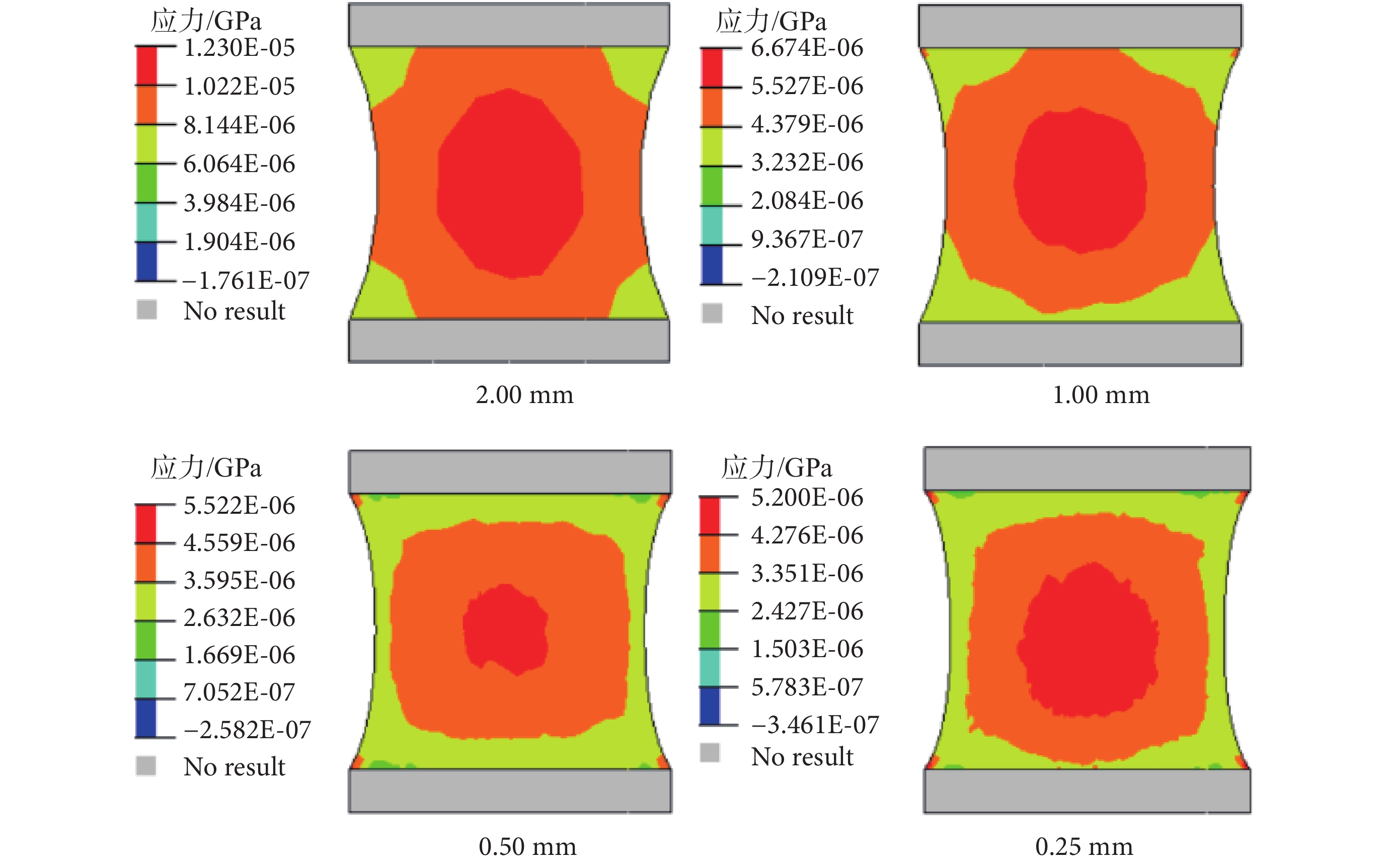
圖 5 和圖 6 所示為應變率為 90 s–1 下的網格收斂性仿真分析結果。由圖 5 可以得知：隨著有限元模型單元平均邊長的減小，當腦組織拉伸率達到 1.3 時仿真預測的工程應力呈現明顯的收斂趨勢。即當單元平均邊長小于 1.00 mm 時，隨著單元邊長的減小，仿真預測的最大工程應力變化較小。同時，腦組織的應力響應云圖（見圖 6）也進一步展示了這一收斂趨勢。然而，隨著單元平均邊長的減小，計算仿真所需要的計算時間會快速增加（圖 5 所示為運用 i7-6700 CPU 計算具有不同單元平均邊長的模型所需要的時間）。考慮到應用遺傳算法進行優化設計時的較大計算量，本文選擇使用有限元模型的單元平均邊長為 1.00 mm。
圖5
網格收斂性分析結果（拉伸率為 1.3 時）
Figure5.
Results of the mesh conversional analysis（at stretch ratio of 1.3）
圖6
腦組織中間剖面拉伸方向應力云圖（拉伸率為 1.3 時）
Figure6.
Contours of predicted stress in the extension direction at the middle cross section of the specimen （at stretch ratio of 1.3）
2.2 材料參數優化求解
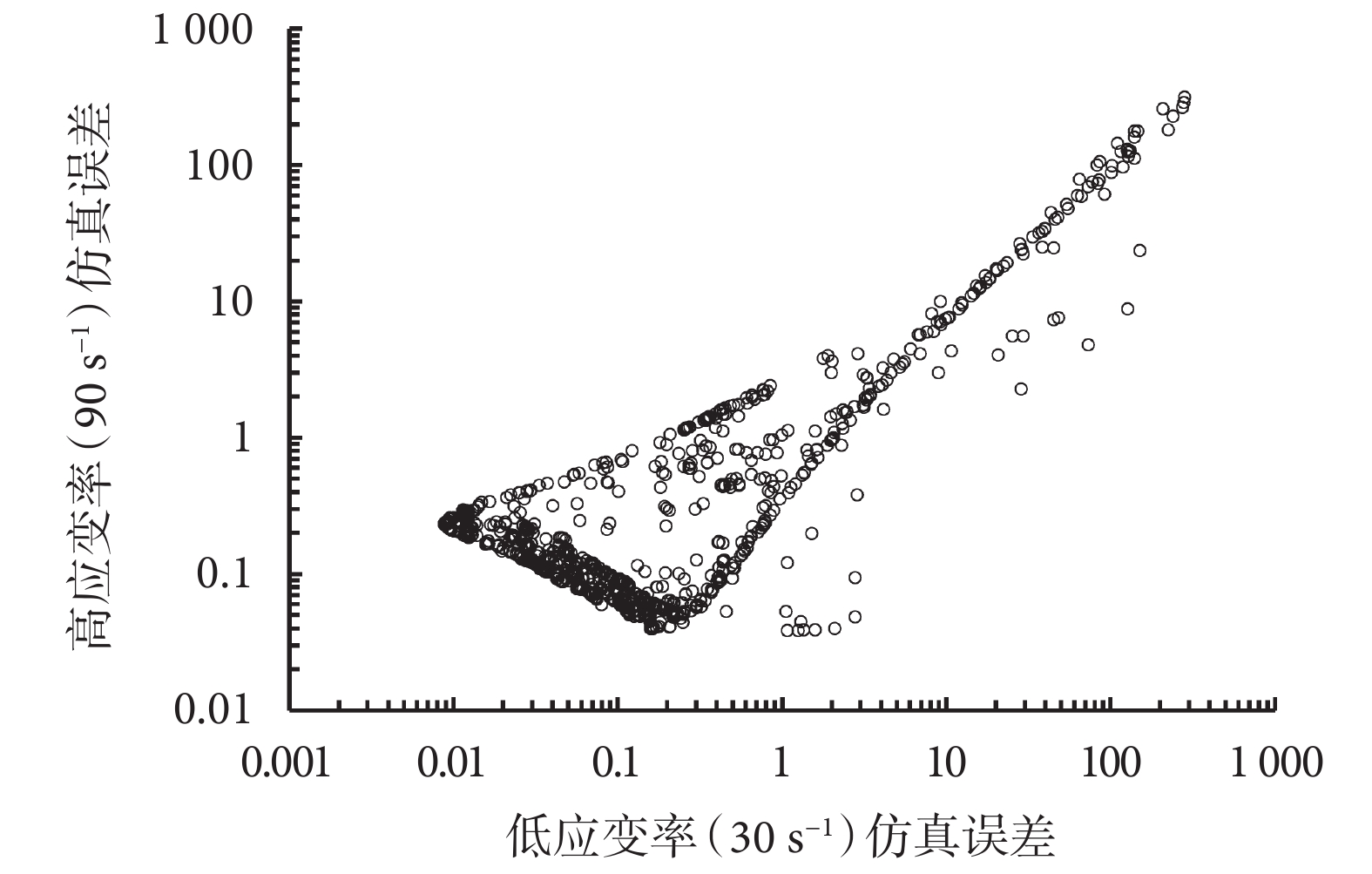
通過進行 20 代的運行，整個優化設計過程共進行 1 200 組（其中有效組數為 1 105）有限元仿真模型的計算，其中每組分別包括一個低應變率（30 s–1）和一個高應變率（90 s–1）的動態單軸拉伸試驗仿真。圖 7 所示為優化設計計算得到的所有樣本點的仿真預測誤差分布，其中某一個樣本點的低應變率仿真誤差和高應變率仿真誤差分別為目標函數公式（6）中的 Fl 和 Fh，即該組有限元仿真模型在相應加載速率下預測的腦組織樣本工程應力–應變曲線與相同加載速率下參考試驗結果均值曲線的誤差。同時，可以看到仿真模型曲線誤差的分布具有明顯的 Pareto 前沿（最優解集）。綜合考慮模型對不同拉伸應變率下腦組織工程應力–應變曲線的擬合精度以及數值計算的穩定性等因素，在曲線擬合誤差均小于 0.1 的 Pareto 最優解集中選擇一組材料參數（如表 2 所示）。
圖 8 所示為應用最優化材料參數的有限元模型在不同拉伸速率下預測的工程應力–應變曲線與參考試驗結果的對比，其中“參考試驗結果區間”是由相應拉伸速率下參考文獻[17]測量的 10 組腦組織應力–應變曲線中具有較高剛度特性和較低剛度特性的兩組試驗曲線構成的工程應力–應變曲線變動區間。如圖 8 所示，在拉伸率小于 1.3 的試驗范圍內，仿真預測的應力–應變曲線均在試驗測量的曲線變動范圍內。尤其是在高應變率情況下，當拉伸率小于 1.25 時，仿真模型與試驗測量數據的均值曲線擬合度較高。
圖7
仿真預測誤差分布
Figure7.
Distribution of the fitting errors
表2
優化得到的粘性-超彈性本構方程材料參數
Table2.
Optimal material constants of the visco-hyperelastic constitutive law
圖8
基于優化得到的材料本構方程的有限元仿真預測結果
Figure8.
The stress-strain relationships predicted by finite element simulations assigned with the novel constitutive material law
3 討論
本文運用了有限元仿真與優化算法相結合的方法來確定腦組織粘性–超彈性本構方程。以仿真預測的應力–應變曲線與試驗獲取的均值曲線的誤差最小化為優化目標，建立多目標遺傳算法和有限元仿真結合的自動化材料參數反求模型，確定了能夠有效預測動態單軸拉伸下腦組織力學特性的粘性–超彈性本構方程。
由于腦組織存在的非線性力學特性，基于粘性–超彈性材料模型構建的腦組織有限元模型相對于單純基于線性粘彈性或超彈性模型構建的有限元模型，能夠更為有效地模擬真實頭部碰撞載荷下的腦組織動力學響應。然而在已有的研究中，研究人員在確定腦組織粘性–超彈性本構方程時，通常是將粘性–超彈性材料模型分為超彈性和線性粘彈性兩部分；然后，依據腦組織力學特性試驗結果分別進行腦組織超彈性本構方程和線性粘彈性本構方程的構建，再合并得到腦組織粘性–超彈性本構方程，如參考文獻[7]、[8]和[11]。然而組合得到的腦組織粘性–超彈性本構方程的力學特性已偏離原始的腦組織力學特性試驗測試結果。相反地，本研究將粘性–超彈性材料模型中的各部分視為一個整體，直接以真實腦組織力學特性試驗結果為目標進行材料模型參數的求解；因此，新確定的腦組織粘性–超彈性本構方程能夠更有效地描述腦組織真實的力學特性。
同時，雖然已有基于單一加載速率的腦組織力學特性試驗測試數據確定的材料本構方程，通常對試驗測量的應力–應變曲線擬合度較高；但是，此類本構方程并不能用于描述其他應變率下的材料力學特性，尤其是基于未考慮材料粘性特性的超彈性材料模型構建的腦組織本構方程（如參考文獻[17]、[20]）。為了能夠適應真實頭部碰撞事故中載荷沖擊速率的變化，本文基于不同加載速率的動態單軸拉伸試驗數據完成了腦組織粘性–超彈性本構方程的構建。圖 8 所示的仿真預測的工程應力–應變曲線與目標均值曲線雖然存在一定程度的偏差，但仿真預測曲線仍在試驗測量結果通道之內，這說明預測精度是可以接受的。值得注意的是，在應變率為 90 s–1 時（見圖 8），當腦組織的拉伸率超過 1.25 后，仿真預測與試驗測量結果均值曲線誤差逐漸增大。導致當前誤差的可能原因是：為了數值計算過程的穩定性，本文在仿真中添加了適當的加載緩沖，延長了加載時間，從而導致了粘性特性中的應力松弛抵消了部分超彈性特性中的應力強化作用。
此外需要指出的是，本文僅研究了單軸拉伸載荷下腦組織的粘性–超彈性本構方程，然而在真實頭部碰撞過程中腦組織會承受更為復雜的載荷形式，需要進一步探究當前本構方程在其他類型沖擊載荷或復合沖擊載荷下的適用性。同時，為了將來更準確地模擬沖擊載荷下的顱內動力學響應，需要考慮基于粘性–超彈性本構方程的腦組織各向異性力學特性的建模。
4 結論
本研究運用有限元仿真與優化算法相結合的方法，通過對腦組織動態拉伸試驗的仿真重現，實現了對腦組織粘性–超彈性材料模型的參數求解。新獲取的腦組織粘性–超彈性本構方程能夠對不同動態拉伸應變率下的腦組織力學特性進行有效的模擬。
