口腔牙齒圖像分割對于牙齒的正畸手術、義齒種植等有重要的意義。由于牙根被牙槽骨包圍,磨牙拓撲結構復雜,以及在牙齒內部有牙髓腔的存在,導致分割時易出現過分割、內部輪廓等問題。為進一步提高分割精度,針對上述問題本文提出了一種基于局部高斯分布擬合與邊緣檢測相結合的分割算法。該算法融合了像素局部鄰域的方差和均值,并將圖像梯度信息引入邊緣檢測,提高了分割算法的穩定性。在實驗中,基于錐形束計算機斷層圖像,完成了對牙根圖像的精確分割,并與當前比較經典的算法進行了對比,結果表明,本文算法能夠更好地區分牙根以及牙根周圍的牙槽骨,能夠更精確地分割出牙根及分裂的磨牙,沒有出現牙髓腔內部輪廓的情況。
引用本文: 劉世偉, 王遠軍. 基于局部高斯分布擬合的牙齒錐形束計算機斷層圖像分割方法. 生物醫學工程學雜志, 2019, 36(2): 291-297, 305. doi: 10.7507/1001-5515.201709042 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
錐形束計算機斷層掃描(cone beam computer tomography,CBCT)在牙科診斷中應用廣泛,與傳統的多層 CT(multi-slice computer tomography,MSCT)相比,CBCT 輻射劑量小,成像速度快,圖像空間分辨率高。牙齒 CBCT 圖像中包含著牙齒的位置和形狀信息。基于 CBCT 牙齒圖像可以重建三維牙齒模型并進行定量分析,這對于牙齒的正畸手術、根管治療、義齒種植等有著重要的意義。基于 CBCT 圖像的牙齒分割對于精確定量分析非常重要。
針對牙齒圖像實現精確分割主要有以下困難[1]:① 牙冠部分,相鄰牙齒之間相互粘連,對于單顆牙齒的分割造成了困難。② 牙根部分,牙齒被牙槽骨包圍,牙齒的灰度與牙槽骨相近,將牙齒與牙槽骨精確區分比較困難。③ 磨牙拓撲結構復雜,在牙根處可能分裂成兩到三個牙齒,對算法要求很高。④ 牙齒內部存在牙髓腔,在牙齒分割過程中容易出現內輪廓。
為了解決牙齒分割的問題,研究者提出了大量的分割方法。在牙冠區域,為解決相鄰牙齒之間相互粘連的問題,Dufour 等[2]提出了耦合水平集。將所有牙齒都用兩個水平集進行表示,相鄰牙齒用不同水平集。在分割時兩個水平集同時演化,這樣相鄰粘連的牙齒分割時就不會相互融合。Heo 等[3]提出了一種自適應閾值方法,利用序列中先驗信息獲取分割閾值,提高了分割的準確性,但是由于圖像灰度分布不均勻,相鄰牙齒相互粘連,閾值選擇比較困難,容易欠分割或過分割。傳統的牙齒分割算法只能分割上下頜不接觸的圖像。Xia 等[4]提出了一種上下頜咬合狀態下的牙齒分割方法。在牙頸牙根處使用混合水平集進行分割,對上下頜接觸處進行分割時重建網格模型,使用閾值和快速分水嶺算法進行分割。當牙齒圖像中存在金屬偽影時,對牙冠區域進行分割時不能準確地分割出單顆牙齒。為此 Xia[5]等對存在金屬偽影的牙冠先用 Radon 變換將單顆牙齒提取出來,再使用水平集方法進行分割。在牙根區域,Akhoodali 等[6]提出了一種基于區域生長的分割方法,Zhang[7]提出了一種基于局部區域生長的方法,但是都不能精確地分割出牙根。對于磨牙的分割,Gao 等[8]和 Gan 等[9]的文章里都有涉及。但是,Gan 等的算法不能精確地識別出第三磨牙,而 Gao 等的算法不能正確地處理牙齒分裂的問題。在牙齒中存在牙髓腔,與牙本質區域相比,牙髓腔區域的灰度值較低,在分割過程中會出現內部邊緣。為此 Gan 等[9]在水平集中引入梯度方向,只有當梯度方向與負水平集的法線方向一致時,邊緣才為有效邊緣。由于牙齒斷層圖像中相鄰斷層圖像的灰度分布非常相似,Gao 等[8]利用上一層斷層圖像中的灰度分布作為當前層的灰度約束項,指導曲線演化,使輪廓上的點自適應地收縮或膨脹。與灰度分布相似,牙齒斷層圖像中相鄰的斷層圖像形狀也是高度相似的,基于此,Gao 等[8]和 Ji 等[10]提出了基于先驗形狀的約束項。將上一層的結果輪廓作為當前層的初始輪廓,當曲線演化到距離初始輪廓較遠時,此約束項的值較大,防止曲線演化到距離上一輪廓較遠的位置。Ji 等[10]在 Gao 等[8]的基礎上改進了先驗區域能量項,用最大后驗概率指導曲線的演化。Hosntalab 等[11]提出了利用三維水平集函數對牙齒圖像進行分割,但是該方法對初始輪廓敏感,分割結果不可控,分割容易出現錯誤。王立新等[12]提出了一種結合自動閾值分割、Chan-Vase(CV)模型與圖割方法的分割方法。對于牙齒與周圍組織灰度值相差較大的圖像有一定的分割效果,但是對于差異較小的則效果較差。在對牙齒序列進行分割時,主要依靠上層牙齒的分割結果指導當前層的分割。如果相鄰層之間的牙齒形狀差距較大,則形狀先驗知識起不到積極的作用。為了解決這個問題,Gan 等[13]提出了一種斜角牙齒的分割方法,根據牙齒的軸線傾斜角度調整為與橫截面垂直,對調整后的牙齒使用水平集進行分割。
為了進一步提高牙根分割精度、磨牙分裂以及牙髓腔內部輪廓等問題,本文提出一種混合水平集分割方法。將局部高斯分布擬合(local Gaussian distribution fitting,LGDF)[14]與邊緣檢測(edge detection)[8, 10]結合起來對牙齒圖像進行分割,并將其與經典的 CV 模型[15]、形狀-強度先驗模型[8]進行實驗對比,驗證本算法的有效性。
1 方法
1.1 水平集分割方法原理
水平集方法最初由 Osher 等[16]提出,用于解決遵循熱力學方程下的火苗變化過程。其方法的核心是用高一維函數的零水平集函數表示低一維的函數。通過獲取高維函數在零水平集中的位置來獲得最終的演化結果。
可以將水平集模型分為基于區域的模型[14-15, 17-18]和基于邊緣的模型[19]。基于邊緣的模型主要利用圖像的邊緣信息來約束曲線的演化。典型的基于邊緣的模型都有一個邊緣停止項來控制曲線的運動。當曲線運動到目標邊緣時,此停止項為零。幾何活動輪廓(geometric active contour,GAC)模型[20]為最常用的邊緣模型,其能量泛函如下:
 |
其中  為水平集閉合曲線的長度,S 為閉合曲線的弧長參數。對上式使用梯度下降法得到零水平集演化方程:
為水平集閉合曲線的長度,S 為閉合曲線的弧長參數。對上式使用梯度下降法得到零水平集演化方程:
 |
其中  為常數,可以加速曲線演化,g 為邊緣停止函數
為常數,可以加速曲線演化,g 為邊緣停止函數  。
。 表示標準偏差為
表示標準偏差為  的高斯核函數。
的高斯核函數。 表示去噪后的圖像。該模型進行曲線演化時受到兩個力的驅動。第一個是內力,即曲率運動,為式(2)的第一項。受到圖像梯度的標量場
表示去噪后的圖像。該模型進行曲線演化時受到兩個力的驅動。第一個是內力,即曲率運動,為式(2)的第一項。受到圖像梯度的標量場  控制,在目標邊緣處為零,因此稱
控制,在目標邊緣處為零,因此稱  為邊緣停止函數。第二個為外力,來自于
為邊緣停止函數。第二個為外力,來自于  的梯度
的梯度  ,為式(2)中的第二項。它可以使水平集函數向著目標邊緣運動。對于目標邊緣較為清晰的圖像分割效果較好。但是該模型對于噪聲比較敏感,圖像邊緣較弱時分割效果較差。
,為式(2)中的第二項。它可以使水平集函數向著目標邊緣運動。對于目標邊緣較為清晰的圖像分割效果較好。但是該模型對于噪聲比較敏感,圖像邊緣較弱時分割效果較差。
基于區域的模型利用圖像的區域信息指導曲線演化,在圖像分割上的表現比基于邊緣的模型要好。比較常用的模型有 CV 模型[15]和局部二值擬合(local binary fitting,LBF)模型[17]。CV 模型是為了解決基于邊緣的水平集函數對邊界模糊和不連續圖像分割效果較差的問題。其能量泛函定義如下:
 |
其中  和
和  分別表示曲線內外灰度的均值。只有當曲線處在目標區域的邊緣時,該泛函才能取到最小值。由于
分別表示曲線內外灰度的均值。只有當曲線處在目標區域的邊緣時,該泛函才能取到最小值。由于  和
和  不能準確地表示一幅圖像,因此該模型對于灰度分布不均勻的圖像分割效果較差,為此 Li 等[17]提出了 LBF 模型。該模型為一種基于局部區域的水平集模型,其能量泛函如下:
不能準確地表示一幅圖像,因此該模型對于灰度分布不均勻的圖像分割效果較差,為此 Li 等[17]提出了 LBF 模型。該模型為一種基于局部區域的水平集模型,其能量泛函如下:
 |
其中  為標準差為
為標準差為  的高斯函數。
的高斯函數。 與
與  分別表示曲線內外的擬合灰度值。該能量方程所考察的區域是以當前點 x 為中心的鄰域范圍。鄰域范圍大小由高斯函數的標準差
分別表示曲線內外的擬合灰度值。該能量方程所考察的區域是以當前點 x 為中心的鄰域范圍。鄰域范圍大小由高斯函數的標準差  決定。當水平集函數演化到目標輪廓時,擬合灰度值近似于區域內曲線內外的灰度值,此時整個區域點的擬合能量值最小。由于本模型是基于局部區域信息,對灰度分布不均勻的圖像分割效果較好。
決定。當水平集函數演化到目標輪廓時,擬合灰度值近似于區域內曲線內外的灰度值,此時整個區域點的擬合能量值最小。由于本模型是基于局部區域信息,對灰度分布不均勻的圖像分割效果較好。
由于牙齒與周圍牙槽骨灰度差異小、磨牙拓撲結構復雜以及相鄰牙齒相互粘連等特點,傳統的水平集方法對于牙齒圖像分割精度較差。例如 CV 模型[11],該模型對于灰度分布均勻的圖像分割效果較好,但是牙齒圖像灰度分布不均勻,使用 CV 模型分割效果很差。針對 CBCT 序列相鄰圖像的相似性,Gao 等[8]提出了一種形狀-強度先驗模型。該模型很好地解決了灰度分布不均勻的問題,對于牙槽骨包埋的牙根分割效果也很精確,但是磨牙分裂的問題還是不能得到很好的解決。為此本文提出了一種基于局部高斯分布擬合與邊緣檢測模型相結合的牙齒分割模型。
1.2 局部高斯分布擬合項
在牙齒圖像分割中,我們假設圖像  由兩部分組成,一部分是牙齒區域,即前景區域,另一部分為背景區域,分別用
由兩部分組成,一部分是牙齒區域,即前景區域,另一部分為背景區域,分別用  和
和  表示。滿足
表示。滿足  ,
, 。在水平集分割的過程中,這兩個區域分別為零水平集的內部和外部,即
。在水平集分割的過程中,這兩個區域分別為零水平集的內部和外部,即  和
和  。
。
在該模型中,對于每一個像素點 x,假設一個以像素點 x 為中心、 為半徑的鄰域。
為半徑的鄰域。
 。根據貝葉斯公式可得:
。根據貝葉斯公式可得:
 |
其中  可以簡化為
可以簡化為  ,表示在區域
,表示在區域  中的灰度分布,i 取值可以為 1 或 2。
中的灰度分布,i 取值可以為 1 或 2。 表示 y 屬于
表示 y 屬于  的先驗概率。
的先驗概率。 表示灰度值
表示灰度值  的先驗概率。因為
的先驗概率。因為  與
與  為定值,可以省略。對得到的最大后驗概率取對數,將最大化轉化為最小化,得到如下能量泛函[14]:
為定值,可以省略。對得到的最大后驗概率取對數,將最大化轉化為最小化,得到如下能量泛函[14]:
 |
式(6)對單點像素構造鄰域最小化函數,對該函數求取最小值實現對該鄰域的最優分割。對于概率密度函數  ,選取高斯密度函數[14]。
,選取高斯密度函數[14]。
 |
其中  和
和  分別為局部強度的均值和方差。
分別為局部強度的均值和方差。
對式(6)引入一個權重函數:
 |
則對式(6)重新定義為:
 |
由于上式是對于一個像素點的計算,如果計算整幅圖像,則需要對上式積分求和:
 |
1.3 邊緣檢測項
為了更準確地分割牙齒圖像,在高斯分布擬合的基礎上引入了邊緣檢測。牙齒主要由兩部分組成。牙齒中間部分,灰度較低,為牙髓腔。在牙髓腔的外部為牙本質區域,灰度值較高。這樣在進行牙齒分割時可能會出現兩個邊緣,一個為牙本質與牙齒外部的邊緣,另一個為牙本質與牙髓腔的內部邊緣。為了避免這一情況,在局部高斯擬合的基礎上引入了邊緣檢測項,并且在邊緣檢測項中引入梯度方向。
 |
其中  表示梯度,
表示梯度, 表示將圖像 I 與高斯核
表示將圖像 I 與高斯核  進行卷積。
進行卷積。 為牙齒的初始輪廓。當圖像的梯度方向與法線方向一致時,此時的邊緣為正確的邊緣。
為牙齒的初始輪廓。當圖像的梯度方向與法線方向一致時,此時的邊緣為正確的邊緣。
同時為了避免初始化與平滑水平集函數引入正則化項以及長度約束項:
 |
 |
總的能量泛函為:
 |
由梯度下降法可得:
 |
其中  和
和  分別為:
分別為:
 |
 |
局部強度為:
 |
 |
局部方差為:
 |
 |
1.4 評價指標
為定量地評價分割結果,本文使用有經驗的臨床醫生手動分割結果作為評價分割準確性的標準。本文使用的定量評價指數分別為 Jaccard 指數(Jaccard Index,Jc)與 Dice 相似性系數(Dice Similarity Index,DSI)。
Jc 指數的定義為:
 |
其中  為臨床醫生手動分割的結果,
為臨床醫生手動分割的結果, 為算法分割的結果。算法分割結果越準確,則 Jc 值越接近 1。
為算法分割的結果。算法分割結果越準確,則 Jc 值越接近 1。
Dice 相似性系數定義為:
 |
與上式一樣,DSI 越接近 1,分割結果越精確。
1.5 實驗步驟
(1)選取初始層。選取初始層時要注意牙齒之間不相互粘連,選取比較好的層面。所以初始層選取在牙頸處,本文采用的序列圖像共 220 層,初始層選取在 73 層。
(2)獲取牙盒。選定待分割的牙齒之后,需要將選定的牙齒從圖像中提取出來。選定初始層之后將圖像顯示出來,確定選定的牙齒之后手動提取該牙齒的中心點,以該點為中心提取出一個一定大小的方形區域,一般選取的大小為  。
。
(3)參數設定。本文的參數主要涉及到迭代步長  ,高斯核函數的截斷系數
,高斯核函數的截斷系數  ,高斯核標準差
,高斯核標準差  ,邊緣檢測項系數
,邊緣檢測項系數  ,長度約束項系數
,長度約束項系數  ,正則化項系數
,正則化項系數  。其中
。其中  和
和  分別為公式(8)中的截斷系數與標準差,
分別為公式(8)中的截斷系數與標準差, 不大于
不大于  。
。 、
、 和
和  分別為公式(15)中第二項、第三項和第四項的系數。實驗中各個參數的取值見下文。
分別為公式(15)中第二項、第三項和第四項的系數。實驗中各個參數的取值見下文。
(4)生成初始輪廓。首先對牙盒進行中值濾波去噪,并且對圖像進行歸一化。對歸一化后的圖像使用閾值分割及圖像的開運算獲得二值模板圖像。將其作為初始層分割的初始輪廓。
(5)序列分割。在對序列圖像進行分割時,將上一層的分割結果作為當前層的初始輪廓。在初始輪廓的基礎上使用本文算法進行曲線的迭代演化,得到最終的結果,一直到將序列圖像分割完成。
2 實驗結果與討論
為驗證本文分割算法的正確性,本文在臨床 CBCT 數據上進行了測試。本文選用十組牙齒 CBCT 數據進行分割實驗,該實驗數據由我們實驗室團隊成員在上海第九人民醫院掃描獲得,符合醫院倫理審查規范,所有參與者對該研究都知情并同意所掃描數據供團隊研究使用。圖像分辨率為 0.25 mm × 0.25 mm × 0.25 mm,圖像為大小為 435 × 435,此序列圖像共 220 層。測試使用的電腦配置為 Intel(R) Core(TM) i7-7700,主頻為 3.60 GHz,內存為 8 GB。測試平臺為 MATLAB2016b。
本文分割算法的默認參數設置為  ,
, ,
, ,
, 。牙齒為磨牙時
。牙齒為磨牙時  = 0.000 1 × 2552,其余牙齒
= 0.000 1 × 2552,其余牙齒  = 0.000 8 × 2552。對于參數
= 0.000 8 × 2552。對于參數  ,牙齒為磨牙時
,牙齒為磨牙時  ,牙齒為前磨牙時
,牙齒為前磨牙時  ,牙齒為尖牙和切牙時
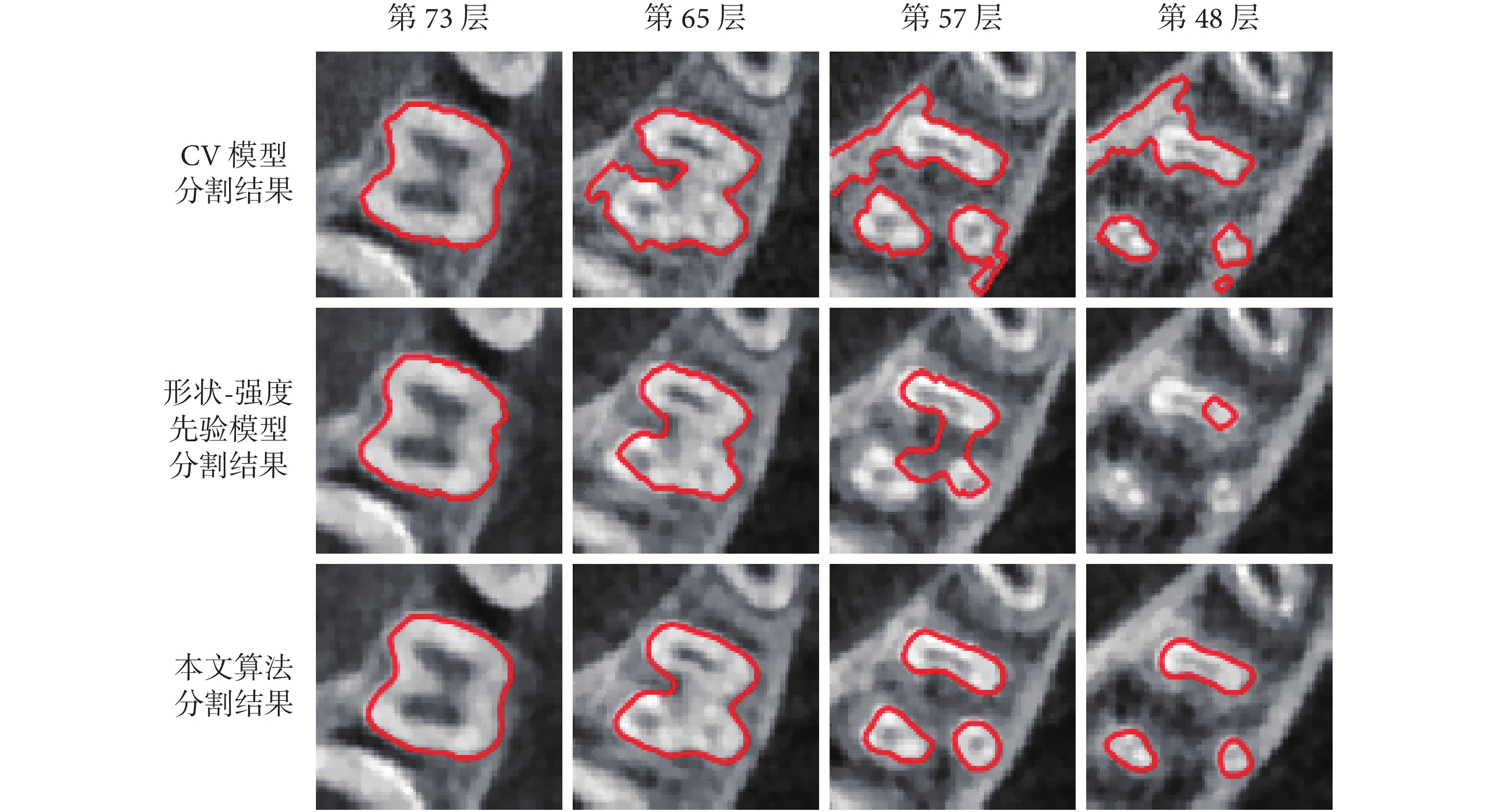
,牙齒為尖牙和切牙時  。本次實驗的對比實驗分別為 CV 模型[15]和形狀-強度先驗模型[8]。在實驗過程中,也有默認參數分割結果不是很好的情況,這種情況下我們通常以上述參數默認值為起點,在以參數默認值為中心的一個局部區間內通過實驗驗證設定更好的參數取值。圖 1 到圖 5 分別為 CV 模型、形狀-強度先驗以及本文算法對磨牙、前磨牙、尖牙、切牙以及整個下頜牙齒的分割結果。表 1 為對三種算法的定量評價。
。本次實驗的對比實驗分別為 CV 模型[15]和形狀-強度先驗模型[8]。在實驗過程中,也有默認參數分割結果不是很好的情況,這種情況下我們通常以上述參數默認值為起點,在以參數默認值為中心的一個局部區間內通過實驗驗證設定更好的參數取值。圖 1 到圖 5 分別為 CV 模型、形狀-強度先驗以及本文算法對磨牙、前磨牙、尖牙、切牙以及整個下頜牙齒的分割結果。表 1 為對三種算法的定量評價。
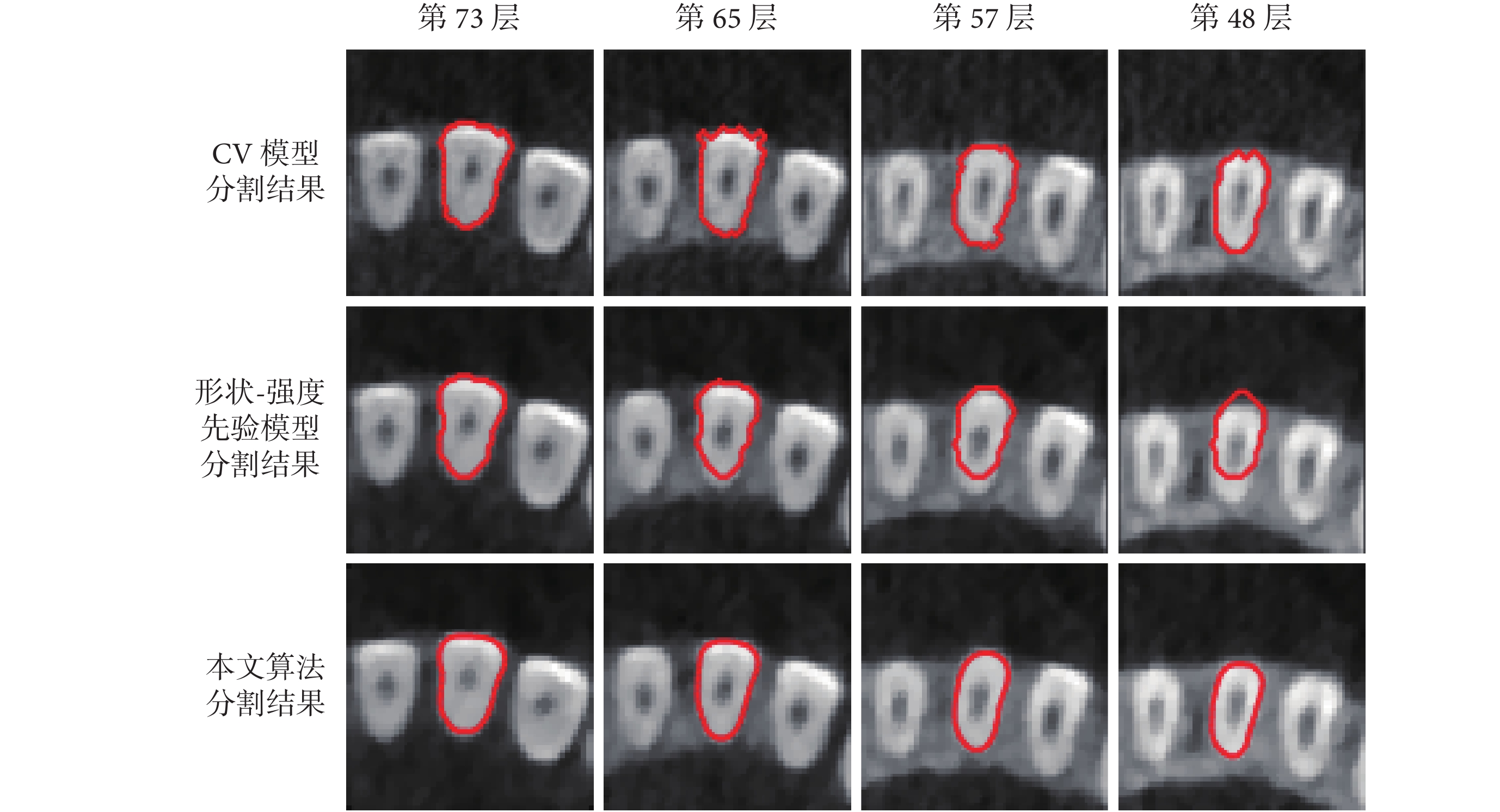
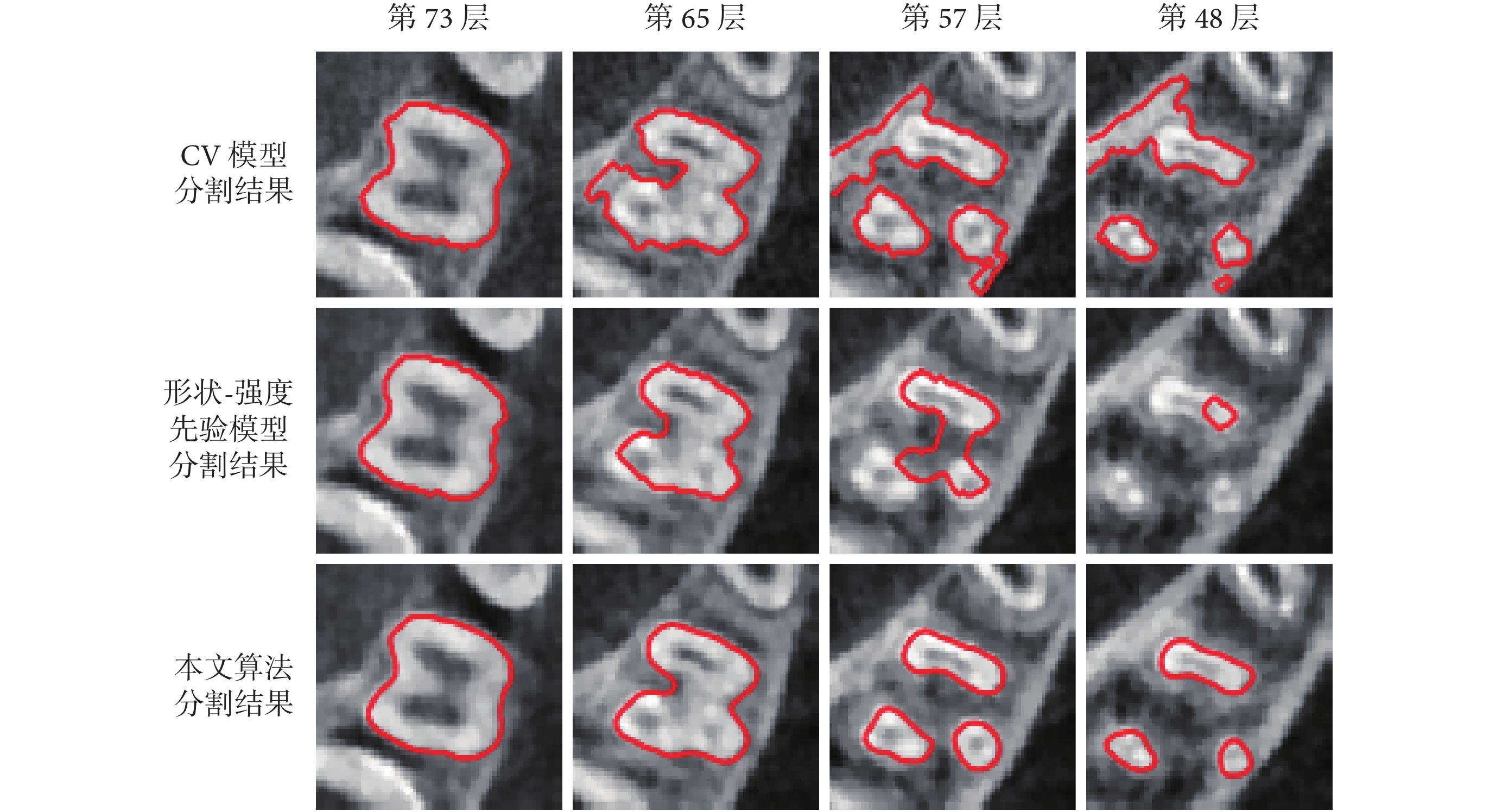 圖1
三種算法對第一磨牙序列的部分分割結果
Figure1.
Partial segmentation results of first molar sequence by three algorithms
圖1
三種算法對第一磨牙序列的部分分割結果
Figure1.
Partial segmentation results of first molar sequence by three algorithms
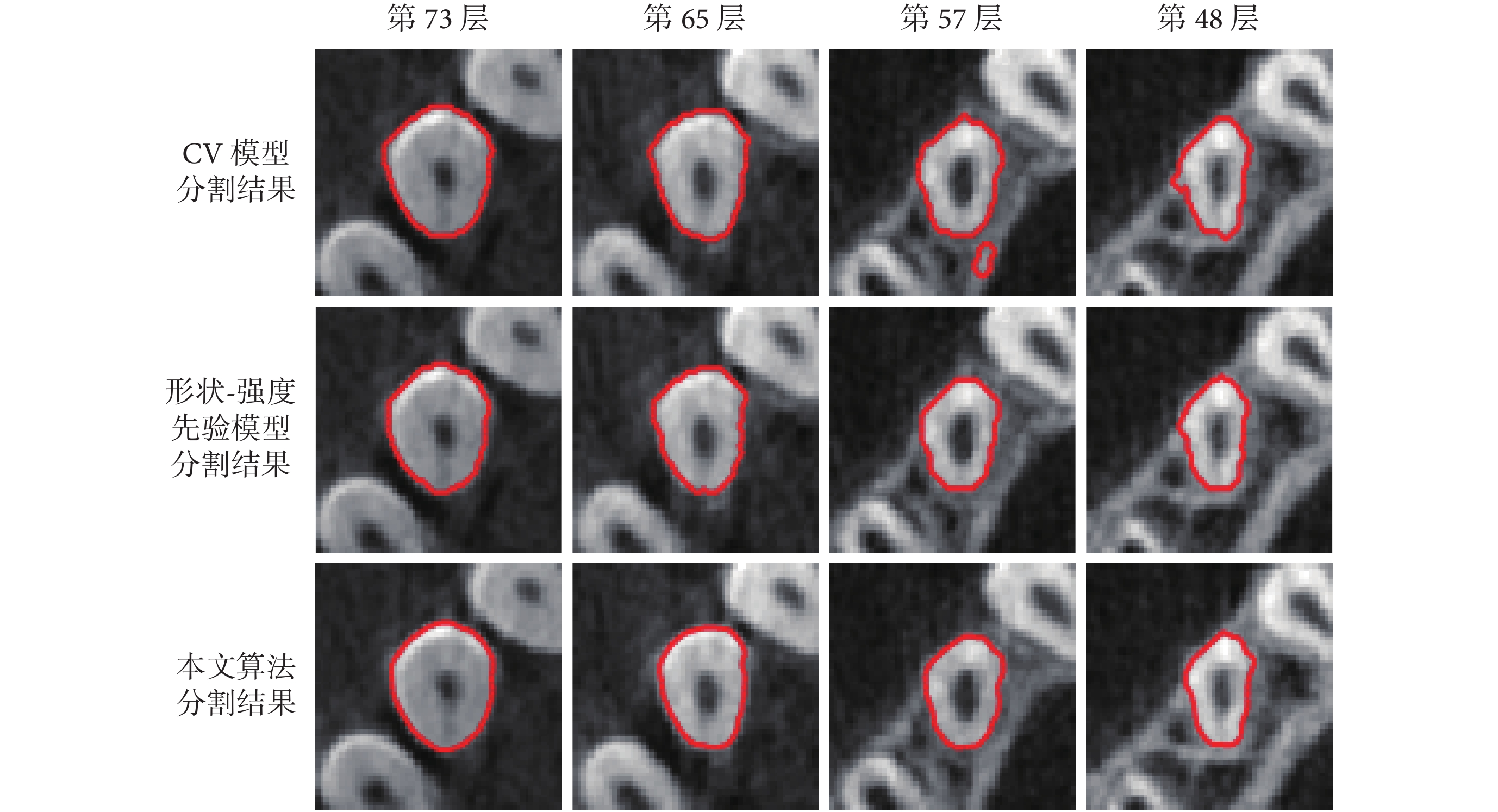
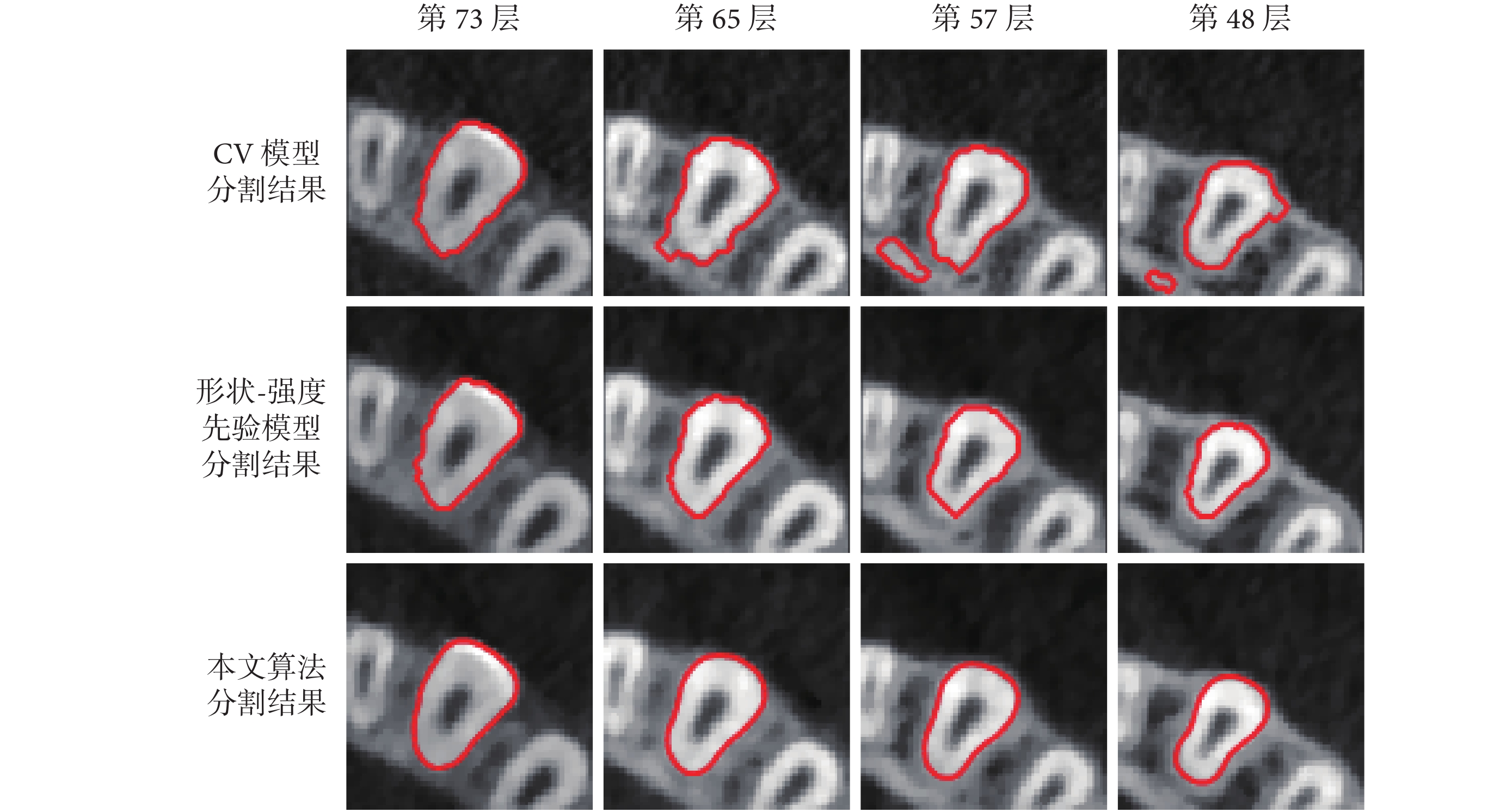 圖3
三種算法對尖牙序列的部分分割結果
Figure3.
Partial segmentation results of canine sequence by three algorithms
圖3
三種算法對尖牙序列的部分分割結果
Figure3.
Partial segmentation results of canine sequence by three algorithms
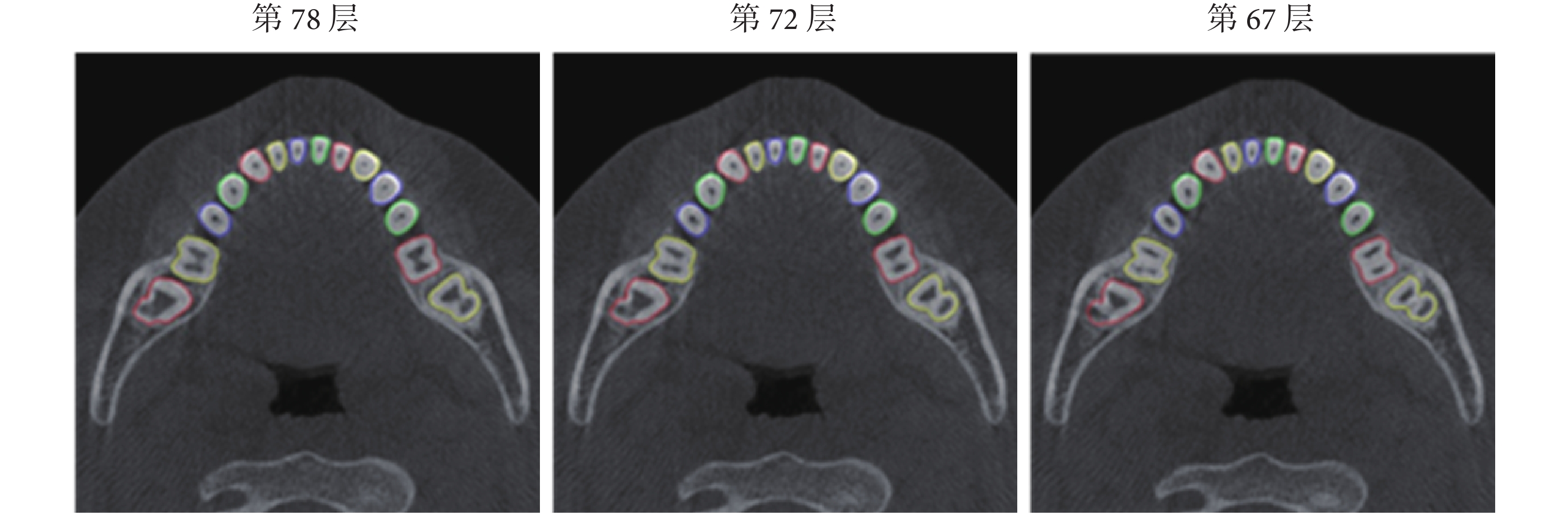
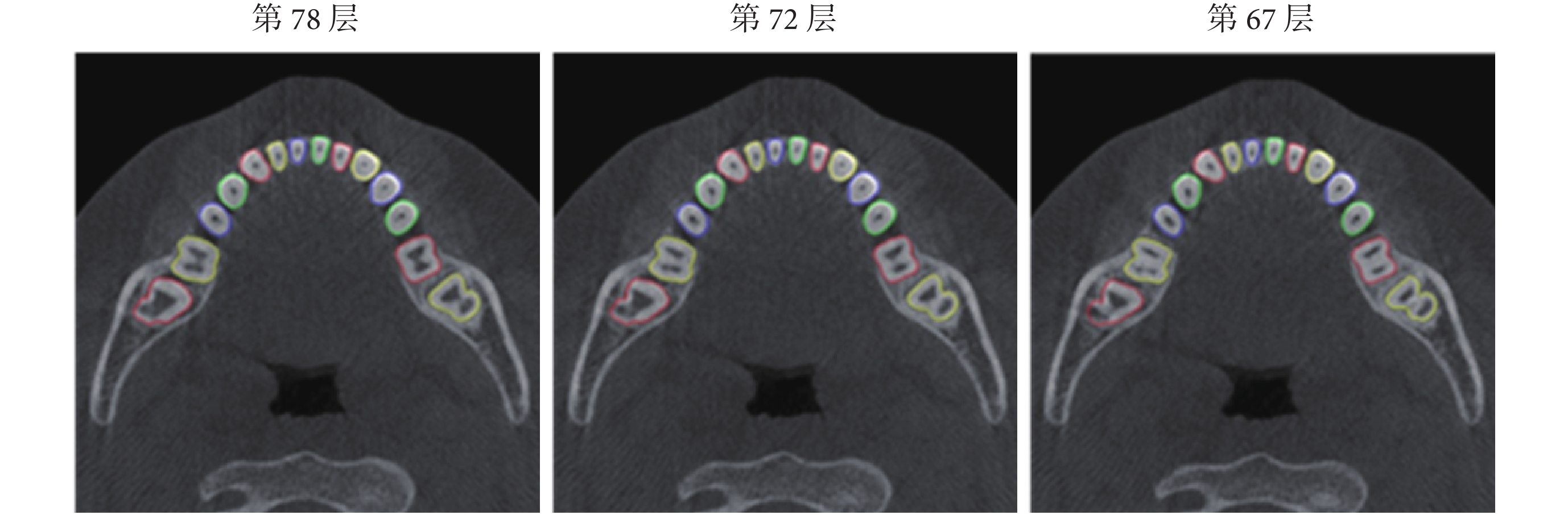 圖5
本文提出的算法對下頜所有牙齒分割部分層面的結果
Figure5.
The segmentation results of the proposed methods for all teeth in samples slices of the mandible
圖5
本文提出的算法對下頜所有牙齒分割部分層面的結果
Figure5.
The segmentation results of the proposed methods for all teeth in samples slices of the mandible
從圖中可以看出本文算法對于牙齒有較好的分割效果,即使牙齒被包埋在牙槽骨中,也可以較精確地將牙齒從牙槽骨中分割出來。磨牙牙根處拓撲結構變化靈活,會分裂成多個牙齒,該模型仍然可以準確分割出分裂的牙齒。CV 模型對于灰度均勻的圖像分割比較準確,對灰度不均勻的圖像分割效果較差。從圖 2 到圖 4 可以看出,CV 模型對牙頸部分進行分割時,分割較為準確,但是當牙齒被牙槽骨包圍時,牙齒灰度與牙槽骨比較接近,此時該模型不能準確地區分牙齒與牙槽骨。尤其是對于磨牙,磨牙在牙頸處就被牙槽骨包圍,且拓撲結構變化靈活,分割效果更差。形狀-強度先驗模型對于前磨牙的分割效果較好。但是對于磨牙,當磨牙開始分裂的時候,不能準確地分割出分裂的牙齒。由于本文涉及到的三種算法采用相同的分割流程,前期預處理的步驟相同,所以算法耗時從自動分割開始算起。本文算法主要是針對牙根圖像進行分割,所展示的時間是整個口腔的 28 顆牙齒從初始層到分割結束所用時間。本文算法、CV 模型和形狀-強度先驗算法的運行時間分別為 45.39、28.56、129.19 s。由于 CV 模型算法計算較為簡單,算法運行時間比本文算法短,但是分割效果太差。本文算法跟形狀-強度先驗模型相比,效率大大提高,且精確度有較大提升。
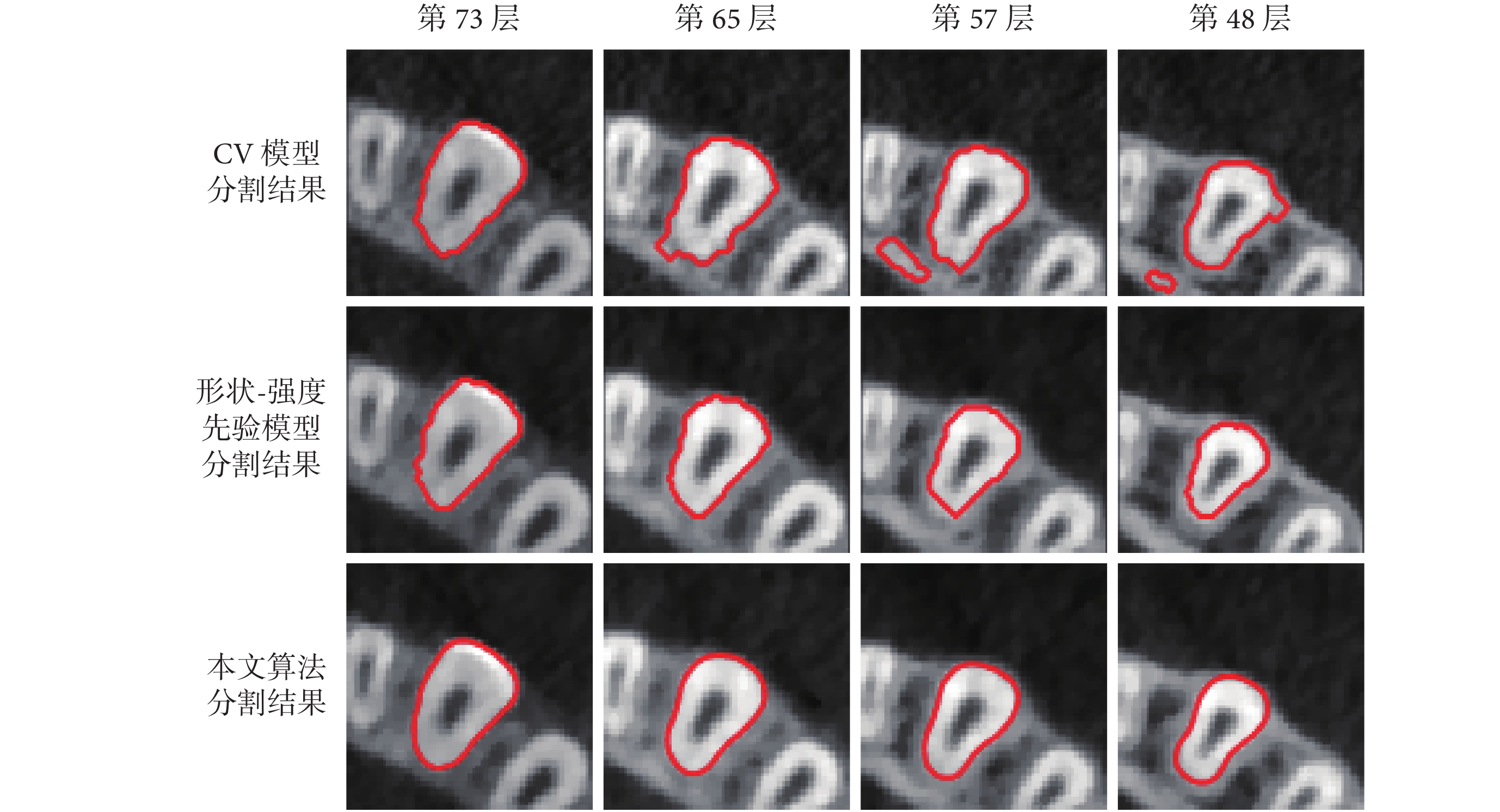
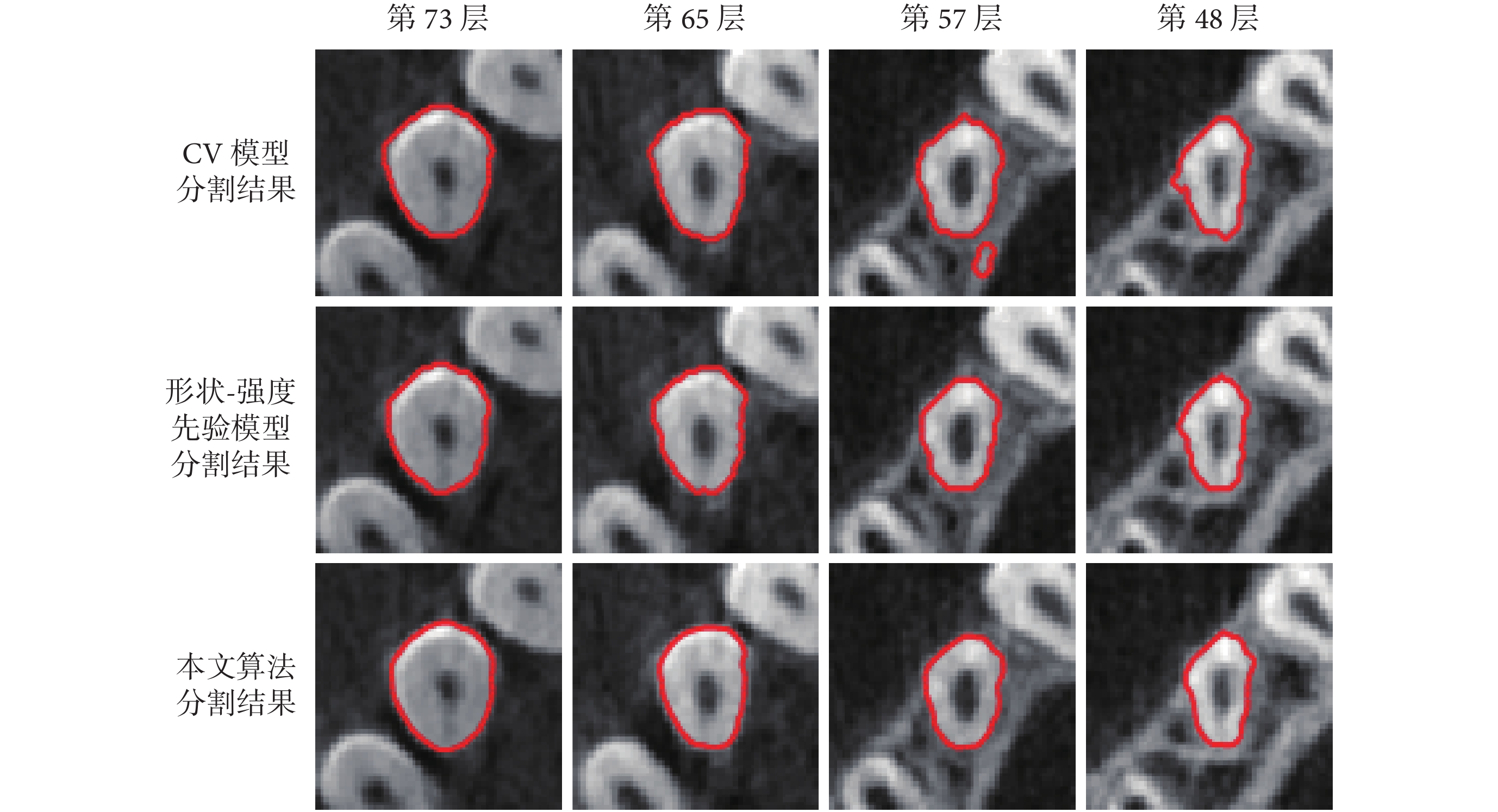 圖2
三種算法對第一前磨牙序列的部分分割結果
Figure2.
Partial segmentation results of first premolar sequence by three algorithms
圖2
三種算法對第一前磨牙序列的部分分割結果
Figure2.
Partial segmentation results of first premolar sequence by three algorithms
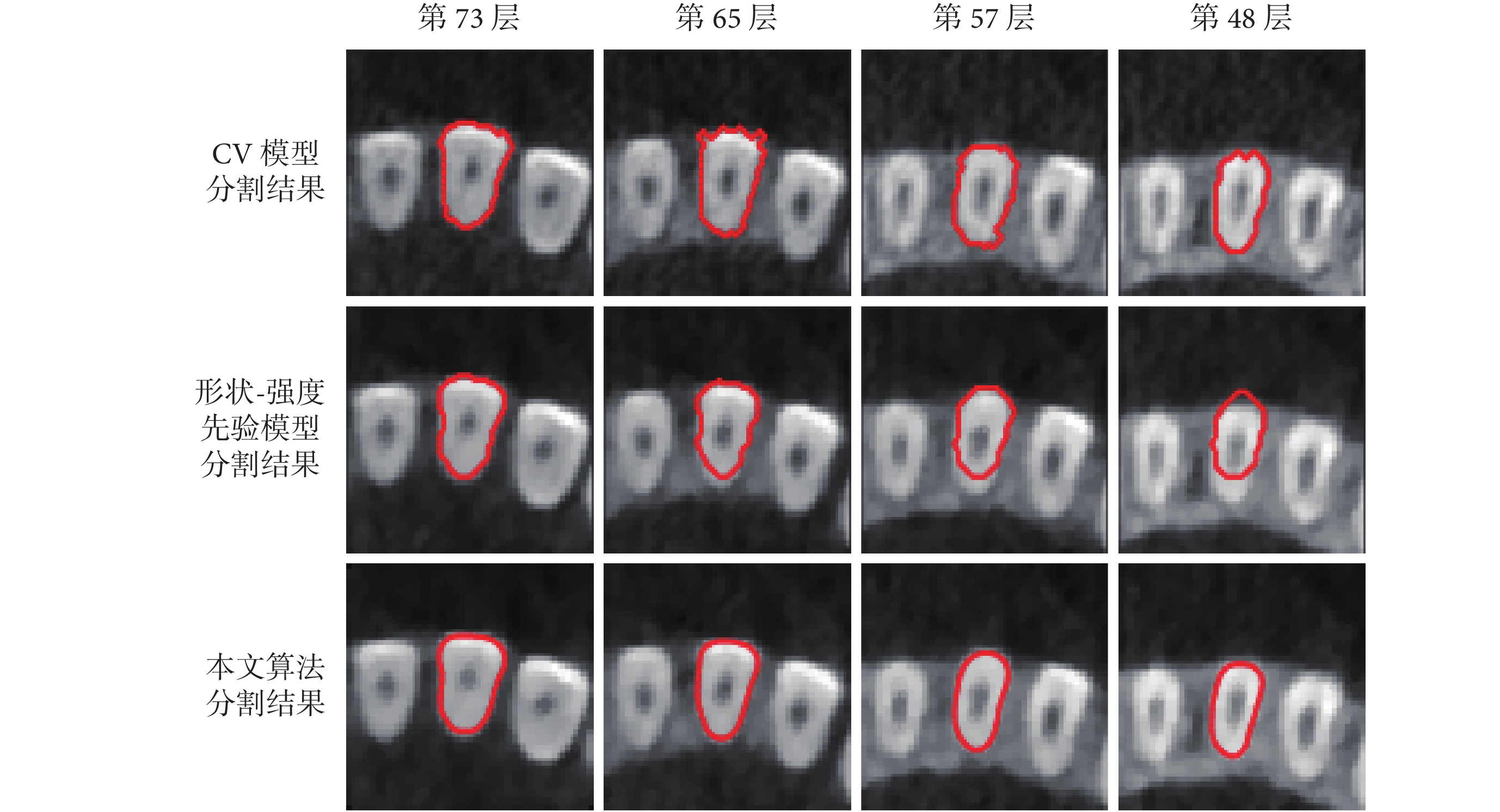 圖4
三種算法切牙序列的部分分割結果
Figure4.
Partial segmentation results of incisor sequence by three algorithms
圖4
三種算法切牙序列的部分分割結果
Figure4.
Partial segmentation results of incisor sequence by three algorithms
3 結論
本文提出了一種基于局部高斯分布擬合模型與邊緣檢測模型的牙齒圖像分割方法。對牙齒圖像使用中值濾波器進行濾波去噪。將目標牙齒從整幅圖像中提取出來,形成牙盒。對牙盒使用區域生長、孔洞填充等操作生成初始輪廓。在對序列圖像進行分割時,以上一層的分割結果作為當前層的初始輪廓指導分割。將本文算法在牙齒圖像上進行驗證,并與 CV 模型、形狀強度先驗模型進行實驗對比。實驗表明,本文提出的方法能夠精確地分割牙齒圖像,尤其是對拓撲結構復雜的磨牙,相對于其他分割方法,分割精度有很大的提高。
引言
錐形束計算機斷層掃描(cone beam computer tomography,CBCT)在牙科診斷中應用廣泛,與傳統的多層 CT(multi-slice computer tomography,MSCT)相比,CBCT 輻射劑量小,成像速度快,圖像空間分辨率高。牙齒 CBCT 圖像中包含著牙齒的位置和形狀信息。基于 CBCT 牙齒圖像可以重建三維牙齒模型并進行定量分析,這對于牙齒的正畸手術、根管治療、義齒種植等有著重要的意義。基于 CBCT 圖像的牙齒分割對于精確定量分析非常重要。
針對牙齒圖像實現精確分割主要有以下困難[1]:① 牙冠部分,相鄰牙齒之間相互粘連,對于單顆牙齒的分割造成了困難。② 牙根部分,牙齒被牙槽骨包圍,牙齒的灰度與牙槽骨相近,將牙齒與牙槽骨精確區分比較困難。③ 磨牙拓撲結構復雜,在牙根處可能分裂成兩到三個牙齒,對算法要求很高。④ 牙齒內部存在牙髓腔,在牙齒分割過程中容易出現內輪廓。
為了解決牙齒分割的問題,研究者提出了大量的分割方法。在牙冠區域,為解決相鄰牙齒之間相互粘連的問題,Dufour 等[2]提出了耦合水平集。將所有牙齒都用兩個水平集進行表示,相鄰牙齒用不同水平集。在分割時兩個水平集同時演化,這樣相鄰粘連的牙齒分割時就不會相互融合。Heo 等[3]提出了一種自適應閾值方法,利用序列中先驗信息獲取分割閾值,提高了分割的準確性,但是由于圖像灰度分布不均勻,相鄰牙齒相互粘連,閾值選擇比較困難,容易欠分割或過分割。傳統的牙齒分割算法只能分割上下頜不接觸的圖像。Xia 等[4]提出了一種上下頜咬合狀態下的牙齒分割方法。在牙頸牙根處使用混合水平集進行分割,對上下頜接觸處進行分割時重建網格模型,使用閾值和快速分水嶺算法進行分割。當牙齒圖像中存在金屬偽影時,對牙冠區域進行分割時不能準確地分割出單顆牙齒。為此 Xia[5]等對存在金屬偽影的牙冠先用 Radon 變換將單顆牙齒提取出來,再使用水平集方法進行分割。在牙根區域,Akhoodali 等[6]提出了一種基于區域生長的分割方法,Zhang[7]提出了一種基于局部區域生長的方法,但是都不能精確地分割出牙根。對于磨牙的分割,Gao 等[8]和 Gan 等[9]的文章里都有涉及。但是,Gan 等的算法不能精確地識別出第三磨牙,而 Gao 等的算法不能正確地處理牙齒分裂的問題。在牙齒中存在牙髓腔,與牙本質區域相比,牙髓腔區域的灰度值較低,在分割過程中會出現內部邊緣。為此 Gan 等[9]在水平集中引入梯度方向,只有當梯度方向與負水平集的法線方向一致時,邊緣才為有效邊緣。由于牙齒斷層圖像中相鄰斷層圖像的灰度分布非常相似,Gao 等[8]利用上一層斷層圖像中的灰度分布作為當前層的灰度約束項,指導曲線演化,使輪廓上的點自適應地收縮或膨脹。與灰度分布相似,牙齒斷層圖像中相鄰的斷層圖像形狀也是高度相似的,基于此,Gao 等[8]和 Ji 等[10]提出了基于先驗形狀的約束項。將上一層的結果輪廓作為當前層的初始輪廓,當曲線演化到距離初始輪廓較遠時,此約束項的值較大,防止曲線演化到距離上一輪廓較遠的位置。Ji 等[10]在 Gao 等[8]的基礎上改進了先驗區域能量項,用最大后驗概率指導曲線的演化。Hosntalab 等[11]提出了利用三維水平集函數對牙齒圖像進行分割,但是該方法對初始輪廓敏感,分割結果不可控,分割容易出現錯誤。王立新等[12]提出了一種結合自動閾值分割、Chan-Vase(CV)模型與圖割方法的分割方法。對于牙齒與周圍組織灰度值相差較大的圖像有一定的分割效果,但是對于差異較小的則效果較差。在對牙齒序列進行分割時,主要依靠上層牙齒的分割結果指導當前層的分割。如果相鄰層之間的牙齒形狀差距較大,則形狀先驗知識起不到積極的作用。為了解決這個問題,Gan 等[13]提出了一種斜角牙齒的分割方法,根據牙齒的軸線傾斜角度調整為與橫截面垂直,對調整后的牙齒使用水平集進行分割。
為了進一步提高牙根分割精度、磨牙分裂以及牙髓腔內部輪廓等問題,本文提出一種混合水平集分割方法。將局部高斯分布擬合(local Gaussian distribution fitting,LGDF)[14]與邊緣檢測(edge detection)[8, 10]結合起來對牙齒圖像進行分割,并將其與經典的 CV 模型[15]、形狀-強度先驗模型[8]進行實驗對比,驗證本算法的有效性。
1 方法
1.1 水平集分割方法原理
水平集方法最初由 Osher 等[16]提出,用于解決遵循熱力學方程下的火苗變化過程。其方法的核心是用高一維函數的零水平集函數表示低一維的函數。通過獲取高維函數在零水平集中的位置來獲得最終的演化結果。
可以將水平集模型分為基于區域的模型[14-15, 17-18]和基于邊緣的模型[19]。基于邊緣的模型主要利用圖像的邊緣信息來約束曲線的演化。典型的基于邊緣的模型都有一個邊緣停止項來控制曲線的運動。當曲線運動到目標邊緣時,此停止項為零。幾何活動輪廓(geometric active contour,GAC)模型[20]為最常用的邊緣模型,其能量泛函如下:
 |
其中  為水平集閉合曲線的長度,S 為閉合曲線的弧長參數。對上式使用梯度下降法得到零水平集演化方程:
為水平集閉合曲線的長度,S 為閉合曲線的弧長參數。對上式使用梯度下降法得到零水平集演化方程:
 |
其中  為常數,可以加速曲線演化,g 為邊緣停止函數
為常數,可以加速曲線演化,g 為邊緣停止函數  。
。 表示標準偏差為
表示標準偏差為  的高斯核函數。
的高斯核函數。 表示去噪后的圖像。該模型進行曲線演化時受到兩個力的驅動。第一個是內力,即曲率運動,為式(2)的第一項。受到圖像梯度的標量場
表示去噪后的圖像。該模型進行曲線演化時受到兩個力的驅動。第一個是內力,即曲率運動,為式(2)的第一項。受到圖像梯度的標量場  控制,在目標邊緣處為零,因此稱
控制,在目標邊緣處為零,因此稱  為邊緣停止函數。第二個為外力,來自于
為邊緣停止函數。第二個為外力,來自于  的梯度
的梯度  ,為式(2)中的第二項。它可以使水平集函數向著目標邊緣運動。對于目標邊緣較為清晰的圖像分割效果較好。但是該模型對于噪聲比較敏感,圖像邊緣較弱時分割效果較差。
,為式(2)中的第二項。它可以使水平集函數向著目標邊緣運動。對于目標邊緣較為清晰的圖像分割效果較好。但是該模型對于噪聲比較敏感,圖像邊緣較弱時分割效果較差。
基于區域的模型利用圖像的區域信息指導曲線演化,在圖像分割上的表現比基于邊緣的模型要好。比較常用的模型有 CV 模型[15]和局部二值擬合(local binary fitting,LBF)模型[17]。CV 模型是為了解決基于邊緣的水平集函數對邊界模糊和不連續圖像分割效果較差的問題。其能量泛函定義如下:
 |
其中  和
和  分別表示曲線內外灰度的均值。只有當曲線處在目標區域的邊緣時,該泛函才能取到最小值。由于
分別表示曲線內外灰度的均值。只有當曲線處在目標區域的邊緣時,該泛函才能取到最小值。由于  和
和  不能準確地表示一幅圖像,因此該模型對于灰度分布不均勻的圖像分割效果較差,為此 Li 等[17]提出了 LBF 模型。該模型為一種基于局部區域的水平集模型,其能量泛函如下:
不能準確地表示一幅圖像,因此該模型對于灰度分布不均勻的圖像分割效果較差,為此 Li 等[17]提出了 LBF 模型。該模型為一種基于局部區域的水平集模型,其能量泛函如下:
 |
其中  為標準差為
為標準差為  的高斯函數。
的高斯函數。 與
與  分別表示曲線內外的擬合灰度值。該能量方程所考察的區域是以當前點 x 為中心的鄰域范圍。鄰域范圍大小由高斯函數的標準差
分別表示曲線內外的擬合灰度值。該能量方程所考察的區域是以當前點 x 為中心的鄰域范圍。鄰域范圍大小由高斯函數的標準差  決定。當水平集函數演化到目標輪廓時,擬合灰度值近似于區域內曲線內外的灰度值,此時整個區域點的擬合能量值最小。由于本模型是基于局部區域信息,對灰度分布不均勻的圖像分割效果較好。
決定。當水平集函數演化到目標輪廓時,擬合灰度值近似于區域內曲線內外的灰度值,此時整個區域點的擬合能量值最小。由于本模型是基于局部區域信息,對灰度分布不均勻的圖像分割效果較好。
由于牙齒與周圍牙槽骨灰度差異小、磨牙拓撲結構復雜以及相鄰牙齒相互粘連等特點,傳統的水平集方法對于牙齒圖像分割精度較差。例如 CV 模型[11],該模型對于灰度分布均勻的圖像分割效果較好,但是牙齒圖像灰度分布不均勻,使用 CV 模型分割效果很差。針對 CBCT 序列相鄰圖像的相似性,Gao 等[8]提出了一種形狀-強度先驗模型。該模型很好地解決了灰度分布不均勻的問題,對于牙槽骨包埋的牙根分割效果也很精確,但是磨牙分裂的問題還是不能得到很好的解決。為此本文提出了一種基于局部高斯分布擬合與邊緣檢測模型相結合的牙齒分割模型。
1.2 局部高斯分布擬合項
在牙齒圖像分割中,我們假設圖像  由兩部分組成,一部分是牙齒區域,即前景區域,另一部分為背景區域,分別用
由兩部分組成,一部分是牙齒區域,即前景區域,另一部分為背景區域,分別用  和
和  表示。滿足
表示。滿足  ,
, 。在水平集分割的過程中,這兩個區域分別為零水平集的內部和外部,即
。在水平集分割的過程中,這兩個區域分別為零水平集的內部和外部,即  和
和  。
。
在該模型中,對于每一個像素點 x,假設一個以像素點 x 為中心、 為半徑的鄰域。
為半徑的鄰域。
 。根據貝葉斯公式可得:
。根據貝葉斯公式可得:
 |
其中  可以簡化為
可以簡化為  ,表示在區域
,表示在區域  中的灰度分布,i 取值可以為 1 或 2。
中的灰度分布,i 取值可以為 1 或 2。 表示 y 屬于
表示 y 屬于  的先驗概率。
的先驗概率。 表示灰度值
表示灰度值  的先驗概率。因為
的先驗概率。因為  與
與  為定值,可以省略。對得到的最大后驗概率取對數,將最大化轉化為最小化,得到如下能量泛函[14]:
為定值,可以省略。對得到的最大后驗概率取對數,將最大化轉化為最小化,得到如下能量泛函[14]:
 |
式(6)對單點像素構造鄰域最小化函數,對該函數求取最小值實現對該鄰域的最優分割。對于概率密度函數  ,選取高斯密度函數[14]。
,選取高斯密度函數[14]。
 |
其中  和
和  分別為局部強度的均值和方差。
分別為局部強度的均值和方差。
對式(6)引入一個權重函數:
 |
則對式(6)重新定義為:
 |
由于上式是對于一個像素點的計算,如果計算整幅圖像,則需要對上式積分求和:
 |
1.3 邊緣檢測項
為了更準確地分割牙齒圖像,在高斯分布擬合的基礎上引入了邊緣檢測。牙齒主要由兩部分組成。牙齒中間部分,灰度較低,為牙髓腔。在牙髓腔的外部為牙本質區域,灰度值較高。這樣在進行牙齒分割時可能會出現兩個邊緣,一個為牙本質與牙齒外部的邊緣,另一個為牙本質與牙髓腔的內部邊緣。為了避免這一情況,在局部高斯擬合的基礎上引入了邊緣檢測項,并且在邊緣檢測項中引入梯度方向。
 |
其中  表示梯度,
表示梯度, 表示將圖像 I 與高斯核
表示將圖像 I 與高斯核  進行卷積。
進行卷積。 為牙齒的初始輪廓。當圖像的梯度方向與法線方向一致時,此時的邊緣為正確的邊緣。
為牙齒的初始輪廓。當圖像的梯度方向與法線方向一致時,此時的邊緣為正確的邊緣。
同時為了避免初始化與平滑水平集函數引入正則化項以及長度約束項:
 |
 |
總的能量泛函為:
 |
由梯度下降法可得:
 |
其中  和
和  分別為:
分別為:
 |
 |
局部強度為:
 |
 |
局部方差為:
 |
 |
1.4 評價指標
為定量地評價分割結果,本文使用有經驗的臨床醫生手動分割結果作為評價分割準確性的標準。本文使用的定量評價指數分別為 Jaccard 指數(Jaccard Index,Jc)與 Dice 相似性系數(Dice Similarity Index,DSI)。
Jc 指數的定義為:
 |
其中  為臨床醫生手動分割的結果,
為臨床醫生手動分割的結果, 為算法分割的結果。算法分割結果越準確,則 Jc 值越接近 1。
為算法分割的結果。算法分割結果越準確,則 Jc 值越接近 1。
Dice 相似性系數定義為:
 |
與上式一樣,DSI 越接近 1,分割結果越精確。
1.5 實驗步驟
(1)選取初始層。選取初始層時要注意牙齒之間不相互粘連,選取比較好的層面。所以初始層選取在牙頸處,本文采用的序列圖像共 220 層,初始層選取在 73 層。
(2)獲取牙盒。選定待分割的牙齒之后,需要將選定的牙齒從圖像中提取出來。選定初始層之后將圖像顯示出來,確定選定的牙齒之后手動提取該牙齒的中心點,以該點為中心提取出一個一定大小的方形區域,一般選取的大小為  。
。
(3)參數設定。本文的參數主要涉及到迭代步長  ,高斯核函數的截斷系數
,高斯核函數的截斷系數  ,高斯核標準差
,高斯核標準差  ,邊緣檢測項系數
,邊緣檢測項系數  ,長度約束項系數
,長度約束項系數  ,正則化項系數
,正則化項系數  。其中
。其中  和
和  分別為公式(8)中的截斷系數與標準差,
分別為公式(8)中的截斷系數與標準差, 不大于
不大于  。
。 、
、 和
和  分別為公式(15)中第二項、第三項和第四項的系數。實驗中各個參數的取值見下文。
分別為公式(15)中第二項、第三項和第四項的系數。實驗中各個參數的取值見下文。
(4)生成初始輪廓。首先對牙盒進行中值濾波去噪,并且對圖像進行歸一化。對歸一化后的圖像使用閾值分割及圖像的開運算獲得二值模板圖像。將其作為初始層分割的初始輪廓。
(5)序列分割。在對序列圖像進行分割時,將上一層的分割結果作為當前層的初始輪廓。在初始輪廓的基礎上使用本文算法進行曲線的迭代演化,得到最終的結果,一直到將序列圖像分割完成。
2 實驗結果與討論
為驗證本文分割算法的正確性,本文在臨床 CBCT 數據上進行了測試。本文選用十組牙齒 CBCT 數據進行分割實驗,該實驗數據由我們實驗室團隊成員在上海第九人民醫院掃描獲得,符合醫院倫理審查規范,所有參與者對該研究都知情并同意所掃描數據供團隊研究使用。圖像分辨率為 0.25 mm × 0.25 mm × 0.25 mm,圖像為大小為 435 × 435,此序列圖像共 220 層。測試使用的電腦配置為 Intel(R) Core(TM) i7-7700,主頻為 3.60 GHz,內存為 8 GB。測試平臺為 MATLAB2016b。
本文分割算法的默認參數設置為  ,
, ,
, ,
, 。牙齒為磨牙時
。牙齒為磨牙時  = 0.000 1 × 2552,其余牙齒
= 0.000 1 × 2552,其余牙齒  = 0.000 8 × 2552。對于參數
= 0.000 8 × 2552。對于參數  ,牙齒為磨牙時
,牙齒為磨牙時  ,牙齒為前磨牙時
,牙齒為前磨牙時  ,牙齒為尖牙和切牙時
,牙齒為尖牙和切牙時  。本次實驗的對比實驗分別為 CV 模型[15]和形狀-強度先驗模型[8]。在實驗過程中,也有默認參數分割結果不是很好的情況,這種情況下我們通常以上述參數默認值為起點,在以參數默認值為中心的一個局部區間內通過實驗驗證設定更好的參數取值。圖 1 到圖 5 分別為 CV 模型、形狀-強度先驗以及本文算法對磨牙、前磨牙、尖牙、切牙以及整個下頜牙齒的分割結果。表 1 為對三種算法的定量評價。
。本次實驗的對比實驗分別為 CV 模型[15]和形狀-強度先驗模型[8]。在實驗過程中,也有默認參數分割結果不是很好的情況,這種情況下我們通常以上述參數默認值為起點,在以參數默認值為中心的一個局部區間內通過實驗驗證設定更好的參數取值。圖 1 到圖 5 分別為 CV 模型、形狀-強度先驗以及本文算法對磨牙、前磨牙、尖牙、切牙以及整個下頜牙齒的分割結果。表 1 為對三種算法的定量評價。
 圖1
三種算法對第一磨牙序列的部分分割結果
Figure1.
Partial segmentation results of first molar sequence by three algorithms
圖1
三種算法對第一磨牙序列的部分分割結果
Figure1.
Partial segmentation results of first molar sequence by three algorithms
 圖3
三種算法對尖牙序列的部分分割結果
Figure3.
Partial segmentation results of canine sequence by three algorithms
圖3
三種算法對尖牙序列的部分分割結果
Figure3.
Partial segmentation results of canine sequence by three algorithms
 圖5
本文提出的算法對下頜所有牙齒分割部分層面的結果
Figure5.
The segmentation results of the proposed methods for all teeth in samples slices of the mandible
圖5
本文提出的算法對下頜所有牙齒分割部分層面的結果
Figure5.
The segmentation results of the proposed methods for all teeth in samples slices of the mandible
從圖中可以看出本文算法對于牙齒有較好的分割效果,即使牙齒被包埋在牙槽骨中,也可以較精確地將牙齒從牙槽骨中分割出來。磨牙牙根處拓撲結構變化靈活,會分裂成多個牙齒,該模型仍然可以準確分割出分裂的牙齒。CV 模型對于灰度均勻的圖像分割比較準確,對灰度不均勻的圖像分割效果較差。從圖 2 到圖 4 可以看出,CV 模型對牙頸部分進行分割時,分割較為準確,但是當牙齒被牙槽骨包圍時,牙齒灰度與牙槽骨比較接近,此時該模型不能準確地區分牙齒與牙槽骨。尤其是對于磨牙,磨牙在牙頸處就被牙槽骨包圍,且拓撲結構變化靈活,分割效果更差。形狀-強度先驗模型對于前磨牙的分割效果較好。但是對于磨牙,當磨牙開始分裂的時候,不能準確地分割出分裂的牙齒。由于本文涉及到的三種算法采用相同的分割流程,前期預處理的步驟相同,所以算法耗時從自動分割開始算起。本文算法主要是針對牙根圖像進行分割,所展示的時間是整個口腔的 28 顆牙齒從初始層到分割結束所用時間。本文算法、CV 模型和形狀-強度先驗算法的運行時間分別為 45.39、28.56、129.19 s。由于 CV 模型算法計算較為簡單,算法運行時間比本文算法短,但是分割效果太差。本文算法跟形狀-強度先驗模型相比,效率大大提高,且精確度有較大提升。
 圖2
三種算法對第一前磨牙序列的部分分割結果
Figure2.
Partial segmentation results of first premolar sequence by three algorithms
圖2
三種算法對第一前磨牙序列的部分分割結果
Figure2.
Partial segmentation results of first premolar sequence by three algorithms
 圖4
三種算法切牙序列的部分分割結果
Figure4.
Partial segmentation results of incisor sequence by three algorithms
圖4
三種算法切牙序列的部分分割結果
Figure4.
Partial segmentation results of incisor sequence by three algorithms
3 結論
本文提出了一種基于局部高斯分布擬合模型與邊緣檢測模型的牙齒圖像分割方法。對牙齒圖像使用中值濾波器進行濾波去噪。將目標牙齒從整幅圖像中提取出來,形成牙盒。對牙盒使用區域生長、孔洞填充等操作生成初始輪廓。在對序列圖像進行分割時,以上一層的分割結果作為當前層的初始輪廓指導分割。將本文算法在牙齒圖像上進行驗證,并與 CV 模型、形狀強度先驗模型進行實驗對比。實驗表明,本文提出的方法能夠精確地分割牙齒圖像,尤其是對拓撲結構復雜的磨牙,相對于其他分割方法,分割精度有很大的提高。