臨床上治療主動脈瓣膜關閉不全的的手術多采用瓣膜移植，但術后患者重建的主動脈根部存在擴張現象，因此瓣膜高度的不足會致使主動脈瓣膜再次關閉不全。本文研究不同主動脈瓣膜高度設計對瓣膜開閉性能的影響，通過體外數值模擬，獲取最佳手術方案，提供技術支持和理論依據。本文以根部直徑 26.0 mm、瓣膜高度 14.0 mm 為參照，建立瓣膜高度增量為 ± 0.5 mm 的六組三維幾何模型。通過對模型最大應力、瓣口面積和接觸力等參數的結構力學計算和分析，獲得合理的幾何尺寸。研究發現，六組模型的最大應力值范圍在 640～690 kPa 之間，與文獻的結果相符合；瓣膜高度分別為 13.5、14.0、14.5 mm 的三組模型的瓣口面積在合理范圍內；六組瓣葉接觸力隨瓣膜高度增加呈增大趨勢。研究表明主動脈瓣膜的高度對主動脈瓣膜關閉性能存在影響，太小或太大的瓣膜高度會減小主動脈收縮期的瓣口面積，影響主動脈開閉功能。
引用本文： 李慧, 潘友聯, 喬愛科, 劉迎龍, 董念國. 瓣膜高度對移植主動脈瓣開閉性能的影響. 生物醫學工程學雜志, 2019, 36(2): 199-205. doi: 10.7507/1001-5515.201709061 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
主動脈瓣膜的存在保證了血液從左心室向主動脈的單向流動。但由于主動脈根部解剖生理的復雜性，導致主動脈瓣膜修復術的療效不盡如人意。Gnyaneshwar 等[1]采用有限元方法仿真模擬了主動脈根部的運行情況，發現在一個心動周期內，瓣膜受到正壓力的作用之前就已經開始開放，這是由于主動脈根部擴張所致。Howard 等[2]研究發現在收縮期中期時，主動脈根部已經開始擴張。由此可見，主動脈根部幾何結構和瓣膜之間存在復雜的相互關系。
近年來，由于主動脈根部擴大造成的主動脈瓣膜關閉不全致使瓣膜反流的問題，得到眾多學者重視。針對嚴重瓣膜疾病，臨床上需要進行瓣膜移植，通過主動脈瓣膜的置換和重構來恢復瓣膜的性能和功能。然而不能排除重建的主動脈根部會在手術后期出現尺寸的擴張，引起瓣膜再次關閉不全。臨床上移植瓣膜的尺寸設計一般保持原有尺寸結構，或是基于臨床醫生的個人經驗去設計瓣膜幾何結構，無法確定患者術后的生理風險，也無法為患者及家屬提供安全可靠的具備理論依據的手術方案。
關于主動脈根部幾何尺寸對主動脈瓣膜開閉性能的影響已有相關學者做過研究。Furukawa 等[3]研究發現主動脈根部的擴張可能導致瓣膜的泄漏，其原因是瓣膜尺寸太小致使瓣膜關閉不全。2002 年 David 等[4]調查發現外科醫生在進行保留主動脈瓣的手術中，為達到恢復患者瓣膜正常生理功能的目的，需按照要求進行特定的瓣膜設計。在 2004 年 Feindel 和 David 發現主動脈根部存在擴張現象，在進行瓣膜保留手術治療時，外科醫生會根據需要擴大瓣膜的尺寸范圍。Hammer 等[5]發現當瓣膜出現嚴重病變需要進行瓣膜移植修復時可針對瓣膜高度進行設計，并得出瓣膜高度的不同使得瓣膜結合高度不同的結論。
目前關于瓣膜高度影響主動脈瓣關閉性能的研究工作較少。為了研究主動脈根部瓣膜關閉不全手術中如何選取主動脈瓣膜幾何尺寸，以及不同主動脈瓣尺寸的設計對瓣膜關閉打開性能的影響，本文采用有限元軟件數值模擬的方法，仿真瓣膜關閉到打開的過程，比較不同瓣膜高度下模型的最大應力、接觸力和瓣膜開口面積。目的是研究不同瓣膜高度的設計對瓣膜開閉性能的影響，獲取瓣膜尺寸的合理設計范圍，為臨床決策提供理論知識和指導。
1 方法
1.1 幾何模型建模
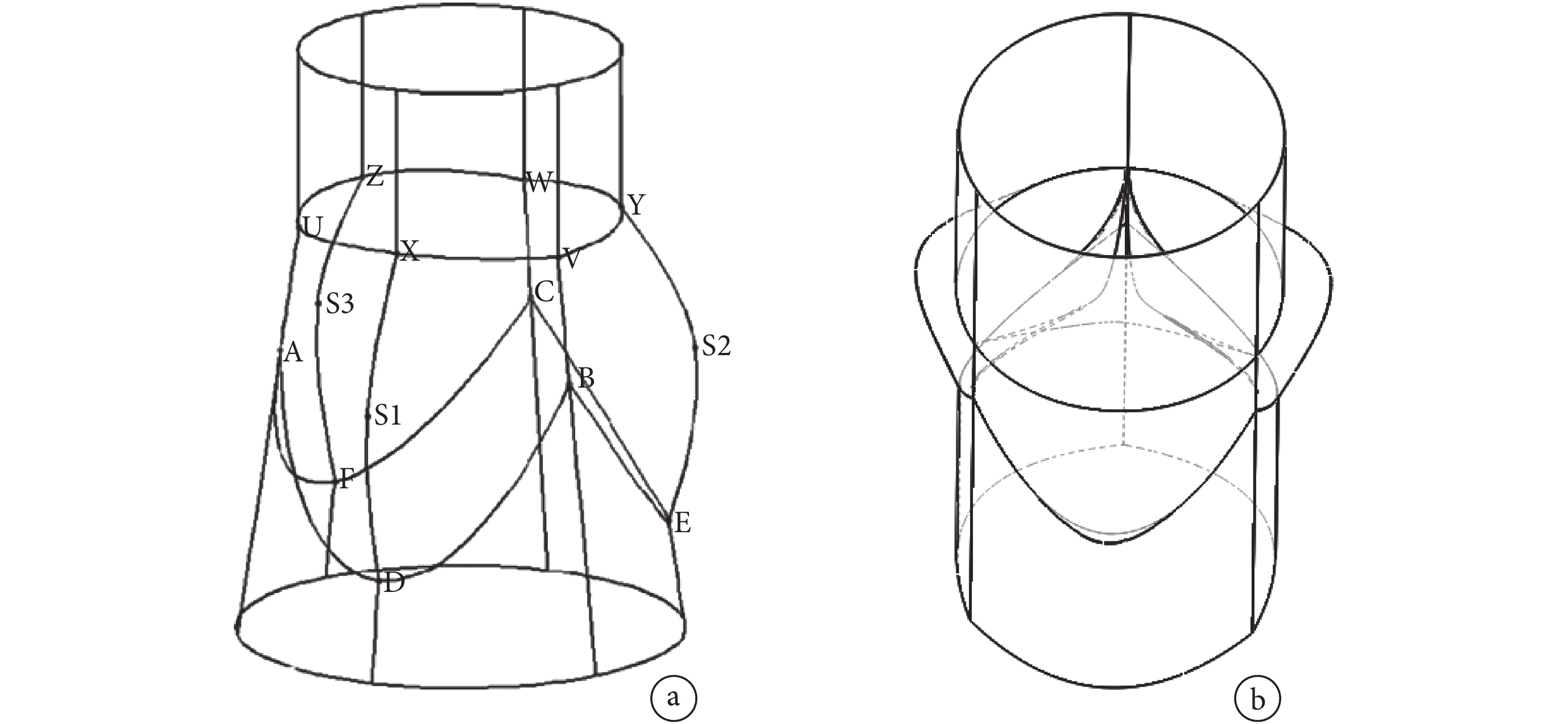
主動脈根部基本結構主要包括瓣環、竇部、瓣膜、竇管交界。在這里采用 Labrosse 等[6]提出的 8 參數 15 坐標點方法（如圖 1a 所示），構建主動脈根部三維幾何模型（如圖 1b 所示）。
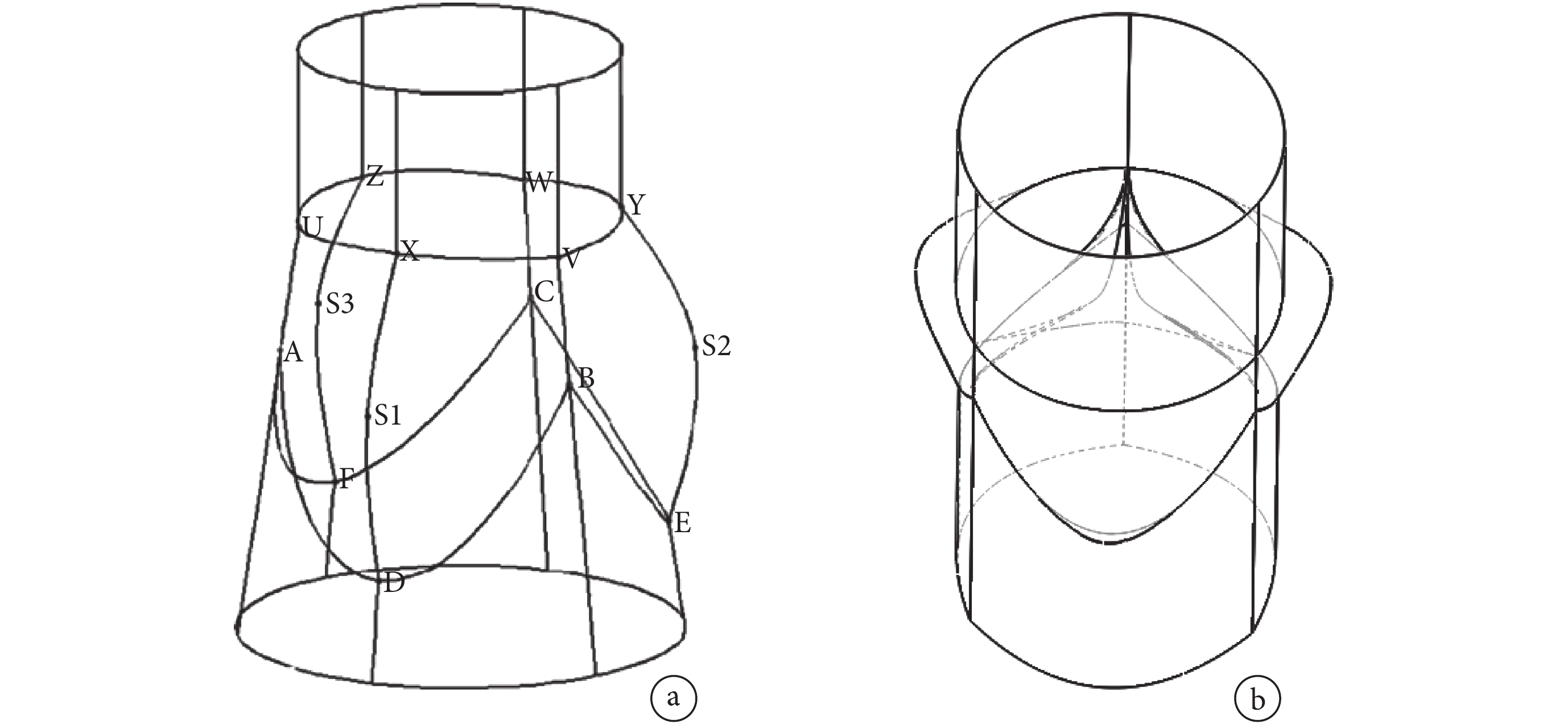圖1
主動脈根部結構圖
a. 主動脈根部 15 坐標模型草圖輪廓線[6]；b. 基于 15 坐標利用有限元軟件建立的主動脈根部三維幾何模型輪廓圖
Figure1. Structure of aortic roota. outline of aortic root model of 15 coordinates; b. three-dimensional geometric model of aortic root established by finite element software through 15 coordinates
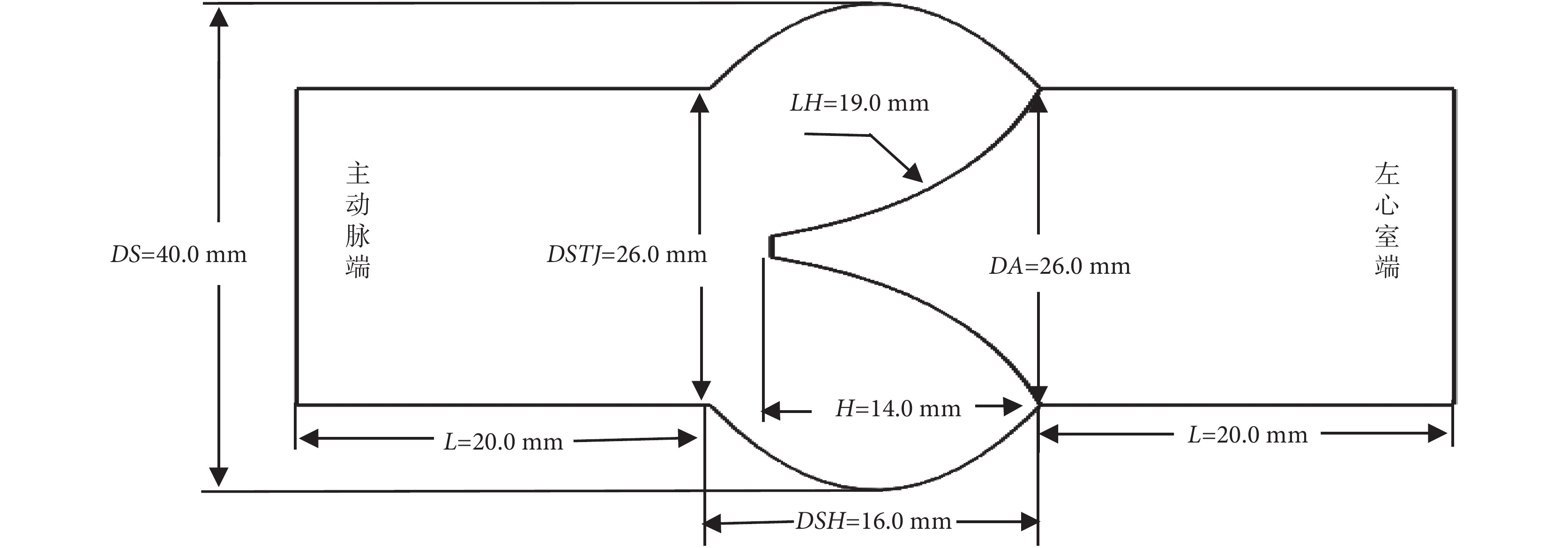
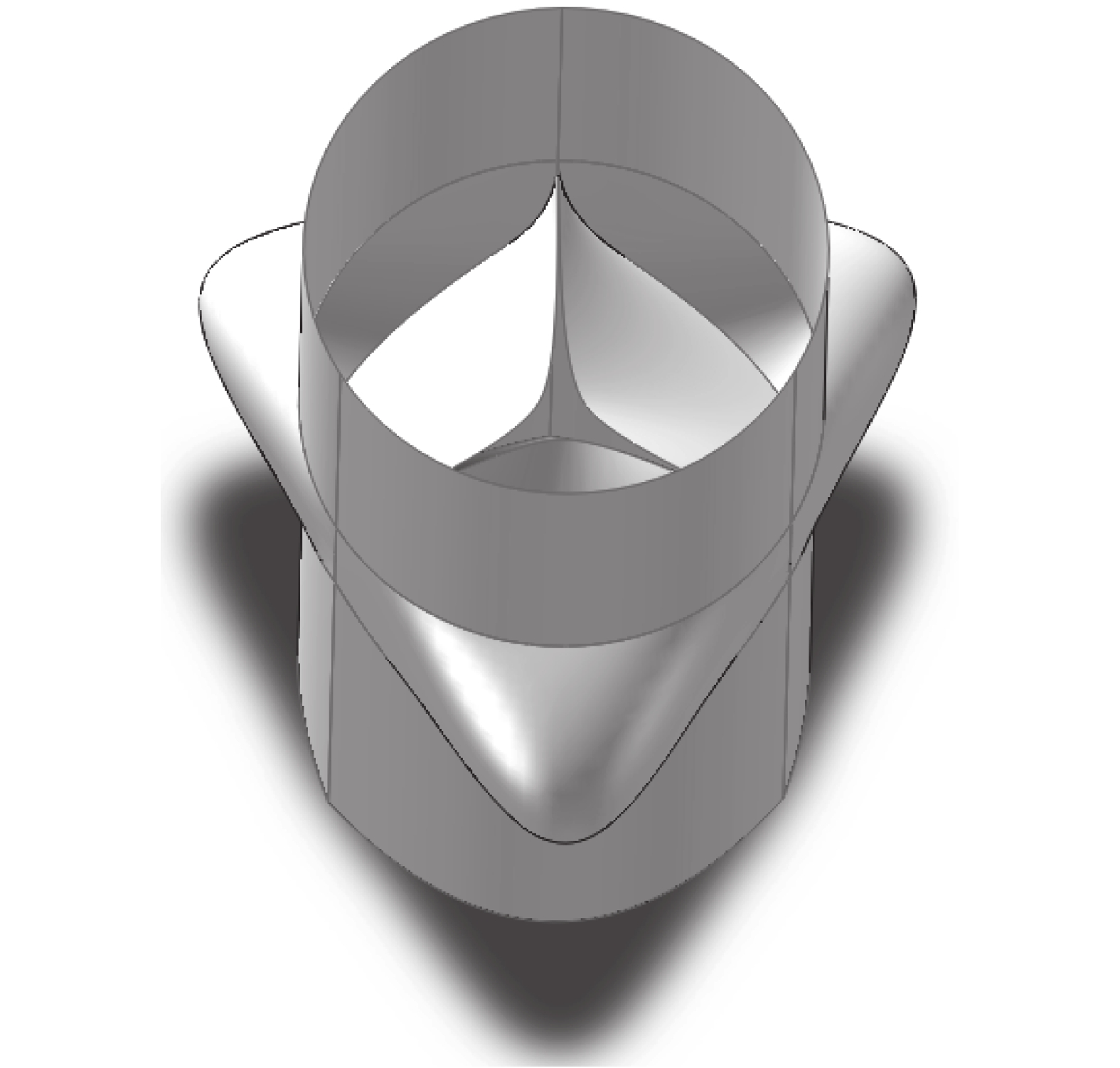
選取 Labrosse 提供的臨床手術指導尺寸數據（如圖 2 所示）[7]。瓣環直徑 DA = 26.0 mm，竇部直徑 DS = 40.0 mm，竇部高度 DSH = 16.0 mm，瓣葉高度 LH = 19.0 mm，瓣膜高度 H = 14.0 mm，竇管交界直徑 DSTJ = 26.0 mm。在模型升主動脈端和左心室端（即主動脈根部的上游和下游）增加 L = 20.0 mm 的血管延長部分，模擬血液的充分發展。三維幾何模型運用 SolidWorks（Concord，MA，美國）軟件構建（如圖 3 所示）。
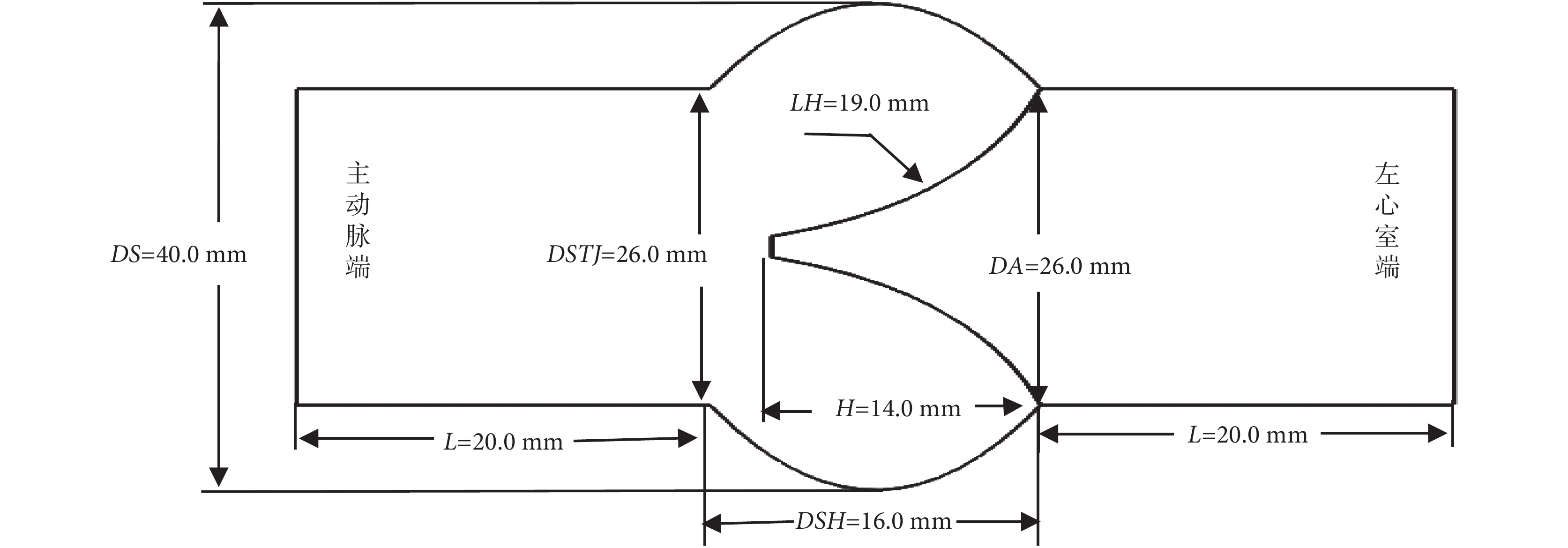圖2
主動脈根部二維平面圖以及各部分結構相關尺寸
Figure2.
Two-dimensional sketch of aortic root and the relative dimensions
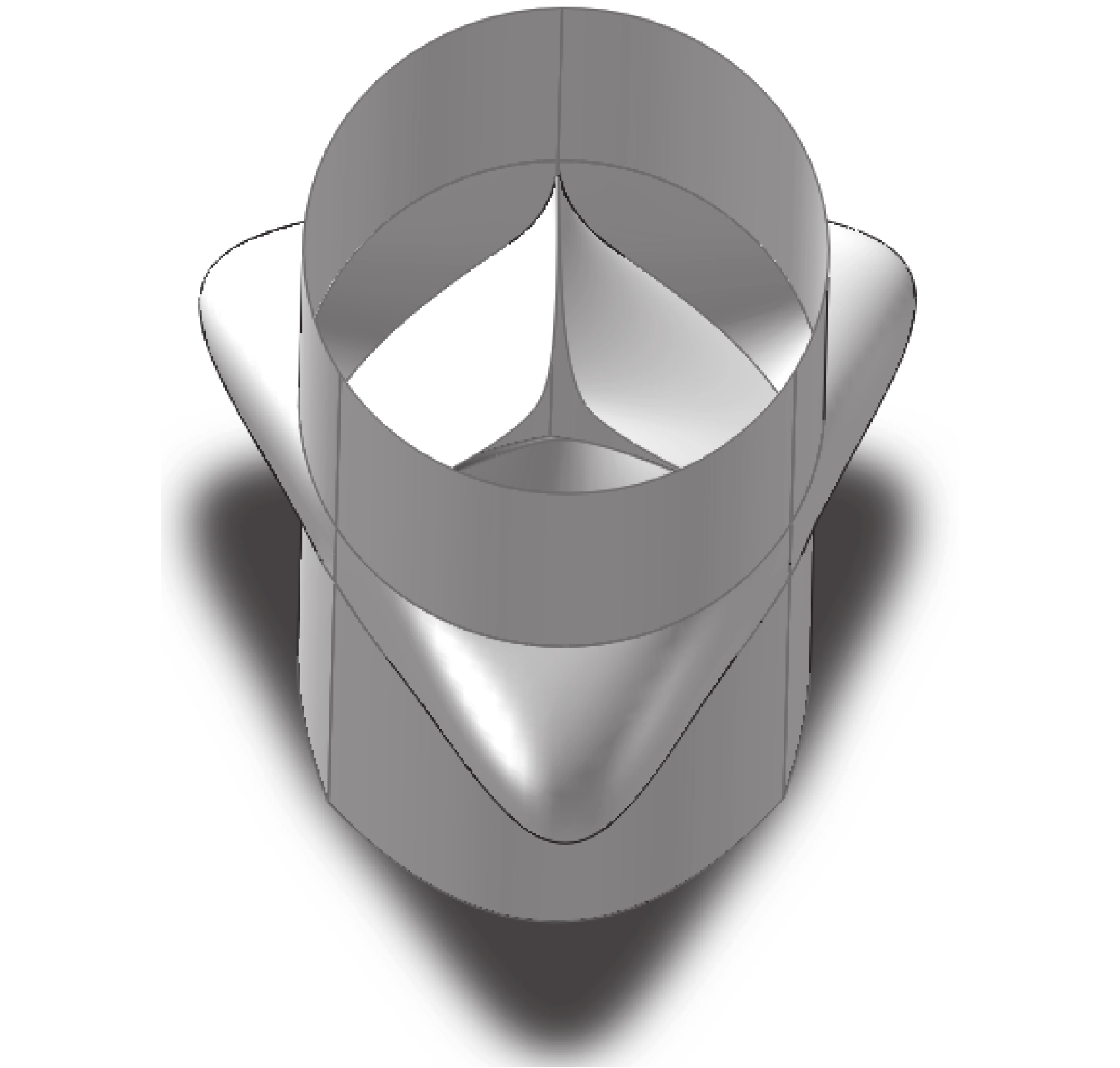圖3
主動脈根部三維幾何模型
Figure3.
Three-dimensional geometric model of aortic root
1.2 實驗模型建立
將 Labrosse 提供的臨床手術指導尺寸作為參考模型 A。保持主動脈根部其他參數的尺寸不變，改變瓣膜高度 H，以增量 ± 0.5 mm 建立 5 組幾何模型，并命名為 B、C、D、E、F。六組主動脈根部幾何模型的瓣膜高度尺寸見表 1。
表1
六組模型的瓣膜高度尺寸和有限元分析結果
Table1.
Valve height and finite element analysis of the six models
六組幾何模型在 SolidWorks 軟件中建立后導入 HyperMesh（Altair Engineering，Troy，MI，美國）進行網格劃分和單元設置等相關操作。對竇部、主動脈端和心室端設置四邊形網格，對瓣膜設置三角形網格；血管壁和瓣膜的單元類型采用殼單元。完成設置后導入 ADINA 9.0（ADINA R&D，Watertown，MA，美國）進行模型的求解和后處理等有限元分析。
1.3 有限元分析
1.3.1 有限元軟件中總體控制參數的設置
在 ADINA9.0 軟件中選擇基于位移參數的隱式動力學方法求解結構模型[8-9]；步長在載荷變化緩慢時段設置為 0.001，載荷變化劇烈時段設置為 0.000 1；收斂原則和迭代方法分別為位移和修正牛頓法；為促進收斂，阻尼系數設置為 0.15；瓣膜關閉存在的接觸采用約束方程接觸法計算，摩擦系數為 0.013。瓣膜和血管壁厚度分別設置為 0.3 mm 和 0.6 mm。
1.3.2 有限元軟件中材料屬性的設置
生理上主動脈根部組織材料為超彈性材料屬性并且各向異性。然而為了簡化計算的復雜性和提高分析的可行性，將模型中的瓣膜和血管壁假設為線彈性、各向同性的材料屬性[10]。瓣膜和主動脈根部其余部分楊氏模量分別為 1 MPa 和 2 MPa，密度分別設置為 1 100 kg/m3和 2 000 kg/m3，泊松比都設置為 0.45。
1.3.3 有限元軟件中邊界條件的設置
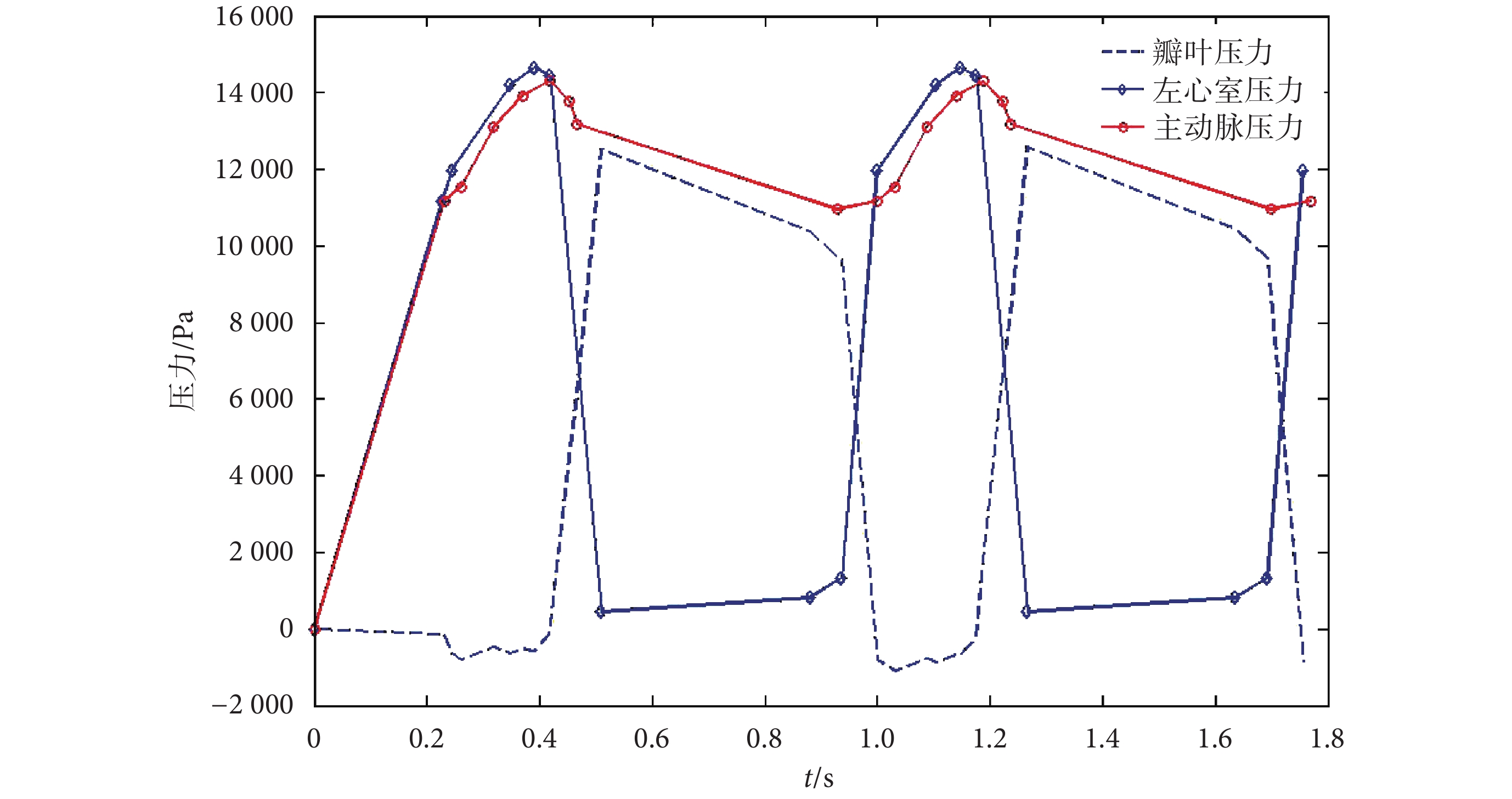
約束：施加全方向的固定約束于主動脈出口端和心室流出端。載荷：對主動脈根部心室端、瓣膜和主動脈端分別施加如圖 4 所示的隨時間變化的壓力載荷。圖中紅色曲線代表主動脈端壓力載荷波形；藍色實曲線代表心室端壓力載荷波形，藍色虛曲線代表瓣膜壓力載荷波形。
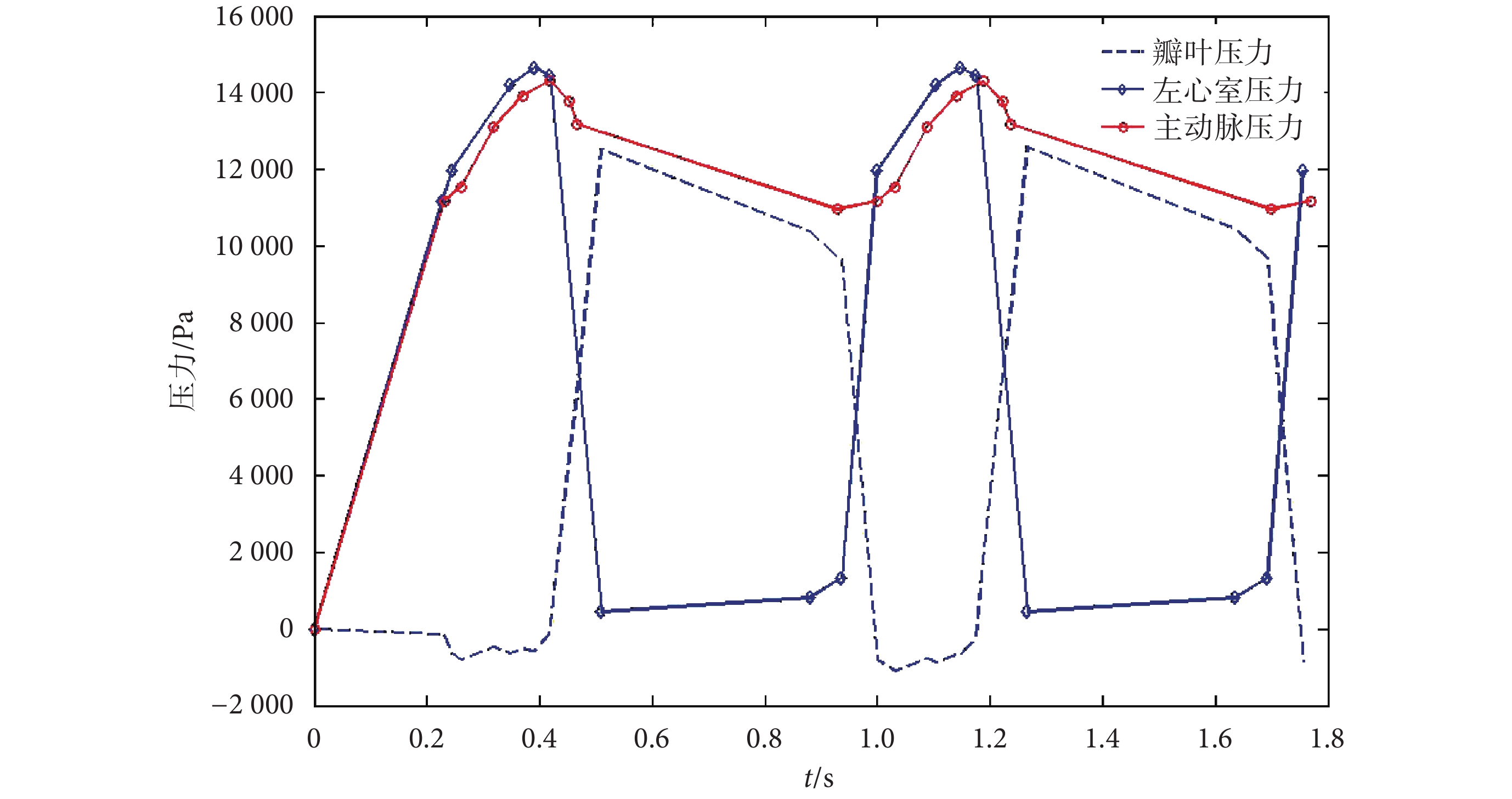圖4
施加到主動脈、左心室和瓣膜的壓力波形
Figure4.
Pressure waves exerted on the aorta, left ventricle and leaflets
為提高計算的精確度，在實現心臟收縮模擬之前要增加 0～0.2 s 的求解階段，使計算從零應力狀態過渡到正常生理壓。在 ADINA9.0 有限元軟件中進行力學行為的計算。有限元模型運算中存在周期依賴性。本課題組前期對周期性問題進行了研究[11-12]，通過逐步增加周期個數，發現兩個周期的函數載荷已經存在很好的收斂效果，增加周期效果相似，相鄰周期誤差小于 5%。為節省計算時間，本研究選取運算兩個周期，獲取收斂結果。
2 計算結果
在主動脈根部瓣膜完全打開和關閉時，提取模型的最大應力值以及分布、瓣口面積、瓣葉接觸力等參數，分析數值模擬結果。
2.1 最大應力值
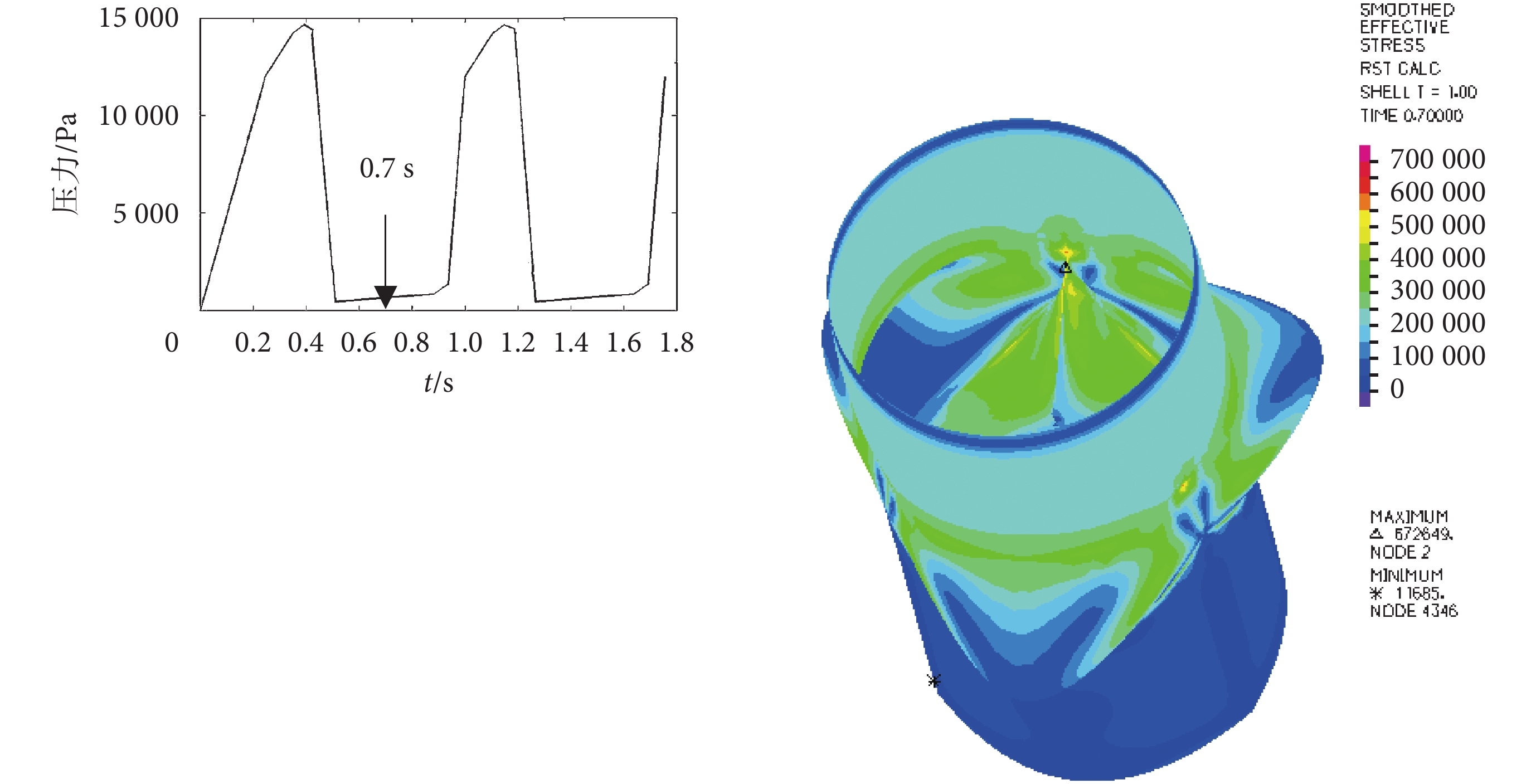
主動脈瓣膜關閉時，竇部、瓣膜之間存在力的相互作用。從不受壓開始的心動周期中，分析主動脈根部三維結構的力學行為。對最大應力值的分析主要針對于瓣膜關閉狀態時。根據 Marom 和 Labrosse 等數值模擬和實體實驗研究發現，主動脈根部最大應力值出現在主動脈瓣膜和主動脈竇的連接線處[6, 13-14]。針對參照模型（DA = 26.0 mm，H = 14.0 mm）進行最大應力分析。通過對不同時刻的最大應力值的查看和對比，發現在兩個心動周期內，在瓣葉和竇部連線處的最大應力出現在 0.7、1.5 s 左右，其值大小相似。在 0.7 s 時刻取值。如圖 5 所示為正常主動脈根部（模型 A）結果，主動脈根部最大應力值出現在瓣膜和竇部連接處，最大應力值約為 672 kPa。B、C、D、E、F 的應力結果如表 1 所示。已有相關研究表示最大應力值是主動脈根部關閉質量評價指標之一[15]，應力值過大會破壞瓣膜性能，影響瓣膜的使用壽命。本文所獲取的最大應力值較小，符合要求。
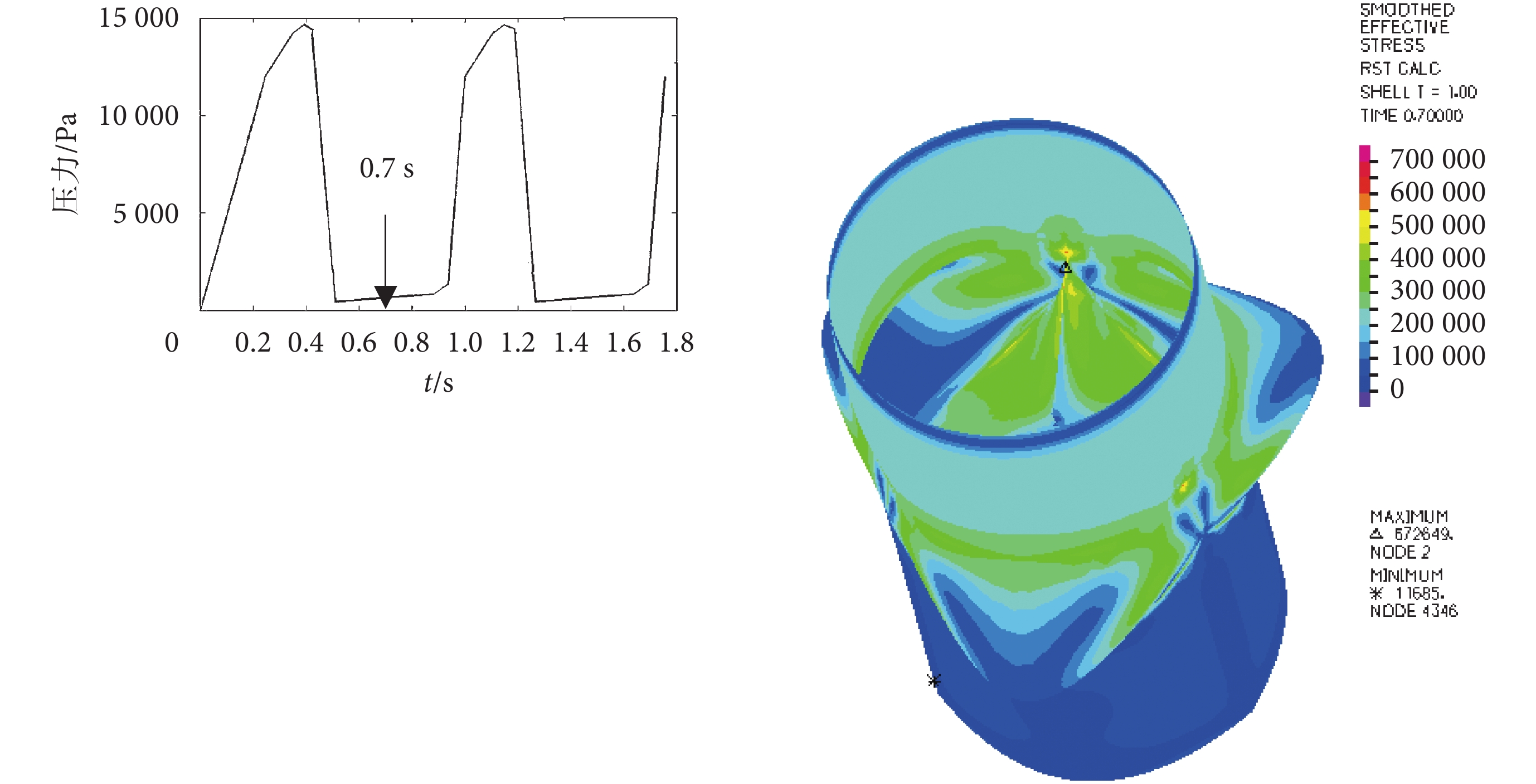圖5
在 0.7 s 時瓣膜完全關閉的主動脈根部應力云圖
Figure5.
Stress contour of aortic root with complete closure at 0.7 s
2.2 瓣開口面積
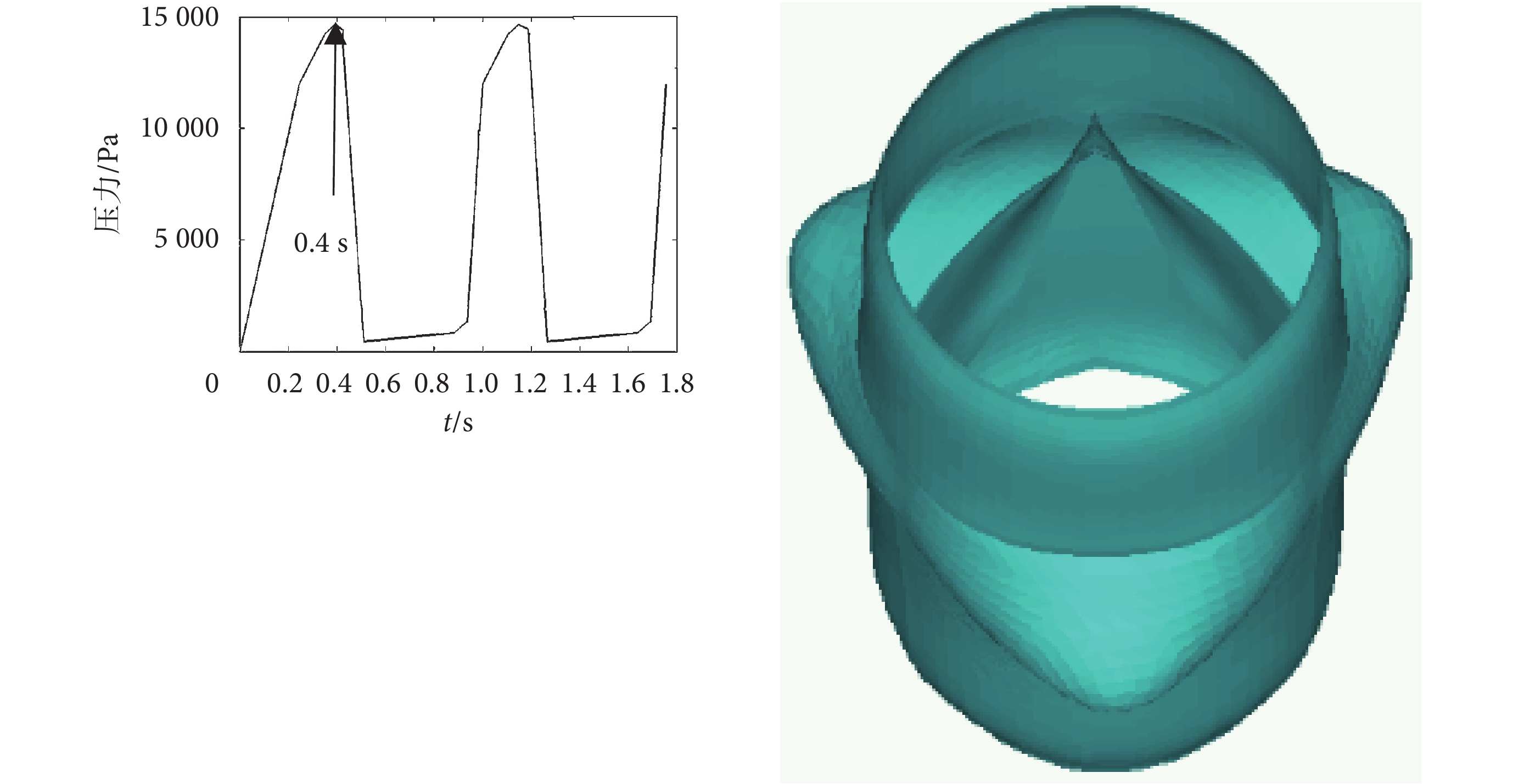
提取 0.4 s 時主動脈瓣膜的打開程度，計算瓣膜完全打開時的面積。如圖 6 所示為正常主動脈根部（模型 A）瓣葉的打開狀態，瓣口面積209.098 mm2。B、C、D、E、F 模型的結果如表 1 所示。正常的主動脈瓣口面積維持著人體正常生理活動。瓣口面積過小會造成心輸出量減少，心室肥大，從而造成暈眩、心絞痛以及心衰等，影響著生命活動。
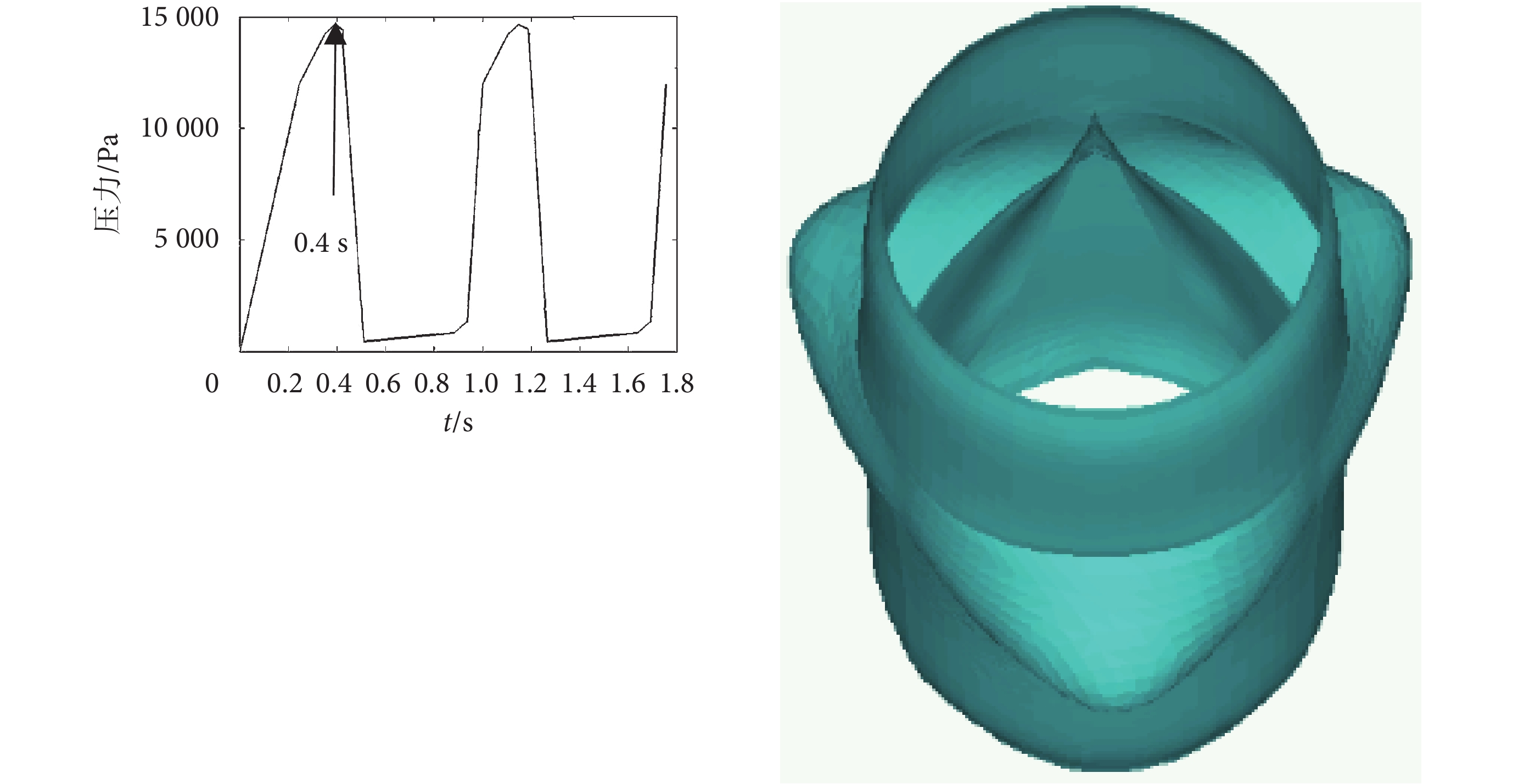圖6
在 0.4 s 時瓣膜完全打開狀態
Figure6.
The valve was fully opened at 0.4 s
2.3 瓣葉接觸力
瓣葉接觸力可以反映瓣膜關閉階段的對合情況[14]。瓣葉接觸應力是求取三個瓣葉完全對合時刻的所有接觸力的總和，模型 A 瓣膜完全關閉在 0.507 s 時，拾取該時刻的瓣葉接觸力，計算大小為 7.09 N。
主動脈瓣膜的正常關閉需要三個瓣葉之間相互作用，接觸力的大小反映著心室舒張期階段的瓣膜關閉性能。6 個模型的瓣葉接觸力的計算結果如表 1 所示。
對比不同瓣膜高度與最大應力、瓣口面積、瓣葉接觸力的變化關系，查看影響程度。研究發現最大應力值的數據變化呈現增大-減小-增大的趨勢；接觸應力值數據趨勢持續增大；瓣口面積值的數據變化隨著瓣膜高度增加呈現先增大后減小的趨勢。通過數據趨勢的對比，六組模型在較小應力值的情況下，達到標準瓣口面積的瓣膜高度在 13.5～15.0 mm 之間，其建立的瓣膜幾何尺寸能夠獲得較好的主動脈瓣膜開閉性能。
3 討論
3.1 研究的合理性和準確性
通過與文獻中的有限元模型和體外實驗研究結果的對比方法來驗證本試驗中計算結果的正確性[16]。
Labrosse 等[13]在 2010 年通過的人體體外實驗獲得了瓣口面積的最大值為（270 ± 0.63）mm2；Garcia 等[16]在 2011 年提出主動脈瓣瓣口面積大于 200 mm 時為正常主動脈瓣的評價標準。本文中參照模型 A 的瓣葉開口面積為 209.098 mm2。瓣口面積結果與上述文獻中的結果接近。
Katayama 等[17]在 2008 年從零應力開始計算瓣膜受力情況，發現舒張期瓣膜和竇部連接處應力值在 600～750 kPa 之間；Marom 等[14]在 2013 年發表的文章中得到的最大應力結果為 800 kPa；本課題組在研究竇管交界和竇部直徑對主動脈根部最大應力和分布位置影響時，獲得的最大應力的變化范圍為 567～601 kPa。本文中參照模型 A 最大應力值為 672 kPa，出現在瓣膜和竇部連接處，數值模擬的最大應力值計算結果與上述幾個研究組的結果相近。
結合以上對比，所設計模型在準確性和可行性方面都已達到要求。
3.2 研究討論
先天性心臟病患者的主動脈瓣會出現逆流、狹窄等瓣膜關閉不全的病情[18]。治療主動脈瓣關閉不全，可采用主動脈瓣修復手術和替換手術兩種方式[19]，在臨床上瓣膜修復多優先考慮瓣膜移植。生命活動是一個動態過程，當外界干擾過大致使血管擴張時，瓣膜有可能再次出現狹窄。考慮到移植瓣膜不會隨著人體生長而生長，本文研究主動脈根部幾何結構時，保持其他結構不變，在增大 ± 0.5 mm 瓣膜高度的情況下研究對主動脈根部瓣膜關閉打開性能的影響，為臨床上瓣膜幾何結構的構建與選取提供理論依據。
評價主動脈根部瓣膜關閉性能的參數有瓣口面積、最大應力值、接觸應力值等。臨床醫學上對于主動脈瓣膜瓣口面積定義三種狀態：當瓣口面積小于 200 mm2、大于 150 mm2時，為輕度狹窄；當瓣口面積小于 150 mm2、大于 100 mm2時，為中度狹窄；當瓣口面積小于 100 mm2時，為重度狹窄；且 Garcia 等[16]在 2011 年制定了瓣口面積的評價標準，即瓣膜開口面積大于 200 mm2時主動脈瓣才能實現正常功能。在本文的研究中六組模型的瓣口面積值隨瓣膜高度的變化呈現先增加后減小的趨勢，結合上述評價標準以及臨床標定，瓣膜幾何高度在 13.5～15.0 mm 之間時，瓣口面積符合要求。
Marom 等[14]研究發現最大應力值的大小對瓣膜使用的長期有效性存在著很大的影響，是評價瓣膜質量的標準之一。應力值過大會降低瓣膜的柔軟性，造成瓣膜撕裂以及鈣化等，引起瓣膜的再度狹窄。在主動脈根部幾何結構性能的數值模擬與分析中，需觀察收縮期瓣膜關閉時主動脈根部的最大應力值。Labrosse 等[13]總結前人研究，認為人體生理情況下主動脈瓣動力學行為顯示最大應力范圍在 300～800 kPa。本文研究幾何結構模型的力學行為所獲取的最大應力值都在 600～700 kPa 之間且偏小，表明采用有限元軟件重建并分析主動脈根部瓣膜的關閉性能是可行的，且六組模型的最大應力值在瓣膜高度 14.5 mm 時最小。
瓣膜接觸力是指瓣膜之間的相互作用，可以反映瓣膜在心動周期中關閉的性能和瓣膜的對合能力。Pan 等[20]在 2014 年研究了改變竇管交界和竇部直徑對瓣膜關閉功能的影響，采用有限元軟件對模型進行結構力學數值模擬，結果發現為使瓣膜正常關閉，主動脈根部竇管交界和竇部直徑增大后，瓣膜接觸力也相應增大，反之亦然，結論是直徑增加不利于主動脈瓣的關閉。通過觀察本組研究數據，隨著瓣膜高度的增加，瓣膜接觸力也隨之增加，與 Pan 等研究結果趨勢相同。因此在設計瓣膜時，需注意瓣膜高度過大不利于瓣膜的關閉。
綜上所述，對比前人研究結果，本研究通過有限元軟件分析主動脈根部改變瓣膜高度的幾何模型的力學行為是可行的，且最佳瓣膜高度的結果在 13.5～15.0 mm 之間。
本文研究的不足之處在于：第一，壓力載荷施加時均勻分布于瓣膜和主動脈根部，而人體生理條件下，壓力分布是不均勻的。第二，本研究中主動脈根部的基礎直徑是 26.0 mm，但人體生理上的血管是處于生長狀態，此研究結論對其他根部尺寸主動脈的適用性尚未可知。因此針對以上不足，下一步工作將構建不同基礎尺寸直徑的主動脈根部模型，從數值模擬結果中獲取瓣口面積、最大應力值以及瓣膜對合高度等評價指標，分析生長狀態下不同主動脈幾何結構對瓣膜關閉性能的影響，為臨床醫生提供最優化的主動脈根部幾何尺寸結構的選擇方案。
4 結論
在改變瓣膜高度的情況下，建立了六組升主動脈根部的幾何模型。利用有限元軟件數值模擬的方法分析了不同瓣膜高度情況下最大應力值、開口面積以及瓣葉接觸力等主動脈瓣膜生物力學性能評價的參數值以及對主動脈瓣開閉性能的影響。研究發現在不影響生命活動的前提下，可結合患者狀態適當改變瓣膜高度，以更好地適應變化的生理環境。就本文所建立的模型而言，主動脈根部瓣膜高度在 13.5～15.0 mm 之間時具有較好的開閉性能，可作為臨床醫生手術規劃的借鑒。
引言
主動脈瓣膜的存在保證了血液從左心室向主動脈的單向流動。但由于主動脈根部解剖生理的復雜性，導致主動脈瓣膜修復術的療效不盡如人意。Gnyaneshwar 等[1]采用有限元方法仿真模擬了主動脈根部的運行情況，發現在一個心動周期內，瓣膜受到正壓力的作用之前就已經開始開放，這是由于主動脈根部擴張所致。Howard 等[2]研究發現在收縮期中期時，主動脈根部已經開始擴張。由此可見，主動脈根部幾何結構和瓣膜之間存在復雜的相互關系。
近年來，由于主動脈根部擴大造成的主動脈瓣膜關閉不全致使瓣膜反流的問題，得到眾多學者重視。針對嚴重瓣膜疾病，臨床上需要進行瓣膜移植，通過主動脈瓣膜的置換和重構來恢復瓣膜的性能和功能。然而不能排除重建的主動脈根部會在手術后期出現尺寸的擴張，引起瓣膜再次關閉不全。臨床上移植瓣膜的尺寸設計一般保持原有尺寸結構，或是基于臨床醫生的個人經驗去設計瓣膜幾何結構，無法確定患者術后的生理風險，也無法為患者及家屬提供安全可靠的具備理論依據的手術方案。
關于主動脈根部幾何尺寸對主動脈瓣膜開閉性能的影響已有相關學者做過研究。Furukawa 等[3]研究發現主動脈根部的擴張可能導致瓣膜的泄漏，其原因是瓣膜尺寸太小致使瓣膜關閉不全。2002 年 David 等[4]調查發現外科醫生在進行保留主動脈瓣的手術中，為達到恢復患者瓣膜正常生理功能的目的，需按照要求進行特定的瓣膜設計。在 2004 年 Feindel 和 David 發現主動脈根部存在擴張現象，在進行瓣膜保留手術治療時，外科醫生會根據需要擴大瓣膜的尺寸范圍。Hammer 等[5]發現當瓣膜出現嚴重病變需要進行瓣膜移植修復時可針對瓣膜高度進行設計，并得出瓣膜高度的不同使得瓣膜結合高度不同的結論。
目前關于瓣膜高度影響主動脈瓣關閉性能的研究工作較少。為了研究主動脈根部瓣膜關閉不全手術中如何選取主動脈瓣膜幾何尺寸，以及不同主動脈瓣尺寸的設計對瓣膜關閉打開性能的影響，本文采用有限元軟件數值模擬的方法，仿真瓣膜關閉到打開的過程，比較不同瓣膜高度下模型的最大應力、接觸力和瓣膜開口面積。目的是研究不同瓣膜高度的設計對瓣膜開閉性能的影響，獲取瓣膜尺寸的合理設計范圍，為臨床決策提供理論知識和指導。
1 方法
1.1 幾何模型建模
主動脈根部基本結構主要包括瓣環、竇部、瓣膜、竇管交界。在這里采用 Labrosse 等[6]提出的 8 參數 15 坐標點方法（如圖 1a 所示），構建主動脈根部三維幾何模型（如圖 1b 所示）。
圖1
主動脈根部結構圖
a. 主動脈根部 15 坐標模型草圖輪廓線[6]；b. 基于 15 坐標利用有限元軟件建立的主動脈根部三維幾何模型輪廓圖
Figure1. Structure of aortic roota. outline of aortic root model of 15 coordinates; b. three-dimensional geometric model of aortic root established by finite element software through 15 coordinates
選取 Labrosse 提供的臨床手術指導尺寸數據（如圖 2 所示）[7]。瓣環直徑 DA = 26.0 mm，竇部直徑 DS = 40.0 mm，竇部高度 DSH = 16.0 mm，瓣葉高度 LH = 19.0 mm，瓣膜高度 H = 14.0 mm，竇管交界直徑 DSTJ = 26.0 mm。在模型升主動脈端和左心室端（即主動脈根部的上游和下游）增加 L = 20.0 mm 的血管延長部分，模擬血液的充分發展。三維幾何模型運用 SolidWorks（Concord，MA，美國）軟件構建（如圖 3 所示）。
圖2
主動脈根部二維平面圖以及各部分結構相關尺寸
Figure2.
Two-dimensional sketch of aortic root and the relative dimensions
圖3
主動脈根部三維幾何模型
Figure3.
Three-dimensional geometric model of aortic root
1.2 實驗模型建立
將 Labrosse 提供的臨床手術指導尺寸作為參考模型 A。保持主動脈根部其他參數的尺寸不變，改變瓣膜高度 H，以增量 ± 0.5 mm 建立 5 組幾何模型，并命名為 B、C、D、E、F。六組主動脈根部幾何模型的瓣膜高度尺寸見表 1。
表1
六組模型的瓣膜高度尺寸和有限元分析結果
Table1.
Valve height and finite element analysis of the six models
六組幾何模型在 SolidWorks 軟件中建立后導入 HyperMesh（Altair Engineering，Troy，MI，美國）進行網格劃分和單元設置等相關操作。對竇部、主動脈端和心室端設置四邊形網格，對瓣膜設置三角形網格；血管壁和瓣膜的單元類型采用殼單元。完成設置后導入 ADINA 9.0（ADINA R&D，Watertown，MA，美國）進行模型的求解和后處理等有限元分析。
1.3 有限元分析
1.3.1 有限元軟件中總體控制參數的設置
在 ADINA9.0 軟件中選擇基于位移參數的隱式動力學方法求解結構模型[8-9]；步長在載荷變化緩慢時段設置為 0.001，載荷變化劇烈時段設置為 0.000 1；收斂原則和迭代方法分別為位移和修正牛頓法；為促進收斂，阻尼系數設置為 0.15；瓣膜關閉存在的接觸采用約束方程接觸法計算，摩擦系數為 0.013。瓣膜和血管壁厚度分別設置為 0.3 mm 和 0.6 mm。
1.3.2 有限元軟件中材料屬性的設置
生理上主動脈根部組織材料為超彈性材料屬性并且各向異性。然而為了簡化計算的復雜性和提高分析的可行性，將模型中的瓣膜和血管壁假設為線彈性、各向同性的材料屬性[10]。瓣膜和主動脈根部其余部分楊氏模量分別為 1 MPa 和 2 MPa，密度分別設置為 1 100 kg/m3和 2 000 kg/m3，泊松比都設置為 0.45。
1.3.3 有限元軟件中邊界條件的設置
約束：施加全方向的固定約束于主動脈出口端和心室流出端。載荷：對主動脈根部心室端、瓣膜和主動脈端分別施加如圖 4 所示的隨時間變化的壓力載荷。圖中紅色曲線代表主動脈端壓力載荷波形；藍色實曲線代表心室端壓力載荷波形，藍色虛曲線代表瓣膜壓力載荷波形。
圖4
施加到主動脈、左心室和瓣膜的壓力波形
Figure4.
Pressure waves exerted on the aorta, left ventricle and leaflets
為提高計算的精確度，在實現心臟收縮模擬之前要增加 0～0.2 s 的求解階段，使計算從零應力狀態過渡到正常生理壓。在 ADINA9.0 有限元軟件中進行力學行為的計算。有限元模型運算中存在周期依賴性。本課題組前期對周期性問題進行了研究[11-12]，通過逐步增加周期個數，發現兩個周期的函數載荷已經存在很好的收斂效果，增加周期效果相似，相鄰周期誤差小于 5%。為節省計算時間，本研究選取運算兩個周期，獲取收斂結果。
2 計算結果
在主動脈根部瓣膜完全打開和關閉時，提取模型的最大應力值以及分布、瓣口面積、瓣葉接觸力等參數，分析數值模擬結果。
2.1 最大應力值
主動脈瓣膜關閉時，竇部、瓣膜之間存在力的相互作用。從不受壓開始的心動周期中，分析主動脈根部三維結構的力學行為。對最大應力值的分析主要針對于瓣膜關閉狀態時。根據 Marom 和 Labrosse 等數值模擬和實體實驗研究發現，主動脈根部最大應力值出現在主動脈瓣膜和主動脈竇的連接線處[6, 13-14]。針對參照模型（DA = 26.0 mm，H = 14.0 mm）進行最大應力分析。通過對不同時刻的最大應力值的查看和對比，發現在兩個心動周期內，在瓣葉和竇部連線處的最大應力出現在 0.7、1.5 s 左右，其值大小相似。在 0.7 s 時刻取值。如圖 5 所示為正常主動脈根部（模型 A）結果，主動脈根部最大應力值出現在瓣膜和竇部連接處，最大應力值約為 672 kPa。B、C、D、E、F 的應力結果如表 1 所示。已有相關研究表示最大應力值是主動脈根部關閉質量評價指標之一[15]，應力值過大會破壞瓣膜性能，影響瓣膜的使用壽命。本文所獲取的最大應力值較小，符合要求。
圖5
在 0.7 s 時瓣膜完全關閉的主動脈根部應力云圖
Figure5.
Stress contour of aortic root with complete closure at 0.7 s
2.2 瓣開口面積
提取 0.4 s 時主動脈瓣膜的打開程度，計算瓣膜完全打開時的面積。如圖 6 所示為正常主動脈根部（模型 A）瓣葉的打開狀態，瓣口面積209.098 mm2。B、C、D、E、F 模型的結果如表 1 所示。正常的主動脈瓣口面積維持著人體正常生理活動。瓣口面積過小會造成心輸出量減少，心室肥大，從而造成暈眩、心絞痛以及心衰等，影響著生命活動。
圖6
在 0.4 s 時瓣膜完全打開狀態
Figure6.
The valve was fully opened at 0.4 s
2.3 瓣葉接觸力
瓣葉接觸力可以反映瓣膜關閉階段的對合情況[14]。瓣葉接觸應力是求取三個瓣葉完全對合時刻的所有接觸力的總和，模型 A 瓣膜完全關閉在 0.507 s 時，拾取該時刻的瓣葉接觸力，計算大小為 7.09 N。
主動脈瓣膜的正常關閉需要三個瓣葉之間相互作用，接觸力的大小反映著心室舒張期階段的瓣膜關閉性能。6 個模型的瓣葉接觸力的計算結果如表 1 所示。
對比不同瓣膜高度與最大應力、瓣口面積、瓣葉接觸力的變化關系，查看影響程度。研究發現最大應力值的數據變化呈現增大-減小-增大的趨勢；接觸應力值數據趨勢持續增大；瓣口面積值的數據變化隨著瓣膜高度增加呈現先增大后減小的趨勢。通過數據趨勢的對比，六組模型在較小應力值的情況下，達到標準瓣口面積的瓣膜高度在 13.5～15.0 mm 之間，其建立的瓣膜幾何尺寸能夠獲得較好的主動脈瓣膜開閉性能。
3 討論
3.1 研究的合理性和準確性
通過與文獻中的有限元模型和體外實驗研究結果的對比方法來驗證本試驗中計算結果的正確性[16]。
Labrosse 等[13]在 2010 年通過的人體體外實驗獲得了瓣口面積的最大值為（270 ± 0.63）mm2；Garcia 等[16]在 2011 年提出主動脈瓣瓣口面積大于 200 mm 時為正常主動脈瓣的評價標準。本文中參照模型 A 的瓣葉開口面積為 209.098 mm2。瓣口面積結果與上述文獻中的結果接近。
Katayama 等[17]在 2008 年從零應力開始計算瓣膜受力情況，發現舒張期瓣膜和竇部連接處應力值在 600～750 kPa 之間；Marom 等[14]在 2013 年發表的文章中得到的最大應力結果為 800 kPa；本課題組在研究竇管交界和竇部直徑對主動脈根部最大應力和分布位置影響時，獲得的最大應力的變化范圍為 567～601 kPa。本文中參照模型 A 最大應力值為 672 kPa，出現在瓣膜和竇部連接處，數值模擬的最大應力值計算結果與上述幾個研究組的結果相近。
結合以上對比，所設計模型在準確性和可行性方面都已達到要求。
3.2 研究討論
先天性心臟病患者的主動脈瓣會出現逆流、狹窄等瓣膜關閉不全的病情[18]。治療主動脈瓣關閉不全，可采用主動脈瓣修復手術和替換手術兩種方式[19]，在臨床上瓣膜修復多優先考慮瓣膜移植。生命活動是一個動態過程，當外界干擾過大致使血管擴張時，瓣膜有可能再次出現狹窄。考慮到移植瓣膜不會隨著人體生長而生長，本文研究主動脈根部幾何結構時，保持其他結構不變，在增大 ± 0.5 mm 瓣膜高度的情況下研究對主動脈根部瓣膜關閉打開性能的影響，為臨床上瓣膜幾何結構的構建與選取提供理論依據。
評價主動脈根部瓣膜關閉性能的參數有瓣口面積、最大應力值、接觸應力值等。臨床醫學上對于主動脈瓣膜瓣口面積定義三種狀態：當瓣口面積小于 200 mm2、大于 150 mm2時，為輕度狹窄；當瓣口面積小于 150 mm2、大于 100 mm2時，為中度狹窄；當瓣口面積小于 100 mm2時，為重度狹窄；且 Garcia 等[16]在 2011 年制定了瓣口面積的評價標準，即瓣膜開口面積大于 200 mm2時主動脈瓣才能實現正常功能。在本文的研究中六組模型的瓣口面積值隨瓣膜高度的變化呈現先增加后減小的趨勢，結合上述評價標準以及臨床標定，瓣膜幾何高度在 13.5～15.0 mm 之間時，瓣口面積符合要求。
Marom 等[14]研究發現最大應力值的大小對瓣膜使用的長期有效性存在著很大的影響，是評價瓣膜質量的標準之一。應力值過大會降低瓣膜的柔軟性，造成瓣膜撕裂以及鈣化等，引起瓣膜的再度狹窄。在主動脈根部幾何結構性能的數值模擬與分析中，需觀察收縮期瓣膜關閉時主動脈根部的最大應力值。Labrosse 等[13]總結前人研究，認為人體生理情況下主動脈瓣動力學行為顯示最大應力范圍在 300～800 kPa。本文研究幾何結構模型的力學行為所獲取的最大應力值都在 600～700 kPa 之間且偏小，表明采用有限元軟件重建并分析主動脈根部瓣膜的關閉性能是可行的，且六組模型的最大應力值在瓣膜高度 14.5 mm 時最小。
瓣膜接觸力是指瓣膜之間的相互作用，可以反映瓣膜在心動周期中關閉的性能和瓣膜的對合能力。Pan 等[20]在 2014 年研究了改變竇管交界和竇部直徑對瓣膜關閉功能的影響，采用有限元軟件對模型進行結構力學數值模擬，結果發現為使瓣膜正常關閉，主動脈根部竇管交界和竇部直徑增大后，瓣膜接觸力也相應增大，反之亦然，結論是直徑增加不利于主動脈瓣的關閉。通過觀察本組研究數據，隨著瓣膜高度的增加，瓣膜接觸力也隨之增加，與 Pan 等研究結果趨勢相同。因此在設計瓣膜時，需注意瓣膜高度過大不利于瓣膜的關閉。
綜上所述，對比前人研究結果，本研究通過有限元軟件分析主動脈根部改變瓣膜高度的幾何模型的力學行為是可行的，且最佳瓣膜高度的結果在 13.5～15.0 mm 之間。
本文研究的不足之處在于：第一，壓力載荷施加時均勻分布于瓣膜和主動脈根部，而人體生理條件下，壓力分布是不均勻的。第二，本研究中主動脈根部的基礎直徑是 26.0 mm，但人體生理上的血管是處于生長狀態，此研究結論對其他根部尺寸主動脈的適用性尚未可知。因此針對以上不足，下一步工作將構建不同基礎尺寸直徑的主動脈根部模型，從數值模擬結果中獲取瓣口面積、最大應力值以及瓣膜對合高度等評價指標，分析生長狀態下不同主動脈幾何結構對瓣膜關閉性能的影響，為臨床醫生提供最優化的主動脈根部幾何尺寸結構的選擇方案。
4 結論
在改變瓣膜高度的情況下，建立了六組升主動脈根部的幾何模型。利用有限元軟件數值模擬的方法分析了不同瓣膜高度情況下最大應力值、開口面積以及瓣葉接觸力等主動脈瓣膜生物力學性能評價的參數值以及對主動脈瓣開閉性能的影響。研究發現在不影響生命活動的前提下，可結合患者狀態適當改變瓣膜高度，以更好地適應變化的生理環境。就本文所建立的模型而言，主動脈根部瓣膜高度在 13.5～15.0 mm 之間時具有較好的開閉性能，可作為臨床醫生手術規劃的借鑒。
