同步腦電—功能磁共振融合技術因其高精度的時空分辨率，在科學研究和臨床領域發揮著重要作用。然而，核磁環境下的心電偽跡嚴重影響了融合結果。本文利用實時技術改進了離線約束獨立成分分析算法，并采用該方法處理了模擬數據和真實靜息態數據。結果表明：對于模擬信號，本方法得到的 Er 值小于平均模板減法等傳統方法（P<0.005）；對于真實信號，本方法得到的 INPS 值高于其他方法（P<0.005）。本文提出的去噪算法為腦電核磁的融合模型研究奠定了技術基礎。
引用本文： 王凱, 嚴瀚瑩, 鄒凌. 基于實時約束獨立成分分析方法的核磁腦電信號去噪研究. 生物醫學工程學雜志, 2019, 36(1): 7-15, 23. doi: 10.7507/1001-5515.201709066 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
在腦科學研究領域，同步腦電（electroencephalogram，EEG）—功能磁共振（functional magnetic resonance imaging，fMRI）融合技術因其高精度的時空分辨率，在科學研究和臨床領域發揮著重要作用[1-3]。但在同步采集過程中，腦電信號會混入大量偽跡，主要有梯度場偽跡（gradient artifact，GA）和心電偽跡（ballistocardiogram artifacts，BCG artifacts）。梯度場偽跡是由磁共振環境下磁場切換引起的周期性偽跡，可以用平均模板相減法（average artifact subtraction，AAS) 去除[4]。心電偽跡因其不穩定的時頻特征，進行特征提取和建模的難度大，一直是核磁腦電信號偽跡去除研究的一大難點。
心電偽跡是由靜態磁場下心跳相關運動所引起的頭部電極移動造成的，與心電信號有類似的特征[5]，其幅值與磁共振掃描儀內的磁場強度成正比，形狀具有時變特征。另一方面，心電偽跡通常對腦電信號 alpha 頻段及其以下頻段產生較大干擾，而 alpha 頻段信號在臨床以及科學研究上有著非常重要的意義。故而，對復雜心電偽跡特征的建模尤為重要，是去除偽跡的關鍵。
心電偽跡去除方法分為空間模式和時域技術兩大類。空間模式技術利用偽跡空間模式下的統計特征進行空域濾波，如主成分分析（principal component analysis，PCA）和獨立成分分析（independent component analysis，ICA）方法[6]。ICA 方法中成分的選取取決于主觀經驗[7]。為解決這類問題，Leclercq 等[8]提出了約束獨立成分分析（constrained ICA，cICA）方法。該方法設置了約束條件，能準確地選取與偽跡相關的成分，且成分選擇減小了主觀因素造成的誤差。然而 cICA 方法沒有考慮到心電偽跡信號的時變性波形、幅值以及規模的影響，故可能存在偽跡去除不凈的問題。時域技術主要利用偽跡時域波形的準周期性去除偽跡，包括 AAS、最優基組法（optimal basis sets，OBS）、移動線性模型以及自適應濾波等[9]。這兩種技術都有局限性，空間模式耗時大，而時域技術要依賴于研究者的經驗。除了上述一些傳統方法外，參考層結合諧波回歸方法、字典學習方法、實時 OBS 方法以及 DRPE 特殊記錄方法也被廣泛運用于心電偽跡去除領域[10-13]。此外，也有研究通過減少電極移動來避免偽跡產生[14]。
本文參照實時 OBS 算法改進了 cICA 方法，提出實時約束獨立成分分析方法（real time-cICA，rt-cICA），處理單導模擬腦電信號以及 64 導真實靜息態核磁腦電信號，并與傳統 AAS、OBS 等方法得到的結果進行時頻分析比較，目的是為了驗證本方法能有效去除心電偽跡，且本算法比傳統方法優越，能為融合技術的進一步實現奠定技術基礎。
1 實驗數據及方法
1.1 實驗數據
1.1.1 模擬核磁腦電信號
模擬數據是將模擬心電偽跡加入到非核磁環境下真實自發腦電中構造，真實自發腦電由美國 EGI 公司生產的 GES 300 MR 腦電放大器和 64 導 HydroCel 電極帽在常規環境下采集。未加噪的腦電信號可作為去噪后腦電信號質量的衡量標準。構造模擬數據的過程可以分為以下三個步驟[12]。
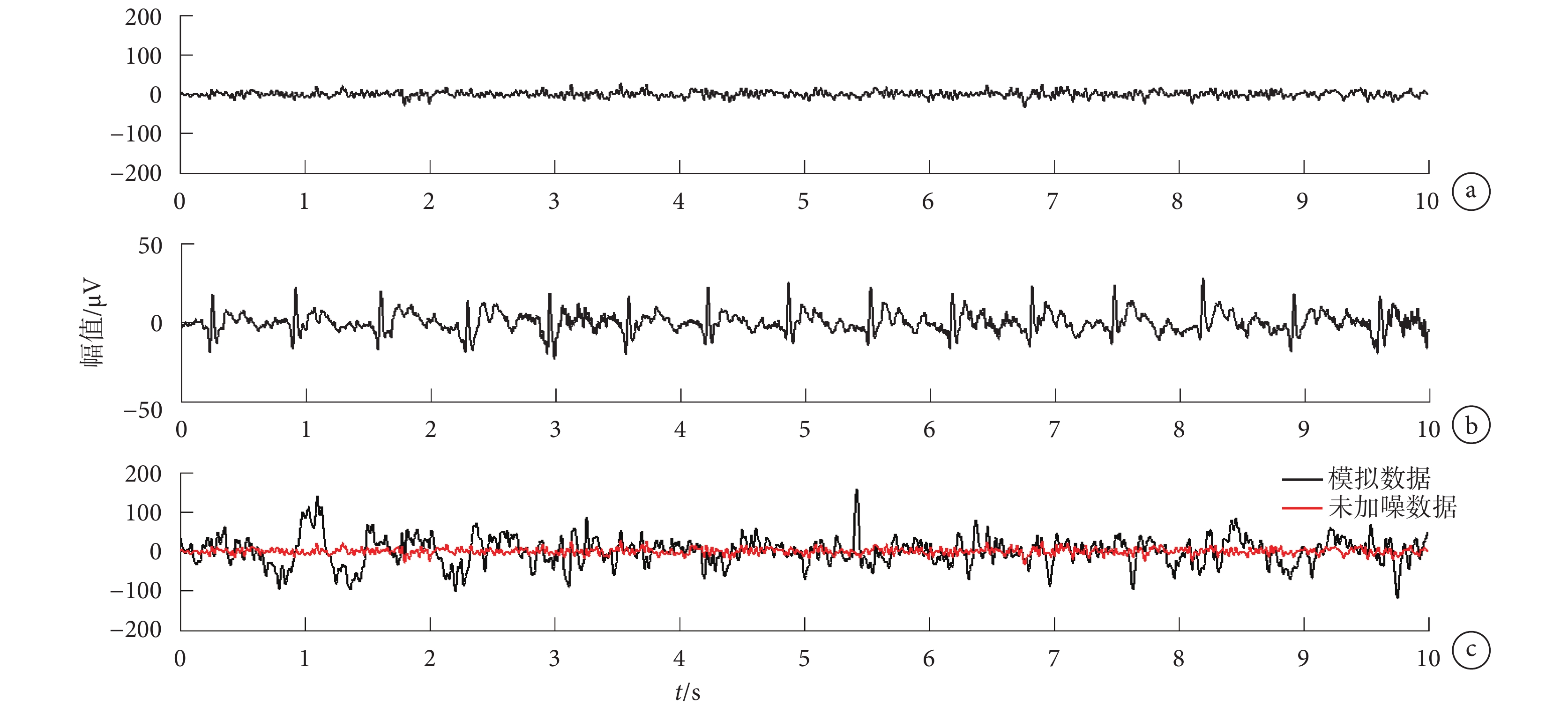
首先，取一導聯沒有去除心電偽跡的真實靜息態核磁腦電數據，以偽跡波峰位置為中心分成若干段進行疊加平均，構造一個偽跡模板；然后獨立隨機地改變模板的形狀和大小，并連續拼接;最后將上述步驟得到的模擬心電偽跡加到非核磁環境下采集的腦電數據中。每個波峰之間的間隔以及偽跡波的大小都是隨機的，如圖 1 所示。圖 1a 是常規環境下采集的用來構造模擬數據的自發腦電，且已濾去了 50 Hz 的工頻干擾。圖 1b 是模擬心電信號，用于檢測圖 1c 模擬混合信號中心電偽跡的波峰位置。圖 1c 是模擬含有偽跡的腦電信號，紅色表示未加噪常規信號，黑色是混合信號。
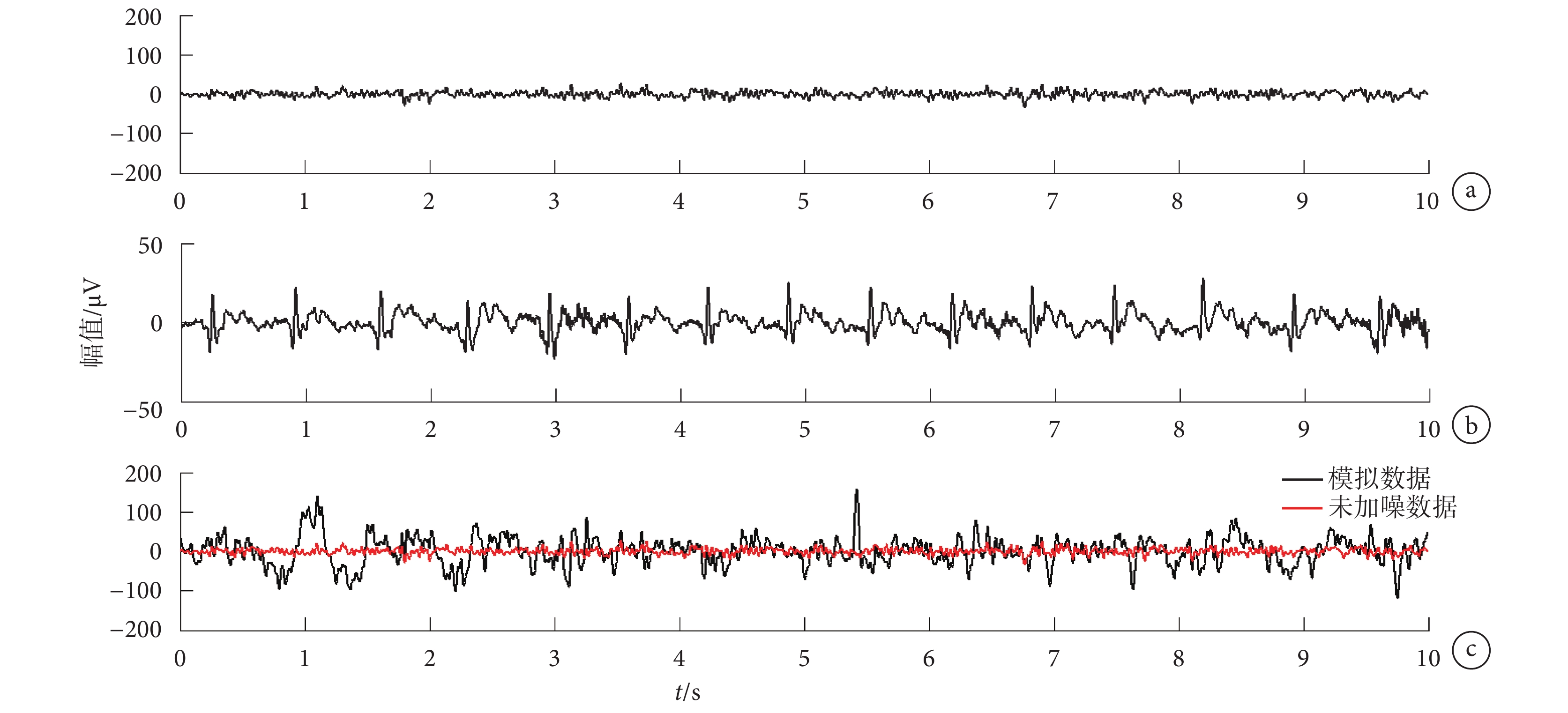圖1
模擬腦電信號
a. 未加噪自發腦電數據；b. 對應的心電信號；c. 混合信號
Figure1. Simulated EEG signalsa. spontaneous EEG data without noise; b. corresponding ECG signals; c. mixed signals
1.1.2 真實核磁腦電信號
為進一步驗證實時約束獨立成分分析方法的有效性，本次實驗采集了 10 名健康被試靜息態的核磁腦電以及心電數據，采集心電數據的目的是為了定位偽跡出現的位置。同步采集得到的核磁腦電數據已使用 AAS 算法去除了梯度場偽跡且采用參考電極標準化技術（reference electrode standardization technique，REST）做預處理[15]。
實驗要求每名被試平躺在核磁室，保持全身放松并且處于閉眼狀態。本次實驗依據《世界醫學協會赫爾辛基宣言》（2000）和常州大學倫理研究委員會批準制定了知情同意書。被試在實驗之前要求簽署知情同意書。
實驗所用到的美國 EGI 公司 64 導腦電放大器以及核磁掃描儀由常州大學生物醫學重點實驗室以及常州第二人民醫院生物醫學技術研究中心提供。功能磁共振圖像由荷蘭飛利浦公司生產的 Achieva 3.0 T 核磁掃描儀采集，其參數為：TR = 2 000 ms，TE = 35 ms，Flip angle = 90°，FOV = 230 mm × 180 mm，一次全腦掃描獲取 24 層圖像，使用平面回波（echo planar imaging，EPI）采集序列。腦電數據由美國 EGI 公司的腦電放大器以及 64 導腦電帽采集，另外還有一導聯同步采集的心電信號，心電電極放在被試的前胸。電極的擺放位置遵循國際 10/10 系統，只是命名規則有所不同。
1.2 方法
在核磁共振室 3.0 T 的環境下，心電偽跡的幅值在 400 μV 左右，是腦電信號的 6～8 倍[4]，僅憑肉眼就能明顯地看出其在腦電信號中的位置，且每一導聯不同時段的心電偽跡差異較大。偽跡去除首先需要定位偽跡位置，準確穩定的心電檢測算法有助于對心電偽跡進行精準定位。
1.2.1 實時心電檢測算法
Allen 等[4]最早提出一個簡單的閾值法來檢測 R 波位置，然而此方法較為耗時，且由于核磁環境的復雜性導致算法精度不高。因此，Christov 等[16]提出了一種組合自適應閾值檢測算法。之后 Niazy 等[9]在此算法的基礎上進行優化改進，首先對每個通道的心電數據進行 7～40 Hz 的帶通濾波，然后利用 k-Teager 能量算子算法處理濾波后的心電信號并且使其負值為 0，從而得到一個復合值，
 |
其中ECG是復合值，n是時間參數，E是濾波后的心電數據，k是頻率選擇參數。接著利用此自適應閾值檢測算法來檢測 R 波。斜率閾值（M）、高頻集合閾值（F）以及心跳預估閾值（R）三者之和作為MFR閾值：
 |
當ECG（n）≥ MFR（n）時就被檢測為一個 QRS 波。
結合自適應閾值檢測算法[9]以及實時技術，本文將實時 R 波檢測算法用于定位心電偽跡波的位置，并結合 rt-cICA、cICA、OBS 以及 AAS 等方法去除心電偽跡。
1.2.2 約束獨立成分分析
cICA 算法假設 EEG 信號只由兩種源成分線性混合而成，即神經信號和偽跡信號。一旦一類源成分被確定，另一類源成分就可以被推導出來［11］。和經典的 ICA 方法類似，cICA 算法的目標也是尋找一個解混矩陣W（W是一個N維方陣，N為導聯數）。但不同點在于該算法必須滿足兩個條件：① 類似經典 ICA 算法，最大化源成分的負熵 
；② 設置約束條件 g（W）≤ 0 并且 h（W） = 0，其中
l 是希望被提取出來的源成分的數量；
g（W） = （g1（w1）
gl（wl）)T，
。其中，i = 1, 
,l；
h（W） = （h1（w1）
hl（wl）)T，hi（wi） = E{si2} ? 1。其中，i = 1,
,l。
第一個約束條件使得每個源成分之間的相關參考距離
保持在一個特定的距離
之內，第二個條件是標準化。此算法采用增廣拉格朗日乘法求解，增廣拉格朗日乘法 L
可知：
 |
其中，
和
是兩組分別用于不等式和等式約束的拉格朗日乘數，
是懲罰參數，確保優化問題在局部凸假設下成立。Newton-like 迭代過程用來求解得到去相關矩陣W：
 '/> |
其中，
是依賴于每個
負熵的向量，
是被記錄腦電信號X的自相關矩陣。
 |
 |
迭代終止條件是W的 2 個連續估計范數之間的相對差值小于 10-5數量級。
W 的行向量可被視為 N 維空間的非正交基。在預處理過程中，正交矩陣 
能由 W 推導出來。識別 
中偽跡相關的行向量可能會找到互補的正交向量的集合。因為神經相關的成分比偽跡相關成分多，所以算法的特點在于使用 Gram-Schmidt 正交化來找到神經相關的源成分，而不是采用計算難度更大的方法去找偽跡相關的源成分。
與經典的 ICA 算法相比，cICA 能識別與給定約束條件最接近的源成分。cICA 算法在偽跡成分估計的穩定性上較經典的 ICA 算法以及多獨立分量分析（multi independent component analysis，MICA）算法有較大的改進，并且沒有增加計算消耗。但算法優勢只局限于偽跡成分的估計，并且也沒有考慮心電偽跡的時變性。總之，cICA 算法的特點在于對偽跡成分的自動識別，減少了主觀因素帶來的誤差。
1.2.3 實時約束獨立成分分析方法
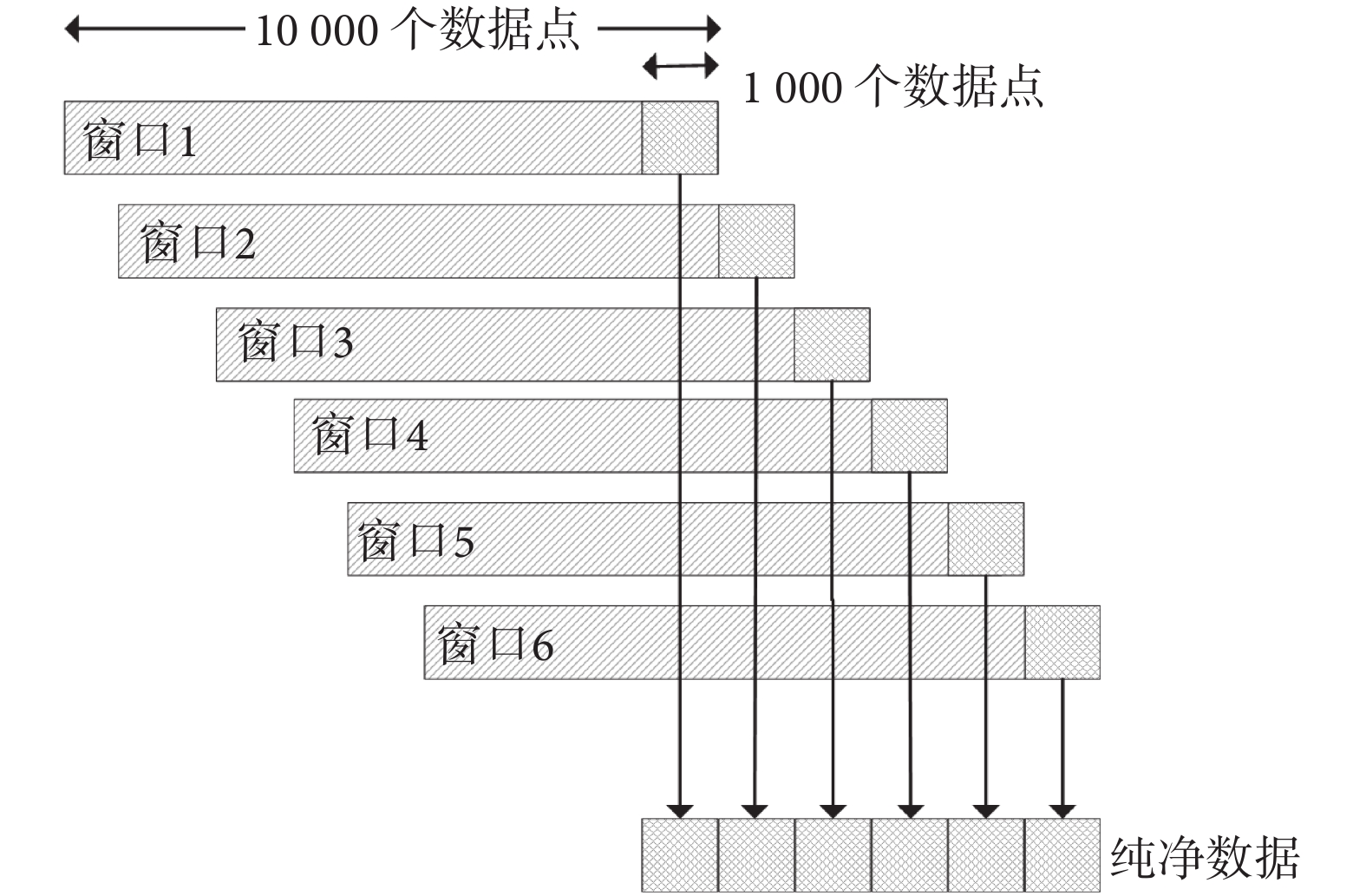
cICA 算法去除心電偽跡是將心電信號作為約束條件，其最大的缺點在于缺少對心電偽跡時變性特征的考慮，即對整體心電信號進行簡單疊加平均后的均值作為約束條件，這樣就忽視了心電信號變異對去噪效果的影響。于是參照實時 OBS 技術，改進了 cICA 方法，提出 rt-cICA。該方法假設短時期內心跳的變化差異性較小，這樣大大減小了時變性對去噪結果帶來的影響。對于實時去噪來說，心電 R 波的間隔隨時間變化明顯，所以找到一個合適的 EEG 信號分段標準尤為重要，為此引入滑動窗來對 EEG 信號進行分段，在每個窗中實時處理心電偽跡，然后滑動至下一個窗中繼續處理。圖 2 是實時處理的一個基本示意圖，首先使用 cICA 算法去除滑窗內數據的心電偽跡，然后選取滑窗最后十分之一段數據作為去除偽跡后的純凈腦電信號，接著滑窗繼續滑動十分之一段大小，按照此流程不斷處理剩下的含噪數據，最終得到純凈的腦電信號[6]。方法性能可能受滑動窗大小影響，不同尺寸的滑動窗得到的去噪效果可能不同，獲得最佳的去噪效果在于找到最合適的滑動窗尺寸。
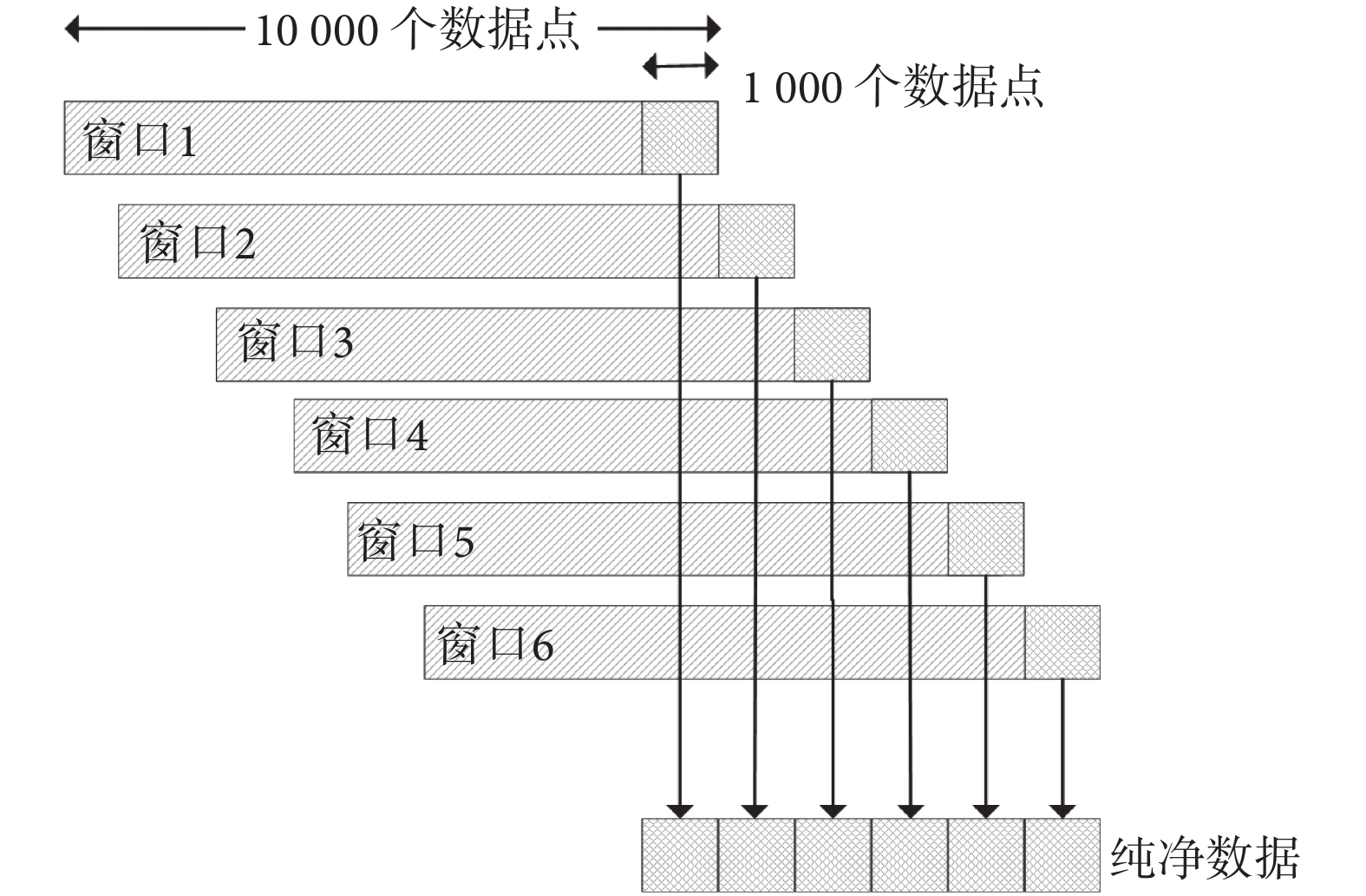圖2
實時處理過程示意圖
Figure2.
Real-time process diagram
心電偽跡波峰一般出現在心電 R 波時刻后的 210 ms[4]，根據這一特點對腦電信號進行分段。在每個尺寸為k的滑動窗中，取相鄰 R 波之間間隔的均值作為腦電分段大小的模板，如公式（7）所示，其中 Ri 為 R 波出現的位置。在確定完平均間隔之后，根據公式（8）即可得到腦電數據的分段 L，L 為以 Ri+Rdelay 為中心、Lrt 為長度的腦電分段。其中 Ri為心電中 R 波出現的位置，Rdelay 為偽跡在 R 波出現后的延時時間，取 210 ms，Lrt 為平均間隔。在偽跡位置檢測出來之后，即可利用 cICA 算法去除心電偽跡。然后對每個滑動窗進行處理，得到較為純凈的腦電信號。
 |
 |
1.3 評價指標
為評價 rt-cICA 方法的有效性，使用了幾種評價分析指標，包括信號幅值誤差（Er）、靈敏度（Se）和特異性（Sp）等指標，不同方法得到的結果進行頻譜分析以及改進的標準化功率譜（improved normalized power spectrum，INPS）分析。
1.3.1 信號幅值誤差
Er 是一項評價不同方法性能的重要指標，偽跡去除后的信號誤差定義為:
 |
其中 x（i）為偽跡去除之后樣本點 i 的幅值，y（i）是對應的參考信號的幅值。對比不同方法的 Er 值可以作為算法去噪效果的評價指標。
1.3.2 靈敏度和特異性
靈敏度和特異性指標用來測試心電 R 波檢測算法的魯棒性[10]。對于心電信號，心電 R 波的出現次數可用肉眼直接觀測，R 波出現的總次數定義為真實主觀數目 TP；未被算法檢測到但真實存在的 R 波定義為假陰性，其數目記為 FN；非 R 波卻被算法誤檢為 R 波定義為假陽性，其數目記為 FP。如果檢測到的 R 波位置發生了一個線性漂移，也都被認為是假陰性或假陽性，例如檢測到 R 波的位置在真實 R 波位置的前面或后面。靈敏度和特異性指標的計算方法如下所示:
 |
 |
1.3.3 功率譜
為比較不同方法的去噪效果，計算去除偽跡前后信號的功率譜值也是一項重要的手段。計算公式如下：
 |
其中 ejw 表示正弦信號和余弦信號的疊加。S（ejw）是功率譜，xl 是每導聯樣本點 l 的值。
1.3.4 改進的標準化功率譜
Tong 等提出的 INPS 指標可以用來評估去噪算法以及去噪后信號的質量，其計算的是信號的功率衰減，計算公式如下:
 |
其中 
和 
是每個特定導聯 Chan 去噪前后以第 j 和第 i 個諧波為中心、窗口大小為 1 Hz 的平均功率值。INPS 表示每個窗口的能量衰減，即心電偽跡能量衰減。INPS 的值越大，說明能量衰減得越多，也就表示去除的心電偽跡越多，但并不是衰減得越多越好，INPS 值過大則可能去除了有用的腦電信號。
2 結果分析
2.1 模擬數據
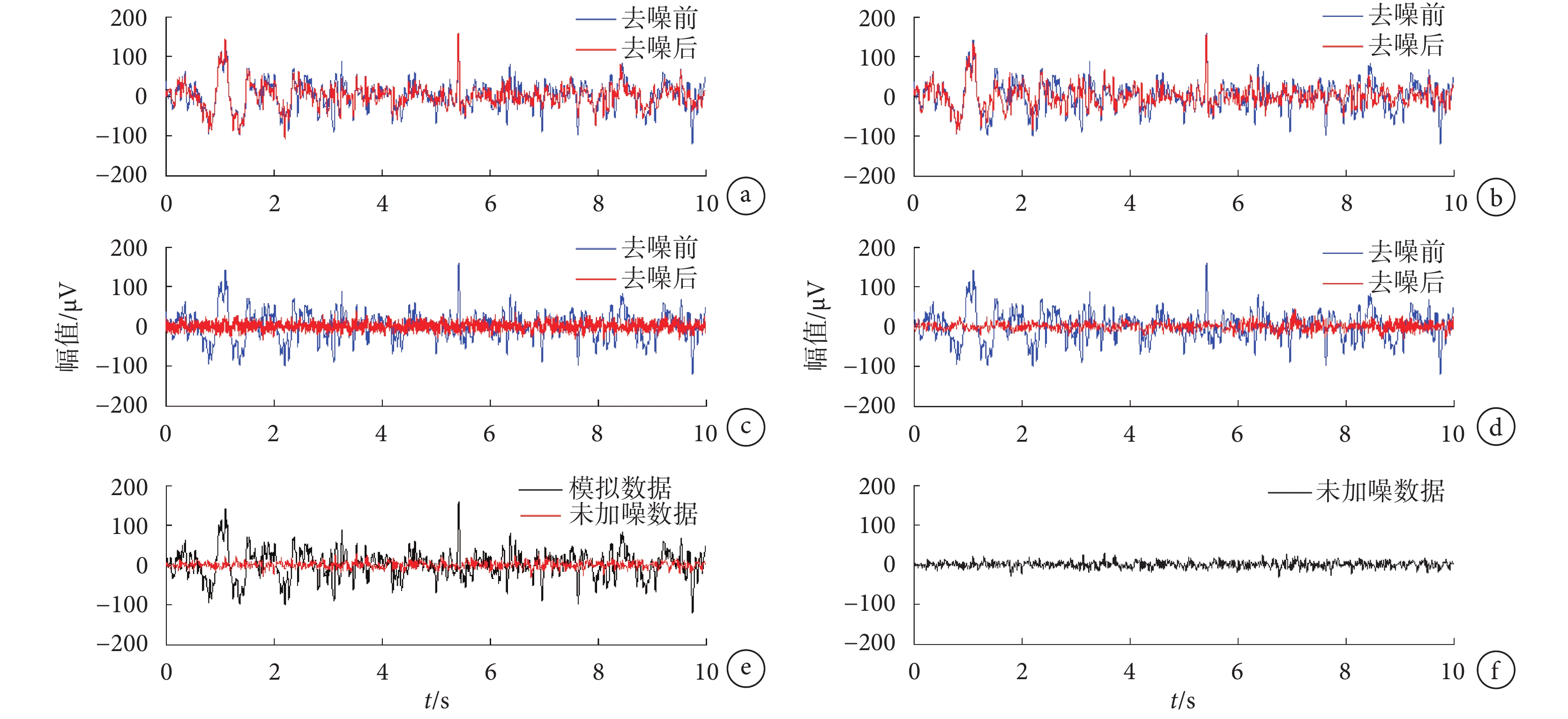
針對模擬數據，比較直觀的評價標準是觀測其時域波形。圖 3 表示分別運用 4 種方法去除心電偽跡前后與原始未加噪聲信號的對比圖。藍色的波形表示去噪前，紅色的表示去噪后。從圖 3a、b 可以直觀地看出，殘留的偽跡相當明顯，并且有些偽跡很難被去除。圖 3c、d 表示的是 cICA 和 rt-cICA 去噪前后的結果圖，兩種方法都去除了絕大部分的心電偽跡，但是綜合圖 3d、e、f 來看，rt-cICA 去噪后信號的趨勢更加接近原始未加噪的信號，而 cICA 方法去除之后信號顯得較密集，有可能是因為部分殘留偽跡所致。故本方法似乎能得到更為純凈的腦電信號，對此結果將進一步進行比較。
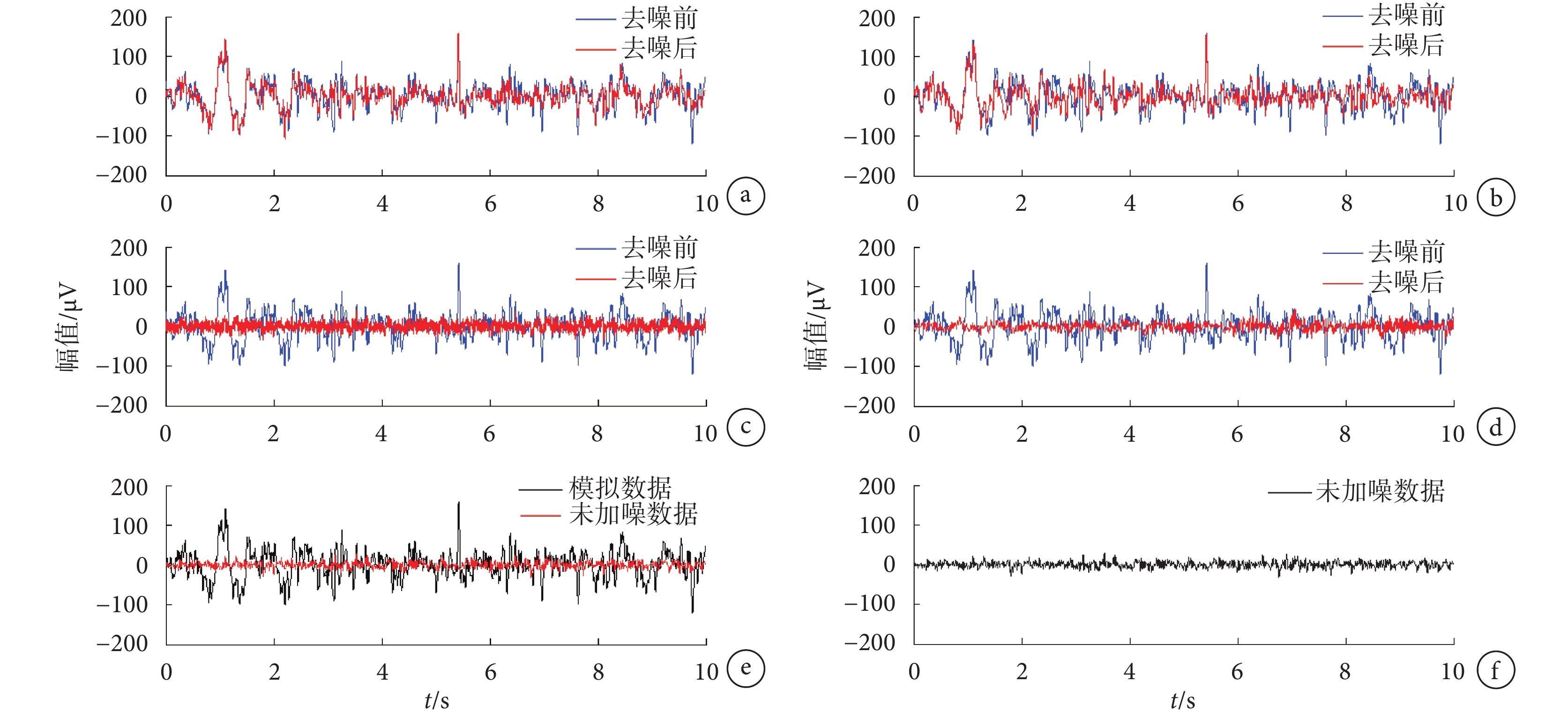圖3
rt-cICA 方法和其他方法去噪效果對比圖
a. AAS 去噪結果；b. OBS（
a. AAS denoising result; b. OBS (
其次，由于模擬數據構成中有未加噪數據作為參考依據，因此，可以用更精確的量化指標，如 Er 值來評估去噪后的信號與未加噪數據的誤差，因此在窗口尺寸相等的情況下，計算了同一腦電數據在不同方法去噪后的 Er 值（對四種方法去除心電偽跡后的 Er 值進行組間雙尾 t 檢驗，P < 0.005）。
窗口尺寸即腦電數據分段的數量，如窗口尺寸 40 表示此窗中有 40 個腦電數據分段。具體見表 1。
表1
不同方法去除心電偽跡之后的 Er 值
Table1.
Er values after removal of BCG artifacts by different methods
從表 1 可以看出，rt-cICA 方法在同一窗口尺寸情況下的 Er 值明顯比其他方法低。鑒于不同窗口大小也是影響去噪效果的一大重要因素，故實驗又選取若干不同大小的窗口，利用 rt-cICA 方法進行對比實驗，計算得到的 Er 值見表 2。
表2
窗口尺寸與 rt-cICA 去噪后的 Er 值
Table2.
Window size and Er value after denoising using rt-cICA
結果顯示，當窗口大小選取為 40 或者 50 時，去噪后的 Er 值較低，并且當窗口尺寸選取過大時，不僅計算消耗會隨之增大，效果也沒有明顯提升，故選取尺寸為 40 或者 50 最為適宜。在最優窗口大小選取完成的情況下，利用同等尺寸窗口以及同樣的心電檢測算法計算不同方法的評價指標。
2.2 真實數據
由于真實靜息態腦電數據是在核磁環境下采集，沒有與之對應的非核磁環境下的腦電數據，故不能使用 Er 值作為評價指標。而真實數據為 10 名被試的靜息態數據，可以計算所有被試數據去噪后的功率譜值和 INPS 值，并利用統計學方法對比本方法和傳統方法。
針對多名被試的真實靜息態腦電數據，為驗證核磁腦電數據質量以及心電檢測算法的魯棒性，計算靈敏度和特異性兩個指標來評估心電數據質量。表 3 列出了 8 名被試心電數據使用 R 波檢測算法后的靈敏度和特異性。前面 7 名被試數據的平均靈敏度和特異性都超過 99%，表明此算法在檢測 R 波時的穩定性較高，被試 8 的數值有明顯差異，可能由于心電電極脫落導致，這類數據在實驗時會加大結果的誤差，故會將其舍棄。
表3
R 波檢測算法的靈敏度和特異性
Table3.
Sensitivity and specificity of the R-peak detection algorithm
2.2.1 rt-cICA 算法去除心電偽跡
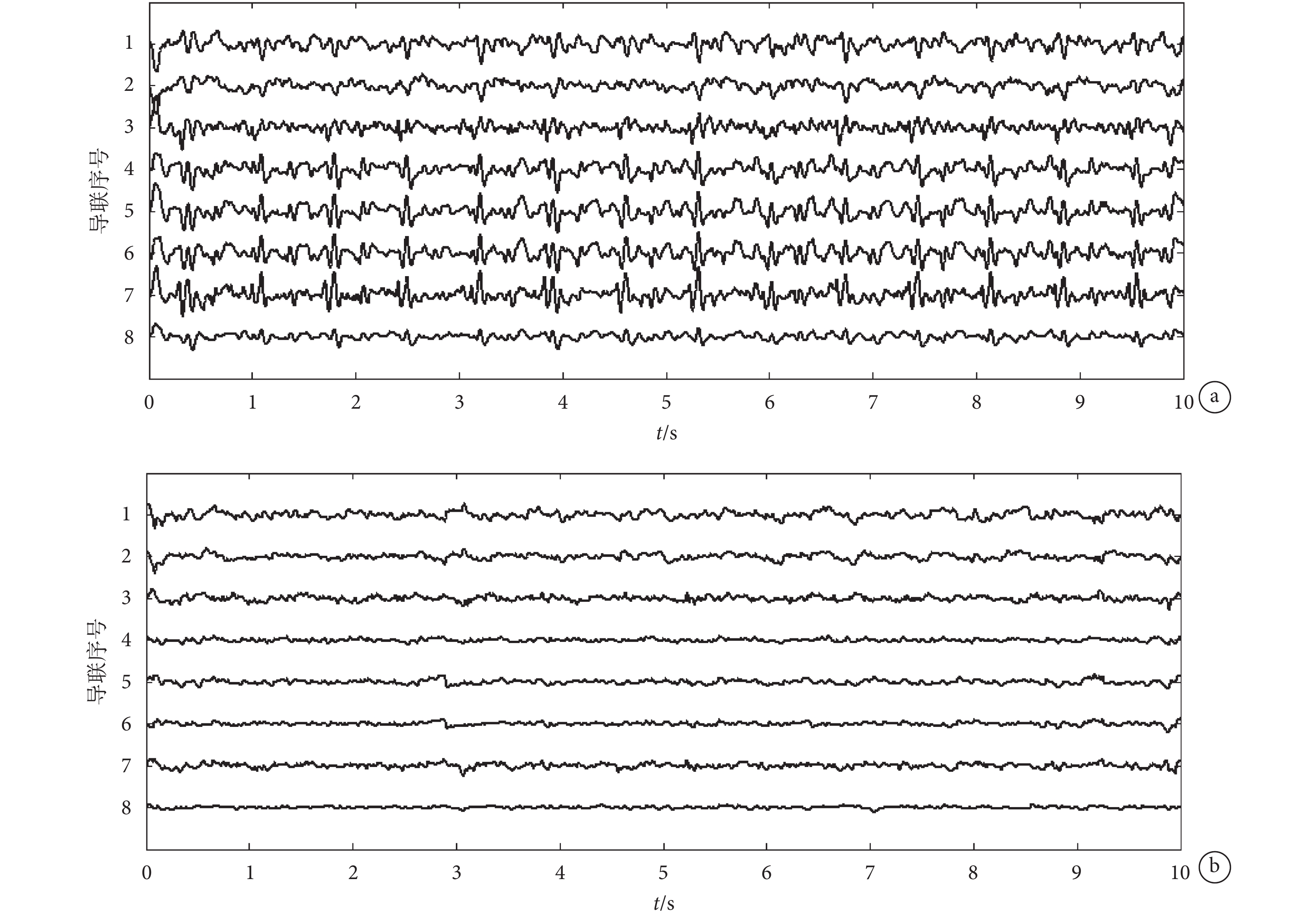
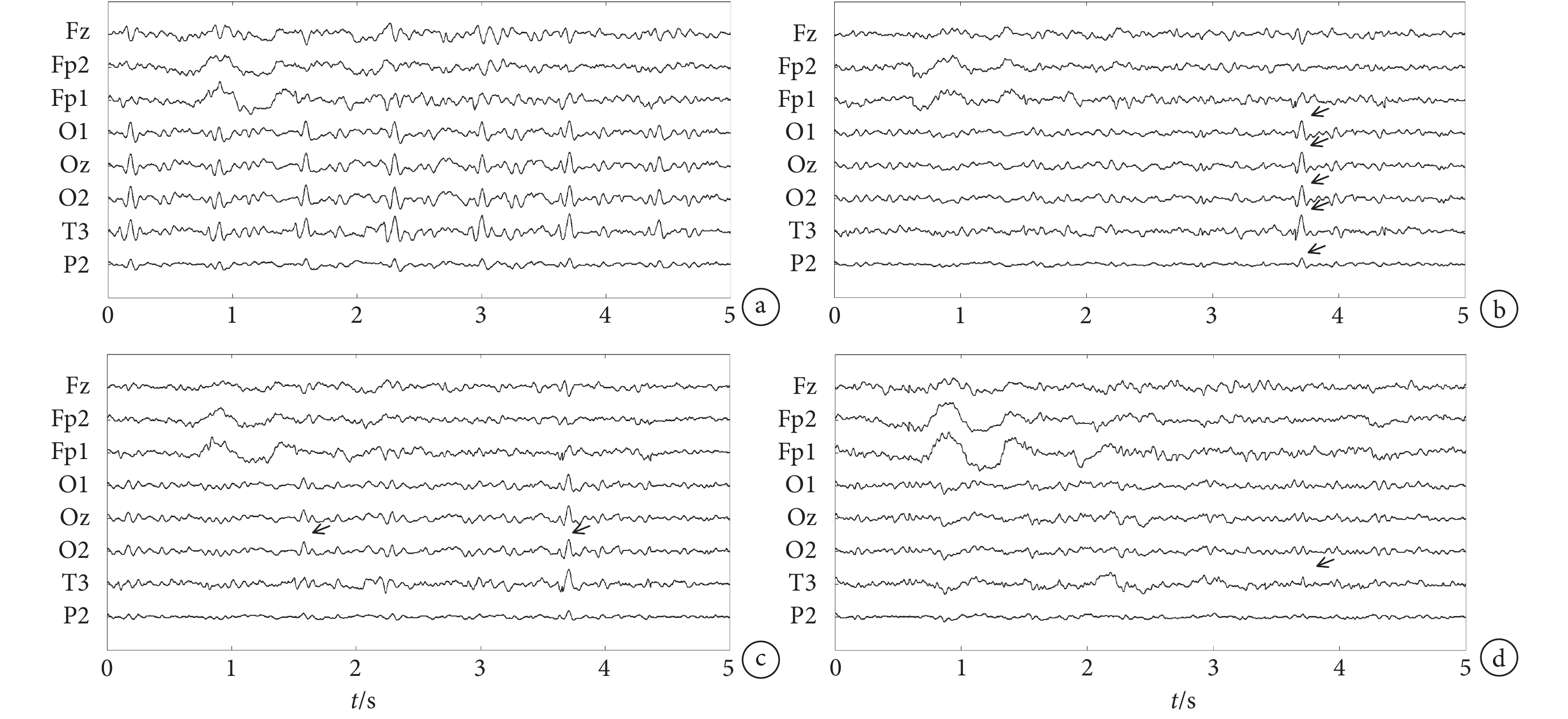
圖 4 表示的是被試 1 閉眼狀態下的 8 導核磁腦電信號（Fz、Fp2、Fp1、O1、Oz、O2、T3、P2）去除偽跡前后的對比圖。圖 4a 是沒有去除心電偽跡的腦電信號，從圖中可以看出有明顯的類似于準周期性心電信號的心電偽跡。圖 4b 是去除偽跡之后的腦電信號。對照偽跡出現的位置可以明顯看出絕大部分偽跡已被去除。
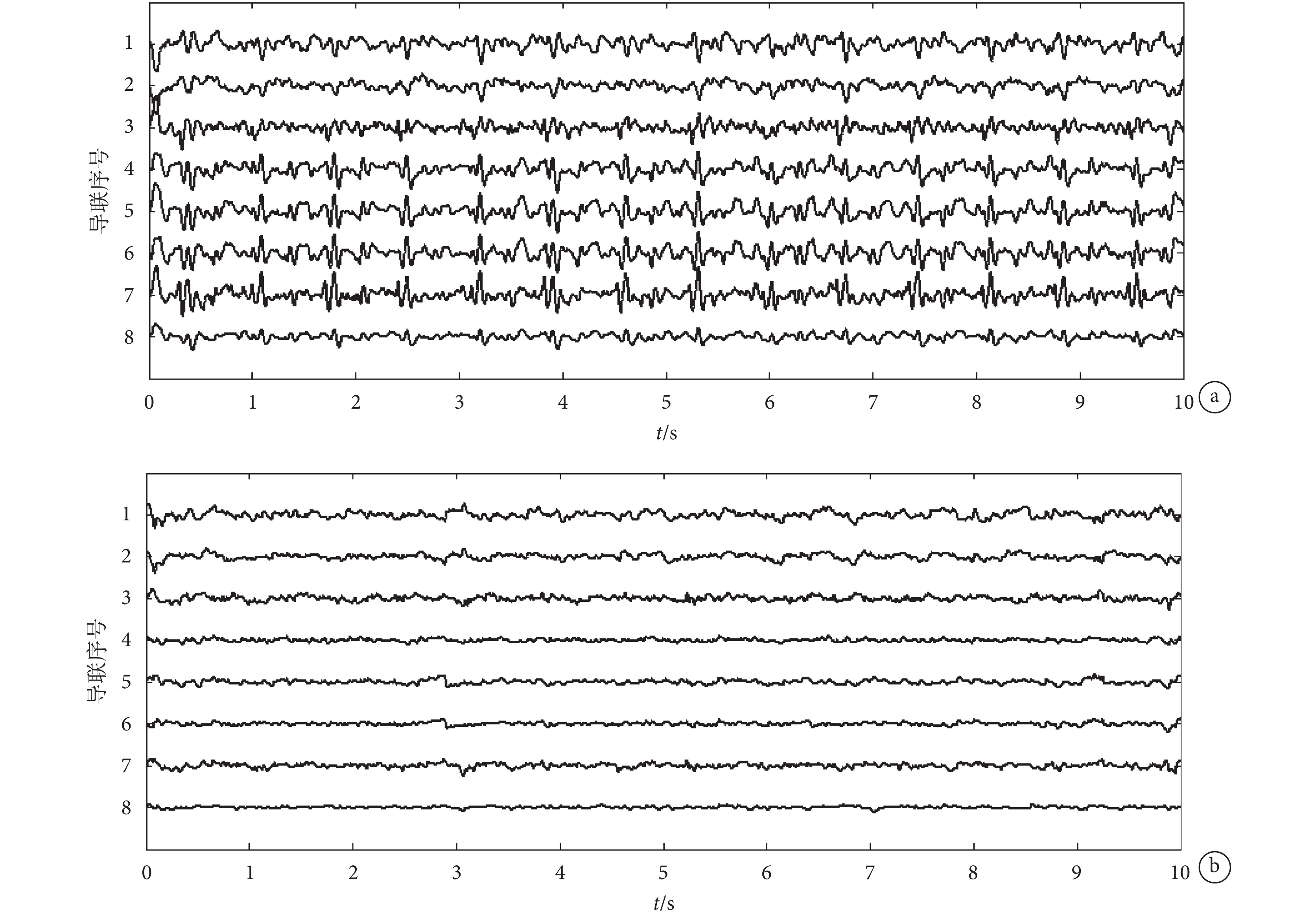圖4
rt-cICA 去除偽跡前后腦電信號對比圖
a.偽跡去除前；b.偽跡去除后
Figure4. Comparison of EEG signals before and after artifacts removal under rt-cICA methoda. before the removal; b. after the removal
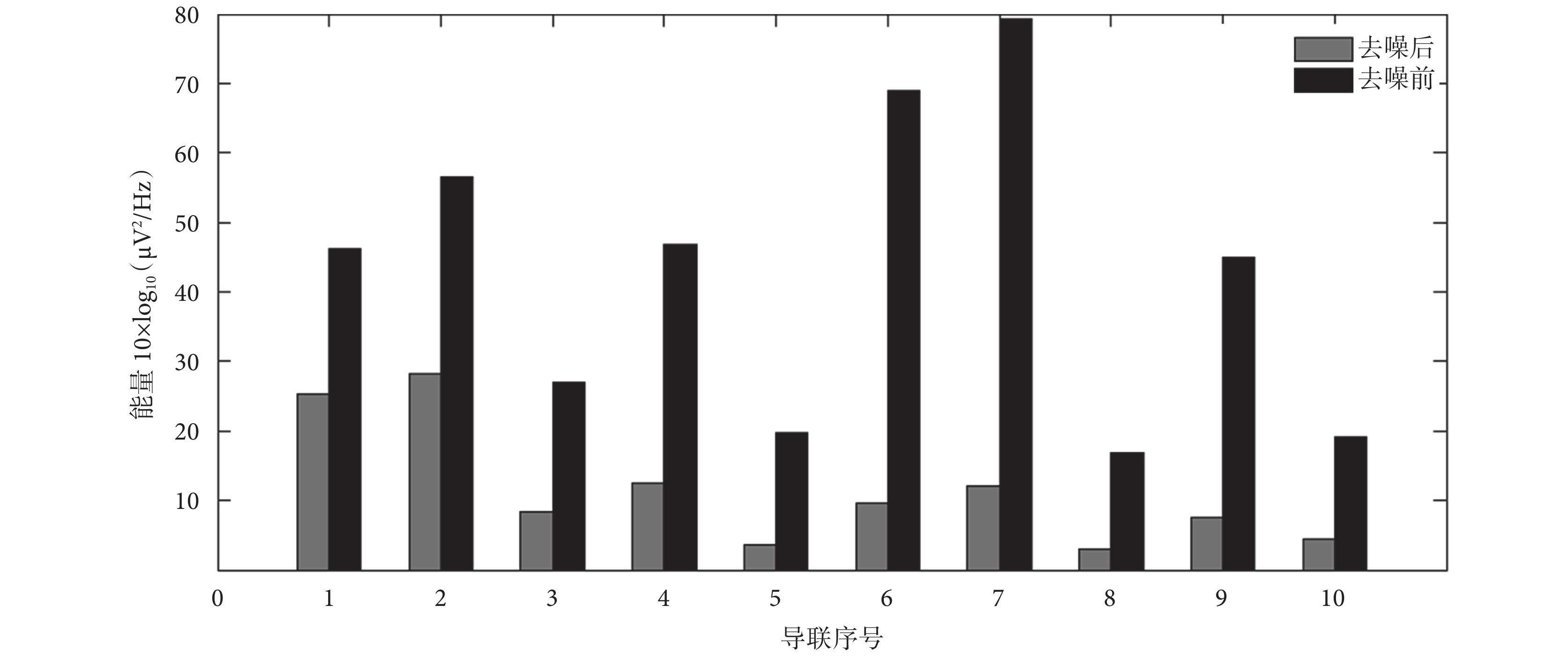
另一方面，計算 rt-cICA 方法去噪前后的功率譜值可以觀測偽跡信號的衰減情況。圖 5 顯示的是 10 個被試 10 個導聯的前 20 Hz 的平均功率譜值，結果顯示去噪后的平均功率譜值明顯低于去噪前，也就表明信號能量得到了明顯的抑制。因為腦電信號幅值較心電偽跡小，所以抑制的信號絕大部分是心電偽跡，也就表明偽跡信號得到了有效的去除。
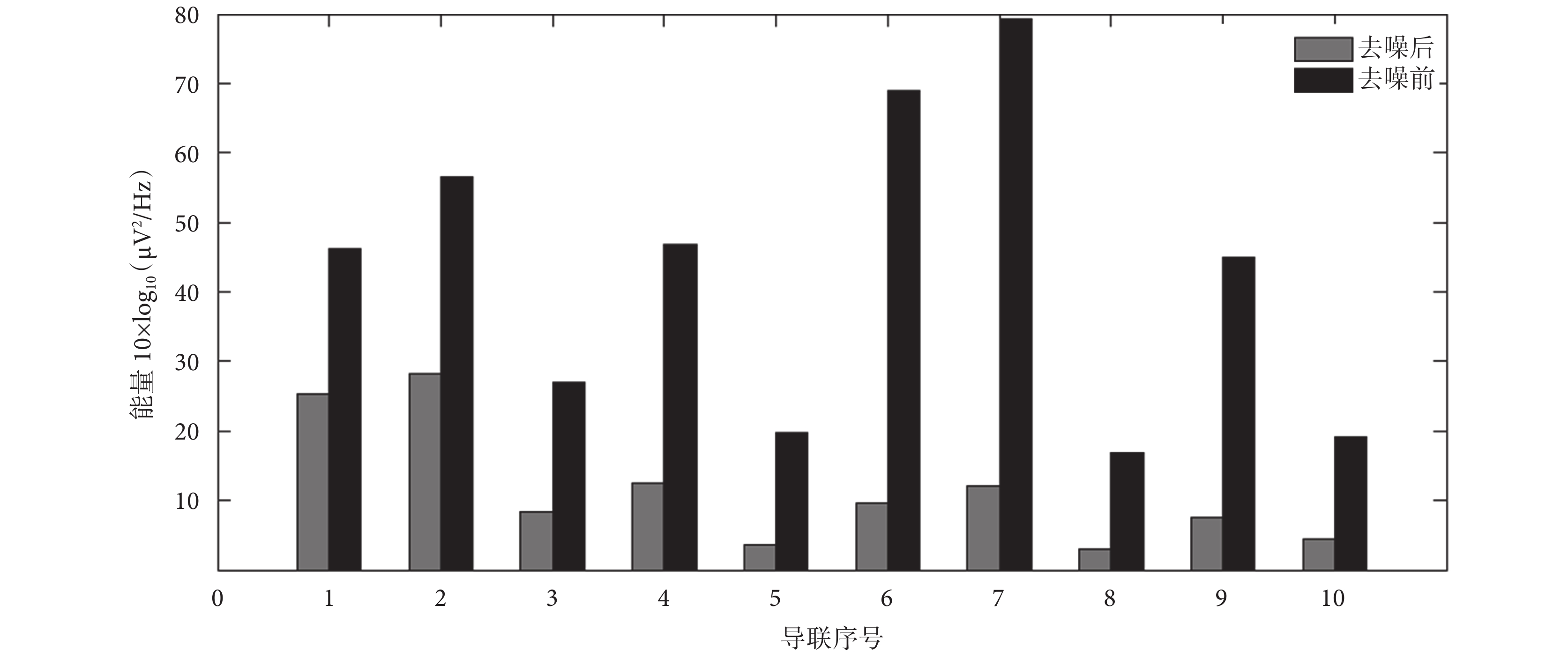圖5
偽跡去除前后的平均功率譜值
Figure5.
Average power spectral values before and after artifacts removal
2.2.2 與 AAS、OBS 以及 cICA 方法的對比
圖 6 顯示的是同一個被試數據在不同方法下得到的八個導聯的時域結果。從圖 6a 可以看出，沒有去除偽跡前的信號有明顯的準周期性的偽跡波。圖 6b 和 c 是利用 OBS 方法和 AAS 方法去除偽跡之后得到的結果，殘留的偽跡非常明顯并且用箭頭標注了出來。結合上文模擬數據得到的結果可以得出，AAS 和 OBS 方法在去除心電偽跡方面魯棒性較差并且效果不太理想。cICA 方法較前兩者來說去除效果較好，但也存在少部分的偽跡未被去除。
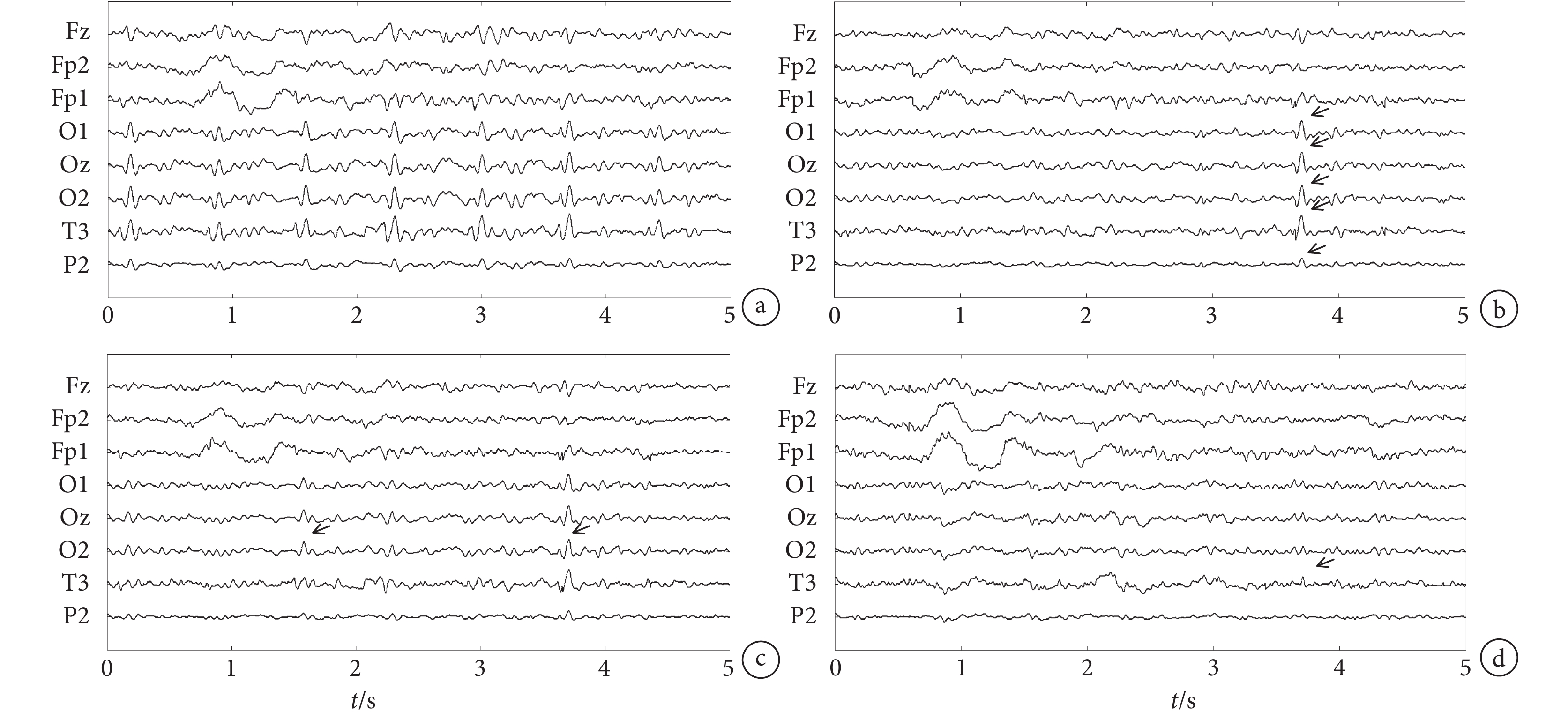圖6
不同方法去除心電偽跡的結果
a.原始信號；b. OBS 方法；c. AAS 方法；d. cICA 方法。殘留偽跡使用箭頭標注
Figure6. BCG artifacts removal by different methodsa. the original signal; b. OBS; c.AAS; d. cICA. Residual artifacts were marked by arrows
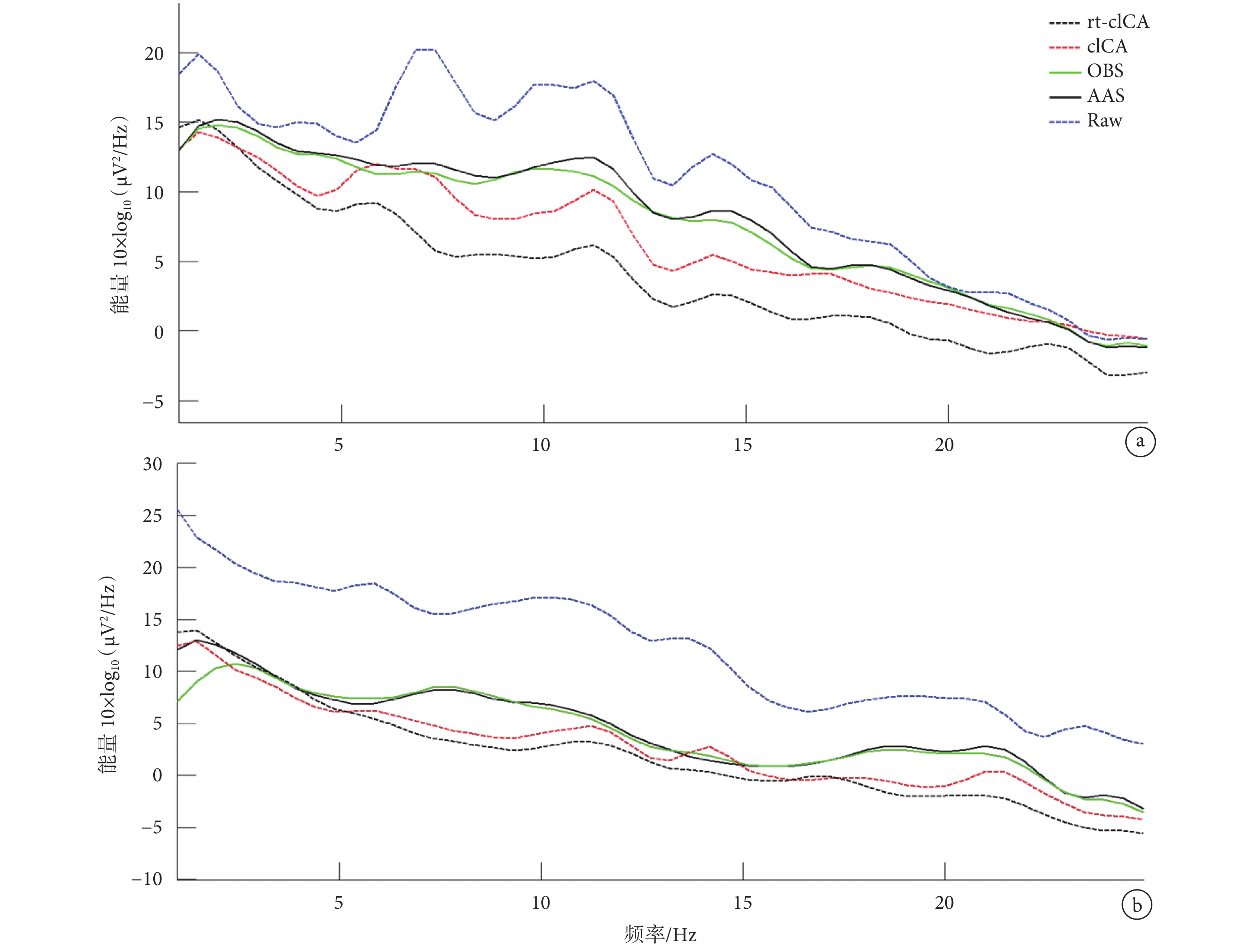
頻域上，所有的去噪方法都抑制了較多的能量，如圖 7 所示。圖 7 是所有 10 名被試數據在使用不同方法去噪前后疊加平均后的頻譜圖。圖 7a 是 O1 電極在使用不同方法去除偽跡后的頻譜圖，圖 7b 則是所有電極平均之后的頻譜圖。從圖 7 中可以看出，rt-cICA 方法和 cICA 方法在各個頻段的去噪效果都比 AAS 和 OBS 方法好，而且在 α 和 β 頻段，rt-cICA 去噪效果更勝一籌。從圖 7 看出 OBS 算法在低頻段的能量明顯比其他方法要低，這是因為它不加限制地去除了睡眠慢波（出現在低頻段，0.8 Hz 附近[7]），而 rt-cICA 方法和 cICA 方法都對此頻段的信號有所保護。綜合來說，cICA 方法在低頻段效果較好，而 rt-cICA 在 α 和 β 頻段效果較好。
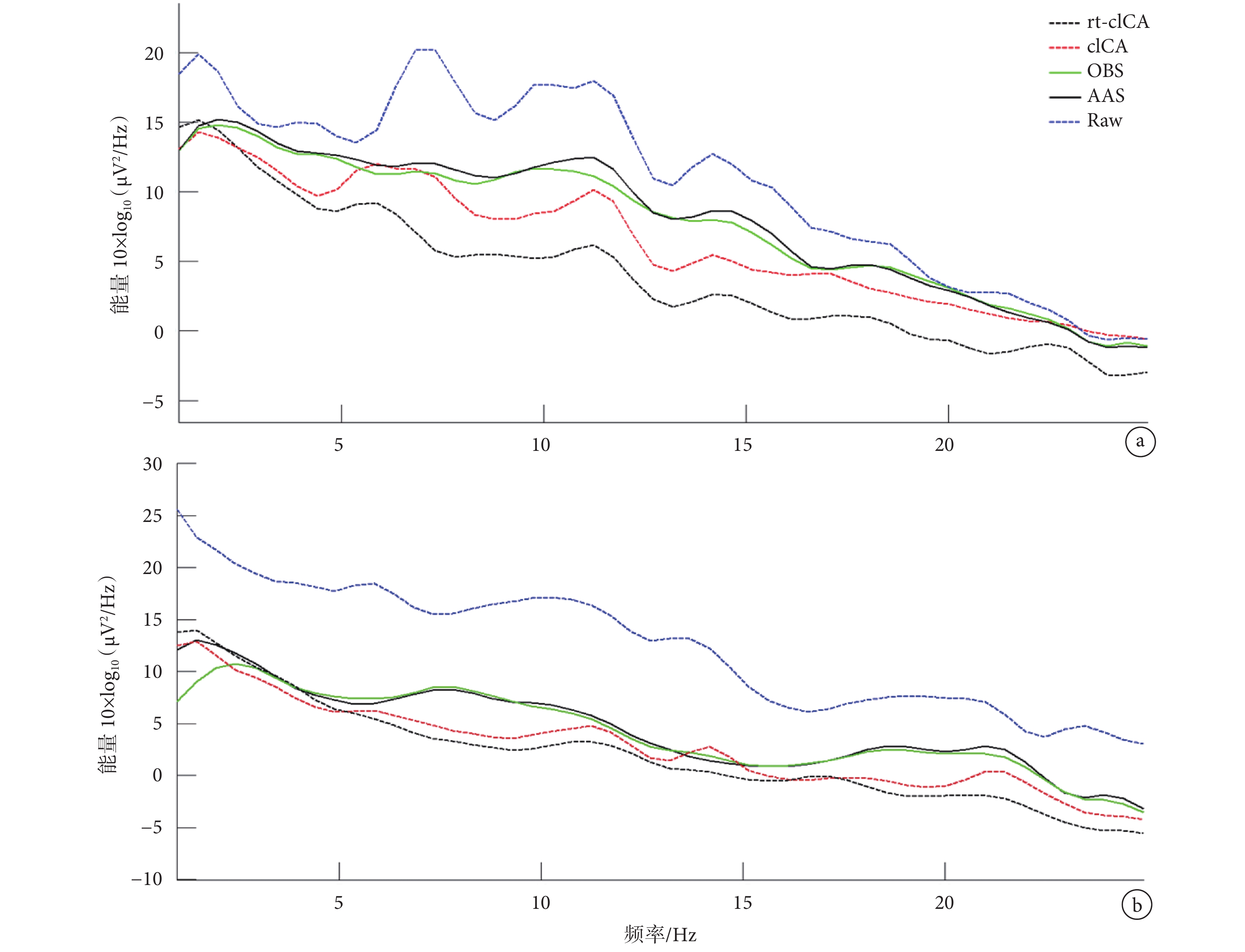圖7
使用不同方法去除偽跡之后的頻譜圖
a. O1 電極；b. 所有導聯平均
Figure7. The spectrum of signals after artifacts removal using different methodsa. O1 electrodes; b. mean of all channels
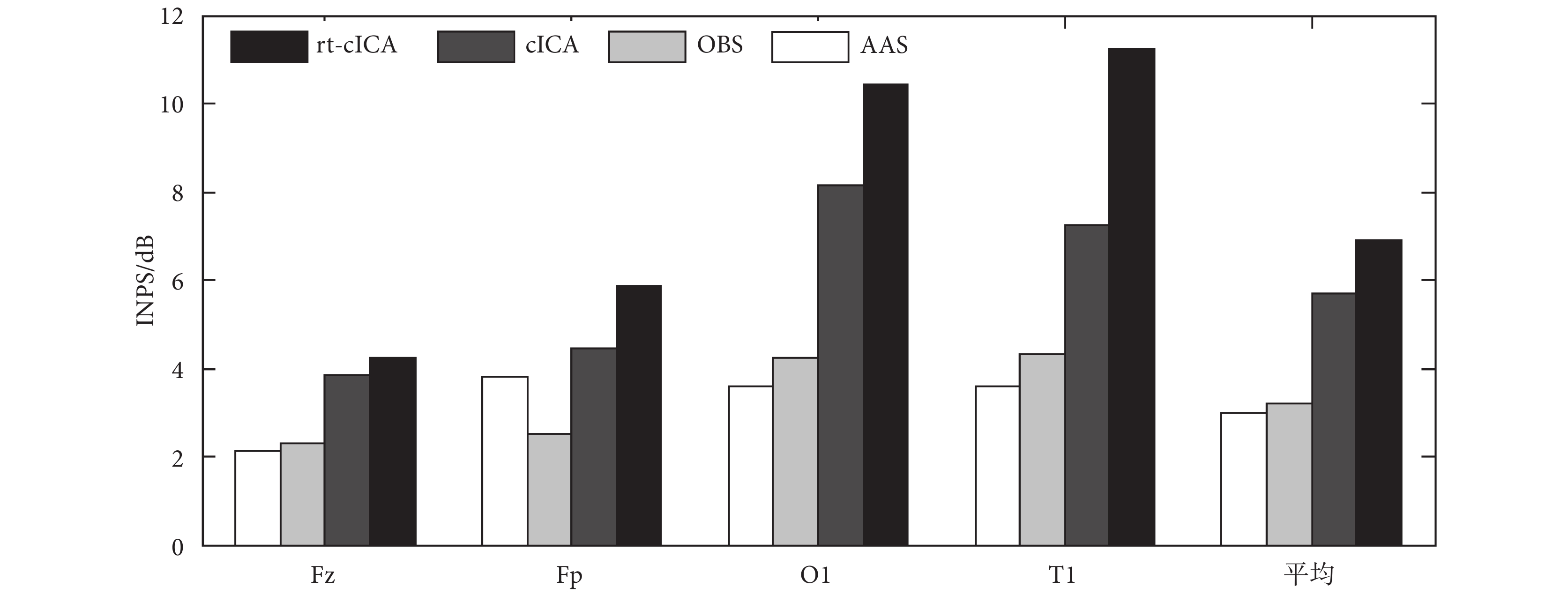
為進一步評價不同方法性能，還計算了 INPS 值。根據公式（13）以及相關文獻介紹，本文選取的參數 N 的值為 5[8]。圖 8 顯示的是去除心電偽跡后的 INPS 值。前 4 列是選取的 10 名被試的四個導聯運用四種不同方法去除偽跡之后得到的平均 INPS 值，第 5 列是所有被試數據平均之后的 INPS 值。從圖 8 得出，rt-cICA 抑制了絕大部分的能量，尤其在枕區以及 α 和 β 頻段效果更好。由此可見，rt-cICA 方法去除心電偽跡效果在各個導聯以及各個頻段似乎都比其他方法要好（對各導聯 rt-cICA 去偽跡的 INPS 值分別與其他方法得到的結果進行雙尾 t 檢驗，P < 0.005）。
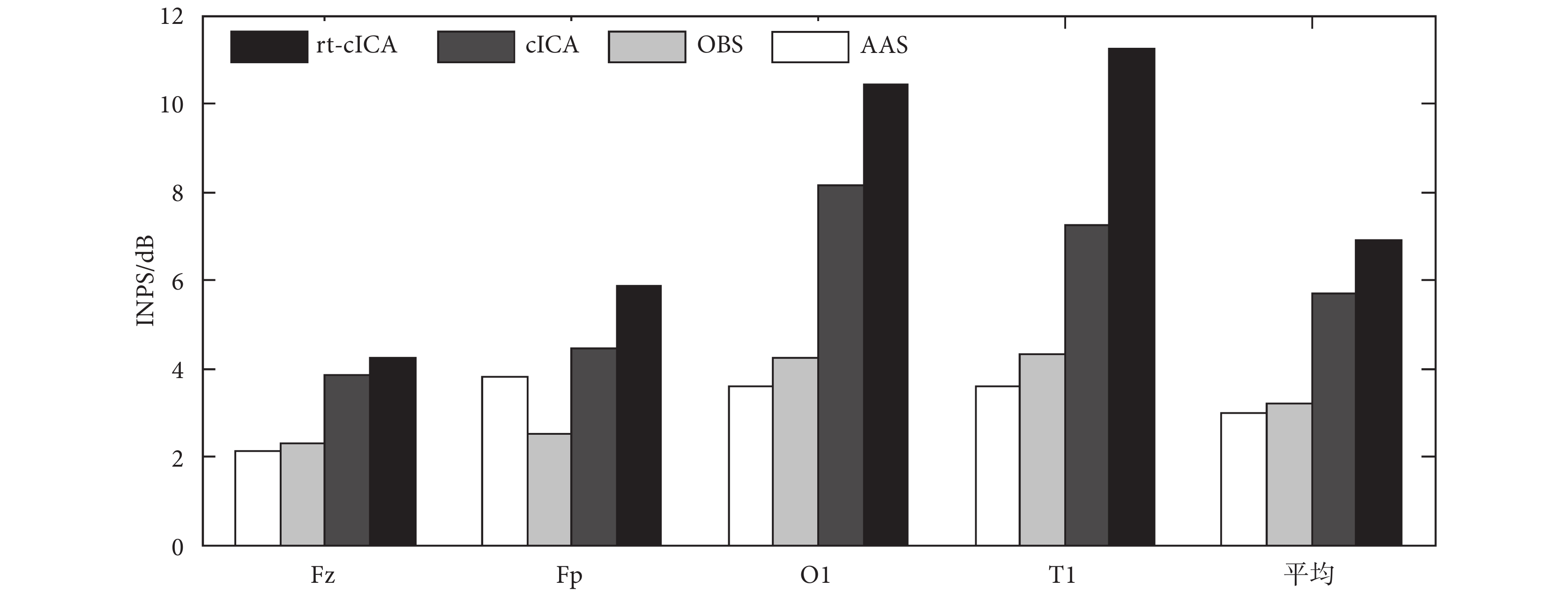圖8
10 名被試的平均 INPS 值
Figure8.
Average INPS for 10 subjects
3 結束語
同步 EEG-fMRI 記錄是一項先進的功能性神經成像技術。在這項技術帶來便利的同時，系統本身成像機制產生的噪聲也錯綜復雜。對結果影響最大的是梯度場偽跡和心電偽跡。本文針對心電偽跡變異性這一特點，在 cICA 的基礎上，提出實時約束獨立成分分析方法（rt-cCIA），在模擬數據以及真實數據上同其他方法對比了多項評價指標，發現 rt-cICA 方法在時域和頻域上去除心電偽跡效果都較其他方法要好，能得到一個更為純凈的腦電信號，為腦電和核磁信號在臨床以及科學領域的融合研究提供了數據基礎。然而，本方法還有待改進的內容，比如不同的參考電極位置（如平均參考或 Cz 參考）可能會對實驗結果產生影響；實時處理的步長，即每次滑動窗滑動距離，也可能影響結果；此外，采樣率以及心電檢測算法也是重要的影響因素。總之，心電偽跡的去除是一項復雜的工作，本方法雖能有效去除心電偽跡，且較其他方法效果要好，有較大的發展空間，但仍需更深層次的探討。
引言
在腦科學研究領域，同步腦電（electroencephalogram，EEG）—功能磁共振（functional magnetic resonance imaging，fMRI）融合技術因其高精度的時空分辨率，在科學研究和臨床領域發揮著重要作用[1-3]。但在同步采集過程中，腦電信號會混入大量偽跡，主要有梯度場偽跡（gradient artifact，GA）和心電偽跡（ballistocardiogram artifacts，BCG artifacts）。梯度場偽跡是由磁共振環境下磁場切換引起的周期性偽跡，可以用平均模板相減法（average artifact subtraction，AAS) 去除[4]。心電偽跡因其不穩定的時頻特征，進行特征提取和建模的難度大，一直是核磁腦電信號偽跡去除研究的一大難點。
心電偽跡是由靜態磁場下心跳相關運動所引起的頭部電極移動造成的，與心電信號有類似的特征[5]，其幅值與磁共振掃描儀內的磁場強度成正比，形狀具有時變特征。另一方面，心電偽跡通常對腦電信號 alpha 頻段及其以下頻段產生較大干擾，而 alpha 頻段信號在臨床以及科學研究上有著非常重要的意義。故而，對復雜心電偽跡特征的建模尤為重要，是去除偽跡的關鍵。
心電偽跡去除方法分為空間模式和時域技術兩大類。空間模式技術利用偽跡空間模式下的統計特征進行空域濾波，如主成分分析（principal component analysis，PCA）和獨立成分分析（independent component analysis，ICA）方法[6]。ICA 方法中成分的選取取決于主觀經驗[7]。為解決這類問題，Leclercq 等[8]提出了約束獨立成分分析（constrained ICA，cICA）方法。該方法設置了約束條件，能準確地選取與偽跡相關的成分，且成分選擇減小了主觀因素造成的誤差。然而 cICA 方法沒有考慮到心電偽跡信號的時變性波形、幅值以及規模的影響，故可能存在偽跡去除不凈的問題。時域技術主要利用偽跡時域波形的準周期性去除偽跡，包括 AAS、最優基組法（optimal basis sets，OBS）、移動線性模型以及自適應濾波等[9]。這兩種技術都有局限性，空間模式耗時大，而時域技術要依賴于研究者的經驗。除了上述一些傳統方法外，參考層結合諧波回歸方法、字典學習方法、實時 OBS 方法以及 DRPE 特殊記錄方法也被廣泛運用于心電偽跡去除領域[10-13]。此外，也有研究通過減少電極移動來避免偽跡產生[14]。
本文參照實時 OBS 算法改進了 cICA 方法，提出實時約束獨立成分分析方法（real time-cICA，rt-cICA），處理單導模擬腦電信號以及 64 導真實靜息態核磁腦電信號，并與傳統 AAS、OBS 等方法得到的結果進行時頻分析比較，目的是為了驗證本方法能有效去除心電偽跡，且本算法比傳統方法優越，能為融合技術的進一步實現奠定技術基礎。
1 實驗數據及方法
1.1 實驗數據
1.1.1 模擬核磁腦電信號
模擬數據是將模擬心電偽跡加入到非核磁環境下真實自發腦電中構造，真實自發腦電由美國 EGI 公司生產的 GES 300 MR 腦電放大器和 64 導 HydroCel 電極帽在常規環境下采集。未加噪的腦電信號可作為去噪后腦電信號質量的衡量標準。構造模擬數據的過程可以分為以下三個步驟[12]。
首先，取一導聯沒有去除心電偽跡的真實靜息態核磁腦電數據，以偽跡波峰位置為中心分成若干段進行疊加平均，構造一個偽跡模板；然后獨立隨機地改變模板的形狀和大小，并連續拼接;最后將上述步驟得到的模擬心電偽跡加到非核磁環境下采集的腦電數據中。每個波峰之間的間隔以及偽跡波的大小都是隨機的，如圖 1 所示。圖 1a 是常規環境下采集的用來構造模擬數據的自發腦電，且已濾去了 50 Hz 的工頻干擾。圖 1b 是模擬心電信號，用于檢測圖 1c 模擬混合信號中心電偽跡的波峰位置。圖 1c 是模擬含有偽跡的腦電信號，紅色表示未加噪常規信號，黑色是混合信號。
圖1
模擬腦電信號
a. 未加噪自發腦電數據；b. 對應的心電信號；c. 混合信號
Figure1. Simulated EEG signalsa. spontaneous EEG data without noise; b. corresponding ECG signals; c. mixed signals
1.1.2 真實核磁腦電信號
為進一步驗證實時約束獨立成分分析方法的有效性，本次實驗采集了 10 名健康被試靜息態的核磁腦電以及心電數據，采集心電數據的目的是為了定位偽跡出現的位置。同步采集得到的核磁腦電數據已使用 AAS 算法去除了梯度場偽跡且采用參考電極標準化技術（reference electrode standardization technique，REST）做預處理[15]。
實驗要求每名被試平躺在核磁室，保持全身放松并且處于閉眼狀態。本次實驗依據《世界醫學協會赫爾辛基宣言》（2000）和常州大學倫理研究委員會批準制定了知情同意書。被試在實驗之前要求簽署知情同意書。
實驗所用到的美國 EGI 公司 64 導腦電放大器以及核磁掃描儀由常州大學生物醫學重點實驗室以及常州第二人民醫院生物醫學技術研究中心提供。功能磁共振圖像由荷蘭飛利浦公司生產的 Achieva 3.0 T 核磁掃描儀采集，其參數為：TR = 2 000 ms，TE = 35 ms，Flip angle = 90°，FOV = 230 mm × 180 mm，一次全腦掃描獲取 24 層圖像，使用平面回波（echo planar imaging，EPI）采集序列。腦電數據由美國 EGI 公司的腦電放大器以及 64 導腦電帽采集，另外還有一導聯同步采集的心電信號，心電電極放在被試的前胸。電極的擺放位置遵循國際 10/10 系統，只是命名規則有所不同。
1.2 方法
在核磁共振室 3.0 T 的環境下，心電偽跡的幅值在 400 μV 左右，是腦電信號的 6～8 倍[4]，僅憑肉眼就能明顯地看出其在腦電信號中的位置，且每一導聯不同時段的心電偽跡差異較大。偽跡去除首先需要定位偽跡位置，準確穩定的心電檢測算法有助于對心電偽跡進行精準定位。
1.2.1 實時心電檢測算法
Allen 等[4]最早提出一個簡單的閾值法來檢測 R 波位置，然而此方法較為耗時，且由于核磁環境的復雜性導致算法精度不高。因此，Christov 等[16]提出了一種組合自適應閾值檢測算法。之后 Niazy 等[9]在此算法的基礎上進行優化改進，首先對每個通道的心電數據進行 7～40 Hz 的帶通濾波，然后利用 k-Teager 能量算子算法處理濾波后的心電信號并且使其負值為 0，從而得到一個復合值，
|
其中ECG是復合值，n是時間參數，E是濾波后的心電數據，k是頻率選擇參數。接著利用此自適應閾值檢測算法來檢測 R 波。斜率閾值（M）、高頻集合閾值（F）以及心跳預估閾值（R）三者之和作為MFR閾值：
|
當ECG（n）≥ MFR（n）時就被檢測為一個 QRS 波。
結合自適應閾值檢測算法[9]以及實時技術，本文將實時 R 波檢測算法用于定位心電偽跡波的位置，并結合 rt-cICA、cICA、OBS 以及 AAS 等方法去除心電偽跡。
1.2.2 約束獨立成分分析
cICA 算法假設 EEG 信號只由兩種源成分線性混合而成，即神經信號和偽跡信號。一旦一類源成分被確定，另一類源成分就可以被推導出來［11］。和經典的 ICA 方法類似，cICA 算法的目標也是尋找一個解混矩陣W（W是一個N維方陣，N為導聯數）。但不同點在于該算法必須滿足兩個條件：① 類似經典 ICA 算法，最大化源成分的負熵 ；② 設置約束條件 g（W）≤ 0 并且 h（W） = 0，其中
l 是希望被提取出來的源成分的數量；
g（W） = （g1（w1）gl（wl）)T，。其中，i = 1, ,l；
h（W） = （h1（w1）hl（wl）)T，hi（wi） = E{si2} ? 1。其中，i = 1,,l。
第一個約束條件使得每個源成分之間的相關參考距離保持在一個特定的距離之內，第二個條件是標準化。此算法采用增廣拉格朗日乘法求解，增廣拉格朗日乘法 L可知：
|
其中，和是兩組分別用于不等式和等式約束的拉格朗日乘數，是懲罰參數，確保優化問題在局部凸假設下成立。Newton-like 迭代過程用來求解得到去相關矩陣W：
| '/> |
其中，是依賴于每個負熵的向量，是被記錄腦電信號X的自相關矩陣。
|
|
迭代終止條件是W的 2 個連續估計范數之間的相對差值小于 10-5數量級。
W 的行向量可被視為 N 維空間的非正交基。在預處理過程中，正交矩陣 能由 W 推導出來。識別 中偽跡相關的行向量可能會找到互補的正交向量的集合。因為神經相關的成分比偽跡相關成分多，所以算法的特點在于使用 Gram-Schmidt 正交化來找到神經相關的源成分，而不是采用計算難度更大的方法去找偽跡相關的源成分。
與經典的 ICA 算法相比，cICA 能識別與給定約束條件最接近的源成分。cICA 算法在偽跡成分估計的穩定性上較經典的 ICA 算法以及多獨立分量分析（multi independent component analysis，MICA）算法有較大的改進，并且沒有增加計算消耗。但算法優勢只局限于偽跡成分的估計，并且也沒有考慮心電偽跡的時變性。總之，cICA 算法的特點在于對偽跡成分的自動識別，減少了主觀因素帶來的誤差。
1.2.3 實時約束獨立成分分析方法
cICA 算法去除心電偽跡是將心電信號作為約束條件，其最大的缺點在于缺少對心電偽跡時變性特征的考慮，即對整體心電信號進行簡單疊加平均后的均值作為約束條件，這樣就忽視了心電信號變異對去噪效果的影響。于是參照實時 OBS 技術，改進了 cICA 方法，提出 rt-cICA。該方法假設短時期內心跳的變化差異性較小，這樣大大減小了時變性對去噪結果帶來的影響。對于實時去噪來說，心電 R 波的間隔隨時間變化明顯，所以找到一個合適的 EEG 信號分段標準尤為重要，為此引入滑動窗來對 EEG 信號進行分段，在每個窗中實時處理心電偽跡，然后滑動至下一個窗中繼續處理。圖 2 是實時處理的一個基本示意圖，首先使用 cICA 算法去除滑窗內數據的心電偽跡，然后選取滑窗最后十分之一段數據作為去除偽跡后的純凈腦電信號，接著滑窗繼續滑動十分之一段大小，按照此流程不斷處理剩下的含噪數據，最終得到純凈的腦電信號[6]。方法性能可能受滑動窗大小影響，不同尺寸的滑動窗得到的去噪效果可能不同，獲得最佳的去噪效果在于找到最合適的滑動窗尺寸。
圖2
實時處理過程示意圖
Figure2.
Real-time process diagram
心電偽跡波峰一般出現在心電 R 波時刻后的 210 ms[4]，根據這一特點對腦電信號進行分段。在每個尺寸為k的滑動窗中，取相鄰 R 波之間間隔的均值作為腦電分段大小的模板，如公式（7）所示，其中 Ri 為 R 波出現的位置。在確定完平均間隔之后，根據公式（8）即可得到腦電數據的分段 L，L 為以 Ri+Rdelay 為中心、Lrt 為長度的腦電分段。其中 Ri為心電中 R 波出現的位置，Rdelay 為偽跡在 R 波出現后的延時時間，取 210 ms，Lrt 為平均間隔。在偽跡位置檢測出來之后，即可利用 cICA 算法去除心電偽跡。然后對每個滑動窗進行處理，得到較為純凈的腦電信號。
|
|
1.3 評價指標
為評價 rt-cICA 方法的有效性，使用了幾種評價分析指標，包括信號幅值誤差（Er）、靈敏度（Se）和特異性（Sp）等指標，不同方法得到的結果進行頻譜分析以及改進的標準化功率譜（improved normalized power spectrum，INPS）分析。
1.3.1 信號幅值誤差
Er 是一項評價不同方法性能的重要指標，偽跡去除后的信號誤差定義為:
|
其中 x（i）為偽跡去除之后樣本點 i 的幅值，y（i）是對應的參考信號的幅值。對比不同方法的 Er 值可以作為算法去噪效果的評價指標。
1.3.2 靈敏度和特異性
靈敏度和特異性指標用來測試心電 R 波檢測算法的魯棒性[10]。對于心電信號，心電 R 波的出現次數可用肉眼直接觀測，R 波出現的總次數定義為真實主觀數目 TP；未被算法檢測到但真實存在的 R 波定義為假陰性，其數目記為 FN；非 R 波卻被算法誤檢為 R 波定義為假陽性，其數目記為 FP。如果檢測到的 R 波位置發生了一個線性漂移，也都被認為是假陰性或假陽性，例如檢測到 R 波的位置在真實 R 波位置的前面或后面。靈敏度和特異性指標的計算方法如下所示:
|
|
1.3.3 功率譜
為比較不同方法的去噪效果，計算去除偽跡前后信號的功率譜值也是一項重要的手段。計算公式如下：
|
其中 ejw 表示正弦信號和余弦信號的疊加。S（ejw）是功率譜，xl 是每導聯樣本點 l 的值。
1.3.4 改進的標準化功率譜
Tong 等提出的 INPS 指標可以用來評估去噪算法以及去噪后信號的質量，其計算的是信號的功率衰減，計算公式如下:
|
其中 和 是每個特定導聯 Chan 去噪前后以第 j 和第 i 個諧波為中心、窗口大小為 1 Hz 的平均功率值。INPS 表示每個窗口的能量衰減，即心電偽跡能量衰減。INPS 的值越大，說明能量衰減得越多，也就表示去除的心電偽跡越多，但并不是衰減得越多越好，INPS 值過大則可能去除了有用的腦電信號。
2 結果分析
2.1 模擬數據
針對模擬數據，比較直觀的評價標準是觀測其時域波形。圖 3 表示分別運用 4 種方法去除心電偽跡前后與原始未加噪聲信號的對比圖。藍色的波形表示去噪前，紅色的表示去噪后。從圖 3a、b 可以直觀地看出，殘留的偽跡相當明顯，并且有些偽跡很難被去除。圖 3c、d 表示的是 cICA 和 rt-cICA 去噪前后的結果圖，兩種方法都去除了絕大部分的心電偽跡，但是綜合圖 3d、e、f 來看，rt-cICA 去噪后信號的趨勢更加接近原始未加噪的信號，而 cICA 方法去除之后信號顯得較密集，有可能是因為部分殘留偽跡所致。故本方法似乎能得到更為純凈的腦電信號，對此結果將進一步進行比較。
圖3
rt-cICA 方法和其他方法去噪效果對比圖
a. AAS 去噪結果；b. OBS（
a. AAS denoising result; b. OBS (
其次，由于模擬數據構成中有未加噪數據作為參考依據，因此，可以用更精確的量化指標，如 Er 值來評估去噪后的信號與未加噪數據的誤差，因此在窗口尺寸相等的情況下，計算了同一腦電數據在不同方法去噪后的 Er 值（對四種方法去除心電偽跡后的 Er 值進行組間雙尾 t 檢驗，P < 0.005）。
窗口尺寸即腦電數據分段的數量，如窗口尺寸 40 表示此窗中有 40 個腦電數據分段。具體見表 1。
表1
不同方法去除心電偽跡之后的 Er 值
Table1.
Er values after removal of BCG artifacts by different methods
從表 1 可以看出，rt-cICA 方法在同一窗口尺寸情況下的 Er 值明顯比其他方法低。鑒于不同窗口大小也是影響去噪效果的一大重要因素，故實驗又選取若干不同大小的窗口，利用 rt-cICA 方法進行對比實驗，計算得到的 Er 值見表 2。
表2
窗口尺寸與 rt-cICA 去噪后的 Er 值
Table2.
Window size and Er value after denoising using rt-cICA
結果顯示，當窗口大小選取為 40 或者 50 時，去噪后的 Er 值較低，并且當窗口尺寸選取過大時，不僅計算消耗會隨之增大，效果也沒有明顯提升，故選取尺寸為 40 或者 50 最為適宜。在最優窗口大小選取完成的情況下，利用同等尺寸窗口以及同樣的心電檢測算法計算不同方法的評價指標。
2.2 真實數據
由于真實靜息態腦電數據是在核磁環境下采集，沒有與之對應的非核磁環境下的腦電數據，故不能使用 Er 值作為評價指標。而真實數據為 10 名被試的靜息態數據，可以計算所有被試數據去噪后的功率譜值和 INPS 值，并利用統計學方法對比本方法和傳統方法。
針對多名被試的真實靜息態腦電數據，為驗證核磁腦電數據質量以及心電檢測算法的魯棒性，計算靈敏度和特異性兩個指標來評估心電數據質量。表 3 列出了 8 名被試心電數據使用 R 波檢測算法后的靈敏度和特異性。前面 7 名被試數據的平均靈敏度和特異性都超過 99%，表明此算法在檢測 R 波時的穩定性較高，被試 8 的數值有明顯差異，可能由于心電電極脫落導致，這類數據在實驗時會加大結果的誤差，故會將其舍棄。
表3
R 波檢測算法的靈敏度和特異性
Table3.
Sensitivity and specificity of the R-peak detection algorithm
2.2.1 rt-cICA 算法去除心電偽跡
圖 4 表示的是被試 1 閉眼狀態下的 8 導核磁腦電信號（Fz、Fp2、Fp1、O1、Oz、O2、T3、P2）去除偽跡前后的對比圖。圖 4a 是沒有去除心電偽跡的腦電信號，從圖中可以看出有明顯的類似于準周期性心電信號的心電偽跡。圖 4b 是去除偽跡之后的腦電信號。對照偽跡出現的位置可以明顯看出絕大部分偽跡已被去除。
圖4
rt-cICA 去除偽跡前后腦電信號對比圖
a.偽跡去除前；b.偽跡去除后
Figure4. Comparison of EEG signals before and after artifacts removal under rt-cICA methoda. before the removal; b. after the removal
另一方面，計算 rt-cICA 方法去噪前后的功率譜值可以觀測偽跡信號的衰減情況。圖 5 顯示的是 10 個被試 10 個導聯的前 20 Hz 的平均功率譜值，結果顯示去噪后的平均功率譜值明顯低于去噪前，也就表明信號能量得到了明顯的抑制。因為腦電信號幅值較心電偽跡小，所以抑制的信號絕大部分是心電偽跡，也就表明偽跡信號得到了有效的去除。
圖5
偽跡去除前后的平均功率譜值
Figure5.
Average power spectral values before and after artifacts removal
2.2.2 與 AAS、OBS 以及 cICA 方法的對比
圖 6 顯示的是同一個被試數據在不同方法下得到的八個導聯的時域結果。從圖 6a 可以看出，沒有去除偽跡前的信號有明顯的準周期性的偽跡波。圖 6b 和 c 是利用 OBS 方法和 AAS 方法去除偽跡之后得到的結果，殘留的偽跡非常明顯并且用箭頭標注了出來。結合上文模擬數據得到的結果可以得出，AAS 和 OBS 方法在去除心電偽跡方面魯棒性較差并且效果不太理想。cICA 方法較前兩者來說去除效果較好，但也存在少部分的偽跡未被去除。
圖6
不同方法去除心電偽跡的結果
a.原始信號；b. OBS 方法；c. AAS 方法；d. cICA 方法。殘留偽跡使用箭頭標注
Figure6. BCG artifacts removal by different methodsa. the original signal; b. OBS; c.AAS; d. cICA. Residual artifacts were marked by arrows
頻域上，所有的去噪方法都抑制了較多的能量，如圖 7 所示。圖 7 是所有 10 名被試數據在使用不同方法去噪前后疊加平均后的頻譜圖。圖 7a 是 O1 電極在使用不同方法去除偽跡后的頻譜圖，圖 7b 則是所有電極平均之后的頻譜圖。從圖 7 中可以看出，rt-cICA 方法和 cICA 方法在各個頻段的去噪效果都比 AAS 和 OBS 方法好，而且在 α 和 β 頻段，rt-cICA 去噪效果更勝一籌。從圖 7 看出 OBS 算法在低頻段的能量明顯比其他方法要低，這是因為它不加限制地去除了睡眠慢波（出現在低頻段，0.8 Hz 附近[7]），而 rt-cICA 方法和 cICA 方法都對此頻段的信號有所保護。綜合來說，cICA 方法在低頻段效果較好，而 rt-cICA 在 α 和 β 頻段效果較好。
圖7
使用不同方法去除偽跡之后的頻譜圖
a. O1 電極；b. 所有導聯平均
Figure7. The spectrum of signals after artifacts removal using different methodsa. O1 electrodes; b. mean of all channels
為進一步評價不同方法性能，還計算了 INPS 值。根據公式（13）以及相關文獻介紹，本文選取的參數 N 的值為 5[8]。圖 8 顯示的是去除心電偽跡后的 INPS 值。前 4 列是選取的 10 名被試的四個導聯運用四種不同方法去除偽跡之后得到的平均 INPS 值，第 5 列是所有被試數據平均之后的 INPS 值。從圖 8 得出，rt-cICA 抑制了絕大部分的能量，尤其在枕區以及 α 和 β 頻段效果更好。由此可見，rt-cICA 方法去除心電偽跡效果在各個導聯以及各個頻段似乎都比其他方法要好（對各導聯 rt-cICA 去偽跡的 INPS 值分別與其他方法得到的結果進行雙尾 t 檢驗，P < 0.005）。
圖8
10 名被試的平均 INPS 值
Figure8.
Average INPS for 10 subjects
3 結束語
同步 EEG-fMRI 記錄是一項先進的功能性神經成像技術。在這項技術帶來便利的同時，系統本身成像機制產生的噪聲也錯綜復雜。對結果影響最大的是梯度場偽跡和心電偽跡。本文針對心電偽跡變異性這一特點，在 cICA 的基礎上，提出實時約束獨立成分分析方法（rt-cCIA），在模擬數據以及真實數據上同其他方法對比了多項評價指標，發現 rt-cICA 方法在時域和頻域上去除心電偽跡效果都較其他方法要好，能得到一個更為純凈的腦電信號，為腦電和核磁信號在臨床以及科學領域的融合研究提供了數據基礎。然而，本方法還有待改進的內容，比如不同的參考電極位置（如平均參考或 Cz 參考）可能會對實驗結果產生影響；實時處理的步長，即每次滑動窗滑動距離，也可能影響結果；此外，采樣率以及心電檢測算法也是重要的影響因素。總之，心電偽跡的去除是一項復雜的工作，本方法雖能有效去除心電偽跡，且較其他方法效果要好，有較大的發展空間，但仍需更深層次的探討。
