胎心宮縮圖是一種臨床常用的評估胎兒健康狀況的電子監護技術，具有易受主觀因素影響導致診斷率較低的缺點。為降低誤診率，輔助醫生做出準確的醫療決策，本文提出了一種基于胎心率信號分析胎兒狀態的智能評估方法。首先，本文將來自捷克技術大學—布爾諾大學醫院公開數據庫的信號進行預處理后，對其中的胎心率信號進行多模態特征提取，然后利用設計的基于 k—最近鄰遺傳算法選擇最優特征子集，最后采用最小二乘支持向量機法對其分類。實驗結果顯示，利用本文提出的方法對胎兒狀態進行分類，其準確度可達 91%，靈敏度為 89%，特異度為 94%，質量指標為 92%，受試者工作特征曲線下面積為 92%，具有較好的分類性能，可輔助臨床醫生對胎兒狀態做出有效評估。
引用本文： 張揚, 趙治棟, 葉海慧. 基于遺傳算法和最小二乘支持向量機的胎兒狀態智能評估. 生物醫學工程學雜志, 2019, 36(1): 131-139. doi: 10.7507/1001-5515.201804046 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
胎心宮縮圖（cardiotocography，CTG）監護，是臨床上監測圍產期胎兒宮內狀態應用最為廣泛的一種胎兒監護方式，主要通過對胎心和宮縮的監測來防止胎兒窘迫情況的發生，以避免對胎兒造成潛在的不良后果[1]。CTG 曲線作為醫學界認證的可實時在線提供胎兒產前和產時狀態信息的連續性信息技術，對降低圍產兒患病率和死亡率起到關鍵作用[2]。
臨床實踐中，對 CTG 的分析主要由產科醫生根據相關指南進行主觀評估，如：國際婦產科聯合會（International Federation of Gynecology and Obstetrics，FIGO）指南等[3]。CTG 評估結果會因為臨床醫師個體主觀認知的不同而存在差異，這是造成近年來剖腹產率上升的主要原因之一。為降低 CTG 曲線分析的差異性，需對臨床醫生進行專業培訓，并開發計算機輔助評估系統。因此有必要找到一種更為客觀的可以輔助臨床醫生進行準確分析胎兒狀態的評估方法，以降低人力物力的消耗，減少主觀分析的差異。
CTG 信號包含胎心率（fetal heart rate，FHR）信號和宮縮（uterine contraction，UC）信號。計算機評估系統通過自動化分析 FHR 信號和 UC 信號，可輔助甚至代替臨床醫生對胎兒狀態做出相對更客觀準確的判斷[4]。此類系統一般分為特征提取和狀態分類兩部分。傳統的特征提取方法中形態學參數不足以完全反映胎兒狀態，而線性時域和頻域以及非線性的眾多參數也能對胎兒狀態評估起到一定的作用[5]。另一方面，近年來不少學者對分類算法進行了深入研究，提出了基于機器學習算法的人工神經網絡（artificial neural network，ANN）、支持向量機（support vector machine，SVM）、決策樹（decision tree，DT）等分類算法，并進一步采用主成分分析、信息增益等降維方法，從原始特征集中選擇最佳參數，以提高分類性能[6-10]。如：陸堯勝等[7]使用常規參數（基線，加減速等）作為待分類的特征，然后采用基于歐式距離的模糊理論分析胎兒狀態。在提取線性和非線性參數的前提下，Georgoulas 等[8]和 Comert 等[10]則分別利用 SVM 和 ANN 對胎兒狀態進行分類。綜上，受前人研究工作的啟發，本文從特征提取、特征選擇和分類器等三個方面研究胎兒狀態智能評估算法。
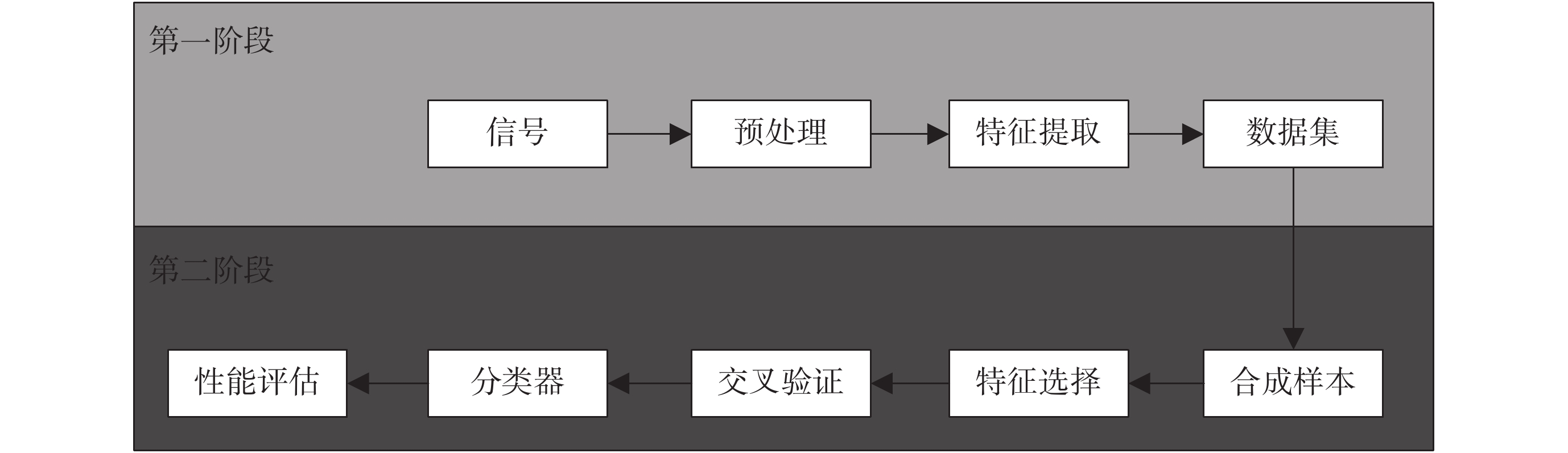
為提高胎兒狀態評估的效果，本文提出了一種基于 FHR 信號分析胎兒狀態的智能評估方法，首先針對預處理后的 FHR 信號提取時域、頻域和非線性特征等參數，基于遺傳算法（genetic algorithm，GA）選擇最優特征，然后通過最小二乘支持向量機（least square support vector machine，LS-SVM）完成胎兒健康的診斷，最后對分類結果進行評估。如圖 1 所示為本文研究內容的基本框架。
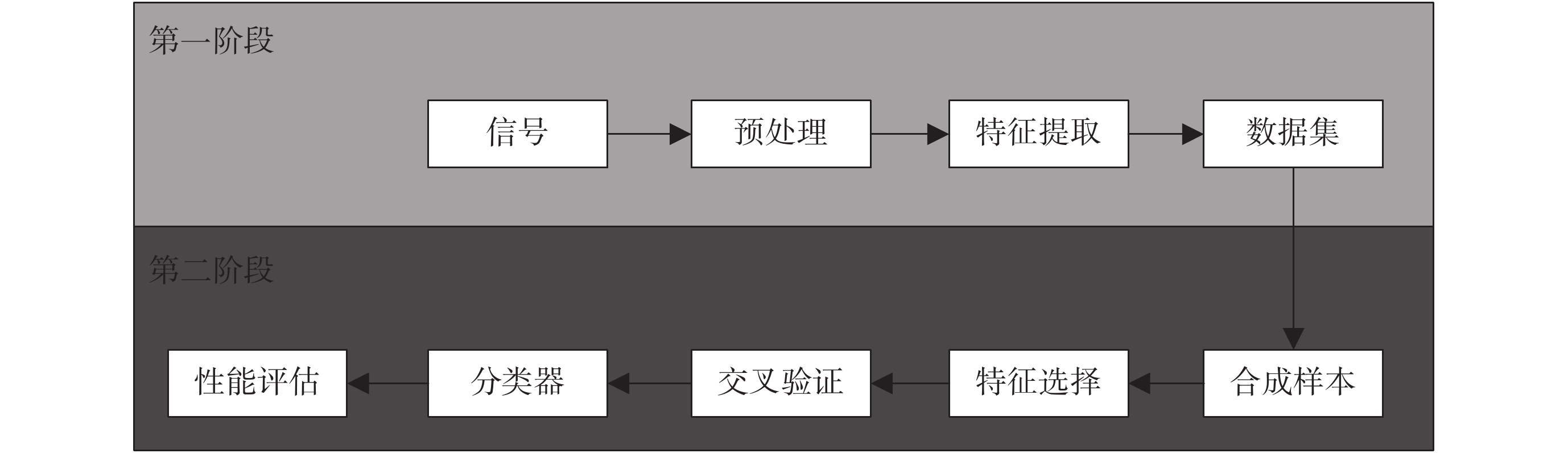圖1
本文研究內容的流程圖
Figure1.
A schematic outline of the research content of this work
1 方法與數據
1.1 實驗數據來源
本文采用了可公開使用的捷克技術大學-布爾諾大學醫院（Czech Technical University-University Hospital in Brno，CTU-UHB）數據庫（網址為：https://www.physionet.org/physiobank/database/ctu-uhb-ctgdb/）中的 CTG 信號來測試提出的算法性能。該數據庫共包含 552 個原始信號，為 2010—2012 年間獲取的 9 164 個產時記錄的子集，所有信號均以 4 Hz 采樣。有關該數據庫的詳細信息可參見文獻[11]。
本文選取胎兒分娩后測量的臍動脈 pH 值對 FHR 信號進行分類，作為后續胎兒分類的真實類別。考慮到病理病例和相關并發癥之間存在的數量關系，將 7.05 選為本研究中用于區分胎兒狀態類別的 pH 閾值。由此得到了該數據庫中包含著 43 個異常胎兒和 509 個正常胎兒的信息。
1.2 信號預處理
臨床 FHR 信號由放置在孕婦腹部的多普勒超聲探頭采集而得[11]。臨床數據采集過程中，獲得的 FHR 信號不可避免會受到多種噪聲干擾，如：孕婦和胎兒的移動、傳感器放置不當和其它外部環境因素等。FHR 信號的干擾噪聲分為尖刺（spiky artifacts）和丟失值（即 FHR 值為 0）兩種表現形式。本文采用插值法對這兩種噪聲進行預處理去噪，具體過程如下：
（1）當 FHR 信號值為 0 且持續時間大于 15 s 時直接移除，否則對其進行線性插值；
（2）當 FHR 信號不穩定，即相鄰兩點的絕對值大于 25 次/min 時，在起始采樣點和下一穩定部分的第一點之間進行插值；
（3）當 FHR 值大于 200 次/min 或者小于 50 次/min 時，用赫爾米特（Hermite）樣條插值進行填補。
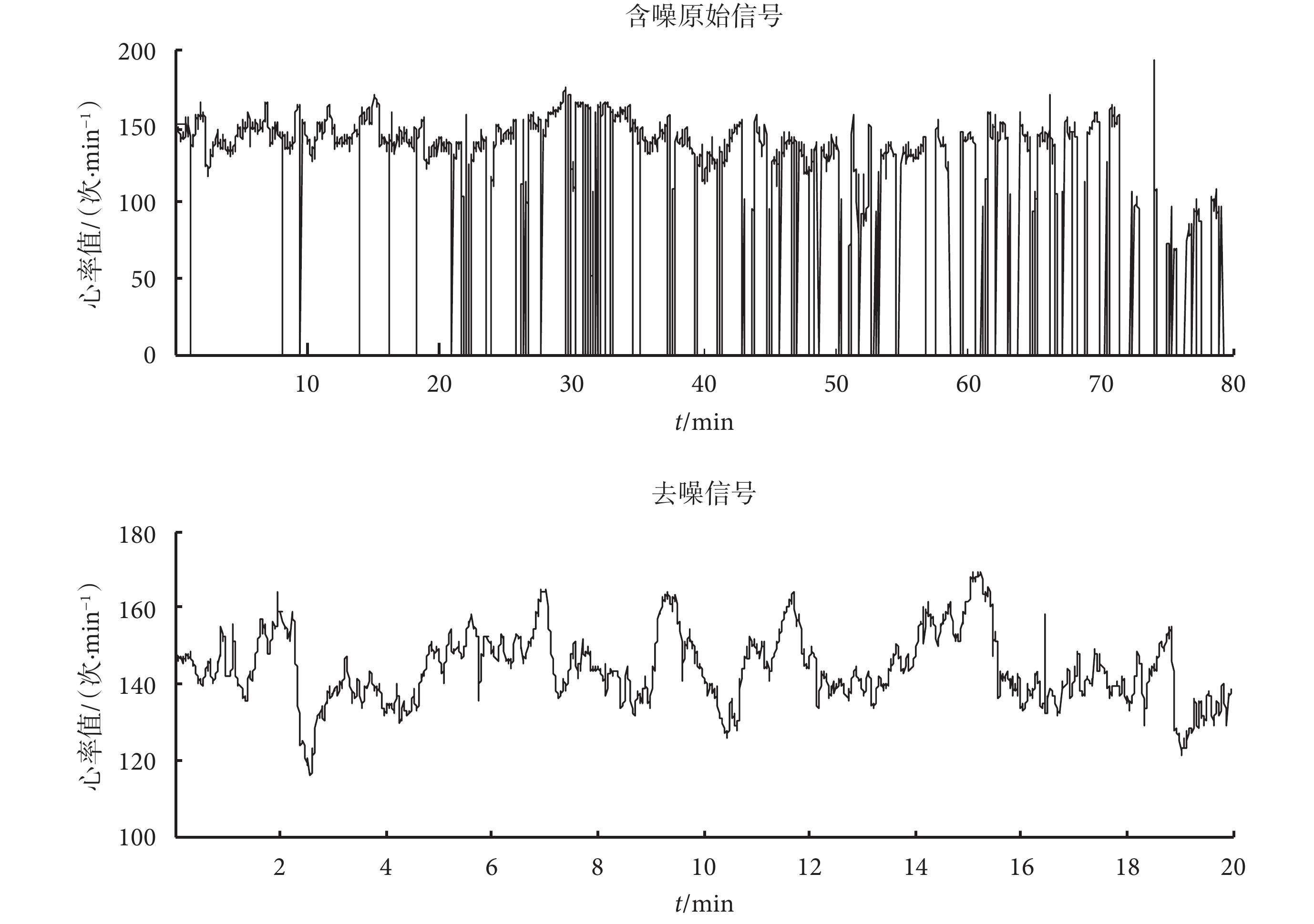
如圖 2 所示是原始信號和預處理后的干凈信號的對比。可見，采用插值法能很好地去除噪聲。
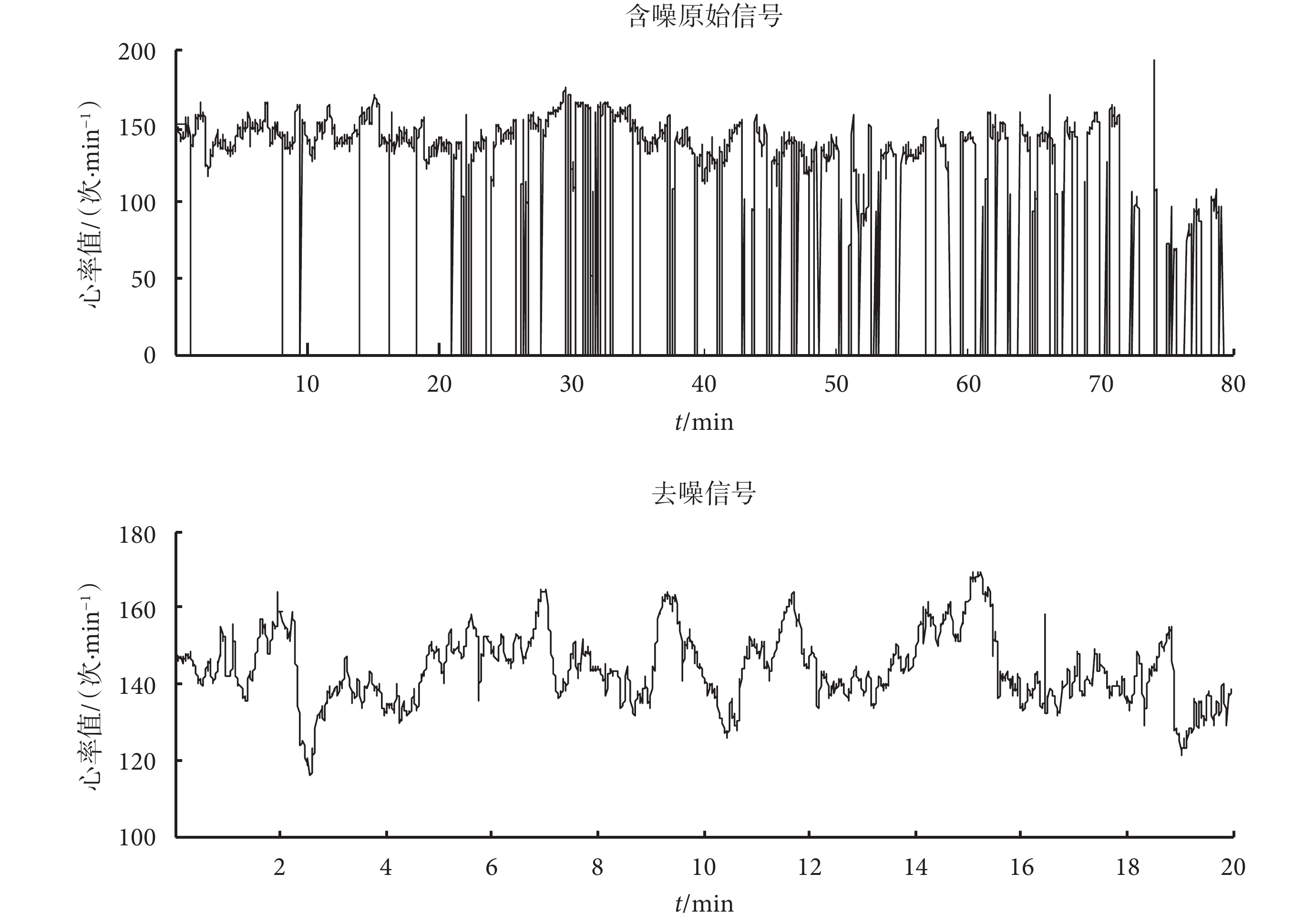圖2
FHR 信號預處理示例
Figure2.
An example of the FHR signal preprocessing
1.3 特征提取
特征提取獲得的參數對下一步的分類來說至關重要。自提出計算機分析系統這一概念以來，不少學者嘗試從 FHR 信號中提取與胎兒狀態相關的不同方面的參數。為了相關特征的完整性和盡可能地提高胎兒分類的準確度，本文采納了近十年來研究人員提出的所有特征，從 FHR 信號中提取線性和非線性等 67 個參數，分別來自于直接計算所得的基礎特征以及通過分析方法間接得到的其它特征，匯總如表 1 所示，為了使用方便，分別編號為 1～67。不同的特征域反映了 CTG 信號的不同分析角度，限于篇幅原因，特征參數的選擇依據和具體含義可參見文獻[5]，簡述如下：
表1
用于分析研究的特征參數
Table1.
Features used for the analysis
（1）基于 FIGO 指南的特征：臨床實踐中醫生最常用的形態學特征，通過視覺觀察得到的宏觀信息，如加、減速等，分別編號為 1～9；
（2）時域特征：臨床醫師容易理解，但不易被肉眼看到的微觀信息，如基線變異程度等，分別編號為 10～22；
（3）頻域特征：本研究中使用維爾奇（Welch）快速傅里葉變換計算 FHR 信號的功率譜密度，從而獲得特征參數，可反映胎兒的自主中樞神經系統平衡行為，包括交感神經和副交感神經兩個分支。FHR 信號的功率譜可以分為 4 個頻帶：甚低頻（very low frequency，VLF）、低頻（low frequency，LF）、中頻（middle frequency，MF）和高頻（high frequency，HF），分別編號為 23～40；
（4）非線性特征：此類特征將 FHR 信號視為非線性信號，通過結合非線性動力學的相關知識，進一步挖掘 FHR 信號中包含的信息，從而更加準確地評估胎兒行為的復雜性，分別編號為 41～67。
顯然，由于特征值的量綱并不完全相同，在下步分析之前需要進行歸一化的預處理。本文使用標準差標準化方法，經過處理后的特征值統一符合標準正態分布，即均值為 0，標準差為 1。
1.4 類不平衡問題
采用機器學習算法進行分類時會存在類不平衡問題。類不平衡，是指在訓練分類器時所使用的訓練集的類別分布不均[12]。例如，本文使用的數據庫包含 552 個 CTG 信號，其中僅有 43 個被評估為負類（胎兒異常），其余皆為正類（胎兒正常），正類和負類之比達 11:1 以上，即任何分類算法的準確度均可達 11/（11 + 1） = 92% 以上，這顯然是不合理的。為避免此類情況發生，現在通常采用的兩種解決方法分別為欠采樣和過采樣。前者是對訓練集里樣本數量較多的類別（多數類，本文中是正類）進行相關處理，即拋棄一些樣本來緩解類不平衡；后者是對訓練集里樣本數量較少的類別（少數類，本文中是負類）進行相關處理，即增加一些樣本使得正負類數目接近。
本文采用合成少數過采樣技術（synthetic minority over-sampling technique，SMOTE），它是由 Chawla 等[13]提出的一種經典的過采樣算法。該方法的主要思想是利用 k-最近鄰和線性插值，在相距較近的兩個少數類樣本間按照一定規則人為地插入新的樣本，以達到使少數類樣本數目增加最終數據集趨于平衡的目的。本文采用此技術后，用于下步分類的數據集變為 552 ? 43 = 509 個正類和 43 × 10 = 430 個負類，樣本數趨于平衡。
1.5 特征選擇
特征提取會產生大量的特征參數（本文 67 個）。在絕大多數模式識別問題中，某些特征包含重疊信息，相關性較高，甚至無法達到預期的信息量，故并不是所有提取的特征對于分類任務都是必需的。因此，在應用分類算法之前，需進行特征選擇，即采用降維處理[14]，從而大大減少構建分類器所需的時間，提高計算效率，同時可以增強分類器的泛化能力。用于分類的特征選擇任務可以描述如下：給定一組有 N 個特征的初始數據集，選擇含 M 個特征的子集，使得 M<<N，并且盡可能保留它們表達的類別不同信息。選擇合適的特征子集是機器學習算法中的關鍵步驟，可使分類器達到近乎最佳的性能。
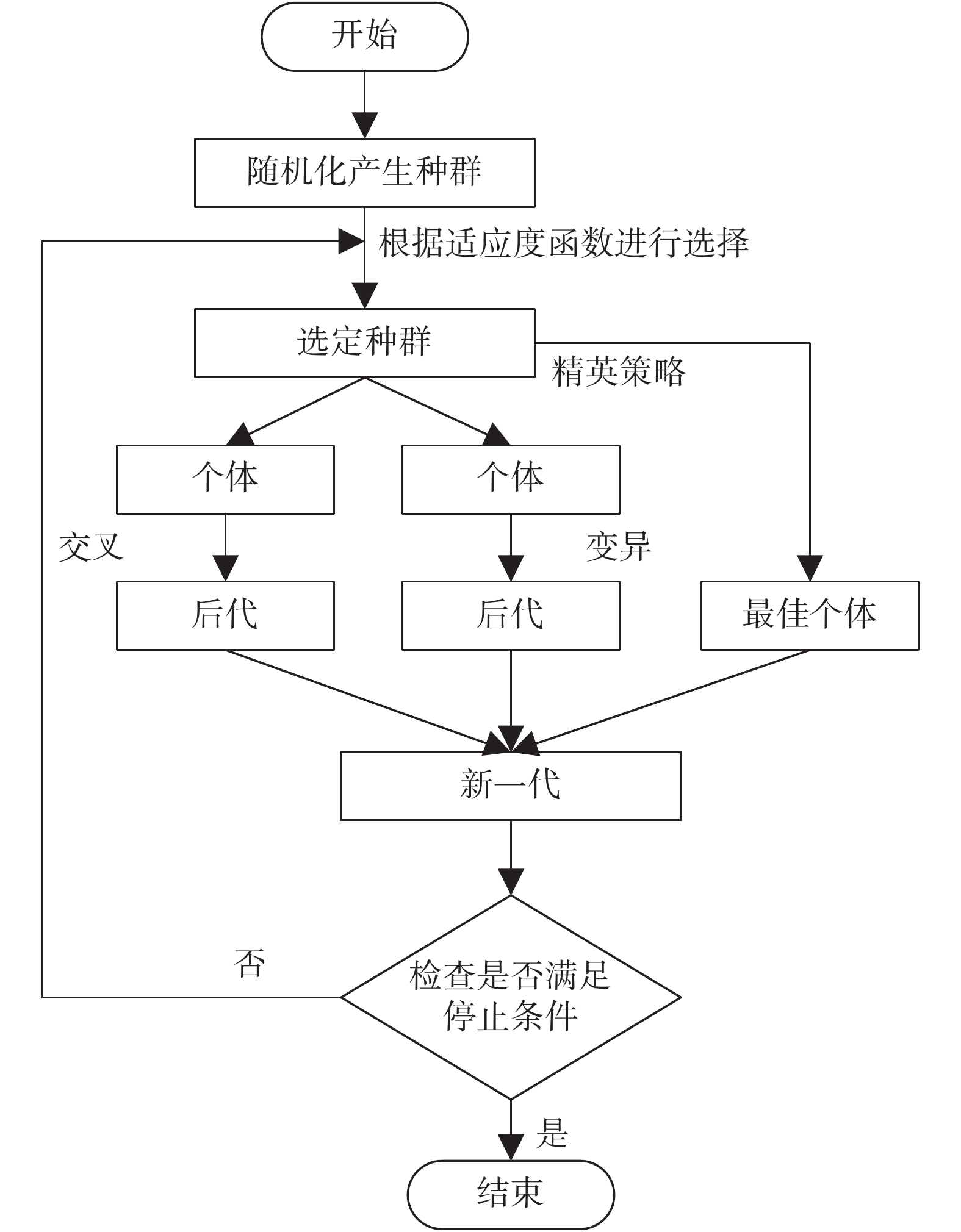
本文設計了基于 k-最近鄰的 GA 算法來選擇最優特征子集。GA 算法是一種基于種群和算法搜索的啟發式方法，實質是模擬人類的自然進化過程[15-16]。GA 算法中的操作是迭代過程，即操控一個染色體群體（候選方案），通過遺傳功能（如交叉、變異）產生新的種群。如圖 3 所示為 GA 算法的流程圖，歸納如下：① 將特征以二進制編碼作為基因組，即“1”表示選擇，“0”表示不選擇，特征種群是隨機產生的；② 使用適應度值對每個特征進行評估，并選擇最佳特征；③ 使用交叉和變異改變最佳特征以形成新一代種群；④ 在停止準則未滿足時，新一代種群繼續執行第二步，反之退出循環。
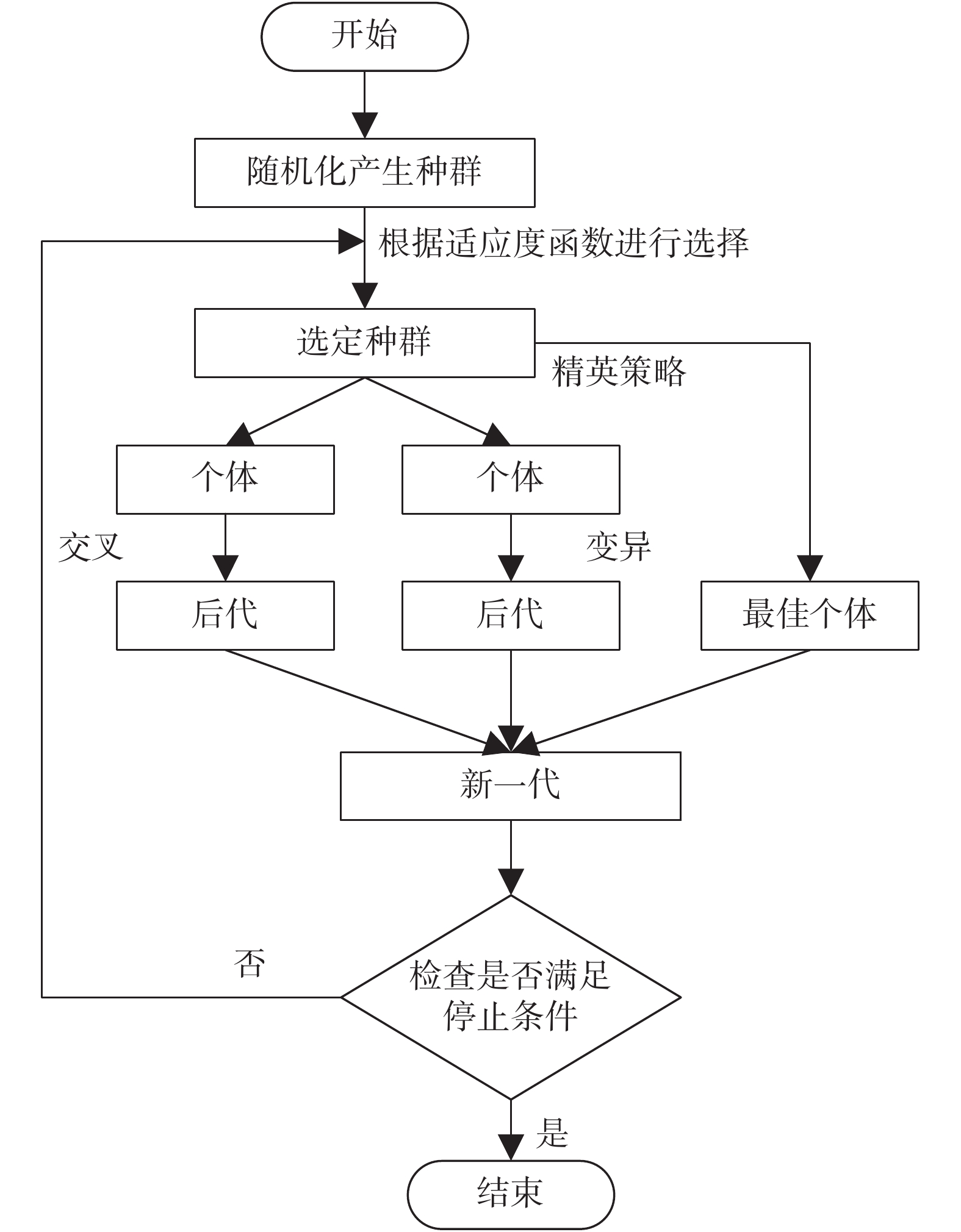圖3
GA 算法的流程圖
Figure3.
Flow chart of the GA algorithm
要得到最終的特征子集，需定義一個適應度函數來評估每個特征子集的判別能力，這是 GA 算法整個過程中最為關鍵的一步。本文設計了基于 k-最近鄰的適應度函數來計算群體中每個個體的適應度。k-最近鄰算法通過查找特征空間中測試數據和訓練集之間的最短距離來解決分類問題。本文使用的數據集可表示為 x = {x1，x2，
，xi，
，xM}，其中 M 是總樣本數（939 = 正類 509 + 負類 430），xi 代表包含 67 個特征參數的矢量，即 xi = {xi1，xi2，
，xij，
，xiN}，N = 67。首先計算測試數據和訓練集之間的歐幾里德（Euclidean）距離（以符號 D 表示），然后找到從訓練集到測試集的最近點（即最短距離），該距離如式（1）所示：
 |
式中，xxtest 和 xi 分別表示測試集和訓練集中包含特征參數的矢量。
本文 k-最近鄰使用 3 個近鄰計算每個類別的類別信息（以符號 count（xm）表示），然后基于如式（2）所示的報告分類結果和誤差，如下：
 |
在每條染色體中，基因值“1”表示選擇“1”的位置索引的特定參數，如果為“0”，則該特征不被選擇用于評估有關的染色體。染色體代表特征的編碼位字符串。隨著 GA 算法的迭代，對當前種群中的個體（組合特征集）進行評估，并根據基于 k-最近鄰的分類錯誤對其適應度進行排序。運行 GA 算法所涉及的迭代可以確保減少錯誤率，并選擇具有最小（即最佳）適應度值的個體，因為其中每個染色體都會報告錯誤率并最終由 GA 算法收集最小的錯誤率，如式（3）所示:
 |
其中 
是基于 k-最近鄰的分類錯誤，Nf 是所選特征的基數。該方程的代數結構確定了 GA 算法的正確學習過程，使得誤差最小化和選擇的特征數量減少。本文使用的 GA 算法是數值計算分析軟件 MATLAB（MathWorks Inc.，美國）中自帶的工具箱[16]。
1.6 分類器
如 1.5 節所述，應用基于 GA 算法的封裝式降維方法來減少特征參數，選擇具有明顯影響的特征，但是并不考慮特征之間的相關性。而 SVM 作為一種分類范例，它不會受到具有相關性的輸入因素影響，故選擇其執行分類任務[17]。
LS-SVM 分類器是采用最小二乘線性系統作為損失函數，代替傳統 SVM 采用的二次規劃方法，在處理中等大小問題時進一步簡化了計算復雜性，并提高了預測結果的準確性[18]。下面簡單敘述 LS-SVM 算法的基本原理和公式推導。
LS-SVM 分類器是將數據映射到更高維空間，然后構建最優分離超平面。給定一組 N 個訓練樣本，{（xi，yi），i = 1，
，N}，其中 xi∈RNf（Nf 是輸入空間維度）和相對應的標簽 yi = {+ 1，– 1}，支持向量旨在構建如式（4）所示形式的分類器：
 |
其中 φ（?）是將輸入空間映射到高維空間的非線性函數，b 是標量值，ω 是與 φ（?）具有相同維度的未知向量。
對于 LS-SVM 分類器，最優化問題如式（5）所示：
 |
其中，e 是誤差變量，γ 是正則化參數，F 是基于結構風險最小化準則的待優化函數。上述公式構建了一個典型的決策函數，如式（6）所示：
 |
這意味著每個訓練數據點都是一個支持向量。sign（t）表示符號函數（當 t > 0 時，sign（t） = 1；當 t < 0 時，sign（t） = –1），K（?，?）是核函數，隱式執行輸入到高維特征空間的映射，ai 是支持向量 xi 對應的拉格朗日乘子（Lagrange multiplier）。
本文使用了徑向基（radial basis function，RBF）核函數，如式（7）所示：
 |
其中，σ 是 RBF 內核的擴展參數。
上述公式在類別平衡的情況下工作良好，但是對于兩類類別分布不平衡的情況，就需要一種補償機制。最簡單的補償機制是對多數類進行二次采樣，但此方法可能導致決策邊界上的信息模式丟失。為了避免這個問題，可以采用基于兩類不等價成本計算的另一種方法。在 LS-SVM 的情形下，補償機制如式（8）、（9）所示：
 |
 |
其中 NP，NN 分別代表正類和分類的訓練樣本數，在輸入參數選擇過程中需要對兩個懲罰因子之間的比率進行微調。
2 實驗與分析
2.1 性能評估
本文采用混淆矩陣（confusion matrix，CM）評估分類模型的性能，如表 2 所示。其中，表格中的“行”為樣本的預測類別，每一行的樣本總數表示預測為該類別的樣本數目，表格中的“列”為樣本的實際歸屬類別，每一列的樣本總數表示實際為該類別的樣本數目[19]。在本文中，胎兒正常表示正類（positive），胎兒異常表示負類（negative）。CM 包括 4 個參數：真正類（true positive，TP）（以符號 TP 表示），定義為正常胎兒被正確分類為正常；假負類（false negative，FN）（以符號 FN 表示），定義為正常胎兒被錯誤分類為異常；假正類（false positive，FP）（以符號 FP 表示），定義為異常胎兒被錯誤分類為正常；真負類（true negative，TN）（以符號 TN 表示），定義為異常胎兒被正確分類為異常。
表2
二分類問題的混淆矩陣
Table2.
A general confusion matrix for a binary problem
CM 中的元素并不能直觀反映分類性能，而需計算基于 CM 的參數指標，如式（10）所示的總體準確度（overall accuracy）（以符號 ACC 表示）。此外，靈敏度（sensitivity）（以符號 SE 表示）和特異度（specificity）（以符號 SP 表示）是醫療領域經常使用的指標，分別表示分類模型對正類、負類樣本的判斷能力，而質量指標（quality index，QI）（以符號 QI 表示）表示 SE 和 SP 的幾何平均值，其計算公式如式（11）～（13）所示。
 |
 |
 |
 |
二分類的分類器經常會忽略少數類，導致分類不平衡情況的發生，需要其它指標來補充衡量分類性能，如平衡誤差率、馬修斯相關性系數等。此外，在醫學工程領域中，本文所采用的受試者工作特征（receiver operating characteristic，ROC）曲線下面積（area under the ROC curve，AUC）也被廣泛用于評估分類結果，其取值范圍為［0，1］，值越大表示模型判斷力越強[20]。理想情況是分類模型的預測結果與胎兒真實狀態完全吻合，此時 AUC 值為 1，而一個基于隨機猜測策略的二分類器的 AUC 值為 0.5。ROC 曲線是以預測結果的每一個值作為可能的判斷閾值，以假陽性率（false positive rate，FPR）為橫坐標，以真陽性率（true positive rate，TPR）為縱坐標繪制而成。
2.2 結果分析
2.2.1 特征選擇
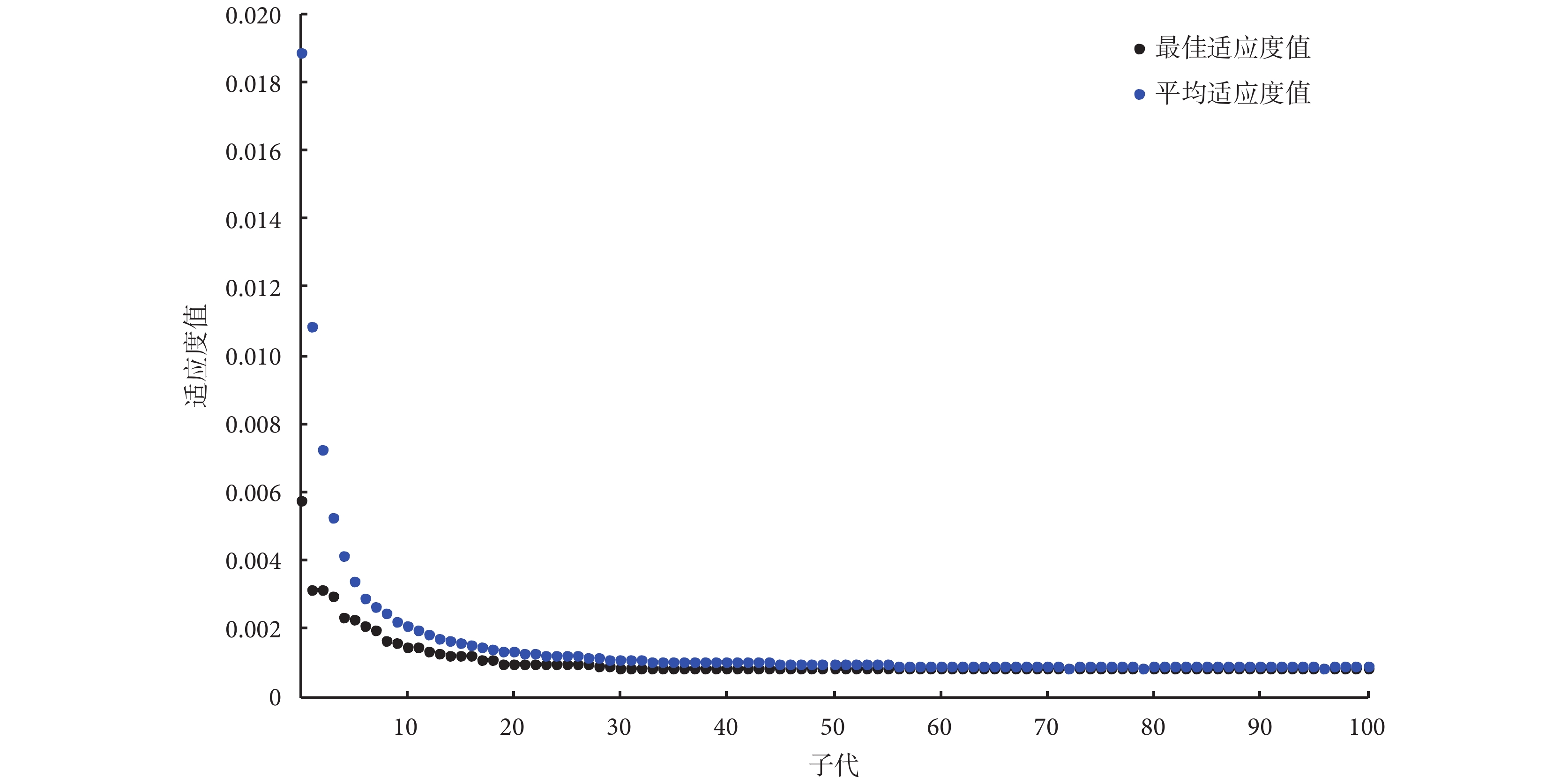
本文所提方法的研究結果可分為兩部分。第一部分是使用 GA 算法作為降維方法，從原始特征集（含 67 個參數）中選擇最優特征子集。如圖 4 所示為 GA 算法運行 1 次時，最佳適應度值和平均適應度值的變化曲線圖。每次 GA 算法的結果會包括 6～8 個特征參量，如表 3 所示為 GA 算法重復運行 20 次后，被選次數最多（以 10 次作為選擇閾值）的 5 個參數，分別為：FHR 曲線的中位數（以符號 FHR_median 表示），表示一段時間內胎兒心率波動的中位數，單位為：次/min；FHR 信號損耗的百分比（以符號 FHR_loss 表示），表示一段時間內因傳感器放置不當等外部因素導致 FHR 信號值為 0 的部分所占的百分比；基線曲線的最小值（以符號 Baseline_min 表示），表示一段時間內 FHR 基線波動的最小值，單位為：次/min；MF 功率（以符號 MF_power 表示），表示對 FHR 信號進行傅里葉變換所得的功率譜中 MF 的功率值，與身體活動（如胎動和孕婦呼吸等）有關，單位為：次2/min；LF 功率（以符號 LF_percent 表示），表示對 FHR 信號進行傅里葉變換所得的功率譜中 LF 的功率值在全頻帶功率值中所占的百分比，反映壓力感受性反射和血壓調節引起的胎兒心率變化。
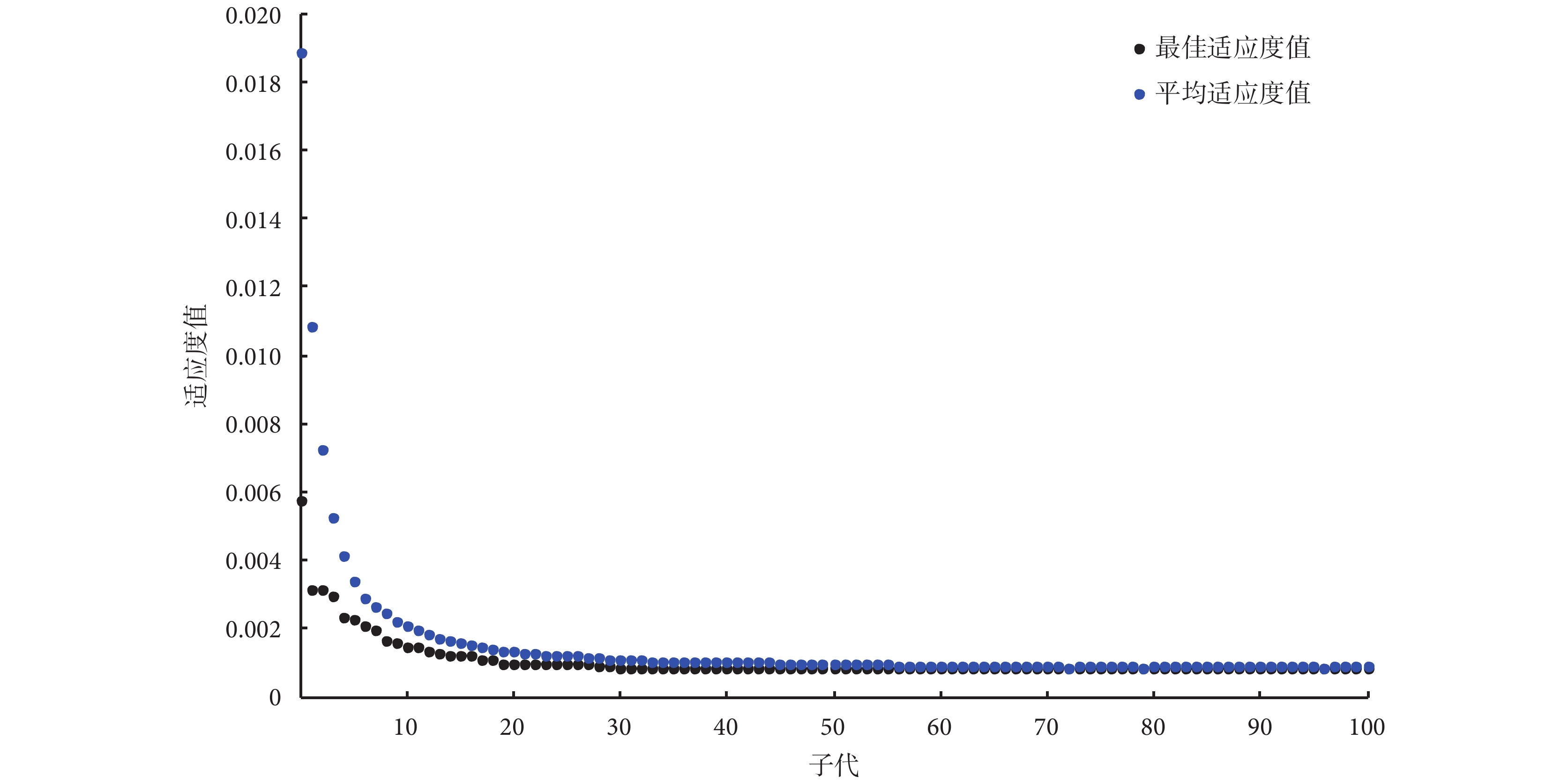圖4
GA 算法運行時最佳適應度值和平均適應度值的變化曲線圖
Figure4.
Change of the best and mean fitness value during the GA process
表3
由 GA 算法選擇的特征
Table3.
Features selected by the GA algorithm
2.2.2 分類結果
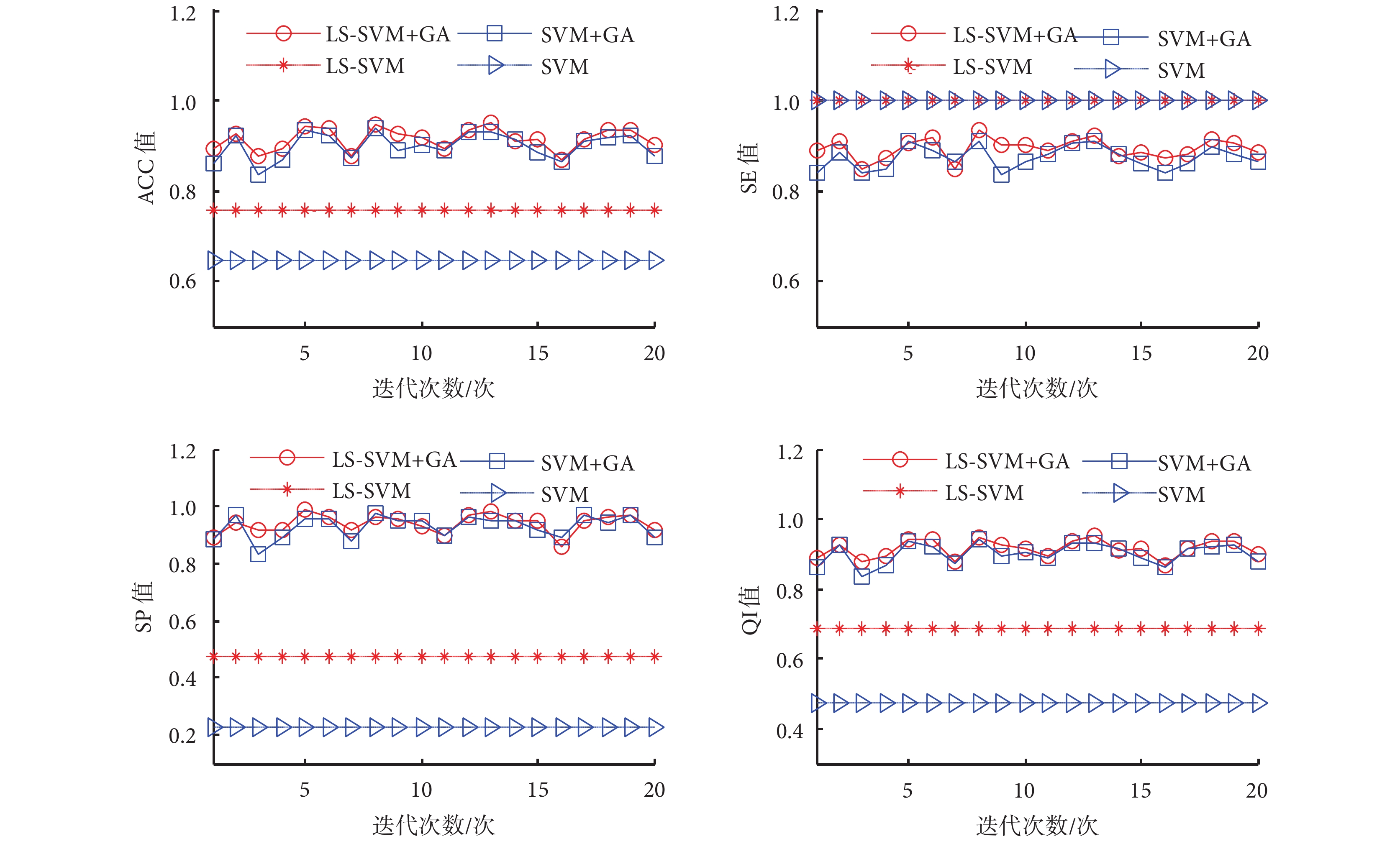
第二部分是對原始特征集和選擇子集分別使用 LS-SVM 和 SVM 進行分類，對所得結果進行二次比較。本文采用 10 階交叉驗證，對分類結果取平均值。隨著 GA 算法的重復運行，所選的特征子集發生變化，使得最后的分類性能也不斷改變，如圖 5 所示。尤為明顯的是，除了 SE 值有微小的上升外，原始特征集（無 GA 算法）的分類性能在 ACC、SP、QI 值上與被選中的特征子集（有 GA 算法）相比呈顯著的下降趨勢。
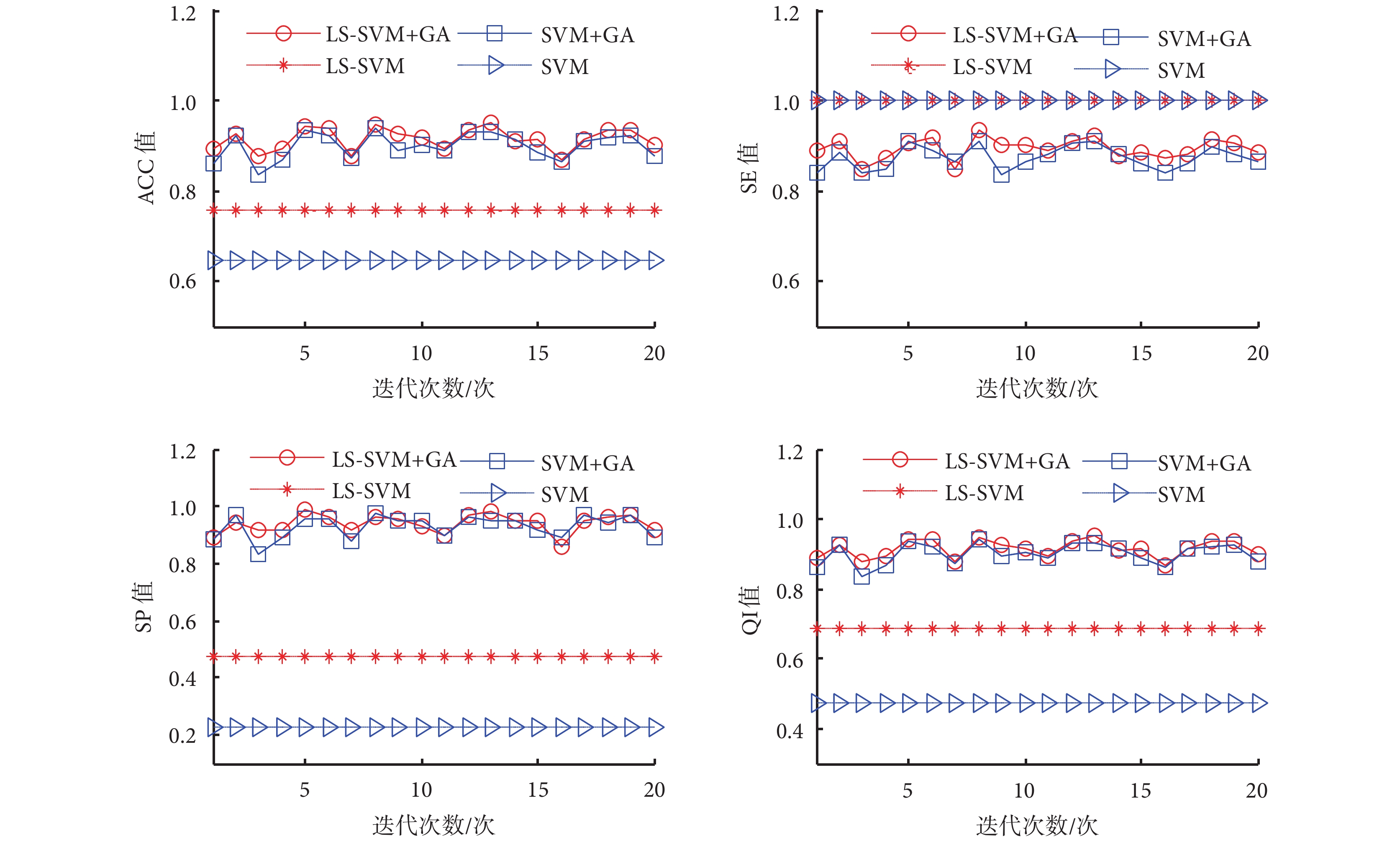圖5
性能指標隨著 GA 算法獲得的特征子集的不同而變化
Figure5.
Performance indexes change with the difference feature subsets obtained by GA algorithm
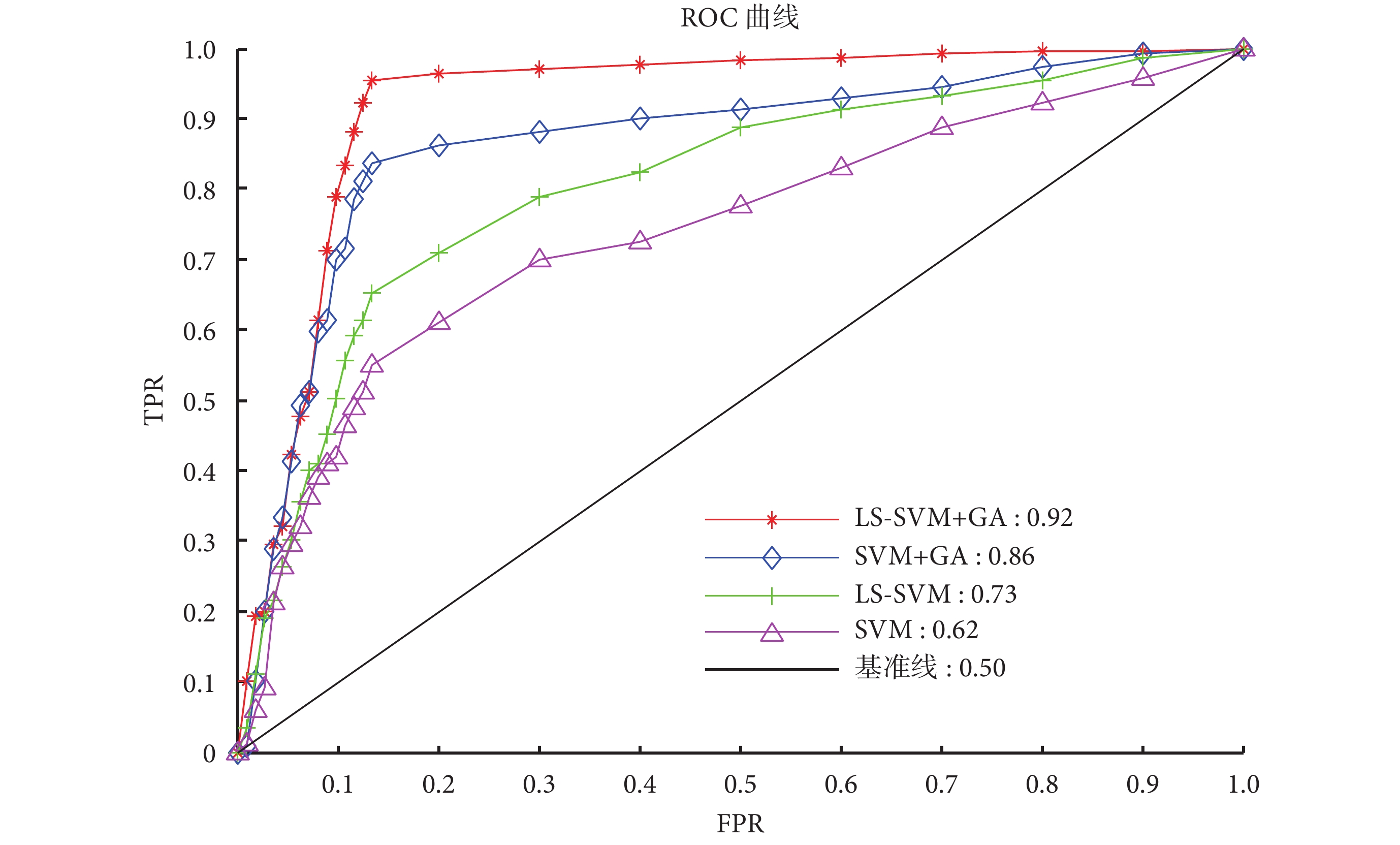
如表 4 所示進一步顯示了本文方法的分類性能，其中對 20 次 GA 算法的分類結果取平均值。如圖 6 所示展示了 ROC 曲線及其對應的 AUC 值。
表4
本文胎兒狀態評估算法的分類結果
Table4.
Classification result of the fetal state assessment algori thm proposed in this work
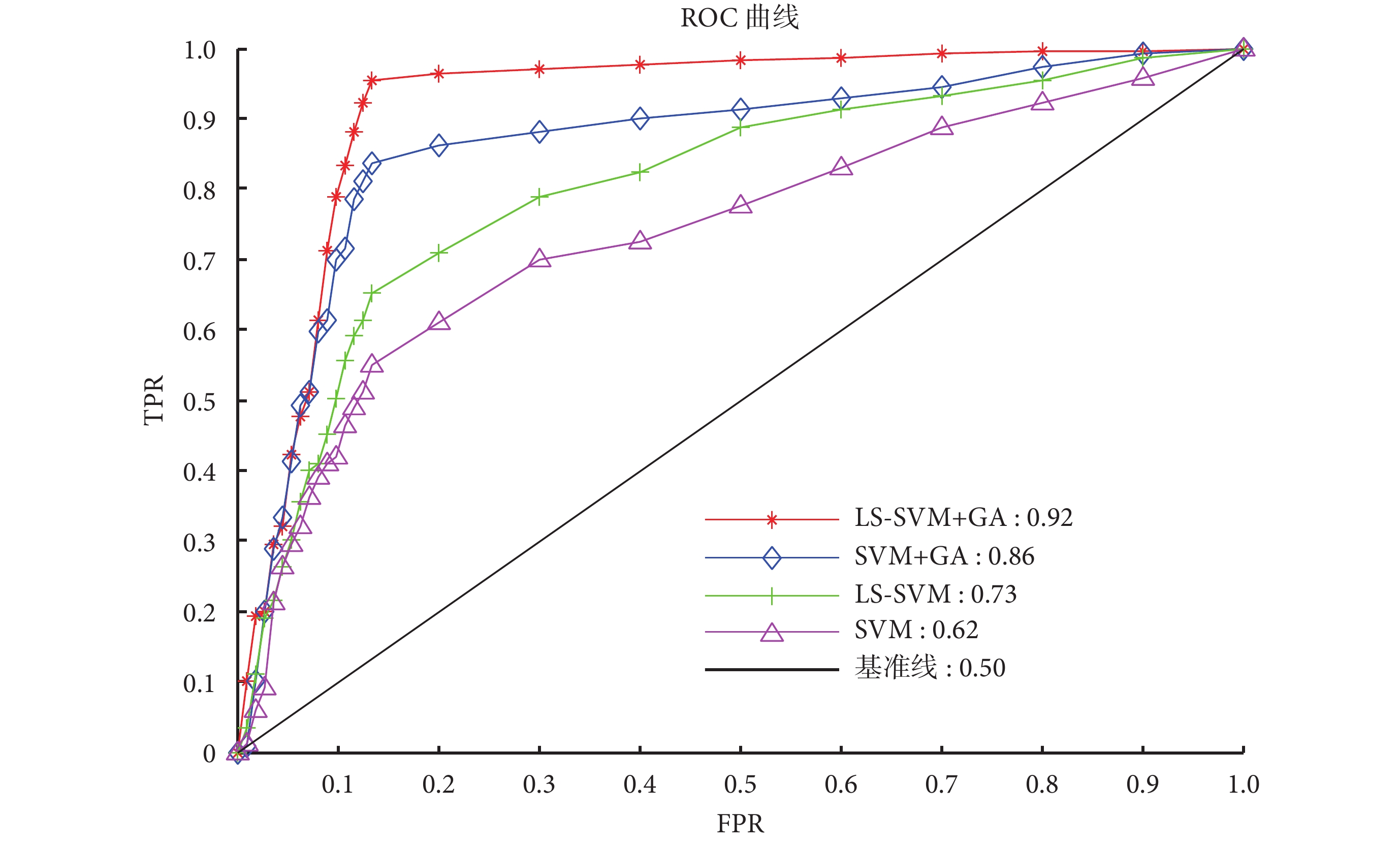圖6
本文算法的 ROC 曲線及其 AUC 值
Figure6.
ROC curve and its AUC value of the proposed algorithm
對比圖 5 和表 4 中發現：無論是 LS-SVM，還是 SVM，當使用 GA 算法選擇最優特征時，除了 SE 值略微減小，ACC、SP、QI 值都有顯著的提高（如 LS-SVM+GA 的 ACC 值相比 LS-SVM 提高了 0.15），證明了 GA 算法的有效性。此外，觀察表 4 和圖 6 可以發現：不管是否采用 GA 算法進行特征選擇時，LS-SVM 的 SE、ACC、SP、QI 值都要高于 SVM（如 LS-SVM 的 ACC 值相比 SVM 提高了 0.11），說明 LS-SVM 的分類性能要高于 SVM。
2.2.3 與前人工作的比較
最后，我們采用相同的數據庫（CTU-UHB），將本文提出的胎兒狀態評估算法與前人工作進行比較分析，得到如表 5 所示結果。觀察可知：與文章[9]的算法相比，在相同分類器（LS-SVM）的情況下，GA 算法大大提升了分類性能；與文章[8]和[10]的算法相比，LS-SVM 的分類性能強于 SVM 和 ANN 等傳統分類器。綜上，通過相互比較證明了本文算法具有一定的優越性。
表5
本文算法與前人工作的分類性能比較
Table5.
Comparison of the classification performance of the pro posed algorithm and previous work
3 結論
臨床實踐中，CTG 監護是應用最為廣泛的一種電子胎兒監護技術。本文提出了一種基于 FHR 信號分析的胎兒狀態智能評估方法，以輔助臨床醫生做出客觀而又準確的醫療決策。該方法通過對預處理后的 FHR 信號進行多模態特征提取，產生一組與胎兒狀態相關的特征集。針對類不平衡問題，本文采用 SMOTE 方法來產生少數類樣本，從而降低因實驗數據不足對分類準確度的影響。而后，設計基于 k-最近鄰的 GA 算法選擇最優特征子集，最后將 LS-SVM 用于胎兒分類。實驗結果表明，使用最佳特征子集的分類性能大大優于原始特征集，而且 LS-SVM 的分類性能也略高于 SVM。其中，基于 LS-SVM 和 GA 的分類算法性能最優：ACC = 0.91，SE = 0.89，SP = 0.94，QI = 0.92，AUC = 0.92。此外，我們對比前人工作，進一步證明了本文算法的有效性和優越性。同時，本文方法亦存在不足之處，一方面是 GA 算法耗時較長，另一方面，LS-SVM 分類算法會發生過擬合情況。因此，通過解決上述問題來提高胎兒評估性能將是筆者未來的研究方向。
引言
胎心宮縮圖（cardiotocography，CTG）監護，是臨床上監測圍產期胎兒宮內狀態應用最為廣泛的一種胎兒監護方式，主要通過對胎心和宮縮的監測來防止胎兒窘迫情況的發生，以避免對胎兒造成潛在的不良后果[1]。CTG 曲線作為醫學界認證的可實時在線提供胎兒產前和產時狀態信息的連續性信息技術，對降低圍產兒患病率和死亡率起到關鍵作用[2]。
臨床實踐中，對 CTG 的分析主要由產科醫生根據相關指南進行主觀評估，如：國際婦產科聯合會（International Federation of Gynecology and Obstetrics，FIGO）指南等[3]。CTG 評估結果會因為臨床醫師個體主觀認知的不同而存在差異，這是造成近年來剖腹產率上升的主要原因之一。為降低 CTG 曲線分析的差異性，需對臨床醫生進行專業培訓，并開發計算機輔助評估系統。因此有必要找到一種更為客觀的可以輔助臨床醫生進行準確分析胎兒狀態的評估方法，以降低人力物力的消耗，減少主觀分析的差異。
CTG 信號包含胎心率（fetal heart rate，FHR）信號和宮縮（uterine contraction，UC）信號。計算機評估系統通過自動化分析 FHR 信號和 UC 信號，可輔助甚至代替臨床醫生對胎兒狀態做出相對更客觀準確的判斷[4]。此類系統一般分為特征提取和狀態分類兩部分。傳統的特征提取方法中形態學參數不足以完全反映胎兒狀態，而線性時域和頻域以及非線性的眾多參數也能對胎兒狀態評估起到一定的作用[5]。另一方面，近年來不少學者對分類算法進行了深入研究，提出了基于機器學習算法的人工神經網絡（artificial neural network，ANN）、支持向量機（support vector machine，SVM）、決策樹（decision tree，DT）等分類算法，并進一步采用主成分分析、信息增益等降維方法，從原始特征集中選擇最佳參數，以提高分類性能[6-10]。如：陸堯勝等[7]使用常規參數（基線，加減速等）作為待分類的特征，然后采用基于歐式距離的模糊理論分析胎兒狀態。在提取線性和非線性參數的前提下，Georgoulas 等[8]和 Comert 等[10]則分別利用 SVM 和 ANN 對胎兒狀態進行分類。綜上，受前人研究工作的啟發，本文從特征提取、特征選擇和分類器等三個方面研究胎兒狀態智能評估算法。
為提高胎兒狀態評估的效果，本文提出了一種基于 FHR 信號分析胎兒狀態的智能評估方法，首先針對預處理后的 FHR 信號提取時域、頻域和非線性特征等參數，基于遺傳算法（genetic algorithm，GA）選擇最優特征，然后通過最小二乘支持向量機（least square support vector machine，LS-SVM）完成胎兒健康的診斷，最后對分類結果進行評估。如圖 1 所示為本文研究內容的基本框架。
圖1
本文研究內容的流程圖
Figure1.
A schematic outline of the research content of this work
1 方法與數據
1.1 實驗數據來源
本文采用了可公開使用的捷克技術大學-布爾諾大學醫院（Czech Technical University-University Hospital in Brno，CTU-UHB）數據庫（網址為：https://www.physionet.org/physiobank/database/ctu-uhb-ctgdb/）中的 CTG 信號來測試提出的算法性能。該數據庫共包含 552 個原始信號，為 2010—2012 年間獲取的 9 164 個產時記錄的子集，所有信號均以 4 Hz 采樣。有關該數據庫的詳細信息可參見文獻[11]。
本文選取胎兒分娩后測量的臍動脈 pH 值對 FHR 信號進行分類，作為后續胎兒分類的真實類別。考慮到病理病例和相關并發癥之間存在的數量關系，將 7.05 選為本研究中用于區分胎兒狀態類別的 pH 閾值。由此得到了該數據庫中包含著 43 個異常胎兒和 509 個正常胎兒的信息。
1.2 信號預處理
臨床 FHR 信號由放置在孕婦腹部的多普勒超聲探頭采集而得[11]。臨床數據采集過程中，獲得的 FHR 信號不可避免會受到多種噪聲干擾，如：孕婦和胎兒的移動、傳感器放置不當和其它外部環境因素等。FHR 信號的干擾噪聲分為尖刺（spiky artifacts）和丟失值（即 FHR 值為 0）兩種表現形式。本文采用插值法對這兩種噪聲進行預處理去噪，具體過程如下：
（1）當 FHR 信號值為 0 且持續時間大于 15 s 時直接移除，否則對其進行線性插值；
（2）當 FHR 信號不穩定，即相鄰兩點的絕對值大于 25 次/min 時，在起始采樣點和下一穩定部分的第一點之間進行插值；
（3）當 FHR 值大于 200 次/min 或者小于 50 次/min 時，用赫爾米特（Hermite）樣條插值進行填補。
如圖 2 所示是原始信號和預處理后的干凈信號的對比。可見，采用插值法能很好地去除噪聲。
圖2
FHR 信號預處理示例
Figure2.
An example of the FHR signal preprocessing
1.3 特征提取
特征提取獲得的參數對下一步的分類來說至關重要。自提出計算機分析系統這一概念以來，不少學者嘗試從 FHR 信號中提取與胎兒狀態相關的不同方面的參數。為了相關特征的完整性和盡可能地提高胎兒分類的準確度，本文采納了近十年來研究人員提出的所有特征，從 FHR 信號中提取線性和非線性等 67 個參數，分別來自于直接計算所得的基礎特征以及通過分析方法間接得到的其它特征，匯總如表 1 所示，為了使用方便，分別編號為 1～67。不同的特征域反映了 CTG 信號的不同分析角度，限于篇幅原因，特征參數的選擇依據和具體含義可參見文獻[5]，簡述如下：
表1
用于分析研究的特征參數
Table1.
Features used for the analysis
（1）基于 FIGO 指南的特征：臨床實踐中醫生最常用的形態學特征，通過視覺觀察得到的宏觀信息，如加、減速等，分別編號為 1～9；
（2）時域特征：臨床醫師容易理解，但不易被肉眼看到的微觀信息，如基線變異程度等，分別編號為 10～22；
（3）頻域特征：本研究中使用維爾奇（Welch）快速傅里葉變換計算 FHR 信號的功率譜密度，從而獲得特征參數，可反映胎兒的自主中樞神經系統平衡行為，包括交感神經和副交感神經兩個分支。FHR 信號的功率譜可以分為 4 個頻帶：甚低頻（very low frequency，VLF）、低頻（low frequency，LF）、中頻（middle frequency，MF）和高頻（high frequency，HF），分別編號為 23～40；
（4）非線性特征：此類特征將 FHR 信號視為非線性信號，通過結合非線性動力學的相關知識，進一步挖掘 FHR 信號中包含的信息，從而更加準確地評估胎兒行為的復雜性，分別編號為 41～67。
顯然，由于特征值的量綱并不完全相同，在下步分析之前需要進行歸一化的預處理。本文使用標準差標準化方法，經過處理后的特征值統一符合標準正態分布，即均值為 0，標準差為 1。
1.4 類不平衡問題
采用機器學習算法進行分類時會存在類不平衡問題。類不平衡，是指在訓練分類器時所使用的訓練集的類別分布不均[12]。例如，本文使用的數據庫包含 552 個 CTG 信號，其中僅有 43 個被評估為負類（胎兒異常），其余皆為正類（胎兒正常），正類和負類之比達 11:1 以上，即任何分類算法的準確度均可達 11/（11 + 1） = 92% 以上，這顯然是不合理的。為避免此類情況發生，現在通常采用的兩種解決方法分別為欠采樣和過采樣。前者是對訓練集里樣本數量較多的類別（多數類，本文中是正類）進行相關處理，即拋棄一些樣本來緩解類不平衡；后者是對訓練集里樣本數量較少的類別（少數類，本文中是負類）進行相關處理，即增加一些樣本使得正負類數目接近。
本文采用合成少數過采樣技術（synthetic minority over-sampling technique，SMOTE），它是由 Chawla 等[13]提出的一種經典的過采樣算法。該方法的主要思想是利用 k-最近鄰和線性插值，在相距較近的兩個少數類樣本間按照一定規則人為地插入新的樣本，以達到使少數類樣本數目增加最終數據集趨于平衡的目的。本文采用此技術后，用于下步分類的數據集變為 552 ? 43 = 509 個正類和 43 × 10 = 430 個負類，樣本數趨于平衡。
1.5 特征選擇
特征提取會產生大量的特征參數（本文 67 個）。在絕大多數模式識別問題中，某些特征包含重疊信息，相關性較高，甚至無法達到預期的信息量，故并不是所有提取的特征對于分類任務都是必需的。因此，在應用分類算法之前，需進行特征選擇，即采用降維處理[14]，從而大大減少構建分類器所需的時間，提高計算效率，同時可以增強分類器的泛化能力。用于分類的特征選擇任務可以描述如下：給定一組有 N 個特征的初始數據集，選擇含 M 個特征的子集，使得 M<<N，并且盡可能保留它們表達的類別不同信息。選擇合適的特征子集是機器學習算法中的關鍵步驟，可使分類器達到近乎最佳的性能。
本文設計了基于 k-最近鄰的 GA 算法來選擇最優特征子集。GA 算法是一種基于種群和算法搜索的啟發式方法，實質是模擬人類的自然進化過程[15-16]。GA 算法中的操作是迭代過程，即操控一個染色體群體（候選方案），通過遺傳功能（如交叉、變異）產生新的種群。如圖 3 所示為 GA 算法的流程圖，歸納如下：① 將特征以二進制編碼作為基因組，即“1”表示選擇，“0”表示不選擇，特征種群是隨機產生的；② 使用適應度值對每個特征進行評估，并選擇最佳特征；③ 使用交叉和變異改變最佳特征以形成新一代種群；④ 在停止準則未滿足時，新一代種群繼續執行第二步，反之退出循環。
圖3
GA 算法的流程圖
Figure3.
Flow chart of the GA algorithm
要得到最終的特征子集，需定義一個適應度函數來評估每個特征子集的判別能力，這是 GA 算法整個過程中最為關鍵的一步。本文設計了基于 k-最近鄰的適應度函數來計算群體中每個個體的適應度。k-最近鄰算法通過查找特征空間中測試數據和訓練集之間的最短距離來解決分類問題。本文使用的數據集可表示為 x = {x1，x2，，xi，，xM}，其中 M 是總樣本數（939 = 正類 509 + 負類 430），xi 代表包含 67 個特征參數的矢量，即 xi = {xi1，xi2，，xij，，xiN}，N = 67。首先計算測試數據和訓練集之間的歐幾里德（Euclidean）距離（以符號 D 表示），然后找到從訓練集到測試集的最近點（即最短距離），該距離如式（1）所示：
|
式中，xxtest 和 xi 分別表示測試集和訓練集中包含特征參數的矢量。
本文 k-最近鄰使用 3 個近鄰計算每個類別的類別信息（以符號 count（xm）表示），然后基于如式（2）所示的報告分類結果和誤差，如下：
|
在每條染色體中，基因值“1”表示選擇“1”的位置索引的特定參數，如果為“0”，則該特征不被選擇用于評估有關的染色體。染色體代表特征的編碼位字符串。隨著 GA 算法的迭代，對當前種群中的個體（組合特征集）進行評估，并根據基于 k-最近鄰的分類錯誤對其適應度進行排序。運行 GA 算法所涉及的迭代可以確保減少錯誤率，并選擇具有最小（即最佳）適應度值的個體，因為其中每個染色體都會報告錯誤率并最終由 GA 算法收集最小的錯誤率，如式（3）所示:
|
其中 是基于 k-最近鄰的分類錯誤，Nf 是所選特征的基數。該方程的代數結構確定了 GA 算法的正確學習過程，使得誤差最小化和選擇的特征數量減少。本文使用的 GA 算法是數值計算分析軟件 MATLAB（MathWorks Inc.，美國）中自帶的工具箱[16]。
1.6 分類器
如 1.5 節所述，應用基于 GA 算法的封裝式降維方法來減少特征參數，選擇具有明顯影響的特征，但是并不考慮特征之間的相關性。而 SVM 作為一種分類范例，它不會受到具有相關性的輸入因素影響，故選擇其執行分類任務[17]。
LS-SVM 分類器是采用最小二乘線性系統作為損失函數，代替傳統 SVM 采用的二次規劃方法，在處理中等大小問題時進一步簡化了計算復雜性，并提高了預測結果的準確性[18]。下面簡單敘述 LS-SVM 算法的基本原理和公式推導。
LS-SVM 分類器是將數據映射到更高維空間，然后構建最優分離超平面。給定一組 N 個訓練樣本，{（xi，yi），i = 1，，N}，其中 xi∈RNf（Nf 是輸入空間維度）和相對應的標簽 yi = {+ 1，– 1}，支持向量旨在構建如式（4）所示形式的分類器：
|
其中 φ（?）是將輸入空間映射到高維空間的非線性函數，b 是標量值，ω 是與 φ（?）具有相同維度的未知向量。
對于 LS-SVM 分類器，最優化問題如式（5）所示：
|
其中，e 是誤差變量，γ 是正則化參數，F 是基于結構風險最小化準則的待優化函數。上述公式構建了一個典型的決策函數，如式（6）所示：
|
這意味著每個訓練數據點都是一個支持向量。sign（t）表示符號函數（當 t > 0 時，sign（t） = 1；當 t < 0 時，sign（t） = –1），K（?，?）是核函數，隱式執行輸入到高維特征空間的映射，ai 是支持向量 xi 對應的拉格朗日乘子（Lagrange multiplier）。
本文使用了徑向基（radial basis function，RBF）核函數，如式（7）所示：
|
其中，σ 是 RBF 內核的擴展參數。
上述公式在類別平衡的情況下工作良好，但是對于兩類類別分布不平衡的情況，就需要一種補償機制。最簡單的補償機制是對多數類進行二次采樣，但此方法可能導致決策邊界上的信息模式丟失。為了避免這個問題，可以采用基于兩類不等價成本計算的另一種方法。在 LS-SVM 的情形下，補償機制如式（8）、（9）所示：
|
|
其中 NP，NN 分別代表正類和分類的訓練樣本數，在輸入參數選擇過程中需要對兩個懲罰因子之間的比率進行微調。
2 實驗與分析
2.1 性能評估
本文采用混淆矩陣（confusion matrix，CM）評估分類模型的性能，如表 2 所示。其中，表格中的“行”為樣本的預測類別，每一行的樣本總數表示預測為該類別的樣本數目，表格中的“列”為樣本的實際歸屬類別，每一列的樣本總數表示實際為該類別的樣本數目[19]。在本文中，胎兒正常表示正類（positive），胎兒異常表示負類（negative）。CM 包括 4 個參數：真正類（true positive，TP）（以符號 TP 表示），定義為正常胎兒被正確分類為正常；假負類（false negative，FN）（以符號 FN 表示），定義為正常胎兒被錯誤分類為異常；假正類（false positive，FP）（以符號 FP 表示），定義為異常胎兒被錯誤分類為正常；真負類（true negative，TN）（以符號 TN 表示），定義為異常胎兒被正確分類為異常。
表2
二分類問題的混淆矩陣
Table2.
A general confusion matrix for a binary problem
CM 中的元素并不能直觀反映分類性能，而需計算基于 CM 的參數指標，如式（10）所示的總體準確度（overall accuracy）（以符號 ACC 表示）。此外，靈敏度（sensitivity）（以符號 SE 表示）和特異度（specificity）（以符號 SP 表示）是醫療領域經常使用的指標，分別表示分類模型對正類、負類樣本的判斷能力，而質量指標（quality index，QI）（以符號 QI 表示）表示 SE 和 SP 的幾何平均值，其計算公式如式（11）～（13）所示。
|
|
|
|
二分類的分類器經常會忽略少數類，導致分類不平衡情況的發生，需要其它指標來補充衡量分類性能，如平衡誤差率、馬修斯相關性系數等。此外，在醫學工程領域中，本文所采用的受試者工作特征（receiver operating characteristic，ROC）曲線下面積（area under the ROC curve，AUC）也被廣泛用于評估分類結果，其取值范圍為［0，1］，值越大表示模型判斷力越強[20]。理想情況是分類模型的預測結果與胎兒真實狀態完全吻合，此時 AUC 值為 1，而一個基于隨機猜測策略的二分類器的 AUC 值為 0.5。ROC 曲線是以預測結果的每一個值作為可能的判斷閾值，以假陽性率（false positive rate，FPR）為橫坐標，以真陽性率（true positive rate，TPR）為縱坐標繪制而成。
2.2 結果分析
2.2.1 特征選擇
本文所提方法的研究結果可分為兩部分。第一部分是使用 GA 算法作為降維方法，從原始特征集（含 67 個參數）中選擇最優特征子集。如圖 4 所示為 GA 算法運行 1 次時，最佳適應度值和平均適應度值的變化曲線圖。每次 GA 算法的結果會包括 6～8 個特征參量，如表 3 所示為 GA 算法重復運行 20 次后，被選次數最多（以 10 次作為選擇閾值）的 5 個參數，分別為：FHR 曲線的中位數（以符號 FHR_median 表示），表示一段時間內胎兒心率波動的中位數，單位為：次/min；FHR 信號損耗的百分比（以符號 FHR_loss 表示），表示一段時間內因傳感器放置不當等外部因素導致 FHR 信號值為 0 的部分所占的百分比；基線曲線的最小值（以符號 Baseline_min 表示），表示一段時間內 FHR 基線波動的最小值，單位為：次/min；MF 功率（以符號 MF_power 表示），表示對 FHR 信號進行傅里葉變換所得的功率譜中 MF 的功率值，與身體活動（如胎動和孕婦呼吸等）有關，單位為：次2/min；LF 功率（以符號 LF_percent 表示），表示對 FHR 信號進行傅里葉變換所得的功率譜中 LF 的功率值在全頻帶功率值中所占的百分比，反映壓力感受性反射和血壓調節引起的胎兒心率變化。
圖4
GA 算法運行時最佳適應度值和平均適應度值的變化曲線圖
Figure4.
Change of the best and mean fitness value during the GA process
表3
由 GA 算法選擇的特征
Table3.
Features selected by the GA algorithm
2.2.2 分類結果
第二部分是對原始特征集和選擇子集分別使用 LS-SVM 和 SVM 進行分類，對所得結果進行二次比較。本文采用 10 階交叉驗證，對分類結果取平均值。隨著 GA 算法的重復運行，所選的特征子集發生變化，使得最后的分類性能也不斷改變，如圖 5 所示。尤為明顯的是，除了 SE 值有微小的上升外，原始特征集（無 GA 算法）的分類性能在 ACC、SP、QI 值上與被選中的特征子集（有 GA 算法）相比呈顯著的下降趨勢。
圖5
性能指標隨著 GA 算法獲得的特征子集的不同而變化
Figure5.
Performance indexes change with the difference feature subsets obtained by GA algorithm
如表 4 所示進一步顯示了本文方法的分類性能，其中對 20 次 GA 算法的分類結果取平均值。如圖 6 所示展示了 ROC 曲線及其對應的 AUC 值。
表4
本文胎兒狀態評估算法的分類結果
Table4.
Classification result of the fetal state assessment algori thm proposed in this work
圖6
本文算法的 ROC 曲線及其 AUC 值
Figure6.
ROC curve and its AUC value of the proposed algorithm
對比圖 5 和表 4 中發現：無論是 LS-SVM，還是 SVM，當使用 GA 算法選擇最優特征時，除了 SE 值略微減小，ACC、SP、QI 值都有顯著的提高（如 LS-SVM+GA 的 ACC 值相比 LS-SVM 提高了 0.15），證明了 GA 算法的有效性。此外，觀察表 4 和圖 6 可以發現：不管是否采用 GA 算法進行特征選擇時，LS-SVM 的 SE、ACC、SP、QI 值都要高于 SVM（如 LS-SVM 的 ACC 值相比 SVM 提高了 0.11），說明 LS-SVM 的分類性能要高于 SVM。
2.2.3 與前人工作的比較
最后，我們采用相同的數據庫（CTU-UHB），將本文提出的胎兒狀態評估算法與前人工作進行比較分析，得到如表 5 所示結果。觀察可知：與文章[9]的算法相比，在相同分類器（LS-SVM）的情況下，GA 算法大大提升了分類性能；與文章[8]和[10]的算法相比，LS-SVM 的分類性能強于 SVM 和 ANN 等傳統分類器。綜上，通過相互比較證明了本文算法具有一定的優越性。
表5
本文算法與前人工作的分類性能比較
Table5.
Comparison of the classification performance of the pro posed algorithm and previous work
3 結論
臨床實踐中，CTG 監護是應用最為廣泛的一種電子胎兒監護技術。本文提出了一種基于 FHR 信號分析的胎兒狀態智能評估方法，以輔助臨床醫生做出客觀而又準確的醫療決策。該方法通過對預處理后的 FHR 信號進行多模態特征提取，產生一組與胎兒狀態相關的特征集。針對類不平衡問題，本文采用 SMOTE 方法來產生少數類樣本，從而降低因實驗數據不足對分類準確度的影響。而后，設計基于 k-最近鄰的 GA 算法選擇最優特征子集，最后將 LS-SVM 用于胎兒分類。實驗結果表明，使用最佳特征子集的分類性能大大優于原始特征集，而且 LS-SVM 的分類性能也略高于 SVM。其中，基于 LS-SVM 和 GA 的分類算法性能最優：ACC = 0.91，SE = 0.89，SP = 0.94，QI = 0.92，AUC = 0.92。此外，我們對比前人工作，進一步證明了本文算法的有效性和優越性。同時，本文方法亦存在不足之處，一方面是 GA 算法耗時較長，另一方面，LS-SVM 分類算法會發生過擬合情況。因此，通過解決上述問題來提高胎兒評估性能將是筆者未來的研究方向。
