為了研究中耳炎引起的鼓膜病變和聽小骨腐蝕對圓窗激振式人工中耳聽力補償的影響,利用計算機斷層掃描(CT)技術和逆向成型技術建立了包含耳蝸不對稱結構的人耳有限元模型,并與相關實驗數據對比,驗證模型的可靠性。基于該模型,通過改變相應的組織結構,分別模擬中耳炎引起的鼓膜病變和聽小骨腐蝕,并對比相應的基底膜特征頻率處的位移響應,來研究中耳炎病變對圓窗激振聽力補償效果的影響。結果表明:鼓膜增厚和鼓膜硬化主要惡化圓窗激振低頻段的聽力補償效果;鼓膜穿孔和未導致聽骨鏈脫離的聽小骨腐蝕,對圓窗激振的影響較小;不同于前述病變類型的影響,聽小骨腐蝕導致聽骨鏈脫離時,將提高圓窗激振低頻段的聽力補償性能。因此,設計圓窗激振作動器時,應綜合考慮中耳炎病變對其聽力補償性能的影響,特別是鼓膜增厚及硬化對其低頻段性能的惡化,適當增大其低頻段的輸出增益,確保其術后的實際聽力補償性能。
引用本文: 薛林, 劉后廣, 王志華, 楊建華, 楊善國, 黃新生, 張虎. 中耳炎病變對圓窗激振聽力補償影響的數值分析. 生物醫學工程學雜志, 2019, 36(5): 745-754. doi: 10.7507/1001-5515.201809056 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
聽力損傷是最常見的疾病之一,世界上有近 5.38 億人患有不同程度的聽力障礙[1]。其中由感音神經性損傷造成的聽力障礙現階段尚無有效藥物及手術治療方法,大部分患者只能通過佩戴助聽器來補償聽力[2]。隨著現代語音處理算法及數字處理芯片的發展,助聽器聽力補償性能得到較大的提高,但仍然存在堵塞耳道、伴有聲反饋、高頻增益小等固有問題,為此許多機構開展了通過直接機械激勵聽小骨來補償聽力的植入式助聽裝置的研究[3-4],這種植入式助聽裝置又稱人工中耳。但是,部分患者伴有聽骨鏈病變,如中耳炎引起的聽小骨腐蝕[5],使得人工中耳作動器無法作用在聽小骨上,進而無法植入人工中耳。針對這類問題,Colletti 等[6]提出并在臨床上首次驗證了避開聽骨鏈直接激勵圓窗來進行聽力補償的可行性,為人工中耳補償伴有聽骨鏈損壞的感音神經性耳聾提供了新思路。
雖然臨床上證明了圓窗激振補償聽力損傷的可行性,但其術后效果針對不同患者表現出較大的個體差異[7]。為找出術后效果不佳的原因,國內外許多學者進行了相關研究。Arnold 等[8]研究了作動器在圓窗上不同的放置方式對耳蝸輸入能量的影響。Schraven 等[9]研究了不同作動器幾何形狀及耦合條件對圓窗激振效率的影響。張虎等[10]通過控制作動器不同大小的初始壓力和改變支撐體剛度,研究其對圓窗激振性能的影響。上述研究為臨床上圓窗激振式人工中耳性能的改進提供了重要參考,但主要針對人工中耳的設計參數和耦合條件,沒有考慮患者因中耳炎等引起的個體病變的影響。人耳具有結構超微、幾何形態復雜的特征,且很難獲得所需病變的人耳標本,這也使得關于中耳炎病變對圓窗激振影響的系統實驗研究不易進行。
針對上述問題,考慮到有限單元法在模擬人耳這種具有結構超微、幾何形態復雜、組織非同質性的復雜生物系統具有的優勢[11-13],本文利用逆向成型技術建立并驗證了人耳傳聲有限元模型,并基于此系統地研究了中耳炎引起的鼓膜病變和聽小骨腐蝕對圓窗激振式人工中耳的聽力補償效果的影響。本文研究結果可為圓窗激振式人工中耳進一步的優化設計提供參考,改進其臨床上的聽力補償效果。
1 材料與方法
1.1 人耳有限元模型
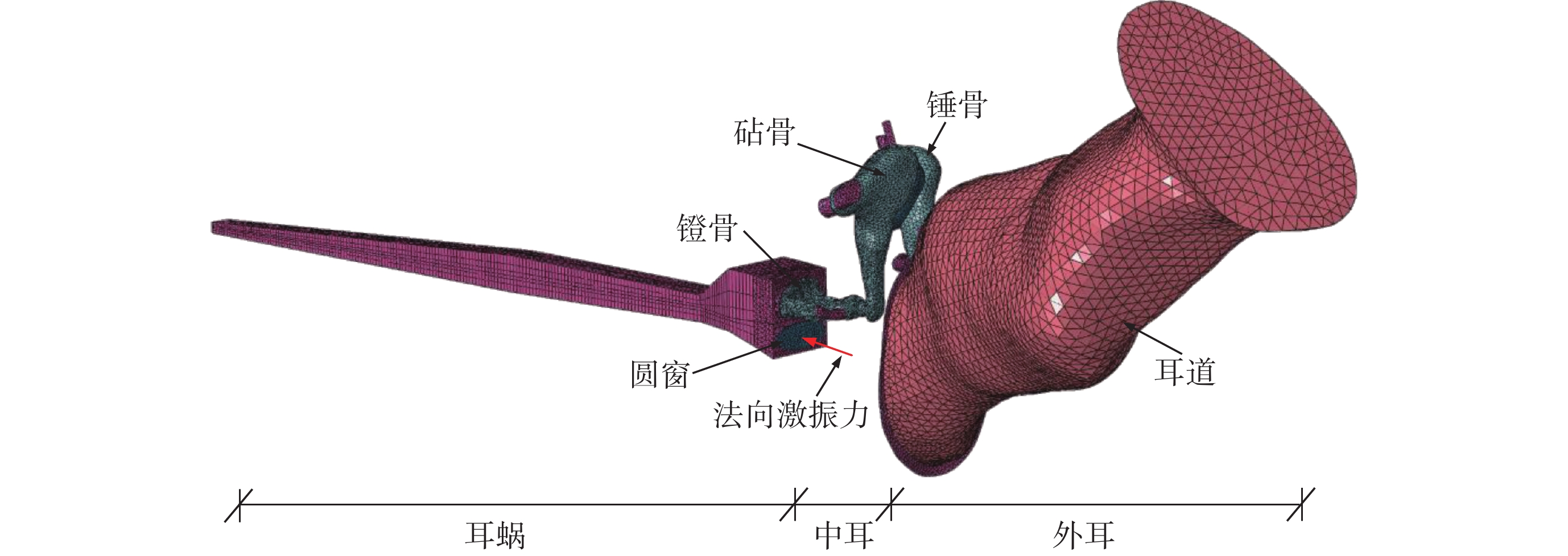
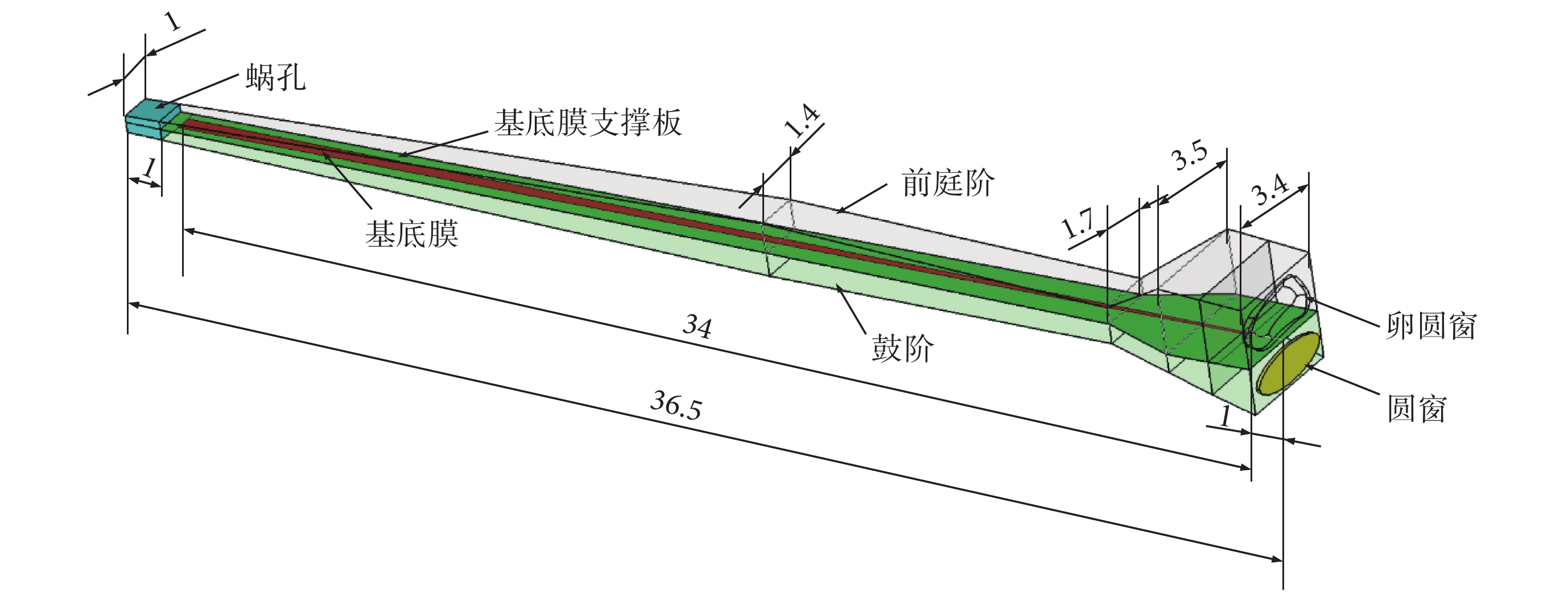
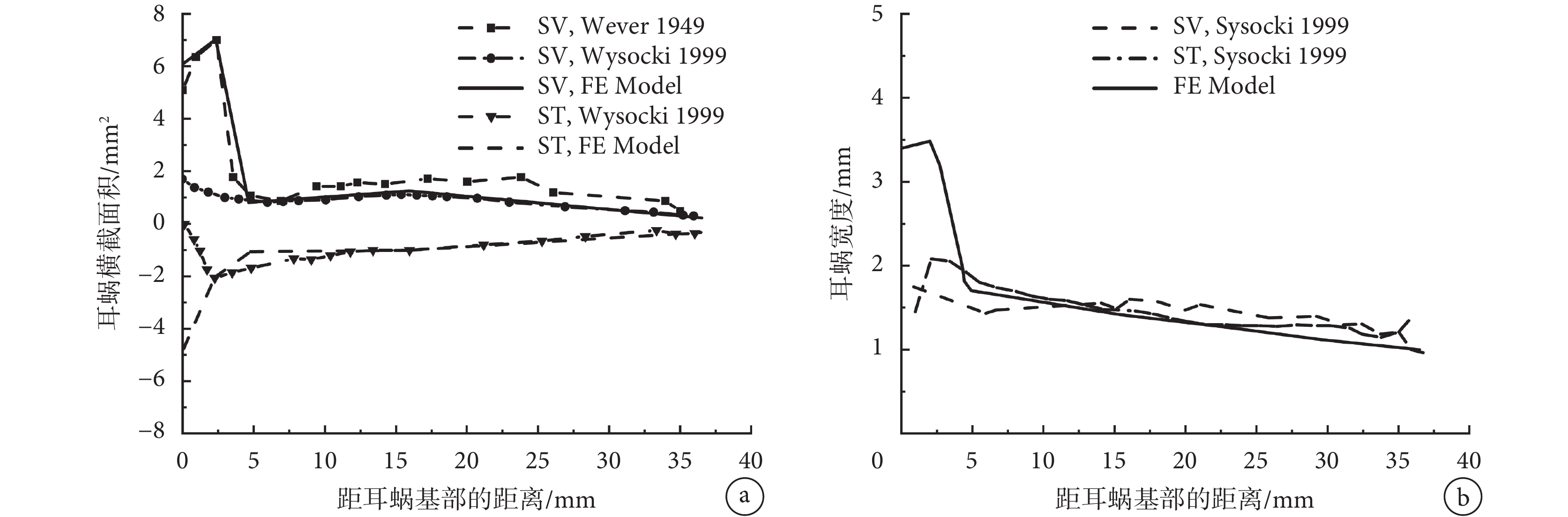
為了輔助分析中耳炎病變對圓窗激振的影響,構建了包括外耳道、中耳、耳蝸三部分的人耳傳聲有限元模型,如圖 1 所示。其中,外耳道和中耳部分是基于人體顳骨計算機斷層掃描(computed tomography,CT)與逆向成型技術所建立,其具體的建模工作先前已經報道[14]。而耳蝸部分,由于 CT 掃描圖像中基底膜分辨率較差,故采用三維軟件近似繪制的方法構建其幾何模型。為了簡化建模過程,忽略了耳蝸內部的前庭膜;考慮到實際耳蝸結構尺寸關于基底膜的不對稱性[15-16],將耳蝸簡化為充滿液體的非螺旋、不對稱的雙腔導管結構,包括鼓階(scala tympani,ST)、前庭階(scala vestibuli,SV)、蝸孔、基底膜、圓窗和卵圓窗。其中,基底膜固定在骨質支撐板上將兩腔體隔開;鼓階和前庭階沿縱向每個斷面的橫截面為長方形,且在蝸頂通過蝸孔相互連通;圓窗和卵圓窗是鼓階和前庭階基部上的膜狀結構,所建立耳蝸實體模型如圖 2 所示。為保證所建耳蝸的幾何尺寸更接近實驗數據,模型中橫截面積和寬度參考 Wever 及 Wysocki 的實驗測量數據[15-16]所確定,如圖 3 所示。模型中基底膜寬度和厚度分別由基部的 150 μm 和 7.5 μm 線性變化到頂部的 500 μm 和 2.5 μm。圓窗膜面積為 2.5 mm2,其厚度為 0.1 mm。耳蝸模型的其余幾何參數如圖 2 所示。
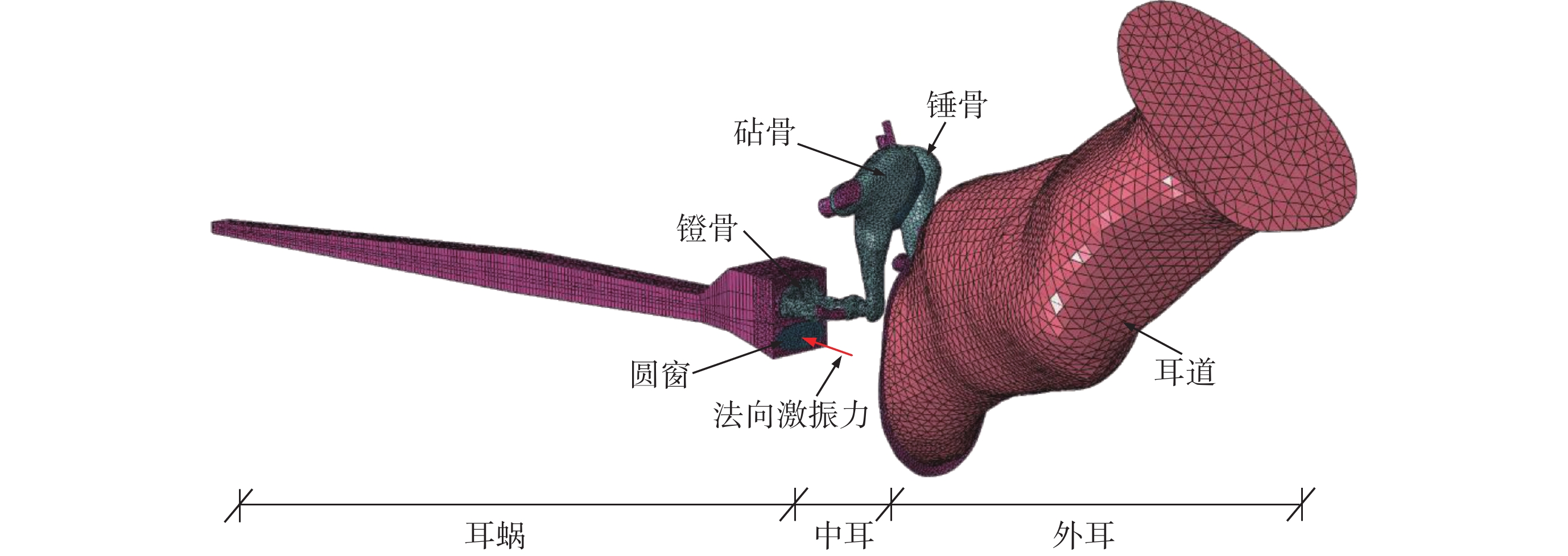 圖1
人耳有限元模型
Figure1.
The constructed human ear finite element model
圖1
人耳有限元模型
Figure1.
The constructed human ear finite element model
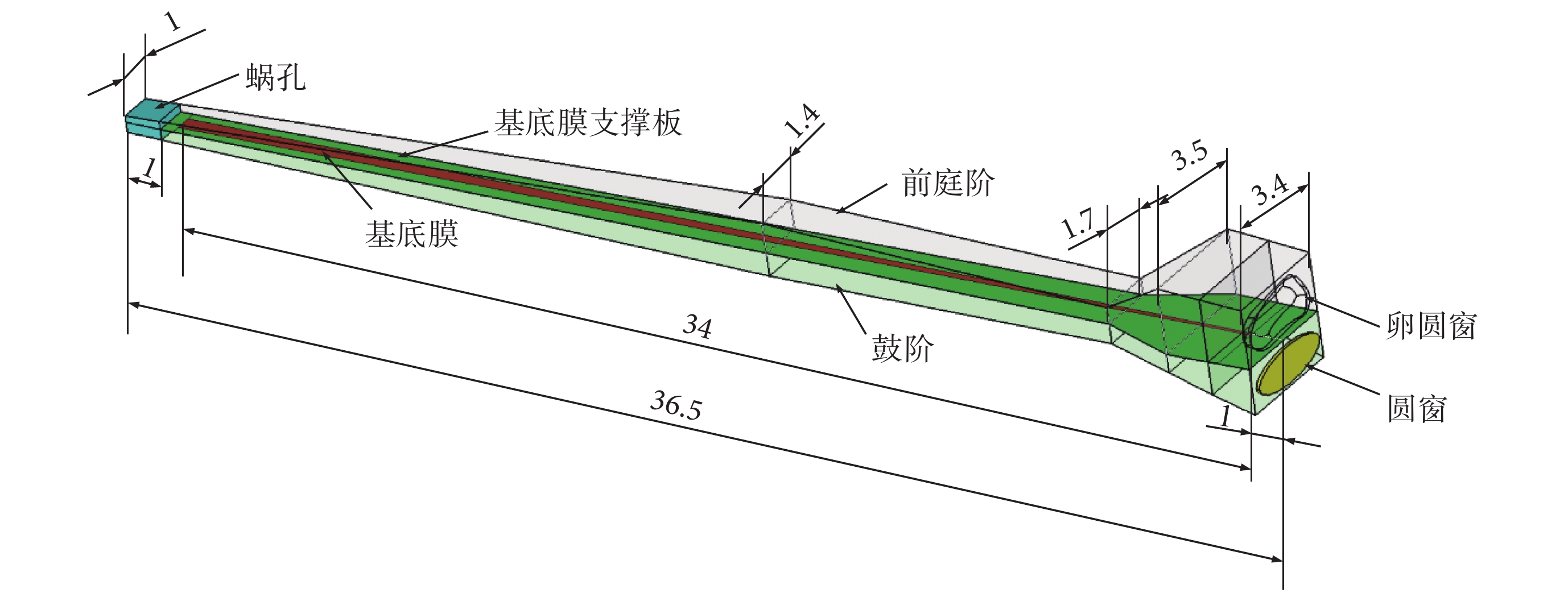 圖2
耳蝸實體模型
Figure2.
Solid model of the cochlea
圖2
耳蝸實體模型
Figure2.
Solid model of the cochlea
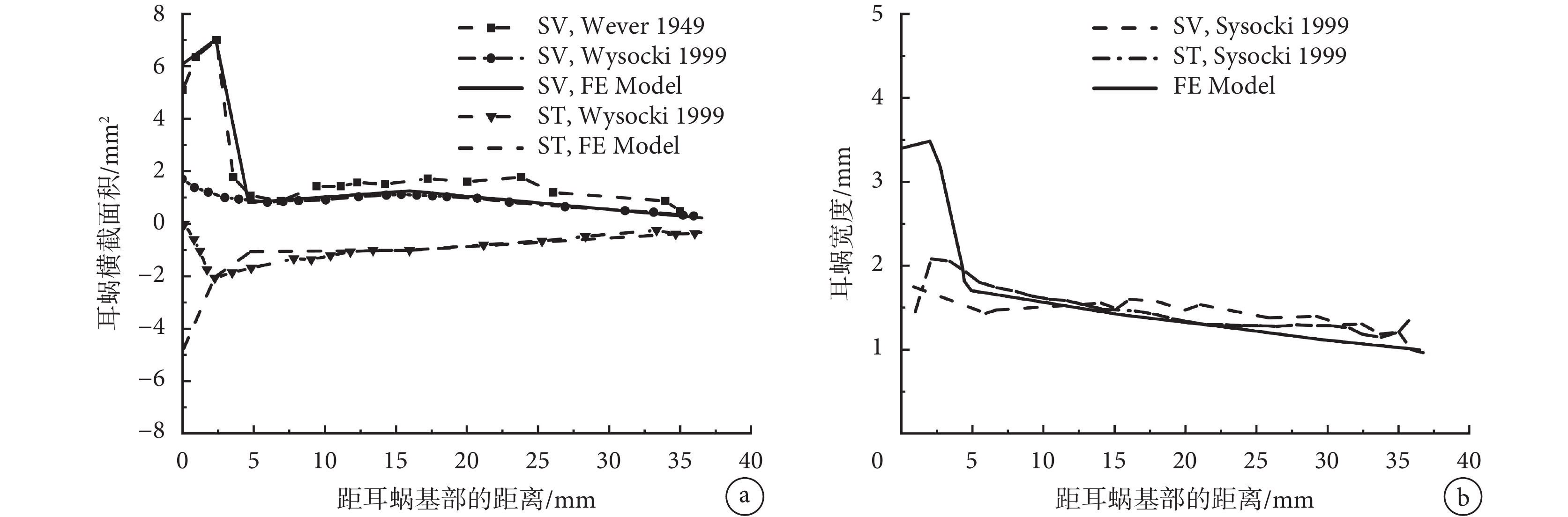 圖3
耳蝸模型幾何尺寸
圖3
耳蝸模型幾何尺寸
a.前庭階和鼓階的橫截面積;b.前庭階和鼓階的寬度
Figure3. The geometric dimensions of the constructed cochlear modela. the cross-sectional areas of the SV and ST; b. the width of SV and ST
1.2 材料屬性
人耳有限元模型中需要定義材料屬性的組織涉及到外耳道、中耳和耳蝸三個部分,其中外耳道氣體的密度和體積模量分別取 1.164 kg/m3 和 0.101 MPa。中耳結構的材料屬性綜合參考文獻報道[17-20]確定,如表 1 所示。耳蝸中鼓階和前庭階液體的流體密度和體積模量分別取 1 000 kg/m3 和 2 250 MPa。基底膜彈性模量由基部的 40 MPa 線性變化到中部的 15 MPa,再變化到頂部的 3 MPa,其能量損耗采用瑞利阻尼形式,阻尼系數為 α = 0 s?1,β = 7.5 × 10?6 s。圓窗膜和基底膜支撐板的彈性模量分別取 1 MPa 和 14 100 MPa。
鼓膜張緊部、鼓膜松弛部、鐙骨環韌帶、砧鐙關節、砧錘關節和圓窗采用線性粘彈性材料模型模擬能量耗散。其松弛模量表達式如式(1)所示。
 |
其中 E0 是表 1 中各組織所對應的彈性模量,e1 和 τ1 為表 2 所示的粘彈性參數[21];中耳其他組織能量耗散均采用瑞利阻尼形式,其阻尼系數為 α = 0 s?1,β = 7.5 × 10?5 s。
1.3 控制方程和邊界條件
在人耳聲傳遞過程中,涉及外耳道聲場與鼓膜的耦合,以及耳蝸內流體分別與鐙骨足板、圓窗和基底膜的耦合。本文建立不同物理場間的耦合關系,并使耦合模型滿足控制方程:
 |
其中:c 為聲音在流體中的速度, (k 表示流體體積模量,ρ 表示流體密度),p 為聲壓,t 為時間。本文中聲音在空氣和耳蝸內流體中的速度分別取 343 m/s 和 1 400 m/s[22],外耳道氣體和耳蝸內流體的密度分別取 1.21、1 000 kg/m3[23]。
(k 表示流體體積模量,ρ 表示流體密度),p 為聲壓,t 為時間。本文中聲音在空氣和耳蝸內流體中的速度分別取 343 m/s 和 1 400 m/s[22],外耳道氣體和耳蝸內流體的密度分別取 1.21、1 000 kg/m3[23]。
邊界條件為外耳道入口處施加壓力載荷模擬正常人耳的聲激勵;模型中鼓膜環韌帶、鼓膜張肌、錘骨側韌帶、錘骨前韌帶、錘骨上韌帶、砧骨后韌帶、砧骨上韌帶、鐙骨肌及鐙骨環韌帶的末端自由度約束為零,基底膜支撐板和圓窗外側周向節點均固定不動;設定耳道骨壁處與耳蝸骨壁處流體法向壓力為零;通過在模型內定義流固耦合面,實現不同物理場之間的耦合作用。文中有限元模型內定義的流體與固體耦合面具體包括:模擬耳道內空氣的聲單元與鼓膜的耦合、鐙骨足板表面與耳蝸流體耦合、基底膜與兩側的前庭階和鼓階內的流體耦合,以及圓窗膜與耳蝸流體耦合。
1.4 圓窗激振模擬及性能評價
考慮到現有臨床報道上圓窗激振式人工中耳所用的作動器主要是電磁式作動器[5, 24],且理想狀態下的電磁作動器作用近似為力激振[25],故通過在圓窗膜上施加法向激振力來模擬作動器激振圓窗。此外,該激振力大小設定為 50 μN[17],以激振起 90 dB 聲壓級(sound pressure level,SPL)鼓膜聲激勵下的等效位移。考慮到模型為線性系統,模型計算時,以包含語音的 250~8 000 Hz 頻率段內的 10 個頻率點為計算頻率點,對模型進行諧波載荷引起的穩態響應譜分析。
傳遞到耳蝸內的振動,以行波的形式沿基底膜從基部向頂部方向傳播。不同頻率的激勵,在基底膜上形成的行波的最大振幅位置不同:高頻響應靠近耳蝸基部,低頻響應靠近耳蝸頂部。對特定的頻率激勵,沿縱向響應最大的基底膜位置稱為該頻率對應的特征位置,該頻率稱之為該基底膜位置的特征頻率。耳蝸便是通過這些沿基底膜縱向的各個特征位置,負責感應從低頻到高頻中的特定頻率的聲音。因此,要使特定頻率的圓窗激振的感聲效果與正常傳聲等效,應該使兩種激勵下對應該頻率的基底膜特征位置處的位移相等。
基于該原理,在正常感聲時,即正向激勵下,當外耳道處輸入頻率為 ω、幅值為 PEC 的聲壓,設其激勵起的基底膜上特征位置 xCF 處的響應位移為  ,則其滿足:
,則其滿足:
 |
其中, 為從外耳道壓力至基底膜位移的人耳感聲正向傳遞函數[22]。考慮在正常感聲聲壓激勵下,人耳近似為線性系統,通過計算文中模型在 90 dB SPL 的耳道聲激勵下的基底膜響應位移
為從外耳道壓力至基底膜位移的人耳感聲正向傳遞函數[22]。考慮在正常感聲聲壓激勵下,人耳近似為線性系統,通過計算文中模型在 90 dB SPL 的耳道聲激勵下的基底膜響應位移  ,得到上述正向傳遞函數:
,得到上述正向傳遞函數:
 |
在圓窗激振時,即耳蝸逆向激勵下,當作動器驅動力 FRW 在圓窗膜后的鼓階內產生 PST 的壓強,則在該壓強驅動下,在基底膜上特征位置 xCF 處激起的響應位移為:
 |
其中, 為耳蝸逆向激振時,從圓窗膜后鼓階內壓力至基底膜位移的人耳感聲逆向傳遞函數[22]。由于本文主要目的是分析中耳炎病變對圓窗激振的影響,為簡化計算,所有頻率的圓窗激振皆統一在圓窗膜上施加幅值為 50 μN 的驅動力。基于模型,得到其激振下的基底膜響應位移
為耳蝸逆向激振時,從圓窗膜后鼓階內壓力至基底膜位移的人耳感聲逆向傳遞函數[22]。由于本文主要目的是分析中耳炎病變對圓窗激振的影響,為簡化計算,所有頻率的圓窗激振皆統一在圓窗膜上施加幅值為 50 μN 的驅動力。基于模型,得到其激振下的基底膜響應位移  。又因為基底膜響應是誘發人耳感聲的主要原因,故其感聲效果等效于在基底膜特征位置處產生同樣幅值響應位移的鼓膜聲激勵。即滿足:
。又因為基底膜響應是誘發人耳感聲的主要原因,故其感聲效果等效于在基底膜特征位置處產生同樣幅值響應位移的鼓膜聲激勵。即滿足:
 |
進而得到其對應的等效鼓膜聲激勵聲壓為:
 |
因此,可以用 SPLEQ,即圓窗激振下基底膜響應的等效鼓膜激振聲壓級,來評估圓窗激振的性能:
 |
進而通過對比研究病變前后圓窗激振該等效聲壓級的變化,來評估中耳炎病變對圓窗激振聽力補償性能的影響。
1.5 中耳炎病變模擬
中耳炎是一種累及中耳全部或部分結構的炎性病變,常表現為鼓膜病變、聽小骨腐蝕甚至消失。其中,鼓膜病變又包括鼓膜增厚、鼓膜硬化及鼓膜穿孔,且鼓膜修復術后同樣會改變其厚度和硬度。為了研究鼓膜增厚的影響,將模型中鼓膜的厚度先后增大為正常厚度的 2 倍和 4 倍,該鼓膜厚度的增大倍數與 Gan 等[26]研究一致。為模擬鼓膜硬化,將其彈性模量變為正常的 10 倍和 100 倍,彈性模量的放大倍數與 Koike 等[27]一致。研究鼓膜穿孔大小對圓窗激振的影響時,在所建模型的鼓膜上分別構建面積為 9.11、28.26、51.93 mm2 的穿孔,各約占鼓膜面積的 15%、45%、85%,鼓膜穿孔大小的比例與 Lee 等[28]一致。
中耳炎造成的聽小骨腐蝕會破壞正常聽骨鏈結構,尤其是錘骨柄、錘骨頭、砧骨長突和鐙骨上部結構的腐蝕發生最多[29-30]。通過刪除模型中對應的組織結構,實現上述常見的聽小骨腐蝕的模擬。
2 結果
2.1 模型可靠性驗證
通過在模型耳道入口處施加 90 dB SPL 的聲壓(0.632 Pa)來模擬人耳正常感聲,以上述圓窗激振模擬時所選取的 10 個頻率點為計算頻率點,對模型進行諧響應分析,并將計算結果與相關實驗數據進行對比,驗證所建人耳模型的可靠性。
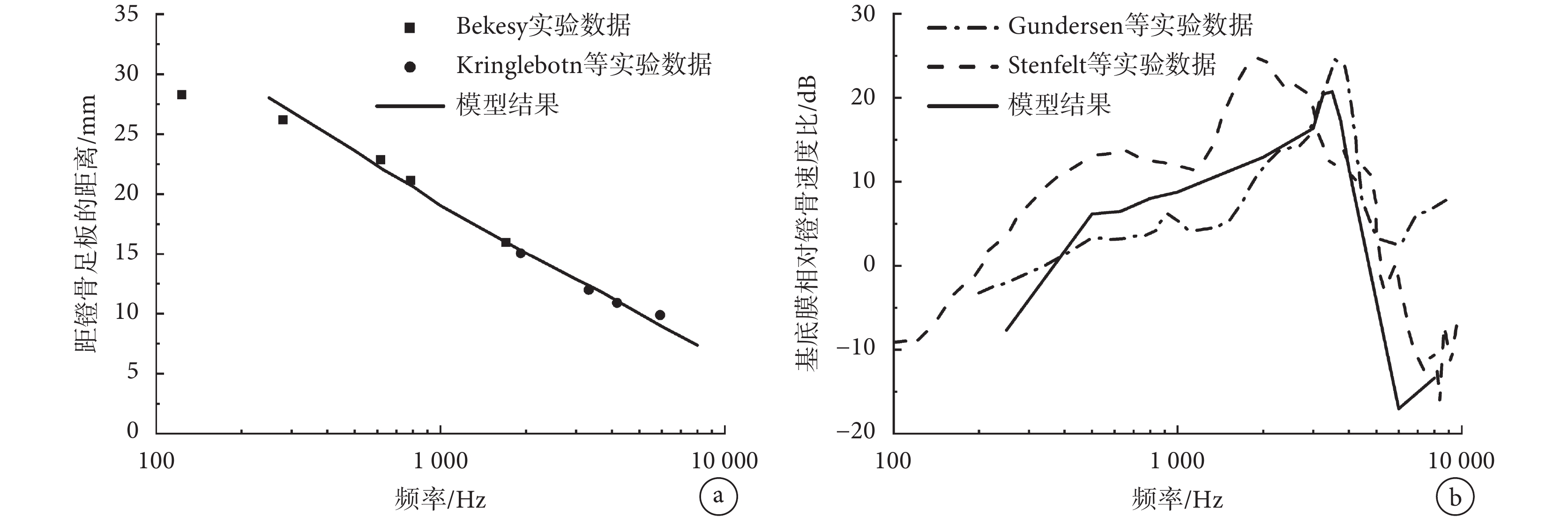
基底膜上特征頻率點的縱向位置關系具體表現為靠近耳蝸基部的基底膜對高頻聲音敏感,而靠近耳蝸頂部的基底膜對低頻聲音敏感,不同頻率的敏感位置沿基底膜縱向位置分布,是驗證所建模型可靠性的重要依據。由圖 4a 可見,模型結果與 Bekesy[31]和 Kringlebotn 等[32]的實驗數據一致。此外,還驗證了基底膜上距鐙骨 12 mm 處的相對運動速度,計算給定聲壓激勵下,基底膜上距耳蝸基部 12 mm 處的速度,與鐙骨足板運動速度的比值,如圖 4b 所示。模型結果和 Gundersen 等[33]數據在中低頻段相符,同 Stenfelt 等[34]數據在高頻段相吻合,并且在全頻段上趨勢一致。
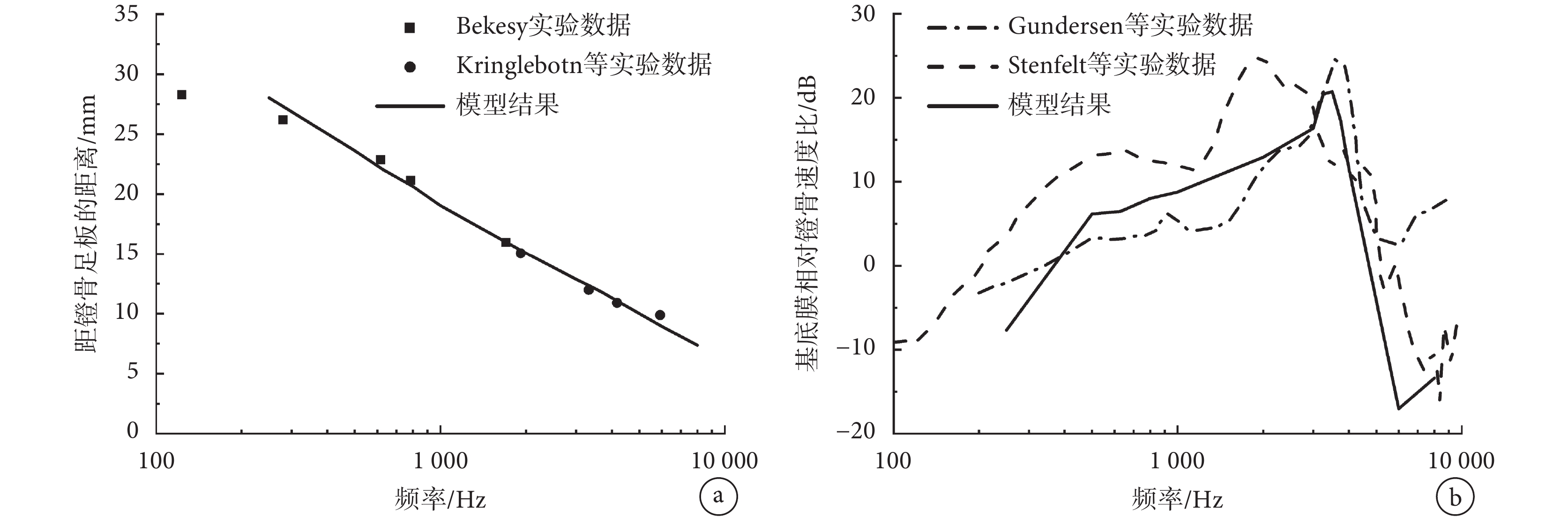 圖4
基底膜響應對比驗證
圖4
基底膜響應對比驗證
a. 基底膜上特征頻率點的縱向位置關系;b.基底膜上距鐙骨 12 mm 處的相對運動速度
Figure4. Comparison of the model predicted basilar membrane’s vibration with experimental dataa. longitudinal position relationship of characteristic frequency points on basilar membrane; b. relative motion velocity at 12 mm from the stapes on the basilar membrane
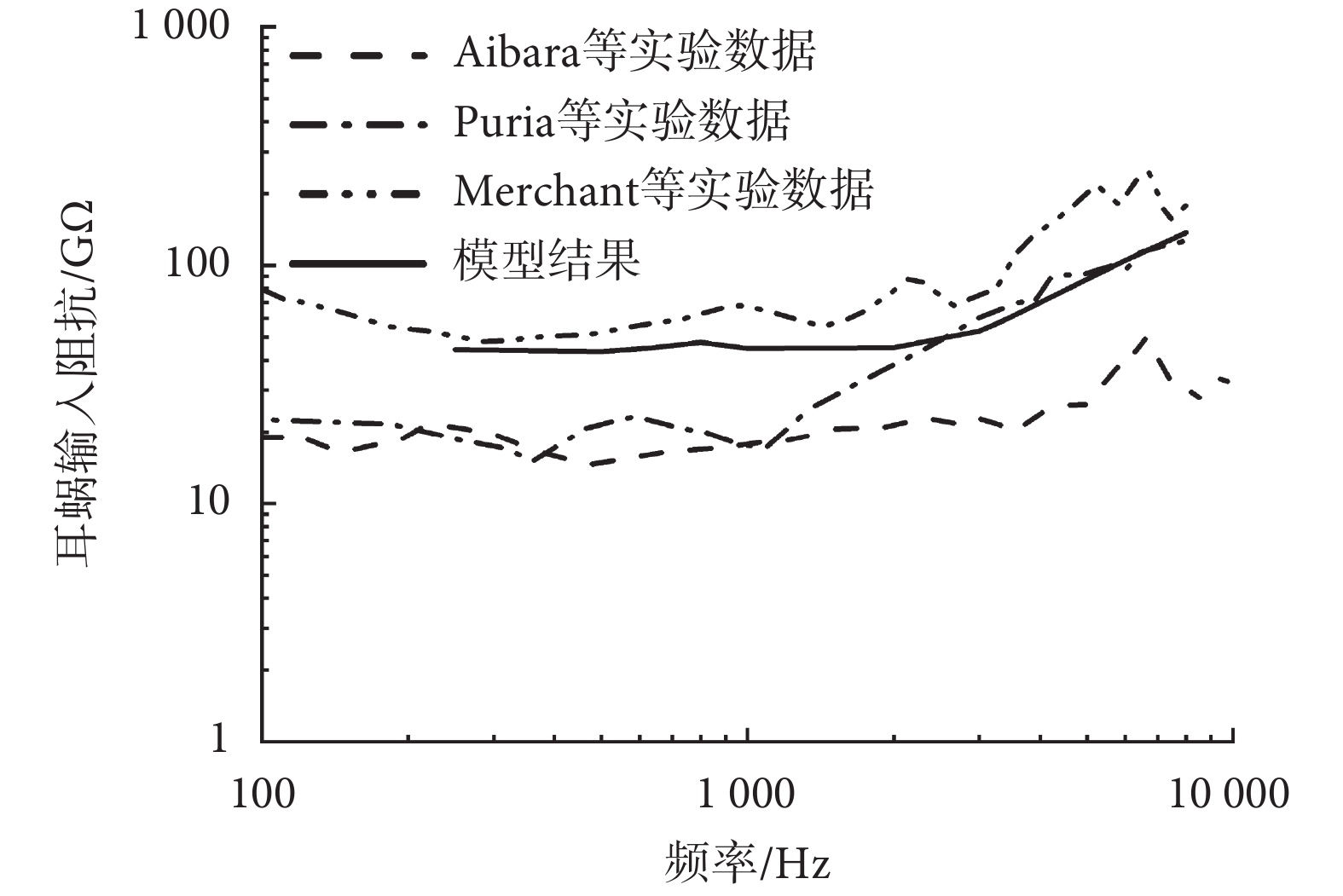
耳蝸輸入阻抗表征的是內耳對中耳的聲阻抗,是評價聲能從中耳傳遞到耳蝸的重要參數。將模型計算結果與文獻的實驗數據[35-37]進行對比,如圖 5 所示。整體趨勢上更逼近 Merchant 等[37]的實驗數據。對比上述三組數據表明,模型計算結果和實驗數據表現出良好的一致性,驗證了所建模型的準確性與可靠性。
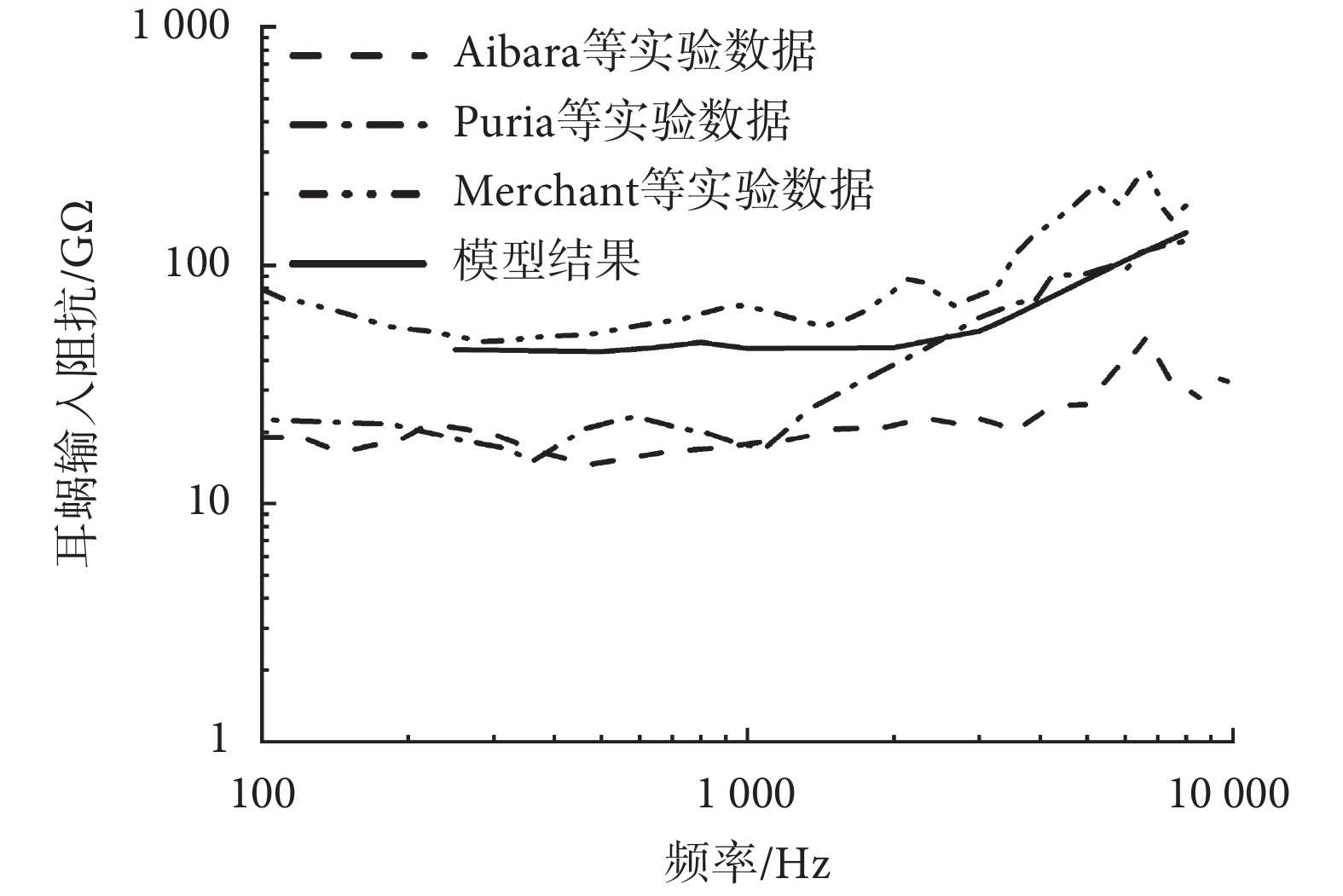 圖5
耳蝸輸入阻抗對比驗證
Figure5.
Comparison of the model predicted cochlear input impedance with the experimental data
圖5
耳蝸輸入阻抗對比驗證
Figure5.
Comparison of the model predicted cochlear input impedance with the experimental data
2.2 鼓膜增厚對圓窗激振的影響
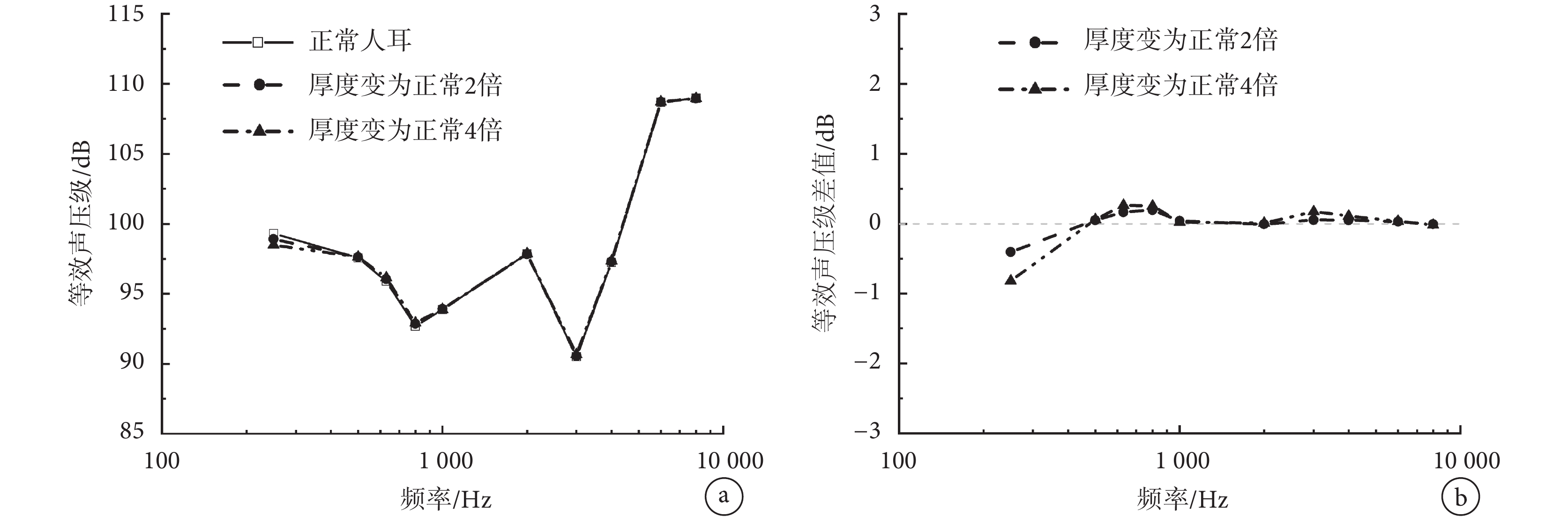
圖 6a 為計算所得的正常鼓膜和病變增厚鼓膜在相同圓窗激振下的等效聲壓級曲線;圖 6b 中曲線為增厚鼓膜與正常情況下的等效聲壓級差值。從圖中可見,鼓膜增厚將惡化圓窗激振低頻(< 500 Hz)響應,且這種惡化隨著鼓膜增厚程度的增大而增大,當鼓膜厚度增加 4 倍時,最大惡化為 0.81 dB;而對中高頻段的圓窗激振效果影響較小。
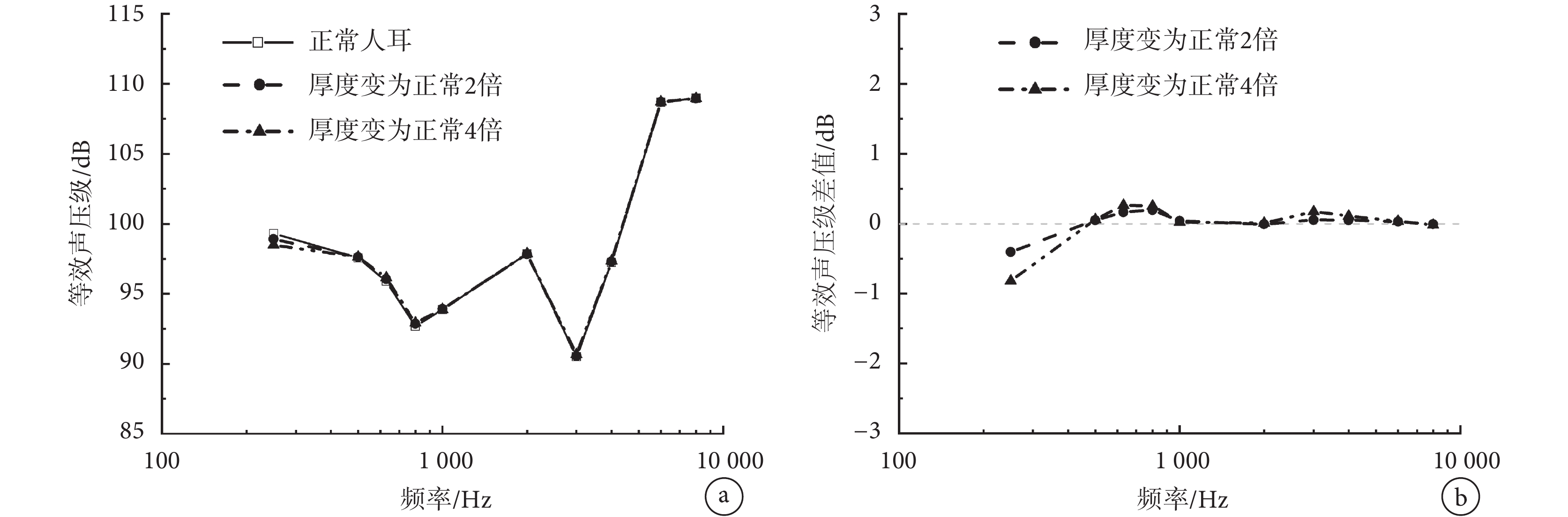 圖6
鼓膜增厚對圓窗激振的影響
圖6
鼓膜增厚對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure6. Effect of increased tympanic membrane thickness on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
2.3 鼓膜硬化對圓窗激振的影響
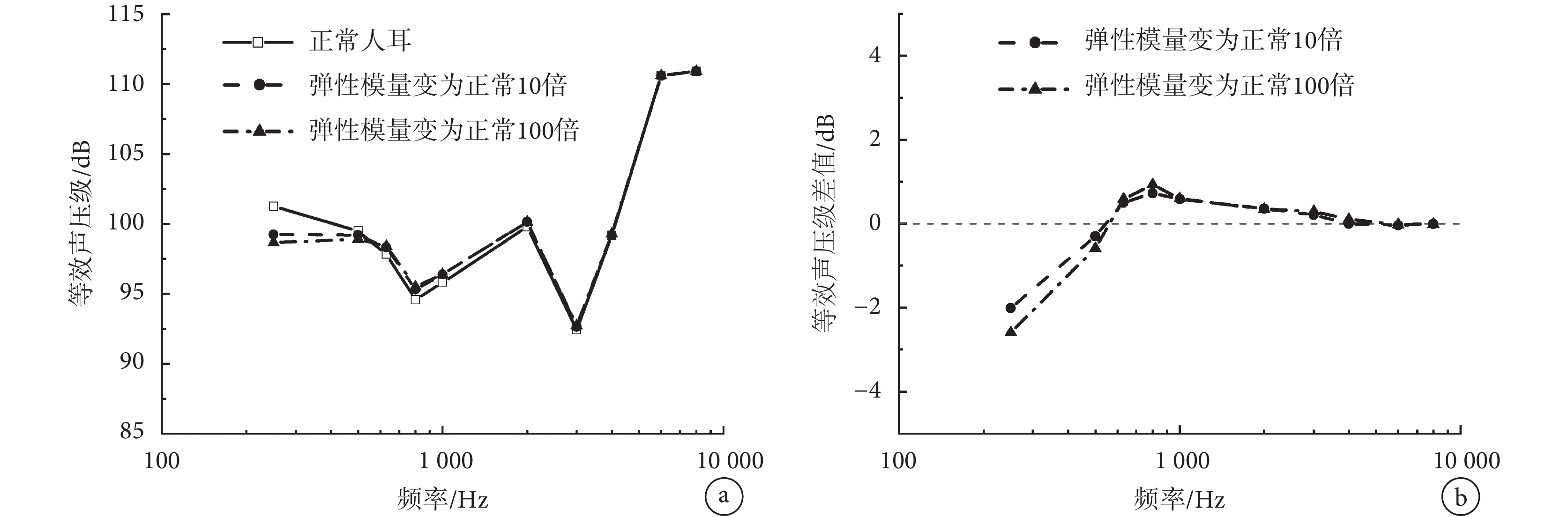
圖 7a 為計算所得的正常鼓膜和鼓膜硬化在相同圓窗激振下的等效聲壓級曲線;圖 7b 中曲線為鼓膜硬化與正常情況下的等效聲壓級差值。從圖中可見,鼓膜硬化將惡化圓窗激振低頻(< 500 Hz)響應,且這種惡化隨著鼓膜硬化程度的增大而增大,當鼓膜彈性模量增大 100 倍時,最大惡化為 2.6 dB;同時略微提高了圓窗激振在 630~3 000 Hz 頻率段的補償效果,在 800 Hz 處提高最大,提高值為 0.93 dB。
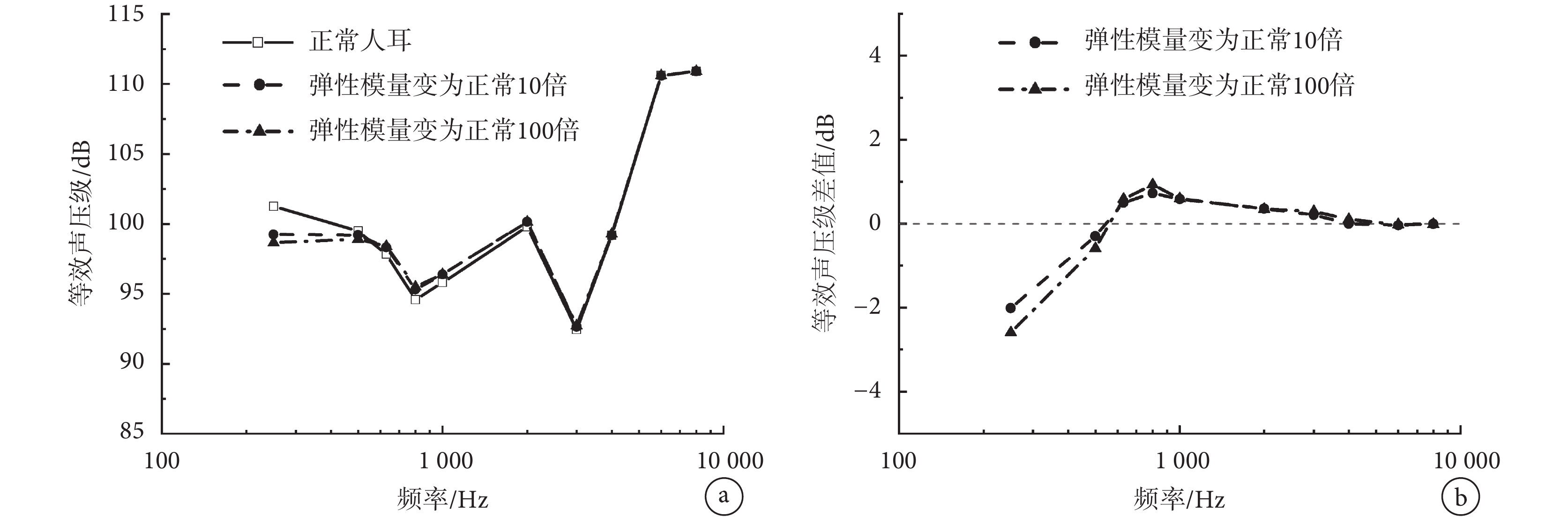 圖7
鼓膜硬化對圓窗激振的影響
圖7
鼓膜硬化對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure7. Effect of tympanosclerosis on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
2.4 鼓膜穿孔對圓窗激振的影響
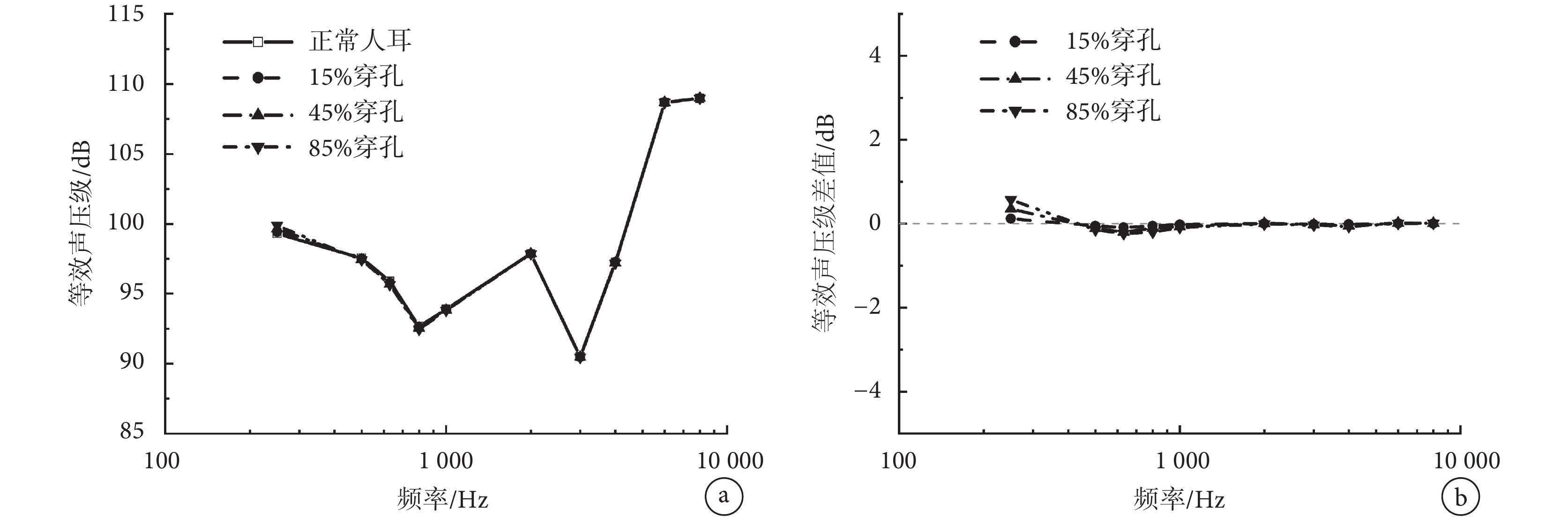
圖 8a 為計算得到的正常鼓膜和不同大小鼓膜穿孔在相同圓窗激振下的等效聲壓級曲線;圖 8b 中曲線為不同大小鼓膜穿孔與正常情況下的等效聲壓級差值。從圖中可見,三個不同大小的穿孔均在 250 Hz 處最大程度地提高了圓窗激振等效聲壓,提高值分別為 0.11、0.35、0.58 dB;同時略微降低了圓窗激振在 500~1 000 Hz 頻段的聽力補償性能,在 630 Hz 處降低最大,降低值分別為 0.08、0.20、0.23 dB。可見穿孔大小對圓窗激振的影響較小。
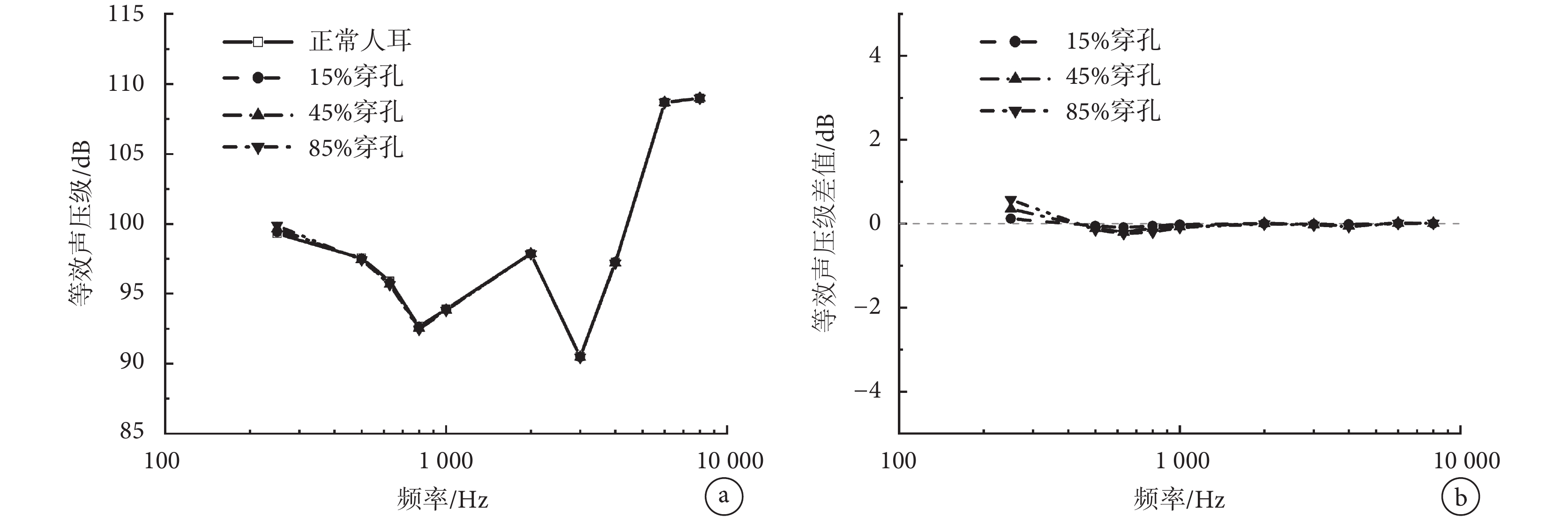 圖8
鼓膜穿孔大小對圓窗激振的影響
圖8
鼓膜穿孔大小對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure8. Effect of tympanic membrane perforation size on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
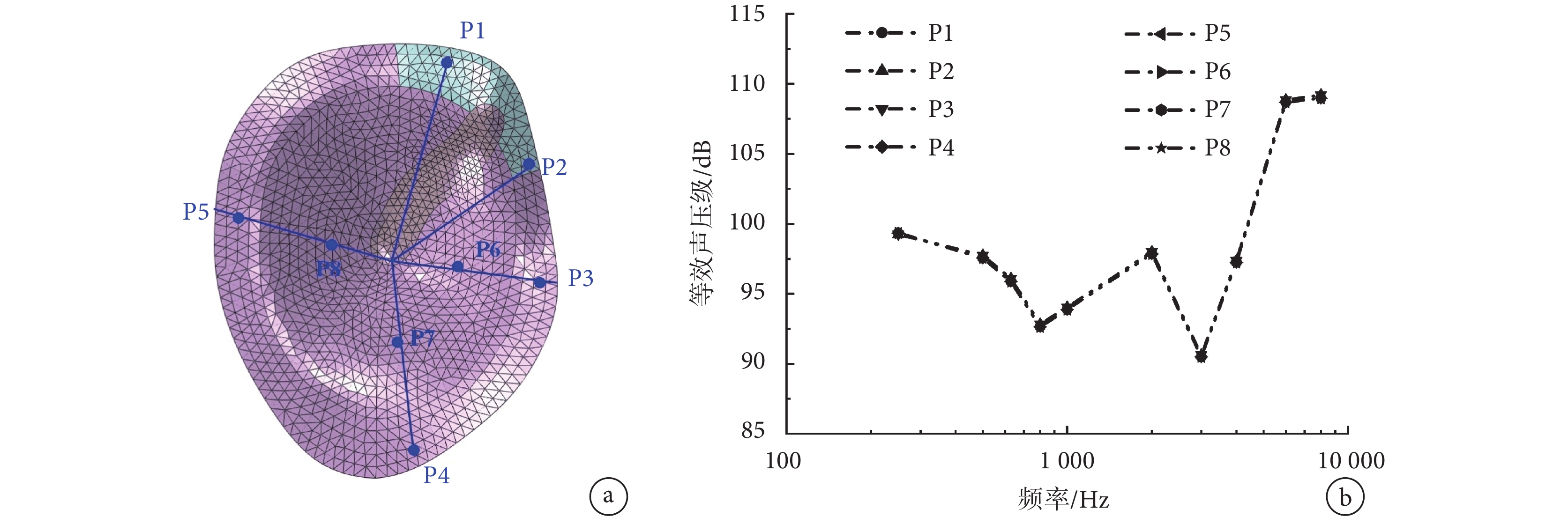
為了進一步研究鼓膜穿孔位置對圓窗激振的影響,在模型鼓膜上的不同部位刪除相應單元。圖 9a 為所研究的鼓膜不同穿孔位置示意圖,圖上標記點 P1 至 P8 位置為模擬穿孔的中心位置。由于前述計算鼓膜穿孔大小對圓窗激振的影響很小,因此本文在模擬穿孔位置對圓窗激振的影響時,只需保證 P1 至 P8 位置穿孔大小一致,統一設定為 0.87 mm2,與孫秀珍等[38]研究報道中所取的大小相近。由圖 9b 可見,鼓膜穿孔位置的改變對圓窗激振聽力補償效果的影響較小。
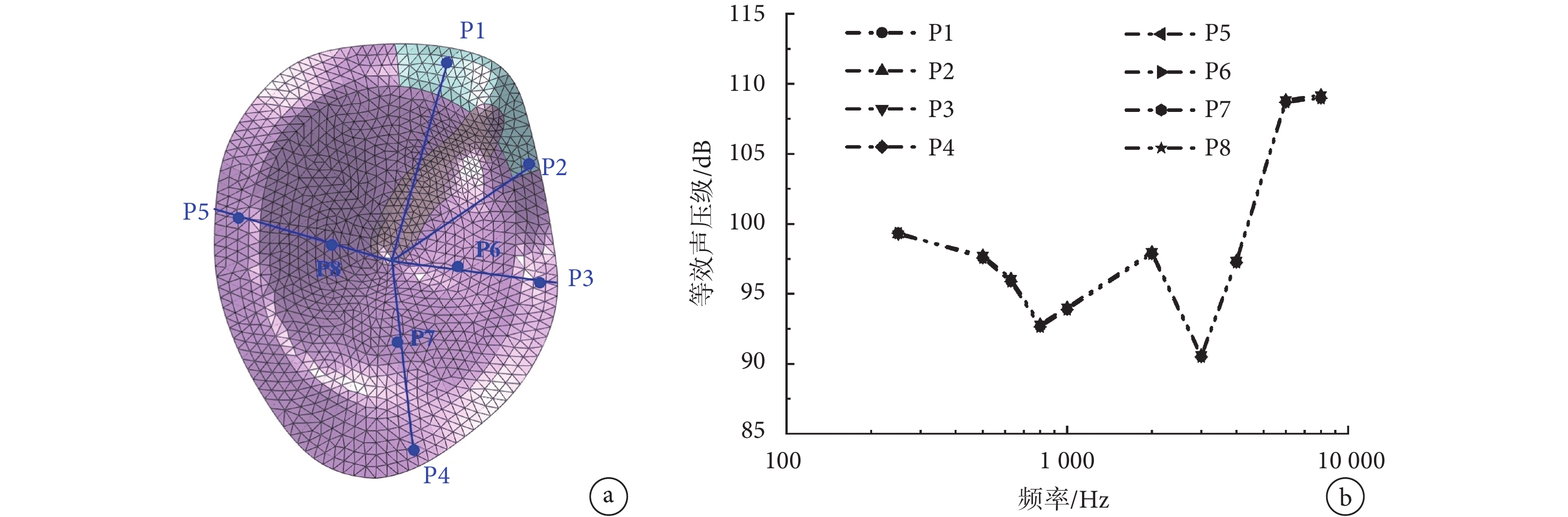 圖9
鼓膜穿孔位置對圓窗激振影響(穿孔面積為 0.87 mm2)
圖9
鼓膜穿孔位置對圓窗激振影響(穿孔面積為 0.87 mm2)
a.鼓膜穿孔位置示意圖;b.等效聲壓級
Figure9. Effect of the position of the tympanic membrane perforation on the performance of round-window stimulation (perforation area is 0.87 mm2)a. schematic diagram of the tympanic membrane perforation’s position; b. equivalent sound pressure level
2.5 聽小骨腐蝕對圓窗激振的影響
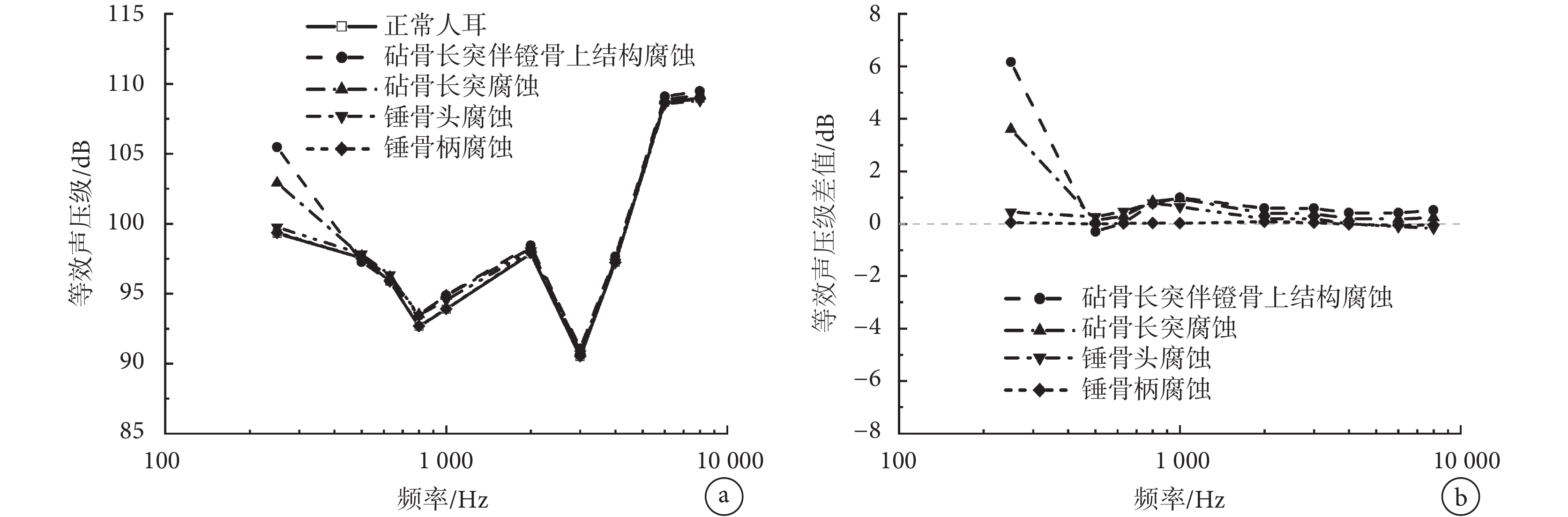
圖 10a 為計算所得的正常人耳和錘骨柄、錘骨頭、砧骨長突和砧骨長突伴鐙骨上部結構腐蝕在相同圓窗激振下的等效聲壓級曲線;圖 10b 為聽小骨腐蝕與正常情況下的等效聲壓級差值。從圖中可見,錘骨柄腐蝕對圓窗激振聽力補償影響很小。錘骨頭腐蝕對圓窗激振的影響略微增大,但最大處也僅提升了 0.79 dB。相對于前兩處聽小骨腐蝕病變的影響,砧骨長突腐蝕和砧骨長突伴鐙骨上部結構腐蝕對圓窗激振影響較大,提高了圓窗激振低頻段的響應,在 250 Hz 處提高最大,提高值分別為 3.61 dB 和 6.16 dB。
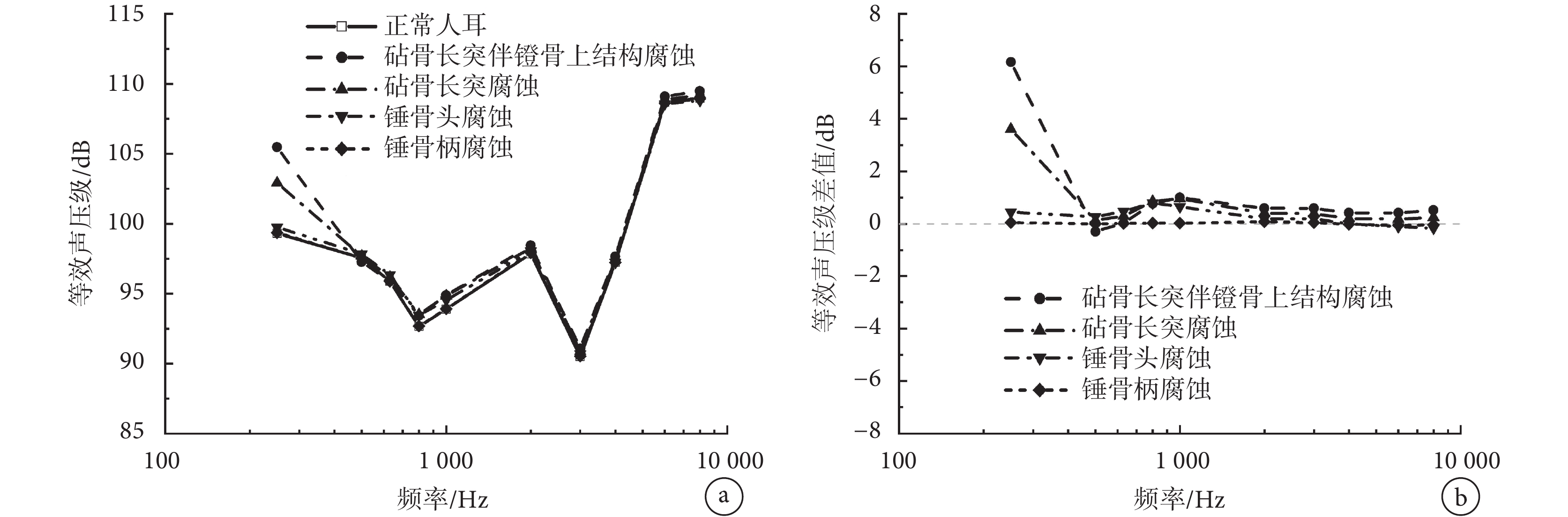 圖10
聽小骨腐蝕對圓窗激振的影響
圖10
聽小骨腐蝕對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure10. Effect of corrosion of ossicular chain on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
3 討論
為了確保本文所建模型更逼近真實人耳,對外耳道和中耳結構采用逆向成型技術進行建模。由于微 CT 影像圖中很難準確識別耳蝸前庭膜和基底膜部分,耳蝸部分采用三維工程軟件繪制的方法對其進行簡化建模。相對于真實耳蝸解剖結構,文中耳蝸模型主要在以下三個方面進行簡化。首先,對于腔體構成進行簡化。實際耳蝸是由三個管腔結構組成,即前庭階、蝸管、鼓階,其中前庭階與蝸管由前庭膜隔開,而蝸管與鼓階通過基底膜隔開。由于前庭膜的主要作用在于隔離前庭階中外淋巴液與蝸管中內淋巴液這兩種離子組成不同的液體,進而使內淋巴液中的聽毛細胞能夠將振動信號轉化為聽神經的生物電信號,而對耳蝸內振動傳遞的影響較小[39],故文中模型忽略了前庭膜,即將三腔耳蝸簡化為兩腔結構。其次,對于腔體橫截面形狀進行簡化。Holmes 等[40]理論研究表明,將這兩腔的橫截面形狀由近似半圓形變為長方形,對基底膜振動的計算結果無較大影響,故模型中兩腔橫截面簡化為長方形的形狀。最后,對于耳蝸空間結構進行簡化。真實的耳蝸是螺旋形狀,而文中將其簡化為直導管。Steele 等[41]學者理論研究顯示,螺旋結構對耳蝸內部響應無較大影響,使得這種直導管耳蝸簡化結構被耳力學研究領域廣泛采用[17, 21, 42]。但 Manoussaki 等[43]近期的研究表明,螺旋結構將增強耳蝸低頻段的感聲性能。因此,文中忽略了螺旋結構,采用直導管結構對耳蝸進行簡化建模,將低估基底膜靠近頂部微段對低頻信號的響應幅值。但由于文中在研究病變對人工中耳性能影響時,前后采用了相同的低幅值的基底膜聲響應對人工中耳激振補償性能進行標定,即對比是在相同的低幅值響應的基礎上展開的,故所得病變對人工中耳性能影響的計算結果不會因為沒考慮螺旋結構而存在較大差異。
關于人工中耳的聽力補償性能,很多學者采用鐙骨足板響應來評估。這種評估方法針對傳統聽骨鏈激振成立,對圓窗激振性能的評估并不可靠。這是因為圓窗激振的傳遞路徑與正常感聲不同:圓窗激振為逆向激勵,其振動能量通過驅動淋巴液流動,進而帶動鐙骨足板運動;而傳統激勵聽骨鏈的人工中耳則為正向激勵,是直接帶動鐙骨運動。由于人耳感受的聽神經沖動是由基底膜運動直接引起[22],故本文采用基底膜位移作為圓窗激振聽力補償性能的評價指標,以保證圓窗激振聽力補償評價的準確性。
針對中耳炎病變對人耳傳聲特性的影響已被多次報道[26-28, 44],但均是對正常感聲影響的研究。由于圓窗激振與正常感聲的聲音傳遞路徑相反,因此中耳炎病變對圓窗激振的影響有待進一步研究。本文研究結果表明,鼓膜增厚和鼓膜硬化主要惡化了圓窗激振的低頻性能,對中高頻影響較小。這主要是因為鼓膜的剛度隨著其彈性模量、厚度的增大而增大,故這兩種鼓膜病變增大了鼓膜的剛度,進而增大圓窗激振的阻抗,惡化了其補償性能。此外,動態系統中,剛度的變化主要影響系統的低頻響應,故這種惡化主要體現在低頻。劉迎曦等[45]和甘超孫等[46]的研究顯示,鼓膜增厚對正常人耳感聲的影響也主要是惡化其低頻響應,與本文得出其對圓窗激振影響的趨勢一致。關于鼓膜穿孔,文中研究結果表明,其對圓窗激振的影響也主要集中在低頻,小幅提升了其性能;小面積的鼓膜穿孔對圓窗激振影響較小,且不受穿孔位置影響。這種對圓窗激振性能的小幅提升,主要是因為鼓膜穿孔造成的整體阻抗降低。與此不同,孫秀珍等[38]研究表明,鼓膜穿孔對正常感聲影響較大,大幅降低了人耳低頻感聲性能。這主要是因為在正常感聲下,鼓膜起感聲作用,其穿孔大大降低了外部聲壓對鼓膜的激振面積,進而顯著降低了傳入人耳的能量。
相對于鼓膜病變對圓窗激振的影響,中耳炎引起的聽小骨腐蝕對圓窗激振的影響更為顯著,特別是砧骨、鐙骨組織的腐蝕。這主要是因為相對于聽小骨、耳蝸的阻抗,鼓膜阻抗在逆向激振總阻抗中占比較小。此外,文中研究結果顯示,相對于未導致聽骨鏈分離的錘骨柄腐蝕和錘骨頭腐蝕,造成聽骨鏈分離的聽小骨腐蝕顯著提高了圓窗激振低頻性能。這是由于聽骨鏈斷裂使斷裂前部的耳組織阻抗從逆向激振負載阻抗中直接去除,進而顯著減小了逆向激振的總阻抗,提高了圓窗激振的性能。不同于聽小骨腐蝕對圓窗激振性能的提升,Liu 等[47]研究顯示,聽小骨中錘骨柄腐蝕會降低正常感聲的性能。出現這種不同,是因為對正常感聲即正向傳聲來說,聽小骨主要起傳聲作用,其腐蝕必將降低其傳聲性能;而對圓窗激振,聽小骨的存在主要以阻抗的形式影響補償性能,其腐蝕會降低負載阻抗,進而提高性能。
4 結論
本文建立并驗證了包含不對稱耳蝸的人耳有限元模型,并基于基底膜特征頻率處的位移響應,研究了中耳炎引起的鼓膜病變和聽小骨腐蝕對圓窗激振聽力補償的影響。研究結果表明,鼓膜增厚和鼓膜硬化主要惡化了圓窗激振低頻段的補償效果;針對這兩類中耳炎病變,在作動器設計時,應該適當增大其低頻段的輸出量,以保證臨床的聽力補償效果。鼓膜穿孔和未導致聽骨鏈脫離的聽小骨腐蝕對圓窗激振的影響很小,而導致聽骨鏈脫離的聽小骨腐蝕對圓窗激振聽力補償效果影響較大,不同于鼓膜增厚和鼓膜硬化的影響,這種中耳炎病變類型卻可以顯著提高圓窗激振低頻段的響應。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
聽力損傷是最常見的疾病之一,世界上有近 5.38 億人患有不同程度的聽力障礙[1]。其中由感音神經性損傷造成的聽力障礙現階段尚無有效藥物及手術治療方法,大部分患者只能通過佩戴助聽器來補償聽力[2]。隨著現代語音處理算法及數字處理芯片的發展,助聽器聽力補償性能得到較大的提高,但仍然存在堵塞耳道、伴有聲反饋、高頻增益小等固有問題,為此許多機構開展了通過直接機械激勵聽小骨來補償聽力的植入式助聽裝置的研究[3-4],這種植入式助聽裝置又稱人工中耳。但是,部分患者伴有聽骨鏈病變,如中耳炎引起的聽小骨腐蝕[5],使得人工中耳作動器無法作用在聽小骨上,進而無法植入人工中耳。針對這類問題,Colletti 等[6]提出并在臨床上首次驗證了避開聽骨鏈直接激勵圓窗來進行聽力補償的可行性,為人工中耳補償伴有聽骨鏈損壞的感音神經性耳聾提供了新思路。
雖然臨床上證明了圓窗激振補償聽力損傷的可行性,但其術后效果針對不同患者表現出較大的個體差異[7]。為找出術后效果不佳的原因,國內外許多學者進行了相關研究。Arnold 等[8]研究了作動器在圓窗上不同的放置方式對耳蝸輸入能量的影響。Schraven 等[9]研究了不同作動器幾何形狀及耦合條件對圓窗激振效率的影響。張虎等[10]通過控制作動器不同大小的初始壓力和改變支撐體剛度,研究其對圓窗激振性能的影響。上述研究為臨床上圓窗激振式人工中耳性能的改進提供了重要參考,但主要針對人工中耳的設計參數和耦合條件,沒有考慮患者因中耳炎等引起的個體病變的影響。人耳具有結構超微、幾何形態復雜的特征,且很難獲得所需病變的人耳標本,這也使得關于中耳炎病變對圓窗激振影響的系統實驗研究不易進行。
針對上述問題,考慮到有限單元法在模擬人耳這種具有結構超微、幾何形態復雜、組織非同質性的復雜生物系統具有的優勢[11-13],本文利用逆向成型技術建立并驗證了人耳傳聲有限元模型,并基于此系統地研究了中耳炎引起的鼓膜病變和聽小骨腐蝕對圓窗激振式人工中耳的聽力補償效果的影響。本文研究結果可為圓窗激振式人工中耳進一步的優化設計提供參考,改進其臨床上的聽力補償效果。
1 材料與方法
1.1 人耳有限元模型
為了輔助分析中耳炎病變對圓窗激振的影響,構建了包括外耳道、中耳、耳蝸三部分的人耳傳聲有限元模型,如圖 1 所示。其中,外耳道和中耳部分是基于人體顳骨計算機斷層掃描(computed tomography,CT)與逆向成型技術所建立,其具體的建模工作先前已經報道[14]。而耳蝸部分,由于 CT 掃描圖像中基底膜分辨率較差,故采用三維軟件近似繪制的方法構建其幾何模型。為了簡化建模過程,忽略了耳蝸內部的前庭膜;考慮到實際耳蝸結構尺寸關于基底膜的不對稱性[15-16],將耳蝸簡化為充滿液體的非螺旋、不對稱的雙腔導管結構,包括鼓階(scala tympani,ST)、前庭階(scala vestibuli,SV)、蝸孔、基底膜、圓窗和卵圓窗。其中,基底膜固定在骨質支撐板上將兩腔體隔開;鼓階和前庭階沿縱向每個斷面的橫截面為長方形,且在蝸頂通過蝸孔相互連通;圓窗和卵圓窗是鼓階和前庭階基部上的膜狀結構,所建立耳蝸實體模型如圖 2 所示。為保證所建耳蝸的幾何尺寸更接近實驗數據,模型中橫截面積和寬度參考 Wever 及 Wysocki 的實驗測量數據[15-16]所確定,如圖 3 所示。模型中基底膜寬度和厚度分別由基部的 150 μm 和 7.5 μm 線性變化到頂部的 500 μm 和 2.5 μm。圓窗膜面積為 2.5 mm2,其厚度為 0.1 mm。耳蝸模型的其余幾何參數如圖 2 所示。
 圖1
人耳有限元模型
Figure1.
The constructed human ear finite element model
圖1
人耳有限元模型
Figure1.
The constructed human ear finite element model
 圖2
耳蝸實體模型
Figure2.
Solid model of the cochlea
圖2
耳蝸實體模型
Figure2.
Solid model of the cochlea
 圖3
耳蝸模型幾何尺寸
圖3
耳蝸模型幾何尺寸
a.前庭階和鼓階的橫截面積;b.前庭階和鼓階的寬度
Figure3. The geometric dimensions of the constructed cochlear modela. the cross-sectional areas of the SV and ST; b. the width of SV and ST
1.2 材料屬性
人耳有限元模型中需要定義材料屬性的組織涉及到外耳道、中耳和耳蝸三個部分,其中外耳道氣體的密度和體積模量分別取 1.164 kg/m3 和 0.101 MPa。中耳結構的材料屬性綜合參考文獻報道[17-20]確定,如表 1 所示。耳蝸中鼓階和前庭階液體的流體密度和體積模量分別取 1 000 kg/m3 和 2 250 MPa。基底膜彈性模量由基部的 40 MPa 線性變化到中部的 15 MPa,再變化到頂部的 3 MPa,其能量損耗采用瑞利阻尼形式,阻尼系數為 α = 0 s?1,β = 7.5 × 10?6 s。圓窗膜和基底膜支撐板的彈性模量分別取 1 MPa 和 14 100 MPa。
鼓膜張緊部、鼓膜松弛部、鐙骨環韌帶、砧鐙關節、砧錘關節和圓窗采用線性粘彈性材料模型模擬能量耗散。其松弛模量表達式如式(1)所示。
 |
其中 E0 是表 1 中各組織所對應的彈性模量,e1 和 τ1 為表 2 所示的粘彈性參數[21];中耳其他組織能量耗散均采用瑞利阻尼形式,其阻尼系數為 α = 0 s?1,β = 7.5 × 10?5 s。
1.3 控制方程和邊界條件
在人耳聲傳遞過程中,涉及外耳道聲場與鼓膜的耦合,以及耳蝸內流體分別與鐙骨足板、圓窗和基底膜的耦合。本文建立不同物理場間的耦合關系,并使耦合模型滿足控制方程:
 |
其中:c 為聲音在流體中的速度, (k 表示流體體積模量,ρ 表示流體密度),p 為聲壓,t 為時間。本文中聲音在空氣和耳蝸內流體中的速度分別取 343 m/s 和 1 400 m/s[22],外耳道氣體和耳蝸內流體的密度分別取 1.21、1 000 kg/m3[23]。
(k 表示流體體積模量,ρ 表示流體密度),p 為聲壓,t 為時間。本文中聲音在空氣和耳蝸內流體中的速度分別取 343 m/s 和 1 400 m/s[22],外耳道氣體和耳蝸內流體的密度分別取 1.21、1 000 kg/m3[23]。
邊界條件為外耳道入口處施加壓力載荷模擬正常人耳的聲激勵;模型中鼓膜環韌帶、鼓膜張肌、錘骨側韌帶、錘骨前韌帶、錘骨上韌帶、砧骨后韌帶、砧骨上韌帶、鐙骨肌及鐙骨環韌帶的末端自由度約束為零,基底膜支撐板和圓窗外側周向節點均固定不動;設定耳道骨壁處與耳蝸骨壁處流體法向壓力為零;通過在模型內定義流固耦合面,實現不同物理場之間的耦合作用。文中有限元模型內定義的流體與固體耦合面具體包括:模擬耳道內空氣的聲單元與鼓膜的耦合、鐙骨足板表面與耳蝸流體耦合、基底膜與兩側的前庭階和鼓階內的流體耦合,以及圓窗膜與耳蝸流體耦合。
1.4 圓窗激振模擬及性能評價
考慮到現有臨床報道上圓窗激振式人工中耳所用的作動器主要是電磁式作動器[5, 24],且理想狀態下的電磁作動器作用近似為力激振[25],故通過在圓窗膜上施加法向激振力來模擬作動器激振圓窗。此外,該激振力大小設定為 50 μN[17],以激振起 90 dB 聲壓級(sound pressure level,SPL)鼓膜聲激勵下的等效位移。考慮到模型為線性系統,模型計算時,以包含語音的 250~8 000 Hz 頻率段內的 10 個頻率點為計算頻率點,對模型進行諧波載荷引起的穩態響應譜分析。
傳遞到耳蝸內的振動,以行波的形式沿基底膜從基部向頂部方向傳播。不同頻率的激勵,在基底膜上形成的行波的最大振幅位置不同:高頻響應靠近耳蝸基部,低頻響應靠近耳蝸頂部。對特定的頻率激勵,沿縱向響應最大的基底膜位置稱為該頻率對應的特征位置,該頻率稱之為該基底膜位置的特征頻率。耳蝸便是通過這些沿基底膜縱向的各個特征位置,負責感應從低頻到高頻中的特定頻率的聲音。因此,要使特定頻率的圓窗激振的感聲效果與正常傳聲等效,應該使兩種激勵下對應該頻率的基底膜特征位置處的位移相等。
基于該原理,在正常感聲時,即正向激勵下,當外耳道處輸入頻率為 ω、幅值為 PEC 的聲壓,設其激勵起的基底膜上特征位置 xCF 處的響應位移為  ,則其滿足:
,則其滿足:
 |
其中, 為從外耳道壓力至基底膜位移的人耳感聲正向傳遞函數[22]。考慮在正常感聲聲壓激勵下,人耳近似為線性系統,通過計算文中模型在 90 dB SPL 的耳道聲激勵下的基底膜響應位移
為從外耳道壓力至基底膜位移的人耳感聲正向傳遞函數[22]。考慮在正常感聲聲壓激勵下,人耳近似為線性系統,通過計算文中模型在 90 dB SPL 的耳道聲激勵下的基底膜響應位移  ,得到上述正向傳遞函數:
,得到上述正向傳遞函數:
 |
在圓窗激振時,即耳蝸逆向激勵下,當作動器驅動力 FRW 在圓窗膜后的鼓階內產生 PST 的壓強,則在該壓強驅動下,在基底膜上特征位置 xCF 處激起的響應位移為:
 |
其中, 為耳蝸逆向激振時,從圓窗膜后鼓階內壓力至基底膜位移的人耳感聲逆向傳遞函數[22]。由于本文主要目的是分析中耳炎病變對圓窗激振的影響,為簡化計算,所有頻率的圓窗激振皆統一在圓窗膜上施加幅值為 50 μN 的驅動力。基于模型,得到其激振下的基底膜響應位移
為耳蝸逆向激振時,從圓窗膜后鼓階內壓力至基底膜位移的人耳感聲逆向傳遞函數[22]。由于本文主要目的是分析中耳炎病變對圓窗激振的影響,為簡化計算,所有頻率的圓窗激振皆統一在圓窗膜上施加幅值為 50 μN 的驅動力。基于模型,得到其激振下的基底膜響應位移  。又因為基底膜響應是誘發人耳感聲的主要原因,故其感聲效果等效于在基底膜特征位置處產生同樣幅值響應位移的鼓膜聲激勵。即滿足:
。又因為基底膜響應是誘發人耳感聲的主要原因,故其感聲效果等效于在基底膜特征位置處產生同樣幅值響應位移的鼓膜聲激勵。即滿足:
 |
進而得到其對應的等效鼓膜聲激勵聲壓為:
 |
因此,可以用 SPLEQ,即圓窗激振下基底膜響應的等效鼓膜激振聲壓級,來評估圓窗激振的性能:
 |
進而通過對比研究病變前后圓窗激振該等效聲壓級的變化,來評估中耳炎病變對圓窗激振聽力補償性能的影響。
1.5 中耳炎病變模擬
中耳炎是一種累及中耳全部或部分結構的炎性病變,常表現為鼓膜病變、聽小骨腐蝕甚至消失。其中,鼓膜病變又包括鼓膜增厚、鼓膜硬化及鼓膜穿孔,且鼓膜修復術后同樣會改變其厚度和硬度。為了研究鼓膜增厚的影響,將模型中鼓膜的厚度先后增大為正常厚度的 2 倍和 4 倍,該鼓膜厚度的增大倍數與 Gan 等[26]研究一致。為模擬鼓膜硬化,將其彈性模量變為正常的 10 倍和 100 倍,彈性模量的放大倍數與 Koike 等[27]一致。研究鼓膜穿孔大小對圓窗激振的影響時,在所建模型的鼓膜上分別構建面積為 9.11、28.26、51.93 mm2 的穿孔,各約占鼓膜面積的 15%、45%、85%,鼓膜穿孔大小的比例與 Lee 等[28]一致。
中耳炎造成的聽小骨腐蝕會破壞正常聽骨鏈結構,尤其是錘骨柄、錘骨頭、砧骨長突和鐙骨上部結構的腐蝕發生最多[29-30]。通過刪除模型中對應的組織結構,實現上述常見的聽小骨腐蝕的模擬。
2 結果
2.1 模型可靠性驗證
通過在模型耳道入口處施加 90 dB SPL 的聲壓(0.632 Pa)來模擬人耳正常感聲,以上述圓窗激振模擬時所選取的 10 個頻率點為計算頻率點,對模型進行諧響應分析,并將計算結果與相關實驗數據進行對比,驗證所建人耳模型的可靠性。
基底膜上特征頻率點的縱向位置關系具體表現為靠近耳蝸基部的基底膜對高頻聲音敏感,而靠近耳蝸頂部的基底膜對低頻聲音敏感,不同頻率的敏感位置沿基底膜縱向位置分布,是驗證所建模型可靠性的重要依據。由圖 4a 可見,模型結果與 Bekesy[31]和 Kringlebotn 等[32]的實驗數據一致。此外,還驗證了基底膜上距鐙骨 12 mm 處的相對運動速度,計算給定聲壓激勵下,基底膜上距耳蝸基部 12 mm 處的速度,與鐙骨足板運動速度的比值,如圖 4b 所示。模型結果和 Gundersen 等[33]數據在中低頻段相符,同 Stenfelt 等[34]數據在高頻段相吻合,并且在全頻段上趨勢一致。
 圖4
基底膜響應對比驗證
圖4
基底膜響應對比驗證
a. 基底膜上特征頻率點的縱向位置關系;b.基底膜上距鐙骨 12 mm 處的相對運動速度
Figure4. Comparison of the model predicted basilar membrane’s vibration with experimental dataa. longitudinal position relationship of characteristic frequency points on basilar membrane; b. relative motion velocity at 12 mm from the stapes on the basilar membrane
耳蝸輸入阻抗表征的是內耳對中耳的聲阻抗,是評價聲能從中耳傳遞到耳蝸的重要參數。將模型計算結果與文獻的實驗數據[35-37]進行對比,如圖 5 所示。整體趨勢上更逼近 Merchant 等[37]的實驗數據。對比上述三組數據表明,模型計算結果和實驗數據表現出良好的一致性,驗證了所建模型的準確性與可靠性。
 圖5
耳蝸輸入阻抗對比驗證
Figure5.
Comparison of the model predicted cochlear input impedance with the experimental data
圖5
耳蝸輸入阻抗對比驗證
Figure5.
Comparison of the model predicted cochlear input impedance with the experimental data
2.2 鼓膜增厚對圓窗激振的影響
圖 6a 為計算所得的正常鼓膜和病變增厚鼓膜在相同圓窗激振下的等效聲壓級曲線;圖 6b 中曲線為增厚鼓膜與正常情況下的等效聲壓級差值。從圖中可見,鼓膜增厚將惡化圓窗激振低頻(< 500 Hz)響應,且這種惡化隨著鼓膜增厚程度的增大而增大,當鼓膜厚度增加 4 倍時,最大惡化為 0.81 dB;而對中高頻段的圓窗激振效果影響較小。
 圖6
鼓膜增厚對圓窗激振的影響
圖6
鼓膜增厚對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure6. Effect of increased tympanic membrane thickness on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
2.3 鼓膜硬化對圓窗激振的影響
圖 7a 為計算所得的正常鼓膜和鼓膜硬化在相同圓窗激振下的等效聲壓級曲線;圖 7b 中曲線為鼓膜硬化與正常情況下的等效聲壓級差值。從圖中可見,鼓膜硬化將惡化圓窗激振低頻(< 500 Hz)響應,且這種惡化隨著鼓膜硬化程度的增大而增大,當鼓膜彈性模量增大 100 倍時,最大惡化為 2.6 dB;同時略微提高了圓窗激振在 630~3 000 Hz 頻率段的補償效果,在 800 Hz 處提高最大,提高值為 0.93 dB。
 圖7
鼓膜硬化對圓窗激振的影響
圖7
鼓膜硬化對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure7. Effect of tympanosclerosis on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
2.4 鼓膜穿孔對圓窗激振的影響
圖 8a 為計算得到的正常鼓膜和不同大小鼓膜穿孔在相同圓窗激振下的等效聲壓級曲線;圖 8b 中曲線為不同大小鼓膜穿孔與正常情況下的等效聲壓級差值。從圖中可見,三個不同大小的穿孔均在 250 Hz 處最大程度地提高了圓窗激振等效聲壓,提高值分別為 0.11、0.35、0.58 dB;同時略微降低了圓窗激振在 500~1 000 Hz 頻段的聽力補償性能,在 630 Hz 處降低最大,降低值分別為 0.08、0.20、0.23 dB。可見穿孔大小對圓窗激振的影響較小。
 圖8
鼓膜穿孔大小對圓窗激振的影響
圖8
鼓膜穿孔大小對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure8. Effect of tympanic membrane perforation size on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
為了進一步研究鼓膜穿孔位置對圓窗激振的影響,在模型鼓膜上的不同部位刪除相應單元。圖 9a 為所研究的鼓膜不同穿孔位置示意圖,圖上標記點 P1 至 P8 位置為模擬穿孔的中心位置。由于前述計算鼓膜穿孔大小對圓窗激振的影響很小,因此本文在模擬穿孔位置對圓窗激振的影響時,只需保證 P1 至 P8 位置穿孔大小一致,統一設定為 0.87 mm2,與孫秀珍等[38]研究報道中所取的大小相近。由圖 9b 可見,鼓膜穿孔位置的改變對圓窗激振聽力補償效果的影響較小。
 圖9
鼓膜穿孔位置對圓窗激振影響(穿孔面積為 0.87 mm2)
圖9
鼓膜穿孔位置對圓窗激振影響(穿孔面積為 0.87 mm2)
a.鼓膜穿孔位置示意圖;b.等效聲壓級
Figure9. Effect of the position of the tympanic membrane perforation on the performance of round-window stimulation (perforation area is 0.87 mm2)a. schematic diagram of the tympanic membrane perforation’s position; b. equivalent sound pressure level
2.5 聽小骨腐蝕對圓窗激振的影響
圖 10a 為計算所得的正常人耳和錘骨柄、錘骨頭、砧骨長突和砧骨長突伴鐙骨上部結構腐蝕在相同圓窗激振下的等效聲壓級曲線;圖 10b 為聽小骨腐蝕與正常情況下的等效聲壓級差值。從圖中可見,錘骨柄腐蝕對圓窗激振聽力補償影響很小。錘骨頭腐蝕對圓窗激振的影響略微增大,但最大處也僅提升了 0.79 dB。相對于前兩處聽小骨腐蝕病變的影響,砧骨長突腐蝕和砧骨長突伴鐙骨上部結構腐蝕對圓窗激振影響較大,提高了圓窗激振低頻段的響應,在 250 Hz 處提高最大,提高值分別為 3.61 dB 和 6.16 dB。
 圖10
聽小骨腐蝕對圓窗激振的影響
圖10
聽小骨腐蝕對圓窗激振的影響
a.等效聲壓級;b.等效聲壓級差值
Figure10. Effect of corrosion of ossicular chain on the performance of round-window stimulationa. equivalent sound pressure level; b. difference of equivalent sound pressure level
3 討論
為了確保本文所建模型更逼近真實人耳,對外耳道和中耳結構采用逆向成型技術進行建模。由于微 CT 影像圖中很難準確識別耳蝸前庭膜和基底膜部分,耳蝸部分采用三維工程軟件繪制的方法對其進行簡化建模。相對于真實耳蝸解剖結構,文中耳蝸模型主要在以下三個方面進行簡化。首先,對于腔體構成進行簡化。實際耳蝸是由三個管腔結構組成,即前庭階、蝸管、鼓階,其中前庭階與蝸管由前庭膜隔開,而蝸管與鼓階通過基底膜隔開。由于前庭膜的主要作用在于隔離前庭階中外淋巴液與蝸管中內淋巴液這兩種離子組成不同的液體,進而使內淋巴液中的聽毛細胞能夠將振動信號轉化為聽神經的生物電信號,而對耳蝸內振動傳遞的影響較小[39],故文中模型忽略了前庭膜,即將三腔耳蝸簡化為兩腔結構。其次,對于腔體橫截面形狀進行簡化。Holmes 等[40]理論研究表明,將這兩腔的橫截面形狀由近似半圓形變為長方形,對基底膜振動的計算結果無較大影響,故模型中兩腔橫截面簡化為長方形的形狀。最后,對于耳蝸空間結構進行簡化。真實的耳蝸是螺旋形狀,而文中將其簡化為直導管。Steele 等[41]學者理論研究顯示,螺旋結構對耳蝸內部響應無較大影響,使得這種直導管耳蝸簡化結構被耳力學研究領域廣泛采用[17, 21, 42]。但 Manoussaki 等[43]近期的研究表明,螺旋結構將增強耳蝸低頻段的感聲性能。因此,文中忽略了螺旋結構,采用直導管結構對耳蝸進行簡化建模,將低估基底膜靠近頂部微段對低頻信號的響應幅值。但由于文中在研究病變對人工中耳性能影響時,前后采用了相同的低幅值的基底膜聲響應對人工中耳激振補償性能進行標定,即對比是在相同的低幅值響應的基礎上展開的,故所得病變對人工中耳性能影響的計算結果不會因為沒考慮螺旋結構而存在較大差異。
關于人工中耳的聽力補償性能,很多學者采用鐙骨足板響應來評估。這種評估方法針對傳統聽骨鏈激振成立,對圓窗激振性能的評估并不可靠。這是因為圓窗激振的傳遞路徑與正常感聲不同:圓窗激振為逆向激勵,其振動能量通過驅動淋巴液流動,進而帶動鐙骨足板運動;而傳統激勵聽骨鏈的人工中耳則為正向激勵,是直接帶動鐙骨運動。由于人耳感受的聽神經沖動是由基底膜運動直接引起[22],故本文采用基底膜位移作為圓窗激振聽力補償性能的評價指標,以保證圓窗激振聽力補償評價的準確性。
針對中耳炎病變對人耳傳聲特性的影響已被多次報道[26-28, 44],但均是對正常感聲影響的研究。由于圓窗激振與正常感聲的聲音傳遞路徑相反,因此中耳炎病變對圓窗激振的影響有待進一步研究。本文研究結果表明,鼓膜增厚和鼓膜硬化主要惡化了圓窗激振的低頻性能,對中高頻影響較小。這主要是因為鼓膜的剛度隨著其彈性模量、厚度的增大而增大,故這兩種鼓膜病變增大了鼓膜的剛度,進而增大圓窗激振的阻抗,惡化了其補償性能。此外,動態系統中,剛度的變化主要影響系統的低頻響應,故這種惡化主要體現在低頻。劉迎曦等[45]和甘超孫等[46]的研究顯示,鼓膜增厚對正常人耳感聲的影響也主要是惡化其低頻響應,與本文得出其對圓窗激振影響的趨勢一致。關于鼓膜穿孔,文中研究結果表明,其對圓窗激振的影響也主要集中在低頻,小幅提升了其性能;小面積的鼓膜穿孔對圓窗激振影響較小,且不受穿孔位置影響。這種對圓窗激振性能的小幅提升,主要是因為鼓膜穿孔造成的整體阻抗降低。與此不同,孫秀珍等[38]研究表明,鼓膜穿孔對正常感聲影響較大,大幅降低了人耳低頻感聲性能。這主要是因為在正常感聲下,鼓膜起感聲作用,其穿孔大大降低了外部聲壓對鼓膜的激振面積,進而顯著降低了傳入人耳的能量。
相對于鼓膜病變對圓窗激振的影響,中耳炎引起的聽小骨腐蝕對圓窗激振的影響更為顯著,特別是砧骨、鐙骨組織的腐蝕。這主要是因為相對于聽小骨、耳蝸的阻抗,鼓膜阻抗在逆向激振總阻抗中占比較小。此外,文中研究結果顯示,相對于未導致聽骨鏈分離的錘骨柄腐蝕和錘骨頭腐蝕,造成聽骨鏈分離的聽小骨腐蝕顯著提高了圓窗激振低頻性能。這是由于聽骨鏈斷裂使斷裂前部的耳組織阻抗從逆向激振負載阻抗中直接去除,進而顯著減小了逆向激振的總阻抗,提高了圓窗激振的性能。不同于聽小骨腐蝕對圓窗激振性能的提升,Liu 等[47]研究顯示,聽小骨中錘骨柄腐蝕會降低正常感聲的性能。出現這種不同,是因為對正常感聲即正向傳聲來說,聽小骨主要起傳聲作用,其腐蝕必將降低其傳聲性能;而對圓窗激振,聽小骨的存在主要以阻抗的形式影響補償性能,其腐蝕會降低負載阻抗,進而提高性能。
4 結論
本文建立并驗證了包含不對稱耳蝸的人耳有限元模型,并基于基底膜特征頻率處的位移響應,研究了中耳炎引起的鼓膜病變和聽小骨腐蝕對圓窗激振聽力補償的影響。研究結果表明,鼓膜增厚和鼓膜硬化主要惡化了圓窗激振低頻段的補償效果;針對這兩類中耳炎病變,在作動器設計時,應該適當增大其低頻段的輸出量,以保證臨床的聽力補償效果。鼓膜穿孔和未導致聽骨鏈脫離的聽小骨腐蝕對圓窗激振的影響很小,而導致聽骨鏈脫離的聽小骨腐蝕對圓窗激振聽力補償效果影響較大,不同于鼓膜增厚和鼓膜硬化的影響,這種中耳炎病變類型卻可以顯著提高圓窗激振低頻段的響應。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。