運動學模型參數偏差是影響神經外科手術機器人精度的主要因素。為獲得更精確的模型參數,本文提出一種自動參數辨識及評價方法,首先基于運動學回路法建立全套神經外科手術機器人運動學參數辨識方程;并設計多次搖尖策略匹配末端工具與測量靶標坐標系;同時提出相對距離誤差和逆解重合誤差用于辨識精度評價;最后構建自動化參數辨識和精度評價系統并用于實驗室原型機和實際神經外科手術機器人參數辨識實驗。研究結果表明,本方法可以穩定自動地實現運動學模型參數辨識和評價,使用辨識后參數控制機器人可將相對距離誤差平均降低 33.96%,逆解重合誤差平均降低 67.30%。
引用本文: 李亮, 丁輝, 王廣志. 神經外科手術機器人運動學模型參數辨識及評價方法. 生物醫學工程學雜志, 2019, 36(6): 994-1002. doi: 10.7507/1001-5515.201810054 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
神經外科手術機器人可以替代傳統神經外科手術中的立體定向頭架,實現自動、快速、精準的電極定位,在癲癇病灶定位、深部腦刺激等手術中具有明顯的優勢[1]。主流的神經外科手術機器人系統均采用多自由度機械臂與末端手術工具組合的方案,如神經外科手術機器人系統 Remebot(柏惠維康 Inc.,中國)、神經外科手術機器人系統 NeuroMate(Renishaw Inc.,英國)、神經外科手術機器人系統 Rosa Brain(Medtech Inc.,法國)等[2-5]。機械臂是保證機器人手術精度的核心部件,但由于加工精度、裝配工藝、零件公差等原因,機械臂本體的實際運動學模型參數與標稱值之間存在一定偏差,導致其絕對定位精度降低[6]。固定在機械臂末端的注冊工具和定位定向工具的標稱尺寸參數與真實值之間也存在一定的偏差,同樣會降低總體定位和測量精度,影響最終手術效果。
準確識別機械臂本體及末端工具的運動學模型參數并據此構建個性化運動控制模型,是提升神經外科手術機器人精度的重要手段,目前已有許多成功報道。劉帥等[7]利用標定箱識別優傲 5 機械臂 UR5(Universal Robots Inc.,丹麥)構成的神經外科手術機器人參數,將其單點定位誤差由 4.05 mm 優化到 0.98 mm。劉達等[8]使用基于視覺的方法對自制的神經外科手術機器人機械臂本體進行了運動學參數標定,使其絕對定位誤差由 8.56 mm 優化到 0.64 mm。陳華等[9]在手術空間內對自建的神經外科手術機器人進行參數優化,使其定位精度達到 1 mm 以內。Vicentini 等[10]對 2 臺協作型機械臂 LWR(KUKA Inc.,德國)構成的雙臂神經外科手術機器人進行參數辨識和精度補償,將端到端靜態精度優化到 0.75 mm。Heinig 等[11]的研究中對框架構型的神經外科手術機器人系統進行參數標定,可以將 95% 的定位誤差控制在 0.50 mm 以內。Haidegger 等[12]對神經外科手術機器人系統 NeuroMate(Renishaw Inc.,英國)進行了精度優化,使其殘余誤差下降了 24%。
參數辨識可以較好地優化神經外科手術機器人精度,但其在臨床環境中應用時仍存在不足:① 辨識方法不完善。目前的研究中僅考慮了機械臂本體的參數辨識,對于末端工具參數的辨識考慮較少。少數研究將手術機器人的末端工具參數簡化為針尖點沿機械臂末端坐標系 X、Y、Z 方向的 3 個平移參數[7],但這并不符合臨床實際,因為神經外科手術機器人定位定向工具需同時描述其位置和姿態,如僅 3 個平移參數則無法完備表示。另外,由于定位定向工具的中空構造,其坐標原點和定向孔軸線方向位置參數無法直接測量,需要進一步提供完善的參數辨識方法。② 缺乏快速有效的精度評價方法。機械臂本體誤差、手術工具參數誤差、運動磨損以及操作不當均可能造成機器人系統精度下降。及時的評估機器人系統的精度水平,有助于醫生了解設備信息,預防意外發生。當前的臨床中仍缺乏快速、直觀、方便實施的手術機器人機械臂精度評價方法。③ 自動化程度低。當前研究大多針對系統樣機進行參數辨識,對辨識方法的人力資源消耗不敏感,自動化程度不高,需要較多的人工參與,操作繁瑣且易引入操作誤差。臨床中的手術機器人還需要滿足術前設備參數校正、定期質量檢定等需求,因此往往需要在醫療機構進行現場參數辨識和精度評價,目前仍缺乏一種自動化的現場參數辨識和精度評價方案。
針對以上問題,本文首先給出了手術機器人正逆運動學模型,提出了運動學模型參數辨識方法與精度評價方法,然后給出了具體實現方案,最后驗證了本文方法的有效性。
1 手術機器人運動學模型
精準的機器人神經外科手術關鍵在于精準的注冊和定位定向,準確的機器人運動學模型是精準的注冊和定位定向的必要條件。本文采用的 6 自由度串聯機械臂及對應末端工具建立了手術機器人運動學模型。從數學模型角度上看,注冊所用探針工具是定位定向工具的特例,故在此僅考慮定位定向工具模型。
本文依據戴南威特-哈特伯格(Denavit-Hartenberg,DH)連桿參數描述方法建立機器人運動學模型[13-14]。機械臂第i、i-1 連桿坐標系之間的變換關系如式(1)所示,φi、di、ai、αi、βi 表示連桿間運動學參數。
 |
其中, 、
、 、
、 表示繞對應坐標軸旋轉的齊次變換矩陣,
表示繞對應坐標軸旋轉的齊次變換矩陣, 、
、 表示沿對應坐標軸平移的齊次變換矩陣。
表示沿對應坐標軸平移的齊次變換矩陣。
設機械臂定位定向工具坐標系到第 6 連桿坐標系的變換矩陣為  ,工具坐標系到基坐標系矩陣為
,工具坐標系到基坐標系矩陣為  。機器人的運動學模型如式(2)所示,表示為
。機器人的運動學模型如式(2)所示,表示為  與關節角度 θ1~6 間函數關系,其中 φ1~6、d1~6、a1~6、α1~6、β1~6、
與關節角度 θ1~6 間函數關系,其中 φ1~6、d1~6、a1~6、α1~6、β1~6、 即為神經外科手術機器人系統待辨識運動學參數。
即為神經外科手術機器人系統待辨識運動學參數。
 |
2 參數辨識方法
2.1 參數辨識流程
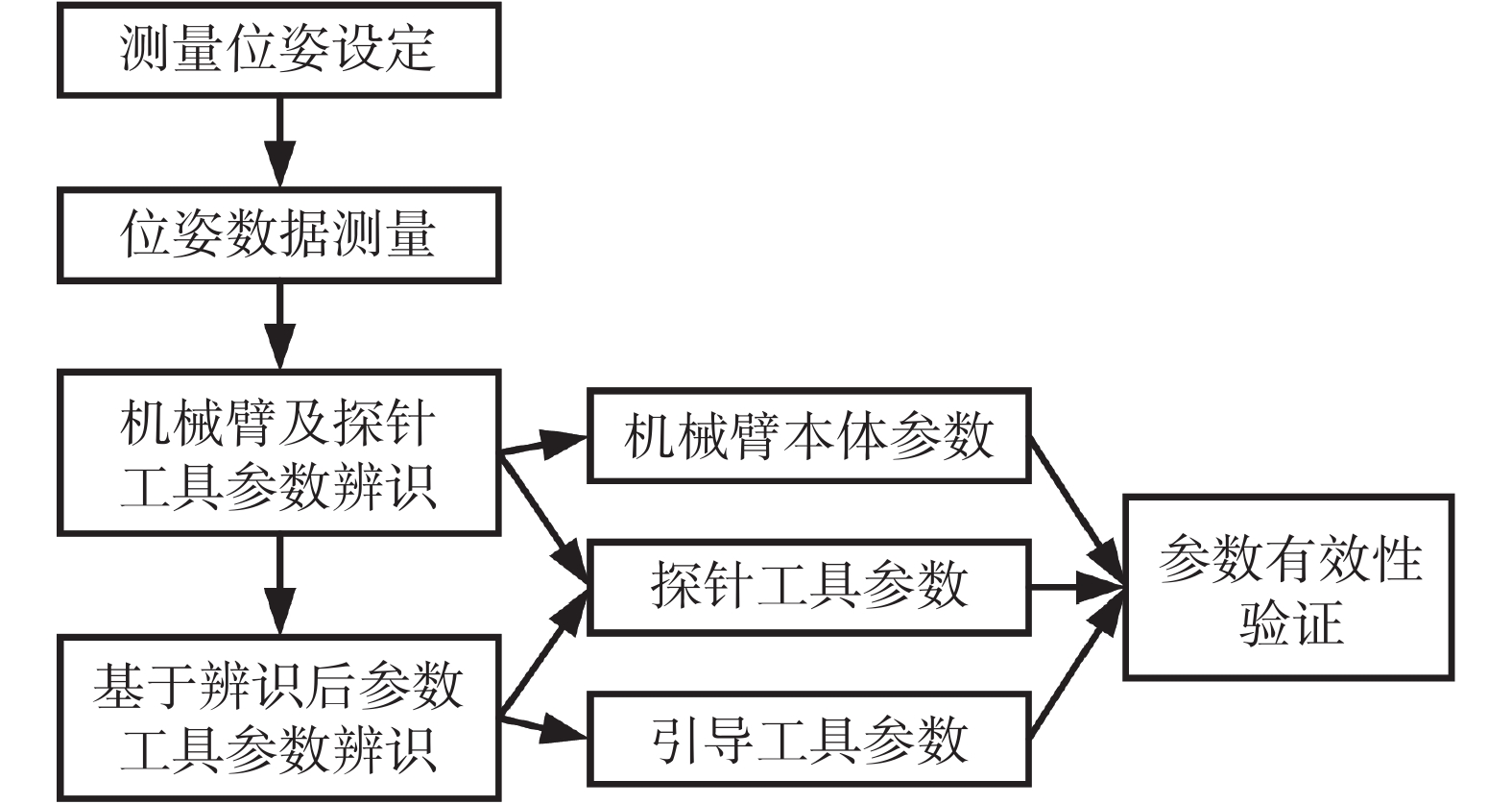
為實現自動化的參數辨識,本文設計如圖 1 所示機器人運動學參數辨識流程。首先設定測量位姿并完成位姿數據自動測量;然后對機械臂探針注冊過程進行聯合參數辨識,獲取機械臂及探針工具運動學參數;最后基于辨識后機械臂運動學參數,對定位定向工具參數進行辨識,進而獲得機器人系統全部運動學參數。
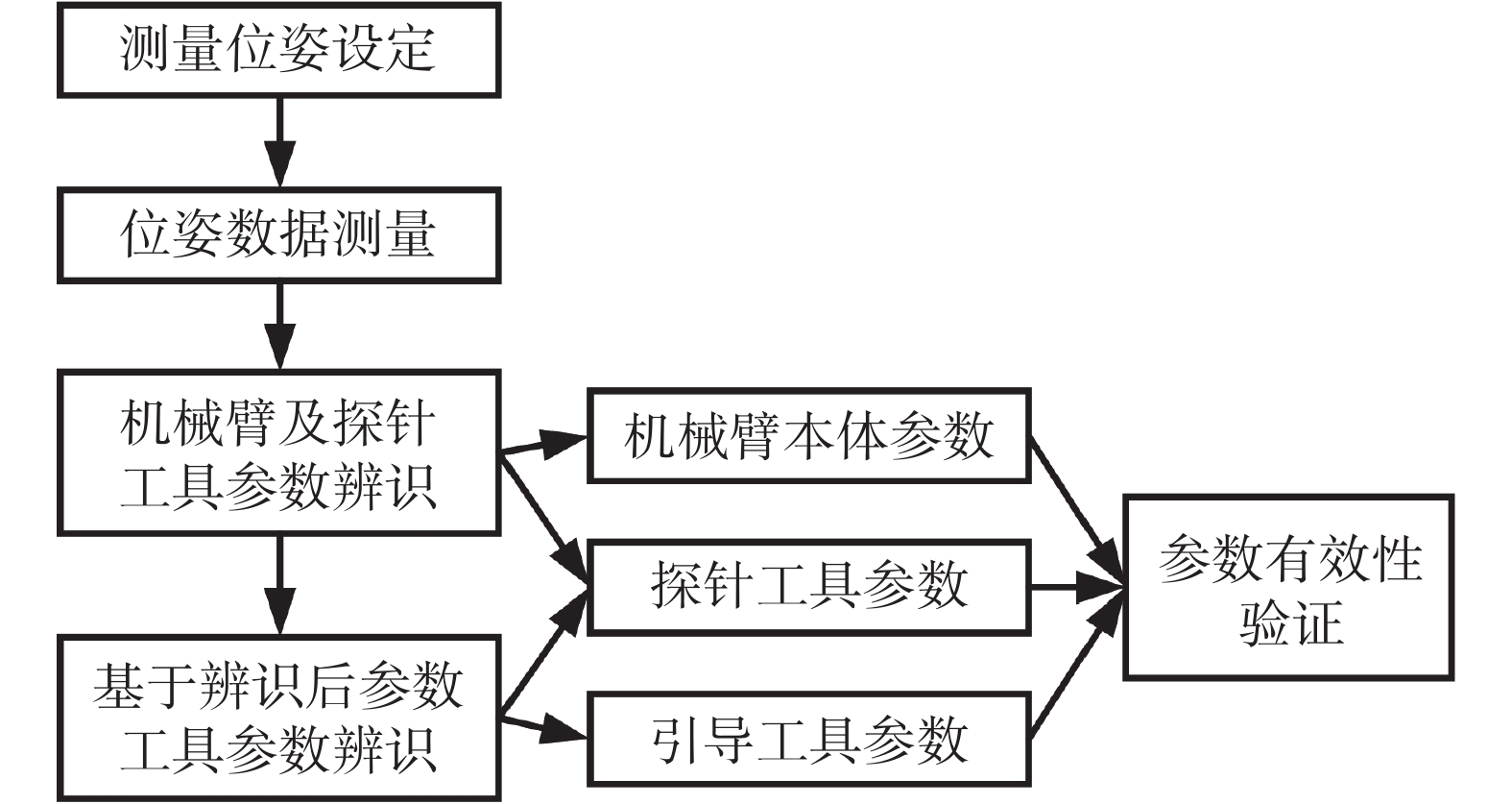 圖1
參數辨識流程
Figure1.
Parameter identification flow chart
圖1
參數辨識流程
Figure1.
Parameter identification flow chart
2.2 機械臂及探針工具參數聯合辨識方法
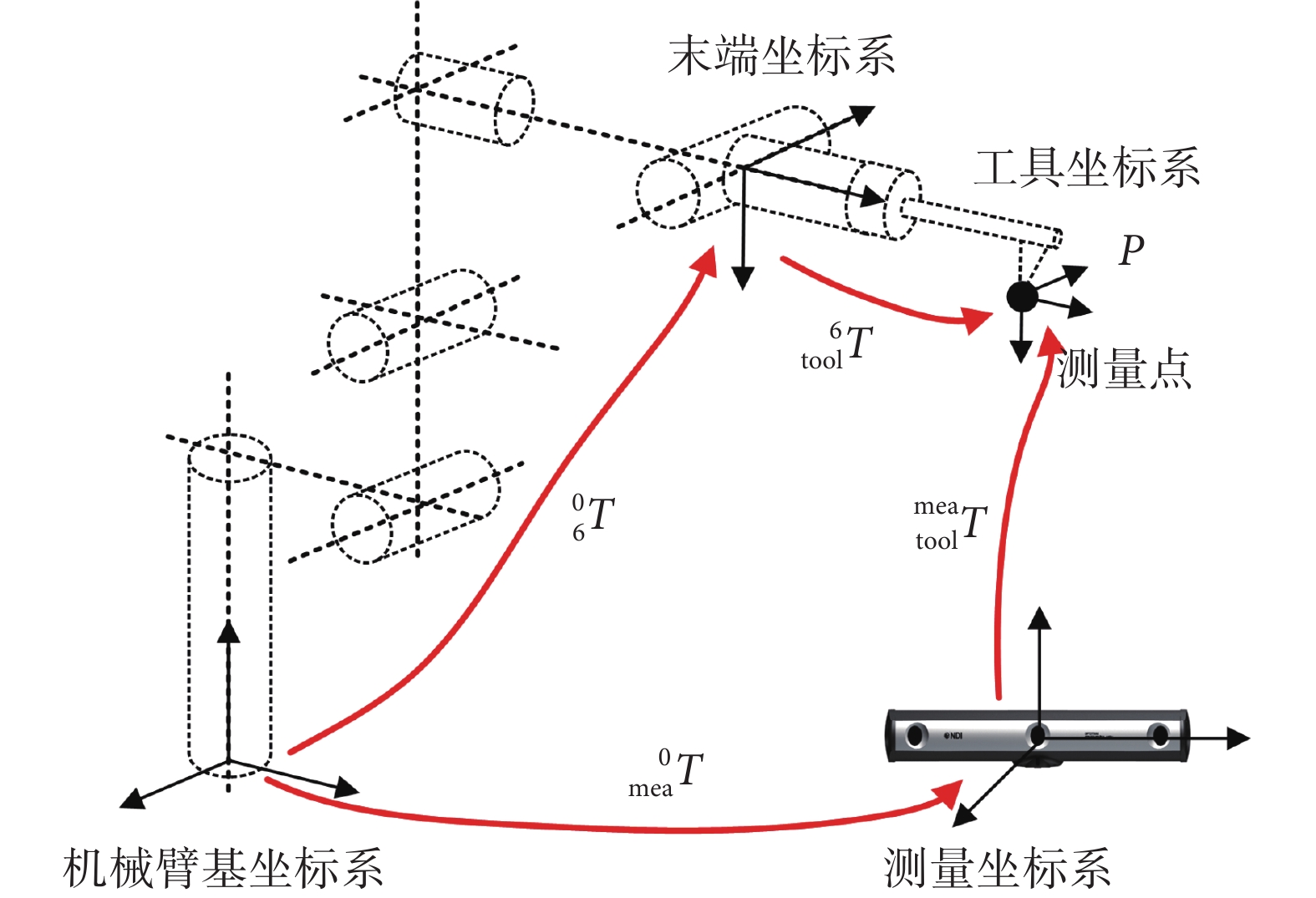
為同步辨識機械臂本體及探針工具參數,本文采用運動學回路法構建待辨識參數方程。設計如圖 2 所示實驗,使用高精度測量設備通過跟蹤靶標獲取機械臂末端工具位姿。首先控制機械臂末端工具移動到某一設定測量點,并由機械臂正運動學模型計算測量點在機械臂基坐標系下的位置坐標P0,如式(3)所示:
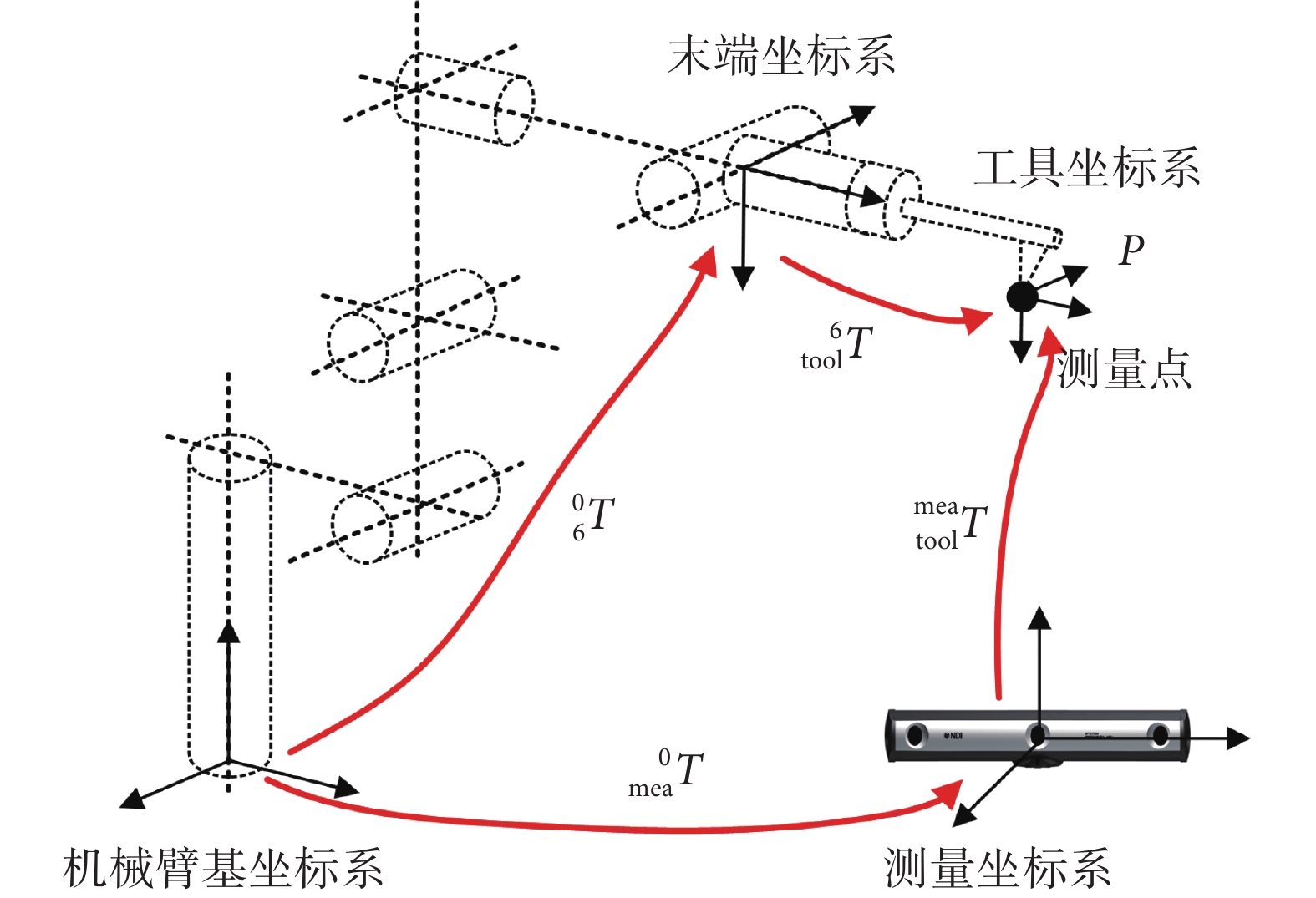 圖2
參數辨識實驗示意圖
Figure2.
Parameter identification experiment diagram
圖2
參數辨識實驗示意圖
Figure2.
Parameter identification experiment diagram
 |
再由測量設備獲取測量點在測量坐標系下的坐標P1,最后通過坐標變換獲得測量點在機械臂坐標系下的坐標值P2。P2 點坐標可得如式(4)所示:
 |
其中, 表示測量設備到機械臂基坐標系間轉換矩陣,
表示測量設備到機械臂基坐標系間轉換矩陣, 表示工具坐標系到測量坐標系間的轉換矩陣。理論上P0 坐標應與P2 相等,由此獲得待辨識參數方程,如式(5)所示:
表示工具坐標系到測量坐標系間的轉換矩陣。理論上P0 坐標應與P2 相等,由此獲得待辨識參數方程,如式(5)所示:
 |
如式(5)所示方程中,P0、P2 項可由式(1)~(4)所示公式代入求得。代入后該方程全部參數為:φ1~6、d1~6、a1~6、α1~6、β1~6、 、
、 。其中待辨識參數共 27 個,包括機械臂本體待辨識參數 18 個:根據 DH 方法,d2、β1、β3~6 均為 0,同時為避免參數耦合,設定d1、φ6、d6、a6、α6 與標稱參數一致,其余為待辨識參數;探針工具到機械臂末端齊次矩陣
。其中待辨識參數共 27 個,包括機械臂本體待辨識參數 18 個:根據 DH 方法,d2、β1、β3~6 均為 0,同時為避免參數耦合,設定d1、φ6、d6、a6、α6 與標稱參數一致,其余為待辨識參數;探針工具到機械臂末端齊次矩陣 中的X、Y、Z方向平移參數 3 個,記為t1~3;測量坐標系到機械臂基坐標系間齊次矩陣
中的X、Y、Z方向平移參數 3 個,記為t1~3;測量坐標系到機械臂基坐標系間齊次矩陣 中包含X、Y、Z方向平移參數 3 個和歐拉角形式旋轉參數 3 個,分別記為tw1~w3和δw1~w3。
中包含X、Y、Z方向平移參數 3 個和歐拉角形式旋轉參數 3 個,分別記為tw1~w3和δw1~w3。
參數辨識實驗如圖 2 所示,經n次重復如圖 2 所示測量實驗,可構建n個如式(5)所示的方程組,該方程組可改寫成如式(6)所示函數形式。
 |
其中, 表示帶求解參數向量,求解該方程組中的未知參數,等價于尋找
表示帶求解參數向量,求解該方程組中的未知參數,等價于尋找 ,使得如式(7)所示函數具有最小值。由此將參數辨識問題轉化為求解非線性最小二乘問題,本文采用萊文貝格-馬夸特(Levenberg-Marquardt,LM)算法對該問題進行優化求解[15-16]。
,使得如式(7)所示函數具有最小值。由此將參數辨識問題轉化為求解非線性最小二乘問題,本文采用萊文貝格-馬夸特(Levenberg-Marquardt,LM)算法對該問題進行優化求解[15-16]。
 |
2.3 基于實際機械臂參數的末端工具參數辨識方法
為進一步根據實際機械臂參數辨識機器人末端工具參數,可將如圖 2 所示的坐標轉換關系改寫成如式(8)所示:
 |
其中, 和
和 分別表示第i次測量中機械臂末端的變換矩陣和測量矩陣,
分別表示第i次測量中機械臂末端的變換矩陣和測量矩陣, 可根據辨識后參數求得,
可根據辨識后參數求得, 為恒定值,
為恒定值, 為參數變換矩陣。多次測量下可獲得如式(9)所示方程:
為參數變換矩陣。多次測量下可獲得如式(9)所示方程:
 |
將其改寫為形如 經典矩陣方程組求解問題,如式(10)所示。
經典矩陣方程組求解問題,如式(10)所示。
 |
本文參考已有經典算法求解該問題,實現工具參數辨識[17]。
2.4 工具坐標系匹配方法
光學測量設備通過測量靶標獲得特定剛體坐標系位姿,僅當靶標坐標系與實際工具坐標系匹配時,測量值才反映真實末端工具位置和姿態,工具參數辨識才有效。本文將分別介紹探針工具和定位定向工具坐標系匹配方法。
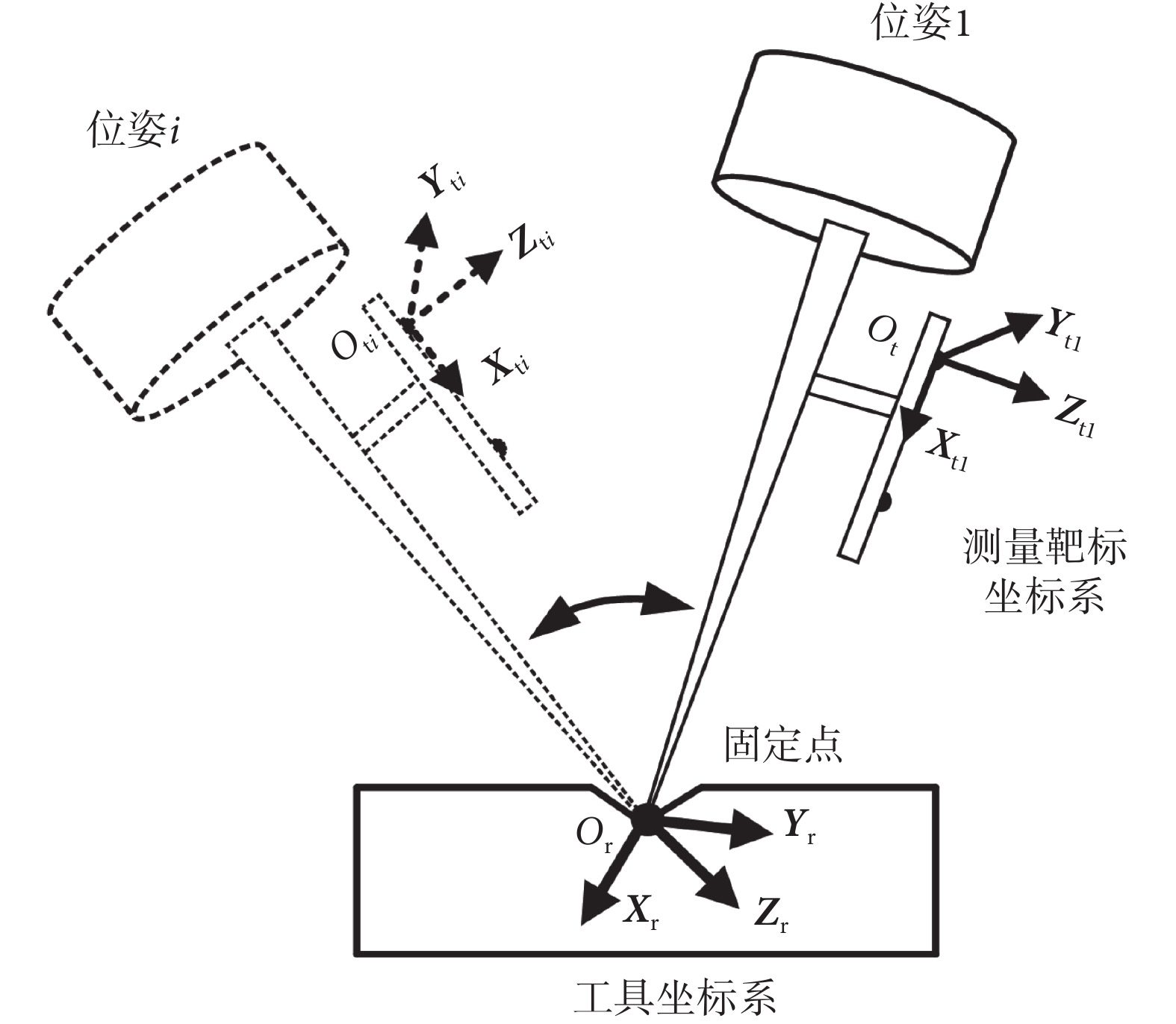
如圖 3 所示,將探針工具與測量靶標剛性固定,保證針尖處于固定點處,同時多次改變探針工具姿態。由于探針針尖相對于靶標坐標系的坐標為固定值,探針姿態改變時,測量設備讀出靶標坐標系應處于以圓心為探針針尖、半徑為探針針尖到靶標坐標系距離的球面上。由此關系可求解探針針尖相對于靶標坐標系間匹配關系。
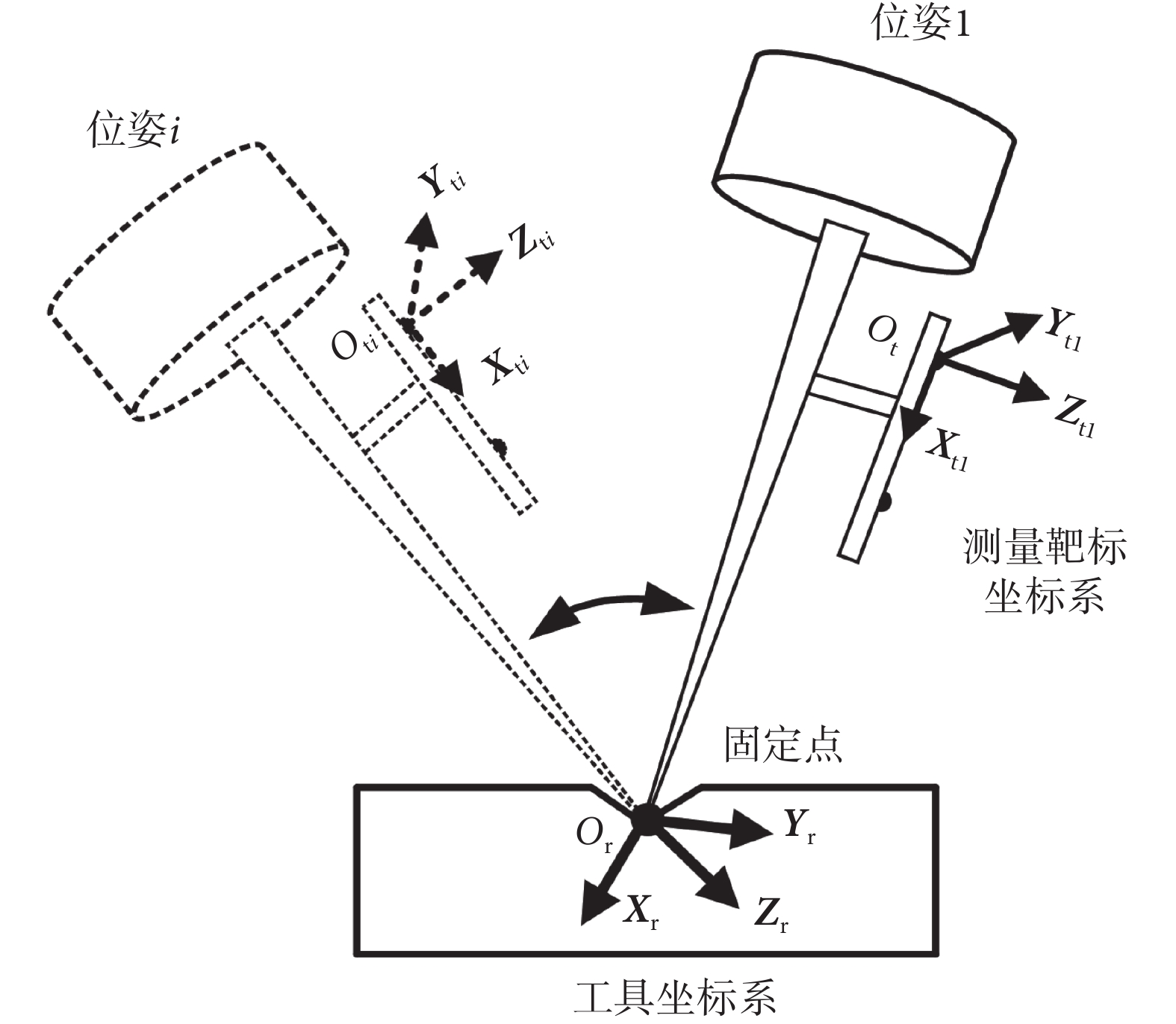 圖3
探針注冊工具坐標系匹配
Figure3.
Registration tool coordinate system matching diagram
圖3
探針注冊工具坐標系匹配
Figure3.
Registration tool coordinate system matching diagram
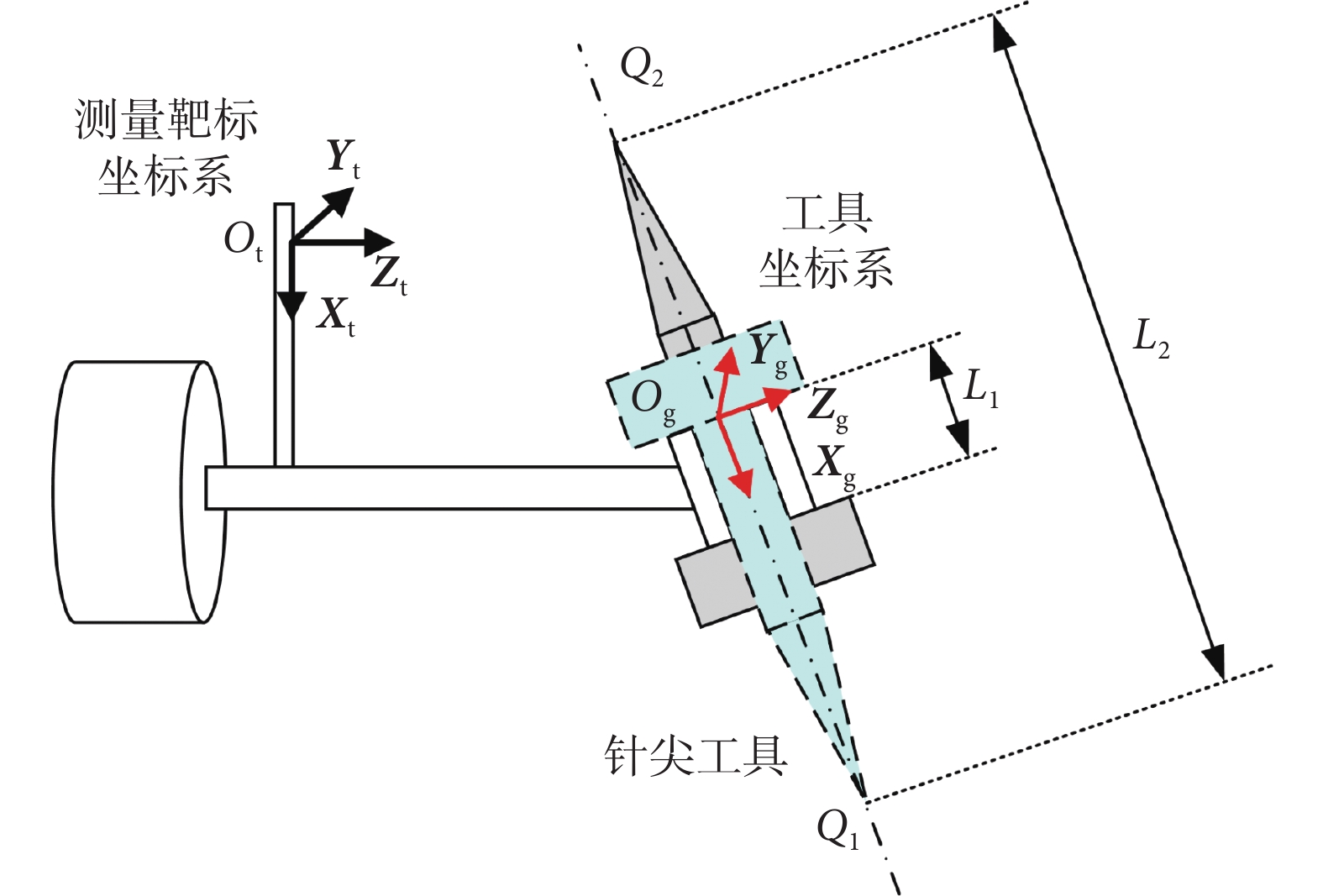
對于定位定向工具坐標系匹配,設計用于匹配的針尖工具,針尖軸與定位定向導向孔滑動配合,針尖位于工具軸心,分別正裝、倒裝在定位定向工具的導向孔中,保證上下端面緊密貼合。使用探針注冊工具坐標系匹配方法,分別確定針尖工具正裝、倒裝時針尖點在測量靶標坐標系下的坐標Q1、Q2。如圖 4 所示,Q1、Q2 連線方向即為工具坐標系X軸方向 ,如式(11)所示。
,如式(11)所示。
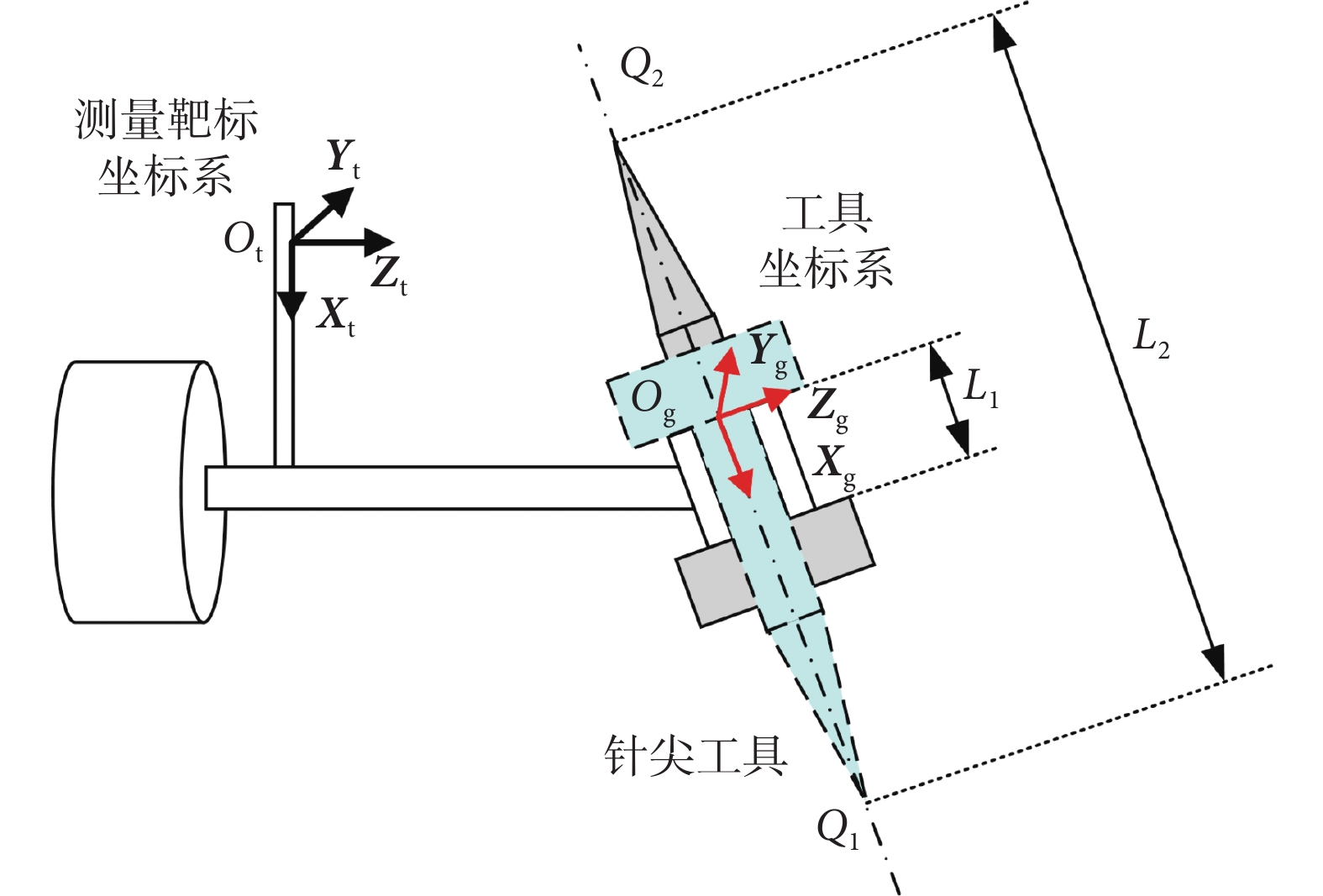 圖4
定位定向工具坐標系匹配
Figure4.
Guiding tool coordinate system matching diagram
圖4
定位定向工具坐標系匹配
Figure4.
Guiding tool coordinate system matching diagram
 |
其中,Q1、Q2 距離L2 可由兩點間距離公式求得,導向孔兩端面距離L1 可由千分尺精確測量,由幾何關系可求得定位定向工具坐標系原點相對于測量靶標的位置關系Og,如式(12)所示。
 |
3 參數辨識精度評價方法
相對于指定位姿的運動準確度和不同逆解到達同一位姿的精度一致性是反映神經外科手術機器人中精度的關鍵指標。據此,本文設計相對距離誤差和逆解重合誤差對手術機器人精度進行評價。隨機選擇一批位姿點,根據機械臂逆運動學模型獲得相應模型學參數下機械臂逆解,控制機械臂運動到該位姿,并用測量設備記錄實際機械臂末端工具位置坐標。計算各位置點相對于某一固定位置點坐標距離與理論距離的差的比值,即為不同位置間相對距離誤差(Errorrelative),如式(13)所示。
 |
其中,Lreal 表示理論距離,Lmeasure 表示測量設備實際測量所得距離。該指標可以反映機械臂的絕對運動精度。
機械臂到達同一位姿點,會有多組可行逆解,定義機械臂在每個逆解控制下所到達位置點與所有逆解到達位置平均點間的距離最大值為同一位姿各逆解重合誤差。該指標可以反映機器人在不同逆解下到達同一位姿的精度一致性。
相對距離誤差和逆解重合誤差評價指標無需測量設備和機器人預先標定,可以借助參數辨識所用的測量設備直接測得,具有快捷直觀、自動化程度高的優點。既可以直接用于臨床作為機器人精度評價,也可以用于參數辨識結果有效性的評估。
4 實驗與結果
本文首先在實驗室環境下完成方法可行性驗證,然后通過對實際神經外科手術機器人進行運動學參數辨識和精度評價以驗證本方法的有效性和實用性。
4.1 數據采集系統構建
為高效獲取參數辨識和精度評價數據,搭建如圖 5 所示的手術機器人末端工具位姿自動測量系統。本文選取光學追蹤設備 Optotrak Certus(Northern Digital Inc,加拿大)進行位姿測量,該系統測量精度 0.1 mm,分辨率 0.01 mm;而采用的機械臂本體為 VS060A3(Denso Inc.,日本)。為實現批量測量,編寫光學追蹤系統和機械臂控制程序,自動完成機械臂運動和相應工具的位姿數據記錄,經測試,系統平均每小時可實現 400 個位姿的批量測量。
 圖5
自動位姿測量系統
Figure5.
Automatic pose measurement system
圖5
自動位姿測量系統
Figure5.
Automatic pose measurement system
4.2 測量位姿設計
為盡可能準確地通過測量位姿反映機械臂運動學模型,測量位姿設計在包含神經外科手術機器人實際工作區域的空間中進行。以機械臂基坐標系Z軸為軸線,在機械臂前方環形圓柱體空間進行測量,設計空間圓柱環張開角度 ? 60~60°,半徑 250~550 mm,高度 200~550 mm。測量位姿點在上述空間中隨機選取,同時在測量靶標與光學追蹤系統平面夾角不至過大的情況下隨機設置機械臂末端姿態,本文設定X、Y、Z三個方向姿態角分別在 ? 30~30°、60~120°、? 30~30° 范圍內。
4.3 實驗室樣機參數辨識結果
采用上述測量系統,分別對機械臂本體、探針工具和定位定向工具進行參數辨識。利用光學追蹤系統的搖尖功能完成工具坐標系與測量靶標坐標系匹配。參數匹配實驗過程如圖 6 所示,三組搖尖數據得到平均誤差分別為 0.06、0.07、0.10 mm,與光學追蹤系統測量精度相當,認為其可接受。根據上述測量位姿設計方法隨機生成 200 個位姿點,根據逆運動學求解獲得 551 個可行測量位姿,用于機械臂和探針工具聯合參數辨識。另外將定位定向工具安裝于機械臂末端,按照相同方法獲取 40 組測量數據,用于定位定向工具單獨參數辨識。基于數值計算軟件 matlab2016a(MathWorks Inc.,美國)編寫參數求解程序實現參數辨識。
 圖6
機械臂末端工具坐標系匹配實驗
Figure6.
Tool coordinate system matching photos
圖6
機械臂末端工具坐標系匹配實驗
Figure6.
Tool coordinate system matching photos
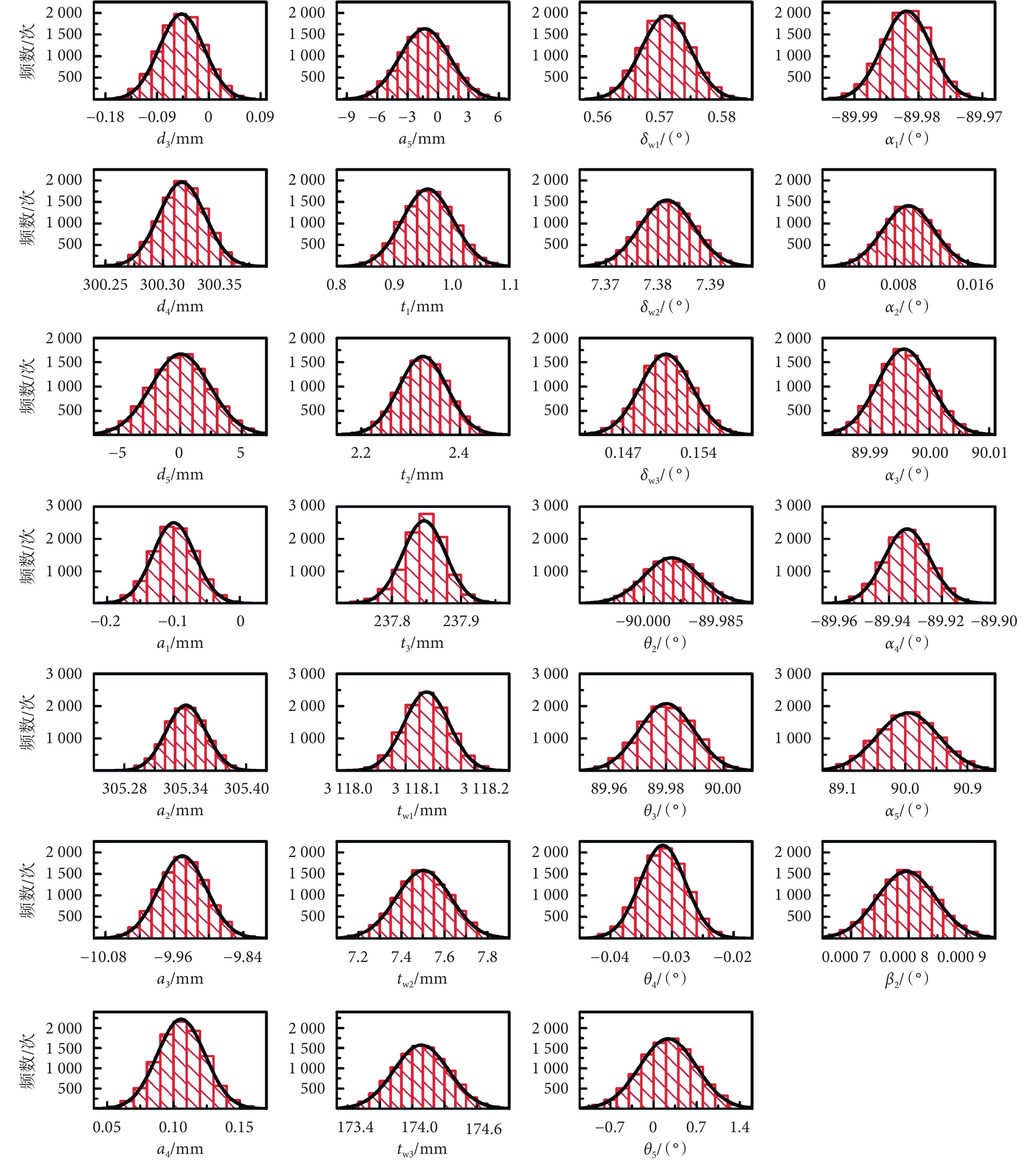
為防止模型參數過擬合,本文從全部數據集合中隨機選取若干組數據作為子集進行參數辨識,獲取模型參數,如此循環重復若干次,根據所得每項數據的分布求取均值,作為最終所得的模型參數。如圖 7 所示為在 551 組數據中隨機選取 200 組數據進行參數辨識,重復 10 000 次,所得 27 個待辨識參數分布情況。可以看出所求參數均符合正態分布,認為參數分布均值反映了參數真實值。
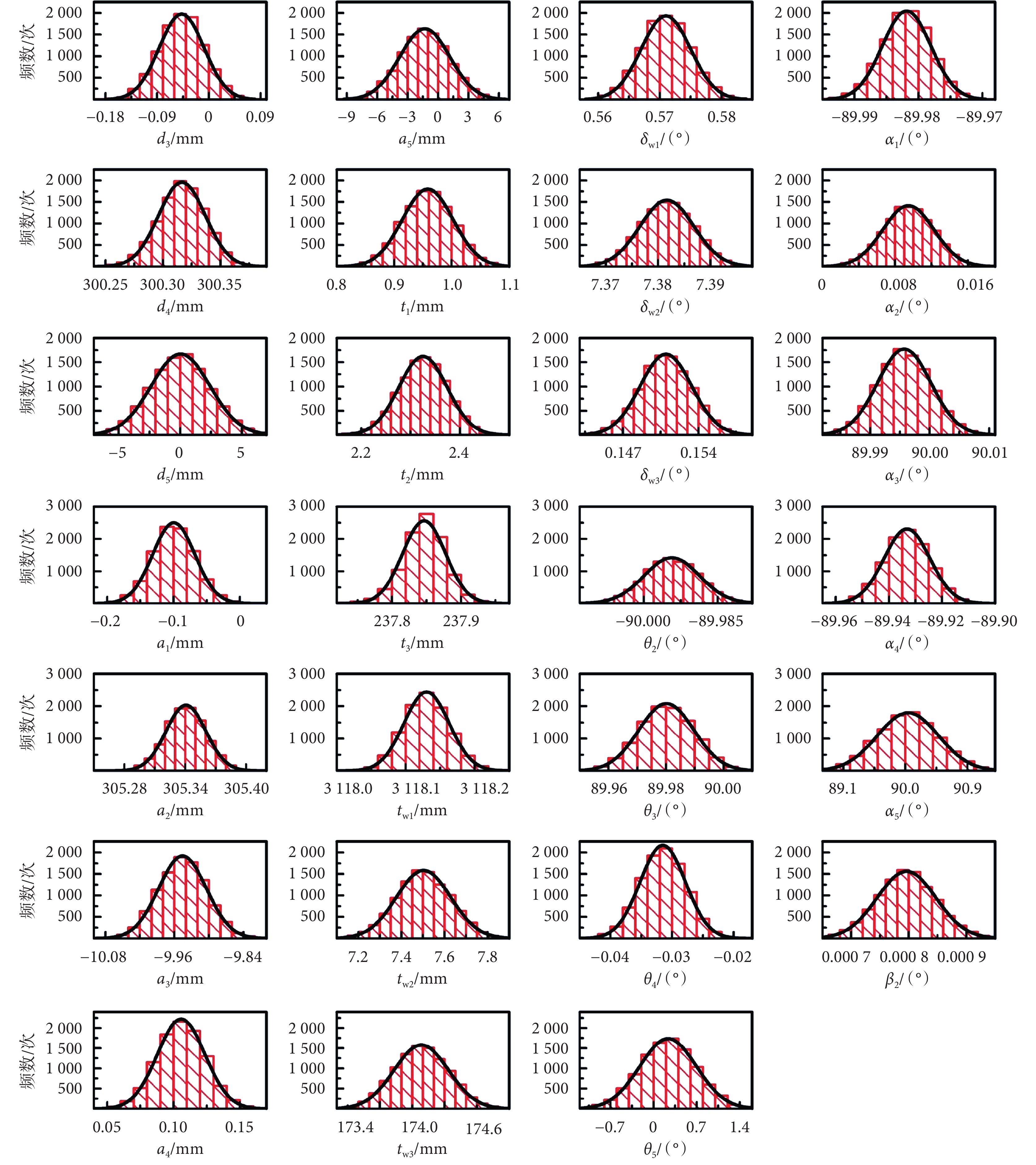 圖7
10 000 次參數辨識后所得運動學參數分布
Figure7.
Kinematic parameter distribution after 10 000 times of parameter identification
圖7
10 000 次參數辨識后所得運動學參數分布
Figure7.
Kinematic parameter distribution after 10 000 times of parameter identification
4.4 實驗室樣機參數辨識精度評價結果
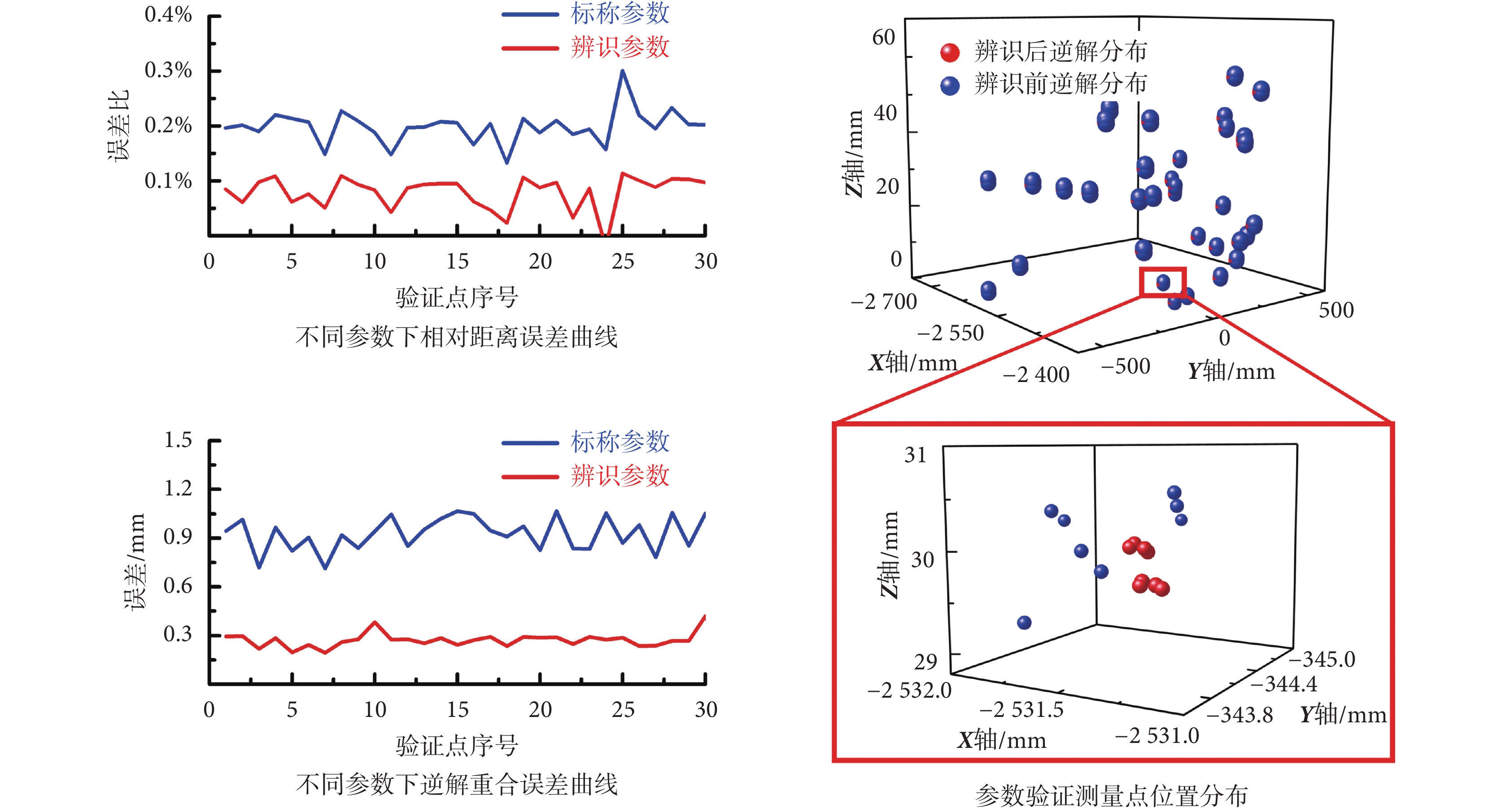
為評價參數辨識精度,在上文所述環形圓柱空間中隨機指定 30 個測量位姿,控制機械臂以所有可行逆解運動到測量位姿,并記錄位置坐標。比較標稱參數和辨識后參數的相對距離誤差和逆解重合誤差。誤差曲線及測量點分布如圖 8 所示。可以看出辨識后機器人相對距離誤差和逆解重合誤差均明顯降低。經統計,兩項誤差均值分別從辨識前的 0.19%、0.93 mm 降低到辨識后的 0.08%、0.27 mm,逆解重合誤差的方差從 0.10 mm 降低到 0.05 mm。從參數驗證測量點位置分布圖中也可以直觀看出,辨識后機器人同一位姿下逆解離散程度明顯減小。
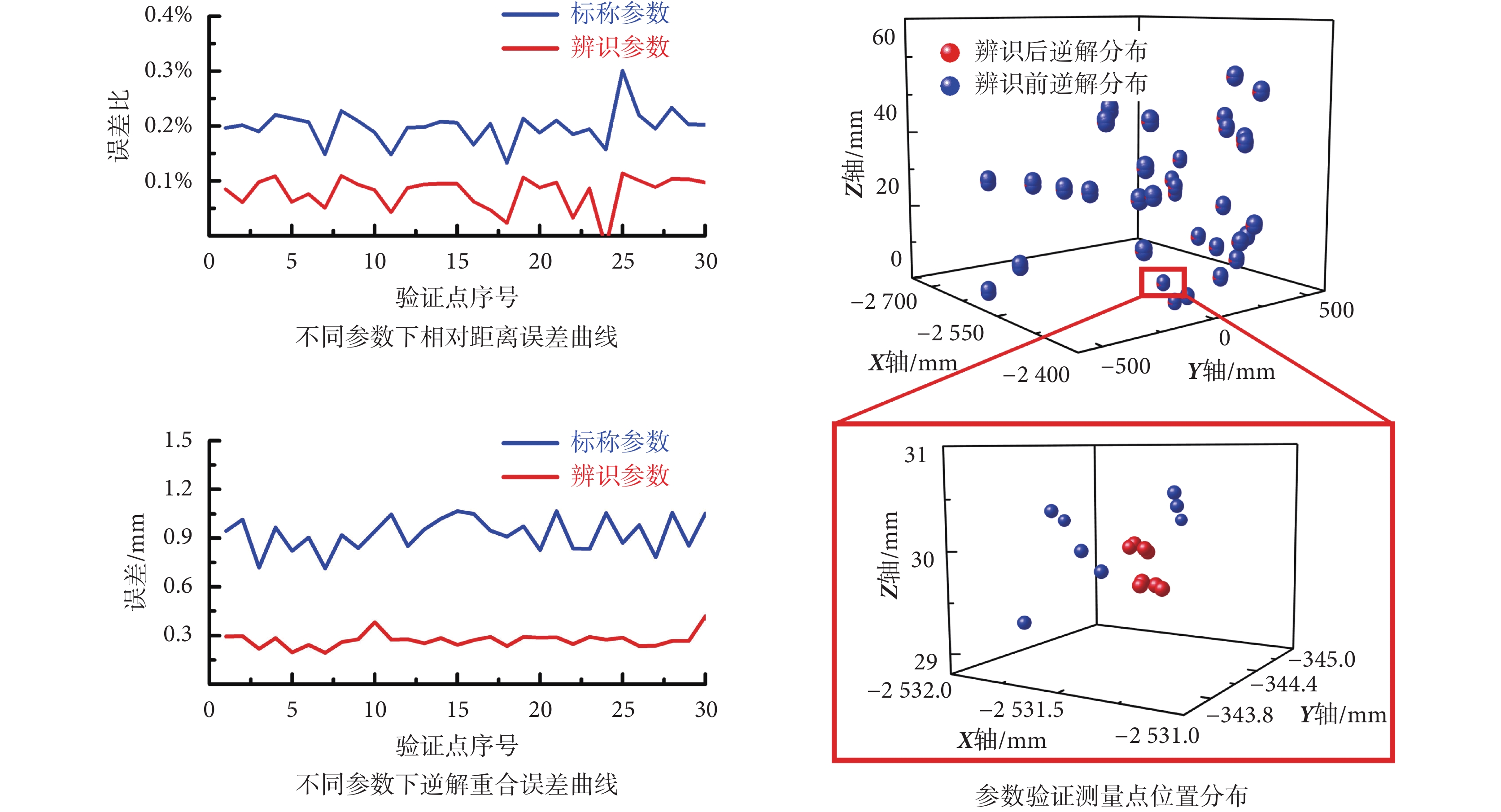 圖8
實驗室樣機精度評價結果
Figure8.
Prototype accuracy evaluation results
圖8
實驗室樣機精度評價結果
Figure8.
Prototype accuracy evaluation results
4.5 手術機器人現場參數辨識與評價結果
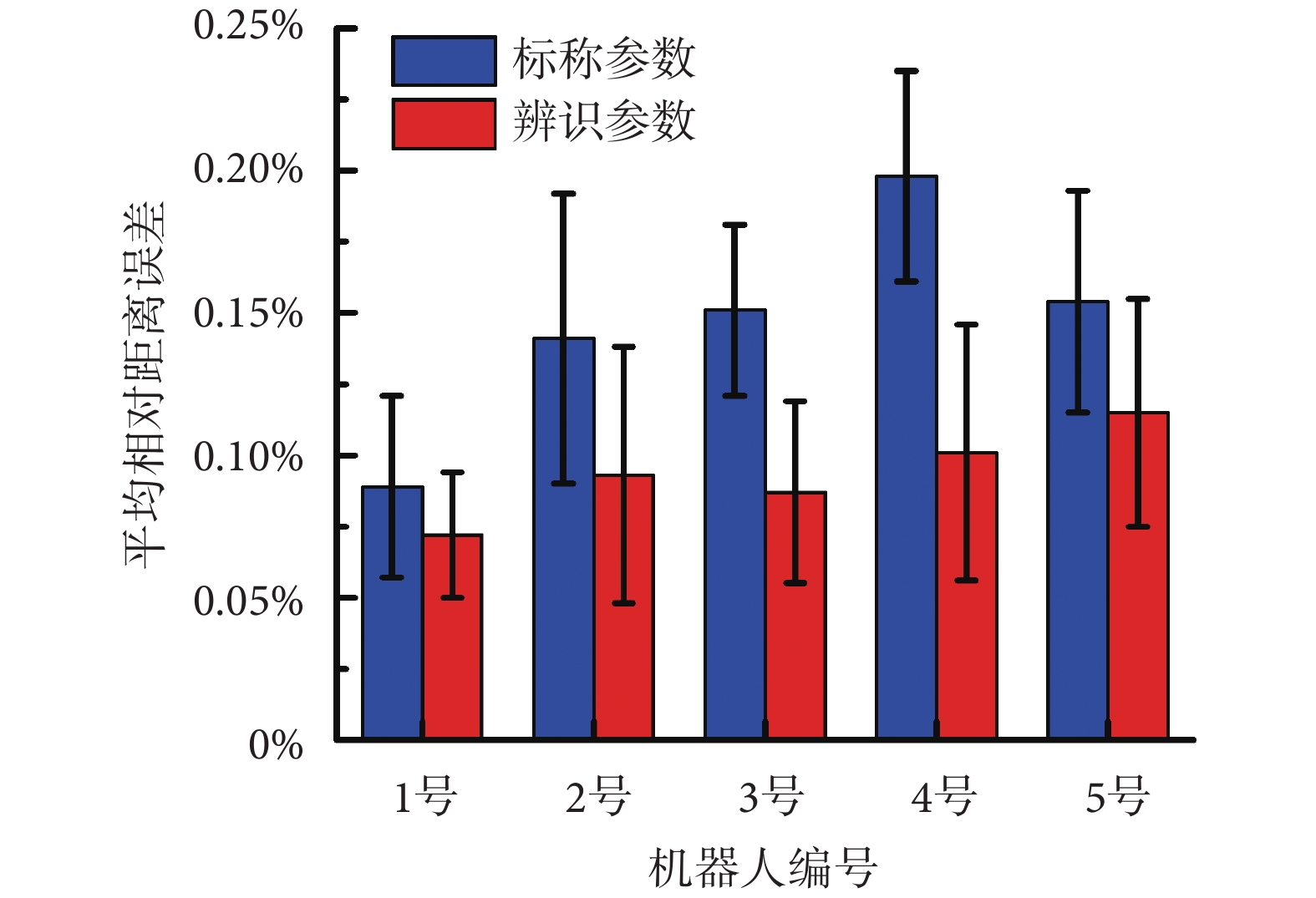
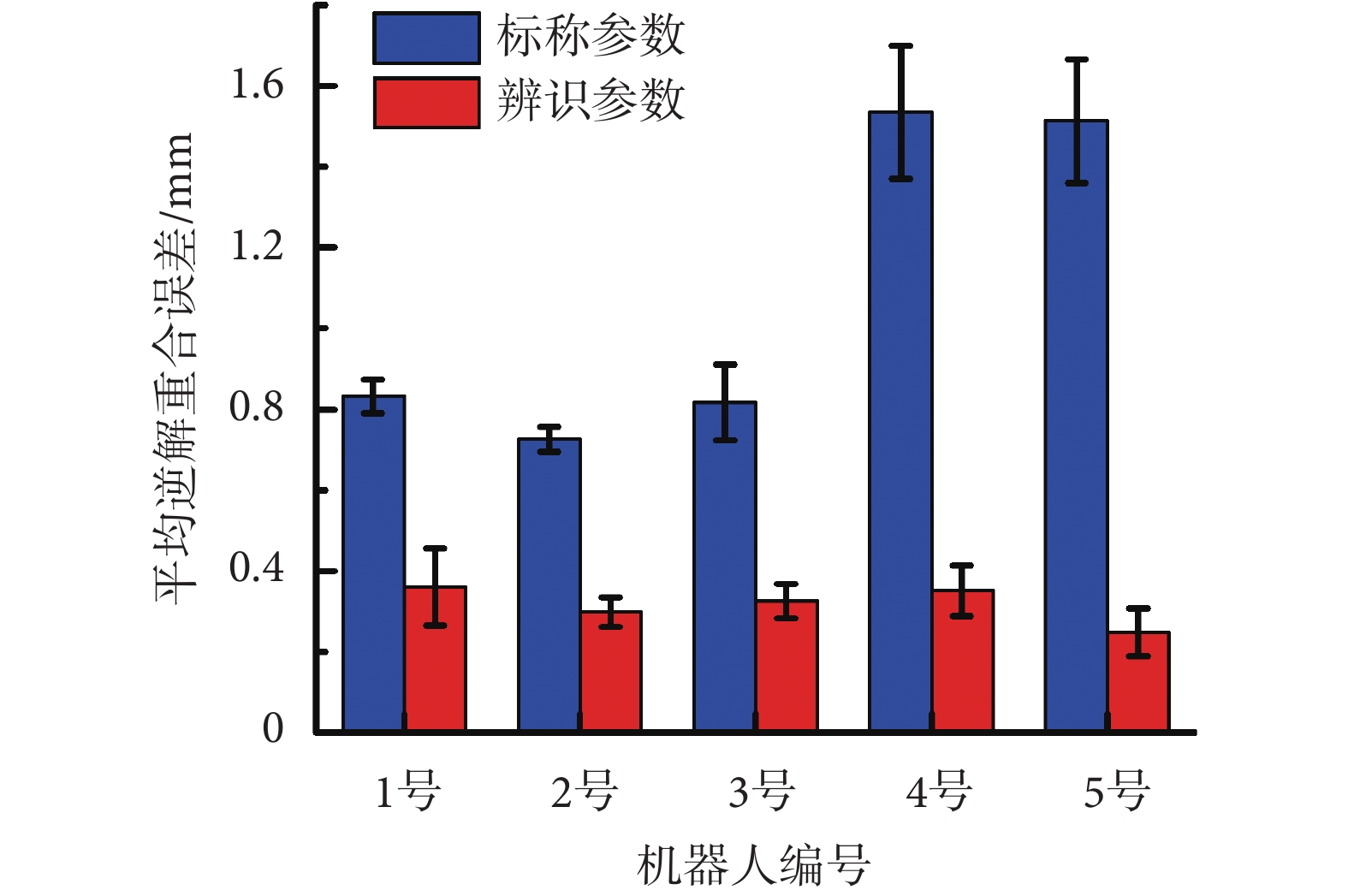
為驗證本方法實際可行性,隨機抽取 5 臺神經外科手術機器人樣機 Sino(華科精準 Inc.,中國)進行批量參數辨識,該型手術機器人機械臂與本文采用機械臂型號一致。選用便攜式光學追蹤系統 Polaris Vega(Northern Digital Inc.,加拿大)(精度 0.15 mm)測量手術機器人末端位姿。每臺機器人選取相同的 300 組數據測量點,隨機挑選 75% 的測量值進行參數辨識,重復 100 次,將均值作為最終參數辨識結果。辨識完成后,隨機設定 20 個測量位姿進行辨識結果驗證,計算每臺機器人標稱參數和辨識后參數的相對距離誤差與逆解重合誤差均值。除加載文件以外,所有辨識過程均由系統自動進行,無需人為干預。如圖 9 所示為現場參數辨識和評價照片,如圖 10 所示為相對距離誤差均值和標準差,如圖 11 所示為逆解重合誤差均值和標準差,如表 1 所示為參數辨識前后誤差優化百分比。
 圖9
機器人現場參數辨識照片
Figure9.
Photos of robot kinematics parameter identification in real applications
圖9
機器人現場參數辨識照片
Figure9.
Photos of robot kinematics parameter identification in real applications
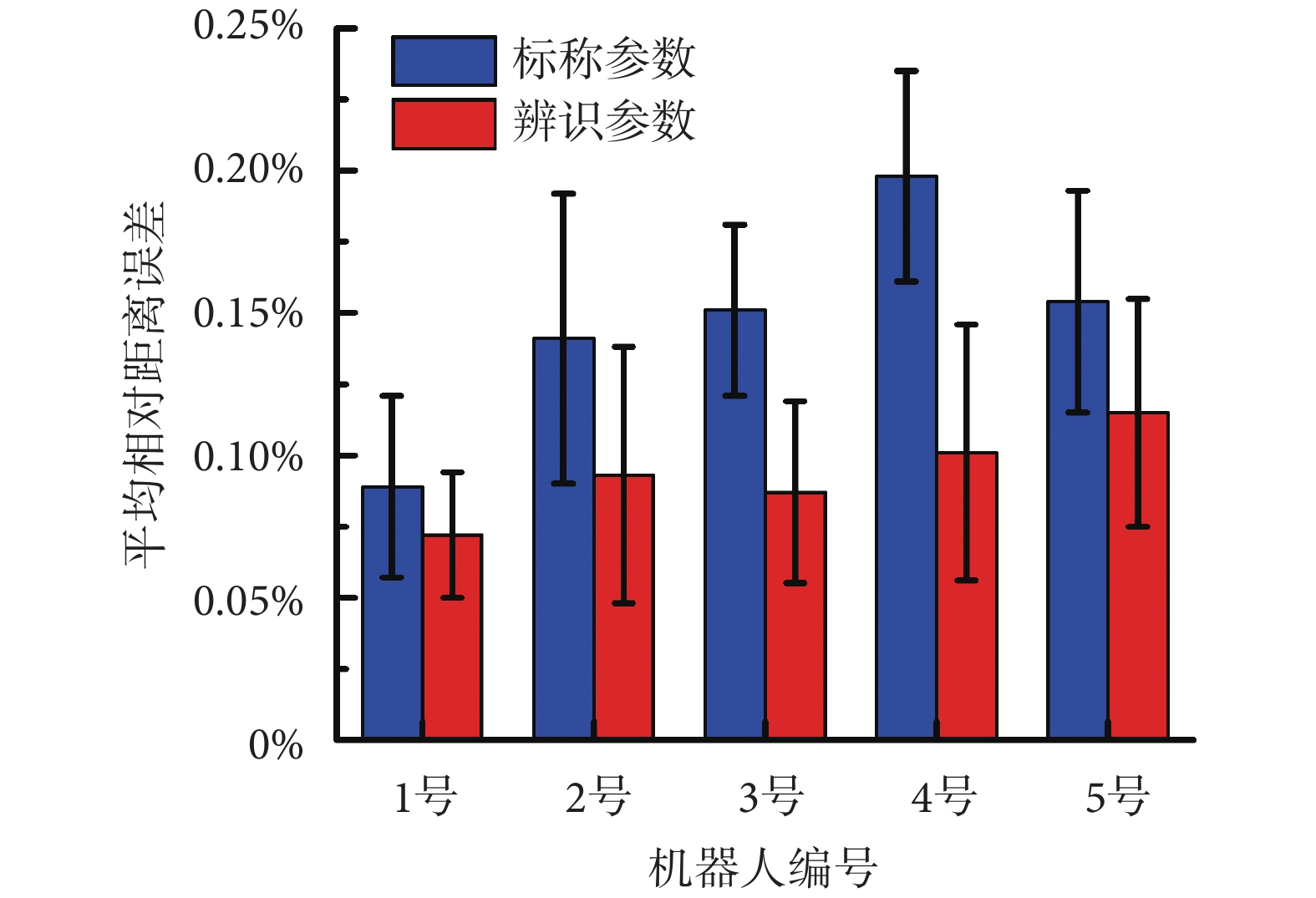 圖10
批量參數辨識機器人相對距離誤差均值與標準差
Figure10.
Mean value and standard deviation of relative distance error of five robots
圖10
批量參數辨識機器人相對距離誤差均值與標準差
Figure10.
Mean value and standard deviation of relative distance error of five robots
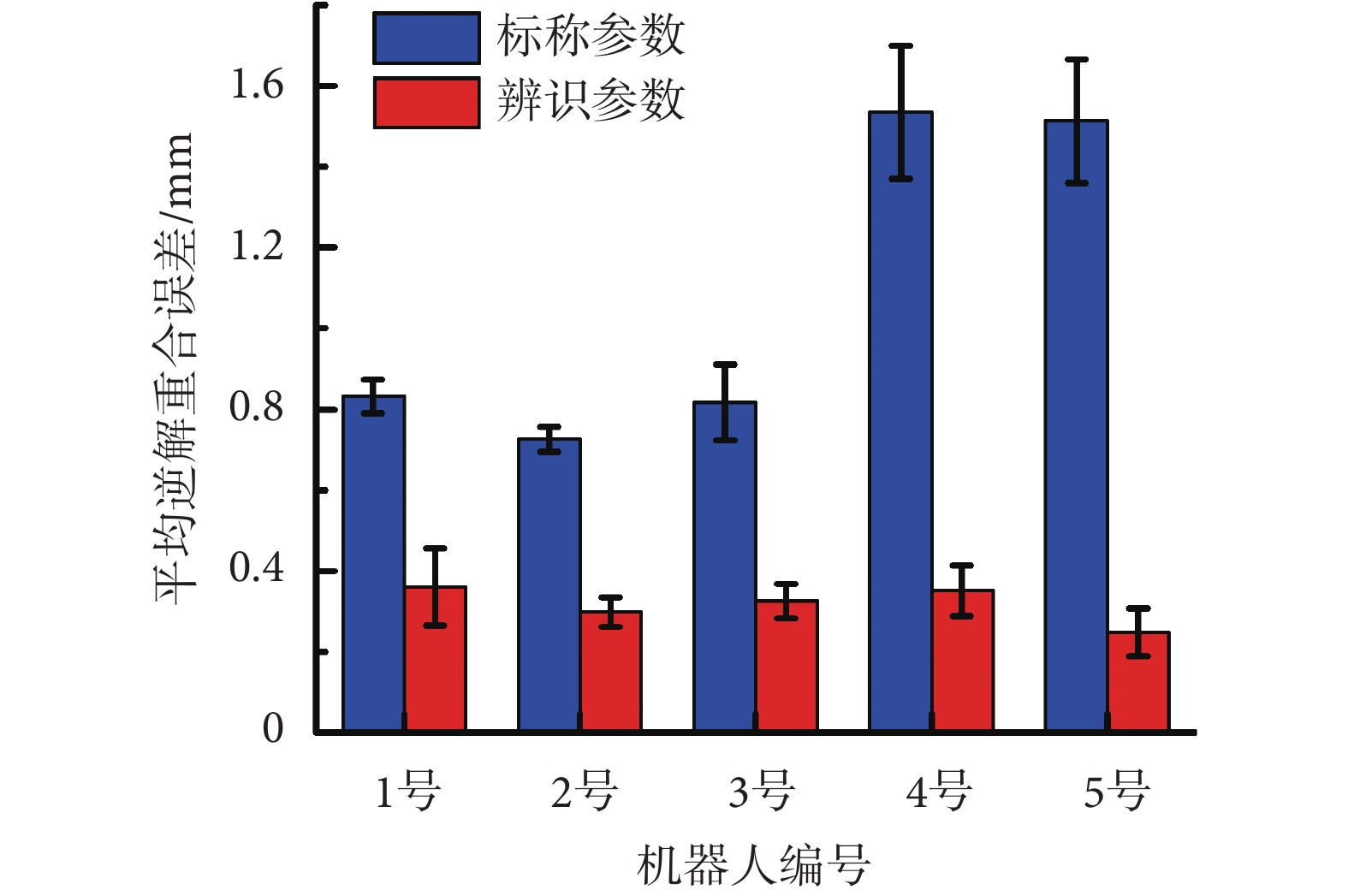 圖11
批量參數辨識機器人逆解重合誤差均值與標準差
Figure11.
Mean value and standard deviation of inverse kine matics consistency error of five robots
圖11
批量參數辨識機器人逆解重合誤差均值與標準差
Figure11.
Mean value and standard deviation of inverse kine matics consistency error of five robots
可以看出,本方法可以保證不同機械臂相對距離誤差在 0.1% 左右,機械臂逆解重合誤差在 0.3 mm 左右。經統計,5 臺機械臂相對距離誤差平均降低 33.96%,機械臂逆解重合誤差平均降低 67.30%。還可以看出,若采用標稱運動學參數,不同機械臂之間精度差異很大。性能較好的 1 號機器人相對距離誤差 0.09% ± 0.02%,逆解重合誤差(0.83 ± 0.04)mm,性能較差的 4 號機器人相對距離誤差 0.20% ± 0.05%,逆解重合誤差(1.54 ± 0.17)mm,評價指標相差兩倍多,這使得機器人之間的精度均一性難以保證,從而大大增加手術風險。采用本文辨識獲得的運動學參數,可以有效降低機械臂不同位置間相對距離誤差和逆解重合誤差,獲得更貼近真實值的手術機器人運動學模型,保證量產的神經外科手術機器人的精度和性能均一性。另外,也可以采用本文方法對在用的手術機器人進行精度的驗證,必要時進行修正。
5 討論
5.1 參數辨識方法
本文設計了兩步參數辨識算法和工具坐標系匹配方法,既可以實現機械臂本體加末端工具的聯合參數辨識,也可以實現基于辨識后機械臂參數的末端工具單獨辨識。本文提出的平均化方法可以很好地提高參數識別的魯棒性,如圖 7 所示,雖然在每次辨識的過程中參數差異性較大,但是在大量實驗過程中,辨識參數服從正態分布,取分布均值作為辨識后參數可以抵消單次參數辨識誤差。另外,本文采用固定數值的方法避免參數耦合,雖然被固定參數誤差無法進行優化,但從本文的結果可以看出,少量的參數固定仍可以實現較大幅度的精度優化。
5.2 精度評價方法
對于神經外科手術機器人精度的評價是保證機器人精度一致性所必需的。本文中采用相對距離誤差反映機器人在定位定向中相對指定參考坐標的定位精度,逆解重合誤差反映機器人在不同逆解下到達指定的一致性。兩項誤差均為相對量,直接在測量設備坐標系中度量,無需測量設備—機械臂配準,不僅可以用于辨識參數有效性的評估,還可以在臨床環境下快速、直觀、方便地完成手術機器人日常精度檢驗。
5.3 自動化程度
對參數的辨識和精度評價過程中的位姿數據測量是一件需要極高認真度且費時費力的工作,手動操作需要投入巨大的人力且易引入不必要的操作誤差。本文對光學追蹤系統和機械臂進行編程控制,可以實現自動化的機器人位姿測量和數據導出,測量中僅需極少的人為參與,同時為參數辨識和精度評價算法設計了人機交互界面,使得非專業人員也可操作完成機器人參數辨識和精度評價,因此通過本系統可以實現醫療機器人現場參數辨識和精度評價。
6 結論
本文通過對機械臂和手術工具運動學參數辨識,獲得更貼近于實際的手術機器人運動學模型,降低手術機器人運動學模型參數實際值與標稱值不一致問題帶來的誤差。本文提出了兩項精度評價指標,用以快速便捷地評價手術機器人精度。本文還建立了自動化的數據測量和參數辨識算法程序。本文所提供的方法可以實現用于現場的手術機器人高效參數辨識和精度評價。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
神經外科手術機器人可以替代傳統神經外科手術中的立體定向頭架,實現自動、快速、精準的電極定位,在癲癇病灶定位、深部腦刺激等手術中具有明顯的優勢[1]。主流的神經外科手術機器人系統均采用多自由度機械臂與末端手術工具組合的方案,如神經外科手術機器人系統 Remebot(柏惠維康 Inc.,中國)、神經外科手術機器人系統 NeuroMate(Renishaw Inc.,英國)、神經外科手術機器人系統 Rosa Brain(Medtech Inc.,法國)等[2-5]。機械臂是保證機器人手術精度的核心部件,但由于加工精度、裝配工藝、零件公差等原因,機械臂本體的實際運動學模型參數與標稱值之間存在一定偏差,導致其絕對定位精度降低[6]。固定在機械臂末端的注冊工具和定位定向工具的標稱尺寸參數與真實值之間也存在一定的偏差,同樣會降低總體定位和測量精度,影響最終手術效果。
準確識別機械臂本體及末端工具的運動學模型參數并據此構建個性化運動控制模型,是提升神經外科手術機器人精度的重要手段,目前已有許多成功報道。劉帥等[7]利用標定箱識別優傲 5 機械臂 UR5(Universal Robots Inc.,丹麥)構成的神經外科手術機器人參數,將其單點定位誤差由 4.05 mm 優化到 0.98 mm。劉達等[8]使用基于視覺的方法對自制的神經外科手術機器人機械臂本體進行了運動學參數標定,使其絕對定位誤差由 8.56 mm 優化到 0.64 mm。陳華等[9]在手術空間內對自建的神經外科手術機器人進行參數優化,使其定位精度達到 1 mm 以內。Vicentini 等[10]對 2 臺協作型機械臂 LWR(KUKA Inc.,德國)構成的雙臂神經外科手術機器人進行參數辨識和精度補償,將端到端靜態精度優化到 0.75 mm。Heinig 等[11]的研究中對框架構型的神經外科手術機器人系統進行參數標定,可以將 95% 的定位誤差控制在 0.50 mm 以內。Haidegger 等[12]對神經外科手術機器人系統 NeuroMate(Renishaw Inc.,英國)進行了精度優化,使其殘余誤差下降了 24%。
參數辨識可以較好地優化神經外科手術機器人精度,但其在臨床環境中應用時仍存在不足:① 辨識方法不完善。目前的研究中僅考慮了機械臂本體的參數辨識,對于末端工具參數的辨識考慮較少。少數研究將手術機器人的末端工具參數簡化為針尖點沿機械臂末端坐標系 X、Y、Z 方向的 3 個平移參數[7],但這并不符合臨床實際,因為神經外科手術機器人定位定向工具需同時描述其位置和姿態,如僅 3 個平移參數則無法完備表示。另外,由于定位定向工具的中空構造,其坐標原點和定向孔軸線方向位置參數無法直接測量,需要進一步提供完善的參數辨識方法。② 缺乏快速有效的精度評價方法。機械臂本體誤差、手術工具參數誤差、運動磨損以及操作不當均可能造成機器人系統精度下降。及時的評估機器人系統的精度水平,有助于醫生了解設備信息,預防意外發生。當前的臨床中仍缺乏快速、直觀、方便實施的手術機器人機械臂精度評價方法。③ 自動化程度低。當前研究大多針對系統樣機進行參數辨識,對辨識方法的人力資源消耗不敏感,自動化程度不高,需要較多的人工參與,操作繁瑣且易引入操作誤差。臨床中的手術機器人還需要滿足術前設備參數校正、定期質量檢定等需求,因此往往需要在醫療機構進行現場參數辨識和精度評價,目前仍缺乏一種自動化的現場參數辨識和精度評價方案。
針對以上問題,本文首先給出了手術機器人正逆運動學模型,提出了運動學模型參數辨識方法與精度評價方法,然后給出了具體實現方案,最后驗證了本文方法的有效性。
1 手術機器人運動學模型
精準的機器人神經外科手術關鍵在于精準的注冊和定位定向,準確的機器人運動學模型是精準的注冊和定位定向的必要條件。本文采用的 6 自由度串聯機械臂及對應末端工具建立了手術機器人運動學模型。從數學模型角度上看,注冊所用探針工具是定位定向工具的特例,故在此僅考慮定位定向工具模型。
本文依據戴南威特-哈特伯格(Denavit-Hartenberg,DH)連桿參數描述方法建立機器人運動學模型[13-14]。機械臂第i、i-1 連桿坐標系之間的變換關系如式(1)所示,φi、di、ai、αi、βi 表示連桿間運動學參數。
 |
其中, 、
、 、
、 表示繞對應坐標軸旋轉的齊次變換矩陣,
表示繞對應坐標軸旋轉的齊次變換矩陣, 、
、 表示沿對應坐標軸平移的齊次變換矩陣。
表示沿對應坐標軸平移的齊次變換矩陣。
設機械臂定位定向工具坐標系到第 6 連桿坐標系的變換矩陣為  ,工具坐標系到基坐標系矩陣為
,工具坐標系到基坐標系矩陣為  。機器人的運動學模型如式(2)所示,表示為
。機器人的運動學模型如式(2)所示,表示為  與關節角度 θ1~6 間函數關系,其中 φ1~6、d1~6、a1~6、α1~6、β1~6、
與關節角度 θ1~6 間函數關系,其中 φ1~6、d1~6、a1~6、α1~6、β1~6、 即為神經外科手術機器人系統待辨識運動學參數。
即為神經外科手術機器人系統待辨識運動學參數。
 |
2 參數辨識方法
2.1 參數辨識流程
為實現自動化的參數辨識,本文設計如圖 1 所示機器人運動學參數辨識流程。首先設定測量位姿并完成位姿數據自動測量;然后對機械臂探針注冊過程進行聯合參數辨識,獲取機械臂及探針工具運動學參數;最后基于辨識后機械臂運動學參數,對定位定向工具參數進行辨識,進而獲得機器人系統全部運動學參數。
 圖1
參數辨識流程
Figure1.
Parameter identification flow chart
圖1
參數辨識流程
Figure1.
Parameter identification flow chart
2.2 機械臂及探針工具參數聯合辨識方法
為同步辨識機械臂本體及探針工具參數,本文采用運動學回路法構建待辨識參數方程。設計如圖 2 所示實驗,使用高精度測量設備通過跟蹤靶標獲取機械臂末端工具位姿。首先控制機械臂末端工具移動到某一設定測量點,并由機械臂正運動學模型計算測量點在機械臂基坐標系下的位置坐標P0,如式(3)所示:
 圖2
參數辨識實驗示意圖
Figure2.
Parameter identification experiment diagram
圖2
參數辨識實驗示意圖
Figure2.
Parameter identification experiment diagram
 |
再由測量設備獲取測量點在測量坐標系下的坐標P1,最后通過坐標變換獲得測量點在機械臂坐標系下的坐標值P2。P2 點坐標可得如式(4)所示:
 |
其中, 表示測量設備到機械臂基坐標系間轉換矩陣,
表示測量設備到機械臂基坐標系間轉換矩陣, 表示工具坐標系到測量坐標系間的轉換矩陣。理論上P0 坐標應與P2 相等,由此獲得待辨識參數方程,如式(5)所示:
表示工具坐標系到測量坐標系間的轉換矩陣。理論上P0 坐標應與P2 相等,由此獲得待辨識參數方程,如式(5)所示:
 |
如式(5)所示方程中,P0、P2 項可由式(1)~(4)所示公式代入求得。代入后該方程全部參數為:φ1~6、d1~6、a1~6、α1~6、β1~6、 、
、 。其中待辨識參數共 27 個,包括機械臂本體待辨識參數 18 個:根據 DH 方法,d2、β1、β3~6 均為 0,同時為避免參數耦合,設定d1、φ6、d6、a6、α6 與標稱參數一致,其余為待辨識參數;探針工具到機械臂末端齊次矩陣
。其中待辨識參數共 27 個,包括機械臂本體待辨識參數 18 個:根據 DH 方法,d2、β1、β3~6 均為 0,同時為避免參數耦合,設定d1、φ6、d6、a6、α6 與標稱參數一致,其余為待辨識參數;探針工具到機械臂末端齊次矩陣 中的X、Y、Z方向平移參數 3 個,記為t1~3;測量坐標系到機械臂基坐標系間齊次矩陣
中的X、Y、Z方向平移參數 3 個,記為t1~3;測量坐標系到機械臂基坐標系間齊次矩陣 中包含X、Y、Z方向平移參數 3 個和歐拉角形式旋轉參數 3 個,分別記為tw1~w3和δw1~w3。
中包含X、Y、Z方向平移參數 3 個和歐拉角形式旋轉參數 3 個,分別記為tw1~w3和δw1~w3。
參數辨識實驗如圖 2 所示,經n次重復如圖 2 所示測量實驗,可構建n個如式(5)所示的方程組,該方程組可改寫成如式(6)所示函數形式。
 |
其中, 表示帶求解參數向量,求解該方程組中的未知參數,等價于尋找
表示帶求解參數向量,求解該方程組中的未知參數,等價于尋找 ,使得如式(7)所示函數具有最小值。由此將參數辨識問題轉化為求解非線性最小二乘問題,本文采用萊文貝格-馬夸特(Levenberg-Marquardt,LM)算法對該問題進行優化求解[15-16]。
,使得如式(7)所示函數具有最小值。由此將參數辨識問題轉化為求解非線性最小二乘問題,本文采用萊文貝格-馬夸特(Levenberg-Marquardt,LM)算法對該問題進行優化求解[15-16]。
 |
2.3 基于實際機械臂參數的末端工具參數辨識方法
為進一步根據實際機械臂參數辨識機器人末端工具參數,可將如圖 2 所示的坐標轉換關系改寫成如式(8)所示:
 |
其中, 和
和 分別表示第i次測量中機械臂末端的變換矩陣和測量矩陣,
分別表示第i次測量中機械臂末端的變換矩陣和測量矩陣, 可根據辨識后參數求得,
可根據辨識后參數求得, 為恒定值,
為恒定值, 為參數變換矩陣。多次測量下可獲得如式(9)所示方程:
為參數變換矩陣。多次測量下可獲得如式(9)所示方程:
 |
將其改寫為形如 經典矩陣方程組求解問題,如式(10)所示。
經典矩陣方程組求解問題,如式(10)所示。
 |
本文參考已有經典算法求解該問題,實現工具參數辨識[17]。
2.4 工具坐標系匹配方法
光學測量設備通過測量靶標獲得特定剛體坐標系位姿,僅當靶標坐標系與實際工具坐標系匹配時,測量值才反映真實末端工具位置和姿態,工具參數辨識才有效。本文將分別介紹探針工具和定位定向工具坐標系匹配方法。
如圖 3 所示,將探針工具與測量靶標剛性固定,保證針尖處于固定點處,同時多次改變探針工具姿態。由于探針針尖相對于靶標坐標系的坐標為固定值,探針姿態改變時,測量設備讀出靶標坐標系應處于以圓心為探針針尖、半徑為探針針尖到靶標坐標系距離的球面上。由此關系可求解探針針尖相對于靶標坐標系間匹配關系。
 圖3
探針注冊工具坐標系匹配
Figure3.
Registration tool coordinate system matching diagram
圖3
探針注冊工具坐標系匹配
Figure3.
Registration tool coordinate system matching diagram
對于定位定向工具坐標系匹配,設計用于匹配的針尖工具,針尖軸與定位定向導向孔滑動配合,針尖位于工具軸心,分別正裝、倒裝在定位定向工具的導向孔中,保證上下端面緊密貼合。使用探針注冊工具坐標系匹配方法,分別確定針尖工具正裝、倒裝時針尖點在測量靶標坐標系下的坐標Q1、Q2。如圖 4 所示,Q1、Q2 連線方向即為工具坐標系X軸方向 ,如式(11)所示。
,如式(11)所示。
 圖4
定位定向工具坐標系匹配
Figure4.
Guiding tool coordinate system matching diagram
圖4
定位定向工具坐標系匹配
Figure4.
Guiding tool coordinate system matching diagram
 |
其中,Q1、Q2 距離L2 可由兩點間距離公式求得,導向孔兩端面距離L1 可由千分尺精確測量,由幾何關系可求得定位定向工具坐標系原點相對于測量靶標的位置關系Og,如式(12)所示。
 |
3 參數辨識精度評價方法
相對于指定位姿的運動準確度和不同逆解到達同一位姿的精度一致性是反映神經外科手術機器人中精度的關鍵指標。據此,本文設計相對距離誤差和逆解重合誤差對手術機器人精度進行評價。隨機選擇一批位姿點,根據機械臂逆運動學模型獲得相應模型學參數下機械臂逆解,控制機械臂運動到該位姿,并用測量設備記錄實際機械臂末端工具位置坐標。計算各位置點相對于某一固定位置點坐標距離與理論距離的差的比值,即為不同位置間相對距離誤差(Errorrelative),如式(13)所示。
 |
其中,Lreal 表示理論距離,Lmeasure 表示測量設備實際測量所得距離。該指標可以反映機械臂的絕對運動精度。
機械臂到達同一位姿點,會有多組可行逆解,定義機械臂在每個逆解控制下所到達位置點與所有逆解到達位置平均點間的距離最大值為同一位姿各逆解重合誤差。該指標可以反映機器人在不同逆解下到達同一位姿的精度一致性。
相對距離誤差和逆解重合誤差評價指標無需測量設備和機器人預先標定,可以借助參數辨識所用的測量設備直接測得,具有快捷直觀、自動化程度高的優點。既可以直接用于臨床作為機器人精度評價,也可以用于參數辨識結果有效性的評估。
4 實驗與結果
本文首先在實驗室環境下完成方法可行性驗證,然后通過對實際神經外科手術機器人進行運動學參數辨識和精度評價以驗證本方法的有效性和實用性。
4.1 數據采集系統構建
為高效獲取參數辨識和精度評價數據,搭建如圖 5 所示的手術機器人末端工具位姿自動測量系統。本文選取光學追蹤設備 Optotrak Certus(Northern Digital Inc,加拿大)進行位姿測量,該系統測量精度 0.1 mm,分辨率 0.01 mm;而采用的機械臂本體為 VS060A3(Denso Inc.,日本)。為實現批量測量,編寫光學追蹤系統和機械臂控制程序,自動完成機械臂運動和相應工具的位姿數據記錄,經測試,系統平均每小時可實現 400 個位姿的批量測量。
 圖5
自動位姿測量系統
Figure5.
Automatic pose measurement system
圖5
自動位姿測量系統
Figure5.
Automatic pose measurement system
4.2 測量位姿設計
為盡可能準確地通過測量位姿反映機械臂運動學模型,測量位姿設計在包含神經外科手術機器人實際工作區域的空間中進行。以機械臂基坐標系Z軸為軸線,在機械臂前方環形圓柱體空間進行測量,設計空間圓柱環張開角度 ? 60~60°,半徑 250~550 mm,高度 200~550 mm。測量位姿點在上述空間中隨機選取,同時在測量靶標與光學追蹤系統平面夾角不至過大的情況下隨機設置機械臂末端姿態,本文設定X、Y、Z三個方向姿態角分別在 ? 30~30°、60~120°、? 30~30° 范圍內。
4.3 實驗室樣機參數辨識結果
采用上述測量系統,分別對機械臂本體、探針工具和定位定向工具進行參數辨識。利用光學追蹤系統的搖尖功能完成工具坐標系與測量靶標坐標系匹配。參數匹配實驗過程如圖 6 所示,三組搖尖數據得到平均誤差分別為 0.06、0.07、0.10 mm,與光學追蹤系統測量精度相當,認為其可接受。根據上述測量位姿設計方法隨機生成 200 個位姿點,根據逆運動學求解獲得 551 個可行測量位姿,用于機械臂和探針工具聯合參數辨識。另外將定位定向工具安裝于機械臂末端,按照相同方法獲取 40 組測量數據,用于定位定向工具單獨參數辨識。基于數值計算軟件 matlab2016a(MathWorks Inc.,美國)編寫參數求解程序實現參數辨識。
 圖6
機械臂末端工具坐標系匹配實驗
Figure6.
Tool coordinate system matching photos
圖6
機械臂末端工具坐標系匹配實驗
Figure6.
Tool coordinate system matching photos
為防止模型參數過擬合,本文從全部數據集合中隨機選取若干組數據作為子集進行參數辨識,獲取模型參數,如此循環重復若干次,根據所得每項數據的分布求取均值,作為最終所得的模型參數。如圖 7 所示為在 551 組數據中隨機選取 200 組數據進行參數辨識,重復 10 000 次,所得 27 個待辨識參數分布情況。可以看出所求參數均符合正態分布,認為參數分布均值反映了參數真實值。
 圖7
10 000 次參數辨識后所得運動學參數分布
Figure7.
Kinematic parameter distribution after 10 000 times of parameter identification
圖7
10 000 次參數辨識后所得運動學參數分布
Figure7.
Kinematic parameter distribution after 10 000 times of parameter identification
4.4 實驗室樣機參數辨識精度評價結果
為評價參數辨識精度,在上文所述環形圓柱空間中隨機指定 30 個測量位姿,控制機械臂以所有可行逆解運動到測量位姿,并記錄位置坐標。比較標稱參數和辨識后參數的相對距離誤差和逆解重合誤差。誤差曲線及測量點分布如圖 8 所示。可以看出辨識后機器人相對距離誤差和逆解重合誤差均明顯降低。經統計,兩項誤差均值分別從辨識前的 0.19%、0.93 mm 降低到辨識后的 0.08%、0.27 mm,逆解重合誤差的方差從 0.10 mm 降低到 0.05 mm。從參數驗證測量點位置分布圖中也可以直觀看出,辨識后機器人同一位姿下逆解離散程度明顯減小。
 圖8
實驗室樣機精度評價結果
Figure8.
Prototype accuracy evaluation results
圖8
實驗室樣機精度評價結果
Figure8.
Prototype accuracy evaluation results
4.5 手術機器人現場參數辨識與評價結果
為驗證本方法實際可行性,隨機抽取 5 臺神經外科手術機器人樣機 Sino(華科精準 Inc.,中國)進行批量參數辨識,該型手術機器人機械臂與本文采用機械臂型號一致。選用便攜式光學追蹤系統 Polaris Vega(Northern Digital Inc.,加拿大)(精度 0.15 mm)測量手術機器人末端位姿。每臺機器人選取相同的 300 組數據測量點,隨機挑選 75% 的測量值進行參數辨識,重復 100 次,將均值作為最終參數辨識結果。辨識完成后,隨機設定 20 個測量位姿進行辨識結果驗證,計算每臺機器人標稱參數和辨識后參數的相對距離誤差與逆解重合誤差均值。除加載文件以外,所有辨識過程均由系統自動進行,無需人為干預。如圖 9 所示為現場參數辨識和評價照片,如圖 10 所示為相對距離誤差均值和標準差,如圖 11 所示為逆解重合誤差均值和標準差,如表 1 所示為參數辨識前后誤差優化百分比。
 圖9
機器人現場參數辨識照片
Figure9.
Photos of robot kinematics parameter identification in real applications
圖9
機器人現場參數辨識照片
Figure9.
Photos of robot kinematics parameter identification in real applications
 圖10
批量參數辨識機器人相對距離誤差均值與標準差
Figure10.
Mean value and standard deviation of relative distance error of five robots
圖10
批量參數辨識機器人相對距離誤差均值與標準差
Figure10.
Mean value and standard deviation of relative distance error of five robots
 圖11
批量參數辨識機器人逆解重合誤差均值與標準差
Figure11.
Mean value and standard deviation of inverse kine matics consistency error of five robots
圖11
批量參數辨識機器人逆解重合誤差均值與標準差
Figure11.
Mean value and standard deviation of inverse kine matics consistency error of five robots
可以看出,本方法可以保證不同機械臂相對距離誤差在 0.1% 左右,機械臂逆解重合誤差在 0.3 mm 左右。經統計,5 臺機械臂相對距離誤差平均降低 33.96%,機械臂逆解重合誤差平均降低 67.30%。還可以看出,若采用標稱運動學參數,不同機械臂之間精度差異很大。性能較好的 1 號機器人相對距離誤差 0.09% ± 0.02%,逆解重合誤差(0.83 ± 0.04)mm,性能較差的 4 號機器人相對距離誤差 0.20% ± 0.05%,逆解重合誤差(1.54 ± 0.17)mm,評價指標相差兩倍多,這使得機器人之間的精度均一性難以保證,從而大大增加手術風險。采用本文辨識獲得的運動學參數,可以有效降低機械臂不同位置間相對距離誤差和逆解重合誤差,獲得更貼近真實值的手術機器人運動學模型,保證量產的神經外科手術機器人的精度和性能均一性。另外,也可以采用本文方法對在用的手術機器人進行精度的驗證,必要時進行修正。
5 討論
5.1 參數辨識方法
本文設計了兩步參數辨識算法和工具坐標系匹配方法,既可以實現機械臂本體加末端工具的聯合參數辨識,也可以實現基于辨識后機械臂參數的末端工具單獨辨識。本文提出的平均化方法可以很好地提高參數識別的魯棒性,如圖 7 所示,雖然在每次辨識的過程中參數差異性較大,但是在大量實驗過程中,辨識參數服從正態分布,取分布均值作為辨識后參數可以抵消單次參數辨識誤差。另外,本文采用固定數值的方法避免參數耦合,雖然被固定參數誤差無法進行優化,但從本文的結果可以看出,少量的參數固定仍可以實現較大幅度的精度優化。
5.2 精度評價方法
對于神經外科手術機器人精度的評價是保證機器人精度一致性所必需的。本文中采用相對距離誤差反映機器人在定位定向中相對指定參考坐標的定位精度,逆解重合誤差反映機器人在不同逆解下到達指定的一致性。兩項誤差均為相對量,直接在測量設備坐標系中度量,無需測量設備—機械臂配準,不僅可以用于辨識參數有效性的評估,還可以在臨床環境下快速、直觀、方便地完成手術機器人日常精度檢驗。
5.3 自動化程度
對參數的辨識和精度評價過程中的位姿數據測量是一件需要極高認真度且費時費力的工作,手動操作需要投入巨大的人力且易引入不必要的操作誤差。本文對光學追蹤系統和機械臂進行編程控制,可以實現自動化的機器人位姿測量和數據導出,測量中僅需極少的人為參與,同時為參數辨識和精度評價算法設計了人機交互界面,使得非專業人員也可操作完成機器人參數辨識和精度評價,因此通過本系統可以實現醫療機器人現場參數辨識和精度評價。
6 結論
本文通過對機械臂和手術工具運動學參數辨識,獲得更貼近于實際的手術機器人運動學模型,降低手術機器人運動學模型參數實際值與標稱值不一致問題帶來的誤差。本文提出了兩項精度評價指標,用以快速便捷地評價手術機器人精度。本文還建立了自動化的數據測量和參數辨識算法程序。本文所提供的方法可以實現用于現場的手術機器人高效參數辨識和精度評價。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。