為了消除運動偽差、高頻噪聲和基線漂移對光電容積脈搏波(PPG)的影響,得到運動狀態下心率的準確值,本文提出了一種基于歸一化最小均方差(NLMS)自適應濾波器聯合集合經驗模態分解(EEMD)分析的 PPG 信號降噪方法。首先,將含有噪聲的 PPG 信號以 3 軸加速度傳感器為參考信號通過自適應濾波器,濾除其中的運動偽差;其次,將 PPG 信號通過 EEMD 分解得到一系列按頻率由高到低的固有模態分量(IMF),通過排列熵(PE)準則判斷信號的閾值范圍,從而濾除其中的高頻噪聲和基線漂移。實驗結果顯示,不同運動狀態下,降噪后 PPG 信號的計算心率和基于心電信號(ECG)的標準心率的皮爾遜相關系數為 0.731,平均絕對誤差百分比為 6.10%,從而表明該方法能夠準確計算出運動狀態的心率,有利于人體運動狀態下的生理監測。
引用本文: 耿讀艷, 趙杰, 王晨旭, 董嘉冀, 寧琦, 王琰. 基于歸一化最小均方差聯合集合經驗模態分解的運動狀態下心率提取算法研究. 生物醫學工程學雜志, 2020, 37(1): 71-79. doi: 10.7507/1001-5515.201812022 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
心率作為衡量心臟搏動能力的參數,其變化與心臟疾病密切相關,是臨床上評價身體健康狀況常用的指標之一[1-3]。在運動狀態下,基于光電容積脈搏波(photoplethysmographic,PPG)的心率測量方法具有方便且靈敏度高的特點。由于脈搏信號微弱而測量裝置的靈敏性較高,以致于測量得到的 PPG 信號易包含運動偽差、高頻噪聲和基線漂移等主要噪聲[4-5]。其中,運動偽差因測量裝置和測量部位的相對運動所產生;高頻噪聲來自于信號采集過程中采集裝置的電磁干擾;基線漂移是由于受試者的呼吸和咳嗽等其它生理活動所導致的[6-7]。因此,消除 PPG 信號所包含的噪聲對于提高運動狀態下人體心率監測的準確率和及時發現人體異常具有重要的意義。
運動狀態下 PPG 信號去噪聲的方法主要有獨立成分分析(independent component analysis,ICA)、小波變換(wavelet transform,WT)、經驗模態分解(empirical mode decomposition,EMD)和自適應濾波器。Kim 等[8]利用 ICA 設計濾波器,將運動偽差和 PPG 信號看作獨立成分后對 PPG 信號進行盲源分離,在強運動下驗證了算法的可行性。Peng 等[9]采用雙通道測量 PPG 信號,使用約束性獨立成分分析(constrained independence component analysis,cICA)方法提取 PPG 信號得到優于單通道 ICA 的實驗結果。Wang 等[10]建立了一種基于小波變換的自適應軟閾值方法濾除 PPG 信號中的主要噪聲,通過選擇合適的小波基后重構出脈搏信號,并與傅里葉變換得到的心率進行比較,取得了較好的實驗結果。王金海等[11]采用 EMD 方法處理微弱運動下的 PPG 信號,通過分析分解得到的固有模態函數(intrinsic mode function,IMF)的波形信息,使用多尺度濾波和累計能量濾波的方法濾除了 PPG 信號中的高頻和基線漂移噪聲,同時解決了在 PPG 信號采集過程中的中斷問題。Ram 等[12]利用傅里葉變換、奇異值分解和 ICA 構造了三種不同的參考信號,同時使用了三種不同的自適應濾波算法來去除 PPG 信號中的運動偽差,取得了良好的實驗效果。
通過上述研究可知,自適應濾波器在濾除 PPG 信號中的運動偽差上表現良好,而 EMD 在濾除 PPG 信號中高頻噪聲和基線漂移時取得了良好的實驗結果。因此,本文提出了一種歸一化最小均方差(normalized least mean square,NLMS)濾波算法和集合經驗模態分解(ensemble empirical mode decomposition,EEMD)算法相聯合的 PPG 信號降噪方法(NLMS-EEMD),同時濾除在運動狀態下 PPG 信號中的運動偽差、高頻噪聲和基線漂移,從而得到心率的準確值,以期實現運動狀態下心率信號的實時監測。
1 算法原理及評價指標
1.1 NLMS-EEMD 算法原理
NLMS 是一種改進的自適應濾波算法,解決了最小均方誤差(least mean square,LMS)算法在收斂速度和穩態誤差對步長要求相互矛盾的問題[13]。其優點是在濾波的初始階段步長大、收斂速度快,而在滿足收斂速度后,減小步長以提高收斂精度[14]。NLMS 濾波器的應用準則是將輸入信號與參考信號進行比較得到誤差,在迭代運算中不斷調整加權濾波器的系數使得均方誤差函數的值達到最小,算法的具體原理如式(1)~式(4)所示。
設輸入信號為  ,則經過濾波器后的輸出信號為
,則經過濾波器后的輸出信號為  ,如式(1)所示:
,如式(1)所示:
 |
其中, 為濾波器權系數的轉置,N 為濾波器階數。
為濾波器權系數的轉置,N 為濾波器階數。 為濾波器權系數。
為濾波器權系數。
將  與期望的參考信號
與期望的參考信號  比較,得到誤差信號
比較,得到誤差信號  ,如式(2)所示:
,如式(2)所示:
 |
在迭代運算中,需要不斷調整加權濾波器的系數,如式(3)、式(4)所示:
 |
其中, 為步長因子,取值范圍
為步長因子,取值范圍  ,
, 為預先設定的矯正量,取值范圍
為預先設定的矯正量,取值范圍  。
。
 |
其中, 為均方誤差。
為均方誤差。
EEMD 通過在原始信號上疊加高斯白噪聲,如式(5)所示,并利用其在分解中的統計特性解決了模態混疊問題,使 IMF 物理意義更加明確[15-16]。對添加白噪聲后的信號進行 EMD 分解,然后重復添加同等幅值的白噪聲再分解,如式(6)所示。計算 IMF 分量的排列熵(permutation entropy,PE),根據 PE 值的大小對 IMF 進行重構可消除信號中的高頻噪聲和基線漂移[17]。
 '/> '/> |
其中, 為添加的白噪聲幅值,
為添加的白噪聲幅值, 為添加的白噪聲,
為添加的白噪聲, 為添加白噪聲后的信號,
為添加白噪聲后的信號, 為實驗次數。
為實驗次數。
 '/> '/> |
其中,IMFi 為第  個 IMF 分量,其值為
個 IMF 分量,其值為  次分解后的均值。
次分解后的均值。 為余項。
為余項。
對  進行相空間重構,如式(7)所示:
進行相空間重構,如式(7)所示:
 |
其中, 為
為  的第
的第  個行向量,
個行向量, 為嵌入維數,
為嵌入維數, 為時間延遲。將
為時間延遲。將  按照升序排列如式(8)所示:
按照升序排列如式(8)所示:
 |
其中, 為重構向量中元素所在列的索引號。此時,任意一個 IMF 分量都可以得到一組序列,如式(9)所示。計算出每種序列出現的概率,即可得到 IMF 分量的 PE 值,如式(10)所示:
為重構向量中元素所在列的索引號。此時,任意一個 IMF 分量都可以得到一組序列,如式(9)所示。計算出每種序列出現的概率,即可得到 IMF 分量的 PE 值,如式(10)所示:
 |
其中, ,
, 是
是  種序列的一種。
種序列的一種。
 |
其中, 為
為  序列出現的概率。
序列出現的概率。
1.2 實驗結果評價指標
本實驗采用皮爾遜相關系數和平均絕對誤差百分比來衡量計算結果和標準結果之間的誤差[18-19]。皮爾遜相關系數可以用于反映兩個變量之間的相關程度,其值通過兩個變量和其離差的積來計算。當皮爾遜相關系數的值在 0.8~1.0 之間時,兩變量為極強相關;在 0.6~0.8 之間時,兩變量為強相關;在 0.4~0.6 之間時,兩變量為中等程度相關;在 0.4 以下時,兩變量為極弱相關或無相關。其計算過程如式(11)所示:
 |
其中,R 為皮爾遜相關系數, 、
、 分別為
分別為  個試驗值,
個試驗值, 、
、 分別為對應的
分別為對應的  個試驗值的均值。
個試驗值的均值。
平均絕對誤差百分比表示計算值和標準值之間偏差絕對值占標準值百分比的平均值。將平均絕對誤差進行百分比,消除了受試者的個體差異性,有助于對比實驗結果的準確性。計算過程如式(12)所示:
 |
其中, 表示平均絕對誤差百分比,
表示平均絕對誤差百分比, 表示計算值,
表示計算值, 表示標準值。
表示標準值。
2 實驗
2.1 實驗數據來源
本研究使用的 PPG 信號來自于麻省理工學院心率失常數據庫(Massachusetts Institute of Technology-Beth Israel Hospital,MIT-BIH)的運動狀態下腕部脈搏波數據庫(網址:https://physionet.org/physiobank/database/wrist/),采樣頻率為 256 Hz,記錄時長為 10 min 左右[20]。數據庫中包含原始的 PPG 信號,同時給出了運動過程中采集的心電(electrocardiogram,ECG)信號、加速度傳感器和陀螺儀傳感器等的同步信號[20]。在原始 ECG 信號采集過程中,使用控制軟件消除電源干擾,且進行了 50 Hz 陷波器處理,保證了數據的完整性以及參考心率計算的準確性。
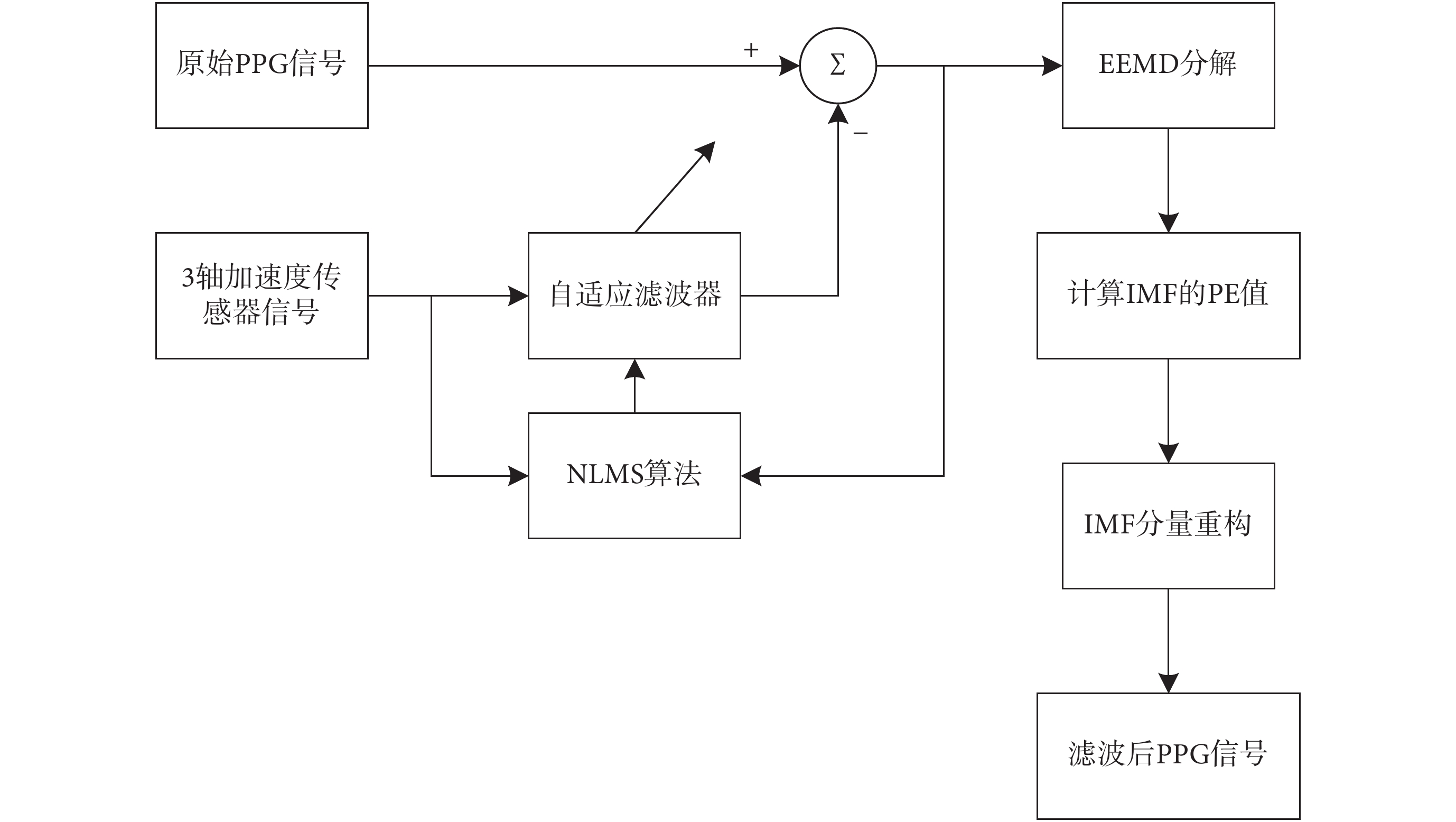
本實驗選擇了低阻騎行、高阻騎行和步行三種運動狀態下的 24 組數據來進行算法驗證。為對降噪效果進行定量說明,分別計算出每組數據同一時間段內 ECG 信號和 PPG 信號的心拍,用 RR 間期和 CC 間期來表示,并計算其相關性。為了評價降噪后 PPG 信號心率檢測方法的準確性,分別計算出每組數據 1 min 內 ECG 信號和 PPG 信號的主峰個數,即標準心率和計算心率,并計算皮爾遜相關性系數和平均絕對誤差百分比。實驗具體過程如圖 1 所示。
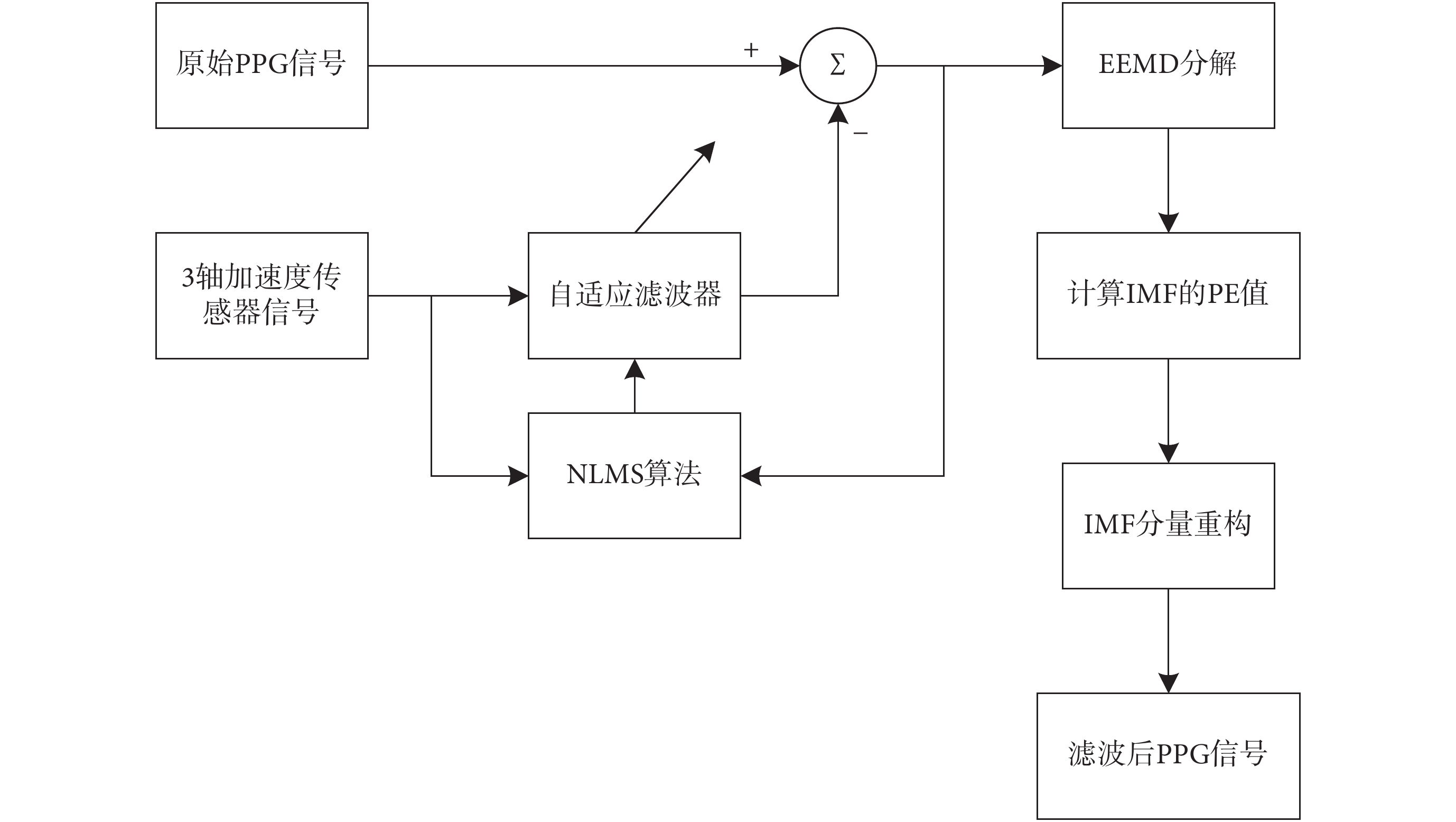 圖1
PPG 信號去噪原理
Figure1.
PPG signal de-noising principle
圖1
PPG 信號去噪原理
Figure1.
PPG signal de-noising principle
2.2 信號處理
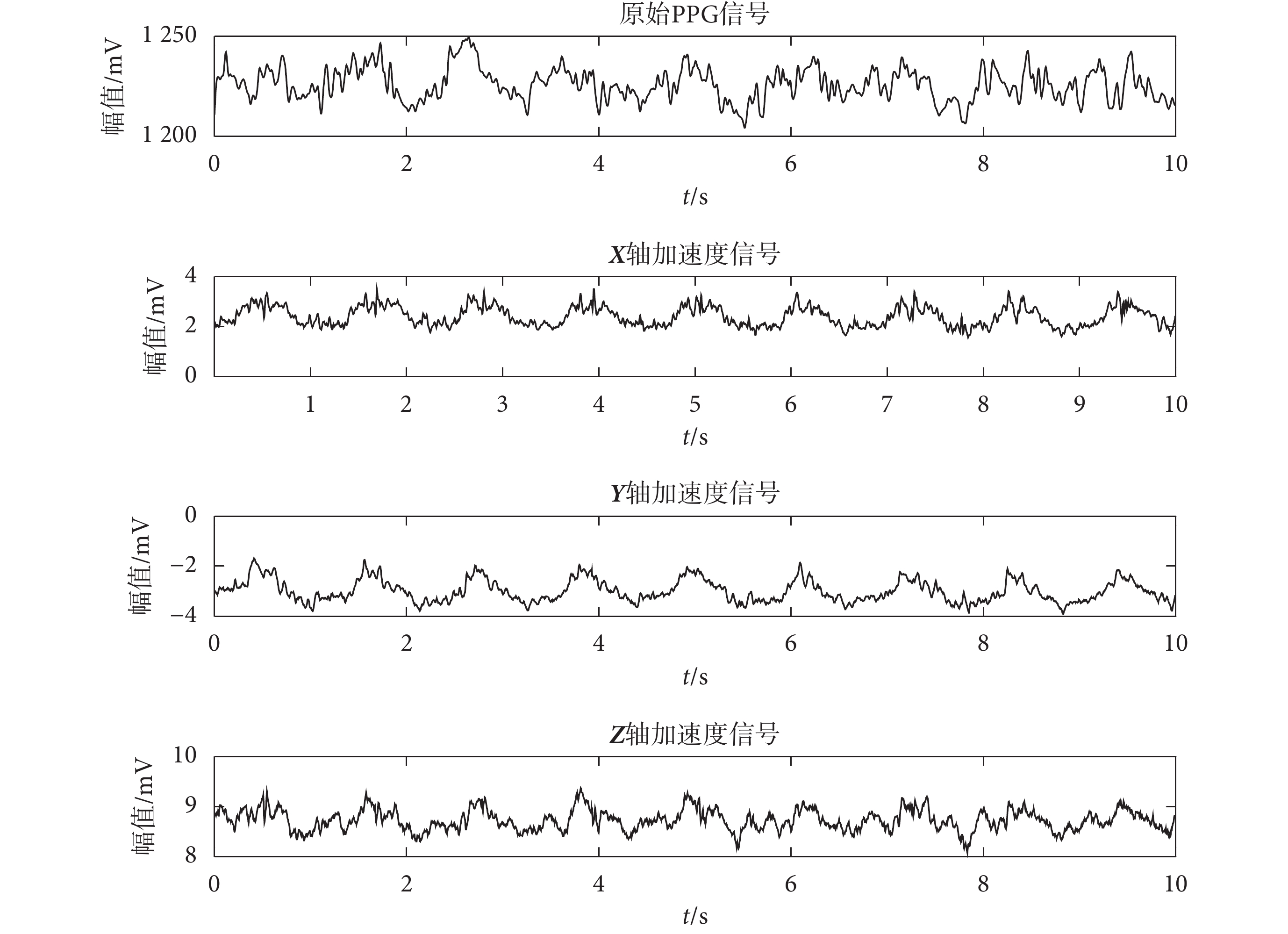
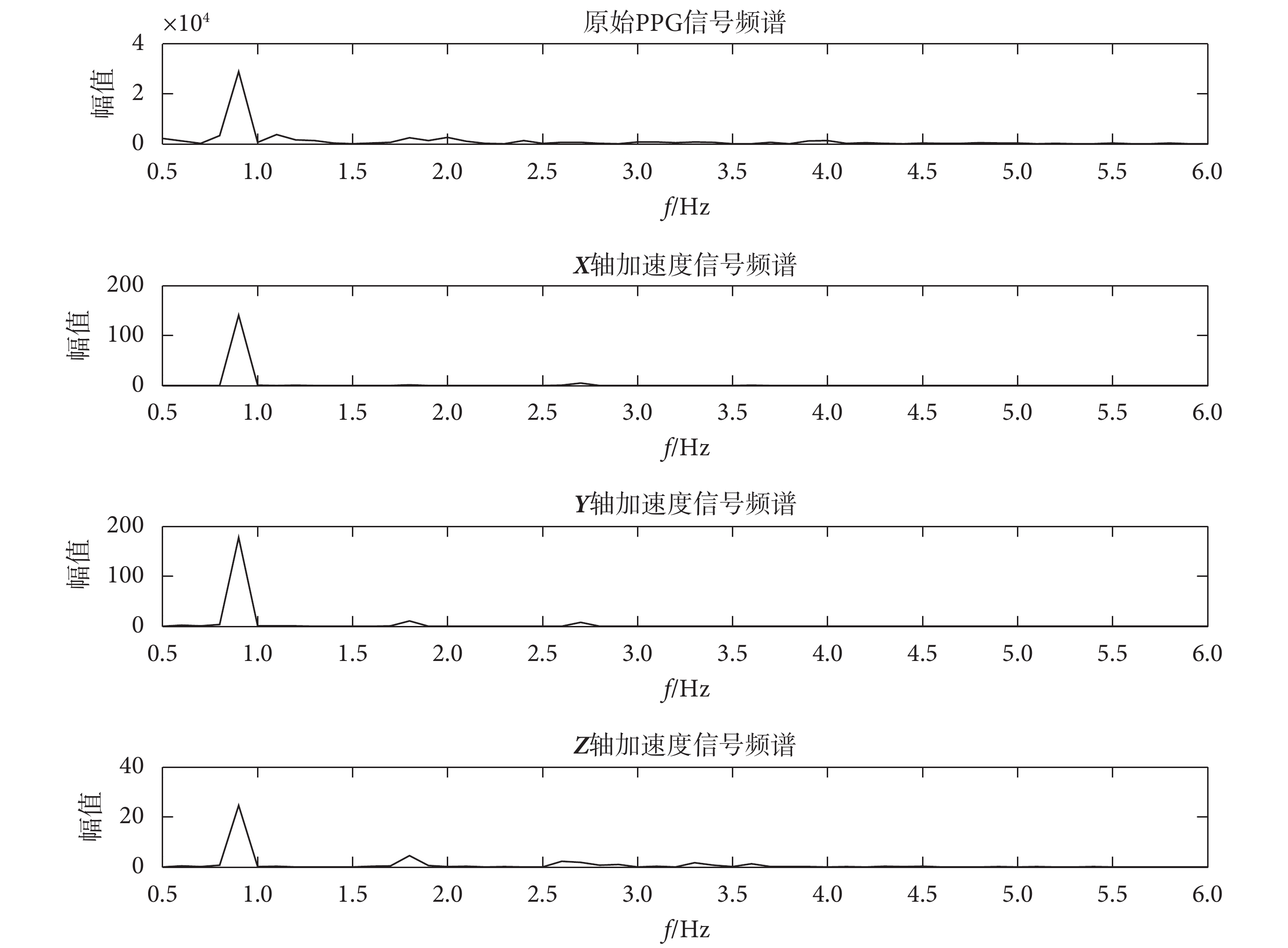
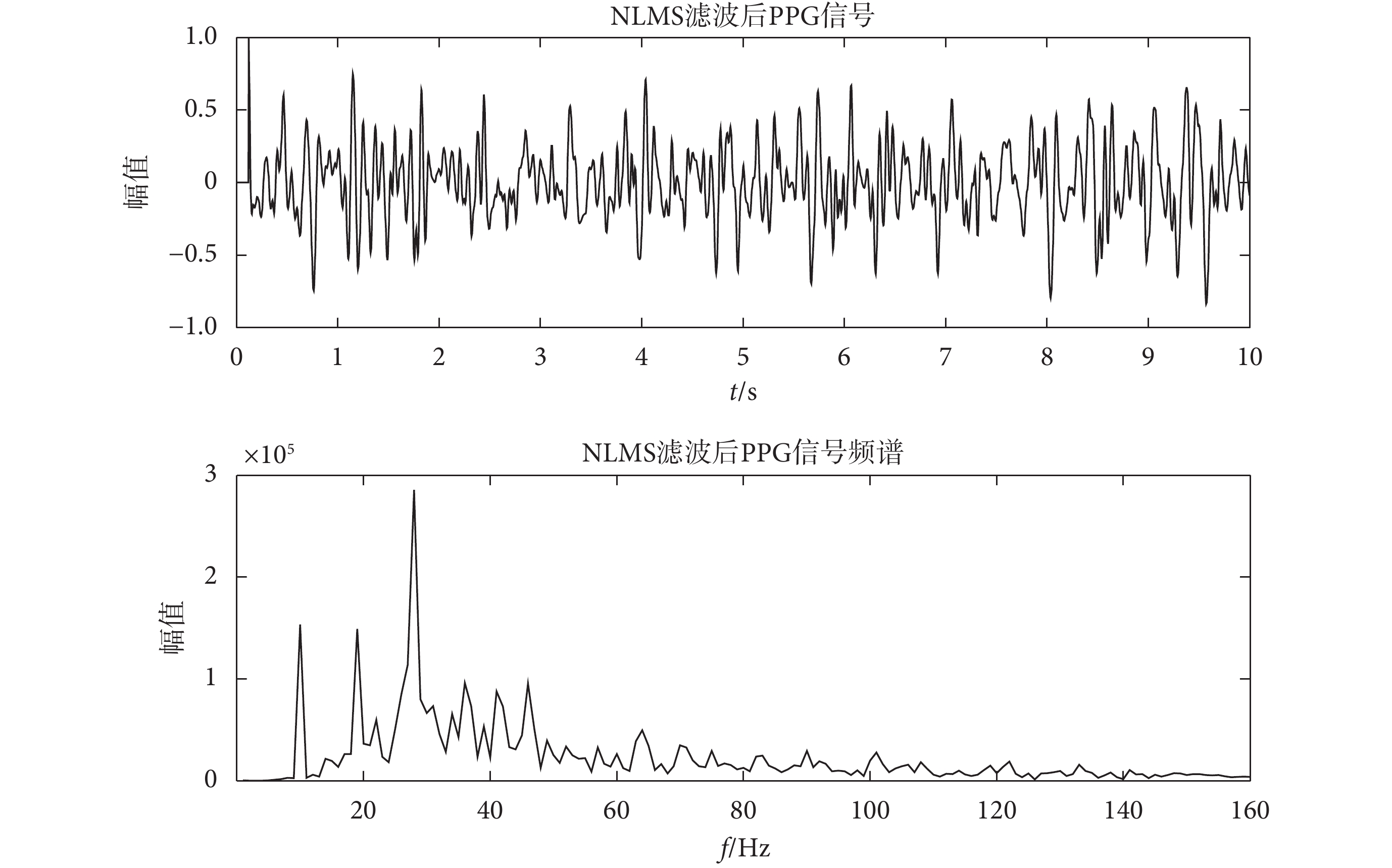
低阻騎行 PPG 信號和 3 軸加速度傳感器信號如圖 2 所示,時長均為 10 s,其中 3 軸加速度傳感器包括 X 軸加速度、Y 軸加速度和 Z 軸加速度。低阻騎行 PPG 信號和 3 軸加速度傳感器信號頻譜如圖 3 所示,當 PPG 信號受到運動偽差的影響后,其頻譜分析結果和 3 軸加速度傳感器信號基本相同,且在時域分析時也無法明確得出主峰個數。經過 NLMS 算法濾波器處理之后的 PPG 信號及其頻譜圖如圖 4 所示,原始 PPG 信號經過以 3 軸加速度傳感器為參考信號的 NLMS 算法濾波器處理后運動噪聲減弱,高頻噪聲和基線漂移表現明顯。
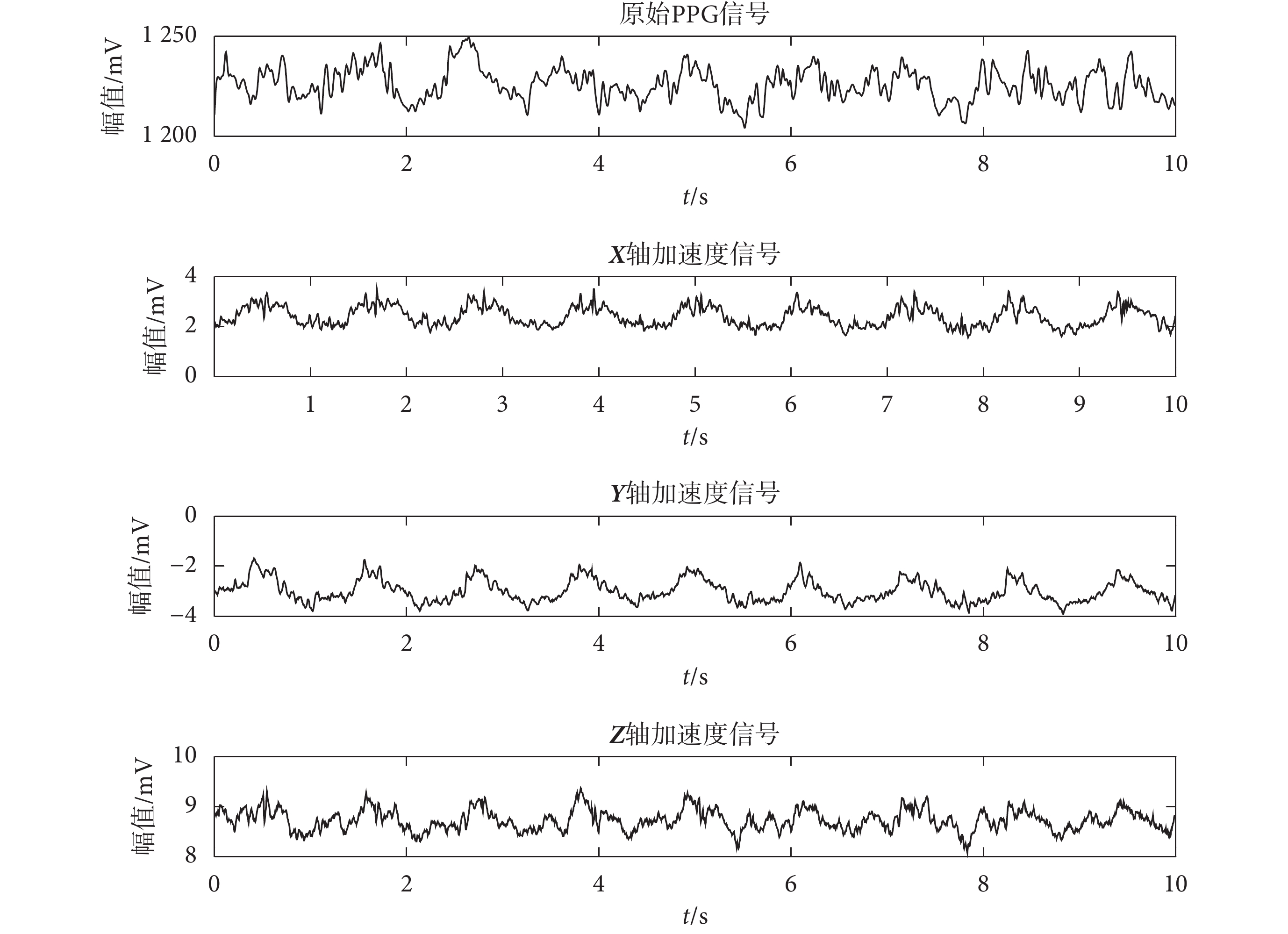 圖2
低阻騎行 PPG 和 3 軸加速度傳感器信號
Figure2.
Low-impedance riding PPG and 3-axis accelerometer signals
圖2
低阻騎行 PPG 和 3 軸加速度傳感器信號
Figure2.
Low-impedance riding PPG and 3-axis accelerometer signals
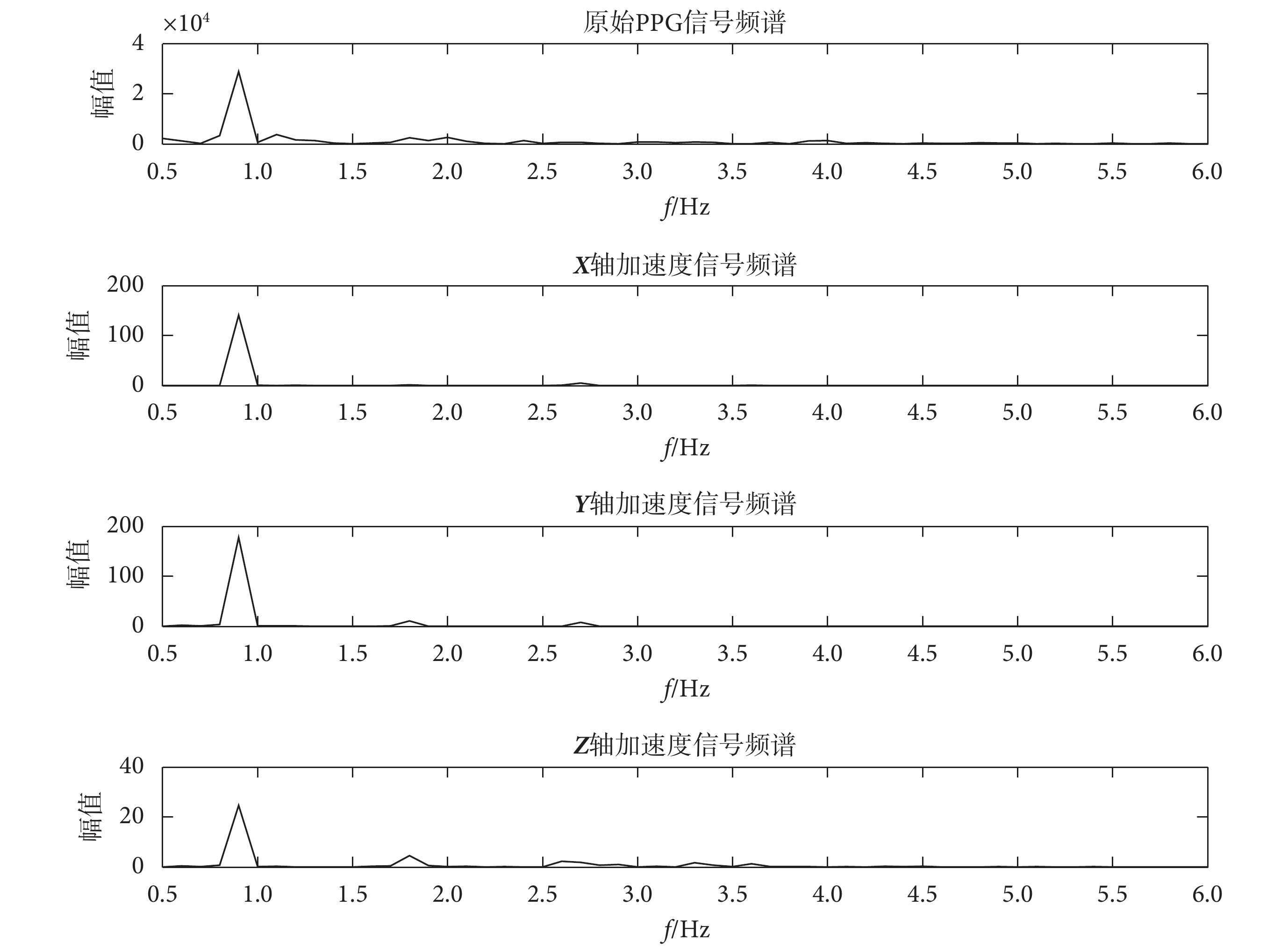 圖3
低阻騎行 PPG 和 3 軸加速度傳感器信號頻譜
Figure3.
Spectrogram of low-impedance riding PPG and 3-axis accelerometer signals
圖3
低阻騎行 PPG 和 3 軸加速度傳感器信號頻譜
Figure3.
Spectrogram of low-impedance riding PPG and 3-axis accelerometer signals
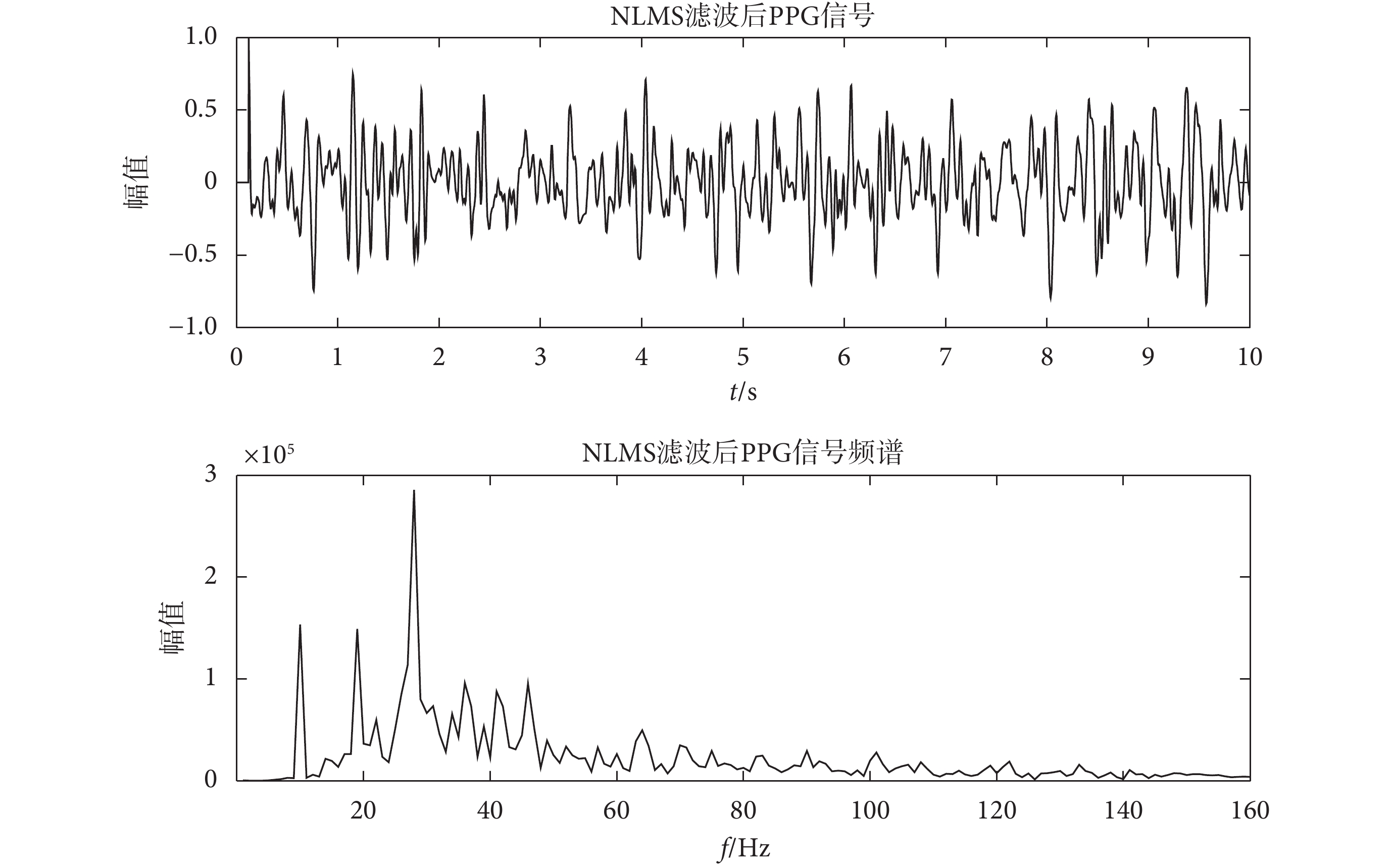 圖4
NLMS 濾波后的 PPG 信號及其對應頻譜
Figure4.
NLMS filtered PPG signal and its spectrum
圖4
NLMS 濾波后的 PPG 信號及其對應頻譜
Figure4.
NLMS filtered PPG signal and its spectrum
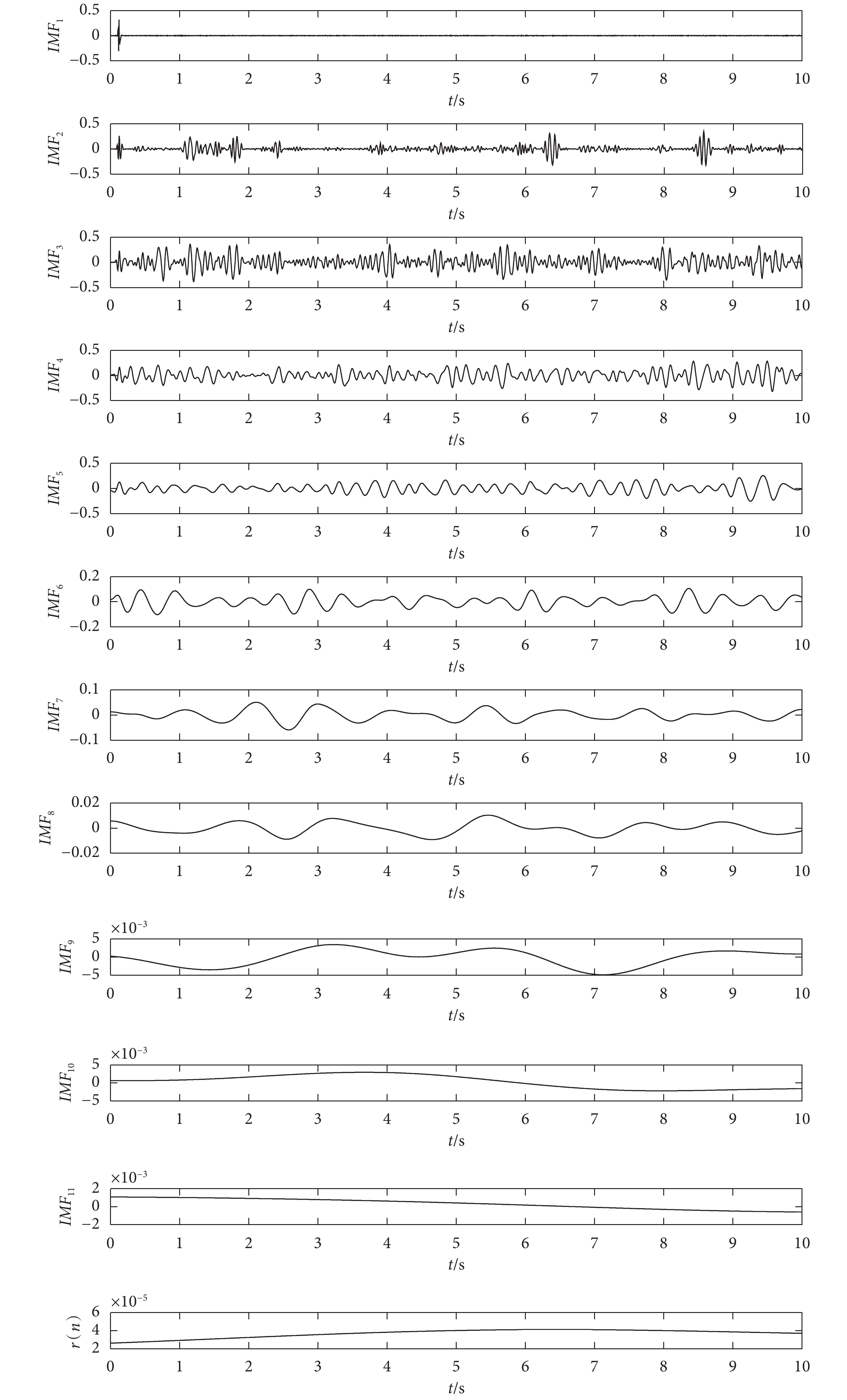
以 NLMS 算法濾波后的 PPG 信號經過 EEMD 分解結果如圖 5 所示。由圖 5 可知,低阻騎行 PPG 信號經 EEMD 分解后得到 11 個 IMF 分量和 1 個余項。根據 EEMD 分解過程可知,噪聲對每個 IMF 分量影響逐漸減弱,對信號的影響逐漸增強。因此,
 可能代表的是高頻噪聲,
可能代表的是高頻噪聲,
 可能代表 PPG 信號分量,
可能代表 PPG 信號分量, 可能代表基線漂移部分。
可能代表基線漂移部分。
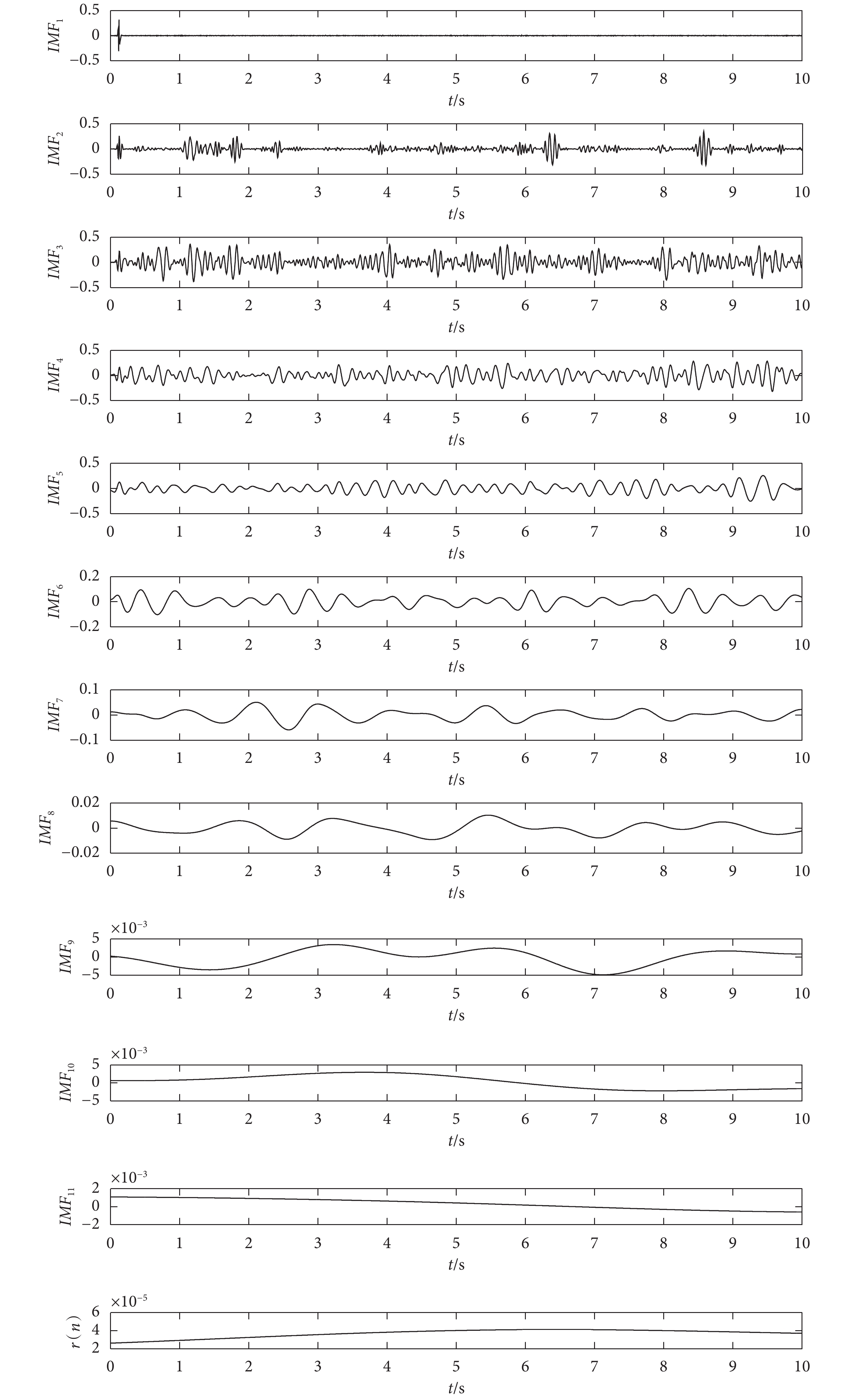 圖5
EEMD 分解圖
Figure5.
EEMD decomposition diagram
圖5
EEMD 分解圖
Figure5.
EEMD decomposition diagram
由多次實驗可知,不同運動狀態下的 IMF 分量個數不同,主觀判斷信號和噪聲之間的分界是不準確的。為減小信號重構誤差,提高心率計算準確率,本實驗采用 PE 值來判斷噪聲和有效信號所占有的 IMF 分量。在計算 PE 值的過程中,需要選擇合適的嵌入維數 α 和時間延遲  ,根據經驗取
,根據經驗取  ,
, [21-22]。不同運動狀態下各 PE 值總體趨勢在減小,據此證實了噪聲對不同的 IMF 支配作用不同。對不同運動狀態下的 PE 值(以符號 pe 表示)進行多次計算,取定的有效信號的閾值為
[21-22]。不同運動狀態下各 PE 值總體趨勢在減小,據此證實了噪聲對不同的 IMF 支配作用不同。對不同運動狀態下的 PE 值(以符號 pe 表示)進行多次計算,取定的有效信號的閾值為  ,當
,當  時為高頻噪聲分量,
時為高頻噪聲分量, 時為低頻基線漂移分量,不同運動狀態下 PE 值如表 1 所示[23-24]。
時為低頻基線漂移分量,不同運動狀態下 PE 值如表 1 所示[23-24]。
3 實驗結果
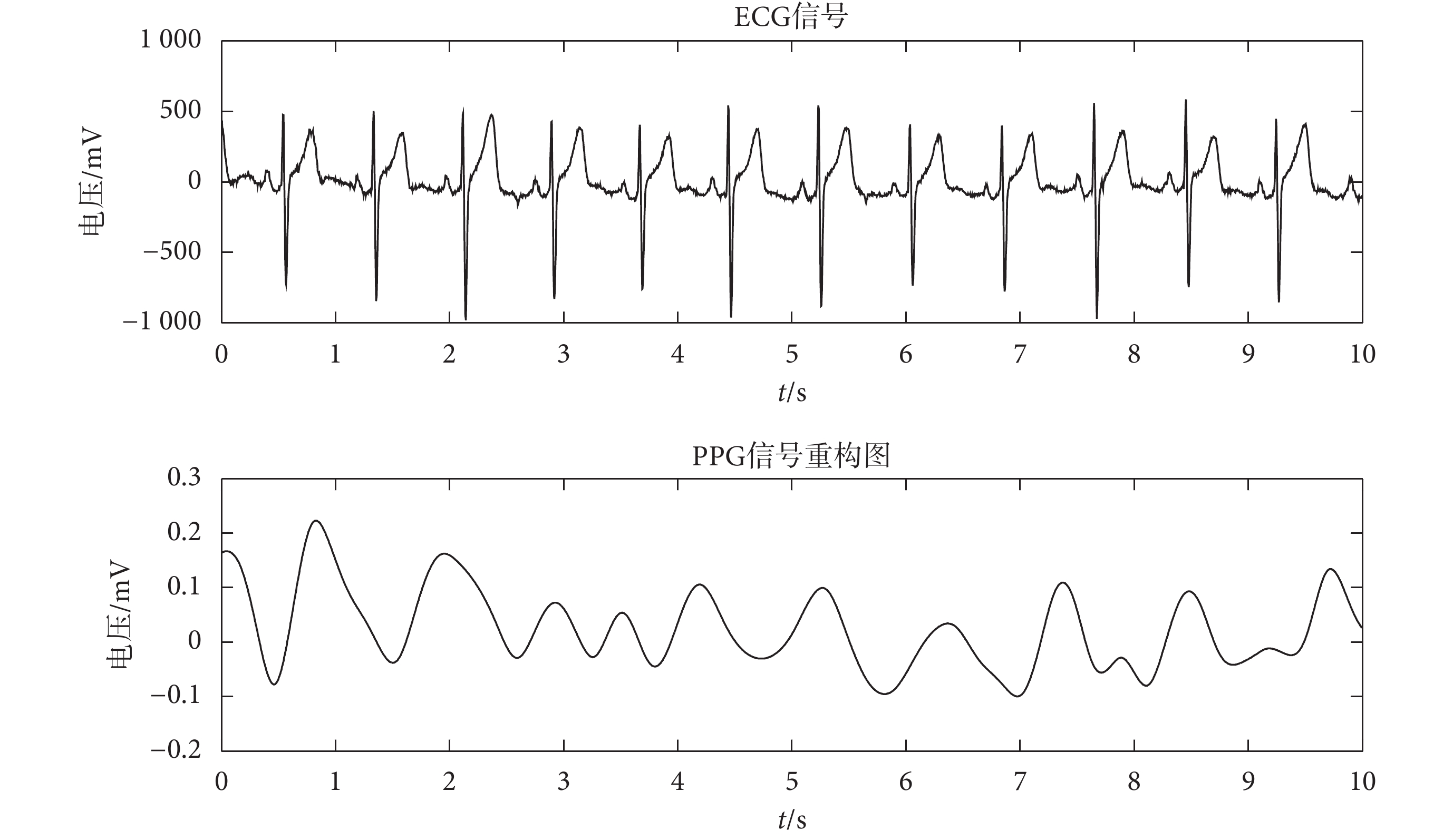
對在閾值范圍內的 IMF 分量進行重構得到 PPG 信號如圖 6 所示,從圖 6 中可以看出,消除了運動偽差、高頻噪聲和基線漂移后的信號更加光滑,主峰突出明顯有利于心率的計算。本實驗選擇的 24 組 PPG 信號包含了低阻騎行、高阻騎行和步行三種運動狀態,分別計算出每組數據的 RR 間期和 CC 間期及其皮爾遜相關系數,如表 2 所示。依次統計不同運動狀態下的皮爾遜相關系數,結果分別為 0.931 ± 0.045、0.904 ± 0.047、0.945 ± 0.041。由此可知,在步行和低阻騎行時,降噪效果好;在高阻騎行時,降噪效果較差。
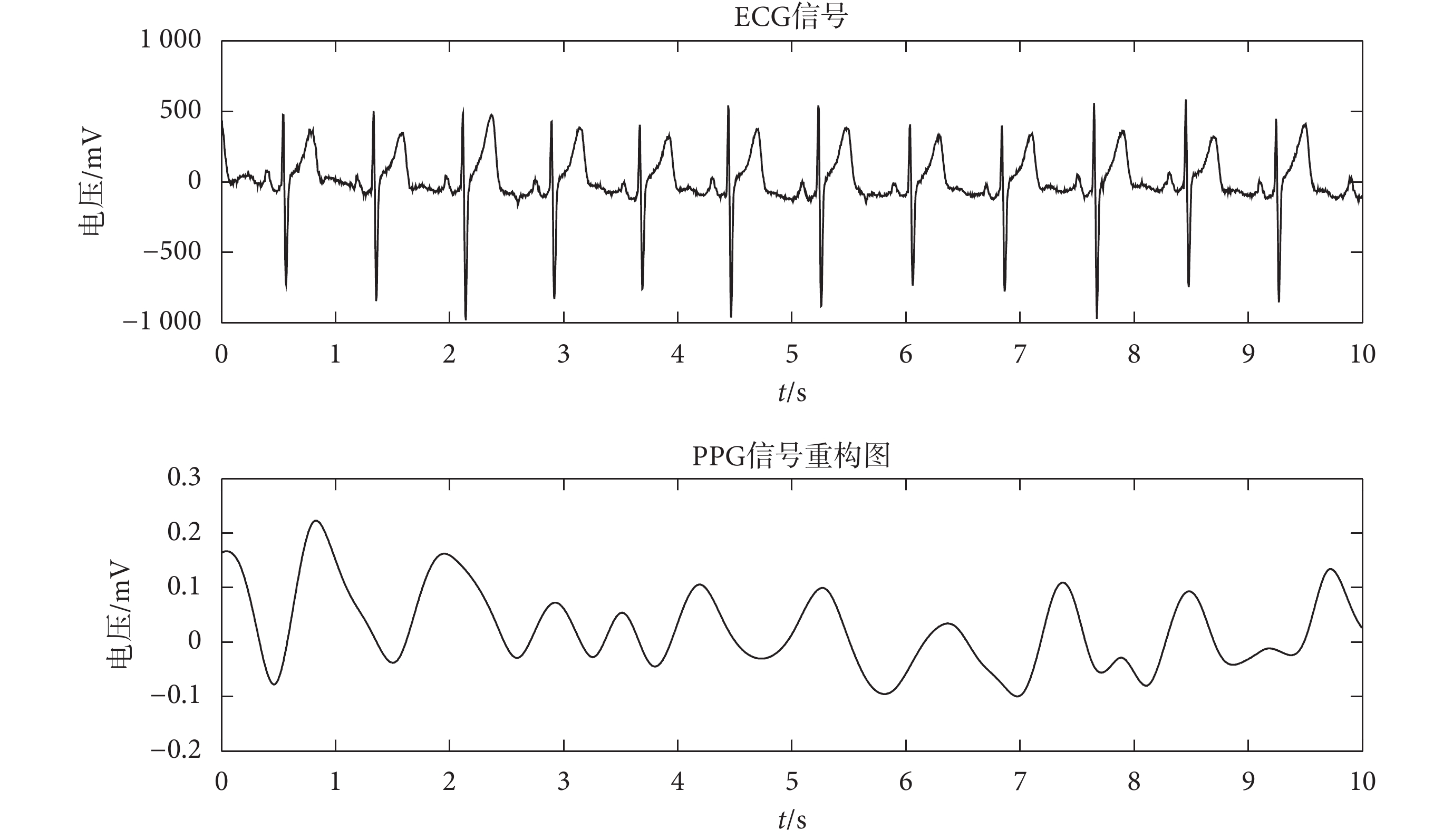 圖6
ECG 和 PPG 同步對比圖
Figure6.
Synchronous comparison between ECG and PPG
圖6
ECG 和 PPG 同步對比圖
Figure6.
Synchronous comparison between ECG and PPG
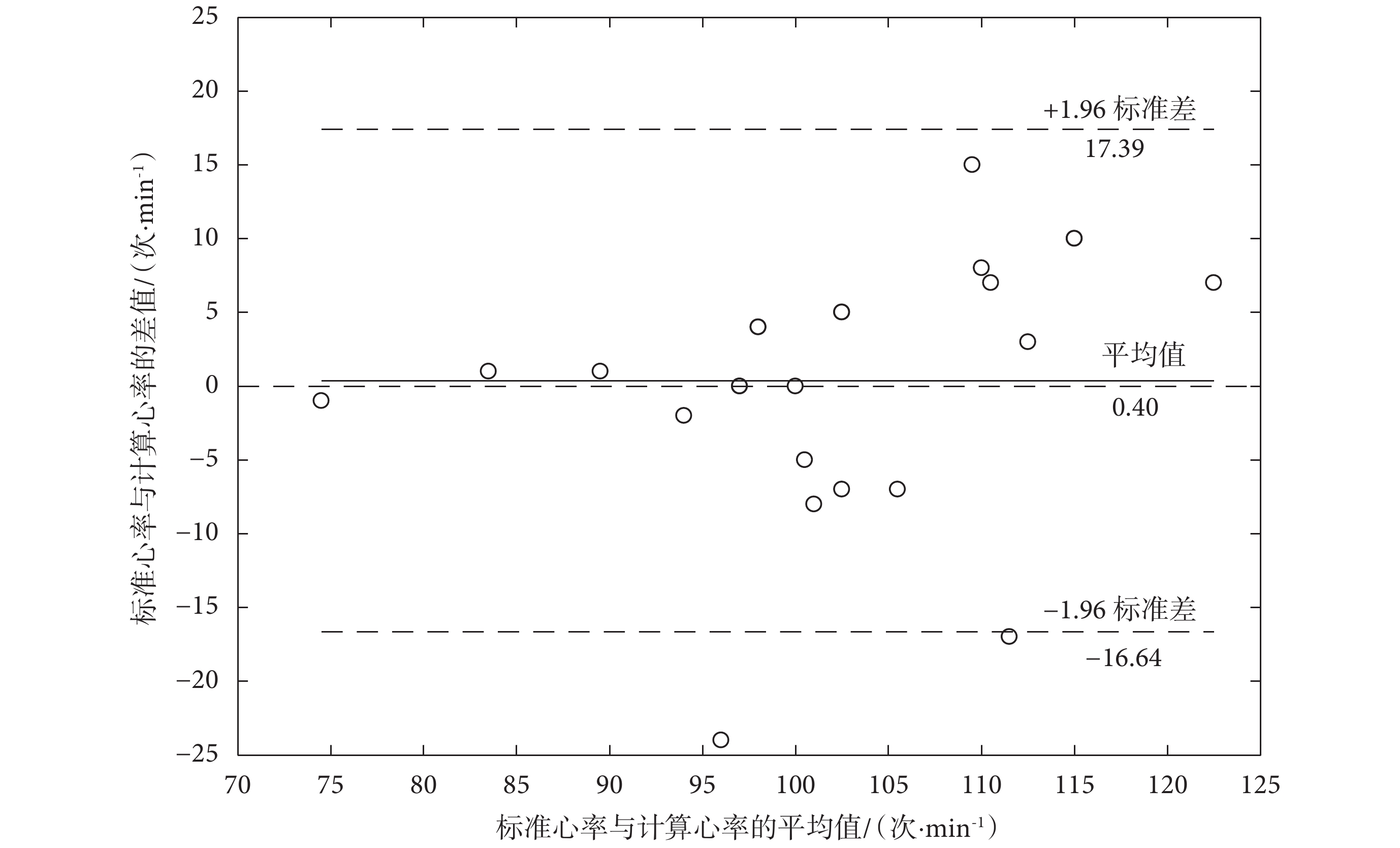
計算標準心率和計算心率的皮爾遜相關系數和平均絕對誤差百分比,并進行偏差統計,其偏差統計結果如圖 7 所示。由圖 7 可知,標準心率和計算心率的相關系數的值為 0.731,表明計算心率和標準心率之間是強相關,平均絕對誤差百分比為 6.10%,表明在不受到個體差異性的影響時,計算心率可以用來代替標準心率。同時,計算心率幾乎全部位于 95% 的置信區間內,證明了本算法的降噪效果具有較高的準確性。
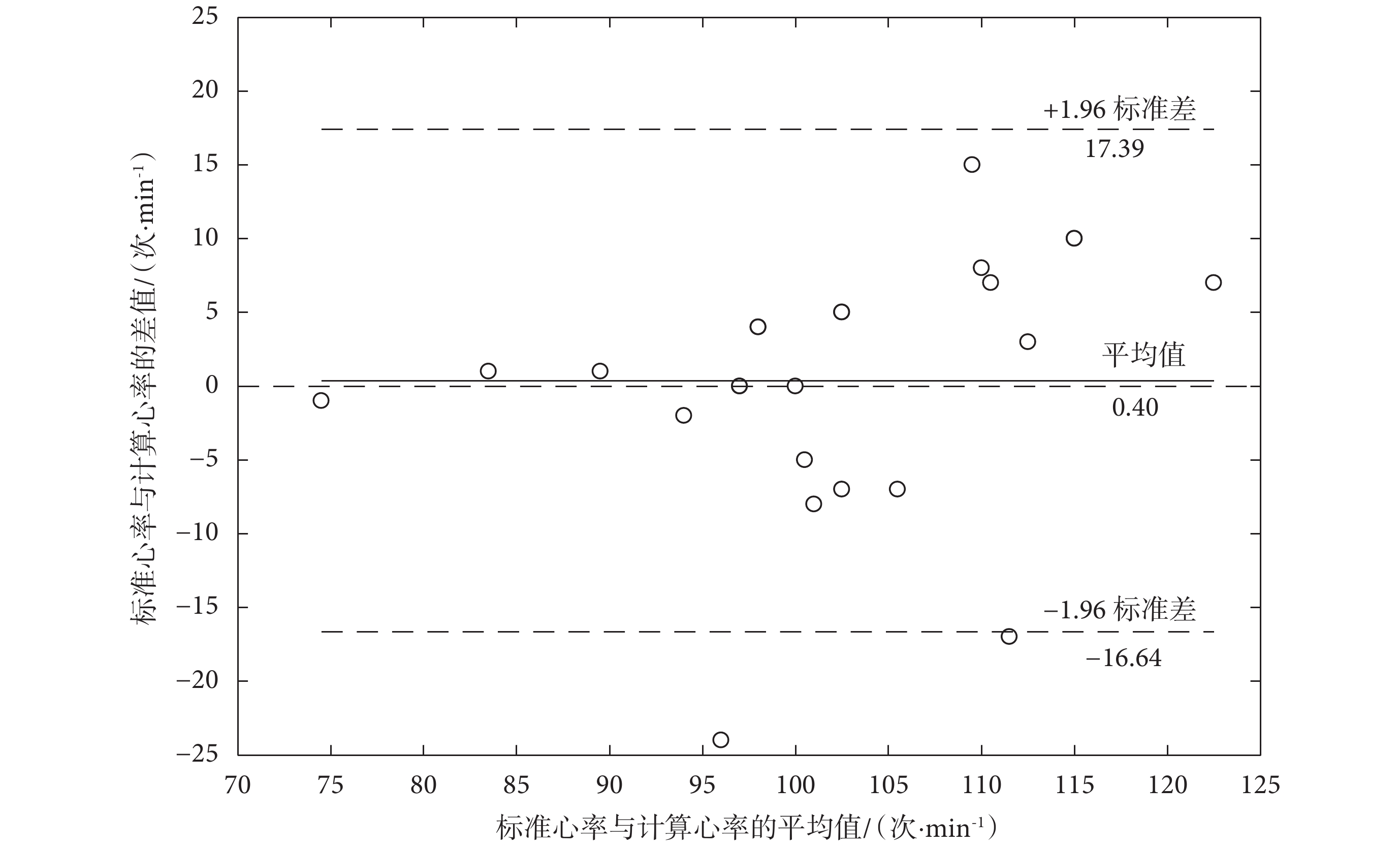 圖7
標準心率和計算心率的偏差統計圖
Figure7.
Statistical figure of heart rate obtained by ECG and PPG
圖7
標準心率和計算心率的偏差統計圖
Figure7.
Statistical figure of heart rate obtained by ECG and PPG
4 討論
由于采集系統和受試者所處環境的影響,PPG 信號中含有不同類型的噪聲,其中對 PPG 信號影響最大的是運動偽差。運動偽差由運動產生,和運動狀態相關但并非線性關系,同時具有非線性、非平穩性的特點。當將運動偽差看作是獨立的成分利用 ICA 或小波變換設計濾波器時,需要考慮運動強度或小波基函數以及分解層數,而實際中運動過程復雜,此類方法會增加計算量和復雜程度,具有一定局限性。當將運動偽差看作是相關成分時,采用自適應算法和奇異值算法構建濾波器可以消除部分運動偽差,得到相對較好的結果,但在此過程中忽略了運動偽差和運動狀態的關系。綜合考慮計算準確率和計算時長,本文將 NLMS 算法和 3 軸加速度參考信號結合來改進自適應濾波器,同時使用 EEMD 和 PE 值結合的方法來自行判斷高頻噪聲、PPG 信號和基線漂移的閾值范圍,極大地提高了計算心率的準確性。
考慮到算法的收斂速度,本實驗使用的 NLMS 算法在極短時間內完成濾波,提高了濾波的時效性。同時,EEMD 算法依據任何信號都是由不同時間尺度的振蕩構成的原理,有效地解決了 EMD 分解帶來的虛假分量和模態混疊問題,但在分解過程中依舊存在端點效應。本實驗從 EEMD 分解過程中對端點效應的影響出發,以平均值來代替測量時間內的心率值可以有效地提高計算心率的準確性。因此,在以后的工作中可以根據不同的運動狀態合理選擇參考信號以提升運動偽差濾除效果,選用改進的 EEMD 算法解決端點效應問題來不斷地減小計算心率的誤差,最終達到在運動狀態下對心率有效監測的目的。
5 結論
本研究結合 NLMS 算法和 EEMD 算法的優點,提出了基于 NLMS-EEMD 的運動狀態下 PPG 信號降噪算法。該方法首先利用 NLMS 濾波器去除原始 PPG 信號中的運動偽差,然后通過 EEMD 分解 PPG 信號得到 IMF 分量,并根據 PE 值確定出 PPG 相關信號的閾值范圍。重構后的 PPG 信號有效地去除了運動偽差、高頻噪聲和基線漂移,提升了在運動過程中心率計算的準確性,對健身或戶外運動過程中監測人體健康狀態具有重要意義。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
心率作為衡量心臟搏動能力的參數,其變化與心臟疾病密切相關,是臨床上評價身體健康狀況常用的指標之一[1-3]。在運動狀態下,基于光電容積脈搏波(photoplethysmographic,PPG)的心率測量方法具有方便且靈敏度高的特點。由于脈搏信號微弱而測量裝置的靈敏性較高,以致于測量得到的 PPG 信號易包含運動偽差、高頻噪聲和基線漂移等主要噪聲[4-5]。其中,運動偽差因測量裝置和測量部位的相對運動所產生;高頻噪聲來自于信號采集過程中采集裝置的電磁干擾;基線漂移是由于受試者的呼吸和咳嗽等其它生理活動所導致的[6-7]。因此,消除 PPG 信號所包含的噪聲對于提高運動狀態下人體心率監測的準確率和及時發現人體異常具有重要的意義。
運動狀態下 PPG 信號去噪聲的方法主要有獨立成分分析(independent component analysis,ICA)、小波變換(wavelet transform,WT)、經驗模態分解(empirical mode decomposition,EMD)和自適應濾波器。Kim 等[8]利用 ICA 設計濾波器,將運動偽差和 PPG 信號看作獨立成分后對 PPG 信號進行盲源分離,在強運動下驗證了算法的可行性。Peng 等[9]采用雙通道測量 PPG 信號,使用約束性獨立成分分析(constrained independence component analysis,cICA)方法提取 PPG 信號得到優于單通道 ICA 的實驗結果。Wang 等[10]建立了一種基于小波變換的自適應軟閾值方法濾除 PPG 信號中的主要噪聲,通過選擇合適的小波基后重構出脈搏信號,并與傅里葉變換得到的心率進行比較,取得了較好的實驗結果。王金海等[11]采用 EMD 方法處理微弱運動下的 PPG 信號,通過分析分解得到的固有模態函數(intrinsic mode function,IMF)的波形信息,使用多尺度濾波和累計能量濾波的方法濾除了 PPG 信號中的高頻和基線漂移噪聲,同時解決了在 PPG 信號采集過程中的中斷問題。Ram 等[12]利用傅里葉變換、奇異值分解和 ICA 構造了三種不同的參考信號,同時使用了三種不同的自適應濾波算法來去除 PPG 信號中的運動偽差,取得了良好的實驗效果。
通過上述研究可知,自適應濾波器在濾除 PPG 信號中的運動偽差上表現良好,而 EMD 在濾除 PPG 信號中高頻噪聲和基線漂移時取得了良好的實驗結果。因此,本文提出了一種歸一化最小均方差(normalized least mean square,NLMS)濾波算法和集合經驗模態分解(ensemble empirical mode decomposition,EEMD)算法相聯合的 PPG 信號降噪方法(NLMS-EEMD),同時濾除在運動狀態下 PPG 信號中的運動偽差、高頻噪聲和基線漂移,從而得到心率的準確值,以期實現運動狀態下心率信號的實時監測。
1 算法原理及評價指標
1.1 NLMS-EEMD 算法原理
NLMS 是一種改進的自適應濾波算法,解決了最小均方誤差(least mean square,LMS)算法在收斂速度和穩態誤差對步長要求相互矛盾的問題[13]。其優點是在濾波的初始階段步長大、收斂速度快,而在滿足收斂速度后,減小步長以提高收斂精度[14]。NLMS 濾波器的應用準則是將輸入信號與參考信號進行比較得到誤差,在迭代運算中不斷調整加權濾波器的系數使得均方誤差函數的值達到最小,算法的具體原理如式(1)~式(4)所示。
設輸入信號為  ,則經過濾波器后的輸出信號為
,則經過濾波器后的輸出信號為  ,如式(1)所示:
,如式(1)所示:
 |
其中, 為濾波器權系數的轉置,N 為濾波器階數。
為濾波器權系數的轉置,N 為濾波器階數。 為濾波器權系數。
為濾波器權系數。
將  與期望的參考信號
與期望的參考信號  比較,得到誤差信號
比較,得到誤差信號  ,如式(2)所示:
,如式(2)所示:
 |
在迭代運算中,需要不斷調整加權濾波器的系數,如式(3)、式(4)所示:
 |
其中, 為步長因子,取值范圍
為步長因子,取值范圍  ,
, 為預先設定的矯正量,取值范圍
為預先設定的矯正量,取值范圍  。
。
 |
其中, 為均方誤差。
為均方誤差。
EEMD 通過在原始信號上疊加高斯白噪聲,如式(5)所示,并利用其在分解中的統計特性解決了模態混疊問題,使 IMF 物理意義更加明確[15-16]。對添加白噪聲后的信號進行 EMD 分解,然后重復添加同等幅值的白噪聲再分解,如式(6)所示。計算 IMF 分量的排列熵(permutation entropy,PE),根據 PE 值的大小對 IMF 進行重構可消除信號中的高頻噪聲和基線漂移[17]。
 '/> '/> |
其中, 為添加的白噪聲幅值,
為添加的白噪聲幅值, 為添加的白噪聲,
為添加的白噪聲, 為添加白噪聲后的信號,
為添加白噪聲后的信號, 為實驗次數。
為實驗次數。
 '/> '/> |
其中,IMFi 為第  個 IMF 分量,其值為
個 IMF 分量,其值為  次分解后的均值。
次分解后的均值。 為余項。
為余項。
對  進行相空間重構,如式(7)所示:
進行相空間重構,如式(7)所示:
 |
其中, 為
為  的第
的第  個行向量,
個行向量, 為嵌入維數,
為嵌入維數, 為時間延遲。將
為時間延遲。將  按照升序排列如式(8)所示:
按照升序排列如式(8)所示:
 |
其中, 為重構向量中元素所在列的索引號。此時,任意一個 IMF 分量都可以得到一組序列,如式(9)所示。計算出每種序列出現的概率,即可得到 IMF 分量的 PE 值,如式(10)所示:
為重構向量中元素所在列的索引號。此時,任意一個 IMF 分量都可以得到一組序列,如式(9)所示。計算出每種序列出現的概率,即可得到 IMF 分量的 PE 值,如式(10)所示:
 |
其中, ,
, 是
是  種序列的一種。
種序列的一種。
 |
其中, 為
為  序列出現的概率。
序列出現的概率。
1.2 實驗結果評價指標
本實驗采用皮爾遜相關系數和平均絕對誤差百分比來衡量計算結果和標準結果之間的誤差[18-19]。皮爾遜相關系數可以用于反映兩個變量之間的相關程度,其值通過兩個變量和其離差的積來計算。當皮爾遜相關系數的值在 0.8~1.0 之間時,兩變量為極強相關;在 0.6~0.8 之間時,兩變量為強相關;在 0.4~0.6 之間時,兩變量為中等程度相關;在 0.4 以下時,兩變量為極弱相關或無相關。其計算過程如式(11)所示:
 |
其中,R 為皮爾遜相關系數, 、
、 分別為
分別為  個試驗值,
個試驗值, 、
、 分別為對應的
分別為對應的  個試驗值的均值。
個試驗值的均值。
平均絕對誤差百分比表示計算值和標準值之間偏差絕對值占標準值百分比的平均值。將平均絕對誤差進行百分比,消除了受試者的個體差異性,有助于對比實驗結果的準確性。計算過程如式(12)所示:
 |
其中, 表示平均絕對誤差百分比,
表示平均絕對誤差百分比, 表示計算值,
表示計算值, 表示標準值。
表示標準值。
2 實驗
2.1 實驗數據來源
本研究使用的 PPG 信號來自于麻省理工學院心率失常數據庫(Massachusetts Institute of Technology-Beth Israel Hospital,MIT-BIH)的運動狀態下腕部脈搏波數據庫(網址:https://physionet.org/physiobank/database/wrist/),采樣頻率為 256 Hz,記錄時長為 10 min 左右[20]。數據庫中包含原始的 PPG 信號,同時給出了運動過程中采集的心電(electrocardiogram,ECG)信號、加速度傳感器和陀螺儀傳感器等的同步信號[20]。在原始 ECG 信號采集過程中,使用控制軟件消除電源干擾,且進行了 50 Hz 陷波器處理,保證了數據的完整性以及參考心率計算的準確性。
本實驗選擇了低阻騎行、高阻騎行和步行三種運動狀態下的 24 組數據來進行算法驗證。為對降噪效果進行定量說明,分別計算出每組數據同一時間段內 ECG 信號和 PPG 信號的心拍,用 RR 間期和 CC 間期來表示,并計算其相關性。為了評價降噪后 PPG 信號心率檢測方法的準確性,分別計算出每組數據 1 min 內 ECG 信號和 PPG 信號的主峰個數,即標準心率和計算心率,并計算皮爾遜相關性系數和平均絕對誤差百分比。實驗具體過程如圖 1 所示。
 圖1
PPG 信號去噪原理
Figure1.
PPG signal de-noising principle
圖1
PPG 信號去噪原理
Figure1.
PPG signal de-noising principle
2.2 信號處理
低阻騎行 PPG 信號和 3 軸加速度傳感器信號如圖 2 所示,時長均為 10 s,其中 3 軸加速度傳感器包括 X 軸加速度、Y 軸加速度和 Z 軸加速度。低阻騎行 PPG 信號和 3 軸加速度傳感器信號頻譜如圖 3 所示,當 PPG 信號受到運動偽差的影響后,其頻譜分析結果和 3 軸加速度傳感器信號基本相同,且在時域分析時也無法明確得出主峰個數。經過 NLMS 算法濾波器處理之后的 PPG 信號及其頻譜圖如圖 4 所示,原始 PPG 信號經過以 3 軸加速度傳感器為參考信號的 NLMS 算法濾波器處理后運動噪聲減弱,高頻噪聲和基線漂移表現明顯。
 圖2
低阻騎行 PPG 和 3 軸加速度傳感器信號
Figure2.
Low-impedance riding PPG and 3-axis accelerometer signals
圖2
低阻騎行 PPG 和 3 軸加速度傳感器信號
Figure2.
Low-impedance riding PPG and 3-axis accelerometer signals
 圖3
低阻騎行 PPG 和 3 軸加速度傳感器信號頻譜
Figure3.
Spectrogram of low-impedance riding PPG and 3-axis accelerometer signals
圖3
低阻騎行 PPG 和 3 軸加速度傳感器信號頻譜
Figure3.
Spectrogram of low-impedance riding PPG and 3-axis accelerometer signals
 圖4
NLMS 濾波后的 PPG 信號及其對應頻譜
Figure4.
NLMS filtered PPG signal and its spectrum
圖4
NLMS 濾波后的 PPG 信號及其對應頻譜
Figure4.
NLMS filtered PPG signal and its spectrum
以 NLMS 算法濾波后的 PPG 信號經過 EEMD 分解結果如圖 5 所示。由圖 5 可知,低阻騎行 PPG 信號經 EEMD 分解后得到 11 個 IMF 分量和 1 個余項。根據 EEMD 分解過程可知,噪聲對每個 IMF 分量影響逐漸減弱,對信號的影響逐漸增強。因此,
 可能代表的是高頻噪聲,
可能代表的是高頻噪聲,
 可能代表 PPG 信號分量,
可能代表 PPG 信號分量, 可能代表基線漂移部分。
可能代表基線漂移部分。
 圖5
EEMD 分解圖
Figure5.
EEMD decomposition diagram
圖5
EEMD 分解圖
Figure5.
EEMD decomposition diagram
由多次實驗可知,不同運動狀態下的 IMF 分量個數不同,主觀判斷信號和噪聲之間的分界是不準確的。為減小信號重構誤差,提高心率計算準確率,本實驗采用 PE 值來判斷噪聲和有效信號所占有的 IMF 分量。在計算 PE 值的過程中,需要選擇合適的嵌入維數 α 和時間延遲  ,根據經驗取
,根據經驗取  ,
, [21-22]。不同運動狀態下各 PE 值總體趨勢在減小,據此證實了噪聲對不同的 IMF 支配作用不同。對不同運動狀態下的 PE 值(以符號 pe 表示)進行多次計算,取定的有效信號的閾值為
[21-22]。不同運動狀態下各 PE 值總體趨勢在減小,據此證實了噪聲對不同的 IMF 支配作用不同。對不同運動狀態下的 PE 值(以符號 pe 表示)進行多次計算,取定的有效信號的閾值為  ,當
,當  時為高頻噪聲分量,
時為高頻噪聲分量, 時為低頻基線漂移分量,不同運動狀態下 PE 值如表 1 所示[23-24]。
時為低頻基線漂移分量,不同運動狀態下 PE 值如表 1 所示[23-24]。
3 實驗結果
對在閾值范圍內的 IMF 分量進行重構得到 PPG 信號如圖 6 所示,從圖 6 中可以看出,消除了運動偽差、高頻噪聲和基線漂移后的信號更加光滑,主峰突出明顯有利于心率的計算。本實驗選擇的 24 組 PPG 信號包含了低阻騎行、高阻騎行和步行三種運動狀態,分別計算出每組數據的 RR 間期和 CC 間期及其皮爾遜相關系數,如表 2 所示。依次統計不同運動狀態下的皮爾遜相關系數,結果分別為 0.931 ± 0.045、0.904 ± 0.047、0.945 ± 0.041。由此可知,在步行和低阻騎行時,降噪效果好;在高阻騎行時,降噪效果較差。
 圖6
ECG 和 PPG 同步對比圖
Figure6.
Synchronous comparison between ECG and PPG
圖6
ECG 和 PPG 同步對比圖
Figure6.
Synchronous comparison between ECG and PPG
計算標準心率和計算心率的皮爾遜相關系數和平均絕對誤差百分比,并進行偏差統計,其偏差統計結果如圖 7 所示。由圖 7 可知,標準心率和計算心率的相關系數的值為 0.731,表明計算心率和標準心率之間是強相關,平均絕對誤差百分比為 6.10%,表明在不受到個體差異性的影響時,計算心率可以用來代替標準心率。同時,計算心率幾乎全部位于 95% 的置信區間內,證明了本算法的降噪效果具有較高的準確性。
 圖7
標準心率和計算心率的偏差統計圖
Figure7.
Statistical figure of heart rate obtained by ECG and PPG
圖7
標準心率和計算心率的偏差統計圖
Figure7.
Statistical figure of heart rate obtained by ECG and PPG
4 討論
由于采集系統和受試者所處環境的影響,PPG 信號中含有不同類型的噪聲,其中對 PPG 信號影響最大的是運動偽差。運動偽差由運動產生,和運動狀態相關但并非線性關系,同時具有非線性、非平穩性的特點。當將運動偽差看作是獨立的成分利用 ICA 或小波變換設計濾波器時,需要考慮運動強度或小波基函數以及分解層數,而實際中運動過程復雜,此類方法會增加計算量和復雜程度,具有一定局限性。當將運動偽差看作是相關成分時,采用自適應算法和奇異值算法構建濾波器可以消除部分運動偽差,得到相對較好的結果,但在此過程中忽略了運動偽差和運動狀態的關系。綜合考慮計算準確率和計算時長,本文將 NLMS 算法和 3 軸加速度參考信號結合來改進自適應濾波器,同時使用 EEMD 和 PE 值結合的方法來自行判斷高頻噪聲、PPG 信號和基線漂移的閾值范圍,極大地提高了計算心率的準確性。
考慮到算法的收斂速度,本實驗使用的 NLMS 算法在極短時間內完成濾波,提高了濾波的時效性。同時,EEMD 算法依據任何信號都是由不同時間尺度的振蕩構成的原理,有效地解決了 EMD 分解帶來的虛假分量和模態混疊問題,但在分解過程中依舊存在端點效應。本實驗從 EEMD 分解過程中對端點效應的影響出發,以平均值來代替測量時間內的心率值可以有效地提高計算心率的準確性。因此,在以后的工作中可以根據不同的運動狀態合理選擇參考信號以提升運動偽差濾除效果,選用改進的 EEMD 算法解決端點效應問題來不斷地減小計算心率的誤差,最終達到在運動狀態下對心率有效監測的目的。
5 結論
本研究結合 NLMS 算法和 EEMD 算法的優點,提出了基于 NLMS-EEMD 的運動狀態下 PPG 信號降噪算法。該方法首先利用 NLMS 濾波器去除原始 PPG 信號中的運動偽差,然后通過 EEMD 分解 PPG 信號得到 IMF 分量,并根據 PE 值確定出 PPG 相關信號的閾值范圍。重構后的 PPG 信號有效地去除了運動偽差、高頻噪聲和基線漂移,提升了在運動過程中心率計算的準確性,對健身或戶外運動過程中監測人體健康狀態具有重要意義。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。