麻醉意識狀態監測是神經科學基礎研究及臨床應用中的重要問題，受到廣泛關注。本研究為尋找臨床麻醉意識狀態監測指標，共采集 14 位全麻手術患者在三種意識狀態（清醒、中度麻醉、深度麻醉）下各 5 min 靜息態腦電數據，對比采用稀疏偏最小二乘（SPLS）和傳統的同步似然（SL）方法計算腦功能連接，通過連接特征來區分麻醉前后三種意識狀態。通過全腦網絡分析，本文 SPLS 方法與傳統 SL 方法得到的不同意識狀態下的網絡參數變化趨勢一致，并且采用 SPLS 方法所得結果的差異具有統計學意義（P<0.05）。對 SPLS 方法得到的連接特征運用支持向量機進行分類，分類準確率為 87.93%，較使用 SL 方法得到的連接特征分類準確率高出 7.69%。本文研究結果顯示，基于 SPLS 方法進行功能連接分析在區分三種意識狀態方面有更好的性能，或可為臨床麻醉監測提供一種新思路。
引用本文： 吳帆, 姜忠義, 畢卉, 張軍, 李世通, 鄒凌. 基于稀疏偏最小二乘的麻醉意識狀態功能連接研究. 生物醫學工程學雜志, 2020, 37(3): 419-426. doi: 10.7507/1001-5515.201904052 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
意識水平的衡量一直是臨床手術監測的重要問題[1]。麻醉手術中，意識水平監測能有效降低術中知曉的發生率，并且能夠幫助麻醉醫生精準控制手術期間患者的意識水平[2]。
為滿足臨床手術中意識狀態監測的需求，近年來麻醉深度監測技術發展迅速，特別是基于腦電圖（electroencephalogram，EEG）的監測技術因其非侵入式、價格適中等優勢，應用更為廣泛。EEG 雙頻指數（bispectral index，BIS）、聽覺誘發電位指數（auditory evoked potentials index，AEP index）、麻醉熵等是臨床上常用的幾種基于 EEG 信號的麻醉深度監測技術[3-4]。但是這幾種麻醉深度監測技術僅適用于 2～4 導聯 EEG 信號，空間分辨率較差，可能會對后續分析造成影響。它們使用的麻醉指標也都為不公開的專利算法，將 EEG 信號中的多種特征融合成為一個數值指標，這就給臨床和科研工作者直接觀察、理解麻醉深度特征帶來了一定困難[5-6]。因此需要對 EEG 信號進一步處理分析，提取更利于觀察的麻醉深度特征。近期，有學者開始利用功能連接來分析麻醉誘導的意識喪失機制[7]。有研究表明，額葉、頂葉區域功能連接對意識感知起重要作用，因此通過功能連接可以對意識水平進行衡量[8]。靜息態 EEG 信號功能連接分析較傳統監測技術能夠更直觀地顯示不同麻醉深度下其連接模式的變化，可以嘗試使用功能連接作為麻醉深度的監測指標來對不同意識狀態進行區分。
功能連接實質上是研究不同神經元活動之間的時間相關性，即大腦各區域之間統計學上的依賴關系[9]。EEG 信號是典型的非平穩信號，適用于非平穩信號傳統的功能連接計算方法主要有同步似然分析（synchronization likelihood，SL）、相位滯后指數等[10-11]。這些傳統方法都是分別對兩兩不同導聯的 EEG 信號計算其連接性，而忽略了其它導聯信號的影響，會產生虛假的較高連接值。本研究引入多元回歸模型計算功能連接，用多個信號對單個信號進行表示，相應的表示系數既能反映信號之間的依賴關系，又可以同時分析單個導聯信號與其它多個導聯信號之間的連接性，有效避免了傳統功能連接方法存在的問題。但是，傳統的多元回歸方法在分析功能連接時，易受 EEG 信號中的噪聲干擾。偏最小二乘法（partial least squares，PLS）是近年來多元回歸模型領域引人關注的方法，可以消除信號間的多重共線性，避免了傳統回歸方法的弊端[12]。PLS 集成了主成分分析（principal component analysis，PCA）和典型相關分析的優點，能夠最大限度挖掘信號內部信息，但該方法在應用于高維數據時模型解釋能力會變差，提取特征時包含噪聲特征。為解決這一問題，有學者提出了稀疏偏最小二乘（sparse partial least squares，SPLS）方法，在傳統 PLS 方法的基礎上引入正則化項，提高了模型的解釋能力并且能夠剔除噪聲特征。Lee 等[13]使用 SPLS 方法對高維數據進行變量選擇和預測，發現 SPLS 較 PLS 方法準確度更高，SPLS 方法在使用高維數據的醫學研究領域更有優勢。但目前尚未有研究報道利用 SPLS 方法計算腦功能連接。
基于以上研究，本文采用功能連接分析對不同意識狀態下的靜息態 EEG 數據進行區分，將 SPLS 方法應用于功能連接的計算，引入超參數調整結果稀疏度，可以保證權重向量不全為零，更易定義參數范圍。首先，本文使用 SPLS 與傳統功能連接計算方法中的 SL 對三種意識狀態（清醒、中度麻醉、深度麻醉）下的靜息態 EEG 數據計算功能連接；其次，基于功能連接計算網絡參數，對比不同意識狀態的差異性；最后，利用支持向量機（support vector machine，SVM）對兩種方法得到的連接特征進行分類，比較兩種功能連接計算方法對不同意識狀態下 EEG 數據的區分度。本文研究嘗試使用功能連接作為麻醉意識狀態區分指標，或可以對臨床麻醉意識狀態的監測提供新的衡量指標。
1 試驗數據及方法
1.1 試驗數據
1.1.1 數據采集
2017 年 1 月 1 日—2017 年 6 月 1 日期間，在復旦大學附屬華山醫院進行全麻手術的患者中招募 14 名受試者。受試者年齡平均（48.0 ± 10.8）歲，男性 10 名，女性 4 名，右利手，沒有麻醉手術史和藥物依賴。
本次試驗依據“世界醫學協會赫爾辛基宣言”（2013），并得到復旦大學附屬華山醫院倫理審查委員會批準，每位受試者在閱讀并理解后簽署了知情同意書。常州市生物醫學信息技術重點實驗室已獲得了數據信息的使用授權。試驗使用 256 導聯 EEG 信號采集設備（Ges300，Electrical Geodesics Inc.，美國），分別采集在丙泊酚誘導下清醒、中度麻醉、深度麻醉三種意識狀態下的閉眼靜息態 5 min EEG 信號。參考電極取 Cz 點，采樣頻率為 1 000 Hz。麻醉采用靜脈靶控輸注，三種意識狀態下開始記錄 EEG 信號及結束記錄時的丙泊酚效應室濃度如表 1 所示。
表1
效應室濃度
Table1.
Effect-site concentration
1.1.2 數據預處理
數據預處理主要使用計算軟件 MATLAB 2014a（MathWorks Inc., 美國）平臺下的電生理信號處理工具箱 EEGLAB 14.1.b 完成，主要步驟如下：
（1）濾波：包括低通濾波和高通濾波，得到頻率范圍在 0.5～48 Hz 的 EEG 信號。
（2）偽跡檢測：使用獨立成分分析工具人工去除因眼動、眨眼等產生的偽跡。
（3）壞通道替換：采用周圍鄰近導聯的平均數據替換壞通道數據。
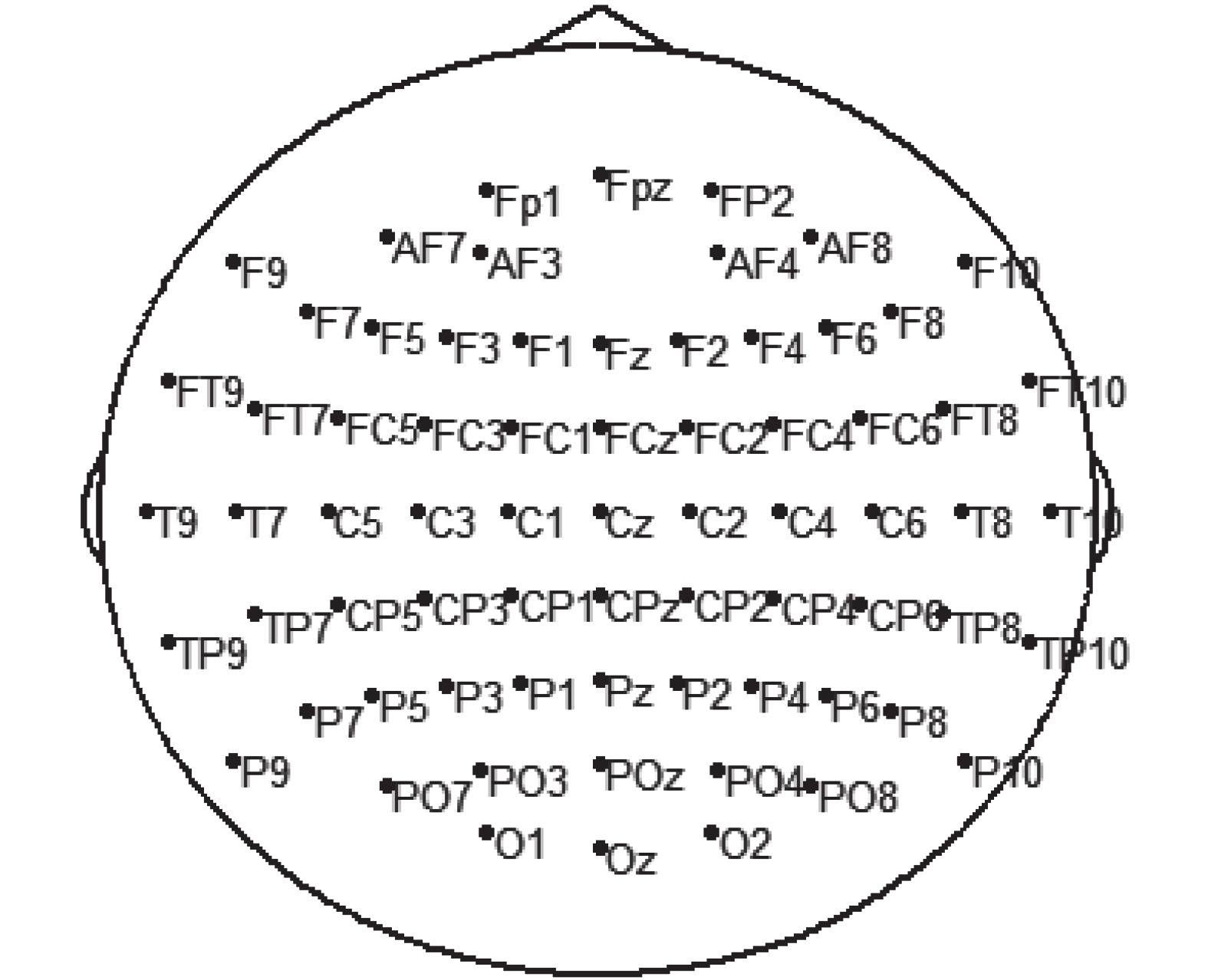
（4）導聯選取：為提高計算速度，依照 10-10 導聯系統中的電極位置在所有導聯中選取了 70 導聯，電極分布如圖 1 所示。
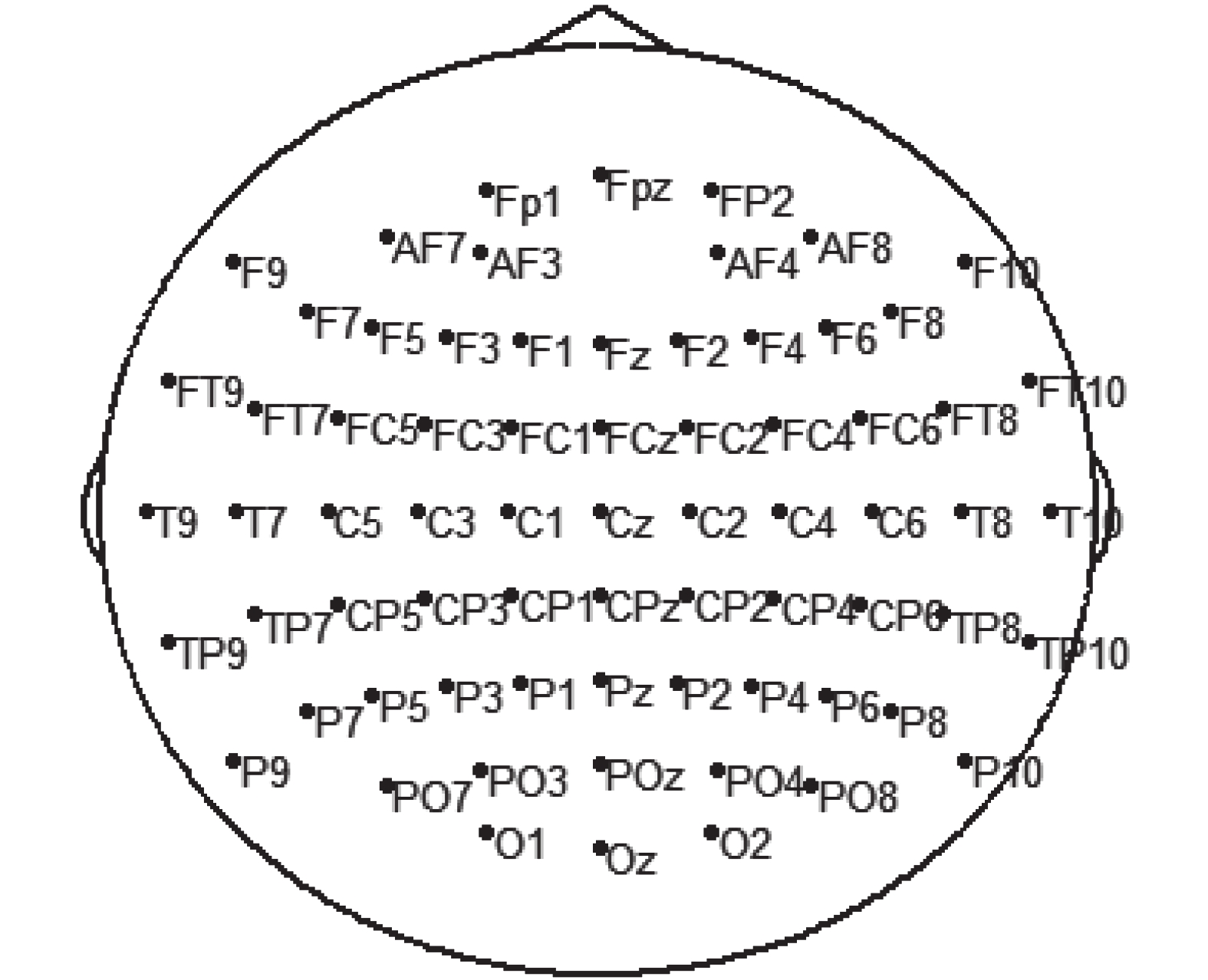圖1
70 導聯電極分布
Figure1.
Electrode distribution of 70-channel map
（5）參考點轉換：轉換為平均參考，將所有電極采集數據的均值作為參考數據。
在每段經預處理后的 5 min EEG 數據中選取 250 s 數據，每個導聯上則有 250 000 個點，用于后續計算。
1.2 方法
1.2.1 同步似然分析法
SL 方法計算功能連接的原理是檢測兩個信號之間相似的可能性[11]。設第 k 導聯 EEG 信號為 
，i 為時間點，共有 N 個時間點，具體步驟如下：
（1）將信號 X 利用時間延遲重建內嵌向量映射到 m 維的狀態空間。
（2）計算時間點 i 和 j 內嵌向量 
和 
之間的歐式距離小于 r 的概率 
，如式（1）所示：
 |
其中，
為 Heaviside 階躍函數，
和 
為兩個窗。
（3）設一共有 M 導聯，則第 k 導聯信號與其他 M－1 導聯信號 i 與 j 時刻的同步似然值 
定義如式（2）所示：
 |
（4）對所有時間點 j 求平均，即得第 k 導聯信號與其它 M－1 導聯信號在 i 時刻的同步似然值，如式（3）所示：
 |
1.2.2 偏最小二乘法
引入多元回歸模型計算功能連接，可以同時計算單個導聯和其它多個導聯的連接性。PLS 方法則能最大程度提取信號內部信息，其最終目的是用多個因變量對多個自變量進行回歸建模[12]。利用 PLS 方法計算功能連接時，將其中某一導聯的信號作為因變量 
，除去該導聯的所有其它導聯信號作為自變量 
。整個回歸建模的過程首先是分別從 X 與 Y 中提取出成分 t 和 u 來研究這兩個矩陣之間的統計關系。t 和 u 必須能盡可能多地攜帶 X 與 Y 中的變異信息，并且兩者之間相關程度也盡可能達到最大。綜合以上兩點要求，實質上就是使得 t 和 u 的協方差達到最大，轉化為求解以下優化問題，如式（4）所示：
 |
其中，X0 和 Y0 分別為 X 與 Y 的標準化矩陣，
與 
分別為 X0 和 Y0 的權重向量，并且是單位向量。求得第一對權重向量 
與 
之后，即能得到第一對主成分 t1 和 u1。其次，建立 X0 和 Y0 對 t1 和 u1 的回歸方程，得到回歸方程的殘差矩陣。將殘差矩陣取代 X0 和 Y0，與第一對主成分求解過程相同，求出 
與 
以及第二對主成分 t2 和 u2。以上步驟一直迭代至殘差矩陣達到設定精度為止，最終轉化為 Y 對 X 的回歸方程，完成了 PLS 回歸建模。
1.2.3 稀疏偏最小二乘法
SPLS 方法在傳統的 PLS 方法基礎上引入了兩個范數 l1、l2 對其進行約束。l1 范數能將部分系數壓縮至零，達到消除微弱虛假連接的目的，l2 范數則能消除 l1 范數約束可能會去除部分相關特征的影響[14]。在式（4）中加入 l1、l2 范數，得到如式（5）所示：
 |
和 
為控制正則化項的超參數，
和 
的值越低，稀疏度越高。為了使得 l1、l2 范數都能發揮作用，超參數的值必須滿足：
、
。求解式（5）的算法步驟如下：
（1）對 X 與 Y 進行標準化得到 X0 和 Y0，令 
。
（2）初始化 
，且滿足
。
（3）重復以下步驟直至收斂。
① 更新 
：
Ⅰ. 
Ⅱ. 
，若
，
；否則
取正的常數使得
② 更新 
：
Ⅰ. 
Ⅱ. 
，若
，
；否則 
取正的常數使得
其中，
為軟閾值函數，定義為：
，符號
表示當
0 時等于
，當
時則等于 0。
SPLS 在功能連接計算過程中，將第 i 導信號作為因變量 Yi，將除去第 i 導的其它導聯信號作為 Xi。因此對于 70 導聯 EEG 信號，
、
，
只能取 1，
。實際上只需對超參數 
進行調節，可以利用交叉驗證法，計算模型的均方誤差（mean-square error，MSE）來確定超參數 
的值。完成 SPLS 回歸建模過程后得到回歸方程系數列向量 soli。將 soli 按順序填充至 70 × 70 矩陣 con 的第 i 列的 1～（i ? 1）行和（i + 1）～70 行，將 con 的第 i 行第 i 列置零。對每一個導聯的信號都如此操作，最后連接矩陣 
。C 中元素 Cjk 表示節點 j 與節點 k 之間的連接強度。利用 MATLAB 2014a（MathWorks Inc.，美國）實現該算法，每計算一個連接矩陣需要 8.59 s。
1.2.4 腦網絡分析
功能連接計算完畢后，得到的也是一個個網絡，為了直觀地觀測計算結果，利用圖論的方法引入復雜網絡分析對結果進行評估，這里選用平均最短路徑長度和平均聚類系數來分析結果。
在二值化網絡中，從節點 i 到節點 j 的長度就是從 i 到 j 要經過的邊數，設節點 i、j 之間的最短路徑長度為 dij，平均最短路徑長度即為網絡所有可能的兩節點之間的最短路徑的平均值。平均最短路徑長度 L 可以衡量全局網絡的整合作用，計算公式如式（6）所示：
 |
聚類系數是評估網絡中節點聚合程度的重要指標，平均聚類系數 C 則是網絡中所有節點聚類系數的平均，其計算方式如式（7）所示：
 |
其中，Ei 表示網絡中與節點 i 連接的邊數。
1.2.5 功能連接對比分析
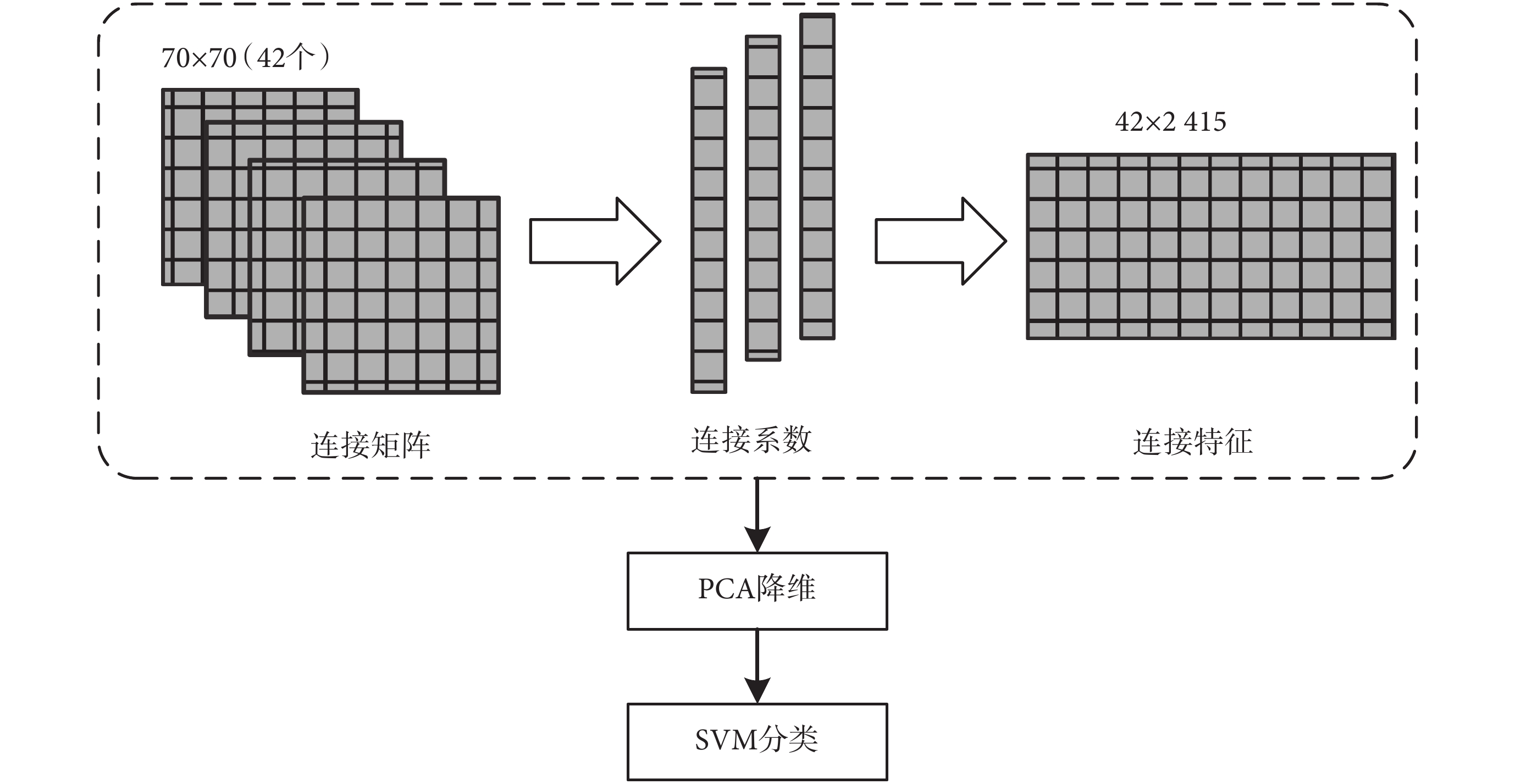
為了驗證兩種方法所計算功能連接對不同意識狀態的區分效果，使用 SVM 分類器分別對連接特征做分類，分類流程如圖 2 所示。原始 EEG 信號經過預處理后，使用 SL 和 SPLS 兩種方法分別對三種意識狀態下的功能連接進行計算，最終每種方法都將得到 42 個連接矩陣，減去重復連接和自身連接，每個連接矩陣得到 2 415 個連接系數。將連接系數整合起來得到連接特征矩陣。使用 PCA 方法對特征進行降維，保留其中有差異的連接特征。之后采用 SVM 分類器對其進行分類，使用 5 折交叉驗證，對比分類準確率。
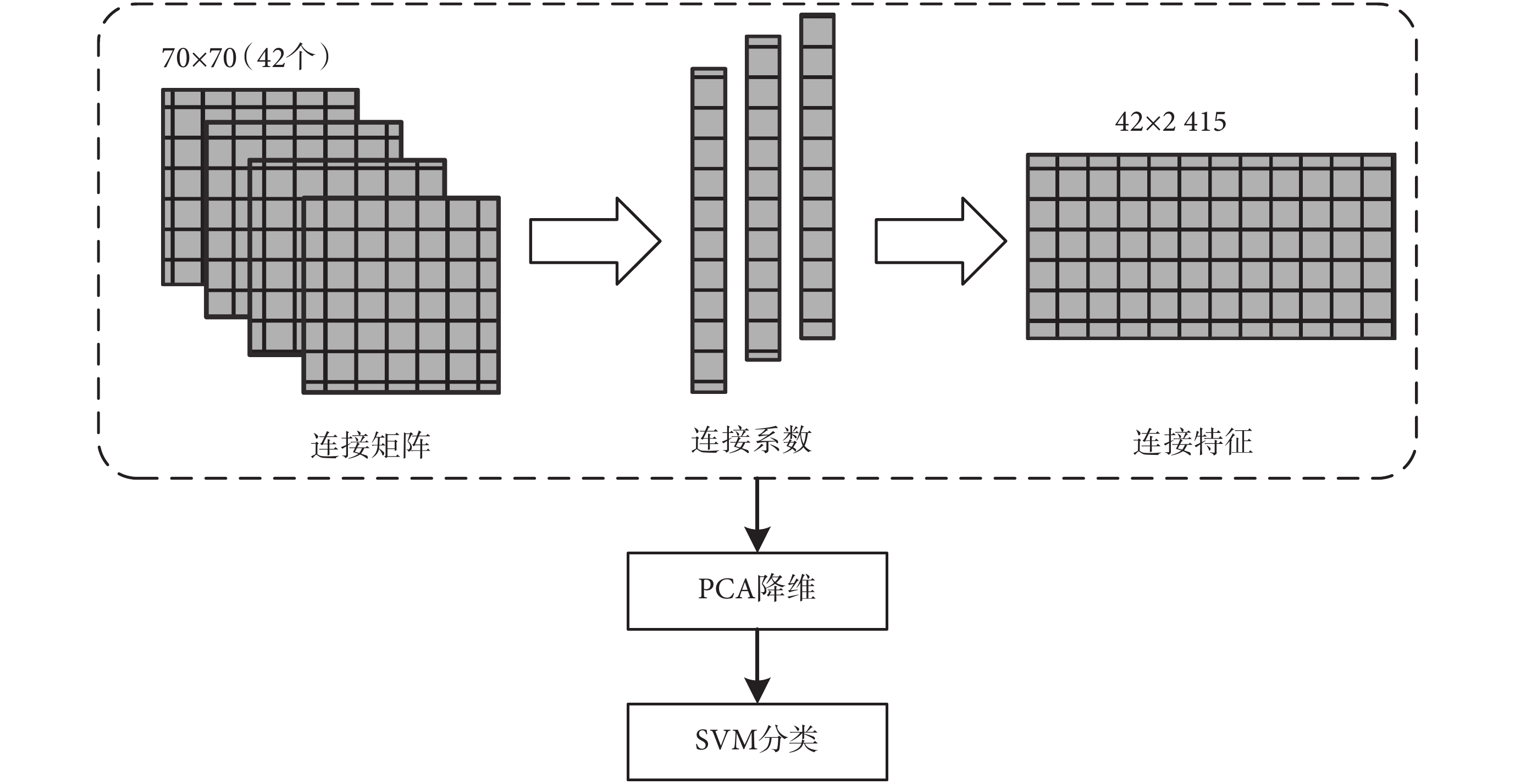圖2
分類流程
Figure2.
Classification process
2 結果分析
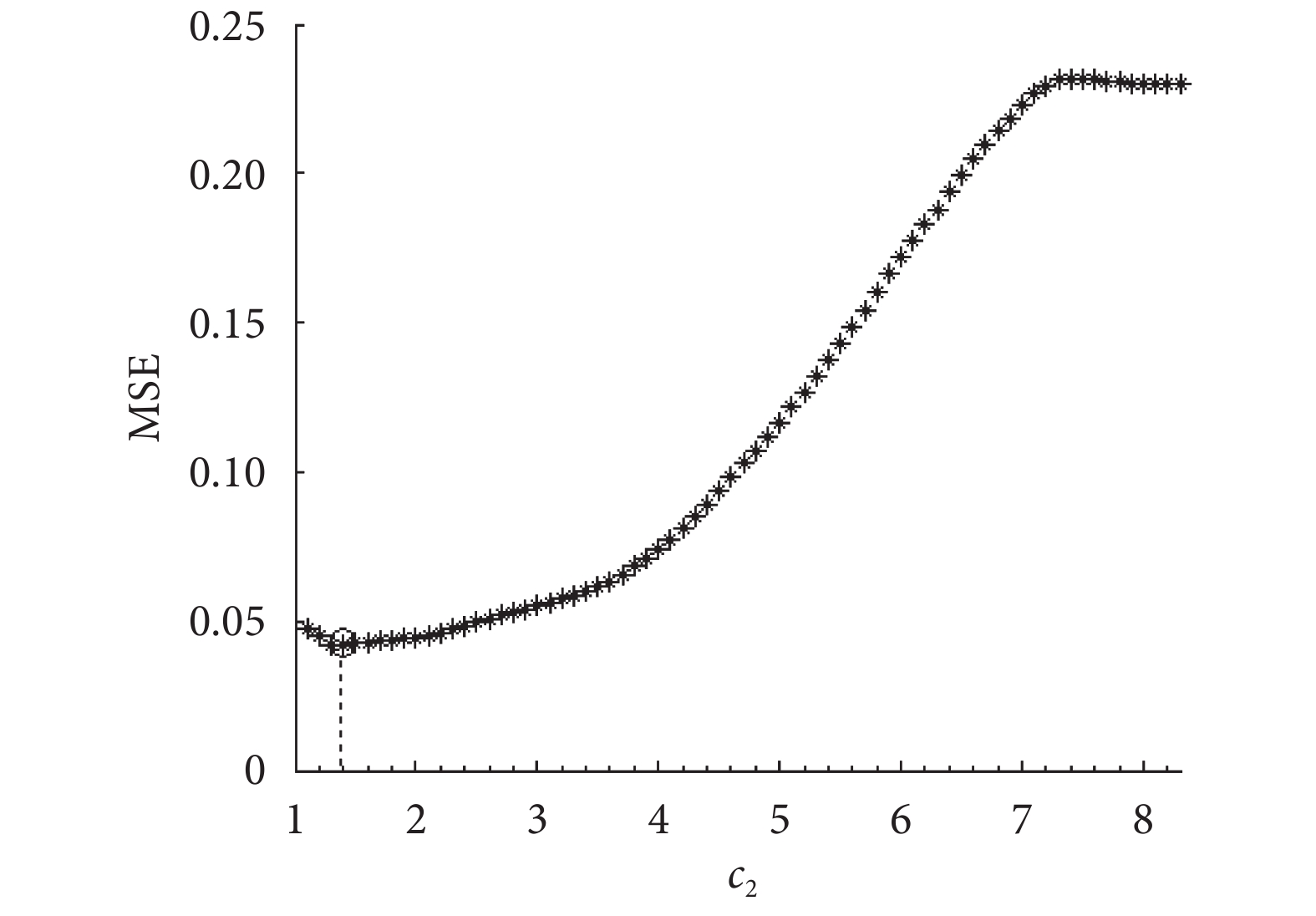
在使用 SPLS 方法計算功能連接時，使用交叉驗證對超參數 
取 1～8.3 時計算回歸模型的 MSE，如圖 3 所示。從圖中可以看出超參數 
的值在取 1.4 時 MSE 值最小，接近于零，因此將超參數 
的值定為 1.4 進行接下來的計算。
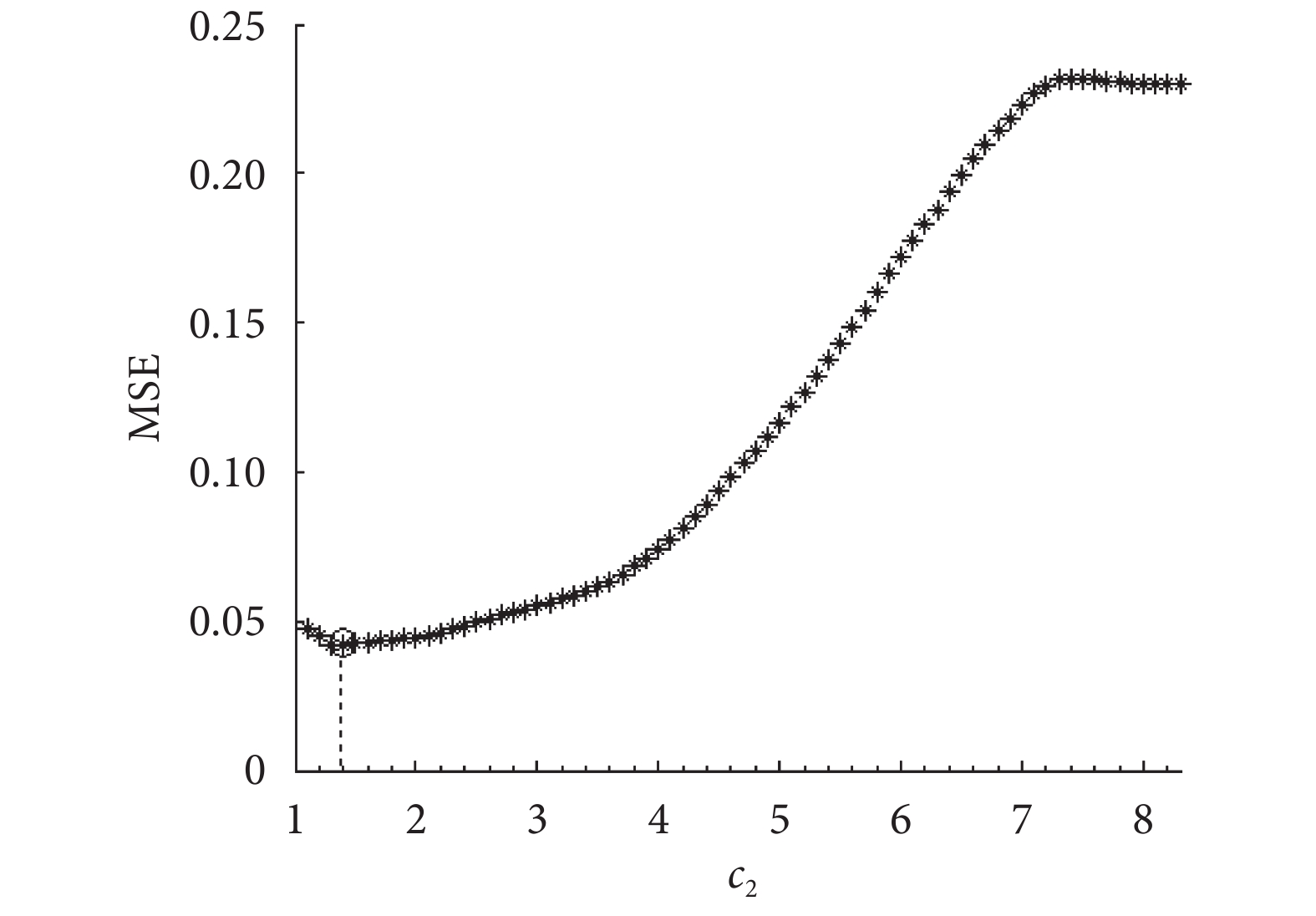圖3
SPLS 均方誤差
Figure3.
MSE of SPLS
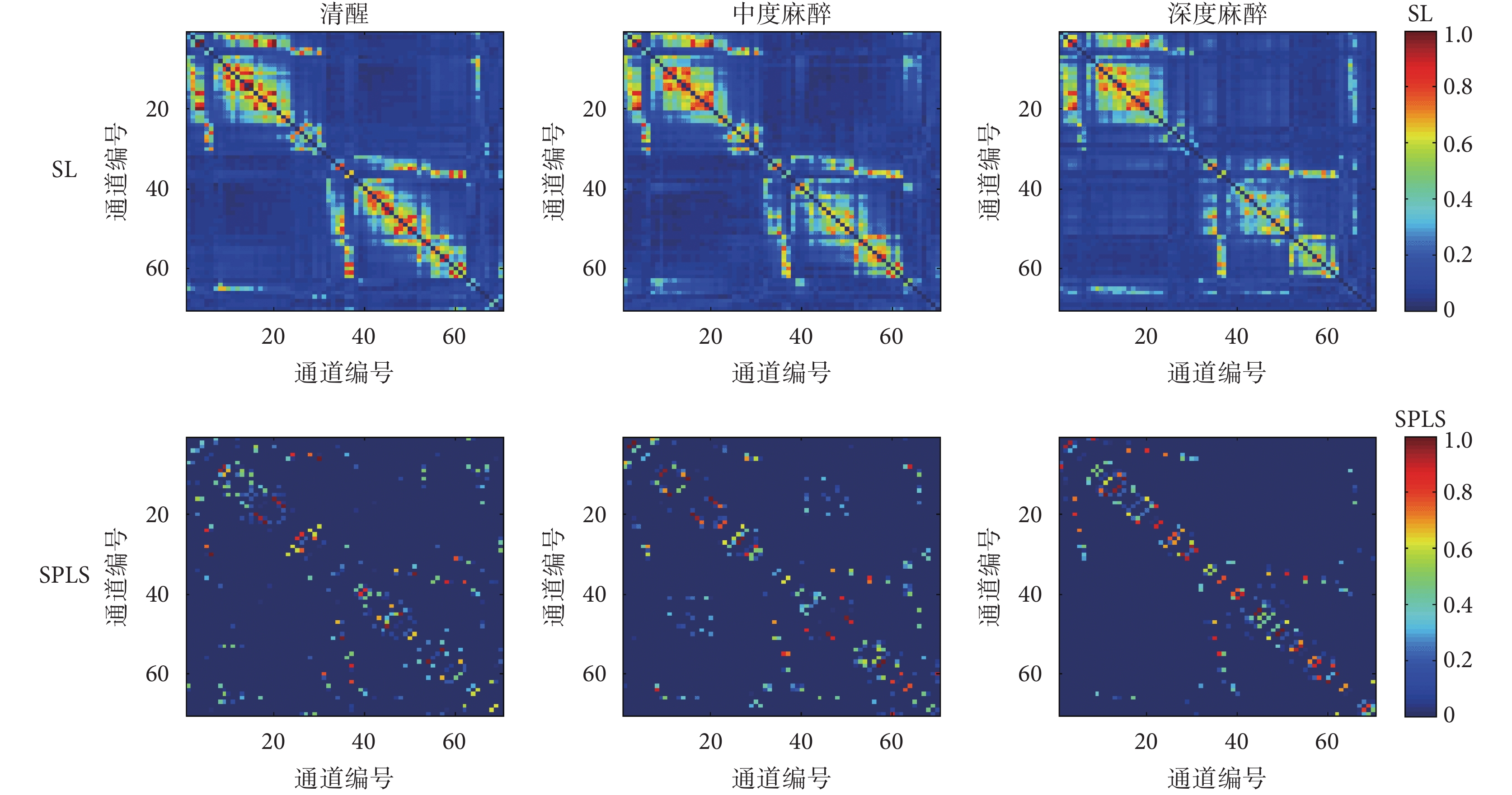
分別采用 SL 和 SPLS 法對三種意識狀態下的 EEG 數據計算功能連接，得到的連接矩陣如圖 4 所示。從圖 4 中可以看出兩種方法得到連接矩陣分布基本一致，只是 SPLS 方法去除了一些虛弱的連接。SL 與 SPLS 方法得到連接矩陣圖中都能較為明顯發現深度麻醉狀態相對其它兩種狀態連接減弱。
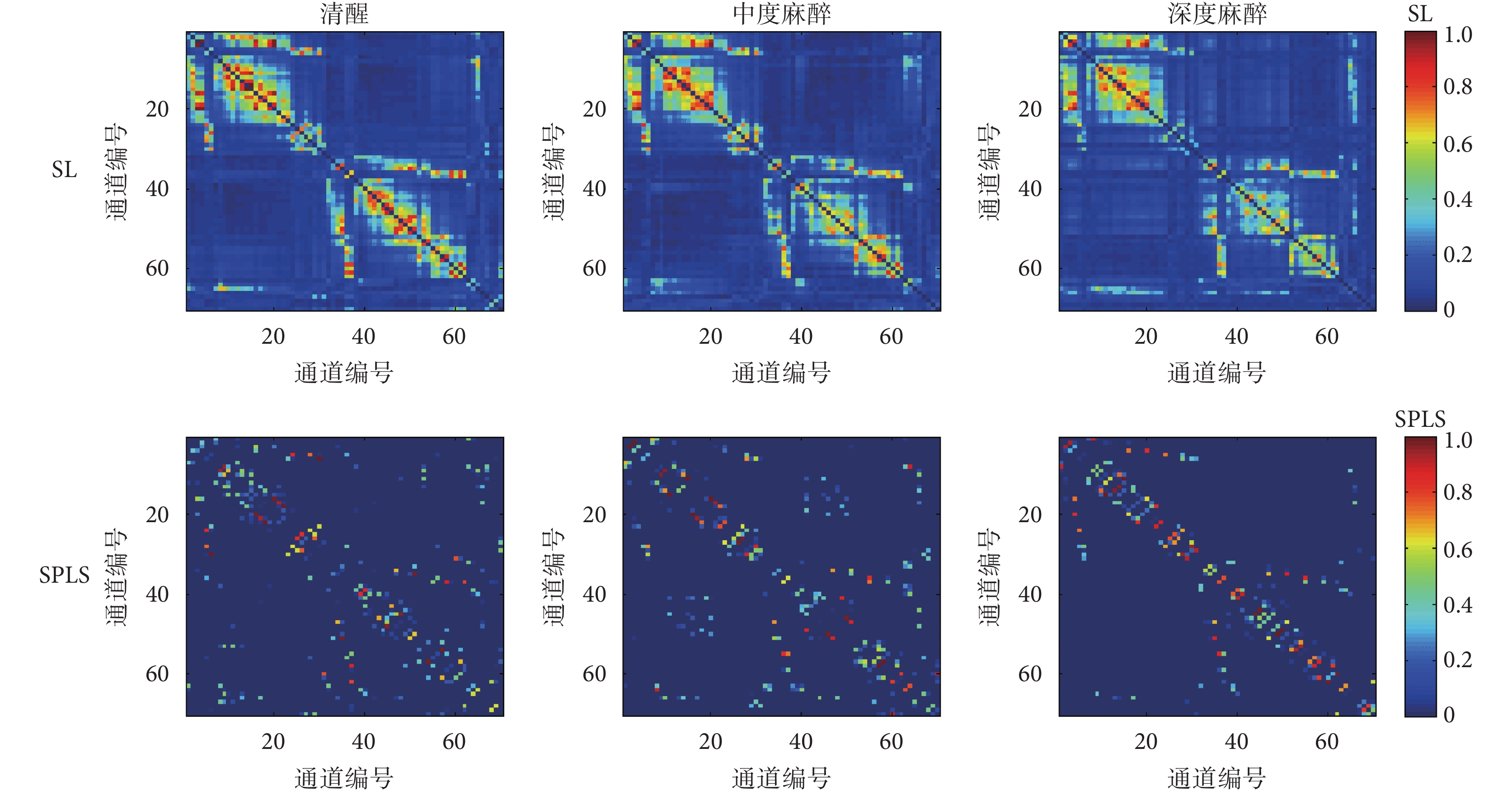圖4
連接矩陣
Figure4.
Connectivity heatmaps
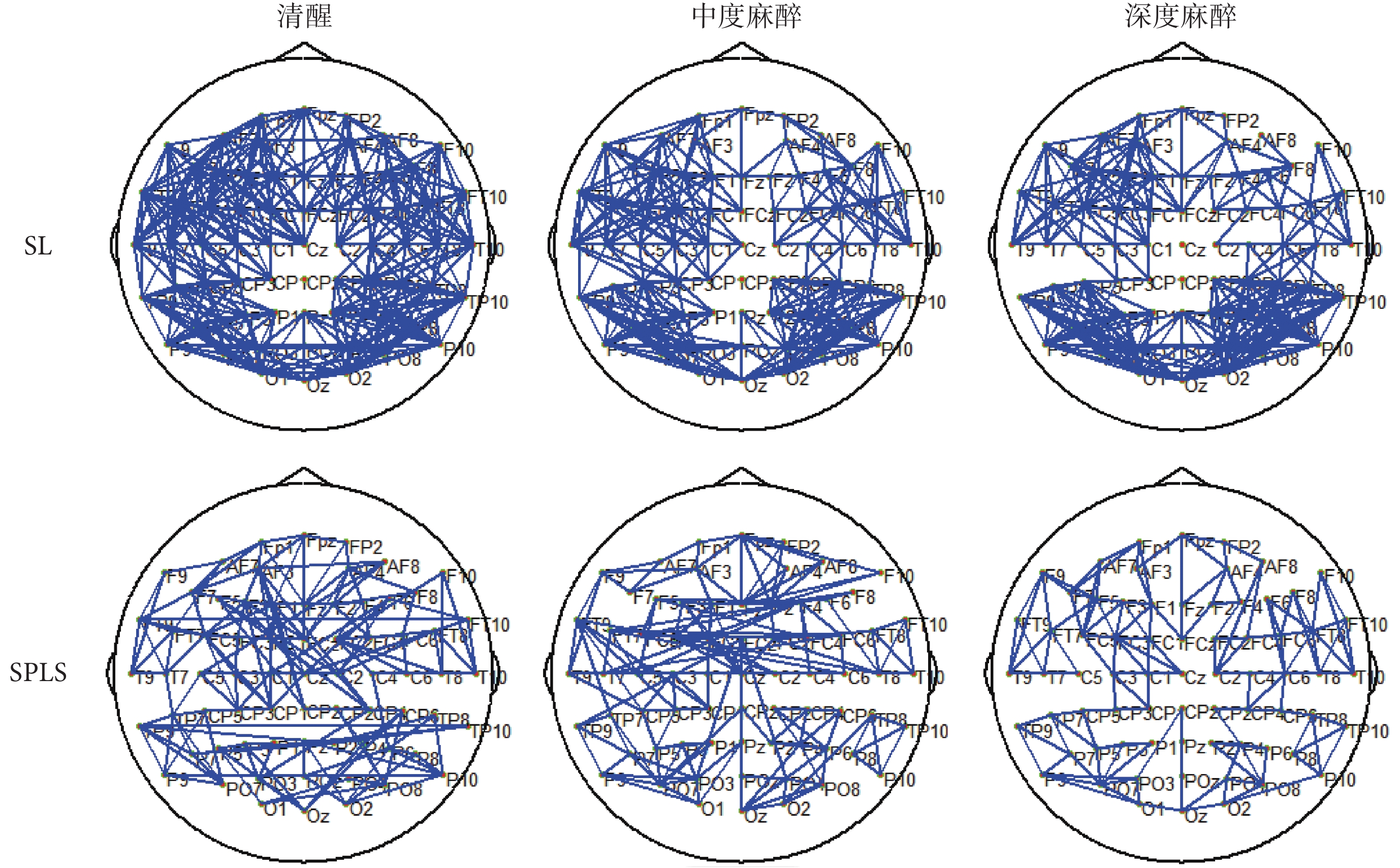
為了更直觀地觀察全腦連接情況，對計算得的連接矩陣畫出連接拓撲圖。SL 方法需要設定閾值，將連接閾值參數設為 0.23，高于這一閾值則將相應的節點對進行連接。SPLS 方法已將虛弱連接去除，因此不需要設定閾值，只需將連接系數大于零的對應節點相連。最終畫出的連接拓撲圖如圖 5 所示。兩種方法得到的連接拓撲圖分布也較為相似，都為清醒狀態連接最密集，中度麻醉次之，深度麻醉最稀疏。
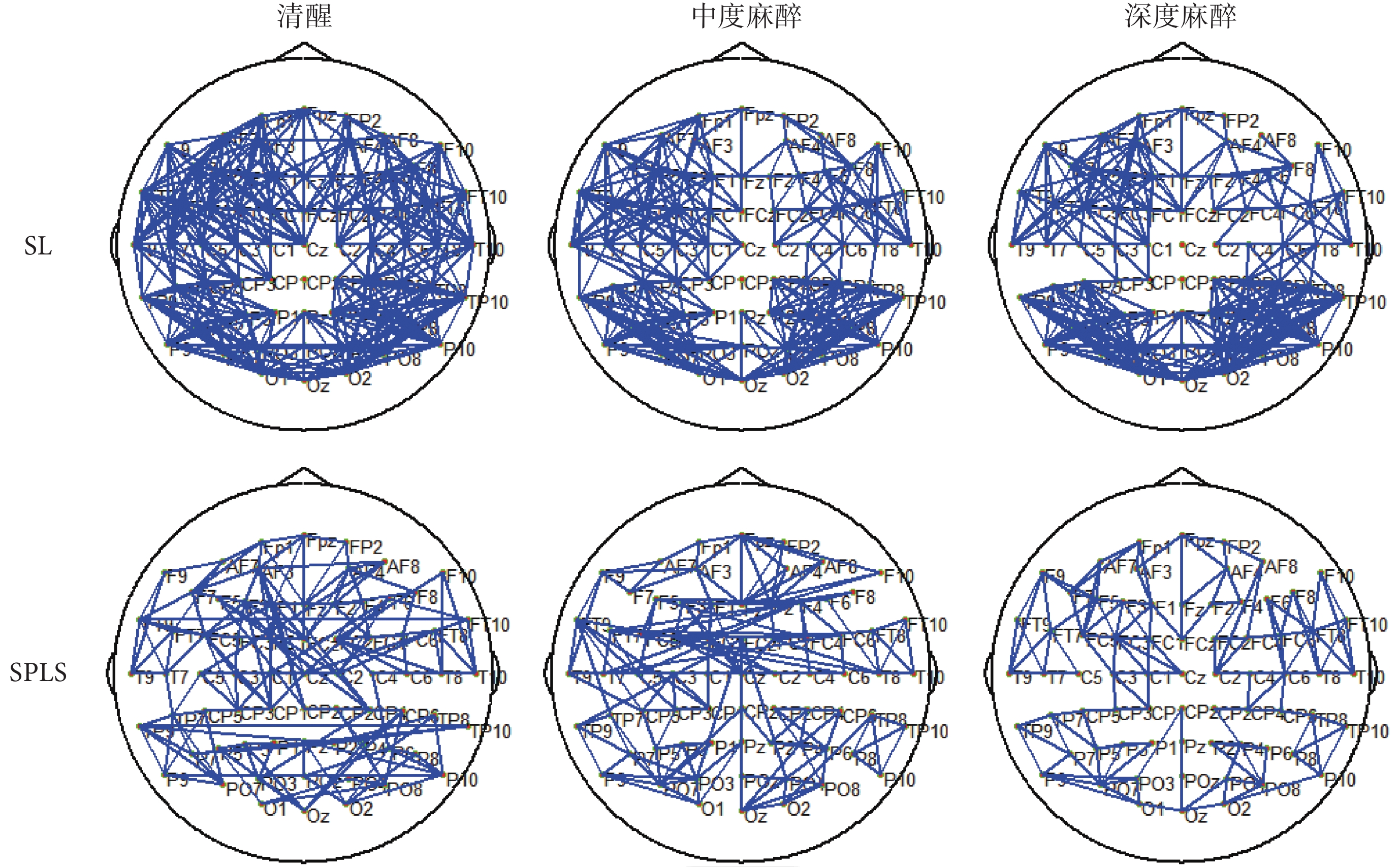圖5
連接拓撲圖
Figure5.
Connection topology
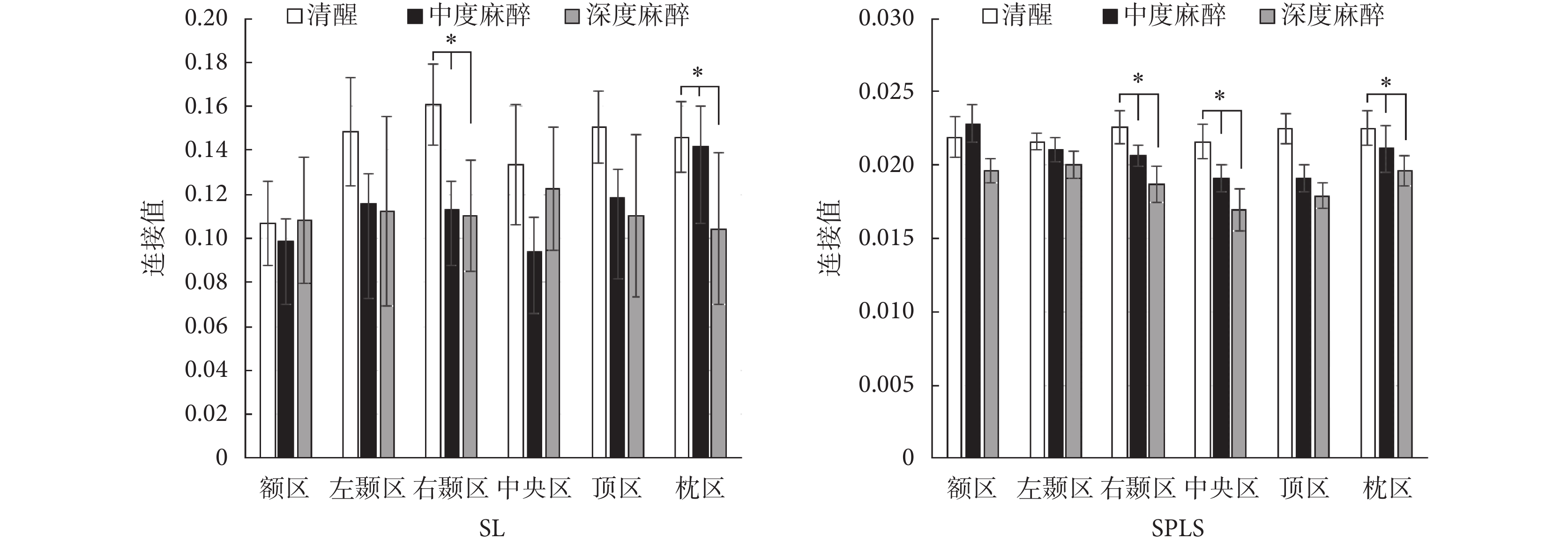
根據解剖位置將 70 個電極劃分為 6 個區域，分別為：額區，包含通道：FPz、FP1、FP2、AF7、AF3、AF4、AF8、F1、F3、F5、Fz、F2、F4、F6；左顳區，包含通道：F9、F7、FT9、FT7、T9、T7、TP9、TP7、P9、P7；右顳區，包含通道：F10、F8、FT10、FT8、T10、T8、TP10、TP8、P10、P8；中央區，包含通道：FC5、FC3、FC1、FCz、FC2、FC4、FC6、C5、C3、C1、Cz、C2、C4、C6；頂區，包含通道：CP5、CP3、CP1、CPz、CP2、CP4、CP6、P5、P3、P1、Pz、P2、P4、P6；枕區，包含通道：PO7、PO3、POz、PO4、PO8、O1、Oz、O2。對這 6 個區域的平均連接值進行統計，結果如圖 6 所示。SL 方法和 SPLS 方法的平均連接值在右顳區、頂區、枕區都是隨麻醉深度的加深而減小的。采用單因素方差分析，其中 SL 方法在右顳區（F = 4.057，P = 0.029）和枕區（F = 7.879，P = 0.002）組間差異具有統計學意義，SPLS 方法在右顳區（F = 18.810，P < 0.001）、中央區（F = 6.674，P = 0.004）和枕區（F = 6.352，P = 0.005）組間差異具有統計學意義。SPLS 方法較 SL 方法連接值差異具有統計學意義的區域更多。
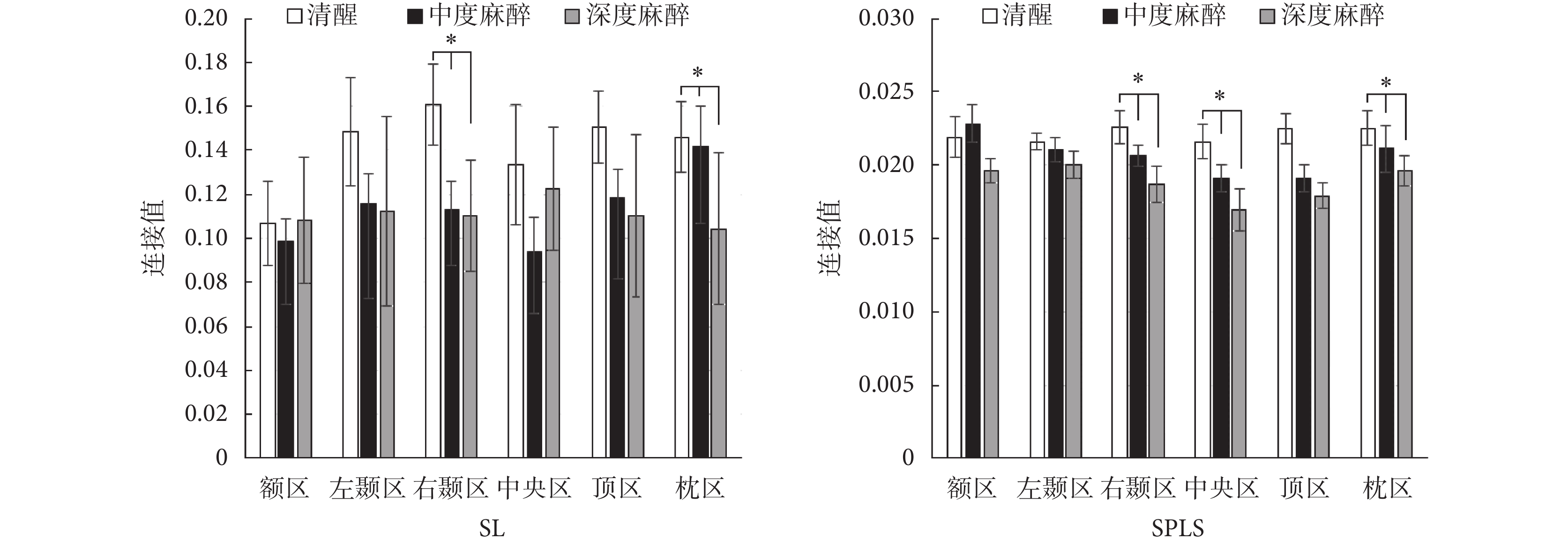圖6
不同腦區平均連接值（*P < 0.05）
Figure6.
Average connectivity value of different brain regions（*P < 0.05）
根據式（6）、（7）對兩種方法得到的連接矩陣計算全腦網絡參數：平均聚類系數 C、平均最短路徑長度 L ，得到的結果如表 2 所示。兩種方法得到不同意識狀態下的網絡參數變化趨勢保持一致，平均聚類系數都為清醒狀態最大、中度麻醉狀態次之、深度麻醉狀態最小；平均最短路徑則都是清醒狀態最小、中度麻醉狀態稍大、深度麻醉狀態最大。對網絡參數做單因素方差分析，其中 SPLS 計算得到的三種意識狀態下的網絡參數差異具有統計學意義（P < 0.05），而 SL 則區分度不大（P > 0.05）。
表2
網絡參數
Table2.
Network parameters
為了驗證兩種方法所計算功能連接對不同意識狀態的區分效果，使用 SVM 分類器分別對特征連接做分類，分類結果如表 3 所示，交叉驗證各折受試者工作特征（receiver operating characteristic，ROC）曲線如圖 7 所示。圖 7 中“fold”表示交叉驗證折數，“mean ROC”表示平均 ROC 曲線，對交叉驗證各折 ROC 曲線計算了曲線下與坐標軸圍成的面積（area under curve, AUC），并以百分比形式寫出。在分類之前使用 PCA 降維的方法選取特征，SPLS 計算出來的特征矩陣雖然更為稀疏，但主成分個數較 SL 方法更多，可能的原因是矩陣稀疏并不會影響其中特征的獨立性。最終使用 SPLS 方法計算功能連接的分類準確率也要高于 SL 方法。
表3
分類結果比較
Table3.
Comparison of classification results
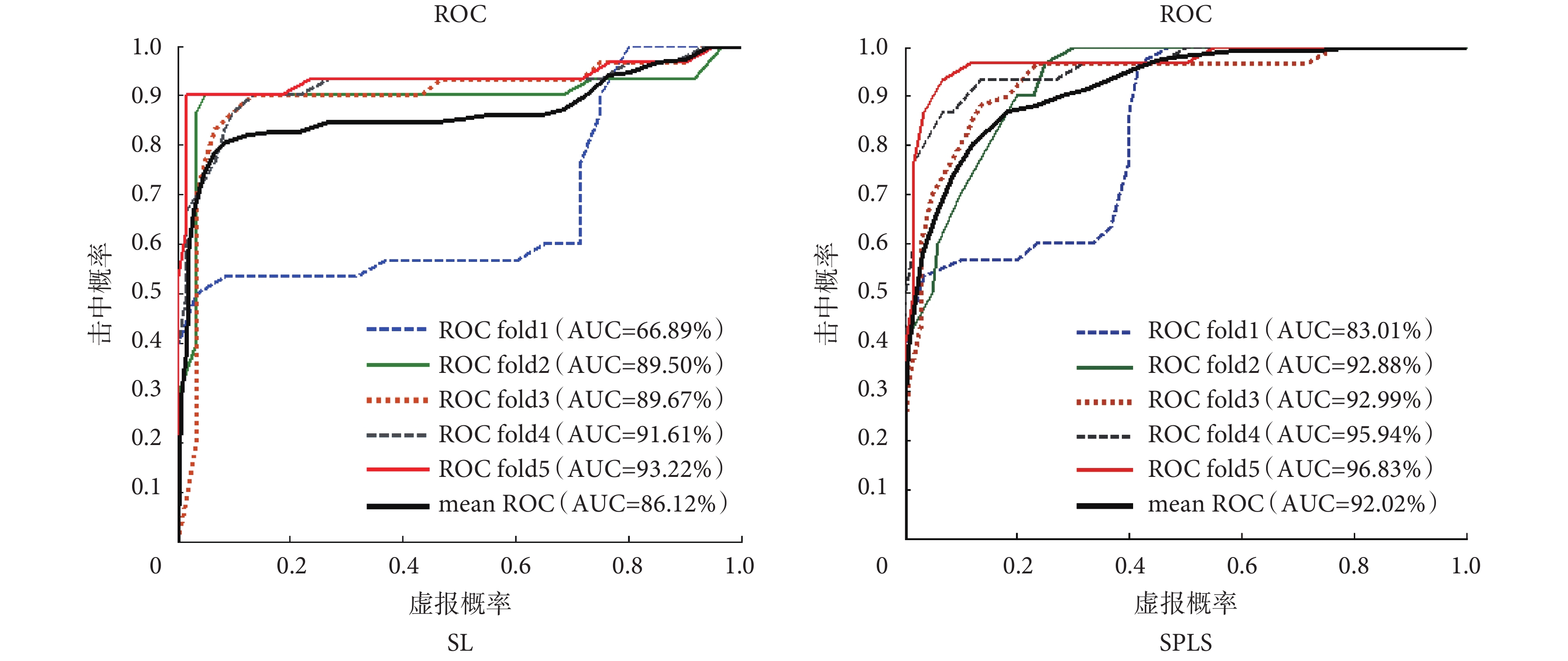圖7
交叉驗證各折 ROC 曲線
Figure7.
Each folding ROC curve of cross-validation
3 結束語
功能連接分析能更直觀地顯示不同麻醉深度下其連接模式的變化，本研究嘗試采用 EEG 信號功能連接分析對不同麻醉深度下的意識狀態進行區分。由于傳統功能連接計算方法都是分別對兩兩不同導聯的 EEG 信號計算連接性，而忽略了其它導聯信號的影響，所以本文引入多元回歸模型計算功能連接，可以同時分析單個導聯信號與其它多個導聯信號之間的連接性。在傳統多元回歸方法 PLS 中加入正則項，使用 SPLS 方法計算不同意識狀態下的 EEG 信號功能連接，提高了其在高維數據上的模型解釋能力。將結果與傳統功能連接方法 SL 計算所得的連接矩陣進行對比。兩種方法得到的結果都為：隨著麻醉深度的加深，全腦連接性整體逐漸減弱；劃分腦區進行討論后發現，右顳區、頂區、枕區隨著麻醉深度的加深，平均連接值逐漸減小，其它腦區的差異則沒有統計學意義。SPLS 方法對比 SL 方法平均連接值差異具有統計學意義的腦區更多。不同意識狀態下其功能連接變化具有特定的模式。對連接矩陣計算網絡參數后，兩種方法不同意識狀態下的網絡參數平均值變化趨勢也保持一致，平均聚類系數會隨意識的減弱而降低，平均最短路徑則會隨意識的減弱而升高，但 SPLS 方法差異具有統計學意義。使用 SVM 分類器對兩種方法得到的連接特征進行分類，SPLS 方法相對傳統功能連接方法 SL 分類準確率更高，達到了 87.93%。研究結果表明，相對于傳統功能連接方法 SL，使用 SPLS 方法計算功能連接，不同意識狀態的區分度更大，可以為意識狀態的衡量、麻醉臨床監測提供一定的技術支持。然而本研究還存在許多待改進的部分，比如受試者數量不多，無法驗證 SPLS 方法對更多數量的受試者是否仍有優勢；只將 SPLS 方法與一種傳統方法 SL 做了對比，并不能說明 SPLS 對比其它傳統方法更有優勢；此外，只研究了丙泊酚一種麻醉藥物，其它麻醉藥物的機制不同可能對其結果產生影響。麻醉意識狀態的衡量是一項非常復雜的工作，本課題組將在今后的研究中進一步深入討論。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
意識水平的衡量一直是臨床手術監測的重要問題[1]。麻醉手術中，意識水平監測能有效降低術中知曉的發生率，并且能夠幫助麻醉醫生精準控制手術期間患者的意識水平[2]。
為滿足臨床手術中意識狀態監測的需求，近年來麻醉深度監測技術發展迅速，特別是基于腦電圖（electroencephalogram，EEG）的監測技術因其非侵入式、價格適中等優勢，應用更為廣泛。EEG 雙頻指數（bispectral index，BIS）、聽覺誘發電位指數（auditory evoked potentials index，AEP index）、麻醉熵等是臨床上常用的幾種基于 EEG 信號的麻醉深度監測技術[3-4]。但是這幾種麻醉深度監測技術僅適用于 2～4 導聯 EEG 信號，空間分辨率較差，可能會對后續分析造成影響。它們使用的麻醉指標也都為不公開的專利算法，將 EEG 信號中的多種特征融合成為一個數值指標，這就給臨床和科研工作者直接觀察、理解麻醉深度特征帶來了一定困難[5-6]。因此需要對 EEG 信號進一步處理分析，提取更利于觀察的麻醉深度特征。近期，有學者開始利用功能連接來分析麻醉誘導的意識喪失機制[7]。有研究表明，額葉、頂葉區域功能連接對意識感知起重要作用，因此通過功能連接可以對意識水平進行衡量[8]。靜息態 EEG 信號功能連接分析較傳統監測技術能夠更直觀地顯示不同麻醉深度下其連接模式的變化，可以嘗試使用功能連接作為麻醉深度的監測指標來對不同意識狀態進行區分。
功能連接實質上是研究不同神經元活動之間的時間相關性，即大腦各區域之間統計學上的依賴關系[9]。EEG 信號是典型的非平穩信號，適用于非平穩信號傳統的功能連接計算方法主要有同步似然分析（synchronization likelihood，SL）、相位滯后指數等[10-11]。這些傳統方法都是分別對兩兩不同導聯的 EEG 信號計算其連接性，而忽略了其它導聯信號的影響，會產生虛假的較高連接值。本研究引入多元回歸模型計算功能連接，用多個信號對單個信號進行表示，相應的表示系數既能反映信號之間的依賴關系，又可以同時分析單個導聯信號與其它多個導聯信號之間的連接性，有效避免了傳統功能連接方法存在的問題。但是，傳統的多元回歸方法在分析功能連接時，易受 EEG 信號中的噪聲干擾。偏最小二乘法（partial least squares，PLS）是近年來多元回歸模型領域引人關注的方法，可以消除信號間的多重共線性，避免了傳統回歸方法的弊端[12]。PLS 集成了主成分分析（principal component analysis，PCA）和典型相關分析的優點，能夠最大限度挖掘信號內部信息，但該方法在應用于高維數據時模型解釋能力會變差，提取特征時包含噪聲特征。為解決這一問題，有學者提出了稀疏偏最小二乘（sparse partial least squares，SPLS）方法，在傳統 PLS 方法的基礎上引入正則化項，提高了模型的解釋能力并且能夠剔除噪聲特征。Lee 等[13]使用 SPLS 方法對高維數據進行變量選擇和預測，發現 SPLS 較 PLS 方法準確度更高，SPLS 方法在使用高維數據的醫學研究領域更有優勢。但目前尚未有研究報道利用 SPLS 方法計算腦功能連接。
基于以上研究，本文采用功能連接分析對不同意識狀態下的靜息態 EEG 數據進行區分，將 SPLS 方法應用于功能連接的計算，引入超參數調整結果稀疏度，可以保證權重向量不全為零，更易定義參數范圍。首先，本文使用 SPLS 與傳統功能連接計算方法中的 SL 對三種意識狀態（清醒、中度麻醉、深度麻醉）下的靜息態 EEG 數據計算功能連接；其次，基于功能連接計算網絡參數，對比不同意識狀態的差異性；最后，利用支持向量機（support vector machine，SVM）對兩種方法得到的連接特征進行分類，比較兩種功能連接計算方法對不同意識狀態下 EEG 數據的區分度。本文研究嘗試使用功能連接作為麻醉意識狀態區分指標，或可以對臨床麻醉意識狀態的監測提供新的衡量指標。
1 試驗數據及方法
1.1 試驗數據
1.1.1 數據采集
2017 年 1 月 1 日—2017 年 6 月 1 日期間，在復旦大學附屬華山醫院進行全麻手術的患者中招募 14 名受試者。受試者年齡平均（48.0 ± 10.8）歲，男性 10 名，女性 4 名，右利手，沒有麻醉手術史和藥物依賴。
本次試驗依據“世界醫學協會赫爾辛基宣言”（2013），并得到復旦大學附屬華山醫院倫理審查委員會批準，每位受試者在閱讀并理解后簽署了知情同意書。常州市生物醫學信息技術重點實驗室已獲得了數據信息的使用授權。試驗使用 256 導聯 EEG 信號采集設備（Ges300，Electrical Geodesics Inc.，美國），分別采集在丙泊酚誘導下清醒、中度麻醉、深度麻醉三種意識狀態下的閉眼靜息態 5 min EEG 信號。參考電極取 Cz 點，采樣頻率為 1 000 Hz。麻醉采用靜脈靶控輸注，三種意識狀態下開始記錄 EEG 信號及結束記錄時的丙泊酚效應室濃度如表 1 所示。
表1
效應室濃度
Table1.
Effect-site concentration
1.1.2 數據預處理
數據預處理主要使用計算軟件 MATLAB 2014a（MathWorks Inc., 美國）平臺下的電生理信號處理工具箱 EEGLAB 14.1.b 完成，主要步驟如下：
（1）濾波：包括低通濾波和高通濾波，得到頻率范圍在 0.5～48 Hz 的 EEG 信號。
（2）偽跡檢測：使用獨立成分分析工具人工去除因眼動、眨眼等產生的偽跡。
（3）壞通道替換：采用周圍鄰近導聯的平均數據替換壞通道數據。
（4）導聯選取：為提高計算速度，依照 10-10 導聯系統中的電極位置在所有導聯中選取了 70 導聯，電極分布如圖 1 所示。
圖1
70 導聯電極分布
Figure1.
Electrode distribution of 70-channel map
（5）參考點轉換：轉換為平均參考，將所有電極采集數據的均值作為參考數據。
在每段經預處理后的 5 min EEG 數據中選取 250 s 數據，每個導聯上則有 250 000 個點，用于后續計算。
1.2 方法
1.2.1 同步似然分析法
SL 方法計算功能連接的原理是檢測兩個信號之間相似的可能性[11]。設第 k 導聯 EEG 信號為 ，i 為時間點，共有 N 個時間點，具體步驟如下：
（1）將信號 X 利用時間延遲重建內嵌向量映射到 m 維的狀態空間。
（2）計算時間點 i 和 j 內嵌向量 和 之間的歐式距離小于 r 的概率 ，如式（1）所示：
|
其中，為 Heaviside 階躍函數， 和 為兩個窗。
（3）設一共有 M 導聯，則第 k 導聯信號與其他 M－1 導聯信號 i 與 j 時刻的同步似然值 定義如式（2）所示：
|
（4）對所有時間點 j 求平均，即得第 k 導聯信號與其它 M－1 導聯信號在 i 時刻的同步似然值，如式（3）所示：
|
1.2.2 偏最小二乘法
引入多元回歸模型計算功能連接，可以同時計算單個導聯和其它多個導聯的連接性。PLS 方法則能最大程度提取信號內部信息，其最終目的是用多個因變量對多個自變量進行回歸建模[12]。利用 PLS 方法計算功能連接時，將其中某一導聯的信號作為因變量 ，除去該導聯的所有其它導聯信號作為自變量 。整個回歸建模的過程首先是分別從 X 與 Y 中提取出成分 t 和 u 來研究這兩個矩陣之間的統計關系。t 和 u 必須能盡可能多地攜帶 X 與 Y 中的變異信息，并且兩者之間相關程度也盡可能達到最大。綜合以上兩點要求，實質上就是使得 t 和 u 的協方差達到最大，轉化為求解以下優化問題，如式（4）所示：
|
其中，X0 和 Y0 分別為 X 與 Y 的標準化矩陣， 與 分別為 X0 和 Y0 的權重向量，并且是單位向量。求得第一對權重向量 與 之后，即能得到第一對主成分 t1 和 u1。其次，建立 X0 和 Y0 對 t1 和 u1 的回歸方程，得到回歸方程的殘差矩陣。將殘差矩陣取代 X0 和 Y0，與第一對主成分求解過程相同，求出 與 以及第二對主成分 t2 和 u2。以上步驟一直迭代至殘差矩陣達到設定精度為止，最終轉化為 Y 對 X 的回歸方程，完成了 PLS 回歸建模。
1.2.3 稀疏偏最小二乘法
SPLS 方法在傳統的 PLS 方法基礎上引入了兩個范數 l1、l2 對其進行約束。l1 范數能將部分系數壓縮至零，達到消除微弱虛假連接的目的，l2 范數則能消除 l1 范數約束可能會去除部分相關特征的影響[14]。在式（4）中加入 l1、l2 范數，得到如式（5）所示：
|
和 為控制正則化項的超參數， 和 的值越低，稀疏度越高。為了使得 l1、l2 范數都能發揮作用，超參數的值必須滿足：、。求解式（5）的算法步驟如下：
（1）對 X 與 Y 進行標準化得到 X0 和 Y0，令 。
（2）初始化 ，且滿足。
（3）重復以下步驟直至收斂。
① 更新 ：
Ⅰ.
Ⅱ. ，若，；否則 取正的常數使得
② 更新 ：
Ⅰ.
Ⅱ. ，若，；否則 取正的常數使得
其中，為軟閾值函數，定義為：，符號表示當 0 時等于，當 時則等于 0。
SPLS 在功能連接計算過程中，將第 i 導信號作為因變量 Yi，將除去第 i 導的其它導聯信號作為 Xi。因此對于 70 導聯 EEG 信號，、， 只能取 1，。實際上只需對超參數 進行調節，可以利用交叉驗證法，計算模型的均方誤差（mean-square error，MSE）來確定超參數 的值。完成 SPLS 回歸建模過程后得到回歸方程系數列向量 soli。將 soli 按順序填充至 70 × 70 矩陣 con 的第 i 列的 1～（i ? 1）行和（i + 1）～70 行，將 con 的第 i 行第 i 列置零。對每一個導聯的信號都如此操作，最后連接矩陣 。C 中元素 Cjk 表示節點 j 與節點 k 之間的連接強度。利用 MATLAB 2014a（MathWorks Inc.，美國）實現該算法，每計算一個連接矩陣需要 8.59 s。
1.2.4 腦網絡分析
功能連接計算完畢后，得到的也是一個個網絡，為了直觀地觀測計算結果，利用圖論的方法引入復雜網絡分析對結果進行評估，這里選用平均最短路徑長度和平均聚類系數來分析結果。
在二值化網絡中，從節點 i 到節點 j 的長度就是從 i 到 j 要經過的邊數，設節點 i、j 之間的最短路徑長度為 dij，平均最短路徑長度即為網絡所有可能的兩節點之間的最短路徑的平均值。平均最短路徑長度 L 可以衡量全局網絡的整合作用，計算公式如式（6）所示：
|
聚類系數是評估網絡中節點聚合程度的重要指標，平均聚類系數 C 則是網絡中所有節點聚類系數的平均，其計算方式如式（7）所示：
|
其中，Ei 表示網絡中與節點 i 連接的邊數。
1.2.5 功能連接對比分析
為了驗證兩種方法所計算功能連接對不同意識狀態的區分效果，使用 SVM 分類器分別對連接特征做分類，分類流程如圖 2 所示。原始 EEG 信號經過預處理后，使用 SL 和 SPLS 兩種方法分別對三種意識狀態下的功能連接進行計算，最終每種方法都將得到 42 個連接矩陣，減去重復連接和自身連接，每個連接矩陣得到 2 415 個連接系數。將連接系數整合起來得到連接特征矩陣。使用 PCA 方法對特征進行降維，保留其中有差異的連接特征。之后采用 SVM 分類器對其進行分類，使用 5 折交叉驗證，對比分類準確率。
圖2
分類流程
Figure2.
Classification process
2 結果分析
在使用 SPLS 方法計算功能連接時，使用交叉驗證對超參數 取 1～8.3 時計算回歸模型的 MSE，如圖 3 所示。從圖中可以看出超參數 的值在取 1.4 時 MSE 值最小，接近于零，因此將超參數 的值定為 1.4 進行接下來的計算。
圖3
SPLS 均方誤差
Figure3.
MSE of SPLS
分別采用 SL 和 SPLS 法對三種意識狀態下的 EEG 數據計算功能連接，得到的連接矩陣如圖 4 所示。從圖 4 中可以看出兩種方法得到連接矩陣分布基本一致，只是 SPLS 方法去除了一些虛弱的連接。SL 與 SPLS 方法得到連接矩陣圖中都能較為明顯發現深度麻醉狀態相對其它兩種狀態連接減弱。
圖4
連接矩陣
Figure4.
Connectivity heatmaps
為了更直觀地觀察全腦連接情況，對計算得的連接矩陣畫出連接拓撲圖。SL 方法需要設定閾值，將連接閾值參數設為 0.23，高于這一閾值則將相應的節點對進行連接。SPLS 方法已將虛弱連接去除，因此不需要設定閾值，只需將連接系數大于零的對應節點相連。最終畫出的連接拓撲圖如圖 5 所示。兩種方法得到的連接拓撲圖分布也較為相似，都為清醒狀態連接最密集，中度麻醉次之，深度麻醉最稀疏。
圖5
連接拓撲圖
Figure5.
Connection topology
根據解剖位置將 70 個電極劃分為 6 個區域，分別為：額區，包含通道：FPz、FP1、FP2、AF7、AF3、AF4、AF8、F1、F3、F5、Fz、F2、F4、F6；左顳區，包含通道：F9、F7、FT9、FT7、T9、T7、TP9、TP7、P9、P7；右顳區，包含通道：F10、F8、FT10、FT8、T10、T8、TP10、TP8、P10、P8；中央區，包含通道：FC5、FC3、FC1、FCz、FC2、FC4、FC6、C5、C3、C1、Cz、C2、C4、C6；頂區，包含通道：CP5、CP3、CP1、CPz、CP2、CP4、CP6、P5、P3、P1、Pz、P2、P4、P6；枕區，包含通道：PO7、PO3、POz、PO4、PO8、O1、Oz、O2。對這 6 個區域的平均連接值進行統計，結果如圖 6 所示。SL 方法和 SPLS 方法的平均連接值在右顳區、頂區、枕區都是隨麻醉深度的加深而減小的。采用單因素方差分析，其中 SL 方法在右顳區（F = 4.057，P = 0.029）和枕區（F = 7.879，P = 0.002）組間差異具有統計學意義，SPLS 方法在右顳區（F = 18.810，P < 0.001）、中央區（F = 6.674，P = 0.004）和枕區（F = 6.352，P = 0.005）組間差異具有統計學意義。SPLS 方法較 SL 方法連接值差異具有統計學意義的區域更多。
圖6
不同腦區平均連接值（*P < 0.05）
Figure6.
Average connectivity value of different brain regions（*P < 0.05）
根據式（6）、（7）對兩種方法得到的連接矩陣計算全腦網絡參數：平均聚類系數 C、平均最短路徑長度 L ，得到的結果如表 2 所示。兩種方法得到不同意識狀態下的網絡參數變化趨勢保持一致，平均聚類系數都為清醒狀態最大、中度麻醉狀態次之、深度麻醉狀態最小；平均最短路徑則都是清醒狀態最小、中度麻醉狀態稍大、深度麻醉狀態最大。對網絡參數做單因素方差分析，其中 SPLS 計算得到的三種意識狀態下的網絡參數差異具有統計學意義（P < 0.05），而 SL 則區分度不大（P > 0.05）。
表2
網絡參數
Table2.
Network parameters
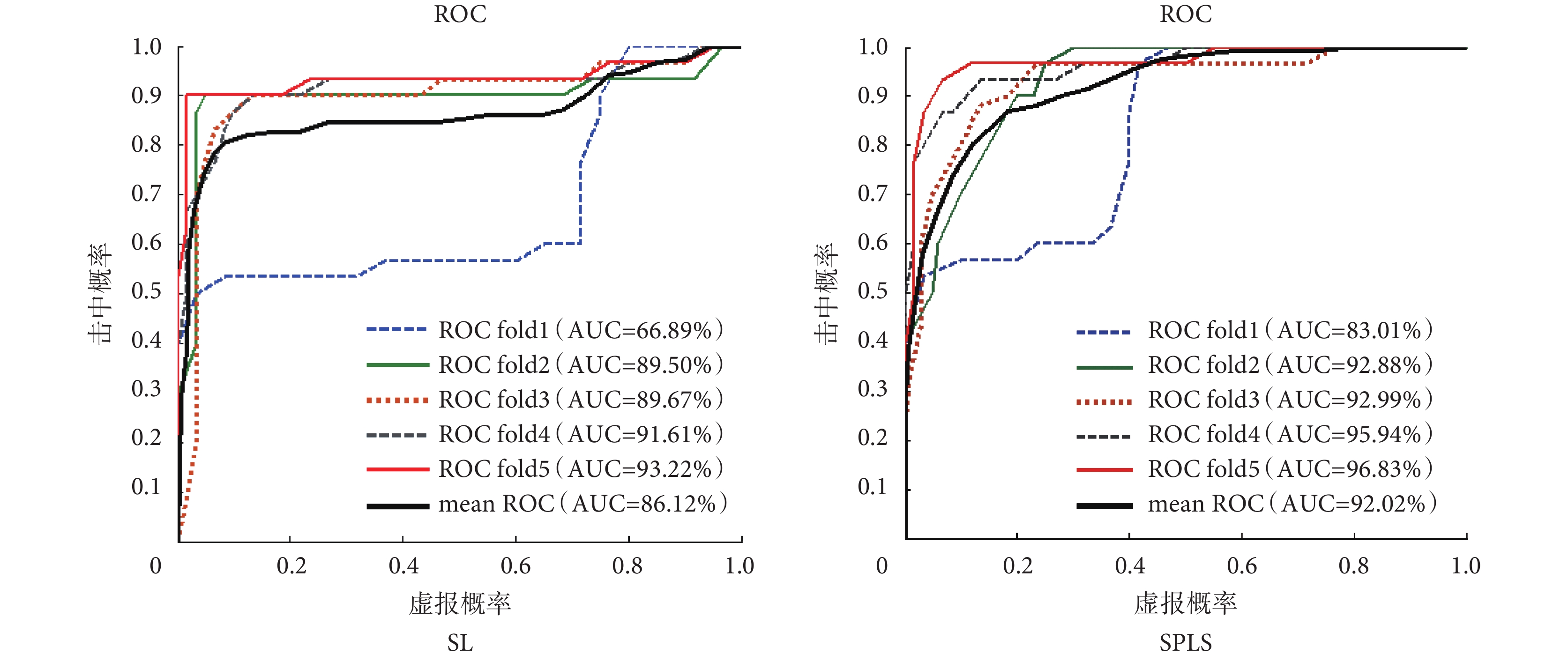
為了驗證兩種方法所計算功能連接對不同意識狀態的區分效果，使用 SVM 分類器分別對特征連接做分類，分類結果如表 3 所示，交叉驗證各折受試者工作特征（receiver operating characteristic，ROC）曲線如圖 7 所示。圖 7 中“fold”表示交叉驗證折數，“mean ROC”表示平均 ROC 曲線，對交叉驗證各折 ROC 曲線計算了曲線下與坐標軸圍成的面積（area under curve, AUC），并以百分比形式寫出。在分類之前使用 PCA 降維的方法選取特征，SPLS 計算出來的特征矩陣雖然更為稀疏，但主成分個數較 SL 方法更多，可能的原因是矩陣稀疏并不會影響其中特征的獨立性。最終使用 SPLS 方法計算功能連接的分類準確率也要高于 SL 方法。
表3
分類結果比較
Table3.
Comparison of classification results
圖7
交叉驗證各折 ROC 曲線
Figure7.
Each folding ROC curve of cross-validation
3 結束語
功能連接分析能更直觀地顯示不同麻醉深度下其連接模式的變化，本研究嘗試采用 EEG 信號功能連接分析對不同麻醉深度下的意識狀態進行區分。由于傳統功能連接計算方法都是分別對兩兩不同導聯的 EEG 信號計算連接性，而忽略了其它導聯信號的影響，所以本文引入多元回歸模型計算功能連接，可以同時分析單個導聯信號與其它多個導聯信號之間的連接性。在傳統多元回歸方法 PLS 中加入正則項，使用 SPLS 方法計算不同意識狀態下的 EEG 信號功能連接，提高了其在高維數據上的模型解釋能力。將結果與傳統功能連接方法 SL 計算所得的連接矩陣進行對比。兩種方法得到的結果都為：隨著麻醉深度的加深，全腦連接性整體逐漸減弱；劃分腦區進行討論后發現，右顳區、頂區、枕區隨著麻醉深度的加深，平均連接值逐漸減小，其它腦區的差異則沒有統計學意義。SPLS 方法對比 SL 方法平均連接值差異具有統計學意義的腦區更多。不同意識狀態下其功能連接變化具有特定的模式。對連接矩陣計算網絡參數后，兩種方法不同意識狀態下的網絡參數平均值變化趨勢也保持一致，平均聚類系數會隨意識的減弱而降低，平均最短路徑則會隨意識的減弱而升高，但 SPLS 方法差異具有統計學意義。使用 SVM 分類器對兩種方法得到的連接特征進行分類，SPLS 方法相對傳統功能連接方法 SL 分類準確率更高，達到了 87.93%。研究結果表明，相對于傳統功能連接方法 SL，使用 SPLS 方法計算功能連接，不同意識狀態的區分度更大，可以為意識狀態的衡量、麻醉臨床監測提供一定的技術支持。然而本研究還存在許多待改進的部分，比如受試者數量不多，無法驗證 SPLS 方法對更多數量的受試者是否仍有優勢；只將 SPLS 方法與一種傳統方法 SL 做了對比，并不能說明 SPLS 對比其它傳統方法更有優勢；此外，只研究了丙泊酚一種麻醉藥物，其它麻醉藥物的機制不同可能對其結果產生影響。麻醉意識狀態的衡量是一項非常復雜的工作，本課題組將在今后的研究中進一步深入討論。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
