多通道微電極陣列記錄的鋒電位（Spike）十分微弱，極易受干擾，其含噪的特性影響了 Spike 檢出的準確率。針對 Spike 檢測過程中通常存在的獨立白噪聲、相關噪聲與有色噪聲，本文結合主成分分析（PCA）、小波分析和自適應時頻分析，提出 PCA-小波（PCAW）與整體平均經驗模態分解（EEMD）聯合的去噪新方法（PCWE）。首先，利用 PCA 提取多通道神經信號通道間的主成分作為相關噪聲去除；然后利用小波閾值法對獨立白噪聲進行去除；最后利用 EEMD 把噪聲分解到各層本質模態函數中，對有色噪聲進行去除。仿真結果表明，PCWE 使信噪比約提高 2.67 dB，標準差約減小 0.4 μV，顯著提高了 Spike 的檢出精確率；實測數據結果表明，PCWE 能使信噪比約提高 1.33 dB，標準差約減小 18.33 μV，表現出良好的去噪性能。本文研究結果表明，PCWE 可以提高 Spike 信號的可靠性，或可為神經信號的編碼解碼提供一種新型有效的鋒電位去噪方法。
引用本文： 周怡君, 胡一凡, 李蒙蒙, 楊莉芳, 尚志剛. 聯合主成分分析-小波與整體平均經驗模態分解的鋒電位去噪方法. 生物醫學工程學雜志, 2020, 37(2): 271-279. doi: 10.7507/1001-5515.201906048 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
鋒電位（Spike）是神經元細胞動作電位的表征[1]，Spike 的發放標志著大腦對感覺與運動事件的信息編碼，因此可靠地識別出同一電極記錄到的 Spike 信號在神經科學研究中具有重要價值[2]。Spike 信號一般通過多通道微電極陣列進行采集，但其十分微弱，幅值一般只有 100～200 μV，極易被環境中各種不同的噪聲污染，導致產生嚴重畸變甚至被淹沒，這對 Spike 信號的檢測與后期的分析處理帶來極大困難。因此，為了提高 Spike 信號的可靠性，需要對其進行有效的去噪，以增加 Spike 信號的信噪比（signal-to-noise ratio，SNR）并減小波形畸變，這對后續神經信號的編碼、解碼和相關的大腦工作機制等研究具有重要意義。
針對 Spike 信號的經典去噪方法有很多，但都具有一定的局限性。常用的主成分分析（principal component analysis，PCA）去噪基于多通道間噪聲的統計特征進行去噪，它通過計算通道間的主成分作為相關噪聲去除，但對相關噪聲以外的其他噪聲成分去噪效果不佳[3]。在此基礎上，吳丹等[4]結合了小波閾值去噪，提出 PCA-小波聯合去噪（principal component analysis-wavelet，PCAW）方法，利用噪聲的小波特征進一步去除信號中的獨立白噪聲，有效提高了 Spike 的 SNR，但其對有色噪聲的去除十分有限。此外，整體平均經驗模態分解（ensemble empirical mode decomposition，EEMD）去噪方法則直接基于數據波形本身，在時域上進行處理[5]，因此具有普適性，對大部分噪聲成分都有一定程度的去噪效果，但其針對性相對較弱，與具有針對性的去噪方法相比，該方法對特定噪聲成分的去噪效果略為遜色。
PCA 與小波閾值法是神經信號處理中十分經典和傳統的去噪方法，而 EEMD 則是自適應濾波的代表，因此在信號處理中都具有一定的代表性，近年來許多新的 Spike 去噪方法都是在此基礎上進行改進或創新的。如 Chen 等[6]提出 EEMD 與典型相關分析（canonical correlation analysis，CCA）相結合的神經信號肌肉偽影去噪方法，該方法可以較好地利用通道信息去除肌肉運動帶來的噪聲，但在噪聲成分中還有可能包含著有用信息。Bhatnagar 等[7]提出 PCA 與獨立成分分析（independent component analysis，ICA）相結合的去噪方法，實驗結果表明該方法比單獨使用 ICA 或小波閾值法更能有效地提高 SNR，但該方法存在收斂性問題，可能存在數據丟失。Li 等[8]針對高壩地震信號的非平穩性和低 SNR 的特點，提出一種基于 EEMD 與奇異譜分析（singular spectrum analysis，SSA）相結合的自適應去噪方法，其去噪結果表明該方法優于 EEMD 和 EEMD-小波閾值去噪算法，然而該算法在神經信號中的應用效果還有待進一步驗證。Bajaj 等[9]則提出了一種基于小波的參數整定偽影去噪算法，該算法以小波包分解為基礎，能夠有效地去除 Spike 中人體運動帶來的噪聲，但在每次進行去噪前都需要單獨進行參數調優。
這些 Spike 去噪方法多是僅針對于某種特定的噪聲成分進行去除，但在 Spike 檢測過程中，通常會同時存在獨立白噪聲、相關噪聲和有色噪聲等多種噪聲成分[3]，為了對以上噪聲進行全面地針對性去噪，本文根據各噪聲特性，結合 PCA、小波分析和自適應時頻分析，提出基于 PCAW 與 EEMD 聯合的去噪新方法（PCWE），先利用 PCAW 針對性地去除通道間的相關噪聲和獨立白噪聲，再利用 EEMD 的普適性去除各通道中的有色噪聲。下面將對仿真數據與從鴿子弓狀皮質尾外側區（nidopallium caudolaterale，NCL）采集到的實測數據進行去噪實驗，對 PCWE 與 PCAW、EEMD 進行性能評估與去噪效果比較，以驗證 PCWE 去噪方法的有效性。最終，期望本文提出的 PCWE 可以為 Spike 信號提供一種可靠的去噪新方法，將有助于更好地開展有效的神經信號編解碼研究。
1 方法和材料
1.1 PCWE 去噪方法原理
PCWE 實際上是把 PCAW 與 EEMD 聯合使用，通過 PCA、小波分析和自適應時頻分析把噪聲的統計特征、小波特征與整體波形特征相結合，使不同的噪聲類型能夠在不同的特征描述下更好地被識別出來，從而實現對各類噪聲的針對性去噪。PCWE 的去噪流程如下：
（1）根據相關噪聲在通道間存在相關性的統計特征，對多通道神經信號利用 PCA 提取通道間的主成分作為相關噪聲成分[3]。假設采樣點數均為 L 的 N 通道記錄信號表示為 S（t，ch）= ［s（t，1），s（t，2），
，s（t，N）］，其中 z 通道信號為 s（t，z）= ［s（1，z），s（2，z），
，s（L，z）］。選擇 z 通道 s（t，z）為目標去噪通道，先計算剩余通道 S（t，chelse）的主成分。對剩余通道信號的協方差 Celse 進行特征根分解，如式（1）所示：
 |
其中，Λelse 為特征根，Uelse 為特征向量，那么 S（t，chelse）的主成分則如式（2）所示：
 |
其中，PCelse（n）的第一個主成分即為相關噪聲。把目標去噪通道 s（t，z）投影到 n 個主成分的空間中，并歸一化計算出每個主成分的投影權重系數[3]，如式（3）所示：
 |
其中，an（z）即為 z 通道上的 n 個投影系數。最后用原信號減去投影后的第一個主成分即能去除通道間的相關噪聲，如式（4）所示：
 '/> |
（2）對每個通道進行小波閾值去噪。信號經離散小波變換后，在每一層小波系數中設置合適閾值，把低于閾值的小波系數置零，即能有效去除通道中的獨立白噪聲[10]。
假設某一通道信號進行離散小波變換后的小波系數記為 xj，k，j 表示原信號被分解為 j 個尺度，k 表示在對應分解尺度下的第 k 個小波系數。那么對 xj，k 設定的閾值如式（5）所示：
 |
其中，σj = MADj/0.674 5 表示每個尺度下噪聲的標準差（standard deviation，SD），MADj 為 j 尺度下小波系數絕對偏差的中位數，0.674 5 為高斯分布校準因子[11]；N（xj）為 j 尺度下小波系數的個數；Tj 即為 j 尺度下小波系數的閾值。
然后使用硬閾值函數去除通道中低于閾值的獨立白噪聲成分，如式（6）所示：
 |
其中，
表示通過閾值去噪后的小波系數。把經過小波閾值去噪后的信號記為 s（t，z）″。
（3）對各通道進行 EEMD 去噪。EEMD 分解不僅能夠避免 Spike 這種間歇性成分帶來的模態混疊現象，還能根據信號整體波形中不同的波動和趨勢特征分解到各層本質模態函數（intrinsic modal function，IMF）中。因此信號經 EEMD 分解步驟處理之后[12]，可以產生 k 層 IMF，如式（7）所示：
 '/> |
其中，hi 表示第 i 層 IMF；rk（t）表示剩余值。
在去除相關噪聲與獨立白噪聲后，信號中的 Spike 成分幅值較大，而有色噪聲幅值較小，且能量主要集中在前幾層 IMF 中，因此選擇前 j 層 IMF 通過式（5）～（6）進行小波閾值去噪，即能把有色噪聲去除，最終去噪結果可表示為如式（8）所示：
 |
其中，
表示小波閾值去噪后的前 j 層 IMF，
表示剩下的 IMF，rk（t）表示剩余值，s（t，z）c 即為 z 通道最終的去噪信號。本文統一選擇前 3 層 IMF 進行小波閾值去噪，即能去除通道中的有色噪聲。
（4）對各通道信號進行重建，完成整體去噪。
1.2 閾值檢測法
對信號進行去噪后，使用閾值法檢測信號中的 Spike 信號。在檢測 Spike 信號時，多使用負閾值，閾值設定如式（9）所示：
 |
其中，b 為閾值系數，L 為 z 通道信號的總采樣點數，s（i，z）表示 z 通道信號中第 i 個點的幅值，
表示 z 通道信號幅值的均值。
1.3 去噪效果評價指標
本文對 PCWE、PCAW 與 EEMD 方法的去噪效果進行評估比較，從信號波形角度，以 SNR 和 SD 作為評價指標；從準確率角度，則以精確率與漏檢率作為評價指標。
1.3.1 SNR 與 SD
SNR（以符號 SNR 表示）為直接評價指標，表示數據中信號與噪聲含量的比值，SNR 值越大，表示去噪效果越好。若通過閾值法檢測出信號中有 N 個 Spike（符號記為：spk），同時每個 Spike 存在相對應的噪聲成分（符號記為：noise），那么該信號的 SNR 值的計算公式如式（10）所示：
 |
其中，N 表示 Spike 總個數，spki 表示第 i 個 Spike，noisei 表示第 i 個 Spike 對應的噪聲成分；max（·）表示取最大值運算，min（·）表示取最小值運算，rms（·）表示均方根運算。在信號采樣率為 30 000 Hz 情況下，一般取每個 Spike 負峰值點前 0.5～2.1 ms 之間的 48 個采樣點作為噪聲部分。
SD（以符號 SD 表示）為間接評價指標，用來衡量 Spike 的畸變程度。理論上微電極陣列中同一個檢測位點對同一個神經元檢測到的 Spike 波形應是相同的[4]，因此 SD 值越小表示去噪效果越好。為區分仿真數據與實測數據的 SD 值差異，把仿真數據的 SD 以符號 SD1 表示；實測數據的 SD 則以符號 SD2 表示。
對于仿真數據，已知模板 Spike 信號（符號記為：SPK），那么 SD1 的計算公式如式（11）所示：
 |
其中，N 表示 Spike 的總個數，M 表示每個 Spike 的采樣點數（每個 Spike 的采樣點數相同），spki，j 表示第 i 個 Spike 的第 j 個采樣點，SPKj 則表示模板 Spike 的第 j 個采樣點。
對于實測數據，若只有一類 Spike，則把檢測到的 N 個 Spike 的均值（符號記為：
）作為模板信號，那么 SD2 的計算公式如式（12）所示：
 |
其中，N、M 和 spki，j 的含義與式（11）相同，
表示 
的第 j 個采樣點。若同一通道上存在多個不同神經元的 Spike 信號，需先對檢測出的 Spike 進行分類，然后對不同類型的 Spike 利用式（12）分別計算其 SD2，最后取其均值作為整體 SD2。
1.3.2 精確率與漏檢率
精確率與漏檢率用于評價信號經不同方法去噪后，檢測出的 Spike 信號的準確性，以及漏檢現象的嚴重性。
假設仿真數據中共設置了 N 個真實 Spike，對信號進行去噪后共檢出 n 個 Spike，其中有 n1 個為真，那么精確率與漏檢率分別如式（13）～（14）所示：
 |
 |
1.4 統計分析
結果中的 SNR 和 SD 均以（
）的形式表示。在統計分析中，先對樣本數據進行正態性檢驗，若樣本總體服從正態分布，利用 t 檢驗度量差異是否具有統計學意義；若樣本總體不服從正態分布，則利用秩和檢驗度量差異是否具有統計學意義。顯著水平均設置為 5%，即 P < 0.05 被認為差異具有統計學意義。
1.5 實驗數據
為了驗證 PCWE 去噪方法的有效性，首先采用仿真數據對算法的去噪性能進行測試，然后結合實測數據的去噪結果，對比分析 PCWE、PCAW 和 EEMD 的去噪性能。
1.5.1 仿真數據生成
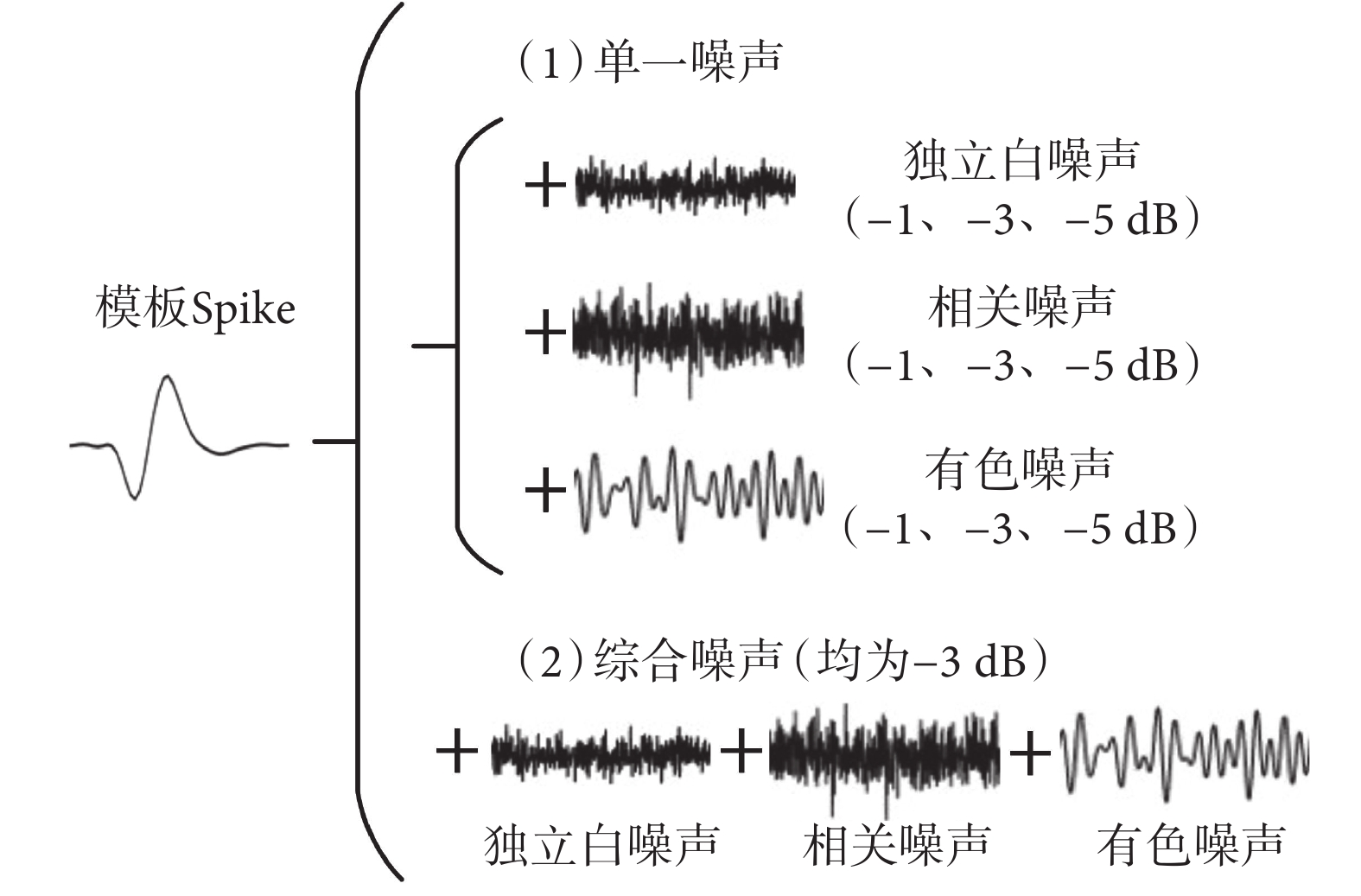
仿真數據由 4 個通道組成，采樣率為 30 000 Hz，時長為 100 ms，各通道隨機設置 10 個模板 Spike。模板 Spike 由商用神經信號模擬發生器（BlackRock MicroSystem，Inc，UT，USA）中的一類 Spike 經平均計算求得，如圖 1 所示。
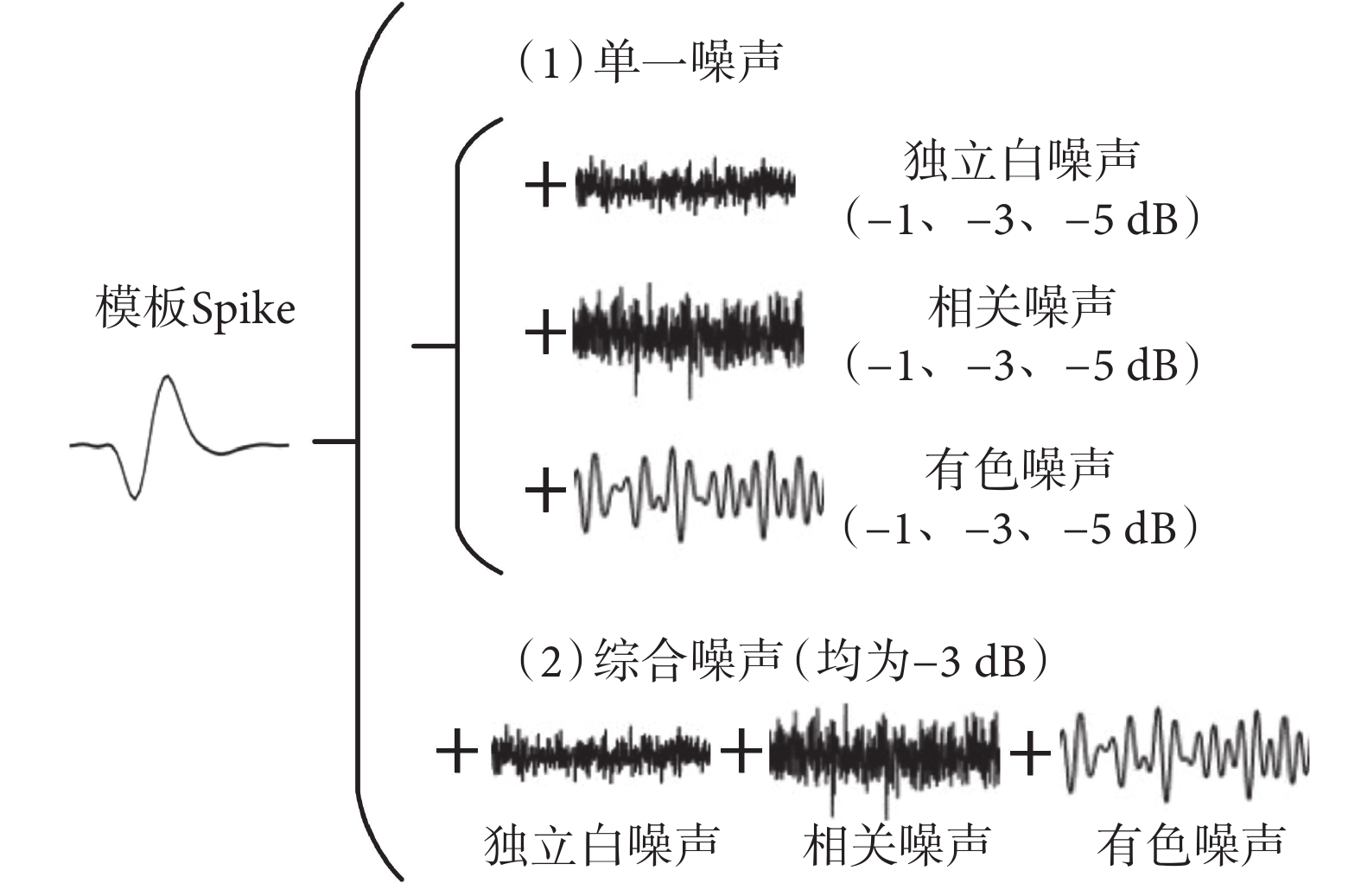圖1
仿真數據示意圖
Figure1.
Schematic diagram of simulation data
（1）單一噪聲仿真數據。往每組仿真數據加入 3 種不同的單一噪聲成分，分別為：① 獨立白噪聲，用于模擬采集系統中的熱噪聲成分；② 相關噪聲，用于模擬外界相同聲源的噪聲成分，如運動噪聲等；③ 頻段為 500～ 1 000 Hz 的有色噪聲，用于模擬與神經信號頻率相關的有源噪聲，如肌電信號等。每種噪聲成分分別設置 3 個噪聲級別，從低到高分別為 ? 1、? 3、? 5 dB。每種噪聲的每一噪聲級別各生成 30 組仿真數據（共 3 × 3 × 30 組）。
（2）綜合噪聲仿真數據。各通道分別加入-3 dB 的綜合噪聲。綜合噪聲同時包括獨立白噪聲、相關噪聲和有色噪聲，共產生 30 組仿真數據。
1.5.2 實測數據采集
本文實驗動物為亞洲原鴿，對成年健康鴿子用濃度為 10% 的水合氯醛進行全身麻醉后，往其 NCL 區植入微電極陣列（4 × 4 排列，共 16 通道），具體手術過程請參考文獻[13]。術后恢復一周后使用 CerebusTM多通道神經信號采集系統（CerebusTM，Blockrock Inc，美國）進行不同狀態下 Spike 信號的采集，采樣率為 30 000 Hz，Spike 濾波范圍為 250～5 000 Hz。分別采集鴿子以下 3 種狀態的神經信號：① 麻醉。用濃度為 10% 的水合氯醛，以 0.3 mL/100 g 的標準對鴿子進行腹腔注射，使鴿子進入麻醉昏迷狀態后采集；② 清醒。結合監控視頻，在鴿子保持正常眨眼與呼吸，無明顯運動時的清醒狀態下進行采集；③ 行走。結合監控視頻，在鴿子清醒且活躍，在熟悉環境中自由行走探索時的狀態下進行采集。三種狀態代表三種不同 SNR 的實測數據，每種狀態分別隨機選取 10 組時長為 1 s 的神經信號進行去噪（共 3 × 10 組）。以上實測數據均由鄭州大學生命科學學院提供。所有實驗動物經鄭州大學生命科學倫理審查委員會審查，符合動物管理使用委員會的各項規定。
2 結果
2.1 仿真數據結果
2.1.1 單一噪聲仿真數據結果
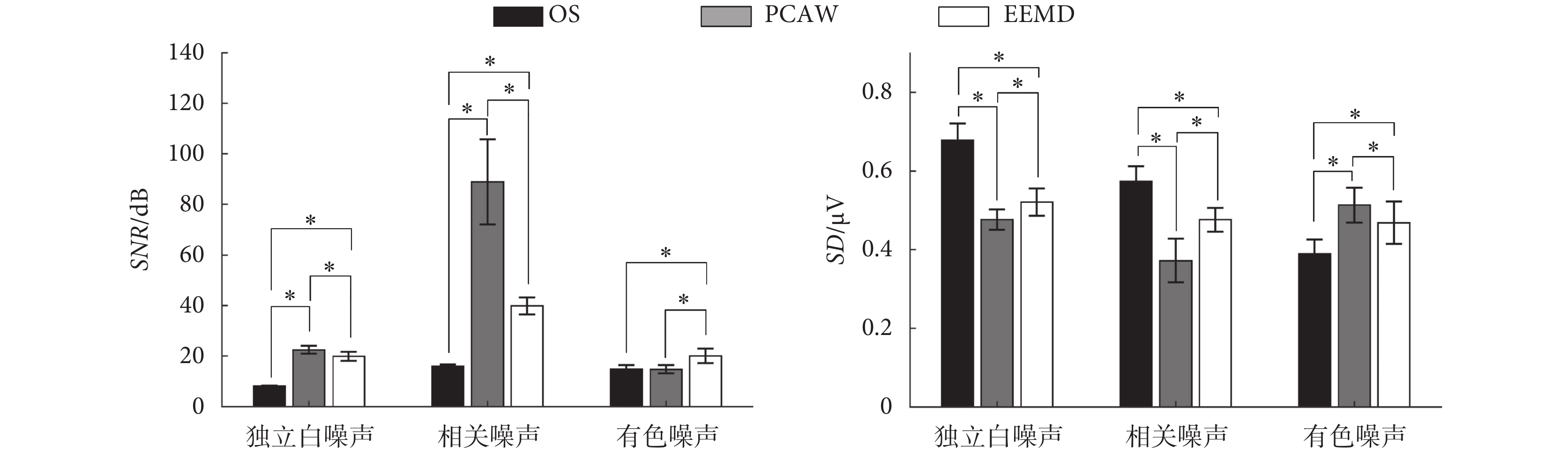
如圖 2 所示，給出了單一噪聲仿真數據在噪聲等級為-3 dB 情況下，PCAW、EEMD 去噪前后的 SNR 與 SD1 統計直方圖，其中第一列為去噪前的原始信號（original signal，OS）。該樣本總體不服從正態分布，使用秩和檢驗檢測各組數據兩兩之間的差異。
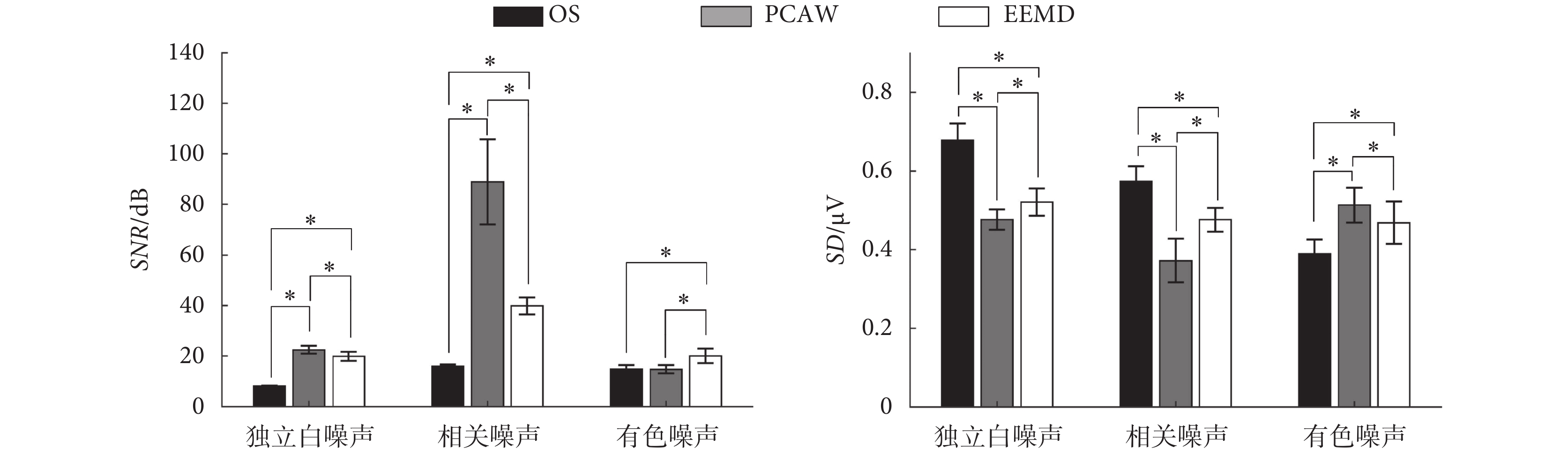圖2
單一噪聲仿真數據去噪前后的 SNR 與 SD1 值 N = 30，*P < 0.01
Figure2.
Change of SNR and SD1 of simulation data with single noise after denoising N = 30，*P < 0.01
由圖 2 可知，對于獨立白噪聲與相關噪聲，經 PCAW 去噪后有效提高了 SNR 并減小 SD1，差異具有統計學意義（P < 0.01）。而對于有色噪聲，只有 EEMD 能夠提高 SNR，且 SD1 增加最少，即帶來的波形畸變最小，且差異具有統計學意義（P < 0.01）。這說明 PCAW 能夠針對性地去除獨立白噪聲與相關噪聲，而 EEMD 則對于有色噪聲的去除更有優勢。在-1 dB 與-5 dB 情況下具有相同的統計結果。顯然，兩者的去噪性能是優勢互補的。
2.1.2 綜合噪聲仿真數據結果
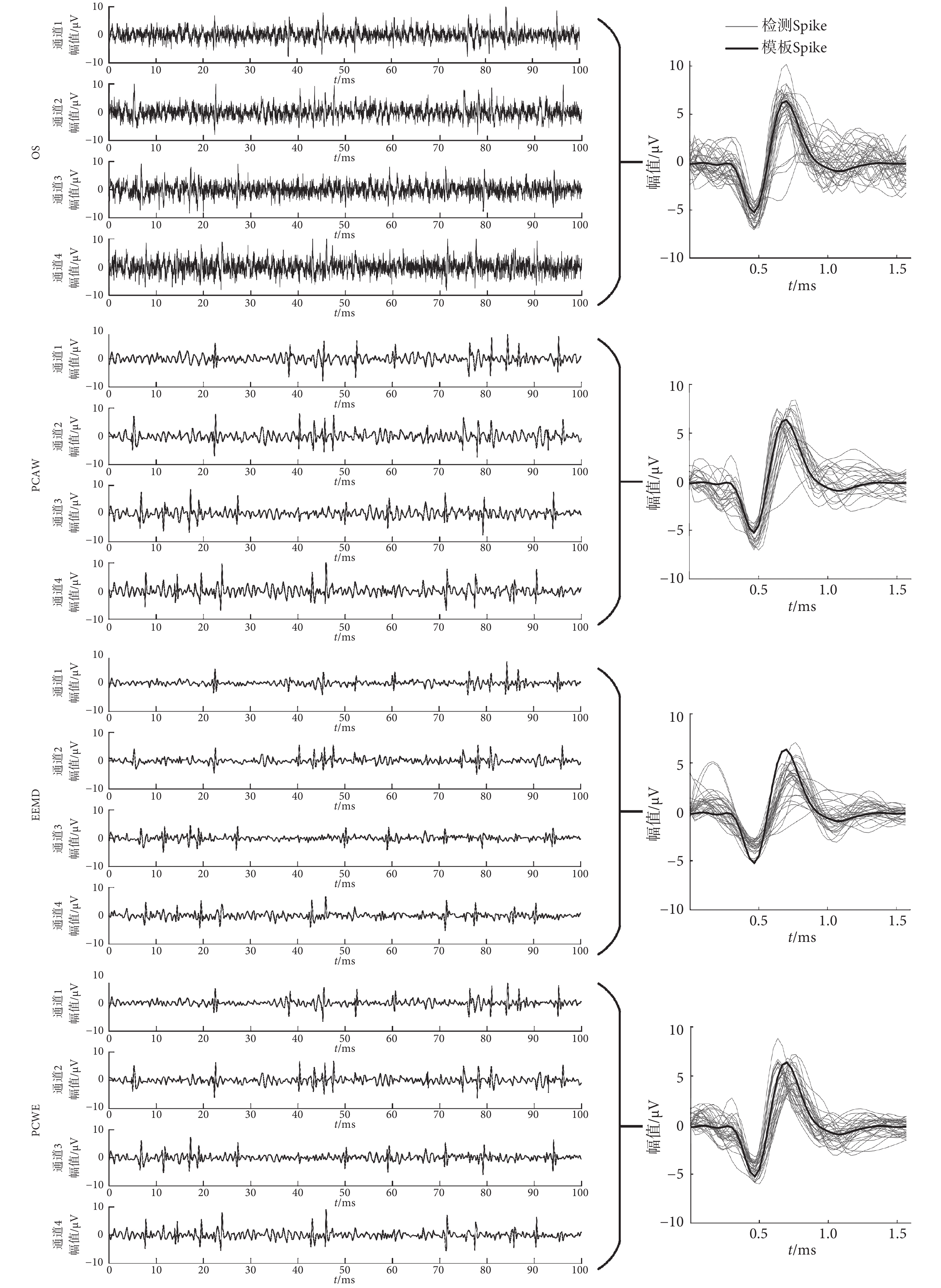
如圖 3 所示，給出了綜合噪聲仿真數據的去噪結果及對應的 Spike 信號。圖中 OS 經 PCAW 去噪后，顯然還存在部分噪聲，但基本保持了 Spike 的幅值水平；EEMD 雖能去除大量噪聲，但對 Spike 信號也存在一定削弱作用，容易導致漏檢現象；PCWE 則兼具兩者優點，既去除了大量噪聲，又能更大程度地保持 Spike 的幅值水平。在檢測 Spike 與模板 Spike 的比較中，顯然經 PCWE 去噪后的 Spike 波形與模板波形重合度最高，即 PCWE 能夠更有效地減小 Spike 的波形畸變。
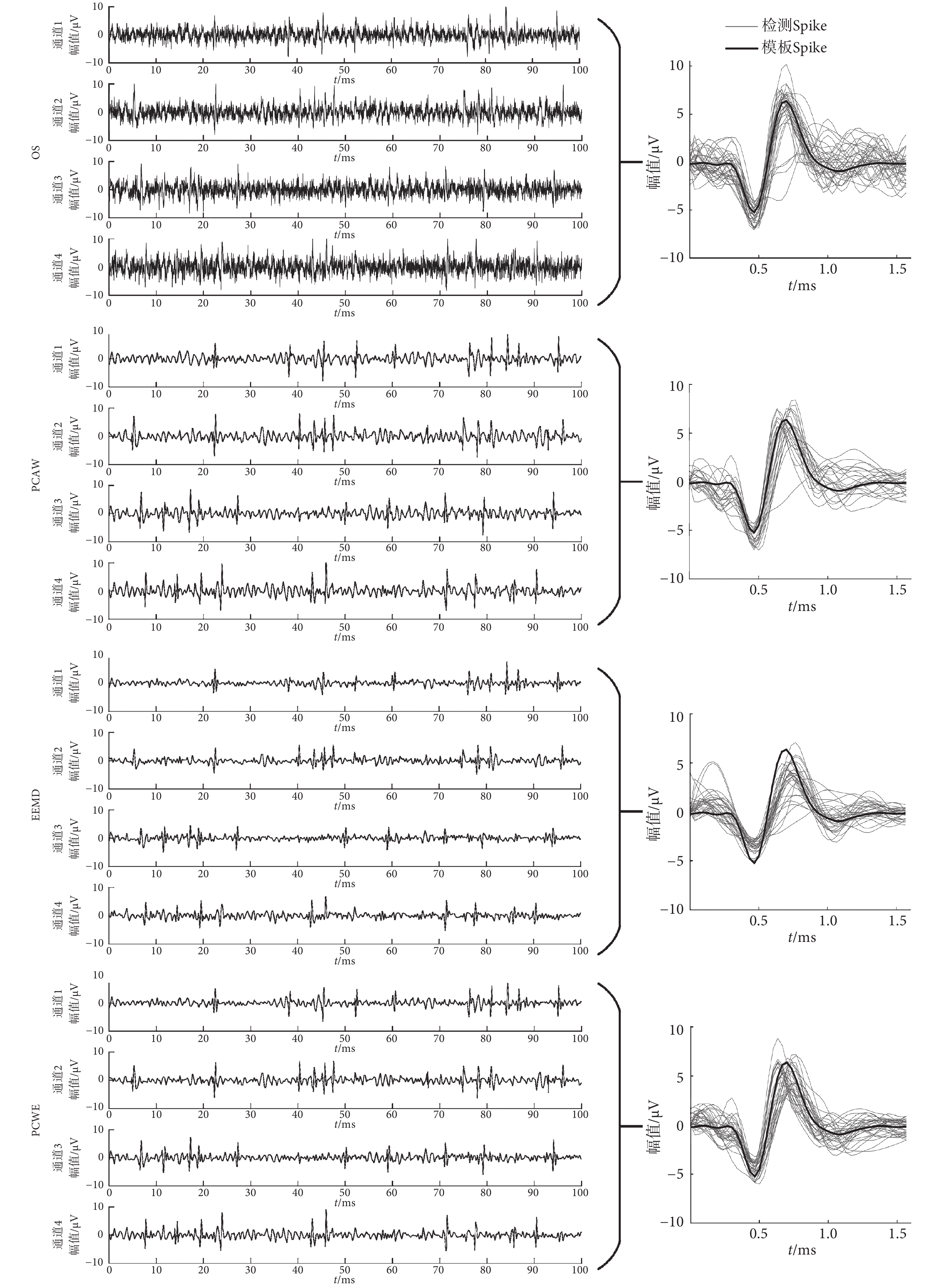圖3
綜合噪聲仿真數據去噪結果及其 Spike 信號
Figure3.
Denoising results of simulation data with comprehensive noise and Spike signal
此外，如圖 4 所示，進一步定量給出了綜合噪聲仿真信號去噪前后 SNR 與 SD1 的統計結果。該樣本總體服從正態分布，使用 t 檢驗檢測各組數據兩兩之間的差異。由圖 4 可知，三種方法對 OS 的 SNR 分別平均提高了 1.84、0.55、2.67 dB，SD1 分別平均減少了 0.26、0.34、0.4 μV，結果具有統計學意義（P < 0.01），顯然 PCWE 能夠更有效地提高 OS 的 SNR，并更大程度地改善了 Spike 波形畸變，表明 PCWE 對綜合噪聲的去噪效果明顯優于 PCAW 與 EEMD。
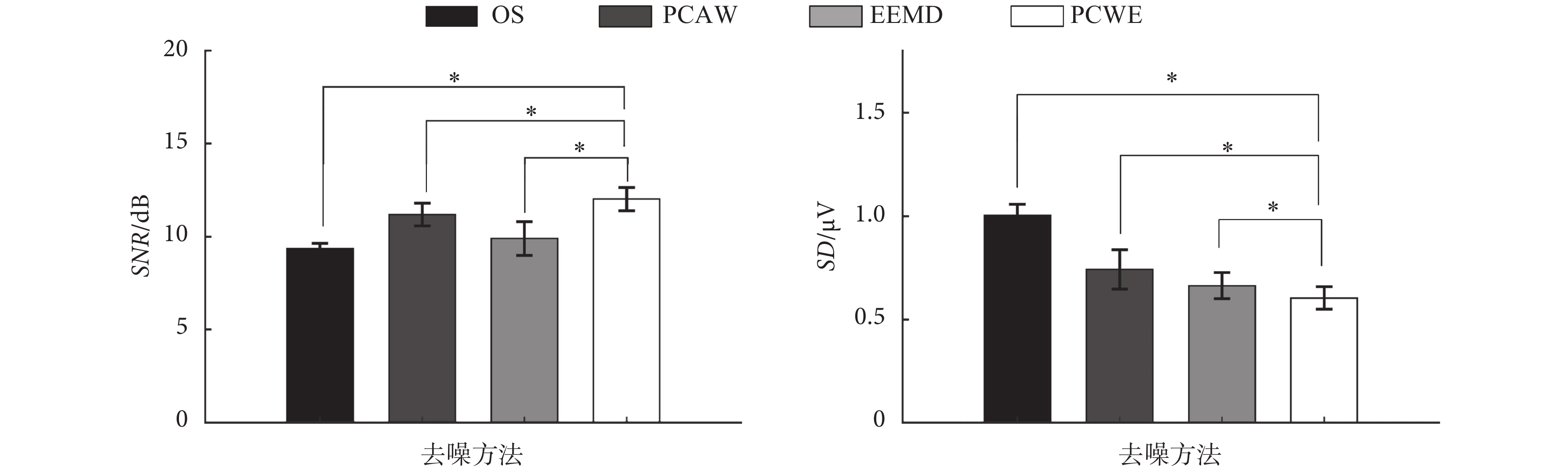圖4
綜合噪聲仿真數據去噪前后的 SNR 與 SD1 值 N = 30，*P < 0.01
Figure4.
Change of SNR and SD1 of simulation data with comprehensive noise after denoising N = 30，*P < 0.01
如表 1 所示，給出了經 3 種方法去噪后，Spike 信號的精確率與漏檢率。結果表明，PCWE 把精確率提高到 96.5%，漏檢率降低到 22.9%，有效提高了 Spike 信號的準確性，并減少了漏檢現象。
表1
3 種方法的 Spike 精確率與漏檢率
Table1.
Spike accuracy rate and missed-alarm rate of three methods
綜合以上分析，從信號的波形角度及 Spike 的準確性角度，PCWE 都表現出比 PCAW、EEMD 更優的去噪性能。
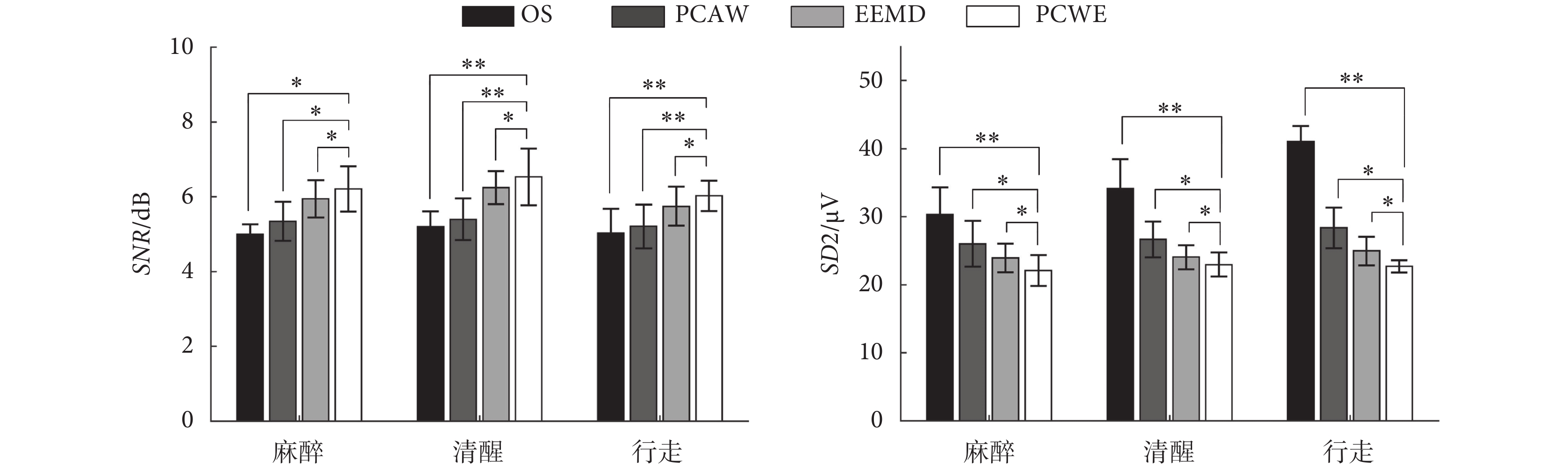
2.2 實測數據結果
實測數據的去噪結果如圖 5 所示，圖中展示了鴿子在麻醉、清醒、行走 3 種狀態下，其中一個通道在 100 ms 內的波形變化，并對去噪前后的信號及 Spike 發放標記圖進行了比較。從波形圖中可以看出，從麻醉、清醒到行走，信號中的噪聲成分越來越多，經 3 種方法去噪后，其中 PCWE 抑制噪聲的效果相對更為明顯，說明 PCWE 更能有效地去除多種噪聲成分。在實測數據中，由于無法得知 Spike 的真實個數，因此無法直接準確地計算出 Spike 的精確率和漏檢率，圖 5 中 Spike 發放標記圖提供了另一種間接評估 Spike 精確率與漏檢率的方法。如圖 5 所示，展示了不同狀態下其中一個通道 1 s 內的 Spike 發放情況，標記處表示在該時間點檢測到一個 Spike，每一個標記圖右側的數值表示 1 s 內檢測到的 Spike 個數。由圖 5 可知，經 PCWE 去噪后檢測出的 Spike 個數最多，且隨著鴿子的狀態從麻醉、清醒到行走，其大腦活躍程度逐步提高，Spike 個數也隨之逐漸增多，這與作為鳥類高級認知區的 NCL 中，Spike 的發放隨認知增強而增多的趨勢是相一致的[14]，而從 OS 中直接檢測出的 Spike 個數則明顯不符合這個趨勢，說明 OS 中的大量噪聲容易導致錯誤的檢測結果。該結果可間接評估，經 PCWE 去噪后檢測出的 Spike 信號具有一定的準確性，且漏檢現象明顯更少。
圖5
實測數據去噪結果比較
Figure5.
Comparison of denoising results of measured data
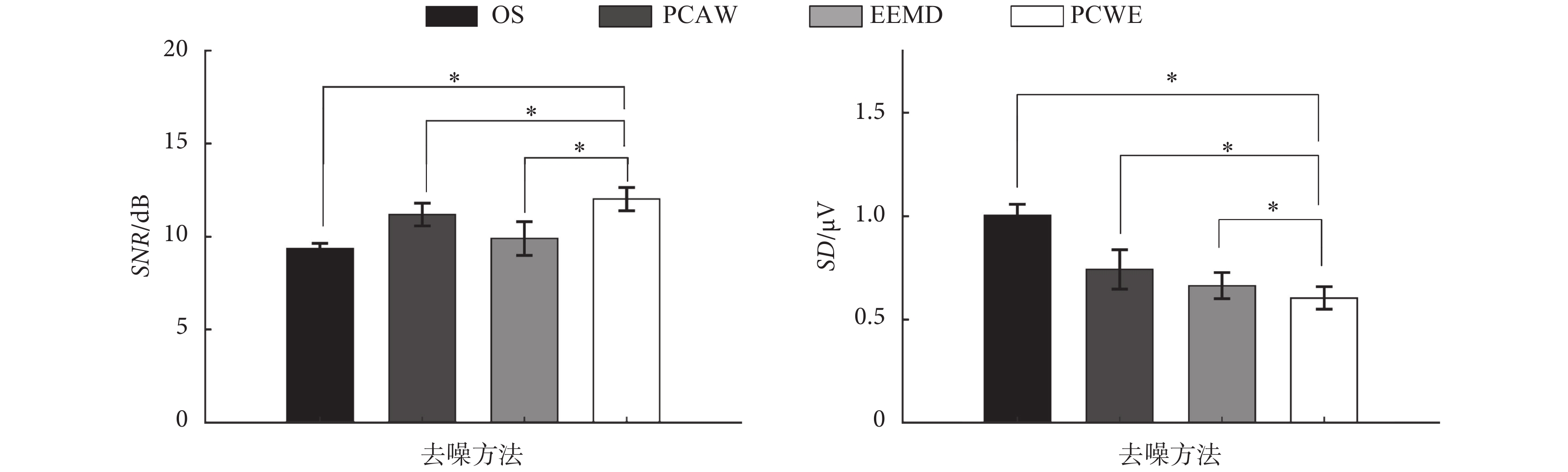
為了進一步說明 PCWE 的有效性，如圖 6 所示，對實測數據去噪前后的 SNR 和 SD2 的統計結果進行定量分析。該樣本總體服從正態分布，使用 t 檢驗檢測各組數據兩兩之間的差異。由圖可見，與 PCAW、EEMD 相比，信號經 PCWE 去噪后能夠更有效地提高 SNR 值和減小 Spike 波形畸變：對于 SNR 值，3 種狀態下分別平均提高了 1.20、1.33、1.00 dB；對于 SD2，3 種狀態下分別平均減小了 8.23、11.18、18.33 μV，結果均具有統計學意義（P < 0.05）。該結果定量表明，PCWE 比 PCAW、EEMD 都更具優越性。
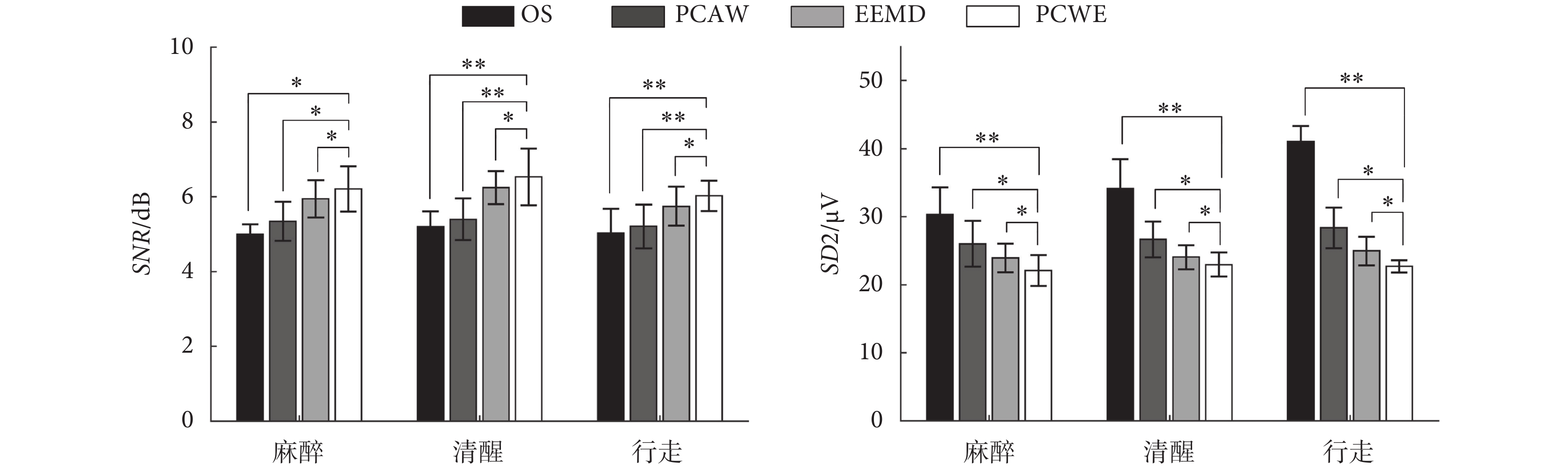圖6
實測數據去噪前后的 SNR 與 SD2 值 N = 10，*P < 0.05，**P < 0.01
Figure6.
Change of SNR and SD2 of measured data after denoising N = 10，*P < 0.05，**P < 0.01
3 討論
本文提出的 PCWE 聯合去噪方法能夠對神經信號進行有效的去噪處理，并增加 Spike 信號的準確率。該方法具有以下特點：
（1）PCWE 方法有效結合了 PCAW 與 EEMD 方法的優點。單一噪聲仿真數據的實驗結果（如圖 2 所示）表明，PCAW 與 EEMD 分別對 3 種噪聲成分有不同的針對性去噪效果，而在綜合噪聲仿真數據實驗結果（如圖 3、圖 4 所示）與實測數據實驗結果（如圖 5、圖 6 所示）中同時表明，PCWE 有效結合了噪聲的統計特征、小波特征與整體波形特征進行去噪，在一定程度上彌補了 PCAW 對有色噪聲去噪效果不明顯、EEMD 的針對性不強的缺點[4-5]，能夠更有效地對 3 種常見噪聲成分進行針對性去除。
（2）PCWE 能夠顯著減少 Spike 的漏檢現象，并提高檢出精確率。PCWE 方法首先采用 PCAW 方法對信號進行處理，可以優先并有效地先去除信號中的大量獨立白噪聲和相關噪聲成分，此時再采用 EEMD 來根據 Spike 的整體波形特征進行分解，能夠更準確地去除有色噪聲成分，使得信號的整體 SD 減小，從而在使用閾值法對信號進行檢測時，能夠顯著降低 Spike 的漏檢率。在綜合噪聲仿真數據結果（如表 1 所示）中，PCAW 與 EEMD 去噪方法在單獨使用時都存在嚴重的漏檢現象，其 Spike 的漏檢率最高甚至達到 41.8%；而 PCWE 方法則把漏檢率降低到 22.9%，顯著改善了漏檢現象。
（3）PCWE 遵循的是從易到難的去噪順序，先把統計特征最明顯的相關噪聲去除，再把小波特征相對明顯的獨立白噪聲去除，此時 Spike 的畸變程度已大大降低，最后再根據整體的波形特征去除有色噪聲，即能夠更有效地對噪聲進行針對性去除。
（4）PCWE 具有普適性，適用于多種噪聲混合的神經信號。但仿真數據和實測數據的處理結果表明，PCWE 去噪前后，實測數據 SNR 值的提升低于仿真數據，這可能是實測數據本身的 SNR 值相對更低，且信號更不平穩所造成。PCWE 在對 SNR 較差的原始信號進行去噪時，去噪效果有所下降，因此后期還需進一步加強該算法的魯棒性。另外，PCWE 在去噪過程中，對信號幅值有一定的削弱作用，導致使用閾值法進行檢測時仍存在一定程度的漏檢現象，在后期進行進一步研究時，可以通過調整閾值法的設置方式來改善這一問題。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
鋒電位（Spike）是神經元細胞動作電位的表征[1]，Spike 的發放標志著大腦對感覺與運動事件的信息編碼，因此可靠地識別出同一電極記錄到的 Spike 信號在神經科學研究中具有重要價值[2]。Spike 信號一般通過多通道微電極陣列進行采集，但其十分微弱，幅值一般只有 100～200 μV，極易被環境中各種不同的噪聲污染，導致產生嚴重畸變甚至被淹沒，這對 Spike 信號的檢測與后期的分析處理帶來極大困難。因此，為了提高 Spike 信號的可靠性，需要對其進行有效的去噪，以增加 Spike 信號的信噪比（signal-to-noise ratio，SNR）并減小波形畸變，這對后續神經信號的編碼、解碼和相關的大腦工作機制等研究具有重要意義。
針對 Spike 信號的經典去噪方法有很多，但都具有一定的局限性。常用的主成分分析（principal component analysis，PCA）去噪基于多通道間噪聲的統計特征進行去噪，它通過計算通道間的主成分作為相關噪聲去除，但對相關噪聲以外的其他噪聲成分去噪效果不佳[3]。在此基礎上，吳丹等[4]結合了小波閾值去噪，提出 PCA-小波聯合去噪（principal component analysis-wavelet，PCAW）方法，利用噪聲的小波特征進一步去除信號中的獨立白噪聲，有效提高了 Spike 的 SNR，但其對有色噪聲的去除十分有限。此外，整體平均經驗模態分解（ensemble empirical mode decomposition，EEMD）去噪方法則直接基于數據波形本身，在時域上進行處理[5]，因此具有普適性，對大部分噪聲成分都有一定程度的去噪效果，但其針對性相對較弱，與具有針對性的去噪方法相比，該方法對特定噪聲成分的去噪效果略為遜色。
PCA 與小波閾值法是神經信號處理中十分經典和傳統的去噪方法，而 EEMD 則是自適應濾波的代表，因此在信號處理中都具有一定的代表性，近年來許多新的 Spike 去噪方法都是在此基礎上進行改進或創新的。如 Chen 等[6]提出 EEMD 與典型相關分析（canonical correlation analysis，CCA）相結合的神經信號肌肉偽影去噪方法，該方法可以較好地利用通道信息去除肌肉運動帶來的噪聲，但在噪聲成分中還有可能包含著有用信息。Bhatnagar 等[7]提出 PCA 與獨立成分分析（independent component analysis，ICA）相結合的去噪方法，實驗結果表明該方法比單獨使用 ICA 或小波閾值法更能有效地提高 SNR，但該方法存在收斂性問題，可能存在數據丟失。Li 等[8]針對高壩地震信號的非平穩性和低 SNR 的特點，提出一種基于 EEMD 與奇異譜分析（singular spectrum analysis，SSA）相結合的自適應去噪方法，其去噪結果表明該方法優于 EEMD 和 EEMD-小波閾值去噪算法，然而該算法在神經信號中的應用效果還有待進一步驗證。Bajaj 等[9]則提出了一種基于小波的參數整定偽影去噪算法，該算法以小波包分解為基礎，能夠有效地去除 Spike 中人體運動帶來的噪聲，但在每次進行去噪前都需要單獨進行參數調優。
這些 Spike 去噪方法多是僅針對于某種特定的噪聲成分進行去除，但在 Spike 檢測過程中，通常會同時存在獨立白噪聲、相關噪聲和有色噪聲等多種噪聲成分[3]，為了對以上噪聲進行全面地針對性去噪，本文根據各噪聲特性，結合 PCA、小波分析和自適應時頻分析，提出基于 PCAW 與 EEMD 聯合的去噪新方法（PCWE），先利用 PCAW 針對性地去除通道間的相關噪聲和獨立白噪聲，再利用 EEMD 的普適性去除各通道中的有色噪聲。下面將對仿真數據與從鴿子弓狀皮質尾外側區（nidopallium caudolaterale，NCL）采集到的實測數據進行去噪實驗，對 PCWE 與 PCAW、EEMD 進行性能評估與去噪效果比較，以驗證 PCWE 去噪方法的有效性。最終，期望本文提出的 PCWE 可以為 Spike 信號提供一種可靠的去噪新方法，將有助于更好地開展有效的神經信號編解碼研究。
1 方法和材料
1.1 PCWE 去噪方法原理
PCWE 實際上是把 PCAW 與 EEMD 聯合使用，通過 PCA、小波分析和自適應時頻分析把噪聲的統計特征、小波特征與整體波形特征相結合，使不同的噪聲類型能夠在不同的特征描述下更好地被識別出來，從而實現對各類噪聲的針對性去噪。PCWE 的去噪流程如下：
（1）根據相關噪聲在通道間存在相關性的統計特征，對多通道神經信號利用 PCA 提取通道間的主成分作為相關噪聲成分[3]。假設采樣點數均為 L 的 N 通道記錄信號表示為 S（t，ch）= ［s（t，1），s（t，2），，s（t，N）］，其中 z 通道信號為 s（t，z）= ［s（1，z），s（2，z），，s（L，z）］。選擇 z 通道 s（t，z）為目標去噪通道，先計算剩余通道 S（t，chelse）的主成分。對剩余通道信號的協方差 Celse 進行特征根分解，如式（1）所示：
|
其中，Λelse 為特征根，Uelse 為特征向量，那么 S（t，chelse）的主成分則如式（2）所示：
|
其中，PCelse（n）的第一個主成分即為相關噪聲。把目標去噪通道 s（t，z）投影到 n 個主成分的空間中，并歸一化計算出每個主成分的投影權重系數[3]，如式（3）所示：
|
其中，an（z）即為 z 通道上的 n 個投影系數。最后用原信號減去投影后的第一個主成分即能去除通道間的相關噪聲，如式（4）所示：
| '/> |
（2）對每個通道進行小波閾值去噪。信號經離散小波變換后，在每一層小波系數中設置合適閾值，把低于閾值的小波系數置零，即能有效去除通道中的獨立白噪聲[10]。
假設某一通道信號進行離散小波變換后的小波系數記為 xj，k，j 表示原信號被分解為 j 個尺度，k 表示在對應分解尺度下的第 k 個小波系數。那么對 xj，k 設定的閾值如式（5）所示：
|
其中，σj = MADj/0.674 5 表示每個尺度下噪聲的標準差（standard deviation，SD），MADj 為 j 尺度下小波系數絕對偏差的中位數，0.674 5 為高斯分布校準因子[11]；N（xj）為 j 尺度下小波系數的個數；Tj 即為 j 尺度下小波系數的閾值。
然后使用硬閾值函數去除通道中低于閾值的獨立白噪聲成分，如式（6）所示：
|
其中， 表示通過閾值去噪后的小波系數。把經過小波閾值去噪后的信號記為 s（t，z）″。
（3）對各通道進行 EEMD 去噪。EEMD 分解不僅能夠避免 Spike 這種間歇性成分帶來的模態混疊現象，還能根據信號整體波形中不同的波動和趨勢特征分解到各層本質模態函數（intrinsic modal function，IMF）中。因此信號經 EEMD 分解步驟處理之后[12]，可以產生 k 層 IMF，如式（7）所示：
| '/> |
其中，hi 表示第 i 層 IMF；rk（t）表示剩余值。
在去除相關噪聲與獨立白噪聲后，信號中的 Spike 成分幅值較大，而有色噪聲幅值較小，且能量主要集中在前幾層 IMF 中，因此選擇前 j 層 IMF 通過式（5）～（6）進行小波閾值去噪，即能把有色噪聲去除，最終去噪結果可表示為如式（8）所示：
|
其中， 表示小波閾值去噪后的前 j 層 IMF， 表示剩下的 IMF，rk（t）表示剩余值，s（t，z）c 即為 z 通道最終的去噪信號。本文統一選擇前 3 層 IMF 進行小波閾值去噪，即能去除通道中的有色噪聲。
（4）對各通道信號進行重建，完成整體去噪。
1.2 閾值檢測法
對信號進行去噪后，使用閾值法檢測信號中的 Spike 信號。在檢測 Spike 信號時，多使用負閾值，閾值設定如式（9）所示：
|
其中，b 為閾值系數，L 為 z 通道信號的總采樣點數，s（i，z）表示 z 通道信號中第 i 個點的幅值， 表示 z 通道信號幅值的均值。
1.3 去噪效果評價指標
本文對 PCWE、PCAW 與 EEMD 方法的去噪效果進行評估比較，從信號波形角度，以 SNR 和 SD 作為評價指標；從準確率角度，則以精確率與漏檢率作為評價指標。
1.3.1 SNR 與 SD
SNR（以符號 SNR 表示）為直接評價指標，表示數據中信號與噪聲含量的比值，SNR 值越大，表示去噪效果越好。若通過閾值法檢測出信號中有 N 個 Spike（符號記為：spk），同時每個 Spike 存在相對應的噪聲成分（符號記為：noise），那么該信號的 SNR 值的計算公式如式（10）所示：
|
其中，N 表示 Spike 總個數，spki 表示第 i 個 Spike，noisei 表示第 i 個 Spike 對應的噪聲成分；max（·）表示取最大值運算，min（·）表示取最小值運算，rms（·）表示均方根運算。在信號采樣率為 30 000 Hz 情況下，一般取每個 Spike 負峰值點前 0.5～2.1 ms 之間的 48 個采樣點作為噪聲部分。
SD（以符號 SD 表示）為間接評價指標，用來衡量 Spike 的畸變程度。理論上微電極陣列中同一個檢測位點對同一個神經元檢測到的 Spike 波形應是相同的[4]，因此 SD 值越小表示去噪效果越好。為區分仿真數據與實測數據的 SD 值差異，把仿真數據的 SD 以符號 SD1 表示；實測數據的 SD 則以符號 SD2 表示。
對于仿真數據，已知模板 Spike 信號（符號記為：SPK），那么 SD1 的計算公式如式（11）所示：
|
其中，N 表示 Spike 的總個數，M 表示每個 Spike 的采樣點數（每個 Spike 的采樣點數相同），spki，j 表示第 i 個 Spike 的第 j 個采樣點，SPKj 則表示模板 Spike 的第 j 個采樣點。
對于實測數據，若只有一類 Spike，則把檢測到的 N 個 Spike 的均值（符號記為：）作為模板信號，那么 SD2 的計算公式如式（12）所示：
|
其中，N、M 和 spki，j 的含義與式（11）相同， 表示 的第 j 個采樣點。若同一通道上存在多個不同神經元的 Spike 信號，需先對檢測出的 Spike 進行分類，然后對不同類型的 Spike 利用式（12）分別計算其 SD2，最后取其均值作為整體 SD2。
1.3.2 精確率與漏檢率
精確率與漏檢率用于評價信號經不同方法去噪后，檢測出的 Spike 信號的準確性，以及漏檢現象的嚴重性。
假設仿真數據中共設置了 N 個真實 Spike，對信號進行去噪后共檢出 n 個 Spike，其中有 n1 個為真，那么精確率與漏檢率分別如式（13）～（14）所示：
|
|
1.4 統計分析
結果中的 SNR 和 SD 均以（）的形式表示。在統計分析中，先對樣本數據進行正態性檢驗，若樣本總體服從正態分布，利用 t 檢驗度量差異是否具有統計學意義；若樣本總體不服從正態分布，則利用秩和檢驗度量差異是否具有統計學意義。顯著水平均設置為 5%，即 P < 0.05 被認為差異具有統計學意義。
1.5 實驗數據
為了驗證 PCWE 去噪方法的有效性，首先采用仿真數據對算法的去噪性能進行測試，然后結合實測數據的去噪結果，對比分析 PCWE、PCAW 和 EEMD 的去噪性能。
1.5.1 仿真數據生成
仿真數據由 4 個通道組成，采樣率為 30 000 Hz，時長為 100 ms，各通道隨機設置 10 個模板 Spike。模板 Spike 由商用神經信號模擬發生器（BlackRock MicroSystem，Inc，UT，USA）中的一類 Spike 經平均計算求得，如圖 1 所示。
圖1
仿真數據示意圖
Figure1.
Schematic diagram of simulation data
（1）單一噪聲仿真數據。往每組仿真數據加入 3 種不同的單一噪聲成分，分別為：① 獨立白噪聲，用于模擬采集系統中的熱噪聲成分；② 相關噪聲，用于模擬外界相同聲源的噪聲成分，如運動噪聲等；③ 頻段為 500～ 1 000 Hz 的有色噪聲，用于模擬與神經信號頻率相關的有源噪聲，如肌電信號等。每種噪聲成分分別設置 3 個噪聲級別，從低到高分別為 ? 1、? 3、? 5 dB。每種噪聲的每一噪聲級別各生成 30 組仿真數據（共 3 × 3 × 30 組）。
（2）綜合噪聲仿真數據。各通道分別加入-3 dB 的綜合噪聲。綜合噪聲同時包括獨立白噪聲、相關噪聲和有色噪聲，共產生 30 組仿真數據。
1.5.2 實測數據采集
本文實驗動物為亞洲原鴿，對成年健康鴿子用濃度為 10% 的水合氯醛進行全身麻醉后，往其 NCL 區植入微電極陣列（4 × 4 排列，共 16 通道），具體手術過程請參考文獻[13]。術后恢復一周后使用 CerebusTM多通道神經信號采集系統（CerebusTM，Blockrock Inc，美國）進行不同狀態下 Spike 信號的采集，采樣率為 30 000 Hz，Spike 濾波范圍為 250～5 000 Hz。分別采集鴿子以下 3 種狀態的神經信號：① 麻醉。用濃度為 10% 的水合氯醛，以 0.3 mL/100 g 的標準對鴿子進行腹腔注射，使鴿子進入麻醉昏迷狀態后采集；② 清醒。結合監控視頻，在鴿子保持正常眨眼與呼吸，無明顯運動時的清醒狀態下進行采集；③ 行走。結合監控視頻，在鴿子清醒且活躍，在熟悉環境中自由行走探索時的狀態下進行采集。三種狀態代表三種不同 SNR 的實測數據，每種狀態分別隨機選取 10 組時長為 1 s 的神經信號進行去噪（共 3 × 10 組）。以上實測數據均由鄭州大學生命科學學院提供。所有實驗動物經鄭州大學生命科學倫理審查委員會審查，符合動物管理使用委員會的各項規定。
2 結果
2.1 仿真數據結果
2.1.1 單一噪聲仿真數據結果
如圖 2 所示，給出了單一噪聲仿真數據在噪聲等級為-3 dB 情況下，PCAW、EEMD 去噪前后的 SNR 與 SD1 統計直方圖，其中第一列為去噪前的原始信號（original signal，OS）。該樣本總體不服從正態分布，使用秩和檢驗檢測各組數據兩兩之間的差異。
圖2
單一噪聲仿真數據去噪前后的 SNR 與 SD1 值 N = 30，*P < 0.01
Figure2.
Change of SNR and SD1 of simulation data with single noise after denoising N = 30，*P < 0.01
由圖 2 可知，對于獨立白噪聲與相關噪聲，經 PCAW 去噪后有效提高了 SNR 并減小 SD1，差異具有統計學意義（P < 0.01）。而對于有色噪聲，只有 EEMD 能夠提高 SNR，且 SD1 增加最少，即帶來的波形畸變最小，且差異具有統計學意義（P < 0.01）。這說明 PCAW 能夠針對性地去除獨立白噪聲與相關噪聲，而 EEMD 則對于有色噪聲的去除更有優勢。在-1 dB 與-5 dB 情況下具有相同的統計結果。顯然，兩者的去噪性能是優勢互補的。
2.1.2 綜合噪聲仿真數據結果
如圖 3 所示，給出了綜合噪聲仿真數據的去噪結果及對應的 Spike 信號。圖中 OS 經 PCAW 去噪后，顯然還存在部分噪聲，但基本保持了 Spike 的幅值水平；EEMD 雖能去除大量噪聲，但對 Spike 信號也存在一定削弱作用，容易導致漏檢現象；PCWE 則兼具兩者優點，既去除了大量噪聲，又能更大程度地保持 Spike 的幅值水平。在檢測 Spike 與模板 Spike 的比較中，顯然經 PCWE 去噪后的 Spike 波形與模板波形重合度最高，即 PCWE 能夠更有效地減小 Spike 的波形畸變。
圖3
綜合噪聲仿真數據去噪結果及其 Spike 信號
Figure3.
Denoising results of simulation data with comprehensive noise and Spike signal
此外，如圖 4 所示，進一步定量給出了綜合噪聲仿真信號去噪前后 SNR 與 SD1 的統計結果。該樣本總體服從正態分布，使用 t 檢驗檢測各組數據兩兩之間的差異。由圖 4 可知，三種方法對 OS 的 SNR 分別平均提高了 1.84、0.55、2.67 dB，SD1 分別平均減少了 0.26、0.34、0.4 μV，結果具有統計學意義（P < 0.01），顯然 PCWE 能夠更有效地提高 OS 的 SNR，并更大程度地改善了 Spike 波形畸變，表明 PCWE 對綜合噪聲的去噪效果明顯優于 PCAW 與 EEMD。
圖4
綜合噪聲仿真數據去噪前后的 SNR 與 SD1 值 N = 30，*P < 0.01
Figure4.
Change of SNR and SD1 of simulation data with comprehensive noise after denoising N = 30，*P < 0.01
如表 1 所示，給出了經 3 種方法去噪后，Spike 信號的精確率與漏檢率。結果表明，PCWE 把精確率提高到 96.5%，漏檢率降低到 22.9%，有效提高了 Spike 信號的準確性，并減少了漏檢現象。
表1
3 種方法的 Spike 精確率與漏檢率
Table1.
Spike accuracy rate and missed-alarm rate of three methods
綜合以上分析，從信號的波形角度及 Spike 的準確性角度，PCWE 都表現出比 PCAW、EEMD 更優的去噪性能。
2.2 實測數據結果
實測數據的去噪結果如圖 5 所示，圖中展示了鴿子在麻醉、清醒、行走 3 種狀態下，其中一個通道在 100 ms 內的波形變化，并對去噪前后的信號及 Spike 發放標記圖進行了比較。從波形圖中可以看出，從麻醉、清醒到行走，信號中的噪聲成分越來越多，經 3 種方法去噪后，其中 PCWE 抑制噪聲的效果相對更為明顯，說明 PCWE 更能有效地去除多種噪聲成分。在實測數據中，由于無法得知 Spike 的真實個數，因此無法直接準確地計算出 Spike 的精確率和漏檢率，圖 5 中 Spike 發放標記圖提供了另一種間接評估 Spike 精確率與漏檢率的方法。如圖 5 所示，展示了不同狀態下其中一個通道 1 s 內的 Spike 發放情況，標記處表示在該時間點檢測到一個 Spike，每一個標記圖右側的數值表示 1 s 內檢測到的 Spike 個數。由圖 5 可知，經 PCWE 去噪后檢測出的 Spike 個數最多，且隨著鴿子的狀態從麻醉、清醒到行走，其大腦活躍程度逐步提高，Spike 個數也隨之逐漸增多，這與作為鳥類高級認知區的 NCL 中，Spike 的發放隨認知增強而增多的趨勢是相一致的[14]，而從 OS 中直接檢測出的 Spike 個數則明顯不符合這個趨勢，說明 OS 中的大量噪聲容易導致錯誤的檢測結果。該結果可間接評估，經 PCWE 去噪后檢測出的 Spike 信號具有一定的準確性，且漏檢現象明顯更少。
圖5
實測數據去噪結果比較
Figure5.
Comparison of denoising results of measured data
為了進一步說明 PCWE 的有效性，如圖 6 所示，對實測數據去噪前后的 SNR 和 SD2 的統計結果進行定量分析。該樣本總體服從正態分布，使用 t 檢驗檢測各組數據兩兩之間的差異。由圖可見，與 PCAW、EEMD 相比，信號經 PCWE 去噪后能夠更有效地提高 SNR 值和減小 Spike 波形畸變：對于 SNR 值，3 種狀態下分別平均提高了 1.20、1.33、1.00 dB；對于 SD2，3 種狀態下分別平均減小了 8.23、11.18、18.33 μV，結果均具有統計學意義（P < 0.05）。該結果定量表明，PCWE 比 PCAW、EEMD 都更具優越性。
圖6
實測數據去噪前后的 SNR 與 SD2 值 N = 10，*P < 0.05，**P < 0.01
Figure6.
Change of SNR and SD2 of measured data after denoising N = 10，*P < 0.05，**P < 0.01
3 討論
本文提出的 PCWE 聯合去噪方法能夠對神經信號進行有效的去噪處理，并增加 Spike 信號的準確率。該方法具有以下特點：
（1）PCWE 方法有效結合了 PCAW 與 EEMD 方法的優點。單一噪聲仿真數據的實驗結果（如圖 2 所示）表明，PCAW 與 EEMD 分別對 3 種噪聲成分有不同的針對性去噪效果，而在綜合噪聲仿真數據實驗結果（如圖 3、圖 4 所示）與實測數據實驗結果（如圖 5、圖 6 所示）中同時表明，PCWE 有效結合了噪聲的統計特征、小波特征與整體波形特征進行去噪，在一定程度上彌補了 PCAW 對有色噪聲去噪效果不明顯、EEMD 的針對性不強的缺點[4-5]，能夠更有效地對 3 種常見噪聲成分進行針對性去除。
（2）PCWE 能夠顯著減少 Spike 的漏檢現象，并提高檢出精確率。PCWE 方法首先采用 PCAW 方法對信號進行處理，可以優先并有效地先去除信號中的大量獨立白噪聲和相關噪聲成分，此時再采用 EEMD 來根據 Spike 的整體波形特征進行分解，能夠更準確地去除有色噪聲成分，使得信號的整體 SD 減小，從而在使用閾值法對信號進行檢測時，能夠顯著降低 Spike 的漏檢率。在綜合噪聲仿真數據結果（如表 1 所示）中，PCAW 與 EEMD 去噪方法在單獨使用時都存在嚴重的漏檢現象，其 Spike 的漏檢率最高甚至達到 41.8%；而 PCWE 方法則把漏檢率降低到 22.9%，顯著改善了漏檢現象。
（3）PCWE 遵循的是從易到難的去噪順序，先把統計特征最明顯的相關噪聲去除，再把小波特征相對明顯的獨立白噪聲去除，此時 Spike 的畸變程度已大大降低，最后再根據整體的波形特征去除有色噪聲，即能夠更有效地對噪聲進行針對性去除。
（4）PCWE 具有普適性，適用于多種噪聲混合的神經信號。但仿真數據和實測數據的處理結果表明，PCWE 去噪前后，實測數據 SNR 值的提升低于仿真數據，這可能是實測數據本身的 SNR 值相對更低，且信號更不平穩所造成。PCWE 在對 SNR 較差的原始信號進行去噪時，去噪效果有所下降，因此后期還需進一步加強該算法的魯棒性。另外，PCWE 在去噪過程中，對信號幅值有一定的削弱作用，導致使用閾值法進行檢測時仍存在一定程度的漏檢現象，在后期進行進一步研究時，可以通過調整閾值法的設置方式來改善這一問題。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
