研究顆粒物在人體肺腺泡區的沉積規律對了解肺部疾病致病機制、促進肺部疾病的預防和治療都有重要意義。現行研究大多關注顆粒物在人體肺腺泡區的最終沉積率，而對其沉積動態過程鮮有涉及。本文建立了 G3～G7 共五個多肺泡模型，引入顆粒物沉積速度評價參數 1/4 沉積時間，通過數值模擬研究了模型級數和結構、顆粒物粒徑、呼吸模式等因素對 0.1～5 μm 粒徑范圍內顆粒物沉積規律的影響，歸納總結了不同粒徑顆粒物的沉積特點，為進一步了解人體肺腺泡區顆粒物的運動規律提供了新視角。結果表明：模型級數和結構是影響各粒徑顆粒物沉積的重要因素。0.1 μm 顆粒物沉積受布朗力主導，沉積率高，沉積速度快，沉積曲線呈對數型分布；5 μm 顆粒物沉積受重力主導，沉積率高，沉積較快，沉積曲線呈“S”型分布；0.3～1 μm 顆粒物沉積則受慣性沖擊影響較大，隨著呼吸模式的改變沉積規律變化明顯。本文的研究方法和結果能為進一步探究肺部疾病致病機制和肺部疾病的預防與治療提供理論依據和數據支持。
引用本文： 李鵬輝, 徐新喜, 李蓉, 喬揚. 多因素影響下的人體肺腺泡區吸入顆粒物沉積規律數值模擬研究. 生物醫學工程學雜志, 2020, 37(5): 793-801. doi: 10.7507/1001-5515.201909004 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
人體肺腺泡是指終末細支氣管以下的肺組織，包括呼吸性細支氣管、肺泡管、肺泡囊和肺泡，是呼吸作用的主要區域。細顆粒物的吸入和沉積會影響肺部健康，引發肺部疾病，因此研究細顆粒物在人體肺腺泡區的沉積規律對肺部疾病致病機制的探究以及肺部疾病的預防和治療都有重要意義。
人體肺腺泡區結構復雜、尺寸微小，尚未獲得真實的計算機模型。現行數值模擬研究多采用簡化的計算機模型，主要分為單肺泡模型和多肺泡模型。單肺泡研究僅對單個肺泡建模，計算量較小，著重關注單個肺泡的內部特性。Sznitman 等[1]對處于不同級數的單肺泡進行了數值模擬研究，發現肺泡內流場形態隨著級數增加由循環狀向輻射狀變化。單肺泡研究只能關注單個肺泡內流場形態和顆粒物沉積狀況，無法探究肺腺泡區的整體特性，因此國內外學者紛紛建立多肺泡模型進行進一步研究。目前，多肺泡模型主要分為四類[2]：“柱狀氣管+球狀肺泡”的多肺泡模型、基于十四面體的多肺泡模型、泰森多邊形法構建的多肺泡模型、計算機成像和重建技術構建的多肺泡模型。Ma 等[3]建立了“柱狀氣管+球狀肺泡”的 5 級多肺泡模型，發現呼吸周期、潮氣量和重力等對顆粒物沉積有較大影響。Longest 等[4]建立了 3 個基于十四面體的多肺泡模型，發現屏氣能大幅度增加顆粒物的沉積率。Hofemeier 等[5]采用泰森多邊形法構建了人體 1/8（第 3～8 級）肺腺泡模型，研究了 0.005～5.0 μm 粒徑范圍內不同大小顆粒物的沉積狀況，發現顆粒物沉積率隨粒徑增加呈先下降后上升的趨勢。Sera 等[6]采用微計算機斷層掃描（micro focal computed tomography system，micro-CT）技術構建了大鼠肺腺泡模型，發現 0.8～1.0 μm 粒徑顆粒物多沉積于肺腺泡入口處，而 0.1～0.2 μm 粒徑顆粒物則主要沉積于模型中部和末端。
上述數值模擬研究大多關注顆粒物在人體肺腺泡區局部或整體的最終沉積率，而對其沉積動態過程鮮有涉及，無法進一步了解人體肺腺泡區顆粒物的運動規律。本文建立了五個“柱狀氣管+球狀肺泡”多肺泡模型，通過數值模擬研究了模型級數和結構、顆粒物粒徑、呼吸模式等因素對 0.1～5 μm 粒徑范圍內顆粒物沉積規律的影響，總結了顆粒物沉積率和沉積速度的變化規律，歸納了沉積曲線特征，以期為進一步研究肺部疾病致病機制和相關疾病的預防與治療提供理論依據和數據支持。
1 模型與方法
1.1 人體肺腺泡模型
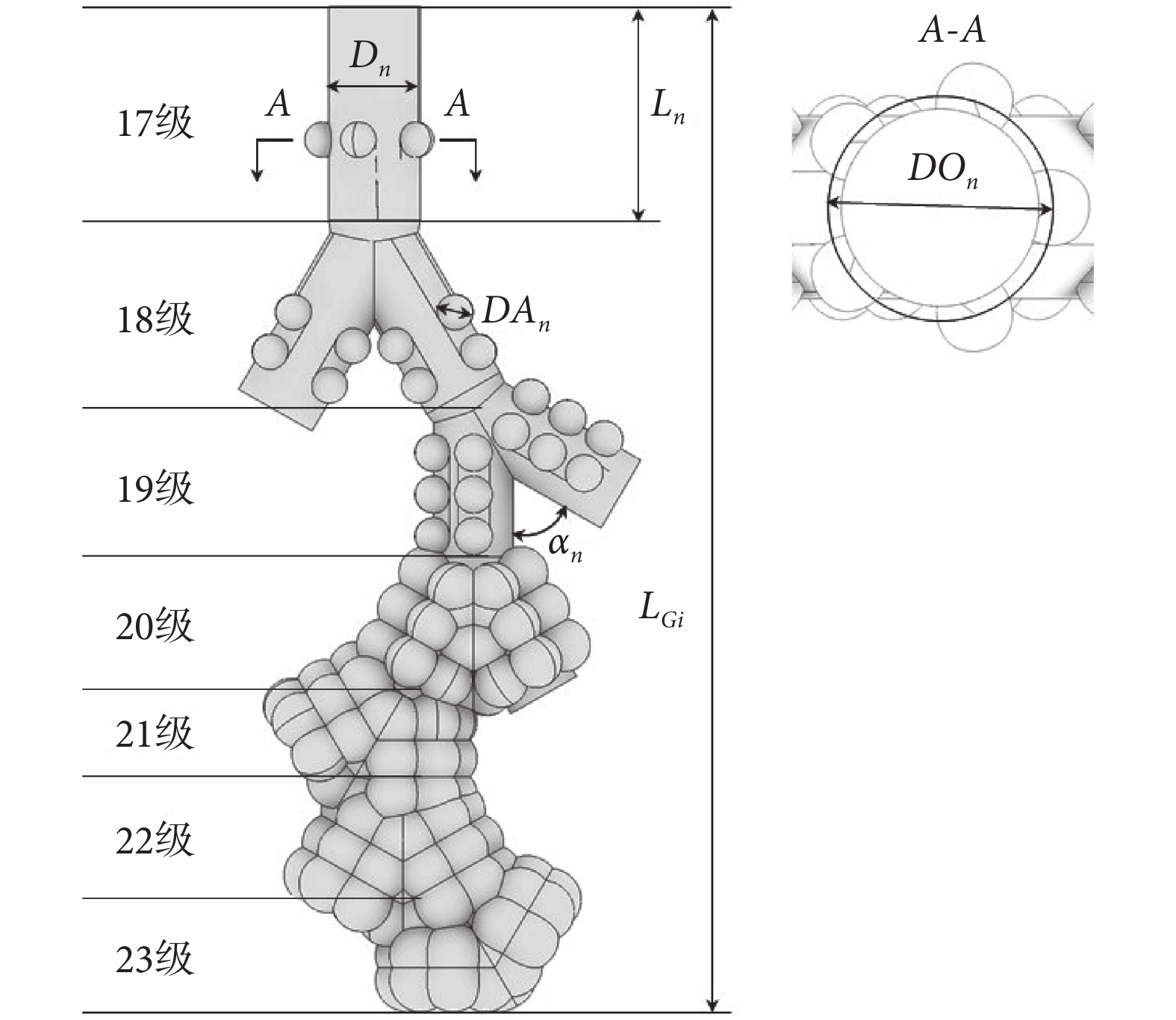
在經典的全肺模型（Weibel A 模型[7]）中，肺部分為 0～23 級。其中，17～23 級部分含有肺泡，是呼吸作用的主要區域，為肺腺泡區。人體肺腺泡區尺寸數據如表 1 所示。
表1
人體肺腺泡區尺寸數據
Table1.
Geometric data of human pulmonary acinus
由表 1 數據可知，肺腺泡區尺寸數據隨級數變化顯著。從 17 級至 23 級，肺腺管長度、管徑數據逐級遞減，最大縮減率分別為 64.54%、24.07%；肺泡直徑和單節肺腺管肺泡數量逐級遞增，最大增長率分別為 79.25%、300%。Sznitman 等[1]研究發現模型尺寸是影響數值模擬結果的重要因素。十四面體多肺泡模型中肺泡形狀、大小一致[8]，僅適用于肺腺泡區局部特性探究或尺寸影響可忽略不計的情況，因而本文采用“柱狀氣管+球狀肺泡”架構，將肺腺管簡化為圓柱狀，肺泡簡化為附著在肺腺管表面的球，建立了如圖 1 所示的多肺泡模型。
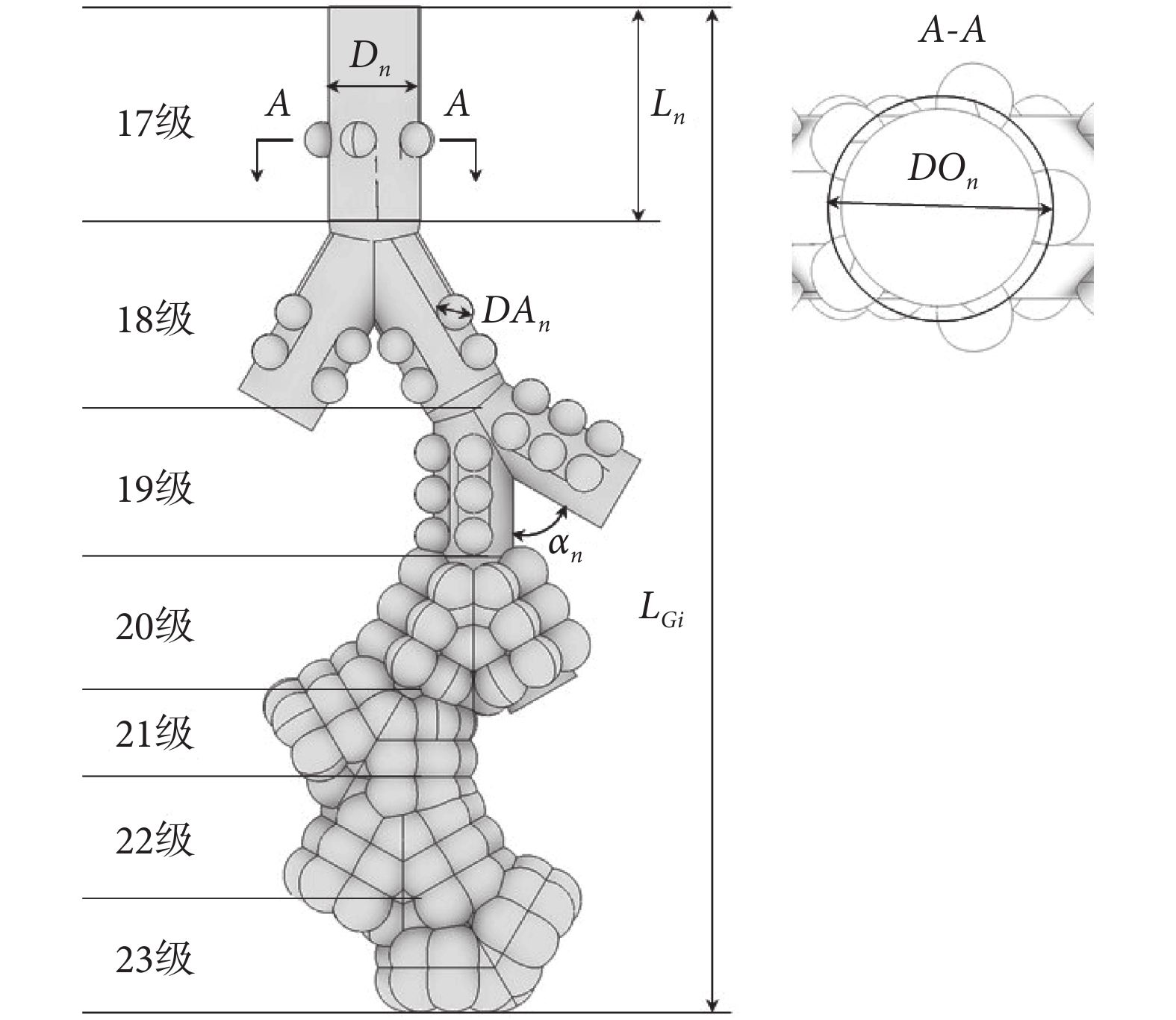圖1
“柱狀氣管+球狀肺泡”架構多肺泡模型
Figure1.
Multi-alveolar model of “columnar trachea + globular alveolar” structure
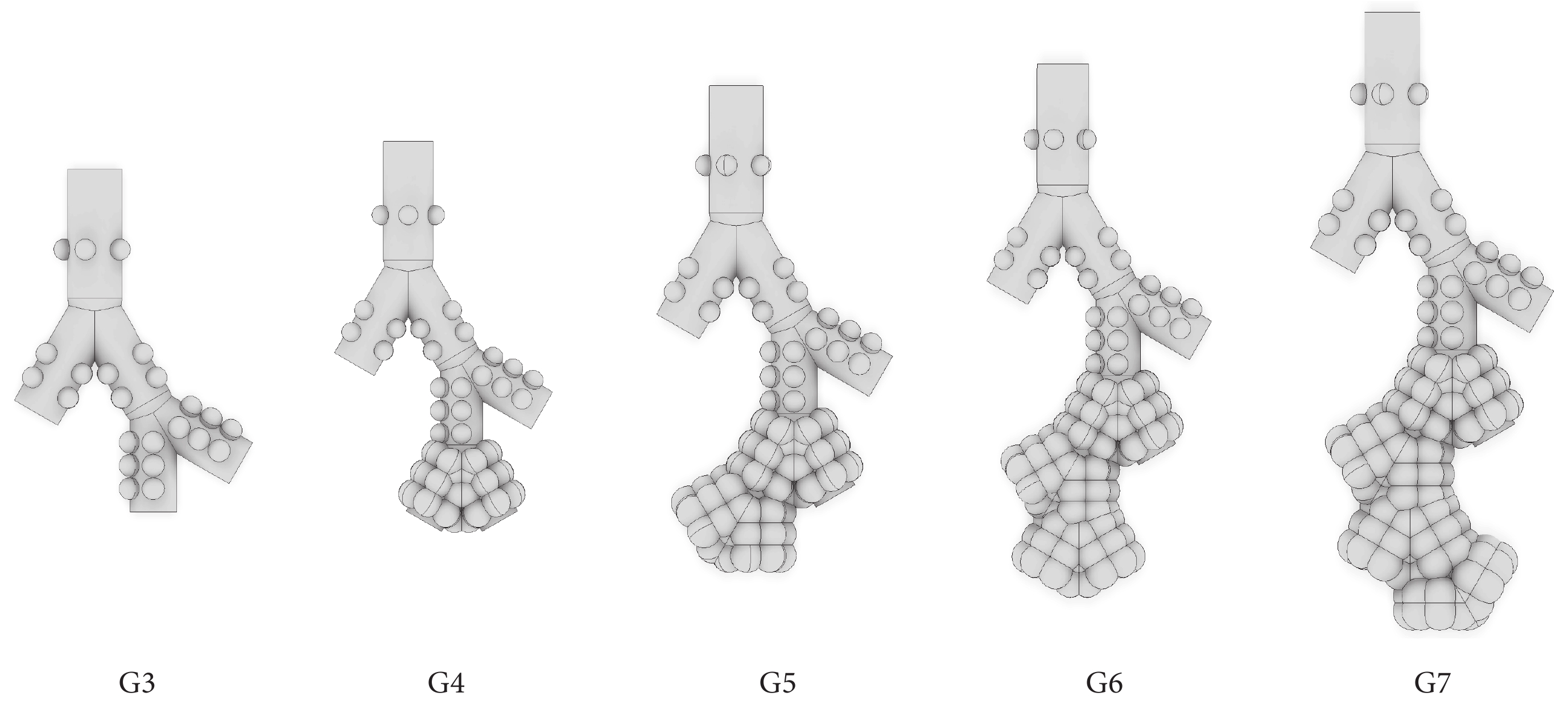
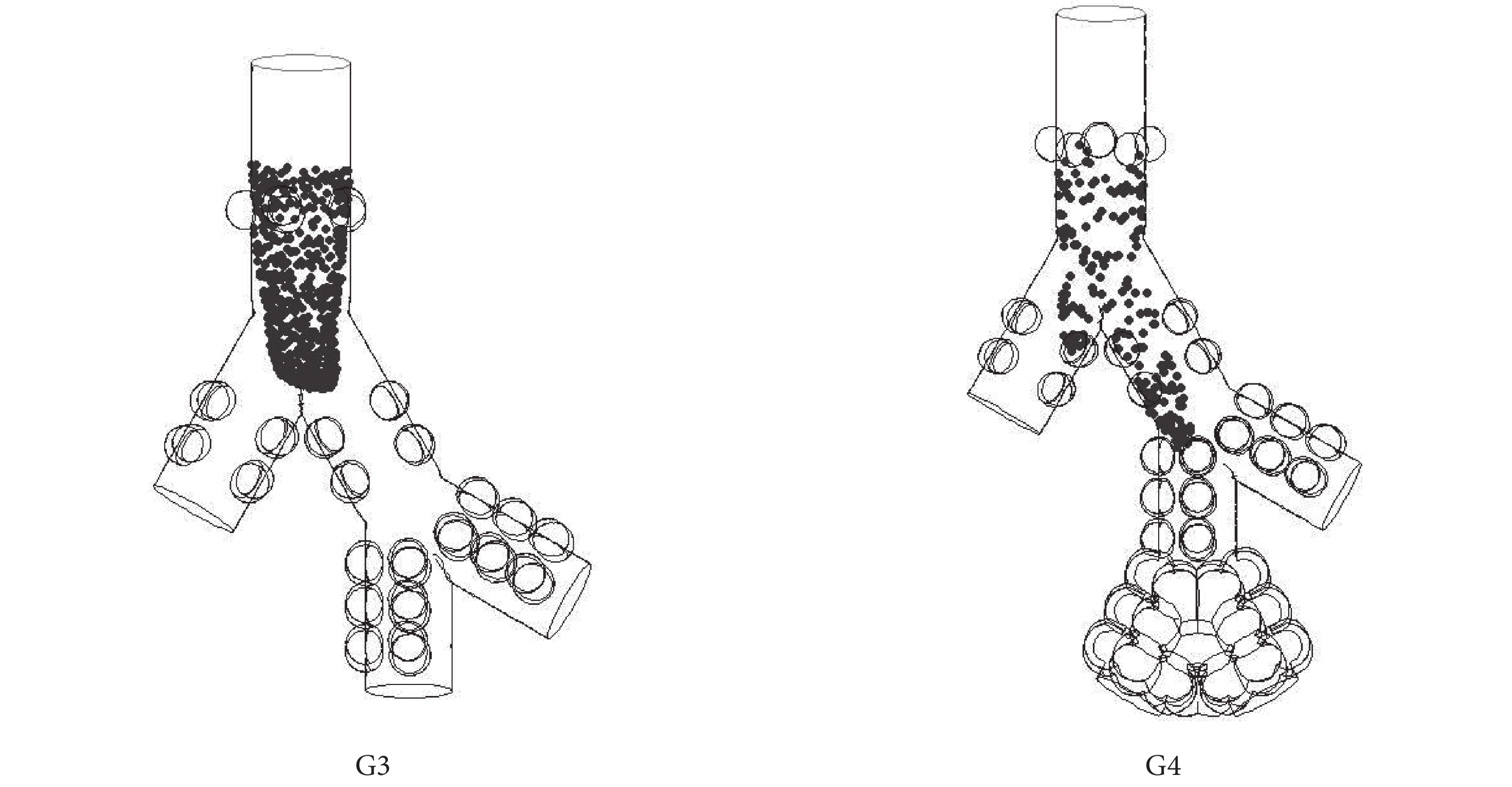
然后，在該模型的基礎上依據表 1 尺寸數據建立了圖 2 所示的 G3（17～19 級）、G4（17～20 級）、G5（17～21 級）、G6（17～22 級）、G7（17～23 級）共 5 個多肺泡模型。各模型所含級數、肺泡數、長度、體積等參數如表 2 所示。
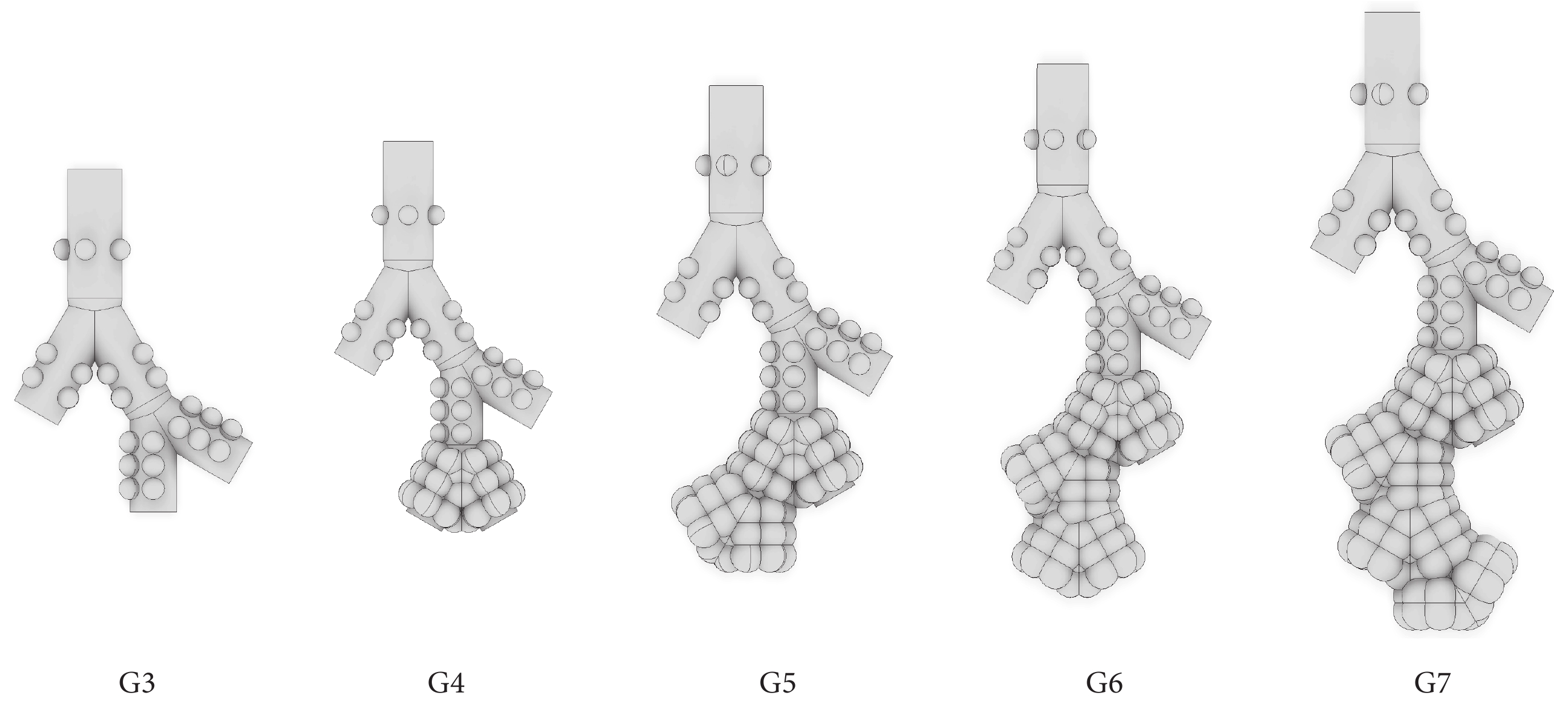圖2
多肺泡模型
Figure2.
Multi-alveolar models
表2
多肺泡模型參數
Table2.
Multi-alveolar models parameters
1.2 數值模擬方法
1.2.1 數值模擬軟件
采用 Inventor 2015 進行多肺泡模型建模，采用 ICEM CFD 15.0 進行模型網格劃分，采用 FLUENT 15.0 進行數值模擬計算。
1.2.2 網格劃分結果
采用非結構網格對 G3～G7 模型進行網格劃分，各模型網格總數及最小網格質量如表 3 所示，最小網格質量均大于 0.3，可以用于數值模擬計算。
表3
G3～G7 模型網格劃分結果
Table3.
Meshing results of G3―G7 models
1.2.3 控制方程
① 流體控制方程：人體肺腺泡區氣流運動為等溫、不可壓縮定常流動。滿足質量、動量守恒方程。
質量守恒方程：
 |
式中，
表示流體密度，
= 1.185 kg/m3，
為流體速度，t為時間。故上式可表示為：
 |
動量守恒方程：
 |
式中，P為流體壓力，
= 1.785e-5 表示運動粘度，
為流體體積力矢量。
② 顆粒物控制方程：本研究中，忽略 Magnus 力、Saffman 力、Basset 力等對顆粒物運動影響較小的力和顆粒物之間的相互影響，僅考慮重力
、布朗力
和流體曳力
的作用效果，因此單個顆粒的運動控制方程為：
 |
 |
 |
 |
其中，其中 
和 
分別為顆粒物的密度和直徑，
為隨機數，
為玻爾茲曼常數，
為空氣熱力學溫度，
為顆粒半徑，
為計算時間間隔。
1.2.4 邊界條件設置
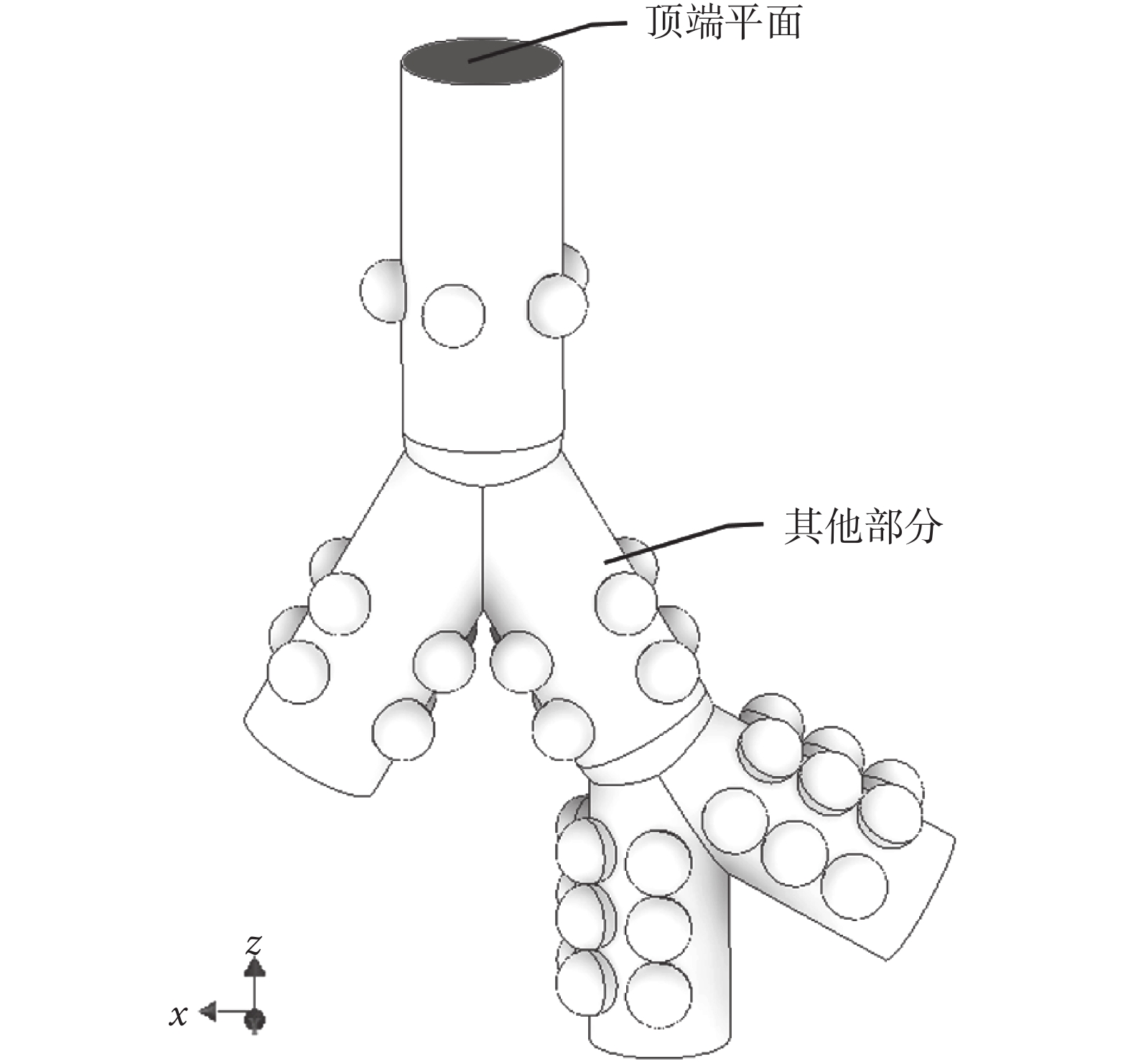
如圖 3 所示，以 G3 模型區域劃分為例，本研究中將模型分為兩部分：頂端平面（黑色陰影部分）和其他部分。其中，頂端平面為氣流和顆粒物入口，采用入口速度函數實現氣流和顆粒物的進入和排出模型，以此模擬呼吸作用下人體肺腺泡區的氣流和顆粒物的運動。其他部分為無滑移壁面，顆粒物在運動過程中接觸壁面會被捕捉，即為沉積。
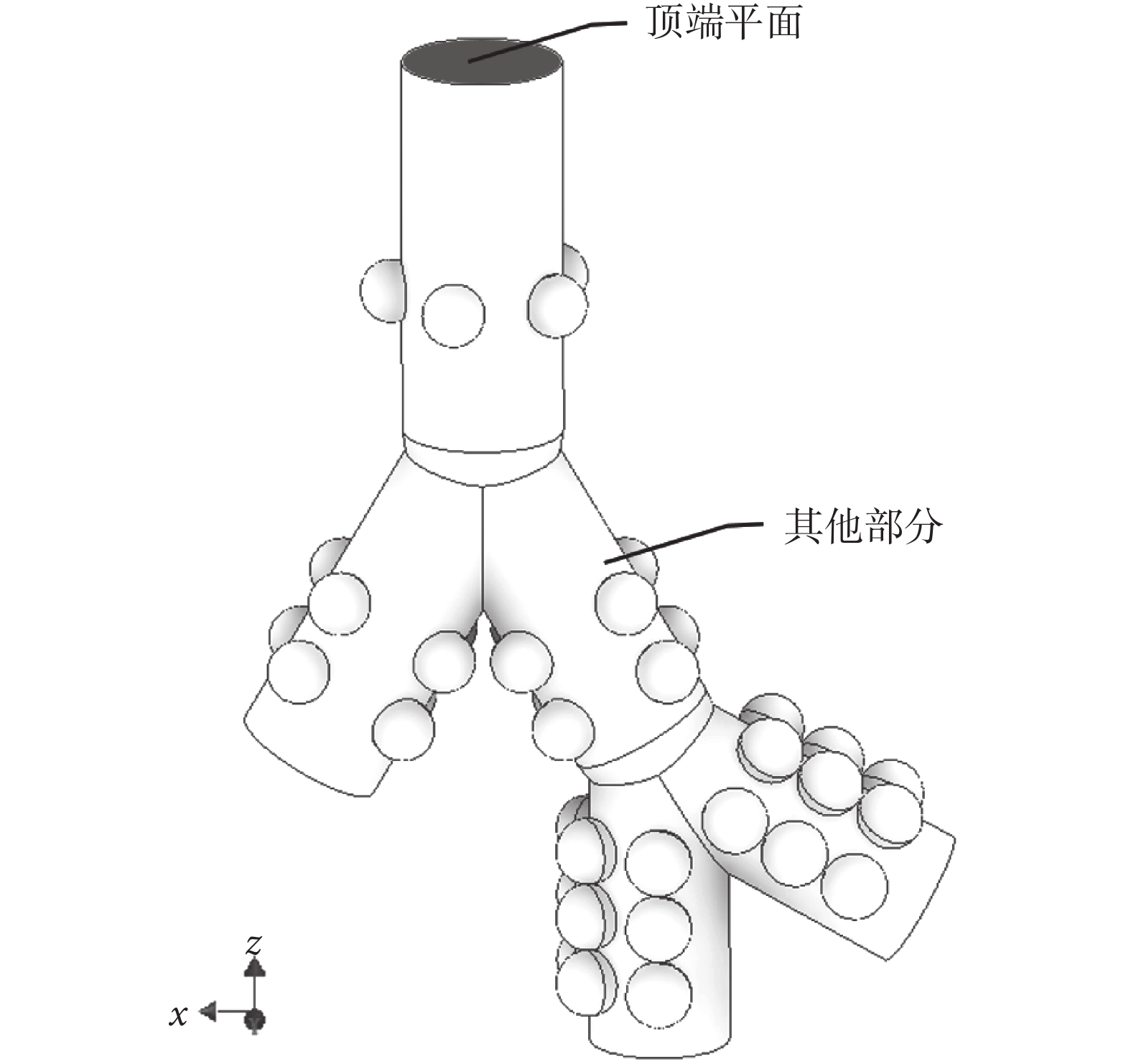圖3
G3 模型區域劃分
Figure3.
Parts of G3 model
1.2.5 入口速度函數
Oakes 等[9]測量了 21 歲健康男性休息狀態下的呼吸流量曲線，近似為正弦曲線，因此本研究中入口速度采用隨時間變化的正弦函數，速度正方向為 ? Z，入口速度 
可表示為:
 |
其中，
為入口氣流最大速度，
為呼吸周期。
則數值模擬一周期模型內氣體最大進入量
為：
 |
積分可得:
 |
其中，
為入口管徑，即 17 級肺腺管管徑。
以上述建立的多肺泡模型代表人體肺腺泡進行數值模擬研究，模型體積
對應功能殘氣量（functional residual capacity，FRC），最大進氣量
對應潮氣量
，則有：
 |
根據 Haefeli-Bleuer 等[10]的測量結果，取人體正常呼吸狀態下功能殘氣量為 3 L，潮氣量為 600 mL，呼吸周期為 4 s。依據式（1）（2）（3）計算可得，正常呼吸狀態下（
= 600 mL，T = 4 s），G3～G7 模型入口氣流最大速度
和入口速度如表 4 所示。
表4
正常呼吸狀態下 G3～G7 模型入口氣流最大速度和入口 速度
Table4.
The maximum velocity and inlet velocity of inlet airflow in G3?G7 models under normal respiratory mode
1.2.6 呼吸模式
當人體處于不同呼吸狀態時，潮氣量和呼吸周期存在明顯差異。由式（1）（2）（3）可知，潮氣量、呼吸周期能直接決定模型入口速度函數，進而影響顆粒物在人體肺腺泡區的沉積規律。從肺腺泡形態結構來說，G7 模型包含級數更多，肺泡數量也更多，更加符合人體實際，因此本研究基于 G7 模型進一步研究呼吸模式對人體肺腺泡區顆粒物運動規律的影響。取呼吸周期為 4 s，潮氣量分別為 300、600、900 mL，代表人體處于淺呼吸、正常呼吸和深呼吸狀態。取潮氣量為 600 mL，呼吸周期分別為 2、4、6 s，代表人體處于急促呼吸、正常呼吸和緩慢呼吸狀態，由式（1）（2）（3）計算可得，不同呼吸模式下 G7 模型入口速度如表 5 所示。
表5
不同呼吸模式下 G7 模型入口速度
Table5.
The velocity of inlet airflow in G7 model under diffe rent respiratory mode
1.2.7 顆粒物設置
數值模擬計算中，將顆粒物簡化為球狀，密度為 1 kg/m3，選取直徑為 0.1、0.3、0.5、0.8、1、3、5 μm 等能夠進入人體肺腺泡區的顆粒物[11]作為研究對象。采用 FLUENT DPM（Discrete Phase Model）模型，激活重力、布朗力、曳力選項。數值模擬開始時，在模型入口平面基于網格釋放顆粒物，使顆粒物均勻地分布在氣流中并隨氣流進入模型。利用 DPM 模型中顆粒物沉積數量統計功能，每 
時間間隔記錄一次顆粒物沉積數量，計算總時長為一個周期。定義 
為t時刻顆粒物沉積率，
為 t 時刻顆粒物沉積數量，
為釋放的顆粒物總量，則：
 |
1.2.8 顆粒物沉積速度評價參數
通常而言，顆粒物沉積速度評價參數是首次沉積發生的時間，即顆粒物首次沉積發生的時間越短，沉積速度越快。但實際上，研究中多采用間隔采樣法對顆粒物沉積率進行記錄，無法得到顆粒物首次沉積發生的具體時間。而且，顆粒物沉積為非線性，顆粒物首次沉積時間并不能真實反映該粒徑顆粒物沉積的快慢。為了更好地評價顆粒物在人體肺腺泡區沉積速度差異，引入顆粒物沉積速度評價參數：1/4 沉積時間，即某粒徑顆粒物沉積率達到 1/4 最終沉積率的時間，記為 
。本研究中數值模擬時間為一周期，T 時刻顆粒物沉積率即為最終沉積率 
，則 1/4 最終沉積率為 
。假定 
、
（
）為兩相鄰記錄時刻，即 
，且這兩時刻沉積率滿足：
 |
那么，1/4 沉積時間位于 
～
之間，假定 
～
內顆粒物沉積速度恒定，為線性沉積，則可利用插值計算估算得：
 |
化簡得：
 |
1/4 沉積時間以顆粒物達到 1/4 最終沉積率的時間作為沉積快慢評價參數，能對顆粒物沉積快慢進行較好地評價。
2 結果和討論
2.1 模型對人體肺腺泡區吸入顆粒物沉積特性的影響
2.1.1 模型級數影響
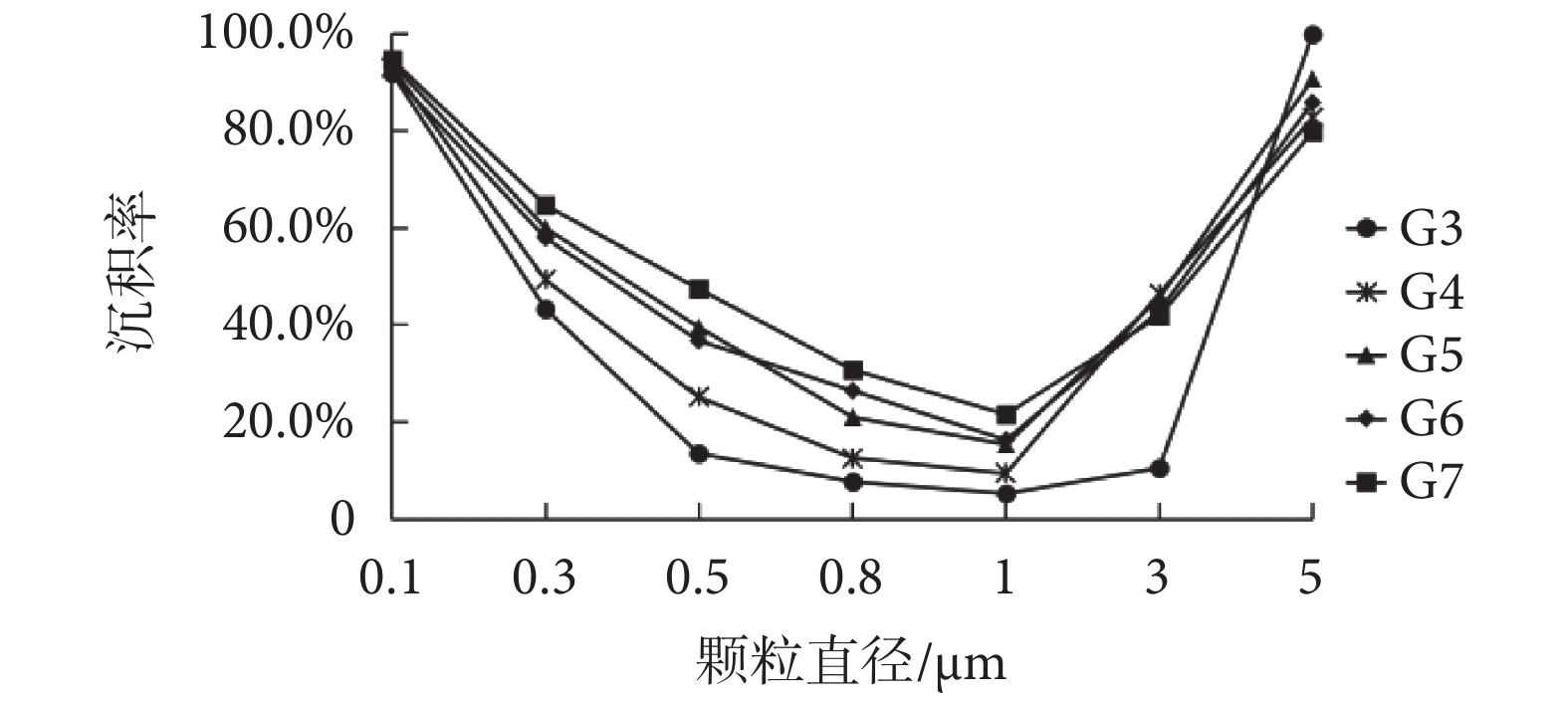
模型的建立是數值模擬研究的前提和基礎，也是影響數值模擬結果的重要因素。由表 2 可知，G3～G7 模型包含肺腺泡級數不同，模型總長度和體積也存在差異，因此研究 G3～G7 模型級數差異對顆粒物沉積特性的影響十分必要。正常呼吸模式下，G3～G7 模型中各粒徑顆粒物最終沉積率如圖 4 所示。由圖 4 可知，由 G3 模型至 G7 模型，隨著模型級數的增加，0.1 μm 粒徑顆粒物最終沉積率呈微弱上升趨勢，整體差異不大；0.3、0.5、0.8、1 μm 粒徑顆粒物最終沉積率呈明顯上升趨勢；3、5 μm 粒徑顆粒物最終沉積率則呈現出下降趨勢。
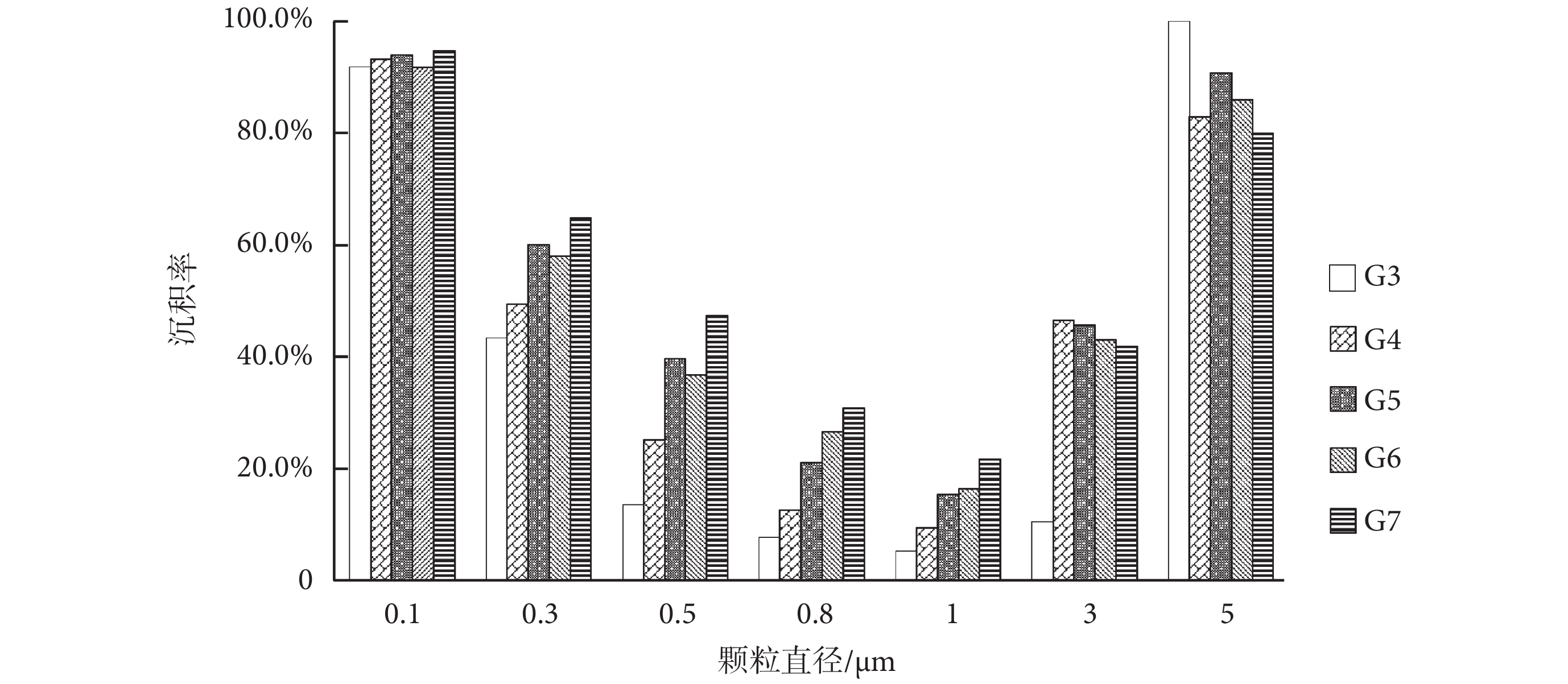圖4
G3～G7 模型中各粒徑顆粒物最終沉積率
Figure4.
Final deposition fraction of particles in G3―G7 models
研究表明，顆粒物在人體肺腺泡區沉積機制主要為布朗擴散、重力沉降和慣性沖擊，而慣性沖擊是影響 0.3～1 μm 粒徑顆粒物沉積的重要因素[12]。由表 4 可知，正常呼吸狀態下，模型所含級數越多，體積越大，則模型入口速度越大，慣性沖擊對顆粒物沉積的影響也相應越大。因此隨著模型級數的增多，0.3～1 μm 粒徑顆粒物最終沉積率呈現出明顯上升趨勢。0.1 μm 粒徑顆粒物沉積由布朗擴散主導，慣性沖擊影響不大，因此沉積率僅微弱上升。由表 2 可知，模型級數的增加不僅體現為體積的增加，還體現在模型總長度的增長。3、5 μm 粒徑顆粒物沉積由重力沉降主導，布朗擴散和重力沉積影響較小，隨著模型總長度的增加，顆粒物沿重力方向沉積所需運動路程相應增加，沉積所需運動時間更長，最終沉積率也相應更低，因而最終沉積率隨模型級數增加呈現出明顯的下降趨勢。Katan 等[13]在研究年齡對肺腺泡區顆粒物沉積狀態的影響時發現，成人肺腺泡模型尺寸較大，顆粒物沉積路徑增加，不利于顆粒物的沉積，因而沉積率較低，與本文研究結果一致。
2.1.2 模型結構影響
由圖 4 可知，上一小節關于模型級數對顆粒物沉積影響規律的描述，只是整體趨勢的歸納和總結。G6 模型中，0.1、0.3、0.5 μm 粒徑顆粒物沉積率較 G5 模型中沉積率稍低，分別相差 2.23%、2.13%、2.90%，鑒于沉積率差值較小，可以認為基本不影響上一小節趨勢的歸納。而 G3 模型中，3 μm 粒徑顆粒物的最終沉積率則與理論值相差甚遠，僅為 10.53%（理論值應大于 G4 模型中 3 μm 粒徑顆粒物最終沉積率，即 > 46.49%），這是模型幾何結構對顆粒物沉積影響的典型體現。如圖 5 所示為
= 2 s 時刻 G3、G4 模型中 3 μm 粒徑顆粒物的分布情況。正常呼吸模式下，2 s 時刻顆粒物運動路徑最長，最容易接觸壁面并沉積。而 G3 模型中，2 s 時刻顆粒物距接觸壁面仍有一定距離，因此沉積率較小。G4 模型中，入口速度增大，運動路徑增加，能夠接觸壁面并沉積，因而沉積率較高。同理，縮減模型中 17 級肺腺管長度（
）或改變重力方向[14]也能大幅度提升 G3 模型中 3 μm 顆粒物的沉積率。
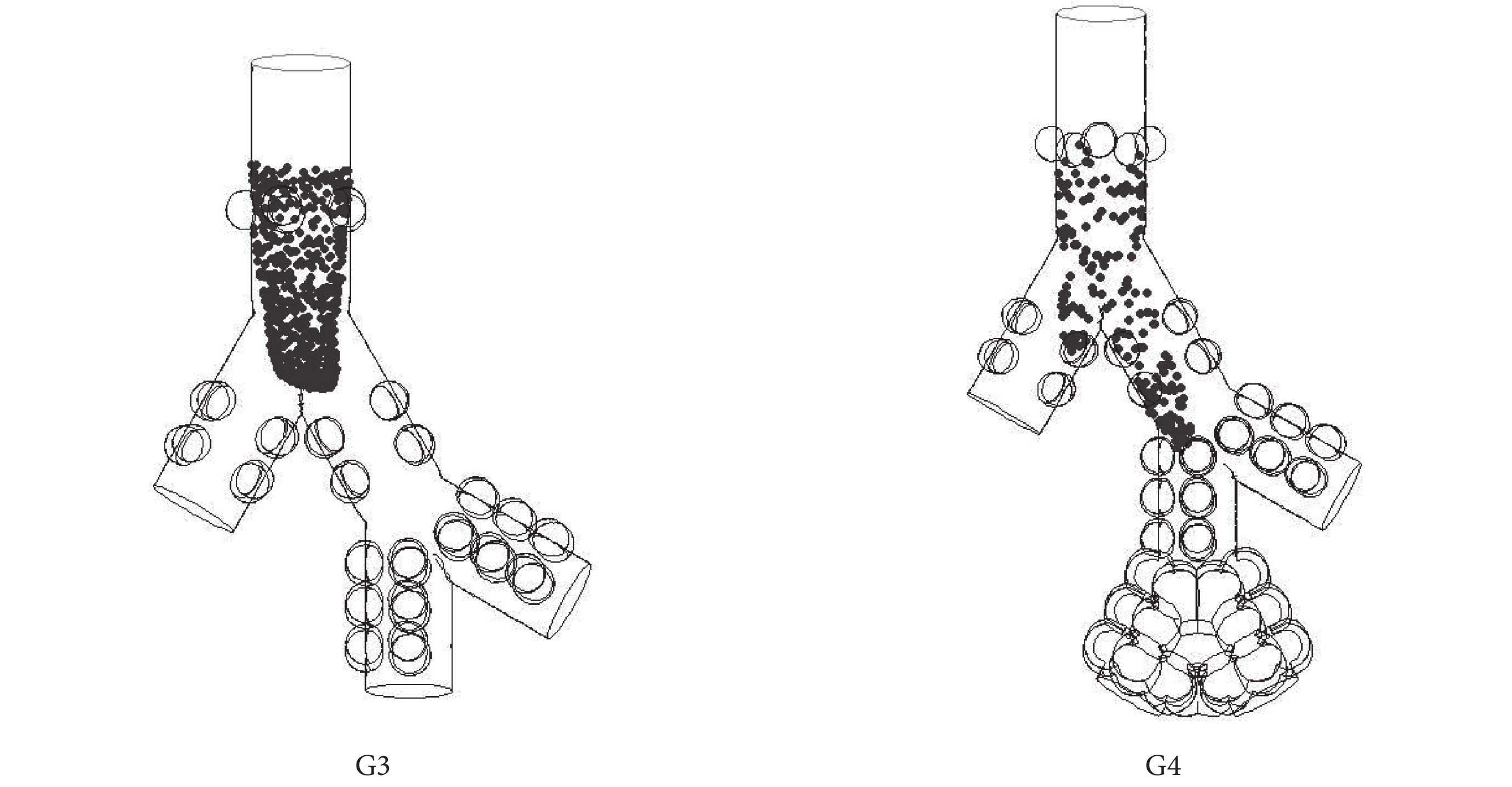圖5
t = 2 s 時刻 G3、G4 模型中 3 μm 粒徑顆粒物分布情況
Figure5.
Distribution of 3 μm particles in G3 and G4 model at t = 2 s
2.2 顆粒物粒徑對人體肺腺泡區吸入顆粒物沉積特性的影響
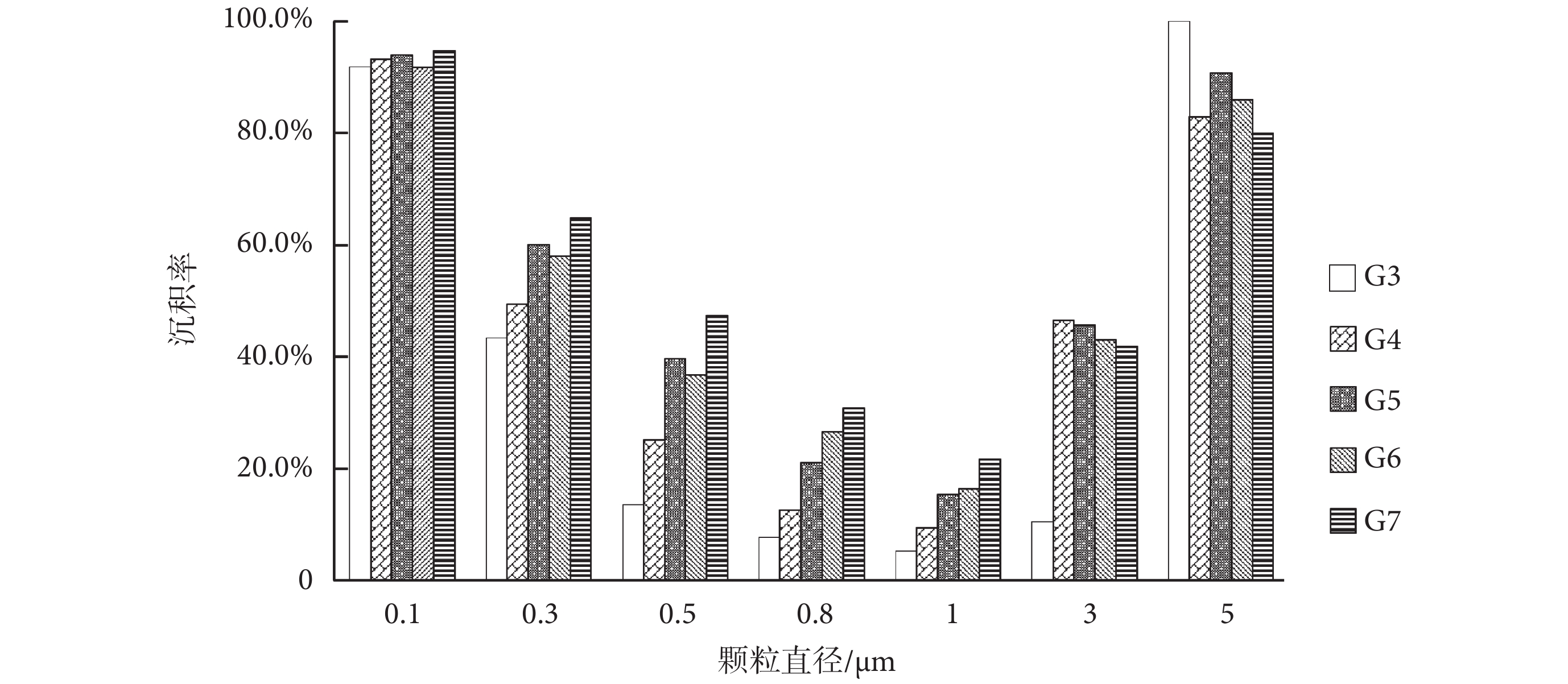
正常呼吸模式下，G3～G7 模型中顆粒物最終沉積率隨粒徑變化趨勢如圖 6 所示，不同模型間各粒徑顆粒物沉積曲線略有差異，但基本形狀均為“U”型，即在顆粒物粒徑為 0.1 μm 時，顆粒物沉積率較高，隨著顆粒物粒徑的增加，沉積率先下降、后上升，并在顆粒物粒徑為 1 μm 左右時沉積率最低，呈現出兩端高、中間低的趨勢，這一趨勢與文獻數據[5, 15-16]保持一致。這是因為，布朗力和重力是影響顆粒物沉積的主要因素。布朗力對微小顆粒物（< 0.1 μm）沉積起主導作用，重力對大顆粒物（> 2 μm）沉積起主導作用。因此，當顆粒物粒徑較小時，沉積受布朗力主導，沉積率較高。顆粒物粒徑較大時，沉積受重力主導，沉積率較高。隨著顆粒物粒徑增加，布朗力作用減弱、重力作用加強，而 1 μm 左右粒徑顆粒物受兩者影響均較小，因而沉積率最低，故沉積曲線呈現為“U”型。
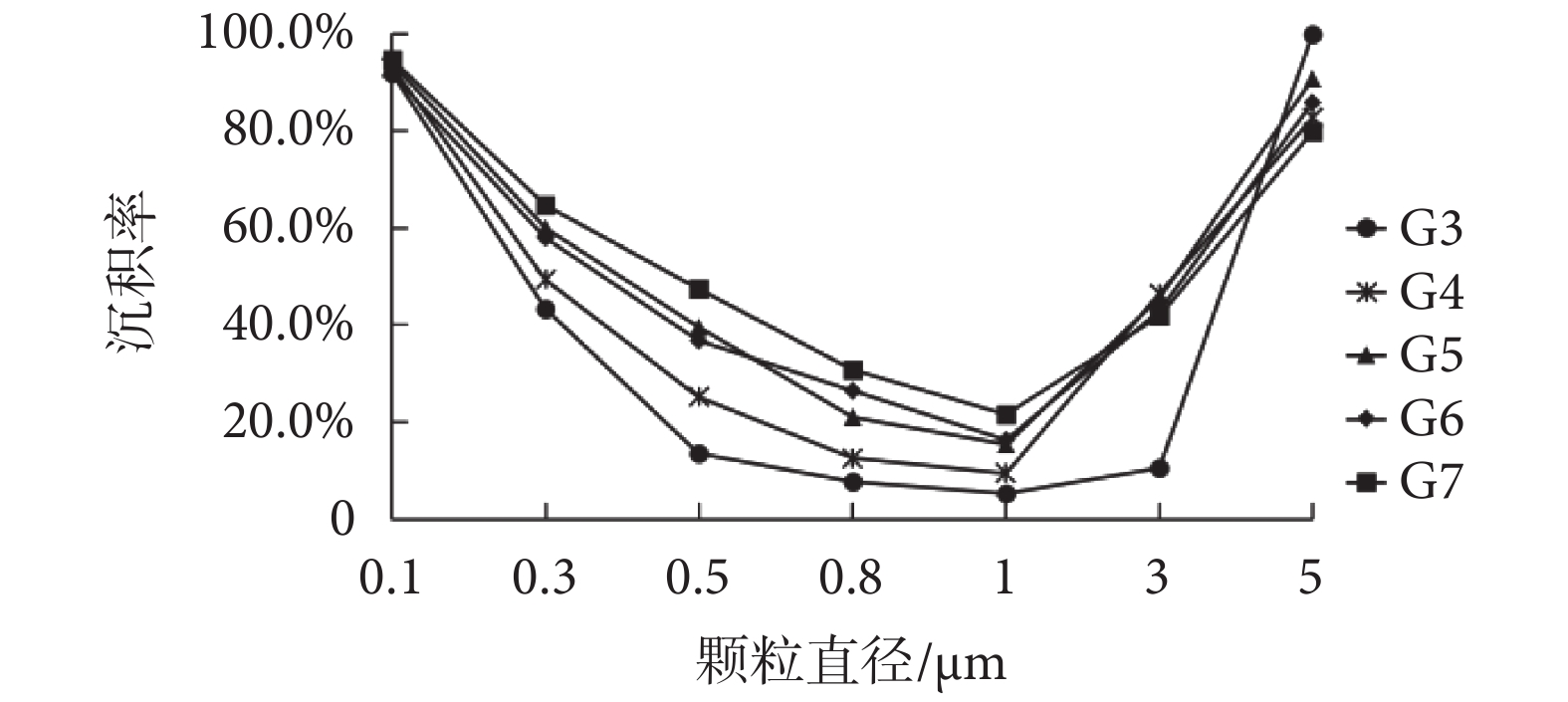圖6
G3～G7 模型中顆粒物最終沉積率隨粒徑變化趨勢
Figure6.
Final deposition fraction of particles as a function of diameter in G3—G7 models
2.3 人體肺腺泡區吸入顆粒物動態沉積特性
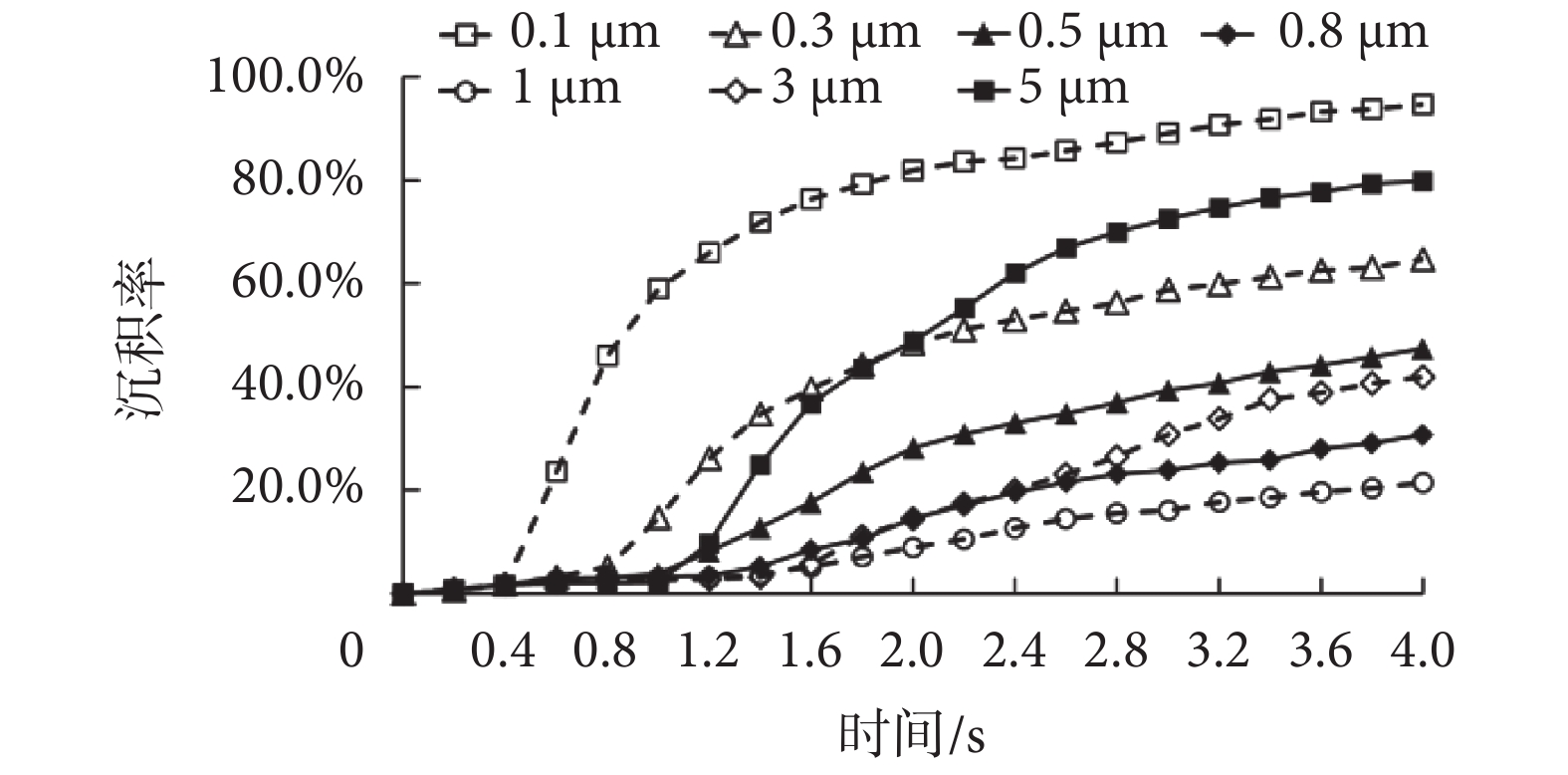
2.1 小節探討了模型級數對人體肺腺泡區顆粒物沉積特性的影響，從肺腺泡形態結構來說，G7 模型包含級數更多，肺泡數量也更多，更加符合人體實際，因此本研究基于 G7 模型進一步研究人體肺腺泡區吸入顆粒物的動態沉積特性和呼吸模式對顆粒物運動規律的影響。正常呼吸模式下（
= 600 mL，T = 4 s），G7 模型中各粒徑顆粒物沉積率隨時間變化曲線如圖 7 所示，G7 模型中各粒徑顆粒物沉積率均隨時間增加，至 4.0 s 時刻達到最大值，即最終沉積率。其中，0.1 μm 顆粒物前期沉積速度快，中后期沉積緩慢并趨于穩定，沉積率變化曲線呈對數型分布。5 μm 顆粒物前期沉積速度慢，中期沉積快速并趨于穩定，后期沉積緩慢，沉積曲線呈“S”型。0.3 μm 顆粒物沉積趨勢與 0.1 μm 基本相似，沉積率相對較低，對數型沉積曲線相對較矮。3 μm 顆粒物沉積曲線與 5 μm 基本相似，沉積率較低，呈較矮的“S”型曲線。其他粒徑顆粒物前期沉積緩慢，中后期沉積率緩慢增長，沉積曲線基本呈折線型。
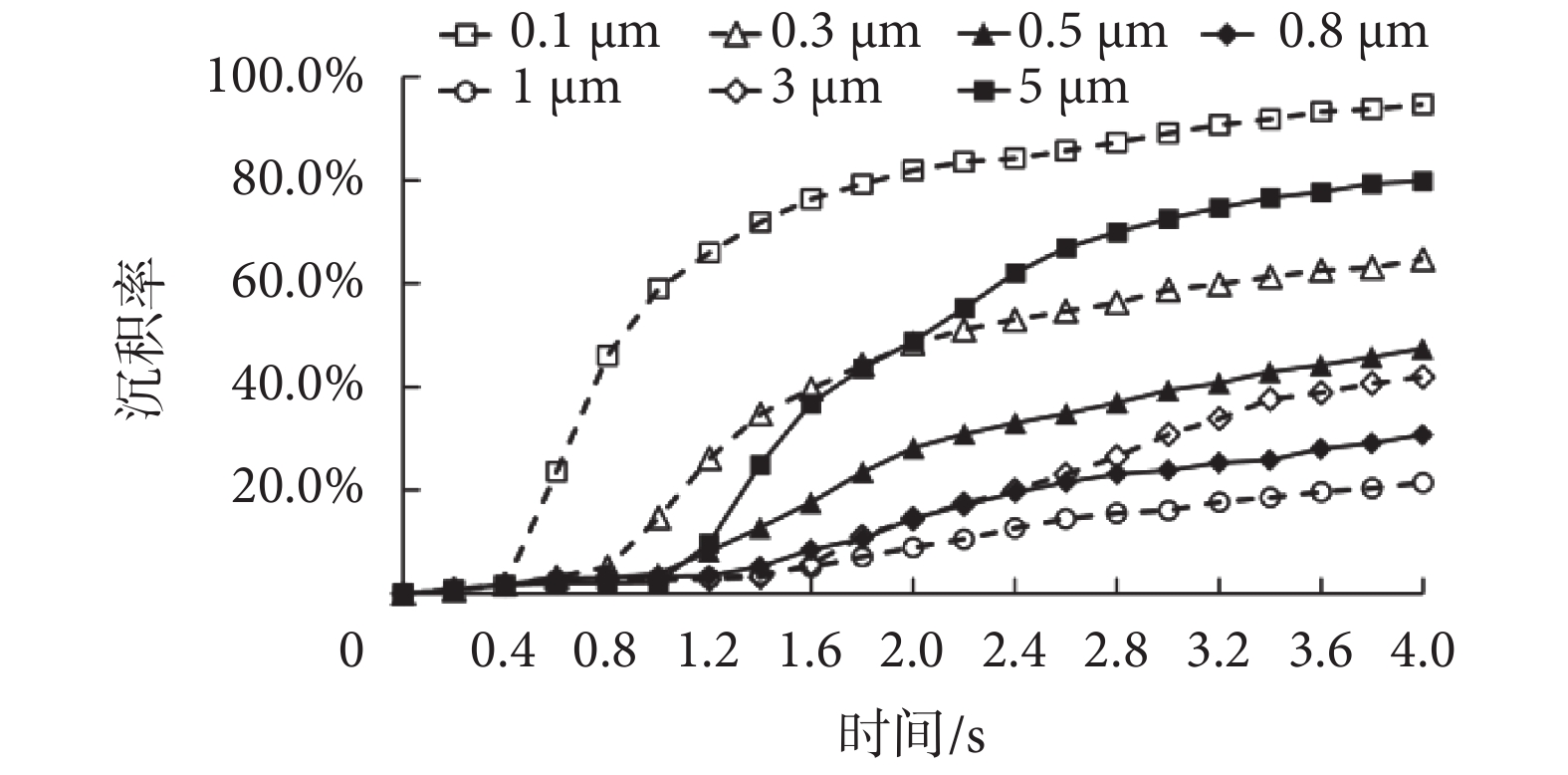圖7
G7 模型各粒徑顆粒物沉積率變化曲線
Figure7.
Variation curves of deposition fraction of particles in G7 model
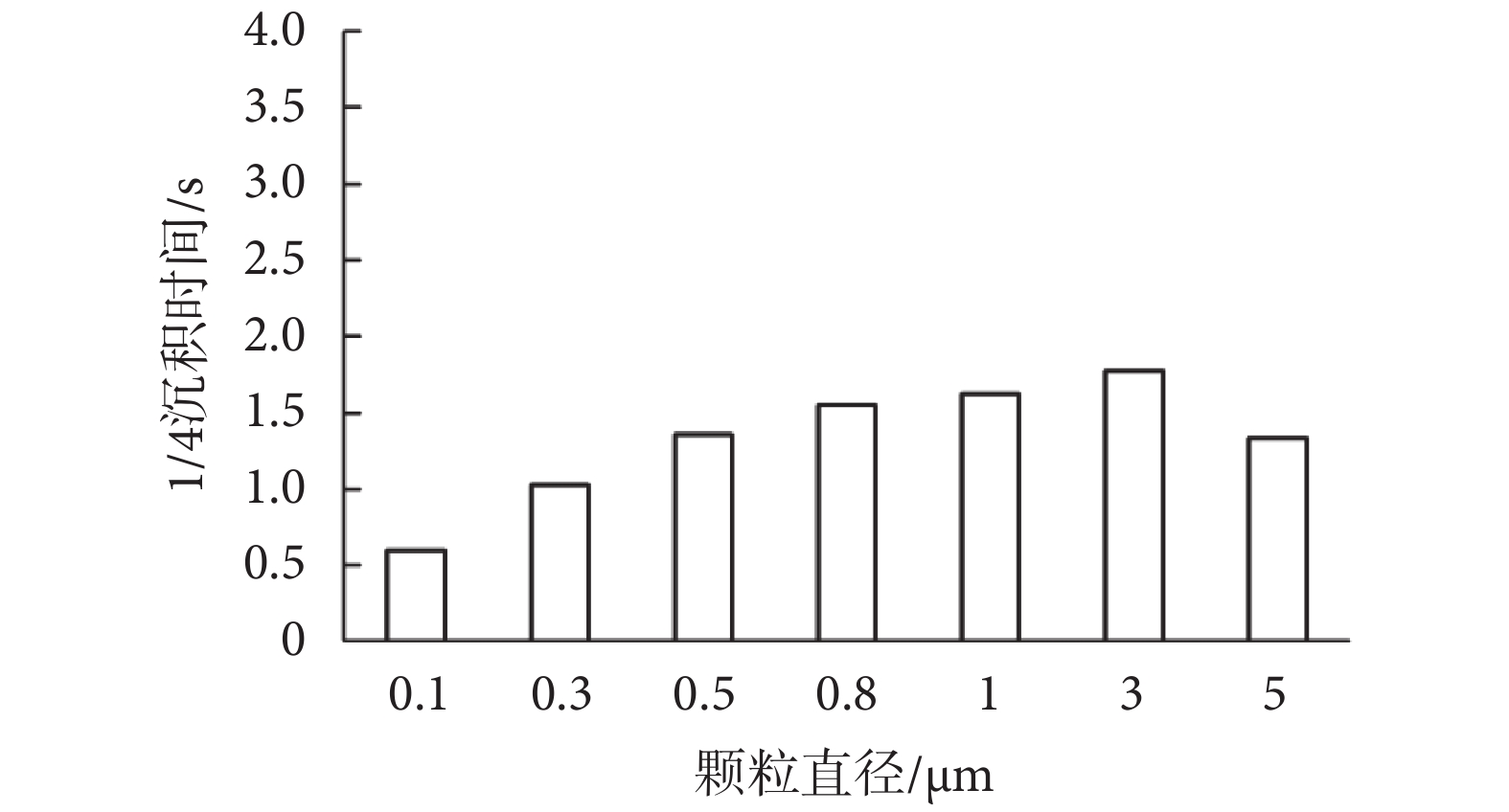
由圖 7 沉積曲線可以看出，0.0～1.0 s 間除 0.1 μm 顆粒物沉積率增長較快外，其他粒徑顆粒物沉積率均較小，很難判斷各粒徑顆粒物沉積速度差異，可見引入合理參數對沉積速度進行評價的必要性。G7 模型中各粒徑顆粒物 1/4 沉積時間如圖 8 所示，從 1/4 沉積時間數值來看，0.1、0.3、5 μm 粒徑顆粒物 1/4 沉積時間相對較短，分別為 0.60、1.03、1.33 s。由此可見，微小顆粒物沉積速度最快，大顆粒物沉積速度次之，而 0.5～3 μm 顆粒物沉積速度則相對較慢。這是因為，數值模擬初期，氣流速度較小，顆粒物速度較小，慣性沖擊影響較小，重力沉降則需要顆粒物沿肺腺管運動一定時間至模型分叉處才能產生沉積。因此，數值模擬初期顆粒物沉積受布朗擴散主導，微小顆粒物沉積速度最快；大顆粒物沉積受重力主導，運動一定時間接觸壁面后開始沉積，沉積速度也相應較快；而其他粒徑顆粒物因數值模擬初期氣流速度小，慣性沖擊影響作用小，沉積較慢。
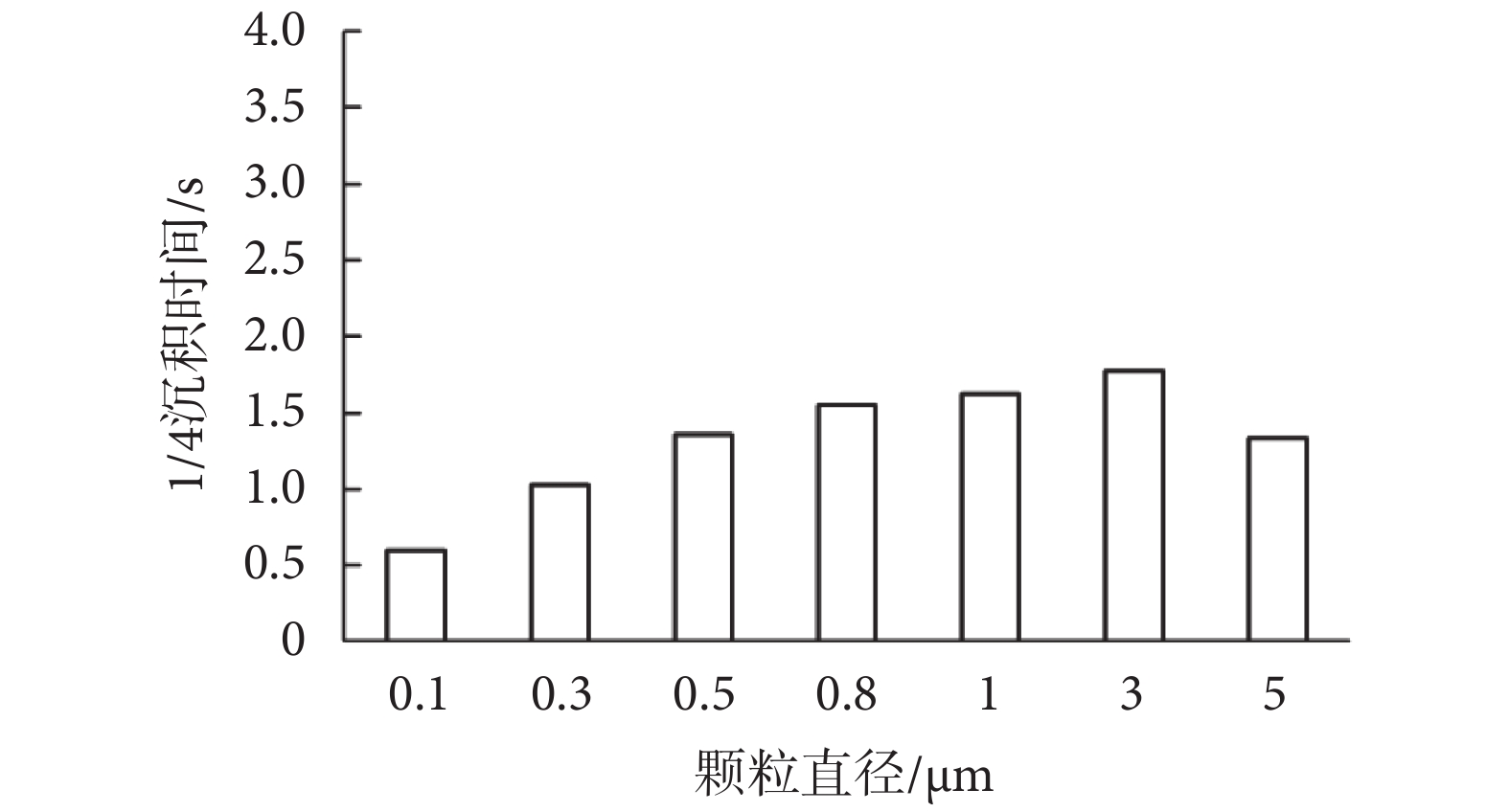圖8
G7 模型中各粒徑顆粒物 1/4 沉積時間
Figure8.
1/4 deposition time of particles in G7 model
2.4 呼吸模式對人體肺腺泡區吸入顆粒物沉積特性的影響
2.4.1 潮氣量影響
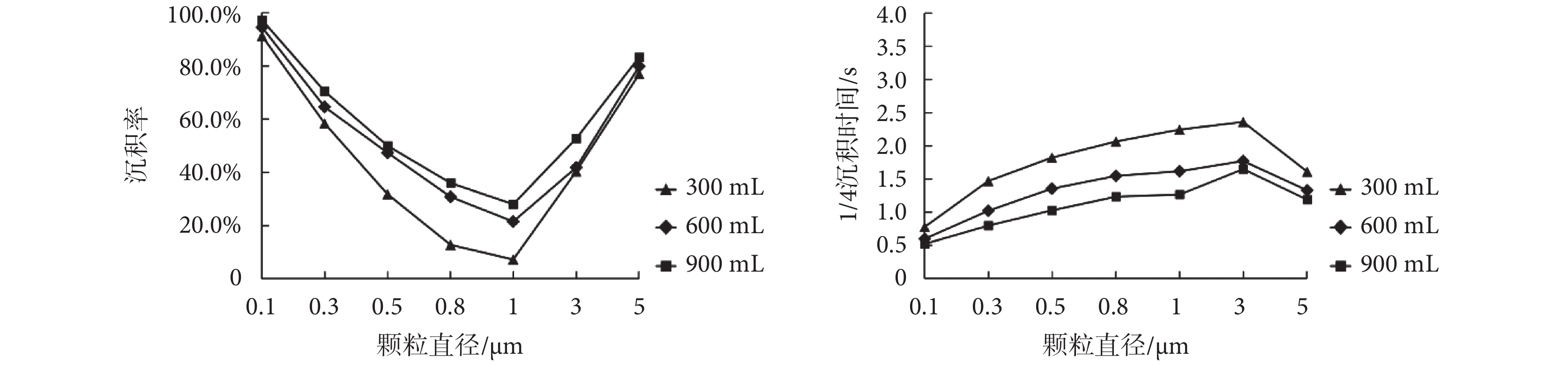
潮氣量分別為 300、600、900 mL 時，G7 模型中各粒徑顆粒物最終沉積率和 1/4 沉積時間如圖 9 所示。
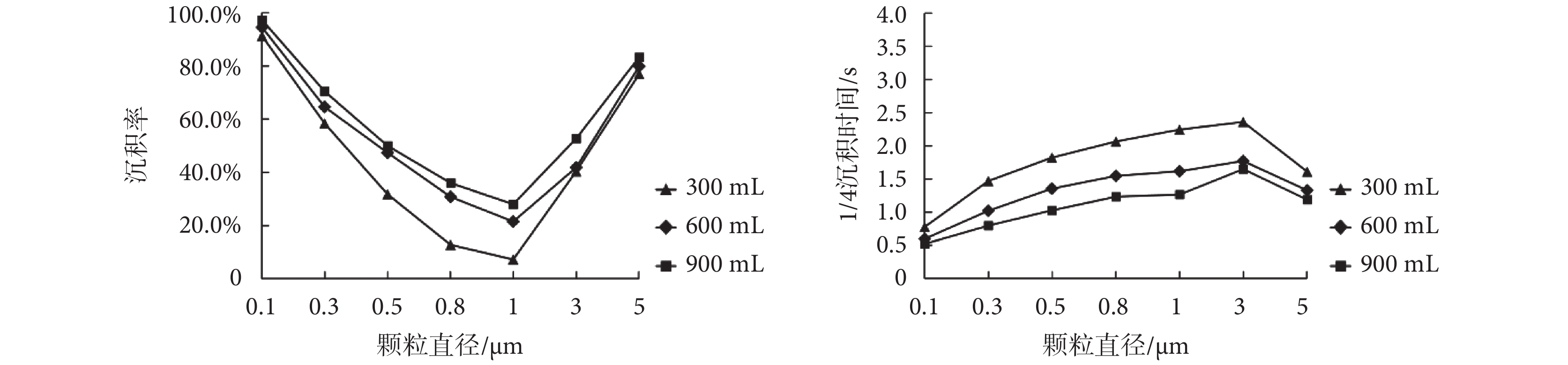圖9
不同潮氣量下顆粒物的最終沉積率和 1/4 沉積時間
Figure9.
Final deposition fraction and 1/4 deposition time of particles under different tidal volume
由圖 9 可知，三種潮氣量下，顆粒物最終沉積率隨粒徑變化趨勢均呈“U”型，1/4 沉積時間的變化趨勢也基本保持一致，說明在人體肺腺泡區潮氣量的變化不會改變流場狀態[17]，仍為充分發展的層流。同一粒徑顆粒物在潮氣量為 300 mL 時最終沉積率最低，1/4 沉積時間最長，潮氣量為 600 mL 時最終沉積率和 1/4 沉積時間次之，潮氣量為 900 mL 時最終沉積率最高，1/4 沉積時間最短。潮氣量對顆粒物沉積規律的影響規律可概括為：潮氣量越大，顆粒物沉積率越高，沉積速度越快。Hofemeier 等[5]分別研究了潮氣量為 500 mL 和潮氣量為 2 500 mL 下的顆粒物沉積狀況，發現潮氣量為 2 500 mL 時顆粒物在肺腺泡內總體沉積率更高，與本文研究結果保持一致。如表 5 所示，潮氣量的增加會導致模型入口速度的增加，受流場曳力影響，顆粒物運動速度隨之增加，慣性沖擊影響作用加大，因而顆粒物沉積數增多，沉積速度加快。
值得注意的是，不同粒徑顆粒物沉積規律率受潮氣量影響程度不同，0.1 和 5 μm 粒徑顆粒物受潮氣量影響較小，沉積率極差量分別為 5.47% 和 6.28%，1/4 沉積時間極差量分別為 0.26 s 和 0.42 s。0.3～1 μm 粒徑顆粒物則受潮氣量影響較大，沉積率極差量分別為 12.12%、18.17%、23.25%、20.85%，1/4 沉積時間極差量分別為 0.68、0.80、0.83、0.98 s。這一結果說明慣性沖擊是影響 0.3～1 μm 顆粒物沉積的關鍵因素，對微小顆粒物和大顆粒物的沉積則影響較小。
2.4.2 呼吸周期影響
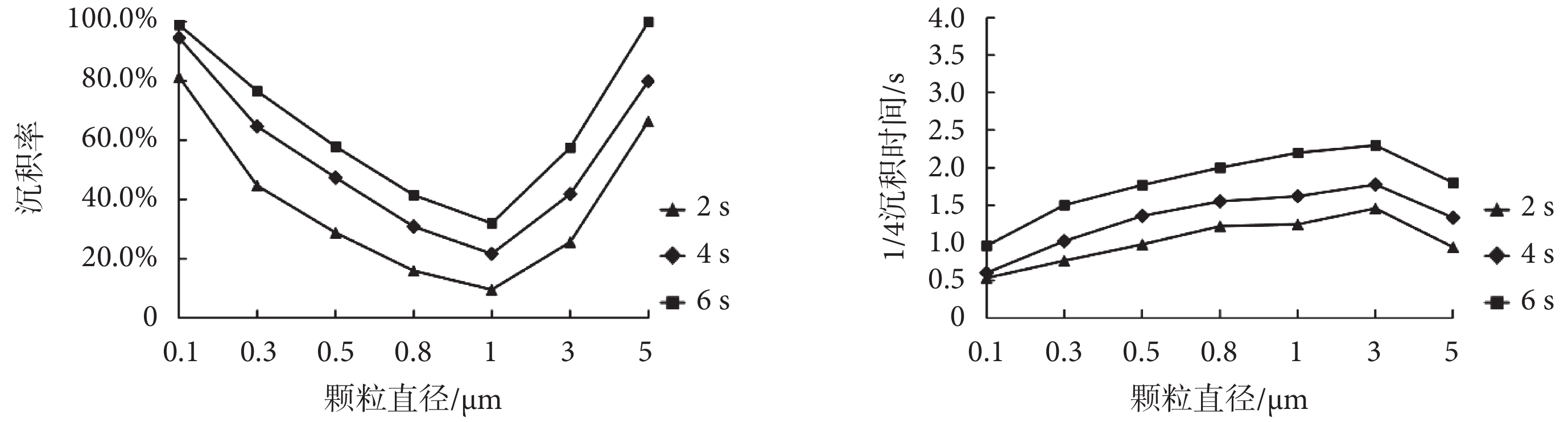
呼吸周期分別為 2、4、6 s 時，G7 模型中各粒徑顆粒物的最終沉積率和 1/4 沉積時間如圖 10 所示，呼吸周期對顆粒物沉積規律的影響與潮氣量影響較為一致，其影響規律可概括為：呼吸周期越長，顆粒物最終沉積率越大，沉積速度越慢，這一結果與文獻[18-19]保持一致。這是因為隨著呼吸周期的增加，數值模擬時間加長，顆粒物沉積更加充分，沉積率相應更高。由表 5 可知，呼吸周期的增加還會導致模型入口氣流速度的減小，慣性沖擊作用減小，因而顆粒物沉積速度減緩，1/4 沉積時間更長。
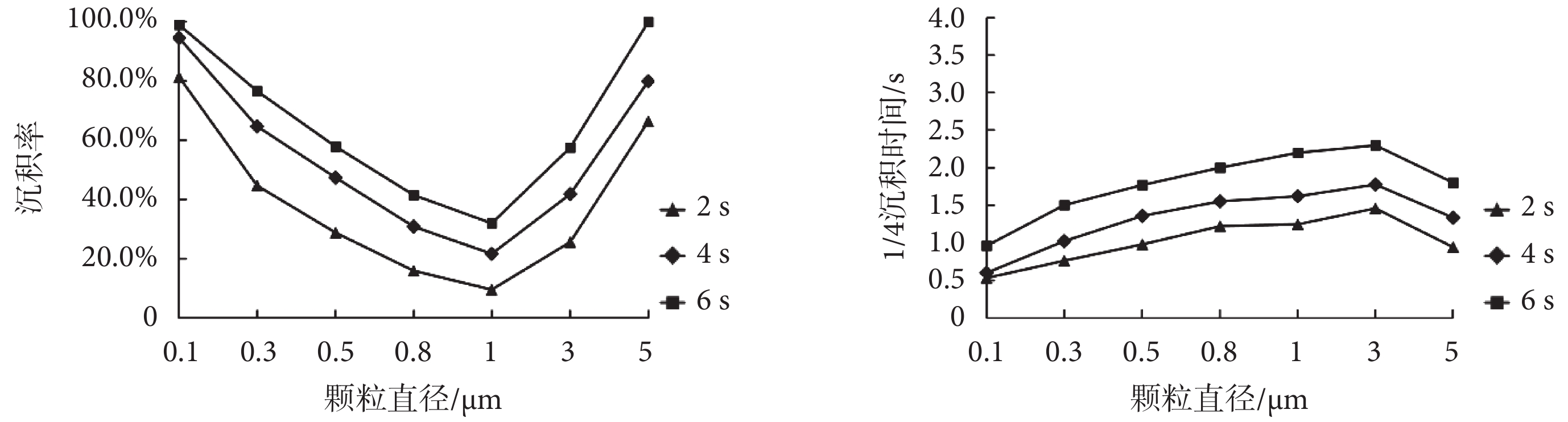圖10
不同呼吸周期下顆粒物的最終沉積率和 1/4 沉積時間
Figure10.
Final deposition fraction and 1/4 deposition time of particles under different respiratory cycle
3 結語
本文一共建立了 G3～G7 五個多肺泡模型，采用數值模擬方法研究了模型級數和結構、顆粒物粒徑、呼吸模式等因素對 0.1～5 μm 粒徑范圍內 7 種顆粒物沉積率和沉積速度的影響。結果表明：模型級數和幾何結構等是造成模型間最終沉積率差異的重要因素。顆粒物沉積率隨粒徑變化曲線呈“U”型，其中，細微顆粒物（0.1 μm）沉積由布朗擴散主導，沉積率高，沉積速度快，沉積曲線呈對數型分布；大顆粒物（5 μm）沉積由重力沉降主導，沉積率高，沉積速度較快，沉積曲線呈“S”型分布；呼吸模式對顆粒物沉積規律的影響體現為：潮氣量越大，顆粒物沉積率越高，沉積越快；呼吸周期越長，顆粒物沉積率越高，沉積越慢，這一結果與文獻數據保持一致。本文建立的“柱狀氣管+球狀肺泡”多肺泡模型和研究方法能為人體肺腺泡區吸入顆粒物運動規律的進一步探究提供參考和借鑒，研究結果和數據能為肺部疾病致病機制的探究、肺部疾病的預防和治療提供理論依據和數據支持。
本文數值模擬過程中，模型壁面剛性固定，以模型入口氣流速度的正弦變化模擬呼吸過程，忽略了真實呼吸過程中肺腺泡模型邊界運動對結果的影響，后期還需進一步研究模型邊界運動的影響。此外，顆粒物沉積的影響因素選取還需進一步細究，考慮更多其他因素，如重力[20]、摒氣時間[21]、肺部病變[22]等的影響。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
人體肺腺泡是指終末細支氣管以下的肺組織，包括呼吸性細支氣管、肺泡管、肺泡囊和肺泡，是呼吸作用的主要區域。細顆粒物的吸入和沉積會影響肺部健康，引發肺部疾病，因此研究細顆粒物在人體肺腺泡區的沉積規律對肺部疾病致病機制的探究以及肺部疾病的預防和治療都有重要意義。
人體肺腺泡區結構復雜、尺寸微小，尚未獲得真實的計算機模型。現行數值模擬研究多采用簡化的計算機模型，主要分為單肺泡模型和多肺泡模型。單肺泡研究僅對單個肺泡建模，計算量較小，著重關注單個肺泡的內部特性。Sznitman 等[1]對處于不同級數的單肺泡進行了數值模擬研究，發現肺泡內流場形態隨著級數增加由循環狀向輻射狀變化。單肺泡研究只能關注單個肺泡內流場形態和顆粒物沉積狀況，無法探究肺腺泡區的整體特性，因此國內外學者紛紛建立多肺泡模型進行進一步研究。目前，多肺泡模型主要分為四類[2]：“柱狀氣管+球狀肺泡”的多肺泡模型、基于十四面體的多肺泡模型、泰森多邊形法構建的多肺泡模型、計算機成像和重建技術構建的多肺泡模型。Ma 等[3]建立了“柱狀氣管+球狀肺泡”的 5 級多肺泡模型，發現呼吸周期、潮氣量和重力等對顆粒物沉積有較大影響。Longest 等[4]建立了 3 個基于十四面體的多肺泡模型，發現屏氣能大幅度增加顆粒物的沉積率。Hofemeier 等[5]采用泰森多邊形法構建了人體 1/8（第 3～8 級）肺腺泡模型，研究了 0.005～5.0 μm 粒徑范圍內不同大小顆粒物的沉積狀況，發現顆粒物沉積率隨粒徑增加呈先下降后上升的趨勢。Sera 等[6]采用微計算機斷層掃描（micro focal computed tomography system，micro-CT）技術構建了大鼠肺腺泡模型，發現 0.8～1.0 μm 粒徑顆粒物多沉積于肺腺泡入口處，而 0.1～0.2 μm 粒徑顆粒物則主要沉積于模型中部和末端。
上述數值模擬研究大多關注顆粒物在人體肺腺泡區局部或整體的最終沉積率，而對其沉積動態過程鮮有涉及，無法進一步了解人體肺腺泡區顆粒物的運動規律。本文建立了五個“柱狀氣管+球狀肺泡”多肺泡模型，通過數值模擬研究了模型級數和結構、顆粒物粒徑、呼吸模式等因素對 0.1～5 μm 粒徑范圍內顆粒物沉積規律的影響，總結了顆粒物沉積率和沉積速度的變化規律，歸納了沉積曲線特征，以期為進一步研究肺部疾病致病機制和相關疾病的預防與治療提供理論依據和數據支持。
1 模型與方法
1.1 人體肺腺泡模型
在經典的全肺模型（Weibel A 模型[7]）中，肺部分為 0～23 級。其中，17～23 級部分含有肺泡，是呼吸作用的主要區域，為肺腺泡區。人體肺腺泡區尺寸數據如表 1 所示。
表1
人體肺腺泡區尺寸數據
Table1.
Geometric data of human pulmonary acinus
由表 1 數據可知，肺腺泡區尺寸數據隨級數變化顯著。從 17 級至 23 級，肺腺管長度、管徑數據逐級遞減，最大縮減率分別為 64.54%、24.07%；肺泡直徑和單節肺腺管肺泡數量逐級遞增，最大增長率分別為 79.25%、300%。Sznitman 等[1]研究發現模型尺寸是影響數值模擬結果的重要因素。十四面體多肺泡模型中肺泡形狀、大小一致[8]，僅適用于肺腺泡區局部特性探究或尺寸影響可忽略不計的情況，因而本文采用“柱狀氣管+球狀肺泡”架構，將肺腺管簡化為圓柱狀，肺泡簡化為附著在肺腺管表面的球，建立了如圖 1 所示的多肺泡模型。
圖1
“柱狀氣管+球狀肺泡”架構多肺泡模型
Figure1.
Multi-alveolar model of “columnar trachea + globular alveolar” structure
然后，在該模型的基礎上依據表 1 尺寸數據建立了圖 2 所示的 G3（17～19 級）、G4（17～20 級）、G5（17～21 級）、G6（17～22 級）、G7（17～23 級）共 5 個多肺泡模型。各模型所含級數、肺泡數、長度、體積等參數如表 2 所示。
圖2
多肺泡模型
Figure2.
Multi-alveolar models
表2
多肺泡模型參數
Table2.
Multi-alveolar models parameters
1.2 數值模擬方法
1.2.1 數值模擬軟件
采用 Inventor 2015 進行多肺泡模型建模，采用 ICEM CFD 15.0 進行模型網格劃分，采用 FLUENT 15.0 進行數值模擬計算。
1.2.2 網格劃分結果
采用非結構網格對 G3～G7 模型進行網格劃分，各模型網格總數及最小網格質量如表 3 所示，最小網格質量均大于 0.3，可以用于數值模擬計算。
表3
G3～G7 模型網格劃分結果
Table3.
Meshing results of G3―G7 models
1.2.3 控制方程
① 流體控制方程：人體肺腺泡區氣流運動為等溫、不可壓縮定常流動。滿足質量、動量守恒方程。
質量守恒方程：
|
式中，表示流體密度， = 1.185 kg/m3，為流體速度，t為時間。故上式可表示為：
|
動量守恒方程：
|
式中，P為流體壓力， = 1.785e-5 表示運動粘度，為流體體積力矢量。
② 顆粒物控制方程：本研究中，忽略 Magnus 力、Saffman 力、Basset 力等對顆粒物運動影響較小的力和顆粒物之間的相互影響，僅考慮重力、布朗力和流體曳力的作用效果，因此單個顆粒的運動控制方程為：
|
|
|
|
其中，其中 和 分別為顆粒物的密度和直徑， 為隨機數， 為玻爾茲曼常數， 為空氣熱力學溫度， 為顆粒半徑， 為計算時間間隔。
1.2.4 邊界條件設置
如圖 3 所示，以 G3 模型區域劃分為例，本研究中將模型分為兩部分：頂端平面（黑色陰影部分）和其他部分。其中，頂端平面為氣流和顆粒物入口，采用入口速度函數實現氣流和顆粒物的進入和排出模型，以此模擬呼吸作用下人體肺腺泡區的氣流和顆粒物的運動。其他部分為無滑移壁面，顆粒物在運動過程中接觸壁面會被捕捉，即為沉積。
圖3
G3 模型區域劃分
Figure3.
Parts of G3 model
1.2.5 入口速度函數
Oakes 等[9]測量了 21 歲健康男性休息狀態下的呼吸流量曲線，近似為正弦曲線，因此本研究中入口速度采用隨時間變化的正弦函數，速度正方向為 ? Z，入口速度 可表示為:
|
其中， 為入口氣流最大速度， 為呼吸周期。
則數值模擬一周期模型內氣體最大進入量為：
|
積分可得:
|
其中，為入口管徑，即 17 級肺腺管管徑。
以上述建立的多肺泡模型代表人體肺腺泡進行數值模擬研究，模型體積對應功能殘氣量（functional residual capacity，FRC），最大進氣量對應潮氣量，則有：
|
根據 Haefeli-Bleuer 等[10]的測量結果，取人體正常呼吸狀態下功能殘氣量為 3 L，潮氣量為 600 mL，呼吸周期為 4 s。依據式（1）（2）（3）計算可得，正常呼吸狀態下（ = 600 mL，T = 4 s），G3～G7 模型入口氣流最大速度和入口速度如表 4 所示。
表4
正常呼吸狀態下 G3～G7 模型入口氣流最大速度和入口 速度
Table4.
The maximum velocity and inlet velocity of inlet airflow in G3?G7 models under normal respiratory mode
1.2.6 呼吸模式
當人體處于不同呼吸狀態時，潮氣量和呼吸周期存在明顯差異。由式（1）（2）（3）可知，潮氣量、呼吸周期能直接決定模型入口速度函數，進而影響顆粒物在人體肺腺泡區的沉積規律。從肺腺泡形態結構來說，G7 模型包含級數更多，肺泡數量也更多，更加符合人體實際，因此本研究基于 G7 模型進一步研究呼吸模式對人體肺腺泡區顆粒物運動規律的影響。取呼吸周期為 4 s，潮氣量分別為 300、600、900 mL，代表人體處于淺呼吸、正常呼吸和深呼吸狀態。取潮氣量為 600 mL，呼吸周期分別為 2、4、6 s，代表人體處于急促呼吸、正常呼吸和緩慢呼吸狀態，由式（1）（2）（3）計算可得，不同呼吸模式下 G7 模型入口速度如表 5 所示。
表5
不同呼吸模式下 G7 模型入口速度
Table5.
The velocity of inlet airflow in G7 model under diffe rent respiratory mode
1.2.7 顆粒物設置
數值模擬計算中，將顆粒物簡化為球狀，密度為 1 kg/m3，選取直徑為 0.1、0.3、0.5、0.8、1、3、5 μm 等能夠進入人體肺腺泡區的顆粒物[11]作為研究對象。采用 FLUENT DPM（Discrete Phase Model）模型，激活重力、布朗力、曳力選項。數值模擬開始時，在模型入口平面基于網格釋放顆粒物，使顆粒物均勻地分布在氣流中并隨氣流進入模型。利用 DPM 模型中顆粒物沉積數量統計功能，每 時間間隔記錄一次顆粒物沉積數量，計算總時長為一個周期。定義 為t時刻顆粒物沉積率， 為 t 時刻顆粒物沉積數量， 為釋放的顆粒物總量，則：
|
1.2.8 顆粒物沉積速度評價參數
通常而言，顆粒物沉積速度評價參數是首次沉積發生的時間，即顆粒物首次沉積發生的時間越短，沉積速度越快。但實際上，研究中多采用間隔采樣法對顆粒物沉積率進行記錄，無法得到顆粒物首次沉積發生的具體時間。而且，顆粒物沉積為非線性，顆粒物首次沉積時間并不能真實反映該粒徑顆粒物沉積的快慢。為了更好地評價顆粒物在人體肺腺泡區沉積速度差異，引入顆粒物沉積速度評價參數：1/4 沉積時間，即某粒徑顆粒物沉積率達到 1/4 最終沉積率的時間，記為 。本研究中數值模擬時間為一周期，T 時刻顆粒物沉積率即為最終沉積率 ，則 1/4 最終沉積率為 。假定 、（）為兩相鄰記錄時刻，即 ，且這兩時刻沉積率滿足：
|
那么，1/4 沉積時間位于 ～ 之間，假定 ～ 內顆粒物沉積速度恒定，為線性沉積，則可利用插值計算估算得：
|
化簡得：
|
1/4 沉積時間以顆粒物達到 1/4 最終沉積率的時間作為沉積快慢評價參數，能對顆粒物沉積快慢進行較好地評價。
2 結果和討論
2.1 模型對人體肺腺泡區吸入顆粒物沉積特性的影響
2.1.1 模型級數影響
模型的建立是數值模擬研究的前提和基礎，也是影響數值模擬結果的重要因素。由表 2 可知，G3～G7 模型包含肺腺泡級數不同，模型總長度和體積也存在差異，因此研究 G3～G7 模型級數差異對顆粒物沉積特性的影響十分必要。正常呼吸模式下，G3～G7 模型中各粒徑顆粒物最終沉積率如圖 4 所示。由圖 4 可知，由 G3 模型至 G7 模型，隨著模型級數的增加，0.1 μm 粒徑顆粒物最終沉積率呈微弱上升趨勢，整體差異不大；0.3、0.5、0.8、1 μm 粒徑顆粒物最終沉積率呈明顯上升趨勢；3、5 μm 粒徑顆粒物最終沉積率則呈現出下降趨勢。
圖4
G3～G7 模型中各粒徑顆粒物最終沉積率
Figure4.
Final deposition fraction of particles in G3―G7 models
研究表明，顆粒物在人體肺腺泡區沉積機制主要為布朗擴散、重力沉降和慣性沖擊，而慣性沖擊是影響 0.3～1 μm 粒徑顆粒物沉積的重要因素[12]。由表 4 可知，正常呼吸狀態下，模型所含級數越多，體積越大，則模型入口速度越大，慣性沖擊對顆粒物沉積的影響也相應越大。因此隨著模型級數的增多，0.3～1 μm 粒徑顆粒物最終沉積率呈現出明顯上升趨勢。0.1 μm 粒徑顆粒物沉積由布朗擴散主導，慣性沖擊影響不大，因此沉積率僅微弱上升。由表 2 可知，模型級數的增加不僅體現為體積的增加，還體現在模型總長度的增長。3、5 μm 粒徑顆粒物沉積由重力沉降主導，布朗擴散和重力沉積影響較小，隨著模型總長度的增加，顆粒物沿重力方向沉積所需運動路程相應增加，沉積所需運動時間更長，最終沉積率也相應更低，因而最終沉積率隨模型級數增加呈現出明顯的下降趨勢。Katan 等[13]在研究年齡對肺腺泡區顆粒物沉積狀態的影響時發現，成人肺腺泡模型尺寸較大，顆粒物沉積路徑增加，不利于顆粒物的沉積，因而沉積率較低，與本文研究結果一致。
2.1.2 模型結構影響
由圖 4 可知，上一小節關于模型級數對顆粒物沉積影響規律的描述，只是整體趨勢的歸納和總結。G6 模型中，0.1、0.3、0.5 μm 粒徑顆粒物沉積率較 G5 模型中沉積率稍低，分別相差 2.23%、2.13%、2.90%，鑒于沉積率差值較小，可以認為基本不影響上一小節趨勢的歸納。而 G3 模型中，3 μm 粒徑顆粒物的最終沉積率則與理論值相差甚遠，僅為 10.53%（理論值應大于 G4 模型中 3 μm 粒徑顆粒物最終沉積率，即 > 46.49%），這是模型幾何結構對顆粒物沉積影響的典型體現。如圖 5 所示為 = 2 s 時刻 G3、G4 模型中 3 μm 粒徑顆粒物的分布情況。正常呼吸模式下，2 s 時刻顆粒物運動路徑最長，最容易接觸壁面并沉積。而 G3 模型中，2 s 時刻顆粒物距接觸壁面仍有一定距離，因此沉積率較小。G4 模型中，入口速度增大，運動路徑增加，能夠接觸壁面并沉積，因而沉積率較高。同理，縮減模型中 17 級肺腺管長度（）或改變重力方向[14]也能大幅度提升 G3 模型中 3 μm 顆粒物的沉積率。
圖5
t = 2 s 時刻 G3、G4 模型中 3 μm 粒徑顆粒物分布情況
Figure5.
Distribution of 3 μm particles in G3 and G4 model at t = 2 s
2.2 顆粒物粒徑對人體肺腺泡區吸入顆粒物沉積特性的影響
正常呼吸模式下，G3～G7 模型中顆粒物最終沉積率隨粒徑變化趨勢如圖 6 所示，不同模型間各粒徑顆粒物沉積曲線略有差異，但基本形狀均為“U”型，即在顆粒物粒徑為 0.1 μm 時，顆粒物沉積率較高，隨著顆粒物粒徑的增加，沉積率先下降、后上升，并在顆粒物粒徑為 1 μm 左右時沉積率最低，呈現出兩端高、中間低的趨勢，這一趨勢與文獻數據[5, 15-16]保持一致。這是因為，布朗力和重力是影響顆粒物沉積的主要因素。布朗力對微小顆粒物（< 0.1 μm）沉積起主導作用，重力對大顆粒物（> 2 μm）沉積起主導作用。因此，當顆粒物粒徑較小時，沉積受布朗力主導，沉積率較高。顆粒物粒徑較大時，沉積受重力主導，沉積率較高。隨著顆粒物粒徑增加，布朗力作用減弱、重力作用加強，而 1 μm 左右粒徑顆粒物受兩者影響均較小，因而沉積率最低，故沉積曲線呈現為“U”型。
圖6
G3～G7 模型中顆粒物最終沉積率隨粒徑變化趨勢
Figure6.
Final deposition fraction of particles as a function of diameter in G3—G7 models
2.3 人體肺腺泡區吸入顆粒物動態沉積特性
2.1 小節探討了模型級數對人體肺腺泡區顆粒物沉積特性的影響，從肺腺泡形態結構來說，G7 模型包含級數更多，肺泡數量也更多，更加符合人體實際，因此本研究基于 G7 模型進一步研究人體肺腺泡區吸入顆粒物的動態沉積特性和呼吸模式對顆粒物運動規律的影響。正常呼吸模式下（ = 600 mL，T = 4 s），G7 模型中各粒徑顆粒物沉積率隨時間變化曲線如圖 7 所示，G7 模型中各粒徑顆粒物沉積率均隨時間增加，至 4.0 s 時刻達到最大值，即最終沉積率。其中，0.1 μm 顆粒物前期沉積速度快，中后期沉積緩慢并趨于穩定，沉積率變化曲線呈對數型分布。5 μm 顆粒物前期沉積速度慢，中期沉積快速并趨于穩定，后期沉積緩慢，沉積曲線呈“S”型。0.3 μm 顆粒物沉積趨勢與 0.1 μm 基本相似，沉積率相對較低，對數型沉積曲線相對較矮。3 μm 顆粒物沉積曲線與 5 μm 基本相似，沉積率較低，呈較矮的“S”型曲線。其他粒徑顆粒物前期沉積緩慢，中后期沉積率緩慢增長，沉積曲線基本呈折線型。
圖7
G7 模型各粒徑顆粒物沉積率變化曲線
Figure7.
Variation curves of deposition fraction of particles in G7 model
由圖 7 沉積曲線可以看出，0.0～1.0 s 間除 0.1 μm 顆粒物沉積率增長較快外，其他粒徑顆粒物沉積率均較小，很難判斷各粒徑顆粒物沉積速度差異，可見引入合理參數對沉積速度進行評價的必要性。G7 模型中各粒徑顆粒物 1/4 沉積時間如圖 8 所示，從 1/4 沉積時間數值來看，0.1、0.3、5 μm 粒徑顆粒物 1/4 沉積時間相對較短，分別為 0.60、1.03、1.33 s。由此可見，微小顆粒物沉積速度最快，大顆粒物沉積速度次之，而 0.5～3 μm 顆粒物沉積速度則相對較慢。這是因為，數值模擬初期，氣流速度較小，顆粒物速度較小，慣性沖擊影響較小，重力沉降則需要顆粒物沿肺腺管運動一定時間至模型分叉處才能產生沉積。因此，數值模擬初期顆粒物沉積受布朗擴散主導，微小顆粒物沉積速度最快；大顆粒物沉積受重力主導，運動一定時間接觸壁面后開始沉積，沉積速度也相應較快；而其他粒徑顆粒物因數值模擬初期氣流速度小，慣性沖擊影響作用小，沉積較慢。
圖8
G7 模型中各粒徑顆粒物 1/4 沉積時間
Figure8.
1/4 deposition time of particles in G7 model
2.4 呼吸模式對人體肺腺泡區吸入顆粒物沉積特性的影響
2.4.1 潮氣量影響
潮氣量分別為 300、600、900 mL 時，G7 模型中各粒徑顆粒物最終沉積率和 1/4 沉積時間如圖 9 所示。
圖9
不同潮氣量下顆粒物的最終沉積率和 1/4 沉積時間
Figure9.
Final deposition fraction and 1/4 deposition time of particles under different tidal volume
由圖 9 可知，三種潮氣量下，顆粒物最終沉積率隨粒徑變化趨勢均呈“U”型，1/4 沉積時間的變化趨勢也基本保持一致，說明在人體肺腺泡區潮氣量的變化不會改變流場狀態[17]，仍為充分發展的層流。同一粒徑顆粒物在潮氣量為 300 mL 時最終沉積率最低，1/4 沉積時間最長，潮氣量為 600 mL 時最終沉積率和 1/4 沉積時間次之，潮氣量為 900 mL 時最終沉積率最高，1/4 沉積時間最短。潮氣量對顆粒物沉積規律的影響規律可概括為：潮氣量越大，顆粒物沉積率越高，沉積速度越快。Hofemeier 等[5]分別研究了潮氣量為 500 mL 和潮氣量為 2 500 mL 下的顆粒物沉積狀況，發現潮氣量為 2 500 mL 時顆粒物在肺腺泡內總體沉積率更高，與本文研究結果保持一致。如表 5 所示，潮氣量的增加會導致模型入口速度的增加，受流場曳力影響，顆粒物運動速度隨之增加，慣性沖擊影響作用加大，因而顆粒物沉積數增多，沉積速度加快。
值得注意的是，不同粒徑顆粒物沉積規律率受潮氣量影響程度不同，0.1 和 5 μm 粒徑顆粒物受潮氣量影響較小，沉積率極差量分別為 5.47% 和 6.28%，1/4 沉積時間極差量分別為 0.26 s 和 0.42 s。0.3～1 μm 粒徑顆粒物則受潮氣量影響較大，沉積率極差量分別為 12.12%、18.17%、23.25%、20.85%，1/4 沉積時間極差量分別為 0.68、0.80、0.83、0.98 s。這一結果說明慣性沖擊是影響 0.3～1 μm 顆粒物沉積的關鍵因素，對微小顆粒物和大顆粒物的沉積則影響較小。
2.4.2 呼吸周期影響
呼吸周期分別為 2、4、6 s 時，G7 模型中各粒徑顆粒物的最終沉積率和 1/4 沉積時間如圖 10 所示，呼吸周期對顆粒物沉積規律的影響與潮氣量影響較為一致，其影響規律可概括為：呼吸周期越長，顆粒物最終沉積率越大，沉積速度越慢，這一結果與文獻[18-19]保持一致。這是因為隨著呼吸周期的增加，數值模擬時間加長，顆粒物沉積更加充分，沉積率相應更高。由表 5 可知，呼吸周期的增加還會導致模型入口氣流速度的減小，慣性沖擊作用減小，因而顆粒物沉積速度減緩，1/4 沉積時間更長。
圖10
不同呼吸周期下顆粒物的最終沉積率和 1/4 沉積時間
Figure10.
Final deposition fraction and 1/4 deposition time of particles under different respiratory cycle
3 結語
本文一共建立了 G3～G7 五個多肺泡模型，采用數值模擬方法研究了模型級數和結構、顆粒物粒徑、呼吸模式等因素對 0.1～5 μm 粒徑范圍內 7 種顆粒物沉積率和沉積速度的影響。結果表明：模型級數和幾何結構等是造成模型間最終沉積率差異的重要因素。顆粒物沉積率隨粒徑變化曲線呈“U”型，其中，細微顆粒物（0.1 μm）沉積由布朗擴散主導，沉積率高，沉積速度快，沉積曲線呈對數型分布；大顆粒物（5 μm）沉積由重力沉降主導，沉積率高，沉積速度較快，沉積曲線呈“S”型分布；呼吸模式對顆粒物沉積規律的影響體現為：潮氣量越大，顆粒物沉積率越高，沉積越快；呼吸周期越長，顆粒物沉積率越高，沉積越慢，這一結果與文獻數據保持一致。本文建立的“柱狀氣管+球狀肺泡”多肺泡模型和研究方法能為人體肺腺泡區吸入顆粒物運動規律的進一步探究提供參考和借鑒，研究結果和數據能為肺部疾病致病機制的探究、肺部疾病的預防和治療提供理論依據和數據支持。
本文數值模擬過程中，模型壁面剛性固定，以模型入口氣流速度的正弦變化模擬呼吸過程，忽略了真實呼吸過程中肺腺泡模型邊界運動對結果的影響，后期還需進一步研究模型邊界運動的影響。此外，顆粒物沉積的影響因素選取還需進一步細究，考慮更多其他因素，如重力[20]、摒氣時間[21]、肺部病變[22]等的影響。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
