口腔正畸研究中,牙頜組織模型對有限元分析結果有著重要影響。目前,常用的牙槽骨有限元模型主要有均質和非均質兩種類型。均質型模型對牙槽骨進行整體材料賦值,每個網格單元的力學特性均相同;而非均質型模型則依據牙槽骨每個網格單元所處的計算機斷層掃描(CT)圖像灰度值對網格單元進行差別賦值。為了探究不同牙槽骨模型對牙周膜生物力學響應的影響,我們選擇一例臨床患者作為研究對象,構建了其下頜尖牙、牙周膜和兩種牙槽骨模型,分別對尖牙施加 1 N 的根向壓入力和 2 Nmm 根向扭矩,分析牙周膜在不同載荷形式下的靜水壓應力和最大對數主應變。研究結果表明無論尖牙平動或轉動,牙周膜的力學響應均會受到牙槽骨模型的影響。相比于均質型模型,當牙槽骨模型為非均質模型時,尖牙沿根向平動時牙周膜的最大應力和應變分別降低了 13.13% 和 35.57%;尖牙沿根向轉動時牙周膜最大應力和應變分別降低了 19.55% 和 35.64%。均質型牙槽骨模型會誘導正畸醫生選擇一個較小的矯治力,非均質牙槽骨模型更能體現真實牙槽骨骨質特性的差異性,更有利于獲得準確的分析結果。
引用本文: 仵健磊, 劉云峰, 李伯休, 王棟才, 董星濤, 周佳麗. 不同牙槽骨有限元模型對牙周膜生物力學響應的影響. 生物醫學工程學雜志, 2021, 38(2): 295-302. doi: 10.7507/1001-5515.202007048 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
臨床正畸治療中,錯位牙齒的矯正主要依靠患者口腔佩戴的正畸矯治器。矯治器形變產生矯治力,矯治力首先作用在錯位牙齒的牙冠上,并通過牙體傳遞給牙周膜,進一步經過牙周膜的緩沖、吸收作用于牙槽骨,進而激發牙槽骨改建,最終在矯治力的作用下,牙齒逐漸移動到理想位置[1-4]。在牙齒移動過程中,牙周膜作為介于牙齒和牙槽骨之間的一層結締纖維組織,在激發骨改建、誘導牙齒移動中起著重要作用[5-6]。有研究表明牙齒矯治過程中的移動速度與牙周膜的應變密切相關[7-8],牙根的吸收情況則與牙周膜的應力有關[9-10]。因此,研究牙周膜受載之后的生物力學響應對于明確正畸矯治機制、優化正畸治療方案具有非常重要的意義。
對于牙周膜生物特性的研究方法主要包括實驗測試和有限元模擬。牙周膜作為人體生物組織,一方面實驗材料來源非常有限;另一方面,牙周膜一般厚度僅有 0.2~0.3 mm[11],極易遭到破壞而失去生物活性,存放條件非常苛刻[12]。另外,對于牙周膜的臨床測試也因患者意愿、裝置結構復雜、跟蹤記錄周期長、數據處理繁瑣等因素難以獲得直接有效的試驗結果[13]。因此,在實驗條件有限的情況下,更多的人采用有限元法對其進行研究。目前有限元法已廣泛用于口腔正畸醫療領域,具有準確度高、重復性好和可操作性強等優點,受到越來越多的研究人員青睞[9, 14]。
在采用有限元法對正畸矯治機制進行研究時,構建牙頜組織有限元模型至關重要。正畸過程中涉及到的牙頜組織主要包括牙齒、牙周膜和牙槽骨。牙齒相比于其他牙頜組織具有很高的硬度,彈性模量可達 20 GPa[15-16],因此在有限元分析中多把牙齒設定為剛體[10, 17]。牙周膜因其厚度較薄、尺寸較小,則一般假定為厚度均勻、均質、各向同性的超-黏彈性體[12, 18]。對于牙槽骨模型的構建方法則主要有兩種:第一種是采用非均勻有理 B 樣條(non-uniform rational b-splines,NURBS)曲面擬合的方式將牙槽骨三角面片網格模型轉化為實體模型,然后將其導入有限元軟件進行整體網格劃分、材料賦值得到牙槽骨有限元模型[3, 19]。這種建模方法獲得牙槽骨模型每個網格單元的材料特性都相同,屬于均質型模型。雖然有些學者按照牙槽骨骨質特性將其人為地分為皮質骨和松質骨[7, 19],但對于整個皮質骨或者松質骨而言,模型的每個單元材料特性也都一樣。另一種方法則直接利用牙槽骨三角面片網格模型生成體網格模型,并依據模型中每個網格單元所處的計算機斷層掃描(computed tomography,CT)圖像灰度值對單元進行差別材料賦值[18, 20],不再利用有限元軟件進行網格劃分和材料賦值,這種建模方法獲得牙槽骨模型每個網格單元的材料特性均不相同,屬于非均質模型。
目前,上述兩種建模方法均有使用,如 Liao 等[9]為了研究牙周膜在正畸力優化中的作用構建了精細的均質型牙槽骨模型,Ashrafi 等[15]、Cozzani 等[16]和 Benaissa 等[19]也都在自己最新的研究中采用了第一種建模方法;而 Wu 等[18]、Liu 等[20]和 Bujtar 等[21]則采用第二種方法構建了非均質牙槽骨模型用于有限元分析計算。Liu 等[20]進一步對比分析了兩種建模方法在構建下頜骨有限元模型中的優劣勢,結果表明非均質模型更有利于構建具有復雜幾何構造的頜骨模型。而針對不同類型的牙槽骨模型,牙周膜受載之后的生物力學響應是否存在差異卻鮮有報道。多數學者習慣采用第一種建模方法構建均質型的牙槽骨模型,對于模型的材料賦值也通常機械式地借鑒他人的材料參數,然而有限元模型的精確度對其分析結果卻有著不可忽視的影響。
為此,我們將基于一例臨床患者的螺旋 CT 圖像數據,選擇其下頜尖牙作為研究對象,構建其牙頜組織有限元模型,分別將其牙槽骨設置為均質型模型和非均質型模型,對尖牙施加牙根向的壓入力和扭矩,研究不同牙槽骨模型作用下的牙周膜應力和應變,進而明確不同牙槽骨仿真模型對牙周膜生物力學響應的影響,協助相關研究人員選擇合適的牙槽骨建模方法,從而提高有限元分析的準確性。
1 材料和方法
1.1 牙頜組織有限元模型構建
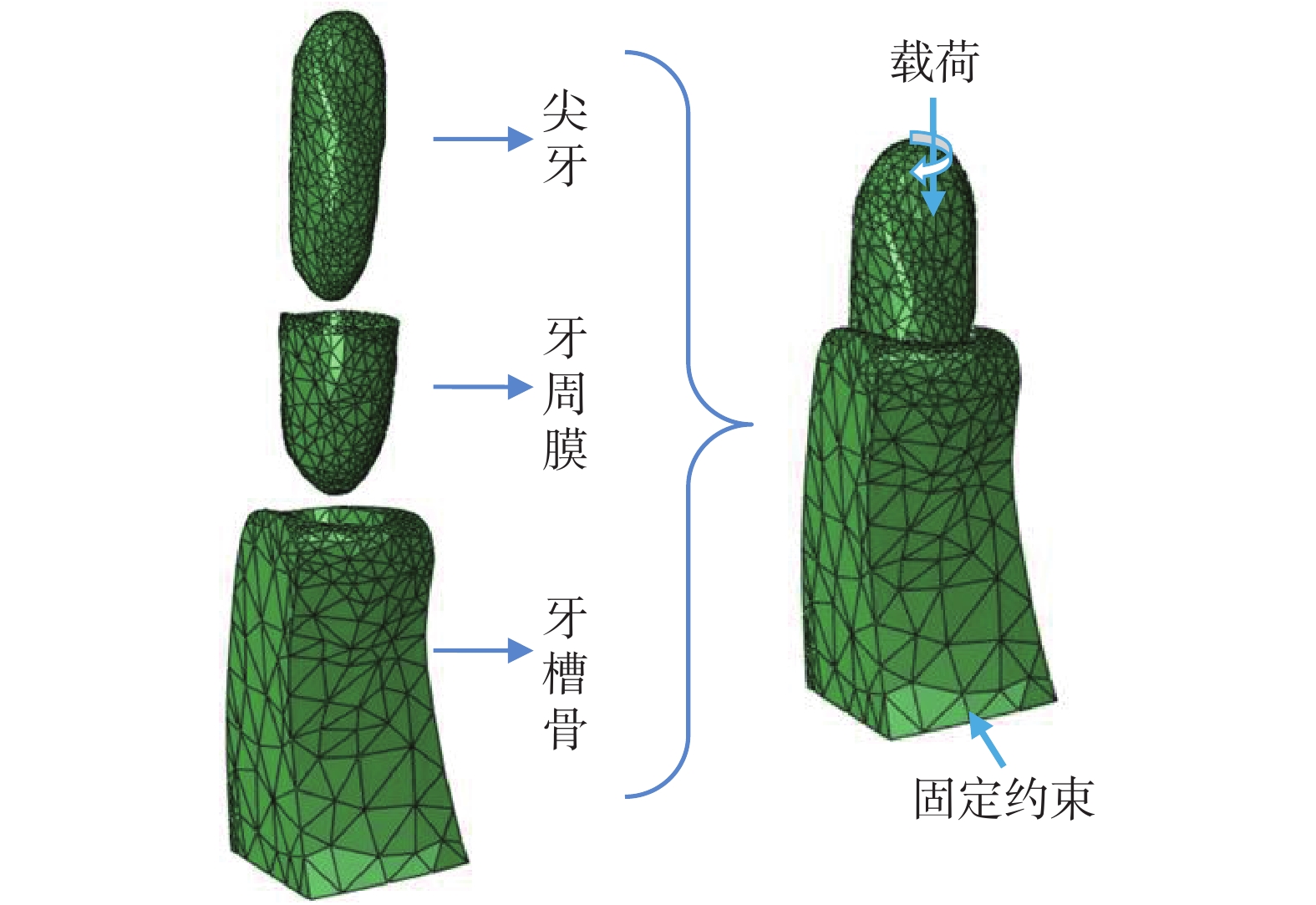
參照醫學倫理審查辦法,在受試者知情同意的前提下選擇浙江大學醫學院第二附屬醫院一例臨床病例作為研究對象,依據患者的螺旋 CT 圖像數據構建其下頜尖牙牙頜組織有限元模型。首先,將患者 CT 數據導入醫學影像處理軟件 Mimics 15.0(Materialise 公司,勒芬,比利時),通過閾值設定、掩膜編輯、區域增長和三維建模等手段建立尖牙及其牙槽骨的三角面片網格模型。接著將尖牙和牙槽骨的三角面片網格模型導入網格模型處理軟件 3-Matic 7.0(Materialise 公司,勒芬,比利時),將尖牙模型向外偏置 0.25 mm 之后與牙槽骨模型求交,然后減去原來的尖牙模型,獲得具有均勻厚度 0.25 mm 的牙周膜三角面片網格模型[18, 22]。進一步利用 3-Matic 7.0 軟件的網格編輯功能,對初步生成的三角面片網格模型進行網格細化、均勻等優化處理,然后基于模型表面的三角網格直接生成體網格模型,該體網格模型可直接被有限元分析軟件 Abaqus 6.13(達索 SIMULIA 公司,波士頓,美國)調用,且不需要再進行網格劃分。導入有限元 Abaqus 6.13 之后牙頜組織模型如圖 1 所示,主要包括尖牙、牙周膜和牙槽骨,其中牙周膜和牙槽骨的網格單元數量分別為 3 416 和 1 915。為了保證模型精度和網格質量,我們進行了相應的模型收斂性分析。當牙周膜和牙槽骨模型進一步精細化,網格數量均增加 1 倍時,牙周膜的最大靜水壓應力變化量小于 5%(模型收斂性測試時的標準誤差)。因此,在這項研究中模型的精度和網格質量是可接受的。模型中網格單元類型均為四節點線性雜交四面體單元(C3D4H)。
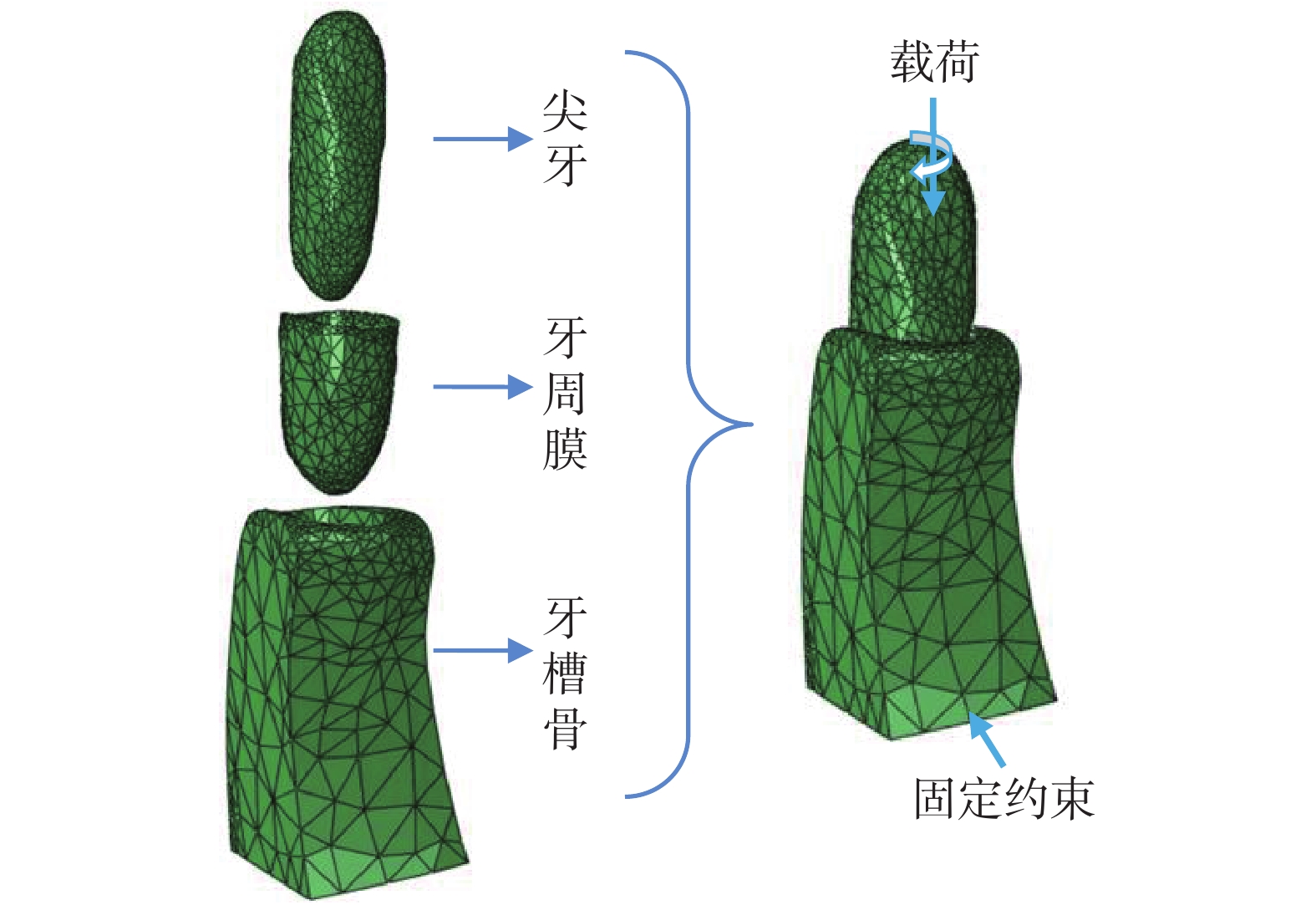 圖1
牙頜組織有限元模型
Figure1.
Finite element models of dental tissues
圖1
牙頜組織有限元模型
Figure1.
Finite element models of dental tissues
1.2 模型材料參數定義
尖牙相比于其他牙頜組織具有更高的硬度和彈性模量,因此在有限元分析中將其設定為剛體[10, 17]。牙周膜具有較薄的厚度和較小的尺寸,不僅具有類似固態橡膠的超彈性,還具有類似液態高分子材料的黏性[23-24],這里將其假定為一種均質的超-黏彈性體,使用二階 Ogden 超彈性模型和均一化的應力松弛函數模型共同描述其生物力學特性,如式(1)和(2)所示[25-26]。其中, 是應變能密度函數,
是應變能密度函數, 、
、 和
和  是應變能的三個主伸長率,
是應變能的三個主伸長率, 且
且  ,
, 是容積率,
是容積率, 是剪切模量,
是剪切模量, 是超彈性材料系數,
是超彈性材料系數, 是體積模量的倒數,
是體積模量的倒數, 是多項式的階數。
是多項式的階數。 是均一化的應力松弛函數,
是均一化的應力松弛函數, 是能量函數的系數,
是能量函數的系數, 是松弛時間常量,
是松弛時間常量, 是時間。公式(1)和(2)中使用的材料參數列于表 1[18, 25-26],G(I)、K(I)和 TAU(I)是牙周膜黏彈性模型參數的 Prony 形式,I 是階數。
是時間。公式(1)和(2)中使用的材料參數列于表 1[18, 25-26],G(I)、K(I)和 TAU(I)是牙周膜黏彈性模型參數的 Prony 形式,I 是階數。
 |
 |
對于牙槽骨模型材料參數的定義將采用兩種方式,一種依據牙槽骨網格單元所處的 CT 圖像灰度值  將其定義為非均質模型,另一種則對整體模型進行統一賦值定義為均質模型。將 1.1 中構建的牙槽骨體網格模型重新導入 Mimics 15.0,利用軟件自帶的材料賦值功能參照經驗公式(3)~(5)對牙槽骨的骨質密度
將其定義為非均質模型,另一種則對整體模型進行統一賦值定義為均質模型。將 1.1 中構建的牙槽骨體網格模型重新導入 Mimics 15.0,利用軟件自帶的材料賦值功能參照經驗公式(3)~(5)對牙槽骨的骨質密度  、彈性模量 E 和泊松比
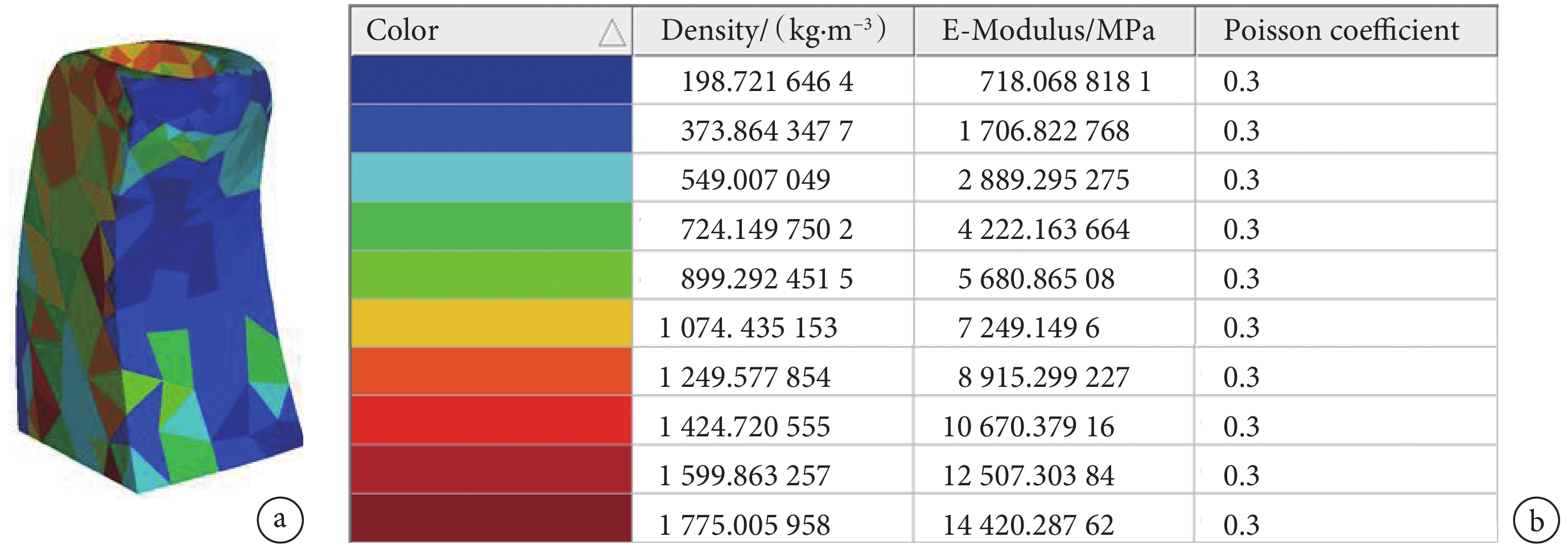
、彈性模量 E 和泊松比  進行定義[20, 27]。賦值完成之后的牙槽骨體網格模型如圖 2a 所示,模型中的網格單元被賦予不同的顏色表示其擁有不同的材料參數,每種顏色代表的材料參數如圖 2b 所示。該材料賦值方法的基本依據是不同骨密度的牙槽骨經掃描會獲得不同灰度值的 CT 圖像,如式(3)所示,骨質越致密其 CT 圖像灰度值就越高。另外,牙槽骨的彈性模量與其骨密度也存在密切聯系,如式(4)所示,牙槽骨骨密度越大其彈性模量越大,因此可以建立牙槽骨 CT 圖像灰度值與彈性模量之間的內在關系,并以此為基礎實現非均質牙槽骨模型的材料賦值,該方法被許多國內外學者所認可[20-21]。對于均質型牙槽骨模型材料參數的定義則直接將非均質模型中的網格單元進行統一賦值,取彈性模量 490 MPa,泊松比 0.3[9],從而保證均質模型和非均質模型具有完全相同的網格單元和節點。在這項對比研究中,除牙槽骨模型的力學特性不同以外,其他設置均完全相同,所以分析結果的差異性可能主要體現在牙槽骨彈性模量上。為此,我們進一步假設將均質型牙槽骨模型的彈性模量提高 10 倍至 4 900 MPa,其大小接近非均質牙槽骨模型中不同區域牙槽骨彈性模量的中間值,研究牙槽骨彈性模量可能對牙周膜力學響應產生的影響。為方便后續的分析討論,將均質型(E = 490 MPa)牙槽骨模型編號為①,非均質型牙槽骨模型編號為②,均質型(E = 4 900 MPa)牙槽骨模型編號為③。在有限元分析過程中,所有模型均假設為各向同性體。
進行定義[20, 27]。賦值完成之后的牙槽骨體網格模型如圖 2a 所示,模型中的網格單元被賦予不同的顏色表示其擁有不同的材料參數,每種顏色代表的材料參數如圖 2b 所示。該材料賦值方法的基本依據是不同骨密度的牙槽骨經掃描會獲得不同灰度值的 CT 圖像,如式(3)所示,骨質越致密其 CT 圖像灰度值就越高。另外,牙槽骨的彈性模量與其骨密度也存在密切聯系,如式(4)所示,牙槽骨骨密度越大其彈性模量越大,因此可以建立牙槽骨 CT 圖像灰度值與彈性模量之間的內在關系,并以此為基礎實現非均質牙槽骨模型的材料賦值,該方法被許多國內外學者所認可[20-21]。對于均質型牙槽骨模型材料參數的定義則直接將非均質模型中的網格單元進行統一賦值,取彈性模量 490 MPa,泊松比 0.3[9],從而保證均質模型和非均質模型具有完全相同的網格單元和節點。在這項對比研究中,除牙槽骨模型的力學特性不同以外,其他設置均完全相同,所以分析結果的差異性可能主要體現在牙槽骨彈性模量上。為此,我們進一步假設將均質型牙槽骨模型的彈性模量提高 10 倍至 4 900 MPa,其大小接近非均質牙槽骨模型中不同區域牙槽骨彈性模量的中間值,研究牙槽骨彈性模量可能對牙周膜力學響應產生的影響。為方便后續的分析討論,將均質型(E = 490 MPa)牙槽骨模型編號為①,非均質型牙槽骨模型編號為②,均質型(E = 4 900 MPa)牙槽骨模型編號為③。在有限元分析過程中,所有模型均假設為各向同性體。
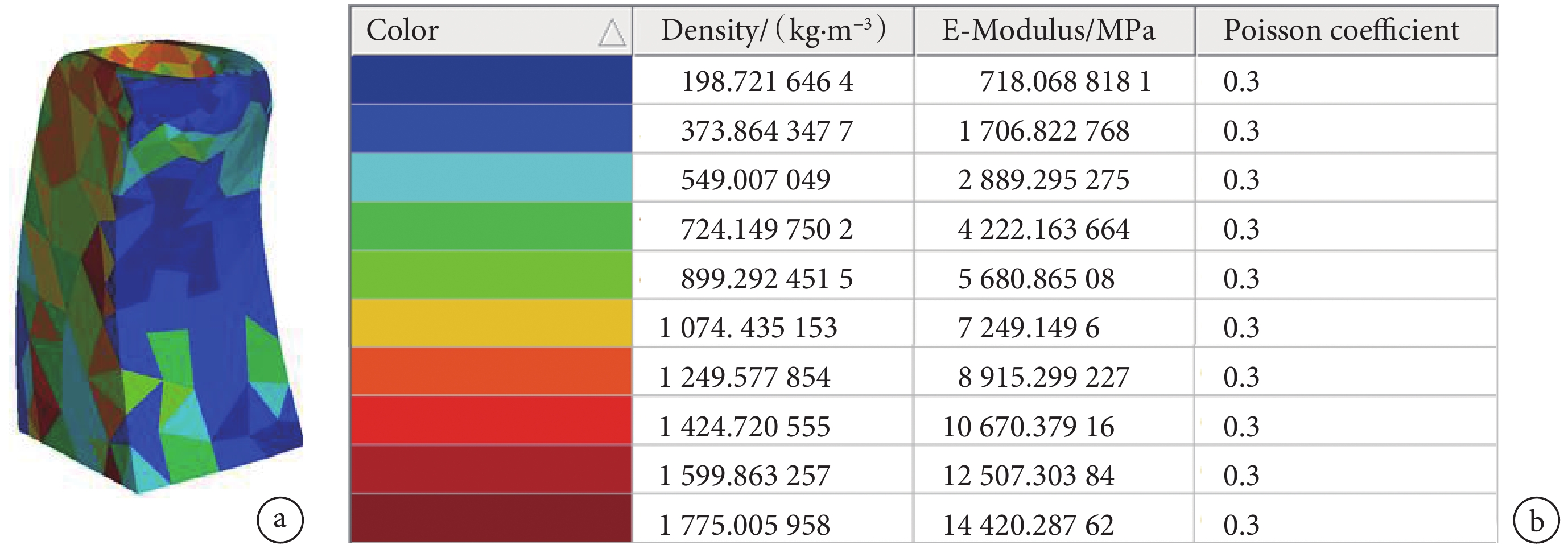 圖2
非均質牙槽骨模型
圖2
非均質牙槽骨模型
a. 牙槽骨體網格模型;b. 不同顏色代表的材料參數
Figure2. Non-uniform model of alveolar bonea. volume mesh model of alveolar bone; b. material parameters represented by colour coding
 |
 |
 |
1.3 有限元模型約束條件及載荷
有限元分析中,牙槽骨的底部完全固定,矯治力施加在尖牙牙冠的中心位置,如圖 1 所示,牙周膜與牙槽骨、牙周膜與尖牙之間的接觸關系均為綁定。臨床正畸治療中,牙齒整體移動所需要的最佳矯治力范圍為 1.0~1.5 N[4],牙齒繞根向轉動所需要的最佳矯治力矩范圍為 2.0~3.0 Nmm[28]。因此,選擇分別對尖牙施加 1 N 的根向壓入力和 2 Nmm 的根向扭矩,研究不同載荷形式下牙周膜對均質型和非均質型牙槽骨模型力學響應的差異,主要參考牙周膜靜水壓應力和最大對數主應變。
2 結果
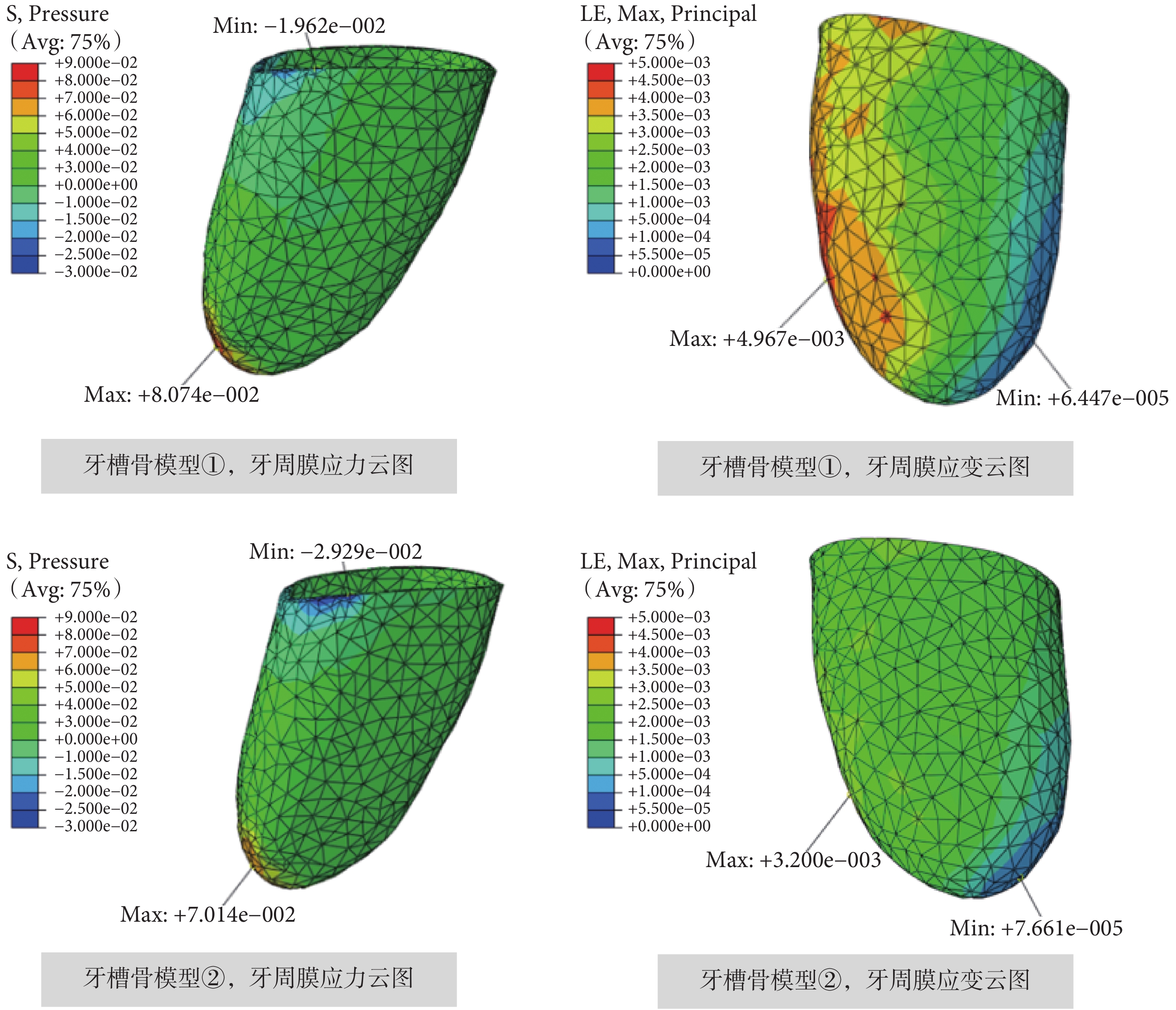
當對尖牙施加 1 N 大小的根向壓入力時,牙周膜對① 均質型(E = 490 MPa)和② 非均質型牙槽骨模型的應力和應變響應如圖 3 所示。牙周膜應力為正值表示牙周膜處于受壓的狀態,反之,牙周膜應力為負值表示牙周膜處于受拉的狀態。牙周膜應變為正值表示牙周膜處于受拉的狀態,而牙周膜應變為負值則表示牙周膜處于受壓的狀態。從圖 3 中可以看出,尖牙受 1 N 根向壓入力時,對于不同類型的牙槽骨模型,牙周膜最大和最小應力應變出現的位置基本相同,但是具體數值卻不一樣。如表 2 所列,與① 均質型牙槽骨模型(E = 490 MPa)相比,當牙槽骨模型為② 非均質模型時,牙周膜的最大應力降低了 13.13%,同時最小應力提高了 49.29%;牙周膜的最大應變降低了 35.57%,最小應變則提高了 18.83%。可見,對于不同類型的牙槽骨模型,在牙齒平動時牙周膜的應力和應變響應均存在一定差異。
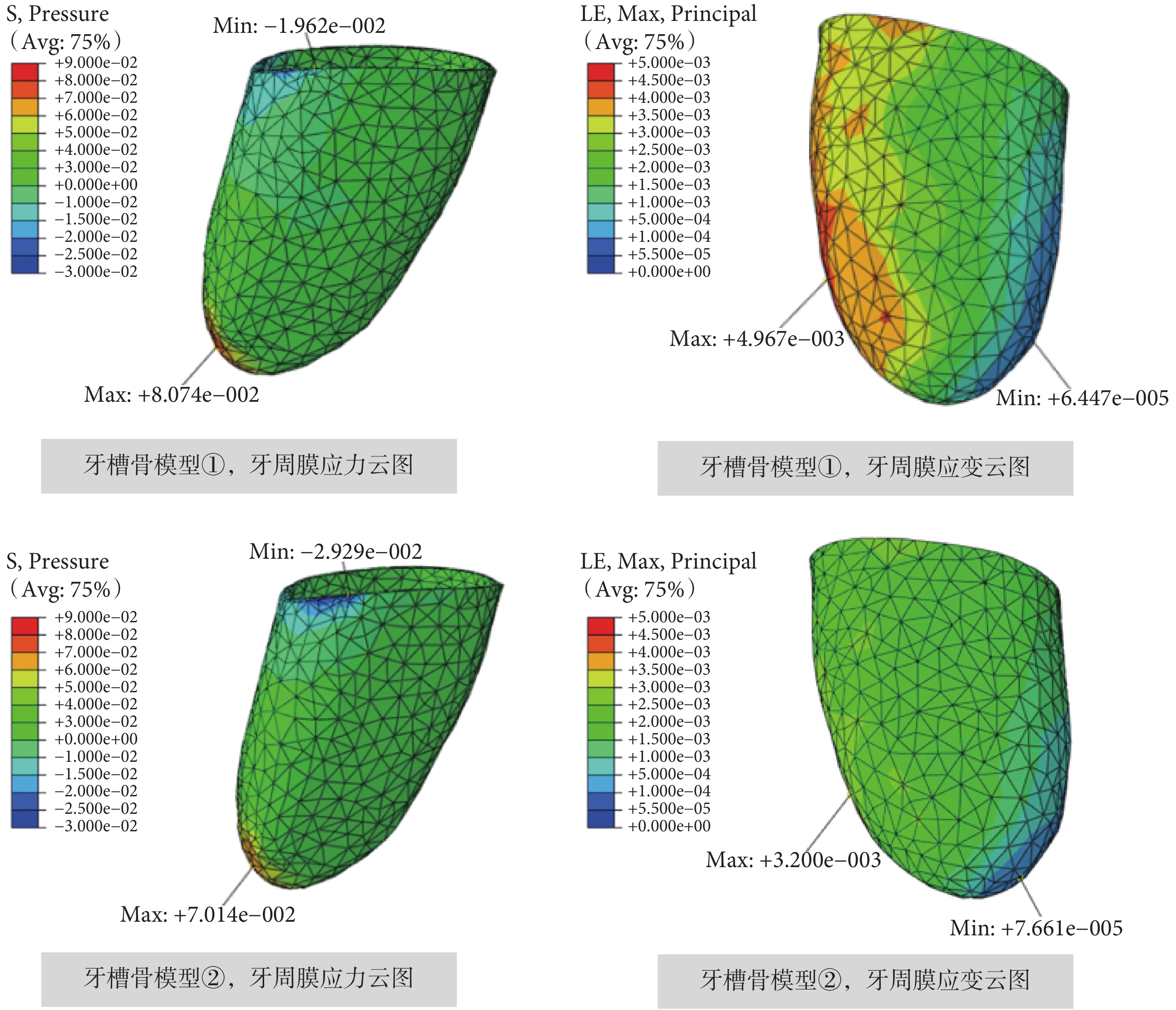 圖3
對尖牙施加 1 N 根向壓入力,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure3.
Loading 1 N force to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
圖3
對尖牙施加 1 N 根向壓入力,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure3.
Loading 1 N force to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
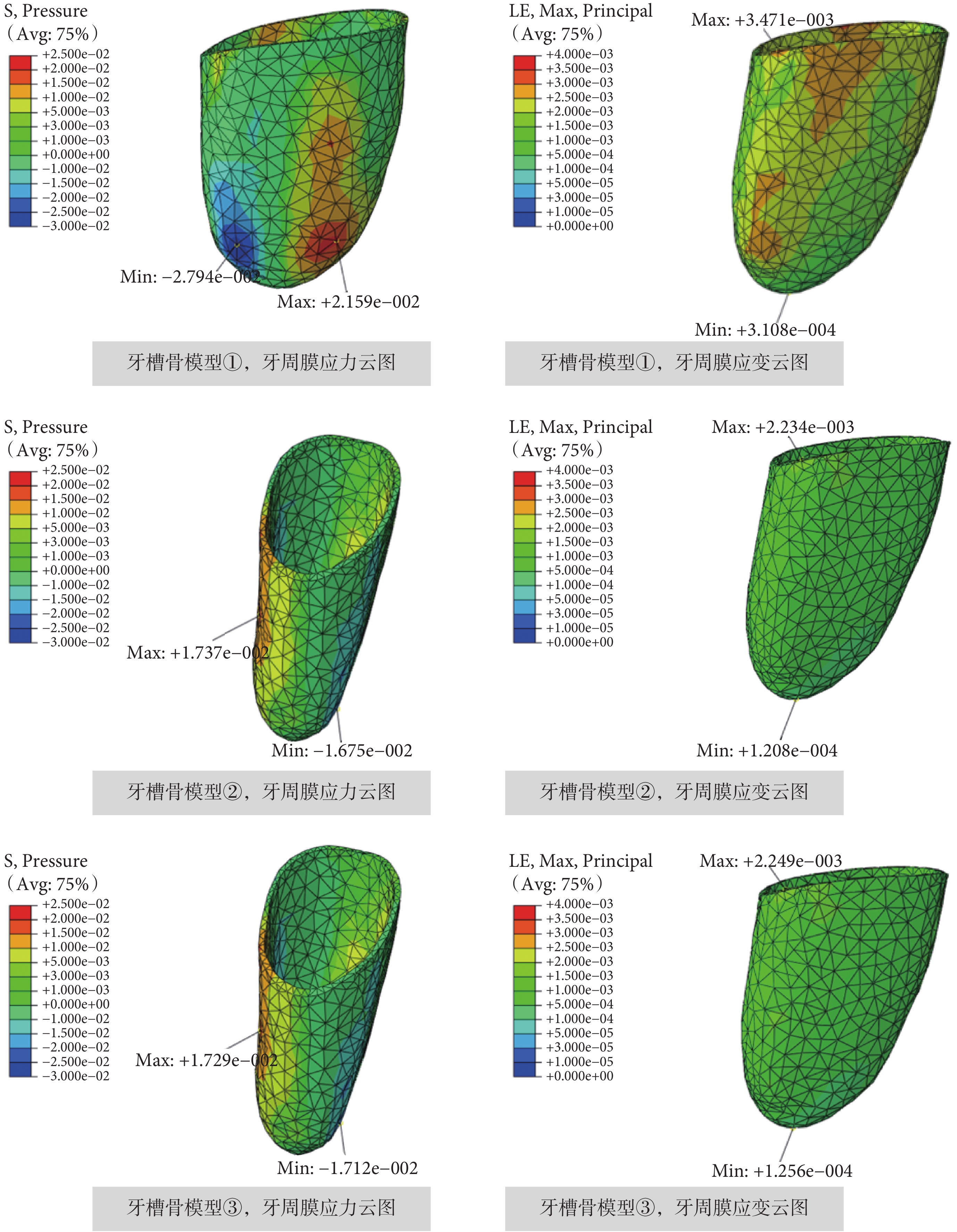
當對尖牙施加 2 Nmm 的根向扭矩時,牙周膜對① 均質型(E = 490 MPa)和② 非均質型牙槽骨模型的應力和應變響應如圖 4 所示。從圖 4 中可以看出對于不同類型牙槽骨模型①和②,牙周膜最小應力、最大和最小應變出現的位置基本相同,但牙周膜最大應力出現的位置卻不相同。此外,牙周膜最大和最小應力應變值也因牙槽骨模型的不同而存在一定差異。如表 2 所列,與① 均質型牙槽骨模型相比,當牙槽骨模型為② 非均質模型時,牙周膜的最大和最小應力分別降低了 19.55% 和 40.05%,牙周膜最大和最小應變分別降低了 35.64% 和 61.13%。可見,對于不同類型的牙槽骨模型,在牙齒轉動時牙周膜的應力和應變響應也存在一定差異。
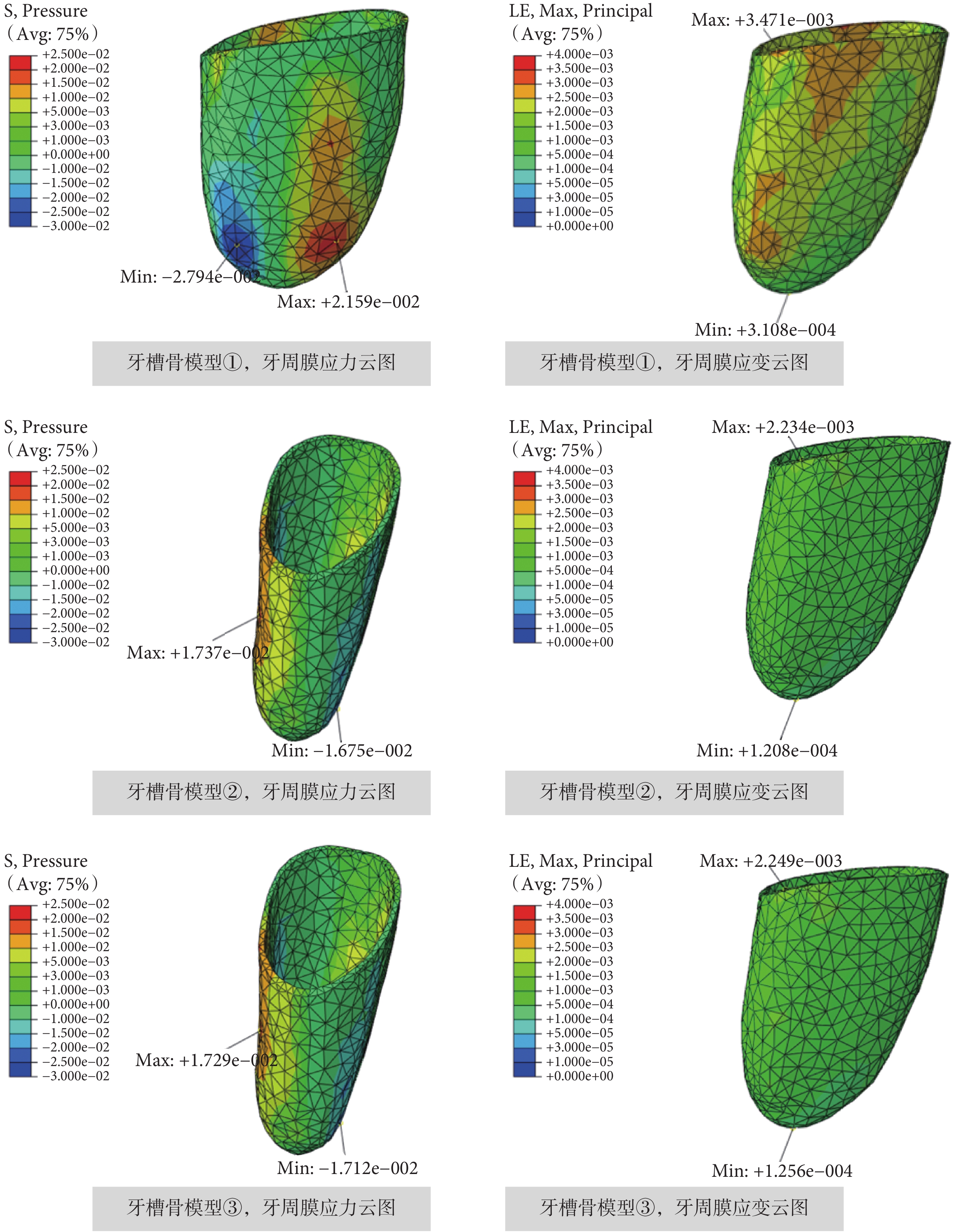 圖4
對尖牙施加 2 Nmm 根向扭矩,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure4.
Loading 2 Nmm moment to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
圖4
對尖牙施加 2 Nmm 根向扭矩,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure4.
Loading 2 Nmm moment to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
如圖 4 所示,當對尖牙施加 2 Nmm 的根向扭矩時,不同彈性模量的均質型牙槽骨模型①和③ 對牙周膜應力應變響應的影響也存在一定差異。當牙槽骨彈性模量提高至 4 900 MPa 之后,所引起的牙周膜最小應力、最大和最小應變出現的位置基本相同,但具體數值因牙槽骨彈性模量的不同而有所差異。如表 2 所列,當牙槽骨的彈性模量提高 10 倍之后,牙周膜的最大和最小應力值分別降低了 19.92% 和 38.73%,牙周膜最大和最小應變值也分別降低了 35.21% 和 59.59%。可見,矯治力作用下牙周膜的生物力學響應很大程度上受牙槽骨彈性模量的影響。
3 討論
通過上述的有限元分析可知,無論在牙齒平動或是轉動時,牙槽骨模型均會對牙周膜的生物力學響應產生影響。當牙槽骨由① 均質模型轉為② 非均質模型時,牙周膜的最大應力值在一定程度上降低了。有研究表明牙周膜的應力與牙齒移動過程中的牙根吸收有關[9-10],當牙周膜應力過大時會造成牙周膜局部血流閉塞,誘發牙根吸收[1-2]。可見采用均質型牙槽骨模型研究矯治力作用下牙周膜的應力時更偏向于獲得較高的應力值,進而選擇一個更保守的矯治力。另一方面,牙周膜的應變與矯治過程中牙齒的移動速度相關,在一定范圍內牙周膜的應變越大則牙齒的移動速度就越快[7-8],當采用均質型牙槽骨模型研究牙周膜的應變分布時會獲得一個較大的應變值,進而認為牙齒已具有較高的移動速度,同樣會引導正畸醫生選擇一個較小的矯治力。矯治力過小會延長正畸治療周期,降低患者配合治療的意愿,難以實現理想的正畸治療[4]。
另外,我們假設將① 均質型牙槽骨模型彈性模量增大 10 倍,重點分析了在尖牙受到 2 Nmm 的根向扭矩時,牙周膜對不同彈性模量的牙槽骨力學響應的差異性。從有限元分析結果(表 2)可以看出在模型網格和節點完全相同的情況下,當牙槽骨彈性模量提高之后,牙周膜的最大應力和最大應變均有所降低。所以,采用高彈性模量的牙槽骨模型進行有限元分析時,分析結果會引導正畸醫生選擇較高的矯治力,相反,低彈性模量的牙槽骨模型則會誘導醫生選擇一個更低的矯治力。然而,更高或者更低的矯治力均不利于正畸治療[4, 8-9]。為了獲得更加安全高效的正畸治療,明確載荷作用下牙周膜的生物力學響應至關重要。因此,根據患者牙槽骨的實際情況,設定合適的牙槽骨力學參數,對于采用有限元法研究正畸治療非常重要。
牙槽骨作為結構復雜的人體生物組織,內部含有神經管、骨小梁、骨髓小腔等組織結構,不同區域的力學特性差異很大[7, 17]。位于牙槽骨表層的骨組織骨質致密、強度高,稱為皮質骨;位于牙槽骨內部的骨組織則骨質疏松,呈海綿狀,稱為松質骨[20, 27]。在認識到牙周膜生物力學響應受牙槽骨力學特性影響的前提下,構建符合人體牙槽骨生物力學特性的有限元模型對于提高有限元分析結果的精確度有著積極促進作用。相比于均質型牙槽骨模型,非均質型牙槽骨模型模糊了皮質骨和松質骨的界限,依據每個網格單元所處的 CT 圖像灰度值對網格單元進行材料賦值,突顯出牙槽骨不同區域骨質特性的差異性,更加貼近牙槽骨實際狀況,有利于獲得更加準確的分析結果。值得注意的是,非均質牙槽骨模型的整體材料屬性在一定程度上受其網格單元尺寸的影響。模型中網格尺寸越小,每個單元越能依據其所在的微小局部 CT 圖像進行個性化材料賦值,越容易獲得更加細致的、差異性的牙槽骨模型。當網格尺寸變大時,其所覆蓋的 CT 圖像區域也更大,即便覆蓋區域的 CT 圖像有一定差異,也無法對該網格單元實現多種材料賦值。如圖 2a 所示,從牙槽骨的橫斷面來看,皮質骨和松質骨的分界面并不明顯,其中一部分原因就是該斷面上牙槽骨網格單元的尺寸過大。不過,從模型收斂性測試結果來看,邊緣區域過大的牙槽骨網格單元并沒有對牙周膜的力學響應產生不可忽視的影響。
在非均質牙槽骨模型中,采用 CT 圖像灰度值進行材料賦值的網格單元中最大的彈性模量是 14 420.28 MPa,其量級與其他研究中報道的皮質骨彈性模量 13 700 MPa 非常接近[7, 17],間接證明了材料賦值公式的準確性。另外,如圖 2a 所示,牙槽骨模型表面的部分區域被表示低彈性模量的藍色所覆蓋,這與處于真實牙槽骨表面的皮質骨力學特性不符。這主要是因為人體牙槽骨外還附著有骨膜和牙齦等組織結構,在牙槽骨模型構建過程中,有一部分口腔軟組織被當作牙槽骨進行了重建,但這并不會對有限元分析結果產生影響,從中我們也可以發現非均質模型的另外一個優點。一般來說,對于牙槽骨模型邊界的劃定主要依靠人工進行手動分割,操作者的熟練程度和工作經驗直接影響著牙槽骨模型的結構和大小,如果采用均質模型進行建模,那么模型構造上可能就與真實的牙槽骨存在結構差異,在一定程度上影響了分析結果。而當采用非均質建模方法時,因模型中的所有網格單元均依據其所在的 CT 圖像灰度值進行材料賦值,即便有一部分外層軟組織或者牙槽骨內部的骨髓小腔、神經管空腔等力學特性遠異于骨組織的組織結構,被誤以為牙槽骨進行有限元建模,也會因其 CT 圖像灰度值偏低被賦予相應的材料參數,不會因模型精度影響有限元分析結果。
4 結論
以一例臨床病例作為研究對象,基于患者的 CT 圖像構建了其尖牙、牙周膜和牙槽骨的有限元模型。其中,牙槽骨模型分別設定為均質模型和非均質模型,其他牙頜組織模型設定均相同。通過對尖牙施加根向矯治力和扭矩探究牙周膜在不同牙槽骨模型下的應力應變響應。結果表明:(1)無論牙齒平動或是轉動,當牙槽骨為均質模型時,牙周膜在同等條件下會產生更大的應力和應變,會誤導正畸醫生選擇一個較小的矯治力;(2)牙周膜的生物力學響應受牙槽骨力學參數影響較為顯著,當牙槽骨彈性模量由 490 MPa 增大 10 倍至 4 900 MPa 時,牙周膜的最大應力和應變值分別降低了 19.92% 和 35.21%;(3)相比于均質牙槽骨模型,非均質牙槽骨模型依據每個網格單元所處的 CT 圖像灰度值對模型進行材料賦值,更能體現真實牙槽骨組織骨質特性的差異性,有助于提高有限元分析的精確性。研究結果為構建更加精確的牙頜組織有限元模型提供了技術支持。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
臨床正畸治療中,錯位牙齒的矯正主要依靠患者口腔佩戴的正畸矯治器。矯治器形變產生矯治力,矯治力首先作用在錯位牙齒的牙冠上,并通過牙體傳遞給牙周膜,進一步經過牙周膜的緩沖、吸收作用于牙槽骨,進而激發牙槽骨改建,最終在矯治力的作用下,牙齒逐漸移動到理想位置[1-4]。在牙齒移動過程中,牙周膜作為介于牙齒和牙槽骨之間的一層結締纖維組織,在激發骨改建、誘導牙齒移動中起著重要作用[5-6]。有研究表明牙齒矯治過程中的移動速度與牙周膜的應變密切相關[7-8],牙根的吸收情況則與牙周膜的應力有關[9-10]。因此,研究牙周膜受載之后的生物力學響應對于明確正畸矯治機制、優化正畸治療方案具有非常重要的意義。
對于牙周膜生物特性的研究方法主要包括實驗測試和有限元模擬。牙周膜作為人體生物組織,一方面實驗材料來源非常有限;另一方面,牙周膜一般厚度僅有 0.2~0.3 mm[11],極易遭到破壞而失去生物活性,存放條件非常苛刻[12]。另外,對于牙周膜的臨床測試也因患者意愿、裝置結構復雜、跟蹤記錄周期長、數據處理繁瑣等因素難以獲得直接有效的試驗結果[13]。因此,在實驗條件有限的情況下,更多的人采用有限元法對其進行研究。目前有限元法已廣泛用于口腔正畸醫療領域,具有準確度高、重復性好和可操作性強等優點,受到越來越多的研究人員青睞[9, 14]。
在采用有限元法對正畸矯治機制進行研究時,構建牙頜組織有限元模型至關重要。正畸過程中涉及到的牙頜組織主要包括牙齒、牙周膜和牙槽骨。牙齒相比于其他牙頜組織具有很高的硬度,彈性模量可達 20 GPa[15-16],因此在有限元分析中多把牙齒設定為剛體[10, 17]。牙周膜因其厚度較薄、尺寸較小,則一般假定為厚度均勻、均質、各向同性的超-黏彈性體[12, 18]。對于牙槽骨模型的構建方法則主要有兩種:第一種是采用非均勻有理 B 樣條(non-uniform rational b-splines,NURBS)曲面擬合的方式將牙槽骨三角面片網格模型轉化為實體模型,然后將其導入有限元軟件進行整體網格劃分、材料賦值得到牙槽骨有限元模型[3, 19]。這種建模方法獲得牙槽骨模型每個網格單元的材料特性都相同,屬于均質型模型。雖然有些學者按照牙槽骨骨質特性將其人為地分為皮質骨和松質骨[7, 19],但對于整個皮質骨或者松質骨而言,模型的每個單元材料特性也都一樣。另一種方法則直接利用牙槽骨三角面片網格模型生成體網格模型,并依據模型中每個網格單元所處的計算機斷層掃描(computed tomography,CT)圖像灰度值對單元進行差別材料賦值[18, 20],不再利用有限元軟件進行網格劃分和材料賦值,這種建模方法獲得牙槽骨模型每個網格單元的材料特性均不相同,屬于非均質模型。
目前,上述兩種建模方法均有使用,如 Liao 等[9]為了研究牙周膜在正畸力優化中的作用構建了精細的均質型牙槽骨模型,Ashrafi 等[15]、Cozzani 等[16]和 Benaissa 等[19]也都在自己最新的研究中采用了第一種建模方法;而 Wu 等[18]、Liu 等[20]和 Bujtar 等[21]則采用第二種方法構建了非均質牙槽骨模型用于有限元分析計算。Liu 等[20]進一步對比分析了兩種建模方法在構建下頜骨有限元模型中的優劣勢,結果表明非均質模型更有利于構建具有復雜幾何構造的頜骨模型。而針對不同類型的牙槽骨模型,牙周膜受載之后的生物力學響應是否存在差異卻鮮有報道。多數學者習慣采用第一種建模方法構建均質型的牙槽骨模型,對于模型的材料賦值也通常機械式地借鑒他人的材料參數,然而有限元模型的精確度對其分析結果卻有著不可忽視的影響。
為此,我們將基于一例臨床患者的螺旋 CT 圖像數據,選擇其下頜尖牙作為研究對象,構建其牙頜組織有限元模型,分別將其牙槽骨設置為均質型模型和非均質型模型,對尖牙施加牙根向的壓入力和扭矩,研究不同牙槽骨模型作用下的牙周膜應力和應變,進而明確不同牙槽骨仿真模型對牙周膜生物力學響應的影響,協助相關研究人員選擇合適的牙槽骨建模方法,從而提高有限元分析的準確性。
1 材料和方法
1.1 牙頜組織有限元模型構建
參照醫學倫理審查辦法,在受試者知情同意的前提下選擇浙江大學醫學院第二附屬醫院一例臨床病例作為研究對象,依據患者的螺旋 CT 圖像數據構建其下頜尖牙牙頜組織有限元模型。首先,將患者 CT 數據導入醫學影像處理軟件 Mimics 15.0(Materialise 公司,勒芬,比利時),通過閾值設定、掩膜編輯、區域增長和三維建模等手段建立尖牙及其牙槽骨的三角面片網格模型。接著將尖牙和牙槽骨的三角面片網格模型導入網格模型處理軟件 3-Matic 7.0(Materialise 公司,勒芬,比利時),將尖牙模型向外偏置 0.25 mm 之后與牙槽骨模型求交,然后減去原來的尖牙模型,獲得具有均勻厚度 0.25 mm 的牙周膜三角面片網格模型[18, 22]。進一步利用 3-Matic 7.0 軟件的網格編輯功能,對初步生成的三角面片網格模型進行網格細化、均勻等優化處理,然后基于模型表面的三角網格直接生成體網格模型,該體網格模型可直接被有限元分析軟件 Abaqus 6.13(達索 SIMULIA 公司,波士頓,美國)調用,且不需要再進行網格劃分。導入有限元 Abaqus 6.13 之后牙頜組織模型如圖 1 所示,主要包括尖牙、牙周膜和牙槽骨,其中牙周膜和牙槽骨的網格單元數量分別為 3 416 和 1 915。為了保證模型精度和網格質量,我們進行了相應的模型收斂性分析。當牙周膜和牙槽骨模型進一步精細化,網格數量均增加 1 倍時,牙周膜的最大靜水壓應力變化量小于 5%(模型收斂性測試時的標準誤差)。因此,在這項研究中模型的精度和網格質量是可接受的。模型中網格單元類型均為四節點線性雜交四面體單元(C3D4H)。
 圖1
牙頜組織有限元模型
Figure1.
Finite element models of dental tissues
圖1
牙頜組織有限元模型
Figure1.
Finite element models of dental tissues
1.2 模型材料參數定義
尖牙相比于其他牙頜組織具有更高的硬度和彈性模量,因此在有限元分析中將其設定為剛體[10, 17]。牙周膜具有較薄的厚度和較小的尺寸,不僅具有類似固態橡膠的超彈性,還具有類似液態高分子材料的黏性[23-24],這里將其假定為一種均質的超-黏彈性體,使用二階 Ogden 超彈性模型和均一化的應力松弛函數模型共同描述其生物力學特性,如式(1)和(2)所示[25-26]。其中, 是應變能密度函數,
是應變能密度函數, 、
、 和
和  是應變能的三個主伸長率,
是應變能的三個主伸長率, 且
且  ,
, 是容積率,
是容積率, 是剪切模量,
是剪切模量, 是超彈性材料系數,
是超彈性材料系數, 是體積模量的倒數,
是體積模量的倒數, 是多項式的階數。
是多項式的階數。 是均一化的應力松弛函數,
是均一化的應力松弛函數, 是能量函數的系數,
是能量函數的系數, 是松弛時間常量,
是松弛時間常量, 是時間。公式(1)和(2)中使用的材料參數列于表 1[18, 25-26],G(I)、K(I)和 TAU(I)是牙周膜黏彈性模型參數的 Prony 形式,I 是階數。
是時間。公式(1)和(2)中使用的材料參數列于表 1[18, 25-26],G(I)、K(I)和 TAU(I)是牙周膜黏彈性模型參數的 Prony 形式,I 是階數。
 |
 |
對于牙槽骨模型材料參數的定義將采用兩種方式,一種依據牙槽骨網格單元所處的 CT 圖像灰度值  將其定義為非均質模型,另一種則對整體模型進行統一賦值定義為均質模型。將 1.1 中構建的牙槽骨體網格模型重新導入 Mimics 15.0,利用軟件自帶的材料賦值功能參照經驗公式(3)~(5)對牙槽骨的骨質密度
將其定義為非均質模型,另一種則對整體模型進行統一賦值定義為均質模型。將 1.1 中構建的牙槽骨體網格模型重新導入 Mimics 15.0,利用軟件自帶的材料賦值功能參照經驗公式(3)~(5)對牙槽骨的骨質密度  、彈性模量 E 和泊松比
、彈性模量 E 和泊松比  進行定義[20, 27]。賦值完成之后的牙槽骨體網格模型如圖 2a 所示,模型中的網格單元被賦予不同的顏色表示其擁有不同的材料參數,每種顏色代表的材料參數如圖 2b 所示。該材料賦值方法的基本依據是不同骨密度的牙槽骨經掃描會獲得不同灰度值的 CT 圖像,如式(3)所示,骨質越致密其 CT 圖像灰度值就越高。另外,牙槽骨的彈性模量與其骨密度也存在密切聯系,如式(4)所示,牙槽骨骨密度越大其彈性模量越大,因此可以建立牙槽骨 CT 圖像灰度值與彈性模量之間的內在關系,并以此為基礎實現非均質牙槽骨模型的材料賦值,該方法被許多國內外學者所認可[20-21]。對于均質型牙槽骨模型材料參數的定義則直接將非均質模型中的網格單元進行統一賦值,取彈性模量 490 MPa,泊松比 0.3[9],從而保證均質模型和非均質模型具有完全相同的網格單元和節點。在這項對比研究中,除牙槽骨模型的力學特性不同以外,其他設置均完全相同,所以分析結果的差異性可能主要體現在牙槽骨彈性模量上。為此,我們進一步假設將均質型牙槽骨模型的彈性模量提高 10 倍至 4 900 MPa,其大小接近非均質牙槽骨模型中不同區域牙槽骨彈性模量的中間值,研究牙槽骨彈性模量可能對牙周膜力學響應產生的影響。為方便后續的分析討論,將均質型(E = 490 MPa)牙槽骨模型編號為①,非均質型牙槽骨模型編號為②,均質型(E = 4 900 MPa)牙槽骨模型編號為③。在有限元分析過程中,所有模型均假設為各向同性體。
進行定義[20, 27]。賦值完成之后的牙槽骨體網格模型如圖 2a 所示,模型中的網格單元被賦予不同的顏色表示其擁有不同的材料參數,每種顏色代表的材料參數如圖 2b 所示。該材料賦值方法的基本依據是不同骨密度的牙槽骨經掃描會獲得不同灰度值的 CT 圖像,如式(3)所示,骨質越致密其 CT 圖像灰度值就越高。另外,牙槽骨的彈性模量與其骨密度也存在密切聯系,如式(4)所示,牙槽骨骨密度越大其彈性模量越大,因此可以建立牙槽骨 CT 圖像灰度值與彈性模量之間的內在關系,并以此為基礎實現非均質牙槽骨模型的材料賦值,該方法被許多國內外學者所認可[20-21]。對于均質型牙槽骨模型材料參數的定義則直接將非均質模型中的網格單元進行統一賦值,取彈性模量 490 MPa,泊松比 0.3[9],從而保證均質模型和非均質模型具有完全相同的網格單元和節點。在這項對比研究中,除牙槽骨模型的力學特性不同以外,其他設置均完全相同,所以分析結果的差異性可能主要體現在牙槽骨彈性模量上。為此,我們進一步假設將均質型牙槽骨模型的彈性模量提高 10 倍至 4 900 MPa,其大小接近非均質牙槽骨模型中不同區域牙槽骨彈性模量的中間值,研究牙槽骨彈性模量可能對牙周膜力學響應產生的影響。為方便后續的分析討論,將均質型(E = 490 MPa)牙槽骨模型編號為①,非均質型牙槽骨模型編號為②,均質型(E = 4 900 MPa)牙槽骨模型編號為③。在有限元分析過程中,所有模型均假設為各向同性體。
 圖2
非均質牙槽骨模型
圖2
非均質牙槽骨模型
a. 牙槽骨體網格模型;b. 不同顏色代表的材料參數
Figure2. Non-uniform model of alveolar bonea. volume mesh model of alveolar bone; b. material parameters represented by colour coding
 |
 |
 |
1.3 有限元模型約束條件及載荷
有限元分析中,牙槽骨的底部完全固定,矯治力施加在尖牙牙冠的中心位置,如圖 1 所示,牙周膜與牙槽骨、牙周膜與尖牙之間的接觸關系均為綁定。臨床正畸治療中,牙齒整體移動所需要的最佳矯治力范圍為 1.0~1.5 N[4],牙齒繞根向轉動所需要的最佳矯治力矩范圍為 2.0~3.0 Nmm[28]。因此,選擇分別對尖牙施加 1 N 的根向壓入力和 2 Nmm 的根向扭矩,研究不同載荷形式下牙周膜對均質型和非均質型牙槽骨模型力學響應的差異,主要參考牙周膜靜水壓應力和最大對數主應變。
2 結果
當對尖牙施加 1 N 大小的根向壓入力時,牙周膜對① 均質型(E = 490 MPa)和② 非均質型牙槽骨模型的應力和應變響應如圖 3 所示。牙周膜應力為正值表示牙周膜處于受壓的狀態,反之,牙周膜應力為負值表示牙周膜處于受拉的狀態。牙周膜應變為正值表示牙周膜處于受拉的狀態,而牙周膜應變為負值則表示牙周膜處于受壓的狀態。從圖 3 中可以看出,尖牙受 1 N 根向壓入力時,對于不同類型的牙槽骨模型,牙周膜最大和最小應力應變出現的位置基本相同,但是具體數值卻不一樣。如表 2 所列,與① 均質型牙槽骨模型(E = 490 MPa)相比,當牙槽骨模型為② 非均質模型時,牙周膜的最大應力降低了 13.13%,同時最小應力提高了 49.29%;牙周膜的最大應變降低了 35.57%,最小應變則提高了 18.83%。可見,對于不同類型的牙槽骨模型,在牙齒平動時牙周膜的應力和應變響應均存在一定差異。
 圖3
對尖牙施加 1 N 根向壓入力,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure3.
Loading 1 N force to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
圖3
對尖牙施加 1 N 根向壓入力,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure3.
Loading 1 N force to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
當對尖牙施加 2 Nmm 的根向扭矩時,牙周膜對① 均質型(E = 490 MPa)和② 非均質型牙槽骨模型的應力和應變響應如圖 4 所示。從圖 4 中可以看出對于不同類型牙槽骨模型①和②,牙周膜最小應力、最大和最小應變出現的位置基本相同,但牙周膜最大應力出現的位置卻不相同。此外,牙周膜最大和最小應力應變值也因牙槽骨模型的不同而存在一定差異。如表 2 所列,與① 均質型牙槽骨模型相比,當牙槽骨模型為② 非均質模型時,牙周膜的最大和最小應力分別降低了 19.55% 和 40.05%,牙周膜最大和最小應變分別降低了 35.64% 和 61.13%。可見,對于不同類型的牙槽骨模型,在牙齒轉動時牙周膜的應力和應變響應也存在一定差異。
 圖4
對尖牙施加 2 Nmm 根向扭矩,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure4.
Loading 2 Nmm moment to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
圖4
對尖牙施加 2 Nmm 根向扭矩,不同牙槽骨模型作用下的牙周膜應力和應變云圖
Figure4.
Loading 2 Nmm moment to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
如圖 4 所示,當對尖牙施加 2 Nmm 的根向扭矩時,不同彈性模量的均質型牙槽骨模型①和③ 對牙周膜應力應變響應的影響也存在一定差異。當牙槽骨彈性模量提高至 4 900 MPa 之后,所引起的牙周膜最小應力、最大和最小應變出現的位置基本相同,但具體數值因牙槽骨彈性模量的不同而有所差異。如表 2 所列,當牙槽骨的彈性模量提高 10 倍之后,牙周膜的最大和最小應力值分別降低了 19.92% 和 38.73%,牙周膜最大和最小應變值也分別降低了 35.21% 和 59.59%。可見,矯治力作用下牙周膜的生物力學響應很大程度上受牙槽骨彈性模量的影響。
3 討論
通過上述的有限元分析可知,無論在牙齒平動或是轉動時,牙槽骨模型均會對牙周膜的生物力學響應產生影響。當牙槽骨由① 均質模型轉為② 非均質模型時,牙周膜的最大應力值在一定程度上降低了。有研究表明牙周膜的應力與牙齒移動過程中的牙根吸收有關[9-10],當牙周膜應力過大時會造成牙周膜局部血流閉塞,誘發牙根吸收[1-2]。可見采用均質型牙槽骨模型研究矯治力作用下牙周膜的應力時更偏向于獲得較高的應力值,進而選擇一個更保守的矯治力。另一方面,牙周膜的應變與矯治過程中牙齒的移動速度相關,在一定范圍內牙周膜的應變越大則牙齒的移動速度就越快[7-8],當采用均質型牙槽骨模型研究牙周膜的應變分布時會獲得一個較大的應變值,進而認為牙齒已具有較高的移動速度,同樣會引導正畸醫生選擇一個較小的矯治力。矯治力過小會延長正畸治療周期,降低患者配合治療的意愿,難以實現理想的正畸治療[4]。
另外,我們假設將① 均質型牙槽骨模型彈性模量增大 10 倍,重點分析了在尖牙受到 2 Nmm 的根向扭矩時,牙周膜對不同彈性模量的牙槽骨力學響應的差異性。從有限元分析結果(表 2)可以看出在模型網格和節點完全相同的情況下,當牙槽骨彈性模量提高之后,牙周膜的最大應力和最大應變均有所降低。所以,采用高彈性模量的牙槽骨模型進行有限元分析時,分析結果會引導正畸醫生選擇較高的矯治力,相反,低彈性模量的牙槽骨模型則會誘導醫生選擇一個更低的矯治力。然而,更高或者更低的矯治力均不利于正畸治療[4, 8-9]。為了獲得更加安全高效的正畸治療,明確載荷作用下牙周膜的生物力學響應至關重要。因此,根據患者牙槽骨的實際情況,設定合適的牙槽骨力學參數,對于采用有限元法研究正畸治療非常重要。
牙槽骨作為結構復雜的人體生物組織,內部含有神經管、骨小梁、骨髓小腔等組織結構,不同區域的力學特性差異很大[7, 17]。位于牙槽骨表層的骨組織骨質致密、強度高,稱為皮質骨;位于牙槽骨內部的骨組織則骨質疏松,呈海綿狀,稱為松質骨[20, 27]。在認識到牙周膜生物力學響應受牙槽骨力學特性影響的前提下,構建符合人體牙槽骨生物力學特性的有限元模型對于提高有限元分析結果的精確度有著積極促進作用。相比于均質型牙槽骨模型,非均質型牙槽骨模型模糊了皮質骨和松質骨的界限,依據每個網格單元所處的 CT 圖像灰度值對網格單元進行材料賦值,突顯出牙槽骨不同區域骨質特性的差異性,更加貼近牙槽骨實際狀況,有利于獲得更加準確的分析結果。值得注意的是,非均質牙槽骨模型的整體材料屬性在一定程度上受其網格單元尺寸的影響。模型中網格尺寸越小,每個單元越能依據其所在的微小局部 CT 圖像進行個性化材料賦值,越容易獲得更加細致的、差異性的牙槽骨模型。當網格尺寸變大時,其所覆蓋的 CT 圖像區域也更大,即便覆蓋區域的 CT 圖像有一定差異,也無法對該網格單元實現多種材料賦值。如圖 2a 所示,從牙槽骨的橫斷面來看,皮質骨和松質骨的分界面并不明顯,其中一部分原因就是該斷面上牙槽骨網格單元的尺寸過大。不過,從模型收斂性測試結果來看,邊緣區域過大的牙槽骨網格單元并沒有對牙周膜的力學響應產生不可忽視的影響。
在非均質牙槽骨模型中,采用 CT 圖像灰度值進行材料賦值的網格單元中最大的彈性模量是 14 420.28 MPa,其量級與其他研究中報道的皮質骨彈性模量 13 700 MPa 非常接近[7, 17],間接證明了材料賦值公式的準確性。另外,如圖 2a 所示,牙槽骨模型表面的部分區域被表示低彈性模量的藍色所覆蓋,這與處于真實牙槽骨表面的皮質骨力學特性不符。這主要是因為人體牙槽骨外還附著有骨膜和牙齦等組織結構,在牙槽骨模型構建過程中,有一部分口腔軟組織被當作牙槽骨進行了重建,但這并不會對有限元分析結果產生影響,從中我們也可以發現非均質模型的另外一個優點。一般來說,對于牙槽骨模型邊界的劃定主要依靠人工進行手動分割,操作者的熟練程度和工作經驗直接影響著牙槽骨模型的結構和大小,如果采用均質模型進行建模,那么模型構造上可能就與真實的牙槽骨存在結構差異,在一定程度上影響了分析結果。而當采用非均質建模方法時,因模型中的所有網格單元均依據其所在的 CT 圖像灰度值進行材料賦值,即便有一部分外層軟組織或者牙槽骨內部的骨髓小腔、神經管空腔等力學特性遠異于骨組織的組織結構,被誤以為牙槽骨進行有限元建模,也會因其 CT 圖像灰度值偏低被賦予相應的材料參數,不會因模型精度影響有限元分析結果。
4 結論
以一例臨床病例作為研究對象,基于患者的 CT 圖像構建了其尖牙、牙周膜和牙槽骨的有限元模型。其中,牙槽骨模型分別設定為均質模型和非均質模型,其他牙頜組織模型設定均相同。通過對尖牙施加根向矯治力和扭矩探究牙周膜在不同牙槽骨模型下的應力應變響應。結果表明:(1)無論牙齒平動或是轉動,當牙槽骨為均質模型時,牙周膜在同等條件下會產生更大的應力和應變,會誤導正畸醫生選擇一個較小的矯治力;(2)牙周膜的生物力學響應受牙槽骨力學參數影響較為顯著,當牙槽骨彈性模量由 490 MPa 增大 10 倍至 4 900 MPa 時,牙周膜的最大應力和應變值分別降低了 19.92% 和 35.21%;(3)相比于均質牙槽骨模型,非均質牙槽骨模型依據每個網格單元所處的 CT 圖像灰度值對模型進行材料賦值,更能體現真實牙槽骨組織骨質特性的差異性,有助于提高有限元分析的精確性。研究結果為構建更加精確的牙頜組織有限元模型提供了技術支持。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。