支架降解與血管重建之間形成的動態耦合關系，不僅影響到支架和血管的結構形態和力學性能，而且影響到支架內再狹窄的形成。本文介紹了支架降解和血管重建方面的生物力學建模分析研究成果；提出了若干值得關注的研究前景問題，建立了基于支架損失函數和血管生長函數的支架-血管動態耦合模型，同時提出了匹配度和風險系數的概念，用于評測支架治療效果，這將為可降解支架的結構設計、力學分析和臨床應用打下科學基礎。
引用本文： 張晗冰, 張愉, 陳詩亮, 崔新陽, 彭坤, 喬愛科. 支架降解與血管重建耦合作用的生物力學建模分析研究綜述. 生物醫學工程學雜志, 2020, 37(6): 956-966. doi: 10.7507/1001-5515.202008007 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
支架內再狹窄（in-stent restenosis，ISR）是制約支架植入術臨床治療效果的主要問題。ISR 主要與炎癥反應、內膜增生、細胞外基質合成及血管重建等因素有關[1]。采用支架對狹窄血管進行擴張，會引起血管壁內皮的損傷，而血管壁對損傷的愈合效應導致血管平滑肌細胞向損傷處遷移增殖，從而引發 ISR[2]。可降解支架具有可降解性及良好的生物相容性，可有效地促進血管重建并恢復其彈性和舒縮功能[3]，在避免 ISR 方面比永久性支架具有更大的潛力。
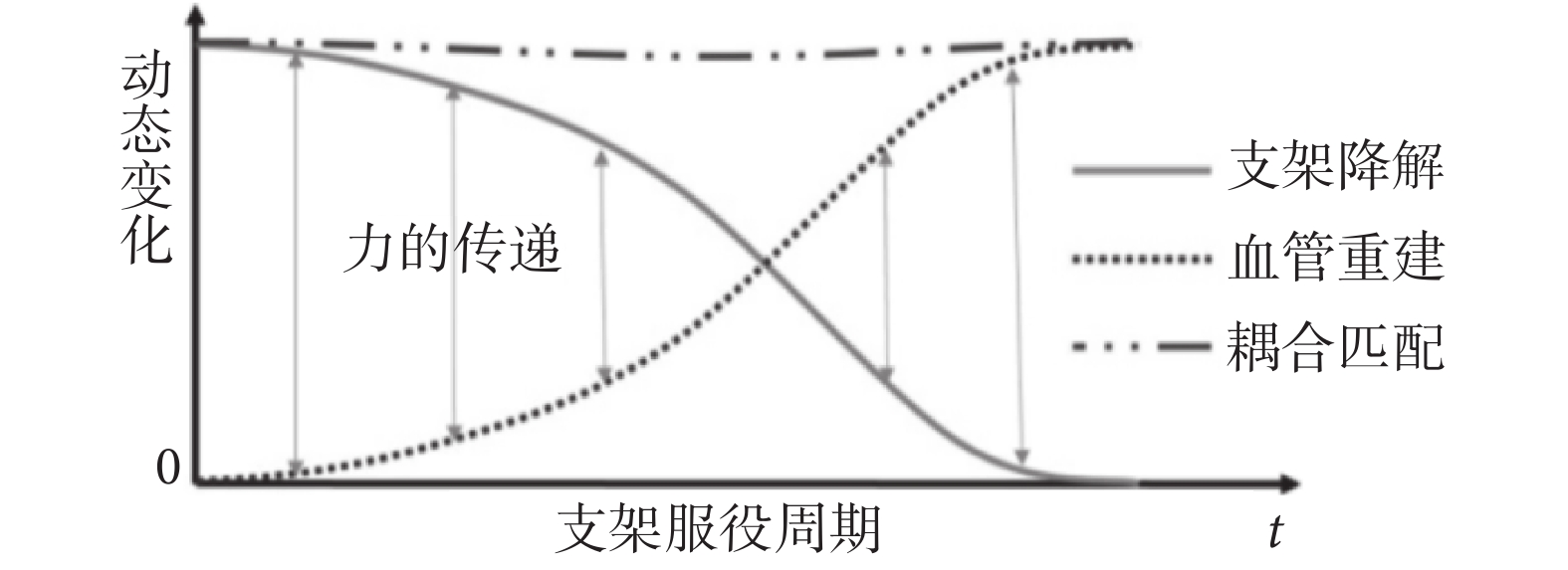
可降解支架在服役過程中，血管重建和支架降解是一個動態耦合的過程，如圖 1 所示。力的傳遞在此過程中發揮了重要的作用。若支架降解速率過快，則血管重建不足，不能單獨承載載荷，將最終導致血管的再塌陷；反之，若支架降解速率過慢，則無法為新生內膜生長騰出空間，造成新陳代謝障礙等問題，也不利于血管重建；這些均有可能導致 ISR 的發生。
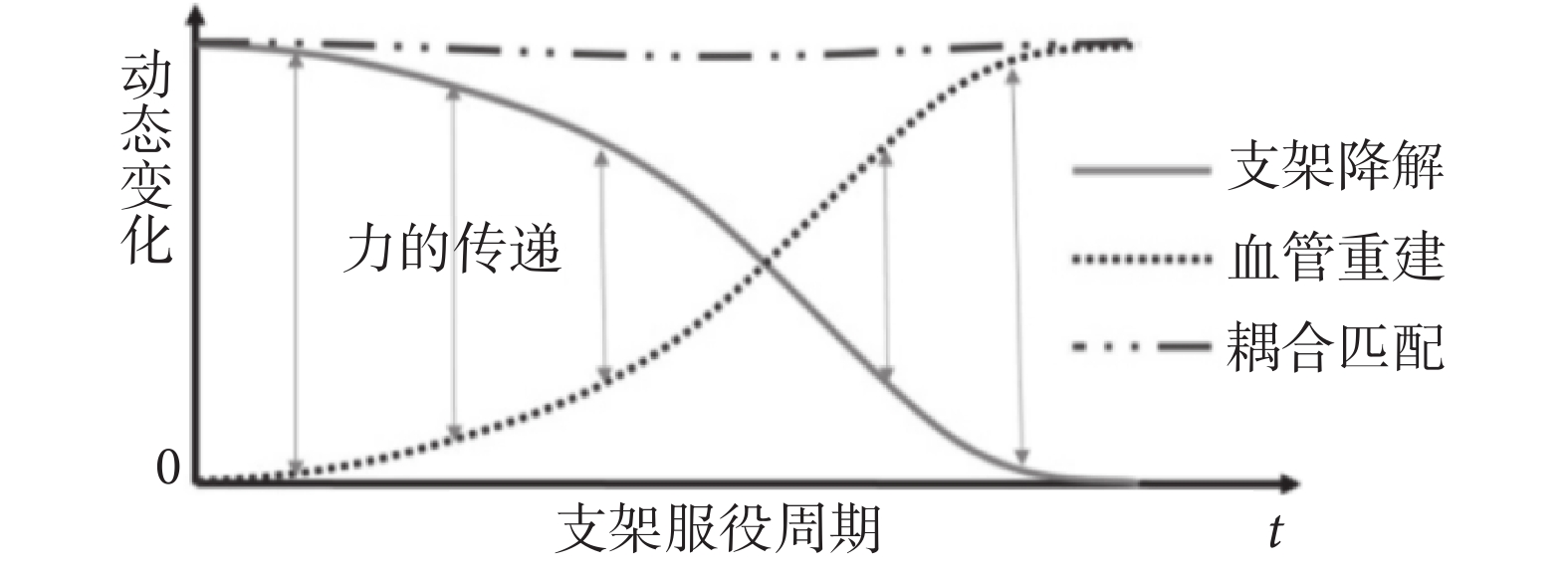圖1
支架與血管力學性能隨時間變化示意圖
Figure1.
Schematic diagram of the temporal change of mechanical performance of stent and vessel.
本文對支架降解、血管重建以及二者動態耦合的生物力學建模分析進行了綜述，并提出了耦合匹配度和 ISR 風險系數的概念，以期對可降解支架的生物力學研究和臨床應用有所啟發。
1 國內外研究現狀
1.1 支架降解過程的建模分析
不同材質的支架植入血液環境中均會發生不同程度的腐蝕，導致材料產生機械損傷，降低材料強度。該腐蝕過程涉及到電化學、金屬物理學、熱動力學、材料學和力學等多學科交叉的問題[4]。支架材料的腐蝕機制一般包括但不局限于微電流腐蝕、點蝕、應力腐蝕和疲勞腐蝕[1]。據此建立的均勻腐蝕模型一般用于描述化學反應或電化學反應引起的腐蝕，即暴露在腐蝕性環境中材料的自由表面受腐蝕的情況；而連續損傷力學（continuous damage mechanics，CDM）法常用于模擬在腐蝕環境中應力/應變作用下材料受侵蝕的情況。下文逐一分類詳述：
（1）均勻腐蝕是支架降解最簡單和理想的狀態。較早的研究中，模擬支架降解較多地采用均勻腐蝕模型。Deshpande[5]采用多物理場方法，開發了兩相金屬鎂合金中微觀電化學活性的數值模型。Grogan 等[6]采用有限元法（finite element method，FEM）在可降解支架外表面通過均勻刪除單元來模擬均勻腐蝕過程，進而利用任意拉格朗日-歐拉（arbitrary Lagrangian-Eulerian，ALE）自適應網格技術，改進了均勻腐蝕模型。
（2）應力/應變腐蝕反映了支架植入血管后在力學作用下的降解行為。聚合物可降解支架在壓握和釋放過程中的應力和應變會對支架內部微結構完整性造成破壞，從而導致不均勻降解和早期崩塌等惡性事件發生[7]，這表明設計支架時應考慮力學因素對支架擴張造成的材料微觀損傷以及支架服役降解的影響。支架擴張結束后產生的殘余應力是支架降解和血管重建的誘導應力[8]。CDM 法從連續介質力學的角度分析支架材料的應力、應變及其誘導的支架材料損傷過程，基于實驗的唯象學結果對模型的參數進行標定，在 FEM 框架中易于實現數值模擬。CDM 法適合于針對可降解支架復雜的三維幾何形狀和加載條件的建模[4]。
舉例來說，Costa-Mattos 等[9]采用 CDM 法建立應力腐蝕模型，將應力腐蝕與均勻腐蝕共同作用到可降解金屬支架上，并通過實驗對該模型進行了驗證。Gastaldi 等[10]的應力腐蝕模型為： σ = 
，其中 σ 為有效應力張量，
為未損傷應力張量，D 為損傷因子；D = DU + DSC，其中 DU 表示均勻腐蝕損傷因子，DSC 表示應力腐蝕損傷因子。D = 0 表示材料無損傷；D = 1 表示材料完全損傷。該模型直觀明了，容易在 FEM 數值模擬中實現，至今仍廣泛用于血管支架的腐蝕降解模擬中。Wu 等[11-12]采用均勻的微電流腐蝕與應力腐蝕共同作用的 FEM 模型，研究兩種可降解金屬支架在應力腐蝕和均勻腐蝕的共同作用下的降解行為，并進行體外腐蝕實驗分析驗證了 FEM 模型在支架設計和性能評估方面的實用性和有效性。
（3）點蝕可能受到支架在制造過程中表面缺陷的位置、在血管成形術中的表面缺陷或應力集中區域的影響[1]，進而影響支架服役過程中的腐蝕降解。Grogan 等[6,13]在均勻腐蝕模型中加入了點蝕模型，研究了一種基于物理學的均勻腐蝕模型，考慮了包括鎂離子運輸的鎂支架降解的多物理過程。Shen 等[4]建立了一種 CDM 模型并采用 FEM 數值模擬鎂合金冠脈支架的疲勞腐蝕，結果表明該模型可以預測降解速率以及損傷誘導的徑向剛度減小等。許多基于 CDM 方法的研究致力于均勻腐蝕、點蝕、應力腐蝕、應變腐蝕，但較少考慮腐蝕和疲勞的協同作用（這會增加問題的復雜性）[14-15]。
由于血液循環引起的傳質和流動剪切應力加速了整體腐蝕（包括局部、均勻、點蝕等）。流動剪切應力提高了平均均勻腐蝕速率、局部腐蝕覆蓋率和深度以及腐蝕坑內腐蝕產物的去除率[16]。對于覆膜支架而言，支架在植入初期的幾個月內，可以不考慮血流沖刷對支架降解的影響；待血管新生內膜覆蓋支架桿之后，血流對支架降解的影響也比較小，當然這是比較理想的狀態。
關于支架降解模型求解方法的問題，應用較為廣泛的還是 FEM。Grogan 等[17]建立了一個可吸收金屬支架的物理降解模型，并利用顯式 FEM 和自適應網格技術，模擬展示了可吸收金屬支架結構在擴散控制腐蝕情況下的變化表面和力學表現。進一步地，Grogan 等[13]基于隱式 FEM 和自適應網格，模擬了擴散控制腐蝕情況下三維可降解鎂支架結構的變化表面。為了擴大基于 FEM 模擬支架降解的方案通用性并縮短計算時間，學者提出了一種隱式的 FEM[18]。該方法被用于預測實驗觀察到的塑性應變介導的質量損失剖面[19]，但局限性是既沒有考慮腐蝕層的形成及其厚度隨時間的變化，也沒有考慮支架壓握、擴張回彈壓力以及動態疲勞載荷作用的影響，而且所計算的應變也是單軸的，而支架在狹窄血管中的應變應該是多軸而復雜的[19]。
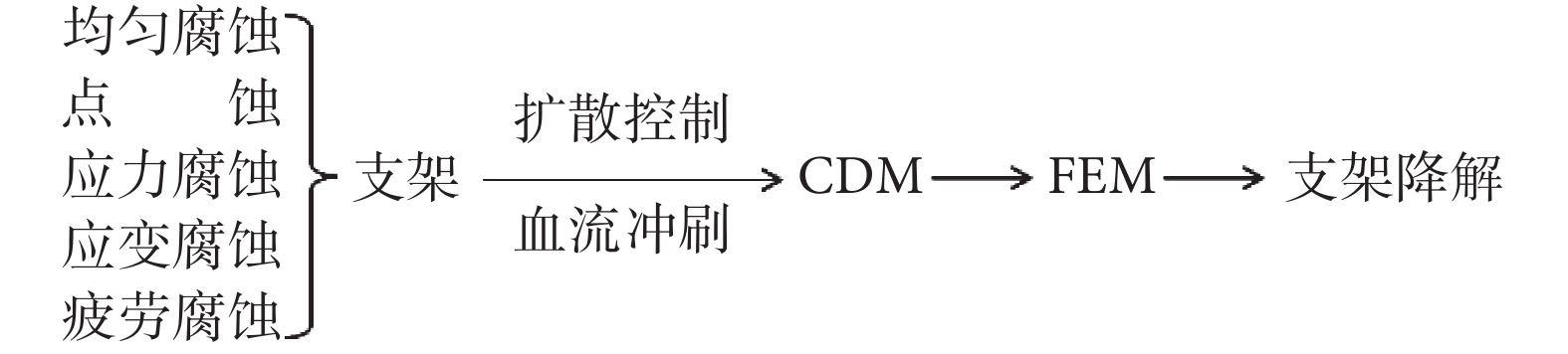
綜合來看，上述關于支架降解的生物力學建模分析的研究，可以歸納為如圖 2 所示的技術路線圖。動脈的個性化幾何形狀、狹窄斑塊的材料屬性、載荷及邊界條件等都是影響支架降解的復雜生物力學環境因素[20]。支架降解動力學建模方面至少存在三個方面的挑戰：一是基于唯象學的經驗數據模型還需要更本質的理論模型支持；二是基于動物實驗的模型不一定符合人體血管和血流的實際；三是如何對離體/在體模型和靜態模型進行合理修正，以便模擬在體、動態的降解過程。
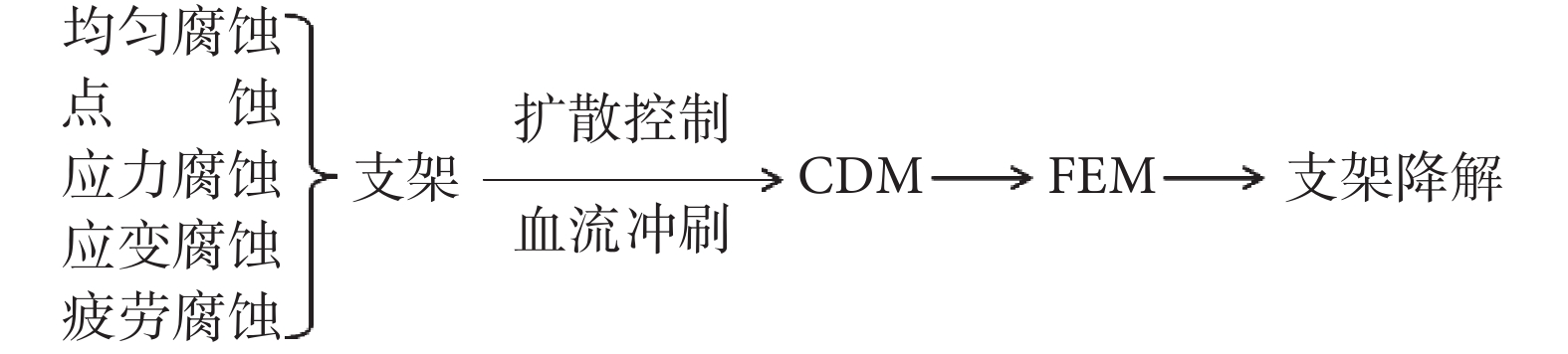圖2
支架降解生物力學建模分析的技術路線圖
Figure2.
Schematic diagram of the biomechanical modeling and analysis of stent degradation
1.2 血管重建的建模分析
血管壁包括內膜、中膜和外膜這三層結構。內皮細胞（endothelial cell，EC）呈單層狀排布于血管內膜表面并對血流剪切應力的變化敏感。血管平滑肌細胞（vascular smooth muscle cell，VSMC）位于血管中膜，VSMC 過度增殖是誘發動脈粥樣硬化以及介入治療后 ISR 的主要病理過程[21-22]。彈性纖維和膠原纖維是外膜的主要成分，血管外膜成纖維細胞在血管損傷后新生內膜的增生中起重要作用。細胞外基質（extracellular matrix，ECM）對細胞起到復雜網絡支持物的作用，并作為一個關鍵的生物化學和生物力學信號的來源，積極參與控制細胞的生長、極性、形狀、遷移、穩定和代謝活動[23]。“生物力學之父”馮元楨先生提出了“應力-生長法則（stress-growth law）” [24]，即包括細胞和 ECM 的生長和吸收在內的血管重建是與血管中的應力/應變相關的，即生長取決于應力和應變。
血管重建是細胞增殖、死亡、遷移以及 ECM 合成和降解所致的血管壁結構動態變化的過程。有人將血管生長和血管重建區分開：血管生長，指的是血管質量的改變；而血管重建，指的是血管結構的改變[25-26]。在這里，將二者統一為血管重建。
從宏觀尺度來看，支架植入后對血管壁的作用力以及管腔內血流對血管壁的切應力驅動了血管重建[27]，一般采用 CDM 法來模擬并利用 FEM 來求解支架擴張后的血管壁應力水平。從微觀尺度來看，ECM 與血管壁各層細胞之間的力學-化學-生物學效應驅動了血管重建，一般采用元胞自動機（cellular automata，CA）或基于代理模型（agent-based model，ABM）來模擬。將宏觀和微觀模型相結合，就組成了血管重建的多尺度模型。下文逐一分類詳述：
（1）宏觀尺度模擬
在血管重建的宏觀尺度模擬方法中有兩種主要的 CDM 方法，即：① 運動學生長模型（kinematic growth model，KGM）：將無載荷體的局部變形分為非彈性和彈性兩部分運動學增長過程[28]；② 約束混合模型（constrained mixture model，CMM）：在附帶預應力的受力物體中加入新生質量，這種預應力與特異性組分的自然幾何結構狀態有關[29]。這兩種方法本質上可以理解為計算應變能和質量密度。KGM 法假設的總變形梯度可以分解成一個彈性部分（確保變形中的力學平衡和幾何相容性）和一個非彈性部分（描述增長）。CMM 法將物體定義為由n個組分組成，每個組分由眾多質量增量組成；在每個體積單元中，不同時間沉積的不同組分的質量增量形成了一個受約束的混合物，也就是說它們呈現同樣的、隨著時間變化的彈性變形[30]。
KGM 法用于模擬整個組織的初始無應力體的生長，即無應力體的大小和形狀的變化可以通過兩個變形來描述：非彈性“生長”變形（梯度）Fg以及隨后的彈性“組裝”變形（梯度）Fa。Fg通過無窮小的體積單元中質量的添加或移除來描繪無應力體的變化；Fa通過將生長的體積元素裝配到無應力的連續體上來確保幾何兼容性。由于其模型簡單而且計算成本低，KGM 法一直被廣泛研究[31-32]。Zahedmanesh 等[33] 據此模擬了血管中層 VSMC 增殖和遷移而導致的 ISR，利用有限元分析軟件 ABAQUS/explicit（Dassault Systemes，法國）求解器與其 VUMAT 子程序進行數值模擬，結果表明支架擴張血管到最大直徑時造成血管損傷的程度對 ISR 發生率起到重要作用。針對力學因素調節膠原纖維的定向生長問題[34-35]、應力-生長動力學關系的異質性和生長穩定性問題[36]、血管成分的各向異性材料屬性引起的趨向性重建問題[37]，均可以通過 KGM 法來模擬。Escuer 等[38]基于重要組分的密度/濃度，如生長因子（growth factor，GF）、基質金屬蛋白酶（matrix metalloprotein，MMP）、ECM 以及 VSMC 等，用耦合擴散-反應偏微分方程組構建了與血管損傷相關的體積增長模型，并利用 FEM 模擬 ISR。KGM 法的一個主要挑戰是確定非彈性“生長”變形（梯度）的本構關系Fg，通常Fg的確定方法是典型的試探性猜測。在自然應力狀態下具有不同的預應力的不同類型組分，其在體的生長和重建往往以不同的速率而產生、去除或重建，然而這些過程沒有在 KGM 法中考慮[30]。
CMM 法因為可以模擬同時存在的多種組分的影響而越來越受到關注，這些組分通常以不同的速率不斷沉積和降解，這對于理解活的軟組織的基本特征很重要，而這些特征是不能被簡單的 KGM 法來描繪的[30]。具有代表性的工作是 Humphrey 等[29]所做的研究，他們建立了一種 CMM 法來解釋組成動脈的不同重要組分的力學性能、自然（無應力）幾何結構以及轉化率和范圍，并將該模型應用于一個不斷發展過程中的顱內梭形動脈瘤的非線性有限元分析（finite element analysis，FEA）。Rivas-Marchena 等[39]構建了一個基于電生物阻抗的數學模型，可以解析地描繪支架植入后的新生內膜的實時組織成分變化。He 等[40-42]采用醫學影像構建了各向異性的血管和狹窄斑塊的幾何模型，用能量損耗密度來評價組織損傷程度。這些工作盡管對模擬血管生長做出了貢獻，但無論從材料屬性、幾何結構，還是從血管組成成分的生長等方面仍然具有局限性。
除了支架作用于血管的應力之外，血流作用于血管的壁面切應力（wall shear stress，WSS）在血管重建中也發揮了重要作用。支架貼壁不良導致支架局部產生主流方向和二次流方向的微觀回流[43]，對 WSS 和血液黏度產生了顯著影響，這與 ISR 密切相關。Ng 等[44]系統分析了流動切變率和 WSS 對血栓和新生內膜等的影響，特別是討論了支架結構以及支架擴張和貼壁情況對局部血流動力學和 ISR 的影響。最近的文獻報道，Boland 等[45]同時考慮了支架擴張對血管壁的應力損傷和血流 WSS 對血管重建的刺激作用，利用 FEM 數值模擬鎂支架支撐三層各向異性結構的動脈，將“虛擬網格”（ghost mesh）置于動脈腔內支架周圍（新生內膜在此發生）；根據 FEA 得到的血管壁應力和 WSS 數值，計算兩者對血管壁的損傷，再將這些變量作為刺激驅動力輸入到血管重建模型中作為細胞負荷，從而誘導動脈中的細胞從動脈擴散到虛擬網格中實現增殖。
CDM 法可用于模擬從細胞到組織的所有水平的生物系統的響應。可以在空間和時間上使用偏微分方程（partial differential equation，PDE）對關鍵的細胞反應（例如細胞密度進化）進行建模，但該方法的一個重要限制是 PDE 可能無法捕獲由單個細胞組成的多細胞生物系統的離散性質，并且在解決復雜問題時涉及多個變量使得計算變得笨重[46]。
（2）微觀尺度模擬
生物系統的整體行為是由細胞水平上發生的離散現象導致的，如細胞遷移、增殖和凋亡等[47]。因此，使用離散方法可以更好地對生物系統進行建模。CA 和 ABM 是用于多細胞生物系統建模的兩種主要離散方法，它們模擬單個細胞的行為和細胞之間的相互作用，從而能夠觀察到生物系統的行為。采用自下而上的方法，每個單獨的細胞都根據為其定義的行為規則而顯式地建模；基于在細胞級別定義的行為規則，系統行為通過細胞之間的局部耦合作用而呈現出來[46]。這兩個系統都是基于規則的，需要定義每個代理或單元的數學關系，以及指定初始和邊界條件[48]。CA 法由具有預定義尺寸的規則單元網格組成，細胞只能通過某些預先定義的網格點移動。相反，ABM 法通常是無網格模型，這意味著單元網格可以位于計算域中的任何位置，這個位置通常是通過求解單個細胞的運動方程來確定的。ABM 法可以在隨機位置初始化代理，也可以在模擬期間創建新的代理。因此，與 CA 法相比，ABM 法可以產生更真實的結果[46, 49]。
ABM 法研究離散的細胞級別的行為和不同分子的生成，模擬血管對生長因子、蛋白酶和其他信號分子水平增減的反應，以及細胞表面黏附分子的強度等[50]，從而揭示單個細胞相互作用的結果是如何綜合形成組織動力學的[51]，而這些是不能依據上述 CDM 法來實現的[52]。
ABM 法將單個細胞用由一組規則控制的格子來表示，細胞和諸如生長因子等其他物種種群的進化通過 PDE 來描述[38]。ABM 法通過求解 PDE 可以整合眾多代理的個體行為和個體之間的相互作用，來預測模型系統（如組織或器官）中代理的復雜集體行為[53]。比如，Boyle 等[54]在格子中模擬 VSMC 的遷移、增殖和分化等活性，在簡化的加載情況下檢驗炎癥方程，論證了基于格子的建模方法具有模擬動脈組織的力學生物學反應的潛力。針對冠狀動脈移植管搭橋術后常發生靜脈移植管動脈化的現象，Garbey 等[55-56]利用 ABM 法等計算模型展示了細胞/組織層次上相互作用的反饋回路和力學環境條件，并以兔子實驗結果中的組織學數據作為參考，在二維計算模型上驗證了所構建模型和方法的可行性。ABM 法相關的研究很多，大家可以參考文獻[51-52]進行延伸閱讀。
針對 ABM 法的模擬仿真已開發了多種軟件，如商業數學軟件 Matlab R2015b（The MathWorks，Inc.，美國）可以模擬動脈壁細胞對機械損傷的集體反應[47]。有些專門基于細胞模型的軟件，可與動脈和支架的有限元模型相結合，預測動脈對支架植入的反應[48]。對于代理數量較大的 ABM 算例，在求解 PDE 時耗時很大。折中的辦法是：限制模擬中細胞的數量，考慮復雜的交互，或者采用更大的細胞集合，簡化交互規則[52]。
雖然 ABM 法可以提供關于生物系統中演化行為的深刻信息，然而 ABM 法要么忽視了力學刺激在調節體內平衡中的作用，要么對應力和應變的計算采用了過于簡單的方法[57]。這與 ABM 法存在的固有缺陷有關，即無法方便地計算出動脈在時變、非均質和復雜幾何結構下的應力和應變。為了解決這個問題，建議將 ABM 法與 CDM 法耦合[53, 58]，這樣就形成了目前更為常見的 ABM-FEM 耦合多尺度模型。
（3）多尺度模擬
FEM-ABM 多尺度模型在血管重建方面的應用越來越盛行[53, 59-60]。其求解思路是：首先采用 FEM 求解 CDM 模型，確定在設定載荷下（或者支架植入后誘導的）血管壁的變形和應力，用于量化計算細胞損傷值，并傳輸到 ABM 模塊；然后采用 ABM 法，模擬血管壁中 VSMC 和 EC 的表型變化、遷移和增殖等行為[61]。
近年來，FEM-ABM 多尺度模型方面的研究成果不少。Boyle 等[62]以 VSMC 為離散代理，通過損傷和炎癥的組合作用來模擬 ISR，其中 CDM 法將支架擴張的 FEA 結果與損傷累積相耦合，用來計算動脈損傷；炎癥模型用常微分方程來建模，描繪因損傷而引起的組織降解、生長因子的生成以及損傷的消除；一個基于格子的 ABM 法用來模擬 VSMC 的表型、增殖、遷移和組織生成。針對支架引起的動脈損傷以及在 ISR 的發展過程中膠原基質重建的研究表明[59]，高應力引起的血管壁損壞上調了 VSMC 細胞的 MMP，從而導致 ECM 降解。Marino 等[63]提出了一個關于動脈生理病理的力學-化學-生物學的框架，解釋組織成分在多尺度層次結構中的精細重構和細胞-細胞信號通路中涉及的分子物種的擴散，重點研究組織結構行為的改變以及擴散性/滲透性對病變情況下非功能性宏觀力學響應的關鍵作用。文獻[64]建立了 ISR 新生內膜質量增長的演化方程，其中考慮了支架誘導損傷對 VSMC 的激活以及激活細胞的增殖速率；利用兩個向量來表征膠原纖維束的方向，通過在質量平衡方程中引入質量演化，得到了生長張量隨時間的演化。通過將包括支架釋放、血流和支架血管組織生長的 FEM 模型與包括描繪 VSMC 增殖和 ECM 產生的 ABM 模型進行耦合，模擬新生內膜的發展[65-67]，并比較模擬結果與豬體內實驗的組織切片數據，這為離體 ISR 模型提供了驗證方法。Cerrolaza 等[49]模擬支架植入后動脈壁的 ISR，其中 ABM 包含兩種相互依賴的 EC 和 VSMC，而它們的行為主要受力學環境的控制。進一步地，Nolan 等[47]探討瞬時加載和循環加載兩種驅動力方式下的損傷誘導細胞增殖的機制，結果表明循環加載損傷模型預示著非生理性、過度增殖性響應，而瞬時加載模型則提示再內皮化可以調節管腔損失。最近，Cheng 等[68]建立了一個將殘余應力與生長模型耦合的數值方法，并研究了殘余應力對冠脈血管組織重建的影響；通過編寫 ABAQUS 子程序來給有限元網格施加殘余應力，利用 UMAT 子例程來指定具有超彈性生長模型的應力和彈性張量；研究結果表明，與無殘余應力的情況相反，殘余應力使血管外壁產生更大的應力和生長因子。
多尺度模型的主要問題是，調試耦合匹配參數的過程復雜，計算工作量大。半侵入式不確定性量化（uncertainty quantification，UQ）方法是一種計算成本更低的方法[69-70]，用于研究多尺度心血管模型的二維 ISR 問題，其計算結果與黑箱擬蒙特卡羅方法的計算結果吻合較好，表明該方法是可靠和有效的。
最近的研究更多地集中在血管重建過程的生長穩定性上（即力學生物學穩定性）。力學生物學穩定性即指在“應力-生長法則”驅動下，血管受到力學刺激而生長所達到的穩定狀態。Erlich 等[36]研究了非均質材料的分層管狀結構生長穩定性問題，結果表明生長穩定性主要取決于生長響應的各向異性。不同學者采用不同的 CMM 法研究動脈血管重建的穩定性，得出一致的結論：在恒定壓力下增大的組織剛度和更高的組織生產率傾向于使血管重建過程保持穩定，而增大的降解速率則會使血管重建不穩定[71-73]。Li 等[74]構建了一種完全雙向耦合的 ABM-FEM 框架，研究血管的力學-化學-生物學因子的相互作用及其在維持體內平衡生長穩定性中的作用；結果表明，將血管曲率和 ECM 的產生包含在模型中對于取得與實驗數據良好的一致性結果至關重要。一種新的基于變化率的三維 CMM 法，適用于研究軟組織在材料組成或施加載荷的瞬時/持續變化下的力學生物學平衡和穩定性[75]。這種基于速率的 CMM 法等價于基于積分的模型，能夠區分可能導致穩定和不穩定的力學生物學響應。
綜合來看，上述關于支架植入后血管重建的生物力學建模分析的研究，可以歸納為如圖 3 所示的技術路線圖。
圖3
支架植入后血管重建的生物力學建模分析的技術路線圖
Figure3.
Schematic diagram of the biomechanical modeling and analysis of blood vessel remodeling after stent intervention.
基于理想化的二維模型來建立支架植入后血管重建的生物力學模型，已經取得了較好的進展。然而，基于三維模型、特別是三維個性化模型來建立支架植入后血管重建的生物力學模型，仍然難度很大。動脈受到力學損傷后，血小板、白細胞、VSMC 等釋放多種類型的 GF：血小板源性 GF、表皮 GF、胰島素樣 GF、轉化 GF、成纖維 GF[76-77]。這些 GF 的力學-化學-生物學協同作用，導致精確構建血管重建的生物力學模型面臨巨大的挑戰。
1.3 支架降解和血管重建的耦合建模分析
支架在服役過程中需要承受血管壁力學-化學-生物學環境的作用以及血流腐蝕作用，支架結構和材料屬性發生腐蝕退化，力學性能變弱，結構發生損傷，血管發生收縮，導致支架與血管之間的相互作用發生動態變化，進一步影響到支架降解和血管重建的耦合過程[78-80]。支架降解和血管重建是既獨立又相互關聯的兩個過程[81]，即形成了一個具有反饋調節機制的閉環系統。
在可降解支架服役過程中，支架降解使材料屬性衰退，而血管新生細胞生長也會對材料屬性造成影響，兩者動態組合出不同性能的新材料。研究表明，干細胞動員、歸巢、分化、增殖是血管內支架植入后血管內皮修復的主要機制，多種血管內因子、力學微環境變化等均參與此過程，進而影響植入部位的再內皮化[82-83]。針對不同內皮覆蓋率和高危因素（包括較厚的支架桿、支架貼壁不良和重疊）對動脈一氧化氮（NO）分布影響的研究發現，內皮覆蓋少、支架桿較厚和支架釋放不當均可能降低 NO 濃度，并導致支架桿附近的 NO 濃度相對較低，進而促進內膜增生[84]。關于鋅材料支架的降解研究發現，支架釋放的鋅離子濃度的高低對 EC 的黏附、聚集和遷移等具有截然相反的作用[85]，可降解鋅表面的氧化物薄膜對可降解鋅材料的早期內膜增生有嚴重影響[86]。Holzapfel 等[87]的實驗研究以及 Boland 等[48]的計算研究發現，被激活的新生內膜的楊氏模量對血管重建后支架的腐蝕及其支撐性能有很大影響，從而也是影響冠狀動脈整體塌陷或回彈的一個重要參數。因此，支架降解和血管重建是相生相長、相互影響的。
關于支架降解和血管重建的耦合建模分析，采用最多的方法是 CDM-ABM 耦合方法。該方法的理想狀態是將“支架降解-血管重建”組合形成一個帶有反饋調節機制的閉環系統模型。這有別于上一節中的 FEM-ABM 多尺度模型，那里僅僅是把 FEM 所得支架對血管壁的作用力傳遞給 ABM 進行血管重建，而沒有考慮支架降解的問題。
由于支架降解和血管重建的耦合建模算法非常復雜，所以目前的相關研究報道還不多。具有代表性的、較為前沿的工作是 Boland 等[45, 48]的研究。他們建立了一個鎂支架植入血管的計算模型框架，其中考慮了導致新生內膜重建的兩種主要生理刺激，即支架作用力和血流 WSS，并與能夠模擬真實情況下支架局部腐蝕的點蝕模型相結合。支架點蝕模型為：
，其中
為腐蝕速率，損傷因子 D 與 
成正比；隨著 D 增加，腐蝕表面單元彈性和塑性會線性下降；
為點蝕系數，
越大表示支架更易受點蝕影響；D ≈ 1 時，單元完全損壞，并更新相鄰單元的點蝕系數 
。新生內膜重建模型為：
，其中 n 為細胞濃度，如果單元中的n超過預定義的閾值，則該單元將被激活而轉化為新生內膜的新材料。公式右邊第一部分就是菲克（Fick）擴散定律，它可以通過熱模擬法與傅里葉（Fourier）熱傳導定律相關聯，并可以在 ABAQUS 中通過耦合熱-位移模擬過程來實現。
和 
分別對應于支架作用力和血流 WSS 誘導的血管壁損傷因子，而 
和 
分別是它們對應的常數。通過反復修改擴散特性，使得大部分新生內膜在 28 d 內形成，這樣就與動物實驗中的結果相匹配。在該模型中，支架降解和血管重建是獨立的，即把支架的腐蝕速率設為一個常數，未討論支架降解與血管重建過程中力的相互作用與匹配度問題；并且純鎂試樣的體外腐蝕實驗表明，覆膜試樣的降解速率比未覆膜試樣慢[88]，所以有必要區別考慮支架降解與血管重建之間的耦合作用。
在動脈的生物力學模型中有兩種非常不同的時間尺度：一種是由心臟周期引起的脈動運動的短期時間尺度——“加載時間尺度”，以秒為單位；另一種是血管重建的長期時間尺度——“生長時間尺度”，以天、周或月為單位。Holzapfel 等[89]在骨骼力學中定義了這兩個“時間”。通過合理假設，可以在血管重建模型中將上面兩種尺度的“時間”聯系起來[26, 45]。準確模擬支架降解和血管重建的關系，探索動態耦合作用下在每個時刻二者的幾何形態和材料匹配度，并在設計可降解支架時保證與組織再生和生物降解性相匹配的降解率[90]，這將是下一步研究的重點。
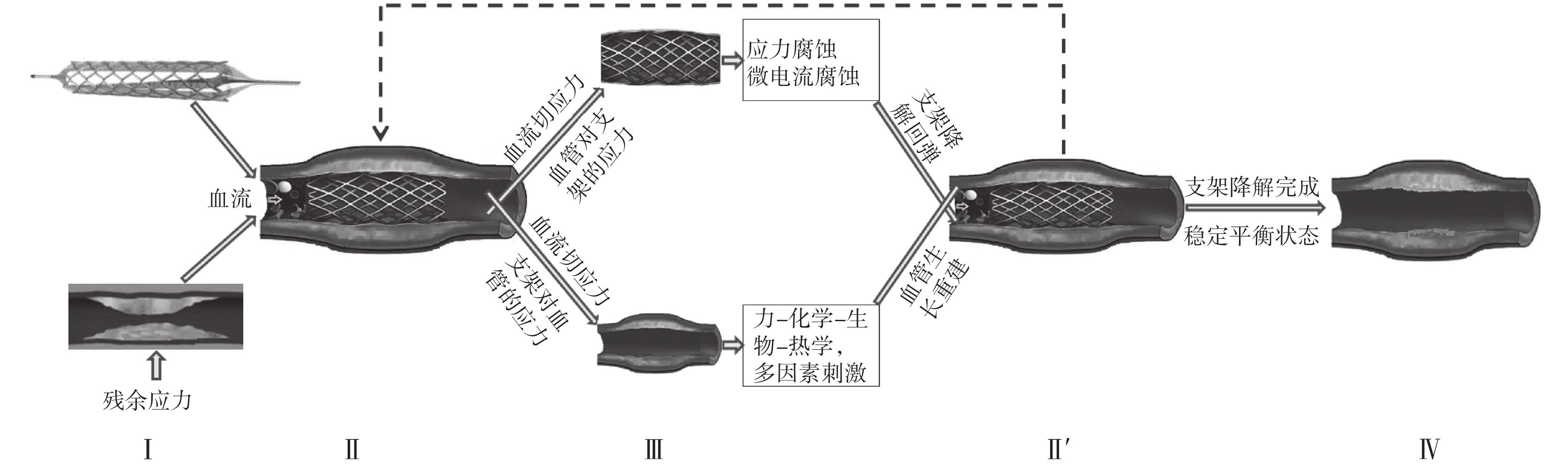
綜合來看，上述關于支架降解和血管重建的動態耦合作用的研究，可以歸納為如圖 4 所示的技術路線圖。在第 I 階段，血管模型需要考慮血管壁的殘余應力，而支架模型需要考慮初始結構尺寸等結構設計因素以保證支架的支撐力及其對血管壁的損傷大小在合理范圍內。在第 II 階段，完成支架在狹窄血管內的釋放，支架和血管的本構關系決定了各自的受力和變形，由此獲得支架與血管壁/斑塊之間的相互作用力以及血流對血管/支架的流動切應力，這些應力將作為輸入驅動條件分別傳遞給支架降解模型和血管重建模型。在第 III 階段，分別模擬支架降解和血管重建過程，此時支架降解模型和血管的“應力-生長法則”發揮作用，由此獲得支架和血管的幾何結構、材料屬性與本構關系的改變結果，這些結果將作為輸入驅動條件傳遞給更新后的支架-血管耦合模型。在 II'階段，支架與血管之間交換幾何、材料和力學等信息，完成更新后的支架-血管耦合模型又回歸到第 II 階段進行新一輪循環的耦合分析。當支架完全降解、達到穩定平衡狀態之后，就進入第 IV 階段，循環才算結束。這樣，如圖 4 所示的過程也就與如圖 1 所示的過程相吻合了。
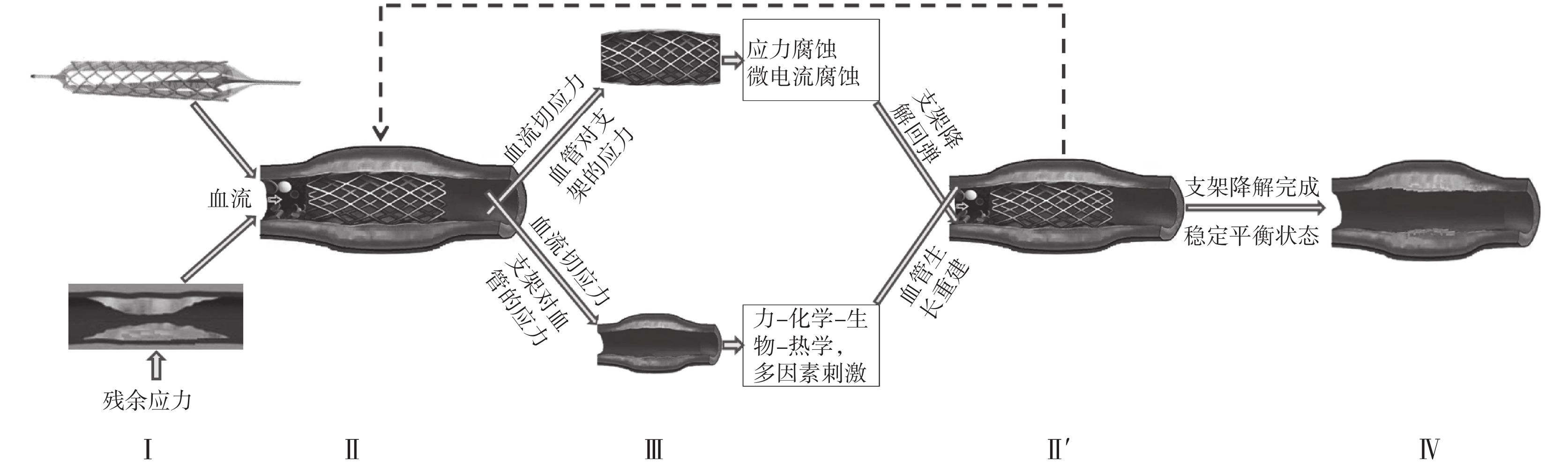圖4
支架降解與血管重建動態耦合生物力學建模分析的技術路線圖
Figure4.
Schematic diagram of the biomechanical modeling and analysis of the dynamic coupling between stent degradation and blood vessel remodeling
2 研究展望
如前所述，支架降解和血管重建之間形成一個復雜的耦合系統，其中涉及到很多時間和空間的跨尺度問題。對一個復雜的系統進行建模和分析，需要由簡單到復雜、“由底層向頂層”和“由頂層向底層”循序漸進的不懈探索。關于這一耦合過程的生物力學建模分析，進一步的深入研究包括但不限于如下幾個需要關注的方面。
（1）耦合過程中的多相材料、多場耦合行為是目前比較新的研究課題。這個耦合系統中涉及到力學（固體力學、流體力學、熱力學）-化學-生物學的綜合相互作用。無論是支架降解還是血管重建，如何分配諸多影響因素之間的貢獻權重，這是必須要考慮的一個問題。要系統地了解支架與血管之間的相互作用，包括腐蝕類型、腐蝕速率、腐蝕產物、氫的演化和局部 pH 值的變化等方面的信息很少，其中關鍵的一步是識別和測試在復雜生物系統中顯著影響支架降解和血管重建行為的相關局部環境參數[16]。針對影響細胞介導血管重建的力學-化學-生物學狀態變量的研究，如不同結構上的重要成分以不同的速率和程度產生和去除，仍然是一個活躍的研究領域[26]。確定適合質量生成和去除的生物力學模型是最重要的開放性問題之一[91]。
（2）將目前描繪動態耦合的開環系統升級為閉環系統，并探討其力學生物學穩定性。血管的力學生物學穩定態（包括不同的組分材料特性、轉化率和幾何結構等）是一個能動的過程：正常的血管組織能適應力學生物學變化、通過反饋調節機制而恢復和維持血管的幾何與材料屬性的穩定平衡狀態；而病變的血管組織則會破壞這種穩定平衡狀態、導致血管重建的惡性循環變化[72, 75, 92-93]。目前的研究基本上還是將耦合系統簡化為一個開環耦合系統，不考慮物質輸運（如新陳代謝、藥物緩釋、組分材料改變等）的力反饋作用，對耦合模型也缺乏嚴格的熱力學平衡約束[63, 94]，沒有實時更新支架-血管之間的幾何、材料和力學交互作用――亦即沒有很好地模擬如圖 4 所示第 II'階段發生的事情。因此，構建具有自適應調節功能的閉環耦合模型是一個系統性的問題。
（3）耦合模型的時間尺度和空間尺度的標定和驗證問題。受應力-生長關系影響的血管重建過程存在滯后效應，力學刺激是個瞬時的過程（以秒計），但生長是個緩慢的過程（以天、月計）；另外，動脈結構和病變（包括創傷和退行性病變等）可能因人而異，以及在細胞生長過程中的遺傳變異，使得不同患者的血管對同一刺激也可能有不同的反應[54]，反過來血管重建對支架受力和降解也有不同的影響。如何在時間尺度和空間尺度上協調統一地標定支架降解與血管重建過程，這是一個挑戰性問題。目前基本上采用抓住主要矛盾、突出主要因素、通過實驗進行唯象學的歸納方法來尋找規則[1, 38, 53]。通過實驗來定量測量影響耦合作用的微觀組分、細胞密度、ECM 和 GF 的濃度是非常困難的。目前文獻中還沒有直接將支架植入引起的應力/應變水平與動脈壁損傷以及 GF 和 MMP 的產生與合成、VSMC 增殖數量等聯系起來的實驗數據[38]。迫切需要更多的力學生物學數據以及材料降解和力學性能的實驗數據，以便建立合適的本構關系來描繪應力誘導的動脈壁不同類型細胞組分的生成和去除[26]。盡管動物的在體實驗研究和器官培養研究可以為損傷性狹窄的定量研究提供更好的幫助，但將其應用于獲取人類數據仍然是一項艱巨的挑戰[59]。
（4）構建接近真實的幾何、材料與力學模型。由于動脈之間存在重要的結構和功能差異，其生物學參數可能因動脈與動脈、物種與物種、患者與患者、甚至同一患者的不同病變而不同[61]。針對支架介入治療動脈狹窄的生物力學模型，應該包含更真實的特征，如患者個性化的三維幾何模型和材料屬性[87]，在本構關系中引入粘彈性，以及動脈粥樣硬化斑塊對血管壁生物力學響應的影響等[64]。這樣便于對模擬結果和實驗數據進行更深層次的模型驗證[93]，也便于充分測試不同的支架設計在預防 ISR 方面的療效[61]。但模型復雜化以后，帶來的弊端是急劇增大計算模擬工作量[59]。另外，動脈在人體內會受到組織的約束，如何確定數值模擬過程中在動脈上施加的約束，也是一個值得研究的力學建模問題。人體內的生理狀態不是一成不變的，如血壓的波動等，這對流固耦合模擬過程中邊界條件的施加會有一定的影響；支架植入后患者會有一定的運動，而身體的運動可能導致動脈的幾何形態或是受力狀態發生變化，如動脈的彎曲、扭轉等，這會導致支架和動脈內應力分布和血液流動狀態發生改變，從而對支架降解速率產生影響，因此對于易發生變形的動脈需要考慮變形對于模擬結果的影響。求解支架降解和血管重建的耦合模型涉及到動邊界、幾何改變、材料屬性改變、動網格、時空迭代算法、求解器的方便應用等問題[93]。對于這樣復雜的動態耦合模型，采用人工智能（artificial intelligence，AI）技術可能是具有吸引力的解決方案。
（5）支架擴張以加大狹窄血管的管腔直徑與血管擴張損傷誘導 ISR 的發生是一對矛盾，如何利用生物力學模型進行優化設計以達到最佳的支架支撐、降解和血管重建能力的匹配，進而獲得最佳治療效果，這是一個面向工程技術和臨床應用的問題，對支架結構設計和支架釋放手術方案具有直接的指導意義。另外，從術后護理與康復建議的角度來看，對易變形動脈患者的合理運動和康復研究存在極大的臨床意義，如身體的運動幅度的限制等。
（6）建立新的無量綱指標——匹配度和風險系數。支架降解喪失支撐力而發生突然崩塌前，血管是否完成重建是支架治療成功與否的關鍵。本文嘗試將這兩個過程用一個初步的數學模型來概括，以更加直觀地反應二者的耦合關系。
假設支架降解過程用一個質量損失函數D（t，σ）來描繪，而血管重建過程用一個質量生長函數G（t，σ）來描繪，D和G至少是時間t和應力σ（或者應變ε）的函數。那么支架治療效果最佳的理想狀態是：在發生崩塌失效時D = G，即在支架突然失效之前血管已經完成重建。當D ≠ G時，支架降解和血管重建的耦合匹配失衡，血管就有發生 ISR 或晚期血栓的風險。為了表示支架降解和血管重建的耦合匹配程度，本文提出一個新的無量綱指標——匹配度M，如式（1）所示。
 |
其中，分子表示D和G的較小者，分母表示D和G的較大者。M值近似為 1，表明耦合匹配程度較好；M值遠小于 1，表示耦合匹配度較差。通過對D和G函數進行歸一化處理，可得到匹配度M的具體數值。
進一步地，本文提出一個新的無量綱指標——風險系數R，來具體表示 ISR 發生的風險大小，如式（2）所示。R越大表示發生 ISR 的風險越大。
 |
盡管上述模型和指標很難全面揭示支架降解和血管重建的動態耦合匹配程度，但至少明確了其中最根本的生物力學核心問題并提出了可能的解決方案。在以后研究中，需要利用生物力學建模、數值分析、離體模型實驗、在體動物實驗等手段，觀測可降解支架動態降解過程中支撐性能變化和血管重建的耦合情況，包括在空間尺度如何考慮局部的損傷和生長對整體性能的影響，從而進一步地優化和修正模型，以揭示支架降解與血管重建之間的力學作用及匹配度變化，這些都將為支架的結構優化與促進血管重建提供科學依據。
3 總結
生物可降解支架相對于現有的永久性支架而言，可降低 ISR 形成的風險，并且適用于兒童患者快速生長的血管，以及促進血管彈性力學性能的恢復，因此成為新一代支架的研究熱點。基于本構關系以及應力-生長關系如何構建支架降解和血管重建的動態耦合模型，并定量評價動態耦合的匹配度和發生 ISR 的風險大小，是其中的核心科學問題。總而言之，利用建模仿真和實驗驗證的方法，研究支架材料損傷退化與生物組織生長重建之間相互作用的動態過程，揭示可降解支架在服役過程中的生物力學影響因素及其作用規律，評測支架服役的動態支撐性能和治療效果，為可降解支架的結構設計、力學分析和臨床應用打下科學基礎并提供重要的生物力學研究技術手段。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
支架內再狹窄（in-stent restenosis，ISR）是制約支架植入術臨床治療效果的主要問題。ISR 主要與炎癥反應、內膜增生、細胞外基質合成及血管重建等因素有關[1]。采用支架對狹窄血管進行擴張，會引起血管壁內皮的損傷，而血管壁對損傷的愈合效應導致血管平滑肌細胞向損傷處遷移增殖，從而引發 ISR[2]。可降解支架具有可降解性及良好的生物相容性，可有效地促進血管重建并恢復其彈性和舒縮功能[3]，在避免 ISR 方面比永久性支架具有更大的潛力。
可降解支架在服役過程中，血管重建和支架降解是一個動態耦合的過程，如圖 1 所示。力的傳遞在此過程中發揮了重要的作用。若支架降解速率過快，則血管重建不足，不能單獨承載載荷，將最終導致血管的再塌陷；反之，若支架降解速率過慢，則無法為新生內膜生長騰出空間，造成新陳代謝障礙等問題，也不利于血管重建；這些均有可能導致 ISR 的發生。
圖1
支架與血管力學性能隨時間變化示意圖
Figure1.
Schematic diagram of the temporal change of mechanical performance of stent and vessel.
本文對支架降解、血管重建以及二者動態耦合的生物力學建模分析進行了綜述，并提出了耦合匹配度和 ISR 風險系數的概念，以期對可降解支架的生物力學研究和臨床應用有所啟發。
1 國內外研究現狀
1.1 支架降解過程的建模分析
不同材質的支架植入血液環境中均會發生不同程度的腐蝕，導致材料產生機械損傷，降低材料強度。該腐蝕過程涉及到電化學、金屬物理學、熱動力學、材料學和力學等多學科交叉的問題[4]。支架材料的腐蝕機制一般包括但不局限于微電流腐蝕、點蝕、應力腐蝕和疲勞腐蝕[1]。據此建立的均勻腐蝕模型一般用于描述化學反應或電化學反應引起的腐蝕，即暴露在腐蝕性環境中材料的自由表面受腐蝕的情況；而連續損傷力學（continuous damage mechanics，CDM）法常用于模擬在腐蝕環境中應力/應變作用下材料受侵蝕的情況。下文逐一分類詳述：
（1）均勻腐蝕是支架降解最簡單和理想的狀態。較早的研究中，模擬支架降解較多地采用均勻腐蝕模型。Deshpande[5]采用多物理場方法，開發了兩相金屬鎂合金中微觀電化學活性的數值模型。Grogan 等[6]采用有限元法（finite element method，FEM）在可降解支架外表面通過均勻刪除單元來模擬均勻腐蝕過程，進而利用任意拉格朗日-歐拉（arbitrary Lagrangian-Eulerian，ALE）自適應網格技術，改進了均勻腐蝕模型。
（2）應力/應變腐蝕反映了支架植入血管后在力學作用下的降解行為。聚合物可降解支架在壓握和釋放過程中的應力和應變會對支架內部微結構完整性造成破壞，從而導致不均勻降解和早期崩塌等惡性事件發生[7]，這表明設計支架時應考慮力學因素對支架擴張造成的材料微觀損傷以及支架服役降解的影響。支架擴張結束后產生的殘余應力是支架降解和血管重建的誘導應力[8]。CDM 法從連續介質力學的角度分析支架材料的應力、應變及其誘導的支架材料損傷過程，基于實驗的唯象學結果對模型的參數進行標定，在 FEM 框架中易于實現數值模擬。CDM 法適合于針對可降解支架復雜的三維幾何形狀和加載條件的建模[4]。
舉例來說，Costa-Mattos 等[9]采用 CDM 法建立應力腐蝕模型，將應力腐蝕與均勻腐蝕共同作用到可降解金屬支架上，并通過實驗對該模型進行了驗證。Gastaldi 等[10]的應力腐蝕模型為： σ = ，其中 σ 為有效應力張量， 為未損傷應力張量，D 為損傷因子；D = DU + DSC，其中 DU 表示均勻腐蝕損傷因子，DSC 表示應力腐蝕損傷因子。D = 0 表示材料無損傷；D = 1 表示材料完全損傷。該模型直觀明了，容易在 FEM 數值模擬中實現，至今仍廣泛用于血管支架的腐蝕降解模擬中。Wu 等[11-12]采用均勻的微電流腐蝕與應力腐蝕共同作用的 FEM 模型，研究兩種可降解金屬支架在應力腐蝕和均勻腐蝕的共同作用下的降解行為，并進行體外腐蝕實驗分析驗證了 FEM 模型在支架設計和性能評估方面的實用性和有效性。
（3）點蝕可能受到支架在制造過程中表面缺陷的位置、在血管成形術中的表面缺陷或應力集中區域的影響[1]，進而影響支架服役過程中的腐蝕降解。Grogan 等[6,13]在均勻腐蝕模型中加入了點蝕模型，研究了一種基于物理學的均勻腐蝕模型，考慮了包括鎂離子運輸的鎂支架降解的多物理過程。Shen 等[4]建立了一種 CDM 模型并采用 FEM 數值模擬鎂合金冠脈支架的疲勞腐蝕，結果表明該模型可以預測降解速率以及損傷誘導的徑向剛度減小等。許多基于 CDM 方法的研究致力于均勻腐蝕、點蝕、應力腐蝕、應變腐蝕，但較少考慮腐蝕和疲勞的協同作用（這會增加問題的復雜性）[14-15]。
由于血液循環引起的傳質和流動剪切應力加速了整體腐蝕（包括局部、均勻、點蝕等）。流動剪切應力提高了平均均勻腐蝕速率、局部腐蝕覆蓋率和深度以及腐蝕坑內腐蝕產物的去除率[16]。對于覆膜支架而言，支架在植入初期的幾個月內，可以不考慮血流沖刷對支架降解的影響；待血管新生內膜覆蓋支架桿之后，血流對支架降解的影響也比較小，當然這是比較理想的狀態。
關于支架降解模型求解方法的問題，應用較為廣泛的還是 FEM。Grogan 等[17]建立了一個可吸收金屬支架的物理降解模型，并利用顯式 FEM 和自適應網格技術，模擬展示了可吸收金屬支架結構在擴散控制腐蝕情況下的變化表面和力學表現。進一步地，Grogan 等[13]基于隱式 FEM 和自適應網格，模擬了擴散控制腐蝕情況下三維可降解鎂支架結構的變化表面。為了擴大基于 FEM 模擬支架降解的方案通用性并縮短計算時間，學者提出了一種隱式的 FEM[18]。該方法被用于預測實驗觀察到的塑性應變介導的質量損失剖面[19]，但局限性是既沒有考慮腐蝕層的形成及其厚度隨時間的變化，也沒有考慮支架壓握、擴張回彈壓力以及動態疲勞載荷作用的影響，而且所計算的應變也是單軸的，而支架在狹窄血管中的應變應該是多軸而復雜的[19]。
綜合來看，上述關于支架降解的生物力學建模分析的研究，可以歸納為如圖 2 所示的技術路線圖。動脈的個性化幾何形狀、狹窄斑塊的材料屬性、載荷及邊界條件等都是影響支架降解的復雜生物力學環境因素[20]。支架降解動力學建模方面至少存在三個方面的挑戰：一是基于唯象學的經驗數據模型還需要更本質的理論模型支持；二是基于動物實驗的模型不一定符合人體血管和血流的實際；三是如何對離體/在體模型和靜態模型進行合理修正，以便模擬在體、動態的降解過程。
圖2
支架降解生物力學建模分析的技術路線圖
Figure2.
Schematic diagram of the biomechanical modeling and analysis of stent degradation
1.2 血管重建的建模分析
血管壁包括內膜、中膜和外膜這三層結構。內皮細胞（endothelial cell，EC）呈單層狀排布于血管內膜表面并對血流剪切應力的變化敏感。血管平滑肌細胞（vascular smooth muscle cell，VSMC）位于血管中膜，VSMC 過度增殖是誘發動脈粥樣硬化以及介入治療后 ISR 的主要病理過程[21-22]。彈性纖維和膠原纖維是外膜的主要成分，血管外膜成纖維細胞在血管損傷后新生內膜的增生中起重要作用。細胞外基質（extracellular matrix，ECM）對細胞起到復雜網絡支持物的作用，并作為一個關鍵的生物化學和生物力學信號的來源，積極參與控制細胞的生長、極性、形狀、遷移、穩定和代謝活動[23]。“生物力學之父”馮元楨先生提出了“應力-生長法則（stress-growth law）” [24]，即包括細胞和 ECM 的生長和吸收在內的血管重建是與血管中的應力/應變相關的，即生長取決于應力和應變。
血管重建是細胞增殖、死亡、遷移以及 ECM 合成和降解所致的血管壁結構動態變化的過程。有人將血管生長和血管重建區分開：血管生長，指的是血管質量的改變；而血管重建，指的是血管結構的改變[25-26]。在這里，將二者統一為血管重建。
從宏觀尺度來看，支架植入后對血管壁的作用力以及管腔內血流對血管壁的切應力驅動了血管重建[27]，一般采用 CDM 法來模擬并利用 FEM 來求解支架擴張后的血管壁應力水平。從微觀尺度來看，ECM 與血管壁各層細胞之間的力學-化學-生物學效應驅動了血管重建，一般采用元胞自動機（cellular automata，CA）或基于代理模型（agent-based model，ABM）來模擬。將宏觀和微觀模型相結合，就組成了血管重建的多尺度模型。下文逐一分類詳述：
（1）宏觀尺度模擬
在血管重建的宏觀尺度模擬方法中有兩種主要的 CDM 方法，即：① 運動學生長模型（kinematic growth model，KGM）：將無載荷體的局部變形分為非彈性和彈性兩部分運動學增長過程[28]；② 約束混合模型（constrained mixture model，CMM）：在附帶預應力的受力物體中加入新生質量，這種預應力與特異性組分的自然幾何結構狀態有關[29]。這兩種方法本質上可以理解為計算應變能和質量密度。KGM 法假設的總變形梯度可以分解成一個彈性部分（確保變形中的力學平衡和幾何相容性）和一個非彈性部分（描述增長）。CMM 法將物體定義為由n個組分組成，每個組分由眾多質量增量組成；在每個體積單元中，不同時間沉積的不同組分的質量增量形成了一個受約束的混合物，也就是說它們呈現同樣的、隨著時間變化的彈性變形[30]。
KGM 法用于模擬整個組織的初始無應力體的生長，即無應力體的大小和形狀的變化可以通過兩個變形來描述：非彈性“生長”變形（梯度）Fg以及隨后的彈性“組裝”變形（梯度）Fa。Fg通過無窮小的體積單元中質量的添加或移除來描繪無應力體的變化；Fa通過將生長的體積元素裝配到無應力的連續體上來確保幾何兼容性。由于其模型簡單而且計算成本低，KGM 法一直被廣泛研究[31-32]。Zahedmanesh 等[33] 據此模擬了血管中層 VSMC 增殖和遷移而導致的 ISR，利用有限元分析軟件 ABAQUS/explicit（Dassault Systemes，法國）求解器與其 VUMAT 子程序進行數值模擬，結果表明支架擴張血管到最大直徑時造成血管損傷的程度對 ISR 發生率起到重要作用。針對力學因素調節膠原纖維的定向生長問題[34-35]、應力-生長動力學關系的異質性和生長穩定性問題[36]、血管成分的各向異性材料屬性引起的趨向性重建問題[37]，均可以通過 KGM 法來模擬。Escuer 等[38]基于重要組分的密度/濃度，如生長因子（growth factor，GF）、基質金屬蛋白酶（matrix metalloprotein，MMP）、ECM 以及 VSMC 等，用耦合擴散-反應偏微分方程組構建了與血管損傷相關的體積增長模型，并利用 FEM 模擬 ISR。KGM 法的一個主要挑戰是確定非彈性“生長”變形（梯度）的本構關系Fg，通常Fg的確定方法是典型的試探性猜測。在自然應力狀態下具有不同的預應力的不同類型組分，其在體的生長和重建往往以不同的速率而產生、去除或重建，然而這些過程沒有在 KGM 法中考慮[30]。
CMM 法因為可以模擬同時存在的多種組分的影響而越來越受到關注，這些組分通常以不同的速率不斷沉積和降解，這對于理解活的軟組織的基本特征很重要，而這些特征是不能被簡單的 KGM 法來描繪的[30]。具有代表性的工作是 Humphrey 等[29]所做的研究，他們建立了一種 CMM 法來解釋組成動脈的不同重要組分的力學性能、自然（無應力）幾何結構以及轉化率和范圍，并將該模型應用于一個不斷發展過程中的顱內梭形動脈瘤的非線性有限元分析（finite element analysis，FEA）。Rivas-Marchena 等[39]構建了一個基于電生物阻抗的數學模型，可以解析地描繪支架植入后的新生內膜的實時組織成分變化。He 等[40-42]采用醫學影像構建了各向異性的血管和狹窄斑塊的幾何模型，用能量損耗密度來評價組織損傷程度。這些工作盡管對模擬血管生長做出了貢獻，但無論從材料屬性、幾何結構，還是從血管組成成分的生長等方面仍然具有局限性。
除了支架作用于血管的應力之外，血流作用于血管的壁面切應力（wall shear stress，WSS）在血管重建中也發揮了重要作用。支架貼壁不良導致支架局部產生主流方向和二次流方向的微觀回流[43]，對 WSS 和血液黏度產生了顯著影響，這與 ISR 密切相關。Ng 等[44]系統分析了流動切變率和 WSS 對血栓和新生內膜等的影響，特別是討論了支架結構以及支架擴張和貼壁情況對局部血流動力學和 ISR 的影響。最近的文獻報道，Boland 等[45]同時考慮了支架擴張對血管壁的應力損傷和血流 WSS 對血管重建的刺激作用，利用 FEM 數值模擬鎂支架支撐三層各向異性結構的動脈，將“虛擬網格”（ghost mesh）置于動脈腔內支架周圍（新生內膜在此發生）；根據 FEA 得到的血管壁應力和 WSS 數值，計算兩者對血管壁的損傷，再將這些變量作為刺激驅動力輸入到血管重建模型中作為細胞負荷，從而誘導動脈中的細胞從動脈擴散到虛擬網格中實現增殖。
CDM 法可用于模擬從細胞到組織的所有水平的生物系統的響應。可以在空間和時間上使用偏微分方程（partial differential equation，PDE）對關鍵的細胞反應（例如細胞密度進化）進行建模，但該方法的一個重要限制是 PDE 可能無法捕獲由單個細胞組成的多細胞生物系統的離散性質，并且在解決復雜問題時涉及多個變量使得計算變得笨重[46]。
（2）微觀尺度模擬
生物系統的整體行為是由細胞水平上發生的離散現象導致的，如細胞遷移、增殖和凋亡等[47]。因此，使用離散方法可以更好地對生物系統進行建模。CA 和 ABM 是用于多細胞生物系統建模的兩種主要離散方法，它們模擬單個細胞的行為和細胞之間的相互作用，從而能夠觀察到生物系統的行為。采用自下而上的方法，每個單獨的細胞都根據為其定義的行為規則而顯式地建模；基于在細胞級別定義的行為規則，系統行為通過細胞之間的局部耦合作用而呈現出來[46]。這兩個系統都是基于規則的，需要定義每個代理或單元的數學關系，以及指定初始和邊界條件[48]。CA 法由具有預定義尺寸的規則單元網格組成，細胞只能通過某些預先定義的網格點移動。相反，ABM 法通常是無網格模型，這意味著單元網格可以位于計算域中的任何位置，這個位置通常是通過求解單個細胞的運動方程來確定的。ABM 法可以在隨機位置初始化代理，也可以在模擬期間創建新的代理。因此，與 CA 法相比，ABM 法可以產生更真實的結果[46, 49]。
ABM 法研究離散的細胞級別的行為和不同分子的生成，模擬血管對生長因子、蛋白酶和其他信號分子水平增減的反應，以及細胞表面黏附分子的強度等[50]，從而揭示單個細胞相互作用的結果是如何綜合形成組織動力學的[51]，而這些是不能依據上述 CDM 法來實現的[52]。
ABM 法將單個細胞用由一組規則控制的格子來表示，細胞和諸如生長因子等其他物種種群的進化通過 PDE 來描述[38]。ABM 法通過求解 PDE 可以整合眾多代理的個體行為和個體之間的相互作用，來預測模型系統（如組織或器官）中代理的復雜集體行為[53]。比如，Boyle 等[54]在格子中模擬 VSMC 的遷移、增殖和分化等活性，在簡化的加載情況下檢驗炎癥方程，論證了基于格子的建模方法具有模擬動脈組織的力學生物學反應的潛力。針對冠狀動脈移植管搭橋術后常發生靜脈移植管動脈化的現象，Garbey 等[55-56]利用 ABM 法等計算模型展示了細胞/組織層次上相互作用的反饋回路和力學環境條件，并以兔子實驗結果中的組織學數據作為參考，在二維計算模型上驗證了所構建模型和方法的可行性。ABM 法相關的研究很多，大家可以參考文獻[51-52]進行延伸閱讀。
針對 ABM 法的模擬仿真已開發了多種軟件，如商業數學軟件 Matlab R2015b（The MathWorks，Inc.，美國）可以模擬動脈壁細胞對機械損傷的集體反應[47]。有些專門基于細胞模型的軟件，可與動脈和支架的有限元模型相結合，預測動脈對支架植入的反應[48]。對于代理數量較大的 ABM 算例，在求解 PDE 時耗時很大。折中的辦法是：限制模擬中細胞的數量，考慮復雜的交互，或者采用更大的細胞集合，簡化交互規則[52]。
雖然 ABM 法可以提供關于生物系統中演化行為的深刻信息，然而 ABM 法要么忽視了力學刺激在調節體內平衡中的作用，要么對應力和應變的計算采用了過于簡單的方法[57]。這與 ABM 法存在的固有缺陷有關，即無法方便地計算出動脈在時變、非均質和復雜幾何結構下的應力和應變。為了解決這個問題，建議將 ABM 法與 CDM 法耦合[53, 58]，這樣就形成了目前更為常見的 ABM-FEM 耦合多尺度模型。
（3）多尺度模擬
FEM-ABM 多尺度模型在血管重建方面的應用越來越盛行[53, 59-60]。其求解思路是：首先采用 FEM 求解 CDM 模型，確定在設定載荷下（或者支架植入后誘導的）血管壁的變形和應力，用于量化計算細胞損傷值，并傳輸到 ABM 模塊；然后采用 ABM 法，模擬血管壁中 VSMC 和 EC 的表型變化、遷移和增殖等行為[61]。
近年來，FEM-ABM 多尺度模型方面的研究成果不少。Boyle 等[62]以 VSMC 為離散代理，通過損傷和炎癥的組合作用來模擬 ISR，其中 CDM 法將支架擴張的 FEA 結果與損傷累積相耦合，用來計算動脈損傷；炎癥模型用常微分方程來建模，描繪因損傷而引起的組織降解、生長因子的生成以及損傷的消除；一個基于格子的 ABM 法用來模擬 VSMC 的表型、增殖、遷移和組織生成。針對支架引起的動脈損傷以及在 ISR 的發展過程中膠原基質重建的研究表明[59]，高應力引起的血管壁損壞上調了 VSMC 細胞的 MMP，從而導致 ECM 降解。Marino 等[63]提出了一個關于動脈生理病理的力學-化學-生物學的框架，解釋組織成分在多尺度層次結構中的精細重構和細胞-細胞信號通路中涉及的分子物種的擴散，重點研究組織結構行為的改變以及擴散性/滲透性對病變情況下非功能性宏觀力學響應的關鍵作用。文獻[64]建立了 ISR 新生內膜質量增長的演化方程，其中考慮了支架誘導損傷對 VSMC 的激活以及激活細胞的增殖速率；利用兩個向量來表征膠原纖維束的方向，通過在質量平衡方程中引入質量演化，得到了生長張量隨時間的演化。通過將包括支架釋放、血流和支架血管組織生長的 FEM 模型與包括描繪 VSMC 增殖和 ECM 產生的 ABM 模型進行耦合，模擬新生內膜的發展[65-67]，并比較模擬結果與豬體內實驗的組織切片數據，這為離體 ISR 模型提供了驗證方法。Cerrolaza 等[49]模擬支架植入后動脈壁的 ISR，其中 ABM 包含兩種相互依賴的 EC 和 VSMC，而它們的行為主要受力學環境的控制。進一步地，Nolan 等[47]探討瞬時加載和循環加載兩種驅動力方式下的損傷誘導細胞增殖的機制，結果表明循環加載損傷模型預示著非生理性、過度增殖性響應，而瞬時加載模型則提示再內皮化可以調節管腔損失。最近，Cheng 等[68]建立了一個將殘余應力與生長模型耦合的數值方法，并研究了殘余應力對冠脈血管組織重建的影響；通過編寫 ABAQUS 子程序來給有限元網格施加殘余應力，利用 UMAT 子例程來指定具有超彈性生長模型的應力和彈性張量；研究結果表明，與無殘余應力的情況相反，殘余應力使血管外壁產生更大的應力和生長因子。
多尺度模型的主要問題是，調試耦合匹配參數的過程復雜，計算工作量大。半侵入式不確定性量化（uncertainty quantification，UQ）方法是一種計算成本更低的方法[69-70]，用于研究多尺度心血管模型的二維 ISR 問題，其計算結果與黑箱擬蒙特卡羅方法的計算結果吻合較好，表明該方法是可靠和有效的。
最近的研究更多地集中在血管重建過程的生長穩定性上（即力學生物學穩定性）。力學生物學穩定性即指在“應力-生長法則”驅動下，血管受到力學刺激而生長所達到的穩定狀態。Erlich 等[36]研究了非均質材料的分層管狀結構生長穩定性問題，結果表明生長穩定性主要取決于生長響應的各向異性。不同學者采用不同的 CMM 法研究動脈血管重建的穩定性，得出一致的結論：在恒定壓力下增大的組織剛度和更高的組織生產率傾向于使血管重建過程保持穩定，而增大的降解速率則會使血管重建不穩定[71-73]。Li 等[74]構建了一種完全雙向耦合的 ABM-FEM 框架，研究血管的力學-化學-生物學因子的相互作用及其在維持體內平衡生長穩定性中的作用；結果表明，將血管曲率和 ECM 的產生包含在模型中對于取得與實驗數據良好的一致性結果至關重要。一種新的基于變化率的三維 CMM 法，適用于研究軟組織在材料組成或施加載荷的瞬時/持續變化下的力學生物學平衡和穩定性[75]。這種基于速率的 CMM 法等價于基于積分的模型，能夠區分可能導致穩定和不穩定的力學生物學響應。
綜合來看，上述關于支架植入后血管重建的生物力學建模分析的研究，可以歸納為如圖 3 所示的技術路線圖。
圖3
支架植入后血管重建的生物力學建模分析的技術路線圖
Figure3.
Schematic diagram of the biomechanical modeling and analysis of blood vessel remodeling after stent intervention.
基于理想化的二維模型來建立支架植入后血管重建的生物力學模型，已經取得了較好的進展。然而，基于三維模型、特別是三維個性化模型來建立支架植入后血管重建的生物力學模型，仍然難度很大。動脈受到力學損傷后，血小板、白細胞、VSMC 等釋放多種類型的 GF：血小板源性 GF、表皮 GF、胰島素樣 GF、轉化 GF、成纖維 GF[76-77]。這些 GF 的力學-化學-生物學協同作用，導致精確構建血管重建的生物力學模型面臨巨大的挑戰。
1.3 支架降解和血管重建的耦合建模分析
支架在服役過程中需要承受血管壁力學-化學-生物學環境的作用以及血流腐蝕作用，支架結構和材料屬性發生腐蝕退化，力學性能變弱，結構發生損傷，血管發生收縮，導致支架與血管之間的相互作用發生動態變化，進一步影響到支架降解和血管重建的耦合過程[78-80]。支架降解和血管重建是既獨立又相互關聯的兩個過程[81]，即形成了一個具有反饋調節機制的閉環系統。
在可降解支架服役過程中，支架降解使材料屬性衰退，而血管新生細胞生長也會對材料屬性造成影響，兩者動態組合出不同性能的新材料。研究表明，干細胞動員、歸巢、分化、增殖是血管內支架植入后血管內皮修復的主要機制，多種血管內因子、力學微環境變化等均參與此過程，進而影響植入部位的再內皮化[82-83]。針對不同內皮覆蓋率和高危因素（包括較厚的支架桿、支架貼壁不良和重疊）對動脈一氧化氮（NO）分布影響的研究發現，內皮覆蓋少、支架桿較厚和支架釋放不當均可能降低 NO 濃度，并導致支架桿附近的 NO 濃度相對較低，進而促進內膜增生[84]。關于鋅材料支架的降解研究發現，支架釋放的鋅離子濃度的高低對 EC 的黏附、聚集和遷移等具有截然相反的作用[85]，可降解鋅表面的氧化物薄膜對可降解鋅材料的早期內膜增生有嚴重影響[86]。Holzapfel 等[87]的實驗研究以及 Boland 等[48]的計算研究發現，被激活的新生內膜的楊氏模量對血管重建后支架的腐蝕及其支撐性能有很大影響，從而也是影響冠狀動脈整體塌陷或回彈的一個重要參數。因此，支架降解和血管重建是相生相長、相互影響的。
關于支架降解和血管重建的耦合建模分析，采用最多的方法是 CDM-ABM 耦合方法。該方法的理想狀態是將“支架降解-血管重建”組合形成一個帶有反饋調節機制的閉環系統模型。這有別于上一節中的 FEM-ABM 多尺度模型，那里僅僅是把 FEM 所得支架對血管壁的作用力傳遞給 ABM 進行血管重建，而沒有考慮支架降解的問題。
由于支架降解和血管重建的耦合建模算法非常復雜，所以目前的相關研究報道還不多。具有代表性的、較為前沿的工作是 Boland 等[45, 48]的研究。他們建立了一個鎂支架植入血管的計算模型框架，其中考慮了導致新生內膜重建的兩種主要生理刺激，即支架作用力和血流 WSS，并與能夠模擬真實情況下支架局部腐蝕的點蝕模型相結合。支架點蝕模型為：，其中 為腐蝕速率，損傷因子 D 與 成正比；隨著 D 增加，腐蝕表面單元彈性和塑性會線性下降； 為點蝕系數， 越大表示支架更易受點蝕影響；D ≈ 1 時，單元完全損壞，并更新相鄰單元的點蝕系數 。新生內膜重建模型為：，其中 n 為細胞濃度，如果單元中的n超過預定義的閾值，則該單元將被激活而轉化為新生內膜的新材料。公式右邊第一部分就是菲克（Fick）擴散定律，它可以通過熱模擬法與傅里葉（Fourier）熱傳導定律相關聯，并可以在 ABAQUS 中通過耦合熱-位移模擬過程來實現。 和 分別對應于支架作用力和血流 WSS 誘導的血管壁損傷因子，而 和 分別是它們對應的常數。通過反復修改擴散特性，使得大部分新生內膜在 28 d 內形成，這樣就與動物實驗中的結果相匹配。在該模型中，支架降解和血管重建是獨立的，即把支架的腐蝕速率設為一個常數，未討論支架降解與血管重建過程中力的相互作用與匹配度問題；并且純鎂試樣的體外腐蝕實驗表明，覆膜試樣的降解速率比未覆膜試樣慢[88]，所以有必要區別考慮支架降解與血管重建之間的耦合作用。
在動脈的生物力學模型中有兩種非常不同的時間尺度：一種是由心臟周期引起的脈動運動的短期時間尺度——“加載時間尺度”，以秒為單位；另一種是血管重建的長期時間尺度——“生長時間尺度”，以天、周或月為單位。Holzapfel 等[89]在骨骼力學中定義了這兩個“時間”。通過合理假設，可以在血管重建模型中將上面兩種尺度的“時間”聯系起來[26, 45]。準確模擬支架降解和血管重建的關系，探索動態耦合作用下在每個時刻二者的幾何形態和材料匹配度，并在設計可降解支架時保證與組織再生和生物降解性相匹配的降解率[90]，這將是下一步研究的重點。
綜合來看，上述關于支架降解和血管重建的動態耦合作用的研究，可以歸納為如圖 4 所示的技術路線圖。在第 I 階段，血管模型需要考慮血管壁的殘余應力，而支架模型需要考慮初始結構尺寸等結構設計因素以保證支架的支撐力及其對血管壁的損傷大小在合理范圍內。在第 II 階段，完成支架在狹窄血管內的釋放，支架和血管的本構關系決定了各自的受力和變形，由此獲得支架與血管壁/斑塊之間的相互作用力以及血流對血管/支架的流動切應力，這些應力將作為輸入驅動條件分別傳遞給支架降解模型和血管重建模型。在第 III 階段，分別模擬支架降解和血管重建過程，此時支架降解模型和血管的“應力-生長法則”發揮作用，由此獲得支架和血管的幾何結構、材料屬性與本構關系的改變結果，這些結果將作為輸入驅動條件傳遞給更新后的支架-血管耦合模型。在 II'階段，支架與血管之間交換幾何、材料和力學等信息，完成更新后的支架-血管耦合模型又回歸到第 II 階段進行新一輪循環的耦合分析。當支架完全降解、達到穩定平衡狀態之后，就進入第 IV 階段，循環才算結束。這樣，如圖 4 所示的過程也就與如圖 1 所示的過程相吻合了。
圖4
支架降解與血管重建動態耦合生物力學建模分析的技術路線圖
Figure4.
Schematic diagram of the biomechanical modeling and analysis of the dynamic coupling between stent degradation and blood vessel remodeling
2 研究展望
如前所述，支架降解和血管重建之間形成一個復雜的耦合系統，其中涉及到很多時間和空間的跨尺度問題。對一個復雜的系統進行建模和分析，需要由簡單到復雜、“由底層向頂層”和“由頂層向底層”循序漸進的不懈探索。關于這一耦合過程的生物力學建模分析，進一步的深入研究包括但不限于如下幾個需要關注的方面。
（1）耦合過程中的多相材料、多場耦合行為是目前比較新的研究課題。這個耦合系統中涉及到力學（固體力學、流體力學、熱力學）-化學-生物學的綜合相互作用。無論是支架降解還是血管重建，如何分配諸多影響因素之間的貢獻權重，這是必須要考慮的一個問題。要系統地了解支架與血管之間的相互作用，包括腐蝕類型、腐蝕速率、腐蝕產物、氫的演化和局部 pH 值的變化等方面的信息很少，其中關鍵的一步是識別和測試在復雜生物系統中顯著影響支架降解和血管重建行為的相關局部環境參數[16]。針對影響細胞介導血管重建的力學-化學-生物學狀態變量的研究，如不同結構上的重要成分以不同的速率和程度產生和去除，仍然是一個活躍的研究領域[26]。確定適合質量生成和去除的生物力學模型是最重要的開放性問題之一[91]。
（2）將目前描繪動態耦合的開環系統升級為閉環系統，并探討其力學生物學穩定性。血管的力學生物學穩定態（包括不同的組分材料特性、轉化率和幾何結構等）是一個能動的過程：正常的血管組織能適應力學生物學變化、通過反饋調節機制而恢復和維持血管的幾何與材料屬性的穩定平衡狀態；而病變的血管組織則會破壞這種穩定平衡狀態、導致血管重建的惡性循環變化[72, 75, 92-93]。目前的研究基本上還是將耦合系統簡化為一個開環耦合系統，不考慮物質輸運（如新陳代謝、藥物緩釋、組分材料改變等）的力反饋作用，對耦合模型也缺乏嚴格的熱力學平衡約束[63, 94]，沒有實時更新支架-血管之間的幾何、材料和力學交互作用――亦即沒有很好地模擬如圖 4 所示第 II'階段發生的事情。因此，構建具有自適應調節功能的閉環耦合模型是一個系統性的問題。
（3）耦合模型的時間尺度和空間尺度的標定和驗證問題。受應力-生長關系影響的血管重建過程存在滯后效應，力學刺激是個瞬時的過程（以秒計），但生長是個緩慢的過程（以天、月計）；另外，動脈結構和病變（包括創傷和退行性病變等）可能因人而異，以及在細胞生長過程中的遺傳變異，使得不同患者的血管對同一刺激也可能有不同的反應[54]，反過來血管重建對支架受力和降解也有不同的影響。如何在時間尺度和空間尺度上協調統一地標定支架降解與血管重建過程，這是一個挑戰性問題。目前基本上采用抓住主要矛盾、突出主要因素、通過實驗進行唯象學的歸納方法來尋找規則[1, 38, 53]。通過實驗來定量測量影響耦合作用的微觀組分、細胞密度、ECM 和 GF 的濃度是非常困難的。目前文獻中還沒有直接將支架植入引起的應力/應變水平與動脈壁損傷以及 GF 和 MMP 的產生與合成、VSMC 增殖數量等聯系起來的實驗數據[38]。迫切需要更多的力學生物學數據以及材料降解和力學性能的實驗數據，以便建立合適的本構關系來描繪應力誘導的動脈壁不同類型細胞組分的生成和去除[26]。盡管動物的在體實驗研究和器官培養研究可以為損傷性狹窄的定量研究提供更好的幫助，但將其應用于獲取人類數據仍然是一項艱巨的挑戰[59]。
（4）構建接近真實的幾何、材料與力學模型。由于動脈之間存在重要的結構和功能差異，其生物學參數可能因動脈與動脈、物種與物種、患者與患者、甚至同一患者的不同病變而不同[61]。針對支架介入治療動脈狹窄的生物力學模型，應該包含更真實的特征，如患者個性化的三維幾何模型和材料屬性[87]，在本構關系中引入粘彈性，以及動脈粥樣硬化斑塊對血管壁生物力學響應的影響等[64]。這樣便于對模擬結果和實驗數據進行更深層次的模型驗證[93]，也便于充分測試不同的支架設計在預防 ISR 方面的療效[61]。但模型復雜化以后，帶來的弊端是急劇增大計算模擬工作量[59]。另外，動脈在人體內會受到組織的約束，如何確定數值模擬過程中在動脈上施加的約束，也是一個值得研究的力學建模問題。人體內的生理狀態不是一成不變的，如血壓的波動等，這對流固耦合模擬過程中邊界條件的施加會有一定的影響；支架植入后患者會有一定的運動，而身體的運動可能導致動脈的幾何形態或是受力狀態發生變化，如動脈的彎曲、扭轉等，這會導致支架和動脈內應力分布和血液流動狀態發生改變，從而對支架降解速率產生影響，因此對于易發生變形的動脈需要考慮變形對于模擬結果的影響。求解支架降解和血管重建的耦合模型涉及到動邊界、幾何改變、材料屬性改變、動網格、時空迭代算法、求解器的方便應用等問題[93]。對于這樣復雜的動態耦合模型，采用人工智能（artificial intelligence，AI）技術可能是具有吸引力的解決方案。
（5）支架擴張以加大狹窄血管的管腔直徑與血管擴張損傷誘導 ISR 的發生是一對矛盾，如何利用生物力學模型進行優化設計以達到最佳的支架支撐、降解和血管重建能力的匹配，進而獲得最佳治療效果，這是一個面向工程技術和臨床應用的問題，對支架結構設計和支架釋放手術方案具有直接的指導意義。另外，從術后護理與康復建議的角度來看，對易變形動脈患者的合理運動和康復研究存在極大的臨床意義，如身體的運動幅度的限制等。
（6）建立新的無量綱指標——匹配度和風險系數。支架降解喪失支撐力而發生突然崩塌前，血管是否完成重建是支架治療成功與否的關鍵。本文嘗試將這兩個過程用一個初步的數學模型來概括，以更加直觀地反應二者的耦合關系。
假設支架降解過程用一個質量損失函數D（t，σ）來描繪，而血管重建過程用一個質量生長函數G（t，σ）來描繪，D和G至少是時間t和應力σ（或者應變ε）的函數。那么支架治療效果最佳的理想狀態是：在發生崩塌失效時D = G，即在支架突然失效之前血管已經完成重建。當D ≠ G時，支架降解和血管重建的耦合匹配失衡，血管就有發生 ISR 或晚期血栓的風險。為了表示支架降解和血管重建的耦合匹配程度，本文提出一個新的無量綱指標——匹配度M，如式（1）所示。
|
其中，分子表示D和G的較小者，分母表示D和G的較大者。M值近似為 1，表明耦合匹配程度較好；M值遠小于 1，表示耦合匹配度較差。通過對D和G函數進行歸一化處理，可得到匹配度M的具體數值。
進一步地，本文提出一個新的無量綱指標——風險系數R，來具體表示 ISR 發生的風險大小，如式（2）所示。R越大表示發生 ISR 的風險越大。
|
盡管上述模型和指標很難全面揭示支架降解和血管重建的動態耦合匹配程度，但至少明確了其中最根本的生物力學核心問題并提出了可能的解決方案。在以后研究中，需要利用生物力學建模、數值分析、離體模型實驗、在體動物實驗等手段，觀測可降解支架動態降解過程中支撐性能變化和血管重建的耦合情況，包括在空間尺度如何考慮局部的損傷和生長對整體性能的影響，從而進一步地優化和修正模型，以揭示支架降解與血管重建之間的力學作用及匹配度變化，這些都將為支架的結構優化與促進血管重建提供科學依據。
3 總結
生物可降解支架相對于現有的永久性支架而言，可降低 ISR 形成的風險，并且適用于兒童患者快速生長的血管，以及促進血管彈性力學性能的恢復，因此成為新一代支架的研究熱點。基于本構關系以及應力-生長關系如何構建支架降解和血管重建的動態耦合模型，并定量評價動態耦合的匹配度和發生 ISR 的風險大小，是其中的核心科學問題。總而言之，利用建模仿真和實驗驗證的方法，研究支架材料損傷退化與生物組織生長重建之間相互作用的動態過程，揭示可降解支架在服役過程中的生物力學影響因素及其作用規律，評測支架服役的動態支撐性能和治療效果，為可降解支架的結構設計、力學分析和臨床應用打下科學基礎并提供重要的生物力學研究技術手段。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
