機器人骨折復位通常是固定骨折近端，機器人帶動骨折遠端按照規劃的復位路徑向近端運動。為提高復位手術的精準性和安全性，有必要了解復位中肌肉力和復位力的變化規律。本文基于骨骼肌組織的肌肉力分析骨折復位力，由 Haeufle 四元素骨骼肌模型，綜合考慮下肢羽狀肌的羽狀角對肌肉力特性的影響，提出一種股骨骨骼肌肉模型 PA-MTM，對比分析不同肌肉模型的骨骼肌的肌肉力。對比仿真分析兩種復位路徑下的肌肉力及復位力變化情況。結果表明，羽狀角越大對肌肉力的影響越大；股骨骨折復位，軸向牽引力最大且股二頭肌短頭起主要作用，軸向牽引力最大值為 472.18 N，復位合力最大值為 497.28 N，驗證了新型骨骼肌肉模型的合理性。
引用本文： 翟宇毅, 于琳, 陳冬冬, 崔澤, 雷靜桃. 基于新型骨骼肌肉模型的肌肉力及損傷股骨復位力分析. 生物醫學工程學雜志, 2021, 38(4): 732-741, 752. doi: 10.7507/1001-5515.202009016 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
股骨骨折是創傷骨科的常見病，且隨著全球老齡化和交通運輸的發展呈逐年增加的趨勢[1]。多由高能量直接損傷所致，如車禍傷、直接暴力打擊、強力擠壓等，也可見于高處墜落傷、機器絞傷等間接暴力導致的損傷；其骨折常伴有重疊、成角及旋轉等，有些還伴有嚴重的軟組織損傷，治療起來比較棘手，而良好的復位手段是股骨干骨折治療的關鍵[2]。傳統人工骨折復位手術，復位過程中醫生牽引和保持骨折的復位狀態，體力消耗比較大，復位效果依賴醫生經驗，而且醫患雙方會多次受到射線輻射影響。隨著醫療科學技術的發展，國內外開始研發機器人輔助骨折復位[3-5]，這不僅大大節省了醫生的體力，而且能有效提高骨折復位精度，并通過遠程操作替代術者的人工復位，減少輻射。
目前，為提高復位精度和復位操作的安全性，術前需要進行精準的復位路徑規劃[6-8]。由于骨折周圍復雜的生物力學環境和解剖力學特性，骨折復位過程中有可能對肌肉等軟組織造成損傷，因而有必要清楚了解骨折骨肌組織的生物力學特性，分析骨折周圍肌肉組織的肌肉力對復位的干擾和影響，分析骨折復位過程中的肌肉力及復位力。
關于骨骼肌肉模型有兩大類：Huxley 模型和 Hill 模型[9]。Huxley 模型是 1957 年由 Huxley 提出的橫橋和肌動蛋白結合的橫橋動力學模型（cross-bridge model），橫橋是指肌球蛋白分子馬達。Huxley 模型是源于肌肉的基本結構，從微觀角度給出了肌肉收縮的本構模型，由于該模型包含多個難以確定的參數，故國內外學者多采用 Hill 肌肉模型。Hill 肌肉模型是 Hill[10]于 1938 年在青蛙肌肉實驗的基礎上提出的宏觀肌肉模型，在一定程度上能反映肌肉的力學特性。但由于該模型過于簡化，與真實肌肉結構相差較大，不能真實反映肌肉力大小。
一些學者對 Hill 模型進行了改進。1989 年，Zajac[11]考慮肌腱對肌肉與骨骼之間力傳遞的影響，將肌腱簡化為串聯彈性元，并引入羽狀角，修正了 Hill 模型。2007 年 Günther 等[12]對仔豬后腿進行實驗研究獲得肌肉參數，通過在串聯單元處引入阻尼元，可抑制肌肉收縮時產生的高頻振蕩，提出了能較為真實反映肌肉力的四元素模型。2013 年 Millard 等[13]對比了彈性肌腱模型、彈性肌腱阻尼模型和剛性肌腱模型等三種骨骼肌模型的計算速度和生物學準確性，表明彈性肌腱阻尼模型的計算速度更快，生物學準確性更高。2014 年 Haeufle 等[14]結合了 Günther 等[12]的研究中在串聯單元處引入阻尼元以及 Van Soest[15]、M?rl 等[16]的研究中對離心收縮力-速度關系的修正，建立骨骼肌的肌肉-肌腱復合體模型（muscle tendon complex，MTC），該模型包括串聯彈性單元、并聯彈性單元、串聯阻尼單元和收縮元，采用該模型進行肘關節的屈曲仿真分析，仿真結果表明該模型較符合真實情況，且該模型同樣適用于部分下肢肌肉。
解剖學中，通常將肌腱與肌纖維間的夾角稱為羽狀角（pinnate angle），反映肌纖維排列方向與肌腱的關系[17]。Folland 等[18]研究表明羽狀角可影響肌肉向肌腱、骨傳遞的力。由于下肢骨骼肌在解剖結構上大多存在羽狀角，Haeufle 四元素模型 MTC 未考慮羽狀角對肌肉力的影響，利用該模型進行下肢含羽狀角骨骼肌的肌肉力分析時可能不夠準確。
機器人骨折復位手術時，由于機器人運行速度比較慢，同時忽略皮膚、血管、神經等組織對復位操作的影響，僅僅考慮肌肉組織對復位的影響，因此骨折復位力主要用于克服肌肉組織的牽拉阻力[19]。國內外學者通過理論分析或實驗對骨折復位力開展研究。2008 年 Graham 等[19]建立搜索最佳復位路徑的模型，可實時輸出斷骨移動時肌肉產生的力和力矩，通過仿真得到中軸骨折復位力最大為 428 N。2011 年 Joung 等[20]為提高機器人骨折復位的安全性，設計能夠計算骨折復位力的骨骼肌肉模型，由導航系統測量髖部和遠端股骨的坐標，由此確定肌肉的長度，基于 Hill 肌肉模型計算肌肉力，模擬髖部骨折復位，獲得兩種復位路徑下的最大復位力分別為 273、382 N。2015 年 Li 等[21]研發長骨骨折復位機器人系統，基于 Hill 肌肉模型和 Kane 方法，建立機器人與肌肉骨骼系統模型，在 Matlab/Simulink 軟件中進行仿真分析，根據規劃的復位路徑模擬骨折復位，模型輸入為斷骨遠端相對于近端的典型位姿，輸出 Stewart 機構支桿的作用力和肌肉力，得到支桿作用力和肌肉力的最大值分別為 600、230 N。研究表明復位過程中，股二頭肌短頭對復位力影響最大，且沿軸向拉伸時復位力的大小變化最為顯著。2018 年朱慶[22]設計了柔性驅動股骨干骨折復位機器人系統，通過觀察復位過程中復位力和力矩的變化確定最佳復位路徑，四種復位路徑下，復位力最大可達 521 N。上述研究表明復位力與復位路徑密切相關，不同的復位路徑，復位力也不同。而上述國內外關于骨折復位力理論研究，大多是基于 Hill 肌肉模型。
本文為提高機器人骨折復位力分析的準確性，基于 Haeufle 四元素模型 MTC，考慮羽狀角對下肢骨骼肌肌肉力特性的影響，建立一種羽狀角-肌肉肌腱骨骼肌模型（pinnate angle-muscle tendon model，PA-MTM），包括主動收縮元、并聯彈性單元、串聯彈性單元、阻尼單元和羽狀角。與 Haeufle 四元素模型 MTC 相比，該模型增加羽狀角，更符合下肢骨骼肌的真實解剖結構。基于新型骨骼肌模型，通過股骨干骨折周圍肌肉群的肌肉力分析，由骨折遠端的力平衡方程確定骨折復位力。根據骨折計算機斷層掃描（computed tomography，CT）數據逆向建模生成三維模型，結合股骨的解剖學模型獲得肌肉附著點坐標，進行骨折復位過程仿真，對比分析不同復位路徑下各肌肉力和復位力，驗證所提出的新型骨骼肌肉模型的合理性，以期為機器人股骨骨折復位的安全性及路徑規劃擇優提供參考。
1 骨骼肌模型及肌肉力
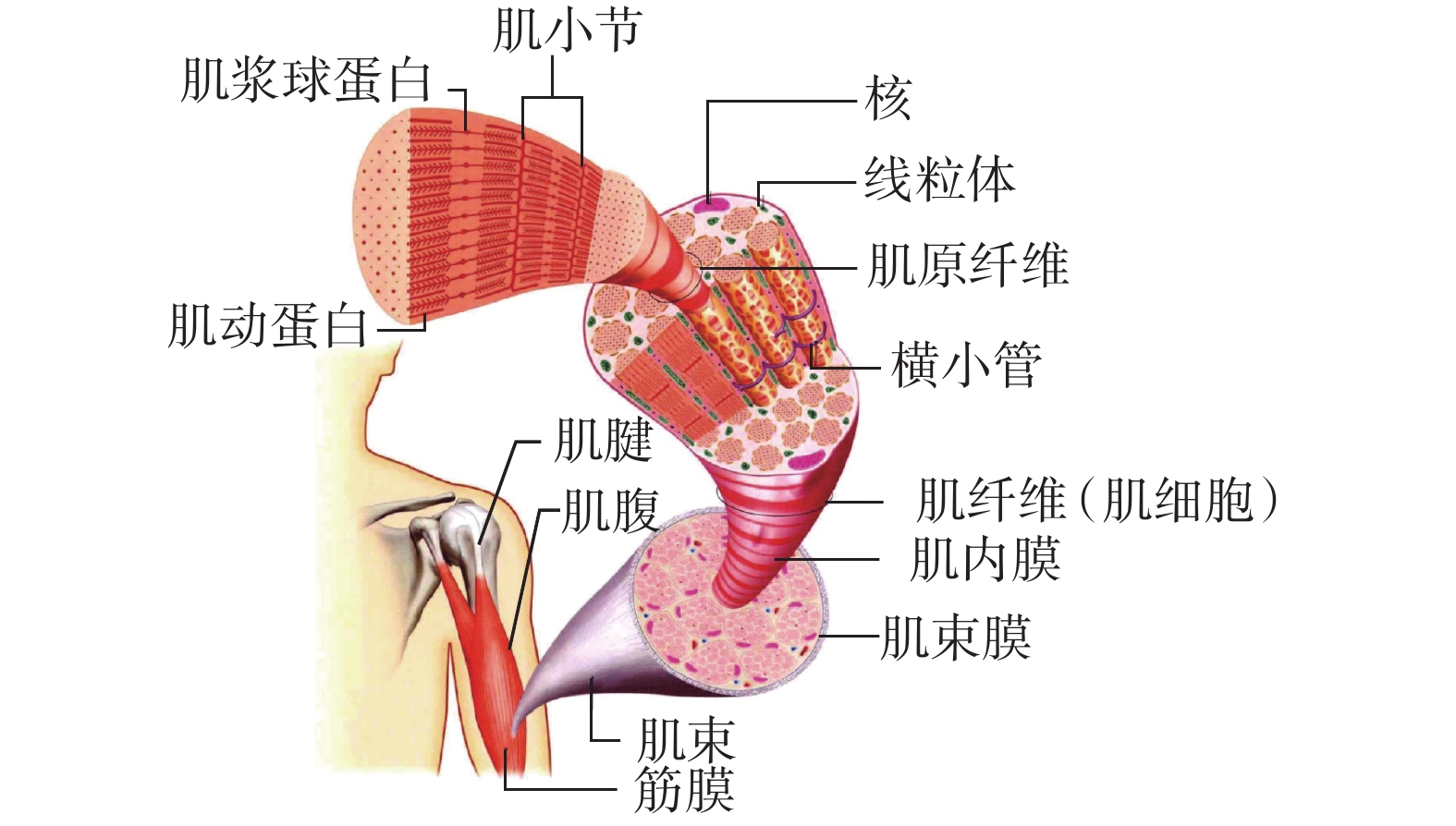
骨骼肌的結構如圖 1 所示，骨骼肌由肌腹和肌腱兩部分組成。肌腹主要由骨骼肌纖維（肌細胞）組成，骨骼肌由肌束并行排列而成，肌束由肌纖維并行排列組成，而肌纖維又由肌原纖維并行排列組成，肌原纖維則由軸向串聯的肌小節組成；微觀上，肌小節主要由粗肌絲和細肌絲構成，構成粗肌絲的肌球蛋白在細肌絲上集體做功，引起了粗細肌絲的相對滑移，即肌小節的收縮，無數肌小節的收縮帶來了肌原纖維的收縮、肌纖維的收縮，從而導致骨骼肌的收縮[23]。肌腱位于肌腹的兩端，連接骨骼和肌腹，在神經系統的支配下，骨骼肌可以實現自主收縮，產生肌肉力，肌肉力在肌腱的傳遞下作用到骨骼上，將肌腹部分產生的力作用于骨骼。
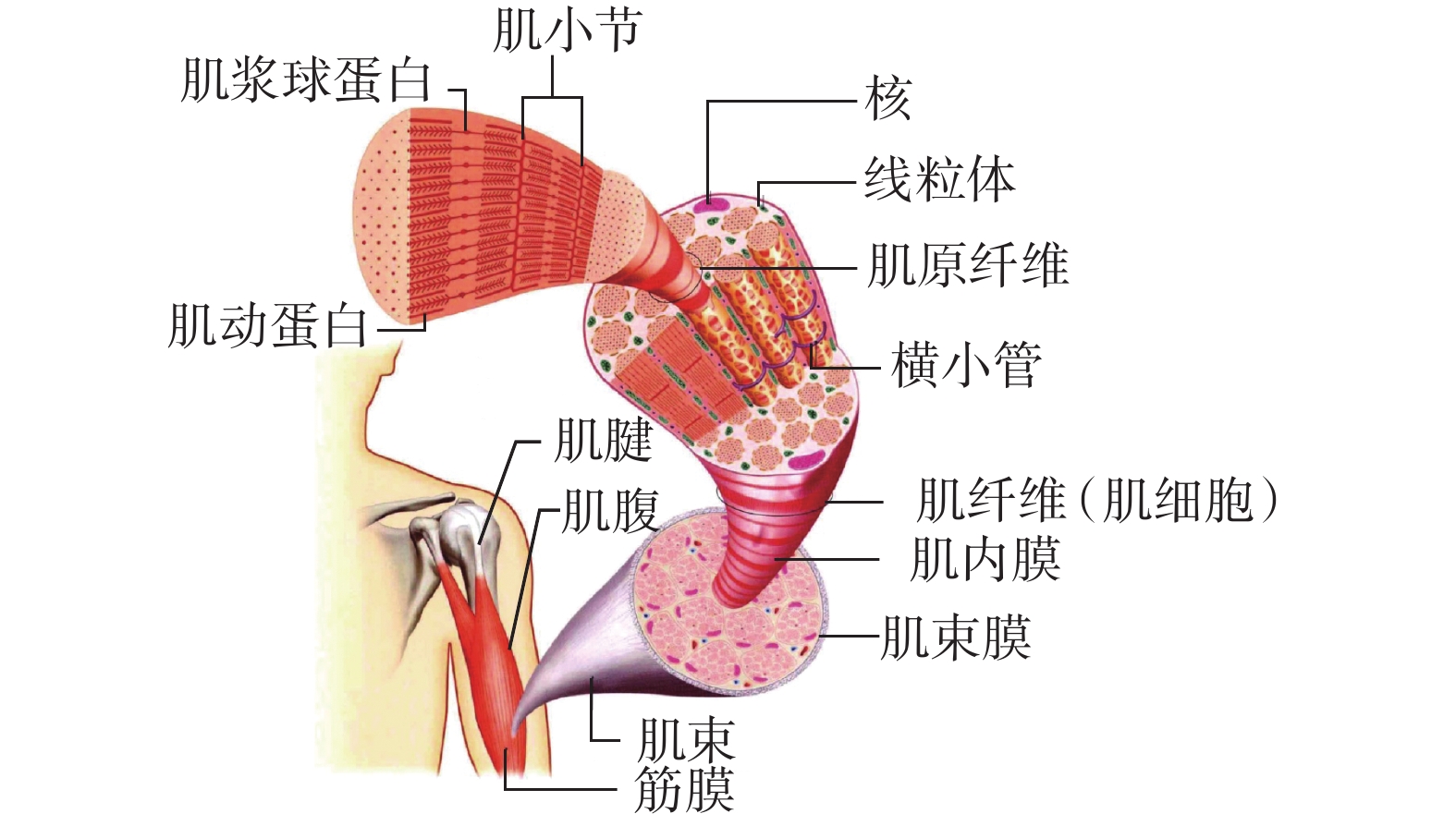圖1
骨骼肌宏觀結構
Figure1.
Structure of skeletal muscle
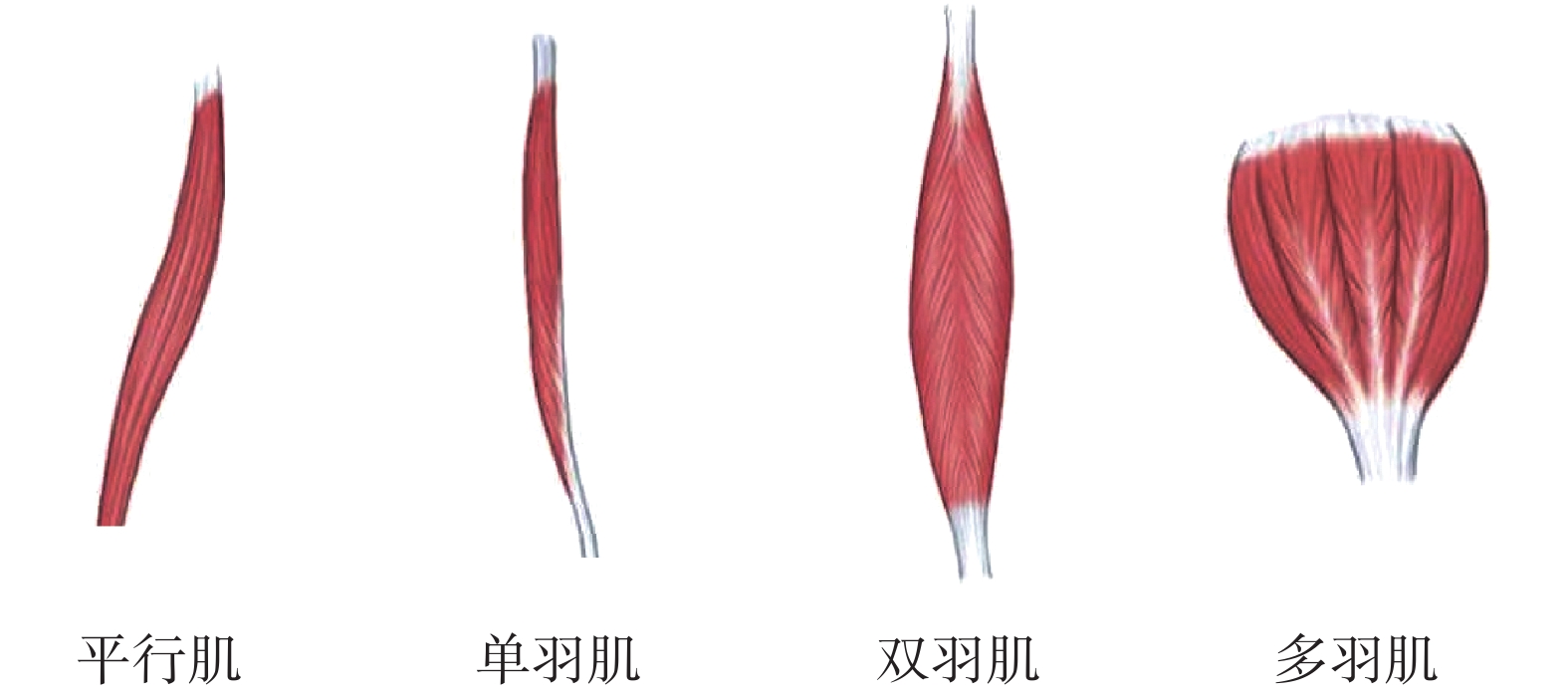
骨骼肌的形態多變，本質上是由肌纖維排列模式的不同造成的。按照肌纖維的排列模式，骨骼肌可分為平行肌和羽狀肌，羽狀肌可分為單羽狀肌、雙羽狀肌和多羽狀肌[24]，如圖 2 所示。羽狀肌的肌纖維較短，生理橫截面積較大，肌力較強，多分布于力量型的下肢；而平行肌的肌纖維較長，生理橫截面積較小，肌力較弱，多分布于發揮靈巧作用的上肢[25]。
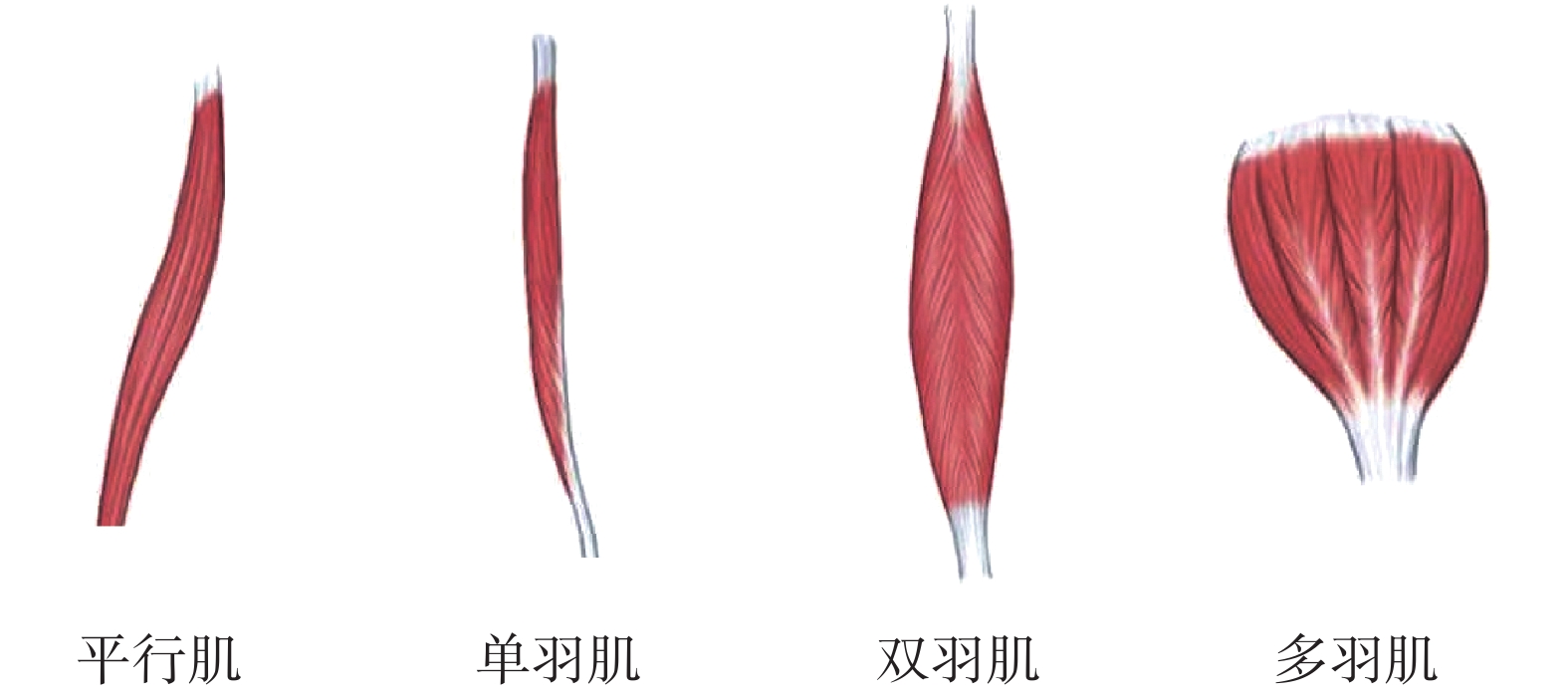圖2
骨骼肌形態的多樣性
Figure2.
Variety of skeletal-muscle shapes
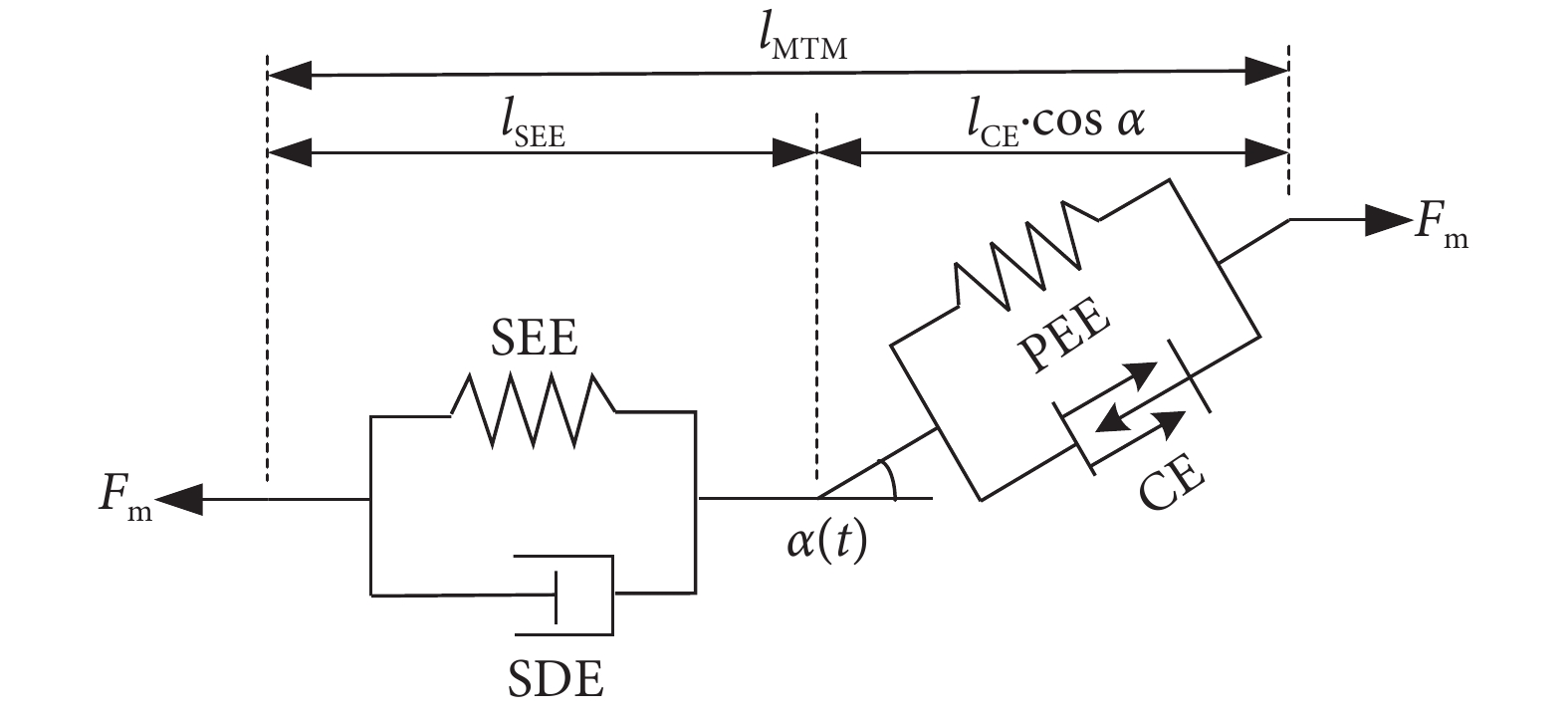
本文基于 Haeufle 等提出的四元素模型 MTC，考慮羽狀角對肌肉力特性的影響，建立適用于下肢骨骼肌的新型肌肉模型 PA-MTM，如圖 3 所示。其中，CE 為收縮元，由肌球蛋白微絲與肌動蛋白微絲組成，在神經系統支配下，可產生主動肌力；PEE 為并聯彈性單元，由肌束膜及肌纖維膜組成，其中結締組織具有彈性，當肌肉處于拉伸狀態時產生彈力，反映肌肉的被動特性；SEE 為串聯彈性單元，表示肌腱、肌節間 Z 盤及肌微絲等組織，反映肌腱的被動特性；SDE 為串聯阻尼單元，用于抑制高頻振蕩；
為羽狀角，描述肌纖維的排列方向與肌腱之間的夾角。
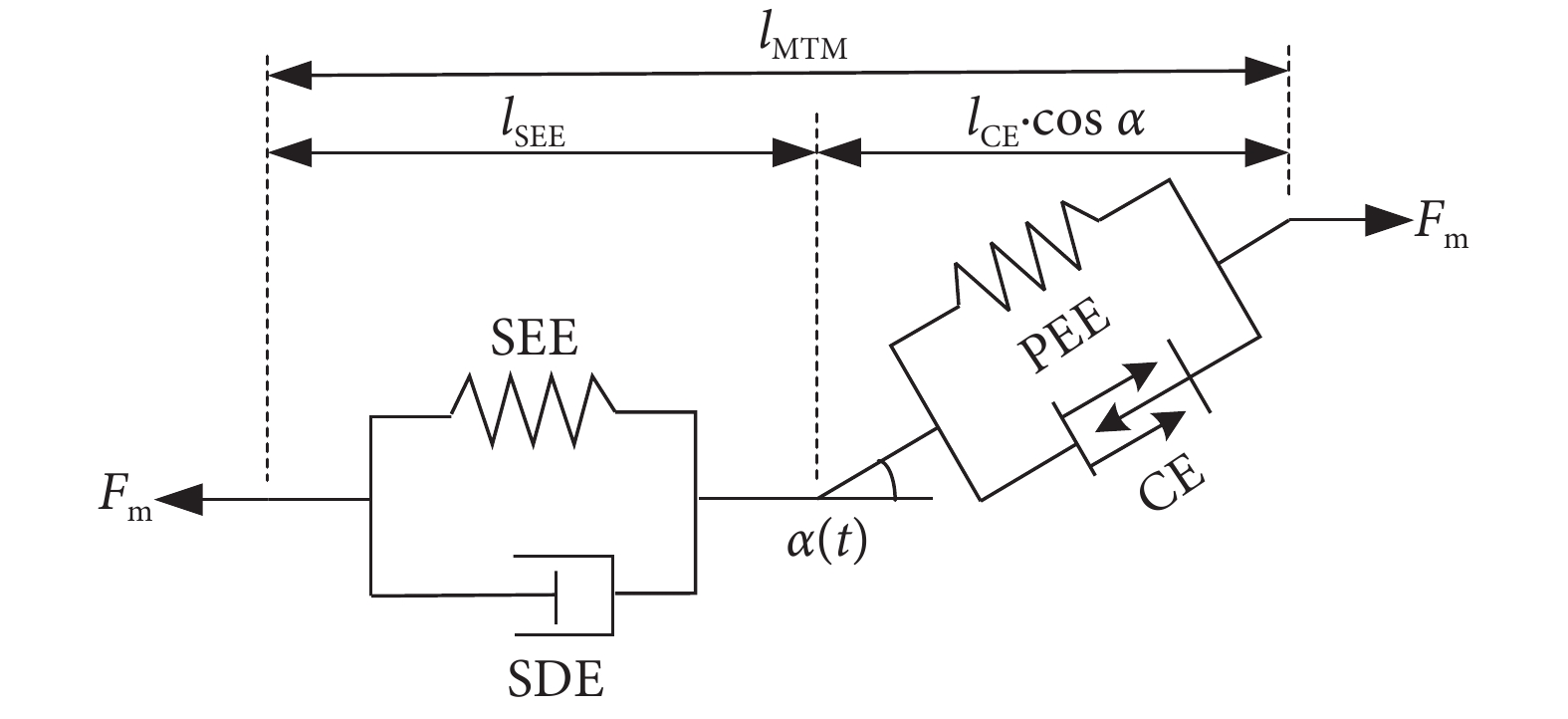圖3
骨骼肌模型 PA-MTM
Figure3.
Skeletal muscle model PA-MTM
則有肌纖維和肌腱單元構成的力平衡方程：
 |
其中，
 |
其中，
為肌肉力，
為收縮單元產生的力，
為與收縮元并聯的彈性單元產生的力，
為肌纖維與肌腱的夾角，
為串聯彈性單元產生的力，
為串聯阻尼單元產生的力。
1.1 PA-MTM 的羽狀角
肌肉收縮時羽狀角并非定值，會隨著肌纖維長度的變化而改變。研究表明[11]，肌肉收縮過程中，肌纖維的長度改變，而寬度不變，如圖 4 所示，則羽狀角 
為：
圖4
羽狀角變化示意圖
Figure4.
Diagram of pinnate angle change
 |
 |
 |
其中，
為肌纖維的寬度，
為肌纖維的當前長度，
為最優肌纖維長度 
處的夾角，
為當前羽狀角。
1.2 PA-MTM 的四元素
主動收縮元、串聯彈性單元、并聯彈性單元和串聯阻尼單元的力分別計算如下[12, 14-15]，式中與下肢肌肉骨骼模型相關的參數如表 1 所示[12]。
為收縮元所產生的主動力，與收縮單元的激活因子 q、長度 
和收縮速度 
相關：
 |
其中，激活因子 q 代表肌肉的激活程度。肌肉激活程度反映的是肌肉在神經系統的刺激下受到激活的程度，激活度越高，表明肌肉的興奮程度越高，肌肉產生的主動收縮力也越大；當 q = 0 時，肌肉不能主動收縮產生主動力，若肌肉處于拉伸狀態，則會產生被動力。
是關于收縮元長度 
的函數，
是當收縮元長度 
為最優肌纖維長度 
時的最大等長力：
 |
為并聯彈性元在被動拉伸時所產生的力：
 |
為串聯彈性元所產生的力，肌腱組織當中也存在與肌腹部分相似的彈性特性：
 |
為串聯阻尼單元所產生的力，它是一種粘性阻尼力：
 |
1.3 PA-MTM 的收縮動力學
由肌纖維和肌腱單元構成的力平衡方程（1），可得肌纖維收縮速度 
的二次方程：
 |
其中，
 |
 |
 |
其中，
 |
解得：
 |
其中，
、
、
是將上面的 
換成 
、
換成 
得到的。
1.4 肌肉力計算
首先，假設初始條件 
，給定肌肉的初始長度 
，其中 
為肌肉的最優肌纖維長度，
為肌腱的松弛長度，肌肉的相關參數見文獻[26]；分別假設激活因子 
、
，則由力平衡方程式（1）得肌肉初始肌纖維長度 
。然后計算其他未知量：
、
、
、
、
、
、
、
、
、
、
、
；得到肌肉的初始肌肉力 
。
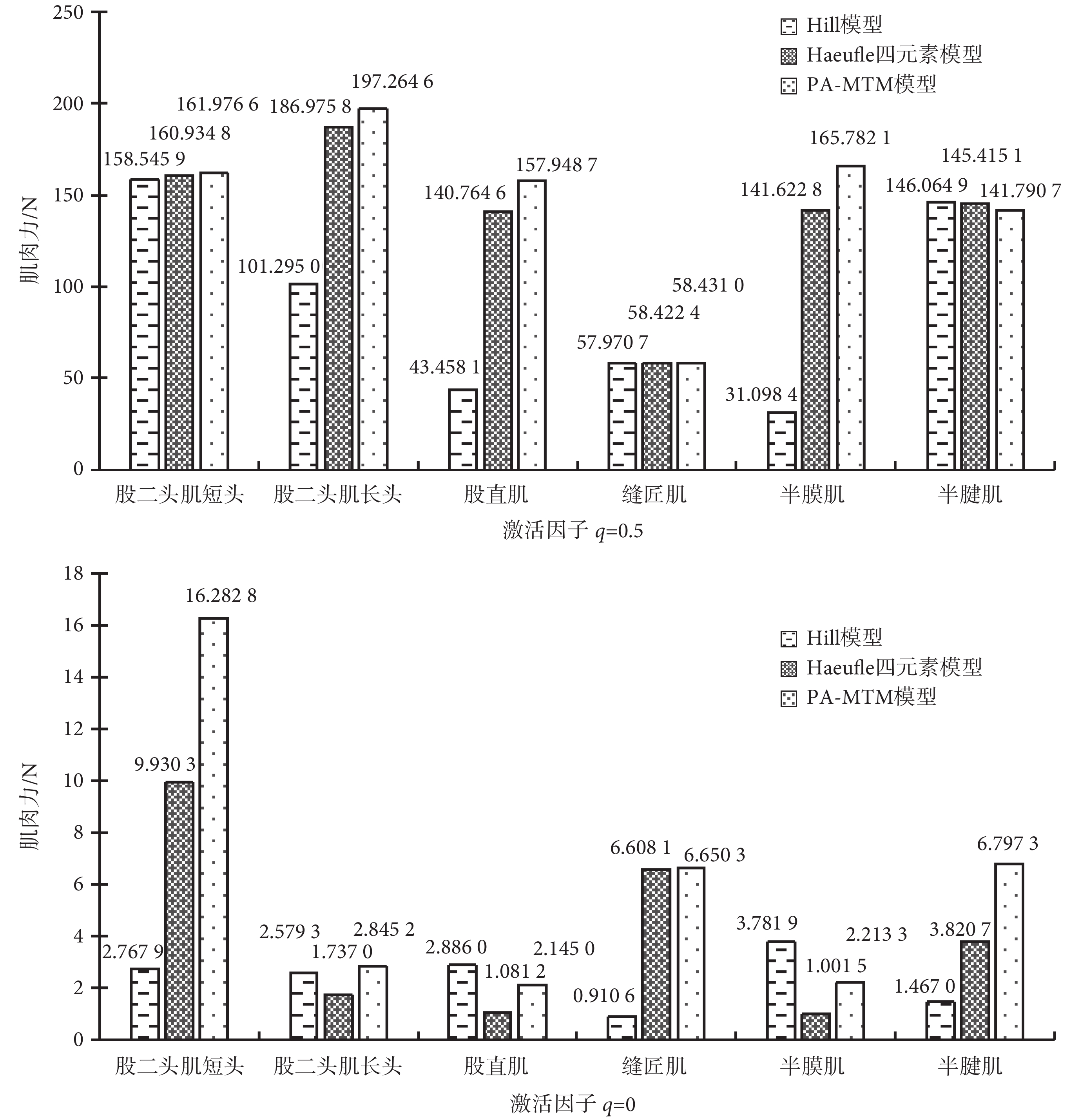
分別采用 Hill 模型、Haeufle 等建立的四元素模型 MTC、本文提出的 PA-MTM 模型，對比分析股二頭肌短頭、股二頭肌長頭、股直肌、縫匠肌、半膜肌、半腱肌的肌肉力，各肌肉的初始條件相同，肌肉力計算結果如圖 5 所示。
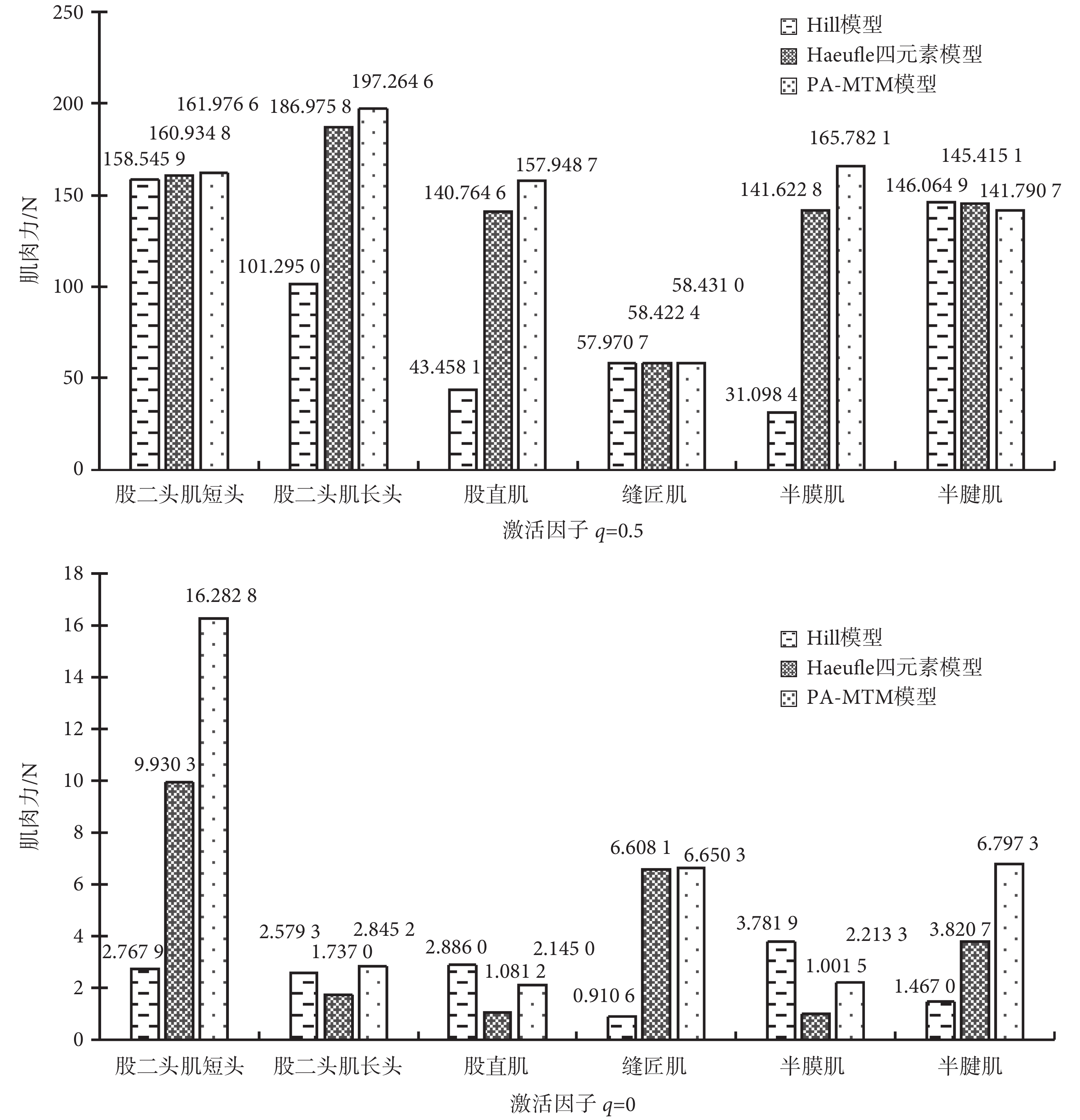圖5
采用不同肌肉模型的肌肉力對比
Figure5.
Comparison of muscle force by different models
在給定的肌肉長度下，當激活因子 q = 0.5 時，此時肌肉既可產生主動力，也可產生被動力。如圖 5 所示，股二頭肌短頭、縫匠肌和半腱肌在三種不同骨骼肌模型下肌肉力相差不大。而股二頭肌長頭、半膜肌和股直肌，采用 PA-MTM 模型比 Haeufle 的四元素模型的肌肉力大 10～25 N，Hill 模型的肌肉力則遠小于另外兩種模型的肌肉力。
在給定的肌肉長度下，當激活因子 q = 0 時，此時肌肉只能產生被動力。如圖 5 所示，除縫匠肌外，股二頭肌短頭、股直肌等肌肉在 Haeufle 等建立的四元素模型 MTC、PA-MTM 模型兩種骨骼肌模型下所計算的肌肉力差別較大，可以看出羽狀角的引入對骨骼肌只存在被動力時所產生的影響較為明顯。
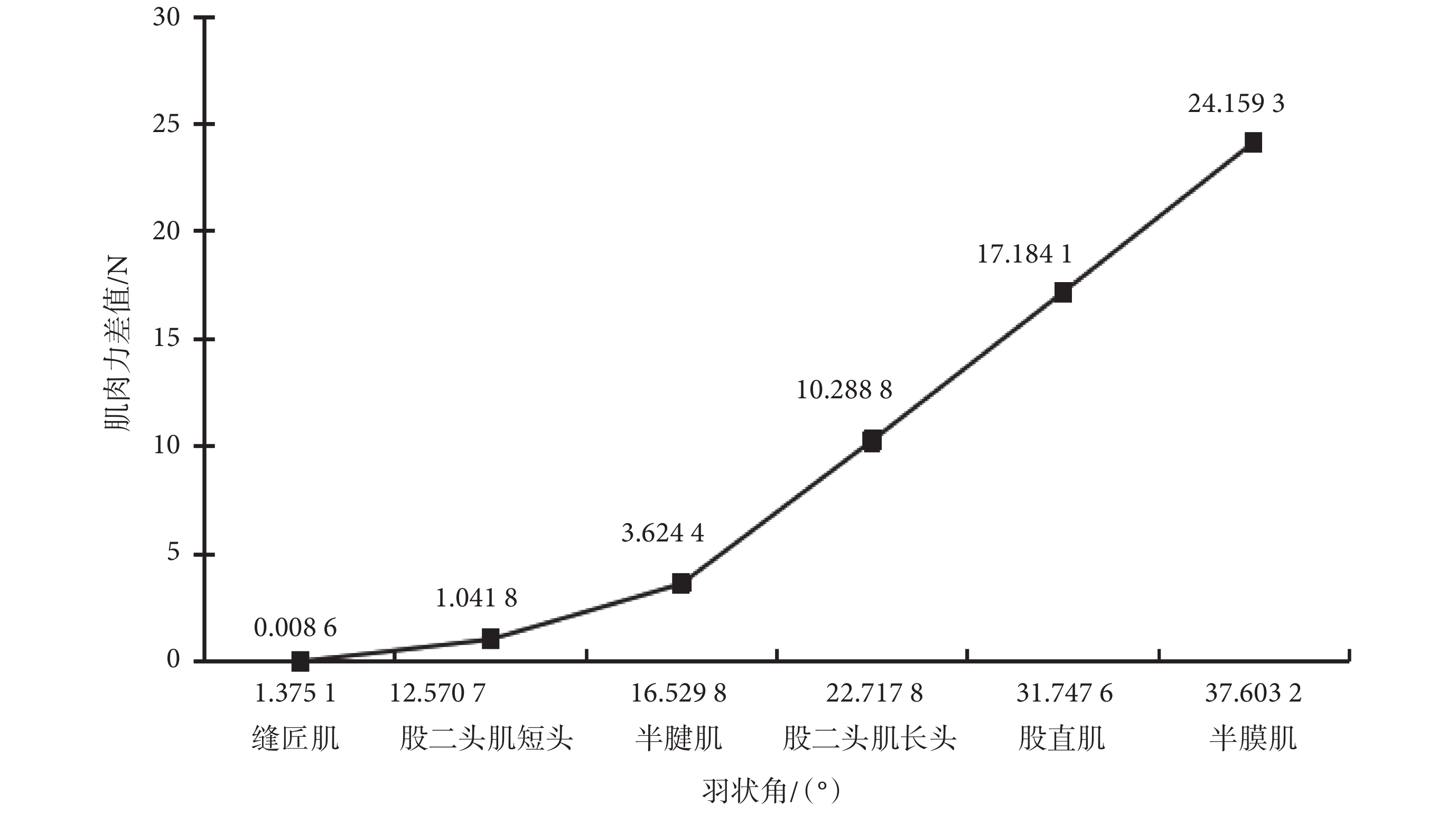
采用 Haeufle 四元素模型、PA-MTM 骨骼肌模型，在激活因子 q = 0.5 時，不同肌肉的肌肉力差值與肌肉羽狀角之間的關系如圖 6 所示，橫坐標為不同肌肉的羽狀角，縱坐標為兩種模型下肌肉力的差值。可以看出，下肢骨骼肌中，肌肉初始條件相同時，肌肉的羽狀角越大，兩模型的肌肉力計算結果差值越大，即羽狀角越大對肌肉力的影響越大。
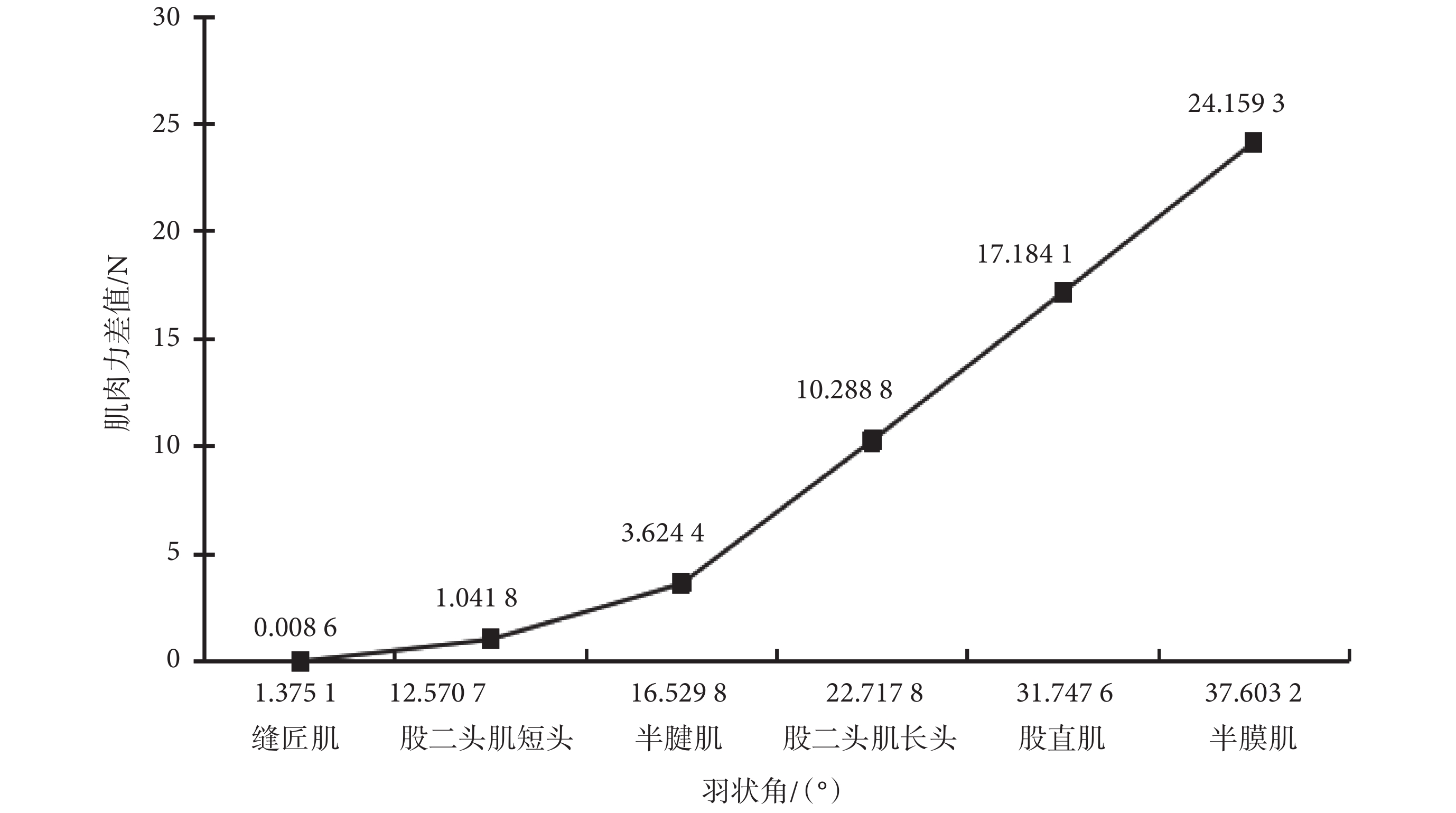圖6
肌肉力差值與羽狀角
Figure6.
The difference in muscle force with pinnate angle
不同骨骼肌的羽狀角是不同的，且羽狀角大小隨肌肉長度變化而變化。由圖 5 和圖 6 可看出，采用不同肌肉模型時，骨骼肌的肌肉力差值因羽狀角的不同而不同。因此，建立肌肉模型時不能忽略羽狀角，尤其是羽狀角比較大的骨骼肌。
2 骨折復位力分析
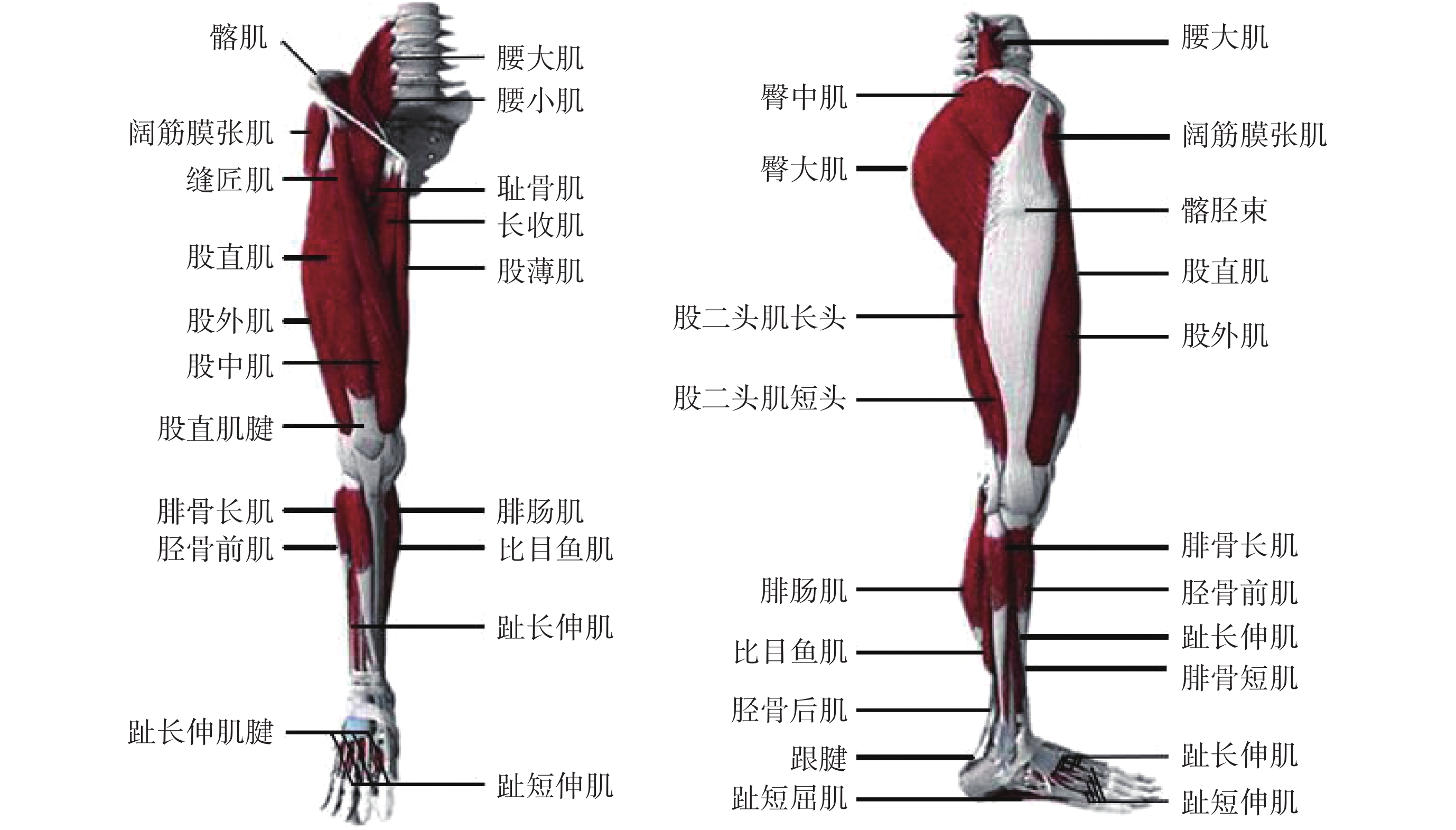
股骨被強有力的骨骼肌包裹著，大腿肌肉是人體最強大、厚實的肌肉群[27]，如圖 7 所示。當在外力作用下，肌肉受到刺激產生收縮力作用在骨折斷骨遠端從而產生移位偏差，骨折復位時，又會產生拉力作用阻礙骨折復位。
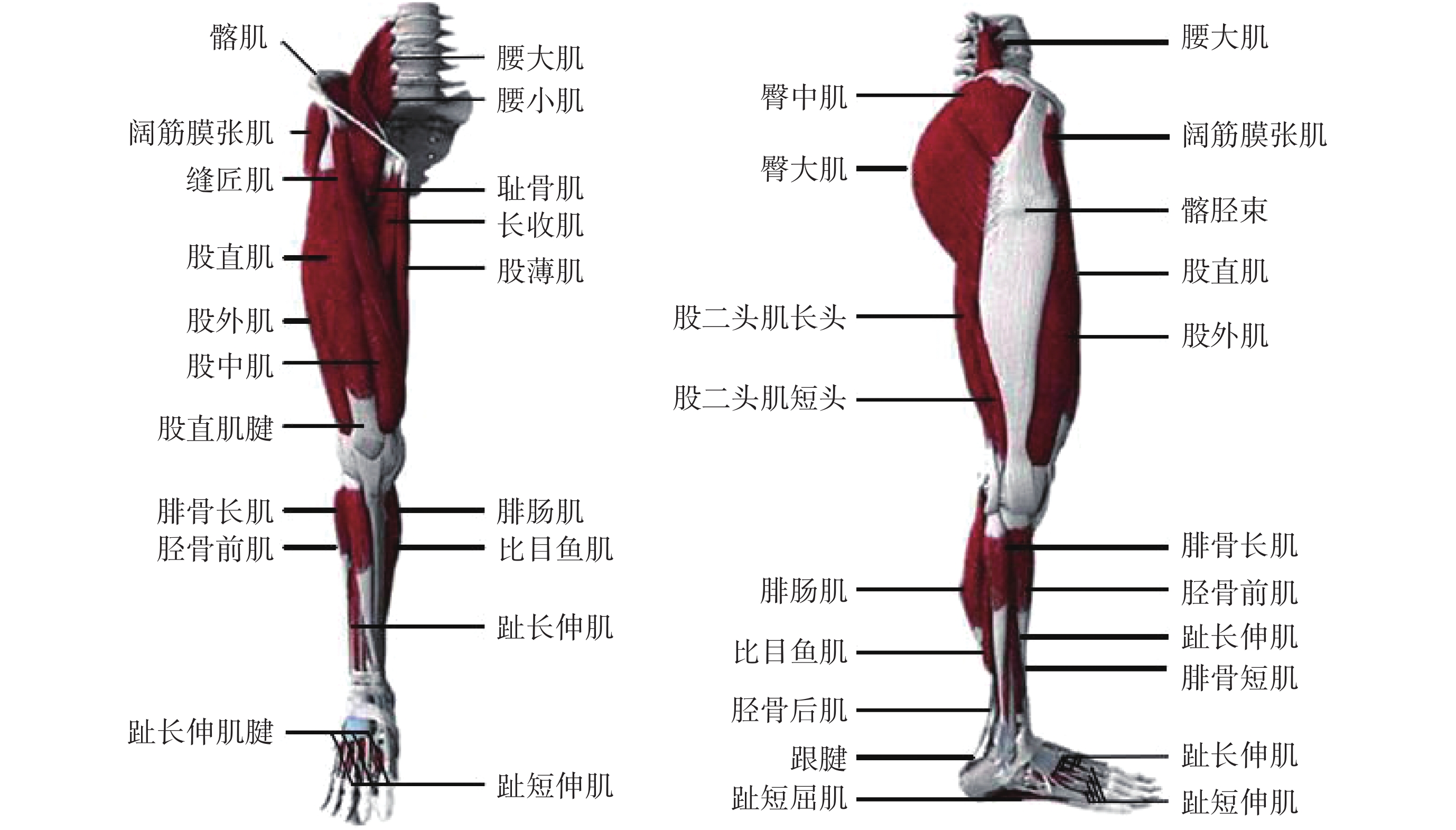圖7
下肢肌肉分布
Figure7.
Muscle distribution in lower limbs
肌肉力與羽狀角 
、肌纖維長度 
、肌肉長度 
等可變參數有關，也與最優羽狀角 
、最優肌纖維長度 
、肌腱的松弛長度 
等不變參數有關[26]。
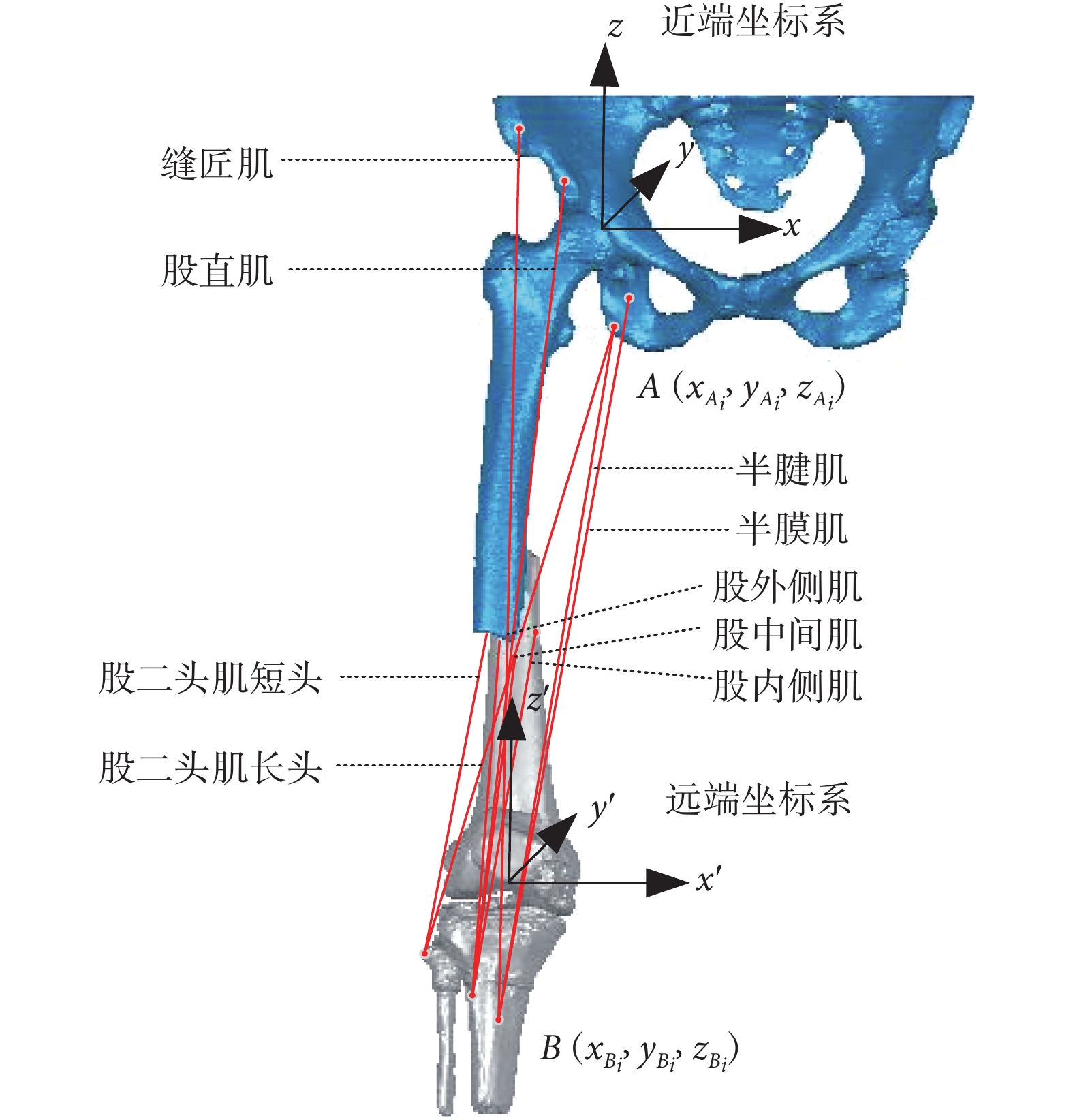
影響股骨骨折復位力的骨骼肌主要有股二頭肌（股二頭肌短頭、股二頭肌長頭）、股四頭肌（股直肌、股中間肌、股外側肌、股內側肌）、縫匠肌、半膜肌、半腱肌等。根據表 2 肌肉的附著點位置以及股骨骨折的逆向模型，確定肌肉起止點的坐標及肌肉的作用線[28]，如圖 8 所示。
表2
肌肉的附著點及坐標
Table2.
The attachment point and coordinates of the muscle
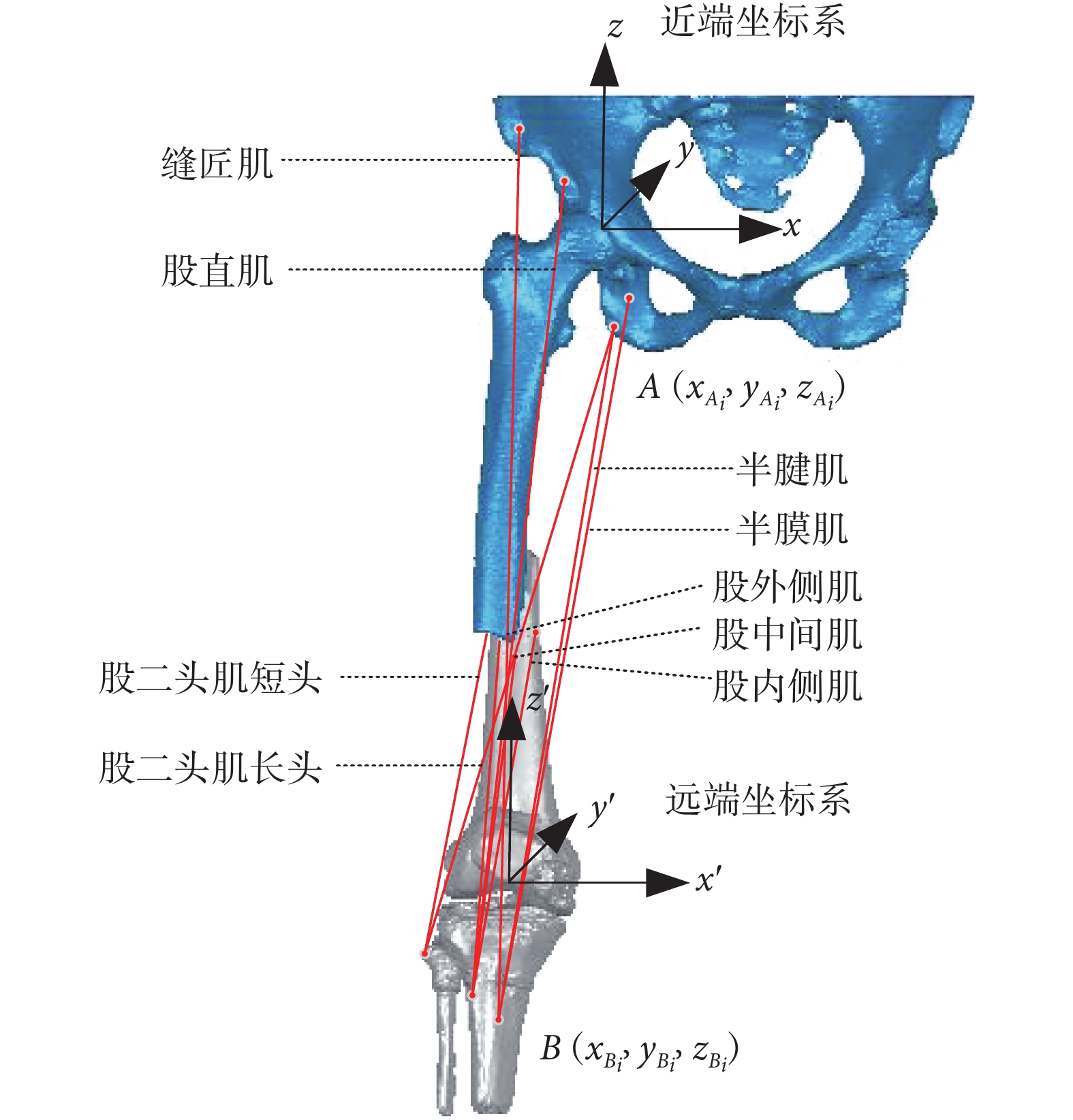圖8
肌肉的附著點和作用線
Figure8.
The attachment points and action lines of the muscles
如圖 8 所示，斷骨近端的坐標系 
固定，遠端坐標系 
移動，遠端坐標系坐標原點 
在近端坐系中的坐標為 
，肌肉 i 的附著點 A、B 在近端坐標系的坐標為 
和 
，點 B 在遠端坐標系的坐標為 
。肌肉 i 的長度為
 |
骨折復位前，通常患者被注射了肌肉松弛劑。復位過程中肌肉處于非激活狀態，收縮元無法主動收縮產生主動力，只有串聯彈性元和并聯彈性元由于肌肉被拉伸而產生被動力[18]。則骨折復位時的骨骼肌力為：
 |
肌肉力 
方向與 xoy 平面的夾角 
為
 |
令 
，即 
在 
平面上的投影。
為 
與 
軸的夾角：
 |
 |
 |
則作用于股骨骨折遠端的肌肉力合力為：
 |
其大小為：
 |
在骨折復位過程中，骨折遠端受力平衡，根據力平衡原理：
 |
其中，
為復位機器人作用在股骨骨折遠端的復位力，
為股骨骨折遠端的重力。
3 復位力仿真分析
3.1 復位路徑
本研究采用醫生提供的一名成年女性患者的下肢 CT 數據，患者為股骨中段骨折，螺旋 CT 獲取原始的 DICOM 數據。患者取仰臥位，位于掃描視野中心位置，沿股骨干長軸方向進行掃描，掃描范圍由髖骨至脛腓骨中段。CT 參數：層厚 0.625 mm、層間距 0.625 mm，數據收集直徑 500 mm，分辨率 512 × 512，共 937 張 CT 圖片，掃描圖像以 DICOM 格式存儲。患者已簽署掃描醫學影像知情同意書。
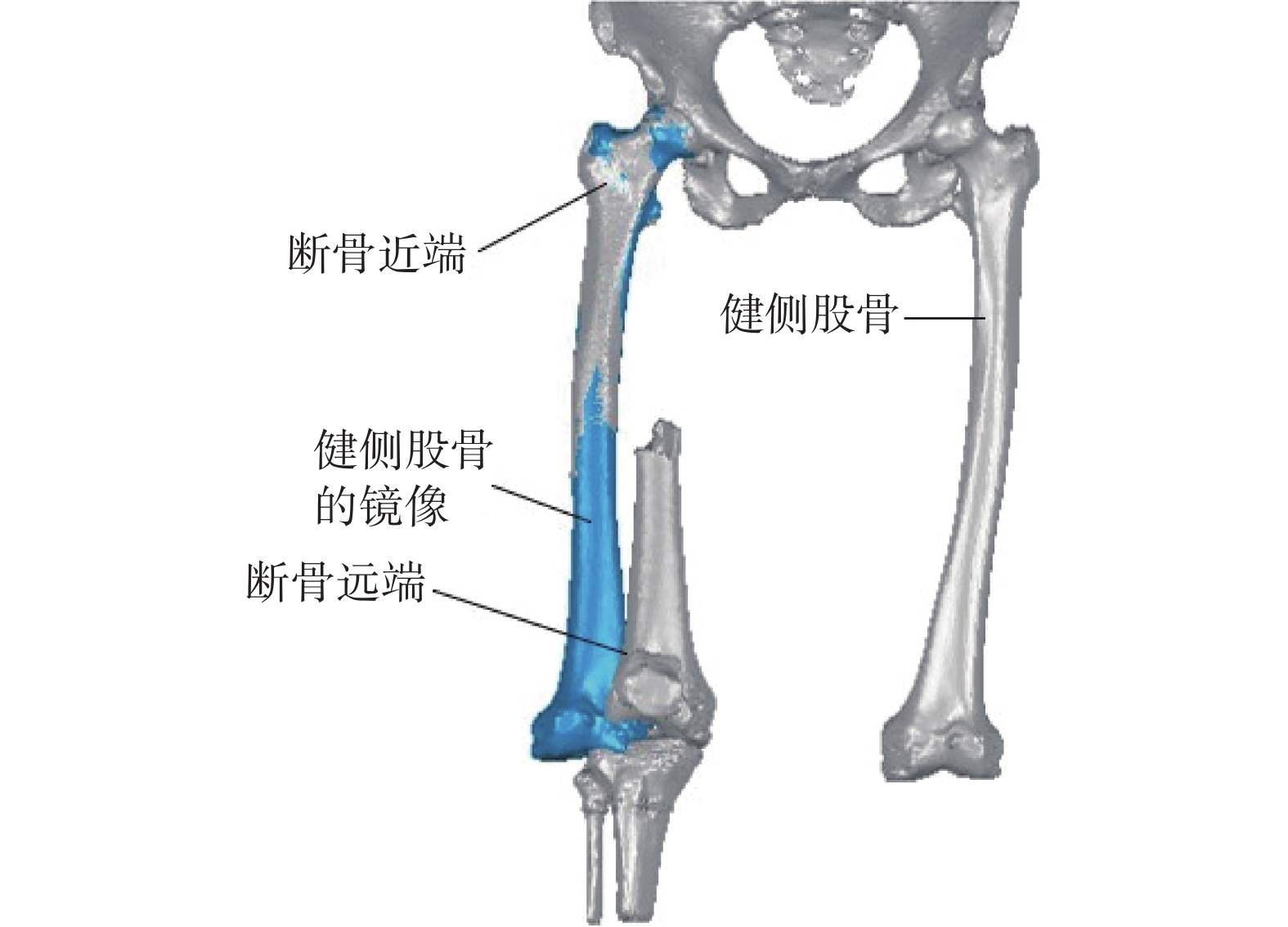
股骨骨折逆向重建的三維模型如圖 9 所示。基于患者股骨骨折的 CT 掃描數據進行逆向建模，建立股骨骨折的三維模型。在 Mimics 20.0 軟件中將 CT 掃描數據進行閾值分割、布爾操作、區域增長、蒙版編輯、空洞填充等操作，建立下肢骨骼蒙板并分割，進而生成 3D 模型，同時將健側股骨的模型關于矢狀面進行鏡像，導出 stl 格式的下肢骨骼點云模型；將點云模型導入 Geomagic studio 軟件中，進行“網格醫生”處理，修復有問題的三角形面片；基于健側股骨的鏡像模型進行患側股骨骨折遠端與近端的擬合配準，根據斷骨遠端的轉換矩陣得到股骨骨折的移位偏差和旋轉偏差，股骨骨折模型繞 x、y、z 軸的旋轉偏差分別為–8.47、3.69、2.18 rad，沿 x、y、z 軸的移位偏差分別為 –8.80、–41.69、–30.02 mm。
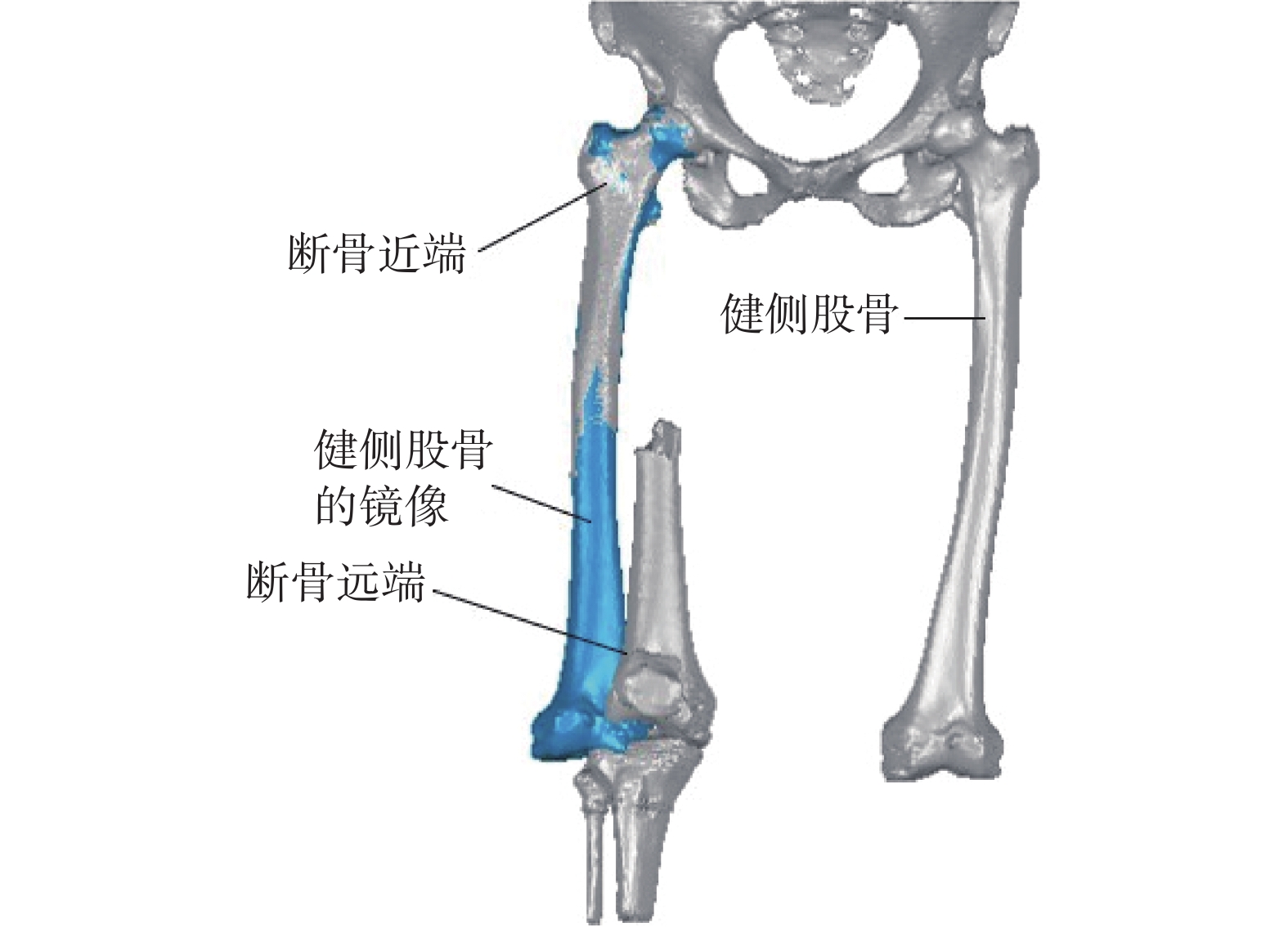圖9
股骨骨折逆向重建的三維模型
Figure9.
Three-dimensional model of reverse reconstruction of femoral fracture
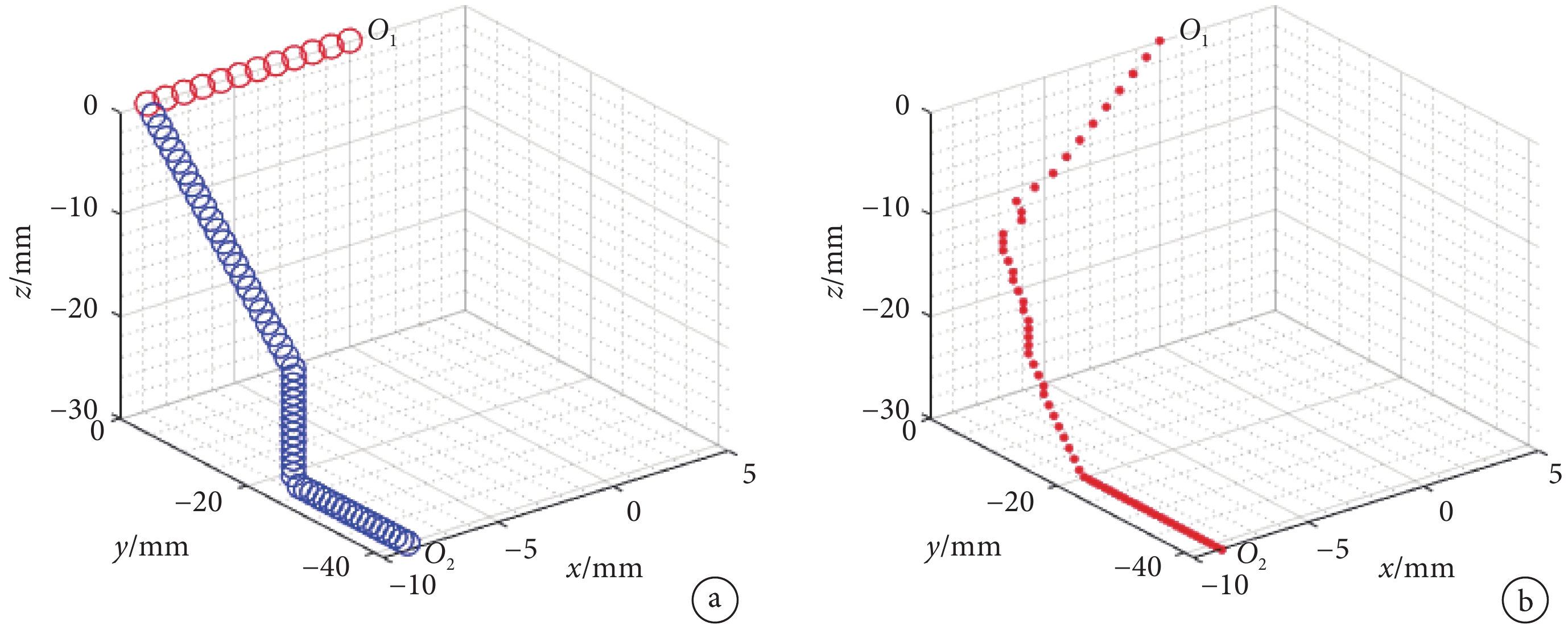
對比分析不同復位路徑下的復位力。采用課題組規劃的雙平面復位路徑[29]（路徑 1），首先將斷骨遠端的姿態與近端姿態調整一致，再根據移位偏差在 xoy 和 yoz 兩個平面內分別進行路徑規劃，得到如圖 10a 所示的復位路徑點，紅圈代表在 xoy 平面內的復位路徑點，藍圈代表在 yoz 平面的復位路徑點；采用課題組規劃的 A*算法的空間復位路徑（路徑 2），得到的復位路徑點如圖 10b 所示；圖中 
為起點，
為終點。
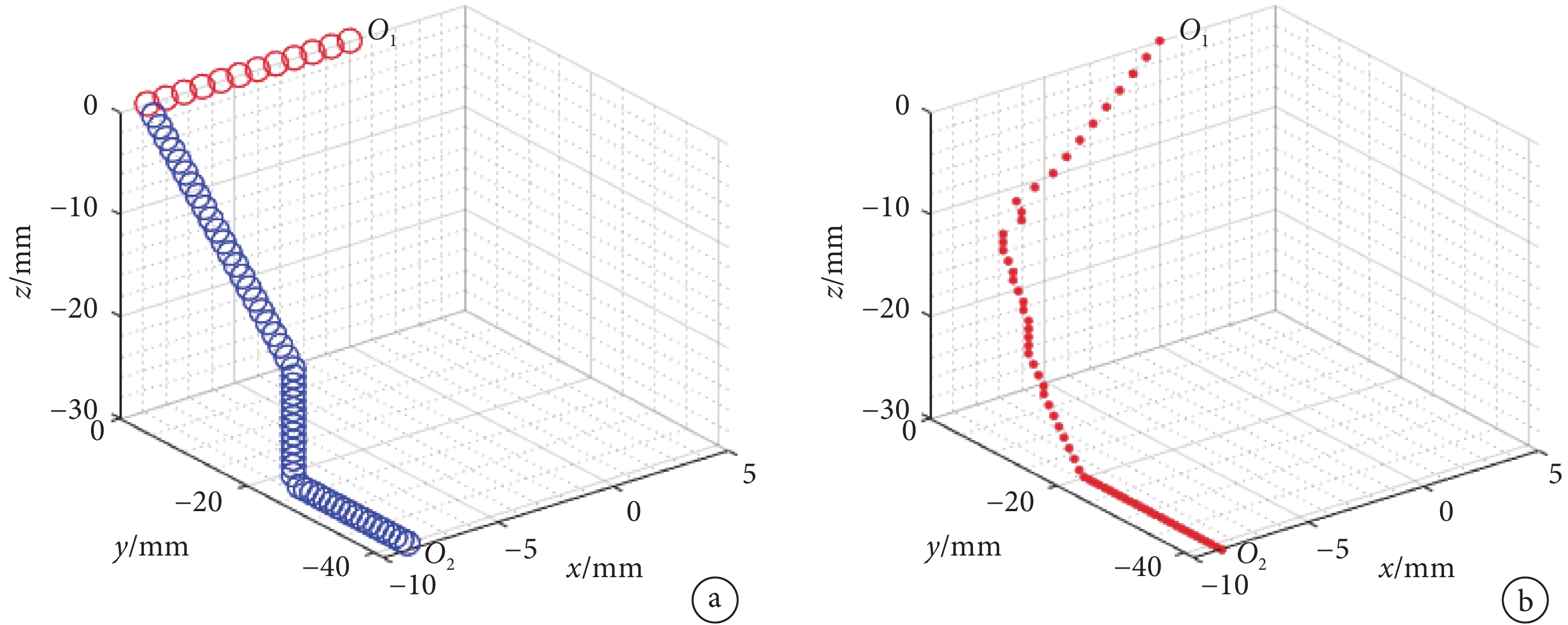圖10
路徑規劃的復位路徑點
a.雙平面復位路徑（路徑 1）；b.空間復位路徑（路徑 2）
Figure10. The reduction path point of path planninga. bi-plane reduction path (path1); b. spatial reduction path (path2)
3.2 復位力仿真
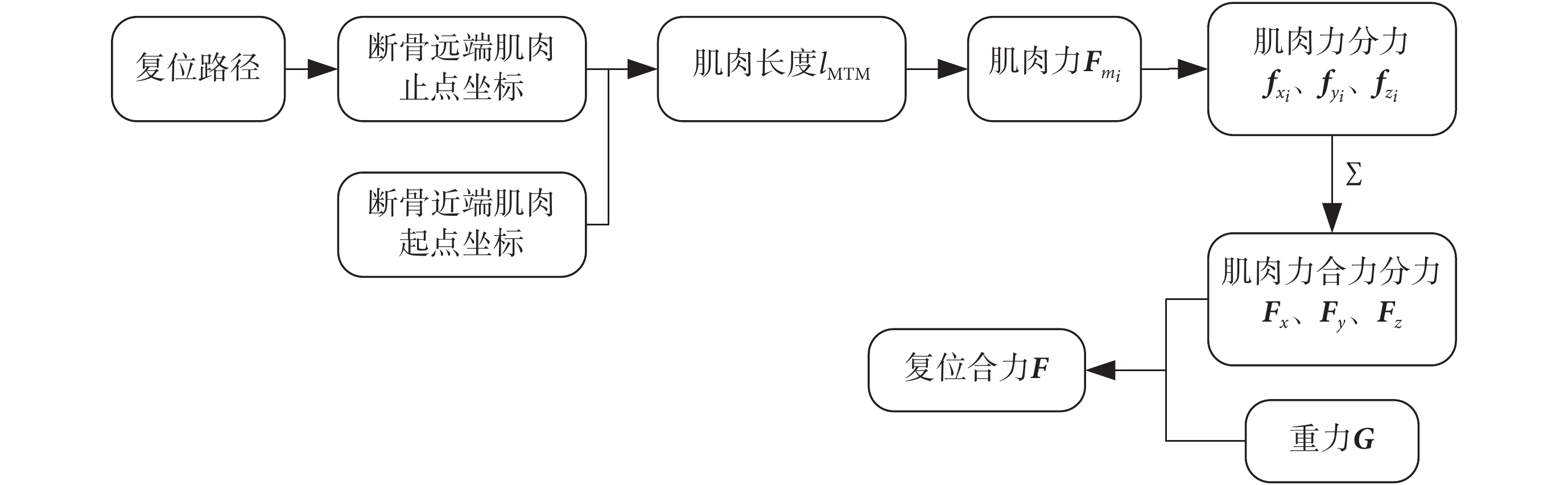
采用 Matlab 軟件編寫計算肌肉力和復位力的函數，在 Simulink 中進行復位力仿真分析[14]，如圖 11 所示為股骨骨折復位仿真流程圖。根據骨骼肌肉的附著點以及該模型的骨折位置可知，影響上述股骨骨折類型復位的骨骼肌主要有股二頭肌短頭、股二頭肌長頭、股直肌、縫匠肌、半膜肌和半腱肌。
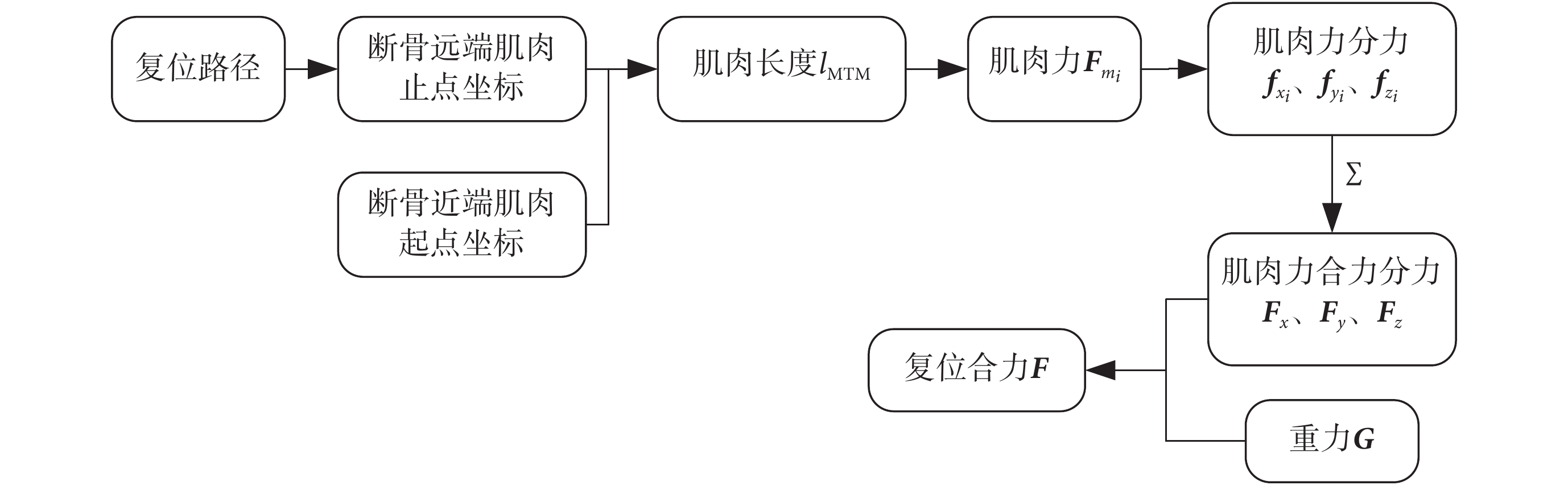圖11
仿真流程圖
Figure11.
Simulation flow chart
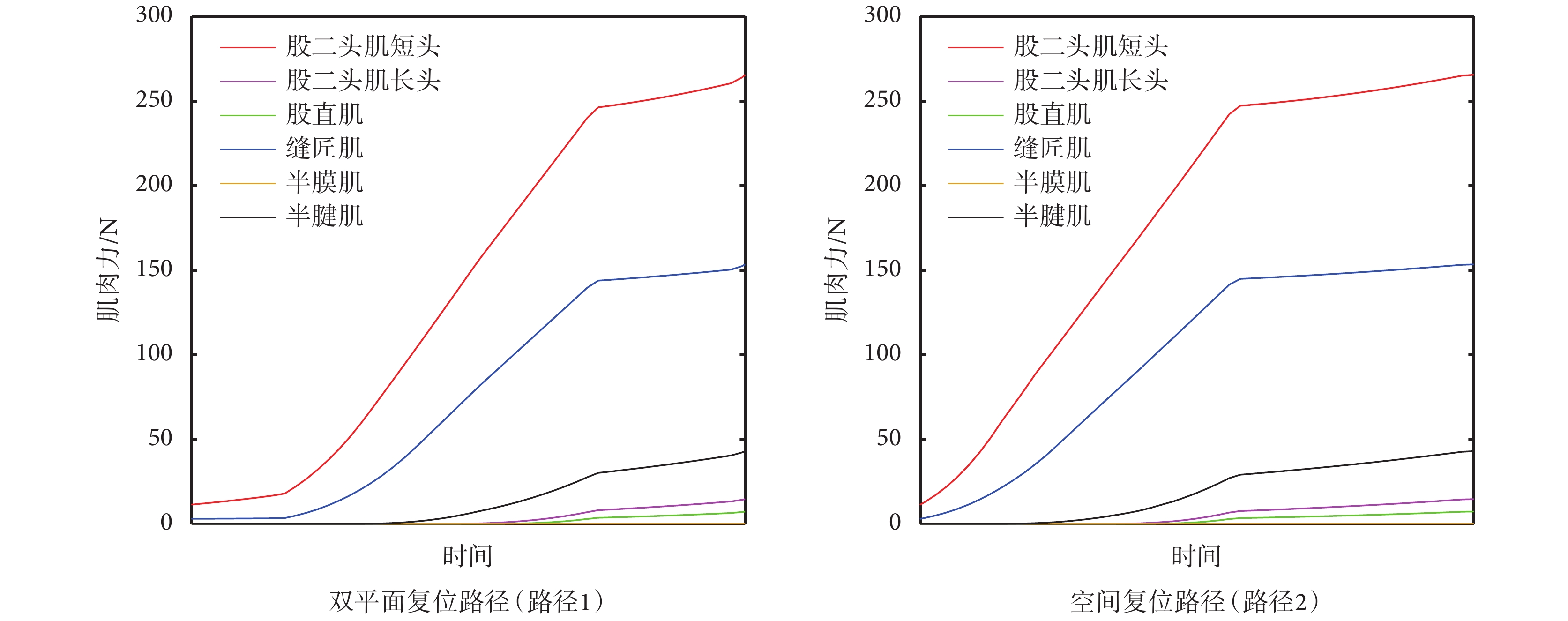
在兩種復位路徑下，各肌肉在復位過程中的肌肉力變化曲線如圖 12 所示。從圖中可看出：在兩種路徑下股二頭肌短頭在復位過程中皆起主要作用，且在復位過程中產生的最大肌肉力為 265.47 N，此時斷骨遠端沿軸向拉伸 30.02 mm。文獻[21]中，骨折的軸向移位偏差為 20 mm，垂直于軸向移位 40 mm，復位過程中，股二頭肌短頭對復位力的影響最大，且軸向拉伸至 20 mm 時，股二頭肌短頭所產生的肌肉力為 230 N。
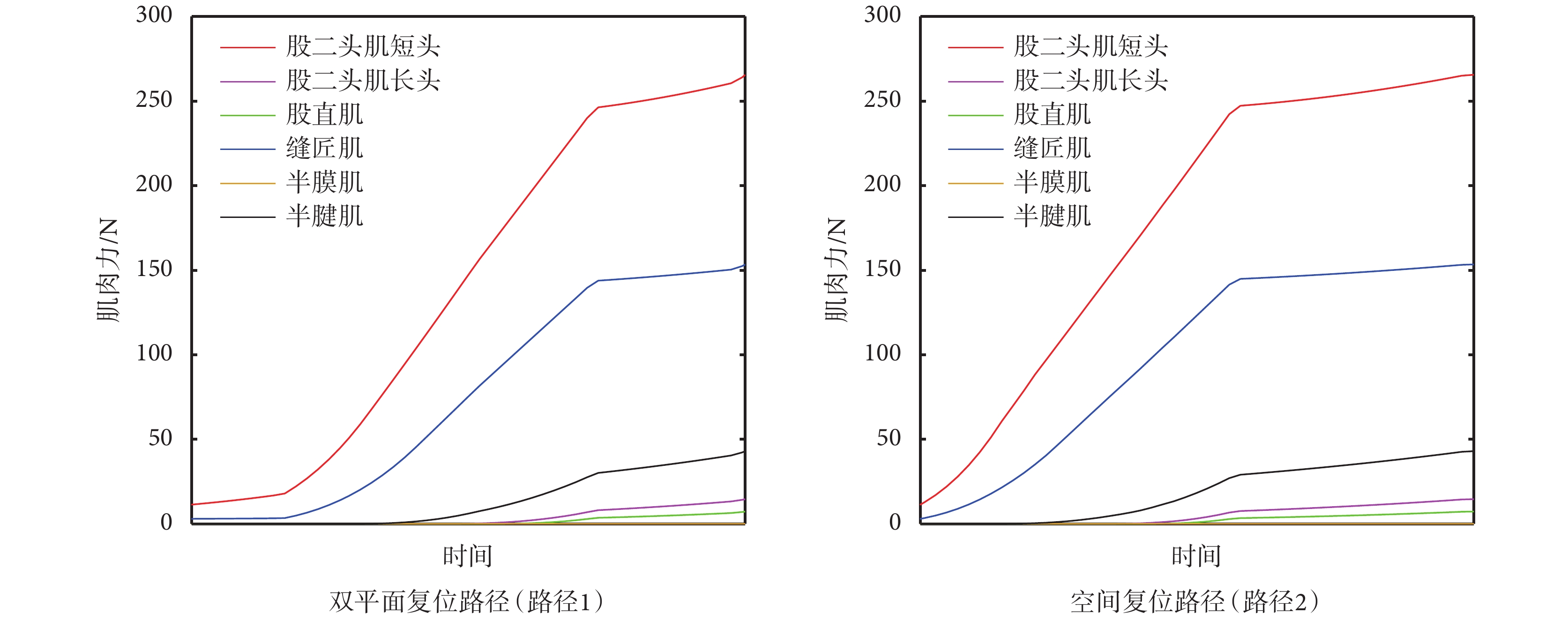圖12
不同復位路徑的肌肉力變化
Figure12.
Muscle force with different reduction path
在股骨骨折復位時，雖然影響骨折復位的主要肌肉——股二頭肌短頭和縫匠肌的羽狀角較小，但其他股直肌、半腱肌等骨骼肌的羽狀角較大，亦影響較大，因此，計算復位力時，也不能忽略羽狀角的影響。
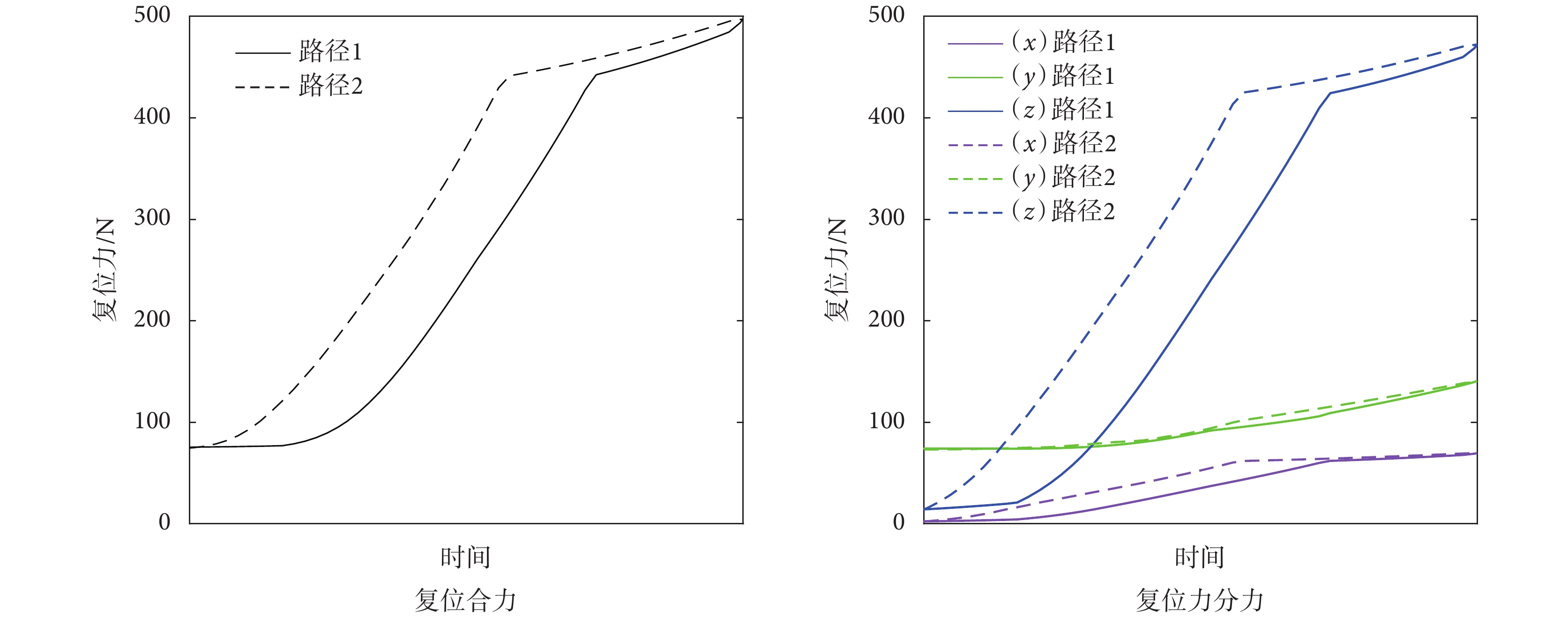
圖 13 為復位過程中復位力及其沿 x、y、z 軸方向的分力的變化曲線，從圖中可以看出，股骨骨折復位過程中，兩種復位路徑下沿股骨干軸向的復位力最大，最大值為 472.18 N，且最大骨折復位合力為 497.28 N。
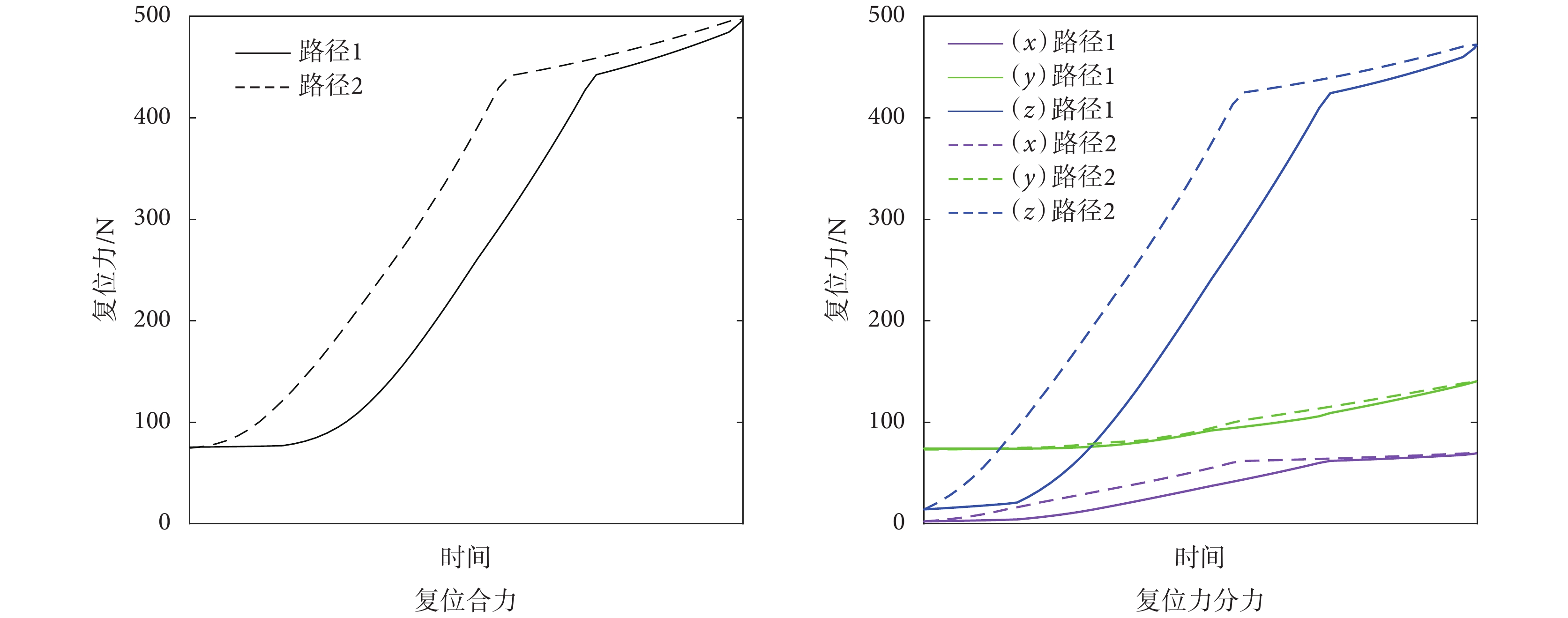圖13
復位力
Figure13.
Reduction force
在復位操作時，肌肉不能產生主動力，只有被動力在起作用，且輔助骨折復位機器人在復位過程中移動緩慢，此時肌肉力的大小只與肌肉長度相關，由于兩種復位路徑的起點和終點相同，從圖 12～13 可以看出，在兩種復位路徑下各力的最小值和最大值相等，而且采用課題組雙平面路徑規劃的路徑 1 進行骨折復位仿真，復位過程中，復位力及肌肉力的變化更加平緩。
采用路徑 1 時，初始階段斷骨遠端在 xoy 平面內僅僅沿 x 軸移動時，肌肉力的變化趨勢較為平緩，當斷骨遠端開始在 yoz 平面內沿著 y 和 z 軸移動時，肌肉力的變化趨勢變得陡峭，而在最后階段又變得比較平緩，此時斷骨遠端沿著 y 軸移動；采用路徑 2 時，初始階段斷骨遠端在三維方向上進行移動，肌肉力的變化趨勢較為陡峭，當斷骨遠端僅沿著 y 軸移動時，肌肉力及復位力的變化趨勢變得平緩，說明軸向位移的變化對復位力的影響最大。
4 結論
本文結合 Haeufle 四元素模型中引入的串聯阻尼、離心收縮力-速度關系以及羽狀角對肌肉力特性的影響，建立一種新型骨骼肌肉模型 PA-MTM，較符合下肢骨骼肌的真實結構。由于肌肉力與骨骼肌的長度 
、肌肉的速度 
、激活程度 
等參數有關，給定各骨骼肌長度、速度及激活程度，對比分析股二頭肌短頭、股二頭肌長頭、股直肌、半膜肌、半腱肌和縫匠肌等六種骨骼肌，在相同肌肉長度下，采用 Hill 模型、Haeufle 四元素模型、PA-MTM 肌肉模型三種不同模型計算的肌肉力。本文所提出 PA-MTM 骨骼肌模型的肌肉力計算結果大于不考慮羽狀角的 Haeufle 四元素骨骼肌模型，且肌肉的羽狀角越大，不同模型下的肌肉力計算結果差值越大。根據股骨骨折模型的骨折偏差，規劃不同復位路徑，進行骨折復位仿真分析，獲得最大復位合力為 497.28 N，最大軸向復位力為 472.18 N，同時，通過與文獻[19, 21, 30]的復位力分析結果對比，驗證了新型骨骼肌模型 PA-MTM 的合理性。本研究可為機器人骨折復位力監控及復位路徑擇優提供參考。
未來將開展下肢骨肌模型肌肉力及復位力實驗測試，進一步驗證該模型的準確性。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
股骨骨折是創傷骨科的常見病，且隨著全球老齡化和交通運輸的發展呈逐年增加的趨勢[1]。多由高能量直接損傷所致，如車禍傷、直接暴力打擊、強力擠壓等，也可見于高處墜落傷、機器絞傷等間接暴力導致的損傷；其骨折常伴有重疊、成角及旋轉等，有些還伴有嚴重的軟組織損傷，治療起來比較棘手，而良好的復位手段是股骨干骨折治療的關鍵[2]。傳統人工骨折復位手術，復位過程中醫生牽引和保持骨折的復位狀態，體力消耗比較大，復位效果依賴醫生經驗，而且醫患雙方會多次受到射線輻射影響。隨著醫療科學技術的發展，國內外開始研發機器人輔助骨折復位[3-5]，這不僅大大節省了醫生的體力，而且能有效提高骨折復位精度，并通過遠程操作替代術者的人工復位，減少輻射。
目前，為提高復位精度和復位操作的安全性，術前需要進行精準的復位路徑規劃[6-8]。由于骨折周圍復雜的生物力學環境和解剖力學特性，骨折復位過程中有可能對肌肉等軟組織造成損傷，因而有必要清楚了解骨折骨肌組織的生物力學特性，分析骨折周圍肌肉組織的肌肉力對復位的干擾和影響，分析骨折復位過程中的肌肉力及復位力。
關于骨骼肌肉模型有兩大類：Huxley 模型和 Hill 模型[9]。Huxley 模型是 1957 年由 Huxley 提出的橫橋和肌動蛋白結合的橫橋動力學模型（cross-bridge model），橫橋是指肌球蛋白分子馬達。Huxley 模型是源于肌肉的基本結構，從微觀角度給出了肌肉收縮的本構模型，由于該模型包含多個難以確定的參數，故國內外學者多采用 Hill 肌肉模型。Hill 肌肉模型是 Hill[10]于 1938 年在青蛙肌肉實驗的基礎上提出的宏觀肌肉模型，在一定程度上能反映肌肉的力學特性。但由于該模型過于簡化，與真實肌肉結構相差較大，不能真實反映肌肉力大小。
一些學者對 Hill 模型進行了改進。1989 年，Zajac[11]考慮肌腱對肌肉與骨骼之間力傳遞的影響，將肌腱簡化為串聯彈性元，并引入羽狀角，修正了 Hill 模型。2007 年 Günther 等[12]對仔豬后腿進行實驗研究獲得肌肉參數，通過在串聯單元處引入阻尼元，可抑制肌肉收縮時產生的高頻振蕩，提出了能較為真實反映肌肉力的四元素模型。2013 年 Millard 等[13]對比了彈性肌腱模型、彈性肌腱阻尼模型和剛性肌腱模型等三種骨骼肌模型的計算速度和生物學準確性，表明彈性肌腱阻尼模型的計算速度更快，生物學準確性更高。2014 年 Haeufle 等[14]結合了 Günther 等[12]的研究中在串聯單元處引入阻尼元以及 Van Soest[15]、M?rl 等[16]的研究中對離心收縮力-速度關系的修正，建立骨骼肌的肌肉-肌腱復合體模型（muscle tendon complex，MTC），該模型包括串聯彈性單元、并聯彈性單元、串聯阻尼單元和收縮元，采用該模型進行肘關節的屈曲仿真分析，仿真結果表明該模型較符合真實情況，且該模型同樣適用于部分下肢肌肉。
解剖學中，通常將肌腱與肌纖維間的夾角稱為羽狀角（pinnate angle），反映肌纖維排列方向與肌腱的關系[17]。Folland 等[18]研究表明羽狀角可影響肌肉向肌腱、骨傳遞的力。由于下肢骨骼肌在解剖結構上大多存在羽狀角，Haeufle 四元素模型 MTC 未考慮羽狀角對肌肉力的影響，利用該模型進行下肢含羽狀角骨骼肌的肌肉力分析時可能不夠準確。
機器人骨折復位手術時，由于機器人運行速度比較慢，同時忽略皮膚、血管、神經等組織對復位操作的影響，僅僅考慮肌肉組織對復位的影響，因此骨折復位力主要用于克服肌肉組織的牽拉阻力[19]。國內外學者通過理論分析或實驗對骨折復位力開展研究。2008 年 Graham 等[19]建立搜索最佳復位路徑的模型，可實時輸出斷骨移動時肌肉產生的力和力矩，通過仿真得到中軸骨折復位力最大為 428 N。2011 年 Joung 等[20]為提高機器人骨折復位的安全性，設計能夠計算骨折復位力的骨骼肌肉模型，由導航系統測量髖部和遠端股骨的坐標，由此確定肌肉的長度，基于 Hill 肌肉模型計算肌肉力，模擬髖部骨折復位，獲得兩種復位路徑下的最大復位力分別為 273、382 N。2015 年 Li 等[21]研發長骨骨折復位機器人系統，基于 Hill 肌肉模型和 Kane 方法，建立機器人與肌肉骨骼系統模型，在 Matlab/Simulink 軟件中進行仿真分析，根據規劃的復位路徑模擬骨折復位，模型輸入為斷骨遠端相對于近端的典型位姿，輸出 Stewart 機構支桿的作用力和肌肉力，得到支桿作用力和肌肉力的最大值分別為 600、230 N。研究表明復位過程中，股二頭肌短頭對復位力影響最大，且沿軸向拉伸時復位力的大小變化最為顯著。2018 年朱慶[22]設計了柔性驅動股骨干骨折復位機器人系統，通過觀察復位過程中復位力和力矩的變化確定最佳復位路徑，四種復位路徑下，復位力最大可達 521 N。上述研究表明復位力與復位路徑密切相關，不同的復位路徑，復位力也不同。而上述國內外關于骨折復位力理論研究，大多是基于 Hill 肌肉模型。
本文為提高機器人骨折復位力分析的準確性，基于 Haeufle 四元素模型 MTC，考慮羽狀角對下肢骨骼肌肌肉力特性的影響，建立一種羽狀角-肌肉肌腱骨骼肌模型（pinnate angle-muscle tendon model，PA-MTM），包括主動收縮元、并聯彈性單元、串聯彈性單元、阻尼單元和羽狀角。與 Haeufle 四元素模型 MTC 相比，該模型增加羽狀角，更符合下肢骨骼肌的真實解剖結構。基于新型骨骼肌模型，通過股骨干骨折周圍肌肉群的肌肉力分析，由骨折遠端的力平衡方程確定骨折復位力。根據骨折計算機斷層掃描（computed tomography，CT）數據逆向建模生成三維模型，結合股骨的解剖學模型獲得肌肉附著點坐標，進行骨折復位過程仿真，對比分析不同復位路徑下各肌肉力和復位力，驗證所提出的新型骨骼肌肉模型的合理性，以期為機器人股骨骨折復位的安全性及路徑規劃擇優提供參考。
1 骨骼肌模型及肌肉力
骨骼肌的結構如圖 1 所示，骨骼肌由肌腹和肌腱兩部分組成。肌腹主要由骨骼肌纖維（肌細胞）組成，骨骼肌由肌束并行排列而成，肌束由肌纖維并行排列組成，而肌纖維又由肌原纖維并行排列組成，肌原纖維則由軸向串聯的肌小節組成；微觀上，肌小節主要由粗肌絲和細肌絲構成，構成粗肌絲的肌球蛋白在細肌絲上集體做功，引起了粗細肌絲的相對滑移，即肌小節的收縮，無數肌小節的收縮帶來了肌原纖維的收縮、肌纖維的收縮，從而導致骨骼肌的收縮[23]。肌腱位于肌腹的兩端，連接骨骼和肌腹，在神經系統的支配下，骨骼肌可以實現自主收縮，產生肌肉力，肌肉力在肌腱的傳遞下作用到骨骼上，將肌腹部分產生的力作用于骨骼。
圖1
骨骼肌宏觀結構
Figure1.
Structure of skeletal muscle
骨骼肌的形態多變，本質上是由肌纖維排列模式的不同造成的。按照肌纖維的排列模式，骨骼肌可分為平行肌和羽狀肌，羽狀肌可分為單羽狀肌、雙羽狀肌和多羽狀肌[24]，如圖 2 所示。羽狀肌的肌纖維較短，生理橫截面積較大，肌力較強，多分布于力量型的下肢；而平行肌的肌纖維較長，生理橫截面積較小，肌力較弱，多分布于發揮靈巧作用的上肢[25]。
圖2
骨骼肌形態的多樣性
Figure2.
Variety of skeletal-muscle shapes
本文基于 Haeufle 等提出的四元素模型 MTC，考慮羽狀角對肌肉力特性的影響，建立適用于下肢骨骼肌的新型肌肉模型 PA-MTM，如圖 3 所示。其中，CE 為收縮元，由肌球蛋白微絲與肌動蛋白微絲組成，在神經系統支配下，可產生主動肌力；PEE 為并聯彈性單元，由肌束膜及肌纖維膜組成，其中結締組織具有彈性，當肌肉處于拉伸狀態時產生彈力，反映肌肉的被動特性；SEE 為串聯彈性單元，表示肌腱、肌節間 Z 盤及肌微絲等組織，反映肌腱的被動特性；SDE 為串聯阻尼單元，用于抑制高頻振蕩； 為羽狀角，描述肌纖維的排列方向與肌腱之間的夾角。
圖3
骨骼肌模型 PA-MTM
Figure3.
Skeletal muscle model PA-MTM
則有肌纖維和肌腱單元構成的力平衡方程：
|
其中，
|
其中， 為肌肉力， 為收縮單元產生的力， 為與收縮元并聯的彈性單元產生的力， 為肌纖維與肌腱的夾角， 為串聯彈性單元產生的力， 為串聯阻尼單元產生的力。
1.1 PA-MTM 的羽狀角
肌肉收縮時羽狀角并非定值，會隨著肌纖維長度的變化而改變。研究表明[11]，肌肉收縮過程中，肌纖維的長度改變，而寬度不變，如圖 4 所示，則羽狀角 為：
圖4
羽狀角變化示意圖
Figure4.
Diagram of pinnate angle change
|
|
|
其中， 為肌纖維的寬度， 為肌纖維的當前長度， 為最優肌纖維長度 處的夾角，為當前羽狀角。
1.2 PA-MTM 的四元素
主動收縮元、串聯彈性單元、并聯彈性單元和串聯阻尼單元的力分別計算如下[12, 14-15]，式中與下肢肌肉骨骼模型相關的參數如表 1 所示[12]。
為收縮元所產生的主動力，與收縮單元的激活因子 q、長度 和收縮速度 相關：
|
其中，激活因子 q 代表肌肉的激活程度。肌肉激活程度反映的是肌肉在神經系統的刺激下受到激活的程度，激活度越高，表明肌肉的興奮程度越高，肌肉產生的主動收縮力也越大；當 q = 0 時，肌肉不能主動收縮產生主動力，若肌肉處于拉伸狀態，則會產生被動力。
是關于收縮元長度 的函數， 是當收縮元長度 為最優肌纖維長度 時的最大等長力：
|
為并聯彈性元在被動拉伸時所產生的力：
|
為串聯彈性元所產生的力，肌腱組織當中也存在與肌腹部分相似的彈性特性：
|
為串聯阻尼單元所產生的力，它是一種粘性阻尼力：
|
1.3 PA-MTM 的收縮動力學
由肌纖維和肌腱單元構成的力平衡方程（1），可得肌纖維收縮速度 的二次方程：
|
其中，
|
|
|
其中，
|
解得：
|
其中，、、 是將上面的 換成 、 換成 得到的。
1.4 肌肉力計算
首先，假設初始條件 ，給定肌肉的初始長度 ，其中 為肌肉的最優肌纖維長度， 為肌腱的松弛長度，肌肉的相關參數見文獻[26]；分別假設激活因子 、，則由力平衡方程式（1）得肌肉初始肌纖維長度 。然后計算其他未知量：、、、、、、、、、、、；得到肌肉的初始肌肉力 。
分別采用 Hill 模型、Haeufle 等建立的四元素模型 MTC、本文提出的 PA-MTM 模型，對比分析股二頭肌短頭、股二頭肌長頭、股直肌、縫匠肌、半膜肌、半腱肌的肌肉力，各肌肉的初始條件相同，肌肉力計算結果如圖 5 所示。
圖5
采用不同肌肉模型的肌肉力對比
Figure5.
Comparison of muscle force by different models
在給定的肌肉長度下，當激活因子 q = 0.5 時，此時肌肉既可產生主動力，也可產生被動力。如圖 5 所示，股二頭肌短頭、縫匠肌和半腱肌在三種不同骨骼肌模型下肌肉力相差不大。而股二頭肌長頭、半膜肌和股直肌，采用 PA-MTM 模型比 Haeufle 的四元素模型的肌肉力大 10～25 N，Hill 模型的肌肉力則遠小于另外兩種模型的肌肉力。
在給定的肌肉長度下，當激活因子 q = 0 時，此時肌肉只能產生被動力。如圖 5 所示，除縫匠肌外，股二頭肌短頭、股直肌等肌肉在 Haeufle 等建立的四元素模型 MTC、PA-MTM 模型兩種骨骼肌模型下所計算的肌肉力差別較大，可以看出羽狀角的引入對骨骼肌只存在被動力時所產生的影響較為明顯。
采用 Haeufle 四元素模型、PA-MTM 骨骼肌模型，在激活因子 q = 0.5 時，不同肌肉的肌肉力差值與肌肉羽狀角之間的關系如圖 6 所示，橫坐標為不同肌肉的羽狀角，縱坐標為兩種模型下肌肉力的差值。可以看出，下肢骨骼肌中，肌肉初始條件相同時，肌肉的羽狀角越大，兩模型的肌肉力計算結果差值越大，即羽狀角越大對肌肉力的影響越大。
圖6
肌肉力差值與羽狀角
Figure6.
The difference in muscle force with pinnate angle
不同骨骼肌的羽狀角是不同的，且羽狀角大小隨肌肉長度變化而變化。由圖 5 和圖 6 可看出，采用不同肌肉模型時，骨骼肌的肌肉力差值因羽狀角的不同而不同。因此，建立肌肉模型時不能忽略羽狀角，尤其是羽狀角比較大的骨骼肌。
2 骨折復位力分析
股骨被強有力的骨骼肌包裹著，大腿肌肉是人體最強大、厚實的肌肉群[27]，如圖 7 所示。當在外力作用下，肌肉受到刺激產生收縮力作用在骨折斷骨遠端從而產生移位偏差，骨折復位時，又會產生拉力作用阻礙骨折復位。
圖7
下肢肌肉分布
Figure7.
Muscle distribution in lower limbs
肌肉力與羽狀角 、肌纖維長度 、肌肉長度 等可變參數有關，也與最優羽狀角 、最優肌纖維長度 、肌腱的松弛長度 等不變參數有關[26]。
影響股骨骨折復位力的骨骼肌主要有股二頭肌（股二頭肌短頭、股二頭肌長頭）、股四頭肌（股直肌、股中間肌、股外側肌、股內側肌）、縫匠肌、半膜肌、半腱肌等。根據表 2 肌肉的附著點位置以及股骨骨折的逆向模型，確定肌肉起止點的坐標及肌肉的作用線[28]，如圖 8 所示。
表2
肌肉的附著點及坐標
Table2.
The attachment point and coordinates of the muscle
圖8
肌肉的附著點和作用線
Figure8.
The attachment points and action lines of the muscles
如圖 8 所示，斷骨近端的坐標系 固定，遠端坐標系 移動，遠端坐標系坐標原點 在近端坐系中的坐標為 ，肌肉 i 的附著點 A、B 在近端坐標系的坐標為 和 ，點 B 在遠端坐標系的坐標為 。肌肉 i 的長度為
|
骨折復位前，通常患者被注射了肌肉松弛劑。復位過程中肌肉處于非激活狀態，收縮元無法主動收縮產生主動力，只有串聯彈性元和并聯彈性元由于肌肉被拉伸而產生被動力[18]。則骨折復位時的骨骼肌力為：
|
肌肉力 方向與 xoy 平面的夾角 為
|
令 ，即 在 平面上的投影。
為 與 軸的夾角：
|
|
|
則作用于股骨骨折遠端的肌肉力合力為：
|
其大小為：
|
在骨折復位過程中，骨折遠端受力平衡，根據力平衡原理：
|
其中， 為復位機器人作用在股骨骨折遠端的復位力， 為股骨骨折遠端的重力。
3 復位力仿真分析
3.1 復位路徑
本研究采用醫生提供的一名成年女性患者的下肢 CT 數據，患者為股骨中段骨折，螺旋 CT 獲取原始的 DICOM 數據。患者取仰臥位，位于掃描視野中心位置，沿股骨干長軸方向進行掃描，掃描范圍由髖骨至脛腓骨中段。CT 參數：層厚 0.625 mm、層間距 0.625 mm，數據收集直徑 500 mm，分辨率 512 × 512，共 937 張 CT 圖片，掃描圖像以 DICOM 格式存儲。患者已簽署掃描醫學影像知情同意書。
股骨骨折逆向重建的三維模型如圖 9 所示。基于患者股骨骨折的 CT 掃描數據進行逆向建模，建立股骨骨折的三維模型。在 Mimics 20.0 軟件中將 CT 掃描數據進行閾值分割、布爾操作、區域增長、蒙版編輯、空洞填充等操作，建立下肢骨骼蒙板并分割，進而生成 3D 模型，同時將健側股骨的模型關于矢狀面進行鏡像，導出 stl 格式的下肢骨骼點云模型；將點云模型導入 Geomagic studio 軟件中，進行“網格醫生”處理，修復有問題的三角形面片；基于健側股骨的鏡像模型進行患側股骨骨折遠端與近端的擬合配準，根據斷骨遠端的轉換矩陣得到股骨骨折的移位偏差和旋轉偏差，股骨骨折模型繞 x、y、z 軸的旋轉偏差分別為–8.47、3.69、2.18 rad，沿 x、y、z 軸的移位偏差分別為 –8.80、–41.69、–30.02 mm。
圖9
股骨骨折逆向重建的三維模型
Figure9.
Three-dimensional model of reverse reconstruction of femoral fracture
對比分析不同復位路徑下的復位力。采用課題組規劃的雙平面復位路徑[29]（路徑 1），首先將斷骨遠端的姿態與近端姿態調整一致，再根據移位偏差在 xoy 和 yoz 兩個平面內分別進行路徑規劃，得到如圖 10a 所示的復位路徑點，紅圈代表在 xoy 平面內的復位路徑點，藍圈代表在 yoz 平面的復位路徑點；采用課題組規劃的 A*算法的空間復位路徑（路徑 2），得到的復位路徑點如圖 10b 所示；圖中 為起點， 為終點。
圖10
路徑規劃的復位路徑點
a.雙平面復位路徑（路徑 1）；b.空間復位路徑（路徑 2）
Figure10. The reduction path point of path planninga. bi-plane reduction path (path1); b. spatial reduction path (path2)
3.2 復位力仿真
采用 Matlab 軟件編寫計算肌肉力和復位力的函數，在 Simulink 中進行復位力仿真分析[14]，如圖 11 所示為股骨骨折復位仿真流程圖。根據骨骼肌肉的附著點以及該模型的骨折位置可知，影響上述股骨骨折類型復位的骨骼肌主要有股二頭肌短頭、股二頭肌長頭、股直肌、縫匠肌、半膜肌和半腱肌。
圖11
仿真流程圖
Figure11.
Simulation flow chart
在兩種復位路徑下，各肌肉在復位過程中的肌肉力變化曲線如圖 12 所示。從圖中可看出：在兩種路徑下股二頭肌短頭在復位過程中皆起主要作用，且在復位過程中產生的最大肌肉力為 265.47 N，此時斷骨遠端沿軸向拉伸 30.02 mm。文獻[21]中，骨折的軸向移位偏差為 20 mm，垂直于軸向移位 40 mm，復位過程中，股二頭肌短頭對復位力的影響最大，且軸向拉伸至 20 mm 時，股二頭肌短頭所產生的肌肉力為 230 N。
圖12
不同復位路徑的肌肉力變化
Figure12.
Muscle force with different reduction path
在股骨骨折復位時，雖然影響骨折復位的主要肌肉——股二頭肌短頭和縫匠肌的羽狀角較小，但其他股直肌、半腱肌等骨骼肌的羽狀角較大，亦影響較大，因此，計算復位力時，也不能忽略羽狀角的影響。
圖 13 為復位過程中復位力及其沿 x、y、z 軸方向的分力的變化曲線，從圖中可以看出，股骨骨折復位過程中，兩種復位路徑下沿股骨干軸向的復位力最大，最大值為 472.18 N，且最大骨折復位合力為 497.28 N。
圖13
復位力
Figure13.
Reduction force
在復位操作時，肌肉不能產生主動力，只有被動力在起作用，且輔助骨折復位機器人在復位過程中移動緩慢，此時肌肉力的大小只與肌肉長度相關，由于兩種復位路徑的起點和終點相同，從圖 12～13 可以看出，在兩種復位路徑下各力的最小值和最大值相等，而且采用課題組雙平面路徑規劃的路徑 1 進行骨折復位仿真，復位過程中，復位力及肌肉力的變化更加平緩。
采用路徑 1 時，初始階段斷骨遠端在 xoy 平面內僅僅沿 x 軸移動時，肌肉力的變化趨勢較為平緩，當斷骨遠端開始在 yoz 平面內沿著 y 和 z 軸移動時，肌肉力的變化趨勢變得陡峭，而在最后階段又變得比較平緩，此時斷骨遠端沿著 y 軸移動；采用路徑 2 時，初始階段斷骨遠端在三維方向上進行移動，肌肉力的變化趨勢較為陡峭，當斷骨遠端僅沿著 y 軸移動時，肌肉力及復位力的變化趨勢變得平緩，說明軸向位移的變化對復位力的影響最大。
4 結論
本文結合 Haeufle 四元素模型中引入的串聯阻尼、離心收縮力-速度關系以及羽狀角對肌肉力特性的影響，建立一種新型骨骼肌肉模型 PA-MTM，較符合下肢骨骼肌的真實結構。由于肌肉力與骨骼肌的長度 、肌肉的速度 、激活程度 等參數有關，給定各骨骼肌長度、速度及激活程度，對比分析股二頭肌短頭、股二頭肌長頭、股直肌、半膜肌、半腱肌和縫匠肌等六種骨骼肌，在相同肌肉長度下，采用 Hill 模型、Haeufle 四元素模型、PA-MTM 肌肉模型三種不同模型計算的肌肉力。本文所提出 PA-MTM 骨骼肌模型的肌肉力計算結果大于不考慮羽狀角的 Haeufle 四元素骨骼肌模型，且肌肉的羽狀角越大，不同模型下的肌肉力計算結果差值越大。根據股骨骨折模型的骨折偏差，規劃不同復位路徑，進行骨折復位仿真分析，獲得最大復位合力為 497.28 N，最大軸向復位力為 472.18 N，同時，通過與文獻[19, 21, 30]的復位力分析結果對比，驗證了新型骨骼肌模型 PA-MTM 的合理性。本研究可為機器人骨折復位力監控及復位路徑擇優提供參考。
未來將開展下肢骨肌模型肌肉力及復位力實驗測試，進一步驗證該模型的準確性。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
