探究雙曲線傳熱模型中弛豫時間對房顫微波消融溫度場的影響,并與采用 Pennes 模型計算得到的心肌組織溫度場進行比較。構建了房顫微波消融的三維模型,弛豫時間(τ)取 0、1、5、8、10、15、20 s,得到心肌組織的溫度場,結果表明,消融開始時,雙曲線模型的心肌組織最高溫度低于 Pennes 模型的心肌組織最高溫度,最大相差 21.8 ℃。隨著消融時間增大,最高溫度逐漸趨于一致。且不同的弛豫時間分別在消融時間達到 3、4、6、7、8、9、10 s 時才開始出現損傷區域。因此雙曲線模型對溫度的影響會隨著消融時間的增大而減小,且在消融開始時弛豫時間會阻礙心肌熱擴散的速度,弛豫時間越大,熱擴散的速度越慢,為雙曲線模型在房顫微波消融中的應用提供參考。
引用本文: 張萌, 田甄, 程妍妍, 劉洪興, 南群. 雙曲線傳熱模型在微波消融治療房顫中的應用研究. 生物醫學工程學雜志, 2021, 38(5): 885-892. doi: 10.7507/1001-5515.202009084 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
心房顫動(簡稱房顫)是臨床上常見的心律失常,可導致卒中、心力衰竭等一系列不良臨床后果[1]。患病率及發病率均隨著年齡的增長而增加[2]。目前研究認為在部分房顫患者中,肺靜脈等異位興奮灶產生的快速沖動是導致房顫發生的原因[3],它不僅參與了房顫的發生,而且在房顫的維持中也起到重要的作用[4]。近年來導管消融術已經成為心房顫動最有效的治療手段。與藥物治療不同,導管消融治療針對的是房顫的發病與維持機制,因此有根治房顫的可能[5]。該方法將能量(如微波、射頻、低溫冷凍)送到肺靜脈口處,對心內膜、心外膜造成不可逆性損傷,從而隔離肺靜脈和左心房電傳導。其中環肺靜脈消融是目前采用的主要手術方式,對陣發性和持續性房顫均有較好的療效[6]。
微波消融是導管消融治療的一種,它通過發射 2.45 GHz 的高頻電磁波,經微波探頭傳到心肌組織,引起雙極性水分子的快速旋轉、震動而摩擦產熱[7]。而心肌組織含水量高,具有較高的導電性,因此心肌更適合微波消融[8]。心肌組織高于 50℃ 會發生不可逆性損傷,通過心肌壞死能阻斷異常電信號傳導從而治療房顫[9]。如果消融不徹底,就會導致房顫的復發,因此心肌組織的熱場分布是決定消融效果的重要因素。
采用數值模擬方法可以得到熱療的溫度場分布,預測熱療的治療效果。目前在多數的熱療數值模擬中,是采用基于傅里葉理論的 Pennes 生物傳熱方程來確定溫度場。傅里葉傳熱定律假設熱的傳遞速度是無限大的[10],介質上的任何熱擾動都會瞬間傳遞到整個介質中,然而這顯然與物理事實不符。因此在生物傳熱過程中,由于生物組織具有各向異性及非均勻介質的特點,在高能量、短時間的熱療中,生物熱傳播速度的有限性是不能忽略的。為了解決傅里葉定律中熱傳播速度無限大這一問題,Cattaneo[11]和 Vernotte[12]提出了傅里葉定律的修改形式,即雙曲線生物傳熱模型。此模型考慮了有限熱傳播的速度的概念,認為熱流矢量與溫度梯度之間存在延遲響應,即存在延遲時間,定義為弛豫時間τ。Tzou 等[13]在加入熱流矢量相位延遲的同時,加入了溫度梯度的相位延遲,以考慮微結構相互作用的影響以及熱傳遞的快速瞬態效應,即雙向滯后非傅里葉傳熱模型。但目前在非傅里葉傳熱效應的研究中,雙曲線生物傳熱模型是最常見、最普遍的模型[14]。
目前已有研究利用雙曲線模型進行了數值分析,Kumar 等[15]采用雙曲線模型探究了肺癌冷凍消融中的相變換熱,發現應用雙曲線模型的組織溫度在消融時間 800 s 內高于 Pennes 傳熱模型,弛豫時間較小時,凍結速度較快。Namakshenas 等[16]采用雙曲線模型模擬聚焦超聲熱消融治療甲狀腺良性腫瘤,結果表明考慮非傅里葉傳熱會導致熱損傷區域減小。Singh 等[17]采用雙曲線模型在生物組織熱消融中研究了一個考慮非傅里葉效應的多物理場耦合模型,結果表明非傅里葉效應會導致消融過程中預測的溫度分布與組織變形減小。以上研究結果皆表明非傅里葉傳熱效應會影響生物傳熱的溫度分布,并且隨著弛豫時間的增加,損傷區域減小,但目前還未有學者探究雙曲線模型對房顫微波消融效果的影響。
本文采用數值模擬的方法,對在微波消融治療房顫中兩種不同的生物傳熱模型(雙曲線模型與 Pennes 模型)得到的熱場進行了比較,同時得到了雙曲線模型中不同弛豫時間對微波消融熱場的影響。
1 研究方法
1.1 幾何模型構建
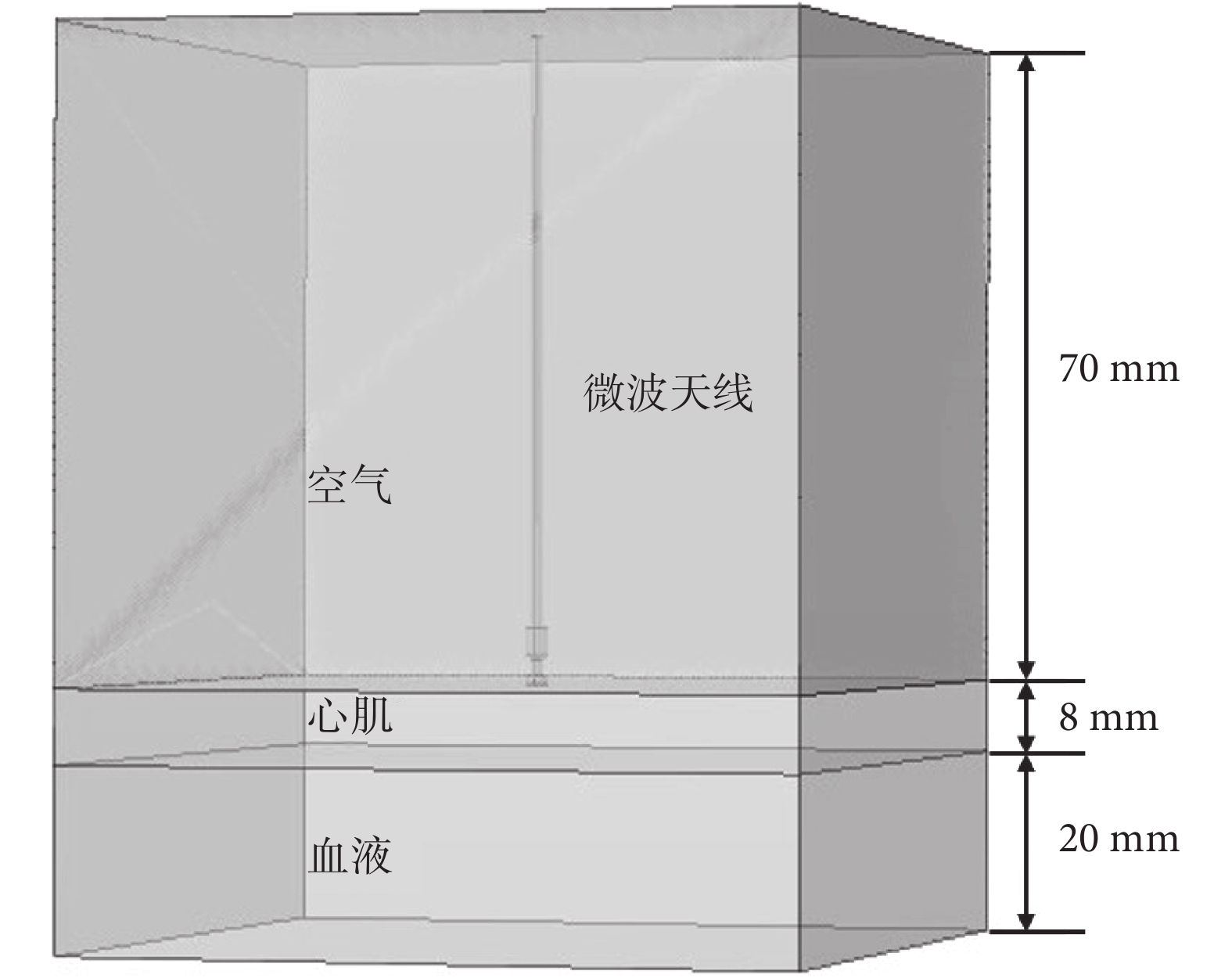
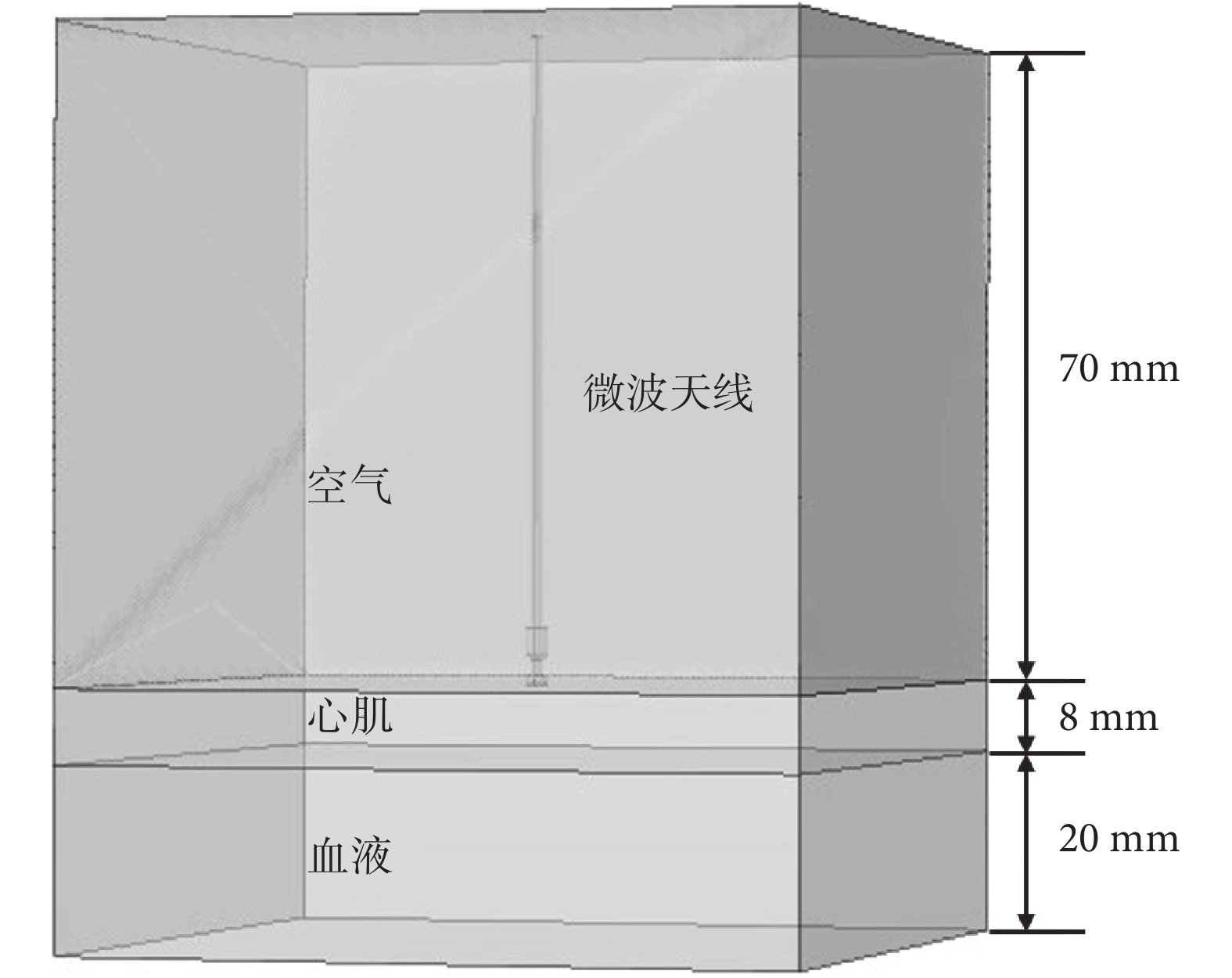
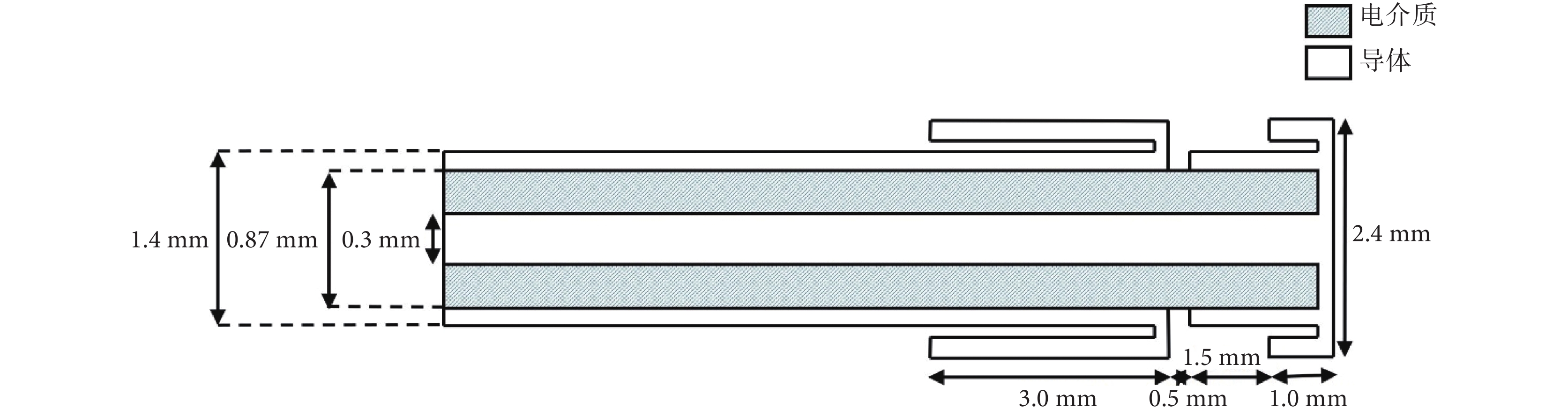
本文采用 COMSOL Multiphysics 多物理場耦合分析軟件,計算采用有限元方法。理想的三維模型中包含心肌、血液、微波天線以及外部環境(空氣)四部分組成。考慮到微波天線的結構,微波天線發出的輻射聚集在頂端周圍,而研究是把電磁場的電磁損耗密度作為溫度場的熱源施加給模型,因此為了得到微波天線完整的電磁場分布,在模型的計算中增加了空氣層。消融方式采用心外膜消融,即由右側胸壁切口進入,置入套管后將消融設備導于心外膜處[18]。心肌厚度選為肺靜脈開口處的心肌厚度 8 mm[19],血液層厚度為 20 mm[20],模型如圖 1 所示。微波天線使用了 Bernardi 等[21]提出的天線模型,天線導體的材料為銅,內外層導體之間由特氟倫構成,結構如圖 2 所示。
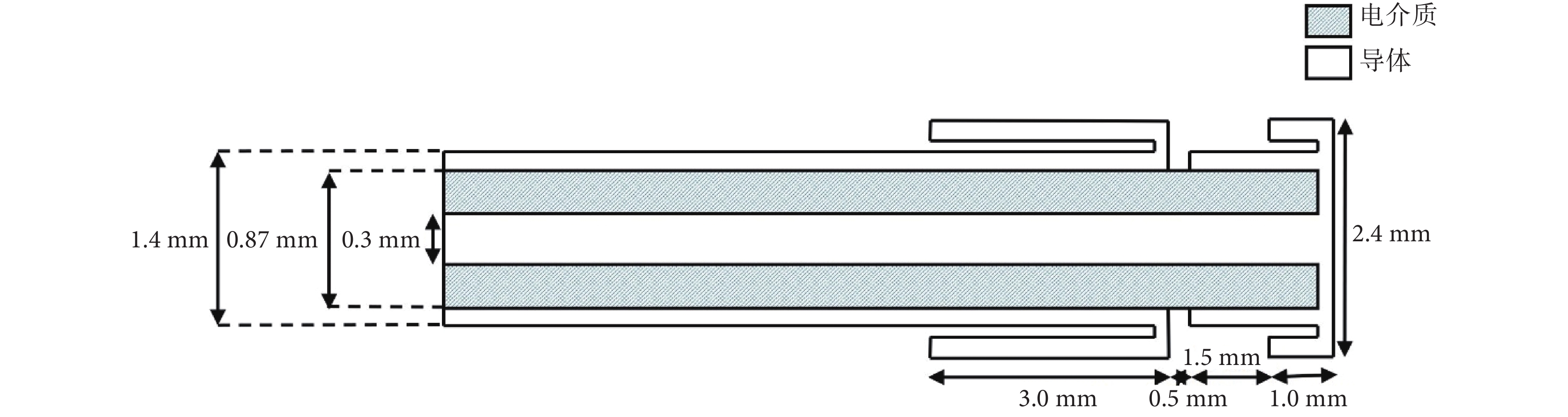 圖2
微波天線幾何結構
Figure2.
Geometry of microwave antenna
圖2
微波天線幾何結構
Figure2.
Geometry of microwave antenna
1.2 數學模型
本研究對電磁場及熱場兩個物理場耦合計算,得到心肌組織的溫度分布。
研究中采用電磁能加熱生物組織,電磁場采用平面橫波,其方程如式(1)所示[22]:
 |
式中 E 為電場矢量,單位為 V/m; 是相對磁導率(
是相對磁導率( = 1);
= 1); 是心肌相對介電常數;
是心肌相對介電常數; 是電導率,單位為 S/m;
是電導率,單位為 S/m; 是真空介電常數,為 8.8542 × 10?12 F/m;
是真空介電常數,為 8.8542 × 10?12 F/m; 為角頻率,單位為 rad/s;
為角頻率,單位為 rad/s; 是自由空間波數,單位為 rad/m。
是自由空間波數,單位為 rad/m。
根據組織中的電磁場分布計算得到的吸收的電磁能( )如式(2)所示[23]:
)如式(2)所示[23]:
 |
大多數研究均采用基于 Pennes 的生物熱模型[24],如式(3)所示:
 |
式中 T、ρ、c、k 分別為溫度、生物組織密度、比熱、熱導率,單位分別為 K、kg/m3、J/(kg·K)、W/(m·K); 、
、 、
、 、
、 分別為血液密度、血液灌注率、血液比熱及血液溫度。血液灌注帶走的熱量,對于微波消融來說,心肌層內部血液灌注帶走的熱量遠小于微波消融產生的熱量及心腔內血液循環帶走的熱量,因此可忽略不計[25]。
分別為血液密度、血液灌注率、血液比熱及血液溫度。血液灌注帶走的熱量,對于微波消融來說,心肌層內部血液灌注帶走的熱量遠小于微波消融產生的熱量及心腔內血液循環帶走的熱量,因此可忽略不計[25]。 為組織新陳代謝產生的熱量,與其他熱量相比,此項可忽略不計[26]。
為組織新陳代謝產生的熱量,與其他熱量相比,此項可忽略不計[26]。 為外部熱源項,即式(2)。
為外部熱源項,即式(2)。
經典傅里葉傳導定律假設熱的傳導速度是無限的。但在實際情況中,任何熱力學過程平衡態的建立都需要一定的弛豫時間,因此得到了雙曲線生物傳熱方程[27],如式(4)所示:
 |
式中  為弛豫時間(s)。
為弛豫時間(s)。
如果雙曲線模型中的 τ = 0,則上述雙曲線模型變為 Pennes 模型即式(3)。
1.3 仿真參數設置
根據文獻中生物組織的實驗研究,參考弛豫時間的不同值,分別設置為 0、1、5、8、10、15、20 s[21,28-30]。研究中的電磁場模塊設置為穩態和頻域,輸出微波頻率穩定為 2.45 GHz,微波天線為同軸微波天線,電介質設置為端口,采用的消融功率為 30 W,總消融時間采用 120 s,時間步長設置 1 s。心肌組織、血液初始溫度為 37℃,微波天線初始溫度為 25℃。微波引起組織損傷的機制是微波能量轉化為熱能,因此在心肌組織上施加的熱源是電磁功率損耗密度。以此獲得不同消融時間下的溫度分布與損傷區域,同時探討不同弛豫時間條件下,心肌組織溫度分布及損傷區域的變化規律。
研究中循環血液流動產生的熱效應考慮成邊界條件[31],如式(5)所示:
 |
其中  為組織-血液邊界的對流換熱系數,設置為 1 417 W/(m2·K),是血液流速為 24 cm/s 時的血液-組織對流換熱系數參考值[32],
為組織-血液邊界的對流換熱系數,設置為 1 417 W/(m2·K),是血液流速為 24 cm/s 時的血液-組織對流換熱系數參考值[32], = 37℃ 為血液溫度。仿真中模型的熱物性參數[21]如表 1 所示。
= 37℃ 為血液溫度。仿真中模型的熱物性參數[21]如表 1 所示。
2 結果
為了探究不同弛豫時間對微波消融房顫的影響,分別從溫度分布及熱損傷區域對比進行了分析。
2.1 溫度場分布
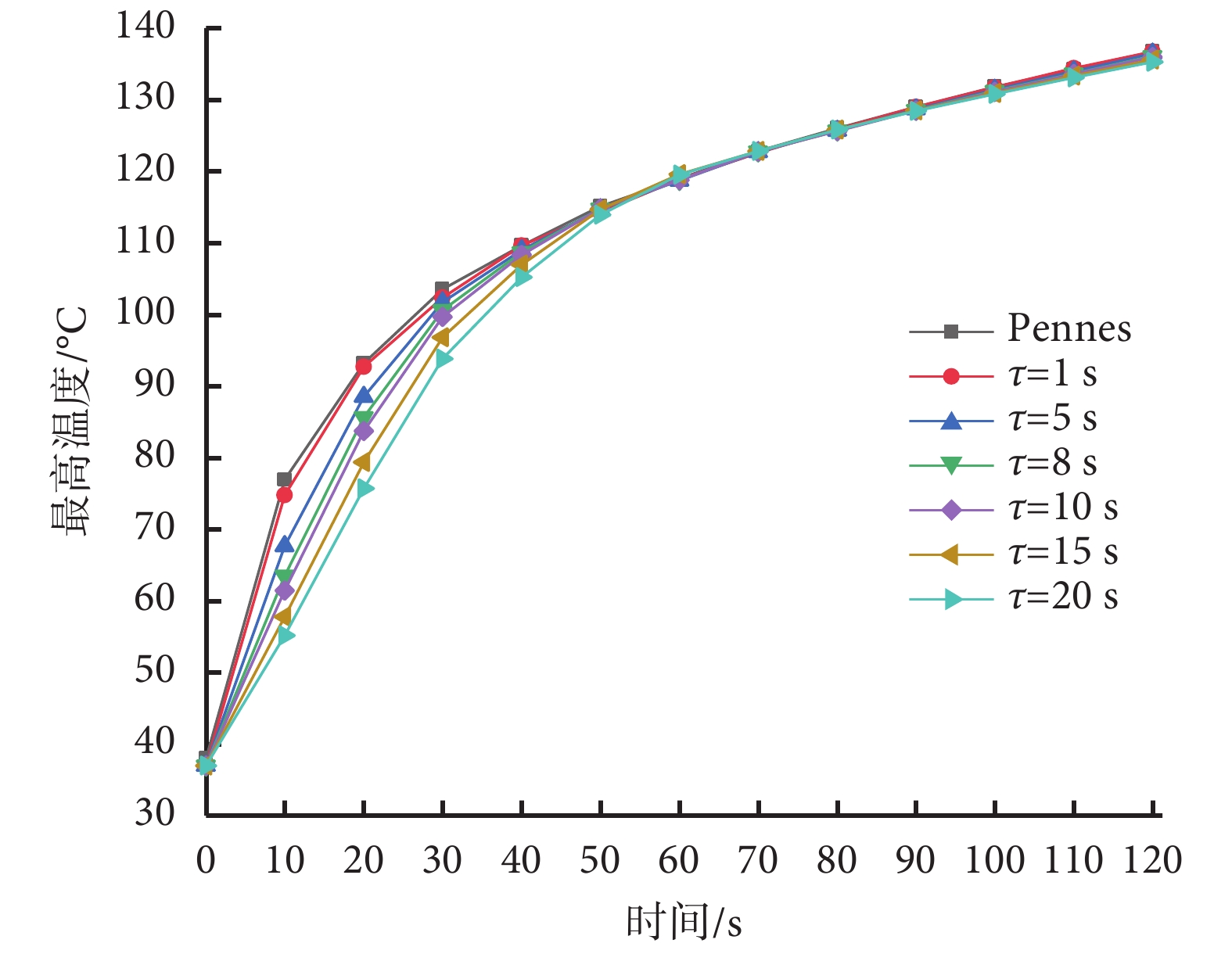
有研究表明心肌細胞興奮性在高于 50℃ 時便會喪失,心肌組織出現不可逆性損傷[9],因此本研究認為高于 50℃ 的區域為損傷區域。不同的弛豫時間導致心肌組織的最高溫度發生變化,圖 3 為心肌組織中最高溫度點變化曲線。從圖中可以看到  = 0 s 與
= 0 s 與  = 1 s 時溫度分布基本一致。然而,隨著弛豫時間的增加,兩種模型結果差異較大,且最高溫度降低。消融時間為 10 s 時,最高溫度差異最大,此時
= 1 s 時溫度分布基本一致。然而,隨著弛豫時間的增加,兩種模型結果差異較大,且最高溫度降低。消融時間為 10 s 時,最高溫度差異最大,此時  = 0、1、5、8、10、15、20 s 時的最高溫度分別為 76.9、74.7、67.6、63.4、61.4、57.7、55.1℃,最大溫差為 21.8℃。隨著消融時間增加,不同弛豫時間下的最高溫度又逐漸趨于一致,當消融時間為 55 s 時,最高溫度分別為 117.0、116.6、116.7、116.8、116.8、117.1、116.7℃。
= 0、1、5、8、10、15、20 s 時的最高溫度分別為 76.9、74.7、67.6、63.4、61.4、57.7、55.1℃,最大溫差為 21.8℃。隨著消融時間增加,不同弛豫時間下的最高溫度又逐漸趨于一致,當消融時間為 55 s 時,最高溫度分別為 117.0、116.6、116.7、116.8、116.8、117.1、116.7℃。
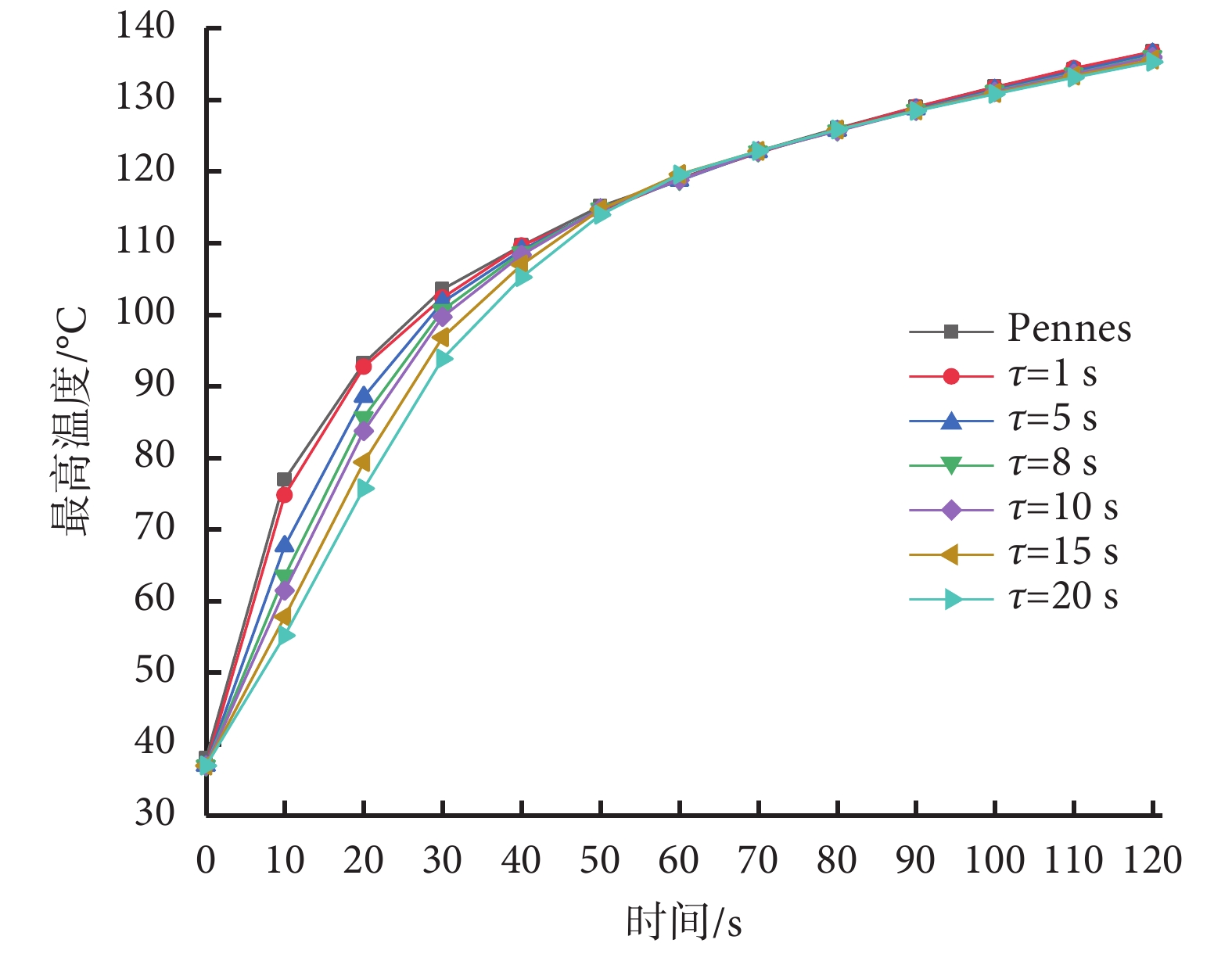 圖3
不同弛豫時間下心肌組織中最高溫度點溫升曲線
Figure3.
Temperature rise curve of the highest temperature point in myocardial tissue under different relaxation time
圖3
不同弛豫時間下心肌組織中最高溫度點溫升曲線
Figure3.
Temperature rise curve of the highest temperature point in myocardial tissue under different relaxation time
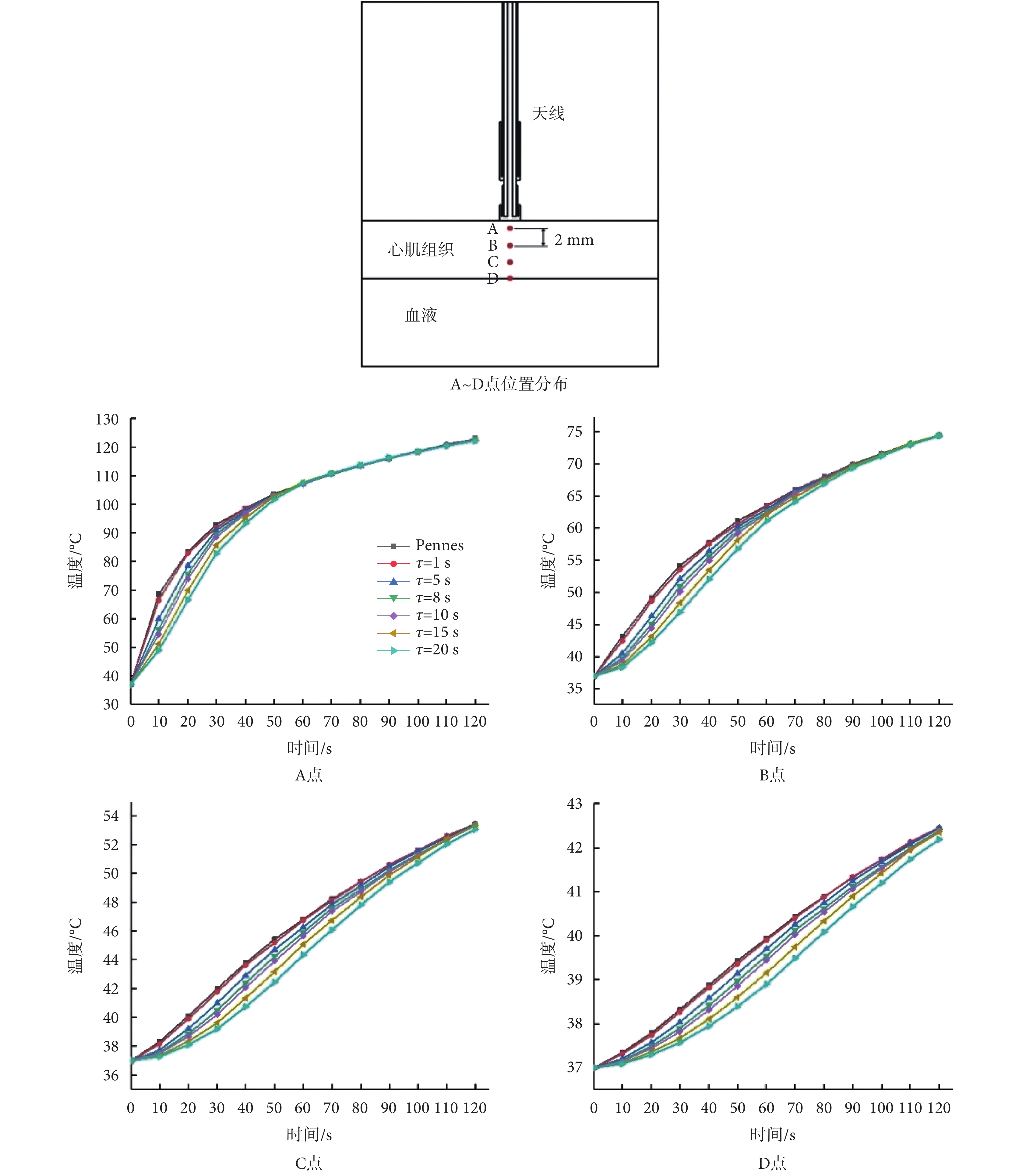
圖 4 為心肌組織不同深度處的溫度分布。取微波天線正下方 1、3、5、7 mm 處,分別為 A~D 點,消融 10 s 時 = 20 s 與
= 20 s 與 = 0 s 在 A、B、C、D 點處溫度分別減小 19.5、4.8、1.0、0.3℃。結果表明不同位置處的溫度分布均受到弛豫時間的影響,在消融開始時,在靠近微波天線的點,弛豫時間對溫度的影響更大。在 A、B、C、D 處,
= 0 s 在 A、B、C、D 點處溫度分別減小 19.5、4.8、1.0、0.3℃。結果表明不同位置處的溫度分布均受到弛豫時間的影響,在消融開始時,在靠近微波天線的點,弛豫時間對溫度的影響更大。在 A、B、C、D 處, = 20 s 與
= 20 s 與 = 0 s 處的溫度相比,溫差最大值分別出現在 10、30、40、50 s 處,分別為 19.5、7.2、3.0、1.0℃。隨著消融時間的增加,不同弛豫時間的溫差逐漸減小,A、B、C、D 點分別在 60、90、110、120 s 后溫度基本一致。因此對于靠近微波天線的點,雙曲線模型計算得到的溫度達到與 Pennes 模型相同溫度所需的消融時間較短。
= 0 s 處的溫度相比,溫差最大值分別出現在 10、30、40、50 s 處,分別為 19.5、7.2、3.0、1.0℃。隨著消融時間的增加,不同弛豫時間的溫差逐漸減小,A、B、C、D 點分別在 60、90、110、120 s 后溫度基本一致。因此對于靠近微波天線的點,雙曲線模型計算得到的溫度達到與 Pennes 模型相同溫度所需的消融時間較短。
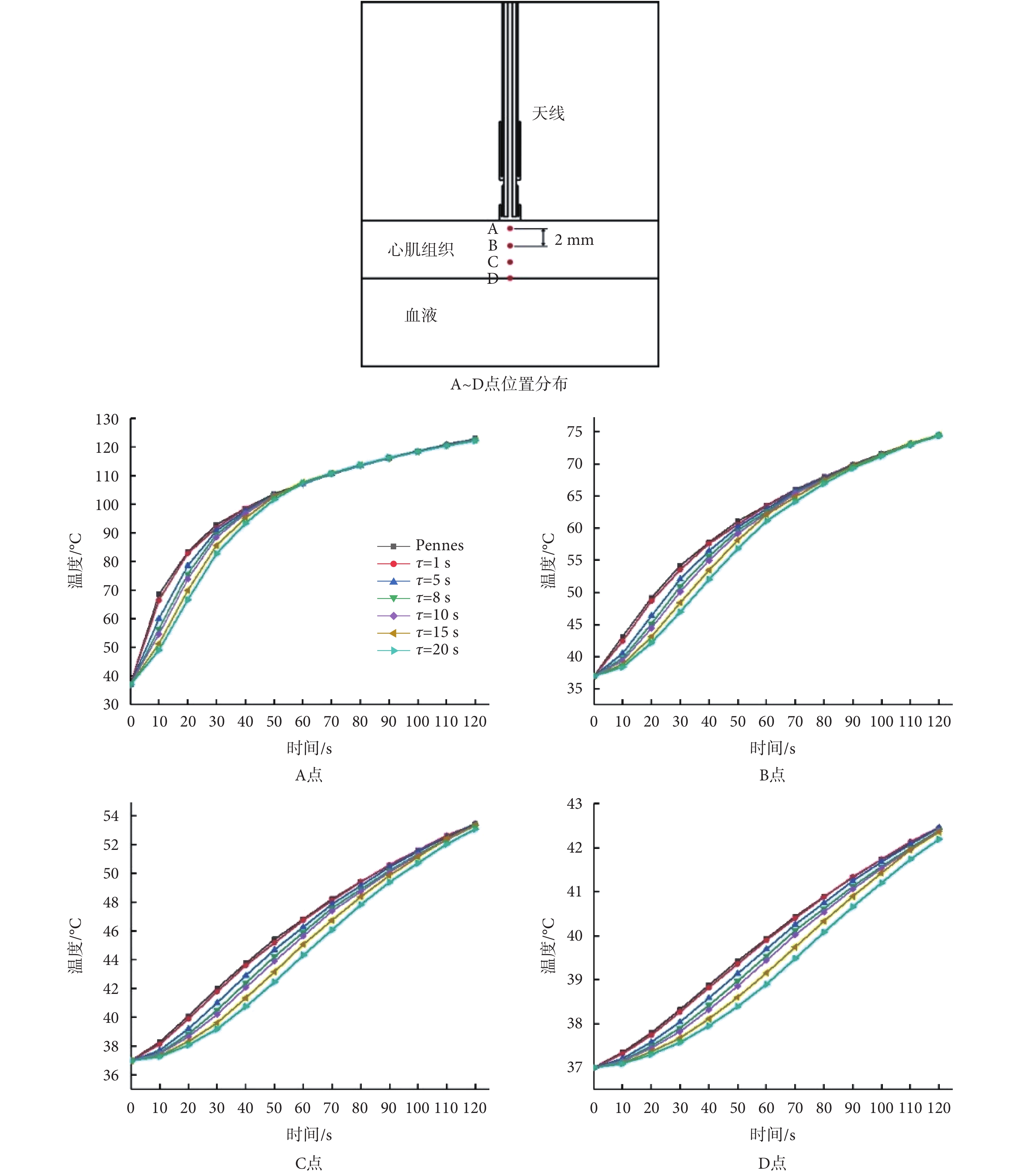 圖4
A~D 位置分布及不同弛豫時間下心肌組織溫升曲線
Figure4.
A–D location distribution and myocardial tissue temperature rise curve under different relaxation time
圖4
A~D 位置分布及不同弛豫時間下心肌組織溫升曲線
Figure4.
A–D location distribution and myocardial tissue temperature rise curve under different relaxation time
2.2 損傷區域對比
通過測量損傷深度及損傷寬度確定心肌的損傷區域,得到不同弛豫時間的損傷寬度、損傷深度變化規律,如圖 5 所示。與心肌組織溫度分布規律一致,消融開始時,損傷寬度與損傷深度隨弛豫時間的增加而增大。與高弛豫時間相比,低弛豫時間時熱擴散到組織中的速度更快,因此損傷區域更大。隨著消融時間的增加,弛豫時間的影響逐漸減小。 = 1、5、8、10、15、20 s 時與采用 Pennes 模型計算得到的組織損傷深度達到一致加熱時間分別為 40、70、80、100、110、120 s。在 120 s 時損傷深度已達到一致,為 5.5 mm;
= 1、5、8、10、15、20 s 時與采用 Pennes 模型計算得到的組織損傷深度達到一致加熱時間分別為 40、70、80、100、110、120 s。在 120 s 時損傷深度已達到一致,為 5.5 mm; = 0、1、5、8、10、15、20 s 時的損傷寬度分別為 11.8、11.8、11.7、11.7、11.7、11.6、11.5 mm,損傷寬度也基本一致。因弛豫時間減小了熱擴散的速度,
= 0、1、5、8、10、15、20 s 時的損傷寬度分別為 11.8、11.8、11.7、11.7、11.7、11.6、11.5 mm,損傷寬度也基本一致。因弛豫時間減小了熱擴散的速度, = 0、1、5、8、10、15、20 s 時分別在 3、4、6、7、8、9、10 s 時才出現損傷區域。例如在消融時間 7 s 時,不同弛豫時間下的溫度分布如圖 6 所示,
= 0、1、5、8、10、15、20 s 時分別在 3、4、6、7、8、9、10 s 時才出現損傷區域。例如在消融時間 7 s 時,不同弛豫時間下的溫度分布如圖 6 所示, = 0、1、5、8 s 時已經形成損傷區域,但
= 0、1、5、8 s 時已經形成損傷區域,但 = 10、15、20 s 時還未形成完整的損傷區域。
= 10、15、20 s 時還未形成完整的損傷區域。
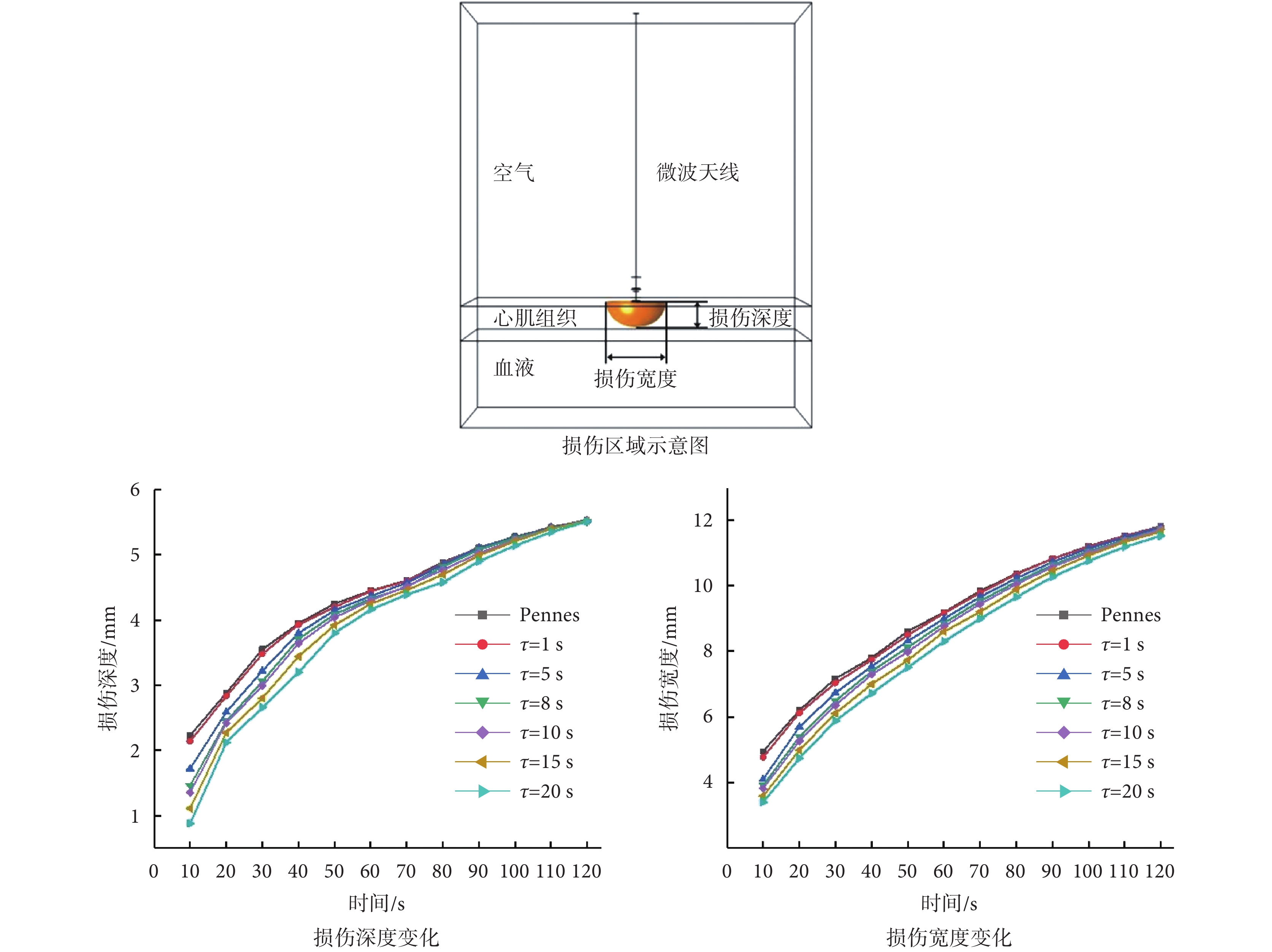 圖5
不同弛豫時間下損傷區域變化
Figure5.
Change of the lesion dimensions under different relaxation time
圖5
不同弛豫時間下損傷區域變化
Figure5.
Change of the lesion dimensions under different relaxation time
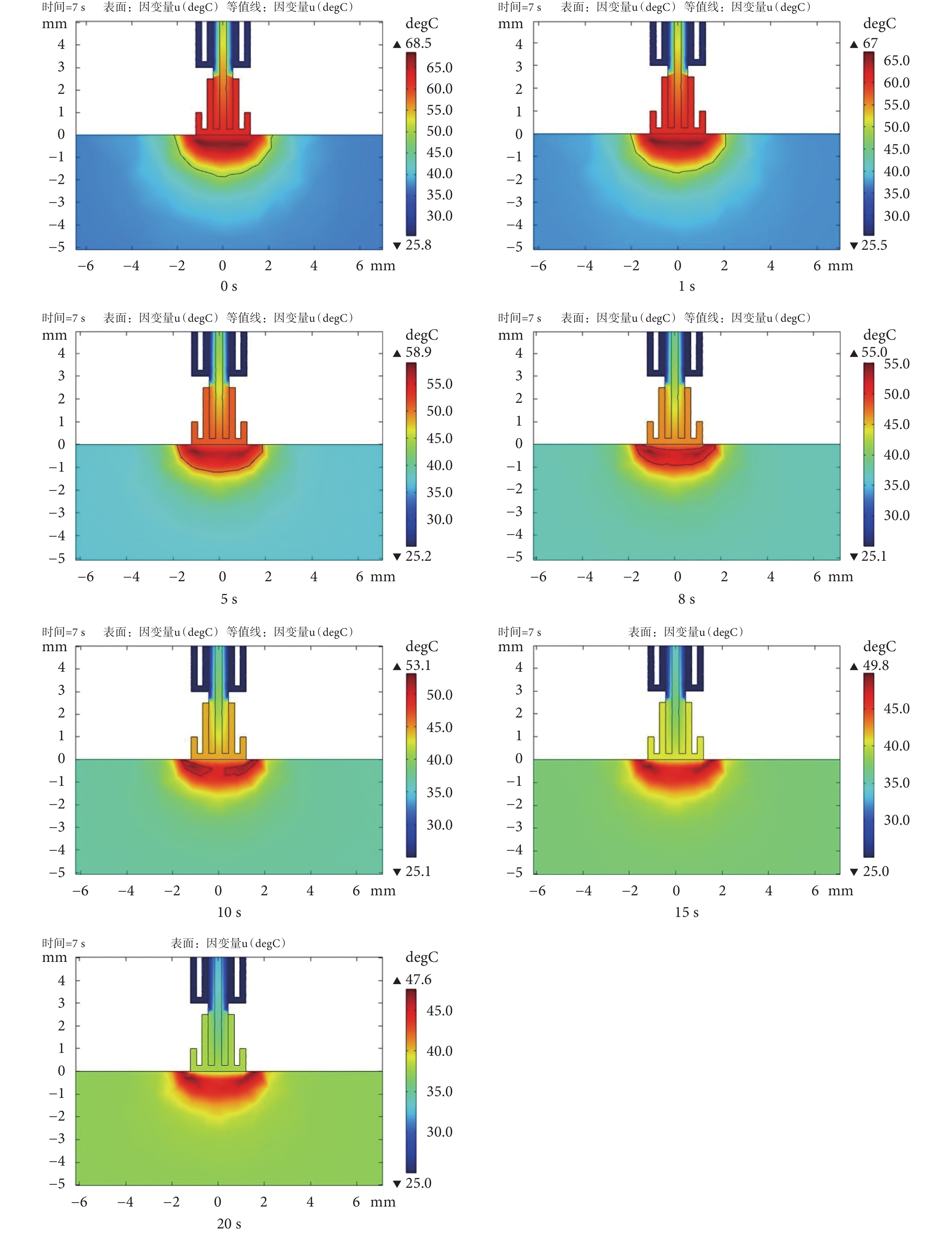 圖6
不同弛豫時間下心肌組織溫度分布圖
Figure6.
Temperature distribution of myocardial tissue at different relaxation times
圖6
不同弛豫時間下心肌組織溫度分布圖
Figure6.
Temperature distribution of myocardial tissue at different relaxation times
表 2 為不同弛豫時間下達到相同心肌損傷深度所需的加熱時間,可以看出達到相同組織損傷深度時, = 0 s 與
= 0 s 與 = 1 s 時所需時間基本相同,但隨著弛豫時間的增加,消融時間也需要增加。反之在相同消融時間下,弛豫時間會影響心肌損傷深度,最終影響消融效果。因此在臨床上若要達到與 Pennes 模型相同的消融效果,應增大消融時間。
= 1 s 時所需時間基本相同,但隨著弛豫時間的增加,消融時間也需要增加。反之在相同消融時間下,弛豫時間會影響心肌損傷深度,最終影響消融效果。因此在臨床上若要達到與 Pennes 模型相同的消融效果,應增大消融時間。
3 討論與結論
經典傅里葉熱傳導理論描述的是瞬時能量沉積的過程,假設熱信號的傳播速度是無限的。而在生物傳熱中,生物組織具有不均勻的結構,需要一段弛豫時間才能將足夠的能量轉移到附近的組織[33],因此生物熱傳播速度的有限性不可忽視。弛豫時間在短消融時間內會影響心肌損傷區域的大小,而臨床使用導管消融旨在用盡可能短的時間獲得透壁性消融損傷[34]。袁彪等[18]對 46 例持續性房顫患者進行了心外膜消融術,術后成功率為 63%,消融效果以及消融線阻斷是否完整是消融成功與否的關鍵。臨床治療及研究中,通常使用消融功率 20~65 W[35-36],消融時間 30~120 s[37-38]。而在此消融時間內,弛豫時間對心肌損傷區域的影響較為明顯。如表 2 中所示,若對 2 mm 的心肌組織進行消融, = 0 s 與
= 0 s 與 = 20 s 時所需的消融時間相差 11 s。如用 Pennes 模型進行心肌損傷評估,可能導致心肌消融不透壁,最終造成房顫復發,因此雙曲線模型對心肌消融效果的影響不可忽視。
= 20 s 時所需的消融時間相差 11 s。如用 Pennes 模型進行心肌損傷評估,可能導致心肌消融不透壁,最終造成房顫復發,因此雙曲線模型對心肌消融效果的影響不可忽視。
在消融短時間內,弛豫時間增大,最高溫度減小,這是由于非傅里葉傳熱的滯后性導致的。傅里葉傳熱不考慮傳熱滯后性,因此 Pennes 模型得到的溫度是最高的。非傅里葉傳熱使熱擴散速度減慢,熱流矢量與溫度梯度之間的延遲越大,熱擴散速度就會越慢。當消融時間增大時,非傅里葉傳熱的延遲性逐漸消失,與傅里葉傳熱速度趨于一致,因此非傅里葉傳熱只在短消融時間內有效。同時由于距離微波天線近的位置微波能量較大,不同弛豫時間對心肌組織溫度的影響也較大。因此與 Pennes 模型相比,雙曲線模型可以更精確地把控心肌組織的溫度分布。
損傷區域會隨著弛豫時間的增加而減小,Pennes 模型的損傷區域最大。當弛豫時間逐漸增大,熱擴散速度的滯后性增強,使得熱量積聚在心肌組織內部,所以損傷區域首先出現在心肌組織內部。表 2 中列出了達到不同心肌損傷深度時需要的消融時間,弛豫時間越大,需要的消融時間就越長。因臨床上對房顫微波消融所需的消融時間較短,所以應充分考慮雙曲線模型對消融效果的影響。Pennes 模型高估了心肌的損傷深度,造成損傷區域不透壁,影響了消融效果,最終會使得房顫復發。
雙曲線傳熱模型對溫度場的影響會隨消融時間的增加而減小,且隨著弛豫時間增加,心肌最高溫度降低;當消融時間達到 55 s 時,不同弛豫時間下的最高溫度基本達到一致。當弛豫時間  = 1、5、8、10、15、20 s 時,消融時間達到 3、4、6、7、8、9、10 s 時才出現損傷區域。弛豫時間會阻礙熱擴散的速度,弛豫時間越大,熱擴散的速度越慢。因此要考慮雙曲線傳熱模型對心肌損傷深度的影響,采用傅里葉傳熱則會影響最終治療效果。
= 1、5、8、10、15、20 s 時,消融時間達到 3、4、6、7、8、9、10 s 時才出現損傷區域。弛豫時間會阻礙熱擴散的速度,弛豫時間越大,熱擴散的速度越慢。因此要考慮雙曲線傳熱模型對心肌損傷深度的影響,采用傅里葉傳熱則會影響最終治療效果。
本文只探究了心外膜微波消融的非傅里葉傳熱效應,并未考慮心內膜微波消融時非傅里葉傳熱的影響。本文弛豫時間的選取在生物組織弛豫時間的選取范圍內,但目前鮮有研究心肌組織的弛豫時間,未來還將對心肌組織的弛豫時間進行探討,并增加離體實驗驗證。非傅里葉傳熱中除雙曲線模型,還包括雙向延遲模型[39]等,未來會考慮不同非傅里葉模型對房顫微波消融的影響。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
心房顫動(簡稱房顫)是臨床上常見的心律失常,可導致卒中、心力衰竭等一系列不良臨床后果[1]。患病率及發病率均隨著年齡的增長而增加[2]。目前研究認為在部分房顫患者中,肺靜脈等異位興奮灶產生的快速沖動是導致房顫發生的原因[3],它不僅參與了房顫的發生,而且在房顫的維持中也起到重要的作用[4]。近年來導管消融術已經成為心房顫動最有效的治療手段。與藥物治療不同,導管消融治療針對的是房顫的發病與維持機制,因此有根治房顫的可能[5]。該方法將能量(如微波、射頻、低溫冷凍)送到肺靜脈口處,對心內膜、心外膜造成不可逆性損傷,從而隔離肺靜脈和左心房電傳導。其中環肺靜脈消融是目前采用的主要手術方式,對陣發性和持續性房顫均有較好的療效[6]。
微波消融是導管消融治療的一種,它通過發射 2.45 GHz 的高頻電磁波,經微波探頭傳到心肌組織,引起雙極性水分子的快速旋轉、震動而摩擦產熱[7]。而心肌組織含水量高,具有較高的導電性,因此心肌更適合微波消融[8]。心肌組織高于 50℃ 會發生不可逆性損傷,通過心肌壞死能阻斷異常電信號傳導從而治療房顫[9]。如果消融不徹底,就會導致房顫的復發,因此心肌組織的熱場分布是決定消融效果的重要因素。
采用數值模擬方法可以得到熱療的溫度場分布,預測熱療的治療效果。目前在多數的熱療數值模擬中,是采用基于傅里葉理論的 Pennes 生物傳熱方程來確定溫度場。傅里葉傳熱定律假設熱的傳遞速度是無限大的[10],介質上的任何熱擾動都會瞬間傳遞到整個介質中,然而這顯然與物理事實不符。因此在生物傳熱過程中,由于生物組織具有各向異性及非均勻介質的特點,在高能量、短時間的熱療中,生物熱傳播速度的有限性是不能忽略的。為了解決傅里葉定律中熱傳播速度無限大這一問題,Cattaneo[11]和 Vernotte[12]提出了傅里葉定律的修改形式,即雙曲線生物傳熱模型。此模型考慮了有限熱傳播的速度的概念,認為熱流矢量與溫度梯度之間存在延遲響應,即存在延遲時間,定義為弛豫時間τ。Tzou 等[13]在加入熱流矢量相位延遲的同時,加入了溫度梯度的相位延遲,以考慮微結構相互作用的影響以及熱傳遞的快速瞬態效應,即雙向滯后非傅里葉傳熱模型。但目前在非傅里葉傳熱效應的研究中,雙曲線生物傳熱模型是最常見、最普遍的模型[14]。
目前已有研究利用雙曲線模型進行了數值分析,Kumar 等[15]采用雙曲線模型探究了肺癌冷凍消融中的相變換熱,發現應用雙曲線模型的組織溫度在消融時間 800 s 內高于 Pennes 傳熱模型,弛豫時間較小時,凍結速度較快。Namakshenas 等[16]采用雙曲線模型模擬聚焦超聲熱消融治療甲狀腺良性腫瘤,結果表明考慮非傅里葉傳熱會導致熱損傷區域減小。Singh 等[17]采用雙曲線模型在生物組織熱消融中研究了一個考慮非傅里葉效應的多物理場耦合模型,結果表明非傅里葉效應會導致消融過程中預測的溫度分布與組織變形減小。以上研究結果皆表明非傅里葉傳熱效應會影響生物傳熱的溫度分布,并且隨著弛豫時間的增加,損傷區域減小,但目前還未有學者探究雙曲線模型對房顫微波消融效果的影響。
本文采用數值模擬的方法,對在微波消融治療房顫中兩種不同的生物傳熱模型(雙曲線模型與 Pennes 模型)得到的熱場進行了比較,同時得到了雙曲線模型中不同弛豫時間對微波消融熱場的影響。
1 研究方法
1.1 幾何模型構建
本文采用 COMSOL Multiphysics 多物理場耦合分析軟件,計算采用有限元方法。理想的三維模型中包含心肌、血液、微波天線以及外部環境(空氣)四部分組成。考慮到微波天線的結構,微波天線發出的輻射聚集在頂端周圍,而研究是把電磁場的電磁損耗密度作為溫度場的熱源施加給模型,因此為了得到微波天線完整的電磁場分布,在模型的計算中增加了空氣層。消融方式采用心外膜消融,即由右側胸壁切口進入,置入套管后將消融設備導于心外膜處[18]。心肌厚度選為肺靜脈開口處的心肌厚度 8 mm[19],血液層厚度為 20 mm[20],模型如圖 1 所示。微波天線使用了 Bernardi 等[21]提出的天線模型,天線導體的材料為銅,內外層導體之間由特氟倫構成,結構如圖 2 所示。
 圖2
微波天線幾何結構
Figure2.
Geometry of microwave antenna
圖2
微波天線幾何結構
Figure2.
Geometry of microwave antenna
1.2 數學模型
本研究對電磁場及熱場兩個物理場耦合計算,得到心肌組織的溫度分布。
研究中采用電磁能加熱生物組織,電磁場采用平面橫波,其方程如式(1)所示[22]:
 |
式中 E 為電場矢量,單位為 V/m; 是相對磁導率(
是相對磁導率( = 1);
= 1); 是心肌相對介電常數;
是心肌相對介電常數; 是電導率,單位為 S/m;
是電導率,單位為 S/m; 是真空介電常數,為 8.8542 × 10?12 F/m;
是真空介電常數,為 8.8542 × 10?12 F/m; 為角頻率,單位為 rad/s;
為角頻率,單位為 rad/s; 是自由空間波數,單位為 rad/m。
是自由空間波數,單位為 rad/m。
根據組織中的電磁場分布計算得到的吸收的電磁能( )如式(2)所示[23]:
)如式(2)所示[23]:
 |
大多數研究均采用基于 Pennes 的生物熱模型[24],如式(3)所示:
 |
式中 T、ρ、c、k 分別為溫度、生物組織密度、比熱、熱導率,單位分別為 K、kg/m3、J/(kg·K)、W/(m·K); 、
、 、
、 、
、 分別為血液密度、血液灌注率、血液比熱及血液溫度。血液灌注帶走的熱量,對于微波消融來說,心肌層內部血液灌注帶走的熱量遠小于微波消融產生的熱量及心腔內血液循環帶走的熱量,因此可忽略不計[25]。
分別為血液密度、血液灌注率、血液比熱及血液溫度。血液灌注帶走的熱量,對于微波消融來說,心肌層內部血液灌注帶走的熱量遠小于微波消融產生的熱量及心腔內血液循環帶走的熱量,因此可忽略不計[25]。 為組織新陳代謝產生的熱量,與其他熱量相比,此項可忽略不計[26]。
為組織新陳代謝產生的熱量,與其他熱量相比,此項可忽略不計[26]。 為外部熱源項,即式(2)。
為外部熱源項,即式(2)。
經典傅里葉傳導定律假設熱的傳導速度是無限的。但在實際情況中,任何熱力學過程平衡態的建立都需要一定的弛豫時間,因此得到了雙曲線生物傳熱方程[27],如式(4)所示:
 |
式中  為弛豫時間(s)。
為弛豫時間(s)。
如果雙曲線模型中的 τ = 0,則上述雙曲線模型變為 Pennes 模型即式(3)。
1.3 仿真參數設置
根據文獻中生物組織的實驗研究,參考弛豫時間的不同值,分別設置為 0、1、5、8、10、15、20 s[21,28-30]。研究中的電磁場模塊設置為穩態和頻域,輸出微波頻率穩定為 2.45 GHz,微波天線為同軸微波天線,電介質設置為端口,采用的消融功率為 30 W,總消融時間采用 120 s,時間步長設置 1 s。心肌組織、血液初始溫度為 37℃,微波天線初始溫度為 25℃。微波引起組織損傷的機制是微波能量轉化為熱能,因此在心肌組織上施加的熱源是電磁功率損耗密度。以此獲得不同消融時間下的溫度分布與損傷區域,同時探討不同弛豫時間條件下,心肌組織溫度分布及損傷區域的變化規律。
研究中循環血液流動產生的熱效應考慮成邊界條件[31],如式(5)所示:
 |
其中  為組織-血液邊界的對流換熱系數,設置為 1 417 W/(m2·K),是血液流速為 24 cm/s 時的血液-組織對流換熱系數參考值[32],
為組織-血液邊界的對流換熱系數,設置為 1 417 W/(m2·K),是血液流速為 24 cm/s 時的血液-組織對流換熱系數參考值[32], = 37℃ 為血液溫度。仿真中模型的熱物性參數[21]如表 1 所示。
= 37℃ 為血液溫度。仿真中模型的熱物性參數[21]如表 1 所示。
2 結果
為了探究不同弛豫時間對微波消融房顫的影響,分別從溫度分布及熱損傷區域對比進行了分析。
2.1 溫度場分布
有研究表明心肌細胞興奮性在高于 50℃ 時便會喪失,心肌組織出現不可逆性損傷[9],因此本研究認為高于 50℃ 的區域為損傷區域。不同的弛豫時間導致心肌組織的最高溫度發生變化,圖 3 為心肌組織中最高溫度點變化曲線。從圖中可以看到  = 0 s 與
= 0 s 與  = 1 s 時溫度分布基本一致。然而,隨著弛豫時間的增加,兩種模型結果差異較大,且最高溫度降低。消融時間為 10 s 時,最高溫度差異最大,此時
= 1 s 時溫度分布基本一致。然而,隨著弛豫時間的增加,兩種模型結果差異較大,且最高溫度降低。消融時間為 10 s 時,最高溫度差異最大,此時  = 0、1、5、8、10、15、20 s 時的最高溫度分別為 76.9、74.7、67.6、63.4、61.4、57.7、55.1℃,最大溫差為 21.8℃。隨著消融時間增加,不同弛豫時間下的最高溫度又逐漸趨于一致,當消融時間為 55 s 時,最高溫度分別為 117.0、116.6、116.7、116.8、116.8、117.1、116.7℃。
= 0、1、5、8、10、15、20 s 時的最高溫度分別為 76.9、74.7、67.6、63.4、61.4、57.7、55.1℃,最大溫差為 21.8℃。隨著消融時間增加,不同弛豫時間下的最高溫度又逐漸趨于一致,當消融時間為 55 s 時,最高溫度分別為 117.0、116.6、116.7、116.8、116.8、117.1、116.7℃。
 圖3
不同弛豫時間下心肌組織中最高溫度點溫升曲線
Figure3.
Temperature rise curve of the highest temperature point in myocardial tissue under different relaxation time
圖3
不同弛豫時間下心肌組織中最高溫度點溫升曲線
Figure3.
Temperature rise curve of the highest temperature point in myocardial tissue under different relaxation time
圖 4 為心肌組織不同深度處的溫度分布。取微波天線正下方 1、3、5、7 mm 處,分別為 A~D 點,消融 10 s 時 = 20 s 與
= 20 s 與 = 0 s 在 A、B、C、D 點處溫度分別減小 19.5、4.8、1.0、0.3℃。結果表明不同位置處的溫度分布均受到弛豫時間的影響,在消融開始時,在靠近微波天線的點,弛豫時間對溫度的影響更大。在 A、B、C、D 處,
= 0 s 在 A、B、C、D 點處溫度分別減小 19.5、4.8、1.0、0.3℃。結果表明不同位置處的溫度分布均受到弛豫時間的影響,在消融開始時,在靠近微波天線的點,弛豫時間對溫度的影響更大。在 A、B、C、D 處, = 20 s 與
= 20 s 與 = 0 s 處的溫度相比,溫差最大值分別出現在 10、30、40、50 s 處,分別為 19.5、7.2、3.0、1.0℃。隨著消融時間的增加,不同弛豫時間的溫差逐漸減小,A、B、C、D 點分別在 60、90、110、120 s 后溫度基本一致。因此對于靠近微波天線的點,雙曲線模型計算得到的溫度達到與 Pennes 模型相同溫度所需的消融時間較短。
= 0 s 處的溫度相比,溫差最大值分別出現在 10、30、40、50 s 處,分別為 19.5、7.2、3.0、1.0℃。隨著消融時間的增加,不同弛豫時間的溫差逐漸減小,A、B、C、D 點分別在 60、90、110、120 s 后溫度基本一致。因此對于靠近微波天線的點,雙曲線模型計算得到的溫度達到與 Pennes 模型相同溫度所需的消融時間較短。
 圖4
A~D 位置分布及不同弛豫時間下心肌組織溫升曲線
Figure4.
A–D location distribution and myocardial tissue temperature rise curve under different relaxation time
圖4
A~D 位置分布及不同弛豫時間下心肌組織溫升曲線
Figure4.
A–D location distribution and myocardial tissue temperature rise curve under different relaxation time
2.2 損傷區域對比
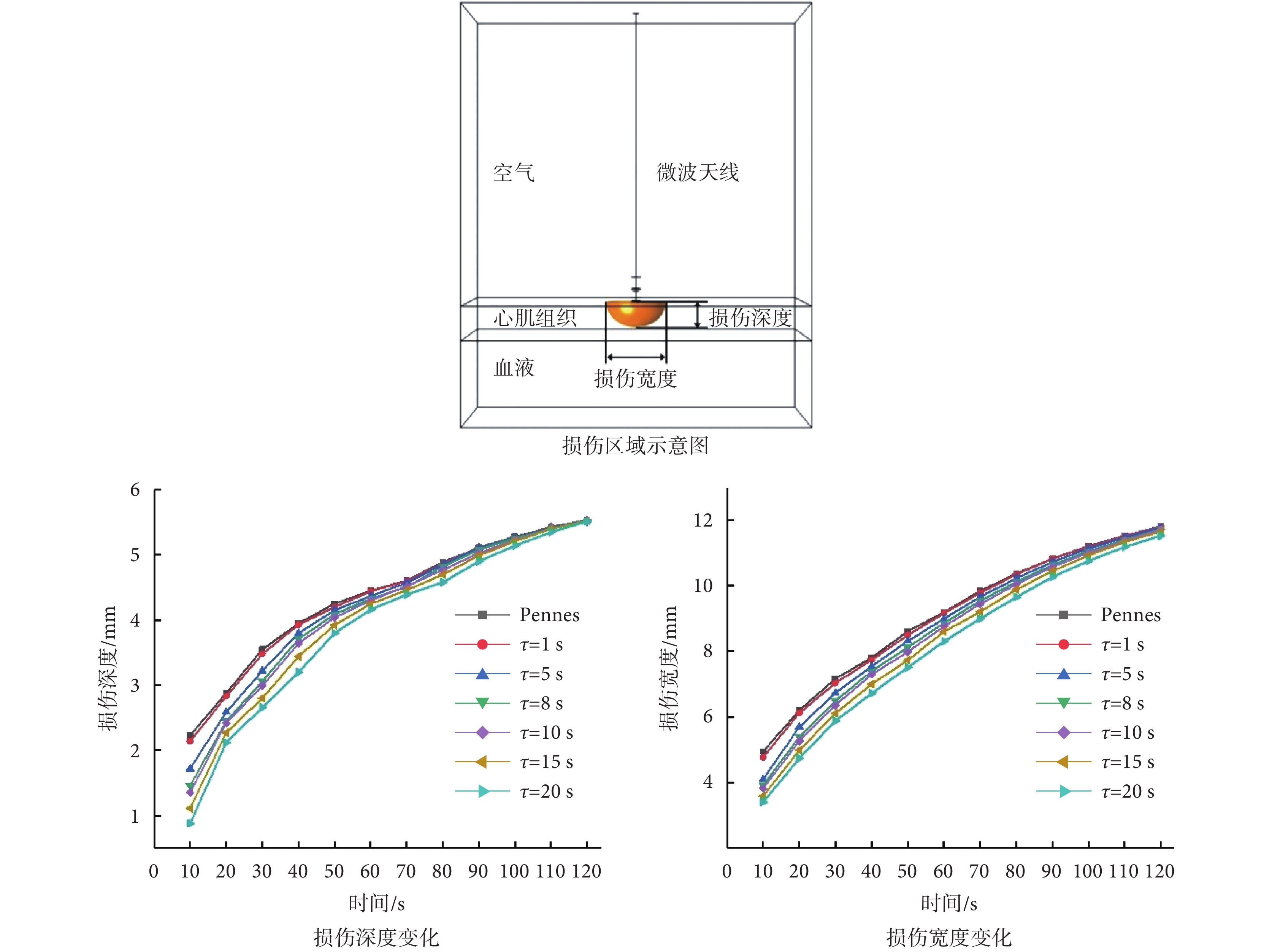
通過測量損傷深度及損傷寬度確定心肌的損傷區域,得到不同弛豫時間的損傷寬度、損傷深度變化規律,如圖 5 所示。與心肌組織溫度分布規律一致,消融開始時,損傷寬度與損傷深度隨弛豫時間的增加而增大。與高弛豫時間相比,低弛豫時間時熱擴散到組織中的速度更快,因此損傷區域更大。隨著消融時間的增加,弛豫時間的影響逐漸減小。 = 1、5、8、10、15、20 s 時與采用 Pennes 模型計算得到的組織損傷深度達到一致加熱時間分別為 40、70、80、100、110、120 s。在 120 s 時損傷深度已達到一致,為 5.5 mm;
= 1、5、8、10、15、20 s 時與采用 Pennes 模型計算得到的組織損傷深度達到一致加熱時間分別為 40、70、80、100、110、120 s。在 120 s 時損傷深度已達到一致,為 5.5 mm; = 0、1、5、8、10、15、20 s 時的損傷寬度分別為 11.8、11.8、11.7、11.7、11.7、11.6、11.5 mm,損傷寬度也基本一致。因弛豫時間減小了熱擴散的速度,
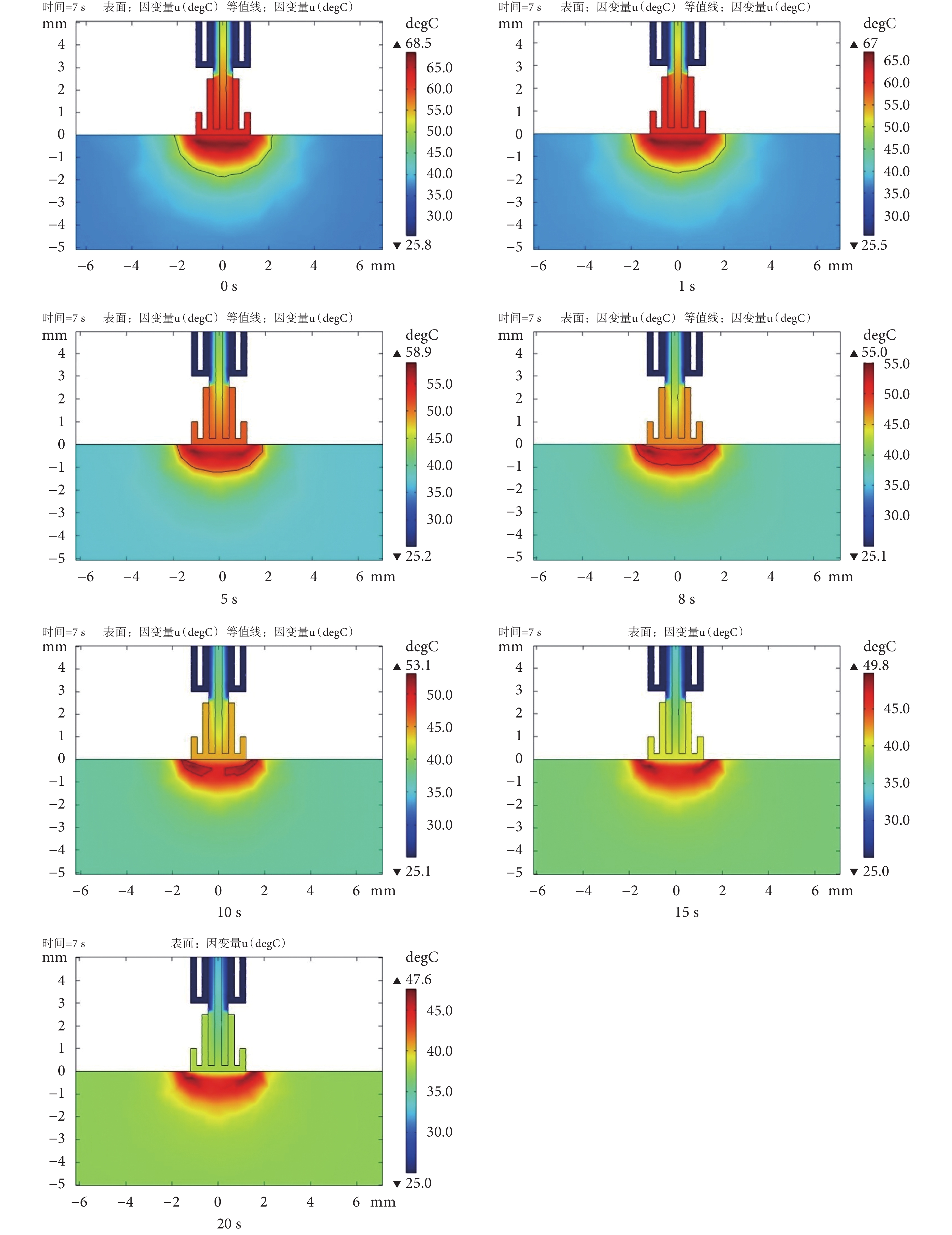
= 0、1、5、8、10、15、20 s 時的損傷寬度分別為 11.8、11.8、11.7、11.7、11.7、11.6、11.5 mm,損傷寬度也基本一致。因弛豫時間減小了熱擴散的速度, = 0、1、5、8、10、15、20 s 時分別在 3、4、6、7、8、9、10 s 時才出現損傷區域。例如在消融時間 7 s 時,不同弛豫時間下的溫度分布如圖 6 所示,
= 0、1、5、8、10、15、20 s 時分別在 3、4、6、7、8、9、10 s 時才出現損傷區域。例如在消融時間 7 s 時,不同弛豫時間下的溫度分布如圖 6 所示, = 0、1、5、8 s 時已經形成損傷區域,但
= 0、1、5、8 s 時已經形成損傷區域,但 = 10、15、20 s 時還未形成完整的損傷區域。
= 10、15、20 s 時還未形成完整的損傷區域。
 圖5
不同弛豫時間下損傷區域變化
Figure5.
Change of the lesion dimensions under different relaxation time
圖5
不同弛豫時間下損傷區域變化
Figure5.
Change of the lesion dimensions under different relaxation time
 圖6
不同弛豫時間下心肌組織溫度分布圖
Figure6.
Temperature distribution of myocardial tissue at different relaxation times
圖6
不同弛豫時間下心肌組織溫度分布圖
Figure6.
Temperature distribution of myocardial tissue at different relaxation times
表 2 為不同弛豫時間下達到相同心肌損傷深度所需的加熱時間,可以看出達到相同組織損傷深度時, = 0 s 與
= 0 s 與 = 1 s 時所需時間基本相同,但隨著弛豫時間的增加,消融時間也需要增加。反之在相同消融時間下,弛豫時間會影響心肌損傷深度,最終影響消融效果。因此在臨床上若要達到與 Pennes 模型相同的消融效果,應增大消融時間。
= 1 s 時所需時間基本相同,但隨著弛豫時間的增加,消融時間也需要增加。反之在相同消融時間下,弛豫時間會影響心肌損傷深度,最終影響消融效果。因此在臨床上若要達到與 Pennes 模型相同的消融效果,應增大消融時間。
3 討論與結論
經典傅里葉熱傳導理論描述的是瞬時能量沉積的過程,假設熱信號的傳播速度是無限的。而在生物傳熱中,生物組織具有不均勻的結構,需要一段弛豫時間才能將足夠的能量轉移到附近的組織[33],因此生物熱傳播速度的有限性不可忽視。弛豫時間在短消融時間內會影響心肌損傷區域的大小,而臨床使用導管消融旨在用盡可能短的時間獲得透壁性消融損傷[34]。袁彪等[18]對 46 例持續性房顫患者進行了心外膜消融術,術后成功率為 63%,消融效果以及消融線阻斷是否完整是消融成功與否的關鍵。臨床治療及研究中,通常使用消融功率 20~65 W[35-36],消融時間 30~120 s[37-38]。而在此消融時間內,弛豫時間對心肌損傷區域的影響較為明顯。如表 2 中所示,若對 2 mm 的心肌組織進行消融, = 0 s 與
= 0 s 與 = 20 s 時所需的消融時間相差 11 s。如用 Pennes 模型進行心肌損傷評估,可能導致心肌消融不透壁,最終造成房顫復發,因此雙曲線模型對心肌消融效果的影響不可忽視。
= 20 s 時所需的消融時間相差 11 s。如用 Pennes 模型進行心肌損傷評估,可能導致心肌消融不透壁,最終造成房顫復發,因此雙曲線模型對心肌消融效果的影響不可忽視。
在消融短時間內,弛豫時間增大,最高溫度減小,這是由于非傅里葉傳熱的滯后性導致的。傅里葉傳熱不考慮傳熱滯后性,因此 Pennes 模型得到的溫度是最高的。非傅里葉傳熱使熱擴散速度減慢,熱流矢量與溫度梯度之間的延遲越大,熱擴散速度就會越慢。當消融時間增大時,非傅里葉傳熱的延遲性逐漸消失,與傅里葉傳熱速度趨于一致,因此非傅里葉傳熱只在短消融時間內有效。同時由于距離微波天線近的位置微波能量較大,不同弛豫時間對心肌組織溫度的影響也較大。因此與 Pennes 模型相比,雙曲線模型可以更精確地把控心肌組織的溫度分布。
損傷區域會隨著弛豫時間的增加而減小,Pennes 模型的損傷區域最大。當弛豫時間逐漸增大,熱擴散速度的滯后性增強,使得熱量積聚在心肌組織內部,所以損傷區域首先出現在心肌組織內部。表 2 中列出了達到不同心肌損傷深度時需要的消融時間,弛豫時間越大,需要的消融時間就越長。因臨床上對房顫微波消融所需的消融時間較短,所以應充分考慮雙曲線模型對消融效果的影響。Pennes 模型高估了心肌的損傷深度,造成損傷區域不透壁,影響了消融效果,最終會使得房顫復發。
雙曲線傳熱模型對溫度場的影響會隨消融時間的增加而減小,且隨著弛豫時間增加,心肌最高溫度降低;當消融時間達到 55 s 時,不同弛豫時間下的最高溫度基本達到一致。當弛豫時間  = 1、5、8、10、15、20 s 時,消融時間達到 3、4、6、7、8、9、10 s 時才出現損傷區域。弛豫時間會阻礙熱擴散的速度,弛豫時間越大,熱擴散的速度越慢。因此要考慮雙曲線傳熱模型對心肌損傷深度的影響,采用傅里葉傳熱則會影響最終治療效果。
= 1、5、8、10、15、20 s 時,消融時間達到 3、4、6、7、8、9、10 s 時才出現損傷區域。弛豫時間會阻礙熱擴散的速度,弛豫時間越大,熱擴散的速度越慢。因此要考慮雙曲線傳熱模型對心肌損傷深度的影響,采用傅里葉傳熱則會影響最終治療效果。
本文只探究了心外膜微波消融的非傅里葉傳熱效應,并未考慮心內膜微波消融時非傅里葉傳熱的影響。本文弛豫時間的選取在生物組織弛豫時間的選取范圍內,但目前鮮有研究心肌組織的弛豫時間,未來還將對心肌組織的弛豫時間進行探討,并增加離體實驗驗證。非傅里葉傳熱中除雙曲線模型,還包括雙向延遲模型[39]等,未來會考慮不同非傅里葉模型對房顫微波消融的影響。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。