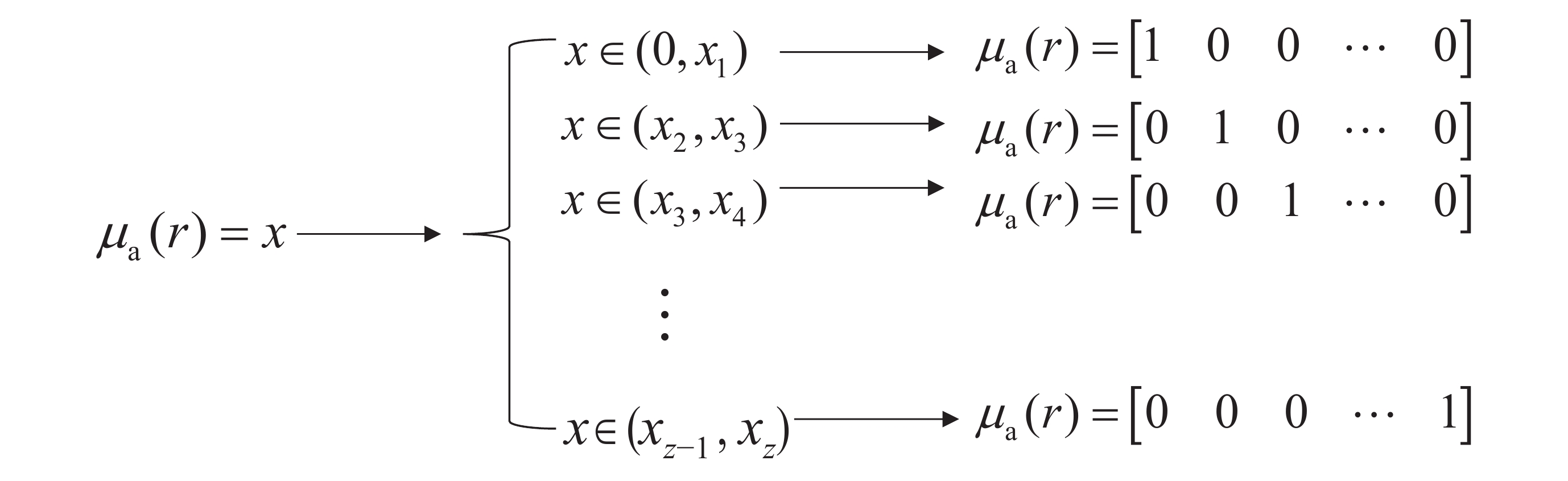擴散光學層析成像（DOT）逆問題病態性嚴重。傳統方法成像精度不高，計算耗時，制約了 DOT 技術的臨床應用。因此，本文提出一種基于棧式自編碼器（SAE）的 DOT 逆問題求解方法。首先采用傳統 SAE 方法代替迭代方法進行逆問題計算，其次改進了 SAE 神經網絡的輸出結構，使用單輸出 SAE 降低單個網絡負擔，最后將改進 SAE 方法與傳統列文伯格-馬夸爾特（LM）迭代方法、傳統 SAE 方法進行仿真比較。結果表明，本文所提方法逆問題求解平均用時只有 LM 迭代方法的 1.67%，實驗模型下均方誤差（MSE）值較迭代方法降低了 46.21%，較傳統 SAE 方法降低了 61.53%，圖像相關系數（ICC）值較傳統方法提升了 4.03%，較傳統 SAE 方法提升了 18.7%，并且在 3% 噪聲條件下具有良好的抗噪性。通過本文的研究結果證明，改進后的 SAE 方法相較于傳統 SAE 方法具有更高的圖像質量及抗噪性，同時相較傳統迭代方法具有較快的計算速度，有利于神經網絡在 DOT 逆問題計算中的應用。
引用本文： 田文旭, 楊丹, 魏竹林, 王驕. 基于改進棧式自編碼器的擴散光學層析成像逆問題求解方法研究. 生物醫學工程學雜志, 2021, 38(4): 774-782. doi: 10.7507/1001-5515.202010041 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
擴散光學層析成像（diffuse optical tomography, DOT）作為一種新興的斷層成像技術，其原理是利用近紅外光在組織體內傳播時與組織的吸收散射效應進行成像，并結合算法獲取被測對象光學參數（吸收系數和散射系數）。正常和病變組織的光學參數具有明顯差異，且 DOT 具有無損、實時、造價低等優點，因此 DOT 技術在動作識別、乳腺腫瘤、腦出血等疾病診斷方面具有潛在的應用價值[1-3]。DOT 技術的研究可分為正問題和逆問題[4]，正問題是指已知光源和被測組織的光學參數分布，根據光在組織中的傳播模型，估計發射光的邊界輻射強度；逆問題則是已知組織體表面光源分布，通過獲取測量邊界的輻射強度，重構被測目標成像區域內光學參數的分布。然而，逆問題具有嚴重的病態性，測量值任意微小的擾動下都會產生很大的波動，快速有效的逆問題求解方法是本領域的研究熱點[5]。
傳統的 DOT 逆問題求解多以迭代算法為主，其中有代表性的是代數重建算法（algebraic reconstruction technique, ART），它是一種基于矩陣的快速穩定逆問題求解算法，包含稀疏矩陣大規模線性方程組求解，1995 年被 Arridge[6]引入 DOT 逆問題中，取得較好效果，可在投影數據不完備且投影角度不均勻的情況下也能獲得髙質量圖像，但該方法計算量大，占用空間內存多，導致逆問題計算速度慢。佟珊珊[7]和唐錦萍[8]提出了混合總變差與 L1、Lp范數正則化的迭代策略，在保持邊界銳利性及穩定性的同時，提高了計算精度，但傳統迭代方法計算速度緩慢及強擾動計算誤差大的問題并沒有得到較好的解決。Vidal-Rosas 等[9-10]提出了在逆問題中使用降階模型用于加速逆問題的迭代速度，通過求解光學參數與輻射強度的非線性關系簡化逆問題計算過程，但降階模型仍然存在可解釋范圍差的問題。近年來，神經網絡的方法被應用到 DOT 逆問題求解中，Feng 等[11]提出了基于反向傳播神經網絡（back propagation neural networks, BPNN）的 DOT 逆問題計算方案，通過直接建立邊界光學信息與成像區域內部的神經網絡求解成像區域光學參數分布，避免了逆問題求解的不適定和速度慢的問題，但 BPNN 擾動吸收系數特異性要求高，泛化能力不足的問題無法得到解決。Yoo 等[12]和 Yedder 等[13]提出了基于卷積神經網絡（convolutional neural networks, CNN）的逆問題求解方案，提高了神經網絡的泛化能力，但 CNN 仍然存在網絡參數過多，計算量大，對計算機要求高等問題。
綜上，為了解決現有的 DOT 逆問題求解泛化能力差、計算精度低等問題，本文提出了一種基于改進棧式自編碼器（stacked autoencoder, SAE）的逆問題求解方法。通過 SAE 對輸入數據進行降維及特征提取，并使用單輸出 SAE 降低傳統 SAE 網絡的任務量，最終期望本文所提的改進 SAE 方法的逆問題求解方法相較于傳統神經網絡能夠具有更高的圖像精度及更好的泛化能力，有利于神經網絡在 DOT 領域中的實際應用。
1 DOT 求解
DOT 求解正問題是根據光在組織中的傳播模型，給定成像區域內不同位置 r 處的光學參數 μ(r)，得到邊界光輻射強度 M，其中 μ（r）與 M 的關系如式（1）～式（2）所示：
 |
 |
其中，μa(r)、μs(r) 分別表示位于成像區域 r 處的吸收系數和散射系數，S、D 表示光源和探測器的數量，
表示光學參數μ(r) 映射到邊界輻射強度M的正向算子，使用輻射傳輸方程（radiative transfer equation, RTE）近似求解，具體形式如式（3）所示：
 |
在體元 X 內，u(r,ω) 表示在 r 處 ω 方向上的單位立體角 dσ(ω) 發射的光子密度，q(r) 表示 r 處入射的光子密度。r 處的擴散系數 κ(r) 如式（4）所示：
 |
其中，g 為已知的各向異性系數。在成像區域邊界 ξ 處光子傳輸如式（5）～式（7）所示：
 |
 |
 |
其中，A 表示邊界處內部與外部折射率之差，n表示邊界處的法向向量，θ（ξ）表示邊界 ξ 處所有方向光子密度的積分。DOT 求解逆問題為，給定邊界光輻射強度M，計算成像區域內的光學參數μ（r）分布。選擇吉洪諾夫（Tikhonov）正則化，正則化矩陣取單位矩陣I時，稱為列文伯格-馬夸爾特（levenberg-marquardt, LM）方法，此時 DOT 逆問題求解如式（8）所示：
 |
其中，
表示成像區域內光學參數分布，P′（μ（k））在此簡寫為J。每次迭代計算 P（μ（k+1））與M的差值，當滿足極小值要求時，迭代結束。
2 提出的方法
2.1 SAE 的 DOT 逆問題求解
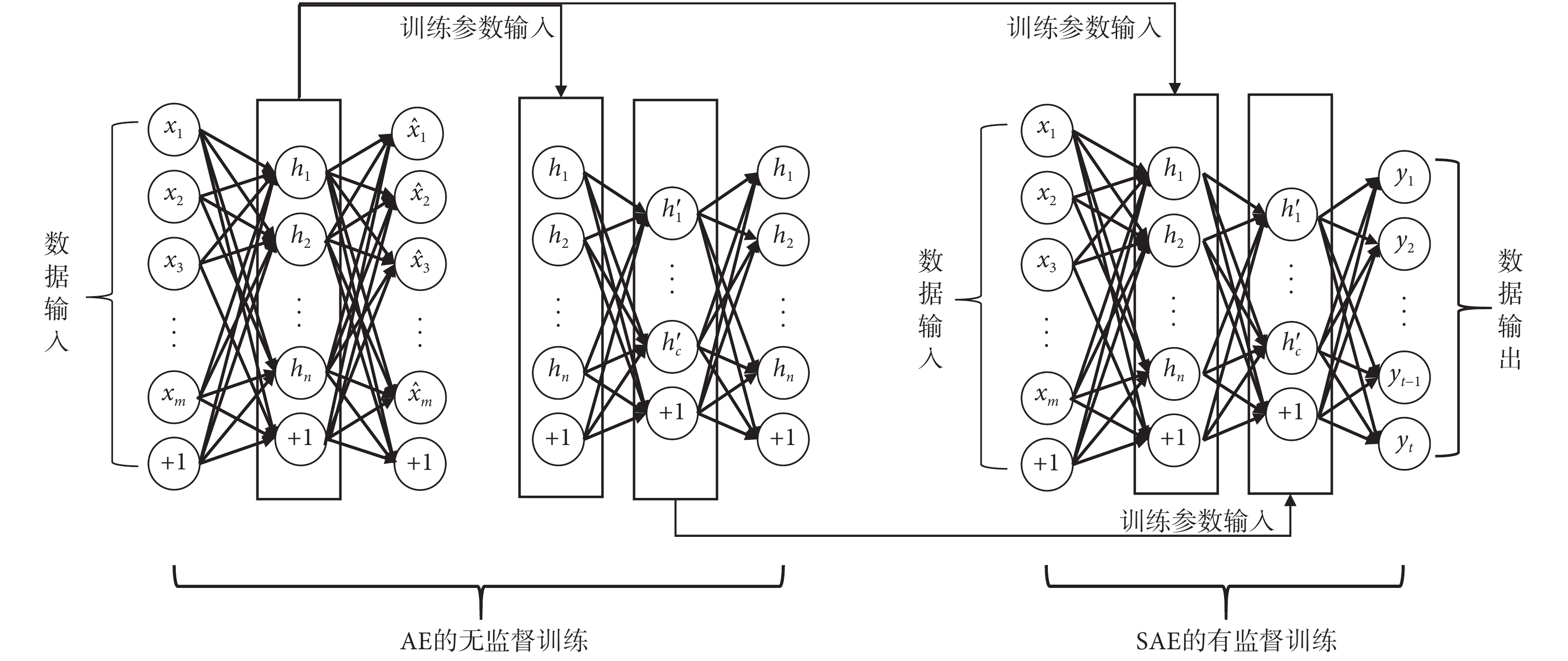
SAE 由多個自編碼器（auto-encoder, AE）堆棧產生，其主要應用在特征提取、數據降維去噪及圖像識別等問題中[14-16]，訓練過程如圖 1 所示。
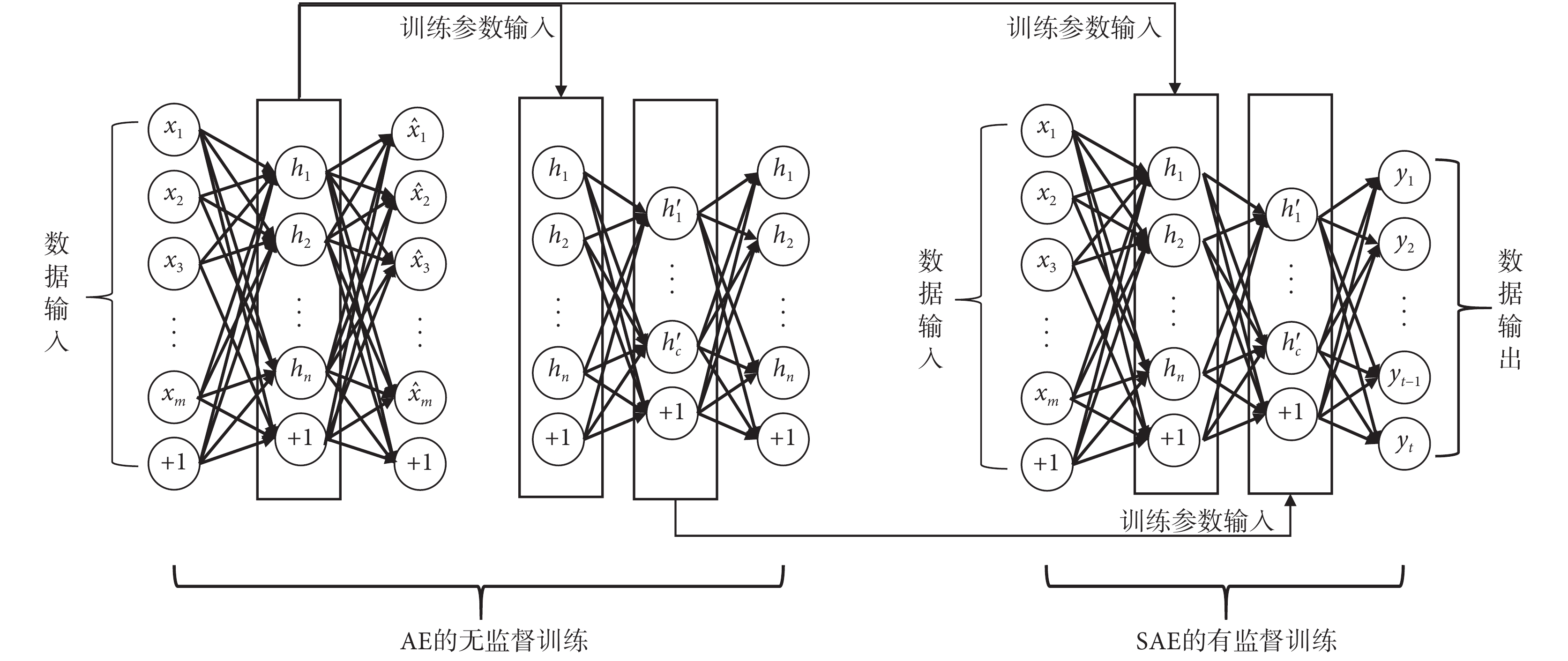圖1
SAE 神經網絡基本結構
Figure1.
Basic structure of SAE neural network
圖 1 中由 AE 網絡構成傳統 SAE 神經網絡并完成神經網絡訓練流程如下：
步驟 1：計算 AE 網絡輸入層到隱藏層的輸出。從輸入層到隱藏層的過程稱為編碼過程，輸入層到隱藏層之間的關系如式（9）～式（11）所示：
 |
 |
 |
其中，上式及圖 1 中
為輸入層一個樣本的 m 維向量，
為隱藏層的 n 維向量，W為從輸入層到隱藏層的權值矩陣，
為隱藏層的偏置向量。
為隱藏層的激活函數，本文使用 tanh 函數作為激活函數，tanh 函數如式（12）所示：
 |
步驟 2：計算 AE 網絡隱藏層到輸出層的輸出。隱藏層到輸出層之間的關系如式（13）～式（15）所示：
 '/> |
 '/> |
 '/> |
其中，
為與輸入向量維度相同的向量，W'為隱藏層到輸出層的權值矩陣，b'為偏置向量。
步驟 3：優化 AE 網絡。通過反向傳播算法迭代更新權值矩陣神經網絡參數，使輸出向量
盡可能等于輸入向量x，損失函數 L（·）如式（16）所示：
 |
步驟 4：AE 網絡堆棧。將隱藏層h作為輸入，重復步驟 1～步驟 3 訓練圖 1 中新的隱藏層
，得到更低維度的信息空間。訓練完成后，舍棄當前輸出層，在隱藏層后加入一個新的輸出層，此時得到完整的傳統 SAE 神經網絡結構。
步驟 5：輸出層的有監督訓練。如圖 1 所示，在無監督訓練完成后，利用有標簽數據集采用有監督學習算法對神經網絡參數進行調優，最終輸出 t 維數據集
。
2.2 改進 SAE 的 DOT 逆問題求解
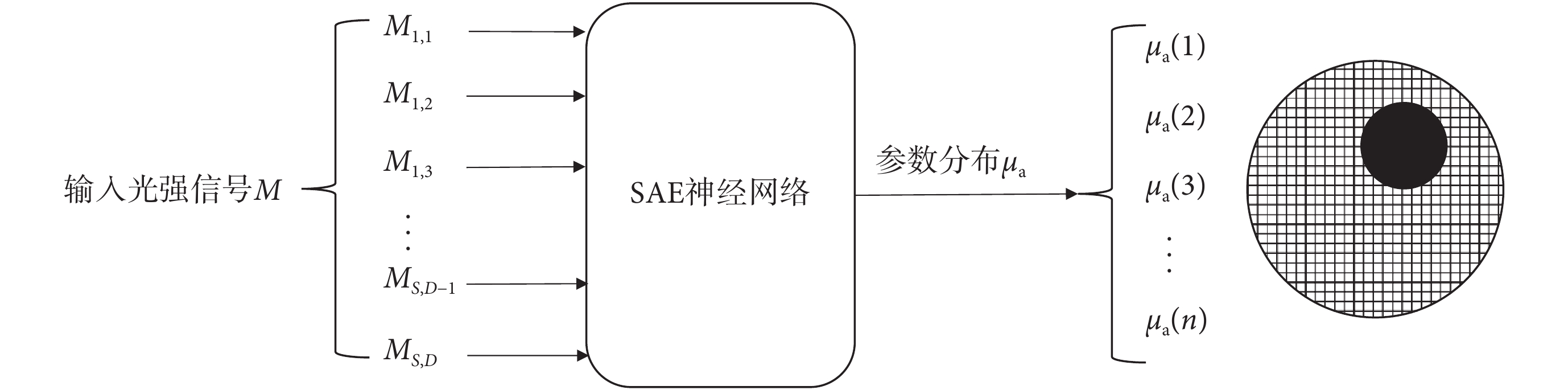
使用 SAE 方法完成 DOT 逆問題求解的過程如圖 2 所示。其中 SAE 神經網絡的數據輸入為已知的 S × D 維歸一化光輻射強度 M，輸出數據為 n 維有限元節點的 μa，傳統的 SAE 方法將 DOT 逆問題視為回歸問題，將輸出數據視為連續值，按照圖 1 的步驟完成 SAE 神經網絡訓練。
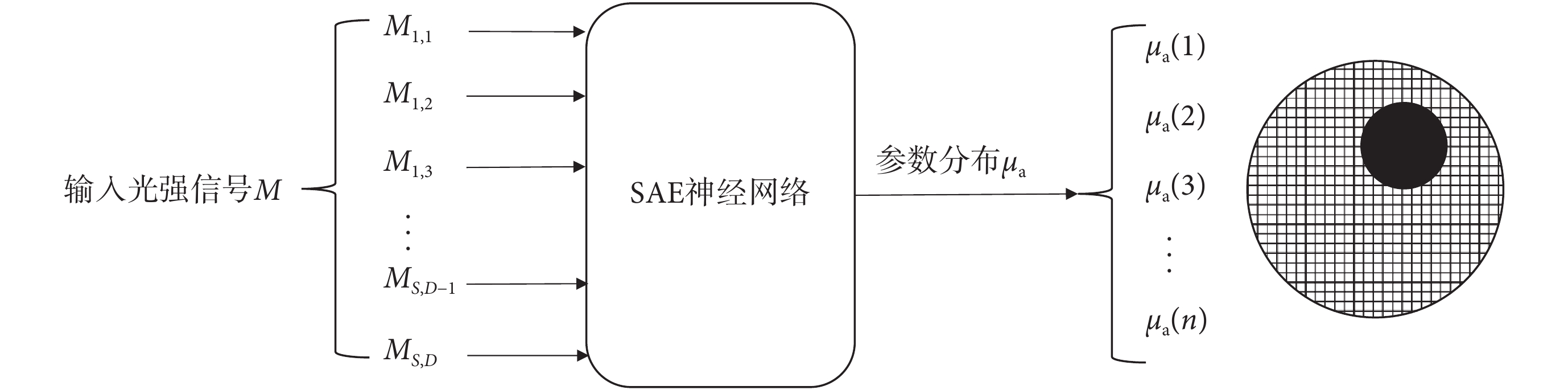圖2
基于傳統 SAE 方法的 DOT 逆問題求解
Figure2.
The calculation of DOT inverse problem based on traditional SAE method
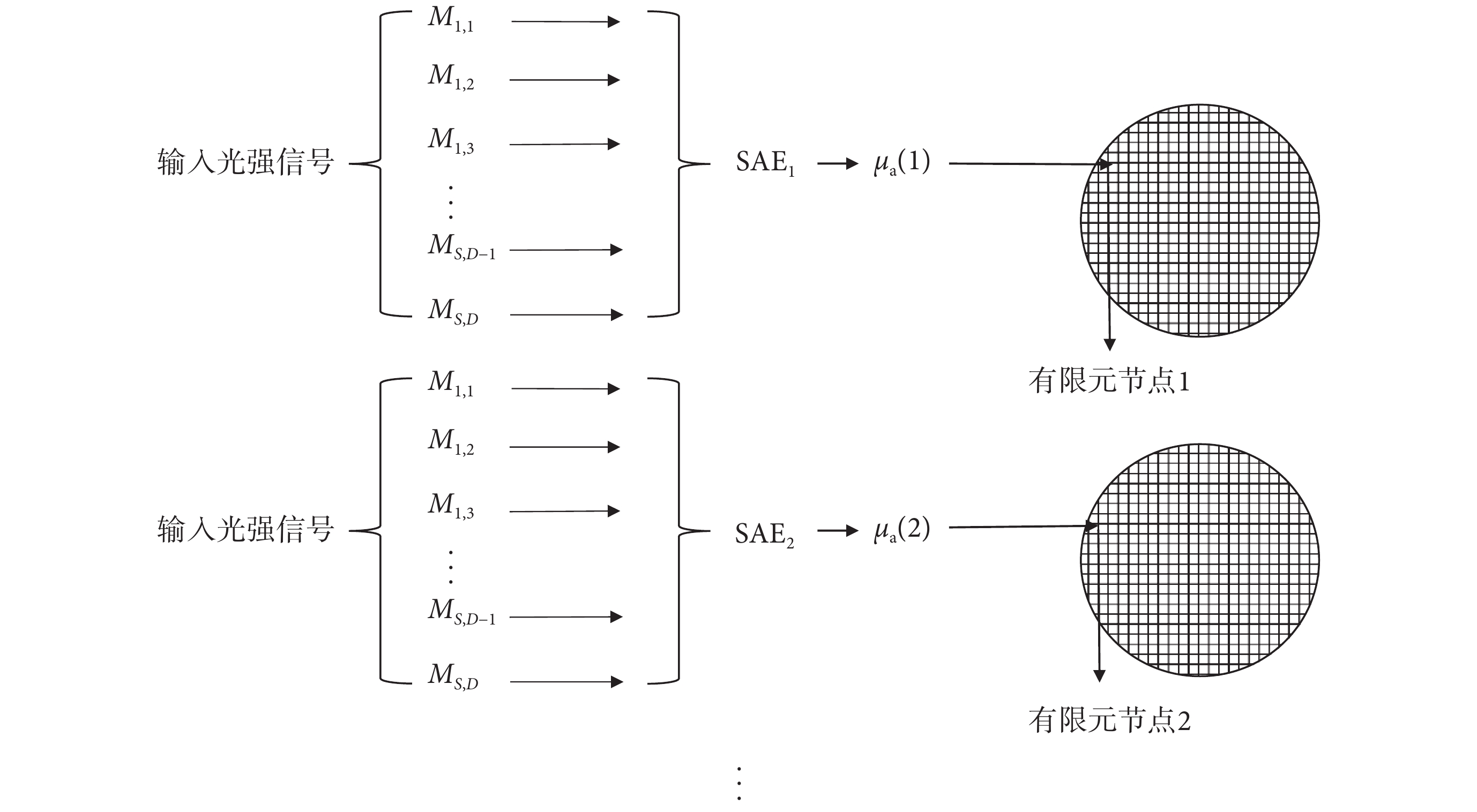
SAE 方法擬合 DOT 逆問題參數分布時，需要擬合所有節點參數分布，SAE 神經網絡負載高，導致輸出擬合結果差。因此，本文提出了一種改進 SAE 方法求解 DOT 逆問題。該方法采用多個子神經網絡計算多個有限元節點，其中每個 SAE 子網絡只計算一個節點，計算過程如圖 3 所示。
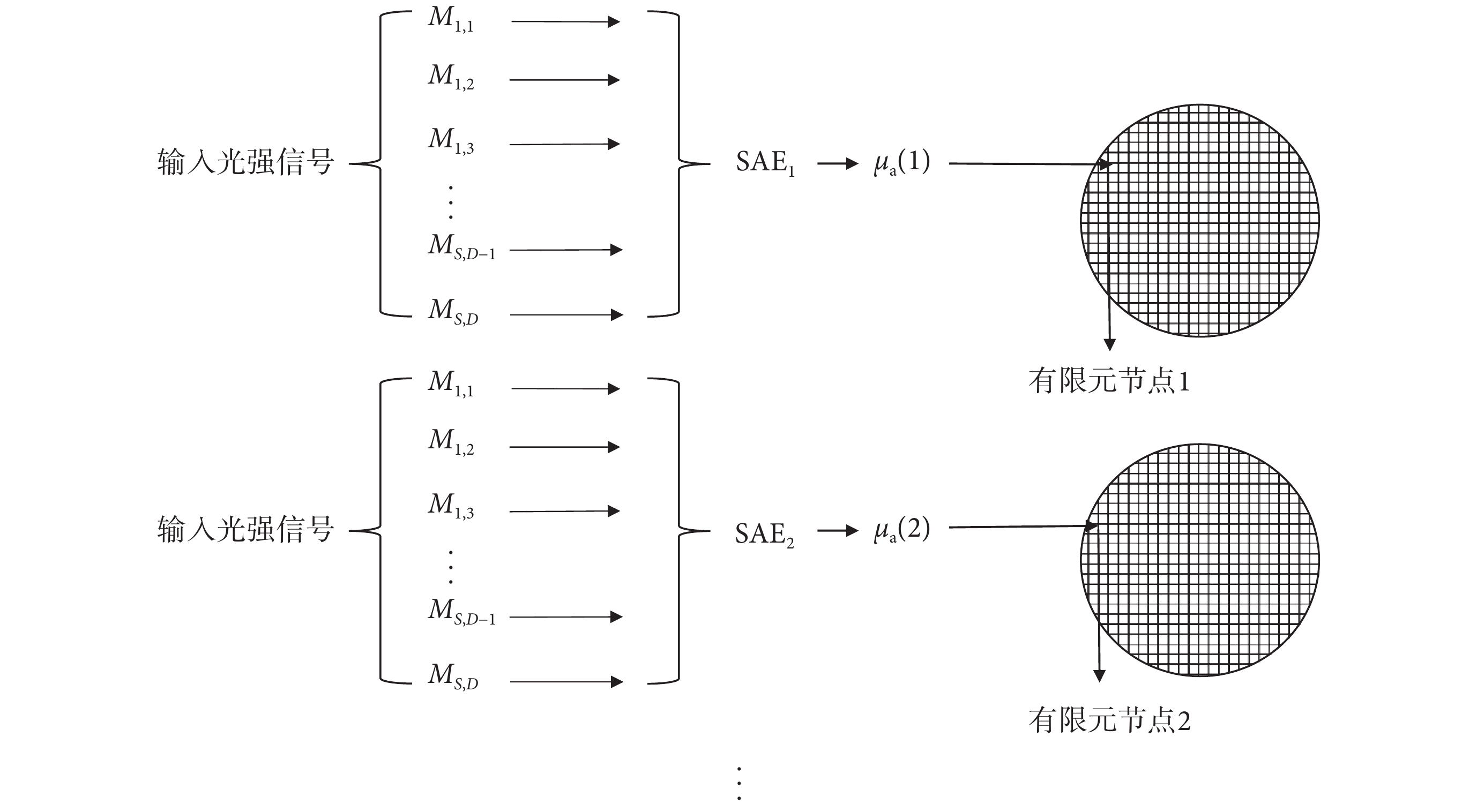圖3
基于改進 SAE 方法的逆問題計算求解
Figure3.
The calculation process of inverse problem based on improved SAE method
在圖 3 中輸入光強信號仍為 S×D 維歸一化輻射強度 M，輸出數據為 1 維的單一有限元節點，此時將輸入數據同時送入 n 個 SAE 網絡，每個網絡都是獨立的，同時每個網絡只計算某一特定有限元節點。
改進 SAE 的數據處理方式如圖 4 所示，在改進的 SAE 方法中，將得到的輸出數據分段表示為獨熱編碼，SAE 子網絡將 μa(r) 的值 x 按大小分為 z 個區間，同時判斷節點 μa（r）所處區間，從而將回歸問題改善為分類問題。改進 SAE 中輸出數據采用 softmax 函數，如式（17）所示：
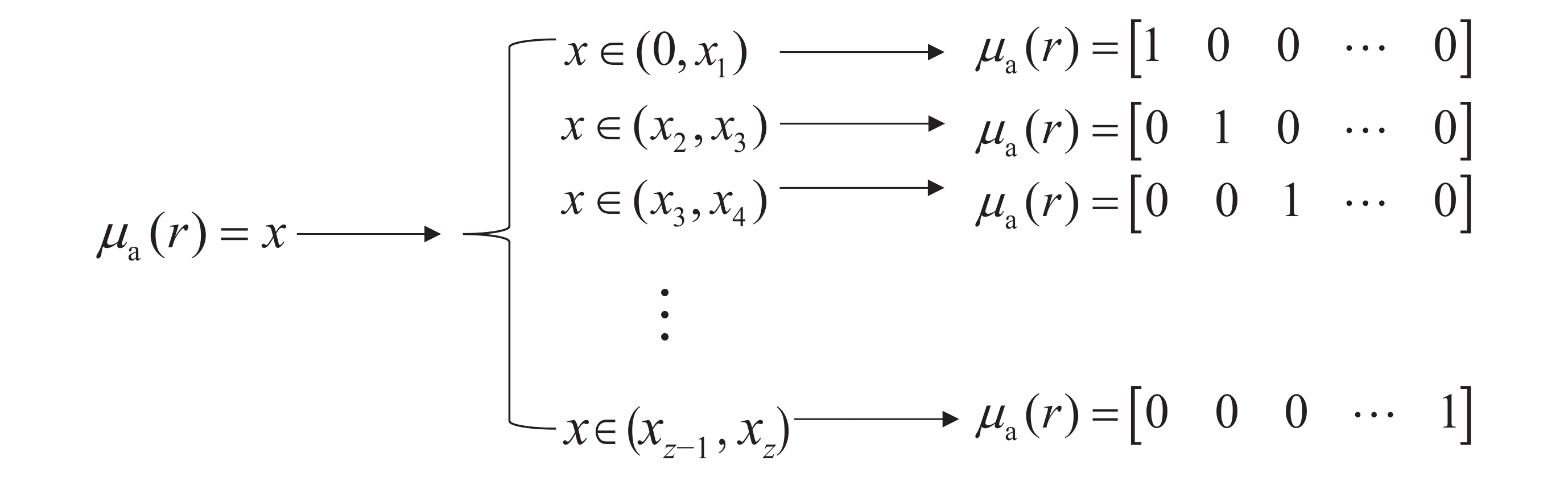圖4
μa 分布的獨熱編碼表示
Figure4.
One-hot encoding representation of μa
 |
其中，z 表示將 μa(r) 分為 z 個區間，f(xi) 表示 μa(r) 屬于第 i 區間的概率。
3 仿真實驗
3.1 參數設置
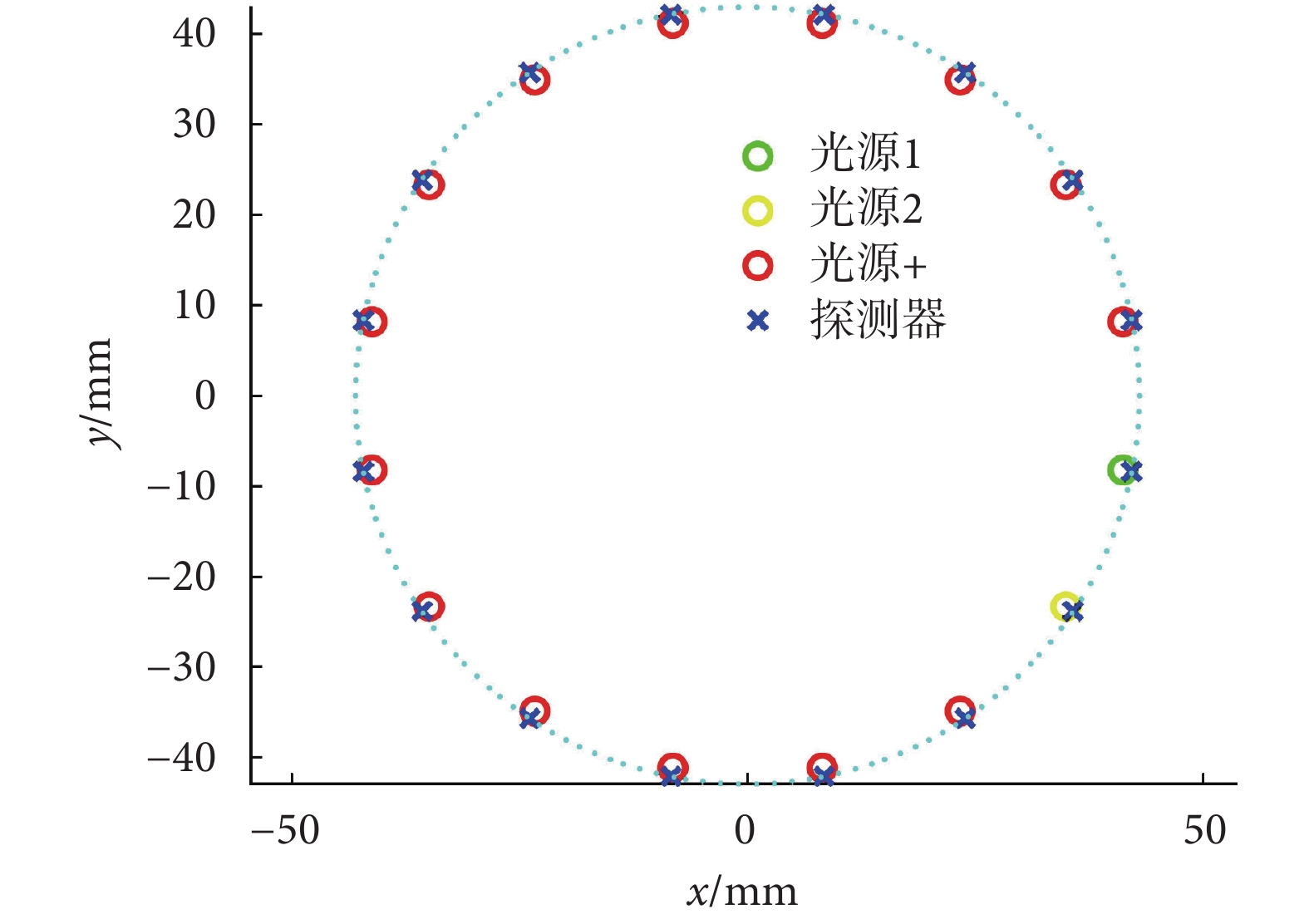
仿真成像區域如圖 5 所示，其具體設計如下：
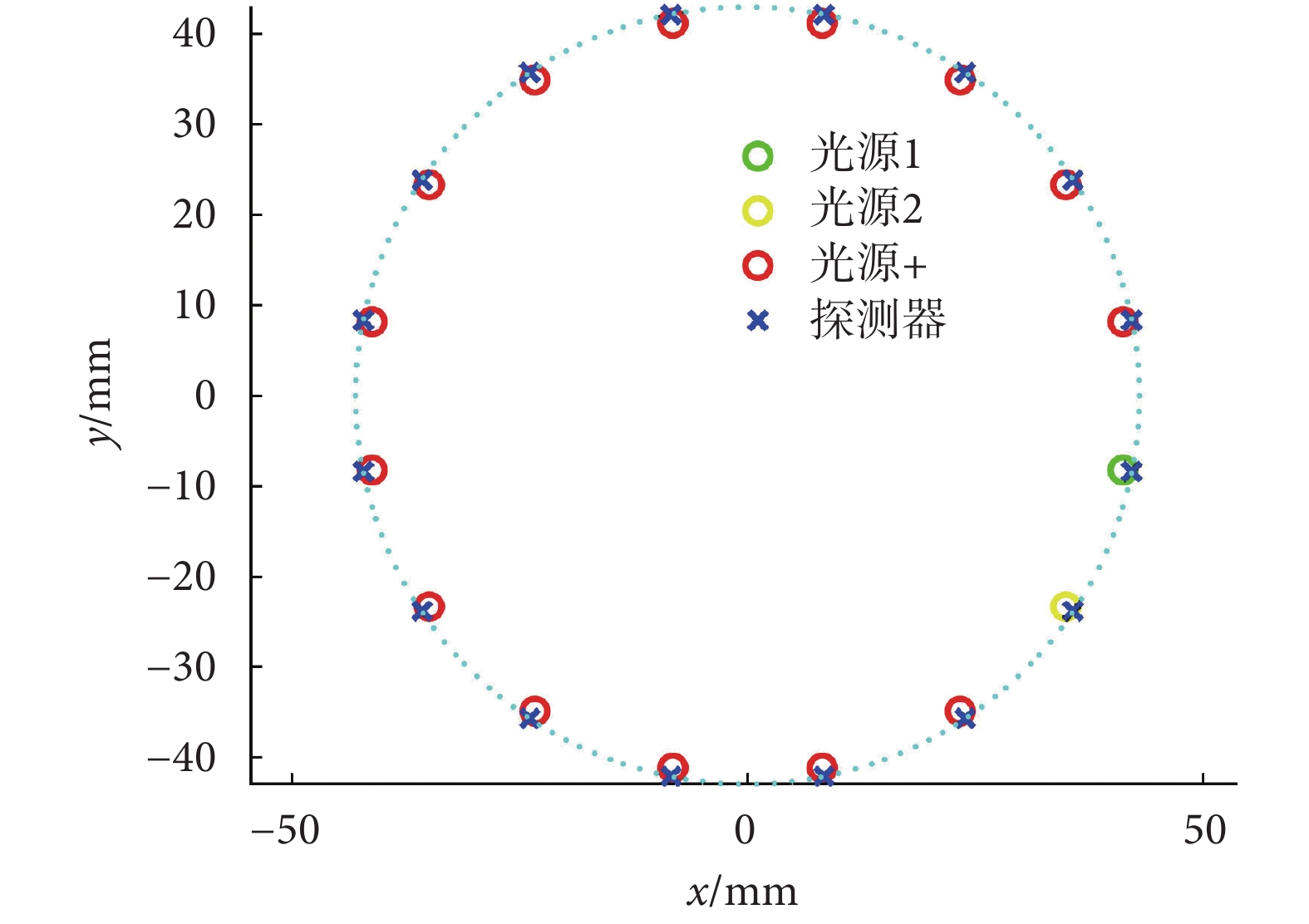圖5
成像區域光源與探測器放置位置（單光源多探測器工 作模式）
Figure5.
The placement of the light sources and detectors in the imaging area (single light source and multiple detectors working mode)
① 傳統 SAE 網絡使用四層結構，每層神經元個數設置為{240, 480, 800, 1 785}。初始學習率為 0.01，迭代 1 000 次。
② 改進 SAE 網絡使用四層結構，每層神經元個數設置為{240, 130, 80, 10}。初始學習率為 0.01，迭代 1 000 次，共 1 785 個單輸出 SAE 子神經網絡。
③ 在圖中背景 μa 和 μs 分別設置為 0.01 mm–1和 1 mm–1。成像區域半徑為 43 mm，在邊界位置處按角度均勻分配 16 個光源和 16 個探測器。
④ 光源的輻射強度為 1 W/mm2，有限元網格數量為 1 785，使用有限元分析軟件 NIRFAST 9.1（Kitware Inc., 美國）得到的 10 000 組數據作為訓練樣本[17-18]。實驗模型中的擾動半徑為 6～18 mm 隨機值，μa 為 0.01～0.1 mm–1隨機值，擾動位置隨機分布在成像區域內，擾動的數量隨機 1～2 個。
3.2 性能比較及結果分析
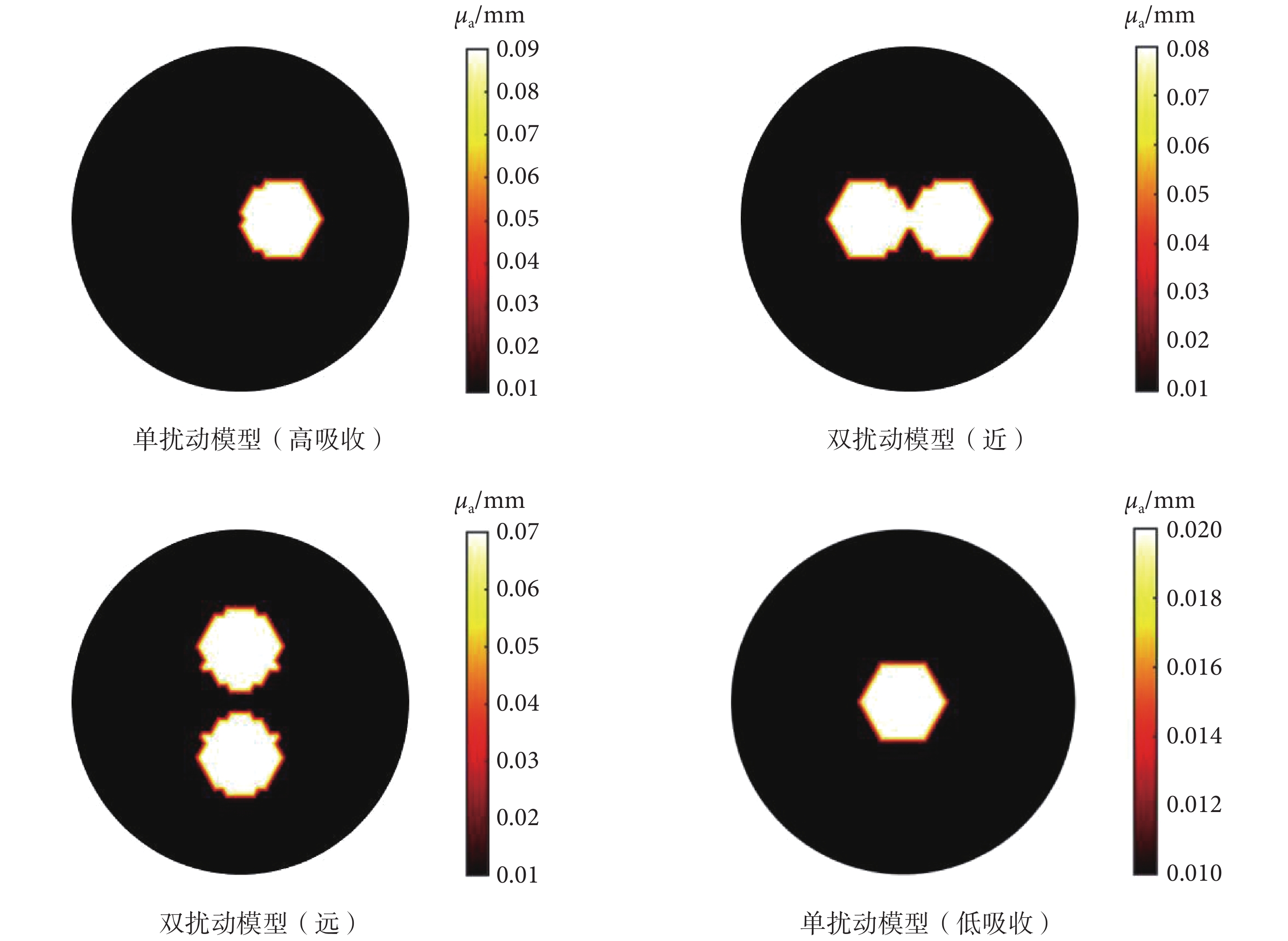
為了驗證所提方法對 DOT 逆問題的求解性能，選取四種擾動模型，擾動的吸收系數分別為 0.09、0.08、0.07、0.02 mm–1，四種模型的設置如圖 6 所示。其中模型一為高吸收系數單一擾動，擾動中心位于 (10, 0)，模型二為相切的兩個擾動球，用于驗證不同方法對鄰近的擾動體分辨能力。模型三為兩個相距 3 mm 的擾動球，用于驗證兩個擾動存在一定距離的條件下不同方法的分辨能力。模型四為位于中心的低吸收系數擾動球，用于驗證在中心深區域低吸收系數擾動的分辨能力。
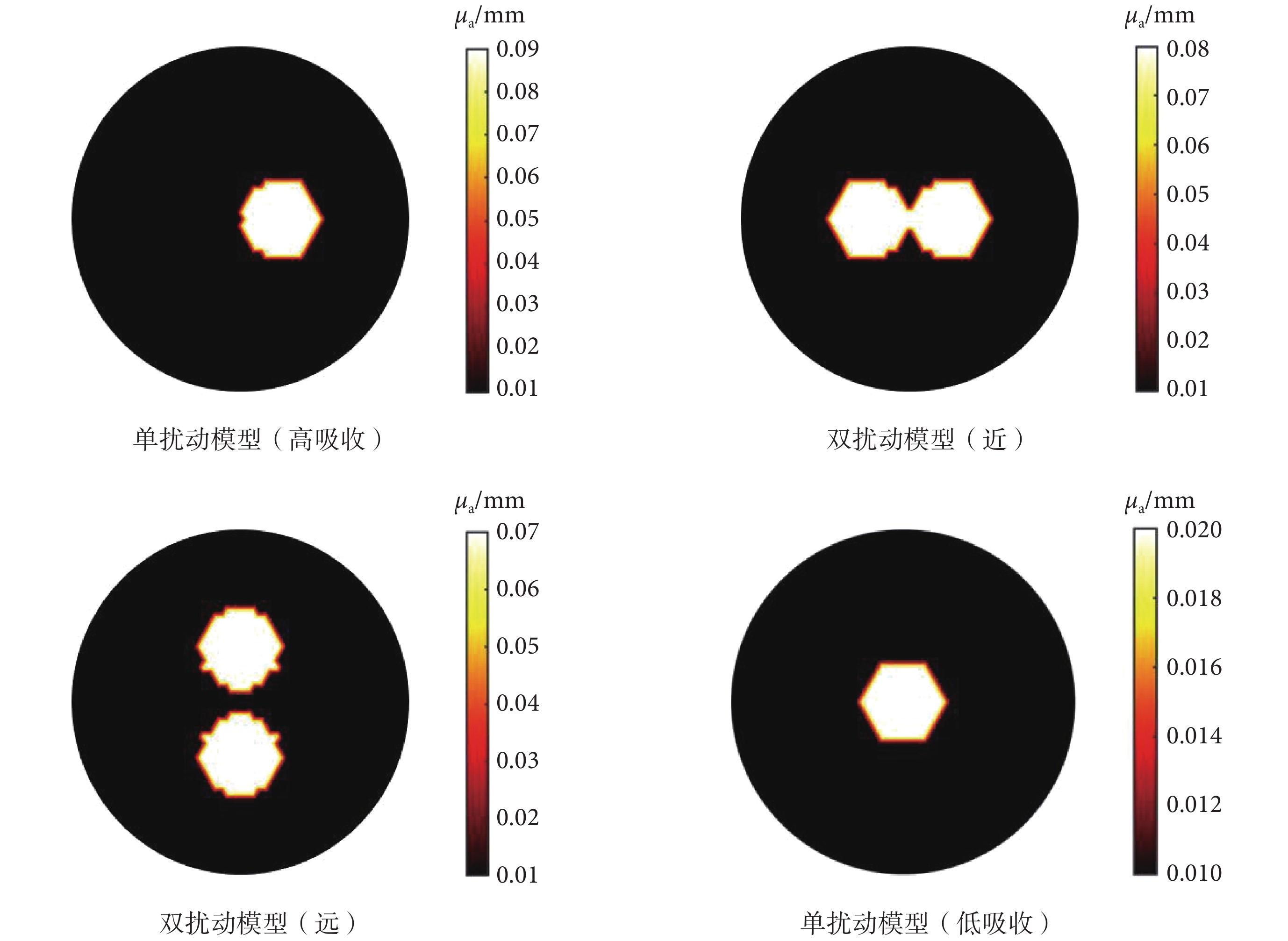圖6
模型背景及擾動設置
Figure6.
Model background and disturbance settings
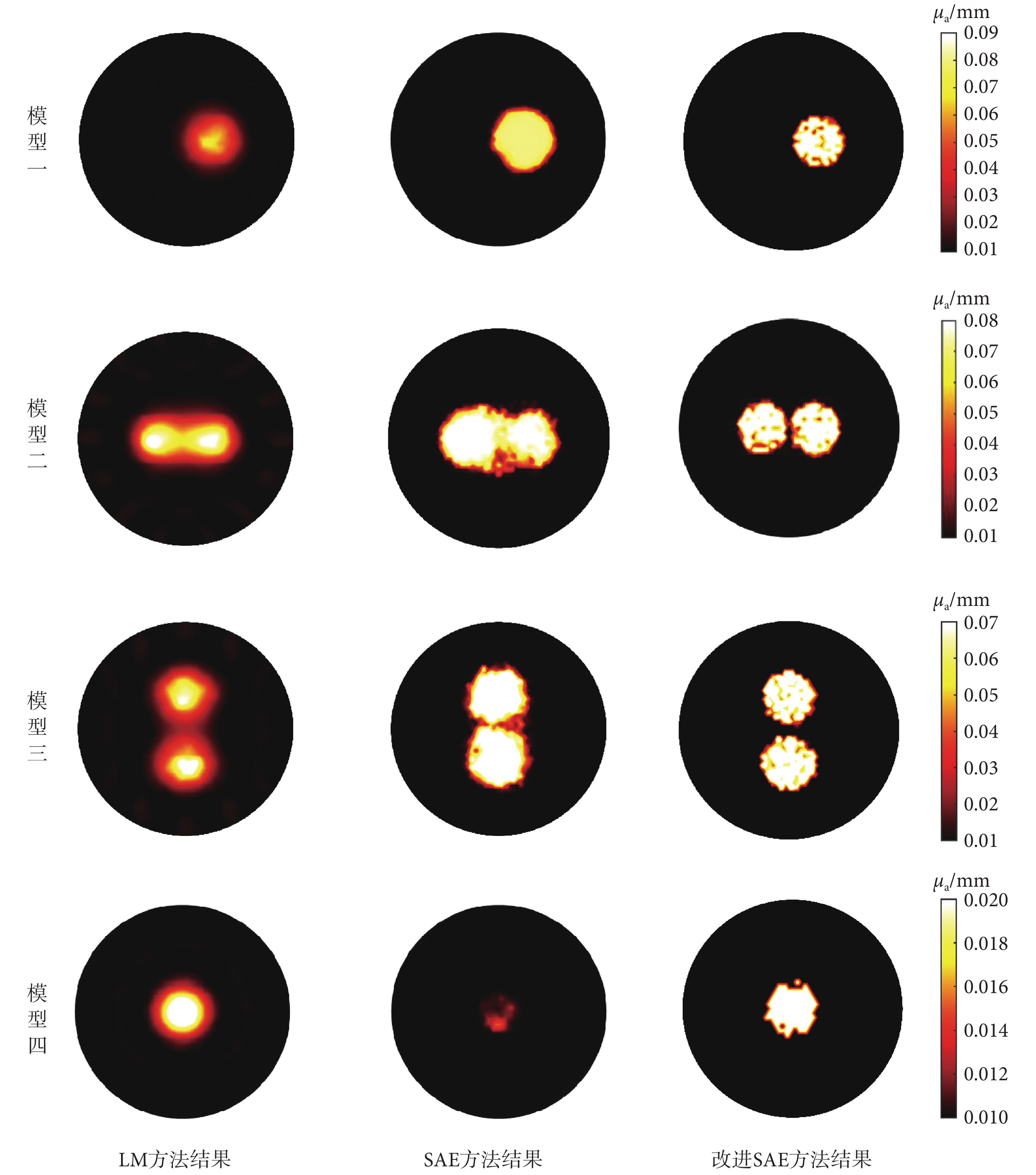
在無噪聲情況下，改進 SAE 方法、LM 方法及 SAE 方法的結果比較如圖 7 所示。對于模型一，由 LM 方法得到的圖像邊界較為模糊，存在分層現象；這是由于 LM 方法采用 L2范數作為懲罰項，導致出現平滑現象。而 SAE 方法會過大估計實際擾動范圍，這是由于網絡對正問題數據進行預估判斷時產生的錯誤計算結果。改進 SAE 方法擾動輪廓具有更小形變，但是會存在部分有限元節點判斷錯誤的情況，進而產生暗點。由于改進 SAE 方法由多個子系統構成，某個系統的錯誤判斷并不會影響到其他系統對輸出的判斷，雖然改進 SAE 方法仍然會有部分節點判斷錯誤產生暗點，但是整體圖像的輪廓和特征并不會受到影響，大部分子系統仍能判斷正確，保持銳利。對于模型二，LM 方法由于 L2范數懲罰限制導致過于平滑的兩個擾動幾乎融合到一起，傳統 SAE 方法仍然會錯誤估計擾動的大小和輪廓，也導致了兩個擾動的融合，而改進 SAE 方法則能較好獲得圖像邊界，圖像較為穩定，兩個擾動的邊界十分清晰。模型三中兩個擾動相距較遠，此時 LM 及傳統 SAE 方法得到改善，能夠分辨兩個擾動的位置，但圖像分層及錯誤估計現象仍然嚴重，改進 SAE 方法仍然保持穩定。對于模型四，擾動吸收系數十分接近背景，此時傳統 LM 方法沒有受到過多影響，但傳統 SAE 方法已經無法判斷擾動的大小，改進 SAE 方法也受到一定影響，有更多的節點存在判斷錯誤的情況，但圖像邊界仍然銳利，大小判斷正確，總體的穩定性仍然超過傳統 SAE 方法。
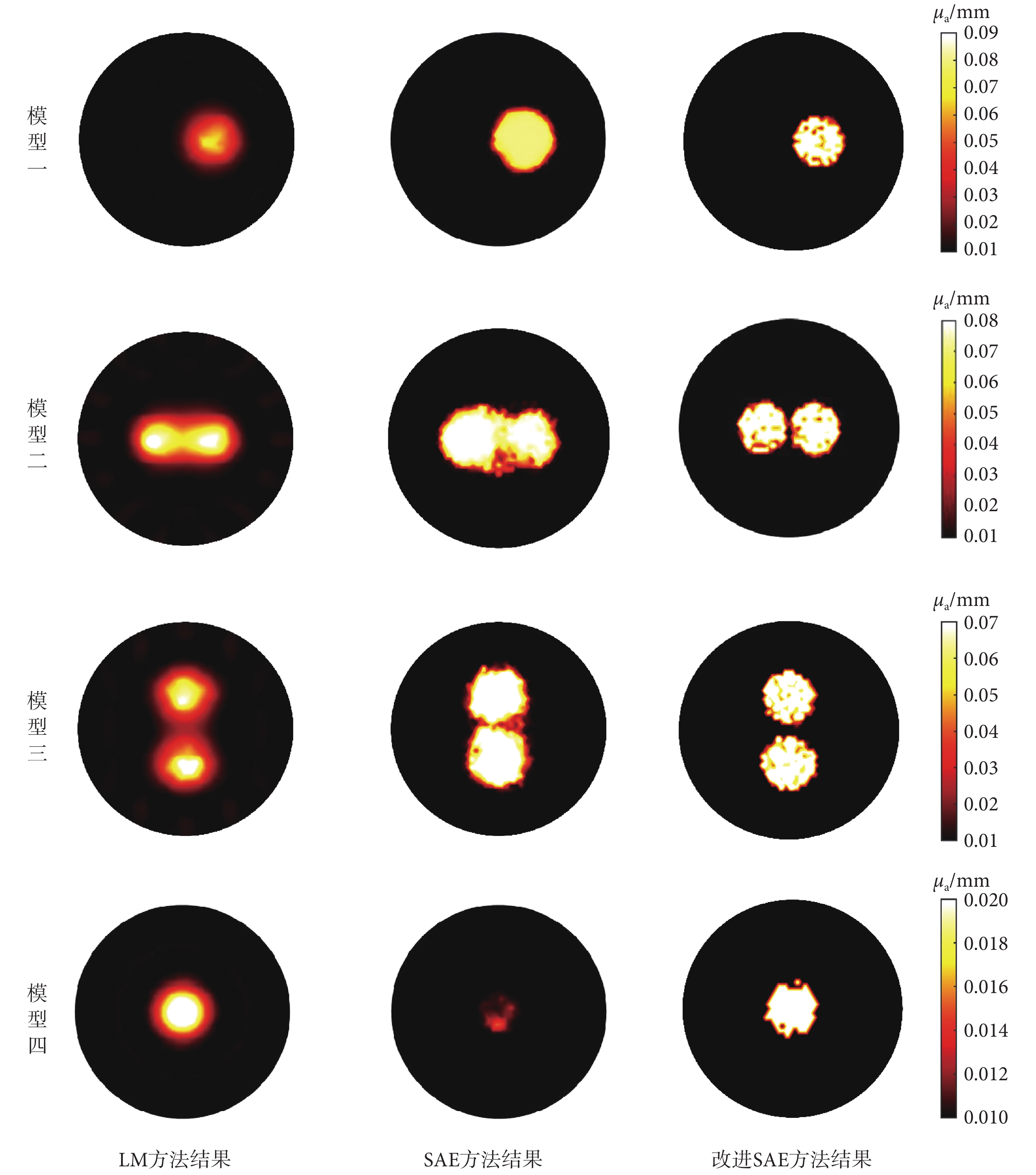圖7
未加噪聲仿真結果比較
Figure7.
Comparison of simulation results without noise
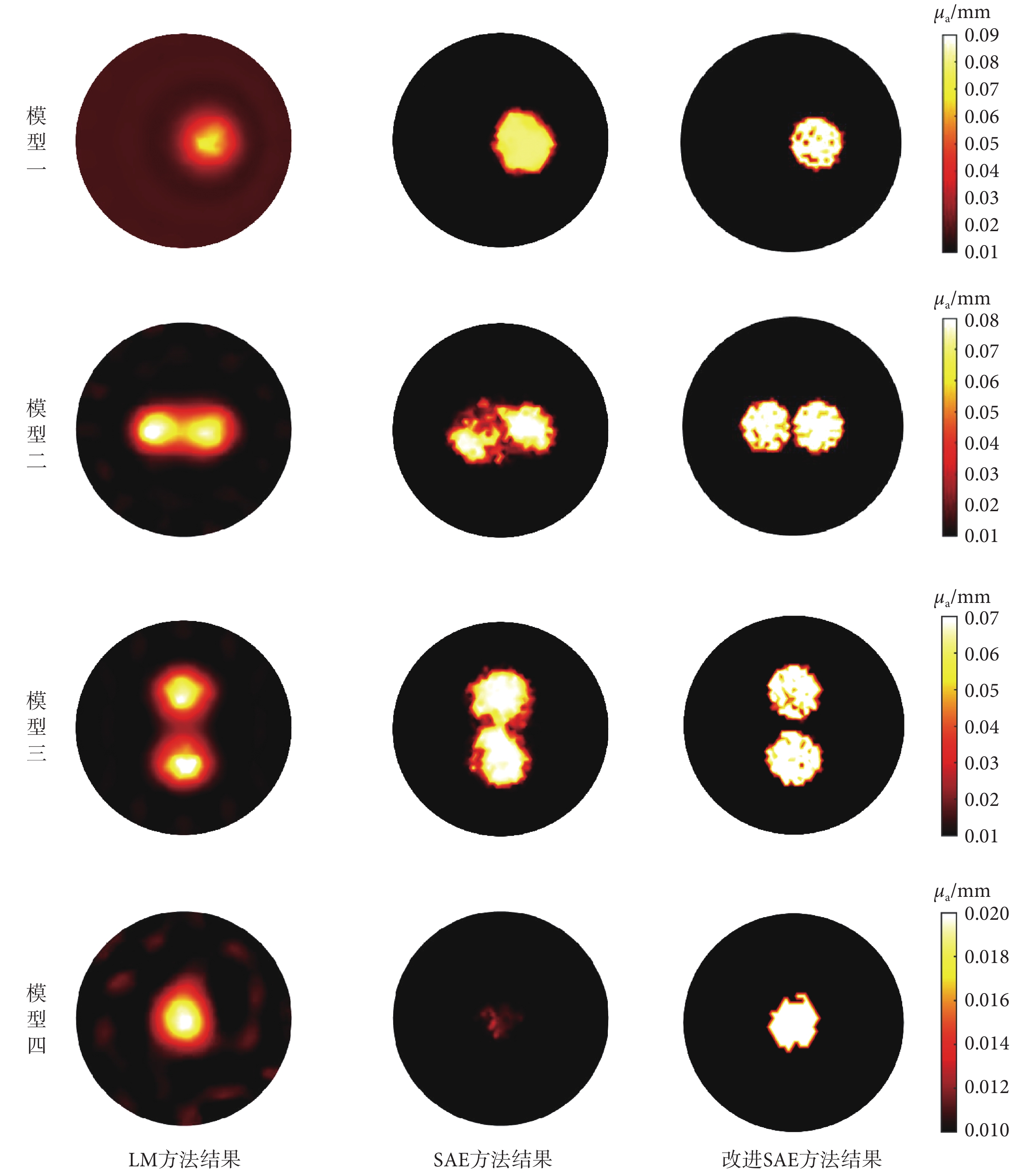
DOT 的硬件系統的噪聲通常在 1% 以下，即使在未添加低頻調制的直流信號檢測中，噪聲也可以限制在 3% 以內[19]。在 3% 隨機噪聲情況下三種方法的結果比較如圖 8 所示，在低信噪比條件下，LM 方法在高吸收擾動條件下幾乎不會受到影響，但隨著擾動吸收系數降低，LM 方法開始產生大量偽影，傳統 SAE 方法則受噪聲影響大，圖像變形嚴重，當存在兩個擾動時，圖像的錯誤估計直接影響了對目標的識別。改進 SAE 方法表現出良好的抗噪能力，在低信噪比條件下也能有清晰的邊界，圖像變形很小。
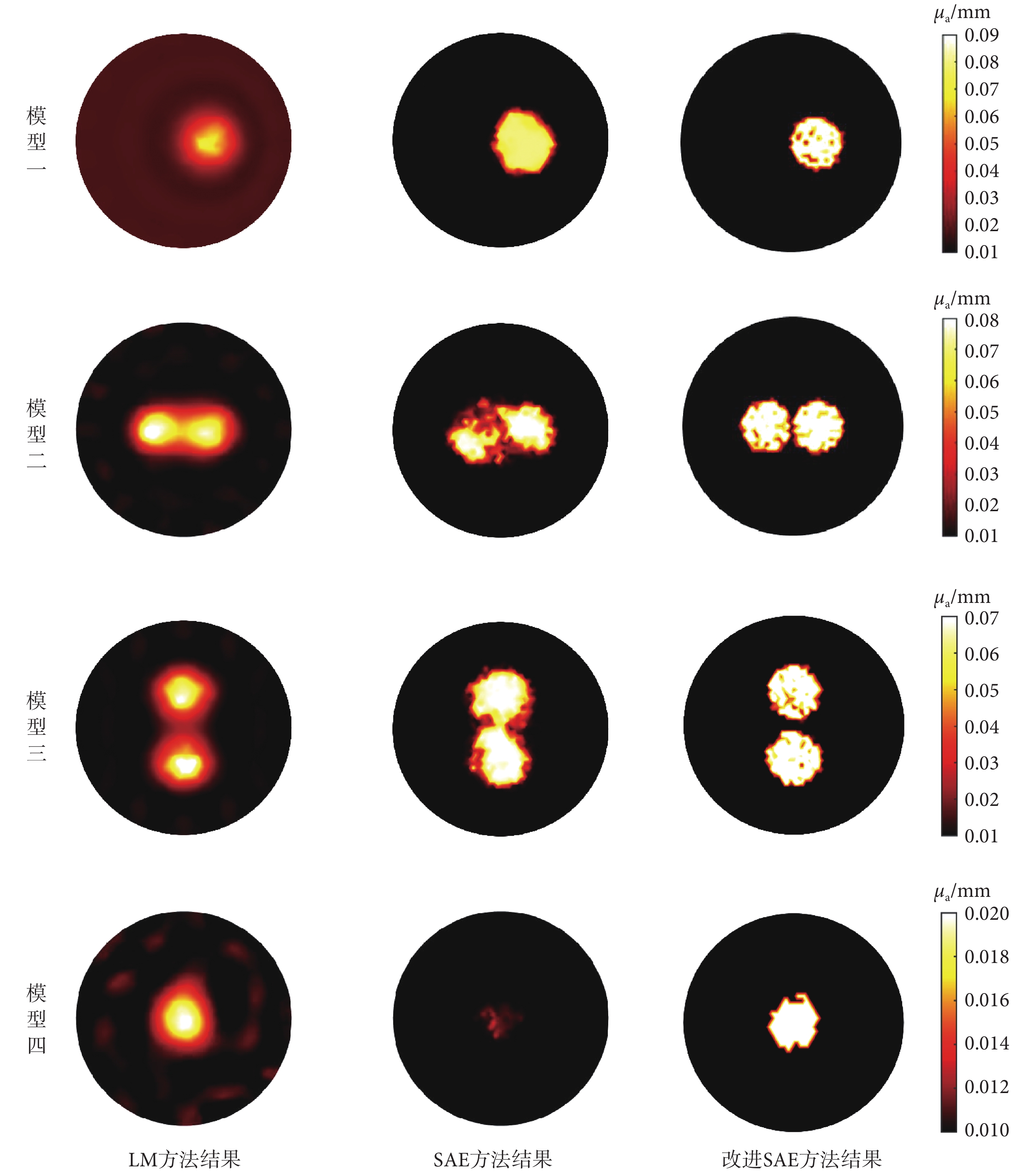圖8
3% 噪聲仿真結果比較
Figure8.
Comparison of simulation results without 3% noise
為了比較所提方法逆問題求解性能，采用了圖像相關系數（image correlation coefficient, ICC）和均方誤差（mean square error, MSE）評價求解的圖像，ICC 計算方法如式（18）所示：
 |
MSE 計算方法如式（19）所示：
 |
其中，
表示實際圖像和結果圖像的 μa 值，
、
表示實際圖像和結果圖像 μa 的平均值。
如表 1 所示，在未添加噪聲時，三種方法在單一擾動條件下都具有較高的 ICC 值及較低的 MSE 值；但在兩個擾動距離較近時，LM 方法及傳統 SAE 方法的 ICC 值下降，MSE 值變大，圖像質量嚴重下降，四個模型條件下，改進 SAE 方法的 MSE 值較 LM 方法降低了 46.21%，較傳統 SAE 方法降低了 61.53%，ICC 值較 LM 方法提升了 4.03%，較傳統 SAE 方法提升了 18.79%，這與圖 7 結果一致。如表 2 所示，加入噪聲后對傳統 SAE 方法圖像質量影響嚴重，ICC 值明顯下降，MSE 值變大，而改進 SAE 方法的 ICC 值與 MSE 值則無明顯變化，表現出更強的抗噪聲能力，四個模型條件下，改進 SAE 方法的 MSE 值較 LM 方法降低了 49.98%，較傳統 SAE 方法降低了 71.94%，ICC 值較 LM 方法提升了 6.38%，較傳統 SAE 方法提升了 57.15%，與圖 8 結果相符合。
表1
MSE 及 ICC 評價結果（未添加噪聲）
Table1.
MSE and ICC evaluation results (no noise added)
表2
MSE 及 ICC 評價結果（3% 隨機噪聲）
Table2.
MSE and ICC evaluation results (3% random noise)
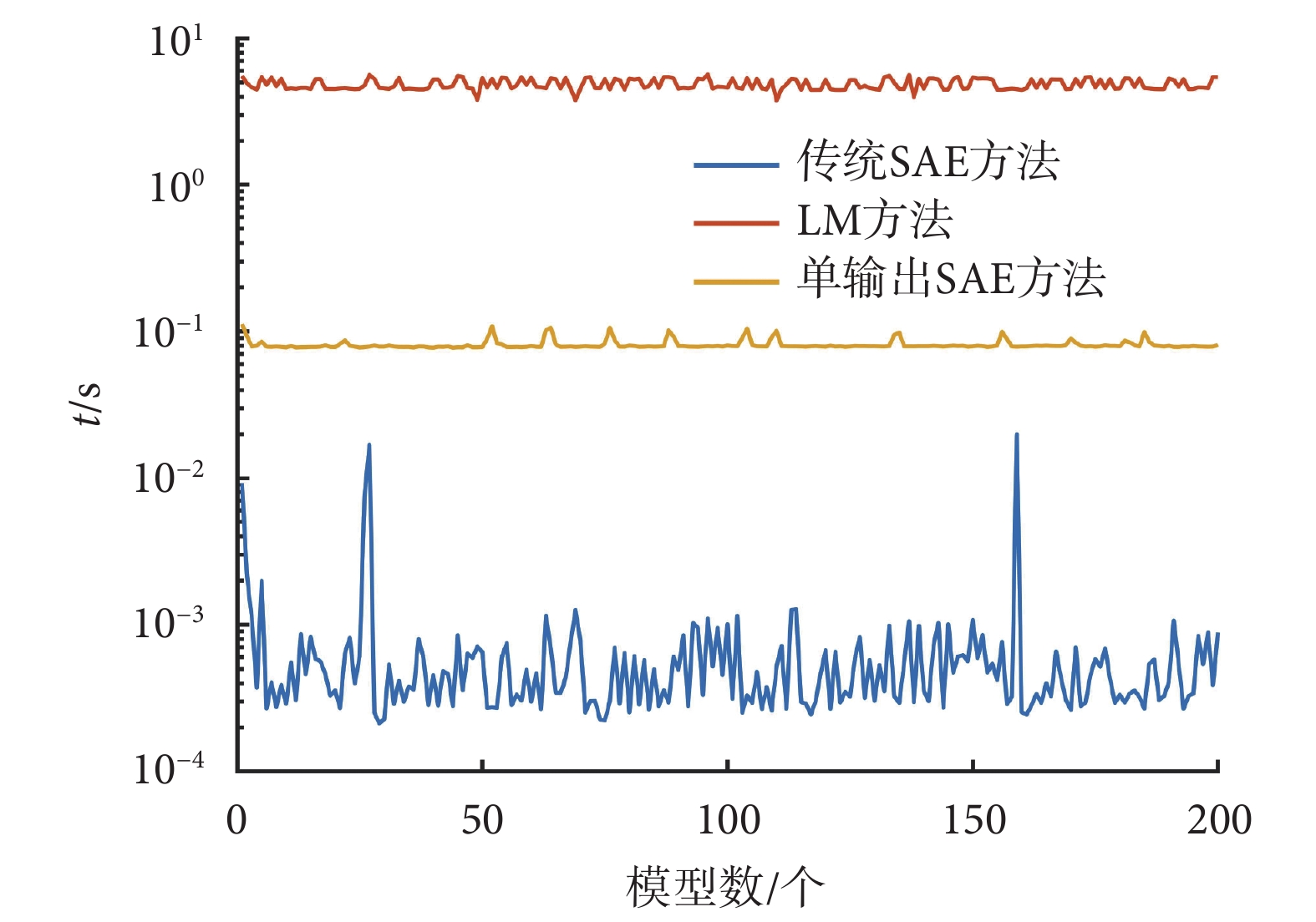
為了驗證不同方法的逆問題求解速度，本文采用了 200 個包含隨機擾動的模型進行實驗，此時 LM 方法、SAE 方法及改進 SAE 方法逆問題計算所用時間 t 如圖 9 所示，改進 SAE 方法平均用時只有 LM 方法的 1.67%，傳統 SAE 方法由于更低的計算量，其時間只有 LM 方法的 0.01%，SAE 及其改進方法的求解速度遠高于 LM 方法。
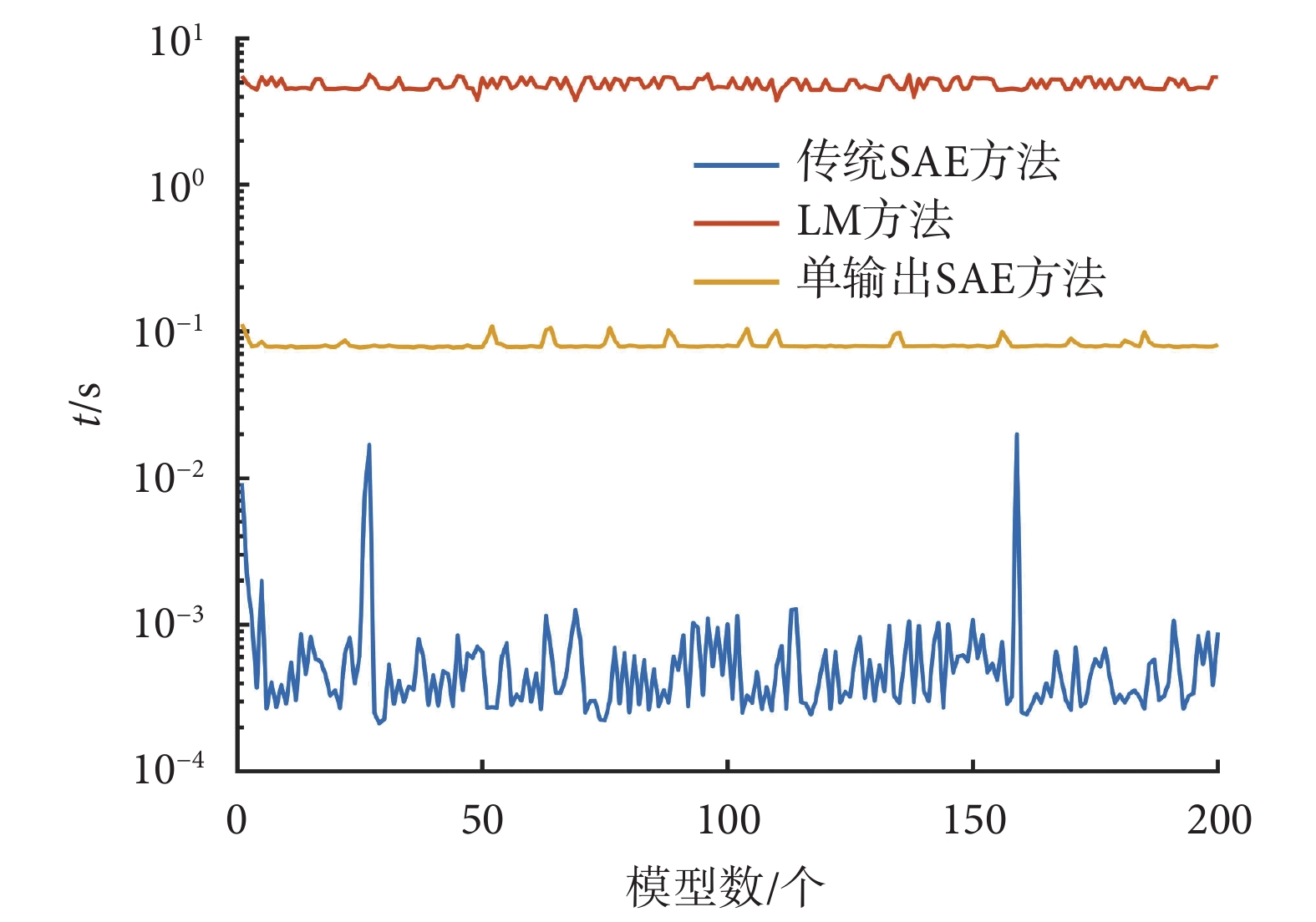圖9
不同擾動模型下逆問題求解時間結果
Figure9.
Results of solving inverse problems under different distributions
4 結論
本文提出了改進 SAE 方法的 DOT 逆問題求解。該方法基于神經網絡對抽象特征的學習，得到光輻射強度與單一節點光學參數之間的非線性特征。雖然基于 SAE 神經網絡的方法需要長久的訓練，但訓練結束后網絡具有極高的計算速度，且病態性的問題也得以避免。另一方面，SAE 神經網絡的抗噪性和圖像質量受到了制約，少量的噪聲就能對網絡產生很大影響，單一網絡完成所有節點的求解極大加重了網絡負擔。為了降低網絡負擔，本文使用多個 SAE 子網絡完成單一節點重建，有效降低了網絡計算量，同時保證了各個節點計算的獨立性。單一網絡的估計錯誤不會影響到其他網絡，從而使圖像質量的失真以像素點為單位，而非以區域為單位，提升了 SAE 網絡的重建精準度。本文提出的新方法避免了 LM 方法逆問題病態性與高耗時的同時，提高了傳統 SAE 方法逆問題求解的 ICC 值，降低了 MSE 值，提升了圖像質量及抗噪聲能力，促進了 DOT 逆問題計算中神經網絡的應用。未來為了實現所提方法的硬件化，需要進一步研究降低單輸出 SAE 網絡的復雜度，提高計算速度。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
擴散光學層析成像（diffuse optical tomography, DOT）作為一種新興的斷層成像技術，其原理是利用近紅外光在組織體內傳播時與組織的吸收散射效應進行成像，并結合算法獲取被測對象光學參數（吸收系數和散射系數）。正常和病變組織的光學參數具有明顯差異，且 DOT 具有無損、實時、造價低等優點，因此 DOT 技術在動作識別、乳腺腫瘤、腦出血等疾病診斷方面具有潛在的應用價值[1-3]。DOT 技術的研究可分為正問題和逆問題[4]，正問題是指已知光源和被測組織的光學參數分布，根據光在組織中的傳播模型，估計發射光的邊界輻射強度；逆問題則是已知組織體表面光源分布，通過獲取測量邊界的輻射強度，重構被測目標成像區域內光學參數的分布。然而，逆問題具有嚴重的病態性，測量值任意微小的擾動下都會產生很大的波動，快速有效的逆問題求解方法是本領域的研究熱點[5]。
傳統的 DOT 逆問題求解多以迭代算法為主，其中有代表性的是代數重建算法（algebraic reconstruction technique, ART），它是一種基于矩陣的快速穩定逆問題求解算法，包含稀疏矩陣大規模線性方程組求解，1995 年被 Arridge[6]引入 DOT 逆問題中，取得較好效果，可在投影數據不完備且投影角度不均勻的情況下也能獲得髙質量圖像，但該方法計算量大，占用空間內存多，導致逆問題計算速度慢。佟珊珊[7]和唐錦萍[8]提出了混合總變差與 L1、Lp范數正則化的迭代策略，在保持邊界銳利性及穩定性的同時，提高了計算精度，但傳統迭代方法計算速度緩慢及強擾動計算誤差大的問題并沒有得到較好的解決。Vidal-Rosas 等[9-10]提出了在逆問題中使用降階模型用于加速逆問題的迭代速度，通過求解光學參數與輻射強度的非線性關系簡化逆問題計算過程，但降階模型仍然存在可解釋范圍差的問題。近年來，神經網絡的方法被應用到 DOT 逆問題求解中，Feng 等[11]提出了基于反向傳播神經網絡（back propagation neural networks, BPNN）的 DOT 逆問題計算方案，通過直接建立邊界光學信息與成像區域內部的神經網絡求解成像區域光學參數分布，避免了逆問題求解的不適定和速度慢的問題，但 BPNN 擾動吸收系數特異性要求高，泛化能力不足的問題無法得到解決。Yoo 等[12]和 Yedder 等[13]提出了基于卷積神經網絡（convolutional neural networks, CNN）的逆問題求解方案，提高了神經網絡的泛化能力，但 CNN 仍然存在網絡參數過多，計算量大，對計算機要求高等問題。
綜上，為了解決現有的 DOT 逆問題求解泛化能力差、計算精度低等問題，本文提出了一種基于改進棧式自編碼器（stacked autoencoder, SAE）的逆問題求解方法。通過 SAE 對輸入數據進行降維及特征提取，并使用單輸出 SAE 降低傳統 SAE 網絡的任務量，最終期望本文所提的改進 SAE 方法的逆問題求解方法相較于傳統神經網絡能夠具有更高的圖像精度及更好的泛化能力，有利于神經網絡在 DOT 領域中的實際應用。
1 DOT 求解
DOT 求解正問題是根據光在組織中的傳播模型，給定成像區域內不同位置 r 處的光學參數 μ(r)，得到邊界光輻射強度 M，其中 μ（r）與 M 的關系如式（1）～式（2）所示：
|
|
其中，μa(r)、μs(r) 分別表示位于成像區域 r 處的吸收系數和散射系數，S、D 表示光源和探測器的數量，表示光學參數μ(r) 映射到邊界輻射強度M的正向算子，使用輻射傳輸方程（radiative transfer equation, RTE）近似求解，具體形式如式（3）所示：
|
在體元 X 內，u(r,ω) 表示在 r 處 ω 方向上的單位立體角 dσ(ω) 發射的光子密度，q(r) 表示 r 處入射的光子密度。r 處的擴散系數 κ(r) 如式（4）所示：
|
其中，g 為已知的各向異性系數。在成像區域邊界 ξ 處光子傳輸如式（5）～式（7）所示：
|
|
|
其中，A 表示邊界處內部與外部折射率之差，n表示邊界處的法向向量，θ（ξ）表示邊界 ξ 處所有方向光子密度的積分。DOT 求解逆問題為，給定邊界光輻射強度M，計算成像區域內的光學參數μ（r）分布。選擇吉洪諾夫（Tikhonov）正則化，正則化矩陣取單位矩陣I時，稱為列文伯格-馬夸爾特（levenberg-marquardt, LM）方法，此時 DOT 逆問題求解如式（8）所示：
|
其中，表示成像區域內光學參數分布，P′（μ（k））在此簡寫為J。每次迭代計算 P（μ（k+1））與M的差值，當滿足極小值要求時，迭代結束。
2 提出的方法
2.1 SAE 的 DOT 逆問題求解
SAE 由多個自編碼器（auto-encoder, AE）堆棧產生，其主要應用在特征提取、數據降維去噪及圖像識別等問題中[14-16]，訓練過程如圖 1 所示。
圖1
SAE 神經網絡基本結構
Figure1.
Basic structure of SAE neural network
圖 1 中由 AE 網絡構成傳統 SAE 神經網絡并完成神經網絡訓練流程如下：
步驟 1：計算 AE 網絡輸入層到隱藏層的輸出。從輸入層到隱藏層的過程稱為編碼過程，輸入層到隱藏層之間的關系如式（9）～式（11）所示：
|
|
|
其中，上式及圖 1 中為輸入層一個樣本的 m 維向量，為隱藏層的 n 維向量，W為從輸入層到隱藏層的權值矩陣，為隱藏層的偏置向量。為隱藏層的激活函數，本文使用 tanh 函數作為激活函數，tanh 函數如式（12）所示：
|
步驟 2：計算 AE 網絡隱藏層到輸出層的輸出。隱藏層到輸出層之間的關系如式（13）～式（15）所示：
| '/> |
| '/> |
| '/> |
其中，為與輸入向量維度相同的向量，W'為隱藏層到輸出層的權值矩陣，b'為偏置向量。
步驟 3：優化 AE 網絡。通過反向傳播算法迭代更新權值矩陣神經網絡參數，使輸出向量盡可能等于輸入向量x，損失函數 L（·）如式（16）所示：
|
步驟 4：AE 網絡堆棧。將隱藏層h作為輸入，重復步驟 1～步驟 3 訓練圖 1 中新的隱藏層，得到更低維度的信息空間。訓練完成后，舍棄當前輸出層，在隱藏層后加入一個新的輸出層，此時得到完整的傳統 SAE 神經網絡結構。
步驟 5：輸出層的有監督訓練。如圖 1 所示，在無監督訓練完成后，利用有標簽數據集采用有監督學習算法對神經網絡參數進行調優，最終輸出 t 維數據集。
2.2 改進 SAE 的 DOT 逆問題求解
使用 SAE 方法完成 DOT 逆問題求解的過程如圖 2 所示。其中 SAE 神經網絡的數據輸入為已知的 S × D 維歸一化光輻射強度 M，輸出數據為 n 維有限元節點的 μa，傳統的 SAE 方法將 DOT 逆問題視為回歸問題，將輸出數據視為連續值，按照圖 1 的步驟完成 SAE 神經網絡訓練。
圖2
基于傳統 SAE 方法的 DOT 逆問題求解
Figure2.
The calculation of DOT inverse problem based on traditional SAE method
SAE 方法擬合 DOT 逆問題參數分布時，需要擬合所有節點參數分布，SAE 神經網絡負載高，導致輸出擬合結果差。因此，本文提出了一種改進 SAE 方法求解 DOT 逆問題。該方法采用多個子神經網絡計算多個有限元節點，其中每個 SAE 子網絡只計算一個節點，計算過程如圖 3 所示。
圖3
基于改進 SAE 方法的逆問題計算求解
Figure3.
The calculation process of inverse problem based on improved SAE method
在圖 3 中輸入光強信號仍為 S×D 維歸一化輻射強度 M，輸出數據為 1 維的單一有限元節點，此時將輸入數據同時送入 n 個 SAE 網絡，每個網絡都是獨立的，同時每個網絡只計算某一特定有限元節點。
改進 SAE 的數據處理方式如圖 4 所示，在改進的 SAE 方法中，將得到的輸出數據分段表示為獨熱編碼，SAE 子網絡將 μa(r) 的值 x 按大小分為 z 個區間，同時判斷節點 μa（r）所處區間，從而將回歸問題改善為分類問題。改進 SAE 中輸出數據采用 softmax 函數，如式（17）所示：
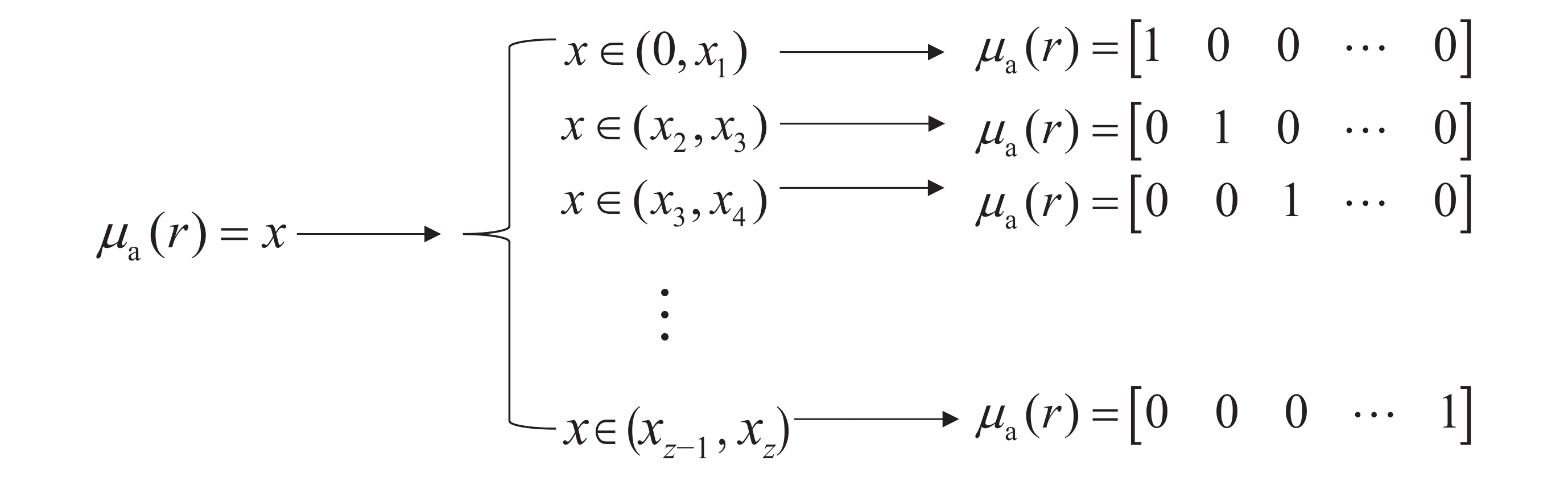圖4
μa 分布的獨熱編碼表示
Figure4.
One-hot encoding representation of μa
|
其中，z 表示將 μa(r) 分為 z 個區間，f(xi) 表示 μa(r) 屬于第 i 區間的概率。
3 仿真實驗
3.1 參數設置
仿真成像區域如圖 5 所示，其具體設計如下：
圖5
成像區域光源與探測器放置位置（單光源多探測器工 作模式）
Figure5.
The placement of the light sources and detectors in the imaging area (single light source and multiple detectors working mode)
① 傳統 SAE 網絡使用四層結構，每層神經元個數設置為{240, 480, 800, 1 785}。初始學習率為 0.01，迭代 1 000 次。
② 改進 SAE 網絡使用四層結構，每層神經元個數設置為{240, 130, 80, 10}。初始學習率為 0.01，迭代 1 000 次，共 1 785 個單輸出 SAE 子神經網絡。
③ 在圖中背景 μa 和 μs 分別設置為 0.01 mm–1和 1 mm–1。成像區域半徑為 43 mm，在邊界位置處按角度均勻分配 16 個光源和 16 個探測器。
④ 光源的輻射強度為 1 W/mm2，有限元網格數量為 1 785，使用有限元分析軟件 NIRFAST 9.1（Kitware Inc., 美國）得到的 10 000 組數據作為訓練樣本[17-18]。實驗模型中的擾動半徑為 6～18 mm 隨機值，μa 為 0.01～0.1 mm–1隨機值，擾動位置隨機分布在成像區域內，擾動的數量隨機 1～2 個。
3.2 性能比較及結果分析
為了驗證所提方法對 DOT 逆問題的求解性能，選取四種擾動模型，擾動的吸收系數分別為 0.09、0.08、0.07、0.02 mm–1，四種模型的設置如圖 6 所示。其中模型一為高吸收系數單一擾動，擾動中心位于 (10, 0)，模型二為相切的兩個擾動球，用于驗證不同方法對鄰近的擾動體分辨能力。模型三為兩個相距 3 mm 的擾動球，用于驗證兩個擾動存在一定距離的條件下不同方法的分辨能力。模型四為位于中心的低吸收系數擾動球，用于驗證在中心深區域低吸收系數擾動的分辨能力。
圖6
模型背景及擾動設置
Figure6.
Model background and disturbance settings
在無噪聲情況下，改進 SAE 方法、LM 方法及 SAE 方法的結果比較如圖 7 所示。對于模型一，由 LM 方法得到的圖像邊界較為模糊，存在分層現象；這是由于 LM 方法采用 L2范數作為懲罰項，導致出現平滑現象。而 SAE 方法會過大估計實際擾動范圍，這是由于網絡對正問題數據進行預估判斷時產生的錯誤計算結果。改進 SAE 方法擾動輪廓具有更小形變，但是會存在部分有限元節點判斷錯誤的情況，進而產生暗點。由于改進 SAE 方法由多個子系統構成，某個系統的錯誤判斷并不會影響到其他系統對輸出的判斷，雖然改進 SAE 方法仍然會有部分節點判斷錯誤產生暗點，但是整體圖像的輪廓和特征并不會受到影響，大部分子系統仍能判斷正確，保持銳利。對于模型二，LM 方法由于 L2范數懲罰限制導致過于平滑的兩個擾動幾乎融合到一起，傳統 SAE 方法仍然會錯誤估計擾動的大小和輪廓，也導致了兩個擾動的融合，而改進 SAE 方法則能較好獲得圖像邊界，圖像較為穩定，兩個擾動的邊界十分清晰。模型三中兩個擾動相距較遠，此時 LM 及傳統 SAE 方法得到改善，能夠分辨兩個擾動的位置，但圖像分層及錯誤估計現象仍然嚴重，改進 SAE 方法仍然保持穩定。對于模型四，擾動吸收系數十分接近背景，此時傳統 LM 方法沒有受到過多影響，但傳統 SAE 方法已經無法判斷擾動的大小，改進 SAE 方法也受到一定影響，有更多的節點存在判斷錯誤的情況，但圖像邊界仍然銳利，大小判斷正確，總體的穩定性仍然超過傳統 SAE 方法。
圖7
未加噪聲仿真結果比較
Figure7.
Comparison of simulation results without noise
DOT 的硬件系統的噪聲通常在 1% 以下，即使在未添加低頻調制的直流信號檢測中，噪聲也可以限制在 3% 以內[19]。在 3% 隨機噪聲情況下三種方法的結果比較如圖 8 所示，在低信噪比條件下，LM 方法在高吸收擾動條件下幾乎不會受到影響，但隨著擾動吸收系數降低，LM 方法開始產生大量偽影，傳統 SAE 方法則受噪聲影響大，圖像變形嚴重，當存在兩個擾動時，圖像的錯誤估計直接影響了對目標的識別。改進 SAE 方法表現出良好的抗噪能力，在低信噪比條件下也能有清晰的邊界，圖像變形很小。
圖8
3% 噪聲仿真結果比較
Figure8.
Comparison of simulation results without 3% noise
為了比較所提方法逆問題求解性能，采用了圖像相關系數（image correlation coefficient, ICC）和均方誤差（mean square error, MSE）評價求解的圖像，ICC 計算方法如式（18）所示：
|
MSE 計算方法如式（19）所示：
|
其中，表示實際圖像和結果圖像的 μa 值，、 表示實際圖像和結果圖像 μa 的平均值。
如表 1 所示，在未添加噪聲時，三種方法在單一擾動條件下都具有較高的 ICC 值及較低的 MSE 值；但在兩個擾動距離較近時，LM 方法及傳統 SAE 方法的 ICC 值下降，MSE 值變大，圖像質量嚴重下降，四個模型條件下，改進 SAE 方法的 MSE 值較 LM 方法降低了 46.21%，較傳統 SAE 方法降低了 61.53%，ICC 值較 LM 方法提升了 4.03%，較傳統 SAE 方法提升了 18.79%，這與圖 7 結果一致。如表 2 所示，加入噪聲后對傳統 SAE 方法圖像質量影響嚴重，ICC 值明顯下降，MSE 值變大，而改進 SAE 方法的 ICC 值與 MSE 值則無明顯變化，表現出更強的抗噪聲能力，四個模型條件下，改進 SAE 方法的 MSE 值較 LM 方法降低了 49.98%，較傳統 SAE 方法降低了 71.94%，ICC 值較 LM 方法提升了 6.38%，較傳統 SAE 方法提升了 57.15%，與圖 8 結果相符合。
表1
MSE 及 ICC 評價結果（未添加噪聲）
Table1.
MSE and ICC evaluation results (no noise added)
表2
MSE 及 ICC 評價結果（3% 隨機噪聲）
Table2.
MSE and ICC evaluation results (3% random noise)
為了驗證不同方法的逆問題求解速度，本文采用了 200 個包含隨機擾動的模型進行實驗，此時 LM 方法、SAE 方法及改進 SAE 方法逆問題計算所用時間 t 如圖 9 所示，改進 SAE 方法平均用時只有 LM 方法的 1.67%，傳統 SAE 方法由于更低的計算量，其時間只有 LM 方法的 0.01%，SAE 及其改進方法的求解速度遠高于 LM 方法。
圖9
不同擾動模型下逆問題求解時間結果
Figure9.
Results of solving inverse problems under different distributions
4 結論
本文提出了改進 SAE 方法的 DOT 逆問題求解。該方法基于神經網絡對抽象特征的學習，得到光輻射強度與單一節點光學參數之間的非線性特征。雖然基于 SAE 神經網絡的方法需要長久的訓練，但訓練結束后網絡具有極高的計算速度，且病態性的問題也得以避免。另一方面，SAE 神經網絡的抗噪性和圖像質量受到了制約，少量的噪聲就能對網絡產生很大影響，單一網絡完成所有節點的求解極大加重了網絡負擔。為了降低網絡負擔，本文使用多個 SAE 子網絡完成單一節點重建，有效降低了網絡計算量，同時保證了各個節點計算的獨立性。單一網絡的估計錯誤不會影響到其他網絡，從而使圖像質量的失真以像素點為單位，而非以區域為單位，提升了 SAE 網絡的重建精準度。本文提出的新方法避免了 LM 方法逆問題病態性與高耗時的同時，提高了傳統 SAE 方法逆問題求解的 ICC 值，降低了 MSE 值，提升了圖像質量及抗噪聲能力，促進了 DOT 逆問題計算中神經網絡的應用。未來為了實現所提方法的硬件化，需要進一步研究降低單輸出 SAE 網絡的復雜度，提高計算速度。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
