針對心音信號非平穩性、非線性的特征，為了更直觀地把心音信號的特征顯示出來，提高分類識別的高效性，提出了一種自適應噪聲完備經驗模態分解（CEEMDAN）排列熵作為心音信號的特征向量，通過支持向量機（SVM）進行心音分類識別的方法。首先，將原始心音信號進行CEEMDAN，得到若干從高頻到低頻的模態分量（IMF）。其次，利用IMF分量與原始信號的相關系數、能量因子和信噪比來優選IMF做Hilbert變換，得到分量信號的瞬時頻率，再計算各IMF排列熵值組成特征向量。最后，將特征向量輸入SVM二分類器進行正常與異常心音信號的分類識別。對源自2016年PhysioNet/CinC挑戰賽的100例心音樣本進行正常與異常的分類，準確度達到87%。研究表明本文方法相比于常用的EMD和EEMD排列熵的方法準確度提高了18%～24%，可見，CEEMDAN排列熵結合SVM的方法能夠有效識別正常和異常心音。
引用本文： 劉美君, 吳全玉, 丁勝, 潘玲佼, 劉曉杰. 自適應噪聲完備經驗模態分解排列熵結合支持向量機的心音分類方法研究. 生物醫學工程學雜志, 2022, 39(2): 311-319. doi: 10.7507/1001-5515.202105065 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
心音信號是心臟收縮舒張時血液與心室和主動脈壁碰撞引起的顫動所形成的一種聲音信號[1-2]，能夠反映出大量的心血管生理信息與病理信息，對臨床評估心臟功能狀態有重大意義[3-5]。由于心音信號的非線性和非平穩性[6-7]，心音信號分析研究的主要方法有時頻分析法和能量分析法，而且通常采用兩種方法相互結合對生理信號進行分析[8-10]。劉麗萍等[11]使用Choi-Williams分布時頻分析結合自回歸模型功率譜的時頻與能量分析方法，提取心音信號的特征向量。尹明等[12]在深入研究希爾伯特-黃變換（Hilbert-Huang transform，HHT）的基礎上，對降噪后的心音信號利用經驗模態分解（empirical mode decomposition，EMD）、希爾伯特變換（Hilbert transform，HT）及歸一化香農能量定理等從多個角度提取心音的特征值。黃林洲等[13]提出EMD與近似熵構成心音信號的特征向量。李宏全等[14]提出EMD與梅爾倒頻譜結合的方法，分類識別舒張期心雜音。Goda等[15]提取了收縮期和舒張期的頻率特性以及重新采樣的小波包絡特征，使用支持向量機（support vector machine，SVM）來對具有幾種訓練集配置的記錄進行分類，達到了80.28%的準確度。Grzegorczyk等[16]提出了基于神經網絡的機器學習算法，心音圖（phonocardiogram，PCG）信號的分割采用基于隱馬爾可夫模型的算法，將重點放在代表信號特征的統計特征上，獲得的最佳總體得分為0.79。Langley等[17]通過小波熵對未分割和短時心電圖進行分類，計算未分段5 s持續時間記錄的小波熵，并根據訓練集確定最佳小波尺度和小波熵閾值，在訓練集上獲得了78％的分數。本團隊[18]提出自適應噪聲完備經驗模態分解（complete ensemble empirical modal decomposition with adaptive noise，CEEMDAN）與盲反卷積結合的算法，分離腦電信號中含有的眼電偽跡。因此，經驗模態分解與時頻、能量分析對復雜的生理信號分析與處理有重大意義[19-20]。Wu等[21]提出了以EMD方法為核心的集總經驗模態分解（ensemble empirical modal decomposition，EEMD），在原始信號上多次加入高斯白噪聲，高斯白噪聲信號是一種便于分析的理想噪聲信號，利用其頻譜均勻分布的特性，使得重構信號在不同的時間尺度上具有連續性，解決了EMD模態混疊的問題。由于EEMD分解效率較低，Yeh等在EEMD的基礎上提出了互補集總經驗模態分解（complete ensemble empirical modal decomposition，CEEMD），在原始信號中加入一個白噪聲，再減去一個白噪聲，這樣很好地消除了重構信號中的殘余噪聲，而且使得集總平均次數減少，提高了分解效率，但是存在虛假的模態分量（intrinsic mode functions，IMF）[22-23]。而CEEMDAN[24]改進了以上方法的缺陷，在各個IMF中添加自適應的高斯白噪聲，使得重構誤差接近于零，分解效率極高而且完整。本團隊的前期工作中將CEEMDAN用在腦電信號的去噪預處理中，本文的改進點在于將CEEMDAN應用于心音信號的特征提取中。
本文提出了一種提取心音信號CEEMDAN模態分量的瞬時頻率排列熵做為特征向量，并通過SVM進行心音正常與異常分類識別的方法。最后，引入Fisher判別法，與SVM進行對比，驗證該方法是否可以有效應用于心音分類。
1 方法
1.1 數據的來源與預處理
本文的心音數據來源于PhysioNet與心臟病計算協會聯合舉辦的“心音記錄的分類—2016年PhysioNet/CinC挑戰賽”所提供的一個大型數據庫（https://www.physionet.org/challenge/2016/）[25-26]。數據庫里包括1 072名受試者中采集的4 430份心音記錄，每個記錄持續時間為5 ～120 s，采樣頻率為2 000 Hz，以*.wav的格式提供。心音記錄通常是從主動脈區、肺動脈區、三尖瓣區和二尖瓣區這四個不同位置之一收集的，記錄分為正常心音和異常心音兩種類型。正常記錄來自健康受試者，異常記錄來自經確診的典型的心臟瓣膜缺陷和冠狀動脈疾病（coronary artery disease，CAD）患者。
本文的實驗硬件配置為華碩FX506LI，CPU為Inter Core I7-10750H，主頻2.60 GHz，內存為DDR4，大小為16 GB，獨立顯卡為NVIDIA GeForce GTX 1650 Ti，顯存為6 GB。軟件配置為Microsoft Windows 10下的Matlab R2018b版本，算法運行時間通過Matlab中的tic和toc指令得到。
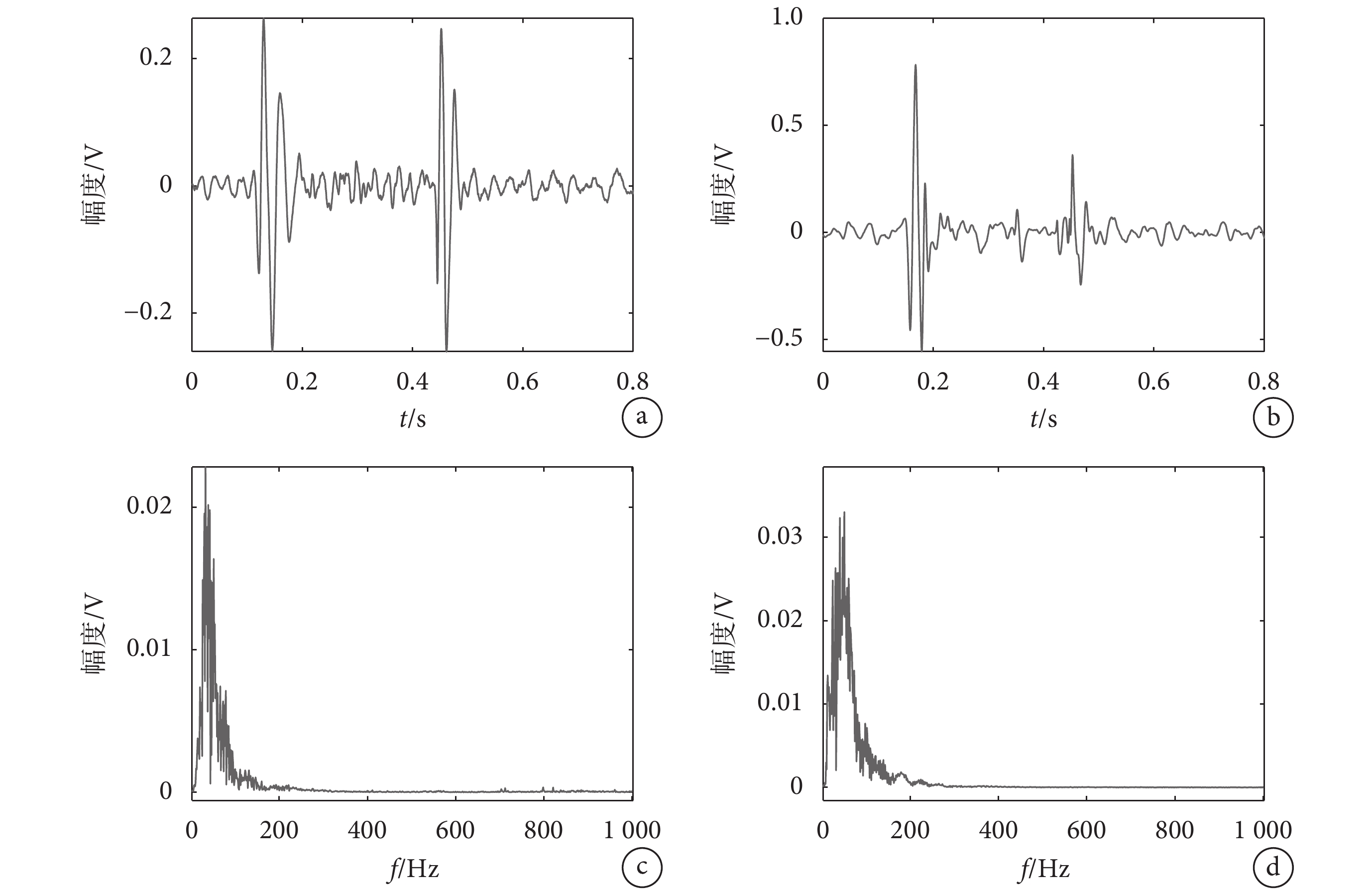
本文選用PhysioNet心音數據庫中300個心音樣本數據進行試驗，正常成年人的心跳周期為0.8 s，而心音數據庫里心音數據的采樣點為0.000 5 s，所以一個心跳周期為1 600個采樣點，為了便于分析，取了7.5個心跳周期進行研究。其中典型的正常與異常心音記錄如圖1所示。由于心音信號采集環境不受控制，許多錄音會包含各種噪音，例如談話、聽診器運動、呼吸和腸道聲音等。所以本文采用巴特沃斯低通濾波器，濾除原始信號中由于操作不當產生的1 000 Hz以上的噪聲；采用陷波器，濾除50 Hz的工頻干擾，對心音信號做預處理。
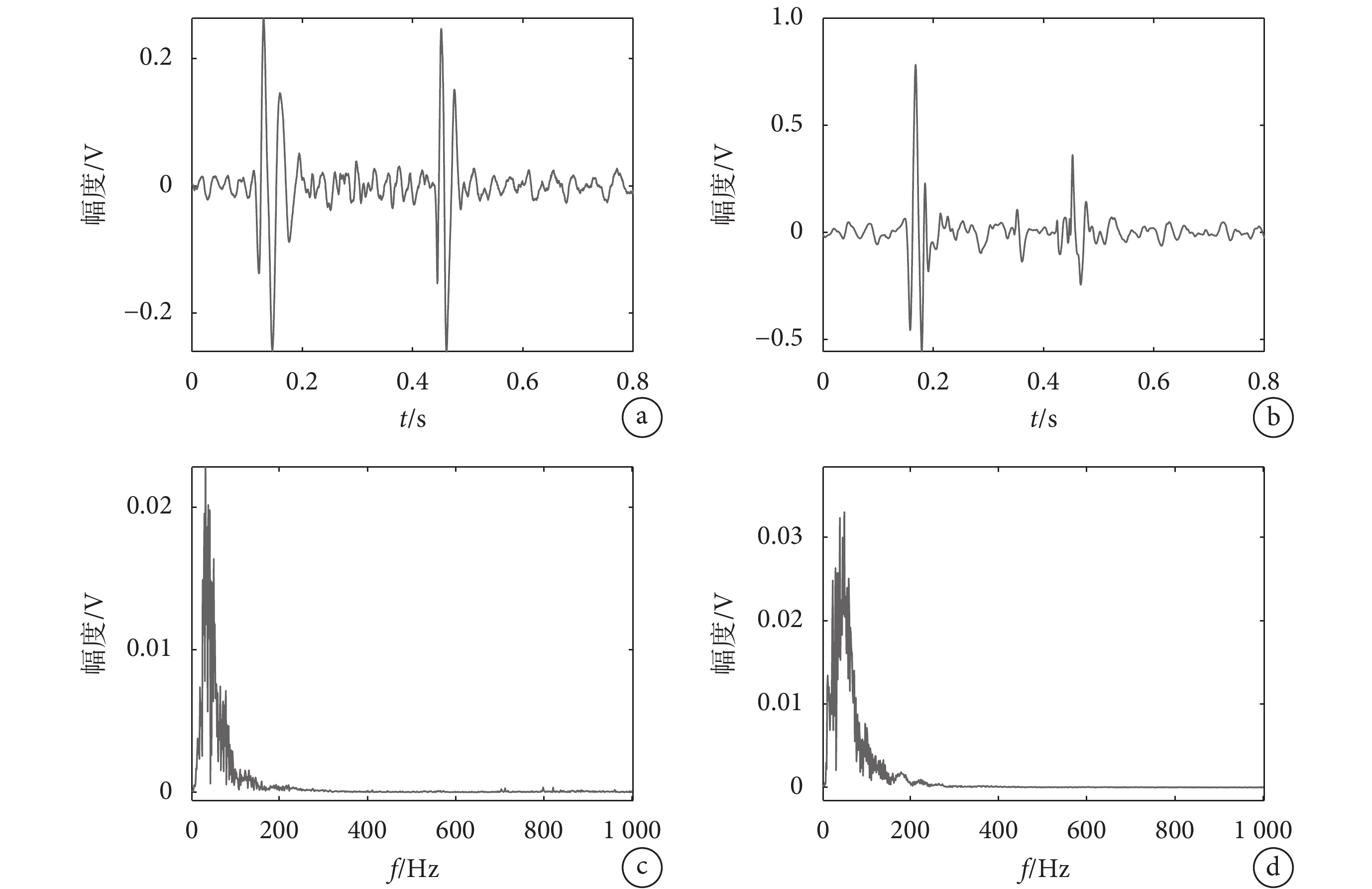圖1
典型的正常與異常心音記錄圖
a. 正常心音時域信號；b. 異常心音時域信號；c. 正常心音頻域曲線；d. 異常心音頻域曲線
Figure1. Typical records of normal and abnormal heart soundsa. normal heart sound time domain signal; b. abnormal signal time domain signal; c. normal heart sound frequency domain curve; d. abnormal heart sound frequency domain curve
1.2 心音信號特征提取
1.2.1 CEEMDAN排列熵原理
CEEMDAN在EMD的基礎上加入了成對的正負白噪聲，消除了虛假的IMF，提高了分解準確性。CEEMDAN算法步驟如下：
① 在原始信號中加入高斯白噪聲組成新的構造信號 
，其中，
為原始信號，
為一階噪聲標準差，
為服從 
分布的白噪聲，表示第j次分解添加的白噪聲，
。
② 對 
進行N次EMD分解，第一次分解結束后取均值，得到一階模態分量 
，如式（1）所示：
 |
同時一階余量信號 
如式（2）所示：
 |
③ 當 
的極值點個數超過2個時，對EMD分解的一階模態算子加入一階余量信號 
構成新的余量信號 
進行EMD分解，得到二階模態分量 
，見式（3）：
 |
其中，
表示二階噪聲標準差，
為對信號進行EMD分解后的第 
階 IMF 模態算子，
為EMD分解產生的一階模態的算子。
④ 循環步驟 ③，直到余量信號不能再分解，原始信號
被分解如式（4）所示：
 |
其中，K 表示模態分解的次數；k表示模態分解的層數，
。
在第 
層分解中，計算 
階余量信號 
如式（5）所示：
 |
階模態分量 
如式（6）所示：
 |
其中，
表示 
階模態分量，
表示 
階噪聲標準差。
HT變換是一種常用的信號處理方法，其定義如式（7）所示。
 |
其中 
為原始信號。
本文將CEEMDAN的IMF作為原始信號進行HT變換，則HT變換 
定義如式（8）所示。
 |
熵是描述信號源不確定度的量。排列熵是描述一維非線性時間序列信號復雜性與混亂程度的熵算法，作為可定量描述時間序列信號復雜程度與混亂程度的熵值參數，信號越復雜，排列熵值越大。因此，可以用排列熵來表示心音信號在不同于原來時間尺度下的不同頻帶出現的情況，排列熵如公式（9）所示。
 |
重構符號序列如公式（10）所示。
 |
式中 
為嵌入維數，
為延遲參數。
1.2.2 特征提取步驟
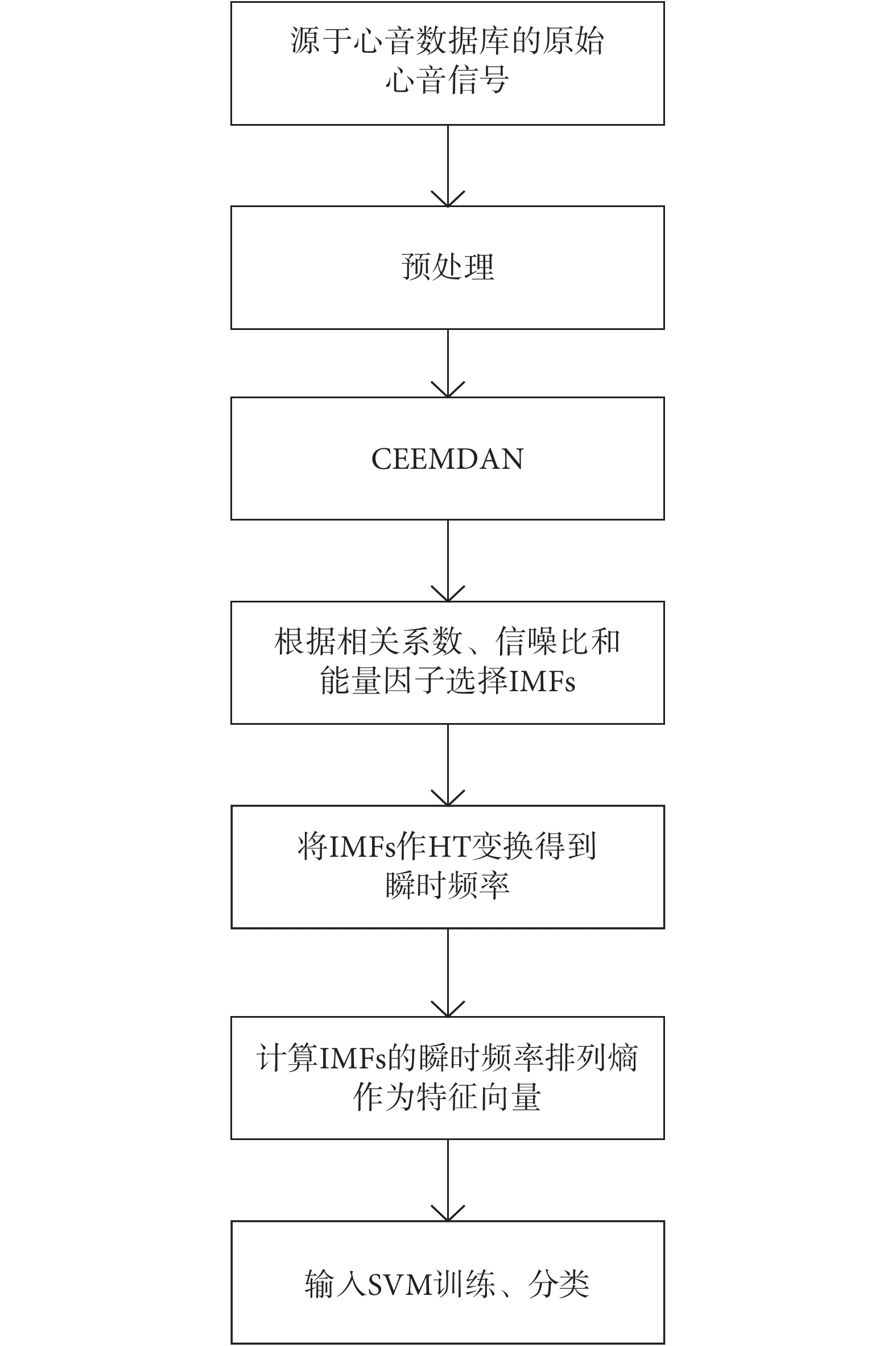
基于CEEMDAN排列熵與SVM的心音分類流程如圖2所示。CEEMDAN可以得到一系列頻率分層的IMF，而能夠反映心臟生理和病理信息的只有一部分IMF，因此，計算各IMF與原始心音信號的相關系數、信噪比與能量因子，挑選能量較大的IMF，并參考分量信號與原始信號的相關程度，分析某階的IMF有效性。本方法中的能量因子是選用DB6小波并進行5層小波分解原始心音信號，通過高頻系數和低頻系數構建原始信號的能量值，作為原始信號能量的頻域分布的指標。將有效的IMF做HT變換，獲得每階IMF在不同于原時域上的頻率分布即瞬時頻率，并計算各IMF的瞬時頻率排列熵，構成一維特征向量，輸入到SVM分類器中，進行分類訓練，實現心音分類診斷。
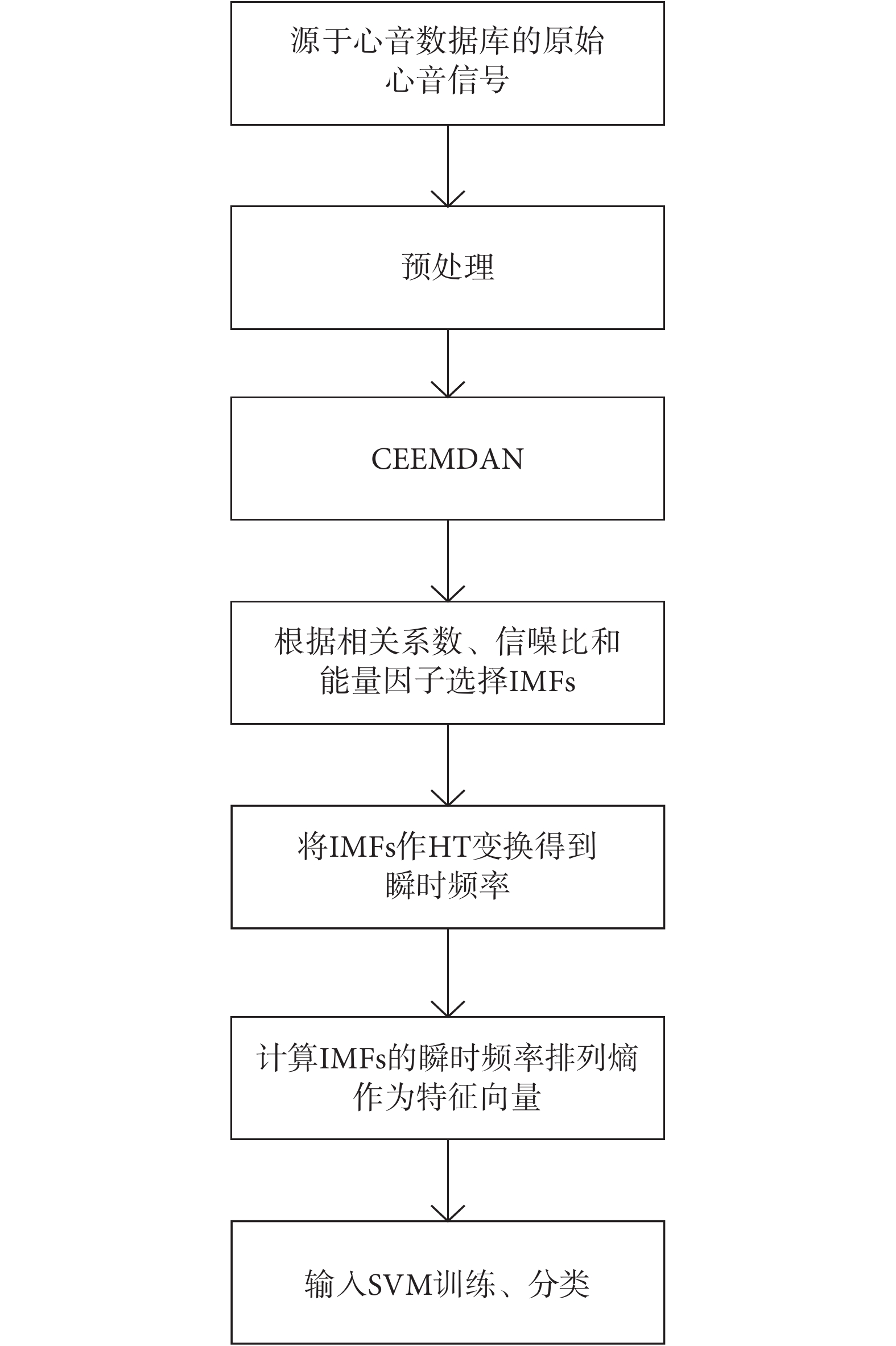圖2
心音分類流程
Figure2.
Flow chart of heart sound classification
2 結果
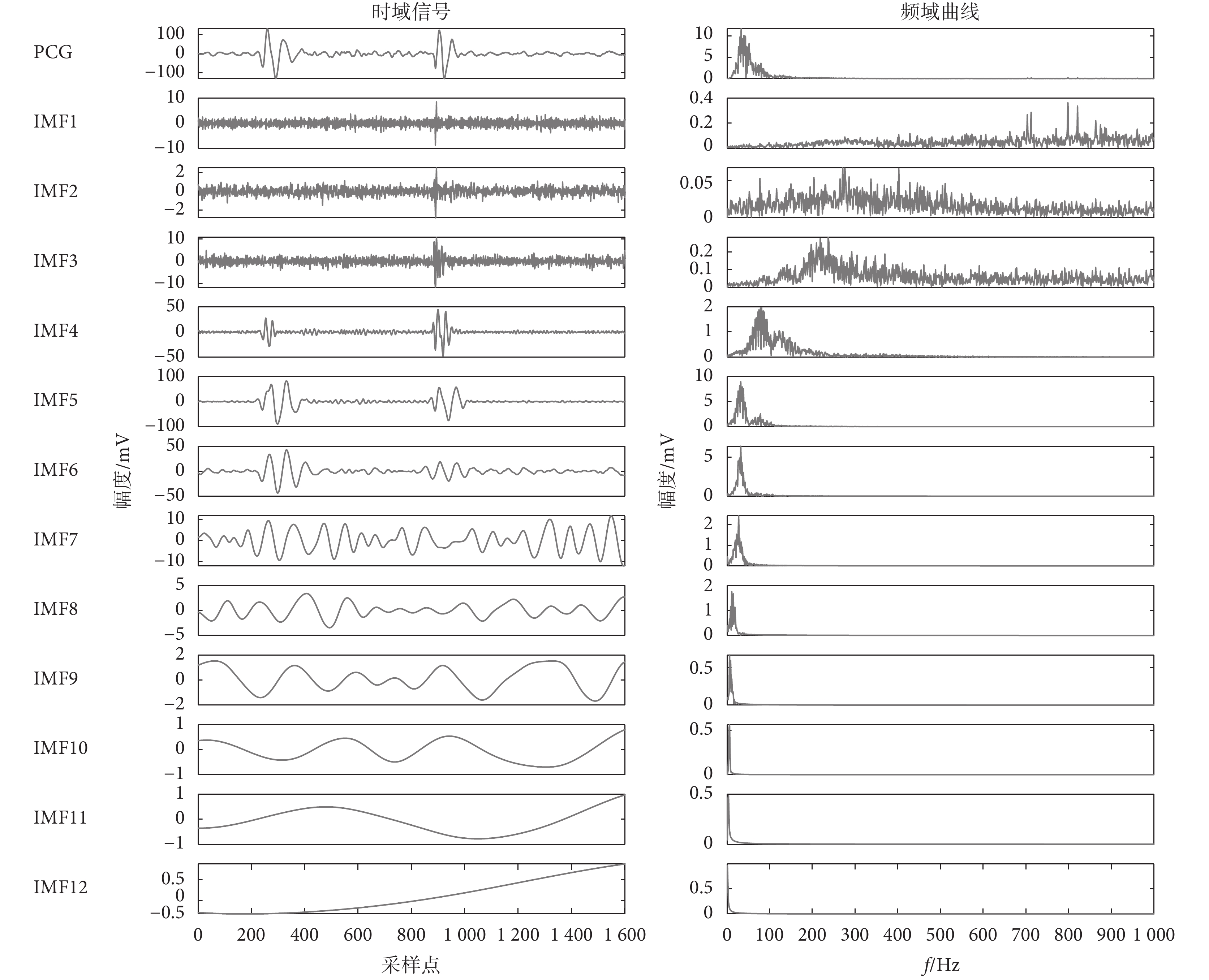
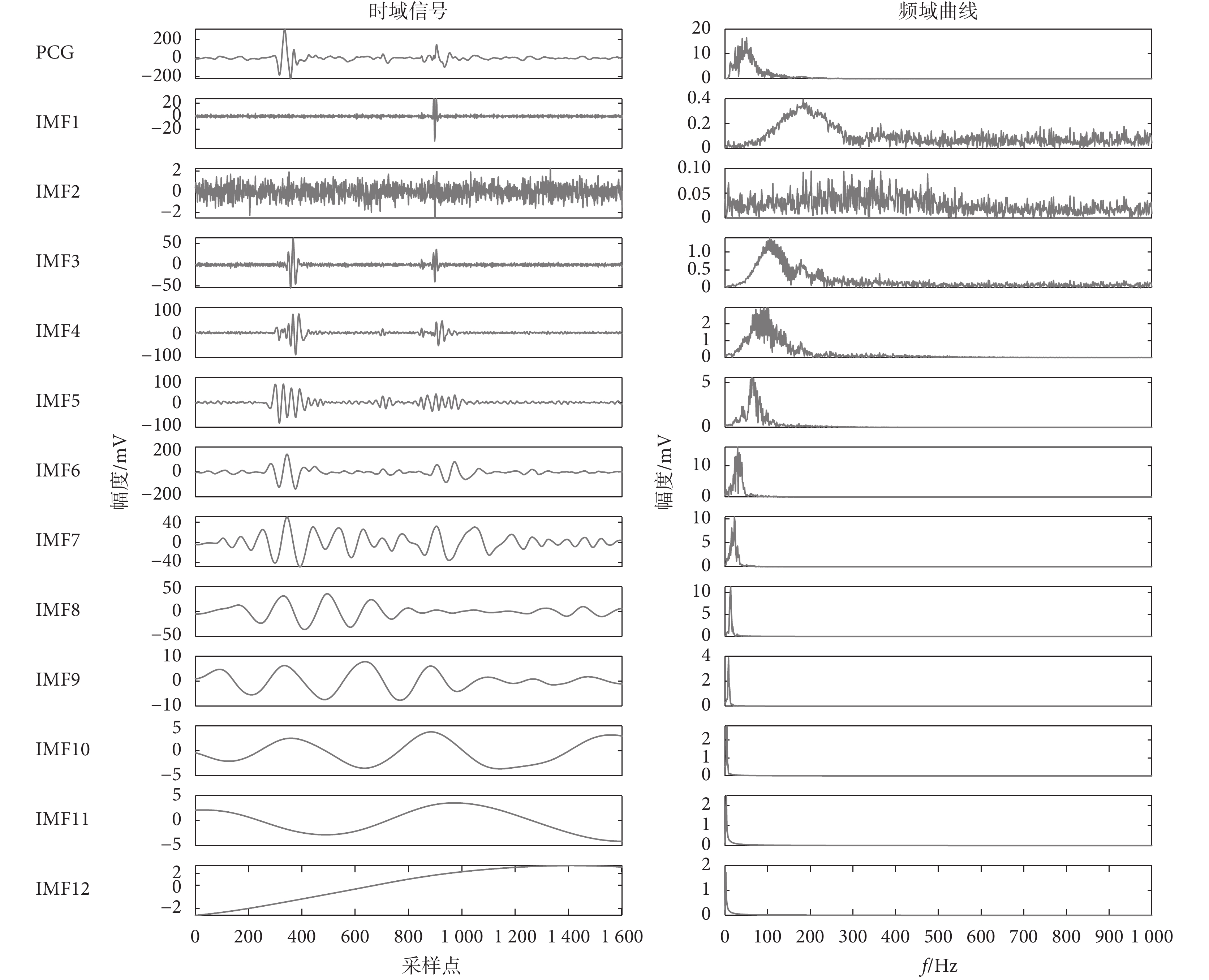
對經過預處理后的正常心音進行CEEMDAN分解，IMF的噪聲標準差為0.2，集總平均次數為50次，典型的正常與異常心音分解結果分別如圖3～4所示。由圖3可知，一個心跳周期的正常心音信號被分解為12個IMF，各IMF的頻譜由大到小、層層遞減，明確了心音信號的主要信息在0～300 Hz集中。由圖4可知，異常心音相比于正常心音分解的頻率分布更傾向于高頻分布，異常心音的分量頻率主要在200～300 Hz。
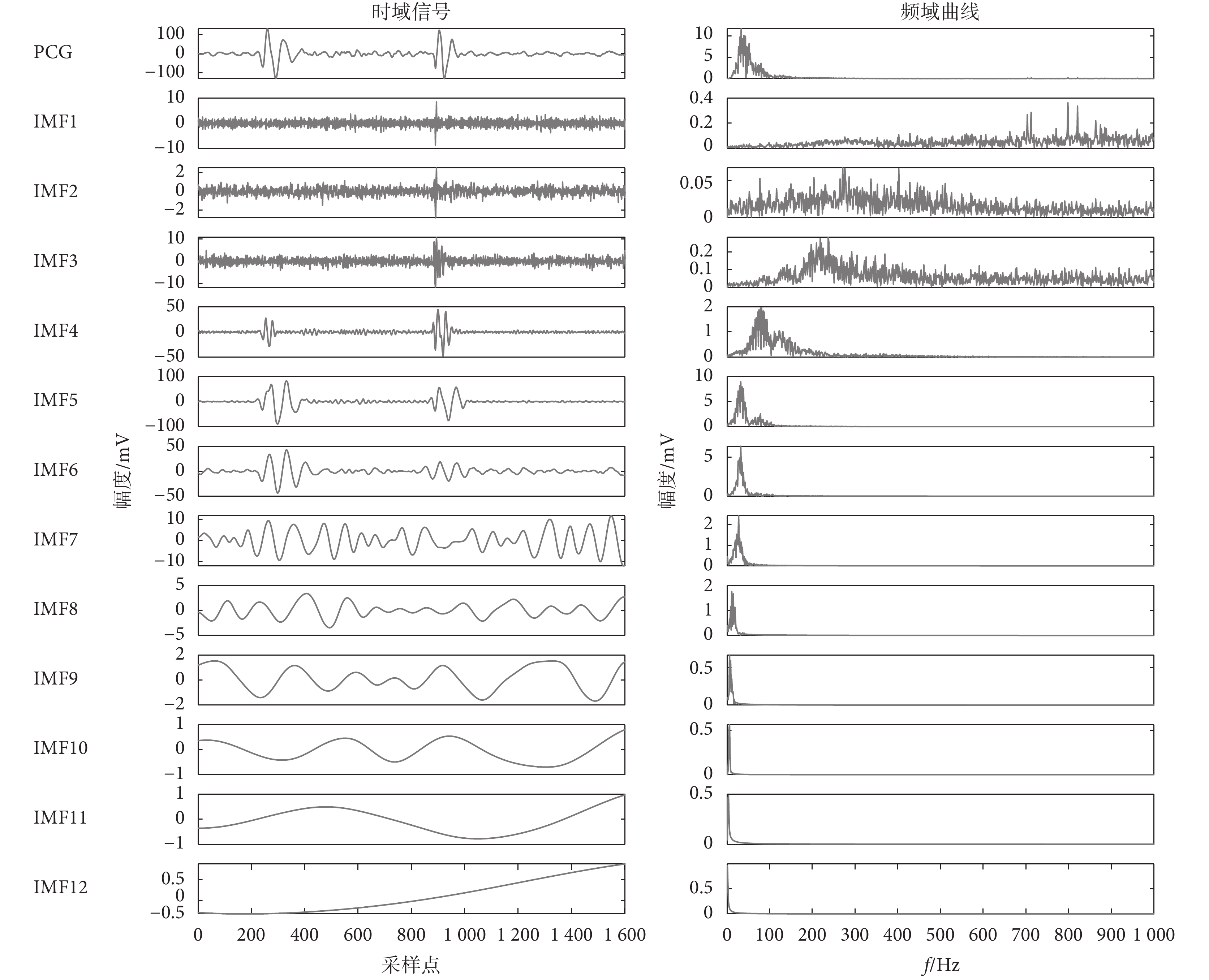圖3
正常心音信號CEEMDAN分解結果
Figure3.
CEEMDAN decomposition result of normal heart sounds signal
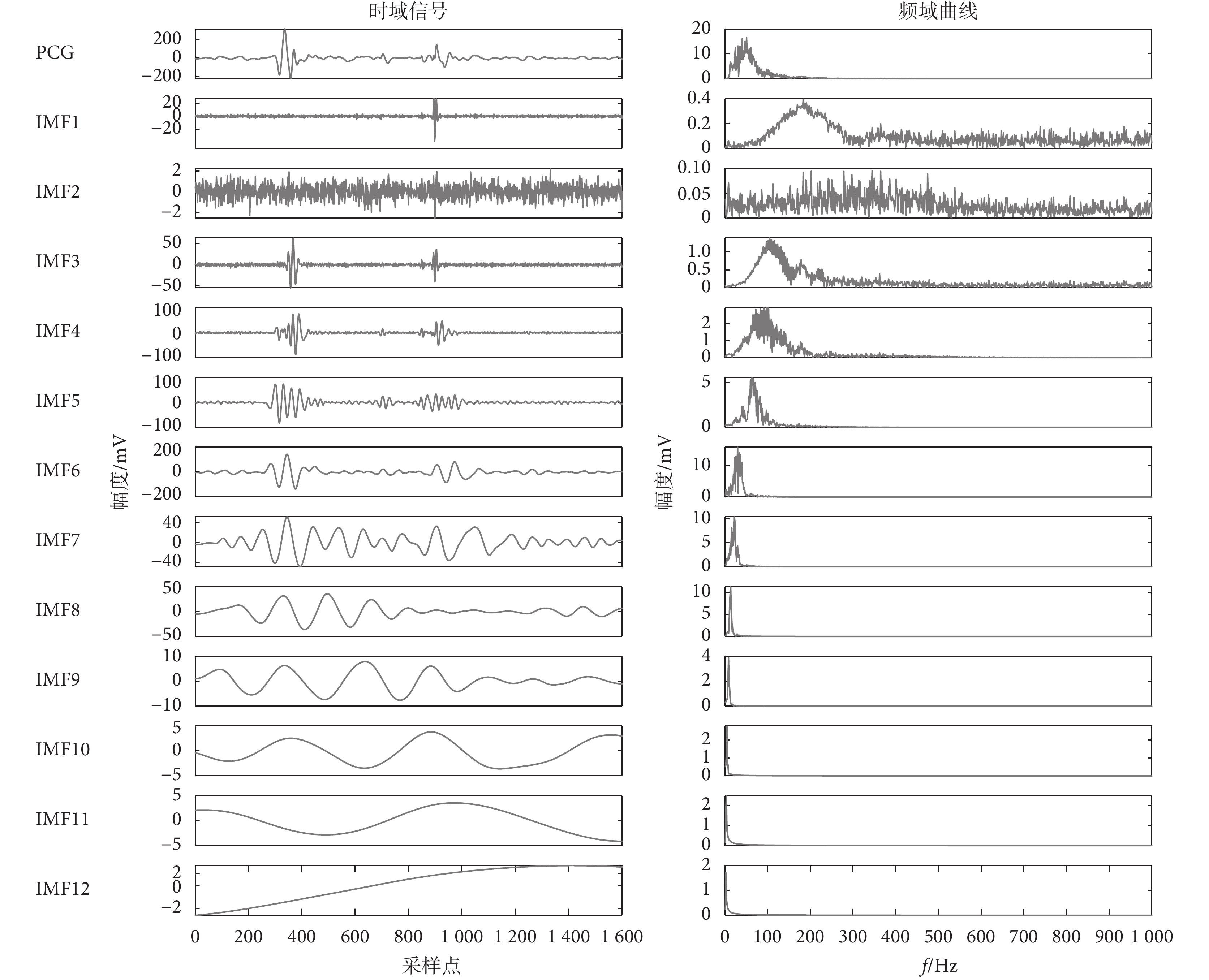圖4
異常心音信號CEEMDAN分解結果
Figure4.
CEEMDAN decomposition result of abnormal heart sounds signal
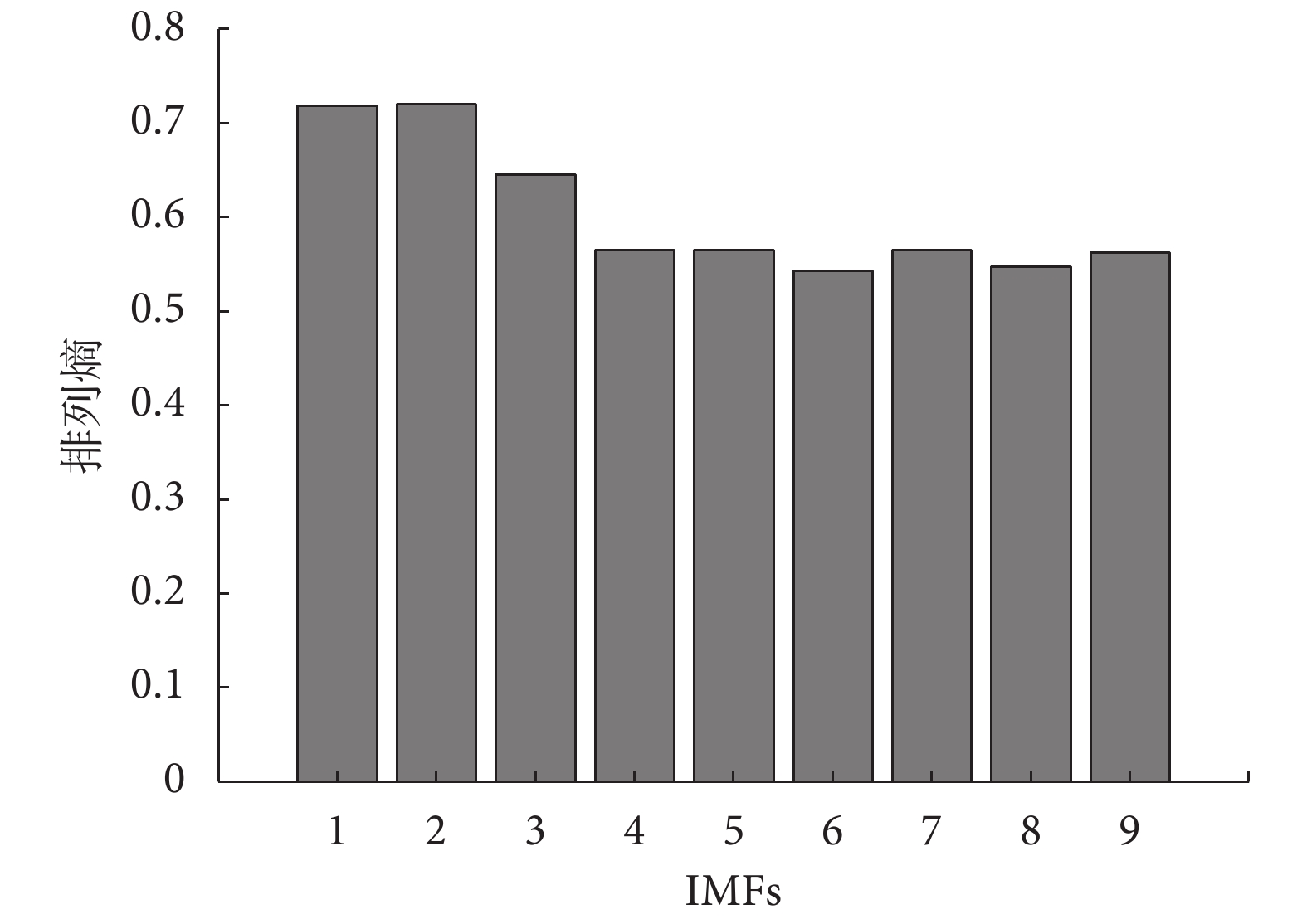
由于篇幅有限，只展示典型正常心音信號分解的各IMF與原始輸入心音信號的相關系數和能量因子值的大小，如表1所示。由表1可知，相關系數與能量因子值以及信噪比的分布都呈現兩頭小中間大的趨勢，考慮到CEEMDAN分解最后的余量信號能量較小，與原始心音信號的相關程度較低，而且信噪比較小，所以本文選擇前九階IMF進行下一步的處理。將前九階IMF做HT變換，取其瞬時頻率計算排列熵，組成一維特征向量。正常心音的前九階瞬時頻率排列熵如圖5所示，由圖5可知瞬時排列熵隨著IMF階數的增大而呈逐漸減小的趨勢，表明其所含信息成分越來越單一，與上述分析相符合。典型的正常心音與異常心音CEEMDAN排列熵對比如圖6所示。由圖6可知，異常心音的排列熵高于正常心音，說明排列熵越高所包含的信息內容越多、越復雜。
表1
各模態分量的相關系數、信噪比和能量因子
Table1.
Correlation coefficient, signal-to-noise ratio and energy factor of each IMF
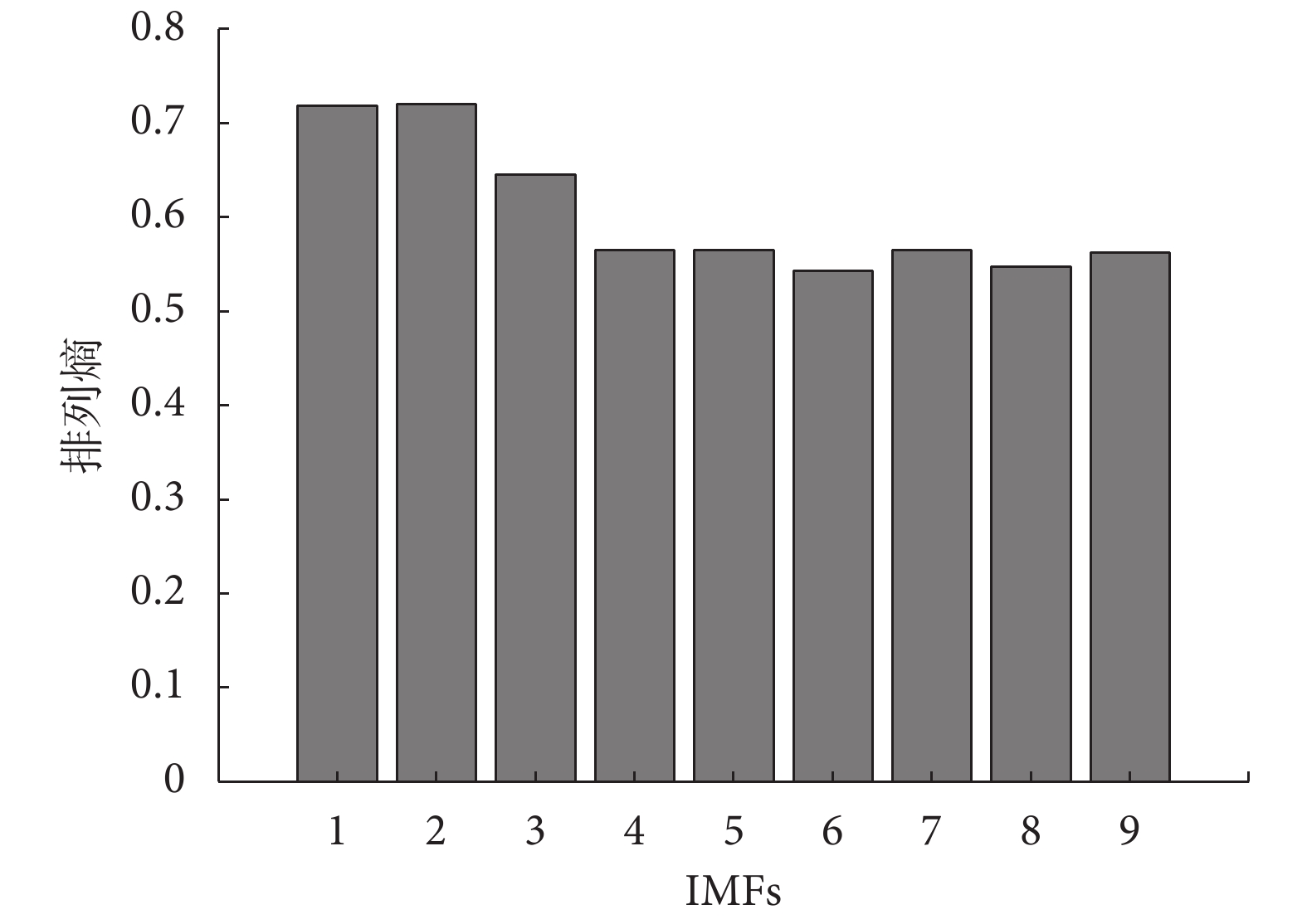圖5
各階IMF瞬時頻率排列熵
Figure5.
Instantaneous frequency permutation entropy of each IMF
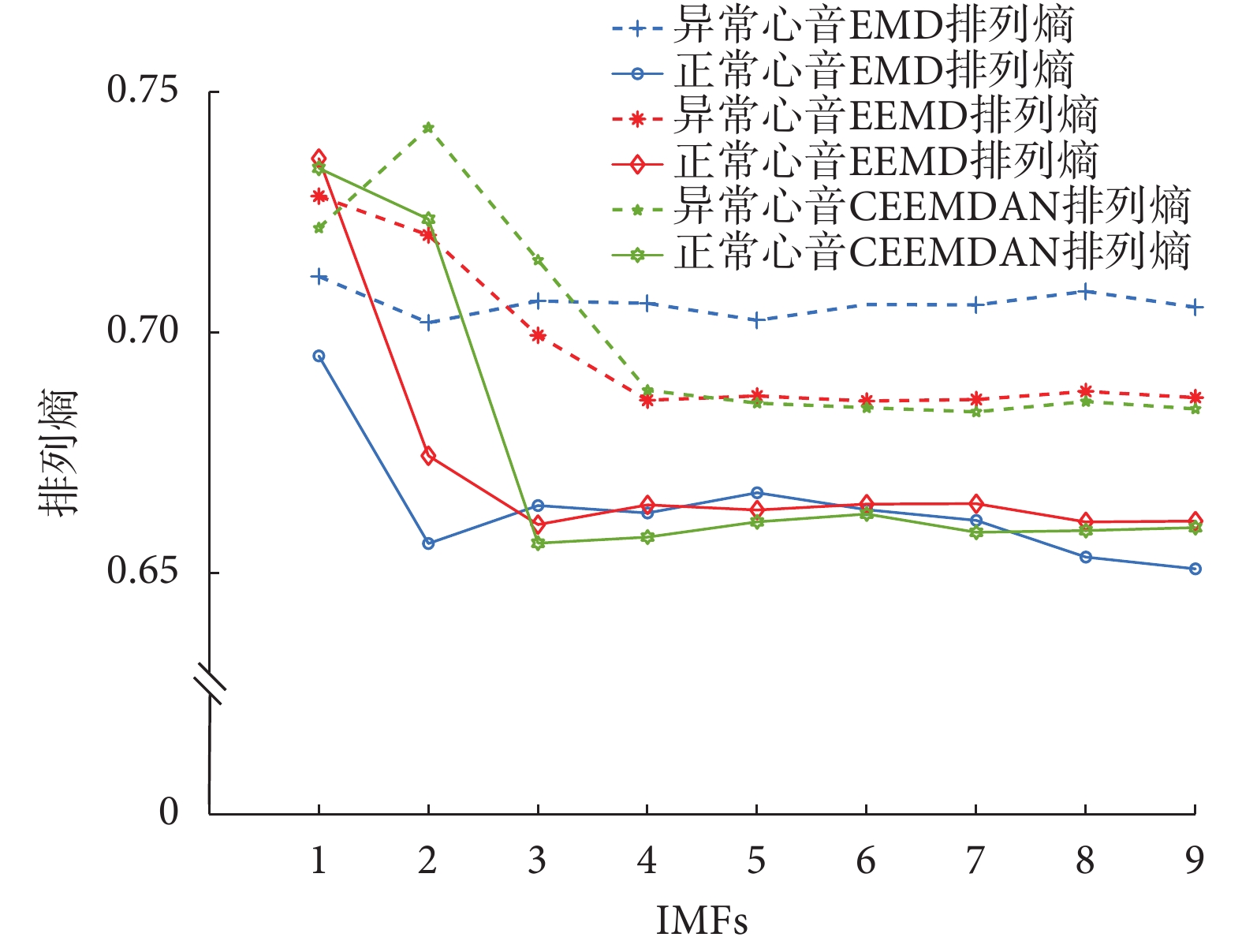
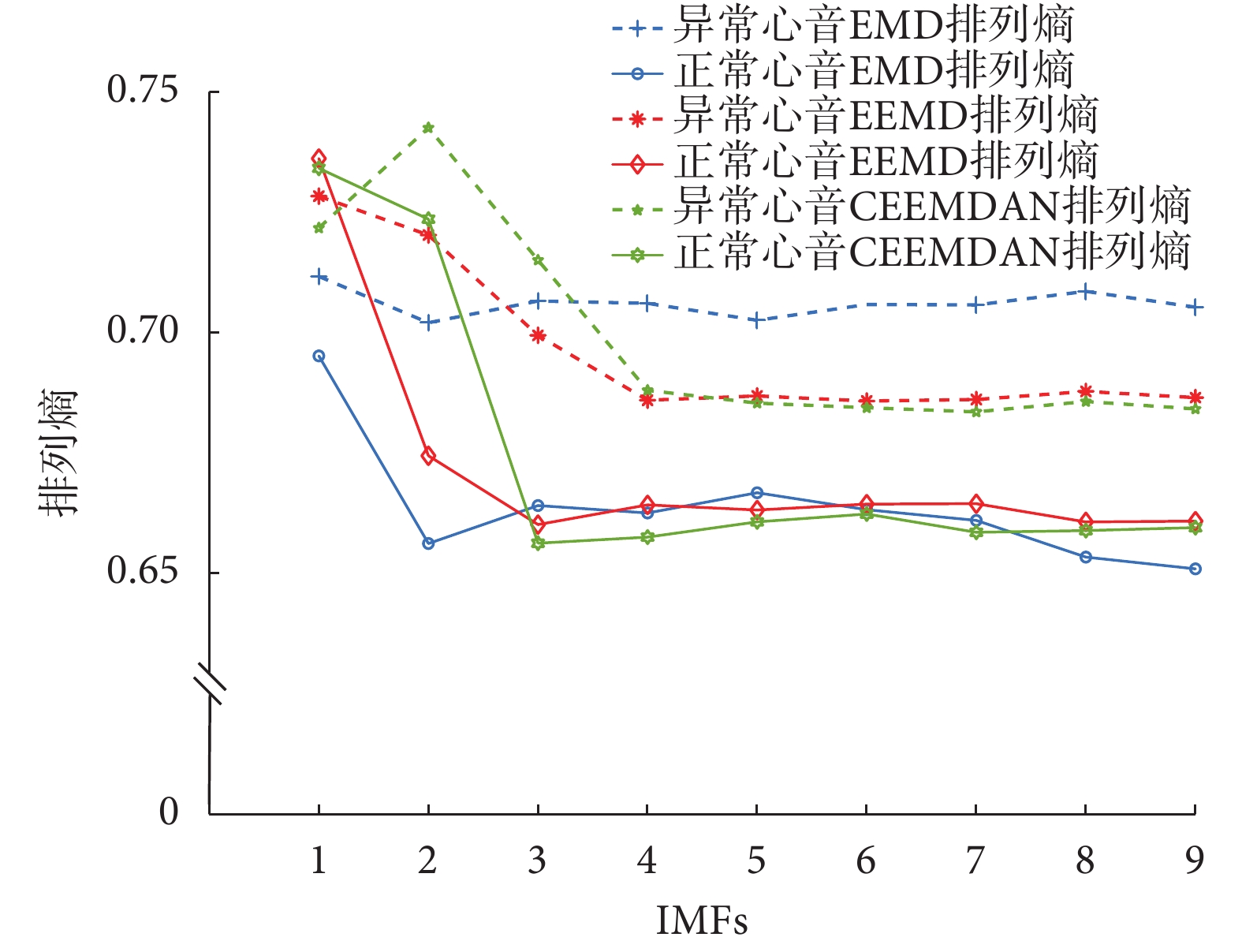圖6
正常心音與異常心音的EMD、EEMD、CEEMDAN排列 熵對比
Figure6.
Comparison of permutation entropy of EMD, EEMD and CEEMDAN of normal and abnormal heart sounds
2.1 評估指標
常用的三個心音分類評估指標為敏感性（sensitivity，Se）、特異性（specificity，Sp）和準確度（modified accuracy，Macc），計算公式分別如公式（11）～（13）所示。
 |
 |
 |
假設將正常心音信號的標簽設置為“1”，異常心音信號的標簽設置為“? 1”，則真陽性（true positive，
）是分類結果為“1”的正常心音信號數目；真陰性（true negative，
）是分類結果為“? 1”的異常心音信號數目；假陽性（false positive，
）是分類結果為“1”的異常心音信號數目；假陰性（false negative，
）是分類結果為“? 1”的正常心音信號數目。
選用分類器性能度量指標ROC曲線和AUC值來展現分類器的分類效果，ROC曲線與坐標軸真陽性率（true positive rate，TPR）和假陽性率（false positive rate，FPR）所圍成的面積（即AUC值）越接近于1，其分類能力越強，其中
，
。
2.2 EMD、EEMD、CEEMDAN排列熵結合SVM結果對比
選取200個原始心音信號作為訓練樣本，其中100個正常心音信號，100個異常心音信號。SVM選擇二分類訓練器，將“1”和“? 1”作為正常和異常心音信號的標簽。選擇高斯徑向基函數（radial basis function，RBF）作為核函數，采用交叉驗證的方法確定懲罰因子C和核函數參數Y，提高預測精度。測試樣本共100個原始心音數據，兩種心音模式各取50個數據，用訓練好的SVM分類器進行心音模式的分類識別。SVM分類結果準確度達到87%，AUC值為0.947 1，如表2所示。正常心音中有4個樣本被錯誤分類為異常心音即
，異常心音中有8個樣本被錯誤分類為正常心音即
。
表2
分類結果對比
Table2.
Comparison of classification results
為驗證本方法的優勢，將這300個樣本分別使用EMD和EEMD進行分解，同樣地選擇前九階IMF計算其瞬時排列熵。正常心音與異常心音信號的EMD、EEMD排列熵對比如圖6所示。由圖6可知，心音信號CEEMDAN排列熵在一階和二階IMF的區分度明顯優于EEMD、EMD，而三者高階IMF熵值的區分程度差異不大。總體來說，CEEMDAN的高階IMF熵值低于EMD、EEMD的高階IMF，而CEEMDAN的低階IMF熵值高于EMD、EEMD的低階IMF，所以，CEEMDAN表現出優異的分解能力，與理論相符。
然后分別將EMD和EEMD排列熵組成的特征向量輸入SVM分類器訓練，得到分類結果分別是66%、71%， AUC值分別為0.692 3、0.705 1，如表2所示。EMD排列熵結合SVM方法分類中 
12，FP = 22，EEMD排列熵結合SVM方法分類中 
，
，相比于CEEMDAN排列熵結合SVM分類，假陰性和假陽性增加明顯，敏感性、特異性和準確度都大幅下降。EMD、EEMD算法的處理效率雖然有所提升，但是分類性能比較CEEMDAN的分類方法下降了0.255、0.242，所以基于CEEMDAN排列熵為特征向量的分類結果高于EMD、EEMD的分類方法，表明了自適應噪聲完備經驗模態分解在心音分類中的優異性。
2.3 EMD、EEMD、CEEMDAN排列熵結合Fisher判別法結果對比
為了體現SVM分類器的優勢，本文將這300個樣本，按照同樣的特征向量提取方法，用Fisher兩類判別法分別對EMD、EEMD和CEEMDAN的IMF的瞬時排列熵進行判別模型的建立，分析后得到CEEMDAN-Fisher兩類判別法的判別函數如式（14）所示。
 |
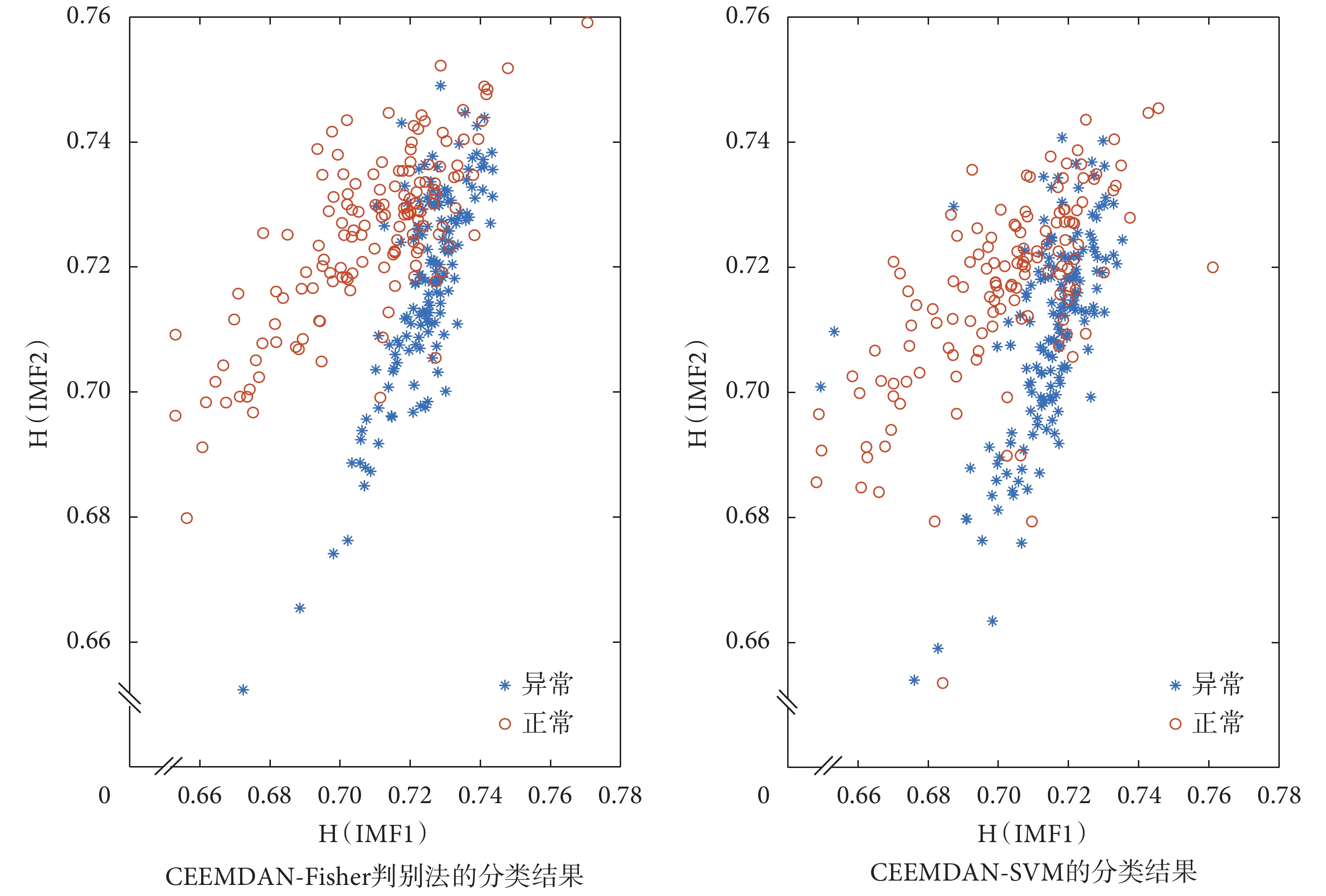
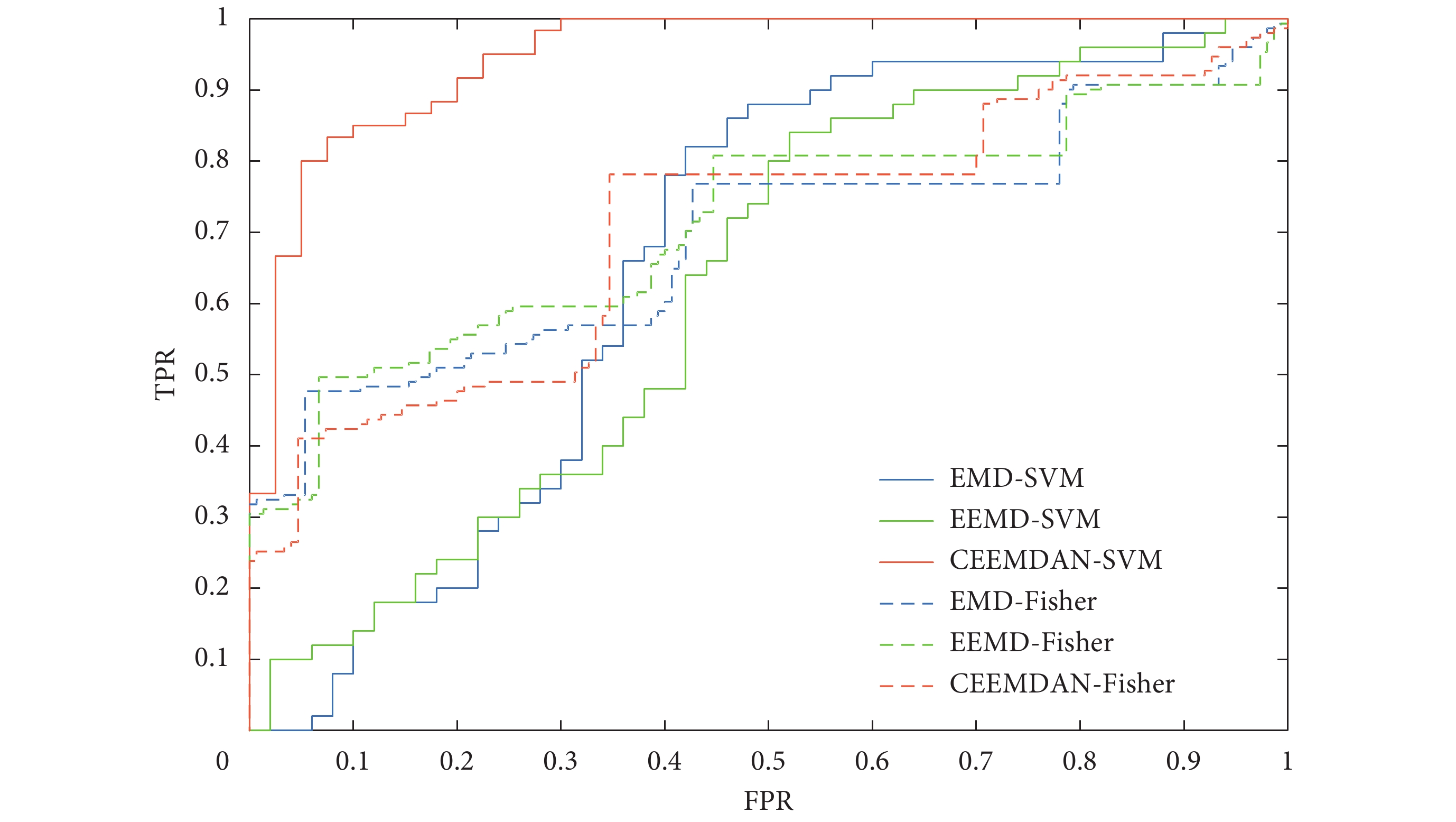
根據判別函數對心音信號的類型進行分類，結果為66.28%，AUC值為0.696 7。同理可得，EMD-Fisher、EEMD-Fisher兩類判別法的分類結果分別為65.61%、65.95%，AUC值分別為0.659 2、0.663 6，與其他算法的結果對比如表2所示。由表2可知，與SVM分類器不同的是，采用Fisher判別法，CEEMDAN排列熵相比EMD、EEMD的敏感性有所下降，特異性有所提高，準確度仍有小幅度增加。圖7是CEEMDAN-Fisher判別法和CEEMDAN-SVM兩種方法根據前兩階IMF熵值，繪制的正常心音與異常心音的分布結果。圖8是Fisher判別法和SVM二分類器的ROC曲線對比圖。由圖7、8分析可知，CEEMDAN-SVM的分類效果明顯優于其他方法。Fisher二類判別法對經驗模態分解的排列熵分類不敏感，不能很好地擬合判別函數，分類效果不佳。而SVM的分類結果優于Fisher二類判別法，能夠快速且較為準確地對心音信號進行分類。
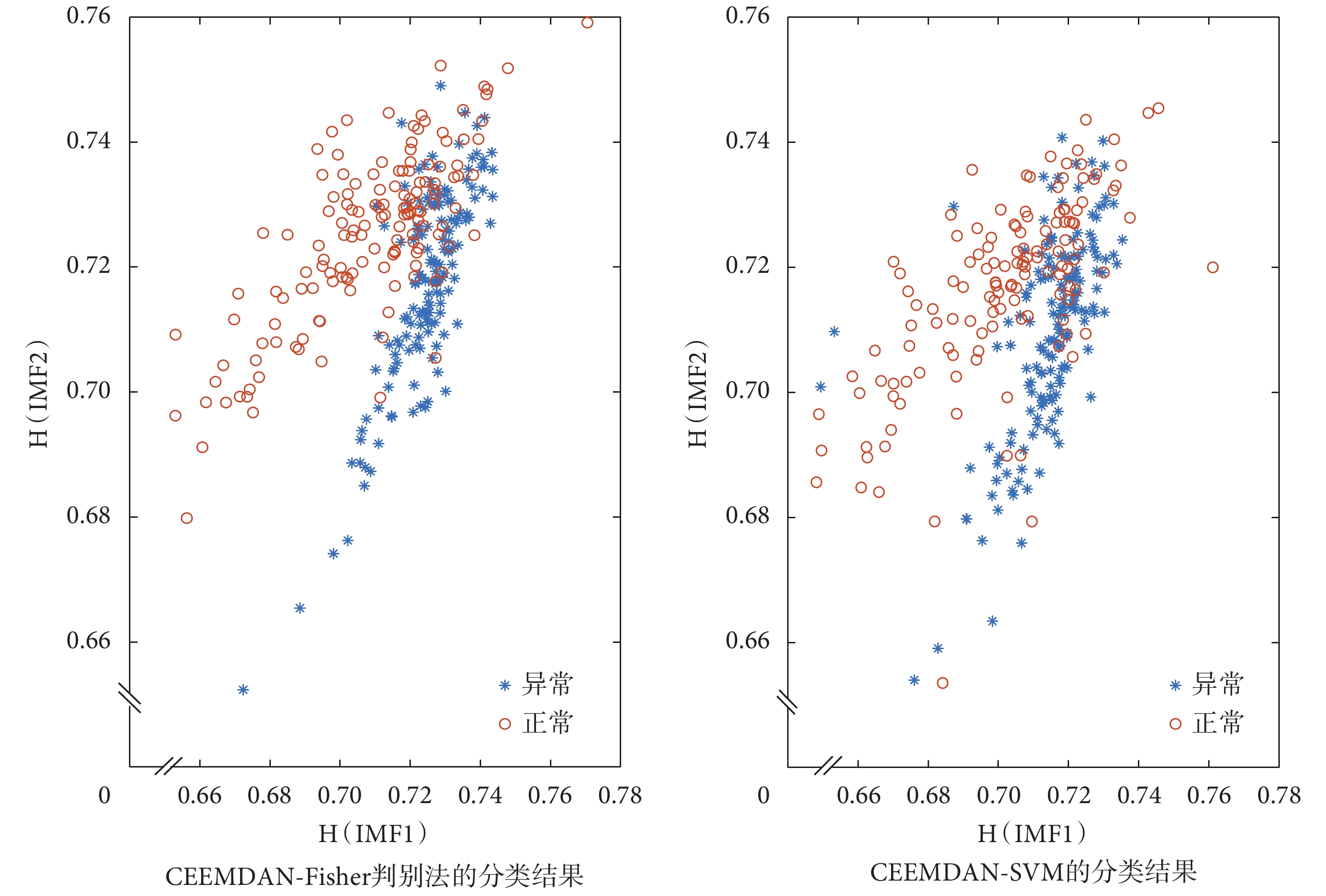圖7
CEEMDAN-Fisher判別法和CEEMDAN-SVM兩種方法的分類結果
Figure7.
Classification results of CEEMDAN-Fisher and CEEMDAN-SVM
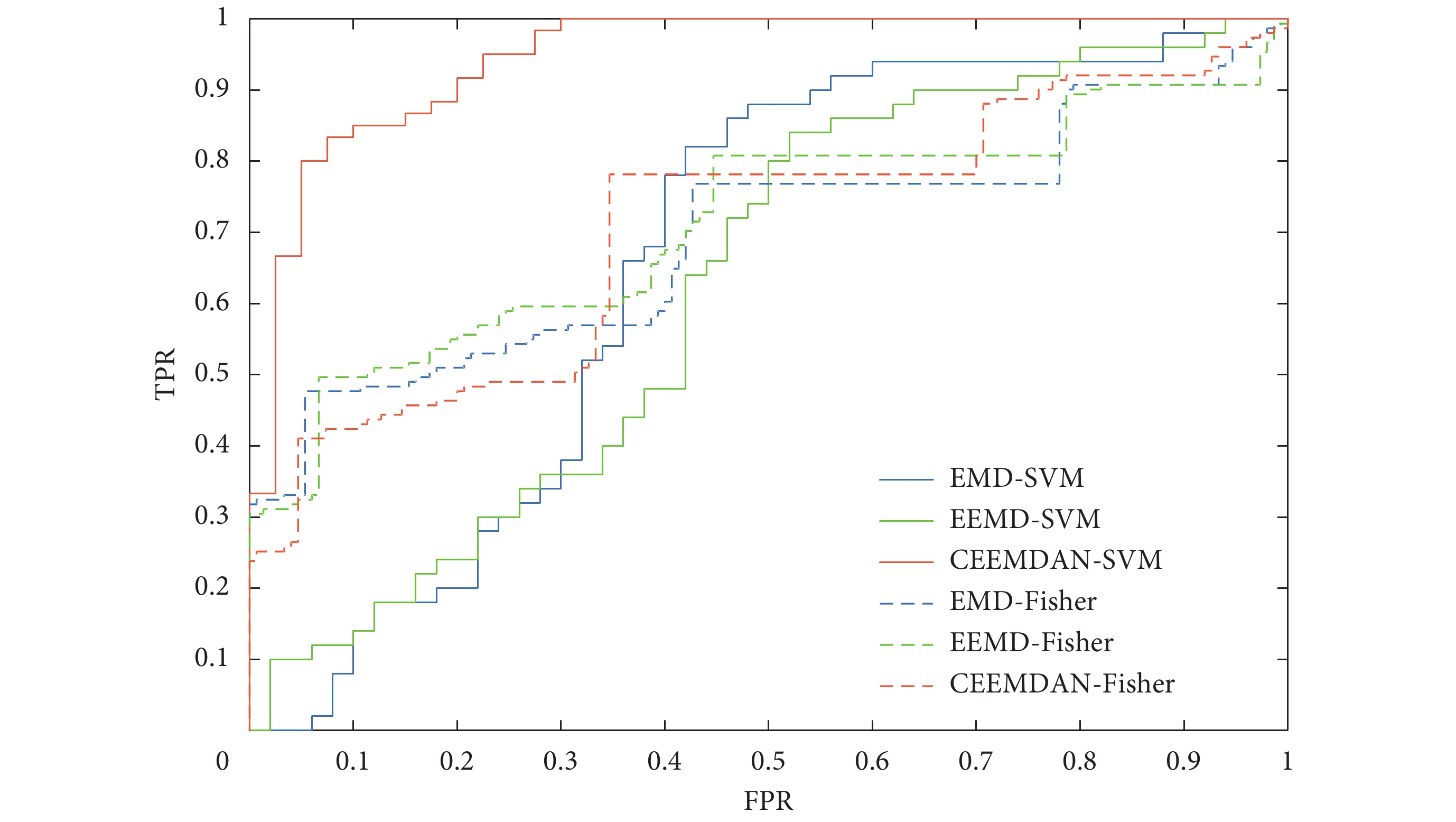圖8
Fisher和SVM兩種分類器的ROC曲線對比
Figure8.
Comparison of ROC curves of Fisher and SVM classifiers
3 討論
心音信號的特征提取是心音信號分類識別的重要內容。心音信號是人體重要的微弱生理信號之一，所包含的信息具有復雜性、非線性和非平穩性，沒有特定的特征提取標準。綜合時頻分析法和能量分析法，本方法避免了文獻[13]中EMD分解心音信號后產生模態混疊和虛假分量的問題，同時加入自適應白噪聲后，使得信號的重構誤差幾乎為零，提高了分量信號與原始信號的相關系數與分解效果。本研究提出將分量信號做HT變換得到瞬時頻率排列熵，計算每個分量中一定序列瞬時頻率出現的概率，相比于原始信號排列熵，分量排列熵更精準地提取了心音信號中頻率分布的信息，更準確地反映了心音信號的本質特征。但是，CEEMDAN分解的前兩階IMF中的幅頻特征存在一定的偽分量，相比于其他階IMF的排列熵較高，所以本方法也存在一定缺陷，有待于在今后的研究中提高特征提取的標準。
心音的分類必須將提取的特征向量與分類器結合才能高效地分類識別。由于Fisher判別分析法借助于方差分析的思想構造一個判別函數，使得投影后的兩組排列熵間標準化距離最大，是高維向低維的映射，不能有效地區別正常與異常心音兩個類別。本研究選擇SVM分類器將兩組特征向量投射到更高維空間，對特征空間劃分最優超平面，非常適用于小樣本、非線性分類。這種方法雖然用到了時頻和能量技術，但是仍然需要手動提取特征值和設置閾值，所以本研究的方法仍有改進的空間，未來工作將致力于卷積神經網絡分類器的研究。此外，本研究心音信號的訓練集與測試集都是來自不同個體的記錄，保證了樣本分布的合理性。
4 結論
本文提出一種CEEMDAN排列熵與SVM結合的心音分類方法，并通過對300例樣本數據進行仿真實驗，證明了該方法的有效性。分析結果表明，CEEMDAN排列熵能夠有效表明心音信號的內在信息排列特征、能量分布特征，可作為心音分類的特征向量，結合SVM可區分正常與異常心音，其分類結果明顯優于EMD和EEMD兩種算法。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：劉美君是本研究的實驗設計者和實驗研究的執行人，完成數據分析和論文寫作；吳全玉是項目的構思者及負責人，指導實驗設計、數據分析、論文修改；丁勝、潘玲佼、劉曉杰參與實驗設計和試驗結果分析。
引言
心音信號是心臟收縮舒張時血液與心室和主動脈壁碰撞引起的顫動所形成的一種聲音信號[1-2]，能夠反映出大量的心血管生理信息與病理信息，對臨床評估心臟功能狀態有重大意義[3-5]。由于心音信號的非線性和非平穩性[6-7]，心音信號分析研究的主要方法有時頻分析法和能量分析法，而且通常采用兩種方法相互結合對生理信號進行分析[8-10]。劉麗萍等[11]使用Choi-Williams分布時頻分析結合自回歸模型功率譜的時頻與能量分析方法，提取心音信號的特征向量。尹明等[12]在深入研究希爾伯特-黃變換（Hilbert-Huang transform，HHT）的基礎上，對降噪后的心音信號利用經驗模態分解（empirical mode decomposition，EMD）、希爾伯特變換（Hilbert transform，HT）及歸一化香農能量定理等從多個角度提取心音的特征值。黃林洲等[13]提出EMD與近似熵構成心音信號的特征向量。李宏全等[14]提出EMD與梅爾倒頻譜結合的方法，分類識別舒張期心雜音。Goda等[15]提取了收縮期和舒張期的頻率特性以及重新采樣的小波包絡特征，使用支持向量機（support vector machine，SVM）來對具有幾種訓練集配置的記錄進行分類，達到了80.28%的準確度。Grzegorczyk等[16]提出了基于神經網絡的機器學習算法，心音圖（phonocardiogram，PCG）信號的分割采用基于隱馬爾可夫模型的算法，將重點放在代表信號特征的統計特征上，獲得的最佳總體得分為0.79。Langley等[17]通過小波熵對未分割和短時心電圖進行分類，計算未分段5 s持續時間記錄的小波熵，并根據訓練集確定最佳小波尺度和小波熵閾值，在訓練集上獲得了78％的分數。本團隊[18]提出自適應噪聲完備經驗模態分解（complete ensemble empirical modal decomposition with adaptive noise，CEEMDAN）與盲反卷積結合的算法，分離腦電信號中含有的眼電偽跡。因此，經驗模態分解與時頻、能量分析對復雜的生理信號分析與處理有重大意義[19-20]。Wu等[21]提出了以EMD方法為核心的集總經驗模態分解（ensemble empirical modal decomposition，EEMD），在原始信號上多次加入高斯白噪聲，高斯白噪聲信號是一種便于分析的理想噪聲信號，利用其頻譜均勻分布的特性，使得重構信號在不同的時間尺度上具有連續性，解決了EMD模態混疊的問題。由于EEMD分解效率較低，Yeh等在EEMD的基礎上提出了互補集總經驗模態分解（complete ensemble empirical modal decomposition，CEEMD），在原始信號中加入一個白噪聲，再減去一個白噪聲，這樣很好地消除了重構信號中的殘余噪聲，而且使得集總平均次數減少，提高了分解效率，但是存在虛假的模態分量（intrinsic mode functions，IMF）[22-23]。而CEEMDAN[24]改進了以上方法的缺陷，在各個IMF中添加自適應的高斯白噪聲，使得重構誤差接近于零，分解效率極高而且完整。本團隊的前期工作中將CEEMDAN用在腦電信號的去噪預處理中，本文的改進點在于將CEEMDAN應用于心音信號的特征提取中。
本文提出了一種提取心音信號CEEMDAN模態分量的瞬時頻率排列熵做為特征向量，并通過SVM進行心音正常與異常分類識別的方法。最后，引入Fisher判別法，與SVM進行對比，驗證該方法是否可以有效應用于心音分類。
1 方法
1.1 數據的來源與預處理
本文的心音數據來源于PhysioNet與心臟病計算協會聯合舉辦的“心音記錄的分類—2016年PhysioNet/CinC挑戰賽”所提供的一個大型數據庫（https://www.physionet.org/challenge/2016/）[25-26]。數據庫里包括1 072名受試者中采集的4 430份心音記錄，每個記錄持續時間為5 ～120 s，采樣頻率為2 000 Hz，以*.wav的格式提供。心音記錄通常是從主動脈區、肺動脈區、三尖瓣區和二尖瓣區這四個不同位置之一收集的，記錄分為正常心音和異常心音兩種類型。正常記錄來自健康受試者，異常記錄來自經確診的典型的心臟瓣膜缺陷和冠狀動脈疾病（coronary artery disease，CAD）患者。
本文的實驗硬件配置為華碩FX506LI，CPU為Inter Core I7-10750H，主頻2.60 GHz，內存為DDR4，大小為16 GB，獨立顯卡為NVIDIA GeForce GTX 1650 Ti，顯存為6 GB。軟件配置為Microsoft Windows 10下的Matlab R2018b版本，算法運行時間通過Matlab中的tic和toc指令得到。
本文選用PhysioNet心音數據庫中300個心音樣本數據進行試驗，正常成年人的心跳周期為0.8 s，而心音數據庫里心音數據的采樣點為0.000 5 s，所以一個心跳周期為1 600個采樣點，為了便于分析，取了7.5個心跳周期進行研究。其中典型的正常與異常心音記錄如圖1所示。由于心音信號采集環境不受控制，許多錄音會包含各種噪音，例如談話、聽診器運動、呼吸和腸道聲音等。所以本文采用巴特沃斯低通濾波器，濾除原始信號中由于操作不當產生的1 000 Hz以上的噪聲；采用陷波器，濾除50 Hz的工頻干擾，對心音信號做預處理。
圖1
典型的正常與異常心音記錄圖
a. 正常心音時域信號；b. 異常心音時域信號；c. 正常心音頻域曲線；d. 異常心音頻域曲線
Figure1. Typical records of normal and abnormal heart soundsa. normal heart sound time domain signal; b. abnormal signal time domain signal; c. normal heart sound frequency domain curve; d. abnormal heart sound frequency domain curve
1.2 心音信號特征提取
1.2.1 CEEMDAN排列熵原理
CEEMDAN在EMD的基礎上加入了成對的正負白噪聲，消除了虛假的IMF，提高了分解準確性。CEEMDAN算法步驟如下：
① 在原始信號中加入高斯白噪聲組成新的構造信號 ，其中， 為原始信號， 為一階噪聲標準差， 為服從 分布的白噪聲，表示第j次分解添加的白噪聲，。
② 對 進行N次EMD分解，第一次分解結束后取均值，得到一階模態分量 ，如式（1）所示：
|
同時一階余量信號 如式（2）所示：
|
③ 當 的極值點個數超過2個時，對EMD分解的一階模態算子加入一階余量信號 構成新的余量信號 進行EMD分解，得到二階模態分量 ，見式（3）：
|
其中， 表示二階噪聲標準差， 為對信號進行EMD分解后的第 階 IMF 模態算子， 為EMD分解產生的一階模態的算子。
④ 循環步驟 ③，直到余量信號不能再分解，原始信號被分解如式（4）所示：
|
其中，K 表示模態分解的次數；k表示模態分解的層數，。
在第 層分解中，計算 階余量信號 如式（5）所示：
|
階模態分量 如式（6）所示：
|
其中， 表示 階模態分量， 表示 階噪聲標準差。
HT變換是一種常用的信號處理方法，其定義如式（7）所示。
|
其中 為原始信號。
本文將CEEMDAN的IMF作為原始信號進行HT變換，則HT變換 定義如式（8）所示。
|
熵是描述信號源不確定度的量。排列熵是描述一維非線性時間序列信號復雜性與混亂程度的熵算法，作為可定量描述時間序列信號復雜程度與混亂程度的熵值參數，信號越復雜，排列熵值越大。因此，可以用排列熵來表示心音信號在不同于原來時間尺度下的不同頻帶出現的情況，排列熵如公式（9）所示。
|
重構符號序列如公式（10）所示。
|
式中 為嵌入維數， 為延遲參數。
1.2.2 特征提取步驟
基于CEEMDAN排列熵與SVM的心音分類流程如圖2所示。CEEMDAN可以得到一系列頻率分層的IMF，而能夠反映心臟生理和病理信息的只有一部分IMF，因此，計算各IMF與原始心音信號的相關系數、信噪比與能量因子，挑選能量較大的IMF，并參考分量信號與原始信號的相關程度，分析某階的IMF有效性。本方法中的能量因子是選用DB6小波并進行5層小波分解原始心音信號，通過高頻系數和低頻系數構建原始信號的能量值，作為原始信號能量的頻域分布的指標。將有效的IMF做HT變換，獲得每階IMF在不同于原時域上的頻率分布即瞬時頻率，并計算各IMF的瞬時頻率排列熵，構成一維特征向量，輸入到SVM分類器中，進行分類訓練，實現心音分類診斷。
圖2
心音分類流程
Figure2.
Flow chart of heart sound classification
2 結果
對經過預處理后的正常心音進行CEEMDAN分解，IMF的噪聲標準差為0.2，集總平均次數為50次，典型的正常與異常心音分解結果分別如圖3～4所示。由圖3可知，一個心跳周期的正常心音信號被分解為12個IMF，各IMF的頻譜由大到小、層層遞減，明確了心音信號的主要信息在0～300 Hz集中。由圖4可知，異常心音相比于正常心音分解的頻率分布更傾向于高頻分布，異常心音的分量頻率主要在200～300 Hz。
圖3
正常心音信號CEEMDAN分解結果
Figure3.
CEEMDAN decomposition result of normal heart sounds signal
圖4
異常心音信號CEEMDAN分解結果
Figure4.
CEEMDAN decomposition result of abnormal heart sounds signal
由于篇幅有限，只展示典型正常心音信號分解的各IMF與原始輸入心音信號的相關系數和能量因子值的大小，如表1所示。由表1可知，相關系數與能量因子值以及信噪比的分布都呈現兩頭小中間大的趨勢，考慮到CEEMDAN分解最后的余量信號能量較小，與原始心音信號的相關程度較低，而且信噪比較小，所以本文選擇前九階IMF進行下一步的處理。將前九階IMF做HT變換，取其瞬時頻率計算排列熵，組成一維特征向量。正常心音的前九階瞬時頻率排列熵如圖5所示，由圖5可知瞬時排列熵隨著IMF階數的增大而呈逐漸減小的趨勢，表明其所含信息成分越來越單一，與上述分析相符合。典型的正常心音與異常心音CEEMDAN排列熵對比如圖6所示。由圖6可知，異常心音的排列熵高于正常心音，說明排列熵越高所包含的信息內容越多、越復雜。
表1
各模態分量的相關系數、信噪比和能量因子
Table1.
Correlation coefficient, signal-to-noise ratio and energy factor of each IMF
圖5
各階IMF瞬時頻率排列熵
Figure5.
Instantaneous frequency permutation entropy of each IMF
圖6
正常心音與異常心音的EMD、EEMD、CEEMDAN排列 熵對比
Figure6.
Comparison of permutation entropy of EMD, EEMD and CEEMDAN of normal and abnormal heart sounds
2.1 評估指標
常用的三個心音分類評估指標為敏感性（sensitivity，Se）、特異性（specificity，Sp）和準確度（modified accuracy，Macc），計算公式分別如公式（11）～（13）所示。
|
|
|
假設將正常心音信號的標簽設置為“1”，異常心音信號的標簽設置為“? 1”，則真陽性（true positive，）是分類結果為“1”的正常心音信號數目；真陰性（true negative，）是分類結果為“? 1”的異常心音信號數目；假陽性（false positive，）是分類結果為“1”的異常心音信號數目；假陰性（false negative，）是分類結果為“? 1”的正常心音信號數目。
選用分類器性能度量指標ROC曲線和AUC值來展現分類器的分類效果，ROC曲線與坐標軸真陽性率（true positive rate，TPR）和假陽性率（false positive rate，FPR）所圍成的面積（即AUC值）越接近于1，其分類能力越強，其中，。
2.2 EMD、EEMD、CEEMDAN排列熵結合SVM結果對比
選取200個原始心音信號作為訓練樣本，其中100個正常心音信號，100個異常心音信號。SVM選擇二分類訓練器，將“1”和“? 1”作為正常和異常心音信號的標簽。選擇高斯徑向基函數（radial basis function，RBF）作為核函數，采用交叉驗證的方法確定懲罰因子C和核函數參數Y，提高預測精度。測試樣本共100個原始心音數據，兩種心音模式各取50個數據，用訓練好的SVM分類器進行心音模式的分類識別。SVM分類結果準確度達到87%，AUC值為0.947 1，如表2所示。正常心音中有4個樣本被錯誤分類為異常心音即，異常心音中有8個樣本被錯誤分類為正常心音即。
表2
分類結果對比
Table2.
Comparison of classification results
為驗證本方法的優勢，將這300個樣本分別使用EMD和EEMD進行分解，同樣地選擇前九階IMF計算其瞬時排列熵。正常心音與異常心音信號的EMD、EEMD排列熵對比如圖6所示。由圖6可知，心音信號CEEMDAN排列熵在一階和二階IMF的區分度明顯優于EEMD、EMD，而三者高階IMF熵值的區分程度差異不大。總體來說，CEEMDAN的高階IMF熵值低于EMD、EEMD的高階IMF，而CEEMDAN的低階IMF熵值高于EMD、EEMD的低階IMF，所以，CEEMDAN表現出優異的分解能力，與理論相符。
然后分別將EMD和EEMD排列熵組成的特征向量輸入SVM分類器訓練，得到分類結果分別是66%、71%， AUC值分別為0.692 3、0.705 1，如表2所示。EMD排列熵結合SVM方法分類中 12，FP = 22，EEMD排列熵結合SVM方法分類中 ，，相比于CEEMDAN排列熵結合SVM分類，假陰性和假陽性增加明顯，敏感性、特異性和準確度都大幅下降。EMD、EEMD算法的處理效率雖然有所提升，但是分類性能比較CEEMDAN的分類方法下降了0.255、0.242，所以基于CEEMDAN排列熵為特征向量的分類結果高于EMD、EEMD的分類方法，表明了自適應噪聲完備經驗模態分解在心音分類中的優異性。
2.3 EMD、EEMD、CEEMDAN排列熵結合Fisher判別法結果對比
為了體現SVM分類器的優勢，本文將這300個樣本，按照同樣的特征向量提取方法，用Fisher兩類判別法分別對EMD、EEMD和CEEMDAN的IMF的瞬時排列熵進行判別模型的建立，分析后得到CEEMDAN-Fisher兩類判別法的判別函數如式（14）所示。
|
根據判別函數對心音信號的類型進行分類，結果為66.28%，AUC值為0.696 7。同理可得，EMD-Fisher、EEMD-Fisher兩類判別法的分類結果分別為65.61%、65.95%，AUC值分別為0.659 2、0.663 6，與其他算法的結果對比如表2所示。由表2可知，與SVM分類器不同的是，采用Fisher判別法，CEEMDAN排列熵相比EMD、EEMD的敏感性有所下降，特異性有所提高，準確度仍有小幅度增加。圖7是CEEMDAN-Fisher判別法和CEEMDAN-SVM兩種方法根據前兩階IMF熵值，繪制的正常心音與異常心音的分布結果。圖8是Fisher判別法和SVM二分類器的ROC曲線對比圖。由圖7、8分析可知，CEEMDAN-SVM的分類效果明顯優于其他方法。Fisher二類判別法對經驗模態分解的排列熵分類不敏感，不能很好地擬合判別函數，分類效果不佳。而SVM的分類結果優于Fisher二類判別法，能夠快速且較為準確地對心音信號進行分類。
圖7
CEEMDAN-Fisher判別法和CEEMDAN-SVM兩種方法的分類結果
Figure7.
Classification results of CEEMDAN-Fisher and CEEMDAN-SVM
圖8
Fisher和SVM兩種分類器的ROC曲線對比
Figure8.
Comparison of ROC curves of Fisher and SVM classifiers
3 討論
心音信號的特征提取是心音信號分類識別的重要內容。心音信號是人體重要的微弱生理信號之一，所包含的信息具有復雜性、非線性和非平穩性，沒有特定的特征提取標準。綜合時頻分析法和能量分析法，本方法避免了文獻[13]中EMD分解心音信號后產生模態混疊和虛假分量的問題，同時加入自適應白噪聲后，使得信號的重構誤差幾乎為零，提高了分量信號與原始信號的相關系數與分解效果。本研究提出將分量信號做HT變換得到瞬時頻率排列熵，計算每個分量中一定序列瞬時頻率出現的概率，相比于原始信號排列熵，分量排列熵更精準地提取了心音信號中頻率分布的信息，更準確地反映了心音信號的本質特征。但是，CEEMDAN分解的前兩階IMF中的幅頻特征存在一定的偽分量，相比于其他階IMF的排列熵較高，所以本方法也存在一定缺陷，有待于在今后的研究中提高特征提取的標準。
心音的分類必須將提取的特征向量與分類器結合才能高效地分類識別。由于Fisher判別分析法借助于方差分析的思想構造一個判別函數，使得投影后的兩組排列熵間標準化距離最大，是高維向低維的映射，不能有效地區別正常與異常心音兩個類別。本研究選擇SVM分類器將兩組特征向量投射到更高維空間，對特征空間劃分最優超平面，非常適用于小樣本、非線性分類。這種方法雖然用到了時頻和能量技術，但是仍然需要手動提取特征值和設置閾值，所以本研究的方法仍有改進的空間，未來工作將致力于卷積神經網絡分類器的研究。此外，本研究心音信號的訓練集與測試集都是來自不同個體的記錄，保證了樣本分布的合理性。
4 結論
本文提出一種CEEMDAN排列熵與SVM結合的心音分類方法，并通過對300例樣本數據進行仿真實驗，證明了該方法的有效性。分析結果表明，CEEMDAN排列熵能夠有效表明心音信號的內在信息排列特征、能量分布特征，可作為心音分類的特征向量，結合SVM可區分正常與異常心音，其分類結果明顯優于EMD和EEMD兩種算法。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：劉美君是本研究的實驗設計者和實驗研究的執行人，完成數據分析和論文寫作；吳全玉是項目的構思者及負責人，指導實驗設計、數據分析、論文修改；丁勝、潘玲佼、劉曉杰參與實驗設計和試驗結果分析。
