自主運動過程中，運動皮層和效應肌之間的功能耦合可以通過計算腦電（EEG）信號和表面肌電（sEMG）信號之間的耦合來量化。最大信息系數算法（MIC）被證明能夠有效量化這種神經信號之間的耦合關系，然而實際使用中也存在計算耗時長的問題。為解決該問題，基于改進的K均值（K-means++）算法的高效聚類特性，本文提出了一種改進的MIC算法用以準確檢測非線性時間序列之間的耦合強度。仿真結果表明，本文所提改進的MIC算法能夠在不同噪聲水平下快速而準確捕獲非線性時間序列之間的耦合關系。基于腦卒中患者的右腳背屈試驗結果表明，改進的MIC算法能準確捕獲EEG信號和sEMG信號在特定頻帶上的耦合強度；相比健康對照組，腦卒中患者組的beta頻段（14～30 Hz）和gamma頻段（31～45 Hz）的皮質肌功能耦合（FCMC）顯著更弱，beta頻段MIC值與福格-邁爾評定量表（FMA）評分正相關。本研究所提算法有望成為腦卒中患者運動功能量化評估的新手段。
引用本文： 梁鐵, 張清愉, 洪磊, 劉曉光, 董斌, 王洪瑞, 劉秀玲. 一種改進的最大信息系數算法在腦卒中患者的皮質肌功能耦合分析中的應用. 生物醫學工程學雜志, 2021, 38(6): 1154-1162. doi: 10.7507/1001-5515.202106062 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
腦卒中由于其高發病率和高致殘率已經成為社會關注的問題。運動功能障礙是腦卒中患者常見的后遺癥。準確評估腦卒中患者運動神經系統功能狀態是提高康復治療效果的基礎。傳統的臨床運動功能評估過分依靠醫生的主觀經驗，存在一定局限性[1-2]。人體大腦運動皮層產生的控制信號驅動效應肌肉動作，從而產生自主運動[3-4]。由于包含了大量的運動控制?響應信息，大腦運動皮層的腦電（electroencephalogram，EEG）信號和效應肌的肌電（electromyography，EMG）信號在自主運動過程中也被證實存在特定頻段的功能耦合[5-7]。近年來，隨著非侵入式檢測技術的快速發展，利用EEG信號和表面肌電 (surface electromyography，sEMG) 信號來探討皮質肌功能耦合（functional corticomuscular coupling，FCMC）已經成為腦卒中康復領域研究的熱點[8-10]。定量分析FCMC能夠為分析運動神經系統功能、評估運動功能障礙患者（如腦卒中患者）的康復效果提供重要手段。
FCMC研究中的一個重要挑戰是準確識別EEG信號和sEMG信號之間的耦合。目前大多數研究主要是基于頻域的相干性算法來評估皮質肌功能耦合[7, 11-12]。一些基于相干性的擴展算法也被提出并應用于FCMC研究，例如Tuncel等[13]提出的時頻相干算法以及Xu等[14]提出的時滯相干算法。然而，EEG信號和sEMG信號屬于典型的神經生理信號，已被證明具有典型的非線性特征[15-16]。相干性方法主要用于測量線性耦合，在研究復雜的非線性的EEG信號和sEMG信號之間功能耦合上有一定局限性。
Reshef等[17]在2011年提出了最大信息系數（maximal information coefficient，MIC）算法來捕捉兩個變量之間的相關關系。近年來，MIC算法已逐漸應用于神經科學領域[18-19]。Su等[18]應用MIC構建腦功能網絡，對精神分裂癥患者進行分類。Tian等[19]將MIC作為皮爾森相關系數的補充方法，揭示了靜息狀態EEG信號腦網絡的潛在機制。這些研究證明了MIC算法在神經科學領域的有效應用。隨后，Liang等[20-21]首次將MIC算法應用于探索健康人群與腦卒中患者的FCMC研究。然而，原MIC算法的核心是通過遍歷方法求出兩個變量指定維數的網格劃分的最大互信息值。這就導致在實際應用中，當數據規模較大或函數關系隨機時，計算復雜度較高，從而導致計算耗時長[22]。考慮到神經生理信號之間的關系大多是隨機非線性的，實際應用中有必要減少MIC算法在計算神經生理信號之間耦合關系時的計算時間。
本研究提出了一種基于K均值（K-means）聚類算法的改進算法（K-means++）的MIC算法，并將其應用于研究腦卒中患者和健康對照者的FCMC分析，并以厄農映射模型進行驗證，期望相比原MIC算法具有更快的計算速度。為證實所提新算法的有效性，本文將其應用于腦卒中患者右腳踝關節背屈任務過程中的FCMC分析，期望本研究能夠擴展FCMC相關研究，為量化評估腦卒中患者運動功能提供新的方法。
1 改進的最大信息系數算法
1.1 最大信息系數算法
MIC算法是Reshef等[17]在2011年提出的，它可以準確捕獲兩個隨機變量之間的線性和非線性相關性。MIC的算法原理是首先對兩變量X和Y聯合樣本的散點圖采取特定規模的網格劃分后，通過計算網格中的邊際概率密度函數和聯合概率密度函數進而計算兩變量的互信息值。數據集D中隨機變量X和Y的互信息計算公式如式（1）所示：
 |
其中，p(x)和p(y)為概率密度函數，p(x,y)為聯合概率密度函數。
在固定網格數的前提下，找出所有網格劃分方式中所得的最大互信息值 
并歸一化為M(D)x,y，如式（2）所示：
 |
已知樣本量為n的數據集D，則在限制網格大小x·y的前提下定義該集合中兩變量 X、Y 的MIC計算公式如式（3）所示：
 |
其中，a通常根據經驗被設置為0.6，以確保算法的普適性。
1.2 改進的最大信息系數算法
原MIC算法的核心是從兩個不同維數的變量網格中尋找到互信息值最大時的網格劃分方式。其計算時間主要耗費在如何根據一個變量的固定網格劃分找到另一個變量的最優網格劃分上。當數據量較大且函數關系為隨機時，尋找最優網格劃分的計算時間較長。因此，本研究提出了一種新的快速計算兩變量間MIC的近似算法。
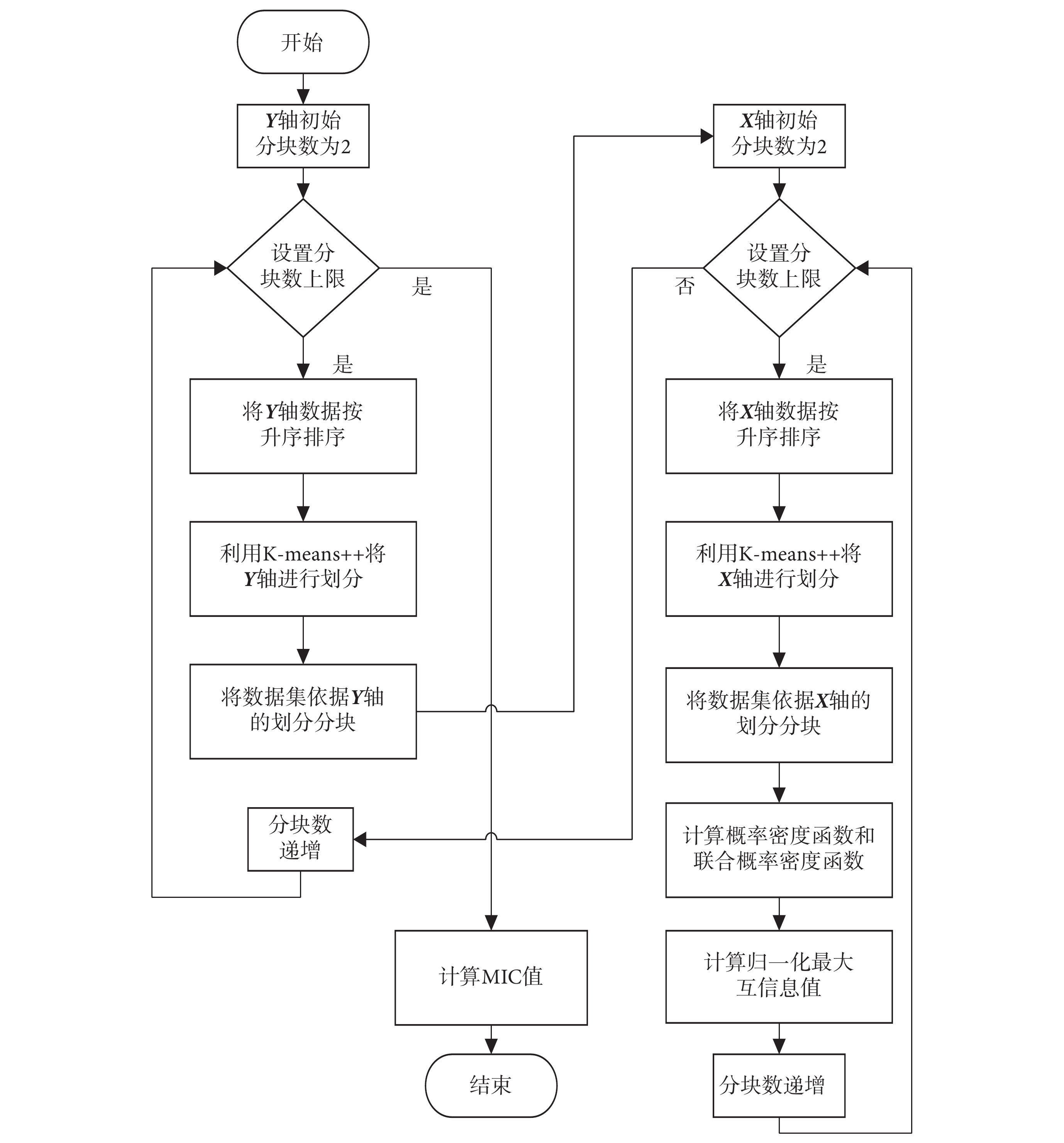
所提算法利用K-means++算法將X軸（變量X）和Y軸（變量Y）分別劃分為x塊和y塊，隨后將所劃分網格中的互信息作為最大的互信息并進行標準化。最后將所有分區方式得到的標準化結果的最大值定義為MIC值。K-means++作為一種高效的聚類算法，引入MIC的計算中，可以減少尋找X軸和Y軸最優劃分方式的計算時間，具體的算法流程如圖1所示。
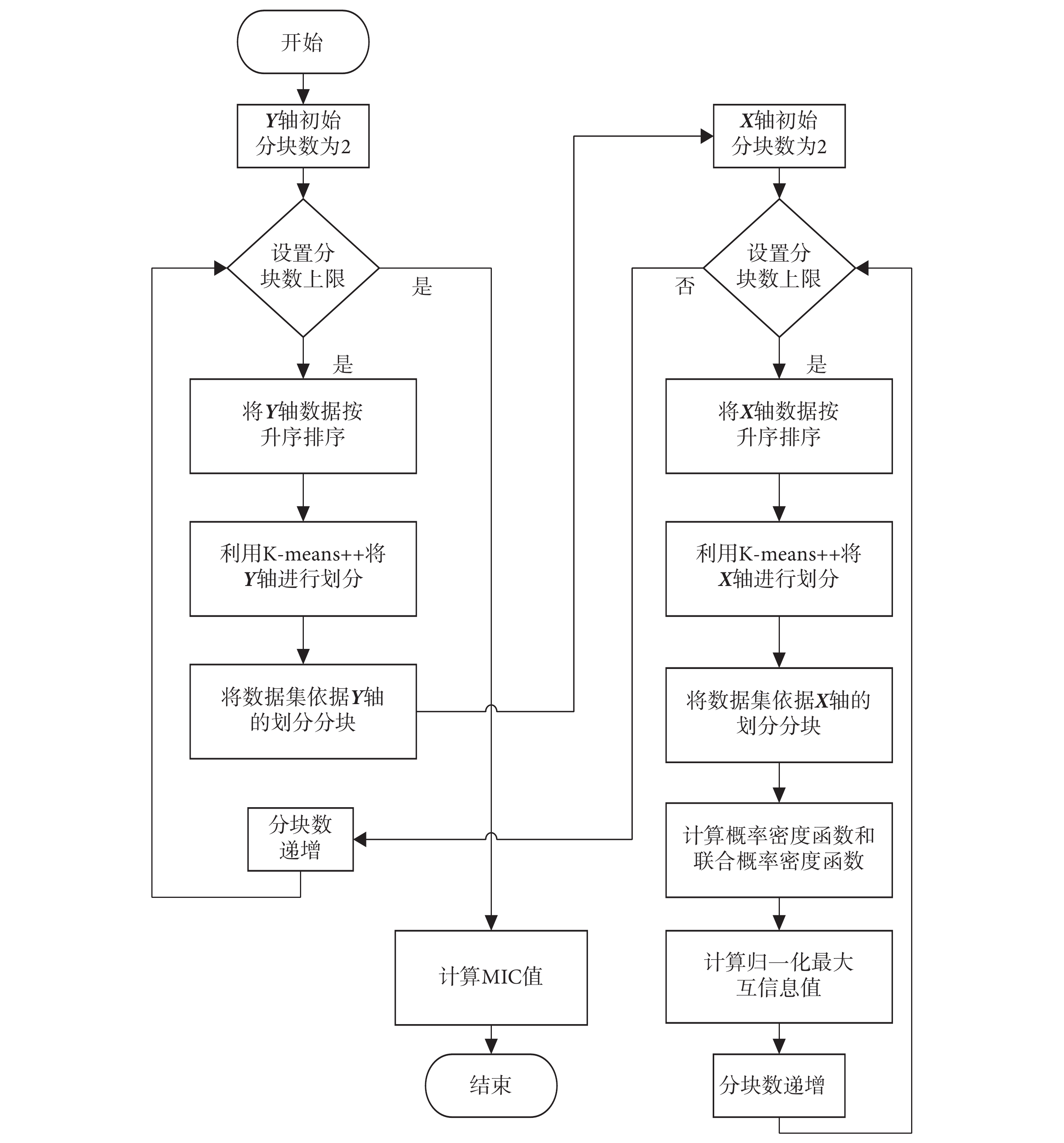圖1
改進的MIC算法流程
Figure1.
The improved MIC algorithm flow
2 算法驗證與應用
2.1 基于厄農映射模型的驗證
本研究中，厄農映射模型被引入來驗證所提算法的有效性。厄農映射作為具有典型混沌動力學和非線性特性的經典模型，廣泛用于驗證新的算法[21, 23-24]。具體的，由厄農映射生成兩個具有單向耦合關系的時間序列X和Y。X和Y分別為驅動系統和響應系統，即Y = F(X)，如式（4）所示:
 |
其中，xi和yi分別為系統X和Y中采樣點i。C代表X和Y系統之間的耦合強度，取值范圍為0～1。當C為1時代表兩個系統完全耦合。參數B決定兩個系統是否相同，即當B = 0.1時，兩系統為不相同系統。式中u i和vi分別代表兩個系統的高斯隨機噪聲。在驗證過程中，系統中xi、yi、ui、vi的初始值在0～1之間隨機生成。
本研究從計算時長和不同噪聲水平下檢測耦合強度變化的能力兩個方面對改進的MIC算法進行了驗證。
2.2 算法在EEG信號和sEMG信號上的應用
本研究將所提算法應用于健康對照者和腦卒中患者進行右腳踝關節背屈任務中beta頻段（14～30 Hz）和gamma頻段（31～45 Hz）的FCMC研究。
2.2.1 試驗范式
本研究招募了10名無任何神經疾病史的健康受試者（年齡范圍：49～67歲，其中包括2名女性）作為健康對照組；10名腦卒中恢復期患者（年齡范圍：50～68歲，其中包括2名女性）作為腦卒中患者組。所有腦卒中患者均表現出右側肢體運動功能障礙，并依據福格?邁爾評定 (Fugl-Meyers assessment, FMA)量表評估了下肢功能。受試者人口學統計信息如表1所示。所有受試者試驗前已簽署試驗知情同意書。該試驗符合《赫爾辛基宣言》，并已得到河北大學附屬醫院倫理審查委員會的批準（HDFY- LL-2020-091）。
表1
腦卒中患者人口學信息
Table1.
Demographics of stroke patients
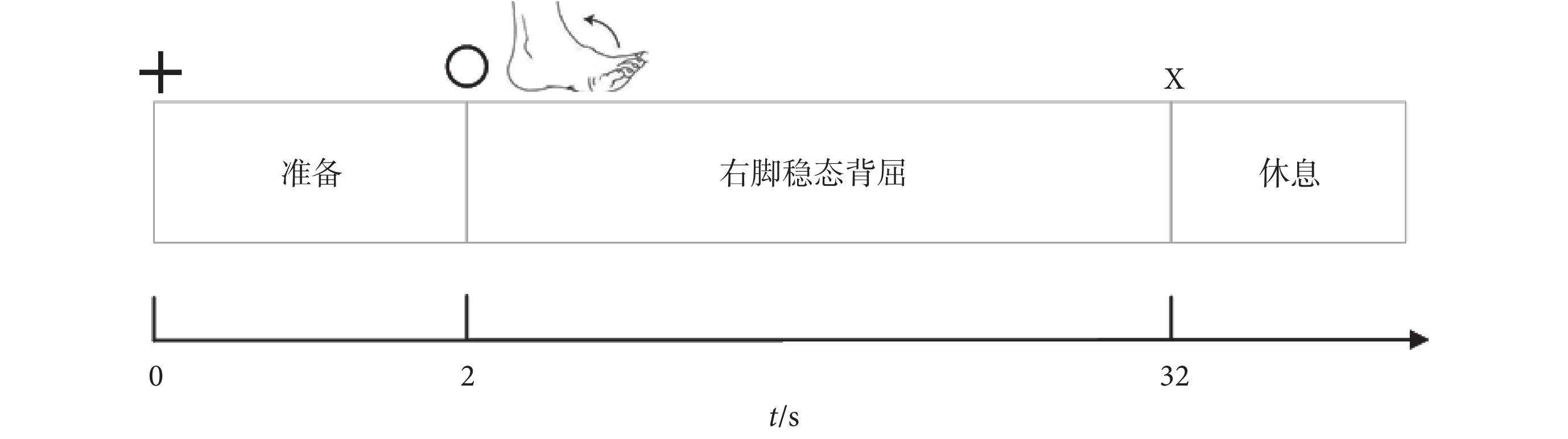
正式試驗中，受試者們被要求在視覺提示下自主進行穩定的右腳背屈。受試者調整為舒適坐姿，雙下肢自然垂直，雙腳掌平放于地面。試驗過程中受試者需平視距離自己90 cm處的電腦屏幕中央。當屏幕中央出現十字標志時，提醒受試者保持注意力。2 s后，屏幕出現圓形標志提示受試者執行保持右腳背屈的任務，持續時間為30 s。每名受試者重復5組上述任務，每組任務中間休息120 s以避免疲勞，試驗范式如圖2所示。
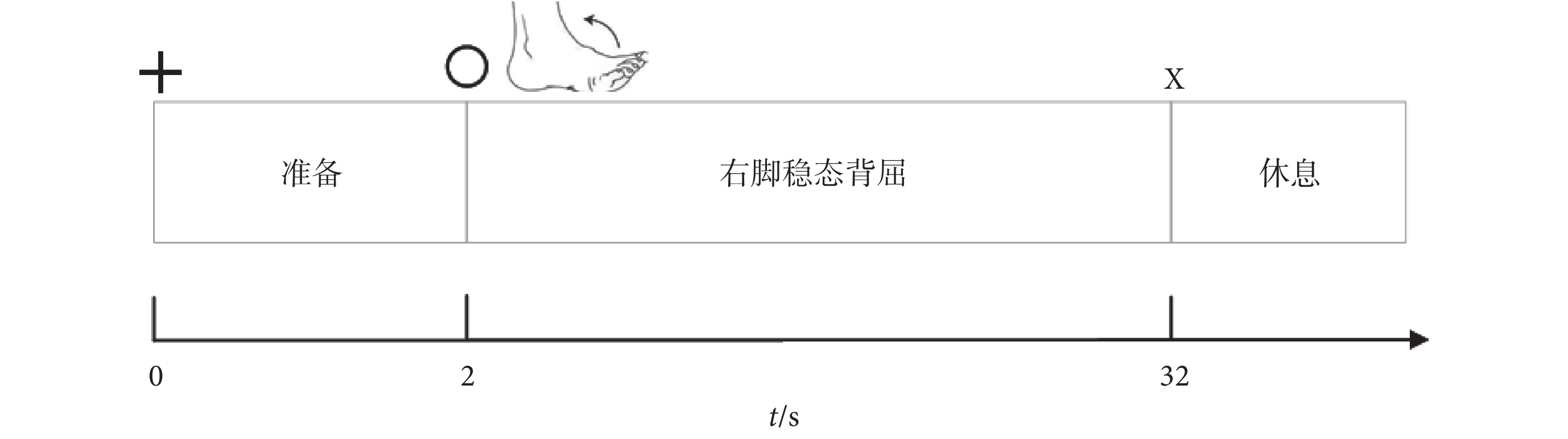圖2
試驗范式
Figure2.
Experimental paradigm
2.2.2 EEG信號與sEMG信號同步采集
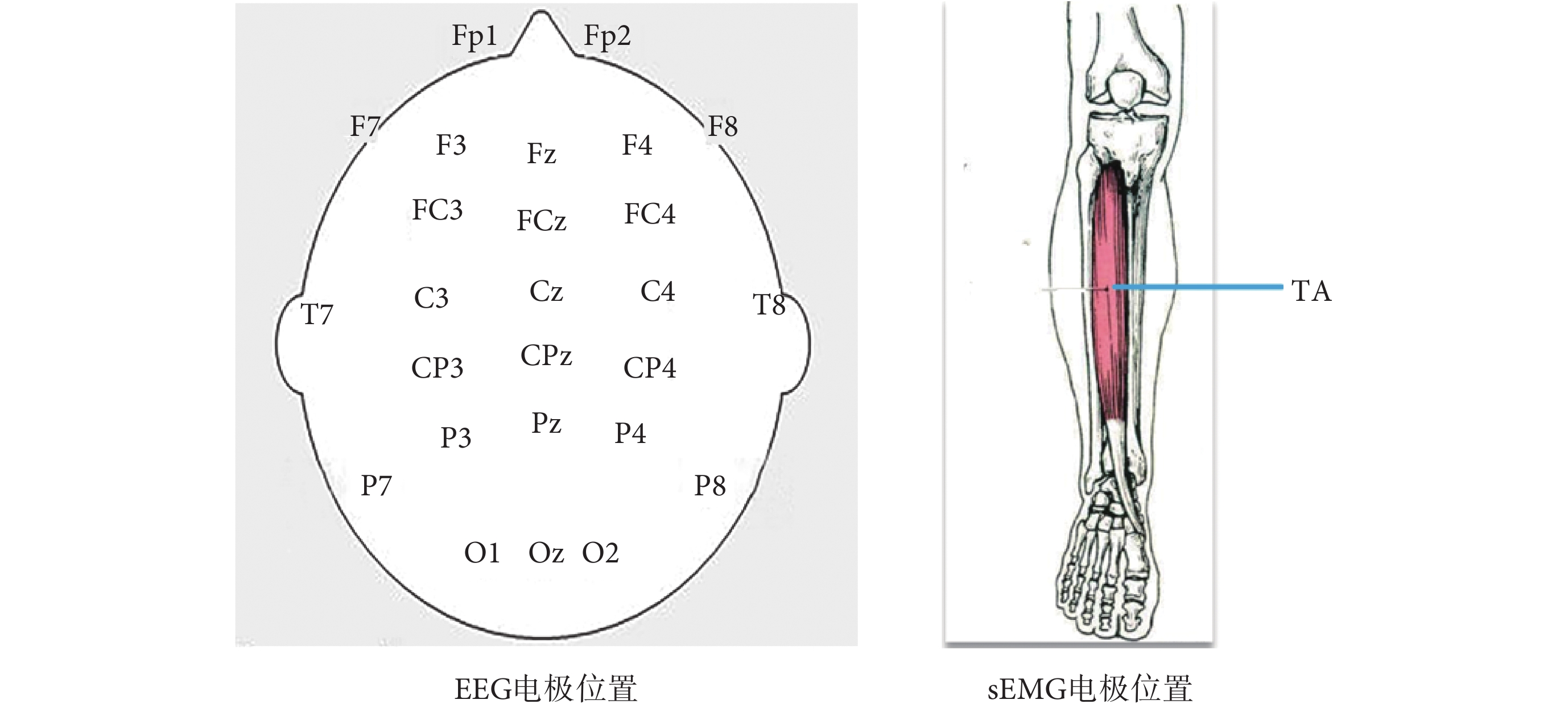
本研究使用便攜式EEG信號采集設備（Grael，Compumedics Neuroscan Inc.，澳大利亞）同步采集EEG信號和sEMG信號，采樣率為1 024 Hz。具體的，利用該設備提供的兩組雙極通道采集左右腿脛骨前肌（tibialis anterior，TA）處sEMG信號。同時依據國際10-20系統的標準，以雙耳乳突M1/M2為參考，選擇采集來自26個通道（FP1、FP2、Fz、F3、F4、F7、F8、FC3、FCz、FC4、C3、Cz、C4、CP3、CPz、CP4、P3、Pz、P4、T7、T8、P7、P8、O1、Oz、O2）的EEG信號，電極安放位置如圖3所示。電極安放前清洗并吹干頭發，用磨砂膏擦拭TA處皮膚，以確保將所有電極與皮膚交界處阻抗降至10 kΩ以下。另外為避免電極導線晃動帶來的噪聲，試驗過程中將導線用膠帶進行必要的固定。試驗過程中盡量避免眨眼、吞咽、轉頭等動作。
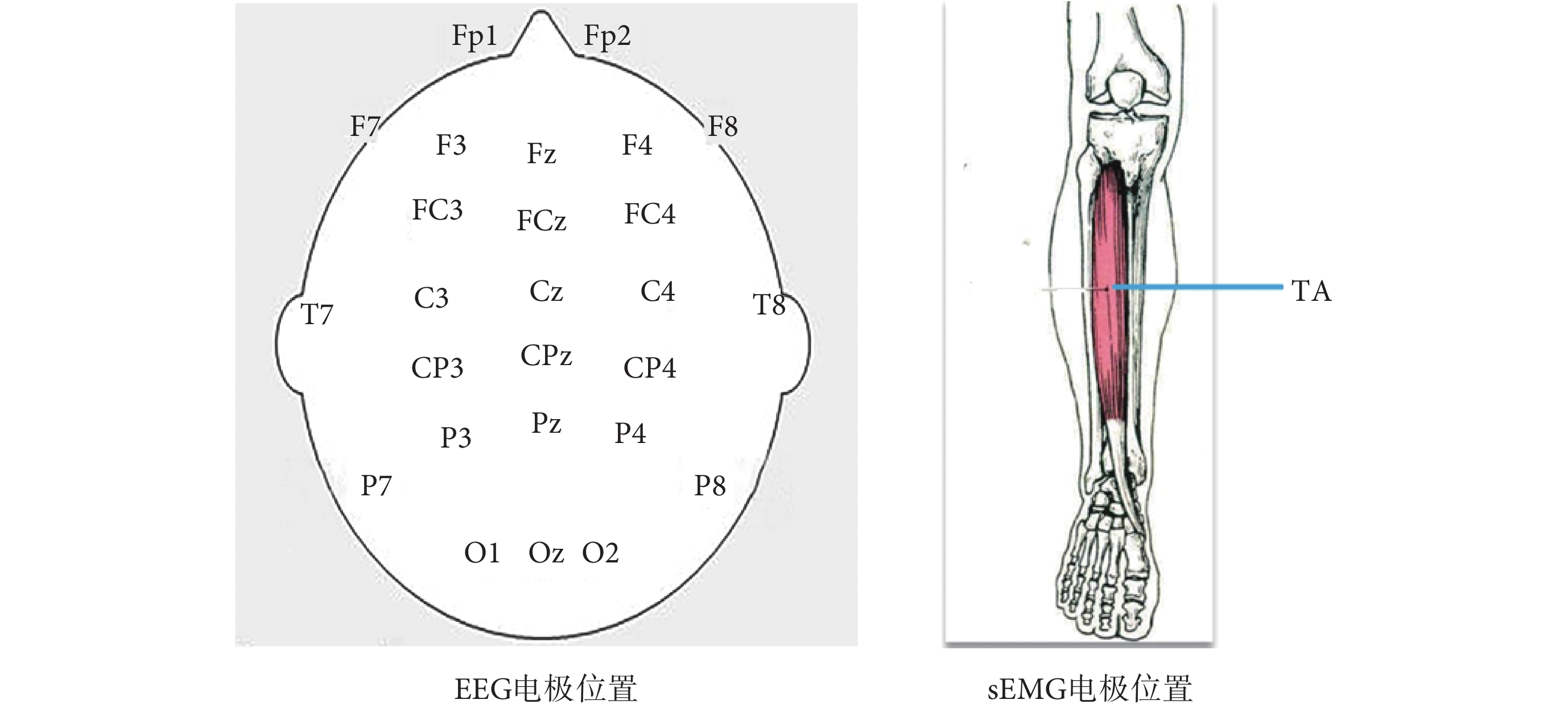圖3
電極安放位置示意
Figure3.
Electrode placement diagram
2.2.3 EEG數據與sEMG數據預處理
按照上述試驗流程采集到的EEG信號和sEMG信號包括2 s的準備階段和30 s的力輸出階段。為了方便下一步數據的分析，只保留了穩定的力輸出時刻的數據。因此，從30 s的力輸出階段數據中截取了第2～29 s時刻的EEG數據和sEMG數據以避免背屈動作起始和結束階段力量動態變化太大造成的影響。最后每位受試者得到了5組28 s的穩定數據。
本研究首先對采集到的EEG數據和sEMG數據去除50 Hz工頻干擾。隨后對數據先進行150 Hz的低通濾波，再進行2 Hz的高通濾波。最后利用獨立成分分析方法（independent component analysis，ICA）去除EEG信號中包括眼動、EMG信號和心電信號在內的偽跡。EEG數據和sEMG數據的上述處理均在開源信號處理工具箱EEGLAB 2020（Swartz Center for Computational Neuroscience，美國）執行。
2.2.4 Morlet小波變換
為同時捕獲EEG信號和sEMG信號在時頻空間的變化，本研究中將濾波處理后的數據進行了Morlet小波變換從而得到信號的時頻能量圖[25]。Morlet小波變換的公式如式（5）所示：
 |
其中，W (t, f)代表轉換后輸出的時頻信號，
為輸入的時域信號，f為返回的頻率向量，t為時間，b為小波函數的平移因子，a為小波函數的尺度因子，
為Morlet小波基函數的復共軛。
如式（6）所示：
 |
上面的 
代表小波基函數，
為小波的中心頻率，i為復頻域表示時的虛數單位，t為時間。
隨后分別計算得到beta頻段和gamma頻段的平均小波功率隨時間變化的新時間序列。最后利用改進的MIC算法計算新生成的時間序列之間的耦合值。考慮到下肢運動過程中大腦運動皮層主要激活區域在Cz電極附近，因此本研究選取Cz電極點進行FCMC分析。EEG信號和sEMG信號的數據處理流程如圖4所示。
圖4
EEG信號和sEMG信號處理流程
Figure4.
The process flow for EEG signal and sEMG signal
2.2.5 統計分析
本研究首先利用排列檢驗進行統計學分析。然后將所得的健康對照組和腦卒中患者組在beta和gamma頻段的MIC值分別使用統計分析軟件SPSS 20.0（IBM SPSS Inc.，美國）進行獨立樣本 t檢驗分析,當P < 0.05，差異具有統計學意義。此外，為了評估MIC值與腦卒中患者運動功能表現可能存在的關系，本研究采用皮爾森相關系數計算了MIC值與FMA量表評分之間的相關性。
3 結果
3.1 仿真結果
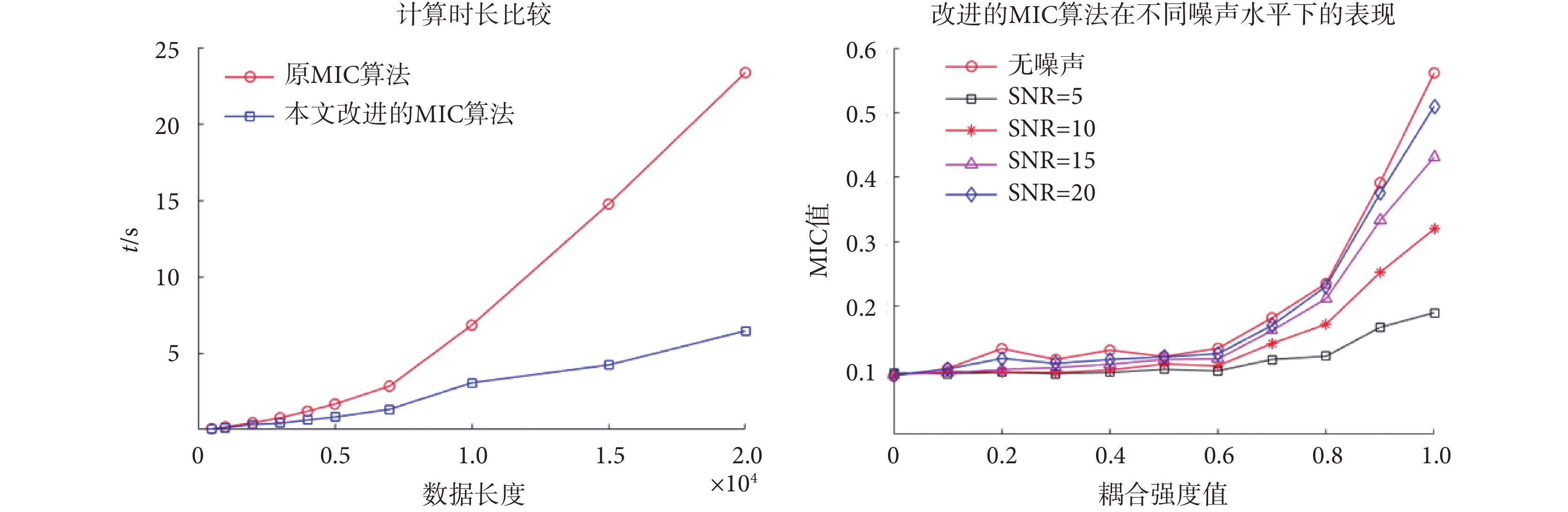
本研究提出的改進算法在數值計算軟件MATLAB R2018a（MathWorks Inc.，美國）中執行。原MIC算法同樣通過MATLAB調用minepy庫文件實現[26]。為方便比較，兩種算法都運行于同一計算平臺上（Windows 10，X64；CPU：i7-1165G7，2.8 G HZ；RAM：16 G）。使用不同系統的厄農映射 (B = 0.1) 生成10個不同數據長度（500、1 000、2 000、3 000, 4 000、5 000、7 000、10 000、15 000、20 000）的數據集，每個數據集獨立生成100次。改進的MIC算法與原算法的平均計算時長差異如圖5所示，本研究提出的算法在數據長度大于6 000時的計算耗時明顯低于原MIC算法。隨著數據規模的增加，原MIC算法計算時長明顯快速增加，而本文所提改進算法計算耗時增長不明顯。
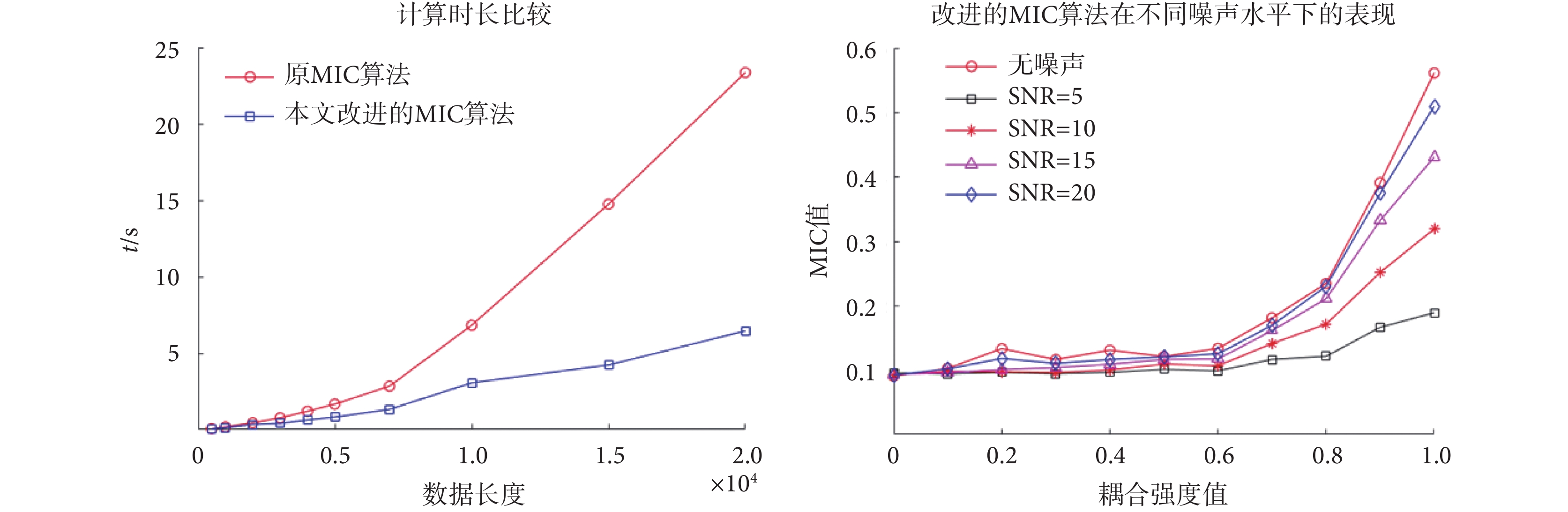圖5
改進的MIC算法的性能表現
Figure5.
The performance of the improved MIC algorithm
進一步，本研究通過添加不同強度的垂直噪聲來驗證改進的MIC算法的魯棒性。不同信噪比（signal to noise ratio，SNR）條件下改進的MIC算法檢測耦合強度的表現如圖5所示。研究結果表明，即便是在低信噪比條件下（例如SNR=5），改進的MIC算法曲線依然能夠跟隨耦合強度值的增加而單調遞增。
3.2 實驗結果
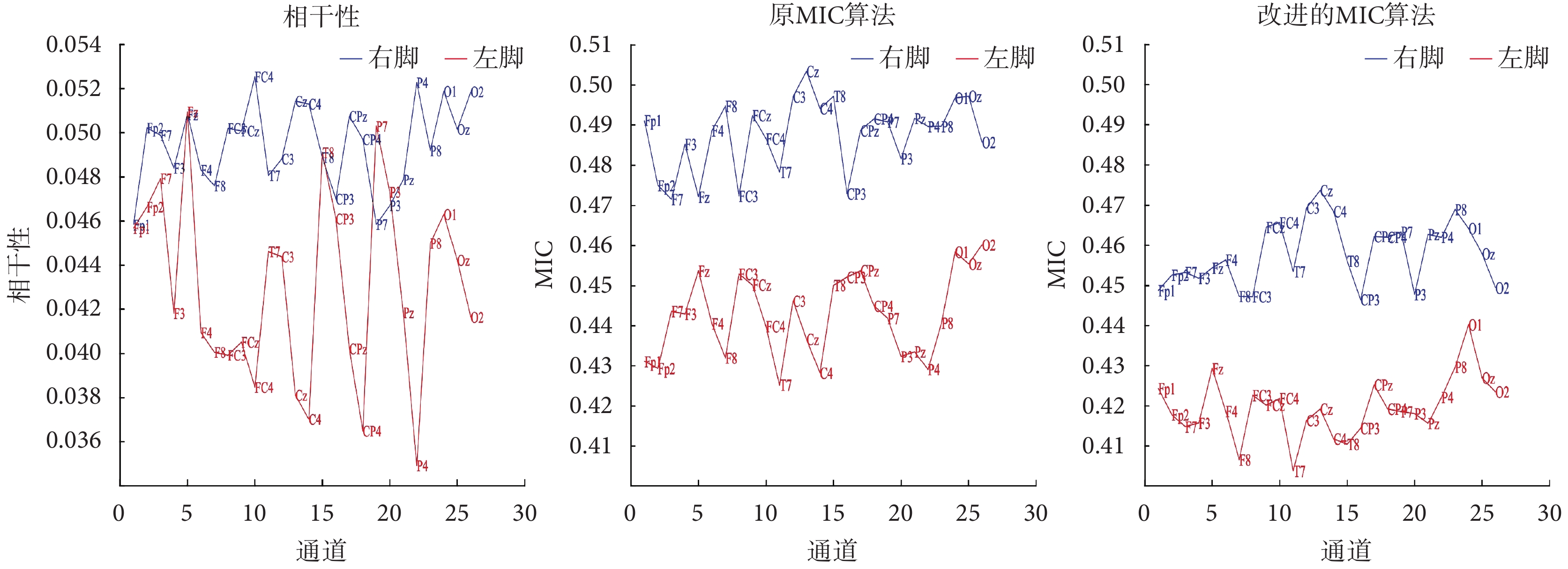
如圖6所示，分別顯示了健康對照組右腳踝關節背屈任務時，在beta頻帶的相干性和改進的MIC算法計算出的總平均耦合強度對比。從圖6可以觀察到，在部分電極位置上（例如Fz、P7和P3），相干性方法無法清晰地區分動作腳(右腳)和靜止腳(左腳)。無論是改進的MIC算法還是原MIC算法都沒有這個問題，與靜止腳（左腳）相比，動作腳TA處sEMG信號與大腦所有電極位置的EEG信號之間均表現出更強的耦合值。相比原MIC算法，改進的MIC算法所得值略低。
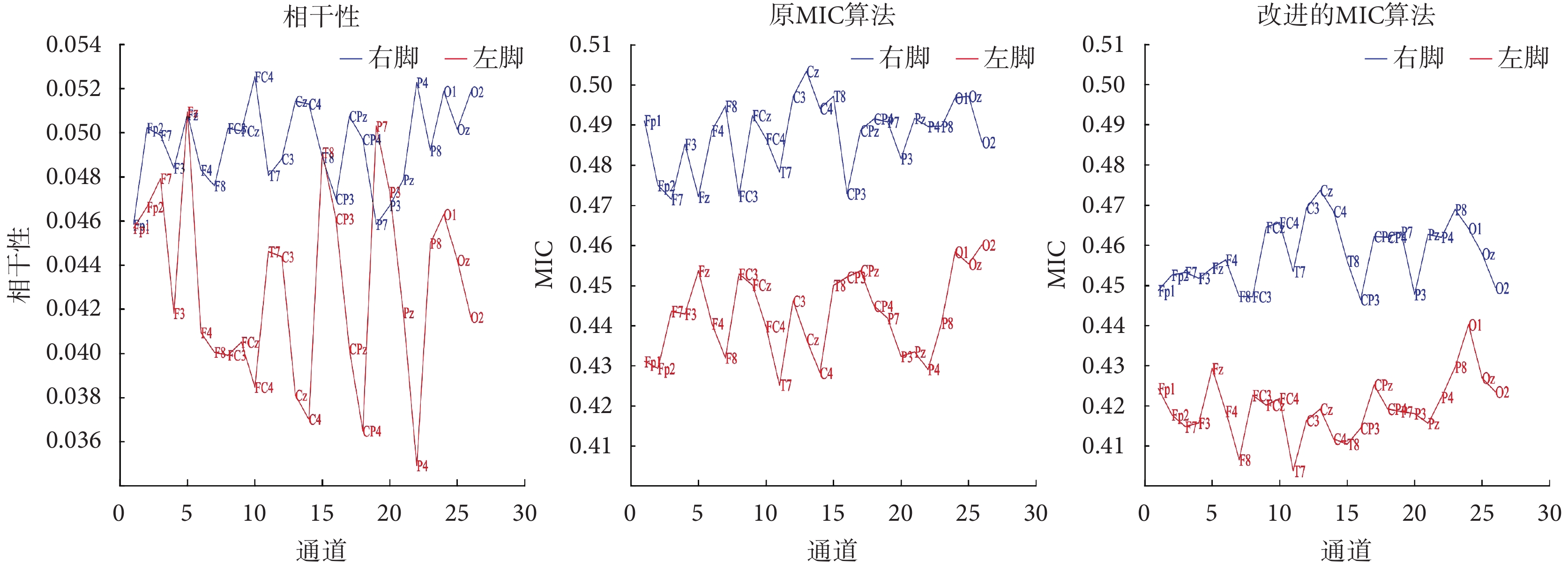圖6
不同算法在計算beta頻段總平均FCMC時的表現對比
Figure6.
Comparison of the performance of different algorithms in calculating the beta-band grand average FCMC
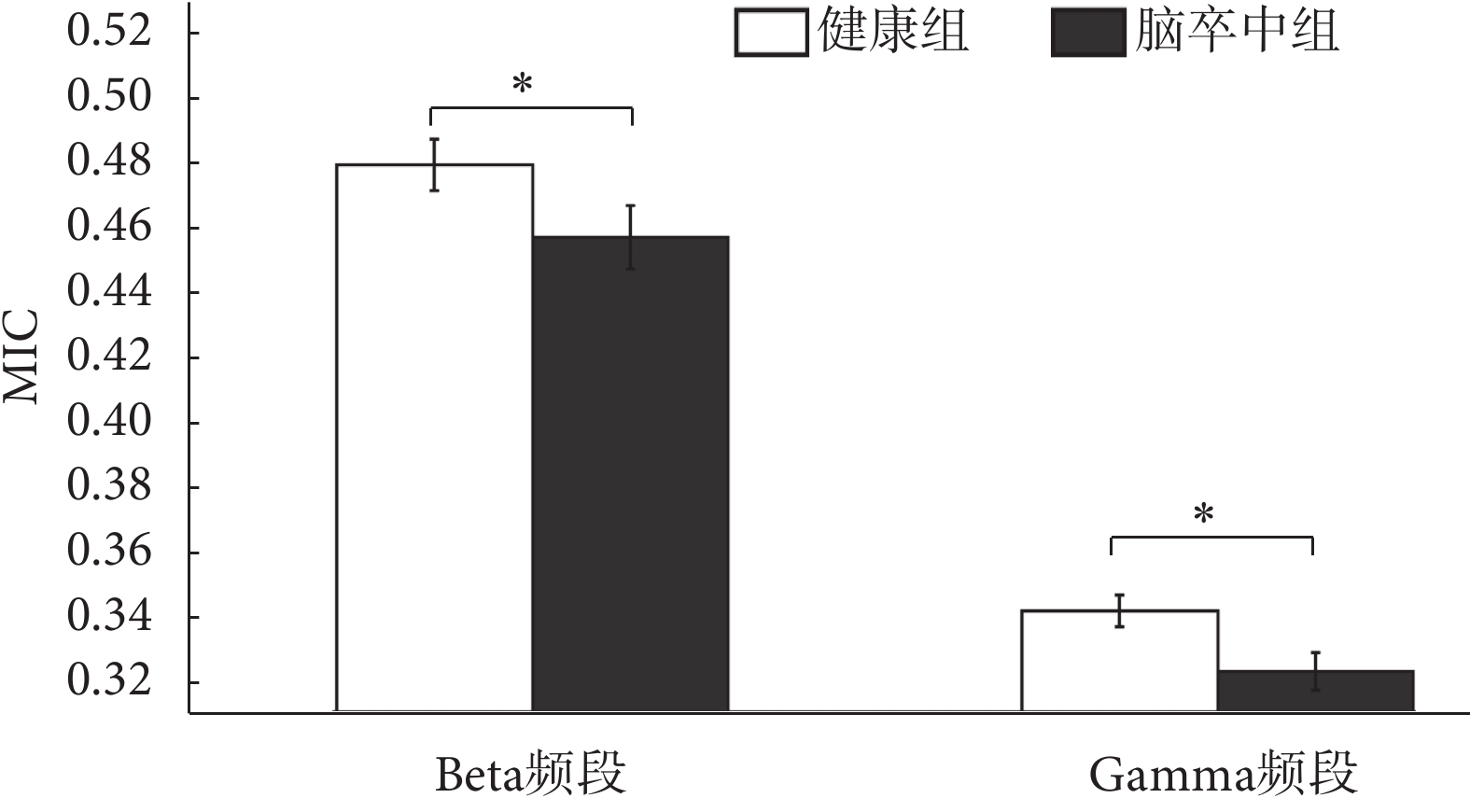
健康對照組和腦卒中患者組在beta頻段和gamma頻段的FCMC差異如圖7所示。相比健康對照組，腦卒中患者組的MIC值無論是在beta頻段還是在gamma頻段都顯著更低。
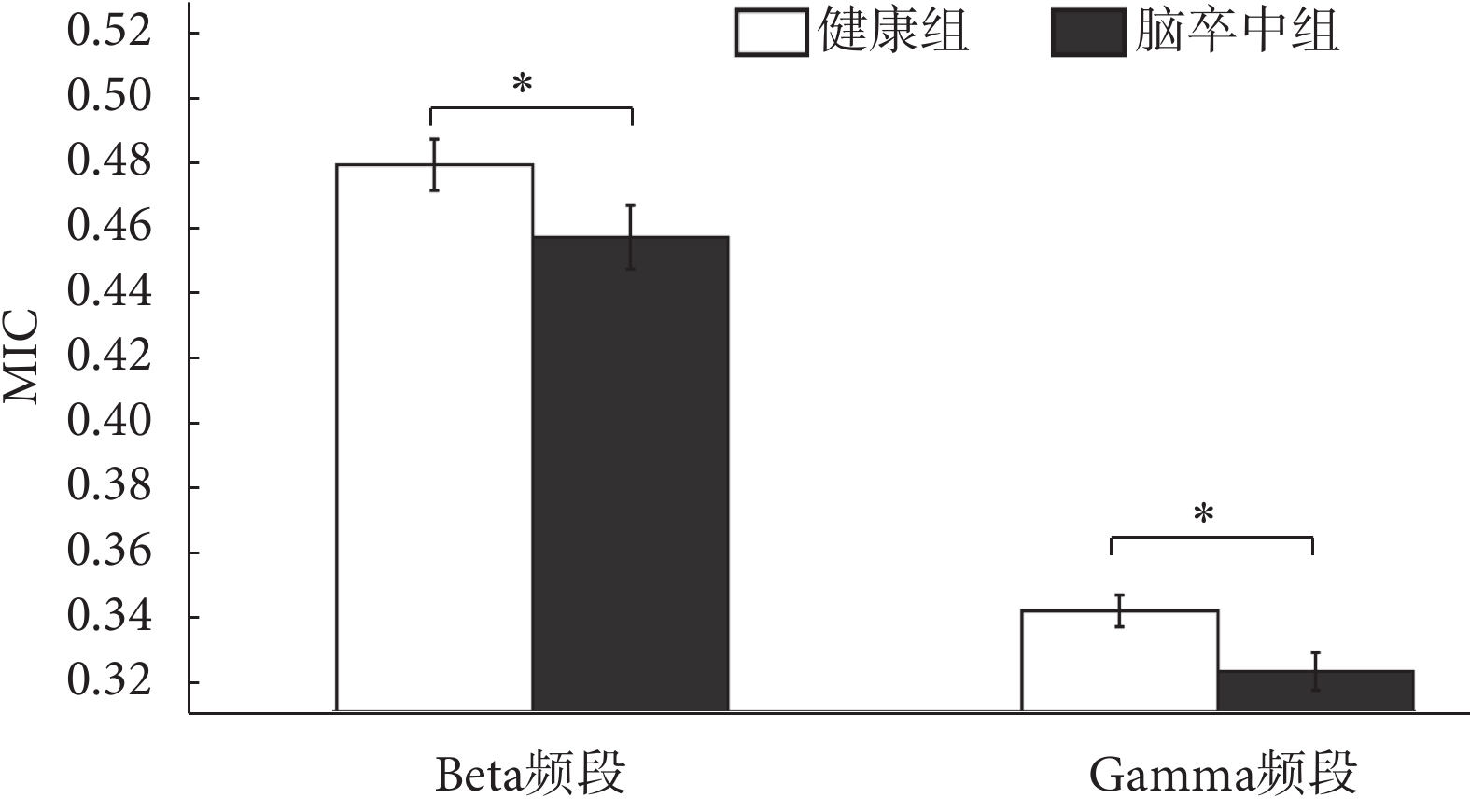圖7
健康對照組和腦卒中組在beta和gamma頻段總平均MIC耦合值的比較
*
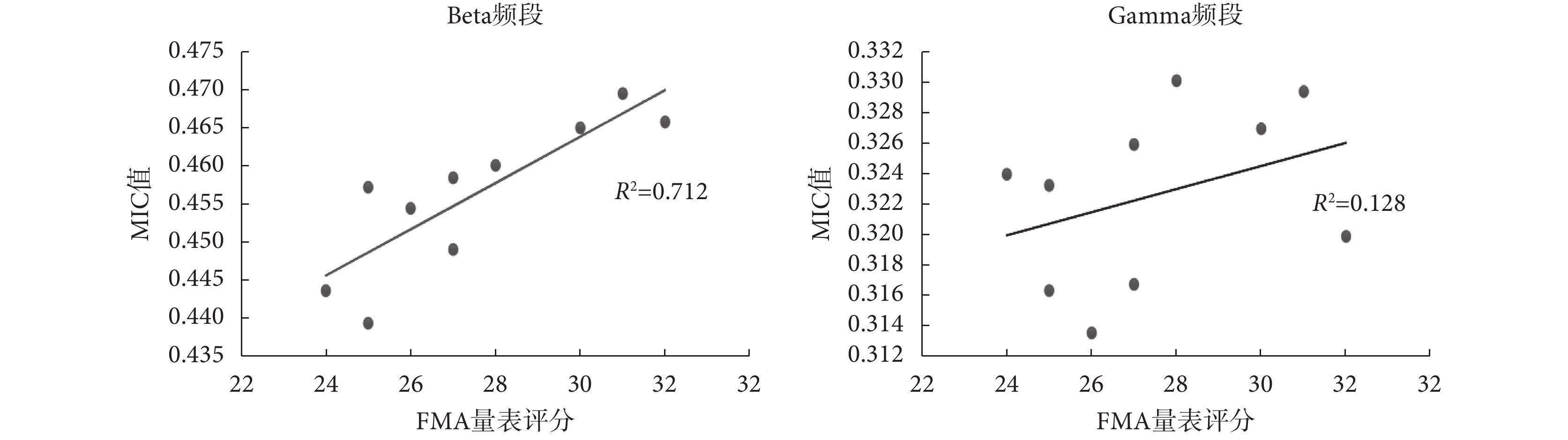
本文進一步研究了MIC值與腦卒中患者運動功能表現的關系。臨床上常用FMA量表進行患者肢體功能評估。如圖8所示，所有患者的beta頻段的MIC值與FMA量表評分之間都存在較強的正相關（r = 0.844，P = 0.002）。而gamma頻段與FMA量表評分之間相關性相對較弱（r = 0.358，P = 0.310）。
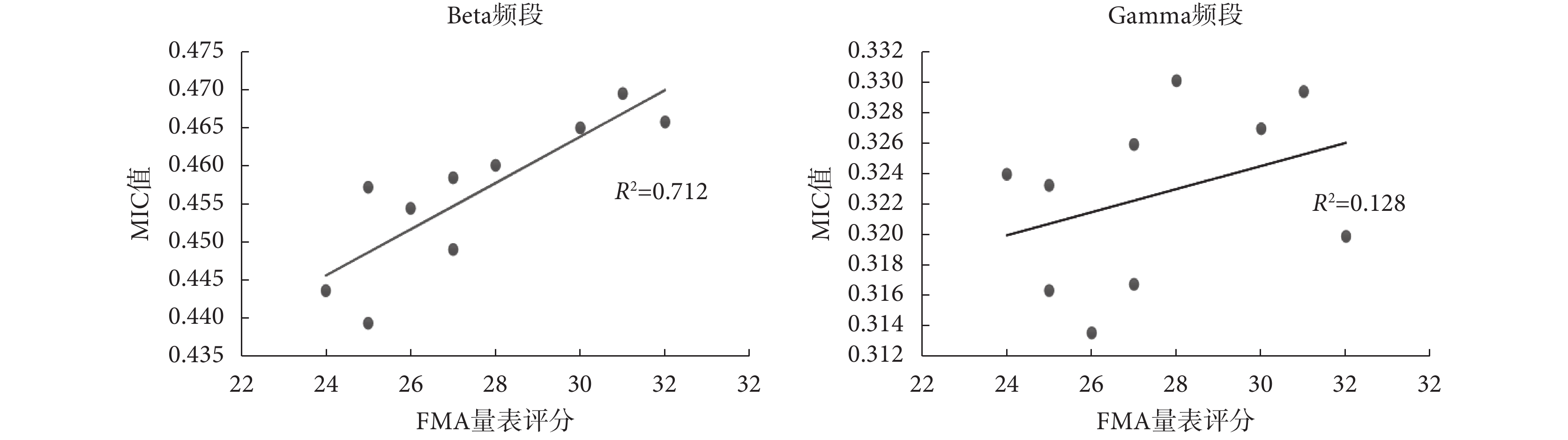圖8
腦卒中患者的MIC值與FMA量表評分的關系
Figure8.
The relationship between the MIC value and the FMA scale score in stroke patients
4 討論
在探討大規模隨機數據中變量之間的相關性時，必須考慮計算時間。原MIC算法的計算時間主要花在利用動態規劃尋找最優的X軸網格劃分方式上。當兩個變量之間關系隨機時，需較長時間才能找到其最優劃分方式。Shao等[22]證明原MIC算法的時間復雜度為O(n2.4)，而基于K-means的MIC算法的時間復雜度為O(n1.6)（當參數a設為0.6時）。但是，在大數據量的情況下，K-means算法存在一些問題，初始聚類中心的選擇會影響結果的準確性和效率。K-means++由Arthur等[27]引入，通過解決K-means算法的分類結果依賴于初始聚類中心的選擇的問題，使K-means++算法比K-means算法更準確、更高效。因此，本研究在MIC計算過程中，使用K-means++來優化X軸和Y軸的網格劃分。仿真結果表明，隨著數據量的增加，改進的MIC算法計算時長遠低于原MIC算法，比較適合分析大樣本隨機變量之間的相關關系。
進一步，利用厄農映射驗證了本文改進的MIC算法檢測兩個系統耦合強度的有效性和魯棒性。厄農映射具有非線性的特點，耦合強度可以通過設置參數C進行調整[28]。改進的MIC算法所得MIC值在低信噪比條件下能夠跟隨耦合參數C的增加而單調遞增，這與原算法結果保持一致。這也表明所提算法能夠滿足非線性系統之間耦合關系的準確檢測。EEG信號和sEMG信號已經被證明具有典型非線性特征，因此本研究所提新算法適用于分析EEG信號和sEMG信號之間的功能耦合。
本研究將改進的MIC算法應用到右腳踝關節背屈試驗中。與相干性方法相比，所提出的MIC算法能更好地識別頭皮所有電極位置與效應肌的運動相關連接。相干性算法依賴于感興趣區域和頻帶選擇，其基于二階統計量的計算原理不適用于非線性動力系統的耦合分析[29-30]。而MIC算法則采用高階統計量來捕獲非線性耦合，其對異常值具有較強的魯棒性是由于其對香農熵和條件熵的估計方法具有較強的魯棒性[31]。特別的，本研究在感興趣的頻段（beta頻段和gamma頻段）內基于EEG信號和sEMG信號的平均功率的時間序列計算MIC值，進一步提高了算法的信噪比[32]。因此所提新方法比相干性算法具有更強的適應性，更適合于任務關聯的耦合識別。需要注意的是，相比原MIC算法，改進的MIC算法由于在尋找變量間最優劃分的時候采用了聚類算法，因此計算所得結果略低于遍歷方式所得結果。盡管如此，觀察到改進的MIC算法與原MIC算法所觀察到的FCMC結果保持一致。這也表明所提算法能夠應用于FCMC研究。
相比健康對照組，腦卒中患者組運動皮層與效應肌之間的功能耦合顯著更弱。這與之前針對腦卒中患者的FCMC研究結果保持一致[8, 33]。腦卒中后運動功能的喪失通常被認為是控制運動的神經網絡受損導致。腦損傷后通過錐體束的神經活動明顯減少，導致突觸前和突觸后活動分離，從而削弱皮質-脊髓連接[34]。這種運動神經網絡的受損可能導致了運動控制信息傳遞的異常，使信號之間發生解耦。Mima等[35]之前的研究也證實了弱耦合主要是因大腦到肌肉的信息傳遞受損引起的。
進一步，本研究探索了MIC值與運動功能表現的相關性。本研究表明，更高的MIC值與更高的FMA量表評分正相關，也說明了更高的MIC值表現了更好的下肢運動功能。之前的研究已經證實更高的運動表現與EEG信號和sEMG信號之間耦合值正相關[9,12]。本研究進一步發現相比gamma頻段的MIC值，beta頻段的MIC值與FMA量表評分相關性更高。這或許與保持背屈的試驗范式設計相關。之前的基于穩態力輸出任務的研究證實了beta頻段的神經震蕩主要負責穩態力的輸出和控制[5, 36]。因此，本研究也表明了beta頻段的MIC值有潛力成為量化腦卒中患者運動神經系統功能狀態的指標，而所提算法有希望成為量化腦卒中患者運動功能評估的有效工具。后續課題組的研究將在增加招募腦卒中志愿者數量基礎上，進一步開展不同康復手段對康復效果影響的量化評估工作。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
腦卒中由于其高發病率和高致殘率已經成為社會關注的問題。運動功能障礙是腦卒中患者常見的后遺癥。準確評估腦卒中患者運動神經系統功能狀態是提高康復治療效果的基礎。傳統的臨床運動功能評估過分依靠醫生的主觀經驗，存在一定局限性[1-2]。人體大腦運動皮層產生的控制信號驅動效應肌肉動作，從而產生自主運動[3-4]。由于包含了大量的運動控制?響應信息，大腦運動皮層的腦電（electroencephalogram，EEG）信號和效應肌的肌電（electromyography，EMG）信號在自主運動過程中也被證實存在特定頻段的功能耦合[5-7]。近年來，隨著非侵入式檢測技術的快速發展，利用EEG信號和表面肌電 (surface electromyography，sEMG) 信號來探討皮質肌功能耦合（functional corticomuscular coupling，FCMC）已經成為腦卒中康復領域研究的熱點[8-10]。定量分析FCMC能夠為分析運動神經系統功能、評估運動功能障礙患者（如腦卒中患者）的康復效果提供重要手段。
FCMC研究中的一個重要挑戰是準確識別EEG信號和sEMG信號之間的耦合。目前大多數研究主要是基于頻域的相干性算法來評估皮質肌功能耦合[7, 11-12]。一些基于相干性的擴展算法也被提出并應用于FCMC研究，例如Tuncel等[13]提出的時頻相干算法以及Xu等[14]提出的時滯相干算法。然而，EEG信號和sEMG信號屬于典型的神經生理信號，已被證明具有典型的非線性特征[15-16]。相干性方法主要用于測量線性耦合，在研究復雜的非線性的EEG信號和sEMG信號之間功能耦合上有一定局限性。
Reshef等[17]在2011年提出了最大信息系數（maximal information coefficient，MIC）算法來捕捉兩個變量之間的相關關系。近年來，MIC算法已逐漸應用于神經科學領域[18-19]。Su等[18]應用MIC構建腦功能網絡，對精神分裂癥患者進行分類。Tian等[19]將MIC作為皮爾森相關系數的補充方法，揭示了靜息狀態EEG信號腦網絡的潛在機制。這些研究證明了MIC算法在神經科學領域的有效應用。隨后，Liang等[20-21]首次將MIC算法應用于探索健康人群與腦卒中患者的FCMC研究。然而，原MIC算法的核心是通過遍歷方法求出兩個變量指定維數的網格劃分的最大互信息值。這就導致在實際應用中，當數據規模較大或函數關系隨機時，計算復雜度較高，從而導致計算耗時長[22]。考慮到神經生理信號之間的關系大多是隨機非線性的，實際應用中有必要減少MIC算法在計算神經生理信號之間耦合關系時的計算時間。
本研究提出了一種基于K均值（K-means）聚類算法的改進算法（K-means++）的MIC算法，并將其應用于研究腦卒中患者和健康對照者的FCMC分析，并以厄農映射模型進行驗證，期望相比原MIC算法具有更快的計算速度。為證實所提新算法的有效性，本文將其應用于腦卒中患者右腳踝關節背屈任務過程中的FCMC分析，期望本研究能夠擴展FCMC相關研究，為量化評估腦卒中患者運動功能提供新的方法。
1 改進的最大信息系數算法
1.1 最大信息系數算法
MIC算法是Reshef等[17]在2011年提出的，它可以準確捕獲兩個隨機變量之間的線性和非線性相關性。MIC的算法原理是首先對兩變量X和Y聯合樣本的散點圖采取特定規模的網格劃分后，通過計算網格中的邊際概率密度函數和聯合概率密度函數進而計算兩變量的互信息值。數據集D中隨機變量X和Y的互信息計算公式如式（1）所示：
|
其中，p(x)和p(y)為概率密度函數，p(x,y)為聯合概率密度函數。
在固定網格數的前提下，找出所有網格劃分方式中所得的最大互信息值 并歸一化為M(D)x,y，如式（2）所示：
|
已知樣本量為n的數據集D，則在限制網格大小x·y的前提下定義該集合中兩變量 X、Y 的MIC計算公式如式（3）所示：
|
其中，a通常根據經驗被設置為0.6，以確保算法的普適性。
1.2 改進的最大信息系數算法
原MIC算法的核心是從兩個不同維數的變量網格中尋找到互信息值最大時的網格劃分方式。其計算時間主要耗費在如何根據一個變量的固定網格劃分找到另一個變量的最優網格劃分上。當數據量較大且函數關系為隨機時，尋找最優網格劃分的計算時間較長。因此，本研究提出了一種新的快速計算兩變量間MIC的近似算法。
所提算法利用K-means++算法將X軸（變量X）和Y軸（變量Y）分別劃分為x塊和y塊，隨后將所劃分網格中的互信息作為最大的互信息并進行標準化。最后將所有分區方式得到的標準化結果的最大值定義為MIC值。K-means++作為一種高效的聚類算法，引入MIC的計算中，可以減少尋找X軸和Y軸最優劃分方式的計算時間，具體的算法流程如圖1所示。
圖1
改進的MIC算法流程
Figure1.
The improved MIC algorithm flow
2 算法驗證與應用
2.1 基于厄農映射模型的驗證
本研究中，厄農映射模型被引入來驗證所提算法的有效性。厄農映射作為具有典型混沌動力學和非線性特性的經典模型，廣泛用于驗證新的算法[21, 23-24]。具體的，由厄農映射生成兩個具有單向耦合關系的時間序列X和Y。X和Y分別為驅動系統和響應系統，即Y = F(X)，如式（4）所示:
|
其中，xi和yi分別為系統X和Y中采樣點i。C代表X和Y系統之間的耦合強度，取值范圍為0～1。當C為1時代表兩個系統完全耦合。參數B決定兩個系統是否相同，即當B = 0.1時，兩系統為不相同系統。式中u i和vi分別代表兩個系統的高斯隨機噪聲。在驗證過程中，系統中xi、yi、ui、vi的初始值在0～1之間隨機生成。
本研究從計算時長和不同噪聲水平下檢測耦合強度變化的能力兩個方面對改進的MIC算法進行了驗證。
2.2 算法在EEG信號和sEMG信號上的應用
本研究將所提算法應用于健康對照者和腦卒中患者進行右腳踝關節背屈任務中beta頻段（14～30 Hz）和gamma頻段（31～45 Hz）的FCMC研究。
2.2.1 試驗范式
本研究招募了10名無任何神經疾病史的健康受試者（年齡范圍：49～67歲，其中包括2名女性）作為健康對照組；10名腦卒中恢復期患者（年齡范圍：50～68歲，其中包括2名女性）作為腦卒中患者組。所有腦卒中患者均表現出右側肢體運動功能障礙，并依據福格?邁爾評定 (Fugl-Meyers assessment, FMA)量表評估了下肢功能。受試者人口學統計信息如表1所示。所有受試者試驗前已簽署試驗知情同意書。該試驗符合《赫爾辛基宣言》，并已得到河北大學附屬醫院倫理審查委員會的批準（HDFY- LL-2020-091）。
表1
腦卒中患者人口學信息
Table1.
Demographics of stroke patients
正式試驗中，受試者們被要求在視覺提示下自主進行穩定的右腳背屈。受試者調整為舒適坐姿，雙下肢自然垂直，雙腳掌平放于地面。試驗過程中受試者需平視距離自己90 cm處的電腦屏幕中央。當屏幕中央出現十字標志時，提醒受試者保持注意力。2 s后，屏幕出現圓形標志提示受試者執行保持右腳背屈的任務，持續時間為30 s。每名受試者重復5組上述任務，每組任務中間休息120 s以避免疲勞，試驗范式如圖2所示。
圖2
試驗范式
Figure2.
Experimental paradigm
2.2.2 EEG信號與sEMG信號同步采集
本研究使用便攜式EEG信號采集設備（Grael，Compumedics Neuroscan Inc.，澳大利亞）同步采集EEG信號和sEMG信號，采樣率為1 024 Hz。具體的，利用該設備提供的兩組雙極通道采集左右腿脛骨前肌（tibialis anterior，TA）處sEMG信號。同時依據國際10-20系統的標準，以雙耳乳突M1/M2為參考，選擇采集來自26個通道（FP1、FP2、Fz、F3、F4、F7、F8、FC3、FCz、FC4、C3、Cz、C4、CP3、CPz、CP4、P3、Pz、P4、T7、T8、P7、P8、O1、Oz、O2）的EEG信號，電極安放位置如圖3所示。電極安放前清洗并吹干頭發，用磨砂膏擦拭TA處皮膚，以確保將所有電極與皮膚交界處阻抗降至10 kΩ以下。另外為避免電極導線晃動帶來的噪聲，試驗過程中將導線用膠帶進行必要的固定。試驗過程中盡量避免眨眼、吞咽、轉頭等動作。
圖3
電極安放位置示意
Figure3.
Electrode placement diagram
2.2.3 EEG數據與sEMG數據預處理
按照上述試驗流程采集到的EEG信號和sEMG信號包括2 s的準備階段和30 s的力輸出階段。為了方便下一步數據的分析，只保留了穩定的力輸出時刻的數據。因此，從30 s的力輸出階段數據中截取了第2～29 s時刻的EEG數據和sEMG數據以避免背屈動作起始和結束階段力量動態變化太大造成的影響。最后每位受試者得到了5組28 s的穩定數據。
本研究首先對采集到的EEG數據和sEMG數據去除50 Hz工頻干擾。隨后對數據先進行150 Hz的低通濾波，再進行2 Hz的高通濾波。最后利用獨立成分分析方法（independent component analysis，ICA）去除EEG信號中包括眼動、EMG信號和心電信號在內的偽跡。EEG數據和sEMG數據的上述處理均在開源信號處理工具箱EEGLAB 2020（Swartz Center for Computational Neuroscience，美國）執行。
2.2.4 Morlet小波變換
為同時捕獲EEG信號和sEMG信號在時頻空間的變化，本研究中將濾波處理后的數據進行了Morlet小波變換從而得到信號的時頻能量圖[25]。Morlet小波變換的公式如式（5）所示：
|
其中，W (t, f)代表轉換后輸出的時頻信號，為輸入的時域信號，f為返回的頻率向量，t為時間，b為小波函數的平移因子，a為小波函數的尺度因子， 為Morlet小波基函數的復共軛。 如式（6）所示：
|
上面的 代表小波基函數， 為小波的中心頻率，i為復頻域表示時的虛數單位，t為時間。
隨后分別計算得到beta頻段和gamma頻段的平均小波功率隨時間變化的新時間序列。最后利用改進的MIC算法計算新生成的時間序列之間的耦合值。考慮到下肢運動過程中大腦運動皮層主要激活區域在Cz電極附近，因此本研究選取Cz電極點進行FCMC分析。EEG信號和sEMG信號的數據處理流程如圖4所示。
圖4
EEG信號和sEMG信號處理流程
Figure4.
The process flow for EEG signal and sEMG signal
2.2.5 統計分析
本研究首先利用排列檢驗進行統計學分析。然后將所得的健康對照組和腦卒中患者組在beta和gamma頻段的MIC值分別使用統計分析軟件SPSS 20.0（IBM SPSS Inc.，美國）進行獨立樣本 t檢驗分析,當P < 0.05，差異具有統計學意義。此外，為了評估MIC值與腦卒中患者運動功能表現可能存在的關系，本研究采用皮爾森相關系數計算了MIC值與FMA量表評分之間的相關性。
3 結果
3.1 仿真結果
本研究提出的改進算法在數值計算軟件MATLAB R2018a（MathWorks Inc.，美國）中執行。原MIC算法同樣通過MATLAB調用minepy庫文件實現[26]。為方便比較，兩種算法都運行于同一計算平臺上（Windows 10，X64；CPU：i7-1165G7，2.8 G HZ；RAM：16 G）。使用不同系統的厄農映射 (B = 0.1) 生成10個不同數據長度（500、1 000、2 000、3 000, 4 000、5 000、7 000、10 000、15 000、20 000）的數據集，每個數據集獨立生成100次。改進的MIC算法與原算法的平均計算時長差異如圖5所示，本研究提出的算法在數據長度大于6 000時的計算耗時明顯低于原MIC算法。隨著數據規模的增加，原MIC算法計算時長明顯快速增加，而本文所提改進算法計算耗時增長不明顯。
圖5
改進的MIC算法的性能表現
Figure5.
The performance of the improved MIC algorithm
進一步，本研究通過添加不同強度的垂直噪聲來驗證改進的MIC算法的魯棒性。不同信噪比（signal to noise ratio，SNR）條件下改進的MIC算法檢測耦合強度的表現如圖5所示。研究結果表明，即便是在低信噪比條件下（例如SNR=5），改進的MIC算法曲線依然能夠跟隨耦合強度值的增加而單調遞增。
3.2 實驗結果
如圖6所示，分別顯示了健康對照組右腳踝關節背屈任務時，在beta頻帶的相干性和改進的MIC算法計算出的總平均耦合強度對比。從圖6可以觀察到，在部分電極位置上（例如Fz、P7和P3），相干性方法無法清晰地區分動作腳(右腳)和靜止腳(左腳)。無論是改進的MIC算法還是原MIC算法都沒有這個問題，與靜止腳（左腳）相比，動作腳TA處sEMG信號與大腦所有電極位置的EEG信號之間均表現出更強的耦合值。相比原MIC算法，改進的MIC算法所得值略低。
圖6
不同算法在計算beta頻段總平均FCMC時的表現對比
Figure6.
Comparison of the performance of different algorithms in calculating the beta-band grand average FCMC
健康對照組和腦卒中患者組在beta頻段和gamma頻段的FCMC差異如圖7所示。相比健康對照組，腦卒中患者組的MIC值無論是在beta頻段還是在gamma頻段都顯著更低。
圖7
健康對照組和腦卒中組在beta和gamma頻段總平均MIC耦合值的比較
*
本文進一步研究了MIC值與腦卒中患者運動功能表現的關系。臨床上常用FMA量表進行患者肢體功能評估。如圖8所示，所有患者的beta頻段的MIC值與FMA量表評分之間都存在較強的正相關（r = 0.844，P = 0.002）。而gamma頻段與FMA量表評分之間相關性相對較弱（r = 0.358，P = 0.310）。
圖8
腦卒中患者的MIC值與FMA量表評分的關系
Figure8.
The relationship between the MIC value and the FMA scale score in stroke patients
4 討論
在探討大規模隨機數據中變量之間的相關性時，必須考慮計算時間。原MIC算法的計算時間主要花在利用動態規劃尋找最優的X軸網格劃分方式上。當兩個變量之間關系隨機時，需較長時間才能找到其最優劃分方式。Shao等[22]證明原MIC算法的時間復雜度為O(n2.4)，而基于K-means的MIC算法的時間復雜度為O(n1.6)（當參數a設為0.6時）。但是，在大數據量的情況下，K-means算法存在一些問題，初始聚類中心的選擇會影響結果的準確性和效率。K-means++由Arthur等[27]引入，通過解決K-means算法的分類結果依賴于初始聚類中心的選擇的問題，使K-means++算法比K-means算法更準確、更高效。因此，本研究在MIC計算過程中，使用K-means++來優化X軸和Y軸的網格劃分。仿真結果表明，隨著數據量的增加，改進的MIC算法計算時長遠低于原MIC算法，比較適合分析大樣本隨機變量之間的相關關系。
進一步，利用厄農映射驗證了本文改進的MIC算法檢測兩個系統耦合強度的有效性和魯棒性。厄農映射具有非線性的特點，耦合強度可以通過設置參數C進行調整[28]。改進的MIC算法所得MIC值在低信噪比條件下能夠跟隨耦合參數C的增加而單調遞增，這與原算法結果保持一致。這也表明所提算法能夠滿足非線性系統之間耦合關系的準確檢測。EEG信號和sEMG信號已經被證明具有典型非線性特征，因此本研究所提新算法適用于分析EEG信號和sEMG信號之間的功能耦合。
本研究將改進的MIC算法應用到右腳踝關節背屈試驗中。與相干性方法相比，所提出的MIC算法能更好地識別頭皮所有電極位置與效應肌的運動相關連接。相干性算法依賴于感興趣區域和頻帶選擇，其基于二階統計量的計算原理不適用于非線性動力系統的耦合分析[29-30]。而MIC算法則采用高階統計量來捕獲非線性耦合，其對異常值具有較強的魯棒性是由于其對香農熵和條件熵的估計方法具有較強的魯棒性[31]。特別的，本研究在感興趣的頻段（beta頻段和gamma頻段）內基于EEG信號和sEMG信號的平均功率的時間序列計算MIC值，進一步提高了算法的信噪比[32]。因此所提新方法比相干性算法具有更強的適應性，更適合于任務關聯的耦合識別。需要注意的是，相比原MIC算法，改進的MIC算法由于在尋找變量間最優劃分的時候采用了聚類算法，因此計算所得結果略低于遍歷方式所得結果。盡管如此，觀察到改進的MIC算法與原MIC算法所觀察到的FCMC結果保持一致。這也表明所提算法能夠應用于FCMC研究。
相比健康對照組，腦卒中患者組運動皮層與效應肌之間的功能耦合顯著更弱。這與之前針對腦卒中患者的FCMC研究結果保持一致[8, 33]。腦卒中后運動功能的喪失通常被認為是控制運動的神經網絡受損導致。腦損傷后通過錐體束的神經活動明顯減少，導致突觸前和突觸后活動分離，從而削弱皮質-脊髓連接[34]。這種運動神經網絡的受損可能導致了運動控制信息傳遞的異常，使信號之間發生解耦。Mima等[35]之前的研究也證實了弱耦合主要是因大腦到肌肉的信息傳遞受損引起的。
進一步，本研究探索了MIC值與運動功能表現的相關性。本研究表明，更高的MIC值與更高的FMA量表評分正相關，也說明了更高的MIC值表現了更好的下肢運動功能。之前的研究已經證實更高的運動表現與EEG信號和sEMG信號之間耦合值正相關[9,12]。本研究進一步發現相比gamma頻段的MIC值，beta頻段的MIC值與FMA量表評分相關性更高。這或許與保持背屈的試驗范式設計相關。之前的基于穩態力輸出任務的研究證實了beta頻段的神經震蕩主要負責穩態力的輸出和控制[5, 36]。因此，本研究也表明了beta頻段的MIC值有潛力成為量化腦卒中患者運動神經系統功能狀態的指標，而所提算法有希望成為量化腦卒中患者運動功能評估的有效工具。后續課題組的研究將在增加招募腦卒中志愿者數量基礎上，進一步開展不同康復手段對康復效果影響的量化評估工作。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
