動脈粥樣硬化斑塊破裂是引發眾多心血管疾病的主要原因，而生物力學因素在斑塊破裂過程中有著重要的作用。在斑塊生物力學的研究中，基于疲勞斷裂破壞理論的研究相對較少，而且大部分相關研究主要關注的是裂紋從萌生直至斑塊破裂的整個疲勞擴展過程，而對疲勞擴展過程中某一時刻下裂紋對斑塊破裂的影響的研究較少。本文針對這個問題建立了二維含裂紋的斑塊模型，基于斷裂力學理論并結合有限元數值模擬方法研究了斑塊中裂紋尖端的應力強度因子（SIF）及相關影響因素，通過SIF來衡量裂紋對斑塊破裂的影響程度。結果表明，裂紋的存在會引發局部應力集中進而增大斑塊破裂風險。斑塊裂尖SIF與血壓呈線性正相關，而與纖維帽厚度和脂質池剛度呈負相關。脂質池厚度和角度對斑塊裂尖SIF的影響均低于4%，可以忽略不計。本研究為含裂紋斑塊的破裂風險評估提供了一定的理論依據。
引用本文： 何家勝, 鐘偉健. 動脈粥樣硬化斑塊的斷裂力學數值模擬研究. 生物醫學工程學雜志, 2021, 38(6): 1097-1102. doi: 10.7507/1001-5515.202106077 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
由動脈粥樣硬化斑塊破裂引發的心肌梗塞等心血管疾病嚴重地危害著人類的健康。在美國，平均每三個死者中就有一個是死于心血管疾病[1]。在我國，心血管疾病死亡占城鄉居民總死亡原因的首位，農村為45.91%，城市為43.56%，并仍處于上升階段[2]。為了探索斑塊破裂機制，眾多學者通過斑塊組織學分析、類血管模擬和小鼠、家兔動物實驗等方法進行了研究[3-8]。目前，斑塊破裂機制仍存在著爭議，但不可否認的是生物力學因素在斑塊破裂的過程中起著主要的作用[9]。隨著有限元數值模擬方法和相關計算機軟件的快速發展，越來越多的研究者普遍接受并選擇使用有限元數值模擬方法進行斑塊的生物力學研究。Polzer等[10]通過有限元計算發現斑塊峰值應力很大程度上由纖維帽厚度決定。Doradla等[11]對30例患者進行了血管內超聲和光學頻域成像，并以此建立了相應的有限元模型，發現斑塊面積與斑塊峰值應力呈正相關。此外，斑塊內鈣化分布特征會改變斑塊的應力分布情況，可能會對斑塊的破裂造成積極的影響[12-14]。也有一些研究，如文獻[15-19]，從血液流體力學角度研究了剪切力對斑塊破裂的影響。
但上述大部分研究中的斑塊模型是不含裂紋缺陷的，且斑塊破裂被視為強度破壞問題，也就是說斑塊的峰值應力超過材料強度極限時才會發生破裂。然而，臨床發現斑塊破裂所需的應力值往往小于斑塊的強度極限[20-21]。此外，考慮到血管環境是一個天然、典型的疲勞系統，血管時刻承受著脈動血壓的作用，斑塊破裂可能是疲勞斷裂的結果。Bank等[22]率先提出了這個觀點，他們認為斑塊破裂是由疲勞損傷引發的微小裂紋發生疲勞擴展導致的。Daemen等[3]通過組織學分析驗證了這一觀點，他們發現一些斑塊中確實存在許多微小裂紋。對于含裂紋的斑塊，基于強度破壞理論的斑塊應力分析可能并不適用于解釋斑塊破裂的問題，因此研究斑塊的斷裂力學行為和性能顯得十分重要。Davis等[23]對纖維帽組織進行了單軸拉伸實驗和微型單邊缺口拉伸實驗，獲得了在單軸拉伸載荷作用下纖維帽微型單邊缺口拉伸試樣破壞時裂紋尖端張開位移等重要數據，并發現裂紋尖端張開位移和裂紋鈍化程度隨著撕裂在組織中的傳播而增加。東南大學李志勇和裴璇等[24-26]、Rezvani-Sharif等[27]和Versluis等[28]采用有限元數值計算方法模擬了斑塊裂紋的疲勞擴展過程，并分析了諸多因素對斑塊裂紋擴展路徑和斑塊剩余壽命的影響。但在他們的研究中更多關注的是斑塊裂紋疲勞擴展的過程，對疲勞擴展過程中某一時刻下裂紋對斑塊破裂影響的研究較少。且實際患者進行診斷時，斑塊中的裂紋正處于疲勞擴展過程的某一階段，分析患者現有斑塊中裂紋對斑塊的影響有助于評估患者體內含裂紋斑塊的破裂風險。
為此，本文建立二維含裂紋的斑塊模型來模擬患者某一階段下已發生裂紋擴展的斑塊，基于斷裂力學理論并結合有限元數值模擬方法研究了含裂紋斑塊的破裂問題，裂紋尖端的應力強度因子（stress intensity factor, SIF）被作為評估斑塊破裂風險的指標，用于判斷裂紋對斑塊的影響程度。考慮到實際患者的血壓、斑塊形態和力學性能存在著差異，還分析了血壓、纖維帽厚度以及脂質池厚度、角度和剛度對斑塊裂尖SIF的影響，或可為臨床診斷和治療提供一定的參考依據。
1 方法
為了探究裂紋對斑塊的影響以及評估含裂紋斑塊的破裂風險，本文以有限元分析軟件ANSYS 17.0（ANSYS Inc.，美國）對含裂紋斑塊進行了有限元數值模擬研究。
1.1 含裂紋斑塊的幾何模型
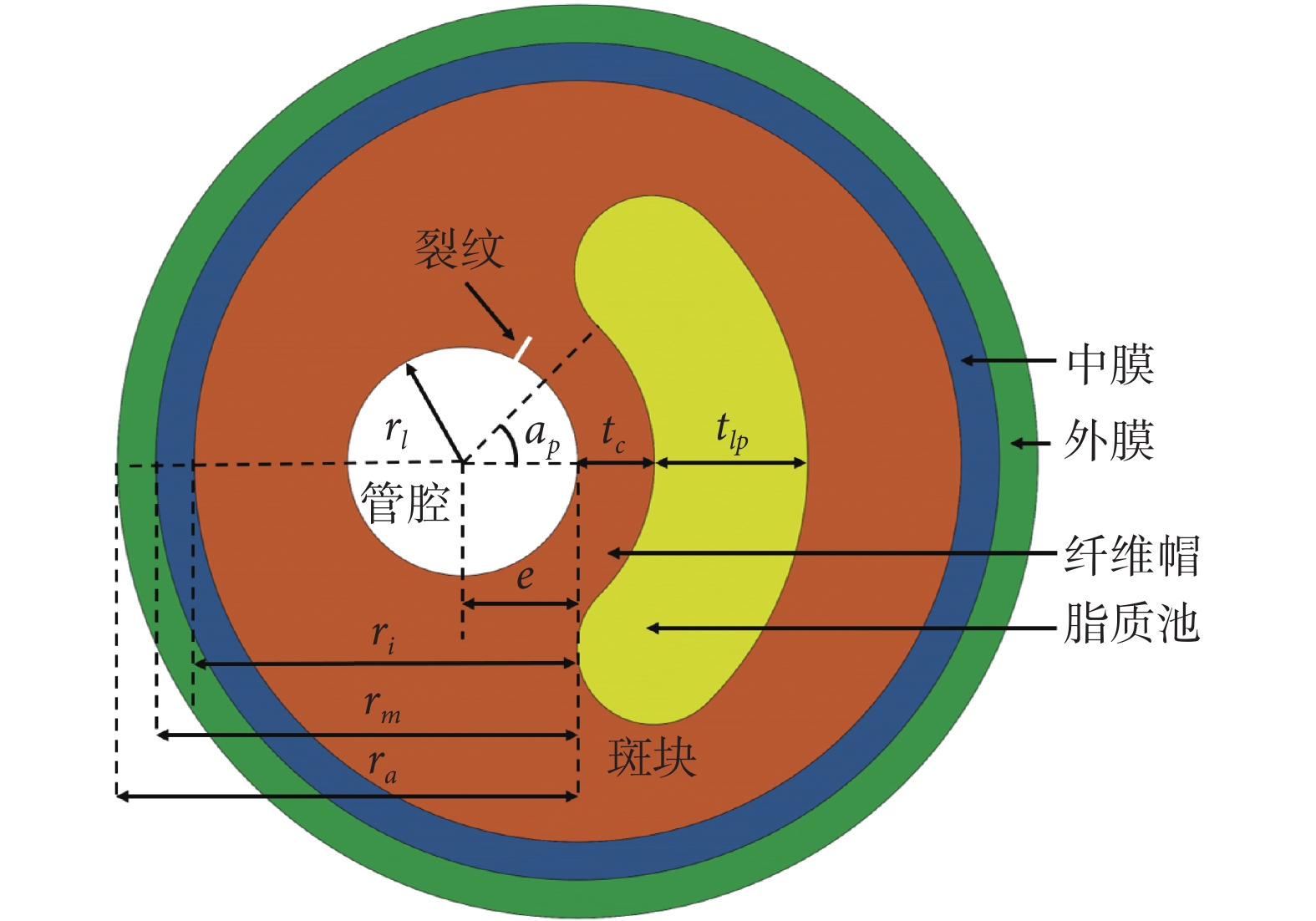
基于Versluis等[28]的實驗數據，本文建立了二維含裂紋斑塊的基線模型（狹窄率為70%），如圖1所示，其包含以下五個部分：血管外膜、中膜、纖維帽、脂質池和管腔。幾何尺寸為：纖維帽厚度tc = 1.0 mm；脂質池的厚度tlp = 2.0 mm；脂質池角度ap = 45 °，它是脂質池肩部和管腔中心的連線與水平線的夾角，和脂質池厚度一起控制著脂質池的尺寸大小；管腔半徑rl = 1.5 mm；管腔的偏心距離e = 1.5 mm；外膜和中膜的各邊界與管芯的距離分別是：ra = 6.0 mm、rm = 5.5 mm和ri = 5.0 mm。對于裂紋位置，本研究假設裂紋萌生在斑塊的最大米塞斯應力位置，因為從生物力學角度而言最大應力處更容易發生損傷和破壞[29]，本文將裂紋長度均假設為0.15 mm。
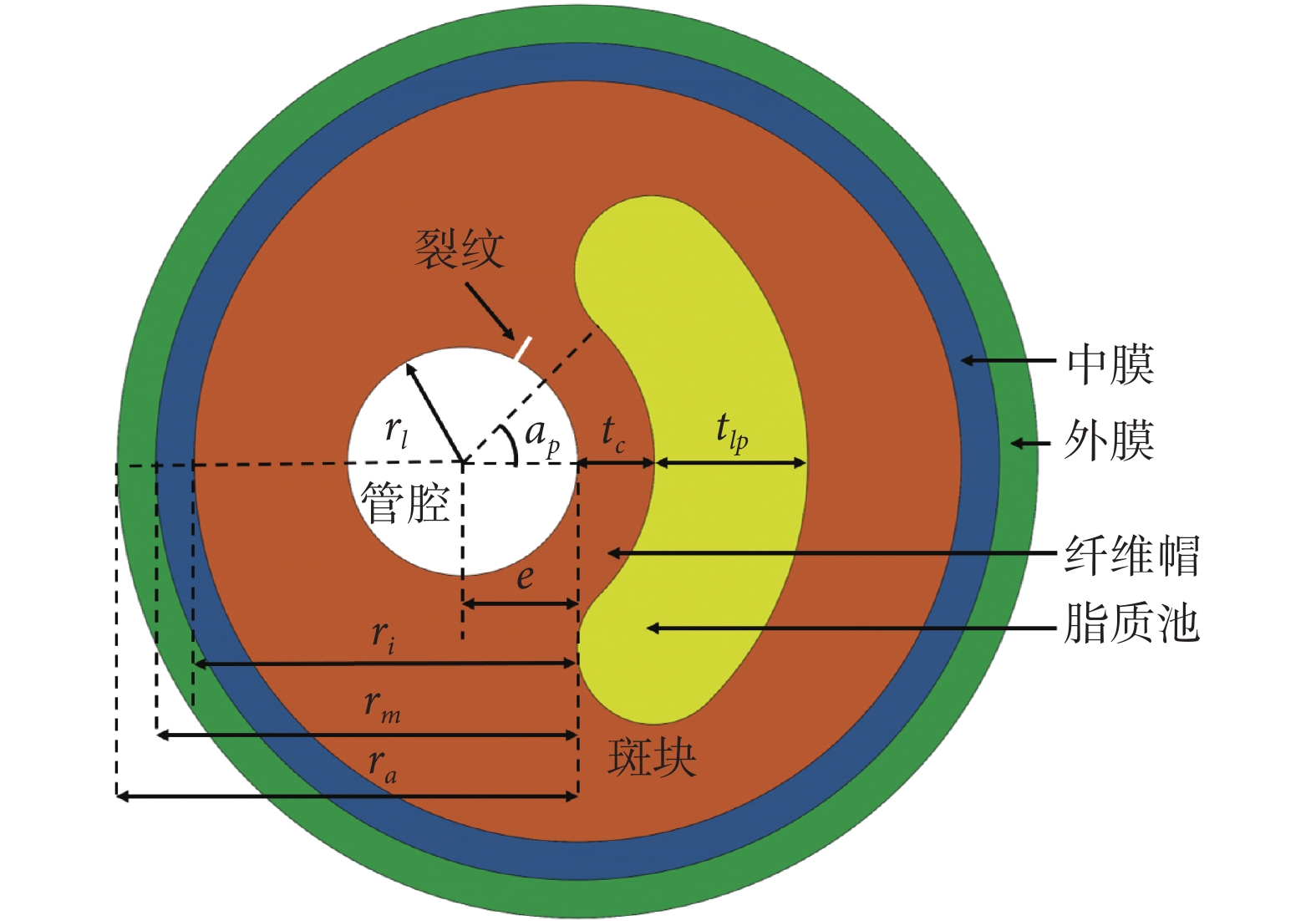圖1
含裂紋斑塊的基線模型
Figure1.
Baseline model of plaque with crack
1.2 材料屬性和網格劃分
含裂紋斑塊模型中的各成分被假設為非線性彈性、各向同性和不可壓縮材料，它們的應力應變關系可以通過如式（1）所示的應變能密度函數WY進行描述：
 |
其中，
為第一應變偏量不變量；J = det(F)為單元變形體積比，F是單元的變形梯度，對于不可壓縮材料J = 1；N、Ci和dk為材料常數。基于Holzapfel等[30]的研究結果，本文取血管外膜和中膜的材料常數N = 3，取纖維帽和脂質池的材料常數N = 1，取血管外膜的材料常數C1 = 2.4 kPa、C2 = 80 kPa、C3 = 345 kPa，取血管中膜的材料常數C1 = 6.3 kPa、C2 = 25 kPa、C3 = 255 kPa，取纖維帽的材料常數C = 166 kPa，取脂質池的材料常數C = 0.166 kPa。
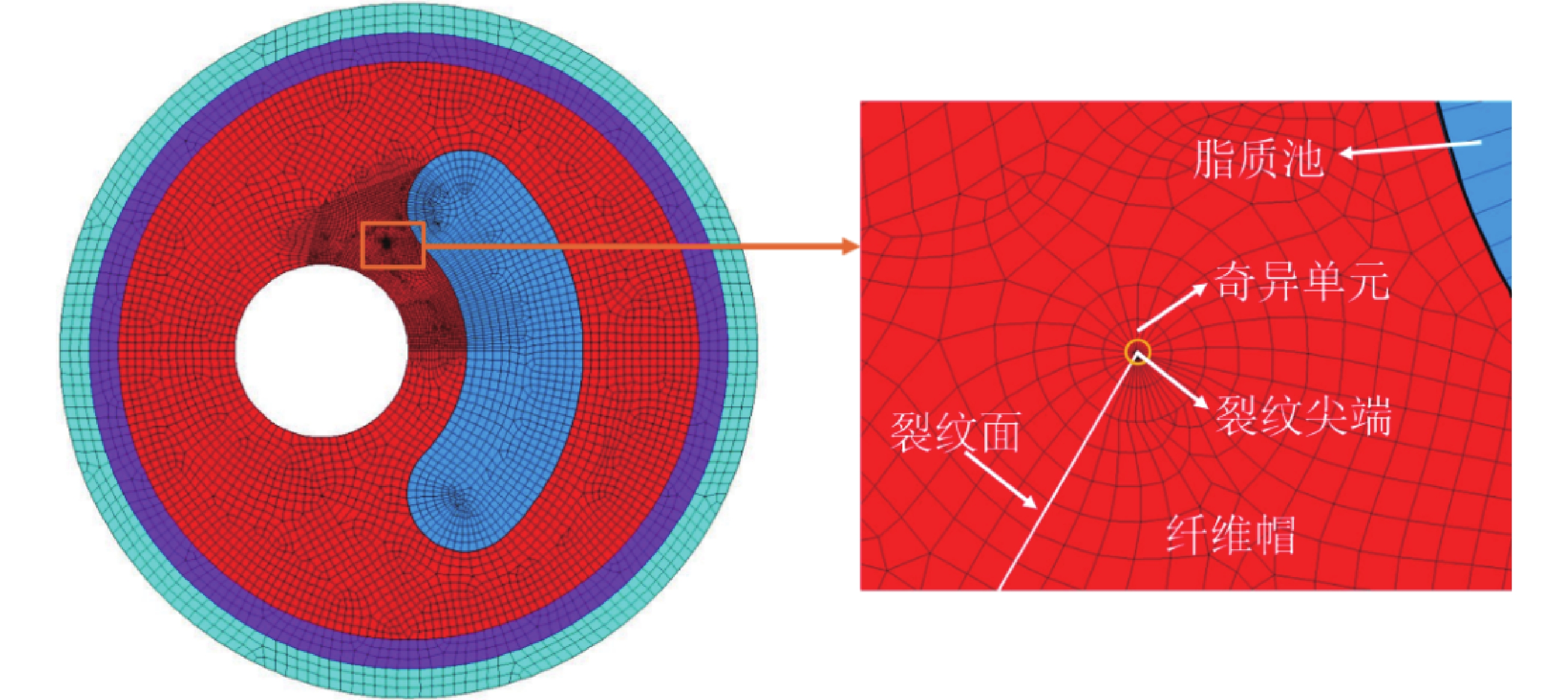
采用平面四邊形8節點單元進行網格劃分。由于裂紋尖端具有應力應變奇異性[31]，為了獲得合理的結果并計算出SIF，裂紋尖端周圍的第一圈單元（奇異單元）采用了四分之一節點法進行設置。基線模型的有限元模型如圖2所示，其包含了45 964個節點和15 266個單元。
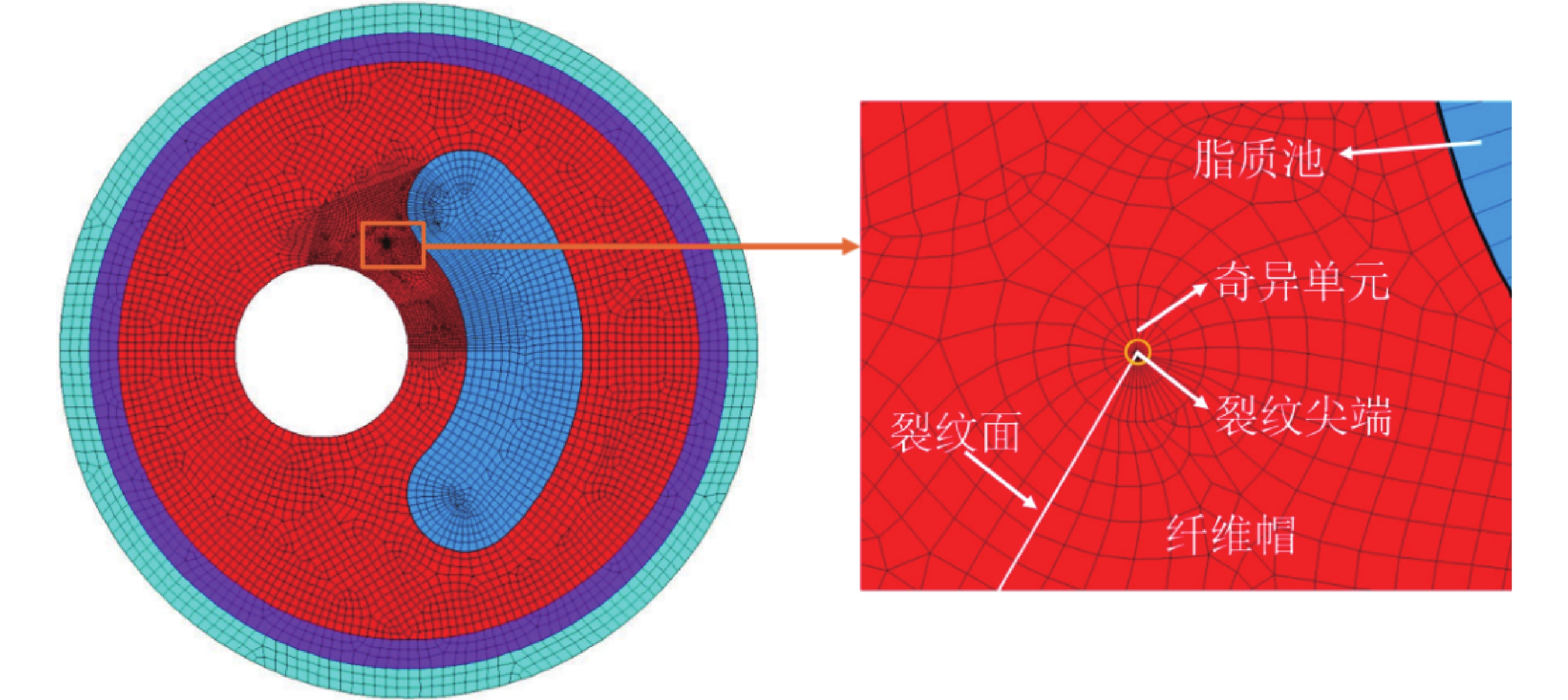圖2
基線模型的有限元模型
Figure2.
Finite element model of baseline model
1.3 邊界條件及SIF的計算
在管腔表面施加100 mm Hg的靜態血壓，在外膜邊界處施加位移約束，以固定它的位置。在有限元分析軟件ANSYS 17.0（ANSYS Inc.，美國）中，SIF是通過相互作用積分法計算所得，相互作用積分I的定義如式（2）所示：
 |
其中，σki和σkj為真實場中的應力，uk,i為真實場中的位移，
、
和 
分別為輔助場中的應力、應變和位移，qi,j為裂紋擴展矢量，qn為裂紋面法向矢量，δij為克羅尼茨符號，V為積分體域，S為積分面域。
再根據相互作用積分I與SIF的關系式，如式（3）所示，求解裂紋尖端SIF：
 |
其中，KⅠ、KⅡ和KⅢ分別是Ⅰ型、Ⅱ型和Ⅲ型SIF，
、
和
分別是輔助場中的Ⅰ型、Ⅱ型和Ⅲ型SIF；對于平面應力問題取E* = E，而對于平面應變問題取E* = E/(1-ν)，其中E為材料的彈性模量，ν為泊松比；μ為剪切模量。本研究屬于平面應變問題，此外，本文計算所得的SIF都是指KⅠ，因為它是三種SIF中最具有危害性的。
1.4 斑塊裂尖SIF的影響因素
在前人的研究中已經證實了血壓、斑塊形態和力學性能等因素對斑塊的應力分布情況有著重要的影響[10-19]。考慮到實際患者血壓和斑塊的多樣性以及本研究的普遍性，本文基于基線模型和各成分的材料常數，通過單獨依次改變靜態血壓值、纖維帽厚度以及脂質池厚度、角度和剛度來研究這些因素對斑塊裂尖SIF的影響，其中脂質池的材料常數C用來表示脂質池剛度，所有影響因素的取值如表1所示。
表1
斑塊裂尖SIF的影響因素的取值
Table1.
Value of influencing factors on SIF at crack tip of plaque
2 結果
2.1 裂紋的存在對斑塊的影響
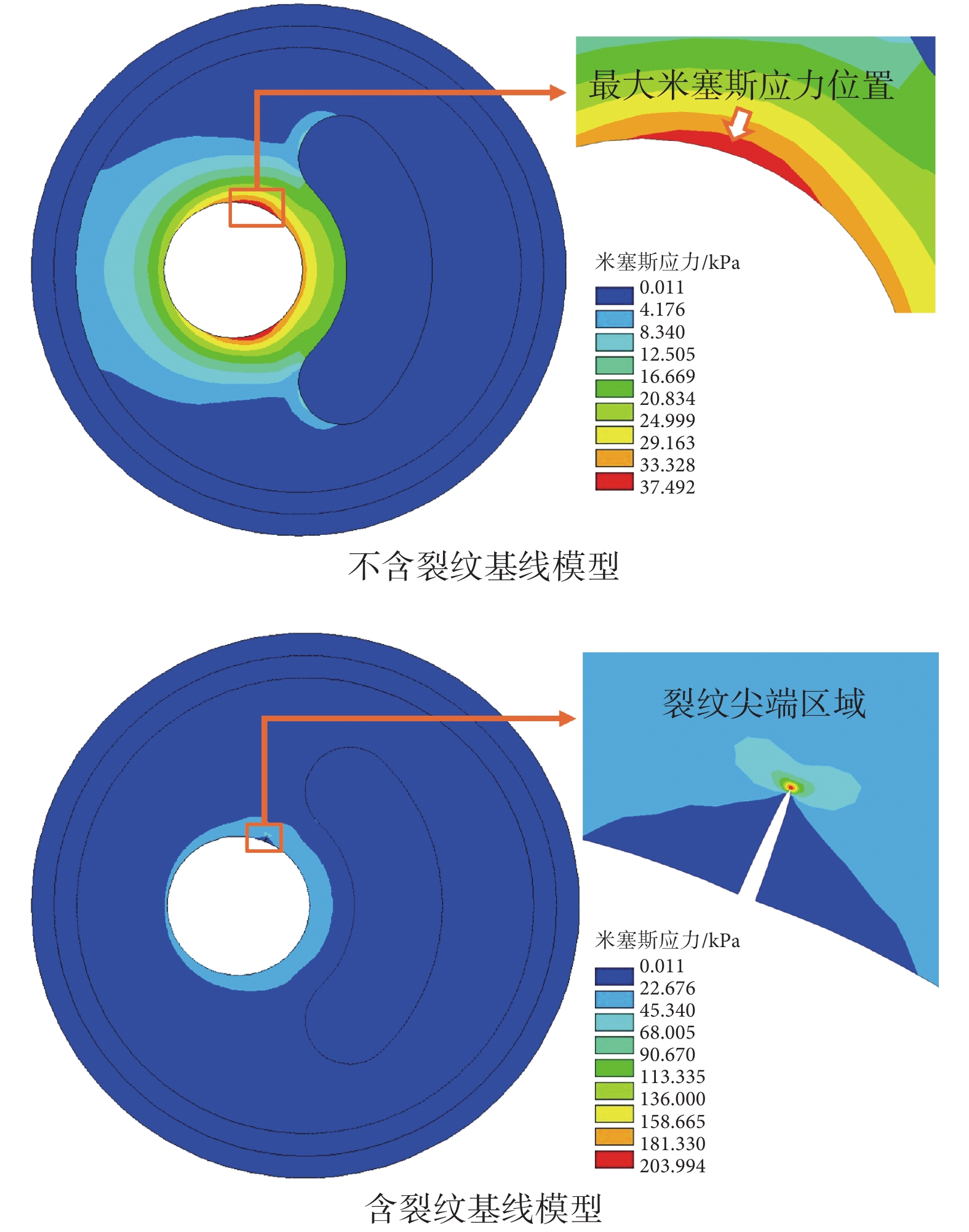
計算了不含裂紋和含裂紋的基線模型在100 mm Hg血壓下的應力分布情況，其應力云圖如圖3所示。前者的最大米塞斯應力出現在肩部區域，其值為37.492 kPa。而裂紋的存在會導致局部應力集中，最大米塞斯應力發生在裂紋尖端，其值為203.994 kPa，是不含裂紋基線模型的5.441倍。要說明的是，計算所得的裂紋尖端應力并沒有實際意義，其值會隨著裂尖網格尺寸發生改變，這種比較只是為了表達裂紋的存在容易導致裂紋尖端發生應力集中。在斷裂力學中通常是采用SIF來表示裂紋尖端應力場強度，基線模型在100 mm Hg 下的裂尖SIF為17.348 kPa·mm0.5。
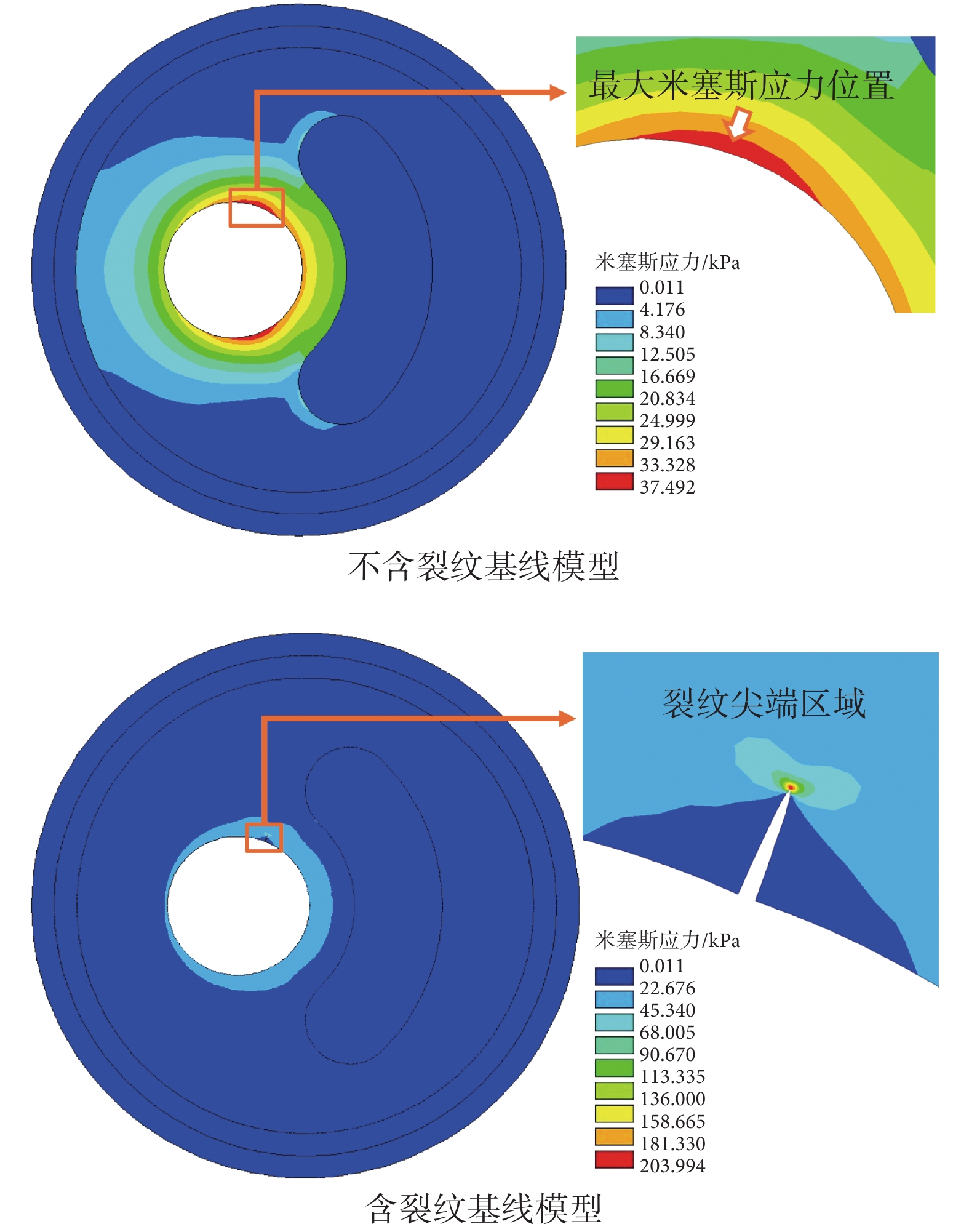圖3
不含裂紋和含裂紋的基線模型在100 mm Hg 血壓下的 應力云圖
Figure3.
Stress nephogram of baseline model without crack and with crack under 100 mm Hg blood pressure
2.2 血壓對斑塊裂尖SIF的影響
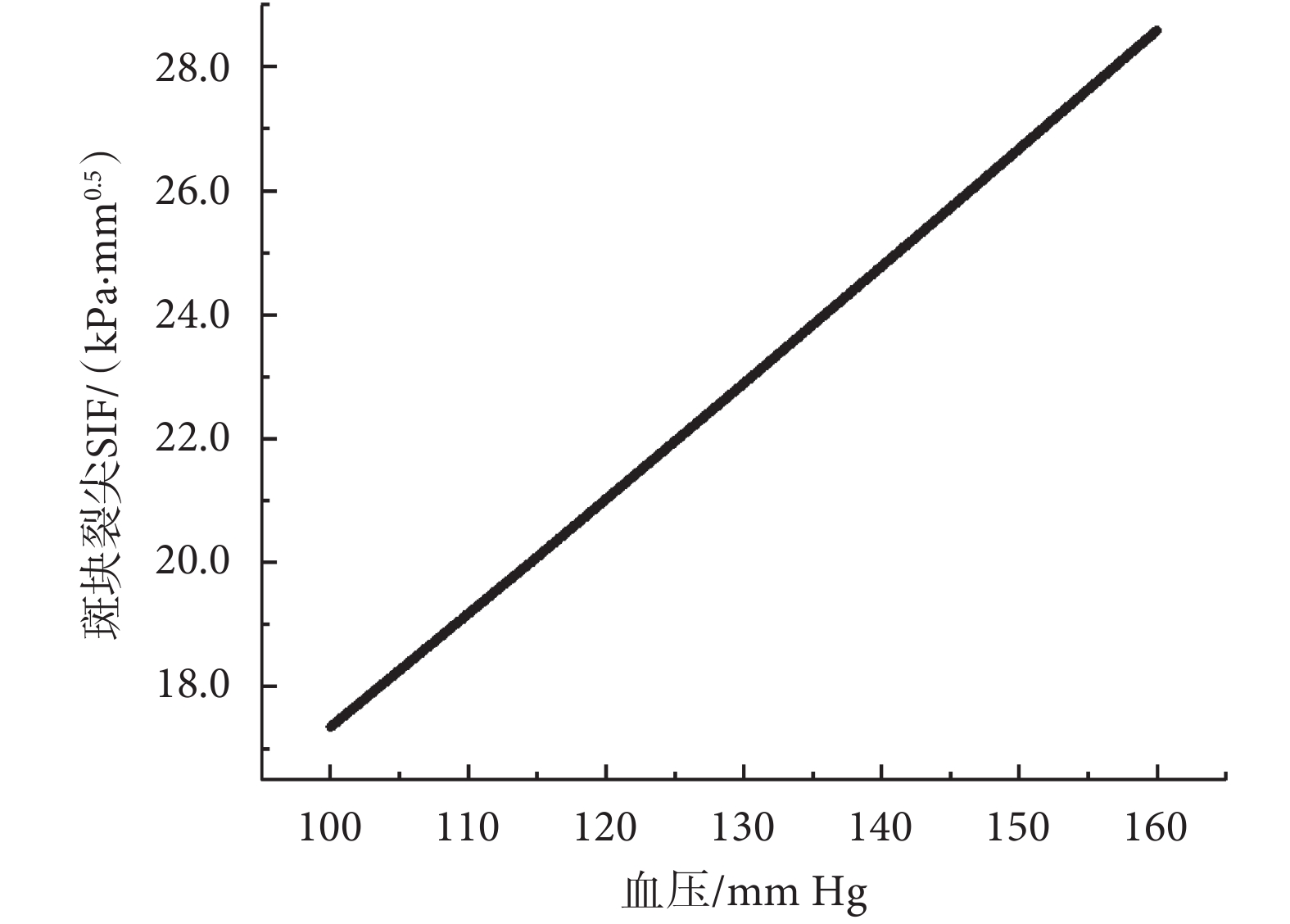
考慮到臨床患者血壓的差異性，研究了血壓對斑塊裂尖SIF的影響。在100~160 mm Hg血壓下基線模型中斑塊裂尖SIF的值如圖4所示。很明顯，斑塊裂尖SIF隨著血壓的增大而線性增加，當血壓由100 mm Hg增大至160 mm Hg 時，斑塊裂尖SIF由17.348 kPa·mm0.5變化到了28.589 kPa·mm0.5，增幅為64.797%。
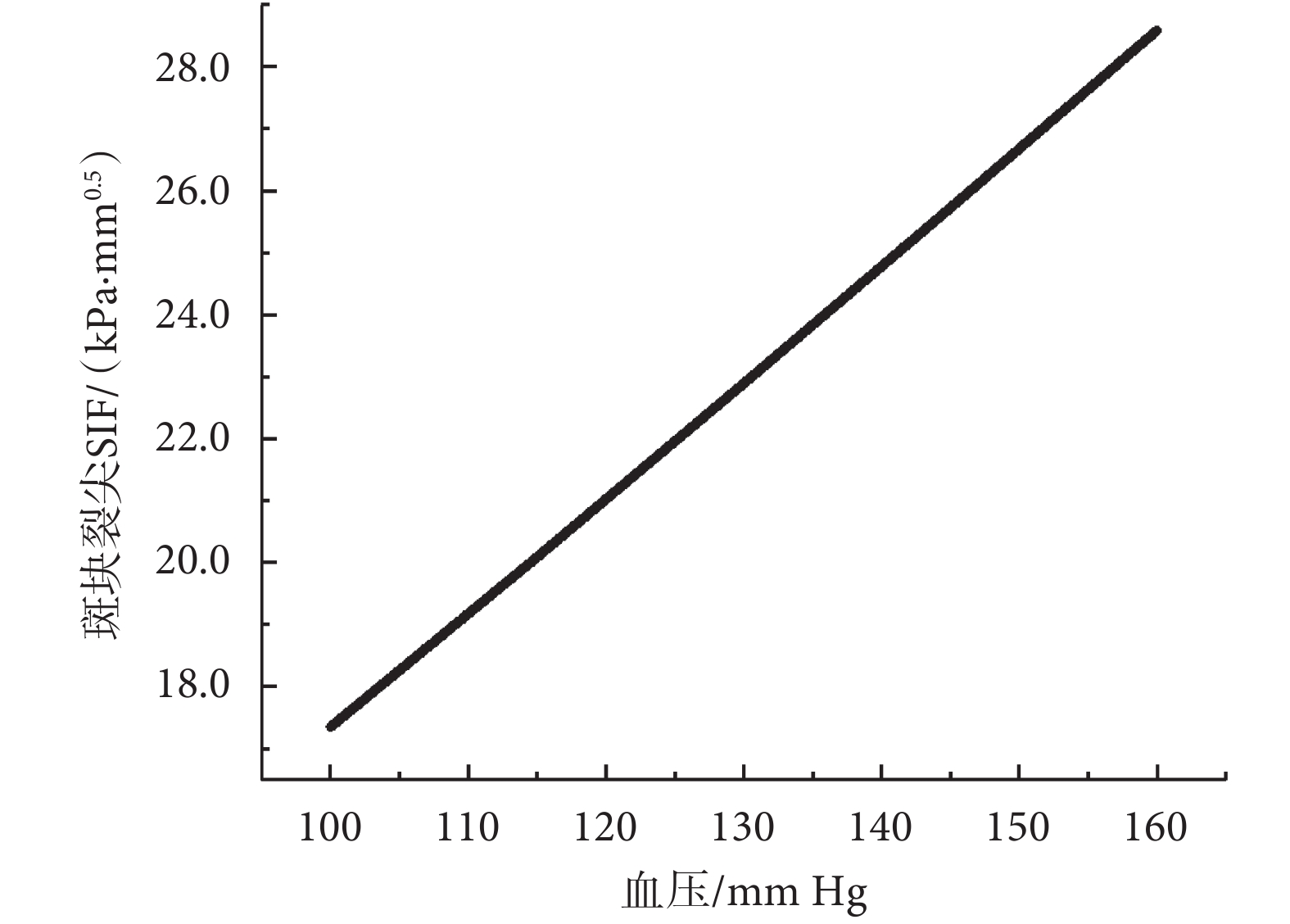圖4
斑塊裂尖SIF隨血壓的變化
Figure4.
The changes of SIF of plaque crack tip with blood pressure
2.3 斑塊形態和力學性能對斑塊裂尖SIF的影響
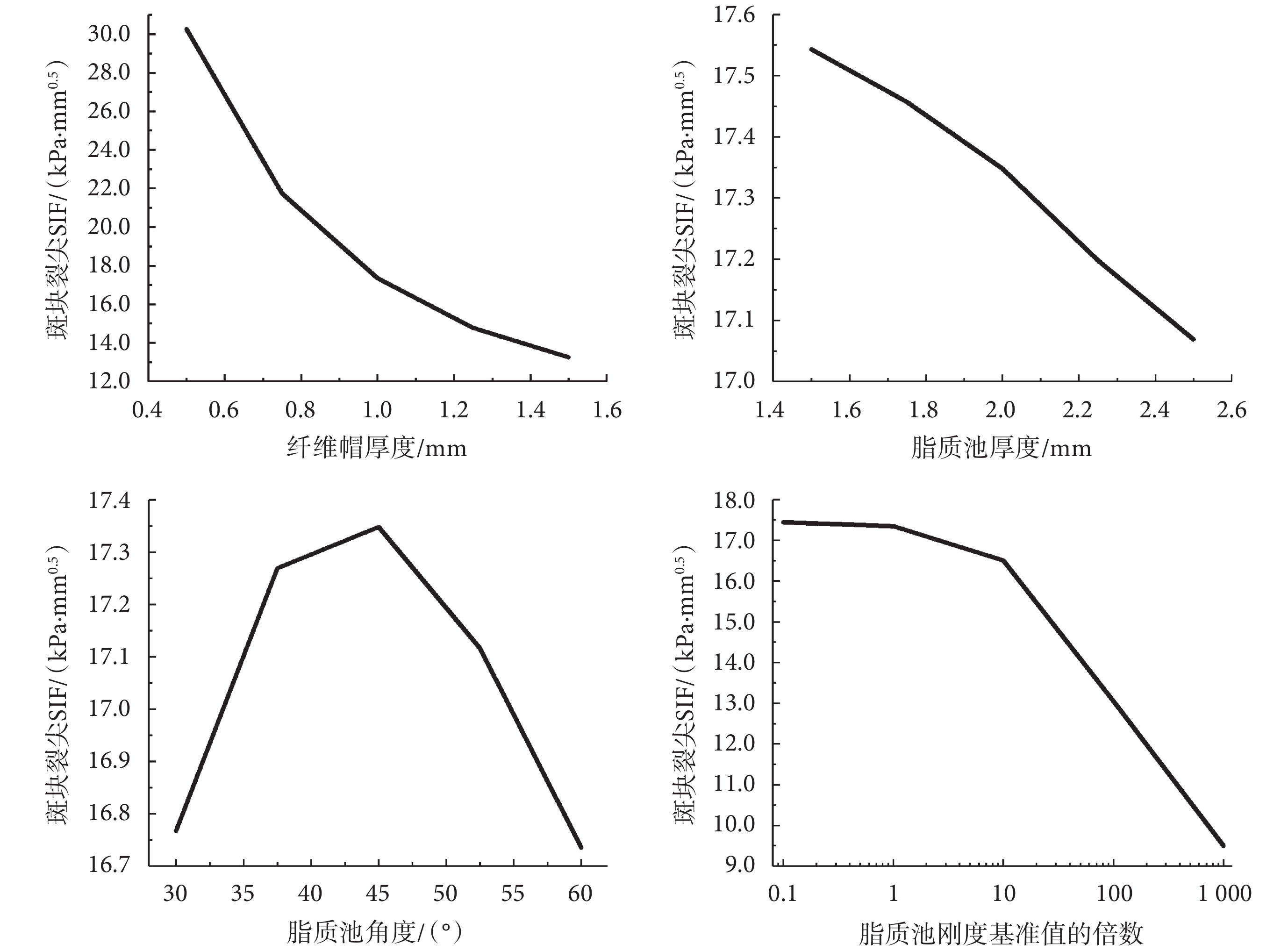
從纖維帽厚度以及脂質池厚度、角度和剛度考察了斑塊形態和力學性能對斑塊裂尖SIF的影響，計算結果如圖5所示。很明顯，纖維帽厚度的減小急劇地增大了斑塊裂尖SIF，當纖維帽厚度從1.5 mm降低至0.5 mm時，斑塊裂尖SIF從13.255 kPa·mm0.5上升至30.262 kPa·mm0.5，增幅為128.306%。脂質池厚度與斑塊裂尖SIF呈負相關，當脂質池厚度由1.5 mm增加至2.5 mm時，斑塊裂尖SIF從17.543 kPa·mm0.5降低至17.069 kPa·mm0.5。脂質池角度與斑塊裂尖SIF呈拋物線關系，當脂質池角度ap為45°時取得最大值，為17.348 kPa·mm0.5。值得注意的是，無論是脂質池厚度還是角度，它們對斑塊裂尖SIF的影響都不超過4%，在一定程度上可以忽略。而降低脂質池剛度會導致斑塊裂尖SIF增大，當脂質池剛度C為基線值0.166 kPa的1 000倍時，也就是脂質池和纖維帽的材料屬性相同時，斑塊裂尖SIF僅為9.5 kPa·mm0.5，而當脂質池剛度C為基線值的0.1倍時，斑塊裂尖SIF高達17.442 kPa·mm0.5，增幅為83.6%。
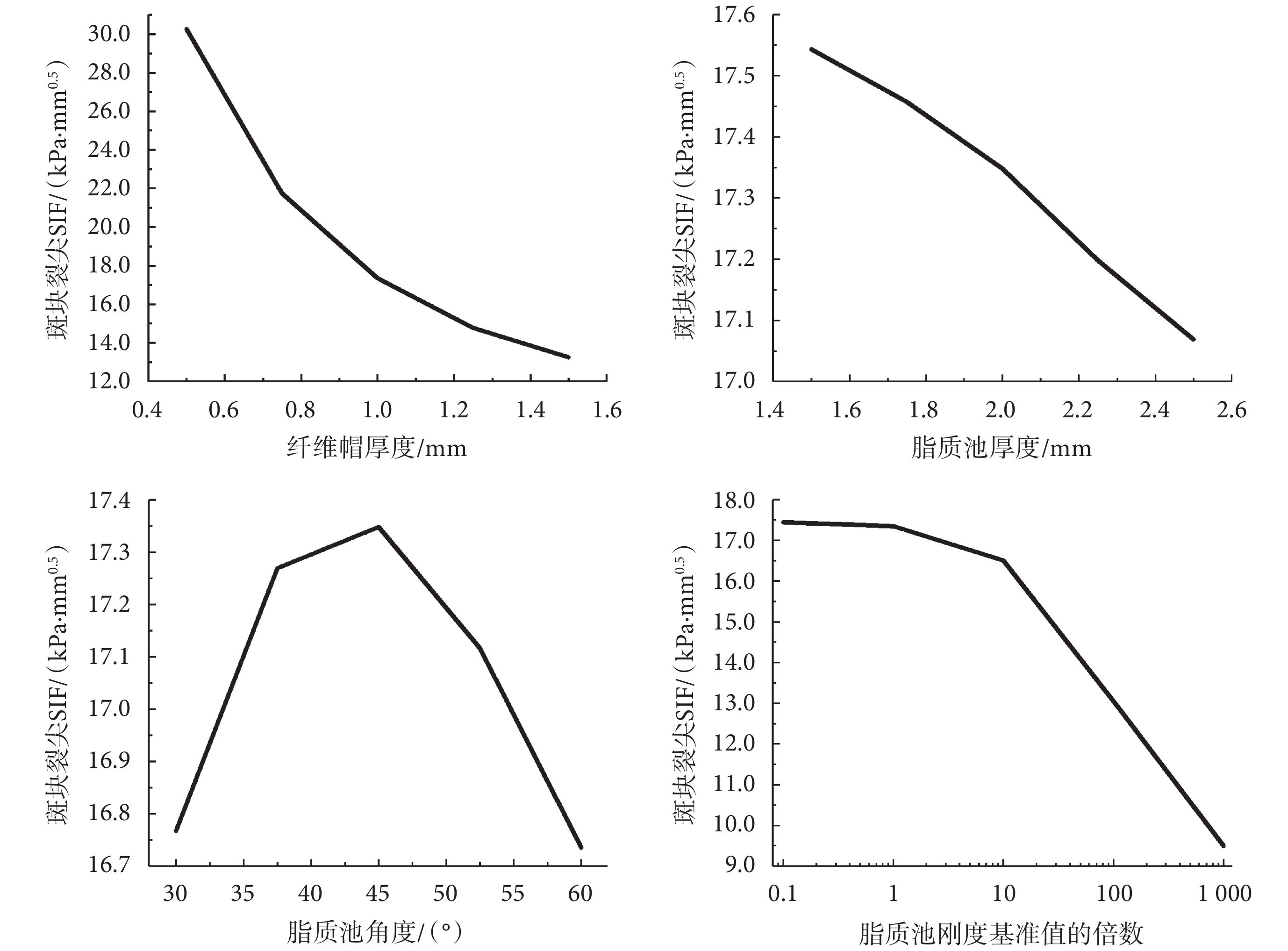圖5
斑塊裂尖SIF隨斑塊形態和力學性能的變化
Figure5.
The changes of SIF of plaque crack tip with plaque morphology
3 討論
近年來，大量研究從生物力學角度探究了動脈粥樣硬化斑塊破裂問題。其中較多研究以強度破壞準則來判斷斑塊破裂風險，并提出了不同的斑塊破裂的應力閾值，如300 kPa[32]。但上述研究往往忽略了裂紋對斑塊破裂的影響，且臨床發現斑塊在低應力狀態下也會發生破裂。為此，陸續有學者從疲勞斷裂理論研究了斑塊破裂問題并分析了含裂紋斑塊疲勞擴展過程。但目前仍然缺少對裂紋疲勞擴展過程中某一時刻下斑塊裂紋的斷裂力學參數的研究。本研究以含裂紋斑塊為研究對象，裂紋被認為萌生在最大米塞斯應力處，通過有限元數值模擬方法計算了斑塊裂尖SIF的值，以此來量化裂紋對斑塊的影響，并分析了一些因素對斑塊裂尖SIF的影響。
研究結果表明，血壓的增加會導致斑塊裂尖SIF的增大，這與以往分析斑塊峰值應力的研究結論相似：血壓的增加會導致斑塊峰值應力上升[33-34]。這說明無論是從SIF還是峰值應力角度來看，血壓的增加都會增大斑塊破裂風險，動脈粥樣硬化患者尤其是高血壓患者要控制血壓、注意飲食和情緒。較薄的纖維帽是易損斑塊的主要特征之一[10]，纖維帽厚度的降低會導致斑塊裂尖SIF的急劇增加，維持一定厚度的纖維帽可能有助于延緩斑塊破裂進程。脂質池尺寸的改變對斑塊裂尖SIF的影響較小，在一定程度上可以忽略。但脂質池剛度的降低會導致斑塊裂尖SIF的增加，這表明脂質池在“由硬到軟”的病變過程中斑塊破裂風險在增加，同時也驗證了使用他汀類藥物減少斑塊成分之間的差異性可以提高動脈粥樣硬化斑塊的穩定性[35]。
從斷裂力學角度而言，裂紋的出現并不意味著斑塊的破裂，當裂尖SIF達到斑塊材料的臨界SIF時斑塊中的裂紋才會發生失穩擴展引發斑塊的破裂。由于目前缺乏人類斑塊的相關實驗研究，尚且不知斑塊的臨界SIF，因此本文并沒有直接判斷斑塊是否發生破裂，但可以肯定的是斑塊裂紋尖端的SIF越大其破裂風險越大。因此，患者應定期進行檢查，做到早發現早治療。但同時，這對醫學成像提出了一定的挑戰，尤其是如何發現處于萌生階段的微小裂紋。此外，本文還對比了100 mm Hg 血壓下含裂紋和無裂紋基線模型中的最大米塞斯應力，前者中的最大米塞斯應力要遠遠大于后者，雖然在前者中計算所得的最大米塞斯應力并沒有實際意義，但這定性地說明了裂紋的存在會導致裂紋尖端區域發生應力集中并產生高應力進而增大斑塊破裂風險。
本研究的一個主要局限在于忽略了斑塊組織的自愈能力。斑塊在自我修復過程中可能會改變裂尖形態和組織的材料性能，因此斑塊裂尖SIF可能也會發生一定的變化，在今后的研究中需要將其考慮進去。此外，本研究所采用的斑塊模型是二維的、理想化的。實際上，斑塊形態具有多樣性，即使是同一個患者，其不同位置處的斑塊都可能是截然不同的。運用患者實際斑塊進行分析確實更有研究價值和指導意義，但這不利于參數化計算，并且會導致計算量的急劇增加。隨著成像技術和有限元分析方法在當代醫療中的深入結合，基于本研究方法的個性化診斷或可能有助于相關疾病的治療。
4 結論
本文建立了二維含裂紋斑塊的有限元模型，完成了不同血壓、斑塊形態和脂質池剛度下斑塊裂尖SIF的計算。結果表明，裂紋的存在可能會導致局部破壞的發生；相比于脂質池尺寸，血壓和脂質池剛度的增大或纖維帽厚度的降低都會顯著地增加斑塊裂尖SIF。創造良性的斑塊環境可以延緩裂紋擴展進程，降低斑塊破裂的風險性。本研究進一步從斷裂力學角度為斑塊破裂問題提供了一些可能的解釋，基于斑塊裂尖SIF的斑塊破裂風險評估方法有望為臨床治療提供一定的指導。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
由動脈粥樣硬化斑塊破裂引發的心肌梗塞等心血管疾病嚴重地危害著人類的健康。在美國，平均每三個死者中就有一個是死于心血管疾病[1]。在我國，心血管疾病死亡占城鄉居民總死亡原因的首位，農村為45.91%，城市為43.56%，并仍處于上升階段[2]。為了探索斑塊破裂機制，眾多學者通過斑塊組織學分析、類血管模擬和小鼠、家兔動物實驗等方法進行了研究[3-8]。目前，斑塊破裂機制仍存在著爭議，但不可否認的是生物力學因素在斑塊破裂的過程中起著主要的作用[9]。隨著有限元數值模擬方法和相關計算機軟件的快速發展，越來越多的研究者普遍接受并選擇使用有限元數值模擬方法進行斑塊的生物力學研究。Polzer等[10]通過有限元計算發現斑塊峰值應力很大程度上由纖維帽厚度決定。Doradla等[11]對30例患者進行了血管內超聲和光學頻域成像，并以此建立了相應的有限元模型，發現斑塊面積與斑塊峰值應力呈正相關。此外，斑塊內鈣化分布特征會改變斑塊的應力分布情況，可能會對斑塊的破裂造成積極的影響[12-14]。也有一些研究，如文獻[15-19]，從血液流體力學角度研究了剪切力對斑塊破裂的影響。
但上述大部分研究中的斑塊模型是不含裂紋缺陷的，且斑塊破裂被視為強度破壞問題，也就是說斑塊的峰值應力超過材料強度極限時才會發生破裂。然而，臨床發現斑塊破裂所需的應力值往往小于斑塊的強度極限[20-21]。此外，考慮到血管環境是一個天然、典型的疲勞系統，血管時刻承受著脈動血壓的作用，斑塊破裂可能是疲勞斷裂的結果。Bank等[22]率先提出了這個觀點，他們認為斑塊破裂是由疲勞損傷引發的微小裂紋發生疲勞擴展導致的。Daemen等[3]通過組織學分析驗證了這一觀點，他們發現一些斑塊中確實存在許多微小裂紋。對于含裂紋的斑塊，基于強度破壞理論的斑塊應力分析可能并不適用于解釋斑塊破裂的問題，因此研究斑塊的斷裂力學行為和性能顯得十分重要。Davis等[23]對纖維帽組織進行了單軸拉伸實驗和微型單邊缺口拉伸實驗，獲得了在單軸拉伸載荷作用下纖維帽微型單邊缺口拉伸試樣破壞時裂紋尖端張開位移等重要數據，并發現裂紋尖端張開位移和裂紋鈍化程度隨著撕裂在組織中的傳播而增加。東南大學李志勇和裴璇等[24-26]、Rezvani-Sharif等[27]和Versluis等[28]采用有限元數值計算方法模擬了斑塊裂紋的疲勞擴展過程，并分析了諸多因素對斑塊裂紋擴展路徑和斑塊剩余壽命的影響。但在他們的研究中更多關注的是斑塊裂紋疲勞擴展的過程，對疲勞擴展過程中某一時刻下裂紋對斑塊破裂影響的研究較少。且實際患者進行診斷時，斑塊中的裂紋正處于疲勞擴展過程的某一階段，分析患者現有斑塊中裂紋對斑塊的影響有助于評估患者體內含裂紋斑塊的破裂風險。
為此，本文建立二維含裂紋的斑塊模型來模擬患者某一階段下已發生裂紋擴展的斑塊，基于斷裂力學理論并結合有限元數值模擬方法研究了含裂紋斑塊的破裂問題，裂紋尖端的應力強度因子（stress intensity factor, SIF）被作為評估斑塊破裂風險的指標，用于判斷裂紋對斑塊的影響程度。考慮到實際患者的血壓、斑塊形態和力學性能存在著差異，還分析了血壓、纖維帽厚度以及脂質池厚度、角度和剛度對斑塊裂尖SIF的影響，或可為臨床診斷和治療提供一定的參考依據。
1 方法
為了探究裂紋對斑塊的影響以及評估含裂紋斑塊的破裂風險，本文以有限元分析軟件ANSYS 17.0（ANSYS Inc.，美國）對含裂紋斑塊進行了有限元數值模擬研究。
1.1 含裂紋斑塊的幾何模型
基于Versluis等[28]的實驗數據，本文建立了二維含裂紋斑塊的基線模型（狹窄率為70%），如圖1所示，其包含以下五個部分：血管外膜、中膜、纖維帽、脂質池和管腔。幾何尺寸為：纖維帽厚度tc = 1.0 mm；脂質池的厚度tlp = 2.0 mm；脂質池角度ap = 45 °，它是脂質池肩部和管腔中心的連線與水平線的夾角，和脂質池厚度一起控制著脂質池的尺寸大小；管腔半徑rl = 1.5 mm；管腔的偏心距離e = 1.5 mm；外膜和中膜的各邊界與管芯的距離分別是：ra = 6.0 mm、rm = 5.5 mm和ri = 5.0 mm。對于裂紋位置，本研究假設裂紋萌生在斑塊的最大米塞斯應力位置，因為從生物力學角度而言最大應力處更容易發生損傷和破壞[29]，本文將裂紋長度均假設為0.15 mm。
圖1
含裂紋斑塊的基線模型
Figure1.
Baseline model of plaque with crack
1.2 材料屬性和網格劃分
含裂紋斑塊模型中的各成分被假設為非線性彈性、各向同性和不可壓縮材料，它們的應力應變關系可以通過如式（1）所示的應變能密度函數WY進行描述：
|
其中， 為第一應變偏量不變量；J = det(F)為單元變形體積比，F是單元的變形梯度，對于不可壓縮材料J = 1；N、Ci和dk為材料常數。基于Holzapfel等[30]的研究結果，本文取血管外膜和中膜的材料常數N = 3，取纖維帽和脂質池的材料常數N = 1，取血管外膜的材料常數C1 = 2.4 kPa、C2 = 80 kPa、C3 = 345 kPa，取血管中膜的材料常數C1 = 6.3 kPa、C2 = 25 kPa、C3 = 255 kPa，取纖維帽的材料常數C = 166 kPa，取脂質池的材料常數C = 0.166 kPa。
采用平面四邊形8節點單元進行網格劃分。由于裂紋尖端具有應力應變奇異性[31]，為了獲得合理的結果并計算出SIF，裂紋尖端周圍的第一圈單元（奇異單元）采用了四分之一節點法進行設置。基線模型的有限元模型如圖2所示，其包含了45 964個節點和15 266個單元。
圖2
基線模型的有限元模型
Figure2.
Finite element model of baseline model
1.3 邊界條件及SIF的計算
在管腔表面施加100 mm Hg的靜態血壓，在外膜邊界處施加位移約束，以固定它的位置。在有限元分析軟件ANSYS 17.0（ANSYS Inc.，美國）中，SIF是通過相互作用積分法計算所得，相互作用積分I的定義如式（2）所示：
|
其中，σki和σkj為真實場中的應力，uk,i為真實場中的位移，、 和 分別為輔助場中的應力、應變和位移，qi,j為裂紋擴展矢量，qn為裂紋面法向矢量，δij為克羅尼茨符號，V為積分體域，S為積分面域。
再根據相互作用積分I與SIF的關系式，如式（3）所示，求解裂紋尖端SIF：
|
其中，KⅠ、KⅡ和KⅢ分別是Ⅰ型、Ⅱ型和Ⅲ型SIF，、和分別是輔助場中的Ⅰ型、Ⅱ型和Ⅲ型SIF；對于平面應力問題取E* = E，而對于平面應變問題取E* = E/(1-ν)，其中E為材料的彈性模量，ν為泊松比；μ為剪切模量。本研究屬于平面應變問題，此外，本文計算所得的SIF都是指KⅠ，因為它是三種SIF中最具有危害性的。
1.4 斑塊裂尖SIF的影響因素
在前人的研究中已經證實了血壓、斑塊形態和力學性能等因素對斑塊的應力分布情況有著重要的影響[10-19]。考慮到實際患者血壓和斑塊的多樣性以及本研究的普遍性，本文基于基線模型和各成分的材料常數，通過單獨依次改變靜態血壓值、纖維帽厚度以及脂質池厚度、角度和剛度來研究這些因素對斑塊裂尖SIF的影響，其中脂質池的材料常數C用來表示脂質池剛度，所有影響因素的取值如表1所示。
表1
斑塊裂尖SIF的影響因素的取值
Table1.
Value of influencing factors on SIF at crack tip of plaque
2 結果
2.1 裂紋的存在對斑塊的影響
計算了不含裂紋和含裂紋的基線模型在100 mm Hg血壓下的應力分布情況，其應力云圖如圖3所示。前者的最大米塞斯應力出現在肩部區域，其值為37.492 kPa。而裂紋的存在會導致局部應力集中，最大米塞斯應力發生在裂紋尖端，其值為203.994 kPa，是不含裂紋基線模型的5.441倍。要說明的是，計算所得的裂紋尖端應力并沒有實際意義，其值會隨著裂尖網格尺寸發生改變，這種比較只是為了表達裂紋的存在容易導致裂紋尖端發生應力集中。在斷裂力學中通常是采用SIF來表示裂紋尖端應力場強度，基線模型在100 mm Hg 下的裂尖SIF為17.348 kPa·mm0.5。
圖3
不含裂紋和含裂紋的基線模型在100 mm Hg 血壓下的 應力云圖
Figure3.
Stress nephogram of baseline model without crack and with crack under 100 mm Hg blood pressure
2.2 血壓對斑塊裂尖SIF的影響
考慮到臨床患者血壓的差異性，研究了血壓對斑塊裂尖SIF的影響。在100~160 mm Hg血壓下基線模型中斑塊裂尖SIF的值如圖4所示。很明顯，斑塊裂尖SIF隨著血壓的增大而線性增加，當血壓由100 mm Hg增大至160 mm Hg 時，斑塊裂尖SIF由17.348 kPa·mm0.5變化到了28.589 kPa·mm0.5，增幅為64.797%。
圖4
斑塊裂尖SIF隨血壓的變化
Figure4.
The changes of SIF of plaque crack tip with blood pressure
2.3 斑塊形態和力學性能對斑塊裂尖SIF的影響
從纖維帽厚度以及脂質池厚度、角度和剛度考察了斑塊形態和力學性能對斑塊裂尖SIF的影響，計算結果如圖5所示。很明顯，纖維帽厚度的減小急劇地增大了斑塊裂尖SIF，當纖維帽厚度從1.5 mm降低至0.5 mm時，斑塊裂尖SIF從13.255 kPa·mm0.5上升至30.262 kPa·mm0.5，增幅為128.306%。脂質池厚度與斑塊裂尖SIF呈負相關，當脂質池厚度由1.5 mm增加至2.5 mm時，斑塊裂尖SIF從17.543 kPa·mm0.5降低至17.069 kPa·mm0.5。脂質池角度與斑塊裂尖SIF呈拋物線關系，當脂質池角度ap為45°時取得最大值，為17.348 kPa·mm0.5。值得注意的是，無論是脂質池厚度還是角度，它們對斑塊裂尖SIF的影響都不超過4%，在一定程度上可以忽略。而降低脂質池剛度會導致斑塊裂尖SIF增大，當脂質池剛度C為基線值0.166 kPa的1 000倍時，也就是脂質池和纖維帽的材料屬性相同時，斑塊裂尖SIF僅為9.5 kPa·mm0.5，而當脂質池剛度C為基線值的0.1倍時，斑塊裂尖SIF高達17.442 kPa·mm0.5，增幅為83.6%。
圖5
斑塊裂尖SIF隨斑塊形態和力學性能的變化
Figure5.
The changes of SIF of plaque crack tip with plaque morphology
3 討論
近年來，大量研究從生物力學角度探究了動脈粥樣硬化斑塊破裂問題。其中較多研究以強度破壞準則來判斷斑塊破裂風險，并提出了不同的斑塊破裂的應力閾值，如300 kPa[32]。但上述研究往往忽略了裂紋對斑塊破裂的影響，且臨床發現斑塊在低應力狀態下也會發生破裂。為此，陸續有學者從疲勞斷裂理論研究了斑塊破裂問題并分析了含裂紋斑塊疲勞擴展過程。但目前仍然缺少對裂紋疲勞擴展過程中某一時刻下斑塊裂紋的斷裂力學參數的研究。本研究以含裂紋斑塊為研究對象，裂紋被認為萌生在最大米塞斯應力處，通過有限元數值模擬方法計算了斑塊裂尖SIF的值，以此來量化裂紋對斑塊的影響，并分析了一些因素對斑塊裂尖SIF的影響。
研究結果表明，血壓的增加會導致斑塊裂尖SIF的增大，這與以往分析斑塊峰值應力的研究結論相似：血壓的增加會導致斑塊峰值應力上升[33-34]。這說明無論是從SIF還是峰值應力角度來看，血壓的增加都會增大斑塊破裂風險，動脈粥樣硬化患者尤其是高血壓患者要控制血壓、注意飲食和情緒。較薄的纖維帽是易損斑塊的主要特征之一[10]，纖維帽厚度的降低會導致斑塊裂尖SIF的急劇增加，維持一定厚度的纖維帽可能有助于延緩斑塊破裂進程。脂質池尺寸的改變對斑塊裂尖SIF的影響較小，在一定程度上可以忽略。但脂質池剛度的降低會導致斑塊裂尖SIF的增加，這表明脂質池在“由硬到軟”的病變過程中斑塊破裂風險在增加，同時也驗證了使用他汀類藥物減少斑塊成分之間的差異性可以提高動脈粥樣硬化斑塊的穩定性[35]。
從斷裂力學角度而言，裂紋的出現并不意味著斑塊的破裂，當裂尖SIF達到斑塊材料的臨界SIF時斑塊中的裂紋才會發生失穩擴展引發斑塊的破裂。由于目前缺乏人類斑塊的相關實驗研究，尚且不知斑塊的臨界SIF，因此本文并沒有直接判斷斑塊是否發生破裂，但可以肯定的是斑塊裂紋尖端的SIF越大其破裂風險越大。因此，患者應定期進行檢查，做到早發現早治療。但同時，這對醫學成像提出了一定的挑戰，尤其是如何發現處于萌生階段的微小裂紋。此外，本文還對比了100 mm Hg 血壓下含裂紋和無裂紋基線模型中的最大米塞斯應力，前者中的最大米塞斯應力要遠遠大于后者，雖然在前者中計算所得的最大米塞斯應力并沒有實際意義，但這定性地說明了裂紋的存在會導致裂紋尖端區域發生應力集中并產生高應力進而增大斑塊破裂風險。
本研究的一個主要局限在于忽略了斑塊組織的自愈能力。斑塊在自我修復過程中可能會改變裂尖形態和組織的材料性能，因此斑塊裂尖SIF可能也會發生一定的變化，在今后的研究中需要將其考慮進去。此外，本研究所采用的斑塊模型是二維的、理想化的。實際上，斑塊形態具有多樣性，即使是同一個患者，其不同位置處的斑塊都可能是截然不同的。運用患者實際斑塊進行分析確實更有研究價值和指導意義，但這不利于參數化計算，并且會導致計算量的急劇增加。隨著成像技術和有限元分析方法在當代醫療中的深入結合，基于本研究方法的個性化診斷或可能有助于相關疾病的治療。
4 結論
本文建立了二維含裂紋斑塊的有限元模型，完成了不同血壓、斑塊形態和脂質池剛度下斑塊裂尖SIF的計算。結果表明，裂紋的存在可能會導致局部破壞的發生；相比于脂質池尺寸，血壓和脂質池剛度的增大或纖維帽厚度的降低都會顯著地增加斑塊裂尖SIF。創造良性的斑塊環境可以延緩裂紋擴展進程，降低斑塊破裂的風險性。本研究進一步從斷裂力學角度為斑塊破裂問題提供了一些可能的解釋，基于斑塊裂尖SIF的斑塊破裂風險評估方法有望為臨床治療提供一定的指導。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
