動作模仿是康復訓練中常見的訓練策略。傳統的康復訓練中患者需要在康復醫師的指導下完成訓練動作，然而由于醫院資源有限，無法滿足所有患者的訓練指導需求。本文針對康復訓練中的動作模仿任務，提出了一種基于Kinect和NAO機器人的跟隨控制方法。該方法通過逆運動學解析實現了Kinect坐標系到NAO機器人坐標系關節角度映射。針對肘關節偏轉角的估計問題，通過構建虛擬空間平面實現了偏轉角的精確估計。最后，基于肘關節的運動偏轉角進行了對比實驗，結果顯示該方法右肘橫軸偏轉和縱軸偏轉的角度估計值均方根誤差分別為2.734°和2.159°，證實了該方法可以實現NAO機器人實時、穩定地跟隨人體動作，從而向患者展示康復訓練方案。
引用本文： 劉曉光, 李思敏, 梁鐵, 李俊, 婁存廣, 王洪瑞, 劉秀玲. 基于Kinect和NAO機器人的人體上肢康復訓練跟隨控制. 生物醫學工程學雜志, 2022, 39(6): 1189-1198. doi: 10.7507/1001-5515.202111009 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
由于中風、帕金森病等疾病和意外事故等原因，我國各類肢體殘疾人數逐漸增加。據2019年中國殘聯發布的殘疾人統計公報顯示，我國肢體殘疾人數為1 989萬，其中上肢殘疾患者約占1 000萬人。上肢殘疾給人的生活帶來了諸多不便，直接影響個人的獨立性和生活質量[1]。臨床研究表明，合理的康復訓練能夠幫助患者恢復肢體的部分功能，一定程度上可恢復其生活和工作能力[2-5]。因此，研究跟隨康復醫師指導訓練動作的智能輔助康復系統已經成為康復醫學領域的研究熱點[6-11]。
近年來，研究人員一直在開發機器人智能輔助康復系統，使人與機器人進行互動[7-17]，從而發揮治療作用。滑少揚[18]利用Kinect傳感器，設計并實現了一種基于解析法的轉化方法，實現了NAO機器人（軟銀機器人，NAO6，法國）跟隨人體姿態變化的控制方案，但沒有解決肘關節偏轉的問題。Zhang等[19]提出并開發了上半身機器人模仿系統，通過基于連桿矢量的幾何分析方法，將人類手臂運動映射到仿人機器人上。Wang等[20]開發了人體上肢和UR5機器人（Universal Robots5）的在線仿真系統，提出了一種基于虛擬關節的方法解決人類手臂與UR5機器人之間的運動學映射問題。Assad-Uz-Zaman M等[21-22]使用體感設備Kinect V2跟蹤人體運動，采用改進的Denavit-Hartenberg（D-H）模型[23-32]對人體上肢進行運動學建模，通過一種完整的幾何解求解關節角度，實現了遠程控制NAO右臂運動，指導患者進行不同的手臂運動練習。目前的康復機器人雖然能夠輔助醫生進行康復訓練，但機器人動作模仿的精度還有待提高，尤其對于關節旋轉角度的估計問題，需進一步研究，從而更好地為輔助康復診療服務。
本文提出了一種基于虛擬空間平面的空間線面角逆運動學解析算法，實現了Kinect（微軟，Kinect V2，美國）坐標系到NAO機器人坐標系關節角度的映射。首先，利用Kinect獲取人體骨架坐標數據。然后，通過逆運動學解析算法，將坐標數據轉化為控制NAO機器人關節運動的角度。針對運動過程中遮擋導致的角度估計失真問題，利用中值濾波對解析的關節角度進行了處理。最后，對估計的角度進行了限幅濾波處理，以保證NAO機器人在安全的前提下跟蹤人體上肢動作。
1 研究平臺和系統設計
1.1 NAO機器人跟隨控制系統
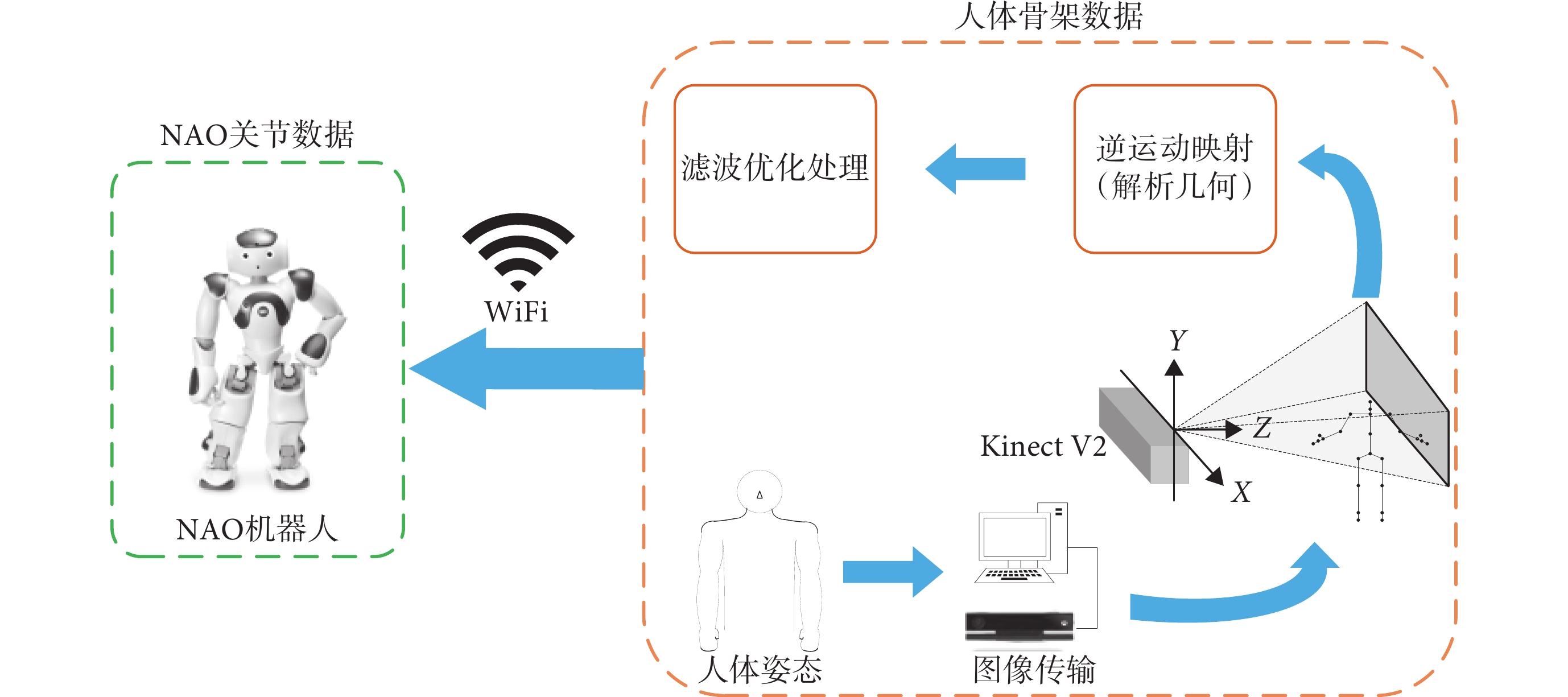
NAO機器人跟隨控制整體流程如圖1所示。為了控制NAO機器人的上肢，利用Kinect的骨骼跟蹤技術，實時采集治療師各骨骼點的笛卡爾坐標信息。然后采用基于逆運動學原理的解析幾何方法，將骨架坐標數據轉化為關節角度。最后對獲取的角度進行濾波處理后通過WiFi傳到NAO機器人的設備通信DCM模塊，實現對NAO機器人上肢各關節的運動控制。
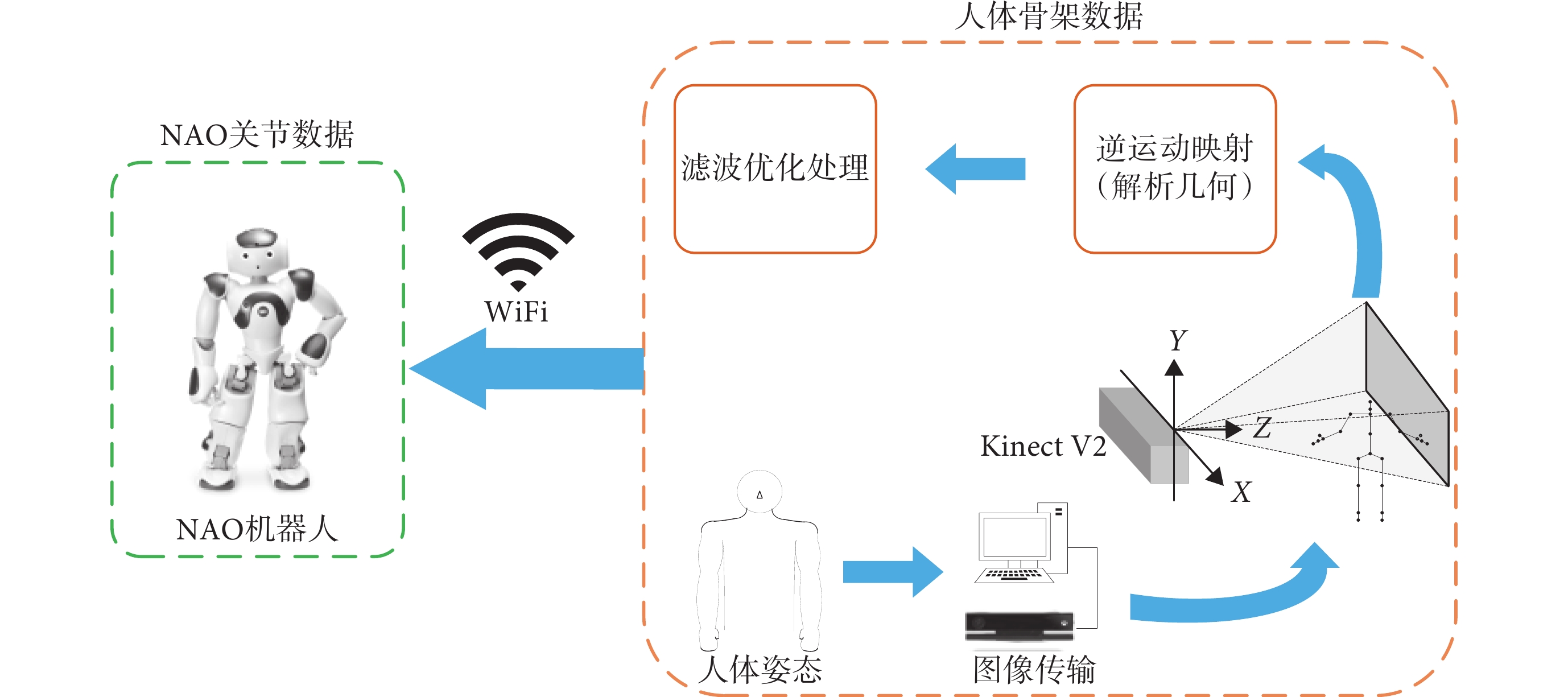圖1
NAO機器人跟隨控制流程圖
Figure1.
The flow chart of NAO robot following control
1.2 Kinect V2概述
為實現追蹤人體上肢運動，采用無標記視覺跟蹤裝置Kinect V2作為傳感器。Kinect V2是一款3D體感設備，能夠獲取RGB彩色圖像和3D深度圖像[33]，其深度圖像能夠提取人體骨架的25個主要關節點信息，并對這25個關節點進行持續追蹤，如圖2所示。Kinect V2以3D深度傳感器中的紅外相機為坐標原點建立三維坐標系，人體關節點數據可以表示為（x，y，z）。根據上肢康復訓練動作，實驗主要利用脊柱肩部、肩關節、肘關節和腕關節點的坐標進行計算，以實現機器人對人體上肢的跟隨控制。
圖2
Kinect V2信息
Figure2.
The information of Kinect V2
1.3 NAO機器人
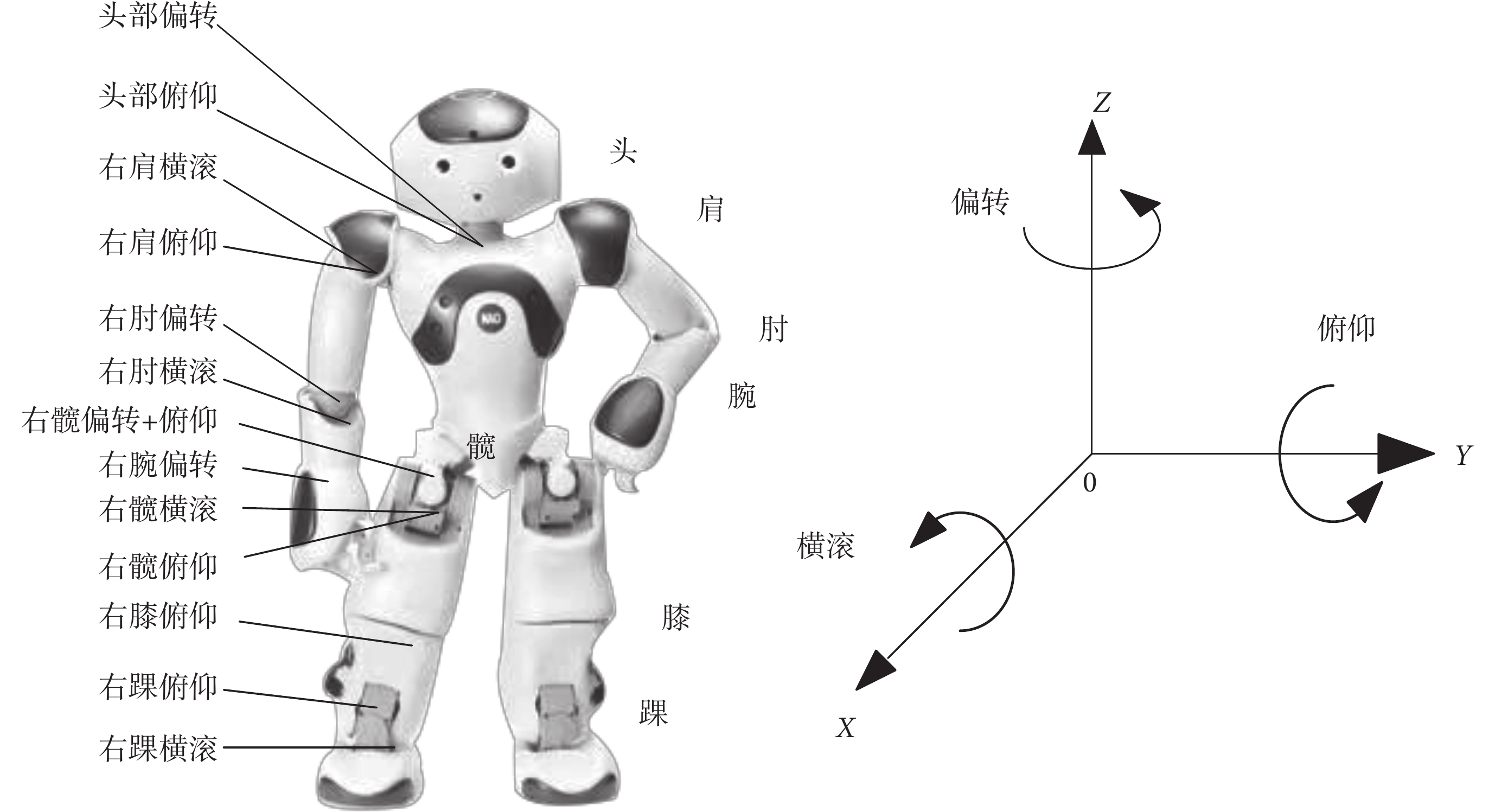
NAO機器人是具有25個自由度的仿人機器人。NAO機器人使用橫滾、俯仰、和偏轉表示運動姿態，分別對應繞X、Y和Z軸方向上的旋轉。每個關節名稱由部件名稱和姿態名稱組成[34]，如圖3所示。
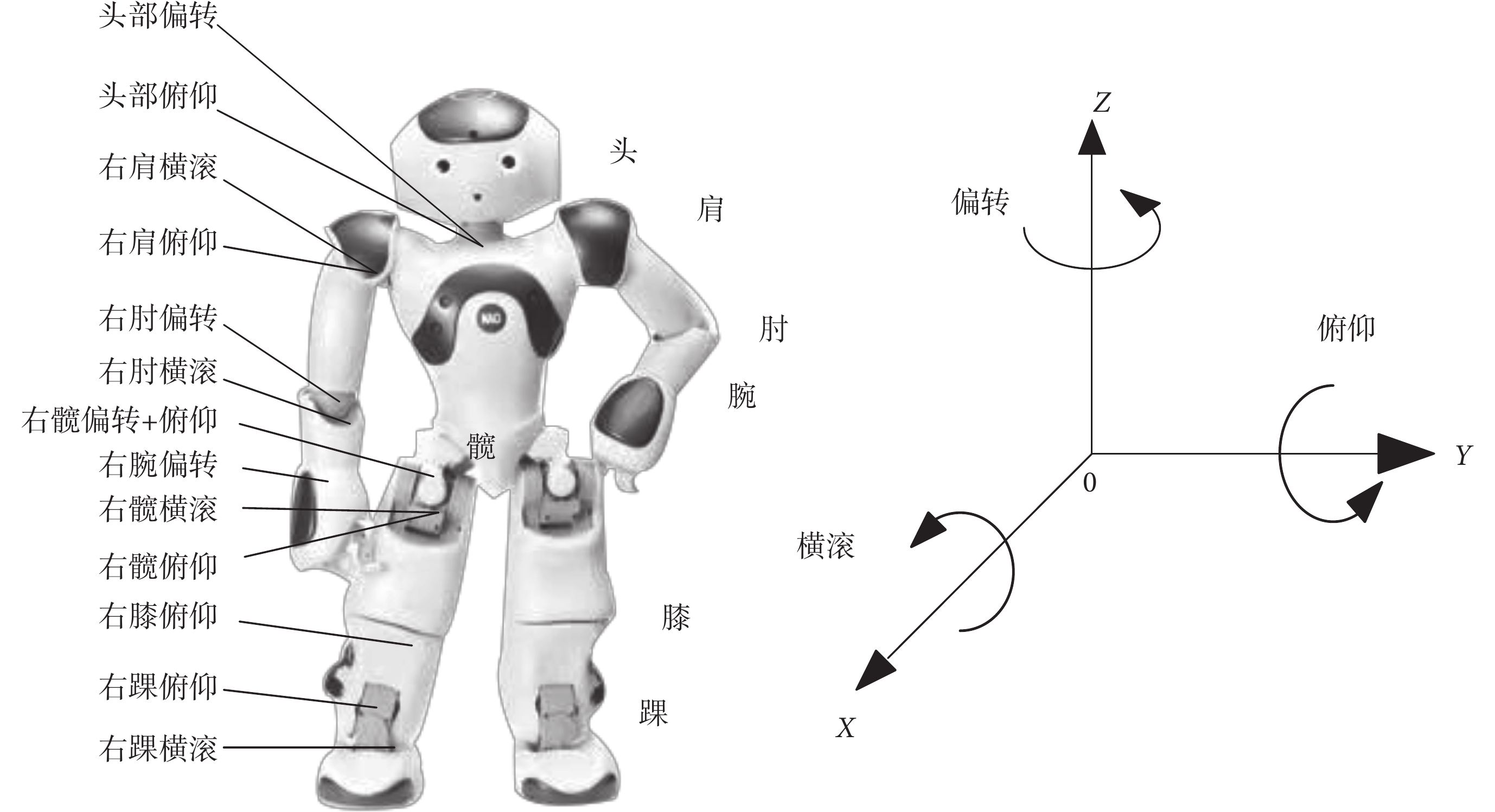圖3
NAO機器人關節
Figure3.
NAO robot joint
2 基于逆運動學解析的關節角度估計
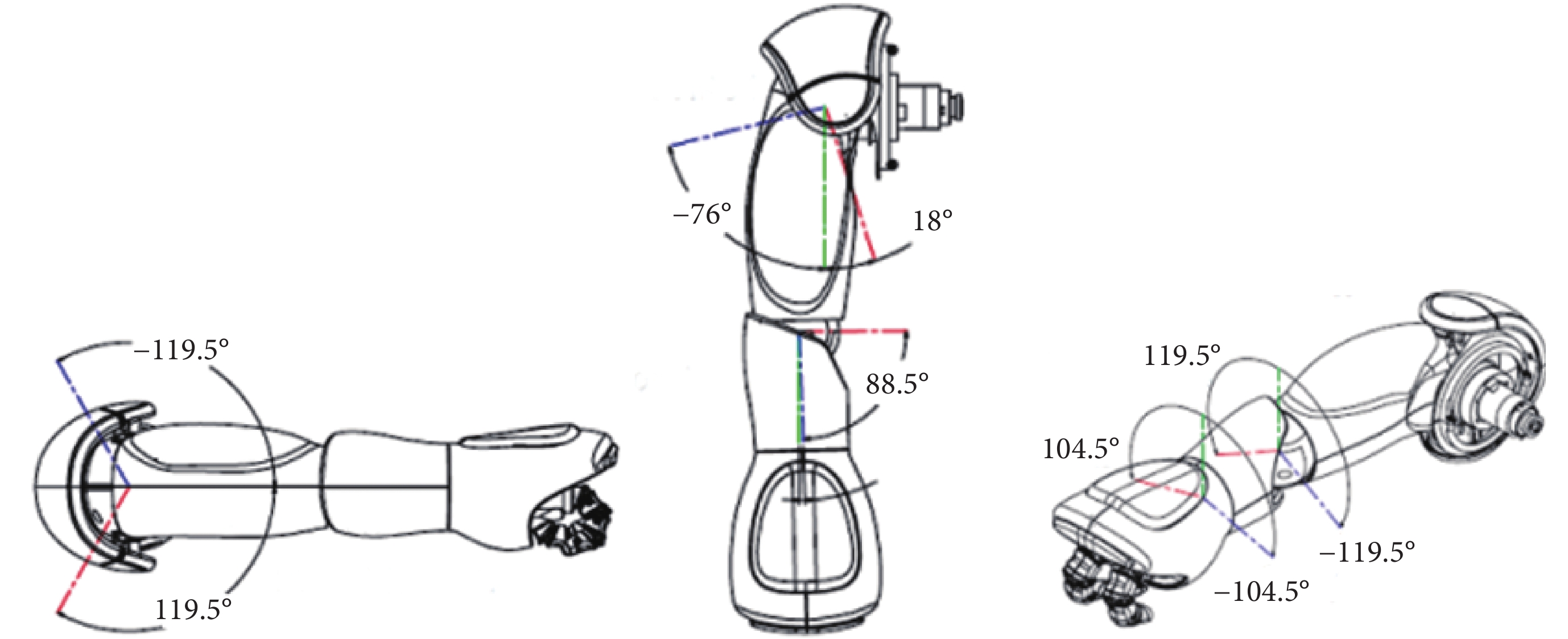
由于個體的體型存在差異，無法直接將獲取的人體骨架坐標映射到NAO機器人。因此，本文通過逆運動學原理對骨架坐標數據進行解析，將其轉換為可控制NAO機器人關節變換的角度，從而實現NAO機器人的實時控制。針對肘關節偏轉角的估計問題，提出了一種構建空間線面角的關節角度估計方法。以右上肢圖4所示的俯仰、橫滾和偏轉運動為例。
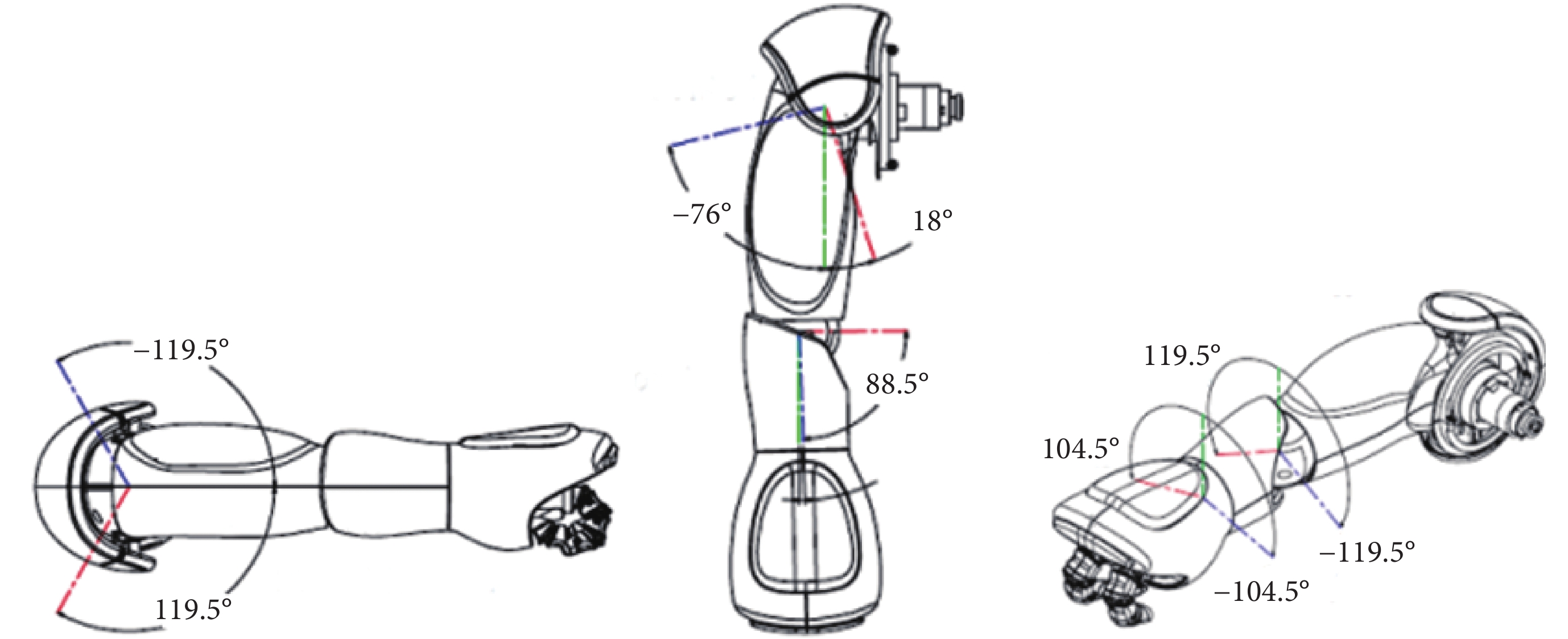圖4
NAO右上肢俯仰、橫滾、偏轉運動
Figure4.
Movement of NAO's right upper limb
利用Kinect坐標系（見圖2右），獲取的肩部脊柱坐標（
）、右肩坐標（
）、右肘坐標（
）和右腕坐標（
）的骨骼點坐標分別用（
，
，
）、（
，
，
）、（
，
，
）、（
，
，
）表示，則肩部脊柱（
）、右肘（
）、右腕（
）相對于肩部關節的坐標分別為：
肩部脊柱坐標：（
，
，
）=（
，
，
）
肘部坐標：（
，
，
）=（
，
，
）
腕部坐標：（
，
，
）=（
，
，
）
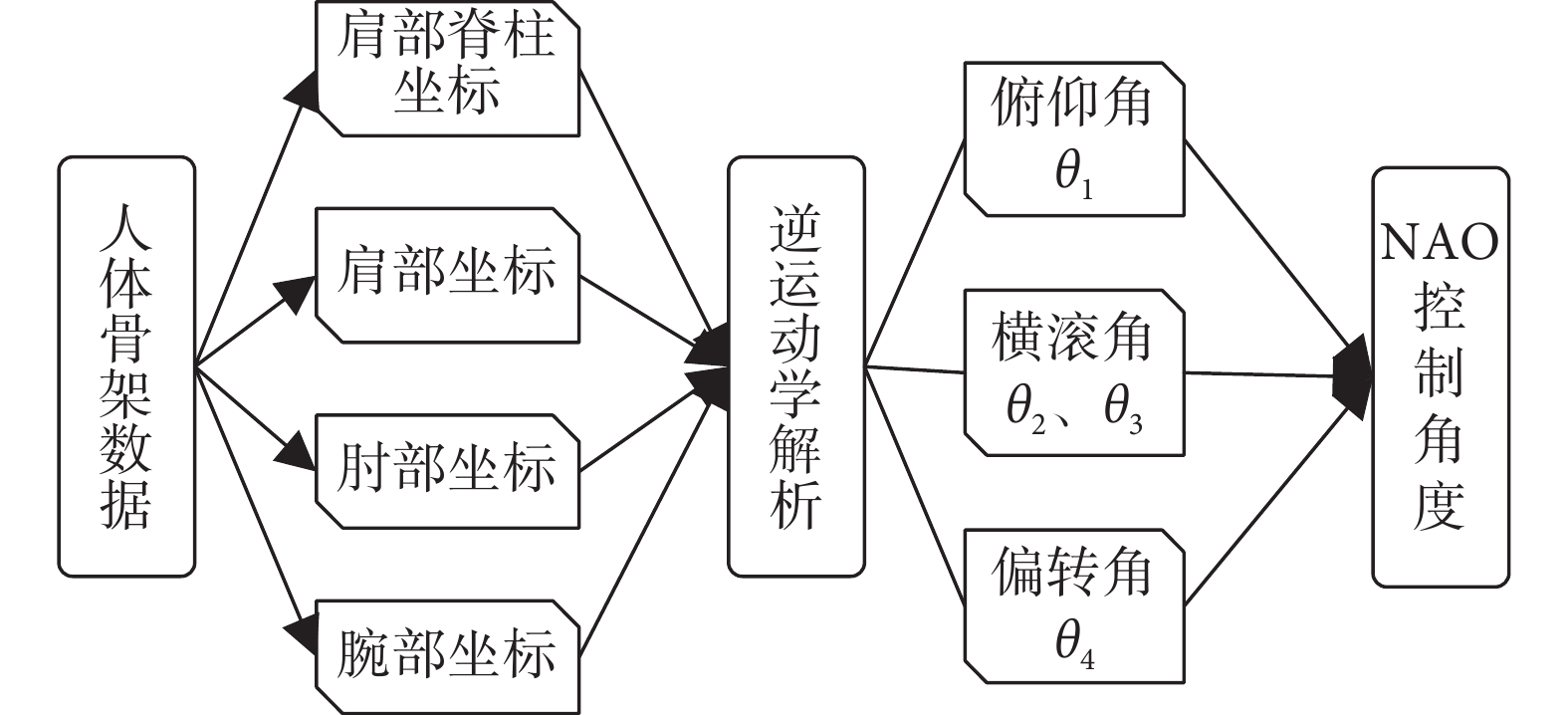
逆運動學解析的流程如圖5所示。
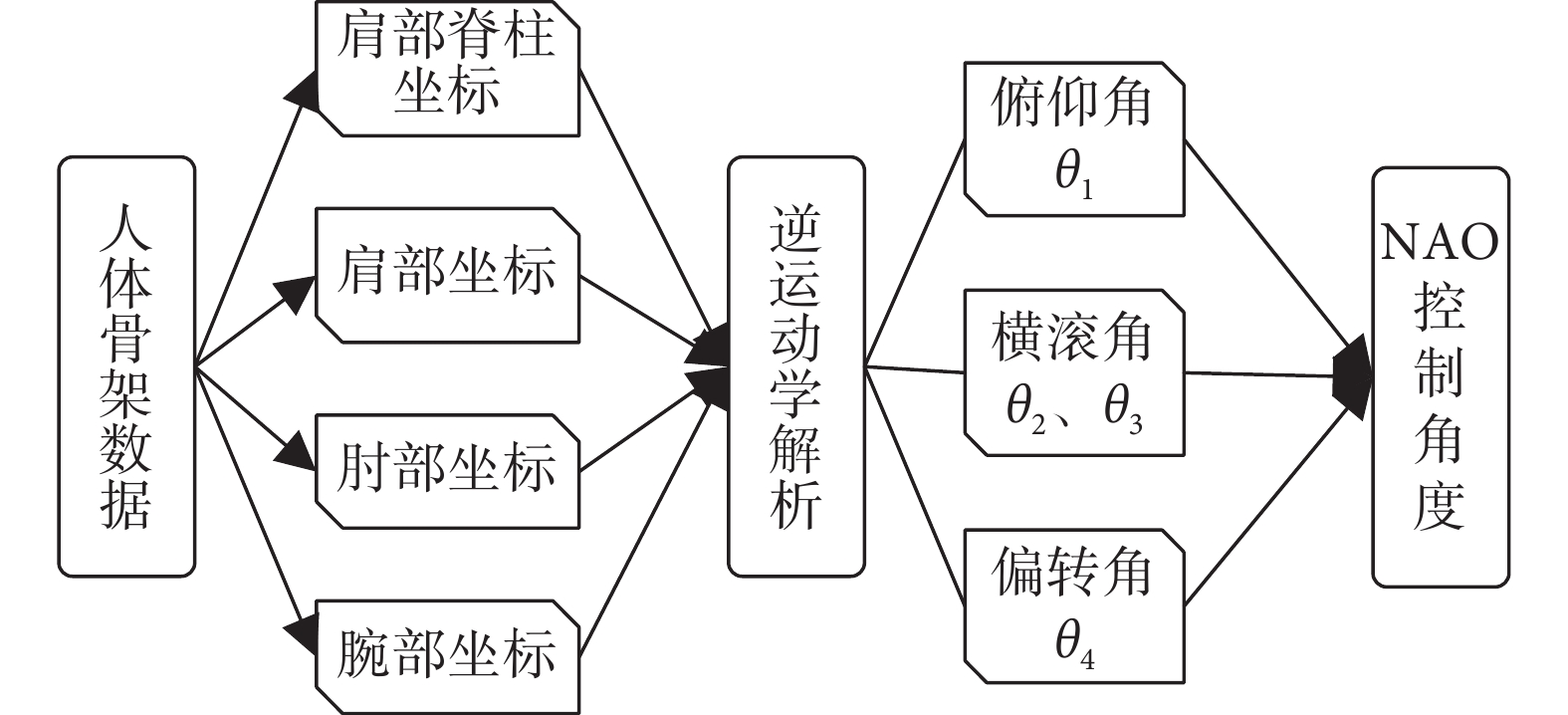圖5
逆運動學解析流程圖
Figure5.
Flow chart of inverse kinematics analysis
2.1 俯仰角與橫滾角
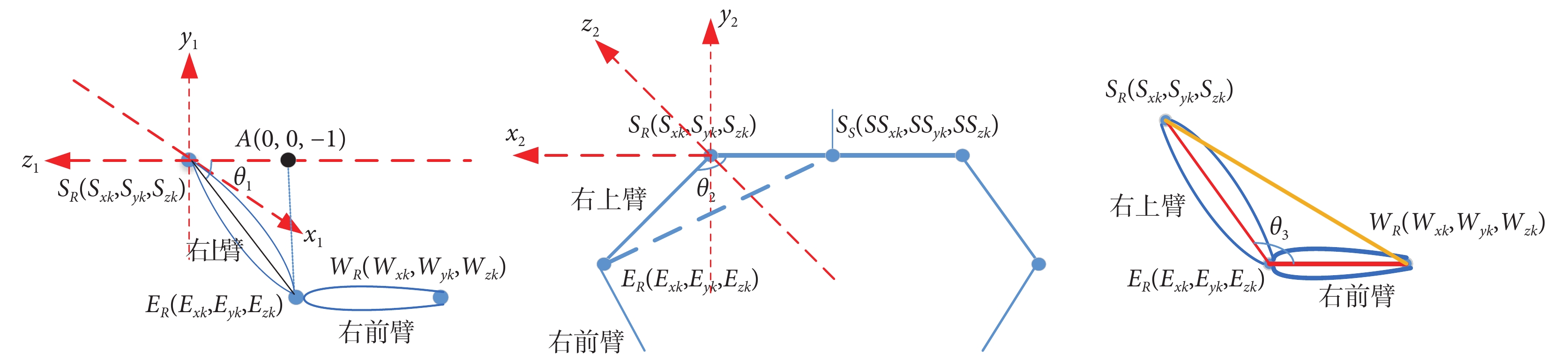
俯仰角即關節上舉或放下，橫滾角即關節外展或內收，效果如圖4所示。以肩部關節為坐標原點，分別建立如圖6所示的坐標系，運用余弦定理，通過構建三角形，求解肩部俯仰角、橫滾角和肘部橫滾角。其中，
為右肩關節俯仰角，
為右肩關節橫滾角，
為右肘關節橫滾角。為方便計算，設定點A在z1軸距原點一個單位長度的負方向上，坐標為（0，0，–1）。
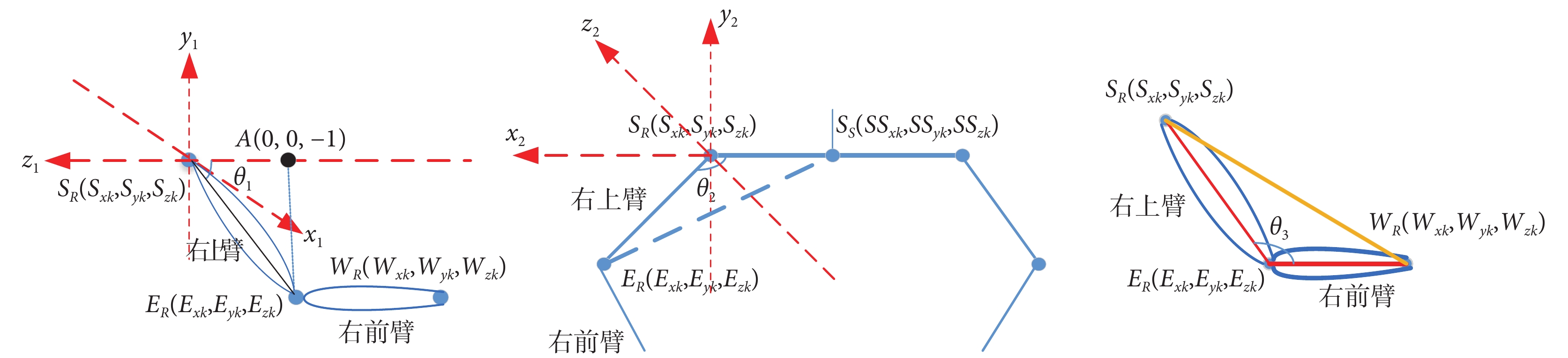圖6
右上肢俯仰角與橫滾角計算
Figure6.
Calculation of pitch angle and roll angle of right upper limb
則構建的三角形各邊邊長分別為：
 |
 |
 |
 |
 |
則各關節角度的絕對值為：
 |
 |
 |
2.2 偏轉角
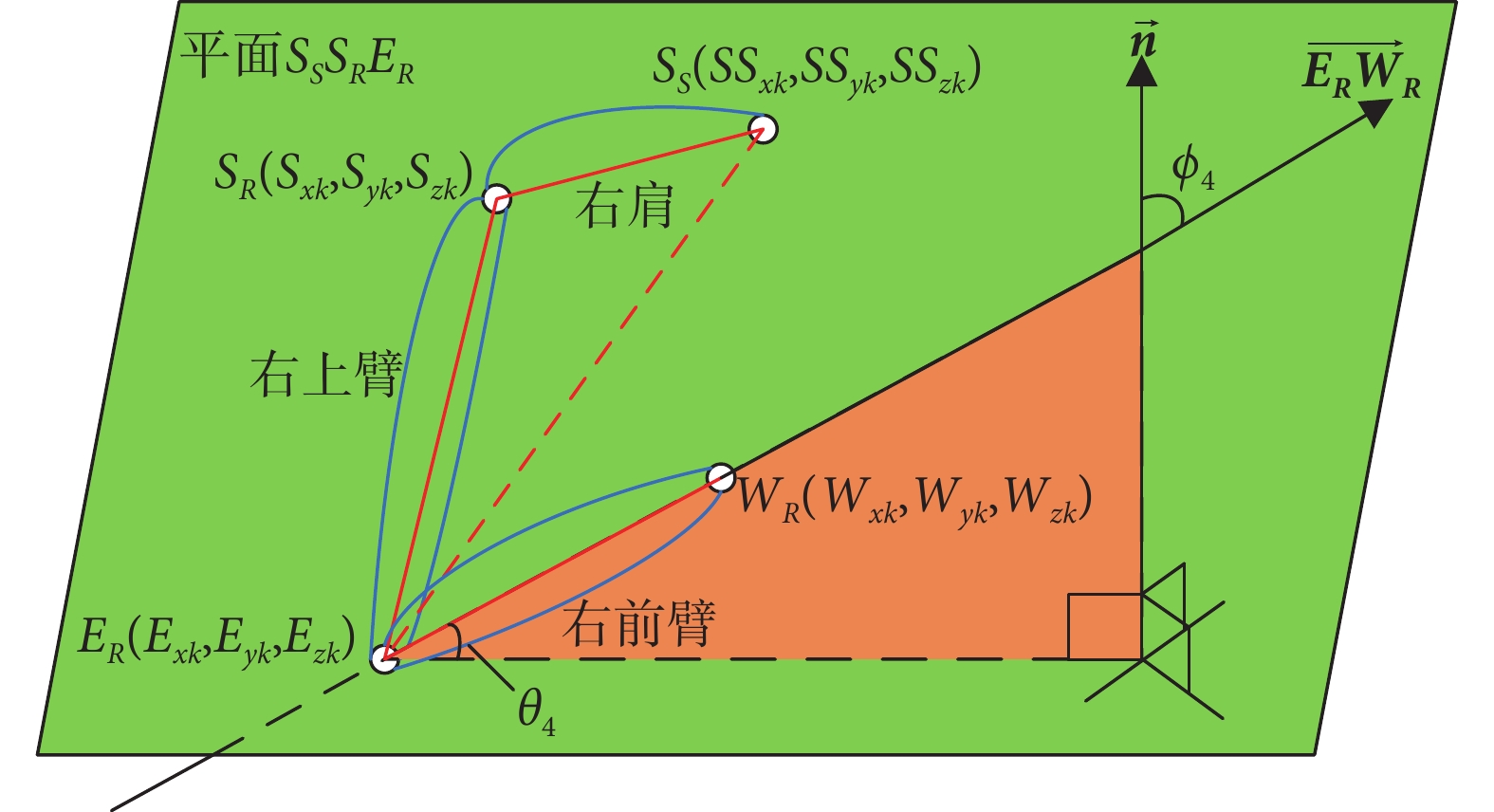
偏轉角即關節內/外旋轉，效果如圖4最右圖所示。由于假設的定點是隨腕關節的位置變化而變化，肘部偏轉角的求解并不能像求解俯仰角一樣設定點構造三角形，所以需要求解腕關節在肩關節、肘關節所成的某一平面上的投影點，然后再進行偏轉角求解。為了提高計算效率，采用空間線面角求解肘部偏轉角。以右肘偏轉為例，如圖7所示，根據NAO機器人肘關節偏轉角度變化，構建 
平面，即NAO機器人肘關節偏轉角0°平面。因此，通過求解右肘到右腕的向量 
與平面 
的夾角 
，間接求得右肘偏轉角 
。
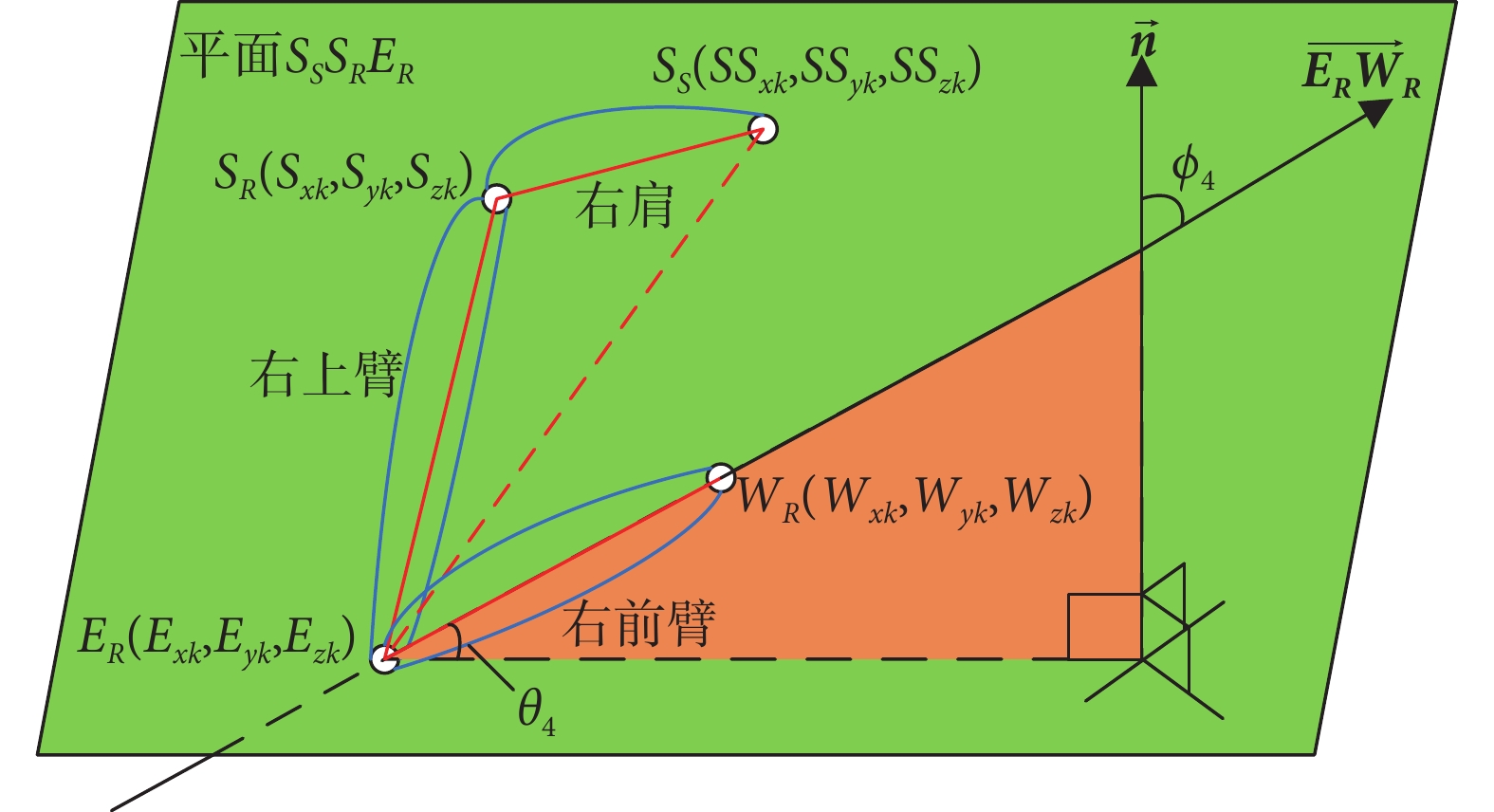圖7
右肘偏轉角計算
Figure7.
Calculation of the right elbow deflection angle
具體過程如下：
（1）構建
平面，其內部向量可表示為式(9)，從而求解出平面
的法向量
，主要過程如下：
 |
設法向量
，則根據平面方程
得：
 |
 |
（2）通過右肘到右腕的向量 
與平面 
的夾角 
，間接求解人體右肘偏轉角 
：
 |
 |
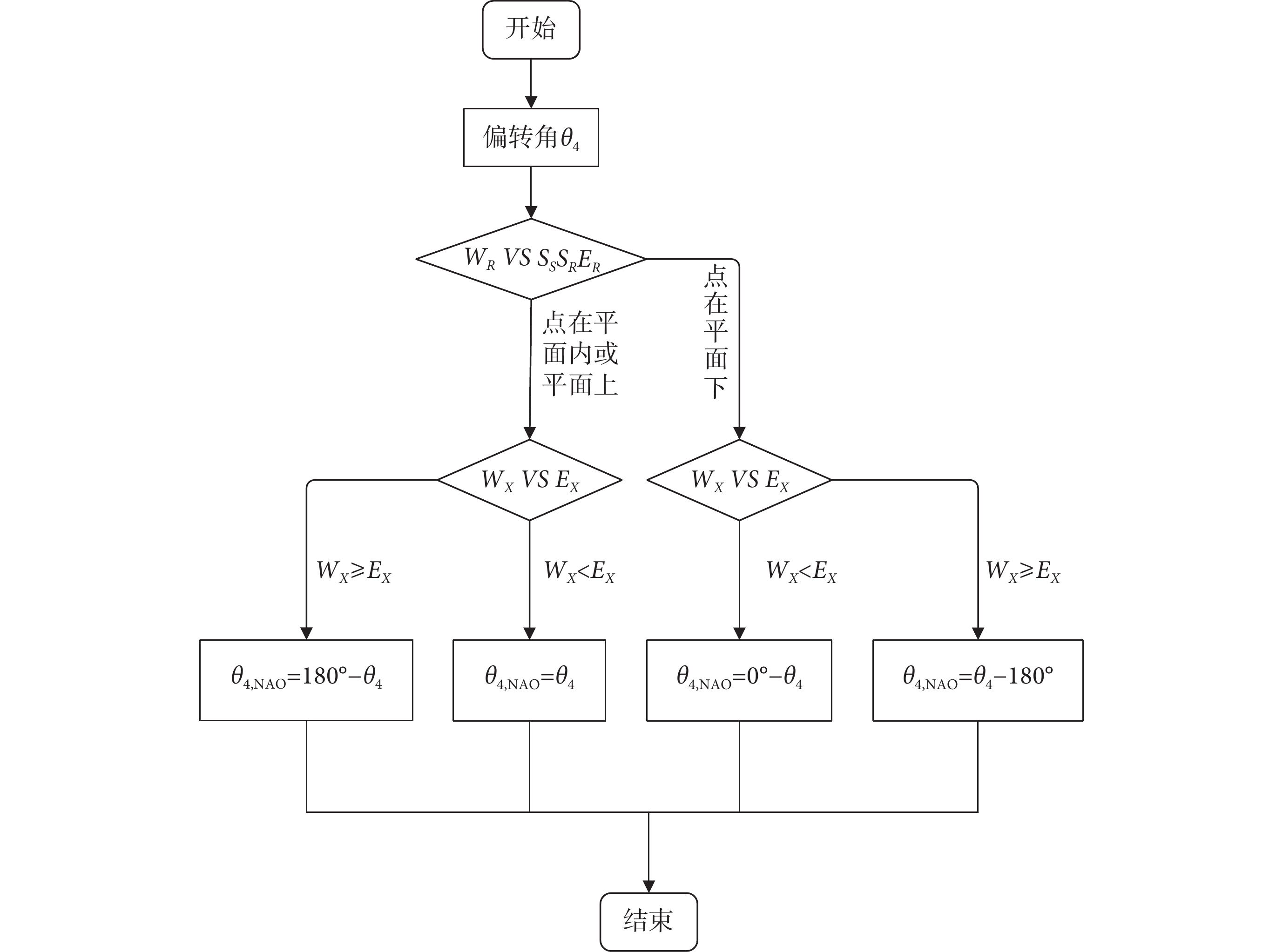
（3）判斷右肘偏轉角的正負：
根據NAO機器人肘關節偏轉角度變化以及線面角 
取值范圍（
[0, 90°]），當人體腕關節在平面 
上或下時，計算得到的右肘關節的偏轉角度 
最高只能達到90°。而實際上，人體與NAO的肘部偏轉關節角度均可以大于90°。所以，結合Kinect V2的笛卡爾坐標系在計算偏轉角中加入腕關節（
）與肘關節（
）大小比較，可判斷肘關節偏轉角度大于90°的情況。右肘偏轉角正負判斷的流程見圖8。
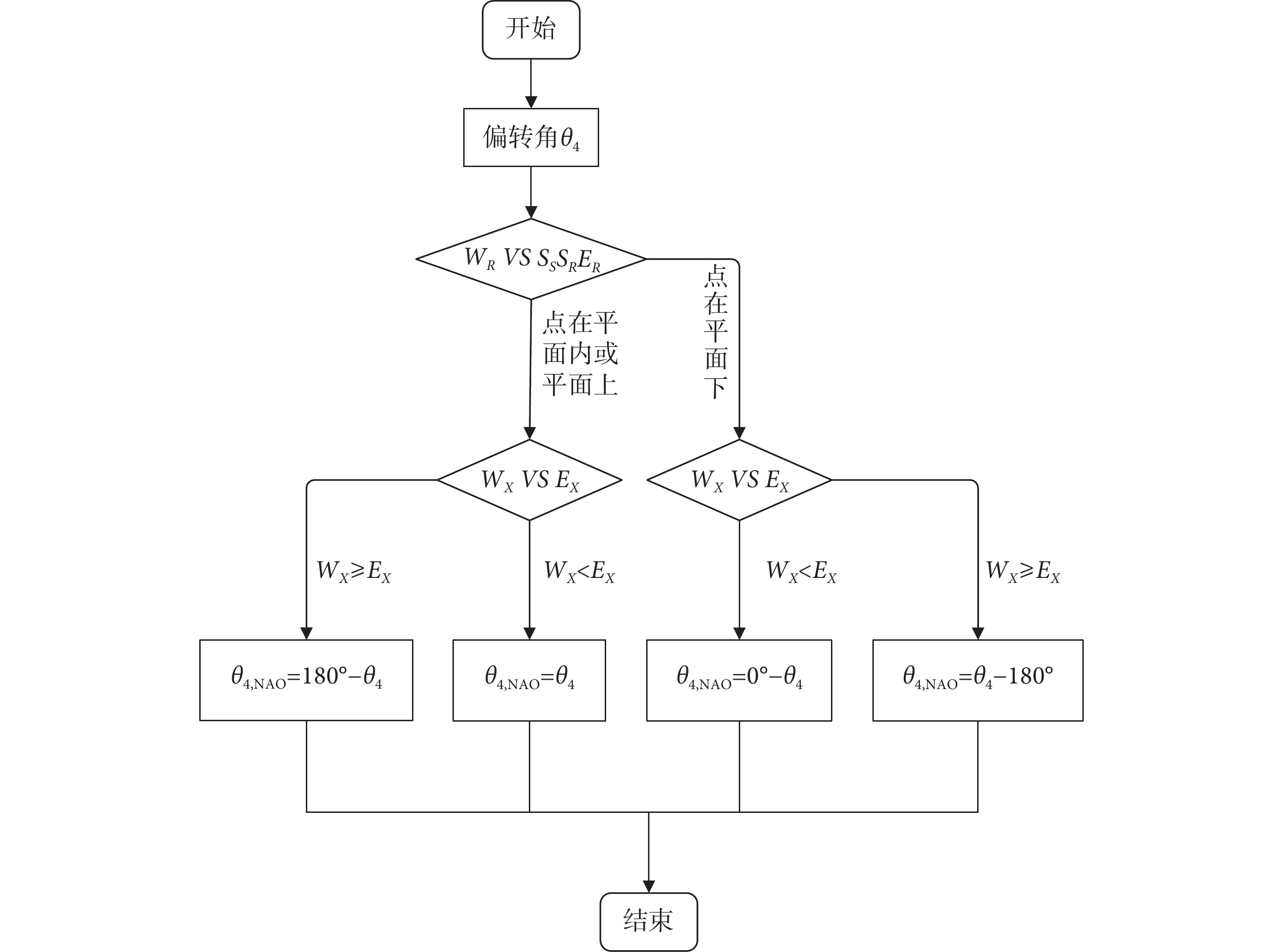圖8
右肘偏轉角正負判斷流程圖
Figure8.
Flow chart for judging the positive and negative deflection angle of right elbow
2.3 控制角度
綜上所述，實現了Kinect的笛卡爾坐標系到NAO機器人坐標系的右上肢運動映射，控制NAO機器人各關節的角度如下：
肩關節俯仰角：
 |
肩關節橫滾角：
 |
肘關節橫滾角：
 |
肘關節偏轉角：
 |
2.4 關節角度濾波處理
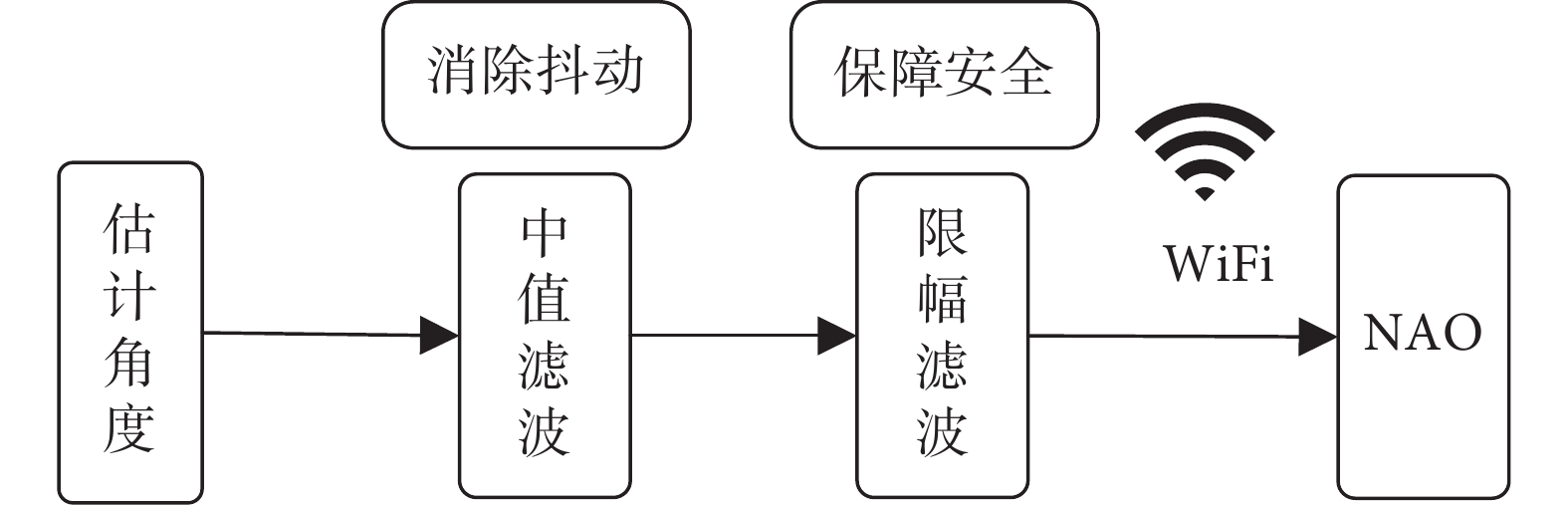
由于利用骨架數據估計獲得的關節角度數據不平滑，直接用于NAO機器人控制導致控制抖動問題嚴重，因此需要對估計的角度數據進行平滑濾波處理。中值濾波是一種能有效抑制噪聲的非線性平滑濾波方法，對于消除較大或較小的孤立異常值非常有效，適用于信號的平滑處理。因此，采用中值濾波的方法對估計角度進行處理。最后為了保證NAO的運動安全，對估計的角度進行了限幅處理，以防止動作幅度過大損壞設備。具體流程如圖9所示。
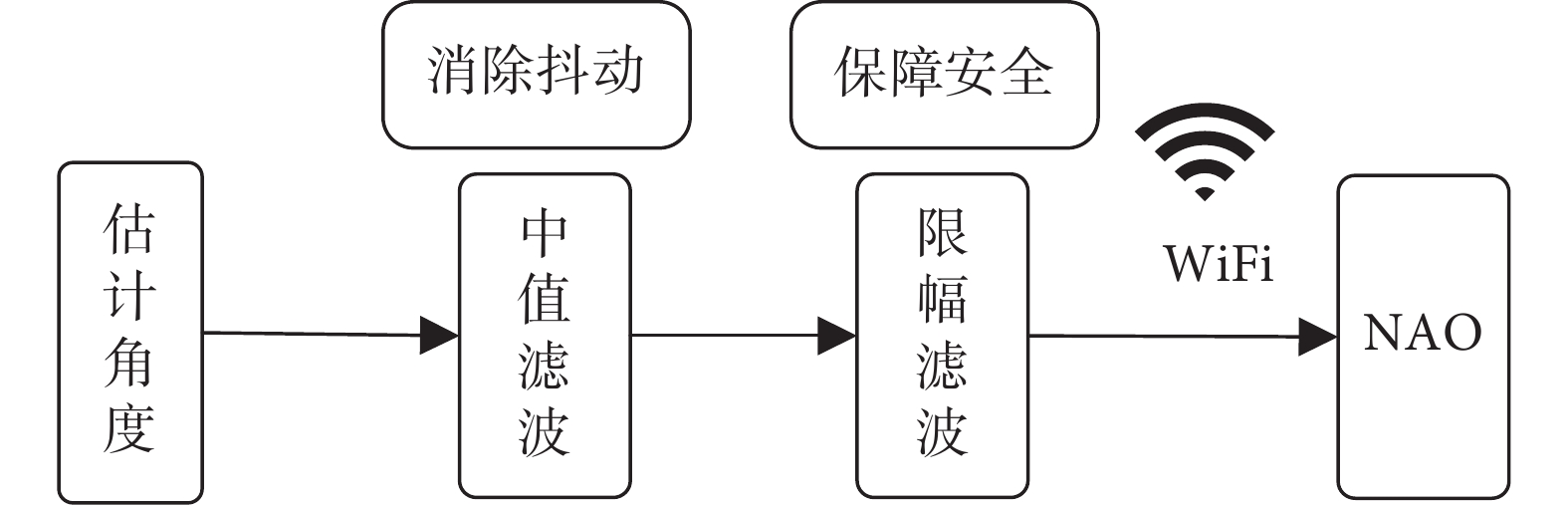圖9
估計角度濾波流程圖
Figure9.
Flow chart for estimating angle filtering
2.4.1 中值濾波
中值濾波主要流程如下：（1）對于每一個關節點，連續采集N次，記作k[a1,a2,....,aN]。
（2）把N次采樣值從小到大排列，當N為奇數時，取中間值為本次有效值輸出；當N為偶數時，取
的平均值為本次有效值輸出。
（3）把每一次得到的新數據放在隊列的尾部，并且丟掉原有隊列中的第一個角度值（遵循先入先出的原則）。
（4）重復步驟（2），進行循環。
2.4.2 限幅濾波
由于人體和NAO機器人的結構不同，人體的運動幅度可能會超出NAO機器人的運動范圍，所以估計的關節角度可能超過NAO機器人關節角度范圍，從而對NAO機器人的關節電機造成損害。為保證NAO的運行安全，采用限幅濾波減少因角度過限對關節電機造成的傷害。表1為NAO機器人（右上肢）與人體（右上肢）的運動范圍。考慮到安全問題，輸入到機器人各關節的控制角度范圍如表1所示。本文以NAO機器人肘關節偏轉角0°時為基本參考平面，當人體肘關節偏轉時并不能一一對應到NAO機器人肘關節范圍，因此NAO機器人肘關節偏轉范圍設定為其肘關節偏轉角度限幅值：–119.5°~119.5°。限幅濾波主要流程：
表1
NAO機器人（右上肢）與人體（右上肢）的運動范圍
Table1.
The range of motion of the NAO robot (upper right limb) and the human body (upper right limb)
（1）當得到的控制角度值超過NAO關節可旋轉的最大角度時，輸出NAO關節角度的最大值驅動相應的關節電機轉動；
（2）當得到的控制角度值小于NAO關節可旋轉的最小角度時，輸出NAO關節角度的最小值驅動相應的關節電機轉動；
（3）當得到的控制角度值在NAO關節可旋轉的角度范圍內時，輸出當前控制角度值驅動相應的關節電機轉動。
3 算法驗證與分析
為了驗證偏轉角度估計算法的有效性，設計了右肘橫軸偏轉、縱軸偏轉兩組動作實驗，每個動作重復三次。具體動作如圖10所示。
圖10
右肘橫軸偏轉、縱軸偏轉實驗動作
Figure10.
Experimental action of transverse axis deflection and longitudinal axis deflection
3.1 實驗對象
為了保證實驗的可靠性，本研究選擇5名男生、5名女生參與實驗，年齡（
）歲，其中，男生的身高為（
）cm，體重為（
）kg，女生的身高為（
）cm，體重為（
）kg。測試者均身體健康，無肌肉損傷等疾病。所有測試者對實驗內容均完全知情且同意。正式實驗前，由實驗組織者告知測試者實驗目的及步驟，并指導測試者完成相應動作。
3.2 方法效果對比
將本文計算肘關節偏轉角的方法（以下稱解析算法）和傳統幾何方法（以下稱傳統算法）分別針對同一右肘偏轉運動進行對比實驗。為保證實驗數據的統一性，實驗將右肘偏轉運動的Kinect骨架數據導出，采用解析算法和傳統算法分別進行右肘偏轉角計算實驗。
3.2.1 Kinect估計值范圍
傳統方法以人體肩肘線垂直地面的平面為0°界面，本文以機器人肘關節偏轉角0°界面為分界線，因人體肘關節范圍隨其他關節運動時不斷發生變化，所以并不能根據NAO機器人的偏轉角范圍進行標定。因此本實驗設定機器人肘關節偏轉電機的最大范圍值（–119.5°~119.5°）。
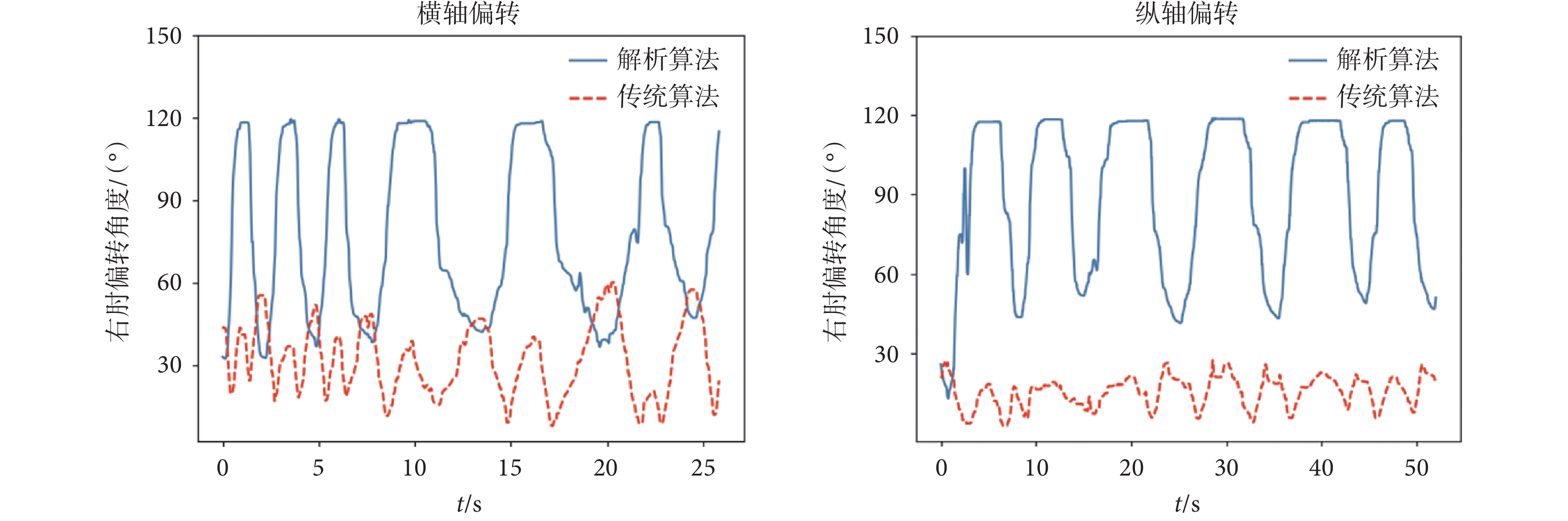
圖11為其中一組實驗的肘部關節偏轉角NAO傳感器數據對比圖。實驗結果表明，右肘關節在橫軸和縱軸兩個方向進行偏轉時，傳統算法肘部偏轉角度范圍較小，而解析算法肘部偏轉角的范圍較大，可以使NAO機器人可以更好地模仿人體肘部關節運動。
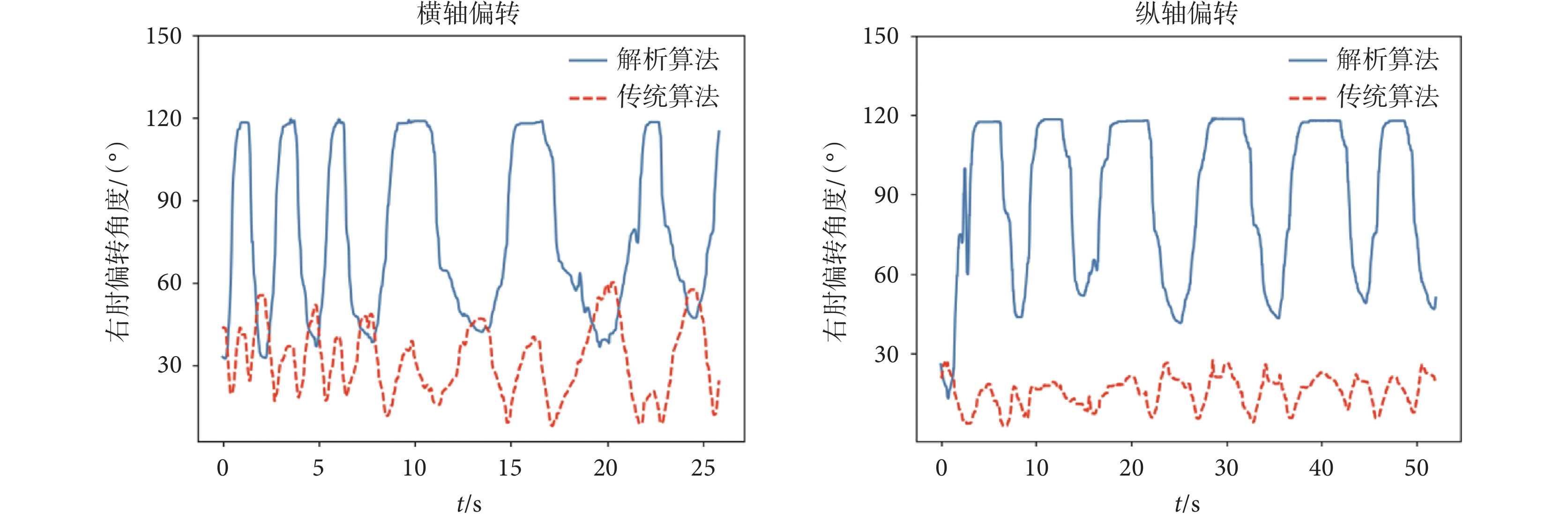圖11
不同方法下右肘橫、縱軸偏轉時NAO傳感器值對比
Figure11.
Comparison of NAO sensor values when the right elbow is deflected in the horizontal and vertical directions under different methods
3.2.2 跟隨控制效果
為了定量顯示NAO機器人的跟隨控制效果，采用均方根誤差指標進行衡量[35]。采用不同方法分別進行右肘橫軸和縱軸偏轉實驗。均方根誤差公式如下：
 |
RMSE表示均方根誤差，N表示數據的個數，
表示限幅濾波后的第i個Kinect估計值，
表示第i個NAO傳感器的值。
在實驗中，采集圖11中數據范圍重疊部分作為數據樣本，用來比較在不同方法下的跟隨控制效果，不同方法下10名測試者的平均均方根誤差對比如表2所示。
表2
不同動作下不同方法的RMSE對比（°）
Table2.
Comparison of RMSE of different methods under different actions (°)
在實驗過程中，當測試者動作變化較快時，Kinect估計值與NAO關節傳感器的值之間存在較大延時。因此，實驗要求測試者動作變化緩慢，但是依然無法保證測試者動作速度的一致性，所以計算所得均方根誤差可能差距較大。由表2可知，在做相同動作時，解析算法的均方根誤差與傳統算法對比，實時動作模仿效果相近。
3.3 濾波有效性
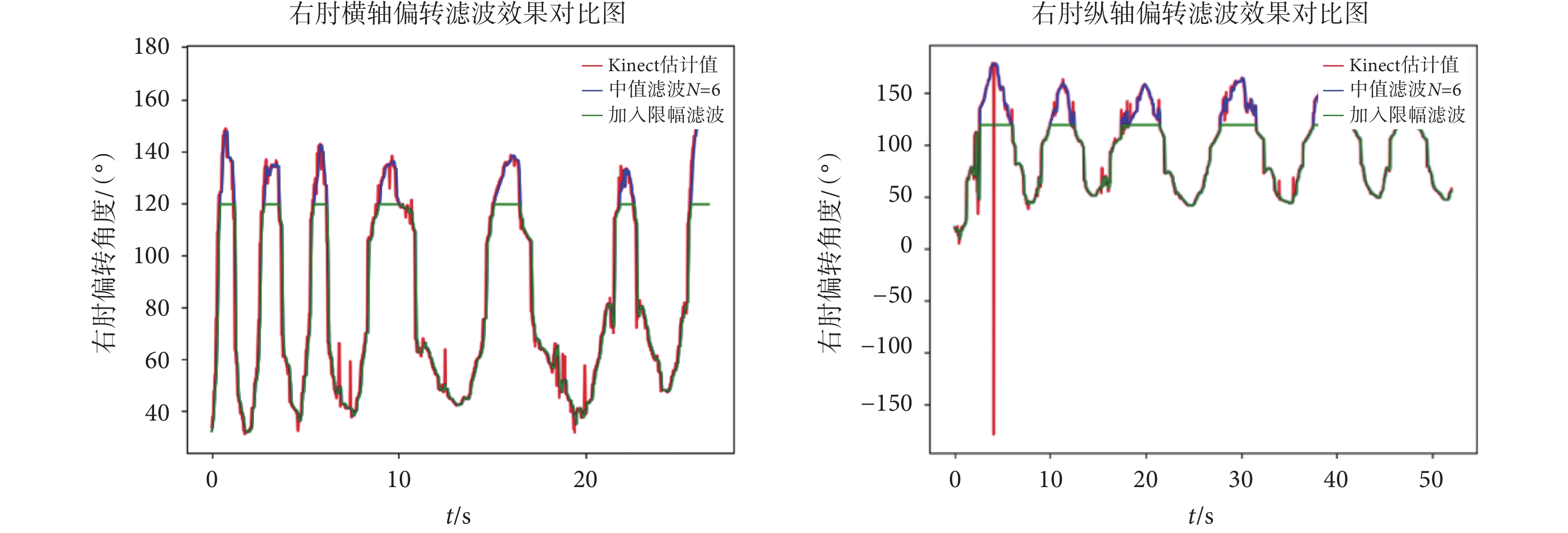
隨機取一名測試者不同動作下的數據，濾波效果如圖12所示。由圖12可以看出Kinect角度估計值存在噪聲，因此要對估計的角度進行濾波處理。中值濾波對孤立的脈沖干擾有較強抑制作用，可以有效解決NAO機器人運動過程中的抖動問題。限幅濾波的加入可以控制超過NAO機器人關節角度范圍的值，防止動作幅度過大，減少對機器人關節電機的傷害，確保NAO機器人運行的安全。
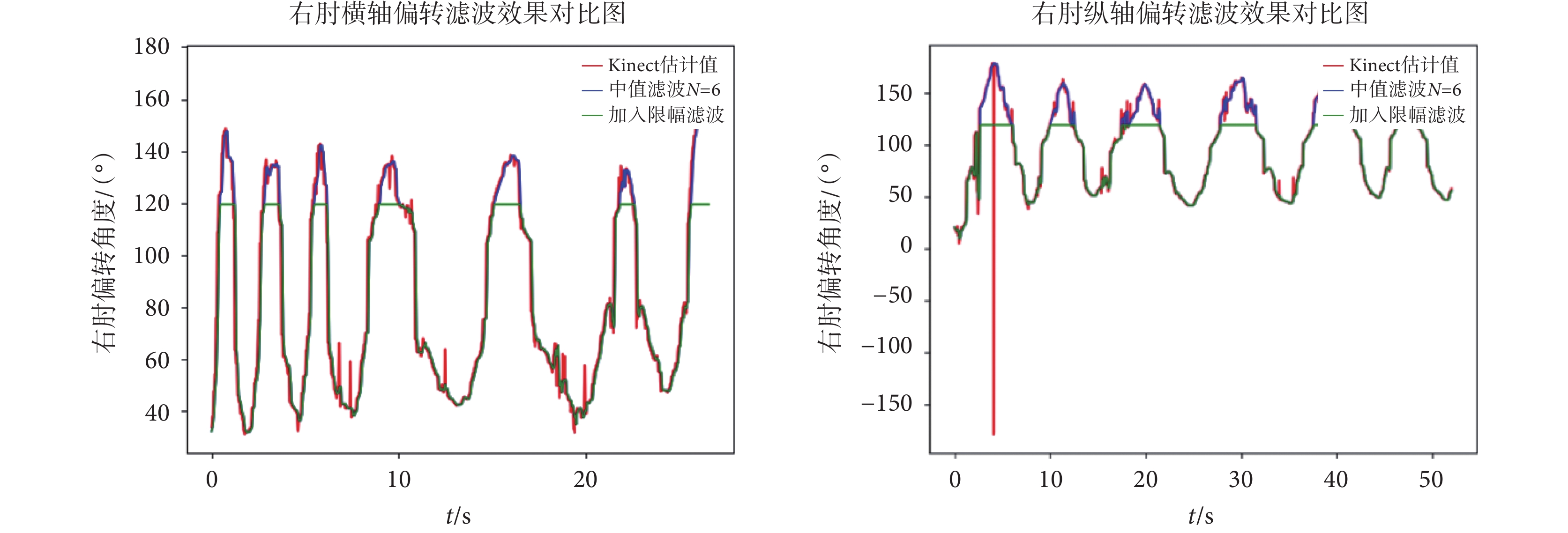圖12
濾波效果圖
Figure12.
Chart of filtering effect
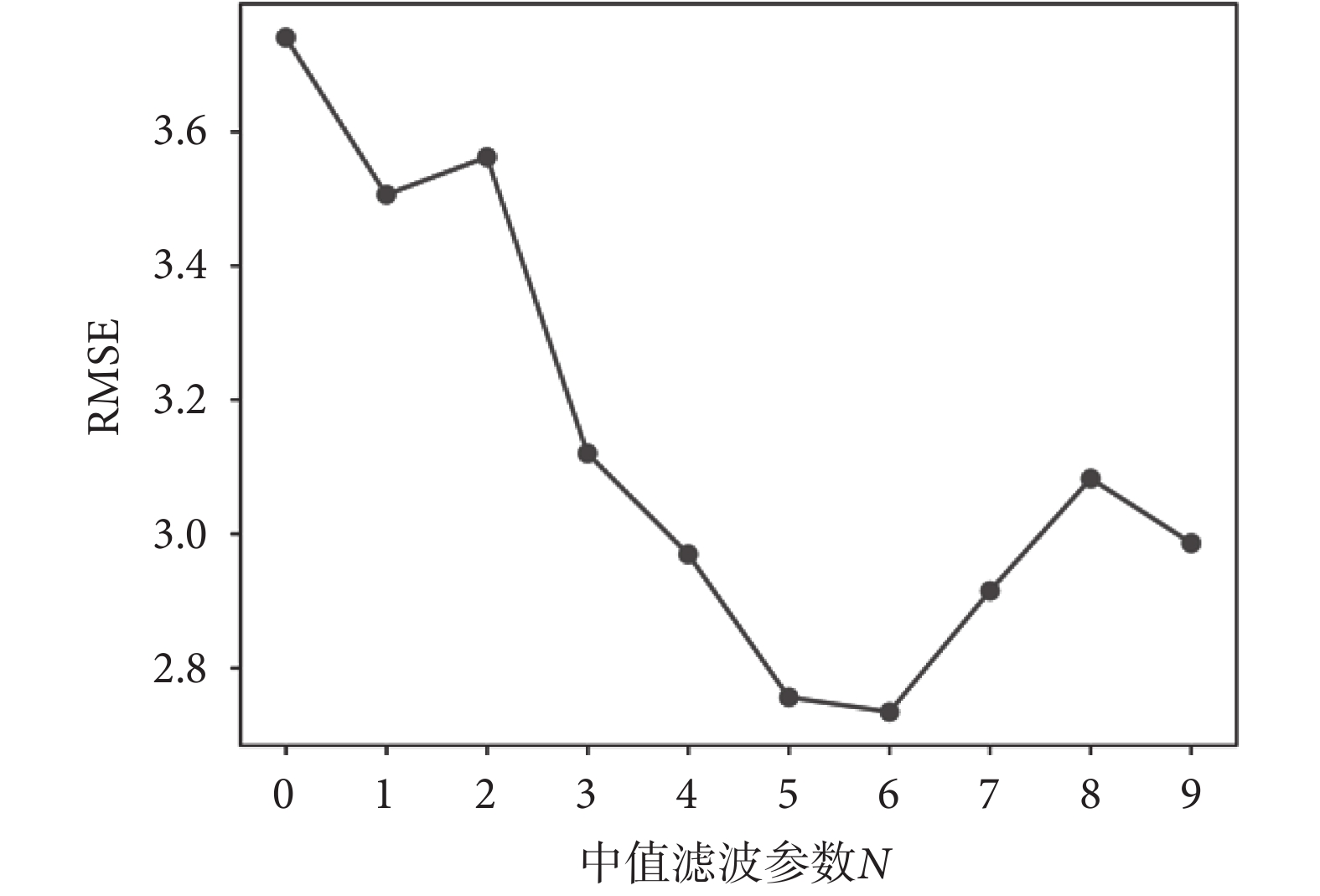
在中值濾波中，滑動窗口N的大小對輸出數據的影響較大。N值越大，輸出數據就越平滑，但同時可能會將有用的數據濾掉。因此，濾波參數N的大小要根據實際情況來確定。本文結合實際情況，對
參數進行實驗，通過對20組實驗數據RMSE的平均值分析來確定濾波參數N的大小，不同濾波參數下RMSE圖實驗結果如圖13所示。然而，這種濾波存在局限性，會造成一段時間的滯后，而滯后時間的長短與濾波參數的大小有關。當動作變化緩慢時，這種滯后在人眼中并不明顯。因此，設定中值濾波參數為6。
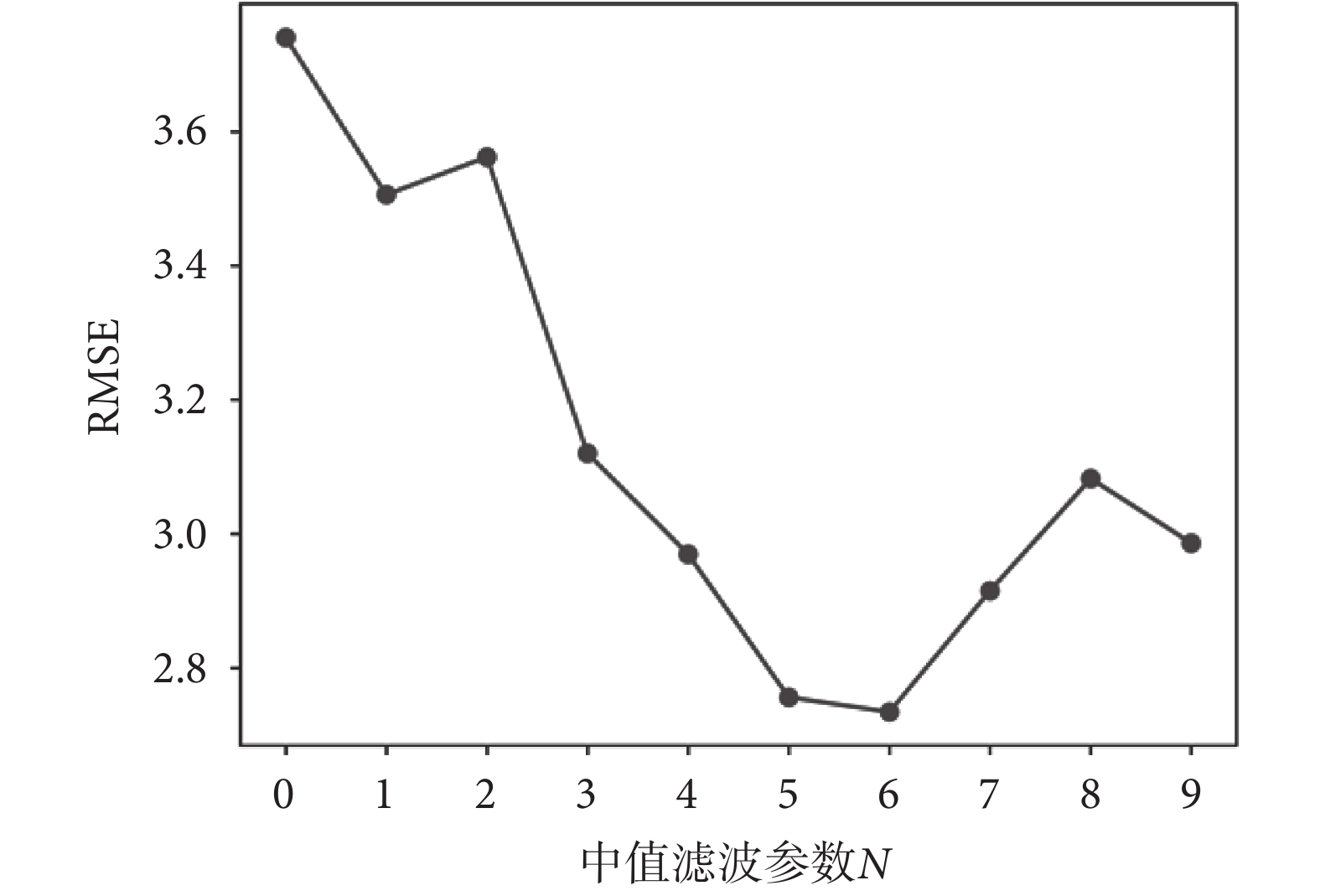圖13
不同中值濾波參數下的RMSE
Figure13.
RMSE with different median filtering parameters
在3.2節的基礎上，實驗加入串聯濾波算法，通過RMSE評價濾波后解析算法與傳統算法的實時效果，實驗結果如表3所示。實驗結果表明，加入濾波后解析算法下10個受試者的RMSE平均值較小。因此，基于串聯濾波的解析算法可以使NAO機器人穩定、實時地模仿人體肘關節偏轉運動。
表3
不同動作下濾波后解析算法與傳統算法RMSE對比（°）
Table3.
Comparison of RMSE between the filtered resolution algorithm and the traditional algorithm under different actions (°)
3.4 實驗平臺分析
本文將經過濾波處理后的控制角度通過軟件系統NAOqi調用對應ALMotion模塊進行數據更新。之后，控制角度由WiFi傳遞到NAO機器人的設備通信模塊DCM，通過DCM發送控制命令[34]，實現NAO機器人的上肢跟隨控制。同時，本實驗中各個模塊均采用Python語言實現，可以減少開發平臺轉換過程中的延時。
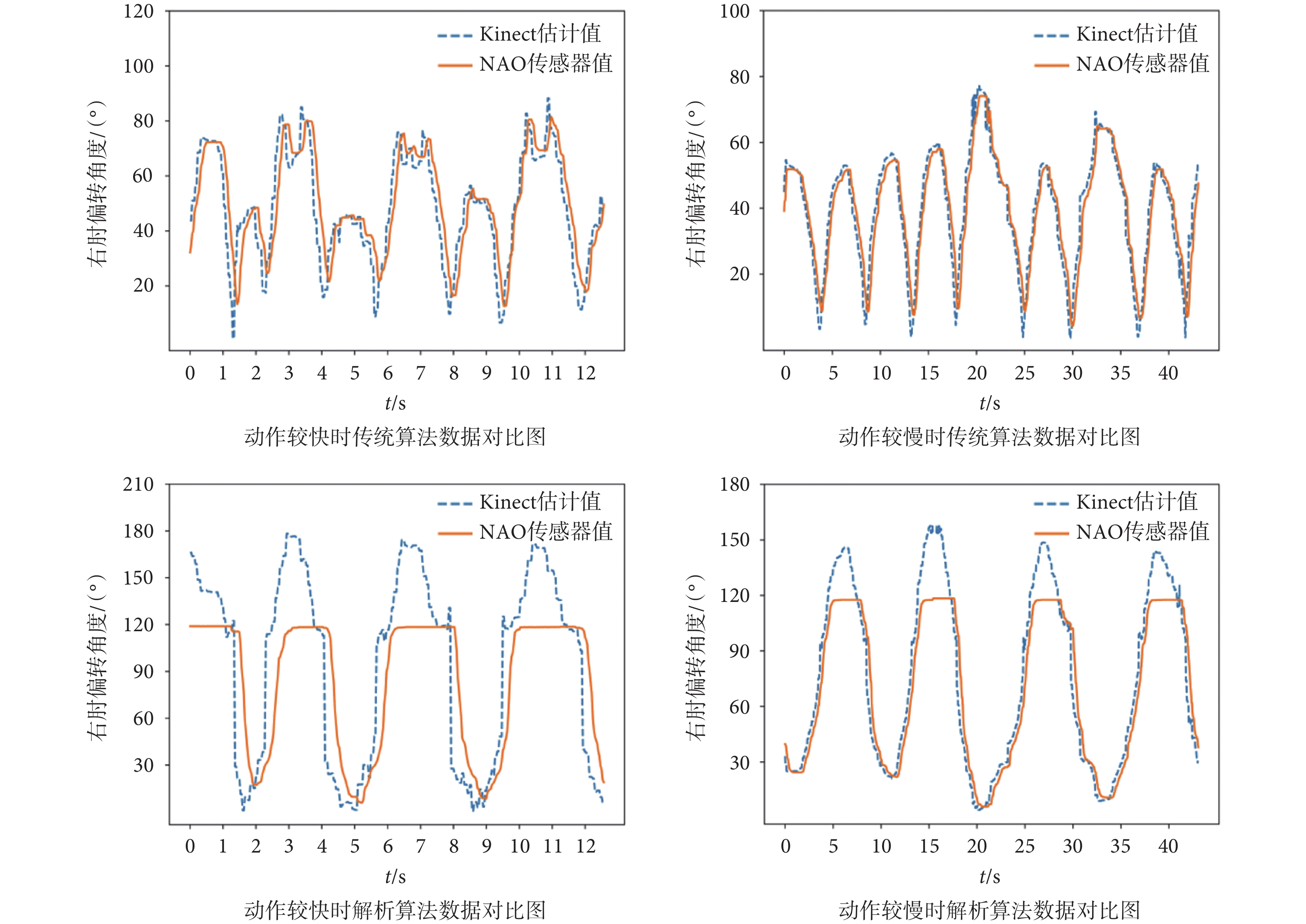
實驗發現，當動作變化速度不同時，從Kinect估計值到NAO傳感器返回值的滯后時間也會不同，實驗結果如圖14所示。當動作變化較緩慢時，從Kinect估計值到NAO傳感器返回值的總滯后時間為240 ms；當動作變化較快時，總滯后時間為267 ms。而在傳統算法下當動作變化較緩慢時，總滯后時間為200 ms；當動作變化較快時，總滯后時間為167 ms。由此可以看出，當動作變化緩慢時，加入濾波后解析算法的NAO機器人內部執行延時與傳統算法的延時相近。
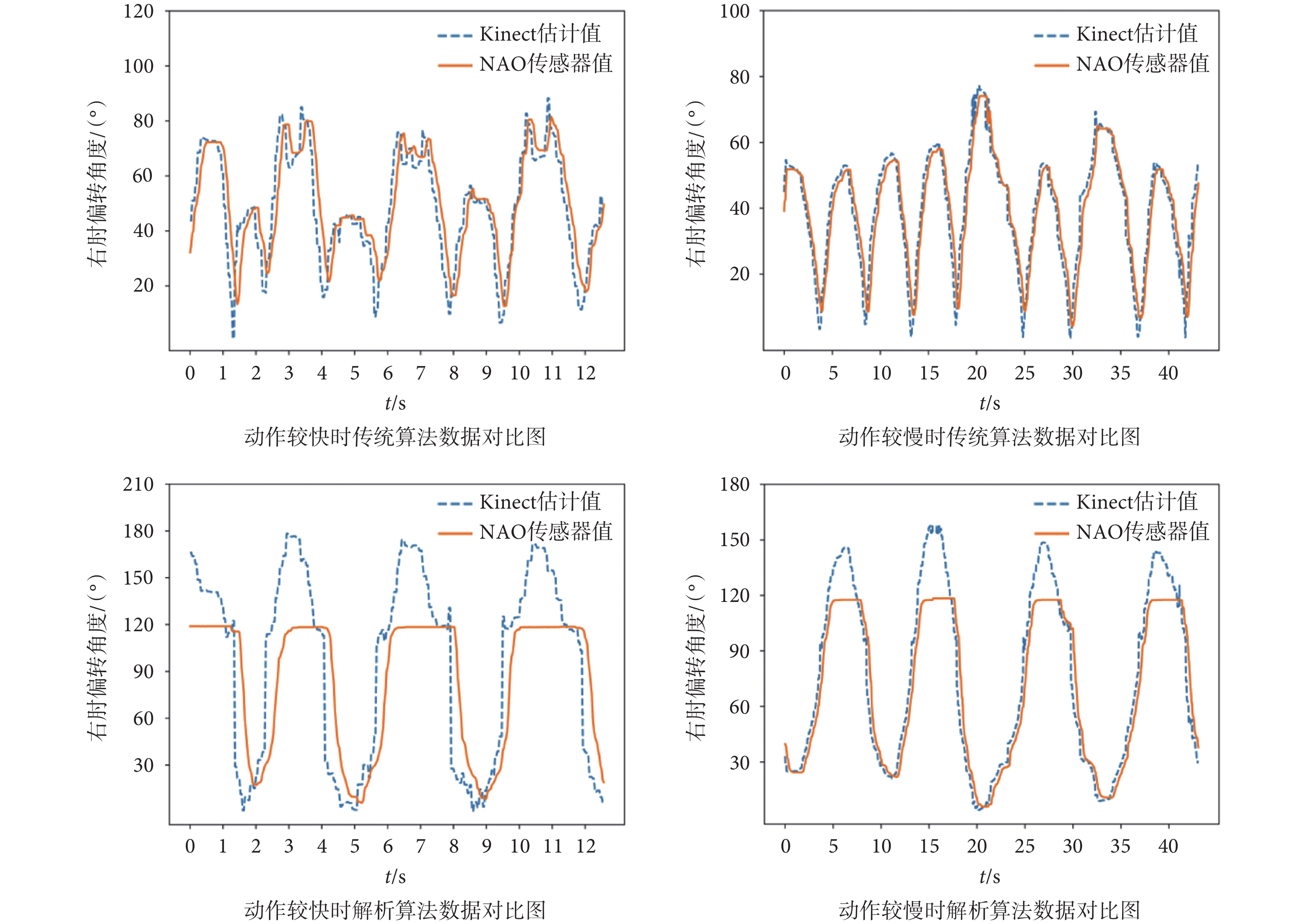圖14
不同速度下不同算法的右肘橫軸偏轉角度與NAO傳感器值對比圖
Figure14.
Comparison of right elbow transverse axis deflection angle and NAO sensor value with different algorithms at different speeds
綜上所述，解析算法的肘關節偏轉范圍較大，所以當動作變化較快時，機器人關節電機需要的執行時間較長，因而造成延時較大。在現實生活中，由于絕大多數動作模仿的過程是相對緩慢的，所以算法執行造成的延時在人眼中并不明顯。因此，從逆運動學算法的準確性、濾波效果和延時三個方面綜合分析，當動作模仿較緩慢時，加入濾波后的解析算法可以保證NAO機器人動作模仿的準確性和實時性。
4 結論
本文將Kinect體感技術與仿人機器人相結合，提出了一種基于虛擬空間平面的空間線面角逆運動學解析算法，實現了NAO機器人的跟隨控制，并進行實驗驗證。首先，基于逆運動學解析算法，克服了傳統算法偏轉角無法精確估計的問題。然后，考慮到運動的平穩性和安全性，利用中值濾波和限幅濾波對估計的角度進行了平滑和限幅處理。最后，在NAO機器人上進行了實際控制實驗。實驗結果表明該方法能夠實現NAO機器人實時、穩定地跟蹤人體上肢動作。這說明NAO機器人跟隨控制系統可以輔助治療師遠程向患者展示上肢康復訓練方案，方便快捷地控制機器人。同時，NAO機器人的3D立體展示可以更好地幫助患者準確地理解并做出康復訓練動作，達到預期的康復效果。當然，實驗中還存在一些不足之處。例如，NAO機器人受自身結構的限制，關節轉動范圍與人體的關節轉動范圍并不相同，所以造成部分康復訓練動作不能實現跟隨控制。相信在不久的將來，隨著機器人技術的發展，這個問題一定會得以解決。下一步的研究方向是利用Kinect和NAO機器人實現監督和指導，從而實現居家康復治療。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：劉曉光主要負責項目主持、平臺搭建、算法程序設計、協調溝通以及計劃安排；李思敏、梁鐵、李俊、婁存廣主要負責實驗流程、數據記錄與分析、論文編寫以及算法程序設計；王洪瑞、劉秀玲主要負責提供實驗指導、數據分析指導和論文審閱修訂。
引言
由于中風、帕金森病等疾病和意外事故等原因，我國各類肢體殘疾人數逐漸增加。據2019年中國殘聯發布的殘疾人統計公報顯示，我國肢體殘疾人數為1 989萬，其中上肢殘疾患者約占1 000萬人。上肢殘疾給人的生活帶來了諸多不便，直接影響個人的獨立性和生活質量[1]。臨床研究表明，合理的康復訓練能夠幫助患者恢復肢體的部分功能，一定程度上可恢復其生活和工作能力[2-5]。因此，研究跟隨康復醫師指導訓練動作的智能輔助康復系統已經成為康復醫學領域的研究熱點[6-11]。
近年來，研究人員一直在開發機器人智能輔助康復系統，使人與機器人進行互動[7-17]，從而發揮治療作用。滑少揚[18]利用Kinect傳感器，設計并實現了一種基于解析法的轉化方法，實現了NAO機器人（軟銀機器人，NAO6，法國）跟隨人體姿態變化的控制方案，但沒有解決肘關節偏轉的問題。Zhang等[19]提出并開發了上半身機器人模仿系統，通過基于連桿矢量的幾何分析方法，將人類手臂運動映射到仿人機器人上。Wang等[20]開發了人體上肢和UR5機器人（Universal Robots5）的在線仿真系統，提出了一種基于虛擬關節的方法解決人類手臂與UR5機器人之間的運動學映射問題。Assad-Uz-Zaman M等[21-22]使用體感設備Kinect V2跟蹤人體運動，采用改進的Denavit-Hartenberg（D-H）模型[23-32]對人體上肢進行運動學建模，通過一種完整的幾何解求解關節角度，實現了遠程控制NAO右臂運動，指導患者進行不同的手臂運動練習。目前的康復機器人雖然能夠輔助醫生進行康復訓練，但機器人動作模仿的精度還有待提高，尤其對于關節旋轉角度的估計問題，需進一步研究，從而更好地為輔助康復診療服務。
本文提出了一種基于虛擬空間平面的空間線面角逆運動學解析算法，實現了Kinect（微軟，Kinect V2，美國）坐標系到NAO機器人坐標系關節角度的映射。首先，利用Kinect獲取人體骨架坐標數據。然后，通過逆運動學解析算法，將坐標數據轉化為控制NAO機器人關節運動的角度。針對運動過程中遮擋導致的角度估計失真問題，利用中值濾波對解析的關節角度進行了處理。最后，對估計的角度進行了限幅濾波處理，以保證NAO機器人在安全的前提下跟蹤人體上肢動作。
1 研究平臺和系統設計
1.1 NAO機器人跟隨控制系統
NAO機器人跟隨控制整體流程如圖1所示。為了控制NAO機器人的上肢，利用Kinect的骨骼跟蹤技術，實時采集治療師各骨骼點的笛卡爾坐標信息。然后采用基于逆運動學原理的解析幾何方法，將骨架坐標數據轉化為關節角度。最后對獲取的角度進行濾波處理后通過WiFi傳到NAO機器人的設備通信DCM模塊，實現對NAO機器人上肢各關節的運動控制。
圖1
NAO機器人跟隨控制流程圖
Figure1.
The flow chart of NAO robot following control
1.2 Kinect V2概述
為實現追蹤人體上肢運動，采用無標記視覺跟蹤裝置Kinect V2作為傳感器。Kinect V2是一款3D體感設備，能夠獲取RGB彩色圖像和3D深度圖像[33]，其深度圖像能夠提取人體骨架的25個主要關節點信息，并對這25個關節點進行持續追蹤，如圖2所示。Kinect V2以3D深度傳感器中的紅外相機為坐標原點建立三維坐標系，人體關節點數據可以表示為（x，y，z）。根據上肢康復訓練動作，實驗主要利用脊柱肩部、肩關節、肘關節和腕關節點的坐標進行計算，以實現機器人對人體上肢的跟隨控制。
圖2
Kinect V2信息
Figure2.
The information of Kinect V2
1.3 NAO機器人
NAO機器人是具有25個自由度的仿人機器人。NAO機器人使用橫滾、俯仰、和偏轉表示運動姿態，分別對應繞X、Y和Z軸方向上的旋轉。每個關節名稱由部件名稱和姿態名稱組成[34]，如圖3所示。
圖3
NAO機器人關節
Figure3.
NAO robot joint
2 基于逆運動學解析的關節角度估計
由于個體的體型存在差異，無法直接將獲取的人體骨架坐標映射到NAO機器人。因此，本文通過逆運動學原理對骨架坐標數據進行解析，將其轉換為可控制NAO機器人關節變換的角度，從而實現NAO機器人的實時控制。針對肘關節偏轉角的估計問題，提出了一種構建空間線面角的關節角度估計方法。以右上肢圖4所示的俯仰、橫滾和偏轉運動為例。
圖4
NAO右上肢俯仰、橫滾、偏轉運動
Figure4.
Movement of NAO's right upper limb
利用Kinect坐標系（見圖2右），獲取的肩部脊柱坐標（）、右肩坐標（）、右肘坐標（）和右腕坐標（）的骨骼點坐標分別用（，，）、（，，）、（，，）、（，，）表示，則肩部脊柱（）、右肘（）、右腕（）相對于肩部關節的坐標分別為：
肩部脊柱坐標：（，，）=（，，）
肘部坐標：（，，）=（，，）
腕部坐標：（，，）=（，，）
逆運動學解析的流程如圖5所示。
圖5
逆運動學解析流程圖
Figure5.
Flow chart of inverse kinematics analysis
2.1 俯仰角與橫滾角
俯仰角即關節上舉或放下，橫滾角即關節外展或內收，效果如圖4所示。以肩部關節為坐標原點，分別建立如圖6所示的坐標系，運用余弦定理，通過構建三角形，求解肩部俯仰角、橫滾角和肘部橫滾角。其中，為右肩關節俯仰角，為右肩關節橫滾角，為右肘關節橫滾角。為方便計算，設定點A在z1軸距原點一個單位長度的負方向上，坐標為（0，0，–1）。
圖6
右上肢俯仰角與橫滾角計算
Figure6.
Calculation of pitch angle and roll angle of right upper limb
則構建的三角形各邊邊長分別為：
|
|
|
|
|
則各關節角度的絕對值為：
|
|
|
2.2 偏轉角
偏轉角即關節內/外旋轉，效果如圖4最右圖所示。由于假設的定點是隨腕關節的位置變化而變化，肘部偏轉角的求解并不能像求解俯仰角一樣設定點構造三角形，所以需要求解腕關節在肩關節、肘關節所成的某一平面上的投影點，然后再進行偏轉角求解。為了提高計算效率，采用空間線面角求解肘部偏轉角。以右肘偏轉為例，如圖7所示，根據NAO機器人肘關節偏轉角度變化，構建 平面，即NAO機器人肘關節偏轉角0°平面。因此，通過求解右肘到右腕的向量 與平面 的夾角 ，間接求得右肘偏轉角 。
圖7
右肘偏轉角計算
Figure7.
Calculation of the right elbow deflection angle
具體過程如下：
（1）構建平面，其內部向量可表示為式(9)，從而求解出平面的法向量，主要過程如下：
|
設法向量，則根據平面方程得：
|
|
（2）通過右肘到右腕的向量 與平面 的夾角 ，間接求解人體右肘偏轉角 ：
|
|
（3）判斷右肘偏轉角的正負：
根據NAO機器人肘關節偏轉角度變化以及線面角 取值范圍（ [0, 90°]），當人體腕關節在平面 上或下時，計算得到的右肘關節的偏轉角度 最高只能達到90°。而實際上，人體與NAO的肘部偏轉關節角度均可以大于90°。所以，結合Kinect V2的笛卡爾坐標系在計算偏轉角中加入腕關節（）與肘關節（）大小比較，可判斷肘關節偏轉角度大于90°的情況。右肘偏轉角正負判斷的流程見圖8。
圖8
右肘偏轉角正負判斷流程圖
Figure8.
Flow chart for judging the positive and negative deflection angle of right elbow
2.3 控制角度
綜上所述，實現了Kinect的笛卡爾坐標系到NAO機器人坐標系的右上肢運動映射，控制NAO機器人各關節的角度如下：
肩關節俯仰角：
|
肩關節橫滾角：
|
肘關節橫滾角：
|
肘關節偏轉角：
|
2.4 關節角度濾波處理
由于利用骨架數據估計獲得的關節角度數據不平滑，直接用于NAO機器人控制導致控制抖動問題嚴重，因此需要對估計的角度數據進行平滑濾波處理。中值濾波是一種能有效抑制噪聲的非線性平滑濾波方法，對于消除較大或較小的孤立異常值非常有效，適用于信號的平滑處理。因此，采用中值濾波的方法對估計角度進行處理。最后為了保證NAO的運動安全，對估計的角度進行了限幅處理，以防止動作幅度過大損壞設備。具體流程如圖9所示。
圖9
估計角度濾波流程圖
Figure9.
Flow chart for estimating angle filtering
2.4.1 中值濾波
中值濾波主要流程如下：（1）對于每一個關節點，連續采集N次，記作k[a1,a2,....,aN]。
（2）把N次采樣值從小到大排列，當N為奇數時，取中間值為本次有效值輸出；當N為偶數時，取的平均值為本次有效值輸出。
（3）把每一次得到的新數據放在隊列的尾部，并且丟掉原有隊列中的第一個角度值（遵循先入先出的原則）。
（4）重復步驟（2），進行循環。
2.4.2 限幅濾波
由于人體和NAO機器人的結構不同，人體的運動幅度可能會超出NAO機器人的運動范圍，所以估計的關節角度可能超過NAO機器人關節角度范圍，從而對NAO機器人的關節電機造成損害。為保證NAO的運行安全，采用限幅濾波減少因角度過限對關節電機造成的傷害。表1為NAO機器人（右上肢）與人體（右上肢）的運動范圍。考慮到安全問題，輸入到機器人各關節的控制角度范圍如表1所示。本文以NAO機器人肘關節偏轉角0°時為基本參考平面，當人體肘關節偏轉時并不能一一對應到NAO機器人肘關節范圍，因此NAO機器人肘關節偏轉范圍設定為其肘關節偏轉角度限幅值：–119.5°~119.5°。限幅濾波主要流程：
表1
NAO機器人（右上肢）與人體（右上肢）的運動范圍
Table1.
The range of motion of the NAO robot (upper right limb) and the human body (upper right limb)
（1）當得到的控制角度值超過NAO關節可旋轉的最大角度時，輸出NAO關節角度的最大值驅動相應的關節電機轉動；
（2）當得到的控制角度值小于NAO關節可旋轉的最小角度時，輸出NAO關節角度的最小值驅動相應的關節電機轉動；
（3）當得到的控制角度值在NAO關節可旋轉的角度范圍內時，輸出當前控制角度值驅動相應的關節電機轉動。
3 算法驗證與分析
為了驗證偏轉角度估計算法的有效性，設計了右肘橫軸偏轉、縱軸偏轉兩組動作實驗，每個動作重復三次。具體動作如圖10所示。
圖10
右肘橫軸偏轉、縱軸偏轉實驗動作
Figure10.
Experimental action of transverse axis deflection and longitudinal axis deflection
3.1 實驗對象
為了保證實驗的可靠性，本研究選擇5名男生、5名女生參與實驗，年齡（）歲，其中，男生的身高為（）cm，體重為（）kg，女生的身高為（）cm，體重為（）kg。測試者均身體健康，無肌肉損傷等疾病。所有測試者對實驗內容均完全知情且同意。正式實驗前，由實驗組織者告知測試者實驗目的及步驟，并指導測試者完成相應動作。
3.2 方法效果對比
將本文計算肘關節偏轉角的方法（以下稱解析算法）和傳統幾何方法（以下稱傳統算法）分別針對同一右肘偏轉運動進行對比實驗。為保證實驗數據的統一性，實驗將右肘偏轉運動的Kinect骨架數據導出，采用解析算法和傳統算法分別進行右肘偏轉角計算實驗。
3.2.1 Kinect估計值范圍
傳統方法以人體肩肘線垂直地面的平面為0°界面，本文以機器人肘關節偏轉角0°界面為分界線，因人體肘關節范圍隨其他關節運動時不斷發生變化，所以并不能根據NAO機器人的偏轉角范圍進行標定。因此本實驗設定機器人肘關節偏轉電機的最大范圍值（–119.5°~119.5°）。
圖11為其中一組實驗的肘部關節偏轉角NAO傳感器數據對比圖。實驗結果表明，右肘關節在橫軸和縱軸兩個方向進行偏轉時，傳統算法肘部偏轉角度范圍較小，而解析算法肘部偏轉角的范圍較大，可以使NAO機器人可以更好地模仿人體肘部關節運動。
圖11
不同方法下右肘橫、縱軸偏轉時NAO傳感器值對比
Figure11.
Comparison of NAO sensor values when the right elbow is deflected in the horizontal and vertical directions under different methods
3.2.2 跟隨控制效果
為了定量顯示NAO機器人的跟隨控制效果，采用均方根誤差指標進行衡量[35]。采用不同方法分別進行右肘橫軸和縱軸偏轉實驗。均方根誤差公式如下：
|
RMSE表示均方根誤差，N表示數據的個數，表示限幅濾波后的第i個Kinect估計值，表示第i個NAO傳感器的值。
在實驗中，采集圖11中數據范圍重疊部分作為數據樣本，用來比較在不同方法下的跟隨控制效果，不同方法下10名測試者的平均均方根誤差對比如表2所示。
表2
不同動作下不同方法的RMSE對比（°）
Table2.
Comparison of RMSE of different methods under different actions (°)
在實驗過程中，當測試者動作變化較快時，Kinect估計值與NAO關節傳感器的值之間存在較大延時。因此，實驗要求測試者動作變化緩慢，但是依然無法保證測試者動作速度的一致性，所以計算所得均方根誤差可能差距較大。由表2可知，在做相同動作時，解析算法的均方根誤差與傳統算法對比，實時動作模仿效果相近。
3.3 濾波有效性
隨機取一名測試者不同動作下的數據，濾波效果如圖12所示。由圖12可以看出Kinect角度估計值存在噪聲，因此要對估計的角度進行濾波處理。中值濾波對孤立的脈沖干擾有較強抑制作用，可以有效解決NAO機器人運動過程中的抖動問題。限幅濾波的加入可以控制超過NAO機器人關節角度范圍的值，防止動作幅度過大，減少對機器人關節電機的傷害，確保NAO機器人運行的安全。
圖12
濾波效果圖
Figure12.
Chart of filtering effect
在中值濾波中，滑動窗口N的大小對輸出數據的影響較大。N值越大，輸出數據就越平滑，但同時可能會將有用的數據濾掉。因此，濾波參數N的大小要根據實際情況來確定。本文結合實際情況，對參數進行實驗，通過對20組實驗數據RMSE的平均值分析來確定濾波參數N的大小，不同濾波參數下RMSE圖實驗結果如圖13所示。然而，這種濾波存在局限性，會造成一段時間的滯后，而滯后時間的長短與濾波參數的大小有關。當動作變化緩慢時，這種滯后在人眼中并不明顯。因此，設定中值濾波參數為6。
圖13
不同中值濾波參數下的RMSE
Figure13.
RMSE with different median filtering parameters
在3.2節的基礎上，實驗加入串聯濾波算法，通過RMSE評價濾波后解析算法與傳統算法的實時效果，實驗結果如表3所示。實驗結果表明，加入濾波后解析算法下10個受試者的RMSE平均值較小。因此，基于串聯濾波的解析算法可以使NAO機器人穩定、實時地模仿人體肘關節偏轉運動。
表3
不同動作下濾波后解析算法與傳統算法RMSE對比（°）
Table3.
Comparison of RMSE between the filtered resolution algorithm and the traditional algorithm under different actions (°)
3.4 實驗平臺分析
本文將經過濾波處理后的控制角度通過軟件系統NAOqi調用對應ALMotion模塊進行數據更新。之后，控制角度由WiFi傳遞到NAO機器人的設備通信模塊DCM，通過DCM發送控制命令[34]，實現NAO機器人的上肢跟隨控制。同時，本實驗中各個模塊均采用Python語言實現，可以減少開發平臺轉換過程中的延時。
實驗發現，當動作變化速度不同時，從Kinect估計值到NAO傳感器返回值的滯后時間也會不同，實驗結果如圖14所示。當動作變化較緩慢時，從Kinect估計值到NAO傳感器返回值的總滯后時間為240 ms；當動作變化較快時，總滯后時間為267 ms。而在傳統算法下當動作變化較緩慢時，總滯后時間為200 ms；當動作變化較快時，總滯后時間為167 ms。由此可以看出，當動作變化緩慢時，加入濾波后解析算法的NAO機器人內部執行延時與傳統算法的延時相近。
圖14
不同速度下不同算法的右肘橫軸偏轉角度與NAO傳感器值對比圖
Figure14.
Comparison of right elbow transverse axis deflection angle and NAO sensor value with different algorithms at different speeds
綜上所述，解析算法的肘關節偏轉范圍較大，所以當動作變化較快時，機器人關節電機需要的執行時間較長，因而造成延時較大。在現實生活中，由于絕大多數動作模仿的過程是相對緩慢的，所以算法執行造成的延時在人眼中并不明顯。因此，從逆運動學算法的準確性、濾波效果和延時三個方面綜合分析，當動作模仿較緩慢時，加入濾波后的解析算法可以保證NAO機器人動作模仿的準確性和實時性。
4 結論
本文將Kinect體感技術與仿人機器人相結合，提出了一種基于虛擬空間平面的空間線面角逆運動學解析算法，實現了NAO機器人的跟隨控制，并進行實驗驗證。首先，基于逆運動學解析算法，克服了傳統算法偏轉角無法精確估計的問題。然后，考慮到運動的平穩性和安全性，利用中值濾波和限幅濾波對估計的角度進行了平滑和限幅處理。最后，在NAO機器人上進行了實際控制實驗。實驗結果表明該方法能夠實現NAO機器人實時、穩定地跟蹤人體上肢動作。這說明NAO機器人跟隨控制系統可以輔助治療師遠程向患者展示上肢康復訓練方案，方便快捷地控制機器人。同時，NAO機器人的3D立體展示可以更好地幫助患者準確地理解并做出康復訓練動作，達到預期的康復效果。當然，實驗中還存在一些不足之處。例如，NAO機器人受自身結構的限制，關節轉動范圍與人體的關節轉動范圍并不相同，所以造成部分康復訓練動作不能實現跟隨控制。相信在不久的將來，隨著機器人技術的發展，這個問題一定會得以解決。下一步的研究方向是利用Kinect和NAO機器人實現監督和指導，從而實現居家康復治療。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：劉曉光主要負責項目主持、平臺搭建、算法程序設計、協調溝通以及計劃安排；李思敏、梁鐵、李俊、婁存廣主要負責實驗流程、數據記錄與分析、論文編寫以及算法程序設計；王洪瑞、劉秀玲主要負責提供實驗指導、數據分析指導和論文審閱修訂。
