支持向量機在進行不同眼動模式分類任務時受參數影響較大，針對這一問題，本文提出一種基于改進鯨魚算法優化支持向量機的算法以提升眼動數據分類性能。根據眼動數據特點，本研究先提取注視、眼跳相關的57個特征，再利用近鄰相關（ReliefF）算法進行特征篩選。針對鯨魚算法收斂精度低，易陷入局部最小值等問題，本文引入慣性權重平衡局部搜索和全局搜索，加快算法收斂速度，同時利用差分變異策略增加個體多樣性，跳出局部最優。本文對8個測試函數進行實驗，結果表明改進鯨魚算法具有最佳的收斂精度和收斂速度。最后，本文將改進鯨魚算法優化支持向量機模型應用于自閉癥眼動數據分類任務，公開數據集實驗結果表明，相較于傳統的支持向量機方法，本文方法的眼動數據分類準確率有著較大提升，相較于標準鯨魚算法和其他優化算法，本文方法優化后的模型具有更高的分類精度，為眼動模式識別提供了新思路與方法。未來或可利用眼動儀獲取的眼動數據，結合本文方法輔助醫療診斷。
引用本文： 沈胤宏, 張暢, 楊林, 李元媛, 鄭秀娟. 改進鯨魚算法尋優支持向量機的眼動數據分類研究. 生物醫學工程學雜志, 2023, 40(2): 335-342. doi: 10.7507/1001-5515.202204066 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
近年來，隨著眼動跟蹤技術的發展，眼動研究開始應用于各個領域，包括閱讀[1]、心理學[2]、眼疾病[3]、精神疾病[4]等。人眼主要有三種基本的行為：注視、眼跳和追隨運動[5]。基于這三種基本的眼球運動，可以衍生出一系列用于量化不同眼動模式的眼動指標[6]。傳統方法通過統計眼動指標的差異來分析眼動模式[7-9]，但是單個指標僅能看出宏觀上的差異，難以實現眼動模式的精確識別，并且無法平衡多維眼動數據的影響。針對這個問題，許多學者對眼動數據提取多種眼動特征，并使用機器學習方法實現對不同眼動模式的分類[10-11]，其中支持向量機（support vector machine，SVM）具有實現簡單、分類精度和計算效率較高、適用于非線性和小樣本場景等優點，因此得到了廣泛應用[12-14]。值得注意的是，SVM分類性能易受關鍵參數影響，盲目選擇超參數可能帶來分類精度低和擬合效率低等問題。
目前，已經有許多研究引入粒子群算法[15]、差分進化算法[16]等智能優化算法對SVM進行超參數尋優，但這些算法本身參數較多，采用經驗取值難以保證尋優結果收斂到全局最優，存在二次調參的風險。鯨魚優化算法（whale optimization algorithm，WOA）是一種新型優化算法[17]，相比粒子群等算法，WOA最大的優點是不需要額外設置參數，并且還具有實現簡單、易于執行等優點，因此本文引入該算法解決SVM參數選取盲目性的問題。但是WOA本身存在易早熟、易陷入局部最優等缺點，所以一些學者對WOA進行了改進。文獻[18]提出使用混沌映射改進種群初始化過程，該方法在一定程度上可以加快收斂速度，但新算法的種群個體搜索能力沒有改變。文獻[19]將萊維飛行引入WOA，可以有效提高種群個體的全局搜索能力，但是無法平衡全局搜索和局部搜索過程。文獻[20]結合自適應權重和模擬退火策略改進WOA，提高了算法的收斂速度和收斂精度，但依然存在容易陷入局部最優的問題。
在前人研究的基礎上，針對WOA收斂速度慢和易陷入局部最優的問題，本文提出使用慣性權重和差分變異擾動改進WOA（inertia weight and differential variation perturbation improve WOA，IDWOA），通過慣性權重來平衡局部搜索和全局搜索過程以提高算法的收斂速度，通過差分變異擾動以增加種群的多樣性，幫助跳出局部最優。本文提出使用IDWOA優化SVM（IDWOA-SVM），構建IDWOA-SVM眼動模式識別模型，為實現高精度的眼動數據分類提供新思路，并利用公開的自閉癥眼動數據集對本研究提出的算法性能進行評估。
1 改進WOA
1.1 標準WOA
標準WOA根據座頭鯨覓食行為進行建模，模擬了包圍捕食、螺旋氣泡捕食和隨機搜索獵物三個主要的覓食行為。鯨魚通過隨機搜索確定目標，然后通過包圍捕食、螺旋氣泡捕食兩種策略圍捕獵物，捕食過程中包圍捕食和螺旋氣泡捕食是同時存在的，為了模擬這種行為，Mirjalili等[17]設置兩種策略的概率相等，通過產生隨機數r∈(0,1)，來決定使用哪種策略。
1.1.1 包圍捕食
當r < 0.5時，鯨魚采取包圍捕食策略，適應度最高的最優個體或最佳候選解帶領其余個體向獵物包圍靠近，該階段的模擬如式(1)、式(2)所示：
 |
 |
式中，D表示種群個體與最優個體之間的向量距離，t為當前迭代次數，
(t)表示第t次迭代時的種群最優個體向量，X(t)表示第t次迭代時的種群個體向量，X(t + 1)表示第t + 1次迭代時的種群個體向量，A，C為系數，如式(3)、式(4)所示：
 |
 |
式中，r為(0,1)之間的隨機數，
，tmax表示最大迭代次數，隨著迭代次數增加，a從2線性遞減到0，當前階段|A| < 1。
1.1.2 隨機搜索策略
在隨機搜索獵物階段，鯨魚種群隨機選擇某一個個體作為參考，其余個體根據該隨機個體更新位置，數學建模如式(5)、式(6)所示：
 |
 |
式中，Xrand(t)為種群隨機個體向量，當前階段|A| ≥ 1。
1.1.3 螺旋氣泡捕食
當r ≥ 0.5時，鯨魚采取螺旋向上的方式靠近獵物，數學模型如式(7)、式(8)所示：
 '/> |
 '/> |
式中，
表示種群個體與最優個體之間的向量距離，e為自然常數，π表示圓周率，b為限定對數螺旋彎曲度的常數，l為[? 1,1]的隨機數。
1.2 改進鯨魚優化算法
1.2.1 慣性權重
WOA使用固定權重進行個體位置更新，在算法迭代后期，種群個體將出現在最優個體附近停留的情況，從而導致局部最優解。本文參考粒子群算法的慣性權重策略[21]，引入一種非線性遞減因子，如式(9)所示。根據粒子群算法當慣性權重w在[0.4, 0.9]變動時收斂效果最好，因此本文將慣性權重歸一化至[0.4, 0.9]，歸一化后的w’如式(10)所示：
 |
 '/> |
式中，當迭代初期 
有較大值，有利于算法在初期進行全局搜索；在迭代后期，權重 
的值非線性遞減，幫助種群個體跳出局部最優區域，加快收斂速度。改進后的鯨魚位置更新公式如式(11)、式(12)所示：
 '/> |
 '/> |
1.2.2 差分變異擾動
差分進化算法具有強大的全局開發能力，而局部開發能力較弱[22]。因此本文利用差分進化算法對種群個體進行差分變異，提高種群的個體多樣性，使算法能跳出局部最優解，快速收斂到全局最優。差分變異策略的基本思想是隨機選取兩個父代進行加權差并與另一個父代進行加和。本文利用差分進化算法對種群最優個體進行變異，如式(13)所示：
 |
式中，V為變異個體，r1，r2，r3為三個隨機數，Xr1，Xr2，Xr3為三個隨機個體，Fc為縮放因子，Fc∈(0, 1)，此處為了保證個體多樣性，擾動應較大，因此本文取Fc = 0.8。
計算變異種群個體與原種群個體的適應度，適應度高的進入下一代，如式(14)所示：
 |
式中，fit(Vi)為變異種群第i個個體的適應度值，fit(Xi)為原種群第i個個體適應度值。
在算法進行迭代更新種群個體位置后，本文使用差分變異擾動在當前種群個體的基礎上生成變異種群個體，選擇適應度值較高的個體進入下一代。
1.3 IDWOA有效性測試
1.3.1 測試函數
為了考察IDWOA的全局搜索和局部開發的能力，本文選取了文獻[17]提到的8個基準測試函數進行測試，其中包括4個單峰函數（只有一個極小值，用于考察算法局部開發能力，F1～F4）和4個多峰函數（具有多個局部極值，用于考察算法全局搜索能力，F5～F8），測試函數信息如表1所示。
表1
測試函數信息
Table1.
Test function information
1.3.2 測試結果
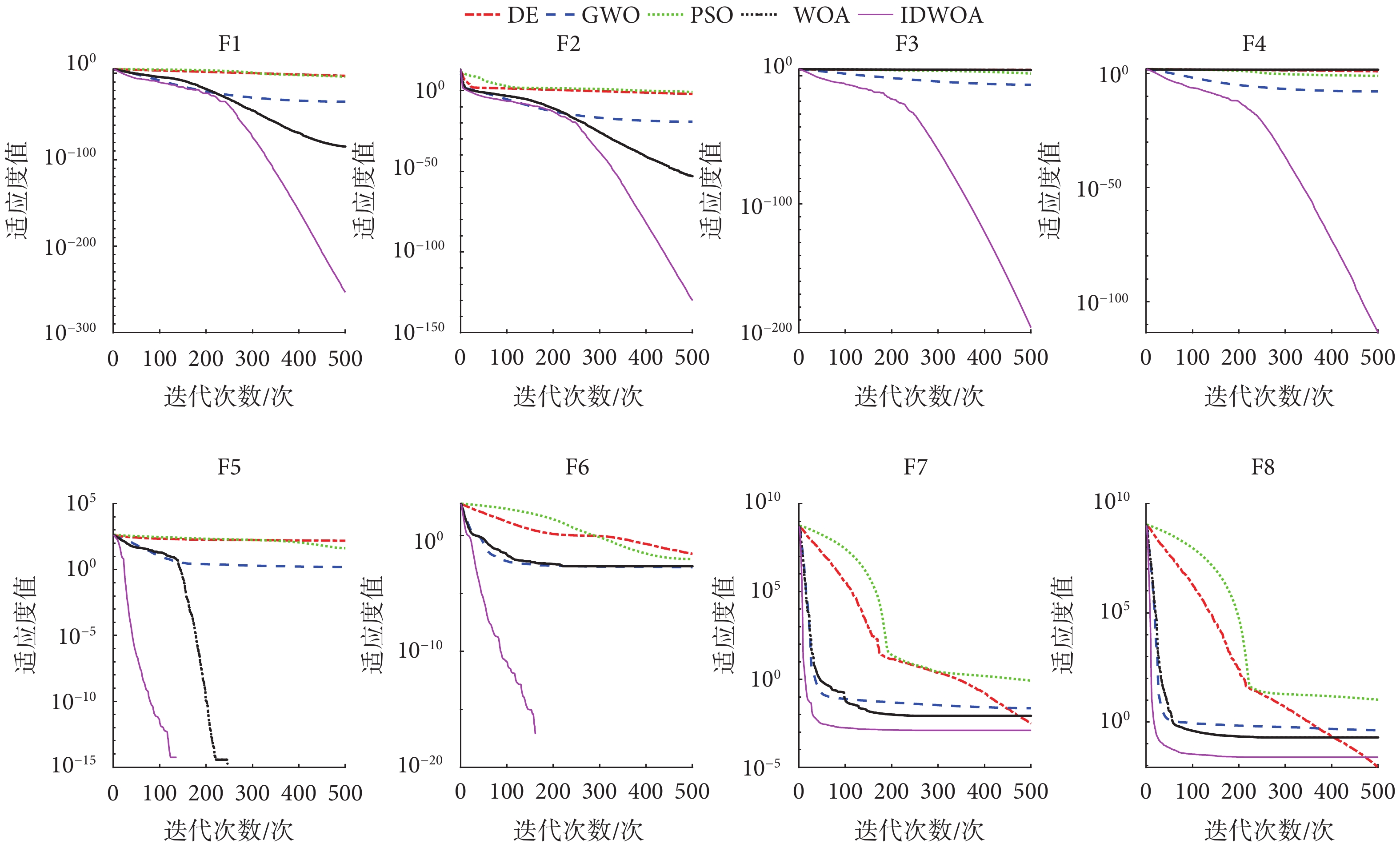
為了驗證本文兩種改進策略的有效性，本文選取了常用的經典尋優算法，包括：標準差分進化（differential evolution，DE）算法、標準粒子群優化（particle swarm optimization，PSO）算法、標準灰狼優化（grey wolf optimizer，GWO）算法、標準 WOA進行測試實驗，各算法的公共參數進行統一設置，種群規模設置為 50，最大迭代次數設置為 500。本文采用8個測試函數對5種優化算法的收斂精度和收斂速度進行測試，5種算法在8個測試函數上的收斂曲線如圖1所示。
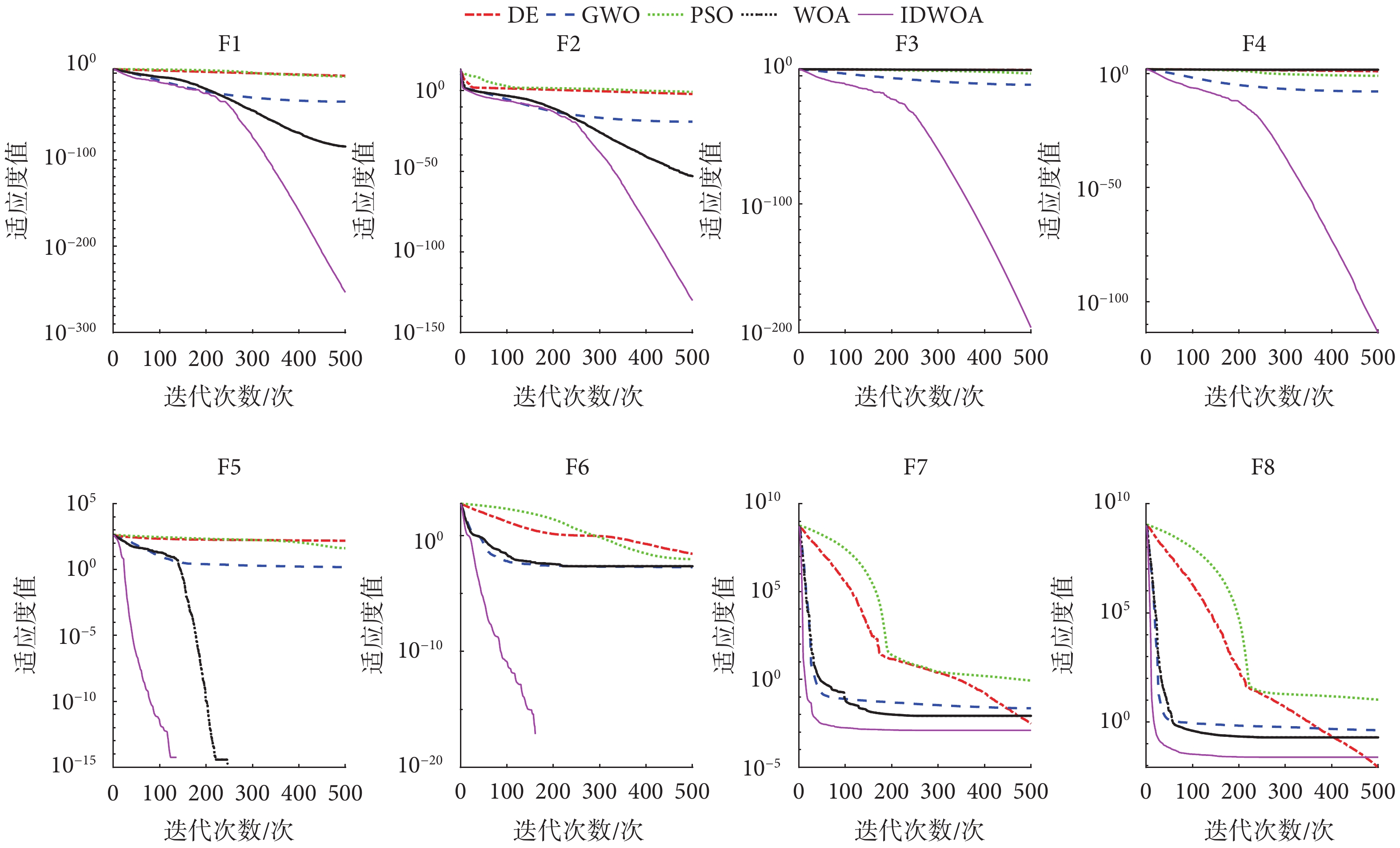圖1
5種算法的收斂曲線圖
Figure1.
Convergence curves of five algorithms
由圖1可知，本文提出的IDWOA在4個單峰測試函數的收斂速度上均優于其他4種算法； 4個單峰測試函數上的收斂精度也優于其他4種算法。IDWOA在4個多峰測試函數上的收斂速度最快；收斂精度在F5、F6、F7上達到了最高，在F8上收斂精度與DE算法相差不大，但是收斂速度相比DE算法更快。綜合來看，IDWOA在8個測試函數具有最快的收斂速度；在7個測試函數上具有最高的收斂精度，因此IDWOA相對其他4種算法具有最佳的局部開發和全局搜索能力。
2 眼動數據與分類模型
2.1 眼動數據
本文采用Hedger等[4]在2021年公開的眼動數據集，該數據收錄于數據分析與研究成果共享平臺（figshare）（網址為：https://figshare.com/），該數據集目前可以免費公開使用。眼動數據集分為兩組：① 30名非自閉癥患者（neurotypical，NT），是從雷丁大學招募而來的學生和教職員工；② 23名自閉癥譜系障礙 （autism spectrum disorder，ASD） 患者，根據《精神障礙診斷與統計手冊》第四版文本修訂版評定入組，每位ASD患者均完成韋氏智力簡寫量表以保證其智力能力和認知能力與NT組無明顯差異。兩組受試者的年齡、性別差異均無統計學意義（P > 0.05）。
數據采集使用的試驗刺激包括60組圖像，分辨率為1 280 × 1 024，每組圖像包括一對社交圖片和非社交圖片。社交圖片涉及幸福的夫妻、嬰兒等場景，非社交圖像涉及食物、自然風光等，兩張圖片在圖像上一左一右進行隨機分布。數據采集時，受試者靜坐于距離顯示器60 cm處，試驗刺激材料的長寬與人眼形成5.59° × 4.19°的夾角，試驗要求受試者在每組刺激中選擇自己感興趣的圖片，每組試驗重復4次，使用眼動儀Tobii T60（Tobii Technology GmbH，瑞典）對眼動數據進行收集。每條眼動數據由具有時間先后順序的坐標點（x, y）組成，每組圖像刺激對應212條眼動數據，其中120條眼動數據來自NT組，其余92條眼動數據來自ASD組。
2.2 眼動特征提取
注視的持續時間和位置信息是描述眼神經系統行為的兩個基本注視特征（S01～S21），如表2所示[23]。這些特征可用于檢查由各個方面共同調節的認知功能。如注視點個數描述了人眼的所有感興趣區域的停留總數，注視時間反映了對當前區域的感興趣程度，注視的位置則反映了感興趣區域分布。多數眼跳都是從一個已知區域朝向新的未知區域，即向前眼跳，但有時還會出現反方向的眼跳，被稱為回視[5]，回視特征（S22～S39）如表2所示。回視特征反映了對感興趣區的再加工情況，回視次數指注視點離開某個興趣區后, 又從其他興趣區域或者位置重新返回到該離開的興趣區域的次數，回視次數的多少反映了感興趣程度或信息理解難易程度。對整體注視位置建模的一種簡單方法是計算注視位置整體樣本的質心、方差以及注視范圍（S40～S50），如表2所示，這些特征反映了數據的總體分布情況。眼跳是非常快速的運動，將眼睛從一個焦點位置旋轉到另一個焦點位置，眼跳特征反映了人的注意力轉移能力（S51～S57），如表2所示。
表2
眼動特征詳細信息
Table2.
Details of eye-movement features
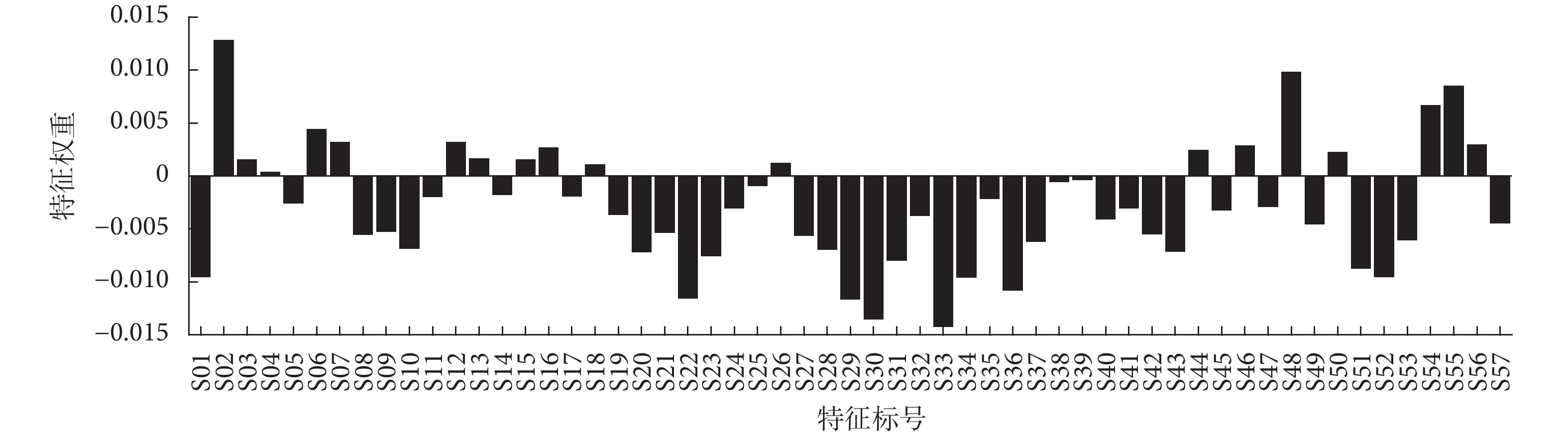
過多的特征會使分類算法的負荷增加，因此需要選取適當且有效的特征構建分類模型。近鄰相關（ReliefF）算法[24]是一種高效的過濾式特征選擇算法，相比包裹式算法具有復雜性低、高效快速、通用性好等優點，經實驗發現，ReliefF算法相比互信息、皮爾遜相關系數等其他過濾式特征選擇算法效果略優，因此本文采用ReliefF算法對輸入特征進行篩選。針對每組圖像刺激下的眼動特征，ReliefF算法對每個特征均返回一個特征權重，如圖2所示。權重值越大表示對分類作用越大，負權重表示該特征不是良好的分類特征。本文特征篩選的標準是：選取特征權重為正值對應的特征用于分類。
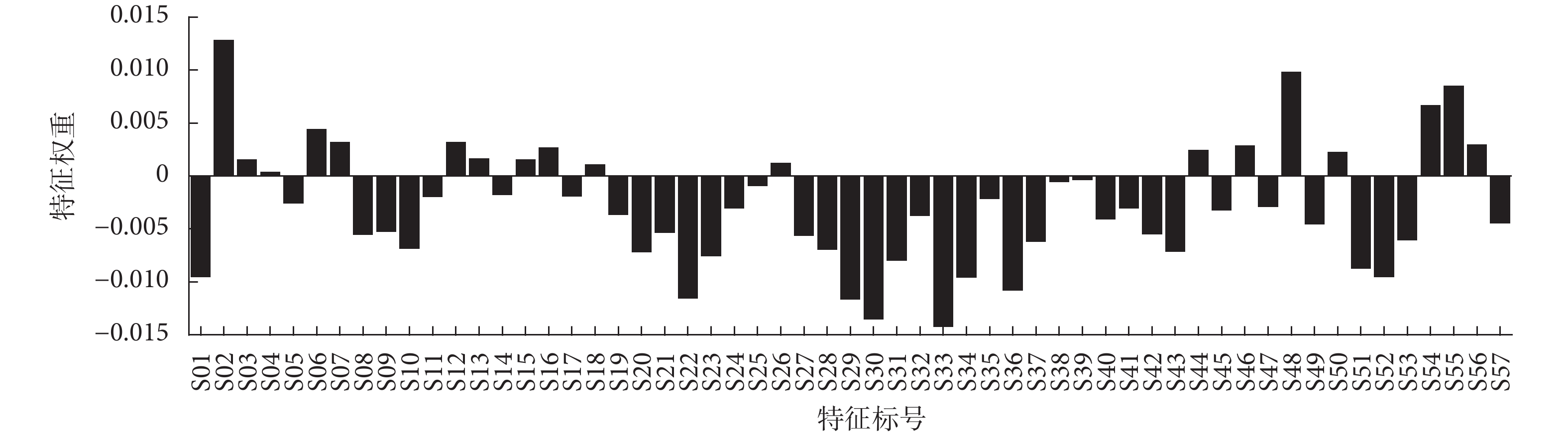圖2
所有特征的特征權重
Figure2.
Feature weights for all features
2.3 分類模型構建
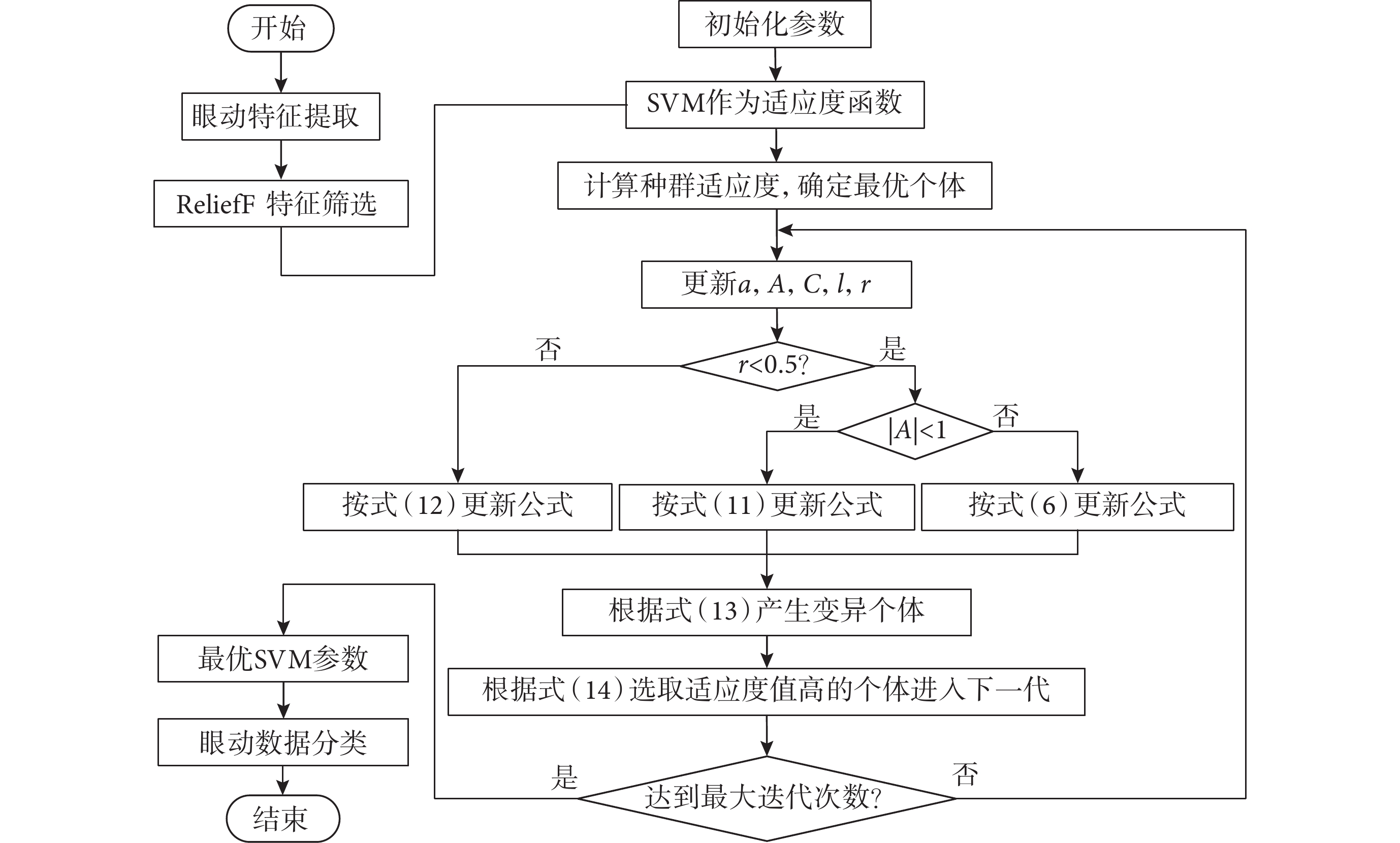
在IDWOA優化SVM過程中，SVM的超參數懲罰因子和核參數的上下限均設置為
，種群規模設置為30、最大迭代次數設置為50，將ReliefF算法提取的眼動特征輸入SVM，以SVM作為適應度函數，使用SVM分類誤差作為適應度值，采用5折交叉驗證。迭代過程中計算種群所有個體的適應度值，確定最優個體并更新所有個體向量，當達到最大迭代次數時返回最優的SVM超參數。本文的IDWOA-SVM眼動數據分類模型整體架構如圖3所示。
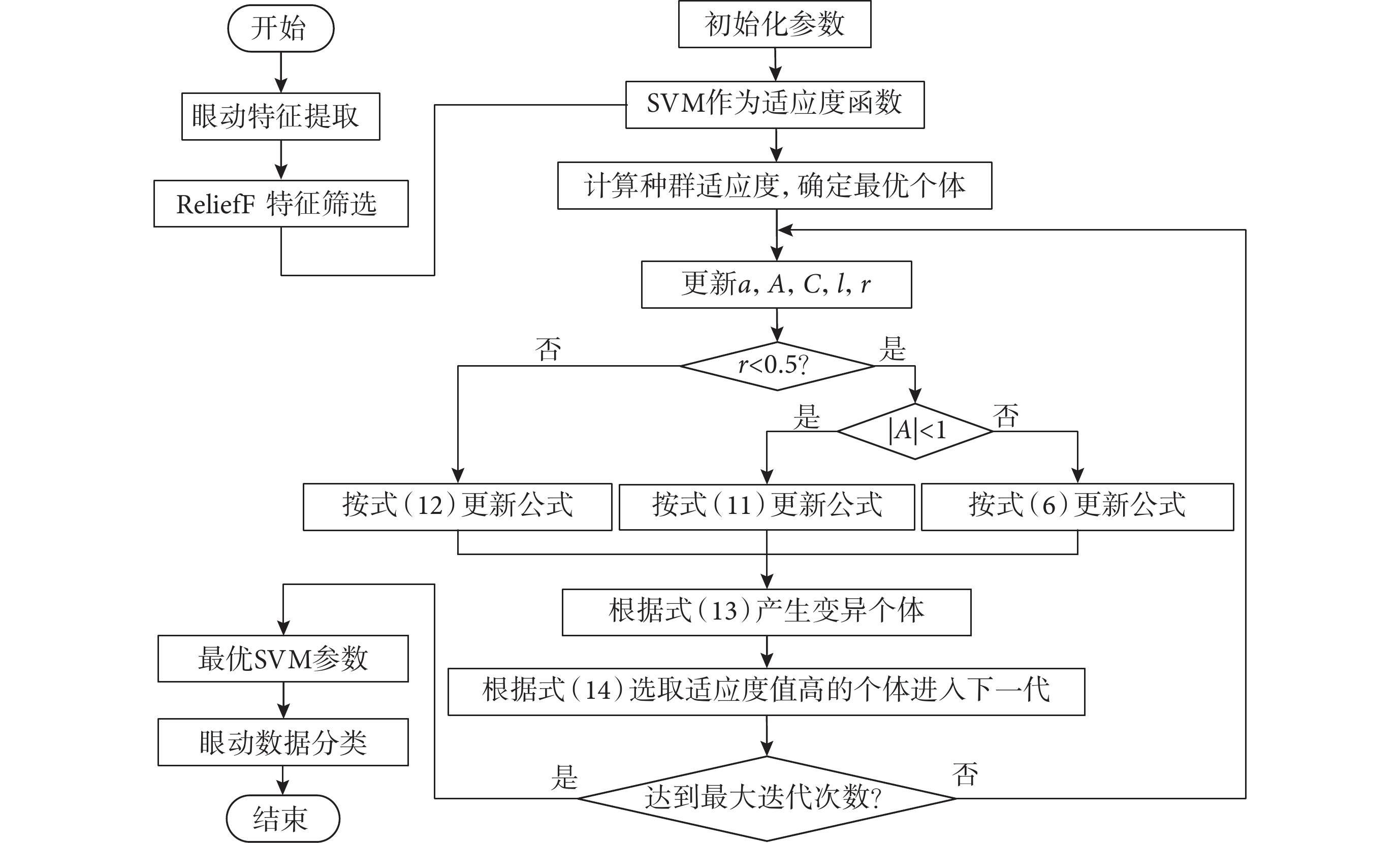圖3
眼動數據分類模型整體架構
Figure3.
The overall architecture of the eye movement data classification model
3 實驗結果與分析
3.1 對比方法與評價指標
為了比較本文提出的IDWOA-SVM眼動數據分類模型的性能優劣，本文將其余四個優化算法與SVM相結合，構建了四個用于比較的分類模型：DE-SVM、PSO-SVM、GWO-SVM、WOA-SVM，同時將SVM方法作為基線。本文針對每條眼動數據提取相應眼動特征，利用ReliefF算法進行特征篩選，然后通過6種分類模型識別兩種人群的眼動數據。
IDWOA有效性測試、眼動特征提取與RelieF特征篩選，以及IDWOA-SVM分類模型有效性驗證均在商業數學軟件MATLAB（2020b，The MathWorks Inc.，美國）平臺進行。實驗測試時種群規模設置為30，最大迭代次數設置為100。為了準確評估算法在分類眼動數據中的表現，本文選取了準確率(accuracy，Acc)、查全率（recall，Rec）、查準率（precision，Pre）、F1分數（F1 score，F1）四個指標進行驗證。計算公式如式(15)～式(18)所示：
 |
 |
 |
 |
式中，真陽性(true positive，TP)表示正類樣本分類正確的數量；真陰性(true negative，TN)表示負類樣本分類正確的數量；假陽性(false positive，FP)表示負類樣本分類錯誤的數量；假陰性(false negative，FN)表示正類樣本分類錯誤的數量。
3.2 ReliefF特征選擇驗證
過多的特征會使系統增加噪聲，提高模型復雜度，因此本文使用ReliefF算法對眼動特征進行篩選，為了驗證ReliefF算法的有效性，本文還引入了互信息（mutual information，MI）、皮爾遜相關系數（Pearson correlation coefficient，PCC）、最小冗余最大相關（minimum redundancy maximum relevance，mRMR）三種過濾式特征選擇加入到對比中，將篩選前后的眼動特征輸入SVM基礎分類模型，60組圖像的平均分類結果如表3所示。
表3
特征篩選前后平均分類結果
Table3.
Average classification accuracy before and after feature selection
根據表3，MI、PCC、mRMR、ReliefF四種特征選擇算法篩選后的結果均優于特征篩選前，說明特征選擇后均能不同程度地去除無用特征，保留有效特征。其中ReliefF算法特征選擇后的分類結果略優于其他三種算法，說明在本實驗場景下ReliefF算法的效果略好。
3.3 IDWOA-SVM分類模型性能驗證
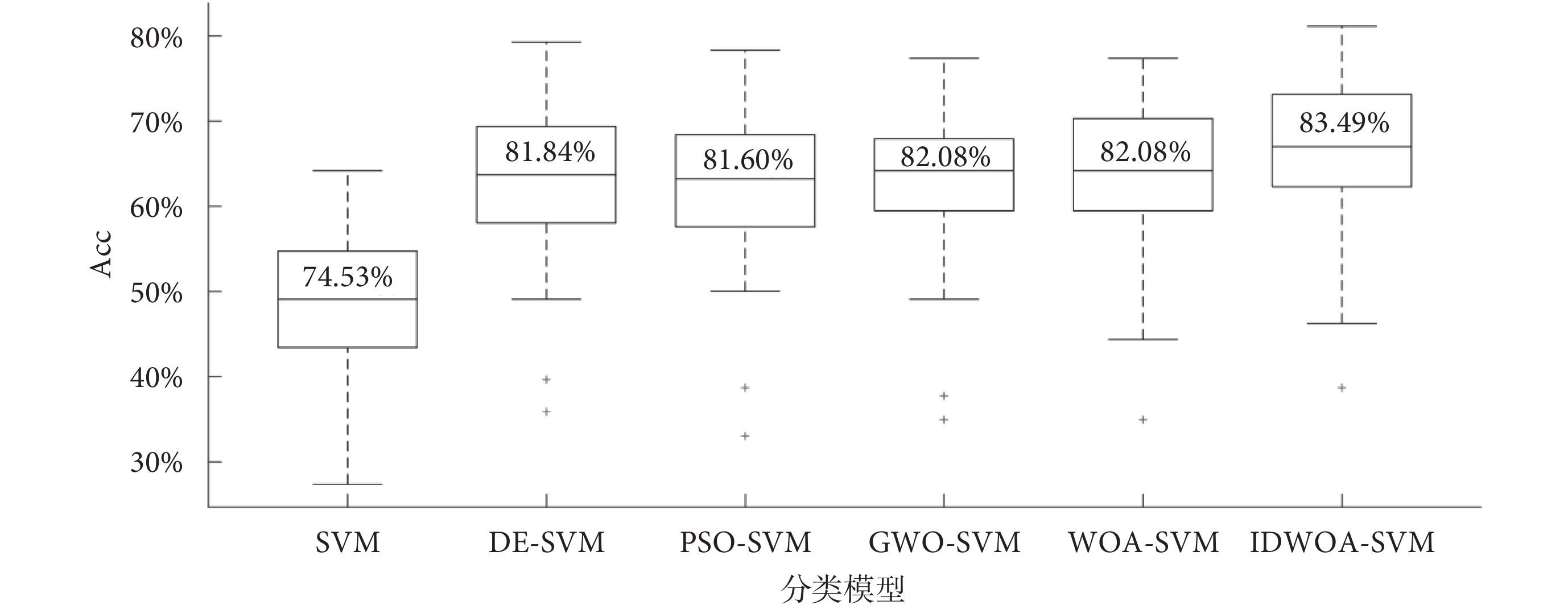
對60組圖像上的分類Acc繪制箱線圖如圖4所示，可以看出DE-SVM、PSO-SVM、GWO-SVM、WOA-SVM、IDWOA-SVM這5種分類模型的分類Acc整體優于標準的SVM，5種方法的下四分位均高于SVM的上四分位，說明優化算法使SVM的參數選取不再具有隨機性和盲目性，Acc大大提高。6種模型的分類Acc中位數分別為74.53%、81.84%、81.60%、82.08%、82.08%、83.49%，IDWOA-SVM分類Acc中位數在所有結果中達到了最優，說明了IDWOA-SVM的分類有效性。
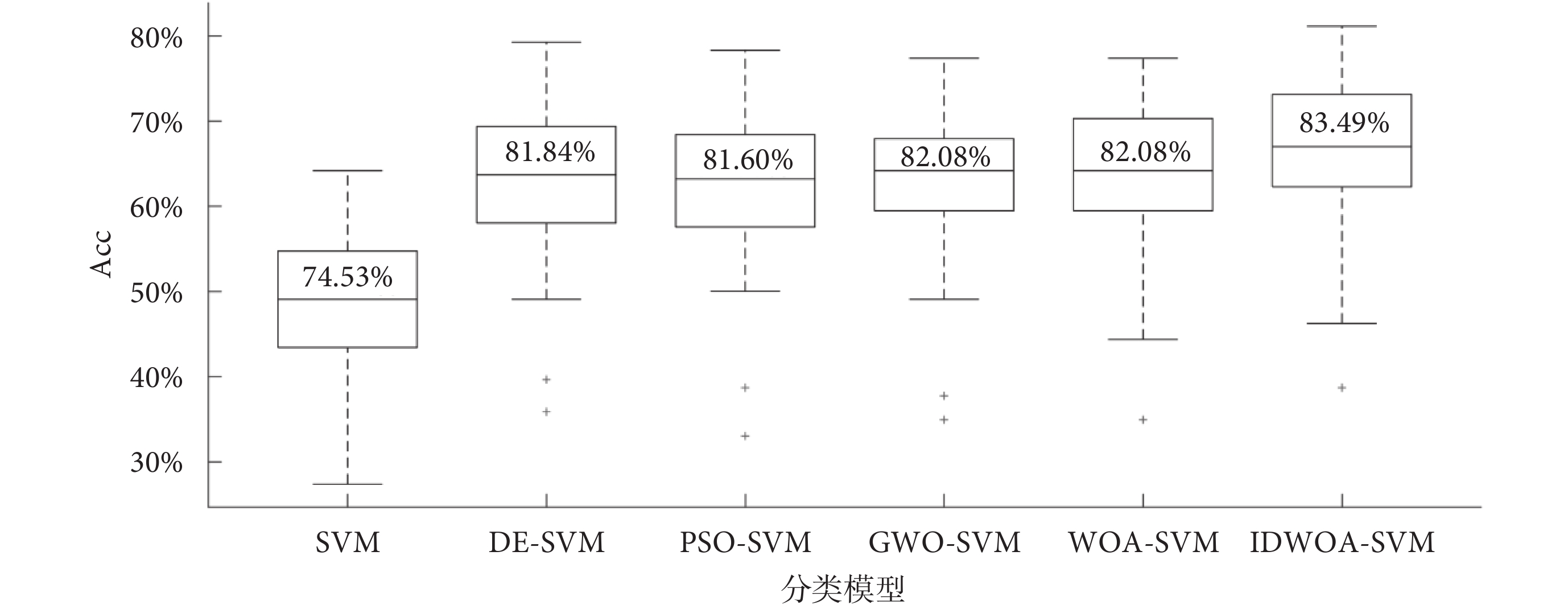圖4
不同模型分類準確率箱線圖
Figure4.
Boxplot of classification accuracy of different models
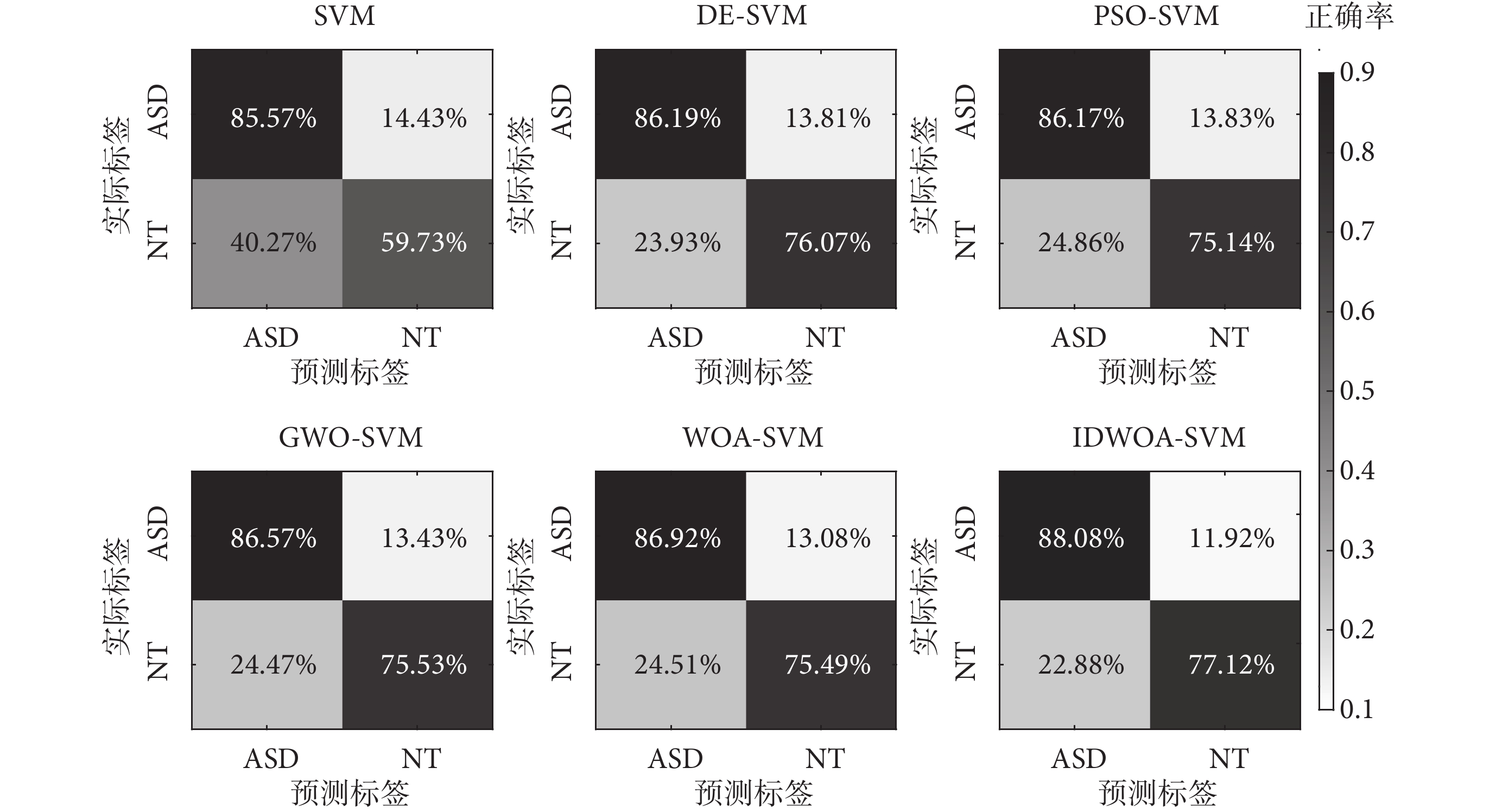
為了更為詳細地驗證IDWOA-SVM分類模型的有效性，計算6種分類模型的Acc、Rec、Pre、F1分數如表4所示。由表4可以看出，在分類兩種不同人群時，6種算法Rec均高于Pre，這是由于ASD組內共性高于NT組，ASD組人群在查看圖像時趨于回避關于社交的內容，而NT組則共性較少，受試者根據自身興趣進行查看，這也在如圖5所示的混淆矩陣中有所體現，ASD組誤分類較少，NT組誤分類較多。
表4
不同模型對比結果
Table4.
Comparison of the results of different models
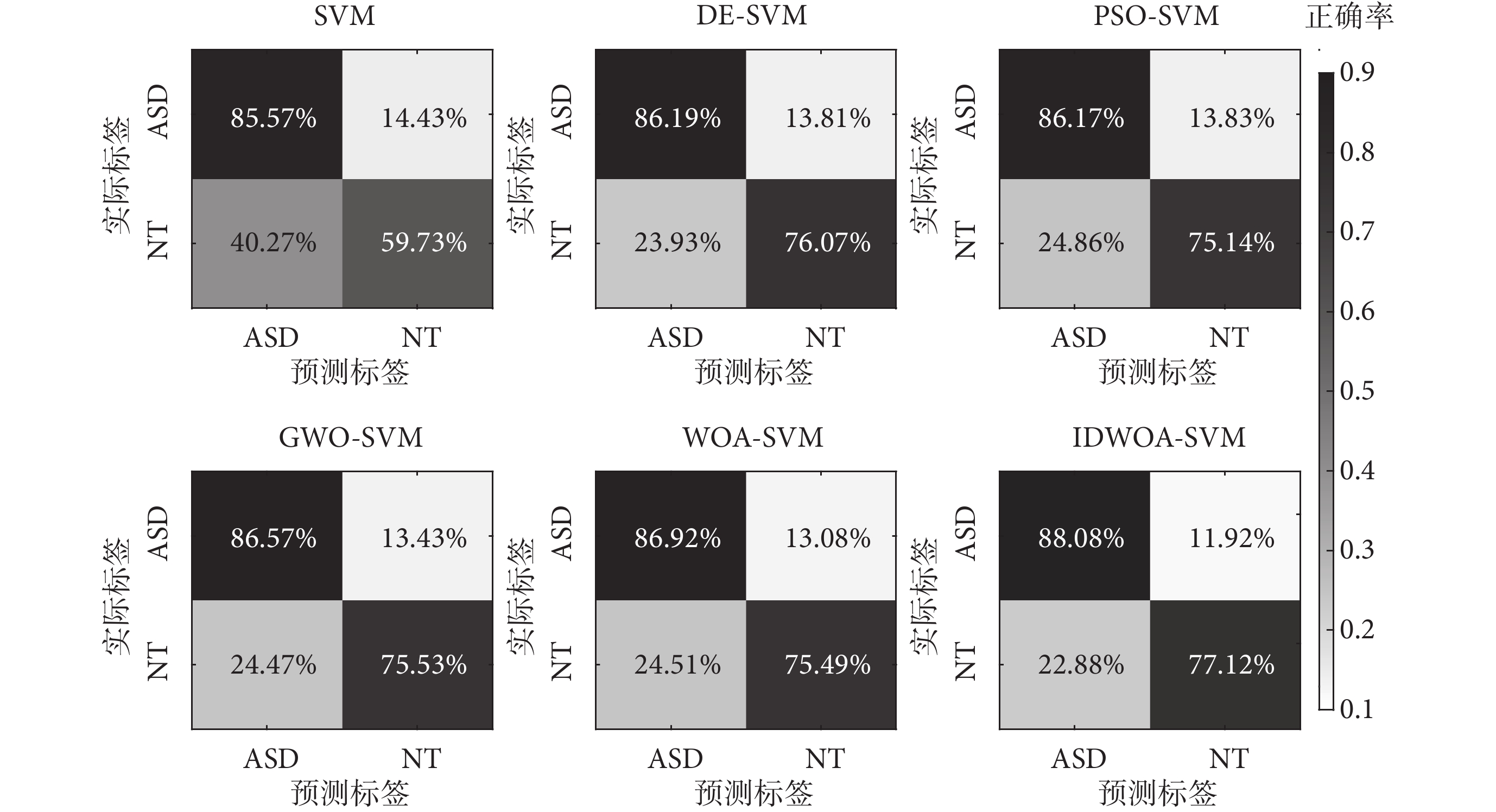圖5
不同模型分類混淆矩陣
Figure5.
Classification confusion matrices of different models
如表4所示，標準的SVM分類性能最差，分類Acc為74.36%，DE-SVM、PSO-SVM、GWO-SVM、WOA-SVM四種算法的分類Acc依次為81.80%、81.38%、81.78%、81.96%，相較于標準的SVM有了較大的提升，說明這4種優化算法能有效進行參數尋優，與SVM結合能提升分類Acc。IDWOA-SVM模型的分類Acc為83.32%，相比WOA-SVM有一定提升，進一步說明了慣性權重和差分變異擾動兩種改進措施的有效性。另外IDWOA-SVM相比DE-SVM、PSO-SVM、GWO-SVM的分類Acc也更高，IDWOA-SVM的Rec、Pre、F1為88.08%、83.56%、85.69%，在6種分類模型中表現最好。
4 結論
本研究提出采用慣性權重和差分變異擾動兩種措施可改進WOA的缺陷，并通過8個測試函數的實驗驗證了IDWOA尋優的性能。本文使用公開的自閉癥眼動數據集驗證IDWOA-SVM眼動模式識別的性能，提取了57個眼動特征并將ReliefF算法篩選后的眼動特征輸入IDWOA-SVM進行分類，實驗結果表明ReliefF算法能有效去除無用的眼動特征，降低模型的復雜度；本文的IDWOA-SVM模型相比傳統的SVM在分類Acc上有較大的提升；相比其他優化算法，IDWOA優化后的SVM具有更高的識別精度，為眼動模式識別提供了新的參考。
但本研究目前僅針對自閉癥眼動數據進行了驗證，對于抑郁癥、閱讀任務、視覺探索任務等眼動數據的效果尚未可知，未來計劃設計不同眼動試驗進行驗證，并進行相應的改進調整，提高方法的泛化能力。另外，本文的眼動特征均是依據眼動儀采集的原始眼動數據進行提取，如何結合眼動數據和相應的眼部圖像內容進行特征提取是一個值得研究的方向。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：沈胤宏負責算法的設計和論文的撰寫；張暢和楊林負責對比方法的整理和測試；李元媛負責指導醫學基礎和分析方法；鄭秀娟負責指導方法理論和算法設計，以及指導論文的撰寫。
0 引言
近年來，隨著眼動跟蹤技術的發展，眼動研究開始應用于各個領域，包括閱讀[1]、心理學[2]、眼疾病[3]、精神疾病[4]等。人眼主要有三種基本的行為：注視、眼跳和追隨運動[5]。基于這三種基本的眼球運動，可以衍生出一系列用于量化不同眼動模式的眼動指標[6]。傳統方法通過統計眼動指標的差異來分析眼動模式[7-9]，但是單個指標僅能看出宏觀上的差異，難以實現眼動模式的精確識別，并且無法平衡多維眼動數據的影響。針對這個問題，許多學者對眼動數據提取多種眼動特征，并使用機器學習方法實現對不同眼動模式的分類[10-11]，其中支持向量機（support vector machine，SVM）具有實現簡單、分類精度和計算效率較高、適用于非線性和小樣本場景等優點，因此得到了廣泛應用[12-14]。值得注意的是，SVM分類性能易受關鍵參數影響，盲目選擇超參數可能帶來分類精度低和擬合效率低等問題。
目前，已經有許多研究引入粒子群算法[15]、差分進化算法[16]等智能優化算法對SVM進行超參數尋優，但這些算法本身參數較多，采用經驗取值難以保證尋優結果收斂到全局最優，存在二次調參的風險。鯨魚優化算法（whale optimization algorithm，WOA）是一種新型優化算法[17]，相比粒子群等算法，WOA最大的優點是不需要額外設置參數，并且還具有實現簡單、易于執行等優點，因此本文引入該算法解決SVM參數選取盲目性的問題。但是WOA本身存在易早熟、易陷入局部最優等缺點，所以一些學者對WOA進行了改進。文獻[18]提出使用混沌映射改進種群初始化過程，該方法在一定程度上可以加快收斂速度，但新算法的種群個體搜索能力沒有改變。文獻[19]將萊維飛行引入WOA，可以有效提高種群個體的全局搜索能力，但是無法平衡全局搜索和局部搜索過程。文獻[20]結合自適應權重和模擬退火策略改進WOA，提高了算法的收斂速度和收斂精度，但依然存在容易陷入局部最優的問題。
在前人研究的基礎上，針對WOA收斂速度慢和易陷入局部最優的問題，本文提出使用慣性權重和差分變異擾動改進WOA（inertia weight and differential variation perturbation improve WOA，IDWOA），通過慣性權重來平衡局部搜索和全局搜索過程以提高算法的收斂速度，通過差分變異擾動以增加種群的多樣性，幫助跳出局部最優。本文提出使用IDWOA優化SVM（IDWOA-SVM），構建IDWOA-SVM眼動模式識別模型，為實現高精度的眼動數據分類提供新思路，并利用公開的自閉癥眼動數據集對本研究提出的算法性能進行評估。
1 改進WOA
1.1 標準WOA
標準WOA根據座頭鯨覓食行為進行建模，模擬了包圍捕食、螺旋氣泡捕食和隨機搜索獵物三個主要的覓食行為。鯨魚通過隨機搜索確定目標，然后通過包圍捕食、螺旋氣泡捕食兩種策略圍捕獵物，捕食過程中包圍捕食和螺旋氣泡捕食是同時存在的，為了模擬這種行為，Mirjalili等[17]設置兩種策略的概率相等，通過產生隨機數r∈(0,1)，來決定使用哪種策略。
1.1.1 包圍捕食
當r < 0.5時，鯨魚采取包圍捕食策略，適應度最高的最優個體或最佳候選解帶領其余個體向獵物包圍靠近，該階段的模擬如式(1)、式(2)所示：
|
|
式中，D表示種群個體與最優個體之間的向量距離，t為當前迭代次數，(t)表示第t次迭代時的種群最優個體向量，X(t)表示第t次迭代時的種群個體向量，X(t + 1)表示第t + 1次迭代時的種群個體向量，A，C為系數，如式(3)、式(4)所示：
|
|
式中，r為(0,1)之間的隨機數， ，tmax表示最大迭代次數，隨著迭代次數增加，a從2線性遞減到0，當前階段|A| < 1。
1.1.2 隨機搜索策略
在隨機搜索獵物階段，鯨魚種群隨機選擇某一個個體作為參考，其余個體根據該隨機個體更新位置，數學建模如式(5)、式(6)所示：
|
|
式中，Xrand(t)為種群隨機個體向量，當前階段|A| ≥ 1。
1.1.3 螺旋氣泡捕食
當r ≥ 0.5時，鯨魚采取螺旋向上的方式靠近獵物，數學模型如式(7)、式(8)所示：
| '/> |
| '/> |
式中， 表示種群個體與最優個體之間的向量距離，e為自然常數，π表示圓周率，b為限定對數螺旋彎曲度的常數，l為[? 1,1]的隨機數。
1.2 改進鯨魚優化算法
1.2.1 慣性權重
WOA使用固定權重進行個體位置更新，在算法迭代后期，種群個體將出現在最優個體附近停留的情況，從而導致局部最優解。本文參考粒子群算法的慣性權重策略[21]，引入一種非線性遞減因子，如式(9)所示。根據粒子群算法當慣性權重w在[0.4, 0.9]變動時收斂效果最好，因此本文將慣性權重歸一化至[0.4, 0.9]，歸一化后的w’如式(10)所示：
|
| '/> |
式中，當迭代初期 有較大值，有利于算法在初期進行全局搜索；在迭代后期，權重 的值非線性遞減，幫助種群個體跳出局部最優區域，加快收斂速度。改進后的鯨魚位置更新公式如式(11)、式(12)所示：
| '/> |
| '/> |
1.2.2 差分變異擾動
差分進化算法具有強大的全局開發能力，而局部開發能力較弱[22]。因此本文利用差分進化算法對種群個體進行差分變異，提高種群的個體多樣性，使算法能跳出局部最優解，快速收斂到全局最優。差分變異策略的基本思想是隨機選取兩個父代進行加權差并與另一個父代進行加和。本文利用差分進化算法對種群最優個體進行變異，如式(13)所示：
|
式中，V為變異個體，r1，r2，r3為三個隨機數，Xr1，Xr2，Xr3為三個隨機個體，Fc為縮放因子，Fc∈(0, 1)，此處為了保證個體多樣性，擾動應較大，因此本文取Fc = 0.8。
計算變異種群個體與原種群個體的適應度，適應度高的進入下一代，如式(14)所示：
|
式中，fit(Vi)為變異種群第i個個體的適應度值，fit(Xi)為原種群第i個個體適應度值。
在算法進行迭代更新種群個體位置后，本文使用差分變異擾動在當前種群個體的基礎上生成變異種群個體，選擇適應度值較高的個體進入下一代。
1.3 IDWOA有效性測試
1.3.1 測試函數
為了考察IDWOA的全局搜索和局部開發的能力，本文選取了文獻[17]提到的8個基準測試函數進行測試，其中包括4個單峰函數（只有一個極小值，用于考察算法局部開發能力，F1～F4）和4個多峰函數（具有多個局部極值，用于考察算法全局搜索能力，F5～F8），測試函數信息如表1所示。
表1
測試函數信息
Table1.
Test function information
1.3.2 測試結果
為了驗證本文兩種改進策略的有效性，本文選取了常用的經典尋優算法，包括：標準差分進化（differential evolution，DE）算法、標準粒子群優化（particle swarm optimization，PSO）算法、標準灰狼優化（grey wolf optimizer，GWO）算法、標準 WOA進行測試實驗，各算法的公共參數進行統一設置，種群規模設置為 50，最大迭代次數設置為 500。本文采用8個測試函數對5種優化算法的收斂精度和收斂速度進行測試，5種算法在8個測試函數上的收斂曲線如圖1所示。
圖1
5種算法的收斂曲線圖
Figure1.
Convergence curves of five algorithms
由圖1可知，本文提出的IDWOA在4個單峰測試函數的收斂速度上均優于其他4種算法； 4個單峰測試函數上的收斂精度也優于其他4種算法。IDWOA在4個多峰測試函數上的收斂速度最快；收斂精度在F5、F6、F7上達到了最高，在F8上收斂精度與DE算法相差不大，但是收斂速度相比DE算法更快。綜合來看，IDWOA在8個測試函數具有最快的收斂速度；在7個測試函數上具有最高的收斂精度，因此IDWOA相對其他4種算法具有最佳的局部開發和全局搜索能力。
2 眼動數據與分類模型
2.1 眼動數據
本文采用Hedger等[4]在2021年公開的眼動數據集，該數據收錄于數據分析與研究成果共享平臺（figshare）（網址為：https://figshare.com/），該數據集目前可以免費公開使用。眼動數據集分為兩組：① 30名非自閉癥患者（neurotypical，NT），是從雷丁大學招募而來的學生和教職員工；② 23名自閉癥譜系障礙 （autism spectrum disorder，ASD） 患者，根據《精神障礙診斷與統計手冊》第四版文本修訂版評定入組，每位ASD患者均完成韋氏智力簡寫量表以保證其智力能力和認知能力與NT組無明顯差異。兩組受試者的年齡、性別差異均無統計學意義（P > 0.05）。
數據采集使用的試驗刺激包括60組圖像，分辨率為1 280 × 1 024，每組圖像包括一對社交圖片和非社交圖片。社交圖片涉及幸福的夫妻、嬰兒等場景，非社交圖像涉及食物、自然風光等，兩張圖片在圖像上一左一右進行隨機分布。數據采集時，受試者靜坐于距離顯示器60 cm處，試驗刺激材料的長寬與人眼形成5.59° × 4.19°的夾角，試驗要求受試者在每組刺激中選擇自己感興趣的圖片，每組試驗重復4次，使用眼動儀Tobii T60（Tobii Technology GmbH，瑞典）對眼動數據進行收集。每條眼動數據由具有時間先后順序的坐標點（x, y）組成，每組圖像刺激對應212條眼動數據，其中120條眼動數據來自NT組，其余92條眼動數據來自ASD組。
2.2 眼動特征提取
注視的持續時間和位置信息是描述眼神經系統行為的兩個基本注視特征（S01～S21），如表2所示[23]。這些特征可用于檢查由各個方面共同調節的認知功能。如注視點個數描述了人眼的所有感興趣區域的停留總數，注視時間反映了對當前區域的感興趣程度，注視的位置則反映了感興趣區域分布。多數眼跳都是從一個已知區域朝向新的未知區域，即向前眼跳，但有時還會出現反方向的眼跳，被稱為回視[5]，回視特征（S22～S39）如表2所示。回視特征反映了對感興趣區的再加工情況，回視次數指注視點離開某個興趣區后, 又從其他興趣區域或者位置重新返回到該離開的興趣區域的次數，回視次數的多少反映了感興趣程度或信息理解難易程度。對整體注視位置建模的一種簡單方法是計算注視位置整體樣本的質心、方差以及注視范圍（S40～S50），如表2所示，這些特征反映了數據的總體分布情況。眼跳是非常快速的運動，將眼睛從一個焦點位置旋轉到另一個焦點位置，眼跳特征反映了人的注意力轉移能力（S51～S57），如表2所示。
表2
眼動特征詳細信息
Table2.
Details of eye-movement features
過多的特征會使分類算法的負荷增加，因此需要選取適當且有效的特征構建分類模型。近鄰相關（ReliefF）算法[24]是一種高效的過濾式特征選擇算法，相比包裹式算法具有復雜性低、高效快速、通用性好等優點，經實驗發現，ReliefF算法相比互信息、皮爾遜相關系數等其他過濾式特征選擇算法效果略優，因此本文采用ReliefF算法對輸入特征進行篩選。針對每組圖像刺激下的眼動特征，ReliefF算法對每個特征均返回一個特征權重，如圖2所示。權重值越大表示對分類作用越大，負權重表示該特征不是良好的分類特征。本文特征篩選的標準是：選取特征權重為正值對應的特征用于分類。
圖2
所有特征的特征權重
Figure2.
Feature weights for all features
2.3 分類模型構建
在IDWOA優化SVM過程中，SVM的超參數懲罰因子和核參數的上下限均設置為，種群規模設置為30、最大迭代次數設置為50，將ReliefF算法提取的眼動特征輸入SVM，以SVM作為適應度函數，使用SVM分類誤差作為適應度值，采用5折交叉驗證。迭代過程中計算種群所有個體的適應度值，確定最優個體并更新所有個體向量，當達到最大迭代次數時返回最優的SVM超參數。本文的IDWOA-SVM眼動數據分類模型整體架構如圖3所示。
圖3
眼動數據分類模型整體架構
Figure3.
The overall architecture of the eye movement data classification model
3 實驗結果與分析
3.1 對比方法與評價指標
為了比較本文提出的IDWOA-SVM眼動數據分類模型的性能優劣，本文將其余四個優化算法與SVM相結合，構建了四個用于比較的分類模型：DE-SVM、PSO-SVM、GWO-SVM、WOA-SVM，同時將SVM方法作為基線。本文針對每條眼動數據提取相應眼動特征，利用ReliefF算法進行特征篩選，然后通過6種分類模型識別兩種人群的眼動數據。
IDWOA有效性測試、眼動特征提取與RelieF特征篩選，以及IDWOA-SVM分類模型有效性驗證均在商業數學軟件MATLAB（2020b，The MathWorks Inc.，美國）平臺進行。實驗測試時種群規模設置為30，最大迭代次數設置為100。為了準確評估算法在分類眼動數據中的表現，本文選取了準確率(accuracy，Acc)、查全率（recall，Rec）、查準率（precision，Pre）、F1分數（F1 score，F1）四個指標進行驗證。計算公式如式(15)～式(18)所示：
|
|
|
|
式中，真陽性(true positive，TP)表示正類樣本分類正確的數量；真陰性(true negative，TN)表示負類樣本分類正確的數量；假陽性(false positive，FP)表示負類樣本分類錯誤的數量；假陰性(false negative，FN)表示正類樣本分類錯誤的數量。
3.2 ReliefF特征選擇驗證
過多的特征會使系統增加噪聲，提高模型復雜度，因此本文使用ReliefF算法對眼動特征進行篩選，為了驗證ReliefF算法的有效性，本文還引入了互信息（mutual information，MI）、皮爾遜相關系數（Pearson correlation coefficient，PCC）、最小冗余最大相關（minimum redundancy maximum relevance，mRMR）三種過濾式特征選擇加入到對比中，將篩選前后的眼動特征輸入SVM基礎分類模型，60組圖像的平均分類結果如表3所示。
表3
特征篩選前后平均分類結果
Table3.
Average classification accuracy before and after feature selection
根據表3，MI、PCC、mRMR、ReliefF四種特征選擇算法篩選后的結果均優于特征篩選前，說明特征選擇后均能不同程度地去除無用特征，保留有效特征。其中ReliefF算法特征選擇后的分類結果略優于其他三種算法，說明在本實驗場景下ReliefF算法的效果略好。
3.3 IDWOA-SVM分類模型性能驗證
對60組圖像上的分類Acc繪制箱線圖如圖4所示，可以看出DE-SVM、PSO-SVM、GWO-SVM、WOA-SVM、IDWOA-SVM這5種分類模型的分類Acc整體優于標準的SVM，5種方法的下四分位均高于SVM的上四分位，說明優化算法使SVM的參數選取不再具有隨機性和盲目性，Acc大大提高。6種模型的分類Acc中位數分別為74.53%、81.84%、81.60%、82.08%、82.08%、83.49%，IDWOA-SVM分類Acc中位數在所有結果中達到了最優，說明了IDWOA-SVM的分類有效性。
圖4
不同模型分類準確率箱線圖
Figure4.
Boxplot of classification accuracy of different models
為了更為詳細地驗證IDWOA-SVM分類模型的有效性，計算6種分類模型的Acc、Rec、Pre、F1分數如表4所示。由表4可以看出，在分類兩種不同人群時，6種算法Rec均高于Pre，這是由于ASD組內共性高于NT組，ASD組人群在查看圖像時趨于回避關于社交的內容，而NT組則共性較少，受試者根據自身興趣進行查看，這也在如圖5所示的混淆矩陣中有所體現，ASD組誤分類較少，NT組誤分類較多。
表4
不同模型對比結果
Table4.
Comparison of the results of different models
圖5
不同模型分類混淆矩陣
Figure5.
Classification confusion matrices of different models
如表4所示，標準的SVM分類性能最差，分類Acc為74.36%，DE-SVM、PSO-SVM、GWO-SVM、WOA-SVM四種算法的分類Acc依次為81.80%、81.38%、81.78%、81.96%，相較于標準的SVM有了較大的提升，說明這4種優化算法能有效進行參數尋優，與SVM結合能提升分類Acc。IDWOA-SVM模型的分類Acc為83.32%，相比WOA-SVM有一定提升，進一步說明了慣性權重和差分變異擾動兩種改進措施的有效性。另外IDWOA-SVM相比DE-SVM、PSO-SVM、GWO-SVM的分類Acc也更高，IDWOA-SVM的Rec、Pre、F1為88.08%、83.56%、85.69%，在6種分類模型中表現最好。
4 結論
本研究提出采用慣性權重和差分變異擾動兩種措施可改進WOA的缺陷，并通過8個測試函數的實驗驗證了IDWOA尋優的性能。本文使用公開的自閉癥眼動數據集驗證IDWOA-SVM眼動模式識別的性能，提取了57個眼動特征并將ReliefF算法篩選后的眼動特征輸入IDWOA-SVM進行分類，實驗結果表明ReliefF算法能有效去除無用的眼動特征，降低模型的復雜度；本文的IDWOA-SVM模型相比傳統的SVM在分類Acc上有較大的提升；相比其他優化算法，IDWOA優化后的SVM具有更高的識別精度，為眼動模式識別提供了新的參考。
但本研究目前僅針對自閉癥眼動數據進行了驗證，對于抑郁癥、閱讀任務、視覺探索任務等眼動數據的效果尚未可知，未來計劃設計不同眼動試驗進行驗證，并進行相應的改進調整，提高方法的泛化能力。另外，本文的眼動特征均是依據眼動儀采集的原始眼動數據進行提取，如何結合眼動數據和相應的眼部圖像內容進行特征提取是一個值得研究的方向。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：沈胤宏負責算法的設計和論文的撰寫；張暢和楊林負責對比方法的整理和測試；李元媛負責指導醫學基礎和分析方法；鄭秀娟負責指導方法理論和算法設計，以及指導論文的撰寫。
