本文提出了一種基于人體肌肉狀態實時監測的自適應人機交互控制方法，用于解決康復外骨骼機器人運動過程中的人機交互問題。為了保證患者的健康監控和康復訓練效率，提出了一種新的疲勞評估算法，該算法利用人體神經肌骨模型，實現了對肌肉疲勞狀態的等級劃分。為了保證人機交互的安全性，提出了一種以該算法作為監督環節的變阻抗控制算法。通過實驗驗證，本文所提出的人機交互控制方法是有效的，具有普遍性，能夠改善穿戴舒適度，提高康復訓練效率，具有廣闊的應用前景。
引用本文： 牛惠祺, 張弼, 劉麗剛, 趙憶文, 趙新剛. 人體肌肉狀態疲勞監測及其在外骨骼交互控制中的應用. 生物醫學工程學雜志, 2023, 40(4): 654-662. doi: 10.7507/1001-5515.202211020 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
隨著經濟社會的發展與信息技術的進步，我國見證了輔助技術從零開始成長到如今相當活躍的水平，而隨著我國社會人口老齡化程度的加劇，由腦卒中等疾病造成的運動功能障礙患者數量急劇增加，對輔助技術的應用需求也越來越大[1-2]。有運動功能障礙的患者主要通過運動康復療法進行康復訓練。對于下肢運動康復，臨床醫生一般使用手動輔助技術幫助患者進行走路等訓練運動，旨在幫助患者恢復正常的生理步態[3]，但是與龐大的患者人數相比，治療師的數量遠遠不足。而隨著機器人技術的高速發展，醫用機器人結合了多學科的發展成果，被廣泛應用于各種醫學領域[2]，其中，康復機器人可以減少手動輔助重復性任務，并可增強步態規范性，提高步態性能。關于使用機器人設備進行步態訓練的有效性已經通過臨床與科學研究驗證[3-5]。因此，使用機器人設備進行康復訓練對于減輕醫護人員的工作量以及提高患者的康復訓練效果具有積極意義。
在康復機器人與患者的人機交互中，首先需要保障的是患者的安全性，對于卒中患者，在康復訓練期間，由于肌肉和認知能力下降，很容易出現疲勞狀態[6]，嚴重的還有可能導致過疲勞現象，對患者健康具有極大風險。肌肉疲勞是一種復雜的生理現象，可以描述為肌肉進行體力活動的能力逐漸下降[7]。肌肉疲勞也是肌肉骨骼問題的危險因素之一，出于對人的健康監控與康復訓練效率考慮，需要在人體工程學與生理學領域對肌肉狀態進行定量評估，進而可以根據監測的肌肉疲勞狀態進行康復訓練方案的優化[6, 8-10]。
關于肌肉疲勞評估目前尚無公認的評估標準體系，針對不同的研究對象存在很多不同的評估方法，根據研究對象的性質可以分為三個方向：化學[11]、生物電[12-14]和機械現象[15]。從化學角度來看，可以通過近紅外光譜技術檢測肌肉血氧飽和度水平的相對變化；從生物電角度來看，表面肌電（surface electromyography，sEMG）信號提供了一種從“源頭”來理解疲勞這一現象的方法；從機械現象角度來看，加速度傳感器從疲勞產生的“結果”出發，可以用于測量運動軌跡變化。
很多研究者將研究對象重點放在sEMG信號上。眾所周知，基于機器人的主動康復訓練不可避免要用到肌電信息，在不附加多余傳感器的情況下，依賴系統設計中已經固有的sEMG信息無疑是非常方便的。Thacham Poyil等[6]通過sEMG的中值頻率對肌肉是否疲勞進行評估，當系統檢測到疲勞時就降低一半的訓練強度以延長訓練時間與效率，通過實驗驗證了控制策略的有效性；Peternel等[9]巧妙地采用一個類RC電路的結構，用電容器電壓代表疲勞進行肌肉疲勞估計，讓機器學習人在正常狀態下的位置/力變化，當系統檢測到肌肉疲勞時，通過學習到的任務執行頻率/力接管任務直至人的狀態恢復。
但是，單一的研究對象可能造成評估結果不準確，因為疲勞是多方面因素相互作用的結果[16]，于是很多學者采用不同研究對象交叉結合的方式來對肌肉疲勞進行評估。Ramos等[17]提出了一種基于sEMG信號和心率變異性（heart rate variability，HRV）參數的疲勞檢測模型；Chandra等[18]利用sEMG和加速度計進行了手部疲勞誘發震顫的評估聚類；Aryal等[19]通過可穿戴式傳感器測量體溫、心率的方式對疲勞進行實時監測。
上述研究成果取得了很大的進展，但是仍存在一定的局限性。一方面，單一的研究對象可能造成評估結果的準確性受限，但是過多研究對象的算法在設計控制系統時又會額外用到大量的傳感器。如何平衡選擇疲勞評估所需的研究對象，對于設計系統的成本具有至關重要的影響。另一方面，現有的疲勞評估方法大部分局限于疲勞閾值的存在，當肌肉狀態達到疲勞閾值時更改或停止任務，并不能做到根據肌肉狀態實時調整控制策略，在系統的容錯機制上有待開發。
為了解決上述問題，本文針對下肢外骨骼康復機器人，提出了一種基于人體肌肉狀態的自適應人機交互控制方法。
1 模型建立
1.1 Hammerstein模型
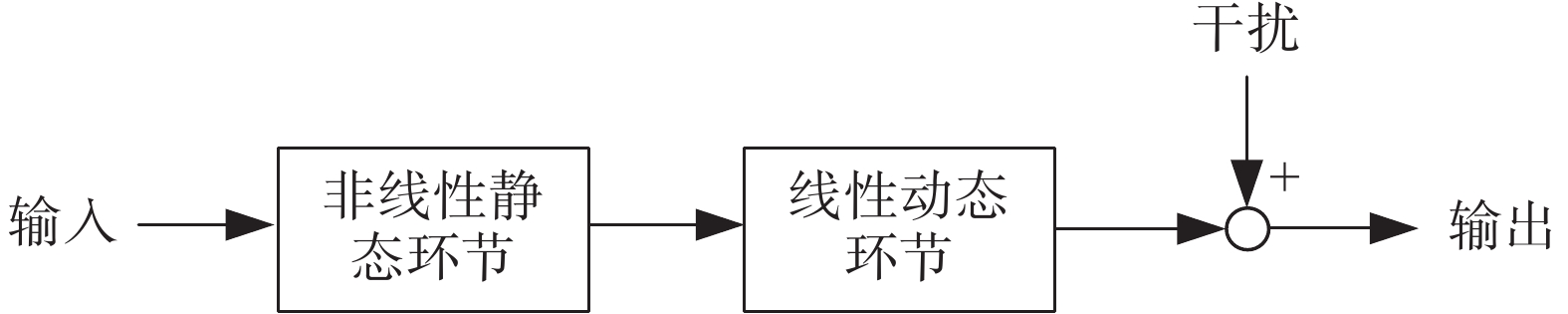
Hammerstein模型是非線性過程中經常使用的典型模型之一，其模型結構由一個非線性靜態部分
與線性動態部分
串聯而成[20]，如圖1所示。其中的輸入非線性可以表示為一組基底選定的基函數的線性加和：
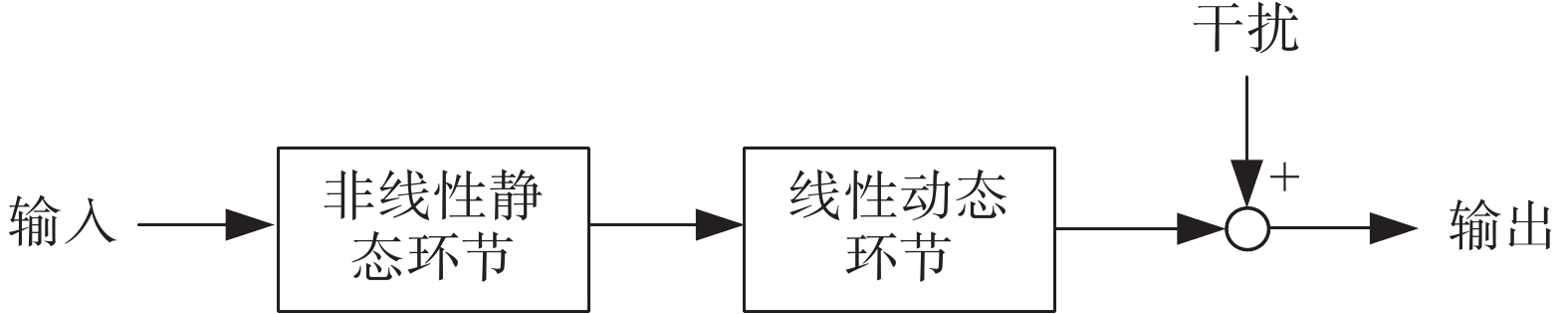圖1
Hammerstein模型結構圖
Figure1.
Structure diagram of Hammerstein model
 |
式中
選取為
。
線性動態部分表示為：
 |
式中的未知多項式
和
定義為：
 |
根據式(1)～(3)，可以得到參數化Hammerstein模型：
 |
其中
為模型輸入，
為模型輸出，
為有界外部干擾，
、
、
均為參數，可通過參數辨識算法進行辨識。
由于與生物物理學對應，與機理模型也近似，而且辨識簡單，Hammerstein模型已被廣泛應用于肌肉疲勞影響下的非線性神經肌肉系統建模[18, 21-25]。
1.2 人體神經肌肉骨骼模型
人體下肢正向動態神經肌肉骨骼模型如圖2所示，通過此模型可以根據神經信號估計或預測肌肉力量，計算關節力矩或關節運動學[26-30]。首先，肌肉的活躍度是通過神經信號激活肌肉的動力學過程來控制的。然后，肌肉的收縮動力學描述了如何將肌肉的活躍度轉化為肌力。最后，通過肌肉骨骼幾何模型，將產生的肌力轉化為關節力矩，并利用運動方程計算出關節的運動。
圖2
下肢神經肌肉骨骼模型
Figure2.
Neuromusculoskeletal model of lower limbs
肌肉激活度直接反映了肌肉的活躍水平，通常引入一個函數表達神經信號與肌肉活躍度之間的非線性關系[29, 31-33]：
 |
其中
表示
時刻的處理后的肌電信號，
表示計算所得的肌肉活躍度特征。
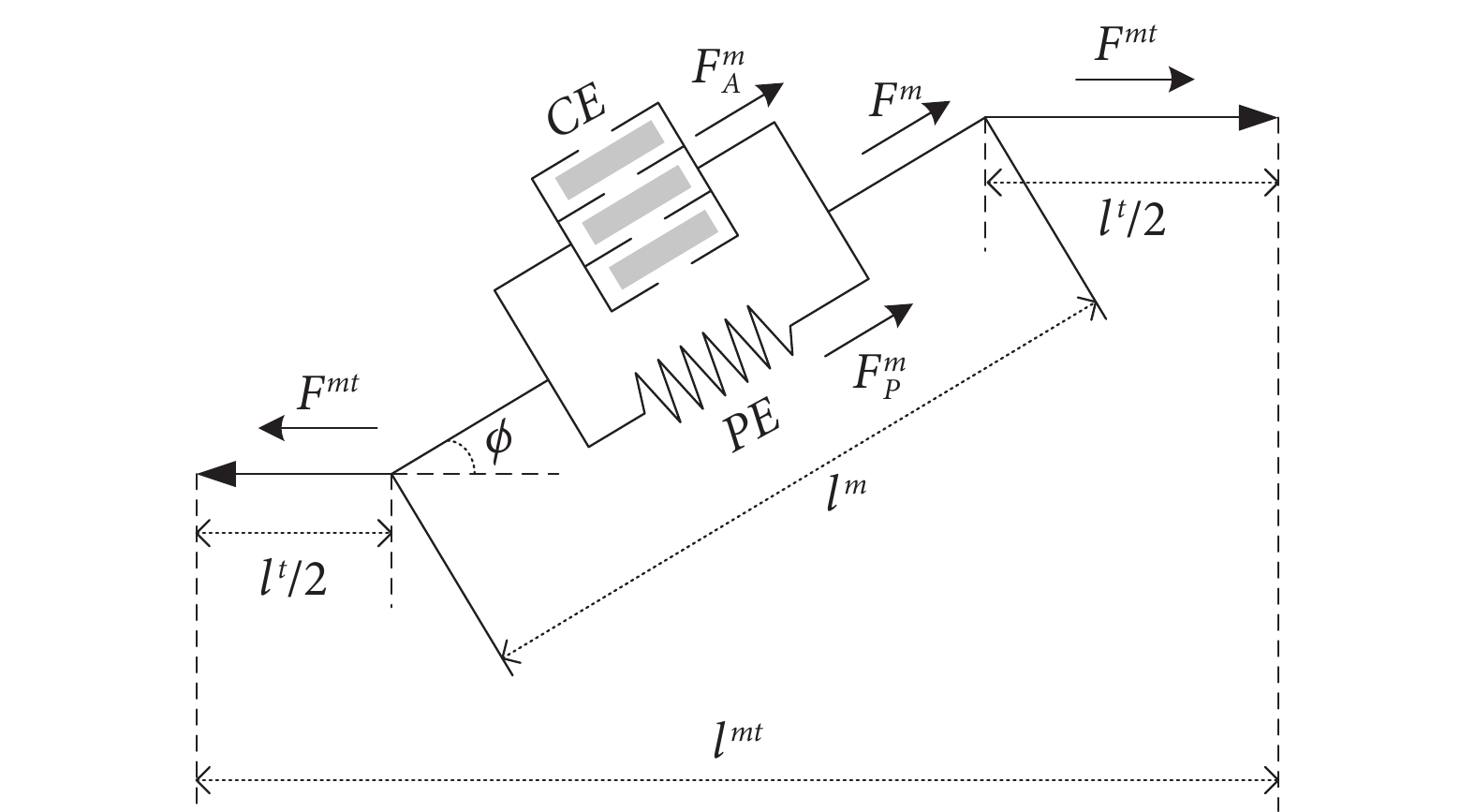
Hill肌肉力模型是通過大量的醫學數據與實驗應用驗證的模型，其模型結構如圖3所示，圖中
表示主動收縮單元，
表示被動彈性單元，
表示肌纖維長度，
表示腱長度，
表示肌腱單元長度，
表示肌肉纖維與腱的夾角，
表示主動收縮力，
表示被動彈性力，
表示肌纖維力，
表示肌腱單元力。可以看出完整的Hill模型十分復雜，包含很多生理學參數，實際應用時難以獲取，因此Han等[31]在保證模型準確性的前提下對模型進行了簡化，計算得到肌腱力
：
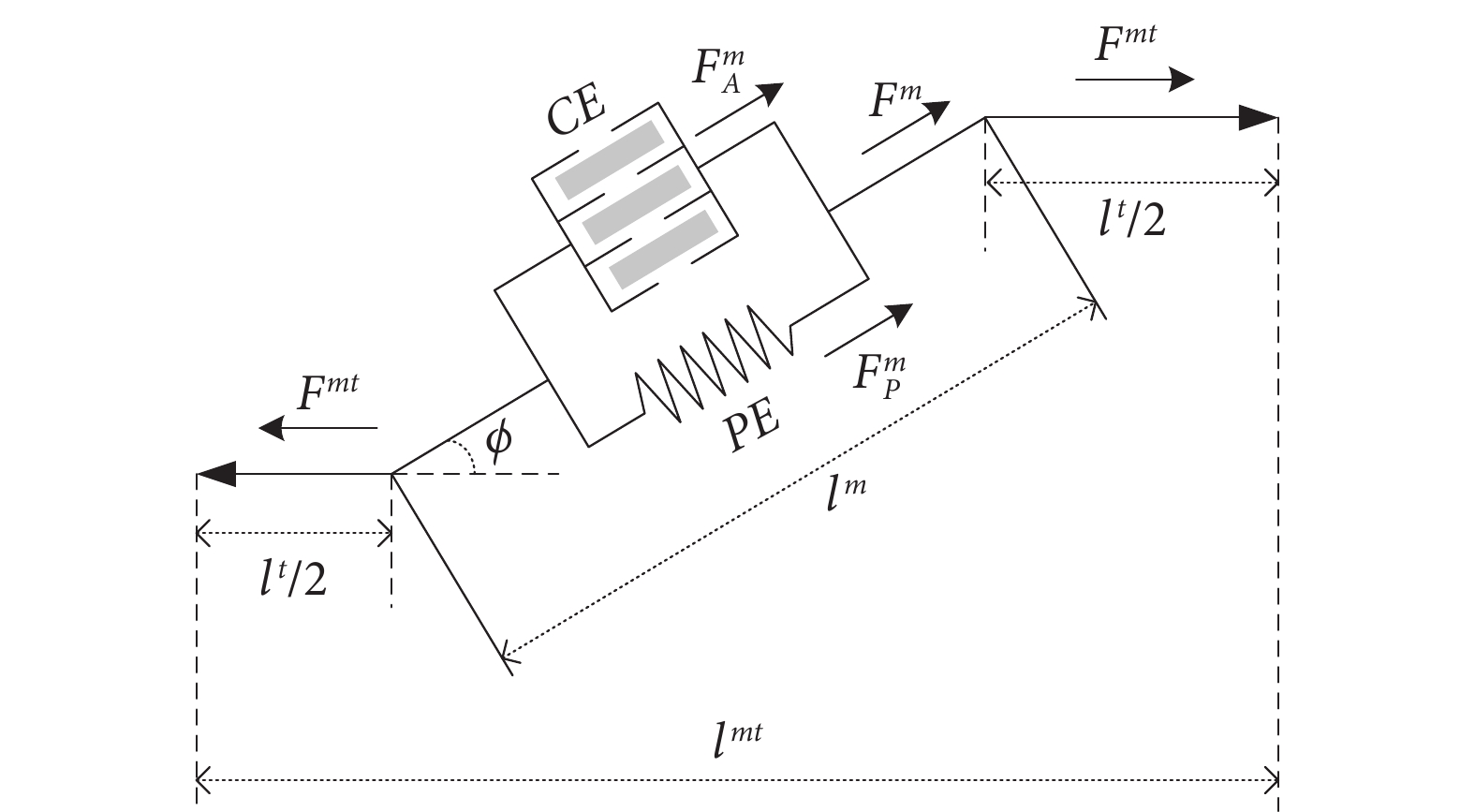圖3
Hill肌肉力模型
Figure3.
Hill-type muscle model
 |
其中 
、
和 
為生理參數關系，可以通過數據擬合，
、
和 
為實際生理參數，均為常值，
為肌肉纖維和腱的夾角。
通過肌肉力可以計算肌肉對其驅動關節的力矩貢獻
：
 |
其中
是常系數，為一階多項式擬合關節角和肌腱長度的一階項系數[31]。
以踝關節為例，通過其肌肉骨骼幾何模型和關節前向動力學可以得到踝關節運動的角加速度：
 |
 |
其中
表示腳相對于踝關節的轉動慣量，假定其為常數，
是外部負載和腳的重力產生的力矩之和，
表示
的最大值。
將公式(1)～(5)聯立并通過三階泰勒級數展開，可以推導由肌電信號計算關節角加速度的離散化方程：
 |
其中
、
均為生理參數及對應關系的常數項，
表示
時刻的sEMG信號，
表示
時刻的關節運動角度，
為系統高階項：
 |
其中
表示生理參數與實際運動之間的非線性關系，
為采樣時間，在實際系統中，采樣周期很短，故該二項式很小。
在數學上，公式(4)的形式與公式(10)相似，公式(4)中
與公式(10)中的
對應，
與
對應；值得指出的是，公式(4)中的
與公式(10)中的高階項對應，由于其包含
項，而實際系統的采樣時間很短，故對系統影響很微弱，即系統擾動較小。
在結構上，如圖1和圖2所示，Hammerstein模型的非線性靜態環節可以代表神經肌肉骨骼模型的神經激活，這是神經信號與肌肉激活之間的靜態增益關系，線性動態環節可以代表肌肉收縮動力學和關節運動學，這使其成為可用于生物系統辨識的可能結構之一[27]。本文也采用Hammerstein模型結構對人體神經肌肉骨骼模型進行擬合。
2 基于疲勞監測的安全保護控制系統
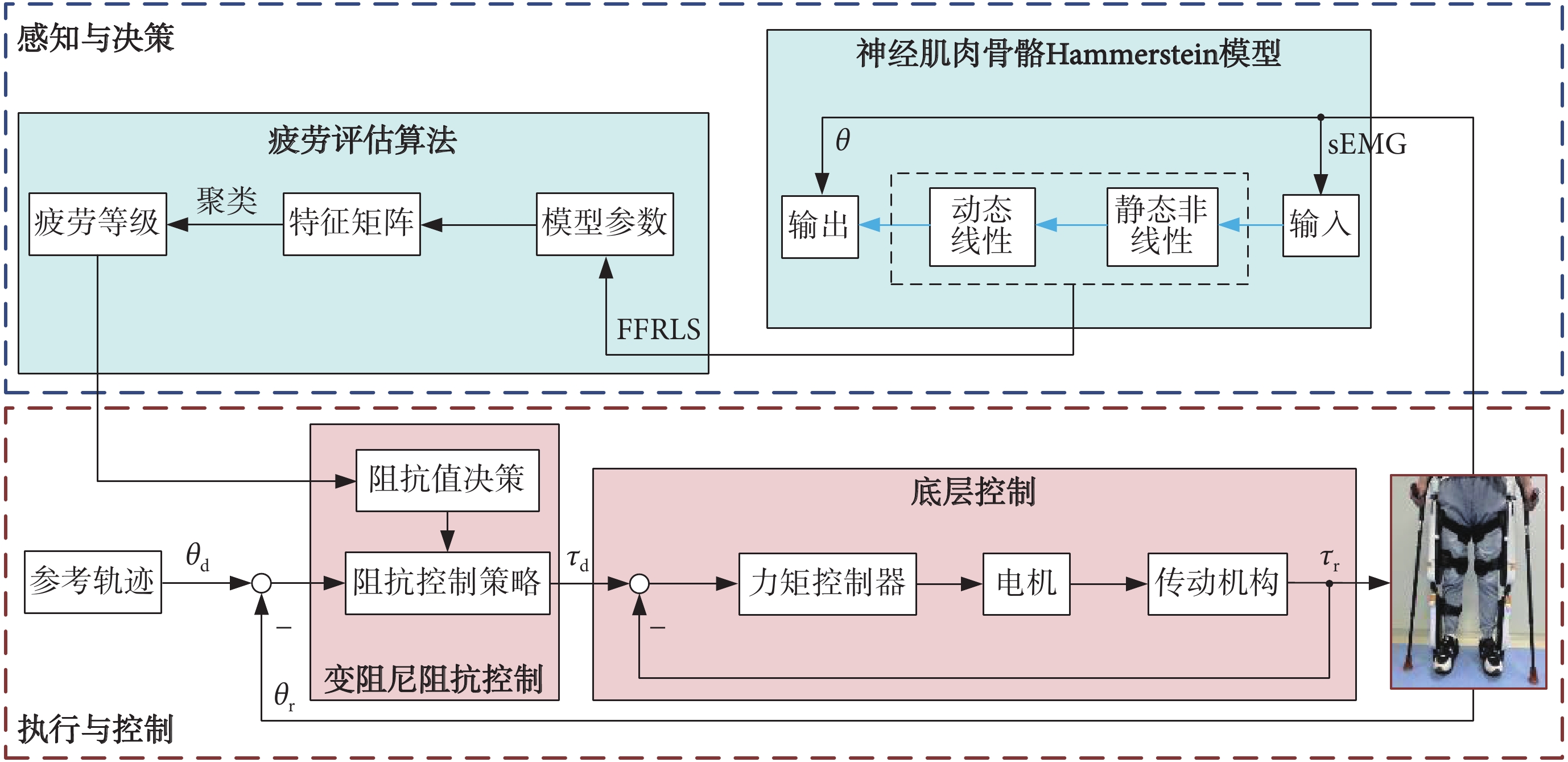
基于人體肌肉狀態的自適應人機交互控制系統流程如圖4所示。首先，探索疲勞過程模型變化規律并進行量化，設計疲勞評估算法，以實現訓練過程實時監測使用者的肌肉狀態。之后，基于評估的肌肉疲勞等級，進行阻抗值決策，在線更新阻抗控制模型阻尼系數。最后，底層控制根據控制策略進行機械驅動并助力，將運動信息反饋給感知與決策環節，形成閉環。本文基于評估肌肉疲勞等級算法，設計人機交互感知與決策環節，在保證既定參考軌跡的前提下，實現變阻尼阻抗控制，確保使用過程中的安全與高效。
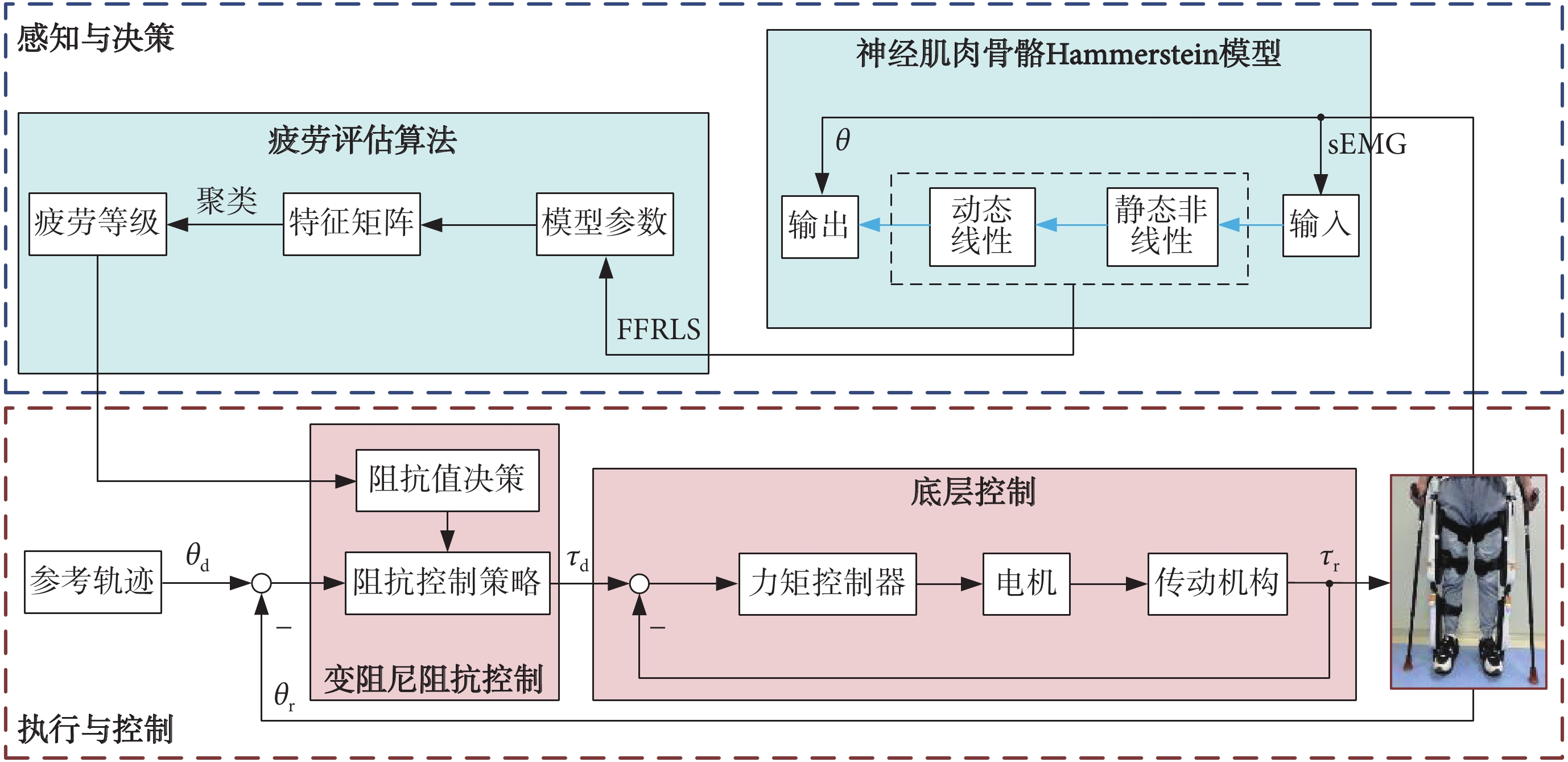圖4
基于疲勞監測的安全保護控制系統
Figure4.
Safety protection control system based on fatigue monitoring
2.1 感知與決策環節
以往建立模型往往是為了進行估計或預測，但在本研究中，注重的是變化過程，而非模型輸出。通過大量實驗采集運動過程的數據，觀測肌肉疲勞過程中模型的變化，并將此變化規律進行量化以設計疲勞評估算法。
在1.2小節中提到Hammerstein模型的非線性靜態部分可以代表神經纖維激活，線性動態部分代表肌肉收縮動力學和關節運動學，而肌肉疲勞主要是受肌肉與外界環境交互過程影響，肌肉收縮能力可以直接反映肌肉的狀態，即在建立的神經肌肉骨骼Hammerstein模型中，疲勞主要與線性動態環節有關。同時，由于非線性靜態部分是無記憶的，不具有任何動態特性，而疲勞是一個動態過程，也可以得出Hammerstein模型的動態線性部分可以體現肌肉狀態。
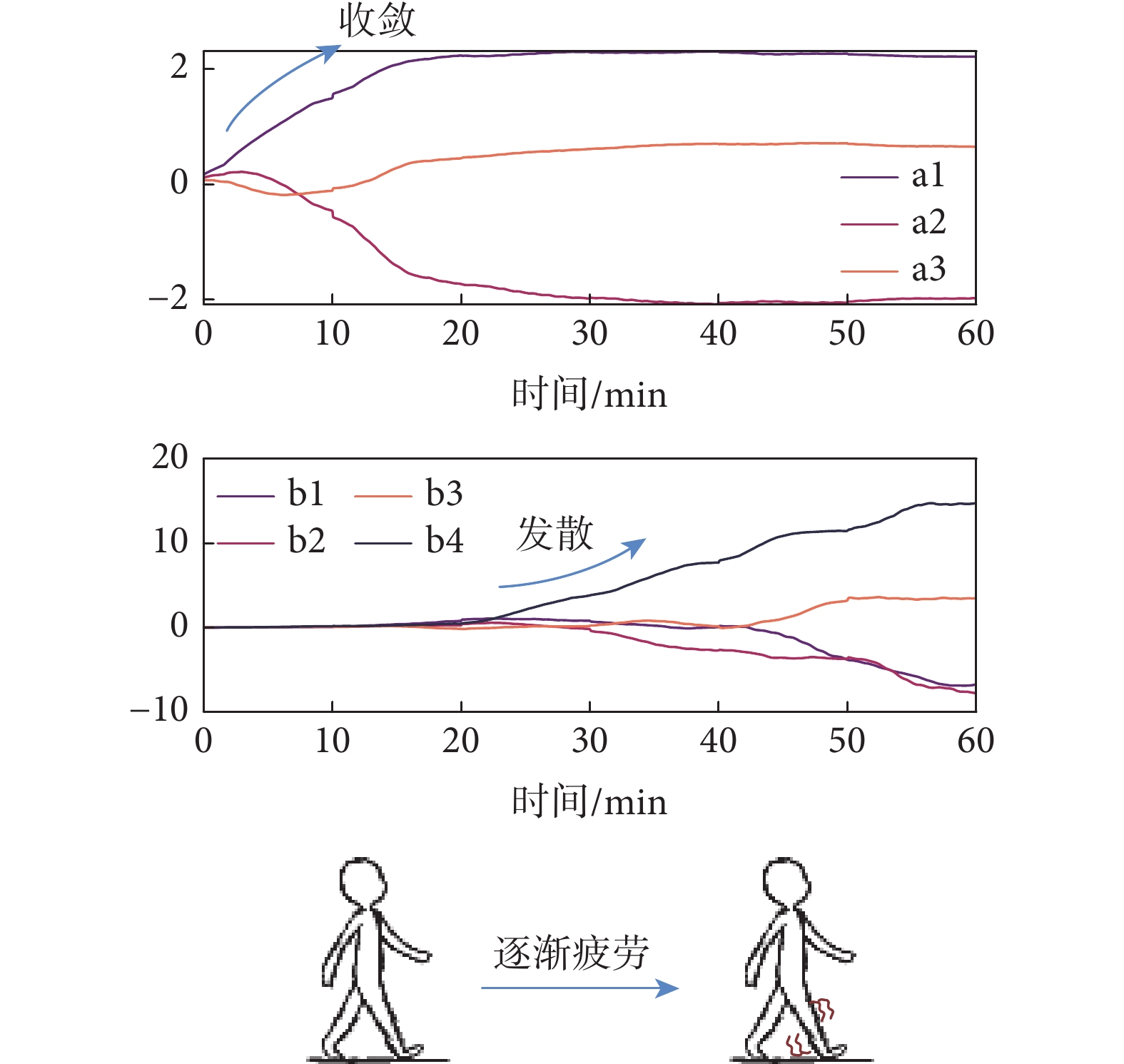
此外，通過設定絕對疲勞趨勢的范式實驗分析辨識的模型參數，結合參數的變化與疲勞過程之間的規律，得到參數隨肌肉狀態的變化如圖5所示，發現建立的Hammerstein模型參數隨著時間的推移有明顯的漸變變化，參數
會隨著疲勞程度的加劇而逐漸趨于平穩（收斂），參數
的變化率會隨著疲勞程度的加劇而變化更加劇烈（發散），而參數
發生無規律變化，與其無記憶性相對應。值得說明的是，此處的參數雖然沒有實際的物理意義，但它們代表了擬合的神經肌肉骨骼模型，它們的變化也就代表了模型的變化，因此結合參數變化表征疲勞過程具備可行性。
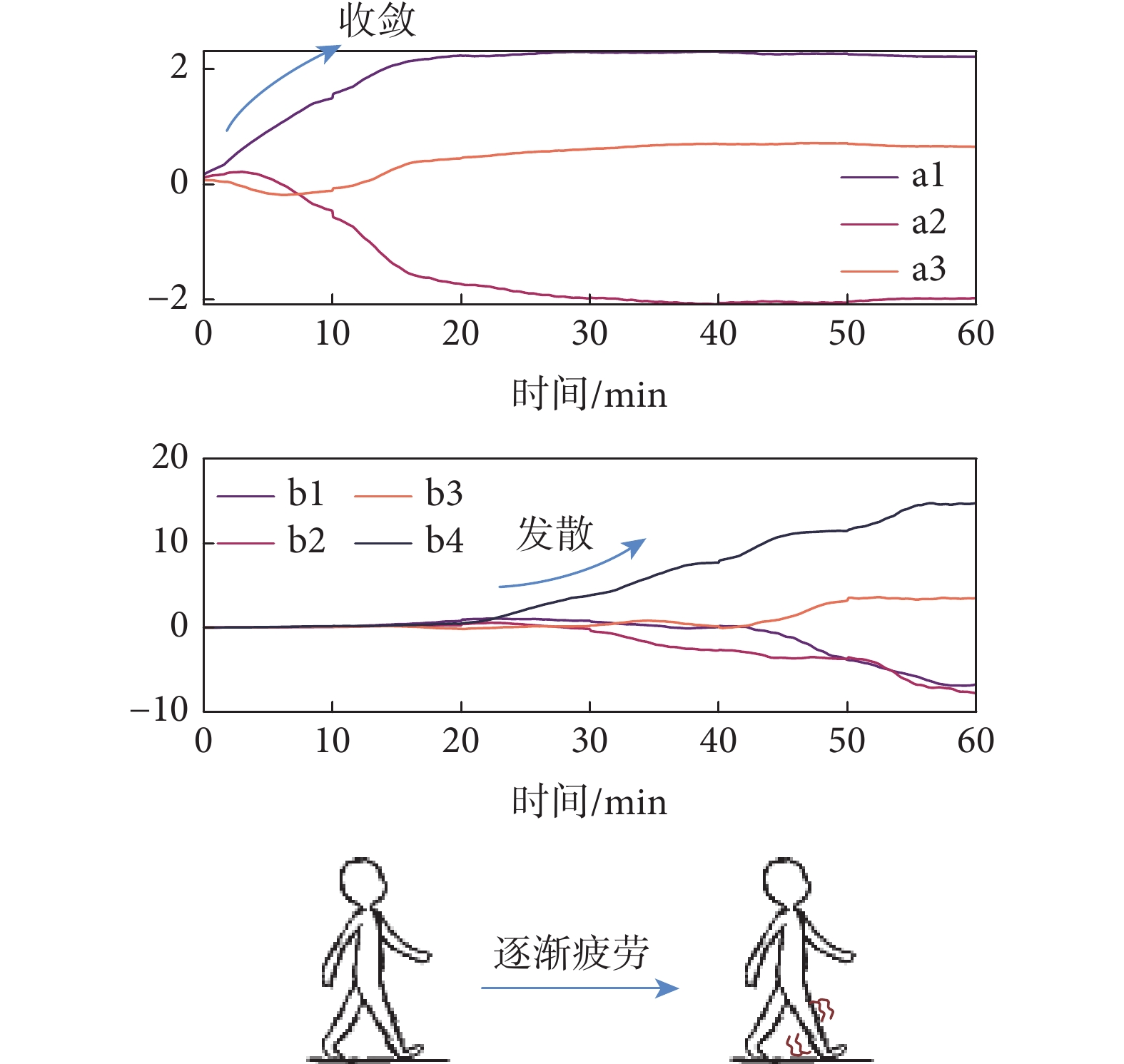圖5
疲勞過程模型參數變化
Figure5.
Variation of model parameters for fatigue process
為了將模型參數的變化規律進行量化，體現其與疲勞程度之間的關系，基于以下三個方面建立參數的特征矩陣
：
（1）參數值：
 |
（2）參數值的變化率：
 |
（3）參數與其瞬時平均值的偏差：
 |
與量化主觀感受疲勞程度的感知勞累程度評定（Rating of Perceived Exertion，RPE）類似[32]，本研究也考慮將疲勞程度評估為疲勞等級，一方面可以直觀地描述肌肉狀態，另一方面，離散的疲勞等級可用于控制系統進行算法實現。基于該特征矩陣采用層次聚類算法對之進行聚類，得到的聚類結果可以用于劃分肌肉疲勞等級。
該疲勞評估算法具體步驟如下：
首先基于使用者的肌電信號與關節運動信息建立神經肌肉骨骼Hammerstein模型[見式（4）]，可變形為：
 |
其中參數矩陣
和信息矩陣
分別定義為：
 |
 |
然后通過遺忘因子遞推最小二乘法（forgetting factor recursive least squares，FFRLS）[33]對其中的參數進行在線辨識：
 |
其中
為參數估計結果，
為實際關節運動角度，
為增益矩陣，
為遺忘因子，
，本文中取
。通過奇異值分解（singular value decomposition，SVD）[34]將耦合的參數
與
進行分解。
最后結合參數
和
及其參數變化特征，構建增廣矩陣，使用層次聚類算法對肌肉的疲勞程度進行聚類，從而評估肌肉的疲勞等級。
選擇歐式距離作為樣本間距離的計算方法：
 |
其中
和
是特征矩陣中的第
個和第
個值。
簇間合并的標準選擇為簇內平方和（cluster sum of square，CSS）：
 |
其中
為簇內樣本，
為每個簇的質心，
為簇內樣本數量，
為簇數。
2.2 執行與控制環節
針對不同肌肉狀態，本小節的任務是：采用分級控制的思想，根據決策層的評估結果，結合環境約束和行為約束進行自適應更新阻抗控制參數。
Hogan等[35]提出了阻抗控制理論，其模型類似于質量塊-彈簧-阻尼器系統，因此具有一定的柔順特性，目前已被廣泛應用在機器人控制領域。
在人-外骨骼控制系統中，阻抗控制的核心思想是將外骨骼等同于物理控制系統，人等同于導納，將外骨骼帶動患者行走的動作等同于阻抗。阻抗控制的數學表達式如下式所示：
 |
其中，
、
、
分別為慣性系數、阻尼系數和剛度系數，
和
分別表示實際關節角和期望關節角，
為帶動患者按預定步態行走的期望的關節力矩。
為了改善患者的穿戴體驗并提高康復效率，本研究讓外骨骼能夠在患者長時間行走時實時調整其助力力矩，以適應穿戴者的肌肉疲勞程度。根據2.1節，通過肌電信號將肌肉疲勞程度分為多個等級，為了在不同級別下提供不同的助力，我們通過調整阻抗控制中的剛度系數
來實現這個目標。
肌肉疲勞等級
越高，代表患者自身能夠提供的行走力矩越低，為了保證他們能夠按照預定軌跡舒適地行走，就需要增大外骨骼助力力矩。由公式(12)阻抗控制關系可知，在關節角度固定的情況下，期望力矩與剛度系數
成正比關系，如下式所示：
 |
其中，在不同的疲勞等級下，通過專家系統[36]在線修改系數
和
從而達到修改期望關節力矩
的目的。
在外骨骼被動控制中，關節力矩控制是實現位置控制的基礎。在理想情況下，電機電流與輸出扭矩成線性關系。但是，當電流超過額定值時，將不再是線性關系，所以本文通過選擇PID控制器控制電機電流
，從而實現控制電機的輸出扭矩
。
由于外骨骼系統各個連桿機械結構運動存在嚴重的滯后，因此舍棄積分項，采用了PD控制器，控制律如下式：
 |
其中，
和
分別是控制器的比例系數和微分系數，
是期望關節力矩。
3 實驗
為了驗證所提出的方法，我們使用下肢康復外骨骼系統，試圖實現基于人體肌肉狀態的自適應人機交互控制策略。
3.1 實驗方案
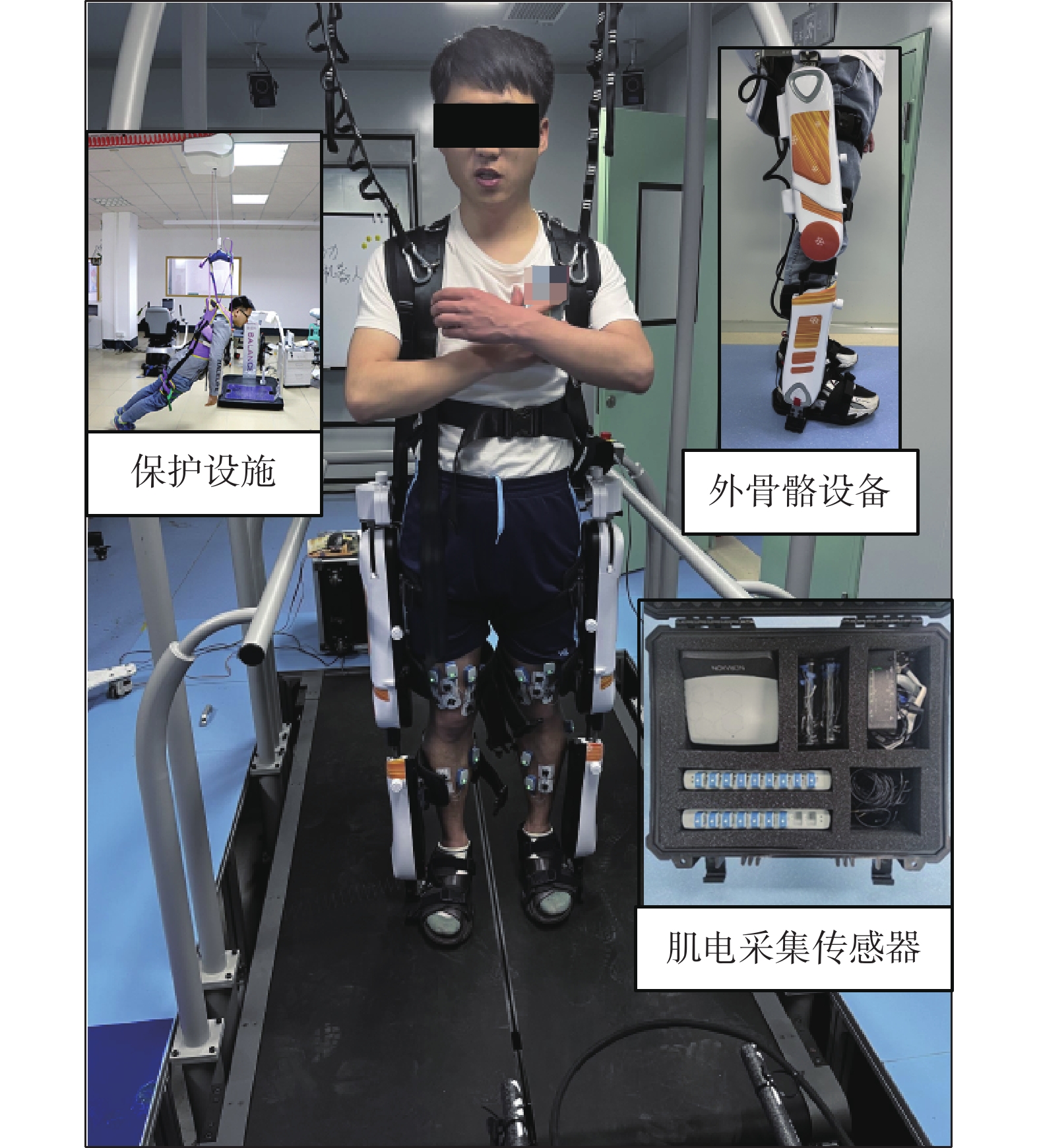
在本實驗中，康復設備采用某商業可穿戴式的下肢外骨骼康復訓練機器人，如圖6所示，由背包控制箱、腰部部件、左腿外骨骼部件、右腿外骨骼部件、觸摸顯示屏及電源適配器等組成，各關節活動范圍如表1所示，通過限位可以避免使用者受傷。肌電信號采集于股直肌、股內外側肌、股二頭肌、半腱肌、內外側腓腸肌和脛骨前肌，雙腿共16通道，所采用的sEMG采集設備為美國NORAXON公司生產的肌電采集傳感器。
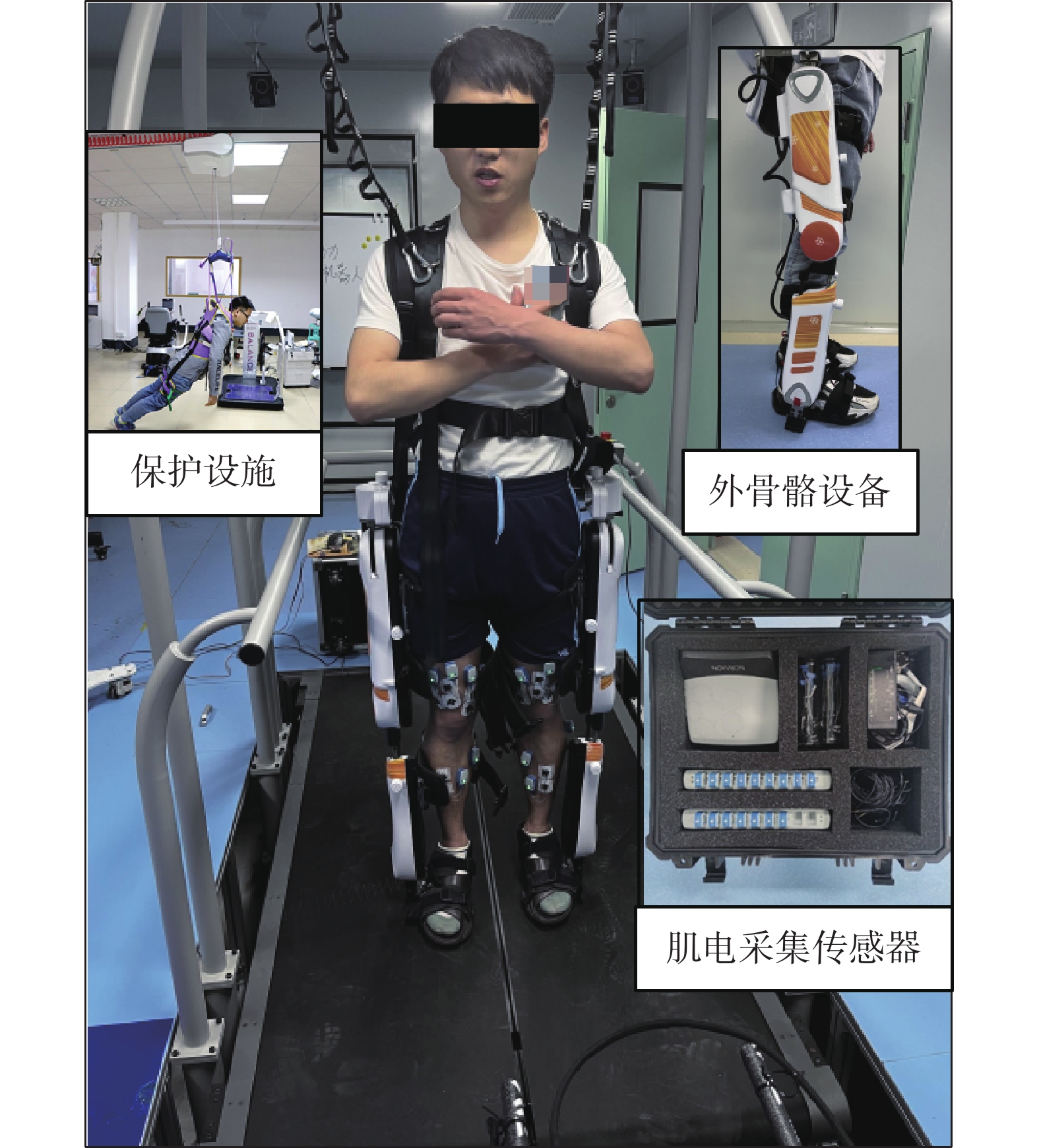圖6
實驗設備
Figure6.
Experiment apparatus
表1
機器人關節活動范圍
Table1.
Robot joint range of motion
為了過濾掉數據采集過程中的干擾信號，將采集到的sEMG信號首先經過25 Hz的高通濾波、全波整流和4 Hz的低通濾波，然后再采用陷波器過濾掉50 Hz的工頻干擾。時間窗與滑動窗分別為100 ms和50 ms，提取每個時間窗的特征值，此處采用均方根（root mean square，RMS）：
 |
其中
為時間窗長度，
為時間窗內第
個sEMG信號值。
將處理后的sEMG和關節角度數據分別作為擬合的參數化神經肌肉骨骼Hammerstein模型[見式（4）]的輸入與輸出，其模型階次選擇為：
 |
我們選擇了10名年齡在21～36歲之間的志愿受試者，其中包括6名男性和4名女性。實驗前，為了更好地進行sEMG信號采集，減少噪聲干擾，需要對受試者的皮膚進行清潔，然后按照肌電信號傳感器放置建議[37]將肌電采集傳感器分別放到對應的肌肉位置。幫助受試者穿戴好外骨骼機器人后，讓他們充分熟悉機器人和環境，并熟讀RPE量表。
RPE量表是一個線性量表，描述從“完全不用力”到“最大用力”，旨在量化受試者的主觀感受，收集他所感知的身體疲勞程度。在RPE量表中加入了言語錨定，使受試者可以根據疾病控制與預防中心（Center of Disease Control and Prevention，CDC）建議的描述來評估自身的運動水平。
在實驗開始時，受試者站立在跑臺上，如圖6所示，通過懸掛的保護設施預防突發情況，保證受試者的安全。每名受試者穿戴或不穿戴外骨骼設備，在跑臺上分別以2 km/h和3 km/h的速度運動60 min，每組實驗之前都充分休息，保證處于放松狀態。在實驗過程中受試者根據自身狀態口頭報告RPE量表疲勞等級，由低到高共分為4個疲勞等級，收集并保存數據。若中途受試者報告達到最高疲勞等級或出現跌倒等突發情況，則立即停止實驗。
3.2 實驗結果
首先驗證算法評估結果的準確性與魯棒性，通過計算本文算法的評估結果與基于RPE量表的評估結果之間的皮爾森相關系數，越接近1代表兩組數據的相關性越強，總體平均皮爾森系數分別為0.936 6和0.921 7，具備強相關性，即本文算法準確可靠。此外，穿戴外骨骼與否對算法的評估結果準確性影響不大，驗證了該算法具備較強魯棒性。
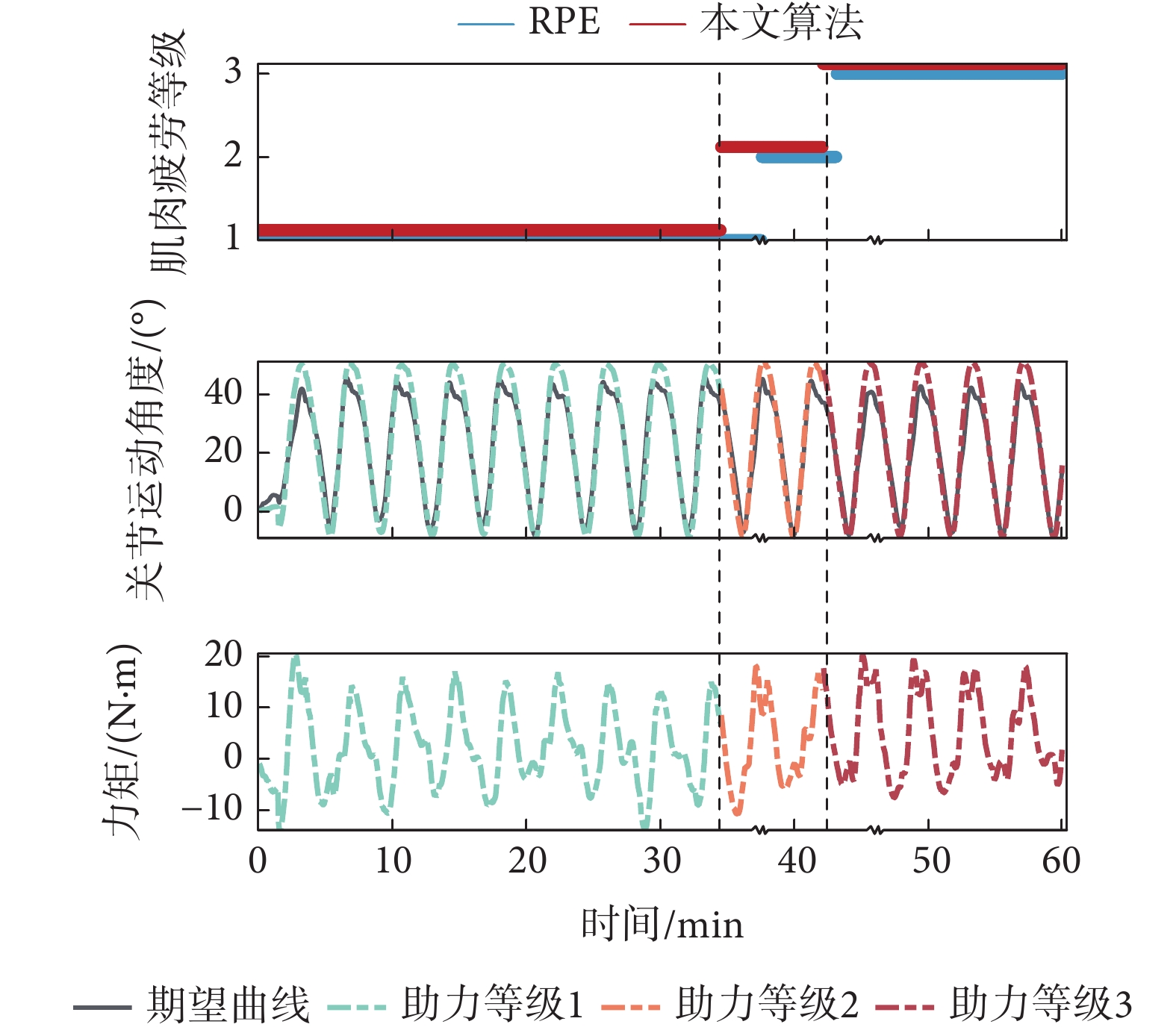
以3號受試者（26歲，男性）為例，其髖關節運動過程的部分實驗數據變化如圖7所示。第一幅圖展示了本文的肌肉狀態評估算法與RPE量表評估的疲勞程度之間的對比，可以直觀看出，本文所提算法與RPE量表評估結果在趨勢上一致，而評估的疲勞等級略超前于RPE量表，這與人體主觀感受滯后于實際肌肉狀態有關。每個疲勞等級所對應的部分關節運動角度與關節力矩如第二、三幅圖所示，橫向觀察難以直觀看出疲勞等級變化前后運動數據的變化。然后計算平均步態周期下各關節運動角度與力矩，置于平均步態周期進行縱向對比，觀測不同助力等級相應的變化，如圖8所示。
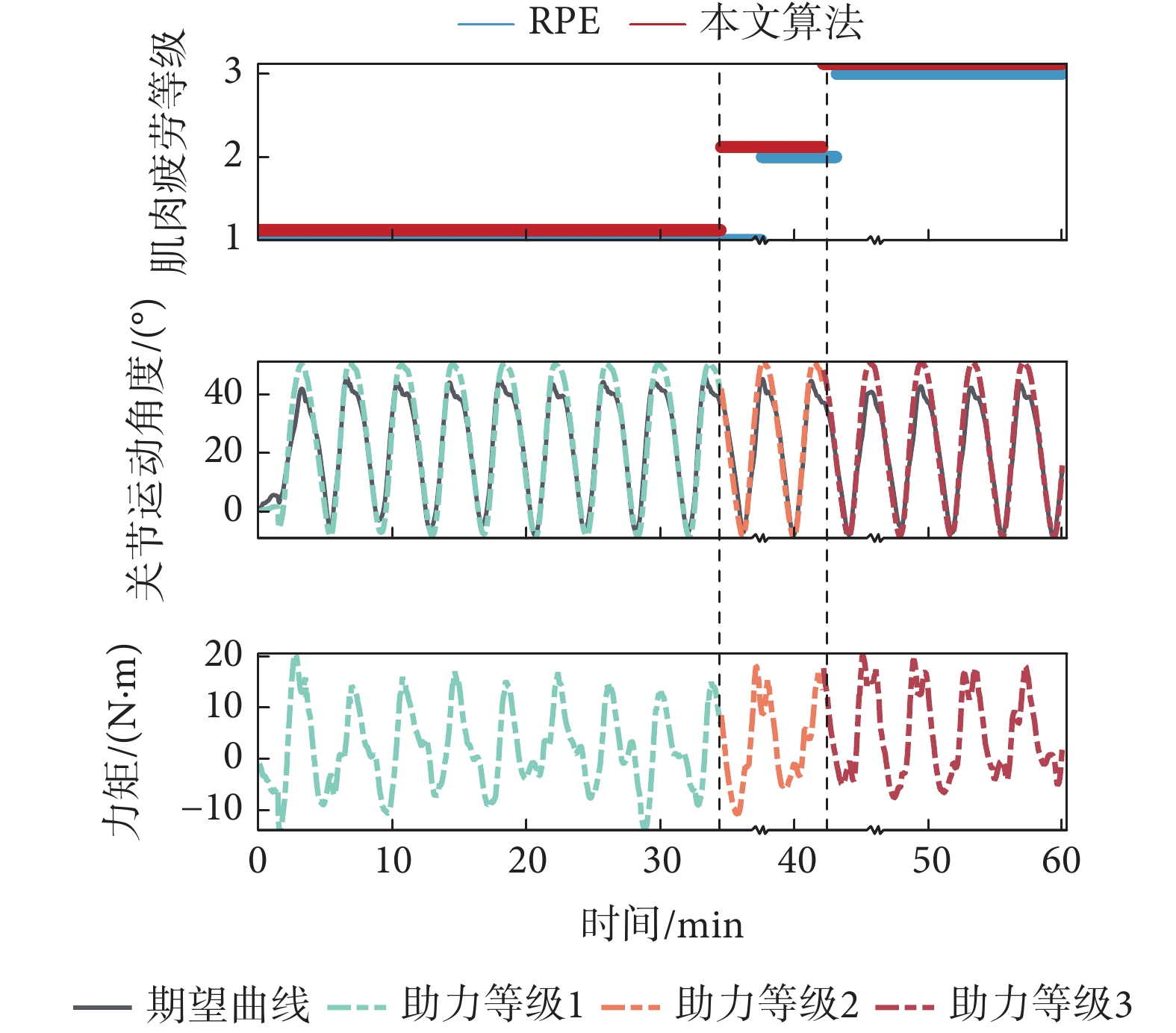圖7
肌肉狀態與運動數據變化（3號受試者，髖關節）
Figure7.
Changes in muscle state and motion data (subject3, hip joint)
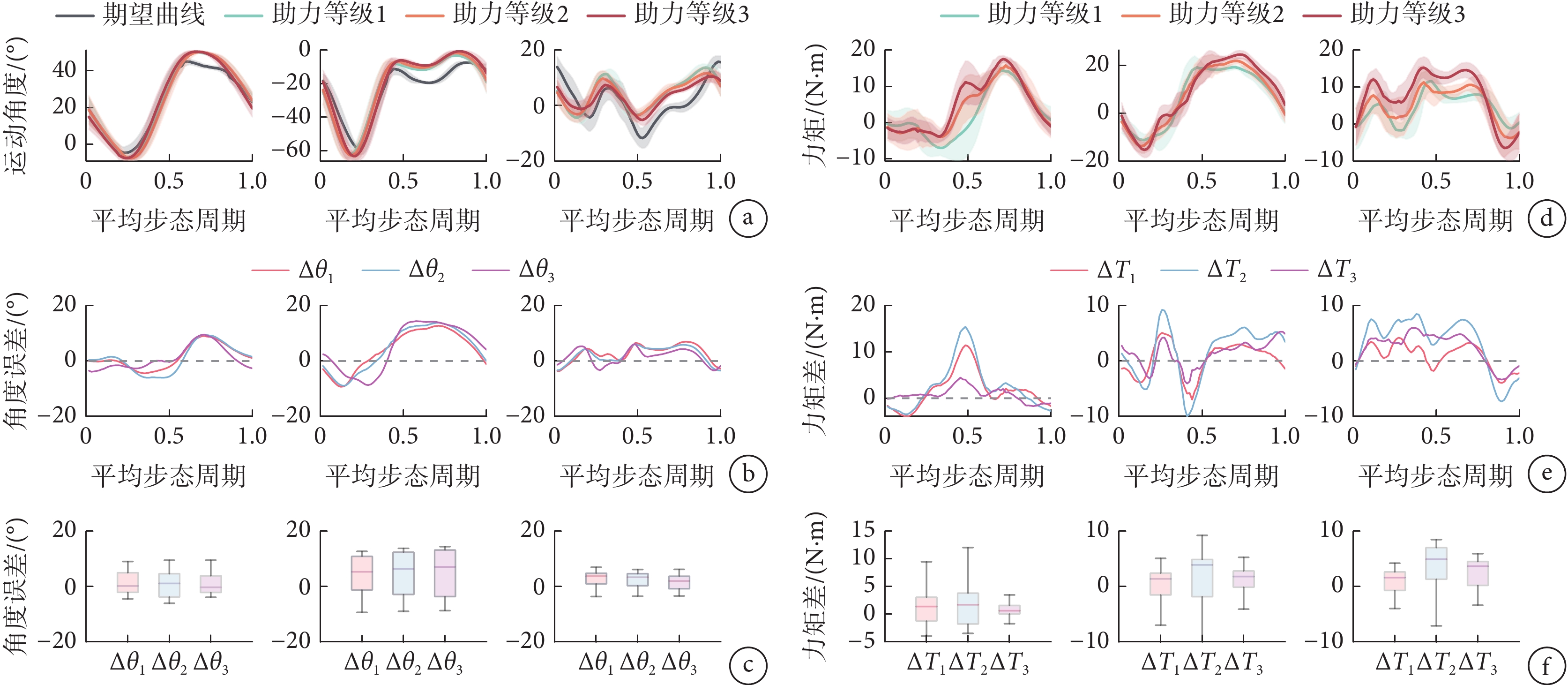圖8
不同助力等級下髖（左）、膝（中）踝（右）關節運動數據對比
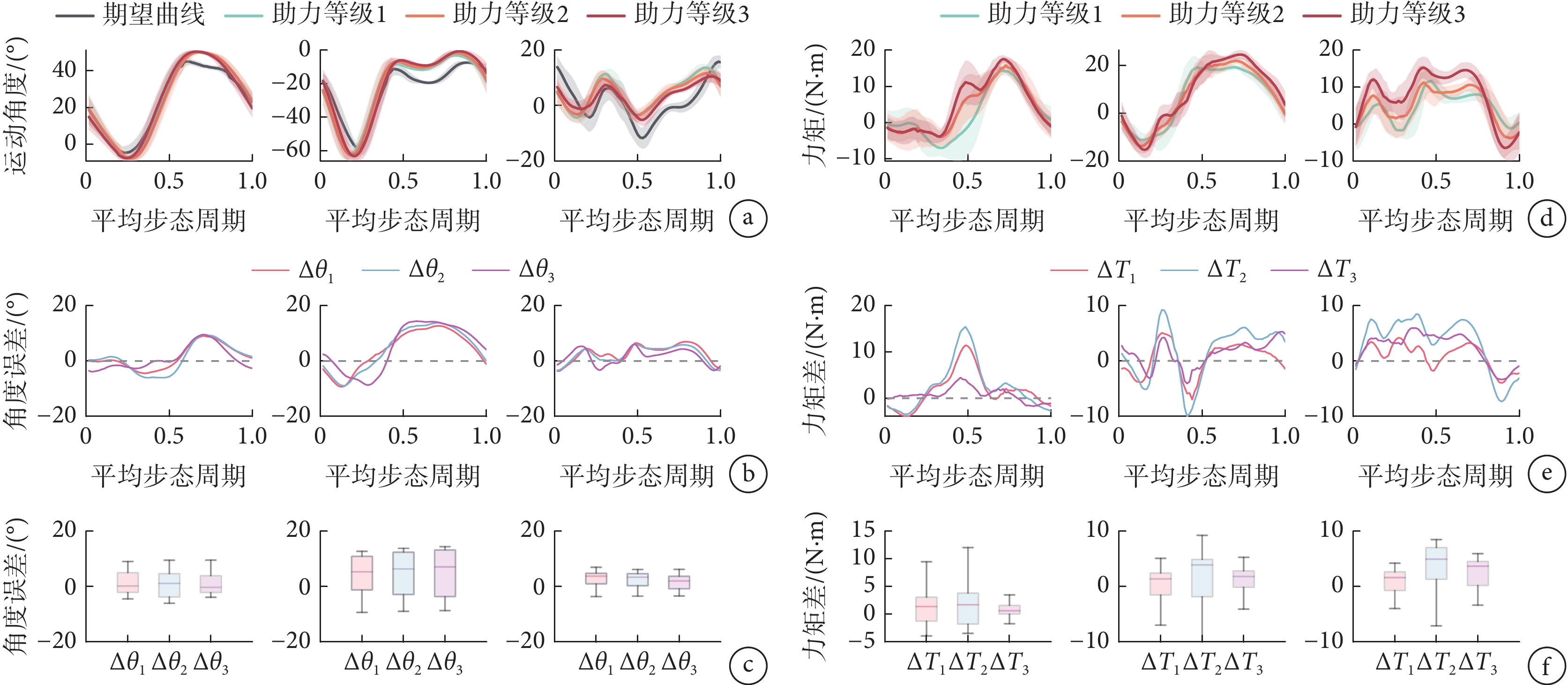
a. 平均步態關節運動角度；b. 平均步態關節運動角度與期望軌跡誤差；c. 平均步態關節運動角度與期望軌跡誤差箱線圖；d. 平均步態關節力矩；e. 平均步態關節力矩差；f. 平均步態關節力矩差箱線圖
Figure8. Comparison of motion data of each joint under different power assistance levelsa. average gait joint motion angle; b. error of average gait joint motion angle and expected trajectory; c. error boxplot of average gait joint motion angle and expected trajectory; d. average gait joint torque; e. average gait joint motion torque difference; f. box plot of average gait joint motion torque difference
在圖8a中，可以看出三種助力等級的平均步態關節運動曲線幾乎一致，且都在期望運動軌跡附近波動。在圖8b中，
、
、
分別為三種助力等級的運動角度與期望軌跡的差，可以看出三種等級下的角度誤差均在0°上下波動，其中最大值為14.400 9°（膝關節，助力等級3），最小值為?9.314 2°（膝關節，助力等級1），膝關節的運動范圍較髖與踝關節更大，其跟蹤誤差也相對較大。在圖8c中，可以看出三組誤差的平均水平均小于10°，隨著助力等級的增加，平均跟蹤誤差相對更小。在圖8d中，可以看出三種助力等級下各關節平均步態力矩在趨勢上一致，助力等級越高踝關節力矩越大。在圖8e中，
為助力等級1與助力等級2的平均步態關節力矩差，
為助力等級1與助力等級3的平均步態關節力矩差，
為助力等級2與助力等級3的平均步態關節力矩差，可以看出三組力矩差大部分數據大于0 
，與關節角度跟蹤誤差一樣，膝關節在不同助力等級下的力矩差也更大。在圖8f中，可以看出三組誤差的平均水平均大于0 
，隨著助力等級的增加，各關節力矩逐漸增大。
統計并分析十位受試者不同助力等級下的跟蹤效果和助力力矩，可以看出，助力等級越高角度誤差越小，跟蹤效果越好；大多數情況下助力等級越高關節力矩越大，助力效果越好。
根據實驗數據與分析結果，本文所提出的控制方法可以在保證關節運動保持跟蹤期望軌跡的基礎上，實時感知肌肉疲勞等級并通過適應性決策改變控制策略，增強助力效果，即增大助力力矩，確保康復訓練過程的安全性與舒適性。
4 結論
本文針對可穿戴式下肢康復外骨骼設備，提出一種基于人體肌肉狀態的自適應人機交互控制方法，可以根據患者的肌肉疲勞程度實時調整控制策略。為保障患者的安全性、增強穿戴舒適度并提高訓練效率，提出一種基于人體肌電信號和運動狀態的疲勞評估算法。基于此算法可以實時監督患者的肌肉疲勞程度，在保證趨勢準確的前提下對疲勞進行等級劃分，并以之作為控制系統的決策層建立變阻尼阻抗控制算法，當系統感知到患者疲勞等級上升時通過決策增大助力力矩。通過實驗驗證了所提出的人機交互控制方法是有效的，未來可應用于柔性外骨骼[38-39]和上肢康復機器人[40]等。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：趙新剛、趙憶文、張弼負責指導實驗設計；牛惠祺負責數據分析、算法設計與論文寫作；劉麗剛負責實驗數據采集。
倫理聲明：本研究通過了遼寧省人民醫院倫理委員會的審批（批文編號：2022HS007）。
0 引言
隨著經濟社會的發展與信息技術的進步，我國見證了輔助技術從零開始成長到如今相當活躍的水平，而隨著我國社會人口老齡化程度的加劇，由腦卒中等疾病造成的運動功能障礙患者數量急劇增加，對輔助技術的應用需求也越來越大[1-2]。有運動功能障礙的患者主要通過運動康復療法進行康復訓練。對于下肢運動康復，臨床醫生一般使用手動輔助技術幫助患者進行走路等訓練運動，旨在幫助患者恢復正常的生理步態[3]，但是與龐大的患者人數相比，治療師的數量遠遠不足。而隨著機器人技術的高速發展，醫用機器人結合了多學科的發展成果，被廣泛應用于各種醫學領域[2]，其中，康復機器人可以減少手動輔助重復性任務，并可增強步態規范性，提高步態性能。關于使用機器人設備進行步態訓練的有效性已經通過臨床與科學研究驗證[3-5]。因此，使用機器人設備進行康復訓練對于減輕醫護人員的工作量以及提高患者的康復訓練效果具有積極意義。
在康復機器人與患者的人機交互中，首先需要保障的是患者的安全性，對于卒中患者，在康復訓練期間，由于肌肉和認知能力下降，很容易出現疲勞狀態[6]，嚴重的還有可能導致過疲勞現象，對患者健康具有極大風險。肌肉疲勞是一種復雜的生理現象，可以描述為肌肉進行體力活動的能力逐漸下降[7]。肌肉疲勞也是肌肉骨骼問題的危險因素之一，出于對人的健康監控與康復訓練效率考慮，需要在人體工程學與生理學領域對肌肉狀態進行定量評估，進而可以根據監測的肌肉疲勞狀態進行康復訓練方案的優化[6, 8-10]。
關于肌肉疲勞評估目前尚無公認的評估標準體系，針對不同的研究對象存在很多不同的評估方法，根據研究對象的性質可以分為三個方向：化學[11]、生物電[12-14]和機械現象[15]。從化學角度來看，可以通過近紅外光譜技術檢測肌肉血氧飽和度水平的相對變化；從生物電角度來看，表面肌電（surface electromyography，sEMG）信號提供了一種從“源頭”來理解疲勞這一現象的方法；從機械現象角度來看，加速度傳感器從疲勞產生的“結果”出發，可以用于測量運動軌跡變化。
很多研究者將研究對象重點放在sEMG信號上。眾所周知，基于機器人的主動康復訓練不可避免要用到肌電信息，在不附加多余傳感器的情況下，依賴系統設計中已經固有的sEMG信息無疑是非常方便的。Thacham Poyil等[6]通過sEMG的中值頻率對肌肉是否疲勞進行評估，當系統檢測到疲勞時就降低一半的訓練強度以延長訓練時間與效率，通過實驗驗證了控制策略的有效性；Peternel等[9]巧妙地采用一個類RC電路的結構，用電容器電壓代表疲勞進行肌肉疲勞估計，讓機器學習人在正常狀態下的位置/力變化，當系統檢測到肌肉疲勞時，通過學習到的任務執行頻率/力接管任務直至人的狀態恢復。
但是，單一的研究對象可能造成評估結果不準確，因為疲勞是多方面因素相互作用的結果[16]，于是很多學者采用不同研究對象交叉結合的方式來對肌肉疲勞進行評估。Ramos等[17]提出了一種基于sEMG信號和心率變異性（heart rate variability，HRV）參數的疲勞檢測模型；Chandra等[18]利用sEMG和加速度計進行了手部疲勞誘發震顫的評估聚類；Aryal等[19]通過可穿戴式傳感器測量體溫、心率的方式對疲勞進行實時監測。
上述研究成果取得了很大的進展，但是仍存在一定的局限性。一方面，單一的研究對象可能造成評估結果的準確性受限，但是過多研究對象的算法在設計控制系統時又會額外用到大量的傳感器。如何平衡選擇疲勞評估所需的研究對象，對于設計系統的成本具有至關重要的影響。另一方面，現有的疲勞評估方法大部分局限于疲勞閾值的存在，當肌肉狀態達到疲勞閾值時更改或停止任務，并不能做到根據肌肉狀態實時調整控制策略，在系統的容錯機制上有待開發。
為了解決上述問題，本文針對下肢外骨骼康復機器人，提出了一種基于人體肌肉狀態的自適應人機交互控制方法。
1 模型建立
1.1 Hammerstein模型
Hammerstein模型是非線性過程中經常使用的典型模型之一，其模型結構由一個非線性靜態部分與線性動態部分串聯而成[20]，如圖1所示。其中的輸入非線性可以表示為一組基底選定的基函數的線性加和：
圖1
Hammerstein模型結構圖
Figure1.
Structure diagram of Hammerstein model
|
式中選取為。
線性動態部分表示為：
|
式中的未知多項式和定義為：
|
根據式(1)～(3)，可以得到參數化Hammerstein模型：
|
其中為模型輸入，為模型輸出，為有界外部干擾，、、均為參數，可通過參數辨識算法進行辨識。
由于與生物物理學對應，與機理模型也近似，而且辨識簡單，Hammerstein模型已被廣泛應用于肌肉疲勞影響下的非線性神經肌肉系統建模[18, 21-25]。
1.2 人體神經肌肉骨骼模型
人體下肢正向動態神經肌肉骨骼模型如圖2所示，通過此模型可以根據神經信號估計或預測肌肉力量，計算關節力矩或關節運動學[26-30]。首先，肌肉的活躍度是通過神經信號激活肌肉的動力學過程來控制的。然后，肌肉的收縮動力學描述了如何將肌肉的活躍度轉化為肌力。最后，通過肌肉骨骼幾何模型，將產生的肌力轉化為關節力矩，并利用運動方程計算出關節的運動。
圖2
下肢神經肌肉骨骼模型
Figure2.
Neuromusculoskeletal model of lower limbs
肌肉激活度直接反映了肌肉的活躍水平，通常引入一個函數表達神經信號與肌肉活躍度之間的非線性關系[29, 31-33]：
|
其中表示時刻的處理后的肌電信號，表示計算所得的肌肉活躍度特征。
Hill肌肉力模型是通過大量的醫學數據與實驗應用驗證的模型，其模型結構如圖3所示，圖中表示主動收縮單元，表示被動彈性單元，表示肌纖維長度，表示腱長度，表示肌腱單元長度，表示肌肉纖維與腱的夾角，表示主動收縮力，表示被動彈性力，表示肌纖維力，表示肌腱單元力。可以看出完整的Hill模型十分復雜，包含很多生理學參數，實際應用時難以獲取，因此Han等[31]在保證模型準確性的前提下對模型進行了簡化，計算得到肌腱力：
圖3
Hill肌肉力模型
Figure3.
Hill-type muscle model
|
其中 、 和 為生理參數關系，可以通過數據擬合，、 和 為實際生理參數，均為常值， 為肌肉纖維和腱的夾角。
通過肌肉力可以計算肌肉對其驅動關節的力矩貢獻：
|
其中是常系數，為一階多項式擬合關節角和肌腱長度的一階項系數[31]。
以踝關節為例，通過其肌肉骨骼幾何模型和關節前向動力學可以得到踝關節運動的角加速度：
|
|
其中表示腳相對于踝關節的轉動慣量，假定其為常數，是外部負載和腳的重力產生的力矩之和，表示的最大值。
將公式(1)～(5)聯立并通過三階泰勒級數展開，可以推導由肌電信號計算關節角加速度的離散化方程：
|
其中、均為生理參數及對應關系的常數項，表示時刻的sEMG信號，表示時刻的關節運動角度，為系統高階項：
|
其中表示生理參數與實際運動之間的非線性關系，為采樣時間，在實際系統中，采樣周期很短，故該二項式很小。
在數學上，公式(4)的形式與公式(10)相似，公式(4)中與公式(10)中的對應，與對應；值得指出的是，公式(4)中的與公式(10)中的高階項對應，由于其包含項，而實際系統的采樣時間很短，故對系統影響很微弱，即系統擾動較小。
在結構上，如圖1和圖2所示，Hammerstein模型的非線性靜態環節可以代表神經肌肉骨骼模型的神經激活，這是神經信號與肌肉激活之間的靜態增益關系，線性動態環節可以代表肌肉收縮動力學和關節運動學，這使其成為可用于生物系統辨識的可能結構之一[27]。本文也采用Hammerstein模型結構對人體神經肌肉骨骼模型進行擬合。
2 基于疲勞監測的安全保護控制系統
基于人體肌肉狀態的自適應人機交互控制系統流程如圖4所示。首先，探索疲勞過程模型變化規律并進行量化，設計疲勞評估算法，以實現訓練過程實時監測使用者的肌肉狀態。之后，基于評估的肌肉疲勞等級，進行阻抗值決策，在線更新阻抗控制模型阻尼系數。最后，底層控制根據控制策略進行機械驅動并助力，將運動信息反饋給感知與決策環節，形成閉環。本文基于評估肌肉疲勞等級算法，設計人機交互感知與決策環節，在保證既定參考軌跡的前提下，實現變阻尼阻抗控制，確保使用過程中的安全與高效。
圖4
基于疲勞監測的安全保護控制系統
Figure4.
Safety protection control system based on fatigue monitoring
2.1 感知與決策環節
以往建立模型往往是為了進行估計或預測，但在本研究中，注重的是變化過程，而非模型輸出。通過大量實驗采集運動過程的數據，觀測肌肉疲勞過程中模型的變化，并將此變化規律進行量化以設計疲勞評估算法。
在1.2小節中提到Hammerstein模型的非線性靜態部分可以代表神經纖維激活，線性動態部分代表肌肉收縮動力學和關節運動學，而肌肉疲勞主要是受肌肉與外界環境交互過程影響，肌肉收縮能力可以直接反映肌肉的狀態，即在建立的神經肌肉骨骼Hammerstein模型中，疲勞主要與線性動態環節有關。同時，由于非線性靜態部分是無記憶的，不具有任何動態特性，而疲勞是一個動態過程，也可以得出Hammerstein模型的動態線性部分可以體現肌肉狀態。
此外，通過設定絕對疲勞趨勢的范式實驗分析辨識的模型參數，結合參數的變化與疲勞過程之間的規律，得到參數隨肌肉狀態的變化如圖5所示，發現建立的Hammerstein模型參數隨著時間的推移有明顯的漸變變化，參數會隨著疲勞程度的加劇而逐漸趨于平穩（收斂），參數的變化率會隨著疲勞程度的加劇而變化更加劇烈（發散），而參數發生無規律變化，與其無記憶性相對應。值得說明的是，此處的參數雖然沒有實際的物理意義，但它們代表了擬合的神經肌肉骨骼模型，它們的變化也就代表了模型的變化，因此結合參數變化表征疲勞過程具備可行性。
圖5
疲勞過程模型參數變化
Figure5.
Variation of model parameters for fatigue process
為了將模型參數的變化規律進行量化，體現其與疲勞程度之間的關系，基于以下三個方面建立參數的特征矩陣：
（1）參數值：
|
（2）參數值的變化率：
|
（3）參數與其瞬時平均值的偏差：
|
與量化主觀感受疲勞程度的感知勞累程度評定（Rating of Perceived Exertion，RPE）類似[32]，本研究也考慮將疲勞程度評估為疲勞等級，一方面可以直觀地描述肌肉狀態，另一方面，離散的疲勞等級可用于控制系統進行算法實現。基于該特征矩陣采用層次聚類算法對之進行聚類，得到的聚類結果可以用于劃分肌肉疲勞等級。
該疲勞評估算法具體步驟如下：
首先基于使用者的肌電信號與關節運動信息建立神經肌肉骨骼Hammerstein模型[見式（4）]，可變形為：
|
其中參數矩陣和信息矩陣分別定義為：
|
|
然后通過遺忘因子遞推最小二乘法（forgetting factor recursive least squares，FFRLS）[33]對其中的參數進行在線辨識：
|
其中為參數估計結果，為實際關節運動角度，為增益矩陣，為遺忘因子，，本文中取。通過奇異值分解（singular value decomposition，SVD）[34]將耦合的參數與進行分解。
最后結合參數和及其參數變化特征，構建增廣矩陣，使用層次聚類算法對肌肉的疲勞程度進行聚類，從而評估肌肉的疲勞等級。
選擇歐式距離作為樣本間距離的計算方法：
|
其中和是特征矩陣中的第個和第個值。
簇間合并的標準選擇為簇內平方和（cluster sum of square，CSS）：
|
其中為簇內樣本，為每個簇的質心，為簇內樣本數量，為簇數。
2.2 執行與控制環節
針對不同肌肉狀態，本小節的任務是：采用分級控制的思想，根據決策層的評估結果，結合環境約束和行為約束進行自適應更新阻抗控制參數。
Hogan等[35]提出了阻抗控制理論，其模型類似于質量塊-彈簧-阻尼器系統，因此具有一定的柔順特性，目前已被廣泛應用在機器人控制領域。
在人-外骨骼控制系統中，阻抗控制的核心思想是將外骨骼等同于物理控制系統，人等同于導納，將外骨骼帶動患者行走的動作等同于阻抗。阻抗控制的數學表達式如下式所示：
|
其中，、、分別為慣性系數、阻尼系數和剛度系數，和分別表示實際關節角和期望關節角，為帶動患者按預定步態行走的期望的關節力矩。
為了改善患者的穿戴體驗并提高康復效率，本研究讓外骨骼能夠在患者長時間行走時實時調整其助力力矩，以適應穿戴者的肌肉疲勞程度。根據2.1節，通過肌電信號將肌肉疲勞程度分為多個等級，為了在不同級別下提供不同的助力，我們通過調整阻抗控制中的剛度系數來實現這個目標。
肌肉疲勞等級越高，代表患者自身能夠提供的行走力矩越低，為了保證他們能夠按照預定軌跡舒適地行走，就需要增大外骨骼助力力矩。由公式(12)阻抗控制關系可知，在關節角度固定的情況下，期望力矩與剛度系數成正比關系，如下式所示：
|
其中，在不同的疲勞等級下，通過專家系統[36]在線修改系數和從而達到修改期望關節力矩的目的。
在外骨骼被動控制中，關節力矩控制是實現位置控制的基礎。在理想情況下，電機電流與輸出扭矩成線性關系。但是，當電流超過額定值時，將不再是線性關系，所以本文通過選擇PID控制器控制電機電流，從而實現控制電機的輸出扭矩。
由于外骨骼系統各個連桿機械結構運動存在嚴重的滯后，因此舍棄積分項，采用了PD控制器，控制律如下式：
|
其中，和分別是控制器的比例系數和微分系數，是期望關節力矩。
3 實驗
為了驗證所提出的方法，我們使用下肢康復外骨骼系統，試圖實現基于人體肌肉狀態的自適應人機交互控制策略。
3.1 實驗方案
在本實驗中，康復設備采用某商業可穿戴式的下肢外骨骼康復訓練機器人，如圖6所示，由背包控制箱、腰部部件、左腿外骨骼部件、右腿外骨骼部件、觸摸顯示屏及電源適配器等組成，各關節活動范圍如表1所示，通過限位可以避免使用者受傷。肌電信號采集于股直肌、股內外側肌、股二頭肌、半腱肌、內外側腓腸肌和脛骨前肌，雙腿共16通道，所采用的sEMG采集設備為美國NORAXON公司生產的肌電采集傳感器。
圖6
實驗設備
Figure6.
Experiment apparatus
表1
機器人關節活動范圍
Table1.
Robot joint range of motion
為了過濾掉數據采集過程中的干擾信號，將采集到的sEMG信號首先經過25 Hz的高通濾波、全波整流和4 Hz的低通濾波，然后再采用陷波器過濾掉50 Hz的工頻干擾。時間窗與滑動窗分別為100 ms和50 ms，提取每個時間窗的特征值，此處采用均方根（root mean square，RMS）：
|
其中為時間窗長度，為時間窗內第個sEMG信號值。
將處理后的sEMG和關節角度數據分別作為擬合的參數化神經肌肉骨骼Hammerstein模型[見式（4）]的輸入與輸出，其模型階次選擇為：
|
我們選擇了10名年齡在21～36歲之間的志愿受試者，其中包括6名男性和4名女性。實驗前，為了更好地進行sEMG信號采集，減少噪聲干擾，需要對受試者的皮膚進行清潔，然后按照肌電信號傳感器放置建議[37]將肌電采集傳感器分別放到對應的肌肉位置。幫助受試者穿戴好外骨骼機器人后，讓他們充分熟悉機器人和環境，并熟讀RPE量表。
RPE量表是一個線性量表，描述從“完全不用力”到“最大用力”，旨在量化受試者的主觀感受，收集他所感知的身體疲勞程度。在RPE量表中加入了言語錨定，使受試者可以根據疾病控制與預防中心（Center of Disease Control and Prevention，CDC）建議的描述來評估自身的運動水平。
在實驗開始時，受試者站立在跑臺上，如圖6所示，通過懸掛的保護設施預防突發情況，保證受試者的安全。每名受試者穿戴或不穿戴外骨骼設備，在跑臺上分別以2 km/h和3 km/h的速度運動60 min，每組實驗之前都充分休息，保證處于放松狀態。在實驗過程中受試者根據自身狀態口頭報告RPE量表疲勞等級，由低到高共分為4個疲勞等級，收集并保存數據。若中途受試者報告達到最高疲勞等級或出現跌倒等突發情況，則立即停止實驗。
3.2 實驗結果
首先驗證算法評估結果的準確性與魯棒性，通過計算本文算法的評估結果與基于RPE量表的評估結果之間的皮爾森相關系數，越接近1代表兩組數據的相關性越強，總體平均皮爾森系數分別為0.936 6和0.921 7，具備強相關性，即本文算法準確可靠。此外，穿戴外骨骼與否對算法的評估結果準確性影響不大，驗證了該算法具備較強魯棒性。
以3號受試者（26歲，男性）為例，其髖關節運動過程的部分實驗數據變化如圖7所示。第一幅圖展示了本文的肌肉狀態評估算法與RPE量表評估的疲勞程度之間的對比，可以直觀看出，本文所提算法與RPE量表評估結果在趨勢上一致，而評估的疲勞等級略超前于RPE量表，這與人體主觀感受滯后于實際肌肉狀態有關。每個疲勞等級所對應的部分關節運動角度與關節力矩如第二、三幅圖所示，橫向觀察難以直觀看出疲勞等級變化前后運動數據的變化。然后計算平均步態周期下各關節運動角度與力矩，置于平均步態周期進行縱向對比，觀測不同助力等級相應的變化，如圖8所示。
圖7
肌肉狀態與運動數據變化（3號受試者，髖關節）
Figure7.
Changes in muscle state and motion data (subject3, hip joint)
圖8
不同助力等級下髖（左）、膝（中）踝（右）關節運動數據對比
a. 平均步態關節運動角度；b. 平均步態關節運動角度與期望軌跡誤差；c. 平均步態關節運動角度與期望軌跡誤差箱線圖；d. 平均步態關節力矩；e. 平均步態關節力矩差；f. 平均步態關節力矩差箱線圖
Figure8. Comparison of motion data of each joint under different power assistance levelsa. average gait joint motion angle; b. error of average gait joint motion angle and expected trajectory; c. error boxplot of average gait joint motion angle and expected trajectory; d. average gait joint torque; e. average gait joint motion torque difference; f. box plot of average gait joint motion torque difference
在圖8a中，可以看出三種助力等級的平均步態關節運動曲線幾乎一致，且都在期望運動軌跡附近波動。在圖8b中，、、分別為三種助力等級的運動角度與期望軌跡的差，可以看出三種等級下的角度誤差均在0°上下波動，其中最大值為14.400 9°（膝關節，助力等級3），最小值為?9.314 2°（膝關節，助力等級1），膝關節的運動范圍較髖與踝關節更大，其跟蹤誤差也相對較大。在圖8c中，可以看出三組誤差的平均水平均小于10°，隨著助力等級的增加，平均跟蹤誤差相對更小。在圖8d中，可以看出三種助力等級下各關節平均步態力矩在趨勢上一致，助力等級越高踝關節力矩越大。在圖8e中，為助力等級1與助力等級2的平均步態關節力矩差，為助力等級1與助力等級3的平均步態關節力矩差，為助力等級2與助力等級3的平均步態關節力矩差，可以看出三組力矩差大部分數據大于0 ，與關節角度跟蹤誤差一樣，膝關節在不同助力等級下的力矩差也更大。在圖8f中，可以看出三組誤差的平均水平均大于0 ，隨著助力等級的增加，各關節力矩逐漸增大。
統計并分析十位受試者不同助力等級下的跟蹤效果和助力力矩，可以看出，助力等級越高角度誤差越小，跟蹤效果越好；大多數情況下助力等級越高關節力矩越大，助力效果越好。
根據實驗數據與分析結果，本文所提出的控制方法可以在保證關節運動保持跟蹤期望軌跡的基礎上，實時感知肌肉疲勞等級并通過適應性決策改變控制策略，增強助力效果，即增大助力力矩，確保康復訓練過程的安全性與舒適性。
4 結論
本文針對可穿戴式下肢康復外骨骼設備，提出一種基于人體肌肉狀態的自適應人機交互控制方法，可以根據患者的肌肉疲勞程度實時調整控制策略。為保障患者的安全性、增強穿戴舒適度并提高訓練效率，提出一種基于人體肌電信號和運動狀態的疲勞評估算法。基于此算法可以實時監督患者的肌肉疲勞程度，在保證趨勢準確的前提下對疲勞進行等級劃分，并以之作為控制系統的決策層建立變阻尼阻抗控制算法，當系統感知到患者疲勞等級上升時通過決策增大助力力矩。通過實驗驗證了所提出的人機交互控制方法是有效的，未來可應用于柔性外骨骼[38-39]和上肢康復機器人[40]等。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：趙新剛、趙憶文、張弼負責指導實驗設計；牛惠祺負責數據分析、算法設計與論文寫作；劉麗剛負責實驗數據采集。
倫理聲明：本研究通過了遼寧省人民醫院倫理委員會的審批（批文編號：2022HS007）。
