現有自動睡眠分期算法存在模型參數量多、訓練耗時長導致分期效率不佳的問題。本文使用單通道腦電信號，提出一種基于遷移學習（TL）的隨機深度（SD）殘差網絡（ResNet）自動睡眠分期算法（TL-SDResNet）。首先，選取16人共30條單通道（Fpz-Cz）腦電信號，在保留有效睡眠片段后，利用巴特沃斯濾波和連續小波變換對原始腦電信號進行預處理，得到包含其時-頻聯合特征的二維圖像作為分期模型的輸入數據。隨后，構建經公開數據集——歐洲數據格式存儲的睡眠數據庫拓展版（Sleep-EDFx）訓練的ResNet50預訓練模型，使用隨機深度策略并修改輸出層以優化模型結構。最后，應用遷移學習對人體整夜睡眠過程進行自動分期。本文算法在進行了多次實驗后，模型分期準確率達到87.95%。實驗表明，TL-SDResNet50可完成少量腦電數據的快速訓練，總體效果優于近年來其他分期算法與經典算法，具有一定的實用價值。
引用本文： 田蘊郅, 周強, 李婉. 基于遷移學習的隨機深度殘差網絡自動睡眠分期算法. 生物醫學工程學雜志, 2023, 40(2): 286-294. doi: 10.7507/1001-5515.202211021 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
睡眠對于人類而言有著不可或缺的作用，占據一生約三分之一的時間[1]，而且在人們的日常學習、工作以及提升生活質量等方面承擔著關鍵的作用[2]。睡眠不足與入睡困難等睡眠障礙問題，一方面對人體身心健康造成了損害[3-5]，另一方面也使社會經濟遭受影響[6]。因此，研究睡眠障礙具有積極的現實意義，而對整個睡眠過程不同階段進行辨識的睡眠分期技術則是研究的基礎。Reschtschaffen和Kales于1968年共同提出了“R & K睡眠分期準則”（簡稱“R & K準則”），即根據多導睡眠圖（polysomnography，PSG）中的各類生物電信號信息進行綜合評判后確立睡眠依據[7]。隨后，美國睡眠醫學學會（American Academy of Sleep Medicine，AASM）對R & K準則進行了修改，將長時間睡眠分為清醒期（wake，W）、非快速眼動期（non-rapid eye movement 1–3，N1–N3）和快速眼動期（rapid eye movement，REM）5個階段[8]。
傳統的睡眠分期方法一是由資深醫師依據上述兩類分期準則，根據受試者的PSG信號，憑借自身經驗對整夜睡眠過程進行人工辨識。這種方法工作強度大，效率低，穩定性弱。二是基于機器學習的自動睡眠分期，主要由睡眠數據采集與預處理、特征提取和分類器三部分組成。睡眠數據特征提取主要采用兼具時間特性和頻率統計特性的時頻分析方法，包括短時傅里葉變換（short-time Fourier transform，STFT）、S變換（Stockwell transform，ST）、連續小波變換（continuous wavelet transform，CWT）、魏格納-威利分布（Wigner-Willi distribution，WVD）、希爾伯特-黃變換（Hilbert-Huang transform，HHT）及其改進算法等。常用分類器主要有隨機森林、支持向量機等[9-10]。睡眠數據具有非平穩隨機性、非線性的特點，隨著深度學習理論的成熟及計算機算力的大幅提升，多數學者開始使用這一手段進行睡眠分期。Tagluk等[11]通過使用多層感知器神經網絡，證明了將之應用于睡眠分期的可行性；Sors等[12]應用卷積神經網絡（convolutional neural network，CNN），提出了一個包含14層結構的CNN模型，具有良好的通用性；金崢等[13]利用循環神經網絡與注意力機制，提取信號時序和通道的融合特征，完成了端對端自動睡眠分期。
上述技術盡管取得了一些成果，但在實際應用中還存在著問題：一是隨著CNN結構的復雜化，需要訓練的參數量會大幅度提升，而訓練一個全新的大型網絡需要的算力及時間成本較高，會導致睡眠分期效率不佳；二是當前常使用睡眠過程中屬于小樣本數據集的腦電信號（electroencephalogram，EEG）作為神經網絡的輸入，在模型上進行訓練時常出現過擬合問題，使得模型的泛化能力受到限制。引入遷移學習（transfer learning，TL）技術可以適當解決此類問題。Abdollahpour等[14]提出了用于數據融合的遷移學習CNN進行分類；Wang等[15]利用遷移學習和網絡融合，構建了由三個子網絡組成的深度睡眠網絡，解決了EEG數據稀缺問題；Heremans等[16]將特征匹配策略應用于可穿戴設備的睡眠分期中，大幅提升了模型的精度。
使用深層網絡的遷移學習時，其模型性能會受限于自身結構的冗余性。因此，本文提出一種基于遷移學習的隨機深度（stochastic depth，SD）殘差網絡（residual network，ResNet）自動睡眠分期算法（TL-SDResNet）。首先，利用CWT將原始EEG信號轉換為可用于計算機視覺（computer vision，CV）的二維時頻圖像；其次，構建經圖像網絡數據集（image network dataset，ImageNet）訓練的ResNet50預訓練模型，在低層參數凍結、高層訓練策略的基礎上，使用隨機深度丟棄部分殘差層；最后，利用遷移學習進行自動睡眠分期，以期有效減少深層網絡訓練所需參數量與訓練時長的問題，并抑制過擬合現象。本文提出的TL-SDResNet分期算法，期望具有快速進行睡眠分期的性能，能夠作為當前睡眠分期的優選方案。
1 本文算法結構
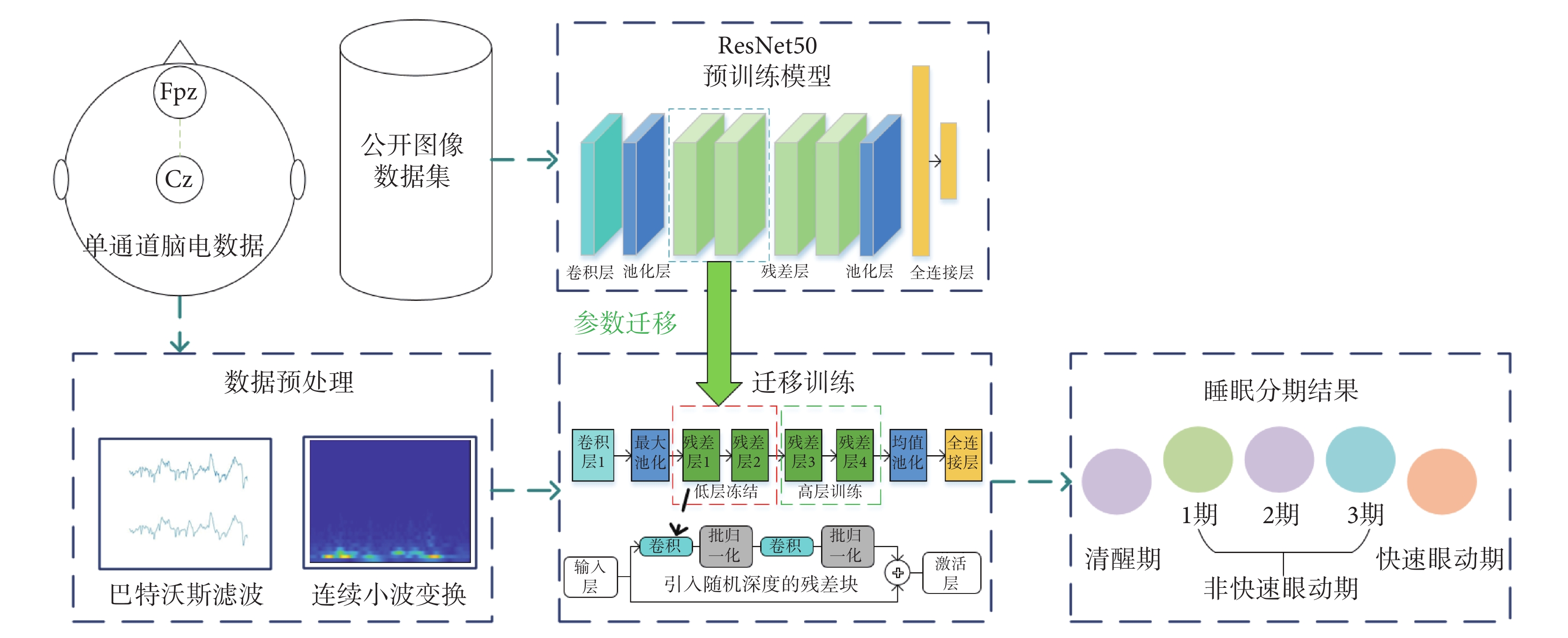
針對小樣本數據在深度學習模型上出現過擬合、深層網絡所需參數量大及訓練時間過多等問題，本文設計并構建了基于遷移學習的隨機深度殘差網絡（TL-SDResNet）自動睡眠分期算法，結構如圖1所示：① 對原始單通道EEG數據利用巴特沃斯濾波與連續小波變化進行預處理，獲取包含時-頻聯合特征的二維彩色圖，作為模型輸入；② 構建以ResNet50為主干的預訓練網絡，采取低層參數凍結、高層遷移訓練策略，以減少訓練所需參數量和算力成本；③ 引入帶隨機深度的殘差塊，在減少ResNet冗余性的同時，提升模型的泛化能力，并保證模型得到較好的分類效果。
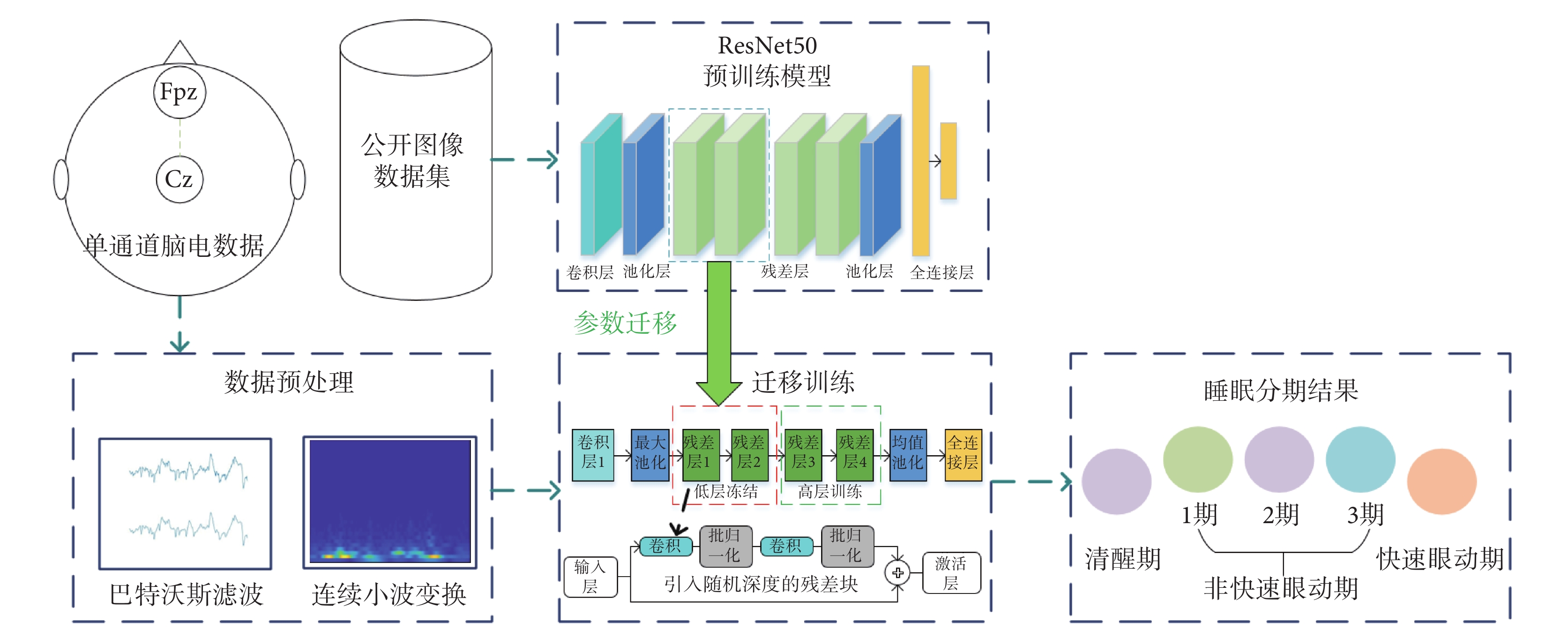圖1
TL-SDResNet結構
Figure1.
The architecture of TL-SDResNet
2 自動睡眠分期算法
2.1 腦電信號預處理
2.1.1 腦電信號去噪
現有的研究多使用包括腦電、眼電（electrooculogram，EOG）和肌電（electromyography，EMG）在內的生物電信號，以多通道形式作為睡眠分期模型的輸入。這些生物電信號在依靠PSG采集的過程中，需要在人體上安裝一定數量的傳感器來獲取，有礙正常的睡眠進程[17]。本文嘗試使用單通道EEG數據作為辨識模型的輸入，通過簡化睡眠信息的采集方式，減輕因外界物體與體表接觸的不適而導致睡眠受到的影響。
在EEG信號采集過程中，常受到EOG、EMG及環境噪聲的影響，為了減少這類信號對分期結果的干擾，需要對原始數據進行預處理。有關研究表明，與人體睡眠相關的EEG頻率范圍為0.5～35 Hz之間[18]，超出這一范圍的信號可被視作偽跡。因此，本文使用數據分析軟件Matlab 2018（MathWorks，美國）對EEG信號進行濾波處理[19]。使用頻帶范圍為0.5～35 Hz的四階巴特沃斯帶通濾波器，用以濾除EEG信號的噪聲與偽影，得到可用于時頻轉換的EEG信號。
2.1.2 腦電信號二維化
EEG信號屬于一維時變信號，而在深度學習的CV領域中，常使用二維彩色圖像數據作為輸入。常用的二維圖像變換方法包括信號拼接和時頻變換，盡管時頻變換方法的速度較信號拼接法慢，但能提供信號時頻域聯合分布信息，因此本文考慮采用并比較如下幾種時頻變換方法。
（1）短時傅里葉變換
STFT可以提取EEG信號在連續時間上的頻率信息，已經被證實可用于各類生物醫學信號處理研究。該方法通過對信號添加可滑動窗函數后做傅里葉變換，得到信號隨時間變換的頻率結構。短時傅里葉變換 
如式(1)所示：
 |
式中 
為原始信號，
是窗函數，本文采用的窗函數包括凱澤窗（Kaiser window，Kaiser）和漢寧窗（Hanning window，Hann）兩種，其定義如式(2)、式(3)所示：
 |
 |
式中I0是零階一類修正貝索函數，N為序列長度，
為可用于調整Kaiser窗外形的任意非負實數。
（2）連續小波變換
CWT既延續了STFT的局部化特點，又克服了窗函數大小不能隨頻率變化的不足，是一種由時間序列中低頻與高頻組成的時頻變換，通過將EEG信號映射至時頻空間，可以更好地對頻率分量進行可見的定位。連續小波變換 
如式(4)所示：
 |
式中 
為原信號，
為母小波，
為尺度，
為平移量。
（3）希爾伯特-黃變換
HHT由兩階段組成，一階段為經驗模態分解（empirical mode decomposition，EMD），二階段是希爾伯特譜分析（Hilbert spectrum analysis，HSA）。HHT利用EMD將給定原始信號 
分解為若干個固有模態函數（intrinsic mode function，IMF）的總和，如式(5)所示：
 |
式中 
為第i個IMF分量，
為剩余分量，N為循環次數。隨后，對每個IMF做HSA以得到其希爾伯特譜，即每個IMF分量在時頻域中的表示，最終得到原始信號的希爾伯特譜如式(6)所示：
 |
（4）魏格納-威利分布
WVD可同時表示具有高時間與頻率分辨率的時頻聯合分布[20]。得到原始信號 
的魏格納分布后，利用希爾伯特變換得到信號的解析形式，最終 
的魏格納-威利分布 
如式(7)所示：
 |
其中 
是積分變量，
是時移，
為頻率。
（5）S變換
ST作為綜合STFT與WT延伸的時頻分析方法，將STFT中窗函數替換為寬度可變的高斯窗[21]。原始信號 
的S變換 
定義如式(8)所示：
 |
式中
為時移參數，
為時間，
為頻率，
為窗函數。
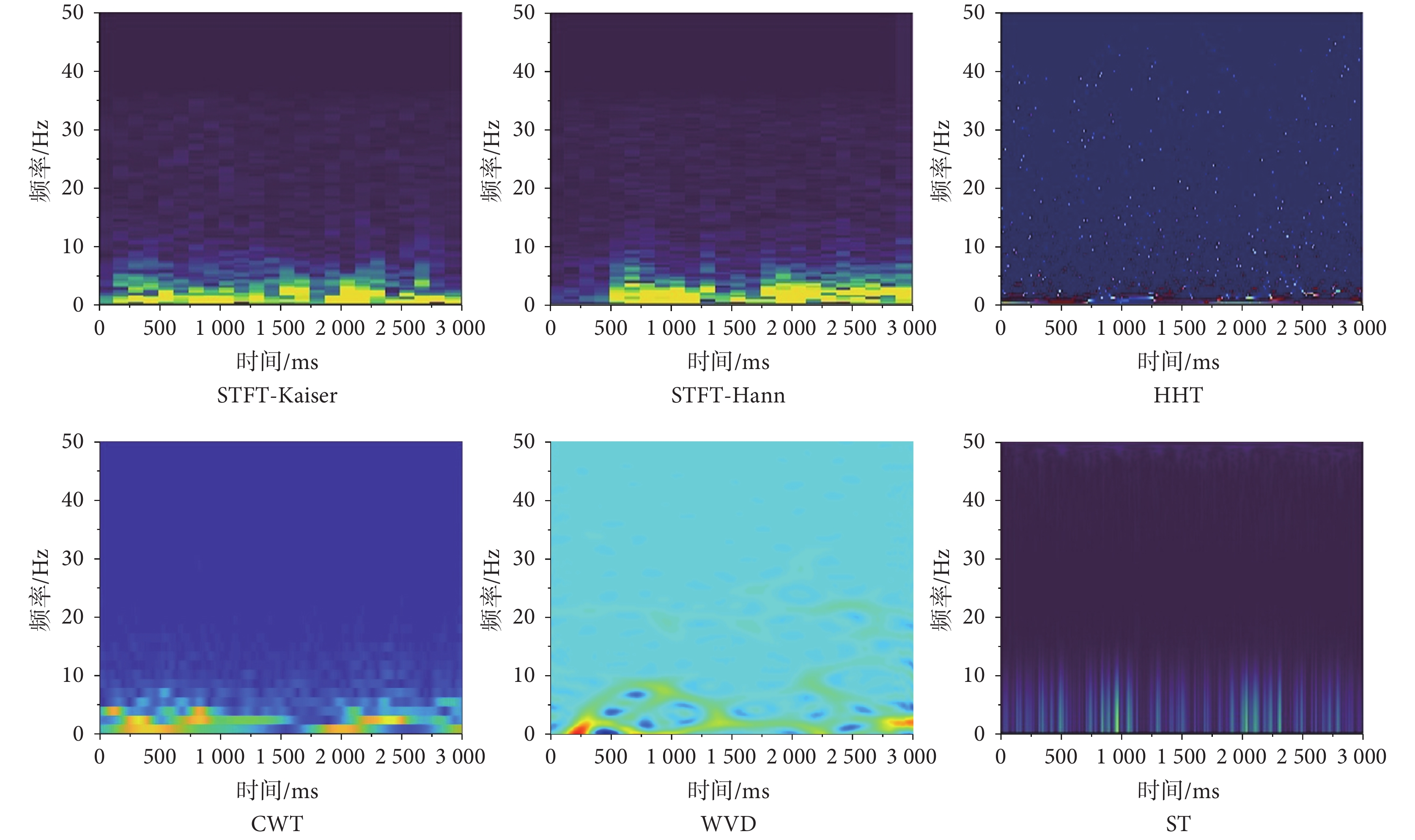
本文利用上述五種時頻分析方法對濾波后的EEG信號進行處理，得到對應的時頻圖，如圖2所示。
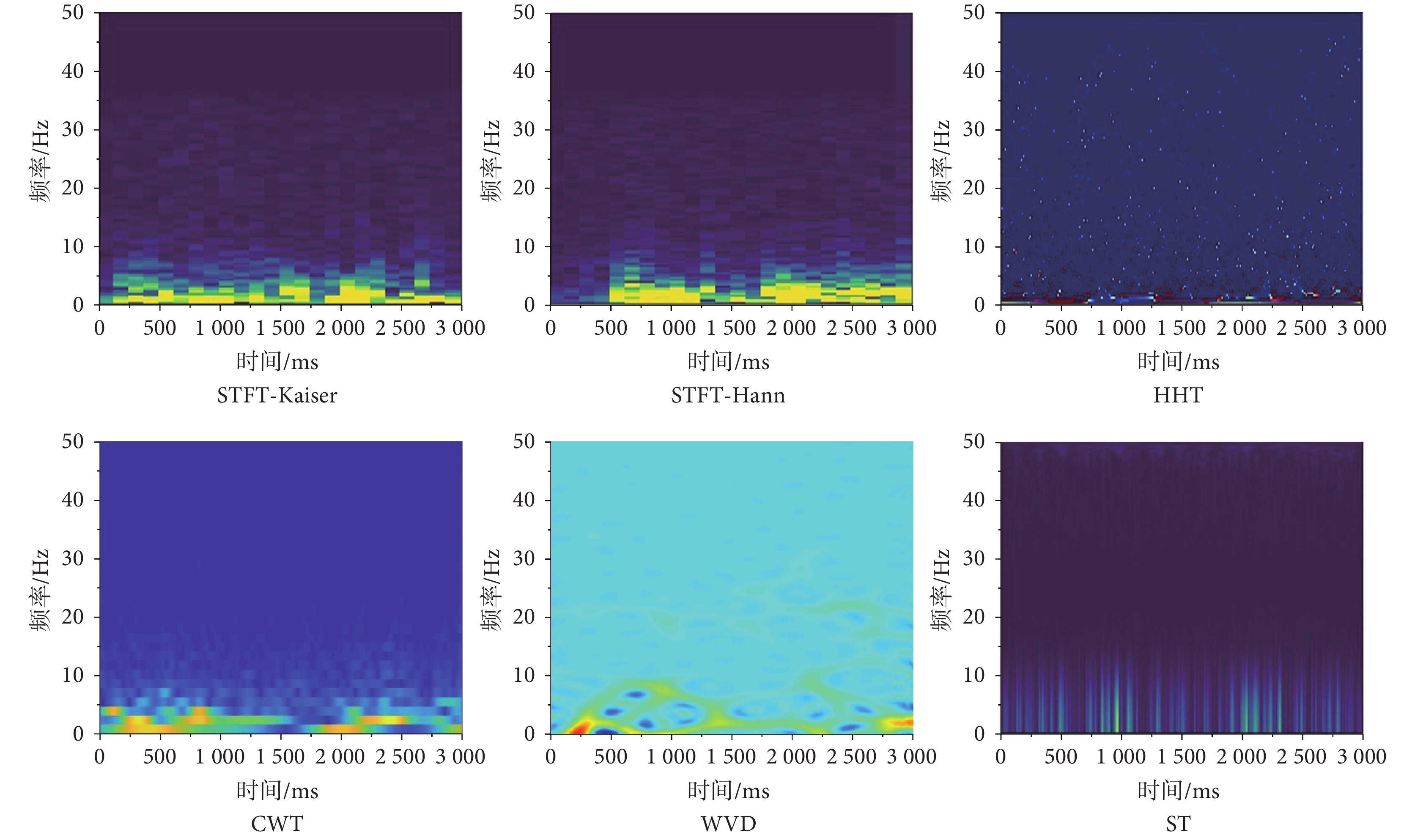圖2
經幾種時頻變換的EEG時頻圖
Figure2.
EEG time-frequency diagram after several time-frequency transformations
在以上非平穩EEG信號的預處理方法中，STFT因窗大小限制了時頻分辨率的同步優化，WVD存在具有強振蕩效應的交叉項干擾，HHT頻率分辨能力不足，ST因其計算復雜度較高在實現時速度較慢。為了同時滿足時頻分析效率與圖像時頻特征細節要求，本文選用CWT對原始EEG進行時頻轉換得到二維特征圖，并將圖像分辨率調整為224*224，與ImageNet數據集圖像保持一致。
2.2 隨機深度殘差網絡
2.2.1 殘差網絡的局限性
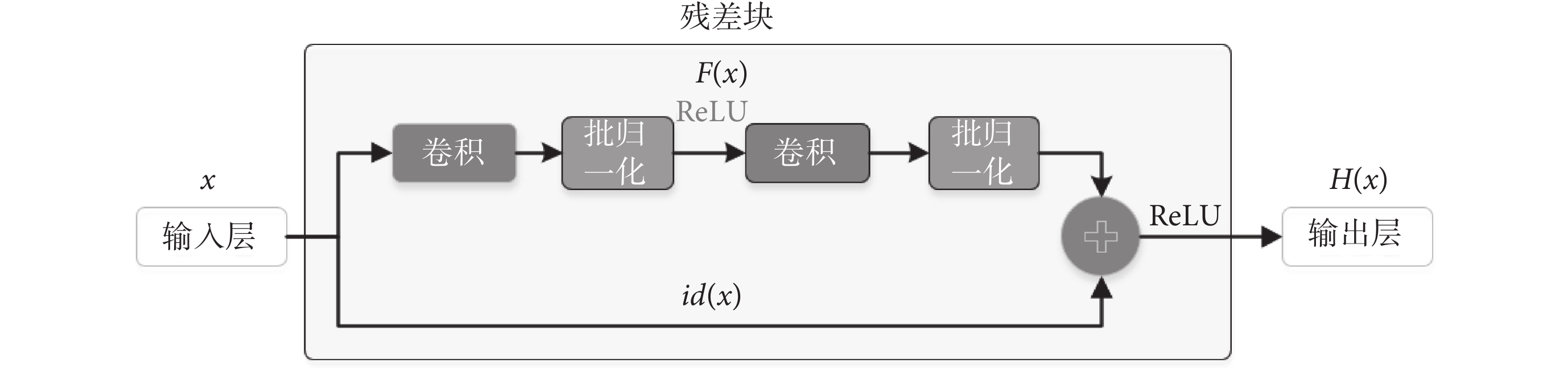
CNN由輸入層、隱藏層和輸出層組成。在CV領域中，輸入層將圖像作為標準化原始像素值輸入。隱藏層包括卷積層、池化層、全連接層和歸一化指數函數（softmax regression，Softmax）分類器[22]。理論上隨著隱藏層加深，神經網絡能獲得更高的感受野，可以更好地提取圖像特征。但實際上，在深層網絡中常出現梯度爆炸與梯度消失問題。為了在使用深層網絡的同時有效地利用圖像特征，ResNet在引入恒等映射計算殘差的同時使用修正線性單元（rectified linear unit，ReLU）作為激活函數來緩解梯度不穩定情況。ResNet最關鍵的部分在于帶殘差連接的殘差塊，即輸出與多個權重層級聯的輸出和恒等映射后的輸入連接，能實現網絡梯度從高至低更好地傳播，可有效避免模型性能減退的問題[23]。殘差塊的結構如圖3所示。
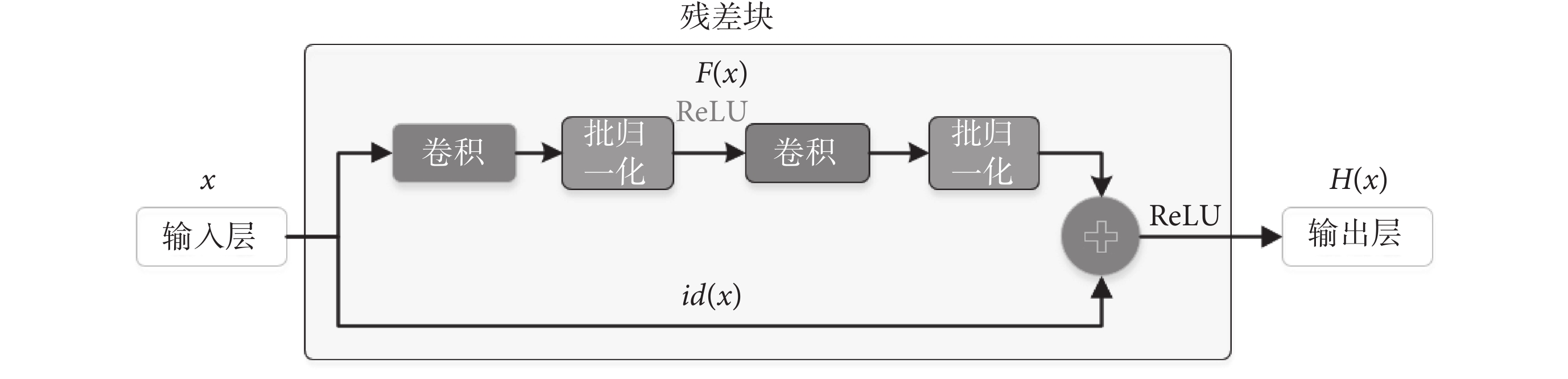圖3
殘差塊結構
Figure3.
The architecture of residual block
圖3中x為輸入值，F(x)為殘差函數，
為恒等映射。輸出H(x)如式(9)所示：
 |
ResNet根據其殘差塊數量與結構的不同，常用的網絡模型包括ResNet18、ResNet50、ResNet101等。本文綜合考量了模型的參數量及訓練效果，選取ResNet50作為預訓練模型，其網絡結構如表1所示。
表1
ResNet50模型結構
Table1.
ResNet50 model structure
在研究使用包括ResNet50在內的深層殘差網絡進行分類任務時，采用EEG信號這類小樣本數據集進行訓練時，仍會產生過擬合現象，導致訓練集與測試集結果差異較大的問題。而殘差網絡層數加深亦會造成訓練耗時過長，并最終影響睡眠分期模型的整體性能。
2.2.2 網絡隨機深度優化
為了解決深層殘差網絡存在的問題，在減少過擬合的同時縮短訓練所需時長，本文使用隨機深度在殘差網絡訓練的過程中以一定的概率任意丟棄殘差塊[24]。通過在訓練時預設一個滿足伯努利分布的二值隨機變量b，給定殘差塊一個激活概率。當b為1時，該殘差塊是原始殘差塊；當b為0時，殘差支路未被激活，此殘差塊將被丟棄。此時式(9)修改為式(10)：
 |
b取1的概率為P，又稱生存概率。本文通過給定P的大小，完成隨機深度殘差網絡的構建。在訓練過程中，P設為殘差層數相關的平滑函數，如式(11)所示：
 |
式中 
表示第 l 層在訓練中的生存概率，L為網絡中殘差層總數。本文設置首殘差層P = 1，并線性遞減到尾殘差層P = 0.5，在模型測試過程中P恒等于1。
2.3 遷移學習訓練
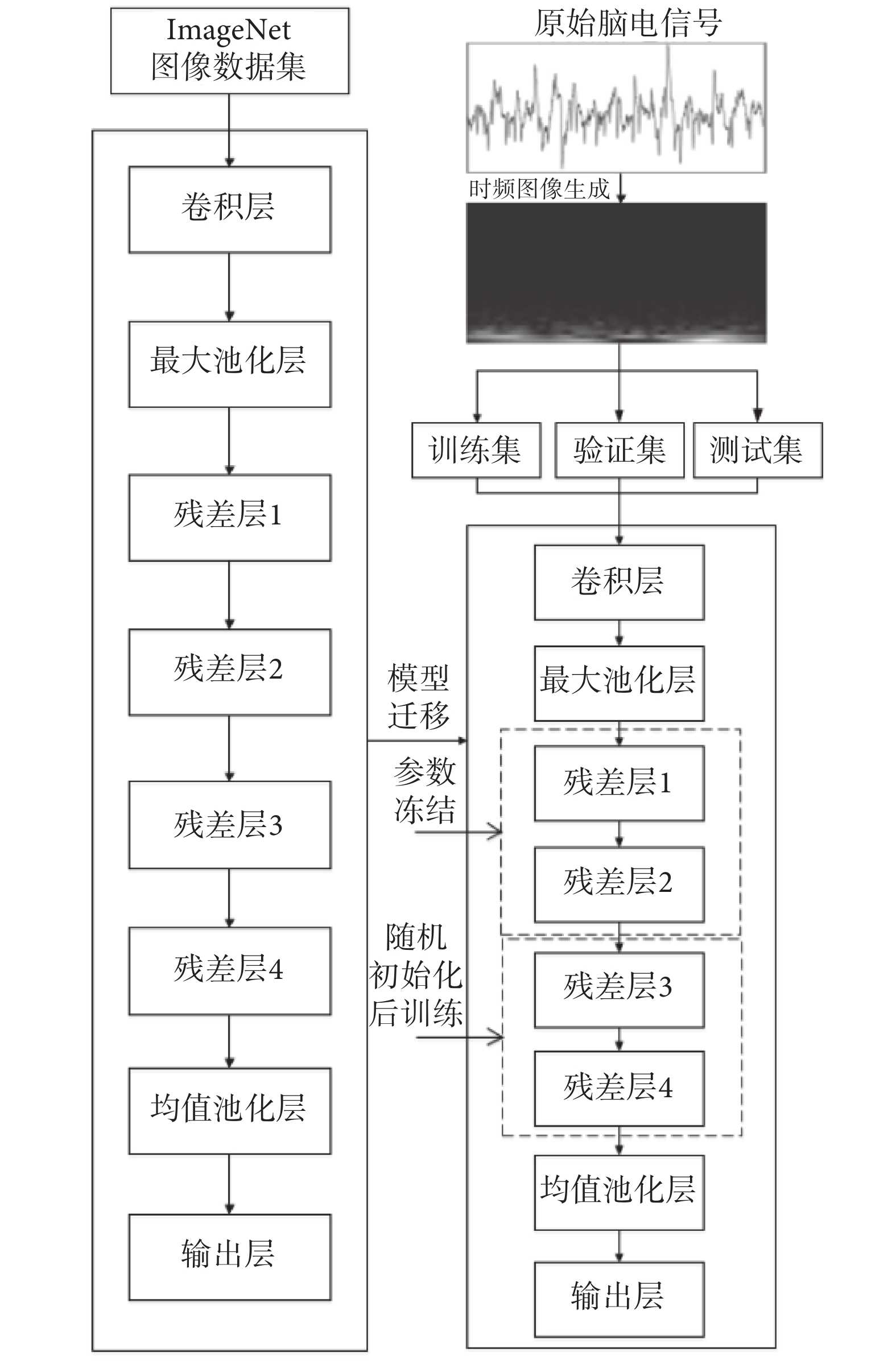
從頭訓練一個神經網絡需要耗費大量的時間和算力，因此常使用遷移學習的方法以提升深度學習效率，即使用模型在大型數據集（如ImageNet）上進行預訓練，用得到的訓練參數來解決相應問題。遷移學習將數據分為源數據與目標數據，源數據通常為與研究任務無關的大樣本數據；目標數據則是與任務相關的小樣本數據。遷移學習就是基于源數據與現有模型，將共用知識用于現有任務中，以充分利用源數據來提高模型在目標數據上的性能[25]。通常低層特征的可遷移能力較佳，而高層特征則呈現出與深度學習任務相關的特性，需要在現有任務上重新訓練。因此，本文采用低層凍結、高層訓練的遷移策略，將ResNet50前兩個殘差層參數與結構凍結，作為低層睡眠各時期特征辨識部分，后兩個殘差層參數進行隨機初始化后，使用經預處理的EEG數據進行訓練，用于學習不同睡眠階段的深度特征。本文設計的遷移學習訓練結構如圖4所示。
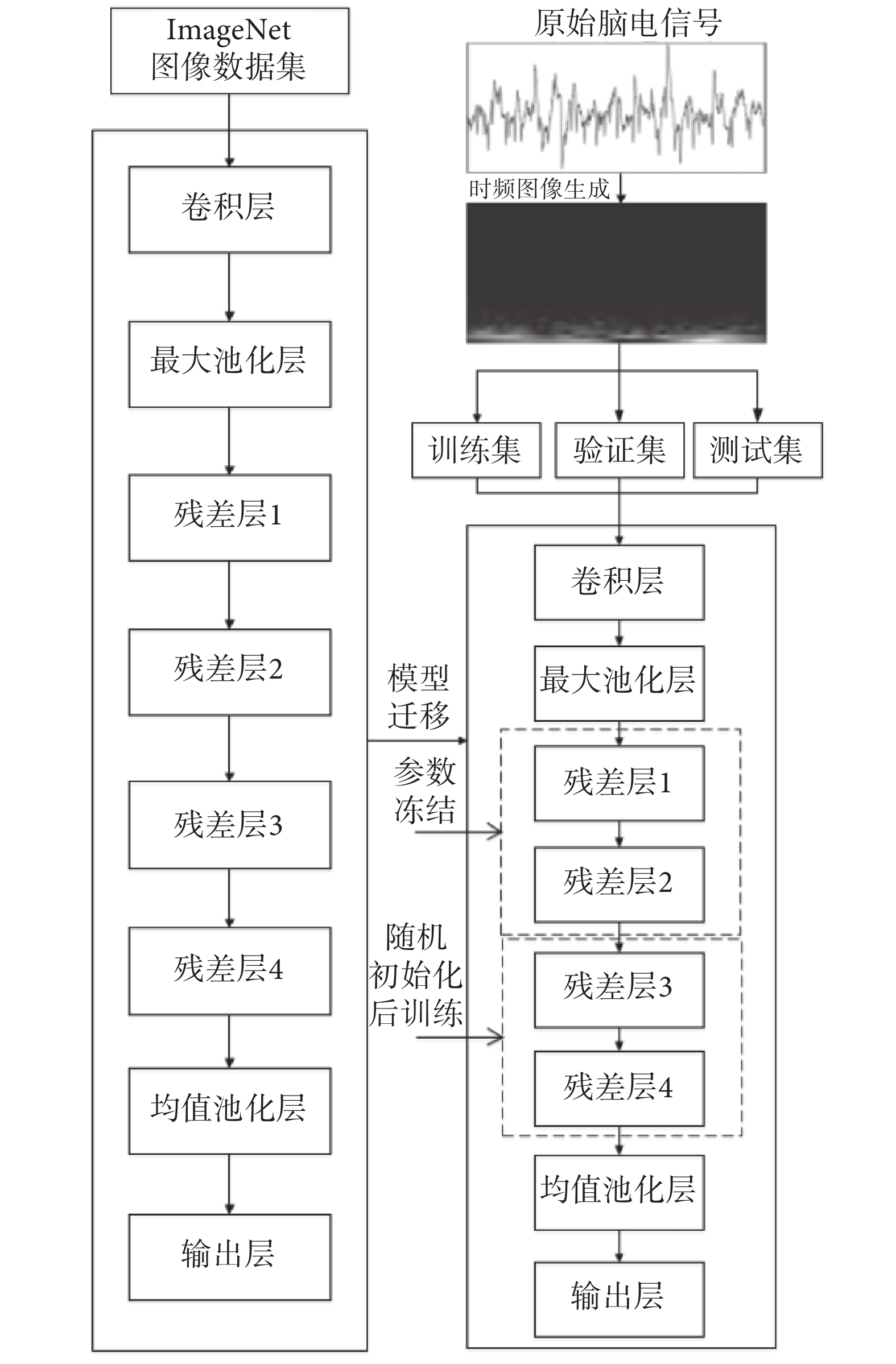圖4
遷移學習訓練結構
Figure4.
Structure of transfer learning training
3 分期實驗及結果分析
為驗證本文所提出的自動睡眠分期算法的可靠性，在硬件設置為圖形處理單元RTX 2080Ti（NVIDIA Inc，美國）、內存32 GB的支持下，使用基于符號數學系統Tensorflow 2.0（Google Inc，美國）框架的計算機編程軟件Python 3.70（Python Software Foundation，美國），進行相關的分期實驗。
綜合現有硬件平臺性能及多輪訓練的效果，實驗設置每輪訓練批大小為32，學習率為0.001，采用適應性矩估計（adaptive moment estimation，Adam）加快收斂速度，損失函數使用交叉熵損失函數。
3.1 實驗條件
3.1.1 實驗數據
本文使用復雜生理信號研究資源網站（Research Resource for Complex Physiologic Signals，PhysioNet）公開可用的歐洲數據格式存儲的睡眠數據庫拓展版（Sleep-European Data Format Database Expanded，Sleep-EDFx）[26]進行實驗。選取數據集中16人共30條單通道（Fpz-Cz）EEG數據，刪去無效信號片段，并只保留入睡前半個小時至清醒后半個小時內的數據。經處理后各時期樣本數與總樣本數如表2所示。
表2
各時期樣本數量與總數量
Table2.
Number of samples in each period and total number
3.1.2 評價指標
為了便于對模型性能進行有效驗證，并與其他同類型研究成果進行對比，本文采用準確率（accuracy，Acc）、精確率（precision rate，PR）、召回率（recall，RE）和F1分數（F1 Score，F1）這些指標用于評估模型性能，采用混淆矩陣用于分析算法效果。
3.2 結果與討論
3.2.1 組合實驗
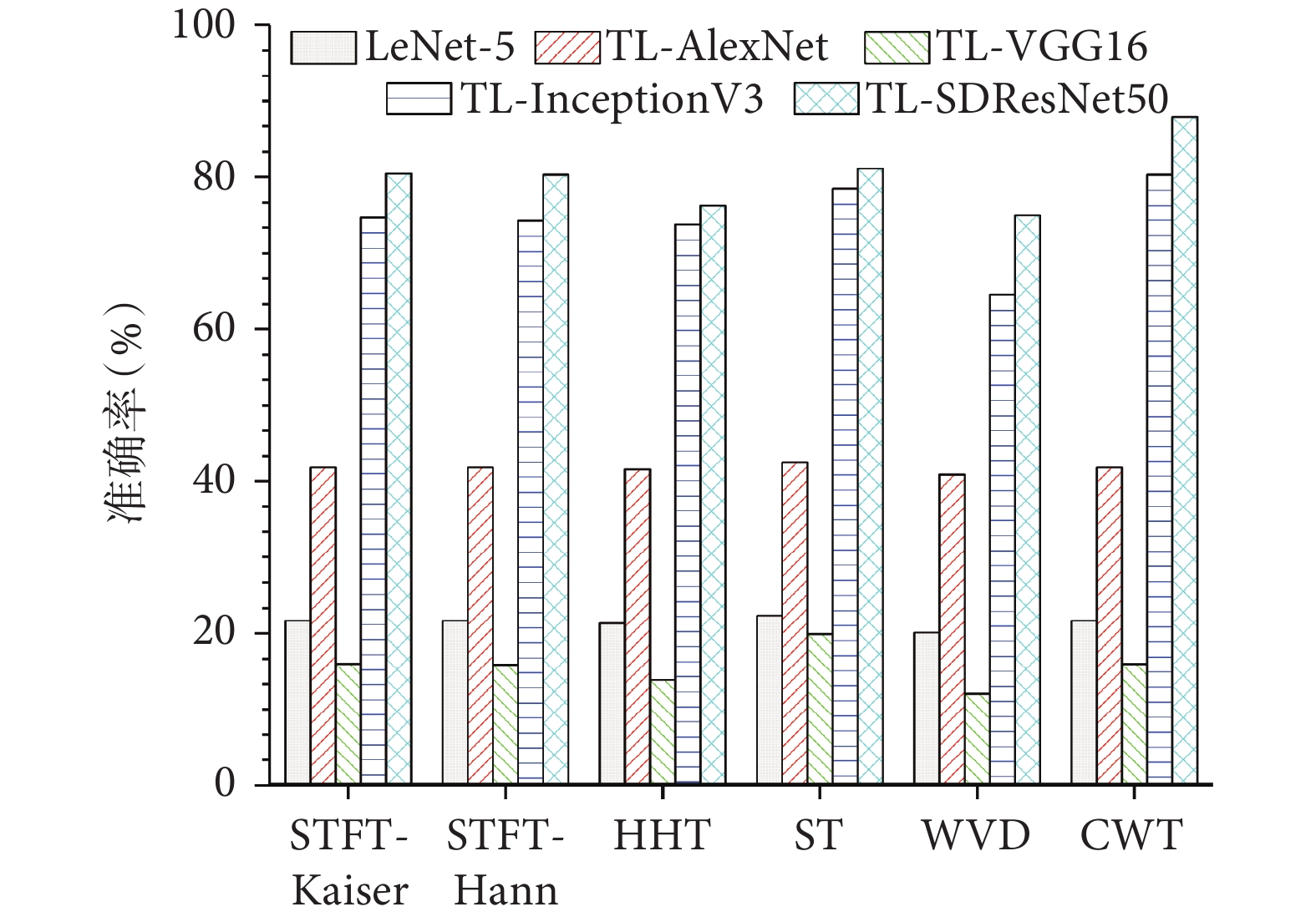
本實驗構建CV領域常用的神經網絡模型LeNet-5、AlexNet、VGG16以及InceptionV3與本文算法進行對比。除LeNet-5因模型簡單外，其余模型皆可在ImageNet數據集上加載預訓練模型。因此，本文采用與ResNet50相同的遷移學習方法，構建了TL-AlexNet、TL-VGG16、TL-InceptionV3、TL-SDResNet50四個遷移學習模型以及LeNet-5模型進行分期實驗。為了驗證本文構建模型的優越性，結合上述分期模型與CWT、HHT、STFT-Kaiser、STFT-Hann、ST、WVD時頻分析方法，在相同的實驗設置條件下進行訓練與測試，得到的實驗結果如圖5所示。
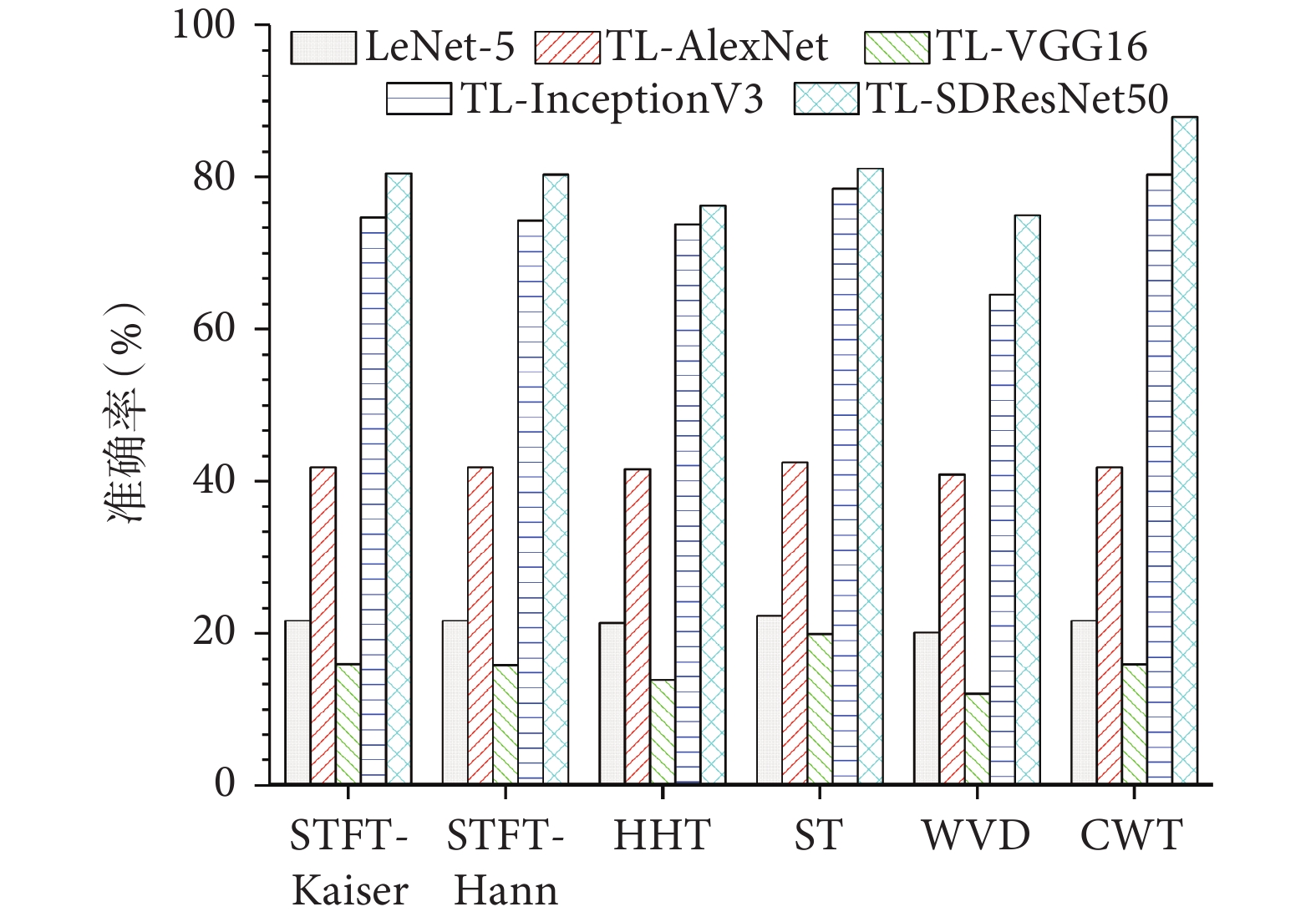圖5
不同時頻分析方法在不同模型上的訓練結果比較
Figure5.
Comparison of training results of different time-frequency analysis methods on various models
可以看出，本文提出的TL-SDResNet50模型無論基于何種時頻分析方法，都能得到較好的分期準確率，性能優于所選基于深度學習的對比模型。基于CWT時頻分析法的不同模型分期結果如表3所示。LeNet-5與TL-AlexNet模型因同屬于“淺層”網絡，盡管訓練時間較短，但其對EEG的特征提取能力有限。而與同屬深層網絡的TL-VGG16、TL-InceptionV3相比，本文提出的TL-SDResNet50大幅度縮短了深層網絡所需的訓練時間，能夠快速地進行自動睡眠分期任務。
表3
基于CWT的不同模型實驗結果對比
Table3.
Comparison of experimental results of different models based on CWT
3.2.2 結果對比及混淆矩陣
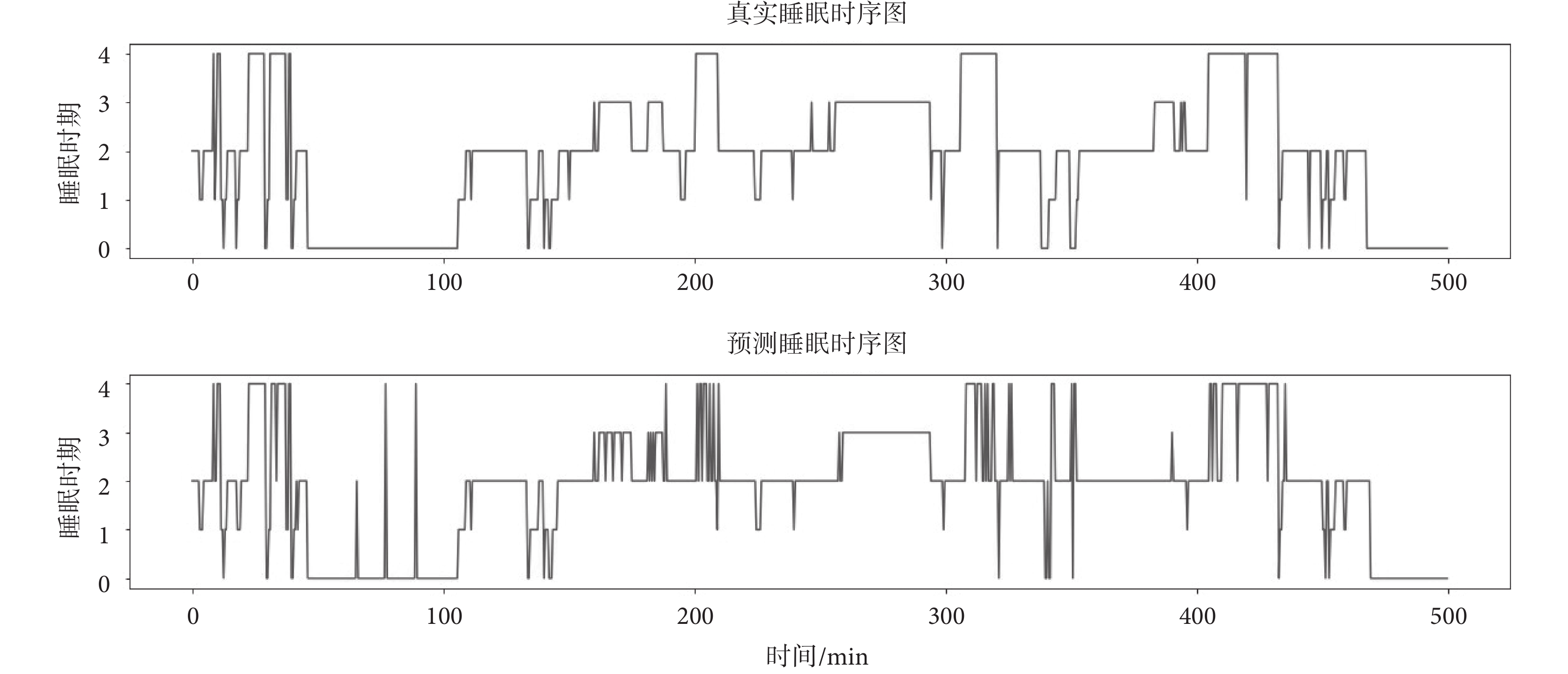
為驗證上述實驗中TL-SDResNet分期模型的可靠性，圖6顯示了由專業醫師手動評估與TL-SDResNet對部分睡眠過程預測的對比結果，這表明本文算法具有良好的睡眠辨識能力，能夠作為實際情況下的自動睡眠分期方法使用。
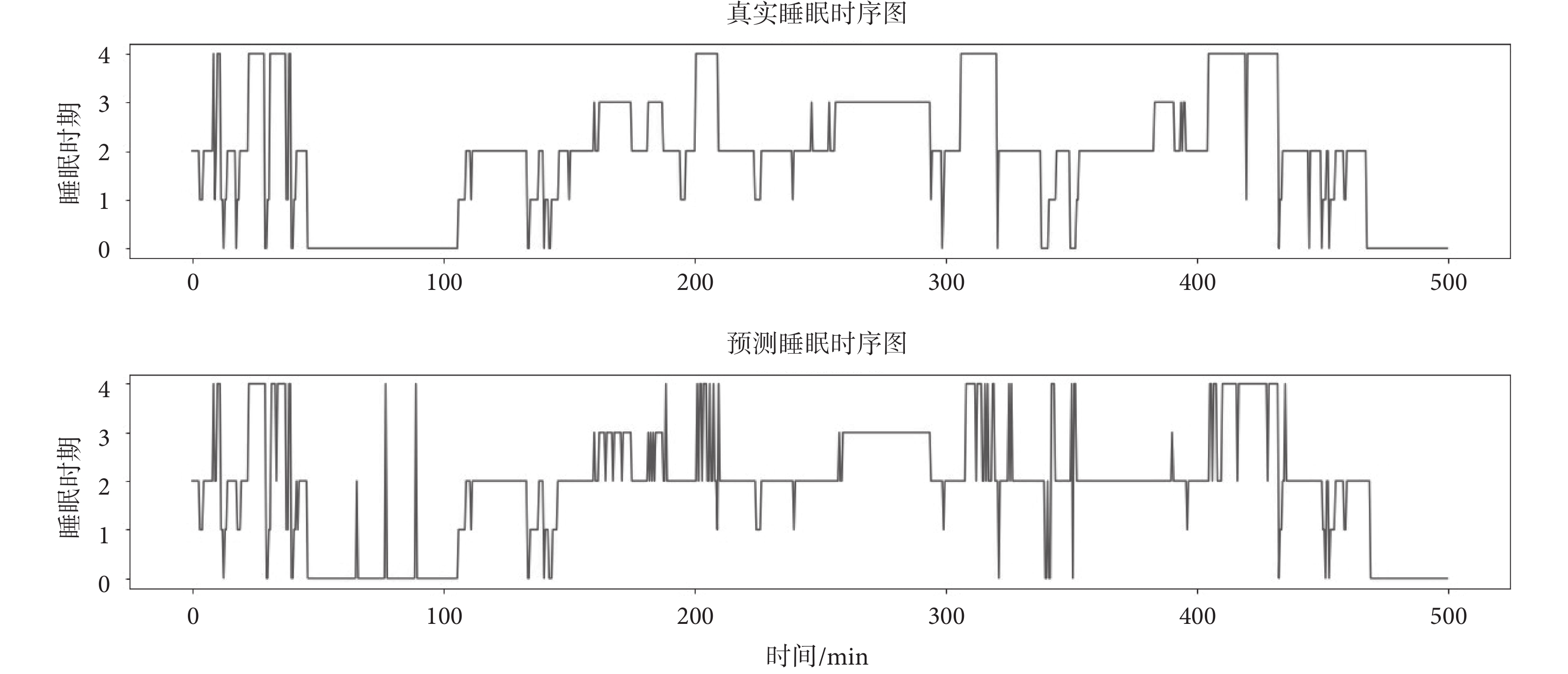圖6
專家評估與TL-SDResNet分期結果對比
Figure6.
Comparison between expert evaluation and TL-SDResNet staging results
進一步驗證模型的性能，對實驗結果進行深度分析。表4所示為TL-SDResNet的分期結果。可以看出，TL-SDResNet在對不同睡眠階段的預測中，都能夠取得較好的辨識效果。除N1期受限于樣本數量不足，模型對其他睡眠時期評估得到的F1均能達到90%左右。
表4
TL-SDResNet模型的混淆矩陣及性能指標
Table4.
Confusion matrix and performance index of TL-SDResNet model
3.2.3 與其他算法的對比
將采用同一數據集的自動睡眠分期算法與TL-SDResNet算法的分期結果進行對比，如表5[10, 27-29]所示。表中包含了基于機器學習與深度學習的不同自動睡眠分期模型，其中文獻[28]提出的深度睡眠網絡屬于睡眠分期領域的經典模型，文獻[29]基于遷移學習將擠壓網絡預訓練模型應用到睡眠分期中。根據對比結果，本文提出的TL-SDResNet分期準確率為87.95%，本文方法相較于其他模型的分類準確率均有所提高，且各時期的F1也有不同程度的提升。
表5
本文提出的自動睡眠分期算法與其他分類算法的比較
Table5.
Comparison between the automatic sleep staging algorithm proposed in this paper and other classification algorithms
4 結論
本文提出了一種基于遷移學習的隨機深度殘差網絡自動睡眠分期算法。該算法利用CWT從單通道腦電數據中提取時頻特征，將其轉換為時頻譜圖作為模型的輸入。在使用經ImageNet數據集上預訓練的ResNet50網絡的基礎上，利用隨機深度優化ResNet，提取深層特征并進行分類。通過組合實驗對比以及相關文獻結論對比的方法，表明了本文所提出模型在自動睡眠分類的準確度與綜合性能上均具有一定優勢，能夠為睡眠障礙的改善、睡眠過程的監督以及睡眠疾病的治療等提供行之有效的輔助工具。
本文使用的Sleep-EDFx數據集中單通道EEG數據經等時間劃分為30 s一段后，因人體睡眠過程本身所具有的特點，導致W期較多、N1期較少，造成了類不平衡問題，會對睡眠分期帶來一定的影響。下一步將對本算法及數據集進行進一步改進，利用數據平衡方法提升數據質量，從而開展進一步的實驗與研究。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：田蘊郅負責方法設計與實驗、數據收集與分析，以及撰寫論文；周強、李婉指導方法理論和實驗設計，以及指導論文撰寫。
0 引言
睡眠對于人類而言有著不可或缺的作用，占據一生約三分之一的時間[1]，而且在人們的日常學習、工作以及提升生活質量等方面承擔著關鍵的作用[2]。睡眠不足與入睡困難等睡眠障礙問題，一方面對人體身心健康造成了損害[3-5]，另一方面也使社會經濟遭受影響[6]。因此，研究睡眠障礙具有積極的現實意義，而對整個睡眠過程不同階段進行辨識的睡眠分期技術則是研究的基礎。Reschtschaffen和Kales于1968年共同提出了“R & K睡眠分期準則”（簡稱“R & K準則”），即根據多導睡眠圖（polysomnography，PSG）中的各類生物電信號信息進行綜合評判后確立睡眠依據[7]。隨后，美國睡眠醫學學會（American Academy of Sleep Medicine，AASM）對R & K準則進行了修改，將長時間睡眠分為清醒期（wake，W）、非快速眼動期（non-rapid eye movement 1–3，N1–N3）和快速眼動期（rapid eye movement，REM）5個階段[8]。
傳統的睡眠分期方法一是由資深醫師依據上述兩類分期準則，根據受試者的PSG信號，憑借自身經驗對整夜睡眠過程進行人工辨識。這種方法工作強度大，效率低，穩定性弱。二是基于機器學習的自動睡眠分期，主要由睡眠數據采集與預處理、特征提取和分類器三部分組成。睡眠數據特征提取主要采用兼具時間特性和頻率統計特性的時頻分析方法，包括短時傅里葉變換（short-time Fourier transform，STFT）、S變換（Stockwell transform，ST）、連續小波變換（continuous wavelet transform，CWT）、魏格納-威利分布（Wigner-Willi distribution，WVD）、希爾伯特-黃變換（Hilbert-Huang transform，HHT）及其改進算法等。常用分類器主要有隨機森林、支持向量機等[9-10]。睡眠數據具有非平穩隨機性、非線性的特點，隨著深度學習理論的成熟及計算機算力的大幅提升，多數學者開始使用這一手段進行睡眠分期。Tagluk等[11]通過使用多層感知器神經網絡，證明了將之應用于睡眠分期的可行性；Sors等[12]應用卷積神經網絡（convolutional neural network，CNN），提出了一個包含14層結構的CNN模型，具有良好的通用性；金崢等[13]利用循環神經網絡與注意力機制，提取信號時序和通道的融合特征，完成了端對端自動睡眠分期。
上述技術盡管取得了一些成果，但在實際應用中還存在著問題：一是隨著CNN結構的復雜化，需要訓練的參數量會大幅度提升，而訓練一個全新的大型網絡需要的算力及時間成本較高，會導致睡眠分期效率不佳；二是當前常使用睡眠過程中屬于小樣本數據集的腦電信號（electroencephalogram，EEG）作為神經網絡的輸入，在模型上進行訓練時常出現過擬合問題，使得模型的泛化能力受到限制。引入遷移學習（transfer learning，TL）技術可以適當解決此類問題。Abdollahpour等[14]提出了用于數據融合的遷移學習CNN進行分類；Wang等[15]利用遷移學習和網絡融合，構建了由三個子網絡組成的深度睡眠網絡，解決了EEG數據稀缺問題；Heremans等[16]將特征匹配策略應用于可穿戴設備的睡眠分期中，大幅提升了模型的精度。
使用深層網絡的遷移學習時，其模型性能會受限于自身結構的冗余性。因此，本文提出一種基于遷移學習的隨機深度（stochastic depth，SD）殘差網絡（residual network，ResNet）自動睡眠分期算法（TL-SDResNet）。首先，利用CWT將原始EEG信號轉換為可用于計算機視覺（computer vision，CV）的二維時頻圖像；其次，構建經圖像網絡數據集（image network dataset，ImageNet）訓練的ResNet50預訓練模型，在低層參數凍結、高層訓練策略的基礎上，使用隨機深度丟棄部分殘差層；最后，利用遷移學習進行自動睡眠分期，以期有效減少深層網絡訓練所需參數量與訓練時長的問題，并抑制過擬合現象。本文提出的TL-SDResNet分期算法，期望具有快速進行睡眠分期的性能，能夠作為當前睡眠分期的優選方案。
1 本文算法結構
針對小樣本數據在深度學習模型上出現過擬合、深層網絡所需參數量大及訓練時間過多等問題，本文設計并構建了基于遷移學習的隨機深度殘差網絡（TL-SDResNet）自動睡眠分期算法，結構如圖1所示：① 對原始單通道EEG數據利用巴特沃斯濾波與連續小波變化進行預處理，獲取包含時-頻聯合特征的二維彩色圖，作為模型輸入；② 構建以ResNet50為主干的預訓練網絡，采取低層參數凍結、高層遷移訓練策略，以減少訓練所需參數量和算力成本；③ 引入帶隨機深度的殘差塊，在減少ResNet冗余性的同時，提升模型的泛化能力，并保證模型得到較好的分類效果。
圖1
TL-SDResNet結構
Figure1.
The architecture of TL-SDResNet
2 自動睡眠分期算法
2.1 腦電信號預處理
2.1.1 腦電信號去噪
現有的研究多使用包括腦電、眼電（electrooculogram，EOG）和肌電（electromyography，EMG）在內的生物電信號，以多通道形式作為睡眠分期模型的輸入。這些生物電信號在依靠PSG采集的過程中，需要在人體上安裝一定數量的傳感器來獲取，有礙正常的睡眠進程[17]。本文嘗試使用單通道EEG數據作為辨識模型的輸入，通過簡化睡眠信息的采集方式，減輕因外界物體與體表接觸的不適而導致睡眠受到的影響。
在EEG信號采集過程中，常受到EOG、EMG及環境噪聲的影響，為了減少這類信號對分期結果的干擾，需要對原始數據進行預處理。有關研究表明，與人體睡眠相關的EEG頻率范圍為0.5～35 Hz之間[18]，超出這一范圍的信號可被視作偽跡。因此，本文使用數據分析軟件Matlab 2018（MathWorks，美國）對EEG信號進行濾波處理[19]。使用頻帶范圍為0.5～35 Hz的四階巴特沃斯帶通濾波器，用以濾除EEG信號的噪聲與偽影，得到可用于時頻轉換的EEG信號。
2.1.2 腦電信號二維化
EEG信號屬于一維時變信號，而在深度學習的CV領域中，常使用二維彩色圖像數據作為輸入。常用的二維圖像變換方法包括信號拼接和時頻變換，盡管時頻變換方法的速度較信號拼接法慢，但能提供信號時頻域聯合分布信息，因此本文考慮采用并比較如下幾種時頻變換方法。
（1）短時傅里葉變換
STFT可以提取EEG信號在連續時間上的頻率信息，已經被證實可用于各類生物醫學信號處理研究。該方法通過對信號添加可滑動窗函數后做傅里葉變換，得到信號隨時間變換的頻率結構。短時傅里葉變換 如式(1)所示：
|
式中 為原始信號， 是窗函數，本文采用的窗函數包括凱澤窗（Kaiser window，Kaiser）和漢寧窗（Hanning window，Hann）兩種，其定義如式(2)、式(3)所示：
|
|
式中I0是零階一類修正貝索函數，N為序列長度， 為可用于調整Kaiser窗外形的任意非負實數。
（2）連續小波變換
CWT既延續了STFT的局部化特點，又克服了窗函數大小不能隨頻率變化的不足，是一種由時間序列中低頻與高頻組成的時頻變換，通過將EEG信號映射至時頻空間，可以更好地對頻率分量進行可見的定位。連續小波變換 如式(4)所示：
|
式中 為原信號， 為母小波， 為尺度， 為平移量。
（3）希爾伯特-黃變換
HHT由兩階段組成，一階段為經驗模態分解（empirical mode decomposition，EMD），二階段是希爾伯特譜分析（Hilbert spectrum analysis，HSA）。HHT利用EMD將給定原始信號 分解為若干個固有模態函數（intrinsic mode function，IMF）的總和，如式(5)所示：
|
式中 為第i個IMF分量， 為剩余分量，N為循環次數。隨后，對每個IMF做HSA以得到其希爾伯特譜，即每個IMF分量在時頻域中的表示，最終得到原始信號的希爾伯特譜如式(6)所示：
|
（4）魏格納-威利分布
WVD可同時表示具有高時間與頻率分辨率的時頻聯合分布[20]。得到原始信號 的魏格納分布后，利用希爾伯特變換得到信號的解析形式，最終 的魏格納-威利分布 如式(7)所示：
|
其中 是積分變量， 是時移， 為頻率。
（5）S變換
ST作為綜合STFT與WT延伸的時頻分析方法，將STFT中窗函數替換為寬度可變的高斯窗[21]。原始信號 的S變換 定義如式(8)所示：
|
式中為時移參數，為時間，為頻率，為窗函數。
本文利用上述五種時頻分析方法對濾波后的EEG信號進行處理，得到對應的時頻圖，如圖2所示。
圖2
經幾種時頻變換的EEG時頻圖
Figure2.
EEG time-frequency diagram after several time-frequency transformations
在以上非平穩EEG信號的預處理方法中，STFT因窗大小限制了時頻分辨率的同步優化，WVD存在具有強振蕩效應的交叉項干擾，HHT頻率分辨能力不足，ST因其計算復雜度較高在實現時速度較慢。為了同時滿足時頻分析效率與圖像時頻特征細節要求，本文選用CWT對原始EEG進行時頻轉換得到二維特征圖，并將圖像分辨率調整為224*224，與ImageNet數據集圖像保持一致。
2.2 隨機深度殘差網絡
2.2.1 殘差網絡的局限性
CNN由輸入層、隱藏層和輸出層組成。在CV領域中，輸入層將圖像作為標準化原始像素值輸入。隱藏層包括卷積層、池化層、全連接層和歸一化指數函數（softmax regression，Softmax）分類器[22]。理論上隨著隱藏層加深，神經網絡能獲得更高的感受野，可以更好地提取圖像特征。但實際上，在深層網絡中常出現梯度爆炸與梯度消失問題。為了在使用深層網絡的同時有效地利用圖像特征，ResNet在引入恒等映射計算殘差的同時使用修正線性單元（rectified linear unit，ReLU）作為激活函數來緩解梯度不穩定情況。ResNet最關鍵的部分在于帶殘差連接的殘差塊，即輸出與多個權重層級聯的輸出和恒等映射后的輸入連接，能實現網絡梯度從高至低更好地傳播，可有效避免模型性能減退的問題[23]。殘差塊的結構如圖3所示。
圖3
殘差塊結構
Figure3.
The architecture of residual block
圖3中x為輸入值，F(x)為殘差函數， 為恒等映射。輸出H(x)如式(9)所示：
|
ResNet根據其殘差塊數量與結構的不同，常用的網絡模型包括ResNet18、ResNet50、ResNet101等。本文綜合考量了模型的參數量及訓練效果，選取ResNet50作為預訓練模型，其網絡結構如表1所示。
表1
ResNet50模型結構
Table1.
ResNet50 model structure
在研究使用包括ResNet50在內的深層殘差網絡進行分類任務時，采用EEG信號這類小樣本數據集進行訓練時，仍會產生過擬合現象，導致訓練集與測試集結果差異較大的問題。而殘差網絡層數加深亦會造成訓練耗時過長，并最終影響睡眠分期模型的整體性能。
2.2.2 網絡隨機深度優化
為了解決深層殘差網絡存在的問題，在減少過擬合的同時縮短訓練所需時長，本文使用隨機深度在殘差網絡訓練的過程中以一定的概率任意丟棄殘差塊[24]。通過在訓練時預設一個滿足伯努利分布的二值隨機變量b，給定殘差塊一個激活概率。當b為1時，該殘差塊是原始殘差塊；當b為0時，殘差支路未被激活，此殘差塊將被丟棄。此時式(9)修改為式(10)：
|
b取1的概率為P，又稱生存概率。本文通過給定P的大小，完成隨機深度殘差網絡的構建。在訓練過程中，P設為殘差層數相關的平滑函數，如式(11)所示：
|
式中 表示第 l 層在訓練中的生存概率，L為網絡中殘差層總數。本文設置首殘差層P = 1，并線性遞減到尾殘差層P = 0.5，在模型測試過程中P恒等于1。
2.3 遷移學習訓練
從頭訓練一個神經網絡需要耗費大量的時間和算力，因此常使用遷移學習的方法以提升深度學習效率，即使用模型在大型數據集（如ImageNet）上進行預訓練，用得到的訓練參數來解決相應問題。遷移學習將數據分為源數據與目標數據，源數據通常為與研究任務無關的大樣本數據；目標數據則是與任務相關的小樣本數據。遷移學習就是基于源數據與現有模型，將共用知識用于現有任務中，以充分利用源數據來提高模型在目標數據上的性能[25]。通常低層特征的可遷移能力較佳，而高層特征則呈現出與深度學習任務相關的特性，需要在現有任務上重新訓練。因此，本文采用低層凍結、高層訓練的遷移策略，將ResNet50前兩個殘差層參數與結構凍結，作為低層睡眠各時期特征辨識部分，后兩個殘差層參數進行隨機初始化后，使用經預處理的EEG數據進行訓練，用于學習不同睡眠階段的深度特征。本文設計的遷移學習訓練結構如圖4所示。
圖4
遷移學習訓練結構
Figure4.
Structure of transfer learning training
3 分期實驗及結果分析
為驗證本文所提出的自動睡眠分期算法的可靠性，在硬件設置為圖形處理單元RTX 2080Ti（NVIDIA Inc，美國）、內存32 GB的支持下，使用基于符號數學系統Tensorflow 2.0（Google Inc，美國）框架的計算機編程軟件Python 3.70（Python Software Foundation，美國），進行相關的分期實驗。
綜合現有硬件平臺性能及多輪訓練的效果，實驗設置每輪訓練批大小為32，學習率為0.001，采用適應性矩估計（adaptive moment estimation，Adam）加快收斂速度，損失函數使用交叉熵損失函數。
3.1 實驗條件
3.1.1 實驗數據
本文使用復雜生理信號研究資源網站（Research Resource for Complex Physiologic Signals，PhysioNet）公開可用的歐洲數據格式存儲的睡眠數據庫拓展版（Sleep-European Data Format Database Expanded，Sleep-EDFx）[26]進行實驗。選取數據集中16人共30條單通道（Fpz-Cz）EEG數據，刪去無效信號片段，并只保留入睡前半個小時至清醒后半個小時內的數據。經處理后各時期樣本數與總樣本數如表2所示。
表2
各時期樣本數量與總數量
Table2.
Number of samples in each period and total number
3.1.2 評價指標
為了便于對模型性能進行有效驗證，并與其他同類型研究成果進行對比，本文采用準確率（accuracy，Acc）、精確率（precision rate，PR）、召回率（recall，RE）和F1分數（F1 Score，F1）這些指標用于評估模型性能，采用混淆矩陣用于分析算法效果。
3.2 結果與討論
3.2.1 組合實驗
本實驗構建CV領域常用的神經網絡模型LeNet-5、AlexNet、VGG16以及InceptionV3與本文算法進行對比。除LeNet-5因模型簡單外，其余模型皆可在ImageNet數據集上加載預訓練模型。因此，本文采用與ResNet50相同的遷移學習方法，構建了TL-AlexNet、TL-VGG16、TL-InceptionV3、TL-SDResNet50四個遷移學習模型以及LeNet-5模型進行分期實驗。為了驗證本文構建模型的優越性，結合上述分期模型與CWT、HHT、STFT-Kaiser、STFT-Hann、ST、WVD時頻分析方法，在相同的實驗設置條件下進行訓練與測試，得到的實驗結果如圖5所示。
圖5
不同時頻分析方法在不同模型上的訓練結果比較
Figure5.
Comparison of training results of different time-frequency analysis methods on various models
可以看出，本文提出的TL-SDResNet50模型無論基于何種時頻分析方法，都能得到較好的分期準確率，性能優于所選基于深度學習的對比模型。基于CWT時頻分析法的不同模型分期結果如表3所示。LeNet-5與TL-AlexNet模型因同屬于“淺層”網絡，盡管訓練時間較短，但其對EEG的特征提取能力有限。而與同屬深層網絡的TL-VGG16、TL-InceptionV3相比，本文提出的TL-SDResNet50大幅度縮短了深層網絡所需的訓練時間，能夠快速地進行自動睡眠分期任務。
表3
基于CWT的不同模型實驗結果對比
Table3.
Comparison of experimental results of different models based on CWT
3.2.2 結果對比及混淆矩陣
為驗證上述實驗中TL-SDResNet分期模型的可靠性，圖6顯示了由專業醫師手動評估與TL-SDResNet對部分睡眠過程預測的對比結果，這表明本文算法具有良好的睡眠辨識能力，能夠作為實際情況下的自動睡眠分期方法使用。
圖6
專家評估與TL-SDResNet分期結果對比
Figure6.
Comparison between expert evaluation and TL-SDResNet staging results
進一步驗證模型的性能，對實驗結果進行深度分析。表4所示為TL-SDResNet的分期結果。可以看出，TL-SDResNet在對不同睡眠階段的預測中，都能夠取得較好的辨識效果。除N1期受限于樣本數量不足，模型對其他睡眠時期評估得到的F1均能達到90%左右。
表4
TL-SDResNet模型的混淆矩陣及性能指標
Table4.
Confusion matrix and performance index of TL-SDResNet model
3.2.3 與其他算法的對比
將采用同一數據集的自動睡眠分期算法與TL-SDResNet算法的分期結果進行對比，如表5[10, 27-29]所示。表中包含了基于機器學習與深度學習的不同自動睡眠分期模型，其中文獻[28]提出的深度睡眠網絡屬于睡眠分期領域的經典模型，文獻[29]基于遷移學習將擠壓網絡預訓練模型應用到睡眠分期中。根據對比結果，本文提出的TL-SDResNet分期準確率為87.95%，本文方法相較于其他模型的分類準確率均有所提高，且各時期的F1也有不同程度的提升。
表5
本文提出的自動睡眠分期算法與其他分類算法的比較
Table5.
Comparison between the automatic sleep staging algorithm proposed in this paper and other classification algorithms
4 結論
本文提出了一種基于遷移學習的隨機深度殘差網絡自動睡眠分期算法。該算法利用CWT從單通道腦電數據中提取時頻特征，將其轉換為時頻譜圖作為模型的輸入。在使用經ImageNet數據集上預訓練的ResNet50網絡的基礎上，利用隨機深度優化ResNet，提取深層特征并進行分類。通過組合實驗對比以及相關文獻結論對比的方法，表明了本文所提出模型在自動睡眠分類的準確度與綜合性能上均具有一定優勢，能夠為睡眠障礙的改善、睡眠過程的監督以及睡眠疾病的治療等提供行之有效的輔助工具。
本文使用的Sleep-EDFx數據集中單通道EEG數據經等時間劃分為30 s一段后，因人體睡眠過程本身所具有的特點，導致W期較多、N1期較少，造成了類不平衡問題，會對睡眠分期帶來一定的影響。下一步將對本算法及數據集進行進一步改進，利用數據平衡方法提升數據質量，從而開展進一步的實驗與研究。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：田蘊郅負責方法設計與實驗、數據收集與分析，以及撰寫論文；周強、李婉指導方法理論和實驗設計，以及指導論文撰寫。
