核與輻射突發事件發生后，在體電子順磁共振（in-vivo EPR）方法可對傷員輻射劑量進行現場、快速、無創檢測。對in-vivo EPR波譜分析，目前常采用人工標記峰值并計算信號強度，存在工作量大、受主觀因素干擾等問題。本研究利用支持向量機（SVM）技術，建立了一種對in-vivo EPR波譜進行自動分類識別的方法，可批量自動識別并篩除in-vivo EPR測量時因振動、牙表面水干擾而產生的無效波譜。本研究利用遺傳算法優化神經網絡（GA-BPNN）建立了一種波譜分析方法，可對in-vivo EPR波譜中的輻射誘發信號進行自動識別，并預測傷員受到輻射的劑量。實驗結果表明，本研究建立的SVM和GA-BPNN波譜處理方法可有效地完成in-vivo EPR波譜自動分類和劑量預測，可滿足核事故應急劑量評估的需求。本研究探索了機器學習方法在電子順磁共振（EPR）波譜處理領域的應用，提高了EPR波譜處理的智能化水平，為提升大批量EPR波譜處理效率提供了支撐。
引用本文： 熊廣為, 陳博, 馬蕾, 賈瀧澎, 陳淑年, 吳可, 寧靜, 朱斌, 郭俊旺. 基于機器學習的在體電子順磁共振波譜分類和輻射劑量預測方法研究. 生物醫學工程學雜志, 2024, 41(5): 995-1002. doi: 10.7507/1001-5515.202302015 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
核與輻射突發事件可能導致在場人員受到電離輻射威脅，進而產生健康損傷；快速估算人員受照射劑量是核應急醫學救援中確定救治方案和合理規劃醫療資源配置的關鍵。利用電子順磁共振（electron paramagnetic resonance，EPR）技術測量牙齒是一種經典的輻射劑量評估方法，具有準確、輻射特異性好等優勢，在體（in-vivo）EPR技術（in-vivo EPR）進一步解決了取樣測量牙齒EPR劑量的難題，在核應急醫學救援中具有良好的應用前景。
EPR波譜處理包括擬合、尋峰標記、信號強度計算等流程[1-2]，最終樣品受到的輻射劑量根據信號強度和經驗曲線獲得。針對EPR波譜處理和輻射劑量評估方法，已有研究者開展了系列相關研究：Bordi等[3]在非線性最小二乘法擬合的基礎上使用列文伯格—馬夸爾特（Levenberg-Marquardt）算法對劑量進行估算；Chumak等[4]和D’Oca等[5]設計了附加劑量技術；Zhumadilov等[6]和Parlato等[7]采用了非線性最小二乘法擬合以及特定函數疊加的方法；Beshir[8]和Kwona等[9]探究了多次擬合方法在劑量評估中的效果；Vanhaelewyn等[10]采用了最大似然估計對EPR波譜進行反卷積和劑量評估；Grün等[11]研究了自然譜法用于信號強度評估；Ivanov等[12]提出了一種基于已知輻射誘發信號（radiation induced signal，RIS）強度的波譜擬合未知劑量波譜的方法；Boyau等[13]開發了基于貝葉斯框架的波譜擬合程序；Ciesielski等[14]和Zou等[15]在EPR波譜處理中利用標準樣品二價錳離子（Mn2+）校正、本底波譜信號扣除、體積校正等方法進一步提高了劑量評估的準確性。上述研究中對EPR波譜處理和劑量評估的方法以擬合或者解析算法為主，目標是將EPR波譜轉化為具有某種特征的曲線，并對特征值進行計算。該方法的優勢是波譜解析性高、結果解釋性好，但也存在波譜處理過程復雜、對特征識別具有人為主觀性偏差等問題。in-vivo EPR波譜數量較大，且因被測人員生理振動、在體樣品含水等特殊干擾導致無效波譜較多[16-20]，用經典擬合或解析方法或將面臨時間開銷過大、波譜選擇和處理中主觀因素干擾多等問題。
支持向量機（support vector machines，SVM）是基于統計學習理論的一種有監督學習的機器學習方法，若在建模前結合主成分分析（principal component analysis，PCA）、線性判別分析（linear discriminant analysis，LDA）等降維方法，可很大程度上解決“維度災難”和“過擬合”的問題，現已廣泛應用于聚類分析、模式識別、機械故障診斷等領域中[21-23]。本研究采用該方法對大量in-vivo EPR波譜進行分類識別，解決在體測量中生理振動、樣品含水等因素影響產生的無效波譜分類問題。反向傳播神經網絡（back propagation neural network，BPNN）具有較高的適應性、魯棒性和擬合能力，通常應用于數據預測及分類識別中，本研究利用遺傳算法（genetic algorithm，GA）優化BPNN的方法（GA-BPNN）對in-vivo EPR波譜進行分析處理，以實現輻射劑量預測，解決EPR波譜中輻射誘發信號特征點選取主觀性強、人工計算速度慢等問題。
1 問題模型
1.1 in-vivo EPR波譜篩選分類
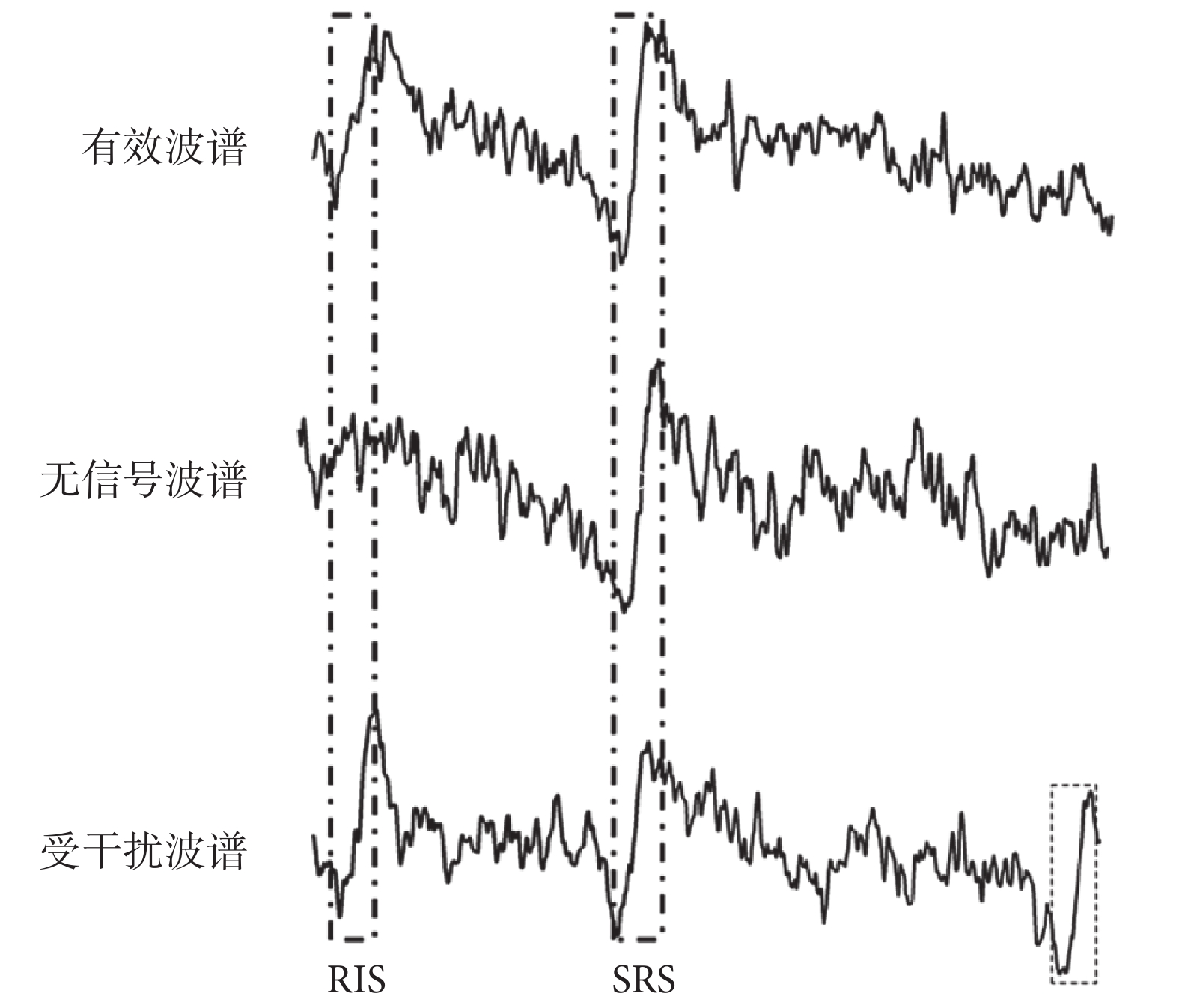
in-vivo EPR測量樣品常為牙齒，受在體測量過程中生理振動、牙表面水等因素影響，波譜中經常會引入對輻射誘發信號產生顯著干擾的噪聲，嚴重情況下可能造成波譜失效。將in-vivo EPR波譜分為有效波譜（記為“0”類）、無信號波譜（記為“1”類）、受干擾波譜（記為“2”類），各類波譜示意如圖1所示。有效波譜具有典型的RIS，可用于輻射劑量評估；人工判別方法是在波譜特定位置（圖1中RIS框位置）觀察是否有特征RIS。無信號波譜中無RIS，其原因是樣品放置不到位或測量參數不當；對此，人工判別方法的依據是波譜特定位置不存在特征RIS。受干擾波譜是in-vivo EPR測量過程中因振動、牙表面水等因素引入顯著干擾噪音的波譜，導致無法進行輻射劑量預測；其人工判別方法是在波譜中尋找是否存在除RIS和標樣信號（standard reference signal，SRS）外的其他強信號。in-vivo EPR測量采用多次短時間重復掃描的策略，故波譜數量較大，依賴人工篩選有效波譜時間代價較大。為提高波譜篩選分類效率，本研究采用SVM方法進行波譜篩選分類。波譜分類準確率如式（1）和式（2）所示：
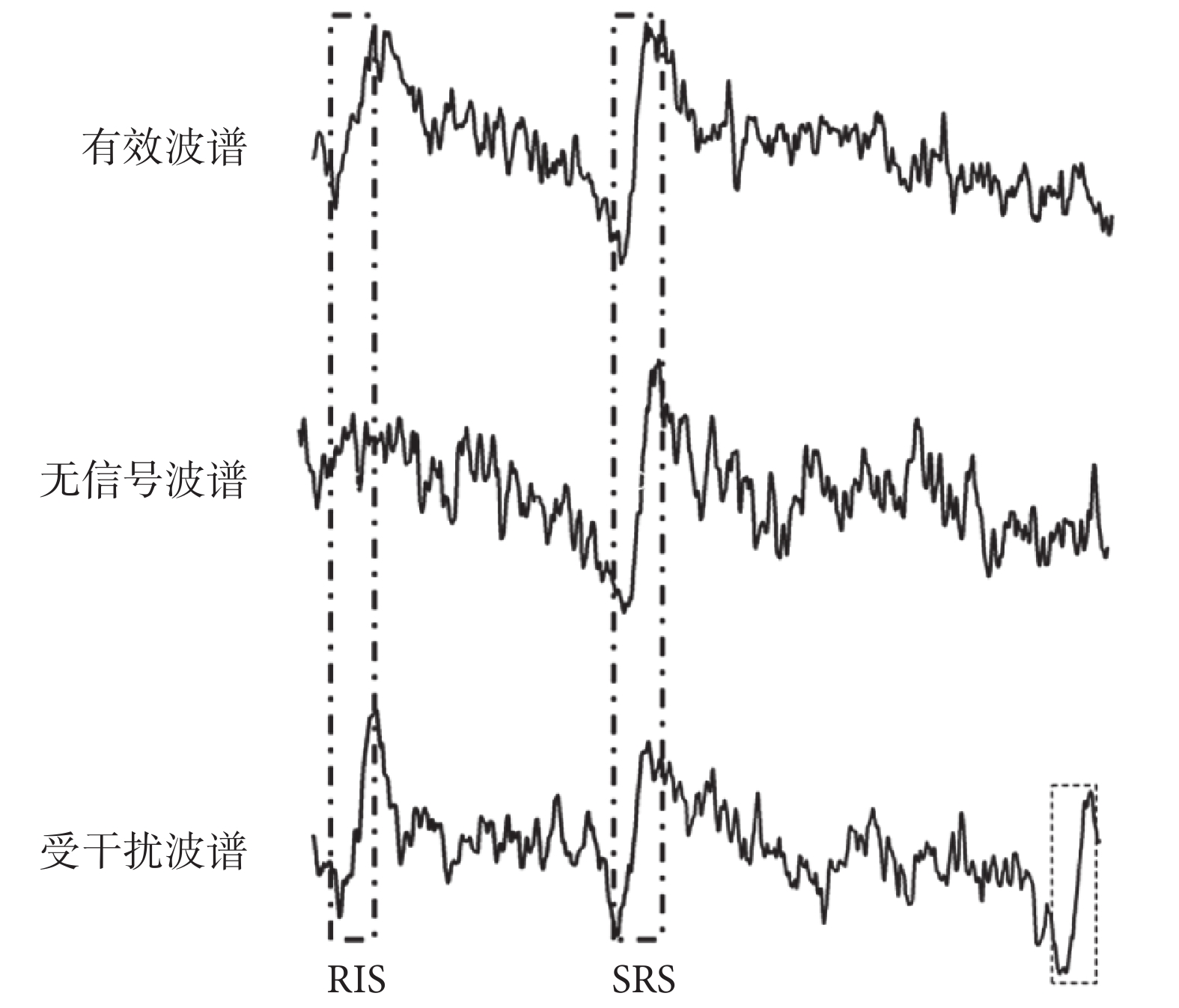圖1
in-vivo EPR波譜分類示意圖
Figure1.
Schematic diagram of in-vivo EPR spectral classification
 |
 |
上式中，Ti為第i類波譜分類的準確率，TPi為第i類波譜分類準確的個數，FPij為將第i類波譜誤分類為第j類波譜的個數，T總為所有波譜分類的準確率。
1.2 輻射劑量預測
牙齒樣品輻射劑量與EPR波譜RIS強度正相關，一般采用人工尋峰的方式確定EPR波譜中的波峰和波谷，波峰波谷相對差值作為RIS強度，結合實驗室建立的曲線推導計算樣品受到照射的劑量。在波譜數量較多時，該方法時間開銷較大且尋峰過程有一定的主觀性。本研究采用GA-BPNN的方法對批量波譜進行輻射劑量預測，預測劑量與實際劑量的相對誤差如式（3）所示：
 |
式中，E為實際劑量與預測劑量的相對誤差，Dr為實際照射劑量，Ds為預測劑量。
1.3 EPR波譜處理流程
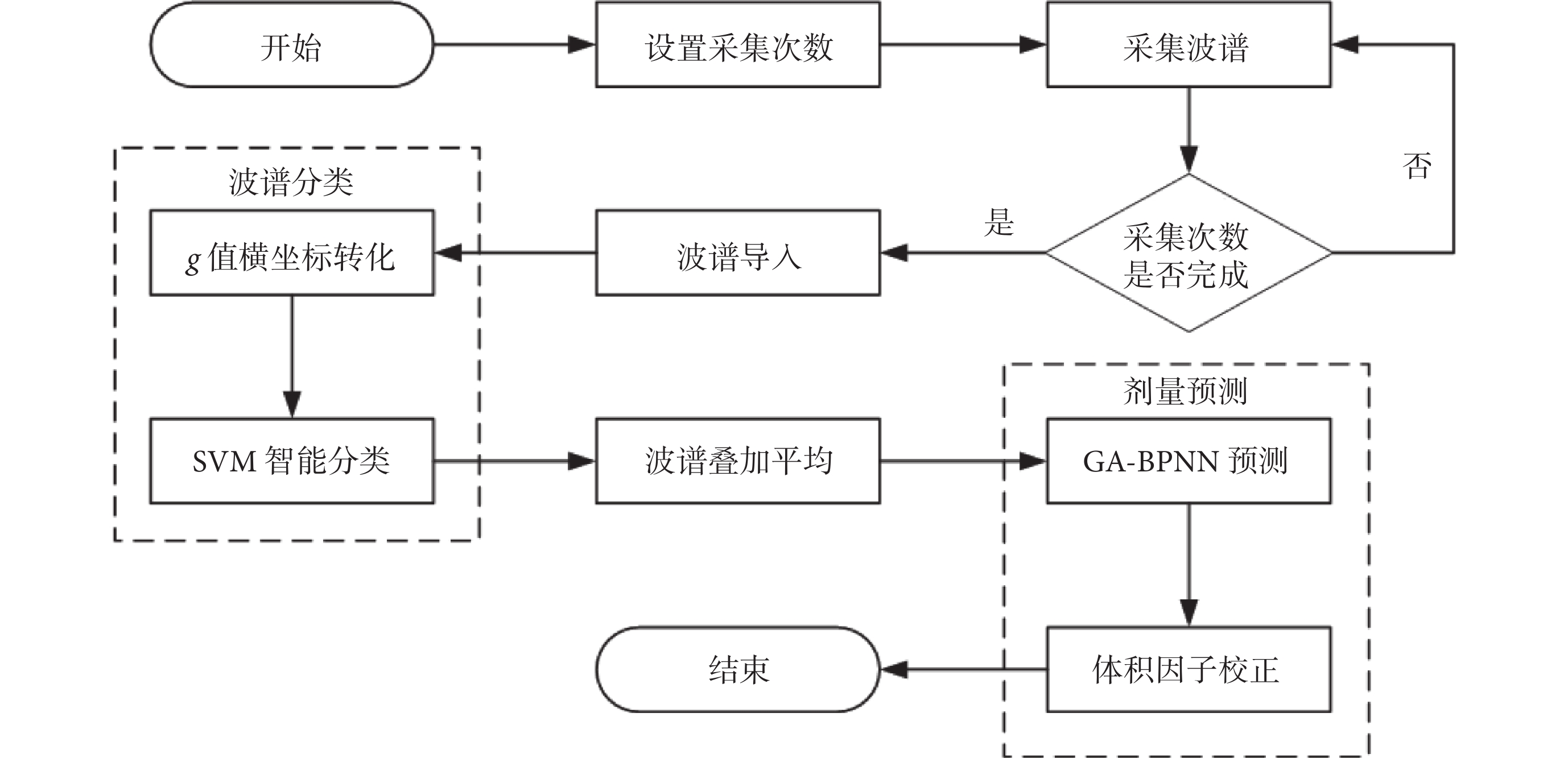
EPR波譜處理過程包括：① 采集一定數量的EPR波譜；② 導入波譜并顯示；③ 將EPR波譜轉化為以g值為橫坐標的標準化波譜；④ 利用SVM算法進行波譜分類；⑤ 將分類后的有效波譜疊加平均處理；⑥ 利用GA-BPNN算法進行初步輻射劑量預測；⑦ 對預測輻射劑量進行體積因子校正。EPR波譜處理流程如圖2所示。
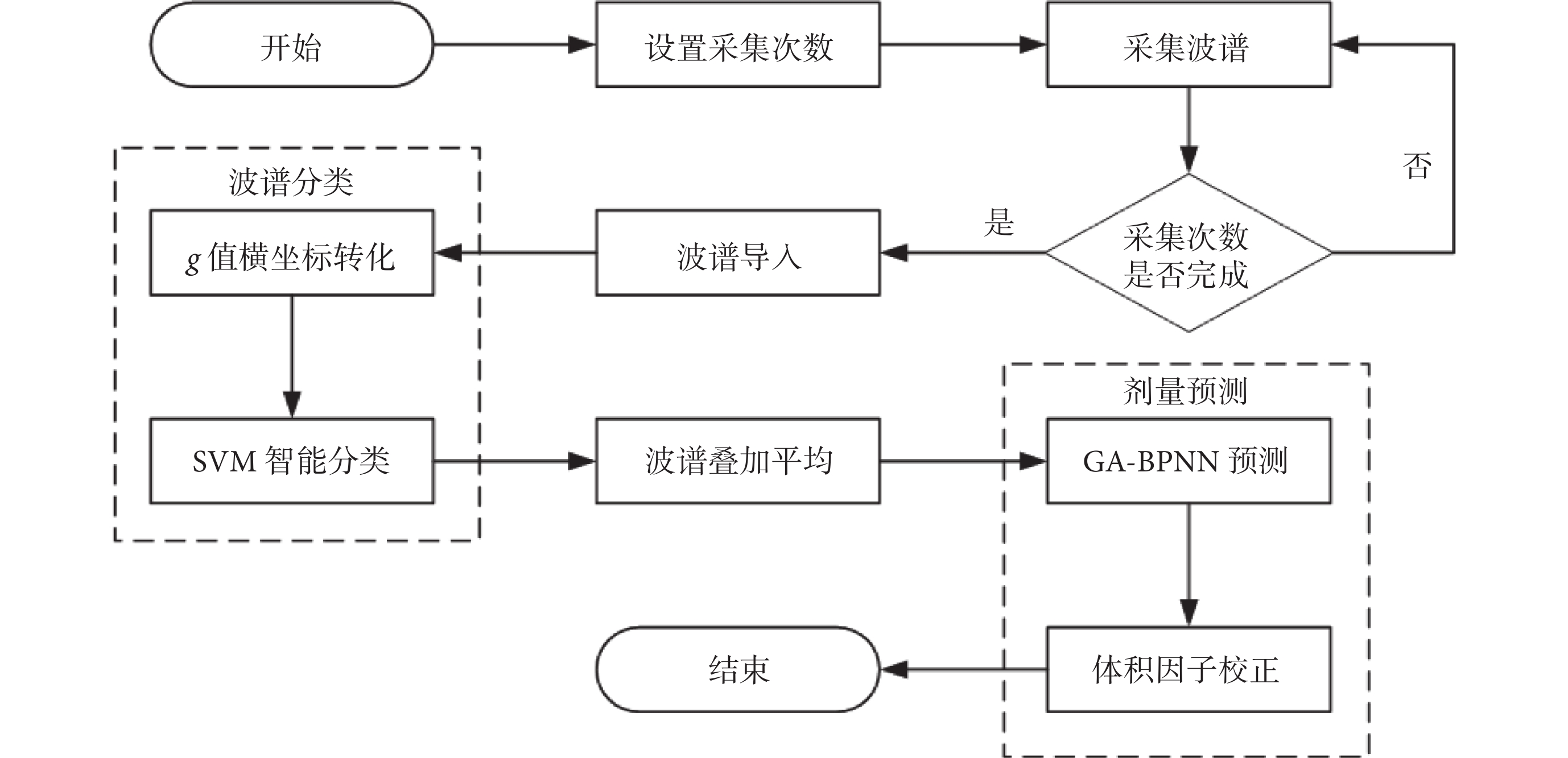圖2
EPR波譜分類和劑量預測流程圖
Figure2.
Flow chart of EPR spectrum classification and dose prediction
2 in-vivo EPR波譜分類方法
2.1 SVM分類模型的建立
為便于SVM和GA-BPNN處理，首先將波譜轉化為橫坐標為g值的標準化波譜，每個波譜選取860個離散數據點。利用PCA方法降低至121個維度，再利用“核函數”將121個維度的in-vivo EPR波譜數據映射到更高維度的空間中，構建一個離訓練樣本點支持集最遠的超平面，從而實現對in-vivo EPR波譜分類。由于in-vivo EPR波譜的形態復雜，可能會存在一些錯分的現象，其求解目標表達式如式（4）所示[24-25]：
 |
式（4）中，w為權重向量，wT為權重向量的轉置，b為偏置向量，c為懲罰系數，ξi為松弛變量，φ為從低維到高維的映射函數，xi為某個EPR波譜數據，yi為某個EPR波譜的標簽。
2.2 波譜分類模型訓練的分析
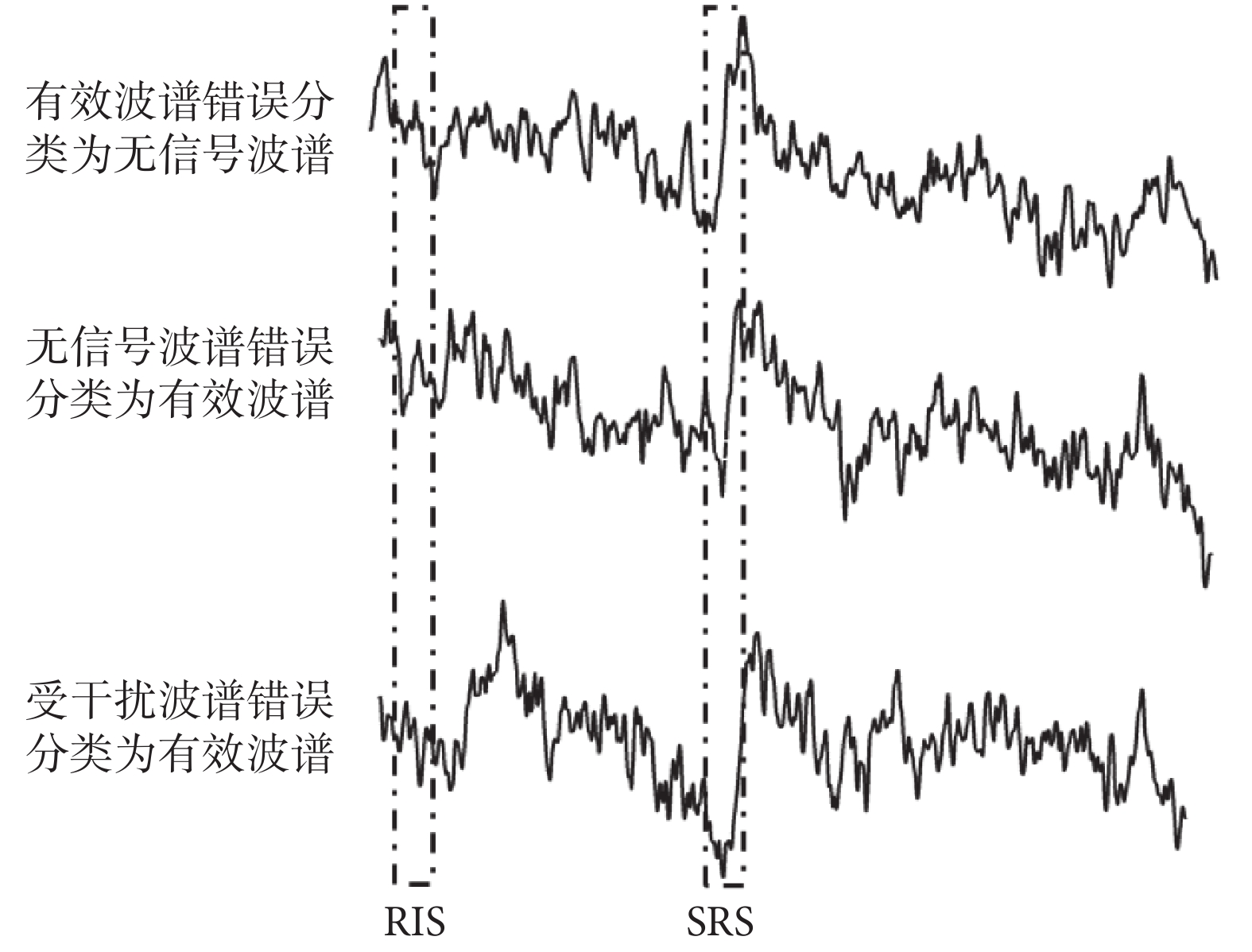
采集一批in-vivo EPR波譜用于波譜分類模型的建立，具體采集方法見后文4.1小節，本次共采集到7 356組波譜數據，其中前5 880組波譜用作模型訓練，剩余波譜用作效果驗證。本文選取高斯核函數作為SVM核函數，根據經驗將SVM的c值設置為1，γ值為特征值的倒數即1/860[26]。實驗驗證所得SVM分類的準確率如表1所示，總準確率為97.56%。對于波譜分類錯誤的示例如圖3所示：當輻射劑量較小時，有效波譜可能被錯誤地分類為無信號波譜；當本底信號過強時，無信號波譜可能被分類為有效波譜；當干擾信號疊加在RIS信號上時，受干擾波譜可能被錯誤地分類為有效波譜。
表1
SVM波譜分類模型驗證的分類準確率
Table1.
Screening accuracy of SVM spectral classification model verification
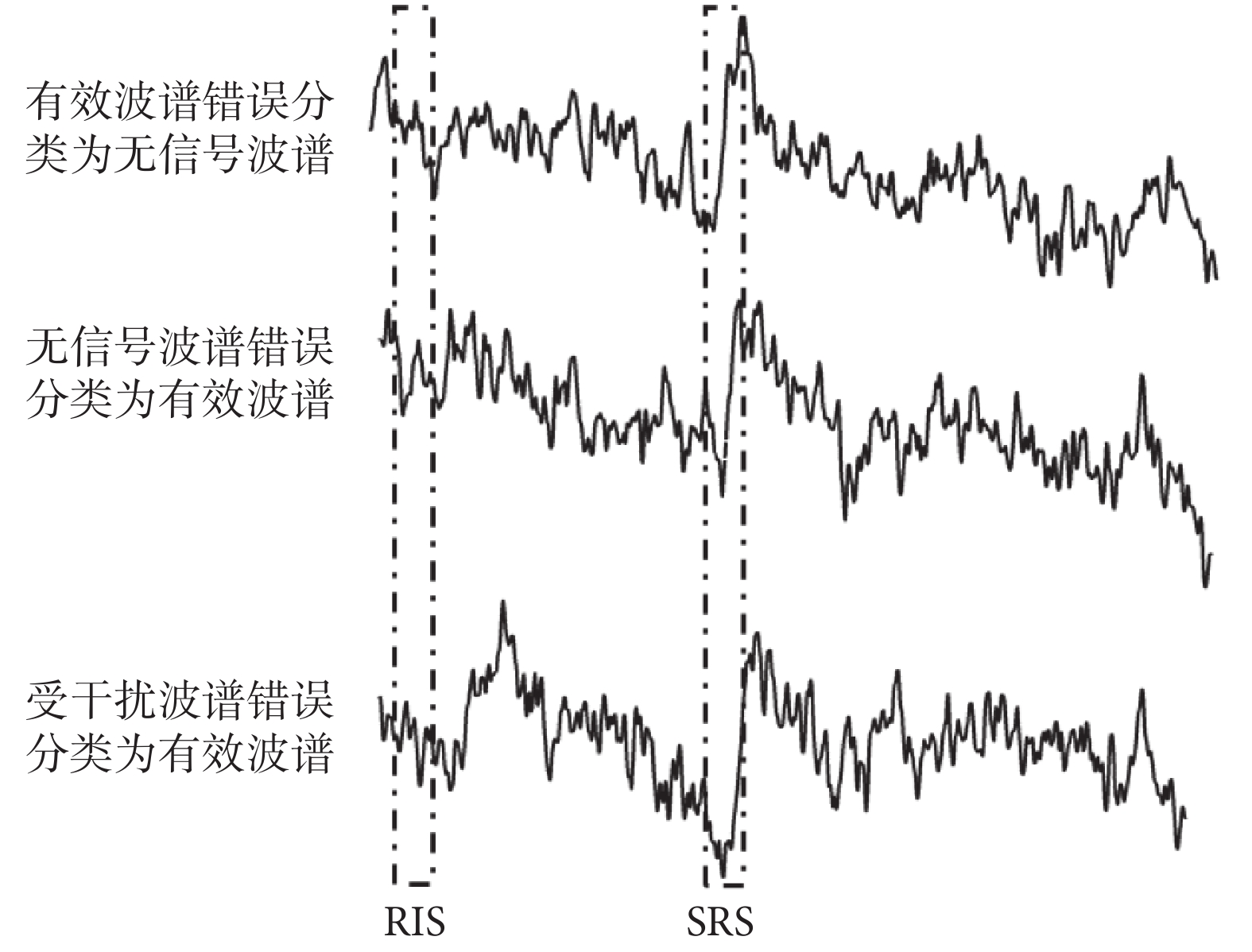圖3
In-vivo EPR波譜分類錯誤示例
Figure3.
The example of incorrect classification of in-vivo EPR spectrum
3 輻射劑量預測方法
3.1 GA-BPNN模型
BPNN由輸入層、隱藏層和輸出層構成，其關系如式（5）所示，網絡可不斷地通過反向傳播來降低損失函數值，使自變量和因變量之間的關系無限逼近一個函數[27]。在利用in-vivo EPR波譜開展輻射劑量預測過程中，輸入層為若干波譜數據，輸出層為輻射劑量。
 |
 |
 |
式中，Ii為神經網絡的輸入層，xi為某個EPR波譜數據，n為輸入層中節點的數量；Hj為網絡的隱藏層，f1為隱藏層激活函數，w1ij為輸入層到隱藏層之間的權值，b1j為輸入層到隱藏層之間的閾值，m為隱藏層中節點的數量；Ok為網絡的輸出層，f2為輸出層激活函數，w2jk為隱藏層到輸出層之間的權值，hj為隱藏層的輸出值，b2k為隱藏層到輸出層之間的閾值，l為輸出層中節點的數量。
針對BPNN在訓練過程可能存在難以確定網絡最優的權值和閾值、收斂時間過長及容易陷入局部尋優等問題[28]，本研究采用GA方法來進一步優化BPNN。采用浮點數編碼的形式對染色體進行編碼，以變異操作對染色體中的某些基因進行變動，從而不斷產生新的個體更新迭代，如式（6）所示：
 |
式中，Cij為第i個染色體的第j個基因，Cmax為基因Cij的上界，Cmin為基因Cij的下界，r為隨機數，
，e為迭代次數，Emax為算法的最大迭代次數。
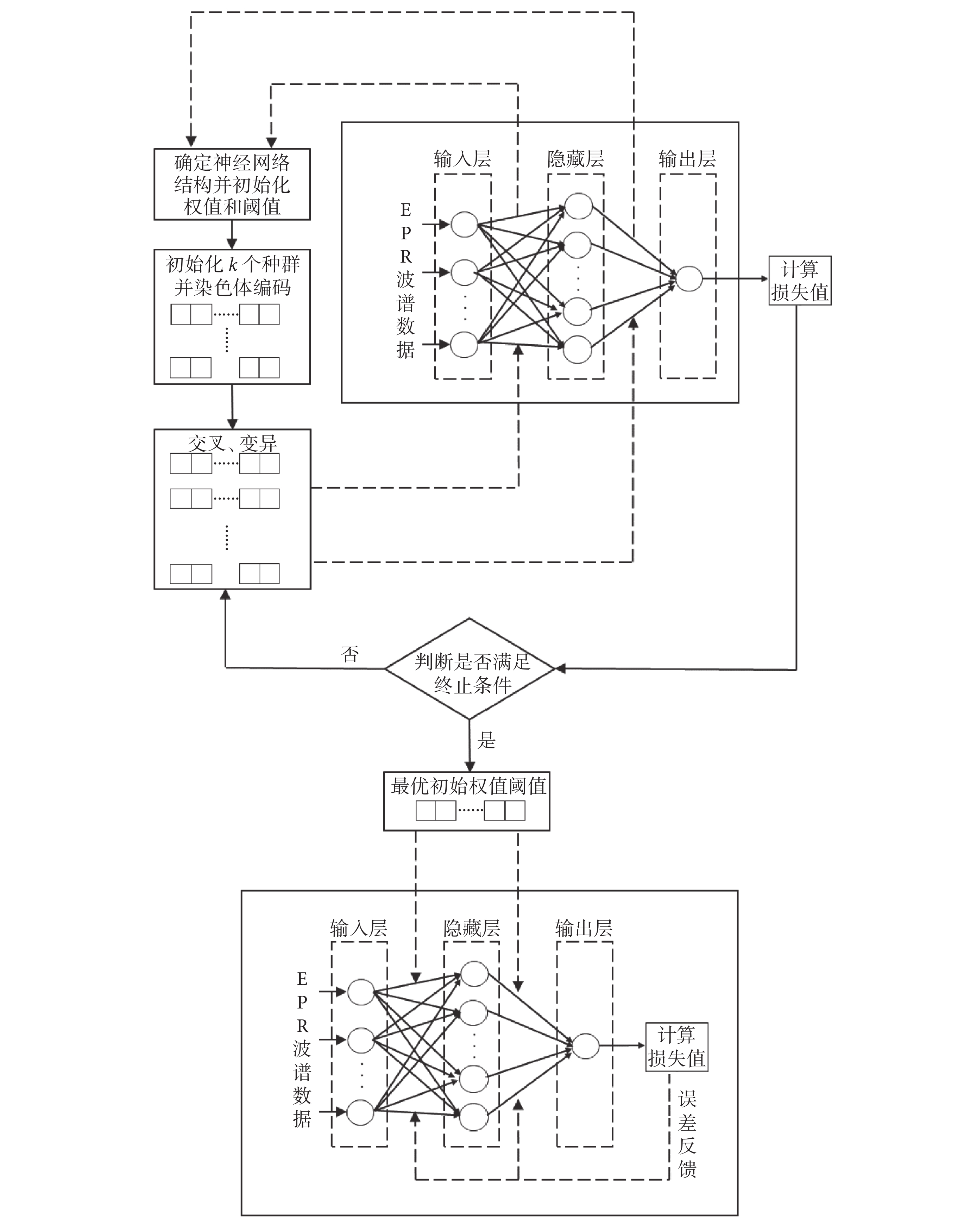
GA-BPNN可分為GA和BPNN兩部分，其核心算法為：將BPNN層與層之間的權值和閾值作為GA中的“種群個體”并進行編碼，通過GA的遺傳操作不斷產生新的種群，最后以神經網絡中的損失值作為評判標準計算個體適應度，從而獲得最優的初始化權值和閾值并帶到網絡中進行訓練[29-30]。最終輻射劑量預測GA-BPNN方法的具體結構如圖4所示。
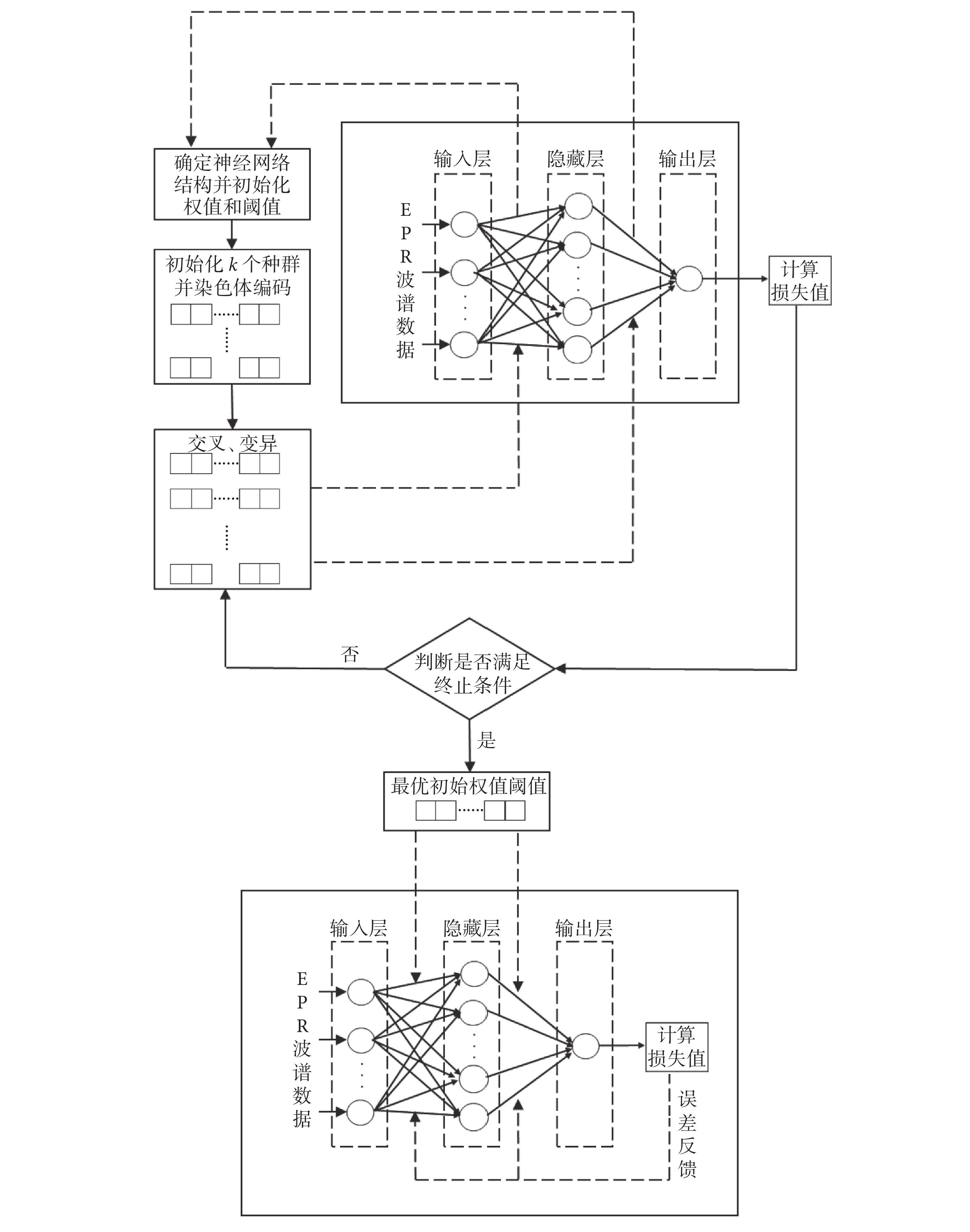圖4
輻射劑量預測GA-BPNN結構圖
Figure4.
Structure chart of GA-BPNN of radiation dose prediction
3.2 牙齒樣品和體積因子校正
本研究中，被測量樣品為33顆沒有明顯蛀齲、金屬填充物或牙髓移植治療史的門牙，牙齒樣品采集于301醫院、307醫院和重慶醫科大學附屬第一醫院。該牙齒作為常規醫療的一部分被移除且被做了匿名處理的患者廢棄，本課題組與患者無任何接觸，不涉及取牙處理，故不涉及倫理審批；且所有牙齒樣品經上述醫院授權，可用于本研究。
由于被測樣品形狀各異，導致樣品進入諧振腔的有效體積存在一定差異，因此需根據樣品被測體積對RIS強度進行校正，具體流程為：首先利用三維掃描儀（Aoralscan 3，先臨三維，中國）對樣品三維形態進行掃描，以獲取牙齒樣品的三維模型；然后，根據牙齒和諧振腔探測口三維模型確定樣品和諧振腔的裝配關系，計算牙齒進入諧振腔探測口部分的樣品體積；最后，根據樣品體積進行RIS校正。
3.3 劑量預測模型訓練
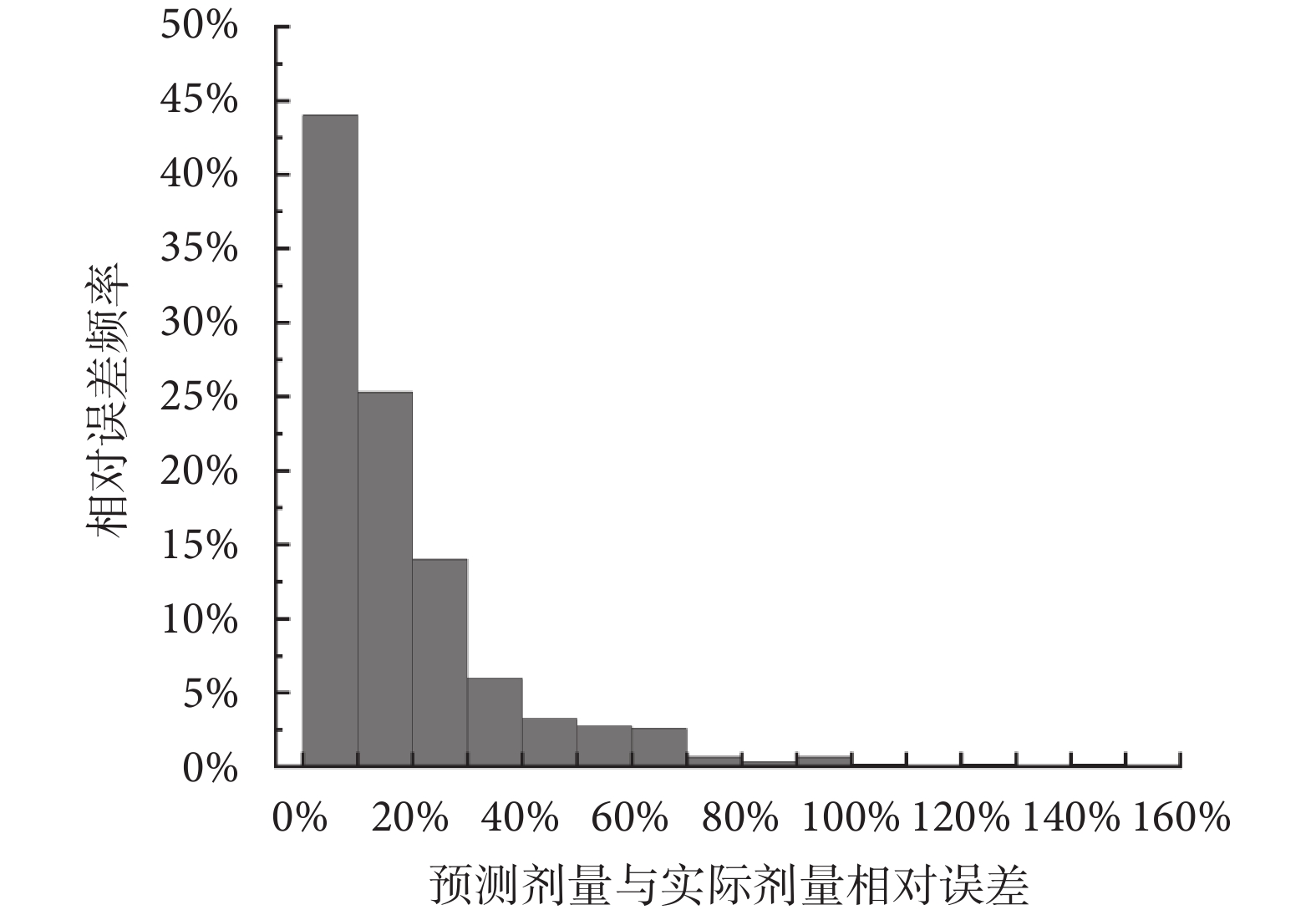
將單個in-vivo EPR波譜數據的860個離散值作為神經網絡輸入層，隱藏層個數為32，采用線性整流函數（rectified linear unit，Relu）作為神經網絡隱藏層和輸出層之間的激活函數，最小平方誤差作為損失函數，GA的種群規模大小為50，交叉概率為0.8，變異概率為0.005，迭代次數為50，最小平方誤差的倒數作為適應度函數。采用循環交叉的方式，對輻照劑量為0~10 Gy的牙齒樣品進行EPR波譜采集，共獲得3 056組波譜數據，其中2 435組用作訓練，其余621組用作驗證。采用上述方法進行8 000次訓練，經測試利用GA-BPNN方法的預測劑量與實際照射劑量相對誤差如圖5所示，預測劑量與實際照射劑量的平均相對誤差為18.6%，其中相對誤差在25%以內的有482組。
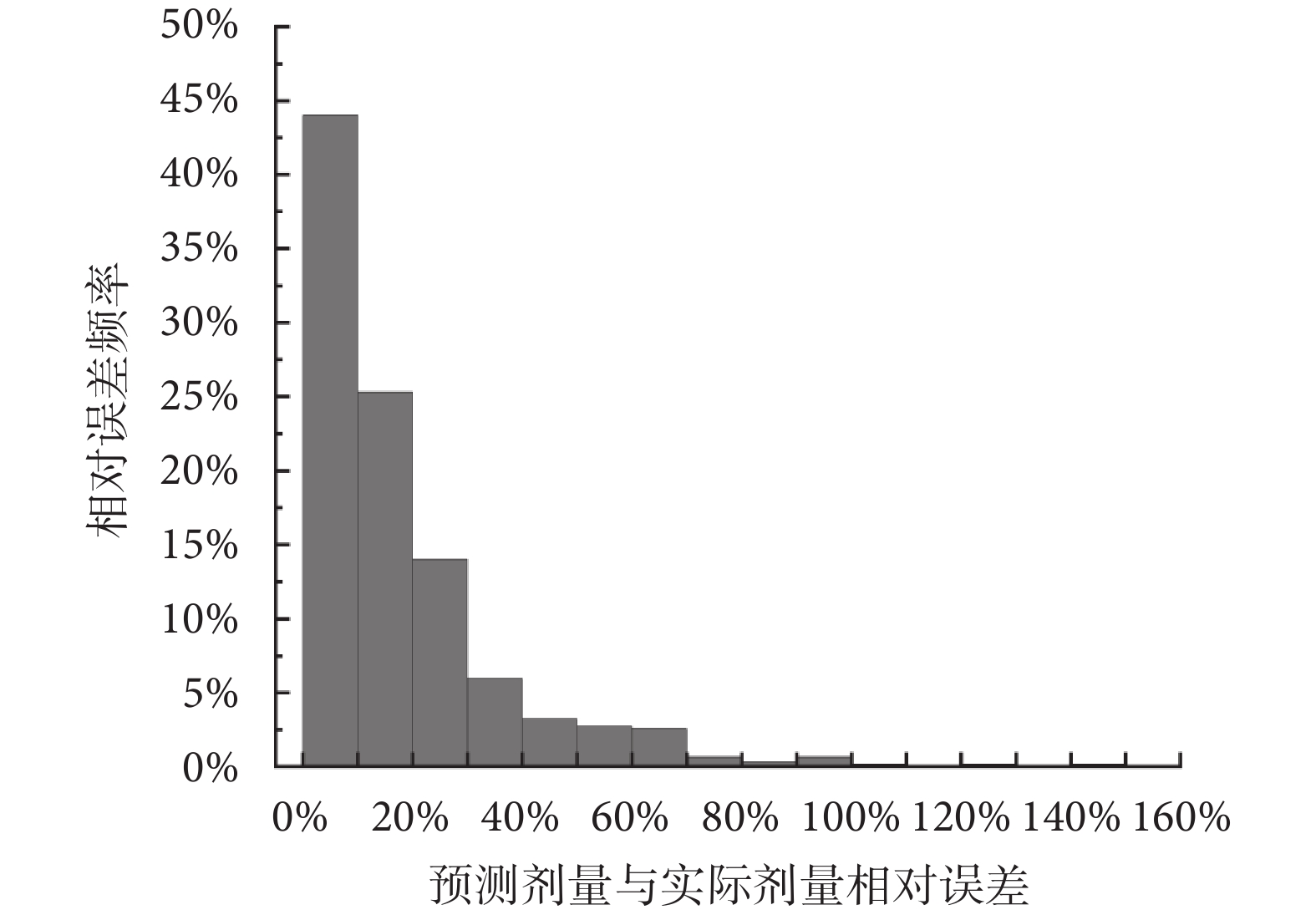圖5
GA-BPNN訓練后輻射劑量預測的相對誤差
Figure5.
Relative error of radiation dose prediction after GA-BPNN training
4 實驗驗證
4.1 牙齒EPR測量
將33顆牙齒樣品分為11組，每組3顆，利用鈷-60（Co-60）放射源分別給予0~10 Gy劑量γ射線照射，組間距為1 Gy。然后，將照射后的牙齒樣品固定于口腔模型進行模擬in-vivo EPR測量實驗。本研究牙齒樣品和模擬in-vivo EPR測量情況，如圖6所示。
圖6
牙齒樣品與模擬in-vivo EPR檢測方法
Figure6.
Tooth samples and the method of simulated in-vivo EPR spectroscopy
4.2 基于SVM的波譜分類效果
再次采集一批in-vivo EPR波譜用于波譜分類效果評價，本次共采集到2 935組in-vivo EPR波譜人工分類，其中有效波譜975組，受干擾波譜1 004組，無信號波譜956組。對2 935組in-vivo EPR波譜利用上文所述SVM方法進行分類，結果如表2所示，總準確率為99.45%。
表2
基于SVM方法的波譜分類結果
Table2.
Spectral classification results based on SVM method
4.3 GA-BPNN的劑量預測效果
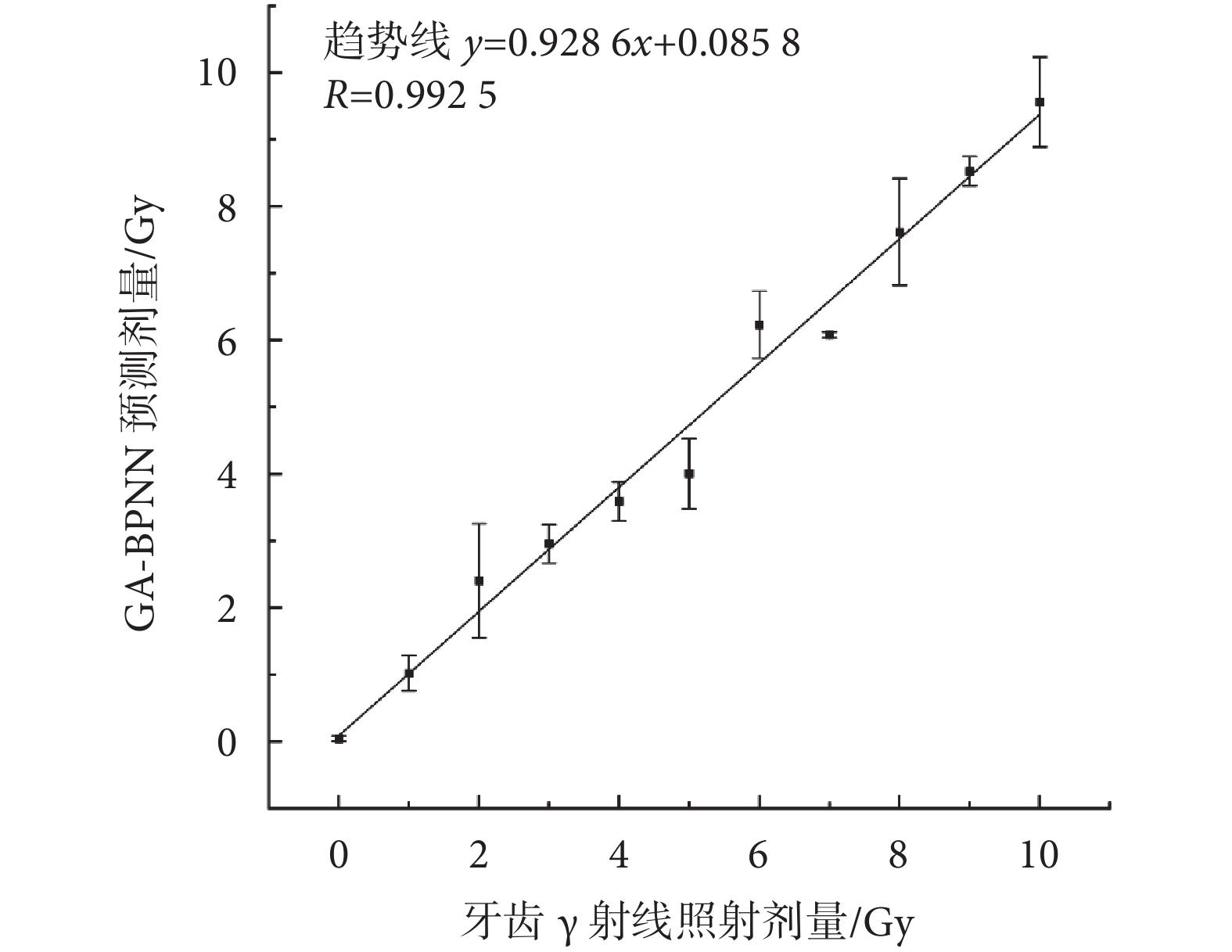
利用上文所述GA-BPNN方法對不同劑量照射牙齒樣品的波譜進行處理和劑量預測，預測劑量與實際照射劑量關系曲線如圖7所示，其中擬合趨勢線公式為y = 0.928 6x + 0.085 8，線性相關系數R為0.992 5，平均相對誤差為11.9%。
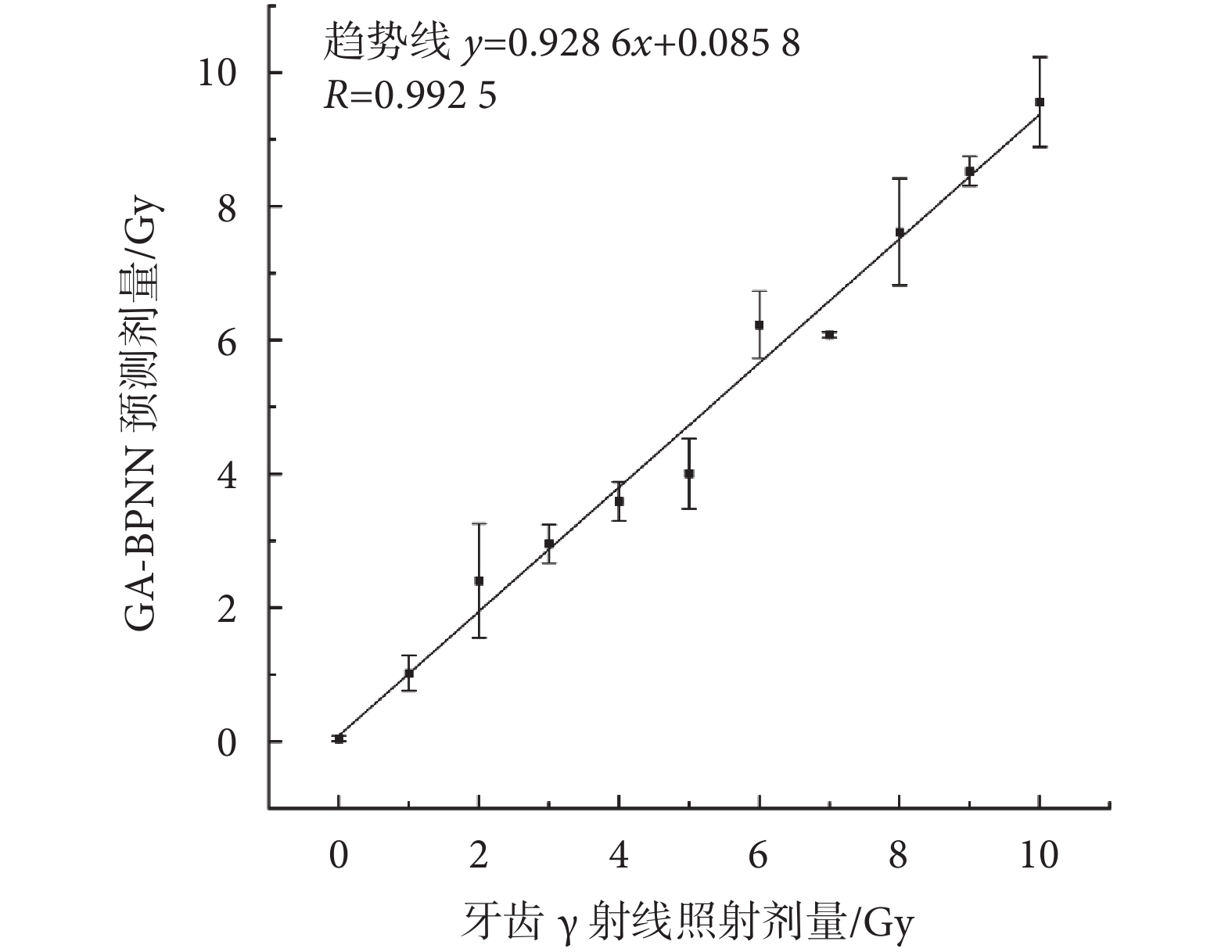圖7
基于GA-BPNN方法的預測劑量與實際照射劑量的關系曲線
Figure7.
Relationship curve between the predicted dose by GA-BPNN method against actual radiation dose
5 結論
in-vivo EPR測量用于核應急醫學救援傷員劑量評估具有輻射特異性高、劑量響應較高等優勢，對于核輻射傷員劑量評估具有良好的潛在應用價值。in-vivo EPR測量中所采用的短時間單次掃描、多次重復累加平均的工作模式會產生數量較多的波譜，同時受到生理振動和牙表面水等干擾因素的影響，往往產生較大比例的無信號波譜和受干擾波譜。依賴人工方法對上述波譜進行篩選分類和劑量評估往往存在時間開銷大、主觀性強等問題。本研究利用SVM方法建立了in-vivo EPR波譜篩選分類方法，實現了從大量波譜中快速自動篩選出具有輻射誘發信號的波譜；同時利用GA-BPNN建立了自動化的輻射劑量預測方法。經實驗驗證，SVM的分類準確率和GA-BPNN的劑量預測誤差可滿足in-vivo EPR波譜分析的需求，同時提高了波譜分析效率，降低了人為因素導致的誤差。該方法不僅適用于in-vivo EPR波譜處理，經適當優化后也可用于通用EPR波譜處理。與現有的解析類波譜分析方法相比，本研究實現了將機器學習新方法用于EPR波譜分析領域，是對機器學習方法的創新應用和對波譜處理方法的拓展延伸。
本文實驗中，發現個別牙齒劑量預測的相對誤差較大，可能與該牙齒本底信號較強、波譜橫坐標g值未對齊以及體積因子校正帶來的誤差有關。下一步算法優化主要包括波譜自動整備（g值對齊）、復雜測量條件下機器學習方法的優化改進，以及改良針對通用樣品EPR波譜處理的神經網絡方法等方面，以期進一步提高EPR劑量評估效率并擴展機器學習方法在EPR波譜處理領域的應用。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：熊廣為，實現了本文所述算法、開展了EPR測量實驗；陳博，優化了算法設計，補充完善了文章；馬蕾、賈瀧澎，參加了EPR測量實驗；陳淑年，修改完善了論文；吳可，設計了in-vivo EPR測量系統；寧靜，指導了γ射線照射和劑量計算；朱斌，指導了神經網絡算法設計；郭俊旺，搭建了in-vivo EPR測量系統，指導了實驗和數據處理，指導寫作和修改了論文。
0 引言
核與輻射突發事件可能導致在場人員受到電離輻射威脅，進而產生健康損傷；快速估算人員受照射劑量是核應急醫學救援中確定救治方案和合理規劃醫療資源配置的關鍵。利用電子順磁共振（electron paramagnetic resonance，EPR）技術測量牙齒是一種經典的輻射劑量評估方法，具有準確、輻射特異性好等優勢，在體（in-vivo）EPR技術（in-vivo EPR）進一步解決了取樣測量牙齒EPR劑量的難題，在核應急醫學救援中具有良好的應用前景。
EPR波譜處理包括擬合、尋峰標記、信號強度計算等流程[1-2]，最終樣品受到的輻射劑量根據信號強度和經驗曲線獲得。針對EPR波譜處理和輻射劑量評估方法，已有研究者開展了系列相關研究：Bordi等[3]在非線性最小二乘法擬合的基礎上使用列文伯格—馬夸爾特（Levenberg-Marquardt）算法對劑量進行估算；Chumak等[4]和D’Oca等[5]設計了附加劑量技術；Zhumadilov等[6]和Parlato等[7]采用了非線性最小二乘法擬合以及特定函數疊加的方法；Beshir[8]和Kwona等[9]探究了多次擬合方法在劑量評估中的效果；Vanhaelewyn等[10]采用了最大似然估計對EPR波譜進行反卷積和劑量評估；Grün等[11]研究了自然譜法用于信號強度評估；Ivanov等[12]提出了一種基于已知輻射誘發信號（radiation induced signal，RIS）強度的波譜擬合未知劑量波譜的方法；Boyau等[13]開發了基于貝葉斯框架的波譜擬合程序；Ciesielski等[14]和Zou等[15]在EPR波譜處理中利用標準樣品二價錳離子（Mn2+）校正、本底波譜信號扣除、體積校正等方法進一步提高了劑量評估的準確性。上述研究中對EPR波譜處理和劑量評估的方法以擬合或者解析算法為主，目標是將EPR波譜轉化為具有某種特征的曲線，并對特征值進行計算。該方法的優勢是波譜解析性高、結果解釋性好，但也存在波譜處理過程復雜、對特征識別具有人為主觀性偏差等問題。in-vivo EPR波譜數量較大，且因被測人員生理振動、在體樣品含水等特殊干擾導致無效波譜較多[16-20]，用經典擬合或解析方法或將面臨時間開銷過大、波譜選擇和處理中主觀因素干擾多等問題。
支持向量機（support vector machines，SVM）是基于統計學習理論的一種有監督學習的機器學習方法，若在建模前結合主成分分析（principal component analysis，PCA）、線性判別分析（linear discriminant analysis，LDA）等降維方法，可很大程度上解決“維度災難”和“過擬合”的問題，現已廣泛應用于聚類分析、模式識別、機械故障診斷等領域中[21-23]。本研究采用該方法對大量in-vivo EPR波譜進行分類識別，解決在體測量中生理振動、樣品含水等因素影響產生的無效波譜分類問題。反向傳播神經網絡（back propagation neural network，BPNN）具有較高的適應性、魯棒性和擬合能力，通常應用于數據預測及分類識別中，本研究利用遺傳算法（genetic algorithm，GA）優化BPNN的方法（GA-BPNN）對in-vivo EPR波譜進行分析處理，以實現輻射劑量預測，解決EPR波譜中輻射誘發信號特征點選取主觀性強、人工計算速度慢等問題。
1 問題模型
1.1 in-vivo EPR波譜篩選分類
in-vivo EPR測量樣品常為牙齒，受在體測量過程中生理振動、牙表面水等因素影響，波譜中經常會引入對輻射誘發信號產生顯著干擾的噪聲，嚴重情況下可能造成波譜失效。將in-vivo EPR波譜分為有效波譜（記為“0”類）、無信號波譜（記為“1”類）、受干擾波譜（記為“2”類），各類波譜示意如圖1所示。有效波譜具有典型的RIS，可用于輻射劑量評估；人工判別方法是在波譜特定位置（圖1中RIS框位置）觀察是否有特征RIS。無信號波譜中無RIS，其原因是樣品放置不到位或測量參數不當；對此，人工判別方法的依據是波譜特定位置不存在特征RIS。受干擾波譜是in-vivo EPR測量過程中因振動、牙表面水等因素引入顯著干擾噪音的波譜，導致無法進行輻射劑量預測；其人工判別方法是在波譜中尋找是否存在除RIS和標樣信號（standard reference signal，SRS）外的其他強信號。in-vivo EPR測量采用多次短時間重復掃描的策略，故波譜數量較大，依賴人工篩選有效波譜時間代價較大。為提高波譜篩選分類效率，本研究采用SVM方法進行波譜篩選分類。波譜分類準確率如式（1）和式（2）所示：
圖1
in-vivo EPR波譜分類示意圖
Figure1.
Schematic diagram of in-vivo EPR spectral classification
|
|
上式中，Ti為第i類波譜分類的準確率，TPi為第i類波譜分類準確的個數，FPij為將第i類波譜誤分類為第j類波譜的個數，T總為所有波譜分類的準確率。
1.2 輻射劑量預測
牙齒樣品輻射劑量與EPR波譜RIS強度正相關，一般采用人工尋峰的方式確定EPR波譜中的波峰和波谷，波峰波谷相對差值作為RIS強度，結合實驗室建立的曲線推導計算樣品受到照射的劑量。在波譜數量較多時，該方法時間開銷較大且尋峰過程有一定的主觀性。本研究采用GA-BPNN的方法對批量波譜進行輻射劑量預測，預測劑量與實際劑量的相對誤差如式（3）所示：
|
式中，E為實際劑量與預測劑量的相對誤差，Dr為實際照射劑量，Ds為預測劑量。
1.3 EPR波譜處理流程
EPR波譜處理過程包括：① 采集一定數量的EPR波譜；② 導入波譜并顯示；③ 將EPR波譜轉化為以g值為橫坐標的標準化波譜；④ 利用SVM算法進行波譜分類；⑤ 將分類后的有效波譜疊加平均處理；⑥ 利用GA-BPNN算法進行初步輻射劑量預測；⑦ 對預測輻射劑量進行體積因子校正。EPR波譜處理流程如圖2所示。
圖2
EPR波譜分類和劑量預測流程圖
Figure2.
Flow chart of EPR spectrum classification and dose prediction
2 in-vivo EPR波譜分類方法
2.1 SVM分類模型的建立
為便于SVM和GA-BPNN處理，首先將波譜轉化為橫坐標為g值的標準化波譜，每個波譜選取860個離散數據點。利用PCA方法降低至121個維度，再利用“核函數”將121個維度的in-vivo EPR波譜數據映射到更高維度的空間中，構建一個離訓練樣本點支持集最遠的超平面，從而實現對in-vivo EPR波譜分類。由于in-vivo EPR波譜的形態復雜，可能會存在一些錯分的現象，其求解目標表達式如式（4）所示[24-25]：
|
式（4）中，w為權重向量，wT為權重向量的轉置，b為偏置向量，c為懲罰系數，ξi為松弛變量，φ為從低維到高維的映射函數，xi為某個EPR波譜數據，yi為某個EPR波譜的標簽。
2.2 波譜分類模型訓練的分析
采集一批in-vivo EPR波譜用于波譜分類模型的建立，具體采集方法見后文4.1小節，本次共采集到7 356組波譜數據，其中前5 880組波譜用作模型訓練，剩余波譜用作效果驗證。本文選取高斯核函數作為SVM核函數，根據經驗將SVM的c值設置為1，γ值為特征值的倒數即1/860[26]。實驗驗證所得SVM分類的準確率如表1所示，總準確率為97.56%。對于波譜分類錯誤的示例如圖3所示：當輻射劑量較小時，有效波譜可能被錯誤地分類為無信號波譜；當本底信號過強時，無信號波譜可能被分類為有效波譜；當干擾信號疊加在RIS信號上時，受干擾波譜可能被錯誤地分類為有效波譜。
表1
SVM波譜分類模型驗證的分類準確率
Table1.
Screening accuracy of SVM spectral classification model verification
圖3
In-vivo EPR波譜分類錯誤示例
Figure3.
The example of incorrect classification of in-vivo EPR spectrum
3 輻射劑量預測方法
3.1 GA-BPNN模型
BPNN由輸入層、隱藏層和輸出層構成，其關系如式（5）所示，網絡可不斷地通過反向傳播來降低損失函數值，使自變量和因變量之間的關系無限逼近一個函數[27]。在利用in-vivo EPR波譜開展輻射劑量預測過程中，輸入層為若干波譜數據，輸出層為輻射劑量。
|
|
|
式中，Ii為神經網絡的輸入層，xi為某個EPR波譜數據，n為輸入層中節點的數量；Hj為網絡的隱藏層，f1為隱藏層激活函數，w1ij為輸入層到隱藏層之間的權值，b1j為輸入層到隱藏層之間的閾值，m為隱藏層中節點的數量；Ok為網絡的輸出層，f2為輸出層激活函數，w2jk為隱藏層到輸出層之間的權值，hj為隱藏層的輸出值，b2k為隱藏層到輸出層之間的閾值，l為輸出層中節點的數量。
針對BPNN在訓練過程可能存在難以確定網絡最優的權值和閾值、收斂時間過長及容易陷入局部尋優等問題[28]，本研究采用GA方法來進一步優化BPNN。采用浮點數編碼的形式對染色體進行編碼，以變異操作對染色體中的某些基因進行變動，從而不斷產生新的個體更新迭代，如式（6）所示：
|
式中，Cij為第i個染色體的第j個基因，Cmax為基因Cij的上界，Cmin為基因Cij的下界，r為隨機數，，e為迭代次數，Emax為算法的最大迭代次數。
GA-BPNN可分為GA和BPNN兩部分，其核心算法為：將BPNN層與層之間的權值和閾值作為GA中的“種群個體”并進行編碼，通過GA的遺傳操作不斷產生新的種群，最后以神經網絡中的損失值作為評判標準計算個體適應度，從而獲得最優的初始化權值和閾值并帶到網絡中進行訓練[29-30]。最終輻射劑量預測GA-BPNN方法的具體結構如圖4所示。
圖4
輻射劑量預測GA-BPNN結構圖
Figure4.
Structure chart of GA-BPNN of radiation dose prediction
3.2 牙齒樣品和體積因子校正
本研究中，被測量樣品為33顆沒有明顯蛀齲、金屬填充物或牙髓移植治療史的門牙，牙齒樣品采集于301醫院、307醫院和重慶醫科大學附屬第一醫院。該牙齒作為常規醫療的一部分被移除且被做了匿名處理的患者廢棄，本課題組與患者無任何接觸，不涉及取牙處理，故不涉及倫理審批；且所有牙齒樣品經上述醫院授權，可用于本研究。
由于被測樣品形狀各異，導致樣品進入諧振腔的有效體積存在一定差異，因此需根據樣品被測體積對RIS強度進行校正，具體流程為：首先利用三維掃描儀（Aoralscan 3，先臨三維，中國）對樣品三維形態進行掃描，以獲取牙齒樣品的三維模型；然后，根據牙齒和諧振腔探測口三維模型確定樣品和諧振腔的裝配關系，計算牙齒進入諧振腔探測口部分的樣品體積；最后，根據樣品體積進行RIS校正。
3.3 劑量預測模型訓練
將單個in-vivo EPR波譜數據的860個離散值作為神經網絡輸入層，隱藏層個數為32，采用線性整流函數（rectified linear unit，Relu）作為神經網絡隱藏層和輸出層之間的激活函數，最小平方誤差作為損失函數，GA的種群規模大小為50，交叉概率為0.8，變異概率為0.005，迭代次數為50，最小平方誤差的倒數作為適應度函數。采用循環交叉的方式，對輻照劑量為0~10 Gy的牙齒樣品進行EPR波譜采集，共獲得3 056組波譜數據，其中2 435組用作訓練，其余621組用作驗證。采用上述方法進行8 000次訓練，經測試利用GA-BPNN方法的預測劑量與實際照射劑量相對誤差如圖5所示，預測劑量與實際照射劑量的平均相對誤差為18.6%，其中相對誤差在25%以內的有482組。
圖5
GA-BPNN訓練后輻射劑量預測的相對誤差
Figure5.
Relative error of radiation dose prediction after GA-BPNN training
4 實驗驗證
4.1 牙齒EPR測量
將33顆牙齒樣品分為11組，每組3顆，利用鈷-60（Co-60）放射源分別給予0~10 Gy劑量γ射線照射，組間距為1 Gy。然后，將照射后的牙齒樣品固定于口腔模型進行模擬in-vivo EPR測量實驗。本研究牙齒樣品和模擬in-vivo EPR測量情況，如圖6所示。
圖6
牙齒樣品與模擬in-vivo EPR檢測方法
Figure6.
Tooth samples and the method of simulated in-vivo EPR spectroscopy
4.2 基于SVM的波譜分類效果
再次采集一批in-vivo EPR波譜用于波譜分類效果評價，本次共采集到2 935組in-vivo EPR波譜人工分類，其中有效波譜975組，受干擾波譜1 004組，無信號波譜956組。對2 935組in-vivo EPR波譜利用上文所述SVM方法進行分類，結果如表2所示，總準確率為99.45%。
表2
基于SVM方法的波譜分類結果
Table2.
Spectral classification results based on SVM method
4.3 GA-BPNN的劑量預測效果
利用上文所述GA-BPNN方法對不同劑量照射牙齒樣品的波譜進行處理和劑量預測，預測劑量與實際照射劑量關系曲線如圖7所示，其中擬合趨勢線公式為y = 0.928 6x + 0.085 8，線性相關系數R為0.992 5，平均相對誤差為11.9%。
圖7
基于GA-BPNN方法的預測劑量與實際照射劑量的關系曲線
Figure7.
Relationship curve between the predicted dose by GA-BPNN method against actual radiation dose
5 結論
in-vivo EPR測量用于核應急醫學救援傷員劑量評估具有輻射特異性高、劑量響應較高等優勢，對于核輻射傷員劑量評估具有良好的潛在應用價值。in-vivo EPR測量中所采用的短時間單次掃描、多次重復累加平均的工作模式會產生數量較多的波譜，同時受到生理振動和牙表面水等干擾因素的影響，往往產生較大比例的無信號波譜和受干擾波譜。依賴人工方法對上述波譜進行篩選分類和劑量評估往往存在時間開銷大、主觀性強等問題。本研究利用SVM方法建立了in-vivo EPR波譜篩選分類方法，實現了從大量波譜中快速自動篩選出具有輻射誘發信號的波譜；同時利用GA-BPNN建立了自動化的輻射劑量預測方法。經實驗驗證，SVM的分類準確率和GA-BPNN的劑量預測誤差可滿足in-vivo EPR波譜分析的需求，同時提高了波譜分析效率，降低了人為因素導致的誤差。該方法不僅適用于in-vivo EPR波譜處理，經適當優化后也可用于通用EPR波譜處理。與現有的解析類波譜分析方法相比，本研究實現了將機器學習新方法用于EPR波譜分析領域，是對機器學習方法的創新應用和對波譜處理方法的拓展延伸。
本文實驗中，發現個別牙齒劑量預測的相對誤差較大，可能與該牙齒本底信號較強、波譜橫坐標g值未對齊以及體積因子校正帶來的誤差有關。下一步算法優化主要包括波譜自動整備（g值對齊）、復雜測量條件下機器學習方法的優化改進，以及改良針對通用樣品EPR波譜處理的神經網絡方法等方面，以期進一步提高EPR劑量評估效率并擴展機器學習方法在EPR波譜處理領域的應用。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：熊廣為，實現了本文所述算法、開展了EPR測量實驗；陳博，優化了算法設計，補充完善了文章；馬蕾、賈瀧澎，參加了EPR測量實驗；陳淑年，修改完善了論文；吳可，設計了in-vivo EPR測量系統；寧靜，指導了γ射線照射和劑量計算；朱斌，指導了神經網絡算法設計；郭俊旺，搭建了in-vivo EPR測量系統，指導了實驗和數據處理，指導寫作和修改了論文。
