深入了解步行過程中的下肢肌肉協作機制是提高神經肌肉功能障礙患者步態康復療效的關鍵。本文研究了步行速度的變化對下肢肌肉協同模式及肌肉功能網絡的影響。招募了8名健康受試者分別以三種不同速度在跑步機上執行步行任務,同步采集右下肢8塊肌肉的表面肌電信號(sEMG),通過非負矩陣分解(NNMF)方法提取肌肉協同模式,利用互信息(MI)方法分別構建alpha頻段(8~13 Hz)、beta頻段(14~30 Hz)和gamma頻段(31~60 Hz)肌肉功能網絡,引入復雜網絡分析方法量化不同網絡差異。肌肉協同分析提取到5個肌肉協同模式,步行速度的變化沒有改變肌肉協同的數量,但導致了肌肉權值的變化;肌肉網絡分析發現在同一速度下,高頻段具有更低的全局效率和聚類系數,隨著步行速度的增加,局部肌肉之間的連接強度增加。研究結果表明不同速度的步行運動存在不同的肌肉協同模式和肌肉功能網絡,本研究為探索不同步行速度下肌肉協同機制提供了新的視野,有望為神經肌肉功能障礙患者的步態功能評估提供理論支撐。
引用本文: 崔彩虹, 繆華聰, 梁鐵, 劉秀玲, 劉曉光. 基于表面肌電信號的不同步行速度下肌肉協同及肌肉功能網絡分析. 生物醫學工程學雜志, 2023, 40(5): 938-944. doi: 10.7507/1001-5515.202303065 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
0 引言
步行是人類日常生活中最基本的活動之一,而基于不同速度的步態研究被證實能夠為步態運動學分析、老年人認知功能預測和康復評估提供有效信息[1-3]。然而,迄今為止不同步行速度背后的神經機制依然不明。隨著非侵入式生理信號采集技術的發展,通過在皮膚表面放置電極記錄肌肉運動過程中產生的表面肌電圖(surface electromyography,sEMG),能夠在一定程度上反映神經肌肉的活動[4]。步行是一種復雜的運動過程,要求中樞神經系統(central nervous system,CNS)和多肌肉高度協調[5]。在此過程中,基于sEMG信號的肌肉協同和肌肉功能網絡的分析,可以有效反映中樞神經系統對肌肉的不同控制過程以及肌肉之間的協作模式。
步行運動涉及多塊下肢肌肉力矩整合和共同協調,這種整合、協調的過程稱為協同[6]。之前研究證實了神經肌肉系統通過共同激活肌肉群構建運動模塊,即肌肉協同作用,從而可以簡化神經系統對多個肌肉的控制[7]。對步行運動來說,中樞神經系統只需控制較少的運動模塊就能控制較多的運動單元和肌肉來實現人體的站立、邁步等動作。因此,廣大研究者針對步行過程中的下肢肌肉開展了肌肉協同分析。Serrancolí等[8]從人體行走任務的sEMG信號中提取了5個肌肉協同模式;Boonstra等[9]在人體站立條件下從下肢sEMG信號中提取到了4個肌肉協同模式;Barroso等[10]通過研究發現步行和騎自行車運動具有相似的肌肉協同模式。上述研究表明,基于sEMG信號可以有效提取步行運動的肌肉協同模式。
構建多肌肉之間的功能網絡是近年發展起來的一種分析肌間協同特性的新方法,旨在進一步解釋肌肉協同作用的神經輸入特性及其簡化運動控制的能力。肌肉網絡分析通過量化分解運動相關肌肉sEMG之間的功能連接,能夠識別由共同神經輸入調節的特定肌肉的頻率特征。相干性是目前用來評估肌肉之間功能耦合的主要方法。然而,sEMG信號是典型的非線性神經生理信號,線性的相干性方法在研究sEMG信號之間功能耦合上存在一定局限性[11]。基于信息論的互信息(mutual information,MI)能夠從復雜性角度有效量化信號間線性和非線性耦合,因此近年來被廣泛應用于構建sEMG信號間的功能網絡。陳玲玲等[12]利用互信息構建了肌肉功能網絡,并全面分析了外骨骼穿戴者的電生理空間分布情況和肌肉協調工作機制。Madeleine等[13]使用互信息方法量化了功能性任務時頸肩痛對肌肉功能連接的影響。上述研究表明,基于互信息方法量化肌肉功能網絡可為分析步行運動下肢的神經肌肉協調機制提供有價值的信息。
本文分析了不同步行速度下肢的肌肉協同模式,并使用互信息方法構建了alpha頻段(8~13 Hz)、beta頻段(14~30 Hz)和gamma頻段(31~60 Hz)的肌肉功能網絡,引入復雜網絡分析方法,探索了不同頻段不同步行速度下肌肉功能網絡拓撲結構的差異以及中樞神經系統對肌肉的協調控制模式。本研究將肌肉協同作用與肌肉功能網絡相結合,有助于發現肌間協同與耦合的內在關聯。本研究旨在為探索不同步行速度下肢肌肉協同機制提供新的視野,以期為神經肌肉功能障礙患者的步態功能評估提供理論支撐。
1 材料與方法
1.1 試驗設計
本研究一共招募8名無任何神經疾病史和運動損傷的健康受試者(男性,年齡21~25歲)參與試驗。所有受試者在試驗前均已知悉試驗步驟并簽署知情同意書。所有受試者在跑步機上以6、8、10 km/h的不同速度執行步行任務。每名受試者執行10組試驗,每組記錄至少10個完整步態周期的sEMG數據。在每組試驗間隙允許受試者休息5 min,以避免肌肉疲勞帶來的影響。本研究符合《赫爾辛基宣言》,并經河北大學附屬醫院倫理審查委員會批準(HDFY-LL-2020-091)。
1.2 數據采集
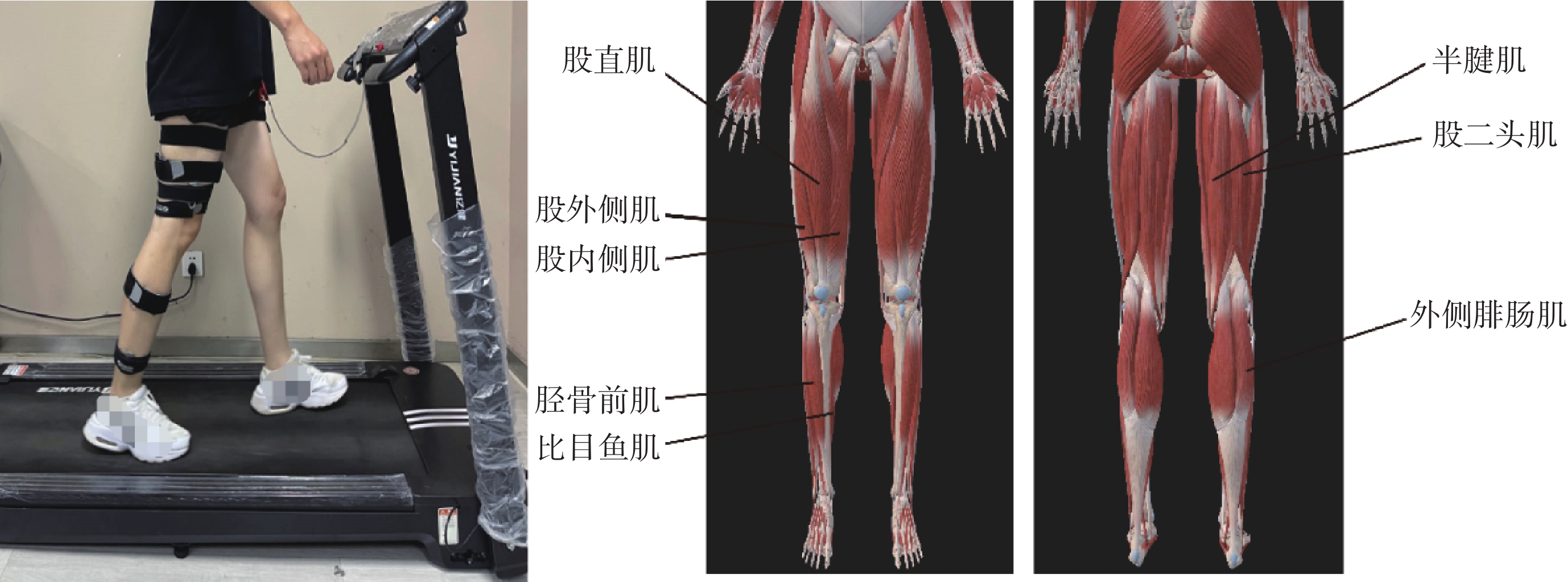
通過Noraxon無線肌電采集系統(美國Noraxon公司)采集任務中受試者右腿的股直肌(rectus femoris,RF)、股內側肌(vastus medialis,VM)、股外側肌(vastus lateralis,VL)、半腱肌(semitendinosus,ST)、股二頭肌(biceps femoris,BF)、脛骨前肌(tibialis anterior,TA)、外側腓腸肌(gastrocnemius,GM)和比目魚肌(soleus,SO)共8塊下肢肌肉位置的sEMG信號,以1 500 Hz的頻率采樣,實驗場景及肌肉位置如圖1所示。
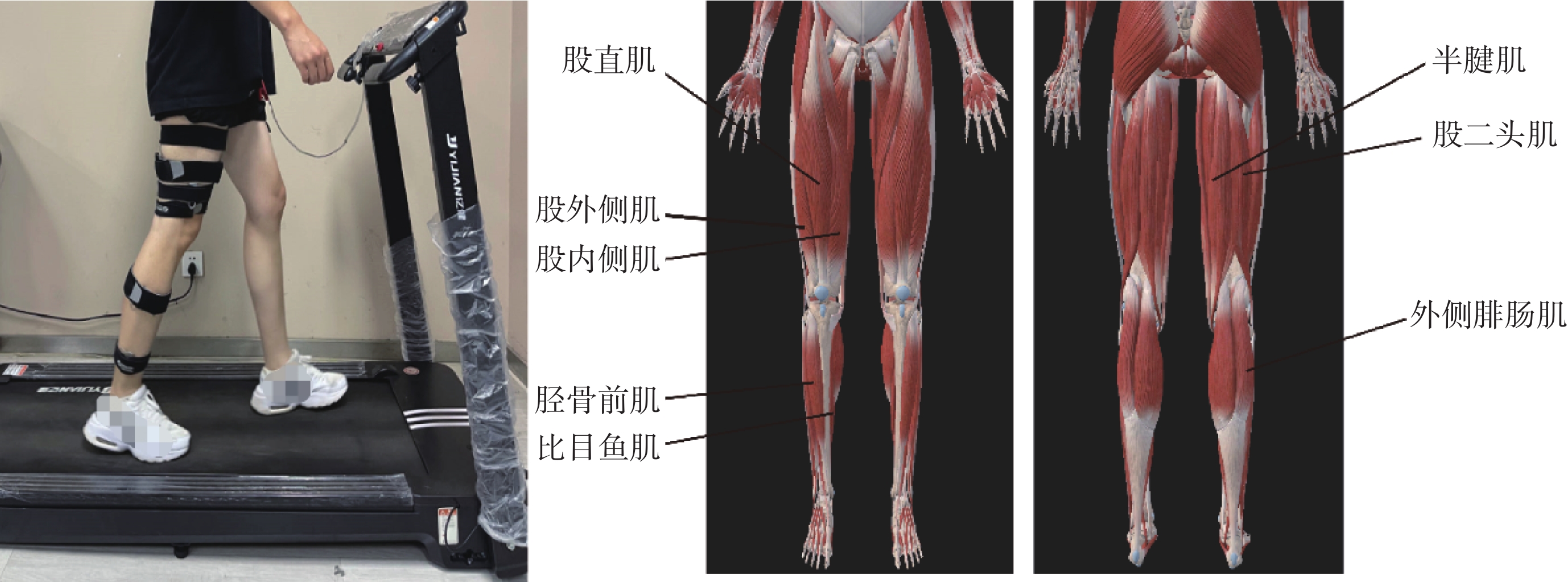 圖1
實驗場景及肌肉位置示意圖
Figure1.
Schematic diagram of the experimental scene and muscle positions
圖1
實驗場景及肌肉位置示意圖
Figure1.
Schematic diagram of the experimental scene and muscle positions
1.3 數據分析
為分析肌肉協同作用,對sEMG信號執行高通濾波處理(截止頻率為20 Hz),隨后使用希爾伯特變換進行整流,整流后的sEMG信號執行低通濾波處理(截止頻率為10 Hz)來確定sEMG包絡。利用sEMG包絡線執行非負矩陣分解來提取肌肉協同效應。sEMG包絡線被分解為兩個非負矩陣,其中一個矩陣反映協同效應,另一個反映相應的激活模式[14]。
 |
其中,矩陣A為sEMG包絡矩陣,W為協同結構矩陣,H為激活系數矩陣。n表示肌肉的數量,t為樣本長度,k表示協同數量。
進而通過解釋方差(variance accounted for,VAF)來確定肌肉協同模塊的個數k:
 |
其中, 為重構矩陣,即為協同結構矩陣W與激活系數矩陣H的乘積。
為重構矩陣,即為協同結構矩陣W與激活系數矩陣H的乘積。
為了構建肌肉功能網絡,使用互信息方法量化sEMG信號間的功能連接。兩個不同通道的sEMG信號x和y之間的互信息如下式所示:
 |
MI(x,y)為x與y的互信息;p(x,y)為x與y的聯合概率密度;p(x)和p(y)分別為x和y的邊際概率密度。互信息非負對稱,即 ,互信息值越大,說明兩個信號之間連接越強,反之則越小。
,互信息值越大,說明兩個信號之間連接越強,反之則越小。
進一步,為評估各個肌肉功能網絡的拓撲特征,本文計算了全局效率和聚類系數兩個網絡屬性[15]。網絡中所有節點對之間的平均最短路徑長度稱為網絡的特征路徑長度,全局效率與特征路徑長度成反比。全局效率值越高表明網絡功能越完整。全局效率的計算公式如下:
 |
其中, 是節點i的效率,N為網絡中所有節點的集合,n為節點數量,
是節點i的效率,N為網絡中所有節點的集合,n為節點數量, 為節點i和j之間的最短路徑長度(距離)。
為節點i和j之間的最短路徑長度(距離)。
聚類系數是用來描述節點之間結集成團程度的系數。具體來說,聚類系數代表一個點與鄰接點之間相互連接的程度。平均聚類系數是衡量一個網絡在整體上的集聚程度[16],聚類系數的計算公式如下:
 |
其中, 為節點i的聚類系數(
為節點i的聚類系數( ),
), 為節點i周圍的三角形的數量,
為節點i周圍的三角形的數量, 為節點i的度。
為節點i的度。
2 結果
2.1 肌肉協同效應
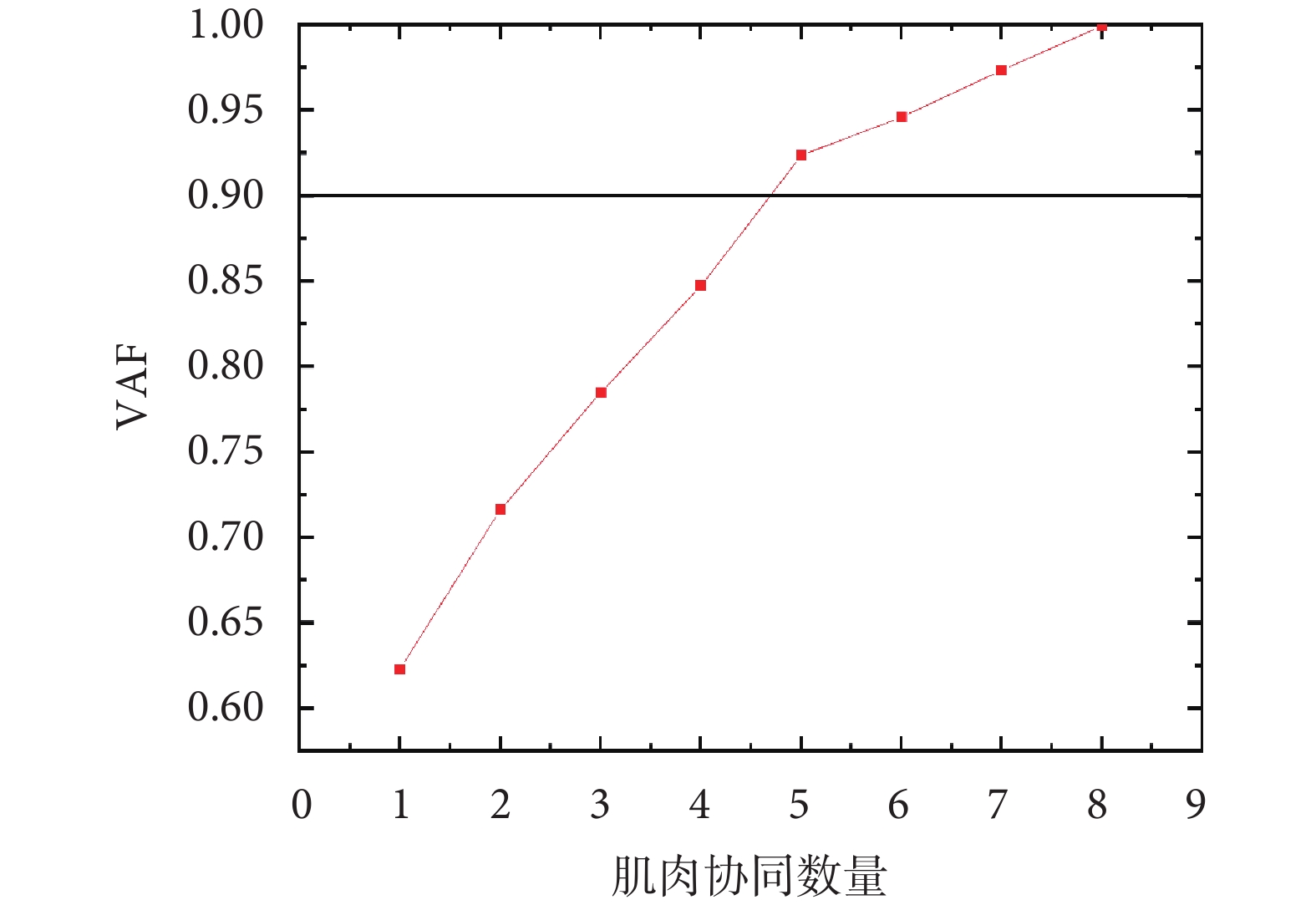
通過使用非負矩陣分解算法對提取的8塊下肢肌肉sEMG包絡進行分解,本研究確定了5個肌肉協同模式(即當  時,
時, ),如圖2所示。
),如圖2所示。
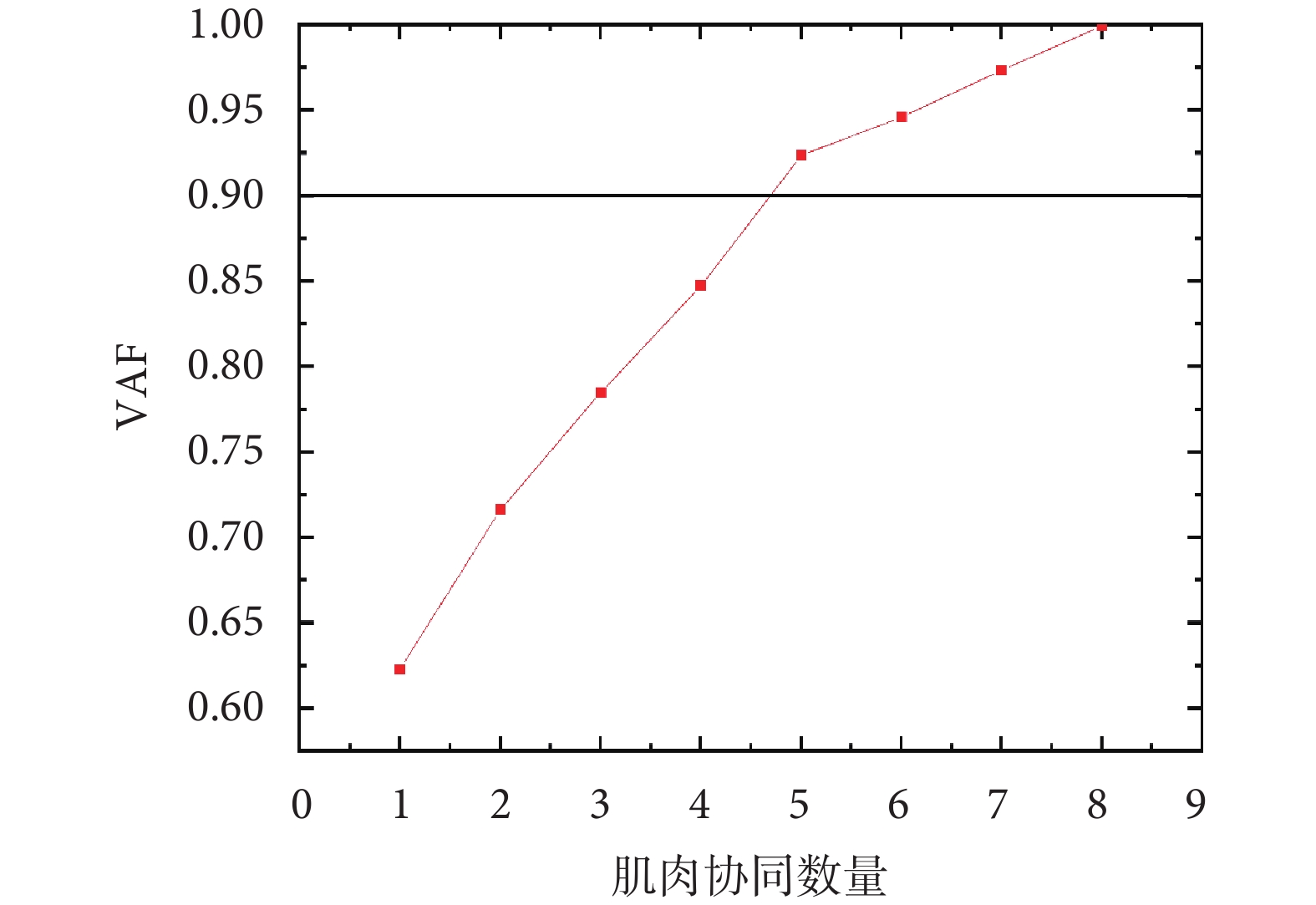 圖2
從sEMG包絡提取的肌肉協同數量
Figure2.
Number of muscle synergies extracted from the sEMG envelope
圖2
從sEMG包絡提取的肌肉協同數量
Figure2.
Number of muscle synergies extracted from the sEMG envelope
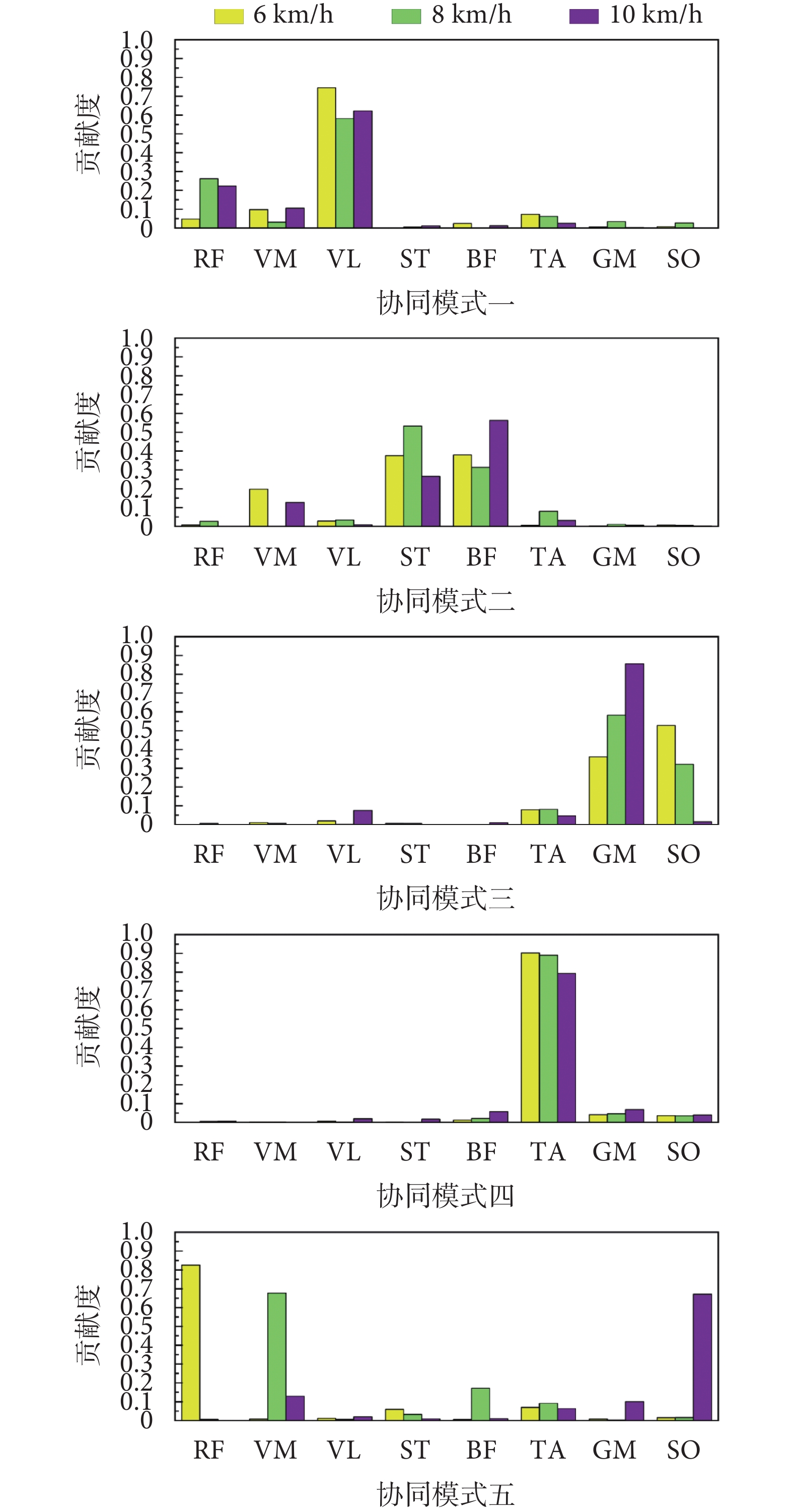
不同步行速度下肌肉協同模式如圖3所示。在6 km/h的步行速度下,協同模式一中股外側肌貢獻相對較大,協同模式二中股內側肌、半腱肌、股二頭肌貢獻相對較大,協同模式三中腓腸肌與比目魚肌貢獻相對較大,協同模式四中脛骨前肌貢獻相對較大,協同模式五中股直肌貢獻相對較大。在8 km/h的步行速度下,協同模式一中股直肌與股外側肌貢獻相對較大,協同模式二中半腱肌與股二頭肌貢獻相對較大,協同模式三中腓腸肌與比目魚肌貢獻相對較大,協同模式四中脛骨前肌貢獻相對較大,協同模式五中股內側肌貢獻相對較大。在10 km/h的步行速度下,協同模式一中股直肌與股外側肌貢獻相對較大,協同模式二中半腱肌與股二頭肌貢獻相對較大,協同模式三中腓腸肌貢獻相對較大,協同模式四中脛骨前肌貢獻相對較大,協同模式五中比目魚肌貢獻相對較大。
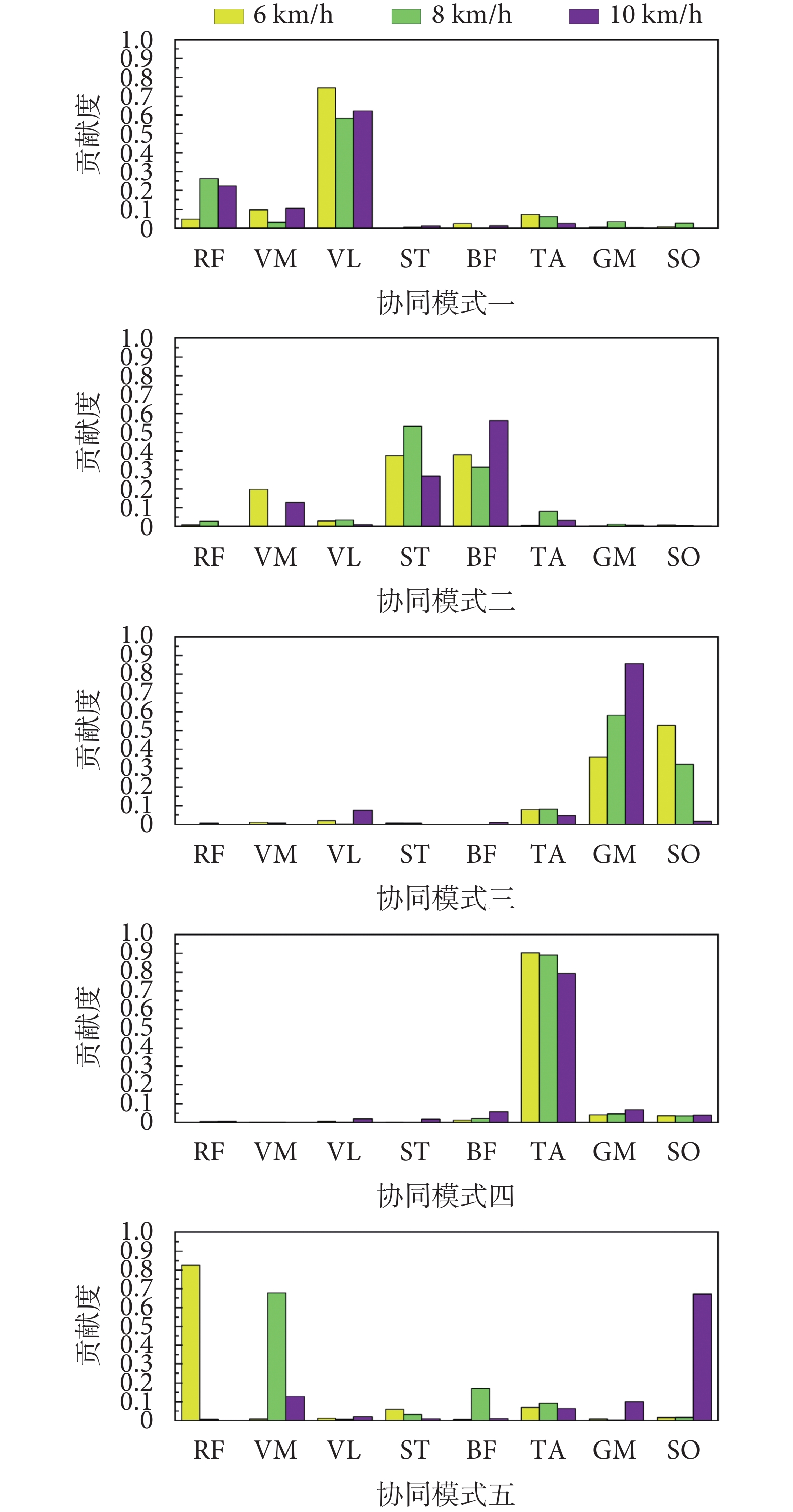 圖3
不同步行速度下的肌肉協同模式
Figure3.
Muscle synergy patterns at different gait speeds
圖3
不同步行速度下的肌肉協同模式
Figure3.
Muscle synergy patterns at different gait speeds
2.2 肌肉網絡分析
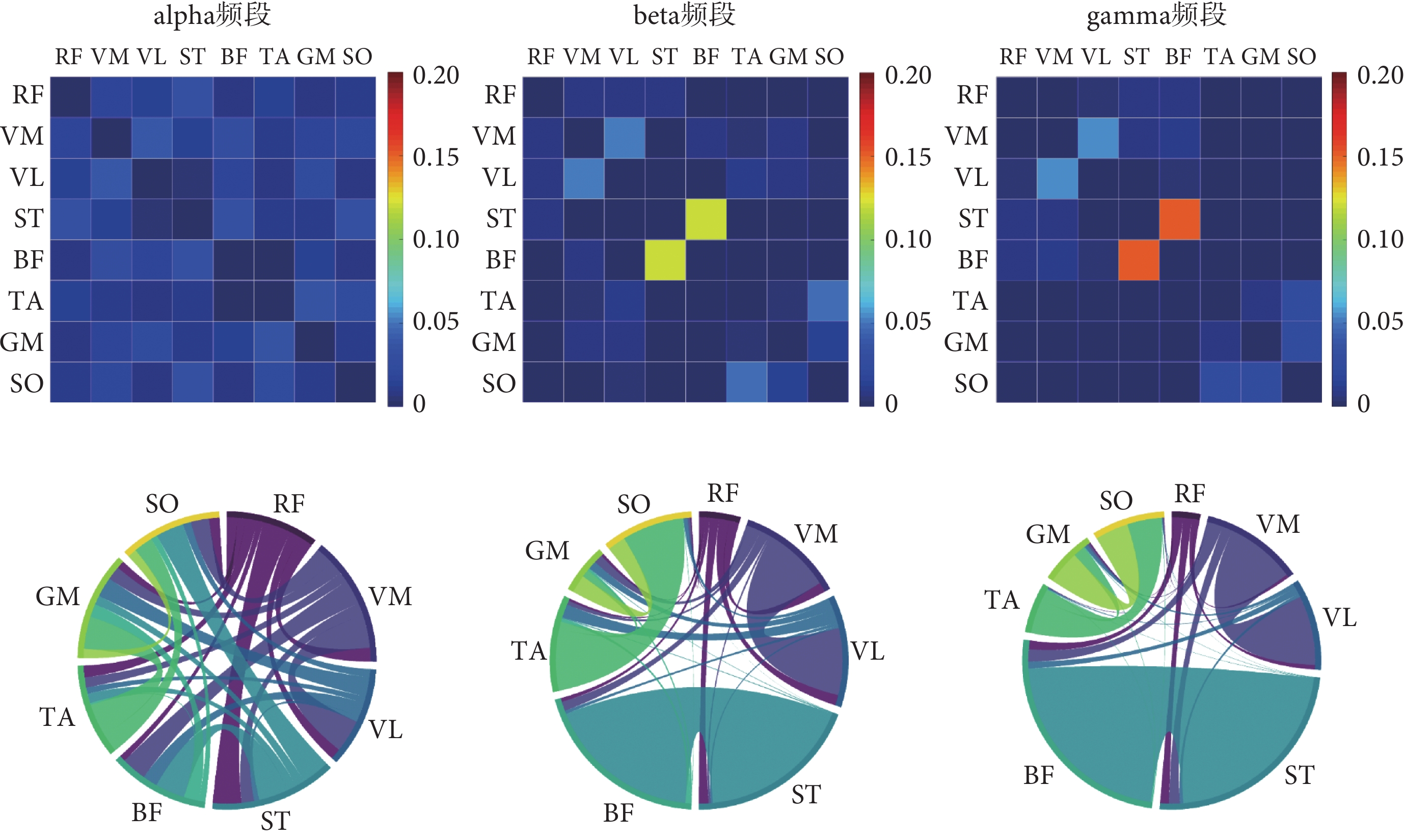
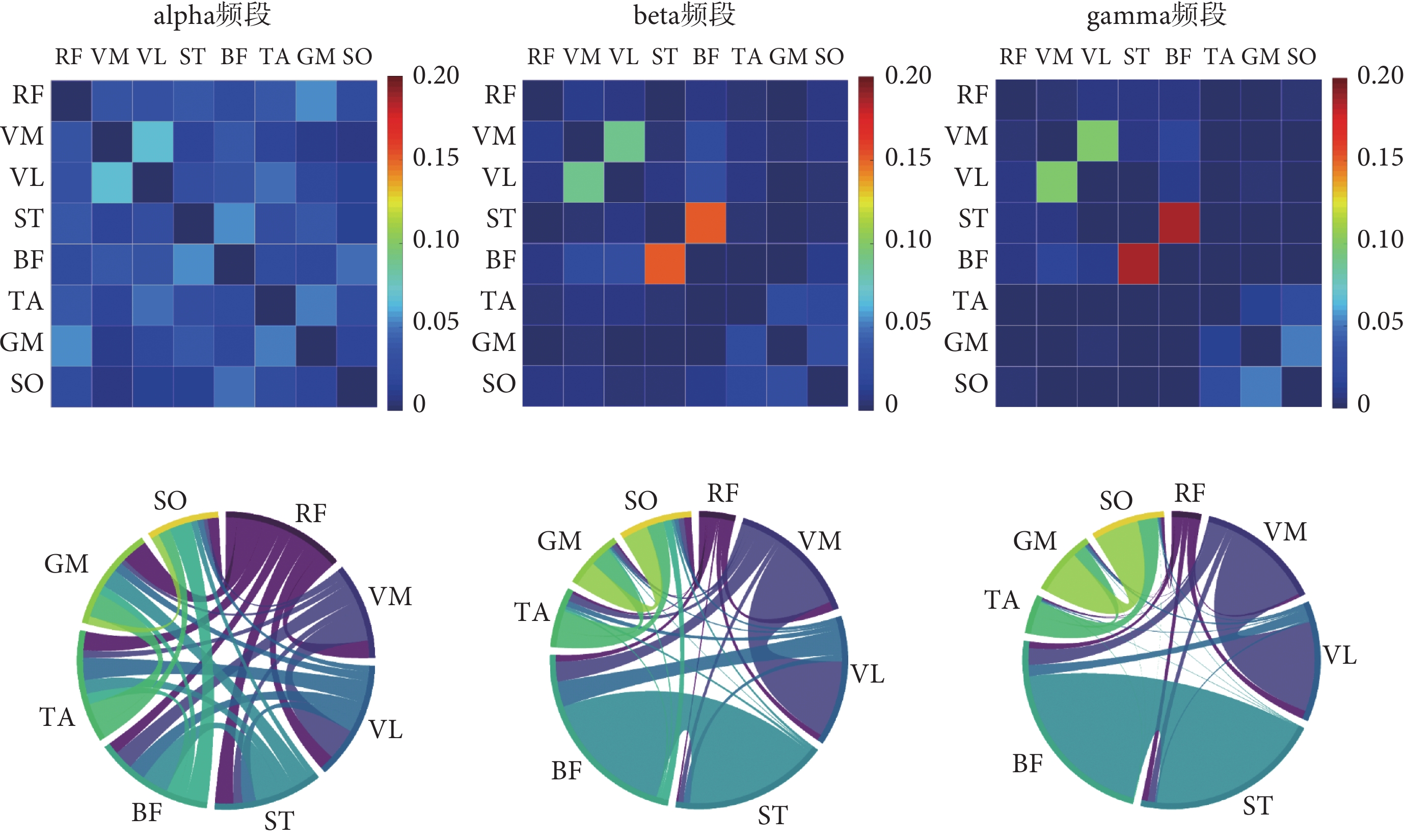
根據前述試驗設計采集到的下肢sEMG信號,本文在不同步行速度下分別構建了alpha頻段、beta頻段和gamma頻段的肌肉功能網絡,結果如圖4~6所示。弦圖主要用于展示多個對象之間的關系,連接圓上任意兩點的線段稱為弦。弦(兩點之間的連線)代表著兩者之間的關聯關系,弦與圓接觸的面積越大則關聯越強。
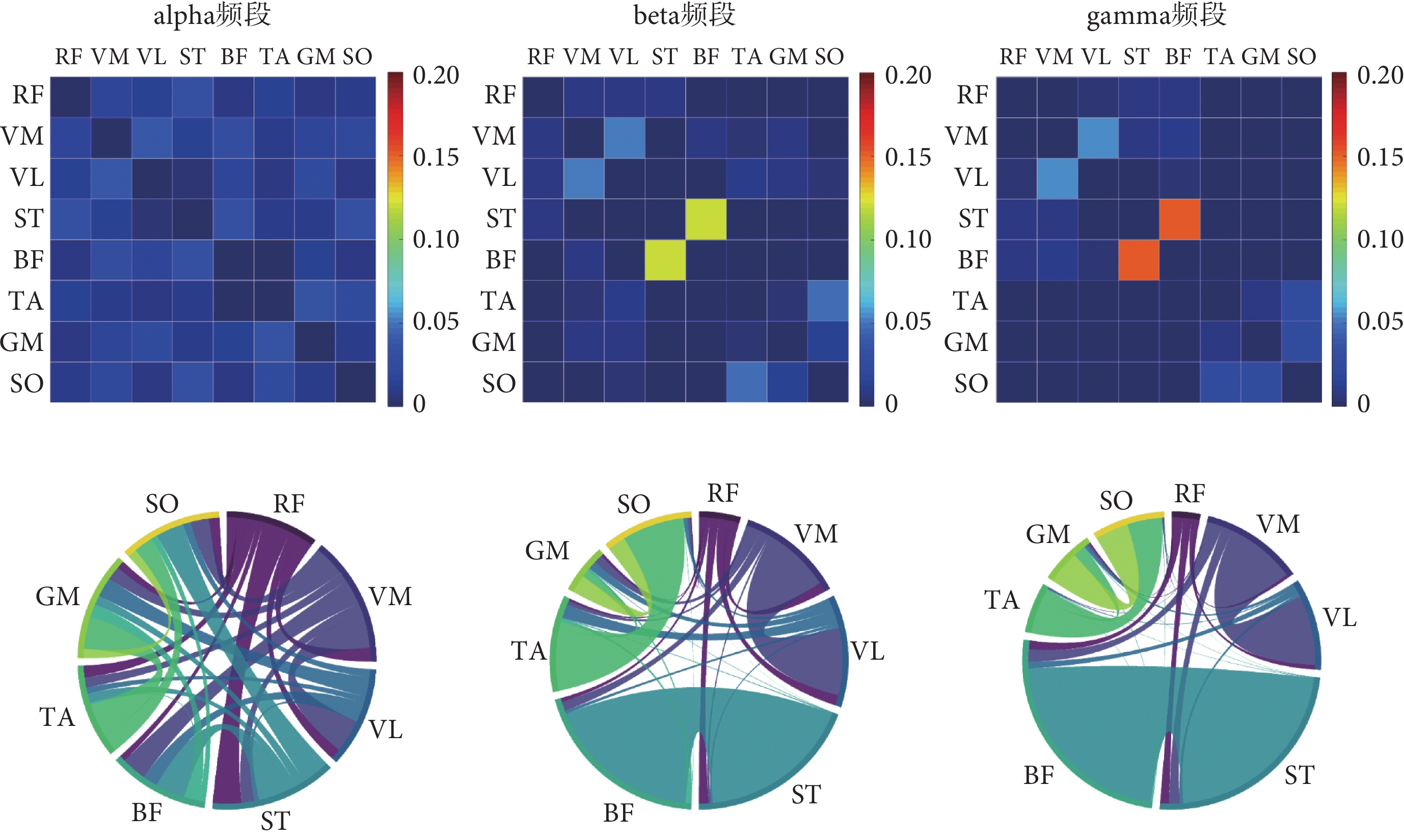 圖4
6 km/h步行速度下的肌肉網絡
Figure4.
Muscle network at 6 km/h gait speed
圖4
6 km/h步行速度下的肌肉網絡
Figure4.
Muscle network at 6 km/h gait speed
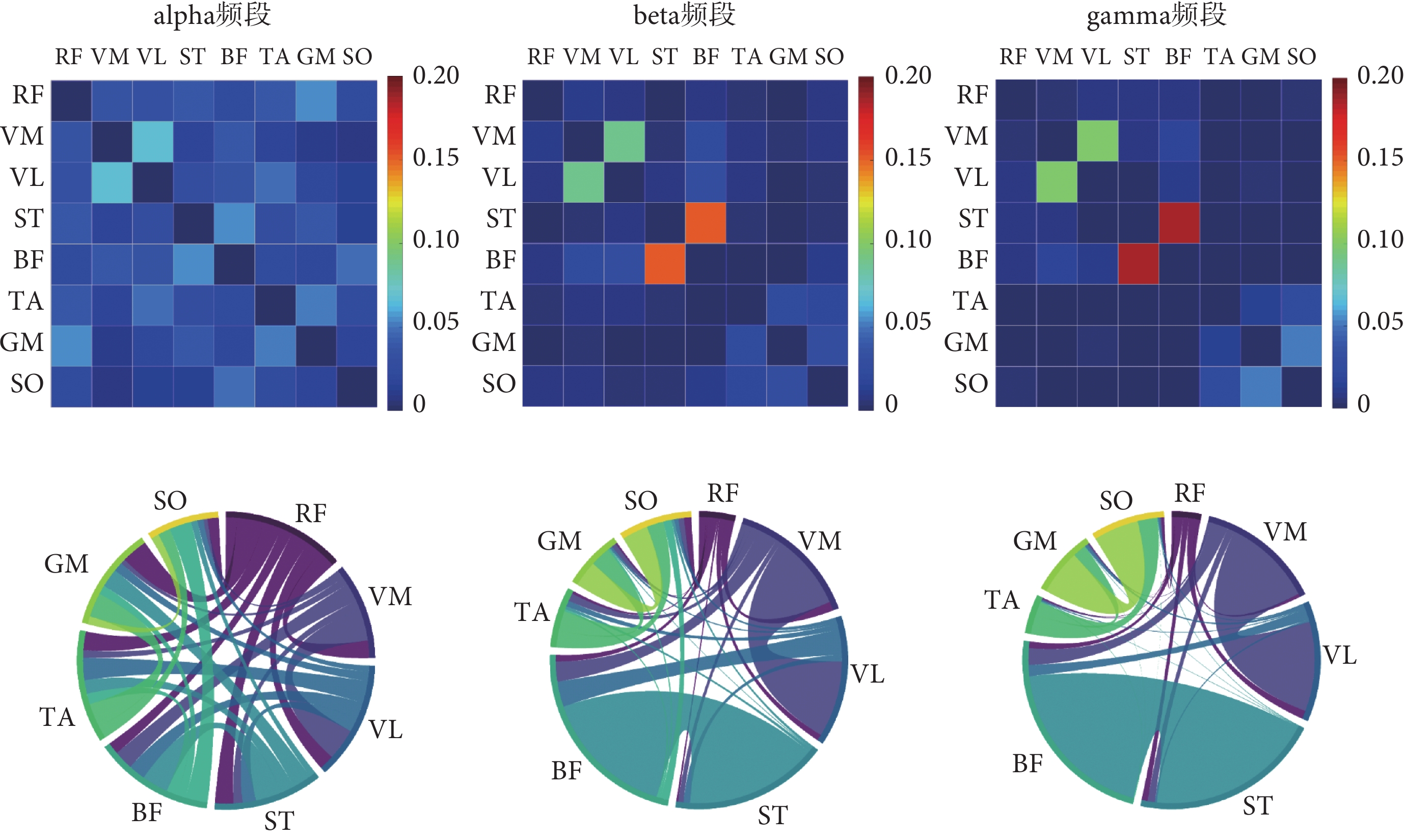 圖5
8 km/h步行速度下的肌肉網絡
Figure5.
Muscle network at 8 km/h gait speed
圖5
8 km/h步行速度下的肌肉網絡
Figure5.
Muscle network at 8 km/h gait speed
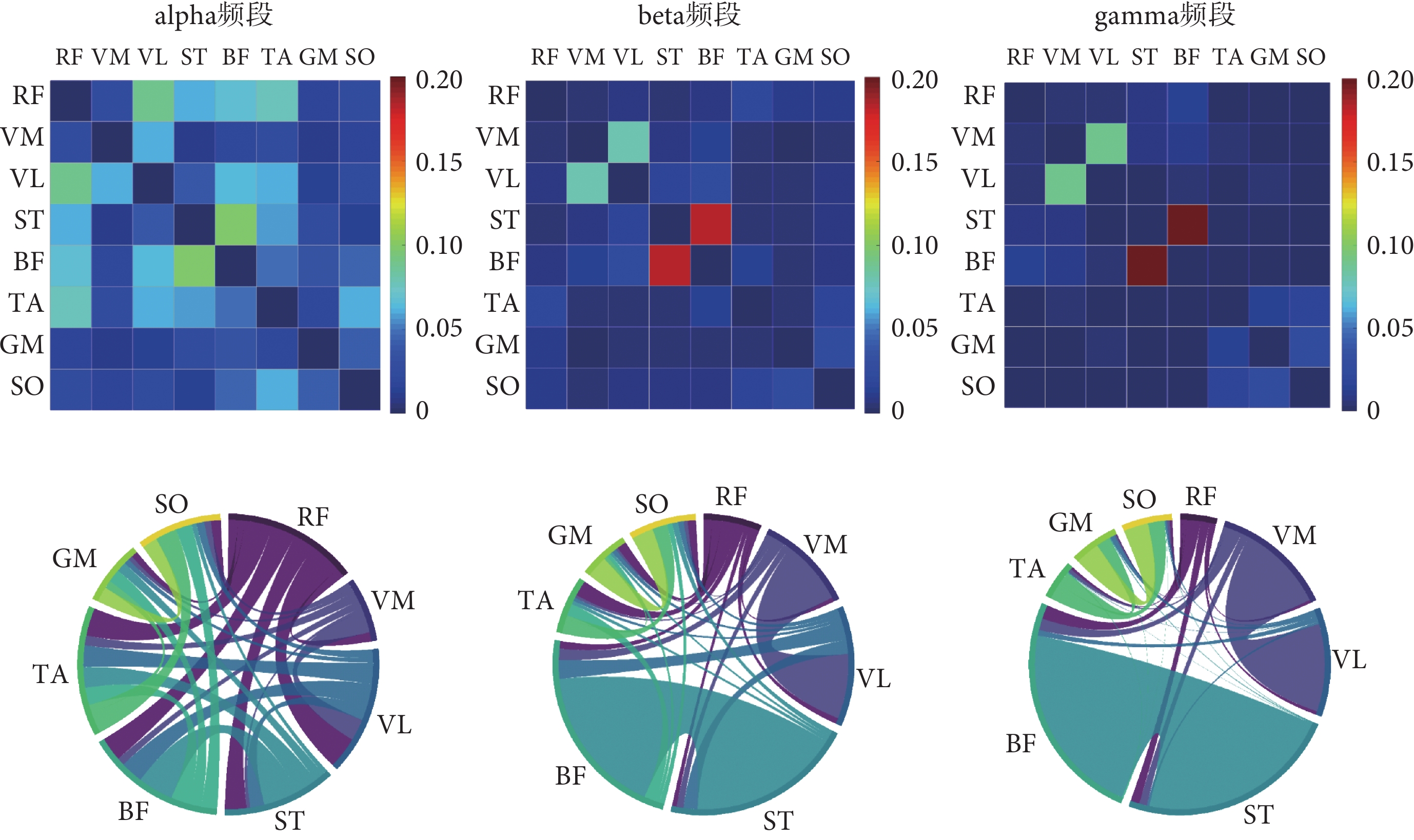 圖6
10 km/h步行速度下的肌肉網絡
Figure6.
Muscle network at 10 km/h gait speed
圖6
10 km/h步行速度下的肌肉網絡
Figure6.
Muscle network at 10 km/h gait speed
如圖4所示,6 km/h的步行速度下,alpha頻段內下肢各個肌肉之間的連接強度普遍較低;而在beta頻段連接強度較高的肌間連接對有VM-VL、ST-BF和TA-SO;在gamma頻段內連接強度較高的肌間連接對為VM-VL和ST-BF,并且與beta頻段相比,ST-BF之間的連接強度更高。
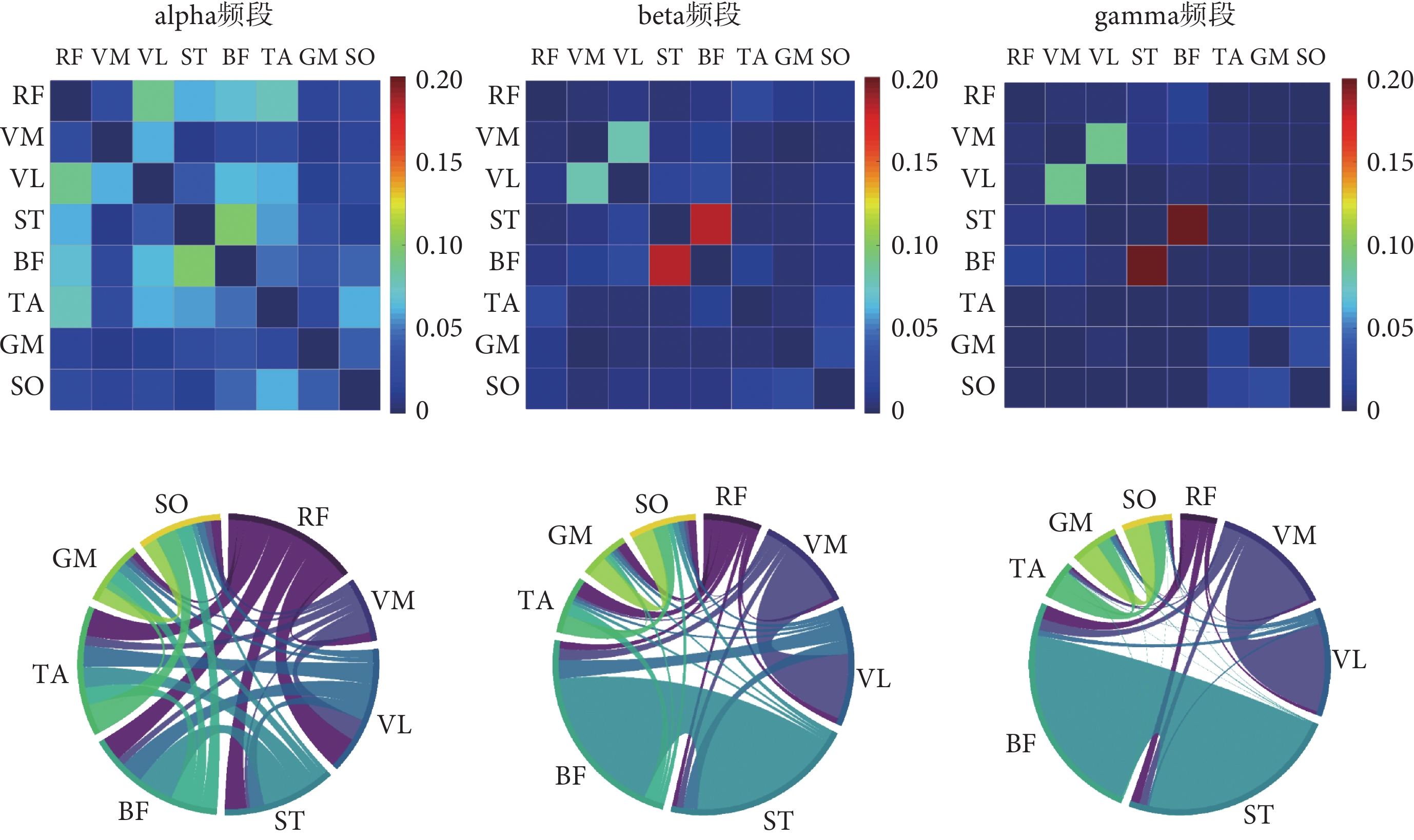
如圖5所示,8 km/h的步行速度下,alpha頻段內各肌肉之間的連接強度較為接近且較低;在beta頻段連接強度較高的肌間連接對為VM-VL和ST-BF;在gamma頻段內同樣觀察到VM-VL和ST-BF肌肉對之間的強連接。
如圖6所示,10 km/h的步行速度下,alpha頻段內連接強度較高的肌間連接有RF-VL、RF-TA和ST-BF;在beta頻段和gamma頻段連接強度較高的肌間連接對為VM-VL和ST-BF。本研究還觀察到無論是哪個頻段,隨著步行速度的增加,VM-VL和ST-BF肌間連接的強度也隨之增加。
2.3 復雜網絡分析
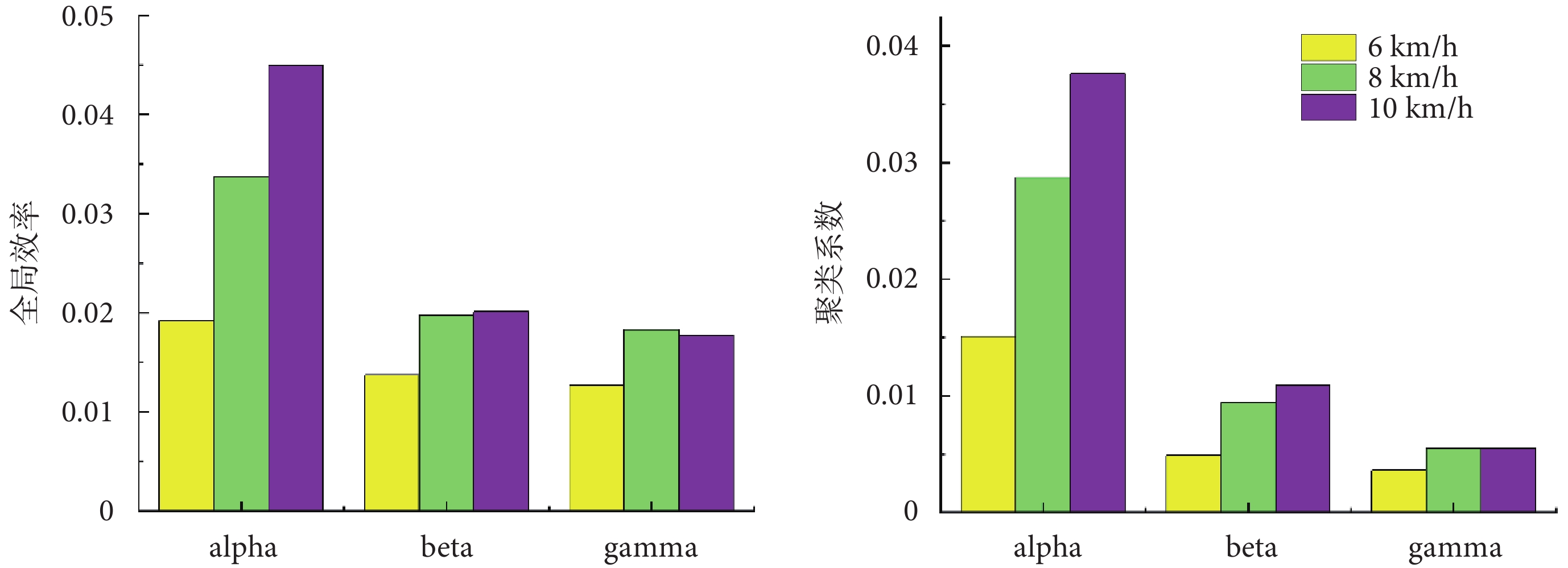
為了進一步量化不同步行速度下肌肉功能網絡的差異,本文計算了各網絡的全局效率以及聚類系數,結果如圖7所示。全局效率越高表明網絡功能越完整,聚類系數越高表明網絡的連通性越好。在alpha頻段內全局效率與聚類系數呈現出隨著步行速度增加而增加的趨勢,在beta和gamma頻段內6 km/h步行速度到8 km/h步行速度下的全局效率與聚類系數有所增加,8 km/h步行速度到10 km/h步行速度下的全局效率與聚類系數較為接近。在同一步行速度下全局效率以及聚類系數隨著頻段的升高而降低,表現為更加局部的肌間強連接。
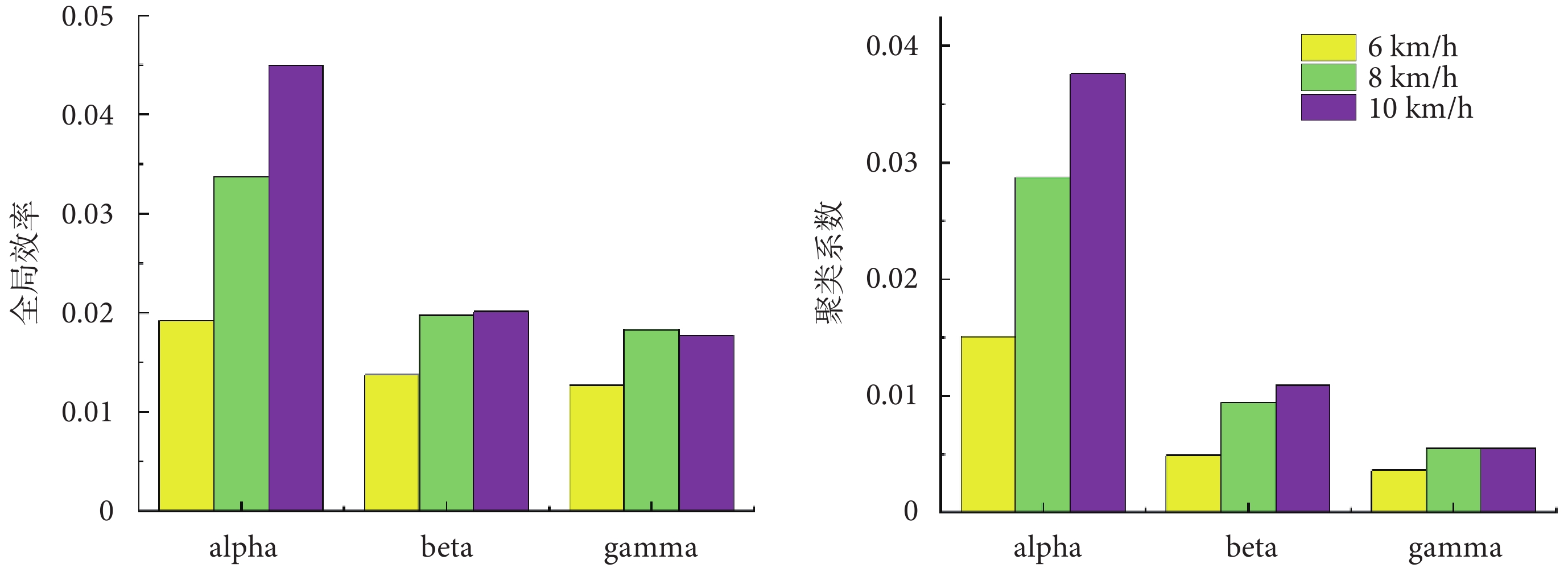 圖7
全局效率及聚類系數分析
Figure7.
Global efficiency and clustering coefficient analysis
圖7
全局效率及聚類系數分析
Figure7.
Global efficiency and clustering coefficient analysis
3 討論和結論
為探索中樞神經系統對多肌肉協調的作用機制,本研究基于不同步行速度下的下肢sEMG信號,利用非負矩陣分解方法提取了肌肉協同效應,分析了不同步行速度對肌肉協同模式的影響。同時,通過互信息方法構建了不同頻段內的肌肉功能網絡,進而引入復雜網絡分析方法,探索了步行速度變化引起的肌肉網絡變化。
本研究提取到5個肌肉協同模式,隨著步行速度的增加,肌肉協同的數量并沒有發生變化。其中協同模式一、二、三、四較為一致,但在不同步行速度下不同肌肉的權值有所改變,而協同模式五的差異最大。本文進一步觀察到,6 km/h步行速度下以股直肌激活為主,8 km/h步行速度下以股內側肌激活為主,10 km/h步行速度下以比目魚肌激活為主,股直肌和股內側肌在步行中主要負責支撐重力,比目魚肌主要負責推動邁步,這可能是由于步行速度的增加進而邁步的頻率增加所致。
通過分析不同步行速度的肌肉網絡,本研究發現在alpha頻段內各個肌肉之間的連接強度相對較低,在弦圖中體現為比較平均的廣泛耦合,beta頻段與gamma頻段內股內側肌與股外側肌、半腱肌與股二頭肌之間的連接強度相對較高,在弦圖中體現為局部的強耦合,這與我們在復雜網絡分析所觀察到的結果一致。在同一步行速度下全局效率和聚類系數隨著頻段的升高而降低,表現為更加局部的肌間強連接,其中較低的頻率范圍反映了更為廣泛的耦合,較高的頻率范圍反映了局部耦合[17]。另外,我們觀察到在所有頻段內,隨著步行速度的增加,肌肉之間的連接強度也隨之增強,這可能說明更劇烈的步態運動需要肌肉之間更強的“交流”。
本文通過對健康受試者不同步行速度下的下肢肌肉協同效應及肌肉網絡進行分析,發現不同步行速度下肌肉協同效應存在一定差異,且更高的步行速度會伴隨著更強的肌間連接。本研究有望為研究神經肌肉功能障礙患者的步態功能評估提供理論支撐。考慮到步態具有周期性,而完整的步態周期又細分為不同的步態時相,在未來的工作中我們將針對完整的步態周期對肌肉協同及肌肉功能網絡展開更細致的研究。
重要聲明
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
作者貢獻聲明:崔彩虹負責試驗設計、數據分析及論文撰寫,繆華聰負責試驗數據采集和論文修改,梁鐵負責提供技術和材料支持,劉秀玲負責論文修改,劉曉光負責整體指導和論文修改。
倫理聲明:本研究通過了河北大學附屬醫院倫理審查委員會批準(批文編號:HDFY-LL-2020-091)。
0 引言
步行是人類日常生活中最基本的活動之一,而基于不同速度的步態研究被證實能夠為步態運動學分析、老年人認知功能預測和康復評估提供有效信息[1-3]。然而,迄今為止不同步行速度背后的神經機制依然不明。隨著非侵入式生理信號采集技術的發展,通過在皮膚表面放置電極記錄肌肉運動過程中產生的表面肌電圖(surface electromyography,sEMG),能夠在一定程度上反映神經肌肉的活動[4]。步行是一種復雜的運動過程,要求中樞神經系統(central nervous system,CNS)和多肌肉高度協調[5]。在此過程中,基于sEMG信號的肌肉協同和肌肉功能網絡的分析,可以有效反映中樞神經系統對肌肉的不同控制過程以及肌肉之間的協作模式。
步行運動涉及多塊下肢肌肉力矩整合和共同協調,這種整合、協調的過程稱為協同[6]。之前研究證實了神經肌肉系統通過共同激活肌肉群構建運動模塊,即肌肉協同作用,從而可以簡化神經系統對多個肌肉的控制[7]。對步行運動來說,中樞神經系統只需控制較少的運動模塊就能控制較多的運動單元和肌肉來實現人體的站立、邁步等動作。因此,廣大研究者針對步行過程中的下肢肌肉開展了肌肉協同分析。Serrancolí等[8]從人體行走任務的sEMG信號中提取了5個肌肉協同模式;Boonstra等[9]在人體站立條件下從下肢sEMG信號中提取到了4個肌肉協同模式;Barroso等[10]通過研究發現步行和騎自行車運動具有相似的肌肉協同模式。上述研究表明,基于sEMG信號可以有效提取步行運動的肌肉協同模式。
構建多肌肉之間的功能網絡是近年發展起來的一種分析肌間協同特性的新方法,旨在進一步解釋肌肉協同作用的神經輸入特性及其簡化運動控制的能力。肌肉網絡分析通過量化分解運動相關肌肉sEMG之間的功能連接,能夠識別由共同神經輸入調節的特定肌肉的頻率特征。相干性是目前用來評估肌肉之間功能耦合的主要方法。然而,sEMG信號是典型的非線性神經生理信號,線性的相干性方法在研究sEMG信號之間功能耦合上存在一定局限性[11]。基于信息論的互信息(mutual information,MI)能夠從復雜性角度有效量化信號間線性和非線性耦合,因此近年來被廣泛應用于構建sEMG信號間的功能網絡。陳玲玲等[12]利用互信息構建了肌肉功能網絡,并全面分析了外骨骼穿戴者的電生理空間分布情況和肌肉協調工作機制。Madeleine等[13]使用互信息方法量化了功能性任務時頸肩痛對肌肉功能連接的影響。上述研究表明,基于互信息方法量化肌肉功能網絡可為分析步行運動下肢的神經肌肉協調機制提供有價值的信息。
本文分析了不同步行速度下肢的肌肉協同模式,并使用互信息方法構建了alpha頻段(8~13 Hz)、beta頻段(14~30 Hz)和gamma頻段(31~60 Hz)的肌肉功能網絡,引入復雜網絡分析方法,探索了不同頻段不同步行速度下肌肉功能網絡拓撲結構的差異以及中樞神經系統對肌肉的協調控制模式。本研究將肌肉協同作用與肌肉功能網絡相結合,有助于發現肌間協同與耦合的內在關聯。本研究旨在為探索不同步行速度下肢肌肉協同機制提供新的視野,以期為神經肌肉功能障礙患者的步態功能評估提供理論支撐。
1 材料與方法
1.1 試驗設計
本研究一共招募8名無任何神經疾病史和運動損傷的健康受試者(男性,年齡21~25歲)參與試驗。所有受試者在試驗前均已知悉試驗步驟并簽署知情同意書。所有受試者在跑步機上以6、8、10 km/h的不同速度執行步行任務。每名受試者執行10組試驗,每組記錄至少10個完整步態周期的sEMG數據。在每組試驗間隙允許受試者休息5 min,以避免肌肉疲勞帶來的影響。本研究符合《赫爾辛基宣言》,并經河北大學附屬醫院倫理審查委員會批準(HDFY-LL-2020-091)。
1.2 數據采集
通過Noraxon無線肌電采集系統(美國Noraxon公司)采集任務中受試者右腿的股直肌(rectus femoris,RF)、股內側肌(vastus medialis,VM)、股外側肌(vastus lateralis,VL)、半腱肌(semitendinosus,ST)、股二頭肌(biceps femoris,BF)、脛骨前肌(tibialis anterior,TA)、外側腓腸肌(gastrocnemius,GM)和比目魚肌(soleus,SO)共8塊下肢肌肉位置的sEMG信號,以1 500 Hz的頻率采樣,實驗場景及肌肉位置如圖1所示。
 圖1
實驗場景及肌肉位置示意圖
Figure1.
Schematic diagram of the experimental scene and muscle positions
圖1
實驗場景及肌肉位置示意圖
Figure1.
Schematic diagram of the experimental scene and muscle positions
1.3 數據分析
為分析肌肉協同作用,對sEMG信號執行高通濾波處理(截止頻率為20 Hz),隨后使用希爾伯特變換進行整流,整流后的sEMG信號執行低通濾波處理(截止頻率為10 Hz)來確定sEMG包絡。利用sEMG包絡線執行非負矩陣分解來提取肌肉協同效應。sEMG包絡線被分解為兩個非負矩陣,其中一個矩陣反映協同效應,另一個反映相應的激活模式[14]。
 |
其中,矩陣A為sEMG包絡矩陣,W為協同結構矩陣,H為激活系數矩陣。n表示肌肉的數量,t為樣本長度,k表示協同數量。
進而通過解釋方差(variance accounted for,VAF)來確定肌肉協同模塊的個數k:
 |
其中, 為重構矩陣,即為協同結構矩陣W與激活系數矩陣H的乘積。
為重構矩陣,即為協同結構矩陣W與激活系數矩陣H的乘積。
為了構建肌肉功能網絡,使用互信息方法量化sEMG信號間的功能連接。兩個不同通道的sEMG信號x和y之間的互信息如下式所示:
 |
MI(x,y)為x與y的互信息;p(x,y)為x與y的聯合概率密度;p(x)和p(y)分別為x和y的邊際概率密度。互信息非負對稱,即 ,互信息值越大,說明兩個信號之間連接越強,反之則越小。
,互信息值越大,說明兩個信號之間連接越強,反之則越小。
進一步,為評估各個肌肉功能網絡的拓撲特征,本文計算了全局效率和聚類系數兩個網絡屬性[15]。網絡中所有節點對之間的平均最短路徑長度稱為網絡的特征路徑長度,全局效率與特征路徑長度成反比。全局效率值越高表明網絡功能越完整。全局效率的計算公式如下:
 |
其中, 是節點i的效率,N為網絡中所有節點的集合,n為節點數量,
是節點i的效率,N為網絡中所有節點的集合,n為節點數量, 為節點i和j之間的最短路徑長度(距離)。
為節點i和j之間的最短路徑長度(距離)。
聚類系數是用來描述節點之間結集成團程度的系數。具體來說,聚類系數代表一個點與鄰接點之間相互連接的程度。平均聚類系數是衡量一個網絡在整體上的集聚程度[16],聚類系數的計算公式如下:
 |
其中, 為節點i的聚類系數(
為節點i的聚類系數( ),
), 為節點i周圍的三角形的數量,
為節點i周圍的三角形的數量, 為節點i的度。
為節點i的度。
2 結果
2.1 肌肉協同效應
通過使用非負矩陣分解算法對提取的8塊下肢肌肉sEMG包絡進行分解,本研究確定了5個肌肉協同模式(即當  時,
時, ),如圖2所示。
),如圖2所示。
 圖2
從sEMG包絡提取的肌肉協同數量
Figure2.
Number of muscle synergies extracted from the sEMG envelope
圖2
從sEMG包絡提取的肌肉協同數量
Figure2.
Number of muscle synergies extracted from the sEMG envelope
不同步行速度下肌肉協同模式如圖3所示。在6 km/h的步行速度下,協同模式一中股外側肌貢獻相對較大,協同模式二中股內側肌、半腱肌、股二頭肌貢獻相對較大,協同模式三中腓腸肌與比目魚肌貢獻相對較大,協同模式四中脛骨前肌貢獻相對較大,協同模式五中股直肌貢獻相對較大。在8 km/h的步行速度下,協同模式一中股直肌與股外側肌貢獻相對較大,協同模式二中半腱肌與股二頭肌貢獻相對較大,協同模式三中腓腸肌與比目魚肌貢獻相對較大,協同模式四中脛骨前肌貢獻相對較大,協同模式五中股內側肌貢獻相對較大。在10 km/h的步行速度下,協同模式一中股直肌與股外側肌貢獻相對較大,協同模式二中半腱肌與股二頭肌貢獻相對較大,協同模式三中腓腸肌貢獻相對較大,協同模式四中脛骨前肌貢獻相對較大,協同模式五中比目魚肌貢獻相對較大。
 圖3
不同步行速度下的肌肉協同模式
Figure3.
Muscle synergy patterns at different gait speeds
圖3
不同步行速度下的肌肉協同模式
Figure3.
Muscle synergy patterns at different gait speeds
2.2 肌肉網絡分析
根據前述試驗設計采集到的下肢sEMG信號,本文在不同步行速度下分別構建了alpha頻段、beta頻段和gamma頻段的肌肉功能網絡,結果如圖4~6所示。弦圖主要用于展示多個對象之間的關系,連接圓上任意兩點的線段稱為弦。弦(兩點之間的連線)代表著兩者之間的關聯關系,弦與圓接觸的面積越大則關聯越強。
 圖4
6 km/h步行速度下的肌肉網絡
Figure4.
Muscle network at 6 km/h gait speed
圖4
6 km/h步行速度下的肌肉網絡
Figure4.
Muscle network at 6 km/h gait speed
 圖5
8 km/h步行速度下的肌肉網絡
Figure5.
Muscle network at 8 km/h gait speed
圖5
8 km/h步行速度下的肌肉網絡
Figure5.
Muscle network at 8 km/h gait speed
 圖6
10 km/h步行速度下的肌肉網絡
Figure6.
Muscle network at 10 km/h gait speed
圖6
10 km/h步行速度下的肌肉網絡
Figure6.
Muscle network at 10 km/h gait speed
如圖4所示,6 km/h的步行速度下,alpha頻段內下肢各個肌肉之間的連接強度普遍較低;而在beta頻段連接強度較高的肌間連接對有VM-VL、ST-BF和TA-SO;在gamma頻段內連接強度較高的肌間連接對為VM-VL和ST-BF,并且與beta頻段相比,ST-BF之間的連接強度更高。
如圖5所示,8 km/h的步行速度下,alpha頻段內各肌肉之間的連接強度較為接近且較低;在beta頻段連接強度較高的肌間連接對為VM-VL和ST-BF;在gamma頻段內同樣觀察到VM-VL和ST-BF肌肉對之間的強連接。
如圖6所示,10 km/h的步行速度下,alpha頻段內連接強度較高的肌間連接有RF-VL、RF-TA和ST-BF;在beta頻段和gamma頻段連接強度較高的肌間連接對為VM-VL和ST-BF。本研究還觀察到無論是哪個頻段,隨著步行速度的增加,VM-VL和ST-BF肌間連接的強度也隨之增加。
2.3 復雜網絡分析
為了進一步量化不同步行速度下肌肉功能網絡的差異,本文計算了各網絡的全局效率以及聚類系數,結果如圖7所示。全局效率越高表明網絡功能越完整,聚類系數越高表明網絡的連通性越好。在alpha頻段內全局效率與聚類系數呈現出隨著步行速度增加而增加的趨勢,在beta和gamma頻段內6 km/h步行速度到8 km/h步行速度下的全局效率與聚類系數有所增加,8 km/h步行速度到10 km/h步行速度下的全局效率與聚類系數較為接近。在同一步行速度下全局效率以及聚類系數隨著頻段的升高而降低,表現為更加局部的肌間強連接。
 圖7
全局效率及聚類系數分析
Figure7.
Global efficiency and clustering coefficient analysis
圖7
全局效率及聚類系數分析
Figure7.
Global efficiency and clustering coefficient analysis
3 討論和結論
為探索中樞神經系統對多肌肉協調的作用機制,本研究基于不同步行速度下的下肢sEMG信號,利用非負矩陣分解方法提取了肌肉協同效應,分析了不同步行速度對肌肉協同模式的影響。同時,通過互信息方法構建了不同頻段內的肌肉功能網絡,進而引入復雜網絡分析方法,探索了步行速度變化引起的肌肉網絡變化。
本研究提取到5個肌肉協同模式,隨著步行速度的增加,肌肉協同的數量并沒有發生變化。其中協同模式一、二、三、四較為一致,但在不同步行速度下不同肌肉的權值有所改變,而協同模式五的差異最大。本文進一步觀察到,6 km/h步行速度下以股直肌激活為主,8 km/h步行速度下以股內側肌激活為主,10 km/h步行速度下以比目魚肌激活為主,股直肌和股內側肌在步行中主要負責支撐重力,比目魚肌主要負責推動邁步,這可能是由于步行速度的增加進而邁步的頻率增加所致。
通過分析不同步行速度的肌肉網絡,本研究發現在alpha頻段內各個肌肉之間的連接強度相對較低,在弦圖中體現為比較平均的廣泛耦合,beta頻段與gamma頻段內股內側肌與股外側肌、半腱肌與股二頭肌之間的連接強度相對較高,在弦圖中體現為局部的強耦合,這與我們在復雜網絡分析所觀察到的結果一致。在同一步行速度下全局效率和聚類系數隨著頻段的升高而降低,表現為更加局部的肌間強連接,其中較低的頻率范圍反映了更為廣泛的耦合,較高的頻率范圍反映了局部耦合[17]。另外,我們觀察到在所有頻段內,隨著步行速度的增加,肌肉之間的連接強度也隨之增強,這可能說明更劇烈的步態運動需要肌肉之間更強的“交流”。
本文通過對健康受試者不同步行速度下的下肢肌肉協同效應及肌肉網絡進行分析,發現不同步行速度下肌肉協同效應存在一定差異,且更高的步行速度會伴隨著更強的肌間連接。本研究有望為研究神經肌肉功能障礙患者的步態功能評估提供理論支撐。考慮到步態具有周期性,而完整的步態周期又細分為不同的步態時相,在未來的工作中我們將針對完整的步態周期對肌肉協同及肌肉功能網絡展開更細致的研究。
重要聲明
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
作者貢獻聲明:崔彩虹負責試驗設計、數據分析及論文撰寫,繆華聰負責試驗數據采集和論文修改,梁鐵負責提供技術和材料支持,劉秀玲負責論文修改,劉曉光負責整體指導和論文修改。
倫理聲明:本研究通過了河北大學附屬醫院倫理審查委員會批準(批文編號:HDFY-LL-2020-091)。