電阻抗斷層成像（EIT）技術在肺通氣監測和區域性肺功能檢測中發揮著重要作用。然而，EIT算法固有的病態特性導致從含有噪聲的電壓數據中求解電導率時存在明顯偏差，難以獲得準確的電導率變化分布圖像以及清晰的邊界輪廓。為了提高EIT在肺通氣監測中的成像質量，本文提出將EIT算法與深度學習算法相結合的方法。首先，引用優化因子對卡爾曼濾波算法進行修正并將吉洪諾夫（Tikhonov）正則化引入算法的狀態空間表達式，以獲得初始肺部重建圖像；其次將初始成像結果輸入生成對抗網絡模型，以重構出精確的肺部輪廓。仿真實驗結果表明，該方法生成的肺部圖像邊界清晰，對噪聲具有更強的魯棒性，基本實現了可視化的效果，可為計算機斷層掃描等影像的診斷提供參考意義。
引用本文： 趙明康, 劉珺, 郭忠圣, 陳祥琪, 張帥, 鄭天予. 結合生成對抗網絡的電阻抗斷層成像技術在肺通氣監測中的應用. 生物醫學工程學雜志, 2024, 41(1): 105-113. doi: 10.7507/1001-5515.202308026 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
電阻抗斷層成像（electrical impedance tomography，EIT）是一種電學測量技術，具有快速成像、無損傷、無輻射等優點[1]。近年來，EIT技術已經被廣泛研究和應用于臨床檢測中，主要用于呼吸系統監測、肺功能成像、肺通氣監測等領域。該技術通過測量邊界電壓并采用適當的成像算法對人體內部電導率分布進行重構，從而實現高分辨率的實時成像[2]。然而在實際測量過程中，由于測量值數量遠少于待求未知量的數量，EIT逆問題具有嚴重的不適定性。傳統成像算法對噪聲和誤差極為敏感，為了提高電導率分布圖像的穩定性，通常需要降低空間分辨率，因此導致重構圖像出現較大的偽影且成像精度較差。目前常用的重構算法包括線性反投影法[3]、一步線性高斯牛頓法[4]等。1998年Vauhkonen等[5]基于隨機游走模型將卡爾曼濾波（Kalman filter，KF）算法引入EIT技術中，將EIT逆問題轉化為狀態估計問題。然而在實際應用中，人們往往難以建立精確的數學模型，EIT的不適定性導致狀態向量的更新過程極易受到噪聲干擾，從而導致傳統KF算法濾波精度下降，進而影響圖像重建的質量。因此，本文提出基于吉洪諾夫（Tikhonov）正則化的修正自適應擴展KF（modified adaptive extended KF with Tikhonov regularization，MAEKF-TR）算法，以期減小過程噪聲對實際數據的影響，改善EIT逆問題的不適定性，完成對肺部組織的圖像重建。
近年來，深度學習算法在計算機視覺、圖像重建等領域取得了長足發展[6]。與傳統方法相比，深度學習網絡模型可以更有效地捕獲圖像的復雜特征，獲得更高的重建性能。因此，許多國內外學者嘗試將深度學習算法用于生物醫學圖像處理領域[7-8]。經典的深度學習算法如卷積神經網絡、U型網絡（U-net）、生成對抗網絡（generative adversarial network，GAN）等，已在計算機斷層掃描（computed tomography，CT）、磁共振成像（magnetic resonance imaging，MRI）等醫學圖像重建領域取得了顯著的成果[9-11]。為了減少傳統EIT算法的重構誤差，降低人為因素對影像診斷的影響，本文提出將GAN與MAEKF-TR算法相結合的方法。具體而言，首先使用卷積神經網絡對包含誤差和偽影的EIT阻抗分布數據進行訓練，通過GAN中生成器與鑒別器之間的對抗訓練所生成的肺部影像能夠更清晰地反映肺部大小和形態等信息，從而減小EIT重建算法引起的偽影干擾。
本文構建了人體肺部仿真數據集，來模擬人類胸腔和常見肺部疾病的電導率分布，以評估所提方法的性能。此外，本文還將以仿真實驗證實，與傳統KF重建算法相比，MAEKF-TR算法與GAN結合，不僅能準確檢測出肺部器官的大小和位置，而且所生成的肺部圖像輪廓邊緣更加清晰，可以降低對EIT重建圖像分析的主觀性影響和誤差。綜上，通過仿真實驗研究結果，期望本研究提出的方法對肺通氣監測相關研究有一定的參考意義。
1 算法描述
1.1 EIT原理
本文采用16個電極的EIT測量系統，采用相鄰電極輸入電流，其他相鄰電極測量電壓值的模式。EIT重建過程可分為兩個主要步驟：正問題求解和逆問題求解。正問題求解，是指在已知物體內EIT分布的情況下求解邊界電壓值；逆問題求解，則是通過邊界電壓差值求解內部電導率的變化分布。圖像重建過程實際上是逆問題的求解過程，EIT線性模型如式(1)所示[12]：
 |
式中，ΔU為測量電壓變化量；J為靈敏度矩陣；Δσ為場域內電導率變化量。逆問題的求解實際是對非線性表達式的求解，而EIT圖像重建過程就是將非線性表達式進行線性化來尋找最優解σ，如式(2)所示：
 |
式中，Z為實際測量數據。
1.2 MAEKF-TR算法
求解EIT逆問題的過程，其實質是對電導率分布的求解。KF標準遞推方程見文獻[13-15]，將KF映射到EIT系統中，電導率σk視為狀態估計量，從而將EIT逆問題轉化為狀態估計問題，如式(3)所示：
 |
式中，
是k時刻的先驗狀態估計量；
是k ? 1時刻的先驗狀態估計量；Fk-1為k–1時刻的狀態傳遞矩陣，wk為k時刻的系統噪聲；Zk為k時刻的實際測量值；Jk為k時刻的觀測矩陣；vk為k時刻的測量噪聲。EIT系統的KF濾波方程如式(4)所示：
 |
式中，
表示估計誤差協方差矩陣k時刻的先驗估計；
表示估計誤差協方差矩陣k – 1時刻的先驗估計；
表示估計誤差協方差矩陣k時刻的后驗估計；
是k時刻的后驗狀態估計量；Rk表示k時刻的測量噪聲協方差；Qk表示k時刻的過程噪聲協方差；Kk表示k時刻的算法增益；I是單位矩陣，T為轉置符號。在實際測量生物組織時，數據信息會發生突變，導致估計的新息矢量發生較大變化。然而算法增益Kk不能實時根據狀態變化進行調整，從而導致濾波精度下降、濾波發散等情況出現。要削減測量噪聲對算法的干擾，就要調整測量噪聲協方差Rk及過程噪聲協方差Qk的權重占比。
本文提出引入優化因子δp[δp∈(0，1)]，對過程噪聲協方差Qk進行修正，將更新的數據給予更多的權重。Qk調整如式(5)所示：
 |
式中，
表示修正后k時刻的過程噪聲協方差；
表示修正后k – 1時刻的過程噪聲協方差；ξk表示在k時刻的新息矢量；Δp表示觀測值與先驗值之間的殘差。以上分析可知，改進后的自適應擴展KF（adaptive extended KF，AEKF）算法考慮了實際噪聲的時變特性對系統的影響，并通過實時數據更新的方式實現了對噪聲的實時修正。
算法增益Kk是最小二乘估計的最優增益，相當于對后驗誤差協方差矩陣的跡進行了最小化[16]。在EIT求解過程中，輸入數據的微小擾動就會對輸出數據產生較大的相對誤差，難以準確求出逆問題的解，體現出嚴重的病態特性。此時AEKF觀測矩陣的病態性會導致重建反演的不穩定，使得濾波值與真值之間存在明顯偏差。因此本文提出基于Tikhonov正則化來修正AEKF算法以克服這一問題，Tikhonov正則化最小化問題如式(6)所示：
 |
式中，γ為正則化參數，參數值可以通過L曲線法來確定；y表示為最小化問題的最優解。L曲線法廣泛應用于選擇最優的正則化參數，參數值越大，其稀疏性約束條件越強。在曲線的拐點處，殘差范數和解范數與正則化參數之間呈現出“L”形曲線，因此選用該點作為正則化控制參數的最優值。基于Tikhonov正則化相應的最小二乘估計值如式(7)所示：
 |
新的正則化觀測矩陣
如式（8）所示：
 |
為了將Tikhonov正則化引入改進的算法中，本文采用偽測量方法[17]，將式(8)替換原始方程引入到遞推的修正AEKF算法中，MAEKF-TR算法更新過程如式(9)所示：
 |
2 結合GAN的后處理
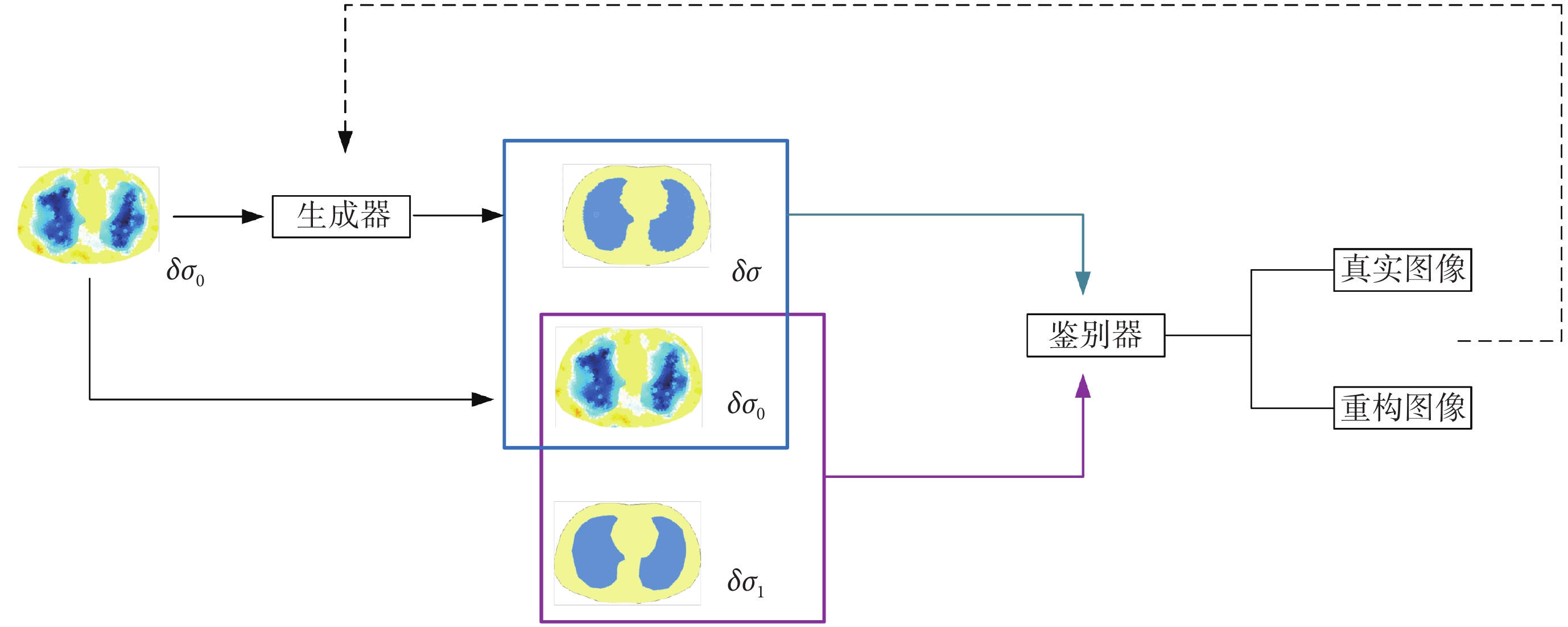
本研究采用MAEKF-TR算法建立邊界電壓與肺部組織電導率分布之間的預映射關系，利用GAN對圖像進行優化，從而提高圖像質量。在EIT算法中，輸入輸出數據必須一一對應，因此使用初始電導率圖像δσ0代替隨機噪聲作為生成器的輸入以生成高質量的重構圖像δσ。鑒別器在學習大量標簽圖像δσ1后對圖像δσ的真實性進行判斷，通過不斷交替更新生成器和鑒別器的參數來優化成像結果[18]。網絡模型結構如圖1所示。
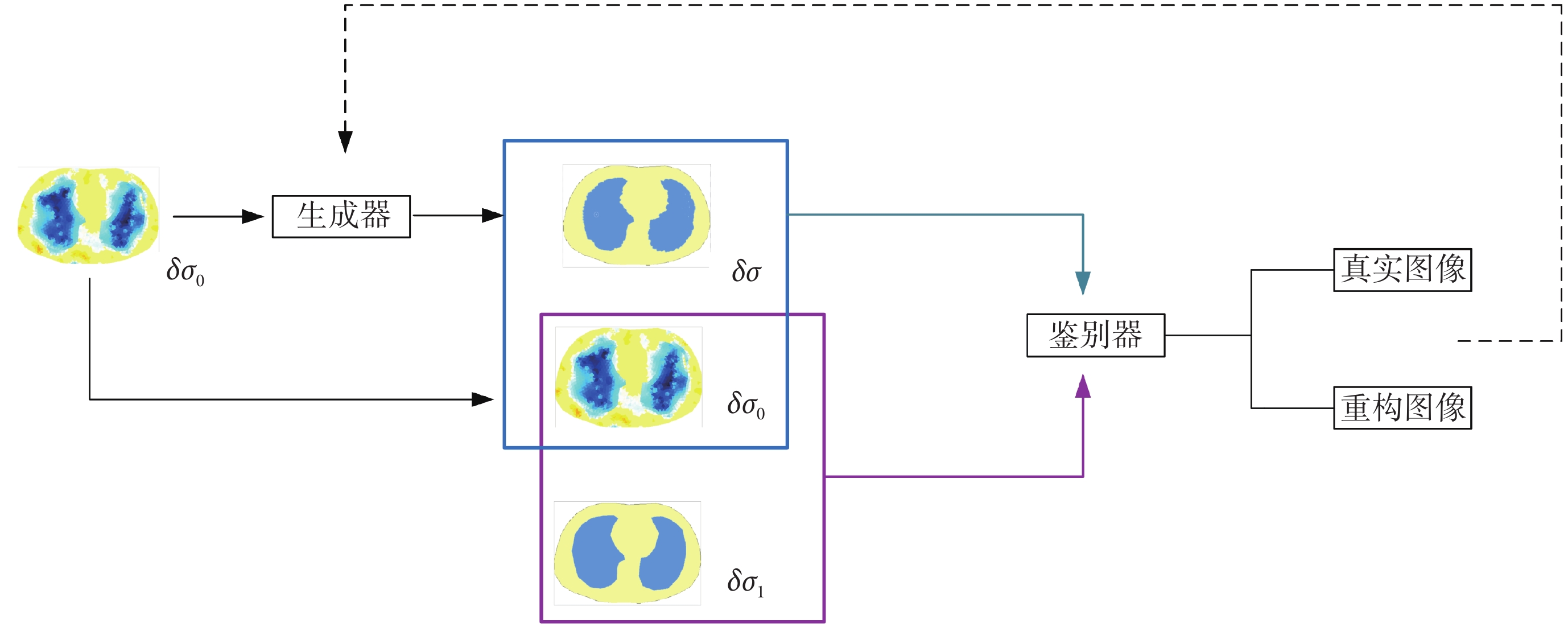圖1
GAN模型整體結構
Figure1.
The overall network architecture of GAN
2.1 GAN模型搭建
鑒于圖像卷積運算（convolution，Conv）能夠有效地利用醫學圖像中的結構信息，因此本文采用U-net作為生成器的網絡結構[19]。輸入輸出均為3通道圖像，網絡結構包括下采樣、上采樣和圖像重構過程。使用4×4的卷積核進行4次卷積與反卷積運算，激活函數為線性整流函數（rectified linear unit，ReLu）。使用全卷積網絡馬爾可夫判別器（PatchGAN）作為模型的鑒別器，將圖片分成固定大小的子圖像，然后獨立處理每個子圖像的內容[20]。PatchGAN的輸入為兩個256 × 256 × 3的數據矩陣，拼接后的數據矩陣先后進行3次組合操作：卷積、批歸一化（batch normalization，BN）、激活函數泄露ReLU（Leaky ReLU），最后通過一次卷積操作提取數據特征，采用邏輯激活函數（Sigmoid）映射到(0, 1)區間。鑒別器結構如表1所示。
表1
鑒別器結構
Table1.
Structure of discriminator
2.2 GAN損失函數
模型采用的損失函數由對抗損失和回歸損失兩部分組成，對抗損失函數 
如式(10)所示：
 |
式中，D為鑒別器，G為生成器；重建圖像的可信度在肺部EIT成像方面非常重要，因此采用L1損失函數來評估重建圖像與真實圖像之間的差值。回歸損失函數 
如式(11)所示：
 |
模型采用的損失函數L如式(12)所示：
 |
式中，D的目標是將式（10）的值最大化，而G則使其值最小。λ1、λ2是平衡對抗損失和回歸損失的加權項，根據經驗選擇設定λ1的值為100，λ2的值為10。
3 實驗結果與分析
3.1 數據集構建
為了驗證算法的有效性，采用兩個肺部公開數據集分別是2016年推出的肺結節分析（lung nodule analysis 16，LUNA 16）數據集[21]和國家肺部篩查試驗（the national lung screening trial，NLST）數據集[22]以及公開癌癥影像數據庫（the cancer imaging archive，TCIA）中的非小細胞肺癌（non‐small cell lung cancer，NSCLC）影像組[23]的肺部CT影像作為EIT仿真模型的樣本。
本文通過區域生長法提取CT影像中的胸腔及肺部輪廓信息，使用有限元仿真軟件COMSOL Multiphysics 6.0（COMSOL Inc.，瑞典）和科學計算軟件MATLAB R2016a（MathWorks Inc.，美國）聯合仿真構建了不同胸腔邊界和肺部形態的仿真模型，建立了人體肺部仿真模型數據庫。在該模型中，將皮下組織電導率設置為0.037 S/m，健康肺部區域電導率設置為0.120～0.142 S/m，病變組織電導率設置為0.200～0.347 S/m [24-25]。在模型邊緣均勻放置了16個激勵電極，電極采用圓形表示，激勵電流設置為1 mA，頻率為50 kHz。通過仿真方法生成的訓練集數據包含5 000個肺部仿真模型，其中健康肺部樣本數與肺部疾病樣本數比例為1:1。將70%的健康肺部和患病肺部的樣本用于訓練集，30%的樣本分配到測試集。本研究的網絡開發環境如下：使用計算機編程語言python 3.8.16（Guido van Rossum，荷蘭）和深度學習框架pytorch 1.4（Facebook Inc，美國）。實驗使用顯卡GPU為NVIDIA GeForce GTX 2080Ti（Nvidia Inc，美國），處理器CPU為Intel（R）Core（TM）i7-6700 CPU @ 3.40 GHz（Intel Inc，美國）。
3.2 評價標準
為了直觀地展示本研究所提出算法的有效性和優越性，可以從定量的角度來比較仿真數據的成像結果。本文使用結構相似性（structural similarity index，SSIM）、峰值信噪比（peak signal to noise ratio，PSNR）、相對誤差（relative error，RE）和相關系數（correlation coefficient，CC）來評估圖像重建的效果。評價指標表達式如式(13)所示：
 |
式中，H和W分別為圖像的長度和寬度，i、j代表標簽與重建圖像的像素指數；
表示圖像真實阻抗值；
表示在第i個單元的真實阻抗值；
表示重建圖像的阻抗值；
表示在第i個單元的重建圖像阻抗值；
和 
表示原始圖像和重建圖像電導率分布的平均值，σi和σj表示原始圖像和重建圖像電導率分布的方差；σij為協方差矩陣；N為重建圖像中像素點的個數。SSIM、PSNR和CC的數值越接近于1，表明重構圖像的質量越高；RE值越接近于0，表明重構圖像與原始圖像之間的相對誤差越小，即圖像重建效果越好。
3.3 無噪聲情況下重構成像
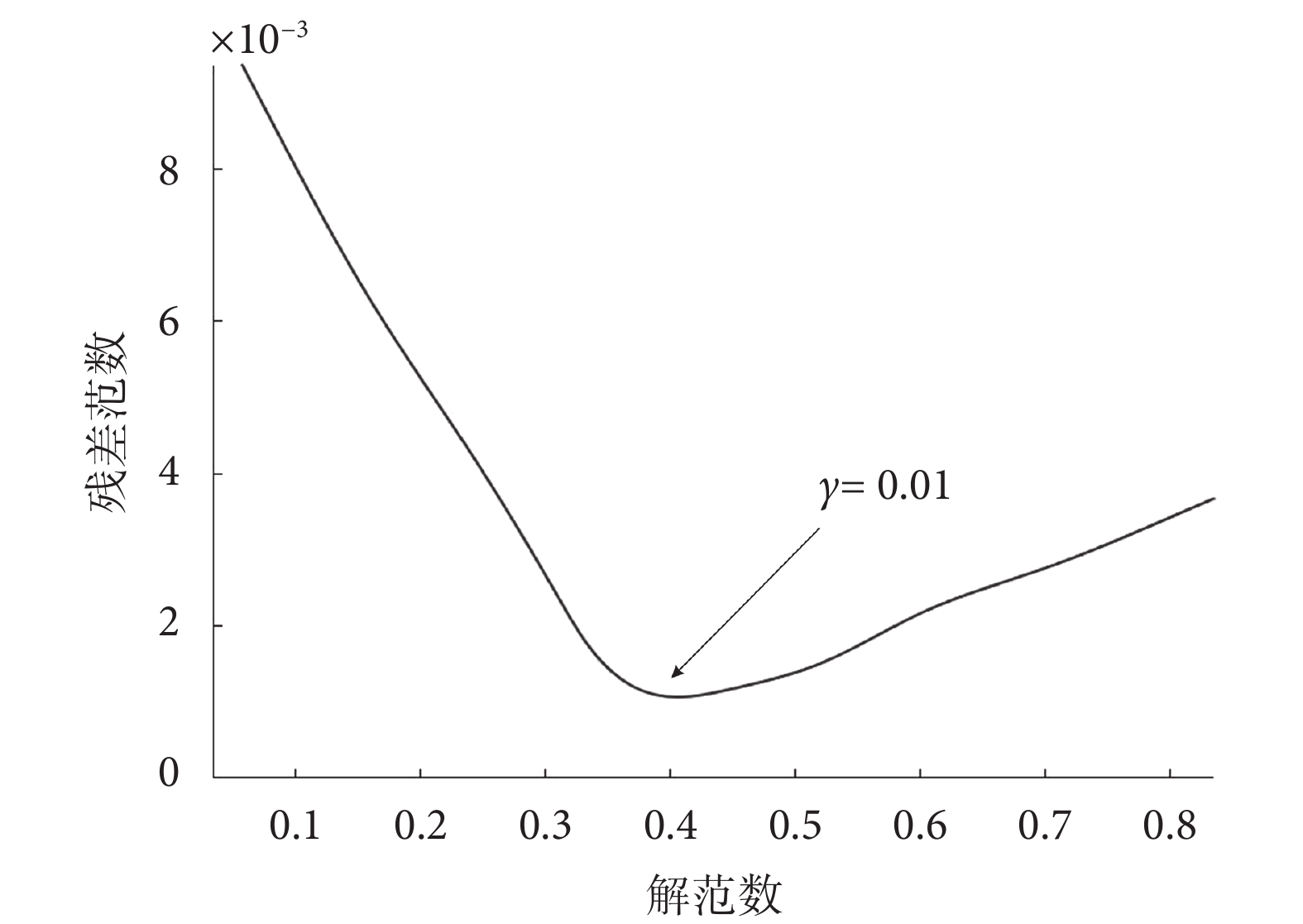
正則化參數的目的是平衡殘差范數和解范數，較小的正則化參數會削弱約束，對殘差項施加較大的懲罰；較大的正則化參數會加強約束，導致正則化項在目標函數中占主導地位。如圖2所示，為觀測到的殘差范數和正則化解范數的L曲線，在拐點處殘差范數和解范數同時達到最小值，因此選取該點作為最優正則化參數，γ值為0.01。
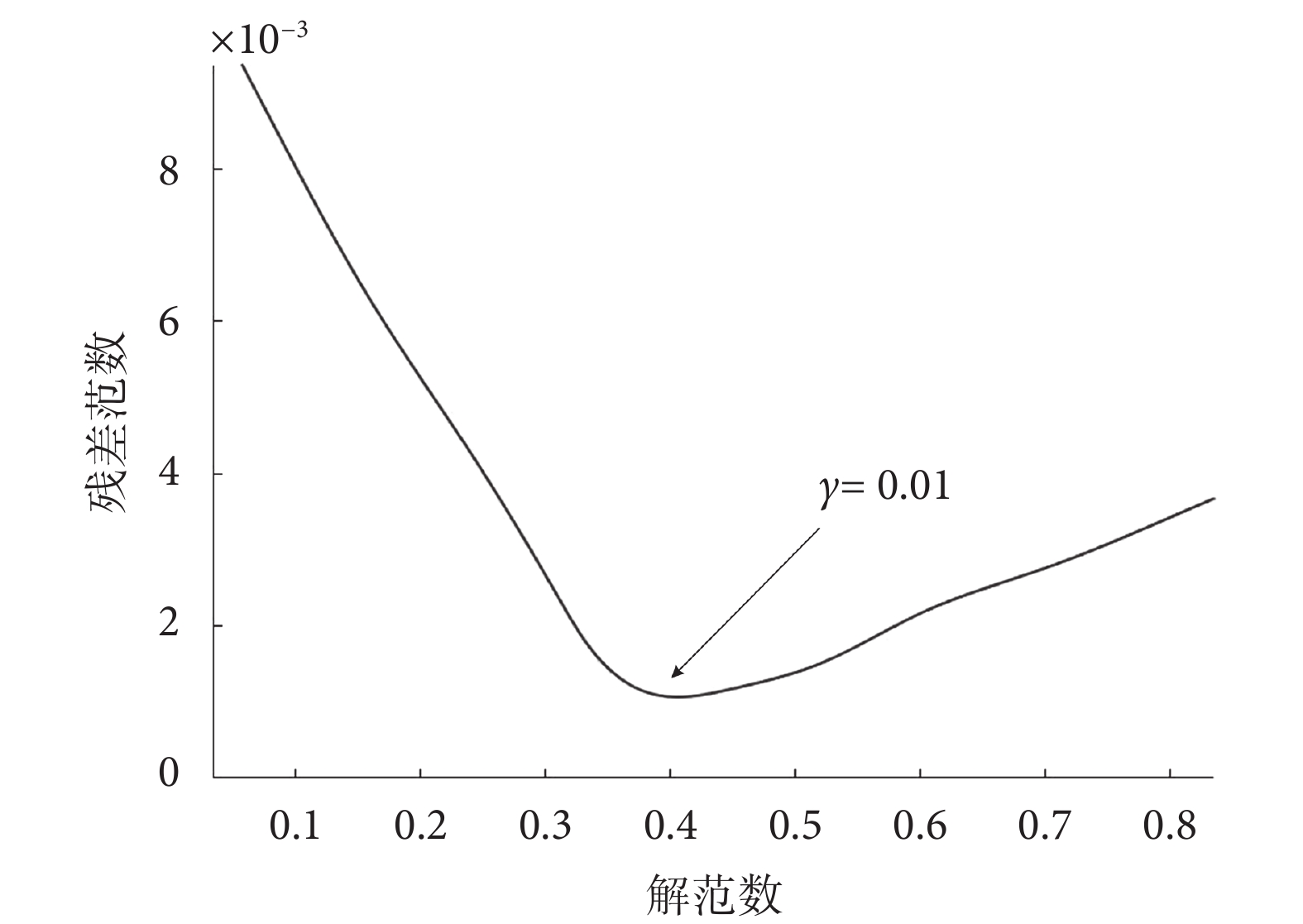圖2
L曲線法確定正則化參數
Figure2.
L-curve method for determining regularization parameter
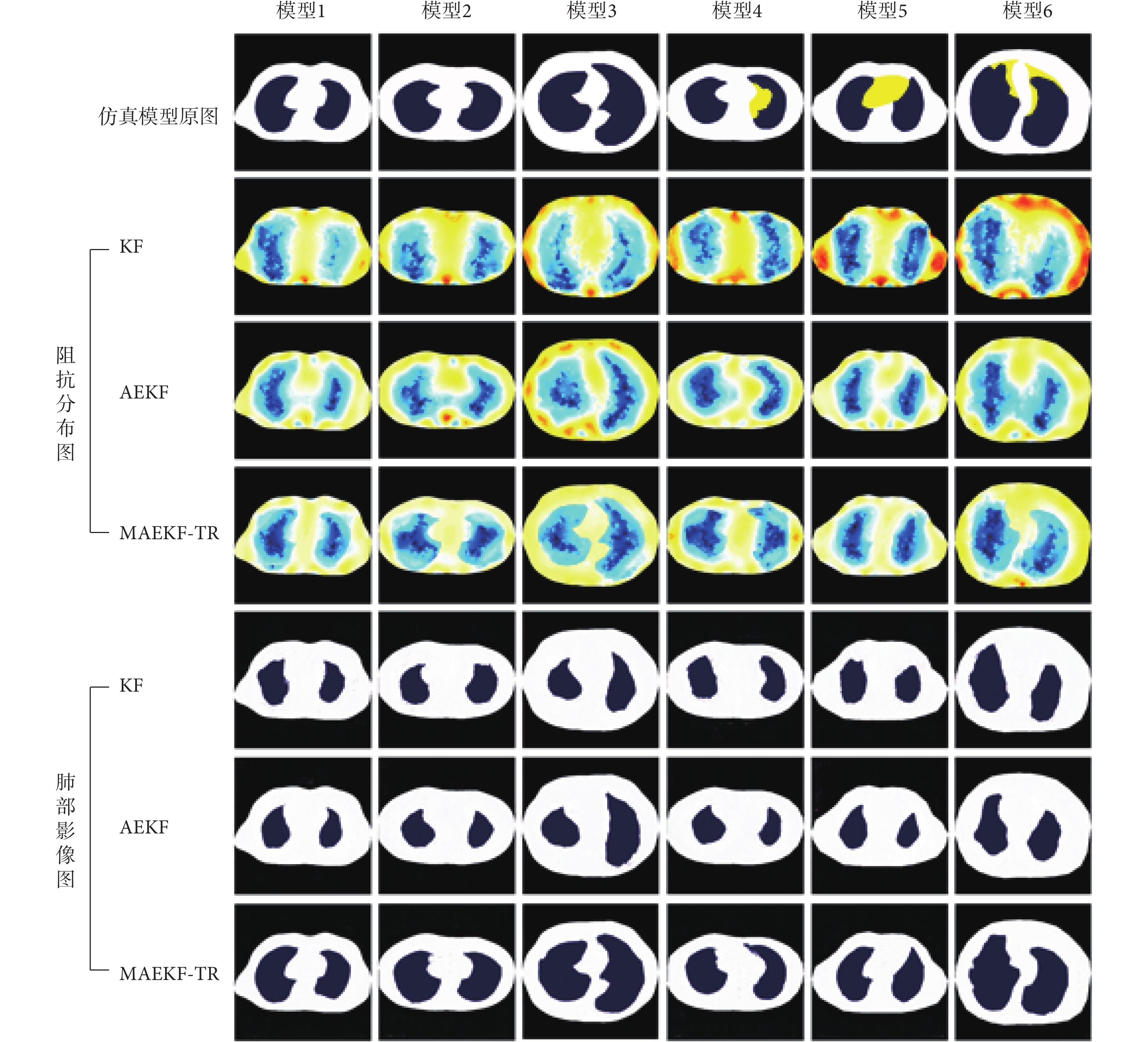
為了驗證本文提出的MAEKF-TR算法的性能，本研究將使用KF算法、AEKF算法和MAEKF-TR算法對人體肺部仿真數據集進行圖像重建，如圖3所示。圖3為六組仿真模型（模型1~模型6）的成像結果，分別展示了EIT阻抗分布數據以及結合GAN模型處理后的肺部影像圖。從阻抗分布圖中可以看出，KF算法能夠檢測到肺部組織，但重建圖像較為模糊，重建效果不佳；AEKF算法相比于KF算法可以重建大致的肺部輪廓，但存在明顯的圖像偽影，無法準確地重現出肺部輪廓。MAEKF-TR算法重建效果最佳，可以較為清晰地重建出肺部邊緣輪廓，更接近真實目標。將三種EIT算法結合GAN模型后得到可視化的肺部影像，可以看到MAEKF-TR算法與GAN模型的組合相比于其他兩種算法能夠更清晰地刻畫肺部輪廓的邊界信息，并且在不同胸腔輪廓模型下成像效果更為穩定，重建圖像的位置大小和邊緣輪廓都更接近真實數據。
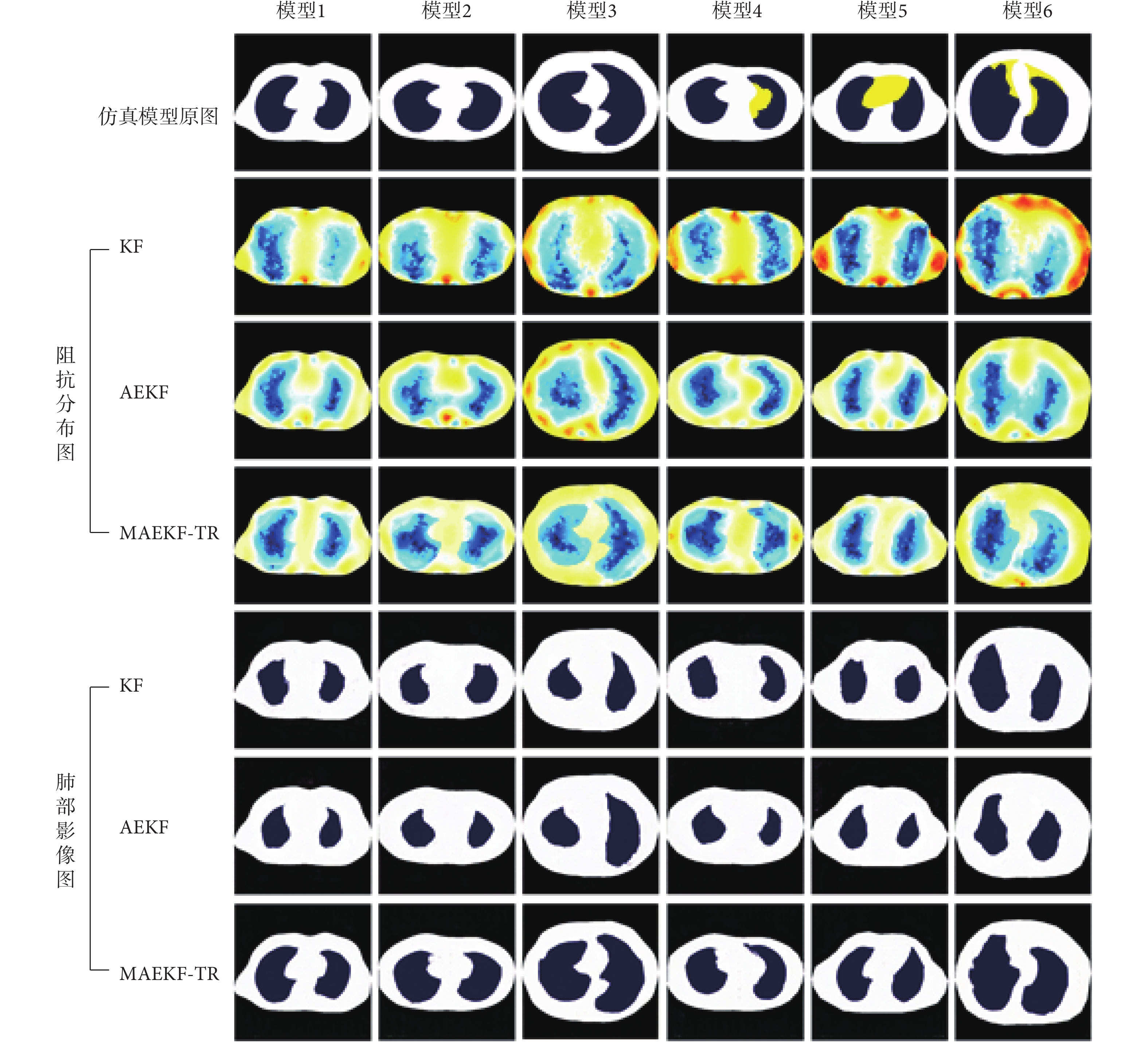圖3
三種算法的仿真成像結果對比
Figure3.
Comparison of simulation imaging results of the three algorithms
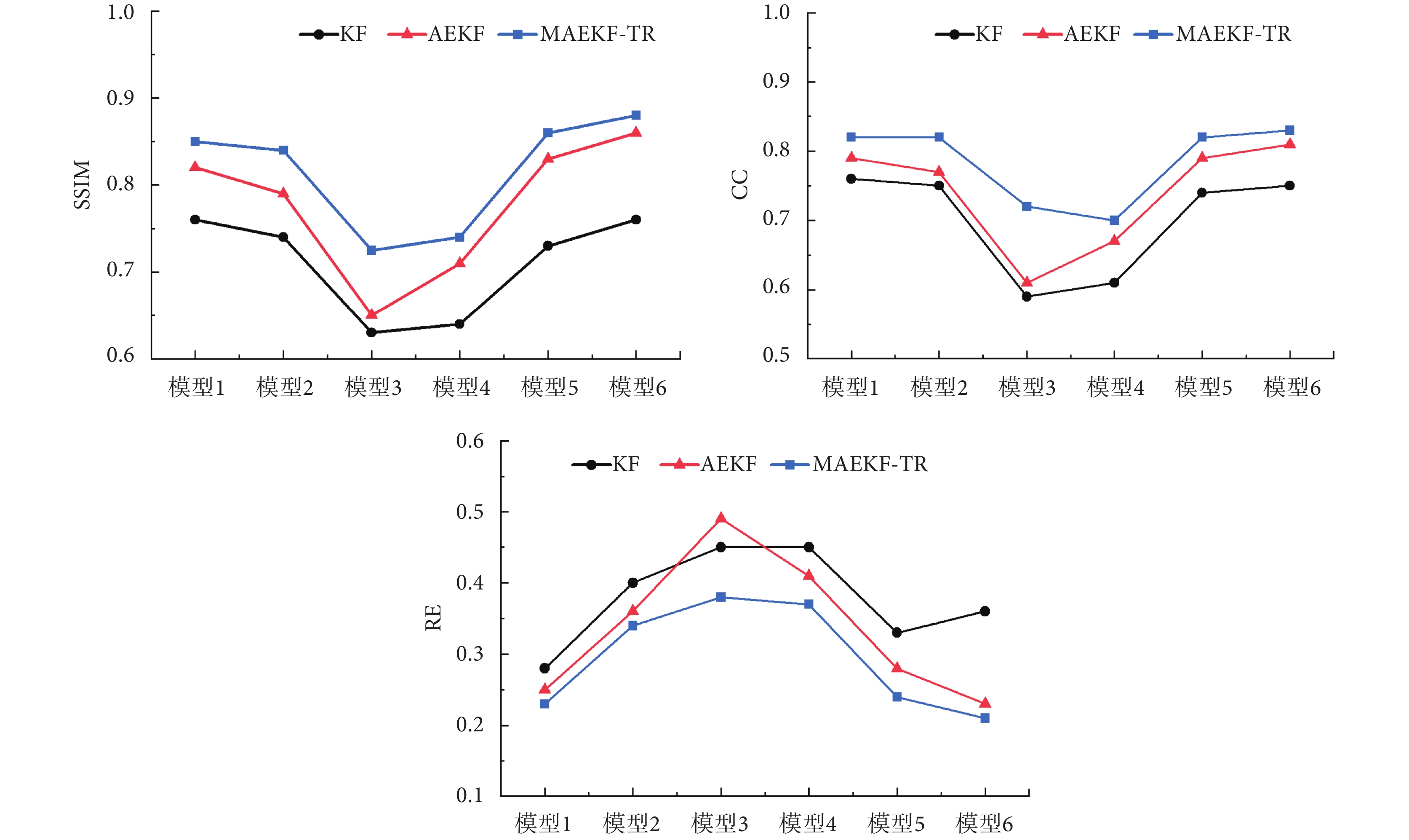
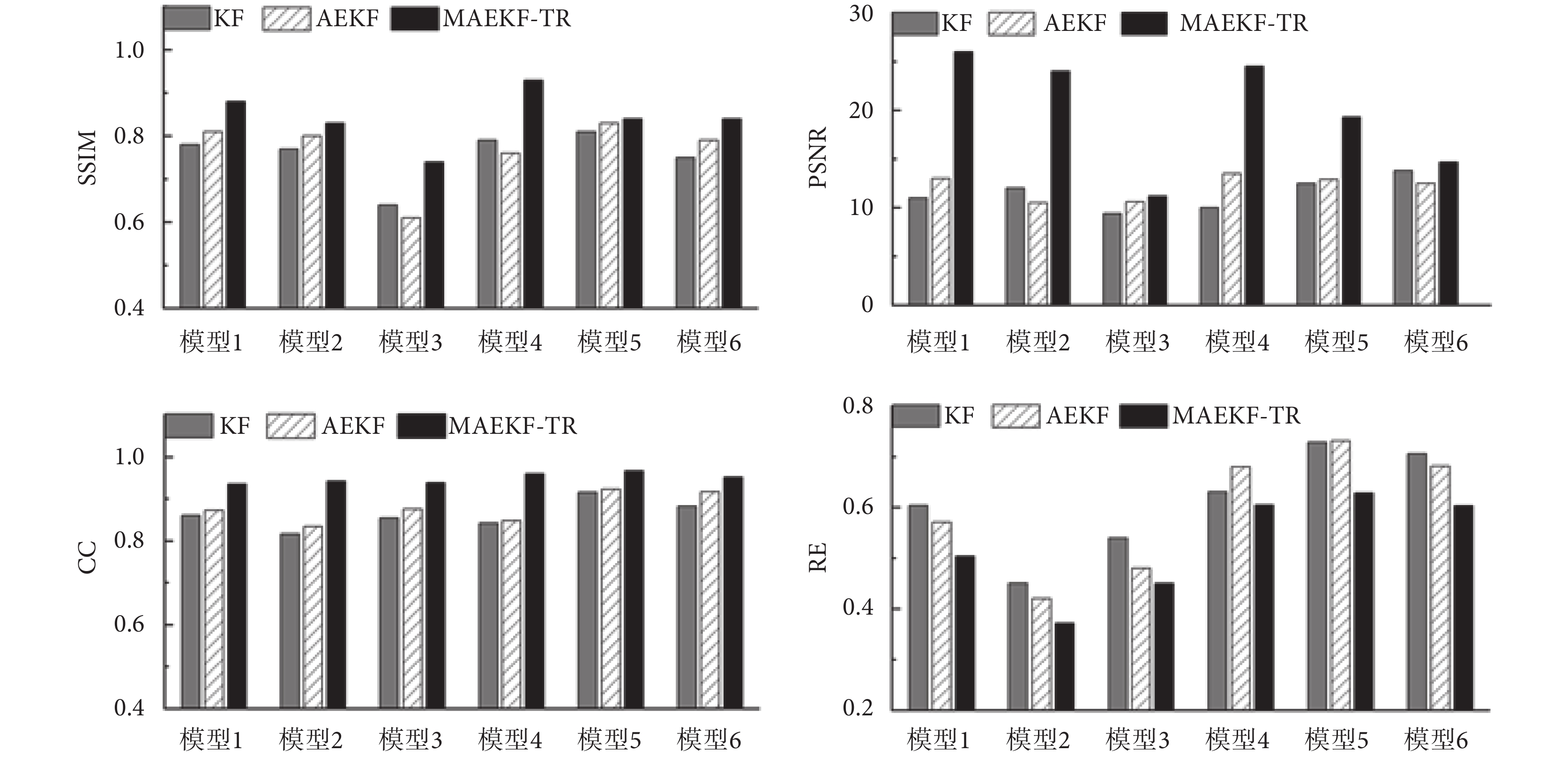
為了定量描述重建圖像質量，本文分別對不同算法的重建圖像進行評估。評價結果如圖4所示，MAEKF-TR算法的SSIM和CC的值接近0.9，顯著優于其他算法，證明了MAEKF-TR算法應用于EIT重建過程的有效性。同時，本文還對三種算法與GAN模型組合后的重建結果進行了評估，結果如圖5所示。對比結果表明，結合GAN模型的MAEKF-TR算法能更加準確地表達胸腔內電特性的參數分布，所成圖像精度更高，并且不易受到肺部疾病等因素導致的模型復雜程度的影響。
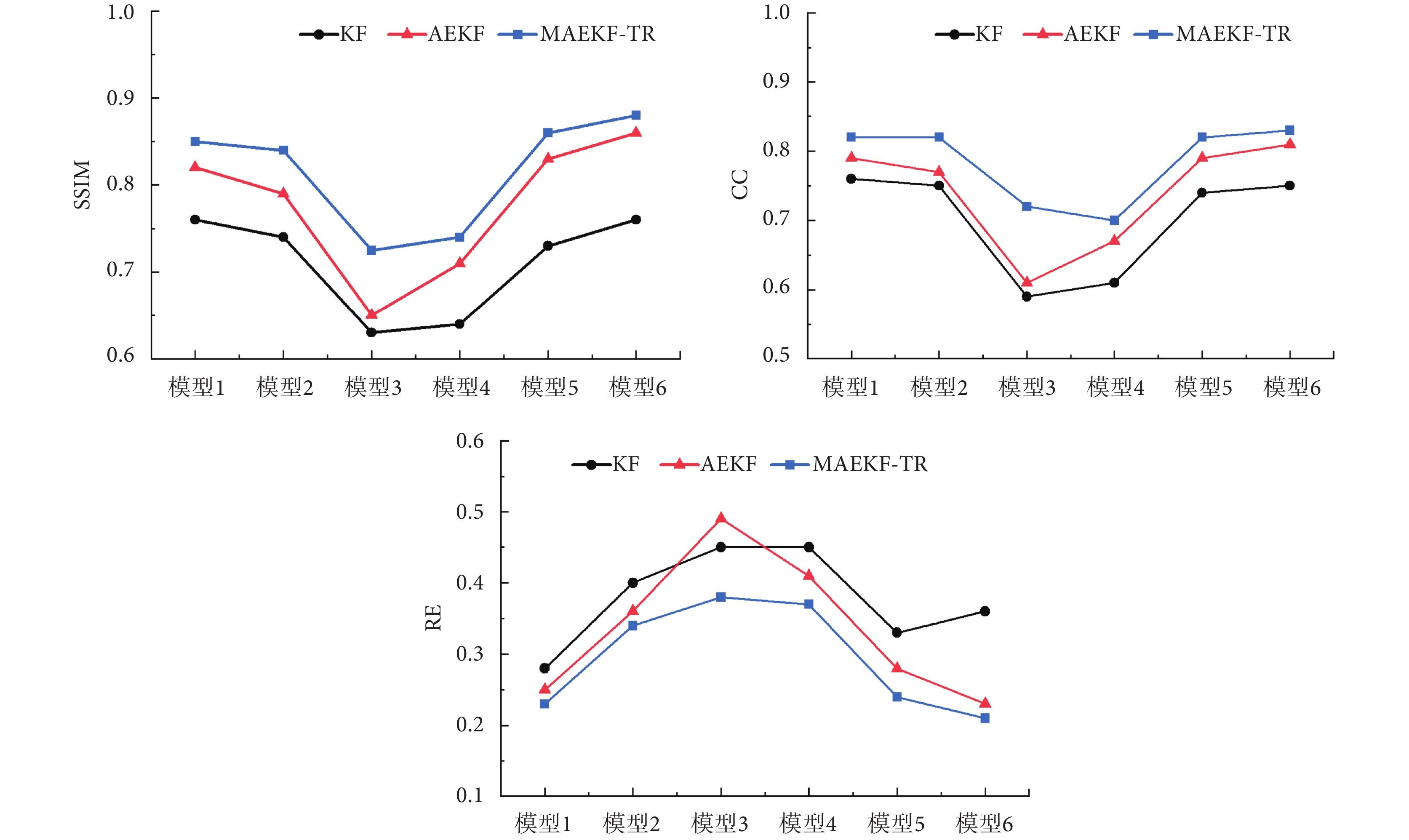圖4
傳統EIT不同算法的重建性能
Figure4.
Reconstruction performance of various algorithms of traditional EIT
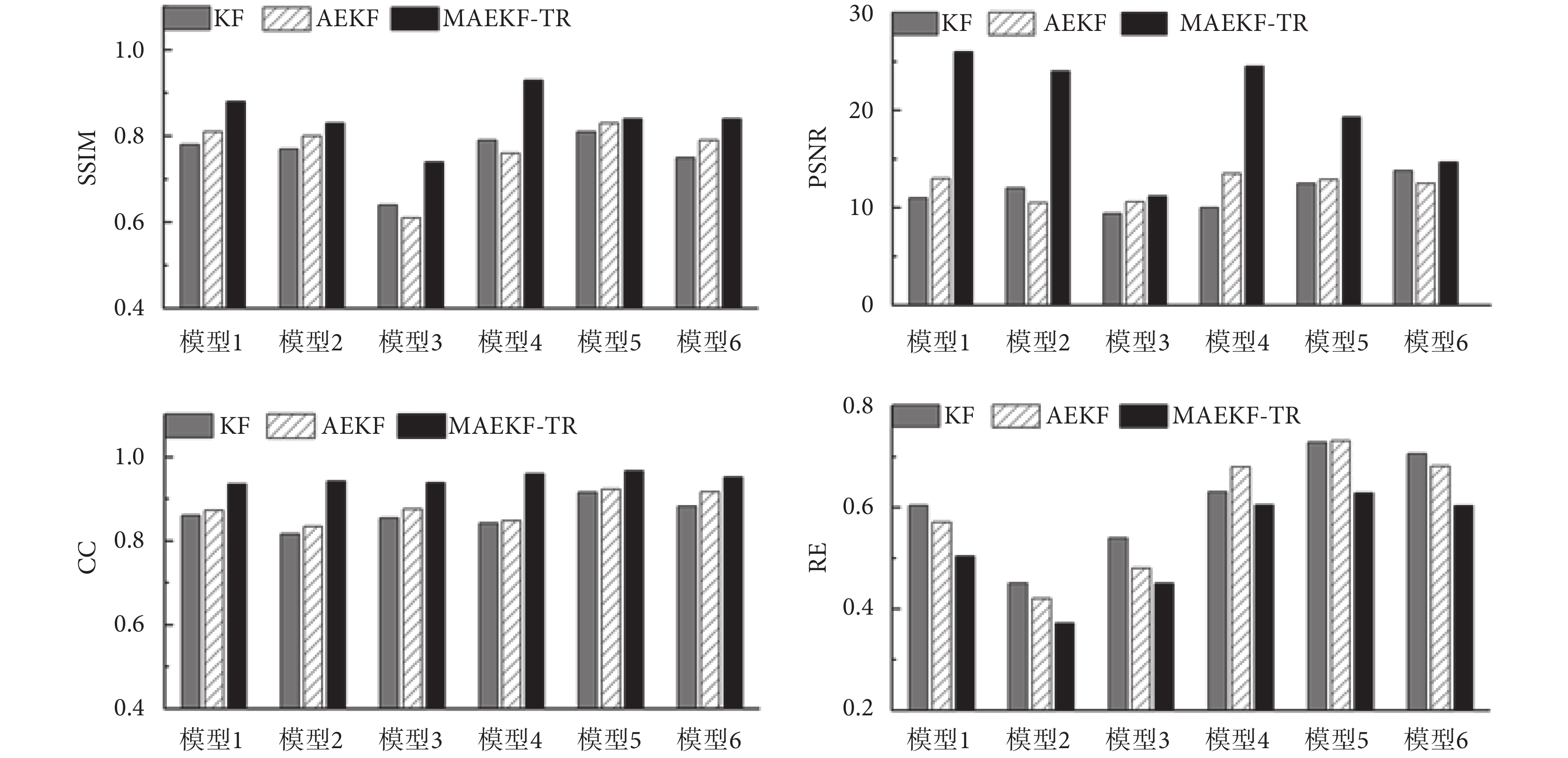圖5
不同算法結合GAN模型的重建性能
Figure5.
Reconstruction performance of various algorithms combined with GAN model
3.4 含噪聲情況下重構成像
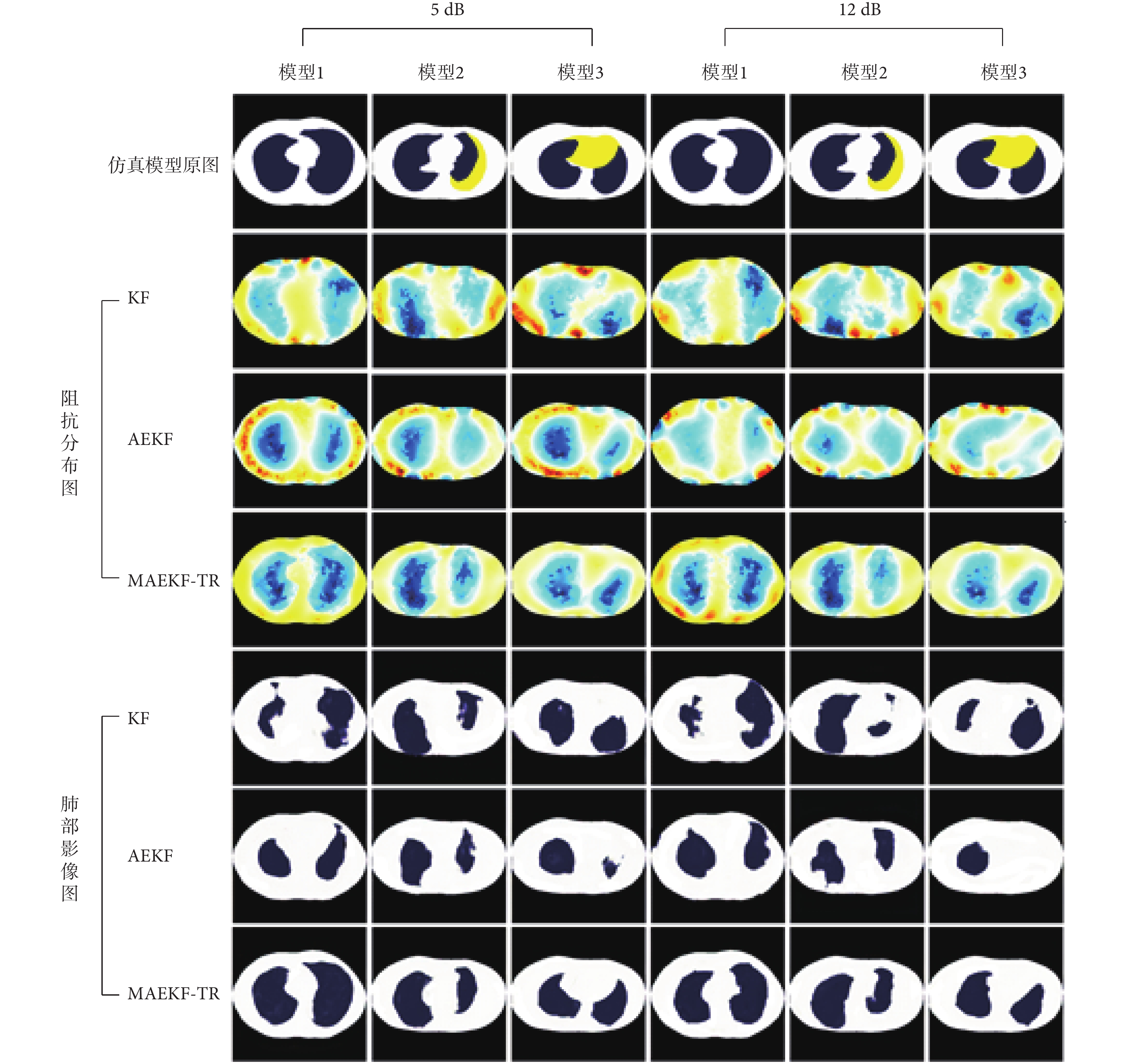
為了驗證MAEKF-TR算法的抗噪性能，本文對仿真數據添加了信噪比為5 dB和12 dB的高斯噪聲。如圖6所示，結合GAN模型的MAEKF-TR算法在噪聲干擾下的重建圖像受到擾動最小，能準確地反映肺部位置，邊緣區域的重建效果較好。而KF算法和AEKF算法的重建圖像受到噪聲的影響均發生了不同程度的畸變，抗干擾能力較差。本文提出的方法在噪聲條件下依舊表現出良好的重建性能，如表2所示，加粗字體表示三種重建算法在噪聲干擾下每個模型的最優性能參數。
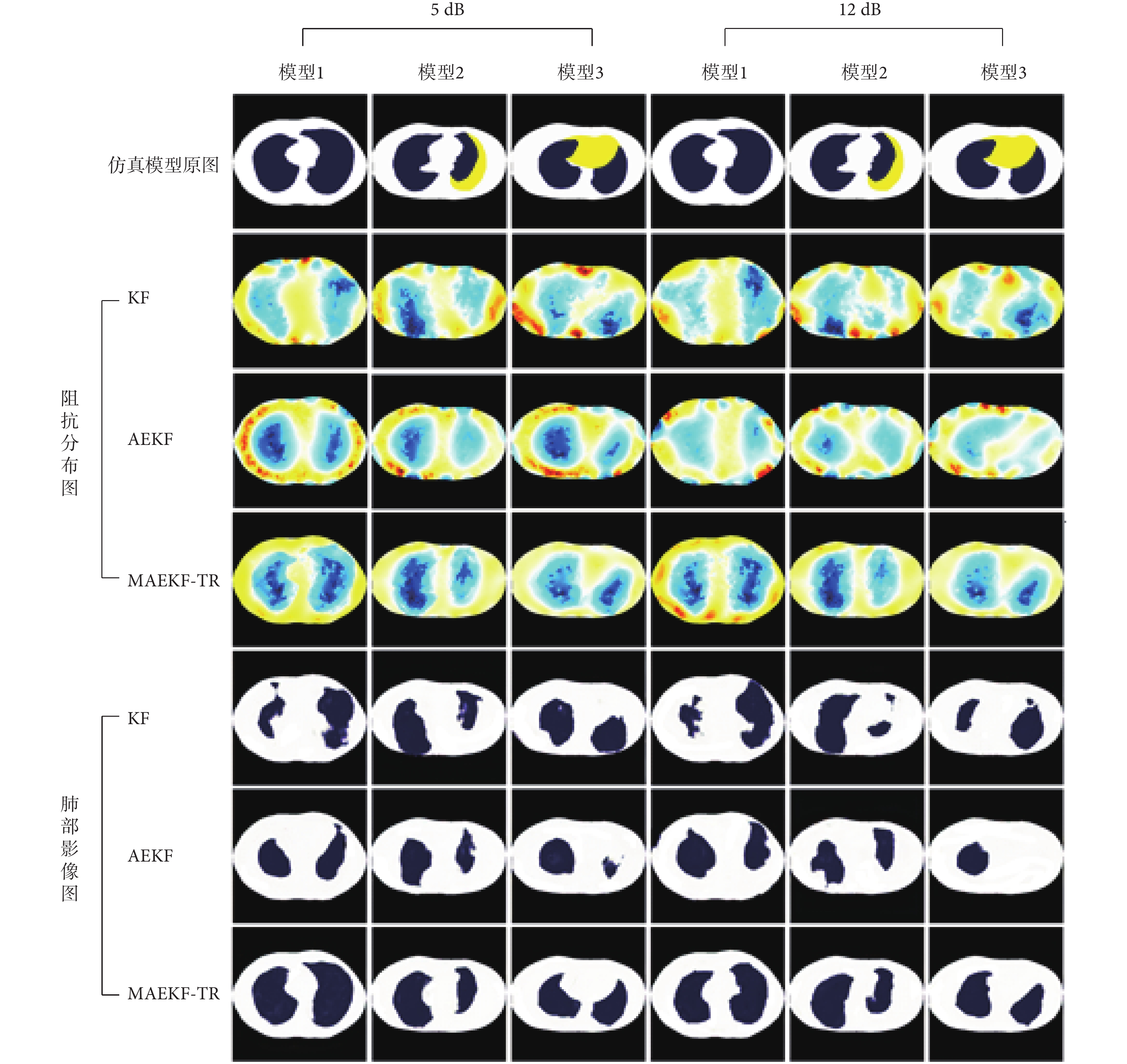圖6
含噪聲情況下不同算法的仿真成像結果對比
Figure6.
Comparison of simulation imaging results of various algorithms in the presence of noise
表2
含噪聲情況下不同算法結合GAN模型的重構性能參數
Table2.
Reconstruction performance metrics of various algorithms combined with GAN model in the presence of noise
4 結論
本文提出了一種結合GAN的MAEKF-TR算法應用于肺通氣監測。首先構建了人體肺部仿真數據集來評估所提出算法的性能，同時將MAEKF-TR算法生成的EIT阻抗分布數據用于GAN模型進行對抗訓練，通過生成器與鑒別器之間的不斷博弈，最終得到了近似人體阻抗分布的肺部重構影像。仿真實驗結果表明，該方法能顯著提升肺部成像的質量，得到邊界完整且位置精確的肺部圖像。綜上，本文所提出的方法為EIT圖像重建提供了新的思路，有望進一步推動EIT在肺部疾病檢測方面的應用。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：本文工作中，趙明康、劉珺負責算法程序設計、數據收集；郭忠圣、陳祥琪負責數據分析；鄭天予負責論文圖像處理；劉珺負責論文寫作；張帥負責論文審閱。
0 引言
電阻抗斷層成像（electrical impedance tomography，EIT）是一種電學測量技術，具有快速成像、無損傷、無輻射等優點[1]。近年來，EIT技術已經被廣泛研究和應用于臨床檢測中，主要用于呼吸系統監測、肺功能成像、肺通氣監測等領域。該技術通過測量邊界電壓并采用適當的成像算法對人體內部電導率分布進行重構，從而實現高分辨率的實時成像[2]。然而在實際測量過程中，由于測量值數量遠少于待求未知量的數量，EIT逆問題具有嚴重的不適定性。傳統成像算法對噪聲和誤差極為敏感，為了提高電導率分布圖像的穩定性，通常需要降低空間分辨率，因此導致重構圖像出現較大的偽影且成像精度較差。目前常用的重構算法包括線性反投影法[3]、一步線性高斯牛頓法[4]等。1998年Vauhkonen等[5]基于隨機游走模型將卡爾曼濾波（Kalman filter，KF）算法引入EIT技術中，將EIT逆問題轉化為狀態估計問題。然而在實際應用中，人們往往難以建立精確的數學模型，EIT的不適定性導致狀態向量的更新過程極易受到噪聲干擾，從而導致傳統KF算法濾波精度下降，進而影響圖像重建的質量。因此，本文提出基于吉洪諾夫（Tikhonov）正則化的修正自適應擴展KF（modified adaptive extended KF with Tikhonov regularization，MAEKF-TR）算法，以期減小過程噪聲對實際數據的影響，改善EIT逆問題的不適定性，完成對肺部組織的圖像重建。
近年來，深度學習算法在計算機視覺、圖像重建等領域取得了長足發展[6]。與傳統方法相比，深度學習網絡模型可以更有效地捕獲圖像的復雜特征，獲得更高的重建性能。因此，許多國內外學者嘗試將深度學習算法用于生物醫學圖像處理領域[7-8]。經典的深度學習算法如卷積神經網絡、U型網絡（U-net）、生成對抗網絡（generative adversarial network，GAN）等，已在計算機斷層掃描（computed tomography，CT）、磁共振成像（magnetic resonance imaging，MRI）等醫學圖像重建領域取得了顯著的成果[9-11]。為了減少傳統EIT算法的重構誤差，降低人為因素對影像診斷的影響，本文提出將GAN與MAEKF-TR算法相結合的方法。具體而言，首先使用卷積神經網絡對包含誤差和偽影的EIT阻抗分布數據進行訓練，通過GAN中生成器與鑒別器之間的對抗訓練所生成的肺部影像能夠更清晰地反映肺部大小和形態等信息，從而減小EIT重建算法引起的偽影干擾。
本文構建了人體肺部仿真數據集，來模擬人類胸腔和常見肺部疾病的電導率分布，以評估所提方法的性能。此外，本文還將以仿真實驗證實，與傳統KF重建算法相比，MAEKF-TR算法與GAN結合，不僅能準確檢測出肺部器官的大小和位置，而且所生成的肺部圖像輪廓邊緣更加清晰，可以降低對EIT重建圖像分析的主觀性影響和誤差。綜上，通過仿真實驗研究結果，期望本研究提出的方法對肺通氣監測相關研究有一定的參考意義。
1 算法描述
1.1 EIT原理
本文采用16個電極的EIT測量系統，采用相鄰電極輸入電流，其他相鄰電極測量電壓值的模式。EIT重建過程可分為兩個主要步驟：正問題求解和逆問題求解。正問題求解，是指在已知物體內EIT分布的情況下求解邊界電壓值；逆問題求解，則是通過邊界電壓差值求解內部電導率的變化分布。圖像重建過程實際上是逆問題的求解過程，EIT線性模型如式(1)所示[12]：
|
式中，ΔU為測量電壓變化量；J為靈敏度矩陣；Δσ為場域內電導率變化量。逆問題的求解實際是對非線性表達式的求解，而EIT圖像重建過程就是將非線性表達式進行線性化來尋找最優解σ，如式(2)所示：
|
式中，Z為實際測量數據。
1.2 MAEKF-TR算法
求解EIT逆問題的過程，其實質是對電導率分布的求解。KF標準遞推方程見文獻[13-15]，將KF映射到EIT系統中，電導率σk視為狀態估計量，從而將EIT逆問題轉化為狀態估計問題，如式(3)所示：
|
式中， 是k時刻的先驗狀態估計量； 是k ? 1時刻的先驗狀態估計量；Fk-1為k–1時刻的狀態傳遞矩陣，wk為k時刻的系統噪聲；Zk為k時刻的實際測量值；Jk為k時刻的觀測矩陣；vk為k時刻的測量噪聲。EIT系統的KF濾波方程如式(4)所示：
|
式中， 表示估計誤差協方差矩陣k時刻的先驗估計； 表示估計誤差協方差矩陣k – 1時刻的先驗估計； 表示估計誤差協方差矩陣k時刻的后驗估計； 是k時刻的后驗狀態估計量；Rk表示k時刻的測量噪聲協方差；Qk表示k時刻的過程噪聲協方差；Kk表示k時刻的算法增益；I是單位矩陣，T為轉置符號。在實際測量生物組織時，數據信息會發生突變，導致估計的新息矢量發生較大變化。然而算法增益Kk不能實時根據狀態變化進行調整，從而導致濾波精度下降、濾波發散等情況出現。要削減測量噪聲對算法的干擾，就要調整測量噪聲協方差Rk及過程噪聲協方差Qk的權重占比。
本文提出引入優化因子δp[δp∈(0，1)]，對過程噪聲協方差Qk進行修正，將更新的數據給予更多的權重。Qk調整如式(5)所示：
|
式中， 表示修正后k時刻的過程噪聲協方差； 表示修正后k – 1時刻的過程噪聲協方差；ξk表示在k時刻的新息矢量；Δp表示觀測值與先驗值之間的殘差。以上分析可知，改進后的自適應擴展KF（adaptive extended KF，AEKF）算法考慮了實際噪聲的時變特性對系統的影響，并通過實時數據更新的方式實現了對噪聲的實時修正。
算法增益Kk是最小二乘估計的最優增益，相當于對后驗誤差協方差矩陣的跡進行了最小化[16]。在EIT求解過程中，輸入數據的微小擾動就會對輸出數據產生較大的相對誤差，難以準確求出逆問題的解，體現出嚴重的病態特性。此時AEKF觀測矩陣的病態性會導致重建反演的不穩定，使得濾波值與真值之間存在明顯偏差。因此本文提出基于Tikhonov正則化來修正AEKF算法以克服這一問題，Tikhonov正則化最小化問題如式(6)所示：
|
式中，γ為正則化參數，參數值可以通過L曲線法來確定；y表示為最小化問題的最優解。L曲線法廣泛應用于選擇最優的正則化參數，參數值越大，其稀疏性約束條件越強。在曲線的拐點處，殘差范數和解范數與正則化參數之間呈現出“L”形曲線，因此選用該點作為正則化控制參數的最優值。基于Tikhonov正則化相應的最小二乘估計值如式(7)所示：
|
新的正則化觀測矩陣如式（8）所示：
|
為了將Tikhonov正則化引入改進的算法中，本文采用偽測量方法[17]，將式(8)替換原始方程引入到遞推的修正AEKF算法中，MAEKF-TR算法更新過程如式(9)所示：
|
2 結合GAN的后處理
本研究采用MAEKF-TR算法建立邊界電壓與肺部組織電導率分布之間的預映射關系，利用GAN對圖像進行優化，從而提高圖像質量。在EIT算法中，輸入輸出數據必須一一對應，因此使用初始電導率圖像δσ0代替隨機噪聲作為生成器的輸入以生成高質量的重構圖像δσ。鑒別器在學習大量標簽圖像δσ1后對圖像δσ的真實性進行判斷，通過不斷交替更新生成器和鑒別器的參數來優化成像結果[18]。網絡模型結構如圖1所示。
圖1
GAN模型整體結構
Figure1.
The overall network architecture of GAN
2.1 GAN模型搭建
鑒于圖像卷積運算（convolution，Conv）能夠有效地利用醫學圖像中的結構信息，因此本文采用U-net作為生成器的網絡結構[19]。輸入輸出均為3通道圖像，網絡結構包括下采樣、上采樣和圖像重構過程。使用4×4的卷積核進行4次卷積與反卷積運算，激活函數為線性整流函數（rectified linear unit，ReLu）。使用全卷積網絡馬爾可夫判別器（PatchGAN）作為模型的鑒別器，將圖片分成固定大小的子圖像，然后獨立處理每個子圖像的內容[20]。PatchGAN的輸入為兩個256 × 256 × 3的數據矩陣，拼接后的數據矩陣先后進行3次組合操作：卷積、批歸一化（batch normalization，BN）、激活函數泄露ReLU（Leaky ReLU），最后通過一次卷積操作提取數據特征，采用邏輯激活函數（Sigmoid）映射到(0, 1)區間。鑒別器結構如表1所示。
表1
鑒別器結構
Table1.
Structure of discriminator
2.2 GAN損失函數
模型采用的損失函數由對抗損失和回歸損失兩部分組成，對抗損失函數 如式(10)所示：
|
式中，D為鑒別器，G為生成器；重建圖像的可信度在肺部EIT成像方面非常重要，因此采用L1損失函數來評估重建圖像與真實圖像之間的差值。回歸損失函數 如式(11)所示：
|
模型采用的損失函數L如式(12)所示：
|
式中，D的目標是將式（10）的值最大化，而G則使其值最小。λ1、λ2是平衡對抗損失和回歸損失的加權項，根據經驗選擇設定λ1的值為100，λ2的值為10。
3 實驗結果與分析
3.1 數據集構建
為了驗證算法的有效性，采用兩個肺部公開數據集分別是2016年推出的肺結節分析（lung nodule analysis 16，LUNA 16）數據集[21]和國家肺部篩查試驗（the national lung screening trial，NLST）數據集[22]以及公開癌癥影像數據庫（the cancer imaging archive，TCIA）中的非小細胞肺癌（non‐small cell lung cancer，NSCLC）影像組[23]的肺部CT影像作為EIT仿真模型的樣本。
本文通過區域生長法提取CT影像中的胸腔及肺部輪廓信息，使用有限元仿真軟件COMSOL Multiphysics 6.0（COMSOL Inc.，瑞典）和科學計算軟件MATLAB R2016a（MathWorks Inc.，美國）聯合仿真構建了不同胸腔邊界和肺部形態的仿真模型，建立了人體肺部仿真模型數據庫。在該模型中，將皮下組織電導率設置為0.037 S/m，健康肺部區域電導率設置為0.120～0.142 S/m，病變組織電導率設置為0.200～0.347 S/m [24-25]。在模型邊緣均勻放置了16個激勵電極，電極采用圓形表示，激勵電流設置為1 mA，頻率為50 kHz。通過仿真方法生成的訓練集數據包含5 000個肺部仿真模型，其中健康肺部樣本數與肺部疾病樣本數比例為1:1。將70%的健康肺部和患病肺部的樣本用于訓練集，30%的樣本分配到測試集。本研究的網絡開發環境如下：使用計算機編程語言python 3.8.16（Guido van Rossum，荷蘭）和深度學習框架pytorch 1.4（Facebook Inc，美國）。實驗使用顯卡GPU為NVIDIA GeForce GTX 2080Ti（Nvidia Inc，美國），處理器CPU為Intel（R）Core（TM）i7-6700 CPU @ 3.40 GHz（Intel Inc，美國）。
3.2 評價標準
為了直觀地展示本研究所提出算法的有效性和優越性，可以從定量的角度來比較仿真數據的成像結果。本文使用結構相似性（structural similarity index，SSIM）、峰值信噪比（peak signal to noise ratio，PSNR）、相對誤差（relative error，RE）和相關系數（correlation coefficient，CC）來評估圖像重建的效果。評價指標表達式如式(13)所示：
|
式中，H和W分別為圖像的長度和寬度，i、j代表標簽與重建圖像的像素指數； 表示圖像真實阻抗值； 表示在第i個單元的真實阻抗值； 表示重建圖像的阻抗值； 表示在第i個單元的重建圖像阻抗值； 和 表示原始圖像和重建圖像電導率分布的平均值，σi和σj表示原始圖像和重建圖像電導率分布的方差；σij為協方差矩陣；N為重建圖像中像素點的個數。SSIM、PSNR和CC的數值越接近于1，表明重構圖像的質量越高；RE值越接近于0，表明重構圖像與原始圖像之間的相對誤差越小，即圖像重建效果越好。
3.3 無噪聲情況下重構成像
正則化參數的目的是平衡殘差范數和解范數，較小的正則化參數會削弱約束，對殘差項施加較大的懲罰；較大的正則化參數會加強約束，導致正則化項在目標函數中占主導地位。如圖2所示，為觀測到的殘差范數和正則化解范數的L曲線，在拐點處殘差范數和解范數同時達到最小值，因此選取該點作為最優正則化參數，γ值為0.01。
圖2
L曲線法確定正則化參數
Figure2.
L-curve method for determining regularization parameter
為了驗證本文提出的MAEKF-TR算法的性能，本研究將使用KF算法、AEKF算法和MAEKF-TR算法對人體肺部仿真數據集進行圖像重建，如圖3所示。圖3為六組仿真模型（模型1~模型6）的成像結果，分別展示了EIT阻抗分布數據以及結合GAN模型處理后的肺部影像圖。從阻抗分布圖中可以看出，KF算法能夠檢測到肺部組織，但重建圖像較為模糊，重建效果不佳；AEKF算法相比于KF算法可以重建大致的肺部輪廓，但存在明顯的圖像偽影，無法準確地重現出肺部輪廓。MAEKF-TR算法重建效果最佳，可以較為清晰地重建出肺部邊緣輪廓，更接近真實目標。將三種EIT算法結合GAN模型后得到可視化的肺部影像，可以看到MAEKF-TR算法與GAN模型的組合相比于其他兩種算法能夠更清晰地刻畫肺部輪廓的邊界信息，并且在不同胸腔輪廓模型下成像效果更為穩定，重建圖像的位置大小和邊緣輪廓都更接近真實數據。
圖3
三種算法的仿真成像結果對比
Figure3.
Comparison of simulation imaging results of the three algorithms
為了定量描述重建圖像質量，本文分別對不同算法的重建圖像進行評估。評價結果如圖4所示，MAEKF-TR算法的SSIM和CC的值接近0.9，顯著優于其他算法，證明了MAEKF-TR算法應用于EIT重建過程的有效性。同時，本文還對三種算法與GAN模型組合后的重建結果進行了評估，結果如圖5所示。對比結果表明，結合GAN模型的MAEKF-TR算法能更加準確地表達胸腔內電特性的參數分布，所成圖像精度更高，并且不易受到肺部疾病等因素導致的模型復雜程度的影響。
圖4
傳統EIT不同算法的重建性能
Figure4.
Reconstruction performance of various algorithms of traditional EIT
圖5
不同算法結合GAN模型的重建性能
Figure5.
Reconstruction performance of various algorithms combined with GAN model
3.4 含噪聲情況下重構成像
為了驗證MAEKF-TR算法的抗噪性能，本文對仿真數據添加了信噪比為5 dB和12 dB的高斯噪聲。如圖6所示，結合GAN模型的MAEKF-TR算法在噪聲干擾下的重建圖像受到擾動最小，能準確地反映肺部位置，邊緣區域的重建效果較好。而KF算法和AEKF算法的重建圖像受到噪聲的影響均發生了不同程度的畸變，抗干擾能力較差。本文提出的方法在噪聲條件下依舊表現出良好的重建性能，如表2所示，加粗字體表示三種重建算法在噪聲干擾下每個模型的最優性能參數。
圖6
含噪聲情況下不同算法的仿真成像結果對比
Figure6.
Comparison of simulation imaging results of various algorithms in the presence of noise
表2
含噪聲情況下不同算法結合GAN模型的重構性能參數
Table2.
Reconstruction performance metrics of various algorithms combined with GAN model in the presence of noise
4 結論
本文提出了一種結合GAN的MAEKF-TR算法應用于肺通氣監測。首先構建了人體肺部仿真數據集來評估所提出算法的性能，同時將MAEKF-TR算法生成的EIT阻抗分布數據用于GAN模型進行對抗訓練，通過生成器與鑒別器之間的不斷博弈，最終得到了近似人體阻抗分布的肺部重構影像。仿真實驗結果表明，該方法能顯著提升肺部成像的質量，得到邊界完整且位置精確的肺部圖像。綜上，本文所提出的方法為EIT圖像重建提供了新的思路，有望進一步推動EIT在肺部疾病檢測方面的應用。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：本文工作中，趙明康、劉珺負責算法程序設計、數據收集；郭忠圣、陳祥琪負責數據分析；鄭天予負責論文圖像處理；劉珺負責論文寫作；張帥負責論文審閱。
