三維牙頜模型的分割是計算機口腔輔助診療系統的關鍵步驟。針對牙齒分割技術普適性差、欠分割的問題，提出一種結合多種子區域生長和邊界延伸的智能牙齒分割方法。該方法結合牙齒的負曲率網格的分布特點獲得新種子點，通過差異性區域生長適應了牙齒頂面和側面間的差異性結構，并結合幾何特征對初次分割的邊界進行延伸，有效彌補了區域生長的欠分割缺陷。在實驗中，通過與當前經典的算法進行對比和消融實驗，表明本文方法能夠更好地分割擁擠的牙頜模型，具有較強算法普適性，已具備滿足口腔診療中實際分割需求的能力。
引用本文： 劉志華, 薛久濤, 唐浩, 廖與禾. 結合多種子區域生長和邊界延伸的智能牙齒分割方法研究. 生物醫學工程學雜志, 2024, 41(3): 520-526. doi: 10.7507/1001-5515.202309030 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
牙齒畸形是口腔疾病中的常見病癥，作為正畸治療的首要步驟，三維牙頜模型分割技術的提升對計算機輔助設計系統在正畸領域的推廣具有重要意義。與傳統的三維分割任務相比，三維牙頜模型在分割過程中存在許多挑戰[1-3]：① 同一類型牙齒的幾何特征因患者個體差異而異；② 牙頜模型中存在牙齒擁擠和排列不齊的問題，導致分割邊界難以確定；③ 缺牙、斷牙、智齒等問題使得模型幾何特征存在不確定性。
為解決上述難題，學者們嘗試了許多方法對牙頜模型進行分割。全自動的分割方法主要基于深度學習網絡[4]。一些方法對數據進行維度轉換，然后利用卷積網絡進行網格的特征提取和預測[5-7]。這類方法的網絡結構簡潔，但是忽略了網格間的拓撲關系，容易出現離散錯誤。為此，有學者通過構建鄰域圖的方法[2, 8]，將網格的鄰接關系融入到語義特征中。然而，上述方法在特征提取過程中過度依賴坐標特征，無法提取到豐富的局部特征，不能較好地適應牙齒形態復雜的情況。
半自動的幾何分割方法中，最常用的算法是基于每顆牙齒的邊界線來實現牙齒分割。通過算法獲取的牙齒邊界點對牙齒的邊界線進行搜尋[9-11]，或者將模型投影到二維平面中[12-13]，再利用圖像分割算法獲取邊界線。這一類方法能夠實現牙齒的快速分割，但是過度依賴于牙齒邊界點的精確性，容易在牙齒排列擁擠時由于邊界點的錯位擬合出錯誤的邊界線。
近些年，隨著區域生長算法在三維模型分割任務中的優異表現[14-17]，一些學者嘗試將它引入牙頜模型分割任務中。例如，范然等[18]通過勾畫種子點，結合多種子點生長的方法實現牙頜模型的分割；馬勇等[19]基于法向量的邊界延伸方法，提高了區域生長后牙齒的邊界光滑度。三維區域生長算法由于其局部貪婪的原則，可以在準確識別和分割牙齒區域的同時處理牙齒擁擠、傾斜以及其他形態復雜的情況。但是，這些方法目前仍然需要較多的人工參與進行種子點勾選并且存在牙齒邊界線模糊的問題，影響了區域生長算法在牙頜模型分割任務中的精度和效率。
為了進一步提高區域生長算法在牙齒邊界的分割精度、提升分割算法對牙齒形態的魯棒性并減少人工參與，本文提出了一種結合多種子區域生長和邊界延伸的智能牙齒分割方法。首先，將牙頜模型曲率分布特征和多種子點區域生長算法結合起來對牙頜模型進行分割；然后，融合幾何特征對分割邊界進行光滑；最后，在牙頜模型數據集上通過消融實驗和對比實驗驗證本文方法的有效性。
1 本文方法
1.1 區域生長算法原理
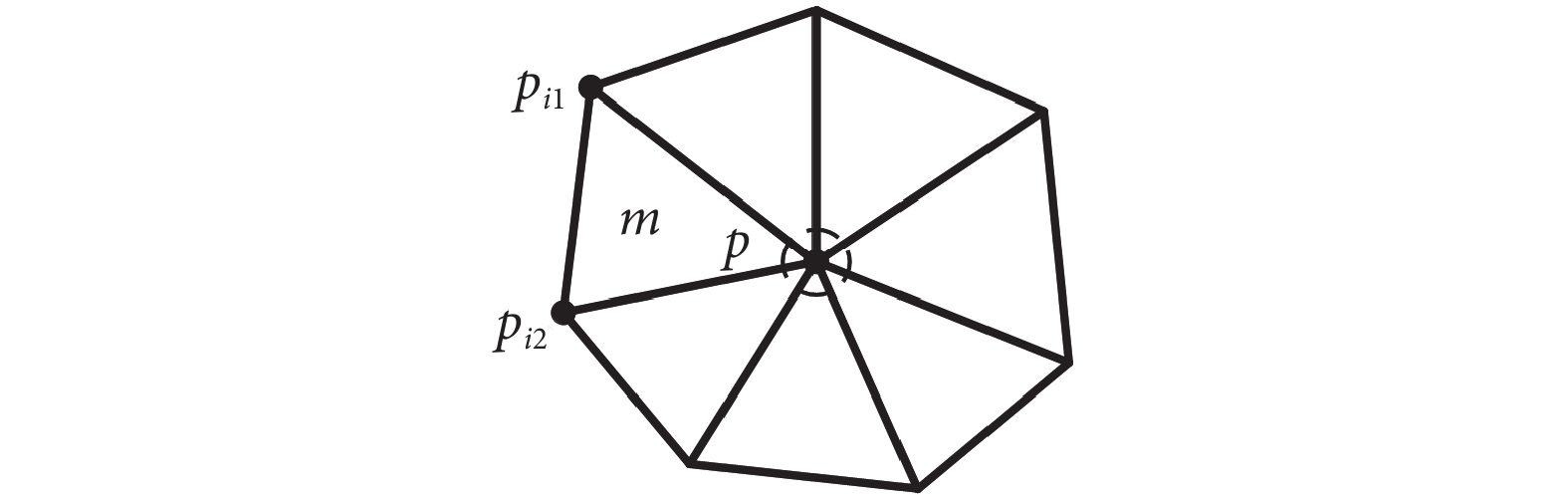
三角網格模型的區域生長算法[20]通過對比種子點和周圍網格頂點的曲率相似性進行區域擴展，直到滿足生長準則為止。圖1顯示了種子點p的相鄰三角網格分布，具體操作如下：① 計算種子點p與所在三角網格m的其他兩個頂點pi1和pi2間的高斯曲率差值的絕對值△c(pi1)和△c(pi2)。② 判斷差值絕對值△c(pi1)和△c(pi2)與設定生長曲率閾值間ct的大小。當兩數值均小于閾值ct時，判定三角網格m屬于當前種子點p的區域。③ 以頂點pi1和pi2為新的種子點重復上述步驟，直至沒有新的三角網格與種子點屬于同一區域。
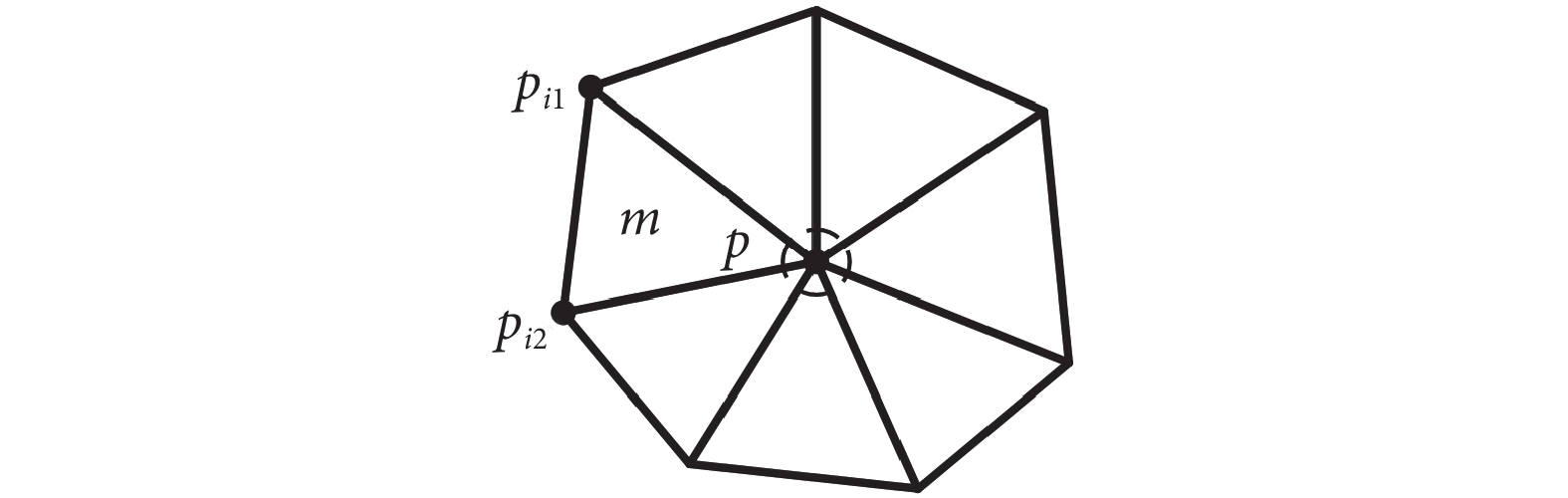圖1
相鄰三角網格分布
Figure1.
Adjacent triangular grid distribution
現有的區域生長算法在三維牙頜模型分割任務中，存在以下不足：① 閾值固定。由于牙齒在頂面和側面的曲率分布差異較大，使用固定的曲率閾值會導致生長停滯的現象。② 魯棒性不足。現有的研究一般將種子點選在牙齒的頂面中心，在分割形狀特殊的牙齒時會造成欠分割問題。③ 邊界粗糙。在分割凹凸不平的牙頜模型時，僅使用曲率信息作為生長條件將陷入局部最優，算法提前停止使得分割邊界粗糙不平。
1.2 結合負曲率分布的多種子點獲取
為充分考慮牙齒的整體結構，提高分割方法對牙齒不同形狀的魯棒性。本文利用人工選定的初始種子點和牙頜模型的二維曲率分布特征，實現多種子點的獲取。在該方法中，需要用戶在每顆牙齒的頂面中心處標記一個初始種子點p，基于初始種子點p的多種子點獲取方式如下。
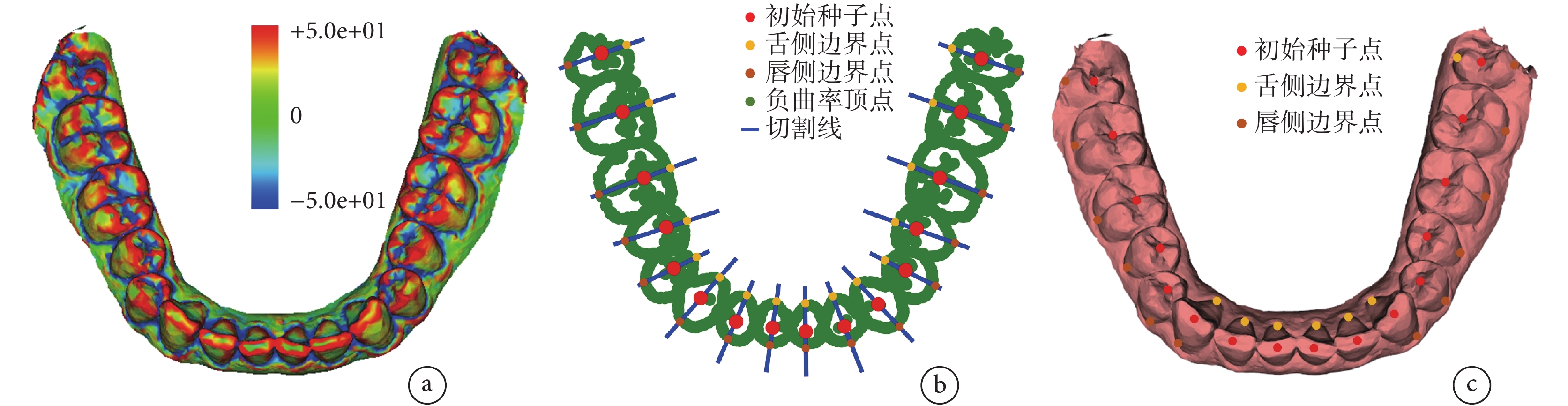
（1）齒齦邊界點獲取。三維牙頜模型的表面是不規則曲面，其齦緣區域和齒間區域呈“谷底”狀分布，存在連續的負曲率三角網格，如圖2a所示。本研究利用牙頜模型的曲率分布特點，以人工選擇的初始種子點p為基礎，為每顆牙齒構建一條切割線，并以牙齒負曲率頂點中接近切割線、相距最遠的兩個點分別作為該牙齒的唇側邊界點pcc和舌側邊界點psc。具體步驟如下。
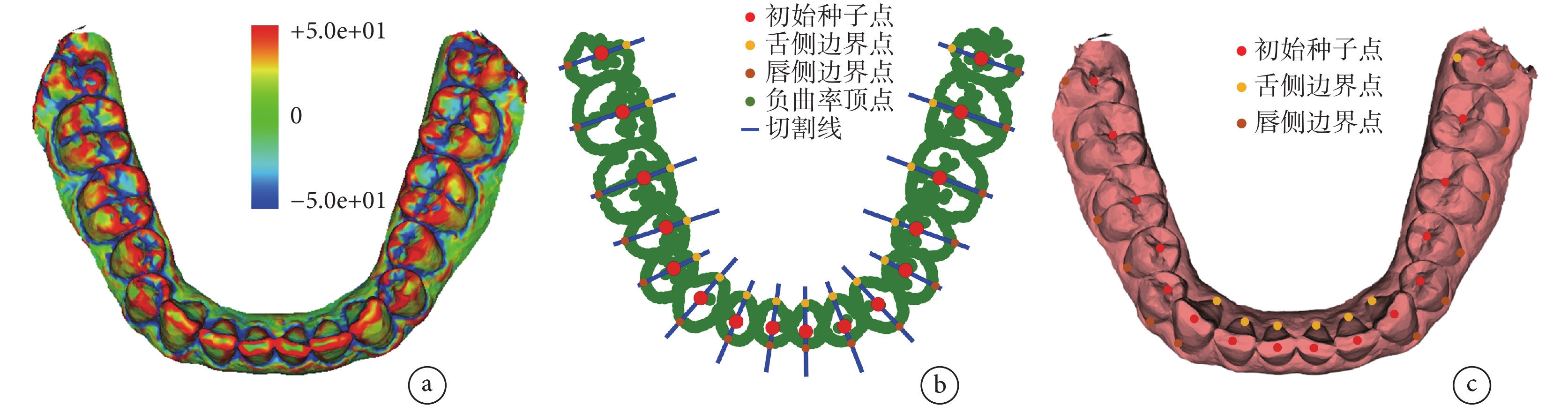圖2
邊界點拾取
a. 曲率分布示意；b. 二維邊界點獲取；c. 牙頜模型選點示意
Figure2. Boundary points pickinga. curvature distribution diagram; b. boundary point acquisition; c. the selection point of the model
Step 1：獲取牙頜模型的負曲率頂點集合Plc={pl1, pl2, ···, pln}，并將其沿模型的高度方向(z軸)進行投影，如圖2b中綠色點所示。其中，頂點pli∈Plc，c(pli)<0。
Step 2：構建切割線。假設3顆相鄰的牙齒上的初始種子點分別為ps1、ps2、ps3，切割線過種子點ps2，其垂線的斜率為
。切割線如圖2b中藍色線所示。
Step 3：獲取離切割線距離1以內的負曲率頂點，以其中距離最遠的兩個頂點pcc和psc分別作為牙齒的唇側邊界點和舌側邊界點。
Step 4：將二維投影中的唇側邊界點pcc和舌側邊界點psc映射至三維模型中，如圖2c所示。
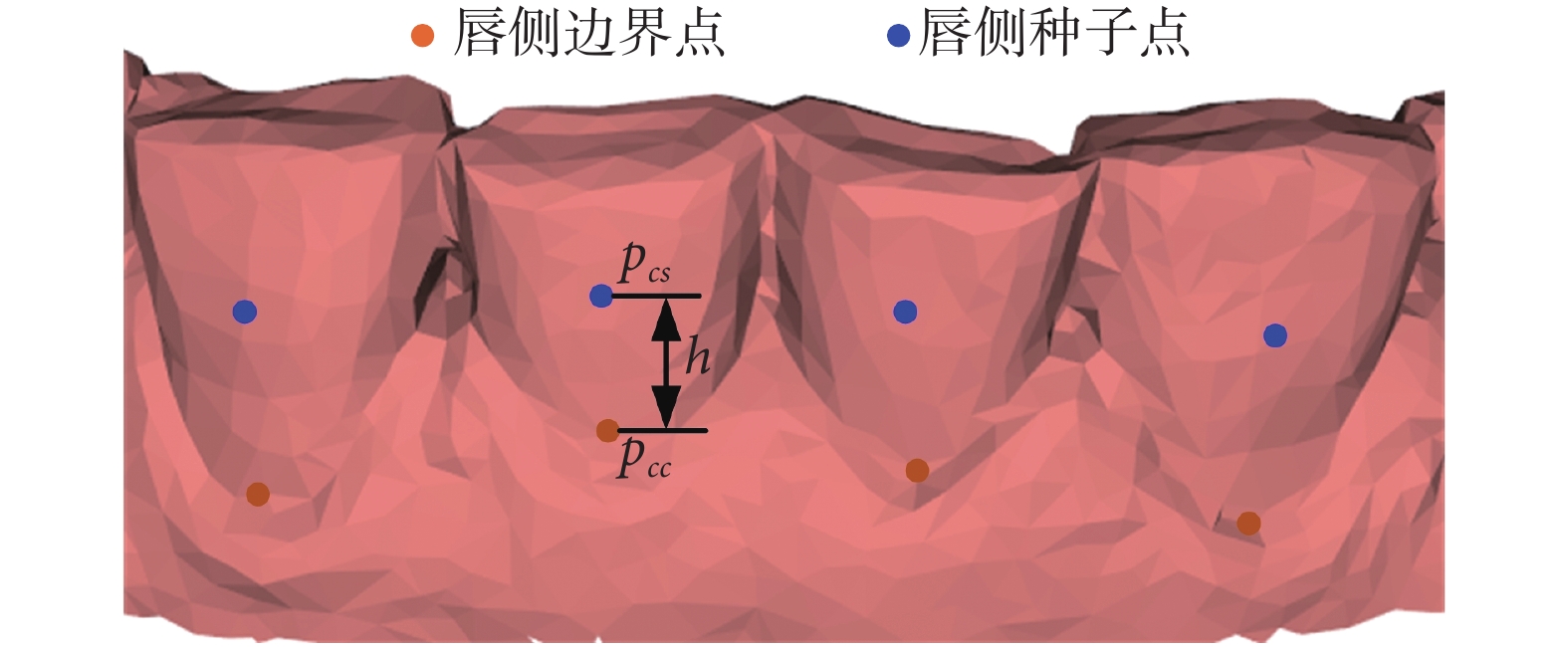
（2）多種子點計算。單種子點的區域生長算法無法適應牙齒的頂面和側面間的巨大結構差異，針對該問題，本文基于初始種子點p、邊界點pcc和psc為每顆牙齒計算兩個側面的種子點。以唇側種子點pcs的獲取為例，以邊界點pcc為基礎沿著模型高度(z軸)方向移動距離h獲得定位點pd，距離h和定位點pd的坐標公式如下：
 |
 |
式中x( )、y( )和z( )分別獲取頂點的x軸、y軸和z軸坐標。然后，計算出模型頂點集合Pall = {p1, p2, ···, pn}中離定位點pd歐式距離最近的頂點作為唇側新種子點pcs，其中n為模型的頂點總數。由于邊界點pcc和psc位于牙齒與牙齦的交接處，以此為基礎進行平移，可以確保種子點位于牙齒側面，如圖3所示。本文提出的多種子點獲取方法充分考慮了牙齒的整體幾何特征，能夠有效避免過多的人工參，提高算法效率。
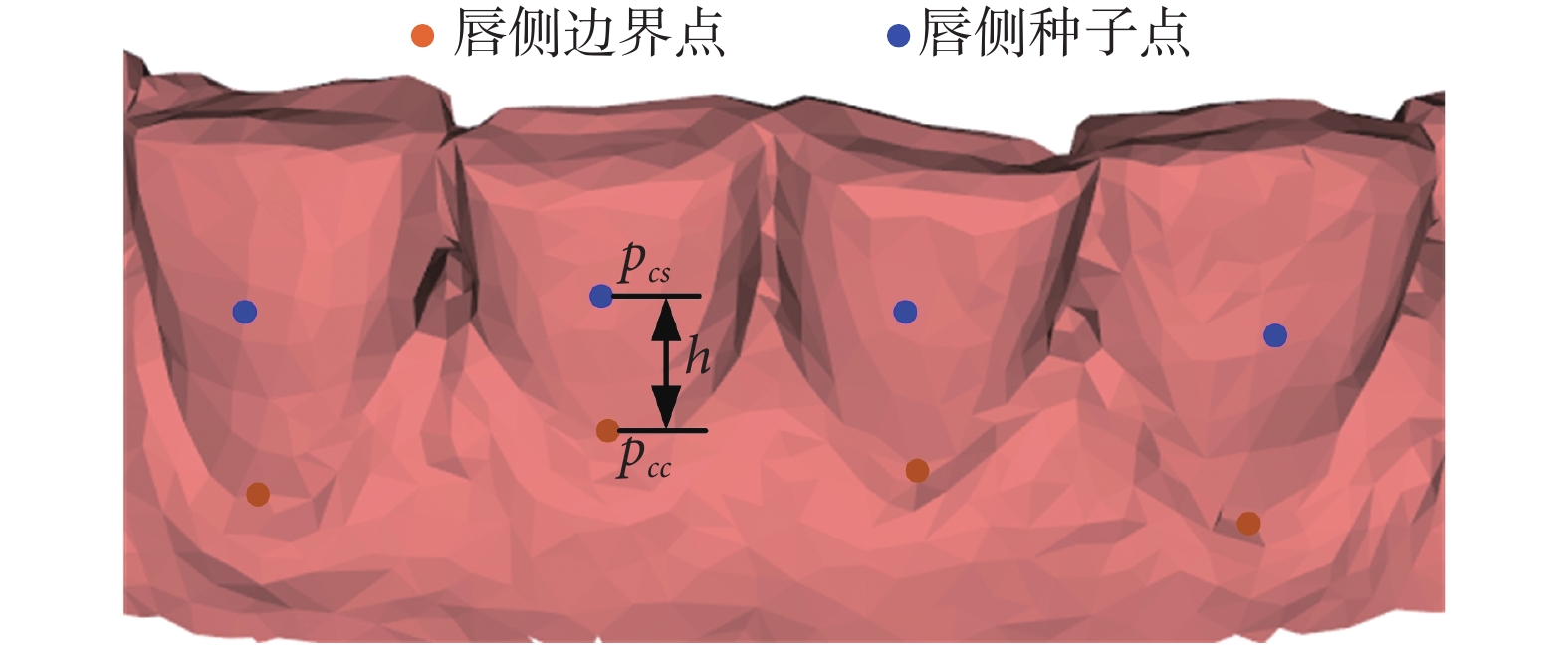圖3
多種子點計算結果
Figure3.
Results of multi-seed point calculation
1.3 結合多種子點的差異性區域生長
1.3.1 數量閾值設定
如圖2a所示，牙齒齒頂處由于咬合面與側面的交接形成了局部凸出的高曲率三角網格，而磨牙中心處由于溝壑的存在形成了大量低曲率三角網格。大幅度的曲率變化會導致區域生長的過程中出現生長停滯現象，即只在初始種子點周圍的小范圍內進行生長。針對該問題，本文為初始種子點設定了數量閾值，使其在牙齒頂面一定范圍內生長時不受限于曲率差值。數量閾值計算公式為：
 |
式中350是網格數為15 000的牙頜模型中切牙和尖牙的頂面網格數統計均值的向下取整數；α是牙齒類型系數，經統計前磨牙和磨牙的牙齒頂面網格數是切牙和尖牙的1.5～2.5，因此當牙齒為切牙和尖牙時α = 1，當牙齒為前磨牙和磨牙時α = 2；γ是模型數量倍率，γ = 模型網格總數/15 000。由于初始種子點是位于牙齒頂面的中心處，基于統計均值計算的數量閾值不僅可以避免生長停滯現象，也可避免無差別生長過度導致的過分割問題。
1.3.2 差異性區域生長
結合多種子點的區域生長算法，核心思想如下：對初始種子點進行數量閾值下的區域生長，即數量閾值內的三角網格歸入對應種子點的初始分割區域，數量閾值外的三角網格則依照常規的區域生長準則來進行判斷；對唇側種子點和舌側種子點則進行常規的區域生長。差異性區域生長準則可表示為：
 |
 |
式中△c(pi1)和△c(pi2)是三角網格頂點間平均曲率差值的絕對值；Ct是區域生長的曲率閾值，經統計試驗設為0.125；L(n)是數量閾值影響系數，n為當前種子點區域內的網格總數；mc(Sk)是數量閾值判斷函數，當種子點屬于唇側種子點或舌側種子點的區域內時mc(Sk) = 0，當種子點屬于初始種子點的區域時mc(Sk) = Sk。
1.4 初始分割區域的邊界延伸
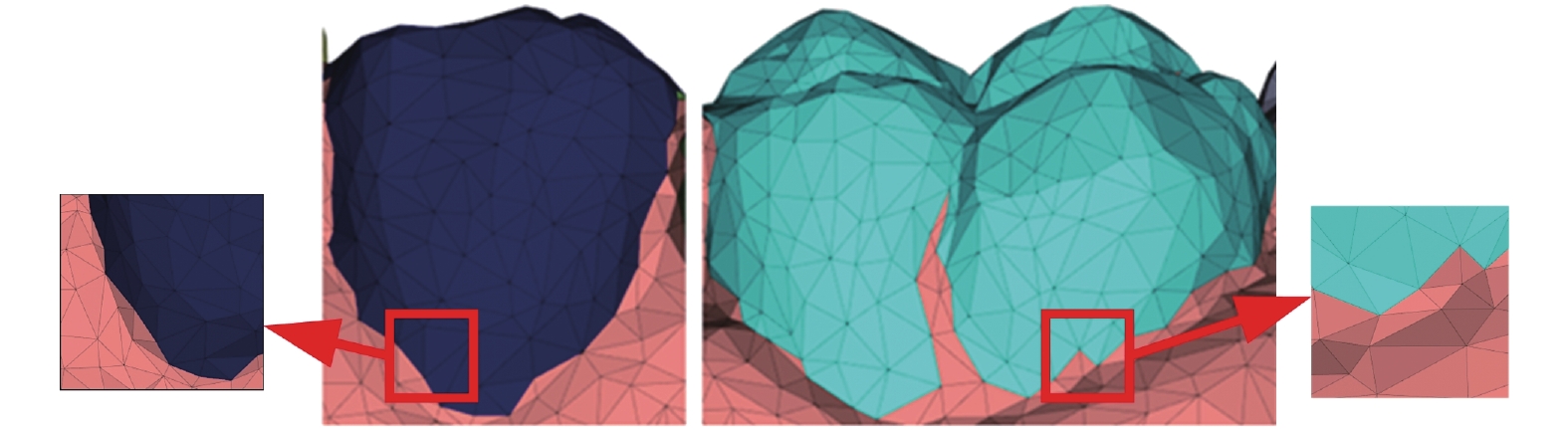
牙頜模型進行區域生長的過程中，齒齦交界處和牙齒側面溝壑處存在明顯的曲率變化，使得區域生長在到達這些網格附近時便提前停止，造成欠分割問題。如圖4中紅色方框的局部放大結果所示，初始分割的邊界處較為粗糙，存在明顯的欠分割。針對這一問題，本文提出基于幾何特征的邊界延伸機制，對牙齒的初始分割區域進行優化。
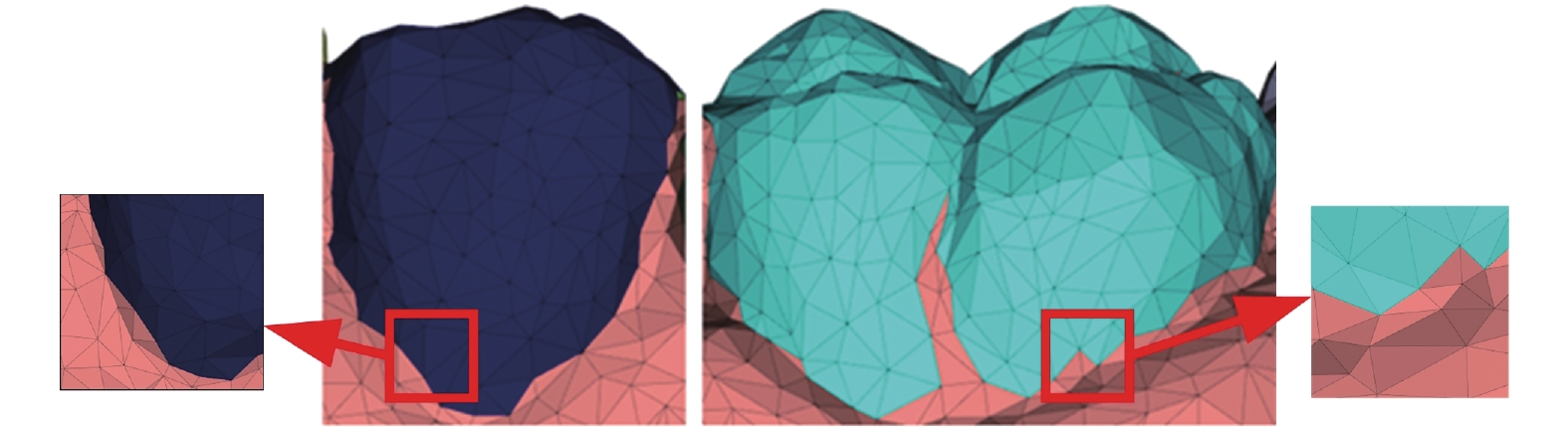圖4
初始分割區域的欠分割結果
Figure4.
Under-segmentation results of the initial partition area
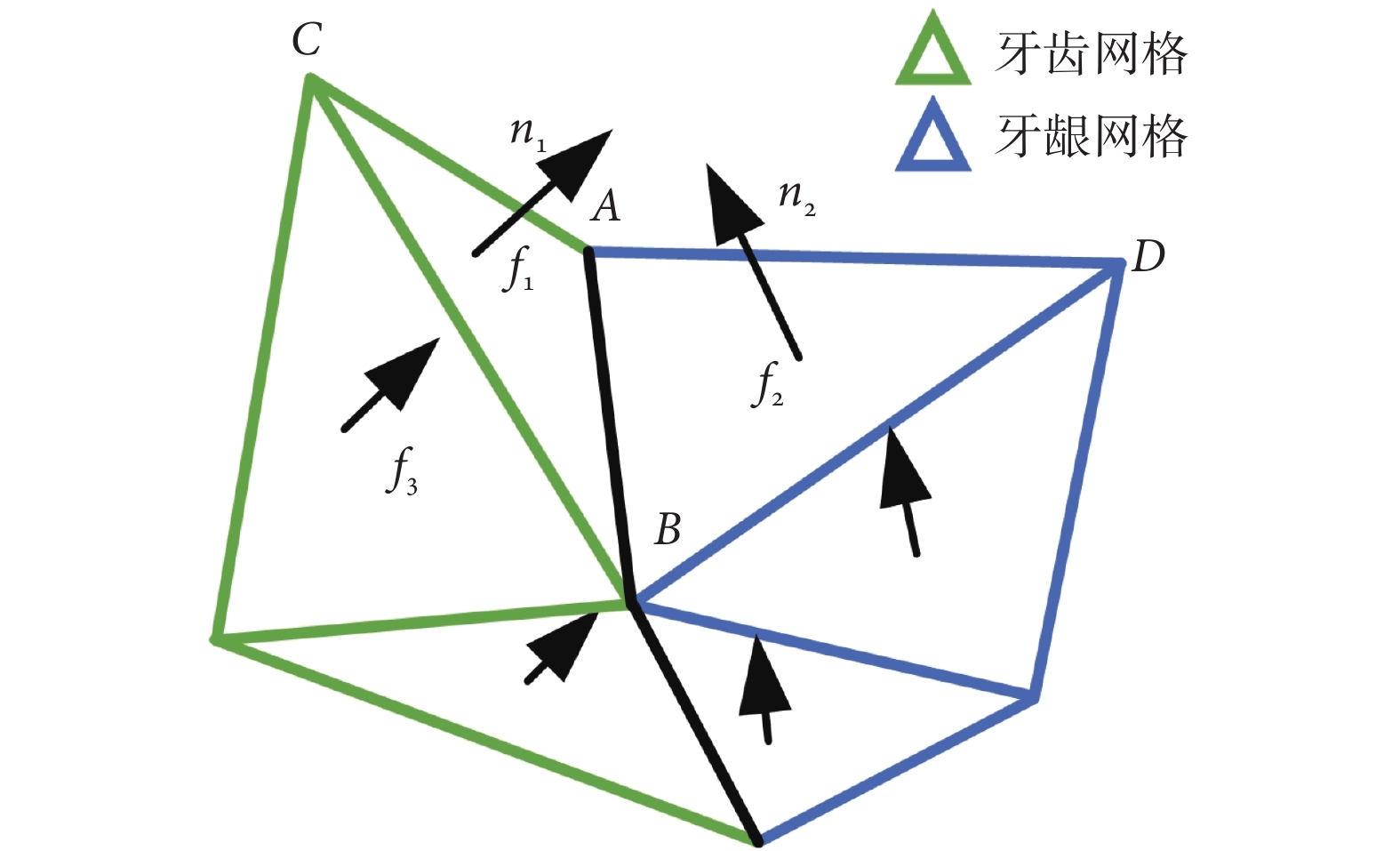
牙頜模型的齦緣區域和齒間區域呈“谷底”分布，這使得邊界處相鄰、異類網格間的法向量夾角驟增，如圖5所示。牙齒的邊界網格f1與近鄰的同類網格f3的法向量夾角較小，而與近鄰的異類邊界網格f2的法向量夾角較大，根據這一特性可以實現邊界處網格的類型劃分。但是，當牙齒畸形較為嚴重時，齒齦邊界處的相鄰、異類網格間的法向量夾角將會變小，這種情況下基于法向量進行延伸會產生過分割問題。考慮到齒齦間網格的曲率是局部極小值[21]，利用該性能對法向量邊界延伸的方位進行引導，使法向量沿著曲率下降的方向延伸，即只對曲率小于當前網格的待生長邊界網格進行法向量判定，可有效避免過分割問題。
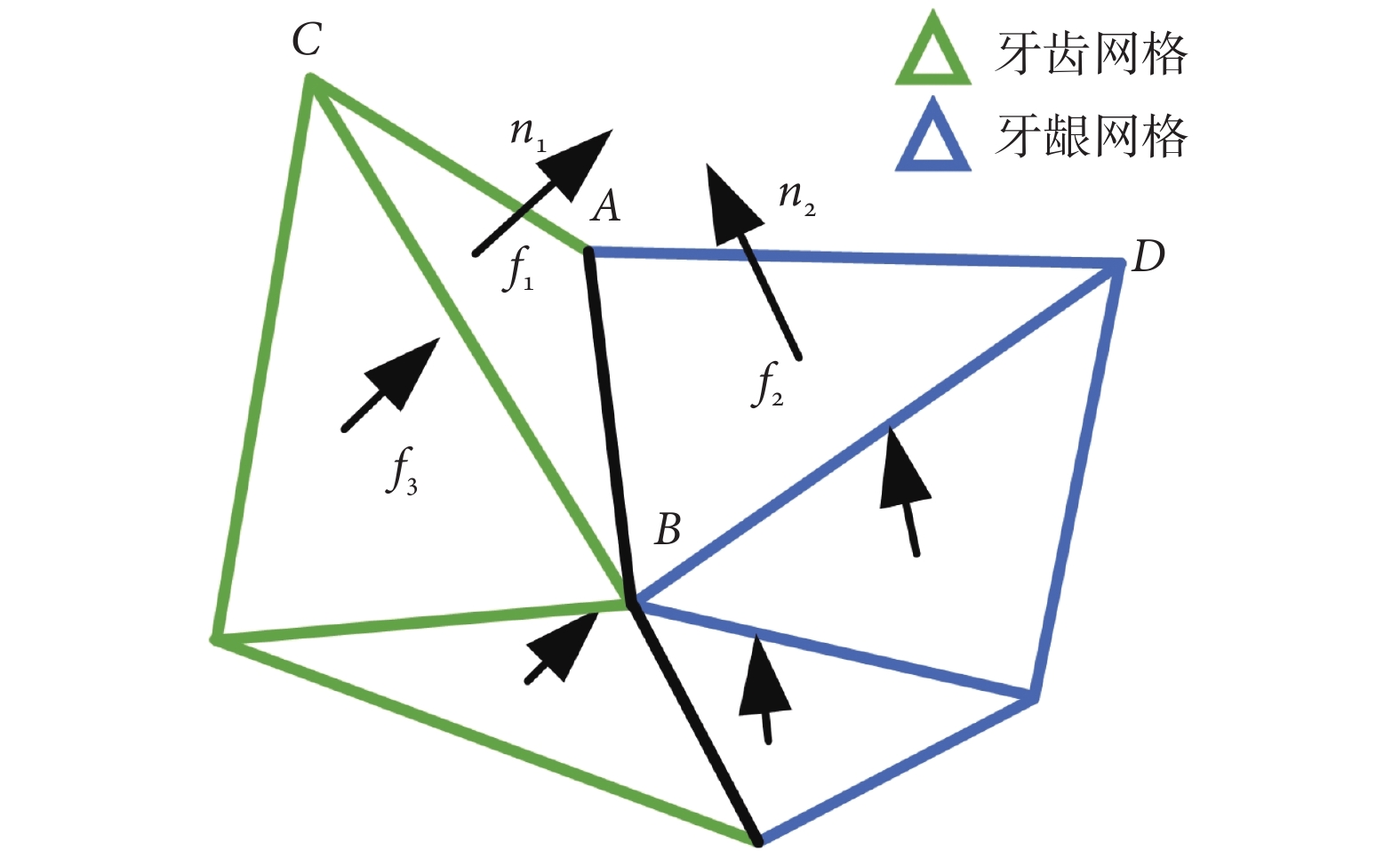圖5
邊界三角網格法向量關系
Figure5.
Normal vector relation of boundary mesh
具體而言，首先，計算邊界網格f2與共邊已標注網格f1的曲率大小；然后，當邊界網格f2的曲率小于共邊已標注網格f1的曲率時，再計算邊界網格f2與共邊已標注網格f1間的法向量夾角，當夾角小于設定的法向量閾值Nt時，邊界網格f2與共邊已標注網格f1屬于同類網格。邊界處的網格類型判斷準則的可表示為：
 |
 |
式中，αc為曲率引導系數；
，其中n1和n2分別為網格f1和f2的法向量，本文采用法向量夾角的余弦值作為指標，評估相鄰三角網格間的相對彎曲程度；
是網格的曲率，c(pi)是網格的頂點平均曲率；法向量閾值Nt根據統計結果設置為Nt = 0.9。結合初始分割邊界處網格的幾何特點，由曲率作為引導方位、法向量作為類型判斷標準，不僅實現了分割邊界的延伸，還可有效避免過分割問題的出現，進而實現牙頜模型的精確分割。
2 實驗結果
2.1 實驗細節
本文算法基于Python語言并利用vedo開源庫實現算法，模型顯示基于Mesh Labeler軟件[22]，硬件環境配置如下：Intel(R) Core(TM) i7-12700F 2.10 GHz處理器，NVIDIA GeForce GTX1660Ti顯卡。本文從Teeth3DS數據庫[23]獲得三維牙頜網格模型，共100個三維牙頜網格模型，出于算力的限制將模型的網格數簡化至15 000個網格。此外，為了定量驗證所提方法的性能，本文使用總體精度（overall accuracy，OA）、交并比（Intersection over Unio，IoU）和均交并比（mIoU）作為評價指標。
2.2 對比實驗
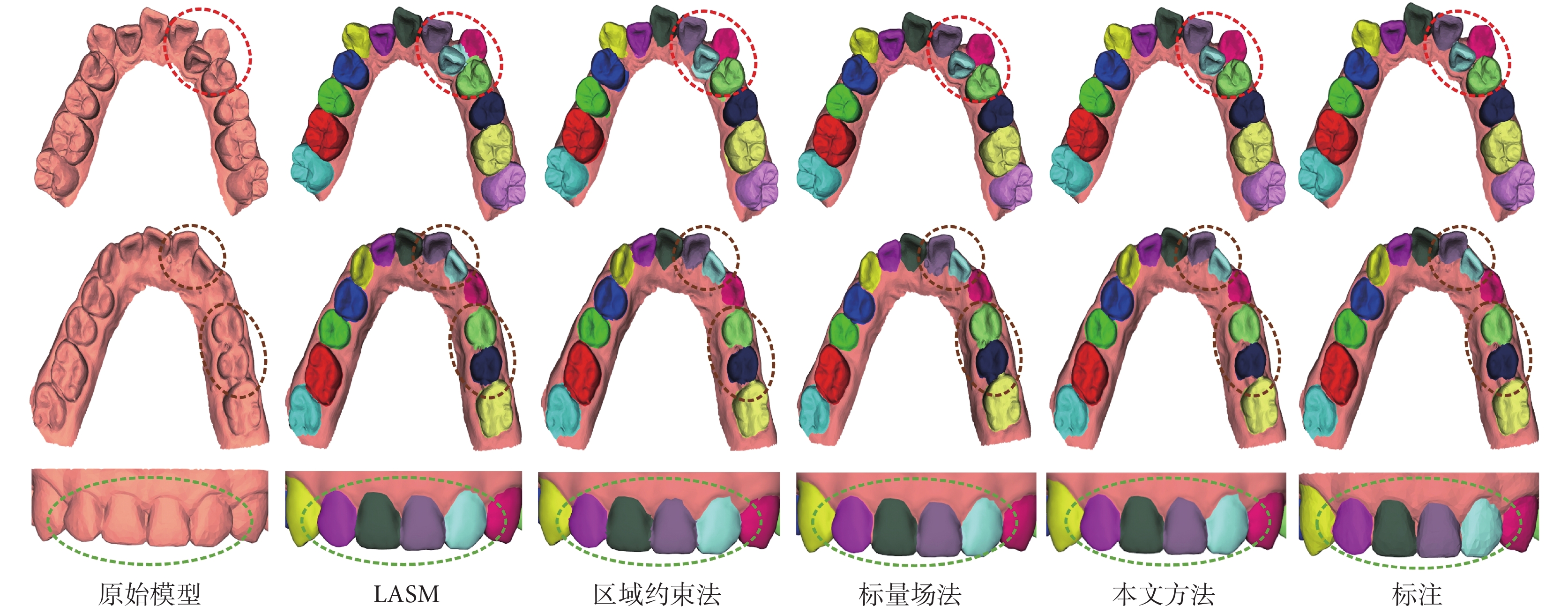
為驗證本文算法優勢，分別與局部信息空間增強模塊（Local Augmentation Spatial Module，LASM）[2]、區域約束法[21]以及標量場法[11]這三種先進的牙齒分割算法進行比較。分割結果通過表1中的OA和mIoU指標進行定量總結，IoU僅顯示左側牙齒（T1-T7）和牙齦（T0）的分割結果。從表1中可以得出以下結論：① 本文方法在每個牙齒分割中都獲得了更高的IoU，證明了本文方法在牙齒精細分割過程中的泛化性能；② 與同樣使用法向量進行邊界優化的區域約束法相比，本文方法的mIoU指標提升了5.36個百分點，因為區域約束法僅使用法向量對邊界進行優化，容易出現過分割問題；③ 與采用邊界線搜尋的標量場法和依賴坐標特征的LASM法相比，本文方法由于不過度依賴網格的坐標信息，在處理擁擠牙齒時擁有更高的精度。
表1
與其他先進方法的比較結果（%）
Table1.
Comparison results with other advanced methods (%)
為進一步體現本文方法的有效性，對分割結果進行了可視化，如圖6所示。首先，如第一行紅色圓圈所示，全自動的LASM法對錯位牙齒的分割精度最低，因為這種方法在特征提取時主要依賴牙齒網格的坐標，擁擠錯位導致網絡在判斷過程中發生混淆進而錯分；而本文方法和其他兩種半自動方法由于預先的人工標注，對于牙齒擁擠的情況能夠保證正確的區域識別，避免大面積錯分。其次，第二行中標量場法在擁有凸起的牙齒邊界處，由于啟發式齦緣線法傾向于獲取更大面積的完整齦緣因此出現了明顯的過分割，而本文使用的區域生長算法在凸起處由于對曲率變化更加敏感，從而有效避免了過分割問題。最后，在第三行的牙齒邊界處和第一行的牙齒擁擠處，可以發現區域約束法的邊界出現了過分割問題，因為它只利用法向量進行邊界線獲取，當邊界網格比較平坦時會出現錯分。
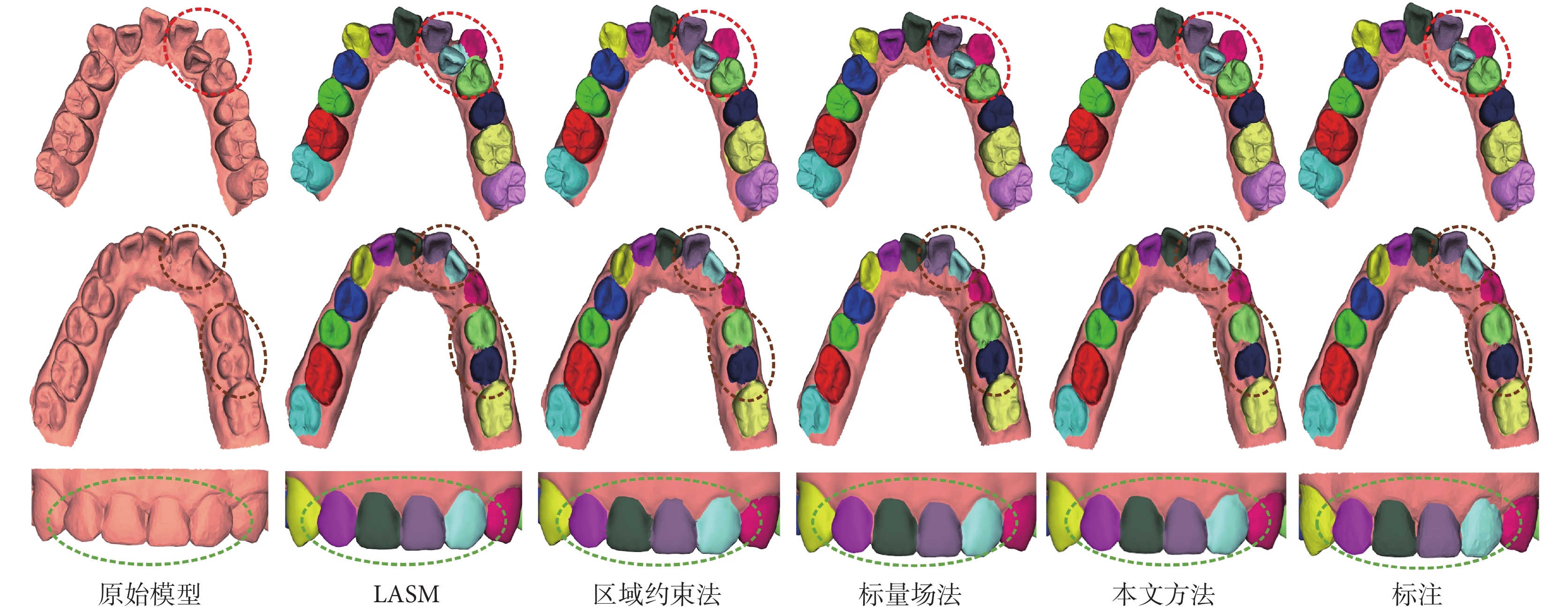圖6
本文方法與三種對比方法的分割結果可視化
Figure6.
Visualization of segmentation results among the proposed method and three comparison methods
2.3 消融實驗
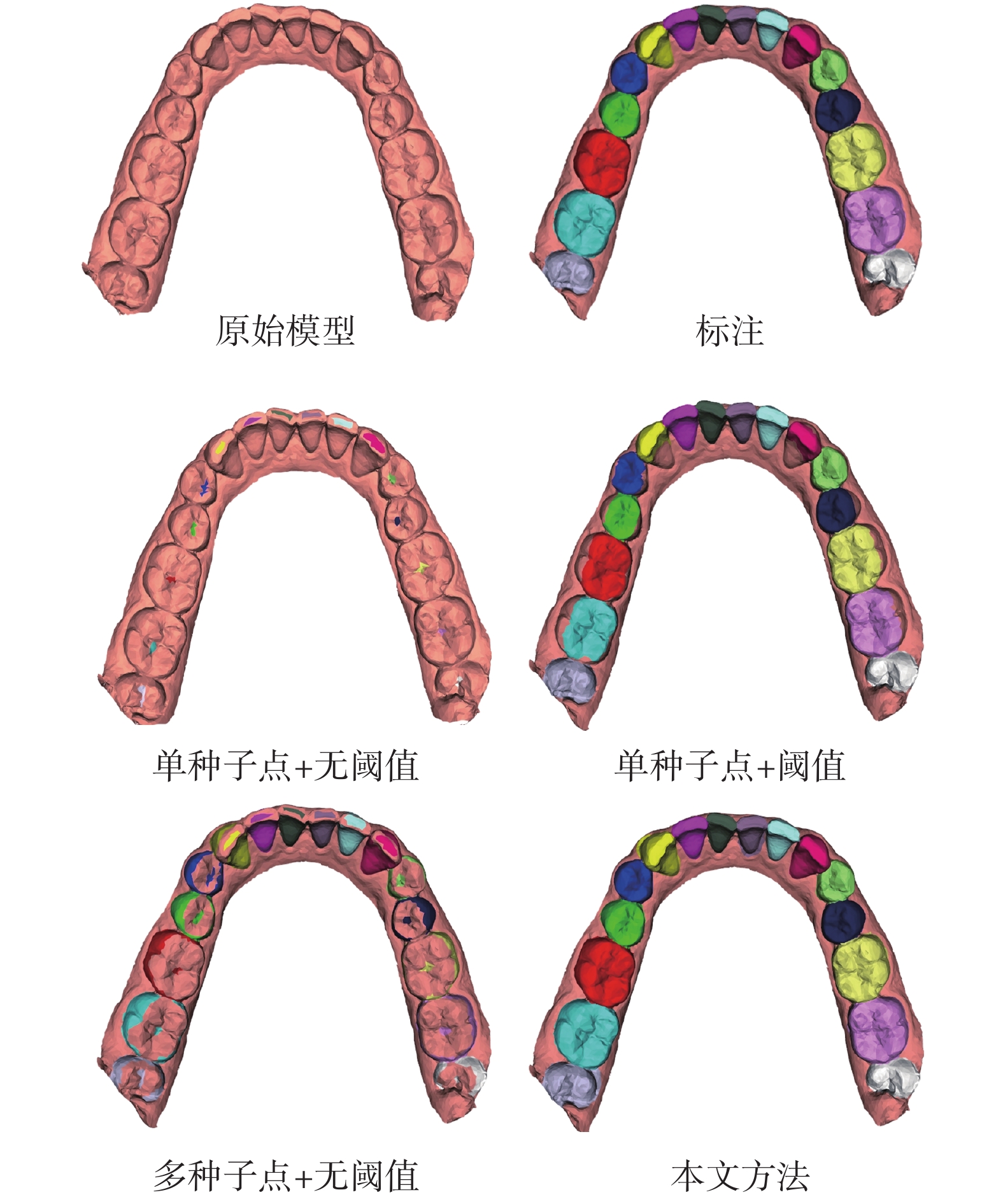
2.3.1 差異性區域生長的有效性
為驗證本文的差異性區域生長算法的有效性，通過不同的生長策略構建了三種變體進行比較：① 僅基于初始種子點進行生長，并取消數量閾值設定；② 僅基于初始種子點進行生長，并包含數量閾值設定；③ 基于多種子點進行生長，并取消數量閾值設定；定性結果如圖7所示。從圖中可以看出，沒有設置數量閾值的模型在牙齒頂面出現了生長停滯的現象，這主要是因為牙齒頂面溝壑處和凸起部位的曲率變化差值大使得算法提前停止。此外，使用單種子點和數量閾值的變體在磨牙的側面均存在明顯的欠分割，這主要是因為牙齒頂面和側面交界處的高曲率網格阻礙了生長的正常進行，單種子點無法適應頂面和側面之間的曲率特征分布差異。與之相比，本文的生長算法通過多種子點和數量閾值針對牙齒的頂面和側面進行不同的生長策略，有效地適應了牙齒幾何結構的差異性。
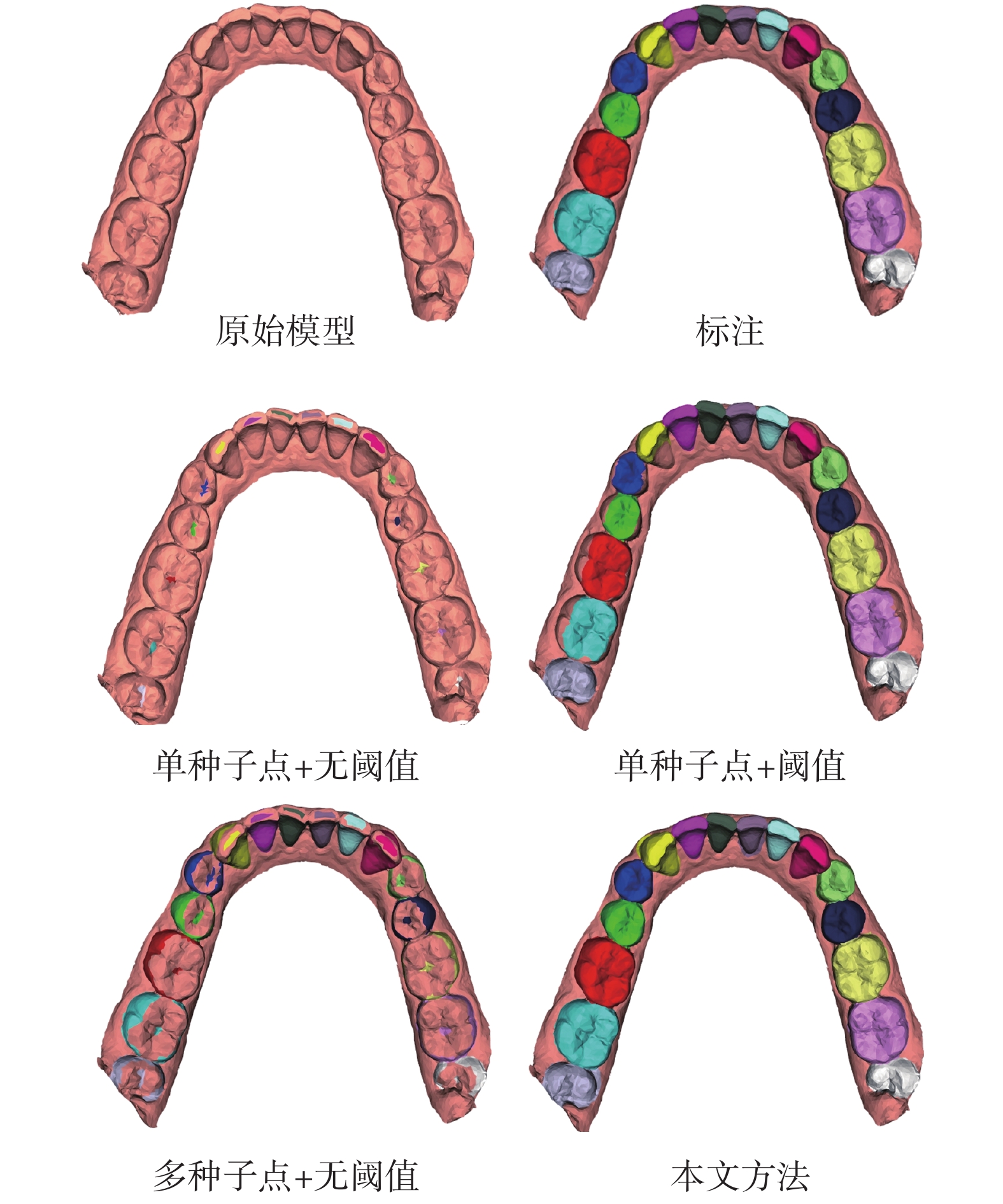圖7
不同生長策略的分割結果
Figure7.
Segmentation results of different growth strategies
2.3.2 邊界延伸策略的有效性
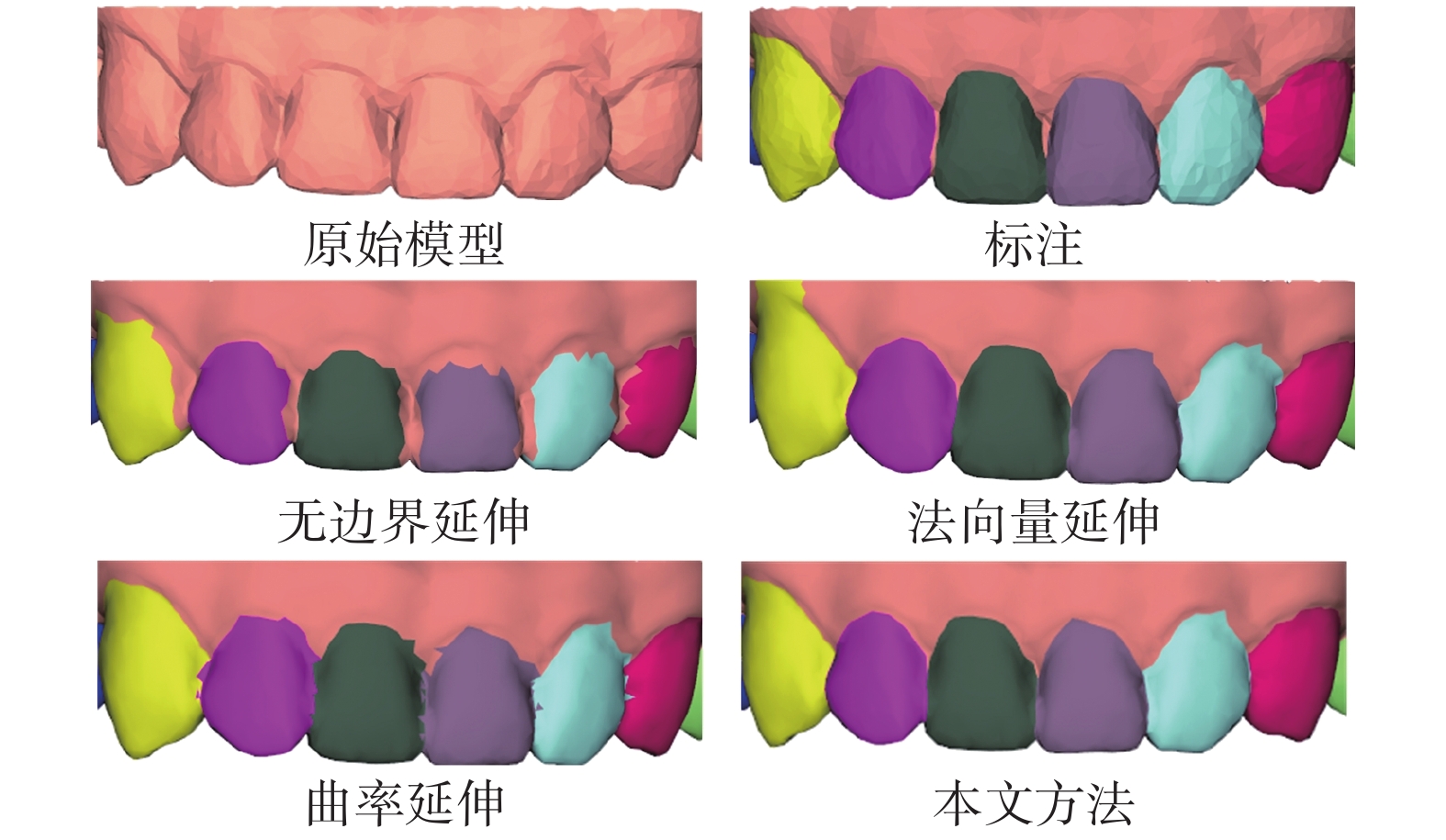
為驗證本文所提的邊界延伸策略的有效性，通過不同的延伸判別條件構建了三種變體進行比較：① 無邊界延伸，即不對網格的初始邊界進行優化；② 法向量延伸，即直接使用法向量夾角判斷進行延伸，不再用網格的曲率變化進行引導；③ 曲率延伸，即直接將曲率小于共邊已標注網格的邊界網格劃分為同類網格。定量結果如表2所示，本文算法的OA和mIoU均有較大的提升。法向量延伸精度小于曲率延伸，主要是因為牙齒嚴重畸形時齒齦邊界處的相鄰、異類網格間的法向量夾角變小，造成大面積過生長降低了分割精度。
表2
不同邊界延伸策略的定量分割結果（%）
Table2.
Quantitative segmentation results with different boundary extension strategies (%)
圖8中展示了上述變體的可視化結果。首先，無邊界延伸的結果在齒間存在明顯的欠分割，這是因為曲率變化大于設定的閾值，導致生長停止。其次，法向量延伸的牙齒邊界比曲率延伸的牙齒邊界光滑，這主要是因為局部極小曲率的網格的類型具有不確定性。最后，法向量延伸的牙齒邊界處有時會存在明顯的過分割，因為齒齦邊界處網格的法向量變化可能較小，進而產生錯誤的分割，而本文方法由于曲率導向的緣故對法向量夾角的變化更加敏感，有效地避免了過分割的錯誤。
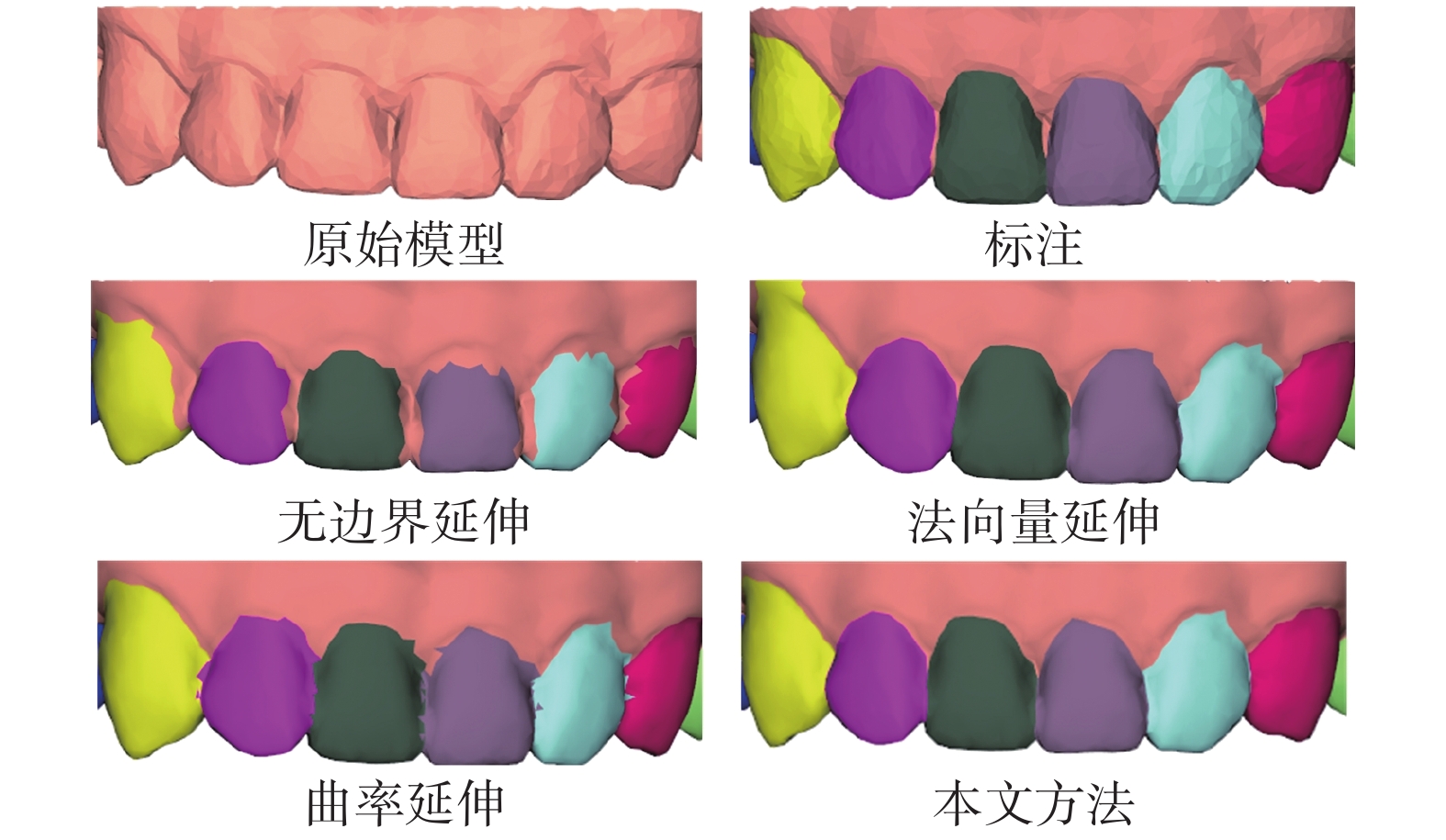圖8
不同邊界延伸策略的可視化分割結果
Figure8.
Visual segmentation results of different boundary extension strategies
3 結語
本文針對牙齒的幾何特征分布和區域生長算法的原理，提出了一種結合多種子區域生長和邊界延伸的牙齒分割方法。該方法結合牙齒的負曲率分布特點獲得新種子點，并通過差異性區域生長有效適應了牙齒頂面和側面間的差異性結構；根據初始分割區域的網格分布特點，結合法向量和曲率特征對邊界進行了延伸，克服了區域生長提前停止的缺陷。此外，本文方法與其他三種優秀的分割方法進行了比較，并通過消融實驗分析了核心技術的有效性，實驗結果證實本文方法具有較少的人工參與和參數調整，適合具有挑戰性的實際情況。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：劉志華和薛久濤構思并設計了研究方案；劉志華實施方案并處理數據；唐浩負責數據收集和文獻調研；劉志華和廖與禾負責論文的撰寫與修改。
0 引言
牙齒畸形是口腔疾病中的常見病癥，作為正畸治療的首要步驟，三維牙頜模型分割技術的提升對計算機輔助設計系統在正畸領域的推廣具有重要意義。與傳統的三維分割任務相比，三維牙頜模型在分割過程中存在許多挑戰[1-3]：① 同一類型牙齒的幾何特征因患者個體差異而異；② 牙頜模型中存在牙齒擁擠和排列不齊的問題，導致分割邊界難以確定；③ 缺牙、斷牙、智齒等問題使得模型幾何特征存在不確定性。
為解決上述難題，學者們嘗試了許多方法對牙頜模型進行分割。全自動的分割方法主要基于深度學習網絡[4]。一些方法對數據進行維度轉換，然后利用卷積網絡進行網格的特征提取和預測[5-7]。這類方法的網絡結構簡潔，但是忽略了網格間的拓撲關系，容易出現離散錯誤。為此，有學者通過構建鄰域圖的方法[2, 8]，將網格的鄰接關系融入到語義特征中。然而，上述方法在特征提取過程中過度依賴坐標特征，無法提取到豐富的局部特征，不能較好地適應牙齒形態復雜的情況。
半自動的幾何分割方法中，最常用的算法是基于每顆牙齒的邊界線來實現牙齒分割。通過算法獲取的牙齒邊界點對牙齒的邊界線進行搜尋[9-11]，或者將模型投影到二維平面中[12-13]，再利用圖像分割算法獲取邊界線。這一類方法能夠實現牙齒的快速分割，但是過度依賴于牙齒邊界點的精確性，容易在牙齒排列擁擠時由于邊界點的錯位擬合出錯誤的邊界線。
近些年，隨著區域生長算法在三維模型分割任務中的優異表現[14-17]，一些學者嘗試將它引入牙頜模型分割任務中。例如，范然等[18]通過勾畫種子點，結合多種子點生長的方法實現牙頜模型的分割；馬勇等[19]基于法向量的邊界延伸方法，提高了區域生長后牙齒的邊界光滑度。三維區域生長算法由于其局部貪婪的原則，可以在準確識別和分割牙齒區域的同時處理牙齒擁擠、傾斜以及其他形態復雜的情況。但是，這些方法目前仍然需要較多的人工參與進行種子點勾選并且存在牙齒邊界線模糊的問題，影響了區域生長算法在牙頜模型分割任務中的精度和效率。
為了進一步提高區域生長算法在牙齒邊界的分割精度、提升分割算法對牙齒形態的魯棒性并減少人工參與，本文提出了一種結合多種子區域生長和邊界延伸的智能牙齒分割方法。首先，將牙頜模型曲率分布特征和多種子點區域生長算法結合起來對牙頜模型進行分割；然后，融合幾何特征對分割邊界進行光滑；最后，在牙頜模型數據集上通過消融實驗和對比實驗驗證本文方法的有效性。
1 本文方法
1.1 區域生長算法原理
三角網格模型的區域生長算法[20]通過對比種子點和周圍網格頂點的曲率相似性進行區域擴展，直到滿足生長準則為止。圖1顯示了種子點p的相鄰三角網格分布，具體操作如下：① 計算種子點p與所在三角網格m的其他兩個頂點pi1和pi2間的高斯曲率差值的絕對值△c(pi1)和△c(pi2)。② 判斷差值絕對值△c(pi1)和△c(pi2)與設定生長曲率閾值間ct的大小。當兩數值均小于閾值ct時，判定三角網格m屬于當前種子點p的區域。③ 以頂點pi1和pi2為新的種子點重復上述步驟，直至沒有新的三角網格與種子點屬于同一區域。
圖1
相鄰三角網格分布
Figure1.
Adjacent triangular grid distribution
現有的區域生長算法在三維牙頜模型分割任務中，存在以下不足：① 閾值固定。由于牙齒在頂面和側面的曲率分布差異較大，使用固定的曲率閾值會導致生長停滯的現象。② 魯棒性不足。現有的研究一般將種子點選在牙齒的頂面中心，在分割形狀特殊的牙齒時會造成欠分割問題。③ 邊界粗糙。在分割凹凸不平的牙頜模型時，僅使用曲率信息作為生長條件將陷入局部最優，算法提前停止使得分割邊界粗糙不平。
1.2 結合負曲率分布的多種子點獲取
為充分考慮牙齒的整體結構，提高分割方法對牙齒不同形狀的魯棒性。本文利用人工選定的初始種子點和牙頜模型的二維曲率分布特征，實現多種子點的獲取。在該方法中，需要用戶在每顆牙齒的頂面中心處標記一個初始種子點p，基于初始種子點p的多種子點獲取方式如下。
（1）齒齦邊界點獲取。三維牙頜模型的表面是不規則曲面，其齦緣區域和齒間區域呈“谷底”狀分布，存在連續的負曲率三角網格，如圖2a所示。本研究利用牙頜模型的曲率分布特點，以人工選擇的初始種子點p為基礎，為每顆牙齒構建一條切割線，并以牙齒負曲率頂點中接近切割線、相距最遠的兩個點分別作為該牙齒的唇側邊界點pcc和舌側邊界點psc。具體步驟如下。
圖2
邊界點拾取
a. 曲率分布示意；b. 二維邊界點獲取；c. 牙頜模型選點示意
Figure2. Boundary points pickinga. curvature distribution diagram; b. boundary point acquisition; c. the selection point of the model
Step 1：獲取牙頜模型的負曲率頂點集合Plc={pl1, pl2, ···, pln}，并將其沿模型的高度方向(z軸)進行投影，如圖2b中綠色點所示。其中，頂點pli∈Plc，c(pli)<0。
Step 2：構建切割線。假設3顆相鄰的牙齒上的初始種子點分別為ps1、ps2、ps3，切割線過種子點ps2，其垂線的斜率為。切割線如圖2b中藍色線所示。
Step 3：獲取離切割線距離1以內的負曲率頂點，以其中距離最遠的兩個頂點pcc和psc分別作為牙齒的唇側邊界點和舌側邊界點。
Step 4：將二維投影中的唇側邊界點pcc和舌側邊界點psc映射至三維模型中，如圖2c所示。
（2）多種子點計算。單種子點的區域生長算法無法適應牙齒的頂面和側面間的巨大結構差異，針對該問題，本文基于初始種子點p、邊界點pcc和psc為每顆牙齒計算兩個側面的種子點。以唇側種子點pcs的獲取為例，以邊界點pcc為基礎沿著模型高度(z軸)方向移動距離h獲得定位點pd，距離h和定位點pd的坐標公式如下：
|
|
式中x( )、y( )和z( )分別獲取頂點的x軸、y軸和z軸坐標。然后，計算出模型頂點集合Pall = {p1, p2, ···, pn}中離定位點pd歐式距離最近的頂點作為唇側新種子點pcs，其中n為模型的頂點總數。由于邊界點pcc和psc位于牙齒與牙齦的交接處，以此為基礎進行平移，可以確保種子點位于牙齒側面，如圖3所示。本文提出的多種子點獲取方法充分考慮了牙齒的整體幾何特征，能夠有效避免過多的人工參，提高算法效率。
圖3
多種子點計算結果
Figure3.
Results of multi-seed point calculation
1.3 結合多種子點的差異性區域生長
1.3.1 數量閾值設定
如圖2a所示，牙齒齒頂處由于咬合面與側面的交接形成了局部凸出的高曲率三角網格，而磨牙中心處由于溝壑的存在形成了大量低曲率三角網格。大幅度的曲率變化會導致區域生長的過程中出現生長停滯現象，即只在初始種子點周圍的小范圍內進行生長。針對該問題，本文為初始種子點設定了數量閾值，使其在牙齒頂面一定范圍內生長時不受限于曲率差值。數量閾值計算公式為：
|
式中350是網格數為15 000的牙頜模型中切牙和尖牙的頂面網格數統計均值的向下取整數；α是牙齒類型系數，經統計前磨牙和磨牙的牙齒頂面網格數是切牙和尖牙的1.5～2.5，因此當牙齒為切牙和尖牙時α = 1，當牙齒為前磨牙和磨牙時α = 2；γ是模型數量倍率，γ = 模型網格總數/15 000。由于初始種子點是位于牙齒頂面的中心處，基于統計均值計算的數量閾值不僅可以避免生長停滯現象，也可避免無差別生長過度導致的過分割問題。
1.3.2 差異性區域生長
結合多種子點的區域生長算法，核心思想如下：對初始種子點進行數量閾值下的區域生長，即數量閾值內的三角網格歸入對應種子點的初始分割區域，數量閾值外的三角網格則依照常規的區域生長準則來進行判斷；對唇側種子點和舌側種子點則進行常規的區域生長。差異性區域生長準則可表示為：
|
|
式中△c(pi1)和△c(pi2)是三角網格頂點間平均曲率差值的絕對值；Ct是區域生長的曲率閾值，經統計試驗設為0.125；L(n)是數量閾值影響系數，n為當前種子點區域內的網格總數；mc(Sk)是數量閾值判斷函數，當種子點屬于唇側種子點或舌側種子點的區域內時mc(Sk) = 0，當種子點屬于初始種子點的區域時mc(Sk) = Sk。
1.4 初始分割區域的邊界延伸
牙頜模型進行區域生長的過程中，齒齦交界處和牙齒側面溝壑處存在明顯的曲率變化，使得區域生長在到達這些網格附近時便提前停止，造成欠分割問題。如圖4中紅色方框的局部放大結果所示，初始分割的邊界處較為粗糙，存在明顯的欠分割。針對這一問題，本文提出基于幾何特征的邊界延伸機制，對牙齒的初始分割區域進行優化。
圖4
初始分割區域的欠分割結果
Figure4.
Under-segmentation results of the initial partition area
牙頜模型的齦緣區域和齒間區域呈“谷底”分布，這使得邊界處相鄰、異類網格間的法向量夾角驟增，如圖5所示。牙齒的邊界網格f1與近鄰的同類網格f3的法向量夾角較小，而與近鄰的異類邊界網格f2的法向量夾角較大，根據這一特性可以實現邊界處網格的類型劃分。但是，當牙齒畸形較為嚴重時，齒齦邊界處的相鄰、異類網格間的法向量夾角將會變小，這種情況下基于法向量進行延伸會產生過分割問題。考慮到齒齦間網格的曲率是局部極小值[21]，利用該性能對法向量邊界延伸的方位進行引導，使法向量沿著曲率下降的方向延伸，即只對曲率小于當前網格的待生長邊界網格進行法向量判定，可有效避免過分割問題。
圖5
邊界三角網格法向量關系
Figure5.
Normal vector relation of boundary mesh
具體而言，首先，計算邊界網格f2與共邊已標注網格f1的曲率大小；然后，當邊界網格f2的曲率小于共邊已標注網格f1的曲率時，再計算邊界網格f2與共邊已標注網格f1間的法向量夾角，當夾角小于設定的法向量閾值Nt時，邊界網格f2與共邊已標注網格f1屬于同類網格。邊界處的網格類型判斷準則的可表示為：
|
|
式中，αc為曲率引導系數；，其中n1和n2分別為網格f1和f2的法向量，本文采用法向量夾角的余弦值作為指標，評估相鄰三角網格間的相對彎曲程度；是網格的曲率，c(pi)是網格的頂點平均曲率；法向量閾值Nt根據統計結果設置為Nt = 0.9。結合初始分割邊界處網格的幾何特點，由曲率作為引導方位、法向量作為類型判斷標準，不僅實現了分割邊界的延伸，還可有效避免過分割問題的出現，進而實現牙頜模型的精確分割。
2 實驗結果
2.1 實驗細節
本文算法基于Python語言并利用vedo開源庫實現算法，模型顯示基于Mesh Labeler軟件[22]，硬件環境配置如下：Intel(R) Core(TM) i7-12700F 2.10 GHz處理器，NVIDIA GeForce GTX1660Ti顯卡。本文從Teeth3DS數據庫[23]獲得三維牙頜網格模型，共100個三維牙頜網格模型，出于算力的限制將模型的網格數簡化至15 000個網格。此外，為了定量驗證所提方法的性能，本文使用總體精度（overall accuracy，OA）、交并比（Intersection over Unio，IoU）和均交并比（mIoU）作為評價指標。
2.2 對比實驗
為驗證本文算法優勢，分別與局部信息空間增強模塊（Local Augmentation Spatial Module，LASM）[2]、區域約束法[21]以及標量場法[11]這三種先進的牙齒分割算法進行比較。分割結果通過表1中的OA和mIoU指標進行定量總結，IoU僅顯示左側牙齒（T1-T7）和牙齦（T0）的分割結果。從表1中可以得出以下結論：① 本文方法在每個牙齒分割中都獲得了更高的IoU，證明了本文方法在牙齒精細分割過程中的泛化性能；② 與同樣使用法向量進行邊界優化的區域約束法相比，本文方法的mIoU指標提升了5.36個百分點，因為區域約束法僅使用法向量對邊界進行優化，容易出現過分割問題；③ 與采用邊界線搜尋的標量場法和依賴坐標特征的LASM法相比，本文方法由于不過度依賴網格的坐標信息，在處理擁擠牙齒時擁有更高的精度。
表1
與其他先進方法的比較結果（%）
Table1.
Comparison results with other advanced methods (%)
為進一步體現本文方法的有效性，對分割結果進行了可視化，如圖6所示。首先，如第一行紅色圓圈所示，全自動的LASM法對錯位牙齒的分割精度最低，因為這種方法在特征提取時主要依賴牙齒網格的坐標，擁擠錯位導致網絡在判斷過程中發生混淆進而錯分；而本文方法和其他兩種半自動方法由于預先的人工標注，對于牙齒擁擠的情況能夠保證正確的區域識別，避免大面積錯分。其次，第二行中標量場法在擁有凸起的牙齒邊界處，由于啟發式齦緣線法傾向于獲取更大面積的完整齦緣因此出現了明顯的過分割，而本文使用的區域生長算法在凸起處由于對曲率變化更加敏感，從而有效避免了過分割問題。最后，在第三行的牙齒邊界處和第一行的牙齒擁擠處，可以發現區域約束法的邊界出現了過分割問題，因為它只利用法向量進行邊界線獲取，當邊界網格比較平坦時會出現錯分。
圖6
本文方法與三種對比方法的分割結果可視化
Figure6.
Visualization of segmentation results among the proposed method and three comparison methods
2.3 消融實驗
2.3.1 差異性區域生長的有效性
為驗證本文的差異性區域生長算法的有效性，通過不同的生長策略構建了三種變體進行比較：① 僅基于初始種子點進行生長，并取消數量閾值設定；② 僅基于初始種子點進行生長，并包含數量閾值設定；③ 基于多種子點進行生長，并取消數量閾值設定；定性結果如圖7所示。從圖中可以看出，沒有設置數量閾值的模型在牙齒頂面出現了生長停滯的現象，這主要是因為牙齒頂面溝壑處和凸起部位的曲率變化差值大使得算法提前停止。此外，使用單種子點和數量閾值的變體在磨牙的側面均存在明顯的欠分割，這主要是因為牙齒頂面和側面交界處的高曲率網格阻礙了生長的正常進行，單種子點無法適應頂面和側面之間的曲率特征分布差異。與之相比，本文的生長算法通過多種子點和數量閾值針對牙齒的頂面和側面進行不同的生長策略，有效地適應了牙齒幾何結構的差異性。
圖7
不同生長策略的分割結果
Figure7.
Segmentation results of different growth strategies
2.3.2 邊界延伸策略的有效性
為驗證本文所提的邊界延伸策略的有效性，通過不同的延伸判別條件構建了三種變體進行比較：① 無邊界延伸，即不對網格的初始邊界進行優化；② 法向量延伸，即直接使用法向量夾角判斷進行延伸，不再用網格的曲率變化進行引導；③ 曲率延伸，即直接將曲率小于共邊已標注網格的邊界網格劃分為同類網格。定量結果如表2所示，本文算法的OA和mIoU均有較大的提升。法向量延伸精度小于曲率延伸，主要是因為牙齒嚴重畸形時齒齦邊界處的相鄰、異類網格間的法向量夾角變小，造成大面積過生長降低了分割精度。
表2
不同邊界延伸策略的定量分割結果（%）
Table2.
Quantitative segmentation results with different boundary extension strategies (%)
圖8中展示了上述變體的可視化結果。首先，無邊界延伸的結果在齒間存在明顯的欠分割，這是因為曲率變化大于設定的閾值，導致生長停止。其次，法向量延伸的牙齒邊界比曲率延伸的牙齒邊界光滑，這主要是因為局部極小曲率的網格的類型具有不確定性。最后，法向量延伸的牙齒邊界處有時會存在明顯的過分割，因為齒齦邊界處網格的法向量變化可能較小，進而產生錯誤的分割，而本文方法由于曲率導向的緣故對法向量夾角的變化更加敏感，有效地避免了過分割的錯誤。
圖8
不同邊界延伸策略的可視化分割結果
Figure8.
Visual segmentation results of different boundary extension strategies
3 結語
本文針對牙齒的幾何特征分布和區域生長算法的原理，提出了一種結合多種子區域生長和邊界延伸的牙齒分割方法。該方法結合牙齒的負曲率分布特點獲得新種子點，并通過差異性區域生長有效適應了牙齒頂面和側面間的差異性結構；根據初始分割區域的網格分布特點，結合法向量和曲率特征對邊界進行了延伸，克服了區域生長提前停止的缺陷。此外，本文方法與其他三種優秀的分割方法進行了比較，并通過消融實驗分析了核心技術的有效性，實驗結果證實本文方法具有較少的人工參與和參數調整，適合具有挑戰性的實際情況。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：劉志華和薛久濤構思并設計了研究方案；劉志華實施方案并處理數據；唐浩負責數據收集和文獻調研；劉志華和廖與禾負責論文的撰寫與修改。
