梯度場作為磁共振成像（MRI）系統的核心磁場之一，由梯度線圈產生，在磁共振圖像空間編碼和回波信號的生成中起關鍵作用。梯度場的均勻性或線性度直接關系到MRI圖像的質量和畸變程度。然而，傳統的單點測量法在梯度場線性度評估方面準確性不足，難以為圖像畸變矯正提供有效參數。本文提出一種基于球面測量的方法，通過在球面上測量磁場分布，進而進行詳盡的磁場計算和線性度分析。本研究應用于評估非對稱頭部梯度線圈的非線性度，顯示出較單點測量法更全面和精確的評估結果。這一進展不僅增強了梯度線圈設計的科學依據，還為MRI圖像的畸變矯正提供了更為可靠的參數和方法。
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
磁共振成像（magnetic resonance imaging，MRI）技術是當代醫學影像領域中最先進的設備之一，對多種臨床疾病的診斷起到了關鍵作用[1]。目前，1.5 T和3.0 T及以上高場強磁共振成像系統已成為臨床上的標準配置，這些系統主要采用超導電磁技術，并以全身通用型系統為主。與此同時，針對專科需求設計的MRI系統也逐漸興起[2-3]，它們能夠解決通用系統難以涉及的特定臨床問題，顯示出其個性化的顯著優勢[4-5]。專科化磁共振成像系統對核心部件提出了更高的要求，如需要更高的梯度強度和更快的梯度切換速度。梯度線圈的設計必須在多個性能指標間做出平衡，這些指標往往相互沖突[6-7]。在實際應用中，為了最大化梯度線圈的效率并減少其電感，通常會犧牲一定程度的梯度均勻度，以優化線圈的成像區域、外形尺寸、受力、噪音及產生的熱量等綜合性能[8]。
MRI系統中的梯度系統負責產生變化的線性梯度場，這些梯度場在成像過程中用于空間編碼以及在梯度回波序列中回波信號的生成，其性能可直接影響成像質量[9-10]。如果梯度磁場的非線性較大，將導致重建圖像的畸變[11]。這種由梯度均勻度引起的圖像畸變和定位不準確的問題通常需通過圖像后處理進行矯正[12-13]。
因此，精確測量梯度場的均勻性是梯度線圈研發和生產過程中的一個關鍵步驟，同時也為圖像畸變的非線性校正和精確定位提供了重要的參考依據[14]。盡管如此，目前對梯度線圈的非線性梯度場進行測量和分析的研究仍相對不足，傳統的點測量法準確性難以滿足現代MRI技術的要求[15-17]。本文旨在通過對特定工藝生產的梯度線圈進行非線性梯度場的測量和分析，評估其磁場均勻性是否達到設計標準。
1 梯度磁場測量
在梯度線圈中通過直流電流，可以在指定的視野（field of view，FOV）內產生變化的梯度磁場，三個獨立的梯度線圈分別沿X、Y、Z方向產生三個相互垂直的獨立梯度場。為了評估梯度場，可以使用測磁儀對FOV內的磁場分布進行精確測量。常用的單點測量法通過在成像區域內選擇特定的采樣點進行測量，并對這些點的磁場進行計算和分析。這種方法中，采樣點的位置和數量是決定測量精度的關鍵因素。單點測量法通常適用于簡單的磁場分析，如測量X、Y、Z軸線上的點并據此進行線性度分析。該方法采用帶單點探頭的磁場測量工具（如瑞士METROlab公司生產的PT2026高精度測磁儀）和定位平臺搭建的三維測量裝置，可以對X、Y、Z軸上的離散采樣點逐一測量。這種方法的優點是成本低，操作簡單，直接獲得所需的磁場值，不需復雜計算，無計算誤差；缺點是受測量設備定位精度的影響較大，改變采樣點分布時需重新測量。
本文提出的球面測量法針對FOV成像區域內球面上的磁場進行測量，通過計算得到成像區域內任意點的磁場強度，進而分析和評估任意線面上的磁場分布。該方法使用帶陣列探頭的磁場測量工具（如瑞士METROlab公司生產的MFC2046陣列測磁儀）和定位平臺組成的測量裝置，能夠對成像區域球面上陣列分布的點進行精確測量。陣列探頭通常布置在半圓弧面上，通過垂直弧面方向旋轉探頭實現全球面的磁場測量。這種方法雖然測量成本較高，但其優勢在于一次測量后，即使改變采樣點分布，也能通過計算獲得新的數據，無需重復測量。此方法依賴磁場計算，可能引入小的舍入誤差，但這些誤差通常可以忽略不計，并且由于依賴計算，該方法受設備定位精度影響較小。
2 梯度磁場計算
梯度線圈在成像區域內產生的梯度磁場屬于空間無源區域磁場，其磁感應強度滿足拉普拉斯（Laplace）方程，可以表示為一組含有球面諧波函數的多項式之和[18-20]。無論梯度場方向為X、Y還是Z，其沿軸向的磁感應強度分量都滿足以下Laplace方程：
 |
其中
，分別代表X、Y、Z方向的梯度線圈產生的梯度場，例如
為X方向梯度場的軸向磁場分量。在球坐標系下求解Laplace方程可得到
的球面諧波函數展開形式：
 |
在此表達式中，
、
、
分別為球坐標系的三個分量，
為n次m階的連帶Legendre多項式，且
，
和
為對應諧波分量的幅值。若已知
和
，則可以計算任意點的磁感應強度。低階次諧波分量的幅值較大，而高階次諧波分量由于幅值相對較小，通常會被忽略，從而
的表達由無限項多項式簡化為有限項。有限的諧波分量幅值
和
可以通過磁場區域的測量進行諧波分析獲得。
下面介紹本文采用的諧波分析方法。為了討論方便，將
中的下標
省略。式(2)中第
次
階的磁場諧波分量記為
：
 |
且有
 |
定義球面諧波函數
，
與
在球面上存在正交關系，即在球面上的積分：
 |
其中
。根據正交性，以上公式左側可以擴展為以下積分：
 |
對應了在半徑為r的球表面進行測量的磁場采樣點。式(6)右側的內層積分可以由
的傅里葉變換（變量為
，固定
）獲得，得到積分結果記為
，而外層積分由高斯數值積分獲得，即為：
 |
其中
為對應采樣點的高斯權重系數，
和
分別對應傅里葉變換的cos和sin函數部分。由于式(2)和式(7)相等，進而推導
和
的表達形式為：
 |
以上公式展示了磁場分布的球諧函數諧波分析結果。通過這些公式，可以利用球面上的磁場測量數據計算出諧波分量的幅值
和
，進而精確計算出球體內任意點的磁感應強度。
3 梯度線性度分析和結果
3.1 梯度非線性度定義
梯度線圈通過電流產生的梯度磁場的非線性度，定義為特定位置的實際磁感應強度與理想線性梯度磁場強度的偏差程度。這一偏差可以通過以下公式表達：
 |
其中，
，分別對應著X、Y、Z方向的梯度場，
為采樣點序號，
是理想梯度場強，
是成像區域的最大半徑。當磁感應強度超過理想值時，非線性度取值為正，反之則為負。在三維成像區域內，理想梯度場應使等磁場強度點在空間中形成一個平面，例如在
的平面上理想梯度磁場強度為0，稱為零平面。然而，實際的梯度場受非線性的影響，這些等梯度磁場強度平面會發生彎曲。在射頻場激發時，存在于這些彎曲平面內的質子會在梯度編碼和相位編碼過程中積累與理想值有差異的相位差，最終導致重建圖像出現扭曲和變形。
3.2 梯度磁場非線性度分析
本文對公司正在開發的3.0 T顱腦專用超導磁共振成像系統中采用的非對稱梯度線圈的非線性度進行了詳細分析。該梯度線圈由英國Tesla公司設計，具有獨特的非對稱結構，其設計擴大了患者端的內孔徑，便于在患者肩部放置，同時使頭部更準確地定位于成像區的中心，該成像區的直徑為26 cm。由于非對稱結構帶來的設計挑戰，為了平衡其他性能參數，梯度線圈在梯度場的均勻性（即線性度）方面做出了一定的妥協。
具體而言，該梯度線圈的非線性度設計指標如下：X線圈為–8.1%～16.6%，Y線圈為–10.6%～16.6%，Z線圈為–7.0%～12.3%，這些數值作為非線性評估的基準范圍。這些設計值是在成像區內一圓柱面上，依據特定密度分布的采樣點，通過式(9)計算得出最大值和最小值。顯然，該梯度線圈的非線性誤差顯著高于常規梯度線圈，這將直接導致成像結果的顯著畸變，因此，在圖像后處理階段必須實施非線性校正技術以優化圖像質量。
本文的重點在于對實際制造完成的梯度線圈的梯度場非線性進行更為詳盡的評估。為此，引入了球面測量法，并將其與傳統的單點測量法進行對比，以全面、準確地評估梯度線圈的非線性度。
3.2.1 單點測量法
本文采用單點測量技術，通過向X、Y、Z梯度線圈分別施加50 A直流電流，生成了三個方向的梯度磁場。隨后，利用單探頭三維測量平臺，以成像區域中心為基準點，沿X、Y、Z軸每隔1 cm設置一個采樣點，直至半徑達到13 cm，每條軸線上設置了27個采樣點進行磁場測量。由于所測磁場值中包含了磁體自身產生的均勻磁場，故需剔除背景場影響，以獲得梯度線圈單獨產生的磁場數據。
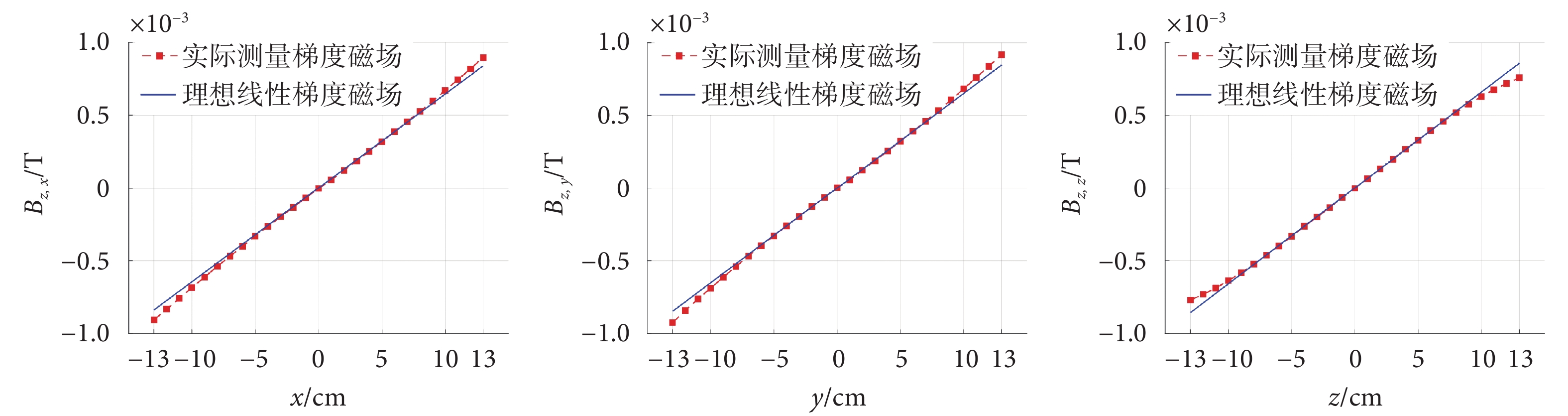
圖1展示了通過單點測量法在X、Y、Z軸線上獲得的梯度磁場測量值與理想線性梯度磁場值的對比。圖中，藍色線條代表理論上的線性梯度磁場，而紅色點則表示實際測量的梯度磁場值。藍色參考線基于梯度線圈效率的設計值繪制，X、Y、Z方向梯度線圈效率的設計值分別為129.1、130.4和131.8 μT/(m·A)，在50 A電流驅動下，產生的梯度場強度依次為6.46、6.52、6.59 mT/m。觀察圖表可知，實際測量的梯度磁場值圍繞理想線性梯度有所偏離，特別是在遠離坐標原點的位置，非線性誤差顯著增大。在測量前，已實施了零點校正，確保測量坐標系與實際梯度磁場坐標系原點一致。
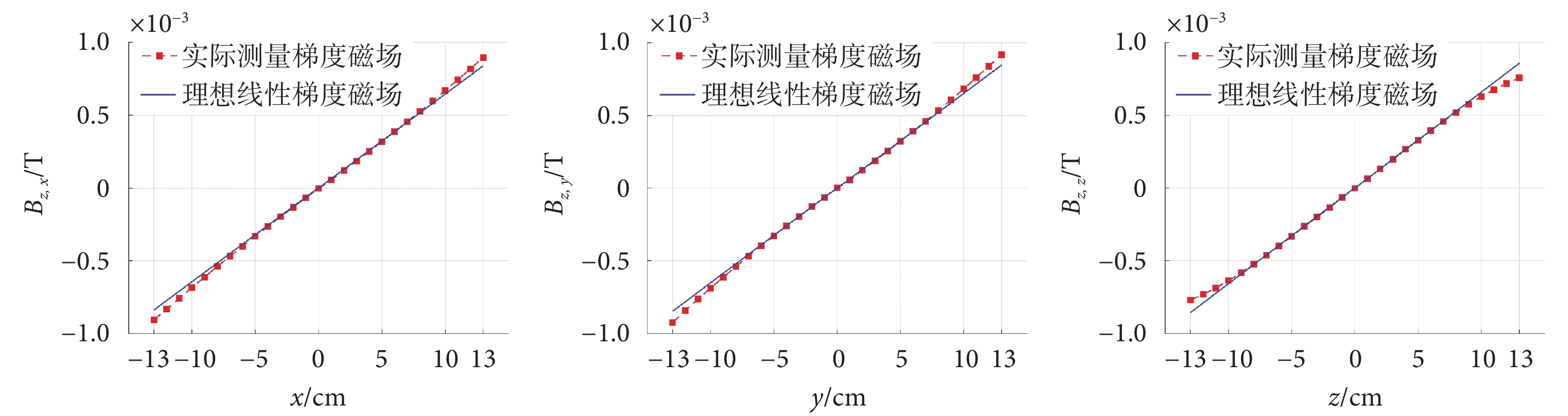圖1
單點測量法測量的梯度磁場分布
Figure1.
Gradient field distribution measured by single-point measurement method
根據本次測量數據，X、Y、Z梯度線圈的最大和最小非線性度分別為X線圈–8.1%～6.8%、Y線圈–9.2%～8.3%、Z線圈–11.6%～10.1%。這些結果顯示，單點測量法得到的結果與設計預期存在較大偏差，尤其是X軸和Y軸的非線性表現優于設計預期，這表明單點測量法在反映實際梯度場非線性特征方面存在局限性。原因包括：① 采樣點數量有限，無法充分揭示非線性特性的最壞情況；② 零點校正方法未能糾正坐標軸的方向偏移；③ 測量工裝存在固有的定位誤差和形變影響。綜上所述，單點測量法在評估梯度非線性度時顯得較為粗略，其測量結果的準確性受到限制。
3.2.2 球面測量法
鑒于單點測量法在全面評估梯度線圈的最大非線性誤差方面的不足，本文提出了一種更為精確的評估方法——球面測量法，以對制作完成的梯度線圈進行更為細致的考量。該方法首先與單點測量法相似，通過直流電源向X、Y、Z梯度線圈分別通入50 A電流，生成對應方向的梯度場。隨后，利用配備24個陣列探頭的測量平臺對梯度磁場進行測量。這些探頭均勻分布在半徑為15 cm的半圓弧上，通過半圓旋轉24個角度（每個角度間隔15 °）進行全方位測量，從而在直徑為30 cm的圓球面上獲取24×24個采樣點的梯度磁場數據。
與單點測量法一致，所測得的磁場值包含了磁體自身產生的均勻磁場，因此需進行背景場剔除處理，以獲得梯度線圈單獨產生的磁場。背景場測量在梯度線圈無電流狀態下進行，采用與梯度場測量相同的方法。基于無源區域磁場的球諧函數諧波展開理論，利用24×24個球面采樣點數據，可以精確計算出23次12階以內的球諧函數諧波分量幅值（更高階次的幅值設為0），即確定
和
（n≤23，m≤12）的取值。
表1詳細列出了X、Y、Z梯度線圈在50 A電流驅動下所產生的梯度磁場的3次以內諧波分量。在理想的線性梯度場中，由于
（X線圈）、
（Y線圈）、
（Z線圈）分別對應X、Y、Z線圈梯度場的一階項，所以其值不為零，其他諧波分量均為零。觀察表１可知，由于高階分量的存在，測量梯度場表現出非線性特征，特別是X線圈的
和Y線圈的
取值較大，成為導致梯度場分布非線性的主要因素。此外，X線圈和Y線圈的非線性程度明顯高于Z線圈。
表1
X、Y、Z梯度線圈梯度場（50 A電流驅動）低階諧波分量
Table1.
Low-order harmonics of gradient fields for X, Y, and Z gradient coils (driven by 50 A current)
值得注意的是，在進行梯度場測量時，陣列探測器的測磁儀裝置無法進行零點和方向性校準。因此，本文在數據分析階段，通過深入分析計算得到的梯度磁場分布，尋找并確定了測量坐標系與梯度坐標系之間的轉換關系，包括零點偏移和旋轉方向，從而實現了測量坐標系與梯度磁場坐標系之間的精確配準。
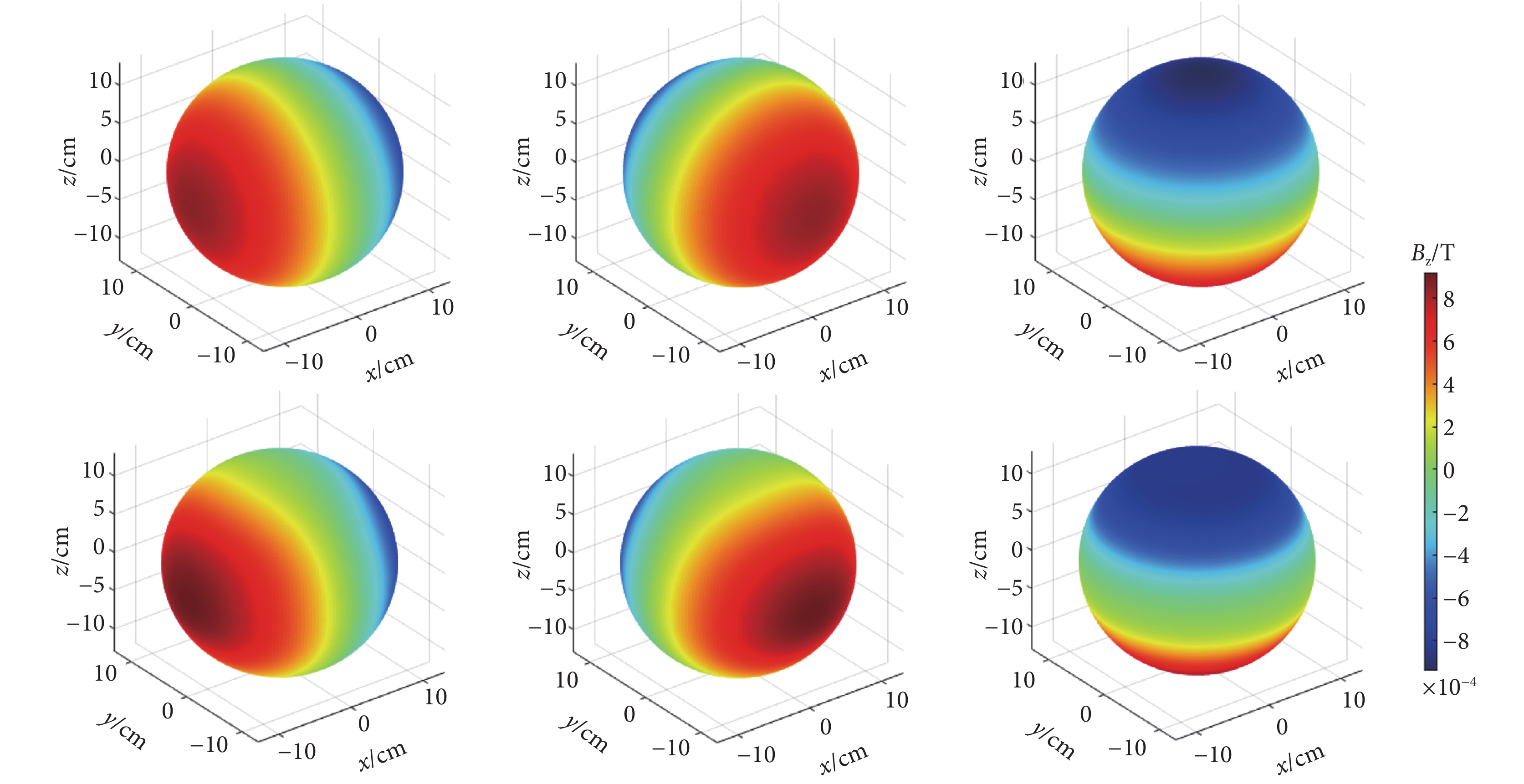
圖2展示了在直徑為26 cm的球體表面上，X、Y、Z梯度線圈所產生的磁場分布情況。具體而言，第一排圖像呈現了理想的梯度磁場分布狀態，而第二排則展示了相應的實際測量磁場分布。在理想狀態下，第一排的梯度磁場分別沿著X、Y、Z軸呈現出線性變化的特征，這種變化在球體表面上以漸變圓環的形式直觀展現。然而，在實際測量中，由于非線性誤差的存在，第二排的磁場分布圓環出現了不同程度的扭曲或偏移。進一步觀察可以發現，X和Y線圈所產生的非線性誤差相較于Z線圈更為顯著。這一細節揭示了在實際應用中，X和Y線圈的磁場分布優化可能面臨更大的挑戰。
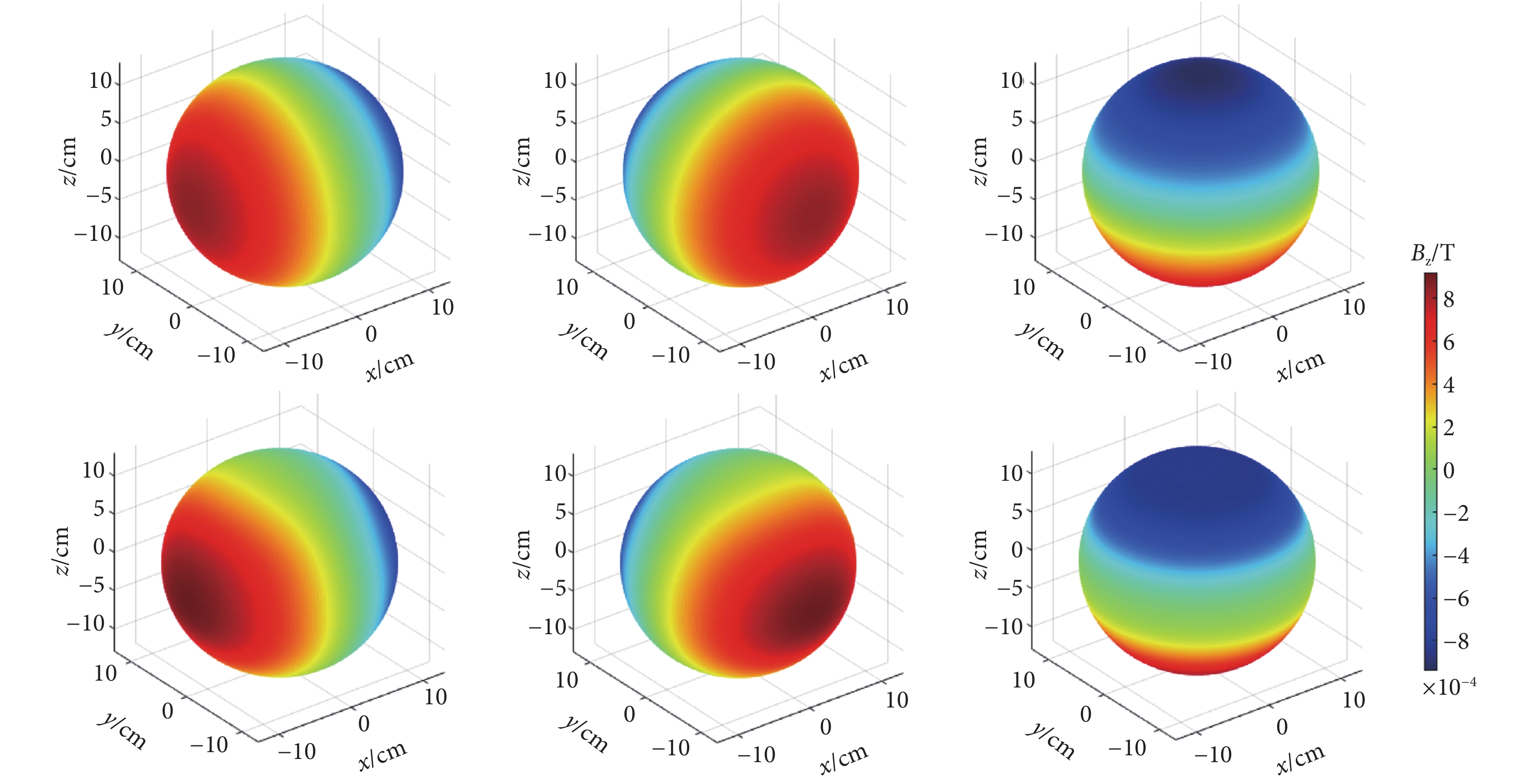圖2
直徑為26 cm球面上的磁場分布（50 A電流驅動）
上圖：理想磁場分布；下圖：測量磁場分布
Figure2. Magnetic field distribution on a sphere with a diameter of 26 cm (driven by 50 A current)top: ideal magnetic field distribution; bottom: measured magnetic field distribution
圖3展示了X、Y、Z梯度線圈分別在
、
、
平面上的磁場分布情況。其中，第一行描繪了理想的梯度磁場分布狀態，而第二行則呈現了實際測量的磁場分布。在理想的梯度磁場中，X、Y、Z方向的梯度場分別與x、y、z坐標線性相關，這種線性關系分別在
、
、
的橫斷面上以清晰的直條紋形式展現。然而，在實際測量的梯度磁場中，這些直條紋因非線性誤差的影響而發生了變形，轉變為圓弧狀或出現了顏色偏移。值得注意的是，條紋的變形或偏移程度直接反映了非線性度的高低。變形或偏移越顯著，非線性度就越高，這在成像過程中將導致更明顯的畸變效應。
圖3
平面上的磁場分布（50 A電流驅動）
上圖：理想磁場分布；下圖：測量磁場分布
Figure3. Magnetic field distribution on planes (driven by 50 A current)top: ideal magnetic field distribution; bottom: measured magnetic field distribution
圖3揭示了一個關鍵現象：在直徑為26 cm的球形區域內，磁場非線性誤差通常隨著距離原點的增大而增大。因此，對球表面的梯度磁場進行評估，能夠有效代表該梯度線圈的最大非線性度。為了全面評估非線性度，在球面上進行了高密度采樣，沿經度和緯度方向各均勻選取了200個點，共計200×200個采樣點。通過計算這些采樣點的磁場強度，并利用式（9），得出了各線圈的非線性度范圍：X線圈為–15.8%～18.62%，Y線圈為–16.2%～19.2%，Z線圈為–12.1%～9.9%。表2對比了不同方法得到的梯度非線性度評估結果。
表2
梯度非線性度評估結果對比
Table2.
Comparison of gradient nonlinearity evaluation results
與設計值相比，采用球面測量法評估得到的非線性度有所增加，這主要歸因于兩點：首先，設計值通常基于柱面采樣點進行評估，而球面測量法則采用了球面上更為密集的采樣點，從而能夠更全面、準確地反映實際梯度線圈的非線性度；其次，由于工藝制作過程中的誤差，實際梯度場分布與設計值之間難免存在差異，而測量法則能更真實地反映由特定工藝制作完成的梯度線圈的實際梯度場分布。
與單點測量法相比，球面測量法的評估結果更接近設計值。單點測量法僅使用軸線上非常有限的采樣點進行評估，因此評估結果可能不夠充分和準確。綜上所述，本文提出的球面測量法為實際梯度線圈產生梯度場的非線性度提供了更為全面、準確的評估方法。
4 結論
本文創新性地提出了一種基于球面測量的MRI梯度線圈非線性梯度場評估方法，涵蓋了測量、磁場計算及非線性度評價。該方法被應用于頭部專用的非對稱梯度線圈，由于非對稱結構的復雜性，在線性度方面做出了一定妥協。通過對比廠商提供的設計值，發現傳統的單點測量法在磁場非線性度評估中準確性欠佳，因為它僅對X、Y、Z軸線上的采樣點進行線性度評估。其優勢在于測量流程簡便、成本低廉，無需復雜的磁場計算，從而避免了計算誤差。然而，單點測量法易受測量裝置定位精度的影響，且一旦改變測量采樣點的分布，就需要重新進行測量。此外，由于采樣點數量有限，該方法難以反映最大非線性度情況。相比之下，本文提出的球面測量法提供了一種更為全面的評估手段。該方法通過測量球面上的磁場，能夠獲取任意點的磁場值，進而可以在任意平面或球面上進行磁場計算和線性度分析。盡管球面測量法的測量成本相對較高，但一次測量后，若需改變采樣點分布，僅需通過計算即可得出結果，無需重復測量。此外，該方法受測量裝置定位精度的影響較小，為后續的非線性矯正提供了更為準確的參考數據，有助于獲得更理想的圖像質量。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：楊曉麗全面負責本文的試驗設計、數據深度分析及論文的整體撰寫工作；王兆連對論文的創新點進行了深入挖掘，并提出了寶貴的建設性意見，同時負責論文的審核工作；王前、張義廷、齊亞飛對論文內容進行了細致的審閱，針對論文的修改提出了富有建設性的意見，并參與了論文的最終審核；宋子軒、張玉昌負責試驗裝置的設計與制作，以及磁場數據的精確測量工作；馬曉鵬為試驗設計和試驗結果的分析提供了關鍵性指導。
0 引言
磁共振成像（magnetic resonance imaging，MRI）技術是當代醫學影像領域中最先進的設備之一，對多種臨床疾病的診斷起到了關鍵作用[1]。目前，1.5 T和3.0 T及以上高場強磁共振成像系統已成為臨床上的標準配置，這些系統主要采用超導電磁技術，并以全身通用型系統為主。與此同時，針對專科需求設計的MRI系統也逐漸興起[2-3]，它們能夠解決通用系統難以涉及的特定臨床問題，顯示出其個性化的顯著優勢[4-5]。專科化磁共振成像系統對核心部件提出了更高的要求，如需要更高的梯度強度和更快的梯度切換速度。梯度線圈的設計必須在多個性能指標間做出平衡，這些指標往往相互沖突[6-7]。在實際應用中，為了最大化梯度線圈的效率并減少其電感，通常會犧牲一定程度的梯度均勻度，以優化線圈的成像區域、外形尺寸、受力、噪音及產生的熱量等綜合性能[8]。
MRI系統中的梯度系統負責產生變化的線性梯度場，這些梯度場在成像過程中用于空間編碼以及在梯度回波序列中回波信號的生成，其性能可直接影響成像質量[9-10]。如果梯度磁場的非線性較大，將導致重建圖像的畸變[11]。這種由梯度均勻度引起的圖像畸變和定位不準確的問題通常需通過圖像后處理進行矯正[12-13]。
因此，精確測量梯度場的均勻性是梯度線圈研發和生產過程中的一個關鍵步驟，同時也為圖像畸變的非線性校正和精確定位提供了重要的參考依據[14]。盡管如此，目前對梯度線圈的非線性梯度場進行測量和分析的研究仍相對不足，傳統的點測量法準確性難以滿足現代MRI技術的要求[15-17]。本文旨在通過對特定工藝生產的梯度線圈進行非線性梯度場的測量和分析，評估其磁場均勻性是否達到設計標準。
1 梯度磁場測量
在梯度線圈中通過直流電流，可以在指定的視野（field of view，FOV）內產生變化的梯度磁場，三個獨立的梯度線圈分別沿X、Y、Z方向產生三個相互垂直的獨立梯度場。為了評估梯度場，可以使用測磁儀對FOV內的磁場分布進行精確測量。常用的單點測量法通過在成像區域內選擇特定的采樣點進行測量，并對這些點的磁場進行計算和分析。這種方法中，采樣點的位置和數量是決定測量精度的關鍵因素。單點測量法通常適用于簡單的磁場分析，如測量X、Y、Z軸線上的點并據此進行線性度分析。該方法采用帶單點探頭的磁場測量工具（如瑞士METROlab公司生產的PT2026高精度測磁儀）和定位平臺搭建的三維測量裝置，可以對X、Y、Z軸上的離散采樣點逐一測量。這種方法的優點是成本低，操作簡單，直接獲得所需的磁場值，不需復雜計算，無計算誤差；缺點是受測量設備定位精度的影響較大，改變采樣點分布時需重新測量。
本文提出的球面測量法針對FOV成像區域內球面上的磁場進行測量，通過計算得到成像區域內任意點的磁場強度，進而分析和評估任意線面上的磁場分布。該方法使用帶陣列探頭的磁場測量工具（如瑞士METROlab公司生產的MFC2046陣列測磁儀）和定位平臺組成的測量裝置，能夠對成像區域球面上陣列分布的點進行精確測量。陣列探頭通常布置在半圓弧面上，通過垂直弧面方向旋轉探頭實現全球面的磁場測量。這種方法雖然測量成本較高，但其優勢在于一次測量后，即使改變采樣點分布，也能通過計算獲得新的數據，無需重復測量。此方法依賴磁場計算，可能引入小的舍入誤差，但這些誤差通常可以忽略不計，并且由于依賴計算，該方法受設備定位精度影響較小。
2 梯度磁場計算
梯度線圈在成像區域內產生的梯度磁場屬于空間無源區域磁場，其磁感應強度滿足拉普拉斯（Laplace）方程，可以表示為一組含有球面諧波函數的多項式之和[18-20]。無論梯度場方向為X、Y還是Z，其沿軸向的磁感應強度分量都滿足以下Laplace方程：
|
其中，分別代表X、Y、Z方向的梯度線圈產生的梯度場，例如為X方向梯度場的軸向磁場分量。在球坐標系下求解Laplace方程可得到的球面諧波函數展開形式：
|
在此表達式中，、、分別為球坐標系的三個分量，為n次m階的連帶Legendre多項式，且，和為對應諧波分量的幅值。若已知和，則可以計算任意點的磁感應強度。低階次諧波分量的幅值較大，而高階次諧波分量由于幅值相對較小，通常會被忽略，從而的表達由無限項多項式簡化為有限項。有限的諧波分量幅值和可以通過磁場區域的測量進行諧波分析獲得。
下面介紹本文采用的諧波分析方法。為了討論方便，將中的下標省略。式(2)中第次階的磁場諧波分量記為：
|
且有
|
定義球面諧波函數，與在球面上存在正交關系，即在球面上的積分：
|
其中。根據正交性，以上公式左側可以擴展為以下積分：
|
對應了在半徑為r的球表面進行測量的磁場采樣點。式(6)右側的內層積分可以由的傅里葉變換（變量為，固定）獲得，得到積分結果記為，而外層積分由高斯數值積分獲得，即為：
|
其中為對應采樣點的高斯權重系數，和分別對應傅里葉變換的cos和sin函數部分。由于式(2)和式(7)相等，進而推導和的表達形式為：
|
以上公式展示了磁場分布的球諧函數諧波分析結果。通過這些公式，可以利用球面上的磁場測量數據計算出諧波分量的幅值和，進而精確計算出球體內任意點的磁感應強度。
3 梯度線性度分析和結果
3.1 梯度非線性度定義
梯度線圈通過電流產生的梯度磁場的非線性度，定義為特定位置的實際磁感應強度與理想線性梯度磁場強度的偏差程度。這一偏差可以通過以下公式表達：
|
其中，，分別對應著X、Y、Z方向的梯度場，為采樣點序號，是理想梯度場強，是成像區域的最大半徑。當磁感應強度超過理想值時，非線性度取值為正，反之則為負。在三維成像區域內，理想梯度場應使等磁場強度點在空間中形成一個平面，例如在的平面上理想梯度磁場強度為0，稱為零平面。然而，實際的梯度場受非線性的影響，這些等梯度磁場強度平面會發生彎曲。在射頻場激發時，存在于這些彎曲平面內的質子會在梯度編碼和相位編碼過程中積累與理想值有差異的相位差，最終導致重建圖像出現扭曲和變形。
3.2 梯度磁場非線性度分析
本文對公司正在開發的3.0 T顱腦專用超導磁共振成像系統中采用的非對稱梯度線圈的非線性度進行了詳細分析。該梯度線圈由英國Tesla公司設計，具有獨特的非對稱結構，其設計擴大了患者端的內孔徑，便于在患者肩部放置，同時使頭部更準確地定位于成像區的中心，該成像區的直徑為26 cm。由于非對稱結構帶來的設計挑戰，為了平衡其他性能參數，梯度線圈在梯度場的均勻性（即線性度）方面做出了一定的妥協。
具體而言，該梯度線圈的非線性度設計指標如下：X線圈為–8.1%～16.6%，Y線圈為–10.6%～16.6%，Z線圈為–7.0%～12.3%，這些數值作為非線性評估的基準范圍。這些設計值是在成像區內一圓柱面上，依據特定密度分布的采樣點，通過式(9)計算得出最大值和最小值。顯然，該梯度線圈的非線性誤差顯著高于常規梯度線圈，這將直接導致成像結果的顯著畸變，因此，在圖像后處理階段必須實施非線性校正技術以優化圖像質量。
本文的重點在于對實際制造完成的梯度線圈的梯度場非線性進行更為詳盡的評估。為此，引入了球面測量法，并將其與傳統的單點測量法進行對比，以全面、準確地評估梯度線圈的非線性度。
3.2.1 單點測量法
本文采用單點測量技術，通過向X、Y、Z梯度線圈分別施加50 A直流電流，生成了三個方向的梯度磁場。隨后，利用單探頭三維測量平臺，以成像區域中心為基準點，沿X、Y、Z軸每隔1 cm設置一個采樣點，直至半徑達到13 cm，每條軸線上設置了27個采樣點進行磁場測量。由于所測磁場值中包含了磁體自身產生的均勻磁場，故需剔除背景場影響，以獲得梯度線圈單獨產生的磁場數據。
圖1展示了通過單點測量法在X、Y、Z軸線上獲得的梯度磁場測量值與理想線性梯度磁場值的對比。圖中，藍色線條代表理論上的線性梯度磁場，而紅色點則表示實際測量的梯度磁場值。藍色參考線基于梯度線圈效率的設計值繪制，X、Y、Z方向梯度線圈效率的設計值分別為129.1、130.4和131.8 μT/(m·A)，在50 A電流驅動下，產生的梯度場強度依次為6.46、6.52、6.59 mT/m。觀察圖表可知，實際測量的梯度磁場值圍繞理想線性梯度有所偏離，特別是在遠離坐標原點的位置，非線性誤差顯著增大。在測量前，已實施了零點校正，確保測量坐標系與實際梯度磁場坐標系原點一致。
圖1
單點測量法測量的梯度磁場分布
Figure1.
Gradient field distribution measured by single-point measurement method
根據本次測量數據，X、Y、Z梯度線圈的最大和最小非線性度分別為X線圈–8.1%～6.8%、Y線圈–9.2%～8.3%、Z線圈–11.6%～10.1%。這些結果顯示，單點測量法得到的結果與設計預期存在較大偏差，尤其是X軸和Y軸的非線性表現優于設計預期，這表明單點測量法在反映實際梯度場非線性特征方面存在局限性。原因包括：① 采樣點數量有限，無法充分揭示非線性特性的最壞情況；② 零點校正方法未能糾正坐標軸的方向偏移；③ 測量工裝存在固有的定位誤差和形變影響。綜上所述，單點測量法在評估梯度非線性度時顯得較為粗略，其測量結果的準確性受到限制。
3.2.2 球面測量法
鑒于單點測量法在全面評估梯度線圈的最大非線性誤差方面的不足，本文提出了一種更為精確的評估方法——球面測量法，以對制作完成的梯度線圈進行更為細致的考量。該方法首先與單點測量法相似，通過直流電源向X、Y、Z梯度線圈分別通入50 A電流，生成對應方向的梯度場。隨后，利用配備24個陣列探頭的測量平臺對梯度磁場進行測量。這些探頭均勻分布在半徑為15 cm的半圓弧上，通過半圓旋轉24個角度（每個角度間隔15 °）進行全方位測量，從而在直徑為30 cm的圓球面上獲取24×24個采樣點的梯度磁場數據。
與單點測量法一致，所測得的磁場值包含了磁體自身產生的均勻磁場，因此需進行背景場剔除處理，以獲得梯度線圈單獨產生的磁場。背景場測量在梯度線圈無電流狀態下進行，采用與梯度場測量相同的方法。基于無源區域磁場的球諧函數諧波展開理論，利用24×24個球面采樣點數據，可以精確計算出23次12階以內的球諧函數諧波分量幅值（更高階次的幅值設為0），即確定和（n≤23，m≤12）的取值。
表1詳細列出了X、Y、Z梯度線圈在50 A電流驅動下所產生的梯度磁場的3次以內諧波分量。在理想的線性梯度場中，由于（X線圈）、（Y線圈）、（Z線圈）分別對應X、Y、Z線圈梯度場的一階項，所以其值不為零，其他諧波分量均為零。觀察表１可知，由于高階分量的存在，測量梯度場表現出非線性特征，特別是X線圈的和Y線圈的取值較大，成為導致梯度場分布非線性的主要因素。此外，X線圈和Y線圈的非線性程度明顯高于Z線圈。
表1
X、Y、Z梯度線圈梯度場（50 A電流驅動）低階諧波分量
Table1.
Low-order harmonics of gradient fields for X, Y, and Z gradient coils (driven by 50 A current)
值得注意的是，在進行梯度場測量時，陣列探測器的測磁儀裝置無法進行零點和方向性校準。因此，本文在數據分析階段，通過深入分析計算得到的梯度磁場分布，尋找并確定了測量坐標系與梯度坐標系之間的轉換關系，包括零點偏移和旋轉方向，從而實現了測量坐標系與梯度磁場坐標系之間的精確配準。
圖2展示了在直徑為26 cm的球體表面上，X、Y、Z梯度線圈所產生的磁場分布情況。具體而言，第一排圖像呈現了理想的梯度磁場分布狀態，而第二排則展示了相應的實際測量磁場分布。在理想狀態下，第一排的梯度磁場分別沿著X、Y、Z軸呈現出線性變化的特征，這種變化在球體表面上以漸變圓環的形式直觀展現。然而，在實際測量中，由于非線性誤差的存在，第二排的磁場分布圓環出現了不同程度的扭曲或偏移。進一步觀察可以發現，X和Y線圈所產生的非線性誤差相較于Z線圈更為顯著。這一細節揭示了在實際應用中，X和Y線圈的磁場分布優化可能面臨更大的挑戰。
圖2
直徑為26 cm球面上的磁場分布（50 A電流驅動）
上圖：理想磁場分布；下圖：測量磁場分布
Figure2. Magnetic field distribution on a sphere with a diameter of 26 cm (driven by 50 A current)top: ideal magnetic field distribution; bottom: measured magnetic field distribution
圖3展示了X、Y、Z梯度線圈分別在、、平面上的磁場分布情況。其中，第一行描繪了理想的梯度磁場分布狀態，而第二行則呈現了實際測量的磁場分布。在理想的梯度磁場中，X、Y、Z方向的梯度場分別與x、y、z坐標線性相關，這種線性關系分別在、、的橫斷面上以清晰的直條紋形式展現。然而，在實際測量的梯度磁場中，這些直條紋因非線性誤差的影響而發生了變形，轉變為圓弧狀或出現了顏色偏移。值得注意的是，條紋的變形或偏移程度直接反映了非線性度的高低。變形或偏移越顯著，非線性度就越高，這在成像過程中將導致更明顯的畸變效應。
圖3
平面上的磁場分布（50 A電流驅動）
上圖：理想磁場分布；下圖：測量磁場分布
Figure3. Magnetic field distribution on planes (driven by 50 A current)top: ideal magnetic field distribution; bottom: measured magnetic field distribution
圖3揭示了一個關鍵現象：在直徑為26 cm的球形區域內，磁場非線性誤差通常隨著距離原點的增大而增大。因此，對球表面的梯度磁場進行評估，能夠有效代表該梯度線圈的最大非線性度。為了全面評估非線性度，在球面上進行了高密度采樣，沿經度和緯度方向各均勻選取了200個點，共計200×200個采樣點。通過計算這些采樣點的磁場強度，并利用式（9），得出了各線圈的非線性度范圍：X線圈為–15.8%～18.62%，Y線圈為–16.2%～19.2%，Z線圈為–12.1%～9.9%。表2對比了不同方法得到的梯度非線性度評估結果。
表2
梯度非線性度評估結果對比
Table2.
Comparison of gradient nonlinearity evaluation results
與設計值相比，采用球面測量法評估得到的非線性度有所增加，這主要歸因于兩點：首先，設計值通常基于柱面采樣點進行評估，而球面測量法則采用了球面上更為密集的采樣點，從而能夠更全面、準確地反映實際梯度線圈的非線性度；其次，由于工藝制作過程中的誤差，實際梯度場分布與設計值之間難免存在差異，而測量法則能更真實地反映由特定工藝制作完成的梯度線圈的實際梯度場分布。
與單點測量法相比，球面測量法的評估結果更接近設計值。單點測量法僅使用軸線上非常有限的采樣點進行評估，因此評估結果可能不夠充分和準確。綜上所述，本文提出的球面測量法為實際梯度線圈產生梯度場的非線性度提供了更為全面、準確的評估方法。
4 結論
本文創新性地提出了一種基于球面測量的MRI梯度線圈非線性梯度場評估方法，涵蓋了測量、磁場計算及非線性度評價。該方法被應用于頭部專用的非對稱梯度線圈，由于非對稱結構的復雜性，在線性度方面做出了一定妥協。通過對比廠商提供的設計值，發現傳統的單點測量法在磁場非線性度評估中準確性欠佳，因為它僅對X、Y、Z軸線上的采樣點進行線性度評估。其優勢在于測量流程簡便、成本低廉，無需復雜的磁場計算，從而避免了計算誤差。然而，單點測量法易受測量裝置定位精度的影響，且一旦改變測量采樣點的分布，就需要重新進行測量。此外，由于采樣點數量有限，該方法難以反映最大非線性度情況。相比之下，本文提出的球面測量法提供了一種更為全面的評估手段。該方法通過測量球面上的磁場，能夠獲取任意點的磁場值，進而可以在任意平面或球面上進行磁場計算和線性度分析。盡管球面測量法的測量成本相對較高，但一次測量后，若需改變采樣點分布，僅需通過計算即可得出結果，無需重復測量。此外，該方法受測量裝置定位精度的影響較小，為后續的非線性矯正提供了更為準確的參考數據，有助于獲得更理想的圖像質量。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：楊曉麗全面負責本文的試驗設計、數據深度分析及論文的整體撰寫工作；王兆連對論文的創新點進行了深入挖掘，并提出了寶貴的建設性意見，同時負責論文的審核工作；王前、張義廷、齊亞飛對論文內容進行了細致的審閱，針對論文的修改提出了富有建設性的意見，并參與了論文的最終審核；宋子軒、張玉昌負責試驗裝置的設計與制作，以及磁場數據的精確測量工作；馬曉鵬為試驗設計和試驗結果的分析提供了關鍵性指導。
