引用本文: 陸舜, 林天燁, 何敏聰, 何曉銘, 何憲順, 田佳慶, 魏騰飛, 詹芝瑋, 林錕, 魏秋實. 基于前外側保留角預測股骨頭壞死塌陷的有限元分析. 中國修復重建外科雜志, 2023, 37(11): 1394-1402. doi: 10.7507/1002-1892.202308072 復制
版權信息: ?四川大學華西醫院華西期刊社《中國修復重建外科雜志》版權所有,未經授權不得轉載、改編
股骨頭壞死(osteonecrosis of the femoral head,ONFH)是一種嚴重威脅中青年人群健康的關節疾病[1],目前發病機制仍不清楚,ONFH進展至中后期常會發生股骨頭塌陷導致髖關節疼痛及功能障礙,最終發展為髖關節骨關節炎,不得不接受髖關節置換手術[2-4]。股骨頭塌陷是ONFH的重要轉折點,在ONFH早期精準預測塌陷風險對判斷疾病預后以及指導制定保髖治療方案有重要意義。股骨頭塌陷是生物因素和生物力學因素共同作用的結果[5-7],壞死股骨頭組織結構破壞意味著頭內生物力學異常改變,導致股骨頭力學支撐性能下降[8]。一旦壞死股骨頭承載負荷超過頭內組織結構屈服強度,軟骨下壞死骨質就會發生應力性骨折導致塌陷。有研究認為ONFH塌陷進程與股骨頭前、外側柱受累程度有顯著相關性[9-12]。本團隊前期研究[13-14]發現,結合髖關節正、蛙位X線片綜合評估前、外側柱保留情況,對ONFH塌陷有較好預測效果。研究進一步發現,可以精確量化前、外側柱保留完整度的前側保留角(anterior preserved angle,APA)和外側保留角(lateral preserved angle,LPA)與塌陷進展顯著相關,APA、LPA臨界值分別為60.53°、60.46°,當APA或LPA 小于臨界值時,提示股骨頭塌陷風險顯著升高[15]。然而根據不同保留角預測ONFH塌陷風險的生物力學機制尚不明確,需要更多力學證據支撐。
有限元生物力學分析在可行性、重復性、可視化方面有顯著優勢,其可靠性已得到驗證[16]。有研究[5]建立不同壞死范圍ONFH模型,分析發現大范圍壞死模型中壞死區深部應力集中更為明顯,提示股骨頭塌陷風險升高,但模型中壞死區位置分布較為模糊。還有研究[17-18]根據中日友好醫院分型,通過股骨頭冠狀位三柱結構建立不同壞死位置模型,發現股骨頭外側負重區域受累時,股骨頭塌陷風險明顯高于其他壞死位置,然而所建模型并未關注壞死區位置對股骨頭前側壁的影響。上述研究結果提示股骨頭塌陷預測中,壞死區的位置與范圍對塌陷預后均有重要意義[19]。本研究基于髖關節正、蛙位X線片描述壞死區位置的保留角,結合壞死區范圍,運用三維有限元分析法探討股骨頭APA和LPA預測塌陷的生物力學機制,為不同保留角精準預測ONFH塌陷風險及指導早期干預治療提供力學依據。報告如下。
1 資料與方法
1.1 研究對象及研究設備、軟件
選擇 1 名 35 歲健康男性志愿者,身高165 cm,體質量58 kg, 排除雙側髖關節、下肢以及全身系統性疾病病史。
Mimics 21.0軟件(Materialise 公司,比利時);Abaqus 2021軟件、Solidworks 2022軟件(Dassault Systemes公司,美國);Geomagic Wrap 2017軟件(Geomagic 公司,美國)。臺式電腦:操作系統Windows10 64 位(DirectX 12);處理器Inter(R)Core(TM)i7-8700 CPU@3.20GHz;RAM 32.0G;主顯卡:NVIDIA GeForce GTX 1080Ti。64排螺旋 CT機(Siemens公司,德國),管電壓120 kV,管電流150 mA,掃描矩陣512×512,層厚1 mm,重建間距1.25 mm。
1.2 影像資料采集
① 受試者仿站立平臥位,雙髂前上棘保持同一水平,雙膝靠攏伸直,雙足并攏成中立位,獲取正位 X 線片及CT數據資料。② 受試者取仰臥位,雙髖、雙膝屈曲,雙足緊密接觸;大腿外展外旋30°,股骨軸線與水平面呈30°,同時保證骨盆所在平面與X線片上的平面平行,獲取蛙位X線片。正位及蛙位X 線片影像的獲取范圍包括髂嵴最高點上緣 1 cm 至小轉子下 5 cm。CT 掃描數據獲取方法:以64 排螺旋 CT 機從雙側髖臼上緣3 cm至小轉子下5 cm 范圍內沿橫斷面連續掃描,生成圖像共 266 幅。將生成的CT圖像文件保存為 DICOM格式,以左側股骨頭CT數據進行以下模型構建及觀測。
1.3 不同保留角ONFH模型建立
1.3.1 建立股骨近端模型
將DICOM 格式的CT數據導入Mimics 21.0軟件中,通過閾值分割(226~1 726),選取股骨近端生成蒙版,保證蒙版與正常骨質輪廓重合,從而獲得整個股骨近端模型。根據皮質骨與松質骨在CT中灰度值不同,重復上述操作,得到松質骨(包含髓腔)模型。對皮質骨和松質骨模型初步光滑處理后,導出為.stl格式,隨后導入Geomagic Wrap 2017軟件中,對模型進行光滑處理,并把模型轉換為NURBS曲面模型(完整股骨近端、松質骨),導出為.stp格式并在Solidworks 2022軟件中打開,進行裝配及布爾運算后,得到正常股骨近端模型。
1.3.2 壞死區模型建立
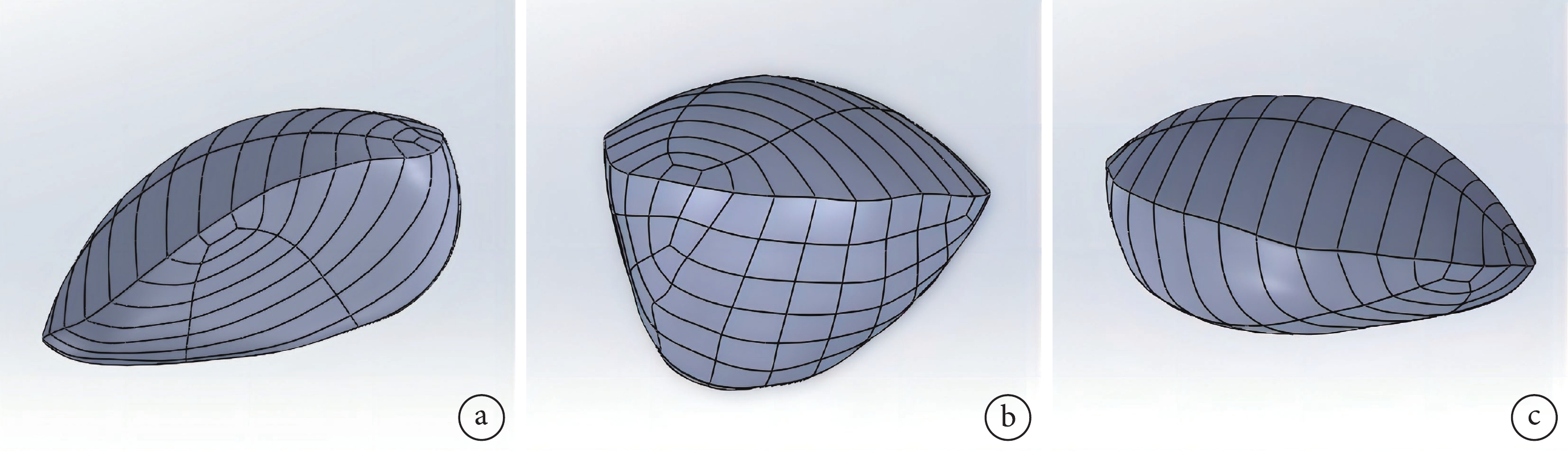
基于ONFH日本厚生省骨壞死研究會(JIC)C1分型前提下,構建3個相同體積且在正位視角中壞死區重心分別靠近股骨頭外側、中部及內側的壞死區模型(記為M1、M2、M3)。方法如下:在同一CT影像數據中,新建左側股骨近端蒙版,參考ONFH JIC C1型壞死區累及股骨頭范圍,在蒙版上逐層勾勒出壞死區范圍后得到目標模型;重復上述過程,初步光滑后,導出為.stl格式在Geomagic Wrap 2017軟件中打開,光滑處理后,使用查詢體積功能查看壞死模型體積,再使用雕刻刀等功能增、減材質;重復以上操作后,得到3個不同形態但體積為(17 700±8)mm3,即占整個股骨頭體積[20]30%的壞死區模型,所建模型最大橫徑為42.175 mm,最大縱徑為24.216 mm。再對模型做NURBS曲面化處理,導出為.stp格式。見圖1。
 圖1
基于ONFH JIC C1分型構建3個相同體積、不同形態的壞死區模型
圖1
基于ONFH JIC C1分型構建3個相同體積、不同形態的壞死區模型
a. M1;b. M2;c. M3
Figure1. Three necrotic area models with the same volume and different morphology were constructed based on ONFH JIC C1 typea. M1; b. M2; c. M3
1.3.3 三維視覺下ONFH模型正位及蛙位視角建立
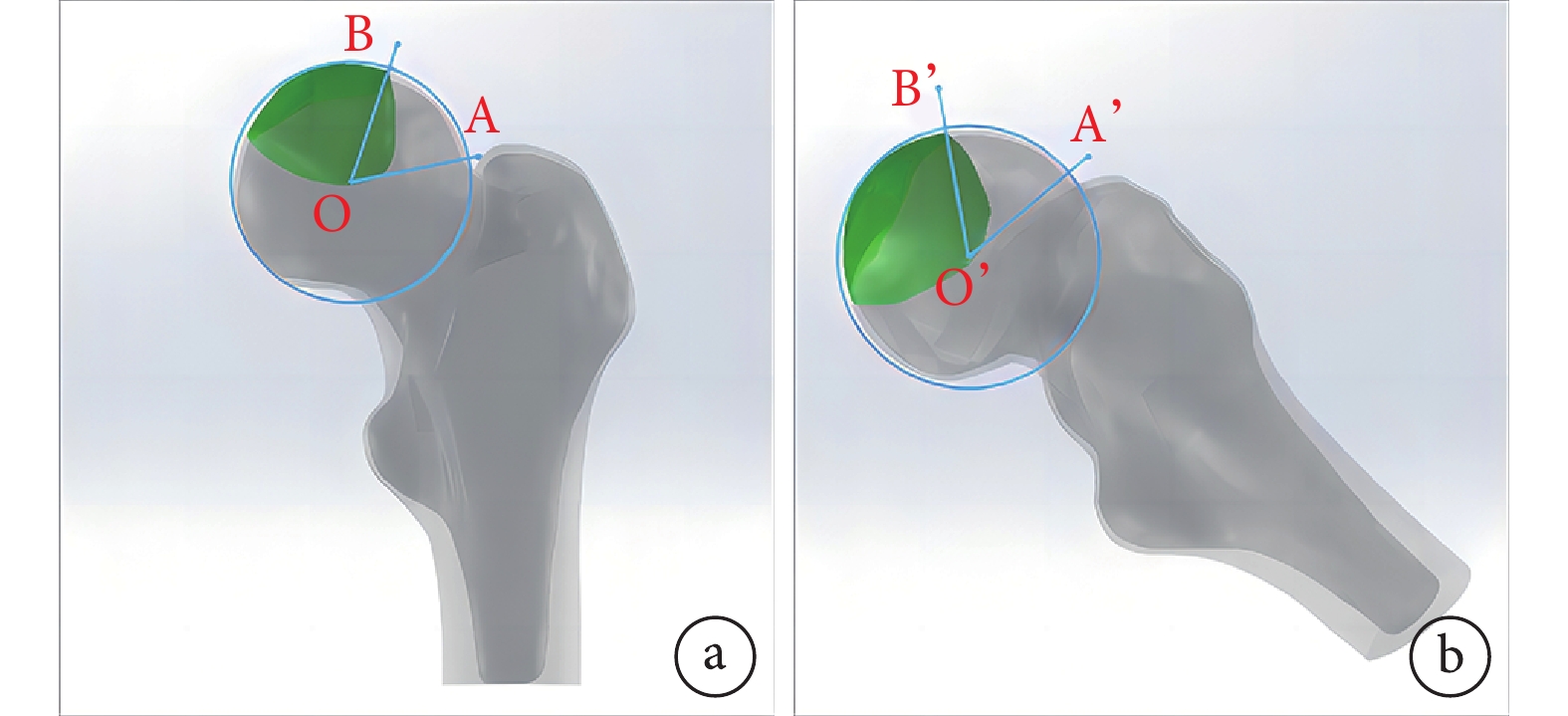
根據本團隊對APA和LPA的定義[21],基于髖關節X線片與股骨近端三維模型正位及蛙位視角進行配準。步驟如下:在Solidworks 2022軟件中,將正常股骨近端模型以裝配體模塊打開,參考正位X線片視角,將股骨近端模型前視面設定為基準面,利用草圖劃圓功能在此基準面上作一個與股骨頭外輪廓相切的圓形,圓心定義為股骨頭中心O,股骨頭外側頭頸交界處為點A,壞死區外側邊緣為點B,線OA與OB的夾角定義為LPA。參考蛙位X線片視角,使用直接編輯中的旋轉實體功能,將股骨近端模型模擬外旋、外展30° 且股骨干長軸與水平面成30° 夾角形成蛙位視角,重復上述作圖連線方法得到線O’A’ 與O’B’ 的夾角,即為股骨頭APA。見圖2。
 圖2
在股骨近端三維模型中構建保留角方法
圖2
在股骨近端三維模型中構建保留角方法
a. LPA;b. APA
Figure2. Constructing the preserved angles in the three-dimensional model of the proximal femura. LPA; b. APA
1.3.4 構建不同保留角模型
基于本團隊前期臨床研究[15],APA、LPA臨界值分別為60.53°、60.46°。故設定一側保留角處于其臨界值,另一側保留角以5° 為單位,在45°~75° 范圍變化,從而模擬當股骨頭前側壁或外側壁保留較完整時,另一側壁的不同完整度情況。根據研究方案構建以下模型:APA為60°,LPA分別為45°、50°、55°、60°、65°、70°、75° 的ONFH有限元模型;LPA為60°,APA分別為45°、50°、55°、60°、65°、70°、75° 的ONFH有限元模型。將1.3.2中構建的3個壞死區模型(M1、M2和M3)導入正常股骨近端模型中,根據上述在股骨近端三維模型中構建保留角的方法,構建不同保留角模型。再將不同保留角ONFH模型通過復制實體、布爾運算、查找干涉等功能,得到由皮質骨、松質骨、壞死區組成的ONFH模型,所構建的模型中壞死區與股骨頭關節面最小間距為0.944 mm,壞死區深部與關節面最大間距為25.625 mm,共構建42個不同保留角ONFH模型。
1.4 有限元模型驗證
1.4.1 網格劃分
將上述模型以.x_t格式導入有限元分析軟件Abaqus 2021進行網格劃分,使用四面體單元劃分模型,網格類型為C3D10M,網格單位2 mm,模型由144 576個四面體單元、224 092個節點構成。
1.4.2 材料屬性賦值
根據文獻 [22] 將股骨近端骨組織定義為各向同性且連續均勻的線彈性材料。皮質骨、松質骨及壞死組織彈性模量分別為15 100、4 457、124.6 MPa,泊松比分別為0.3、0.22、0.152。
1.4.3 邊界條件及載荷
約束股骨遠端所有節點的 6 個自由度為 0,本團隊前期研究[23]根據Genda等[24]提出的“髖臼接觸理論”構建出股骨頭表面精確受力區域。本研究運用此方法在股骨頭圓頂及前外側建立了面積為1 464.37 mm2的受力區域,在研究[23]得到的股骨頭表面受力面積1 218.63~1 871.06 mm2范圍內,提示本模型受力區域建模基本符合實際。人體在單腿直立靜力狀態時,股骨頭需承載自重的3~4倍負荷[21],載荷設定考慮到受試者真實體質量及股骨近端肌肉收縮力量的影響,在股骨頭表面負重區施加與股骨干成25° 夾角[25]、方向向下且大小為受試者3.5倍體質量的合力[5]。見圖3。
 圖3
ONFH模型邊界條件及載荷
Figure3.
Boundary conditions and loading force settings of the ONFH mode
圖3
ONFH模型邊界條件及載荷
Figure3.
Boundary conditions and loading force settings of the ONFH mode
1.4.4 模型網格收斂及檢測指標
研究中ONFH有限元模型由Abaqus 2021軟件進行網格劃分,共設置5種網格單元,分別為1.0、1.5、2.0、 2.5、3.0 mm。經過網格收斂性分析,確定模型網格尺寸為2.0 mm時,在運算速度與結果準確性上取得平衡。故網格劃分單位尺寸為2 mm,并對模型輸出結果準確性進行驗證。根據Abaqus 2021運算結果,分別檢測各ONFH有限元模型的股骨頭表面最大應力、壞死區最大應力和股骨頭負重區最大位移。
1.5 統計學方法
采用SPSS27.0統計軟件進行分析。計量資料經Shapiro-Wilk正態性檢驗,均符合正態分布,數據以均數±標準差表示,同側保留角下不同角度ONFH有限元模型間比較采用單因素方差分析。檢驗水準α=0.05。
2 結果
2.1 模型有效性驗證
LPA 60°、APA 45° 模型和APA 60°、LPA 45° 模型的股骨頭表面應力集中區應力峰值分別為(21.16±0.31)、(20.79±0.25)MPa,與既往研究[22]基于ONFH JIC C1分型構建模型的股骨頭表面應力峰值(20.19±1.01)MPa 接近,提示此次構建的ONFH模型基本符合ONFH力學情況。
2.2 APA為60° 時不同LPA模型的應力和位移情況
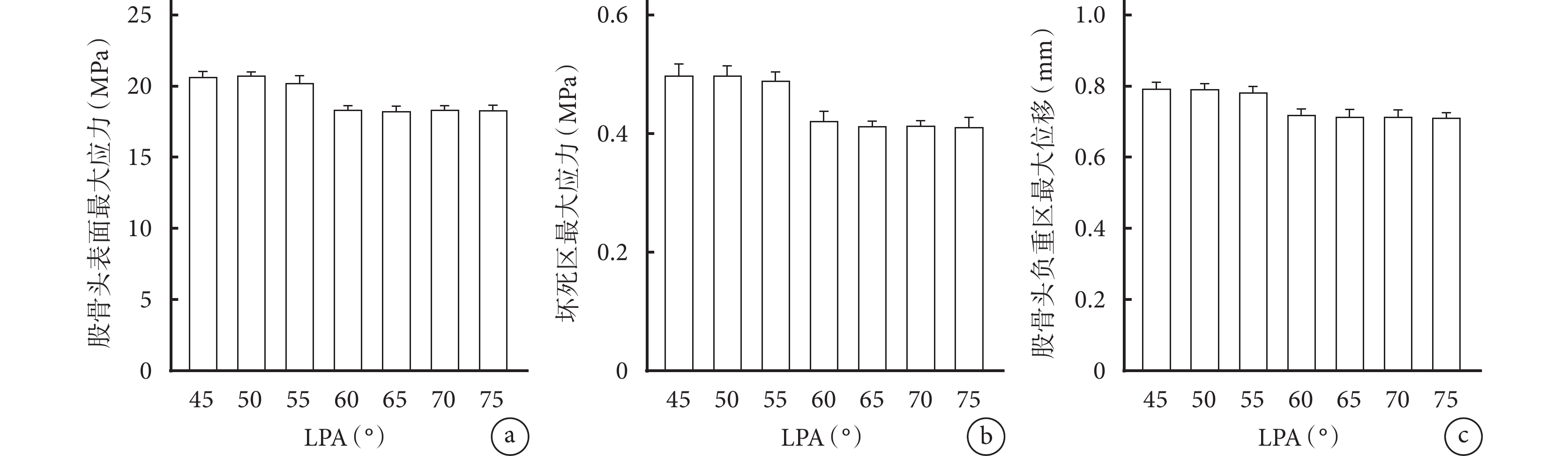
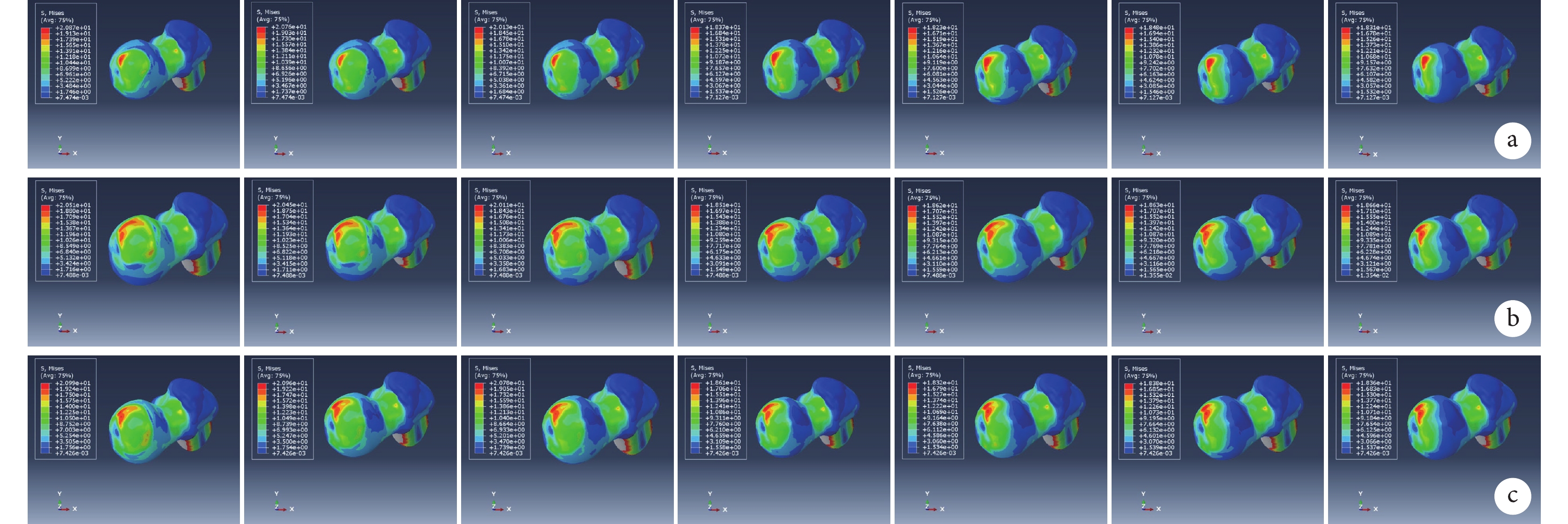
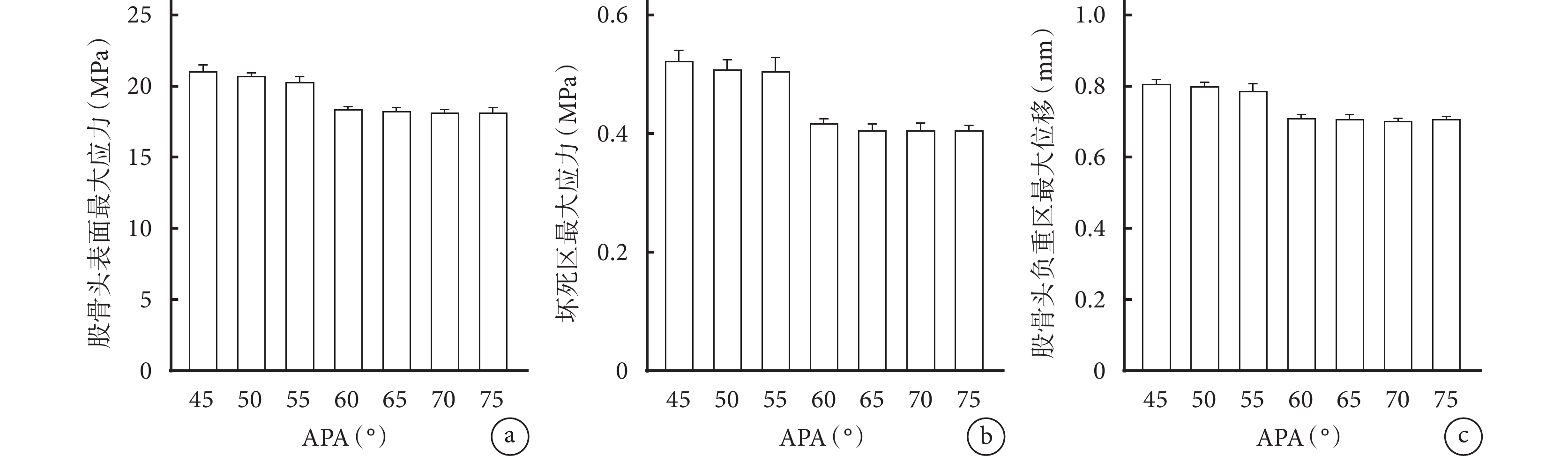
在相同載荷條件下,壞死區周圍均有應力集中現象,LPA為45° 時模型應力集中最明顯。隨著LPA逐漸增大,模型的股骨頭表面、壞死區最大應力和股骨頭負重區最大位移總體呈下降趨勢。LPA<60° 模型的上述各指標明顯高于LPA≥60° 模型,差異有統計學意義(P<0.05);LPA≥60° 模型間各指標比較差異均無統計學意義(P>0.05)。見圖4~6。
 圖4
APA為60° 時不同LPA模型的應力和位移
圖4
APA為60° 時不同LPA模型的應力和位移
a. 股骨頭表面最大應力;b. 壞死區最大應力;c. 股骨頭負重區最大位移
Figure4. Von Mises stress and displacement of different LPA models with APA of 60°a. The maximum Von Mises stress of the surface of the femoral head; b. The maximum Von Mises stress of the necrotic area; c. The maximum displacement of the femoral head
 圖5
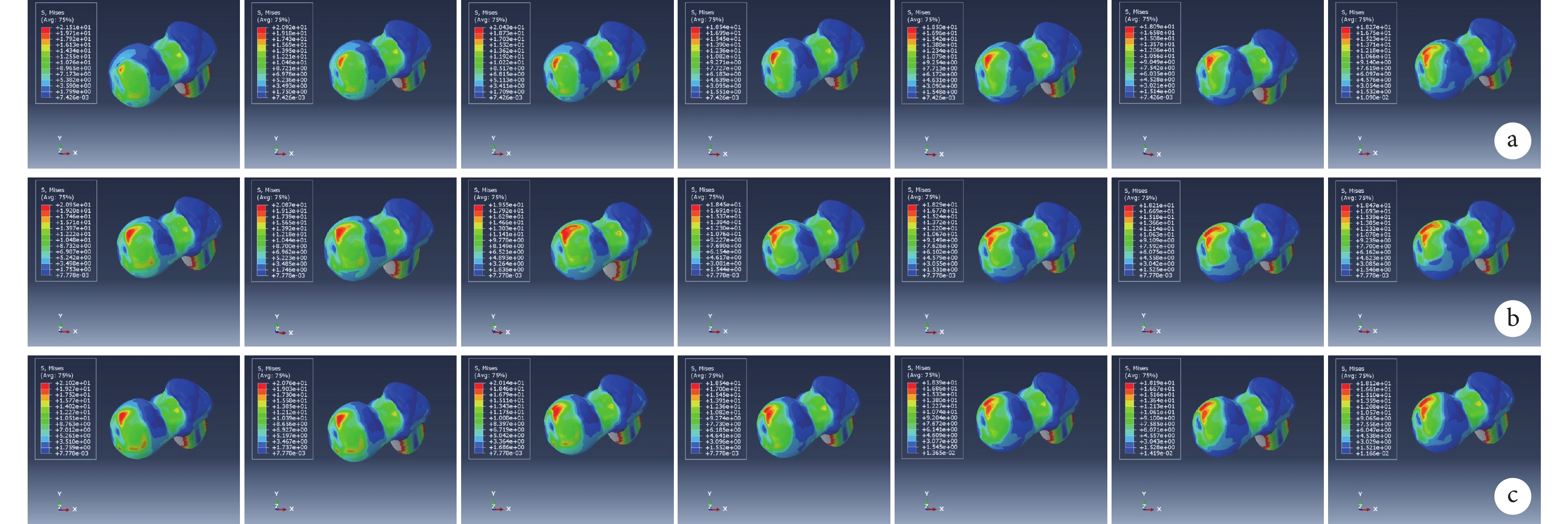
APA為60° 時不同LPA模型股骨頭表面應力分布云圖
圖5
APA為60° 時不同LPA模型股骨頭表面應力分布云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure5. Von Mises stress distribution nephogram of the surface of the femoral head in different LPA models with APA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
 圖6
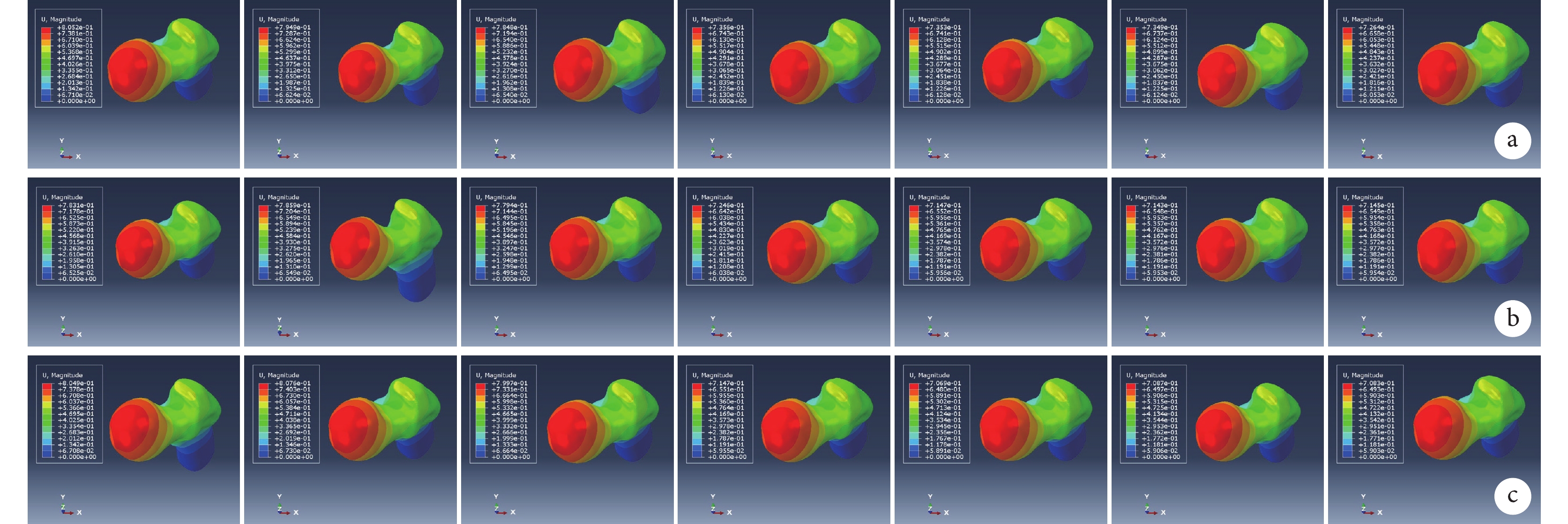
APA為60° 時不同LPA模型股骨頭負重區最大位移云圖
圖6
APA為60° 時不同LPA模型股骨頭負重區最大位移云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure6. The maximum displacement nephogram of weight-bearing area of the femoral head in different LPA models with APA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
2.3 LPA為60° 時不同APA模型的應力和位移情況
在相同載荷條件下,壞死區周圍均有應力集中現象,APA為45° 時,模型應力集中最明顯。隨著APA逐漸增大,模型的股骨頭表面、壞死區最大應力和股骨頭負重區最大位移總體呈下降趨勢。APA<60° 模型的上述各指標明顯高于APA≥60° 模型,差異有統計學意義(P<0.05);APA≥60° 模型間各指標比較差異均無統計學意義(P>0.05)。見圖7~9。
 圖7
LPA為60° 時不同APA模型的應力和位移
圖7
LPA為60° 時不同APA模型的應力和位移
a. 股骨頭表面最大應力;b. 壞死區最大應力;c. 股骨頭負重區最大位移
Figure7. Von Mises stress and displacement of different APA models with LPA of 60°a. The maximum Von Mises stress of the surface of the femoral head; b. The maximum Von Mises stress of the necrotic area; c. The maximum displacement of the femoral head
 圖8
LPA為60° 時不同APA模型股骨頭表面應力分布云圖
圖8
LPA為60° 時不同APA模型股骨頭表面應力分布云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure8. Von Mises stress distribution nephogram of the surface of the femoral head in different APA models with LPA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
 圖9
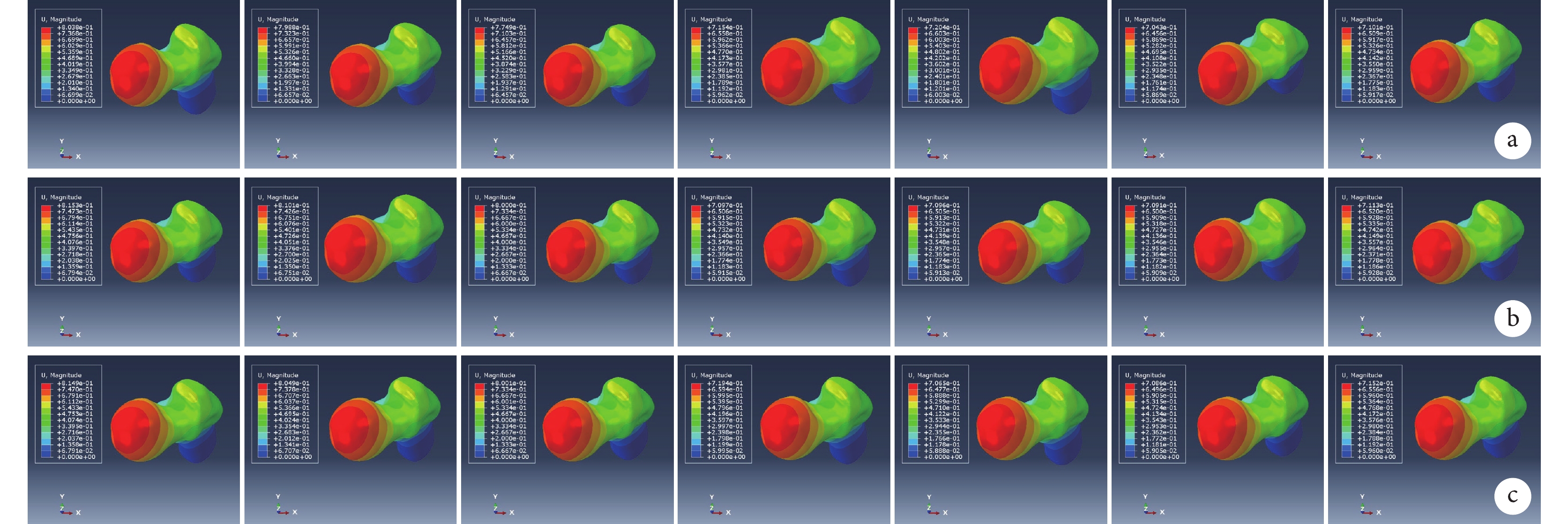
LPA為60° 時不同APA模型股骨頭負重區最大位移云圖
圖9
LPA為60° 時不同APA模型股骨頭負重區最大位移云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure9. The maximum displacement nephogram of weight-bearing area of the femoral head in different APA models with LPA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
3 討論
通過ONFH的生物因素和生物力學因素來預測股骨頭塌陷和判斷預后,一直是國內外研究熱點[26]。ONFH發生后,壞死區域破骨細胞活躍而成骨細胞活性降低,導致壞死骨組織結構薄弱,形成囊性變[8,27],使得頭內組織結構惡化。相應地,壞死骨組織應力水平較正常骨下降,承載負荷能力降低,壞死區周圍應力集中,軟骨下骨板應力代償,股骨頭表面應力峰值則會增高。ONFH 塌陷遵循應力集中→骨小梁微骨折→斷層骨折→塌陷的自然病理過程,一旦壞死區應力峰值超過其屈服應力,導致一點或者幾點骨小梁突然斷裂,進一步降低壞死組織的屈服應力,就會由此出現“多米諾骨牌效應”,造成不可逆轉的大范圍骨小梁斷裂,導致股骨頭塌陷[28]。生物因素及生物力學因素對ONFH的影響是聯系的,塌陷是骨重建和力學因素反復作用的結果。
無論是生物力學研究還是臨床研究,既往結果均表明股骨頭前、外側柱保留完整度,是決定ONFH是否塌陷的關鍵因素,即使外側柱保留完整的壞死股骨頭,其前側柱受累時也有塌陷風險[29-30]。在臨床診療中,保留角通過髖關節正、蛙位X線片精準預測ONFH塌陷風險,對指導早期ONFH干預治療有較大意義。但目前尚無生物力學證據支撐這一結論,故本研究運用有限元分析探討其生物力學機制。
有限元生物力學分析在ONFH塌陷預測等研究[17,22]中得到廣泛運用。構建模型的有效性及客觀性是影響有限元分析結果的重要因素[31],建立符合實際情況的有限元模型是生物力學分析的前提。本研究建立的壞死區體積占股骨頭體積的30%,雖然有一定局限性,但可以反映早期ONFH應力情況,且控制了壞死范圍對股骨頭應力分布的影響,有利于直觀地分析壞死位置與塌陷的關系。有限元分析中,施加載荷的位置對模型輸出結果的準確性至關重要,此次根據本團隊前期建模方法[23],成功建立了股骨頭精確受力區域。此方法在不增加建模難度的情況下,對股骨頭表面受力區進行精確識別和量化,提高了股骨近端三維有限元分析的準確性和可重復性。JIC分型作為經典的ONFH分型系統,其根據壞死區是否累及外側負重區進行分型[32],基于JIC C1分型建立3個不同形態且在正位視角中壞死區重心分別靠近股骨頭外側、中部及內側的壞死區模型,可以有效避免壞死模型的幾何特征對股骨頭應力分布的影響,且此種壞死區建模方法也比較符合臨床中ONFH病灶不規則的特點。基于髖關節正位X線片,保留角可以清晰、快捷描述壞死區對股骨頭前、外側壁的累及程度,構建了APA為60° 且LPA分別為45°、50°、55°、60°、65°、70°、75° 的3種不同壞死形態、相同體積的ONFH 三維模型,模擬壞死股骨頭前側柱完整、外側柱不同受累程度時的生物力學情況。而股骨頭前側壁受累程度對塌陷的影響同樣得到關注,故構建了LPA為60° 且APA分別為45°、50°、55°、60°、65°、70°、75° 的3種不同壞死形態、相同體積的ONFH 三維模型,模擬壞死股骨頭外側柱完整、前側柱不同受累程度時的生物力學情況。因此,本研究構建的ONFH模型在控制壞死范圍前提下,能夠較為客觀地反映壞死病灶對前、外側負重區不同程度累及情況。
有研究[33-34]指出,股骨頭位移增量是骨壞死前后某一點垂直距離的變化,當位移增量越大時,股骨頭越容易塌陷。股骨頭的骨組織結構應力水平與ONFH預后顯著相關,應力越集中,塌陷風險越高[27]。因此,股骨頭前、外側柱作為股骨頭承重區,ONFH患者前、外側柱受累程度越嚴重,則股骨頭表面、壞死區最大應力及負重區最大位移越大,提示股骨頭發生塌陷的風險越大。本研究通過比較當APA為60° 時,LPA為45°、50°、55°、60°、65°、70°、75° 模型的股骨頭表面、壞死區最大應力及負重區最大位移值差異,發現隨著LPA從45° 逐漸增大至60° 時,各指標呈明顯降低趨勢,而LPA從60° 逐漸增大至75° 時,各指標變化趨勢不明顯。通過比較當LPA為60° 時,APA為45°、50°、55°、60°、65°、70°、75° 模型的應力、位移峰值變化,發現與前者有相同趨勢。不同保留角ONFH模型的應力變化趨勢與本團隊前期臨床研究結果[15]基本一致,提示本研究結果在生物力學方面可以較為有效、客觀地為保留角精確量化前、外側柱保留完整度,從而預測ONFH患者股骨頭塌陷提供力學依據。
本研究的局限性:首先,本研究構建的是股骨近端骨性模型,主要考慮了松質骨、皮質骨、壞死骨的有效彈性模量,而缺少了對肌肉與韌帶的處理。其次,受限于技術,只能手動調整壞死區空間位置構建不同保留角的ONFH模型,建模無法達到絕對精確。我們認為這也是在相同分析條件下,相同保留角度下各模型之間的應力及位移峰值有誤差的原因。再次,模型加載負荷只考慮了人體單腿直立靜力狀態的力學情況,完整行走步態周期的股骨近端生物力學有待進一步驗證。最后,為了避免壞死范圍對研究的影響,只設計了壞死區體積占比股骨頭30%的ONFH模型,不同壞死范圍對保留角預測塌陷的影響有待進一步研究。
綜上述,基于生物力學角度,當ONFH保留角小于臨界值時,股骨頭應力集中現象更為明顯;而當保留角大于臨界值后,股骨頭應力處于較低且相對穩定的狀態。提示ONFH保留角小于臨界值時,壞死股骨頭發生塌陷風險更高。
利益沖突 在課題研究和文章撰寫過程中不存在利益沖突;項目經費支持沒有影響文章觀點和對研究數據客觀結果的分析及其報道
倫理聲明 研究方案經廣州中醫藥大學第三附屬醫院倫理審查委員會批準(PJ-KY-20211207-001);研究對象知情同意
作者貢獻聲明 魏秋實:研究設計、經費支持;林天燁、何敏聰:研究設計;何曉銘:數據統計分析;何憲順、田佳慶、魏騰飛、詹芝瑋、林錕:進行有限元分析并負責數據獲取;陸舜:文稿撰寫
股骨頭壞死(osteonecrosis of the femoral head,ONFH)是一種嚴重威脅中青年人群健康的關節疾病[1],目前發病機制仍不清楚,ONFH進展至中后期常會發生股骨頭塌陷導致髖關節疼痛及功能障礙,最終發展為髖關節骨關節炎,不得不接受髖關節置換手術[2-4]。股骨頭塌陷是ONFH的重要轉折點,在ONFH早期精準預測塌陷風險對判斷疾病預后以及指導制定保髖治療方案有重要意義。股骨頭塌陷是生物因素和生物力學因素共同作用的結果[5-7],壞死股骨頭組織結構破壞意味著頭內生物力學異常改變,導致股骨頭力學支撐性能下降[8]。一旦壞死股骨頭承載負荷超過頭內組織結構屈服強度,軟骨下壞死骨質就會發生應力性骨折導致塌陷。有研究認為ONFH塌陷進程與股骨頭前、外側柱受累程度有顯著相關性[9-12]。本團隊前期研究[13-14]發現,結合髖關節正、蛙位X線片綜合評估前、外側柱保留情況,對ONFH塌陷有較好預測效果。研究進一步發現,可以精確量化前、外側柱保留完整度的前側保留角(anterior preserved angle,APA)和外側保留角(lateral preserved angle,LPA)與塌陷進展顯著相關,APA、LPA臨界值分別為60.53°、60.46°,當APA或LPA 小于臨界值時,提示股骨頭塌陷風險顯著升高[15]。然而根據不同保留角預測ONFH塌陷風險的生物力學機制尚不明確,需要更多力學證據支撐。
有限元生物力學分析在可行性、重復性、可視化方面有顯著優勢,其可靠性已得到驗證[16]。有研究[5]建立不同壞死范圍ONFH模型,分析發現大范圍壞死模型中壞死區深部應力集中更為明顯,提示股骨頭塌陷風險升高,但模型中壞死區位置分布較為模糊。還有研究[17-18]根據中日友好醫院分型,通過股骨頭冠狀位三柱結構建立不同壞死位置模型,發現股骨頭外側負重區域受累時,股骨頭塌陷風險明顯高于其他壞死位置,然而所建模型并未關注壞死區位置對股骨頭前側壁的影響。上述研究結果提示股骨頭塌陷預測中,壞死區的位置與范圍對塌陷預后均有重要意義[19]。本研究基于髖關節正、蛙位X線片描述壞死區位置的保留角,結合壞死區范圍,運用三維有限元分析法探討股骨頭APA和LPA預測塌陷的生物力學機制,為不同保留角精準預測ONFH塌陷風險及指導早期干預治療提供力學依據。報告如下。
1 資料與方法
1.1 研究對象及研究設備、軟件
選擇 1 名 35 歲健康男性志愿者,身高165 cm,體質量58 kg, 排除雙側髖關節、下肢以及全身系統性疾病病史。
Mimics 21.0軟件(Materialise 公司,比利時);Abaqus 2021軟件、Solidworks 2022軟件(Dassault Systemes公司,美國);Geomagic Wrap 2017軟件(Geomagic 公司,美國)。臺式電腦:操作系統Windows10 64 位(DirectX 12);處理器Inter(R)Core(TM)i7-8700 CPU@3.20GHz;RAM 32.0G;主顯卡:NVIDIA GeForce GTX 1080Ti。64排螺旋 CT機(Siemens公司,德國),管電壓120 kV,管電流150 mA,掃描矩陣512×512,層厚1 mm,重建間距1.25 mm。
1.2 影像資料采集
① 受試者仿站立平臥位,雙髂前上棘保持同一水平,雙膝靠攏伸直,雙足并攏成中立位,獲取正位 X 線片及CT數據資料。② 受試者取仰臥位,雙髖、雙膝屈曲,雙足緊密接觸;大腿外展外旋30°,股骨軸線與水平面呈30°,同時保證骨盆所在平面與X線片上的平面平行,獲取蛙位X線片。正位及蛙位X 線片影像的獲取范圍包括髂嵴最高點上緣 1 cm 至小轉子下 5 cm。CT 掃描數據獲取方法:以64 排螺旋 CT 機從雙側髖臼上緣3 cm至小轉子下5 cm 范圍內沿橫斷面連續掃描,生成圖像共 266 幅。將生成的CT圖像文件保存為 DICOM格式,以左側股骨頭CT數據進行以下模型構建及觀測。
1.3 不同保留角ONFH模型建立
1.3.1 建立股骨近端模型
將DICOM 格式的CT數據導入Mimics 21.0軟件中,通過閾值分割(226~1 726),選取股骨近端生成蒙版,保證蒙版與正常骨質輪廓重合,從而獲得整個股骨近端模型。根據皮質骨與松質骨在CT中灰度值不同,重復上述操作,得到松質骨(包含髓腔)模型。對皮質骨和松質骨模型初步光滑處理后,導出為.stl格式,隨后導入Geomagic Wrap 2017軟件中,對模型進行光滑處理,并把模型轉換為NURBS曲面模型(完整股骨近端、松質骨),導出為.stp格式并在Solidworks 2022軟件中打開,進行裝配及布爾運算后,得到正常股骨近端模型。
1.3.2 壞死區模型建立
基于ONFH日本厚生省骨壞死研究會(JIC)C1分型前提下,構建3個相同體積且在正位視角中壞死區重心分別靠近股骨頭外側、中部及內側的壞死區模型(記為M1、M2、M3)。方法如下:在同一CT影像數據中,新建左側股骨近端蒙版,參考ONFH JIC C1型壞死區累及股骨頭范圍,在蒙版上逐層勾勒出壞死區范圍后得到目標模型;重復上述過程,初步光滑后,導出為.stl格式在Geomagic Wrap 2017軟件中打開,光滑處理后,使用查詢體積功能查看壞死模型體積,再使用雕刻刀等功能增、減材質;重復以上操作后,得到3個不同形態但體積為(17 700±8)mm3,即占整個股骨頭體積[20]30%的壞死區模型,所建模型最大橫徑為42.175 mm,最大縱徑為24.216 mm。再對模型做NURBS曲面化處理,導出為.stp格式。見圖1。
 圖1
基于ONFH JIC C1分型構建3個相同體積、不同形態的壞死區模型
圖1
基于ONFH JIC C1分型構建3個相同體積、不同形態的壞死區模型
a. M1;b. M2;c. M3
Figure1. Three necrotic area models with the same volume and different morphology were constructed based on ONFH JIC C1 typea. M1; b. M2; c. M3
1.3.3 三維視覺下ONFH模型正位及蛙位視角建立
根據本團隊對APA和LPA的定義[21],基于髖關節X線片與股骨近端三維模型正位及蛙位視角進行配準。步驟如下:在Solidworks 2022軟件中,將正常股骨近端模型以裝配體模塊打開,參考正位X線片視角,將股骨近端模型前視面設定為基準面,利用草圖劃圓功能在此基準面上作一個與股骨頭外輪廓相切的圓形,圓心定義為股骨頭中心O,股骨頭外側頭頸交界處為點A,壞死區外側邊緣為點B,線OA與OB的夾角定義為LPA。參考蛙位X線片視角,使用直接編輯中的旋轉實體功能,將股骨近端模型模擬外旋、外展30° 且股骨干長軸與水平面成30° 夾角形成蛙位視角,重復上述作圖連線方法得到線O’A’ 與O’B’ 的夾角,即為股骨頭APA。見圖2。
 圖2
在股骨近端三維模型中構建保留角方法
圖2
在股骨近端三維模型中構建保留角方法
a. LPA;b. APA
Figure2. Constructing the preserved angles in the three-dimensional model of the proximal femura. LPA; b. APA
1.3.4 構建不同保留角模型
基于本團隊前期臨床研究[15],APA、LPA臨界值分別為60.53°、60.46°。故設定一側保留角處于其臨界值,另一側保留角以5° 為單位,在45°~75° 范圍變化,從而模擬當股骨頭前側壁或外側壁保留較完整時,另一側壁的不同完整度情況。根據研究方案構建以下模型:APA為60°,LPA分別為45°、50°、55°、60°、65°、70°、75° 的ONFH有限元模型;LPA為60°,APA分別為45°、50°、55°、60°、65°、70°、75° 的ONFH有限元模型。將1.3.2中構建的3個壞死區模型(M1、M2和M3)導入正常股骨近端模型中,根據上述在股骨近端三維模型中構建保留角的方法,構建不同保留角模型。再將不同保留角ONFH模型通過復制實體、布爾運算、查找干涉等功能,得到由皮質骨、松質骨、壞死區組成的ONFH模型,所構建的模型中壞死區與股骨頭關節面最小間距為0.944 mm,壞死區深部與關節面最大間距為25.625 mm,共構建42個不同保留角ONFH模型。
1.4 有限元模型驗證
1.4.1 網格劃分
將上述模型以.x_t格式導入有限元分析軟件Abaqus 2021進行網格劃分,使用四面體單元劃分模型,網格類型為C3D10M,網格單位2 mm,模型由144 576個四面體單元、224 092個節點構成。
1.4.2 材料屬性賦值
根據文獻 [22] 將股骨近端骨組織定義為各向同性且連續均勻的線彈性材料。皮質骨、松質骨及壞死組織彈性模量分別為15 100、4 457、124.6 MPa,泊松比分別為0.3、0.22、0.152。
1.4.3 邊界條件及載荷
約束股骨遠端所有節點的 6 個自由度為 0,本團隊前期研究[23]根據Genda等[24]提出的“髖臼接觸理論”構建出股骨頭表面精確受力區域。本研究運用此方法在股骨頭圓頂及前外側建立了面積為1 464.37 mm2的受力區域,在研究[23]得到的股骨頭表面受力面積1 218.63~1 871.06 mm2范圍內,提示本模型受力區域建模基本符合實際。人體在單腿直立靜力狀態時,股骨頭需承載自重的3~4倍負荷[21],載荷設定考慮到受試者真實體質量及股骨近端肌肉收縮力量的影響,在股骨頭表面負重區施加與股骨干成25° 夾角[25]、方向向下且大小為受試者3.5倍體質量的合力[5]。見圖3。
 圖3
ONFH模型邊界條件及載荷
Figure3.
Boundary conditions and loading force settings of the ONFH mode
圖3
ONFH模型邊界條件及載荷
Figure3.
Boundary conditions and loading force settings of the ONFH mode
1.4.4 模型網格收斂及檢測指標
研究中ONFH有限元模型由Abaqus 2021軟件進行網格劃分,共設置5種網格單元,分別為1.0、1.5、2.0、 2.5、3.0 mm。經過網格收斂性分析,確定模型網格尺寸為2.0 mm時,在運算速度與結果準確性上取得平衡。故網格劃分單位尺寸為2 mm,并對模型輸出結果準確性進行驗證。根據Abaqus 2021運算結果,分別檢測各ONFH有限元模型的股骨頭表面最大應力、壞死區最大應力和股骨頭負重區最大位移。
1.5 統計學方法
采用SPSS27.0統計軟件進行分析。計量資料經Shapiro-Wilk正態性檢驗,均符合正態分布,數據以均數±標準差表示,同側保留角下不同角度ONFH有限元模型間比較采用單因素方差分析。檢驗水準α=0.05。
2 結果
2.1 模型有效性驗證
LPA 60°、APA 45° 模型和APA 60°、LPA 45° 模型的股骨頭表面應力集中區應力峰值分別為(21.16±0.31)、(20.79±0.25)MPa,與既往研究[22]基于ONFH JIC C1分型構建模型的股骨頭表面應力峰值(20.19±1.01)MPa 接近,提示此次構建的ONFH模型基本符合ONFH力學情況。
2.2 APA為60° 時不同LPA模型的應力和位移情況
在相同載荷條件下,壞死區周圍均有應力集中現象,LPA為45° 時模型應力集中最明顯。隨著LPA逐漸增大,模型的股骨頭表面、壞死區最大應力和股骨頭負重區最大位移總體呈下降趨勢。LPA<60° 模型的上述各指標明顯高于LPA≥60° 模型,差異有統計學意義(P<0.05);LPA≥60° 模型間各指標比較差異均無統計學意義(P>0.05)。見圖4~6。
 圖4
APA為60° 時不同LPA模型的應力和位移
圖4
APA為60° 時不同LPA模型的應力和位移
a. 股骨頭表面最大應力;b. 壞死區最大應力;c. 股骨頭負重區最大位移
Figure4. Von Mises stress and displacement of different LPA models with APA of 60°a. The maximum Von Mises stress of the surface of the femoral head; b. The maximum Von Mises stress of the necrotic area; c. The maximum displacement of the femoral head
 圖5
APA為60° 時不同LPA模型股骨頭表面應力分布云圖
圖5
APA為60° 時不同LPA模型股骨頭表面應力分布云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure5. Von Mises stress distribution nephogram of the surface of the femoral head in different LPA models with APA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
 圖6
APA為60° 時不同LPA模型股骨頭負重區最大位移云圖
圖6
APA為60° 時不同LPA模型股骨頭負重區最大位移云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure6. The maximum displacement nephogram of weight-bearing area of the femoral head in different LPA models with APA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
2.3 LPA為60° 時不同APA模型的應力和位移情況
在相同載荷條件下,壞死區周圍均有應力集中現象,APA為45° 時,模型應力集中最明顯。隨著APA逐漸增大,模型的股骨頭表面、壞死區最大應力和股骨頭負重區最大位移總體呈下降趨勢。APA<60° 模型的上述各指標明顯高于APA≥60° 模型,差異有統計學意義(P<0.05);APA≥60° 模型間各指標比較差異均無統計學意義(P>0.05)。見圖7~9。
 圖7
LPA為60° 時不同APA模型的應力和位移
圖7
LPA為60° 時不同APA模型的應力和位移
a. 股骨頭表面最大應力;b. 壞死區最大應力;c. 股骨頭負重區最大位移
Figure7. Von Mises stress and displacement of different APA models with LPA of 60°a. The maximum Von Mises stress of the surface of the femoral head; b. The maximum Von Mises stress of the necrotic area; c. The maximum displacement of the femoral head
 圖8
LPA為60° 時不同APA模型股骨頭表面應力分布云圖
圖8
LPA為60° 時不同APA模型股骨頭表面應力分布云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure8. Von Mises stress distribution nephogram of the surface of the femoral head in different APA models with LPA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
 圖9
LPA為60° 時不同APA模型股骨頭負重區最大位移云圖
圖9
LPA為60° 時不同APA模型股骨頭負重區最大位移云圖
a. M1壞死區;b. M2壞死區;c. M3壞死區
Figure9. The maximum displacement nephogram of weight-bearing area of the femoral head in different APA models with LPA of 60°a. Necrotic area with M1; b. Necrotic area with M2; c. Necrotic area with M3
3 討論
通過ONFH的生物因素和生物力學因素來預測股骨頭塌陷和判斷預后,一直是國內外研究熱點[26]。ONFH發生后,壞死區域破骨細胞活躍而成骨細胞活性降低,導致壞死骨組織結構薄弱,形成囊性變[8,27],使得頭內組織結構惡化。相應地,壞死骨組織應力水平較正常骨下降,承載負荷能力降低,壞死區周圍應力集中,軟骨下骨板應力代償,股骨頭表面應力峰值則會增高。ONFH 塌陷遵循應力集中→骨小梁微骨折→斷層骨折→塌陷的自然病理過程,一旦壞死區應力峰值超過其屈服應力,導致一點或者幾點骨小梁突然斷裂,進一步降低壞死組織的屈服應力,就會由此出現“多米諾骨牌效應”,造成不可逆轉的大范圍骨小梁斷裂,導致股骨頭塌陷[28]。生物因素及生物力學因素對ONFH的影響是聯系的,塌陷是骨重建和力學因素反復作用的結果。
無論是生物力學研究還是臨床研究,既往結果均表明股骨頭前、外側柱保留完整度,是決定ONFH是否塌陷的關鍵因素,即使外側柱保留完整的壞死股骨頭,其前側柱受累時也有塌陷風險[29-30]。在臨床診療中,保留角通過髖關節正、蛙位X線片精準預測ONFH塌陷風險,對指導早期ONFH干預治療有較大意義。但目前尚無生物力學證據支撐這一結論,故本研究運用有限元分析探討其生物力學機制。
有限元生物力學分析在ONFH塌陷預測等研究[17,22]中得到廣泛運用。構建模型的有效性及客觀性是影響有限元分析結果的重要因素[31],建立符合實際情況的有限元模型是生物力學分析的前提。本研究建立的壞死區體積占股骨頭體積的30%,雖然有一定局限性,但可以反映早期ONFH應力情況,且控制了壞死范圍對股骨頭應力分布的影響,有利于直觀地分析壞死位置與塌陷的關系。有限元分析中,施加載荷的位置對模型輸出結果的準確性至關重要,此次根據本團隊前期建模方法[23],成功建立了股骨頭精確受力區域。此方法在不增加建模難度的情況下,對股骨頭表面受力區進行精確識別和量化,提高了股骨近端三維有限元分析的準確性和可重復性。JIC分型作為經典的ONFH分型系統,其根據壞死區是否累及外側負重區進行分型[32],基于JIC C1分型建立3個不同形態且在正位視角中壞死區重心分別靠近股骨頭外側、中部及內側的壞死區模型,可以有效避免壞死模型的幾何特征對股骨頭應力分布的影響,且此種壞死區建模方法也比較符合臨床中ONFH病灶不規則的特點。基于髖關節正位X線片,保留角可以清晰、快捷描述壞死區對股骨頭前、外側壁的累及程度,構建了APA為60° 且LPA分別為45°、50°、55°、60°、65°、70°、75° 的3種不同壞死形態、相同體積的ONFH 三維模型,模擬壞死股骨頭前側柱完整、外側柱不同受累程度時的生物力學情況。而股骨頭前側壁受累程度對塌陷的影響同樣得到關注,故構建了LPA為60° 且APA分別為45°、50°、55°、60°、65°、70°、75° 的3種不同壞死形態、相同體積的ONFH 三維模型,模擬壞死股骨頭外側柱完整、前側柱不同受累程度時的生物力學情況。因此,本研究構建的ONFH模型在控制壞死范圍前提下,能夠較為客觀地反映壞死病灶對前、外側負重區不同程度累及情況。
有研究[33-34]指出,股骨頭位移增量是骨壞死前后某一點垂直距離的變化,當位移增量越大時,股骨頭越容易塌陷。股骨頭的骨組織結構應力水平與ONFH預后顯著相關,應力越集中,塌陷風險越高[27]。因此,股骨頭前、外側柱作為股骨頭承重區,ONFH患者前、外側柱受累程度越嚴重,則股骨頭表面、壞死區最大應力及負重區最大位移越大,提示股骨頭發生塌陷的風險越大。本研究通過比較當APA為60° 時,LPA為45°、50°、55°、60°、65°、70°、75° 模型的股骨頭表面、壞死區最大應力及負重區最大位移值差異,發現隨著LPA從45° 逐漸增大至60° 時,各指標呈明顯降低趨勢,而LPA從60° 逐漸增大至75° 時,各指標變化趨勢不明顯。通過比較當LPA為60° 時,APA為45°、50°、55°、60°、65°、70°、75° 模型的應力、位移峰值變化,發現與前者有相同趨勢。不同保留角ONFH模型的應力變化趨勢與本團隊前期臨床研究結果[15]基本一致,提示本研究結果在生物力學方面可以較為有效、客觀地為保留角精確量化前、外側柱保留完整度,從而預測ONFH患者股骨頭塌陷提供力學依據。
本研究的局限性:首先,本研究構建的是股骨近端骨性模型,主要考慮了松質骨、皮質骨、壞死骨的有效彈性模量,而缺少了對肌肉與韌帶的處理。其次,受限于技術,只能手動調整壞死區空間位置構建不同保留角的ONFH模型,建模無法達到絕對精確。我們認為這也是在相同分析條件下,相同保留角度下各模型之間的應力及位移峰值有誤差的原因。再次,模型加載負荷只考慮了人體單腿直立靜力狀態的力學情況,完整行走步態周期的股骨近端生物力學有待進一步驗證。最后,為了避免壞死范圍對研究的影響,只設計了壞死區體積占比股骨頭30%的ONFH模型,不同壞死范圍對保留角預測塌陷的影響有待進一步研究。
綜上述,基于生物力學角度,當ONFH保留角小于臨界值時,股骨頭應力集中現象更為明顯;而當保留角大于臨界值后,股骨頭應力處于較低且相對穩定的狀態。提示ONFH保留角小于臨界值時,壞死股骨頭發生塌陷風險更高。
利益沖突 在課題研究和文章撰寫過程中不存在利益沖突;項目經費支持沒有影響文章觀點和對研究數據客觀結果的分析及其報道
倫理聲明 研究方案經廣州中醫藥大學第三附屬醫院倫理審查委員會批準(PJ-KY-20211207-001);研究對象知情同意
作者貢獻聲明 魏秋實:研究設計、經費支持;林天燁、何敏聰:研究設計;何曉銘:數據統計分析;何憲順、田佳慶、魏騰飛、詹芝瑋、林錕:進行有限元分析并負責數據獲取;陸舜:文稿撰寫